密度经典例题解析
八年级物理密度经典例题

八年级物理密度经典例题当涉及到物理密度的经典例题时,有很多不同的题目可以选择。
下面我将为你提供几个典型的例题,并从多个角度进行解答。
例题1,一个物体的质量为120g,体积为40cm³,求该物体的密度。
解答,密度的定义是物体的质量除以物体的体积。
根据题目给出的数据,质量为120g,体积为40cm³。
所以,该物体的密度可以通过计算质量除以体积得到。
即,密度 = 质量 / 体积 = 120g /40cm³ = 3g/cm³。
例题2,一块物体的密度为2.5g/cm³,质量为500g,求该物体的体积。
解答,体积的计算可以通过密度乘以质量得到。
根据题目给出的数据,密度为2.5g/cm³,质量为500g。
所以,该物体的体积可以通过计算密度乘以质量得到。
即,体积 = 密度× 质量 =2.5g/cm³ × 500g = 1250cm³。
例题3,一个物体的密度为0.8g/cm³,体积为200cm³,求该物体的质量。
解答,质量的计算可以通过密度乘以体积得到。
根据题目给出的数据,密度为0.8g/cm³,体积为200cm³。
所以,该物体的质量可以通过计算密度乘以体积得到。
即,质量 = 密度× 体积 = 0.8g/cm³ × 200cm³ = 160g。
通过以上三个例题,我们可以看到密度的计算方法是一致的,即质量除以体积。
根据已知的数据,可以计算出未知的质量、体积或密度。
这些例题涵盖了基本的密度计算方法,帮助学生理解密度的概念和计算方法。
此外,在解答这些例题时,需要注意单位的转换。
在计算密度时,要确保质量和体积的单位一致,通常使用克和立方厘米。
如果单位不一致,需要进行换算。
希望以上解答能够帮助你理解物理密度的经典例题。
如果你还有其他问题,欢迎继续提问。
密度计算应用题及解答

密度计算应用题及解答密度是描述物质紧密程度的物理量,通常表示为单位体积内的质量。
在科学实验和工程领域中,密度计算是一个常见且重要的计算问题。
本文将介绍几个与密度计算相关的应用题,并提供详细的解答过程。
**应用题一:**某实验室得到一块体积为300 cm³的未知固体样品,称重后得到质量为450 g。
请计算该固体的密度,并以适当的单位表示。
**解答:**根据密度的定义,密度=质量/体积。
将已知数据代入公式中进行计算:密度 = 450 g / 300 cm³ = 1.5 g/cm³因此,该固体样品的密度为1.5 g/cm³。
**应用题二:**一块铁块的质量为800 g,将它放入水中浸泡后,水面上升高了40 cm。
已知水的密度为1 g/cm³,求铁的密度。
**解答:**铁块浸泡在水中时,会受到浮力的作用,使得铁块所排开的水的质量等于铁块的质量。
因此,铁块的质量等于浸泡后水的质量减去铁块放入前水的质量。
铁块的质量 = 浸泡后水的质量 - 浸泡前水的质量根据水的密度和水面上升高度,可以计算出铁块的体积。
将铁块的质量和体积代入密度的定义中进行计算,即可得到铁块的密度。
**应用题三:**某种液体的密度为0.8 g/cm³,若在容器中注入200 cm³的液体,求液体的质量是多少?**解答:**根据密度的定义,密度=质量/体积。
将已知数据代入公式中进行计算:质量 = 密度 x 体积质量 = 0.8 g/cm³ x 200 cm³ = 160 g因此,200 cm³的该液体的质量为160g。
通过以上三个应用题及解答,我们可以看到密度计算在实际问题中的应用广泛性。
掌握密度计算方法对于科学研究和工程实践具有重要意义。
希望本文可以帮助读者更深入地理解密度计算的原理与方法。
初三物理密度试题答案及解析

初三物理密度试题答案及解析1.某液体质量为365kg,体积为0.5m3,其密度为 kg/m3;一个圆柱形容器底面积为20cm2,盛满水,有一个金属块浸没水中,溢出水的质量为100g,取出金属块后,容器底部受到的液体压强减小了 Pa.(g=9.8N/kg)【答案】730;490.【解析】由密度公式金属块浸没水中,溢出水的体积为液面上升的高度取出金属块后,容器底部受到的液体压强减小了△p=ρgh=1.0×103kg/m3×9.8N/kg×0.05m=490Pa.【考点】密度的计算;液体的压强的计算2.阿基米德采用排水法解决了王冠掺假问题,现有一个金和银做成的王冠,用排水法测量出其体积为56.9cm3,若与王冠质量相同的纯金块和纯银块的体积分别为52.5cm3和96.5cm3,则王冠中银的质量和金的质量之比为()A.1:8B.1:9C.1:10D.1:11【答案】B【解析】由于与王冠相同质量的纯金块的体积为52.5cm3,所以王冠的质量为:,王冠的体积为金和银的体积之和,设其中金和银的质量分别为m1和m2,则,即:且,解得:,即,则,所以。
【考点】平均密度3.(6分)如图甲所示,石料在钢绳拉力的作用下从水面上方以恒定的速度下降,直至全部没入水中,如图乙所示是钢绳拉力随时间t变化的图象,若不计水的阻力(g=10N/kg,ρ水=1.0×103kg/m3),求:(1)石料全部没入水中时受到的浮力是多少?(2)石料的体积是多少?(3)石料的密度是多少?【答案】(1)石料浸没水中时受到的浮力为500N;(2)石料的体积为5×10﹣2m3;(3)石料的密度是2.8×103kg∕m3.【解析】(1)由图乙可知,当石块没有浸入水中时,拉力等于重力,即:F=G=1400N,g=10N/kg,石料的质量:m石=G/g=1400N/10N/kg=140kg,当石块全浸入后,拉力F′=900N,等于重力减去浮力,则F浮=G﹣F′=1400N﹣900N=500N;(2)根据阿基米德原理,F浮=ρ水gV排,ρ水=1.0×103kg/m3得:,因为石料完全浸没,石料的体积:V石=V排=5×10﹣2m3;(3)石料的密度:。
初中物理密度题讲解

初中物理密度题讲解密度是初中物理中的重要概念,理解和掌握密度的计算对于学习物理具有重要意义。
下面,我将通过一些典型的初中物理密度题,为大家详细讲解密度的计算方法和解题技巧。
一、密度的定义及公式密度是指单位体积的某种物质的质量,用符号ρ表示。
密度的计算公式为:ρ= m / V其中,ρ表示密度,m表示质量,V表示体积。
二、常见题型及解题方法1.计算物体的密度例题:一个物体的质量为200g,体积为100cm,求该物体的密度。
解题步骤:(1)根据密度的公式,代入已知数据:ρ = 200g / 100cm。
(2)进行单位换算,将g和cm转换为国际单位制:ρ = 0.2kg / 0.1m。
(3)计算得出密度:ρ = 2kg/m。
2.已知密度和质量,求体积例题:某物体的密度为2g/cm,质量为120g,求该物体的体积。
解题步骤:(1)根据密度的公式,代入已知数据:V = m / ρ = 120g / 2g/cm。
(2)进行单位换算,将g和cm转换为国际单位制:V = 0.12kg /2kg/m。
(3)计算得出体积:V = 0.06m。
3.已知密度和体积,求质量例题:一个物体的密度为0.8g/cm,体积为500cm,求该物体的质量。
解题步骤:(1)根据密度的公式,代入已知数据:m = ρ × V = 0.8g/cm ×500cm。
(2)进行单位换算,将g和cm转换为国际单位制:m = 0.8kg/m × 0.5m。
(3)计算得出质量:m = 0.4kg。
三、总结通过以上典型例题的讲解,我们可以发现,解决初中物理密度题的关键在于熟练掌握密度的定义和计算公式,以及注意单位换算。
在实际解题过程中,要根据题目所给的信息,灵活运用公式,进行计算。
密度十大类型计算题(含答案)

= 2.46 × 104kg
类型四:鉴别问题
有一只金戒指,用量筒测得其体积为 0.24������������3,用天平称出其质量为4.2g,试问 这只戒指是否是纯金制成的?
金 19.3 103 kg / m3
解:这个金戒指的密度 ������ 4.2������
������ = ������ = 0.24������������3 = 10 ������Τ������������3 = 10 × 103 ������������Τ������3 ∵ 10 × 103 ������������Τ������3 ≠ ������金 = 19.3 × 103 kgΤ������3 ∴ 这只戒指不是纯金制成的。
=
������金 ������金
540g = ������������������������������������
= ������. ������ ������������������������
= ������. ������ × ������������������������������Τ������������
类型十:配置问题
思路与方法:求两种物质的混合密度: 老板派小姚去订购酒精,合同上要求酒精的
密度小于或者是等于0.82g/cm3就算达标,小 姚在抽样检查时,取酒精的样本500ml,称得 的质量是420g. 请你通过计算说明小姚的结论 是 (A 达标 B 不达标,含水太多) 你认为小姚 该怎么办?如何配置500ml密度为0.82g/������������3的 酒精?(������酒=0.8×103 kg/m3 ρ水=1.0×103 kg/m3)
500cm3−������水
500������������3
《密度常考题型归类》

密度常考题型归类题型一:气体密度一般情况下,物质密度不变,质量、体积同比增加或减小。
但气体很特殊,需容器盛装,体积会随容积大小的改变而变化。
根据=m Vρ,容器体积V 增大,气体密度ρ减小。
例1.氧气瓶里的氧气原来的密度是ρ,用去一半后,剩余氧气的密度为( )A.ρB.12ρC.2ρD.14ρ 解析:氧气质量减半,体积等于瓶的容积不变,密度ρ同比减半。
答案:B 。
例2.某医院急诊室的氧气瓶中,氧气的密度为5kg/m 3,给急救病人供氧用去了氧气质量的一半,则瓶内剩余氧气的密度是________kg/m 3;病 人需要冰块进行物理降温,取450g 水凝固成冰后使用,其体积增大了________cm 3。
(ρ冰=0.9×103kg/m 3)解析:思路一:根据质量不变,列等式,ρ水V 水=ρ冰V 冰,求解相减得体积差。
思路二:质量不变,ρ、V 反比,有:ρ水∶ρ冰=10∶9→V 水∶V 冰=9∶10,则体积差为19V 水。
例3. 2020年初新型冠状病毒肆虐,某ICU 重症监护室内配有充满氧气的钢瓶,供急救病人时使用,钢瓶内氧气的质量m =3kg ,其密度ρ=6kg/m 3,若某次抢救病人用去了氧气质量的13,求: (1)钢瓶内剩余氧气的质量;(2)钢瓶的容积;(3)钢瓶内剩余氧气的密度。
解析:钢瓶容积=氧气体积(1)(1-13)×3kg=2kg (2)333kg ====0.5m 6kg/m m V V ρ瓶氧氧(3)332kg ===4kg/m 0.5mm V ρ余余 题型二:比例问题(直接赋值比/图像比值)比例问题可直接把比值的数字看作实际值带入公式中。
例1.如图所示,由不同物质制成的甲、乙两种实心球体积相等,此时天平衡,则制成甲、乙两种球的物质密度之比为( )A.3∶5B.5∶3C.2∶1D.3∶1解析:体积不变,密度和质量同比;m 左=m 右→2甲+乙=甲+4乙→m 甲=3m 乙。
初二物理密度试题答案及解析

初二物理密度试题答案及解析1.(6分)如图所示,将实心正方体木块轻轻地放入已侧倾放置且水已满的大烧杯内,待木块静止时,从杯中溢出75g水,该木块质地均匀,边长为5cm,木块吸收的水忽略不计,g取10N/kg。
求:(1)木块受到的浮力;(2)木块排开水的体积;(3)木块的密度。
【答案】(1)0.75N (2)75 cm3(3)0.6×103 kg/m3【解析】(1)(2)由题意知:从杯中溢出水的质量为m排=75g=0.075kg,水的密度ρ水=1.0×103 kg/m3,g=10N/kg,根据阿基米德原理知木块受到的浮力F浮=m排g=0.075kg×10N/kg=0.75N;木块排开水的体积。
(3)由题意可知:木块处于漂浮状态,所受的浮力等于重力,即G=F浮=0.75N,木块的体积V=(5cm)3=0.000125m3,g=10N/kg,则木块的密度。
【考点】浮力、密度的综合计算2.如图所示,一装有水的小桶放在水平面上,桶与水的总重为50N,用测力计吊着一个体积为300cm的实心金属球,将金属球缓慢浸没在水中,使其在水中静止,且不与桶壁、桶底接触,此时测力计的示数为12N。
则下列不正确的是( )A.金属球所受浮力为3N B.金属球的重力为15NC.金属球的密度为5×10kg/m D.桶对水平面的压力为65N【答案】D【解析】根据阿基米德原理,金属球受到的浮力,A 选项正确。
金属球的重力,B选项正确。
金属球的质量,金属球的密度,C选项正确。
由于相互作用力的大小相等,水对金属球的浮力为3N,金属球对水的作用力也是3N,桶对水平面的压力,D选项错误。
正确的选择是D。
【考点】浮力密度压力3.在常温常压下,冰的密度是0.9×103kg/m3,它表示_________________________现将体积为1.8m3的水结成冰后质量是____kg,体积为_____________m3。
初中物理密度计算典型题

初中物理密度计算典型题1.一个容积V0=500cm3、质量m=0.5kg的瓶子里装有水,乌鸦为了喝到瓶子里的水,就衔了很多的小石块填到瓶子里,让水面上升到瓶口。
若瓶内有质量m=0.4kg的水。
求:(水的密度ρ水=1.0×103kg/m3,石块密度ρ石块=2.6×103kg/m3)(1)瓶中水的体积V1;(2)乌鸦投入瓶子中的石块的体积V2;(3)乌鸦投入石块后,瓶子、石块和水的总质量m。
解:(1)由ρ=得瓶内水的体积:V1==4×10﹣4m3=400cm3;答:瓶中水的体积为400cm3;(2)石块总体积:V2=V﹣V1=500cm3﹣400cm3=100cm3;答:乌鸦投入瓶子中的石块的体积为100cm3;(3)由ρ=得石块的质量:m石=ρ石V2=2.6g/cm3×100cm3=260g=0.26kg,乌鸦投入石块后,瓶子、石块和水的总质量:m=m水+m瓶+m石=0.4kg+0.5kg+0.26kg=1.16kg=1160g。
答:乌鸦投入石块后,瓶子、石块和水的总质量为1160g。
2.有一只玻璃瓶,它的质量为0.1kg,当瓶内装满水时,瓶和水的总质量为0.4kg.在此空玻璃瓶中装入一些合金滚珠,瓶和合金滚珠的总质量为0.8kg,此时再往瓶中灌入水到瓶口止,瓶、合金滚珠和水的总质量为0.9kg,g=10N/kg,求:(1)玻璃瓶的容积;(2)合金滚珠的总质量;(3)合金滚珠的密度。
解:(1)玻璃瓶装满水:m水=0.4kg﹣0.1kg=0.3kg=300g,玻璃瓶容积:V=V水===300cm3,答:玻璃瓶的容积为300cm3;(2)合金滚珠的质量:m合金=m总﹣m瓶=0.8kg﹣0.1kg=0.7kg =700g,答:合金滚珠的总质量为700g;(3)瓶中装了合金滚珠后再装满水,水的体积:V水′==100cm3,合金滚珠的体积:V合金=V﹣V水´=300cm3﹣100cm3=200cm3,合金滚珠的密度:ρ===3.5g/cm3。
八年级上册物理密度计算题

八年级上册物理密度计算题密度是物质的一种固有属性,是指单位体积的物质的质量。
在物理学中,密度通常用符号ρ表示,单位为千克/立方米(kg/m³)。
密度的计算公式为:密度=质量/体积,即ρ = m/V。
下面我将给出一些八年级上册物理密度计算题的例题和解答,希望能帮助您更好地理解和掌握密度的计算方法。
例题1:一块物体的质量为200克,体积为100立方厘米,求该物体的密度是多少?解答:首先要将质量转换为千克,200克 = 0.2千克。
体积单位是立方厘米,要将其转换为立方米,100立方厘米 = 0.0001立方米。
然后,代入密度的计算公式ρ= m/V,即可得到密度为0.2/0.0001 = 2000 kg/m³。
例题2:一个物体的密度为8000 kg/m³,体积为0.5立方米,求该物体的质量是多少?解答:直接代入密度的计算公式ρ = m/V,8000 = m/0.5,解方程可得质量m = 8000 * 0.5 = 4000千克,即该物体的质量为4000千克。
例题3:一块金属的密度为7200 kg/m³,质量为90克,求该金属的体积是多少?解答:首先将质量转换为千克,90克 = 0.09千克。
代入密度的计算公式ρ =m/V,可得0.09/V = 7200,解方程可得体积V = 0.09/7200 = 0.0000125立方米,即该金属的体积为0.0000125立方米。
通过以上例题和解答,希望您能对八年级上册物理密度计算题有更清晰的认识,掌握密度的计算方法,为学习物理打下坚实的基础。
如果有更多问题,欢迎随时向我提问。
祝您学业进步,取得优异的成绩!。
部编物理八年级上册6.2密度(知识点+例题)(解析版)含答案
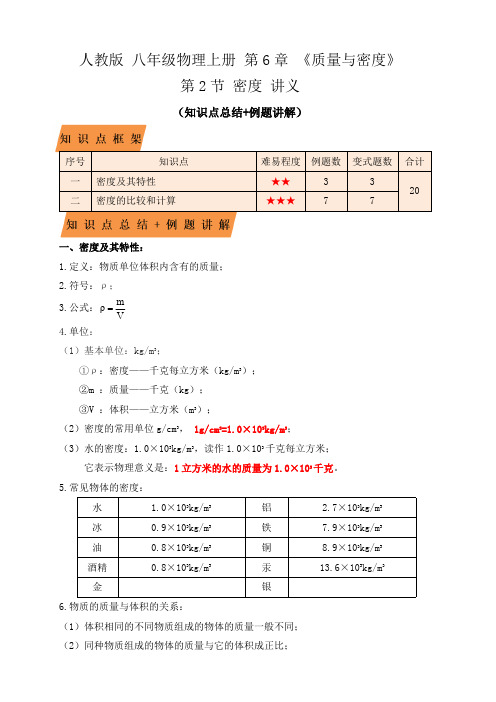
人教版 八年级物理上册 第6章 《质量与密度》第2节 密度 讲义(知识点总结+例题讲解)一、密度及其特性:1.定义:物质单位体积内含有的质量;2.符号:ρ;3.公式:Vm ρ 4.单位:(1)基本单位:kg/m 3;①ρ:密度——千克每立方米(kg/m 3);②m :质量——千克(kg );③V :体积——立方米(m 3);(2)密度的常用单位g/cm 3, 1g/cm 3=1.0×103kg/m 3;(3)水的密度:1.0×103kg/m 3,读作1.0×103千克每立方米;它表示物理意义是:1立方米的水的质量为1.0×103千克。
5.常见物体的密度:水 1.0×103kg/m 3铝 2.7×103kg/m 3冰0.9×103kg/m 3铁7.9×103kg/m 3油0.8×103kg/m 3铜8.9×103kg/m 3酒精0.8×103kg/m 3汞13.6×103kg/m 3金银6.物质的质量与体积的关系:(1)体积相同的不同物质组成的物体的质量一般不同;(2)同种物质组成的物体的质量与它的体积成正比;7.密度反映了不同物质的不同特性:(1)一种物质的质量与体积的比值是一定的;(2)物质不同,其比值一般不同。
【例题1】木雕是我国历史悠久、技艺精湛的雕刻工艺,是我国工艺美术中一项珍贵的艺术遗产。
如图所示,这是一名工艺师正在一个质地均匀的木头上进行雕刻。
雕刻过程中不发生变化的是( )A.木头的质量B.木头的体积C.木头的密度D.木头的质量和密度【答案】C【解析】解:由题意知,一名工艺师正在一个质地均匀的木头上进行雕刻过程中,木头的质量和体积会变小;密度是物质的一种特性,同种物质,密度相同,所以密度不变,故C正确,ABD错误。
故选:C。
【变式1】一瓶矿泉水,喝掉半瓶,对于剩下的水,不变的物理量是( )A.质量 B.体积 C.密度 D.对瓶底的压强【答案】C【解析】解:一瓶矿泉水喝掉半瓶后,AB、物质总量减少,所以质量变小,同时所占空间变小,所以体积也变小。
密度习题解析答案

密度习题解析答案密度习题解析答案密度是物理学中一个重要的概念,用来描述物体的质量与体积之间的关系。
在学习密度的过程中,我们常常会遇到一些习题,下面我将为大家解析一些常见的密度习题。
1. 问题:一个物体的质量是200克,体积是100毫升,求其密度。
解析:密度的计算公式是密度=质量/体积。
根据题目中的数据,将质量和体积代入公式,可以得到密度=200克/100毫升=2克/毫升。
2. 问题:一个物体的密度是0.8克/立方厘米,体积是500毫升,求其质量。
解析:根据密度的计算公式,质量=密度*体积。
将密度和体积代入公式,可以得到质量=0.8克/立方厘米*500毫升=400克。
3. 问题:一个物体的质量是600克,密度是2克/毫升,求其体积。
解析:根据密度的计算公式,体积=质量/密度。
将质量和密度代入公式,可以得到体积=600克/2克/毫升=300毫升。
4. 问题:一个物体的密度是1.2克/立方厘米,体积是250毫升,求其质量。
解析:根据密度的计算公式,质量=密度*体积。
将密度和体积代入公式,可以得到质量=1.2克/立方厘米*250毫升=300克。
通过以上几个例题,我们可以看出,密度的计算方法是比较简单的,只需要将已知的质量和体积代入相应的公式即可。
但是在实际应用中,我们还需要注意一些细节问题。
首先,密度的单位。
在国际单位制中,质量的单位是克,体积的单位是立方厘米或毫升,因此密度的单位就是克/立方厘米或克/毫升。
在计算中,我们要保持单位的一致性,避免出现单位不匹配的错误。
其次,密度的测量。
通常情况下,我们可以通过称量质量和测量体积来计算密度。
质量可以使用天平进行测量,而体积则可以通过容器的形状和尺寸来计算。
需要注意的是,对于不规则形状的物体,可以使用水位法或排水法来测量体积。
最后,密度的应用。
密度是物质的固有属性,可以用来区分不同的物质。
在实际应用中,我们常常利用密度来鉴别物质的真伪或进行物质的分离。
例如,通过密度的差异可以将沉淀和液体分离,或者用密度测量仪器来检测某种物质的纯度。
密度经典例题1

密度经典例题【例1】甲、乙两物体质量相等,已知甲物体积为V0,乙物体的体积V乙=5V甲,甲物密度是乙物密度的4倍,若两物中只有一个空心的,则[ ]A.甲物一定是空心的B.乙物一定是空心的C.空心体积是V0 D.空心体积是0.8V0【解答】B、C。
【例2】一只空瓶质量50g,装满水后总质量是1.3kg,装满某种液体后总质量1.05kg,求这种液体的密度。
求出水的体积即瓶的容积,即可求得液体的密度。
【解答】m水=m水瓶-m瓶=1300g-50g=1250g,m液=m液瓶-m瓶=1050g-50g=1000g。
这种液体的密度是0.8g/cm3【说明】本题还可以直接应用比例关系求出ρ液而避免瓶容积大小的【例3】体育用铅球实际上是铜和铁的混合物。
一个质量是8kg的铅球,体积是0.84dm3,求这个铅球内铅的含量是多少?(ρ铁=7.9×103kg/m3,ρ铅=11.3×103kg/m3)。
铅的含量是4.53kg.【说明】上述计算中过程比较复杂,也可分成两步,即先求出铅在球中所占的体积,再求铅的质量。
解法如下:m=ρ铁(V-V铅)+ρ铅V铅按密度定义,任何物质的密度都是等于单位体积的质量,因此,混合物质的密度等于混合物的总质量与总体积之比。
设某混合物两个部分的质量分别为m1、m2;两部分所占体积V1、【例4】测得体育课上使用的铅球质量为4千克,体积约为0.57分米3,判断此球是用纯铅制成吗?(铅的密度为11.3×103千克/米3)【分析】要判断此球是否为纯铅的,需根据已知条件计算出此球的密度值。
用此值与物质铅的密度值比较,就可判断此球是否为纯铅的了。
已:m铅球=4千克,V铅球=0.57分米3=0.57×10-3米3,求:ρ铅球=?铅球不是用纯铅制的。
【例5】有一捆横截面积是2.5毫米2的铜丝,质量为89千克,不用尺子量,计算出这捆铜丝的长度。
【分析】因为物体体积与长度有关系。
密度公式计算应用典型题目(带答案)

1、一个空瓶的质量是20g,装满水后,称得总质量是120g,把水到干净后,瓶中再装满酒精,则其总质量是多少?(ρ酒精=0.8×103kg/m 3)2、一个空瓶子的质量是150g ,当装满水时,瓶和水的总质量是400g ;当装满另一种液体时,瓶和液体的总质量是350g 。
求:⑴这个瓶子的容积 ⑵液体的密度3、如图所示,乌鸦为了喝到瓶中的水,每次将一个质量为0.01kg 的小石头投入容积为3×10-4m 3盛有0.2kg 的水的瓶中,当投入25个相同的小石头后,水面恰好升到瓶口,已知水的密度ρ水=1.0×103kg/m 3,求:(1)瓶内小石头的总体积;(2)小石头的密度。
4、一辆载重汽车的车厢容积为3.5m ×2m ×0.6m ,额定载重量为4t 。
求:(1)如果车厢装满泥沙(泥沙的体积等于车厢容积),汽车载重量为多少?(2)已知泥沙的密度为2.4×103 kg /m 3.为了行车安全,汽车不能超载,如果不超载,此车最多能装多少立方米的泥沙?m 总=20g+80g=100g (2) (1)V 容=V 水=250cm 35、“五•一”黄金周,王海栋和妈妈到无锡旅游,买了一只宜兴茶壶,如图所示.他听说宜兴茶壶是用宜兴特有的泥土材料制成的,很想知道这种材料的密度.于是他用天平测出壶盖的质量为44.4g,再把壶盖放入装满水的溢水杯中,并测得溢出水的质量是14.8g。
(1)请你帮王海栋算出这种材料的密度是多少?(2)若测得整个空茶壶的质量为159g,则该茶壶所用材料的体积为多大?6、今年陈传祥家种植柑橘获得了丰收。
他想:柑橘的密度是多少呢?于是,他将柑橘带到学校实验室,用天平、溢水杯来测量柑橘的密度。
他用天平测出一个柑橘的质量是114g,测得装满水的溢水杯的总质量是360g;然后借助牙签使这个柑橘浸没在溢水杯中,当溢水杯停止排水后再取出柑橘,接着测得溢水杯的总质量是240g。
密度计算案例与解答

密度计算案例与解答密度是物质的一种重要性质,它反映了单位体积物质的质量。
在化学实验和日常生活中,密度计算是一个常见且必须掌握的技能。
本篇文章将通过实际案例,详细介绍密度计算的相关知识和解答方法。
案例一:求解物质密度假设有一块铁块,其质量为200克,体积为50立方厘米,现要求解该铁块的密度。
解答:首先,根据密度的定义,密度(ρ)等于物质的质量(m)除以体积(V)。
因此,铁块的密度可以用以下公式表示:ρ = m / V将题目中给出的质量和体积代入公式中,可得:ρ = 200克 / 50立方厘米 = 4克/立方厘米因此,该铁块的密度为4克/立方厘米。
案例二:混合物密度计算现有一瓶密度为0.8克/毫升的甲醇,一瓶密度为1.2克/毫升的乙醇,现要将这两种液体混合在一起,求混合后液体的密度。
解答:首先,由于混合液体的密度是各组分密度的加权平均,可以用以下公式计算混合后密度(ρ'):ρ' = (m1 * ρ1 + m2 * ρ2) / (m1 + m2)其中,m1和m2分别为两种液体的质量,ρ1和ρ2分别为两种液体的密度。
假设混合后液体的总质量为100克,则根据质量守恒,可以得到:m1 + m2 = 100克再根据题目给出的密度和总质量,代入公式中计算混合后液体的密度:ρ' = (80克 * 0.8克/毫升 + 20克 * 1.2克/毫升) / 100克= (64毫升 + 24毫升) / 100克= 88毫升 / 100克= 0.88克/毫升因此,混合后液体的密度为0.88克/毫升。
结语通过以上案例的详细解答,相信读者对密度计算有了更深入的理解。
在实践中,掌握密度计算方法可以帮助我们更准确地了解物质的性质,为化学实验和科研工作提供有力支持。
希望本文能为读者提供实用的帮助,谢谢阅读!。
八年级上密度典型例题

zhm
物
第六章
理
密度典型例题
【例1】一支蜡烛,燃烧掉 一半,剩下的半支与原来的相 比( )
A.质量减半,密度减半 B.质量减半,密度不变 C.质量不变,密度减半 D.质量不变,密度不变
【例2】市场出售的“洋河酒”, 包装上注明的净含量为500mL,酒 精度为55%,求这瓶酒的质量。
分析:(1)洋河酒可以看 做是纯酒精和纯水的混合。 (2)55%指的是酒精和这瓶酒 的体积比。
•
【例3】甲、乙两种物 质的密度分别为 ρ1和ρ2, 现将这两种等质量物质 混合,求混合后的密度。 (设混合前后体积它们的质量之比为2:3, 体积之比为1:2,求它们的密 度之比。 【例5】在氧气瓶中装满密 3 度的4kg/m 的氧气,若用去 一半,剩余部分氧气的密度是 3 ______kg/m 。
•
【例6】只用量筒, 不用天平,如何量得 80g的酒精?写出实验 步骤。(ρ酒=0.8×103kg/m3 )
【例7】给你一架天 平(配有砝码盒)、烧 杯和水,如何测出煤油 的密度,写出实验步骤 和表达式。
祝同学们 不断进步!
密度例题讲解

密度知识总结及常见题型1.密度定义:单位体积的某种物质的质量叫做该物质的密度。
.(1)密度是物质的固有属性,与物体的形状、体积、质量无关,即对于同一物质而言,密度值是不变的。
(2)密度的大小只由材料决定。
(如:一杯水和一桶水的密度是一样的;)(3)不同的物质,密度一般不同;相同物质,密度一般相同;但状态不同,密度不同。
(水和冰的密度不同)2.密度的公式:ρ = m / v(公式变形:m=ρv v=m / ρ)(1)ρ表示密度,m表示质量(单位:千克或克),v 表示体积(单位:m³或cm³)(2)密度的物理意义:水银的密度为13.6×10³千克/m³,它所表示的意义是1m³的水银的质量是13.6×10³千克。
3.密度的单位:(1)密度的单位:kg/m³或g/cm³,(2)两者的关系:1g/cm³=1000kg/m³1kg/m³=1×103-g/cm³(3)水的密度:1×10³kg/m³或1g/cm³1毫升=1cm³= 1×106-m³1升=1 dm³=103-m³(4)单位转化:4.密度的测量(1)测量原理:ρ=m/v(2)测量步骤:①用天平称量物体的质量;②用量筒或量杯测量物体的体积;③计算5.密度知识的应用:(1)在密度公式中,知道其中任意两个量,即可求得第三个量。
(2)可用于鉴别物质的种类。
例题解析单位换算7.8×103kg/m 3= g/cm 3,2.7g/cm 3= 103kg/m 3。
密度概念理解1.对于公式m Vρ=的物理意义,下列叙述中正确的是( ) A .物质的密度与其质量成正比,质量越大,密度越大B .物质的密度与其体积成反比,体积越小,密度越小C .同种物质组成的物体,其密度是确定的,与其质量多少或体积大小无关D .以上说法都不对2.用了多年的铅球,其表面磨损了一些,未发生变化的是铅球的( )A.质量B.体积C. 表面积D. 密度3.一瓶矿泉水喝去半瓶,则剩下的半瓶矿泉水( )A .质量减半,密度减半B .质量减半,密度不变C .体积减半,密度也减半D .质量、体积、密度均减半气体密度变化1.一钢瓶中储质量为m 、密度为ρ的氧气,当住院病人用去3分之一的氧气后,瓶内剩余氧的密度是( )A 、ρB 、ρ/3C 、2ρ/3D 、3ρ2. 气体是很易被压缩的,一定质量的气体,当它的体积被压缩后,它的密度( )A. 增大B. 不变C. 减小D. 不确定3、一气球在升空的过程中,体积逐渐变大,则气球内的气体的密度如何变化( )A 、不变B 、变大C 、变小D 、无法判断瓶子问题(液体体积不变)1.一个质量为0.25 kg 的玻璃瓶,盛满水时称得质量是1.5kg ,若盛满某液体时称得质量是1.75kg,那么这种液体的密度是( )A. 1.0×103 kg/m3B.1.16×103 kg/m3C. 1.75×103 kg/m3D. 1.2×103kg/m32. 一只空瓶装满水时的总质量是400g ,装满酒精时的总质量是350g ,则该空瓶的容积是(ρ水=1g/cm 3,ρ酒精=0.8g/cm 3)( ) A 、400cm 3 B 、350cm 3 C 、250cm 3 D 、200cm3 3. 我国名酒五粮液素有“三杯下肚浑身爽,一滴沾唇满口香”的赞誉,曾经获得世博会两届金奖。
有关密度例题

有关密度例题【例1】将一瓶油倒掉一些后 [ ]A.质量变小、密度变小 B.质量不变、密度不变C.质量变小、密度不变 D.质量变小、密度变大【分析】质量是物体的特性,密度是物质的特性。
一瓶油倒掉一些后,作为物体已经发生了变化,但作为物质却没有发生变化。
【解答】C.【例2】一块铝的密度是2.7×103kg/m3,将这块铝平分成二块,则其中一块的密度是 [ ]A.1.35×103kg/m3 B.2.7×103g/cm3C.5.4×103kg/m3 D.2.7g/cm3【分析】密度是物质的特性,一块铝与半块铝的物质不变,所以密度也不变。
【解答】D.【例3】某金属板长1m,宽50cm,厚8mm,测得其质量是35.6kg,问这是什么金属?【分析】判断是什么金属,可以先求出其密度,然后参照密度表对照.【解答】因50cm=0.5m,8mm=0.008m,体积为V=1m×0.5m×0.008m=0.004m3,查表得该金属是铜.【说明】也可将质量化为35600g,体积用cm3单位,得到ρ=8.9g/cm31.密度的实用单位除g/cm3外还可用kg/dm3和t/m3,有时使用这些单位能使计算简化.2.密度公式的意义包含有:(1)不同物质的物体,质量相等时,密度较大的物体其体积较小。
如:质量相等铜块和铁块,铜块体积小于铁块体积。
(2)不同物质的物体,体积相等时,密度较大的物体其质量较大。
如:同一个瓶装满水和装满油相比较,装满水的质量大。
【例4】试说明质量和密度是不同的物理概念。
【解答】质量表示物体内所含物质的多少。
物体所含物质越多,物体的质量就越大。
物体质量的大小与物质的种类无类。
单位体积内物质的质量,称为该物质的密度。
根据ρ=m/V可知,对于由同一种物质组成的物体来说,当它的体积增大时,它的质量和质量无关。
物质不同,密度不同。
提到质量,应称为物体质量。
如桌子的质量是20千克;杯子的质量是0.2千克等。
密度典型例题解析(详细解析)

密度典型例题解析例1 关于密度公式ρ=Vm,下列说法中正确的是 ( ) A .由公式可知ρ与m 成正比,m 越大ρ越大 B .由公式可知ρ与m 成反比,m 越大ρ越小C .由公式可知当物质的质量m 一定时,ρ与 V 成正比,当物质的体积一定时,ρ与m 成正比D .由公式可知物质的质量 m 与物质的体积V 的比值是定值解析:密度是物质的一种特性,各种物质的密度都是一定的,不同物质的密度一般是不同的.物质的密度等于质量跟体积的比值即ρ=Vm,但与其质量m 和体积V 无关.所以选项D 是正确的.点拨:密度是反映某种物质单位体积的质量的物理量.密度的概念在初中物理有着广泛的应用,是后面要学习的“液体的压强”、“固体的压强”、“浮力”等知识的基础.例2 测石块的密度(1)用调节好的天平称石块的质量.把石块放在天平的左盘内,当右盘内有50克的砝码一个,游码在标尺上的位置如图示时,天平平衡,则石块的质量是________克.(2)把石块放入盛有40厘米3水的量筒以后,水面所到达的位置如图3—6所示,则石块的体积是________厘米3.(3)石块的密度是________千克/米3.解析:石块的质量是砝码的总质量50克加上游码在标尺上所对的刻度值3.4克,得出石块的质量.(1)53.4克;石块的体积是用石块放入量筒后水面所达到的刻度60厘米3减去没有放入石块前水面所对的刻度值40厘米3,得出石块的体积.(2)20厘米3;根据ρ=Vm求出石块的密度.(3)2.67×103. 点拨:读取量筒的数据时,若液面是凹形的,观察时以凹形底部为准;若液面是凸形的,以凸形的顶部为准.例如:用量筒测水的体积时,水面是凹面,如图1—3—2示.若用量筒测银的体积时,水银面则是凸面,如图示.例3 质量相等半径相同的空心铜球、铁球和铝球各一个(ρ铜>ρ铁>ρ铝),则空心部分体积最大的球是 ( )A .铜球B .铁球C .铝球D .条件不足无法确定 解析:根据密度计算公式ρ=Vm;质量相等的不同物质,密度大的体积小.因为ρ铜>ρ铁>ρ铝,质量相等半径相同的(体积相等)空心铜球、铁球和铝球,含有物质部分的体积最小的是铜球,所以中间空心部分体积最大的是铜球,如图示.选项A 是正确的.点拨:利用密度判断物体空、实心情况有下列几种方法:(1)用公式ρ物体=Vm求物体的平均密谋,若ρ物体=ρ物质为实心,ρ物体<ρ物质为空心.(2)用公式V物质=ρm求出物体中含物质的体积,若V 物质=V 实际为实心,V 物质<V 实际为空心.常见的稍有难度的题型如“例2”、还有如“若是空心的,空心部分的体积是多少”、“在空心部分铸满铝,质量又是多少”等题型.所以一般情况下,做这种题型常选第(3)种方法.例4 在调好的天平两盘上各放一铝块和铁块,天平恰能保持平衡,则铝块与铁块的质量之比m 铝∶m 铁=________,体积之比V 铝∶V 铁=________.(ρ铝=2.7×103千克/米3,ρ铁=7.8×103千克/米3)解析:天平平衡后左、右盘的物体的质量相等m 铝=m 铁,所以质量比是1∶1.根据公式V =ρm和铁与铝的密度值,可得体积之比是78∶27.点拨:利用天平判断物体的密度关系、体积关系、质量关系是常见的题型,能反映出我们综合运用知识的能力.例5 一个瓶子最多能装下500克水,则这个瓶子能装下500克的下列哪种物质( ) A .浓硫酸B .酒精C .煤油D .汽油解析:这个瓶子能装下比水的密度大的物质,因为瓶的容积为V =水水ρm =3/1500厘米克克=500厘米3,在相同质量时,密度大于1克/厘米3的物质体积才能小于500厘米3,所以正确答案为A .点拨:这是一个关于密度应用的题目,借助水的密度可把瓶子的容积求出,这样就可以在质量相等的情况下对比密度判断出体积大小,密度小于水的物质不能装下,而密度大于水的物质可以装下,因为它的体积小于500厘米3.例6 把一块金属块放入盛满酒精的杯中时,从杯中溢出10克酒精(ρ酒精=0.8克/厘米3),若将这块金属块从酒精中取出放入盛满水的杯中,则从水杯中溢出水的质量 ( ) A .大于10克 小于10克 C .等于10克 D .无法确定 解析:由ρ=Vm得V =ρm =3/8.010厘米克克=12.5厘米3,溢出水的质量m =ρ水·V =1克/厘米3×12.5厘米3=12.5克>10克,所以正确答案为A .点拨:此类型题解决问题的突破口是求出杯的容积V ,它是沟通酒精和水的桥梁,两种液体的体积相等,利用这个关系就可以找出水的质量.例7 有一只玻璃瓶,它的质量为0.1千克,当瓶内装满水时,瓶和水的总质量为0.4千克.用此瓶装金属颗粒若干,瓶和金属颗粒的总质量为0.8千克,若在装金属颗粒的瓶中再装满水时,瓶、金属颗粒和水的总质量为0.9千克.求:(1)玻璃瓶的容积.(2)金属颗粒的质量.(3)金属颗粒的. 解析:由密度公式ρ=Vm (1)V 瓶=V 水=水水ρm =33/101.04.0米千克千克千克-=3×10—4米3 (2)m 金=0.8千克-0.1千克=0.7千克 (3)瓶内装金属粒后倒进去的水的体积V 水=水水ρm =33/108.09.0米千克千克千克-=10—4米3 金属粒体积V金=V瓶—V水=3×10—4—10—4米3=2×10—4米3所以ρ金=金金V m =341027.0米千克-⨯=3.5×103千克/米3答:玻璃瓶的容积为3×10—4米3,金属颗粒的质量是0.7千克;金属颗粒的密度是3.5×10—4米3.点拨: 对这种有一定难度的题目,要认真审题,挖掘题目所给的隐含条件,以图助思,将题目所述情景再现于图中,以求帮助我们建立起已知量和待求量的联系.由题意可画出图1—3—5该题的第(3)问中,求金属颗粒的密度难度较大,但可以从图1—3—5找出解法.尤其是金属颗粒的体积不好求,但可以从求它所排开水的体积为线索,这个难点便能突破了.例8 用天平测一木块的质量,操作正确,所用砝码和游码位置如图示.用量筒测测其体积,量筒中水面的位置如图1—3—6示,则所测木块的质量为________千克,体积为________米3,木块的密度为________千克/米3.解析:由题意知木块的质量是0.018千克,木块体积为V =80厘米3—60厘米3=20厘米3=2×10—5米3,木块的ρ=V m=35102018.0米千克-⨯=0.9×103千克/米3 点拨:本实验是测不易浸水木块的密度,木块的质量可直接测,木块的体积可利用“沉锤法”,借助于能沉入水下的铁块把木块的体积测出,测试时一定要注意V 木=V 2—V 1,即两次量筒的示数差.例9 用一架天平,一只空瓶和适量纯水测定牛奶的密度.(1)应测的物理量为________.(2)用测出的物理量写出计算牛奶密度的计算式:________________________. 解析:(1)应测的物理量为:空瓶质量m ,装满纯水后瓶子的质量m 1,装满牛奶后瓶子的质量m 2.(2)牛奶的体积V =水ρmm -1牛奶的密度ρ牛奶=Vmm -2或ρ牛奶=m m m m --12ρ水点拨:此题是一个自行设计的测牛奶密度的实验.我们要根据ρ=Vm这一公式,充分利用题中给出的工具由天平可测出牛奶的质量.在没有量筒的情况下要知道体积,就得借助纯水,因为它的密度是已知的,这是解决问题的突破口.由水可求出瓶的容积V =水水ρm ,也是牛奶的体积.在写牛奶密度的表达式时要用实验中已测量出的物理量具体表示.例10 有一团长细铁丝,用天平称出它的质量是150克,测得铁丝的直径是1毫米,这团铁丝有多长?(ρ铁=7.9克/厘米3) 解析:铁丝的体积,由ρ=Vm得V =ρm=3/9.7150厘米克克铁丝的截面积S =πr 2=π(2d )2 根据V =SL 可得L =SV=223)05.0(14.3/9.7150厘米厘米克克⨯⨯ =2419厘米≈24米点拨:利用密度可以解决一些不易直接测量的问题.该题中细铁丝长度不容易用刻度尺测量,但用天平或秤测量铁丝的质量很方便,这样就可以利用密度公式V =ρm求出体积,长度就可以算出来.在实际中常采用秤称出几千米金属线或电线的质量来的方法,就是根据上述道理.例11 质量相等的甲、乙两种注体,甲液体的密度为ρ1,乙液体的密度为ρ2,将两种液体混合(混合时总体积的微小变化略去不计),则混合液的密度为 ( ). A .221ρρ+ B .21ρρ+ C .2121ρρρρ+⋅ D .21212ρρρρ+⋅解析:由密度公式ρ=Vm知,需要先求出混合液的质量和体积.甲、乙两种液体质量相等,设分别为m ,则甲的体积是V 甲=1ρm,则乙的体积是V 乙=2ρm,混合液的质量是2m ,体积是V 甲+V 乙=1ρm+2ρm,把质量和体积代入密度公式即可求出混合密度.答案为D .点拨:若把体积相等的两种液体混合,则混合液体的密度为21(ρ1+ρ2).例12 给你一台已调好的天平和一盒砝码,一只烧杯,适量的水和盐水,现要测量盐水的密度请说出你的办法.解析:①用天平称出空烧杯的质量m 1;②用天平称出烧杯装适量的水的总质量m 2,并做记号;③烧杯内水的质量为m 水=m 2-m 1;④用天平称出烧杯内装入和水体积相同的盐水的质量m ;⑤烧杯内盐水的质量为m 盐水=m 3-m 1;⑥利用ρ=Vm,算出烧杯内水的体积即盐水的体积. V 盐水=V 水=水水ρm =水ρ12m m -⑦盐水的密度是ρ盐水=盐水盐水V m =水ρ1213m m m m --=1213)(m m m m --水ρ点拨:测量密度,需要测量质量和体积,质量可以用天平测量,但体积的测量没有量筒或量杯,而是给了适量的水,所以只有通过天平和水来间接地测量盐水的体积,所以本题需要采取等体积代换的方法,用天平测量与盐水体积相等的水的质量,算出水(水的密度作为已知条件)的体积即是盐水的体积.例13 一只正在燃烧的蜡烛,它的 ( )A .质量不断减少,密度不变B .质量不断减少,密度也减小C .密度不变,质量不变D .质量不变,密度减小解析:这道题同时考查质量和密度的概念.蜡烛在燃烧过程中,质量减少.但蜡烛这种物质没有改变,所以密度不变. 答案:A例14 (北京市中考试题)对于密度的计算公式ρ=vm,下面说法正确的是 ( ) A .密度与物体的质量成正比 B .密度与物体的体积成反比C .物质的密度与质量成正比,与体积成反比D .密度是物质的一种特性,其大小等于物质的质量与体积的比值解析:对密度的概念应从物理意义上去理解,而学生容易从数学公式的角度去分析,而选择C 选项.ρ=vm是定义密度、计算密度大小的公式,但它不能决定某种物质密度的大小.例如:质量是1kg 的水,密度为1.0×103kg /m 3,质量为2kg 的水,密度仍为1.0×103kg /m 3.因为当某种物质的质量为原来2倍时,体积也相应为原来的2倍,质量与体积的比值不变. 所以不能说某种物质的密度跟它的质量成正比,跟它的体积成反比. 答案:D例15 (南京市中考试题) A 、B 、C 三种物质的质量m 与体积V 的关系图像,如图所示.由图可知,A 、B 、C 三种物质的密度ρA 、ρB 、ρC 和水密度ρ水之间的关系是 ( )A .ρA >ρB >ρC ,且ρA >ρ水, B .ρA >ρB >ρC ,且ρA <ρ水, C .ρA <ρB <ρC ,且ρA >ρ水,D .ρA <ρB <ρC ,且ρA >ρ水,解析:此题是用图像来求物理量,是数学知识应用于物理的一种常用方法,但在平时的学习中,学生不够重视.图像中,横轴表示体积,单位是cm 3,纵轴是质量,单位是g ,整个图像表示了质量随体积的变化. 根据密度公式ρ=vm,我们可以从体积为10 cm 3处作纵轴m 的平行线,如图l —3—8所示,并与A 、B 、C 三条直线交于点C 1、C 2和C 3,再分别过点作横轴V 的平行线,从图中就可以看出:ρA >ρB >ρC ,又因为ρ水=1g /cm 3,而图中ρA 约为2g / cm 3,ρB 约为1g / cm 3,ρC 则小于l g / cm 3.答案:A例16 (上海初中物理竞赛试题)在测定液体密度的实验中,液体的体积(V )及液体和容器的总质量(m 总)可分别由量筒和天平测得,某同学通过改变液体的体积得到几组数据,画出有关的图线,在图中能正确反映液体和容器的总质量跟液体的体积关系的是 ( )ABCD解析:这道题考查学生是否会观察m -V 图像,是否会通过图像分析问题的正确性. 当所测液体体积V 增大时,液体质量m l 一定增大,由公式m =ρV ,m l 和V 为正比关系,且V =0时,m l =0,图线A 应过原点.但m 总=m 1+m 0(m 0为容器质量),m 总=ρV +m 0,当V =0时,m l =m 0,图线B 恰好反映了这种情况,此时的质量代表了容器本身的质量,而图像的斜率代表了此种液体的密度.C 图中,V ≠0时,m 总=0,和实际不符.D 图中,随着V 的增大,m 总减少,也和实际不符. 答案:B例17 为测定黄河水的含沙量,某校课外活动小组取了10dm 3的黄河水,称其质量是10.18kg .已知沙子的密度ρ沙=2.5×103kg /m 3,问黄河水的含沙量是多少?(即每立方米黄河水中含沙多少千克)解析:此题是沙掺在水中,但两者不相混合,可以先求出10dm 3黄河水中的沙子的质量,进而求出1 m 3中沙子的质量.考查了学生灵活掌握密度知识去解决问题的能力. 已知:V =10dm 3-1×104cm 3,m =10.18kg =10180g . 求:1 m 3中含沙质量m 沙′解:⎩⎨⎧+=+=沙水沙水V V V m m m由①得m 沙=m -ρ水V 水=m —ρ水(V —V 秒) =m -ρ水V —ρ水沙沙ρm整理得 m 沙=水沙水沙ρρρρ--)(V m代入数据 m 沙=333343/1/5.2)/110110180(/5.2cmg cm g cm g cm g cm g -⨯⨯- 答案:1 m 3中含沙量为30kg .例18 (北京市中考试题)为节约用水,某同学家采取了多种节水措施,减少了用水量.4月底查水表时,水表显示的数字325m 3,4月份这个同学家的用水量为8t .5月底查水表时,水表显示的数字为332 m 3,则5月份这个同学家的用水量比4月份少________吨. 解析:5月份用水体积V =332 m 3-325 m 3=7 m 3,则5月份用水质量m =ρ水V =1 t /m3×7 m 3=7t .此时选择t /m 3为密度单位,比选用国际单位要方便. 5月比4月用水量少了8t -7t =1 t . 答案:1 t例19 一个瓶子装满水时,水的质量为1kg ,这个瓶子最多能装下多少千克的酒精?(ρ酒精=0.8×103kg /m 3) 已知:m 酒精. 解 ρ酒精=0.8×103kg /m 3=0.8kg /dm 3ρ水=1.0×103kg /m 3=1 kg /dm 3此时选择kg /dm 3为密度单位,可使计算过程简化.V 水=水水ρm =3/11dmkg kg=1 kg /dm 3 瓶子的容积一定:V 酒精=V 水m 酒精=ρ水V 酒精=0.8kg /m 3×1 dm 3=0.8kg 答案:这个瓶子最多能装下0.8kg 酒精例20 (四川省中考试题)一个空瓶的质量为400g ,装满水后两者的总质量为800g ;当装满油后的总质量为720g ,求:油的密度是多少?解析:用同样的瓶分别装水和装油,水和油体积相同,可以用V 一定时,21m m =21ρρ关系去做.已知:m 水=800g -400g =400g ,m 油=720g -400g =320g . 求ρ油. 解 V 水=V 油水油m m =水油ρρ(ρ水取1g /cm 3)g g 400320=3/1cm g 油ρ(ρ油取0.8g /cm 3) 答案:油的密度为0.8 g /cm3例21 (天津市中考试题)甲、乙两金属块,甲的密度是乙的52,乙的质量是甲的2倍,则甲的体积是乙的体积的 ( )A .0.8倍B .1.25倍C .0.2倍D .5倍解析:这种根据公式求化值的试题,在平时的考查中也多次出现.首先要把题中文字叙述的比值,用数学形式表示出来,如甲的密度是乙的52,即乙甲ρρ=52,乙的质量是甲的2倍,即m 乙=2m 甲,推得乙甲m m =21. 求:乙甲V V .解法1乙甲V V =乙乙甲甲ρρm m =乙甲m m ×甲乙ρρ=21×25=45=1.25 解法2 因为在比值中,各物理量的单位是统一的.所以这种题也可以用“设数”法做.则 乙甲V V =5221=45=1.25答案:B这种方法是将物理公式的繁索推导转化为简单的数学运算.当“填空”或“选择”题中出现类似问题时,可以用此方法,但它的中间过程从理论上看不够严密.例22 5m 3的冰熔化成水后,体积是多少?体积变化与原体积比是多少?如果是水结成冰,体积变化与原体积比是多少?(ρ冰=0.9×103kg /m 3) 解析:冰熔成水,质量不变,密度增大,体积减小.已知:V 冰=5m 3,ρ冰=0.9t /m 3求:V 冰,1V V △,2V V△ 解 冰化成水后: m 水=m 冰利用前面的比例式:冰水V V =水冰ρρ V 水=V 冰×水冰ρρ=5m 3×109=4.5 m 3 1V V △=冰水冰V V V -=333m5m 5.4m 5-=101水结成冰后,质量不变水冰V V =冰水ρρ=109∴ V 冰=109V 水2V V △=水水冰V V V -=水水水V V V -910=91【注意】 与前面答案不同.答案:体积是4.5m 3,所求值分别101和91例23 (北京市中考试题)一个装满水的水杯,杯和水总质量为600g ,将一些金属粒倒入杯中沉底后从杯中共溢出水200g ,待水溢完测得此时水杯总质量为900g ,则金属粒密度为多少立方米每千克?解析:可借助于画图来帮助理解题目当中几个质量的意义及各质量之间的关系.如图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第七章 质量和密度综合练习(二)【例题精选】:1、托盘天平的调节和使用 例1:对放在水平桌面上的托盘天平进行调节时,发现指针指在分度盘中央的左侧,这时应将横梁上的平衡螺母向 调节(填:“左”或“右”)。
用调节后的天平测某物体的质量,所用砝码和游码的位置如图3所示,那么该物体的质量是 克。
分析与解:调节天平时,指针指在分度盘中央的左侧,说明左盘低,应将横梁上的平衡螺母向右移动。
被测物体的质量为112.2克。
说明:读游码对应的刻度值时,也应先认清标尺的量程及最小刻度值。
根据游码左侧对应的刻度线读数。
图3中,标尺的量程是5克,每一大格表示1克,最小刻度值为0.2克。
游码对应的刻度值为2.4克。
所以物体的总质量为112.2克。
2、正确理解密度是物质的一种特性特性是指物质本身具有且能与其它物质相互区别的一种性质。
密度是物质的一种力学特性。
它表示在体积相同的情况下,不同物质的质量不同;或者说在质量相同的情况下,不同物质体积不同的一种性质,通常情况下每种物质都有一定的密度,不同的物质密度一般是不同的。
当温度、状态等不同时,同种物质的密可能不同,如一定质量的水结成冰,它的质量不变,但体积变大、密度变小。
例2:体积是20厘米3,质量是178克的铜,它的密度是多少千克/米3?若去掉一半,剩下一半铜的密度多大?分析:利用公式ρ=mV可以算出铜的密度,可用克/厘米3作密度单位进行计算,再利用1克/厘米3 = 103千克/米3,换算得出结果。
解:ρ====⨯m V 178208989103333克厘米克厘米千克米././ 铜的密度是891033./⨯千克米 因为密度是物质的特性,去掉一半的铜,密度值不变。
所以密度仍为891033./⨯千克米。
说明:去掉一半铜的体积是10厘米3,而它的质量也仅为原来的二分之一,为89克,利用密度公式ρ=mV计算,也可得出剩余一半铜的密度仍为891033./⨯千克米,由此看出物质的密度跟它的体积大小、质量的多少无关。
密度公式ρ=mV是定义密度、计算密度大小的公式,但它不能决定某种物质密度的大小。
所以说,某种物质的密度既不跟它的质量成正比,也不跟它的体积成反比。
在学习密度公式时,要明确它的物理意义,这一点十分重要。
3、会用比例关系解密度问题 密度知识中有三个比例关系: (1)同一种物质,密度相同,体积大的质量也大,物质的质量跟它的体积成正比。
即:当ρ一定时,m m VV 1212=。
(2)不同的物质,密度不同,在体积相同的情况下,密度大的质量也大,物质的质量跟它的密度成正比。
即:当V 一定时,m m 1212=ρρ(3)不同的物质,密度不同,在质量相同的情况下,密度大的体积反而小。
物体的体积跟它的密度成反比,即:当m 一定时,V V 1221=ρρ例3:一个瓶子装满水时,水的质量是1千克,这个瓶子最多能装下多少酒精?(ρ酒精=⨯08103.千克/米3) 分析与解:题中隐含的已知条件是,瓶的容积一定,则水的体积和酒精的体积相等。
分步解法如下: 解法一:V m 水水水千克千克米米==⨯=-ρ1110103333/V V m V 酒精水酒精酒精酒精米千克米米千克===-=⨯⨯=--1008101008333333ρ./.可采用比例法求解:解法二:V V m m m m 酒精水酒精水酒精水酒精水酒精水·千克千克米千克米千克=∴=∴==⨯⨯⨯=ρρρρ10810110083333.//.说明:(1)解题要认真审题,注意挖掘题目中隐含的已知条件。
对于这道题来说,明确水的体积与酒精的体积相等这一隐含条件是解题的关键。
(2)在运用公式解题时,要注意各物理量之间的对应关系,即在运用密度公式ρ=mV或其变形公式m V =ρ、V m =ρ解题时,m 、V 、ρ的量值必须是同一物体,在同一物理状态时的量值。
如果在一道题里出现两个或两个以上不同物体,在运用公式解题时,应在各物理量的字母的右下方添加角标以区别。
(3)运用比例法求解,必须具备成比例的条件。
解题时,要先写出成比例的条件,再写出比例关系式。
4、运用密度公式解决有关问题 例4:甲、乙两物体的质量之比为3∶1,它们的密度之比为1∶3,则甲、乙两物体的体积之比为 。
分析与解:这是利用密度公式求比值的问题。
其解题步骤是:①把未知量写在等号的左边;②将未知量的表达式写在等号右边;③化简;④代入数据,运算,得出结果。
具体解法如下:V V m m m m 甲乙甲甲乙乙甲甲乙乙·===⨯⨯=ρρρρ331191例5:体积是30厘米3的铁球,质量是79克,这个铁球是空心的还是实心的,如果是空心的,空心部分的体积多大? 分析:判断这个球是空心的还是实心的,可以从密度、质量或体积三个方面去考虑。
解法一:密度比较法。
根据密度公式求出此球的密度,再跟铁的密度相比较。
ρρρ球球球球铁克厘米克厘米千克米千克米千克米====⨯⨯<⨯<m V 79302626102610791033333333....∴铁球是空心的 解法二:质量比较法。
假设这个铁球是实心的,利用密度公式求出实心铁球的质量,再跟这个球的实际质量相比较。
m V 球铁球克厘米厘米克==⨯=ρ793023733.237克 > 79克m m 实球>∴铁球是空心的 解法三:体积比较法。
根据题目给出的铁球的质量,利用密度公式计算出实心铁球应具有的体积,再跟实际铁球的体积相比较。
V m V V 实球铁实球克克厘米厘米厘米厘米===<<ρ79791010303333.∴铁球是空心的 空心部分体积:V V V 空球实厘米厘米厘米=-=-=301020333答:这个球是空心的。
空心部分的体积是20厘米3。
例6:一个空瓶质量是200克,装满水称,瓶和水的总质量是700克。
将瓶里的水倒出,先在空瓶内装入一些金属的颗粒,称出瓶和金属的总质量是为878克,然后将瓶内装满水,称出瓶水和金属粒总质量是1318克。
求瓶内金属的密度多大? 分析:本题可运用分析法从所求量入手,逐步推导,运用密度公式,直至推到已知条件满足求解为止。
设:瓶的质量为m 瓶,装满水时水的质量为m 水,水的体积V 水,水和瓶总质量m 瓶+m 水。
金属粒的质量为m 金。
装入金属粒且装入金属粒后,再装满水时水的质量,对应的体积为'V 水。
V 水-'V 水则为金属粒占有的体积。
分析法推导思路:而瓶的质量、瓶与水的总质量、瓶与金属的总质量,以及瓶、金属加入水后的总质量、水的密度均已知。
此题即可解。
已知:m 瓶=200克 m m 瓶水+=700克m m 瓶金+=878克 m m m m 总瓶金水=++=1318克求:ρ金解:利用分步求解: ()m m m m 金金瓶瓶=+-=878克-200克 = 678克 ()m mm m水水瓶瓶=+-=700克-200克 = 500克瓶的容积与装满水时水的体积相等,即V V 瓶水=。
V V m 瓶水水水克克厘米厘米====ρ500150033()()'='++-+=m m m m m m 水水金瓶金瓶1318克-878克 = 440克瓶内装金属粒后所剩余的空间V V 空水=''='==V m 水水水克克厘米ρ44013440厘米3 V V V V V 金空水水=-=-'=550厘米3 -440厘米3 = 60厘米3ρ金金金克厘米克厘米===m V 6786011333. 答:这种金属的密度为1133.克厘米或11.3×103千克/米3。
说明:测物质的密度一般需用天平测出物体的质量,量筒测出其体积,利用ρ=mV求出物质的密度。
而本题中需天平、水和一个瓶子就可以测出固体的密度。
天平可以直接测出质量。
这里利用密度公式,间接求出固体的体积,再计算出密度。
【综合练习】:一、填空题: 1、在物理学中,我们把 叫做质量。
在国际单位制中,质量的单位是 。
常用的还有 、 、 。
2、请给下列各量写上恰当的单位。
(1)成人身体的质量是50~70。
(2)鲸的质量可达1.2×102 。
(3)一只鸡的质量大约是1~2 。
(4)一枚大头针的质量大约是5×10-2。
3、在调节托盘天平时,游码置于零刻线处时,指针仍偏右,此时应将天平右端的螺母向 边调。
4、有一个实心金属球的质量是2.825千克,体积是250厘米3,这个金属球的密度是 ,若把这个金属球分成体积相等的两个半球的密度是。
5、用同种材料制成的两个实心物体,若两物体的质量之比是4∶3。
那么这两个物体的体积之比是 ,两物体的密度之比是 。
6、某种物质的 的质量叫做这种物质的密度,计算密度的公式是 ,密度的单位是 或 ,根据密度的物理意义可知,ρ与m 、V 。
7、有一装满油的玻璃瓶总质量为1.46千克,已知瓶的容积为1.2分米3,空瓶的质量是0.5千克,这种油的密度为。
8、一个正方体铅块,它的质量是90.4克,则此铅块的边长为厘米。
(ρ铅千克米=⨯1131033.)二、选择题:1、托盘天平的横梁上都有标尺和游码,移动游码的作用是A.调节横梁平衡B.代替指针指示的位置C.相当于向左盘上加小砝码D.相当于向右盘加上小砝码2、下列物体接近5×10-5千克的是A.一枚大头针B.一只鸡蛋C.一本物理书D.一块橡皮3、已知铁的密度是7.9克/厘米3,铜的密度为8.9×103克/厘米3,那么790克的铁块和890克的铜块相比较:A.铜块的体积大B.铁块的体积大C.铜块和铁块的体积一样大D.条件不足,无法比较4、甲、乙两个物体的质量之比是2∶3,体积之比是4∶5,则甲乙两种物质的密度之比为A.6∶5 B.5∶6 C.5∶3 D.8∶155、平放在水平地面上的一块砖,切去一半,则剩下的半块砖:A.质量减少一半,密度减少一半B.质量减少一半,密度不变C.体积减少一半,密度减少一半D.以上的说法均不正确6、一只能装2千克酒精的瓶子(ρ酒千克米=⨯081033.),如果用来装水,则瓶内水的质量为A.小于2千克B.大于2千克C.等于2千克D.无法判断7、一个空瓶装满水后质量为32克,装满酒精后质量为28克,则空瓶的质量和容积分别为A.14克,14厘米3B.12克,20厘米3C.28克,28厘米3D.24克,40厘米3三、实验题:1、下面是调节天平和使用天平的步骤,请把正确的排列顺序写在横线上。
A.把物体放在左盘,砝码放在右盘并移动游码使天平平衡。
B.调节天平横梁右端的平衡螺母,使指针指在刻度盘的中线处。
C.盘中砝码的总质量加上游码在标尺上所对的刻度值,算出被测物体的质量。
D.把天平放在水平台上,把游码放在标尺左端的零刻线处。
