2018年天津市河东区高考一模文科数学试卷及答案 精品
2018年天津高考文科数学(含参考答案)

2018年普通高等学校招生全国统一考试(天津卷)数学(文史类)本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试用时120分钟。
第Ⅰ卷1至2页,第Ⅱ卷3至5页。
答卷前,考生务必将自己的姓名、准考证号填写在答题考上,并在规定位置粘贴考试用条形码。
答卷时,考生务必将答案涂写在答题卡上,答在试卷上的无效。
考试结束后,将本试卷和答题卡一并交回。
祝各位考生考试顺利!第Ⅰ卷注意事项:1.每小题选出答案后,再选涂其他答案标号。
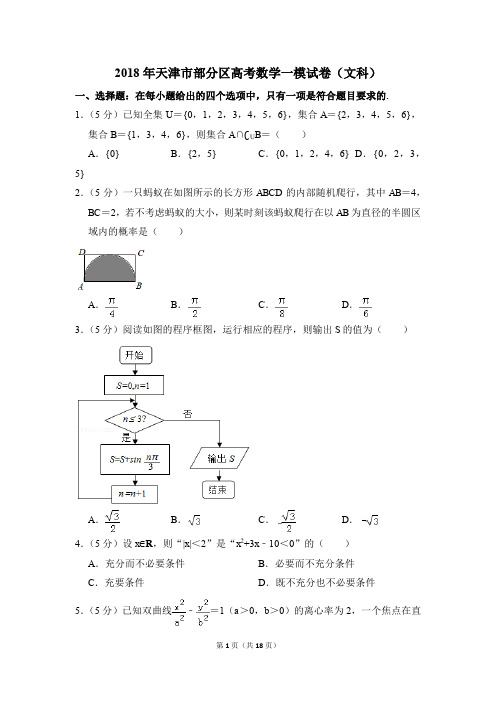
2.本卷共8参考公式:·如果事件.h 表示棱柱的高.h 表示棱锥的高.一..(1|12}x x ∈-≤<R ,则()A B C = (A ){1,1}-(C ){1,0,1}-(D ){2,3,4}(2)设变量,x y 满足约束条件52410x y x y x y y +≤⎧⎪-≤⎪⎨-+≤⎪⎪≥⎩,,,,则目标函数35z x y =+的最大值为(A )6 (B )19 (C )21(D )45(3)设x ∈R ,则“38x >”是“||2x >”的 (A )充分而不必要条件(B )必要而不充分条件(C )充要条件(D )既不充分也不必要条件(4)阅读如图所示的程序框图,运行相应的程序,若输入N 的值为20,则输出T 的值为 (A )1(B )2(C )3(D )4(5)已知13313711log ,(),log 245a b c ===,则,,a b c 的大小关系为(A )a>(6(A (C (7),A B 两点(A )23x -(C )24x -(8)·OM 的值为 (A )15-(C )6-(D )0第Ⅱ卷注意事项:1.用黑色墨水的钢笔或签字笔将答案写在答题卡上。
2.本卷共12小题,共110分。
二.填空题:本大题共6小题,每小题5分,共30分. (9)i 是虚数单位,复数67i12i++=__________.(10)已知函数f (x )=e x ln x ,f?′(x )为f (x )的导函数,则f?′(1)的值为__________. (11)如图,已知正方体ABCD –A 1B 1C 1D 1的棱长为1,则四棱柱A 1–BB 1D 1D 的体积为__________. (12)在平面直角坐标系中,经过三点(0,0),(1,1),(2,0)的圆的方程为__________. (13)已知a ,b ∈R ,且a –3b +6=0,则2a +18b的最小值为__________. (14)已知a ∈R ,函数()22220220x x a x f x x x a x ⎧++-≤⎪=⎨-+->⎪⎩,,,.若对任意x ∈[–3,+∞),f (x )≤x 恒成立,则a 的取值范围是__________.三.解答题:本大题共6小题,共80(15)(本小题满分13分)中抽取7名同学去某敬老院参加献爱心活动.(Ⅱ)设抽出的7名同学分别用A ,B ,C ,D ,E ,的卫生工作.(i(ii )设M (16在△ABC .已知b sin A =a cos(B –π6). (Ⅰ)求教(Ⅱ)设a (17如图,ABC ⊥平面ABD ,点M 为棱AB 的中点,AB =2,AD =(Ⅰ)求证:AD ⊥BC ;(Ⅱ)求异面直线BC 与MD 所成角的余弦值; (Ⅲ)求直线CD 与平面ABD 所成角的正弦值. (18)(本小题满分13分)设{a n }是等差数列,其前n 项和为S n (n ∈N *);{b n }是等比数列,公比大于0,其前n 项和为T n (n ∈N *).已知b 1=1,b 3=b 2+2,b 4=a 3+a 5,b 5=a 4+2a 6.(Ⅰ)求S n 和T n ;(Ⅱ)若S n +(T 1+T 2+…+T n )=a n +4b n ,求正整数n 的值. (19)(本小题满分14分)设椭圆22221(0)x y a b a b+=>>的右顶点为A ,上顶点为B .已知椭圆的离心率为3,||AB =(I )求椭圆的方程;(II )设直线:(0)l y kx k =<与椭圆交于,P Q 两点,l 与直线AB 交于点M ,且点P ,M 均在第四象限.若BPM △(20)设函数(f x (I )若2t =(II )若d (III . 参考答案(1)C (5)D(9)4–i (12)2x y +三、解答题(15)本小题主要考查随机抽样、用列举法计算随机事件所含的基本事件数、古典概型及其概率计算公式等基本知识.考查运用概率知识解决简单实际问题的能力.满分13分.(Ⅰ)解:由已知,甲、乙、丙三个年级的学生志愿者人数之比为3∶2∶2,由于采用分层抽样的方法从中抽取7名同学,因此应从甲、乙、丙三个年级的学生志愿者中分别抽取3人,2人,2人. (Ⅱ)(i )解:从抽出的7名同学中随机抽取2名同学的所有可能结果为{A ,B },{A ,C },{A ,D },{A ,E },{A ,F },{A ,G },{B ,C },{B ,D },{B ,E },{B ,F },{B ,G },{C ,D },{C ,E },{C ,F },{C ,G },{D ,E },{D ,F },{D ,G },{E ,F },{E ,G },{F ,G },共21种.(ii )解:由(Ⅰ),不妨设抽出的7名同学中,来自甲年级的是A ,B ,C ,来自乙年级的是D ,E ,来自丙年级的是F ,G ,则从抽出的7名同学中随机抽取的2名同学来自同一年级的所有可能结果为{A ,B },{A ,C },{B ,C },{D ,E },{F ,G },共5种.学@科网 所以,事件M 发生的概率为P (M )=521. (16)(Ⅰ)解:在△ABC中,由正弦定理sin sin a b A B =π)6-,得πsin cos()6a B a B =-,即πsin cos()6B B =-,可得tanB(Ⅱ)解:在△ABC 中,由余弦定理及a =2,c =3 由sin b A a =2cos22cosA =所以,sin(217- (17考13分.=AB ,AD ⊥AB ,可得AD ⊥平面ABC ,故AD ⊥BC . M 为棱AB 的中点,故MN ∥BC .所以∠DMN (或在Rt △DAM 中,AM =1,故DM AD ⊥平面ABC ,故AD ⊥AC . 在Rt △DAN 中,AN =1,故DN .在等腰三角形DMN 中,MN =1,可得12cos MNDMN DM ∠==. 所以,异面直线BC 与MD(Ⅲ)解:连接CM .因为△ABC 为等边三角形,M 为边AB 的中点,故CM ⊥AB ,CM 面ABC ⊥平面ABD ,而CM ⊂平面ABC ,故CM ⊥平面AB D .所以,∠CDM 为直线CD 与平面ABD 所成的角.在Rt △CAD 中,CD .在Rt △CMD 中,sin CM CDM CD ∠==.所以,直线CD 与平面ABD . (18(I 因为0q >设等差数列16,d =从而11,a d ==(II 131(222)2n n n T n +++=+++-=由1(n n S T b ++可得1(1)222n n n n n n +++--=+整理得240,n --=解得(19(I||AB =,从而3,2a b ==.所以,椭圆的方程为22194x y +=. (II )解:设点P 的坐标为11(,)x y ,点M 的坐标为22(,)x y ,由题意,210x x >>, 点Q 的坐标为11(,).x y --由BPM △的面积是BPQ △面积的2倍,可得||=2||PM PQ , 从而21112[()]x x x x -=--,即215x x =.易知直线AB 的方程为236x y +=,由方程组236,,x y y kx +=⎧⎨=⎩消去y ,可得2632x k =+.由方程组221,94,x y y kx ⎧+⎪=⎨⎪=⎩消去y,可得1x =.由215x x =5(32)k =+,两边平方,整理得2182580k k ++=,解得89k =-,或12k =-.当89k =-时,290x =-<,不合题意,舍去;当12k =-时,212x =,1125x =,符合题意.(20,又y =0. f (x故(f '当x (III )解:曲线y =f (x )与直线y =?(x ?t 2有三个互异的公共点等价于关于x 的方程(x ?t 2+d )(x ?t 2)(x ?t 2?d )+(x ?t 2有三个互异的实数解,令u =x ?t 2,可得u 3+(1?d 2)u =0. 设函数g (x )=x 3+(1?d 2)x ,则曲线y =f (x )与直线y =?(x ?t 2有三个互异的公共点等价于函数y =g (x )有三个零点.()g'x =3x 3+(1?d 2).当d 2≤1时,()g'x ≥0,这时()g'x 在R 上单调递增,不合题意.当d 2>1时,()g'x =0,解得x 1=,x 2.易得,g (x )在(?∞,x 1)上单调递增,在[x 1,x 2]上单调递减,在(x 2,+∞)上单调递增,g (x )的极大值g (x 1)=g (+g (x )若g (x 2若2()0,g x <12||,(d x g -<()y g x =所以d 10)(10,+∞。
2018天津高考文科数学试题及答案(Word版)

绝密★启用前2018年普通高等学校招生全国统一考试(天津卷)数学(文史类)本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试用时120分钟。
第Ⅰ卷1至2页,第Ⅱ卷3至5页。
答卷前,考生务必将自己的姓名、准考证号填写在答题考上,并在规定位置粘贴考试用条形码。
答卷时,考生务必将答案涂写在答题卡上,答在试卷上的无效。
考试结束后,将本试卷和答题卡一并交回。
祝各位考生考试顺利!第Ⅰ卷注意事项:1.每小题选出答案后,用铅笔将答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
2.本卷共8小题,每小题5分,共40分。
参考公式:·如果事件 A ,B 互斥,那么 P (A ∪B )=P (A )+P (B ). ·棱柱的体积公式V =Sh . 其中S 表示棱柱的底面面积,h 表示棱柱的高. ·棱锥的体积公式13V Sh =,其中S 表示棱锥的底面积,h 表示棱锥的高. 一.选择题:在每小题给出的四个选项中,只有一项是符合题目要求的. (1)设集合{1,2,3,4}A =,{1,0,2,3}B =-,{|12}C x x =∈-≤<R ,则()A B C =(A ){1,1}-(B ){0,1}(C ){1,0,1}-(D ){2,3,4}(2)设变量,x y 满足约束条件52410x y x y x y y +≤⎧⎪-≤⎪⎨-+≤⎪⎪≥⎩,,,,则目标函数35z x y =+的最大值为(A )6 (B )19 (C )21(D )45(3)设x ∈R ,则“38x >”是“||2x >” 的(A )充分而不必要条件 (B )必要而不充分条件 (C )充要条件(D )既不充分也不必要条件(4)阅读如图所示的程序框图,运行相应的程序,若输入N 的值为20,则输出T 的值为(A )1(B )2(C )3(D )4(5)已知13313711log ,(),log 245a b c ===,则,,a b c 的大小关系为(A )a b c >> (B )b a c >> (C )c b a >>(D )c a b >>(6)将函数sin(2)5y x π=+的图象向右平移10π个单位长度,所得图象对应的函数 (A )在区间[,]44ππ- 上单调递增 (B )在区间[,0]4π上单调递减(C )在区间[,]42ππ 上单调递增 (D )在区间[,]2ππ 上单调递减(7)已知双曲线22221(0,0)x y a b a b-=>> 的离心率为2,过右焦点且垂直于x 轴的直线与双曲线交于,A B两点.设,A B 到双曲线的同一条渐近线的距离分别为1d 和2d ,且126,d d += 则双曲线的方程为(A )22139x y -=(B )22193x y -=(C )221412x y -=(D )221124x y -= (8)在如图的平面图形中,已知 1.2,120OM ON MON ==∠=,2,2,BM MA CN NA ==则·BC OM 的值为(A )15- (B )9- (C )6-(D )0第Ⅱ卷注意事项:1.用黑色墨水的钢笔或签字笔将答案写在答题卡上。
2018年高考天津卷文科数学(含答案)

绝密★启用前2018年普通高等学校招生全国统一考试(天津卷)数学(文史类)本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试用时120分钟。
第Ⅰ卷1至2页,第Ⅱ卷3至5页。
答卷前,考生务必将自己的姓名、准考证号填写在答题考上,并在规定位置粘贴考试用条形码。
答卷时,考生务必将答案涂写在答题卡上,答在试卷上的无效。
考试结束后,将本试卷和答题卡一并交回。
祝各位考生考试顺利!第Ⅰ卷注意事项:1.每小题选出答案后,用铅笔将答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
2.本卷共8小题,每小题5分,共40分。
参考公式:·如果事件 A ,B 互斥,那么 P (A ∪B )=P (A )+P (B ). ·棱柱的体积公式V =Sh . 其中S 表示棱柱的底面面积,h 表示棱柱的高. ·棱锥的体积公式13V Sh =,其中S 表示棱锥的底面积,h 表示棱锥的高. 一.选择题:在每小题给出的四个选项中,只有一项是符合题目要求的. (1)设集合{1,2,3,4}A =,{1,0,2,3}B =-,{|12}C x x =∈-≤<R ,则()A B C =(A ){1,1}-(B ){0,1}(C ){1,0,1}-(D ){2,3,4}(2)设变量,x y 满足约束条件52410x y x y x y y +≤⎧⎪-≤⎪⎨-+≤⎪⎪≥⎩,,,,则目标函数35z x y =+的最大值为(A )6 (B )19 (C )21(D )45(3)设x ∈R ,则“38x >”是“||2x >” 的(A )充分而不必要条件 (B )必要而不充分条件 (C )充要条件(D )既不充分也不必要条件(4)阅读如图所示的程序框图,运行相应的程序,若输入N 的值为20,则输出T 的值为(A )1(B )2(C )3(D )4(5)已知13313711log ,(),log 245a b c ===,则,,a b c 的大小关系为(A )a b c >> (B )b a c >> (C )c b a >>(D )c a b >>(6)将函数sin(2)5y x π=+的图象向右平移10π个单位长度,所得图象对应的函数 (A )在区间[,]44ππ- 上单调递增 (B )在区间[,0]4π上单调递减(C )在区间[,]42ππ 上单调递增 (D )在区间[,]2ππ 上单调递减(7)已知双曲线22221(0,0)x y a b a b-=>> 的离心率为2,过右焦点且垂直于x 轴的直线与双曲线交于,A B两点.设,A B 到双曲线的同一条渐近线的距离分别为1d 和2d ,且126,d d += 则双曲线的方程为(A )22139x y -=(B )22193x y -=(C )221412x y -=(D )221124x y -= (8)在如图的平面图形中,已知 1.2,120OM ON MON ==∠=,2,2,BM MA CN NA ==则·BC OM 的值为(A )15- (B )9- (C )6-(D )0第Ⅱ卷注意事项:1.用黑色墨水的钢笔或签字笔将答案写在答题卡上。
[历年真题](精校版)2018年天津文数高考试题文档版(含答案)
2018年天津文数高考试题文档版(含答案)](https://img.taocdn.com/s3/m/7327da8fc281e53a5902ff0c.png)
绝密★启用前2018年普通高等学校招生全国统一考试(天津卷)数学(文史类)本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试用时120分钟.第Ⅰ卷1至2页,第Ⅱ卷3至5页.答卷前,考生务必将自己的姓名、准考证号填写在答题考上,并在规定位置粘贴考试用条形码.答卷时,考生务必将答案涂写在答题卡上,答在试卷上的无效.考试结束后,将本试卷和答题卡一并交回. 祝各位考生考试顺利!第Ⅰ卷注意事项:1.每小题选出答案后,用铅笔将答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.2.本卷共8小题,每小题5分,共40分. 参考公式:·如果事件 A ,B 互斥,那么 P (A ∪B )=P (A )+P (B ). ·棱柱的体积公式V =Sh . 其中S 表示棱柱的底面面积,h 表示棱柱的高. ·棱锥的体积公式13V Sh =,其中S 表示棱锥的底面积,h 表示棱锥的高. 一.选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.(1)设集合{1,2,3,4}A =,{1,0,2,3}B =-,{|12}C x x =∈-≤<R ,则()A B C =U I (A ){1,1}-(B ){0,1}(C ){1,0,1}-(D ){2,3,4}(2)设变量,x y 满足约束条件52410x y x y x y y +≤⎧⎪-≤⎪⎨-+≤⎪⎪≥⎩,,,,则目标函数35z x y =+的最大值为(A )6 (B )19 (C )21(D )45(3)设x ∈R ,则“38x >”是“||2x >” 的(A )充分而不必要条件 (B )必要而不充分条件 (C )充要条件(D )既不充分也不必要条件(4)阅读如图所示的程序框图,运行相应的程序,若输入N 的值为20,则输出T 的值为(A )1(B )2(C )3(D )4(5)已知13313711log ,(),log 245a b c ===,则,,a b c 的大小关系为(A )a b c >> (B )b a c >> (C )c b a >>(D )c a b >>(6)将函数sin(2)5y x π=+的图象向右平移10π个单位长度,所得图象对应的函数 (A )在区间[,]44ππ- 上单调递增 (B )在区间[,0]4π上单调递减(C )在区间[,]42ππ 上单调递增 (D )在区间[,]2ππ 上单调递减(7)已知双曲线22221(0,0)x y a b a b-=>> 的离心率为2,过右焦点且垂直于x 轴的直线与双曲线交于,A B两点.设,A B 到双曲线的同一条渐近线的距离分别为1d 和2d ,且126,d d += 则双曲线的方程为(A )22139x y -=(B )22193x y -=(C )221412x y -=(D )221124x y -= (8)在如图的平面图形中,已知 1.2,120OM ON MON ==∠=o,2,2,BM MA CN NA ==u u u u r u u u r u u u r u u u r则·BC OM u u u r u u u u r 的值为(A )15- (B )9- (C )6-(D )0第Ⅱ卷注意事项:1.用黑色墨水的钢笔或签字笔将答案写在答题卡上. 2.本卷共12小题,共110分.二.填空题:本大题共6小题,每小题5分,共30分. (9)i 是虚数单位,复数67i12i++=__________. (10)已知函数f (x )=e x ln x ,f ′(x )为f (x )的导函数,则f ′(1)的值为__________.(11)如图,已知正方体ABCD –A 1B 1C 1D 1的棱长为1,则四棱柱A 1–BB 1D 1D 的体积为__________.(12)在平面直角坐标系中,经过三点(0,0),(1,1),(2,0)的圆的方程为__________. (13)已知a ,b ∈R ,且a –3b +6=0,则2a +18b的最小值为__________.(14)已知a ∈R ,函数()22220220x x a x f x x x a x ⎧++-≤⎪=⎨-+->⎪⎩,,,.若对任意x ∈[–3,+∞),f (x )≤x 恒成立,则a 的取值范围是__________.三.解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤. (15)(本小题满分13分)已知某校甲、乙、丙三个年级的学生志愿者人数分别为240,160,160.现采用分层抽样的方法从中抽取7名同学去某敬老院参加献爱心活动.(Ⅰ)应从甲、乙、丙三个年级的学生志愿者中分别抽取多少人?(Ⅱ)设抽出的7名同学分别用A ,B ,C ,D ,E ,F ,G 表示,现从中随机抽取2名同学承担敬老院的卫生工作. (i )试用所给字母列举出所有可能的抽取结果;(ii )设M 为事件“抽取的2名同学来自同一年级”,求事件M 发生的概率. (16)(本小题满分13分)在△ABC 中,内角A ,B ,C 所对的边分别为a,b,c .已知b sin A =a cos(B –π6). (Ⅰ)求教B 的大小;(Ⅱ)设a =2,c =3,求b 和sin(2A –B )的值. (17)(本小题满分13分)如图,在四面体ABCD 中,△ABC 是等边三角形,平面ABC ⊥平面ABD ,点M 为棱AB 的中点,AB =2,AD =23,∠BAD =90°. (Ⅰ)求证:AD ⊥BC ;(Ⅱ)求异面直线BC 与MD 所成角的余弦值; (Ⅲ)求直线CD 与平面ABD 所成角的正弦值.(18)(本小题满分13分)设{a n }是等差数列,其前n 项和为S n (n ∈N *);{b n }是等比数列,公比大于0,其前n 项和为T n (n ∈N *).已知b 1=1,b 3=b 2+2,b 4=a 3+a 5,b 5=a 4+2a 6.(Ⅰ)求S n 和T n ;(Ⅱ)若S n +(T 1+T 2+…+T n )=a n +4b n ,求正整数n 的值. (19)(本小题满分14分)设椭圆22221(0)x y a b a b+=>> 的右顶点为A ,上顶点为B .||AB =(I )求椭圆的方程;(II )设直线:(0)l y kx k =<与椭圆交于,P Q 两点,l 与直线AB 交于点M ,且点P ,M 均在第四象限.若BPM △的面积是BPQ △面积的2倍,求k 的值.(20)(本小题满分14分)设函数123()=()()()f x x t x t x t ---,其中123,,t t t ∈R ,且123,,t t t 是公差为d 的等差数列. (I )若20,1,t d == 求曲线()y f x =在点(0,(0))f 处的切线方程; (II )若3d =,求()f x 的极值;(III )若曲线()y f x = 与直线 12()y x t =---有三个互异的公共点,求d 的取值范围. 参考答案一、选择题:本题考查基本知识和基本运算.每小题5分,满分40分. (1)C (2)C (3)A (4)B (5)D(6)A(7)A(8)C二、填空题:本题考查基本知识和基本运算.每小题5分,满分30分. (9)4–i(10)e (11)13(12)2220x y x +-= (13)14(14)[18,2]三、解答题(15)本小题主要考查随机抽样、用列举法计算随机事件所含的基本事件数、古典概型及其概率计算公式等基本知识.考查运用概率知识解决简单实际问题的能力.满分13分.(Ⅰ)解:由已知,甲、乙、丙三个年级的学生志愿者人数之比为3∶2∶2,由于采用分层抽样的方法从中抽取7名同学,因此应从甲、乙、丙三个年级的学生志愿者中分别抽取3人,2人,2人. (Ⅱ)(i )解:从抽出的7名同学中随机抽取2名同学的所有可能结果为{A ,B },{A ,C },{A ,D },{A ,E },{A ,F },{A ,G },{B ,C },{B ,D },{B ,E },{B ,F },{B ,G },{C ,D },{C ,E },{C ,F },{C ,G },{D ,E },{D ,F },{D ,G },{E ,F },{E ,G },{F ,G },共21种.(ii )解:由(Ⅰ),不妨设抽出的7名同学中,来自甲年级的是A ,B ,C ,来自乙年级的是D ,E ,来自丙年级的是F ,G ,则从抽出的7名同学中随机抽取的2名同学来自同一年级的所有可能结果为{A ,B },{A ,C },{B ,C },{D ,E },{F ,G },共5种.学@科网所以,事件M 发生的概率为P (M )=521. (16)本小题主要考查同角三角函数的基本关系,两角差的正弦与余弦公式,二倍角的正弦与余弦公式,以及正弦定理、余弦定理等基础知识,考查运算求解能力.满分13分. (Ⅰ)解:在△ABC 中,由正弦定理sin sin a b A B =,可得sin sin b A a B =,又由πsin cos()6b A a B =-,得πsin cos()6a B a B =-,即πsin cos()6B B =-,可得tan 3B =.又因为(0π)B ∈,,可得B =π3.(Ⅱ)解:在△ABC 中,由余弦定理及a =2,c =3,B =π3,有2222cos 7b a c ac B =+-=,故b =7. 由πsin cos()6b A a B =-,可得3sin 7A =.因为a <c ,故cos 7A =.因此43sin 22sin cos A A A ==,21cos22cos 17A A =-=. 所以,sin(2)sin 2cos cos2sin AB A B A B -=-=431133327⨯-⨯=.(17)本小题主要考查异面直线所成的角、直线与平面所成的角、平面与平面垂直等基础知识.考查空间想象能力、运算求解能力和推理论证能力.满分13分.(Ⅰ)由平面ABC ⊥平面ABD ,平面ABC ∩平面ABD =AB ,AD ⊥AB ,可得AD ⊥平面ABC ,故AD ⊥BC . (Ⅱ)解:取棱AC 的中点N ,连接MN ,ND .又因为M 为棱AB 的中点,故MN ∥BC .所以∠DMN (或其补角)为异面直线BC 与MD 所成的角.在Rt △DAM 中,AM =1,故DM 22=13AD AM +AD ⊥平面ABC ,故AD ⊥AC .在Rt △DAN 中,AN =1,故DN在等腰三角形DMN 中,MN =1,可得12cos MNDMN DM ∠==. 所以,异面直线BC 与MD(Ⅲ)解:连接CM .因为△ABC 为等边三角形,M 为边AB 的中点,故CM ⊥AB ,CMABC ⊥平面ABD ,而CM ⊂平面ABC ,故CM ⊥平面AB D .所以,∠CDM 为直线CD 与平面ABD 所成的角. 在Rt △CAD 中,CD. 在Rt △CMD 中,sin CM CDM CD ∠==. 所以,直线CD 与平面ABD. (18)本小题主要考查等差数列、等比数列的通项公式及前n 项和公式等基础知识.考查数列求和的基本方法和运算求解能力.满分13分.(I )解:设等比数列{}n b 的公比为q ,由b 1=1,b 3=b 2+2,可得220q q --=. 因为0q >,可得2q =,故12n n b -=.所以122112nn n T -==--. 设等差数列{}n a 的公差为d .由435b a a =+,可得134a d +=.由5462b a a =+,可得131316,a d += 从而11,1a d ==,故n a n =,所以(1)2n n n S +=. (II )解:由(I ),知13112(222)2 2.n n n T T T n n ++++=+++-=--L L由12()4n n n n S T T T a b ++++=+L 可得11(1)2222n n n n n n ++++--=+, 整理得2340,n n --= 解得1n =-(舍),或4n =.所以n 的值为4.学&科网(19)本小题主要考查椭圆的标准方程和几何性质、直线方程等基础知识.考查用代数方法研究圆锥曲线的性质.考查运算求解能力,以及用方程思想解决问题的能力.满分14分.(I )解:设椭圆的焦距为2c ,由已知得2259c a =,又由222a b c =+,可得23.a b =由||AB ==,从而3,2a b ==.所以,椭圆的方程为22194x y +=. (II )解:设点P 的坐标为11(,)x y ,点M 的坐标为22(,)x y ,由题意,210x x >>, 点Q 的坐标为11(,).x y -- 由BPM △的面积是BPQ △面积的2倍,可得||=2||PM PQ , 从而21112[()]x x x x -=--,即215x x =.易知直线AB 的方程为236x y +=,由方程组236,,x y y kx +=⎧⎨=⎩ 消去y ,可得2632x k =+.由方程组221,94,x y y kx ⎧+⎪=⎨⎪=⎩消去y ,可得1x =.由215x x =,5(32)k =+,两边平方,整理得2182580k k ++=,解得89k =-,或12k =-.当89k =-时,290x =-<,不合题意,舍去;当12k =-时,212x =,1125x =,符合题意.所以,k 的值为12-.(20)本小题主要考查导数的运算、导数的几何意义、运用导数研究函数的性质等基础知识和方法,考查函数思想和分类讨论思想,考查综合分析问题和解决问题的能量,满分14分.(Ⅰ)解:由已知,可得f (x )=x (x −1)(x +1)=x 3−x ,故f ‵(x )=3x −1,因此f (0)=0,(0)f '=−1,又因为曲线y =f (x )在点(0, f (0))处的切线方程为y −f (0)= (0)f ' (x −0),故所求切线方程为x +y =0. (Ⅱ)解:由已知可得f (x )=(x −t 2+3)( x −t 2) (x −t 2−3)=( x −t 2)3−9 ( x −t 2)=x 3−3t 2x 2+(3t 22−9)x − t 22+9t 2. 故()f x '= 3x 3−6t 2x +3t 22−9.令()f x '=0,解得x = t 2或x = t 2当x 变化时,f ‵(x ),f (x )的变化如下表:所以函数f (x )的极大值为f (t 23−9×(函数小值为f (t 2)3−9×−.(III )解:曲线y =f (x )与直线y =−(x −t 2)−有三个互异的公共点等价于关于x 的方程(x −t 2+d ) (x −t 2) (x −t 2−d )+(x −t 2有三个互异的实数解,令u = x −t 2,可得u 3+(1−d 2)u =0.设函数g (x )= x 3+(1−d 2)x 则曲线y =f (x )与直线y =−(x −t 2)−y =g (x )有三个零点.()g'x =3 x 3+(1−d 2).当d 2≤1时,()g'x ≥0,这时()g'x 在R 上单调递增,不合题意.当d 2>1时,()g'x =0,解得x 1=,x 2.易得,g (x )在(−∞,x 1)上单调递增,在[x 1, x 2]上单调递减,在(x 2, +∞)上单调递增,g (x )的极大值g (x 1)= g (+g (x )的极小值g (x 2)= g)=+若g (x 2) ≥0,由g (x )的单调性可知函数y =f (x )至多有两个零点,不合题意.若2()0,g x <即322(1)27d ->,也就是||d >此时2||d x >,(||)||0,g d d =+> 且312||,(2||)6||2||0d x g d d d -<-=--+<-<,从而由()g x 的单调性,可知函数()y g x = 在区间1122(2||,),(,),(,||)d x x x x d -内各有一个零点,符合题意.学科……网所以d 的取值范围是(,).-∞+∞U。
2018年普通高等学校招生统一考试文科数学真题及参考答案(天津卷)

2018年普通高等学校招生全国统一考试(天津卷、)数学试卷(文史类)注意事项:1.答卷前,考生务必将自己姓名和准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
4.本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试用时120分钟。
第Ⅰ卷1至2页,第Ⅱ卷3至5页。
第Ⅰ卷注意事项:1.每小题选出答案后,用铅笔将答题卡上对应题目答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
2.本卷共8小题,每小题5分,共40分。
参考公式:·如果事件A ,B 互斥,那么P (A ∪B )=P (A )+P (B ). ·棱柱体积公式V =Sh ,其中S 表示棱柱底面面积,h 表示棱柱高. ·棱锥体积公式13V Sh =,其中S 表示棱锥底面积,h 表示棱锥高. 一.选择题:在每小题给出四个选项中,只有一项是符合题目要求. (1)设集合{1,2,3,4}A =,{1,0,2,3}B =-,{|12}C x x =∈-≤<R ,则()AB C =(A ){1,1}- (B ){0,1} (C ){1,0,1}-(D ){2,3,4}(2)设变量,x y 满足约束条件52410x y x y x y y +≤⎧⎪-≤⎪⎨-+≤⎪⎪≥⎩,,,,则目标函数35z x y =+最大值为(A )6(B )19(C )21 (D )45(3)设x ∈R ,则“38x >”是“||2x >”(A )充分而不必要条件 (B )必要而不充分条件 (C )充要条件(D )既不充分也不必要条件(4)阅读如图所示程序框图,运行相应程序,若输入N 值为20,则输出T 值为(A )1(B )2(C )3(D )4(5)已知13313711log ,(),log 245a b c ===,则,,a b c 大小关系为(A )a b c >> (B )b a c >> (C )c b a >>(D )c a b >>(6)将函数sin(2)5y x π=+图象向右平移10π个单位长度,所得图象对应函数 (A )在区间[,]44ππ-上单调递增 (B )在区间[,0]4π-上单调递减(C )在区间[,]42ππ上单调递增 (D )在区间[,]2ππ上单调递减(7)已知双曲线22221(0,0)x y a b a b-=>> 离心率为2,过右焦点且垂直于x 轴直线与双曲线交于,A B 两点.设,A B 到双曲线同一条渐近线距离分别为1d 和2d ,且126,d d +=则双曲线方程为(A )22139x y -=(B )22193x y -= (C )221412x y -=(D )221124x y -= (8)在如图平面图形中,已知1,2,120OM ON MON ==∠=,2,2,BM MA CN NA ==则·BC OM 值为(A )15- (B )9- (C )6-(D )0第Ⅱ卷注意事项:1.用黑色墨水钢笔或签字笔将答案写在答题卡上。
天津市2018河东区一模数学试卷答案

2018河东区一模考试数学试题答案词东区初辫中考-帙n c " 子 85 A G. A2. A 牛 8 /Q 6 II. 6 De .雄.^3-30/215. z 仏胜冲/.刃& (工)略(丄)劣7-失 .........Gt ) .1 I 、.,),-5 -*f -3 喫-I 。
1 2 3 十 5OV?女"& g 切;五(JL )乎井数-机5十例。
卄2X/5十/OX 刀十艘J 二/& %)5。
众薮將款应欲为/。
元剧双* /从,死載景A 角从氽版为2肽.毕及薮物捐款孟嶽井溢増厥存撫夙,好K 及B 绑 /",就顶队g =毕=}"m 不釦h /。
无 階摇/。
无)脅占函百次此*缪,够 朴入心:2彻*怎%千实丿二以以入)層:妹*相损簡就蠲M 初出泌鬲人划/诜入-4任)虛辰挥以,。
13,'•‘ PA 、卩堰出袖如加且丄怦宓衍 「'膈册嵐瞄:加歹叶罹同飒布对朗斜f 跃'锢-精:<\ M 二仲g -'瓷拝感=I. D7. D 3 -•睡誣2&. -r -IT ?-■解答题. /?.④ %阪慎智康、'、AD -亨® =2 | 乏、'、pD 二 如乙二少+勿二片巨二% •,■ % 二》AB 琅_、' S 如矽砌p - W/ZWp” 宇:22. CL )在 Ri^BCl 冲,厶CBD*", BD^O'"'CD= 0。
.洌5。
CD -5-2 Cm )咨•'》华与他餾垒直心C 闭醵云2m. 皿)在R 必能T%、:屜十二勺s .''•A7--二 BJ BOBOSSN Ml 祀IM)'' Ab 二/Q7-十庞 + CD - /,,3 十 // 您*Z ■!飾)詹''棒餾離AB ".阮.^3 -心根•据瓯憲得:畐M 牛&Z 沽/0)十初彻二归、例十%1二5.斗以沖。
2018年天津市河东区高考数学一模文科试卷含答案解析 精品

2018年天津市河东区高考数学一模试卷(文科)一、选择题:本题共8个小题,每小题5分,共40分.每小题给出的四个选项只有一个符合题目要求.1.设集合I={x||x|<3,x∈Z},A={1,2},B={﹣2,﹣1,2},则A∪(C I B)=()A.{1} B.{1,2} C.{2} D.{0,1,2}2.取一根长度为3m的绳子,拉直后在任意位置剪断,那么剪得两段的长都不小于1m的概率是()A.B.C.D.不确定3.一个直棱柱被一个平面截去一部分后所剩几何体的三视图如图所示,则该几何体的体积为()A.9 B.10 C.11 D.4.在△ABC中,b=5,∠B=,tanA=2,则a的值是()A.10B.2C. D.5.如果执行如图所示的程序框图,那么输出的S=()A.190 B.94 C.46 D.226.已知函数f(x)=a x+x﹣b的零点x0∈(n,n+1)(n∈Z),其中常数a,b满足0<b<1<a,则n的值为()A.2 B.1 C.﹣2 D.﹣l7.图是函数y=Asin(ωx+φ)(x∈R)在区间上的图象,为了得到这个函数的图象,只要将y=sinx(x∈R)的图象上所有的点()A.向左平移个单位长度,再把所得各点的横坐标缩短到原来的倍,纵坐标不变B.向左平移个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变C.向左平移个单位长度,再把所得各点的横坐标缩短到原来的倍,纵坐标不变D.向左平移个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变8.已知,且函数y=f(x)﹣2x恰有3个不同的零点,则实数a 的取值范围是()A.[﹣4,0]B.[﹣8,+∞)C.[﹣4,+∞)D.(0,+∞)二、填空题(本大题共6个小题,每小题5分,共30分.把答案填在题中横线上.)9.若(1+2ai)i=1﹣bi,其中a、b∈R,i是虚数单位,则|a+bi|=.10.某高校甲、乙、丙、丁四个专业分别有150、150、400、300名学生,为了解学生的就业倾向,用分层抽样的方法从该校这四个专业共抽取40名学生进行调查,应在丙专业抽取的学生人数为.11.已知双曲线=1(a>0,b>0)的一条渐近线方程是y=x,它的一个焦点与抛物线y2=16x 的焦点相同.则双曲线的方程为.12.如图,PA切⊙O于点A,割线PBC经过圆心O,OB=PB=1,OA绕点O逆时针旋转60°到OD,则PD的长为.13.若实数a,b,c满足2a+2b=2a+b,2a+2b+2c=2a+b+c,则c的最大值是.14.在平面四边形ABCD中,点E、F分别是边AD、BC的中点,且AB=1,EF=,CD=,若•=15,则•的值为.三、解答题:(本大题6个题,共80分)15.某木器厂生产圆桌和衣柜两种产品,现有两种木料,第一种有72m3,第二种有56m3,假设生产每种产品都需要用两种木料,生产一只圆桌和一个衣柜分别所需木料如表所示.每生产一只圆桌可获利6元,生产一个衣柜可获利10元,木器厂在现有木料条件下,圆桌和衣柜各生产多少,才使获得利润最多,利润最多为多少?16.已知函数f(x)=2sinωxcosωx﹣2sin2ωx+(ω>0),直线x=x1,x=x2是函数y=f(x)的图象的任意两条对称轴,且|x1﹣x2|的最小值为.(Ⅰ)求ω的值;(Ⅱ)求函数f(x)的单调增区间;(Ⅲ)若f(α)=,求sin(π﹣4α)的值.17.如图,在四棱锥P﹣ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,E为AD的中点,M是棱PC的中点,PA=PD=2,,.(1)求证:PE⊥平面ABCD;(2)求直线BM与平面ABCD所成角的正切值;(3)求直线BM与CD所成角的余弦值.18.已知椭圆C:的离心率为,椭圆短轴的一个端点与两个焦点构成的三角形的面积为.(1)求椭圆C的方程;(2)已知动直线y=k(x+1)与椭圆C相交于A、B两点.①若线段AB中点的横坐标为,求斜率k的值;②已知点,求证:为定值.19.已知函数f(x)=,数列{a n}满足a1=1,a n+1=f(),n∈N*,(1)求数列{a n}的通项公式;(2)令T n=a1a2﹣a2a3+a3a4﹣a4a5+…﹣a2n a2n+1,求T n;(3)令b n=(n≥2),b1=3,S n=b1+b2+…+b n,若S n<对一切n∈N*成立,求最小正整数m.20.已知函数f(x)=lnx﹣ax2﹣bx.(I)当a=﹣1时,若函数f(x)在其定义域内是增函数,求b的取值范围;(Ⅱ)若f(x)的图象与x轴交于A(x1,0),B(x2,0)(x1<x2)两点,且AB的中点为C(x0,0),求证:f′(x0)<0.2018年天津市河东区高考数学一模试卷(文科)参考答案与试题解析一、选择题:本题共8个小题,每小题5分,共40分.每小题给出的四个选项只有一个符合题目要求.1.设集合I={x||x|<3,x∈Z},A={1,2},B={﹣2,﹣1,2},则A∪(C I B)=()A.{1} B.{1,2} C.{2} D.{0,1,2}【考点】交、并、补集的混合运算.【专题】计算题.【分析】把集合A用列举法表示,然后求出C I B,最后进行并集运算.【解答】解:因为I={x||x|<3,x∈Z}={﹣2,﹣1,0,1,2},B={﹣2,﹣1,2},所以,C I B={0,1},又因为A={1,2},所以A∪(C I B)={1,2}∪{0,1}={0,1,2}.故选D.【点评】本题考查了并集和补集的混合运算,考查了学生对集合运算的理解,是基础题.2.取一根长度为3m的绳子,拉直后在任意位置剪断,那么剪得两段的长都不小于1m的概率是()A.B.C.D.不确定【考点】几何概型;任意角的三角函数的定义.【专题】计算题.【分析】根据题意确定为几何概型中的长度类型,将长度为3m的绳子分成相等的三段,在中间一段任意位置剪断符合要求,从而找出中间1m处的两个界点,再求出其比值.【解答】解:记“两段的长都不小于1m”为事件A,则只能在中间1m的绳子上剪断,剪得两段的长都不小于1m,所以事件A发生的概率.故选B【点评】本题主要考查概率中的几何概型长度类型,关键是找出两段的长都不小于1m的界点来.3.一个直棱柱被一个平面截去一部分后所剩几何体的三视图如图所示,则该几何体的体积为()A.9 B.10 C.11 D.【考点】棱柱、棱锥、棱台的体积.【专题】空间位置关系与距离.【分析】根据得出该几何体是在底面为边长是2的正方形、高是3的直四棱柱的基础上,截去一个底面积为×2×1=1、高为3的三棱锥形成的,运用直棱柱减去三棱锥即可得出答案.【解答】解:.由三视图可知该几何体是在底面为边长是2的正方形、高是3的直四棱柱的基础上,==1,截去一个底面积为×2×1=1、高为3的三棱锥形成的,V三棱锥所以V=4×3﹣1=11.故选:C【点评】本题考查了空间几何体的性质,求解体积,属于计算题,关键是求解底面积,高,运用体积公式.4.在△ABC中,b=5,∠B=,tanA=2,则a的值是()A.10B.2C. D.【考点】正弦定理.【专题】解三角形.【分析】由条件利用同角三角函数的基本关系求得sinA=,再由正弦定理求得a的值.【解答】解:∵在△ABC中,b=5,∠B=,tanA==2,sin2A+cos2A=1,∴sinA=.再由余弦定理可得=,解得a=2,故选B.【点评】本题主要考查同角三角函数的基本关系、正弦定理的应用,属于中档题.5.如果执行如图所示的程序框图,那么输出的S=()A.190 B.94 C.46 D.22【考点】循环结构;程序框图.【专题】算法和程序框图.【分析】根据框图的流程依次计算运行的结果,直到满足条件i>5,退出循环体,计算输出S的值.【解答】解:由程序框图知:第一次运行i=2,S=2×(1+1)=4;第二次运行i=2+1=3,S=2×(4+1)=10;第三次运行i=3+1=4,S=2×(10+1)=22;第四次运行i=4+1=5,S=2×(22+1)=46;第五次运行i=5+1=6,S=2×(46+1)=94.满足条件i>5,退出循环体,输出S=94.故选:B.【点评】本题考查了循环结构的程序框图,根据框图的流程依次计算运行的结果是解答此类问题的常用方法.6.已知函数f(x)=a x+x﹣b的零点x0∈(n,n+1)(n∈Z),其中常数a,b满足0<b<1<a,则n的值为()A.2 B.1 C.﹣2 D.﹣l【考点】函数零点的判定定理.【专题】函数的性质及应用.【分析】根据指数函数,一次函数的单调性,及增+增=增,可得函数f(x)=a x+x﹣b为增函数,结合常数a,b满足0<b<1<a,可得f(﹣1)<0,f(0)>0,进而可得n值.【解答】解:∵函数f(x)=a x+x﹣b为增函数,常数a,b满足0<b<1<a,∴f(﹣1)=﹣1﹣b<0,f(0)=1﹣b>0,∴函数f(x)=a x+x﹣b在(﹣1,0)内有一个零点,故n=﹣1,故选:D【点评】本题主要考查了函数零点的判定定理以及指数与对数的互化,函数f(x)=a x+x﹣b是增函数,单调函数最多只有一个零点,是解题的关键,属中档题.7.图是函数y=Asin(ωx+φ)(x∈R)在区间上的图象,为了得到这个函数的图象,只要将y=sinx(x∈R)的图象上所有的点()A.向左平移个单位长度,再把所得各点的横坐标缩短到原来的倍,纵坐标不变B.向左平移个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变C.向左平移个单位长度,再把所得各点的横坐标缩短到原来的倍,纵坐标不变D.向左平移个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变【考点】由y=Asin(ωx+φ)的部分图象确定其解析式.【专题】综合题.【分析】先根据函数的周期和振幅确定w和A的值,再代入特殊点可确定φ的一个值,进而得到函数的解析式,再进行平移变换即可.【解答】解:由图象可知函数的周期为π,振幅为1,所以函数的表达式可以是y=sin(2x+φ).代入(﹣,0)可得φ的一个值为,故图象中函数的一个表达式是y=sin(2x+),即y=sin2(x+),所以只需将y=sinx(x∈R)的图象上所有的点向左平移个单位长度,再把所得各点的横坐标缩短到原来的倍,纵坐标不变.故选A.【点评】本题主要考查三角函数的图象与图象变换的基础知识,属于基础题题.根据图象求函数的表达式时,一般先求周期、振幅,最后求φ.三角函数图象进行平移变换时注意提取x的系数,进行周期变换时,需要将x的系数变为原来的8.已知,且函数y=f(x)﹣2x恰有3个不同的零点,则实数a 的取值范围是()A.[﹣4,0]B.[﹣8,+∞)C.[﹣4,+∞)D.(0,+∞)【考点】根的存在性及根的个数判断.【专题】计算题;压轴题;函数的性质及应用.【分析】当x≥0时,f(x)=f(x﹣2),可得当x≥0时,f(x)在[﹣2,0)重复的周期函数,根据x∈[﹣2,0)时,y=a﹣x2﹣4x=4+a﹣(x+2)2,对称轴x=﹣2,顶点(﹣2,4+a),进而可进行分类求实数a的取值范围.【解答】解:因为当x≥0的时候,f(x)=f(x﹣2),当x∈[0,2)时,x﹣2∈[﹣2,0),此时f(x)=f(x﹣2)=a﹣(x﹣2)2﹣4(x﹣2)当x∈[2,4)时,x﹣4∈[﹣2,0),此时f(x)=f(x﹣2)=f(x﹣4)=a﹣(x﹣4)2﹣4(x﹣4)依此类推,f(x)在x<0时为二次函数a﹣x2﹣4x=﹣(x+2)2+a+4,在x≥0上为周期为2的函数,重复部分为a﹣x2﹣4x=﹣(x+2)2+a+4在区间[﹣2,0)上的部分.二次函数a﹣x2﹣4x=﹣(x+2)2+a+4顶点为(﹣2,a+4),y=f(x)﹣2x恰有3个不同的零点,即f(x)与y=2x恰有3个不同的交点,需满足f(x)与y=2x在x<0时有两个交点且0≤a+4≤4或f(x)与y=2x在x<0时有两个交点且a+4>4∴﹣4≤a≤0或a>0综上可得a≥﹣4故选C【点评】本题重点考查函数的零点与方程根的关系,考查函数的周期性,有一定的难度.二、填空题(本大题共6个小题,每小题5分,共30分.把答案填在题中横线上.)9.若(1+2ai)i=1﹣bi,其中a、b∈R,i是虚数单位,则|a+bi|=.【考点】复数求模.【专题】数系的扩充和复数.【分析】由(1+2ai)i=1﹣bi化简求出a、b的值,然后由复数模的公式即可求出|a+bi|的值.【解答】解:由(1+2ai)i=1﹣bi,得﹣1﹣2a+(1+b)i=0.∴.解得:.设z=a+bi(a、b∈R),则z=﹣﹣i,∴|a+bi|=.故答案为:.【点评】本题考查了复数的基本概念,考查了复数模的求法,是基础的计算题.10.某高校甲、乙、丙、丁四个专业分别有150、150、400、300名学生,为了解学生的就业倾向,用分层抽样的方法从该校这四个专业共抽取40名学生进行调查,应在丙专业抽取的学生人数为16.【考点】分层抽样方法.【专题】概率与统计.【分析】根据四个专业各有的人数,得到本校的总人数,根据要抽取的人数,得到每个个体被抽到的概率,利用丙专业的人数乘以每个个体被抽到的概率,得到丙专业要抽取的人数.【解答】解:∵高校甲、乙、丙、丁四个专业分别有150、150、400、300名学生∴本校共有学生150+150+400+300=1000,∵用分层抽样的方法从该校这四个专业共抽取40名学生进行调查∴每个个体被抽到的概率是=,∵丙专业有400人,∴要抽取400×=16故答案为:16【点评】本题考查分层抽样方法,是一个基础题,解题的依据是在抽样过程中每个个体被抽到的概率是相等的,这种题目经常出现在高考卷中.11.已知双曲线=1(a>0,b>0)的一条渐近线方程是y=x,它的一个焦点与抛物线y2=16x的焦点相同.则双曲线的方程为=1.【考点】双曲线的标准方程.【专题】圆锥曲线的定义、性质与方程.【分析】先由双曲线的渐近线方程为y=±x,易得,再由抛物线y2=16x的焦点为(4,0)可得双曲线中c=4,最后根据双曲线的性质c2=a2+b2列方程组,解得a2、b2即可.【解答】解:由双曲线渐近线方程可知①因为抛物线的焦点为(4,0),所以c=4②又c2=a2+b2③联立①②③,解得a2=4,b2=12,所以双曲线的方程为.故答案为.【点评】本题主要考查双曲线和抛物线的标准方程及几何性质.12.如图,PA切⊙O于点A,割线PBC经过圆心O,OB=PB=1,OA绕点O逆时针旋转60°到OD,则PD的长为.【考点】与圆有关的比例线段.【专题】综合题;压轴题;综合法.【分析】解法一:如图根据题设条件可求得角DOP的大小,由于OD=1,OP=2,由余弦定理求长度即可.解法二:由图形知,若能求得点D到线段OC的距离DE与线段OE的长度,在直角三角形PED中用勾股定理求PD即可.【解答】解:法一:∵PA切⊙O于点A,B为PO中点,∴AB=OB=OA,∴∠AOB=60°,∴∠POD=120°,在△POD中由余弦定理,得:PD2=PO2+DO2﹣2PO•DOcos∠POD=.∴.法二:过点D作DE⊥PC垂足为E,∵∠POD=120°,∴∠DOC=60°,可得,,在Rt△PED中,有.【点评】本题考点是与圆有关的比例线段,本题考查求线段的长度,平面几何中求线段长度一般在三角形中用正弦定理与余弦定理求解,本题中法一的特征用的是余弦定理求长度,法二在直角三角形中用勾股定理求长度,在三角形中求长度时应该根据题意选取适当的方法求解,做题后要注意总结方法选取的规律.13.若实数a,b,c满足2a+2b=2a+b,2a+2b+2c=2a+b+c,则c的最大值是2﹣log23.【考点】基本不等式在最值问题中的应用.【专题】计算题;压轴题.【分析】由基本不等式得2a+2b≥,可求出2a+b的范围,再由2a+2b+2c=2a+b+c=2a+b2c=2a+b+2c,2c可用2a+b表达,利用不等式的性质求范围即可.【解答】解:由基本不等式得2a+2b≥,即2a+b≥,所以2a+b≥4,令t=2a+b,由2a+2b+2c=2a+b+c可得2a+b+2c=2a+b2c,所以2c=因为t≥4,所以,即,所以故答案为:2﹣log23【点评】本题考查指数的运算法则,基本不等式求最值、不等式的性质等问题,综合性较强.14.在平面四边形ABCD中,点E、F分别是边AD、BC的中点,且AB=1,EF=,CD=,若•=15,则•的值为13.【考点】平面向量数量积的运算.【专题】平面向量及应用.【分析】画出图形,结合图形,先求出•的值,再利用•=15,求出•的值.【解答】解:如图所示,设AB∩DC=O,∵=++=+,=++=+,两式相加得=;∵AB=1,EF=,CD=,平方得2=;∴•=2;又∵•=15,即(﹣)•(﹣)=15;∴•﹣•﹣•+•=15,∴•+•=15+•+•,∴•=(﹣)•(﹣)=•﹣•﹣•+•=(15+•+•)﹣•﹣•=15+•(﹣)+•(﹣)=15+•+•=15+•(﹣)=15+•=15﹣•=15﹣2=13.故答案为:13.【点评】本题考查了两个向量的加减运算的应用问题,也考查了平面向量的几何意义以及平面向量的数量积的应用问题,是中档题.三、解答题:(本大题6个题,共80分)15.某木器厂生产圆桌和衣柜两种产品,现有两种木料,第一种有72m3,第二种有56m3,假设生产每种产品都需要用两种木料,生产一只圆桌和一个衣柜分别所需木料如表所示.每生产一只圆桌可获利6元,生产一个衣柜可获利10元,木器厂在现有木料条件下,圆桌和衣柜各生产多少,才使获得利润最多,利润最多为多少?【考点】简单线性规划的应用.【专题】计算题;应用题;作图题;不等式的解法及应用.【分析】由题意,设生产圆桌x只,衣柜y个,获得利润为z元;从而可得,z=6x+10y;利用线性规划求解.【解答】解:由题意,设生产圆桌x只,衣柜y个,获得利润为z元;则,z=6x+10y;做其平面区域如下,则由y=800﹣2x,x=700﹣3.5y得,x=350,y=100;答:应生产圆桌350只,生产衣柜100个,能使利润总额达到最大,利润最多3100元.【点评】本题考查了线性规划在实际问题中的应用,属于中档题.16.已知函数f(x)=2sinωxcosωx﹣2sin2ωx+(ω>0),直线x=x1,x=x2是函数y=f(x)的图象的任意两条对称轴,且|x1﹣x2|的最小值为.(Ⅰ)求ω的值;(Ⅱ)求函数f(x)的单调增区间;(Ⅲ)若f(α)=,求sin(π﹣4α)的值.【考点】三角函数中的恒等变换应用;由y=Asin(ωx+φ)的部分图象确定其解析式;复合三角函数的单调性.【专题】计算题;三角函数的图像与性质.【分析】(I)利用二倍角公式即辅助角公式,化简函数,利用直线x=x1,x=x2是函数y=f(x)的图象的任意两条对称轴,且|x1﹣x2|的最小值为,可得函数的最小正周期为π,根据周期公式,可求ω的值;(II)利用正弦函数的单调性,可得函数f(x)的单调增区间;(III)由f(a)=,可得sin(2a+)=,根据sin(π﹣4a)=sin[﹣2(2a+)]=﹣cos[2(2a+)]=2sin2(2a+)﹣1,即可求得结论.【解答】解:(I)∵f(x)=2sinωxcosωx﹣2sin2ωx+=sin2ωx+cos2ωx=2sin(2ωx+)∵直线x=x1,x=x2是函数y=f(x)的图象的任意两条对称轴,且|x1﹣x2|的最小值为,∴函数的最小正周期为π∴=π∴ω=1;(II)由(I)知,f(x)=2sin(2x+)∴﹣+2kπ≤2x+≤+2kπ,k∈Z∴﹣+kπ≤x≤+kπ,k∈Z∴函数f(x)的单调增区间为[﹣+kπ,+kπ],k∈Z;(III)∵f(a)=,∴sin(2a+)=∴sin(π﹣4a)=sin[﹣2(2a+)]=﹣cos[2(2a+)]=2sin2(2a+)﹣1=﹣.【点评】本题考查函数的周期性,考查函数解析式的确定,考查函数的单调性,考查学生的计算能力,周期确定函数解析式是关键.17.如图,在四棱锥P﹣ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,E为AD的中点,M是棱PC的中点,PA=PD=2,,.(1)求证:PE⊥平面ABCD;(2)求直线BM与平面ABCD所成角的正切值;(3)求直线BM与CD所成角的余弦值.【考点】直线与平面所成的角;异面直线及其所成的角;直线与平面垂直的判定.【专题】证明题;转化思想;综合法;空间角.【分析】(1)推导出PE⊥AD,平面PAD⊥平面ABCD,由此能证明PE⊥平面ABCD.(2)连结EC,取EC中点H,连结MH、HB,则MH∥PE,从而∠MBH即为BM与平面ABCD 所成角,由此能求出直线BM与平面ABCD所成角的正切值.(3)由CD∥BE,得直线BM与CD所成角即为直线BM与BE所成角,由此能求出直线BM与CD 所成角的余弦值.【解答】证明:(1)∵PA=PD,E为AD的中点,∴PE⊥AD,又∵平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD,∴PE⊥平面ABCD.解:(2)连结EC,取EC中点H,连结MH、HB,∵M是PC的中点,H是EC的中点,∴MH∥PE,由(1)知PE⊥平面ABCD,∴MH⊥平面ABCD,∴HB是BM在平面ABCD内的射影,∴∠MBH即为BM与平面ABCD所成角,∵AD∥BC,BC=AD,E为AD的中点,∠ADC=90°,∴四边形BCDE为矩形,∴EC=2,HB=,又∵MH=PE=,∴△MHB中,tan=,∴直线BM与平面ABCD所成角的正切值为.(3)由(2)知CD∥BE,∴直线BM与CD所成角即为直线BM与BE所成角连接ME,Rt△MHE中,,Rt△MHB中,,又,∴△MEB中,,∴直线BM与CD所成角的余弦值为.【点评】本题考查线面垂直的证明,考查线面角的正弦值和线线角的余弦值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.18.已知椭圆C:的离心率为,椭圆短轴的一个端点与两个焦点构成的三角形的面积为.(1)求椭圆C的方程;(2)已知动直线y=k(x+1)与椭圆C相交于A、B两点.①若线段AB中点的横坐标为,求斜率k的值;②已知点,求证:为定值.【考点】直线与圆锥曲线的综合问题;椭圆的标准方程.【专题】综合题;压轴题.【分析】(1)根据椭圆的离心率,三角形的面积及椭圆几何量之间的关系,建立等式,即可求得椭圆的标准方程;(2)①直线方程代入椭圆方程,利用韦达定理及线段AB中点的横坐标为,即可求斜率k的值;②利用韦达定理,及向量的数量积公式,计算即可证得结论.【解答】(1)解:因为满足a2=b2+c2,,…根据椭圆短轴的一个端点与两个焦点构成的三角形的面积为,可得.从而可解得,所以椭圆方程为…(2)证明:①将y=k(x+1)代入中,消元得(1+3k2)x2+6k2x+3k2﹣5=0…△=36k4﹣4(3k2+1)(3k2﹣5)=48k2+20>0,…因为AB中点的横坐标为,所以,解得…②由①知,所以…==…===…【点评】本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查向量的数量积,考查学生的运算能力,综合性强.19.已知函数f(x)=,数列{a n}满足a1=1,a n+1=f(),n∈N*,(1)求数列{a n}的通项公式;(2)令T n=a1a2﹣a2a3+a3a4﹣a4a5+…﹣a2n a2n+1,求T n;(3)令b n=(n≥2),b1=3,S n=b1+b2+…+b n,若S n<对一切n∈N*成立,求最小正整数m.【考点】数列的求和;数列递推式;数列与不等式的综合.【专题】计算题;转化思想;综合法;等差数列与等比数列.【分析】(1)通过代入函数解析式化简可知a n+1=a n+,进而计算可得结论;(2)通过(1)可知T n=a1a2﹣a2a3+a3a4﹣a4a5+…﹣a2n a2n+1=a2(a1﹣a3)+a4(a3﹣a5)+…+a2n(a2n﹣1﹣a2n+1),进而计算可得结论;(3)当n≥2时裂项可知b n=(﹣),进而并项相加可知S n=,从而可知<,进而问题转化为解不等式≥,计算即得结论.【解答】解:(1)依题意,a n+1==a n+,∴数列{a n}是以为公差的等差数列,又∵a1=1,∴a n=n+;(2)由(1)可知T n=a1a2﹣a2a3+a3a4﹣a4a5+…﹣a2n a2n+1=a2(a1﹣a3)+a4(a3﹣a5)+…+a2n(a2n﹣a2n+1)﹣1=﹣(a2+a4+…+a2n)=﹣•=﹣(2n2+3n);(3)当n≥2时,b n===(﹣),又∵b1=3=×(1﹣)满足上式,∴S n=b1+b2+…+b n=×(1﹣+﹣+…+﹣)=(1﹣)=,∵S n<对一切n∈N*成立,即<,又∵=(1﹣)递增,且<,∴≥,即m≥2018,∴最小正整数m=2018.【点评】本题考查数列的通项及前n项和,考查运算求解能力,考查裂项相消法,注意解题方法的积累,属于中档题.20.已知函数f(x)=lnx﹣ax2﹣bx.(I)当a=﹣1时,若函数f(x)在其定义域内是增函数,求b的取值范围;(Ⅱ)若f(x)的图象与x轴交于A(x1,0),B(x2,0)(x1<x2)两点,且AB的中点为C(x0,0),求证:f′(x0)<0.【考点】函数的单调性与导数的关系;导数在最大值、最小值问题中的应用.【专题】计算题;综合题;转化思想.【分析】(I)将f(x)在(0,+∞)上递增,转化成f′(x)≥0对x∈(0,+∞)恒成立,即b≤+2x对x∈(0,+∞)恒成立,只需b≤即可,根据基本不等式可求出;(II)根据f(x)的图象与x轴交于A(x1,0),B(x2,0)(x1<x2)两点,得到,两式相减,可得,利用中点坐标公式和导数,即可证明结论.【解答】解:(Ⅰ)依题意:f(x)=lnx+x2﹣bx∵f(x)在(0,+∞)上递增,∴f′(x)=+2x﹣b≥0对x∈(0,+∞)恒成立即b≤+2x对x∈(0,+∞)恒成立,∴只需b≤∵x>0,∴+2x≥2当且仅当x=时取“=”,∴b≤2,∴b的取值范围为(﹣∞,2];(II)证明:由已知得,即,两式相减,得:⇒,由f′(x)=﹣2ax﹣b及2x0=x1+x2,得f′(x0)=﹣2ax0﹣b===,令t=∈(0,1),且φ(t)=,∵φ′(t)=,∴φ(t)是(0,1)上的减函数,∴φ(t)>φ(1)=0,又x1<x2,∴f'(x0)<0.【点评】本题主要考查导函数的正负与原函数的单调性之间的关系,即当导函数大于0时原函数单调递增,当导函数小于0时原函数单调递减,同时考查了转化与划归的思想,分析问题解决问题的能力,属于中档题.。
2018高考天津文科数学带答案

2018高考天津文科数学带答案绝密★启用前2018年普通高等学校招生全国统一考试(天津卷)数学(文史类)本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试用时120分钟。
答卷前,考生务必将自己的姓名、准考证号填写在答题考上,并在规定位置粘贴考试用条形码。
答卷时,考生务必将答案涂写在答题卡上,答在试卷上的无效。
考试结束后,将本试卷和答题卡一并交回。
祝各位考生考试顺利!第Ⅰ卷注意事项:1.每小题选出答案后,用铅笔将答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
2.本卷共8小题,每小题5分,共40分。
参考公式:·如果事件A,B互斥,那么P(A∪B)=P(A)+P(B).·棱柱的体积公式V=Sh. 其中S表示棱柱的底面面积,h 表示棱柱的高.·棱锥的体积公式13V Sh =,其中S 表示棱锥的底面积,h 表示棱锥的高.一.选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.(1)设集合{1,2,3,4}A =,{1,0,2,3}B =-,{|12}C x x =∈-≤<R ,则()A B C =(A ){1,1}- (B ){0,1}(C ){1,0,1}- (D ){2,3,4}(2)设变量,x y 满足约束条件52410x y x y x y y +≤⎧⎪-≤⎪⎨-+≤⎪⎪≥⎩,,,,则目标函数35z x y =+的最大值为(A )6 (B )19(C )21 (D )45(3)设x ∈R ,则“38x>”是“||2x >” 的 (A )充分而不必要条件 (B )必要而不充分条件(C )充要条件 (D )既不充分也不必要条件(4)阅读如图所示的程序框图,运行相应的程序,若输入N 的值为20,则输出T 的值为(A )1 (B )2 (C )3(D )4(5)已知13313711log ,(),log 245a b c ===,则,,a b c 的大小关系为(A )a b c >> (B )b a c >> (C )c b a >>(D )c a b >>(6)将函数sin(2)5y x π=+的图象向右平移10π个单位长度,所得图象对应的函数(A )在区间[,]44ππ- 上单调递增 (B )在区间[,0]4π 上单调递减(C )在区间[,]42ππ 上单调递增 (D )在区间[,]2ππ 上单调递减(7)已知双曲线22221(0,0)x y a b a b -=>> 的离心率为2,过右焦点且垂直于x 轴的直线与双曲线交于,A B 两点.设,A B 到双曲线的同一条渐近线的距离分别为1d 和2d ,且126,d d += 则双曲线的方程为(A )22139x y -= (B )22193x y -= (C )221412x y -= (D )221124x y -=(8)在如图的平面图形中,已知1.2,120OM ON MON ==∠=,2,2,BM MA CN NA ==则·BC OM 的值为(A )15- (B )9-(C )6- (D )0第Ⅱ卷注意事项:1.用黑色墨水的钢笔或签字笔将答案写在答题卡上。
2018年天津市河东区高考一模文科数学试卷及答案

河东区 2018 年高考一模考试数学试卷(文史类)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试用时120分钟.第Ⅰ卷1至2页,第Ⅱ卷3至6页.答题前,考生务必将自己的姓名、准考证号涂写在答题卡上,并在规定位置粘贴考试用条形码。
答卷时,考生务必将答案涂写在答题卡上,答在试卷上的无效。
考试结束后,将本试卷和答题卡一并交回。
祝各位考生考试顺利!第Ⅰ卷(选择题共40分)注意事项:1. 每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
2.本题共8个小题,每小题5分,共40分.每小题给出的四个选项只有一个符合题目要求. 1.复数2()2iz ii-=+为虚数单位在复平面内对应的点所在象限为()A.第一象限 B.第二象限 C.第三象限 D.第四象限2.已知变量x y,满足约束条件21110x yx yy,,.⎧+≥⎪-≤⎨⎪-≤⎩则2z x y=-的最大值为()A.-3 B. 0C.1 D.33.某程序框图如图1所示,则输出的结果S=()A.26 B.57C.120 D.2474.函数()|2|lnf x x x=--在定义域内的零点的个数为()A.0 B.1 C.2 D.35.下列说法正确的是个数为( )①1=a是直线0=-ayx与直线0=+ayx互相垂直的充要条件②直线12π=x是函数)62sin(2π-=xy的图象的一条对称轴③ 已知直线l :20x y ++=与圆C :22(1)(1)2x y -++=,则圆心C 到直线l的距离是④若命题P :“存在∈0x R ,0102>--x x”,则命题P的否定:“任意R x ∈,012≤--x x”A .1B .2C .3D .46.已知双曲线22221x y a b-=的渐近线方程为y =,则以它的顶点为焦点,焦点为顶点的椭圆的离心率等于( ) A .12B.2CD .17.在R 上定义运算).1(:y x y x -=⊗⊗若对任意2x >,不等式()2x a xa -⊗≤+都成立,则实数a 的取值范围是( ) A .17,⎡⎤-⎣⎦B .(3,⎤-∞⎦C .(7,⎤-∞⎦D .()17,,⎤⎡-∞-+∞⎦⎣8.若直角坐标系内A 、B 两点满足:(1)点A 、B 都在f (x )的图像上;(2)点A 、B 关于原点对称,则称点对(A ,B )是函数f (x )的一个“姊妹点对”(点对(A ,B )与(B ,A )可看作一个“姊妹点对”。
【数学】天津市河东区2018年高考一模考试数学试题(文史类)

河东区2018年高考一模考试数学试卷(文史类)第Ⅰ卷(选择题 共40分)一、选择题:本大题共8个小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 设集合{1,2,3,4,5,6}M =,{|26}N x R x =∈≤≤,那么下列结论正确的是( )A .M N M =B .M N N ÙC .M N N =D .M N M Ø2. ABC ∆中,3AB =,BC =4AC =,则ABC ∆的面积是( )A ..2C .3D .32 3. 阅读如图的程序框图,并判断运行结果为( )A .55B .5C .-5D .-554. 设,a b R ∈,则“2a ≥且2b ≥”是“224a b +≥”的( )A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件5. 设双曲线的焦点在x 轴上,两条渐近线为13y x =±,则该双曲线的离心率e =( )A .10B .2 D .36.设等差数列{}n a 的前n 项和为n S ,且满足20140S >,20150S <,对任意正整数n ,都有n k a a ≥,则k 的值为( )A .1006B .1007C .1008D .10097. 设P 是ABC ∆边BC 上的任意一点,Q 为AP 的中点,若AQ AB AC λμ=+,则λμ+=( )A .14 B .13 C .12D .1 8. 设正实数a ,b ,c 满足22340a ab b c -+-=,则当ab c 取得最大值时,212a b c +-最大值为( )A .0B .1C .94D .3 第Ⅱ卷(非选择题 共110分)二、填空题:本大题共6小题,每小题5分,共30分.把答案填在题中横线上.9.在复平面内,复数1i i+对应的点位于第 象限. 10.若过曲线()ln f x x x =上的点P 的切线的斜率为2,则点P 的坐标是 .11.某几何体的三视图如图(其中侧视图中的圆弧是半圆),则该几何体的表面积为 .12.已知A ,(1,0)B ,点P 为圆2220x y x ++=上的任意一点,则PAB ∆面积的最大值为 .13.已知关于x 的不等式220x ax a -+>在R 上恒成立,则实数a 的取值范围是 .14.设()f x 是定义在R 上的奇函数,且()y f x =的图象关于直线12x =对称,则(1)(2)(3)f f f ++(4)(5)f f ++= .三、解答题:本大题共6小题,共80分.解答应写出文字说明、证明过程或演算步骤.15.某餐厅装修,需要大块胶合板20张,小块胶合板50张,已知市场出售A 、B 两种不同规格的胶合板。
2018年天津市部分区高考一模数学试卷(文科)【解析版】
2018年天津市部分区高考数学一模试卷(文科)一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)已知全集U={0,1,2,3,4,5,6},集合A={2,3,4,5,6},集合B={1,3,4,6},则集合A∩∁U B=()A.{0}B.{2,5}C.{0,1,2,4,6}D.{0,2,3,5}2.(5分)一只蚂蚁在如图所示的长方形ABCD的内部随机爬行,其中AB=4,BC=2,若不考虑蚂蚁的大小,则某时刻该蚂蚁爬行在以AB为直径的半圆区域内的概率是()A.B.C.D.3.(5分)阅读如图的程序框图,运行相应的程序,则输出S的值为()A.B.C.D.4.(5分)设x∈R,则“|x|<2”是“x2+3x﹣10<0”的()A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件5.(5分)已知双曲线﹣=1(a>0,b>0)的离心率为2,一个焦点在直线x+y﹣2=0上,则该双曲线的方程为()A.B.C.x2D.6.(5分)在△ABC中,∠BAC=60°,AB=6,AC=9,若E,F为边BC的三等分点,则等于()A.18B.20C.26D.417.(5分)已知函数f(x)是定义在R上的偶函数,且在区间[0,+∞)上对于任意两个不相等的实数x1,x2恒有成立,若实数a满足f (log6a)≥f(﹣1),则a的取值范围是()A.[]B.[)C.(0,6]D.(﹣∞,6]8.(5分)将函数f(x)=2sin(ωx+)(ω>0)的图象向右平移个单位长度,得到y=g(x)的图象.若y=g(x)的图象关于原点对称,且在[﹣]上不是单调函数,则ω的最小整数值为()A.9B.11C.17D.25二、填空题:本大题共有6小题,每小题5分,共30分.9.(5分)已知a∈R,i为虚数单位,若复数是实数,则a的值为.10.(5分)设函数f(x)=(x+a)lnx,若曲线y=f(x)在点(1,f(1))处的切线与直线2x﹣y=0平行,则实数a的值为.11.(5分)已知圆x2+y2+mx﹣3=0(m>0)与抛物线x2=8y的准线相切,则圆的方程是.12.(5分)如图,四棱锥E﹣ABCD的五个顶点都在同一个球的球面上,且EA ⊥平面ABCD,AB⊥BC,AB=3,BC=4,EA=5,则这个球的表面积为.13.(5分)已知正实数a,b满足ab=a+2,那么2a+b的最小值为.14.(5分)已知函数f(x)=,若关于x的方程f(x)=2x+m (m∈R)恰有三个不相等的实数解,则m的取值范围是.三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤.15.(13分)设△ABC的内角A,B,C所对的边分别为a,b,c,且a=3,sin B =2sin A,cos C=.(Ⅰ)求c和sin A的值;(Ⅱ)求cos(2A)的值.16.(13分)某大型企业计划在A、B两市举行新产品推介会,受产品时效性和成本影响,新产品推介会总时间不能超过30天,且在A市时间不少于B市,推介会总费用不超过5万元.在A、B两市举行新产品推介会的费用分别为每天0.2万元和0.1万元,销售纯收益分别为每天3万元和2万元.分别用x,y 表示该企业计划在A、B两市举行新产品推介会的天数.(Ⅰ)用x,y列出满足条件的数学关系式,并画出相应的平面区域;(Ⅱ)该企业如何分配在A、B两市做新产品推介会的天数,才能使企业获得的销售纯收益最大?最大销售纯收益是多少?17.(13分)如图,四棱锥A﹣DCBE中,DE∥CB,∠DCB=∠ADE=90°,CB=2DE=2,AD=CD,二面角C﹣DE﹣A为60°,且AC=.(Ⅰ)求证:BC⊥平面ACD;(Ⅱ)求异面直线AB与DE所成角的余弦值;(Ⅲ)求直线CE与平面ADE所成角的正弦值.18.(13分)已知数列{a n}的前n项和为S n,且2a n=S n﹣n+1(n∈N*),a1=.(Ⅰ)证明数列{a n﹣1}是等比数列,并求数列{a n}的通项公式;(Ⅱ)设b n=(n∈N*),数列{b n}的前n项和为T n,证明:T n<4.19.(14分)已知椭圆C:+=1(a>b>0),点M(,)在椭圆C 上,且椭圆的离心率为.(Ⅰ)求椭圆C的方程;(Ⅱ)直线l:y=kx+m(km≠0)与椭圆C相交于A,B两点,线段AB的中点N在直线3x+4y=0上,求△OAB面积的最大值(其中O为坐标原点).20.(14分)已知函数f(x)=ax2﹣(2+a)x+1+lnx(a>0),g(x)=.(Ⅰ)求g(x)的极值;(Ⅱ)证明:对任意x1∈(0,]均存在x2∈(0,1],使得f(x1)<g(x2)成立;(Ⅲ)证明:ln(2×3×4×…×2018)<2019.2018年天津市部分区高考数学一模试卷(文科)参考答案与试题解析一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)已知全集U={0,1,2,3,4,5,6},集合A={2,3,4,5,6},集合B={1,3,4,6},则集合A∩∁U B=()A.{0}B.{2,5}C.{0,1,2,4,6}D.{0,2,3,5}【解答】解:∵全集U={0,1,2,3,4,5,6},集合A={2,3,4,5,6},集合B={1,3,4,6},∴∁U B={0,2,5},集合A∩∁U B={2,5}.故选:B.2.(5分)一只蚂蚁在如图所示的长方形ABCD的内部随机爬行,其中AB=4,BC=2,若不考虑蚂蚁的大小,则某时刻该蚂蚁爬行在以AB为直径的半圆区域内的概率是()A.B.C.D.【解答】解:如图,∵AB=4,BC=2,∴S ABCD=4×2=8,阴影部分半圆的面积为,∴某时刻该蚂蚁爬行在以AB为直径的半圆区域内的概率是.故选:A.3.(5分)阅读如图的程序框图,运行相应的程序,则输出S的值为()A.B.C.D.【解答】解:模拟程序的运行,可得程序框图的功能是计算并输出S=sin+sin的值,可得S=sin+sin=++0=.故选:B.4.(5分)设x∈R,则“|x|<2”是“x2+3x﹣10<0”的()A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件【解答】解:由|x|<2得﹣2<x<2,由x2+3x﹣10<0得(x﹣2)(x+5)<0,得﹣5<x<2,则“|x|<2”是“x2+3x﹣10<0”的充分不必要条件,故选:A.5.(5分)已知双曲线﹣=1(a>0,b>0)的离心率为2,一个焦点在直线x+y﹣2=0上,则该双曲线的方程为()A.B.C.x2D.【解答】解:双曲线﹣=1(a>0,b>0)的离心率为2,一个焦点在直线x+y﹣2=0上,可得c=2,则a=1,b=,则该双曲线的方程为:x2.故选:C.6.(5分)在△ABC中,∠BAC=60°,AB=6,AC=9,若E,F为边BC的三等分点,则等于()A.18B.20C.26D.41【解答】解:如图所示,△ABC中,∠BAC=60°,AB=6,AC=9,且E,F为边BC的三等分点,则=(+)•(+)=(+)•(﹣)=(+﹣)•(﹣+)=(+)•(+)=++=×62+×92+×6×9×cos60°=41.故选:D.7.(5分)已知函数f(x)是定义在R上的偶函数,且在区间[0,+∞)上对于任意两个不相等的实数x1,x2恒有成立,若实数a满足f(log6a)≥f(﹣1),则a的取值范围是()A.[]B.[)C.(0,6]D.(﹣∞,6]【解答】解:根据题意,函数f(x)在区间[0,+∞)上有成立,则函数f(x)在区间[0,+∞)上是减函数,又由函数为偶函数,则f(log6a)≥f(﹣1)⇒|log6a|≤1⇒﹣1≤log6a≤1,解可得:≤a≤6;故选:A.8.(5分)将函数f(x)=2sin(ωx+)(ω>0)的图象向右平移个单位长度,得到y=g(x)的图象.若y=g(x)的图象关于原点对称,且在[﹣]上不是单调函数,则ω的最小整数值为()A.9B.11C.17D.25【解答】解:函数f(x)=2sin(ωx+)(ω>0)的图象向右平移个单位长度,∴y=2sin[ω(x﹣)+]=2sin(ωx+),∴y=g(x)=2sin(ωx+),若y=g(x)的图象关于原点对称,则=kπ,k∈Z;解得ω=1﹣8k,k∈Z①;又g(x)在[﹣]上不是单调函数,∴<×2,得T<,即<,∴ω>9②;由①②知,ω的最小整数值为17.故选:C.二、填空题:本大题共有6小题,每小题5分,共30分.9.(5分)已知a∈R,i为虚数单位,若复数是实数,则a的值为.【解答】解:∵=是实数,∴,则a=﹣.故答案为:.10.(5分)设函数f(x)=(x+a)lnx,若曲线y=f(x)在点(1,f(1))处的切线与直线2x﹣y=0平行,则实数a的值为1.【解答】解:函数f(x)=(x+a)lnx的导数为f′(x)=lnx+,可得曲线y=f(x)在点(1,f(1))处的切线斜率为k=1+a,由切线与直线2x﹣y=0平行,可得1+a=2,解得a=1,故答案为:1.11.(5分)已知圆x2+y2+mx﹣3=0(m>0)与抛物线x2=8y的准线相切,则圆的方程是x2+y2±2x﹣3=0.【解答】解:圆x2+y2+mx﹣3=0(m>0)转化为(x+)2+y2=,∵圆x2+y2+mx﹣3=0(m>0)与抛物线x2=8y的准线相切,抛物线x2=8y的准线为y=﹣2,∴=2,解得m=±2.∴圆x2+y2±2x﹣3=0.故答案为:x2+y2±2x﹣3=0.12.(5分)如图,四棱锥E﹣ABCD的五个顶点都在同一个球的球面上,且EA⊥平面ABCD,AB⊥BC,AB=3,BC=4,EA=5,则这个球的表面积为50π.【解答】解:由题意可知,ABCD的外接圆的圆心在AC的中点,EA⊥平面ABCD,所以EC的中点是外接球的球心,所以球的半径为:=.则这个球的表面积为:4=50π.故答案为:50π.13.(5分)已知正实数a,b满足ab=a+2,那么2a+b的最小值为5.【解答】解:根据题意,正实数a,b满足ab=a+2,则b=1+,则2a+b=2a+1+=2a++1≥2(a+)+1≥2×2+1=5,即2a+b的最小值为5;故答案为:5.14.(5分)已知函数f(x)=,若关于x的方程f(x)=2x+m(m∈R)恰有三个不相等的实数解,则m的取值范围是(﹣1,0).【解答】解:方程f(x)=2x+m(m∈R)恰有三个不相等的实数解⇔方程f(x)﹣2x=m(m∈R)恰有三个不相等的实数解令g(x)=f(x)﹣2x=.当x≤0时,函数h(x)=ln(x+1)﹣x,h′(x)=﹣1=,可知函数h(x)在(0,+∞)递减,函数g(x)的图象如下,由图可知g(﹣1)<m<0,∴﹣1<m<0,故答案为:(﹣1,0).三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤.15.(13分)设△ABC的内角A,B,C所对的边分别为a,b,c,且a=3,sin B =2sin A,cos C=.(Ⅰ)求c和sin A的值;(Ⅱ)求cos(2A)的值.【解答】解:(Ⅰ)由a=3,sin B=2sin A,得b=2a=6,又cos C=,∴=36.∴c=6.由cos C=,得sin C=,由正弦定理可得:,即,得sin A=;(Ⅱ)由(Ⅰ)得,sin A=,∵a<c,∴cos A=.则sin2A=2sin A cos A=,cos2A=.∴cos(2A)=cos2A cos﹣sin2A sin=.16.(13分)某大型企业计划在A、B两市举行新产品推介会,受产品时效性和成本影响,新产品推介会总时间不能超过30天,且在A市时间不少于B市,推介会总费用不超过5万元.在A、B两市举行新产品推介会的费用分别为每天0.2万元和0.1万元,销售纯收益分别为每天3万元和2万元.分别用x,y表示该企业计划在A、B两市举行新产品推介会的天数.(Ⅰ)用x,y列出满足条件的数学关系式,并画出相应的平面区域;(Ⅱ)该企业如何分配在A、B两市做新产品推介会的天数,才能使企业获得的销售纯收益最大?最大销售纯收益是多少?【解答】解:(Ⅰ)根据题意知,x,y满足的条件为,目标函数是z=3x+2y,画出不等式组表示的平面区域,如图所示;(Ⅱ)根据图形知,当目标函数过点M时,z取得最大值;由,解得M(20,10),即企业在A市推销20天,B市推销10天,才能使企业获得的销售纯收益最大,且最大销售纯收益是z=3×20+2×10=80(万元).17.(13分)如图,四棱锥A﹣DCBE中,DE∥CB,∠DCB=∠ADE=90°,CB=2DE=2,AD=CD,二面角C﹣DE﹣A为60°,且AC=.(Ⅰ)求证:BC⊥平面ACD;(Ⅱ)求异面直线AB与DE所成角的余弦值;(Ⅲ)求直线CE与平面ADE所成角的正弦值.【解答】证明:(Ⅰ)∵四棱锥A﹣DCBE中,DE∥CB,∠DCB=∠ADE=90°,∴BC⊥DC,AD⊥DE,∴BC⊥AD,∵DC∩AD=D,∴BC⊥平面ACD.解:(Ⅱ)∵BC⊥平面ACD,DE∥CB,∴DE⊥平面ACD,∠ABC是异面直线AB与DE所成角(或所成角的补角),∵BC⊥平面ACD,∴∠ACB=90°,∵AC=,BC=2,∴AB==,∴cos∠ABC===,∴异面直线AB与DE所成角的余弦值为.(Ⅲ)∵DE⊥平面ADC,二面角C﹣DE﹣A为60°,∴∠ADC=60°,∵CB=2DE=2,AD=CD,二面角C﹣DE﹣A为60°,且AC=.∴△ADC是边长为的等边三角形,取CD中点O,以O为原点,OC为x轴,过O作DE平行线为y轴,OA为z 轴,建立空间直角坐标系,C(,0,0),E(﹣,1,0),D(﹣,0,0),A(0,0,),=(0,1,0),=(,0,),=(,﹣1,0),设平面ADE的法向量=(x,y,z),则,取x=,得=(,0,﹣1),设直线CE与平面ADE所成角为θ,则sinθ===.∴直线CE与平面ADE所成角的正弦值为.18.(13分)已知数列{a n}的前n项和为S n,且2a n=S n﹣n+1(n∈N*),a1=.(Ⅰ)证明数列{a n﹣1}是等比数列,并求数列{a n}的通项公式;(Ⅱ)设b n=(n∈N*),数列{b n}的前n项和为T n,证明:T n<4.【解答】证明:(Ⅰ)数列{a n}的前n项和为S n,且2a n=S n﹣n+1①(n∈N*),则:2a n﹣1=S n﹣1﹣n+1+1②,①﹣②得:a n=2a n﹣1﹣1,整理得:a n﹣1=2(a n﹣1﹣1),所以:=2(常数),所以:数列{a n﹣1}是等比数列,则:a n﹣1=,由于:a1=.则:,证明:(Ⅱ)由于:,由于:==则:T n=①,=②①﹣②得:,解得:T n=4(1﹣)﹣<4.故不等式成立.19.(14分)已知椭圆C:+=1(a>b>0),点M(,)在椭圆C 上,且椭圆的离心率为.(Ⅰ)求椭圆C的方程;(Ⅱ)直线l:y=kx+m(km≠0)与椭圆C相交于A,B两点,线段AB的中点N在直线3x+4y=0上,求△OAB面积的最大值(其中O为坐标原点).【解答】解:(I)由题意可得:+=1,=,a2=b2+c2,联立解得:a=2,b2=3,c=1.∴椭圆C的方程为:+=1.(II)设A(x1,y1),B(x2,y2),线段AB的中点N(x0,y0).联立,化为:(3+4k2)x2+8kmx+4m2﹣12=0,△=64k2m2﹣4(3+4k2)(4m2﹣12)>0.(*)∴x1+x2=﹣,x1x2=.∴x0=,y0=kx0+m=.∵线段AB的中点N在直线3x+4y=0上,∴+=0,km≠0,化为:k=1.∴7﹣m2>0.∴|AB|===.点O到AB的距离d=.=d|AB|=×=∴S△AOB≤=.当且仅当m2=时取等号.∴△OAB面积的最大值为.20.(14分)已知函数f(x)=ax2﹣(2+a)x+1+lnx(a>0),g(x)=.(Ⅰ)求g(x)的极值;(Ⅱ)证明:对任意x1∈(0,]均存在x2∈(0,1],使得f(x1)<g(x2)成立;(Ⅲ)证明:ln(2×3×4×…×2018)<2019.【解答】解:(Ⅰ)g(x)=的导数为g′(x)=,当0<x<e时,g′(x)>0,g(x)递增,当x>e时,g′(x)<0,g(x)递减,可得g(x)在x=e处取得极大值,且为,无极小值;(Ⅱ)证明:由(Ⅰ)可得g(x)在(0,1]递增,即有g(x)的最大值为g(1)=0;即证ax2﹣(2+a)x+1+lnx(a>0)<0,即为a(x2﹣x)<2x﹣1﹣lnx,由a>0,0<x≤,可得a(x2﹣x)<0,由y=2x﹣1﹣lnx的导数为y′=2﹣<0在(0,]恒成立,即有函数y递减,可得最小值为﹣ln=ln2>0,则a(x2﹣x)<2x﹣1﹣lnx恒成立,可得对任意x1∈(0,]均存在x2∈(0,1],使得f(x1)<g(x2)成立;(Ⅲ)证明:由函数y=lnx﹣x+1的导数为y′=﹣1,可得x>1时,函数y递减;0<x<1时,函数y递增,可得x=1处函数y取得极大值,且为最大值0,即有lnx≤x﹣1,可得ln2≤1,ln3≤2,ln4≤3,…,ln2018≤2017,即有ln2+ln3+…+ln2018≤1+2+…+2017=×2017×2018=2017×1009<2019×1009,可得ln(2×3×4×…×2018)<2019×1009,即为ln(2×3×4×…×2018)<2019.。
天津市河东区2018高三一模试题解析

河东区2018高三一模文综政治1、【答案】A【命题立意】本题考查生产与消费的关系。
【解析】①正确,享有三天的试驾体验,车主可以在这个时间段考虑是否购买此车。
说明“天猫汽车超市”的推出有利于提升消费体验,促进传统商业模式创新;②正确,只需要通过手机进行下单,然后通过支付宝完成付款,再到天猫汽车超市进行提车即可,全程没有任何导购员或服务员。
说明“天猫汽车超市”的推出有利于降低零售经营成本,提高商品和资金流动效率。
③不符合题意,材料所述并没有去除商品流通中间环节,实现直接交换。
④错误,劳动者在生产力发展中起决定性作用。
故选:A。
2、【答案】B【命题立意】本题考查全面提高开放型经济水平;经济全球化【解析】①③符合题意,根据题意,“金砖实践”有利于建设开放型世界经济体系,促进贸易和投资自由化、便利化;推动经济全球化朝开放、包容、普惠、平衡、共贏方向发展;②表述错误,“金砖实践”并不能化解全球金融风险和保障发展中国家的经济稳定与安全;④不符合题意,世贸组织提供解决各国贸易摩擦的场所,实现要素的有序、自由流动,故排除;故选:B。
3、【答案】D【命题立意】本题考查:收入分配的社会公平【解析】扩大中等收入者的数量可以缩小社会总体的收入差距,实现社会公平,从而提高社会总体消费水平,②③④符合题意。
我国的基本分配制度不是扩大中等收入者数量的原因,①不符合题意。
4、【答案】C【命题立意】本题考查政府的职能。
【解析】材料中统筹全国养老保险属于政府的社会职能,蓝天保卫战属于生态文明职能,高中和高等教育属于政府的文化建设职能,①③④符合题意。
②说法错误,为人民服务是政府的宗旨。
5、【答案】B【命题立意】本题考查全面推进依法治国【解析】为国歌立法国歌的尊严和权威将受到法律的保护,做到了有法可依,有利于维护国家尊严,提升公民的国家观念和爱国意识,有利于增加公民的责任感和使命感,①②④符合题意; ③错误,全国人大具有最高立法权; 所以B选项是正确的.6、【答案】D【命题立意】本题考查新型民族关系及处理民族关系的原则【解析】①表述错误,我国平等、团结、互助、和谐的社会主义新型民族关系早已建立;②表述错误,西藏新疆人民的自身努力是西藏新疆繁荣稳定的关键;③④符合题意,天津市高度重视,积极做好国家扶贫援藏援疆工作是因为国家的强盛需要各民族共同繁荣,民族共同繁荣是民族平等、民族团结的物质保证;故选:D。
天津市河东高考数学一模试卷(文科)有答案

天津市河东区高考数学一模试卷(文科)一、选择题:本题共8个小题,每小题5分,共40分.每小题给出的四个选项只有一个符合题目要求.1.设集合I={x||x|<3,x∈Z},A={1,2},B={﹣2,﹣1,2},则A∪(C I B)=()A.{1} B.{1,2} C.{2} D.{0,1,2}2.取一根长度为3m的绳子,拉直后在任意位置剪断,那么剪得两段的长都不小于1m的概率是()A.B.C.D.不确定3.一个直棱柱被一个平面截去一部分后所剩几何体的三视图如图所示,则该几何体的体积为()A.9 B.10 C.11 D.4.在△ABC中,b=5,∠B=,tanA=2,则a的值是()A.10B.2C. D.5.如果执行如图所示的程序框图,那么输出的S=()A.190 B.94 C.46 D.226.已知函数f(x)=a x+x﹣b的零点x0∈(n,n+1)(n∈Z),其中常数a,b满足0<b<1<a,则n的值为()A.2 B.1 C.﹣2 D.﹣l7.图是函数y=Asin(ωx+φ)(x∈R)在区间上的图象,为了得到这个函数的图象,只要将y=sinx(x∈R)的图象上所有的点()A.向左平移个单位长度,再把所得各点的横坐标缩短到原来的倍,纵坐标不变B.向左平移个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变C.向左平移个单位长度,再把所得各点的横坐标缩短到原来的倍,纵坐标不变D.向左平移个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变8.已知,且函数y=f(x)﹣2x恰有3个不同的零点,则实数a 的取值范围是()A.[﹣4,0]B.[﹣8,+∞)C.[﹣4,+∞)D.(0,+∞)二、填空题(本大题共6个小题,每小题5分,共30分.把答案填在题中横线上.)9.若(1+2ai)i=1﹣bi,其中a、b∈R,i是虚数单位,则|a+bi|=.10.某高校甲、乙、丙、丁四个专业分别有150、150、400、300名学生,为了解学生的就业倾向,用分层抽样的方法从该校这四个专业共抽取40名学生进行调查,应在丙专业抽取的学生人数为.11.已知双曲线=1(a>0,b>0)的一条渐近线方程是y=x,它的一个焦点与抛物线y2=16x 的焦点相同.则双曲线的方程为.12.如图,PA切⊙O于点A,割线PBC经过圆心O,OB=PB=1,OA绕点O逆时针旋转60°到OD,则PD的长为.13.若实数a,b,c满足2a+2b=2a+b,2a+2b+2c=2a+b+c,则c的最大值是.14.在平面四边形ABCD中,点E、F分别是边AD、BC的中点,且AB=1,EF=,CD=,若•=15,则•的值为.三、解答题:(本大题6个题,共80分)15.某木器厂生产圆桌和衣柜两种产品,现有两种木料,第一种有72m3,第二种有56m3,假设生产每种产品都需要用两种木料,生产一只圆桌和一个衣柜分别所需木料如表所示.每生产一只圆桌可获利6元,生产一个衣柜可获利10元,木器厂在现有木料条件下,圆桌和衣柜各生产多少,才使获得利润最多,利润最多为多少?16.已知函数f(x)=2sinωxcosωx﹣2sin2ωx+(ω>0),直线x=x1,x=x2是函数y=f(x)的图象的任意两条对称轴,且|x1﹣x2|的最小值为.(Ⅰ)求ω的值;(Ⅱ)求函数f(x)的单调增区间;(Ⅲ)若f(α)=,求sin(π﹣4α)的值.17.如图,在四棱锥P﹣ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,E为AD的中点,M是棱PC的中点,PA=PD=2,,.(1)求证:PE⊥平面ABCD;(2)求直线BM与平面ABCD所成角的正切值;(3)求直线BM与CD所成角的余弦值.18.已知椭圆C:的离心率为,椭圆短轴的一个端点与两个焦点构成的三角形的面积为.(1)求椭圆C的方程;(2)已知动直线y=k(x+1)与椭圆C相交于A、B两点.①若线段AB中点的横坐标为,求斜率k的值;②已知点,求证:为定值.19.已知函数f(x)=,数列{a n}满足a1=1,a n+1=f(),n∈N*,(1)求数列{a n}的通项公式;(2)令T n=a1a2﹣a2a3+a3a4﹣a4a5+…﹣a2n a2n+1,求T n;(3)令b n=(n≥2),b1=3,S n=b1+b2+…+b n,若S n<对一切n∈N*成立,求最小正整数m.20.已知函数f(x)=lnx﹣ax2﹣bx.(I)当a=﹣1时,若函数f(x)在其定义域内是增函数,求b的取值范围;(Ⅱ)若f(x)的图象与x轴交于A(x1,0),B(x2,0)(x1<x2)两点,且AB的中点为C(x0,0),求证:f′(x0)<0.天津市河东区高考数学一模试卷(文科)参考答案与试题解析一、选择题:本题共8个小题,每小题5分,共40分.每小题给出的四个选项只有一个符合题目要求.1.设集合I={x||x|<3,x∈Z},A={1,2},B={﹣2,﹣1,2},则A∪(C I B)=()A.{1} B.{1,2} C.{2} D.{0,1,2}【考点】交、并、补集的混合运算.【专题】计算题.【分析】把集合A用列举法表示,然后求出C I B,最后进行并集运算.【解答】解:因为I={x||x|<3,x∈Z}={﹣2,﹣1,0,1,2},B={﹣2,﹣1,2},所以,C I B={0,1},又因为A={1,2},所以A∪(C I B)={1,2}∪{0,1}={0,1,2}.故选D.【点评】本题考查了并集和补集的混合运算,考查了学生对集合运算的理解,是基础题.2.取一根长度为3m的绳子,拉直后在任意位置剪断,那么剪得两段的长都不小于1m的概率是()A.B.C.D.不确定【考点】几何概型;任意角的三角函数的定义.【专题】计算题.【分析】根据题意确定为几何概型中的长度类型,将长度为3m的绳子分成相等的三段,在中间一段任意位置剪断符合要求,从而找出中间1m处的两个界点,再求出其比值.【解答】解:记“两段的长都不小于1m”为事件A,则只能在中间1m的绳子上剪断,剪得两段的长都不小于1m,所以事件A发生的概率.故选B【点评】本题主要考查概率中的几何概型长度类型,关键是找出两段的长都不小于1m的界点来.3.一个直棱柱被一个平面截去一部分后所剩几何体的三视图如图所示,则该几何体的体积为()A.9 B.10 C.11 D.【考点】棱柱、棱锥、棱台的体积.【专题】空间位置关系与距离.【分析】根据得出该几何体是在底面为边长是2的正方形、高是3的直四棱柱的基础上,截去一个底面积为×2×1=1、高为3的三棱锥形成的,运用直棱柱减去三棱锥即可得出答案.【解答】解:.由三视图可知该几何体是在底面为边长是2的正方形、高是3的直四棱柱的基础上,==1,截去一个底面积为×2×1=1、高为3的三棱锥形成的,V三棱锥所以V=4×3﹣1=11.故选:C【点评】本题考查了空间几何体的性质,求解体积,属于计算题,关键是求解底面积,高,运用体积公式.4.在△ABC中,b=5,∠B=,tanA=2,则a的值是()A.10B.2C. D.【考点】正弦定理.【专题】解三角形.【分析】由条件利用同角三角函数的基本关系求得sinA=,再由正弦定理求得a的值.【解答】解:∵在△ABC中,b=5,∠B=,tanA==2,sin2A+cos2A=1,∴sinA=.再由余弦定理可得=,解得a=2,故选B.【点评】本题主要考查同角三角函数的基本关系、正弦定理的应用,属于中档题.5.如果执行如图所示的程序框图,那么输出的S=()A.190 B.94 C.46 D.22【考点】循环结构;程序框图.【专题】算法和程序框图.【分析】根据框图的流程依次计算运行的结果,直到满足条件i>5,退出循环体,计算输出S的值.【解答】解:由程序框图知:第一次运行i=2,S=2×(1+1)=4;第二次运行i=2+1=3,S=2×(4+1)=10;第三次运行i=3+1=4,S=2×(10+1)=22;第四次运行i=4+1=5,S=2×(22+1)=46;第五次运行i=5+1=6,S=2×(46+1)=94.满足条件i>5,退出循环体,输出S=94.故选:B.【点评】本题考查了循环结构的程序框图,根据框图的流程依次计算运行的结果是解答此类问题的常用方法.6.已知函数f(x)=a x+x﹣b的零点x0∈(n,n+1)(n∈Z),其中常数a,b满足0<b<1<a,则n的值为()A.2 B.1 C.﹣2 D.﹣l【考点】函数零点的判定定理.【专题】函数的性质及应用.【分析】根据指数函数,一次函数的单调性,及增+增=增,可得函数f(x)=a x+x﹣b为增函数,结合常数a,b满足0<b<1<a,可得f(﹣1)<0,f(0)>0,进而可得n值.【解答】解:∵函数f(x)=a x+x﹣b为增函数,常数a,b满足0<b<1<a,∴f(﹣1)=﹣1﹣b<0,f(0)=1﹣b>0,∴函数f(x)=a x+x﹣b在(﹣1,0)内有一个零点,故n=﹣1,故选:D【点评】本题主要考查了函数零点的判定定理以及指数与对数的互化,函数f(x)=a x+x﹣b是增函数,单调函数最多只有一个零点,是解题的关键,属中档题.7.图是函数y=Asin(ωx+φ)(x∈R)在区间上的图象,为了得到这个函数的图象,只要将y=sinx(x∈R)的图象上所有的点()A.向左平移个单位长度,再把所得各点的横坐标缩短到原来的倍,纵坐标不变B.向左平移个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变C.向左平移个单位长度,再把所得各点的横坐标缩短到原来的倍,纵坐标不变D.向左平移个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变【考点】由y=Asin(ωx+φ)的部分图象确定其解析式.【专题】综合题.【分析】先根据函数的周期和振幅确定w和A的值,再代入特殊点可确定φ的一个值,进而得到函数的解析式,再进行平移变换即可.【解答】解:由图象可知函数的周期为π,振幅为1,所以函数的表达式可以是y=sin(2x+φ).代入(﹣,0)可得φ的一个值为,故图象中函数的一个表达式是y=sin(2x+),即y=sin2(x+),所以只需将y=sinx(x∈R)的图象上所有的点向左平移个单位长度,再把所得各点的横坐标缩短到原来的倍,纵坐标不变.故选A.【点评】本题主要考查三角函数的图象与图象变换的基础知识,属于基础题题.根据图象求函数的表达式时,一般先求周期、振幅,最后求φ.三角函数图象进行平移变换时注意提取x的系数,进行周期变换时,需要将x的系数变为原来的8.已知,且函数y=f(x)﹣2x恰有3个不同的零点,则实数a 的取值范围是()A.[﹣4,0]B.[﹣8,+∞)C.[﹣4,+∞)D.(0,+∞)【考点】根的存在性及根的个数判断.【专题】计算题;压轴题;函数的性质及应用.【分析】当x≥0时,f(x)=f(x﹣2),可得当x≥0时,f(x)在[﹣2,0)重复的周期函数,根据x∈[﹣2,0)时,y=a﹣x2﹣4x=4+a﹣(x+2)2,对称轴x=﹣2,顶点(﹣2,4+a),进而可进行分类求实数a的取值范围.【解答】解:因为当x≥0的时候,f(x)=f(x﹣2),当x∈[0,2)时,x﹣2∈[﹣2,0),此时f(x)=f(x﹣2)=a﹣(x﹣2)2﹣4(x﹣2)当x∈[2,4)时,x﹣4∈[﹣2,0),此时f(x)=f(x﹣2)=f(x﹣4)=a﹣(x﹣4)2﹣4(x﹣4)依此类推,f(x)在x<0时为二次函数a﹣x2﹣4x=﹣(x+2)2+a+4,在x≥0上为周期为2的函数,重复部分为a﹣x2﹣4x=﹣(x+2)2+a+4在区间[﹣2,0)上的部分.二次函数a﹣x2﹣4x=﹣(x+2)2+a+4顶点为(﹣2,a+4),y=f(x)﹣2x恰有3个不同的零点,即f(x)与y=2x恰有3个不同的交点,需满足f(x)与y=2x在x<0时有两个交点且0≤a+4≤4或f(x)与y=2x在x<0时有两个交点且a+4>4∴﹣4≤a≤0或a>0综上可得a≥﹣4故选C【点评】本题重点考查函数的零点与方程根的关系,考查函数的周期性,有一定的难度.二、填空题(本大题共6个小题,每小题5分,共30分.把答案填在题中横线上.)9.若(1+2ai)i=1﹣bi,其中a、b∈R,i是虚数单位,则|a+bi|=.【考点】复数求模.【专题】数系的扩充和复数.【分析】由(1+2ai)i=1﹣bi化简求出a、b的值,然后由复数模的公式即可求出|a+bi|的值.【解答】解:由(1+2ai)i=1﹣bi,得﹣1﹣2a+(1+b)i=0.∴.解得:.设z=a+bi(a、b∈R),则z=﹣﹣i,∴|a+bi|=.故答案为:.【点评】本题考查了复数的基本概念,考查了复数模的求法,是基础的计算题.10.某高校甲、乙、丙、丁四个专业分别有150、150、400、300名学生,为了解学生的就业倾向,用分层抽样的方法从该校这四个专业共抽取40名学生进行调查,应在丙专业抽取的学生人数为16.【考点】分层抽样方法.【专题】概率与统计.【分析】根据四个专业各有的人数,得到本校的总人数,根据要抽取的人数,得到每个个体被抽到的概率,利用丙专业的人数乘以每个个体被抽到的概率,得到丙专业要抽取的人数.【解答】解:∵高校甲、乙、丙、丁四个专业分别有150、150、400、300名学生∴本校共有学生150+150+400+300=1000,∵用分层抽样的方法从该校这四个专业共抽取40名学生进行调查∴每个个体被抽到的概率是=,∵丙专业有400人,∴要抽取400×=16故答案为:16【点评】本题考查分层抽样方法,是一个基础题,解题的依据是在抽样过程中每个个体被抽到的概率是相等的,这种题目经常出现在高考卷中.11.已知双曲线=1(a>0,b>0)的一条渐近线方程是y=x,它的一个焦点与抛物线y2=16x的焦点相同.则双曲线的方程为=1.【考点】双曲线的标准方程.【专题】圆锥曲线的定义、性质与方程.【分析】先由双曲线的渐近线方程为y=±x,易得,再由抛物线y2=16x的焦点为(4,0)可得双曲线中c=4,最后根据双曲线的性质c2=a2+b2列方程组,解得a2、b2即可.【解答】解:由双曲线渐近线方程可知①因为抛物线的焦点为(4,0),所以c=4②又c2=a2+b2③联立①②③,解得a2=4,b2=12,所以双曲线的方程为.故答案为.【点评】本题主要考查双曲线和抛物线的标准方程及几何性质.12.如图,PA切⊙O于点A,割线PBC经过圆心O,OB=PB=1,OA绕点O逆时针旋转60°到OD,则PD的长为.【考点】与圆有关的比例线段.【专题】综合题;压轴题;综合法.【分析】解法一:如图根据题设条件可求得角DOP的大小,由于OD=1,OP=2,由余弦定理求长度即可.解法二:由图形知,若能求得点D到线段OC的距离DE与线段OE的长度,在直角三角形PED中用勾股定理求PD即可.【解答】解:法一:∵PA切⊙O于点A,B为PO中点,∴AB=OB=OA,∴∠AOB=60°,∴∠POD=120°,在△POD中由余弦定理,得:PD2=PO2+DO2﹣2PO•DOcos∠POD=.∴.法二:过点D作DE⊥PC垂足为E,∵∠POD=120°,∴∠DOC=60°,可得,,在Rt△PED中,有.【点评】本题考点是与圆有关的比例线段,本题考查求线段的长度,平面几何中求线段长度一般在三角形中用正弦定理与余弦定理求解,本题中法一的特征用的是余弦定理求长度,法二在直角三角形中用勾股定理求长度,在三角形中求长度时应该根据题意选取适当的方法求解,做题后要注意总结方法选取的规律.13.若实数a,b,c满足2a+2b=2a+b,2a+2b+2c=2a+b+c,则c的最大值是2﹣log23.【考点】基本不等式在最值问题中的应用.【专题】计算题;压轴题.【分析】由基本不等式得2a+2b≥,可求出2a+b的范围,再由2a+2b+2c=2a+b+c=2a+b2c=2a+b+2c,2c可用2a+b表达,利用不等式的性质求范围即可.【解答】解:由基本不等式得2a+2b≥,即2a+b≥,所以2a+b≥4,令t=2a+b,由2a+2b+2c=2a+b+c可得2a+b+2c=2a+b2c,所以2c=因为t≥4,所以,即,所以故答案为:2﹣log23【点评】本题考查指数的运算法则,基本不等式求最值、不等式的性质等问题,综合性较强.14.在平面四边形ABCD中,点E、F分别是边AD、BC的中点,且AB=1,EF=,CD=,若•=15,则•的值为13.【考点】平面向量数量积的运算.【专题】平面向量及应用.【分析】画出图形,结合图形,先求出•的值,再利用•=15,求出•的值.【解答】解:如图所示,设AB∩DC=O,∵=++=+,=++=+,两式相加得=;∵AB=1,EF=,CD=,平方得2=;∴•=2;又∵•=15,即(﹣)•(﹣)=15;∴•﹣•﹣•+•=15,∴•+•=15+•+•,∴•=(﹣)•(﹣)=•﹣•﹣•+•=(15+•+•)﹣•﹣•=15+•(﹣)+•(﹣)=15+•+•=15+•(﹣)=15+•=15﹣•=15﹣2=13.故答案为:13.【点评】本题考查了两个向量的加减运算的应用问题,也考查了平面向量的几何意义以及平面向量的数量积的应用问题,是中档题.三、解答题:(本大题6个题,共80分)15.某木器厂生产圆桌和衣柜两种产品,现有两种木料,第一种有72m3,第二种有56m3,假设生产每种产品都需要用两种木料,生产一只圆桌和一个衣柜分别所需木料如表所示.每生产一只圆桌可获利6元,生产一个衣柜可获利10元,木器厂在现有木料条件下,圆桌和衣柜各生产多少,才使获得利润最多,利润最多为多少?【考点】简单线性规划的应用.【专题】计算题;应用题;作图题;不等式的解法及应用.【分析】由题意,设生产圆桌x只,衣柜y个,获得利润为z元;从而可得,z=6x+10y;利用线性规划求解.【解答】解:由题意,设生产圆桌x只,衣柜y个,获得利润为z元;则,z=6x+10y;做其平面区域如下,则由y=800﹣2x,x=700﹣3.5y得,x=350,y=100;答:应生产圆桌350只,生产衣柜100个,能使利润总额达到最大,利润最多3100元.【点评】本题考查了线性规划在实际问题中的应用,属于中档题.16.已知函数f(x)=2sinωxcosωx﹣2sin2ωx+(ω>0),直线x=x1,x=x2是函数y=f(x)的图象的任意两条对称轴,且|x1﹣x2|的最小值为.(Ⅰ)求ω的值;(Ⅱ)求函数f(x)的单调增区间;(Ⅲ)若f(α)=,求sin(π﹣4α)的值.【考点】三角函数中的恒等变换应用;由y=Asin(ωx+φ)的部分图象确定其解析式;复合三角函数的单调性.【专题】计算题;三角函数的图像与性质.【分析】(I)利用二倍角公式即辅助角公式,化简函数,利用直线x=x1,x=x2是函数y=f(x)的图象的任意两条对称轴,且|x1﹣x2|的最小值为,可得函数的最小正周期为π,根据周期公式,可求ω的值;(II)利用正弦函数的单调性,可得函数f(x)的单调增区间;(III)由f(a)=,可得sin(2a+)=,根据sin(π﹣4a)=sin[﹣2(2a+)]=﹣cos[2(2a+)]=2sin2(2a+)﹣1,即可求得结论.【解答】解:(I)∵f(x)=2sinωxcosωx﹣2sin2ωx+=sin2ωx+cos2ωx=2sin(2ωx+)∵直线x=x1,x=x2是函数y=f(x)的图象的任意两条对称轴,且|x1﹣x2|的最小值为,∴函数的最小正周期为π∴=π∴ω=1;(II)由(I)知,f(x)=2sin(2x+)∴﹣+2kπ≤2x+≤+2kπ,k∈Z∴﹣+kπ≤x≤+kπ,k∈Z∴函数f(x)的单调增区间为[﹣+kπ,+kπ],k∈Z;(III)∵f(a)=,∴sin(2a+)=∴sin(π﹣4a)=sin[﹣2(2a+)]=﹣cos[2(2a+)]=2sin2(2a+)﹣1=﹣.【点评】本题考查函数的周期性,考查函数解析式的确定,考查函数的单调性,考查学生的计算能力,周期确定函数解析式是关键.17.如图,在四棱锥P﹣ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,E为AD的中点,M是棱PC的中点,PA=PD=2,,.(1)求证:PE⊥平面ABCD;(2)求直线BM与平面ABCD所成角的正切值;(3)求直线BM与CD所成角的余弦值.【考点】直线与平面所成的角;异面直线及其所成的角;直线与平面垂直的判定.【专题】证明题;转化思想;综合法;空间角.【分析】(1)推导出PE⊥AD,平面PAD⊥平面ABCD,由此能证明PE⊥平面ABCD.(2)连结EC,取EC中点H,连结MH、HB,则MH∥PE,从而∠MBH即为BM与平面ABCD 所成角,由此能求出直线BM与平面ABCD所成角的正切值.(3)由CD∥BE,得直线BM与CD所成角即为直线BM与BE所成角,由此能求出直线BM与CD 所成角的余弦值.【解答】证明:(1)∵PA=PD,E为AD的中点,∴PE⊥AD,又∵平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD,∴PE⊥平面ABCD.解:(2)连结EC,取EC中点H,连结MH、HB,∵M是PC的中点,H是EC的中点,∴MH∥PE,由(1)知PE⊥平面ABCD,∴MH⊥平面ABCD,∴HB是BM在平面ABCD内的射影,∴∠MBH即为BM与平面ABCD所成角,∵AD∥BC,BC=AD,E为AD的中点,∠ADC=90°,∴四边形BCDE为矩形,∴EC=2,HB=,又∵MH=PE=,∴△MHB中,tan=,∴直线BM与平面ABCD所成角的正切值为.(3)由(2)知CD∥BE,∴直线BM与CD所成角即为直线BM与BE所成角连接ME,Rt△MHE中,,Rt△MHB中,,又,∴△MEB中,,∴直线BM与CD所成角的余弦值为.【点评】本题考查线面垂直的证明,考查线面角的正弦值和线线角的余弦值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.18.已知椭圆C:的离心率为,椭圆短轴的一个端点与两个焦点构成的三角形的面积为.(1)求椭圆C的方程;(2)已知动直线y=k(x+1)与椭圆C相交于A、B两点.①若线段AB中点的横坐标为,求斜率k的值;②已知点,求证:为定值.【考点】直线与圆锥曲线的综合问题;椭圆的标准方程.【专题】综合题;压轴题.【分析】(1)根据椭圆的离心率,三角形的面积及椭圆几何量之间的关系,建立等式,即可求得椭圆的标准方程;(2)①直线方程代入椭圆方程,利用韦达定理及线段AB中点的横坐标为,即可求斜率k的值;②利用韦达定理,及向量的数量积公式,计算即可证得结论.【解答】(1)解:因为满足a2=b2+c2,,…根据椭圆短轴的一个端点与两个焦点构成的三角形的面积为,可得.从而可解得,所以椭圆方程为…(2)证明:①将y=k(x+1)代入中,消元得(1+3k2)x2+6k2x+3k2﹣5=0…△=36k4﹣4(3k2+1)(3k2﹣5)=48k2+20>0,…因为AB中点的横坐标为,所以,解得…②由①知,所以…==…===…【点评】本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查向量的数量积,考查学生的运算能力,综合性强.19.已知函数f(x)=,数列{a n}满足a1=1,a n+1=f(),n∈N*,(1)求数列{a n}的通项公式;(2)令T n=a1a2﹣a2a3+a3a4﹣a4a5+…﹣a2n a2n+1,求T n;(3)令b n= (n≥2),b1=3,S n=b1+b2+…+b n,若S n<对一切n∈N*成立,求最小正整数m.【考点】数列的求和;数列递推式;数列与不等式的综合.【专题】计算题;转化思想;综合法;等差数列与等比数列.【分析】(1)通过代入函数解析式化简可知a n+1=a n+,进而计算可得结论;(2)通过(1)可知T n=a1a2﹣a2a3+a3a4﹣a4a5+…﹣a2n a2n+1=a2(a1﹣a3)+a4(a3﹣a5)+…+a2n(a2n﹣1﹣a2n+1),进而计算可得结论;(3)当n≥2时裂项可知b n=(﹣),进而并项相加可知S n=,从而可知<,进而问题转化为解不等式≥,计算即得结论.【解答】解:(1)依题意,a n+1==a n+,∴数列{a n}是以为公差的等差数列,又∵a1=1,∴a n=n+;(2)由(1)可知T n=a1a2﹣a2a3+a3a4﹣a4a5+…﹣a2n a2n+1=a2(a1﹣a3)+a4(a3﹣a5)+…+a2n(a2n﹣a2n+1)﹣1=﹣(a2+a4+…+a2n)=﹣•=﹣(2n2+3n);(3)当n≥2时,b n===(﹣),又∵b1=3=×(1﹣)满足上式,∴S n=b1+b2+…+b n=×(1﹣+﹣+…+﹣)=(1﹣)=,∵S n<对一切n∈N*成立,即<,又∵=(1﹣)递增,且<,∴≥,即m≥2016,∴最小正整数m=2016.【点评】本题考查数列的通项及前n项和,考查运算求解能力,考查裂项相消法,注意解题方法的积累,属于中档题.20.已知函数f(x)=lnx﹣ax2﹣bx.(I)当a=﹣1时,若函数f(x)在其定义域内是增函数,求b的取值范围;(Ⅱ)若f(x)的图象与x轴交于A(x1,0),B(x2,0)(x1<x2)两点,且AB的中点为C(x0,0),求证:f′(x0)<0.【考点】函数的单调性与导数的关系;导数在最大值、最小值问题中的应用.【专题】计算题;综合题;转化思想.【分析】(I)将f(x)在(0,+∞)上递增,转化成f′(x)≥0对x∈(0,+∞)恒成立,即b≤+2x 对x∈(0,+∞)恒成立,只需b≤即可,根据基本不等式可求出;(II)根据f(x)的图象与x轴交于A(x1,0),B(x2,0)(x1<x2)两点,得到,两式相减,可得,利用中点坐标公式和导数,即可证明结论.【解答】解:(Ⅰ)依题意:f(x)=lnx+x2﹣bx∵f(x)在(0,+∞)上递增,∴f′(x)=+2x﹣b≥0对x∈(0,+∞)恒成立即b≤+2x对x∈(0,+∞)恒成立,∴只需b≤∵x>0,∴+2x≥2当且仅当x=时取“=”,∴b≤2,∴b的取值范围为(﹣∞,2];(II)证明:由已知得,即,两式相减,得:⇒,由f′(x)=﹣2ax﹣b及2x0=x1+x2,得f′(x0)=﹣2ax0﹣b===,令t=∈(0,1),且φ(t)=,∵φ′(t)=,∴φ(t)是(0,1)上的减函数,∴φ(t)>φ(1)=0,又x1<x2,∴f'(x0)<0.【点评】本题主要考查导函数的正负与原函数的单调性之间的关系,即当导函数大于0时原函数单调递增,当导函数小于0时原函数单调递减,同时考查了转化与划归的思想,分析问题解决问题的能力,属于中档题.。
天津市河东区高考数学一模试卷(文科)

高考数学一模试卷(文科)一、选择题(本大题共8小题,共24.0分)1.已知i是虚数单位,x∈R,复数z=(x+i)(2+i)为纯虚数,则2x-i的模等于()A. 1B.C.D. 22.已知x,y满足不等式组,则z=x+3y的最小值等于()A. 3B. 6C. 9D. 123.若某程序框图如图所示,则输出的n的值是()A. 3B. 4C. 5D. 64.设x∈R,则“1<x<2”是“|x﹣2|<1”的()A. 充分而不必要条件B. 必要而不充分条件C. 充要条件D. 既不充分也不必要条件5.已知偶函数f(x)在[0,2]上递减,试比a=f(1),b=f(),c=f(log2)大小()A. a>b>cB. a>c>bC. b>a>cD. c>a>b6.为了得到函数y=3cos2x图象,只需把函数图象上所有点()A. 向右平行移动个单位长度B. 向右平行移动个单位长度C. 向左平行移动个单位长度D. 向左平行移动个单位长度7.已知F1、F2分别是双曲线-=1(a>0,b>0)的左、右焦点,过点F2与双曲线的一条渐近线平行的直线交双曲线另一条渐近线于点M,若点M在以线段F1F2为直径的圆外,则双曲线离心率的取值范围是()A. (1,)B. (,+∞)C. (,2)D. (2,+∞)8.定义域为R的函数f(x)满足f(x+2)=2f(x),当x∈[0,2)时,f(x)=,若当x∈[-4,-2)时,不等式f(x)≥恒成立,则实数t的取值范围是()A. [2,3]B. [1,3]C. [1,4]D. [2,4]二、填空题(本大题共6小题,共18.0分)9.集合A={0,1,2,3},B={x|x2-2x≤0},则A∩B=______.10.已知函数f(x)的导函数,满足f(x)=2xf'(1)+x3,则f'(1)等于______.11.如图,圆柱内有一个直三棱柱,三棱柱的底面在圆柱底面内,且底面是正三角形.如果三棱柱的体积为,圆柱的底面直径与母线长相等,则圆柱的侧面积为______.12.已知直线y=mx与圆C:(x-m)2+(y-1)2=m2-1交于A,B两点,∠ACB=60°,则圆的面积为______.13.如图,在平行四边形ABCD中,已知AB=8,AD=5,=3,=2,则的值是______.14.若实数x,y满足2cos2(x+y-1)=,则xy的最小值为______.三、解答题(本大题共6小题,共72.0分)15.在△ABC中,角A,B,C所对的边分别为a,b,c,f(x)=2sin(x-A)cos x+sin(B+C)(x∈R),函数f(x)的图象关于点(,0)对称.(Ⅰ)当x∈(0,)时,求f(x)的值域;(Ⅱ)若a=7且sin B+sin C=,求△ABC的面积.16.某校从高一年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40的整数)分成六段:[40,50),[50,60),…,[90,100]后得到如图的频率分布直方图.(1)求图中实数a的值;(2)若该校高一年级共有学生640人,试估计该校高一年级期中考试数学成绩不低于60分的人数;(3)若从数学成绩在[40,50)与[90,100]两个分数段内的学生中随机选取两名学生,①列出所有可能的结果;②求这两名学生的数学成绩之差的绝对值不大于10的概率.17.如图,四棱柱ABCD-A1B1C1D1的底面ABCD为正方形,CC1⊥平面ABCD.(1)求证:BD⊥平面ACC1A1;(2)若二面角C1-BD-C的大小为60°,求异面直线BC1与AC所成角的余弦值.18.在等差数列{a n}中,已知公差d=2,a2是a1与a4的等比中项.(Ⅰ)求数列{a n}的通项公式;(Ⅱ)若数列{b n}满足:,求数列{b n}的通项公式;(Ⅲ)令(n∈N*),求数列{c n}的前n项和T n.19.已知椭圆C:+=1(a>b>0)的短轴的一个顶点与两个焦点构成正三角形,且该三角形的面积为.(1)求椭圆C的方程;(2)设F1,F2是椭圆C的左右焦点,若椭圆C的一个内接平行四边形的一组对边过点F1和F2,求这个平行四边形的面积最大值.20.已知f(x)=mx-a ln x-m,g(x)=,其中m,a均为实数,(1)求g(x)的极值;(2)设m=1,a=0,求证对|恒成立;(3)设a=2,若对∀给定的x0∈(0,e],在区间(0,e]上总存在t1,t2(t1≠t2)使得f(t1)=f(t2)=g(x0)成立,求m的取值范围.答案和解析1.【答案】B【解析】解:∵z=(x+i)(2+i)=(2x-1)+(x+2)i为纯虚数,∴,即x=.∴2x-i=1-i,则2x-i的模等于.故选:B.利用复数代数形式的乘除运算化简,由实部为0且虚部不为0求得x,代入2x-i,再由复数模的计算公式求解.本题考查复数代数形式的乘除运算,考查复数的基本概念,考查复数模的求法,是基础题.2.【答案】A【解析】解:画出满足条件的平面区域,如图示:,由z=x+3y得:y=-x+,显然直线过(3,0)时,z最小,z的最小值是3,故选:A.画出满足条件的平面区域,将直线变形为y=-x+,通过图象读出即可.本题考察了简单的线性规划问题,考察数形结合思想,是一道基础题.3.【答案】C【解析】解:由程序框图知:算法的功能是求满足P=1+3+…+(2n-1)>20的最小n 值,∵P=1+3+…+(2n-1)=×n=n2>20,∴n≥5,故输出的n=5.故选:C.算法的功能是求满足P=1+3+…+(2n-1)>20的最小n值,利用等差数列的前n项和公式求得P,根据P>20,确定最小的n值.本题考查了循环结构的程序框图,根据框图的流程判断算法的功能是关键.4.【答案】A【解析】【分析】本题考查了简单的不等式的求解,充分必要条件的定义,属于容易题.求解:|x-2|<1,得出“1<x<2”,根据充分必要条件的定义判断即可.【解答】解:∵|x-2|<1,∴1<x<3,∵“1<x<2”∴根据充分必要条件的定义可得出:“1<x<2”是“|x-2|<1”的充分不必要条件.故选A.5.【答案】D【解析】解:∵,∴∵f(x)在[0,2]上递减,∴f()>f(1)>f(2)又∵f(x)是偶函数,f()=f(-)=∴>f(1)>,即c>a>b故选:D.由对数的定义,可得b=f(2),c=f(-)=f().再结合函数函数f(x)在[0,2]上递减,即可得到a、b、c的大小关系.本题给出偶函数在[0,2]上递减,要求我们比较三个函数值的大小,考查了函数奇偶性与单调性和对数的运算性质等知识,属于基础题.6.【答案】D【解析】解:把函数图象上所有点向左平行移动个单位长度,可得函数y=3cos2x=3sin(2x+)图象,故选:D.由题意利用诱导公式,函数y=A sin(ωx+φ)的图象变换规律,得出结论.本题主要考查诱导公式的应用,函数y=A sin(ωx+φ)的图象变换规律,统一这两个三角函数的名称,是解题的关键,属于基础题.7.【答案】D【解析】解:双曲线-=1的渐近线方程为y=±x,不妨设过点F2与双曲线的一条渐过线平行的直线方程为y=(x-c),与y=-x联立,可得交点M(,-),∵点M在以线段F1F2为直径的圆外,∴|OM|>|OF2|,即有>c2,∴b2>3a2,∴c2-a2>3a2,即c>2a.则e=>2.∴双曲线离心率的取值范围是(2,+∞).故选:D.根据斜率与平行的关系即可得出过焦点F2的直线,与另一条渐近线联立即可得到交点M的坐标,再利用点M在以线段F1F2为直径的圆外和离心率的计算公式即可得出.本题考查的知识点是双曲线的简单性质,熟练掌握双曲线的渐近线、离心率的计算公式、点与圆的位置关系是解题的关键.8.【答案】B【解析】解:当x∈[0,1)时,f(x)=x2-x∈[-,0],当x∈[1,2)时,f(x)=-(0.5)|x-1.5|∈[-1,],∴当x∈[0,2)时,f(x)的最小值为-1,又∵函数f(x)满足f(x+2)=2f(x),当x∈[-2,0)时,f(x)的最小值为-,当x∈[-4,-2)时,f(x)的最小值为-,若x∈[-4,-2]时,f(x)≥-t+恒成立,∴≥-t+恒成立.即t2-4t+3≤0,即(t-3)(t-1)≤0,即1≤t≤3,即t∈[1,3],故选:B.根据条件,只要求出函数f(x)在x∈[-4,-2)上的最小值即可得到结论.本题考查的知识点是函数恒成立问题,函数的最值,一元二次不等式的解法,难度较大.9.【答案】{0,1,2}【解析】解:∵集合A={0,1,2,3},B={x|x2-2x≤0}={x|0≤x≤2},∴A∩B={0,1,2}.故答案为:{0,1,2}.先分别求出集合A和B,由此能求出A∩B.本题考查交集的求法,考查交集定义、不等式性质等基础知识,考查运算求解能力,是基础题.10.【答案】-3【解析】解:∵f(x)=2xf′(1)+x3,∴f′(x)=2f′(1)+3x2,令x=1,则f′(1)=2f′(1)+3×12=2f′(1)+3,即f′(1)=-3.故答案为:-3求函数的导数,让x=1,建立关于f′(1)的方程,即可求解.本题主要考查导数的计算和求值,利用f′(1)为常数,建立关于f′(1)的方程是解决本题的关键,比较基础.11.【答案】16π【解析】解:设圆柱的底面半径为r,则其高为2r.三棱柱的底面是正三角形,内接于圆,如图:连接OA,OB,过O作OD垂直于AB,垂足为D,因为三角形ABC为等边三角形,所以∠OAB=30°,在直角三角形中,AD=OA×cos30°=,∴AB=r,∴三棱柱的体积为=12.解得r=2,所以圆柱的侧面积为:2πr×2r=2π×2×4=16π.故填:16π.根据已知条件求出底面半径,同时得到圆柱的母线长,进而得到圆柱的侧面积.本题考察圆柱侧面积的简单计算,属于基础题.12.【答案】6π【解析】解:根据题意,圆C:(x-m)2+(y-1)2=m2-1,则其圆心为(m,1),半径为,直线y=mx与圆C交于A,B两点,且∠ACB=60°,则△ABC为等边三角形,则圆心到直线y=mx的距离d=r,即=×,解可得:m2=7,则圆的半径r==,则圆的面积S=πr2=6π;故答案为:6π.根据题意,分析圆C的圆心与半径,结合直线与圆的位置关系可得圆心到直线y=mx的距离d=r,进而可得=×,解可得m的值,由圆的面积公式计算可得答案.本题考查直线与圆的位置关系,注意分析弦长与圆心到直线的距离,半径的关系,属于基础题.13.【答案】22【解析】【分析】本题考查向量在几何中的应用,平面向量数量积的运算,属于中档题.由=3,可得=+,=-,进而由AB=8,AD=5,=3,•=2,构造方程,进而可得答案.【解答】解:∵=3,∴=+=+,=-,又∵AB=8,AD=5,∴=(+)(-)=||2--||2=25--12=2,故•=22,故答案为22.14.【答案】【解析】解:∵,∴2cos2(x+y-1)=∴2cos2(x+y-1)=,故2cos2(x+y-1)==(x-y+1)+,由基本不等式可得(x-y+1)+≥2,或(x-y+1)+≤-2,∴2cos2(x+y-1)≥2,由三角函数的有界性可得2cos2(x+y-1)=2,故cos2(x+y-1)=1,即cos(x+y-1)=±1,此时x-y+1=1,即x=y∴x+y-1=kπ,k∈Z,故x+y=2x=kπ+1,解得x=,故xy=x•x=,当k=0时,xy的最小值,故答案为:配方可得2cos2(x+y-1)==(x-y+1)+,由基本不等式可得(x+y+1)+≤2,或(x-y+1)+≤-2,进而可得cos(x+y-1)=±1,x=y=,由此可得xy的表达式,取k=0可得最值.本题考查基本不等式在最值问题中的应用,余弦函数的单调性,得出cos(x+y-1)=±1是解决问题的关键,属中档题.15.【答案】解:(Ⅰ)f(x)=2sin(x-A)cos x+sin(B+C)=2(sin x cos A-cos x sin A)cos x+sin A=2sin x cosxcos A-2cos2x sin A+sin A=sin2x cos A-cos2x sin A=sin(2x-A),由于函数f(x)的图象关于点(,0)对称,则f()=0,即有sin(-A)=0,由0<A<π,则A=,则f(x)=sin(2x-),由于x∈(0,),则2x-∈(-,),即有-<sin(2x-)≤1.则值域为(-,1];(Ⅱ)由正弦定理可得===,则sin B=b,sin C=c,sin B+sin C=(b+c)=,即b+c=13,由余弦定理可得a2=b2+c2-2bc cos A,即49=b2+c2-bc=(b+c)2-3bc,即有bc=40,则△ABC的面积为S=bc sin A=×40×=10.【解析】(Ⅰ)运用两角差的正弦公式和诱导公式,结合二倍角公式,化简f(x),再由对称性,计算可得A,再由x的范围,结合正弦函数的图象和性质,即可得到值域;(Ⅱ)运用正弦定理和余弦定理,可得bc=40,再由面积公式即可计算得到.本题重点考查正弦定理和余弦定理以及面积公式的运用,考查两角和差的正弦公式和二倍角公式的运用,考查正弦函数的图象和性质,考查运算能力,属于中档题.16.【答案】解:(1)由频率分布直方图得:(0.010+0.015+0.015+a+0.025+0.005)×10=1,解得a=0.03.(2)由频率分布直方图得不低于60分的学生的频率为:1-(0.010+0.015)×10=0.75,∴估计该校高一年级期中考试数学成绩不低于60分的人数为:0.75×640=480.(3)①数学成绩在[40,50)的学生人数为:0.010×10×40=4人,设为A,B,C,D,数学成绩在[90,100]的学生人数为:0.005×10×40=2人,设为a,b,数学成绩在[40,50)与[90,100]两个分数段内的学生中随机选取两名学生,所有可能的结果有15种,分别为:(A,B),(A,C),(A,D),(A,a),(A,b),(B,C),(B,D),(B,a),(B,b),(C,D),(C,a),(C,b),(D,a),(D,b),(a,b).②这两名学生的数学成绩之差的绝对值不大于10包含的基本事件有7种,分别为:(A,B),(A,C),(A,D),(B,C),(B,D),(C,D),(a,b)∴这两名学生的数学成绩之差的绝对值不大于10的概率p=.【解析】本题考查实数值、频数、概率的求法,考查频率分布直方图、概率、列举法,考查运算求解能力,属于中档题.(1)由频率分布直方图能求出a.(2)由频率分布直方图得不低于60分的学生的频率为0.75,由此能估计该校高一年级期中考试数学成绩不低于60分的人数.(3)①数学成绩在[40,50)的学生人数为4人,设为A,B,C,D,数学成绩在[90,100]的学生人数为2人,设为a,b,数学成绩在[40,50)与[90,100]两个分数段内的学生中随机选取两名学生,利用列举法能求出所有可能的结果.②这两名学生的数学成绩之差的绝对值不大于10包含的基本事件有7种,这两名学生的数学成绩之差的绝对值不大于10的概率.17.【答案】证明:(1)∵四棱柱ABCD-A1B1C1D1的底面ABCD为正方形,∴AC⊥BD,∵CC1⊥平面ABCD,∴CC1⊥BD,∵AC∩CC1=C,∴BD⊥平面ACC1A1.解:(2)以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,设AB=BC=1,AA1=t,则D(0,0,0),B(1,1,0),C1(0,1,t),C(0,1,0),=(1,1,0),=(0,1,t),=(0,1,0),设平面DBC1的法向量=(x,y,z),则,取x=1,得=(1,-1,),平面BDC的法向量=(0,0,1),∵二面角C1-BD-C的大小为60°,∴cos60°==,解得t=,∴B(1,1,0),C1(0,1,),A(1,0,0),C(0,1,0),=(-1,0,),=(-1,1,0),设异面直线BC1与AC所成角为θ,则cosθ===.∴异面直线BC1与AC所成角的余弦值为.【解析】(1)推导出AC⊥BD,CC1⊥BD,由此能证明BD⊥平面ACC1A1.(2)以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,利用向量法能求出异面直线BC1与AC所成角的余弦值.本题考查线面垂直的证明,考查异面直线所成角的余弦值的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,是中档题.18.【答案】解:(Ⅰ)等差数列{a n}的公差d=2,a2是a1与a4的等比中项,可得a22=a1a4,即(a1+2)2=a1(a1+6),解得a1=2,则a n=a1+(n-1)d=2+2(n-1)=2n;(Ⅱ)数列{b n}满足:,可得a1=,即b1=8;n≥2时,a n-1=++…+,与,相减可得2=,即有b n=2(3n+1),上式对n=1也成立,可得b n=2(3n+1),n∈N*;(Ⅲ)=n(3n+1),则前n项和T n=(1•3+2•32+…+n•3n)+(1+2+…+n),设S n=1•3+2•32+…+n•3n,3S n=1•32+2•33+…+n•3n+1,相减可得-2S n=3+32+…+3n-n•3n+1=-n•3n+1,化简可得S n=,则T n=+n(n+1).【解析】(Ⅰ)运用等差数列{a n}的通项公式和等比数列中项性质,解方程可得首项,可得所求通项公式;(Ⅱ)令n=1可得数列b1,n≥2时,将n换为n-1,作差可得所求通项公式;(Ⅲ)求得=n(3n+1),运用数列的分组求和和错位相减法,结合等差数列和等比数列的求和公式,即可得到所求和.本题考查等差数列和等比数列的通项公式和求和公式的运用,考查数列的求和方法:分组求和和错位相减法,考查化简整理的运算能力,属于中档题.19.【答案】20.(本小题满分12分)解:(1)∵椭圆C:+=1(a>b>0)的短轴的一个顶点与两个焦点构成正三角形,且该三角形的面积为,∴依题意,解得a=2,b=,c=1,∴椭圆C的方程为:.…(5分)(2)设过椭圆右焦点F2的直线l:x=ty+1与椭圆交于A,B两点,则,整理,得:(3t2+4)y2+6ty-9=0,由韦达定理,得:,,∴|y1-y2|===,∴==,椭圆C的内接平行四边形面积为S=4S△OAB=,令m=≥1,则S=f(m)==,注意到S=f(m)在[1,+∞)上单调递减,∴S max=f(1)=6,当且仅当m=1,即t=0时等号成立.故这个平行四边形面积的最大值为6.…(12分)【解析】(1)由椭圆的短轴的一个顶点与两个焦点构成正三角形,且该三角形的面积为,列出方程组,求出a,b,由此能求出椭圆C的方程.(2)设过椭圆右焦点F2的直线l:x=ty+1与椭圆交于A,B两点,由,得:(3t2+4)y2+6ty-9=0,由此利用韦达定理、弦长公式、平行四边形面积、函数单调性,能求出平行四边形面积的最大值.本题考查椭圆方程的求法,考查平行四边形的面积的最大值的求法,是中档题,解题时要认真审题,注意椭圆性质、韦达定理、弦长公式、平行四边形面积、函数单调性的合理运用.20.【答案】解:(1)∵,∴,∴(-∞,1)↑,(1,+∞)↓,∴g(x)极大值g(1)=1,无极小值;…(4分)(2)∵m=1,a=0,∴f(x)=x-1,在[3,4]上是增函数∴,在[3,4]上是增函数设3≤x1<x2≤4,则原不等式转化为即…(6分)令,即证∀x1<x2,h(x2)<h(x1),即h(x)在[3,4]↓∵h′(x)=1-e x<0在[3,4]恒成立即h(x)在[3,4]↓,即所证不等式成立.…(9分)(3)由(1)得g(x)在(0,1)↑(1,e)↓,g(x)max=g(1)=1所以,g(x)∈(0,1]又不符合题意当m>0时,要∃t1,t2使得f(t1)=f(t2),那么由题意知f(x)的极值点必在区间(0,e)内,即得,且函数f(x)在由题意得g(x)在(0,e)上的值域包含于f(x)在上的值域,∴内,,下面证时,f(t)≥1,取t=e-m,先证.令w(x)=2e x-x,∴内恒成立,∴w(x)↑,∴,∴2e m-m>0,再证f(e-m)≥1,∵,∴.…(14分)【解析】(1)求出函数的导数,利用导函数的符号判断函数的单调性,然后求解极值.(2)通过m=1,a=0,化简f(x)=x-1,利用函数的单调性,转化原不等式转化,构造函数,利用新函数的导数的单调性,证不等式成立.(3)由(1)得g(x)的最大值,求出函数f(x)的导数,判断m≤0,不满足题意;当m>0时,要∃t1,t2使得f(t1)=f(t2),f(x)的极值点必在区间(0,e)内,求出m的范围,当,利用g(x)在(0,e)上的值域包含于f(x)在上的值域,推出关系式,通过构造函数w(x)=2e x-x,通过导数求解函数的最值,然后推出.本题考查函数的导数的综合应用,函数的极值以及函数的单调性的判断与应用,新函数以及构造法的应用,考查综合分析问题解决问题的能力.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
河 东 区 2018 年 高 考 一 模 考 试数学试卷(文史类)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试用时120分钟.第Ⅰ卷1至2页,第Ⅱ卷3至6页.答题前,考生务必将自己的姓名、准考证号涂写在答题卡上,并在规定位置粘贴考试用条形码。
答卷时,考生务必将答案涂写在答题卡上,答在试卷上的无效。
考试结束后,将本试卷和答题卡一并交回。
祝各位考生考试顺利!第Ⅰ卷(选择题 共40分)注意事项:1. 每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
2.本题共8个小题,每小题5分,共40分.每小题给出的四个选项只有一个符合题目要求.1.复数2()2iz i i-=+为虚数单位在复平面内对应的点所在象限为( )A .第一象限B .第二象限C .第三象限D .第四象限2.已知变量x y ,满足约束条件21110x y x y y ,,.⎧+≥⎪-≤⎨⎪-≤⎩则2z x y =-的最大值为( ) A . -3 B . 0 C .1 D .3 3.某程序框图如图1所示,则输出的结果S =( )A .26B .57C .120D .2474.函数()|2|ln f x x x=--在定义域内的零点的个数为( )A .0B .1C .2D .35.下列说法正确的是个数为( )① 1=a 是直线0=-ay x 与直线0=+ay x 互相垂直的充要条件② 直线12π=x 是函数)62sin(2π-=x y 的图象的一条对称轴密封装 订 线密 封 线 内 不 要 答 题学校 班级 姓③ 已知直线l :20x y ++=与圆C :22(1)(1)2x y -++=,则圆心C 到直线l的距离是④若命题P :“存在∈0x R ,0102>--x x”,则命题P的否定:“任意R x ∈,012≤--x x”A .1B .2C .3D .46.已知双曲线22221x y a b-=的渐近线方程为y =,则以它的顶点为焦点,焦点为顶点的椭圆的离心率等于( ) A .12B.2CD .17.在R 上定义运算).1(:y x y x -=⊗⊗若对任意2x >,不等式()2x a xa -⊗≤+都成立,则实数a 的取值范围是( ) A .17,⎡⎤-⎣⎦B .(3,⎤-∞⎦C .(7,⎤-∞⎦D .()17,,⎤⎡-∞-+∞⎦⎣8.若直角坐标系内A 、B 两点满足:(1)点A 、B 都在f (x )的图像上;(2)点A 、B 关于原点对称,则称点对(A ,B )是函数f (x )的一个“姊妹点对”(点对(A ,B )与(B ,A )可看作一个“姊妹点对”。
已知函数f (x )=22(0)2(0)x x x x x e⎧+<⎪⎨≥⎪⎩,则f (x )的“姊妹点对”有( )A .1个B .2个C .3个D .4个河 东 区 2018 年 高 考 一 模 考 试数学试卷(文史类) 第Ⅱ卷(非选择题 共110分)二、填空题(本大题共6个小题,每小题5分,共30分.把答案填在答题卡横线上.)9.一支田径队有男运动员 56 人,女运动员 42 人,若用分层抽样的方法从全体运动员中抽出一个容量为 28 的样本,则样本中女运动员的人数为 人.10.某几何体的三视图如图所示,则该几何体的体积为 .11.如右图3,AB 是圆O 的直径,直线CE 和圆O 相切于点C ,AD CE ⊥于D ,若AD=1,30ABC ∠=,则圆O 的面积是 .12.函数()101xy a a a -=>≠,的图象恒过定点A ,若点A 在直线()100mx ny mn +-=>上,则11mn+的最小值为 .13.已知()f x 是定义在R 上的奇函数,当0x ≥时,2()2f x x x=+,若2(2)()f a f a ->,则实数a 的取值范围是 14.在ABC ∆中,0120=∠BAC ,2=AB ,1=AC ,D 是边BC 上一点,BD DC 2=,则=⋅ . 三、解答题:(本大题6个题,共80分) 15. (本小题满分13分)袋中有五张卡片,其中红色卡片三张,标号分别为1,2,3;蓝色卡片两张,标号分别为1,2.(1)从以上五张卡片中任取两张,求这两张卡片颜色不同且标号之和小于4的概率;(2)现袋中再放入一张标号为0的绿色卡片,从这六张卡片中任取两张,求这两张卡片颜色不同且标号之和小于4的概率.16. (本小题满分13分)已知函数x x x x x f cos sin 2)sin (cos 3)(22+-=.(1)求()f x 的最小正周期;(2)设[,]33x ππ∈-,求()f x 的值域和单调递减区间.图317. (本小题满分13分)如图, 在直三棱柱ABC-A1B1C1中,AC=3,BC=4,5=AB,AA1=4,点D是AB的中点.(1)求证:AC⊥BC1;(2)求证:AC 1//平面CDB1;(3)求二面角B-CD-B1 正切值的大小。
18.(本小题满分13分)已知各项均为正数的数列{a n}的前n项的和为S n,且对任意的n∈N*,都有2S n=2na+a n(1)求数列{a n}的通项公式;(2)数列{b n}满足b1=1,2b n+1-b n=0,(n∈N*).若c n=a n b n,求数列{c n}的前n项和T n19. (本小题满分14分)已知函数).(111)(Raxaaxnxxf∈--+-=(1)当处的切线方程;,在点(时,求曲线))2(2)(1fxfya=-=(2)当12a≤时,讨论()f x的单调性.20. (本小题满分14分)设21FF,分别是椭圆22221(0)x ya ba b+=>>的左、右焦点,P为椭圆上的任意一点,满足821=+PFPF,21FPF∆的周长为12.密封装订线密封线内不要答题(1)求椭圆的方程;(2)求21PF PF ⋅的最大值和最小值;(3)已知点()08,A ,()02,B ,是否存在过点A 的直线l 与椭圆交于不同的两点D C ,,使得BD BC =?若存在,求直线l 的方程;若不存在,请说明理由.河东区2014年高考一模试卷 数 学 答 案(文史类)一、选择题:本题共8个小题,每小题5分,共40分。
每小题给出的四个选项只有一个符合题目要求。
二、填空题:每小题5分,共30分.9. 12 ,10.108+3π,11. 4π ,12. 4 ,13. —2<a<1 ,14.83-三、解答题:本大题6个题,共80分15.解 (1)从五张卡片中任取两张的所有可能情况有如下10种:红1红2,红1红3,红1蓝1, 红1蓝2,红2红3,红2蓝1,红2蓝2,红3蓝1,红3蓝2,蓝1蓝2.其中两张卡片的颜色不同且标号之和小于4的有3种情况,故所求的概率为310P =.(2)加入一张标号为0的绿色卡片后,从六张卡片中任取两张,除上面的10种情况外,多出5种情况:红1绿0,红2绿0,红3绿0,蓝1绿0,蓝2绿0,即共有15种情况,其中颜色不同且标号之和小于4的有8种情况,所以概率为815P =.16. 解:(1)∵()sin 2f x x x =2sin(2)3x π=+ )(x f ∴的最小正周期为π. (2)∵[,]33x ππ∈-, 233x πππ∴-≤+≤,1)32sin(23≤+≤-∴πx . )(x f ∴的值域为[.()f x 的递减区间为⎥⎦⎤⎢⎣⎡3,12ππ.17.证明:(1)由勾股定理逆定理得,AC BC ⊥,因为直三棱柱中1ABC CC ⊥平面,1AC CC∴⊥,11AC BB C C ∴⊥平面,1AC BC ∴⊥;(2)假设11BC B C=O ,连结OD ,由中位线得OD ∥1A C ,所以1A C ∥平面1CDB ;(3)作BE ⊥CD 延长线于E 连结1B E ,易知1B EB ∠即为二面角平面角,在直角三角形1B EB 中,1B B =4,BE=125,所以11B B 5tan B EB==BE 3∠。
18. 解:(1)当n=1时,由2a 1=2S 1=211a a +,a 1>0,得a 1=1当n ≥2时,由2a n =2S n -2S n-1=(2na +a n )-(211n n aa --+)得(a n +a n-1)(a n -a n-1-1)=0 因为a n +a n-1>0,所以a n -a n-1=1故a n =1+(n-1)×1=n (2)由b 1=1,112n nb b +=,得b n =11()2n -,则c n =n 11()2n -因为 T n =12111112()3()()222n n -+++⋅⋅⋅+, 所以 21111112()(1)()()22222n n n T n n -=++⋅⋅⋅+-+得 21111111()()()22222n n n T n -=+++⋅⋅⋅+-=2-(n+2)1()2n 所以 T n =4-(n+2)11()2n - 19. 解:(1) 当=-=)(1x f a 时,),,0(,12ln +∞∈-++x xx x所以)('x f 222,(0,)x x x x+-=∈+∞ 因此,,)(12=f即 曲线.1))2(2)(,处的切线斜率为,在点(f x f y = 又 ,22ln )2(+=f 所以曲线.02ln ,2)22(ln ))2(2)(=+--=+-=y x x y f x f y 即处的切线方程为,在点((2)因为 11ln )(--+-=xaax x x f , 所以211)('x a a x x f -+-=221x ax ax -+--= ),0(+∞∈x ,令 ,1)(2a x axx g -+-=),,0(+∞∈x(1)当0,()1,(0,)a h x x x ==-+∈+∞时所以,当(0,1),()0,()0x h x f x '∈><时此时,函数()f x 单调递减; 当(1,)x ∈+∞时,()0h x <,此时()0,f x '>函数f(x)单调递 (2)当0a '≠时,由f (x)=0 即210axx a -+-=,解得1211,1x x a==- ①当12a =时,12,()0xx h x =≥恒成立,此时()0f x '≤,函数()f x 在(0,+∞)上单调递减; ②当110,1102a a<<->>时(0,1)x ∈时,()0,()0,()h x f x f x '><此时函数单调递减; 1(1,1)x a ∈-时,()0,()0,()h x f x f x '<>此时函数单调递增;1(1,),()0x h x a∈-+∞>时,此时()0f x '<,函数()f x 单调递减; ③当0a <时,由于110a-<(0,1)x ∈时,()0h x >,此时()0f x '<,函数()f x 单调递减;(1,)x ∈+∞时,()0h x <,此时()0f x '>,函数()f x 单调递增。
