2018年天津文数高考试题文档版(含答案)
2018年天津高考文科数学(含参考答案)

2018年普通高等学校招生全国统一考试(天津卷)数学(文史类)本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试用时120分钟。
第Ⅰ卷1至2页,第Ⅱ卷3至5页。
答卷前,考生务必将自己的姓名、准考证号填写在答题考上,并在规定位置粘贴考试用条形码。
答卷时,考生务必将答案涂写在答题卡上,答在试卷上的无效。
考试结束后,将本试卷和答题卡一并交回。
祝各位考生考试顺利!第Ⅰ卷注意事项:1.每小题选出答案后,再选涂其他答案标号。
2.本卷共8参考公式:·如果事件.h 表示棱柱的高.h 表示棱锥的高.一..(1|12}x x ∈-≤<R ,则()A B C = (A ){1,1}-(C ){1,0,1}-(D ){2,3,4}(2)设变量,x y 满足约束条件52410x y x y x y y +≤⎧⎪-≤⎪⎨-+≤⎪⎪≥⎩,,,,则目标函数35z x y =+的最大值为(A )6 (B )19 (C )21(D )45(3)设x ∈R ,则“38x >”是“||2x >”的 (A )充分而不必要条件(B )必要而不充分条件(C )充要条件(D )既不充分也不必要条件(4)阅读如图所示的程序框图,运行相应的程序,若输入N 的值为20,则输出T 的值为 (A )1(B )2(C )3(D )4(5)已知13313711log ,(),log 245a b c ===,则,,a b c 的大小关系为(A )a>(6(A (C (7),A B 两点(A )23x -(C )24x -(8)·OM 的值为 (A )15-(C )6-(D )0第Ⅱ卷注意事项:1.用黑色墨水的钢笔或签字笔将答案写在答题卡上。
2.本卷共12小题,共110分。
二.填空题:本大题共6小题,每小题5分,共30分. (9)i 是虚数单位,复数67i12i++=__________.(10)已知函数f (x )=e x ln x ,f?′(x )为f (x )的导函数,则f?′(1)的值为__________. (11)如图,已知正方体ABCD –A 1B 1C 1D 1的棱长为1,则四棱柱A 1–BB 1D 1D 的体积为__________. (12)在平面直角坐标系中,经过三点(0,0),(1,1),(2,0)的圆的方程为__________. (13)已知a ,b ∈R ,且a –3b +6=0,则2a +18b的最小值为__________. (14)已知a ∈R ,函数()22220220x x a x f x x x a x ⎧++-≤⎪=⎨-+->⎪⎩,,,.若对任意x ∈[–3,+∞),f (x )≤x 恒成立,则a 的取值范围是__________.三.解答题:本大题共6小题,共80(15)(本小题满分13分)中抽取7名同学去某敬老院参加献爱心活动.(Ⅱ)设抽出的7名同学分别用A ,B ,C ,D ,E ,的卫生工作.(i(ii )设M (16在△ABC .已知b sin A =a cos(B –π6). (Ⅰ)求教(Ⅱ)设a (17如图,ABC ⊥平面ABD ,点M 为棱AB 的中点,AB =2,AD =(Ⅰ)求证:AD ⊥BC ;(Ⅱ)求异面直线BC 与MD 所成角的余弦值; (Ⅲ)求直线CD 与平面ABD 所成角的正弦值. (18)(本小题满分13分)设{a n }是等差数列,其前n 项和为S n (n ∈N *);{b n }是等比数列,公比大于0,其前n 项和为T n (n ∈N *).已知b 1=1,b 3=b 2+2,b 4=a 3+a 5,b 5=a 4+2a 6.(Ⅰ)求S n 和T n ;(Ⅱ)若S n +(T 1+T 2+…+T n )=a n +4b n ,求正整数n 的值. (19)(本小题满分14分)设椭圆22221(0)x y a b a b+=>>的右顶点为A ,上顶点为B .已知椭圆的离心率为3,||AB =(I )求椭圆的方程;(II )设直线:(0)l y kx k =<与椭圆交于,P Q 两点,l 与直线AB 交于点M ,且点P ,M 均在第四象限.若BPM △(20)设函数(f x (I )若2t =(II )若d (III . 参考答案(1)C (5)D(9)4–i (12)2x y +三、解答题(15)本小题主要考查随机抽样、用列举法计算随机事件所含的基本事件数、古典概型及其概率计算公式等基本知识.考查运用概率知识解决简单实际问题的能力.满分13分.(Ⅰ)解:由已知,甲、乙、丙三个年级的学生志愿者人数之比为3∶2∶2,由于采用分层抽样的方法从中抽取7名同学,因此应从甲、乙、丙三个年级的学生志愿者中分别抽取3人,2人,2人. (Ⅱ)(i )解:从抽出的7名同学中随机抽取2名同学的所有可能结果为{A ,B },{A ,C },{A ,D },{A ,E },{A ,F },{A ,G },{B ,C },{B ,D },{B ,E },{B ,F },{B ,G },{C ,D },{C ,E },{C ,F },{C ,G },{D ,E },{D ,F },{D ,G },{E ,F },{E ,G },{F ,G },共21种.(ii )解:由(Ⅰ),不妨设抽出的7名同学中,来自甲年级的是A ,B ,C ,来自乙年级的是D ,E ,来自丙年级的是F ,G ,则从抽出的7名同学中随机抽取的2名同学来自同一年级的所有可能结果为{A ,B },{A ,C },{B ,C },{D ,E },{F ,G },共5种.学@科网 所以,事件M 发生的概率为P (M )=521. (16)(Ⅰ)解:在△ABC中,由正弦定理sin sin a b A B =π)6-,得πsin cos()6a B a B =-,即πsin cos()6B B =-,可得tanB(Ⅱ)解:在△ABC 中,由余弦定理及a =2,c =3 由sin b A a =2cos22cosA =所以,sin(217- (17考13分.=AB ,AD ⊥AB ,可得AD ⊥平面ABC ,故AD ⊥BC . M 为棱AB 的中点,故MN ∥BC .所以∠DMN (或在Rt △DAM 中,AM =1,故DM AD ⊥平面ABC ,故AD ⊥AC . 在Rt △DAN 中,AN =1,故DN .在等腰三角形DMN 中,MN =1,可得12cos MNDMN DM ∠==. 所以,异面直线BC 与MD(Ⅲ)解:连接CM .因为△ABC 为等边三角形,M 为边AB 的中点,故CM ⊥AB ,CM 面ABC ⊥平面ABD ,而CM ⊂平面ABC ,故CM ⊥平面AB D .所以,∠CDM 为直线CD 与平面ABD 所成的角.在Rt △CAD 中,CD .在Rt △CMD 中,sin CM CDM CD ∠==.所以,直线CD 与平面ABD . (18(I 因为0q >设等差数列16,d =从而11,a d ==(II 131(222)2n n n T n +++=+++-=由1(n n S T b ++可得1(1)222n n n n n n +++--=+整理得240,n --=解得(19(I||AB =,从而3,2a b ==.所以,椭圆的方程为22194x y +=. (II )解:设点P 的坐标为11(,)x y ,点M 的坐标为22(,)x y ,由题意,210x x >>, 点Q 的坐标为11(,).x y --由BPM △的面积是BPQ △面积的2倍,可得||=2||PM PQ , 从而21112[()]x x x x -=--,即215x x =.易知直线AB 的方程为236x y +=,由方程组236,,x y y kx +=⎧⎨=⎩消去y ,可得2632x k =+.由方程组221,94,x y y kx ⎧+⎪=⎨⎪=⎩消去y,可得1x =.由215x x =5(32)k =+,两边平方,整理得2182580k k ++=,解得89k =-,或12k =-.当89k =-时,290x =-<,不合题意,舍去;当12k =-时,212x =,1125x =,符合题意.(20,又y =0. f (x故(f '当x (III )解:曲线y =f (x )与直线y =?(x ?t 2有三个互异的公共点等价于关于x 的方程(x ?t 2+d )(x ?t 2)(x ?t 2?d )+(x ?t 2有三个互异的实数解,令u =x ?t 2,可得u 3+(1?d 2)u =0. 设函数g (x )=x 3+(1?d 2)x ,则曲线y =f (x )与直线y =?(x ?t 2有三个互异的公共点等价于函数y =g (x )有三个零点.()g'x =3x 3+(1?d 2).当d 2≤1时,()g'x ≥0,这时()g'x 在R 上单调递增,不合题意.当d 2>1时,()g'x =0,解得x 1=,x 2.易得,g (x )在(?∞,x 1)上单调递增,在[x 1,x 2]上单调递减,在(x 2,+∞)上单调递增,g (x )的极大值g (x 1)=g (+g (x )若g (x 2若2()0,g x <12||,(d x g -<()y g x =所以d 10)(10,+∞。
2018年高考天津卷文科数学(含答案)

绝密★启用前2018年普通高等学校招生全国统一考试(天津卷)数学(文史类)本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试用时120分钟。
第Ⅰ卷1至2页,第Ⅱ卷3至5页。
答卷前,考生务必将自己的姓名、准考证号填写在答题考上,并在规定位置粘贴考试用条形码。
答卷时,考生务必将答案涂写在答题卡上,答在试卷上的无效。
考试结束后,将本试卷和答题卡一并交回。
祝各位考生考试顺利!第Ⅰ卷注意事项:1.每小题选出答案后,用铅笔将答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
2.本卷共8小题,每小题5分,共40分。
参考公式:·如果事件 A ,B 互斥,那么 P (A ∪B )=P (A )+P (B ). ·棱柱的体积公式V =Sh . 其中S 表示棱柱的底面面积,h 表示棱柱的高. ·棱锥的体积公式13V Sh =,其中S 表示棱锥的底面积,h 表示棱锥的高. 一.选择题:在每小题给出的四个选项中,只有一项是符合题目要求的. (1)设集合{1,2,3,4}A =,{1,0,2,3}B =-,{|12}C x x =∈-≤<R ,则()A B C =(A ){1,1}-(B ){0,1}(C ){1,0,1}-(D ){2,3,4}(2)设变量,x y 满足约束条件52410x y x y x y y +≤⎧⎪-≤⎪⎨-+≤⎪⎪≥⎩,,,,则目标函数35z x y =+的最大值为(A )6 (B )19 (C )21(D )45(3)设x ∈R ,则“38x >”是“||2x >” 的(A )充分而不必要条件 (B )必要而不充分条件 (C )充要条件(D )既不充分也不必要条件(4)阅读如图所示的程序框图,运行相应的程序,若输入N 的值为20,则输出T 的值为(A )1(B )2(C )3(D )4(5)已知13313711log ,(),log 245a b c ===,则,,a b c 的大小关系为(A )a b c >> (B )b a c >> (C )c b a >>(D )c a b >>(6)将函数sin(2)5y x π=+的图象向右平移10π个单位长度,所得图象对应的函数 (A )在区间[,]44ππ- 上单调递增 (B )在区间[,0]4π上单调递减(C )在区间[,]42ππ 上单调递增 (D )在区间[,]2ππ 上单调递减(7)已知双曲线22221(0,0)x y a b a b-=>> 的离心率为2,过右焦点且垂直于x 轴的直线与双曲线交于,A B两点.设,A B 到双曲线的同一条渐近线的距离分别为1d 和2d ,且126,d d += 则双曲线的方程为(A )22139x y -=(B )22193x y -=(C )221412x y -=(D )221124x y -= (8)在如图的平面图形中,已知 1.2,120OM ON MON ==∠=,2,2,BM MA CN NA ==则·BC OM 的值为(A )15- (B )9- (C )6-(D )0第Ⅱ卷注意事项:1.用黑色墨水的钢笔或签字笔将答案写在答题卡上。
2018年天津市高考数学试卷(文科)

2018年天津市高考数学试卷(文科)一.选择题:在每小题给出的四个选项中.只有一项是符合题目要求的.1.(5分)设集合A={1.2.3.4}.B={﹣1.0.2.3}.C={x∈R|﹣1≤x<2}.则(A∪B)∩C=()A.{﹣1.1} B.{0.1} C.{﹣1.0.1} D.{2.3.4}2.(5分)设变量x.y满足约束条件.则目标函数z=3x+5y的最大值为()A.6 B.19 C.21 D.453.(5分)设x∈R.则“x3>8”是“|x|>2”的()A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件4.(5分)阅读如图的程序框图.运行相应的程序.若输入N的值为20.则输出T 的值为()A.1 B.2 C.3 D.45.(5分)已知a=log3.b=().c=log.则a.b.c的大小关系为()A.a>b>c B.b>a>c C.c>b>a D.c>a>b6.(5分)将函数y=sin(2x+)的图象向右平移个单位长度.所得图象对应的函数()A.在区间[]上单调递增B.在区间[﹣.0]上单调递减C.在区间[]上单调递增D.在区间[.π]上单调递减7.(5分)已知双曲线=1(a>0.b>0)的离心率为2.过右焦点且垂直于x轴的直线与双曲线交于A.B两点.设A.B到双曲线的同一条渐近线的距离分别为d1和d2.且d1+d2=6.则双曲线的方程为()A.﹣=1 B.﹣=1 C.﹣=1 D.﹣=18.(5分)在如图的平面图形中.已知OM=1.ON=2.∠MON=120°.=2.=2.则的值为()A.﹣15 B.﹣9 C.﹣6 D.0二.填空题:本大题共6小题.每小题5分.共30分.9.(5分)i是虚数单位.复数= .10.(5分)已知函数f(x)=e x lnx.f′(x)为f(x)的导函数.则f′(1)的值为.11.(5分)如图.已知正方体ABCD﹣A1B1C1D1的棱长为1.则四棱锥A1﹣BB1D1D的体积为.12.(5分)在平面直角坐标系中.经过三点(0.0).(1.1).(2.0)的圆的方程为.13.(5分)已知a.b∈R.且a﹣3b+6=0.则2a+的最小值为.14.(5分)己知a∈R.函数f(x)=.若对任意x∈[﹣3.+∞).f(x)≤|x|恒成立.则a的取值范围是.三.解答题:本大题共6小题.共80分.解答应写出文字说明.证明过程或演算步骤.15.(13分)己知某校甲、乙、丙三个年级的学生志愿者人数分别为240.160.160.现采用分层抽样的方法从中抽取7名同学去某敬老院参加献爱心活动.(Ⅰ)应从甲、乙、丙三个年级的学生志愿者中分别抽取多少人?(Ⅱ)设抽出的7名同学分别用A.B.C.D.E.F.G表示.现从中随机抽取2名同学承担敬老院的卫生工作.(i)试用所给字母列举出所有可能的抽取结果;(ii)设M为事件“抽取的2名同学来自同一年级”.求事件M发生的概率.16.(13分)在△ABC中.内角A.B.C所对的边分别为a.b.c.已知bsinA=acos (B﹣).(Ⅰ)求角B的大小;(Ⅱ)设a=2.c=3.求b和sin(2A﹣B)的值.17.(13分)如图.在四面体ABCD中.△ABC是等边三角形.平面ABC⊥平面ABD.点M为棱AB的中点.AB=2.AD=2.∠BAD=90°.(Ⅰ)求证:AD⊥BC;(Ⅱ)求异面直线BC与MD所成角的余弦值;(Ⅲ)求直线CD与平面ABD所成角的正弦值.18.(13分)设{an }是等差数列.其前n项和为Sn(n∈N*);{bn}是等比数列.公比大于0.其前n项和为Tn (n∈N*).已知b1=1.b3=b2+2.b4=a3+a5.b5=a4+2a6.(Ⅰ)求Sn 和Tn;(Ⅱ)若Sn +(T1+T2+……+Tn)=an+4bn.求正整数n的值.19.(14分)设椭圆+=1(a>b>0)的右顶点为A.上顶点为B.已知椭圆的离心率为.|AB|=.(Ⅰ)求椭圆的方程;(Ⅱ)设直线l:y=kx(k<0)与椭圆交于P.Q两点.1与直线AB交于点M.且点P.M均在第四象限.若△BPM的面积是△BPQ面积的2倍.求k的值.20.(14分)设函数f(x)=(x﹣t1)(x﹣t2)(x﹣t3).其中t1.t2.t3∈R.且t1.t2.t3是公差为d的等差数列.(Ⅰ)若t2=0.d=1.求曲线y=f(x)在点(0.f(0))处的切线方程;(Ⅱ)若d=3.求f(x)的极值;(Ⅲ)若曲线y=f(x)与直线y=﹣(x﹣t2)﹣6有三个互异的公共点.求d 的取值范围.2018年天津市高考数学试卷(文科)参考答案与试题解析一.选择题:在每小题给出的四个选项中.只有一项是符合题目要求的.1.(5分)设集合A={1.2.3.4}.B={﹣1.0.2.3}.C={x∈R|﹣1≤x<2}.则(A∪B)∩C=()A.{﹣1.1} B.{0.1} C.{﹣1.0.1} D.{2.3.4}【解答】解:∵A={1.2.3.4}.B={﹣1.0.2.3}.∴(A∪B)={1.2.3.4}∪{﹣1.0.2.3}={﹣1.0.1.2.3.4}.又C={x∈R|﹣1≤x<2}.∴(A∪B)∩C={﹣1.0.1}.故选:C.2.(5分)设变量x.y满足约束条件.则目标函数z=3x+5y的最大值为()A.6 B.19 C.21 D.45【解答】解:由变量x.y满足约束条件.得如图所示的可行域.由解得A(2.3).当目标函数z=3x+5y经过A时.直线的截距最大.z取得最大值.将其代入得z的值为21.故选:C.3.(5分)设x∈R.则“x3>8”是“|x|>2”的()A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件【解答】解:由x3>8.得x>2.则|x|>2.反之.由|x|>2.得x<﹣2或x>2.则x3<﹣8或x3>8.即“x3>8”是“|x|>2”的充分不必要条件.故选:A.4.(5分)阅读如图的程序框图.运行相应的程序.若输入N的值为20.则输出T 的值为()A .1B .2C .3D .4【解答】解:若输入N=20. 则i=2.T=0.==10是整数.满足条件.T=0+1=1.i=2+1=3.i ≥5不成立.循环.=不是整数.不满足条件..i=3+1=4.i ≥5不成立. 循环.==5是整数.满足条件.T=1+1=2.i=4+1=5.i ≥5成立.输出T=2. 故选:B .5.(5分)已知a=log 3.b=().c=log.则a.b.c 的大小关系为( )A .a >b >cB .b >a >cC .c >b >aD .c >a >b【解答】解:∵a=log 3.c=log=log 35.且5.∴.则b=()<.∴c>a>b.故选:D.6.(5分)将函数y=sin(2x+)的图象向右平移个单位长度.所得图象对应的函数()A.在区间[]上单调递增B.在区间[﹣.0]上单调递减C.在区间[]上单调递增D.在区间[.π]上单调递减【解答】解:将函数y=sin(2x+)的图象向右平移个单位长度.所得图象对应的函数解析式为y=sin[2(x﹣)+]=sin2x.当x∈[]时.2x∈[.].函数单调递增;当x∈[.]时.2x∈[.π].函数单调递减;当x∈[﹣.0]时.2x∈[﹣.0].函数单调递增;当x∈[.π]时.2x∈[π.2π].函数先减后增.故选:A.7.(5分)已知双曲线=1(a>0.b>0)的离心率为2.过右焦点且垂直于x轴的直线与双曲线交于A.B两点.设A.B到双曲线的同一条渐近线的距离分别为d1和d2.且d1+d2=6.则双曲线的方程为()A.﹣=1 B.﹣=1 C.﹣=1 D.﹣=1【解答】解:由题意可得图象如图.CD是双曲线的一条渐近线y=.即bx﹣ay=0.F(c.0).AC⊥CD.BD⊥CD.FE⊥CD.ACDB是梯形.F是AB的中点.EF==3.EF==b.所以b=3.双曲线=1(a>0.b>0)的离心率为2.可得.可得:.解得a=.则双曲线的方程为:﹣=1.故选:A.8.(5分)在如图的平面图形中.已知OM=1.ON=2.∠MON=120°.=2.=2.则的值为()A.﹣15 B.﹣9 C.﹣6 D.0【解答】解:不妨设四边形OMAN是平行四边形.由OM=1.ON=2.∠MON=120°.=2.=2.知=﹣=3﹣3=﹣3+3.∴=(﹣3+3)•=﹣3+3•=﹣3×12+3×2×1×cos120°=﹣6.故选:C.二.填空题:本大题共6小题.每小题5分.共30分.9.(5分)i是虚数单位.复数= 4﹣i .【解答】解:====4﹣i.故答案为:4﹣i10.(5分)已知函数f(x)=e x lnx.f′(x)为f(x)的导函数.则f′(1)的值为 e .【解答】解:函数f(x)=e x lnx.则f′(x)=e x lnx+•e x;∴f′(1)=e•ln1+1•e=e.故答案为:e.11.(5分)如图.已知正方体ABCD﹣A1B1C1D1的棱长为1.则四棱锥A1﹣BB1D1D的体积为.【解答】解:由题意可知四棱锥A1﹣BB1D1D的底面是矩形.边长:1和.四棱锥的高:A1C1=.则四棱锥A1﹣BB1D1D的体积为:=.故答案为:.12.(5分)在平面直角坐标系中.经过三点(0.0).(1.1).(2.0)的圆的方程为(x﹣1)2+y2=1(或x2+y2﹣2x=0).【解答】解:【方法一】根据题意画出图形如图所示.结合图形知经过三点(0.0).(1.1).(2.0)的圆.其圆心为(1.0).半径为1.则该圆的方程为(x﹣1)2+y2=1.【方法二】设该圆的方程为x2+y2+Dx+Ey+F=0.则.解得D=﹣2.E=F=0;∴所求圆的方程为x2+y2﹣2x=0.故答案为:(x﹣1)2+y2=1(或x2+y2﹣2x=0).13.(5分)已知a.b∈R.且a﹣3b+6=0.则2a+的最小值为.【解答】解:a.b∈R.且a﹣3b+6=0.可得:3b=a+6.则2a+==≥2=.当且仅当2a=.即a=﹣3时取等号.函数的最小值为:.故答案为:.14.(5分)己知a∈R.函数f(x)=.若对任意x∈[﹣3.+∞).f(x)≤|x|恒成立.则a的取值范围是[] .【解答】解:当x≤0时.函数f(x)=x2+2x+a﹣2的对称轴为x=﹣1.抛物线开口向上.要使x≤0时.对任意x∈[﹣3.+∞).f(x)≤|x|恒成立.则只需要f(﹣3)≤|﹣3|=3.即9﹣6+a﹣2≤3.得a≤2.当x>0时.要使f(x)≤|x|恒成立.即f(x)=﹣x2+2x﹣2a.则直线y=x的下方或在y=x上.由﹣x2+2x﹣2a=x.即x2﹣x+2a=0.由判别式△=1﹣8a≤0.得a≥.综上≤a≤2.故答案为:[.2].三.解答题:本大题共6小题.共80分.解答应写出文字说明.证明过程或演算步骤.15.(13分)己知某校甲、乙、丙三个年级的学生志愿者人数分别为240.160.160.现采用分层抽样的方法从中抽取7名同学去某敬老院参加献爱心活动.(Ⅰ)应从甲、乙、丙三个年级的学生志愿者中分别抽取多少人?(Ⅱ)设抽出的7名同学分别用A.B.C.D.E.F.G表示.现从中随机抽取2名同学承担敬老院的卫生工作.(i)试用所给字母列举出所有可能的抽取结果;(ii)设M为事件“抽取的2名同学来自同一年级”.求事件M发生的概率.【解答】解:(Ⅰ)由已知得甲、乙、丙三个年级的学生志愿者人数之比为3:2:2.由于采用分层抽样的方法从中抽取7名同学.∴应从甲、乙、丙三个年级的学生志愿意者中分别抽取得人.2人.2人.(Ⅱ)(i)从抽取的7名同学中抽取2名同学的所有可能结果为:{A.B}.{A.C}.{A.D}.{A.E}.{A.F}.{A.G}.{B.C}.{B.D}.{B.E}.{B.F}.{B.G}.{C.D}.{C.E}.{C.F}.{C.G}.{D.E}.{D.F}.{D.G}.{E.F}.{E.G}.{F.G}.共21个.(i)设抽取的7名学生中.来自甲年级的是A.B.C.来自乙年级的是D.E.来自丙年级的是F.G.M为事件“抽取的2名同学来自同一年级”.则事件M包含的基本事件有:{A.B}.{A.C}.{B.C}.{D.E}.{F.G}.共5个基本事件.∴事件M发生的概率P(M)=.16.(13分)在△ABC中.内角A.B.C所对的边分别为a.b.c.已知bsinA=acos (B﹣).(Ⅰ)求角B的大小;(Ⅱ)设a=2.c=3.求b和sin(2A﹣B)的值.【解答】解:(Ⅰ)在△ABC中.由正弦定理得.得bsinA=asinB.又bsinA=acos(B﹣).∴asinB=acos(B﹣).即sinB=cos(B﹣)=cosBcos+sinBsin=cosB+.∴tanB=.又B∈(0.π).∴B=.(Ⅱ)在△ABC中.a=2.c=3.B=.由余弦定理得b==.由bsinA=acos(B﹣).得sinA=.∵a<c.∴cosA=.∴sin2A=2sinAcosA=.cos2A=2cos2A﹣1=.∴sin(2A﹣B)=sin2AcosB﹣cos2AsinB==.17.(13分)如图.在四面体ABCD中.△ABC是等边三角形.平面ABC⊥平面ABD.点M为棱AB的中点.AB=2.AD=2.∠BAD=90°.(Ⅰ)求证:AD⊥BC;(Ⅱ)求异面直线BC与MD所成角的余弦值;(Ⅲ)求直线CD与平面ABD所成角的正弦值.【解答】(Ⅰ)证明:由平面ABC⊥平面ABD.平面ABC∩平面ABD=AB.AD⊥AB.得AD⊥平面ABC.故AD⊥BC;(Ⅱ)解:取棱AC的中点N.连接MN.ND.∵M为棱AB的中点.故MN∥BC.∴∠DMN(或其补角)为异面直线BC与MD所成角.在Rt△DAM中.AM=1.故DM=.∵AD⊥平面ABC.故AD⊥AC.在Rt△DAN中.AN=1.故DN=.在等腰三角形DMN中.MN=1.可得cos∠DMN=.∴异面直线BC与MD所成角的余弦值为;(Ⅲ)解:连接CM.∵△ABC为等边三角形.M为边AB的中点.故CM⊥AB.CM=.又∵平面ABC⊥平面ABD.而CM⊂平面ABC.故CM⊥平面ABD.则∠CDM为直线CD与平面ABD所成角.在Rt△CAD中.CD=.在Rt△CMD中.sin∠CDM=.∴直线CD与平面ABD所成角的正弦值为.18.(13分)设{an }是等差数列.其前n项和为Sn(n∈N*);{bn}是等比数列.公比大于0.其前n项和为Tn (n∈N*).已知b1=1.b3=b2+2.b4=a3+a5.b5=a4+2a6.(Ⅰ)求Sn 和Tn;(Ⅱ)若Sn +(T1+T2+……+Tn)=an+4bn.求正整数n的值.【解答】解:(Ⅰ)设等比数列{bn }的公比为q.由b1=1.b3=b2+2.可得q2﹣q﹣2=0.∵q>0.可得q=2.故.;设等差数列{an }的公差为d.由b4=a3+a5.得a1+3d=4.由b5=a4+2a6.得3a1+13d=16.∴a1=d=1.故an=n.;(Ⅱ)由(Ⅰ).可得T1+T2+……+Tn==2n+1﹣n﹣2.由Sn +(T1+T2+……+Tn)=an+4bn.可得.整理得:n2﹣3n﹣4=0.解得n=﹣1(舍)或n=4.∴n的值为4.19.(14分)设椭圆+=1(a>b>0)的右顶点为A.上顶点为B.已知椭圆的离心率为.|AB|=.(Ⅰ)求椭圆的方程;(Ⅱ)设直线l:y=kx(k<0)与椭圆交于P.Q两点.1与直线AB交于点M.且点P.M均在第四象限.若△BPM的面积是△BPQ面积的2倍.求k的值.【解答】解:(1)设椭圆的焦距为2c.由已知可得.又a2=b2+c2.解得a=3.b=2.∴椭圆的方程为:.(Ⅱ)设点P(x1.y1).M(x2.y2).(x2>x1>0).则Q(﹣x1.﹣y1).∵△BPM的面积是△BPQ面积的2倍.∴|PM|=2|PQ|.从而x2﹣x1=2[x1﹣(﹣x1)].∴x2=5x1.易知直线AB的方程为:2x+3y=6.由.可得>0.由.可得.⇒.⇒18k2+25k+8=0.解得k=﹣或k=﹣.由>0.可得k.故k=﹣.20.(14分)设函数f(x)=(x﹣t1)(x﹣t2)(x﹣t3).其中t1.t2.t3∈R.且t1.t2.t3是公差为d的等差数列.(Ⅰ)若t2=0.d=1.求曲线y=f(x)在点(0.f(0))处的切线方程;(Ⅱ)若d=3.求f(x)的极值;(Ⅲ)若曲线y=f(x)与直线y=﹣(x﹣t2)﹣6有三个互异的公共点.求d 的取值范围.【解答】解:(Ⅰ)函数f(x)=(x﹣t1)(x﹣t2)(x﹣t3).t2=0.d=1时.f(x)=x(x+1)(x﹣1)=x3﹣x.∴f′(x)=3x2﹣1.f(0)=0.f′(0)=﹣1.∴y=f(x)在点(0.f(0))处的切线方程为y﹣0=﹣1×(x﹣0).即x+y=0;(Ⅱ)d=3时.f(x)=(x﹣t2+3)(x﹣t2)(x﹣t2﹣3)=﹣9(x﹣t2)=x3﹣3t2x2+(3﹣9)x﹣+9t2;∴f′(x)=3x2﹣6t2x+3﹣9.令f′(x )=0.解得x=t 2﹣或x=t 2+;当x 变化时.f′(x ).f (x )的变化情况如下表;+∴f (x )的极大值为f (t 2﹣)=﹣9×(﹣)=6.极小值为f (t 2+)=﹣9×=﹣6;(Ⅲ)曲线y=f (x )与直线y=﹣(x ﹣t 2)﹣6有三个互异的公共点.等价于关于x 的方程(x ﹣t 2+d )(x ﹣t 2)(x ﹣t 2﹣d )+(x ﹣t 2)﹣6=0有三个互异的实数根.令u=x ﹣t 2.可得u 3+(1﹣d 2)u+6=0; 设函数g (x )=x 3+(1﹣d 2)x+6.则曲线y=f (x )与直线y=﹣(x ﹣t 2)﹣6有3个互异的公共点.等价于函数y=g (x )有三个不同的零点; 又g′(x )=3x 2+(1﹣d 2).当d 2≤1时.g′(x )≥0恒成立.此时g (x )在R 上单调递增.不合题意; 当d 2>1时.令g′(x )=0.解得x 1=﹣.x 2=;∴g (x )在(﹣∞.x 1)上单调递增.在(x 1.x 2)上单调递减. 在(x 2.+∞)上也单调递增; ∴g (x )的极大值为g (x 1)=g (﹣)=+6>0;极小值为g (x 2)=g ()=﹣+6;若g (x 2)≥0.由g (x )的单调性可知. 函数g (x )至多有两个零点.不合题意;若g(x2)<0.即>27.解得|d|>.此时|d|>x2.g(|d|)=|d|+6>0.且﹣2|d|<x1;g(﹣2|d|)=﹣6|d|3﹣2|d|+6<0.从而由g(x)的单调性可知.函数y=g(x)在区间(﹣2|d|.x1).(x1.x2).(x2.|d|)内各有一个零点.符合题意;∴d的取值范围是(﹣∞.﹣)∪(.+∞).。
(精校版)2018年天津文数高考试题文档版(含答案)
2018年普通高等学校招生全国统一考试(天津卷)数学(文史类)一.选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.(1)设集合{1,2,3,4}A =,{1,0,2,3}B =-,{|12}C x x =∈-≤<R ,则()A B C =(A ){1,1}- (B ){0,1} (C ){1,0,1}-(D ){2,3,4}(2)设变量,x y 满足约束条件52410x y x y x y y +≤⎧⎪-≤⎪⎨-+≤⎪⎪≥⎩,,,,则目标函数35z x y =+的最大值为(A )6 (B )19 (C )21(D )45(3)设x ∈R ,则“38x >”是“||2x >”的(A )充分而不必要条件 (B )必要而不充分条件 (C )充要条件(D )既不充分也不必要条件(4)阅读如图所示的程序框图,运行相应的程序,若输入N 的值为20,则输出T 的值为(A )1(B )2(C )3(D )4(5)已知13313711log ,(),log 245a b c ===,则,,a b c 的大小关系为(A )a b c >> (B )b a c >> (C )c b a >>(D )c a b >>(6)将函数sin(2)5y x π=+的图象向右平移10π个单位长度,所得图象对应的函数 (A )在区间[,]44ππ-上单调递增 (B )在区间[,0]4π-上单调递减(C )在区间[,]42ππ上单调递增 (D )在区间[,]2ππ上单调递减(7)已知双曲线22221(0,0)x y a b a b-=>> 的离心率为2,过右焦点且垂直于x 轴的直线与双曲线交于,A B两点.设,A B 到双曲线的同一条渐近线的距离分别为1d 和2d ,且126,d d +=则双曲线的方程为(A )22139x y -=(B )22193x y -= (C )221412x y -=(D )221124x y -= (8)在如图的平面图形中,已知1,2,120OM ON MON ==∠=,2,2,BM MA CN NA == 则·BC OM的值为(A )15- (B )9- (C )6-(D )0二.填空题:本大题共6小题,每小题5分,共30分. (9)i 是虚数单位,复数67i12i++=__________. (10)已知函数f (x )=e xln x ,f ′(x )为f (x )的导函数,则f ′(1)的值为__________.(11)如图,已知正方体ABCD –A 1B 1C 1D 1的棱长为1,则四棱锥A 1–BB 1D 1D 的体积为__________.(12)在平面直角坐标系中,经过三点(0,0),(1,1),(2,0)的圆的方程为__________.(13)已知a ,b ∈R ,且a –3b +6=0,则2a+18b的最小值为__________. (14)已知a ∈R ,函数()22220220x x a x f x x x a x ⎧++-≤⎪=⎨-+->⎪⎩,,,.若对任意x ∈[–3,+∞),f (x )≤x 恒成立,则a 的取值范围是__________.三.解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤. (15)(本小题满分13分)已知某校甲、乙、丙三个年级的学生志愿者人数分别为240,160,160.现采用分层抽样的方法从中抽取7名同学去某敬老院参加献爱心活动.学&科网(Ⅰ)应从甲、乙、丙三个年级的学生志愿者中分别抽取多少人?(Ⅱ)设抽出的7名同学分别用A ,B ,C ,D ,E ,F ,G 表示,现从中随机抽取2名同学承担敬老院的卫生工作.(i )试用所给字母列举出所有可能的抽取结果;(ii )设M 为事件“抽取的2名同学来自同一年级”,求事件M 发生的概率. (16)(本小题满分13分)在△ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c .已知b sin A =a cos(B –π6). (Ⅰ)求角B 的大小;(Ⅱ)设a =2,c =3,求b 和sin(2A –B )的值. (17)(本小题满分13分)如图,在四面体ABCD 中,△ABC 是等边三角形,平面ABC ⊥平面ABD ,点M 为棱AB 的中点,AB =2,AD =23,∠BAD =90°.(Ⅰ)求证:AD ⊥BC ;(Ⅱ)求异面直线BC 与MD 所成角的余弦值; (Ⅲ)求直线CD 与平面ABD 所成角的正弦值.(18)(本小题满分13分)设{a n }是等差数列,其前n 项和为S n (n ∈N *);{b n }是等比数列,公比大于0,其前n 项和为T n (n ∈N *).已知b 1=1,b 3=b 2+2,b 4=a 3+a 5,b 5=a 4+2a 6. (Ⅰ)求S n 和T n ;(Ⅱ)若S n +(T 1+T 2+…+T n )=a n +4b n ,求正整数n 的值. (19)(本小题满分14分)设椭圆22221(0)x y a b a b +=>>的右顶点为A ,上顶点为B .已知椭圆的离心率为53,||13AB =.(I )求椭圆的方程;(II )设直线:(0)l y kx k =<与椭圆交于,P Q 两点,l 与直线AB 交于点M ,且点P ,M 均在第四象限.若BPM △的面积是BPQ △面积的2倍,求k 的值. (20)(本小题满分14分)设函数123()=()()()f x x t x t x t ---,其中123,,t t t ∈R ,且123,,t t t 是公差为d 的等差数列. (I )若20,1,t d ==求曲线()y f x =在点(0,(0))f 处的切线方程; (II )若3d =,求()f x 的极值;(III )若曲线()y f x =与直线2()63y x t =---有三个互异的公共点,求d 的取值范围.参考答案一、(1)C (2)C (3)A (4)B (5)D (6)A (7)A (8)C 二、(9)4–i (10)e (11)13(12)2220x y x +-=(13)14(14)[18,2]三、解答题(15)(Ⅰ)解:由已知,甲、乙、丙三个年级的学生志愿者人数之比为3∶2∶2,由于采用分层抽样的方法从中抽取7名同学,因此应从甲、乙、丙三个年级的学生志愿者中分别抽取3人,2人,2人. (Ⅱ)(i )解:从抽出的7名同学中随机抽取2名同学的所有可能结果为{A ,B },{A ,C },{A ,D },{A ,E },{A ,F },{A ,G },{B ,C },{B ,D },{B ,E },{B ,F },{B ,G },{C ,D },{C ,E },{C ,F },{C ,G },{D ,E },{D ,F },{D ,G },{E ,F },{E ,G },{F ,G },共21种.(ii )解:由(Ⅰ),不妨设抽出的7名同学中,来自甲年级的是A ,B ,C ,来自乙年级的是D ,E ,来自丙年级的是F ,G ,则从抽出的7名同学中随机抽取的2名同学来自同一年级的所有可能结果为{A ,B },{A ,C },{B ,C },{D ,E },{F ,G },共5种. 所以,事件M 发生的概率为P (M )=521. (16)本小题主要考查同角三角函数的基本关系,两角差的正弦与余弦公式,二倍角的正弦与余弦公式,以及正弦定理、余弦定理等基础知识,考查运算求解能力.满分13分. (Ⅰ)解:在△ABC 中,由正弦定理sin sin a b A B =,可得sin sin b A a B =,又由πsin cos()6b A a B =-,得πsin cos()6a B a B =-,即πsin cos()6B B =-,可得tan 3B =.又因为(0π)B ∈,,可得B =π3.(Ⅱ)解:在△ABC 中,由余弦定理及a =2,c =3,B =π3,有2222cos 7b a c ac B =+-=,故b =7. 由πsin cos()6b A a B =-,可得3sin 7A =.因为a <c ,故2cos 7A =.因此43sin 22sin cos 7A A A ==,21cos22cos 17A A =-=. 所以,sin(2)sin 2cos cos 2sin AB A B A B -=-=4311333727214⨯-⨯=. (17)本小题主要考查异面直线所成的角、直线与平面所成的角、平面与平面垂直等基础知识.考查空间想象能力、运算求解能力和推理论证能力.满分13分.(Ⅰ)证明:由平面ABC ⊥平面ABD ,平面ABC ∩平面ABD =AB ,AD ⊥AB ,可得AD ⊥平面ABC ,故AD ⊥BC .(Ⅱ)解:取棱AC 的中点N ,连接MN ,ND .又因为M 为棱AB 的中点,故MN ∥BC .所以∠DMN (或其补角)为异面直线BC 与MD 所成的角.在Rt △DAM 中,AM =1,故DM =22=13AD AM +.因为AD ⊥平面ABC ,故AD ⊥AC . 在Rt △DAN 中,AN =1,故DN =22=13AD AN +.在等腰三角形DMN 中,MN =1,可得1132cos 26MNDMN DM ∠==.所以,异面直线BC 与MD 所成角的余弦值为1326. (Ⅲ)解:连接CM .因为△ABC 为等边三角形,M 为边AB 的中点,故CM ⊥AB ,CM =3.又因为平面ABC ⊥平面ABD ,而CM ⊂平面ABC ,故CM ⊥平面ABD .所以,∠CDM 为直线CD 与平面ABD 所成的角.在Rt △CAD 中,CD =22AC AD +=4. 在Rt △CMD 中,3sin 4CM CDM CD ∠==. 所以,直线CD 与平面ABD 所成角的正弦值为34. (18)本小题主要考查等差数列、等比数列的通项公式及前n 项和公式等基础知识.考查数列求和的基本方法和运算求解能力.满分13分.(I )解:设等比数列{}n b 的公比为q ,由b 1=1,b 3=b 2+2,可得220q q --=. 因为0q >,可得2q =,故12n n b -=.所以,122112nn n T -==--. 设等差数列{}n a 的公差为d .由435b a a =+,可得134a d +=.由5462b a a =+,可得131316,a d +=从而11,1a d ==,故n a n =,所以,(1)2n n n S +=. (II )解:由(I ),有131122(12)(222)=2 2.12n nn n T T T n n n +⨯-+++=+++--=---由12()4n n n n S T T T a b ++++=+ 可得11(1)2222n n n n n n ++++--=+, 整理得2340,n n --=解得1n =-(舍),或4n =.所以n 的值为4.(19)本小题主要考查椭圆的标准方程和几何性质、直线方程等基础知识.考查用代数方法研究圆锥曲线的性质.考查运算求解能力,以及用方程思想解决问题的能力.满分14分.(I )解:设椭圆的焦距为2c ,由已知得2259c a =,又由222a b c =+,可得23a b =.由22||13AB a b =+=,从而3,2a b ==.所以,椭圆的方程为22194x y +=. (II )解:设点P 的坐标为11(,)x y ,点M 的坐标为22(,)x y ,由题意,210x x >>, 点Q 的坐标为11(,)x y --.由BPM △的面积是BPQ △面积的2倍,可得||=2||PM PQ , 从而21112[()]x x x x -=--,即215x x =.学*科网 易知直线AB 的方程为236x y +=,由方程组236,,x y y kx +=⎧⎨=⎩消去y ,可得2632x k =+.由方程组221,94,x y y kx ⎧+⎪=⎨⎪=⎩消去y ,可得12694x k =+.由215x x =,可得2945(32)k k +=+,两边平方,整理得2182580k k ++=,解得89k =-,或12k =-. 当89k =-时,290x =-<,不合题意,舍去;当12k =-时,212x =,1125x =,符合题意. 所以,k 的值为12-.(20)本小题主要考查导数的运算、导数的几何意义、运用导数研究函数的性质等基础知识和方法,考查函数思想和分类讨论思想,考查综合分析问题和解决问题的能力,满分14分.(Ⅰ)解:由已知,可得f (x )=x (x −1)(x +1)=x 3−x ,故()f x '=3x 2−1,因此f (0)=0,(0)f '=−1,又因为曲线y =f (x )在点(0,f (0))处的切线方程为y −f (0)=(0)f '(x −0),故所求切线方程为x +y =0. (Ⅱ)解:由已知可得f (x )=(x −t 2+3)(x −t 2)(x −t 2−3)=(x −t 2)3−9(x −t 2)=x 3−3t 2x 2+(3t 22−9)x −t 23+9t 2. 故()f x '=3x 2−6t 2x +3t 22−9.令()f x '=0,解得x =t 2−3,或x =t 2+3.当x 变化时,()f x ',f (x )的变化如下表:x(−∞,t 2−3)t 2−3 (t 2−3,t 2+3)t 2+3 (t 2+3,+∞)()f x '+ 0 − 0 + f (x )↗极大值↘极小值↗所以函数f (x )的极大值为f (t 2−3)=(−3)3−9×(−3)=63;函数f (x )的极小值为f (t 2+3)=(3)3−9×(3)=−63.(Ⅲ)解:曲线y =f (x )与直线y =−(x −t 2)−63有三个互异的公共点等价于关于x 的方程(x −t 2+d )(x −t 2)(x −t 2 −d )+(x −t 2)+ 63=0有三个互异的实数解,令u =x −t 2,可得u 3+(1−d 2)u +63=0.学科.网设函数g (x )=x 3+(1−d 2)x +63,则曲线y =f (x )与直线y =−(x −t 2)−63有三个互异的公共点等价于函数y =g (x )有三个零点.()g'x =3x 3+(1−d 2).当d 2≤1时,()g'x ≥0,这时()g x 在R 上单调递增,不合题意.当d 2>1时,()g'x =0,解得x 1=213d --,x 2=213d -.易得,g (x )在(−∞,x 1)上单调递增,在[x 1,x 2]上单调递减,在(x 2,+∞)上单调递增.g (x )的极大值g (x 1)=g (213d --)=32223(1)639d -+>0. g (x )的极小值g (x 2)=g (213d -)=−32223(1)639d -+. 若g (x 2)≥0,由g (x )的单调性可知函数y =g (x )至多有两个零点,不合题意.若2()0,g x <即322(1)27d ->,也就是||10d >,此时2||d x >,(||)||630,g d d =+>且312||,(2||)6||2||636210630d x g d d d -<-=--+<-+<,从而由()g x 的单调性,可知函数()y g x =在区间1122(2||,),(,),(,||)d x x x x d -内各有一个零点,符合题意.所以,d 的取值范围是(,10)(10,)-∞-+∞ .。
2018年高考文科数学天津卷(含答案与解析)

数学试卷 第1页(共14页) 数学试卷 第2页(共14页)绝密★启用前天津市2018年普通高等学校招生全国统一考试文科数学第I 卷本试卷分为第I 卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试用时120分钟. 参考公式:·如果事件A ,B 互斥,那么()()()P AB P A P B =+.·棱柱的体积公式V Sh =.其中S 表示棱柱的底面面积,h 表示棱柱的高.·棱锥的体积公式13V Sh =,其中S 表示棱锥的底面积,h 表示棱锥的高.一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合{1,2,3,4}A =,{1,0,2,3}B =-,{|12}C x x =∈-<R ≤,则()A B C =( )A .{1,1}-B .{0,1}C .{1,0,1}-D .{2,3,4}2.设变量x ,y 满足约束条件5,24,1,0,x y x y x y y +⎧⎪-⎪⎨-+⎪⎪⎩≤≤≤≥则目标函数35z x y =+的最大值为 ( )A .6B .19C .21D .45 3.设x ∈R ,则“38x >”是“||2x >”的( )A .充分而不必要条件B .必要而不充分条件C .充要条件D .既不充分也不必要条件4.阅读如图所示的程序框图,运行相应的程序,若输入N 的值为20,则输出T 的值为( )A .1B .2C .3D .4 5.已知37log 2a =,131()4b =,131log 5c =,则a ,b ,c 的大小关系为( )A .a b c >>B .b a c >>C .c b a >>D .c a b >>6.将函数sin 25y x π⎛⎫=+ ⎪⎝⎭的图象向右平移10π个单位长度,所得图象对应的函数( )A .在区间,44ππ⎡⎤-⎢⎥⎣⎦上单调递增B .在区间,04π⎡⎤⎢⎥⎣⎦上单调递减C .在区间,42ππ⎡⎤⎢⎥⎣⎦上单调递增D .在区间,2π⎡⎤π⎢⎥⎣⎦上单调递减毕业学校_____________ 姓名________________ 考生号________________________________ _____________-------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------数学试卷 第3页(共14页) 数学试卷 第4页(共14页)7.已知双曲线22221(0,0)x y a b a b-=>>的离心率为2,过右焦点且垂直于x 轴的直线与双曲线交于A ,B 两点.设A ,B 到双曲线的同一条渐近线的距离分别为1d 和2d ,且126d d +=,则双曲线的方程为( )A .22139x y -=B .22193x y -= C .221412x y -=D .221124x y -= 8.在如图的平面图形中,已知1OM =,2ON =,120MON ∠=︒,2BM MA =,2CN NA =则BC OM 的值为( )A .-15B .-9C .-6D .0第Ⅱ卷二、填空题:本大题共6小题,每小题5分,共30分.9.i 是虚数单位,复数67i12i+=+ . 10.已知函数()e x f x lnx =,()f x '为()f x 的导函数,则(1)f '的值为 . 11.如图,已知正方体1111–ABCD A B C D 的棱长为1,则四棱柱111–A BB D D 的体积为 .12.在平面直角坐标系中,经过三点(0,0),(1,1),(2,0)的圆的方程为 .13.已知a ,b ∈R ,且–360a b +=,则218a b+的最小值为 . 14.已知a ∈R ,函数2222,0,()22,0x x a x f x x x a x ⎧++-⎪=⎨-+->⎪⎩≤.若对任意)[3,x ∈-+∞,()||f x x ≤恒成立,则a 的取值范围是 .三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤. 15.(本小题满分13分)已知某校甲、乙、丙三个年级的学生志愿者人数分别为240,160,160.现采用分层抽样的方法从中抽取7名同学去某敬老院参加献爱心活动. (Ⅰ)应从甲、乙、丙三个年级的学生志愿者中分别抽取多少人?(Ⅱ)设抽出的7名同学分别用A ,B ,C ,D ,E ,F ,G 表示,现从中随机抽取2名同学承担敬老院的卫生工作。
2018年全国高等院校同一招生考试天津文科数学试卷(含答案)

绝密★启用前2018年普通高等学校招生全国统一考试(天津卷)数学(文史类)本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试用时120分钟。
第Ⅰ卷1至2页,第Ⅱ卷3至5页。
答卷前,考生务必将自己的姓名、准考证号填写在答题考上,并在规定位置粘贴考试用条形码。
答卷时,考生务必将答案涂写在答题卡上,答在试卷上的无效。
考试结束后,将本试卷和答题卡一并交回。
祝各位考生考试顺利!第Ⅰ卷注意事项:1.每小题选出答案后,用铅笔将答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
2.本卷共8小题,每小题5分,共40分。
参考公式:·如果事件 A ,B 互斥,那么 P (A ∪B )=P (A )+P (B ). ·棱柱的体积公式V =Sh . 其中S 表示棱柱的底面面积,h 表示棱柱的高. ·棱锥的体积公式13V Sh =,其中S 表示棱锥的底面积,h 表示棱锥的高. 一.选择题:在每小题给出的四个选项中,只有一项是符合题目要求的. (1)设集合{1,2,3,4}A =,{1,0,2,3}B =-,{|12}C x x =∈-≤<R ,则()A B C =(A ){1,1}-(B ){0,1}(C ){1,0,1}-(D ){2,3,4}(2)设变量,x y 满足约束条件52410x y x y x y y +≤⎧⎪-≤⎪⎨-+≤⎪⎪≥⎩,,,,则目标函数35z x y =+的最大值为(A )6 (B )19 (C )21(D )45(3)设x ∈R ,则“38x >”是“||2x >” 的(A )充分而不必要条件 (B )必要而不充分条件 (C )充要条件(D )既不充分也不必要条件(4)阅读如图所示的程序框图,运行相应的程序,若输入N 的值为20,则输出T 的值为(A )1(B )2(C )3(D )4(5)已知13313711log ,(),log 245a b c ===,则,,a b c 的大小关系为(A )a b c >> (B )b a c >> (C )c b a >>(D )c a b >>(6)将函数sin(2)5y x π=+的图象向右平移10π个单位长度,所得图象对应的函数 (A )在区间[,]44ππ- 上单调递增 (B )在区间[,0]4π上单调递减(C )在区间[,]42ππ 上单调递增 (D )在区间[,]2ππ 上单调递减(7)已知双曲线22221(0,0)x y a b a b-=>> 的离心率为2,过右焦点且垂直于x 轴的直线与双曲线交于,A B两点.设,A B 到双曲线的同一条渐近线的距离分别为1d 和2d ,且126,d d += 则双曲线的方程为(A )22139x y -=(B )22193x y -=(C )221412x y -=(D )221124x y -= (8)在如图的平面图形中,已知 1.2,120OM ON MON ==∠=,2,2,BM MA CN NA ==则·BC OM 的值为(A )15- (B )9- (C )6-(D )0第Ⅱ卷注意事项:1.用黑色墨水的钢笔或签字笔将答案写在答题卡上。
2018天津高考文科数学试卷含答案

2018天津文一.选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合A ={1,2,3,4},B ={-1,0,2,3},C ={x ∈R|-1≤x <2},则(A ∪B )∩C = A .{-1,1} B .{0,1} C .{-1,0,1} D .{2,3,4}【解析】由并集的定义可得:A ∪B ={-1,0,1,2,3,4},结合交集的定义可知:(A ∪B )∩C ={-1,0,1}.本题选择C 选项.点睛:本题主要考查并集运算、交集运算等知识,意在考查学生的计算求解能力. 2.设变量x ,y 满足约束条件⎩⎪⎨⎪⎧x +y ≤5,2x -y ≤4,-x +y ≤1,y ≥0,则目标函数z =3x +5y 的最大值为A . 6B . 19C . 21D . 45【解析】绘制不等式组表示的平面区域如图所示,结合目标函数的几何意义可知目标函数在点A 处取得最大值,联立直线方程:⎩⎪⎨⎪⎧-x +y =1,x +y =5,,可得点A 的坐标为:A (2,3),据此可知目标函数的最大值为:z max =3×2+5×3=21.本题选择C 选项.3.设x ∈R ,则“x 3>8”是“|x |>2” 的 A . 充分而不必要条件 B . 必要而不充分条件 C . 充要条件 D . 既不充分也不必要条件【解析】求解不等式x 3>8可得x >2,求解绝对值不等式|x |>2可得x >2或x <-2,据此可知:“x 3>8”是“|x |>2”的充分而不必要条件.本题选择A 选项.点睛:本题主要考查绝对值不等式的解法,充分不必要条件的判断等知识,意在考查学生的转化能力和计算求解能力.4.阅读如图所示的程序框图,运行相应的程序,若输入N 的值为20,则输出T 的值为A . 1B . 2C . 3D . 4【解析】结合流程图运行程序如下:首先初始化数据:N =20,i =2,T =0,Ni =10,结果为整数,执行T =T +1=1,i =i +1=3,此时不满足i ≥5;N i =203,结果不为整数,执行i =i +1=4,此时不满足i ≥5;Ni =5,结果为整数,执行T =T +1=2,i =i +1=5,此时满足i ≥5;跳出循环,输出T =2.本题选择B 选项.点睛:识别、运行程序框图和完善程序框图的思路: (1)要明确程序框图的顺序结构、条件结构和循环结构. (2)要识别、运行程序框图,理解框图所解决的实际问题. (3)按照题目的要求完成解答并验证.5.已知a =log 372,b =(14)13,c =log 1315,则a ,b ,c 的大小关系为A .a >b >cB .b >a >cC .c >b >aD .c >a >b【解析】由题意可知:log 33<log 372<log 39,即1<a <2,0<(14)1<(14)13<(14)0,即0<b <1,log 1315=log 35>log 372,即c >a ,综上可得:c >a >b .本题选择D 选项.点睛:对于指数幂的大小的比较,我们通常都是运用指数函数的单调性,但很多时候,因幂的底数或指数不相同,不能直接利用函数的单调性进行比较.这就必须掌握一些特殊方法.在进行指数幂的大小比较时,若底数不同,则首先考虑将其转化成同底数,然后再根据指数函数的单调性进行判断.对于不同底而同指数的指数幂的大小的比较,利用图像法求解,既快捷,又准确. 6.将函数y =sin(2x +π5)的图像向右平移π10个单位长度,所得图像对应的函数单调增区间是A .在区间[-π4,π4]上单调递增B .在区间[-π4,0]上单调递减C .在区间[π4,π2]上单调递增D .在区间[π2,π]上单调递减【解析】把函数y =sin(2x +π5)的图像向右平移π10个单位长度得函数g (x )=sin[2(x -π10)+π5]=sin 2x的图像,由-π2+2k π≤2x ≤π2+2k π(k ∈Z )得-π4+k π≤x ≤π4+k π(k ∈Z ),故函数的单调增区间为[-π4+k π,π4+k π],k ∈Z .点睛:本题主要考查三角函数的平移变换,三角函数的单调区间等知识,意在考查学生的转化能力和计算求解能力.7.已知双曲线x 2a 2-y 2b 2=1(a >0,b >0)的离心率为2,过右焦点且垂直于x 轴的直线与双曲线交于A ,B 两点.设A ,B 到双曲线的同一条渐近线的距离分别为d 1和d 2,且d 1+d 2=6,则双曲线的方程为A .x 23-y 29=1B .x 29-y 23=1C .x 24-y 212=1D . x 212-y 24=1【解析】由题意不妨设A (c ,b 2a ),B (c ,-b 2a ),不妨设双曲线的一条渐近线方程为y =ba x ,即bx -ay =0,则d 1=|bc -b 2|a 2+b 2,d 2=|bc +b 2|a 2+b 2,故d 1+d 2=|bc -b 2|a 2+b 2+|bc +b 2|a 2+b 2=bc -b 2+bc +b 2c =2b =6,故b =3.又ca =c 2a 2=a 2+b 2a 2=1+b 2a 2=2,故b 2=3a 2,得a 2=3.故双曲线的方程为x 23-y 29=1.点睛:求双曲线的标准方程的基本方法是待定系数法.具体过程是先定形,再定量,即先确定双曲线标准方程的形式,然后再根据a ,b ,c ,e 及渐近线之间的关系,求出a ,b 的值.如果已知双曲线的渐近线方程,求双曲线的标准方程,可利用有公共渐近线的双曲线方程为x 2a 2+y 2b 2=λ(λ≠0),再由条件求出λ的值即可.8.在如图的平面图形中,已知OM =1,ON =2,∠MON =120°,BM →=2MA →,CN →=2NA →,则BC →·OM→的值为( )【解析】由BM →=2MA →,可知|BM →||MA →|=2,故|BA →||MA →|=3,由CN →=2NA →,可知|CN →||NA →|=2,故|CA →||NA →|=3,故|BA →||MA →|=|CA →||NA →|=3,连接MN ,则BC ∥MN 且|BC →|=3|MN →|.故BC →=3MN →=3(ON →-OM →),故BC →·OM →=3(ON →-OM →)·OM →=3(ON →·OM →-OM →2)=3(|ON →|·|OM →|cos 120°-|OM →|2)=-6.故选C .点睛:求两个向量的数量积有三种方法:利用定义;利用向量的坐标运算;利用数量积的几何意义.具体应用时可根据已知条件的特征来选择,同时要注意数量积运算律的应用. 二.填空题:本大题共6小题,每小题5分,共30分. 9.i 是虚数单位,复数6+7i1+2i =___________.【解析】由复数的运算法则得:6+7i 1+2i =(6+7i )(1-2i )(1+2i )(1-2i )=20-5i5=4-i .点睛:本题主要考查复数的运算法则及其应用,意在考查学生的转化能力和计算求解能力. 10.已知函数f (x )=e x ln x ,f ′(x )为f (x )的导函数,则f ′(1)的值为__________. 【解析】由题意得,f ′(x )=e x ln x +e x ·1x,则f ′(1)=e .点睛:本题主要考查导数的运算法则,基本初等函数的导数公式等知识,意在考查学生的转化能力和计算求解能力.11. 如图,已知正方体ABCD –A 1B 1C 1D 1的棱长为1,则四棱柱A 1–BB 1D 1D 的体积为__________.【解析】法一 连接A 1C 1交B 1D 1于点E ,则A 1E ⊥B 1D 1,A 1E ⊥BB 1,则A 1E ⊥平面BB 1D 1D ,所以A 1E 为四棱锥A 1-BB 1D 1D 的高,且A 1E =22,矩形BB 1D 1D 的长和宽分别为2,1,故V A 1-BB 1D 1D =13×1×2×22=13.法二 连接BD 1,则四棱锥A 1-BB 1D 1D 分成两个三棱锥B -A 1DD 1与B -A 1B 1D 1,V A 1-BB 1D 1D =V B-A 1DD 1+V B -A 1B 1D 1=13×12×1×1×1+13×12×1×1×1=13.点睛:本题主要考查棱锥体积的计算,空间想象能力等知识,意在考查学生的转化能力和计算求解能力.12.在平面直角坐标系中,经过三点(0,0),(1,1),(2,0)的圆的方程为__________.【解析】法一 设圆的方程为x 2+y 2+Dx +Ey +F =0(D 2+E 2-4F >0),则⎩⎪⎨⎪⎧F =0,1+1+D +E +F =0,4+2D +F =0,解得D =-2,E =0,F =0,故圆的方程为x 2+y 2-2x =0. 法二 设O (0,0),A (1,1),B (2,0),所以k OA =1,k AB =1-01-2=-1,所以k OA ·k AB =-1,所以OA ⊥AB .所以OB 为所求圆的直径,所以圆心坐标为(1,0),半径为1.故所求圆的方程为(x -1)2+y 2=1,即x 2+y 2-2x =0.点睛:求圆的方程,主要有两种方法:(1)几何法:具体过程中要用到初中有关圆的一些常用性质和定理.如:①圆心在过切点且与切线垂直的直线上;②圆心在任意弦的中垂线上;③两圆相切时,切点与两圆心三点共线.(2)待定系数法:根据条件设出圆的方程,再由题目给出的条件,列出等式,求出相关量.一般地,与圆心和半径有关,选择标准式,否则,选择一般式.不论是哪种形式,都要确定三个独立参数,所以应该有三个独立等式.13.已知a ,b ∈R ,且a -3b +6=0,则2a +18b 的最小值为__________.【解析】由题知a -3b =-6,因为2a >0,8b >0,所以2a +18b ≥2×2a ×18b =2×2a -3b =22-6=14,当且仅当2a =18b ,即a =-3,b =1时取等号. 点睛:在应用基本不等式求最值时,要把握不等式成立的三个条件,就是“一正——各项均为正;二定——积或和为定值;三相等——等号能否取得”,若忽略了某个条件,就会出现错误.14.已知a ∈R ,函数f (x )=⎩⎪⎨⎪⎧x 2+2x +a -2,x ≤0,-x 2+2x -2a ,x >0.若对任意x ∈[-3,+∞),f (x )≤|x |恒成立,则a的取值范围是__________.【解析】当-3≤x ≤0时,f (x )≤|x |恒成立等价转化为x 2+2x +a -2≤-x 恒成立,即a ≤-x 2-3x +2恒成立,所以a ≤(-x 2-3x +2)min =2;当x >0时,f (x )≤|x |恒成立等价转化为-x 2+2x -2a ≤x 恒成立,即a ≥-x 2+x 2恒成立,所以a ≥(-x 2+x 2)min =18.综上,a 的取值范围是[18,2].点睛:对于恒成立问题,常用到以下两个结论:(1)a ≥f (x )恒成立⇔a ≥f (x )max ;(2)a ≤f (x )恒成立⇔a ≤f (x )min .有关二次函数的问题,数形结合,密切联系图像是探求解题思路的有效方法.一般从:①开口方向;②对称轴位置;③判别式;④端点函数值符号四个方面分析.三.解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤. 15.已知某校甲、乙、丙三个年级的学生志愿者人数分别为240,160,160.现采用分层抽样的方法从中抽取7名同学去某敬老院参加献爱心活动.(Ⅰ)应从甲、乙、丙三个年级的学生志愿者中分别抽取多少人?(Ⅱ)设抽出的7名同学分别用A ,B ,C ,D ,E ,F ,G 表示,现从中随机抽取2名同学承担敬老院的卫生工作.(i )试用所给字母列举出所有可能的抽取结果;(ii )设M 为事件“抽取的2名同学来自同一年级”,求事件M 发生的概率.【解析】(Ⅰ)由已知,甲、乙、丙三个年级的学生志愿者人数之比为3∶2∶2,由于采用分层抽样的方法从中抽取7名同学,因此应从甲、乙、丙三个年级的学生志愿者中分别抽取3人,2人,2人.(Ⅱ)(i )从抽出的7名同学中随机抽取2名同学的所有可能结果为{A ,B },{A ,C },{A ,D },{A ,E },{A ,F },{A ,G },{B ,C },{B ,D },{B ,E },{B ,F },{B ,G },{C ,D },{C ,E },{C ,F },{C ,G },{D ,E },{D ,F },{D ,G },{E ,F },{E ,G },{F ,G },共21种.(ii )由(Ⅰ),不妨设抽出的7名同学中,来自甲年级的是A ,B ,C ,来自乙年级的是D ,E ,来自丙年级的是F ,G ,则从抽出的7名同学中随机抽取的2名同学来自同一年级的所有可能结果为{A ,B },{A ,C },{B ,C },{D ,E },{F ,G },共5种.所以,事件M 发生的概率为P (M )=521.点睛:本小题主要考查随机抽样、用列举法计算随机事件所含的基本事件数、古典概型及其概率计算公式等基本知识.考查运用概率知识解决简单实际问题的能力.16.△ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c .已知b sin A =a cos(B -π6).(1)求角B 的大小;(2)设a =2,c =3,求b 和sin(2A -B )的值. 【解析】(1)在△ABC 中,由正弦定理a sin A =b sin B ,得b sin A =a sin B ,又由b sin A =a cos(B -π6),得a sin B =a cos(B -π6),即sin B =cos(B -π6),可得tan B =3.又B ∈(0,π),可得B =π3.(2)在△ABC 中,由余弦定理及a =2,c =3,B =π3,有b 2=a 2+c 2-2ac cos B =7,故b =7.由b sinA =a cos(B -π6),可得sin A =37.因a <c ,故cos A =27.因此sin 2A =2sin A cos A =437,cos 2A=2cos 2A -1=17.所以,sin(2A -B )=sin 2A cos B -cos 2A sin B =437×12-17×32=3314.点睛:在处理三角形中的边角关系时,一般全部化为角的关系,或全部化为边的关系.题中若出现边的一次式一般采用到正弦定理,出现边的二次式一般采用到余弦定理.应用正、余弦定理时,注意公式变式的应用.解决三角形问题时,注意角的限制范围.17.如图,在四面体ABCD 中,△ABC 是等边三角形,平面ABC ⊥平面ABD ,点M 为棱AB 的中点,AB =2,AD =23,∠BAD =90°. (Ⅰ)求证:AD ⊥BC ;(Ⅱ)求异面直线BC 与MD 所成角的余弦值; (Ⅲ)求直线CD 与平面ABD 所成角的正弦值.【解析】(Ⅰ)由平面ABC ⊥平面ABD ,平面ABC ∩平面ABD =AB ,AD ⊥AB ,可得AD ⊥平面ABC ,故AD ⊥BC .(Ⅱ)取棱AC 的中点N ,连接MN ,ND .又因为M 为棱AB 的中点,故MN ∥BC .所以∠DMN (或其补角)为异面直线BC 与MD 所成的角.在Rt △DAM 中,AM =1,故DM =13.因为AD ⊥平面ABC ,故AD ⊥AC .在Rt △DAN 中,AN =1,故DN =13.在等腰三角形DMN 中,MN =1,可得cos ∠DMN =13/26.所以,异面直线BC 与MD 所成角的余弦值为13/26.(Ⅲ)连接CM .因为△ABC 为等边三角形,M 为边AB 的中点,故CM ⊥AB ,CM =3.又因为平面ABC ⊥平面ABD ,而CM ⊂平面ABC ,故CM ⊥平面ABD .所以,∠CDM 为直线CD 与平面ABD 所成的角.在Rt △CAD 中,CD =4.在Rt △CMD 中,sin ∠CDM =34.所以,直线CD 与平面ABD所成角的正弦值为34. 点睛:本小题主要考查异面直线所成的角、直线与平面所成的角、平面与平面垂直等基础知识.考查空间想象能力、运算求解能力和推理论证能力.18.设{a n }是等差数列,其前n 项和为S n (n ∈N *);{b n }是等比数列,公比大于0,其前n 项和为T n (n ∈N *).已知b 1=1,b 3=b 2+2,b 4=a 3+a 5,b 5=a 4+2a 6. (1)求S n 和T n ;(2)若S n +(T 1+T 2+…+T n )=a n +4b n ,求正整数n 的值.【解析】(1)设等比数列{b n }的公比为q (q >0).由b 1=1,b 3=b 2+2,可得q 2-q -2=0.因为q >0,可得q =2,故b n =2n -1.所以T n =1-2n 1-2=2n-1.设等差数列{a n }的公差为d .由b 4=a 3+a 5,可得a 1+3d =4.由b 5=a 4+2a 6,可得3a 1+13d =16,从而a 1=1,d =1,故a n =n .所以S n =n (n +1)2.(2)由(1),有T 1+T 2+…+T n =(21+22+…+2n )-n =2×(1-2n )1-2-n =2n +1-n -2.由S n +(T 1+T 2+…+T n )=a n +4b n 可得n (n +1)2+2n +1-n -2=n +2n +1,整理得n 2-3n -4=0,解得n =-1(舍),或n =4.所以n 的值为4.19.设椭圆x 2a 2+y 2b 2=1(a >b >0)的右顶点为A ,上顶点为B .已知椭圆的离心率为53,|AB |=13.(1)求椭圆的方程;(2)设直线l :y =kx (k <0)与椭圆交于P ,Q 两点,l 与直线AB 交于点M ,且点P ,M 均在第四象限.若△BPM 的面积是△BPQ 面积的2倍,求k 的值.解 (1)设椭圆的焦距为2c ,由已知有c 2a 2=59,又由a 2=b 2+c 2,可得2a =3b .由|AB |=a 2+b 2=13,从而a =3,b =2.所以,椭圆的方程为x 29+y 24=1.(2)设点P 的坐标为(x 1,y 1),点M 的坐标为(x 2,y 2),由题意,x 2>x 1>0,点Q 的坐标为(-x 1,-y 1).由△BPM 的面积是△BPQ 面积的2倍,可得|PM |=2|PQ |,从而x 2-x 1=2[x 1-(-x 1)],即x 2=5x 1.易知直线AB 的方程为2x +3y =6,由方程组⎩⎪⎨⎪⎧2x +3y =6,y =kx ,消去y ,可得x 2=63k +2.由方程组⎩⎪⎨⎪⎧x 29+y 24=1,y =kx ,消去y ,可得x 1=69k 2+4.由x 2=5x 1,可得9k 2+4=5(3k +2),两边平方,整理得18k 2+25k +8=0,解得k =-89,或k =-12.当k =-89时,x 2=-9<0,不合题意,舍去;当k=-12时,x 2=12,x 1=125,符合题意.所以,k 的值为-12.20.设函数f (x )=(x -t 1)(x -t 2)(x -t 3),其中t 1,t 2,t 3∈R ,且t 1,t 2,t 3是公差为d 的等差数列. (1)若t 2=0,d =1,求曲线y =f (x )在点(0,f (0))处的切线方程; (2)若d =3,求f (x )的极值.(III)若曲线y =f (x )与直线y =-(x -t 2)-63有三个互异的公共点,求d 的取值范围.【解析】(1)由已知,得f (x )=x (x -1)(x +1)=x 3-x ,故f ′(x )=3x 2-1.因此f (0)=0,f ′(0)=-1,又因为曲线y =f (x )在点(0,f (0))处的切线方程为y -f (0)=f ′(0)(x -0),故所求切线方程为x +y =0.(2)由已知得f (x )=(x -t 2+3)(x -t 2)(x -t 2-3)=(x -t 2)3-9(x -t 2)=x 3-3t 2x 2+(3t 22-9)x -t 32+9t 2.故f ′(x )=3x 2-6t 2x +3t 22-9.令f ′(x )=0,解得x =t 2-3,或x =t 2+3.当x 变化时,f ′(x ),f (x )的变化情况如下表:所以函数f (x )的极大值为f (t 2-3)=(-3)3-9×(-3)=63;函数f (x )的极小值为f (t 2+3)=(3)3-9×3=-63.(Ⅲ)曲线y =f (x )与直线y =-(x -t 2)-63有三个互异的公共点等价于关于x 的方程(x -t 2+d )(x -t 2)(x -t 2-d )+(x -t 2)+63=0有三个互异的实数解,令u =x -t 2,可得u 3+(1-d 2)u +63=0. 设函数g (x )=x 3+(1-d 2)x +63,则曲线y =f (x )与直线y =-(x -t 2)-63有三个互异的公共点等价于函数y =g (x )有三个零点.g ′(x )=3x 3+(1-d 2).当d 2≤1时,g ′(x )≥0,这时g (x )在R 上单调递增,不合题意.当d 2>1时,g ′(x )=0,解得x 1=-d 2-13,x 2=d 2-13.易得,g (x )在(-∞,x 1)上单调递增,在[x 1,x 2]上单调递减,在(x 2,+∞)上单调递增.g (x )的极大值g (x 1)=g (-d 2-13)=23(d 2-1)329+63>0.g (x )的极小值g (x 2)=g (d 2-13)=-23(d 2-1)329+63.若g (x 2)≥0,由g (x )的单调性可知函数y =g (x )至多有两个零点,不合题意.若g (x 2)<0,即(d 2-1)32>27,也就是|d |>10,此时|d |>x 2,g (|d |)=|d |+63>0,且-2|d |<x 1,g (-2|d |)=-6|d |3-2|d |+63<-6210+63<0,从而由g (x )的单调性,可知函数g (x )在区间(-2|d |,x 1),(x 1,x 2),(x 2,|d |)内各有一个零点,符合题意. 所以,d 的取值范围是(-∞,-10)∪(10,+∞).点睛:导数是研究函数的单调性、极值(最值)最有效的工具,而函数是高中数学中重要的知识点,所以在历届高考中,对导数的应用的考查都非常突出 ,本专题在高考中的命题方向及命题角度 从高考来看,对导数的应用的考查主要从以下几个角度进行: (1)考查导数的几何意义,往往与解析几何、微积分相联系.(2)利用导数求函数的单调区间,判断单调性;已知单调性,求参数.(3)利用导数求函数的最值(极值),解决生活中的优化问题.(4)考查数形结合思想的应用.。
2018年高考文科数学天津卷及答案解析

数学试卷 第1页(共14页) 数学试卷 第2页(共14页)绝密★启用前天津市2018年普通高等学校招生全国统一考试文科数学第I 卷本试卷分为第I 卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试用时120分钟. 参考公式:·如果事件A ,B 互斥,那么()()()P AB P A P B =+.·棱柱的体积公式V Sh =.其中S 表示棱柱的底面面积,h 表示棱柱的高.·棱锥的体积公式13V Sh =,其中S 表示棱锥的底面积,h 表示棱锥的高.一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合{1,2,3,4}A =,{1,0,2,3}B =-,{|12}C x x =∈-<R ≤,则()A B C =( )A .{1,1}-B .{0,1}C .{1,0,1}-D .{2,3,4}2.设变量x ,y 满足约束条件5,24,1,0,x y x y x y y +⎧⎪-⎪⎨-+⎪⎪⎩≤≤≤≥则目标函数35z x y =+的最大值为 ( )A .6B .19C .21D .45 3.设x ∈R ,则“38x >”是“||2x >”的( )A .充分而不必要条件B .必要而不充分条件C .充要条件D .既不充分也不必要条件4.阅读如图所示的程序框图,运行相应的程序,若输入N 的值为20,则输出T 的值为( )A .1B .2C .3D .4 5.已知37log 2a =,131()4b =,131log 5c =,则a ,b ,c 的大小关系为( )A .a b c >>B .b a c >>C .c b a >>D .c a b >>6.将函数sin 25y x π⎛⎫=+ ⎪⎝⎭的图象向右平移10π个单位长度,所得图象对应的函数( )A .在区间,44ππ⎡⎤-⎢⎥⎣⎦上单调递增B .在区间,04π⎡⎤⎢⎥⎣⎦上单调递减C .在区间,42ππ⎡⎤⎢⎥⎣⎦上单调递增D .在区间,2π⎡⎤π⎢⎥⎣⎦上单调递减毕业学校_____________ 姓名________________ 考生号________________________________ _____________-------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------数学试卷 第3页(共14页) 数学试卷 第4页(共14页)7.已知双曲线22221(0,0)x y a b a b-=>>的离心率为2,过右焦点且垂直于x 轴的直线与双曲线交于A ,B 两点.设A ,B 到双曲线的同一条渐近线的距离分别为1d 和2d ,且126d d +=,则双曲线的方程为( )A .22139x y -=B .22193x y -= C .221412x y -=D .221124x y -= 8.在如图的平面图形中,已知1OM =,2ON =,120MON ∠=︒,2BM MA =,2CN NA =则BC OM 的值为( )A .-15B .-9C .-6D .0第Ⅱ卷二、填空题:本大题共6小题,每小题5分,共30分.9.i 是虚数单位,复数67i12i+=+ . 10.已知函数()e x f x lnx =,()f x '为()f x 的导函数,则(1)f '的值为 . 11.如图,已知正方体1111–ABCD A B C D 的棱长为1,则四棱柱111–A BB D D 的体积为 .12.在平面直角坐标系中,经过三点(0,0),(1,1),(2,0)的圆的方程为 .13.已知a ,b ∈R ,且–360a b +=,则218a b+的最小值为 . 14.已知a ∈R ,函数2222,0,()22,0x x a x f x x x a x ⎧++-⎪=⎨-+->⎪⎩≤.若对任意)[3,x ∈-+∞,()||f x x ≤恒成立,则a 的取值范围是 .三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤. 15.(本小题满分13分)已知某校甲、乙、丙三个年级的学生志愿者人数分别为240,160,160.现采用分层抽样的方法从中抽取7名同学去某敬老院参加献爱心活动. (Ⅰ)应从甲、乙、丙三个年级的学生志愿者中分别抽取多少人?(Ⅱ)设抽出的7名同学分别用A ,B ,C ,D ,E ,F ,G 表示,现从中随机抽取2名同学承担敬老院的卫生工作。
2018年高考文科数学天津卷-答案

天津市2018年普通高等学校招生全国统一考试文科数学答案解析一、选择题 1.【答案】C【解析】由于1,0,1,2,},4{3A B =- ,所以{()1,0,1}A B C -= . 【考点】集合的运算 2.【答案】C【解析】做出不等式组5,24,1,0x y x y x y y +⎧⎪-⎪⎨-+⎪⎪⎩≤≤≤≥,所表示的可行域,其是由(00)O ,,(2,0)A ,(3,2)B ,(2,3)C ,(0,1)D 围成的五边形区域(包括边界),对于目标函数35x x y =+;结合图象可知过点C 时取得最大值,最大值为325321⨯+⨯=. 【考点】简单的线性规划 3.【答案】A【解析】由38>解得2x >;由||2x >解得2x <-或2x >,所以“8x >”是“||2x >”的充分而不必要条件。
【考点】不等式的求解、充分必要条件的判定 4.【答案】B【解析】输人2020N i T ===,,,此时10Ni=是整数,则有011213T i =+==+=,,此时不满足条件5i ≥;接下来有203N i =不是整数,则有314i =+=,此时.不满足条件5i ≥;接下来有5Ni=是整数,则有112415T i =+==+=,,此时满足条件5i ≥,结束循环,输出2T =. 【考点】算法的程序框图.模拟程序框图的运行 5.【答案】D【解析】根据函数的图象与性质可知13133331711log log 5log log 315244⎛⎫⎛⎫=>>==> ⎪ ⎪⎝⎭⎝⎭,则c a b >>. 【考点】代数值的大小比较、函数的图象与性质 6.【答案】A【解析】将函数πsin 25y x ⎛⎫=+⎪⎝⎭的图象向右平移π10个单位长度得到ππsin 2sin 2105y x x ⎡⎤⎛⎫=-+= ⎪⎢⎥⎝⎭⎣⎦由ππ2π22π+,22k x k k -+∈Z ≤≤,解得ππππ+,44k x k k -+∈Z ≤≤,当0k =时,则知函数在区间ππ,44⎡⎤-⎢⎥⎣⎦上单调递增.【考点】三角函数图象的平移变换、三角函数的图象与性质 7.【答案】A【解析】由双曲线的离心率2c e a==,可得2c a =,则知b =,将2x a =代人双曲线222213x y a a -=,可得3y a =±,设点(2,3)(2,3)A d a B a a -,0y +=,可得12d d ====,,所以126d d +===,解得a =,故双曲线的方程为22139x y -=. 【考点】双曲线的方程与几何性质、点到直线的距离公式 8.【答案】C【解析】根据题目可得:22((33)3()33()33321cos120=31=6BC OM AC AB OM AN AM OM AN AM OMMN OM ON OM OM ON OM OM =-=-=-==-=-=⨯⨯⨯︒⨯-) 【考点】平面向量的线性运算与数量积 二、填空题 9.【答案】4i - 【解析】由题可得67i (67i)(12i)205i4i 12i (12i)(12i)5++--===-++-. 【考点】复数的四则运算 10.【答案】e【解析】由于()e ln x f x x =则有1()e ln e x x f x x x '=+ ,所以111(1)e ln1e e 1f '=+= . 【考点】导数及其应用、函数值的求解 11.13【答案】【解析】由题可知四棱锥111A BB D D -,1111A BB D D -的体为11133V =⨯=. 【考点】空间几何体的性质、空间几何体的体积12.【答案】2220x y x +-=【解析】由于圆经过三点(0,0)(1,1)(2,0)O A B ,,,可知OA AB ⊥,则知OB 为圆的直径,则圆心(1,0)C ,半径1r =,可得圆的方程为22(1)1x y -+=,即2220x y x +-=. 【考点】圆的方程13.【答案】14【解析】由于360a b -+=;可得366a -=-,结合基本不等式可得33112222284a ab b --+=+==== ≥,当且仅当322a b -=,即33a b =-=-. 【考点】基本不等式 14.【答案】1,28⎡⎤⎢⎥⎣⎦【解析】当[]3,0-时,由()||f x x ≤恒成立可得22x x a x ++-≤-即232x x a ++-≤0,结合图象可知99200020a a -+-⎧⎨++-⎩≤≤,解得2a ≤;当·(0,)x ∈+∞时,由()||f x x ≤恒成立可得222x x a x -+-≤,即²20x x a -+≥,结合图象可知2412(1)041a ⨯⨯--⨯≥,解得a 18a ≥;综上分析可得128a ≤≤. 【考点】分段函数、函数的图象与性质、不等式恒成立 三、解答题15.【答案】(Ⅰ)解:由已知,甲、乙、丙三个年级的学生志愿者人数之比为3:2:2,由于采用分层抽样的方法从中抽取7名同学,因此应从甲、乙、丙三个年级的学生志愿者中分别抽取3人,2人,2人. (Ⅱ)(ⅰ)解:从抽出的7名同学中随机抽取2名同学的所有可能结果为{A ,B },{A ,C },{A ,D },{A ,E },{A ,F },{A ,G },{B ,C },{B ,D },{B ,E },{B ,F },{B ,G },{C ,D },{C ,E },{C ,F },{C ,G },{D ,E },{D ,F },{D ,G },{E ,F },{E ,G },{F ,G },共21种.(ⅱ)解:由(Ⅰ),不妨设抽出的7名同学中,来自甲年级的是A ,B ,C ,来自乙年级的是D ,E ,来自丙年级的是F ,G ,则从抽出的7名同学中随机抽取的2名同学来自同一年级的所有可能结果为{A ,B },{A ,C },{B ,C },{D ,E },{F ,G },共5种. 所以,事件M 发生的概率为5(2)1P M =. 【考点】随机抽样、用列举法计算随机事件所含的基本事件数、古典概型及其概率计算公式等基本知识 16.【答案】(Ⅰ)解:在ABC △中,由正弦定理sin sin a bA B=,可得sin sin b A a B =,又由πsin cos 6b A a B ⎛⎫=- ⎪⎝⎭,得πsin cos 6a B a B ⎛⎫=- ⎪⎝⎭,即πsin cos 6B B ⎛⎫=- ⎪⎝⎭,可得tan B =(0π)B ∈,,可得π3B =. (Ⅱ)解:在ABC △中,由余弦定理及23π3a c B ===,,,有2222cos 7b a c ac B =+-=,故b =. 由πsin cos 6b A a B ⎛⎫=-⎪⎝⎭,可得sin A =.因为a c <,故cos A =sin 22sin cos A A A ==,21cos22cos 17A A =-=.所以,11sin(2)sin 2cos cos 2sin 27A B A B A B -=-=-= 【考点】考查同角三角函数的基本关系,两角差的正弦与余弦公式,二倍角的正弦与余弦公式,以及正弦定理、余弦定理等基础知识17.【答案】(Ⅰ)由平面ABC ⊥平面ABD ,平面ABC ∩平面ABD =AB ,AD ⊥AB ,可得AD ⊥平面ABC ,故AD ⊥BC .(Ⅱ)解:取棱AC 的中点N ,连接MN ,ND .又因为M 为棱AB 的中点,故MN ∥BC .所以∠DMN (或其补角)为异面直线BC 与MD 所成的角.在Rt △DAM 中,1AM =,故DM =.因为AD ⊥平面ABC ,故AD AC ⊥. 在Rt △DAN 中,1AN =,故DN =在等腰三角形DMN 中,1MN =,可得12cos MNDMN DM ∠==. 所以,异面直线BC 与MD(Ⅲ)解:连接CM .因为△ABC 为等边三角形,M 为边AB 的中点,故CM ⊥AB,CM .又因为平面ABC ⊥平面ABD ,而CM ⊂平面ABC ,故CM ⊥平面AB D .所以,∠CDM 为直线CD 与平面ABD 所成的角.在Rt △CAD 中,4CD ==.在Rt △CMD中,sin CM CDM CD ∠=. 所以,直线CD 与平面ABD. 【考点】异面直线所成的角、直线与平面所成的角、平面与平面垂直等基础知识18.【答案】(I )解:设等比数列{}n b 的公比为q ,由13212b b b ==+,,可得220q q --=. 因为0q >,可得2q =,故12n n b -=.所以122112nn n T -==--.设等差数列{}n a 的公差为d .由435b a a =+,可得134a d +=.由5462b a a =+,可得131316,a d += 从而11,1a d ==,故n a n =,所以(1)2n n n S +=. (II )解:由(I ),知13112(222)2 2.n n n T T T n n ++++=+++-=-- 由12()4n n n n S T T T a b ++++=+ 可得11(1)2222n n n n n n ++++--=+, 整理得2340,n n --= 解得1n =-(舍),或4n =.所以n 的值为4. 【考点】等差数列、等比数列的通项公式及前n 项和公式等基础知识19.【答案】(I )解:设椭圆的焦距为2c ,由已知得2259c a=,又由222a b c =+,可得23.a b =由||AB ==,从而3,2a b ==. 所以,椭圆的方程为22194x y +=.(II )解:设点P 的坐标为11(,)x y ,点M 的坐标为22(,)x y ,由题意,210x x >>, 点Q 的坐标为11(,).x y -- 由BPM △的面积是BPQ △面积的2倍,可得||=2||PM PQ , 从而21112[()]x x x x -=--,即215x x =.易知直线AB 的方程为236x y +=,由方程组236,,x y y kx +=⎧⎨=⎩消去y ,可得2632x k =+.由方程组221,94,x y y kx ⎧+⎪=⎨⎪=⎩消去y,可得1x =由215x x =5(32)k =+,两边平方,整理得2182580k k ++=,解得89k =-,或12k =-.当89k =-时,290x =-<,不合题意,舍去;当12k =-时,212x =,1125x =,符合题意. 所以,k 的值为12-.【考点】标准方程和几何性质、直线方程等基础知识,用代数方法研究圆锥曲线的性质,运算求解能力,以及用方程思想解决问题的能力20.【答案】(Ⅰ)解:由已知,可得3()(11))(x f x x x x x +=-=-,故()31f x x '=-,因此(0)0f =,(0)1f '=-,又因为曲线()y f x =在点(0, f (0))处的切线方程为()(0)0(0)f y f x -'-=,故所求切线方程为0x y +=.(Ⅱ)解:由已知可得33222222222222()3 39 3399()()()()().)(f x x t x t x t x t x t x t x t x t t =-+---=---=-+--+故3222363()9x t x t f x =+'--.令()0f x '=,解得2x t =,或2x t =.当x所以函数f (x )的极大值为23((9(f t =-⨯=;函数小值为23(9f t +=-⨯=(III)解:曲线()y f x =与直线2()y x t =---有三个互异的公共点等价于关于x 的方程2222 ()()()()0x t d x t x t d x t -+---+-+=有三个互异的实数解,令2u x t =-,可得32()01u d u ++=-.设函数()321()g x x d x =+-+,则曲线()y f x =与直线2()y x t =---有三个互异的公共点等价于函数()y g x =有三个零点.32()()31g d 'x x =+-.当21d ≤时,()0g'x ≥,这时()g'x 在R 上单调递增,不合题意.当21d >时,()0g'x =,解得1x =,2x =.易得,g (x )在(−∞,x 1)上单调递增,在[x 1, x 2]上单调递减,在(x 2, +∞)上单调递增,g (x )的极大值1)0(g x g ⎛> ⎝=.g (x )的极小值2()g g x =+=. 若2()0g x ≥,由g (x )的单调性可知函数()y f x =至多有两个零点,不合题意.若2()0,g x <即322(1)27d->,也就是||d >2||d x >,(||)||0,g d d =+> 且312||,(2||)6||2||0d x g d d d -<-=--+<-+<,从而由()g x 的单调性,可知函数()y g x =在区间1122(2||,),(,),(,||)d x x x x d -内各有一个零点,符合题意所以d 的取值范围是(,).-∞+∞【考点】导数的运算、导数的几何意义、运用导数研究函数的性质等基础知识和方法,函数思想和分类讨论思想,综合分析问题和解决问题的能力。
2018年天津高考数学文科真题答案

2018年普通高等学校招生全国统一考试(天津卷)数学(文史类)答案一、选择题:本题考查基本知识和基本运算.每小题5分,满分40分.(1)C (2)C (3)A (4)B (5)D (6)A (7)A (8)C二、填空题:本题考查基本知识和基本运算.每小题5分,满分30分.(9)4–i (10)e (11)13(12)2220+-=(13)14(14)[18,2]x y x三、解答题(15)本小题主要考查随机抽样、用列举法计算随机事件所含的基本事件数、古典概型及其概率计算公式等基本知识.考查运用概率知识解决简单实际问题的能力.满分13分.(Ⅰ)解:由已知,甲、乙、丙三个年级的学生志愿者人数之比为3∶2∶2,由于采用分层抽样的方法从中抽取7名同学,因此应从甲、乙、丙三个年级的学生志愿者中分别抽取3人,2人,2人.(Ⅱ)(i)解:从抽出的7名同学中随机抽取2名同学的所有可能结果为{A ,B },{A ,C },{A ,D },{A ,E },{A ,F },{A ,G },{B ,C },{B ,D },{B ,E },{B ,F },{B ,G },{C ,D },{C ,E },{C ,F },{C ,G },{D ,E },{D ,F },{D ,G },{E ,F },{E ,G },{F ,G },共21种. (ii )解:由(Ⅰ),不妨设抽出的7名同学中,来自甲年级的是A ,B ,C ,来自乙年级的是D ,E ,来自丙年级的是F ,G ,则从抽出的7名同学中随机抽取的2名同学来自同一年级的所有可能结果为{A ,B },{A ,C },{B ,C },{D ,E },{F ,G },共5种.所以,事件M 发生的概率为P (M )=521.(16)本小题主要考查同角三角函数的基本关系,两角差的正弦与余弦公式,二倍角的正弦与余弦公式,以及正弦定理、余弦定理等基础知识,考查运算求解能力.满分13分. (Ⅰ)解:在△ABC 中,由正弦定理sin sin a bA B=,可得sin sin b A a B =,又由πsin cos()6b A a B =-,得πsin cos()6a B a B =-,即πsin cos()6B B =-,可得tan B =.又因为(0π)B ∈,,可得B =π3.(Ⅱ)解:在△ABC 中,由余弦定理及a =2,c =3,B =π3,有2222cos 7b a c ac B =+-=,故b由πsin cos()6b A a B =-,可得sin A =.因为a <c ,故cos A =sin 22sin cos A A A =21cos22cos 17A A =-=.所以,sin(2)sin 2cos cos2sin A B A B A B -=-=1127-(17)本小题主要考查异面直线所成的角、直线与平面所成的角、平面与平面垂直等基础知识.考查空间想象能力、运算求解能力和推理论证能力.满分13分.(Ⅰ)由平面ABC ⊥平面ABD ,平面ABC ∩平面ABD =AB ,AD ⊥AB ,可得AD ⊥平面ABC ,故AD ⊥BC .(Ⅱ)解:取棱AC 的中点N ,连接MN ,ND .又因为M 为棱AB 的中点,故MN ∥BC .所以∠DMN (或其补角)为异面直线BC 与MD 所成的角.在Rt △DAM 中,AM =1,故DMAD ⊥平面ABC ,故AD ⊥AC .在Rt △DAN 中,AN =1,故DN在等腰三角形DMN 中,MN=1,可得12cos MNDMN DM ∠==.所以,异面直线BC 与MD(Ⅲ)解:连接CM .因为△ABC 为等边三角形,M 为边AB 的中点,故CM ⊥AB ,CMABC ⊥平面ABD ,而CM ⊂平面ABC ,故CM ⊥平面AB D .所以,∠CDM 为直线CD 与平面ABD 所成的角.在Rt △CAD 中,CD.在Rt △CMD 中,sin CMCDM CD ∠==.所以,直线CD 与平面ABD .(18)本小题主要考查等差数列、等比数列的通项公式及前n 项和公式等基础知识.考查数列求和的基本方法和运算求解能力.满分13分. (I )解:设等比数列{}n b 的公比为q ,由b 1=1,b 3=b 2+2,可得220q q --=.因为0q >,可得2q =,故12n n b -=.所以122112nn n T -==--. 设等差数列{}n a 的公差为d .由435b a a =+,可得134a d +=.由5462b a a =+,可得131316,a d += 从而11,1a d ==,故n a n =,所以(1)2n n n S +=.(II )解:由(I ),知13112(222)2 2.n n n T T T n n ++++=+++-=--由12()4n n n n S T T T a b ++++=+可得11(1)2222n n n n n n ++++--=+, 整理得2340,n n --= 解得1n =-(舍),或4n =.所以n 的值为4.(19)本小题主要考查椭圆的标准方程和几何性质、直线方程等基础知识.考查用代数方法研究圆锥曲线的性质.考查运算求解能力,以及用方程思想解决问题的能力.满分14分. (I )解:设椭圆的焦距为2c ,由已知得2259c a =,又由222a b c =+,可得23.a b = 由||AB =,从而3,2a b ==.所以,椭圆的方程为22194x y +=.(II )解:设点P 的坐标为11(,)x y ,点M 的坐标为22(,)x y ,由题意,210x x >>,点Q 的坐标为11(,).x y -- 由BPM △的面积是BPQ △面积的2倍,可得||=2||PM PQ ,从而21112[()]x x x x -=--,即215x x =.易知直线AB 的方程为236x y +=,由方程组236,,x y y kx +=⎧⎨=⎩ 消去y ,可得2632x k =+.由方程组221,94,x y y kx ⎧+⎪=⎨⎪=⎩消去y,可得1x =由215x x =,可得5(32)k =+,两边平方,整理得2182580k k ++=,解得89k =-,或12k =-. 当89k =-时,290x =-<,不合题意,舍去;当12k =-时,212x =,1125x =,符合题意. 所以,k 的值为12-.(20)本小题主要考查导数的运算、导数的几何意义、运用导数研究函数的性质等基础知识和方法,考查函数思想和分类讨论思想,考查综合分析问题和解决问题的能量,满分14分.(Ⅰ)解:由已知,可得f (x )=x (x −1)(x +1)=x 3−x ,故f ‵(x )=3x −1,因此f (0)=0,(0)f '=−1,又因为曲线y =f (x )在点(0, f (0))处的切线方程为y −f (0)=(0)f ' (x −0),故所求切线方程为x +y =0.(Ⅱ)解:由已知可得f (x )=(x −t 2+3)( x −t 2) (x −t 2−3)=( x −t 2)3−9 ( x −t 2)=x 3−3t 2x 2+(3t 22−9)x − t 22+9t 2.故()f x '= 3x 3−6t 2x +3t 22−9.令()f x '=0,解得x = t 2x = t 2.当x 变化时,f ‵(x ),f (x )的变化如下表:所以函数f (x )的极大值为f (t 2)3−9×(;函数小值为f (t 2)=(3−9×()=−(III )解:曲线y =f (x )与直线y =−(x −t 2)−价于关于x 的方程(x −t 2+d ) (x −t 2) (x −t 2−d )+ (x −t 2=0有三个互异的实数解,令u = x −t 2,可得u 3+(1−d 2)u 设函数g (x )= x 3+(1−d 2)x +6,则曲线y =f (x )与直线y =−(x −t 2)−6y =g (x )有三个零点.()g'x =3 x 3+(1−d 2).当d 2≤1时,()g'x ≥0,这时()g'x 在R 上单调递增,不合题意.当d 2>1时,()g'x =0,解得x 1=,x 2.易得,g (x )在(−∞,x 1)上单调递增,在[x 1, x 2]上单调递减,在(x 2, +∞)上单调递增,g (x )的极大值g (x1)= g (+g (x )的极小值g (x2)= g)=−+若g (x 2) ≥0,由g (x )的单调性可知函数y =f (x )至多有两个零点,不合题意. 若2()0,g x <即322(1)27d->,也就是||d >2||d x >,(||)||0,g d d =+>且312||,(2||)6||2||0d x g d d d -<-=--+<-<,从而由()g x 的单调性,可知函数()y g x = 在区间1122(2||,),(,),(,||)d x x x x d -内各有一个零点,符合题意.所以d 的取值范围是(,(10,).-∞+∞。
2018年高考文科数学天津卷-答案

天津市2018年普通高等学校招生全国统一考试文科数学答案解析一、选择题 1.【答案】C【解析】由于1,0,1,2,},4{3A B =-U ,所以{()1,0,1}A B C -=U I . 【考点】集合的运算 2.【答案】C【解析】做出不等式组5,24,1,0x y x y x y y +⎧⎪-⎪⎨-+⎪⎪⎩≤≤≤≥,所表示的可行域,其是由(00)O ,,(2,0)A ,(3,2)B ,(2,3)C ,(0,1)D 围成的五边形区域(包括边界),对于目标函数35x x y =+;结合图象可知过点C 时取得最大值,最大值为325321⨯+⨯=. 【考点】简单的线性规划 3.【答案】A【解析】由38>解得2x >;由||2x >解得2x <-或2x >,所以“8x >”是“||2x >”的充分而不必要条件。
【考点】不等式的求解、充分必要条件的判定 4.【答案】B【解析】输人2020N i T ===,,,此时10Ni=是整数,则有011213T i =+==+=,,此时不满足条件5i ≥;接下来有203N i =不是整数,则有314i =+=,此时.不满足条件5i ≥;接下来有5N i =是整数,则有112415T i =+==+=,,此时满足条件5i ≥,结束循环,输出2T =. 【考点】算法的程序框图.模拟程序框图的运行 5.【答案】D【解析】根据函数的图象与性质可知13133331711log log 5log log 315244⎛⎫⎛⎫=>>==> ⎪ ⎪⎝⎭⎝⎭,则c a b >>. 【考点】代数值的大小比较、函数的图象与性质 6.【答案】A【解析】将函数πsin 25y x ⎛⎫=+ ⎪⎝⎭的图象向右平移π10个单位长度得到ππsin 2sin 2105y x x ⎡⎤⎛⎫=-+= ⎪⎢⎥⎝⎭⎣⎦由ππ2π22π+,22k x k k -+∈Z ≤≤,解得ππππ+,44k x k k -+∈Z ≤≤,当0k =时,则知函数在区间ππ,44⎡⎤-⎢⎥⎣⎦上单调递增.【考点】三角函数图象的平移变换、三角函数的图象与性质 7.【答案】A【解析】由双曲线的离心率2c e a==,可得2c a =,则知b ,将2x a =代人双曲线222213x y a a -=,可得3y a =±,设点(2,3)(2,3)A d a B a a -,0y +=,可得12d d ====,,所以126d d +=+==,解得a =,故双曲线的方程为22139x y -=. 【考点】双曲线的方程与几何性质、点到直线的距离公式 8.【答案】C【解析】根据题目可得:22((33)3()33()33321cos120=31=6BC OM AC AB OM AN AM OM AN AM OMMN OM ON OM OM ON OM OM =-=-=-==-=-=⨯⨯⨯︒⨯-u u u r u u u u r u u u r u u u r u u u u r u u u r u u u u r u u u u r u u u r u u u u r u u u u rg g g g u u u u u r u u u u r u u u u r u u u r u u u u r u u u u r u u u r u u u u rg g g ) 【考点】平面向量的线性运算与数量积 二、填空题 9.【答案】4i -【解析】由题可得67i (67i)(12i)205i 4i 12i(12i)(12i)5++--===-++-.【考点】复数的四则运算 10.【答案】e【解析】由于()e ln x f x x =则有1()e ln e x x f x x x '=+g ,所以111(1)e ln1e e 1f '=+=g g .【考点】导数及其应用、函数值的求解11.13【答案】 【解析】由题可知四棱锥111A BB D D -,1,则四棱锥111A BB D D -的体为11133V =⨯=. 【考点】空间几何体的性质、空间几何体的体积 12.【答案】2220x y x +-=【解析】由于圆经过三点(0,0)(1,1)(2,0)O A B ,,,可知OAAB ⊥,则知OB 为圆的直径,则圆心(1,0)C ,半径1r =,可得圆的方程为22(1)1x y -+=,即2220x y x +-=. 【考点】圆的方程13.【答案】14【解析】由于360a b -+=;可得366a -=-,结合基本不等式可得33112222284a a b b --+=+==g ≥,当且仅当322a b -=,即33a b =-=-.【考点】基本不等式14.【答案】1,28⎡⎤⎢⎥⎣⎦【解析】当[]3,0-时,由()||f x x ≤恒成立可得22x x a x ++-≤-即232x x a ++-≤0,结合图象可知99200020a a -+-⎧⎨++-⎩≤≤,解得2a ≤;当·(0,)x ∈+∞时,由()||f x x ≤恒成立可得222x x a x -+-≤,即²20x x a -+≥,结合图象可知2412(1)041a ⨯⨯--⨯≥,解得a 18a ≥;综上分析可得128a ≤≤.【考点】分段函数、函数的图象与性质、不等式恒成立 三、解答题15.【答案】(Ⅰ)解:由已知,甲、乙、丙三个年级的学生志愿者人数之比为3:2:2,由于采用分层抽样的方法从中抽取7名同学,因此应从甲、乙、丙三个年级的学生志愿者中分别抽取3人,2人,2人. (Ⅱ)(ⅰ)解:从抽出的7名同学中随机抽取2名同学的所有可能结果为{A ,B },{A ,C },{A ,D },{A ,E },{A ,F },{A ,G },{B ,C },{B ,D },{B ,E },{B ,F },{B ,G },{C ,D },{C ,E },{C ,F },{C ,G },{D ,E },{D ,F },{D ,G },{E ,F },{E ,G },{F ,G },共21种.(ⅱ)解:由(Ⅰ),不妨设抽出的7名同学中,来自甲年级的是A ,B ,C ,来自乙年级的是D ,E ,来自丙年级的是F ,G ,则从抽出的7名同学中随机抽取的2名同学来自同一年级的所有可能结果为{A ,B },{A ,C },{B ,C },{D ,E },{F ,G },共5种. 所以,事件M 发生的概率为5(2)1P M =.【考点】随机抽样、用列举法计算随机事件所含的基本事件数、古典概型及其概率计算公式等基本知识16.【答案】(Ⅰ)解:在ABC △中,由正弦定理sin sin a bA B=,可得sin sin b A a B =,又由πsin cos 6b A a B ⎛⎫=- ⎪⎝⎭,得πsin cos 6a B a B ⎛⎫=- ⎪⎝⎭,即πsin cos 6B B ⎛⎫=- ⎪⎝⎭,可得tan B(0π)B ∈,,可得π3B =. (Ⅱ)解:在ABC △中,由余弦定理及23π3a c B ===,,,有2222cos 7b a c ac B =+-=,故b =.由πsin cos 6b A a B ⎛⎫=- ⎪⎝⎭,可得sin A =.因为a c <,故cos A =sin 22sin cos A A A =,21cos22cos 17A A =-=.所以,11sin(2)sin 2cos cos 2sin 27A B A B A B -=-=-= 【考点】考查同角三角函数的基本关系,两角差的正弦与余弦公式,二倍角的正弦与余弦公式,以及正弦定理、余弦定理等基础知识17.【答案】(Ⅰ)由平面ABC ⊥平面ABD ,平面ABC ∩平面ABD =AB ,AD ⊥AB ,可得AD ⊥平面ABC ,故AD ⊥BC .(Ⅱ)解:取棱AC 的中点N ,连接MN ,ND .又因为M 为棱AB 的中点,故MN ∥BC .所以∠DMN (或其补角)为异面直线BC 与MD 所成的角.在Rt △DAM 中,1AM =,故DM =AD ⊥平面ABC ,故AD AC ⊥. 在Rt △DAN 中,1AN =,故DN =在等腰三角形DMN 中,1MN =,可得12cos MNDMN DM ∠==. 所以,异面直线BC 与MD(Ⅲ)解:连接CM .因为△ABC 为等边三角形,M 为边AB 的中点,故CM ⊥AB,CM =面ABC ⊥平面ABD ,而CM ⊂平面ABC ,故CM ⊥平面AB D .所以,∠CDM 为直线CD 与平面ABD 所成的角.在Rt △CAD 中,4CD =.在Rt △CMD中,sin CM CDM CD ∠=. 所以,直线CD 与平面ABD. 【考点】异面直线所成的角、直线与平面所成的角、平面与平面垂直等基础知识 18.【答案】(I )解:设等比数列{}n b 的公比为q ,由13212b b b ==+,,可得220q q --=.因为0q >,可得2q =,故12n nb -=.所以122112nn n T -==--.设等差数列{}n a 的公差为d .由435b a a =+,可得134a d +=.由5462b a a =+,可得131316,a d += 从而11,1a d ==,故n a n =,所以(1)2n n n S +=. (II )解:由(I ),知13112(222)2 2.n n n T T T n n ++++=+++-=--L L由12()4n n n n S T T T a b ++++=+L 可得11(1)2222n n n n n n ++++--=+, 整理得2340,n n --= 解得1n =-(舍),或4n =.所以n 的值为4. 【考点】等差数列、等比数列的通项公式及前n 项和公式等基础知识19.【答案】(I )解:设椭圆的焦距为2c ,由已知得2259c a=,又由222a b c =+,可得23.a b =由||AB ,从而3,2a b ==.所以,椭圆的方程为22194x y +=. (II )解:设点P 的坐标为11(,)x y ,点M 的坐标为22(,)x y ,由题意,210x x >>, 点Q 的坐标为11(,).x y -- 由BPM △的面积是BPQ △面积的2倍,可得||=2||PM PQ , 从而21112[()]x x x x -=--,即215x x =. 易知直线AB 的方程为236x y +=,由方程组236,,x y y kx +=⎧⎨=⎩消去y ,可得2632x k =+.由方程组221,94,x y y kx ⎧+⎪=⎨⎪=⎩消去y,可得1x =.由215x x =5(32)k =+,两边平方,整理得2182580k k ++=,解得89k =-,或12k =-. 当89k =-时,290x =-<,不合题意,舍去;当12k =-时,212x =,1125x =,符合题意. 所以,k 的值为12-.【考点】标准方程和几何性质、直线方程等基础知识,用代数方法研究圆锥曲线的性质,运算求解能力,以及用方程思想解决问题的能力20.【答案】(Ⅰ)解:由已知,可得3()(11))(x f x x x x x +=-=-,故()31f x x '=-,因此(0)0f =,(0)1f '=-,又因为曲线()y f x =在点(0, f (0))处的切线方程为()(0)0(0)f y f x -'-=,故所求切线方程为0x y +=.(Ⅱ)解:由已知可得33222222222222()3 39 3399()()()()().)(f x x t x t x t x t x t x t x t x t t =-+---=---=-+--+故3222363()9x t x t f x =+'--.令()0f x '=,解得2x t =2x t =当x所以函数f (x )的极大值为23((9(f t =-⨯=23(9f t =-⨯=(III )解:曲线()y f x =与直线2()y x t =---有三个互异的公共点等价于关于x 的方程2222 ()()()()0x t d xt x t d x t -+---+-+有三个互异的实数解,令2u x t =-,可得32()01u d u ++=-.设函数()321()g x x d x =+-+()y f x =与直线2()y x t =---函数()y g x =有三个零点.32()()31g d 'x x =+-.当21d ≤时,()0g'x ≥,这时()g'x 在R 上单调递增,不合题意.当21d >时,()0g'x =,解得1x =,2x =. 易得,g (x )在(−∞,x 1)上单调递增,在[x 1, x 2]上单调递减,在(x 2, +∞)上单调递增,g (x )的极大值1)0(g x g ⎛=> ⎝=.g (x )的极小值32221)9()g g d x -=+=若2()0g x ≥,由g (x )的单调性可知函数()y f x =至多有两个零点,不合题意.若2()0,g x <即322(1)27d->,也就是||d >2||d x >,(||)||0,g d d =+ 且312||,(2||)6||2||0d x g d d d -<-=--+-<,从而由()g x 的单调性,可知函数()y g x =在区间1122(2||,),(,),(,||)d x x x x d -内各有一个零点,符合题意所以d 的取值范围是(,).-∞+∞U【考点】导数的运算、导数的几何意义、运用导数研究函数的性质等基础知识和方法,函数思想和分类讨论思想,综合分析问题和解决问题的能力。
2018年天津市高考数学试卷(文科)

2018年天津市高考数学试卷(文科)一.选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)设集合A={1,2,3,4},B={﹣1,0,2,3},C={x∈R|﹣1≤x<2},则(A∪B)∩C=()A.{﹣1,1}B.{0,1}C.{﹣1,0,1}D.{2,3,4}2.(5分)设变量x,y满足约束条件,则目标函数z=3x+5y的最大值为()A.6 B.19 C.21 D.453.(5分)设x∈R,则“x3>8”是“|x|>2”的()A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件4.(5分)阅读如图的程序框图,运行相应的程序,若输入N的值为20,则输出T的值为()A.1 B.2 C.3 D.45.(5分)已知a=log3,b=(),c=log,则a,b,c的大小关系为()A.a>b>c B.b>a>c C.c>b>a D.c>a>b6.(5分)将函数y=sin(2x+)的图象向右平移个单位长度,所得图象对应的函数()A.在区间[]上单调递增B.在区间[﹣,0]上单调递减C.在区间[]上单调递增D.在区间[,π]上单调递减7.(5分)已知双曲线=1(a>0,b>0)的离心率为2,过右焦点且垂直于x轴的直线与双曲线交于A,B两点.设A,B到双曲线的同一条渐近线的距离分别为d1和d2,且d1+d2=6,则双曲线的方程为()A.﹣=1 B.﹣=1 C.﹣=1 D.﹣=18.(5分)在如图的平面图形中,已知OM=1,ON=2,∠MON=120°,=2,=2,则的值为()A.﹣15 B.﹣9 C.﹣6 D.0二.填空题:本大题共6小题,每小题5分,共30分.9.(5分)i是虚数单位,复数=.(1)的值为.(x)为f(x)的导函数,则f′10.(5分)已知函数f(x)=e x lnx,f′11.(5分)如图,已知正方体ABCD﹣A1B1C1D1的棱长为1,则四棱锥A1﹣BB1D1D 的体积为.12.(5分)在平面直角坐标系中,经过三点(0,0),(1,1),(2,0)的圆的方程为.13.(5分)已知a,b∈R,且a﹣3b+6=0,则2a+的最小值为.14.(5分)己知a∈R,函数f(x)=.若对任意x∈[﹣3,+∞),f(x)≤|x|恒成立,则a的取值范围是.三.解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤.15.(13分)己知某校甲、乙、丙三个年级的学生志愿者人数分别为240,160,160.现采用分层抽样的方法从中抽取7名同学去某敬老院参加献爱心活动.(Ⅰ)应从甲、乙、丙三个年级的学生志愿者中分别抽取多少人?(Ⅱ)设抽出的7名同学分别用A,B,C,D,E,F,G表示,现从中随机抽取2名同学承担敬老院的卫生工作.(i)试用所给字母列举出所有可能的抽取结果;(ii)设M为事件“抽取的2名同学来自同一年级”,求事件M发生的概率.16.(13分)在△ABC中,内角A,B,C所对的边分别为a,b,c.已知bsinA=acos (B﹣).(Ⅰ)求角B的大小;(Ⅱ)设a=2,c=3,求b和sin(2A﹣B)的值.17.(13分)如图,在四面体ABCD中,△ABC是等边三角形,平面ABC⊥平面ABD,点M为棱AB的中点,AB=2,AD=2,∠BAD=90°.(Ⅰ)求证:AD⊥BC;(Ⅱ)求异面直线BC与MD所成角的余弦值;(Ⅲ)求直线CD与平面ABD所成角的正弦值.18.(13分)设{a n}是等差数列,其前n项和为S n(n∈N*);{b n}是等比数列,公比大于0,其前n项和为T n(n∈N*).已知b1=1,b3=b2+2,b4=a3+a5,b5=a4+2a6.(Ⅰ)求S n和T n;(Ⅱ)若S n+(T1+T2+……+T n)=a n+4b n,求正整数n的值.19.(14分)设椭圆+=1(a>b>0)的右顶点为A,上顶点为B.已知椭圆的离心率为,|AB|=.(Ⅰ)求椭圆的方程;(Ⅱ)设直线l:y=kx(k<0)与椭圆交于P,Q两点,1与直线AB交于点M,且点P,M均在第四象限.若△BPM的面积是△BPQ面积的2倍,求k的值.20.(14分)设函数f(x)=(x﹣t1)(x﹣t2)(x﹣t3),其中t1,t2,t3∈R,且t1,t2,t3是公差为d的等差数列.(Ⅰ)若t2=0,d=1,求曲线y=f(x)在点(0,f(0))处的切线方程;(Ⅱ)若d=3,求f(x)的极值;(Ⅲ)若曲线y=f(x)与直线y=﹣(x﹣t2)﹣6有三个互异的公共点,求d 的取值范围.2018年天津市高考数学试卷(文科)参考答案与试题解析一.选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)设集合A={1,2,3,4},B={﹣1,0,2,3},C={x∈R|﹣1≤x<2},则(A∪B)∩C=()A.{﹣1,1}B.{0,1}C.{﹣1,0,1}D.{2,3,4}【解答】解:∵A={1,2,3,4},B={﹣1,0,2,3},∴(A∪B)={1,2,3,4}∪{﹣1,0,2,3}={﹣1,0,1,2,3,4},又C={x∈R|﹣1≤x<2},∴(A∪B)∩C={﹣1,0,1}.故选:C.2.(5分)设变量x,y满足约束条件,则目标函数z=3x+5y的最大值为()A.6 B.19 C.21 D.45【解答】解:由变量x,y满足约束条件,得如图所示的可行域,由解得A(2,3).当目标函数z=3x+5y经过A时,直线的截距最大,z取得最大值.将其代入得z的值为21,故选:C.3.(5分)设x∈R,则“x3>8”是“|x|>2”的()A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件【解答】解:由x3>8,得x>2,则|x|>2,反之,由|x|>2,得x<﹣2或x>2,则x3<﹣8或x3>8.即“x3>8”是“|x|>2”的充分不必要条件.故选:A.4.(5分)阅读如图的程序框图,运行相应的程序,若输入N的值为20,则输出T的值为()A.1 B.2 C.3 D.4【解答】解:若输入N=20,则i=2,T=0,==10是整数,满足条件.T=0+1=1,i=2+1=3,i≥5不成立,循环,=不是整数,不满足条件.,i=3+1=4,i≥5不成立,循环,==5是整数,满足条件,T=1+1=2,i=4+1=5,i≥5成立,输出T=2,故选:B.5.(5分)已知a=log3,b=(),c=log,则a,b,c的大小关系为()A.a>b>c B.b>a>c C.c>b>a D.c>a>b【解答】解:∵a=log3,c=log=log35,且5,∴,则b=()<,∴c>a>b.故选:D.6.(5分)将函数y=sin(2x+)的图象向右平移个单位长度,所得图象对应的函数()A.在区间[]上单调递增B.在区间[﹣,0]上单调递减C.在区间[]上单调递增D.在区间[,π]上单调递减【解答】解:将函数y=sin(2x+)的图象向右平移个单位长度,所得图象对应的函数解析式为y=sin[2(x﹣)+]=sin2x.当x∈[]时,2x∈[,],函数单调递增;当x∈[,]时,2x∈[,π],函数单调递减;当x∈[﹣,0]时,2x∈[﹣,0],函数单调递增;当x∈[,π]时,2x∈[π,2π],函数先减后增.故选:A.7.(5分)已知双曲线=1(a>0,b>0)的离心率为2,过右焦点且垂直于x轴的直线与双曲线交于A,B两点.设A,B到双曲线的同一条渐近线的距离分别为d1和d2,且d1+d2=6,则双曲线的方程为()A.﹣=1 B.﹣=1 C.﹣=1 D.﹣=1【解答】解:由题意可得图象如图,CD是双曲线的一条渐近线y=,即bx﹣ay=0,F(c,0),AC⊥CD,BD⊥CD,FE⊥CD,ACDB是梯形,F是AB的中点,EF==3,EF==b,所以b=3,双曲线=1(a>0,b>0)的离心率为2,可得,可得:,解得a=.则双曲线的方程为:﹣=1.故选:A.8.(5分)在如图的平面图形中,已知OM=1,ON=2,∠MON=120°,=2,=2,则的值为()A.﹣15 B.﹣9 C.﹣6 D.0【解答】解:不妨设四边形OMAN是平行四边形,由OM=1,ON=2,∠MON=120°,=2,=2,知=﹣=3﹣3=﹣3+3,∴=(﹣3+3)?=﹣3+3?=﹣3×12+3×2×1×cos120°=﹣6.故选:C.二.填空题:本大题共6小题,每小题5分,共30分.9.(5分)i是虚数单位,复数=4﹣i.【解答】解:====4﹣i,故答案为:4﹣i10.(5分)已知函数f(x)=e x lnx,f′(x)为f(x)的导函数,则f′(1)的值为e.【解答】解:函数f(x)=e x lnx,则f′(x)=e x lnx+?e x;∴f′(1)=e?ln1+1?e=e.故答案为:e.11.(5分)如图,已知正方体ABCD﹣A1B1C1D1的棱长为1,则四棱锥A1﹣BB1D1D 的体积为.【解答】解:由题意可知四棱锥A1﹣BB1D1D的底面是矩形,边长:1和,四棱锥的高:A1C1=.第11页(共20页)。
2018天津高考文科数学试题及答案

2018天津高考文科数学试题及答案编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(2018天津高考文科数学试题及答案)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为2018天津高考文科数学试题及答案的全部内容。
2018年普通高等学校招生全国统一考试(天津卷)数学(文史类)本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试用时120分钟。
第Ⅰ卷1至2页,第Ⅱ卷3至5页.答卷前,考生务必将自己的姓名、准考证号填写在答题考上,并在规定位置粘贴考试用条形码。
答卷时,考生务必将答案涂写在答题卡上,答在试卷上的无效。
考试结束后,将本试卷和答题卡一并交回。
祝各位考生考试顺利!第Ⅰ卷注意事项:1.每小题选出答案后,用铅笔将答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号。
2.本卷共8小题,每小题5分,共40分。
参考公式:·如果事件 A,B 互斥,那么P(A∪B)=P(A)+P(B).·棱柱的体积公式V=Sh. 其中S表示棱柱的底面面积,h表示棱柱的高.(A)1 (B)2 (C)3 (D)4第Ⅱ卷注意事项:1.用黑色墨水的钢笔或签字笔将答案写在答题卡上. 2.本卷共12小题,共110分。
二.填空题:本大题共6小题,每小题5分,共30分.三.解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤.(15)(本小题满分13分)已知某校甲、乙、丙三个年级的学生志愿者人数分别为240,160,160.现采用分层抽样的方法从中抽取7名同学去某敬老院参加献爱心活动.(Ⅰ)应从甲、乙、丙三个年级的学生志愿者中分别抽取多少人?(Ⅱ)设抽出的7名同学分别用A,B,C,D,E,F,G表示,现从中随机抽取2名同学承担敬老院的卫生工作.(i)试用所给字母列举出所有可能的抽取结果;(ii)设M为事件“抽取的2名同学来自同一年级”,求事件M发生的概率.(16)(本小题满分13分)在△ABC中,内角A,B,C所对的边分别为a,b,c.已知bsinA=acos(B–π/6).(Ⅰ)求教B的大小;(Ⅱ)设a=2,c=3,求b和sin(2A–B)的值.。
2018年天津市高考文科数学试题及答案

2018年天津市⾼考⽂科数学试题及答案绝密★启⽤前2018年普通⾼等学校招⽣全国统⼀考试(天津卷)数学(⽂史类)本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(⾮选择题)两部分,共150分,考试⽤时120分钟。
第Ⅰ卷1⾄2页,第Ⅱ卷3⾄5页。
答卷前,考⽣务必将⾃⼰的姓名、准考证号填写在答题考上,并在规定位置粘贴考试⽤条形码。
答卷时,考⽣务必将答案涂写在答题卡上,答在试卷上的⽆效。
考试结束后,将本试卷和答题卡⼀并交回。
祝各位考⽣考试顺利!第Ⅰ卷注意事项:1.每⼩题选出答案后,⽤铅笔将答题卡上对应题⽬的答案标号涂⿊。
如需改动,⽤橡⽪擦⼲净后,再选涂其他答案标号。
2.本卷共8⼩题,每⼩题5分,共40分。
参考公式:·如果事件A,B互斥,那么P(A∪B)=P(A)+P(B).·棱柱的体积公式V=Sh.其中S表⽰棱柱的底⾯⾯积,h表⽰棱柱的⾼.·棱锥的体积公式,其中表⽰棱锥的底⾯积,h表⽰棱锥的⾼.⼀.选择题:在每⼩题给出的四个选项中,只有⼀项是符合题⽬要求的.(1)设集合,,,则(A)(B)(C)(D)(2)设变量满⾜约束条件则⽬标函数的最⼤值为(A)6(B)19(C)21(D)45(3)设,则“”是“”的(A)充分⽽不必要条件(B)必要⽽不充分条件(C)充要条件(D)既不充分也不必要条件(4)阅读如图所⽰的程序框图,运⾏相应的程序,若输⼊的值为20,则输出的值为(A)1(B)2(C)3(D)4(5)已知,则的⼤⼩关系为(A)(B)(C)(D)(6)将函数的图象向右平移个单位长度,所得图象对应的函数(A)在区间上单调递增(B)在区间上单调递减(C)在区间上单调递增(D)在区间上单调递减(7)已知双曲线的离⼼率为2,过右焦点且垂直于轴的直线与双曲线交于两点.设到双曲线的同⼀条渐近线的距离分别为和,且则双曲线的⽅程为(A)(B)(C)(D)(8)在如图的平⾯图形中,已知,则的值为(A)(B)(C)(D)0第Ⅱ卷注意事项:1.⽤⿊⾊墨⽔的钢笔或签字笔将答案写在答题卡上。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
绝密★启用前2018年普通高等学校招生全国统一考试(天津卷)数学(文史类)本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试用时120分钟。
第Ⅰ卷1至2页,第Ⅱ卷3至5页。
答卷前,考生务必将自己的姓名、准考证号填写在答题考上,并在规定位置粘贴考试用条形码。
答卷时,考生务必将答案涂写在答题卡上,答在试卷上的无效。
考试结束后,将本试卷和答题卡一并交回。
祝各位考生考试顺利!第Ⅰ卷注意事项:1.每小题选出答案后,用铅笔将答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
2.本卷共8小题,每小题5分,共40分。
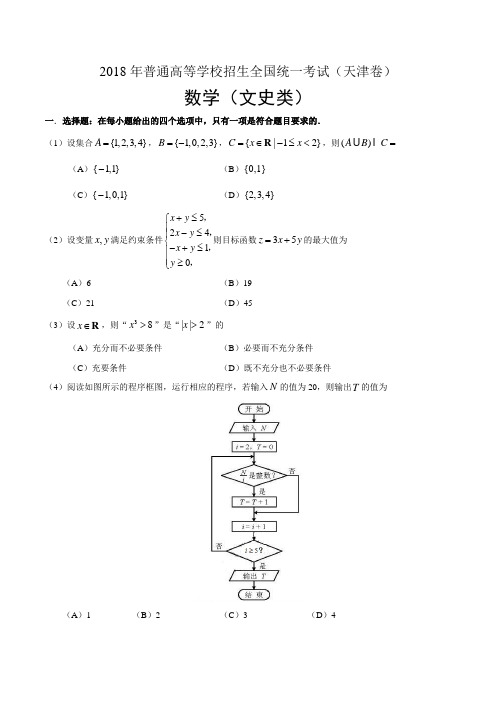
参考公式:·如果事件 A ,B 互斥,那么 P (A ∪B )=P (A )+P (B ). ·棱柱的体积公式V =Sh . 其中S 表示棱柱的底面面积,h 表示棱柱的高. ·棱锥的体积公式13V Sh =,其中S 表示棱锥的底面积,h 表示棱锥的高. 一.选择题:在每小题给出的四个选项中,只有一项是符合题目要求的. (1)设集合{1,2,3,4}A =,{1,0,2,3}B =-,{|12}C x x =∈-≤<R ,则()A B C =(A ){1,1}-(B ){0,1}(C ){1,0,1}-(D ){2,3,4}(2)设变量,x y 满足约束条件52410x y x y x y y +≤⎧⎪-≤⎪⎨-+≤⎪⎪≥⎩,,,,则目标函数35z x y =+的最大值为(A )6 (B )19 (C )21(D )45(3)设x ∈R ,则“38x >”是“||2x >” 的(A )充分而不必要条件 (B )必要而不充分条件 (C )充要条件(D )既不充分也不必要条件(4)阅读如图所示的程序框图,运行相应的程序,若输入N 的值为20,则输出T 的值为(A )1(B )2(C )3(D )4(5)已知13313711log ,(),log 245a b c ===,则,,a b c 的大小关系为(A )a b c >> (B )b a c >> (C )c b a >>(D )c a b >>(6)将函数sin(2)5y x π=+的图象向右平移10π个单位长度,所得图象对应的函数 (A )在区间[,]44ππ- 上单调递增 (B )在区间[,0]4π上单调递减(C )在区间[,]42ππ 上单调递增 (D )在区间[,]2ππ 上单调递减(7)已知双曲线22221(0,0)x y a b a b-=>> 的离心率为2,过右焦点且垂直于x 轴的直线与双曲线交于,A B两点.设,A B 到双曲线的同一条渐近线的距离分别为1d 和2d ,且126,d d += 则双曲线的方程为(A )22139x y -=(B )22193x y -=(C )221412x y -=(D )221124x y -= (8)在如图的平面图形中,已知 1.2,120OM ON MON ==∠=,2,2,BM MA CN NA ==则·BC OM 的值为(A )15- (B )9- (C )6-(D )0第Ⅱ卷注意事项:1.用黑色墨水的钢笔或签字笔将答案写在答题卡上。
2.本卷共12小题,共110分。
二.填空题:本大题共6小题,每小题5分,共30分. (9)i 是虚数单位,复数67i12i++=__________. (10)已知函数f (x )=e xln x ,f ′(x )为f (x )的导函数,则f ′(1)的值为__________.(11)如图,已知正方体ABCD –A 1B 1C 1D 1的棱长为1,则四棱柱A 1–BB 1D 1D 的体积为__________.(12)在平面直角坐标系中,经过三点(0,0),(1,1),(2,0)的圆的方程为__________.(13)已知a ,b ∈R ,且a –3b +6=0,则2a+18b的最小值为__________.(14)已知a ∈R ,函数()22220220x x a x f x x x a x ⎧++-≤⎪=⎨-+->⎪⎩,,,.若对任意x ∈[–3,+∞),f (x )≤x 恒成立,则a 的取值范围是__________.三.解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤. (15)(本小题满分13分)已知某校甲、乙、丙三个年级的学生志愿者人数分别为240,160,160.现采用分层抽样的方法从中抽取7名同学去某敬老院参加献爱心活动.(Ⅰ)应从甲、乙、丙三个年级的学生志愿者中分别抽取多少人?(Ⅱ)设抽出的7名同学分别用A ,B ,C ,D ,E ,F ,G 表示,现从中随机抽取2名同学承担敬老院的卫生工作.(i )试用所给字母列举出所有可能的抽取结果;(ii )设M 为事件“抽取的2名同学来自同一年级”,求事件M 发生的概率. (16)(本小题满分13分)在△ABC 中,内角A ,B ,C 所对的边分别为a,b,c .已知b sin A =a cos(B –π6). (Ⅰ)求教B 的大小;(Ⅱ)设a =2,c =3,求b 和sin(2A –B )的值. (17)(本小题满分13分)如图,在四面体ABCD 中,△ABC 是等边三角形,平面ABC ⊥平面ABD ,点M 为棱AB 的中点,AB =2,AD =23,∠BAD =90°. (Ⅰ)求证:AD ⊥BC ;(Ⅱ)求异面直线BC 与MD 所成角的余弦值; (Ⅲ)求直线CD 与平面ABD 所成角的正弦值.(18)(本小题满分13分)设{a n }是等差数列,其前n 项和为S n (n ∈N *);{b n }是等比数列,公比大于0,其前n 项和为T n (n ∈N *).已知b 1=1,b 3=b 2+2,b 4=a 3+a 5,b 5=a 4+2a 6. (Ⅰ)求S n 和T n ;(Ⅱ)若S n +(T 1+T 2+…+T n )=a n +4b n ,求正整数n 的值. (19)(本小题满分14分)设椭圆22221(0)x y a b a b +=>> 的右顶点为A ,上顶点为B .已知椭圆的离心率为53,||13AB =.(I )求椭圆的方程;(II )设直线:(0)l y kx k =<与椭圆交于,P Q 两点,l 与直线AB 交于点M ,且点P ,M 均在第四象限.若BPM △的面积是BPQ △面积的2倍,求k 的值.(20)(本小题满分14分)设函数123()=()()()f x x t x t x t ---,其中123,,t t t ∈R ,且123,,t t t 是公差为d 的等差数列. (I )若20,1,t d == 求曲线()y f x =在点(0,(0))f 处的切线方程; (II )若3d =,求()f x 的极值;(III )若曲线()y f x = 与直线 12()63y x t =---有三个互异的公共点,求d 的取值范围. 参考答案一、选择题:本题考查基本知识和基本运算.每小题5分,满分40分. (1)C (2)C (3)A (4)B (5)D(6)A(7)A(8)C二、填空题:本题考查基本知识和基本运算.每小题5分,满分30分. (9)4–i(10)e (11)13(12)2220x y x +-= (13)14(14)[18,2]三、解答题(15)本小题主要考查随机抽样、用列举法计算随机事件所含的基本事件数、古典概型及其概率计算公式等基本知识.考查运用概率知识解决简单实际问题的能力.满分13分.(Ⅰ)解:由已知,甲、乙、丙三个年级的学生志愿者人数之比为3∶2∶2,由于采用分层抽样的方法从中抽取7名同学,因此应从甲、乙、丙三个年级的学生志愿者中分别抽取3人,2人,2人. (Ⅱ)(i )解:从抽出的7名同学中随机抽取2名同学的所有可能结果为{A ,B },{A ,C },{A ,D },{A ,E },{A ,F },{A ,G },{B ,C },{B ,D },{B ,E },{B ,F },{B ,G },{C ,D },{C ,E },{C ,F },{C ,G },{D ,E },{D ,F },{D ,G },{E ,F },{E ,G },{F ,G },共21种. (ii )解:由(Ⅰ),不妨设抽出的7名同学中,来自甲年级的是A ,B ,C ,来自乙年级的是D ,E ,来自丙年级的是F ,G ,则从抽出的7名同学中随机抽取的2名同学来自同一年级的所有可能结果为{A ,B },{A ,C },{B ,C },{D ,E },{F ,G },共5种.学@科网 所以,事件M 发生的概率为P (M )=521. (16)本小题主要考查同角三角函数的基本关系,两角差的正弦与余弦公式,二倍角的正弦与余弦公式,以及正弦定理、余弦定理等基础知识,考查运算求解能力.满分13分. (Ⅰ)解:在△ABC 中,由正弦定理sin sin a b A B =,可得sin sin b A a B =,又由πsin cos()6b A a B =-,得πsin cos()6a B a B =-,即πsin cos()6B B =-,可得tan 3B =.又因为(0π)B ∈,,可得B =π3.(Ⅱ)解:在△ABC 中,由余弦定理及a =2,c =3,B =π3,有2222cos 7b a c ac B =+-=,故b =7. 由πsin cos()6b A a B =-,可得3sin 7A =.因为a <c ,故2cos 7A =.因此43sin 22sin cos 7A A A ==,21cos22cos 17A A =-=. 所以,sin(2)sin 2cos cos 2sin AB A B A B -=-=4311333727214⨯-⨯=. (17)本小题主要考查异面直线所成的角、直线与平面所成的角、平面与平面垂直等基础知识.考查空间想象能力、运算求解能力和推理论证能力.满分13分.(Ⅰ)由平面ABC ⊥平面ABD ,平面ABC ∩平面ABD =AB ,AD ⊥AB ,可得AD ⊥平面ABC ,故AD ⊥BC . (Ⅱ)解:取棱AC 的中点N ,连接MN ,ND .又因为M 为棱AB 的中点,故MN ∥BC .所以∠DMN (或其补角)为异面直线BC 与MD 所成的角.在Rt △DAM 中,AM =1,故DM =22=13AD AM +.因为AD ⊥平面ABC ,故AD ⊥AC . 在Rt △DAN 中,AN =1,故DN =22=13AD AN +.在等腰三角形DMN 中,MN =1,可得1132cos 26MNDMN DM ∠==. 所以,异面直线BC 与MD 所成角的余弦值为1326. (Ⅲ)解:连接CM .因为△ABC 为等边三角形,M 为边AB 的中点,故CM ⊥AB ,CM =3.又因为平面ABC ⊥平面ABD ,而CM ⊂平面ABC ,故CM ⊥平面AB D .所以,∠CDM 为直线CD 与平面ABD 所成的角. 在Rt △CAD 中,CD =22AC AD +=4. 在Rt △CMD 中,3sin 4CM CDM CD ∠==. 所以,直线CD 与平面ABD 所成角的正弦值为34. (18)本小题主要考查等差数列、等比数列的通项公式及前n 项和公式等基础知识.考查数列求和的基本方法和运算求解能力.满分13分.(I )解:设等比数列{}n b 的公比为q ,由b 1=1,b 3=b 2+2,可得220q q --=. 因为0q >,可得2q =,故12n n b -=.所以122112nn n T -==--. 设等差数列{}n a 的公差为d .由435b a a =+,可得134a d +=.由5462b a a =+,可得131316,a d += 从而11,1a d ==,故n a n =,所以(1)2n n n S +=. (II )解:由(I ),知13112(222)2 2.n n n T T T n n ++++=+++-=--由12()4n n n n S T T T a b ++++=+可得11(1)2222n n n n n n ++++--=+, 整理得2340,n n --= 解得1n =-(舍),或4n =.所以n 的值为4.学&科网(19)本小题主要考查椭圆的标准方程和几何性质、直线方程等基础知识.考查用代数方法研究圆锥曲线的性质.考查运算求解能力,以及用方程思想解决问题的能力.满分14分.(I )解:设椭圆的焦距为2c ,由已知得2259c a =,又由222a b c =+,可得23.a b = 由22||13AB a b =+=,从而3,2a b ==.所以,椭圆的方程为22194x y +=. (II )解:设点P 的坐标为11(,)x y ,点M 的坐标为22(,)x y ,由题意,210x x >>, 点Q 的坐标为11(,).x y -- 由BPM △的面积是BPQ △面积的2倍,可得||=2||PM PQ , 从而21112[()]x x x x -=--,即215x x =.易知直线AB 的方程为236x y +=,由方程组236,,x y y kx +=⎧⎨=⎩ 消去y ,可得2632x k =+.由方程组221,94,x y y kx ⎧+⎪=⎨⎪=⎩消去y ,可得12694x k =+.由215x x =,可得2945(32)k k +=+,两边平方,整理得2182580k k ++=,解得89k =-,或12k =-.当89k =-时,290x =-<,不合题意,舍去;当12k =-时,212x =,1125x =,符合题意.所以,k 的值为12-.(20)本小题主要考查导数的运算、导数的几何意义、运用导数研究函数的性质等基础知识和方法,考查函数思想和分类讨论思想,考查综合分析问题和解决问题的能量,满分14分.(Ⅰ)解:由已知,可得f (x )=x (x −1)(x +1)=x 3−x ,故f ‵(x )=3x −1,因此f (0)=0,(0)f '=−1,又因为曲线y =f (x )在点(0, f (0))处的切线方程为y −f (0)= (0)f ' (x −0),故所求切线方程为x +y =0. (Ⅱ)解:由已知可得f (x )=(x −t 2+3)( x −t 2) (x −t 2−3)=( x −t 2)3−9 ( x −t 2)=x 3−3t 2x 2+(3t 22−9)x − t 22+9t 2. 故()f x '= 3x 3−6t 2x +3t 22−9.令()f x '=0,解得x = t 2−3,或x = t 2+3. 当x 变化时,f ‵(x ),f (x )的变化如下表:x(−∞,t 2−3) t 2−3 (t 2−3,t 2+3) t 2+3 (t 2+3,+∞) ()f x '+ 0 − 0 + f (x )↗极大值↘极小值↗所以函数f (x )的极大值为f (t 2−3)=(−3)3−9×(−3)=63;函数小值为f (t 2+3)=(3)3−9×(3)=−63.(III )解:曲线y =f (x )与直线y =−(x −t 2)−63有三个互异的公共点等价于关于x 的方程(x −t 2+d ) (x −t 2) (x −t 2−d )+ (x −t 2)+ 63=0有三个互异的实数解,令u = x −t 2,可得u 3+(1−d 2)u +63=0.设函数g (x )= x 3+(1−d 2)x +63,则曲线y =f (x )与直线y =−(x −t 2)−63有三个互异的公共点等价于函数y =g (x )有三个零点.()g'x =3 x 3+(1−d 2).当d 2≤1时,()g'x ≥0,这时()g'x 在R 上单调递增,不合题意.当d 2>1时,()g'x =0,解得x 1=213d --,x 2=213d -.易得,g (x )在(−∞,x 1)上单调递增,在[x 1, x 2]上单调递减,在(x 2, +∞)上单调递增,g (x )的极大值g (x 1)= g (213d --)=32223(1)639d -+>0. g (x )的极小值g (x 2)= g (213d -)=−32223(1)639d -+. 若g (x 2) ≥0,由g (x )的单调性可知函数y =f (x )至多有两个零点,不合题意.若2()0,g x <即322(1)27d ->,也就是||10d >,此时2||d x >,(||)||630,g d d =+> 且312||,(2||)6||2||636210630d x g d d d -<-=--+<-+<,从而由()g x 的单调性,可知函数()y g x = 在区间1122(2||,),(,),(,||)d x x x x d -内各有一个零点,符合题意.学科……网所以d 的取值范围是(,10)(10,).-∞-+∞。
