中国海洋大学资料物理习题答案习题2
(完整word版)中国海洋大学大学物理I3A

2005-2006学年第 1 学期试题名称:大学物理Ⅰ(3)共5 页第 1 页IIAA ′O+-2005-2006学年第 1 学期 试题名称 :大学物理Ⅰ(3) 共 5 页 第 2 页 6.(本题3分)(3368) 一束光强为I 0的自然光垂直穿过两个偏振片,且此两偏振片的偏振化方向成45°角,则穿过两个偏振片后的光强I 为 (A) 4/0I 2 . (B) I 0 / 4.(C) I 0 / 2. (D) 2I 0 / 2. [ ]7.(本题3分)(4351) 宇宙飞船相对于地面以速度v 作匀速直线飞行,某一时刻飞船头部的宇航员向飞船尾部发出一个光讯号,经过∆t (飞船上的钟)时间后,被尾部的接收器收到,则由此可知飞船的固有长度为 (c 表示真空中光速) (A) c ·∆t (B) v ·∆t (C)2)/(1c t c v -⋅∆(D) 2)/(1c t c v -⋅⋅∆ [ ]8.(本题3分)(4359) (1)对某观察者来说,发生在某惯性系中同一地点、同一时刻的两个事件,对于相对该惯性系作匀速直线运动的其它惯性系中的观察者来说,它们是否同时发生? (2)在某惯性系中发生于同一时刻、不同地点的两个事件,它们在其它惯性系中是否同时发生?关于上述两个问题的正确答案是: (A) (1)同时,(2)不同时. (B) (1)不同时,(2)同时. (C) (1)同时,(2)同时.(D) (1)不同时,(2)不同时. [ ]二、填空题(共21分) 9.(本题5分)(1206) 一平行板电容器,充电后与电源保持联接,然后使两极板间充满相对介电常量为εr 的各向同性均匀电介质,这时两极板上的电荷是原来的________倍;电场强度是原来的 _________倍;电场能量是原来的____________倍.10.(本题3分)(1391) 一个半径为R 的薄金属球壳,带有电荷q ,壳内充满相对介电常量为εr 的各向同性均匀电介质.设无穷远处为电势零点,则球壳的电势U = ________________________________.11.(本题3分)(2564) 如图,两根导线沿半径方向引到铁环的上A 、A ′两点,并在很远处与电源相连,则环中心的磁感强度为_________________.中国海洋大学命题专用纸2005-2006学年第 1 学期试题名称:大学物理Ⅰ(3)共 5 页第 3 页中国海洋大学命题专用纸2005-2006学年第 1 学期试题名称:大学物理Ⅰ(3)共 5 页第 4 页16 (本题10分)设光栅平面和透镜都与屏幕平行,在平面透射光栅上每厘米有5000条刻线,用它来观察钠黄光(λ=589 nm)的光谱线.(1)当光线垂直入射到光栅上时,能看到的光谱线的最高级次k m是多少?(2)当光线以30°的入射角(入射线与光栅平面的法线的夹角)斜入射到光栅上时,能看k'是多少?(1nm=10-9m)到的光谱线的最高级次mv0.99c (c为真空中光速)的速率运动.试求:17.(本题8分)(4500)一电子以=(1) 电子的总能量是多少?(2) 电子的经典力学的动能与相对论动能之比是多少?(电子静止质量m e=9.11×10-31 kg)中国海洋大学命题专用纸。
大学物理II2-B试题及答案马丽珍

中国海洋大学命题专用纸(附页A)中国海洋大学命题专用纸(附页C)2006-2007学年第 2 学期试题名称:大学物理II2 (B)共6页第 4 页三、计算题(共36分)10 C·m-3求距球心17、(本题12分)均匀带电球壳内半径6cm,外半径10cm,电荷体密度为2×55cm,8cm ,12cm 各点的场强.中国海洋大学命题专用纸(附页E)2006-2007学年第 2 学期试题名称:大学物理II2 (B)共6页第 6 页19、(本题12分)白光垂直照射到空气中一厚度为3800oA的肥皂膜上,设肥皂膜的折射率为1.33,试问该膜的正面呈现什么颜色?背面呈现什么颜色?四、简答题(共7分)20、(本题7分)光电效应和康普顿效应都包含了电子和光子的相互作用,试问这两个过程有什么不同?06-07学年第二学期大学物理II2(B )参考答案及评分标准一、选择题 (每题3分,共27分)1B 2C 3D 4B 5D 6B 7C 8A 9D二、填空题 (共30分)00010.()0,(2E (2,(2,(2,(2,(2(2,(2,(2(2sin sin 2,(2sin 2(26,(2(216.41(243(2r r r m E r rI I f qv lvtB t lvB t σεεεεμμα=⨯00R 分)(r)=分)11.分)分)分)12.分)0,分)2分)13.分)v B 分)14.分)分)15.分)明,分),分),分)三、计算题 (共36分)17. 均匀带电球壳内半径6cm ,外半径10cm ,电荷体密度为2×510-C ·m -3求距球心5cm ,8cm ,12cm 各点的场强.解: 高斯定理0d ε∑⎰=⋅q S E s ,02π4ε∑=q r E (4分)当5=r cm 时,0=∑q ,0=E(2分)8=r cm 时,∑q 3π4p=3(r )3内r - ∴ ()2023π43π4rr r E ερ内-=41048.3⨯≈1C N -⋅, 方向沿半径向外.(3分) 12=r cm 时,3π4∑=ρq -3(外r )内3r ∴ ()420331010.4π43π4⨯≈-=rr r E ερ内外 1C N -⋅ 沿半径向外. (3分) 18.两平行长直导线相距d =40cm ,每根导线载有电流1I =2I =20A ,如题图所示.求: (1)两导线所在平面内与该两导线等距的一点A 处的磁感应强度; (2)通过图中斜线所示面积的磁通量.(1r =3r =10cm, l =25cm).解:(1) 52010104)2(2)2(2-⨯=+=d I d I B A πμπμ T 方向⊥纸面向外 (6分)(2)取面元 r l S d d =612010110102.23ln 31ln 23ln 2])(22[1211-+⨯=πμ=πμ-πμ=-πμ+πμ=⎰lI l I l I ldr r d I r I r r r ΦWb (6分) 19.白光垂直照射到空气中一厚度为3800 oA 的肥皂膜上,设肥皂膜的折射率为1.33,试问该膜的正面呈现什么颜色?背面呈现什么颜色? 解: 由反射干涉相长公式有λλk ne =+22 ),2,1(⋅⋅⋅=k (4分) 得 122021612380033.14124-=-⨯⨯=-=k k k ne λ 2=k , 67392=λo A (红色) (2分) 3=k , 40433=λ oA (紫色) (2分)所以肥皂膜正面呈现紫红色.由透射干涉相长公式 λk ne =2),2,1(⋅⋅⋅=k (2分) 所以 kk ne 101082==λ 当2=k 时, λ =5054oA (绿色) (2分)故背面呈现绿色.四、简答题(共7分)20. 光电效应和康普顿效应都包含了电子和光子的相互作用,试问这两个过程有什么不同?答:光电效应是指金属中的电子吸收了光子的全部能量而逸出金属表面,是电子处于原子中束缚态时所发生的现象.遵守能量守恒定律.(4分)而康普顿效应则是光子与自由电子(或准自由电子)的弹性碰撞,同时遵守能量与动量守恒定律(3分).。
(完整word版)中国海洋大学大学物理电磁学I3B

中国海洋大学命题专用纸2005-2006学年第 1 学期试题名称:大学物理Ⅰ(3)共5页第 1 页授课教师命题教师或命题负责人签字院系负责人签字年月日中国海洋大学命题专用纸2005-2006学年第 1 学期试题名称:大学物理Ⅰ(3)共5页第 2 页中国海洋大学命题专用纸2005-2006学年第 1 学期试题名称:大学物理Ⅰ(3)共 5 页第 3 页12.(本题5分)(3230)要使一束线偏振光通过偏振片之后振动方向转过90°,至少需要让这束光通过__________块理想偏振片.在此情况下,透射光强最大是原来光强的______________________倍.13.(本题3分)(4353)已知惯性系S'相对于惯性系S系以0.5 c的匀速度沿x轴的负方向运动,若从S'系的坐标原点O'沿x轴正方向发出一光波,则S系中测得此光波在真空中的波速为____________________________________.14.(本题5分)(4732)观察者甲以0.8c的速度(c为真空中光速)相对于静止的观察者乙运动,若甲携带一质量为1 kg的物体,则(1)甲测得此物体的总能量为____________;(2)(2) 乙测得此物体的总能量为_________.二、计算题(共38分)15.如图所示,一厚为b的“无限大”带电平板,其电荷体密度分布为 =kx (0≤x≤b ),式中k为一正的常量.求:(1) 平板外两侧任一点P1和P2处的电场强度大小;(2) 平板内任一点P处的电场强度;(3) 场强为零的点在何处?中国海洋大学命题专用纸2005-2006学年第 1 学期试题名称:大学物理Ⅰ(3)共5 页第 4 页中国海洋大学命题专用纸2005-2006学年第 1 学期试题名称:大学物理Ⅰ(3)共5 页第 4 页v0.99c (c为真空中光速)的速率运动.试求:17.(本题8分)(4500)一电子以(1) 电子的总能量是多少?(2) 电子的经典力学的动能与相对论动能之比是多少?(电子静止质量m e=9.11×10-31 kg)三、简述题(共15分)18(本题5分)(3762)光栅的衍射光谱和棱镜的色散光谱主要有什么不同?19(本题5分)19—6你能否举一些日常生活中所见到的例子.来说明物体热辐射的各种波长中,单色辐射强度最大的波长随温度的升高而减小?20(本题5分)光电效应和康普顿效应都是光子与电子间的相互作用,你是怎样区别这两个过程的?。
中国海洋大学 大学物理3 期末考试试题和答案81

Φ 2
2d
d
0I 2r
drΒιβλιοθήκη 0 Id 2
ln 2
d
总磁通量
Φ
Φ1
Φ2
0 Id 2
ln
4 3
4分
感应电动势为:
dΦ 0d (ln 4) d I 0d ln 4
2分
d t 2 3 d t 2 3
由 >0 和回路正方向为顺时针,所以 的绕向为顺时针方向,线圈中的感应电流
dEx=-dEcos
dEy=-dEsin
对各分量分别求和
Ex
0 4 0 R
sin cos d =0
0
E y
0 4 0 R
sin
2
d
0
0
8 0 R
∴
E
Exi
Ey
j
0 8 0 R
j
y
dq R
d
O
x
dEy
1分 1分 2分
对于'=600 nm 的光,连同附加光程差,在 A 处两反射光的光程差为
2e4
1 2
,它与波长 之比为 2e4
/
1 2
3.0
.所以
A
处是明纹
3分
(3) 棱边处仍是暗纹,A 处是第三条明纹,所以共有三条明纹,三条暗纹.
2分
四、问答题(共 13 分)
1、(5 分)
答:因 k =±4 的主极大出现在=±90°的方向上,实际观察不到.
亦是顺时针方向.
2分
中国海洋大学 大学物理3 期末考试试题和答案41

感应电动势.
O
x
2、(12 分)图示一平面简谐波在 t = 0 时刻的波形图,求 (1) 该波的波动表达式; (2) P 处质点的振动方程.
y (m) u = 0.08 m/s
O -0.04
P
x (m)
0.20 0.40 0.60
3、(10 分)一衍射光栅,每厘米 200 条透光缝,每条透光缝宽为 a=2×10-3 cm,在光栅后放 一焦距 f=1 m 的凸透镜,现以=600 nm (1 nm=10-9 m)的单色平行光垂直照射光栅,求:
S,S 边线所在平面 的磁通量(取弯面向
外为正)为
(A) r2B.
. (B) 2r2B.
(C) -r2Bsin.
(D) -r2Bcos.
[
]
2、四条皆垂直于纸面的载流细长直导线,每条中的电流皆为 I.这四条导
线被纸面截得的断面,如图所示,它们组成了边长为 2a 的正方形的四个 角顶,每条导线中的电流流向亦如图所示.则在图中正方形中心点 O 的
院系负责人 签字
年月日
中 国 海 洋 大 学 命 题 专 用 纸(附页)
2006-2007 学年第 1 学期
试题名称 :大学物理Ⅱ2 (A 卷) 共 4 页 第 2 页
5、一弹簧振子作简谐振动,总能量为 E1,如果简谐振动振幅增加为原来的两倍,重物的质量
增为原来的四倍,则它的总能量 E2 变为
(A) E1/4.
--AAO12
为________________________________.
3、(3 分)如图所示,波源 S1 和 S2 发出的波在 P 点相遇,P 点距波源 S1 和 S2 的距离分别为 3和 103 ,为两列波在介质中的波长,若
中国海洋大学资料物理习题答案习题17

习题1617-1 按照原子核的质子一中子模型,组成原子核X AZ 的质子数和中子数各是多少?核内共有多少个核子?这种原子核的质量数和电荷数各是多少?答:组成原子核X A Z 的质子数是Z ,中子数是Z A -.核内共有A 个核子.原子核的质量数是A ,核电荷数是Z .17-2 原子核的体积与质量数之间有何关系?这关系说明什么?答:实验表明,把原子核看成球体,其半径R 与质量数A 的关系为310A R R =,说明原子核的体积与质量数A 成正比关系.这一关系说明一切原子核中核物质的密度是一个常数.即单位体积内核子数近似相等,并由此推知核的平均结合能相等.结合能正比于核子数,就表明核力是短程力.如果核力象库仑力那样,按照静电能的公式,结合能与核子数A 的平方成正比,而不是与A 成正比.17-3 什么叫原子核的质量亏损?如果原子核X AZ 的质量亏损是m ∆,其平均结合能是多少?解:原子核的质量小于组成原子核的核子的质量之和,它们的差额称为原子核的质量亏损.设原子核的质量为x M ,原子核X A Z 的质量亏损为:x n p M m Z A Zm m --+=∆])([平均结合能为 Am c A E E 20ΔΔ== 17-4 已知Th 23290的原子质量为u 232.03821,计算其原子核的平均结合能. 解:结合能为MeV 5.931])([ΔH ⨯--+=M m Z A Zm E nTh 23290原子u M 03821.232=,90=Z ,232=A ,氢原子质量u m 007825.1H =,u m n 008665.1=MeV1.766.56MeV5.931]03821.232008665.1)90232(007825.190[Δ=⨯-⨯-+⨯=∴E∴平均结合能为 MeV 614.723256.1766Δ0===A E E 17-5什么叫核磁矩?什么叫核磁子(N μ)?核磁子N μ和玻尔磁子B μ有何相似之处?有何区别?质子的磁矩等于多少核磁子?平常用来衡量核磁矩大小的核磁矩I μ'的物理意义是什么?它和核的g 因子、核自旋量子数的关系是什么?解:原子核自旋运动的磁矩叫核磁矩,核磁子是原子核磁矩的单位,定义为:227m A 10.05.51.18361π4⋅⨯===-B p N m eh μμ式中p m 是质子的质量.核磁子与玻尔磁子形式上相似,玻尔磁子定义为eB m ehπμ4=,式中e m 是电子的质量.质子的磁矩不等于N μ.质子的磁矩N P μμ79273.2=.平常用来衡量核磁矩大小的是核磁矩在外磁场方向分量的最大值I μ',它和原子核g 因子、自旋量子数的关系是N I I I g μμ='.17-6 核自旋量子数等于整数或半奇整数是由核的什么性质决定?核磁矩与核自旋角动量有什么关系?核磁矩的正负是如何规定的?解:原子核是由质子和中子组成.质子和中子的自旋均为21.因此组成原子核的质子和中子数的奇、偶数决定了核自旋量子数为零或21的奇、偶倍数. 核磁矩与自旋角动量的关系是:I pII P m eg 2=μ I μ的正负取决于I g 的正负.当I μ与I P 平行时I μ 为正,当I μ 与I P 反平行时,I μ为负. 17-7 什么叫核磁共振?怎样利用核磁共振来测量核磁矩?解:原子核置于磁场中,磁场和核磁矩相互作用的附加能量使原子核能级发生分裂.当核在电磁辐射场中时,辐射场是光子组成的,当光子的能量hv 等于核能级间隔时,原子核便吸收电磁场的能量,称为共振吸收,这一现象称为核磁共振.在磁场中核能级间隔为:B g E N I μ=∆共振吸收时,B g E h N I μυ=∆=通常用核磁矩在磁场方向分量的最大值I μ'来衡量磁矩的大小,N I I I g μμ=',则有B Ih Iμυ'=∴Bh II υμ=',已测出I ,υ,现测得B 就可以算出I μ'. 17-8 什么叫核力?核力具有哪些主要性质?答:组成原子核的核子之间的强相互作用力称为核力.核力的主要性质:(1)是强相互作用力,主要是引力.(2)是短程力,作用距离小于m 1015-,(3)核力与核子的带电状况无关.(4)具有饱和性.17-9 什么叫放谢性衰变?α,β,γ射线是什么粒子流?写出U 23890的α衰变和Th 23490的β衰变的表示式.写出α衰变和β衰变的位移定则.解:不稳定的原子核都会自发地转变成另一种核而同时放出射线,这种变化叫放射性衰变.α射线是带正电的氦核He 42粒子流,β射线是高速运动的正、负电子流,γ射线是光子流.ee υ~Pa T h HeT h 012349123490422349023892++→+→-α衰变和β衰变的位移定则为:α衰变 He Y X 4242+→--A z A zβ衰变的位移定则为:e A z A z υ~e Y X 0++→-+e A z A zυ++→+-e Y X 01117-10 什么叫原子核的稳定性?哪些经验规则可以预测核的稳定性?答:原子核的稳定性是指原子核不会自发地从核中发出射线而转变成另一种原子核的性质. 以下经验规则可预测核的稳定性:(1)原子序数大于84的核是不稳定的.(2)原子序数小于84的核中质子数和中子数都是偶数的核稳定.(3)质子或中子数等于幻数2、8、20、28、50、82、126的原子核特别稳定.(4)质子数和中子数之比1=pn的核稳定.比值越大,稳定性越差. 17-11 写出放射性衰变定律的公式.衰变常数λ的物理意义是什么?什么叫半衰期21T ?21T 和λ有什么关系?什么叫平均寿命τ?它和半衰期21T 、和λ有什么关系?解:t N N λ-0e =,衰变常数NtN d /d -=λ.的物理意义是表示在某时刻,单位时间内衰变的原子数与该时刻原子核数的比值.是表征衰变快慢的物理常数.原子核每衰变一半所需的时间叫半衰期.λT 2ln 21=平均寿命τ是每个原子核衰变前存在时间的平均值.λτ1=2ln 21τ=T .17-12 测得地壳中铀元素U 23592只点0.72%,其余为U 23892,已知U 23892的半衰期为4.468×109年,U 23592的半衰期为7.038×108年,设地球形成时地壳中的U 23892和U 23592是同样多,试估计地球的年龄.解:按半衰期 λλ693.02ln ==T对年:/110847.910038.7693.0693.0U 10181123592-⨯=⨯==T λ 对年:/110551.110468.4693.0693.0U 1092223892-⨯=⨯==T λ 按衰变定律t N N λ-=e 0,可得ttt N N N N )(00211221e ee λλλλ---== 则地球年龄: 1221lnλλ-=N N t年9101094.510)847.9551.1(28.9972.0ln⨯=⨯-=-17-13 放射性同位素主要应用有哪些?答:放射性同位素主要在以下几个方面应用较广泛:医学上用于放射性治疗和诊断;工业上用于无损检测;农业上用放射性育种;考古学、地质学中用于计算生物或地质年代;生物学中作示踪原子等等.17-14 为什么重核裂变或轻核聚变能够放出原子核能?答:轻核和重核的平均结合能较小,而中等质量)60~40(=A 的核平均结合能较大,因此将重核裂变成两个中等质量的核或轻核聚变成质量数较大的核时平均结合能升高,从而放出核能.17-15 原子核裂变的热中子反应堆主要由哪几部分组成?它们各起什么作用?答:热中子反应堆的主要组成部份有堆芯、中子反射层、冷却系统、控制系统、防护层.堆芯是放置核燃料和中子减速剂的核心部份,维持可控链式反应,释放原子核能. 冷却系统与换能系统合二为一,再通过冷却系统将堆芯释放出的核能输送到堆芯以外. 控制系统是通过控制棒插入堆芯的长度,控制参加反应的中子数,使反应堆保持稳定的功率.中子反射层是阻挡中子从反应堆中逸出. 防护层是反应堆的安全屏障.17-16 试举出在自然界中存在负能态的例子.这些状态与狄拉克真空,结果产生1 MeV 的电子,此时还将产生什么?它的能量是多少?答:例如物体在引力场中所具有的引力势能;正电荷在负电荷电场中的静电能,都是自然界中的负能态.这些负能态是能够观测到的,具有可观测效应.狄拉克的负能态是观测不到的,没有可观测效应.17-17 将3MeV 能量的γ光子引入狄拉克真空,结果产生1MeV 的电子,此时还将产生什么?它的能量是多少?答:把能量大于电子静能两倍MeV 022.1220=>c m E 的γ光子引入真空,它有可能被负能量电子的一个电子所吸收,吸收了这么多能量的电子有可能越过禁区而跃迁到正能量区,并表现为一个正能量的负电子-e ;同时,留下的空穴表现为一个正能量的正电子+e .这一过程称为电子偶的产生,可写为-++→e e γ按题意,根据能量守恒,正电子的能量为MeV 217-18 试证明任何能量的γ光子在真空中都不可能产生正、负电子对.答:证明:设由γ光子转化成的一对正负电子其动量分别为1p 和2p ,在电子的质心系中应有021=+p p并且正负电子的总能量应大于22c m e .按照相对论,光子动量与能量的关系为pc E =,动量等于零而能量不等于零的光子是不存在的.显然γ光子转换成正负电子,同时满足能量守恒和动量守恒是不可能的,即在真空中无论γ光子能量多大,都不可能产生正负电子对.但是γ光子与重原子核作用时便可转化为正负电子对.。
中国海洋大学资料物理习题答案习题13

习题十三13-1 衍射的本质是什么?衍射和干涉有什么联系和区别?答:波的衍射现象是波在传播过程中经过障碍物边缘或孔隙时所发生的展衍现象.其实质是由被障碍物或孔隙的边缘限制的波阵面上各点发出的无数子波相互叠加而产生.而干涉则是由同频率、同方向及位相差恒定的两列波的叠加形成.13-2 在夫琅禾费单缝衍射实验中,如果把单缝沿透镜光轴方向平移时,衍射图样是否会 跟着移动?若把单缝沿垂直于光轴方向平移时,衍射图样是否会跟着移动?答:把单缝沿透镜光轴方向平移时,衍射图样不会跟着移动.单缝沿垂直于光轴方向平移时,衍射图样不会跟着移动.13-3 什么叫半波带?单缝衍射中怎样划分半波带?对应于单缝衍射第3级明条纹和第4级暗 条纹,单缝处波面各可分成几个半波带?答:半波带由单缝A \B 首尾两点向ϕ方向发出的衍射线的光程差用2λ来划分.对应于第3级明纹和第4级暗纹,单缝处波面可分成7个和8个半波带.∵由272)132(2)12(sin λλλϕ⨯=+⨯=+=k a ,284sin λλϕ⨯==a 13-4 在单缝衍射中,为什么衍射角ϕ愈大(级数愈大)的那些明条纹的亮度愈小? 答:因为衍射角ϕ愈大则ϕsin a 值愈大,分成的半波带数愈多,每个半波带透过的光通量就愈小,而明条纹的亮度是由一个半波带的光能量决定的,所以亮度减小.13-5 若把单缝衍射实验装置全部浸入水中时,衍射图样将发生怎样的变化?如果此时用公式),2,1(2)12(sin =+±=k k a λϕ来测定光的波长,问测出的波长是光在空气中的还是在水中的波长?解:当全部装置浸入水中时,由于水中波长变短,对应='='λϕk a sin n k λ,而空气中为λϕk a =sin ,∴ϕϕ'=sin sin n ,即ϕϕ'=n ,水中同级衍射角变小,条纹变密. 如用)12(sin +±=k a ϕ2λ),2,1(⋅⋅⋅=k 来测光的波长,则应是光在水中的波长.(因ϕsin a 只代表光在水中的波程差).13-6 在单缝夫琅禾费衍射中,改变下列条件,衍射条纹有何变化?(1)缝宽变窄;(2)入 射光波长变长;(3)入射平行光由正入射变为斜入射.解(1)缝宽变窄,由λϕk a =sin 知,衍射角ϕ变大,条纹变稀;(2)λ变大,保持a ,k 不变,则衍射角ϕ亦变大,条纹变稀;(3)由正入射变为斜入射时,因正入射时λϕk a =sin ;斜入射时,λθϕk a '=-)sin (sin ,保持a ,λ不变,则应有k k >'或k k <'.即原来的k 级条纹现为k '级.13-7 单缝衍射暗条纹条件与双缝干涉明条纹的条件在形式上类似,两者是否矛盾?怎样 说明?答:不矛盾.单缝衍射暗纹条件为k k a 2sin ==λϕ2λ,是用半波带法分析(子波叠加问题).相邻两半波带上对应点向ϕ方向发出的光波在屏上会聚点一一相消,而半波带为偶数,故形成暗纹;而双缝干涉明纹条件为λθk d =sin ,描述的是两路相干波叠加问题,其波程差为波长的整数倍,相干加强为明纹.13-8 光栅衍射与单缝衍射有何区别?为何光栅衍射的明条纹特别明亮而暗区很宽?答:光栅衍射是多光束干涉和单缝衍射的总效果.其明条纹主要取决于多光束干涉.光强与缝数2N 成正比,所以明纹很亮;又因为在相邻明纹间有)1(-N 个暗纹,而一般很大,故实际上在两相邻明纹间形成一片黑暗背景.13-9 试指出当衍射光栅的光栅常数为下述三种情况时,哪些级次的衍射明条纹缺级?(1) a+b=2a;(2)a+b=3a;(3)a+b=4a.解:由光栅明纹条件和单缝衍射暗纹条件同时满足时,出现缺级.即 ⎩⎨⎧=''±==±=+)2,1(sin ),2,1,0(sin )( k k a k k b a λϕλϕ可知,当k a b a k '+=时明纹缺级. (1)a b a 2=+时,⋅⋅⋅=,6,4,2k 偶数级缺级;(2)a b a 3=+时,⋅⋅⋅=,9,6,3k 级次缺级;(3)a b a 4=+,⋅⋅⋅=,12,8,4k 级次缺级.13-10 若以白光垂直入射光栅,不同波长的光将会有不同的衍射角.问(1)零级明条纹能 否分开不同波长的光?(2)在可见光中哪种颜色的光衍射角最大?不同波长的光分开程度与什 么因素有关?解:(1)零级明纹不会分开不同波长的光.因为各种波长的光在零级明纹处均各自相干加强.(2)可见光中红光的衍射角最大,因为由λϕk b a =+sin )(,对同一k 值,衍射角λϕ∞. 13-11 一单色平行光垂直照射一单缝,若其第三级明条纹位置正好与6000οA 的单色平行光的第二级明条纹位置重合,求前一种单色光的波长.解:单缝衍射的明纹公式为)12(sin +=k a ϕ 2λ当6000=λo A 时,2=k x λλ=时,3=k 重合时ϕ角相同,所以有)132(26000)122(sin +⨯=+⨯=ϕa 2x λ,得4286600075=⨯=x λo A 13-12 单缝宽0.10mm ,透镜焦距为50cm ,用5000=λoA 的绿光垂直照射单缝.求:(1)位于透镜焦平面处的屏幕上中央明条纹的宽度和半角宽度各为多少?(2)若把此装置浸入水中(n=1.33),中央明条纹的半角宽度又为多少? 解:中央明纹的宽度为f na x λ2=∆半角宽度为naλθ1sin -=(1)空气中,1=n ,所以3310100.51010.01050005.02---⨯=⨯⨯⨯⨯=∆x m ,33101100.51010.0105000sin ----⨯=⨯⨯=θ rad (2)浸入水中,33.1=n ,所以有33101076.31010.033.110500050.02---⨯≈⨯⨯⨯⨯⨯=∆x m331011076.3101.033.1105000sin ----⨯≈⨯⨯⨯=θ rad 13-13 用橙黄色的平行光垂直照射一宽为a=0.60mm 的单缝,缝后凸透镜的焦距f=40.0cm ,观察屏幕上形成的衍射条纹.若屏上离中央明条纹中心1.40mm 处的P 点为一明条纹;求:(1)入射光的波长;(2)P 点处条纹的级数;(3)从P 点看,对该光波而言,狭缝处的波面可分成几个半波带?解:(1)由于P 点是明纹,故有2)12(sin λϕ+=k a ,⋅⋅⋅=3,2,1k 由ϕϕsin tan 105.34004.13≈=⨯==-f x ,故3105.3126.0212sin 2-⨯⨯+⨯=+=k k a ϕλ 3102.4121-⨯⨯+=k mm ,当 3=k ,得60003=λo A ,4=k ,得47004=λo A (2)若60003=λo A ,则P 点是第3级明纹;若47004=λo A ,则P 点是第4级明纹.(3)由2)12(sin λϕ+=k a 可知,当3=k 时,单缝处的波面可分成712=+k 个半波带;当4=k 时,单缝处的波面可分成912=+k 个半波带.13-14 用5900=λoA 的钠黄光垂直入射到每毫米有500条刻痕的光栅上,问最多能看到第几级明条纹?解:5001=+b a mm 3100.2-⨯= mm 4100.2-⨯=o A ,由λϕk b a =+sin )(知,最多见到的条纹级数max k 对应的2πϕ=,,所以有39.35900100.24max ≈⨯=+=λb a k ,即实际见到的最高级次为3max =k . 13-15 波长为5000o A 的平行单色光垂直照射到每毫米有200条刻痕的光栅上,光栅后的透镜焦距为60cm . 求:(1)屏幕上中央明条纹与第一级明条纹的间距;(2)当光线与光栅法线成 30°斜入射时,中央明条纹的位移为多少? 解:3100.52001-⨯==+b a mm 6100.5-⨯m (1)由光栅衍射明纹公式 λϕk b a =+sin )(,因1=k ,又f x ==ϕϕtan sin ,所以有λ=+fx b a 1)( 即 62101100.51060105000---⨯⨯⨯⨯=+=b a fx λ2100.6-⨯=m 6= cm (2)对应中央明纹,有0=k正入射时,0sin )(=+ϕb a ,所以0sin =≈ϕϕ斜入射时,0)sin )(sin (=±+θϕb a ,即0sin sin =±θϕ因︒=30θ,∴21tan sin ±==≈f x ϕϕ 故22103010602121--⨯=⨯⨯==f x m 30= cm 这就是中央明条纹的位移值.13-16 波长6000=λo A 的单色光垂直入射到一光栅上,第二、第三级明条纹分别20.0sin =ϕ与30.0sin =ϕ处,第四级缺级.求:(1)光栅常数;(2)光栅上狭缝的宽度;(3)在90°>ϕ>-90°范围内,实际呈现的全部级数.解:(1)由λϕk b a =+sin )(式对应于20.0sin 1=ϕ与30.0sin 2=ϕ处满足:101060002)(20.0-⨯⨯=+b a ,101060003)(30.0-⨯⨯=+b a得6100.6-⨯=+b a m(2)因第四级缺级,故此须同时满足λϕk b a =+sin )(,λϕk a '=sin 解得k k b a a '⨯='+=-6105.14,取1='k ,得光栅狭缝的最小宽度为6105.1-⨯m (3)由λϕk b a =+sin )(,λϕsin )(b a k += 当2πϕ=,对应max k k =∴ 10106000100.6106max =⨯⨯=+=--λb a k 因4±,8±缺级,所以在︒︒<<-9090ϕ范围内实际呈现的全部级数为9,7,6,5,3,2,1,0±±±±±±±=k 共15条明条纹(10±=k 在︒±=90k 处看不到).13-17 一双缝,两缝间距为0.1mm ,每缝宽为0.02mm ,用波长为4800oA 的平行单色光垂直入射双缝,双缝后放一焦距为50cm 的透镜.试求:(1)透镜焦平面上单缝衍射中央明条纹的宽度;(2)单缝衍射的中央明条纹包迹内有多少条双缝衍射明条纹?解:(1)中央明纹宽度为 02.010501048002270⨯⨯⨯⨯==-f a l λmm 4.2=cm (2)由缺级条件λϕk a '=sinλϕk b a =+sin )(知k k a b a k k '='=+'=502.01.0 ⋅⋅⋅=',2,1k 即⋅⋅⋅=,15,10,5k 缺级. 中央明纹的边缘对应1='k ,所以单缝衍射的中央明纹包迹内有4,3,2,1,0±±±±=k 共9条双缝衍射明条纹.13-18 在夫琅禾费圆孔衍射中,设圆孔半径为0.10mm ,透镜焦距为50cm ,所用单色光波长为5000oA ,求在透镜焦平面处屏幕上呈现的爱里斑半径.解:由爱里斑的半角宽度 47105.302.010500022.122.1--⨯=⨯⨯==D λθ ∴ 爱里斑半径5.1105.30500tan 24=⨯⨯=≈=-θθf f d mm 13-19 已知天空中两颗星相对于一望远镜的角距离为4.84×10-6rad ,它们都发出波长为5500oA 的光,试问望远镜的口径至少要多大,才能分辨出这两颗星?解:由最小分辨角公式 D λθ22.1=∴ 86.131084.4105.522.122.165=⨯⨯⨯==--θλD cm 13-20 已知入射的X 射线束含有从0.95~1.30o A 范围内的各种波长,晶体的晶格常数为2.75o A ,当X 射线以45°角入射到晶体时,问对哪些波长的X 射线能产生强反射? 解:由布喇格公式 λϕk d =sin 2 得kd ϕλsin 2=时满足干涉相长 当1=k 时, 89.345sin 75.22=⨯⨯=︒λoA2=k 时,91.1245sin 75.22=⨯⨯=︒λo A 3=k 时,30.1389.3==λo A 4=k 时, 97.0489.3==λo A 故只有30.13=λo A 和97.04=λo A 的X 射线能产生强反射.。
中国海洋大学 大学物理3 期末考试试题和答案72

2005-2006学年第 2 学期 大学物理II2(B ) 评分标准一 选择题(共18分,每题3分)B B ACD C二.填空题(共23分)1. 0 (4分) 2.221010,....3arctg π-⨯-,(4分)3. 2 (3分)4. 030 (3分) 5. 20.25e m c (3分) . 6 .)(20νν-m h(3分) 7.actg 2 (3分)三.计算题(共44分)3.2 解:设第三级暗纹在ϕ3方向上,则有a sin ϕ3 = 3λ 5分此暗纹到中心的距离为 x 3 = f tg ϕ3 3分因为ϕ3很小,可认为tg ϕ3≈sin ϕ3,所以x 3≈3f λ / a .两侧第三级暗纹的距离是 2 x 3 = 6f λ / a = 8.0mm∴ λ = (2x 3) a / 6f= 500 nm 2分3.3解:(1) ∆x =20 D λ / a 4分=0.11 m 2分(2) 覆盖云玻璃后,零级明纹应满足(n -1)e +r 1=r 2 3分设不盖玻璃片时,此点为第k 级明纹,则应有r 2-r 1=k λ 2分所以 (n -1)e = k λ k =(n -1) e / λ=6.96≈7零级明纹移到原第7级明纹处 1分3.4 解;3.1 解:(1)2v F m qvBRP mv qBR h p λ=====h mvλ=四.问答题(共15分) 4.1略4.2 答:没对准. 3分根据相对论同时性,如题所述在K '系中同时发生,但不同地点(x '坐标不同)的两事件(即A '处的钟和B '处的钟有相同示数),在K 系中观测并不同时;因此,在K 系中某一时刻同时观测,这两个钟的示数必不相同. 5分。
中国海洋大学 大学物理3 期末考试试题和答案52

一、选择题(24 分,每题 3 分)
1、C 2、C 3、C 4、B 5、E 6、B 7、C
二、填空题(共 23 分)
1、2v /(分)
L
、(分)
8、A
t
3、22.6 J·m-3
(3 分)
4、电磁波能流密度矢量
S EH
(2 分) (1 分)
5、2-1 = 3-2=2/3
2分
5、(5 分)解:
EK p2 /(2me ) (h / )2 /(2me )
3
分
=5.0×10-6 eV
2分
四、问答题(共 10 分)
1、(5 分)解:(1) x = 0 点
0
1 2
;
1分
x=2点
2
1 ; 2
1分
y
x =3 点 3 ;
(2) 如图所示.
1分 2分
0 时刻,O 处质点
0 Acos , 0 v0 A sin ,
故
1
3分
2
又 t = 2 s,O 处质点位移为
A / 2 Acos(4 1 ) 2
所以
1 4 1 , = 1/16 Hz
2分
4
2
振动方程为
y0
A cos(t
/8
旋转矢量图见图
2分
振动曲线见图
3分
1T 5T
12
12
1?
x1 2
x
x3
x1
x3
t
7 ?
6
6
1x2 -A
T
1 12
T
T T 3T T 4 24
中国海洋大学 大学物理3 期末考试试题和答案ab

(1) P 点的位移电流密度的方向为____________.
×E ×
O ×
×P
(2) P 点感生磁场的方向为____________.
中 国 海 洋 大 学 命 题 专 用 纸(附页)
2006-2007 学年第 1 学期
试题名称 :电磁学(A 卷) 共 6 页 第 3 页
三 计算题(30 分)
(A) U1.
(B) U2.
(C)U1+ U2.
(D)
1 2
(U1
U
2
)
.
[
]
4、附图中,M、P、O 为由软磁材料制成的棒,三者在同一平面
内, 当 K 闭合后,
(A) M 的左端出现 N 极. (B) P 的左端出现 N 极.
P
(C) O 的右端出现 N 极. (D) P 的右端出现 N 极.
M O
a
d
1
2
满其内.如忽略边缘效应,介质中的场强应为____________________.
3、(4 分)在一根通有电流 I 的长直导线旁,与之共面地放着一个长、宽 各 b
I
为 a 和 b 的矩形线框,线框的长边与载流长直导线平行,且二者相距
b
为 b,如图所示.在此情形中,线框内的磁通量 =______________. a
1、(10 分)一导体球带电 q,半径为 R,导体球外面有两种均匀电介质,一种是介质
厚
r1
度为 d;另一种是空气 r 2 =1,且充满其余整个空间。求:
1. 各部分电场强度和电势的分布。 2. 第一种电介质两界面上的极化电荷面密度。
中 国 海 洋 大 学 命 题 专 用 纸(附页)
中国海洋大学最全历年物理3(下)真题

N D P C +q M -q O a b c d a b c d a bc d v v v ⅠⅢⅡ I2005-2006学年第 1 学期 试题名称 :大学物理III (下) 共6页 第1页专业年级: 学号 姓名 授课教师名 分数(请将计算题的答案写在答题纸上,其余直接作在试卷上) 一、选择题(共27分,每题3分)1、在边长为a 的正方体中心处放置一点电荷Q ,设无穷远处为电势零点,则在正方体顶角处的电势为:(A)aQ 034επ .(B) a Q032επ.(C) a Q 06επ. (D) aQ012επ . [ ]2、如图所示,直线MN 长为2l ,弧OCD 是以N 点为中心,l 为半径的半圆弧,N 点有正电荷+q ,M 点有负电荷-q .今将一试验电荷+q 0从O 点出发沿路径OCDP 移到无穷远处,设无穷远处电势为零,则电场力作功(A) A <0 , 且为有限常量. (B) A >0 ,且为有限常量.(C) A =∞. (D) A =0. [ ] 3、一块铜板垂直于磁场方向放在磁感强度正在增大的磁场中时,铜板中出现的涡流(感应电流)将(A) 加速铜板中磁场的增加. (B) 减缓铜板中磁场的增加.(C) 对磁场不起作用. (D) 使铜板中磁场反向. [ ]4、在无限长的载流直导线附近放置一矩形闭合线圈,开始时线圈与导线在同一平面内,且线圈中两条边与导线平行,当线圈以相同的速率作如图所示的三种不同方向的平动时,线圈中的感应电流(A) 以情况Ⅰ中为最大. (B) 以情况Ⅱ中为最大. (C) 以情况Ⅲ中为最大.(D) 在情况Ⅰ和Ⅱ中相同. [ ]a a ′b b ′ a a ′ b b ′ 图(1) 图(2)B O2005-2006学年第 1 学期 试题名称 :大学物理III (下) 共 6 页 第2页5、一束波长为λ的单色光由空气垂直入射到折射率为n 的透明薄膜上,透明薄膜放在空气中,要使反射光得到干涉加强,则薄膜最小的厚度为(A) λ / 4 . (B) λ / (4n ).(C) λ / 2 . (D) λ / (2n ). [ ]6、在双缝干涉实验中,用单色自然光,在屏上形成干涉条纹.若在两缝后放一个偏振片,则 (A) 干涉条纹的间距不变,但明纹的亮度加强. (B) 干涉条纹的间距不变,但明纹的亮度减弱. (C) 干涉条纹的间距变窄,且明纹的亮度减弱.(D) 无干涉条纹. [ ]7、磁介质有三种,用相对磁导率μr 表征它们各自的特性时, (A) 顺磁质μr >0,抗磁质μr <0,铁磁质μr >>1. (B) 顺磁质μr >1,抗磁质μr =1,铁磁质μr >>1. (C) 顺磁质μr >1,抗磁质μr <1,铁磁质μr >>1.(D) 顺磁质μr <0,抗磁质μr <1,铁磁质μr >0. [ ]8、圆铜盘水平放置在均匀磁场中,B的方向垂直盘面向上.当铜盘绕通过中心垂直于盘面的轴沿图示方向转动时,(A) 铜盘上有感应电流产生,沿着铜盘转动的相反方向流动.(B) 铜盘上有感应电流产生,沿着铜盘转动的方向流动.(C) 铜盘上产生涡流.(D) 铜盘上有感应电动势产生,铜盘边缘处电势最高.(E) 铜盘上有感应电动势产生,铜盘中心处电势最高. [ ]9、在一中空圆柱面上绕有两个完全相同的线圈aa ′和bb ′,当线圈aa ′和bb ′如图(1)绕制及联结时,ab 间自感系数为L 1;如图(2)彼此重叠绕制及联结时,ab 间自感系数为L 2.则(A) L 1 = L 2 =0. (B) L 1 = L 2 ≠ 0.(C) L 1 = 0,L 2 ≠ 0.(D) L 1 ≠ 0,L 2 = 0. [ ]中 国 海 洋 大 学 命 题 专 用 纸(附页)2005-2006学年第 1 学期 试题名称 :大学物理III (下) 共6页 第3页二、填空题(共33分,每题3分)1、在国际单位制中,磁场强度的单位是__________.磁感强度的单位是______,用H B ⋅21表示的单位体积内储存的磁能的单位是__________.2、如右图,单色平行光垂直入射到双缝上.观察屏上P 点到两缝的距离分别为r 1和r 2.设双缝和屏之间充满折射率为n 的媒质,则P 点处二相干光线的光程差为________________.3、在单缝的夫琅禾费衍射实验中,屏上第三级暗纹对应于单缝处波面可划分为_________________ 个半波带,若将缝宽缩小一半,原来第三级暗纹处将是____________纹.4、一无铁芯的长直螺线管,在保持其半径和总匝数不变的情况下,把螺线管拉长一些,则它的自感系数将____________________.5、图示一充电后的平行板电容器,A 板带正电,B 板带负电.当将开关K 合上放电时,AB 板之间的电场方向为________________,位移电流的方向为____________________(按图上所标x 轴正方向来回答) .6、如图,有一N 匝载流为I 的平面线圈(密绕),其面积为S ,则在图示均匀磁场B的作用下,线圈所受到的磁力矩为______________.线圈法向矢量n将转向________________.7、一金属球壳的内、外半径分别为R 1和R 2,带电荷为Q .在球心处有一电荷为q 的点电荷,则球壳内表面上的电荷面密度σ =______________.pd r 1r 2S 2S 1nRK x A BI O zy xBnS 1 S 2 S 3+q -q2005-2006学年第 1 学期 试题名称 :大学物理III (下) 共6页 第4页8、如图所示,一半径为r 的很小的金属圆环,在初始时刻与一半径为a (a >>r )的大金属圆环共面且同心.在大圆环中通以恒定的电流I ,方向如图.如果小圆环以匀角速度ω绕其任一方向的直径转动,并设小圆环的电阻为R ,则任一时刻t 通过小圆环的磁通量Φ =______________________.小圆环中的感应电流i =______________________________.9、三个平行的“无限大”均匀带电平面,其电荷面密度都是+σ,如图所示,则A 、B 、C 、D 三个区域的电场强度分别为: E A =_________________,E B =_____________,E C =_______________,E D =_________________(设方向向右为正).10、在点电荷+q 和-q 的静电场中,作出如图所示的三个闭合面S 1、S 2、S 3,则通过这些闭合面的电场强度通量分别是: Φ1=________,Φ2=___________,Φ3=__________.11、一个密绕的细长螺线管,每厘米长度上绕有10匝细导线,螺线管的横截面积为10 cm 2.当在螺线管中通入10 A 的电流时,它的横截面上的磁通量为_________________________.(真空磁导率μ0 =4π³10-7 T ²m/A)ωa rI +σ +σ +σ A B C DOS 1 S 2 n 2 n 1r 1 r 2 d2005-2006学年第 1 学期 试题名称 :大学物理III (下) 共6页 第5页三、计算题(共30分)(请将计算题的答案写在答题纸上)1、在一半径R =1.0 cm 的无限长半圆筒形金属薄片中,沿长度方向有横截面上均匀分布的电流I = 5.0 A 通过.试求圆柱轴线任一点的磁感强度.(μ0 =4π³10-7 N/A 2) (本题6分)2、用波长为589.3 nm (1 nm = 10-9 m)的钠黄光垂直入射在每毫米有500 条缝的光栅上,求第一级主极大的衍射角. (本题6分)3、在图示的双缝干涉实验中,若用薄玻璃片(折射率n 1=1.4)覆盖缝S 1,用同样厚度的玻璃片(但折射率n 2=1.7)覆盖缝S 2,将使原来未放玻璃时屏上的中央明条纹处O 变为第五级明纹.设单色光波长λ=480 nm(1nm=109m ),求玻璃片的厚度d (可认为光线垂直穿过玻璃片).(本题7分)4、磁感应强度为B的均匀磁场充满一半径为R 的圆柱形空间,一金属杆放在图中位置,杆长为2R ,其中一半位于磁场内、另一半在磁场外.当tBd d >0时,求:杆两端的感应电动势的大小和方向.(本题6分)5、当电子的德布罗意波长与可见光波长( λ =5500 Å)相同时,求它的动能是多少电子伏特?(电子质量m e =9.11³10-31 kg ,普朗克常量h =6.63³10-34 J ²s, 1 eV =1.60³10-19 J) (本题5分)2005-2006学年第 1 学期试题名称:大学物理III(下)共6页第6 页四、简答题(共10分,每题5分)1、已知铂的逸出电势为8 V,今用波长为300 nm (1 nm = 10-9 m)的紫外光照射,问能否产生光电效应?为什么?2、某单色光从空气射入水中,其频率、波速、波长是否变化?怎样变化?学年第 2学期 试题名称 : 大学物理III2-A 共 2 页 第1页专业年级: 学号 姓名 授课教师名 分数题1:如图,半径为R 的圆柱形空间内分布有沿圆柱轴线方向的均匀磁场,磁场方向垂直纸面向里,其变化率为dtdB 。
中国海洋大学 大学物理3 期末考试试题和答案32

大学物理Ⅱ2A 答案一、选择题1、C2、D3、C4、C5、D6、A 二、填空题1、5.00×10-5T2、v BL sin θ a3、π-21或π234、π5、46、I 0/87、48、2/112)2/(eU m h e 三、计算题1、2、解:(1) 振动方程 )22cos(06.00π+π=ty )cos(06.0π+π=t (SI) 3分(2) 波动表达式 ])/(cos[06.0π+-π=u x t y 3分])21(cos[06.0π+-π=x t (SI)(3) 波长 4==uT λ m 2分 3、解:双缝干涉条纹:(1) 第k 级亮纹条件: d sin θ =k λ第k 级亮条纹位置:x k = f tg θ ≈f sin θ ≈kf λ / d相邻两亮纹的间距:∆x = x k +1-x k =(k +1)f λ / d -kf λ / d =f λ / d=2.4×10-3 m=2.4 mm 5分 (2) 单缝衍射第一暗纹: a sin θ1 = λ单缝衍射中央亮纹半宽度:∆x 0 = f tg θ1≈f sin θ1 ≈f λ / a =12 mm∆x 0 / ∆x =5 ∴ 双缝干涉第±5极主级大缺级. 3分∴在单缝衍射中央亮纹范围内,双缝干涉亮纹数目N = 9 1分分别为k = 0,±1,±2,±3,±4级亮纹1分或根据d / a = 5指出双缝干涉缺第±5级主大,同样得该结论的3分.四、问答题1、不是,解释略2、答案略3、答案略4、答:成功:从理论上解释了氢原子光谱的实验规律,并从理论上算出里德伯常量.1分玻尔首先提出了原子系统能量量子化的概念和角动量量子化的假设.1分玻尔创造性的提出了定态、跃迁等重要概念,为近代量子物理的建立奠定了基础.1分局限性:由于未能预见微观粒子的波粒二象性,虽然提出正确的量子假设,但未能完全脱离经典理论的影响,仍采用经典理论的思想和处理方法,因此不能正确说明氢原子内部的微观粒子运动.2分。
中国海洋大学大学物理试题及答案
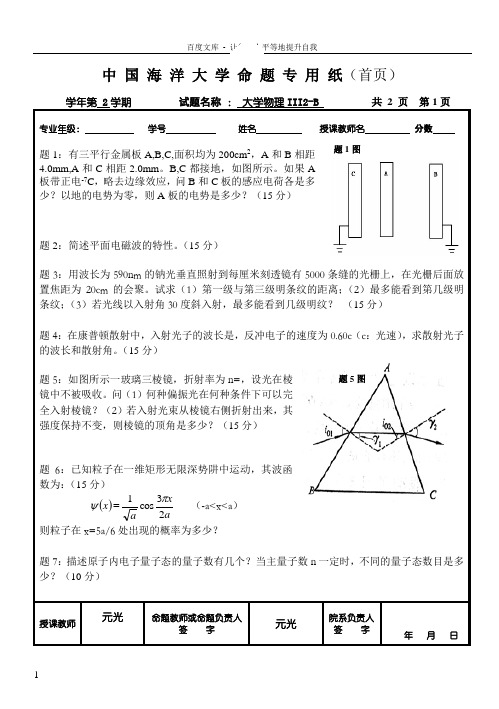
中 国 海 洋 大 学 命 题 专 用 纸(首页)学年第 2学期 试题名称 : 大学物理III2-B 共 2 页 第1页专业年级: 学号 姓名 授课教师名 分数 题1:有三平行金属板A,B,C,面积均为200cm 2,A 和B 相距4.0mm,A 和C 相距2.0mm 。
B,C 都接地,如图所示。
如果A板带正电-7C ,略去边缘效应,问B 和C 板的感应电荷各是多少?以地的电势为零,则A 板的电势是多少?(15分)题2:简述平面电磁波的特性。
(15分)题3:用波长为590nm 的钠光垂直照射到每厘米刻透镜有5000条缝的光栅上,在光栅后面放置焦距为20cm 的会聚。
试求(1)第一级与第三级明条纹的距离;(2)最多能看到第几级明条纹;(3)若光线以入射角30度斜入射,最多能看到几级明纹? (15分)题4:在康普顿散射中,入射光子的波长是,反冲电子的速度为0.60c (c :光速),求散射光子的波长和散射角。
(15分)题5:如图所示一玻璃三棱镜,折射率为n=,设光在棱镜中不被吸收。
问(1)何种偏振光在何种条件下可以完全入射棱镜?(2)若入射光束从棱镜右侧折射出来,其强度保持不变,则棱镜的顶角是多少?(15分)题6:已知粒子在一维矩形无限深势阱中运动,其波函数为:(15分)()a x ax 23cos 1πψ= (-a<x<a ) 则粒子在x=5a/6处出现的概率为多少?题7:描述原子内电子量子态的量子数有几个?当主量子数n 一定时,不同的量子态数目是多少?(10分)授课教师 元光 命题教师或命题负责人签 字元光院系负责人 签 字 年 月 日题5图 题1图中国海洋大学命题专用纸(附页)学年第 2学期试题名称:大学物理III2-B 共 2 页第2页注:电子质量:m≈*10-31 kg;普朗克常数: h≈*10-34 ;真空光速:c≈3*108 m/s玻尔兹曼常数:k≈*10-23 J/K电子电荷:e≈×10-19 C;答案:题-1:解: 如题图示,令A 板左侧面电荷面密度为1σ,右侧面电荷面密度为2σ题8-22图 (1)∵ AB AC U U =,即 ∴ AB AB AC AC E E d d =∴ 2d d 21===ACAB AB AC E E σσ 且 1σ+2σSq A = 得 ,32S q A =σ Sq A 321=σ 而 7110232-⨯-=-=-=A C q S q σC C 10172-⨯-=-=S q B σ (2)301103.2d d ⨯===AC AC AC A E U εσV题-2:1.E 和H 互相垂直,且均与传播方向垂直。
中国海洋大学 大学物理3 期末考试试题和答案31

(A) L1∶L2=1∶1,Wm1∶Wm2 =1∶1.
(B) L1∶L2=1∶2,Wm1∶Wm2 =1∶1.
(C) L1∶L2=1∶2,Wm1∶Wm2 =1∶2.
(D) L1∶L2=2∶1,Wm1∶Wm2 =2∶1.
[
]
2、一劲度系数为 k 的轻弹簧,下端挂一质量为 m 的物体,系统的振动周期为 T1.若
4、试简述玻尔氢原子理论的成功之处和局限是什么?
单缝处的波面可划分为______________个半波带.
优选专业优年选级专业X年XX级XXXXXXX XXXX
学号 学号
姓名 姓名
授课教师授课教师
座号 座号
--------------------------------------装装----------装-装-----------------------------订订----------订-订-----------------------------线线----------线-线---------------------------------------
中国海洋大学 2007-2008 学年 第 X 学期 期末考试试卷
信息 学院《大学物理Ⅱ2》课程试题(A 卷)
6、(3 分)使光强为 I0 的自然光依次垂直通过三块偏振片 P1,P2 和 P3.P1 与 P2 的偏 振化方向成 45°角,P2 与 P3 的偏振化方向成 45°角.则透过三块偏振片的
光强 I 为______________.
合回路,可得 L B dl 0 ,由此结果能否说在闭合回路上各点的磁感强度为零?给出解
释。
L Il
I
2、试从以下三个方面来比较静电场与有旋电场:(1)产生原因;(2)电场线的特点;(2) 对导体中电荷的作用。
中国海洋大学 大学物理3 期末考试试题和答案71
[
]
4. 自然光以布儒斯特角由空气入射到一玻璃表面上,反射光是
(A) 在入射面内振动的完全线偏振光.
(B) 平行于入射面的振动占优势的部分偏振光.
(C) 垂直于入射面振动的完全线偏振光.
(D) 垂直于入射面的振动占优势的部分偏振光
[
]
5 .有下列几种说法: (1) 所有惯性系对物理基本规律都是等价的. (2) 在真空中,光的速度与光的频率、光源的运动状态无关. (3)在任何惯性系中,光在真空中沿任何方向的传播速率都相同.
(真空的磁导率0 =4×10-7 T·m/A,铜的相对磁导率r≈1)
S
2 (10 分) 某种单色平行光垂直入射在单缝上,单缝宽 a = 0.15 mm.缝后放一个焦距 f = 400 mm 的凸透镜,在透镜的焦平面上,测得中央明条纹两侧的两个第三级暗条纹之间的距离为 8.0 mm,求入射光的波长.(要求作出示意图)
中 国 海 洋 大 学 命 题 专 用 纸(附页)
学年第 学期
试题名称 :大学物理 II2(B)
共4页 第4 页
四.问答题(共 15 分) 1 (7 分)试用具体例子说明楞次定律确定的感应电流方向是符合能量守恒定律的.
2(8 分) 两个惯性系 K 与 K'坐标轴相互平行,K'系相对于 K 系沿 x 轴作匀速运动,在 K' 系的 x'轴上,相距为 L'的 A'、B'两点处各放一只已经彼此对准了的钟,试问在 K 系中的 观测者看这两只钟是否也是对准了?为什么?
管单位长度上的匝数相等.设 R = 2r,则两螺线管中的磁感强度大小 BR 和 Br 应满足:
(A) BR = 2 Br.
(B) BR = Br.
(C) 2BR = Br.
(D) BR = 4 Br.
中国海洋大学资料物理习题答案习题12

习题十二12-1 某单色光从空气射入水中,其频率、波速、波长是否变化?怎样变化?解: υ不变,为波源的振动频率;n n 空λλ=变小;υλn u =变小.12-2 在杨氏双缝实验中,作如下调节时,屏幕上的干涉条纹将如何变化?试说明理由.(1)使两缝之间的距离变小;(2)保持双缝间距不变,使双缝与屏幕间的距离变小;(3)整个装置的结构不变,全部浸入水中;(4)光源作平行于1S ,2S 联线方向上下微小移动;(5)用一块透明的薄云母片盖住下面的一条缝.解: 由λdD x =∆知,(1)条纹变疏;(2)条纹变密;(3)条纹变密;(4)零级明纹在屏幕上作相反方向的上下移动;(5)零级明纹向下移动. 12-3 什么是光程? 在不同的均匀媒质中,若单色光通过的光程相等时,其几何路程是否相同?其所需时间是否相同?在光程差与位相差的关系式∆λπϕ∆2= 中,光波的波长要用真空中波长,为什么?解:nr =∆.不同媒质若光程相等,则其几何路程定不相同;其所需时间相同,为Ct ∆=∆.因为∆中已经将光在介质中的路程折算为光在真空中所走的路程。
12-4 如题12-4图所示,A ,B 两块平板玻璃构成空气劈尖,分析在下列情况中劈尖干涉条纹将如何变化?(1) A 沿垂直于B 的方向向上平移[见图(a)];(2) A 绕棱边逆时针转动[见图(b)].题12-4图解: (1)由l 2λθ=,2λk e k =知,各级条纹向棱边方向移动,条纹间距不变;(2)各级条纹向棱边方向移动,且条纹变密.12-5 用劈尖干涉来检测工件表面的平整度,当波长为λ的单色光垂直入射时,观察到的干涉条纹如题12-5图所示,每一条纹的弯曲部分的顶点恰与左邻的直线部分的连线相切.试说明工件缺陷是凸还是凹?并估算该缺陷的程度.解: 工件缺陷是凹的.故各级等厚线(在缺陷附近的)向棱边方向弯曲.按题意,每一条纹弯曲部分的顶点恰与左邻的直线部分连线相切,说明弯曲部分相当于条纹向棱边移动了一条,故相应的空气隙厚度差为2λ=∆e ,这也是工件缺陷的程度.题12-5图 题12-6图12-6 如题12-6图,牛顿环的平凸透镜可以上下移动,若以单色光垂直照射,看见条纹向中 心收缩,问透镜是向上还是向下移动?解: 条纹向中心收缩,透镜应向上移动.因相应条纹的膜厚k e 位置向中心移动. 12-7 在杨氏双缝实验中,双缝间距d =0.20mm ,缝屏间距D =1.0m ,试求:(1)若第二级明条纹离屏中心的距离为6.0mm ,计算此单色光的波长;(2)相邻两明条纹间的距离.解: (1)由λk d D x =明知,λ22.01010.63⨯⨯=,∴3106.0-⨯=λmm o A 6000= (2)3106.02.010133=⨯⨯⨯==∆-λd D x mm 12-8 在双缝装置中,用一很薄的云母片(n=1.58)覆盖其中的一条缝,结果使屏幕上的第七级明条纹恰好移到屏幕中央原零级明纹的位置.若入射光的波长为5500oA ,求此云母片的厚度. 解: 设云母片厚度为e ,则由云母片引起的光程差为e n e ne )1(-=-=δ 按题意 λδ7=,∴610106.6158.1105500717--⨯=-⨯⨯=-=n e λm 6.6=m μ 12-9 洛埃镜干涉装置如题12-9图所示,镜长30cm ,狭缝光源S 在离镜左边20cm 的平面内,与镜面的垂直距离为2.0mm ,光源波长=λ7.2×10-7m ,试求位于镜右边缘的屏幕上第一条明条纹到镜边缘的距离.题12-9图解: 镜面反射光有半波损失,且反射光可视为虚光源S '发出.所以由S 与S '发出的两光束到达屏幕上距镜边缘为x 处的光程差为22)(12λλδ+=+-=D x d r r ,第一明纹处,对应λδ= ∴25105.44.0250102.72--⨯=⨯⨯⨯==d Dx λmm 12-10 一平面单色光波垂直照射在厚度均匀的薄油膜上,油膜覆盖在玻璃板上.油的折射率为1.30,玻璃的折射率为1.50,若单色光的波长可由光源连续可调,可观察到5000 o A 与7000 oA 这两个波长的单色光在反射中消失.试求油膜层的厚度.解: 油膜上、下两表面反射光的光程差为ne 2,由反射相消条件有λλ)21(2)12(2+=+=k k ne ),2,1,0(⋅⋅⋅=k ① 当50001=λo A 时,有2500)21(21111+=+=λλk k ne ② 当70002=λo A 时,有3500)21(22222+=+=λλk k ne ③ 因12λλ>,所以12k k <;又因为1λ与2λ之间不存在3λ满足 33)21(2λ+=k ne 式,即不存在 132k k k <<的情形,所以2k 、1k 应为连续整数,即112-=k k ④,由②、③、④式可得:51)1(75171000121221+-=+=+=k k k k λλ得 31=k ,2112=-=k k 可由②式求得油膜的厚度为67312250011=+=nk e λo A 12-11 白光垂直照射到空气中一厚度为3800 o A 的肥皂膜上,设肥皂膜的折射率为1.33,试问该膜的正面呈现什么颜色?背面呈现什么颜色?解: 由反射干涉相长公式有λλk ne =+22),2,1(⋅⋅⋅=k ,得122021612380033.14124-=-⨯⨯=-=k k k ne λ,2=k ,67392=λo A (红色) 3=k ,40433=λoA (紫色,所以肥皂膜正面呈现紫红色,由透射干涉相长公式λk ne =2),2,1(⋅⋅⋅=k 所以k k ne 101082==λ当2=k 时λ=5054o A 绿色)故背面呈现绿色. 12-12 在折射率1n =1.52的镜头表面涂有一层折射率2n =1.38的Mg 2F 增透膜,如果此膜适用于波长λ=5500 oA 的光,问膜的厚度应取何值?解: 设光垂直入射增透膜,欲透射增强,则膜上、下两表面反射光应满足干涉相消条件,即 λ)21(22+=k e n ),2,1,0(⋅⋅⋅=k ,∴222422)21(n n k n k e λλλ+=+= )9961993(38.14550038.125500+=⨯+⨯=k k o A ,令0=k ,得膜的最薄厚度为996o A . 当k 为其他整数倍时,也都满足要求.12-13 如题12-13图,波长为6800oA 的平行光垂直照射到L =0.12m 长的两块玻璃片上,两玻璃片一边相互接触,另一边被直径d =0.048mm 的细钢丝隔开.求:(1)两玻璃片间的夹角=θ?(2)相邻两明条纹间空气膜的厚度差是多少?(3)相邻两暗条纹的间距是多少?(4)在这0.12 m 内呈现多少条明条纹?解: (1)由图知,d L =θsin ,即d L =θ故 43100.41012.0048.0-⨯=⨯==L d θ(弧度) (2)相邻两明条纹空气膜厚度差为7104.32-⨯==∆λe m ,3)相邻两暗纹间距641010850100.421068002---⨯=⨯⨯⨯==θλl m 85.0= mm (4)141≈=∆l L N 条 12-14 用=λ 5000o A 的平行光垂直入射劈形薄膜的上表面,从反射光中观察,劈尖的 棱边是暗纹.若劈尖上面媒质的折射率1n 大于薄膜的折射率n (n =1.5).求:(1)膜下面媒质的折射率2n 与n 的大小关系;(2)第10条暗纹处薄膜的厚度;(3)使膜的下表面向下平移一微小距离e ∆,干涉条纹有什么变化?若e ∆=2.0 μm ,原来的第10条暗纹处将被哪级暗纹占据?解: (1)n n >2.因为劈尖的棱边是暗纹,对应光程差2)12(22λλ+=+=∆k ne ,膜厚0=e 处,有0=k ,只能是下面媒质的反射光有半波损失2λ才合题意; (2)3105.15.12500092929-⨯=⨯⨯==⨯=∆n e nλλ mm (因10个条纹只有9个条纹间距) (3)膜的下表面向下平移,各级条纹向棱边方向移动.若0.2=∆e μm ,原来第10条暗纹处现对应的膜厚为)100.2105.1(33--⨯+⨯='∆e mm ,21100.55.12105.3243=⨯⨯⨯⨯='∆=∆--n e N λ 现被第21级暗纹占据.12-15 (1)若用波长不同的光观察牛顿环,1λ=6000o A ,2λ=4500o A ,观察到用1λ时的第k 个暗环与用2λ时的第k+1个暗环重合,已知透镜的曲率半径是190cm .求用1λ时第k 个暗环的半径.(2)又如在牛顿环中用波长为5000o A 的第5个明环与用波长为2λ的第6个明环重合,求未知波长2λ.解: (1)由牛顿环暗环公式λkR r k =据题意有 21)1(λλR k kR r +==∴212λλλ-=k ,代入上式得2121λλλλ-=R r 10101010210450010600010450010600010190-----⨯-⨯⨯⨯⨯⨯⨯=31085.1-⨯=m (2)用A 50001 =λ照射,51=k 级明环与2λ的62=k 级明环重合,则有 2)12(2)12(2211λλR k R k r -=-= ∴ 4091500016215212121212=⨯-⨯-⨯=--=λλk k o A 12-16 当牛顿环装置中的透镜与玻璃之间的空间充以液体时,第十个亮环的直径由1d =1.40×10-2m 变为2d =1.27×10-2m ,求液体的折射率. 解: 由牛顿环明环公式2)12(21λR k D r -==空 n R k D r 2)12(22λ-==液 两式相除得n D D =21,即22.161.196.12221≈==D D n 12-17 利用迈克耳逊干涉仪可测量单色光的波长.当1M 移动距离为0.322mm 时,观察到干涉条纹移动数为1024条,求所用单色光的波长.解: 由 2λN d ∆=∆得102410322.0223-⨯⨯=∆∆=N d λ 710289.6-⨯=m 6289=oA12-18 把折射率为n =1.632的玻璃片放入迈克耳逊干涉仪的一条光路中,观察到有150条干涉条纹向一方移过.若所用单色光的波长为λ= 5000o A ,求此玻璃片的厚度.解: 设插入玻璃片厚度为d ,则相应光程差变化为 λN d n ∆=-)1(2∴ )1632.1(2105000150)1(210-⨯⨯=-∆=-n N d λ5109.5-⨯=m 2109.5-⨯=mm。
中国海洋大学资料物理化学学习指导及课后答案

第一章化学热力学基础1.1 本章学习要求1. 掌握化学热力学的基本概念和基本公式2. 复习热化学内容;掌握Kirchhoff公式3. 掌握熵变的计算;了解熵的统计意义1.2内容概要1.2.1热力学基本概念1. 体系和环境体系(system):热力学中,将研究的对象称为体系。
热力学体系是大量微观粒子构成的宏观体系。
环境(surroundings):体系之外与体系密切相关的周围部分称作环境。
体系与环境之间可以有明显的界面,也可以是想象的界面。
①敞开体系(open system):体系与环境间既可有物质交换,又可有能量交换。
②封闭体系(closed system):体系与环境间只有能量交换,没有物质交换。
体系中物质的量守恒。
③孤立体系(isolated system):体系与环境间既无物质交换,又无能量交换。
2. 体系的性质(property of system)用来描述体系状态的宏观物理量称为体系的性质(system properties)。
如T、V、p、U、H、S、G、F等等。
①广度性质(extensive properties):体系这种性质的数值与体系物质含量成正比,具有加和性。
②强度性质(intensive properties):这种性质的数值与体系物质含量无关,无加和性。
如T、p、d(密度)等等。
3. 状态及状态函数状态(state):是体系的物理性质及化学性质的综合表现,即体系在一定条件下存在的形式。
热力学中常用体系的宏观性质来描述体系的状态。
状态函数(state function):体系性质的数值又决定于体系的状态,它们是体系状态的单值函数,所以体系的性质又称状态函数。
根据经验知,一个纯物质体系的状态可由两个状态变量来确定,T、p、V是最常用的确定状态的三个变量。
例如,若纯物质体系的状态用其中的任意两个物理量(如T、p)来确定,则其它的性质可写成T、p的函数Z = f (T、p)。
状态函数的微小变化,在数学上是全微分,并且是可积分的。
大学海洋科学专业《大学物理(二)》期末考试试题 附答案

大学海洋科学专业《大学物理(二)》期末考试试题附答案姓名:______ 班级:______ 学号:______考试须知:1、考试时间:120分钟,本卷满分为100分。
2、请首先按要求在试卷的指定位置填写您的姓名、班级、学号。
一、填空题(共10小题,每题2分,共20分)1、动量定理的内容是__________,其数学表达式可写__________,动量守恒的条件是__________。
2、一质点作半径为0.1m的圆周运动,其运动方程为:(SI),则其切向加速度为=_____________。
3、从统计的意义来解释, 不可逆过程实质上是一个________________的转变过程, 一切实际过程都向着________________ 的方向进行。
4、将热量Q传给一定量的理想气体:(1)若气体的体积不变,则热量转化为_____________________________。
(2)若气体的温度不变,则热量转化为_____________________________。
(3)若气体的压强不变,则热量转化为_____________________________。
5、图示为三种不同的磁介质的B~H关系曲线,其中虚线表示的是的关系.说明a、b、c各代表哪一类磁介质的B~H关系曲线:a代表__________________________的B~H关系曲线b代表__________________________的B~H关系曲线c代表__________________________的B~H关系曲线6、一质点作半径为0.1m的圆周运动,其角位置的运动学方程为:,则其切向加速度大小为=__________第1秒末法向加速度的大小为=__________。
7、设在某一过程P中,系统由状态A变为状态B,如果________________________________________,则过程P为可逆过程;如果_________________________________________则过程P为不可逆过程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
习题二2-1 一细绳跨过一定滑轮,绳的一边悬有一质量为1m 的物体,另一边穿在质量为2m 的圆柱体的竖直细孔中,圆柱可沿绳子滑动.今看到绳子从圆柱细孔中加速上升,柱体相对于绳子以匀加速度a '下滑,求1m ,2m 相对于地面的加速度、绳的张力及柱体与绳子间的摩擦力(绳轻且不可伸长,滑轮的质量及轮与轴间的摩擦不计).解:因绳不可伸长,故滑轮两边绳子的加速度均为1a ,其对于2m 则为牵连加速度,又知2m 对绳子的相对加速度为a ',故2m 对地加速度,由图(b)可知,为a a a '-=12 ①又因绳的质量不计,所以圆柱体受到的摩擦力f 在数值上等于绳的张力T ,由牛顿定律,有111a m T g m =- ②222a m g m T =- ③联立①、②、③式,得2121211212212211)2()()(m m a g m m T f m m a m g m m a m m a m g m m a +'-==+'--=+'+-=讨论 (1)若0='a ,则21a a =表示柱体与绳之间无相对滑动.(2)若g a 2=',则0==f T ,表示柱体与绳之间无任何作用力,此时1m , 2m 均作自由落体运动.题2-1图2-2 一个质量为P 的质点,在光滑的固定斜面(倾角为α)上以初速度0v 运动,0v 的方向与斜面底边的水平线AB解: 物体置于斜面上受到重力mg ,斜面支持力N .建立坐标:取0v方向为X 轴,平行斜面与X 轴垂直方向为Y 轴.如图2-2.题2-2图X 方向: 0=x F t v x 0= ①Y方向: y yma mg F ==αsin ②0=t 时 0=y 0=y v2sin 21t g y α=由①、②式消去t ,得220sin 21x g v y ⋅=α 2-3 质量为16 kg 的质点在xOy 平面内运动,受一恒力作用,力的分量为x f =6 N ,y f =-7 N ,当t =0时,==y x0,x v =-2 m ·s-1,y v =0.求当t = 2 s(1)位矢;(2)解: 2s m 83166-⋅===m f a x x2s m 167-⋅-==mf a y y (1)⎰⎰--⋅-=⨯-=+=⋅-=⨯+-=+=20101200s m 872167s m 452832dt a v v dt a v v y y y x x x于是质点在s 2时的速度1s m 8745-⋅--=ji v(2)m874134)167(21)4832122(21)21(220j i j i jt a i t a t v r y x--=⨯-+⨯⨯+⨯-=++=2-4 质点在流体中作直线运动,受与速度成正比的阻力kv (k 为常数)作用,t =0时质点的速度为0v ,证明(1) t 时刻的速度为v =t mkev )(0-;(2) 由0到t 的时间内经过的距离为x=(km v 0)[1-t mk e)(-];(3)停止运动前经过的距离为)(0kmv ;(4)证明当k m t =时速度减至0v 的e1,式中m 为质点的质量. 答: (1)∵ tvm kv a d d =-=分离变量,得m tk v v d d -=即 ⎰⎰-=v v t m tk vv 00d d m kt e v v -=ln ln 0∴ tkev v-=0(2) ⎰⎰---===tt tm k m k e kmv t ev t v x00)1(d d(3)质点停止运动时速度为零,即t →∞, 故有 ⎰∞-=='0d km v t ev x tk(4)当t=km 时,其速度为ev e v ev v m k 0100===-⋅-即速度减至0v 的e1. 2-5 升降机内有两物体,质量分别为1m ,2m ,且2m =21m .用细绳连接,跨过滑轮,绳子不可伸长,滑轮质量及一切摩擦都忽略不计,当升降机以匀加速a =21g 上升时,求:(1) 1m 和2m 相对升降机的加速度.(2)在地面上观察1m ,2m 的加速度各为多少?解: 分别以1m ,2m 为研究对象,其受力图如图(b)所示. (1)设2m 相对滑轮(即升降机)的加速度为a ',则2m 对地加速度a a a -'=2;因绳不可伸长,故1m 对滑轮的加速度亦为a ',又1m 在水平方向上没有受牵连运动的影响,所以1m 在水平方向对地加速度亦为a ',由牛顿定律,有)(22a a m T g m -'=-a m T '=1题2-5图联立,解得g a ='方向向下(2) 2m 对地加速度为22ga a a =-'= 方向向上 1m 在水面方向有相对加速度,竖直方向有牵连加速度,即牵相绝a a a+=' ∴ g g g a a a 25422221=+=+'=a a '=arctanθo 6.2621arctan ==,左偏上. 2-6一质量为m 的质点以与地的仰角θ=30°的初速0v从地面抛出,若忽略空气阻力,求质点落地时相对抛射时的动量的增量.解: 依题意作出示意图如题2-6图题2-6图在忽略空气阻力情况下,抛体落地瞬时的末速度大小与初速度大小相同,与轨道相切斜向下, 而抛物线具有对y 轴对称性,故末速度与x 轴夹角亦为o 30,则动量的增量为0v m v m p -=∆由矢量图知,动量增量大小为v m ,方向竖直向下.2-7 一质量为m 的小球从某一高度处水平抛出,落在水平桌面上发生弹性碰撞.并在抛出1 s ,跳回到原高度,速度仍是水平方向,速度大小也与抛出时相等.求小球与桌面碰撞过程中,桌面给予小球的冲量的大小和方向.并回答在碰撞过程中,小球的动量是否守恒?解: 由题知,小球落地时间为s 5.0.因小球为平抛运动,故小球落地的瞬时向下的速度大小为g gt v 5.01==,小球上跳速度的大小亦为g v 5.02=.设向上为y 轴正向,则动量的增量 12v m v m p-=∆方向竖直向上,大小mg mv mv p =--=∆)(12碰撞过程中动量不守恒.这是因为在碰撞过程中,小球受到地面给予的冲力作用.另外,碰撞前初动量方向斜向下,碰后末动量方向斜向上,这也说明动量不守恒.2-8 作用在质量为10 kg 的物体上的力为i t F)210(+=N ,式中t 的单位是s ,(1)求4s 后,这物体的动量和速度的变化,以及力给予物体的冲量.(2)为了使这力的冲量为200 N ·s ,该力应在这物体上作用多久,试就一原来静止的物体和一个具有初速度j6-m ·s -1的物体,回答这两个问题.解: (1)若物体原来静止,则i t i t t F p t10401s m kg 56d )210(d -⋅⋅=+==∆⎰⎰,沿x 轴正向,ip I imp v111111s m kg 56s m 6.5--⋅⋅=∆=⋅=∆=∆ 若物体原来具有6-1s m -⋅初速,则⎰⎰+-=+-=-=t t t F v m t m F v m p v m p 000000d )d (,于是⎰∆==-=∆t p t F p p p 0102d,同理, 12v v ∆=∆,12I I=这说明,只要力函数不变,作用时间相同,则不管物体有无初动量,也不管初动量有多大,那么物体获得的动量的增量(亦即冲量)就一定相同,这就是动量定理. (2)同上理,两种情况中的作用时间相同,即⎰+=+=tt t t t I 0210d )210(亦即 0200102=-+t t解得s 10=t,(s 20='t 舍去)2-9 一质量为m 的质点在xOyj t b i t a rωωsin cos +=求质点的动量及t =0 到ωπ2=t解: 质点的动量为)cos sin (j t b i t a m v m pωωω+-==将0=t 和ωπ2=t 分别代入上式,得j b m pω=1,i a m p ω-=2 ,则动量的增量亦即质点所受外力的冲量为)(12j b i a m p p p I+-=-=∆=ω2-10 一颗子弹由枪口射出时速率为10sm -⋅v ,当子弹在枪筒内被加速时,它所受的合力为 F=(bt a -)N(b a ,为常数),其中t 以秒为单位:(1)假设子弹运行到枪口处合力刚好为零,试计算子弹走完枪筒全长所需时间;(2)求子弹所受的冲量.(3)求子弹的质量. 解: (1)由题意,子弹到枪口时,有0)(=-=bt a F ,得ba t =(2)子弹所受的冲量⎰-=-=t bt at t bt a I 0221d )(将bat =代入,得 ba I 22=(3)由动量定理可求得子弹的质量202bv a v I m ==2-11 一炮弹质量为m ,以速率v 飞行,其内部炸药使此炮弹分裂为两块,爆炸后由于炸药使弹片增加的动能为T ,且一块的质量为另一块质量的kv +mkT 2, v -kmT 2证明: 设一块为1m ,则另一块为2m ,21km m =及m m m =+21于是得 1,121+=+=k mm k km m ① 又设1m 的速度为1v , 2m 的速度为2v ,则有2222211212121mv v m v m T -+=② 2211v m v m mv += ③联立①、③解得12)1(kv v k v -+= ④将④代入②,并整理得21)(2v v kmT-= 于是有 kmT v v 21±= 将其代入④式,有mkT v v 22±=又,题述爆炸后,两弹片仍沿原方向飞行,故只能取kmTv v m kT v v 2,221-=+= 证毕.2-12 设N 67j i F -=合.(1) 当一质点从原点运动到m 1643k j i r++-=时,求F 所作的功.(2)如果质点到r 处时需0.6s ,试求平均功率.(3)如果质点的质量为1kg ,试求动能的变化. 解: (1)由题知,合F为恒力,∴ )1643()67(k j i j i r F A++-⋅-=⋅=合J 452421-=--= (2) w 756.045==∆=t A P (3)由动能定理,J 45-==∆A E k2-13 以铁锤将一铁钉击入木板,设木板对铁钉的阻力与铁钉进入木板内的深度成正比,在铁锤击第一次时,能将小钉击入木板内1 cm解: 以木板上界面为坐标原点,向内为y 坐标正向,如题2-13图,则铁钉所受阻力为题2-13图ky f -=第一锤外力的功为1A⎰⎰⎰==-='=ssky ky y f y f A 112d d d ① 式中f '是铁锤作用于钉上的力,f 是木板作用于钉上的力,在0d →t时,f 'f-=.设第二锤外力的功为2A ,则同理,有⎰-==21222221d y k ky y ky A ②由题意,有2)21(212kmv A A =∆== ③即 222122kk ky =-所以, 22=y于是钉子第二次能进入的深度为cm 414.01212=-=-=∆y y y2-14 设已知一质点(质量为m )在其保守力场中位矢为r 点的势能为n P r k r E /)(=, 试求质点所受保守力的大小和方向.解: 1d )(d )(+-==n rnkr r E r F方向与位矢r的方向相反,即指向力心. 2-15 一根劲度系数为1k 的轻弹簧A 的下端,挂一根劲度系数为2k 的轻弹簧B ,B 的下端一重物C ,C 的质量为M ,如题2-15图.求这一系统静止时两弹簧的伸长量之比和弹性势解: 弹簧B A 、及重物C 受力如题2-15图所示平衡时,有题2-15图Mg F F B A ==又 11x k F A∆= 22x k F B ∆=所以静止时两弹簧伸长量之比为1221k k x x =∆∆弹性势能之比为12222211121212k kx k x k E E p p =∆∆= 2-16 (1)试计算月球和地球对m 物体的引力相抵消的一点P ,距月球表面的距离是多少?地球质量5.98×1024kg ,地球中心到月球中心的距离3.84×108m ,月球质量7.35×1022kg ,月球半径1.74×106m .(2)如果一个1kg 的物体在距月球和地球均为无限远处的势能为零,那么它在P 点的势能为多少?解: (1)设在距月球中心为r 处地引月引F F =,由万有引力定律,有 ()22r R mM Gr mM G -=地月经整理,得R M M M r 月地月+==2224221035.71098.51035.7⨯+⨯⨯81048.3⨯⨯m 1032.386⨯=则P 点处至月球表面的距离为m 1066.310)74.132.38(76⨯=⨯-=-=月r r h(2)质量为kg 1的物体在P 点的引力势能为()r R M GrM GE P ---=地月()72411722111083.34.381098.51067.61083.31035.71067.6⨯-⨯⨯⨯-⨯⨯⨯⨯-=-J 1028.16⨯=2-17 由水平桌面、光滑铅直杆、不可伸长的轻绳、轻弹簧、理想滑轮以及质量为1m 和2m 的滑块组成如题2-17图所示装置,弹簧的劲度系数为k ,自然长度等于水平距离BC ,2m 与桌面间的摩擦系数为μ,最初1m 静止于A 点,AB=BC =h ,绳已拉直,现令滑块落下1m ,求它下落到B 处时的速率.解: 取B 点为重力势能零点,弹簧原长为弹性势能零点,则由功能原理,有])(21[)(21212212l k gh m v m m gh m ∆+-+=-μ 式中l ∆为弹簧在A 点时比原长的伸长量,则h BC AC l )12(-=-=∆联立上述两式,得()()212221122m m kh gh m m v +-+-=μ题2-17图2-18 如题2-18图所示,一物体质量为2kg ,以初速度0v =3m ·s -1从斜面A 点处下滑,它与斜面的摩擦力为8N ,到达B 点后压缩弹簧20cm 后停止,然后又被弹回,求弹簧的劲度系数和物体最后能回到的高度. 解: 取木块压缩弹簧至最短处的位置为重力势能零点,弹簧原 长处为弹性势能零点。
