算法流程(循环结构)
合集下载
人教版高中数学循环结构
（2）循环结构特征图： 说明：1、先判断所给条
A
P N
Y
件P是否成立，若P成立， 则执行A，再判断条件P 是否成立，若P仍成立， 则又执行A如此反复，知 道某一次条件P不成立时 为止，这种循环结构称 为当型循环 2、当型循环的特点：
（1）先判断后操作
（2）Y进入循环，N退出循环
例1.写出求1×2×3×4×5的一个算法.
i≤99 N 输出S
S←S+i Y
结束
1、本节课主要讲述了当型循环结构。 小结：
2、当型循环结构的特点是：
（1）先判断后操作 （2）Y进入循环，N退出循环 3、循环结构要在某个条件下终止循环， 这就需要选择结构来判断。因此，循环 结构中一定包含选择结构，但不允许 “死循环”。
温馨提示：
画循环结构流程图前：
①确定循环变量和初始条件； ②确定算法中反复执行的部分，即循环体；
③确定循环的转向位置；
④确定循环的终止条件.
课后探究：将下述算法用流程图表示，并说 出这个算法的意义． 算法 S1 S ← 0； S2 I ← 1； S3 输入G； S4 S ← S＋G； S5 I ← I＋1； S6 若I大于10，转S7, 否则，转S3； S7 A ← S/10； S8 输出A.
思路2:选择循环结构，用变量T存放相乘的结果，变 量i作为计数变量 S1 T←1； S2 i ←2；
S3 S4 S5
S6
否则转S6。 如果i ≤ 5,那么转S4，
T←T×i； i←i+1, 转S3
输出T； 试画出算法2的流程图. ；
算法2的优点是什么?
算法2流程图:
算法2:
开始 T←1
S1
算法(流程图)的三种基本结构
功能
表示一个算法的 开始和结束
表示一个算法的 输入和输出信息
赋值，执行计算语句， 结果的传送
表示判断某一个条件 是否成立
表示执行步骤的路径 流程进行的方向
程序的三种结构
程序的三种结构
顺序结构
选择结构
循环结构
顺序结构
各操作是按先后顺序执行的。是最简单的一种基本结构。
A
B
其中A和B两个框是顺序执行的。即在完成A框所指定 的操作后，必然接着执行B框所指定的操作，
没有判断框和回指的流程线。
选择结构
又称分支结构。根据是否满足给定条件而从两组操作中选择执行 一种操作。至少有一个判断框，没有回指的流程线。 入口
成立
不成立
P
A
B
出口
选择结构
某一部分的操作可以为空操作。 入口成立Fra bibliotek不成立
P
A
出口
选择结构
某一部分的操作可以为空操作。 入口
成立
不成立
P
B
出口
再来看一个“求较小数”的流程图和程序代码。
循环结构
又称重复结构。用来描述反复执行某一部分算法的操作。 循环结构又分为直到型结构和当型结构。 有回指的流程线
当型结构
条件成立时，反复执行某一部分的操作，当条件不成立时退出 环。 特点：A可能一次也没执行到。 入口
不成立
P
成立
A
出口
直到型结构
先执行某一部分的操作，再判断条件，当条件成立时，退出循 环；条件不成立时，继续循环。
2.用表格描述算法 表格是一种常用的事物关联结构描述方法，在程 序设计中，用来表现规律化算法的一种方式，适合表 达模块关系、数据传递关系、函数变量关系等内容。
流程图——循环结构
试画出算法2的流程图 该算法为何结构 试画出算法 的流程图.该算法为何结构 的流程图 该算法为何结构?
算法2流程图: 开始 T←1 I←2 T←T×I I←I+1 I>5 Y 输出T
结束
思考： 思考 此流程图使用那 一种循环结构？ 如何用当型循环 来描述同样问题？
开始 当型循环 T←1 I←2 I←I+1 T←T×I
S ←0
S ← S + 400
S ≥ 10000
Y
N
开始
开始
S ←0
S ← S + 400
S ←0
S ← S + 400
S<10000 N 结束
问题： 问题：
Y
S ≥ 10000
Y 结束
N
仔细观察上述两个算法，有何区别与联系？ 仔细观察上述两个算法，有何区别与联系？
像这种需要重复执行同一操作 重复执行同一操作的结构称为循环结构 循环结构. 重复执行同一操作 循环结构 那么这两个循环结构有什么区别呢？
N
X ← S / 10
—
输出 X
—
结束
结束
小结
1．本节课主要讲述了算法的循环结构。算法的 基本逻辑结构有三种，即顺序结构、条件结构和 循环结构。其中顺序结构是最简单的结构，也是 最基本的结构，循环结构必然包含条件结构，所 以这三种基本逻辑结构是相互支撑的，它们共同 构成了算法的基本结构，无论怎样复杂的逻辑结 构，都可以通过这三种结构来表达 。 2．循环结构要在某个条件下终止循环，这就需要 条件结构来判断。因此，循环结构中一定包含条件 结构，但不允许“死循环”。
N
I≤5 N 输出T
结束
Y
延伸、设计一个计算 ， ， ， 的平均数的算法. 延伸、设计一个计算1，2，3，﹍，10的平均数的算法 的平均数的算法 分析:先设计一个循环依次输入 分析 先设计一个循环依次输入1-10，再用一个变量存 先设计一个循环依次输入 ， 放这些数的累加和，最后除以10。 放这些数的累加和，最后除以 。 解： S1 S2 S3 S4 S5 S←0 I←1 S←S+I I←I+1 如果I大于 大于10,转 否则返回 否则返回S3. 如果 大于 转S6,否则返回
循环结构
S=3 S=5
S=S+2 S=5 S=7
问题： 如何变化？ 问题：（2）i如何变化？ 变量i从第1步开始每次增加1 直至100 100， 变量i从第1步开始每次增加1，直至100，故可视为 计数变量。 计数变量。 由此，可以得出循环体是： 由此，可以得出循环体是： S=S+i,i=i+1
S=0,i=1
反复执行的步骤称为循环体. 反复执行的步骤称为循环体 注意:循环结构不能是永无终止的“ 注意 循环结构不能是永无终止的“死循 循环结构不能是永无终止的 一定要在某个条件下终止循环,这 环”,一定要在某个条件下终止循环 这 一定要在某个条件下终止循环 就需要条件结构来作出判断,因此 因此,循环 就需要条件结构来作出判断 因此 循环 结构中一定包含条件结构与顺序结构。 结构中一定包含条件结构与顺序结构。
S=1,i=1 S=3,i=2 S=S+i
S=1,i=2 i=i+1 S=3,i=3
（二）初始化变量
问题：（3 的初始值是什么？ 的初始值是什么？ 问题：（3）S的初始值是什么？i的初始值是什么？ ：（ 由第1步可知S的初始值可定为0 的初始值可定为1. 由第1步可知S的初始值可定为0，i的初始值可定为1.
程序框图： 程序框图：
开始 n=2005 a=200 t=0.05a a=a+t n=n+1 a>300? 是 输出n 输出n 结束 否
思考:该程序框图反映的实际问题是什么？ 思考:该程序框图反映的实际问题是什么？
开始 n=1 S=0 n=n+1 S=S-n×n - × 是 n≤100？ ？ 否 输出S 输出 结束 是 n是偶数 是偶数? 是偶数 否 S=S+n×n + ×
程序框图及逻辑结构——循环结构
为了方便有效地表示上述过程,我 们引进一个变量S来表示每一步 的计算结果,i表示第i步运算
方法1：算法设计：
开始
第一步，令i=1，S=0. 第二步，计算S=S+i， 第三步，计算i=i+1， 第四步，判断i>100是否成立
i=1 S=0
S=S+i
i=i+1 否
. 若是，则输出S，结束算法； 否则，返回第二步.
算法分析：
第一步，输入2005年的年生产总值. 第二步，计算下一年的年生产总值. 第三步，判断所得的结果是否大于300. 若是，则输出该年的年份；否则， 返回第二步.
循环结构：
（1）循环体:设a为某年的年生产总值， t为年生产总值的年增长量,n为年份,则 t=0.05a，a=a+t，n=n+1.
（2）初始值:n=2005,a=200.
是
否
在每次执行循环 体前，对条件进 行判断，当条件 满足时，就执行 循环体，否则终 止循环.
这种循环结构称为当型循环结构，你能指出 当型循环结构的特征吗？ 先判断后执行
两种循环结构异同：
循环体
循环体 满足条件？
否
满足条件？
是
是
否
直到型
当 型
注意:循环结构不能是永无终止的“死循 环”,一定要在某个条件下终止循环,这 就需要条件结构来作出判断,因此,循环 结构中一定包含条件结构.
某些循环结构用程序框图可以表示为：
循环体
满足条件？
否
是
在执行了一次循环 体后，对条件进行 判断，如果条件不 满足，就继续执行 循环体，直到条件 满足时终止循环.
这种循环结构称为直到型循环结构，你能指出直 到型循环结构的特征吗？ 先执行后判断
第四章 循环结构程序设计
while(i<=100)
{ i++;
程序运行结果： sum=5050
sum=sum+i;
}
6
4.3 do-while语句
do-while语句的结构 do 语句 while(表达式);
例如： do
x-=1; while(x>0);
功能：
1）执行“语句”。 2）计算“表达式”的值。如果值为非0，转1）；否则转3）。
}
8
4.3 do-while语句
1）循环体如果包含一个以上的语句，要用复合语句表示。 2）在循环体中应有使循环趋于结束的语句。 3）while语句的特点是先执行循环体，然后判断表达式的值。 4）一般情况下，用while语句和用do-while语句处理同一 个问题时，若二者的循环体部分一样，其结果也一样。但如
18
4.7 goto语句以及用goto语句构成循环结构
goto语句的一般格式：
goto 语句标号;
例如： goto loop;
功能：程序执行到goto语句时，将程序流程转到语句标号指定的 语句去执行。
有标号的语句的格式：
语句标号: 语句
例如： loop: sum=sum+i;
19
4.7 goto语句以及用goto语句构成循环结构
【例4-9】用goto语句实现求1～100累加和。
#include <stdio.h>
main() { int n=1, sum=0; loop: sum += n; n++;
if(n<=100) goto loop;
printf("sum=%d\n",sum); }
人教A版 高中数学 必修3 第一章 1.1.2 循环结构的程序框图课件(共16张PPT)
巩固提高
1、设计一算法，求 积:1×2×3×…×100， 画出流程图
思考：该流程图与前面 的例1中求和的流程图有 何不同？
开始 i=0，S=1
i=i+1 S=S*i 否 i>=100?
是 输出S 结束
巩固提高
2、设计一算法输出1~1000以内能被3整除的整数
开始
算法：
i=0
S1：确定i的初始值为0；
开始 i=0，S=0
否 i<100? 是 i=i+1 S=S+ i
输出S 结束
思考:将步骤A和步骤B交换位 置，结果会怎样？能达到预期结果 吗？为什么？要达到预期结果，还 需要做怎样的修改？
步骤A
步骤B 答：达不到预期结果；
当i = 100时，退出循环，i 的值未能加入到S中；修 改的方法是将判断条件改 为i<101
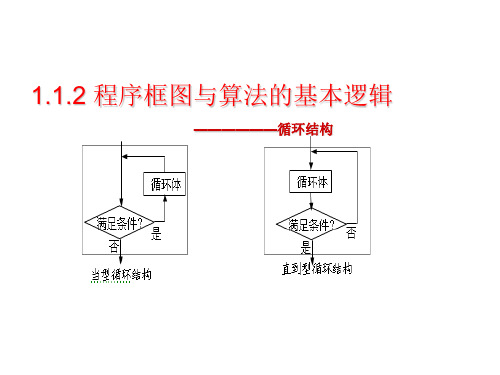
1.1.2 程序框图与算法的基本逻辑
——————循环结构
复习回顾
1、程序框图（流程图）的概念： 2、算法的三种逻辑结构： 3、顺序结构的概念及其程序框图： 4、条件结构的概念及其程序框图：
复习回顾
i) 顺序结构
ii) 条件结构
Yp N A
A
B
B
循环结构
循环结构：在一些算法中，也经常会出现从某处开始，
小结：
4．画循环结构流程图前： ①确定循环变量和初始条件； ②确定算法中反复执行的部分，即循环体； ③确定循环的转向位置； ④确定循环的终止条件.
循环结构的三要素：
循环变量，循环体、循环的终止条件。
其中顺序结构是最简单的结构，也是最基 本的结构，循环结构必然包含条件结构，所以 这三种基本逻辑结构是相互支撑的，无论怎样 复杂的逻辑结构，都可以通过这三种结构来表 达。
算法与程序框图(循环结构)
输出S 结束
程序框图:
开始
开始
i=1 S=0 S=S+i
i=i+1 直到 型循 环结 构 否
i>100?
i=1 S=0 i=i+1
S=S+i
i≤100?
是
是 输出S
结束
否 输出S
结束
当型循环 结构
开始
i=1 初始值 计数变量 S=0
i=i+1
循环体
S=S+i
循环条件
i≤100?
Y
N 输出S
结束
累计变量
循环体
开始 投票 有一城市过半票
淘汰得票最少者 否
是 选出该城市
结束
例1 设计一个计算1×2×3+……×100的值的算法,
算法分析:
并画出程序框图. 观察各步骤的共同点 第(i-1)步的结果×i=第i步的结果
第1步:1×2 =2;
S=1 第2步: 2×3 =6; S=S × 2 S=S × 3 第3步: 6×4 =24; S=S × i S=S × 4 第4步: 24×5 =120 … S=S × 100 i=i+1 …… 为了方便有效地表示上述过程,我们 引进一个变量S来表示每一步的计算 结果,从而把第i步表示为S=S×i
奥运会主办权投票过程的算法: S1 ：投票；
S2 ：计票. 如果有一个城市得票超过一半，
那么这个城市取得主办权，进入S3 ；
否则淘汰得票数最少的城市，转入S1；
S3 ：宣布主办城市.
奥运会主办权投票表决流程图：
开始 投票 有一城市过半票 是 选出该城市 结束
淘汰得票最少者 否
循环结构
以上算法中, 出现从某处开始,按照一定条件, 反复执行某些步骤的情况.这就是循环结构.反复 执行的步骤称为循环体.
算法流程图(循环结构)
算法流程图(循环结 构)
目录
• 循环结构的概述 • 循环流程图的绘制 • 常见的循环结构算法 • 循环结构的应用场景 • 循环结构的注意事项 • 案例分析
01
循环结构的概述
循环结构的定义
循环结构是算法流程图中的一种基本结构，用于 01 重复执行一段代码，直到满足某个条件为止。
循环结构由三个基本部分组成：初始化、循环体 02 和终止条件。
详细描述
在for循环中，首先定义一个计数器变量和循环次数，然后在每次循 环中执行指定的操作，直到计数器达到设定的循环次数为止。
示例
以下是一个简单的for循环算法，用于计算1到10的累加和
for循环算法
```
sum = sum + i
for i = 1 to 10 do
for循环算法
end for ```
VS
详细描述
for循环通常用于已知循环次数的情况， 它包含三个基本部分：初始化、条件和后 续操作。在流程图中，for循环通常以矩 形表示，并在其中标明循环变量、初始值 、条件表达式和增量。例如，计算1到10 的累加和可以使用以下for循环实现
for循环的案例分析
```
for (int i = 1; i <= 10; i) {
控制条件的绘制
01 绘制一个菱形，标注为“条件”，表示循环的控
制条件。
02
在条件菱形内标注判断的具体内容，如“i<10” 。
循环次数的表示
使用一个数字标注在控制条件旁边，表示循环的 次数。
如果循环次数是动态变化的，可以使用变量代替 数字，如“n”。
03
常见的循环结构算法
for循环算法
总结词
for循环是一种预先设定循环次数的循环结构，通常用于已知循环次 数的情况。
目录
• 循环结构的概述 • 循环流程图的绘制 • 常见的循环结构算法 • 循环结构的应用场景 • 循环结构的注意事项 • 案例分析
01
循环结构的概述
循环结构的定义
循环结构是算法流程图中的一种基本结构，用于 01 重复执行一段代码，直到满足某个条件为止。
循环结构由三个基本部分组成：初始化、循环体 02 和终止条件。
详细描述
在for循环中，首先定义一个计数器变量和循环次数，然后在每次循 环中执行指定的操作，直到计数器达到设定的循环次数为止。
示例
以下是一个简单的for循环算法，用于计算1到10的累加和
for循环算法
```
sum = sum + i
for i = 1 to 10 do
for循环算法
end for ```
VS
详细描述
for循环通常用于已知循环次数的情况， 它包含三个基本部分：初始化、条件和后 续操作。在流程图中，for循环通常以矩 形表示，并在其中标明循环变量、初始值 、条件表达式和增量。例如，计算1到10 的累加和可以使用以下for循环实现
for循环的案例分析
```
for (int i = 1; i <= 10; i) {
控制条件的绘制
01 绘制一个菱形，标注为“条件”，表示循环的控
制条件。
02
在条件菱形内标注判断的具体内容，如“i<10” 。
循环次数的表示
使用一个数字标注在控制条件旁边，表示循环的 次数。
如果循环次数是动态变化的，可以使用变量代替 数字，如“n”。
03
常见的循环结构算法
for循环算法
总结词
for循环是一种预先设定循环次数的循环结构，通常用于已知循环次 数的情况。
流程图(循环结构)课件
←p+i
t←t+1
i←i+t
否
i >46?
是
输出p
流程图(循环结构)
结束
此课件下载可自行编辑修改，供参考！ 感谢您的支持，我们努力做得更好！
流程图(循环结构)
流程图(循环结构)
开始
投票
有一个城市 得票数超过总票
数的一半
Y
输出该城市
淘汰得票数 最少的城市
N
结束
流程图(循环结构)
循环结构及框图表示
1.循环结构的概念
循环结构是指在算法中从某处开始,按 照一定的条件反复执行某一处理步骤的结 构.在科学计算中,有许多有规律的重复计算, 如累加求和、累乘求积等问题要用到循环 结构.
流程图(循环结构)
设计一算法，求和: 1 2 3 L 1 0 0 .
开始
开始
i←1，S←0
i←1，S←0
S←S + i
i←i+1 否
i>100? 是
输出S
结束
i≤100? 否 是 S←S + i
i←i+1
输出S
流程图(循环结构)
结束
2.循环结构的算法流程图
直
到
型
语句A
循
环
结 构
条件 N
Y
直到型循环执行了一次循环体之后,对控 制循环条件进行判断,当条件不满足时执行循 环体,满足则停止.
流程图(循环结构)
设计一个求1+2+4+7+…+46的算法,并画出相应 的程序框图.
算法如下:
第一步:P←0; 第二步:i←1; 第三步:t←0; 第四步:p←p+i; 第五步:t←t+1; 第六步:i←i+t. 第七步:如果i不大于46,返回第四步;否 则,跳出循环结束程序.
t←t+1
i←i+t
否
i >46?
是
输出p
流程图(循环结构)
结束
此课件下载可自行编辑修改，供参考！ 感谢您的支持，我们努力做得更好！
流程图(循环结构)
流程图(循环结构)
开始
投票
有一个城市 得票数超过总票
数的一半
Y
输出该城市
淘汰得票数 最少的城市
N
结束
流程图(循环结构)
循环结构及框图表示
1.循环结构的概念
循环结构是指在算法中从某处开始,按 照一定的条件反复执行某一处理步骤的结 构.在科学计算中,有许多有规律的重复计算, 如累加求和、累乘求积等问题要用到循环 结构.
流程图(循环结构)
设计一算法，求和: 1 2 3 L 1 0 0 .
开始
开始
i←1，S←0
i←1，S←0
S←S + i
i←i+1 否
i>100? 是
输出S
结束
i≤100? 否 是 S←S + i
i←i+1
输出S
流程图(循环结构)
结束
2.循环结构的算法流程图
直
到
型
语句A
循
环
结 构
条件 N
Y
直到型循环执行了一次循环体之后,对控 制循环条件进行判断,当条件不满足时执行循 环体,满足则停止.
流程图(循环结构)
设计一个求1+2+4+7+…+46的算法,并画出相应 的程序框图.
算法如下:
第一步:P←0; 第二步:i←1; 第三步:t←0; 第四步:p←p+i; 第五步:t←t+1; 第六步:i←i+t. 第七步:如果i不大于46,返回第四步;否 则,跳出循环结束程序.
循环结构的流程图
谈算法中“循环结构的流程图”的学习策略）高中数学新教材增加了算法知识，其中流程图是算法中的重点，而相对于顺序结构和选择结构的流程图来说，循环结构的流程图教学难度较大。
这是因为，程序设计中的循环结构与学生熟悉的重复运算存在一定的区别，学生对循环体和终止条件的学习还是比较困难的。
因此，加强对算法中循环结构的分析与研究很有必要，下面结合具体问题谈谈对循环结构的流程图认识及学习策略。
一、理解两类循环结构及相互转化循环结构是指在算法中从某处开始，按照一定的条件反复执行某一处理步骤的结构。
循环结构有两类，当型循环和直到型循环。
如图1所示为当型循环结构表示“当条件p满足时，反复执行A框操作，直到条件P不成立时才停止循环”；如图2所示直到型循环结构表示“先执行A框操作，再判断给定的条件P是否成立，若条件P不成立，则执行A，如此反复，直到条件P成立为止”。
直到型循环的特点是至少执行一次操作，当事先不能确定是否至少执行一次循环的情况下，用当型循环较好。
两类循环结构是可以相互转化的。
二、关注循环结构的三要素及其对程序的影响(1)循环前，初始化变量的值，并关注其对程序的影响所谓循环变量，是指在算法执行过程中，被反复赋值修改的变量。
例如，在上述两类循环结构中，都先给变量s、i分别赋初值0、1，当然也可以给变量s、i分别赋初值1、3。
(2)确定循环体，并关注其对程序的影响循环体就是在循环结构中反复执行的操作步骤，例如，上述循环结构中的循环体是“S←S+I，I←I+2”(3)设置循环终止条件，并关注其对程序的影响循环结构不能是永无终止的，一定要在某个条件下终止循环，这就需要条件结构来做出判断，因此，i≤”都是终止条件。
循环结构中一定包含条件结构。
例如，上述循环结构中的“i>99”、“99如果把上述循环结构中的循环体“S←S+i，i←i+2”改成“i←i+2，S←S+i”，则循环终止条件也要作出相应的改变，程序流程图如下：流程图如下：作者简介：孟庆东（1980-），男，江苏涟水人,江苏省淮阴中学教师，学士通讯地址：江苏省淮安市解放东路99号江苏省淮阴中学孟庆东（收）邮编：本人联系电话：邮箱：hymqd2003@。
算法的基本逻辑结构-循环结构讲解
第五步，判断[a，b]的长度是否小于d或f(m)是否 等于0.若是，则m是方程的近似解；否则，返回第 三步.
思考1:该算法中哪几个步骤可以用顺序 结构来表示？这个顺序结构的程序框图 如何？
f(x)=x2-2
输入精确度d 和初始值a，b
m ab 2
思考2:该算法中第四步是什么逻辑结构 ？这个步骤用程序框图如何表示？
赋值、计算
)
判断框
判断某一条件是否成立,成立时 在出口处标明“是”或“Y”,不 成立时标明“否”或“N”.
流程线
连接程序框
连结点
连接程序框图的两部分
6
开始
顺
输入n
序
i=2
结
构
求n除以i的余数
循
i的值增加1,仍用i表示
环
i>n-1或r=0?
否
结
构
是
r=0?
否
条
是
件
结
n不是质数
n是质数 构
结束
2、算法的三种基本逻辑结构 顺序结构、条件结构、循环结构。
第三步，判断所得的结果是否大于300. 若是，则输出该年的年份； 否则，返回第二步.
循环结构：
（1）循环体：设a为某年的年生产总值
，t为年生产总值的年增长量，n为年份 ，则t=0.05a，a=a+t，n=n+1.
（2）初始值：n=2005，a=200.
（3）设定循环控制条件：当“a>300” 时终止循环.
否 a=m
f(a)f(m)<0? 是
b=m
思考3:该算法中哪几个步骤构成循环结 构？这个循环结构用程序框图如何表示 ？
第三步
第四步
|a-b|<d或
思考1:该算法中哪几个步骤可以用顺序 结构来表示？这个顺序结构的程序框图 如何？
f(x)=x2-2
输入精确度d 和初始值a，b
m ab 2
思考2:该算法中第四步是什么逻辑结构 ？这个步骤用程序框图如何表示？
赋值、计算
)
判断框
判断某一条件是否成立,成立时 在出口处标明“是”或“Y”,不 成立时标明“否”或“N”.
流程线
连接程序框
连结点
连接程序框图的两部分
6
开始
顺
输入n
序
i=2
结
构
求n除以i的余数
循
i的值增加1,仍用i表示
环
i>n-1或r=0?
否
结
构
是
r=0?
否
条
是
件
结
n不是质数
n是质数 构
结束
2、算法的三种基本逻辑结构 顺序结构、条件结构、循环结构。
第三步，判断所得的结果是否大于300. 若是，则输出该年的年份； 否则，返回第二步.
循环结构：
（1）循环体：设a为某年的年生产总值
，t为年生产总值的年增长量，n为年份 ，则t=0.05a，a=a+t，n=n+1.
（2）初始值：n=2005，a=200.
（3）设定循环控制条件：当“a>300” 时终止循环.
否 a=m
f(a)f(m)<0? 是
b=m
思考3:该算法中哪几个步骤构成循环结 构？这个循环结构用程序框图如何表示 ？
第三步
第四步
|a-b|<d或
算法的三种基本逻辑结构和框图
处输理出结S果 结束
iS 10 100 1+ …1 +100
1021 退退出 出
概念深化—循环 一起看一下如何进行循环的。
引例分析
例2 如何求1+2+4+……+263的值？
开始
开始
初始值
条件 否 是
累计变量 计数变量
处理结果 结束
初始S=值0怎,i=么1 取？
初始值
累计变量
SS==SS++22ii 循环累终计止变i<>条量6件43怎怎么么取取？？
萨·班·达依尔。国王问他想要什么，他对国王说：“陛下，请 您在这张棋盘的第1个小格里赏给我一粒麦子，在第2个小格 里给2粒，第3个小格给4粒，以后每一小格都比前一小格加一 倍。请您把这样摆满棋盘上所有64格的麦粒，都赏给您的仆 人吧！” 设计程序求国王需要奖赏多少麦子。
谢谢指导
循环体
循环体
满足条件？ 是
否 当型循环结构
满足条件？
否
是 直到型循环结构
差异:循环终止条件不同,检验条件是否成立的先后次序也不同. 当型循环结构:先判断后执行循环体. 直到型循环结构:先执行循环体后判断条件是否成立.
循环结构分为当型循环结构和直到型循环结构
循环体
循环体
满足条件？ 是
否 当型循环结构
（2） S=S+i，i=i+1分别有何作用？
（3）能用直到型结构画出框图么？
曲径通幽
如果改为直到型结构如何修改？
开始
开始
初SS=始=00值,i,=i=11 i≤条1件00 否
是 累S计=变S+量i
计数i=i变+1量
C语言循环结构
for (<初始表达式>)；<条件表达式>；<循环表达式>） <循环体语句>
功能：先计算<初始表达式>的值，然后判断<条件表达式> 的值，若该值为“假”，则退出循环，执行循环体下面的 语句；若该值为“真”，则执行<循环体语句>，然后计算 <循环表达式>的值，再判断<条件表达式>的值，重复以上 的操作。
total = total + grade;
num++;
Enter grades: 67 88 73 54 82 -1
scanf (“%lf”, &grade); }
Grade average is 72.80
if(num != 0)
printf(“Grade average is %.2f\n", total/num);
/*exam5_4.c 用while求简单几何级数的和*/ #include <stdio.h>
main()
{
int i=1,sum=0; while(i<=100) {
程序运行结果： sum=5050
sum=sum+i;
i++; } printf("sum=%d\n",sum); }
【例5-5】输入一个正整数n，求n!。
<循环语句体>：是用一对花括号括起来的复合语句。
注意：在<循环语句体>中要有使<表达式>的值为假 （或<表达式>的值为零）的语句，否则会使程序出现 无限循环而发生错误。
注意：由于while循环是先判断<表达式>的值，后决 定是否执行<循环语句>，因此，有可能一次也不执 行<循环语句>。
功能：先计算<初始表达式>的值，然后判断<条件表达式> 的值，若该值为“假”，则退出循环，执行循环体下面的 语句；若该值为“真”，则执行<循环体语句>，然后计算 <循环表达式>的值，再判断<条件表达式>的值，重复以上 的操作。
total = total + grade;
num++;
Enter grades: 67 88 73 54 82 -1
scanf (“%lf”, &grade); }
Grade average is 72.80
if(num != 0)
printf(“Grade average is %.2f\n", total/num);
/*exam5_4.c 用while求简单几何级数的和*/ #include <stdio.h>
main()
{
int i=1,sum=0; while(i<=100) {
程序运行结果： sum=5050
sum=sum+i;
i++; } printf("sum=%d\n",sum); }
【例5-5】输入一个正整数n，求n!。
<循环语句体>：是用一对花括号括起来的复合语句。
注意：在<循环语句体>中要有使<表达式>的值为假 （或<表达式>的值为零）的语句，否则会使程序出现 无限循环而发生错误。
注意：由于while循环是先判断<表达式>的值，后决 定是否执行<循环语句>，因此，有可能一次也不执 行<循环语句>。
循环结构.
结束
i←i+1
Y i=0，1，2，3，4，5，6，7，8，9
S 1 2 3 10
例2:设计一个计算10个数平均数的算法，并画出流程图．
分析：由于需要依次输入10个数，并计算它们的和，因此， 需要用一个循环结构，并用一个变量存放数的累加和。在求
出10个数的总和后，再除以10，就得到10个数的平均数。
结束 S 1 2 3 9
开始 S←0 i←0
i ← i +1
i≤10
N 输出S
结束
S← S +i Y
S 1 3 5 99
开始
当
型
S ←0
后
计
数
i ←1
开始
直 到
型
S←0
后
计
i← 1
数
开始
直 到
型
S ←1
先
计
i← 1
数
开始
当
型
S ←1
先
计
数
i←1
i ← i +2
解 算法： S1 x ← 0；
S2 x ← x＋1；
S3 y ← 316－x；
S4 如果x能被11整除，且y能被13整除，转到S5， 否则转到S2；
S5 输出x，y，算法结束．
流程图（直到型）： 开始 x←0
x ← x＋1 y ← 316－x
x能被11整除，且y能
N
被13整除
Y
输出x，y
结束
流程图（当型）: 开始 x←1
开始
算法为：
T←1
S1 T ← 1； S2 I ← 3；
I←3
S3 T ← T×I；
计算机算法的5种表达形式
计算机算法的5种表达形式
一、用自然语言表示算法
例如：
S1：令t=1；
S2：令i=2；
S3：使t与i相乘，将结果放在t中；
S4：使i值加1；
S5：若i的值不大于5，返回重新执行S3、S4与S5；若i的值大于5，则算法结束。
二、用流程图表示算法
（一）基本概念及简单实例
①起止框：表示算法的开始与结束。
②判断框：对一个给定的条件进行判断，根据给定的条件是否成立决定如何执行其后的操作。
③输入输出框：表示算法的输入与输出操作。
④连接点：用于将画在不同地方的流程线连接起来，同时表示算法的执行顺序。
（二）三种基本结构
（1）顺序结构
（2）选择结构
（3）循环结构
三、用N-S图表示算法
N-S图又称N-S结构化流程图、盒图，它将全部算法写在一个矩形框内，在该框内可包含它的从属框。
也就是说，由一些基本框可以组成一个大的矩形框，即N-S图。
四、用伪代码表示算法
伪代码是用介于自然语言与计算机语言之间的文字和符号来描述算法。
它无固定的、严格的语法规则，书写格式自由，且易于修改，只要表达清楚意思即可。
五、用计算机语言表示算法
该方法必须严格遵循所用语言的语法规则。
算法流程图(循环结构)
流 程 图
i) 顺序结构
三种基本算法结构
ii) 选择结构
Y A B A
p
N B
循环结构
算法2流程图:
算法2:
开始 T←1
S1
S2
T←1；
S←2；
S←2
T←T×S S←S+1 S>5 Y 输出T 结束 N
S3
S4 S5
T←T×S；
S←S+1； 如果S不大于5,返 回 S3,否则输出T。
开始
开始
i ← 0，Sum ← 0
2010辽宁文数如果执行下图左的程序框图输入那么输出的等于a720b360c240d12010aa1b2b1输出b结束缚目录点击添加标题点击添加标题点击添加标题点击添加标题添加文本点击添加文本点击添加文本点击添加文本点击添加文本点击添加文本点击添加文本添加文本点击添加文本点击添加文本点击添加文本点击添加文本添加文本点击添加文本点击添加文本点击添加文本添加文本点击添加文本点击添加文本点击添加文本点击添加文本点击添加文本点击添加文本添加文本点击添加文本点击添加文本点击添加文本点击添加文本点击添加文本添加文本点击添加文本点击添加文本点击添加文本添加文本点击添加文本点击添加文本点击添加文本点击添加文本点击添加文本点击添加文本点击添加文本01020304添加标添加文本点击添加文本点击添加文本点击添加文本点击添加文本会议基调年会视频
开始 Sum←0,i←1 Sum←Sum+1 i←i+1 否 i>100 是 输出Sum 结束
1.【2010· 浙江理数】 某程序框图如左图所 示，若输出的S=57， 则判断框内位（ ） A. k＞4? B.k＞5? C. k＞6? D.k＞7?
2.【2010· 辽宁文数】 如果执行下图（左）的 程序框图，输入 n 6 , m 4那么输出的 等于（ ） A.720 B.360 C.240 D.120
i) 顺序结构
三种基本算法结构
ii) 选择结构
Y A B A
p
N B
循环结构
算法2流程图:
算法2:
开始 T←1
S1
S2
T←1；
S←2；
S←2
T←T×S S←S+1 S>5 Y 输出T 结束 N
S3
S4 S5
T←T×S；
S←S+1； 如果S不大于5,返 回 S3,否则输出T。
开始
开始
i ← 0，Sum ← 0
2010辽宁文数如果执行下图左的程序框图输入那么输出的等于a720b360c240d12010aa1b2b1输出b结束缚目录点击添加标题点击添加标题点击添加标题点击添加标题添加文本点击添加文本点击添加文本点击添加文本点击添加文本点击添加文本点击添加文本添加文本点击添加文本点击添加文本点击添加文本点击添加文本添加文本点击添加文本点击添加文本点击添加文本添加文本点击添加文本点击添加文本点击添加文本点击添加文本点击添加文本点击添加文本添加文本点击添加文本点击添加文本点击添加文本点击添加文本点击添加文本添加文本点击添加文本点击添加文本点击添加文本添加文本点击添加文本点击添加文本点击添加文本点击添加文本点击添加文本点击添加文本点击添加文本01020304添加标添加文本点击添加文本点击添加文本点击添加文本点击添加文本会议基调年会视频
开始 Sum←0,i←1 Sum←Sum+1 i←i+1 否 i>100 是 输出Sum 结束
1.【2010· 浙江理数】 某程序框图如左图所 示，若输出的S=57， 则判断框内位（ ） A. k＞4? B.k＞5? C. k＞6? D.k＞7?
2.【2010· 辽宁文数】 如果执行下图（左）的 程序框图，输入 n 6 , m 4那么输出的 等于（ ） A.720 B.360 C.240 D.120
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
五、小结
算法的执行流程
循环结构
循环三要素： 1 初始化： 2 条件： 3 循环体：①循环部分
②修正部分 （没有的话否则可能造成死循环）
在一个循环结构中，以上三个部分缺一不可。
六、作业
用算法实现
输出由30个“=”组成的 一行分割线
初始化 循环条件 循环体
六、作业
输出由30个“=”组成的一行分割线
结束
算法的执行流程
三、循环结构
有需要重复执行步骤的结构
循环结构
流程图的画法： 伪代码：
条件 y 循环体
n
Do while 条件 循环体 loop
每个循环结构都是一个入口，一个出口
开始 I=0 I<33
循环结构
N
方法1
Y 输入 cj 输出 cj I=I+1
I=0 Do while I<33 输入 cj 输出 cj I=I+1 loop
结束
开始 I=1
循环结构方法2
N
I<=33 Y 输入 cj 输出 cj I=I+1
I=1 Do while I<=33 输入 cj 输出 cj I=I+1 loop
结束
循环结构（三要素）
循环初始状态 循环条件 循环体
①循环部分 ②修正部分
四、课堂练习
练习1：用算法实现
输入某班每个学生的语文月 考考试的成绩并输出.
一、作业讲评： 西瓜价格为1.2元/千克,
若一次购买大于100千克小于200千 克着价格为0.9元/千克;
若一次购买200千克及以上着价格为 0.8元/千克; 输入西瓜重量(千克), 计算并输出应付金额。
开始
填空
输入 w n n W<200 y P=w*1.2 ② ① y
P=w*0.8
输出 p 结束
3
二、用算法实现 1 .输入自己的语文月考考试 成绩并输出.
2 .输入本组的每个成员语文 月考考试的成绩并输出.
3 编程实现：
输入本班的每个成员语文月 考考试的成绩并输出. 能不能只用一条输入和一条输 出语句概括描述全班的语文月 考考试成绩的输入和输出
开始 I=0 I<33 Y 输入 cj 输出 cj I=I+1 N
初始化 ： C=0 输入 n c<n 条件： 输入 cj ,输出 cj 循环体： c=c+1
练习2:用算法实现 求某班的语文月考考 试成绩的总和。
1 循环初始化 s=0,C=0,输入 n 2 循环条件 c<n 3 循环体 输入cj ,s=s+cj c=c+1
输出 s
开始 S=0:c=0
输入 n
n
C<n
输入 cj
y
S=s+cj c=c+1 输出 S 结束
开始 S=0:c=0
输入 n
练习3:用算法实现
求某班某一学科考试 的平均成绩。
n
C<n
输入 cj
y p=s/c
S=s+cj c=c+1 输出 p 结束
s=0；c=0 输入 n Do while c<n 输入 cj s=s+cj c=c+1 Loop p=s/c 输出 p