风险偏好与效用函数

风险中性定价理论中的期望效用函数研究

风险中性定价理论中的期望效用函数研究在金融领域，风险中性定价理论是一种重要的定价模型，通过衡量投资者的偏好和预期，来确定金融资产的合理价格。

在这个理论中，期望效用函数是一个关键的概念，它用于描述投资者在不确定条件下做出决策时所追求的效用最大化原则。

1. 期望效用函数的基本概念和性质期望效用函数是描述投资者偏好的一种数学工具，它把投资者对于资产收益的期望和风险的偏好程度进行了量化。

该函数通常表示为U(W)，其中W表示财富水平，U(W)表示投资者对于这个财富水平所获得的效用。

期望效用函数是从财富到效用的映射关系，而财富又是从资产收益到财富的映射关系，因此期望效用函数可以用于描述投资者对于资产收益的偏好。

期望效用函数具有以下几个基本性质：(1) 非线性性质：期望效用函数一般是非线性的，并且通常是递增但递减边际效益。

这意味着随着财富的增加，投资者对于每增加的单位财富的效用递减。

(2) 风险厌恶性质：期望效用函数体现了投资者的风险厌恶性质，即对于相同的期望收益，投资者倾向于选择风险较小的投资策略。

这体现了投资者对于风险的厌恶程度。

(3) 增量效用递减性：期望效用函数具有增量效用递减性，即对于相同的财富增加，其效用的增加逐渐减少。

这意味着投资者对于财富增加的效用增加程度逐渐变小。

(4) 风险规避程度的度量：期望效用函数的斜率可以用来度量投资者对风险的规避程度。

斜率越大，表示投资者对风险的规避程度越高。

2. 期望效用函数在风险中性定价理论中的应用风险中性定价理论是基于投资者风险厌恶性质的假设建立的，而期望效用函数则是衡量投资者风险厌恶程度的一种工具。

在风险中性定价理论中，期望效用函数被用来确定金融资产的合理价格。

在传统的资产定价模型中，投资者通常是理性且风险厌恶的，他们的决策依据是最大化期望效用。

在这种情况下，通过将投资者的效用函数与风险资产的概率分布函数相结合，可以推导出资产的期望回报率和风险溢价。

这些结果可以用来估计资产的合理价格和投资者对于不同资产的需求。

金融经济学第二章-偏好、效用与风险厌恶

的理论部分讲解。
（1）风险补偿
（2）绝对风险厌恶与相对风险厌恶
• 绝对风险厌恶
• Arrow（1970）和Pratt（1964）首先提出将
A(w)定义为风险厌恶程度的度量，所以也称
为Arrow-Pratt风险厌恶测度。
（2）绝对风险厌恶与相对风险厌恶
• 绝对风险厌恶
• 我们可以根据绝对风险厌恶函数关于w的增减性
Marshall
边际效用价值论
奥地利学派
效用价值论稍占上风
引言
效用的表达：

基数效用论
边际效用学派
序数效用论
新古典综合派
（一般均衡论）
序数效用论占上风
2.1
偏好关系
问题的提出：
微观经济学中如何用数学的语言来描述
个人的选择问题：
偏好的假定？
偏好与效用函数之间在什么条件下可以
存在对应关系？
比投资者2的效用函数更厉害。定理2.4的4条
判别准则其实说的都是这同一个道理。
第二章小结
偏好、选择的理性基础
以效用表示偏好
不确定性条件下的偏好关系与期望效用函数

第二章小结

理性ቤተ መጻሕፍቲ ባይዱ非理性：独立性公理
第二章小结
风险厌恶
风险补偿
风险厌恶的比较

第二章小结
期望效用函数的存在性
定理 2.2：对于建立在有限概率分布空间 P 上
的偏好关系 p ，满足 2.3 节所述的三条行为公
理（理性选择、独立性、阿基米德性），则期
望效用函数存在，且在严格正的仿射变换意义
下是唯一的。
小结
小结
小结
小结
2.5 阿里亚斯悖论

FRM模型丨效用函数和风险偏好的辨析

FRM模型丨效用函数和风险偏好的辨析1.效用历史沿革效用的概念是丹尼尔·伯努利（不是数学家伯努利，但是他们都是伯努利家族的。

）在解释圣彼得堡悖论时提出的，目的是挑战以金额期望值作为决策的标准，证明期望收益并不是人们在做决策时的唯一衡量标准。

经济学家对于效用的理解是有一个过程的。

●19世纪的威廉姆·斯坦利·杰文斯、里昂·瓦尔拉斯和阿尔弗雷德·马歇尔等早期经济学家认为效用如同人们的身高和体重一样是可以测量的。

●而约翰·希克斯则尝试了只在序数性效用的假定下，也取得了很多的研究成果。

希克斯认为，效用的数值表现只是为了表达偏好的顺序，并非效用的数值。

因此，从分析消费者行为的方法来看，基数效用论者采用边际效用分析方法，序数效用论者采用无差异曲线分析方法。

从教科书等内容判断，现在比较通用的应该是后者的序数性效用。

1.1.效用概念的提出——圣彼得堡悖论圣彼得堡悖论是尼古拉·伯努利在1738年提出的一个概率期望值悖论。

它来自于一种掷币游戏，圣彼得堡游戏。

游戏规则为：掷出正面或者反面为成功，游戏者如果投掷成功，得奖金2元，游戏结束；若不成功，继续投掷，二次成功得奖金4元，游戏结束；这样，游戏者如果投掷不成功就反复继续投掷，直到成功，游戏结束。

如果n 次投掷成功，得奖金2n 元，游戏结束。

首先，我们用公式1()k kk E X x p ∞==∑来计算这个游戏收益的数学期望值：23423411111()2222222222n n E X n n ==⨯+⨯+⨯+⨯++⨯= 从理论上来说，该游戏的期望值是无穷大的。

按照概率的理论，多次试验的结果将会接近于其数学期望。

这就出现了计算的期望值与实际情况的“矛盾”。

如果仅仅以期望值标准，我们将无法给这个游戏进行定价。

圣彼得堡悖论反映了决策理论和实际之间的差别。

人们总是不自觉地把模型与实际问题进行比较，但决策理论模型与实际问题并不是一个东西；圣彼得堡问题的理论模型是一个概率模型，它不仅是一种理论模型，而且本身就是一种统计的 “近似的”模型。

金融经济学第四章效用函数与风险厌恶

不确定性：是指发生结果尚未不知的所有情形，也即那些决策的结果明显地依赖于不能由决策者控制的事件，并且仅在做出决策后，决策者才知道其决策结果的一类问题。即知道未来世界的可能状态（结果），但对于每一种状态发生的概率不清楚。 Knight 的观点并未被普遍接受。但是这一观点成为研究方法上的区别。
34
不难发现，抛硬币选择A或B的结果的概率分布于彩票C的分布完全相同。因此我们可以将投资者的偏好概括如下：C偏好 A；A偏好A或B各50%；但是A和B各 50%又恰好与C一样好。因此C明确偏好 A, A明确偏好C—矛盾。
35
例20美元； ❖ 方案B:
（1）x y弱偏好于x，x 至少与y 一样好。
（2）x y 强偏好于x ； x y x y 但， y x 不成立。
（3）x y无差异于x 、y；即：
x yxy 和 yx
5
2.偏好应满足的基本公理（Axiom）条件：（1）完备性（completeness）
x, y C y x x y x y
q (q1, , qm, , qM ) RM
max u(.) s.t.z C RM : qc W
上述约束式为瓦尔拉斯（walrasian budget set）预算集。
16
最优解：
u q 0
C C
W qC 0
MRSi, j
u / Ci u / C j
qi qj
17
❖ 得到5000000美元的概率是0.1 ❖ 得到1000000美元的概率是0.89 ❖ 得到0美元的概率是0.01
36
他发现，在A和B中，他的受试者偏好于 A。于是，他进一步要求受试着考虑一下情形：
❖ 方案C：以0.11的概率得到1000000美元

效用、风险与风险态度简介

效用、风险与风险态度简介效用是指个体对各种选择或决策结果的主观评价，也可以理解为满足程度或心理感受。

效用理论是经济学中一个重要的概念，用来描述个体在面临选择时如何进行决策。

根据效用理论，人们在做决策时会选择能够带来最大效用的选项。

风险是指在不确定性条件下，预期可能发生的不确定结果。

在风险决策中，个体往往需要在多个可能的结果之间做出选择，每个结果都有相应的概率。

风险与效用理论密切相关，因为个体会考虑不同结果的效用大小来决定选择哪个风险。

风险态度是指个体对风险的态度和偏好。

不同的人对风险会有不同的态度。

有些人可能更喜欢谨慎的决策，更倾向于避免风险，他们会选择较为确定的选项。

而有些人可能更愿意冒险，更容忍风险，他们愿意冒更高的风险来追求更高的收益。

风险态度可以分为三类：风险厌恶、风险中性和风险偏好。

风险厌恶者倾向于选择较为保守的选项，他们对于风险敏感，更倾向于避免风险。

风险中性者对风险持中立态度，他们会权衡风险与回报，选择平衡的选项。

而风险偏好者则更愿意承担风险，他们会选择更高的概率获得更高回报的选项。

风险态度会对决策产生影响。

不同的风险态度会导致不同的选择。

对于企业来说，了解员工的风险态度可以帮助管理者更好地分配任务和确定激励措施。

对于投资者来说，了解自己的风险态度可以帮助他们选择适合自己的投资组合。

然而，风险在决策中也存在一定的风险。

一些决策者可能会过于乐观或过于悲观地估计风险。

过于乐观的估计可能会导致对风险的低估，而过于悲观的估计则可能会导致对风险的高估。

这种偏差估计可能导致做出错误的决策或选择。

综上所述，效用、风险和风险态度是决策中非常重要的概念。

了解效用理论、风险和自身的风险态度可以帮助个体更好地进行决策，并在不确定条件下做出最优的选择。

然而，在决策中也需要注意风险的偏差和错误估计的可能性。

效用、风险和风险态度是现代经济学和决策理论中的重要概念，对于个体和组织的决策过程具有重要的影响。

在经济学和金融学中，效用函数常常用来衡量个体对不同选择或决策结果的主观评价。

风险厌恶系数[1]

PPT文档演模板
风险厌恶系数[1]
阿罗-普拉特度量
阿罗-普拉特度量是对一个决策者的风险厌恶程度的度量。它由肯尼思·阿罗和约翰·普拉特的名字命名。
设是一个可微分的效用函数, 那么一个绝对风险厌恶的阿罗-普拉特度量被定义为：
PPT文档演模板
风险厌恶系数[1]
l ARA为正，表明具有此效用函数的投资者或者消费者是风险厌恶者；
为风险中性，只有极少部分的个体为风险爱好，并且高度风
险爱好的个体基本不存在，同时也可以发现个体的风险偏好具有较强的异质性。
PPT文档演模板
风险厌恶系数[1]
• 从表3可以看出，采用 MPL 和 OLS 设计所测度出的个体风险厌恶中值并没有明显差异，但是要显著低于 iMPL 设计所测度出的个体风险厌恶中值，这表明实验中所测度的个体的风险态度可能会受到测度方法的影响。
• 个体普遍是风险厌恶的这一结论是不受影响并且是稳健的。 Carlsson 等（2009）同样采用Holt和Laury （2002）的设计对中国贵州农村个体的风险厌恶进行了测度，但实验中的收益是本文中的 10 倍，作者研究发现这主要是激励的差异所造成的，该结论表明了使用学生作为被试的实验数据同样具有代表性。
风险厌恶系数[1]
基于以上分析，财富概念应为包含房产、人力资本后的财富净值，由金融财富净值、房产和人力资本等构成。为了检验三类财富对风险庆恶系数分别产生的影响，分析模型III 的拟合结果如表8 所示。
PPT文档演模板
风险厌恶系数[1]
2.3 考量居民主观风险偏好对于风险厌恶系数大小的影响为了方便模型数据的拟合，本文需要首先量化每一心理测试题的各个选项，如对于第一题中的A 、B 、C 和D 四个选项分别赋予1 、3 ，5 和9 分;随后累加四道心理测试题受访者所勾选项对应的分值，并将该总分值赋予变量X ，即居民的风险偏好态度为X。

第二章风险偏好及选择

一条自左下方向右上方倾斜的曲线。退出返回目录
dr 0 表明无差异曲线具有正的斜率，它是 d
上一页
下一页
第二章风险偏好及选择
第四节无差异曲线
dr 0 的经济含义为：增加单位风险时，投资者所要求 d
的收益补偿量，按经济学相关边际原则，可将其定义为边际补偿率MRS。边际补偿率大于0，刻画了风险与收益之间的对称性，即高收益常常与高风险相伴。下凸曲线一般请况下，随着风险的增大，人们所要求的收益补偿会越来越高。这就是说，人们的投资行为通常符合边际补偿率递增法则。依据MRS递增法则，有 dMRS 0 d 返回目录上一页下一页退出
大小可定义为 E R (r ) rdF (r ) rf (r )dr

R
R
离散情况下，风险为 E R (r ) Pi ri

R
退出
返回目录
上一页
下一页
第二章风险偏好及选择
第二节风险的度量
一个例子
P0 购买了总金额为 W 在股票市场中,你以某一价格
的某一只股票,且你认为该股价格的变动服从均值
所谓无差异曲线是指：能够使投资者得到同样满足程度的不同投资方案风险与收益组合的轨迹，用效用函数表示，无差异曲线就是等效用函数。
U , r k

为风险，r为预期收益或收益率，k为常数
退出
返回目录
上一页
下一页
第二章风险偏好及选择
第四节无差异曲线
r关于的函数 r g ( ) 所对应的曲线即为无差异曲线，它表明该曲线上任何一点给投资者带来的满足程度都是相同的。在无差异曲线族中，位于左上方向的无差异曲线优于右下方向的无差异曲线。退出

投资者的效用函数 (I)

调查问卷法
通过设计问卷，收集投资者的风险偏好、投资目标、资产配置等方面的数据，分析投资者对不同投资组合的效用评价。
实验法
在实验室环境下模拟投资场景，观察和记录投资者的决策行为，分析投资者对风险和收益的权衡。
大数据挖掘
利用大数据技术，对投资者的交易数据进行分析，挖掘投资者的风险偏好和投资行为模式。
投资者行为受到多种因素的影响，包括个人性格、经验、风险偏好、信息获取等，这些因素会影响投资者对投资机会和风险的认知和判断。
效用函数对投资者行为的影响
01
效用函数是描述投资者对风险和收益的偏好关系的函数，它反映了投资者对风险和收益的权衡取舍。
02
效用函数对投资者行为的影响主要体现在投资者会根据自己的
实证研究还发现，投资者在决策过程中存在许多非理性因素，如过度自信、损失厌恶等，这些因素会影响投资者的决策和行为。
对投资者的启示
1 2
了解自己的风险偏好和投资目标
投资者应了解自己的风险偏好和投资目标，以便选择适合自己的投资产品和策略。
多元化投资分散风险
投资者可以通过多元化投资分散风险，降低单一资产的风险暴露。
效用函数来选择最优的投资组合，以达到最大的效用。
不同投资者的效用函数可能存在差异，因此他们的投资行为也
03
会有所不同。
投资者行为与市场表现
投资者行为对市场表现有着重要的影响，一些不理性的投资者行为可能会导致市场的波动和不稳
定。
例如，羊群效应、过度交易等行为可能会加剧市场的波动，而理性的投资者行为则有助于市场的
研究如何将效用函数应用到更广泛的投资者群体和投资场景中，包括不同类型的投资者、不同的资产类别等。

效用、损失与风险函数

效用、损失与风险函数效用函数（Utility Function）是一种经济学概念，用于评估个人或组织对不同选择的偏好程度。

它衡量的是个体对于不同结果的满意程度或福利水平。

损失函数（Loss Function）是一种数学函数，用于评估模型预测结果与实际结果之间的差距。

风险函数（Risk Function）则是指损失函数的期望值，用于评估模型的整体表现。

效用函数的应用范围非常广泛，不仅限于经济学领域。

在经济学中，效用函数可以用来评估个体在消费决策中的偏好。

例如，一个消费者在购买商品时，可以根据效用函数来判断对于不同商品的满意程度，从而做出最优的购买选择。

在生产决策中，效用函数也可用于评估企业的利润或效益。

此外，效用函数在公共政策制定中也有重要的应用。

政府可以通过对不同政策措施的效用函数分析，来选择最优的政策方案。

然而，效用函数也存在一定的局限性。

首先，效用函数是基于个人的主观偏好进行评估，因此不同个体对于相同选择可能有不同的效用函数。

这使得在集体决策中，如何综合不同个体的效用函数成为了一个问题。

其次，效用函数往往是根据个体的经验和认知进行建模的，因此可能忽视了一些隐含的因素。

例如，某个人可能会根据过去的经验来评估未来的效用，但如果未来情况发生变化，这种评估就会失效。

损失函数在机器学习中有着广泛的应用。

在监督学习任务中，模型通过学习数据集中的样本和相应的标签，来预测新样本的标签。

损失函数用于衡量模型预测结果与实际结果之间的差距。

常见的损失函数有均方差损失函数和交叉熵损失函数等。

通过最小化损失函数，可以找到最优的模型参数，从而提高模型的预测准确性。

然而，损失函数的选择也是有风险的。

不同的损失函数适用于不同的情况，选择不当可能导致模型产生误导性的结果。

例如，在处理分类问题时，使用错误的损失函数可能导致模型过于关注错误分类的样本，而忽视其他分类结果。

此外，某些损失函数对异常值（Outlier）较为敏感，一旦输入数据中存在异常值，模型的训练过程就可能受到影响。

效用、损失与风险函数

效用、损失与风险函数效用、损失与风险函数在决策理论和风险管理中起着重要的作用，帮助人们做出理性的决策和进行有效的风险管理。

效用函数是用来衡量个体对不同结果或决策方案的偏好程度的函数。

它反映了个体对不同结果的偏好、满足程度或效用水平。

通过建立有效的效用函数，我们可以在选择不同的决策方案时，根据效用的大小来做出最优决策。

例如，在投资决策中，我们可以建立一个效用函数，根据预期回报以及风险程度，来评估不同投资方案的风险收益比，从而选择最优的投资方案。

损失函数是用来衡量预测结果与真实结果之间差异的函数。

它通常用于机器学习和统计建模中，用于评估模型的预测精度。

通过选择适当的损失函数，我们可以训练和优化模型，使其能够最小化预测误差，提高预测准确性。

例如，在二分类问题中，我们可以使用交叉熵损失函数来评估分类模型的预测结果与实际标签之间的差异。

风险函数是用来衡量不同风险事件或决策方案的风险程度的函数。

它通常用于风险管理中，用于评估不同风险事件可能造成的损失大小。

通过建立合理的风险函数，我们可以对不同的风险事件进行量化和比较，从而制定有效的风险管理策略。

例如，在金融风险管理中，我们可以使用价值-at-risk（VaR）或期望损失等风险函数来评估投资组合的风险水平，从而帮助投资者作出合理的投资决策。

然而，使用效用、损失和风险函数也存在一定的局限性和风险。

首先，构建准确的效用函数、损失函数和风险函数需要对决策者的偏好、预测准确性和风险承受能力进行准确的量化和建模，这可能会受到主观因素的影响。

其次，使用这些函数进行决策和风险管理时，需要准确的数据和模型，否则会产生误导性的结果。

最后，由于不确定性和未知风险的存在，预测准确性和风险评估可能存在一定的误差和不确定性。

总而言之，效用、损失和风险函数在决策理论和风险管理中起到了重要的作用，帮助人们做出理性的决策和进行有效的风险管理。

然而，它们也存在一定的局限性和风险，需要在实际应用中结合具体情况进行衡量和权衡。

风险、不确定性及个人效用函数分析

关系（preference relationship）（续）
PPT文档演模板
风险、不确定性及个人效用函数分析
➢期望效用准则
贝努力提出期望效用准则方法：用期望效用作为最大化的目标，假设投资者关心的是期末财富的效用，从而成功解决了圣彼得堡悖论问题。
用期末财富的对数形式或指数形式作为效用函数，则 alog(w) 或 w1/2表示效用函数，w表示财富。那么通过简单的计算，可以发现人们的确定等价财富的确在2-3 元之间。
• 也就是说，风险与不确定性有区别，但在操作上，我们引入主观概率或设定概率分布的概念，其二者的界线就模糊了，几乎成为一个等同概念。
PPT文档演模板
风险、不确定性及个人效用函数分析
（二）风险来源的不同看法
• 风险与不确定性联系在一起。一项经济活动的风险可以由其收益的不可预测性的波动性来定义，而不管收益波动采取什么样的形式。
• 有的二元关系所涉及的两个元素有相同的性质，有的二元关系所涉及的两个元素则属于不同性质的集合。
• 有的二元关系满足一定的性质，如完全性、传递性、自反性、（非）对称性。我们主要考虑前三者。
PPT文档演模板
风险、不确定性及个人效用函数分析
一、二元关系(binary relations)与偏好
们愿意付出的金额在2-3之间。 • 因此，期望收益最大原则并不能解决一切的不确定性
问题。
PPT文档演模板
风险、不确定性及个人效用函数分析
➢ 对于证券投资来讲，只追求期望收益最大化的投资者绝不会选择一个多元化的资产组合。如果一种证券具有最高的期望收益，这个投资者会把他的全部资金投资于这种证券。如果几种证券具有相同的最大化期望收益，对这个投资者来说，投资于若干这些证券的组合或者只是其中的某一种证券是无差别的。由此可见，如果我们认为多元化是投资的基本原则的话，我们必须否定仅仅最大化期望收益原则的目标假定。

风险不确定性及个人效用函数分析

风险不确定性及个人效用函数分析风险不确定性是经济学中一个重要的概念，指的是决策者在面对未来的各种可能性时所面临的不确定性程度。

个人效用函数则是用来描述个人对风险不确定性的态度和对不同结果的偏好程度。

在这篇文章中，我们将探讨风险不确定性及个人效用函数的分析。

首先，我们来讨论风险不确定性。

在现实生活中，人们常常面临各种风险和不确定性，比如投资、职业选择、购买决策等。

在这些决策中，决策者可能无法准确预测未来的结果，并且不同结果的概率分布也可能不一样。

这种不确定性给决策者带来了风险，因为他们的决策可能会受到不可控因素的影响，从而导致结果与预期不符。

为了对风险不确定性进行分析，经济学家引入了概率论和统计学的工具。

通过对可能结果的概率分布进行量化，可以计算出风险的大小，并从中选择最优的决策。

这种分析方法被称为风险分析。

在风险分析中，个人效用函数起着重要的作用。

个人效用函数是描述个人对不同结果的偏好程度的数学函数。

通过个人效用函数，可以量化个人对不同结果的喜好程度，从而在不确定性的环境下进行决策。

个人效用函数可以是线性的、非线性的，也可以是凸的或凹的，取决于个体的偏好。

个人效用函数的形式不同，会对决策结果产生重要影响。

比如，在风险回避的个人效用函数中，个人对较低的收益有较高的偏好，对较高的收益有较低的偏好。

这意味着，对于相同的风险水平，决策者更倾向于选择较为保守的决策，而回避可能带来较大风险的选择。

而在风险偏好的个人效用函数中，个人对较高的收益有较高的偏好，对较低的收益有较低的偏好。

这意味着，对于相同的风险水平，决策者更倾向于选择较为冒险的决策，从而追求更大的收益。

此外，个人效用函数还可以反映出决策者对风险的态度。

比如，风险厌恶的个人效用函数会对不确定性和风险给予较高的负面效用，而风险喜好的个人效用函数则对不确定性和风险给予较高的正面效用。

这种态度的差异会影响决策者在面对风险时的选择。

风险不确定性及个人效用函数的分析在经济学中有着广泛的应用。

资产定价、风险偏好、效用函数与“股权溢价之谜”研究

Ａｆｔｅｒｉｎｔｅｒｐｒｅｔｉｎｇｒｅｌａｔｅｄｌｉｔｅｒａｔｕｒｅｉｎｄｅｔａｉｌ，ｔｈｉｓｐａｐｅｒｂｅｌｉｅｖｅｓｔｈａｔｔｈｅｒｅａｒｅｔｗｏ
ｒｅａｓｏｎｓｇｉｖｉｎｇｒｉｓｅｔｏｔｈｅＥｑｕｉｔｙＰｒｅｍｉｕｍＰｕｚｚｌｅ．Ｏｎｔｈｅｏｎｅｈａｎｄ，ｔｈｅｈｙｐｏｔｈｅｓｉｓｏｆ
ｓｉｔｕａｔｉｏｎ．Ｏｎｈｙｐｏｔｈｅｓｉｓｉｓｆａｒａｗａｙｆｒｏｍａｃｔｕａｌ
ｔｈｅｏｔｈｅｒｈａｎｄ，ｔｈｅｆｏｍｅｒｌｉｔｅｒａｔｕｒｅｓ
ｄｅｍｏｎｓｔｒａｔｅｄｔｈｅｅｑｕｉｔｙｐｒｅｍｉｕｍｕｄｅｒｅｎｄｏｗｍｅｎｔｅｃｏｎｏｍｙ，ｗｈｉｃｈｍｅａｎｓｔｈｅａｃｔｕａｌ
ＩＩＩ
ｐａｒａｍｅｔｅｒｓｗｈｉｃｈａｒｅｎｏｔｏｎｌｙａｃｃｏｒｄｉｎｇｗｉｔｌｌｔｈｅＢｏｕｎｄｅｄＲａｔｉｏｎａｌｉｔｙ’Ｓｍｏｄｅｌｂｕｔａｌｓｏｆｉｔｆｏｒｔｈｅｅｃｏｎｏｍｉｃａｌｈｉｓｔｏｒｉｃａｌｄａｔａ，ＥｑｕｉｔｙＰｒｅｍｉｕｍＰｕｚｚｌｅｗｉｌｌｂｅｅｘｐｌａｉｎｅｄｖｅｒｙｗｅｌｌ．Ｔｈｉｓｐａｐｅｒｄｅｖｅｌｏｐｓｈｙｐｏｔｈｅｓｉｓｂｙｍｅａｎｓｏｆｉｎｖｅｓｔｉｇａｔｉｏｎａｎｄｇｏｅｓｏｎｔｈｅｏｒｅｔｉｃａｌｄｅｄｕｃｉｎｇ
ａｃｃｏｒｄｉｎｇｔｏｍａｘｉｍｉｚａｔｉｏｎｏｆＢｏｕｎｄｅｄＲａｔｉｏｎａｌｉｔｙ’Ｓｕｔｉｌｉｔｙｆｕｎｃｔｉｏｎ．Ｏｎｔｈｅｂａｓｉｓｏｆ
ＣｈｉｎｅｓｅａｎｄＡｍｅｒｉｃａｎｄａｔａ，ｔｈｉｓｐａｐｅｒｈａｓｄｅｖｅｌｏｐｅｄｄｅｍｏｎｓｔｒａｔｉｏｎａｂｏｕｔＢｏｕｎｄｅｄＲａｔｉｏｎａｌｉｔｙｍｏｄｅｌ．Ａｎｄｔｈｅｒｅｓｕｌｔｉｓｔｈａｔｔｈｅｒｅｅｘｉｓｔｓｓｔａｂｌｅｐｒｅｆｅｒｅｎｃｅｏｎｃｏｎｓｕｍｐｔｉｏｎａｎｄ

重点总结-投资理论

投资理论效用函数凹性函数——风险厌恶者——一阶导数>0，二阶导数<0。

凸性函数——风险偏好者——一阶导数>0，二阶导数>0。

线性函数——风险中性者——一阶导数>0，二阶导数=0。

投资者的最优投资组合两种风险资产构造的投资组合其中121=+w w两种风险资产构造的最小方差投资组合最小方差投资组合为可行集边界的顶点当时，当时，当时，不存在最小方差投资组合一种无风险资产与一种风险资产构造的投资组合一种无风险资产与一种风险资产构造的最优投资组合投资者效用最大化投资组合实际上就是其效用无差异曲线与资本配置线的切点效用函数公式（1）资本配置线公式（2）将（2）代入（1）得到令一阶导数=0，可求出在风险资产上的投资比例因二阶导数一定<0，因此不用计算校验。

求出的投资比例代回公式（2）可得到最优投资组合的收益与风险。

一种无风险资产与两种风险资产构造的最优投资组合第一步，构造最优风险资产组合P ：目标函数（1）约束条件（2）将（2）代入（1）令一阶导数=0，可得在其中一种风险资产上的投资比例进而代回（2）求出P 点坐标，即该点收益与风险。

从而得到资本配置线。

第二步，构造投资者的最优投资组合C ：效用函数（1）资本配置线（2）将（2）代入（1）令一阶导数=0，可求出在风险资产上的投资比例求出的投资比例代回公式（2）可得到最优投资组合的收益与风险。

市场模型及β风险的定价市场模型是资本资产定价模型在实际中的“替代品”，可用统计数据估算β值。

市场模型公式：其中，R i 表示第i 项资产的收益率，R I 表示市场指数的收益率，e i 表示第i 项资产的随机扰动项，a i 和b i 分别表示截距参数和斜率参数。

斜率参数b i 是系数βi 的估计值。

公式两边随机变量取方差得到如果已求出β值，也可表示为总风险 = 系统风险+非系统风险如果两两资产随机扰动项之间不相关、市场指数与各项资产随机扰动项不相关，那么两两资产协方差关系为 )()()(2211R E w R E w R E p +=12212222212122σσσσw w w w p ++=211221222221212σσρσσw w w w ++=112-=ρ1112<<-ρ112=ρ212*1σσσ+=w 211222212112221222211222*122σσρσσσσρσσσσσσ-+-=-+-=w)()1()(R yE R y R E f p +-=σσy p =2005.0)(pp A R E U σ-=)()1()(R yE R y R E f p +-=22005.0])([σAy R R E y R U f f --+=2*01.0)(σA R R E y f-=⇒σσy p =pf p p R R E MaxS σ-=)()()1()()(2111R E w R E w R E p -+=1211222121212)1(2)1(σσσσw w w w p -+-+=1221221212122221*1]2)()([])([])([])([])([σσσσσf f f f f R R E R E R R E R R E R R E R R E w -+--+----=2005.0)(cc A R E U σ-=)()1()(p f c R yE R y R E +-=p c y σσ=2*01.0)(pfp A R R E y σ-=⇑iI i i i e R b a R ++=2222eiI i i b σσσ+=2222e I i i σσβσ+=2Mj i ij σββσ=因素模型公式其中，R i 表示资产i 的收益率，E(R i )表示实际投资资产i 获得的预期收益率，F j 表示第j 个影响因素的意外变化，即该因素的实际值与预期值的偏差，b ji 表示资产i 对第j 个影响因素的敏感度的估计值，j=1,2，…，k ，e i 表示资产i 的随机扰动项。

风险偏好与效用函数

效用
3.等
风险中立者
• 效用 • 效用函数
效用函数
效用函数
凹性凸性线性来自风险风险厌恶风险追求风险中立
（一）凹性效用函数
AB AC
老年人
风险厌恶者
2013年：厂房、设备维护：
43亿美元投资收购：
2.44亿美元
（二）凸性效用函数
AB
中青年人
风险追求者
2014年上半年：投资：
268亿元
（初创企业）
（三）线性效用函数
小结
效用函数
凹性
凸性线性
风险
风险厌恶风险追求风险中立
课后任务
微访谈：结合本课所学知识，判断身边的亲朋好友各自属于哪种风险偏好的投资者，效用函数如何？
Thank You!
部分资料从网络收集整理而来，供大家参考，
感谢您的关注！
风险偏好与效用函数风险偏好与效用函数财政金融系潍柴动力000338风险偏好风险偏好风险厌恶者风险中立者风险追求者效用效用函数风险风险厌恶风险追求效用函数一凹性效用函数一凹性效用函数老年人风险厌恶者2013年
风险偏好与效用函数
财政金融系陈月
潍柴动力（000338）
风险偏好
1.卖
风险厌恶者
2.买
风险追求者

第十四章决策风险偏好与效用理论

面對期望收益是無限大的賭博，為何大家只願意付出有 2n 限的代價，甚至非常低的費用？
EMV
P(n)V (n)
n1
n1
(
1 2n
)(2n
)
0.5 反面
0.5反面
決策者並非用期望金
0.5正面
23
錢價值來評估上述賭
0.5反面
0.5正面
博方案的決策
22
0.5正面
2
$?
決策分析研究室 .tw
決策分析研究室 .tw
4
® Enabling A+ Decisions ®
確定等值
當效用函數為 U (x) x1/ 2
則期望效用值為
1 n1 ( 2n )U
2n
1 n1 ( 2n )(
2n )
1 2 1
令 x1 2 1
2 1
則 x 1 2 6 2 1
12
® Enabling A+ Decisions ®
實數效用函數
滿足個公理時，我們可以證明實數效用函數存在，在P集合中之p和q在偏好順序上存在實數函數
Hale Waihona Puke p f q ( p) f (q)p (1 ) q ( p) (1 ) (q)
其中μ為正線性轉換函數，當Pi為Xi發生之機率時，則
2
® Enabling A+ Decisions ®
大綱
效用期望效用理論
• 期望效用理論的公理 • 屬性效用值的衡量決策者偏好與風險態度 • 決策者對風險之態度 • 風險補償值 • 效用函數型態多屬性效用模式
風險下的決策應用實例—生產組合之決策分析
分析風險決策時可能的錯誤

投资者的效用函数名词解释

投资者的效用函数名词解释随着投资市场的不断发展和投资理论的不断推陈出新，投资者的效用函数成为了一个重要的概念。

本文将对投资者的效用函数进行解释，并讨论其在投资决策中的作用。

一、什么是效用函数？效用函数是一种描述投资者偏好和决策行为的数学模型。

它是投资者为实现自身目标和满足自身需求进行决策时所依据的工具。

效用函数将投资者的偏好转化为数值表达，从而帮助投资者权衡不同的风险和回报，并做出相应的投资决策。

二、效用函数的构成要素1. 资产收益资产收益是效用函数中的一个重要要素。

投资者通过投资不同的资产可以获得不同的收益。

效用函数将这些收益转化为投资者的满足程度，从而形成投资者对不同收益水平的偏好排序。

2. 风险偏好风险偏好是衡量投资者承受风险程度的指标。

不同的投资者对风险有着不同程度的接受能力，从而形成不同的风险偏好。

效用函数将投资者对风险的态度转化为数值表达，帮助投资者在面对不同风险水平时做出决策。

3. 时间偏好时间偏好是指投资者对资产收益的时间分布偏好程度。

有些投资者更倾向于短期获得较高收益，而有些投资者则更注重长期稳定的回报。

效用函数将投资者对不同时间分布的收益偏好进行量化，为投资者的决策提供依据。

三、效用函数的作用1. 投资决策效用函数在投资决策中起着重要作用。

通过对不同资产收益、风险偏好和时间偏好的综合考量，效用函数帮助投资者确定最优的投资组合。

投资者可以根据效用函数的指导，选择最适合自己的投资策略，最大化自己的效用。

2. 风险管理效用函数也发挥着风险管理的作用。

通过量化投资者对风险的偏好，效用函数帮助投资者选取适合自己风险承受能力的投资组合，避免过度承担风险或风险不足。

同时，效用函数还可以帮助投资者进行风险控制和资产组合调整，以期实现更好的风险收益平衡。

3. 个性化投资建议效用函数还可以为投资顾问提供个性化的投资建议。

通过对投资者的效用函数进行分析，投资顾问可以根据投资者的偏好和目标，量身定制投资方案，提供更加符合投资者需求的建议。

消费者风险偏好

消费者风险偏好
一、风险偏好类型
消费者的风险态度分为3类：风险偏好者、风险厌恶者、风险中立者。

假定消费者面临一种彩票具有两种可能结果，并且事后发生且仅仅发生一种结果。

第一种结果发生的概率为p，第一种结果发生时，消费者所拥有的财富量为W1；第二种结果发生的概率为1-p，第二种结果发生时消费者多拥有的财富量为W2，0<p<1，且消费者在无风险条件下（不买彩票时）可以持有的确定的货币财富量等于彩票的期望值即：pW1+（1-p）W2
1.风险偏好者：如果消费者认为在无风险条件下持有这笔确定的货币财富量的效用小于在风险条件下彩票的期望效用，称之为风险偏好者，即U（pW1+（1-p）W2）< pU(W1)+（1-p）U（W2），其效用函数特征为：凸函数，且二阶导大于零。

2.风险中立者：如果消费者认为在无风险条件下持有这笔确定的货币财富量的效用等于在风险条件下彩票的期望效用，称之为风险中立者，即U（pW1+（1-p）W2）=pU(W1)+（1-p）U（W2），其效用函数特征：线性函数，二阶导等于零。

3.风险厌恶者：如果消费者认为在无风险条件下持有这笔确定的货币财富量的效用大于在风险条件下彩票的期望效用，称之为风险厌恶者，即U（pW1+（1-p）W2）＞pU(W1)+（1-p）U（W2），其效用函数特征：凹函数，且二阶导小于零。

二、结论
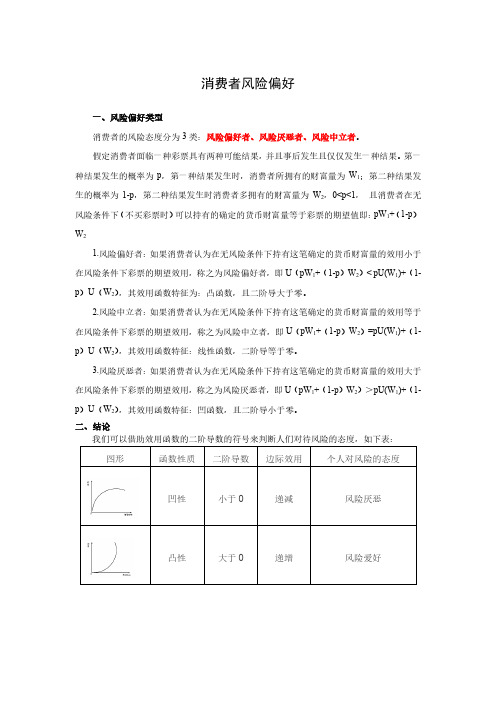
我们可以借助效用函数的二阶导数的符号来判断人们对待风险的态度，如下表：
【例题】消费者B的效用函数为U(x)=4x2+6x，那么该消费者是（）。

A.风险爱好者
B.风险中性者
C.风险厌恶者
D.无法确定
【答案】A。