第一章 特殊平行四边形 检测卷
第一章特殊平行四边形检测题

第一早《特殊平仃四边形》检测题一、选择题(每小题3分,共27分)1.从菱形的钝角顶点向对角的两条边作垂线,垂足恰好是该边的中点,贝U 菱形的内角中 钝角的度数是(2.顺次连接一个四边形的各边中点,得到了一个矩形,则下列四边形中满足条件的是: ①平行四边形:②菱形;③矩形;④对角线互相垂直的四边形.( )3.已知一矩形的两边长分别为10 cm 和15 cm,其中一个内角的平分线分长边为两部分, 这两部分的长为( )则图中阴影部分的面积为(7.矩形、菱形、正方形都具有的性质是(A.每一条对角线平分一组对角B.对角线相等 8.如图,将一个长为iO 口口,宽为S cm 的矩形纸片先按照从左向右对折, 再按照从下向 上的方向对折两次后,沿所得矩形两邻边中点的连线(虚线)剪下(如图( 1)),再打开,得到如图(2)所示的小菱形的面积为( B. 20 C 宦 C. 4" cni" A.150 ° B. 135C. 120 °D. 100 ° A.①③B.②③C.③④D.②④A.6 cm 和 9 cmB. 5 cm 和 10 cmC. 4 cm 和 11 cmD. 7 cm 和 8 cm 4.如图,在矩形A 肚D 中,匚几 G H 分别为边AS. DA. CD •,班的中点.若45 = 2=4 , A.3 C.6 5.如图,在菱形磁D 中,= = 3,则对角线」〔等于( ) A.20 B.15 C.10 D.56.若正方形的对角线长为2 cm , 则这个正方形的面积为(B.2 口口卫C.住 cm-D.C. 对角线互相平分D. 对角线互相垂直 D. 30 cini"C CDD.8第5题图9.如图是一张矩形纸片A5CD = IDcm ,若将纸片沿折叠,使必落在血上,点C的对应点为点F ,若却£ =临n 口,则CD =、填空题(每小题4分,共32 分)10.已知菱形的边长为6, —个内角为60°则菱形的较短对角线的长是11•如图,在菱形ABCD 中,/ 60°点E , F 分别从点B , D 同时以同样的速度沿边 BC , DC 向点C 运动.给出以下四个结论:①肛=AF ;② /闊F = /CF£;③ 当点E , F 分别为边BC , DC 的中点时,△ AEF 是等边三角形;④ 当点E , F 分别为边BC , DC 的中点时,△ AEF 的面积最大.上述正确结论的序号有13.如图,矩形屈™的两条对角线交于点。
特殊的平行四边形试题及参考答案

第一章特殊平行四边形检测题一、 选择题(每小题3分,共30分)1.下列四边形中,对角线一定不相等的是(D )A.正方形B.矩形C.等腰梯形D.直角梯形3.顺次连接一个四边形的各边中点,得到了一个矩形,则下列四边形中满足条件的是(D ) ①平行四边形;②菱形;③等腰梯形;④对角线互相垂直的四边形.A.①③B.②③C.③④D.②④4.已知一矩形的两边长分别为10 cm 和15 cm ,其中一个内角的平分线分长边为两部分,这两部分的长为(B )A.6 cm 和9 cmB.5 cm 和10 cmC.4 cm 和11 cmD.7 cm 和8 cm5.如图,在矩形中,分别为边的中点.若,,则图中阴影部分的面积为(B )A .3B .4C .6D.86.如图,在菱形中,,∠,则对角线等于(D )A .20B .15C .10D .57.若正方形的对角线长为2 cm ,则这个正方形的面积为(B )A.4B .2C .D .8.矩形、菱形、正方形都具有的性质是( C )A .每一条对角线平分一组对角B .对角线相等C .对角线互相平分D .对角线互相垂直A. B . C . D .(1) (2)一、 填空题(每小题3分,共24分)11.已知菱形的边长为6,一个内角为60°,则菱形的较短对角线的长是___6______.13.如图,四边形ABCD 是正方形,延长AB 到点E ,使,则∠BCE 的度数是22.5°.14.如图,矩形的两条对角线交于点,过点作的垂线,分别交,于点,,连接,已知△的周长为24 cm ,则矩形的周长是48cm.15.已知,在四边形ABCD 中,90A B C ∠=∠=∠=︒,若添加一个条件即可判定该四边形是正方形,那么这个条件可以是____________. 16.已知菱形的周长为,一条对角线长为,则这个菱形的面积为____96_____.17.如图,在矩形ABCD 中,对角线与相交于点O ,且,则BD 的长为____4____cm ,BC 的长为_______cm.三、解答题(共66分)19.(8分)如图,在△ABC 中,AB =AC ,AD 是△ABC 外角的平分线,已知∠BAC =∠ACD .(1)求证:△ABC ≌△CDA ;(2)若∠B =60°,求证:四边形ABCD 是菱形.证明:(1)∵AB =AC ,∴∠B =∠ACB ,∴∠FAC =∠B +∠ACB =2∠BCA .第5题图 第6题图∵AD平分∠FAC,∴∠FAC=2∠CAD,∴∠CAD=∠ACB.在△ABC和△CDA中,∠BAC=∠DCA,AC=AC,∠DAC=∠ACB,∴△ABC≌△CDA.(2)∵∠FAC=2∠ACB,∠FAC=2∠DAC,∴∠DAC=∠ACB,∴AD∥BC.∵∠BAC=∠ACD,∴AB∥CD,∴四边形ABCD是平行四边形.∵∠B=60°,AB=AC,∴△ABC是等边三角形,∴AB=BC,∴平行四边形ABCD是菱形.20.(8分)如图,在□ABCD中,E为BC边上的一点,连接AE、BD且AE=AB.(1)求证:∠ABE=∠EAD;(2)若∠AEB=2∠ADB,求证:四边形ABCD是菱形.证明:(1)在□ABCD中,AD∥BC,∴∠AEB=∠EAD.∵AE=AB,∴∠ABE=∠AEB,∴∠ABE=∠EAD.(2)∵AD∥BC,∴∠ADB=∠DBE.∵∠ABE=∠AEB,∠AEB=2∠ADB,∴∠ABE=2∠ADB,∴∠ABD=∠ABE-∠DBE=2∠ADB-∠ADB=∠ADB,∴AB=AD.又∵四边形ABCD是平行四边形,∴四边形ABCD是菱形.22.(8分)如图,正方形ABCD的边长为3,E,F分别是AB,BC边上的点,且∠EDF=45°.将△DAE 绕点D逆时针旋转90°,得到△DCM.(1)求证:EF=FM;(2)当AE=1时,求EF的长.(1)证明:∵△DAE逆时针旋转90°得到△DCM,∴∠FCM=∠FCD+∠DCM=180°,∴F,C,M三点共线,DE=DM,∠EDM=90°,∴∠EDF+∠FDM=90°.∵∠EDF=45°,∴∠FDM=∠EDF=45°.在△DEF和△DMF中,DE=DM,∠EDF=∠MDF,DF=DF,∴△DEF≌△DMF(SAS),∴EF=MF.(2)解:设EF=MF=x,∵AE=CM=1,且BC=3,∴BM=BC+CM=3+1=4,∴BF=BM-MF=BM-EF=4-x.∵EB=AB-AE=3-1=2,在Rt△EBF中,由勾股定理得EB2+BF2=EF2,即22+(4-x)2=x2,解得:x=,即EF=.23.(8分)如图,在矩形中,相交于点,平分,交于点.若,求∠的度数.解:因为平分,所以.又知,所以因为,所以△为等边三角形,所以因为,所以△为等腰直角三角形,所以.所以,,所以=75°24.(8分)如图所示,在矩形ABCD中,E,F分别是边AB,CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC.(1)求证:OE=OF;(2)若BC=23,求AB的长.25.(8分)已知:如图,在四边形中,∥,平分∠,,为的中点.试说明:互相垂直平分.解:如图,连接∵AB⊥AC,∴∠BAC=90°.因为在Rt△中,是的中点,所以是R t△的斜边BC上的中线,所以,所以.因为平分,所以,所以所以∥.又AD∥BC,所以四边形是平行四边形.又,所以平行四边形是菱形,所以互相垂直平分.。
第一章 特殊平行四边形 单元测试(含答案)

第一章特殊平行四边形一、选择题1. 下列四边形对角线相等但不一定垂直的是( )A.平行四边形B.矩形C.菱形D.正方形2. 平行四边形ABCD中,AC,BD是两条对角线,如果添加一个条件,即可推出平行四边形ABCD是矩形,那么这个条件是( )A.AB=BC B.AC=BD C.AC⊥BD D.AB⊥BD3. 如图,菱形ABCD的两条对角线AC,BD相交于点O,若AC=4,BD=6,则菱形ABCD的周长为( )A.16B.24C.413D.8134. 如图,点O是矩形ABCD的对角线AC的中点,OM∥AB交AD于点M,若OM=3,BC=10,则OB的长为( )D.34 A.5B.4C.3425. 如图,菱形ABCD的对角线AC,BD的长分别为6 cm,8 cm,则这个菱形的周长为( )A.5 cm B.10 cm C.14 cm D.20 cm6. 如图,点P是矩形ABCD的边上的一动点,矩形的两条边AB,BC的长分别是6和8,则点P到矩形的两条对角线AC和BD的距离之和是( )A.4.8B.5C.6D.7.27. 如图,点E是正方形ABCD中CD上的一点,把△ADE绕点A顺时针旋转90∘到△ABF的位置,若四边形AECF的面积为16,DE=1,则EF的长是( )A.4B.5C.217D.348. 如图,在矩形ABCD中,EG垂直平分BD于点G,若AB=4,BC=3,则线段EG的长度是( )A.32B.158C.52D.39. 如图,正方形ABCD的边长为2,点E,F分别为边AD,BC上的点,且EF=5,点G,H 分别边AB,CD上的点,连接GH交EF于点P.若∠EPH=45∘,则线段GH的长为( )A.5B.2103C.253D.710. 如图,在矩形ABCD中,AB=3,AD=4,以BC为斜边在矩形的外部作直角三角形BEC,点F是CD的中点,则EF的最大值为( )A.732B.4C.5D.92二、填空题11. 菱形的对角线长为6和8,则菱形的高为.12. 如图,连接四边形ABCD各边中点,得到四边形EFGH,只要添加条件,就能保证四边形EFGH是矩形.13. 在菱形ABCD中,对角线AC,BD交于点O,点F为BC中点,过点F作FE⊥BC于点F交BD于点E,连接CE,若∠BDC=34∘,则∠ECA=.14. 如图,矩形纸片ABCD中,已知AD=8,折叠纸片使AB边与对角线AC重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为.15. 在矩形ABCD中,AB=4,BC=3,折叠矩形ABCD,使点B与点D重合,则BF的长为.16. 如图,菱形ABCD中,AB=2,∠BAD=60∘,点E是边AB的中点,点P在对角线AC上移动.则PB+PE的最小值是.三、解答题17. 已知如图,在菱形ABCD中,对角线AC,BD相交于点O,DE∥AC,AE∥BD.(1) 求证:四边形AODE是矩形.(2) 若AB=6,∠BCD=120∘,求四边形AODE的面积.18. 如图,在正方形ABCD中,点F是BC延长线上一点,过点B作BE⊥DF于点E,交CD于点G,连接CE.(1) 若正方形ABCD边长为3,DF=4,求CG的长.(2) 求证:EF+EG=2CE.19. 在平行四边形ABCD中,对角线AC,BD相交于点O.EF过点O且与ABCD分别相交于点E,F.(1) 如图①,求证:OE=OF;(2) 如图②,若EF⊥DB,垂足为O,求证:四边形BEDF是菱形.20. 回答下列问题.(1) 提出问题:如图1,在正方形ABCD中,点E,H分别在BC,AB上,若AE⊥DH于点O,求证:AE=DH.(2) 类比探究:如图2,在正方形ABCD中,点H,E,G,F分别在AB,BC,CD,DA上,若EF⊥HG 于点O,探究线段EF与HG的数量关系,并说明理由.21. 如图,矩形ABCD中,点E,F分别在边AB,CD上,点G,H在对角线AC上,EF与AC相交于点O,AG=CH,BE=DF.(1) 求证:四边形EGFH是平行四边形.(2) 当EG=EH时,连接AF.①求证:AF=FC.②若DC=8,AD=4,求AE的长.答案一、选择题1. B2. B3. C4. D5. D6. A7. D8. B9. B10. D二、填空题11. 24512. AC⊥BD13. 2214. 615. 25816. 3三、解答题17.(1) 因为DE∥AC,AE∥BD,所以四边形AODE是平行四边形,因为在菱形ABCD中,AC⊥BD,所以∠AOD=90∘,所以四边形AODE是矩形.(2) 因为∠BCD=120∘,AB∥CD,所以∠ABC=180∘−120∘=60∘,因为AB=BC,所以△ABC是等边三角形,所以OA=12×6=3,OB=32×6=33,因为四边形ABCD是菱形,所以OD=OB=33,所以四边形AODE的面积=OA⋅OD=3×33=93.18.(1) ∵四边形ABCD是正方形,∴∠BCG=∠DCB=∠DCF=90∘,BC=DC,∵BE⊥DF,∴∠CBG+∠F=∠CDF+∠F,∴∠CBG=∠CDF,在△CBG和△CDF中,{∠BCG=∠DCF=90∘,BC=CD,∠CBG=∠CDF,∴△CBG≌△CDF(ASA),∴BG=DF=4,∴在Rt△BCG中,CG2+BC2=BG2,∴CG=42−32=7.(2) 过点C作CM⊥CE交BE于点M,∵△CBG≌△CDF,∴CG=CF,∠F=∠CGB,∵∠MCG+∠DCE=∠ECF+∠DCE=90∘,∴∠MCG=∠ECF,在 △MCG 和 △ECF 中,{∠MCG =∠ECF,CG =CF,∠F =∠CGB,∴△MCG ≌△ECF (ASA),∴MG =EF ,CM =CE ,∴△CME 是等腰直角三角形,∴ME =2CE ,又 ∵ME =MG +EG =EF +EG , ∴EF +EG =2CE .19.(1) ∵ 四边形 ABCD 是平行四边形, ∴OB =OD ,AB ∥CD ,∴∠EBO =∠FDO ,在 △OBE 与 △ODF 中,{∠EBO =∠FDO,OB =OD,∠BOE =∠DOF, ∴△OBE ≌△ODF (ASA),∴OE =OF ;(2) ∵OB =OD ,OE =OF , ∴ 四边形 BEDF 是平行四边形, ∵EF ⊥BD ,∴ 四边形 BEDF 是菱形.20.(1) ∵ 四边形 ABCD 是正方形, ∴AB =DA ,∠ABE =90∘=∠DAH , ∴∠HAO +∠OAD =90∘,∵AE⊥DH,∴∠ADO+∠OAD=90∘,∴∠HAO=∠ADO,在△ABE和△DAH中,{∠BAE=∠HDA,AB=AD,∠B=∠HAD,∴△ABE≌△DAH(ASA),∴AE=DH.(2) EF=GH,理由:将PE平移到AM处,则AM∥EF,AM=EF,将GH平移到DN处,则DN∥GH,DN=GH,∵EF⊥GH,∴AM⊥DN,根据(1)的结论得AM=DN,∴EF=GH.21.(1) ∵矩形ABCD中,AB∥CD,∴∠FCH=∠EAG,又∵CD=AB,BE=DF,∴CF=AE,且CH=AG,∠FCH=∠EAG,∴△AEG≌△CFH(SAS),∴GE=FH,∠CHF=∠AGE,∴∠FHG=∠EGH,∴FH∥GE,∴四边形EGFH是平行四边形.(2) ①连接AF,∵EG=EH,四边形EGFH是平行四边形,∴四边形GFHE为菱形,∴EF垂直平分GH,又∵AG=CH,∴EF垂直平分AC,∴AF=CF=AE.②设AE=x,则FC=AF=x,DF=8−x,在Rt△ADF中,AD2+DF2=AF2,∴42+(8−x)2=x2,解得x=5,∴AE=5.。
(典型题)初中数学九年级数学上册第一单元《特殊平行四边形》测试卷(包含答案解析)

一、选择题1.如图,已知△ABC 中,AB =AC ,AD 是∠BAC 的平分线,AE 是∠BAC 的外角平分线,ED ∥AB 交AC 于点G .下列结论:①AD ⊥BC ;②AE ∥BC ;③AE =AG ;④AD 2+AE 2=4AG 2,其中正确结论的个数是( )A .1B .2C .3D .42.如图,ABCD 的对角线AC 、BD 交于点O ,顺次连接ABCD 各边中点得到一个新的四边形,如果添加下列四个条件中的一个条件:①AC BD ⊥;②ΔΔABO CBO C C =;③DAO CBO ∠=∠;④DAO BAO ∠=∠,可以使这个新的四边形成为矩形,那么这样的条件个数是( )A .1个B .2个C .3个D .4个 3.如图所示,在菱形ABCD 中,5AC =,120BCD ∠=︒,则菱形ABC 的周长是( ).A .20B .15C .10D .54.如图,四边形ABCD 中,90A B ∠=∠=︒,60C ∠=°,2CD AD =,4AB =,点P 是AB 上一动点,则PC PD +的最小值是( )A.4B.6C.8D.105.如图,菱形ABCD的对角线AC,BD相交于点O,过点A作AE⊥BC于点E,连接OE.若OB=6,菱形ABCD的面积为54,则OE的长为()A.4 B.4.5 C.8 D.96.如图,公路,AC BC互相垂直,公路AB的中点M与点C被湖隔开,若测得AB的长为4.8km,则,M C两点间的距离为()A.1.2km B.2.4km C.3.6km D.4.8km7.如图,将长方形纸片ABCD沿AE折叠,使点D恰好落在BC边上点F处.若6AB=,10AD=,则EC的长为()A.2 B.83C.3 D.1038.给出下列命题,其中错误命题的个数是()①四条边相等的四边形是正方形;②四边形具有不稳定性;③有两个锐角对应相等的两个直角三角形全等;④一组对边平行的四边形是平行四边形.A .1B .2C .3D .49.如图,矩形ABCD 的对角线相交于点O ,过点O 作OG AC ⊥,交AB 于点G ,连接CG ,若15BOG ∠=,则BCG ∠的度数是( )A .15B .15.5C .20D .37.510.如图,在菱形ABCD 中,对角线AC 、BD 相交于点O ,延长CB 至E 使BE=CB ,连续AE .下列结论①AE=2OE ;②90EAC ∠=︒;③四边形ADBE 为平行四边形;④34AEBO ABCD S S =四边形菱形中,正确的个数有( )A .1个B .2个C .3个D .4个11.如图,四边形ABCD 中,∠BAD =∠C =90°,AB =AD ,AE ⊥BC ,垂足是E ,若线段AE =4,则四边形ABCD 的面积为( )A .12B .16C .20D .2412.如图,正方形OABC 的两边OA 、OC 分别在x 轴、y 轴上,点D (5,3)在边AB 上,以C 为中心,把CDB 旋转90°,则旋转后点D 的对应点D 的坐标是( )A .(2,10)B .(﹣2,0)C .(2,10)或(﹣2,0)D .(10,2)或(﹣2,0)二、填空题13.如图,在菱形ABCD 中,2,60AB BAD =∠=︒,将菱形ABCD 绕点A 逆时针方向旋转,对应得到菱形,AEFG 点E 在AC 上.EF 与CD 交于点,P 则PE 的长是____.14.如图,在菱形ABCD 中,E 、F 分别是AC 、BC 的中点,如果EF =5,那么菱形ABCD 的周长_____.15.如图所示,在矩形ABCD 中,AB a ,BC b =,两条对角线相交于点O ,OB 、OC 为邻边作第1个平行四边形1OBB C ,对角线相交于点1A ,以为11A B 、1A C 邻边作第2个平行四边形111A B C C ,对角线相交于1O ;再以11O B 、11O C 为邻边作第3个平行四边形1121O B B C ……此类推,第2020个平行四边形的面积__________.16.如图,矩形ABOC 的顶点B 、C 分别在x 轴、y 轴上,顶点A 在第一象限,点B 的坐标30),将线段OC 绕点O 顺时针旋转60°至线段OD ,若反比例函数k y x=(k ≠0)的图象进过A 、D 两点,则k 值为_____.17.如图,△ABC 中,13AB AC ==,10BC =,AD 平分∠BAC 交BC 于点D ,点E 为AC 的中点,连接DE ,则△CDE 的周长是________.18.如图,点H 在菱形ABCD 的边BC 上,连结AH ,把菱形ABCD 沿AH 折叠,使B 点落在边BC 上的点E 处,若∠B=70°,则∠AED 的度数为_____.19.如下图,在平面直角坐标系中有一边长为l 的正方形OABC ,边OA 、OC 分别在x 轴、y 轴上,如果以对角线OB 为边作第二个正方形OBB 1C 1,再以对角线OB l 为边作第三个正方形OB l B 2C 2,照此规律作下去,则点B 2020的纵坐标为_______.20.请你写出一个原命题与它的逆命题都是真命题的命题____________________ .三、解答题21.已知矩形ABCD 中,点F 在AD 边上,四边形EDCF 是平行四边形,请仅用无刻度的直尺分别按下列要求画图(保留画图痕迹,不必写画法).(1)在图1画出BCD △中DC 边上的中线BG ;(2)在图2中画出线段AF 的垂直平分线.22.如图,过ABC 边AC 的中点O ,作OE AC ⊥,交AB 于点E ,过点A 作//AD BC ,与BO 的延长线交于点D ,连接CD ,CE ,若CE 平分ACB ∠,CE BO ⊥于点F .(1)求证:①OC BC =,②四边形ABCD 是矩形;(2)若3BC =,求DE 的长.23.如图所示,平行四边形,ABCD 对角线BD 平分ABC ∠;()1求证:四边形ABCD 为菱形;()2已知AE BC ⊥于E ,若24CE BE ==,求BD .24.已知:如图,在矩形ABCD 中,M 、N 分别是边AD 、BC 的中点,E 、F 分别是线段BM 、CM 的中点.(1)求证:△ABM ≌△DCM ;(2)当AB :AD 的值为多少时,四边形MENF 是正方形?请说明理由.25.如图,在ABC 中,已知105BAC ∠=︒,45ACB ∠=︒,AD 是BC 边上的高线,CE 是AB 边上的中线,DG CE 于点G ,且42AC =.(1)求AB 的长;(2)求证:CG EG .26.如图,E 、F 分别是矩形ABCD 的边 BC 、AD 上的点,且BE = DF .(1)求证:四边形 AECF 是平行四边形;(2)若四边形 AECF 是菱形,且 CE = 10,AB = 8,求线段BE 的长.【参考答案】***试卷处理标记,请不要删除一、选择题1.C解析:C【分析】连接EC ,根据等腰三角形的性质得出AD ⊥BC ,即可判断①;求出∠FAE=∠B ,再根据平行线的性质得出AE ∥BC ,即可判断②;求出四边形ABDE 是平行四边形,根据平行四边形的性质得出AE=BD ,求出AE=CD ,根据矩形的判定推出四边形ADCE 是矩形,根据矩形的性质得出AC=DE ,AG=CG ,DG=EG ,求出DG=AG=CG=EG ,根据勾股定理判断④即可;根据AE=BD=12BC 和AG=12AC 判断③即可. 【详解】解:连接EC ,∵AB=AC,AD是∠BAC的平分线,∴AD⊥BC,故①正确;∵AB=AC,∴∠B=∠ACB,∵AE平分∠FAC,∴∠FAC=2∠FAE,∵∠FAC=∠B+∠ACB,∴∠FAE=∠B,∴AE∥BC,故②正确;∵AE∥BC,DE∥AB,∴四边形ABDE是平行四边形,∴AE=BD,∵AB=AC,AD⊥BC,∴CD=BD,∴AE=CD,∵AE∥BC,∠ADC=90°,∴四边形ADCE是矩形,∴AC=DE,AG=CG,DG=EG,∴DG=AG=CG=EG,在Rt△AED中,AD2+AE2=DE2=AC2=(2AG)2=4AG2,故④正确;∵AE=BD=12BC,AG=12AC,∴AG=AE错误(已知没有条件AC=BC),故③错误;即正确的个数是3个,故选:C.【点睛】本题考查了勾股定理,等腰三角形的性质,平行线的性质和判定,平行四边形的性质和判定,矩形的性质和判定等知识点,能综合运用知识点进行推理是解此题的关键.2.C解析:C【分析】根据顺次连接四边形的中点,得到的四边形形状和四边形的对角线位置、数量关系有关,利用三角形中位线性质可得:当对角线垂直时,所得新四边形是矩形.逐一对四个条件进行判断.【详解】解:顺次连接四边形的中点,得到的四边形形状和四边形的对角线位置、数量关系有关,利用三角形中位线性质可得:当对角线垂直时,所得新四边形是矩形.①,AC BD ⊥∴新的四边形成为矩形,符合条件; ②四边形ABCD 是平行四边形,,AO OC BO DO ∴==.ΔΔ,ABO CBO C C AB BC =∴=.根据等腰三角形的性质可知,BO AC BD AC ⊥∴⊥.所以新的四边形成为矩形,符合条件; ③四边形ABCD 是平行四边形,CBO ADO ∠∠∴=.,DAO CBO ADO DAO ∠∠∠∠=∴=.AO OD ∴=.,AC BD ∴=∴四边形ABCD 是矩形,连接各边中点得到的新四边形是菱形,不符合条件;④,DAO BAO BO DO ∠∠==,AO BD ∴⊥,即平行四边形ABCD 的对角线互相垂直,∴新四边形是矩形.符合条件.所以①②④符合条件.故选:C .【点睛】本题考查特殊四边形的判定与性质,掌握矩形、平行四边形的判定与性质是解题的关键. 3.A解析:A【分析】根据题意可得出∠B=60︒,结合菱形的性质可得BA=BC ,判断出△ABC 是等边三角形即可得出菱形的周长.【详解】解:∵四边形ABCD 是菱形,∴//BA CD ,又∵∠BCD=120︒,∴∠B=180︒-∠BCD= 60︒,又∵四边形ABCD 是菱形,∴BA=BC ,∴△ABC 是等边三角形,∴BA=BC=AC=5,故可得菱形的周长=4AB=20.故选:A .【点睛】本题考查了菱形的性质及等边三角形的判定与性质,根据菱形的性质判断出△ABC是等边三角形是解答本题的关键,难度一般.4.C解析:C【分析】作D点关于AB的对称点D',连接CD'交AB于P,根据两点之间线段最短可知此时PC+PD 最小;再作D'E⊥BC于E,则EB=D'A=AD,先根据等边对等角得出∠DCD'=∠DD'C,然后根据平行线的性质得出∠D'CE=∠DD'C,从而求得∠D'CE=∠DCD',得出∠D'CE=30°,根据30°角的直角三角形的性质求得D'C=2D'E=2AB,即可求得PC+PD的最小值.【详解】作D点关于AB的对称点D',连接CD'交AB于P,P即为所求,此时PC+PD=PC+PD'=CD',根据两点之间线段最短可知此时PC+PD最小.作D'E⊥BC于E,则EB=D'A=AD.∵CD=2AD,∴DD'=CD,∴∠DCD'=∠DD'C.∵∠DAB=∠ABC=90°,∴四边形ABED'是矩形,∴DD'∥EC,D'E=AB=4,∴∠D'CE=∠DD'C,∴∠D'CE=∠DCD'.∵∠DCB=60°,∴∠D'CE=30°,∴在Rt△D'CE中,D'C=2D'E=2×4=8,∴PC+PD的最小值为8.故选:C.【点睛】本题考查了轴对称﹣最短路线问题,轴对称的性质,矩形的判定和性质,等腰三角形的性质,平行线的性质,含30°角的直角三角形的性质等,确定出P点是解答本题的关键.5.B解析:B【分析】由菱形的性质得出BD=12,由菱形的面积得出AC=9,再由直角三角形斜边上的中线性质即可得出结果.【详解】解:∵四边形ABCD是菱形,∴OA=OC,OB=OD=12BD,BD⊥AC,∴BD=2OB=12,∵S菱形ABCD═12AC×BD=54,∴AC=9,∵AE⊥BC,∴∠AEC=90°,∴OE=12AC=4.5,故选:B.【点睛】本题主要考查了菱形的性质、直角三角形斜边上的中线性质;熟练掌握菱形的性质是解题的关键.6.B解析:B【分析】根据直角三角形斜边上的中线性质得出CM=12AB,代入求出即可.∵AC⊥BC,∴∠ACB=90°,∵M为AB的中点,∴CM=12AB,∵AB=4.8km,∴CM=2.4km,故选:B.【点睛】本考考查了直角三角形斜边上的中线性质,能根据直角三角形斜边上的中线性质得出CM=12AB是解此题的关键.7.B解析:B【分析】由翻折可知:AD=AF=10.DE=EF,设EC=x,则DE=EF=6-x.在Rt△ECF中,利用勾股定理构建方程即可解决问题.【详解】解:∵四边形ABCD是矩形,∴AD=BC=10,AB=CD=6,∴∠B=∠BCD=90°,由翻折可知:AD=AF=10,DE=EF,设EC=x,则DE=EF=6-x.在Rt△ABF中,8BF===,∴CF=BC-BF=10-8=2,在Rt△EFC中,EF2=CE2+CF2,∴(6-x)2=x2+22,∴x=83,∴EC=83.故选:B.【点睛】本题考查了折叠的性质,矩形的性质,勾股定理,熟练掌握方程的思想方法是解题的关键.8.C解析:C【分析】利用正方形的判定、直角三角形全等的判定、平行四边形的判定定理对每个选项依次判定【详解】①四条边相等的四边形是菱形,故①错误;②四边形具有不稳定性,故②正确;③两直角三角形隐含一个条件是两直角相等,两个锐角对应相等,因此构成了AAA ,不能判定全等,故③错误;④一组对边平行且相等的四边形是平行四边形,故④错误;综上,错误的命题有①③④共3个.故选:C .【点睛】本题考查了命题与定理的知识,解题的关键是了解正方形的判定、平行四边形的判定及直角三角形全等的判定.9.A解析:A【分析】根据矩形的性质求出OCB ∠的度数,从而得到GAC ∠的度数,再根据垂直平分线的性质得到GCA GAC ∠=∠,最后求出BCG ∠的度数.【详解】解:∵OG AC ⊥,∴90COG ∠=︒,∵15BOG ∠=︒,∴901575COB COG BOG ∠=∠-∠=︒-︒=︒,∵四边形ABCD 是矩形,∴AC BD =,12OC OA AC ==,12OB OD BD ==,//AB DC ,90BCD ∠=︒, ∴OC OB =, ∴1801807552.522COB OCB OBC ︒-∠︒-︒∠=∠===︒, ∴37.5ACD BCD OCB ∠=∠-∠=︒, ∵//AB CD ,∴37.5GAC ACD ∠=∠=︒,∵OG AC ⊥,OA OC =,∴GO 是AC 的垂直平分线,∴AG CG =,∴37.5GCA GAC ∠=∠=︒,∴52.537.515BCG OCB GCA ∠=∠-∠=︒-︒=︒.故选:A .【点睛】本题考查矩形的性质,垂直平分线的性质,解题的关键是熟练掌握这些性质定理,并结合题目条件进行证明.10.D解析:D【分析】先判定四边形AEBD 是平行四边形,再根据平行四边形的性质以及菱形的性质,即可得出结论.【详解】 解:四边形ABCD 是菱形,AD BC ∴=,//AD BC ,2BD DO =,又BC BE =,AD BE ∴=,∴四边形AEBD 是平行四边形,故③正确,AE BD ∴=,2AE DO ,故①正确;四边形AEBD 是平行四边形,四边形ABCD 是菱形,//AE BD ∴,AC BD ⊥,AE AC ∴⊥,即90CAE ∠=︒,故②正确;四边形AEBD 是平行四边形, 12ABE ABD ABCD S S S 菱形, 四边形ABCD 是菱形,14ABO ABCDS S 菱形, 34ABE ABO AEBO ABCDS S S S 四边形菱形,故④正确; 故选:D .【点睛】本题主要考查了菱形的性质以及平行四边形的判定与性质,熟悉相关性质是解题的关键. 11.B解析:B【分析】延长CD ,作AF CD ⊥的延长线于点F ,构造出全等三角形,()ABE ADF AAS ≅,即可得到四边形ABCD 的面积就等于正方形AECF 的面积.【详解】解:如图,延长CD ,作AF CD ⊥的延长线于点F ,∵AE BC ⊥,∴90AEC AEB ∠=∠=︒,∵AF CD ⊥,∴90AFC ∠=︒,∵90C ∠=︒,∴四边形AECF 是矩形,∴90EAF ∠=︒,∵BAD EAF ∠=∠,∴BAD EAD EAF EAD ∠-∠=∠-∠,即BAE DAF ∠=∠,在ABE △和ADF 中,BAE DAF AEB AFD AB AD ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴()ABE ADF AAS ≅,∴AE AF =,∴四边形AECF 是正方形,∵ABE ADF S S ,∴216ABCD AECF S S AE ===.故选:B .【点睛】本题考查全等三角形的性质和判定,正方形的性质和判定,解题的关键是作辅助线构造全等三角形.12.C解析:C【分析】分顺时针旋转和逆时针旋转两种情况讨论解答即可.【详解】解:∵点D (5,3)在边AB 上,∴BC =5,BD =5﹣3=2,①若顺时针旋转,则点D 在x 轴上,O D =2,所以,D (﹣2,0),②若逆时针旋转,则点D 到x 轴的距离为10,到y 轴的距离为2,所以,D (2,10),综上所述,点D 的坐标为(2,10)或(﹣2,0).故选:C .【点睛】本题考查了坐标与图形变化﹣旋转,正方形的性质,难点在于分情况讨论.二、填空题13.【分析】连接BD 交AC 于O 由菱形的性质得出CD=AB=2∠BCD=∠BAD=60°由直角三角形的性质求出OB=AB=1由直角三角形的性质得出由旋转的性质得出AE=AB=2∠EAG=∠BAD=60°求 解析:31- 【分析】连接BD 交AC 于O ,由菱形的性质得出CD=AB=2,∠BCD=∠BAD=60°,1ACD 302︒∠=∠=∠=BAC BAD ,由直角三角形的性质求出OB=12AB=1,由直角三角形的性质得出23AC =,由旋转的性质得出AE=AB=2,∠EAG=∠BAD=60°,求出CE=AC-AE 232=-,证出∠CPE=90°,由直角三角形的性质得出PE 的长【详解】解:连接BD 交AC 于O ,如图所示:∵四边形ABCD 是菱形,∴CD=AB=2,∠BCD=∠BAD=60°,1ACD 302︒∠=∠=∠=BAC BAD ,OA=OC ,AC ⊥BD , ∴112OB AB == ∴33,==OA OB∴23AC =由旋转的性质得:AE=AB=2,∠EAG=∠BAD=60°,∴232,=-=CE AC AE∵四边形AEFG 是菱形,∴EF ∥AG ,∴∠CEP=∠EAG=60°,∴∠CEP+∠ACD=90°,∴∠CPE=90°,∴112PE CE ==1【点睛】本题考查了菱形的性质、旋转的性质、含30°角的直角三角形的性质、平行线的性质等知识;熟练掌握旋转的性质和菱形的性质是解题的关键.14.40【分析】根据三角形的中位线平行于第三边并且等于第三边的一半可得AB =2EF 然后根据菱形的四条边都相等列式计算即可得解【详解】解:∵EF 分别是ACBC 的中点∴EF 是△ABC 的中位线∴AB =2EF =解析:40【分析】根据三角形的中位线平行于第三边并且等于第三边的一半可得AB =2EF ,然后根据菱形的四条边都相等列式计算即可得解.【详解】解:∵E 、F 分别是AC 、BC 的中点,∴EF 是△ABC 的中位线,∴AB =2EF =2×5=10,∴菱形ABCD 的周长=4×10=40.故答案为:40.【点睛】本题考查了菱形的性质,三角形的中位线平行于第三边并且等于第三边的一半,熟记性质与定理是解题的关键.15.【分析】结合题意根据矩形性质得平行四边形为菱形从而依次计算前4个平行四边形的面积并通过归纳计算规律即可得到第2020个平行四边形的面积【详解】∵矩形中两条对角线相交于点∴∵为邻边作第1个平行四边形∴ 解析:20202ab【分析】结合题意,根据矩形性质,得平行四边形1OBB C 为菱形,从而依次计算前4个平行四边形的面积,并通过归纳计算规律,即可得到第2020个平行四边形的面积.【详解】∵矩形ABCD 中,AB a ,BC b =,两条对角线相交于点O∴OB OC OA ==∵OB 、OC 为邻边作第1个平行四边形1OBB C∴11OB OC BB CB ===∴平行四边形1OBB C 为菱形∵平行四边形1OBB C ,对角线相交于点1A ,∴1OA BC ⊥,1112BA CA BC ==,111OA A B = ∵OC OA = ∴11122OA AB a == ∴第1个平行四边形1OBB C 面积112BC OA a b =⨯=⨯ ∴第2个平行四边形111A B C C 面积1111122AC A B a b =⨯=⨯ 同理,得第3个平行四边形1121O B B C 面积21111122222a b a b ⎛⎫=⨯⨯=⨯ ⎪⎝⎭第4个平行四边形2221A B C C 面积2221111122222a b a b ⎛⎫⎛⎫⎛⎫=⨯⨯=⨯ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭以此类推,第2020个平行四边形2221A B C C 面积为:10101010202020201112222ab a b ab ⎛⎫⎛⎫⎛⎫⨯== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ 故答案为:20202ab . 【点睛】 本题考查了数字及图形规律、三角形中位线、幂的乘方、平行四边形、矩形、菱形的知识;解题的关键是熟练掌握数字及图形规律、幂的乘方、平行四边形、矩形的性质,从而完成求解.16.4【分析】过点D 作DH ⊥x 轴于H 四边形ABOC 是矩形由性质有AB =CO ∠COB =90°将OC 绕点O 顺时针旋转60°OC =OD ∠COD =60°可得∠DOH =30°设DH =x 点D (xx )点A (2x )反比解析:【分析】过点D 作DH ⊥x 轴于H ,四边形ABOC 是矩形,由性质有AB =CO ,∠COB =90°, 将OC 绕点O 顺时针旋转60°,OC =OD ,∠COD =60°,可得∠DOH =30°,设DH =x ,点D ,x ),点A ,2x ),反比例函数k y x=(k ≠0)的图象经过A 、D 两点,构造方程求出即可.【详解】解:如图,过点D 作DH ⊥x 轴于H ,∵四边形ABOC是矩形,∴AB=CO,∠COB=90°,∵将线段OC绕点O顺时针旋转60°至线段OD,∴OC=OD,∠COD=60°,∴∠DOH=30°,∴OD=2DH,OH3,设DH=x,∴点D3,x),点A32x),∵反比例函数kyx=(k≠0)的图象经过A、D两点,∴3×x3x,∴x=2,∴点D(32),∴k=3=3故答案为:3【点睛】本题考查反比例函数解析式问题,关键利用矩形的性质与旋转找到AB=CO=OD,∠DOH =30°,DH=x,会用x表示点D3,x),点A3,2x),利用A、D在反比例函数kyx=(k≠0)的图象上,构造方程使问题得以解决.17.18【详解】根据等腰三角形三线合一的性质可得AD⊥BCDC=BC再根据直角三角形的性质可得DE=EC=AC=65然后可得答案【解答】解:∵AB=ACAD平分∠BAC∴AD⊥BCDC=BC∵BC=10解析:18【详解】根据等腰三角形三线合一的性质可得AD⊥BC,DC=12BC,再根据直角三角形的性质可得DE=EC=12AC=6.5,然后可得答案.【解答】解:∵AB=AC,AD平分∠BAC,∴AD⊥BC,DC=12BC,∵BC=10,∴DC=5,∵点E为AC的中点,∴DE=EC=12AC=6.5,∴△CDE的周长为:DC+EC+DE=13+5=18,故答案为:18.【点睛】此题主要考查了等腰三角形的性质,以及直角三角形的性质,关键是掌握在直角三角形中,斜边上的中线等于斜边的一半.18.55°【分析】根据翻折变换的性质可得AB=AE然后根据等腰三角形两底角相等求出∠B=∠AEB=70°根据菱形的四条边都相等可得AB=AD菱形的对角相等求出∠ADC再求出∠DAE然后根据等腰三角形两底解析:55°【分析】根据翻折变换的性质可得AB=AE,然后根据等腰三角形两底角相等求出∠B=∠AEB=70°,根据菱形的四条边都相等可得AB=AD,菱形的对角相等求出∠ADC,再求出∠DAE,然后根据等腰三角形两底角相等求出∠AED.【详解】解:∵菱形ABCD沿AH折叠,B落在BC边上的点E处,∴AB=AE,∵∠B=70°,∴∠AEB=70°在菱形ABCD中,AB=AD,∠ADC=∠B=70°,AD∥BC,∴∠DAE=∠AEB=70°,∵AB=AE,AB=AD,∴AE=AD,∴∠AED=12(180°-∠DAE)=12(180°-70°)=55°.故答案为:55°.【点睛】本题考查了翻折变换的性质,菱形的性质,等腰三角形两底角相等的性质,翻折前后对应边相等,菱形的四条边都相等,对角相等.19.【分析】首先求出B1B2B3B4B5B6B7B8B9的坐标找出这些坐标的之间的规律然后根据规律计算出点B2020的坐标【详解】解:∵正方形OABC边长为1∴OB=∵正方形OBB1C1是正方形OABC解析:10102-【分析】首先求出B1、B2、B3、B4、B5、B6、B7、B8、B9的坐标,找出这些坐标的之间的规律,然后根据规律计算出点B2020的坐标.【详解】解:∵正方形OABC边长为1,∴,∵正方形OBB1C1是正方形OABC的对角线OB为边,∴OB1=2,∴B1点坐标为(0,2),同理可知OB2,B2点坐标为(-2,2),同理可知OB3=4,B3点坐标为(-4,0),B4点坐标为(-4,-4),B5点坐标为(0,-8),B6(8,-8),B7(16,0)B8(16,16),B9(0,32),由规律可以发现,每经过8次作图后,点的坐标符号与第一次坐标符号相同,每次正方形倍,∵2020÷8=252…4,∴B2020的纵横坐标符号与点B4的相同,横坐标为负值,纵坐标是负值,∴B2020的坐标为(-21010,-21010).故答案为:10102-.【点睛】本题主要考查正方形的性质和坐标与图形的性质的知识点,解答本题的关键是由点坐标的规律发现每经过8次作图后,点的坐标符号与第一次坐标符号相同,每次正方形的边长变倍,此题难度较大.20.对角线互相平分且相等的四边形是矩形(答案不唯一)【分析】命题由题设和结论两部分组成题设是已知事项结论是由已知事项推出的事项;题设成立结论也成立的叫真命题而题设成立结论不成立的为假命题把一个命题的题设解析:对角线互相平分且相等的四边形是矩形(答案不唯一)【分析】命题由题设和结论两部分组成.题设是已知事项,结论是由已知事项推出的事项;题设成立,结论也成立的叫真命题,而题设成立,结论不成立的为假命题,把一个命题的题设和结论互换即可得到其逆命题.【详解】解:如命题:对角线互相平分且相等的四边形是矩形,真命题,逆命题是矩形的对角线互相平分且相等,真命题,故答案为:对角线互相平分且相等的四边形是矩形(答案不唯一).【点睛】本题考查了命题与定理:判断事物的语句叫命题;题设与结论互换的两个命题互为逆命题;正确的命题叫真命题,错误的命题叫假命题.三、解答题21.(1)见解析(2)见解析【分析】(1)(1)延长EF交BC于H,连结DH,交CF于N,连结AH,FB交于M,过M、N作直线交DC于G,连结BG即可;(2)连接AH,BF,相交于M,连接BE并交AD于N,由四边形EDCF是平行四边形,矩形ABCD,可得EF=CD=AB,EF∥CD∥AB,可证△ANB≌△FNE(AAS),可得AN=FN过M、N作直线l即可.【详解】解:(1)如图,延长EF交BC于H,连结DH,交CF于N,连结AH,FB交于M过M、N作直线交DC于G连结BG如图1,线段BG即为所求作;(2)如图,连接AH,BF,相交于M,连接BE并交AD于N,∵四边形EDCF是平行四边形,矩形ABCD∴EF=CD=AB,EF∥CD∥AB∴∠ABN=∠FEN,∠ANB=∠FNE∴△ANB≌△FNE(AAS)∴AN=FN过M、N作直线l如图2,直线l即为所求作.【点睛】本题考查的是利用无刻度的直尺作图,平行四边形的性质,矩形的性质,三角形的中位线的性质,三角形的中线的概念,线段垂直平分线,掌握以上知识是解题的关键. 22.(1)①证明见解析;②证明见解析;(2)21DE =【分析】(1)①运用ASA 证明OCF BCF ≌△△即可得出结论;②先证明四边形ABCD 是平行四边形,再证明90EBC ∠=︒即可得出结论;(2)证明△OCB 是等边三角形,得∠ECB=30°,求出3AE 的长,再运用勾股定理求出DE 的长即可.【详解】证明:(1)①∵CE 平分BCA ∠,∴OCE BCE ∠=∠.∵BO CE ⊥,∴90∠∠==︒CFO CFB .又∵CF CF =,∴()≌OCF BCF ASA △△∴OC BC =.②∵O 是AC 的中点,∴OA OC =.又∵//AD BC .∴DAO BCO ∠=∠,ADO CBO ∠=∠.∴()≌OAD OCB ASA △△.∴AD BC =.∵//AD BC ,∴四边形ABCD 是平行四边形.∵OE AC ⊥,∴90EOC ∠=︒∵OCE BCE ∠=∠,CE CE =,OC BC =,∴()≌OCE BCE ASA △△.∴90∠∠==︒EBC EOC .∴四边形ABCD 是矩形.(2)∵四边形ABCD 是矩形,∴3AD BC ==,90DAB ∠=︒,AC BD =.∴OB OC =.∵OC BC =,∴OB OC BC ==.∴OBC 是等边三角形.∴60OCB ∠=︒ ∴1302∠∠︒==ECB OCB . ∵90EBC ∠=︒, ∴12=EB EC . ∵222BE BC EC +=,3BC =. ∴EB =EC = ∵OE AC ⊥,OA OC =, ∴==EC EA .在Rt ADE △中,90DAB ∠=︒,∴===DE 【点睛】此题主要考查了全等三角形的判定与性质,矩形的判定与性质,勾股定理以及直角三角形的性质,熟练掌握矩形的判定与性质是解答此题的关键.23.(1)证明见解析;(2)BD =【分析】(1)由角平分线的定义得ABD CBD ∠=∠,再证明CDB CBD ∠=∠,从而得BC DC =,即可利用一组邻边相等的平行四边形是菱形证明出四边形ABCD 是菱形; (2)分别求出BE EC BC AB AE AC 、、、、、,再根据菱形的面积等于平行四边形的面积求解即可.【详解】解:(1)∵BD 平分ABC ∠∴ABD CBD ∠=∠∵四边形ABCD 是平行四边形∴//AB CD∴CDB ABD ∠=∠∴CDB CBD ∠=∠∴BC DC =∴四边形ABCD 是菱形;(2)连接AC ,如图,∵ABCD 是菱形∴3BC AB BE EC BE ==+=又∵24BE EC ==∴2BE =∴246BC BE EC AB =+=+==又AE BC ⊥ ∴22226242AE AB BE =-=-=2222(42)443AC AE EC =+=+= ∴642242ABCD S BC AE =⨯=⨯= 而242ABCD ABCD S S==菱形 ∴114324222BD AC BD ⨯=⨯= ∴6BD =【点睛】此题主要考查了菱形的性质与判定,关键是掌握菱形的判定定理.24.(1)见解析;(2)当AB :AD =1:2时,四边形MENF 是正方形,理由见解析【分析】(1)求出AB =DC ,∠A =∠D =90°,AM =DM ,根据全等三角形的判定定理推出即可; (2)求出∠EMF =90°,根据正方形的判定推出即可.【详解】(1)证明:∵四边形ABCD 是矩形,∴AB =DC ,∠A =∠D =90°,∵M 为AD 中点,∴AM =DM ,在△ABM 和△DCM ,AM DM A D AB CD =⎧⎪∠=∠⎨⎪=⎩,∴△ABM ≌△DCM (SAS );(2)解:当AB :AD =1:2时,四边形MENF 是正方形,理由:当四边形MENF 是正方形时,则∠EMF =90°,∵△ABM≌△DCM,∴∠AMB=∠DMC=45°,∴△ABM、△DCM为等腰直角三角形,∴AM=DM=AB,∴AD=2AB,即当AB:AD=1:2时,四边形MENF是正方形.【点睛】本题考查了正方形的判定,全等三角形的判定和性质,等腰直角三角形的性质,熟练掌握全等三角形的判定和性质定理是解题的关键.25.(1)8;(2)见解析【分析】(1)证明△ADC是等腰直角三角形,求出AD和CD,根据∠BAC的度数求出∠BAD,根据直角三角形的性质可得AB;(2)连接DE,求出DE的长,再根据三线合一的性质证明即可.【详解】解:(1)∵AD是BC边上的高线,∴AD⊥BC,∴∠ADB=∠ADC=90°,∵∠ACB=45°,∴△ADC是等腰直角三角形,∴AD=CD=2AC=4,∠DAC=45°,2∵∠BAC=105°,∴∠BAD=∠BAC-∠DAC=60°,∴∠ABD=30°,∴AB=2AD=8;(2)连接DE,∵CE是AB边上中线,∴E是AB中点,在Rt△ABD中,E是斜边AB中点,∴DE=1AB=4,2∵DC=4,∴DE=DC,∵DG ⊥CE ,∴CG =EG .【点睛】本题考查了直角三角形斜边中线的性质,30度的直角三角形的性质,等腰三角形三线合一的性质,属于基本定理,解题的关键是利用好“中点”这样的条件.26.(1)见解析;(2)6【分析】(1)证明AF EC =,利用一组对边平行且相等证明平行四边形;(2)根据菱形的性质得到10AE CE ==,再用勾股定理求出BE 的长.【详解】解:(1)∵四边形ABCD 是矩形,∴AD BC =,//AD BC ,∵BE DF =,∴AD DF BC BE -=-,即AF EC =,∵//AF EC ,∴四边形AECF 是平行四边形;(2)∵四边形AECF 是菱形,∴10AE CE ==,在Rt ABE △中,6BE ===. 【点睛】本题考查平行四边形的判定,矩形的性质,菱形的性质,解题的关键是掌握这些性质定理进行证明求解.。
第一章 特殊平行四边形单元评价检测(含答案解析)

第一章特殊平行四边形评价检测(45分钟100分)一、选择题(每小题4分,共28分)1.矩形、菱形、正方形都具有的性质是()A.每一条对角线平分一组对角;B.对角线相等;C.对角线互相平分;D.对角线互相垂直【解析】选C.∵矩形、菱形、正方形都是特殊的平行四边形,∴平行四边形具有的性质就是矩形,菱形,正方形都具有的性质,∴矩形、菱形、正方形都具有的性质是对角线互相平分.【知识归纳】矩形、菱形、正方形对角线性质的区别(1)矩形的对角线相等但不垂直.(2)菱形的对角线垂直但不相等.(3)正方形的对角线相等而且垂直.2.如图,矩形ABCD中,E在AD上,且EF⊥EC,EF=EC,DE=2,矩形的周长为16,则AE的长是()A.3B.4C.5D.7【解题指南】解答本题的三个关键(1)由矩形的性质和EF⊥EC,EF=EC,得出△AEF≌△DCE.(2)由全等得AE=CD,再结合矩形的周长,求出A D.(3)用AD减DE得出AE的长.【解析】选A.∵矩形ABCD中,EF⊥EC,∴∠DEC+∠DCE=90°,∠DEC+∠AEF=90°,∴∠AEF=∠DCE,又∵EF=EC,∴△AEF≌△DCE,∴AE=CD,∵矩形的周长为16,即2CD+2AD=16,∴CD+AD=8,∴AD-2+AD=8,AD=5,∴AE=AD-DE=5-2=3.3.下列说法正确的是()A.对角线相等且互相垂直的四边形是菱形B.对角线互相垂直且平分的四边形是正方形C.对角线互相垂直的四边形是平行四边形D.对角线相等且互相平分的四边形是矩形【解析】选D.∵对角线相互平分且互相垂直的四边形是菱形,∴A,B选项错误;∵对角线互相垂直的四边形不一定是平行四边形,∴C选项错误;D选项正确,故选D.4.如图,在矩形ABCD中,BC=2,AE⊥BD,垂足为E,∠BAE=30°,那么△ECD的面积是()A.2B.C.D.【解析】选C.如图,过点C作CF⊥BD于F.∵矩形ABCD中,BC=2,AE⊥BD,∠BAE=30°,∴∠ABE=∠CDF=60°,AB=CD,AD=BC=2,∠AEB=∠CFD=90°.∴△ABE≌△CDF.∴AE=CF.∵∠ADE=∠BAE=30°,∴AE=AD=1,∴DE==,∴S△ECD=ED·CF=ED·AE=.【变式训练】如图,在矩形ABCD中,E是BC的中点,∠BAE=30°,AE=2,则矩形ABCD的面积为.【解析】在Rt△ABE中,AE=2,∠BAE=30°,∴BE=AE=1,∴AB===.∵E是BC的中点,∴BC=2BE=2,∴矩形ABCD的面积=AB×BC=2.答案:25.如图,已知菱形ABCD与△ABE,其中D在BE上.若AB=17,BD=16,AE=25,则DE的长度为()A.8B.9C.11D.12【解析】选D.连接AC,设AC交BD于O点,∵四边形ABCD为菱形,∴AC⊥BD,且BO=DO==8,在△AOD中,∵∠AOD=90°,∴AO===15,在△AOE中,∵∠AOE=90°,∴OE===20,又OD=8,∴DE=OE-OD=20-8=12.6.如图,在矩形ABCD中,AB=10,BC=5,点E,F分别在AB,CD上,将矩形ABCD沿EF折叠,使点A,D分别落在矩形ABCD外部的点A1,D1处,则阴影部分图形的周长为()A.15B.20C.25D.30【解析】选 D.根据折叠的性质,A1E=AE,A1D1=AD,D1F=DF;所以阴影部分的周长=矩形的周长=2(10+5)=30.7.如图,正方形ABCD中,AB=3,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG,CF.下列结论:①点G是BC的中点;②FG=FC;③S△FGC=.其中正确的是()A.①②B.①③C.②③D.①②③【解析】选B.①正确.理由:∵正方形ABCD中,AB=3,CD=3DE,∴ED=CD=1.∴EC=2.由对折得△AFE≌△ADE.进而得,AF=AD,EF=ED =1,∠AFE=∠D=90°.∴可证△ABG≌△AFG.设BG=x,则FG=x,GC=3-x.在Rt△EGC中,由勾股定理得GC2+ EC2=EG2,即(3-x)2+22=(1+x)2.解得x=,即BG=B C.②不正确.理由:∵GF=,EF=1,∴点F不是GE的中点.假设FG=FC,则∠FGC=∠FCG.由等角的余角相等,得∠FEC=∠FCE.∴EF=F C.∴FG=EF.这与前面的结论:点F不是GE的中点相矛盾.所以假设不成立.③正确.理由:△GFC中,设GC边上的高为h,则h=·EC=.S△GFC=GC·h=××=.二、填空题(每小题5分,共25分)8.等边三角形、平行四边形、矩形、正方形四个图形中,既是轴对称图形又是中心对称图形的是.【解析】等边三角形是轴对称图形,不是中心对称图形;平行四边形不是轴对称图形,是中心对称图形;矩形、正方形是轴对称图形,也是中心对称图形.答案:矩形和正方形【易错提醒】平行四边形是中心对称图形,但不是轴对称图形,本题易误认为平行四边形既是轴对称图形又是中心对称图形.【知识归纳】特殊平行四边形的对称性(1)矩形、菱形、正方形既是轴对称图形又是中心对称图形.(2)矩形与菱形有两条对称轴,正方形有四条对称轴.(3)对角线的交点是它们的对称中心,过对称中心的任一条直线均把原图形分成面积相等的两部分.9.如图所示,平行四边形ABCD的对角线AC,BD相交于点O,试添加一个条件:,使得平行四边形ABCD是菱形.【解析】添加AC⊥BD,则对角线互相垂直的平行四边形是菱形;添加AD=DC,则一组邻边相等的平行四边形是菱形.答案:AC⊥BD(或AD=DC,答案不唯一)10.如图,在矩形ABCD中,对角线AC,BD相交于点O,点E,F分别是AO,AD的中点,若AB=6cm,BC=8cm,则△AEF的周长=.【解析】在Rt△ABC中,AC==10(cm),∵点E,F分别是AO,AD的中点,∴EF是△AOD的中位线,EF=OD=BD=AC=2.5(cm),AF=AD=BC=4(cm),AE=AO=AC=2.5(cm),∴△AEF的周长=AE+AF+EF=9cm.答案:9cm【变式训练】如图,顺次连接菱形ABCD的各边中点E,F,G,H.若AC=a,BD=b,则四边形EFGH的面积是.【解析】∵点E,F分别是菱形边AB,BC的中点,∴EF是△ABC的中位线,∴EF=AC,且EF∥A C.同理,HG=AC,且HG∥AC,∴EF=HG,且EF∥HG.∴四边形EFGH是平行四边形,且EH∥FG,EH=FG=B D.又∵四边形ABCD是菱形,∴AC⊥BD,∴EF⊥EH,∴四边形EFGH的面积=EF·EH=a·b=a b.答案:ab11.如图,在矩形ABCD中,AE=AF,过点E作EH⊥EF交DC于点H,过F作FG⊥EF交BC于G,连接GH,当AD,AB满足时,四边形EFGH为矩形.【解析】∵四边形ABCD是矩形,∴∠A=90°.∵AE=AF,∴∠AFE=∠AEF=45°.又∵EH⊥EF,FG⊥EF∴∠GFB=∠HED=45°,∴△DHE和△BGF都是等腰直角三角形.如果四边形EFGH是矩形,则EH=FG,∴ED=FB,又∵AE=AF,∴AD=A B.答案:AD=AB12.如图,四边形ABCD与AEFG都是菱形,其中点C在AF上,点E,G分别在BC,CD上,若∠BAD=135°,∠EAG=75°,则=.【解析】作EH⊥AB于H,由对称性知,两菱形分别关于AF对称,∴∠BAE=∠DAG=(∠BAD-∠EAG)=30°,∠B=180°-∠BAD=45°.在Rt△BHE中,∠B=∠BEH=45°,设BH=x,则EH=BH=x,在Rt△EHA中,∠BAE=30°,AE=2HE=2x,AH===x.∴AB=BH+AH=x+x,故==.答案:三、解答题(共47分)13.(10分)如图,在四边形ABFC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且CF=AE.(1)求证:四边形BECF是菱形.(2)若四边形BECF为正方形,求∠A的度数.【解析】(1)∵BC的垂直平分线EF交BC于点D,∴BF=FC,BE=E C.又∵∠ACB=90°,∴EF∥A C.∴=.∵D为BC中点,∴==,∴E为AB中点,即BE=AE,∵CF=AE,∴CF=BE,∴CF=FB=BE=CE,∴四边形BECF是菱形.(2)∵四边形BECF为正方形,∴∠BEC=90°.又AE=CE,∴∠A=45°.【互动探究】四边形BECF的面积与△ABC的面积有什么关系?为什么?提示:四边形BECF的面积与△ABC的面积相等,理由如下:∵四边形BECF是菱形,∴CF∥A B.∵CF=AE,∴S△CFB=S△AEC,∴S△CFB+S△CEB=S△AEC+S△CEB,即:四边形BECF的面积=△ABC的面积.14.(12分)如图,已知菱形ABCD,AB=AC,E,F分别是BC,AD的中点,连接AE,CF.(1)证明:四边形AECF是矩形.(2)若AB=8,求菱形的面积.【解析】(1)∵四边形ABCD是菱形,∴AB=BC,又∵AB=AC,∴△ABC是等边三角形,∵E是BC的中点,∴AE⊥BC,∴∠AEC=90°,∵E,F分别是BC,AD的中点,∴AF=AD,EC=BC,∵四边形ABCD是菱形,∴AD∥BC且AD=BC,∴AF∥EC且AF=EC,∴四边形AECF是平行四边形,又∵∠AEC=90°,∴四边形AECF是矩形.(2)在Rt△ABE中,AE==4,所以,S菱形=8×4=32.15.(12分)(2014·新民市一模)已知:如图,在四边形ABCD中,点G在边BC的延长线上,CE平分∠BCD,CF平分∠GCD,EF∥BC交CD于点O.(1)求证:OE=OF.(2)若点O为CD的中点,求证:四边形DECF是矩形.【解析】(1)∵CE平分∠BCD,CF平分∠GCD,∴∠BCE=∠DCE,∠DCF=∠GCF,∵EF∥BC,∴∠BCE=∠FEC,∠EFC=∠GCF,∴∠DCE=∠FEC,∠EFC=∠DCF,∴OE=OC,OF=OC,∴OE=OF.(2)∵点O为CD的中点,∴OD=OC,又OE=OF,∴四边形DECF是平行四边形,∵CE平分∠BCD,CF平分∠GCD,∴∠DCE=∠BCD,∠DCF=∠DCG,∴∠DCE+∠DCF==90°,即∠ECF=90°,∴四边形DECF是矩形.16.(13分)(2013·青岛中考)已知:如图,在矩形ABCD中,M,N分别是边AD,BC的中点,E,F分别是线段BM,CM 的中点.(1)求证:△ABM≌△DCM.(2)判断四边形MENF是什么特殊四边形,并证明你的结论.(3)当AD∶AB=时,四边形MENF是正方形(只写结论,不需证明) 【解析】(1)在矩形ABCD中,∵AB=CD,∠A=∠D=90°,又∵M是AD的中点,∴AM=DM,∴△ABM≌△DCM(SAS).(2)四边形MENF是菱形.证明:∵E,F,N分别是BM,CM,CB的中点,∴NF∥ME,NF=ME,∴四边形MENF是平行四边形,由(1)得BM=CM,∴ME=MF,∴□MENF是菱形.(3)2∶1.。
特殊平行四边形检测试卷

第一章 特殊平行四边形检测试卷一、选择题1. 不能判定四边形ABCD 为平行四边形的题设是( ) (A )AB 平行且等于CD 。
(B )∠A=∠C ,∠B=∠D 。
(C )AB=AD ,BC=CD 。
(D )AB=CD ,AD=BC 。
2.矩形、菱形、正方形都具有的性质是 ( ) A.每一条对角线平分一组对角 B.对角线相等 C.对角线互相平分 D.对角线互相垂直3. 如图,在平行四边形ABCD 中,对角线AC 、BD 相交于点O ,若BD 、AC 的和为cm 18,CD :DA=2:3,△AOB 的周长为cm 13,那么BC 的长是 ( ) A. cm 6 B. cm 9 C. cm 3 D. cm 124.在直角三角形ABC 中,∠ACB =︒90,∠B =︒60,AC =cm 3,则AB 边上的中线长为 ( ) A. cm 1 B. cm 2 C. cm5.1 D. cm 3 5. 下列说法错误的是( )A.一组对边平行且一组对角相等的四边形是平行四边形.B.每组邻边都相等的四边形是菱形.C.对角线互相垂直的平行四边形是正方形.D.四个角都相等的四边形是矩形. 6.下列命题中,真命题是 ( )A .两条对角线垂直的四边形是菱形B .对角线垂直且相等的四边形是正方形C .两条对角线相等的四边形是矩形D .两条对角线相等的平行四边形是矩形 7.将两块能完全重合的两张等腰直角三角形纸片拼成下列图形:①平行四边形(不包括菱形、矩形、正方形)②矩形③正方形④等边三角形⑤等腰直角三角形 ( )A .①③⑤B .②③⑤C .①②③D .①③④⑤8.如图,已知菱形ABCD 与△ABE,其中D 在BE 上.若AB=17,BD=16,AE=25,则DE 的长度为 ( )A.8B.9C.11D.129. 如图在矩形ABCD 中,AB=10,BC=5,点E,F 分别在AB,CD 上,将矩形ABCD 沿EF 折叠,使点A,D 分别落在矩形ABCD 外部的点A 1,D 1处,则阴影部分图形的周长为 ( ) A.15B.20C.25D.3010.如图,菱形ABCD 中,对角线AC 、BD 相交于点O ,H 为AD 边中点,菱形ABCD 的周长为28,则OH 的长等于( )A. 3.5B. 4C. 7D. 1411.给出以下三个命题:①对角线相等的四边形是矩形;②对角线互相垂直的四边形是菱形;③对角线互相垂直的矩形是正方形;④菱形对角线的平方和等于边长平方的4倍,其中真命题的是( )A .③B .①②C .②③D .③④ 12.如图,正方形ABCD 中,AB=3,点E 在边CD 上,且CD=3DE.将△ADE 沿AE 对折至△AFE,延长EF 交边BC 于点G,连接AG,CF.下列结论: ①点G 是BC 的中点; ②FG=FC; ③∠GAE =︒45. 其中正确的是 ( )A.①②B.①③C.②③D.①②③ABCDO二、填空题:13.①等边三角形②菱形③平行四边形④矩形(5)正方形五个图形中,既是轴对称图形又是中心对称图形的是 (填写序号).14. 在Rt⊿ABC中,∠ACB =90°,∠A =30°,AC =32,则AB边上的中线为,高为15.菱形ABCD的边长为8cm,∠BAD=120°,则AC= ,BD= ,面积= 。
第一章 特殊平行四边形 单元测试卷(含答案) 北师大版九年级上册数学

共有( )
A.1 对
B.2 对
C.3 对
D.4 对
3.如图,AC、BD 是四边形 ABCD 的两条对角线,顺次连接四边形 ABCD 各边中点得到四边形 EFGH,要使四边
形 EFGH 为矩形,应添加的条件是( )
A.AC⊥BD
B.AB=CD
C.AB∥CD
D.AC=BD
4.如图,在正方形 ABCD 中, CE MN , MCE 36 ,那么 ANM 等于( )
的最小值为
.
三、解答题(共 6 小题,每题 8 分,满分 48 分) 19.如图,小亮将升旗的绳子拉到杆底端,绳子末刚好接触地面,然后将绳子末端拉到距离旗杆 8m 处,发现此时 绳子末端距离地面 2m .请你求出杆的高度(滑轮上方的高度忽略不计,解题时请在图中标注字母)
20.如图,将一张长方形纸片 ABCD 沿 CE 折叠,使点 B 与 AD 边上的点 B′重合.过点 B′作 B′F//EB 交 CE 于点 F, 连接 EB′与 BF.
24.(1)
y1
2t 0
16 2t
t 4 4 t
8
;
y2
t
0
t
8
(2)①当 0 t 4 时, y1 随时间 t 的增大而增大,当 4 t 8 时, y1 随时间 t 的增大而减小;② 0 t 16
3
周长多 4,则 AC 的长是(
A.2 3
B.4 3
C.2 7
D. 4 7
8.如图,边长为 4 和 10 的两个正方形 ABCD 与 CEFG 并排在一起,连接 BD 并延长交 EF 于 H,交 EG 于 I,则 GI 的长为( )
A.3
B.7
C.3 2
初中数学北师大版九年级上册 第一章 特殊平行四边形 单元测试(含答案)

第一章特殊平行四边形一、单选题1.如图,要使平行四边形ABCD成为菱形,需添加的一个条件是( )A.AB=BC B.AC=BD C.∠ABC=90°D.AC与BD互相平分2.如图,矩形ABCD中,对角线AC,BD交于O点.若∠BOC=120°,AC=8,则AB的长为()A.6B.4C.43D.423.如图在Rt△ABC中,∠ACB=90°,AB=10cm,点D是AB的中点,则CD的长度是()A.7cm B.6cm C.5cm D.4cmCD的长为半径4.如图,矩形ABCD中,AB=10,BC=6,分别以C,D为圆心,以大于12作弧,两弧分别交于G,H两点,作直线GH交CD于点E,连接AE,点D关于AE的对称点为点M,作射线AM交BC于点N,则CN的长为()A .253B .4C .256D .55.如图,在长方形ABCD 中,AB=3,BC=4,若沿折痕EF 折叠,使点C 与点A 重合,则折痕EF 的长为( )A .158B .154C .152D .156.如图,在四边形ABCD 中,AB ∥CD ,AB =CD ,对角线AC 与BD 交于点O ,点E 是AD 的中点,连接OE ,△ABD 的周长为12cm ,则下列结论错误的是( )A .OE ∥ABB .四边形ABCD 是中心对称图形C .△EOD 的周长等于3cmD .若∠ABC =90°,则四边形ABCD 是轴对称图形7.如图,在△ABC 中,AB =5,AC =12,BC =13,P 为边BC 上一动点,PE ⊥AB 于E ,PF ⊥AC 于F ,M 为EF 中点,则AM 的最小值为( )A.6013B.3013C.2413D.12138.如图,正方形ABCD的周长为24,P为对角线AC上的一个动点,E是CD的中点,则PE+PD 的最小值为()A.35B.32C.6D.5二、填空题9.菱形的周长为12cm,它的一个内角为60°,则菱形的面积为.10.如图,在菱形ABCD中,对角线AC,BD相交于点O,H为BC中点,AC=3,BD=4,则线段OH的长为.11.如图,在△ABC中,点D在BC上过点D分别作AB、AC的平行线,分别交AC、AB于点E、F①如果要得到矩形AEDF,那么△ABC应具备条件:;②如果要得到菱形AEDF,那么△ABC应具备条件:.12.已知,如图,四边形ABCD是正方形,BE=AC,则∠BED=度.13.如图,矩形ABCD内有一点P,连接AP,DP,CP,延长CP交AB于点E,若∠APD=90°,AD=8,CP=CD=6,则AE的长是.OA,把矩形OABC沿OB折叠,14.如图,四边形OABC是矩形,点A的坐标为(8,0),AB=12点C落在点D处,BD交OA于点E,则点E的坐标为.15.如图,已知点E在菱形ABCD的边AB上,以BE为边向菱形ABCD外部作菱形BEFG,连接DF,M,N分别是DC,DF的中点,连接MN.若AB=5,BE=2,∠ABC=120°,则MN=.16.如图,在边长为10的正方形ABCD中,E是BC的中点,连接AE,过点B作AE的垂线,交AE于点G,交CD于点H,F是BH上一点,连接EF,若BE=FE,则FH的长为.17.如图,矩形ABCD 中,AB =10,BC =24,点P 在BC 边上,PE ⊥BD ,PF ⊥AC ,则PE +PF = .18.已知:如图,在正方形ABCD 外取一点E ,连接AE 、BE 、DE .过点A 作AE 的垂线交DE 于点P .若AE =AP =1,BP =5.下列结论:①△APD ≌△AEB ;②点B 到直线AE 的距离为2;③S △APD +S △APB =12+62;④S 正方形ABCD =4+6.其中正确结论的序号是 .三、解答题19.如图,四边形ABCD 中,对角线AC 、BD 相交于点O ,AO =CO ,BO =DO ,且∠ABC=90°.(1)求证:四边形ABCD 是矩形.(2)若∠ACB=30°,AB=1,求①∠AOB 的度数;②四边形ABCD 的面积.20.如图,在菱形ABCD中,∠A=60∘,AB=4,O是对角线BD的中点,过O点作OE丄AB,垂足为E.(1)求∠ABD的度数;(2)求线段BE的长;(3)求菱形ABCD的面积.21.如图,在平行四边形ABCD中,两条对角线相交于点O,EF经过O且垂直于AC,分别与边AD、BC交于点F、E.(1)求证:四边形AECF为菱形;(2)若AD=3,CD=2,且∠ADC=60°,求菱形AECF的面积.22.十一国庆节,某校各班都在开展丰富多彩的庆祝活动,八年级(1)班开展了手工制作竞赛,每个同学都在规定时间内完成一件手工作品.武玥同学在制作手工作品的第一、二个步骤是:①先裁下了一张长BC=20cm,宽AB=16cm的长方形纸片ABCD;②如图,将纸片沿着直线AE折叠,点D恰好落在BC边上的F处.请你根据①②步骤计算EC,FC的长.23.综合与实践:【问题情境】某数学兴趣小组在学完《平行四边形》之后,研究了新人教版数学教材第64页的数学活动1.其内容如下:如果我们身旁没有量角器或三角尺,又需要作60°,30°,15°等大小的角,可以采用下面的方法(如图1);(1)对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展平.(2)再一次折叠纸片,使点A落在EF上,并使折痕经过点B,得到折痕BM.同时,得到了线段BN.【知识运用】请根据上述过程完成下列问题:(1)已知矩形纸片ABCD,AB=43,AM=4,求线段BM的长;(2)通过观察猜测∠NBC的度数是多少?并进行证明;【综合提升】(3)乐乐在探究活动的第(2)步基础上再次动手操作(如图2),将MN延长交BC于点G.将△BMG沿MG折叠,点B刚好落在AD边上点H处,连接GH,把纸片再次展平.请判断四边形BGHM的形状,并说明理由.参考答案:1.A2.B3.C4.C5.B6.C7.B8.Acm29.93210.5411.∠BAC=90∘AD平分∠BAC 12.22.513.8314.(5,0)15.67216.517.1201318.①③④19.解:(1)证明:∵AO=CO,BO=DO∴四边形ABCD是平行四边形,∴∠ABC=∠ADC,∵∠ABC=90°,∴四边形ABCD是矩形;(2)∵∠ABC=90°,∠ACB=300,AB=1∴∠BAC=60°,AC=2,BC=3又∵矩形ABCD中,OA=OB∴∠AOB=180°-2∠BAC=60°S□ABCD=1×3=320.解:(1)在菱形ABCD中,∵AB=AD,∠A=60∘,∴△ABD为等边三角形,∴∠ABD=60∘;(2)∵O是对角线BD的中点,BD=2,∴OB=12∵∠ABD=60∘,=1;∴BE=OBcos60∘=2×12(3)过D作DF⊥AB于点F,由(2)可得:OE=OBsin60∘=3,∵OE⊥AB,点O为BD中点,∴DF=2OE=23,则S菱形ABCD=AB⋅DF=4×23=83.21.(1)证明:∵四边形ABCD为平行四边形,∴OA=OC,AD∥BC,∴∠FAC=∠ACE,∠AFE=∠CEF,∴△AOF≌△COE,∴AF=CE,∴四边形AECF为平行四边形,∵EF经过O且垂直于AC,∴EF是对角线AC的垂直平分线,∴AF=CF,∴四边形AECF为菱形;(2)解:过C作CH⊥AD于H,则∠CHD=∠CHF=90°,∵∠ADC=60°,∴∠HCD=30°,∴HD=12CD=1,∴CH=CD2−HD2=3,∵AD=3,∴AH=2,∵四边形AECF是菱形,∴AF=CF,设AF=CF=x,则FH=2−x,在Rt△CHF中,由勾股定理得:CF2=FH2+CH2,即x2=(2−x)2+(3)2,解得:x=74,∴AF=CF=74,∴菱形AECF的面积为:AF×CH=74×3=734.22.解:∵△ADE由△AFE关于AE对称,∴△ADE≌△AFE,∴DE=FE,AD=AF,∵四边形ABCD是矩形,∴BC=AD=AF=20cm,AB=CD=16cm,在Rt△ABF中,由勾股定理:BF=AF2−AB2=202−162=12cm,∴CF=BC-BF=20-12=8cm.∵四边形ABCD是矩形,∴∠C=90°.设CE=x,则DE=EF=16-x,在Rt△CEF中,由勾股定理:EF2=CE2+CF2,代入数据:(16-x)2=x2+64,解得:x=6.∴EC=6cm.综上所述,线段EC=6cm,CF=8cm.23.解:(1)∵四边形ABCD为矩形,∴∠A=90°,∵AB=43,AM=4,∴BM=AB2+AM2=8;(2)猜测:∠NBC=30°,证明:连接AN:∵EF为折痕,∴EF垂直平分AB,∴AN=BN,∵△BMN由△BMA折叠所得,∴AB=BN,∴AN=BN=AB,∴△ABN为等边三角形,∴∠ABN=60°,∴∠NBC=90°−60°=30°;(3)四边形BGHM为菱形,理由:∵△BMN由△BMA折叠所得,∴∠ABM=∠NBM,∠BAM=∠MNB=90°,∵∠ABN=∠ABM+∠NBM=60°,∴∠ABM=∠NBM=30°,∵∠NBC=30°,∴∠NBM=∠NBC=30°,∴∠MBG=60°,∴△BMG是等边三角形,∴BM=BG,∵将△BMG沿MG折叠,点B刚好落在AD边上点H处,连接GH,∴△BMG≌△HGM,BH⊥MG,∴MH=BM,∴MH=BM=BG,∵MH∥BG,∴四边形BGHM是平行四边形,∵BM=BG,∴四边形BGHM是菱形.。
第一章《特殊平行四边形》单元测试卷(含答案解析)

第一章《特殊平行四边形》单元测试卷班级:___________ 姓名:___________ 得分:___________一.选择题:(每小题3分,共36分)1.菱形具有而矩形不一定具有的性质是()A.对角线互相垂直B.对角线相等C.对角线互相平分D.对角互补2.矩形具有而菱形不一定具有的性质是()A.内角和等于3600B.对角互补C.对边平行且相等D.对角线互相平分3.已知四边形ABCD是平行四边形,下列结论不正确的是()A.当AC=BD时,它是菱形B.当AC⊥BD时,它是菱形C.当∠ABC=90°时,它是矩形D.当AB=BC时,它是菱形4.如图所示,四边形ABCD的对角线互相平分,要使四边形ABCD成为矩形,需要添加的条件是()A.AB=CD B.AD=BD C.AB=BC D.AC=BD(第4题) (第5题) (第6题)5.如图,矩形ABCD的对角线AC=8cm,∠AOD=120°,则AB的长为()A.cm B.2cm C.2cm D.4cm6.如图,四边形ABCD是平行四边形,下列说法不正确的是()A.当AC=BD时,四边形ABCD是矩形;B.当AB=BC时,四边形ABCD是菱形;C.当AC⊥BD时,四边形ABCD是菱形;D.当∠DAB=90°时,四边形ABCD是正方形7.正方形具有而菱形不具有的性质是()A.对角线平分一组对角B.对角线相等C.对角线互相垂直平分D.四条边相等N 分别是边AB 、BC 的中点,则PM +PN 的最小值是( ) A .5 B .10 C .14 D .不确定(第8题) (第9题) (第10题)9.如图所示,在菱形ABCD 中,AC 、BD 相交于点O ,E 为AB 的中点,若OE =4,则菱形ABCD 的周长是( )A .8B .16C .24D .3210.如图,AC 、BD 是矩形ABCD 的对角线,过点D 作DE ∥AC ,交BC 的延长线于E ,则图中与△ABC 全等的三角形共有( )A .1个B .2个C .3个D .4个11.如图,在菱形ABCD 中,∠BAD =82°,AB 的垂直平分线交对角线AC 于点F ,垂足为E ,连接DF ,则∠CDF 等于( )A.67°B.57°C.60°D.87°(第11题) (第12题)12.如图,将n 个边长都为1cm 的正方形按如图所示摆放,点A 1、A 2、…、A n 分别是正方形的中心,则n 个这样的正方形重叠部分的面积和为( ) A .41cm 2 B .4n cm 2 C .41 n cm 2D .n )41( cm 2 二.填空题:(每小题3分,共12分13.如图,四边形 ABCD 中,点E 、F 、G 、H 分别为边 AB 、BC 、CD 、DA 的中点,请你(第13题) (第14题) (第15题)14.如图,l∥m,矩形ABCD的顶点B在直线m上,则∠α= 度.15.如图,E是边长为1的正方形ABCD对角线BD上一点,且BE=BC,P为CE上任意一点,PQ⊥BC于点Q,PR⊥BD于点R,则PQ+PR的值为。
(典型题)初中数学九年级数学上册第一单元《特殊平行四边形》检测卷(答案解析)

一、选择题1.菱形的一条对角线与它的边相等,则它的锐角等于( )A .30°B .45°C .60°D .75°2.如图,把矩形ABCD 沿EF 对折,若112,AEF ∠=︒则1∠等于( )A .43B .44C .45︒D .46︒3.如图,在平面直角坐标系中,将边长为a 的正方形OABC 绕点O 顺时针旋转45︒后得到正方形111OA B C ,依此方式连续旋转2021次得到正方形202120212021OA B C ,那么点2021A 的坐标是( )A .22,22a a ⎛⎫ ⎪⎝⎭B .22,22a a ⎛⎫- ⎪⎝⎭C .22,22a a ⎛⎫-- ⎪⎝⎭D .22,22a a ⎛⎫- ⎪⎝⎭ 4.如图所示,△ABC 是等边三角形,AQ=PQ ,PR=PS ,PR ⊥AB 于R ,PS ⊥AC 于S ,则四个结论正确的是( )①点 P 在∠A 的平分线上; ②AS=AR ; ③QP //AR ; ④△BRP ≌△QSP .A .全部正确B .①②正确C .①②③正确D .①③正确5.如图,已知菱形OABC 的顶点()0,0O ,()2,0C 且60AOC ∠=︒,若菱形绕点O 逆时针旋转,每秒旋转45︒,则第2020秒时,菱形的对角线交点D 的坐标为( )A .()3,3-B .()1,3--C .()2,3D .33,22⎛⎫-- ⎪ ⎪⎝⎭6.如图,在矩形ABCD 中,23,4AB BC ==,E 为BC 的中点,连接,,,AE DE P Q 分别是,AE DE 上的点,且PE DQ =.设EPQ ∆的面积为y ,PE 的长为x ,则y 关于x 的函数关系式的图象大致是 ( )A .B .C .D .7.如图,已知正方形ABCD 与正方形AEFG 的边长分别为4和1,若将正方形AEFG 绕点A 旋转,则在旋转过程中,点,C E 之间的最小距离为 ( )A .3B .421-C .321-D .42 8.如图,将长方形纸片ABCD 沿AE 折叠,使点D 恰好落在BC 边上点F 处.若6AB =,10AD =,则EC 的长为( )A .2B .83C .3D .1039.如图,以△ABC 的三条边为边,分别向外作正方形,连接EF ,GH ,DJ ,如果△ABC 的面积为8,则图中阴影部分的面积为( )A .28B .24C .20D .1610.□ABCD 中,AC 、BD 是两条对角线,如果添加一个条件,可推出□ABCD 是菱形,那么这个条件可以是( )A .AB=CDB .AC=BDC .AC ⊥BD D .AB ⊥BD 11.如图所示,将矩形纸片ABCD 折叠,使点D 与点B 重合,点C 落在点C '处,折痕为EF ,若122EFC '∠=︒,那么ABE ∠的度数为( )A .24︒B .32︒C .30D .26︒12.如图,矩形ABCD 中,3AB =,4BC =,点E 是BC 边上一点,连接AE ,把B 沿AE 折叠,使点B 落在点'B 处,当'CEB ∆为直角三角形时,BE 的长为( )A .3B .32C .2或3D .3或32二、填空题13.如图,正方形ABCD 中,点E 在边AD 上,点F 在边CD 上,若BEF EBC ∠=∠,3AB AE =,则下列结论:①DF FC =;②AE DF EF +=;③45ABE CBF ∠+∠=︒;④::3:4:5DF DE EF =;其中结论正确的序号有_____.14.如图,将矩形ABCD 沿DE 折叠,使A 点落在BC 上的F 处,若∠EFB =60°,则∠CFD =_____.15.如图,在平面直角坐标系中,边长为1的正方形1111D C B A (记为第1个正方形)的顶点1A 与原点重合,点1B 在y 轴上,点1D 在x 轴上,点1C 在第一象限内,以1C 为顶点作等边122C A B ,使得点2A 落在x 轴上,22A B x ⊥轴,再以22A B 为边向右侧作正方形2222A B C D (记为第2个正方形),点2D 在x 轴上,以2C 为顶点作等边233C A B ,使得点3A 落在x 轴上,33A B x ⊥轴,若按照上述的规律继续作正方形,则第2021个正方形的边长为_________.16.如图,在△ABC 中,∠BAC =45°,AB=AC =4,P 为AB 边上一动点,以PA ,PC 为邻边作平行四边形PAQC ,则对角线PQ 的最小值为___________.17.如图,将一个装有水的杯子斜放在水平的桌面上,其截面可看作一个宽BC =6厘米的矩形.当水面触到杯口边缘时,水面宽度BE =12厘米,此时杯子的倾斜角α等于_____度.18.如图,矩形ABOC 的顶点B 、C 分别在x 轴、y 轴上,顶点A 在第一象限,点B 的坐标为(3,0),将线段OC 绕点O 顺时针旋转60°至线段OD ,若反比例函数k y x= (k ≠0)的图象进过A 、D 两点,则k 值为_____.19.如图,在矩形纸片ABCD 中,AD =3,将矩形纸片折叠,边AD 、边BC 与对角线BD 重合,点A 与点C 恰好落在同一点处,则矩形纸片ABCD 的周长是______.20.如图,正方形ABCD 的边长为6,点E ,F 分别是边AB ,CD 上的点,且60CFE ∠=︒.将四边形BCFE 沿EF 翻折,得到B C FE '',点C '恰好落在AD 边上,B C ''交AB 于点G ,则GE 的长是_______.三、解答题21.如图,点D 是Rt ABC 斜边AB 的中点,过点B ,C 分别作//BE CD ,//CE BD ,连接DE .(1)若60A ∠=︒,3AC =,求CD 的长;(2)求证:BC DE ⊥.22.如图,矩形EFGH 的顶点,E G 分别在菱形ABCD 的边,AD BC 上,顶点,F H 在菱形ABCD 的对角线BD 上.(1)求证:BG DE =;(2)若E 为AD 中点,5,12FG GH ==,求菱形ABCD 的周长;23.如图,E 是正方形ABCD 中CD 边上一点,以点A 为中心把ADE ∆顺时针旋转90︒.(1)在图中画出旋转后的图形;(2)若旋转后E 点的对应点记为M ,点F 在BC 上,且45EAF ︒∠=,连接EF . ①求证:AMF AEF ∆≅∆;②若正方形的边长为6,35AE =,求EF .24.如图,矩形ABCD 中,AB =6,BC =8,E 为BC 上一动点.将△ABE 沿AE 翻折后得到AFE ,延长AF 交CD 所在直线于点G ,设BE =x .(1)若点G 在CD 边上,求x 的取值范围;(2)若x =5,求CG 的长.25.如图,正方形ABCD 的边AB 在数轴上,数轴上点A 表示的数为-1,正方形ABCD 的面积为16.(1)数轴上点B 表示的数为 ;(2)将正方形ABCD 沿数轴水平移动,移动后的正方形记为''''A B C D ,移动后的正方形''''A B C D 与原正方形ABCD 重叠部分的面积记为S.① 当S =4时,画出图形,并求出数轴上点'A 表示的数;② 设正方形ABCD 的移动速度为每秒2个单位长度,点E 为线段'AA 的中点,点F 在线段'BB上,且. 经过t秒后,点E,F所表示的数互为相反数,求出t的值.26.已知:如图,P是正方形ABCD内一点,在正方形ABCD外有一点E,满足∠ABE=∠CBP,BE=BP.≌;.求证:(1)CPB AEB(2)PB⊥BE(3)请你连接PE,猜想线段PB与线段PE的数量关系,并说明理由.【参考答案】***试卷处理标记,请不要删除一、选择题1.C解析:C【分析】由菱形的性质可得这条对角线与菱形的两边组成等边三角形,从而求得锐角的度数等于60°.【详解】解:由菱形的性质得,菱形相邻的两边相等,则与这条对角线组成等边三角形,则它的锐角等于60°,故选C.【点睛】此题主要考查菱形的性质:四边相等.2.B解析:B【分析】根据矩形的对边平行,可得∠AEF+∠BFE=180°,继而求得∠BFE=68°,再利用折叠的性质和平角的定义求解即可.【详解】∵四边形ABCD 是矩形,∴AD ∥BC ,∴∠AEF+∠BFE=180°,∵112AEF ∠=︒,∴∠BFE=68°,∴∠1=180°-2∠BFE=44°,故选B .【点睛】本题考查了折叠问题,矩形的性质,平行线的性质,平角的定义,熟练掌握折叠的性质是解题的关键.3.C解析:C【分析】由正方形的性质和旋转的性质探究规律,利用规律解决问题即可.【详解】解:∵四边形OABC 是正方形,且OA=1,∴A (0,a ),∵将正方形OABC 绕点O 顺时针旋转45°后得到正方形OA 1B 1C 1,∴A 122),A 2(a ,0),A 322),A 4(0,-a )…, 发现是8次一循环,∵2021÷8=252…5,∴点A 2021的坐标为22,22a ⎛⎫-- ⎪⎝⎭, 故选:C .【点睛】本题考查了正方形的性质、旋转的性质、坐标与图形的变化、规律型:点的坐标等知识,解题的关键是学会从特殊到一般的探究规律的方法,属于中考常考题型.4.A解析:A【分析】因为△ABC 为等边三角形,根据已知条件可推出Rt △ARP ≌Rt △ASP ,则AR =AS ,故②正确,∠BAP =∠CAP ,所以AP 是等边三角形的顶角的平分线,故①正确,根据等腰三角形的三线合一的性质知,AP 也是BC 边上的高和中线,即点P 是BC 的中点,因为AQ =PQ ,所以点Q 是AC 的中点,所以PQ 是边AB 对的中位线,有PQ ∥AB ,故③正确,又可推出△BRP ≌△QSP ,故④正确.【详解】解:∵PR ⊥AB 于R ,PS ⊥AC 于S∴∠ARP =∠ASP =90°∵PR =PS ,AP =AP∴Rt △ARP ≌Rt △ASP∴AR =AS ,故②正确,∠BAP =∠CAP∴AP 是等边三角形的顶角的平分线,故①正确∴AP 是BC 边上的高和中线,即点P 是BC 的中点∵AQ =PQ∴点Q 是AC 的中点∴PQ 是边AB 对的中位线∴PQ ∥AB ,故③正确∵Q 是AC 的中点,∴QC=QP ,∵∠C=60°,∴△QPC 是等边三角形,∴PB=PC=PQ ,∵PR =PS ,∠BRP =∠QSP =90°,∴△BRP ≌△QSP ,故④正确∴全部正确.故选:A .【点睛】本题利用了等边三角形的性质:三线合一,全等三角形的判定和性质,中位线的性质,熟练掌握上述性质和判定方法是解题的关键.5.D解析:D【分析】过A 作AE ⊥OC 于E ,由菱形OABC 的顶点()0,0O ,()2,0C 且60AOC ∠=︒,求出A(1D 为AC 中点,可求D (12458=360︒⨯︒,转8次回到原位置,菱形绕点O 逆时针旋转,每秒旋转45︒,则第2020秒时,2020445=45252+88⎛⎫︒⨯︒ ⎪⎝⎭,相当于旋转454=180︒⨯︒,菱形旋转180°。
北师版九年级数学 第一章 特殊平行四边形(单元综合测试卷)

第一章特殊平行四边形(单元重点综合测试)班级___________姓名___________学号____________分数____________考试范围:全章的内容;考试时间:120分钟;总分:120分一、单选题(本大题共10小题,每小题3分,共30分)1.矩形具有而菱形不一定具有的性质是()A .对角线互相平分B .对边平行且相等C .对角线相等D .对角相等2.如图,正方形ABCD 的对角线相交于点O ,则AOB ∠的度数是()A .30︒B .45︒C .60︒D .90︒3.已知矩形的较短边长为6,对角线相交成60°角,则这个矩形的较长边的长是()A .B .C .9D .124.如图,在菱形ABCD 中,对角线AC ,BD 相交于点O ,若110BAD ∠=︒,则OBC ∠的度数为()A .30︒B .35︒C .55︒D .70︒5.下面说法正确的是()A .有一组邻边相等的四边形是菱形B .对角线互相垂直的四边形是菱形C .矩形的对角线相等D .对角线互相垂直平分的四边形是正方形6.如图,已知菱形ABCD 的对角线AC 、BD 的长分别为6cm 、8cm ,AE ⊥BC 于点E ,则AE 的长是()A .5cmB .6cmC .485cm D .245cm ;7.如图,矩形ABCD 中,AB =2,BC =4,对角线AC 的垂直平分线分别交AD 、BC 于点E 、F ,连接CE ,则△DCE 的面积为()A .52B .32C .2D .18.如图,点B 、C 分别在两条直线y kx =和6y x =-上,点A 、D 是x 轴上两点,若四边形ABCD 是正方形,则k 的值为()A .6B .5C .56D .659.如图,在菱形ABCD 中,∠A =60°,点E 、F 分别为AD 、DC 上的动点,∠EBF =60°,点E 从点A 向点D 运动的过程中,AE+CF 的长度().A .逐渐增加B .逐渐减小C .保持不变且与EF 的长度相等D .保持不变且与AB 的长度相等10.如图,在正方形ABCD 中,O 是对角线AC 与BD 的交点,M 是BC 边上的动点(点M 不与B 、C 重合),过点C 作CN 垂直DM 交AB 于点N ,连结OM 、ON 、MN .下列四个结论:①CNB DMC △≌△;②ON OM =;③ON OM ⊥;④222AN CM MN +=.其中结论正确的有()个A .1B .2C .3D .4二、填空题(本大题共8小题,每小题3分,共24分)11.菱形ABCD 的边长为5,对角线6AC =,则菱形ABCD 的面积是.12.要使矩形ABCD 成为正方形,可添加的条件是(写一个即可).13.如图,E 是正方形ABCD 的边BC 延长线上一点,且CE=AC ,AE 交CD 于点F ,则∠E=14.如图,一张长8cm ,宽6cm 的矩形纸片,将它沿某直线折叠使得A 、C 重合,则折痕EF 的长为.15.如图,在矩形ABCD 中,AB =8,BC =6,点P 为边AB 上任意一点,过点P 作PE ⊥AC ,PF ⊥BD ,垂足分别为E 、F ,则PE +PF =.16.已知,矩形ABCD ,点F 在边BC 上,点E 在边AB 上,连接CE 、AF 交于点G .若12AB =,9BC =,3BE =,45AGE ∠=︒.则BF =.17.如图,在平面直角坐标系中,四边形OABC 是边长为1的正方形,顶点,A C 分别在x y ,轴的正半轴上.点Q 在对角线OB 上,且OQ OC =,连接CQ 并延长CQ 交边AB 于点P ,则点P 的坐标为.18.如图,矩形ABCD 中,5,7AD DC ==,点H 在边AD 上,1AH =,E 为边AB 上一个动点,连HE .以HE 为一边在HE 的右上方作菱形HEFG ,使点G 落在边DC 上,连结CF .(1)当菱形HEFG 为正方形时,DG 的长为;(2)在点E 的运动过程中,△FCG 的面积S 的取值范围为.三、解答题(本大题共9小题,共66分)19.如图,在正方形ABCD 中,E 是边AB 的中点,F 是边BC 的中点,连接CE 、DF .求证:CE DF =.20.如图,四边形ABCD 是菱形,∠ACD=30°,BD=6.求:(1)∠BAD ,∠ABC 的度数;(2)AB ,AC 的长.21.如图,在6×6的方格纸中,请按要求作图.(1)图1中,A ,B 是方格纸中的格点,以AB 为一边作一个矩形ABCD ,要求C ,D 两点也在格点上;(2)图2中,E ,F 是方格纸中的格点,以EF 为一边作一个菱形EFGH ,要求G ,H 两点也在格点上.22.如图,四边形ABCD 是正方形,E 、F 分别是DC 和CB 的延长线上的点,且DE =BF ,连接AE ,AF ,EF .(1)求证:△ADE ≌△ABF ;(2)若BC =8,DE =6,求EF 的长.23.如图,菱形ABCD 的对角线AC BD ,交于点O ,CE BD ∥,DE AC ∥.(1)求证:四边形OCED 是矩形;(2)连接BE ,若2AC =,BD =,求BE 的长.24.如图,在矩形ABCD 中,3cm AB =,6cm BC =.点P 从点D 出发向点A 运动,运动到点A 即停止;同时,点Q 从点B 出发向点C 运动,运动到点C 即停止,点P 、Q 的速度都是1cm s .连接PQ 、AQ 、CP .设点P 、Q 运动的时间为t s .(1)当t 为何值时,四边形ABQP 是矩形,请说明理由;(2)当t 为何值时,四边形AQCP 是菱形,请说明理由;(3)直接写出(2)中菱形AQCP 的周长和面积,周长是______cm ,面积是______2cm .25.如图,在菱形ABCD 中60ABC ∠=︒,E 为对角线AC 上一点,F 是BC 延长线上一点,连接BE ,DE ,AF ,DF ,60EDF ∠=︒.(1)求证:AE CF =;(2)若点G 为BE 的中点,连接AG ,求证:2AF AG =.26.如图,在矩形ABCD 中,CD a =,E 为边CD 上一点,点P 在线段BE 上,且满足90CPD ∠=︒,延长CP 交边BA 于点M .(1)若点E 为CD 的中点,线段PE 的长为________(用含a 的代数式表示);(2)连接AP ,若AP AD =,求证AM BM =;(3)当BC =4a =时,求BP 的最小值.27.如图1,四边形ABCD 为菱形,120ABC ∠=︒.()B ,)C,()03D ,.(1)点A 坐标为,四边形ABOD 的面积为;(2)如图2,点E 在线段AC 上运动,DEF 为等边三角形.①求证:AF BE =,并求AF 的最小值;②点E 在线段AC 上运动时,点F 的横坐标是否发生变化?若不变,请求出点F 的横坐标.若变化,请说明理由.28.已知正方形ABCD ,2AB =,点E 是BC 边上的一个动点(不与B C 、重合),将EA 绕点E 顺时针旋转90︒至EF ,连接AF ,设EF 交CD 于点P ,AF 交CD 于点Q .(1)如图1,若BE DQ =,求BAE ∠的度数;(2)如图2,①点E 在BC 上运动的过程中,线段EQ BE 、与DQ 之间有怎样的数量关系,请证明你的发现;②若222BE =,求此时BAE ∠的度数.(3)如图3,连接DF ,则AF DF +的最小值是____________(直接写出答案......);第一章特殊平行四边形(单元重点综合测试)班级___________姓名___________学号____________分数____________考试范围:全章的内容;考试时间:120分钟;总分:120分一、单选题1.矩形具有而菱形不一定具有的性质是()A .对角线互相平分B .对边平行且相等C .对角线相等D .对角相等【答案】C【分析】根据矩形和菱形都是特殊的平行四边形,所以平行四边形所具有的性质,矩形和菱形都具有即可解答.【解析】解: 矩形和菱形是平行四边形,∵A 、B 、D 是二者都具有的性质,∴对角线相等是矩形具有而菱形不一定具有的性质.故选:C .【点睛】本题主要考查了矩形、菱形的性质,掌握矩形、菱形与平行四边形的关系是解答本题的关键.2.如图,正方形ABCD 的对角线相交于点O ,则AOB ∠的度数是()A .30︒B .45︒C .60︒D .90︒【答案】D【分析】直接利用正方形的性质求解即可.【解析】解:∵四边形ABCD 是正方形,∴AC BD ⊥,∴90AOB ∠=︒,故选:D .【点睛】本题考查正方形的性质,熟练掌握正方形的性质是解决问题的关键.3.已知矩形的较短边长为6,对角线相交成60°角,则这个矩形的较长边的长是()A .B .C .9D .12【解析】AB=6,∠AOB=60°,∵四边形是矩形,AC ,BD 是对角线,OA=OB=OC=OD=12BD=12AC 中,OA=OB ,∠AOB=60°4.如图,在菱形ABCD 中,对角线AC ,BD 相交于点O ,若110BAD ∠=︒,则OBC ∠的度数为()A .30︒B .35︒C .55︒D .70︒5.下面说法正确的是()A.有一组邻边相等的四边形是菱形B.对角线互相垂直的四边形是菱形C.矩形的对角线相等D.对角线互相垂直平分的四边形是正方形【答案】C【分析】根据菱形,矩形,正方形的性质和判定定理,逐个进行判断即可.【解析】解:A、有一组邻边相等的平行四边形是菱形,故A不正确,不符合题意;B、对角线互相垂直的平行四边形是菱形,故B不正确,不符合题意;C、矩形的对角线相等,故C正确,符合题意;D、对角线相等且互相垂直平分的四边形是正方形,故D不正确,不符合题意;故选:C.【点睛】本题主要考查了菱形、矩形、正方形的判定和性质,解题的关键是熟练掌握相关定理和性质.6.如图,已知菱形ABCD的对角线AC、BD的长分别为6cm、8cm,AE⊥BC于点E,则AE的长是()A.5cm B.6cm C.485cm D.245cm;【点睛】此题主要考查了菱形的性质以及勾股定理,正确得利用三角形面积求出AE 的长是解题关键.7.如图,矩形ABCD 中,AB =2,BC =4,对角线AC 的垂直平分线分别交AD 、BC 于点E 、F ,连接CE ,则△DCE 的面积为()A .52B .32C .2D .18.如图,点B 、C 分别在两条直线y kx =和6y x =-上,点A 、D 是x 轴上两点,若四边形ABCD 是正方形,则k 的值为()A .6B .5C .56D .65【答案】D 【分析】设点(),B b bk ,根据正方形的性质可得=C bk y ,再代入6y x =-求得,6bk C bk ⎛⎫- ⎪⎝⎭,再根据6==66bk bk b AD b ++,=AB bk ,列方程求解即可.【解析】解:∵点B 、C 分别在两条直线y kx =和6y x =-上,设点(),B b bk ,∵四边形ABCD 是正方形,∴AB CD BC AD ===,∴把y bk =代入6y x =-得,=6bk x -,∴,6bk C bk ⎛⎫- ⎪⎝⎭,∴6==66bk bk b AD b ++,=AB bk ,∴6=6bk b bk +,∴65k =,故选:D .9.如图,在菱形ABCD 中,∠A =60°,点E 、F 分别为AD 、DC 上的动点,∠EBF =60°,点E 从点A 向点D 运动的过程中,AE+CF 的长度().A .逐渐增加B .逐渐减小C .保持不变且与EF 的长度相等D .保持不变且与AB 的长度相等【答案】D【分析】证明△ABE ≌△DBF (AAS ),可得AE =DF ;结合图形可知:AE+CF =AB ,AB 是一定值,从而完成求解.【解析】连接BD∵四边形ABCD 是菱形,∴AB =AD =CD ,∵∠A =60°∴△ABD 是等边三角形∴AB =BD ,∠ABD =60°∵DC ∥AB∴∠CDB =∠ABD =60°∴∠A =∠CDB∵∠EBF =60°∴∠ABE+∠EBD =∠EBD+∠DBF∴∠ABE =∠DBF∵A BDF ABE DBF AB BD ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△ABE ≌△DBF (AAS )∴AE =DF∴AE+CF =DF+CF =CD =AB故选:D .【点睛】本题考察了菱形、等边三角形、全等三角形的知识;求解的关键是熟练掌握菱形、等边三角形、全等三角形的性质,从而完成求解.10.如图,在正方形ABCD 中,O 是对角线AC 与BD 的交点,M 是BC 边上的动点(点M 不与B 、C 重合),过点C 作CN 垂直DM 交AB 于点N ,连结OM 、ON 、MN .下列四个结论:①CNB DMC △≌△;②ON OM =;③ON OM ⊥;④222AN CM MN +=.其中结论正确的有()个A .1B .2C .3D .4【答案】D 【分析】本题考查正方形的性质,全等三角形的性质和判定,勾股定理应用,解题关键是全等三角形的性质和判定,根据正方形的性质,依次判定CNB DMC △≌△,OCM OBN ≌,根据全等三角形的性质以及勾股定理进行计算即可得出结论.【解析】解:①正方形ABCD 中,CD BC =,90BCD ∠=︒,90BCN DCN ∴∠+∠=︒,又CN DM ⊥ ,90CDN DCN \Ð+Ð=°,∴BCN CDM ∠=∠,90CBN DCM ∠=∠=︒ ,∴()ASA CNB DMC ≌;故①正确;②③根据CNB DMC △≌△,可得CM BN =,45OCM OBN ∠=∠=︒ ,OC OB =,()SAS OCM OBN ∴ ≌,OM ON ∴=,COM BON ∠=∠,BOM COM BOM BON ∴∠+∠=∠+∠,即90NOM BOC ∠=∠=︒,ON OM ∴⊥;故②和③正确;④AB BC = ,CM BN =,BM AN ∴=,Rt BMN 中,222BM BN MN +=,222AN CM MN ∴+=,故④正确;本题正确的结论有:①②③④;故选:D .二、填空题11.菱形ABCD 的边长为5,对角线6AC =,则菱形ABCD 的面积是.∵菱形ABCD 的边长为5,∴5AD AB DC BC ====,AC BD ⊥,又∵6AC =,∴3AO =,∴22534DO =-=,∴8BD =,∴菱形ABCD 的面积116824AC BD ==⨯⨯= .12.要使矩形ABCD 成为正方形,可添加的条件是(写一个即可).【答案】AB=BC ;BC=CD ;CD=AD ;AD=AB ;AC ⊥BD (挑选一个即可)【分析】根据正方形的判定定理进行添加即可.【解析】从边上添加:有AB=BC,BC=CD,CD=DA,DA=AB(有一组领边相等的矩形为正方形)从对角线上添加:有AC⊥BD(对角线互相垂直的矩形为正方形).故答案为:AB=BC;BC=CD;CD=AD;AD=AB;AC⊥BD(挑选一个即可)【点睛】本题考查了由矩形得到正方形的判定,熟知其判定定理是解题的关键.13.如图,E是正方形ABCD的边BC延长线上一点,且CE=AC,AE交CD于点F,则∠E=14.如图,一张长8cm,宽6cm的矩形纸片,将它沿某直线折叠使得A、C重合,则折痕EF的长为.=,由翻折可知,AF CF∥,∵AD BC∠=∠,∴OAF OCE15.如图,在矩形ABCD中,AB=8,BC=6,点P为边AB上任意一点,过点P作PE⊥AC,PF⊥BD,垂足分别为E、F,则PE+PF=.【答案】245【分析】连接OP .由勾股定理得出AC =10,可求得OA =OB =5,由矩形的性质得出S 矩形ABCD =AB •BC =48,S △AOB =14S 矩形ABCD =12,OA =OB =5,由S △AOB =S △AOP +S △BOP =12OA •PE +12OB •PF =12OA (PE +PF )=12×5×(PE +PF )=12求得答案.【解析】解:连接OP ,如图:∵四边形ABCD 是矩形,∴∠ABC =90°,OA =OC ,OB =OD ,AC =BD ,∴OA =OB ,AC =222286AB BC +=+=10,∴S 矩形ABCD =AB •BC =48,S △AOB =14S 矩形ABCD =12,OA =OB =5,∴S △AOB =S △AOP +S △BOP =12OA •PE +12OB •PF =12OA (PE +PF )=12×5×(PE +PF )=12,∴PE +PF =245;故答案为:245.【点睛】本题考查了矩形的性质、勾股定理.注意掌握辅助线的作法,注意掌握数形结合思想的应用.16.已知,矩形ABCD ,点F 在边BC 上,点E 在边AB 上,连接CE 、AF 交于点G .若12AB =,9BC =,3BE =,45AGE ∠=︒.则BF =.【答案】6【分析】过点E 作EH EC ⊥,垂足为E ,交AD 于点H ,证明AEH BCE ≌,得出EHC △是等腰直角三角形,进而得出四边形AFCH 是平行四边形,即可求解.【解析】解:如图所示,过点E 作EH EC ⊥,垂足为E ,交AD 于点H ,∵四边形ABCD 是矩形,∴90A B ∠=∠=︒,AD BC∥∴90AEH BEC BCE ∠=∠︒-=∠,∵12AB =,9BC =,3BE =,∴1239AE AB BE BC =-=-==,∴AEH BCE≌∴EH EC =,3AH BE ==,∴EHC △是等腰直角三角形,∴45HCE ∠=︒,∵45AGE ∠=︒,∴AF CH ∥,又∵AD BC ∥,∴四边形AFCH 是平行四边形,∴AH FC =,∴936BF BC FC BC BE =-=-=-=,故答案为:6.【点睛】本题考查了矩形的性质,全等三角形的性质与判定,平行四边形的性质与判定,正确的添加辅助线是解题的关键.,轴的正半轴上.点17.如图,在平面直角坐标系中,四边形OABC是边长为1的正方形,顶点,A C分别在x y=,连接CQ并延长CQ交边AB于点P,则点P的坐标为.Q在对角线OB上,且OQ OC本特征是解题关键.18.如图,矩形ABCD中,5,7==,点H在边AD上,1AD DCAH=,E为边AB上一个动点,连HE.以HE.为一边在HE的右上方作菱形HEFG,使点G落在边DC上,连结CF(1)当菱形HEFG为正方形时,DG的长为;(2)在点E的运动过程中,△FCG的面积S的取值范围为.三、解答题19.如图,在正方形ABCD 中,E 是边AB 的中点,F 是边BC 的中点,连接CE 、DF .求证:CE DF =.【答案】见详解【分析】本题考查正方形的性质、全等三角形的判定和性质,解题的关键是熟练掌握正方形的性质以及全等三角形的判定和性质,属于基础题,中考常考题型.欲证明CE DF =,只要证明CEB DFC ≌即可.【解析】证明:ABCD 是正方形,AB BC CD ∴==,90EBC FCD ∠=∠=︒,又E 、F 分别是AB 、BC 的中点,BE CF ∴=,在CEB 和DFC 中,BC CD B DCF BE CF =⎧⎪∠=∠⎨⎪=⎩,∴△≌△CEB DFC ,CE DF ∴=.20.如图,四边形ABCD 是菱形,∠ACD=30°,BD=6.求:(1)∠BAD ,∠ABC 的度数;(2)AB ,AC 的长.【答案】(1)∠BAD=60°,∠ABC=120°;(2)AB=6cm,AC=63【分析】(1)根据∠ACD=30°和菱形的性质求出AD//BC,即可得出答案;(2)根据菱形的性质求出∠DBC,然后根据三角形内角和定理求出CD即可得到AB,进而求出AC.【解析】解:(1)∵∠ACD=30°∴∠BCD=60°(菱形对角线平分对角)∴∠BAD=60°(菱形对角相等)∴AD//BC(菱形对边平行)∴∠ABC=120°(,两直线平行,同旁内角互补)(2)∵∠ABC=120°∴∠DBC=60°(菱形对角线平分对角)∵∠DBC+∠BCD+∠BDC=180°(三角形内角和为180°)∴∠DBC=∠BCD=∠BDC=60°∴BD=BC=CD=6cm∴AB=CD=6cm(菱形对边相等)∵AC⊥BD且AO=CO(菱形对角线互相垂直平分)∴AO=33(直角三角形30°角定理)∴AC=63【点睛】本题考查了菱形的性质、三角形内角和定理和30°直角三角形等知识点,能灵活运用菱形的性质进行推理是解此题的关键.21.如图,在6×6的方格纸中,请按要求作图.(1)图1中,A,B是方格纸中的格点,以AB为一边作一个矩形ABCD,要求C,D两点也在格点上;(2)图2中,E,F是方格纸中的格点,以EF为一边作一个菱形EFGH,要求G,H两点也在格点上.【答案】(1)见解析;(2)见解析【分析】(1)根据网格,以AB为边在图1中即可画一个以A,B,C,D为顶点的矩形;(2)根据网格,分别以E,F为顶点,画1×2格对角线即可在图2中作一个菱形EFGH.【解析】解:(1)如图1,四边形ABCD即为所求作的矩形;(2)如图2,四边形EFGH即为所求作的菱形;.【点睛】本题考查了作图-应用与设计作图,矩形的判定与性质,菱形的判定与性质等知识,解题的关键是理解题意,灵活运用所学知识解决问题.22.如图,四边形ABCD是正方形,E、F分别是DC和CB的延长线上的点,且DE=BF,连接AE,AF,EF.(1)求证:△ADE ≌△ABF ;(2)若BC =8,DE =6,求EF 的长.【答案】(1)见解析(2)102【分析】(1)利用正方形的性质结合全等三角形的判定与性质得出答案;(2)首先利用去等三角形的性质得出CE ,CF 的长,再利用勾股定理得出答案.【解析】(1)证明:∵四边形ABCD 是正方形,∴∠ADE =∠ABC =90°=∠ABF ,AD =AB在△ADE 和△ABF 中,AD AB D ABF DE BF =⎧⎪∠=∠⎨⎪=⎩,∴△ADE ≌△ABF (SAS );(2)解:∵△ADE ≌△ABF ,DE =6,∴BF =DE =6,∵BC =DC =8,∴CE =8﹣6=2,CF =8+6=14,在Rt △FCE 中,EF =22CF +CE =22142+=102.【点睛】此题主要考查了正方形的性质以及全等三角形的判定与性质以及勾股定理,正确应用正方形的性质是解题关键.23.如图,菱形ABCD 的对角线AC BD ,交于点O ,CE BD ∥,DE AC ∥.(1)求证:四边形OCED 是矩形;(2)连接BE ,若2AC =,BD =,求BE 的长. 112AO OC AC ∴===,∵四边形OCED 是矩形∴1ED OC BDE ==∠,24.如图,在矩形ABCD 中,3cm AB =,6cm BC =.点P 从点D 出发向点A 运动,运动到点A 即停止;同时,点Q 从点B 出发向点C 运动,运动到点C 即停止,点P 、Q 的速度都是1cm s .连接PQ 、AQ 、CP .设点P 、Q 运动的时间为t s .(1)当t 为何值时,四边形ABQP 是矩形,请说明理由;(2)当t 为何值时,四边形AQCP 是菱形,请说明理由;(3)直接写出(2)中菱形AQCP 的周长和面积,周长是______cm ,面积是______2cm .【答案】(1)当3t =时,四边形ABQP 为矩形(2)当94t =时,四边形AQCP 为菱形(3)15;454【分析】(1)根据题意用t 表示出BQ 、AP 、CQ ,根据矩形的判定定理列出方程,解方程得到答案;(2)根据邻边相等的平行四边形是菱形、勾股定理列式计算即可;(3)根据(2)中求出的t 的值,求出CQ ,根据菱形的周长公式、面积公式计算即可.【解析】(1)解:由题意得,BQ DP t ==,则6AP CQ t ==-,四边形ABCD 是矩形,90B ∴∠=︒,AD BC ∥,∴当BQ AP =时,四边形ABQP 为矩形,6t t ∴=-,解得,3t =,故当3t =时,四边形ABQP 为矩形;(2)解:由(1)可知,四边形AQCP 为平行四边形,∴当AQ CQ =时,四边形AQCP 为菱形,即2236t t +=-时,四边形AQCP 为菱形,解得,94t =,故当94t =时,四边形AQCP 为菱形;(3)解:当94t =时,1564CQ t =-=,25.如图,在菱形ABCD 中60ABC ∠=︒,E 为对角线AC 上一点,F 是BC 延长线上一点,连接BE ,DE ,AF ,DF ,60EDF ∠=︒.(1)求证:AE CF =;(2)若点G 为BE 的中点,连接AG ,求证:2AF AG =.【答案】(1)证明见解析;(2)证明见解析.【分析】(1)根据菱形的性质,得到AD=CD ,∠ABC=∠ADC=∠ACD=∠CAD=60°,然后根据等式的性质求得∠ADE=∠CDF ,从而利用ASA 定理判定三角形全等,问题得解;(2)过点B 作BH ∥AC ,交AG 的延长线于点H ,根据菱形的性质结合(1)中的结论判定△ABE ≌△ADE ≌△CDF ,利用ASA 定理判定△BHG ≌△EAG ,利用SAS 定理判定△ABH ≌△ACF ,从而得到AH=AF ,使问题得解.【解析】解:在菱形ABCD 中,∵60ABC ∠=︒∴AD=CD ,∠ABC=∠ADC=∠ACD=∠CAD=∠ACB=60°∴∠DCF=60°又∵60EDF ∠=︒∴∠ADE+∠EDC=∠CDF+∠EDC=60°∴∠ADE=∠CDF ,在△ADE 和△CDF 中ADE CDF AD CD EAD DCF ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△ADE ≌△CDF∴AE CF =;(2)过点B 作BH ∥AC ,交AG 的延长线于点H在菱形ABCD 中,∠ABE=∠ADE ,AB=AD ,AE=AE 又由(1)可知△ADE ≌△CDF∴△ABE ≌△ADE ≌△CDF∴AE=CF∵BH ∥AC ,点G 是BE 的中点∴∠H=∠GAE ,BG=EG ,∠HBG=∠ACB=60°∴∠ABH=∠ACF=120°又∵∠AGE=∠HGB∴△BHG ≌△EAG∴BH=AE=CF ,AG=GH又∵AB=AC∴△ABH ≌△ACF∴AH=AF=AG+GH=2AG即2AF AG =.【点睛】本题考查菱形的性质及三角形全等的判定,正确添加辅助线证明三角形全等是本题的解题关键.26.如图,在矩形ABCD 中,CD a =,E 为边CD 上一点,点P 在线段BE 上,且满足90CPD ∠=︒,延长CP 交边BA 于点M .(1)若点E 为CD 的中点,线段PE 的长为________(用含a 的代数式表示);(2)连接AP ,若AP AD =,求证AM BM =;(3)当2BC =4a =时,求BP 的最小值.【答案】(1)12a (2)证明过程见解析(3)232-【分析】(1)根据直角三角形的性质求解即可;(2)延长CM 、DA 交于点F ,根据等腰三角形的性质可得12∠=∠,利用等量代换可得3F ∠=∠,由等腰三角形的判定可得==AP AF AD ,再根据矩形的性质和平行线的性质可得4F ∠=∠,BC AF =,由对顶角相等得=CMB FMA ∠∠,从而证得AFM BCM ≌,即可得证;(3)取CD 的中点H ,连接BH 、PH ,根据直角三角形的性质可得1====22PH CH HD CD ,利用勾股定理求得23BH =,再根据三角形三边关系可得BP BH PH ≥-,从而可得当B 、P 、H 三点共线时,BH 的值最小,即可求解.【解析】(1)解:∵90CPD ∠=︒,点E 为CD 的中点,∴11==22PE CD a ,故答案为:12a ;(2)解:如图,延长CM 、DA 交于点F ,∵AP AD =,∴12∠=∠,∵90CPD ∠=︒,∴=13=90DPF ∠∠+∠︒,∴290F ∠+∠=︒,(3)解:如图,取CD ∴90CPD ∠=︒,∴1===2PH CH HD CD ∴()22222BH =+=又∵BP BH PH ≥-,当B 、P 、H 三点共线时,【点睛】本题考查直角三角形的性质、矩形的性质、对顶角相等、等腰三角形的判定与性质、勾股定理、三角形的三边关系、勾股定理、全等三角形的判定与性质,熟练掌握相关定理是解题的关键.27.如图1,四边形ABCD 为菱形,120ABC ∠=︒.()B ,)C ,()03D ,.(1)点A 坐标为,四边形ABOD 的面积为;(2)如图2,点E 在线段AC 上运动,DEF 为等边三角形.①求证:AF BE =,并求AF 的最小值;②点E 在线段AC 上运动时,点F 的横坐标是否发生变化?若不变,请求出点F 的横坐标.若变化,请说明理由.∴60EDF ADB ∠=∠=︒,∴ADF BDE ∠=∠.∵AD DB DF DE ==,,∴()SAS ADF BDE ≌,∴AF BE =,【点睛】本题主要考查了坐标与图形,菱形的性质,等边三角形的判定和性质,三角形全等的判定和性质,含30度角的直角三角形的性质等知识,综合性强.正确作出辅助线是解题关键.28.已知正方形ABCD ,2AB =,点E 是BC 边上的一个动点(不与B C 、重合),将EA 绕点E 顺时针旋转90︒至EF ,连接AF ,设EF 交CD 于点P ,AF 交CD 于点Q .(1)如图1,若BE DQ =,求BAE ∠的度数;(2)如图2,①点E 在BC 上运动的过程中,线段EQ BE 、与DQ 之间有怎样的数量关系,请证明你的发现;②若2BE =,求此时BAE ∠的度数.(3)如图3,连接DF ,则AF DF +的最小值是____________(直接写出答案......);∵四边形ABCD是正方形,∠=∠∴AB AD=,ABC∵四边形ABCD 是正方形,∴2AB BC ==,90B Ð=∴(222AM CE ==--∴135AME ∠=︒,∵(222EM BE ==⨯∵90AEF ∠=︒,∴90AEB CEF ∠+∠=︒,∵90AEB BAE ∠+∠=︒,∴CEF MAE ∠=∠,∵AE EF =,。
九年级上册数学第一章特殊平行四边形检测卷(北师大含答案)

九年级上册数学第一章特殊平行四边形检测卷(北师大含答案)★精品文档★九年级上册数学第一章特殊平行四边形检测卷(北师大含答案)一、选择题(每小题3分,共45分)1.下列四边形中,对角线互相垂直平分的是()a.平行四边形、菱形b.矩形、菱形c.矩形、正方形d.菱形、正方形2.在四边形abcd中,ab=bc=cd=da,如果嵌入一个条件,即可面世该四边形就是正方形,那么这个条件可以就是()a.ac⊥bdb.ab∥cdc.∠a=90°d.∠a=∠c3.若矩形的一条对角线与一边的夹角就是40°,则两条对角线平行阿芒塔的锐角就是()a.20°b.40°c.80°d.100°4.如图,在矩形abcd中,对角线ac,bd交于点o,下列说法错误的是()a.ab∥dcb.ac=bdc.ac⊥bdd.oa=oc第4题图第5题图第6题图5.如图,点p是菱形abcd对角线bd上一点,pe⊥ab于点e,且pe=2.连接pc,若菱形的周长为24.则△bcp的面积为()2021全新精品资料-全新公文范文-全程指导文学创作c独家原创1/9★精品文档★a.4b.6c.8d.126.例如图,在△abc中,bc=12,ac=5,ab=13,点d就是ab的中点,则cd的短为()a.6.5b.6c.2.5d.无法确认7.如图,已知面积为1的正方形abcd的对角线相交于点o,过点o任意作一条直线分别交ad,bc于e,f,则阴影部分的面积是()a.1b.0.5c.0.25d.无法确认第7题图第8题图第9题图8.如图,在矩形abcd中,对角线ac、bd相交于点o.若∠acb=30°,ab=2,则bd的长为()a.4b.3c.2d.19.菱形oabc在平面直角坐标系则中的边线如图所示,∠aoc=45°,点a的座标为(2,0),则点b的座标为()a.(2,1)b.(1,2)c.(1,2+1)d.(2+1,1)10.例如图,四边形abcd就是正方形,点e在对角线bd上,且be=bc,则∠ace的度数等同于()a.20°b.22.5°c.25°d.30°第10题图第11题图2021全新精品资料-全新公文范文-全程指导写作c独家原创2/9★精品文档★第12题图11.如图,在菱形abcd中,对角线ac、bd相交于点o,作oe∥ab,交bc于点e,则oe的长一定等于()a.beb.aoc.add.ob12.例如图,四边形abcd就是正方形,be⊥ef,df⊥ef,be=2.5d,df=4d,那么ef的短为()a.6.5db.6dc.5.5dd.4d13.顺次连接对角线相等的四边形各边中点所得四边形是()a.矩形b.平行四边形c.菱形d.任一四边形14.如图,将边长为2c的菱形abcd沿边ab所在的直线l翻折得到四边形abef,若∠dab=30°,则四边形cdfe的面积为()a.2c2b.3c2c.4c2d.6c2第14题图第15题图15.如图,四边形abcd为矩形纸片,把纸片abcd折叠,使点b恰好落在cd边的中点e处,折痕为af.若cd=6,则af等于()a.43b.33c.42d.8二、填空题(每小题5分,共25分)2021全新精品资料-全新公文范文-全程指导文学创作c独家原创3/9★精品文档★16.rt△abc中,如果斜边上的中线cd=4c,那么斜边ab=c.17.例如图,一个平行四边形的活动框架,对角线就是两根橡皮筋.若发生改变框架的形状,则∠α也随之变化,两条对角线长度也在出现发生改变.当∠α为度时,两条对角线长度成正比.第17题图18.矩形的对角线相交成的角中,有一个角是60°,这个角所对的边长为1c,则其对角线长为c,矩形的面积为c2.19.如图,在正方形abcd的外侧,作等边△ade,则∠bed的度数是.第19题图第20题图20.例如图,菱形abcd的边长为4,且ae⊥bc于e,af⊥cd于f,∠b=60°,则菱形abcd的面积为.三、答疑题(共80分后)21.(8分)如图,点o是菱形abcd对角线的交点,de∥ac,ce∥bd,连接oe.求证:oe=bc.22.(8分后)例如图,正方形abcd中,e为cd边上一点,f为bc延长线上一点,且ce=cf.澄清:△bce≌△dcf.2021全新精品资料-全新公文范文-全程指导写作c独家原创4/9★精品文档★23.(10分后)例如图,在矩形abcd中,对角线ac,bd平行于点o,ae⊥bd于点e,be∶ed=1∶3,ad=6c,谋ae的长.24.(12分)如图,等腰三角形abc中,ab=ac,ah⊥bc,点e是ah上一点,延长ah至点f,使fh=eh.(1)求证:四边形ebfc是菱形;(2)如果∠bac=∠ecf,求证:ac⊥cf.25.(12分后)例如图,在矩形abcd中,沿ef将矩形卷曲,并使a,c重合,点d落到点g处为,ac与ef处设点h.(1)澄清:△abe≌△agf;(2)若ab=6,bc=8,求△abe的面积.26.(14分后)未知梯形abcd中,ad∥bc,ab=ad(如图所示).(1)在右图中,用尺规并作∠bad的平分线ae交bc于点e,相连接de(留存作图痕迹,不文学创作法),并证明四边形abed就是菱形;(2)若∠abc=60°,ec=2be.求证:ed⊥dc.27.(16分后)例如图,未知△abc,直线pq垂直平分ac,与边ab处设点e,相连接ce,过点c作cf平行于ba交pq于点f,相连接af.(1)澄清:△aed≌△cfd;2021全新精品资料-全新公文范文-全程指导写作c独家原创5/9。
九年级数学上册《第一章 特殊平行四边形》单元测试卷带答案(北师大版)

九年级数学上册《第一章 特殊平行四边形》单元测试卷带答案(北师大版)学校:___________班级:___________姓名:___________考号:___________一、选择题:(本题共8小题,每小题5分,共40分.)1.对角线互相垂直平分的四边形是( )A .菱形、正方形B .矩形、菱形C .矩形、正方形D .平行四边形、菱形2.在ABC 中,点D 是边AC 的中点,连结BD 并延长到E ,使DE DB =,连结AE ,CE .则下列说法不正确的是( )A .四边形ABCE 是平行四边形B .当90ABC ∠=︒时,四边形ABCE 是矩形C .当AB BC =时,四边形ABCE 是菱形D .当AB BC CA ==时,四边形ABCE 是正方形3.如图,在矩形ABCD 中(AD >AB ),点E 是BC 上一点,且DE=DA ,AF ⊥DE ,垂足为点F ,在下列结论中,不一定正确的是( )A .△AFD ≌△DCEB .AF=12AD C .AB=AF D .BE=AD ﹣DF 4.如图,在菱形ABCD 中,点E 是AB 的中点,点F 是AC 的中点,连接EF ,如果4EF =,那么菱形ABCD 的周长为( )A .4B .8C .16D .325.如图,正方形ABCD 中,AB=6,G 是BC 的中点.将△ABG 沿AG 对折至△AFG ,延长GF 交DC 于点E ,则DE 的长是( )A .1B .1.5C .2D .2.56.如图,在菱形ABCD 中,对角线AC ,BD 分别为16和12,DE AB ⊥于点E ,则DE =( )A .485B .965C .10D .87.如图,在正方形ABCD 中,AB=4,E ,F 分别为边AB BC ,的中点,连接AF DE ,,点G ,H 分别为DE AF ,的中点,连接GH ,则GH 的长为( )A .2B .1CD .28.如图,在矩形ABCD 中,在CD 上取点E ,连接AE ,在AE ,AB 上分别取点F ,G ,连接DF ,GF ,AG GF =将ADF 沿FD 翻折,点A 落在BC 边的A '处,若//GF A D ',且3AB =,AD=5,AF 的长是( )A B C .52 D 二、填空题:(本题共5小题,每小题3分,共15分.)9.菱形的边长为5,一条对角线长为8,则此菱形的面积是 .10.如图,在ABCD 中,对角线AC BD 、相交于点O ,在不添加任何辅助线的情况下,请你加一个条件 ,使ABCD 是菱形.11.如图,点M 是正方形ABCD 内位于对角线BD 上方的一点2MAD ∠=∠,则AMD ∠的度数为 .12.如图,矩形ABCD 中,AB =4,AD =3,点E 是边BC 的中点,连接AE ,把△ABE 沿AE 对折得到△AFE ,延长AF 与CD 交于点G ,则DG 的长为 .13.如图,正方形ABCD 的边长为2,将正方形ABCD 绕点A 逆时针旋转角()α0α180︒<<︒得到正方形A B C D '''',连接D C ',当点B '恰好落在线段D C '上时,线段D C '的长度是 .(结果保留根号)三、解答题:(本题共5题,共45分)14.如图,在菱形ABCD 中,∠BAD =80°,AB 的垂直平分线交对角线AC 于点F ,点E 为垂足,连接DF ,求∠CDF 的度数.15.如图,矩形ABCD 中,AB=4,BC=10,E 在AD 上,连接BE ,CE ,过点A 作AG ∥CE ,分别交BC ,BE 于点G ,F ,连接DG 交CE 于点H .若AE=2,求证:四边形EFGH 是矩形.16.把一张矩形ABCD 纸片按如图方式折叠,使点A 与点E 重合,点C 与点F 重合(E 、F 两点均在BD 上),折痕分别为BH 、DG .(1)求证:△BHE ≌△DGF ;(2)若AB=6cm ,BC=8cm ,求线段FG 的长.17.如图,菱形ABCD的对角线AC,BD相交于点O,E是AD的中点,点F,G在AB上,EF⊥AB,OG∥EF.(1)求证:四边形OEFG是矩形;(2)若AD=10,EF=4,求BG的长.18.如图1,在正方形ABCD中,P是对角线BD上的点,点E在AB上,且PA=PE.(1)求证:PC=PE;(2)求∠CPE的度数;(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,试探究∠CPE与∠ABC之间的数量关系,并说明理由参考答案:1.A 2.D 3.B 4.D 5.C 6.A 7.C 8.A9.2410.AB BC =(答案不唯一)11.135°12.5516136214.解答:解:如图,连接BF ,在△BCF 和△DCF 中,∵CD =CB ,∠DCF =∠BCF ,CF =CF ,∴△BCF ≌△DCF ,∴∠CBF =∠CDF ,∵FE 垂直平分AB ,∠BAF = ×80°=40°∴∠ABF =∠BAF =40°,∵∠ABC =180°-80°=100°,∠CBF =100°-40°=60°,∴∠CDF =60°.15.解:∵四边形ABCD 是矩形∴∠BAD=∠ADC=90°∵AB=4,AE=2∴22AE AB +5,22DE CD +221024-+()5∴BE 2+CE 2=BC 2∴∠BEC=90°∵AG ∥CE ,AE ∥CG∴四边形AECG 是平行四边形∴CG=AE=2,5同理∠AGD=90°∵AG ∥CE∴∠EFG=∠FEH=90°∴四边形EFGH 是矩形.16.(1)证明:∵四边形ABCD 是矩形∴AB=CD ,∠A=∠C=90°,∠ABD=∠BDC∵△BEH 是△BAH 翻折而成∴∠ABH=∠EBH ,∠A=∠HEB=90°,AB=BE∵△DGF 是△DGC 翻折而成∴∠FDG=∠CDG ,∠C=∠DFG=90°,CD=DF∴∠DBH=12∠ABD ,∠BDG=12∠BDC ∴∠DBH=∠BDG∴△BEH 与△DFG 中∠HEB=∠DFG ,BE=DF ,∠DBH=∠BDG∴△BEH ≌△DFG(2)解:∵四边形ABCD 是矩形,AB=6cm ,BC=8cm∴AB=CD=6cm ,AD=BC=8cm∴22BC CD +2286+∵由(1)知,FD=CD ,CG=FG∴BF=10-6=4cm设FG=x ,则BG=8-x在Rt △BGF 中BG 2=BF 2+FG 2,即(8-x )2=42+x 2解得x=3,即FG=3cm .17.(1)解:四边形ABCD 是菱形OB OD ∴= E 是AD 的中点OE ∴是ΔABD 的中位线//OE FG ∴//OG EF∴四边形OEFG 是平行四边形EF AB ⊥90EFG ∴∠=︒∴平行四边形OEFG 是矩形;(2)解:四边形ABCD 是菱形BD AC ∴⊥ 10AB AD ==90AOD ∴∠=︒ E 是AD 的中点152OE AE AD ∴===;由(1)知,四边形OEFG 是矩形5FG OE ∴==5AE = 4EF =223AF AE EF ∴=-=10352BG AB AF FG ∴=--=--=.18.(1)证明:在正方形ABCD 中,AB=BC∠ABP=∠CBP=45°在△ABP 和△CBP 中AB BCABP CBP PB PB=⎧⎪∠=∠⎨⎪=⎩∴△ABP ≌△CBP (SAS )∴PA=PC∵PA=PE∴PC=PE ;(2)解:由(1)知,△ABP ≌△CBP ,∴∠BAP=∠BCP ,∵PA=PE ,∴∠PAE=∠PEA∴∠CPB=∠AEP∵∠AEP+∠PEB=180°,∴∠PEB+∠PCB=180°∴∠ABC+∠EPC=180°∵∠ABC=90°,∴∠EPC=90°(3)∠ABC+∠EPC=180°,理由:解:在菱形ABCD 中,AB=BC ,∠ABP=∠CBP=60°,在△ABP 和△CBP 中,AB BC ABP CBPPB PB =⎧⎪∠=∠⎨⎪=⎩ ,∴△ABP ≌△CBP (SAS ),∴∠BAP=∠BCP ,∵PA=PE∴∠DAP=∠DCP∴∠PAE=∠PEA ,∴∠CPB=∠AEP ,∵∠AEP+∠PEB=180°,∴∠PEB+∠PCB=180°,∴∠ABC+∠EPC=180°。
第1章 特殊的平行四边形单元测试卷(含解析)

绝密★启用前特殊的平行四边形单元测试卷题号一二三总分得分注意事项:1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上第Ⅰ卷(选择题)请点击修改第I卷的文字说明评卷人得分一.选择题(共10小题,每小题3分,共30分)1.已知平行四边形ABCD,下列条件中,不能判定这个平行四边形为矩形的是()A.∠A=∠B B.∠A=∠C C.AC=BD D.AB⊥BC2.菱形不具备的性质是()A.四条边都相等B.对角线一定相等C.是轴对称图形D.是中心对称图形3.如图,菱形ABCD的对角线AC、BD的长分别为6和8,则这个菱形的周长是()A.20 B.24 C.40 D.484.下列说法中,正确的是()A.两条直线被第三条直线所截,内错角相等B.对角线相等的平行四边形是正方形C.相等的角是对顶角D.角平分线上的点到角两边的距离相等5.如图,矩形ABCD中,AB=3,BC=4,EF∥DF且BE与DF之间的距离为3,则AE的长是()A.B.C.D.6.如图,在菱形ABCD中,E是AC的中点,EF∥CB,交AB于点F,如果EF=3,那么菱形ABCD的周长为()A.24 B.18 C.12 D.97.如图,点P是矩形ABCD的对角线AC上一点,过点P作EF∥BC,分别交AB,CD于E、F,连接PB、PD.若AE=2,PF=8.则图中阴影部分的面积为()A.10 B.12 C.16 D.188.如图,在正方形ABCD中,A、B、C三点的坐标分别是(﹣1,2)、(﹣1,0)、(﹣3,0),将正方形ABCD向右平移3个单位,则平移后点D的坐标是()A.(﹣6,2)B.(0,2)C.(2,0)D.(2,2)9.如图,正方形ABCD的边长为1,点E,F分别是对角线AC上的两点,EG⊥AB.EI⊥AD,FH⊥AB,FJ⊥AD,垂足分别为G,I,H,J.则图中阴影部分的面积等于()A.1 B.C.D.10.矩形ABCD与CEFG如图放置,点B,C,E共线,点C,D,G共线,连接AF,取AF 的中点H,连接GH.若BC=EF=2,CD=CE=1,则GH=()A.1 B.C.D.第Ⅱ卷(非选择题)请点击修改第Ⅱ卷的文字说明评卷人得分二.填空题(共8小题,每小题3分,共24分)11.如图,在平行四边形ABCD中,添加一个条件使平行四边形ABCD是菱形.12.若菱形两条对角线的长分别是6cm和8cm,则其面积为cm2.13.以正方形ABCD的边AD作等边△ADE,则∠BEC的度数是.14.如图,在正方形ABCD中,AB=3,点E,F分别在CD,AD上,CE=DF,BE,CF相交于点G.若图中阴影部分的面积与正方形ABCD的面积之比为2:3,则△BCG的周长为.15.如图,平面直角坐标系中,矩形OABC的顶点A(﹣6,0),C(0,2).将矩形OABC绕点O顺时针方向旋转,使点A恰好落在OB上的点A1处,则点B的对应点B1的坐标为.16.对于一个位置确定的图形,如果它的所有点都在一个水平放置的矩形内部或边上,且该图形与矩形的每条边都至少有一个公共点(如图1),那么这个矩形水平方向的边长称为该图形的宽,铅锤方向的边长称为该矩形的高.如图2,菱形ABCD的边长为1,边AB水平放置.如果该菱形的高是宽的,那么它的宽的值是.17.如图,点E、F、G分别在菱形ABCD的边AB,BC,AD上,AE=AB,CF=CB,AG=AD.已知△EFG的面积等于6,则菱形ABCD的面积等于.18.如图,在矩形ABCD中,AB=4,AD=2,点E在CD上,DE=1,点F是边AB上一动点,以EF为斜边作Rt△EFP.若点P在矩形ABCD的边上,且这样的直角三角形恰好有两个,则AF的值是.评卷人得分三.解答题(共6小题,共46分)19.(6分)如图,在▱ABCD中,E,F分别是AD,BC上的点,且DE=BF,AC⊥EF.求证:四边形AECF是菱形.20.(6分)如图,在正方形ABCD中,点E,F分别在BC,CD上,且BE=CF,求证:△ABE≌△BCF.21.(8分)在矩形ABCD中,点E在BC上,AE=AD,DF⊥AE,垂足为F.(1)求证:DF=AB;(2)若∠FDC=30°,且AB=4,求AD.22.(8分)如图,在菱形ABCD中,对角线AC与BD交于点O.过点C作BD的平行线,过点D作AC的平行线,两直线相交于点E.(1)求证:四边形OCED是矩形;(2)若CE=1,DE=2,则菱形ABCD的面积是.23.(8分)已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,连接DE交AC于点F.(1)求证:四边形ADCE为矩形;(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.(3)在(2)的条件下,若AB=AC=2,求正方形ADCE周长.24.(10分)四边形ABCD为正方形,点E为线段AC上一点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.(1)如图1,求证:矩形DEFG是正方形;(2)若AB=2,CE=,求CG的长度;(3)当线段DE与正方形ABCD的某条边的夹角是30°时,直接写出∠EFC的度数.参考答案与试题解析1.解:A、∠A=∠B,∠A+∠B=180°,所以∠A=∠B=90°,可以判定这个平行四边形为矩形,正确;B、∠A=∠C不能判定这个平行四边形为矩形,错误;C、AC=BD,对角线相等,可推出平行四边形ABCD是矩形,故正确;D、AB⊥BC,所以∠B=90°,可以判定这个平行四边形为矩形,正确;故选:B.2.解:菱形的四条边相等,是轴对称图形,也是中心对称图形,对角线垂直不一定相等,故选:B.3.解:由菱形对角线性质知,AO=AC=3,BO=BD=4,且AO⊥BO,则AB==5,故这个菱形的周长L=4AB=20.故选:A.4.解:A、两条平行线被第三条直线所截,内错角才相等,错误,故本选项不符合题意;B、对角线相等的四边形是矩形,不一定是正方形,错误,故本选项不符合题意;C、相等的角不一定是对顶角,错误,故本选项不符合题意;D、角平分线上的点到角的两边的距离相等,正确,故本选项符合题意;故选:D.5.解:如图所示:过点D作DG⊥BE,垂足为G,则GD=3.∵∠A=∠G,∠AEB=∠GED,AB=GD=3,∴△AEB≌△GED.∴AE=EG.设AE=EG=x,则ED=4﹣x,在Rt△DEG中,ED2=GE2+GD2,x2+32=(4﹣x)2,解得:x=.故选:C.6.解:∵E是AC中点,∵EF∥BC,交AB于点F,∴EF是△ABC的中位线,∴EF=BC,∴BC=6,∴菱形ABCD的周长是4×6=24.故选:A.7.解:作PM⊥AD于M,交BC于N.则有四边形AEPM,四边形DFPM,四边形CFPN,四边形BEPN都是矩形,∴S△ADC =S△ABC,S△AMP=S△AEP,S△PBE=S△PBN,S△PFD=S△PDM,S△PFC=S△PCN,∴S△DFP =S△PBE=×2×8=8,∴S阴=8+8=16,故选:C.8.解:∵在正方形ABCD中,A、B、C三点的坐标分别是(﹣1,2)、(﹣1,0)、(﹣3,0),∴D(﹣3,2),∴将正方形ABCD向右平移3个单位,则平移后点D的坐标是(0,2),故选:B.9.解:∵四边形ABCD是正方形,∴直线AC是正方形ABCD的对称轴,∵EG⊥AB.EI⊥AD,FH⊥AB,FJ⊥AD,垂足分别为G,I,H,J.∴根据对称性可知:四边形EFHG的面积与四边形EFJI的面积相等,∴S阴=S正方形ABCD=,故选:B.10.解:如图,延长GH交AD于点P,∵四边形ABCD和四边形CEFG都是矩形,∴∠ADC=∠ADG=∠CGF=90°,AD=BC=2、GF=CE=1,∴AD∥GF,∴∠GFH=∠PAH,又∵H是AF的中点,∴AH=FH,在△APH和△FGH中,∵,∴△APH≌△FGH(ASA),∴AP=GF=1,GH=PH=PG,∴PD=AD﹣AP=1,∵CG=2、CD=1,∴DG=1,则GH=PG=×=,故选:C.11.解:当AB=BC或AC⊥BD时,四边形ABCD是菱形.故答案为AB=BC或AC⊥BD.12.解:∵菱形的两条对角线分别是6cm和8cm,∴这个菱形的面积是:×6×8=24(cm2).故答案为:24.13.解:如图1,∵四边形ABCD为正方形,△ADE为等边三角形,∴AB=BC=CD=AD=AE=DE,∠BAD=∠ABC=∠BCD=∠ADC=90°,∠AED=∠ADE=∠DAE=60°,∴∠BAE=∠CDE=150°,又AB=AE,DC=DE,∴∠AEB=∠CED=15°,则∠BEC=∠AED﹣∠AEB﹣∠CED=30°.如图2,∵△ADE是等边三角形,∴AD=DE,∵四边形ABCD是正方形,∴AD=DC,∴DE=DC,∴∠CED=∠ECD,∴∠CDE=∠ADC﹣∠ADE=90°﹣60°=30°,∴∠CED=∠ECD=(180°﹣30°)=75°,∴∠BEC=360°﹣75°×2﹣60°=150°.故答案为:30°或150°.14.解:∵阴影部分的面积与正方形ABCD的面积之比为2:3,∴阴影部分的面积为×9=6,∴空白部分的面积为9﹣6=3,由CE=DF,BC=CD,∠BCE=∠CDF=90°,可得△BCE≌△CDF,∴△BCG的面积与四边形DEGF的面积相等,均为×3=,设BG=a,CG=b,则ab=,又∵a2+b2=32,∴a2+2ab+b2=9+6=15,即(a+b)2=15,∴a+b=,即BG+CG=,∴△BCG的周长=+3,故答案为:+3.15.解:连接OB1,作B1H⊥OA于H,由题意得,OA=6,AB=OC=2,则tan∠BOA==,∴∠BOA=30°,∴∠OBA=60°,由旋转的性质可知,∠B1OB=∠BOA=30°,∴∴∠B1OH=60°,在△AOB和△HB1O,,∴△AOB≌△HB1O,∴B1H=OA=6,OH=AB=2,∴点B1的坐标为(﹣2,6),故答案为:(﹣2,6).16.解:在菱形上建立如图所示的矩形EAFC,设AF=x,则CF=x,在Rt△CBF中,CB=1,BF=x﹣1,由勾股定理得:BC2=BF2+CF2,,解得:x=或0(舍),即它的宽的值是,故答案为:.17.解:在CD上截取一点H,使得CH=CD.连接AC交BD于O,BD交EF于Q,EG 交AC于P.∵=,∴EG∥BD,同法可证:FH∥BD,∴EG∥FH,同法可证EF∥GF,∴四边形EFGH是平行四边形,∵四边形ABCD是菱形,∴AC⊥BD,∴EF⊥EG,∴四边形EFGH是矩形,易证点O在线段FG上,四边形EQOP是矩形,=6,∵S△EFG=3,即OP•OQ=3,∴S矩形EQOP∵OP:OA=BE:AB=2:3,∴OA=OP,同法可证OB=3OQ,=•AC•BD=×3OP×6OQ=9OP×OQ=27.∴S菱形ABCD故答案为27.18.解:∵△EFP是直角三角形,且点P在矩形ABCD的边上,∴P是以EF为直径的圆O与矩形ABCD的交点,①当AF=0时,如图1,此时点P有两个,一个与D重合,一个交在边AB上;②当⊙O与AD相切时,设与AD边的切点为P,如图2,此时△EFP是直角三角形,点P只有一个,当⊙O与BC相切时,如图4,连接OP,此时构成三个直角三角形,则OP⊥BC,设AF=x,则BF=P1C=4﹣x,EP1=x﹣1,∵OP∥EC,OE=OF,∴OG=EP1=,∴⊙O的半径为:OF=OP=,在Rt△OGF中,由勾股定理得:OF2=OG2+GF2,∴,解得:x=,∴当1<AF<时,这样的直角三角形恰好有两个,③当AF=4,即F与B重合时,这样的直角三角形恰好有两个,如图5,综上所述,则AF的值是:0或1<AF或4.故答案为:0或1<AF或4.19.证明:∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC,∵DE=BF,∴AE=CF,∵AE∥CF,∴四边形AECF是平行四边形,∵AC⊥EF,∴四边形AECF是菱形.20.证明:∵四边形ABCD是正方形,∴AB=BC,∠ABE=∠BCF=90°,在△ABE和△BCF中,,∴△ABE≌△BCF.21.证明:(1)在矩形ABCD中,∵AD∥BC,∴∠AEB=∠DAF,又∵DF⊥AE,∴∠DFA=90°,∴∠DFA=∠B,又∵AD=EA,∴△ADF≌△EAB,∴DF=AB.(2)∵∠ADF+∠FDC=90°,∠DAF+∠ADF=90°,∴∠FDC=∠DAF=30°,∴AD=2DF,∵DF=AB,∴AD=2AB=8.22.(1)证明:∵四边形ABCD是菱形,∴AC⊥BD,∴∠COD=90°.∵CE∥OD,DE∥OC,∴四边形OCED是平行四边形,又∠COD=90°,∴平行四边形OCED是矩形;(2)由(1)知,平行四边形OCED是矩形,则CE=OD=1,DE=OC=2.∵四边形ABCD是菱形,∴AC=2OC=4,BD=2OD=2,∴菱形ABCD的面积为:AC•BD=×4×2=4.故答案是:4.23.(1)证明:∵AB=AC,AD⊥BC,垂足为点D,∴∠CAD=∠BAC.∵AN是△ABC外角∠CAM的平分线,∴∠CAE=∠CAM.∵∠BAC与∠CAM是邻补角,∴∠BAC+∠CAM=180°,∴∠CAD+∠CAE=(∠BAC+∠CAM)=90°.∵AD⊥BC,CE⊥AN,∴∠ADC=∠CEA=90°,∴四边形ADCE为矩形;(2)∠BAC=90°且AB=AC时,四边形ADCE是一个正方形,证明:∵∠BAC=90°且AB=AC,AD⊥BC,∴∠CAD=∠BAC=45°,∠ADC=90°,∴∠ACD=∠CAD=45°,∴AD=CD.∵四边形ADCE为矩形,∴四边形ADCE为正方形;(3)解:由勾股定理,得=AB,AD=CD,即AD=2,AD=2,正方形ADCE周长4AD=4×2=8.24.(1)证明:作EP⊥CD于P,EQ⊥BC于Q,∵∠DCA=∠BCA,∴EQ=EP,∵∠QEF+∠FEC=45°,∠PED+∠FEC=45°,∴∠QEF=∠PED,在Rt△EQF和Rt△EPD中,,∴Rt△EQF≌Rt△EPD,∴EF=ED,∴矩形DEFG是正方形;(2)如图2中,在Rt△ABC中.AC=AB=2,∵EC=,∴AE=CE,∴点F与C重合,此时△DCG是等腰直角三角形,易知CG=.(3)①当DE与AD的夹角为30°时,∠EFC=120°,②当DE与DC的夹角为30°时,∠EFC=30°综上所述,∠EFC=120°或30°.。
(好题)初中数学九年级数学上册第一单元《特殊平行四边形》检测卷(包含答案解析)
一、选择题1.如图,依据尺规作图的痕迹,则α∠是( )A .54°B .36°C .28°D .72° 2.正方形具有而矩形没有的性质是( ) A .对角线互相平分B .每条对角线平分一组对角C .对角线相等D .对边相等3.如图,在矩形ABCD 中,点E 在DC 上,将矩形沿AE 折叠,使点D 落在BC 边上的点F 处.若AB =3,BC =5,则DE 的长为( )A .12B .53C .25D .134.如图,在矩形ABCD 中,23,4AB BC ==,E 为BC 的中点,连接,,,AE DE P Q 分别是,AE DE 上的点,且PE DQ =.设EPQ ∆的面积为y ,PE 的长为x ,则y 关于x 的函数关系式的图象大致是 ( )A .B .C .D .5.如图,将等边ABC 与正方形DEFG 按图示叠放,其中D ,E 两点分别在AB ,BC 上,且BD BE =.若6AB =,2DE =,则EFC 的面积为( )A .4B .23C .2D .16.如图,在正方形ABCD 中,E F 、分别在CD AD 、边上,且CE DF =,连接BE CF 、相交于G 点.则下列结论:①BE CF =;②BCG DFGE S S ∆=四边形;③2CG BG GE =⋅;④当E 为CD 中点时,连接DG ,则45FGD ∠=︒;正确结论的个数是( )A .1B .2C .3D .47.已知菱形ABCD 的对角线AC ,BD 相交于点O ,8AC =,6BD =,则菱形ABCD 的周长为( )A .30B .20C .15D .128.如图,Rt △ABC 中,∠ACB =90°,AC =6,BC =8,D 是AB 的中点,E 是BC 的中点,EF ⊥CD 于点F ,则EF 的长是( )A .3B .4C .5D .125 9.如图,四边形ABCD 中,∠BAD =∠C =90°,AB =AD ,AE ⊥BC ,垂足是E ,若线段AE =4,则四边形ABCD 的面积为( )A .12B .16C .20D .2410.如图,在等腰直角三角形ABC 中,90ABC ∠=︒,2AB =,点D 是边AC 的中点,连接BD ,点E 为AC 延长线上的一点,连接BE ,30E ∠=︒,则CE 的长为( )A .2622-B .62-C .6D .211.如图,将n 个边长都为2的正方形按如图所示摆放,点A 1,A 2,…A n 分别是正方形的中心,则这n 个正方形重叠部分的面积之和是( )A .nB .n -1C .(14)n -1D .14n 12.如图,AB AF ⊥,EF AF ⊥,BE 与AF 交于点C ,点D 是BC 的中点,2AEB B ∠=∠.若8BC =,7EF =AF 的长是( )A .6B .7C .3D .5二、填空题13.如图,AC 是菱形ABCD 的对角线,P 是AC 上的一个动点,过点P 分别作AB 和BC 的垂线,垂足分别是点F 和E ,若菱形的周长是12cm ,面积是6cm 2,则PE +PF 的值是_____cm .14.如图,将正方形OABC 放在平面直角坐标系中,O 是原点,A 的坐标为(1,3),则点C 的坐标为______.15.我国古代数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的三角形,如图所示,已知∠A =90°,正方形ADOF 的面积为4, CF =6,则BD 的长是_______.16.请你写出一个原命题与它的逆命题都是真命题的命题____________________ . 17.如图,四边形ABCD 中,30,120B D ∠=︒∠=︒,且,6AB AC AD CD ⊥+=,则四边形ABCD 周长的最小值是_______________________.18.如图,矩形ABCD 中,AC 与BD 交于点O ,BE AC ⊥于点E ,DF 平分ADC ∠,交EB 的延长线于点F ,3BC =,6CD =,则BE BF=_________.19.如图,在矩形ABCD 纸片中,点E 是BC 边的中点,沿直线AE 折叠,点B 落在矩形内部的点B '处,连接AB '并延长交CD 于点F .已知4CF =,5DF =,则AD 的长为__________.20.如图,在正方形ABCD 中,已知2AB =,点,E G 分别是边,AD CD 的中点,点F 是边BC 上的动点,连接EF ,将正方形ABCD 沿EF 折叠,,A B 的对应点分别为,A B '',则线段GB '的最小值是_____.三、解答题21.我们可以沿直角三角形纸片的斜边中线把它剪成两个等腰三角形.(初步思考)(1)任意三角形纸片都可以剪成4个等腰三角形,在图①中画出分割线,并作适当的标注;(深入思考)(2)任意三角形纸片都可以剪成5个等腰三角形,在图②中画出分割线,并作适当的标注;(回顾反思)(3)在把一个三角形纸片剪成5个等腰三角形时,我们发现图②中的分割方法不能用于等边三角形.因此,我们需要为等边三角形想一种分割方案,请在图③中画出分割线,并作适当的标注;(4)我们发现,不是所有三角形纸片都能剪成3个等腰三角形.当∠A=110°,∠B为多少度时,△ABC能被剪成3个等腰三角形,请画出两种分割方案,并标注∠B和∠C的度数.22.△ABC是等腰三角形,其中AB=BC,将△ABC绕顶点B逆时针旋转50°到△A1BC1的位置,AB与A1C1相交于点D,AC与A1C1,BC1分别相交于点E,F.(1)求证:△BCF≌△BA1D;(2)当∠C=50°时,判断四边形A1BCE的形状并说明理由.23.在△ABC中,AB=AC,∠BAC=90°,点D在射线BC上(与B、C两点不重合),以AD为边作正方形ADEF,使点E与点B在直线AD的异侧,射线BA与直线CF相交于点G.(1)若点D 在线段BC 上,如图(1),判断:线段BC 与线段CG 的数量关系 ,位置关系 ;(2)如图(2),①若点D 在线段BC 的延长线上,(1)中判断线段BC 与线段CG 的数量关系与位置关系是否仍然成立,并说明理由;②当G 为CF 中点,BC =2时,求线段AD 的长.24.如图,在平行四边形ABCD 中,E ,F 分别是AD ,BC 上的点,且DE BF =,AC EF ⊥.求证:四边形AECF 是菱形.25.如图,ABC ∆在坐标系的网格中,且三点均在格点上.(1)C 点的坐标为 ;(2)作ABC ∆关于y 轴的对称三角形111A B C ∆;(3)取11B C 的中点D ,连接A 1D ,则A 1D 的长为 .26.如图,点O是线段AB上的一点,OA=OC,OD平分∠AOC交AC于点D,OF平分∠COB,CF⊥OF于点F.求证:四边形CDOF是矩形.【参考答案】***试卷处理标记,请不要删除一、选择题1.A解析:A【分析】先根据矩形的性质得出AD∥BC,故可得出∠DAC的度数,由角平分线的定义求出∠EAF的度数,再由EF是线段AC的垂直平分线得出∠AEF的度数,根据三角形内角和定理得出∠AFE的度数,进而可得出结论.【详解】解:如图,∵四边形ABCD是矩形,∴AD∥BC,∴∠DAC=∠ACB=72°.∵由作法可知,AF是∠DAC的平分线,∠DAC=36°.∴∠EAF=12∵由作法可知,EF是线段AC的垂直平分线,∴∠AEF=90°,∴∠AFE=90°-36°=54°,∴∠α=54°.故选:A.【点睛】本题考查的是作图-基本作图,熟知角平分线及线段垂直平分线的作法是解答此题的关键.解析:B【分析】首先要知道正方形和矩形的性质,正方形是四边相等的矩形,正方形对角线平分对角,且对角线互相垂直.【详解】解:A、正方形和矩形对角线都互相平分,故A不符合题意,B、正方形对角线平分对角,而矩形对角线不平分对角,故B符合题意,C、正方形和矩形对角线都相等,故C不符合题意,D、正方形和矩形的对边都相等,故D不符合题意.故选:B.【点睛】本题主要考查正方形对角线相互垂直平分相等的性质和长方形对角线平分相等性质的比较.3.B解析:B【分析】先根据矩形的性质得AD=BC=5,AB=CD=3,再根据折叠的性质得AF=AD=5,EF=DE,在Rt△ABF中,利用勾股定理计算出BF=4,则CF=BC﹣BF=1,设CE=x,则DE=EF=3﹣x,然后在Rt△ECF中根据勾股定理得到x2+12=(3﹣x)2,解方程即可得到DE的长.【详解】解:∵四边形ABCD为矩形,∴AD=BC=5,AB=CD=3,∵矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上的F处,∴AF=AD=5,EF=DE,在Rt△ABF中,BF4,∴CF=BC﹣BF=5﹣4=1,设CE=x,则DE=EF=3﹣x,在Rt△ECF中,CE2+FC2=EF2,∴x2+12=(3﹣x)2,解得x=43,∴DE=3﹣x=53,故选:B.【点睛】本题考查了翻折变换、矩形的性质、勾股定理等知识,属于常考题型,灵活运用这些性质进行推理与计算是解题的关键.解析:C【分析】过点P 作PH ED ⊥于点H ,用勾股定理求出AE=DE=4,可得ADE ∆为等边三角形,用x 表示出PE 和EQ 的长,在Rt PEH 中利用三角函数用含x 的式子表示出PH 的长,再利用12S EQ PH =⋅△PEQ 可列出y 与x 的函数关系,在结合二次函数性质即可解答. 【详解】∵4BC =,E 为BC 的中点,∴2BE =.在Rt ABE ∆中,23,2AB BE ==,则4AE =,同理可得4ED AE AD ===,故ADE ∆为等边三角形,则60AED ︒∠=, ∵PE QD x ==,∴4QE x =-,如图,在PQE ∆中,过点P 作PH ED ⊥于点H .3·sin ?sin 60PH PE AED x x =∠=︒=, ∴()21133432224y PH EQ x x x x ==⨯⨯-=-+ 因此该函数的图象为开口向下的抛物线,当32232b x a =-==-⨯时,y 有最大值3.故选C .【点睛】本题考查了等边三角形的判定和性质,矩形的性质,三角函数解直角三角形,二次函数的性质,解题关键是用含x 的式子表示出PQE ∆的底和高,列出y 与x 的函数关系. 5.C解析:C【分析】过F 作FQ ⊥BC 于Q ,根据等边三角形的性质和判定和正方形的性质求出BE =2,∠BED =60°,∠DEF =90°,EF =2,求出∠FEQ ,求出CE 和FQ ,即可求出答案.【详解】过F作FQ⊥BC于Q,则∠FQE=90°,∵△ABC是等边三角形,AB=6,∴BC=AB=6,∠B=60°,∵BD=BE,DE=2,∴△BED是等边三角形,且边长为2,∴BE=DE=2,∠BED=60°,∴CE=BC−BE=4,∵四边形DEFG是正方形,DE=2,∴EF=DE=2,∠DEF=90°,∴∠FEC=180°−60°−90°=30°,∴QF=12EF=1,∴△EFC的面积=12×CE×FQ=12×4×1=2,故选:C.【点睛】本题考查了等边三角形的性质和判定、正方形的性质等知识点,能求出CE和FQ的长度是解此题的关键.6.D解析:D【分析】证明△BCE≌△CDF可判断①;利用△BCE≌△CDF可得S△BCE=S△CDF,从而可判断②;证明△BCG∽△CEG得CG GEBG CG=,可判断③;过D作DM⊥FG于M,证明MD=MG即可判断④,从而可得结论.【详解】解:∵四边形ABCD是正方形∴BC=CD,∠BCE=∠CDF又CE=DF∴△BCE≌△CDF∴BE CF=,故①正确;②∵△BCE ≌△CDF∴S △BCE =S △CDF ,∴S △BCE -S △CGE =S △CDF -S △CG ,∴BCG DFGE S S ∆=四边形;③∵△BCE ≌△CDF∴∠CBE=∠FCD∵∠BCG+90GCE ∠=︒,∴∠90BCG CBG +∠=︒∴∠90BGC =︒又∵∠BGC=∠CGE=90°,∠GBC=∠GCE∴△BCG ∽△CEG ∴CG GE BG CG=, ∴2CG BG GE =⋅,故③正确;④过D 作DM ⊥FG 于M ,如图所示,设DF=a ,则AD=2a∵CE=DF ∴225BE BC CE a =+=利用面积法可得1122BC CE BE CG = ∴255CG a = 同理可得,255DM a = ∴225FM DF DM =-=∴255a ∴MD=MG∵∠DMG=90° ∴45FGD ∠=︒,故④正确∴正确的结论有4个,【点睛】此题主要考查了运用正方形的有关性质进行讲明和求解,熟练掌握正方形的性质是解答此题的关键.7.B解析:B【分析】由菱形的性质,得到AC ⊥BD ,4AO =,3BO =,然后利用勾股定理求出AB=5,即可求出周长.【详解】解:∵四边形ABCD 是菱形,∴AC ⊥BD ,118422AO AC ==⨯=,116322BO BD ==⨯=; 在直角△ABO 中,由勾股定理,得 22435AB ,∴菱形的周长为:4520⨯=;故选:B .【点睛】本题考查了菱形的性质,勾股定理的应用,解题的关键是掌握菱形的性质进行解题. 8.D解析:D【分析】根据勾股定理得出AB ,进而利用直角三角形的性质得出:BD=DC=AD=5,利用三角形面积公式解答即可.【详解】∵在Rt △ABC 中,∠ACB =90°,AC =6,BC =8,∴10AB =,∵D 是AB 的中点,∴BD=DC=AD=5,1116812222BDC BAC SS ==⨯⨯⨯=, 连接DE ,∵E 是BC 的中点,∴162DEC BDC SS ==, ∵115622DEC S DC EF EF ==⨯⨯= ∴125EF =【点睛】本题主要考查的是勾股定理,直角三角形斜边上的中线,关键是根据勾股定理解出AB ,进而利用直角三角形的性质解答.9.B解析:B【分析】延长CD ,作AF CD ⊥的延长线于点F ,构造出全等三角形,()ABE ADF AAS ≅,即可得到四边形ABCD 的面积就等于正方形AECF 的面积.【详解】解:如图,延长CD ,作AF CD ⊥的延长线于点F ,∵AE BC ⊥,∴90AEC AEB ∠=∠=︒,∵AF CD ⊥,∴90AFC ∠=︒,∵90C ∠=︒,∴四边形AECF 是矩形,∴90EAF ∠=︒,∵BAD EAF ∠=∠,∴BAD EAD EAF EAD ∠-∠=∠-∠,即BAE DAF ∠=∠,在ABE △和ADF 中,BAE DAF AEB AFD AB AD ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴()ABE ADF AAS ≅,∴AE AF =,∴四边形AECF 是正方形,∵ABE ADF S S ,∴216ABCD AECF S S AE ===.故选:B .【点睛】本题考查全等三角形的性质和判定,正方形的性质和判定,解题的关键是作辅助线构造全等三角形.10.B解析:B【分析】根据等腰直角三角形和三角形内角和性质,得45A ACB ∠=∠=︒,即AB BC =,再根据勾股定理的性质计算,得AC ;根据直角三角形斜边中线的性质,得AD CD BD ==;结合30E ∠=︒,根据含30角的直角三角形的性质,得BE ,最后根据勾股定理计算,即可得到答案.【详解】∵ABC 是等腰直角三角形,2AB =∴90ABC ∠=︒,∴45A ACB ∠=∠=︒,∴2AB BC == ,∴AC ==∵ABC 是等腰直角三角形,D 是AC 的中点, ∴AD CD BD ===90BDC ∠=︒, ∵30E ∠=︒, ∴2BE BD == ,∴DE == ∴CE DE CD =-=故选:B .【点睛】本题考查了等腰三角形、三角形内角和、勾股定理、直角三角形的知识;解题的关键是熟练掌握等腰三角形、三角形内角和、勾股定理、直角三角形的性质,从而完成求解. 11.B解析:B【分析】过中心作阴影另外两边的垂线可构建两个全等三角形(ASA ),由此可知阴影部分的面积是正方形的面积的14,已知两个正方形可得到一个阴影部分,则n 个这样的正方形重叠部分即为(n -1)个阴影部分的和,即可求解.如图作正方形边的垂线,由ASA 可知同正方形中两三角形全等, 利用割补法可知一个阴影部分面积等于正方形面积的14 , 即是12214⨯⨯=, n 个这样的正方形重叠部分(阴影部分)的面积和为:()111n n ⨯-=-.故选:B .【点睛】本题考查了正方形的性质、全等三角形的判定与性质.解题的关键是得到n 个这样的正方形重叠部分(阴影部分)的面积和的计算方法,难点是求得一个阴影部分的面积. 12.C解析:C【分析】根据直角三角形的性质和等腰三角形的判定和性质即可得到结论.【详解】∵AB ⊥AF ,∴∠FAB=90°,∵点D 是BC 的中点,∴AD=BD=12BC=4, ∴∠DAB=∠B , ∴∠ADE=∠B+∠BAD=2∠B ,∵∠AEB=2∠B ,∴∠AED=∠ADE ,∴AE=AD ,∴AE=AD=4,∵7,EF ⊥AF ,∴()222247AE EF -=-=3,故选:C .本题考查了直角三角形斜边中线的性质,三角形的外角性质,等腰三角形的判定和性质,勾股定理,正确的识别图形是解题的关键.二、填空题13.2【分析】连接BP 根据菱形的面积公式和三角形的面积公式得S △ABC =S △ABP +S △BPC =S △ABP +S △BPC =AB•PE +BC•PE 把相应的值代入即可【详解】解:连接BP ∵四边形ABCD 是菱形解析:2【分析】连接BP ,根据菱形的面积公式和三角形的面积公式得S △ABC =S △ABP +S △BPC =12ABCD S 菱形,S △ABP +S △BPC =12AB•PE +12BC•PE 把相应的值代入即可. 【详解】解:连接BP ,∵ 四边形ABCD 是菱形,且周长是12cm ,面积是6cm 2∴AB =BC =14×12=3(cm ), ∵AC 是菱形ABCD 的对角线, ∴ S △ABC =S △ABP +S △BPC =12ABCD S 菱形=3(cm 2), ∴S △ABP +S △BPC =12AB•PE +12BC•PE =3(cm 2), ∴12×3×PE +12×3×PF =3, ∴PE +PF =3×23=2(cm ), 故答案为:2.【点睛】 此题考查菱形的性质,S △ABP +S △BPC =S △ABC =12ABCDS 菱形是解题的关键.注意掌握辅助线的作法和数形结合思想的应用.14.【分析】如图作AF ⊥x 轴于FCE ⊥x 轴于E 先证明△COE ≌△OAF 推出CE =OFOE =AF 由此即可解决问题【详解】解:如图作AF ⊥x 轴于FCE ⊥x 轴于E ∵四边形ABCO 是正方形∴OA =OC ∠AOC = 解析:()3,1-【分析】如图作AF ⊥x 轴于F ,CE ⊥x 轴于E ,先证明△COE ≌△OAF ,推出CE =OF ,OE =AF ,由此即可解决问题.【详解】解:如图作AF ⊥x 轴于F ,CE ⊥x 轴于E .∵四边形ABCO 是正方形,∴OA =OC ,∠AOC =90°,∵∠COE +∠AOF =90°,∠AOF +∠OAF =90°,∴∠COE =∠OAF ,在△COE 和△OAF 中,CEO AFO COE OAF OC OA ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△COE ≌△OAF , ∴CE =OF ,OE =AF ,∵A (13∴CE =OF =1,OE =AF 3∴点C 坐标()3,1-, 故答案为:()3,1-.【点睛】 本题考查全等三角形的判定与性质,作出辅助线构造全等三角形是解题的关键. 15.4【分析】根据正方形的性质可得AD=AF=2设BD=x 由全等三角形的性质可得CE=6BC=6+x 然后根据勾股定理可以求得BD 的长【详解】解:∵正方形ADOF 的面积为4∴AD=AF=2设BD=x 则AB解析:4【分析】根据正方形的性质可得AD=AF=2,设BD=x,由全等三角形的性质可得CE=6,BC=6+x,然后根据勾股定理可以求得BD的长.【详解】解:∵正方形ADOF的面积为4,∴AD=AF=2,设BD=x,则AB=x+2,∵△BDO≌△BEO,△CEO≌△CFO,∴BD=BE,CF=CE,∴CE=6,BC=6+x,∵∠A=90°,∴AB2+AC2=BC2,∴ (x+2)2+82=(x+6)2,解得,x=4,即BD=4,故答案为:4.【点睛】本题考查正方形的性质、全等三角形的性质、勾股定理,解答本题的关键是明确题意,利用数形结合的思想解答.16.对角线互相平分且相等的四边形是矩形(答案不唯一)【分析】命题由题设和结论两部分组成题设是已知事项结论是由已知事项推出的事项;题设成立结论也成立的叫真命题而题设成立结论不成立的为假命题把一个命题的题设解析:对角线互相平分且相等的四边形是矩形(答案不唯一)【分析】命题由题设和结论两部分组成.题设是已知事项,结论是由已知事项推出的事项;题设成立,结论也成立的叫真命题,而题设成立,结论不成立的为假命题,把一个命题的题设和结论互换即可得到其逆命题.【详解】解:如命题:对角线互相平分且相等的四边形是矩形,真命题,逆命题是矩形的对角线互相平分且相等,真命题,故答案为:对角线互相平分且相等的四边形是矩形(答案不唯一).【点睛】本题考查了命题与定理:判断事物的语句叫命题;题设与结论互换的两个命题互为逆命题;正确的命题叫真命题,错误的命题叫假命题.17.【分析】延长AD至点E使得连接CE过点C作证明△CDE为等边三角形分别求出四边形ABCD的边长判断即可;【详解】如图所示延长AD至点E使得连接CE过点C作∵∴又∵∴△CDE为等边三角形∴设则∵∴则∴解析:15【分析】延长AD 至点E ,使得DE CD =,连接CE ,过点C 作CH AE ⊥,证明△CDE 为等边三角形,分别求出四边形ABCD 的边长判断即可;【详解】如图所示,延长AD 至点E ,使得DE CD =,连接CE ,过点C 作CH AE ⊥,∵120ADC =∠︒,∴180********EDC ADC ∠=︒-∠=︒-︒=︒,又∵DE CD =,∴△CDE 为等边三角形,∴CD DE CE ==,60E ∠=︒,设CE x =,则CD DE x ==,∵CH DE ⊥,∴9030ECH E ∠=︒-∠=︒, 则1122EH CE x ==, ∴=+-=+-=-11622AH AD DE EH AD CD x x , 22221342CH CE EH x x x =-=-=, ∴()⎛⎫=+=-+=-+≥ ⎪⎝⎭222221363273324AC AH CH x x x , ∴当3x =时,AC 取得最小值为33 此时,3AD CD x ===,∵AB AC ⊥,∴90BAC =︒,又30B ∠=︒, ∴12AC BC =,即2BC AC =,AB ===,∴四边形ABCD 周长AD CD AB BC=+++, ()2AD CD AC =+++, ))626215AC =++≥++⨯=+;∴四边形ABCD 的最小值为15+故答案是15+【点睛】本题主要考查了四边形综合,等边三角形的判定和性质,含30度角的直角三角形的性质,勾股定理等知识,解答本题的关键是明确题意,找出所求问题需要的条件.18.【分析】由矩形的性质可得结合角平分线的定义可求得可证明结合矩形的性质可得根据三角形的面积公式得到于是得到结论【详解】解:四边形为矩形设与相交于点平分又又故答案为:【点睛】本题主要考查矩形的性质掌握矩 解析:25【分析】由矩形的性质可得2COB CDO ∠=∠,EBO BDF F ∠=∠+∠,结合角平分线的定义可求得F BDF ∠=∠,可证明BF BD =,结合矩形的性质可得AC BF =,根据三角形的面积公式得到BE ,于是得到结论.【详解】 解:四边形ABCD 为矩形,设DF 与AC 相交于点M ,AC BD ∴=,90ADC ∠=︒,OA OD =,6AB CD ==,3AD BC ==, DF 平分ADC ∠,ADG AGD ∴∠=∠,又CDB CAB ∠=∠,CMF CAB DGA ∠=∠+∠,CMF ADG CDB ∴∠=∠+∠,又90BDF ADG CDB ∠+∠+∠=︒,90BDF CMF ∴∠+∠=︒,90CMF F ∠+∠=︒,BDF F ∴∠=∠,BF BD ∴=,AC BF ∴=,6AB CD ==,3AD BC ==, 226335BF AC ∴==+=,1122ABC S AC BE AB BC ∆==, 355BE ∴==,∴25535BE BF ==, 故答案为:25.【点睛】本题主要考查矩形的性质,掌握矩形的四个角都是直角、对角线互相平分且相等是解题的关键,注意三角形外角性质的应用.19.【分析】连接EF 根据矩形的性质可得AB=CD=9∠B=∠C=∠D=90°根据折叠的性质可得=∠B=90°利用HL 证出Rt △≌Rt △FCE 从而求出即可求出AF 最后利用勾股定理即可求出结论【详解】解:连解析:12【分析】连接EF ,根据矩形的性质可得AB=CD=9,∠B=∠C=∠D=90°,根据折叠的性质可得9AB AB '==,B E BE '=,AB E '∠=∠B=90°,利用HL 证出Rt △FB E '≌Rt △FCE ,从而求出B F ',即可求出AF ,最后利用勾股定理即可求出结论.【详解】解:连接EF ,∵4CF =,5DF =,∴CD=CF +DF=9∵四边形ABCD 为矩形,∴AB=CD=9,∠B=∠C=∠D=90°由折叠的性质可得9AB AB '==,B E BE '=,AB E '∠=∠B=90°∴FB E '∠=90°=∠C∵点E 为BC 的中点∴BE=CE∴B E CE '=在Rt △FB E '和Rt △FCE 中B E CE EF EF '=⎧⎨=⎩∴Rt △FB E '≌Rt △FCE∴4B F CF '==∴AF=AB '+B F '=13在Rt △AFD 中,AD=22AF DF -=12故答案为:12.【点睛】此题考查的是矩形与折叠问题,掌握矩形的性质、折叠的性质、利用HL 判定两个三角形全等和勾股定理是解题关键. 20.【分析】如图连接EGEB′求出EGEB′的长可以判定点B′在EG 的延长线上时GB′的值最小最小值=即可解决问题【详解】解:如图连接EGEB′∵四边形ABCD 是正方形∴∠A=∠D=90°AD=DC=A解析:52-【分析】如图,连接EG ,EB ′.求出EG ,EB ′的长,可以判定点B ′在EG 的延长线上时,GB ′的值最小,最小值=52-,即可解决问题.【详解】解:如图,连接EG ,EB ′,∵四边形ABCD 是正方形,∴∠A =∠D =90°,AD =DC =AB =2,∵AE =DE =1,DG =GC =1,∴EG = 22DE DG +=2211+=2,由翻折的性质可知,∠A ′=∠A =90°,A ′E =AE =1,A ′B ′=AB =2,∴EB ′=22'''A E A B +=2212+ =5,∴当点B ′在EG 的延长线上时,GB ′的值最小,最小值=52-, 故答案为52-.【点睛】 本题考查正方形的性质,翻折变换,勾股定理等知识,解题的关键是学会用转化的思想思考问题,属于中考填空题中的压轴题.三、解答题21.(1)详见解析;(2)详见解析;(3)详见解析;(4)详见解析【分析】(1)先作直角三角形,然后利用直角三角形斜边上的中线等于斜边的一半解答;(2)先作AD ⊥BC 于D ,然后在DC 上取点F ,使AF=FC ,然后再利用直角三角形斜边上的中线等于斜边的一半解答;(3)先作AD ⊥BC 于D ,然后在AD 上取点F ,使AF=FC ,然后再利用直角三角形斜边上的中线等于斜边的一半解答;(4)作∠BAD ,使∠BAD=∠B ,同时使∠DAC 为90°时,可得到∠B 和∠C 的大小,再借助直角三角形斜边上的中线等于斜边的一半解答;作∠CAD ,使∠CAD=∠C ,同时使∠ADC 为90°时,可得到∠B 和∠C 的大小,再借助直角三角形斜边上的中线等于斜边的一半解答.【详解】解:(1)如图①,过A 作AD ⊥BC 于D ,分别取AB 中点E ,AC 中点F ,连接ED ,DF ,EB =ED ,EA =ED ,FA =FD ,FC =FD ;(2)如图②,过A 作AD ⊥BC 于D ,取AB 中点E ,在DC 上取点F 使AF=FC ,取AF 的中点G ,连接ED ,DG ,EB =ED ,EA =ED ,FA =FC ,GA =GD ,GF =GD ;(3)如图③,过A 作AD ⊥BC 于D ,取AB 中点E ,在AD 上取点F 使AF=FC ,取CF 的中点G,连接ED,DG,EB=ED,EA=ED,FA=FC,GF=GD,GC=GD;(4)第一种分割方案如图④,DA=DB,EA=ED,EA=EC;第二种分割方案如图⑤DA=DC,EB=ED,EA=ED.【点睛】本题考查了等腰三角形的性质,直角三角形的性质,找到两边相等或两角相等是解题的关键.22.(1)见解析;(2)四边形A1BCE是菱形,理由见解析.【分析】(1)根据等腰三角形的性质得到AB=BC,∠A=∠C,由旋转的性质得到A1B=AB=BC,∠A=∠A1=∠C,∠A1BD=∠CBC1,根据全等三角形的判定定理得到△BCF≌△BA1D;(2)由旋转的性质得到∠A1=∠A,根据平角的定义得到∠DEC=180°-50=130º,根据四边形的内角和得到∠ABC=360°-∠A1-∠C-∠A1EC=180°-50=130º,证得四边形A1BCE是平行四边形,由于A1B=BC,即可得到四边形A1BCE是菱形.【详解】解:(1)证明:∵△ABC是等腰三角形,∴AB=BC,∠A=∠C,∵将等腰△ABC绕顶点B逆时针方向旋转50度到△A1BC1的位置,∴A1B=AB=BC,∠A=∠A1=∠C,∠A1BD=∠CBC1,在△BCF与△BA1D中,111A C AB BCA BD CBF ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴△BCF ≌△BA 1D (ASA );(2)四边形A 1BCE 是菱形,理由:∵将等腰△ABC 绕顶点B 逆时针方向旋转50度到△A 1BC 1的位置,∴∠A 1=∠A ,∵∠ADE=∠A 1DB ,∴∠AED=∠A 1BD=50º,∴∠DEC=180°-50º=130º,∵∠C=50º,∴∠A 1=50º,∴∠A 1BC=360°-∠A 1-∠C-∠A 1EC=180°-50º=130º,∴∠A 1=∠C ,∠A 1BC=∠A 1EC ,∴四边形A 1BCE 是平行四边形,∴A 1B=BC ,∴四边形A 1BCE 是菱形.【点睛】本题考查了旋转的性质,全等三角形的判定和性质,等腰三角形的性质,正确的理解题意是解题的关键.23.(1)BC =BG ,BC ⊥BG ;(2)①(1)中结论仍然成立,理由见解析;【分析】(1)由题意易得∠ACB =∠B =45°,AD =AF ,∠DAF =90°,则有∠BAD =∠CAF ,进而可证△ABD ≌△ACF ,然后问题可求解;(2)①由题意易得∠ACB =∠B =45°,AD =AF ,∠DAF =90°,则有∠BAD =∠CAF ,进而可证△ABD ≌△ACF ,则问题可求解;②过点A 作AM ⊥BD 于M ,由题意易得AM =12BC =1,CG =2,由①△ABD ≌△ACF ,则有BD =CF ,进而可得BD =CF =4,DM =BD ﹣AM =3,最后根据勾股定理可求解.【详解】解:(1)在△ABC 中,AB =AC ,∠BAC =90°,∴∠ACB =∠B =45°,∵四边形ADEF 是正方形,∴AD =AF ,∠DAF =90°,∴∠CAF =90°﹣∠CAD ,∵∠BAC =90°,∴∠BAD =90°﹣∠CAD ,∴∠BAD =∠CAF ,∵AB =AC ,∴△ABD≌△ACF(SAS),∴∠ACF=∠B=45°,∴∠B CG=90°,∴BC⊥CG,∠G=90°﹣∠B=45°=∠B,∴BC=BG,故答案为:BC=BG,BC⊥BG;(2)①(1)中结论仍然成立,理由:在△ABC中,AB=AC,∠BAC=90°,∴∠ACB=∠B=45°,∵四边形ADEF是正方形,∴AD=AF,∠DAF=90°,∴∠CAF=90°+∠CAD,∵∠BAC=90°,∴∠BAD=90°+∠CAD,∴∠BAD=∠CAF,∵AB=AC,∴△ABD≌△ACF(SAS),∴∠ACF=∠B=45°,∴∠B CG=90°,∴BC⊥CG,∠G=90°﹣∠B=45°=∠B,∴BC=BG;②如图,过点A作AM⊥BD于M,∵BC=2,△ABC是等腰直角三角形,∴AM=1BC=1,2∵BC=CG,∴CG=2,由①△ABD≌△ACF,∴BD=CF,∵点G是CF的中点,∴CF=2CG=4,∴BD=CF=4,∴DM=BD﹣AM=3,在Rt△AMD中,根据勾股定理得,AD.【点睛】本题主要考查正方形的性质、勾股定理及等腰直角三角形的性质,熟练掌握正方形的性质、勾股定理及等腰直角三角形的性质是解题的关键.24.见详解【分析】先证明四边形AECF 是平行四边形,再结合AC EF ⊥,即可得到结论成立.【详解】证明:在平行四边形ABCD 中,有AD ∥BC ,AD=BC ,∵DE BF =,∴AD DE BC BF -=-,∴AE CF =,∵AD ∥BC ,∴四边形AECF 是平行四边形,∵AC EF ⊥,∴四边形AECF 是菱形.【点睛】本题考查了菱形的判定和性质、平行四边形的判定与性质等知识;本题综合性强,熟练掌握平行四边形的判定与性质是解决问题的关键.25.(1)(4,-2);(2)作图见解析;(3)52. 【分析】(1)根据图象可得C 点坐标;(2)根据关于y 轴对称的点,横坐标互为相反数,纵坐标相等描出三个顶点,再依次连接即可;(3)先利用勾股定理逆定理证明111A B C ∆为直角三角形,再根据直角三角形斜边上的中线等于斜边的一半即可求得A 1D .【详解】解:(1)由图可知,C (4,-2)故答案为:(4,-2);(2)111A B C ∆如图所示,(3)由图可知,222222222111111125,2420,3425,A B A C C B ∴222111111A B A C C B ,即111A B C ∆为直角三角形, ∴1111522A D B C . 故答案为:52. 【点睛】本题考查坐标与图形变化轴对称,勾股定理逆定理,直角三角形斜边上的中线.(3)中能证明三角形为直角三角形,并理解直角三角形斜边上的中线等于斜边的一半是解题关键. 26.见解析.【分析】利用角平分线的性质、平角的定义可以求得∠DOF=90°;由等腰三角形的“三合一”的性质可推知OD ⊥AC ,即∠CDO=90°;根据已知条件“CF ⊥OF”知∠CFO=90°;则三个角都是直角的四边形是矩形.【详解】证明:∵OD 平分∠AOC ,OF 平分∠COB ,∴∠AOC=2∠COD ,∠COB=2∠COF ,∵∠AOC+∠BOC=180°,∴2∠COD+2∠COF=180°,∴∠COD+∠COF=90°,∴∠DOF=90°;∵OA=OC ,OD 平分∠AOC ,∴OD ⊥AC ,AD=DC ,∴∠CDO=90°,∵CF ⊥OF ,∴∠CFO=90°∴四边形CDOF 是矩形【点睛】本题考查了矩形的判定、角平分线的定义、等腰三角形的性质等知识,熟练掌握矩形的判定是解题的关键.。
第一章特殊平行四边形学业质量评价试题2024-2025学年北师大版数学九年级上册

数学 九年级上册第一章学业质量评价一、选择题1. 已知▱ABCD ,其对角线的交点为O ,则下面说法正确的是( ).A. 当OA=OB 时, ▱ABCD 为矩形B. 当AB=AD 时, ▱ABCD 为正方形C. 当∠ABC=90°时, ▱ABCD 为菱形D. 当AC⊥BD 时, ▱ABCD 为正方形2. 如图, 在四边形 ABCD 中,对角线AC, BD 相交于点O, AO=CO, BO=DO.添加下列条件,不能判定四边形 ABCD 是菱形的是( ).A. AB=ADB. AC=BDC. AC⊥BDD.∠ABO=∠CBO3. 如图, 将矩形纸片ABCD 折叠, 使顶点B 落在边AD 的点E 处, 折痕FG 交BC 于点G, 交AB 于点F, 若∠AEF=30°, 则∠FGB 的度数为( ).A.25°B.30°C.35°D.40°4. 如图, 在正方形ABCD 中, A, B, C 三点的坐标分别是(--1, 2), (--1, 0),(--3,0),将正方形ABCD 向右平移3个单位长度,则平移后点 D 的坐标是( ).A.(-6, 2)B.(0, 2)C.(2, 0)D.(2, 2)5. 如图,正方形 ABCD 的边长为9,将正方形折叠,使顶点 D 落在BC 边上的点E 处, 折痕为GH.若BE: EC=2:1, 则线段CH 的长是( ).A.3B.4C.5D.66. 如图, 正方形 ABCD 的边长为1, 点 E, F 分别是对角线 AC 上的两点,EG⊥AB, EI ⊥AD, FH⊥AB, FJ⊥AD, 垂足分别为G, I, H, J. 则图中阴影部分的面积等于( ).A.1 B 12 C 13 D 14二、填空题7. 如图,在平行四边形 ABCD 中,添加一个条件 ,使平行四边形ABCD 是矩形.8. 如图, 在菱形 ABCD 中, 对角线AC与BD 相交于点O,AC=8,BD=6,OE⊥AD于点E, 交BC于点F, 则EF的长为 .9. 如图, 在矩形 ABCD 中,∠ABC的平分线交AD 于点E,连接CE. 若BC=7,AE=4 ,则CE=.10. 如图, 菱形ABCD 的面积为120cm²,,正方形AECF的面积为72cm²,则菱形的边长为 .(结果中如有根号保留根号)11. 如图, 在正方形 ABCD 中,AB=3,, 点 E, F 分别在CD, AD 上,CE=DF,BE,C F相交于点G. 若图中阴影部分的面积与正方形ABCD 的面积之比为2:3,则△BCG的周长为 .12. 如图, 矩形OABC的顶点A, C 分别在坐标轴上, B(8, 7), D(5, 0), 点 P 是边AB 或边BC 上的一点, 连接OP, DP, 当△ODP 为等腰三角形时, 点 P 的坐标为 .三、解答题13.在四边形 ABCD中,对角线AC, BD相交于点O, 过点O的两条直线分别交边AB, CD,AD, BC于点E, F, G, H.【感知】如图①, 若四边形 ABCD 是正方形, 且.AG=BE=CH=DF,则S四边形AEOG= S正方形ABCD;【拓展】如图②, 若四边形 ABCD 是矩形, 且S四边形AEOG=14S矩形ABCD,设AB=a,AD=b,BE=m,求AG的长(用含a, b, m的代数式表示);【探究】如图③,若四边形ABCD 是平行四边形,且.AB=3,AD=5,BE=1,,试确定F, G, H的位置, 使直线EF, GH 把四边形ABCD 的面积四等分.14.(1)如图①, P 为正方形ABCD 内一点, 且PA:PB:PC=1:2:3,求∠APB的度数.小明同学的想法是:不妨设.PA=x,PB=2x,PC=3x,设法把PA, PB, PC相对集中,于是他将△BCP绕点 B 顺时针旋转90°得到△BAE(如图②),然后连接PE,问题得以解决.请你回答图②中∠APB=.(2)请你参考小明同学的方法,解答下列问题.如图③,P 是等边三角形ABC 内一点,PA:PB:PC=3:4:5,那么∠APB= .请写出推理过程.15.如图, 在平行四边形ABCD中,AC⊥AD,, 延长 DA 到点E, 使得DA=AE, 连接BE.(1)求证: 四边形 AEBC 是矩形;(2)过点E作AB的垂线分别交AB, AC于点F, G, 连接CE交AB于点O, 连接OG, 若AB=6,∠CAB=30°,求△OGC的面积.16.已知在四边形 ABCD 中,AD∥BC,AD=CD,E 是对角线BD 上一点,且EA=EC.(1)如图①, 求证: 四边形 ABCD是菱形;(2)如图②, 延长AE交BC的延长线于点F, 交DC于点G, 若BE=BC,且∠CBE:∠BCE=1:2,在不添加其他辅助线的情况下,请直接写出图中的所有与,△BCE全等的三角形.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章检测卷
班级:__________姓名:__________
一、选择题
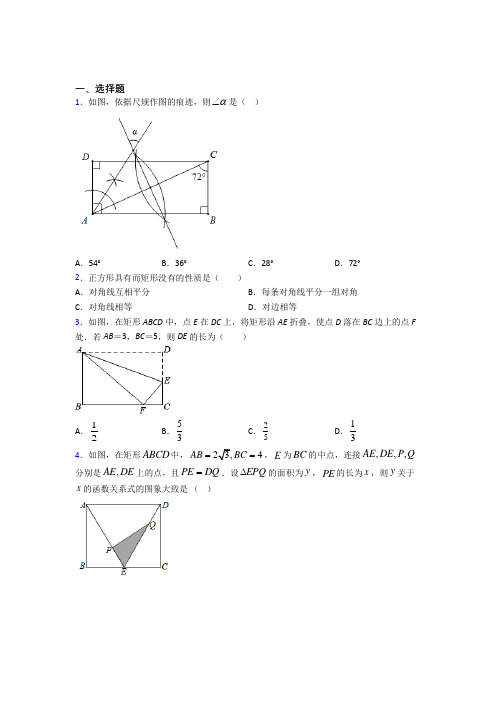
1.下列四边形中,对角线互相垂直平分的是()
A.平行四边形、菱形B.矩形、菱形C.矩形、正方形D.菱形、正方形2.在四边形ABCD中,AB=BC=CD=DA,如果添加一个条件,即可推出该四边形是正方形,那么这个条件可以是()
A.AC⊥BD B.AB∥CD C.∠A=90°D.∠A=∠C
3.若矩形的一条对角线与一边的夹角是40°,则两条对角线相交所成的锐角是()
A.20°B.40°C.80°D.100°
4.如图,在矩形ABCD中,对角线AC,BD交于点O,下列说法错误的是()A.AB∥DC B.AC=BD C.AC⊥BD D.OA=OC
4 5 6
5.如图,点P是菱形ABCD对角线BD上一点,PE⊥AB于点E,且PE=2.连接PC,若菱形的周长为24.则△BCP的面积为()
A.4 B.6 C.8 D.12
6.如图,在△ABC中,BC=12,AC=5,AB=13,点D是AB的中点,则CD 的长为()
A.6.5 B.6 C.2.5 D.不能确定
7.如图,已知面积为1的正方形ABCD的对角线相交于点O,过点O任意作一条直线分别交AD,BC于E,F,则阴影部分的面积是()
A.1 B.0.5 C.0.25 D.无法确定
7
8.如图,在矩形ABCD中,对角线AC、BD相交于点O.若∠ACB=30°,AB=2,则BD的长为()
A.4 B.3 C.2 D.1
9.菱形OABC在平面直角坐标系中的位置如图所示,∠AOC=45°,点A的坐标为(2,0),则点B的坐标为()
A.(2,1) B.(1,2) C.(1,2+1) D.(2+1,1)
10.如图,四边形ABCD是正方形,点E在对角线BD上,且BE=BC,则∠ACE 的度数等于()
A.20°B.22.5°C.25°D.30°
11.顺次连接对角线相等的四边形各边中点所得四边形是()
A.矩形B.平行四边形C.菱形D.任意四边形
12.如图,将边长为2cm的菱形ABCD沿边AB所在的直线l翻折得到四边形ABEF,若∠DAB=30°,则四边形CDFE的面积为()
A.2cm2B.3cm2C.4cm2D.6cm2
13.如图,四边形ABCD为矩形纸片,把纸片ABCD折叠,使点B恰好落在CD边的中点E处,折痕为AF.若CD=6,则AF等于()
A.4 3 B.3 3 C.4 2 D.8
14.一个菱形的周长是20cm,两条对角线的比是4:3,则这个菱形的面积是()A.12 B.96 C.48 D.24
二、填空题
1.如图,一个平行四边形的活动框架,对角线是两根橡皮筋.若改变框架的形状,则∠α也随之变化,两条对角线长度也在发生改变.当∠α为度时,两条对角线长度相等.
2.如图,在正方形ABCD的外侧,作等边△ADE,则∠BED的度数是. 3.如图,菱形ABCD的边长为4,且AE⊥BC于E,AF⊥CD于F,∠B=60°,则菱形ABCD的面积为.
4.如图所示,平行四边形ABCD的对角线AC、BD相交于点O,试添加一个条件,使得平行四边形ABCD为菱形.
5.如图,在矩形ABCD中,对角线AC、BD相交于点O,点E、F分别是AO、AD的中点,若AB=6cm,BC=8cm,则△AEF的周长=cm.
三、解答题
1.如图,点O是菱形ABCD对角线的交点,DE∥AC,CE∥BD,连接OE.求证:OE=BC.
2.如图:在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB上一点,过点D作DE⊥BC,交直线MN于点E,垂足为F,连结CD,BE,
(1)当点D是AB的中点时,四边形BECD是什么特殊四边形?说明你的理由
(2)在(1)的条件下,当∠A=时四边形BECD是正方形.
3.已知:如图,在矩形ABCD中,M、N分别是边AD、BC的中点,E、F分别是线段BM、CM 的中点.
(1)求证:BM=CM;
(2)判断四边形MENF是什么特殊四边形,并证明你的结论;
(3)当AD:AB= 时,四边形MENF是正方形(只写结论,不需证明).
4、
23.(10分)如图,在矩形ABCD中,对角线AC,BD相交于点O,AE⊥BD 于点E,BE∶ED=1∶3,AD=6cm,求AE的长.
24. (12分)如图,等腰三角形ABC中,AB=AC,AH⊥BC,点E是AH上一点,延长AH至点F,使FH=EH.
(1)求证:四边形EBFC是菱形;
(2)如果∠BAC=∠ECF,求证:AC⊥CF.
25.(12分)如图,在矩形ABCD中,沿EF将矩形折叠,使A,C重合,点D落在点G处,AC与EF交于点H.
(1)求证:△ABE≌△AGF;
(2)若AB=6,BC=8,求△ABE的面积.
26.(14分)已知梯形ABCD中,AD∥BC,AB=AD(如图所示).
(1)在下图中,用尺规作∠BAD的平分线AE交BC于点E,连接DE(保留作图痕迹,不写作法),并证明四边形ABED是菱形;
(2)若∠ABC=60°,EC=2BE.求证:ED⊥DC.
27.(16分)如图,已知△ABC,直线PQ垂直平分AC,与边AB交于点E,连接CE,过点C作CF平行于BA交PQ于点F,连接AF.
(1)求证:△AED≌△CFD;
(2)求证:四边形AECF是菱形;
(3)若AD=3,AE=5,则菱形AECF的面积是多少?。
