浙江省衢州市中考数学第一轮总复习讲义函数及其图像精选资料
衢州市中考数学第一轮总复习讲义:解直角三角形(一)

浙江考情分析解直角三角形(一)典型考题考点一成比例线段与比例的基本性质若2a=3b=4c,且abc≠0,则a+b的值是( ) c-2bA.2 B.-2 C.3 D.-3变式:(2015·乐山)如图,l1∥l2∥l3,两条直线与这三条平行线分别交于点A,B,C 和D,E,F.已知AB=3,则DE的值为( )BC 2 DFA.32B.23C.25D.35考点二 相似多边形的性质如果两个相似多边形面积的比为 1∶5,则它们的相似比为()A .1∶25B .1∶5C .1∶2.5D .1∶ 5变式 1: 如图 1 所示的两个四边形相似,则∠α的度数是()A .87°B .60°C .75°D .120°图 1图 2变式 2:如图 2,四边形 ABCD 与四边形 A 1B 1C 1D 1 相似, AB =12,CD =15,A 1B 1=9,则边 C 1D 1 的长是() A .10B .12C.454考点三 相似三角形的性质与判定D. 365(·庆阳)如图,在△ABC 中,两条中线 BE ,CD相交于点 O ,则 S △DOE ∶S △COB =()A .1∶4B .2∶3C .1∶3D .1∶2变式 1: (2015·重庆)已知△ABC ∽△DEF ,若△ABC 与 △DEF 的相似比为 2∶3,则△ABC 与△DEF 对应边上的中 线的比为.变式2:(·南京)如图,△ABC 中,CD 是边AB 上的高,且CD2=AD·DB.(1)求证:△ACD∽△CBD;(2)求∠ACB 的大小.考点四相似图形的应用(·菏泽)如图,M,N 为山两侧的两个村庄,为了两村交通方便,根据国家的惠民政策,政府决定打一直线涵洞,工程人员为计算工程量,必须计算M,N 两点之间的直线距离,选择测量点A,B,C,点B,C 分别在AM,AN 上,现测得AM=1 千米、AN=1.8 千米、AB=54 米、BC=45 米、AC=30 米,求M,N 两点之间的直线距离.变式1:如图,在一场羽毛球比赛中,站在场内M 处的运动员林丹把球从N 点击到了对方内的B 点,已知网高OA =1.52 米,OB=4 米,OM=5 米,则林丹起跳后击球点N 离地面的距离NM=米.变式2:有一支夹子如图所示,AB=2BC,BD=2BE,在夹子前面有一个长方体硬物,厚PQ 为6 cm,如果想用夹子的尖端A,D 两点夹住P,Q 两点,那么手握的地方EC 至少要张开cm.随堂巩固1.(·安顺)如图,▱ABCD 中,点E 是边AD 的中点,EC交对角线BD 于点F,则EF∶FC 等于( )A.3∶2 B.3∶1C.1∶1 D.1∶2第1 题第2 题2.如图,等边三角形ABC 的边长为3,P 为BC 上一点,且BP=1,D 为AC 上一点,若∠APD=60°,则CD 的长为.3.如图,在方格纸中,△ABC 和△EPD 的顶点均在格点上,要使△ABC∽△EPD,则点P 所在的格点为( ) A.P1 B.P2 C.P3 D.P4第3 题第4 题4.(2015·南通)如图,AB 为⊙O 的直径,C 为⊙O 上一点,弦AD 平分∠BAC,交BC 于点E,AB=6,AD=5,则AE 的长为( )A.2.5 B.2.8 C.3 D.3.25.如图,在矩形ABCD 中,F 是DC 上的一点,AE 平分∠BAF 交BC 于点E,且DE⊥AF,垂足为点M,BE=3,AE=2 6,则MF 的长是( )A. 15B.1510C.1 D.1515第5 题第6 题6.(2015·金华外国语学校模拟)如图,已知矩形ABCD 中,AB=1,在BC 上取一点E,沿AE 将△ABE 向上折叠,使B 点落在AD 上的F 点,若四边形EFDC 与矩形ABCD 相似,则AD=.7.(·绍兴鲁迅中学模拟)如图,四边形ABCD 中,AC ⊥BD 交BD 于点E,点F,M 分别是AB,BC 的中点,BN 平分∠ABE 交AM 于点N ,AB=AC=BD,连结MF,NF.(1)判断△BMN 的形状,并证明你的结论;(2)判断△MFN 与△BDC 之间的关系,并说明理由.8.(·安徽)如图①,在四边形ABCD 中,点E,F 分别是AB ,CD 的中点.过点E 作AB 的垂线,过点F 作CD 的垂线,两垂线交于点G,连结GA,GB,GC,GD,EF.若∠AGD=∠BGC.(1)求证:AD=BC;(2)求证:△AGD∽△EGF;AD(3)如图②,若AD,BC 所在的直线互相垂直,求的值.EF。
《中考大一轮数学复习》课件 反比例函数及其图像

中考大一轮复习讲义◆ 数学
2
夯实基本
中考大一轮复习讲义◆ 数学 知识结构梳理
知已知彼
1 2
3
3
夯实基本
中考大一轮复习讲义◆ 数学
知已知彼
基础知识回顾 1. 反比例函数的概念 定义:形如____________的函数称为反比例函数,其中 x 是自变量,y 是函数,自变量的取值范 围是不等于 0 的一切实数. 温馨提示 反比例函数的另外两种形式为 y=kx-1(k≠0),xy=k(k≠0). 2. 反比例函数的图像和性质 k 的符号 图像的大致位 置 经过象限 性质 3. k 的几何含义 k k 反比例函数 y= (k≠0)中比例系数 k 的几何意义, 即过双曲线 y= (k≠0)上任意一点 P 作 x 轴、 x x y 轴垂线,设垂足分别为 A,B,则所得矩形 OAPB 的面积为__________;连 OP,则△OAP 的面积为 __________. 第______象限 在每一象限内 y 随 x 的增大而 ______ 第______象限 在每一象限内 y 随 x 的增大而 ______ k>0 k<0
C
)
1 2
6 6. (2013²湖南邵阳)下列四个点中,在反比例函数 y=- 的图-2)
B. (3,2)
C. (2,3)
D. (-2,-3)
3
中考大一轮复习讲义◆ 数学
k 7. (2014²广东汕尾)已知反比例函数 y= 的图像经过点 M(2,1). x (1)求该函数的表达式. (2)当 2<x<4 时,求 y 的取值范围(直接写出结果).
1 2 3
A
)
k 4. (2013²山东滨州)若点 A(1,y1),B(2,y2)都在反比例函数 y= (k>0)的图像上,则 y1,y2 的 x 大小关系为( A. y1<y2
浙江省衢州市中考数学第一轮总复习讲义函数及其图像(无答案)

函数及其图像浙江考情分析典型考题考点一平面内点的坐标(2015·南京)在平面直角坐标系中,点A 的坐标是(2,-3),作点A 关于x 轴的对称点得到点A′,再作点A′关于y 轴的对称点,得到点A″,则点A″的坐标是变式1:(2015·天津)在平面直角坐标系中,把点P(-3,2)绕原点O顺时针旋转180°,所得到的对应点P′的坐标为( )A.(3,2) B.(2,-3) C.(-3,-2) D.(3,-2)变式2:如图,在平面直角坐标系中,一动点从原点O 出发,按向上、向右、向下、向右的方向依次不断地移动,每次移动一个单位,得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),…,那么点A4n+1(n 是自然数)的坐标为.考点二函数自变量的取值范围(2015·内江)函数y=2-x+1中自变量x 的取值范围是( )x-1A.x≤2 B.x≤2 且x≠1 C.x<2 且x≠1 D.x≠1变式:在函数y=x+2中,自变量x 的取值范围是( )x-1A.x>1 B.x≥1 C.x>-2 D.x≥-2考点三函数的图象及应用(2015·济宁)匀速地向一个容器内注水,最后把容器注满,在注水过程中,水面高度h 随时间t 的变化规律如图所示(图中OABC 为一折线),这个容器的形状是下图中的( )变式:如图,在Rt△ABC 中,∠C=90°,AC=1 cm,BC=2 cm,点P从点A 出发,以1 cm/s 的速度沿折线AC→CB→BA 运动,最终回到A 点.设点P 的运动时间为x(s),线段AP 的长度为y(cm),则能反映y 与x 之间函数关系的图象大致是( )随堂巩固1.(2015·营口)函数y=x+3中自变量x 的取值范围是( )x-5A.x≥-3 B.x≠5 C.x≥-3 或x≠5 D.x≥-3 且x≠52.(2015·衢州实验中学调研)如图,在5×4 的方格纸中,每个小正方形边长为1,点O,A,B 在方格线的交点(格点)上.在第四象限内的格点上找点C,使△ABC 的面积为3,则这样的点C 共有( )A.2 个B.3 个C.4 个D.5 个 3.如图,在平面直角坐标系中,点A,B 的坐标分别为(-6,0),(0,8).以点A 为圆心,以AB 长为半径画弧交x 轴正半轴于点C,则点C的坐标为( )4.如图,动点P 从点A 出发,沿线段AB 运动至点B 后,立即按原路返回,点P 在运动过程中速度不变,则以点B 为圆心,线段BP 长为半径的圆的面积S 与点P 的运动时间t 的函数图象大致为( )5.小聪骑车从飞瀑出发前往宾馆,速度为20 km/h,途中遇见小慧时,小慧恰好游完一景点后乘车前往下一景点,上午10:00 小聪到达宾馆.图②中的图象分别表示两人离宾馆的路程s(km)与时间t(h)的函数关系.试结合图中信息回答:(1)小聪上午几点钟从飞瀑出发?(2)试求线段AB,GH 的交点B 的坐标,并说明它的实际意义.(3)如果小聪到达宾馆后,立即以30 km/h 的速度按原路返回,那么返回途中他几点钟遇见小慧?。
第三单元 函数及其图象中考数学第一轮 中考考点复习课件详解 1

6.抒发的感情真诚感人,不写自己的 品学兼 优、勤 奋用功 ,而是 如实地 展现自 己的天 生的野 性,充 满了阅 读和学 习“生 活”这 本大书 所得到 的欢欣 鼓舞的 生命体 验,表 现了对 自然和 生命无 比好奇 和热爱 以及泰 然面对 一切残 忍和苦 难的生 活观。
7. 学习了这篇传记让我们了解到了沈 从文从 小如何 “读社 会这本 大书” ,感受 到他青 春期的 悲欢得 失。由 于传主 生活经 历的太 多苦难 ,加上 作者在 回忆中 不时融 入淳厚 的情感 ,让我 们读来 有某种 沉重与 辛酸, 也让我 们学生 受到启 发:对 于强者 ,生活 中的风 霜雨雪 也和阳 光雨露 一样, 都从不 同侧面 或者以 不同的 方式滋 润着我 们的生 命,现 实中的 曲折、 坎坷、 苦难可 能拓展 人的精 神空间 ,让人 能更加 以阔大 的心胸 与坚强 的意志 ,去感 受
|y| |x|
C 四
A
C B
第三单元 函数及其图象中考数学第一轮 中考考点复习课件详解 1 第三单元 函数及其图象中考数学第一轮 中考考点复习课件详解 1
第三单元 函数及其图象中考数学第一轮 中考考点复习ห้องสมุดไป่ตู้件详解 1 第三单元 函数及其图象中考数学第一轮 中考考点复习课件详解 1
第三单元 函数及其图象中考数学第一轮 中考考点复习课件详解 1 第三单元 函数及其图象中考数学第一轮 中考考点复习课件详解 1
四象限角平分线上的点的横、纵坐标__互__为__相__反___数__. 对称点:(1)点P(x,y)关于x轴的对称点的坐标为__(_x__,__-__y_)__. (2)点P(x,y)关于y轴的对称点的坐标为__(_-___x_,__y_)_____. (3)点P(x,y)关于原点的对称点的坐标为_(_-___x_,__-__y_)____. (4)点P(x,y)关于第一、三象限角平分线的对称点的坐标为__(_y_,__x_)_____. (5)点P(x,y)关于第二、四象限角平分线的对称点的坐标为_(_-__y__,__-__x_)_.
浙江省衢州市中考数学第一轮总复习讲义解直角三角形2精选资料

解直角三角形课前预习(2014·嘉兴、舟山)如图,在地面上的点 A 处测得树顶 B 的仰角为α度,AC =7 米,则树高 BC 为 米(用含α 的代数式表示).浙江考情分析典型例题:例 1.(2015·乐山)如图,已知△ABC 的三个顶点均在格点上, 则 cos A 的值为( )A. 3 3 5 5 2 3 3 2 5 5变式:1.(2015·兰州)如图,在△ABC 中,∠B =90°,BC =2AB ,则cos A =( )52 1 2 2 5 5 55 32.(2015·庆阳)在△ABC 中,若∠A ,∠B 满足|cos A - 2 |+(1-tan B )2=0,则∠C 的大小是( )A . 45°B . 60°C . 75°D .105°例 2.(2015·武威) 如图①所示,将直尺摆放在三角尺 A BC 上, 使直尺与三角尺的边分别交于点 D ,E ,F ,G ,量得∠CGD=42°.(1)求∠CEF 的度数; (2)将直尺向下平移,使直尺的边缘通过三角尺的顶点 B ,交 AC 边于点 H ,如图②所示,点 H ,B 在直尺上的读数分别 为 4,13.4,求 BC 的长(结果保留两位小数).(参考数据:sin 42°≈0.67,cos 42°≈0.74,tan 42°≈0.90)变式: 3.如图,△ABC 中,∠C =90°,AB =8,cos A = ,则 BC 的4长是 ..如图,已知在 Rt △ABC 中,∠ACB =90°,CD 是斜边 AB 上的中线,过点 A 作 AE ⊥CD ,AE 分别与 CD ,CB 相交于点 H ,E ,AH =2CH .(1)求 sin B 的值;(2)如果 CD = 5,求 BE 的值.例 3.(2015·天水)2015 年 4 月 25 日 14 时 11 分,尼泊尔发生8.1 级地震,震源深度 20 千米.中国救援队火速赶往灾区救 援,探测出某建筑物废墟下方点 C 处有生命迹象.在废墟一 侧某面上选两探测点 A ,B ,AB 相距 2 米,探测线与该面的夹角分别是 30°和 45°(如图).试确定生命所在点 C 与探测面的距离.(参考数据 2≈1.41, 3≈1.73)变式:1.河堤横断面如图所示,堤高B C=6 米,迎水坡AB 的坡比为1∶3,则AB 的长为( )A.12 米B.4 3米C.5 3米D.6 3米2.如图,在电线杆上的C 处引拉线CE,CF 固定电线杆.拉线CE 和地面成60°角,在离电线杆6 米处安置测角仪AB,在A 处测得电线杆上C 处的仰角为30°.已知测角仪AB 的高为1.5 米,求拉线CE 的长.(结果保留根号)随堂巩固1.(2015·温州)如图,在△ABC 中,∠C =90°,AB =5,BC =3,则 cos A 的值是( )3 4 4 3 3 5 452.(2015·丽水)如图,点 A 为∠α边上的任意一点,作 A C ⊥ BC 于点 C ,CD ⊥AB 于点 D ,下列用线段比表示 cos α的 值,错误的是( )BD BC BC AB AD AC CDAC3.(2014·衢州、丽水)如图,河坝横断面迎水坡 A B 的坡比 1∶3(坡比是坡面的铅直高度 BC 与水平宽度 AC 之比),坝高 BC=3 m ,则坡面 AB 的长度是( )A .9 mB .6 mC .6 3 mD .3 3 m4.(2015·宁波)如图,在数学活动课中,小敏为了测量校园内 旗杆 AB 的高度,站在教学楼的 C 处测得旗杆底端 B 的俯角 为 45°,测得旗杆顶端 A 的仰角为 30°,若旗杆与教学楼的距 离为 9 m ,则旗杆 AB 的高度是 (结果保留根号).5.(2014·宁波)如图,从 A 地到 B 地的公路需经过 C 地,图 中 A C =10 千米,∠CAB =25°,∠CBA =37°.因城市规划的需 要,将在 A ,B 两地之间修建一条笔直的公路. (1)求改直后的公路 A B 的长; (2) 问 公 路 改 直 后 比 原 来 缩 短 了 多 少 千 米 ? (sin 25° ≈0.42,cos 25°≈0.91,sin 37°≈0.60,tan 37°≈0.75)。
最新衢州市中考数学第一轮总复习讲义:全等三角形.doc
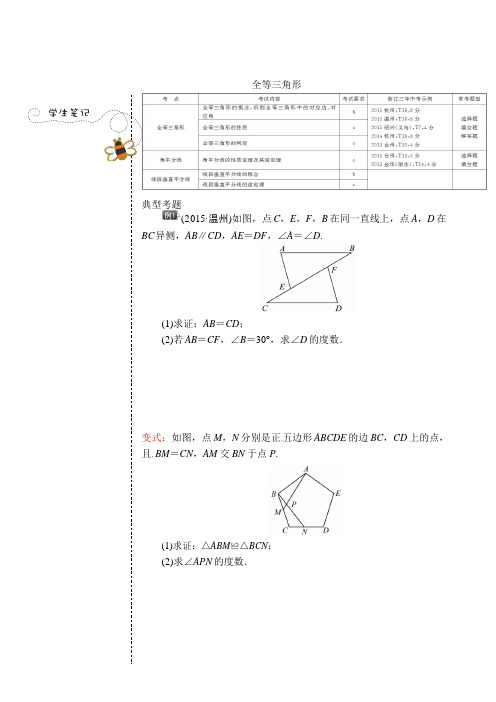
全等三角形典型考题(2015·温州)如图,点 C ,E ,F ,B 在同一直线上,点 A ,D 在 BC 异侧,AB ∥CD ,AE =DF ,∠A =∠D .(1)求证:AB =CD ;(2)若 AB =CF ,∠B =30°,求∠D 的度数.变式:如图,点 M ,N 分别是正五边形 ABCDE 的边 BC ,CD 上的点, 且 BM =CN ,AM 交 BN 于点 P .(1)求证:△ABM ≌△BCN ; (2)求∠APN 的度数.(2015·茂名)如图,OC 是∠AOB 的平分线,P 是 OC 上一点, PD ⊥OA 于点 D ,PD =6,则点 P 到边 OB 的距离为()A .6B .5C .4D .3变式:在 Rt △ABC 中,∠A =90°,∠ABC 的平分线 BD 交 AC 于点 D ,AD =3,BC =10,则△BDC 的面积是.如图,已知点 A ,F ,E ,C 在同一直线上,AB ∥CD ,∠ABE =∠CDF ,AF =CE.(1)从图中任找两组全等三角形; (2)从(1)中任选一组进行证明.变式:(2015·黔东南)如图,在四边形 ABCD 中,AB ∥CD ,连结 BD .请 添加一个适当的条件 使△ABD≌△CDB (只需写一个).随堂巩固1.(2015·随州)如图,△ABC 中,AB=5,AC=6,BC=4,边AB 的垂直平分线交AC 于点D,则△BDC 的周长是( C)A.8 B.9 C.10 D.112.(2015·金华外国语学校检测)如图,点E 是矩形AB CD 的边AD 延长线上的一点,且AD=DE,连结BE 交CD 于点O,连结AO,下列结论不正确的是()A.△AOB≌△BOC B.△BOC≌△EOD C.△AOD≌△EOD D.△AOD≌△BOC3.如图,△ABC 和△DEF 中,AB=DE,∠B=∠DEF,添加下列哪一个条件无法证明△ABC≌△DEF( C )A.AC∥DF B.∠A=∠DC.AC=D F D.∠ACB=∠F4.(2015·达州)如图,△ABC 中,BD 平分∠ABC,BC 的中垂线交BC 于点E,交BD 于点F,连结CF.若∠A=60°,∠AB D=24°,则∠ACF 的度数为()A.48°B.36°C.30°D.24°5.(2015·衢州华茂外国语学校调研)课间,小明拿着老师的等腰三角尺玩,不小心掉到两墙之间,如图.(1)求证:△ADC≌△CEB;(2)从三角板的刻度可知AC=25 cm,请你帮小明求出砌墙砖块的厚度a 的大小(每块砖的厚度相等).。
衢州市中考数学第一轮总复习讲义:图形的平移与旋转
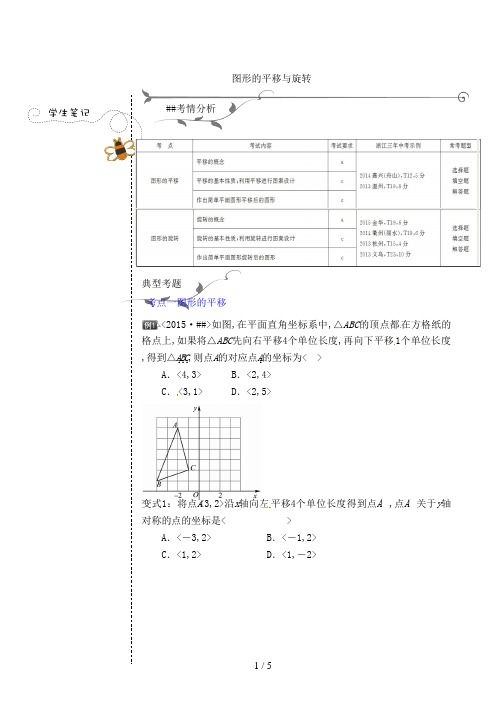
图形的平移与旋转##考情分析典型考题考点一图形的平移<2015·##>如图,在平面直角坐标系中,△ABC的顶点都在方格纸的格点上,如果将△ABC先向右平移4个单位长度,再向下平移1个单位长度,得到△A1B1C1,则点A的对应点A1的坐标为< >A.<4,3> B.<2,4>C.<3,1> D.<2,5>变式1:将点A<3,2>沿x轴向左平移4个单位长度得到点A′,点A′关于y轴对称的点的坐标是< >A.<-3,2> B.<-1,2>C.<1,2> D.<1,-2>变式2:如图,在边长为1的正方形网格中,将△ABC向右平移2个单位长度得到△A′B′C′,则与点B′关于x轴对称的点的坐标是< > A.<0,-1> B.<1,1>2>C.<2,-1> D.<1,-<2015·##>如图,已知Rt△ABC中,∠ACB=90°,AC=6,BC=4,将△AB C绕直角顶点C顺时针旋转90°得到△DEC,若点F是D E的中点,连结AF,则AF=.时针旋转至△A′B′C,使得点A′恰好落在AB上,则旋转角度为< >变式2:如图,在△ABC中,∠BAC=45°,AB=4cm,将△ABC绕点B按逆时针.方向旋转45°后得到△A′BC′,则阴影部分的面积为 cm2考点三利用平移或旋转作图<2015·##>如图,在边长均为1的正方形网格纸上有一个△ABC,顶点A,B,C与点O均在格点上,请按要求完成以下操作或运算:<1>将△AB C向上平移4个单位,得到△A1B1C1<不写作法,但要标出字母>; <2>将△ABC绕点O旋转180°,得到△A2B2C2<不写作法,但要标出字母>; <3>求点A绕点O旋转到点A2所经过的路径长.变式:如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A<-3,2>, B<0,4>,C<0,2>.<1>将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C ;平移△ABC,若点A的对应点A2的坐标为<0,-4>,画出平移后对应的△A2B2C2; <2>若将△A1B1C绕某一点旋转可以得到△A2B2C2,请直接写出旋转中心的坐标;<3>在x轴上有一点P,使得PA+PB的值最小,请直接写出点P的坐标.随堂巩固1..<2015·##>在平面直角坐标系中,点A的坐标是<0,3>,点B在x轴上,将△AOB绕点A逆时针旋转90°得到△AEF,点O,B的对应点分别是点E,F.<1>若点B坐标是<-4,0>,请在图中画出△AEF,并写出点E,F的坐标; <2>当点F落在x轴的上方时,试写出一个符合条件的点B的坐标.2.把一副三角尺按如图甲放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边AB=6,D C=7,把三角尺DCE绕着点C顺时针旋转15°得到△D1CE1<如图乙>,此时A B与CD1交于点O,则线段AD1的长为< >A.32 B.5 C.4 D.31图甲图乙5.<2015·日照>如图,已知,在△ABC中,CA=CB,∠ACB=90°,E,F分别是CA,CB 边的三等分点,将△ECF绕点C逆时针旋转α度<0°<α<90°>,得到△MCN,连结AM,BN.<1>求证:AM=BN;<2>当MA∥CN时,试求旋转角α的余弦值。
浙江省中考数学一轮复习 第11课 函数及其图象课件

探究提高
要学会阅读图象,正确理解图象中点的坐标的实际意义, 由图象分析变量的变化趋势,从而确定实际情况.分析变量 之间的关系、加深对图象表示函数的理解,进一步提高从图 象中获取信息的能力,运用数形结合的思想观察图象求解.
•
题型分类 题型一 确定自变量的取值范围
【例 1】 函数 y=x-x1中,自变量 x 的取值范围是_x_≥__0_且__x_≠__1_. x
解析 x中 x 作为被开方数,x≥0;x-1中 x-1 作为分母, x-1≠0,∴x≥0 且 x≠1.
探究提高
代数式有意义的条件问题: (1)若解析式是整式,则自变量取全体实数; (2)若解析式是分式,则自变量取使分母不为0的全体实数; (3)若解析式是偶次根式,则自变量只取使被开方数为非负数 的全体实数; (4)若解析式含有零指数或负整数指数幂,则自变量应是使底 数不等于0的全体实数; (5)若解析式是由多个条件限制,必须首先求出式子中各部分 自变量的取值范围,然后再取其公共部分,此类问题要特别注 意,只能就已知的解析式进行求解,而不能进行化简变形,特 别是不能轻易地乘或除以含自变量的因式.
3.函数自变量取值范围: 由解析式给出的函数,自变量取值范围应使解析式有意 义;对于实际意义的函数,自变量取值范围还应使实际 问题有意义.
要点梳理
4.函数的图象和函数表示方法: (1)函数的图象:一般地,对于一个函数,如果把自变 量x与函数y的每对对应值分别作为点的横坐标与纵 坐标,在坐标平面内描出这些点,用光滑曲线连接 这些点所组成的图形,就是这个函数的图象. (2)函数的表示法:①_解__析__法__;②_列__表__法__;③_图__象__法__.
浙江省中考数学一轮复习 第12课 一次函数及其图象课件

(2)若直线 y=-x+b 与 x 轴交于点(2,0),则关于 x 的不 等式-x+b&g 直线 y=-x+b 与 x 轴交于(2,0), 可知 x=2 时,y=0, 所以不等式-x+b>0 的解是 x<2.
探究提高
进一步熟悉函数图象的作法,通过图象体会一 次函数与一元一次方程,一元一次不等式的内在联 系,提高识图能力.一次函数 y=kx+b,当 y=0, 则 kx+b=0,得到一元一次方程,当 y>0,则有 kx+b>0,得到一元一次不等式.
解析 ∵a+b+c=0,且 a<b<c, ∴a<0,c>0(b 的正负情况不能确定). a<0,则函数 y=ax+c 图象经过第二、四象限; c>0,则函数 y=ax+c 的图象与 y 轴正半轴相交. 纵观各选项,只有 A 选项符合.
基础自测
4.(2012·陕西) 下列四组点中,可以在同一个正比例函
<c,则函数 y=ax+c 的图象可能是
( A)
•1、纪律是集体的面貌,集体的声音,集体的动作,集体的表情,集体的信念。 •2、知之者不如好之者,好之者不如乐之者。 •3、反思自我时展示了勇气,自我反思是一切思想的源泉。 •4、在教师手里操着幼年人的命运,便操着民族和人类的命运。一年之计,莫如树谷;十年之计,莫如树木;终身之计,莫如树人。 •5、诚实比一切智谋更好,而且它是智谋的基本条件。 •6、做老师的只要有一次向学生撒谎撒漏了底,就可能使他的全部教育成果从此为之失败。2022年1月2022/1/152022/1/152022/1/151/15/2022 •7、凡为教者必期于达到不须教。对人以诚信,人不欺我;对事以诚信,事无不成。2022/1/152022/1/15January 15, 2022 •8、教育者,非为已往,非为现在,而专为将来。2022/1/152022/1/152022/1/152022/1/15
中考数学 第一讲、函数及其图象知识点分析浙教版

第一讲、函数及其图象知识点1:理解函数的概念,认识函数关系在一个变化过程中,有两个变量(如、),对于自变量()的每一个确定值,函数()都有唯一确定的值与它对应,这时,就是的函数。
如何判断函数关系:第一:是不是一个变化过程 第二:是不是有两个变量第三:自变量每取一个值函数有几个值与它对应例1.下面的表分别给出了变量与之间的对应关系,判断是的函数吗如果不是,说明出理由.知识点2:认识函数关系式中的常量、自变量与函数常量:在变化过程中,始终保持不变的量;变量:在变化过程中,可以取不同数值的量;通常在表达时,等式左边的是函数,等式右边的是自变量。
例2.指出下列函数中的自变量、函数和常量:(1)x y 2-=; (2)613-=x y ;(3)2732+-=x x y ; (4)qp 51=.知识点3:自变量的取值范围一般来说,用解析法表示的函数,自变量的取值范围就是使代数式有意义的范围。
(1)分母不为零;(2)被开方数必须是非负数。
例3.求下列函数中自变量的取值范围:(1)x y 5-=;(2)132+=x y ;(3)xy -=21;(4)12+=x y . 知识点4:函数值的讨论函数值随着自变量取值的变化而变化;反之,函数的取值也决定着自变量的取值。
(1)自变量的每一个值对应着唯一一个函数值; (2)函数的每一个值对应着相应的自变量值。
难点:当给出一个量的取值范围,求另一个量的取值时,要结合不等式(或不等式组)加以讨论。
例4.写出下列函数中自变量的取值范围,并分别求出当自变量取2时函数的值:(1)5312+=x y ;(2)1035-=t y ;(3)1-+=x x y . 例5.按要求填空:(1)在=5-3中,当满足 时,≤2。
(2)在=2-中,若3≤≤6,则的取值为 。
知识点5:实际问题中函数关系式的列法及自变量取值范围的限制(一)函数式的列法:关键是要弄清各数量之间的关系(二)实际问题的自变量取值范围:不但要使得出的函数式有意义,还必须考虑到使实际问题有意义。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
函数及其图像
浙江考情分析
典型考题
考点一平面内点的坐标
(2015·南京)在平面直角坐标系中,点A 的坐标是(2,-3),作点A 关于x 轴的对称点得到点A′,再作点A′关于y 轴的对称点,得到点A″,则点A″的坐标是
变式1:(2015·天津)在平面直角坐标系中,把点P(-3,2)绕原点O
顺时针旋转180°,所得到的对应点P′的坐标为( )
A.(3,2) B.(2,-3) C.(-3,-2) D.(3,-2)
变式2:如图,在平面直角坐标系中,一动点从原点O 出发,按向上、向右、向下、向右的方向依次不断地移动,每次移动一个单位,得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),…,那么点A4n+1(n 是自然数)
的坐标为.
考点二 函数自变量的取值范围
(2015·内江)函数 y = 2-x +
1 中自变量 x 的取值范围是( ) x -1 A .x ≤
2 B .x ≤2 且 x ≠1 C .x <2 且 x ≠1 D .x ≠1
变式: 在函数 y = x +2 中,自变量 x 的取值范围是( )
x -1
A .x >1
B .x ≥1
C .x >-2
D .x ≥-2
考点三 函数的图象及应用
(2015·济宁)匀速地向一个容器内注水,最后把容器注满,在注 水过程中,水面高度 h 随时间 t 的变
化规律如图所示(图中 OABC 为一 折线),这个容器的形状是下图中的( )
变式:如图,在 Rt △ABC 中,∠C =90°,AC =1 cm ,BC =2 cm , 点 P 从点 A 出发,以 1 cm/s 的速度沿折线 AC →CB →BA 运动,最终回 到 A 点.设点 P 的运动时间为 x (s),线段 AP 的长度为 y (cm),则能反 映 y 与 x 之间函数关系的图象大致是( )
随堂巩固
1.(2015·营口)函数 y = x +3中自变量 x 的取值范围是( ) x -5 A .x ≥-3 B .x ≠5 C .x ≥-3 或 x ≠5 D .x ≥-3 且 x ≠5 2.(2015·衢州实验中学调研)如图,在 5×4 的方格纸中,每个小 正方形边长为 1,点 O ,A ,B 在方格线的交点(格点)上.在第四象限内 的格点上找点 C ,使△ABC 的面积为 3,则这样的点 C 共有
( )
A .2 个
B .3 个
C .4 个
D .5 个 3.如图,在平面直角坐标系中,点 A ,B 的坐标分别为(-6,0),(0, 8).以点 A 为圆心,以 AB 长为半径画弧交 x 轴正半轴于点 C ,则点 C
的坐标为( )
4.如图,动点 P 从点 A 出发,沿线段 AB 运动至点 B 后,立即按原 路返回,点 P 在运动过程中速度不变,则以点 B 为圆心,线段 BP 长为 半径的圆的面积 S 与点 P 的运动时间 t 的函数图象大致为
( )
5.小聪骑车从飞瀑出发前往宾馆,速度为 20 km/h ,途中遇见小慧 时,小慧恰好游完一景点后乘车前往下一景点,上午 10:00 小聪到达 宾馆.图②中的图象分别表示两人离宾馆的路程 s (km)与时间 t (h)的函 数关系.试结合图中信息回答:
(1)小聪上午几点钟从飞瀑出发?
(2)试求线段 AB ,GH 的交点 B 的坐标,并说明它的实际意义.
(3)如果小聪到达宾馆后,立即以 30 km/h 的速度按原路返回,那么 返回途中他几点钟遇见小慧?。
