机械制图 平面与回转体相交
田凌清华大学机械制图8 平面及直线与立体相交

《机械制图》
第8章 平面及直线与立体相交
16
8.3.2 直线与回转体相交
如果直线或回转体表面的投影有积聚性,可直接求出交 点的投影;如无法直接利用积聚性投影,一般则要通过作 辅助面的方法,才能作出直线与回转体的交点。 【例】求直线AB与圆锥的交点。 分析:
直线和圆锥的投影都不具备积聚性, 故要利用辅助面进行作图。 包含直线AB和锥顶S作辅助面与圆锥 面交于两条素线,这两条素线与AB的交 点即为直线AB与圆锥的交点。
《机械制图》
第8章 平面及直线与立体相交
12
8.2.3 平面与圆球相交
平面与圆球相交,截交线始终为圆;依据截平面相对于投影 面的不同位置,截交线的投影可为圆、椭圆或者积聚为直线。 分析: 两个侧平面和一个水平面截切圆球, 【例】求作圆球截切后的俯 截交线分别为侧平圆弧和水平圆弧; 视图、左视图。 侧平截面和水平截面的交线为正垂线;
18
要点小结
• 平面截切平面体时,截交线的特点及作法 • 平面截切回转体时,截交线的性质和作法 • 直线与平面体或回转体时,交点的作法
《机械制图》
第8章 平面及直线与立体相交
19
8.1 平面与平面体相交
(4) 2
1
4
1 3
分析:
截平面与四棱柱的四条棱线相 交,截交线为四边形。 截平面为正垂面,截交线的正 面投影积聚,水平投影、侧面投 影为类似的四边形图形。
2
3
Ⅳ 4 Ⅲ 1 Ⅱ
Ⅰ
作图步骤:
* 利用主视图中截平面的积聚性, 找出截交线4个顶点的正面投影: * 利用“三等”关系,在棱线上作出 截交线顶点的侧面和水平投影; * 顺序连接各顶点,画出截交线; * 补全棱线的投影。
平面与回转体相交

平面与回转体相交
平面与球相交
1.平面与球面的截交情况 球体被平面截切后的截交线是个圆。
平面与回转体相交
平面与球相交
2.作图举例
例 完成半球上部开 槽后的俯视图和左视图。
平面与回转体相交
平面与球相交
2.作图举例
例 完成半球上部开 槽后的俯视图和左视图。
分析:半球上部的 缺口是由一个水平面和 两个侧平面切割半球体 形成的。
平面与回转体相交
平面与回转体相交
回转体的截交线 平面与圆柱相交 平面与圆锥相交 平面与球相交
平面与回转体相交
回转体的截交线
1.截交线的特点 平面与回转体相交产生的截交线通常是一条封闭的平面曲线,
或曲线和直线围成的平面图形或多边形。
平面与回转体相交
回转体的截交线
1.截交线的特点
平面与回转体相交产生的截交线通常是一条封闭的平面曲线, 或曲线和直线围成的平面图形或多边形。
平面与回转体相交
平面与球相交
2.作图举例
例 完成半球上部开 槽后的俯视图和左视图。
作图:判断截交线 的可见性及球面轮廓线 投影范围,完成全图。
平面与回转体相交
小结
回转体的截交线 平面与圆柱相交 平面与圆锥相交 平面与球相交
2.求截交线的步骤 ★ 空间及投影分析
确定截交 线的形状
☆ 截平面与轴线的相对位置 ☆ 截平面与投影面的相对位置
确定截交线 的投影特性
平面与回转体相交
回转体的截交线
2.求截交线的步骤
★ 空间及投影分析 ★ 画截交线的步骤
转向轮廓线上的点
☆求截交线的特殊点: 极限位置点 截交线的形状特殊点
☆求一般点
平面与回转体相交
机械制图 第三章 立体及立体表面交线

第三章立体及立体表面交线目的要求:1)掌握平面立体和回转体的投影特性,以及表面取点线的方法2)熟悉立体表面上常见交线的画法(截交线、相贯线)重点难点:1)掌握和熟练运用各种立体的投影特性求解表面取点线的方法2)熟练求解立体表面上截交线和相贯线授课学时:8学时主要作图练习:1)完成平面立体、回转体的三面投影,平面立体、回转体表面找点、找线。
2)单个截平面截棱柱、棱锥后的三面投影。
3)多个截平面(切口)截棱柱、棱锥的三面投影,尤其是长方体截切后的三面投影。
4)单个和多个截平面截切圆柱、圆锥、圆球后的三面投影,尤以带槽的圆柱和圆球为主。
5)圆柱与圆柱相贯、同轴回转体相贯的各种情况作图、综合作图。
6)授课内容:机件形状是多种多样的,经过分析,都是由一些基本几何体所组成。
而几何体又是由一些表面所围成,根据这些表面的性质,几何体可分为两类:平面立体——由若干个平面所围成的几何体,如棱柱、棱锥等。
曲面立体——由曲面或曲面与平面所围成的几何体,最常见的是回转体,如圆柱、圆锥、圆球、圆环等。
用投影图表示一个立体,就是把围成立体的这些平面和曲面表达出来,然后根据可见性判别哪些线是可见的,哪些线是不可见的,把其投影分别画成粗实线和虚线,即可得立体的投影图。
§3-1 平面立体的投影平面立体各表面都是平面图形,各平面图形均由棱线围成,棱线又由其端点确定。
因此,平面立体的投影是由围成它的各平面图形的投影表示的,其实质是作各棱线与端点的投影。
一、棱柱以正六棱柱为例,其顶面、底面均为水平面,它们的水平投影反映实形,正面及侧面投影积聚为一直线。
棱柱有六个侧棱面,前后棱面为正平面,它们的正面投影反映实形,水平投影及侧面投影积聚为一直线。
棱柱的其它四个侧棱面均为铅垂面,水平投影积聚为直线,正面投影和侧面投影为类似形。
图3-1 正六棱柱的投影二、棱锥以四棱锥为例,其底面为一长方形,呈水平位置,水平投影反映底面的实形。
左右两个棱面是正垂面,其正面投影积聚为直线,水平和侧面投影均为类似三角形,前后两个棱面为侧垂面,其侧面投影积聚为直线,水平和正面投影同样为类似的三角形。
机械制图第3章

第 3 章 基本体及其表面交线
3.3 平面与立体相交
平面与平面体相交 3.3.1 平面与平面体相交 平面与立体表面相交而产生的交线称为截交线。 这个截 交线是一个平面多边形,此多边形的各个顶点就是截平面与平 面体的棱线的交点, 称为贯穿点。在求作棱柱或棱锥的截交线 时,常常先求出贯穿点, 即侧棱线或底棱与截平面的交点, 然 后依次连成截交线。 棱柱的截交线 1. 棱柱的截交线 例 3-1 图3-7所示的L形棱柱被正垂面P切割, 求作切割后 棱柱的三视图。
第 3 章 基本体及其表面交线
图 3-1 正三棱柱及其表面上点的投影
第 3 章 基本体及其表面交线 投影分析 1. 投影分析 如图3-1所示,正三棱柱的两端面(顶面和底面)平行于水平 面, 后侧棱面平行于正面, 另外两个棱面垂直于水平面。 在这 种位置下, 三棱柱的投影特征是: 顶面和底面的水平投影重合, 并反映实形——正三角形。三个侧棱面的水平投影积聚为三角 形的三条边。
第 3 章 基本体及其表面交线
图 3-10 正垂面切割三棱锥的截交线的作图步骤
第 3 章 基本体及其表面交线 作图 作图 (1) 根据三棱锥的三视图以及p′的位置, 由s′a′和s′c′与p′的交 点d′和f′,分别在sa、 sc和s″a″、s″c″上直接求出d、 f和d″、 f″, 如图3-10(a)所示。 (2) 由于SB是侧平线, 因此必须由s′b′与p′的交点e′在s″b″ 上求出e″, 再由45°线或利用宽相等的投影关系在sb上求出e, 如 图3-10(b)所示。 (3) 连接各点的同面投影即为所求交线的三面投影,擦去作 图线, 将切割后三棱锥的图线描深, 如图3-10(c)所示。
第 3 章 基本体及其表面交线 2. 作图方法 作图方法 画圆锥的三视图时, 应先画各投影的中心线, 再画底面圆的 各投影, 然后画出锥顶的投影和等腰三角形, 完成圆锥的三视图。 3. 圆锥体表面上点的投影 圆锥体表面上点的投影 如图3-5所示,已知圆锥体表面上点M的正面投影m′,求作m和 m″。根据M点的位置和可见性, 可确定点M在前、左方圆锥面上, 点M的三面投影均为可见。
《机械制图》模拟考试题(附答案)

《机械制图》模拟考试题(附答案)一、判断题(共100题,每题1分,共100分)1、推拔销之锥度为 1 : 50 。
A、正确B、错误正确答案:A2、退刀槽和砂轮越程槽可按“槽宽×直径”的形式标注。
A、正确B、错误正确答案:A3、装配图必须有明细栏A、正确B、错误正确答案:A4、水平面的水平投影积聚为直线。
A、正确B、错误正确答案:B5、尺寸公差有可能是负值A、正确B、错误正确答案:B6、螺钉旋转一周,就沿轴向位移三个螺距者为三线螺纹。
A、正确B、错误正确答案:A7、同一标称直径之细螺纹,可有不同之节距。
A、正确B、错误正确答案:A8、用剖视图来表示物体内部特征,比用虚线表示之视图要清楚。
A、正确B、错误正确答案:A9、装配图上已注明的尺寸,零件图上可以省略。
A、正确B、错误正确答案:B10、420×594为4张A4的大小。
A、正确B、错误正确答案:A11、汉字的书写应求端正划一,大小间隔适当,清晰易认即可。
A、正确B、错误正确答案:A12、在相同工件条件下,钻头直径愈小,转速要愈快。
A、正确B、错误正确答案:A13、与他件组合有关之尺寸称为功能尺寸。
A、正确B、错误正确答案:A14、一个实心小圆点,有时可以代替相邻的两箭头。
A、正确B、错误正确答案:A15、沿垂直轴线方向所量得之螺峰与螺谷间的距离称为螺距。
A、正确B、错误正确答案:B16、平面与回转体相交,截交线在特殊情况时可能由直线和曲线或完全由直线组成A、正确B、错误正确答案:A17、薄片弯曲物体,仅用一视图表示即可。
B、错误正确答案:B18、槽孔之表面符号可用指引线引至适当位置标注。
A、正确B、错误正确答案:A19、多个同方向之位置尺寸,应用基准面标注法标注之。
A、正确B、错误正确答案:A20、一物体之各视图,剖面线需保持相同的间隔与方向。
A、正确B、错误正确答案:A21、机件表面局部特殊处理之范围须加细链线表明。
A、正确B、错误正确答案:B22、长仿宋体汉字,字宽为字高的 4 / 3 倍。
画法几何与机械制图1章图文 (6)

第6章 立体与立体表面相交
(1) 利用积聚性:两立体相交,当其中有一个立体的表 面(平面或圆柱面)垂直于某一投影面时,立体的表面具有积 聚性(积聚为直线或圆),相贯线在这个投影面上的投影则重 合在有积聚性的直线或圆上,即相贯线在这个投影面上的投 影是已知的,从而可利用积聚性求出相贯线在其它投影面上 的投影,即可作出相贯线。
两圆柱体相交有三种形式:两外表面相交、两内表面相 交、外表面与内表面相交。图6-4给出了圆柱体相交的常见 三种形式,其相贯线的分析和作图与例6-2相同。
第6章 立体与立体表面相交
从以上几种圆柱相贯线的作图结果可总结出以下规律: (1) 当直径不等,轴线垂直相交的两圆柱相贯时,在圆 柱面有积聚性的视图中,相贯线为已知,在两圆柱面均无积 聚性的视图中(如图6-3、图6-4中的主视图),相贯线待求。 (2) 相贯线总是发生在直径较小的圆柱周围(见图6-4主 视图)。 (3) 相贯线总是向直径较大圆柱的轴线方向凸起(见图64主视图)。 当相交的两个圆柱体的直径和两轴线的相对位置发生变 化时,相贯线的形状也随之发生变化,但是其相贯线的分析 和作图方法是类似的。
【例6-1】 如图6-2(a)所示,已知三棱柱与半球相贯, 试完成相贯体的三视图(主视图和左视图中的双点画线表示 立体未确定的图线)。
第6章 立体与立体表面相交
【解】(1) 空间情况和投影分析。由已知条件可知,相 贯体左右对称,因此相贯线也左右对称。三棱柱在俯视图中 具有积聚性,所以相贯线的水平投影是已知的,可利用积聚 性求出其它投影。三棱柱与半球相贯,可以看做半球被三棱 柱的三个棱面(截平面)切割,每一个棱面切割半球面产生一 条截交线,求出每一条截交线的投影,即得到相贯线的投影。 三棱柱的三个棱面均垂直于水平面,因此相贯线的水平投影 重合在三个棱面有积聚性的直线上。三个棱面分别切割半球 所产生的截交线实形均为圆弧,因棱面M和N为铅垂面,它 倾斜于正面和侧面,所以截交线的正面投影和侧面投影都是 椭圆弧;
工程制图第四章

例2:正垂面截切六棱柱,完成截切后的三面投影。
6'(7') 4' (5') 5" 2' (3') 1' 3 5 7 1 6 2 4 3" 1" 7" 6" 4" 2" 分析:由图可知,截交线的 正面投影积聚为一直线。水 平投影,除顶面上的截交线 外,其余各段截交线都积聚 在六边形上。
完成后的投影图
截平面与圆锥轴线 平行或倾角θ<α, 截交线为双曲线。
截平面过锥顶截 交线为三角形。
例1:已知圆锥体的正面投影和部分水平面投影,求斜切圆 锥体的水平投影和侧面投影。
c'(d ') b' • a' •
•• k'l'
b" d" • • • c" • • l" • •k" •
a"
ld •••
a
•
•
kc
•••
e'
a'
d f h •••
a• ec
例2:已知带通槽半球的正面投影,完成水平和侧面投影。
分析:半球的通槽由三个平面构成, 一个水平面和两个侧平面截切圆球, 它们与球面的截交线都是分别平行于 投影面的圆弧。 作图的关键是确定截交圆弧的半径, 可根据截平面位置确定。 1、通槽的水平投影作图:过槽底部 作辅助水平面,水平投影为圆,并 在圆周上截取与正面投影相对应的 前后两段圆弧。 2、通槽侧面投影的作图:两侧平面 距球心等远,两圆弧的半径相等, 两段圆弧的侧面投影重合。
b' g'(h' ) • c'(d') • (f ') • 分析:截平面为正垂面,截交线的正面投影为 直线,水平投影为椭圆。 作图:1.求特殊点 截交线的最低点A和最 高点B也是最左点和最右点,还是截交线水平 投影椭圆短轴的端点,水平投影a、b在其正面 投影轮廓线的水平投影上。 e'f'是截交线与球的水平投影轮廓线的正 面投影的交点,其水平投影ef在球的水平投影 轮廓线上。 • b • •• g a'b'的中点 c ' d'是截交线的水平投影椭 圆长轴端点的正面投影,其水平投影c、d投影 在辅助纬圆上。 2.求一般点 选择适当位置作辅助水平面, 与 a'b'的交点g' 、h'为截交线上两个点的正 面投影,其水平投影g、h投影在辅助纬圆上。
《机械制图习题集》习题答案——第2章
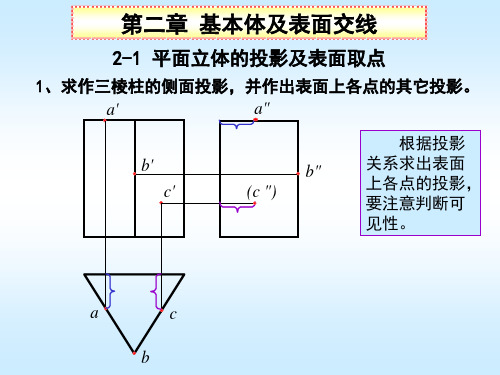
由于棱
锥体的棱面 无积聚性, 表面取点要 利用辅助线 法。
2-2 回转体的投影及表面取点
完成回转体的投影,并作出表面上各点的三面投影。
(1
)
a'
a"
b'
(b")
(b) a
回转体表面取点, 根据已知点的可见性 判断点所处的位置, 按投影关系,找出各 点的投影。
(2 )
(c') 1'
a'
b'
1" c" a"
4、完成相贯体的三视图。
1'
5'(6') 3'(4') 2' 7'(8')
1"
5" 6"
4"
3"
8"
7" 2"
4 86 21
75 3
圆锥体与圆
柱形孔正交。因 圆锥面的投影无 积聚性,利用辅 助平面求一般位 置的点。
5、完成相贯体的三视图。
1'
5'(6') 3'(4') 7'(8') 2'
1"
6"
b"
c
a
b
圆锥面的投
影无积聚性,表 面取点利用辅助 素线或辅助纬圆 法求解。底面上 的点可利用投影 关系直接求出。
(3 )
a'
b'
a" (b")
1a
圆锥台的表面
2 b
投影无积聚性,表 面上取点利用辅助
纬圆法。
(4 )
《机械制图》试题库及答案

《机械制图》试题库及答案一、单选题(共10题,每题1分,共10分)1、当孔的公差带与轴的公差带相交时,属于( )A、过渡配合B、间隙配合C、过盈配合D、不明确性质正确答案:A2、在图纸上的图框必须用()画出。
A、细虚线B、细点画线C、细实线D、粗实线正确答案:D3、机械图样中,表示断裂处边界线、视图与剖视图的分界线采用()。
A、细实线B、波浪线C、粗实线D、细点画线正确答案:B4、轴套类零件的加工,大部分工序是在车床或磨床上进行,因此一般将其轴线()放置画出主视图。
A、任意位置B、水平C、倾斜D、垂直正确答案:B5、在圆柱(或圆锥)外表面形成的螺纹,称为()。
A、标准螺纹B、表面螺纹C、外螺纹D、内螺纹正确答案:C6、在圆柱(或圆锥)内表面形成的螺纹,称为()。
A、标准螺纹B、表面螺纹C、内螺纹D、外螺纹正确答案:C7、斜视图仅表达倾斜表面的真实形状,其他部分用()断开。
A、粗实线B、细实线C、波浪线D、点划线正确答案:C8、某调整螺旋,采用双线粗牙螺纹,螺距为3mm,为使螺母相对螺杆沿轴向移动12mm,螺杆应转( )圈。
A、2.5B、3C、4D、2正确答案:D9、为了将物体的外部形状表达清楚,一般采用()个视图来表达。
A、五B、四C、三D、六正确答案:C10、锯齿形螺纹常用于()。
A、连接管道B、单方向传递动力C、锯销D、连接零件正确答案:B二、多选题(共10题,每题1分,共10分)1、与一个投影面平行的平面,一定与其它两个投影面垂直,这种平面称为投影面的平行面,具体可分为()。
A、特殊面B、中心面C、正平面D、侧平面E、水平面正确答案:CDE2、零件有长宽高三个方向的尺寸,主视图上只能反映零件的()A、高B、前C、长D、都不对E、宽正确答案:AC3、两点的相对位置,是指在三面投影体系中,一个点处于另一个点的()位置问题。
A、左右B、角度C、前后D、南北E、上下正确答案:ACE4、断面图与剖视图的区别()A、断面图仅画出被切断处的断面形状B、剖视图仅画出被切断处的断面形状C、左视图D、断面图还须画出可见轮廓线E、剖视图还须画出可见轮廓线正确答案:AE5、Φ50+0.025 表示( )A、最大尺寸是Φ50.025 ㎜B、最大尺寸是Φ50.00 ㎜C、实际尺寸是Φ50 ㎜D、基本尺寸是Φ50 ㎜E、最小尺寸是Φ50.025㎜正确答案:AD6、M20×2—5g6g—LH表示()A、细牙B、螺距C、长的旋合长度D、粗牙E、普通螺纹正确答案:ACE7、平面图形的尺寸按其在平面图形中所起的作用,可分为()。
机械制图讲义之第二章_立体的投影
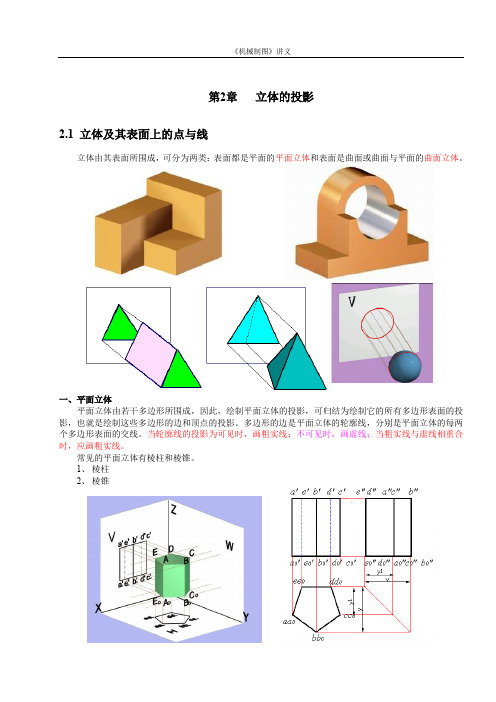
第2章立体的投影2.1 立体及其表面上的点与线立体由其表面所围成,可分为两类:表面都是平面的平面立体和表面是曲面或曲面与平面的曲面立体。
一、平面立体平面立体由若干多边形所围成,因此,绘制平面立体的投影,可归结为绘制它的所有多边形表面的投影,也就是绘制这些多边形的边和顶点的投影。
多边形的边是平面立体的轮廓线,分别是平面立体的每两个多边形表面的交线。
当轮廓线的投影为可见时,画粗实线;不可见时,画虚线;当粗实线与虚线相重合时,应画粗实线。
常见的平面立体有棱柱和棱锥。
1、棱柱2、棱锥平面立体的投影的外围轮廓总是可见的,应画粗实线;而在投影的外围轮廓内部的图线,则应根据线、面的投影分析,按前遮后、上遮下、左遮右直接判断投影的可见性,决定画粗实线或虚线,必要时还可利用交叉两直线的重影点的可见性进行判断。
二、曲面立体曲面立体由曲面或曲面与平面所围成。
有的曲面立体有轮廓线,即表面之间的交线,如圆柱;有的曲面立体有尖点,如圆锥;有的曲面立体全部由光滑的曲面所围成,如圆球。
在画曲面立体的投影时,除了画出轮廓线和尖点外,还要画出曲面投影的转向轮廓线。
曲面立体的转向轮廓线是切于曲面的诸投射线与投影面的交点的集合,也就是这些投射线所组成的平面或柱面与曲面的切线的投影,常常是曲面的可见投影和不可见投影的分界线。
曲面立体的投影就是它的所有曲面表面或曲面表面与平面表面的投影,也就是曲面立体的轮廓线、尖点的投影和曲面投影的转向轮廓线。
常见的曲面立体有圆柱、圆锥、圆球,圆环。
1、圆柱圆柱由圆柱面、顶面和底面所围成。
圆柱面由直线绕与它平行的轴线旋转而成。
因此,画圆柱的投影就是画顶面和底面及轮廓线、圆柱面投影的转向轮廓线、轴线。
当圆柱的轴线与投影面垂直时,圆柱面在轴线垂直的投影面上的投影具有积聚性。
因此,作圆柱表面2、 圆锥圆锥由圆锥面和底面所围成。
圆锥面由直线绕与它相交的轴线旋转而成。
因此,画圆锥的投影就是画尖点(即锥顶)、底面及轮廓线、圆锥面投影的转向轮廓线、轴线。
机械工程图学-基本立体的投影(2)

Wang chenggang
3-7/46
3.3 基本回转体的投影—3.3.1 圆柱的投影
圆柱的三面投影图中转向轮廓线与轴线的关系
图3-19 圆柱的三面投影
Wang chenggang
3-8/46
3.3 基本回转体的投影—3.3.1 圆柱的投影
圆柱投影的可见性
对正面投影而言,以 最左、最右素线(转向线)
Wang chenggang
b″
3-4/46
3.3 基本回转体的投影—3.3.1 圆柱的投影
3.3.1 圆柱的投影
1. 圆柱的三面投影图 圆柱由圆柱面和上、下两个底面(圆形平面)所围成。
Wang chenggang
3-5/46
3.3 基本回转体的投影—3.3.1 圆柱的投影
圆柱三面投影图的形成 圆柱的轴线垂直于H面, 其上下底面为水平面,水 平投影反映实形,其正面 和侧面投影积聚为一直线。
平投影。
(3)依次光滑连接各点 的同面投影,即可得到曲线 ADF的水平投影abcdef,其侧 面投影与圆柱面的积聚性投 影(圆)重合。
图3-21 圆柱表面上线的投影(续)
Wang chenggang
3-16/46
3.3 基本回转体的投影—3.3.1 圆柱的投影
本节课的重点:
圆柱的三面投影图、圆柱表面上点和线的投影。
图3-27 求作空心圆柱被水平面Q、R 和侧平面S截切后的水平投影
Wang chenggang
3-38/46
3.3 基本回转体的投影—3.3.1 圆柱的投影 在正面投影中,
空心圆柱位于侧平面 S左边的中心线被切 掉,则其水平投影相 应的内外转向轮廓线 都应被切掉。
4.3平面立体与回转体相交平面立体与圆柱体相交

平面与立体表面的交线称为截交线。
立体与立体表面的交线称Байду номын сангаас相贯线。
4.1 平面立体的截切
一、截交线的性质
1、截交线是由直线组成的平面图形(封闭多边形)。 2、多边形的各边是立体表面与截平面的交线。
3、多边形的各顶点是立体各棱线与截平面的交点。
截断面
截平面
截交线
分析圆筒内外交线投影
[例10]补画视图中所缺的图线。
[例10]补画视图中所缺的图线。
[例11] 已知主、俯视图,补画左视图。
[例12] 已知主、俯视图,补画左视图。
[例13] 已知主、俯视图,补画左视图。
●
●
1、空间及投影分析。
截平面与体的相对位置。 截平面与投影面的相对位置。
●
2、求截交线。
[例18] 画出球体开槽的三视图。
[例18] 画出球体开槽的三视图。
4.3 平面立体与回转体相交
平面立体与圆柱体相交,内外交线画法分析
4.4 两回转体相交
两回转体相交产生的交线称为相贯线。
相贯线的性质
1、一般情况下,相贯线是封闭的空间曲线,在特 殊情况下,可以是平面曲线或直线。
2、相贯线是两回转体表面的共有线,也是相贯体 两表面的分界线,相贯线上所有点都是两曲面 体的共有点。
分析切割式平面立体的形成
[例2] 根据物体的立体图,画出三视图。
b´ a´
a b
b" a"
B
[例3] 已知物体的主、左视图,补画出俯视图。
[例3] 已知物体的主、左视图,补画出俯视图。
a'
b'
P´
c' d'
《机械制图》第五章教案解析

第五章组合体视图第一讲组合体的画图1.知识要点(1)组合体的组合方式;(2)形体分析法;(3)线面分析法2.教学设计:在讲解组合体的画图方法时,要紧紧抓住两个顺序(①组合体的各基本几何体的画图顺序。
一般按组合体的生成过程先画基础形体,再画局部细节;②同一个形体三个视图的画图顺序。
一般先画形状特征最明显的那个视图,或有积聚性的视图)。
可先给出模型或实体仿真模型,引导同学作形体分析,然后按形体分析的过程绘制三视图。
这个过程要反复进行几次,可停下来让同学画一个模型的三视图,教师观察同学的画图方法,对不正确的方法给予纠正,直到同学掌握正确的观察方法和画图方法为止。
线面分析法是形体分析的补充。
3.课前准备:上课之前要准备好模型,模型要能够充分体现形体分析法的特点。
4.教学内容(1)组合体的组成方式(形体分析法)叠加如图5-1所示图5-1叠加切割如图5-2所示图5-2切割相切如图5-3所示图5-3相切图5-4为常见的画图错误,主视图上的错误原因是因为没有认识到立体是一个实体,即由各种材料制造成的立体,板和柱面的结合部分柱面已经消失,所以不存在转向轮廓线。
左视图上的错误原因是没有考虑宽相等,不作形体分析。
图5-4常见错误画法.综合如图5-5所示图5-5综合(2)用线面分析法绘制组合体的三视图(图5-6和图5-7)图5-6平面立体的线面分析图5-7曲面立体的线面分析5.作业习题集:按模型或立体图绘制三视图。
第二讲圆柱截交线教学内容圆柱体与平面相交有三种情况:1)当截平面与圆柱体的轴线垂直时,截交线为圆或圆弧;2)当截平面与圆柱体的轴线平行时,截交线为两条线段;3)当截平面与圆柱体的轴线倾斜时,截交线为椭圆或椭圆弧。
表4-1圆柱截交线[例1]根据立体图绘制三视图(利用课件中的动画讲解)【形体分析】基本形体为圆柱体,先用一个侧平面和水平面切去一角,侧平面和柱面的交线为线段,水平面和柱面的交线为圆弧;再用两个正平面和水平面切去一个矩形槽,矩形槽的侧面和柱面的交线为线段,槽的底面与柱面的交线为圆弧。
机械制图-两回转体相交

三、相贯线的特殊情况
1、两回转体具有公共轴线时(过球心),其相贯线为垂直轴线 的圆。
相贯线 相贯线
相贯线
圆球与圆锥台相贯
2、两曲面立体相交,一般情况下相贯线为空间曲线,但 特殊情况下可能是平面曲线或直线。
A. 当两回转体相交并公切于一球时,相贯线为平面曲线 (椭圆)。
B.当两圆锥共锥顶或者两圆柱轴线平行时,相贯线为直线。
3.5 两回转体表面相交
一、相贯线概述
二、利用积聚性法求相贯线 三、相贯线的特殊情况
一、相贯线的概述
相贯线 ——立体相交后表面产生的交线。
性质:(表面性、共有性、封 闭性) 1)是相交两回转体表面的 共有线。相贯线上的点是两 回转体表面的共有点。
相贯线 圆台
2)一般来说交线是一封闭的 空间曲线,特殊情况下是平面 曲线或直线。
分析:当圆柱直径变化时,相贯线的变化趋势。
垂直直径<水平直径 上下两条空间曲线
直径相等 两条平面曲线(椭圆)
垂直直径>水平直径 左右两条空间曲线
相贯线投影关于小圆柱轴线对称,弯向大圆柱的轴线
例:补全主视图
1. 两外表面相贯(直径相等) 2. 一内表面和一外表面相贯(直径不等)
1’(2’)
● ●
2’’ 4’
●
1’’
3’
3’’( 4’’)
(2)
(3)
(4) (1)●
●
二)圆柱与圆锥、圆球相贯
相贯线
共有性
柱面上的曲线
积聚性
已知相贯线的 一个投影
锥(球)面上的曲线
也即已知锥(球)面上 曲线的一个投影
求相贯线即转化为锥(球) 面上求点、线。
例:已知圆柱与圆锥相交,完成H面投影。
机械制图 (8)

例3:求圆筒截切后的水平投影
具体步骤: 例4:斜切圆柱的截交线
5’
6”
5” 4” 3”
8”
4’
3’
2’ 1’ 8 1 2
(7)’
7”
2” 1”
(1)先作出截交线上的 特殊点—找齐 由于平面与圆柱的轴线 斜交,因此截交线为一椭圆。 (2)再作出适当数量 截交线的正面投影重影为一 的一般点。 直线,水平投影与圆柱面的 (3)将这些点的投影 投影重影为圆。侧面投影可 依次光滑的连接起来。 根据圆柱表面取点的方法求 (4)补全侧面投影中 出。 的转向轮廓线。
球体截切实例
例1:求半球体截切后的水平和侧面投影。
两个侧平面截圆球的截 水平面截圆球的截交线 交线的投影,在侧视图 的投影,在俯视图上为 上为部分圆弧,在俯视 部分圆弧,在侧视图上 图上积聚为直线。 积聚为直线。
首页
水平面截切圆球, 例1:求半球体截切后的水平和侧面投影。 截交线在H面的投 影为圆
分析:截交线的正面投影为双曲线. 作图: 1. 求特殊点。
1ˊ 最高点、最低点—找齐
2 .求一般点。
3. 连线。
4.整理轮廓 线,完成 全图
1
例2 过锥顶的截平面斜截圆锥,已知它的正 面投影,求其 余两个投影。
解题步骤:
(1) 画出完整圆锥的投影。 (2)求截交线的投影。 (3)整理轮廓线,判别可见性。 (4)检查加深,完成全图。
截交线
截平面
截平面
截交线
截交线都是封闭的平面图形,是截平面与回转体表面的共 有线其形状取决于回转体表面的形 状及截平面与回转体轴线的 相对位置。 求平面与回转体的截交线的一般步骤
(1)空间及投影分析
☆ 分析回转体的形状以及截平面与回转体轴线的相对位置,以便确定截 交线的形状。 ☆ 分析截平面与投影面的相对位置,明确截交线的投影特性,如积聚 性、类似性等。找出截交线的已知投影,明确待求投影。 (2)画出截交线的投影 当截交线的投影为非圆曲线时,其作图步骤为: ☆ 先找特殊点,补充中间点。 ☆ 将各点光滑地连接起来,并判断截交线的可 见性。
