第十章习题课曲线曲面积分

合集下载

高等数学课后习题及参考答案(第十章)

高等数学课后习题及参考答案（第十章）习题 10-11. 设在xOy 面内有一分布着质量的曲线弧L , 在点(x , y )处它的线密度为μ(x , y ), 用对弧长的曲线积分分别表达:(1)这曲线弧对x 轴、对y 轴的转动惯量I x , I y ; (2)这曲线弧的重心坐标x , y .解在曲线弧L 上任取一长度很短的小弧段ds (它的长度也记做ds ), 设(x , y )为小弧段ds 上任一点.曲线L 对于x 轴和y 轴的转动惯量元素分别为 dI x =y 2μ(x , y )ds , dI y =x 2μ(x , y )ds . 曲线L 对于x 轴和y 轴的转动惯量分别为 ⎰=Lx ds y x y I ),(2μ, ⎰=Ly ds y x x I ),(2μ.曲线L 对于x 轴和y 轴的静矩元素分别为 dM x =y μ(x , y )ds , dM y =x μ(x , y )ds . 曲线L 的重心坐标为⎰⎰==L L y dsy x ds y x x M M x ),(),(μμ, ⎰⎰==LL x ds y x dsy x y M M y ),(),(μμ. 2. 利用对弧长的曲线积分的定义证明: 如果曲线弧L 分为两段光滑曲线L 1和L 2, 则⎰⎰⎰+=12),(),(),(LL L ds y x f ds y x f ds y x f .证明划分L , 使得L 1和L 2的连接点永远作为一个分点, 则∑∑∑+===∆+∆=∆111111),(),(),(n n i i i i ni n i i i i i i i s f s f s f ηξηξηξ.令λ=max{∆s i }→0, 上式两边同时取极限∑∑∑+=→=→=→∆+∆=∆nn i i i i n i i i i ni i i i s f s f s f 111011),(lim),(lim ),(lim ηξηξηξλλλ,即得⎰⎰⎰+=12),(),(),(LL L ds y x f ds y x f ds y x f .3. 计算下列对弧长的曲线积分:(1)⎰+Ln ds y x )(22, 其中L 为圆周x =a cos t , y =a sin t (0≤t ≤2π);解⎰+L nds y x)(22⎰+-+=π20222222)cos ()sin ()sin cos (dt t a t a t a t a n=⎰+-+π20222222)cos ()sin ()sin cos (dt t a t a t a t a n ⎰++==ππ2012122n n a dt a .(2)⎰+Lds y x )(, 其中L 为连接(1, 0)及(0, 1)两点的直线段;解 L 的方程为y =1-x (0≤x ≤1);⎰⎰'-+-+=+102])1[(1)1()(dx x x x ds y x L22)1(1=-+=⎰dx x x .(3)xdx L⎰, 其中L 为由直线y =x 及抛物线y =x 2所围成的区域的整个边界; 解 L 1: y =x 2(0≤x ≤1), L 2: y =x (0≤x ≤1) .xdx L ⎰xdx xdx LL ⎰⎰+=21⎰⎰'++'+=102122)(1])[(1dx x x dx x x⎰⎰++=10102241xdx dx x x )12655(121-+=.(4)ds ey x L22+⎰, 其中L 为圆周x 2+y 2=a 2, 直线y =x 及x 轴在第一象限内所围成的扇形的整个边界; 解 L =L 1+L 2+L 3, 其中 L 1: x =x , y =0(0≤x ≤a ),L 2: x =a cos t , y =a sin t )40(π≤≤t ,L 3: x =x , y =x )220(a x ≤≤,因而ds eds eds eds ey x L y x L y x L y x L22322222122++++⎰⎰⎰⎰++=,⎰⎰⎰+++-++=axa ax dx e dt t a t a e dx e 220222402202211)cos ()sin (01π2)42(-+=a e a π.(5)⎰Γ++ds z y x 2221, 其中Γ为曲线x =e t cos t , y =e t sin t , z =e t 上相应于t 从0变到2的这段弧;解 dt dtdz dt dydt dx ds 222)()()(++=dt e t e t e t e t e t t t t t 222)cos sin ()sin cos (+++-=dt e t 3=,⎰⎰++=++Γ20222222223sin cos 11dt e et e t e ds z y x t t t t ⎰----=-==2220)1(23]23[23e e dt e t t .(6)⎰Γyzds x 2, 其中Γ为折线ABCD , 这里A 、B 、C 、D 依次为点(0, 0, 0)、 (0, 0, 2)、(1, 0, 2)、(1, 3, 2); 解 Γ=AB +BC +CD , 其中 AB : x =0, y =0, z =t (0≤t ≤1), BC : x =t , y =0, z =2(0≤t ≤3), CD : x =1, y =t , z =2(0≤t ≤3), 故yzds x yzds x yzds x yzds x CD BC AB 2222⎰⎰⎰⎰++=Γ9010200322231=++++=⎰⎰⎰dt t dt dt .(7)⎰Lds y 2, 其中L 为摆线的一拱x =a (t -sin t ), y =a (1-cos t )(0≤t ≤2π);解⎰⎰'+'--=L dt t a t t a t a ds y π2022222])(cos [])sin ([)cos 1(⎰--=π2023cos 1)cos 1(2dt t t a 315256a =.(8)⎰+Lds y x )(22, 其中L 为曲线x =a (cos t +t sin t ), y =a (sin t -t cos t )(0≤t ≤2π).解 dt dtdydt dx ds 22)()(+=atdt dt t at t at =+=22)sin ()cos (atdt t t t a t t t a ds y x L ])cos (sin )sin (cos [)(22202222-++=+⎰⎰π⎰+=+=πππ2023223)21(2)1(a tdt t a .4. 求半径为a , 中心角为2ϕ的均匀圆弧(线密度μ=1)的重心. 解建立坐标系如图10-4所示, 由对称性可知0=y , 又 ⎰==L x xds a M M x ϕ21⎰-⋅=ϕϕθθϕad a a cos 21ϕϕsin a =, 所以圆弧的重心为)0 ,sin (ϕϕa5. 设螺旋形弹簧一圈的方程为x =a cos t , y =a sin t , z =kt , 其中0≤1≤2π, 它的线密度ρ(x , y , z )=x 2+y 2+z 2, 求:(1)它关于z 轴的转动惯量I z ; (2)它的重心. 解 dt t z t y t x ds )()()(222'+'+'=dt k a 22+=. (1)⎰+=Lz ds z y x y x I ),,()(22ρds z y x y x L))((22222+++=⎰dt k a t k a a ⎰++=π20222222)()43(32222222k a k a a ππ++=. (2)⎰⎰++==LLds z y x ds z y x M )(),,(222ρ⎰++=π2022222)(dt k a t k a)43(3222222k a k a ππ++=, ds z y x x M x L)(1222⎰++=⎰++=π2022222)(cos 1dt k a t k a t a M2222436k a ak ππ+=, ds z y x y M y L)(1222⎰++=⎰++=π2022222)(sin 1dt k a t k a t a M2222436k a ak ππ+-=, ds z y x z M z L)(1222⎰++=⎰++=π2022222)(1dt k a t k a kt M22222243)2(3k a k a k πππ++=,故重心坐标为)43)2(3 ,436 ,436(22222222222222k a k a k k a ak k a ak πππππππ+++-+.习题 10-21. 设L 为xOy 面内直线x =a 上的一段, 证明:⎰=L dx y x P 0),(.证明设L 是直线x =a 上由(a , b 1)到(a , b 2)的一段, 则L : x =a , y =t , t 从b 1变到b 2. 于是00) ,())( ,(),(2121⎰⎰⎰=⋅==b b b b L dt t a P dt dtda t a P dx y x P . 2. 设L 为xOy 面内x 轴上从点(a , 0)到(b , 0)的一段直线, 证明⎰⎰=Lbadx x P dx y x P )0 ,(),(.证明L : x =x , y =0, t 从a 变到b , 所以⎰⎰⎰='=baL b adx x P dx x x P dx y x P )0 ,())(0 ,(),(.3. 计算下列对坐标的曲线积分:(1)⎰-Ldx y x )(22, 其中L 是抛物线y =x 2上从点(0, 0)到点(2, 4)的一段弧;解 L : y =x 2, x 从0变到2, 所以⎰⎰-=-=-L dx x x dx y x2042221556)()(.(2)⎰Lxydx , 其中L 为圆周(x -a )2+y 2=a 2(a >0)及x 轴所围成的在第一象限内的区域的整个边界(按逆时针方向绕行); 解 L =L 1+L 2, 其中L 1: x =a +a cos t , y =a sin t , t 从0变到π, L 2: x =x , y =0, x 从0变到2a , 因此⎰⎰⎰+=21L L L xydx xydx xydx⎰⎰+'++=adx dt t a a t a t a 200)cos (sin )cos 1(π3020232)sin sin sin (a t td tdt a πππ-=+-=⎰⎰.(3)⎰+Lxdy ydx , 其中L 为圆周x =R cos t , y =R sin t 上对应t 从0到2π的一段弧;解 ⎰⎰+-=+L dt t tR R t R t R xdy ydx ]cos cos )sin (sin [20π⎰==20202cos πtdt R .(4)⎰+--+L y x dy y x dx y x 22)()(, 其中L 为圆周x 2+y 2=a 2(按逆时针方向绕行);解圆周的参数方程为: x =a cos t , y =a sin t , t 从0变到2π, 所以⎰+--+L yx dyy x dx y x 22)()( ⎰---+=π202)]cos )(sin cos ()sin )(sin cos [(1dt t a t a t a t a t a t a a ⎰-=-=ππ202221dt a a .(5)ydz zdy dx x -+⎰Γ2, 其中Γ为曲线x =k θ, y =a cos θ, z =a sin θ上对应θ从0到π的一段弧; 解⎰⎰--+=-+Γπθθθθθθ022]cos cos )sin (sin )[(d a a a a k k ydz zdy dx x233220331)(a k d a k ππθθπ-=-=⎰.(6)dz y x ydy xdx )1(-+++⎰Γ, 其中Γ是从点(1, 1, 1)到点(2, 3, 4)的一段直线;解 Γ的参数方程为x =1+t , y =1+2t , z =1+3t , t 从0变到1.⎰Γ-+++dz y x ydy xdx )1(⎰-+++++++=1)]1211(3)21(2)1[(dt t t t t⎰=+=1013)146(dt t .(7)⎰Γ+-ydz dy dx , 其中Γ为有向闭折线ABCA , 这里的A , B , C依次为点(1, 0, 0), (0, 1, 0), (0, 0, 1); 解 Γ=AB +BC +CA , 其中AB : x =x , y =1-x , z =0, x 从1变到0, BC : x =0, y =1-z , z =z , z 从0变到1, CA : x =x , y =0, z =1-x , x 从0变到1, 故ydz dy dx ydz dy dx ydz dy dx ydz dy dx CA BC AB +-++-++-=+-⎰⎰⎰⎰Γ⎰⎰⎰+-+'--+'--=101010)]1()1([])1(1[dx dt z z dx x 21=.(8)dy xy y dx xy x L)2()2(22-+-⎰, 其中L 是抛物线y =x 2上从(-1, 1)到(1, 1)的一段弧.解 L : x =x , y =x 2, x 从-1变到1, 故⎰-+-L dy xy y dx xy x )2()2(22⎰--+-=113432]2)2()2[(dx x x x x x 1514)4(21042-=-=⎰dx x x 4. 计算⎰-++Ldy x y dx y x )()(, 其中L 是:(1)抛物线y =x 2上从点(1, 1)到点(4, 2)的一段弧; 解 L : x =y 2, y =y , y 从1变到2, 故⎰-++L dy x y dx y x )()(⎰=⋅-+⋅+=2122334]1)(2)[(dy y y y y y . (2)从点(1, 1)到点(4, 2)的直线段; 解 L : x =3y -2, y =y , y 从1变到2, 故⎰-++L dy x y dx y x )()(11]1)23()23[(21=⋅+-+⋅+-=⎰dy y y y y y(3)先沿直线从点(1, 1)到(1, 2), 然后再沿直线到点(4, 2)的折线; 解 L =L 1+L 2, 其中L 1: x =1, y =y , y 从1变到2, L 2: x =x , y =2, x 从1变到4, 故⎰-++L dy x y dx y x )()(dy x y dx y x dy x y dx y x L L )()()()(21-+++-++=⎰⎰14)2()1(4121=++-=⎰⎰dx x dy y .(4)沿曲线x =2t 2+t +1, y =t 2+1上从点(1, 1)到(4, 2)的一段弧. 解 L : x =2t 2+t +1, y =t 2+1, t 从0变到1, 故⎰-++L dy x y dx y x )()(332]2)()14)(23[(1022=⋅--++++=⎰dt t t t t t t .5. 一力场由沿横轴正方向的常力F 所构成, 试求当一质量为m 的质点沿圆周x 2+y 2=R 2按逆时针方向移过位于第一象限的那一段时场力所作的功.解已知场力为F =(|F |, 0), 曲线L 的参数方程为 x =R cos θ, y =R sin θ,θ从0变到2π, 于是场力所作的功为R F d R F dx F d W LL||)sin (||||20-=-⋅==⋅=⎰⎰⎰πθθr F .6. 设z 轴与力方向一致, 求质量为m 的质点从位置(x 1, y 1, z 1) 沿直线移到(x 2, y 2, z 2)时重力作的功.解已知F =(0, 0, mg ). 设Γ为从(x 1, y 1, z 1)到(x 2, y 2, z 2)的直线, 则重力所作的功为⎰⎰⎰ΓΓ-==++=⋅=21)(0012z z z z mg dz mg mgdz dy dx d W r F .7. 把对坐标的曲线积分⎰+Ldy y x Q dx y x P ),(),(化成对弧长的曲线积分, 其中L 为:(1)在xOy 面内沿直线从点(0, 0)到(1, 1); 解 L 的方向余弦214cos cos cos ===πβα,故⎰+L dy y x Q dx y x P ),(),(ds y x Q y x P L]cos ),(cos ),([βα+=⎰⎰+=L ds y x Q y x P 2),(),(.(2)沿抛物线y =x 2从点(0, 0)到(1, 1);解曲线L 上点(x , y )处的切向量为τ=(1, 2x ), 单位切向量为 )412,411()cos ,(cos 22x x x ++==τβαe ,故⎰+L dy y x Q dx y x P ),(),(ds y x Q y x P L ]cos ),(cos ),([βα+=⎰⎰++=L ds xy x xQ y x P 241),(2),(. (3)沿上半圆周x 2+y 2=2x 从点(0, 0)到(1, 1). 解 L 的方程为22x x y -=, 其上任一点的切向量为 )21 ,1(2x x x --=τ, 单位切向量为)1 ,2()cos ,(cos 2x x x --==τβαe ,故⎰+L dy y x Q dx y x P ),(),(ds y x Q y x P L ]cos ),(cos ),([βα+=⎰⎰-+-=Lds y x Q x y x P x x )],()1(),(2[2.8. 设Γ为曲线x =t , y =t 2, z =t 3上相应于t 从0变到1的曲线弧,把对坐标的曲线积分⎰Γ++Rdz Qdy Pdx 化成对弧长的曲线积分.解曲线Γ上任一点的切向量为 τ=(1, 2t , 3t 2)=(1, 2x , 3y ), 单位切向量为)3 ,2 ,1(9211)cos ,cos ,(cos 22y x yx ++==τγβαe ,ds R Q P Rdz Qdy Pdx L ]cos cos cos [γβα++=++⎰⎰Γ⎰++++=L ds y x yRxQ P 2294132.习题 10-31. 计算下列曲线积分, 并验证格林公式的正确性:(1)⎰++-ldy y x dx x xy )()2(22, 其中L 是由抛物线y =x 2及y 2=x 所围成的区域的正向边界曲线; 解 L =L 1+L 2, 故⎰++-L dy y x dx x xy )()2(22⎰⎰++-+++-=21)()2()()2(2222L L dy y x dx x xy dy y x dx x xy⎰⎰++-+++-=112243423)](2)2[(]2)()2[(dy y y y y y dx x x x x x301)242()22(1010245235=++--++=⎰⎰dy y y y dx x x x ,而dxdy x dxdy yPx Q DD)21()(-=∂∂-∂∂⎰⎰⎰⎰⎰⎰-=102)21(y y dx x dy301)(42121=+--=⎰dy y y y y , 所以⎰⎰⎰+=∂∂-∂∂l DQdy Pdx dxdy yPx Q )(.(2)⎰-+-ldy xy y dx xy x )2()(232, 其中L 是四个顶点分别为(0, 0)、 (2, 0)、(2, 2)、和(0, 2)的正方形区域的正向边界.解 L =L 1+L 2+L 3+L 4, 故⎰-+-L dy xy y dx xy x )2()(232dy xy y dx xy x L L L L )2())((2324321-+-+++=⎰⎰⎰⎰ ⎰⎰⎰⎰+-+-+=202002022222)8()4(dy y dx x x dy y y dx x 8482020=-+=⎰⎰ydy xdx , 而 dxdy xy y dxdy y P x Q DD )32()(2+-=∂∂-∂∂⎰⎰⎰⎰ ⎰⎰+-=20220)32(dy xy y dx 8)48(20=-=⎰dx x , 所以 ⎰⎰⎰+=∂∂-∂∂l D Qdy Pdx dxdy yP x Q )(. 2. 利用曲线积分, 求下列曲线所围成的图形的面积:(1)星形线x =a cos 3t , y =a sin 3t ;解 ⎰⎰-⋅⋅-=-=L dt t t a t a ydx A π2023)sin (cos 3sin ⎰==ππ20224283cos sin 3a tdt t a . (2)椭圆9x 2+16y 2=144;解椭圆9x 2+16y 2 =144的参数方程为x =4cos θ, y =3sin θ, 0≤θ≤2π, 故⎰-=Lydx xdy A 21 ⎰-⋅-⋅=πθθθθθ20)]sin 4(sin 3cos 3cos 4[21d ⎰==ππθ20126d . (3)圆x 2+y 2=2ax .解圆x 2+y 2=2ax 的参数方程为x =a +a cos θ, y =a sin θ, 0≤θ≤2π,故 ⎰-=Lydx xdy A 21 ⎰-⋅-⋅+=πθθθθθ20)]sin (sin cos )cos 1([21d a a a a 2202)cos 1(2a d a ⎰=+=ππθθ.3. 计算曲线积分⎰+-L y x xdy ydx )(222, 其中L 为圆周(x -1)2+y 2=2, L 的方向为逆时针方向.解 )(222y x y P +=, )(222y x x Q +-=. 当x 2+y 2≠0时 y P x Q ∂∂=∂∂0)(2)(22222222222=+--+-=y x y x y x y x . 在L 内作逆时针方向的ε小圆周l : x =εcos θ, y =εsin θ(0≤θ≤2π),在以L 和l 为边界的闭区域D ε上利用格林公式得0)(=∂∂-∂∂=+⎰⎰⎰-+dxdy y P x Q Qdy Pdx D l L ε, 即 ⎰⎰⎰+=+-=+-lL l dy Pdx Qdy Pdx Qdy Pdx . 因此 ⎰⎰+-=+-l L y x xdy ydx y x xdy ydx )(2)(22222⎰--=πθεθεθε20222222cos sin d ⎰-=-=ππθ2021d .4. 证明下列曲线积分在整个xOy 面内与路径无关, 并计算积分值:(1)⎰-++)3 ,2()1 ,1()()(dy y x dx y x ;解 P =x +y , Q =x -y , 显然P 、Q 在整个xOy 面内具有一阶连续偏导数, 而且1=∂∂=∂∂xQ y P , 故在整个xOy 面内, 积分与路径无关.取L 为点(1, 1)到(2, 3)的直线y =2x -1, x 从1变到2, 则⎰⎰-+-=-++)3 ,2()1 ,1(21)]1(2)13[()()(dx x x dy y x dx y x ⎰=+=2125)1(dx x . (2)⎰-+-)4 ,3()2 ,1(2232)36()6(dy xy y x dx y xy ;解 P =6xy 2-y 3, Q =6x 2y -3xy 2, 显然P 、Q 在整个xOy 面内具有一阶连续偏导数, 并且2312y xy xQ y P -=∂∂=∂∂, 故积分与路径无关, 取路径 (1, 2)→(1, 4)→(3, 4)的折线, 则⎰-+-)4 ,3()2 ,1(2232)36()6(dy xy y x dx y xy236)6496()3642312=-+-=⎰⎰dx x dy y y .(3)⎰-++-)1 ,2()0 ,1(324)4()32(dy xy x dx y xy .解 P =2xy -y 4+3, Q =x 2-4xy 3, 显然P 、Q 在整个xOy 面内具有一阶连续偏导数, 并且342y x xQ y P -=∂∂=∂∂, 所以在整个xOy 面内积分与路径无关, 选取路径为从(1, 0)→(1, 2)→(2, 1)的折线, 则⎰-++-)1 ,2()0 ,1(324)4()32(dy xy x dx y xy⎰⎰=++-=102135)1(2)41(dx x dy y .5. 利用格林公式, 计算下列曲线积分:(1)⎰-+++-Ldy x y dx y x )635()42(, 其中L 为三顶点分别为(0, 0)、 (3, 0)和(3, 2)的三角形正向边界;解 L 所围区域D 如图所示, P =2x -y +4, Q =5y +3x -6,4)1(3=--=∂∂-∂∂yP x Q , 故由格林公式,得⎰-+++-L dy x y dx y x )6315()42(dxdy y P x Q D)(∂∂-∂∂=⎰⎰ 124==⎰⎰dxdy D.(2)⎰-+-+Lx x dy ye x x dx e y x xy x y x )2sin ()sin 2cos (222, 其中L 为正向星形线323232a y x =+(a >0);解 x e y x xy x y x P 22sin 2cos -+=, x ye x x Q 2sin 2-=,0)2cos sin 2()2cos sin 2(22=-+--+=∂∂-∂∂x x ye x x x x ye x x x x yP x Q , 由格林公式⎰-+-+L x x dy ye x x dx e y x xy x y x )2sin ()sin 2cos (2220)(=∂∂-∂∂=⎰⎰dxdy yP x Q D . (3)⎰+-+-Ldy y x x y dx x y xy )3sin 21()cos 2(2223, 其中L 为在抛物线 2x =πy 2上由点(0, 0)到)1 ,2(π的一段弧; 解 x y xy P cos 223-=, 223sin 21y x x y Q +-=,0)cos 26()6cos 2(22=--+-=∂∂-∂∂x y xy xy x y yP x Q , 所以由格林公式0)(=∂∂-∂∂=+⎰⎰⎰++-dxdy yP x Q Qdy Pdx D OB OA L , 其中L 、OA 、OB 、及D 如图所示.故 ⎰⎰++=+AB OA L Qdy Pdx Qdy Pdx4)4321(02201022πππ=+-+=⎰⎰dy y y dx . (4)⎰+--L dy y x dx y x )sin ()(22, 其中L 是在圆周22x x y -=上由点(0, 0)到点(1, 1)的一段弧.解 P =x 2-y , Q =-x -sin 2y ,0)1(1=---=∂∂-∂∂y P x Q , 由格林公式有0)(=∂∂-∂∂-=+⎰⎰⎰++dxdy y P x Q Qdy Pdx DBO AB L , 其中L 、AB 、BO 及D 如图所示.故 ⎰⎰++--=+--L OB BA dy y x dx y x dy y x dx y x )sin ()()sin ()(22222sin 4167)sin 1(102102+-=++-=⎰⎰dx x dy y .6. 验证下列P (x , y )dx +Q (x , y )dy 在整个xOy 平面内是某一函数u (x , y )的全微分, 并求这样的一个u (x , y ):(1)(x +2y )dx +(2x +y )dy ;证明因为yP x Q ∂∂==∂∂2, 所以P (x , y )dx +Q (x , y )dy 是某个定义在整个xOy 面内的函数u (x , y )的全微分.⎰++++=),()0,0()2()2(),(y x C dy y x dx y x y x u C y xy x +++=22222. (2)2xydx +x 2dy ;解因为y P x x Q ∂∂==∂∂2, 所以P (x , y )dx +Q (x , y )dy 是某个定义在整个 xOy 面内的函数u (x , y )的全微分.⎰++=),()0,0(22),(y x C dy x xydx y x u ⎰⎰+=++=y yC y x C xydx dy 00220. (3)4sin x sin3y cos xdx –3cos3y cos2xdy解因为yP x y x Q ∂∂==∂∂2sin 3cos 6, 所以P (x , y )dx +Q (x , y )dy 是某个定义在整个xOy 平面内的函数u (x , y )的全微分.⎰+-=),()0,0(2cos 3cos 3cos 3sin sin 4),(y x C xdy y xdx y x y x u C y x C xdy y dx xy +-=+-+=⎰⎰3sin 2cos 2cos 3cos 3000. (4)dy ye y x x dx xy y x y )128()83(2322++++解因为yP xy x x Q ∂∂=+=∂∂1632, 所以P (x , y )dx +Q (x , y )dy 是某个定义在整个xOy 平面内的函数u (x , y )的全微分. ⎰+++++=),()0,0(232)128()823(),(y x y C dy ye y x x dx xy iy xh y x u C dx xy y x dy ye yx y +++=⎰⎰0022)83(12C e ye y x y x y y +-++=)(124223.(5)dy y x x y dx x y y x )sin sin 2()cos cos 2(22-++解因为yP y x x y x Q ∂∂=-=∂∂sin 2cos 2, 所以P (x , y )dx +Q (x , y )dy 是某个函数u (x , y )的全微分 ⎰⎰+-+=x y C dy y x x y xdx y x u 002)sin sin 2(2),( C y x x y ++=cos sin 22.7. 设有一变力在坐标轴上的投影为X =x +y 2, Y =2xy -8, 这变力确定了一个力场, 证明质点在此场内移动时, 场力所做的功与路径无关. 解场力所作的功为⎰Γ-++=dy xy dx y x W )82()(2. 由于yX y x Y ∂∂==∂∂2, 故以上曲线积分与路径无关, 即场力所作的功与路径无关.习题10-41. 设有一分布着质量的曲面∑, 在点(x , y , z )处它的面密度为μ(x , y , z ), 用对面积的曲面积分表达这曲面对于x 轴的转动惯量.解. 假设μ(x , y , z )在曲面∑上连续, 应用元素法, 在曲面∑上任意一点(x , y , z )处取包含该点的一直径很小的曲面块dS (它的面积也记做dS ), 则对于x 轴的转动惯量元素为dI x =(y 2+z 2)μ(x , y , z )dS ,对于x 轴的转动惯量为dS z y x z y I x ),,()(22μ+=∑⎰⎰.2. 按对面积的曲面积分的定义证明公式dS z y x f dS z y x f dS z y x f ),,(),,(),,(21∑∑∑⎰⎰⎰⎰⎰⎰+=,其中∑是由∑1和∑2组成的.证明划分∑1为m 部分, ∆S 1, ∆S 2, ⋅⋅⋅, ∆S m ;划分∑2为n 部分, ∆S m +1, ∆S m +2, ⋅⋅⋅, ∆S m +n ,则∆S 1, ⋅⋅⋅, ∆S m , ∆S m +1, ⋅⋅⋅, ∆S m +n 为∑的一个划分, 并且i i i i nm m i i i i i m i i i i i n m i S f S f S f ∆∑+∆∑=∆∑++==+=),,(),,(),,(111ζηξζηξζηξ. 令}{max 11i mi S ∆=≤≤λ, }{max 12i n m i m S ∆=+≤≤+λ, } ,max{21λλλ=, 则当 λ→0时, 有dS z y x f dS z y x f dS z y x f ),,(),,(),,(21∑∑∑⎰⎰⎰⎰⎰⎰+=.3. 当∑是xOy 面内的一个闭区域时, 曲面积分dSz y x f ),,(∑⎰⎰与二重积分有什么关系？解 ∑的方程为z =0, (x , y )∈D ,dxdy dxdy z z dS y x=++=221, 故 dxdy z y x f dS z y x f D),,(),,(⎰⎰⎰⎰=∑.4. 计算曲面积分dS z y x f ),,(∑⎰⎰, 其中∑为抛物面z =2-(x 2+y 2)在xOy 面上方的部分, f (x , y , z )分别如下:(1) f (x , y , z )=1;解 ∑: z =2-(x 2+y 2), D xy : x 2+y 2≤2,dxdy y x dxdy z z dS y x22224411++=++=. 因此 dxdy y x dS z y x f xyD 22441),,(++=⎰⎰⎰⎰∑ ⎰⎰+=πθ2020241rdr r d ππ313])41(121[2202/32=+=r . (2) f (x , y , z )=x 2+y 2;解 ∑: z =2-(x 2+y 2), D xy : x 2+y 2≤2, dxdy y x dxdy z z dS y x22224411++=++=. 因此 dxdy y x y x dS z y x f xyD 2222441)(),,(+++=⎰⎰⎰⎰∑ ⎰⎰+=πθ2020241rdr r d ππ301494122022=+=⎰rdr r r . (3) f (x , y , z )=3z .解 ∑: z =2-(x 2+y 2), D xy : x 2+y 2≤2,dxdy y x dxdy z z dS y x22224411++=++=. 因此 dS z y x f ),,(∑⎰⎰dxdy y x y x xyD 2222441)](2[3+++-=⎰⎰⎰⎰+-=πθ20202241)2(3rdr r r d ππ1011141)2(62022=+-=⎰rdr r r . 5. 计算dS y x )(22+∑⎰⎰, 其中∑是: (1)锥面22y x z +=及平面z =1所围成的区域的整个边界曲面;解将∑分解为∑=∑1+∑2, 其中∑1: z =1 , D 1: x 2+y 2≤1, dS =dxdy ;∑1:22y x z +=, D 2: x 2+y 2≤1, dxdy dxdy z z dS y x2122=++=. dS y x dS y x dS y x )()()(22222221+++=+∑∑∑⎰⎰⎰⎰⎰⎰ dxdy y x dxdy y x D D )()(222221+++=⎰⎰⎰⎰⎰⎰=πθ20103dr r d +⎰⎰πθ201032dr r d πππ221222+=+=. 提示: dxdy dxdy yx y y x x dS 21222222=++++=.(2)锥面z 2=3(x 2+y 2)被平面z =0及z =3所截得的部分. 解 ∑:223y x z +=, D xy : x 2+y 2≤3,dxdy dxdy z z dS y x2122=++=, 因而 πθπ922)()(302202222==+=+⎰⎰⎰⎰⎰⎰∑rdr r d dxdy y x dS y x xy D . 提示: dxdy dxdy y x y y x x dS 2])(326[])(326[1222222=++++=.6. 计算下面对面积的曲面积分:(1)dS y x z )342(++∑⎰⎰, 其中∑为平面1432=++z y x 在第一象限中的部分;解 y x z 3424:--=∑, x y x D xy 2310 ,20 :-≤≤≤≤, dxdy z z dS y x 221++=dxdy 361=, 61436143614)342(==⋅=++⎰⎰⎰⎰⎰⎰∑dxdy dxdy dS y x z xy xyD D . (2)dS z x x xy )22(2+--∑⎰⎰, 其中∑为平面2x +2y +z =6在第一象限中的部分;解 ∑: z =6-2x -2y , D xy : 0≤y ≤3-x , 0≤x ≤3,dxdy dxdy z z dS y x3122=++=, dS z x x xy )22(2+--∑⎰⎰ dxdy y x x x xy xyD 3)22622(2--+--=⎰⎰⎰⎰--+--=x dy y xy x x dx 30230)22236(3 427)9103(33023-=+-=⎰dx x x . (3)dS z y x )(++∑⎰⎰, 其中∑为球面x 2+y 2+z 2=a 2上z ≥h (0<h <a )的部分;解 ∑:222y x a z --=, D xy : x 2+y 2≤a 2-h 2,dxdy z z dS y x 221++=dxdy y x a a 222--=,dxdy yx a a y x a y x dS z y x xy D 222222)()(----++=++⎰⎰⎰⎰∑ )(||22h a a D a adxdy xy D xy-===⎰⎰π(根据区域的对称性及函数的奇偶性).提示: dxdy yx a y y x a x dS 22222222)()(1+--++--+=dxdy y x a a 222--=, (4)dS zx yz xy )(++∑⎰⎰, 其中∑为锥面22y x z +=被x 2+y 2=2ax所截得的有限部分.解 ∑: 22y x z +=, D xy : x 2+y 2≤2ax ,dxdy dxdy z z dS y x2122=++=, dxdy y x y x xy dS zx yz xy xyD ])([2)(22+++=++⎰⎰⎰⎰∑ ⎰⎰++=-θππθθθθcos 202222)]sin (cos cos sin [2a rdr q r r dθθθθθθππd a )cos sin cos cos (sin 24422554⎰-++= 421564a =. 提示: dxdy yx y y x x dS 2222221++++=. 7. 求抛物面壳)10)((2122≤≤+=z y x z 的质量, 此壳的面密度为μ=z .解 ∑: )(2122y x z +=, D xy : x 2+y 2≤2, dxdy y x dxdy z z dS y x222211++=++=.故 dxdy y x y x zdS M xyD 22221)(21+++==⎰⎰⎰⎰∑ ⎰⎰+=πθ202022121rdr r r d )136(152+=π. 8. 求面密度为μ0的均匀半球壳x 2+y 2+z 2=a 2(z ≥0)对于z 轴的转动惯量. 解 ∑: 222y x a z --=, D xy : x 2+y 2≤a 2,dxdy z z dS y x 221++=dxdy yx a a 222--=, dxdy y x a a y x dS y x I z 222022022)()(--+=+=∑∑⎰⎰⎰⎰μμ ⎰⎰-=a dr ya r d a 0223200πθμ 4034a πμ=.提示:dxdy yx a y y x a x dS 22222222)()(1---+---+=dxdy y x a a 222--=.习题10-51. 按对坐标的曲面积分的定义证明公式:dydz z y x P z y x P )],,(),,([21±∑⎰⎰dydz z y x P dydz z y x P )],,(),,(21∑∑⎰⎰⎰⎰±=.解证明把∑分成n 块小曲面∆S i (∆S i 同时又表示第i 块小曲面的面积), ∆S i 在yOz 面上的投影为(∆S i )yz , (ξi , ηi ,ζi )是∆S i 上任意取定的一点, λ是各小块曲面的直径的最大值, 则dydzz y x P z y x P )],,(),,([21±∑⎰⎰ yz i i i i i i i n i S P P ))](,(),([lim ,2,110∆±==→∑ζηξζηξλyz i i i i ni yz i i i i n i S P S P ))(,(lim ))(,(lim ,210,110∆±∆==→=→∑∑ζηξζηξλλ dydz z y x P dydz z y x P )],,(),,(21∑∑⎰⎰⎰⎰±=.2. 当∑为xOy 面内的一个闭区域时, 曲面积分dxdy z y x R ),,(∑⎰⎰与二重积分有什么关系？解因为∑: z =0, (x , y )∈D xy , 故dxdy z y x R dxdy z y x R xyD ),,(),,(⎰⎰⎰⎰±=∑,当∑取的是上侧时为正号, ∑取的是下侧时为负号.3. 计算下列对坐标的曲面积分:(1)zdxdy y x 22∑⎰⎰其中∑是球面x 2+y 2+z 2=R 2的下半部分的下侧;解 ∑的方程为222y x R z ---=, D xy : x 2+y 2≤R , 于是zdxdy y x 22∑⎰⎰dxdy y x R y x xyD )(22222----=⎰⎰ ⎰⎰⋅-⋅⋅=πθθθ20222202sin cos rdr r R r r d R⎰⎰-=πθθ20052222sin 41R dr r r R d 71052R π=. (2)ydzdx xdydz zdxdy ++∑⎰⎰, 其中z 是柱面x 2+y 2=1被平面z =0及z =3所截得的第一卦限内的部分的前侧;解 ∑在xOy 面的投影为零, 故0=∑⎰⎰zdxdy .∑可表示为21y x -=, (y , z )∈D yz ={(y , z )|0≤y ≤1, 0≤z ≤3}, 故 ⎰⎰⎰⎰⎰⎰⎰-=-=-=∑3010102221311dy y dy y dz dydz y xdyz yz D ∑可表示为21x y -=, (z , x )∈D zx ={(z , x )|0≤z ≤3, 0≤x ≤1}, 故dzdx x ydzdx zx D 21-=⎰⎰⎰⎰∑⎰⎰⎰-=-=30101022131dx x dx x dz . 因此 ydzdx xdydz zdxdy ++∑⎰⎰)13(2102dx x ⎰-=ππ2346=⨯=. 解法二 ∑前侧的法向量为n =(2x , 2y , 0), 单位法向量为)0 , ,(1)cos ,cos ,(cos 22y x y x +=γβα, 由两种曲面积分之间的关系,dS z y x ydzdx xdydz zdxdy )cos cos cos (γβα++=++∑∑⎰⎰⎰⎰π23)(222222==+=+⋅++⋅=∑∑∑⎰⎰⎰⎰⎰⎰dS dS y x dS y x y y y x x x . 提示: dS ∑⎰⎰表示曲面的面积.(3)dxdy z z y x f dzdx y z y x f dydz x z y x f ]),,([]),,(2[]),,([+++++∑⎰⎰, 其中f (x , y , z )为连续函数, ∑是平面x -y +z =1在第四卦限部分的上侧; 解曲面∑可表示为z =1-x +y , (x , y )∈D xy ={(x , y )|0≤x ≤1, 0≤y ≤x -1}, ∑上侧的法向量为n =(1, -1, 1), 单位法向量为)31 ,31 ,31()cos ,cos ,(cos -=γβα, 由两类曲面积分之间的联系可得dxdy z z y x f dzdx y z y x f dydz x z y x f ]),,([]),,(2[]),,([+++++∑⎰⎰dS z f y f x f ]cos )(cos )2(cos )[(γβα+++++=∑⎰⎰dS z f y f x f ]31)()31()2(31)(⋅++-⋅++⋅+=∑⎰⎰ 2131)(31===+-=⎰⎰⎰⎰⎰⎰∑∑dxdy dS dS z y x xyD .(4)⎰⎰∑++yzdzdx xydydz xzdxdy , 其中∑是平面x =0, y =0, z =0, x +y +z =1所围成的空间区域的整个边界曲面的外侧.解 ∑=∑1+∑2+∑3+∑4, 其中∑1: x =0, D yz : 0≤y ≤1, 0≤z ≤1-y ,∑2: y =0, D zx : 0≤z 1, 0≤x ≤1-z ,∑3: z =0, D xy : 0≤x ≤1, 0≤y ≤1-x ,∑4: z =1-x -y , D xy : 0≤x ≤1, 0≤y ≤1-x ,于是 ⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰∑∑∑∑∑+++=4321xzdxdy xzdxdy 4000∑⎰⎰+++= dxdy y x x xy D )1(--=⎰⎰⎰⎰-=--=1010241)1(x dy y x xdx . 由积分变元的轮换对称性可知241⎰⎰⎰⎰∑∑==yzdzdx xydydz . 因此⎰⎰∑=⨯=++812413yzdzdx xydydz xzdxdy .解 ∑=∑1+∑2+∑3+∑4, 其中∑1、∑2、∑3是位于坐标面上的三块; ∑4: z =1-x -y , D xy : 0≤x ≤1, 0≤y ≤1-x .显然在∑1、∑2、∑3上的曲面积分均为零, 于是⎰⎰∑++yzdzdx xydydz xzdxdyyzdzdx xydydz xzdxdy ++=∑⎰⎰4dS xz yz xy )cos cos cos (4γβα++=∑⎰⎰dS xz yz xy )(34++=∑⎰⎰81)]1)(([3=--++=⎰⎰dxdy y x y x xy xyD . 4. 把对坐标的曲面积分dxdy z y x R dzdx z y x Q dydz z y x P ),,(),,(),,(++∑⎰⎰化成对面积的曲面积分:(1)∑为平面63223=++z y x 在第一卦限的部分的上侧;解令63223),,(-++=z y x z y x F , ∑上侧的法向量为:)32 ,2 ,3(),,(==z y x F F F n ,单位法向量为)32 ,2 ,3(51)cos ,cos ,(cos =γβα, 于是 Rdxdy Qdzdx Pdydz ++∑⎰⎰dS R Q P )cos cos cos (γβα++=∑⎰⎰dS R Q P )3223(51++=∑⎰⎰. (2)∑是抛物面z =8-(x 2+y 2)在xOy 面上方的部分的上侧.解令F (x , y , z )=z +x 2+y 2-8, ∑上侧的法向量n =(F x , F y , F z )=(2x , 2y , 1),单位法向量为)1 ,2 ,2(4411)cos ,cos ,(cos 22y x y x ++=γβα, 于是 Rdxdy Qdzdx Pdydz ++∑⎰⎰dS R Q P )cos cos cos (γβα++=∑⎰⎰dS R yQ xP yx )22(441122++++=∑⎰⎰.10-61. 利用高斯公式计算曲面积分:(1)⎰⎰∑++dxdy z dzdx y dydz x 222, 其中∑为平面x =0, y =0, z =0, x =a ,y =a , z =a 所围成的立体的表面的外侧;解由高斯公式原式dv z y x dv z R y Q x P )(2)(++=∂∂+∂∂+∂∂=ΩΩ⎰⎰⎰⎰⎰⎰ ⎰⎰⎰⎰⎰⎰===Ωaa a a dz dy xdx xdv 0400366(这里用了对称性).(2)⎰⎰∑++dxdy z dzdx y dydz x 333, 其中∑为球面x 2+y 2+z 2=a 2的外侧;解由高斯公式原式dv z y x dv z R y Q x P )(3)(222++=∂∂+∂∂+∂∂=ΩΩ⎰⎰⎰⎰⎰⎰ ⎰⎰⎰=ππϕϕθ20004sin 3a dr r d d 5512a π=. (3)⎰⎰∑++-+dxdy z y xy dzdx z y x dydz xz )2()(2322, 其中∑为上半球体 x 2+y 2≤a 2, 2220y x a z --≤≤的表面外侧;解由高斯公式原式dv y x z d z R y Q x P )()(222++=∂∂+∂∂+∂∂=ΩΩ⎰⎰⎰⎰⎰⎰ ⎰⎰⎰=ππϕϕθ2020022sin a dr r r d d 552a π=. (4)⎰⎰∑++zdxdy ydzdx xdydz 其中∑界于z =0和z =3之间的圆柱体x 2+y 2≤9的整个表面的外侧;解由高斯公式原式π813)(==∂∂+∂∂+∂∂=ΩΩ⎰⎰⎰⎰⎰⎰dv dv z R y Q x P . (5)⎰⎰∑+-yzdxdy dzdx y xzdydz 24,其中∑为平面x =0, y =0, z =0, x =1,y =1, z =1所围成的立体的全表面的外侧.解由高斯公式原式dv y y z dv z R y Q x P )24()(+-=∂∂+∂∂+∂∂=ΩΩ⎰⎰⎰⎰⎰⎰ ⎰⎰⎰=-=10101023)4(dz y z dy dx . 2. 求下列向量A 穿过曲面∑流向指定侧的通量: (1)A =yz i +xz j +xy k , ∑为圆柱x +y 2≤a 2(0≤z ≤h )的全表面, 流向外侧; 解 P =yz , Q =xz , R =xy ,⎰⎰∑++=Φxydxdy xzdzdx yzdydzdv z xy y xz x yz ))()()((∂∂+∂∂+∂∂=Ω⎰⎰⎰00==Ω⎰⎰⎰dv . (2)A =(2x -z )i +x 2y j - xz 2k , ∑为立方体0≤x ≤a , 0≤y ≤a , 0≤z ≤a ,的全表面, 流向外侧;解 P =2x -z , Q =x 2y , R =-xz 2,⎰⎰∑++=ΦRdxdy Qdzdx Pdydzdv xz x dv z r y Q x P )22()(2-+=∂∂+∂∂+∂∂=ΩΩ⎰⎰⎰⎰⎰⎰ ⎰⎰⎰-=-+=a a a a a dz xz x dy dx 023200)62()22(. (3)A =(2x +3z )i -(xz +y )j +(y 2+2z )k , ∑是以点(3, -1, 2)为球心, 半径R =3的球面, 流向外侧.解 P =2x +3z , Q =-(xz +y ), R =y 2+2z ,⎰⎰∑++=ΦRdxdy Qdzdx Pdydzdv dv z R y Q x P )212()(+-=∂∂+∂∂+∂∂=ΩΩ⎰⎰⎰⎰⎰⎰π1083==Ω⎰⎰⎰dv . 3. 求下列向量A 的散度:(1)A =(x 2+yz )i +(y 2+xz )j +(z 2+xy )k ;解 P =x 2+yz , Q =y 2+xz , R =-z 2+xy ,)(2222div z y x z y x zR y Q x P ++=++=∂∂+∂∂+∂∂=A . (2)A =e xy i +cos(xy )j +cos(xz 2)k ;解 P =e xy , Q =cos(xy ), R =cos(xz 2),)sin(2sin div 2xz xz xy x ye zR y Q x P xy --=∂∂+∂∂+∂∂=A . (3)A =y 2z i +xy j +xz k ;解 P =y 2, Q =xy , R =xz ,x x x zR y Q x P 20div =++=∂∂+∂∂+∂∂=A . 4. 设u (x , y , z )、v (x , y , z )是两个定义在闭区域Ω上的具有二阶连续偏导数的函数, n u ∂∂, nv ∂∂依次表示u (x , y , z )、v (x , y , z )沿∑的外法线方向的方向导数. 证明dS n u v n v u dxdydz u v v u )()∂∂-∂∂=∆-∆⎰⎰⎰⎰⎰∑Ω, 其中∑是空间闭区间Ω的整个边界曲面, 这个公式叫作林第二公式. 证明由第一格林公式(见书中例3)知dxdydz z v y v x v u )(222222∂∂+∂∂+∂∂Ω⎰⎰⎰ dxdydz z v z u y v y u x v x u dS n v u )(∂∂∂∂+∂∂∂∂+∂∂∂∂-∂∂=⎰⎰⎰⎰⎰∑Ω, dxdydz z u y u x u v )(222222∂∂+∂∂+∂∂Ω⎰⎰⎰dxdydz z v z u y v y u x v x u dS n u v )(∂∂∂∂+∂∂∂∂+∂∂∂∂-∂∂=⎰⎰⎰⎰⎰∑Ω. 将上面两个式子相减, 即得dxdyd z u y u x u v z v y v x v u )]()([222222222222∂∂+∂∂+∂∂-∂∂+∂∂+∂∂Ω⎰⎰⎰ ⎰⎰∑∂∂-∂∂=dS n u v n v u )(. 5. 利用高斯公式推证阿基米德原理: 浸没在液体中所受液体的压力的合力(即浮力)的方向铅直向上, 大小等于这物体所排开的液体的重力. 证明取液面为xOy 面, z 轴沿铅直向下, 设液体的密度为ρ, 在物体表面∑上取元素dS 上一点, 并设∑在点(x , y , z )处的外法线的方向余弦为cos α, cos β, cos γ, 则dS 所受液体的压力在坐标轴x , y , z 上的分量分别为-ρz cos αdS , -ρz cos β dS , -ρz cos γ dS ,∑所受的压力利用高斯公式进行计算得00cos ==-=Ω∑⎰⎰⎰⎰⎰dv dS z F x αρ,00cos ==-=Ω∑⎰⎰⎰⎰⎰dv dS z F y βρ,||cos Ω-=-=-=-=ΩΩ∑⎰⎰⎰⎰⎰⎰⎰⎰ρρργρdv dv dS z F z ,其中|Ω|为物体的体积. 因此在液体中的物体所受液体的压力的合力, 其方向铅直向上, 大小等于这物体所排开的液体所受的重力, 即阿基米德原理得证.习题10-71. 利用斯托克斯公式, 计算下列曲线积分:(1)⎰Γ++xdz zdy ydx , 其中Γ为圆周x 2+y 2+z 2=a 2, , 若从z 轴的正向看去, 这圆周取逆时针方向;解设∑为平面x +y +z =0上Γ所围成的部分, 则∑上侧的单位法向量为)31,31,31()cos ,cos ,(cos ==γβαn .于是 ⎰Γ++xdz zdy ydx dS x z y zy x ∂∂∂∂∂∂=∑⎰⎰γβαcos cos cos 2333)cos cos cos (a dS dS πγβα-=-=---=∑∑⎰⎰⎰⎰.提示:dS ∑⎰⎰表示∑的面积, ∑是半径为a 的圆.(2)⎰Γ-+-+-dz y x dy x z dz z y )()()(, 其中Γ为椭圆x 2+y 2=a 2, 1=+b z a x(a >0, b >0), 若从x 轴正向看去, 这椭圆取逆时针方向;解设∑为平面1=+b z a x 上Γ所围成的部分, 则∑上侧的单位法向量为) ,0 ,()cos ,cos ,(cos 2222b a b b a b ++==γβαn . 于是 ⎰Γ-+-+-dz y x dy x z dx z y )()()(dS y x x z z y zy x ---∂∂∂∂∂∂=∑⎰⎰γβαcos cos cos dS b a b a dS ∑∑⎰⎰⎰⎰++-=---=22)(2)cos 2cos 2cos 2(γβα)(2)(2)(22222b a a dxdy a b a dxdy a b a b a b a xyxyD D +-=+-=+++-=⎰⎰⎰⎰π.提示: ∑(即x ab b z -=)的面积元素为dxdy a b a dxdy a b dS 222)(1+=+=.(3)⎰Γ+-dz yz xzdy ydx 23, 其中Γ为圆周x 2+y 2=2z , z =2, 若从z 轴的正向看去, 这圆周是取逆时针方向;解设∑为平面z =2上Γ所围成的部分的上侧, 则⎰Γ+-dz yz xzdy ydx 2323yz xz y zy x dxdydzdx dydz -∂∂∂∂∂∂=∑⎰⎰ ππ2025)3()(22-=⨯-=+-+=∑⎰⎰dxdy z dydz x z .(4)⎰Γ-+dz z xdy ydx 232, 其中Γ为圆周x 2+y 2+z 2=9, z =0, 若从z 轴的正向看去, 这圆周是取逆时针方向.解设∑为xOy 面上的圆x 2+y 2≤9的上侧, 则⎰Γ-+dz z xdy ydx 232232z x y zy x dxdydzdx dydz -∂∂∂∂∂∂=∑⎰⎰ π9===⎰⎰⎰⎰∑dxdy dxdy xyD .2. 求下列向量场A 的旋度: (1)A =(2z -3y )i +(3x -z )j +(-2x )k ;解 k j i kj i A 6422332++=---∂∂∂∂∂∂=x y z x y z z y x rot . (2)A =(sin y )i -(z -x cos y )k ;解 j i kji A +=--+∂∂∂∂∂∂=0)cos (sin y x z y z z yx rot . (3)A =x 2sin y i +y 2sin(xz )j +xy sin(cos z )k .解 )sin(cos )sin(sin 22z xy xz y y x z y x ∂∂∂∂∂∂=kj i A rot=[x sin(cos z )-xy 2cos(xz )]i -y sin(cos z )j +[y 2z cos(xz )-x 2cos y ]k . 3. 利用斯托克斯公式把曲面积分dS n A ⋅∑⎰⎰rot 化为曲线积分, 并计算积分值,其中A 、∑及n 分别如下:(1)A =y 2i +xy j +xz k , ∑为上半球面221y x z --=, 的上侧, n 是∑的单位法向量;解设∑的边界Γ : x 2+y 2=1, z =0, 取逆时针方向, 其参数方程为 x =cos θ, y =sin θ, z =0(0≤θ≤2π, 由托斯公式dS n A ⋅∑⎰⎰rot ⎰Γ++=Rdz Qdy Pdx ⎰Γ++=xzdz xydy dx y 2⎰=+-=πθθθθθ20220]sin cos )sin ([sin d .(2)A =(y -z )i +yz j -xz k , ∑为立方体0≤x ≤2, 0≤y ≤2, 0≤z ≤2的表面外侧去掉xOy 面上的那个底面, n 是∑的单位法向量. 解dS n A ⋅∑⎰⎰rot ⎰Γ++=Rdz Qdy Pdx⎰Γ-++-=dz xz yzdy dx x y )()(⎰⎰Γ-===0242dx ydx .4. 求下列向量场A 沿闭曲线Γ(从z 轴正向看依逆时针方向)的环流量: (1)A =-y i +x j +c k (c 为常量), Γ为圆周x 2+y 2=1, z =0; 解θθθθθπd cdz xdy ydx L ]cos cos )sin ()(sin [(20+--=++-⎰⎰⎰==ππθ202d .(2)A =(x -z )i +(x 3+yz )j -3xy 2k , 其中Γ为圆周222y x z +-=, z =0. 解有向闭曲线Γ的参数方程为x =2cos θ, y =2sin θ, z =0(0≤π≤2π). 向量场A 沿闭曲线Γ的环流量为⎰⎰-++-=++LL dz xy dy yz x dx z x Rdz Qdy Pdx 223)()(。

曲线积分与曲面积分习题课0657

提示:
完整ppt
23
首上下返回束
提示: 方法1 利用称性
完整ppt
24
首上下返回束
方法2 利用斯托克斯公式三角形区域 , 方向向上,
完整ppt
25
首上下返回束
提示: 以半球底面助面 ,
且取下 , 半球域 ,利用
高斯公式有
完整ppt
7
首上下返回束
或：
注: 格林公式(斯托克斯公式)反映的是平面区域 D(空曲面 Σ)上重分 (曲面分 )与界曲上曲分之关系 .
完整ppt
8
首上下返回束
2. 基本技巧
(1) 利用称性化算 ;
(2) 利用分与路径无关的等价条件 ;
于曲分
直段 (合 P、Q考 ).
(3) 利用格林公式(适用于封曲 )化定分 .
注: 若曲 L不是封的 ,直接算又困 , 可考添
加
助曲 C, 使L+C完封整ppt 曲 , 再利用格林公式.6
首上下返回束
(4) 利用斯托克斯公式(适用空封曲分 ). 利用行列式号可：
L参数方程
L直角坐方程
完整ppt
L极坐方程
4
首上下返回束
坐的曲分算方法： (1) 直接化参量的定分
注: 下限起点 , 上限点
完整ppt
5
首上下返回束
(2) 利用分与路径无关的条件
若
, 分只与 L的起点与点有关
,故可取便于算的路径 ,如折段、弧段、
完整ppt
2
首上下返回束
弧的曲分解步： (1) 写出曲 L方程及相弧微分公式 ds ① L参数方程 :

辽宁工业大学高数习题课(10)

（这里 L 为区域 D 的正向边界曲线) 3．利用积分与路径无关的条件计算法.
c . Pdx Qdy 与路径无关 Pdx Qdy 0 ，为区域内任意闭曲线
L
c

P Q , ( x, y ) G ─单连域. y x
du Pdx Qdy, ( x, y ) G —单连域.
所以

AB
dx dy ydz [1 (1 x )]dx 2;
1
0

BC
dx dy ydz [(1 z ) (1 z )z ]dz ( 2 z )dz
0
0
1
1
3 2
CA
dx dy ydz 1 dx 1
采用框图中线路2→21的方法计算；此时应注意首先要利
用积分曲线方程将被积函数中的分母化简，去掉奇点，使其满足格林公式的条件。
解法1：化为定积分计算。
x a cos t L 的参数方程为： , t 从 0 变到 2 . 则 y a sint
( x y )dx ( x y )dy I L x2 y2 1 2 2 [(a cos t a sint )(a cos t ) (a cos t a sint )(a sint )]dt a 0 1 2 2 [( a 2 )dt 2 a 0
0
1
从而
I

dx dy ydz (
3 1 1 2 2
AB

BC
) dx dy ydz
CA
2
解法2：利用斯托克斯公式计算. 设为平面 x y z 1 上 L AB BC CA 所围成部分的上侧，

《高数》第十章习题课-线面积分的计算

12
练习题: P184 题 3(5) ; P185 题6; 10 3(5). 计算
其中L为上半圆周提示:
沿逆时针方向.
I ex sin y d x (ex cos y 2)dy 2 ydx
L
L

2 ydx
L AB AB
L
L
:
xy

a a
(1 cos sin t
其中L为上半圆周
沿逆时针方向.
P185 6 . 设在右半平面 x > 0 内, 力
构成力场,其中k 为常数,
场力所作的功与所取的路径无关.
证明在此力场中
P185 10. 求力
沿有向闭曲线所作的
功, 其中为平面 x + y + z = 1 被三个坐标面所截成三
角形的整个边界, 从 z 轴正向看去沿顺时针方向.
3
16
二、曲面积分的计算法
1. 基本方法
曲面积分

第一类( 第二类(
对面积对坐标
) )
转化
二重积分
(1) 统一积分变量 — 代入曲面方程
(2)
积分元素投影

第一类: 第二类:
始终非负有向投影
(3) 确定二重积分域
— 把曲面积分域投影到相关坐标面
17
2. 基本技巧
(1) 利用对称性及重心公式简化计算重心公式
20
例4. 设为简单闭曲面, a 为任意固定向量, n 为的单位外法向向量, 试证
证明: 设 n (cos , cos , cos )
(常向量)
则 cos( n ,a ) d S n a 0 dS

第十章曲线积分与曲面积分习题课

理论上的联系
1.定积分与不定积分的联系
b
a f ( x ) d F x ( b ) F ( a )( F ( x ) f ( x ))
牛顿--莱布尼茨公式
2.二重积分与曲线积分的联系
D( Q x P y)dx d L Py dQ xd (沿 y L 的)正向
格林公式
2020/6/3
3.三重积分与曲面积分的联系
思路:
ILPdxQdy
(x,y)
非闭
I PdxQdy (x0,y0)
P
Q
P
定义
n
n
f(x,y,z)d sl i0 im 1f(i,i,i) si R (x ,y,z)dx l d i0i m 1 y R (i,i,i)( S i)xy
联系
PdydQzdzdRxdxd (yP c oQ sco s R co)dsS
计
f(x, y,z)ds
R(x,y,z)dxdy
算
a y 1 (x ) z 1 (x ,y )
f(x ,y )d s bf[x ,y (x )1 ] y 2 d,(d x 线 s ( 曲元 ))
L
a
f(x ,y )d x bf[x ,y (x )d ],(d x 线 x (投元 ))影素
L
a
2020/6/3
f(x ,y ,z)d S f[x ,y ,z(x ,y )]1 zx 2 zy2 dxd
旋度 rA o ( tR Q )i ( P R ) j ( Q P )k y z z x x y
2020/6/3
二、典型例题
例 1 计算 I (x22x)ydx (x2y4)d, y L
其中 L为由点 O(0,0)到点 A(1,1)的曲线 ysi nx. 2

§10.习题课(曲面积分)

环流量 Pdx Qdy Rdz 旋度
R Q P R Q P rotA ( )i ( )j ( )k y z z x x y
线积分典型例题
例1 计算
e
L
x y
2
2
ds L : x y a , y x , y 0
2 2
其中L为
①不包围也不通过原点的任意闭曲线(可直接用格林公式) ②以原点为中心的正向单位圆周 ③包围原点的任意正向闭曲线(挖去小圆)
解 ① P x y2 2
x y
P y Q x
2
Q
2
y x x y
2
2 2
2

x y 2 xy (x y )
2
1) 因为
2
2

L l
-

l
-
l
-

D
(
Q x

P y
) dxdy

2
-

2
（ x y ) dx ( x y ) dy
l

x y
2

（ x y ) dx ( x y ) dy
l
这里的x,y就是小圆的
x y
2
2

0
(cos sin )( sin ) (sin cos )(cos ) cos sin
( 0 ,0 ) D
则由Green公式
Qdy 0
Pdx
L
②
I
L
2
x y 1
2 2

第十章曲面积分习题课

3d x d y d z 0 xdydz ydzdx zdxdy
3 2 R3 0 2 R3
3
9
例. 设是四面体 x y z 1 , x 0 , y 0 , z 0的表
面, 计算
z1
解: 在四面体的四个面上
平面方程
dS
1 o 1y 投影域 x
z 1 x y 3dx dy Dxy : 0 x 1, 0 y 1 x
59
和平面 z = y 下方的那部分的侧面积
解一易见曲面对称于 yoz 面
A dS 2dS
1
:
x2 5
y2 9
1,x
1
0, y
0,0
z
y
1 在 yoz 面的投影
D : 0 y 3,0 z y
12
x 5 9 y2 3
A 2
1
x
2 y
xz2dydz
D
2 81 y2 dydz
6
关于对称性
对面积的曲面积分与侧无关，具有与三重积分相类似的奇偶性
你对称，我奇偶
积分曲面对称于坐标面，被积函数关于另一个变量具有奇偶性
对坐标的曲面积分的对称性比较复杂，一般不直接使用，可利用两类曲面积分之间的关系先化为对面积的曲面积分，再使用对称性
7
P184 题2. 设
一卦限中的部分, 则有( C ).
lim
0 i1
f (i ,i , i )Si
n
R(
x,
y,
z)dxdy
lim
0
i 1
R(i
,i
,
i
)(Si
)xy
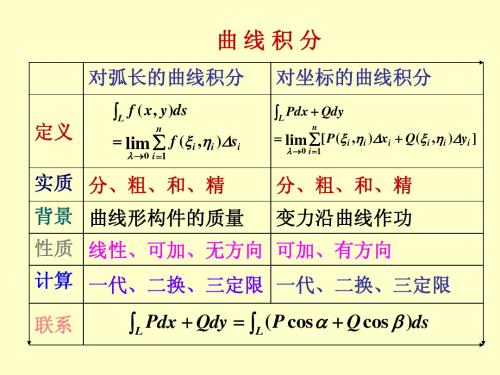
分、粗、和、精
分、粗、和、精
背景性质计算

大一高数课件第十章 10-习题课-1

L
半圆周 ( x − a ) 2 + y 2 = a 2 , y ≥ 0 ,沿逆时针方向 .
三、证明: 证明:
xdx + ydy 在整个 xoy 平面除去 y 的负半轴及 2 2 x +y
内是某个二元函数的全微分, 原点的开区域 G 内是某个二元函数的全微分,并求出一个这样的二元函数 .
测验题答案
(2) I2 = ∫ ( x2 − y+ y2)d x + ( y2 − x)d y L
= ∫ ( x2 − y)d x + ( y2 − x)dy + ∫ y2 dx
L L
L: x = acost, y = asint ,
t : 0 →π
= I − ∫ a sin3 t d t = −2a3
0
π 3
非闭
I = ∫ Pdx + Qdy =0
L
闭合
∂P ∂Q ∂P = ≠ ∂y ∂x ∂y ∂x非闭补充曲线或用公式
∂Q ∂P 闭合 I = ∫∫ ( − )dxdy ∂x ∂y ∂Q D
解
由 I = ∫ ( x2 + 2xy)dx + ( x2 + y4 )dy
1
y
A
∂P ∂ 2 知 = ( x + 2 xy ) = 2 x ∂ y ∂y ∂Q ∂ 2 = ( x + y4 ) = 2 x x ∂x ∂x o 1 ∂P ∂Q 1 2 1 , 即 = 故原式 = ∫ x dx + ∫ (1 + y 4 )dy = 23 . ∂y ∂x 0 0
λ→0 i=1
n
∫ P( x, y)dx+ Q( x, y)dy

大一高数课件第十章10-习题课-2

1
(C) z 2dxdy 2 z 2dxdy.

1
2、若为 z 2 ( x 2 y 2 )在 xoy面上方部分的曲面 ,
则 ds等于( C ).
(A)
2
d
r
1 4r 2 rdr ;(B)
2
d
2
1 4r 2 rdr;
0
0

*

(
P x

Q y

R z
)dxdydz
2
o1

*
y
3
x
(8 y 1 4 y 4 y)dxdydz dv

3
dxdz 1 z2 x2 dy
Dxz
2 d
0
2 d
0
3
1 2 dy
2 0 2 (2 3 )d 2 ,
0
0
(C)
2
d
2 1 4r 2 rdr.
0
0
3、若为球面x 2 y 2 z 2 R2 的外侧,则 x 2 y 2 zdxdy 等于( A ).
(A) 2 x2 y2 R2 x2 y2dxd;y
Dxy
(B) x 2 y 2 R2 x 2 y 2 dxdy ;
3
3
3
I

{

1[ 3
f
( x,
y,z)
x]
1 [2 f ( x, y, z) y] 1 [ f ( x, y, z) z]}dS
3
3

1 3
(x

高数第十章曲线积分与曲面积分

曲线积分
计算
定积分
计算
Stokes公式计算曲面积分 Gauss公式
重积分
16
积分概念的联系

定积分
f ( M )d lim f ( M ) i , f ( M )点函数
0
i 1
n
当 R1上区间 a, b]时, f ( M )d f ( x )dx. [
5
基本问题：如何熟练掌握各种积分的计算
首先判断准确要求的是哪一类积分重要的是牢牢记住各种积分的计算方法
1、I

L
f ( x , y )ds 代入曲线的方程以及ds，从而化为定积分解之
2、I Pdx Qdy 代入曲线的方程，化为定积分解之 L
P Q 闭合 y x 非闭

( y 2 z 2 ) dS; I z

( x 2 y 2 ) dS
曲面质心：曲面形心：
x
x
dS ; y
S
;y

ydS ydS

dS ; z
S
;z
dS S
dS zzdS

15
（二）各种积分之间的联系
积分是
P cos Q cos R cos ds
，其中，，为有向曲面上点
x, y, z 处的
法方向的方向角。
20
2.选择以下各题中给出的四个结论中一个正确的结论：
(1)设曲面是上半球面 : x 2 y 2 z 2 R 2 , z 0, 曲面 1 是曲面在第一卦限中的部分 , 则有 C .
条件等

高等数学第10章课后习题答案(科学出版社)

第十章曲线积分与曲面积分习题详解习题10—11 计算下列对弧长的曲线积分：（1）LI xds =⎰，其中L 是圆221x y +=中(0,1)A到B 之间的一段劣弧；解: L AB =的参数方程为：cos ,sin x y θθ==()42ππθ-≤≤，于是2cos I ππθ-=⎰4cos (1d ππθθ-==+⎰．（2）(1)Lx y ds ++⎰ ，其中L 是顶点为(0,0),(1,0)O A 及(0,1)B 所成三角形的边界；解: L 是分段光滑的闭曲线，如图9－2所示，根据积分的可加性，则有(1)Lx y ds ++⎰(1)OAx y ds =++⎰(1)ABx y ds +++⎰ (1)BOx y ds +++⎰，由于OA :0y =，01x ≤≤，于是ds dx ===，故 103(1)(01)2x y ds x dx ++=++=⎰⎰OA，而:AB 1y x =-,01x ≤≤，于是ds ==．故10(1)[(1)ABx y ds x x ++=+-+=⎰⎰，同理可知:BO 0x =（01y ≤≤），0d s =，则13(1)[01]2BOx y ds y dy ++=++=⎰⎰． xyoABC综上所述33(1)322Lx y ds -+=+=+⎰ （3）⎰，其中L 为圆周22x y x +=；解直接化为定积分．1L 的参数方程为11cos 22x θ=+,1sin 2y θ=（02θπ≤≤）, 且12ds d θθ==．于是201cos222d πθθ=⋅=⎰⎰．（4）2 Lx yzds ⎰，其中L 为折线段ABCD ，这里(0,0,0)A ，(0,0,2),B (1,0,2),C(1,2,3)D ；解如图所示， 2222 LABBCCDx yzds x yzds x yzds x yzds =++⎰⎰⎰⎰．线段AB 的参数方程为 0,0,2(01)x y z t t ===≤≤，则ds =2dt ==，故02200 12=⋅⋅⋅=⎰⎰dt t yzds x AB．线段BC 的参数方程为,0,2(01)x t y z t ===≤≤，则,ds dt ==故122 0020BCx yzds t dt =⋅⋅⋅=⎰⎰，线段CD 的参数方程为1,2,2x y t z t===+)10(≤≤t ，则ds ==，故1122012(2))x yzds t t t t dt =⋅⋅+=+=⎰⎰ 2 (2所以2222LBB CC Dx y z d s x y z d sx y z d sd s =++⎰⎰⎰⎰2 求八分之一球面2221(0,0,0)x y z x y z ++=≥≥≥的边界曲线的重心，设曲线的密度1ρ=。

第10章曲线积分和曲面积分参考解答

第10章曲线积分和曲⾯积分参考解答1l ()()213122001211418312l xds x ==?+= ()1211212Ll l xds xdsxds =+=+??蜒? （2）()22234Lxy x y ds ++??，L 为椭圆22143x y +=，其周长为a 。

解：()()22222342341212LLy ds xyds x y ds ds a ++=++==蜒蜒注意第⼀类曲线积分的对称性：若曲线关于x （y ）轴对称，⽽被积函数关于y （x ）为奇函数，则曲线积分为零！（3）L，L 为圆周22x y ax +=（0a >）。

解：圆周之参数⽅程为cos 22sin 2a a x t a y t ?=+=??（02t π≤≤），故22200cos22La tdtππ==2222002cos cos cos2a u du a udu udu aππππ（4）Lzds，L为()0 cossin0x t ty t t t tz t==≤≤=解：()322123tLzds t==+-Lx ds，L圆周为2222x y z ax y z++=++=解：因222L L Lx ds y ds z ds==蜒?，故()222223112333L L Lx ds x y z ds a ds aπ=++==蜒?2、计算下列对坐标的曲线积分：（1）()()2222Lx y dx x y dy++-1,1再到点()2,0的⼆线段。

x解：()1:01L y x x=≤≤，()2:212L y x x=-≤≤()()2222LI x y dx x y dy=++-()()()()1222222222L Lx y dx x y dy x y dx x y dy =++-+++-()()()()1222222=++----()122201222x dx x dx =+-??43=（作代换2t x =-，知第⼆个定积分与第⼀个相等）（2）23Lydx xzdy yz dz -+??，L 是圆周2222x y zz ?+=?=?，从z 轴正向看去，该圆周取逆时针⽅向。

第十章-曲线曲面积分(习题及解答)

第十章曲线曲面积分§10．1对弧长的曲线积分一、选择题1. 设曲线弧段AB 为，则曲线积分有关系( ).(A)(,)d (,)d ABBAf x y s f x y s =-⎰⎰； (B )(,)d (,)d A BB Af x y s f x y s =⎰⎰；(C )(,)d (,)d A B B Af x y s f x y s +=⎰⎰；(D)(,)d (,)d AB BAf x y s f x y s =--⎰⎰．答(B).2. 设有物质曲线23:,,(01),23t t C x t y z t ===≤≤其线密度为ρ=,它的质量M =( ).(A)10t ⎰; (B )1t t ⎰;(C)t ⎰; (D)t ⎰. 答(A).3.设OM 是从(0,0)O 到(1,1)M 的直线段,则与曲线积分OMI s=⎰不相等的积分是( ).(A)10x ⎰; (B)10y ⎰;(C)d r r ⎰; (D)10e r ⎰答(D).4 .设L 是从(0,0)A 到(4,3)B 的直线段,则曲线积分()d Lx y s -=⎰( ).(A)403d 4x x x ⎛⎫- ⎪⎝⎭⎰; (B)303d 4y y y ⎛⎫- ⎪⎝⎭⎰;(C)3034y y y ⎛- ⎝⎰; (D)4034x x x ⎛- ⎝⎰. 答(D).5. 设L 为抛物线2y x =上从点(0,0)到点(1,1)的一段弧,则曲线积分s =⎰( ).(A)x ⎰; (B)y ⎰;(C)10x ⎰; (D)y ⎰. 答(C).6. 设L 是从(1,0)A 到(1,2)B -的直线段,则曲线积分()d Lx y s +=⎰( ).(A); (B)2; (C) (D) 答(D).二、填空题1. 设L 是圆周221x y +=,则31d LI x s =⎰与52d LI x s =⎰的大小关系是.答:12.I I =2. 设L 是连接(1,0)A 与(0,1)B 两点的直线段, 则()d Lx y s +=⎰.3. 设:cos ,sin (02),L x a t y a t t π==≤≤则22()d n Lx y s +=⎰.答：212a a π+.4. 设:cos ,sin (02),L x a t y a t t π==≤≤则22()d Lx y s -=⎰.答：0.5. 设L 是圆周221x y +=,则2d LI x s ==⎰.答：π.6. 设:cos ,sin ,t t t x e t y e t z e Γ===,上相应于t 从0变到2的这段弧,则曲线积分22()d Lx y s -=⎰.答:2)e --. 7. 设L 为曲线24y x =上从点(0,0)A 到点(1,2)B 的弧段,则Ls =⎰.答：3. 三、解答题1.计算下列对弧长的曲线积分： (1)d Lx s ⎰其中为由直线y x =与抛物线2y x =所围区域的整个边界.答： 11)12.(2)22d x y Les +⎰其中L 为圆周222x y a +=，直线y x =及x 轴在第一象限内所围成的扇形的整个边界.答： 2 2.4a a e π⎛⎫+- ⎪⎝⎭(3)2d x yz s Γ⎰，其中Γ为折线ABCD ，这里,,,A B C D 依次为点(0,0,0)、(0,0,2)、(1,0,2)、(1,3,2).答：9. (4)2d Ly s ⎰其中L 为摆线一拱(sin ),(1cos )(02)x a t t y a t t π=-=-≤≤.答： 34232.53a ⋅⋅(5)22()d Lx y s +⎰其中L 为曲线(cos sin )(sin cos )x a t t t y a t t t =+⎧⎨=-⎩(02)t π≤≤. 答： 2322(12).a ππ+§10．2对坐标的曲线积分一、选择题1. 设AB 为由(0,)A π到(,0)B π的直线段,则sin d sin d ABy x x y +=⎰( ).(A)2; (B)1-; (C)0; (D)1. 答(C). 2. 设C 表示椭圆22221x y a b+=,其方向为逆时针,则2()d C x y x +=⎰ ( ).(A)ab π; (B)0; (C)2a b +; (D)1. 答(B). 3. 设C 为由(1,1)A 到(2,3)B 的直线段,则(3)d (2)d Cx y x y x y +++=⎰( ).(A)21[(2)(23)]d x x x x x +++⎰； (B)21[(21)(213)]d x x x x x +-+-+⎰(C)21[(73)2(51)]d x x x -+-⎰; (D)21[(73)(51)]d x x x -+-⎰. 答(C).4. 设曲线C 的方程为x y =(0)2t π≤≤,则22d d Cx y y y x x -=⎰( )(A)20[cos sin t π⎰； (B)2220(cos sin )d t t t π-⎰(C)2200cos sin ππ-⎰⎰(D)201d 2t π⎰.答(D).5. 设()f u 连续可导,L 为以原点为心的单位圆,则必有( ).(A)22()(d d )0Lf x y x x y y ++=⎰；(B)22()(d d )0Lf x y x y y x ++=⎰(C)22()(d d )0Lf x y x y y ++=⎰; (D)22()(d d )0Lf x y x x y ++=⎰.答(A).6. 设C 是从(0,0)O 沿折线11y x =--到(2,0)A 到的折线段,则d d Cx y y x -=⎰( )(A)0; (B)1-; (C)2-; (D)2. 答(C).二、填空题1. L 为xoy 平面内直线x a =上的一段,则(,)d LP x y x =⎰.答：0.2. 设L 为2y x =上从(0,0)O 到(2,4)A 的一段弧,则22()d Lx y x -=⎰.答：5615-. 3. 设L 为2y x =上从(0,0)O 到(2,4)A 的一段弧,则22()d Lx y y -=⎰.答：403-.4．L 为圆弧y (2,2)A 的一段弧,则d Lxy y =⎰ .答：43. 5．设L 为圆周222()(0)x a y a a -+=>及x 轴所围成的在第一象限的区域的整个边界(按逆时针方向绕行),则d Lxy y =⎰.答：32a π-.6．设(2)d (23)d 9Lx y x x y y -++=-⎰,其中L 为xoy 平面上简单闭曲线,方向为逆时针.则L 所围成的平面区域D 的面积等于.答：32. 三、解答题1．计算()d ()d Lx y x y x y ++-⎰,其中L 为:(1) 抛物线2y x =上从(1,1)到(4,2)的一段弧; (2) 从点(1,1)到点(4,2)的一直线段;(3) 先沿直线从点(1,1)到点(1,2),然后再沿直线到点(4,2)的折线; (4) 曲线2221,1x t t y t =++=+上从点(1,1)到点(4,2)的一段弧. 答案：3432(1);(2)11;(3)14;(4).332．计算d d Ly x x y +⎰其中L 为圆周cos ,sin x R t y R t ==上对应t 从0到2π的一段弧.答：0. 3．计算22()d ()d L x y x x y yx y+--+⎰,其中L 为圆周222x y a +=(方向按逆时针). 答：2π-.4．计算d d (1)d x x y y x y z Γ+++-⎰其中Γ为从点(1,1,1)到点(2,3,4)的直线段.答：13.5. 计算22(2)d (2)d Lx xy x y xy y -+-⎰,其中L 是2y x =上从点(1,1)-到点(1,1)的一段弧.答：1415-. §10．3 格林公式一、选择题1. 设C 是圆周222x y R +=,方向为逆时针方向,则22d d Cx y x xy y -+⎰用格林公式计算可化为( ).(A)230d d Rr r πθ⎰⎰； (B)2200d d Rr r πθ⎰⎰;(C)230d 4sin cos d Rr r πθθθ-⎰⎰; (D)220d d RR r r πθ⎰⎰. 答(A).2. 设L 是圆周222x y a +=,方向为负向,则3223()d ()d Lx x y x xy y y -+-⎰= ( ).(A)323a π; (B)4a π-; (C); (D)42a π-. 答(D). 3. 设L 是从(0,0)O 沿折线22y x =--到(4,0)A 到的折线段,则d d Cx y y x -=⎰( )(A)8; (B)8-; (C)4-; (D)4. 答(B).4. 设(,),(,)P x y Q x y 在单连通区域D 内具有一阶连续偏导数,则d d LP x Q y +⎰在D 内与路径无关的充分必要条件是在D 内恒有( ).(A)0Q P x y ∂∂+=∂∂; (B)0Q Px y∂∂-=∂∂; (C)0P Q x y ∂∂-=∂∂; (D)0P Q x y∂∂+=∂∂. 答(B). 5. 设L 为一条不过原点,不含原点在内的简单闭曲线, 则22d d 4L x y y xx y -=+⎰( ).(A)4π; (B)π; (C)2π; (D)0. 答(D).6. 设L 为一条包含原点在内的简单闭曲线,则22d d 4L x y y xI x y -==+⎰( ).(A)因为Q P x y ∂∂=∂∂,所以0I =; (B)因为,Q Px y∂∂∂∂不连续,所以I 不存在; (C)2π; (D)因为Q Px y∂∂≠∂∂,所以沿不同的L ,I 的值不同. 答(C). 7. 表达式(,)d (,)d P x y x Q x y y -为某函数(,)U x y 的全微分的充分心要条件是( ).(A)P Q x y ∂∂=∂∂; (B)P Q y x∂∂=∂∂; (C)P Q x y ∂∂=-∂∂; (D)P Q y x∂∂=-∂∂. 答(D). 8. 已知2()d d ()x ay x y yx y +++为某函数(,)U x y 的全微分,则a =( ).(A)0; (B)2; (C)1-; (D)1. 答(B). 9. 设L 是从点(1,1)A 到点(2,3)B 的直线段,则(3)d (3)d Lx y x y x y +++=⎰( ).(A)2311(3)d (6)d x x y y +++⎰⎰; (B)21[(6)(23)]d x x x x x +++⎰;(C)23111(31)d (3)d 2y x x y y ++++⋅⎰⎰; (D)21[(31)(51)]d x x x -++⎰. 答(A).10*. 设()f x 连续可导,且(0)1f =,曲线积分(,)43(0,0)()tan d ()d I yf x x x f x y ππ=-⎰与路径无关,则()f x =( ).(A)1cos x +; (B)1cos x -; (C)cos x ; (D)sin x . 答(C).二、填空题1. 设区域D 的边界为L ,方向为正向, D 的面积为σ. 则d d Lx y y x -=⎰.答: 2σ.2. 设(,)f x y 在22:14x D y +≤上具有二阶连续偏导数, L 是D 的边界正向,则(,)d [3(,)]d y x Lf x y y y f x y x -+=⎰.答: 6π.3. 设L 是圆周229x y +=,方向为逆时针, 则2(2)d (4)d Lxy y x x x y -+-=⎰.答: 27π-.4. 设L 为闭曲线2x y +=方向为逆时针,,a b 为常数, 则d d L ax y by x x y -+⎰=.答: 4()a b +.5. 设ABCDA 为以点(1,0),(0,1),(1,0),(0,1)A B C D --为顶点的正方形逆时针方向一周,则d d Lx yx y++⎰=.答: 0.6. 设L 为圆周221x y +=上从(1,0)A 到(0,1)B 再到(1,0)C -的曲线段,则2d y Le y =⎰.答: 0. 7.(2,2)2(0,0)2d (3)d xy x x y +-=⎰.答: 2.8. 设L 为直线y x =从(0,0)O 到(2,2)A 的一段, 则22d 2d y y Le x xye y +=⎰.答: 42e .9*. 设L 为抛物线上一段弧,试将积分(,)d (,)d LP x y x Q x y y +⎰化为对弧长的曲线积分,其中(,),(,)P x y Q x y 在L 上连续.答:22d 14L P xQ s x ++⎰.10*. 设()f x 连续可导,且(0)0f =,曲线积分[()]sin d ()cos d x Lf x e y x f x y y --⎰与路径无关,则()f x =.答: 2x xe e --.三、解答题1. 计算22d d 2()L y x x y x y -+⎰，其中L 为圆周22(1)2x y -+=的正向.答:π-. 2. 计算(24)d (536)d Lx y x y x y -+++-⎰，其中L 是顶点分别为(0,0)、(3,0)和(3,2)的三角形正向边界.答:12. 3. 计算3222(2c o s )d (12s i n3)d Lx y y x x y x x y y -+-+⎰,其中L 为抛物线22x y π=上由点(0,0)到,12π⎛⎫⎪⎝⎭的一段弧.答:24π.4. 计算22()d (sin )d Lx y x x y y --+⎰，其中L 是圆周y 上由(0,0)到(1,1)的一段弧. 答:7sin 264-+.5. 证明下列曲线积分与路径无关,并计算积分值:(1) (2,3)(1,1)()d ()d x y x x y y ++-⎰.答:52. (2)(2,1)423(1,0)(23)d (4)d xy y x x xy y -++-⎰.答: 5.6. 验证下列(,)d (,)d P x y x Q x y y +在整个xoy 平面内是某函数(,)u x y 的全微分,并求函数(,)u x y .(1) (2)d (2)d x y x x y y +++. (2) 22d d xy x x y +.(3) 22(2cos cos )d (2sin sin )d x y y x x y x x y y ++-.答: (1) 22222x y xy ++; (2) 2x y ; (3)22cos sin x y y x +. 7. 用格林公式计算223()d (2)d Lx x y x xy y y -+-+⎰，其中L 是圆周y (2,0)A 到(0,0)O 的一段弧.答:324π-.8. 用格林公式计算423(23)d (4)d Lxy y x x x xy y -+++-⎰，其中L 是圆周y (1,0)A 到(1,0)B -的一段弧.答:62π-.§10．4 对面积的曲面积分一、选择题1. 设∑是xoy 平面上的一个有界闭区域xy D ,则曲面积分(,,)d f x y z S ∑⎰⎰与二重积分(,)d d xyD f x y x y ⎰⎰的关系是 ( ).(A)(,,0)d f x y S ∑⎰⎰=(,)d d xyD f x y x y ⎰⎰;(B)(,,0)d f x y S ∑⎰⎰=(,)d d xyD f x y x y -⎰⎰;(C)(,,0)d f x y S ∑<⎰⎰(,)d d xyD f x y x y ⎰⎰;(D)(,,0)d f x y S ∑>⎰⎰(,)d d xyD f x y x y ⎰⎰.答(A).2. 设∑是抛物面22(04)z x y z =+≤≤,则下列各式正确的是( ).(A)(,,)d f x y z S ∑⎰⎰=22224(,,)d d x y f x y x y x y +≤+⎰⎰;(B)(,,)d f x y z S ∑⎰⎰=22224(,,d x y f x y x y x y +≤+⎰⎰;(C)(,,)d f x y z S ∑=⎰⎰22224(,,d x y f x y x y x y +≤+⎰⎰;(D)(,,)d f x y z S ∑=⎰⎰22224(,,d x y f x y x y x y +≤+⎰⎰. 答(D).3.设2222:(0)x y z a z ∑++=≥,1∑是∑在第一卦限中的部分,则有( ).(A)1d 4d x S x S ∑∑=⎰⎰⎰⎰;(B)1d 4d y S x S ∑∑=⎰⎰⎰⎰;(C)1d 4d z S z S ∑∑=⎰⎰⎰⎰;(D)1d 4d xyz S xyz S ∑∑=⎰⎰⎰⎰. 答(C).4. 设∑是锥面1)z z =≤≤,则22()d x y S ∑+=⎰⎰( ).(A)22()d x y S ∑+=⎰⎰2120d d r r r πθ⋅⎰⎰;(B)22()d xy S ∑+=⎰⎰120d d r r r πθ⋅⎰⎰;(C)22()d xy S ∑+=⎰⎰21200d d r r πθ⎰;(D)22()d x y S ∑+=⎰⎰2120d d r r r πθ⋅⎰;. 答(D).5. 设∑为平面1234x y z++=在第一卦限内的部分, 则42d 3z x y S ∑⎛⎫++= ⎪⎝⎭⎰⎰( ).(A)4d d xyD x y ⎰⎰;(B)4d d 3xyD x y ⋅⎰⎰; (C)23004d d x y ⎰; (D)32004d d x y ⎰;. 答(B). 6. 设∑为曲面222()z x y =-+在xoy 平面上方的部分,则d z S ∑=⎰⎰().(A)222200d (2)d r r r r πθ--⋅⎰⎰;(B)2220d (2d r r r πθ-⎰⎰;(C)220d )d r r r πθ-⋅⎰⎰; (D)220d d r r r πθ-⎰⎰. 答(D).7. 设∑为球面2222x y z z ++=,则下列等式错误的是( ).(A)22()d 0x yz S ∑+=⎰⎰; (B )22()d 0y y z S ∑+=⎰⎰;(C)22()d 0z x y S ∑+=⎰⎰; (D)2()d 0x y z S ∑+=⎰⎰. 答(C). 二、填空题1. 设2222:x y z a ∑++=,则222()d x y z S ∑++=⎰⎰.答: 44a π.2. 设∑为球面2222x y za ++=,则222d xy z S ∑=⎰⎰.答: 0.3. 设∑为上半球面z ,则d z S ∑=⎰⎰.答: 3a π.4. 设∑为下半球面z =,则d z S ∑=⎰⎰.答: 3a π.5 设∑为球面2222x y z a ++=,则d z S ∑=⎰⎰.答: 23a π.6. 设∑为上半球面z ,则d x S ∑=⎰⎰.答: 0. 7. 设∑为平面1232x y z ++=在第一卦限部分,则2d 3z y x S ∑⎛⎫++=⎪⎝⎭⎰⎰.答:8. 设∑为平面1x y z ++=在第一卦限部分,则d z S ∑=⎰⎰.答:. 9. 设∑为平面226x y z ++=在第一卦限部分, 则(522)d x y z S ∑---=⎰⎰.答: 272-. 三、解答题1. 计算曲面积分(,,)d f x y z S ∑⎰⎰,其中∑为抛物面222()z x y =-+在xoy 面上方部分,(,,)f x y z 分别如下:(1) (,,)1f x y z =; (2) 22(,,)f x y z x y =+; (3) (,,)2f x y z z =. 答: (1) 136π; (2) 14930π; (3) 11110π. 2. 计算22()d x y S ∑+⎰⎰,其中∑是锥面z =1z =所围成的区域的整个边界曲面.答:.3. 计算22()d x y S ∑+⎰⎰,其中∑是锥面222z x y =+被平面0z =和3z =所截得的部分.答: 9π.4. 计算42d 3z x y S ∑⎛⎫++ ⎪⎝⎭⎰⎰,其中∑为平面1234x y z ++=在第一卦限中的部分.答: 5. 计算()d x y z S ∑++⎰⎰,其中∑为球面2222x y z a ++=上(0)z h h a ≥<<的部分.答: 22()a a h π-.§10．5 对坐标的曲面积分一、选择题1. 设∑是球面2222x y z a ++=外侧,222:xy D x y a +≤,则下列结论正确的是( ).(A) 2d d z x y ∑=⎰⎰222()d d xyD ax y x y --⎰⎰;(B)2d d z x y ∑=⎰⎰2222()d d xyD a x y x y --⎰⎰; (C)2d d z x y ∑=⎰⎰0;(D )(A)(B)(C)都不对. 答(C). 2. 设∑为柱面222x y a +=被平面0z =及3z =所截得的部分外侧,则d d d d d d z x y x y z y x z ∑++=⎰⎰( ).(A) 3d d z x y ∑⎰⎰; (B)3d d x y z ∑⎰⎰;(C)3d d y x z ∑⎰⎰0; (D)d d d d x y z y x z ∑+⎰⎰. 答(D).3. 设∑为柱面222x y a +=被平面0z =及3z =所截得的部分外侧在第一卦限内的部分,则d d d d d d z x y x y z y x z ∑++=⎰⎰( ).(A)303d y x ⎰⎰;(B)302d z y ⎰⎰;(C)30d z x ⎰⎰; (D)30d zx ⎰⎰. 答(B).4. 设2222:x y z a ∑++=,1:z ∑=∑取外侧, 1∑取上侧.下列结论正确的是( ).(A) 12222()d d d d xy z x y a x y ∑∑++=⎰⎰⎰⎰;(B)12222()d d 2d d x y z x y a x y ∑∑++=⎰⎰⎰⎰;(C)2222222()d d 2d d x y a x y z x y a x y ∑+≤++=⎰⎰⎰⎰; (D) 0. 答(D).5. 已知∑为平面1x y z ++=在第一卦限内的下侧,则d d z x y ∑=⎰⎰( ).(A) 1100d (1)d x x x y y ----⎰⎰; (B)110d (1)d x x x y y ---⎰⎰;(C)110d (1)d xy x y x ---⎰⎰; (D) 110d (1)d x y x y x ----⎰⎰. 答(A).6. 曲面积分2d d z x y ∑⎰⎰在数值上等于( ).(A)向量2z i 穿过曲面∑的流量;(B)密度为2z 的曲面∑的质量;(C)向量2z k 穿过曲面∑的流量;(D)向量2z j 穿过曲面∑的流量. 答(C).二、填空题1. 设∑是xoy 平面上的闭区域0101x y ≤≤⎧⎨≤≤⎩的上侧,则()d d x y z y z ∑++=⎰⎰.答: 0.2. 设∑是xoy 平面上的闭区域0101x y ≤≤⎧⎨≤≤⎩的上侧,则()d d x y z x y ∑++=⎰⎰.答: 1.3. 设∑为球面2222x y z a ++=取外侧, 则222()d d xy z x y ∑++=⎰⎰..答: 0.4. 设∑为球面2222x y z a ++=取外侧, 则d d z x y ∑=⎰⎰..答:343a π. 5. 设∑为球面2222()()()x a yb zc R -+-+-=取外侧, 则曲面积分d d z x y ∑=⎰⎰..答:343R π. 6. 设∑为球面2222x y z a ++=取外侧, 则222()d d xy z x y ∑++=⎰⎰.答: 0. 三、解答题1. 计算22d d x y z x y ∑⎰⎰,其中∑是球面2222x y z R ++=的下半部分的下侧.答:77426422453753105R R ππ⎛⎫⋅-⋅⋅= ⎪⎝⎭. 2. 计算d d d d d d z x y x y z y z x ∑++⎰⎰,其中∑是柱面221x y +=被平面0z =及3z =所截得的在第一卦限内的部分的前侧.答: 32π.3. 计算d d d d d d xz x y xy y z yz z x ∑++⎰⎰,其中∑是平面0x =,0y =,0z =,及1x y z ++=所围成的空间区域的整个边界曲面的外侧.答:18. 4*. 把对坐标的曲面积分(,,)d d (,,)d d (,,)d d P x y z y z Q x y z z x R x y z x y∑++⎰⎰化成对面积的曲面积分,其中:(1) ∑是平面326x y ++=在第一卦限部分的上侧. (2) ∑是抛物面228()z x y =-+在xoy 面上方部分的上侧. 答: (1)32d 55P Q S ∑⎛⎫++ ⎪ ⎪⎝⎭⎰⎰; (2) S ∑.§10．6 高斯公式一、选择题1. 设空间闭区域Ω的边界是分片光滑的闭曲面∑围成, ∑取外侧，则Ω的体积V =( ).(A)1d d d d d d 3y y z z z x x x y ∑++⎰⎰; (B )1d d d d d d 3x y z y z x z x y∑++⎰⎰; (C)1d d d d d d 3z y z z z x y x y ∑++⎰⎰; (D) 1d d d d d d 3x y z z z x y x y ∑++⎰⎰.答(B). 2.设∑是长方体{}:(,,)0,0,0,x y z x a y b z c Ω≤≤≤≤≤≤的整个表面的外侧,则222d d d d d d x y z y z x z x y ∑++=⎰⎰( ). (A) 2a bc ; (B)2ab c ; (C)2abc ; (D) ()a b c abc ++. 答(D).3. 在高斯定理的条件下,下列等式不成立的是( ).(A)d d d P Q R x y z x y z Ω⎛⎫∂∂∂++= ⎪∂∂∂⎝⎭⎰⎰⎰(cos cos cos )d P Q R S αβγ∑++⎰⎰;(B)d d d d d d P y z Q z x R x y ∑++=⎰⎰d d d P Q R x y z x y z Ω⎛⎫∂∂∂++ ⎪∂∂∂⎝⎭⎰⎰⎰; (C)d d d d d d P y z Q z x R x y ∑++=⎰⎰d d d R Q P x y z x y z Ω⎛⎫∂∂∂++ ⎪∂∂∂⎝⎭⎰⎰⎰; (D)d d d d d d P y z Q z x R x y ∑++=⎰⎰(cos cos cos )d P Q R S αβγ∑++⎰⎰.答(C).4. 若∑是空间区域Ω的外表面,下述计算用高斯公式正确的是( ).(A) 2d d (2)d d x y z z y x y ∑++=⎰⎰(22)d d d x x y z Ω+⎰⎰⎰;(B)3()d d 2d d d d xyz y z xy z x z x y ∑--+=⎰⎰2(321)d d d xx x y z Ω-+⎰⎰⎰;(C) 2d d (2)d d x y z z y z x ∑++=⎰⎰(21)d d d x x y z Ω+⎰⎰⎰;(D)2d d (2)d d x x y z y y z ∑++=⎰⎰(22)d d d x x y z Ω+⎰⎰⎰. 答(B).二、填空题1. 设∑是球面2222x y z a ++=外侧, 则d d z x y ∑=⎰⎰.答:343a π. 2. 设∑是球面2222x y z a ++=外侧, 则333d d d d d d x y z y z x z x y ∑++=⎰⎰.答:525a π. 3. 设∑是长方体{}:(,,)0,0,0,x y z x a yb zc Ω≤≤≤≤≤≤的整个表面的外侧,则d d d d d d x y z y z x z x y ∑++=⎰⎰.答: 3abc .4. 设∑是长方体{}:(,,)0,0,0,x y z x a y b z c Ω≤≤≤≤≤≤的整个表面的外侧,则222d d d d d d x y z y z x z x y ∑++=⎰⎰.答: ()a b c abc ++.5. 向量A yzi zxj xyk =++穿过圆柱222(0)x y a z h +=≤≤全表面∑流向外侧的通量Φ=.答: 0.6.向量2(23)()(2)A x z i xz y j y z k =+-+++穿过球面222(3)(1)(2)9x y z -+++-=∑流向外侧的通量Φ=.答: 108π.三、解答题1. 计算222d d d d d d x y z y z x z x y ∑++⎰⎰,其中∑为平面0x =,0y =,0z =及x a =,y a =,z a =所围成的立体的表面外侧.答: 43a . 2. 计算333d d d d d d x y z y z x z x y ∑++⎰⎰,其中∑为球面2222xy z a ++=外侧.答:525a π. 3. 计算2232d d ()d d (2)d d xz y z xy z z x xy y z x y ∑+-++⎰⎰,其中∑为上半球体222x y a +≤,0z ≤.答:525a π. 4. 计算d d d d d d x y z y z x z x y ∑++⎰⎰,其中∑是界于0z =和3z =之间的圆柱体223x y +≤的整个表面外侧. 答: 81π.5. 计算24d d d d d d xz y z y z x yz x y ∑-+⎰⎰,其中∑是平面0x =,0y =,0z =与平面1x =,1y =,1z =所围成的立方体的全表面外侧. 答:32. 6. 计算22d d (2)d d d d 2zx y z z xy z x x y ∑+-+⎰⎰,其中∑为曲面22z x y =+与平面1z =所围成的立体的表面外侧. 答:4π. 7. 计算曲面积分3333d d (2)d d ()d d x y z y z x z x x y ∑+++-⎰⎰,其中∑为曲面z =z .答: 326(1cos2)5π⋅⋅-.8. 计算曲面积分222d d d d (1)d d xy y z z z x z xx y ∑++-⎰⎰,其中∑为由曲面z =0z =所围成的空间区域的整个边界表面外侧.答: 322161625335πππ⋅⋅-=. 9*.用Gauss 公式计算曲面积分2()d d d d z x y z z x y ∑+-⎰⎰,其中∑是旋转抛物面221()2z x y =+介于平面0z =及2z =之间部分的下侧. 答: 8π.§10．7 斯托克斯公式一、选择题1. 在斯托克斯定理的条件下,下列等式不成立的是( ).(A) d d d P x Q y R z Γ++=⎰d d d d d d y z z x x y x y z P Q R ∑∂∂∂∂∂∂⎰⎰; (B) d d d P x Q y R z Γ++=⎰cos cos cos d S x y z PQ Rαβγ∑∂∂∂∂∂∂⎰⎰; (C)d d d P x Q y R z Γ++=⎰{}cos ,cos ,cos d i j k S x y z P Q Rαβγ∑∂∂∂⋅∂∂∂⎰⎰; (D)d d d P x Q y R z Γ++=⎰{}d ,d ,d i j k x y z x y z PQR∑∂∂∂⋅∂∂∂⎰⎰. 答(D). 2. 设Γ是从点(,0,0)a 到点(0,,0)a 再到(0,0,)a 最后回到(,0,0)a 的三角形边界(0a >),则()d ()d ()d z y x x z y y x z Γ-+-+-=⎰( ).(A) 23a ; (B )26a ; (C )22a ; (D) 2a . 答(A).3. 设Γ为圆周2229,0x y z z ++==,若从z 轴正向看去, Γ为逆时针方向.则22d 3d d y x x y z z Γ+-=⎰( ).(A) π; (B)6π; 9π; (D) 0. 答(C).二、填空题1. 设Γ为圆周2222,0x y z a z ++==,若从z 轴正向看去, Γ为逆时针方向.22d 2d d y x x y z z Γ+-=⎰.答: 0.2. 设u xy yz zx xyz =+++, 则(1)grad u =.答: {},,y z yz z x xz x y xy ++++++(2) div(grad )u = .答: 0.(3) rot(grad )u = . 答: 0.3. 设向量场(23)(3)(2)A z y i x z j y x k =-+-+-,则rot A =.答: 246i j k ++.4. 设向量场22sin sin()sin(cos )A x yi y xz j xy z k =++, 则rot A =.答: 222[sin(cos )cos()]sin(cos )[cos()cos ]x z xy xz i y z j y z xz x y k --+-. 三、解答题1. 计算d d d y x z y x z Γ++⎰,其中Γ为圆周2222,0x y z a x y z ++=++=,若高等数学第十章曲线曲面积分第 21 页学院专业学号姓名从z 轴正向看去, Γ为逆时针方向.答: 2a .2*. 计算()d ()d ()d yz x z x y x y z Γ+-+-⎰,其中Γ为椭圆222x y a +=, 1(0,0)x y a b a b+=>>,若从x 轴正向看去, Γ为逆时针方向.答: π3. 计算23d d d y x xz y yz z Γ-+⎰,其中Γ为圆周222,2x y z z +==,若从z 轴正向看去, Γ为逆时针方向.答: 20π-.4. 计算22d 3d d y x x y z z Γ+-⎰,其中Γ为圆周2229,0x y z z ++==,若从z轴正向看去, Γ为逆时针方向.答: 9π.5*. 利用斯托克斯公式把曲面积分rot d A n S ∑⋅⎰⎰化为曲线积分,并计算积分值,其中A 、∑及n 分别如下:(1) 2A y i xyj xzk =++,∑为上半球面z , n 是∑的单位法向量.(2) ()A y z i yzj xzk =-+-,∑为{}(,,)02,02,02x y z x y z ≤≤≤≤≤≤的表面外侧去掉xoy 平面上的那个底面,, n 是∑的单位法向量.答: (1) 0. (2) 4-.。

(完整版)第十章曲线积分与曲面积分练习题

第十章曲线积分与曲面积分§10.1 对弧长曲线的积分一、判断题1．若f(x)在（-+∞∞,）内连续，则⎰badx x f )(也是对弧长的曲线积分。

（）2．设曲线L 的方程为x=)(y ϕ在[βα,]上连续可导则⎰⎰'+=Ldyy y y f ds y x f βαϕϕ2)]([1)),((),(（）二、填空题1.将⎰+Lds y x)(22，其中L 为曲线x=a(cost+tsint),y=a(sint-tcost)()20π≤≤t 化为定积分的结果是。

2.⎰+L ds y x )(= ，其中L 为连接（1，0）和（0，1）两点的直线段。

三、选择题1．⎰+Lds y x )(22=（），其中L 为圆周122=+y x （A ）⎰02πθd （B ）⎰πθ2d （C ）⎰πθ22d r （D ）⎰πθ22d2．⎰Lxds =（），L 为抛物线2x y =上10≤≤x 的弧段。

（A ）)155(121- （B ）)155(- （C ）121 （D ）)155(81-四、计算⎰+Cds y x )(，其中C 为连接点（0，0）、（1，0）、（0，1）的闭折线。

五、计算⎰++L ds z y x )2(22，其中L 为⎩⎨⎧=++=++02222z y x R z y x六、计算⎰+Ln ds y x)(22，L 为上半圆周：)(222N n R y x ∈=+七、计算⎰+Ly x ds e22，其中L 为圆周222a y x =+，直线y=x 和y=0在第一象限内围成扇形的边界。

八、求半径为a ，中心角为ϕ2的均匀圆弧（ρ=1）的重心。

§10.2 对坐标的曲线积分一、判断题1．定积分也是对坐标的曲线积分。

（） 2．022=+-⎰L y x ydx xdy ，其中L 为圆周122=+y x 按逆时针方向转一周。

（）二、填空题1．ydz x dy y dx x 2233++⎰Γ= ，其中Γ是从点A （1，2，3）到点B （0，0，0）的直线段AB 。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

而
2 2 L
2
L
L 2
L
例4 计算曲线积分
( z y )dx ( x z )dy ( x y )dz
x2 y2 1 , 从z轴正向看去，其中L是曲线 x y z 2
L
L取顺时针方向. 解这里L由一般方程给出，首先要将一般方程化为参数方程. 注意到 x y 1 因此可令 x cos t , y sin t , 再由 z 2 x y 得 z 2 cos t sin t , t 从2 变到0.
在所学过的积分中区域无向的积分有：重积分,第一类曲线积分和第一类曲面积分区域有向的积分有：定积分,第二类曲线积分和第二类曲面积分. 曲线的方向是由起点到终点（定积分）
或切向量的方向来确定,曲面的方向则由曲
面上点的法向量所指向的侧来确定.
问题3 设是半球面 x y z R ( y 0)
第十章习题课
曲线积分与曲面积分
一基本要求
1．理解两类曲线和曲面积分的概念,了解两类积分的性质以及两类积分的关系. 2．掌握计算两类曲线、曲面积分的方法. 3．掌握格林公式并会运用平面曲线积分与路径无关的条件. 4.了解高斯公式,并会用公式求曲面积分. 5．会用曲线积分和曲面积分求一些几何量与物理量（弧长,质量,重心,转动惯量, 引力、功和流量等）.
y
x 准线L : y y( x )
四典型题目
例1 计算
0,1
y
。
1 L x y ds 2 L x y dx
o
1,0 x
L : x y 1, 从 1,0 到 0,1
解
2 dx 2dx 1 L : y 1 x, ds 1 y
y=y(x) （准线y=y(x)为底边，z=f (x,y)为高的面积）

L
f ( x , y )ds
x
y
平面上对弧长的曲线积分几何意义：

L
f ( x , y )ds 表示柱面y y( x )介于
平面z 0与z f ( x , y )之间部分的面积.
z z f ( x, y )
O
柱面： y(x ) y
P Q R ( x y z )dv Pdydz Qdzdx Rdxdy
为外侧.
三
2 2
问题与思考
问题1 设为平面
2
x z a 在柱面
x y a 内那一部分的上侧，
下面两个积分的解法是否正确？
(1) ( x z )dS a dS a 的面积 2 a 3
2．曲面积分的计算（化为二重积分）
（1）对面积（第一类）的曲面积分若 : z z( x , y )
f ( x , y , z )dS
f x, y, z( x, y ) 1 z ( x, y ) z ( x, y )dxdy
2 x 2 y Dxy

: x x( y, z ), dS 1 x x dydz
.
对于

xdydz : x
4 y (1 z 3) 前侧
2
在yoz面上的投影区域为 Dyz ( y, z) | 2 y 2,1 z 3
xdydz 4 y 2 dydz 故
D yz
dz
3 1
2
2
4 y 2 dy
解原式= 2xyds (3 x 4 y )ds
2 2
L
因为积分曲线L关于y轴对称，函数 2xy是x 的奇函数，因此有 2xyds 0
L
L
(3 x 4 y )ds 12ds 12a 所以 (2xy 3 x 4 y )ds 12a
x y ds 1 2dx 或 x y ds 1ds ds 2 L : y 1 x, x :1 0,
1 L 0
L L L
2
2
x y dx 1 1 dx 1 L
0
例2 求 x y
2 L 2
Dzx z , x | 1 z 3, 0 x 2
1 : y 4 x ( x 0,1 z 3)
2
而侧相反，故
zdzdx zdzdx zdzdx zdzdx zdzdx 0
1 2 Dzx Dzx
2 2

解下向xoy面的投影区域Dxy : x y 1
2 2
x 2 y 2 z x 2 y 2 dxdy = x 2 y 2 dxdy
Dxy

2
0
2 d d 0 3
1 2
例7 求
xdydz zdzdx y zdxdy 2 2 是 x y 4 x 0介于 1 z 3
a D的面积 a 如果是下侧，则

D
3
D: x y a
2 2
2
( x z )dxdy a dxdy a
D
3
问题2. 如何正确理解两类曲线积分和曲面积分的概念？答：由于实际需要,曲线积分与曲面积分为两种
类型,有关质量﹑重心﹑转动惯量等数量积分问题导出第一类线面积分;有关变力作功,流体流过曲面的流量等向量问题导出第二类线、面积分. 前者被积函数化为数量函数沿区域积分,无需考虑方向性,而后者被积函数是向量函数,必须考虑方向.因此,一个函数的积分可以由积分区域的有向或无向分为两种类型的积分.

2
ds,
n 2
L: y a x
2 2
上半圆周
2
解改写L：x y a , y 0
x
L
2
y
2
ds a ds
n 2 n L
a
2n

L
ds a
2 n 1
x2 y2 1, 其周长为a，求例3 设L为椭圆 4 3 (2xy 3 x 2 4 y 2 )ds

若 : z z( x , y ) P ( x, y, z )dydz P x( y, z ), y, z dydz
D yz
: y y( x, z ), Q( x , y, z )dzdx Q x . y( z , x ), z dzdx
x dS
2

Rx dxdy R x y
2 2 2
2
D
2
xy
: x y R , x 0, y 0
2 2 2 2

Dxy
R d
2 0

R
cos
3 2
0
R
2
d

6
R
4
解法2 由对称性（轮换性）
x 2 dS y 2 dS z 2 dS
2
之间的部分，它的法向量指向前侧. 解由于曲面在xoy面的投影为一半圆周曲线，面积为0，所以
z

y zdxdy 0
2
x
y
对于 zdzdx ,

分为两块
2
z
1
右侧 y 2 ( x 0,1 z 3) x 2 : y 4 x 左侧 1 与 2 在xoz面上的投影区域相同,即
因此，原积分 4 0 0 4
1 2 22 4 . 2
2 2
x cos t , L参数方程 y sin t , t 从2 变到0. z 2 cos t sin t ,
于是
0 2
( z y )dx ( x z )dy ( x y )dz
L
[(2 cos t )( sin t ) (2cos t 2 sin t ) cos t

正确
(2) ( x z )dxdy a dxdy a 的面积 2 a

3
错误
( x z )dS

2 a ,
3
( x z )dxdy

2 a
3
因为第二个积分是对坐标的曲面积分，其中的微元 dxdy 是 dS 在xoy面上的投影，故正确的作法是： ( x z )dxdy a dxdy a dxdy

1 2 2 2 x dS 3 x y z dS
2
R2 3
R2 1 4 2 dS 3 8 4 R 6 R
例6 求 x y z x y dxdy，
2 2 2 2
: z 1 x y z 0 的下侧.
（2）对坐标（第二类）设L： x (t ), y (t ),
从A , 到B ,

L
P ( x , y )dx Q( x , y )dy

P (t ), (t ) (t ) Q (t ), (t ) (t )dt
2 2 2 2
的外侧.有人说：“由对称性知 zdS 0 故同样也有不对
zdxdy 0 ”,

对吗?
讨论题
已知一柱面的准线（平面曲线）和高，可以利用积分求出它的面积吗？由此给出对弧长的曲线积分的几何意义. 提示：由定积分的几何意义推广. 答：柱面的侧面积
z
O
z f ( x, y )
(cos t sin t )(sin t cos t )]dt