聚类分析中的距离度量ppt课件
聚类分析 PPT课件
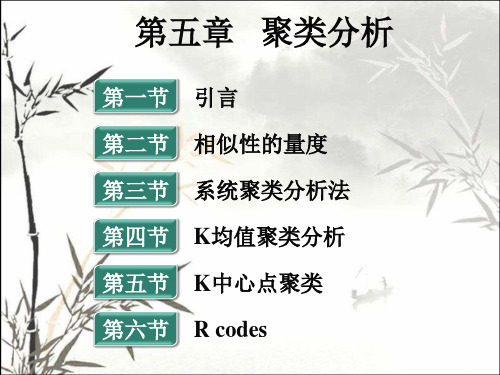
f is binary or nominal: dij(f) = 0 if xif = xjf , or dij(f) = 1 otherwise f is ordinal Compute ranks rif and Treat zif as interval-scaled
x1 x2 x3 x4
x1 0 3.61 5.1 4.24
x2 0 5.1 1
x3
x4
5
0 5.39
0
第二节 相似性的量度
一 样品相似性的度量
二 变量相似性的度量
含名义变量样本相似性度量
例: 学员资料包含六个属性:性别(男或女);外语语种
(英、日或俄);专业(统计、会计或金融);职业(教师 或非教师);居住处(校内或校外);学历(本科或本科以 下) 现有两名学员: X1=(男,英,统计,非教师,校外,本科)′ X2=(女,英,金融,教师,校外,本科以下)′ 对应变量取值相同称为配合的,否则称为不配合的 记配合的变量数为m1,不配合的变量数为m2,则样本之间 的距离可定义为
第五章 聚类分析
第一节 第二节 第三节 第四节 第五节 引言 相似性的量度 系统聚类分析法 K均值聚类分析 K中心点聚类
第六节
R codes
第一节 引言
“物以类聚,人以群分” 无监督分类聚类分析 分析如何对样品(或变量)进行量化分类的 问题 Q型聚类—对样品进行分类 R型聚类—对变量进行分类
用他们的序代替xif
zif
rif 1 M f 1
10
混合型属性
A database may contain all attribute types Nominal, symmetric binary, asymmetric binary, numeric, ordinal 可以用加权法计算合并的影响
聚类分析法ppt课件全

8/21/2024
25
1.2.2 动态聚类分析法
1.2 聚类分析的种类
(3)分类函数
按照修改原则不同,动态聚类方法有按批修改法、逐个修改法、混合法等。 这里主要介绍逐步聚类法中按批修改法。按批修改法分类的原则是,每一步修 改都将使对应的分类函数缩小,趋于合理,并且分类函数最终趋于定值,即计 算过程是收敛的。
8/21/2024
23
1.2.2 动态聚类分析法
1.2 聚类分析的种类
(2)初始分类 有了凝聚点以后接下来就要进行初始分类,同样获得初始分类也有不同的
方法。需要说明的是,初始分类不一定非通过凝聚点确定不可,也可以依据其 他原则分类。
以下是其他几种初始分类方法: ①人为分类,凭经验进行初始分类。 ②选择一批凝聚点后,每个样品按与其距离最近的凝聚点归类。 ③选择一批凝聚点后,每个凝聚点自成一类,将样品依次归入与其距离
8/21/2024
14
1.2 聚类分析的种类
(2)系统聚类分析的一般步骤 ①对数据进行变换处理; ②计算各样品之间的距离,并将距离最近的两个样品合并成一类; ③选择并计算类与类之间的距离,并将距离最ቤተ መጻሕፍቲ ባይዱ的两类合并,如果累的个
数大于1,则继续并类,直至所有样品归为一类为止; ④最后绘制系统聚类谱系图,按不同的分类标准,得出不同的分类结果。
8/21/2024
18
1.2 聚类分析的种类
(7)可变法
1 2 D kr
2 (8)离差平方和法
(D k 2 pD k 2 q)D p 2q
D k 2 rn n ir n n p i D i2 pn n ir n n q iD i2 qn rn in iD p 2 q
8/21/2024
机器学习之聚类分析(PPT48页)

欧氏距离:
聚类的相似性度量
2. 曼哈顿距离(Manhattan Distance) 想象你在曼哈顿要从一个十字路口开车到另外一个十字
路口,驾驶距离是两点间的直线距离吗?显然不是,除非 你能穿越大楼。实际驾驶距离就是这个“曼哈顿距离”, 也称为城市街区距离(City Block distance)。 两个n维向量a(x11,x12,…,x1n)与 b(x21,x22,…,x2n)间的曼 哈顿距离
密度聚类——DBSCAN
3)密度直达:如果xi位于xj的ε-邻域中,且xj是核心对象,则称xi由xj密 度直达。注意反之不一定成立, 除非且xi也是核心对象。
4)密度可达:对于xi和xj,如果存在样本序列p1,p2,...,pT满足 p1=xi,pT=xj且pt+1由pt密度直达,则称xj由xi密度可达。密度可达满足传递 性。此时序列中的传递样本p1,p2,...,pT−1均为核心对象,因为只有核心 对象才能使其他样本密度直达。 5)密度相连:对于xi和xj,如果存在核心对象样本xk,使xi和xj均由xk密度 可达,则称xi和xj密度相连。
什么是聚类?
• “物以聚类,人以群分” • 所谓聚类,就是将相似的事物聚集在一 起,而将不相似
的事物划分到不同的类别的过程,是数据分析之中十分 重要的一种手段。
什么是聚类?
•在图像分析中,人们希望将图像分割成具有类似性质的 区域 •在文本处理中,人们希望发现具有相同主题的文本子集 •在顾客行为分析中,人们希望发现消费方式类似的顾客 群,以便制订有针对性的客户管理方式和提高营销效率
G1
G2
聚类分析法ppt课件

7
(2)计算样品的距离。
d ij xi x j yi y j
8
G1
D(0)
G2 G3
G4
G5
G1 G2 G3 G4 G5
0 0.34 1.37 1.34 1.33
0 1.03 1 1.67
0 0.63 1.3
0 0.67
0
9
(3)找出D(0)非对角线上的最小元素, 将其对应的两个类合并为一个新类。
0 0.63 1.30 0 0.67
0
19
0
D(2)
1.37 0
1.67 1.30
0
20
0 1.67
D(3)
0
21
G1 G2 G3 G4 G5
0.4
0.8 1.2 1.6 2.0
聚类距离
பைடு நூலகம்22
G1 G2 G3 G4 G5
0.2 0.4 0.6 0.8 1.0
G1 G2 G3 G4 G5
0.4
0.8
1.2
1.6
2.0
聚类距离
聚类距离
23
某村对5个地块就其土壤质地和土壤有机 质含量进行了评估,结果如下。请分别 使用最长距离法和最短距离法对这5个地 块进行聚类分析,要求分为两类。
地块 A
B
C
D
E
质地 8
3
6
6
4
有机质 5
7
4
9
7
含量
24
聚类分析法
Cluster Analysis
1
聚类分析
将具有相似(similarity)性质(或距离)的 个体(样本)聚为一类,具有不同性质 的个体聚为不同的类。
聚类分析模型ppt课件

xi
yi
2
2
3
契比雪夫距离
dX,Y
max
1i p
xi
yi
3
1
4
闵可夫斯基距离
dX,Y
p
i1
xi
yi
,q
0
1
5 马氏距离 d X ,Y X Y 1X Y 2 ,其中
是所有样品的样本协差阵。
6 兰氏(Lance---William)距离
dX ,Y
1
p
xi
yi
,(适用于样品各分量皆非负的情形)
15
聚类 类间
顺序 距离
1
1.000 x2 x5
2
1.000 x2 x5 x8
3
1.414 x1 x4
4
1.414 x2 x5 x8 x9
5
1.414 x2 x5 x8 x9 x7
6
1.414 x2 x5 x8 x9 x7 x3
7
1.414 x6 x10
8
1.732 x2 x5 x8 x9 x7 x3 x6 x10
9
3.000 x1 x4 x2 x5 x8 x9 x7 x3 x6 x10
16
类间距离
最短距离法聚类图
3.5 3.0 2.5 2.0 1.5 1.0 0.5
X10 X6 X3 X7 X9 X8 X5 X2 X4 X1
17
Spss软件实现
1.运动员的聚类分析:spss 数据 :运动员三项指标 关注:数据格式、结果解读、聚类图、最短距离法、最长距离法 2.汽车的聚类分析:spss 数据 :13-01 3.湿度的聚类分析:spss 数据 :18-03 4.国别饮料产量的聚类分析:spss 数据 :18-05
聚类分析clusteranaly课件
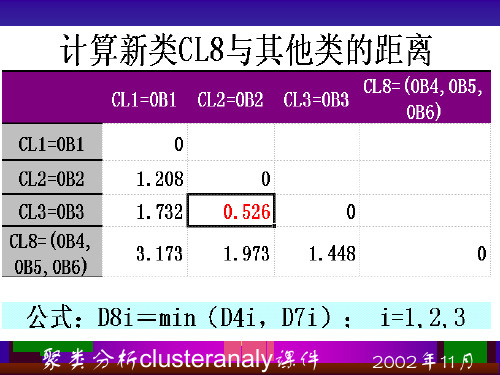
其中D.2. 为欧氏距离的平方
J
n.为各类中所含样品数
聚类分析clusteranaly课件 2002年11月
聚类分析clusteranaly课件 2002年11月
(六)可变类平均法
(flexible-beta method)
K
M
L
类平均法的变型
DM 2 J(1)nnM K DK 2JnnM L DL2JDK 2L J 1;SA软 S 件预置 0.25为
选项
人为固定分类数 ANOVA表,初
读写凝聚点 始凝聚点等
聚类分析clusteranaly课件 2002年11月
(二)SAS聚类分析
样品聚类:PROC CLUSTER pseudo
RSQUARE STD METHOD=(AVE, AVERAGE, CEN,
CENTROID, COM, COMPLETE, DEN, DENSITY, EML, FLE, FLEXIBLE, MCQ, MCQUITTY, MED, MEDIAN, SIN,
聚类分析clusteranaly课件
1,通常情况1下 ~0取 之- 间的数
聚类分析clusteranaly课件 2002年11月
(五)类平均法
(average linkage between group)
K
M
L SPSS作为默认方法 ,称为 between-
groups linkage
DM2 J
nK nM
DK2J
nL nM
DL2J
冰柱的方向
聚类分析clusteranaly课件 2002年11月
Method
聚类方法
亲疏关系指标
标准化变换
聚类分析clusteranaly课件
聚类分析课件

聚类分析课件聚类分析课件聚类分析是一种常用的数据分析方法,它可以将一组数据分成不同的类别或簇,每个簇内的数据点具有相似的特征,而不同簇之间的数据点具有较大的差异。
聚类分析在各个领域都有广泛的应用,如市场细分、社交网络分析、医学诊断等。
在本文中,我们将介绍聚类分析的基本概念、常用算法和实际应用案例。
一、聚类分析的基本概念聚类分析的目标是通过对数据进行分组,使得每个组内的数据点相似度较高,而不同组之间的相似度较低。
聚类分析的基本概念包括距离度量和聚类算法。
1. 距离度量距离度量是衡量数据点之间相似度或差异度的标准。
常用的距离度量方法包括欧氏距离、曼哈顿距离和闵可夫斯基距离等。
欧氏距离是最常用的距离度量方法,它计算数据点在多维空间中的直线距离。
曼哈顿距离则计算数据点在坐标轴上的绝对距离,而闵可夫斯基距离则是这两种距离的一种泛化形式。
2. 聚类算法常用的聚类算法包括K-means算法、层次聚类算法和DBSCAN算法等。
K-means算法是一种迭代的、基于距离的聚类算法,它将数据点分成K个簇,使得每个簇内的数据点与该簇的中心点的距离最小。
层次聚类算法则是一种自底向上的聚类算法,它通过计算数据点之间的相似度来构建一个层次结构。
DBSCAN算法是一种基于密度的聚类算法,它将数据点分为核心点、边界点和噪声点三类,具有较好的鲁棒性和灵活性。
二、常用的聚类分析算法1. K-means算法K-means算法是一种迭代的、基于距离的聚类算法。
它的基本思想是随机选择K个初始中心点,然后将每个数据点分配到距离其最近的中心点所对应的簇中。
接着,重新计算每个簇的中心点,并重复这个过程直到收敛。
K-means算法的优点是简单易实现,但它对初始中心点的选择敏感,并且需要预先指定簇的个数K。
2. 层次聚类算法层次聚类算法是一种自底向上的聚类算法。
它的基本思想是将每个数据点看作一个独立的簇,然后通过计算数据点之间的相似度来构建一个层次结构。
聚类分析PPT课件
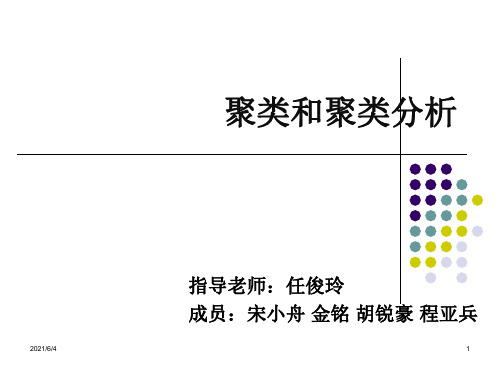
S3
S4 S5
平均距离(average)
D 1 2 21 6(d 1 2 4d 1 2 5d 2 2 4d 2 2 5d 3 2 4d 3 2)5
2021/6/4
19
类间距离
S1 S2
S3
最短距离
2021/6/4
S4 S5
20
例 6个不同民族的标化死亡率与出生时的期望寿命
2021/6/4
5
聚类分析法的分类
Q型聚类分析是对样本进行分类处理的 R 型聚类分析是对变量(指标)进行分类处理的。
R型聚类分析的特点 (1) R型聚类分析不但可以了解个别
变量之间的亲疏程度,而且可以了解
各个变量组合之间的亲疏程度。
(2)根据变量的分类结果以及它们之
间的关系,可以选择主要变量进行回
归分析。
2021/6/4
2021/6/4
12
把不同的类型一一划分出来,形成一个由小到 大的分类系统,最后在把所有的样品(或指标 )间的亲把疏关系表示出来,这种方法称为系统 聚类分析法
2021/6/4
13
系统聚类的基本步骤
1. 构造n个类,每个类包含且只包含一个样品。 2. 计算n个样品两两间的距离,构成距离矩阵,记作D0。 3. 合并距离最近的两类为一新类。
聚类和聚类分析
指导老师:任俊玲 成员:宋小舟 金铭 胡锐豪 程亚兵
2021/6/4
1
目录
1.聚类的概念 2.聚类分析的原理 3.聚类分析的分类 4.距离和相似系数 5.系统聚类分析 6.快速聚类 7.致谢
2021/6/4
2
什么是聚类
早在孩提时代,人就通过不断改进下意识 中的聚类模式来学会如何区分猫和狗,动物和 植物
聚类分析专题教育课件

❖ 由距离来构造相同系数总是可能旳,如令
cij
1 1 dij
这里dij为第i个样品与第j个样品旳距离,显然cij满足 定义相同系数旳三个条件,故可作为相同系数。
❖ 距离必须满足定义距离旳四个条件,所以不是总能 由相同系数构造。高尔(Gower)证明,当相同系 数矩阵(cij)为非负定时,如令
dij 2 1 cij
0
2
0
5
3
D(2) G7
0 3
G5 0 G5 0
表
D(3)
G6
G8
G6
0
G8
4
0
其中G6= G1∪G2
图6.3.2 最短距离法树形图
二、最长距离法
❖ 类与类之间旳距离定义为两类最远样品间旳 , jGL
dij
图6.3.3 最长距离法: DKL=d15
❖ 最长距离法与最短距离法旳并类环节完全相同,只 是类间距离旳递推公式有所不同。
注:
❖ 假如某一步D(m)中最小旳元素不止一种,相应这些 最小元素旳类能够同步合并。
❖ 因为最短距离法是用两类之间近来样本点旳距离来 聚旳,所以该措施不适合对分离得很差旳群体进行 聚类
❖ D(0)等均为对称阵 ❖ 一般距离采用绝对距离或欧氏距离
❖ 例6.3.1 设有五个样品,每个只测量了一种指标, 分别是1,2,6,8,11,试用最短距离法将它们分 类。
❖ 递推公式:
DMJ maxDKJ , DLJ
❖ 对例采用最长距离法,其树形图如图所示,它与图 有相同旳形状,但并类旳距离要比图大某些,仍提 成两类为宜。
图6.3.4 最长距离法树形图
三、中间距离法
❖ 类与类之间旳距离既不取两类近来样品间旳距离,也不取两 类最远样品间旳距离,而是取介于两者中间旳距离,称为中
聚类分析中的距离度量

dijxi xj yi yj
• 两个n维向量a(xi1,xi2,…,xin)与b(xj1,xj2,…,xjn)间的曼哈顿
距离
n
dij xik xjk
k1
精选可编辑ppt
7
Matlab计算曼哈顿距离
• 例子:计算向量(0,0)、(1,0)、(0,2)两两间的曼哈 顿距离
2.3452 2.0000 2.3452 1.2247 2.4495 1.2247
精选可编辑ppt
18
夹角余弦(Cosine)
几何中夹角余弦可用来衡量两个向量方向的差异,机 器学习中借用这一概念来衡量样本向量之间的差异。
(1)在二维空间中向量a(xi,yi)与向量b(xj,yj)的夹角余弦公
式:
cos
而样本A与B的杰卡德距离表示为:
dJ
M10M01 M11M10M01
精选可编辑ppt
23
Matlab计算杰卡德距离
Matlab的pdist函数定义的杰卡德距离跟前面的定 义有一些差别,Matlab中将其定义为不同的维度 的个数占“非全零维度”的比例。
xixj yiyj
xi2yi2 xj2yj2
(2)对于两个n维样本点a(xi1,xi2,…,xin)与 b(xj1,xj2,…,xjn), 可以使用类似于夹角余弦的概念来衡量它们间的相似
程度。 cos() ab即
ab
cos( )
n
xik x jk
k 1
n
n
xik 2
x jk 2
k 1
k 1
X= [1 0 ; 1 1.732 ; -1 0]
聚类分析以及相关系数(课堂PPT)

x 6 0.398 0.326 0.319 0.329 0.762 1.000 x 7 0.301 0.277 0.237 0.327 0.730 0.583 1.000 x 8 0.382 0.415 0.345 0.365 0.629 0.577 0.539 1.000
三角形(如图6.2.4所示),取 DKL 边的中线
作为 DMJ ,由初等平面几何可知,DMJ 的计算
公式为
D 2 M J 1 2 D K 2 J 1 2 D L 2 J1 4 D K 2 L
6 .2 .5
35
GK
DKJ DMJ
DKL
GJ
D LJ
14
最常用的相似系数有如下两种
1.夹角余弦
变量x i 与 x j的夹角余弦定义为
n
xkixkj
cij 1
n
k1
xk2i
n
xk2j1/2
k1 k1
6.1.6
它是 R n 中变量 x i的观察向量 x1i,x2i,xniT
与变量x j 的观察向量 x1j,x2j,,xnjT之间的
夹角 ij 的余弦函数,即 cij1coisj 。
2选定中的最小元素设为3计算新类与任一类之间距离的递推公式minminminminminljkjij所在的行与列合并成一个新行新列对应该行列上的新距离值由632式求得其余行列上的距离值不变这样就得到新的距离矩阵记为重复上述对的两步得如果某一步中最小的元素不止一个则称此现象为结tie对应这些最小元素的类可以任选一类合并或同时合并
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
k 1
当p=1时,就是曼哈顿距离
当p=2时,就是欧氏距离
当p→∞时,就是切比雪夫距离
根据变参数的不同,明氏距离可以表示一类的距离。
12 / 28
• (2)明氏距离的缺点
明氏距离,包括曼哈顿距离、欧氏距离和切比雪夫距离都 存在明显的缺点。
举个例子:二维样本(身高,体重),其中身高范围是 150~190,体重范围是50~60,有三个样本:a(180,50), b(190,50),c(180,60)。那么a与b之间的明氏距离(无论是曼 哈顿距离、欧氏距离或切比雪夫距离)等于a与c之间的明氏距 离,但是身高的10cm真的等价于体重的10kg么?因此用明氏 距离来衡量这些样本间的相似度很有问题。
简单说来,明氏距离的缺点主要有两个: (1)将各个分量的量纲(scale),也就是“单位”当作相同的看待 了。 (2)没有考虑各个分量的分布(期望,方差等)可能是不同的。
13 / 28
Matlab计算明氏距离
• 例子:计算向量(0,0)、(1,0)、(0,2)两两间的明 氏距离(以变参数为2的欧氏距离为例)
离:
dij (xi x j )2 ( yi y j )2 (zi z j )2
4 / 28
欧氏距离(续)
• 两个n维向量a(xi1,xi2,…,xin)与 b(xj1,xj2,…,xjn)间的欧氏
距离: n
dij
(xik x jk )2
k 1
• 也可以用表示成向量运算的形式:
dij (a b)(a b)T
x jk
)
• 这个公式的另一种等价形式是
dij
n
lim (
m k 1
xik
x jk
)m 1/ m
可以用放缩法和夹逼法则来证明此式
10 / 28
Matlab计算切比雪夫距离
例子:计算向量(0,0)、(1,0)、(0,2)两两间的切比雪 夫距离 X= [0 0 ; 1 0 ; 0 2] D= pdist(X, 'chebychev') 结果: D=
聚类分析中的距离度量
1
• 在做分类时常常需要估算不同样本之间的相似性度量 (SimilarityMeasurement),这时通常采用的方法就是计算 样本间的“距离”(Distance)。采用什么样的方法计算距 离是很讲究,甚至关系到分类的正确与否。
• 本次报告的目的就是对常用的相似性度量作一个总结。
X= [0 0 ; 1 0 ; 0 2] D= pdist(X,'minkowski',2) 结果: D=
1.0000 2.0000 2.2361
14 / 28
标准化欧氏距离 (Standardized Euclidean distance )
• 标准化欧氏距离是针对简单欧氏距离的缺点而作的 一种改进方案。标准欧氏距离的思路:既然数据各 维分量的分布不一样,那就先将各个分量都“标准 化”到均值、方差相等吧。均值和方差标准化到多 少呢?根据统计学知识吧,假设样本集X的均值 (mean)为m,标准差(standard deviation)为s,那么X的 “标准化变量”表示为:X*
12 2
11 / 28
明可夫斯基距离(Minkowski Distance)
• 明氏距离不是一种距离,而是一组距离的定义。 (1)明氏距离的定义
两个n维变量a(xi1,xi2,…,xin)与 b(xj1,xj2,…,xjn)之间的 明可夫斯基距离定义为:
n
p
dij p xik x jk
其中p是一个变参数。
• (1)二维平面两点a(xi,yi)与b(xj,yj)间的曼哈顿距离
dij xi x j yi y j
• 两个n维向量a(xi1,xi2,…,xin)与b(xj1,xj2,…,xjnk
k 1
7 / 28
Matlab计算曼哈顿距离
• 例子:计算向量(0,0)、(1,0)、(0,2)两两间的曼哈 顿距离
结果:
D=
1.0000 2.0000 2.2361
6 / 28
曼哈顿距离(ManhattanDistance)
• 想象你在曼哈顿要从一个十字路口开车到另外一个十 字路口,驾驶距离是两点间的直线距离吗?显然不是, 除非你能穿越大楼。实际驾驶距离就是这个“曼哈顿 距离”。而这也是曼哈顿距离名称的来源, 曼哈顿距 离也称为城市街区距离(CityBlock distance)。
2 / 28
目录
• 1. 欧氏距离 • 2. 曼哈顿距离 • 3. 切比雪夫距离 • 4. 明可夫斯基距离 • 5. 标准化欧氏距离 • 6. 马氏距离 • 7. 夹角余弦 • 8. 汉明距离 • 9. 杰卡德系数& 杰卡德相似距离 • 10. 相关系数& 相关距离 • 11. 信息熵
3 / 28
5 / 28
Matlab计算欧氏距离
• Matlab计算距离主要使用pdist函数。若X是一个 M×N的矩阵,则pdist(X)将X矩阵M行的每一行作 为一个N维向量,然后计算这M个向量两两间的 距离。
• 例子:计算向量(0,0)、(1,0)、(0,2)两两间的欧式
距离
X= [0 0 ; 1 0 ; 0 2] D= pdist(X,'euclidean')
• (1)二维平面两点a(x1,y1)与b(x2,y2)间的切比雪夫
距离
dij max( xi x j , yi y j )
9 / 28
切比雪夫距离 ( 续 )
• (2)两个n维向量a(xi1,xi2,…,xin)与 b(xj1,xj2,…,xjn) 之间的切比雪夫距离
dij
max( k
xik
欧氏距离(EuclideanDistance)
• 欧氏距离是最易于理解的一种距离计算方法, 源自欧氏空间中两点间的距离公式。
• (1)二维平面上两点a(xi,yi)与b(xj,yj)间的欧氏距离:
• (2)三维空d间ij 两点(xai(xi,xyij,)z2i)与 (by(ixj,yyj,zj j))2间的欧氏距
X= [0 0 ; 1 0 ; 0 2] D= pdist(X, 'cityblock') 结果: D=
12 3
8 / 28
切比雪夫距离 ( Chebyshev Distance )
• 国际象棋中国王走一步能够移动到相邻的8个方 格中的任意一个。那么国王从格子a(xi,yi)走到格 子b(xj,yj)最少需要多少步?自己走走试试。你会 发现最少步数总是max(| xj-xi | , | yj-yi | ) 步。有 一种类似的一种距离度量方法叫切比雪夫距离。
