江苏省无锡市天一中学2020学年高三数学11月月考试卷(含解析)
2020年江苏省无锡市锡山区天一中学高考数学第一次模拟测试试卷 (解析版)

2020年高考数学第一次模拟试卷一、填空题(共14个小题)1.已知集合A={x|0<x<2},B={x|﹣1<x<1},则A∩B=.2.复数z=(i为虚数单位)的虚部为.3.函数的定义域为.4.在编号为1,2,3,4,5且大小和形状均相同的五张卡片中,一次随机抽取其中的两张,则抽取的两张卡片编号之和是偶数的概率为.5.在平面直角坐标系xOy中,若双曲线(a>0,b>0)的离心率为,则该双曲线的渐近线方程为.6.某种圆柱形的如罐的容积为128π个立方单位,当它的底面半径和高的比值为时,可使得所用材料最省.7.在平面直角坐标系xOy中,双曲线的右准线与渐近线的交点在抛物线y2=2px 上,则实数p的值为.8.已知α是第二象限角,且,tan(α+β)=﹣2,则tanβ=.9.已知等差数列{a n}的前n项和为S n,若S3=6,S6=﹣8,则S9=.10.在平面直角坐标系xOy中,已知直线l:y=与函数f(x)=sin(ωx+)(ω>0)的图象在y轴右侧的公共点从左到右依次为A1,A2…,若点A1的横坐标为1.则点A2的横坐标为.11.设P为有公共焦点F1,F2的椭圆C1与双曲线C2的一个交点,且PF1⊥PF2,椭圆C1的离心率为e1,双曲线C2的离心率为e2,若e2=3e1,则e1=.12.如图,在△ABC中,AB=AC=2,,,AE的延长线交BC边于点F,若,则=.13.已知函数f(x)是定义在R上的奇函数,其图象关于直线x=1对称,当x∈(0,1]时,f(x)=﹣e ax(其中e是自然对数的底数),若f(2020﹣ln2)=8,则实数a的值为.14.已知函数(其中e为自然对数的底数),若关于x的方程f2(x)﹣3a|f(x)|+2a2=0恰有5个相异的实根,则实数a的取值范围为.二、解答题15.如图,在斜三棱柱ABC﹣A1B1C1中,已知△ABC为正三角形,D,E分别是AC,CC1的中点,平面AA1C1C⊥平面ABC,A1E⊥AC1.(1)求证:DE∥平面AB1C1;(2)求证:A1E⊥平面BDE.16.在△ABC中,角A,B,C的对边分别为a,b,c,且.(1)若a=5,,求b的值;(2)若,求tan2C的值.17.截至1月30日12时,湖北省累计接收揭赠物资615.43万件,包括医用防护服2.6万套,N95口罩47.9万个,医用一次性口罩172.87万个,护目镜3.93万个等.某运输队接到给武汉运送物资的任务,该运输队有8辆載重为6t的A型卡车,6辆载重为10t的B型卡车,10名驾驶员,要求此运输队每天至少运送720t物资.已知每辆卡车每天往返的次数:A型卡车16次,B型卡车12次;每辆卡车每天往返的成本:A型卡车240元,B型卡车378元.求每天派出A型卡车与B型卡车各多少辆,运输队所花的成本最低?18.在平面直角坐标系xOy中,椭圆C:的右准线方程为x=2,且两焦点与短轴的一个顶点构成等腰直角三角形.(1)求椭圆C的方程;(2)假设直线l:y=kx+m与椭圆C交于A,B两点.①若A为椭圆的上顶点,M为线段AB中点,连接OM并延长交椭圆C于N,并且,求OB的长;②若原点O到直线l的距离为1,并且,当时,求△OAB的面积S的范围.19.设函数f(x)=2x2+alnx,(a∈R)(Ⅰ)若曲线y=f(x)在点(1,f(1))处的切线方程为y=2x+m,求实数a,m的值(Ⅱ)若f(2x﹣1)+2>2f(x)对任意x∈[2,+∞)恒成立,求实数a的取值范围;(Ⅲ)关于x的方程f(x)+2cos x=5能否有三个不同的实根?证明你的结论20.已知f(x)=x3+ax2+bx,a,b∈R.(1)若b=1,且函数f(x)在区间(﹣1,)上单调递增,求实数a的范围;(2)若函数f(x)有两个极值点x1,x2,x1<x2,且存在x0满足x1+2x0=3x2,令函数g (x)=f(x)﹣f(x0),试判断g(x)零点的个数并证明你的结论.[选做题]本题包括A、B、C三小题,请选定其中两题.[选修4-2:矩阵与变换]21.已知矩阵M=的一个特征值为4,求矩阵M的逆矩阵M﹣1.[选修4-4:坐标系与参数方程]22.在平面直角坐标系xOy中,已知直线l的参数方程为(t为参数),在以坐标原点O为极点,x轴的非负半轴为极轴,且与直角坐标系长度单位相同的极坐标系中,曲线C的极坐标方程是.(1)求直线l的普通方程与曲线C的直角坐标方程;(2)若直线l与曲线C相交于两点A,B,求线段AB的长.[选修4-5:不等式选讲」23.已知x1,x2,x3∈(0,+∞),且满足x1+x2+x3=3x1x2x3,证明:x1x2+x2x3+x3x1≥3.[必做题]第22题、第23题,每题10分,共计20分.24.如图,在平面直角坐标系xOy中,已知抛物线:C:y2=2px(p>0)的焦点F在直线x+y﹣1=0上,平行于x轴的两条直线l1,l2分别交抛物线线C于A,B两点,交该抛物线的准线于D,E两点.(1)求抛物线C的方程;(2)若F在线段AB上,P是DE的中点,证明:AP∥EF.25.在开展学习强国的活动中,某校高三数学教师成立了党员和非党员两个学习组,其中党员学习组有4名男教师、1名女教师,非党员学习组有2名男教师、2名女教师,高三数学组计划从两个学习组中随机各选2名教师参加学校的挑战答题比赛.(1)求选出的4名选手中恰好有一名女教师的选派方法数;(2)记X为选出的4名选手中女教师的人数,求X的概率分布和数学期望.参考答案一、填空题1.已知集合A={x|0<x<2},B={x|﹣1<x<1},则A∩B={x|0<x<1}.解:∵A={x|0<x<2},B={x|﹣1<x<1},∴A∩B={x|0<x<1}.故答案为:{x|0<x<1}.2.复数z=(i为虚数单位)的虚部为1.解:z==i+1的虚部为1.故答案为:1.3.函数的定义域为[4,+∞)..解:函数f(x)=有意义,只需log2x﹣2≥0,且x>0,解得x≥4.则定义域为[4,+∞).故答案为:[4,+∞).4.在编号为1,2,3,4,5且大小和形状均相同的五张卡片中,一次随机抽取其中的两张,则抽取的两张卡片编号之和是偶数的概率为.解:在编号为1,2,3,4,5且大小和形状均相同的五张卡片中,一次随机抽取其中的两张,基本事件总数为n==10,抽取的两张卡片编号之和是偶数包含的基本事件个数:m==4,则抽取的两张卡片编号之和是偶数的概率为p=.故答案为:.5.在平面直角坐标系xOy中,若双曲线(a>0,b>0)的离心率为,则该双曲线的渐近线方程为.解:因为双曲线(a>0,b>0)的离心率为,可得=,所以=,所以渐近线方程为y=±x.故答案为:y=±x.6.某种圆柱形的如罐的容积为128π个立方单位,当它的底面半径和高的比值为时,可使得所用材料最省.解:如图所示,设圆柱的高为h,底面半径为r.由题意,128π=πr2•h,∴S=2πr2+2πr•h==≥3.当且仅当,即当r=4时取等号.此时h==8.∴它的底面半径和高的比值为.故答案为:.7.在平面直角坐标系xOy中,双曲线的右准线与渐近线的交点在抛物线y2=2px 上,则实数p的值为.解:双曲线的右准线x=,渐近线y=x,双曲线的右准线与渐近线的交点(,),交点在抛物线y2=2px上,可得:=3p,解得p=.故答案为:.8.已知α是第二象限角,且,tan(α+β)=﹣2,则tanβ=﹣.解:∵α是第二象限角,且sinα=,∴cosα=﹣=﹣,tanα=﹣,∵tan(α+β)===﹣2;∴tanβ=﹣.故答案为:﹣.9.已知等差数列{a n}的前n项和为S n,若S3=6,S6=﹣8,则S9=﹣42.解:由题意可得:2×(﹣8﹣6)=6+S9﹣(﹣8),解得S9=﹣42.故答案为:﹣42.10.在平面直角坐标系xOy中,已知直线l:y=与函数f(x)=sin(ωx+)(ω>0)的图象在y轴右侧的公共点从左到右依次为A1,A2…,若点A1的横坐标为1.则点A2的横坐标为3.解:因为点A1的横坐标为1,即当x=1时,f(x)=sin(ω+)=,所以ω+=2kπ+或ω+=2kπ+(k∈Z),又直线l:y=与函数f(x)=sin(ωx+)(ω>0)的图象在y轴右侧的公共点从左到右依次为A1,A2…,所以ω+=,故ω=,所以:函数的关系式为f(x)=sin().当x2=3时,f(3)=sin()=,即点A2的横坐标为3,(3,)为二函数的图象的第二个公共点.故答案为:3.11.设P为有公共焦点F1,F2的椭圆C1与双曲线C2的一个交点,且PF1⊥PF2,椭圆C1的离心率为e1,双曲线C2的离心率为e2,若e2=3e1,则e1=.解:如图,由椭圆定义及勾股定理得,,可得=b12,∵e1=,∴a1=,∴b12=a12﹣c2=c2(),同理可得=b22,∵e2=,∴a2=,∴b22=c2﹣a22=c2(1﹣),∴c2(﹣1)=c2(1﹣),即,∵e2=3e1,∴e1=.故答案为:.12.如图,在△ABC中,AB=AC=2,,,AE的延长线交BC边于点F,若,则=.解:作DG∥AF交BC于G;∴,∴FE=DG;BF=FG;①∵,∴DG=AF;FG=GC;②联立①②可得EF=AF;AE=AF;BF=BC;∵=(+)•=﹣[+(﹣)]•()=﹣(+)•()=﹣[﹣﹣]=﹣[×22﹣•﹣×22]∴=;则=•=×()•=×(•+)=×(×+×22)=;故答案为:.13.已知函数f(x)是定义在R上的奇函数,其图象关于直线x=1对称,当x∈(0,1]时,f(x)=﹣e ax(其中e是自然对数的底数),若f(2020﹣ln2)=8,则实数a的值为3.解:根据题意,f(x)的图象关于x=1对称,所以f(1+x)=f(1﹣x)又由f(x)是R上的奇函数,所以f(x+1)=﹣f(x﹣1),则有f(x+2)=﹣f(x),f(x+4)=﹣f(x+2)=f(x).则f(x)是周期为4的函数,故f(2020﹣ln2)=f(﹣ln2)=﹣f(ln2)=﹣(﹣e x•ln2)=8,变形可得:2x=8,解可得x=3;故答案为:314.已知函数(其中e为自然对数的底数),若关于x的方程f2(x)﹣3a|f(x)|+2a2=0恰有5个相异的实根,则实数a的取值范围为{}∪[,).解:当x≤2时,令f′(x)==0,解得x=1,所以当x≤1时,f′(x)>0,则f(x)单调递增,当1≤x≤2时,f′(x)<0,则f (x)单调递减,当x>2时,f(x)==单调递减,且f(x)∈[0,)作出函数f(x)的图象如图:(1)当a=0时,方程整理得f2(x)=0,只有2个根,不满足条件;(2)若a>0,则当f(x)<0时,方程整理得f2(x)+3af(x)+2a2=[f(x)+2a][f(x)+a]=0,则f(x)=﹣2a<0,f(x)=﹣a<0,此时各有1解,故当f(x)>0时,方程整理得f2(x)﹣3af(x)+2a2=[f(x)﹣2a][f(x)﹣a]=0,f(x)=2a有1解同时f(x)=a有2解,即需2a=1,a=,因为f(2)==>,故此时满足题意;或f(x)=2a有2解同时f(x)=a有1解,则需a=0,由(1)可知不成立;或f(x)=2a有3解同时f(x)=a有0解,根据图象不存在此种情况,或f(x)=2a有0解同时f(x)=a有3解,则,解得,故a∈[,)(3)若a<0,显然当f(x)>0时,f(x)=2a和f(x)=a均无解,当f(x)<0时,f(x)=﹣2a和f(x)=﹣a无解,不符合题意.综上:a的范围是{}∪[,)故答案为{}∪[,)二、解答题:共6小题,共90分,请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.15.如图,在斜三棱柱ABC﹣A1B1C1中,已知△ABC为正三角形,D,E分别是AC,CC1的中点,平面AA1C1C⊥平面ABC,A1E⊥AC1.(1)求证:DE∥平面AB1C1;(2)求证:A1E⊥平面BDE.解:(1)证明:D,E分别是AC,CC1的中点,∴DE∥AC1,DE⊈平面AB1C1,∵AC1⫋平面AB1C1,故DE∥平面AB1C1;(2)证明:△ABC为正三角形,所以BD⊥AC,因为平面AA1C1C⊥平面ABC,平面AA1C1C∩平面ABC=AC,故BD⊥平面AA1C1C,A1E⊂平面AA1C1C,所以BD⊥A1E,又A1E⊥AC1,DE∥AC1,所以A1E⊥DE,又BD∩DE=D,所以A1E⊥平面BDE.16.在△ABC中,角A,B,C的对边分别为a,b,c,且.(1)若a=5,,求b的值;(2)若,求tan2C的值.解:(1)在△ABC中,由余弦定理b2+c2﹣2bc cos A=a2,得,即b2﹣4b﹣5=0,解得b=5或b=﹣1(舍),所以b=5.(2)由及0<A<π得,,所以,又因为0<C<π,所以,从而,所以.17.截至1月30日12时,湖北省累计接收揭赠物资615.43万件,包括医用防护服2.6万套,N95口罩47.9万个,医用一次性口罩172.87万个,护目镜3.93万个等.某运输队接到给武汉运送物资的任务,该运输队有8辆載重为6t的A型卡车,6辆载重为10t的B型卡车,10名驾驶员,要求此运输队每天至少运送720t物资.已知每辆卡车每天往返的次数:A型卡车16次,B型卡车12次;每辆卡车每天往返的成本:A型卡车240元,B型卡车378元.求每天派出A型卡车与B型卡车各多少辆,运输队所花的成本最低?解:设每天派出A型卡车x辆,B型卡车y辆,运输队所花成本为z元,则,且x∈N,y∈N,化简得:,目标函数z=240x+378y,画出满足条件的可行域如图中阴影部分所示:由图可知,当直线z=240x+378y经过点A时,截距z最小,解方程组,得点A的坐标为(,0),又∵x∈N,y∈N,∴点A(,0)不是最优解,∵在可行域的整数点中,点(8,0)使z取得最小值,即z min=240×8+378×0=1920,∴每天排除A型卡车8辆,B型卡车0辆,运输队所花的成本最低,最低成本为1920元,答:每天派出A型卡车8辆,B型卡车0辆,运输队所花的成本最低,最低成本为1920元.18.在平面直角坐标系xOy中,椭圆C:的右准线方程为x=2,且两焦点与短轴的一个顶点构成等腰直角三角形.(1)求椭圆C的方程;(2)假设直线l:y=kx+m与椭圆C交于A,B两点.①若A为椭圆的上顶点,M为线段AB中点,连接OM并延长交椭圆C于N,并且,求OB的长;②若原点O到直线l的距离为1,并且,当时,求△OAB的面积S的范围.解:(1)因为两焦点与短轴的一个顶点的连线构成等腰直角三角形,所以a=,又由右准线方程为x=2,得到=2,解得a=,所以b2=a2﹣c2=1所以,椭圆C的方程为+y2=1(2)设B(x1,y1),而A(0,1),则M(,),∵=,∴N(,),因为点B,N都在椭圆上,所以,解得:y1=,x=所以(3)由原点O到直线l的距离为1,得=1,化简得:1+k2=m2联立直线l的方程与椭圆C的方程:,得(1+2k2)x2+4kmx+2m2﹣2=0设A(x1,y1),B(x2,y2),则x1+x2=﹣,x1x2=,且△=8k2>0,∴•=x1x2+y1y2=x1x2+(kx1+m)(kx2+m)=(1+k2)x1x2+km(x1+x2)+m2=(1+k2)﹣+m2====λ所以k2=,所以△OAB的面积S=1×AB=|x1﹣x2|====,因为S=在[,]为单调减函数,并且当λ=时,S=,当λ=时,S=,所以△OAB的面积S的范围为19.设函数f(x)=2x2+alnx,(a∈R)(Ⅰ)若曲线y=f(x)在点(1,f(1))处的切线方程为y=2x+m,求实数a,m的值(Ⅱ)若f(2x﹣1)+2>2f(x)对任意x∈[2,+∞)恒成立,求实数a的取值范围;(Ⅲ)关于x的方程f(x)+2cos x=5能否有三个不同的实根?证明你的结论解:(I)∵f(x)=2x2+alnx,∴f′(x)=4x,由题意可得,f′(1)=2,f(1)=2∴4+a=2,2+m=2∴a=﹣2,m=0,(II)∵f(2x﹣1)+2>2f(x)对任意x∈[2,+∞)恒成立,2(2x﹣1)2+aln(2x﹣1)+2>2(2x2+alnx),整理可得,4(x﹣1)2﹣a[2lnx﹣ln(2x﹣1)]>0对任意x∈[2,+∞)恒成立,∴4﹣a(n4﹣ln3)>0即a当a时,4(x﹣1)2﹣a[2lnx﹣ln(2x﹣1)]设g(x)=4(x﹣1)2﹣,则g′(x)=8(x﹣1)[(2x2﹣x)﹣]∵x≥2,∴x﹣1>0,,∴g′(x)>0,即g(x)单调递增,g(x)>g(2)=0综上可得,a(III)不可能有三个不同的实根,证明如下:令g′(x)=f(x)+2cos x,若g(x)=5有三个不同的实数根,则g(x)至少要有三个单调区间,则g′(x)=0至少有两个不等实根,所以只要证明g′(x)=0在(0,+∞)至多1个实根,g′(x)=4x,g′′(x)=4﹣2cos x﹣∵,∴g′′(x)>0,∴g′(x)在(0,+∞)上单调递增,∴g′(x)=0至多1个根,当a≥0时,(4x﹣2sin x)′=4﹣2cos x>0,∴y=4x﹣2sin x在(0,+∞)上单调递增,∴y=4x﹣2sin x>0,又因为a≥0时,∴>0,g′(x)=0g′(x)在(0,+∞)上没有实数根综上可得,g′(x)=0(0,+∞)上至多一个实数根,得证20.已知f(x)=x3+ax2+bx,a,b∈R.(1)若b=1,且函数f(x)在区间(﹣1,)上单调递增,求实数a的范围;(2)若函数f(x)有两个极值点x1,x2,x1<x2,且存在x0满足x1+2x0=3x2,令函数g (x)=f(x)﹣f(x0),试判断g(x)零点的个数并证明你的结论.解:f′(x)=3x2+2ax+b,(x∈R),(1)当b=1时,f′(x)=3x2+2ax+1,因为f(x)在区间(﹣1,)上单调递增所以当x∈(﹣1,)时,f′(x)=3x2+2ax+1≥0恒成立.函数f′(x)=3x2+2ax+1的对称轴为x=﹣.①﹣<﹣1,即a>3时,f′(﹣1)≥0,即3﹣2a+1≥0,解之得a,解集为空集;②﹣1,即﹣时,f即,解之得,所以﹣③﹣,即a时,f≥0即3+a+1≥0,解之得a≥﹣,所以﹣综上所述,当﹣函数f(x)在区间(﹣1,)上单调递增.…(2)∵f(x)有两个极值点x1,x2,∴x1,x2是方程f′(x)=3x2+2ax+b=0的两个根,且函数f(x)在区间(﹣∞,x1)和(x2,+∞)上单调递增,在(x1,x2)上单调递减.∵g′(x)=f′(x)∴函数g(x)也是在区间(﹣∞,x1)和(x2,+∞)上单调递增,在(x1,x2)上单调递减∵g(x0)═f(x0)﹣f(x0)=0,∴x0是函数g(x)的一个零点.…由题意知:x1+2x0=3x2,g(x2)=f(x2)﹣f(x0)∵x1+2x0=3x2,∴2x0﹣2x2=x2﹣x1>0,∴x0>x2∴f(x2)<f(x0),∴g(x2)=f(x2)﹣f(x0)<0又g(x1)=f(x1)﹣f(x0)=x13+ax12+bx1﹣(x03+ax02+bx0)=(x1﹣x0)(x12+x1x0+x02+ax1+ax0+b)=(x1﹣x0)(x12+x1•+()2+ax1+a•+b)=(x1﹣x0)(3x12+2ax1+b+9x22+6ax2+3b)∵x1,x2是方程f′(x)=3x2+2ax+b=0的两个根,∴3x12+2ax1+b=0,3x22+2ax2+b=0…∴g(x1)=f(x1)﹣f(x0)=0∵函数g(x)图象连续,且在区间(﹣∞,x1)上单调递增,在(x1,x2)上单调递减,在(x2,+∞)上单调递增∴当x∈(﹣∞,x1)时,g(x)<0,当x∈(x1,x0)时g(x)<0,当x∈(x0,+∞)时g(x)>0,∴函数g(x)有两个零点x0和x1.…(16分)[选做题]本题包括A、B、C三小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分,解答时应写出文字说明、证明过程或演算步骤.[选修4-2:矩阵与变换]21.已知矩阵M=的一个特征值为4,求矩阵M的逆矩阵M﹣1.解:矩阵M的特征多项式为f(λ)==(λ﹣2)(λ﹣1)﹣3t;因为矩阵M的一个特征值为4,所以方程f(λ)=0有一根为4;即f(4)=2×3﹣3t=0,解得t=2;所以M=,设M﹣1=,则MM﹣1==,由,解得;由,解得;所以M﹣1=.[选修4-4:坐标系与参数方程](本小题满分10分)22.在平面直角坐标系xOy中,已知直线l的参数方程为(t为参数),在以坐标原点O为极点,x轴的非负半轴为极轴,且与直角坐标系长度单位相同的极坐标系中,曲线C的极坐标方程是.(1)求直线l的普通方程与曲线C的直角坐标方程;(2)若直线l与曲线C相交于两点A,B,求线段AB的长.解:(1)已知直线l的参数方程为(t为参数),转换为直角坐标方程为:,曲线C的极坐标方程是.由,得ρ2=4ρcosθ+4ρsinθ,整理的直角坐标方程为:x2+y2=4x+4y,所以曲线C:(x﹣2)2+(y﹣2)2=8.(2)由(1)知圆C半径,利用圆心到直线的距离,所以.[选修4-5:不等式选讲」23.已知x1,x2,x3∈(0,+∞),且满足x1+x2+x3=3x1x2x3,证明:x1x2+x2x3+x3x1≥3.【解答】证明:∵x1+x2+x3=3x1x2x3,∴,∴,当且仅当“x1=x2=x3=1”时取等号,故x1x2+x2x3+x3x1≥3,即得证.[必做题]第22题、第23题,每题10分,共计20分.请在答卷卡指定区域内作答.解答应写出文字说明、证明过程或演算步骤.24.如图,在平面直角坐标系xOy中,已知抛物线:C:y2=2px(p>0)的焦点F在直线x+y﹣1=0上,平行于x轴的两条直线l1,l2分别交抛物线线C于A,B两点,交该抛物线的准线于D,E两点.(1)求抛物线C的方程;(2)若F在线段AB上,P是DE的中点,证明:AP∥EF.解:(1)抛物线C的焦点F坐标为,且该点在直线x+y﹣1=0上,所以,解得p=2,故所求抛物线C的方程为y2=4x;(2)由点F在线段AB上,可设直线l1,l2的方程分别为y=a和y=b且a≠0,b≠0,a≠b.则,,D(﹣1,a),E(﹣1,b)∵P是DE的中点,∴直线AB的方程为,即4x﹣(a+b)y+ab=0,又点F(1,0)在线段AB上,∴ab=﹣4,,,由于AP,EF不重合,所以AP∥EF.25.在开展学习强国的活动中,某校高三数学教师成立了党员和非党员两个学习组,其中党员学习组有4名男教师、1名女教师,非党员学习组有2名男教师、2名女教师,高三数学组计划从两个学习组中随机各选2名教师参加学校的挑战答题比赛.(1)求选出的4名选手中恰好有一名女教师的选派方法数;(2)记X为选出的4名选手中女教师的人数,求X的概率分布和数学期望.【解答】角:(1)某校高三数学教师成立了党员和非党员两个学习组,其中党员学习组有4名男教师、1名女教师,非党员学习组有2名男教师、2名女教师,高三数学组计划从两个学习组中随机各选2名教师参加学校的挑战答题比赛.选出的4名选手中恰好有一名女教师的选派方法数为:m=+=28.(2)记X为选出的4名选手中女教师的人数,则X的可能取值为0,1,2,3,P(X=0)==,P(X=1)==,P(X=2)==,P(X=3)==,∴X的概率分布为:X0123PX的数学期望E(X)==.。
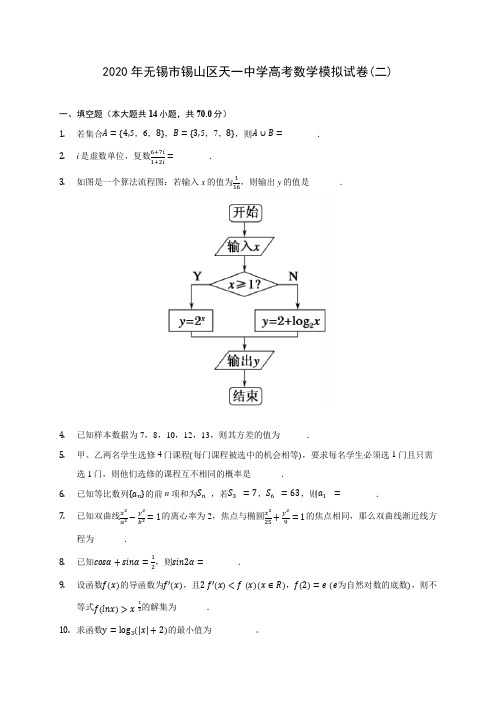
江苏省无锡市天一中2018-2019学年高三11月月考数学试卷

㈠ 䦸 吠和
㈠䦸 吠 t 䦸 ㈮ t 存在相同的极值点,
而
在
㈠
䦸㈮处有极大值,
吠
所以
䦸㈮ 吠
㈠
,所以
ㄼ
㈠ ㄼ,故答案为 3.
【点睛】
本题主要考查利用导数判断函数的单调性以及函数的极值,属于中档题.求函数 极值的步骤: (1) 确定函数的定义域;(2) 求导数 ;(3) 解方程 ㈠ h㤰求出函数定义域内的所有根;(4) 列 表检查 在 ㈠ h 的根 h左右两侧值的符号,如果左正右负(左增右减),那么 在 h处取 极大值,如果左负右正(左减右增),那么 在 h处取极小值. (5)如果只有一个极值点,则在 该处即是极值也是最值.
10.
3
【解析】试题分析:由 tanxtany 2 可得 sinxsiny 2 .又因为 sinxsiny 1 所以 cosxcosy 1 .
cosxcosy
3
6
又因为 cos x y cosxcosy sinxsiny 1 .又因为 0 y x 所以 0 x y .所以
㈠ 吠 t 是偶函数,则实数 ㈠______.
吠
6.已知 t h,函数
㈠ 䦸 吠和
㈠䦸 吠 t 䦸 ㈮ t 存在相同的极值点,则
㈠________.
7.已知函数 ㈠ 吠sin t
t hh.若 ㄼ ㈠ h㤰 吠 ㈠ 吠,则实数 的最小值为______.
8.已知函数 ㈠ sin
h㤰 与函数
㈠ ㈮ tan 的图象交于 㤰〳㤰 三点,则 〳 的面
㤰
h 有零点,且所有零点的和不 th
14.设函数 h ㈠ 䦸 h 䦸 䦸 则 的取值范围是____.
t 吠 t ㈮( h).若存在 h 䦸 ㈮ , ㈮ ,使 hh h,
江苏省天一中学2018-2019学年高三11月月考(含详细解答)

江苏省天一中学2018-2019高三11月月考一、填空题:本大题共14小题,每小题5分,共70分.请把答案直接填写在答题卡相....应位置上.....1.设集合,则_______.【分析】直接利用集合并集的定义求解即可.【详解】因为集合,所以,故答案为.【点睛】研究集合问题,一定要抓住元素,看元素应满足的属性.研究两集合的关系时,关键是将两集合的关系转化为元素间的关系,本题实质求满足属于集合或属于集合的元素的集合.2.命题:“使得”的否定为__________.【分析】根据特称命题的否定是全称命题,既要改写量词,又要否定结论,可得原命题的否定形式.【详解】因为特称命题的否定是全称命题,既要改写量词,又要否定结论,故命题“”的否定是,故答案为.【点睛】本题主要考查特称命题的否定,属于简单题.全称命题与特称命题的否定与命题的否定有一定的区别,否定全称命题和特称命题时,一是要改写量词,全称量词改写为存在量词、存在量词改写为全称量词;二是要否定结论,而一般命题的否定只需直接否定结论即可.3.函数的定义域为_________.【分析】直接由根式内部的代数式大于等于0 ,分式的分母不等于0 ,列不等式求解即可得结果.【详解】要使函数有意义,则,解得,函数的定义域为,故答案为.【点睛】本题主要考查具体函数的定义域、不等式的解法,属于中档题.定义域的三种类型及求法:(1)已知函数的解析式,则构造使解析式有意义的不等式(组)求解;(2) 对实际问题:由实际意义及使解析式有意义构成的不等式(组)求解;(3) 若已知函数的定义域为,则函数的定义域由不等式求出.4.曲线在处的切线的斜率为_________.【分析】求出原函数的导函数,可得到曲线在处的导数值,根据导数的几何意义可得结果.【详解】因为曲线在处的切线的斜率就是曲线在处的导数值,由得,,即曲线在处的切线的斜率为1,故答案为1.【点睛】本题考查了利角导数研究曲线上某点处的切线斜率,曲线在某点处的导数值,即为曲线上以该点为切点的切线的斜率,是中档题.5.若函数是偶函数,则实数______.【分析】由函数是偶函数,利用求得,再验证即可得结果.【详解】是偶函数,,即,解得,当时,是偶函数,合题意,故答案为1.【点睛】本题主要考查函数的奇偶性,属于中档题. 已知函数的奇偶性求参数,主要方法有两个,一是利用:(1)奇函数由恒成立求解,(2)偶函数由恒成立求解;二是利用特殊值:奇函数一般由求解,偶函数一般由求解,用特殊法求解参数后,一定要注意验证奇偶性.6.已知,函数和存在相同的极值点,则________.【分析】(1)求出函数的导数,可得极值点,通过与有相同的极值点,列方程求的值.【详解】,则,令,得或,可得在上递增;可得在递减,极大值点为,极小值点为,因为函数和存在相同的极值点,而在处有极大值,所以,所以,故答案为3.【点睛】本题主要考查利用导数判断函数的单调性以及函数的极值,属于中档题.求函数极值的步骤:(1) 确定函数的定义域;(2) 求导数;(3) 解方程求出函数定义域内的所有根;(4) 列表检查在的根左右两侧值的符号,如果左正右负(左增右减),那么在处取极大值,如果左负右正(左减右增),那么在处取极小值. (5)如果只有一个极值点,则在该处即是极值也是最值.7.已知函数.若,则实数的最小值为______.试题分析:由题意得,实数的最小值为考点:三角函数周期8.已知函数和函数的图像相交于三点,则的面积为__________.【解析】联立方程与可得,解之得,所以,因到轴的距离为,所以的面积为,应填答案。
天一联考高三数学试卷答案

一、选择题1. 答案:D解析:由题意可知,函数在区间[0,1]上单调递增,在区间[1,2]上单调递减,因此函数的最大值出现在x=1时,最大值为2。
2. 答案:A解析:由题意可知,a,b,c成等差数列,且abc=1,则b=1/3,a+c=2b=2/3,又因为a+c≥2√ac,代入ac=1/9得a+c≥2/3,所以a+c=2/3。
3. 答案:C解析:由题意可知,|x+1|≥2,所以x≥1或x≤-3。
又因为x+1≠0,所以x≠-1。
综合以上条件,解得x≥1。
4. 答案:B解析:由题意可知,函数f(x)在区间[-1,1]上单调递增,且f(0)=0,所以f(x)>0。
又因为g(x)=x^2-2x+1,所以g(x)在区间[-1,1]上单调递减,且g(0)=1,所以g(x)<1。
因此,f(x)g(x)>0。
5. 答案:A解析:由题意可知,等差数列{an}的前n项和为Sn,公差为d,首项为a1。
则Sn=n/2[2a1+(n-1)d],Sn+1=n/2[2a1+nd]。
两式相减得d=2,代入Sn+1得Sn+1=2n+1。
二、填空题6. 答案:-2解析:由题意可知,函数f(x)在x=1处取得极小值,因此f'(1)=0。
又因为f(x)=x^3-3x^2+2x,所以f'(x)=3x^2-6x+2。
代入x=1得f'(1)=0,解得x=1。
所以f(x)在x=1处取得极小值,即f(1)=-2。
7. 答案:3解析:由题意可知,圆的方程为x^2+y^2-4x-2y+5=0,圆心坐标为(2,1)。
点P到圆心的距离为√[(x-2)^2+(y-1)^2]。
要使点P在圆上,需满足距离等于圆的半径,即√[(x-2)^2+(y-1)^2]=√(4-5)=-1。
由于距离不能为负,所以不存在满足条件的点P。
8. 答案:1/2解析:由题意可知,数列{an}的前n项和为Sn,公差为d,首项为a1。
则Sn=n/2[2a1+(n-1)d],Sn+1=n/2[2a1+nd]。
江苏省天一中学2020届高三第一次模拟考试数学试答案

5)2 2
5
,…8 分
5
5
5
所以
cos C
cos(
(
A
B))
cos( A
)
2 (cos A sin A)
10
,
42
10
又因为 0 C ,所以 sin C
1 cos2 C
1(
10 )2
3
10
,
10
10
3 10 从而 tan C sin C 10 3 ,………………………………………………12 分
即
,解之得
,所以
③
,即
时,
即
,解之得
,所以
综上所述,当
函数 在区间
上单调递增.
(2)∵ 有两个极值点
,
∴
是方程
的两个根,且函数 在区间
和
上单调递增,在 ∵
上单调递减.
∴函数 也是在区间
和
上单调递增,在
∵
,∴ 是函数 的一个零点.
由题意知:
∵
,∴
,∴
∴
又
上单调递减 ,∴
∵
是方程
的两个根,
∴
,
,
∴
∵函数 图像连续,且在区间
所以 p 1 0 ,解得 p 2 2
故所求抛物线 C 的方程为 y 2 4x (2)由点 F 在线段 AB 上, 可设直线 l1 , l2 的方程分别为 y a 和 y b 且 a 0,b 0, a b .
则 A ( a2 ,a) ,B (b2 ,b) ,D (1,a) ,E (1,b)
S
的范围为
10 , 2
2 .
6 5
19.(1).a=-2,m=0………………………………………2 分
江苏省天一中学2018-2019高三11月月考 数学(含答案)

江苏省天一中学2018-2019高三第一次诊断性测试一、填空题:本大题共14小题,每小题5分,共70分.请把答案直接填写在答题卡相应.....位置上.... 1. 设集合{1,2,3,5},{2,3,6}A B ==,则AB = ▲ .2.命题:“ 0,x ∃>使得10x +>”的否定为 ▲3. 函数y =的定义域为 ▲ 4. 曲线sin y x x =-在2x π=处的切线的斜率为 ▲5. 若函数()22xxaf x =+是偶函数,则实数a 等于 ▲ . 6. 已知0a >,函数2()()f x x x a =-和2()(1)g x x a x a =-+-+存在相同的极值点,则a = ▲ .7. 已知函数f (x )=2sin(ωx +φ)(ω>0).若f (π3)=0,f (π2)=2,则实数ω的最小值为▲ .8.已知函数()sin ([0,])f x x x π=∈和函数1()tan 3g x x =的图像相交于,,A B C 三点,则ABC ∆的面积为 ▲ .9. 已知f (x )是定义在R 上的偶函数,且在区间(-∞,0)上单调递增.若实数a 满足1(2)(a f f ->,则a 的取值范围是__ ▲ ____10. 已知0πy x <<<,且tan tan 2x y =,1sin sin 3x y =,则x y -= ▲ .11. 在平行四边形ABCD 中,若3AC AD AC BD ⋅=⋅=,则线段AC 的长为▲ 12. 已知24παπ<<,24πβπ<<,且22sin sin sin()cos cos αβαβαβ=+,则t a n ()αβ+的最大值为 ▲ . 13.设0a ≠,e 是自然对数的底数,函数2,0,(),0xae x x f x x ax a x ⎧-≤⎪=⎨-+>⎪⎩有零点,且所有零点的和不大于6,则a 的取值范围为 ▲ .14. 设函数()()21f x x a x a x x a =---++(0a <).若存在[]011x ∈-,,使0()0f x ≤,则a 的取值范围是 ▲ .二、解答题:本大题共6小题,共90分.请在答题卡指定区域.......内作答. 解答时应写出文字说明、证明过程或演算步骤.15. (本小题满分14分)已知sin cos θθ+=,ππ44θ⎛⎫∈- ⎪⎝⎭,. (1)求θ的值;(2)设函数()22()sin sin f x x x θ=-+,x ∈R ,求函数()f x 的单调增区间.16. (本小题满分14分)如图,在ABC ∆中,已知7,45AC B =∠=o ,D 是边AB 上的一点,3,120AD ADC =∠=o . 求: (1)CD 的长; (2)ABC ∆的面积.ADCB17. (本小题满分14分)在平面直角坐标系xOy 中,已知向量=a (1,0),=b (0,2).设向量=+x a (1cos θ-)b ,k =-y a 1sin θ+b ,其中0πθ<<.(1)若4k =,π6θ=,求x ⋅y 的值;(2)若x //y ,求实数k 的最大值,并求取最大值时θ的值.18. (本小题满分16分)对于函数,若在定义域内存在实数x ,满足,则称为“局部奇函数”.(1)已知二次函数,试判断是否为“局部奇函数”?并说明理由; (2)若是定义在区间上的“局部奇函数”,求实数m 的取值范围; (3)若为定义域上的“局部奇函数”,求实数m 的取值范围()f x ()()f x f x -=-()f x 2()24()f x ax x a a =+-∈R ()f x ()2x f x m =+[]1,1-12()423x x f x m m +=-+-R19..如图,A 、B 是海岸线OM 、ON 上的两个码头,Q 为海中一小岛,在水上旅游线AB上.测得tan 3MON ∠=-,6km OA =,Q 到海岸线OM 、ON 的距离分别为2km.(1)求水上旅游线AB 的长;(2)海中P (6PQ km =,且)PQ OM ⊥处的某试验产生的强水波圆P ,生成t 小时时的半径为r =.若与此同时,一艘游轮以/小时的速度自码头A 开往码头B ,试研究强水波是否波及游轮的航行?20. 已知函数()()42ln f x x x =+,()245g x x x =+-.(1)求曲线()y f x =在点()()1,1f 处的切线方程;(2)证明:当1x ≠时,曲线()y f x =恒在曲线()y g x =的下方;(3)当(]0,x k ∈时,不等式()()()()2121k f x x g x +⋅≤+⋅恒成立,求实数k 的取值范围.(第19题图)M江苏省天一中学2018届数学阶段测试答案1、{1,2,3,5,6}2、0,10x x ∀>+≤3、(0,1]4、15、16、37、38 9、13(,)22 10、3π 11 12、-4 13、(,0)[4,6]-∞14、[2]-15. (本小题满分14分)解:(1)由sin cos θθ+,得2(sin cos )1θθ+=即22sin 2sin cos cos 1θθθθ++=,所以sin 2θ=.因为()ππθ∈-,,所以()ππ222θ∈-,,所以π23θ=-,即π6θ=-. (2)由(1)知,()22π()sin sin 6f x x x =--,所以()()11π()1cos21cos 2223f x x x ⎡⎤=----⎢⎥⎣⎦()1πcos 2cos2x x ⎡⎤=--⎢⎥⎣⎦112cos222x x ⎫=-⎪⎭()1πsin 226x =-.令πππ2π22π+262k x k --≤≤,得ππππ+63k x k -≤≤,所以函数()f x 的单调增区间是ππππ+k k ⎡⎤-⎢⎥⎣⎦,,Z k ∈.16.解:(1)在ACD ∆中,由余弦定理得2222cos AC AD CD AD CD ADC =+-⋅∠,2227323cos120CD CD =+-⨯⋅o ,解得5CD =.(2)在BCD ∆中,由正弦定理得sin sin BD CD BCD B =∠,5sin 75sin 45BD =o o,解得52BD +=,所以BDC BD CD ADC CD AD S S S BCD ACD ABC ∠⋅+∠⋅=+=∆∆∆sin 21sin 2111535sin120560222+=⨯⨯+⨯⨯o o 758+=17..解:(1)(方法1)当4k =,π6θ=时,(123=-,x ,=y (44-,), …… 2分则⋅=x y (1(4)244⨯-+-⨯=- …… 6分(方法2)依题意,0⋅=a b , 2分则⋅=x y (()(22142421⎡⎤+⋅-+=-+⨯⎢⎥⎣⎦a b a b a b(42144=-+⨯⨯=- . …… 6分 (2)依题意,()122cos θ=-,x ,()2k θ=-,y , 因为x //y ,所以2(22cos )sin k θθ=--,整理得,()1sin cos 1kθθ=-, … 9分令()()sin cos 1f θθθ=-,则()()cos cos 1sin (sin )f θθθθθ'=-+-22cos cos 1θθ=--()()2cos 1cos 1θθ=+-. …… 11分令()0f θ'=,得1cos θ=-或cos 1θ=,又0πθ<<,故2π3θ=.列表:故当2π3θ=时,m i n ()f θ=,此时实数k 取最大值…… 14分 (注:第(2)小问中,得到()122cos θ=-,x ,()2sin k θ=-,y ,及k 与θ的等式,各1分.)18.(本小题满分16分)解:为“局部奇函数”等价于关于x 的方程有解. (Ⅰ)当时,方程即有解, 所以为“局部奇函数”. …………… 3分(Ⅱ)当时,可化为,因为的定义域为,所以方程在上有解. (5)分令,则.设,则,当时,,故在上为减函数,当时,,故在上为增函数. (7)分所以时,. 所以,即. (9)分()f x ()()0f x f x +-=2()24()f x ax x a a =+-∈R ()()0f x f x +-=22(4)0a x -=2x =±()f x ()2x f x m =+()()0f x f x +-=2220x xm -++=()f x []1,1-2220x xm -++=[]1,1-12[,2]2xt =∈12m t t -=+1()g t t t =+22211()1t g t t t-'=-=(0,1)t ∈()0g t '<()g t (0,1)(1,)t ∈+∞()0g t '>()g t (1,)+∞1[,2]2t ∈5()[2,]2g t ∈52[2,]2m -∈5[,1]4m ∈--θ()2π0 3, 2π3()2π π3, ()f θ'-+fθ(Ⅲ)当时,可化为 .,则,从而在有解即可保证为“局部奇函数”. (11)分令,1° 当,在有解,由,即,解得; ………… 13分2° 当时,在有解等价于解得. (15)分(说明:也可转化为大根大于等于2求解)综上,所求实数m 的取值范围为. …………… 16分 19.解:(1)以点O 为坐标原点,直线OM 为x 轴,建立直角坐标系如图所示. 则由题设得:(6,0)A ,直线ON 的方程为3y x =-,00(,2)(0)Q x x >, ………2分,及00x >得04x =,(4,2)Q ∴ ………4分 ∴直线AQ 的方程为(6)y x =--,即60x y +-=, ………6分由3,60y x x y =-⎧⎨+-=⎩得3,9,x y =-⎧⎨=⎩即(3,9)B -,AB ∴=AB的长为. ………8分 (2)设试验产生的强水波圆P ,生成t 小时时,游轮在线段AB 上的点C 处,则AC =,102t ≤≤,(618,18)C t t ∴-, ………10分令22()h t r PC =-, 则(4,8)P,r =222()[(218)(188)]h t t t ∴=--+-3218(123620)68t t t =-+-,102t ≤≤, ………12分2()18(12336220)h t t t '∴=⨯-⨯+12()423x x f x m m +=-+-()()0f x f x +-=2442(22)260x x x x m m --+-++-=22[2,)x x t -=+∈+∞2442x x t -+=-222280t mt m -+-=[2,)+∞()f x 22()228F t t mt m =-+-(2)0F ≤222280t mt m -+-=[2,)+∞(2)0F ≤22440m m --≤11m ≤(2)0F >222280t mt m -+-=[2,)+∞2244(28)0,2,(2)0,m m m F ⎧∆=--⎪>⎨⎪>⎩≥1m≤1m ≤272(9185)t t =-+ 72(31)(35)t t =--,102t ≤≤, ………14分 由()0h t '=得1t =或5t =(舍去)∴3322max [()]()6()[(26)(68)]12033h t h ==⨯--+-=-<,102t ∴≤≤时,()0h t <,即r PC <恒成立,亦即强水波不会波及游轮的航行. ………16分20. 20. 解:(1)()24ln 4f x x x'=++,()16f '=, ………………………………………2分故切线方程是66y x =-. …………………………………………………………………3分 (4)分 (5)分 (6)分 (8)分 (9)分’ (10)分 (12)分 (13)分 (14)分 (15)分 (16)分。
2018-2019学年江苏省无锡市锡山区天一中学高三(上)11月月考数学试卷

2018-2019学年江苏省无锡市锡山区天一中学高三(上)11月月考数学试卷试题数:20.满分:1601.(填空题.5分)设集合A={1.2.3.5}.B={2.3.6}.则A∪B=___ . 2.(填空题.5分)命题:“∃x >0.使得x+1>0”的否定为___ 3.(填空题.5分)函数 y =√1−xx的定义域为___ . 4.(填空题.5分)曲线y=x-sinx 在 x =π2 处的切线的斜率为___ 5.(填空题.5分)若函数 f (x )=2x +m2x 为偶函数.则实数m=___ .6.(填空题.5分)已知a >0.函数f (x )=x (x-a )2和g (x )=-x 2+(a-1)x+a 存在相同的极值点.则a=___ .7.(填空题.5分)已知函数f (x )=2sin (ωx+φ)(ω>0).若 f (π3)=0,f (π2)=2 .则实数ω的最小值为___ .8.(填空题.5分)已知函数f (x )=sinx (x∈[0.π])和函数g (x )= 13 tanx 的图象相交于A.B.C 三点.则△ABC 的面积为___ .9.(填空题.5分)已知f (x )是定义在R 上的偶函数.且在区间(-∞.0)上单调递增.若实数a 满足f (2|a-1|)>f (- √2 ).则a 的取值范围是___ .10.(填空题.5分)已知0<y <x <π.且tanxtany=2. sinxsiny =13.则x-y=___ .11.(填空题.5分)在平行四边形ABCD 中. AC ⃗⃗⃗⃗⃗ •AD ⃗⃗⃗⃗⃗ =AC ⃗⃗⃗⃗⃗ •BD ⃗⃗⃗⃗⃗⃗ =3.则线段AC 的长为___ . 12.(填空题.5分)已知 π4 <α< π2 . π4 <β< π2 .且sin 2αsin 2β=sin (α+β)cosαcosβ.则tan (α+β)的最大值为___ .13.(填空题.5分)设a≠0.e 是自然对数的底数.函数f (x )= {ae x −x ,x ≤0x 2−ax +a ,x >0 有零点.且所有零点的和不大于6.则a 的取值范围为___ .14.(填空题.5分)设函数f (x )=(x-a )|x-a|-x|x|+2a+1(a <0.)若存在x 0∈[-1.1].使f (x 0)≤0.则a 的取值范围为___ .15.(问答题.14分)已知sinθ+cosθ= √3−12 .θ∈(- π4 . π4). (1)求θ的值:(2)设函数f (x )=sin 2x-sin 2(x+θ)x∈R .求函数f (x )的单调增区间.16.(问答题.14分)如图.在△ABC 中.已知AC=7.∠B=45°.D 是边AB 上的一点.AD=3.∠ADC=120°.求: (1)CD 的长; (2)△ABC 的面积.17.(问答题.14分)在平面直角坐标系xOy 中.已知向量 a =(1.0). b ⃗ =(0.2).设向量 x =a +(1-cosθ)b ⃗ . y =-k a + 1sinθ b⃗ .其中0<θ<π. (1)若k=4.θ= π6 .求 x • y 的值;(2)若 x || y .求实数k 的最大值.并求取最大值时θ的值.18.(问答题.16分)对于函数f (x ).若在定义域内存在实数x.满足f (-x )=-f (x ).则称f (x )为“局部奇函数”.(Ⅰ)已知二次函数f (x )=ax 2+2x-4a (a∈R ).试判断f (x )是否为“局部奇函数”?并说明理由;(Ⅱ)若f (x )=2x +m 是定义在区间[-1.1]上的“局部奇函数”.求实数m 的取值范围; (Ⅲ)若f (x )=4x -m•2x+1+m 2-3为定义域R 上的“局部奇函数”.求实数m 的取值范围.19.(问答题.16分)如图.A、B是海岸线OM、ON上的两个码头.Q为海中一小岛.在水上旅游km.线AB上.测得tan∠MON=-3.OA=6km.Q到海岸线OM、ON的距离分别为2km. 7√105(1)求水上旅游线AB的长;(2)海中P(PQ=6km.且PQ⊥OM)处的某试验产生强水波圆P.生成t小时的半径为r=6√6t32 km.若与此同时.一艘游轮以18 √2 km/小时的速度自码头A开往码头B.试研究强水波是否波及游轮的航行?20.(问答题.16分)已知函数f(x)=(4x+2)lnx.g(x)=x2+4x-5.(1)求曲线y=f(x)在点(1.f(1))处的切线方程;(2)证明:当x≠1时.曲线y=f(x)恒在曲线y=g(x)的下方;(3)当x∈(0.k]时.不等式(2k+1)•f(x)≤(2x+1)•g(x)恒成立.求实数k的取值范围.2018-2019学年江苏省无锡市锡山区天一中学高三(上)11月月考数学试卷参考答案与试题解析试题数:20.满分:1601.(填空题.5分)设集合A={1.2.3.5}.B={2.3.6}.则A∪B=___ . 【正确答案】:[1]{1.2.3.5.6}【解析】:直接利用集合的并集的定义求解即可.【解答】:解:集合A={1.2.3.5}.B={2.3.6}.则A∪B={1.2.3.5.6}. 故答案为:{1.2.3.5.6}.【点评】:本题考查集合的基本运算.并集定义的应用.是基础题. 2.(填空题.5分)命题:“∃x >0.使得x+1>0”的否定为___ 【正确答案】:[1]∀x >0.x+1≤0【解析】:根据含有量词的命题的否定定义即可得到结论【解答】:解:全称特称量词命题的否定:量词互换再否定结论. 故:“∃x >0.使得x+1>0”的否定为:∀x >0.x+1≤0 故答案为:∀x >0.x+1≤0【点评】:本题主要考查含有量词的命题的否定.比较基础. 3.(填空题.5分)函数 y =√1−xx的定义域为___ . 【正确答案】:[1](0.1]【解析】:直接由根式内部的代数式大于等于0.分式的分母不等于0.求解即可答案.【解答】:解:要使原函数有意义. 则 {1−x ≥0x >0.解得0<x≤1.∴函数y= √1−x√x的定义域为:(0.1].【点评】:本题考查了函数的定义域及其求法.考查了不等式的解法.是基础题.4.(填空题.5分)曲线y=x-sinx在x=π2处的切线的斜率为___【正确答案】:[1]1【解析】:根据题意.求出函数的导数.进而求出y′ |x=π2的值.由导数的几何意义分析可得答案.【解答】:解:根据题意.曲线y=x-sinx.其导数y′=1-cosx.则有y′ |x=π2 =1-cos π2=1.即曲线y=x-sinx在x=π2处的切线的斜率k=1;故答案为:1.【点评】:本题考查利用导数分析切线的斜率.关键是掌握导数的几何意义.属于基础题.5.(填空题.5分)若函数f(x)=2x+m2x为偶函数.则实数m=___ .【正确答案】:[1]1【解析】:直接根据偶函数的定义得到2−x+m2−x = 2x+m2x.即可得到所求的值.【解答】:解:由题意. 2−x+m2−x = 2x+m2x.∴m=1.故答案为1.【点评】:本题重点考查了偶函数的概念和基本性质.属于基础题.6.(填空题.5分)已知a>0.函数f(x)=x(x-a)2和g(x)=-x2+(a-1)x+a存在相同的极值点.则a=___ .【正确答案】:[1]3【解析】:由函数f(x)=x(x-a)2和g(x)=-x2+(a-1)x+a存在相同的极值点.则f′(x)=0.g′(x)=0.存在相同的根.求出根讨论即可得a的值.【解答】:解:∵f′(x)=3x2-4ax+a2=(x-a)(3x-a)=0.∴x=a.或x= a3.∵g′(x)=-2x+a-1=0.∴x= a−12.∵函数f(x)=x(x-a)2和g(x)=-x2+(a-1)x+a存在相同的极值点. ∴则f′(x)=0.g′(x)=0.存在相同的根.∴a= a−12或a3= a−12.∴a=-1或a=3.∵a>0.∴a=3.经检验当a=3时符合题意.故答案为:3.【点评】:本题考查函数极值点的含义.关键是转化为f′(x)=0.g′(x)=0存在相同的根.属于中档题.7.(填空题.5分)已知函数f(x)=2sin(ωx+φ)(ω>0).若f(π3)=0,f(π2)=2 .则实数ω的最小值为___ .【正确答案】:[1]3【解析】:直接利用f(π3)=0,f(π2)=2 .列出方程.然后求解ω的值.求出最小值.【解答】:解:函数f(x)=2sin(ωx+φ)(ω>0).若f(π3)=0,f(π2)=2 .所以2sin(ω× π3+φ)=0.2sin(ω× π2+φ)=2.ω× π3+φ=kπ.ω× π2+φ=2kπ +π2.所以π6ω=kπ +π2.所以实数ω的最小值为:3.故答案为:3.【点评】:本题考查三角函数解析式的求法.三角函数值的应用.考查分析问题解决问题的能力.8.(填空题.5分)已知函数f(x)=sinx(x∈[0.π])和函数g(x)= 13tanx的图象相交于A.B.C 三点.则△ABC的面积为___ .【正确答案】:[1] √23π【解析】:根据题意.令sinx= 13tanx.结合x∈[0.π]求出x的值.得出三个点A、B、C的坐标.即可计算△ABC的面积.【解答】:解:根据题意.令sinx= 13 tanx.即sinx(1- 13cosx)=0.解得sinx=0.或1- 13cosx=0.即sinx=0或cosx= 13.又x∈[0.π].∴x=0或x=π.或x=arccos 13 .∴点A(0.0).B(π.0).C(arccos 13. 2√23).∴△ABC的面积为12•|AB|•|y C|= 12•π•2√23= √23π.故答案为:√2π3.【点评】:本题考查了三角函数的图象与性质的应用问题.属于中档题.9.(填空题.5分)已知f(x)是定义在R上的偶函数.且在区间(-∞.0)上单调递增.若实数a 满足f(2|a-1|)>f(- √2).则a的取值范围是___ .【正确答案】:[1](12 . 32)【解析】:根据函数奇偶性和单调性之间的关系将不等式进行转化进行求解即可.【解答】:解:∵f(x)是定义在R上的偶函数.且在区间(-∞.0)上单调递增.∴f(x)在区间[0.+∞)上单调递减.则f(2|a-1|)>f(- √2).等价为f(2|a-1|)>f(√2).即- √2<2|a-1|<√2 .则|a-1|<12 .即12<a<32.故答案为:(12 . 32)【点评】:本题主要考查不等式的求解.根据函数奇偶性和单调性之间的关系将不等式进行转化是解决本题的关键.10.(填空题.5分)已知0<y<x<π.且tanxtany=2. sinxsiny=13.则x-y=___ .【正确答案】:[1] π3【解析】:由题意可得cosxcosy= 16 .进而可得cos(x-y)=cosxcosy+sinxsiny= 12.由余弦函数可知x-y的值.【解答】:解:由题意可得tanxtany= sinxsinycosxcosy=2.解得cosxcosy= 16 .故cos(x-y)=cosxcosy+sinxsiny= 16+13=12故x-y=2kπ± π3.k∈Z.又0<y <x <π.所以0<x-y <π. 所以x-y= π3 故答案为: π3【点评】:本题考查同角三角函数的基本关系.以及两角和与差的余弦函数.属基础题. 11.(填空题.5分)在平行四边形ABCD 中. AC ⃗⃗⃗⃗⃗ •AD ⃗⃗⃗⃗⃗ =AC ⃗⃗⃗⃗⃗ •BD ⃗⃗⃗⃗⃗⃗ =3.则线段AC 的长为___ . 【正确答案】:[1] √3【解析】:根据题意.易得 AC ⃗⃗⃗⃗⃗ •AB ⃗⃗⃗⃗⃗ =0 .建立直角坐标系.设D (x.y ).则C (0.y ).(-x.0).则 AC ⃗⃗⃗⃗⃗ •AD ⃗⃗⃗⃗⃗ =y 2=3.解出 |AC ⃗⃗⃗⃗⃗ | 即可.【解答】:解:根据题意.得 AC ⃗⃗⃗⃗⃗ •BD ⃗⃗⃗⃗⃗⃗ = AC ⃗⃗⃗⃗⃗ •(AD ⃗⃗⃗⃗⃗ −AB ⃗⃗⃗⃗⃗ ) = AC ⃗⃗⃗⃗⃗ •AD ⃗⃗⃗⃗⃗ −AC ⃗⃗⃗⃗⃗ •AB ⃗⃗⃗⃗⃗ . 又∵ AC ⃗⃗⃗⃗⃗ •AD ⃗⃗⃗⃗⃗ =AC ⃗⃗⃗⃗⃗ •BD ⃗⃗⃗⃗⃗⃗ ∴ AC⃗⃗⃗⃗⃗ •AB ⃗⃗⃗⃗⃗ =0 . 又四边形ABCD 为平行四边形.建立直角坐标系如右图. 设D (x.y ).则C (0.y ).B (-x.0). 则 AC ⃗⃗⃗⃗⃗ =(0.y ). AD ⃗⃗⃗⃗⃗ =(x.y ). 所以 AC ⃗⃗⃗⃗⃗ •AD ⃗⃗⃗⃗⃗ =y 2=3.从而线段AC 的长为 |AC ⃗⃗⃗⃗⃗ | = √y 2 = √3 . 故答案为: √3 .【点评】:本题考查向量数量积的坐标表示.建立直角坐标系是解决本题的关键.属中档题. 12.(填空题.5分)已知 π4 <α< π2 . π4 <β< π2 .且sin 2αsin 2β=sin (α+β)cosαcosβ.则tan (α+β)的最大值为___ . 【正确答案】:[1]-4【解析】:由已知可得.tanαtanβ= sinαsinβcosαcosβ = sin (α+β)sinαsinβ .然后结合和角正弦公式及同角基本关系化简可得tan (α+β)= tanα+tanβ1−tanαtanβ = (tanαtanβ)21−tanαtanβ .利用换元法.结合基本不等式可求.【解答】:解:∵ π4 <α< π2 . π4 <β< π2 .且sin 2αsin 2β=sin (α+β)cosαcosβ. ∴tanαtanβ= sinαsinβcosαcosβ = sin (α+β)sinαsinβ . =sinαcosβ+sinβcosαsinαsinβ . = tanα+tanβtanαtanβ .∴(tanαtanβ)2=tanα+tanβ.∵tan (α+β)= tanα+tanβ1−tanαtanβ = (tanαtanβ)21−tanαtanβ ① . 令t=tanαtanβ.则t >1. ① 可得. t 21−t =(1−t )2−2(1−t )+11−t .=1-t+ 11−t −2 . =-[(t-1)+1t−1]-2 ≤−2√(t −1)•1t−1−2 =-4.当且仅当t-1= 1t−1 即t=2时取等号.此时tanαtanβ=2. 则tan (α+β)的最大值-4. 故答案为:-4.【点评】:本题主要考查了三角函数.两角和与差的三角函数及利用基本不等式求解最值.属于中档试题.13.(填空题.5分)设a≠0.e 是自然对数的底数.函数f (x )= {ae x −x ,x ≤0x 2−ax +a ,x >0 有零点.且所有零点的和不大于6.则a 的取值范围为___ . 【正确答案】:[1](-∞.0)∪[4.6]【解析】:分a >0和a <0两种情况.结合函数的图象讨论可得.【解答】:解:当a >0时.x≤0时.f (x )=ae x -x >0恒成立.f (x )无零点;x >0时.f (x )=x 2-ax+a 必有零点.设为x 1.x 2.∴ {△=a 2−4a ≥0x 1+x 2=a ≤6.解得4≤a≤6;当a <0时.x≤0时.f (x )=ae x -x 的零点为负值.x >0时.f (x )=x 2-ax+a 的对称轴在y 轴左边.f (0)=a <0.f (1)=1-a+a=1>0.f (x )只有一个零点小于1.满足所有零点不大于6.综上a 的取值范围时(-∞.0)∪[4.6]. 故答案为:(-∞.0)∪[4.6].【点评】:本题考查了分段函数的应用.属中档题.14.(填空题.5分)设函数f (x )=(x-a )|x-a|-x|x|+2a+1(a <0.)若存在x 0∈[-1.1].使f (x 0)≤0.则a 的取值范围为___ . 【正确答案】:[1][-3.-2+ √2 ]【解析】:化简f (x )的解析式.判断f (x )的单调性.讨论f (x )的单调区间与区间[-1.1]的关系.求出f (x )在[-1.1]上的最小值.令最小值小于或等于零解出a .【解答】:解:∵存在x 0∈[-1.1].使f (x 0)≤0. ∴f min (x )≤0.x∈[-1.1].当x≤a 时.f (x )=(x-a )(a-x )+x 2+2a+1=2ax-a 2+2a+1. ∴f (x )在(-∞.a]上单调递减;当a <x <0时.f (x )=(x-a )2+x 2+2a+1=2x 2-2ax+a 2+2a+1. ∴f (x )在(a. a 2)上单调递减.在( a 2.0)上单调递增; 当x≥0时.f (x )=(x-a )2-x 2+2a+1=-2ax+a 2+2a+1. ∴f (x )在[0.+∞)上单调递增.(1)若 a2≤ -1.即a≤-2时.f (x )在[-1.1]上单调递增. ∴f min (x )=f (-1)=a 2+4a+3≤0. 解得-3≤a≤-1.∴-3≤a≤-2;(2)若 −1<a2<0 .即-2<a <0时.f (x )在[-1. a2 ]上单调递减.在( a2 .1]上单调递增. ∴f min (x )=f ( a2 )= a 22 +2a+1≤0. 解得-2- √2 ≤a≤-2+ √2 .∴-2<a≤-2+ √2 . 综上.a 的取值范围是[-3.-2+ √2 ]. 故答案为:[-3.-2+ √2 ].【点评】:本题考查了二次函数的单调性与最值.函数恒成立问题.分类讨论思想.属于中档题. 15.(问答题.14分)已知sinθ+cosθ= √3−12 .θ∈(- π4 . π4). (1)求θ的值:(2)设函数f (x )=sin 2x-sin 2(x+θ)x∈R .求函数f (x )的单调增区间.【正确答案】:【解析】:(1)由sinθ+cosθ= √3−12 .可得(sinθ+cosθ)2=sin 2θ+cos 2θ+2sinθcosθ= 2−√32.可得sin2θ= −√32.结合范围θ∈(- π4 . π4 ).即可解得θ=- π6 .(2)由(1)可得θ=- π6 .则f (x )=sin 2x-sin 2(x- π6 ).利用倍角公式.两角差的余弦函数公式以及辅助角公式化简可得f (x )= 12 sin (2x- π6 ).令2k π−π2 ≤2x - π6 ≤2kπ+ π2 .k∈Z .解得k π−π6 ≤x≤kπ+ π3.k∈Z .可得函数的单调增区间.【解答】:解:(1)因为sinθ+cosθ=√3−12. 所以(sinθ+cosθ)2=sin 2θ+cos 2θ+2sinθcosθ=1+sin2θ=( √3−12 )2= 2−√32. 即sin2θ= −√32. 又θ∈(- π4 . π4 ). 所以2 θ∈(−π2,π2) . 所以2θ=- π3 .θ=- π6 . (2)由(1)可得θ=- π6 . 则f (x )=sin 2x-sin 2(x- π6 ).所以f (x )= 12 (1-cos2x )- 12 [1-cos (2x- π3 )] = 12−12 cos2x- 12 + 12 cos (2x- π3 ) =- 12 cos2x+ 12 ( 12 cos2x+ √32 sin2x ) = √34 sin2x- 14 cos2x = 12( √32sin2x- 12cos2x ) = 12 sin (2x- π6 ).令2k π−π2≤2x - π6≤2kπ+ π2.k∈Z . 则k π−π6 ≤x≤kπ+ π3 .k∈Z .所以函数的单调增区间为[k π−π6 .kπ+ π3].k∈Z.【点评】:本题主要考查三角函数、倍角公式与半角公式以及两角和与差公式的综合应用.考查了正弦函数的性质.考查了计算能力和转化思想.属于中档题.16.(问答题.14分)如图.在△ABC中.已知AC=7.∠B=45°.D是边AB上的一点.AD=3.∠ADC=120°.求:(1)CD的长;(2)△ABC的面积.【正确答案】:【解析】:(1)在△ACD中.由余弦定理即可解得CD的值.(2)在△BCD中.由正弦定理得:BDsin∠BCD = CDsinB. BDsin75°= 5sin45°.解得BD的值.利用三角形的面积公式可求S△ABC=S△ACD+S△BCD的值.【解答】:解:(1)在△ACD中.由余弦定理得:AC2=AD2+CD2-2AD•CD•cos∠ADC. 可得:72=32+CD2-2×3×CD×cos120°.解得CD=5.(2)在△BCD中.由正弦定理得:BDsin∠BCD = CDsinB. BDsin75°= 5sin45°.解得:BD= 5+5√32.所以:S△ABC=S△ACD+S△BCD= 12AD•CD•sin∠ADC + 12CD•BD•sin∠BDC = 12×3×5×sin120°+12×5×5+5√32×sin60°= 75+55√38.【点评】:本题主要考查了正弦定理.余弦定理在解三角形中的应用.考查了计算能力和数形结合思想.属于基础题.17.(问答题.14分)在平面直角坐标系xOy中.已知向量a =(1.0). b⃗ =(0.2).设向量x =a +(1-cosθ)b⃗ . y =-k a + 1b⃗ .其中0<θ<π.sinθ.求x• y的值;(1)若k=4.θ= π6(2)若x || y .求实数k的最大值.并求取最大值时θ的值.【正确答案】:时.用坐标表示向量x、y .代入计算即可;【解析】:(1)当k=4. θ=π6=sinθ(cosθ−1) .令f(θ)=sinθ(cosθ-1).(2)用坐标表示出向量x、y .由x∥y .可得1k问题转化为求f(θ)的最小值.时. x =(1.2- √3). y =(-4.4).【解答】:解:(1)当k=4. θ=π6则x•y = 1×(−4)+(2−√3)×4 = 4−4√3.).(2)依题意. x =(1.2-2cosθ). y =(-k. 2sinθ=−k(2−2cosθ) .因为x∥y .所以2sinθ=sinθ(cosθ−1) .整理得. 1k令f(θ)=sinθ(cosθ-1).则f′(θ)=cosθ(cosθ-1)+sinθ(-sinθ)=2cos2θ-cosθ-1=(2cosθ+1)(cosθ-1).或cosθ=1.令f′(θ)=0.得cosθ=−12.又0<θ<π.故θ=2π3列表如下:当θ=3min √4.√9【点评】:本题考查向量的坐标运算.将问题转化为求三角函数的最小值是解题的关键.属中档题.18.(问答题.16分)对于函数f(x).若在定义域内存在实数x.满足f(-x)=-f(x).则称f(x)为“局部奇函数”.(Ⅰ)已知二次函数f(x)=ax2+2x-4a(a∈R).试判断f(x)是否为“局部奇函数”?并说明理由;(Ⅱ)若f(x)=2x+m是定义在区间[-1.1]上的“局部奇函数”.求实数m的取值范围;(Ⅲ)若f(x)=4x-m•2x+1+m2-3为定义域R上的“局部奇函数”.求实数m的取值范围.【正确答案】:【解析】:利用局部奇函数的定义.建立方程关系.然后判断方程是否有解即可.【解答】:解:f(x)为“局部奇函数”等价于关于x的方程f(-x)=-f(x)有解.(Ⅰ)当f(x)=ax2+2x-4a(a∈R).时.方程f(-x)=-f(x)即2a(x2-4)=0.有解x=±2.所以f(x)为“局部奇函数”.(Ⅱ)当f(x)=2x+m时.f(-x)=-f(x)可化为2x+2-x+2m=0.因为f(x)的定义域为[-1.1].所以方程2x+2-x+2m=0在[-1.1]上有解.令t=2x∈[12,2] .则−2m=t+1t.设g(t)=t+ 1t .则g'(t)=1- 1t2=t2−1t2.当t∈(0.1)时.g'(t)<0.故g(t)在(0.1)上为减函数.当t∈(1.+∞)时.g'(t)>0.故g(t)在(1.+∞)上为增函数.所以t∈[ 12,2 ]时.g(t)∈[2,52].所以 −2m ∈[2,52] .即 m ∈[−54,−1] .(Ⅲ)当f (x )=4x -m2x+1+m 2-3时.f (-x )=-f (x )可化为4x +4-x -2m (2x +2-x )+2m 2-6=0. t=2x +2-x ≥2.则4x +4-x =t 2-2.从而t 2-2mt+2m 2-8=0在[2.+∞)有解即可保证f (x )为“局部奇函数”. 令F (t )=t 2-2mt+2m 2-8.1° 当F (2)≤0.t 2-2mt+2m 2-8=0在[2.+∞)有解.由当F (2)≤0.即2m 2-4m-4≤0.解得1- √3≤m ≤1+√3 ; 2° 当F (2)>0时.t 2-2mt+2m 2-8=0在[2.+∞)有解等价于 {△=4m 2−4(2m 2−8)≥0m >2F (2)>0解得 1+√3≤m ≤2√2 . (说明:也可转化为大根大于等于2求解)综上.所求实数m 的取值范围为 1−√3≤m ≤2√2 .【点评】:本题主要考查新定义的应用.利用新定义.建立方程关系.然后利用函数性质进行求解是解决本题的关键.考查学生的运算能力.19.(问答题.16分)如图.A 、B 是海岸线OM 、ON 上的两个码头.Q 为海中一小岛.在水上旅游线AB 上.测得tan∠MON=-3.OA=6km.Q 到海岸线OM 、ON 的距离分别为2km. 7√105km . (1)求水上旅游线AB 的长;(2)海中P (PQ=6km.且PQ⊥OM )处的某试验产生强水波圆P .生成t 小时的半径为r=6 √6 t 32 km.若与此同时.一艘游轮以18 √2 km/小时的速度自码头A 开往码头B.试研究强水波是否波及游轮的航行?【正确答案】:【解析】:(1)利用△AOB 的面积列出等式求出OB.然后使用余弦定理求出AB ;(2)求出AP.∠PAQ .假设航行t 小时候到达D 点.使用余弦定理求出PD.比较PD 与r 的大小关系即可判断强水波是否波及航行.【解答】:解:(1)连结OQ.则S △OAQ = 12×OA × 2=6.S △OBQ = 12×OB × 7√105 = 7√1010OB . ∵tan∠MON=-3.∴sin∠MON=3√1010 .cos∠MON=- √1010. ∴S △AOB = 12×OA ×OB ×sin∠MON = 9√1010OB . ∴6+7√1010 OB= 9√1010OB .∴OB=3 √10 . ∴AB= √OA 2+OB 2−2OA •OBcos∠MON = √162 =9 √2 . (2)在△ABO 中.由正弦定理得OBsinA=AB sin∠MON .即3√10sinA=9√23√1010.∴sinA= √22. 延长PQ 交OA 于C.连结AP.则QC=2.AQ=2 √2 .cos∠AQP=-cos∠AQC=-sinA=-√22 .∴sin∠AQP= √22. ∴AP= √AQ 2+PQ 2−2AQ •PQcos∠AQP =2 √17 . ∵PQ sin∠PAQ=AP sin∠AQP .∴sin∠PAQ= 3√3434 .∴cos∠PAQ= 5√3434.假设t 小时候游轮航行到D 处.连结PD.则0≤t ≤12 .AD=18 √2 t. ∴PD= √AP 2+AD 2−2AP •ADcos∠PAQ = √648t 2−360t +68 . 令f (t )=PD 2-r 2=648t 2-360t+68-216t 3.则f′(t )=-648t 2-1296t-360. 令f′(t )=0解得t= 13 或t= 53 (舍).当 0≤t <13 时.f′(t )<0.当 13 <t ≤12 时.f′(t )>0. ∴f min (t )=f ( 13 )=12>0.∴PD 2-r 2>0.即PD >r 恒成立. ∴强水波不会波及游轮的航行.【点评】:本题考查了正弦定理.余弦定理在解三角形中的应用.函数值的大小比较.属于中档题.20.(问答题.16分)已知函数f(x)=(4x+2)lnx.g(x)=x2+4x-5.(1)求曲线y=f(x)在点(1.f(1))处的切线方程;(2)证明:当x≠1时.曲线y=f(x)恒在曲线y=g(x)的下方;(3)当x∈(0.k]时.不等式(2k+1)•f(x)≤(2x+1)•g(x)恒成立.求实数k的取值范围.【正确答案】:【解析】:(1)结合导数的几何意义可求切线斜率.进而可求切线方程.(2)要证当x≠1时.曲线y=f(x)恒在曲线y=g(x)的下方.即证f(x)<g(x)恒成立.构造函数.结合导数与单调性关系即可.(3)由题意可知不等式(2k+1)•f(x)≤(2x+1)•g(x)可转化为2(2k+1)lnx≤x2+4x-5.构造函数H (x)=2(2k+1)lnx-(x2+4x-5).转化为求解最值.【解答】:解:(1)f′(x)=4lnx+2x+4 .f'(1)=6.故切线方程是y=6x-6.(2)要证明当x≠1时.曲线y=f(x)恒在曲线y=g(x)的下方.即证f(x)<g(x).(x≠1).设F(x)=f(x)-g(x)=(4x+2)lnx-4x+5-x2.则F′(x)=4lnx+ 2x−2x令G(x)=4lnx+ 2x −2x .则G′(x)= −2(x−1)2x2≤0恒成立.∴F′(x)在(0.+∞)上单调递减且F′(1)=0.∴x∈(0.1)时.F′(x)>0.F(x)单调递增.当x∈(1.+∞)时.F′(x)<0.F(x)单调递减. 当x=1时.函数F(x)取得最大值F(1)=0.当x≠1时.F(x)<F(1)=0.∴曲线y=f(x)恒在曲线y=g(x)的下方.(3)由题意可知.k>0.2x+1>0.不等式(2k+1)•f(x)≤(2x+1)•g(x)可转化为2(2k+1)lnx≤x2+4x-5.令H (x)=2(2k+1)lnx-(x2+4x-5).∴H′(x)= 4k+2x −2x−4 = −2x2−4x+4k+2x.∵y=-2x2-4x+4k+2的对称轴x=-1.开口向下.且过定点(0.4k+2).与x轴交点的横坐标x1= −1−√2k+2(舍).x2= −1+√2k+2 .① 当x2= −1+√2k+2<k即k<-1(舍)或k>1时.此时当x∈(0.x2)时.H′(x)>0.H(x)单调递增.当x∈(x2.k)时.H′(x)<0.H(x)单调递减.函数取得最大值.记为H1(x)max=H1(x2)=2(2k+1)lnx2- x22 -4x2+5.由x2= −1+√2k+2 .可得2k+1= x22+2x2 .∴H1(x2)=2(x22+2x2)lnx2- x22 -4x2+5≤0.而H1′(x2)=4(1+x2)lnx2.x2∈(0.1)时.H1′(x2)<0.H1(x2)单调递减.当x2∈(1.+∞)时.H1′(x2)>0.H1(x2)单调递增.故H(x)在(0.k]取得最大值.记为H2(k)=2(2k+1)lnk-k2-4k+5所以H1(x2)在x2=1处取得最小值0所以只有x2=1符合题意.此时解得k=1不符合题意.舍去② 当x2=k时.解得k=1.当x∈(0.1)时.H′(x)>0.H(x)单调递增.在(0.1]取得最大值H(1)=0.即H(x)≤0恒成立.原不等式成立.③ 当x2>k时.解可得0<k<1当x∈(0.k)时.H′(x)>0.H(x)单调递增.H(x)在(0.k]取得最大值.记为H2(k)=2(2k+1)lnk-k2-4k+5由(2)可证H2(k)与F(x)的图象相同.所以当0<k<1时.H2(k)<H2(1)=0.原不等式成立实数k的取值范围(0.1].【点评】:本题主要考查了导数几何意义的应用及利用导数与单调性关系证明不等式.求解函数最值.体现了分类讨论与转化思想的应用.。
试题 江苏省无锡市天一中学2018--2019学年高三11月月考 数学试题 Word版含解析

2018-2019学年江苏省无锡市天一中学高三11月月考 数学试题数学注意事项:1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题的作答:每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4.考试结束后,请将本试题卷和答题卡一并上交。
一、填空题1.设集合A ={1,2,3,5},B ={2,3,6},则A ∪B =_______. 2.命题:“ ∃x >0,使得x +1>0”的否定为__________. 3.函数y =√1−x x的定义域为_________.4.曲线y =x −sinx 在x =π2处的切线的斜率为_________. 5.若函数f (x )=2x +a2x 是偶函数,则实数a =______.6.已知a >0,函数f (x )=x (x −a )2和g (x )=−x 2+(a −)1x +a 存在相同的极值点,则a =________.7.已知函数f (x )=2sin (ωx +φ)(ω>0).若f (π3)=0,f (π2)=2,则实数ω的最小值为______. 8.已知函数f (x )=sinx (x ∈[0,π])与函数g (x )=13tanx 的图象交于A,B,C 三点,则ΔABC 的面积为________.9.已知f (x )是定义在R 上的偶函数,且在区间(−∞,0)上单调递增.若实数a 满足f (2|a-1|)>f (−√2),则a 的取值范围是______.10.已知0y x π<<<,且tan tan 2x y =, 1sin sin 3x y =,则x y -=______.11.在平行四边形ABCD 中,AC AD AC BD ⋅=⋅3=,则线段AC 的长为 .12.已知π4<α<π2,π4<β<π2,且sin 2αsin 2β=sin (α+β)cosαcosβ,则tan (α+β)的最大值为______.13.设a ≠0,e 是自然对数的底数,函数f(x)={ae x −x,x ≤0x 2−ax +a,x >0有零点,且所有零点的和不大于6,则a 的取值范围为______.14.设函数f(x)=(x −a)|x −a |−x |x |+2a +1(a <0).若存在x 0∈[−1 , 1],使f(x 0)≤0, 则a 的取值范围是____.二、解答题15.已知sinθ+cosθ=√3−12,θ∈(−π4 , π4).(1)求θ的值;(2)设函数f(x)=sin 2x −sin 2(x +θ),x ∈R ,求函数f(x)的单调增区间.16.如图,在△ABC 中,已知AC =7,∠B =45∘,D 是边AB 上的一点,AD =3,∠ADC =120∘,求:(1)CD 的长; (2)△ABC 的面积.17.在平面直角坐标系xOy 中,已知向量a ⃑=(1,0),b ⃑⃑=(0,2),设向量x =a ⃑+(1−cosθ)b ⃑⃑,y =−ka ⃑+1sinθb⃑⃑,其中0<θ<π. (1)若k =4,θ=π6,求x ⋅y 的值;(2)若x//y ,求实数k 的最大值,并求取最大值时θ的值.18.对于函数f(x),若在定义域内存在实数x ,满足f(−x)=−f(x),则称f(x)为“局部奇函数”. (Ⅰ)已知二次函数f(x)=ax 2+2x −4a(a ∈R),试判断f(x)是否为“局部奇函数”?并说明理由;(Ⅱ)若f(x)=2x +m 是定义在区间[−1,1]上的“局部奇函数”,求实数m 的取值范围; (Ⅲ)若f(x)=4x −m2x+1+m 2−3为定义域R 上的“局部奇函数”,求实数m 的取值范围. 19.如图,A 、B 是海岸线OM 、ON 上的两个码头,Q 为海中一小岛,在水上旅游线AB 上.测得tan∠MON =−3,OA =6km ,Q 到海岸线OM 、ON 的距离分别为2km ,7√105km . 此卷只装订不密封班级 姓名 准考证号 考场号 座位号(1)求水上旅游线AB的长;(2)海中P(PQ=6km,且PQ⊥OM)处的某试验产生的强水波圆P,生成t小时时的半径为r= 6√6t32km.若与此同时,一艘游轮以18√2km/小时的速度自码头A开往码头B,试研究强水波是否波及游轮的航行?20.已知函数f(x)=(4x+2)lnx,g(x)=x2+4x−5.(1)求曲线y=f(x)在点(1,f(1))处的切线方程;(2)证明:当x≠1时,曲线y=f(x)恒在曲线y=g(x)的下方;(3)当x∈(0,k]时,不等式(2k+1)⋅f(x)≤(2x+1)⋅g(x)恒成立,求实数k的取值范围.2018-2019学年江苏省无锡市天一中学高三11月月考数学试题数学答案参考答案1.{1,2,3,5,6}【解析】【分析】直接利用集合并集的定义求解即可.【详解】因为集合A={1,2,3,5},B={2,3,6},所以A∪B={1,2,3,5,6},故答案为{1,2,3,5,6}.【点睛】研究集合问题,一定要抓住元素,看元素应满足的属性.研究两集合的关系时,关键是将两集合的关系转化为元素间的关系,本题实质求满足属于集合A或属于集合B的元素的集合.2.∀x>0,x+1≤0【解析】【分析】根据特称命题的否定是全称命题,既要改写量词,又要否定结论,可得原命题的否定形式.【详解】因为特称命题的否定是全称命题,既要改写量词,又要否定结论,故命题“ ∃x>0,x+1>0”的否定是∀x>0,x+1≤0,故答案为∀x>0,x+1≤0.【点睛】本题主要考查特称命题的否定,属于简单题.全称命题与特称命题的否定与命题的否定有一定的区别,否定全称命题和特称命题时,一是要改写量词,全称量词改写为存在量词、存在量词改写为全称量词;二是要否定结论,而一般命题的否定只需直接否定结论即可.3.(0,1]【解析】【分析】直接由根式内部的代数式大于等于0 ,分式的分母不等于0 ,列不等式求解即可得结果.【详解】要使函数y=√1−xx有意义,则{1−xx≥0x≠0⇒{(1−x)x≥0x≠0解得0<x≤1,∴函数y=√1−xx的定义域为(0,1],故答案为(0,1].【点睛】本题主要考查具体函数的定义域、不等式的解法,属于中档题.定义域的三种类型及求法:(1)已知函数的解析式,则构造使解析式有意义的不等式(组)求解;(2) 对实际问题:由实际意义及使解析式有意义构成的不等式(组)求解;(3) 若已知函数f(x)的定义域为[a,b],则函数f(g(x))的定义域由不等式a≤g(x)≤b求出.4.1【解析】【分析】求出原函数的导函数,可得到曲线y=x−sinx在x=π2处的导数值,根据导数的几何意义可得结果.【详解】因为曲线y=x−sinx在x=π2处的切线的斜率就是曲线y=x−sinx在x=π2处的导数值,由y=x−sinx得y′=1−cosx,∴y′|x=π2=1−cosπ2=1,即曲线y=x−sinx在x=π2处的切线的斜率为1,故答案为1.【点睛】本题考查了利角导数研究曲线上某点处的切线斜率,曲线在某点处的导数值,即为曲线上以该点为切点的切线的斜率,是中档题.5.1【解析】【分析】由函数f(x)=2x+a2x是偶函数,利用f(−1)=f(1)求得a=1,再验证即可得结果.【详解】∵f(x)=2x+a2x是偶函数,∴f (−1)=f (1),即2+a 2=12+2a ,解得a =1, 当a =1时,f (−x )=2−x+12−x=2x+12x是偶函数,合题意,故答案为1.【点睛】本题主要考查函数的奇偶性,属于中档题. 已知函数的奇偶性求参数,主要方法有两个,一是利用:(1)奇函数由f (x )+f (−x )=0 恒成立求解,(2)偶函数由 f (x )−f (−x )=0 恒成立求解;二是利用特殊值:奇函数一般由f (0)=0 求解,偶函数一般由f (1)−f (−1)=0求解,用特殊法求解参数后,一定要注意验证奇偶性.6.3 【解析】 【分析】(1)求出函数y =f (x )的导数,可得极值点,通过与y =g (x )【详解】f (x )=x (x −a )2=x 3−2ax 2+a 2x , 则f′(x )=3x 2−4ax +a 2=(3x −a )(x −a ), 令f′(x )=0,得x =a 或a 3, 可得f (x )在(−∞,a3),(a,+∞)上递增;可得f (x )在(a3,a)递减,极大值点为a3,极小值点为a ,因为函数f (x )=x (x −a )2和g (x )=−x 2+(a −)1x +a 而g (x )在x =a−12处有极大值,所以a−12=a 3,所以 a =3,故答案为 3.【点睛】(1)确定函数的定义域;(2) 求导数f ′(x );(3) 解方程f ′(x )=0,求出函数定义域内的所有根;(4) 列表检查f ′(x )在f ′(x )=0的根x 0左右两侧值的符号,如果左正右负(左增右减),那么f (x )在x 0处取极大值,如果左负右正(左减右增),那么f (x )在x 0处取极小值. (5)如果只有一个极值点,则在该处即是极值也是最值.7.3 【解析】试题分析:由题意得T4≤π2−π3⇒T ≤2π3⇒ω=2πT≥3,实数ω的最小值为3考点:三角函数周期 8.√2π3【解析】联立方程f(x)=sinx 与g(x)=13tanx 可得13tanx =sinx ,解之得x =0,π,cosx =13⇒sinx =2√23,所以A(0,0),B(π,0),C(x,sinx),因AB =π,C(x,sinx)到x 轴的距离为sinx =2√23,所以ΔABC 的面积为S =12×π×2√23=√2π3,应填答案√2π3。
2020年江苏省无锡市锡山区天一中学高考数学第一次模拟测试试卷(解析版)

2021年高考数学第一次模拟试卷一、填空题(共14个小题)1,集合A={x|0vxv2}, B= {x| -1 vxv 1},那么A n B =.… 2i , .......... ........ .. ..2 .复数z=m- (i为虚数单位)的虚部为_______________ .1+13 .函数仪由寸1口言/-2的定义域为.4 .在编号为1, 2, 3, 4, 5且大小和形状均相同的五张卡片中,一次随机抽取其中的两张, 那么抽取的两张卡片编号之和是偶数的概率为 .2 2I ।匚直y 55.在平面直角坐标系xOy中,假设双曲线—z ---------- -- 1 (a>0, b> 0)的离心率为;那么该双1 b q曲线的渐近线方程为.6 .某种圆柱形的如罐的容积为128兀个立方单位,当它的底面半径和高的比值为时,可使得所用材料最省.27 .在平面直角坐标系xOy中,双曲线上-了的右准线与渐近线的交点在抛物线y2=2px上,那么实数p的值为.8 .a是第二象限角,且出inCL三", tan (o+3) = -2,那么tan 3= ____________________ .59 .等差数列{an}的前n项和为Sn,假设S3=6, S6= - 8,那么S9=.10.在平面直角坐标系xOy中,直线l:与函数f (x) = sin ( wx+的图象在y轴右侧的公共点从左到右依次为A I, A2…,假设点A1的横坐标为1 ,那么点A2的横坐标为.11 .设P为有公共焦点F1, F2的椭圆C I与双曲线C2的一个交点,且PF11PF2,椭圆C I 的离心率为双曲线C2的离心率为e2,假设e2=3e〔,那么e[ =.12 .如图,在^ ABC 中,AB=AC=2, AT)= DC, DE=2E§, AE 的延长线交BC 边于点F, 假设陆二千,那么AE・AC=.□CA D13 .函数f (x)是定义在R 上的奇函数,其图象关于直线 x=1对称,当xC (0, 1]时, f(x) = -e ax (其中e 是自然对数的底数),假设f(2021-ln2) =8,那么实数a 的值为.工x<2X14 .函数六公乂 S(其中e 为自然对数的底数),假设关于 x 的方程f 2 (x)-3a|f (x) |+2a 2=0恰有5个相异的实根,那么实数 a 的取值范围为 . 二、解做题15.如图,在斜三棱柱 ABC-A i B i C i 中,△ ABC 为正三角形,D, E 分别是 AC, CC i 的中点,平面 AA 1C 1C ,平面ABC, A 1EXAC 1.(1)求证:DE //平面 AB 1C 1; (2)求证:A 1E,平面BDE .(1)假设 a=5, c=2<5,求 b 的值;17.截至1月30日12时,湖北省累计接收揭赠物资 615.43万件,包括医用防护服 2.6万套,N95 口罩47.9万个,医用一次性口罩 172.87万个,护目镜 3.93万个等.某运输队 接到给武汉运送物资的任务,该运输队有8辆载重为6t 的A 型卡车,6辆载重为10t 的B 型卡车,10名驾驶员,要求此运输队每天至少运送720t 物资.每辆卡车每天往返的次数:A 型卡车16次,B 型卡车12次;每辆卡车每天往返的本钱:A 型卡车240元,B 型卡车378元.求每天派出 A 型卡车与B 型卡车各多少辆,运输队所花的本钱最低?且两焦点与短轴的一个顶点构成等腰直角三角形.16.在^ ABC 中,角A, B, C 的对边分别为a, b,-口」西C,且 I l318.在平面直角坐标系 xOy 中,椭圆C :22力lCa>b>0的右准线方程为 a bx= 2,求tan2 C 的值.(1)求椭圆C的方程;(2)假设直线l: y=kx+m与椭圆C交于A, B两点.①假设A为椭圆的上顶点,M为线段AB中点,连接OM并延长交椭圆C于N,并且而考L而,求OB的长;②假设原点O到直线l的距离为1 ,并且演后二卜,当言< 九"时,求^ OAB的面积S的范围.□019 .设函数f (x) = 2x2+alnx , (aCR)(I)假设曲线y=f (x)在点(1, f (1))处的切线方程为y=2x+m,求实数a, m的值(n)假设f (2x- 1) +2>2f (x)对任意x€[2, +8)恒成立,求实数a的取值范围;(m)关于x的方程f (x) +2cosx=5能否有三个不同的实根?证实你的结论20 .f (x) =x3+ax,bx, a, b CR.(1)假设b=1,且函数f (x)在区间(-1,二)上单调递增,求实数a的范围;(2)假设函数f (x)有两个极值点x1,x2, x1<x2,且存在x o满足x1+2x o = 3x2,令函数g(X) =f (x) - f(X.),试判断g (x)零点的个数并证实你的结论.[选做题]此题包括A、B、C三小题,请选定其中两题.[选彳4-2:矩阵与变换]121.矩阵M= 的一个特征值为4,求矩阵M的逆矩阵M 1.-t41 )■ ■[选彳4-4:坐标系与参数方程]22 .在平面直角坐标系xOy中,直线l的参数方程为后(t为参数),在以[12坐标原点.为极点,x轴的非负半轴为极轴,且与直角坐标系长度单位相同的极坐标系中,曲线C的极坐标方程是P二孰用5五式丁+ 3 ) .(1)求直线I的普通方程与曲线C的直角坐标方程;(2)假设直线I与曲线C相交于两点A, B,求线段AB的长.[选彳4-5:不等式选讲」23 .x1, x2, x3C (0, +oo),且满足x1+x2+x3= 3x1x2x3,证实:x1x2+x2x3+x3x1 > 3.[必做题]第22题、第23题,每题10分,共计20分.24 .如图,在平面直角坐标系xOy中,抛物线:C: y2 = 2px (p>0)的焦点F在直线x+y-1 = 0上,平行于x轴的两条直线11, 12分别交抛物线线C于A, B两点,交该抛物线的准线于D, E两点.(1)求抛物线C的方程;(2)假设F在线段AB上,P是DE的中点,证实:AP // EF .25 .在开展学习强国的活动中,某校高三数学教师成立了党员和非党员两个学习组,其中党员学习组有4名男教师、1名女教师,非党员学习组有2名男教师、2名女教师,高三数学组方案从两个学习组中随机各选2名教师参加学校的挑战做题比赛.(1)求选出的4名选手中恰好有一名女教师的选派方法数;(2)记X为选出的4名选手中女教师的人数,求X的概率分布和数学期望.、填空题1,集合 A={x|0vxv2}, B={x| 一1 vxv 1},那么 AnB= {x|0vx<1}解:••・ A={x|0vxv2}, B = {x|- 1<x<1}, An B = {x|0<x< 1}. 故答案为:{x|0<x<1}.2 .复数z=-j ,(i 为虚数单位)的虚部为1 .故答案为:1.3 .函数£—)=={1口总252的定义域为 [4, +8)..解:函数f (x) =,10目〞-2有意义, 只需 log2x - 2>0,且 x>0, 解得x>4.那么定义域为[4, +8). 故答案为:[4, +8).4 .在编号为1, 2, 3, 4, 5且大小和形状均相同的五张卡片中,一次随机抽取其中的两张,|2那么抽取的两张卡片编号之和是偶数的概率为 -T .-5 - 解:在编号为1,2, 3, 4, 5且大小和形状均相同的五张卡片中, 一次随机抽取其中的两张, 根本领件总数为n = C^ = 10,抽取的两张卡片编号之和是偶数包含的根本领件个数: n 2士 , m = Uj2=4,,一,……一…,…,… I 4 2那么抽取的两张卡片编号之和是偶数的概率为 p=T7--. 1U □故答案为:告.J 255 .在平面直角坐标系 xOy 中,假设双曲线■^-'=1 (a>0, b>.)的离心率为那么该双解:z=2id-n1+i Cl+i) Ci _i)=i+1的虚部为1.三;7-工^"= [ (a >0, b >0)的离心率为 与,可得一产4所以渐近线方程为 y=±4x- 4故答案为:y= 土二x.46 .某种圆柱形的如罐的容积为 128兀个立方单位,当它的底面半径和高的比值为 二■—时,可使得所用材料最省. 解:如下图,设圆柱的高为h ,底面半径为r. 由题意,128兀=兀「2? h,•.S=2/+2兀r?卜=2兀1与2兀/罩=2兀工'^^=2日卫生 3U 也冗/■江.且44冗声. rry r r当且仅当2兀r W'n ,即当r = 4时取等号.r….12^ .此时h =2 =8.r_ _ __ ___ _ ______ 4 1,它的底面半径和图的比值为 一=—.o Z故答案为:方.7 .在平面直角坐标系 xOy 中,双曲线今--了2=1的右准线与渐近线的交点在抛物线y 2=2px上,那么实数p 的值为_^一解:双曲线亭-了2, L 的右准线x=—,渐近线y= 土.x,曲线的渐近线方程为 一了一土彳 X —解:由于双曲线所以总a.c 3• tan 3= —7.4故答案为:一*的横坐标为 3左到右依次为 A i, A2…,所以«+-7T交点在抛物线y 2=2px 上, 可得:二=3p,4解得P=彳.4故答案为:8.“是第二象限角,且si n CL =解:: a 是第二象限角,且 sin a= , tan (0+3) = - 2,贝U tan 3=5V5tan ( a+ 3)=亭向61-(—tan P=—2;9.等差数列{a n }的前n 项和为S n,假设 S 3=6, S 6= - 8,贝U S 9= - 42 解:由题意可得:2X (-8-6) =6+S9- ( - 8),解得S 9 = - 42.故答案为:-42.10.在平面直角坐标系 xOy 中,直线l: y=3■与函数f,、・,兀、,- (x) = sin ( wx+7-) ( co>0) b的图象在y 轴右侧的公共点从左到右依次为A i, A 2…,假设点A i 的横坐标为1 .那么点A 2解:由于点A i 的横坐标为1,即当x=1时,7Tf (x) = sin ( 3+ 6 ) 所以co7T ~6=2k TT + 兀~6 (kCZ),又直线l : y =(3>0)的图象在y 轴右侧的公共点从双曲线2=[的右准线与渐近线的交点(,tan a=• •.COSa= -/ 口 =-2炳5(x) = sin (故答案为:3.的离心率为e i,双曲线 C 2的离心率为e 2,假设e 2=3e i,那么ei = _r^-—.O解:如图,由椭圆定义及勾股定理得,. e i =同理可得S 迪PF,% = b22, e2 =• •c 2 (2 - i )= c 2 ( i -2),e l e2- e2= 3ei,所以:函数的关系式为 f (x) = sin ( 当 X2=3 时,f (3)=sin (即点A 2的横坐标为 3, 空~32JT 兀(3, 4-)为二函数的图象的第二个公共点.故答案为:11 .设P 为有公共焦点F i, F 2的椭圆C i 与双曲线 C 2的一个交点,且 PFi±PF 2,椭圆C ice2b 22=c 2 — a 22 = c 2 (1 —2)GZb 12= a 12 —c 2 = c 2 ,a i =即e l e212.如图,在^ ABC 中,AB=AC=2, AT )= DC, DE =2EB , AE 的延长线交 BC 边于点 F, • .FE = BF =AD=DC,DG =^AF ; FG =GC ; 擀AF ; BF =-^-BC ; o5 i 二 *4 ••・内・[] — — □=(IS +-BC) ? BC=-[商+卷(AC-AB) ]? (AB-AC) =-(+够+:族)? (AB ,-AC)=-[^2 -1'屈-AC--5 AC 21那么冠•囊=涓?标联立①②可得EF =AF; AE = 力-翁?^-*22]= -^x -X 6 5229 '作出函数f (x)的图象如图:13.函数f (x)是定义在R 上的奇函数,其图象关于直线 x=1对称,当xC (0, 1]时, f(x)=- e ax (其中e 是自然对数的底数),假设f (2021—ln2) =8,贝U 实数a 的值为 3 解:根据题意,f (x)的图象关于x=1对称,所以f (1 + x) = f (1- x) 又由f (x)是R 上的奇函数,所以 f (x+1) = - f (x-1),那么有f (x+2) = - f (x), f (x+4) = - f (x+2) = f (x). 那么f (x)是周期为4的函数, 故 f (2021— ln2) = f ( — ln2) = - f (In 2) = 一 (— e x . 1n2) = 8, 变形可得:2x= 8,解可得x=3; 故答案为:3 14.函数 驾K2X e 笔生,x>2 5x(其中e 为自然对数的底数),假设关于 x 的方程f 2 (x) -3a|f (x) |+2a2=0恰有5个相异的实根,那么实数a 的取值范围为 45 _ , 一,人, e .解:当x< 2时,令f' (x) =--1 = 0,解得ex= 1, 所以当x< 1时,f' (x) >0,那么f (x)单调递增,当 1WxW2时,,(x) <0,那么f (x)单调递减, 当 x>2 时,f (x)= f (x)q .,*— 5x(46 5 ABCX 22)IM(1)当a=0时,方程整理得f2 (x) =0,只有2个根,不满足条件;(2)假设a>0,那么当f (x) <0 时,方程整理得f2(x) +3af (x) +2a2=[f (x) +2a][f (x)+a]= 0,那么 f (x) = - 2a< 0, f (x) = - av 0,此时各有 1 解,故当 f (x) >0 时,方程整理得f2 (x) - 3af (x) +2a2= [f (x) - 2a][f (x) - a]=0,—,,、 1 …一四2f (x) = 2a有1 解同时f (x) = a 有2 解,即需2a= 1, a=~ ,由于f (2) = o =— >2 日口言,故此时满足题意;或f (x) = 2a有2解同时f (x) = 2有1解,那么需a= 0,由(1)可知不成立;或f (x) = 2a有3解同时f (x) = 2有0解,根据图象不存在此种情况,f2a>l或f (x) = 2a有0解同时f (x) = 2有3解,那么{2x 〞4 ,解得一龟—三^2\6 JI良5故 a qy")(3)假设a<0,显然当f (x) > 0 时,f (x) = 2a 和f (x) = a 均无解,当f (x) v 0时,f (x) =- 2a和f (x) =- a无解,不符合题意.综上:a的范围是{^^U I^-,言)故答案为&U看,看)、解做题:共6小题,共90分,请在做题卡指定区域内作答,解答时应写出文字说明、证实过程或演算步骤.15 .如图,在斜三棱柱ABC-A1B1C1中,△ ABC为正三角形,D, E分别是AC, CC1的中点,平面AA1C1C,平面ABC, A1EXAC1.(1)求证:DE //平面AB1C1;解:(1)证实:D, E分别是AC, CC i的中点,.. DE // AC i, DE?平面AB i C i,.. AC i?平面AB i C i,故DE //平面AB i C i;(2)证实:△ ABC为正三角形,所以BD XAC,由于平面AA i C i C,平面ABC ,平面AA i C i CA平面ABC = AC,故BDL平面AA i C i C, A i E?平面AA i C i C,所以BDXA i E,又A i EXAC i, DE // AC i,所以A i EXDE,又BD A DE = D ,所以A i EL平面BDE .16 .在^ ABC中,角A, B, C的对边分别为a, b, c, HcasA^(i)假设a=5, c=2V5,求b 的值;兀I q -(2)假设求tan2c 的值.解:(i)在^ ABC 中,由余弦定理b2+c2- 2bccosA=a2, 得b*+20-2K2^X 假设即b2-4b - 5= 0,解得b= 5或b = - i (舍),所以b= 5.(2)求证:A i E,平面BDE .(2)由eosA二■及OvAv所以cosC=cos (冗4 (MB))三又由于0V Cv兀,所以口Y 3 J 1匹、.也/A.A、®10cr“ 2tanC3| 所以 tm2C= ------- 丁= ------ 7=^T .1-tan^C 1-3J417 .截至1月30日12时,湖北省累计接收揭赠物资 615.43万件,包括医用防护服 2.6万套,N95 口罩47.9万个,医用一次性口罩 172.87万个,护目镜 3.93万个等.某运输队 接到给武汉运送物资的任务,该运输队有8辆载重为6t 的A 型卡车,6辆载重为10t 的B 型卡车,10名驾驶员,要求此运输队每天至少运送720t 物资.每辆卡车每天往返的次数:A 型卡车16次,B 型卡车12次;每辆卡车每天往返的本钱:A 型卡车240元,B 型卡车378元.求每天派出 A 型卡车与B 型卡车各多少辆,运输队所花的本钱最低? 解:设每天派出 A 型卡车x 辆,B 型卡车y 辆,运输队所花本钱为 z 元,r o<x<8 I10为 x 16K+12X 10X >72CrO<5f<8内.xE N目标函数z= 240x+378y,画出满足条件的可行域如图中阴影局部所示: 由图可知,当直线 z=240x+378y 经过点A 时,截距z 最小,一一「急+5 产 3. 口-15 解方程组 〜,得点A 的坐标为〔上〕,0〕,[y=02「 〜 - 一■ 15 .………又「xa, yCN, •••点A 〔―, 0〕不是最优解,•・•在可行域的整数点中,点〔8, 0〕使Z 取得最小值, 即 Z min = 240X 8+378X 0= 1920,・•・每天排除A 型卡车8辆,B 型卡车0辆,运输队所花的本钱最低,从而3 A「一」匚 二 一.,且 xCN, yCN,化简得:最低本钱为1920元,答:每天派出A 型卡车8辆,B 型卡车0辆,运输队所花的本钱最低,最低本钱为(1)求椭圆C 的方程;(2)假设直线l: y=kx+m 与椭圆C 交于A, B 两点.①假设A 为椭圆的上顶点,M 为线 段AB 中点,连接OM 并延长交椭圆C 于N,并且加吟血,求OB 的长;②假设原点I J K IO 到直线l 的距离为1 ,并且而,当信< 九爱时,求^ OAB 的面积S 的范围. D O 解:(1)由于两焦点与短轴的一个顶点的连线构成等腰直角三角形,所以 an 匹d,2又由右准线方程为 x = 2,得到月—=2,C解得 a =JL 白=1,所以 b 2= a 2 - c 2= 1 所以,椭圆C 的方程为答1(2)设 B ⑶,y1),而 A (0, 1),那么 M , —,1920x = 2,且V G的右准线方程为 两焦点与短轴的一个顶点构成等腰直角三角形.N.4 s由于S=在[丁,一]为单调减函数,□ c4 2^/9并且当上一时,S=—^,当□ 5所以△ OAB 的面积S 的范围为[乂更.2些] 6 5 19.设函数 f (x) = 2x 2+alnx , (aCR)(I)假设曲线y=f (x)在点(1, f (1))处的切线方程为 y=2x+m,求实数a, m 的 值由于点B, N 都在椭圆上,所以町2 z—+yl =13xi 2 3(l+yi)2— ----------- -- =1 16 8所以g/町& 华吗) 2_V17 =_y(3)由原点O 到直线l 的距离为1,得/ ---------- ^=1,化简得:1 + k 2= m 2联立直线l 的方程与椭圆C 的方程:1+2k 2) x 2+4kmx+2m 2 — 2= 0设 A (xi, yi) , B (x2, y2),那么 xi+x2=-4k in1+2 7'X 1X 2 = 2m 2-2 1+2 k 3心=8k 2>0,- -* " - *•1- OA ? 0B =x 1x 2+ y i y 2 = x i x 2+ (kx i +m)(kx 2+m) = ( 1 + k 2) x i x 2+km2(x i +x 2) +m3m 2-2-2k 2l+2k 221n2-2 +2k 2m 2-2k 2-4k 2m 2^m 2+2k 2m 2l+2k 2所以k 2=所以△ OAB 的面积i-X 1 x 2ABx 2|81?J(l+2k 2)2(H2k 2) 2272 2=入/2、2 m 2 T (1 + k 2) ---------- 彳1+2 k 22,. x>2, . . x- 1 >0,,g' (x) > 0,即 g (x)单调递增,g (x) > g (2) = 0综上可得,a(III)不可能有三个不同的实根,证实如下: 令 g' (x) =f (x) +2cosx,假设g (x) =5有三个不同的实数根,那么 g (x)至少要有三个单调区间,那么 g' (x) =0 至少有两个不等实根,所以只要证实g' (x) =0在(0, +8)至多1个实根,• •g (x) > 0,(n)假设f (2x- 1) +2>2f (x)对任意x€[2, +8)恒成立,求实数 a 的取值范围; (m)关于x 的方程f (x) +2cosx=5能否有三个不同的实根?证实你的结论 解:(I) 1.1 f (x) = 2x 2+ainx ,• ・f' (x) =4xj, Ji 由题意可得,f' ( 1) =2, f (1) = 2,4+a=2, 2+m=2m= 0,(II ) ••• f (2x-1) +2>2f (x)对任意 xq2, +8)恒成立, 2 ( 2x T)2+aln (2x — 1) +2 > 2 (2x 2 + alnx),整理可得, 4 (x-1) 2- a[2lnx - In (2x-1) ]>0对任意 x€[2, +8)恒成立, • .4-a (n4-ln3) > 0 即 a< 4 In4*ln3当a —一时时,4 (x-1) 2- a[2lnx - In (2x-1) ]>4O1)J oin4-ino设 g (x) = 4 (x — 1)4-, ,•一 .......................... ...1「,口 [21n 左-1门(2广1)],那么 g (x) = 8 (x-1) [ (2x 2—x)IndTnMg' ( x) = 4x 「-2fin 工,g (x) = 4— 2cosx 一・•・g' (x)在(0, +8)上单调递增,,g' (x) = 0至多1个根,当a>0 时,(4x— 2sinx) ' = 4—2cosx>0,,y= 4x-2sinx 在(0, +oo)上单调递增,1. y= 4x - 2sinx> 0,又由于2>0时二:,0,吕(x)= >0,xg' ( x) = 0g' (x)在(0, +8)上没有实数根综上可得,g' (x) =0 (0, +8)上至多一个实数根,得证20.f (x) =x3+ax2+bx, a, b CR.(1)假设b=1,且函数f (x)在区间(-1, 丁)上单调递增,求实数a的范围;(2)假设函数f (x)有两个极值点x i , x2, x i<x2,且存在x0满足x i+2x0 = 3x2,令函数g(x) =f (x) - f (x.),试判断g (x)零点的个数并证实你的结论.解:f' ( x) = 3x2+2ax+b, (xCR),(1)当b=1时,1 (x) = 3x2+2ax+1,由于f (x)在区间(-1, 4)上单调递增所以当xC ( - 1,])时,f' (x) = 3x2+2ax+1>0 恒成立.函数f' (x) = 3x2+2ax+1的对称轴为x=-①一—1,即a> 3 时,f' ( - 1) >0,即3-2a+1>0,解之得a?中,解集为空集;②T?用4士即-台时,一(号2 0IP 3---+-2a-(-y)41>0,解之得-强所以—二4■?无j③-即aV"时,—得)>0 O 占旦£r 1 .、2 7 -即3〞2解之得所以一综上所述,当- 太太册函数f (x)在区间(-1, U)上单调递增.♦・・(2) ••• f (x)有两个极值点x1,x2,,x1, x2是方程f' ( x) = 3x2+2ax+b= 0的两个根,且函数f (x)在区间x1)和〔X2, +8〕上单调递增,在〔X1, X2〕上单调递减. ,「g'〔X 〕=f' 〔X 〕,函数g 〔X 〕也是在区间〔-巴xi 〕和〔X2,+oo 〕上单调递增,在〔X 1, X2〕上单调递减•1g 〔X0〕—f 〔X0〕— f 〔X0〕= 0,,X0是函数 g 〔X 〕的一个零点.…由题意知:X I +2X0=3X2, g 〔X2〕= f 〔X2〕- f 〔X0〕 -- X i +2X 0= 3X 2,2X 0 — 2X 2=X 2— X 1> 0,X 0> X 2f 〔X2〕< f 〔X0〕,.二g 〔X2〕= f 〔X2〕— f 〔X0〕< 0又 g (XI ) = f (XI ) - f (X 0)= X i 3+aX i 2+bX i - ( X 03+aX 02+bX 0) (X i 2+X i X 0+X 02+aX i +aX 0+b)(X/+X 1?-二七 + (上士) 2+aX i +a? 土二L+b )2222 2(3X I +2aX i +b+9X 2 +6aX 2+3b)•' X i, X 2是方程 f' (x) = 3x 2+2ax+b= 0 的两个根,•1- 3x i 2+2ax i +b= 0, 3x 22+2ax 2+b= 0 --・ • g 〔X 1〕= f 〔x i 〕 - f〔X 0〕= 0・•・函数g 〔x 〕图象连续,且在区间〔-8, Xi 〕上单调递增,在〔xi, X2〕上单调递减,在〔X 2, +oo 〕上单调递增 ・•・当 x C 〔— 8, X i 〕时,g 〔x 〕 V 0,当 X € 〔X i, X 0〕时 g 〔X 〕< 0,当 X € 〔X 0, +OO 〕 时 g〔x 〕 > 0, ・•・函数g 〔x 〕有两个零点 X 0和Xi .…〔i6分〕[选做题]此题包括 A 、B 、C 三小题,请选定其中两题,并在相应的做题区域内作答.假设多 做,那么按作答的前两题评分,解答时应写出文字说明、证实过程或演算步骤. [选彳4-2:矩阵与变换]i2i,矩阵 M=七]的一个特征值为 4,求矩阵M 的逆矩阵M i .M k 吠 钻吐:\ -2 -3 解:矩阵 M 的特征多项式为 f 〔 X 〕=1 T =〔入―2〕〔入-i 〕 - 3t;-t A -1由于矩阵M 的一个特征值为 4,所以方程f 〔入〕=0有一^为4; 即 f (4)= 2X 3- 3t=0,解得 t = 2; 所以M = 设M1==(X1-X0)=(X1-X0)=(X 1 — X0)坐标原点.为极点,X 轴的非负半轴为极轴,且与直角坐标系长度单位相同的极坐标系 中,曲线C 的极坐标方程是〔1〕求直线l 的普通方程与曲线 C 的直角坐标方程; 〔2〕假设直线l 与曲线C 相交于两点A, B,求线段AB 的长.ir i解:〔1〕直线l 的参数方程为 L〔t 为参数〕,转换为直角坐标方程为:卜多2i/^K-y+S=O,l 兀,J-TT 一曲线C 的极坐标方程是 R 二翡用+白〕.由P 二如展in 〔q~ +日〕,得P 2 = 4 pcos 9+4 psin 0,整理的直角坐标方程为: x 2+y 2=4x+4y, 所以曲线 C: 〔x-2〕 2+ 〔y-2〕 2=8.〔2〕由〔1〕知圆C 半径r=2正,利用圆心到直线的距离 把但9 2-2 |』,所以雄二2用匚濯=2低. [选彳4-5:不等式选讲」23. x 1, x 2, x 3C (0, +8),且满足 x 1+x 2+x 3= 3x 1x 2x 3,证实:x [x 2+x 2x 3+x 3x1 > 3.【解答】证实:; x I + x 2+x 3= 3x 1x 2x 3,2^^3c 2b +3d 2a-He 2b+d[选彳4-4:坐标系与参数方程 ]〔本小题总分值10分〕22.在平面直角坐标系xOy 中,直线l 的参数方程为 〔t 为参数〕,在以那么 MM 1=勺五2十工〞3十打工1 7(町也十.打十句町) ,4〔1寸1十1)2= 3,当且仅当" Xi = X2=X3=1〞时取等号,故X1X2+X2X3+X3X1 >3,即得证.[必做题]第22题、第23题,每题10分,共计20分.请在答卷卡指定区域内作答.解容许写出文字说明、证实过程或演算步骤.24.如图,在平面直角坐标系XOy中,抛物线:C: y2 = 2pX (p>0)的焦点F在直线X+y-1 = 0上,平行于X轴的两条直线11, 12分别交抛物线线C于A, B两点,交该抛物线的准线于D, E两点.(1)求抛物线C的方程;(2)假设F在线段AB上,P是DE的中点,证实:AP // EF .I■L产解:(1)抛物线C的焦点F坐标为(4,0),且该点在直线X+y-1 = 0上,所以一T=0,解得P=2,故所求抛物线C的方程为y2=4X;(2)由点F在线段AB上,可设直线11, 12的方程分别为y=a和y=b且aw0, bw0, awb.・•・P是DE的中点,・•. P〔T,当上), 2椁—Q Q直线AB的方程为y-a=―§ -- 丁(工一丁)b -a 4即 4x- ( a+b) y+ab=0,又点F (1, 0)在线段 AB 上,,ab= - 4,a.+b 4 . "Z /2一=^—a a +4 d_L -4由于AP, EF 不重合,所以 AP // EF .25.在开展学习强国的活动中,某校高三数学教师成立了党员和非党员两个学习组,其中 党员学习组有4名男教师、1名女教师,非党员学习组有 2名男教师、2名女教师,高三 数学组方案从两个学习组中随机各选 2名教师参加学校的挑战做题比赛.(1)求选出的4名选手中恰好有一名女教师的选派方法数;(2)记X 为选出的4名选手中女教师的人数,求 X 的概率分布和数学期望.【解答】角:(1)某校高三数学教师成立了党员和非党员两个学习组,其中党员学习组有 4名男教师、1名女教师,非党员学习组有 2名男教师、2名女教师, 高三数学组方案从两个学习组中随机各选 2名教师参加学校的挑战做题比赛. 选出的4名选手中恰好有一名女教师的选派方法数为:m =C :cH +C :C ;C ; = 28.(2)记X 为选出的4名选手中女教师的人数,那么X 的可能取值为0, 1, 2, 3,P (X=0) 28 = 60,22——— — 60'P (X= 1) C :c 沟+总c ;cP (X=2)=r 2p2 P (X=3)X的概率分布为:X 0 1P J L28 2260 60: 60X 的数学期望E (X) = 0X^+ix-^-+2X^-+-3X-^-=-.60 60 60 60 54 60。
江苏省无锡市天一中学2019届高三上学期11月月考数学试题

江苏省天一中学2018-2019高三第一次诊断性测试一、填空题:本大题共14小题,每小题5分,共70分.请把答案直接填写在答题卡相应.....位置上....1.设集合,则_______.【答案】【解析】【分析】直接利用集合并集的定义求解即可.【详解】因为集合,所以,故答案为.【点睛】研究集合问题,一定要抓住元素,看元素应满足的属性.研究两集合的关系时,关键是将两集合的关系转化为元素间的关系,本题实质求满足属于集合或属于集合的元素的集合.2.命题:“ 使得”的否定为__________.【答案】【解析】【分析】根据特称命题的否定是全称命题,既要改写量词,又要否定结论,可得原命题的否定形式. 【详解】因为特称命题的否定是全称命题,既要改写量词,又要否定结论,故命题“ ”的否定是,故答案为.【点睛】本题主要考查特称命题的否定,属于简单题.全称命题与特称命题的否定与命题的否定有一定的区别,否定全称命题和特称命题时,一是要改写量词,全称量词改写为存在量词、存在量词改写为全称量词;二是要否定结论,而一般命题的否定只需直接否定结论即可.3.函数的定义域为_________.【答案】【解析】【分析】直接由根式内部的代数式大于等于0 ,分式的分母不等于0 ,列不等式求解即可得结果. 【详解】要使函数有意义,则解得,函数的定义域为,故答案为.【点睛】本题主要考查具体函数的定义域、不等式的解法,属于中档题.定义域的三种类型及求法:(1)已知函数的解析式,则构造使解析式有意义的不等式(组)求解;(2) 对实际问题:由实际意义及使解析式有意义构成的不等式(组)求解;(3) 若已知函数的定义域为,则函数的定义域由不等式求出.4.曲线在处的切线的斜率为_________.【答案】1【解析】【分析】求出原函数的导函数,可得到曲线在处的导数值,根据导数的几何意义可得结果.【详解】因为曲线在处的切线的斜率就是曲线在处的导数值,由得 ,,即曲线在处的切线的斜率为1,故答案为1.【点睛】本题考查了利角导数研究曲线上某点处的切线斜率,曲线在某点处的导数值,即为曲线上以该点为切点的切线的斜率,是中档题.5.若函数是偶函数,则实数______.【答案】1【解析】【分析】由函数是偶函数,利用求得,再验证即可得结果.【详解】是偶函数,,即,解得,当时,是偶函数,合题意,故答案为1.【点睛】本题主要考查函数的奇偶性,属于中档题. 已知函数的奇偶性求参数,主要方法有两个,一是利用:(1)奇函数由恒成立求解,(2)偶函数由恒成立求解;二是利用特殊值:奇函数一般由求解,偶函数一般由求解,用特殊法求解参数后,一定要注意验证奇偶性.6.已知,函数和存在相同的极值点,则________.【答案】3【解析】【分析】(1)求出函数的导数,可得极值点,通过与有相同的极值点,列方程求的值. 【详解】,则,令,得或,可得在上递增;可得在递减,极大值点为,极小值点为,因为函数和存在相同的极值点,而在处有极大值,所以,所以,故答案为3.【点睛】本题主要考查利用导数判断函数的单调性以及函数的极值,属于中档题.求函数极值的步骤:(1) 确定函数的定义域;(2) 求导数;(3) 解方程求出函数定义域内的所有根;(4) 列表检查在的根左右两侧值的符号,如果左正右负(左增右减),那么在处取极大值,如果左负右正(左减右增),那么在处取极小值. (5)如果只有一个极值点,则在该处即是极值也是最值.7.已知函数.若,则实数的最小值为______.【答案】【解析】试题分析:由题意得,实数的最小值为考点:三角函数周期8.已知函数与函数的图象交于三点,则的面积为________.【答案】【解析】联立方程与可得,解之得,所以,因到轴的距离为,所以的面积为,应填答案。
江苏省无锡市天一中学2020届高三数学第一次模拟考试试题含解析

【解析】
【分析】
设每天派出A型卡车 辆,则派出B型卡车 辆,由题意列出约束条件,作出可行域,求出使目标函数取最小值的整数解,即可得解。
【详解】设每天派出A型卡车 辆,则派出B型卡车 辆,运输队所花成本为 元,
由题意可知, ,
整理得 ,
1.已知集合 , ,则 _________。
【答案】
【解析】
【分析】
根据交集的定义即可写出答案.
【详解】 , ,
故填
【点睛】本题考查集合的交集,需熟练掌握集合交集的定义,属于基础题.
2。复数 为虚数单位)的虚部为__________.
【答案】1
【解析】
试题分析: ,即虚部为1,故填:1。
考点:复数的代数运算
18.在平面直角坐标系xOy中,椭圆C: 的右准线方程为x=2,且两焦点与短轴的一个顶点构成等腰直角三角形.
(1)求椭圆C的方程;
(2)假设直线l: 与椭圆C交于A,B两点.①若A为椭圆的上顶点,M为线段AB中点,连接OM并延长交椭圆C于N,并且 ,求OB的长;②若原点O到直线l的距离为1,并且 ,当 时,求△OAB的面积S的范围.
【答案】3
【解析】
【分析】
当 时, 得 ,或 ,依题意可得 ,可求得 ,继而可得答案.
【详解】因为点 的横坐标为1,即当 时, ,
所以 或 ,
又直线 与函数 的图象在 轴右侧的公共点从左到右依次为 , ,
所以 ,
故 ,
所以函数的关系式为 .
当 时, (3) ,
即点 的横坐标为3, 为二函数的图象的第二个公共点.
目标函数 ,
如图所示,为不等式组表示的可行域,
江苏省无锡市天一中学高三11月月考数学试题(解析版)

2018-2019学年江苏省无锡市天一中学高三11月月考 数学试题数学注意事项:1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4.考试结束后,请将本试题卷和答题卡一并上交。
一、填空题1.设集合A ={1,2,3,5},B ={2,3,6},则A ∪B =_______. 2.命题:“ ∃x >0,使得x +1>0”的否定为__________. 3.函数y =√1−x x的定义域为_________.4.曲线y =x −sinx 在x =π2处的切线的斜率为_________. 5.若函数f (x )=2x +a2x 是偶函数,则实数a =______.6.已知a >0,函数f (x )=x (x −a )2和g (x )=−x 2+(a −)1x +a 存在相同的极值点,则a =________.7.已知函数f (x )=2sin (ωx +φ)(ω>0).若f (π3)=0,f (π2)=2,则实数ω的最小值为______. 8.已知函数f (x )=sinx (x ∈[0,π])与函数g (x )=13tanx 的图象交于A,B,C 三点,则ΔABC 的面积为________.9.已知f (x )是定义在R 上的偶函数,且在区间(−∞,0)上单调递增.若实数a 满足f (2|a-1|)>f (−√2),则a 的取值范围是______.10.已知0y x π<<<,且tan tan 2x y =, 1sin sin 3x y =,则x y -=______. 11.在平行四边形ABCD 中,AC AD AC BD ⋅=⋅3=,则线段AC 的长为 .12.已知π4<α<π2,π4<β<π2,且sin 2αsin 2β=sin (α+β)cosαcosβ,则tan (α+β)的最大值为______.13.设a ≠0,e 是自然对数的底数,函数f(x)={ae x −x,x ≤0x 2−ax +a,x >0有零点,且所有零点的和不大于6,则a 的取值范围为______.14.设函数f(x)=(x −a)|x −a |−x |x |+2a +1(a <0).若存在x 0∈[−1 , 1],使f(x 0)≤0, 则a 的取值范围是____.二、解答题15.已知sinθ+cosθ=√3−12,θ∈(−π4 , π4).(1)求θ的值;(2)设函数f(x)=sin 2x −sin 2(x +θ),x ∈R ,求函数f(x)的单调增区间.16.如图,在△ABC 中,已知AC =7,∠B =45∘,D 是边AB 上的一点,AD =3,∠ADC =120∘,求:(1)CD 的长; (2)△ABC 的面积.17.在平面直角坐标系xOy 中,已知向量a ⃑=(1,0),b ⃑⃑=(0,2),设向量x =a ⃑+(1−cosθ)b ⃑⃑,y =−ka ⃑+1sinθb⃑⃑,其中0<θ<π. (1)若k =4,θ=π6,求x ⋅y 的值;(2)若x//y ,求实数k 的最大值,并求取最大值时θ的值.18.对于函数f(x),若在定义域内存在实数x ,满足f(−x)=−f(x),则称f(x)为“局部奇函数”. (Ⅰ)已知二次函数f(x)=ax 2+2x −4a(a ∈R),试判断f(x)是否为“局部奇函数”?并说明理由;(Ⅱ)若f(x)=2x +m 是定义在区间[−1,1]上的“局部奇函数”,求实数m 的取值范围; (Ⅲ)若f(x)=4x −m2x+1+m 2−3为定义域R 上的“局部奇函数”,求实数m 的取值范围.19.如图,A 、B 是海岸线OM 、ON 上的两个码头,Q 为海中一小岛,在水上旅游线AB 上.测得tan∠MON =−3,OA =6km ,Q 到海岸线OM 、ON 的距离分别为2km ,7√105km . 此卷只装订不密封班级 姓名 准考证号 考场号 座位号(1)求水上旅游线AB的长;(2)海中P(PQ=6km,且PQ⊥OM)处的某试验产生的强水波圆P,生成t小时时的半径为r= 6√6t32km.若与此同时,一艘游轮以18√2km/小时的速度自码头A开往码头B,试研究强水波是否波及游轮的航行?20.已知函数f(x)=(4x+2)lnx,g(x)=x2+4x−5.(1)求曲线y=f(x)在点(1,f(1))处的切线方程;(2)证明:当x≠1时,曲线y=f(x)恒在曲线y=g(x)的下方;(3)当x∈(0,k]时,不等式(2k+1)⋅f(x)≤(2x+1)⋅g(x)恒成立,求实数k的取值范围.2018-2019学年江苏省无锡市天一中学高三11月月考数学试题数学答案参考答案1.{1,2,3,5,6}【解析】【分析】直接利用集合并集的定义求解即可.【详解】因为集合A={1,2,3,5},B={2,3,6},所以A∪B={1,2,3,5,6},故答案为{1,2,3,5,6}.【点睛】研究集合问题,一定要抓住元素,看元素应满足的属性.研究两集合的关系时,关键是将两集合的关系转化为元素间的关系,本题实质求满足属于集合A或属于集合B的元素的集合.2.∀x>0,x+1≤0【解析】【分析】根据特称命题的否定是全称命题,既要改写量词,又要否定结论,可得原命题的否定形式.【详解】因为特称命题的否定是全称命题,既要改写量词,又要否定结论,故命题“ ∃x>0,x+1>0”的否定是∀x>0,x+1≤0,故答案为∀x>0,x+1≤0.【点睛】本题主要考查特称命题的否定,属于简单题.全称命题与特称命题的否定与命题的否定有一定的区别,否定全称命题和特称命题时,一是要改写量词,全称量词改写为存在量词、存在量词改写为全称量词;二是要否定结论,而一般命题的否定只需直接否定结论即可.3.(0,1]【解析】【分析】直接由根式内部的代数式大于等于0 ,分式的分母不等于0 ,列不等式求解即可得结果.【详解】要使函数y=√1−xx有意义,则{1−xx≥0x≠0⇒{(1−x)x≥0x≠0解得0<x≤1,∴函数y=√1−xx的定义域为(0,1],故答案为(0,1].【点睛】本题主要考查具体函数的定义域、不等式的解法,属于中档题.定义域的三种类型及求法:(1)已知函数的解析式,则构造使解析式有意义的不等式(组)求解;(2) 对实际问题:由实际意义及使解析式有意义构成的不等式(组)求解;(3) 若已知函数f(x)的定义域为[a,b],则函数f(g(x))的定义域由不等式a≤g(x)≤b求出.4.1【解析】【分析】求出原函数的导函数,可得到曲线y=x−sinx在x=π2处的导数值,根据导数的几何意义可得结果.【详解】因为曲线y=x−sinx在x=π2处的切线的斜率就是曲线y=x−sinx在x=π2处的导数值,由y=x−sinx得y′=1−cosx,∴y′|x=π2=1−cosπ2=1,即曲线y=x−sinx在x=π2处的切线的斜率为1,故答案为1.【点睛】本题考查了利角导数研究曲线上某点处的切线斜率,曲线在某点处的导数值,即为曲线上以该点为切点的切线的斜率,是中档题.5.1【解析】【分析】由函数f(x)=2x+a2x是偶函数,利用f(−1)=f(1)求得a=1,再验证即可得结果.【详解】∵f(x)=2x+a2x是偶函数,∴f(−1)=f(1),即2+a2=12+2a,解得a=1,当a=1时,f(−x)=2−x+12−x =2x+12x是偶函数,合题意,故答案为1.【点睛】本题主要考查函数的奇偶性,属于中档题. 已知函数的奇偶性求参数,主要方法有两个,一是利用:(1)奇函数由f(x)+f(−x)=0恒成立求解,(2)偶函数由f(x)−f(−x)=0恒成立求解;二是利用特殊值:奇函数一般由f(0)=0求解,偶函数一般由f(1)−f(−1)=0求解,用特殊法求解参数后,一定要注意验证奇偶性.6.3【解析】【分析】(1)求出函数y=f(x)的导数,可得极值点,通过与y=g(x)有相同的极值点,列方程求a的值.【详解】f(x)=x(x−a)2=x3−2ax2+a2x,则f′(x)=3x2−4ax+a2=(3x−a)(x−a),令f′(x)=0,得x=a或a3,可得f(x)在(−∞,a3),(a,+∞)上递增;可得f(x)在(a3,a)递减,极大值点为a3,极小值点为a,因为函数f(x)=x(x−a)2和g(x)=−x2+(a−)1x+a存在相同的极值点,而g(x)在x=a−12处有极大值,所以a−12=a3,所以a=3,故答案为3.【点睛】本题主要考查利用导数判断函数的单调性以及函数的极值,属于中档题.求函数f(x)极值的步骤:(1) 确定函数的定义域;(2) 求导数f′(x);(3) 解方程f′(x)=0,求出函数定义域内的所有根;(4) 列表检查f′(x)在f′(x)=0的根x0左右两侧值的符号,如果左正右负(左增右减),那么f(x)在x0处取极大值,如果左负右正(左减右增),那么f(x)在x0处取极小值. (5)如果只有一个极值点,则在该处即是极值也是最值.7.3【解析】试题分析:由题意得T4≤π2−π3⇒T≤2π3⇒ω=2πT≥3,实数ω的最小值为3考点:三角函数周期8.√2π3【解析】联立方程f(x)=sinx与g(x)=13tanx可得13tanx=sinx,解之得x=0,π,cosx=13⇒sinx=2√23,所以A(0,0),B(π,0),C(x,sinx),因AB=π,C(x,sinx)到x轴的距离为sinx=2√23,所以ΔABC的面积为S=12×π×2√23=√2π3,应填答案√2π3。
2020年江苏省无锡市重点中学高三数学理月考试题含解析

2020年江苏省无锡市重点中学高三数学理月考试题含解析一、 选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 在△ABC 中,∠BAC=60°,AB=2,AC=1,E ,F 为边BC 的三等分点,则=( ).B .C .D参考答案:A 略2. 设全集U 是实数集R ,,则 (A)(B)(C)(D)参考答案:A3. 已知函数有三个不同的零点,(其中),则的值为( )A .B .C .-1D .1参考答案:D4. 的展开式的系数是 ( )A.B.C.0D.3参考答案: A5. 函数恰有两个零点,则实数k 的范围是( )A.(0,1)B.(0,l )U (1,2)C. (1,+oo ) D 、(一oo,2)参考答案:B【知识点】函数的零点与方程根的关系.B9解析:由题意,令f (x )=0,则令,,则y1==,图象如图所示表示过点(0,0)的直线,结合图像以及斜率的意义,∴k 的取值范围是(0,1)∪(1,2), 故选B.【思路点拨】令f (x )=0,则,构建函数,作出函数的图象,即可求得k 的取值范围.6. 对于函数f (x)和g(x),其定义域为[a, b],若对任意的x∈[a, b]总 有 |1-|≤, 则称f (x)可被g(x)置换,那么下列给出的函数中能置换f (x)= x∈[4,16]的是()A. g(x)=2x+6 x∈[4,16]B. g(x)=x 2+9 x∈[4,16]C. g(x)=(x+8) x∈[4,16] D. g(x)=(x+6) x∈[4,16]参考答案:D7. 设为两个非零向量、的夹角,已知对任意实数,的最小值为1( )A.若确定,则唯一确定B.若确定,则唯一确定C.若确定,则唯一确定D.若确定,则唯一确定参考答案:D8. 设是两条直线,是两个平面,则的一个充分条件是()A.B.C.D.参考答案:C9. 若实数a,b满足,则ab的最小值为()A.B.2 C.D.4参考答案:A【考点】基本不等式.【分析】利用基本不等式的性质即可得出.【解答】解:实数满足,∴a,b>0,∴≥2,化为:ab,当且仅当b=2a=.则ab的最小值为.故选:A.10. 若实数a,b,c,d满足,则的最小值为()A.B.8 C.D.2参考答案:B二、填空题:本大题共7小题,每小题4分,共28分11. 已知三棱锥的所有棱长都相等,现沿桑涛侧棱剪开,将其表面展开成一个平面图形,若这个平面图形外接圆的半径为,则三棱锥的内切球的表面积为参考答案:12. 已知曲线f(x)=2x2+1在点M(x0,y0)处的瞬时变化率为﹣8,则点M的坐标为.参考答案:(﹣2,9)【考点】导数的几何意义.【分析】求导函数,令其值为﹣8,即可求得结论.【解答】解:∵y=2x2+1,∴y′=4x,令4x0=﹣8,则x0=﹣2,∴y0=9,∴点M的坐标是(﹣2,9),故答案为:(﹣2,9).13. 在平面直角坐标系xOy中,过x轴上的点P作双曲线C:的一条渐近线的垂线,垂足为M,若,则双曲线C的离心率的值是参考答案:14. (极坐标系与参数方程)极坐标系下曲线表示圆,则点到圆心的距离为;参考答案:曲线方程的直角坐标方程为,所以圆心为(0,2),又点的直角坐标方程为,所以点A 与圆心的距离为。
天一大联考2020届高三数学(文)上学期11月阶段性测试卷

天一大联考2020届高三上学期11月阶段性测数学(文)试卷―、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有上项是符合题目要求的.1.已知集合A={0<31|x x -},B={1|2+=x y y },则=B A A.{3<1|x x ≤} B.{1<<0|x x }C.{3<0|x x ≤}D.{3<<1|x x }2.下列命题中,真命题是A.命题“若1y >+x ,则y >x ,的逆否命题为“若y ≤x ,则1y >+x B.若12≥x ,则1-≤x 或1≥x C.若020192=-x x ,则2019=x D.若b a >,则b1<1a 3.已知20191.05.01.01.0log ,5.0,2===c b a ,则A.a >b >c B.c>a>b C.a>c>b D.c>b>a4.函数x x x f cos )(-=在2π=x 处的切线方程为A.042=--πy xB.02=-y x πC.014=--y x π D.024=--πy x 5.朱世杰是历史上最伟大的数学家之一,他所著的《四元玉鉴》卷中“如像招数”五问有如下表述今有官司差夫一千八百六十四人筑堤,只云初日差六十四人,次日转多七人,每人日支米三升其大意为“官府陆续派遣1864人前往修筑堤坝,第一天派出64人,从第二天开始每天派出的人数比前一天多7人,修筑堤坝的每人每天分发大米3升”,则前3天共分发大米A.234升B.468升C.639升D.903升6.函数||ln 10)(3x x x f -=的图象大致为7.已知0)2cos(21)37sin(=---x x ππ,则=-)3tan(x πA.51 B.53 C.532 D.38.已知)(x g 函数是R 上的奇函数,当0<x 时,)1ln()(x x g --=,且⎩⎨⎧≤=0>),(0,)(3x x g x x x f ,若)(>)2(2x f x f -,则实数x 的取值范围是A.(-1,2)B.(1,2)C.(-2,-1)D.(-2,1)9.已知y x ,满足约束条件⎪⎩⎪⎨⎧≥-+≤-+≥+-02203042y x y x y x ,则目标函数y x z 2-2=的最大值为A.128B.64C.641D.128110.要想得到函数)62sin(π+=x y 的图象,只需将函数)sin (cos )sin (cos x x x x y +⋅-=的图像A.向右平移6π个单位长度 B.向左平移3π个单位长度C.向右平移3π个单位长度 D.向左平移6π个单位长度11.已知菱形ABCD 的边长为4,060=∠ABC ,E 是BC 的中点,AF DF 2-=,则=⋅BF AE A.24B.-7C.-10 D.-1212.已知函数⎪⎩⎪⎨⎧≤-++=0,1)2(0>,4)(2x x x x x x f ,若方程02)(=-m x f 恰有三个不同的实数根,则实数m 的取值范围是A.),2(-∞B.),4(+∞C.)4,2(D.)4,3(二、填空题:本题共4小题,每小题5分,共20分.13.已知向量)23,21(=a ,向量b a ,的夹角是43π,且1-=⋅b a ,则=||b .14.△ABC 的内角A,B,C 的对边分别为a,b,c,已知a =5,c =6,cos B =54,则sin A =.15.已知8a +2b =l(a>0,b >0),则ab 的最大值为.16.记数列{n a }的前n 项和为n S ,已知)2(92,411≥+-==-n a a a n n .若对任意的4)3(,≥-*∈n S N n n λ恒成立,则实数λ的最小值为.三、解答题:共70分.解答应写出文字说明,证明过程或演算步骤.17.(10分)已知:p 指数函数x a x f )12()(-=在R 上单调递减,关于x 的方程012322=++-a ax x 的两个实根均大于0.若“p 或q ”为真命题,“p 且q ”为假命题,求实数a 的取值范围.18.(12分)△ABC 的内角A,B,C 所对的边分别为a,b,c,已知B A B A sin tan cos tan +=.(I)若8=+c a ,△ABC 的面积为6,求B sin ;(II)若223a b =,求B.19.(12分)已知正项等比数列{n a },6,92324=-=a a a a .(I)求数列{n a }的通项公式;(II)若n n na b =,求数列{n b }的前n 项和n T .20.(12分)记数列{n a }的前n 项和为n S ,已知)2(32,311≥+-=-n S S S a n n n .(I)求数列{n a }的通项公式;(II)求使81≥n a 成立的n 的最大值.21.(12分)已知函数R a x a x x f ∈-=,ln )()(2.(I)设正实数T 满足)0()(f T f =,求T 的最小值;(II)当]3,4(ππ-∈x 时,求)(x f 的值域.22.(12分)已知函数x x x f 2ln )(+=.(I)求)(x f 的极小值.(II)已知函数x x a x x f x g 223)()(2--+=,其中a 为常数且0≠a ,若函数)(x g 在区间[1,2]上为单调增函数,求实数a 的取值范围。
2020年无锡市锡山区天一中学高考数学模拟试卷(二)(含答案解析)
2020年无锡市锡山区天一中学高考数学模拟试卷(二)一、填空题(本大题共14小题,共70.0分)1.若集合A={4,5,6,8},B={3,5,7,8},则A∪B=______ .2.i是虚数单位,复数6+7i1+2i=________.3.如图是一个算法流程图:若输入x的值为116,则输出y的值是______ .4.已知样本数据为7,8,10,12,13,则其方差的值为______.5.甲、乙两名学生选修4门课程(每门课程被选中的机会相等),要求每名学生必须选1门且只需选1门,则他们选修的课程互不相同的概率是______ .6.已知等比数列{a n}的前n项和为S n,若S3=7,S6=63,则a1=________.7.已知双曲线x2a2−y2b2=1的离心率为2,焦点与椭圆x225+y29=1的焦点相同,那么双曲线渐近线方程为______ .8.已知cosα+sinα=12,则sin2α=______ .9.设函数f(x)的导函数为f′(x),且2f′(x)<f(x)(x∈R),f(2)=e(e为自然对数的底数),则不等式f(lnx)>x 12的解集为______ .10.求函数y=log3(|x|+2)的最小值为__________。
11. 已知函数f(x)=e x−2+x −3(e 为自然对数的底数),g(x)=x 2−(a +1)x −a +7,若存在实数x 1、x 2、x 3(x 2≠x 3),使得f(x 1)=g(x 2)=g(x 3)=0,且|x 1−x 2|≤1和|x 1−x 3|≤1同时成立,则实数a 的取值范围是__________.12. 若−4<a <−1,2<b <3,则ab 的取值范围是 . 13. 已知函数f(x)=4−xln3x ,则当x =__________时,f(x)有最大值.14. 已知A ,B 是圆C 1:x 2+y 2=1上的动点,AB =√3,P 是圆C 2:(x −3)2+(y −4)2=1上的动点,则|PA ⃗⃗⃗⃗⃗ +PB ⃗⃗⃗⃗⃗ |的取值范围为________.二、解答题(本大题共6小题,共90.0分)15. 已知函数f(x)=2sinx ⋅cosx −cos 2x +sin 2x ,x ∈R .(1)求f(x)的最小正周期及单调递减区间;(2)求f(x)在区间[0,π2]上的最大值和最小值.16. 在四棱锥M −ABCD 中,平面MAD ⊥平面ABCD ,底面ABCD 为矩形,AB =2,AM =AD =3,MD =3√2,E ,F 分别为线段BC ,MD 上一点,且CE =1,DF =√2.(1)证明:AM ⊥BD ;(2)证明:EF//平面MAB,并求三棱锥D−AEF的体积.17.如图,将边长为6的等边三角形各切去一个全等的四边形,再沿虚线折起,做成一个无盖的正三棱柱形的容器.(1)若这个容器的底面边长为x,容积为y,写出y关于x的函数关系式并注明定义域;(2)求这个容器容积的最大值.18.已知椭圆C:x2a2+y2b2=1(a>b>0)的离心率为14,左顶点为A,右焦点为F,且AF=5.(1)求椭圆C的方程;(2)已知圆M的圆心M(−78,0),半径为r.点P为椭圆上的一点,若圆M与直线PA,PF都相切,求此时圆M的半径r.19.已知数列{a n}的前n项和为S n,满足a1=1,S n+1=S n+2a n+5.(1)证明:{a n+5}是等比数列;(2)若S n+5n>128,求n的最小值.x3+ax2+(2a−1)x(a∈R).20.已知函数f(x)=13(Ⅰ)若f(x)在点(0,0)处的切线方程为y=x,求a的值;(Ⅱ)求f(x)的单调区间;(Ⅲ)当a=−1时,设f(x)在x1,x2(x1<x2)处取到极值,记M(x1,f(x1)).A(0,f(0)),B(1,f(1)),C(2,f(2)),判断直线AM、BM、CM与函数f(x)的图象各有几个交点(只需写出结论).【答案与解析】1.答案:{3,4,5,6,7,8}解析:解:∵集合A={4,5,6,8},B={3,5,7,8},∴A∪B={3,4,5,6,7,8}.故答案为:{3,4,5,6,7,8}.利用并集的性质求解.本题考查并集的求法,解题时要认真审题,是基础题.2.答案:4−i解析:本题考查复数的四则运算,根据复数除法的运算法则直接计算即可,属于基础题.解:6+7i1+2i =(6+7i)(1−2i)(1+2i)(1−2i)=6+14+7i−12i5=20−5i5=4−i.故答案为4−i.3.答案:−2解析:本题考查程序框图,属于基础题.直接模拟程序即得结论.解:初始值x=116,不满足判断条件,则.故答案为−2.4.答案:265解析:本题考查了方差的公式,属于基础题.将数据直接代入方差计算公式可得答案.解:因为样本平均数x=7+8+10+12+135=10,故方差s2=15[(7−10)2+(8−10)2+(10−10)2+(12−10)2+(13−10)2]=265,故答案为265.5.答案:34解析:此题考查了古典概型概率计算公式,掌握古典概型概率公式:概率=所求情况数与总情况数之比是解题的关键.利用分步乘法原理,分别计算出甲、乙两名学生任选一门选修课程的情况总数和满足他们选修的课程互不相同的情况数,代入古典概型概率计算公式,可得答案.解:设选修4门课程名称为A,B,C,D甲、乙两名学生选修课程名称记为(x,y),则共有4×4=16种不同情况,其中他们选修的课程互不相同的事件有4×3=12种不同情况,故他们选修的课程互不相同的概率P=1216=34,故答案为:34.6.答案:1解析:本题考查等比数列的前n项和公式以及应用,注意分析q是否为1.根据题意,由等比数列前n项和公式可得S3=a1(1−q3)1−q =7,S6=a1(1−q6)1−q=63;变形可得1+q3=9,解可得q的值,将q的值代入S3=a1(1−q3)1−q=7,计算可得答案.解:根据题意,等比数列{a n}满足S3=7,S6=63,则其公比q≠1,若S3=7,则a1(1−q3)1−q=7;S6=63,则a1(1−q6)1−q=63;变形可得:1+q 3=9,解可得q =2;又由a 1(1−q 3)1−q =7,解可得a 1=1.故答案为17.答案:y =±√3x解析:解:∵椭圆x 225+y 29=1的焦点为(4,0)(−4,0),故双曲线中的c =4,且满足c a =2,故a =2,b =√c 2−a 2=2√3,所以双曲线的渐近线方程为y =±b a x =±√3x故答案为:y =±√3x先根据椭圆的方程求出焦点坐标,得到双曲线的c 值,再由离心率求出a 的值,最后根据b =√c 2−a 2得到b 的值,可得到渐近线的方程.本题主要考查圆锥曲线的基本元素之间的关系问题,同时双曲线、椭圆的相应知识也进行了综合性考查.8.答案:−34解析:解:∵cosα+sinα=12,平方可得1+sin2α=14,则sin2α=−34,故答案为:−34.把所给的等式平方,利用同角三角函数的基本关系,二倍角的正弦公式求得sin2α的值. 本题主要考查同角三角函数的基本关系,二倍角的正弦公式的应用,属于基础题. 9.答案:(0,e 2)解析:解:可构造函数F(x)=f(x)e x 2, F′(x)=f′(x)−12f(x)e x 2,由2 f′(x)<f (x),可得F′(x)<0,即有F(x)在R 上递减,不等式f(lnx)>x 12即为f(lnx)e lnx 2>1,(x >0), 即有F(2)=f(2)e =1,即为F(lnx)>F(2),由F(x)在R 上递减,可得lnx <2,解得0<x <e 2,故答案为:(0,e 2).构造函数F(x),求出导数,判断F(x)在R 上的单调性.原不等式等价为F(lnx)>F(2),运用单调性,可得lnx <2,运用对数不等式的解法,即可得到所求解集.本题考查导数的运用:求单调性,考查构造法的运用,以及单调性的运用,对数不等式的解法. 10.答案:log 32解析:令t =|x |+2≥2,所以y =log 3t ≥log 32,所以函数y =log 3(|x |+2)的最小值为log 32. 11.答案:(3,134]解析:本题主要考查函数与方程的综合知识,首先求出函数f(x)的导数,可得f(x)单调递增,解得f(x)=0的解为x 1=2,由题意可得g(x)=x 2−(a +1)x −a +7=0在1≤x ≤3上有两个不等的根,通过判别式对称轴等可求得a 的取值范围,难度中等.解:函数f(x)=e x−2+x −3的导数为f ′(x)=e x−2+1>0,∴f(x)在R 上单调递增,由f(2)=0,可得x 1=2,又存在实数x 1、x 2、x 3(x 2≠x 3),使得f(x 1)=g(x 2)=g(x 3)=0,且|x 1−x 2|⩽1和|x 1−x 3|⩽1同时成立,∴存在实数x 2、x 3(x 2≠x 3),使得g(x 2)=g(x 3)=0,且|2−x 2|⩽1和|2−x 3|⩽1同时成立, 即g(x)=x 2−(a +1)x −a +7=0在1≤x ≤3上有两个不等的根,则{ g (1)=−2a +7≥0g (3)=−4a +13≥0Δ=(a +1)2−4(−a +7)>01<a+12<3,解得3<a ≤134, 即a 的取值范围为(3,134] 12.答案:−12<ab <−2解析:【试题解析】本题考查了不等式的性质,属于基础题.根据不等式的基本性质先求出−ab 的范围,即可求得ab 的取值范围.解:∵−4<a <−1,∴1<−a <4,又2<b <3,∴2<−ab <12,∴−12<ab <−2.故答案为−12<ab <−2.13.答案:13e解析:依题意知:原函数的定义域为(0,+∞),f′(x)=−ln3x −x ⋅33x=−ln3x −1,令f′(x)>0,⇒0<x <13e .令f′(x)<0⇒x >13e ,所以函数f(x)在(0,13e )单调递增,在(13e ,+∞)单调递减,∴当x =13e 时,f(x)有最大值.14.答案:[7,13]解析:本题考查了平面向量中向量的数量积知识点.取AB 的中点H ,则|PA +PB|=2|PD|,|C 1D|=√1−34=12,根据圆的对称性,可得C 1,C 2,P,D 共线时,|PD|取得最值,可得结论.解:因为A ,B 是圆C 1:x 2+y 2=1上的动点,AB =√3,所以线段AB 的中点H 在圆O :x 2+y 2=14上,且|PA ⃗⃗⃗⃗⃗ +PB ⃗⃗⃗⃗⃗ |=2|PH⃗⃗⃗⃗⃗⃗ |. 因为点P 是圆C 2:(x −3)2+(y −4)2=1上的动点,所以5−32≤|PH ⃗⃗⃗⃗⃗⃗ |≤5+32,即72≤|PH ⃗⃗⃗⃗⃗⃗ |≤132, 所以7≤2|PH⃗⃗⃗⃗⃗⃗ |≤13, 从而|PA ⃗⃗⃗⃗⃗ +PB ⃗⃗⃗⃗⃗ |的取值范围是[7,13].15.答案:解:(1)f(x)=sin2x−cos2x=√2sin(2x−π4).所以函数f(x)的最小正周期为T=2π2=π.令2kπ+π2≤2x−π4≤2kπ+3π2得kπ+38π≤x≤kπ+78π,k∈Z.所以函数f(x)的单调减区间为[kπ+3π8,kπ+7π8],k∈Z.(2)因为0≤x≤π2,所以−π4≤2x−π4≤3π4.所以当2x−π4=π2,即x=3π8时,函数f(x)有最大值f(3π8)=√2,当2x−π4=−π4,即x=0时,函数f(x)有最小值f(0)=−1.解析:本题考查二倍角公式、两角和与差的三角函数及正弦函数的图象与性质,考查了学生的计算能力,培养了学生分析问题与解决问题的能力.(1)利用二倍角公式及两角和与差的三角函数可得f(x)==√2sin(2x−π4),进而利用正弦函数的图象与性质即可求得结果;(2)根据题意可得−π4≤2x−π4≤3π4,进而利用正弦函数的性质即可求得结果.16.答案:证明:(1)∵AM=AD=3,MD=3√2,∴AM2+AD2=MD2,∴AM⊥AD,∵平面MAD⊥平面ABCD,平面MAD∩平面ABCD=AD,,∴AM⊥平面ABCD,又BD在平面ABCD内,∴AM⊥BD.(2)在棱AD上取一点N,使得ND=1,连接NE,NF,∵CE=1,∴CE=ND,又BC//AD,∴EC//ND,∴四边形CEND为平行四边形,∴EN//CD,又AB//CD,∴EN//AB,∵NDAD =FDMD=13,∴FN//AM,∵FN∩EN=N,.,∴平面ENF//平面MAB,又EF⊂平面ENF,∴EF//平面MAB,∵AM⊥平面ABCD,且FD=13MD,AM=3,∴F 到平面ABCD 的距离为13AM =1,∴V D−AEF =V F−ADE =13×1×12×3×2=1.解析:本题考查线线垂直的证明,考查三棱锥的体积的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,是中档题.(1)推导出AM ⊥AD ,从而AM ⊥平面ABCD ,由此能证明AM ⊥BD ;(2)在棱AD 上取一点N ,使得ND =1,连接NE ,NF ,可得EN//AB ,FN//AM ,从而平面ENF//平面MAB ,进而EF//平面MAB ,由V D−AEF =V F−ADE ,能求出三棱锥D −AEF 的体积.17.答案:解:(1)∵容器的底面边长为x ,则高为√3(6−x)6(0<x <6), ∴容积y =√34x 2⋅√3(6−x)6=6x 2−x 38(0<x <6); (2)由(1)得,y ′=18(−3x 2+12x)(0<x <6),令y ′=0,则x =0(舍),或x =4,∴函数y 在(0,4)上单调递增,在(4,6)上单调递减,∴当x =4时,y max =4,∴这个容器的体积最大为4.解析:本题考查了棱柱的体积和利用导数研究函数的单调性与最值,属基础题.根据已知中箱子的制作方法,y 的解析式后求导,根据单调性得到最值点即可.18.答案:解:(1)∵椭圆离心率为14,左顶点为A ,右焦点为F ,且AF =5. ∴{c a =14a +c =5, 解得:{a =4c =1 ,∴b 2=15 , ∴椭圆C 的方程为:x 216+y 215=1 . (2)由题意得:A(−4,0),F(1,0),设点P 的坐标为(x 0,y 0),则x 0216+y 0215=1. ①当x 0=1时,直线PF:x =1,与圆M 相切,则R =1−(−78)=158, 不妨取P(1,154),直线PA:y =1541−(−4)(x +4),即3x −4y +12=0. ∴点M 到直线PF 的距离为|3×(−78)+12|√32+42=158=r ,∴直线PF 与圆M 相切∴当r =158时,圆M 与直线PA,PF 都相切. ②当x 0=−4时,点P 与点A 重合,不符合题意;③当x 0≠1且x 0≠−4时,直线PA:y =y 0x 0+4(x +4),PF:y =y 0x 0−1(x −1)化简得:PA:y 0x −(x 0+4)y +4y 0=0,PF:y 0x −(x 0−1)y −y 0=0,∵圆M 与直线PA,PF 都相切 ∴|−78y +4y |0202=|−78y −y |0202=r . ∵y 0≠0,又y 02=15(1−x 0216)代入化简得:x 02−122x 0+121=0, 解得:x 0=1或x 0=121,∵−4<x 0<4且x 0≠1, ∴无解 .综上:r =158.解析:本题主要考查椭圆的标准方程与性质,以及直线与椭圆的位置关系,题目有难度.(1)由已知,{c a =14a +c =5,解得:{a =4c =1 ,∴b 2=15 ,可得椭圆的标准方程; (2)设点P 的坐标为(x 0,y 0),讨论x 0的取值,求得直线PA,PF 的方程,若圆M 与直线PA,PF 都相切,求得圆心M 与直线直线PA,PF 的距离,求得r . 19.答案:解:(1)因为S n+1=S n +2a n +5,所以a n+1=2a n +5,则a n+1+5=2(a n +5),所以a n+1+5a n +5=2a n +10a n +5=2,而a 1+5=6,所以{a n +5}是以6为首项,2为公比的等比数列.(2)由(1)得a n +5=6×2n−1=3×2n ,a n =3×2n −5,∴S n =3×(2+22+23+⋯+2n )−5n=3×2×(1−2n )1−2−5n =6×2n −6−5n ,由S n +5n =6×2n −6>128,得2n >673, 因为25>673>24,所以S n +5n >128时,n 的最小值为5.解析:本题考查数列的递推关系式以及数列求和,考查分析问题解决问题的能力,属于中档题.(1)利用已知条件推出a n+1=2a n +5,然后证明{a n +5}是等比数列;(2)求出数列的通项公式和数列的前n 项和,然后化简不等式求解即可.20.答案:解:(Ⅰ)由题意f′(x)=x2+2ax+2a−1,…(1分)因为f(x)在(0,0)点处切线方程为y=x,所以f′(0)=2a−1=1,解得a=1,经检验a=1时满足条件.…(3分)(Ⅱ)由(I)f′(x)=x2+2ax+2a−1=(x+1)(x+2a−1)令f′(x)=0,则x=−1或x=1−2a,…(4分)①当a>1时,1−2a<−1,令f′(x)>0,解得x<1−2a或x>−1;令f′(x)<0,解得1−2a<x<−1.所以函数f(x)的单调增区间为(−∞,1−2a)和(−1,+∞),单调减区间为(1−2a,−1).…(6分)②当a=1时,1−2a=−1,此时,f′(x)≥0恒成立,且仅在x=−1处f′(x)=0,故函数f(x)的单调增区间为(−∞,+∞).…(7分)③当a<1时,1−2a>−1,同理可得函数f(x)的单调增区间为(−∞,−1)和(1−2a,+∞),单调减区间为(−1,1−2a).…(9分)(Ⅲ)直线AM与f(x)的图象的交点个数是3个;…(10分)直线BM与f(x)的图象的交点个数是3个;…(11分)直线CM与f(x)的图象的交点个数是2个.…(13分)解析:(Ⅰ)求出函数的导数,根据切线方程求出a的值即可;(Ⅱ)通过讨论a的范围,解关于导函数的不等式,求出函数的单调区间即可;(Ⅲ)a=−1时,求出直线和f(x)的交点个数,写出结论即可.本题考查了切线方程问题,考查函数的单调性、最值问题,考查导数的应用以及分类讨论思想,是一道综合题.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2020学年江苏省无锡市天一中学高三11月月考数学试题注意事项:1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4.考试结束后,请将本试题卷和答题卡一并上交。
一、填空题1.设集合,则_______.2.命题:“使得”的否定为__________.3.函数的定义域为_________.4.曲线在处的切线的斜率为_________.5.若函数是偶函数,则实数______.6.已知,函数和存在相同的极值点,则________.7.已知函数.若,则实数的最小值为______.8.已知函数与函数的图象交于三点,则的面积为________.9.已知f (x )是定义在R 上的偶函数,且在区间(−,0)上单调递增.若实数a 满足f(2|a-1|)>f (),则a 的取值范围是______.10.已知0y x π<<<,且tan tan 2x y =, 1sin sin 3x y =,则x y -=______. 11.在平行四边形ABCD 中,AC AD AC BD ⋅=⋅u u u r u u u r u u u r u u u r3=,则线段AC 的长为 .12.已知,,且,则的最大值为______.13.设是自然对数的底数,函数有零点,且所有零点的和不大于6,则的取值范围为______.14.设函数().若存在,使,则的取值范围是____.二、解答题15.已知,.(1)求的值;(2)设函数,,求函数的单调增区间. 16.如图,在中,已知是边上的一点,,,求:(1)的长;(2)的面积.17.在平面直角坐标系中,已知向量,设向量,其中.此卷只装订不密封班级 姓名 准考证号 考场号 座位号(1)若,,求的值;(2)若,求实数的最大值,并求取最大值时的值.18.对于函数,若在定义域内存在实数,满足,则称为“局部奇函数”.(Ⅰ)已知二次函数,试判断是否为“局部奇函数”?并说明理由;(Ⅱ)若是定义在区间上的“局部奇函数”,求实数的取值范围;(Ⅲ)若为定义域上的“局部奇函数”,求实数的取值范围.19.如图,、是海岸线、上的两个码头,为海中一小岛,在水上旅游线上.测得,,到海岸线、的距离分别为,.(1)求水上旅游线的长;(2)海中,且处的某试验产生的强水波圆,生成小时时的半径为.若与此同时,一艘游轮以小时的速度自码头开往码头,试研究强水波是否波及游轮的航行?20.已知函数,.(1)求曲线在点处的切线方程;(2)证明:当时,曲线恒在曲线的下方;(3)当时,不等式恒成立,求实数的取值范围.2020学年江苏省无锡市天一中学高三11月月考数学试题数学答案参考答案1.【解析】【分析】直接利用集合并集的定义求解即可.【详解】因为集合,所以,故答案为.【点睛】研究集合问题,一定要抓住元素,看元素应满足的属性.研究两集合的关系时,关键是将两集合的关系转化为元素间的关系,本题实质求满足属于集合或属于集合的元素的集合.2.【解析】【分析】根据特称命题的否定是全称命题,既要改写量词,又要否定结论,可得原命题的否定形式.【详解】因为特称命题的否定是全称命题,既要改写量词,又要否定结论,故命题“ ”的否定是,故答案为.【点睛】本题主要考查特称命题的否定,属于简单题.全称命题与特称命题的否定与命题的否定有一定的区别,否定全称命题和特称命题时,一是要改写量词,全称量词改写为存在量词、存在量词改写为全称量词;二是要否定结论,而一般命题的否定只需直接否定结论即可.3.【解析】【分析】直接由根式内部的代数式大于等于0 ,分式的分母不等于0 ,列不等式求解即可得结果.【详解】要使函数有意义,则解得,函数的定义域为,故答案为.【点睛】本题主要考查具体函数的定义域、不等式的解法,属于中档题.定义域的三种类型及求法:(1)已知函数的解析式,则构造使解析式有意义的不等式(组)求解;(2) 对实际问题:由实际意义及使解析式有意义构成的不等式(组)求解;(3) 若已知函数的定义域为,则函数的定义域由不等式求出.4.1【解析】【分析】求出原函数的导函数,可得到曲线在处的导数值,根据导数的几何意义可得结果.【详解】因为曲线在处的切线的斜率就是曲线在处的导数值,由得 ,,即曲线在处的切线的斜率为1,故答案为1.【点睛】本题考查了利角导数研究曲线上某点处的切线斜率,曲线在某点处的导数值,即为曲线上以该点为切点的切线的斜率,是中档题.5.1【解析】【分析】由函数是偶函数,利用求得,再验证即可得结果.【详解】是偶函数,,即,解得,当时,是偶函数,合题意,故答案为1.【点睛】本题主要考查函数的奇偶性,属于中档题. 已知函数的奇偶性求参数,主要方法有两个,一是利用:(1)奇函数由恒成立求解,(2)偶函数由恒成立求解;二是利用特殊值:奇函数一般由求解,偶函数一般由求解,用特殊法求解参数后,一定要注意验证奇偶性.6.3【解析】【分析】(1)求出函数的导数,可得极值点,通过与有相同的极值点,列方程求的值.【详解】,则,令,得或,可得在上递增;可得在递减,极大值点为,极小值点为,因为函数和存在相同的极值点,而在处有极大值,所以,所以,故答案为3.【点睛】本题主要考查利用导数判断函数的单调性以及函数的极值,属于中档题.求函数极值的步骤:(1) 确定函数的定义域;(2) 求导数;(3) 解方程求出函数定义域内的所有根;(4) 列表检查在的根左右两侧值的符号,如果左正右负(左增右减),那么在处取极大值,如果左负右正(左减右增),那么在处取极小值. (5)如果只有一个极值点,则在该处即是极值也是最值.7.【解析】试题分析:由题意得,实数的最小值为考点:三角函数周期8.【解析】联立方程与可得,解之得,所以,因到轴的距离为,所以的面积为,应填答案。
9.【解析】试题分析:由题意在上单调递减,又是偶函数,则不等式可化为,则,,解得.【考点】利用函数性质解不等式【名师点睛】利用数形结合解决不等式问题时,在解题时既要想形又要以形助数,常见的“以形助数”的方法有:(1)借助数轴,运用数轴的有关概念,解决与绝对值有关的问题,解决数集的交、并、补运算非常有效.(2)借助函数图象的性质,利用函数图象分析问题和解决问题是数形结合的基本方法,需要注意的问题是准确把握代数式的几何意义实现由“数”向“形”的转化.10.3π【解析】试题分析:由tan tan 2x y =可得sin sin 2cos cos x yx y =.又因为1sin sin 3x y =所以1cos cos 6x y =.又因为()1cos cos cos sin sin 2x y x y x y -=+=.又因为0y x π<<<所以0x y π<-<.所以3x y π-=.本小题关键是角的和差的余弦公式的正逆方向的应用.考点:1.余弦和差公式的应用.2.解三角方程. 11.3 【解析】试题分析:由AC AD AC BD ⋅=⋅u u u r u u u r u u u r u u u r 得()0AC AD BD ⋅-=u u u r u u u r u u u r,即0AC AB ⋅=u u u r u u u r ,所以AC AB ⊥,于是AC CD ⊥,又22()AC AD AC AC CD AC AC CD AC ⋅=⋅+=+⋅=u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r ,即23AC =u u u r ,所以3AC =;考点:1.向量的数量积; 12.【解析】 【分析】利用同角三角函数的关系以及两角和的正弦公式化简可得,由此得,利用基本不等式可得结果.【详解】,,, 可得,,,,,故答案为-4.【点睛】本题主要考查同角三角函数的关系以及两角和的正弦公式、两角和的正切公式以及利用基本不等式求最值,属于难题.求最值问题往往先将所求问题转化为函数问题,然后根据:配方法、换元法、不等式法、三角函数法、图象法、函数单调性法求解,,利用基本不等式求最值,注意应用基本不等式的条件是“一正二定三相等”.13.【解析】【分析】对分四种情况讨论,分别判断函数的单调性与最值,根据单调性、最值,判断函数是否有零点,若函数有零点,判断所有零点的和是否不大于6,综合各种讨论结果,即可得结论.【详解】①,时,在单调递减,且在有一个小于0的零点;时,在单调递增,,在有一个小于1的零点,因此满足条件.②(1)时,在单调递减,在上没有零点.又,故在上也没有零点,因此不满足题意.(2)时,在上单调递减,在上单调递增,在上没有零点.又,故在上也没有零点,因此不满足题意.(3)时,在上没有零点,在上只有零点2,满足条件.(4)时,在上没有零点,在上有两个不相等的零点,且和为,故满足题意的范围是.综上所述,的取值范围为,故答案为.【点睛】本题主要考查利用导数研究函数的单调性与零点以及分类讨论思想的应用.属于难题.分类讨论思想解决高中数学问题的一种重要思想方法,是中学数学四种重要的数学思想之一,尤其在解决含参数问题发挥着奇特功效,大大提高了解题能力与速度.运用这种方法的关键是将题设条件研究透,这样才能快速找准突破点. 充分利用分类讨论思想方法能够使问题条理清晰,进而顺利解答,希望同学们能够熟练掌握并应用与解题当中.14.【解析】【分析】存在, 使,等价于,化简的解析式,判断的单调性,讨论的单调区间与区间的关系,求出在上的最小值,令最小值小于或等于零解出即可.【详解】存在, 使,,当时,,在上单调递减;当时,,在上单调递减,在上单调递增;当时,,在上单调递增,(1) 若,即时,在上单调递增,,解得;(2)若,即时,在上单调递减,在上单调递增,,解得,综上,的取值范围是,故答案为.【点睛】本题主要考查不等式有解问题以及利用导数研究函数的单调性、求函数最值,考查了分类讨论思想的应用,属于难题.不等式有解问题不能只局限于判别式是否为正,不但可以利用一元二次方程根的分布解题,还可以转化为有解(即可)或转化为有解(即可).15.(1);(2),【解析】【分析】(1)由,两边平方可得,结合,可得,即;(2)由(1)知,,利用二倍角的余弦公式以及两角和与差的正弦公式将函数化为,利用正弦函数的单调性解不等式,可得到函数的递增区间.【详解】(1)由,得,即,所以.因为,所以,所以,即.(2)由(1)知,,所以.令,得,所以函数的单调增区间是,.【点睛】本题主要考查三角函数的单调性、二倍角的正弦公式、二倍角的余弦公式以及正弦函数的单调性,属于中档题.函数的单调区间的求法:(1) 代换法:①若,把看作是一个整体,由求得函数的减区间,求得增区间;②若,则利用诱导公式先将的符号化为正,再利用①的方法,或根据复合函数的单调性规律进行求解;(2) 图象法:画出三角函数图象,利用图象求函数的单调区间.16.(1)5;(2).【解析】【分析】(1)在中,, ,由余弦定理得,解得;(2)在中,由正弦定理得,解得,利用三角形面积公式可得结果.【详解】(1)在中,由余弦定理得,解得.(2)在中,由正弦定理得,,解得,所以.【点睛】本题主要考查正弦定理、三角形面积公式以及余弦定理的应用,属于中档题. 对余弦定理一定要熟记两种形式:(1);(2),同时还要熟练掌握运用两种形式的条件.另外,在解与三角形、三角函数有关的问题时,还需要记住等特殊角的三角函数值,以便在解题中直接应用.17.(1);(2);【解析】试题分析:(1)向量数量积问题可以先求向量的坐标,再利用坐标运算;或者先符号运算进行化简,再代入坐标;(2)由向量共线得到与的关系式,用表示出,再利用导数求该函数的最大值,为了便于运算,可以求的最小值;试题解析:(1)(方法1)当,时,,(),则.(方法2)依题意,,则.(2)依题意,,,因为x y,所以,整理得,,令,则.令,得或,又,故.列表:↘极小值↗故当时,,此时实数取最大值.考点:1.向量数量积的坐标公式;2.向量共线的坐标公式;3利用导数求函数的最值;18.(1)是“局部奇函数”,理由见解析;(2);(3)【解析】试题分析:(Ⅰ)判断方程是否有解;(Ⅱ)在方程有解时,通过分离参数求取值范围;(Ⅲ)在不便于分离参数时,通二次函数的图象判断一元二次方程根的分布.试题解析:为“局部奇函数”等价于关于的方程有解.(Ⅰ)当时,方程即有解,所以为“局部奇函数”. 3分(Ⅱ)当时,可化为,因为的定义域为,所以方程在上有解. 5分令,则.设,则,当时,,故在上为减函数,当时,,故在上为增函数,. 7分所以时,.所以,即. 9分(Ⅲ)当时,可化为.设,则,从而在有解即可保证为“局部奇函数”. 11分令,1° 当,在有解,由,即,解得; 13分2° 当时,在有解等价于解得. 15分(说明:也可转化为大根大于等于2求解)综上,所求实数m的取值范围为. 16分考点:函数的值域、方程解的存在性的判定.19.(1);(2)强水波不会波及游轮的航行.【解析】【分析】(1)以点为坐标原点,直线为轴,建立直角坐标系,直线的方程为,,由点到直线距离公式得求得直线的方程为,可得交点,结合由两点间距离公式可得的长;(2) 设试验产生的强水波圆,生成小时,游轮在线段上的点处,令,求得,,利用导数证明,即恒成立,从而可得结果.【详解】(1)以点为坐标原点,直线为轴,建立直角坐标系如图所示.则由题设得:,直线的方程为,,由,及得,直线的方程为,即,由得即,,即水上旅游线的长为.(2)设试验产生的强水波圆,生成小时,游轮在线段上的点处,则,,,令,则,,,,,,由得或(舍去)+ -,时,,即恒成立,亦即强水波不会波及游轮的航行.【点睛】本题主要考查阅读能力、数学建模能力和化归思想以及直线方程、点到直线距离公式以及利用导数研究函数的单调性求函数的最值,属于难题.与实际应用相结合的题型也是高考命题的动向,这类问题的特点是通过现实生活的事例考查书本知识,解决这类问题的关键是耐心读题、仔细理解题,只有吃透题意,才能将实际问题转化为数学模型进行解答.20.(1);(2)证明见解析;(3).【解析】【分析】(1)求出,求出的值可得切点坐标,求出的值,可得切线斜率,利用点斜式可得曲线在点处的切线方程;(2)要使得当时,曲线恒在曲线的下方,即需证,不妨设,则,利用导数证明取得最大值即可得结果;(3)由题意可知,可得不等式可转化为,构造函数,分类讨论,利用导数研究函数的单调性,可证明的最大值小于零,从而可得结论.【详解】(1),,故切线方程是.(2)要使得当时,曲线恒在曲线的下方,即需证,不妨设,则,,令,恒成立,^在单调递减,v又时,;当时,,在上单调递增,在上单调递减,即当时,取得最大值,当时,,即,当时,曲线恒在曲线的下方,(3)由题意可知,不等式可转化为,构造函数,,在二次函数中,开口向下,对称轴,且过定点,解得,得(舍去),.①当时,即 (舍去)或,此时当时,;时,;当时,取得最大值,记为,由得,,而,当时,,即在上递减,当时,,即在上递增,在处取得最小值,只有符合条件,此时解得,不合条件,舍去;②当时,解得,当时,在时取得最大值,即当时,恒成立,原不等式恒成立;③当时,解得,当时,,在时取得最大值,记为,由(2)可知的图象与的图象相同,当时,,原不等式恒成立;综上所述,实数的取值范围是.【点睛】本题是以导数的运用为背景的函数综合题,主要考查了函数思想,化归思想,抽象概括能力,综合分析问题和解决问题的能力,属于较难题,近来高考在逐年加大对导数问题的考查力度,不仅题型在变化,而且问题的难度、深度与广度也在不断加大,本部分的要求一定有三个层次:第一层次主要考查求导公式,求导法则与导数的几何意义;第二层次是导数的简单应用,包括求函数的单调区间、极值、最值等;第三层次是综合考查,包括解决应用问题,将导数内容和传统内容中有关不等式甚至数列及函数单调性有机结合,设计综合题.。
