离散数学作业
离散数学练习题(含答案)

离散数学试题第一部分选择题一、单项选择题1.下列是两个命题变元p,q的小项是( C )A.p∧┐p∧q B.┐p∨qC.┐p∧q D.┐p∨p∨q2.令p:今天下雪了,q:路滑,则命题“虽然今天下雪了,但是路不滑”可符号化为( D )A.p→┐q B.p∨┐qC.p∧q D.p∧┐q3.下列语句中是命题的只有( A )A.1+1=10 B.x+y=10C.sinx+siny<0 D.x mod 3=24.下列等值式不正确的是( C )A.┐(∀x)A⇔(∃x)┐AB.(∀x)(B→A(x))⇔B→(∀x)A(x)C.(∃x)(A(x)∧B(x))⇔(∃x)A(x)∧(∃x)B(x)D.(∀x)(∀y)(A(x)→B(y))⇔(∃x)A(x)→(∀y)B(y)5.谓词公式(∃x)P(x,y)∧(∀x)(Q(x,z)→(∃x)(∀y)R(x,y,z)中量词∀x的辖域是( C )A.(∀x)Q(x,z)→(∃x)(∀y)R(x,y,z))B.Q(x,z)→(∀y)R(x,y,z)C.Q(x,z)→(∃x)(∀y)R(x,y,z)D.Q(x,z)6.设A={a,b,c,d},A上的等价关系R={<a,b>,<b,a>,<c,d>,<d,c>}∪I A,则对应于R的A的划分是( D )A.{{a},{b,c},{d}} B.{{a,b},{c},{d}}C.{{a},{b},{c},{d}} D.{{a,b},{c,d}}7.设A={Ø},B=P(P(A)),以下正确的式子是( A )A.{Ø,{Ø}}∈B B.{{Ø,Ø}}∈BC.{{Ø},{{Ø}}}∈B D.{Ø,{{Ø}}}∈B8.设X,Y,Z是集合,一是集合相对补运算,下列等式不正确的是( A )A.(X-Y)-Z=X-(Y∩Z)B.(X-Y)-Z=(X-Z)-YC.(X-Y)-Z=(X-Z)-(Y-Z)D.(X-Y)-Z=X-(Y∪Z)9.在自然数集N上,下列定义的运算中不可结合的只有( D )A.a*b=min(a,b)B.a*b=a+bC.a*b=GCD(a,b)(a,b的最大公约数)02324# 离散数学试题第1 页共4页02324# 离散数学试题 第 2 页 共4页D .a*b=a(mod b)10.设R 和S 是集合A 上的关系,R ∩S 必为反对称关系的是( A ) A .当R 是偏序关系,S 是等价关系; B .当R 和S 都是自反关系; C .当R 和S 都是等价关系; D .当R 和S 都是传递关系11.设R 是A 上的二元关系,且R ·R ⊆R,可以肯定R 应是( D ) A .对称关系; B .全序关系; C .自反关系; D .传递关系第二部分 非选择题二、填空题1.设论域是{a,b,c},则(∀x)S(x)等价于命题公式 S(a)∧S(b)∧S(c) ;(x ∃)S(x)等价于命题公式 S(a)∨S(b) ∨S(c) 。
离散数学期末考试卷

离散数学期末考试卷一、选择题(每题2分,共20分)1. 在集合论中,下列哪个选项不是集合的基本运算?A. 并集B. 交集C. 差集D. 幂集2. 命题逻辑中,下列哪个命题不是合取命题?A. (p ∧ q)B. (p ∨ q)C. (p → q)D. (p ↔ q)3. 关系R在集合A上是自反的,这意味着:A. 对于所有a∈A,(a, a)∈RB. R是对称的C. R是传递的D. R是反对称的4. 在图论中,下列哪个不是图的基本概念?A. 顶点B. 边C. 路径D. 矩阵5. 布尔代数中,下列哪个操作不是基本操作?A. 与(AND)B. 或(OR)C. 非(NOT)D. 模(MOD)6. 函数f: A → B,下列哪个条件不是函数的一一对应的必要条件?A. 对于A中不同的元素,它们的函数值不同B. 对于B中的每个元素,A中至少有一个元素映射到它C. 对于A中的每个元素,B中只有一个元素映射到它D. A和B的元素数量相同7. 在组合数学中,下列哪个是排列的定义?A. 从n个不同元素中取出r个元素的所有可能组合B. 从n个不同元素中取出r个元素的所有可能排列C. 从n个元素中取出r个元素的所有可能组合,不考虑顺序D. 从n个元素中取出r个元素的所有可能排列,考虑顺序8. 逻辑等价是指两个命题:A. 总是同时为真或同时为假B. 在所有可能的真值分配下都具有相同的真值C. 只有在某些真值分配下具有相同的真值D. 至少在一个真值分配下具有相同的真值9. 递归函数的特点是:A. 只能通过迭代来实现B. 必须有一个或多个基本情况C. 只能通过递归调用自身来实现D. 不能包含任何循环结构10. 在证明中,归纳法的基本步骤是:A. 基础步骤和归纳步骤B. 假设步骤和证明步骤C. 假设步骤和归纳步骤D. 基础步骤和假设步骤二、填空题(每空2分,共20分)11. 集合{1, 2, 3}的幂集包含元素个数为______。
离散数学作业标准答案

离散数学作业一、选择题1、下列语句中哪个就是真命题(C )。
A.我正在说谎。
B.如果1+2=3,那么雪就是黑色的。
C.如果1+2=5,那么雪就是白色的。
D.严禁吸烟!2、设命题公式))((r q p p G →∧→=,则G 就是( C )。
A 、 恒假的B 、 恒真的C 、 可满足的D 、 析取范式 3、谓词公式),,(),,(z y x yG x z y x F ∃∀→中的变元x ( C )。
A.就是自由变元但不就是约束变元 B.既不就是自由变元又不就是约束变元 C.既就是自由变元又就是约束变元 D.就是约束变元但不就是自由变元4、设A={1,2,3},则下列关系R 不就是等价关系的就是(C ) A.R={<1,1>,<2,2>,<3,3>}B.R={<1,1>,<2,2>,<3,3>,<2,3>,<3,2>}C.R={<1,1>,<2,2>,<3,3>,<1,4>}D.R={<1,1>,<2,2>,<3,3>,<1,2>,<1,3>,<2,3>,<2,1>,<3,1>,<3,2>} 5、设R 为实数集,映射σ=R →R,σ(x)= -x 2+2x-1,则σ就是( D )。
A.单射而非满射B.满射而非单射C.双射D.既不就是单射,也不就是满射 6、下列二元运算在所给的集合上不封闭的就是( D ) A 、 S={2x-1|x ∈Z +},S 关于普通的乘法运算 B 、 S={0,1},S 关于普通的乘法运算 C 、 整数集合Z 与普通的减法运算D 、 S={x | x=2n ,n ∈Z +},S 关于普通的加法运算7、*运算如下表所示,哪个能使({a,b},*)成为含幺元半群( D )b b b a a a b a * a b b b a a b a *8( A )A B C D 9、下列各组数中,能构成无向图的度数列就是( D ) A.1,1,1,2,4 B.1,2,3,4,5 C.0,1,0,2,4 D.1,2,3,3,510、一棵树有2个4度顶点,3个3度顶点,其余都就是树叶,则该树中树叶的个数就是( B )A 、8B 、9C 、 10D 、 11 11、“所有的人都就是要死的。
(完整版)离散数学题目及答案

数理逻辑习题判断题1.任何命题公式存在惟一的特异析取范式 ( √ ) 2. 公式)(q p p →⌝→是永真式 ( √ ) 3.命题公式p q p →∧)(是永真式 ( √ ) 4.命题公式r q p ∧⌝∧的成真赋值为010 ( × ) 5.))(()(B x A x B x xA →∃=→∀ ( √ )6.命题“如果1+2=3,则雪是黑的”是真命题 ( × ) 7.p q p p =∧∨)( ( √ )8.))()((x G x F x →∀是永真式 ( × ) 9.“我正在撒谎”是命题 ( × ) 10. )()(x xG x xF ∃→∀是永真式( √ )11.命题“如果1+2=0,则雪是黑的”是假命题 ( × ) 12.p q p p =∨∧)( ( √ )13.))()((x G x F x →∀是永假式 ( × )14.每个命题公式都有唯一的特异(主)合取范式 ( √ ) 15.若雪是黑色的:p ,则q →p 公式是永真式 ( √ ) 16.每个逻辑公式都有唯一的前束范式 ( × ) 17.q →p 公式的特异(主)析取式为q p ∨⌝ ( × ) 18.命题公式 )(r q p →∨⌝的成假赋值是110 ( √ ) 19.一阶逻辑公式)),()((y x G x F x →∀是闭式( × )单项选择题1. 下述不是命题的是( A )A.花儿真美啊! B.明天是阴天。
C.2是偶数。
D.铅球是方的。
2.谓词公式(∀y)(∀x)(P(x)→R(x,y))∧∃yQ(x,y)中变元y (B)A.是自由变元但不是约束变元B.是约束变元但不是自由变元C.既是自由变元又是约束变元D.既不是自由变元又不是约束变元3.下列命题公式为重言式的是( A )A.p→ (p∨q)B.(p∨┐p)→qC.q∧┐q D.p→┐q4.下列语句中不是..命题的只有(A )A.花儿为什么这样红?B.2+2=0C.飞碟来自地球外的星球。
离散数学练习题(含答案)

离散数学练习题(含答案)题目1. 对于集合 $A={1,2,3,...,10}$ 和 $B={n|n是偶数,2<n<8}$,求 $A \cap B$ 的元素。
2. 存在三个可识别的状态A,B,C。
置换群 $S_3$ 作用在状态集上。
定义四个动作:$α: A → C, β: A → B, γ: C→ A, δ: B→ C$。
确定式子,描述 $\{α,β,γ,δ\}$ 的乘法表。
3. 证明 $\forall n \in \mathbb{N}$,合数的个数不小于$n$。
4. 给定一个无向带权图,图中每个节点编号分别是$1,2,...,n$,证明下列结论:a. 如果从节点$i$到$j$只有一条权值最小的路径,则这条路径的任意子路径都是最短路径。
b. 如果从节点$i$到$j$有两条或两条以上权值相等的路径,则从$i$到$j$的最短路径可能不唯一。
答案1. $A \cap B = \{2,4,6\}$。
2. 乘法表:3. 对于任意$n$,我们可以选择$n+1$个连续的自然数$k+1,k+2,...,k+n,k+n+1$中的$n$个数,其中$k \in \mathbb{Z}$。
这$n$个数构成的$n$个正整数均为合数,因为它们都至少有一个小于它自身的因子,所以不是质数。
所以合数的个数不小于任意$n$。
4.a. 根据题意,从$i$到$j$只有一条权值最小的路径,即这条最短路径已被确定。
如果从这条路径中任意取出一段子路径,假设这段子路径不是这个节点到$j$的最短路径,那么存在其他从$i$到$j$的路径比这段子路径更优,又因为这条路径是最短路径,所以这段子路径也一定不优于最短路径,矛盾。
所以从这条路径中任意取出的子路径都是最短路径。
b. 如果从节点$i$到$j$有多条权值相等的路径,则这些路径权值都是最短路径的权值。
因为所有最短路径的权值相等,所以这些路径的权值就是最短路径的权值。
所以从$i$到$j$的最短路径可能不唯一。
《离散数学》典型例题
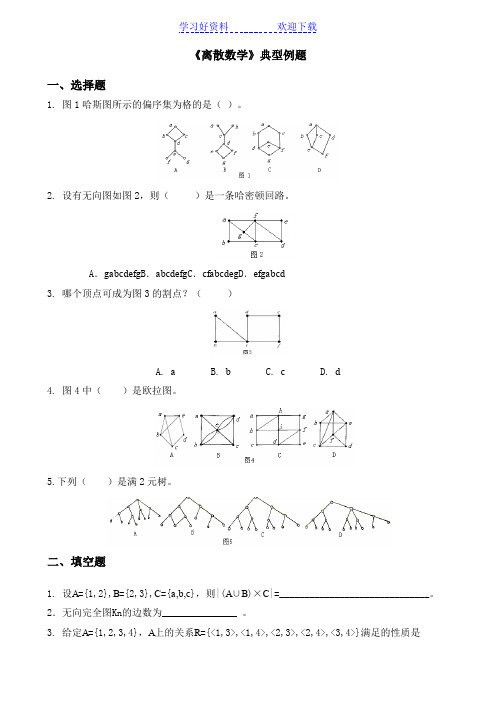
《离散数学》典型例题一、选择题1. 图1哈斯图所示的偏序集为格的是()。
2. 设有无向图如图2,则()是一条哈密顿回路。
A.gabcdefg B.abcdefg C.cfabcdeg D.efgabcd3. 哪个顶点可成为图3的割点?()A. aB. bC. cD. d4. 图4中()是欧拉图。
5.下列()是满2元树。
二、填空题1. 设A={1,2},B={2,3},C={a,b,c},则|(A∪B)×C|=______________________________。
2.无向完全图Kn的边数为_______________ 。
3. 给定A={1,2,3,4},A上的关系R={<1,3>,<1,4>,<2,3>,<2,4>,<3,4>}满足的性质是_________________________。
4. 设A ={a,b,c },F 是A 上的二元关系,F ={<a,a >,<b,b >,<c,c >},则其自反闭包为r (F )=______________________________。
5. 设A 和B 是有穷集合,|A |=m ,|B |=n ,A 到B 有_______多少个不同一对一映射。
三、判断题1.每个正整数都可以唯一地表示为素数的乘积。
( )2.集合X 上的关系R 如果是自反的、反对称的、传递的则称此关系为相容关系。
( )3.一条基本回路一定是简单回路,但一条简单回路不一定是基本回路。
( )4.树是不包含回路的连通图,在(n ,m )树中必有m=n+1( )5.一个有限群<G ,*>的阶n 一定被它的任一个子群的阶m 所等分。
( )四 、综合题1. 求公式(~P →Q) →(Q →~P)的主析取范式和主合取范式。
2. 6个人一起吃饭,围绕圆桌就餐,有多少种就座方式?如果要从4种不同的菜系中点足6道菜,问有多少种点法?3. 一个面包店里有5种不同口味的面包,要挑选8个面包,并且至少有2个奶油味面包和不超过2个咸味面包。
离散数学考试题及答案

离散数学考试题及答案一、选择题(每题5分,共20分)1. 下列哪个选项不是离散数学的研究对象?A. 图论B. 组合数学C. 微积分D. 逻辑学答案:C2. 在逻辑学中,下列哪个命题是真命题?A. 如果今天是周一,那么明天是周二。
B. 如果今天是周一,那么明天是周三。
C. 如果今天是周一,那么明天是周四。
D. 如果今天是周一,那么明天是周五。
答案:A3. 在集合论中,下列哪个符号表示集合的并集?A. ∩B. ∪C. ⊆D. ⊂答案:B4. 在图论中,下列哪个术语描述的是图中的顶点集合?A. 边B. 路径C. 子图D. 顶点答案:D二、填空题(每题5分,共20分)1. 如果一个集合A包含5个元素,那么它的子集个数是______。
答案:322. 在逻辑学中,如果命题P和命题Q都是真命题,那么复合命题“P且Q”的真值是______。
答案:真3. 在图论中,如果一个图的顶点数为n,那么它的最大边数是______。
答案:n(n-1)/24. 如果一个二叉树的深度为3,那么它最多包含______个节点。
答案:7三、简答题(每题10分,共30分)1. 请简述什么是图的连通性,并给出一个例子。
答案:图的连通性是指在图中任意两个顶点之间都存在一条路径。
例如,在一个完全图K3中,任意两个顶点之间都可以通过一条边直接连接,因此它是连通的。
2. 解释什么是逻辑蕴含,并给出一个例子。
答案:逻辑蕴含是指如果一个命题P为真,则另一个命题Q也必须为真。
例如,命题P:“如果今天是周一”,命题Q:“明天是周二”。
如果今天是周一,那么根据逻辑蕴含,明天必须是周二。
3. 请描述什么是二叉搜索树,并给出它的一个性质。
答案:二叉搜索树是一种特殊的二叉树,其中每个节点的左子树只包含小于当前节点的数,右子树只包含大于当前节点的数。
它的一个性质是中序遍历可以得到一个有序序列。
四、计算题(每题15分,共30分)1. 给定一个集合A={1, 2, 3, 4, 5},请计算它的幂集,并列出所有元素。
离散数学试题总汇及答案

离散数学试题总汇及答案一、单项选择题(每题2分,共20分)1. 在集合{1,2,3}和{3,4,5}的笛卡尔积中,元素(2,4)是否存在?A. 存在B. 不存在C. 无法确定D. 以上都不对2. 函数f: A→B是单射的,当且仅当对于任意的a1, a2∈A,若f(a1)=f(a2),则a1=a2。
A. 正确B. 错误C. 无法确定D. 以上都不对3. 以下哪个命题是真命题?A. 所有的狗都会游泳。
B. 有些狗不会游泳。
C. 所有的狗都不会游泳。
D. 以上都不是真命题。
4. 如果p蕴含q为假,那么p和q的真值可以是?A. p为真,q为假B. p为假,q为真C. p为真,q为真D. p为假,q为假5. 以下哪个图是连通图?A. 一个孤立点B. 两个不相连的点C. 一个包含三个点且每对点都相连的图D. 以上都不是连通图6. 在有向图中,如果存在从顶点u到顶点v的路径,那么称v是u的后继顶点。
A. 正确B. 错误C. 无法确定D. 以上都不对7. 以下哪个等价关系是集合{1,2,3}上的?A. {(1,1), (2,2), (3,3)}B. {(1,2), (2,1), (2,2), (3,3)}C. {(1,1), (2,3), (3,2), (3,3)}D. {(1,1), (2,2), (3,3), (1,3)}8. 以下哪个命题是假命题?A. 所有的鸟都有羽毛。
B. 有些鸟不会飞。
C. 所有的哺乳动物都是温血动物。
D. 以上都不是假命题。
9. 在图论中,一个图的生成树是包含图中所有顶点的最小连通子图。
A. 正确B. 错误C. 无法确定D. 以上都不对10. 如果命题p和q互为逆否命题,那么它们具有相同的真值。
A. 正确B. 错误C. 无法确定D. 以上都不对二、填空题(每题2分,共20分)1. 集合{1,2,3}和{3,4,5}的并集是________。
2. 函数f: A→B是满射的,当且仅当对于任意的b∈B,存在a∈A,使得f(a)=________。
苏XI友离散数学作业(13篇)

作业6
补充作业:用等值演算证明下列等值式. (1)∃x∃y¬ (F(x)∧¬ G(y))∀xF(x)→∃yG(y). 证.∃x∃y¬ (F(x)∧¬ G(y))
∃x∃y(¬ F(x)∨G(y))或 ∃x(¬ F(x)∨∃yG(y)) ∃x∃y(F(x)→G(y)) ∃x¬ F(x)∨∃yG(y) ∃x(F(x)→∃yG(y)) ¬ ∀xF(x)∨∃yG(y) ∀xF(x)→∃yG(y). ∀xF(x)→∃yG(y)
2020
感谢 观看
*北京林业大学信息学院 苏喜友
作业6
P55-2.15 求下列各式的前束范式, 要求使用自 由变项换名规则.
(2)∃x(F(x)∧∀yG(x,y,z))→∃zH(x,y,z) 解.∃x(F(x)∧∀yG(x,y,z))→∃zH(x,y,z)
∃x(F(x)∧∀yG(x,y,u))→∃zH(v,w,z) ∃x∀y(F(x)∧G(x,y,u))→∃zH(v,w,z) ∀x∃y((F(x)∧G(x,y,u))→∃zH(v,w,z)) ∀x∃y∃z((F(x)∧G(x,y,u))→H(v,w,z)).
作业1
P33-1.7 (7)设A=(p∨¬ p)→((q∧¬ q)∧¬ r)
p q r ¬ p ¬ q ¬ r p∨¬ p q∧¬ q (q∧¬ q)∧¬ r A
000 1 1 1 1
0
0
0
001 1 1 0 1
0
0
0
010 1 0 1 1
0
0
0
011 1 0 0 1
0
0
0
100 0 1 1 1
0
*北京林业大学信息学院 苏喜友
作业5
(5)任何金属都可以溶解在某种液体中. 设M(x):x是金属, L(x):x是液体, R(x,y):x 溶解在y中. 符号化为: ∀x(M(x)→∃y(L(y)∧R(x,y))).
离散数学试题及答案解析

离散数学试题及答案解析一、选择题1. 在集合{1,2,3,4}中,含有3个元素的子集有多少个?A. 4B. 8C. 16D. 32答案:B解析:含有3个元素的子集可以通过组合数公式C(n, k) = n! / [k!(n-k)!]来计算,其中n为集合的元素个数,k为子集中的元素个数。
在本题中,n=4,k=3,所以C(4, 3) = 4! / [3!(4-3)!] = 4。
2. 下列哪个命题是真命题?A. 所有偶数都是整数。
B. 所有整数都是偶数。
C. 所有整数都是奇数。
D. 所有奇数都是整数。
答案:A解析:偶数是指能被2整除的整数,因此所有偶数都是整数,选项A是真命题。
选项B、C和D都是错误的,因为并非所有整数都是偶数或奇数。
二、填空题1. 逻辑运算符“非”(NOT)的真值表是:当输入为真时,输出为______;当输入为假时,输出为真。
答案:假解析:逻辑运算符“非”(NOT)是一元运算符,它将输入的真值取反。
如果输入为真,则输出为假;如果输入为假,则输出为真。
2. 命题逻辑中,合取词“与”(AND)的真值表是:当两个命题都为真时,输出为真;否则输出为______。
答案:假解析:合取词“与”(AND)是二元运算符,只有当两个命题都为真时,输出才为真;如果其中一个或两个命题为假,则输出为假。
三、简答题1. 解释什么是等价关系,并给出一个例子。
答案:等价关系是定义在集合上的一个二元关系,它满足自反性、对称性和传递性。
例如,考虑整数集合上的“同余”关系。
对于任意整数a,b,如果a和b除以同一个正整数n后余数相同,则称a和b模n同余。
这个关系是自反的(a同余a),对称的(如果a同余b,则b同余a),并且是传递的(如果a同余b且b同余c,则a同余c)。
2. 什么是图的连通性?一个图是连通的需要满足什么条件?答案:图的连通性是指在无向图中,任意两个顶点之间都存在一条路径。
一个图是连通的需要满足以下条件:图中的任意两个顶点v和w,都可以通过图中的边相互到达。
离散数学课程作业(3)

《离散数学》课程作业(3)——第三部分图论一、填空题1、一个无向图表示为G=(P,L),其中P是____________的集合,L是________________________的集合,并且要求________________。
2、设G=(P,L)是图,如果G是____________,并且____________,则G是树。
如果根树T的每个点v最多有两棵子树,则称T为____________。
3、设G是完全二叉树,G有15个点,其中8个叶结点,则G的总度数为____________,分枝点数为____________。
二、单项选择题1、已知图G的相邻矩阵为,则G有()。
A. 5点,8边;B. 6点,7边;C. 5点,7边;D. 6点,8边2、设图G是有6个顶点的连通图,总度数为20,则从G中删去()边后使之变成树。
A .10;B. 5;C. 3;D. 23、已知图G的相邻矩阵为,则G的边数与分枝数为()。
A. 5,3 ;B.4,2;C.5,1;D.6,4三、计算题1、设无向图个G=(P,L),P={v1,v2,¼v6},L={(v1,v2),(v2,v2),(v2,v4),(v4,v5),(v3,v4),(v1,v3),(v3,v1)}。
(1)画出G的图形;(2)求出G中各顶点的度及奇数度顶点的个数。
2、设T是如下的二叉树,试写出对T先根遍历,中根遍历和后根遍历时访问所有点的顺序。
(从上到下,从左至右,节点依次为A、B、C、…、O、P)3、求图中A到其余各顶点的最短路径,并写出它们的权。
4、用迪克斯特拉算法求出下面有限权图中从A到D的最短路,要求用图示方法给出求解过程。
5、设有5个城市v1,v2,v3,v4,v5,任意两城市之间铁路造价如下:(以百万元为单位)w(v1,v2)=4,w(v1,v3)=7,w(v1,v4)=16,w(v1,v5)=10,w(v2,v3)=13,w(v2,v4)=8,w(v2,v5)=17,w(v3,v4)=3,w(v3,v5,)=10,w(v4,v5)=12试求出连接5个城市的且造价最低的铁路网。
《离散数学》作业

A. 0
B. 1
C. 2
D. 不能确定
18.设无向图 G 有 16 条边且每个顶点的度数都是 2,则图 G 有(D )个顶点。
A. 10
B. 4
C. 8
D. 16
19.A,B,C是三个集合,则下列哪几个推理正确:(A)
A. A B,B C=> A C
B. A B,B C=> A∈B C. A∈B,B∈C=> A∈C
(3),(4)
(6) Q→S
前提
(7) S
(5),(6)
(8) R S
CP,(1),(8)
2.A→(C B),B→ A,D→ C => A→ D
第 5 页 共 13 页 在您完成作业过程中,如有疑难,请登录学院网站“辅导答疑”栏目,与老师进行交流讨论!
证明:(1) (2) (3) (4) (5) (6) (7) (8) (9)
A. m-n+2
B. n-m-2
C. n+m-2
D. m+n+2。
24.设无向图 G 有 18 条边且每个顶点的度数都是 3,则图 G 有( D )个顶点。
A. 10
B. 4
C. 8
D. 12
25、A,B,C 是三个集合,则下列哪个推理正确?( 1 )
(1) A B,B C A C
(2) A B,B C A B
D. xy(y=2x) ( T )
3.有 n 个结点的树,其结点度数之和是( 2n-2
)。
4.举出集合 A 上的既是等价关系又是偏序关系的一个例子。( IA ) 5.群<G,*>的等幂元是( 单位元 ),有( 1 )个。
6.下面给出的集合中,哪一个不是前缀码( A )。
离散数学期末考试题及答案

离散数学期末考试题及答案一、单项选择题(每题2分,共20分)1. 集合{1, 2, 3}的子集个数是:A. 3B. 4C. 8D. 2^3答案:C2. 命题逻辑中,命题p∧(q∨¬p)的真值表中,真值个数为:A. 1B. 2C. 3D. 4答案:B3. 函数f: A→B中,若A={1, 2},B={a, b},则f是单射的必要条件是:A. |A| ≤ |B|B. |A| < |B|C. |A| = |B|D. |A| > |B|答案:B4. 以下哪个图是无向图?A. 有向图B. 无向图C. 完全图D. 树答案:B5. 在图论中,一个图的生成树是:A. 包含图中所有顶点的最小连通子图B. 包含图中所有边的最小连通子图C. 包含图中所有顶点和边的连通子图D. 包含图中所有顶点和边的无环子图答案:A6. 以下哪个命题是真命题?A. 所有偶数都是整数B. 所有整数都是偶数C. 所有奇数都是整数D. 所有整数都是奇数答案:A7. 在布尔代数中,以下哪个运算符表示逻辑与?A. ∨B. ∧C. ¬D. →答案:B8. 有限状态机中,状态的转移是由以下哪个决定的?A. 当前状态B. 输入符号C. 当前状态和输入符号D. 输出符号答案:C9. 以下哪个是图的遍历算法?A. 深度优先搜索B. 广度优先搜索C. 动态规划D. 分治算法答案:A10. 在集合论中,以下哪个符号表示集合的交集?A. ∪B. ∩C. ×D. ÷答案:B二、填空题(每题2分,共20分)1. 集合{1, 2, 3}的幂集是{∅, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3}},其中包含元素个数最多的子集是_。
答案:{1, 2, 3}2. 在命题逻辑中,如果p和q都为真,则p∨q的真值为_。
答案:真3. 函数f: A→B中,若A={1, 2},B={a, b, c},则f是满射的必要条件是_。
离散数学作业

第一章 命题逻辑的基本概念一、单项选择题1.下列语句中不是命题的有( ).A 9+5≤12 B. 1+3=5 C. 我用的电脑CPU 主频是1G 吗D.我要努力学习。
2. 下列语句是真命题为( ).A. 1+2=5当且仅当2是偶数B. 如果1+2=3,则2是奇数C. 如果1+2=5,则2是奇数D. 你上网了吗3. 设命题公式)(r q p∧→⌝,则使公式取真值为1的p ,q ,r 赋值分别是( ) 0,0,1)D (0,1,0)C (1,0,0)B (0,0,0)A ( 4. 命题公式q q p →∨)(为 ( )(A) 矛盾式 (B) 仅可满足式 (C) 重言式 (D) 合取范式5. 设p:我将去市里,q :我有时间.命题“我将去市里,仅当我有时间时”符号化为为( )q p q p q p p q ⌝∨⌝↔→→)D ()C ()B ()A (6.设P :我听课,Q :我看小说. “我不能一边听课,一边看小说”的符号为( )A. Q P ⌝→ ;B. Q P →⌝;C. P Q ⌝∧⌝ ;D. )(Q P ∧⌝二、判断下列语句是否是命题,若是命题是复合命题则请将其符号化(1)中国有四大发明。
(2)2是有理数。
(3)“请进!”(4)刘红和魏新是同学。
(5)a+b(6)如果买不到飞机票,我哪儿也不去。
(8)侈而惰者贫,而力而俭者富。
(韩非:《韩非子显学》)(9)火星上有生命。
(10)这朵玫瑰花多美丽啊!二、将下列命题符号化,其中p:2<1,q:3<2(1)只要2<1,就有3<2。
(2)如果2<1,则32。
(3)只有2<1,才有32。
(4)除非2<1,才有32。
(5)除非2<1,否则32。
(6)2<1仅当3<2。
三、将下列命题符号化(1)小丽只能从筐里拿一个苹果或一个梨。
(2)王栋生于1992年或1993年。
四、设p、q的真值为0;r、s的真值为1,求下列各命题公式的真值。
离散数学考试试题及答案

离散数学考试试题及答案一、单项选择题(每题5分,共20分)1. 在离散数学中,以下哪个概念不是布尔代数的基本元素?A. 逻辑与B. 逻辑或C. 逻辑非D. 逻辑异或答案:D2. 下列哪个命题不是命题逻辑中的命题?A. 所有学生都是勤奋的B. 有些学生是勤奋的C. 学生是勤奋的D. 勤奋的学生答案:D3. 在集合论中,以下哪个符号表示集合的并集?A. ∩B. ∪C. ⊆D. ⊂答案:B4. 以下哪个图不是无向图?A. 简单图B. 完全图C. 有向图D. 多重图答案:C二、填空题(每题5分,共20分)1. 如果一个命题的逆否命题为真,则原命题的________为真。
答案:逆命题2. 在图论中,如果一个图的任意两个顶点都由一条边连接,则称这个图为________图。
答案:完全3. 一个集合的幂集是指包含该集合的所有________的集合。
答案:子集4. 如果一个函数的定义域和值域都是有限集合,那么这个函数被称为________函数。
答案:有限三、简答题(每题10分,共30分)1. 请简述什么是图的欧拉路径。
答案:欧拉路径是一条通过图中每条边恰好一次的路径。
2. 解释什么是二元关系,并给出一个例子。
答案:二元关系是指定义在两个集合之间的关系,它将第一个集合中的元素与第二个集合中的元素联系起来。
例如,小于关系就是一个二元关系。
3. 请说明什么是递归函数,并给出一个简单的例子。
答案:递归函数是一种通过自身定义来计算函数值的函数。
例如,阶乘函数就是一个递归函数,定义为:n! = n * (n-1)!,其中n! = 1当n=0时。
四、计算题(每题10分,共30分)1. 计算以下逻辑表达式:(P ∧ Q) ∨ ¬R答案:首先计算P ∧ Q,然后计算¬R,最后计算两者的逻辑或。
2. 给定集合A = {1, 2, 3},B = {2, 3, 4},求A ∪ B。
答案:A ∪ B = {1, 2, 3, 4}3. 已知函数f(x) = 2x + 3,求f(5)。
《离散数学》试卷及答案精选全文完整版

H(x):x是身体健康的;
S(x):x是科学家
C(x):x是事业获得成功的人
置换规则。
3、设集合|A|=101,S ,且|S|为奇数,则这样的S有2101/2或2100个。
4、设mi是公式G的的主析取范式中的一个极小项,则mi的对偶式不一定是(填“是”/“不是”/“不一定是” ) G的主合取范式中的一个极大项。
5、由3个元素组成的有限集上所有的等价关系有5个
6、给定解释I如下: (1) Di:={2,3}; (2) a=3; (3) 函数f(x)为f(2)=2,f(3)=3; (4) 谓词:F(x)为F(2):=1,F(3):=0;G(x,y)为当i=j时,G(i,j):=1;当i≠j时,G(i,j):=0;其中i,j=2,3;
ac>0并且cu>0
若u>0,则c>0,a>0,因此有ac>0;
若u<0,则c<0,a<0, 也有ac>0;
因此有(a+bi)R(u+vi)
所以R在C*是传递的。所以R是C*上的等价关系。
2、在一阶逻辑自然推理系统F中,构造下面推理的证明。个体域是人的集合。
“每位科学家都是勤奋的,每个勤奋又身体健康的人在事业中都会获得成功。存在着身体健康的科学家。所以,存在着事业获得成功的人。”(15分)
2.设A={1,2,3…10},定义A上的二元关系R={<x,y>|x,y∈A∩x+y=10},试讨论R关于关系的五个方面的性质并说明理由(5分)
解答:R={<1,9>,<9,1>,<2,8>,<8, 2 >,<3,7>,<7,3>,<4,6>,<6, 4 >,<5, 5 >}
离散数学作业标准答案

一、选择题1、以下语句中哪个是真命题〔C 〕. A.我正在说谎.B.如果1+2=3,那么雪是黑色的.C.如果1+2=5,那么雪是白色的.D.严禁吸烟!2、设命题公式G p 〔p 〔q r 〕〕,那么6是〔C 〕. A.恒假的 B.恒真的 C,可满足的D.析取范式 3、谓词公式F 〔x,y,z 〕 x yG 〔x, y,z 〕中的变元 x 〔 C 〕. A.是自由变元但不是约束变元 B.既不是自由变元又不是约束变元 C.既是自由变元又是约束变元 D.是约束变元但不是自由变元5、设R 为实数集,映射=RR 〔x 〕 = -x 2+2x-1,那么是〔D 〕A.单射而非满射B.满射而非单射C.双射D.既不是单射,也不是满射6、以下二元运算在所给的集合上不封闭的是〔 D 〕A. S={2x-1|x Z +〕, S 关于普通的乘法运算B. S={0 1}, S 关于普通的乘法运算C.整数集合Z 和普通的减法运算D. S={x | x=2, n Z +}, S 关于普通的加法运算7、*运算如下表所示,哪个能使〔{a,b}, *〕成为含幺元半群〔 D 〕离散数学作业4、设人={1, 2, 3},那么以下关系 R 不是等价关系的是〔C 〕 A. B. C. D.R={<1, 1>, R={<1, 1> R={<1, 1> R={<1, 1><3, <2, 2>, <3, <2, 2>, <3, <2, 2>, <3, <2, 2>, <3, 1) <3, 2>}3>}3) <2, 3>, 3> <1, 4>} 3>, <1 , 2>,<3, 2>} <1 3)<2, 3>, <2,1)A B8、以下图中是欧拉图的是〔 A 〕9、以下各组数中,能构成无向图的度数列是( D )A. 1,1,1,2,4B. 1,2,3,4,5C. 0,1,0,2,4D. 1,2,3,3,510、一棵树有2个4度顶点,3个3度顶点,其余都是树叶,那么该树中树叶的个数是(B )A .8 B.9 C. 10 D. 1111、〞所有的人都是要死的.苏格拉底是人,所以苏格拉底是要死的. 〞那么该句话(B )A.不是命题B.是真命题C.是假命题D.是悖论12、一个公式在等价意义下,下面哪个写法是唯一的( C )0A.析取范式B.合取范式C.主析取范式D.以上答案都不对13、设论域E={a, b},且P(a,a)=1 P(a,b)=0 P(b,a)=1 P(b,b)=0 那么在以下公式中真值为1的是(D )A.$x"yP(x,y)B."x"yP(x,y)C."xP(x,x)D. "x$yP(x,y)14、设集合A={1,2, 3 }, A 上的关系R={<1, 1 >,<2, 2 > ,}那么R 不具有(A ) 性质.A.自反卜t B对称卜t C传递性D.反对称性15、设集合A={a,b,c,d},B={1,2,3,4}那么从A到B 的函数f={<a,2>,<b,1>,<c,3 >,<d,2 >} 是(D ).A.双射函数B.单射函数C.满射函数D.即不是满射又是不是单射函数16、下面给出的一阶逻辑等值式中,(B )是错的.A. x(A(x) B(x)) xA(x) xB(x);B. x(A(x) B(x)) xA(x) xB(x);C. xA(x) x( A(x));D.A xB(x) x(A B(x)).17、以下各代数系统中,不含零元素的是(C )A. M n(R), , M n(R)是全体n阶实矩阵集合, 是矩阵乘法运算B. p(S), , p(S)是集合S的募集合, 是集合的并运算.C. R, , R是有理数集, 是数的加法运算.D. I, , I是整数集, 是数的乘法运算.(A) {群}{独异点}{半群}(B) {独异点}{半群}{群}(C) {独异点}{群}{半群}(D) {半群}{独异点}{群}22.设集合A={1,2, 3 }, A上的关系R={<1, 1 >,<2, 2 >,<3,3>}那么R不具有以下性(D)质中的aa ab ba b a bab25.(A)设P:张三可以做这件事,b(B)Q:李四可以做这件事.命题(D)〞张三或李四可以18、设图G是有6个顶点的连通图,后使之变成树.总度数为20,那么从G中删去(B )边19、A .10 B. 5 C. 3在具有n个结点的无向连通图中,D. 2 (B )0A.恰好有n条边C.最多有n条边B.恰好有n-1条边D.至少有n条边20、21.半群、群及独异点的关系是卜列图是欧拉图的是(C )做这件事〞符号化为 ........................(A) P Q (B) P ~ Q (C) P Q ......... ( A(D) ~ (~ P ~ Q) 26. 27. G 是连通的平面图,有5个顶点,6个面,那么G 的边数为 ............ (C) (A) 6 (B) 5 (C) 9 (D) 11 28. 以下句子中是命题的有 ................................... (D) (A)上课时请不要说话! (B)我在说谎.(C)你吃饭了吗(D)上海是中国的 首都. (C) 1 (q-q)Ap (D) 30 .图 的生成子图为 ................ 0^0(A) (B) (C) 31 .如以下图所示的有界格中,元素 b 的补元是(D)(A) a q . (B) 0(C) c 」 (D) d 32 .设人二缶口©,那么卜列是集合A 的划分的是(D) (A) {{b,c},{c}} (B) {{a,b},{a,c}} (C) {{a,b},c} 33 .整数集合Z 上“〈〞关系的自反闭包是关系 (A) = (B)w (C)> 34 .以下式子正确的选项是(B) (A) C (B) (C){ } 35 .设i 是虚数,•是复数乘法运算,那么 G=<{1,-1,i,-i}, • 是(A) (A) <{1}, • > (B)〈{-1}, •〉 (C) <{i} 36 .集合A={1, 2}的募集P(A)的基数是 ................1 (qVi p)一(pAi p) …・…(C )(D) (D) {{a},{b,c}} (D ) (D) <(D){ }C>是群,卜列是G 的子群,〉 (D) <{-i}, •〉 ..................... (D )29.以下命题公式中,为永假式的是(C )(A)「(pVq V r) (B) 61 p)—i p(A) 0 (B) 1 (C) 2 (D) 437 .以下哪个联结词运算不可交换............................ (A)(A) 一(B) (C) V (D) A38 .设集合A={1, 2, 3,…,10},以下定义的哪种运算关于集合A是不封闭的(D )(A) x*y=max{x,y} (B) x*y=(x,y)即x,y 的最大公约数(C) x*y=min{x,y} (D) x*y=[x,y]即x,y 的最小公倍数39 .设R为实数集,函数f: R- R, f(x)=2x,那么£是(B )A.满射函数B,单射函数C,双射函数D,非单射非满射40 .假设<人*>是一个代数系统,且满足结合律,那么<人*>必为...... (A )(A)半群(B)独异点(C)群(D)交换群41 .设R是A上的等价关系,即R是................................... (D)(A)反自反的,对称的,传递的(B)自反的,反对称的,传递的(C)反自反的,反对称的传递的(D)自反的,对称的传递的42 .以下哪一组命题公式是等价的.................................. (B )(A)〜P 〜Q, P Q (B) A (B A),〜A (A - B)(C) Q (P Q),〜Q (P Q) (D)〜A (A B) , B43 .设S={0,1}那么S .......................................................................... ( A )(A)在普通乘法下封闭,在普通加法下不封闭(B)在普通加法和乘法下都封闭;(C)在普通加法下封闭,在普通乘法下不封闭;(D)在普通加法和乘法下都不封闭;44 .下面谓词公式是前束范式的是(A ). x y z(B(x, y) A(z)) B. x y(B(x, y)A. x y z(B(x, y) A(z)) D. x(B(x, y) yB(y))C45 .整数集合Z上关系的自反闭包是关系(D)(A)= (B)w (C)>(D)<11.以下图既是欧拉图,又是哈密顿图的是(A)(B)(C)(D)47.以下式子正确的选项是(设A(x):x 是运发动,B(x):x 是强壮的.命题“没有一个运发动不是强壮的〞可符号化为设集合 A={1,2,3}±两个二元关系为 R I ={< 1,3>, <2,1>, <3,2>}和 於={<1,2>, <2,3>, <3,1>},那么 R?=t(R)5、集合Z m ={[0],[1],[2],…,[m-1]},在Z m 上定义运算+m 为:对任意的[i] , [j] €Z m 有:[i]+m [j]=[ (i+j) (modm)],那么<加,+m >的幺元是[0] e Zm 的逆元是—[m-i] 6、无向图G 如图1所示,那么G 的点连通度为 146.设A={a,b,c}, A 上二元关系 包S(R 足(C ) R={ <a,a>, <b,b> , <a,c> },那么关系 R 的对称闭(A) RUIA(B) R (C) RJ { <c,a> } (D) RAIA(A) e (B) (C) { } (D) { }C48 .以下句子是命题的是( (A)水开了吗(B)这朵花多好看呀! 49 .函数f : A B 可逆的充要条件是(A) A=B (B)A 与B 有相同的基数二、填空题 (C) 2是常数.(D)我正在说谎D )(Cf 为满射 (D)f 为双射1、公式(PA QH(RV S 滇值表中共有 16, 种真值指派.2、 3、是公式xF(y,x) yG(y)的前束范式.4、 R I7、有向图D 如图2所示,那么有向图D 的邻接矩阵A=, D 中长度为2的回路有 2 条. 8、设p : 1+1=5, q :明天是阴天.那么命题“只要1+1=5,那么明天是阴天〞可符号化为,其真值为 1.9、设F(x):x 是兔子,G y : y 是乌龟,H (x, y): x 比y 跑得快,那么“并不是所有的兔子都比乌龟跑得快.〞可符号化为1 2 110、设有向图D 的邻接矩阵A(D)= 00 10 0 0 0 0 1x y x y 4 一y { ,那么(Z 4,)的生成元x y 4 x y 4是 1 或 3 .12、具有16个结点的完全无向图其边数一定为120 条13、设集合A {2,3,4,6,8,12,24}, R 为A 上的整除关系,集合A 中的极大元是在;极小元建工;14、整数加群的幺元是__0 .15假设人={1,2,3 }, x, y A,x y min{ x, y},那么* 的运算表为 16 .设 A={a,{a}}, A 的募集 P(A)是.17 .设G 是n 阶无向完全图,那么该图的边数为 . 18 .在一棵根树中,仅有一个结点的入度为 _0_,称为树根,其余结点的入度均为 1.19 .设 A 、B 是两个集合,其中 A={ a,b,c},B={ 1,2},那么 AX B= 20 .设个体域A={a,b},公式xP(x) xS(x)在A 中消去量词后应是,那么长度为2的通路有10条.1 011、设 Z 4 {0,1,2,3}, x图221 .设M(x):x 是人,D(x):x 是要死的,那么命题“所有的人都是要死的〞可符号化 为,其中量词的辖域是22 .画出完全图K 5 __________________________________________________________________________ 23 .设A={a,b,c}那么AX A 中的元素有 9________ 上.24 .设集合 A={1,2,3 ,4}R 为 A 上的一个二元关系,R={<1,1>,<1,2>, <2,1>,<3,3加R 的关系矩阵为:25 .设G 是m 阶有向完全图,那么该图的边数为 m(m-1)26 .设P(x): x 非常聪明;Q(x):x 非常能干;a :小李;那么命题“小李非常聪明和 能干〞的为谓词表达式为.27 .设 A, B 是两个集合,A={1,2, 3,4}, B={2, 3, 5},那么 A B=[1.4.5}. 28 .公式A 一( x)B(x ?勺前束范式为29 . 一个简单连通无向图有n 个节点,它的边数至少有 n-1条.30 .画出完全图K 3,3 ___________________________________________三、计算题1、求公式(p q) r 的主析取范式和主合取范式 解:方法一(等值演算法)(p q) r((p q) r) (r (p q))((p q) r) ( p q r)(p q r) ( p r) (q r)r) ( p q r) ( p q r) (p q r)m 〔 m 3 m 4 m 7方法二(真值表法) 公式(p q) r 真值表如下:((P q) r) (( p q)r)(p q根据真值表可以得到主析取范式为:m1 m3 m4 m72、列出命题公式((p q) p) p的真值表.解:3、设集合A= 1,2,3 , R 为A上的二元关系,R=£ 1,2>< 3,1 >,<2,3>},求R2,r(R) , s(R), t(R)的集合表达式.解:由于R={<1,2>,<2,3>,<3,1>所以R2={<1,3>,<2,1>,<3,2>}r(R)={<1,1>,<2,2>,<3,3>,<1,2>,<2,3>,<3,1>}s(R)={<1,2>,<2,1>,<2,3>,<3,2>,<3,1>,<1,3>}t(R)=E A4、在偏序集<A,0 >中,其中A={1,2,3,4,6,8,12,14! <是A中的整除关系,求集合D={2,3,4,6加勺极大元,极小元,最大元,最小元,上界,下界,最小上界和最大下界. 解:极大元:4, 6;极小元:2, 3;最大元:无;最小元:无;上界:12;下界1 :最小上界:12;最大下界:15、求带权为1,3, 6, 7,8,11的最优二叉树,编一个最正确2元前缀码,并求其权数解:最优二叉树如以下图所示:编码:1: 0000 ; 3: 0001 ; 6: 001; 7: 10; 8: 11; 11: 01最小生成树的权数为其权W(T)=(1+3)*4+6*3+(11+7+8)*12=866、用Kruskal算法求以下权图的最小生成树,并求最小生成树的权数,要求写出解的过程.解:取数的由小到大的排列为1<2<3<4<5<7<9B 2C最小生成树如下图:最小生成树的权数为其权W(T)=127、设A={a,b,c,d},R={<a,b>,<b,a>,<b,c>,<c,d>就用关系图表示R 及R 的传递闭包.8、设G=< a>是10阶循环群,求出G的所有子群.解:由于10的正因子是1,2,5, 10所以G的子群有4个,分别是< a10>={e}< a5>={e, a5}< a2>={e, a2, a4, a6, a8 }< a>=G9、(1)在一棵有2个2度顶点,4个3度顶点,其余顶点都是树叶的无向树中, 应该有几片树叶(2)画出两棵非同构的满足(1)中顶点度数的无向树T1和T2解:(1)设树有n个顶点,那么有n-6片树叶根据握手定理可知2 2 43 (n 6) 2(n 1)于是n=12因此有6片树叶.⑵两棵非同构的树为T1 T210、A、B、C D四个人中要派两个人出差,需满足如下条件:(1)假设A去,那么C和D中要去一人;(2) B和C不能都去;(3) C去那么D要留下.问有几种派法如何派解:用A、B、G D分别表示A去,B去,C去,D去出差,那么命题符号化如下:(1) A- (COD)(.表示异或,可用其它符号)(2) (BA[ C) V ([ BA C)(3) 81 D出差的派法要同时满足上述三个条件,故G= (A一(COD) A ( (BA n C) V (n BA C)) A ( C-n D)列该公式的真值表如下:(可以去掉所有不满足条件的,只剩6种情况如下:)0 0 1 1 1 1 0 0 0 1 0 1 1 1 1 1 0 1 1 0 1 0 1 0 1 0 0 1 0 1 1 0 1111111 1 0 0 0 1 1 0 由真值表知有两种派法 A, C 去或B, D 去.11、设A={1,2,3,6,12}对于整除关系构成偏序集 R (1)作出偏序关系R 的哈斯图(2)令B={2,3,6},求B 的最大,最小元,极大、极小元,上界,最小上界,下界, 最大下界.12、一棵树有2个4度结点,3个3度结点,其余结点是叶子,求该树的叶子数. 解:设树的叶子数为x,于是T 中有x+2+3个顶点,有(x+2+3)-1条边,x yd(v )由握手定理知T 中所有顶点的度数之和i 1=2[(x+2+3)-1]2*4+3*3+x*1=2*[(2+3+x)-1]X=913、求带权为2, 3, 5, 7,8,9的最优二叉树,并编一个最正确2元前缀码.解:最优二叉树如以下图所示:编码:2: 0000; 3: 0001 5: 001 7: 10 8: 11 9: 01G 如下,求G 的最小生成树T 及T 的权总和,要求写出解的过程17解:取数的由小到大的排列为 1 < 3< 4< 8< 9< 15< 16<17<20<23<28<3614、带权无向图最小生成树如下图:最小生成树的权数为其权W(T)=4815、求](P-Q) (P-[ Q)的主合取范式并给出所有使命题为真的赋值.解:原式(](P-Q户(P-i Q))A((P-i Q)fi (P^Q))((P-Q)V (P-1 Q))A(i (P-[ Q)V] (P^Q))(i PVQVn PV[ Q)A(i 〞 PV n Q)V(PA n Q))(i (PA[ Q)V(PA[ Q))(PAQ)V (PAi Q)PA(QVi Q)PV (QAi Q)(PV Q)A(PV[ Q)命题为真的赋值是P=1,Q=0和P=1,Q=116、某班有学生60人,其中有38人选修Visual C+磔程,有16人选修Visual Basic 课程.有21人选修Java课程;有3人这三门课程都选修,有2人这三门课程都不选修,问仅选修两门课程的学生人数是多少解设选修Visual C+钟程的学生为集合A;选修Visual Basic课程的学生为集合B;选修Java课程的学生为集合Co由题意可知:|A| =38 |B| =16 |C| =21|A A BA C| = 3 60-|A UBUC| = 2由于|A U BU C| = |A|+|B|+|C|-|A A B|-|A A C|-|B A C|+|A A BA C|所以有:|A n B|+|A n C|+|B n C|=20.所以仅选修两门课程的学生数是|A nB|+|A nC|+|B nC|-31A n BAC|=II.17、设〈A,R〉为一个偏序集,其中A={1, 2, 3, 4, 6, 9, 24, 54} , R是A上的整除关系.(1)画出〈A,R〉的哈斯图;(2)求R关于A的极大元;(3)求B={4,6,9} 的最小上界和最大下界.18、设G=< a>是12阶循环群,求出G的所有子群.解:由于12的正因子是1,2,5, 10所以G的子群有4个,分别是< a10>={e}< a5>={e, a5}< a2>={e, c2, a4, a6, a8 }<a>=G四、证实题1、设R1, R2为A上的关系,证实:(R, R2) 1 R,1 R21 o证实:对任意的x,y A ,有1x,y (R1 R2)y, x R1 R2( y, x R1 ) ( y, x R2 )11( x, y R1 1 ) ( x, y R2 1)11x, y R1 R2故(R1 R2) 1 R11 R212、设R1, R2为A上的关系,证实:(R R2) 1R/ R21.证实:对任意的x, y A ,有x, y (R1 R2) 1y, x R1 R2( y, x R1 ) ( y, x R2 )( x, y R1 1 ) ( x, y R2 1)11x, y R1 R2故(R1 R2) 1 R11 R213、在自然推理系统P中,构造下面推理的证实:只要A曾到过受害者房间并且11点以前没离开,A就犯了谋杀罪.A曾到过受害者房间.如果A在11点以前离开,看门人会看见他.看门人没有看见他, 所以A犯了谋杀罪.证实:命题符号化:p: A曾到过受害者房间q:A11点以前离开r : A犯了谋杀罪s:看门人会看见他前提:(pA[ q) 一r, p, q-s, i s结论:r证实:①]s②q-s③1q④p⑤(pAi q)⑥(pA[ q) —r⑦r4、设C*={a+bi | a,b为实数,且aw 0}.其中i是虚数单位.在C*上定义:R={<a+bi c+di>| a+bi €C*A c+diC C* A ac>0}(1)证实:R是C*上的等价关系;(2)给出R产生的等价类.证实:(1)对任意的a+biCC*,aw0aa>0 (a+bi) R (a+bi)所以R是自反的.(2)对任意的a+bi, c+diCC\(a+bi) R (c+di) ac>0 ca>0 (c+di) R (a+bi)所以R是对称的.(3)对任意的a+bi, c+di, e+fiCC*,(a+bi) R (c+di), (c+di) R (e+fi) ac>0, ce>0ae>0(a+bi) R (e+fi)所以R是传递的.综上R是一个等价关系.R有两个不同的等价类.设为K I, K2K={ (a+bi) Aa>0}, K2={ (a+bi) Na< 0}5、证实:6阶群中必含3阶元.证实:设G是6阶群,由L一定理白5t论1知G中元素的阶只可能是1, 2,3, 6.假设G中含有6阶元,设该元素为a,那么a2为3阶元.假设G中不含有6阶元,下面证实G中必含有3阶元.假设不然G中只含有1 阶和2阶元,即对任意a€ G,有a2=e,那么G是Abel群,取G中两个不同的2阶元a,b,令H={e,a,b,ab},那么H是G的子群,但|H|=4 , |G|=6 , 4不整除6,矛盾.故G中必含有3阶元.6、构造下面推理的证实:前提:x(F(x) H(x)), x(G(x) H(x)).结论:x(G(x) F(x)).证实:(1) x(F(x) H(x)) 前提引入(2) x( F(x) H(x))⑴置换(3) x(H(x) F(x))(2)置换(4) H(y)F(y))⑶UI(5) x(G(x) H(x)) 前提弓I入(6) G(y) H (y))(5)UI(7) G(y)F(y))(6)(4)假言三段论(8) x(G(x) F(x)). (7)UG7、、构造以下推理的证实.前提:p q, p r,s t, s r, t结论:q证实:(1)s t 前提引入(9) t 前提引入(10) s(1)(2)拒取式(11) s r前提引入(5)r(3)(4)假言推理(6)p r 前提引入(12) p (5)(6)拒取式(8)p q前提引入(9)q(7)(8)析取三段论8、设Z为整数集合,在Z上定义二元运算*, x, y Z有x y x y 1证实:g *)是群.证实:(1)封闭性:(2)可结合性:(3)幺元为1 :(4)x的逆元为X 1 2 x9、试证:任一棵非平凡树G至少有两片树叶.证实:设T中有x片树叶,y个分支点.于是T中有x+y个顶点,有x+y-1条边,由握手定理知T中所有顶点的度数之和「" =2(x+y-1).又树叶的度为1,任一分支点的度大于等于2于是x yd(v)>x . 1+2yi 1从而2(x+y-1户x+2yx> 2证毕.10、设Q为有理数集合,在Q-{1}上定义二元运算*, x,y Q-{1}有x y x y xy证实:<Q-{1},*>是群.证实:(1)封闭性:(2)可结合性:(3)幺元为0 :(4)x的逆元为x 1—x—x 111、有代数系统V1 =<R十>,V2=<R , >,其中+ ,为普通加法和乘法,令j :Rf R j (x)=e x,试证j映射为同构映射.x y x _ y -一「一证实:(1)" x,y€ R,j(x+ y)= e = e e =j(x)j(y),所以,j 是V1到V2的同态.x y(2) " x,y€ R, x y 那么有 e e,即j(x) j(y),所以,j 是V1 到V2的单射(3) " y€ R ,有x=lnyC R ,所以,j是V1到V2的满射综上三点,所以j是V1到V2的同构映射12、在自然推理系统F中,构造下面推理的证实:任何人如果喜欢音乐就不喜欢体育.每个人或者喜欢体育或者喜欢美术.有的人不喜欢美术,因而有的人不喜欢音乐.(个体域为人类集合)命题符号化:F(x): x喜欢音乐G(x): x喜欢体育H(x): x喜欢美术前提:x(F(x) G(x)), x(G(x) H(x)) 结论:x H (x) x F (x)证实:附加前提证实法①x H(x)②H(c)③x(G(x) H(x))④G(c) H(c)⑤G(c)附加前提引入EI规那么前提引入UI规那么②④析取三段论⑥x(F(x) G(x)) 前提引入⑧ F(c) ⑨ x F(x)13、设R 是A 上的自反的和传递的,如下定义 A 上的关系T,使得x, y A , x, y T x, y R y, x R证实:T 是A 上的等价关系证实:由于R 具有自反性,所以对任意的x A, x,x R 故x, x R x, x R x, x T 所以T 具有自反性.对任意的 x, y T ,有x, y T x, y R y, x R y, x R x, yRy, xT所以T 具有对称性;利用R 具有传递性,假设 x,y , y,z T ,那么x, y Ty,zT( x, y R y, x R) ( y, z R z, y R) ( x, y Ry, zR) ( z, y R y, x R)x, z R z, x R x, z T所以T 具有传递性;由于T 具有自反性、对称性和传递性,所以 R 是一个等价关系 14、设Z 为整数集合,在Z 上定义二元运算 如下:x, y Z, x y x y 2证实:Z 关于运算构成群. 证实:由于对任意的x,y Z ,有x y 2 Z ,所以整数集合Z 关于运算 封闭 对 x, y,z Z 有( x y ) z ( x y 2) z x y z 4 x (y z)x ( y z 2)x y z 4故(x y) z (x y) z,即运算 满足结合律.2 Z,且对任意的x Z 有x2 2 x x ,所以2是乙的单位元.⑦ F(c)G(c) UI 规那么 ⑤⑦拒取 EG 规那么对任意的x Z 有4 x Z,且x(4 x) (4 x) x 2,即x1 4 x 综合上述可知Z关于运算构成群.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章命题逻辑的基本概念一、判断下列语句是否是命题,若是命题是复合命题则请将其符号化(1)中国有四大发明。
(2)2是有理数。
(3)“请进!”(4)刘红和魏新是同学。
(5)a+b(6)你去图书馆吗?(7)如果买不到飞机票,我哪儿也不去。
(8)侈而惰者贫,而力而俭者富。
(韩非:《韩非子•显学》)(9)火星上有生命。
(10)这朵玫瑰花多美丽啊!二、将下列命题符号化,其中p:2<1,q:3<2(1)只要2<1,就有3<2。
(2)如果2<1,则3≥2。
(3)只有2<1,才有3≥2。
(4)除非2<1,才有3≥2。
(5)除非2<1,否则3≥2。
(6)2<1仅当3<2。
三、将下列命题符号化(1)小丽只能从筐里拿一个苹果或一个梨。
(2)王栋生于1992年或1993年。
四、设p、q的真值为0;r、s的真值为1,求下列各命题公式的真值。
(1)p∨(q∧r)(2)(p↔r)∧(﹁q∨s)(3)(⌝p∧⌝q∧r)↔(p∧q∧﹁r)(4)(⌝r∧s)→(p∧⌝q)五.判断下面一段论述是否为真:“π是无理数。
并且,如果3是无理数,则2也是无理数。
另外6能被2整除,6才能被4整除。
”六、用真值表判断下列公式的类型:(1) p∧(p→q)∧(p→⌝q)(2) (p∧r) ↔(⌝p∧⌝q)(2)((p→q) ∧(q→r)) →(p→r)第二章命题逻辑等值演算一、用等值演算法判断下列公式的类型,对不是重言式的可满足式,再用真值表法求出成真赋值.(1) ⌝(p∧q→q)(2)(p→(p∨q))∨(p→r)(3)(p∨q)→(p∧r)二、用等值演算法证明下面等值式(1)(p→q)∧(p→r)⇔(p→(q∧r))(2)(p∧⌝q)∨(⌝p∧q)⇔(p∨q) ∧⌝(p∧q)三、用等值演算求下列公式的主析取范式与主合取范式,并求成真赋值(1)(⌝p→q)→(⌝q∨p)(2)⌝(p→q)∧q∧r(3)(p∨(q∧r))→(p∨q∨r)四、用真值表法求下列公式的主析取范式,再用主析取范式求主合取范式(1) (p∨q)∧r (2)p→(p∨q∨r)第三章命题逻辑的推理理论一、填空1.数理逻辑的的主要任务是。
推理是指,前提是,结论是。
2.推理正确是指:3.命题公式A1,A,2, ,A,k推B的推理正确当且仅当二、先把下列命题符号化,再写出前提、结论、推理的形式结构,然后用3种方法证明(真值表法、等值演算法、主析取范式法)证明下列推理是正确的。
若a是奇数,则a不能被2整除。
若a是偶数,则a能被2整除。
因此,若a 是偶数,则a不是奇数。
设p: a是奇数,q: a能被2整除,r: a是偶数三、在自然推理系统下用直接法或用附加前提法或用归谬法构造下列推理的证明(1)前提:p→q,⌝(q∧r),r结论:⌝p (2)前提:q→p,q↔s,s↔t,t∧r结论:p∧q(3)前提:p→(q→r),s→p,q (4)前提:p→⌝q,⌝r∨q,r∧⌝s 结论:s→r 结论:⌝p四、在自然推理系统下构造下列推理的证明如果我学习,那么我数学不会不及格。
如果不热衷于玩游戏,那么我将学习。
但我数学不及格。
因此我热衷于玩游戏。
第四章 一阶逻辑的基本概念一、将下列命题用0元谓词符号化.(1) 小王学过英语和法语。
(2)除非李建是东北人,否则他一定怕冷。
(3)2大于3仅当2大于4。
(4)3不是偶数。
(5)2或3是素数。
二、在一阶逻辑中将下面将下面命题符号化,并分别讨论个体域限制为(a),(b)条件时命题的真值:(1) 对于任意x,均有)2)(2(22-+=-x x x(2) 存在x,使得x+5=9.其中(a)个体域为自然数集合.(b)个体域为实数集合.三、在一阶逻辑中将下列命题符号化:(1) 没有不能表示成分数的有理数。
(2) 在北京卖菜的人不全是外地人。
(3)乌鸦都是黑的。
(4)有的人天天锻炼身体。
四、给定解释I如下:(a) 个体域D为实数集合R.(b) D中特定元素a=0.(c) 特定函数f(x,y)=x-y,x,y D∈(d) 特定谓词F(x,y):x=y, G(x,y):x<y,x,y D∈.说明下列公式在I下的含义,并指出各公式的真值: (1)))Gxyy∀∀x⌝→)(,,(x(yF(2)))fxyFa∀x→y∀,)(,),(x(y(G(3) ))yxyFx⌝→),∀∀fG)((,(y(a,x(4) ))fxyGya∀x→∀(),F,,)x(y((五、给定下列各公式一个成真的解释,一个成假的解释。
(1) ∀x(F(x)∨G(x))(2) ∃x(F(x) ∨G(x) ∧H(x))六、判断下列公式的类型(1) F(x,y)→(G(x,y)→F(x,y))(2) ∀x∃y F(x,y)→∃x∀y F(x,y)第五章 一阶逻辑的等值演算与推理一、设个体域D={a,b,c},消去下列各式的量词(1) ∀x ∃y(F(x) ∧G(y))(2) ∀x ∃y(F(x) ∨G(y))(3) ∀x F(x) →∃y G(y)二、求下列公式的前束范式(1)∀x F(x) →∀y G(x,y)(2)∀x(F(x,y) →∃y G(x,y,z))三、设个体域D={1,2,3,4},F(x):x 是2的倍数,G(x):x 是奇数。
将命题∀x (F(x) →⌝ G(y))中的量词消去,并讨论命题的真值。
四、在自然推理系统下用直接法或用附加前提法或用归谬法构造下列推理的证明❑1.全称量词消去规则(UI) ❑2.全称量词引入规则(UG) ❑3. 存在量词引入规则(EG) ❑4.存在量词消去规则(EI) )()()()(c A x xA y A x xA ∴∀∴∀或)()(x xA y A ∀∴)()(x xA c A ∃∴)()(c A x xA ∴∃(1)前提:∀x (F(x) →G(x)), ∀x F(x)结论:∀x G(x)(2)前提:∀x(F(x)→G(x))结论:∀xF(x)→∀x G(x)(3)前提:∀x(F(x)∨G(x)),┐∃x G(x)结论:∃x F(x)五、在自然推理系统下构造下列推理的证明没有白色的乌鸦,北京鸭都是白色的。
因此,北京鸭都不是乌鸦。
第六章集合论一、单项选择题1.若集合A={a,b},B={ a,b,{ a,b }},则().A.A⊂B,且A∈B B.A∈B,但A⊄BC.A⊂B,但A∉B D.A⊄B,且A∉B2.若集合A={2,a,{ a },4},则下列表述正确的是( ).A.{a,{ a }}∈A B.{ a }⊆AC.{2}∈A D.∅∈A3.若集合A={ a,{a},{1,2}},则下列表述正确的是( ).A.{a,{a}}∈A B.{2}⊆AC.{a}⊆A D.∅∈A4.若集合A={a,b,{1,2 }},B={1,2},则().A.B⊂ A,且B∈A B.B∈ A,但B⊄AC.B ⊂ A,但B∉A D.B⊄ A,且B∉A5.设集合A = {1, a },则P(A) = ( ).A.{{1}, {a}} B.{∅,{1}, {a}}C.{∅,{1}, {a}, {1, a }} D.{{1}, {a}, {1, a }}6.若集合A的元素个数为10,则其幂集的元素个数为().A.1024 B.10 C.100 D.1二、1.设集合A有n个元素,那么A的幂集合P(A)的元素个数为.2.设集合A={a,b},那么集合A的幂集是.三、(1)B、C为任意的三个集合,如果A∪B=A∪C,判断结论B=C是否成立?并说明理由.(2)B、C为任意的三个集合,如果A⊕B=A⊕C,判断结论B=C是否成立?并说明理由.- 11 -四、1.设集合A={a, b, c},B={b, d, e},求(1)B⋂A;(2)A⋃B;(3)A-B;(4)B⊕A.2.设A={{a, b}, 1, 2},B={ a, b, {1}, 1},试计算(1)(A-B)(2)(A∪B)(3)(A∪B)-(A∩B)五.证明集合等式:A⋃ (B⋂C)=(A⋃B) ⋂ (A⋃C)六、某班有25个学生,其中14人会打篮球,12人会打排球,6人会打篮球和排球,5人会打篮球和网球,还有2人会打这三种球。
已知6个会打网球的人都会打篮球或排球。
求不会打球的人数。
- 12 -第七章二元关系(1)一、单项选择题1.集合A={1, 2, 3, 4, 5, 6, 7, 8}上的关系R={<x,y>|x+y=10且x, y∈A},则R 的性质为().A.自反的B.对称的C.传递且对称的D.反自反且传递的2.设集合A = {1,2,3,4,5,6 }上的二元关系R ={<a , b>⎢a , b∈A , 且a +b = 8},则R具有的性质为().A.自反的B.对称的C.对称和传递的D.反自反和传递的3.如果R1和R2是A上的自反关系,则R1∪R2,R1∩R2,R1-R2中自反关系有()个.A.0 B.2 C.1 D.34.设集合A={1 , 2 , 3 , 4}上的二元关系R = {<1 , 1>,<2 , 2>,<2 , 3>,<4 , 4>},S = {<1 , 1>,<2 , 2>,<2 , 3>,<3 , 2>,<4 , 4>},则S是R的()闭包.A.自反B.传递C.对称D.以上都不对二、填空题1.设集合A={0, 1, 2, 3},B={2, 3, 4, 5},R是A到B的二元关系,∈R⋂xxy<且=且>∈∈{B,,}AyyBxA则R的有序对集合为.2.设集合A={0, 1, 2},B={0, 2, 4},R是A到B的二元关系,∈R⋂yx∈∈且=且<>y{B,x}A,AyBx则R的关系矩阵M R=.3.设集合A={a,b,c},A上的二元关系R={<a, b>,<c. a>},S={<a, a>,<a, b>,<c, c>}则(R•S)-1=.4.设集合A={a,b,c},A上的二元关系R={<a, b>, <b, a>, <b, c>, <c, d>},则二元关系R具有的性质是.- 13 -- 14 -三、设A={a ,b},构成集合ρ(A )×A 。
四、(1)列出集合A={2,3,4}上的恒等关系I A ,全域关系E A ,小于或等于关系L A ,整除关系D A .(2)设A={a,b,c,d},1R ,2R 为A 上的关系,其中1R ={},,,,,a a a b b d{}2,,,,,,,R a db c b d c b=求23122112,,,R R R R R R o o 。
