解的存在唯一性定理证明
解的存在唯一性定理证明

存在唯一性定理 如(,)f x y 在R 上连续且关于y 满足利普希茨条件,则方程(,),dyf x y dx=在区间0x x h -≤上存在唯一解00(),()y x x y ϕϕ==,其中(,)min ,,max (,)xy R bh a M f x y M∈⎛⎫== ⎪⎝⎭逐步迫近法 微分方程(,)dyf x y dx=等价于积分方程00(,)xxy y f x y dx =+⎰取00()x y ϕ=,定义001()(,()),1,2,xn n x x y f x x dx n ϕϕ-=+=⎰ 可证明lim ()()n n x x ϕϕ→∞=的()y x ϕ=满足积分方程。
通过逐步迫近法可证明解的存在唯一性。
命题1 先证积分方程与微分方程等价:设()y x ϕ=是微分方程(,)dyf x y dx =定义于区间00x x x h ≤≤+上满足初值条件00()x y ϕ=的解,则()y x ϕ=是积分方程000(,),xx y y f x y dx x x x h =+≤≤+⎰定义于区间00x x x h ≤≤+上的连续解。
反之亦然。
证 因()y x ϕ=是微分方程(,)dyf x y dx=的解,有 ()(,())d x f x x dxϕϕ= 两边从0x 到0x h +取定积分0000()()(,()),xx x x f x x dx x x x h ϕϕϕ-=≤≤+⎰代入初值条件00()x y ϕ=得0000()(,()),xx x y f x x dx x x x h ϕϕ=+≤≤+⎰即()y x ϕ=是积分方程0000(,),xx y y f x y dx x x x h =+≤≤+⎰定义于区间00x x x h ≤≤+上的连续解。
反之,则有0000()(,()),xx x y f x x dx x x x h ϕϕ=+≤≤+⎰微分之()(,())d x f x x dxϕϕ= 且当0x x =时有00()x y ϕ=。
一阶线性微分方程解的存在唯一性证明

一阶线形微分方程解的存在唯一性定理的证明)()(x q y x p dxdy +=摘要:从分析方法入手,来证明满足初值条件下一阶线形微分方程解的存在唯一性定理的证明.引言:我们学习了能用初等解法的一阶方程的若干类型,但同时知道大量的一阶方程是不能用初等解法求出它的通解,而实际问题中所需要的往往是要求满足某种初始条件的解,因此对初值问题的研究被提到重要地位,自然要问:初值问题的解是否存在?如果存在是否唯一?首先,我们令f(x,y)=p(x)y+q(x) 这里f(x,y)是在矩形域R:上的连续函数.b y y a x x ≤-≤-00,函数f(x,y)称为在R 上关于y 满足利普希兹条件,如果存在常数L>0使不等式对于所有的 都成立,L 称2121),(),(y y L y x f y x f -≤-R y x y x ∈),(),,(21为利普希兹常数下面我们给出一阶线形微分方程(1)解的存在唯一性)()(x q y x p dxdy+=定理:如果f(x,y)=p(x)y+q(x)在R 上连续且关于y 满足利普希兹条件,则方程(1)存在唯一的解,定义于区间上,连续)(x y ϕ=h x x ≤-0且满足初始条件:这里 00)(y x =ϕ),min(Mba h =),(max y x f M =R y x ∈),(我们采用皮卡的逐步逼近法来证明这个定理,为了简单起见,只就区间来讨论,对于的讨论完全一样.h x x x +≤≤0000x x h x ≤≤-现在简单叙述一下运用逐步逼近法证明定理的主要思想,首先证明求微分方程的初值问题的解等价于求积分方程的连续解这里我们用f(x,y)=p(x)y+q(x)来[]⎰++=x x dx x q y x p y y 0)()(0替代,因此也就等价于求积分方程 的连续解,然⎰+=xx dx y x f y y 0),(0后去证明积分方程的解的存在唯一性.任取一个连续函数 代入上面的积分方程右端的y 就得)(0x ϕ到函数dx x x f y x xx ))(,()(0001⎰+≡ϕϕ显然也是连续解,如果那么就是积分方)(1x ϕ)(1x ϕ≡)(0x ϕ)(0x ϕ程的解.否则,我们又把代入积分方程右端的y 得到)(1x ϕ dxx x f y x xx ))(,()(0102⎰+≡ϕϕ如果 ,那么就是积分方程的解,否则我们继≡)(2x ϕ)(1x ϕ)(1x ϕ续这个步骤.一般地做函数 (2)dx x x f y x xx n n ))(,()(010⎰-+≡ϕϕ这样就得到连续函数序列,……)(0x ϕ)(1x ϕ)(x n ϕ如果那么就是积分方程的解,如果始终不发生这种≡+)(1x n ϕ)(x n ϕ)(x n ϕ情况,我们可以证明上面的函数序列有一个极限函数即)(x ϕ 存在因此对(2)取极限就得到)()(lim x x n n ϕϕ=∞→dxx x f y x xx n n n n ))(,(lim )(lim 010⎰-∞→∞→+=ϕϕ =dxx x f y xx n n ))(,(lim 010⎰-∞→+ϕ =dxx x f y xx ))(,(00⎰+ϕ即 dxx x f y x xx ))(,()(00⎰+≡ϕϕ这就是说是积分方程的解,这种一步一步地求出方程的解的方法)(x ϕ就成为逐步逼近法,由(2)所确定的函数称为问题(1)的n 次近)(x n ϕ似解,在定理的假设条件下以上步骤是可以实现的下面我们分四个命题来证明这个定理.命题1,设是一阶线形微分方程(1)的定义于区间)(x y ϕ=上的,且满足初始条件的解,则是积分方h x x x +≤≤0000)(y x =ϕ)(x y ϕ=程()的定义于上的连续解,反⎰+=xx dx y x f y y 0),(0h x x x +≤≤00h x x x +≤≤00之亦然.因为是一阶线形微分方程(1)的解故有)(x y ϕ=))(,()(x x f dxx d ϕϕ=两边从到x 取定积分得到0x dx x x f x x x x ))(,()()(00⎰≡-ϕϕϕhx x x +≤≤00把代上式,即有00)(y x =ϕ dx x x f y x xx ))(,()(00⎰+≡ϕϕhx x x +≤≤00因此, 是积分方程定义于上的)(x y ϕ=⎰+=xx dx y x f y y 0),(0h x x x +≤≤00连续解反之如果是积分方程的连续解,则有)(x y ϕ=⎰+=xx dx y x f y y 0),(0 (3)dx x x f y x xx ))(,()(00⎰+≡ϕϕh x x x +≤≤00微分之,得到))(,()(x x f dxx d ϕϕ=又把代入(3)得到0x x =00)(y x =ϕ因此是方程(1)的定义于 上且满足初始条件)(x y ϕ=h x x x +≤≤00的解.命题1证毕.00)(y x =ϕ现在取,构造皮卡逐步逼近函数序列如下:00)(y x =ϕ ⎪⎩⎪⎨⎧+==⎰-x x n nd f y x y x 0))(,()()(1000ξξϕξϕϕh x x x +≤≤00(n=1,2,…)(4)命题2 函数序列在上是一致收敛的{})(x n ϕh x x x +≤≤00证明:我们考虑级数 (5)[]∑∞=--+110)()()(k k k x x x ϕϕϕh x x x +≤≤00它的部分和为=[]∑=--+nk k k x x x 110)()()(ϕϕϕ)(x ϕ因此,要证明序列在上一致收敛,只需证明级数(5)在{})(x n ϕh x x x +≤≤00上一致收敛.为此,我们进行如下估计.由(4)有h x x x +≤≤00 (6))())(,()()(00001⎰-≤≤-xx x x M d f x x ξξϕξϕϕ及 ⎰-≤-xx d f f x x 0))(,())(,()()(0112ξξϕξξϕξϕϕ利用利普希兹条件及(6)得到⎰-≤-xx d L x x 0)()()()(0112ξξϕξϕϕϕ =ξξd x M L x x ⎰-≤0)(020)(!2x x ML-设对于正整数n,不等式nn n n x x n ML x x )(!)()(011-≤---ϕϕ成立,则有利普希兹条件,当时,有h x x x +≤≤00 ⎰-+-≤-x x n n n n d f f x x 0))(,())(,()()(11ξξϕξξϕξϕϕ⎰--≤xx n n d L 0)()(1ξξϕξϕ100)()!1()(!+-+=-≤⎰n n xx nnx x n ML d x n ML ξξ于是,由数学归纳法得知,对于所有的正整数k,有如下的估计(7)k k k k x x k ML x x )(!)()(011-≤---ϕϕh x x x +≤≤00从而可知,当时h x x x +≤≤00 (8)kk k k h k ML x x !)()(11--≤-ϕϕ(8)的右端是正项收敛级数∑∞=1!k kkk h ML的一般项,由维尔斯特拉斯判别法级数(5)在上一h x x x +≤≤00致收敛,因而序列也在上一致收敛,命题2证毕.{})(x n ϕh x x x +≤≤00命题3 是积分方程(2)的定义于上的连续解.)(x ϕh x x x +≤≤00证明: 由利普希兹条件)()())(,())(,(x x L x x f x x f n n ϕϕϕϕ-≤-以及在上一致收敛于,即知序列{})(x n ϕh x x x +≤≤00)(x ϕ{}{})(,()(x x f x f n n ϕ≡在上一致收敛于.因而对于(4)两边取极h x x x +≤≤00{})(,(x x f ϕ限,得到dxx x f y x xx n n n n ))(,(lim )(lim 010⎰-∞→∞→+≡ϕϕ =⎰-∞→+xx n n d f y 0))(,(lim 10ξξϕξ即⎰+=xx d f y x 0))(,()(0ξξϕξϕ这就是说是积分方程(2)的定义于上的连续解.命)(x ϕh x x x +≤≤00题3证毕.命题4 设是积分方程(2)的定义于上的一个连)(x φh x x x +≤≤00续解,则 , )()(x x ϕφ≡hx x x +≤≤00证明:我们首先证明也是序列的一致收敛极限函数.)(x φ{})(x n ϕ为此,从0)(y x =ϕ (n=1,2,…)⎰+=xx n d f y x 0))(,()(0ξξϕξϕ ξξφφd x f y x xx ))(,()(00⎰+≡我们可以进行如下估计)()(,()()(000x x M d f x x xx -≤≤-⎰ξξφξφϕξξφξξϕξφϕd f f x x x x ⎰-≤-0))(,())(,()()(01 ξξφξϕd L xx ⎰-≤0)()(0 200)(!2)(0x x MLd x ML xx -=-≤⎰ξξ现设,则有n n n x x n ML x x )(!)()(011-≤---φϕ ξξφξξϕξφϕd f f x x xx n n ⎰-≤--0))(,())(,()()(1 ξξφξϕd L xx n ⎰-≤-0)()(1 100)()!1()(!+-+=-≤⎰n xx Nx x n MLd x n ML ξξ故有数学归纳法得知,对于所有的正整数n,有下面的估计式(10)10)()!1()()(+-+≤-n nn x x n ML x x φϕ因此,在上有h x x x +≤≤00 (11)1)!1()()(++≤-n n n h n ML x x φϕ是收敛级数的公项,故因而1)!1(++n n h n ML 0)!1(1→+∞→+n n h n ML n 时在上一致收敛于,根据极限的唯一性,即得{})(x n ϕh x x x +≤≤00)(x φ)()(x x ϕφ≡h x x x +≤≤00命题4证毕.综合1-4,即得到一阶线性微分方程解的存在唯)()(x q y x p dxdy+=一定理的证明.。
常微分方程12解的存在唯一性

1 x2
),
y(x) 0 ,
c2
exp(
1 x2
)
,
x 0. x 0. x 0.
3
1.2.1例子和思路
例 4: 证明初值问题
dy y, dx
的解存在且惟一。
y(0) 1
(1 .2 .1)
证:若 y y(x) 是初始值问题的解, (1 .2 .1) 两端积分
y ( x ) 满足 y(x)=1+ xy(s)ds 0
y 1 , 1 x
x( ,1).
初值问题 yy2,y(0)2的解:
y
2 1 2x
.
它的存在区间为
(
1 2
,
)
例2: 初值问题 yx,y(0)a(a0)的解为: y
y a2 x2存在区间为 (a,a)
2
例3:初始值问题:
2y yx3
x0 ,
0 x0
y(0)0
有无穷多解,存在区间为: (,).
c1
exp(
x 2 (x )1 (x )x 0f(s ,1 (s )) f(s ,0 (s ))d s 13
x 2 (x )1 (x )x 0f(s ,1 (s )) f(s ,0 (s ))d s
x
L 2
其中第二个不等式由Lipschitz条件可以得到,
( 1 x) =y0+xx0 f(s,0(s))ds ( 2 x) M =y0+xx0 f(s,1(s))ds ( n x) =y0+xx0 f(s,n1(s))ds
这样就得到一个连续函数列 n ( x)
它称为 Picard迭代序列。
11
( 3 ) Picard 序列的收敛性
引理1.1 对于一切 n 和 x [x0,x0h],n(x)
一阶线性微分方程解的存在唯一性证实[解答]
![一阶线性微分方程解的存在唯一性证实[解答]](https://img.taocdn.com/s3/m/deca9e0afbd6195f312b3169a45177232f60e402.png)
一阶线形微分方程)()(x q y x p dxdy+=解的存在唯一性定理的证明摘要:从分析方法入手,来证明满足初值条件下一阶线形微分方程解的存在唯一性定理的证明.引言:我们学习了能用初等解法的一阶方程的若干类型,但同时知道大量的一阶方程是不能用初等解法求出它的通解,而实际问题中所需要的往往是要求满足某种初始条件的解,因此对初值问题的研究被提到重要地位,自然要问:初值问题的解是否存在?如果存在是否唯一?首先,我们令f(x,y)=p(x)y+q(x) 这里f(x,y)是在矩形域 R:b y y a x x ≤-≤-00,上的连续函数.函数f(x,y)称为在R 上关于y 满足利普希兹条件,如果存在常数L>0使不等式2121),(),(y y L y x f y x f -≤- 对于所有的R y x y x ∈),(),,(21 都成立,L 称为利普希兹常数下面我们给出一阶线形微分方程)()(x q y x p dxdy+=(1)解的存在唯一性定理:如果f(x,y)=p(x)y+q(x)在R 上连续且关于y 满足利普希兹条件,则方程(1)存在唯一的解)(x y ϕ=,定义于区间h x x ≤-0上,连续且满足初始条件:00)(y x =ϕ 这里 ),min(Mba h = ),(max y x f M = Ry x ∈),(我们采用皮卡的逐步逼近法来证明这个定理,为了简单起见,只就区间h x x x +≤≤00来讨论,对于00x x h x ≤≤-的讨论完全一样.现在简单叙述一下运用逐步逼近法证明定理的主要思想,首先证明求微分方程的初值问题的解等价于求积分方程[]⎰++=xx dx x q y x p y y 0)()(0的连续解这里我们用f(x,y)=p(x)y+q(x)来替代,因此也就等价于求积分方程 ⎰+=xxdx y x f y y 0),(0 的连续解,然后去证明积分方程的解的存在唯一性.任取一个连续函数)(0x ϕ 代入上面的积分方程右端的y 就得到函数dx x x f y x xx))(,()(0001⎰+≡ϕϕ 显然)(1x ϕ也是连续解,如果)(1x ϕ≡)(0x ϕ那么)(0x ϕ就是积分方程的解.否则,我们又把)(1x ϕ代入积分方程右端的y 得到dx x x f y x xx ))(,()(0102⎰+≡ϕϕ如果 ≡)(2x ϕ)(1x ϕ,那么)(1x ϕ就是积分方程的解,否则我们继续这个步骤.一般地做函数 dx x x f y x xx n n ))(,()(010⎰-+≡ϕϕ (2)这样就得到连续函数序列,)(1x ϕ…)(x n ϕ…如果≡+)(1x n ϕ)(x n ϕ那么)(x n ϕ就是积分方程的解,如果始终不发生这种情况,我们可以证明上面的函数序列有一个极限函数)(x ϕ即)()(lim x x n n ϕϕ=∞→ 存在因此对(2)取极限就得到dx x x f y x xx n n n n ))(,(lim )(lim 010⎰-∞→∞→+=ϕϕ=dxx x f y xx n n ))(,(lim 010⎰-∞→+ϕ=dxx x f y xx))(,(00⎰+ϕ即 dxx x f y x xx))(,()(00⎰+≡ϕϕ这就是说)(x ϕ是积分方程的解,这种一步一步地求出方程的解的方法就成为逐步逼近法,由(2)所确定的函数)(x n ϕ称为问题(1)的n 次近似解,在定理的假设条件下以上步骤是可以实现的下面我们分四个命题来证明这个定理.命题1,设)(x y ϕ=是一阶线形微分方程(1)的定义于区间h x x x +≤≤00上的,且满足初始条件00)(y x =ϕ的解,则)(x y ϕ=是积分方程⎰+=xx dx y x f y y 0),(0(h x x x +≤≤00)的定义于h x x x +≤≤00上的连续解,反之亦然.因为)(x y ϕ=是一阶线形微分方程(1)的解故有))(,()(x x f dxx d ϕϕ= 两边从0x 到x 取定积分得到dx x x f x x xx ))(,()()(00⎰≡-ϕϕϕ h x x x +≤≤00把00)(y x =ϕ代上式,即有dx x x f y x xx ))(,()(00⎰+≡ϕϕ h x x x +≤≤00因此, )(x y ϕ=是积分方程⎰+=xx dx y x f y y 0),(0定义于h x x x +≤≤00上的连续解反之如果)(x y ϕ=是积分方程⎰+=xx dx y x f y y 0),(0的连续解,则有dx x x f y x xx))(,()(00⎰+≡ϕϕ h x x x +≤≤00 (3)微分之,得到))(,()(x x f dxx d ϕϕ= 又把0x x =代入(3)得到00)(y x =ϕ因此)(x y ϕ=是方程(1)的定义于 h x x x +≤≤00上且满足初始条件00)(y x =ϕ的解.命题1证毕.现在取00)(y x =ϕ,构造皮卡逐步逼近函数序列如下:⎪⎩⎪⎨⎧+==⎰-x x n nd f y x y x 0))(,()()(1000ξξϕξϕϕ h x x x +≤≤00 (n=1,2,…)(4)命题2 函数序列{})(x n ϕ在h x x x +≤≤00上是一致收敛的证明:我们考虑级数[]∑∞=--+110)()()(k k k x x x ϕϕϕ h x x x +≤≤00(5)它的部分和为[]∑=--+nk k k x x x 110)()()(ϕϕϕ=)(x ϕ因此,要证明序列{})(x n ϕ在h x x x +≤≤00上一致收敛,只需证明级数(5)在h x x x +≤≤00上一致收敛.为此,我们进行如下估计.由(4)有)())(,()()(00001⎰-≤≤-xx x x M d f x x ξξϕξϕϕ (6)及 ⎰-≤-xxd f f x x 0))(,())(,()()(0112ξξϕξξϕξϕϕ利用利普希兹条件及(6)得到⎰-≤-xx d L x x 0)()()()(0112ξξϕξϕϕϕ ξξd x M L xx⎰-≤0)(0=20)(!2x x ML-设对于正整数n,不等式n n n n x x n ML x x )(!)()(011-≤---ϕϕ成立,则有利普希兹条件,当h x x x +≤≤00时,有⎰-+-≤-xxn n n n d f f x x 0))(,())(,()()(11ξξϕξξϕξϕϕ⎰--≤xx n n d L 0)()(1ξξϕξϕ100)()!1()(!0+-+=-≤⎰n n xx nn x x n ML d x n ML ξξ于是,由数学归纳法得知,对于所有的正整数k,有如下的估计k k k k x x k ML x x )(!)()(011-≤---ϕϕ h x x x +≤≤00 (7)从而可知,当h x x x +≤≤00时kk k k h k ML x x !)()(11--≤-ϕϕ (8)(8)的右端是正项收敛级数∑∞=1!k kkk h ML的一般项,由维尔斯特拉斯判别法级数(5)在h x x x +≤≤00上一致收敛,因而序列{})(x n ϕ也在h x x x +≤≤00上一致收敛,命题2证毕.命题3 )(x ϕ是积分方程(2)的定义于h x x x +≤≤00上的连续解.证明: 由利普希兹条件)()())(,())(,(x x L x x f x x f n n ϕϕϕϕ-≤-以及{})(x n ϕ在h x x x +≤≤00上一致收敛于)(x ϕ,即知序列{}{})(,()(x x f x f n n ϕ≡在h x x x +≤≤00上一致收敛于{})(,(x x f ϕ.因而对于(4)两边取极限,得到dx x x f y x xx n n n n ))(,(lim )(lim 010⎰-∞→∞→+≡ϕϕ=⎰-∞→+xx n n d f y 0))(,(lim 10ξξϕξ即⎰+=xx d f y x 0))(,()(0ξξϕξϕ这就是说)(x ϕ是积分方程(2)的定义于h x x x +≤≤00上的连续解.命题3证毕.命题4 设)(x φ是积分方程(2)的定义于h x x x +≤≤00上的一个连续解,则)()(x x ϕφ≡ , hx x x +≤≤00证明:我们首先证明)(x φ也是序列{})(x n ϕ的一致收敛极限函数.为此,从00)(y x =ϕ⎰+=xx n d f y x 0))(,()(0ξξϕξϕ (n=1,2,…)ξξφφd x f y x xx))(,()(00⎰+≡我们可以进行如下估计)()(,()()(000x x M d f x x x x -≤≤-⎰ξξφξφϕ ξξφξξϕξφϕd f f x x xx ⎰-≤-0))(,())(,()()(01ξξφξϕd L xx⎰-≤0)()(0200)(!2)(0x x MLd x ML xx -=-≤⎰ξξ 现设n n n x x n ML x x )(!)()(011-≤---φϕ,则有ξξφξξϕξφϕd f f x x xx n n ⎰-≤--0))(,())(,()()(1ξξφξϕd L xxn ⎰-≤-0)()(1100)()!1()(!+-+=-≤⎰n xx Nx x n MLd x n ML ξξ 故有数学归纳法得知,对于所有的正整数n,有下面的估计式10)()!1()()(+-+≤-n nn x x n ML x x φϕ (10)因此,在h x x x +≤≤00上有1)!1()()(++≤-n n n h n ML x x φϕ (11)1)!1(++n n h n ML 是收敛级数的公项,故0)!1(1→+∞→+n n h n ML n 时因而{})(x n ϕ在h x x x +≤≤00上一致收敛于)(x φ,根据极限的唯一性,即得)()(x x ϕφ≡ h x x x +≤≤00命题4证毕.综合1-4,即得到一阶线性微分方程)()(x q y x p dxdy+=解的存在唯一定理的证明.。
2.2解的存在唯一性定理

常微分方程
绵阳师范学院
下面分五个命题来证明定理,为此先给出 下面分五个命题来证明定理 为此先给出 积分方程 如果一个数学关系式中含有定积分符号且在定积分符 号下含有未知函数, 则称这样的关系式为积分方程. 号下含有未知函数 则称这样的关系式为积分方程
如 : y = e + ∫ y( t )dt , 就是一个简单的积分方程 .
0
x
≤ L ∫ n (ξ ) n 1 (ξ ) dξ
x0
x
MLn ≤ n!
MLn n (ξ x0 ) dξ = ( x x0 ) n +1 , ∫x0 (n + 1)!
x
17
常微分方程
绵阳师范学院
于是由数学归纳法得知,对所有正整数 有 于是由数学归纳法得知 对所有正整数n,有 对所有正整数
则 (x, y)在 上 于 满 Lipschitz条 . f R 关 y 足 件 f (x, y1) f (x, y2 ) = f y (x, y2 +θ ( y1 y2 )) y1 y2 ≤ L y1 y2
2
常微分方程
绵阳师范学院
b (2) 定理中h = min{a , }的几何意义 M 在矩形R中有 f ( x , y ) ≤ M ,
故初值问题(2.1)的解曲线的斜率必介于 M 与M 之间,
过点( x0 , y0 )分别作斜率为 M 和M的直线,
b 当M ≤ 时(如图(a ) a 所示 ), 解y = ( x )在 x0 a ≤ x ≤ x0 + a 中有定义;
3
常微分方程
绵阳师范学院
b 而当M > 时(如图(b)所示), 不能保证解y = ( x )在 a x0 a ≤ x ≤ x0 + a中有定义;它有可能在区间内跑到矩形 b b R外去, 使得无意义, 只有当x0 ≤ x ≤ x0 + 时, 才能保 M M 证解y = ( x )在R内.
解的存在唯一性定理证明

存在唯一性定理 如(,)f x y 在R 上连续且关于y 满足利普希茨条件,则方程(,),dyf x y dx=在区间0x x h -≤上存在唯一解00(),()y x x y ϕϕ==,其中(,)min ,,max (,)xy R bh a M f x y M∈⎛⎫== ⎪⎝⎭逐步迫近法 微分方程(,)dyf x y dx=等价于积分方程00(,)xxy y f x y dx =+⎰取00()x y ϕ=,定义001()(,()),1,2,xn n x x y f x x dx n ϕϕ-=+=⎰ 可证明lim ()()n n x x ϕϕ→∞=的()y x ϕ=满足积分方程。
通过逐步迫近法可证明解的存在唯一性。
命题1 先证积分方程与微分方程等价:设()y x ϕ=是微分方程(,)dyf x y dx =定义于区间00x x x h ≤≤+上满足初值条件00()x y ϕ=的解,则()y x ϕ=是积分方程000(,),xx y y f x y dx x x x h =+≤≤+⎰定义于区间00x x x h ≤≤+上的连续解。
反之亦然。
证 因()y x ϕ=是微分方程(,)dyf x y dx=的解,有 ()(,())d x f x x dxϕϕ= 两边从0x 到0x h +取定积分0000()()(,()),xx x x f x x dx x x x h ϕϕϕ-=≤≤+⎰代入初值条件00()x y ϕ=得0000()(,()),xx x y f x x dx x x x h ϕϕ=+≤≤+⎰即()y x ϕ=是积分方程0000(,),xx y y f x y dx x x x h =+≤≤+⎰定义于区间00x x x h ≤≤+上的连续解。
反之,则有0000()(,()),xx x y f x x dx x x x h ϕϕ=+≤≤+⎰微分之()(,())d x f x x dxϕϕ= 且当0x x =时有00()x y ϕ=。
解的存在唯一性定理

一阶微分方程解的存在性定理的其它证明方法姜旭东摘要 本文在文[1]对一阶微分方程初值问题解得存在唯一性定理证明的基础上,应用压缩映像原理,Schauder 不动点定理,以及Euler 折线法,给出了一阶微分方程解得存在唯一性定理的其它几种证法.关键词 一阶微分方程 不动点定理 解的存在性 唯一性 1、引言微分方程来源于生活实际,研究微分方程的目的在于掌握它所反映的客观规律。
在文[1]第二章里,介绍了能用初等解法求解的一阶方程的若干类型,但同时指出,大量的一阶方程一般是不能用初等解法求解它的通解,而实际问题需要的往往是要求满足某种初始条件的解. 本文在文[1]对一阶微分方程初值问题解的存在唯一性定理证明的基础上,应用压缩映像原理,Schauder 不动点定理,以及Euler 折线法,给出了一阶微分方程解的存在唯一性定理的其它几种证法.考虑一阶微分方程 (,)dyf x y dx= (1.1)这里(,)f x y 是在矩形区域00:||,||R x x a y y b -≤-≤ (1.2)上的连续函数.函数(,)f x y 在R 上满足Lipschitz 条件,即存在常数L >0,使得不等式1212|(,)(,)|||f x y f x y L y y -≤- (1.3)对所有12(,),(,)x y x y R ∈都成立, L 称为Lipschitz 常数。
定理1.1、如果(,)f x y 在R 上连续且关于y 满足Lipschitz 条件,则方程(1.1)存在唯一的解()y x ϕ=,定义于区间0||x x h -≤上,连续且满足初始条件00()x y ϕ=这里min(,)bh a M=,(,)max |(,)|x y R M f x y ∈=.文[1]中采用皮卡逐步逼近法来证明这个定理.为了简单起见,只就区间00x x x h≤≤+来讨论,对于00x h x x -≤≤的讨论完全一样.分五个命题来证明这个定理:命题1、设()y x ϕ=是方程(1.1)定义于区间00x x x h ≤≤+上满足初始条件00()x y ϕ=的解,则()y x ϕ=是积分方程0(,)xx y y f x y dx =+⎰ 00x x x h ≤≤+ (1.4)的定义于00x x x h ≤≤+上的连续解.反之亦然. 现在取00()x y ϕ=,构造皮卡逐步逼近函数序列如下:0000100()()(,())x nn x x y x y f d x x x hϕϕξϕξξ-=⎧⎪⎨=+≤≤+⎪⎩⎰ (1.5)(n=1,2,…)命题2 、对于所有的n ,(1.5)中()n x ϕ在00x x x h ≤≤+上有定义、且满足不等式0|()|n x y b ϕ-≤命题3 、函数序列{}()n x ϕ在00x x x h ≤≤+上是一致收敛的. 命题4 、()x ϕ是积分方程(1.4)的定义于00x x x h ≤≤+上的连续解.命题5 、()x ψ是积分方程(1.4)的定义于00x x x h ≤≤+上的一个连续解,则()()x x ϕψ=,00x x x h ≤≤+.综合命题1—5,即得到存在唯一性定理.本文在方程(1.1)在满足定理1.1条件下,应用应用压缩映像原理,Schauder 不动点定理,以及Euler 折线法,给出了一阶微分方程解得存在唯一性定理的其它几种证法.2、预备知识定义 2.1、 定义在t αβ≤≤上的实值(m 维)向量函数族{}()F f t =,如果存在数M >0,使得对任一f F ∈,都有()f t M ≤,当t αβ≤≤时,则称函数族F 在t αβ≤≤上是一致有界的.定义2.2 、定义在t αβ≤≤上的实值(m 维)向量函数族{}()F f t =,如果对于任给的ε﹥0,总存在δ﹥0,使得对任一f F ∈和任意的12,[,]t t αβ∈,只要12|,|t t -<δ就有12()()f t f t -<ε则称函数族F 在 t αβ≤≤上是同等连续.定义2.3、设X 是度量空间,M 是X 中子集,若M 是X 中紧集,则称M 是X 中相对紧集。
常微分方程解的存在唯一性定理证明

常微 分方 程是 一 门应用 性较 强 的课 程 ,它在 数学 、物 理 、天 文 和工程 技术 等领 域有 着 广 泛应 用 .一 阶微 分 方程 初值 问题 解 的存 在 唯 一 性 定 理 既是 微 分 方 程 的理 论 基 础 ,又 是 常 微 分 方 程 的精 华 所 在 ,在 很 多教 材 中¨ 都 是作 为重 点章 节来 讲述 ,而且 一 阶微 分 方 程 解 的存 在 唯 一性 的应 用 也很 广泛 .此处 从 几 个 不 同
1,由敛.故由Weierstrass 0法得级 ㈤+蠢 ) ㈤]一致收敛.
命题 3 lim (t)= ( )是 积分 方程 的解 . 证 明 由于{ (t))在 【t0,to+ 】上 一致 收敛 ,令lim (t)= (t),由 Lipschitz条 件知道
= o 十I,(s, ( ))ds,£0≤t≤t0+h
to
构 造 picard序 列 { (t)},即令
(2)
收 稿 日期 :2014-08—19:修 回 日期 :2014-09—25. 基金项 目:安徽省高等学校省级 自然科学基金项 目(KJ2013B105);安徽新华 学院质量 工程 (2012jgkcx03);安徽新 华学 院
(2)函数 t,X)在 R上关于 满足 Lipschitz条件 ,即存在常数 L>0,使得对所有(t, ),(t, )∈R都有
l £ ) , )l≤L l X1-X2 l成立,则初值问题(1)在区间[t-to I≤ 上存在唯一解,其中 :min{n, ),
Banach空间中常微分方程解的存在与唯一性定理(参考模板)

Banach 空间中常微分方程解的存在唯一性定理魏婷婷(天水师范学院 数学与统计学院,甘肃,天水,741000)摘要: 在Banach 空间中, 常微分方程解的存在唯一性定理中},1min{M b L h =,初值问题的解)(t y 的变量t 在h t t h t +≤≤-00上变化,把t 的变化范围扩大为Mbt t Mbt +≤≤-00,为此给出t 变化范围后的Banach 空间中常微分方程解的存在唯一性定理,并对定理给予明确的证明.关键词: 存在唯一;常微分方程;数学归纳法;皮卡逐步逼近法;Banach 空间引言常微分方程解的存在唯一性定理明确地肯定了在一定条件下方程的解的存在性和唯一性,它是常微分方程理论中最基本且实用的定理,有其重大的理论意义,另一方面,它也是近似求解法的前提和理论基础.对于人们熟知的Banach 空间中常微分方程解的存在唯一性定理,解的存在区间较小, 只限制在一个小的球形邻域内,(球形邻域的半径若为δ,还需满足1<δL ,且解只在以0y 为中心以δ为半径的闭球δδ≤-∈=00)(y y X y y B 存在唯一,其中X 是Banach 空间)因此在应用过程中受到了一定的限制.如今我们尝试扩大了解的存在范围,从而使此重要的定理今后有更加广泛的应用.1 预备定理我们给出Banach 空间中常微分方程解的存在唯一性定理如下设X 是Banach 空间, X U ⊂是一个开集. X U f →:上关于y 满足利普希茨)(Lipschitz 条件,即存在常数0>L ,使得不等式2121),(),(y y L y t f y t f -≤-,对于所有U y y ∈21,都成立.取U y ∈0,在U 内,以0y 为中心作一个半径为b 的闭球b y y X y y B b ≤-∈=00)(,对所有的)(0y B y b ∈都成立,且有M y f ≤)(,取},1min{Mb L h =,则存在唯一的1C 曲线)(t y ,使得在h t t h t +≤≤-00上满足)(0y B y b ∈,并有),(y t f y =',00)(y t y =.2 结果与证明笔者通过改进对h 的限制,即仅取Mb h =,预备定理仍然成立,从而使定理的应用进一步广泛.2.1改进条件后的定理定理 假设条件同上预备定理,设初值为),(00y t ,则存在唯一的1C 曲线)(t y ,对任意的Mbt t Mbt +≤≤-00,满足)(0y B y b ∈,且使得),(y t f y =',00)(y t y =.显然可有],[],[0000Mbt M bt h t h t +-⊂+-,且},1min{MbL h =.2.2定理的证明证明 证明过程中我们利用皮卡)(Picard 逐步逼近法.为了简单起见,只就区间00t t Mbt ≤≤-进行讨论,对于区间Mbt t t +≤≤00的讨论完全一样.2.2.1定理证明的思想现在先简单叙述一下运用皮卡逐步逼近法证明的主要思想. 首先证明条件),(y t f y =',00)(y t y =等价于求积分方程dt y t f y t y t t ),()(00⎰+=.(1)再证明积分方程的解的存在唯一性.任取一个)(0t y 为连续函数,将它代入方程(1)的右端),(y t f ,可得到函数dt y t f y t y t t ),()(0010⎰+=,显然,)(1t y 也为连续函数.若)()(01t y t y =,则可知)(0t y 就是方程(1)的解.若不然,我们又把)(1t y 代入积分方程(1)的右端),(y t f ,可得到函数dt y t f y t y t t ),()(1020⎰+=.若)()(12t y t y =,则可知)(1t y 就是方程(1)的解.若不然,我们如此下去,可作连续函数,dt y t f y t y n t t n ),()(100-⎰+=. (2)这样就得到连续函数列),(,),(),(),(210t y t y t y t y n若)()(1t y t y n n =+,那么)(t y n 就是积分方程的解,如果始终不发生这种情况,我们可以证明上面的函数序列有一个极限函数)(t y ,即)()(lim t y t y n n =∞→存在,因而对(2)式两边取极限时,就得到dt y t f y dt y t f y dt y t f y t y t t n n t t n t t n n n ⎰⎰⎰+=+=+=-∞→-∞→∞→),(),(lim ),(lim )(lim 00001010,即dt y t f y t y t t ),()(00⎰+=,这就是说,)(t y 是积分方程的解.在定理的假设条件下,以上的步骤是可以实现的. 2.2.2定理证明的步骤下面我们分五个命题来证明定理.命题1 设)(t y y =是),(y t f y ='的定义于区间00t t Mbt ≤≤-上,满足初值条件00)(y t y = (3) 的解,则)(t y y =是积分方程dt y t f y t y t t ),()(00⎰+=定义于00t t M b t ≤≤-上的连续解,反之亦然.证明 因为)(t y y =是方程),(y t f y ='的解,故有),()(y t f dtt dy =. 对上式两边从0t 到t 取定积分得到dt y t f t y t y t t ⎰=-),()()(00,00t t M b t ≤≤-,把(3)式代入上式,即有dt y t f y t y t t ⎰+=),()(00,00t t M b t ≤≤-. (4)因此, )(t y y =是(4)的定义于00t t Mbt ≤≤-上的连续解.反之,如果)(t y y =是(4)的连续解, dt y t f y t y t t ⎰+=),()(00,00t t M b t ≤≤-.微分之,得到),()(y t f dtt dy =. 又把0t t =代入(4)式,得到00)(y t y =,因此, )(t y y =是方程),(y t f y ='的定义于区间00t t Mbt ≤≤-,且满足初值条件(3)的解.命题1证毕.现在取00)(y t y =,构造皮卡逐步逼近函数序列如下⎪⎩⎪⎨⎧=≤≤-+==⎰-),2,1(,),()()(0010000 n t t M b t dt y t f y t y y t y n t t n(5) 命题2 对于所有的n ,(5)中函数)(t y n 在00t t Mb t ≤≤-上有定义,连续且满足不等式b y t y n ≤-0)(.证明 用数学归纳法可以证明,如下)()(0y B t y b n ∈,对于任意N n ∈,00t t Mbt ≤≤-,当1=n 时, ξξd y f y t y t t ),()(0010⎰+=,显然)(1t y 在00t t Mb t ≤≤-上有定义,连续且有b t t M d y f d y f y t y t t t t ≤-≤≤=-⎰⎰)(),(),()(0000100ξξξξ.设当k n =时有)()(0y B t y b k ∈,也即)(t y k 在00t t Mbt ≤≤-上有定义,连续且满足不等式b y t y k ≤-0)(,这时ξξd y f y t y k t t k ),()(001⎰+=+.由假设,命题2当k n =时成立,则可知)(1t y k +在00t t Mb t ≤≤-上有定义,连续且有当1+=k n 时b t t M d y f d y f y t y k t t k t t k ≤-≤≤=-⎰⎰+)(),(),()(00100ξξξξ,即命题2当1+=k n 时也成立,从而得知命题2对于所有的n 均成立.命题2证毕.命题3 函数序列)}({t y n 在00t t Mb t ≤≤-上是一致收敛的.证明 我们考虑级数∑∞=--+110)]()([)(k k k t y t y t y ,00t t Mbt ≤≤-,(6)(6)式级数的部分和为)()]()([)(110t y t y t y t y n nk k k =-+∑=-,因此,要证明函数序列)}({t y n 在00t t Mbt ≤≤-上一致收敛,我们仅证明级数(6)在00t t Mbt ≤≤-上一致收敛.因此,我们可进行如下计算,由)(),(),()(0000100t t M d y f d y f y t y t t t t -≤≤=-⎰⎰ξξξξ, (7)及ξξξd y f y f t y t y t t ⎰-≤-),(),()()(01120,利用利普希茨)(Lipschitz 条件及(7)式可知对于任意的n 为正整数,不等式n n n n t t n ML t y t y )(!)()(011-≤---成立. 则由利普希茨条件,当00t t Mbt ≤≤-时,有为此,由数学归纳法可知,对于所有的正整数k ,可有如下的式子成立,k k k k t t k ML t y t y )(!)()(011-≤---,00t t M b t ≤≤-.因此可有,当k k kk k k M b k ML t t k ML t y t y )(!)(!)()(1011---≤-≤-, (8) (8)式右端为收敛的正项级数∑∞=-11)(!k k k M bk ML 的一般项. 由魏尔斯特拉斯)(s Weierstras 判别法,级数(6)在00t t Mb t ≤≤-上是一致收敛的,因此序列)}({t y n 也在00t t Mbt ≤≤-上一致收敛,命题3证毕.现设)()(lim t y t y n n =∞→,为此)(t y 也在00t t Mbt ≤≤-上连续,且由命题2又可知b y t y ≤-0)(,命题4 )(t y 是积分方程dt y t f y t y t t ),()(00⎰+=的定义在区间00t t M b t ≤≤-上的连续解.证明 由利普希茨条件)()(),(),(t y t y L y t f y t f n n -≤-以及)}({t y n 在2000112)(!2)()()()()(0t t ML d t M L d y y L t y t y t t t t -=-≤-≤-⎰⎰ξξξξξ100111)()!1()(!)()(),(),()()(000+--+-+=-≤-≤-≤-⎰⎰⎰n nnt t n n n t t n n t t n n t t n ML d t n ML d y y L d y f y f t y t y ξξξξξξξξ00t t Mbt ≤≤-上一致收敛于)(t y ,且函数列)}({t y n 逐项连续,即知序列))}(({t y f n 在00t t Mbt ≤≤-上一致收敛于))((t y f .因而对(5)式两边取极限,得到ξξξξd y f y d y f y t y n n t t n t t n n n ),(lim ),(lim )(lim 101000-∞→-∞→∞→⎰⎰+=+=即ξξd y f y t y t t ),()(00⎰+=,这就是说, )(t y 是积分方程dt y t f y t y t t ),()(00⎰+=的定义于00t t Mbt ≤≤-上的连续解.命题4证毕.命题5 (证明解的唯一性)设)(t x 是积分方程dt y t f y t y t t ),()(00⎰+=定义于00t t Mbt ≤≤-上的另一个连续解,则)()(t x t y =,00t t Mbt ≤≤-.证明 现在我们证明)(t x 也是序列)}({t y n 的一致收敛极限函数.为此,从00)(y t y =,.),()(100ξξd y f y t y n t t n ⎰-+= )1(≥n ,ξξd x f y t x t t ),()(00⎰+=,可以进行如下的估计,)(),(),()()(0000t t M d x f d x f t x t y t t t t -≤≤=-⎰⎰ξξξξ200001)(!2)()()(),(),()()(000t t MLd t ML d x y L d x f y f t x t y t t t t t t -=-≤-≤-≤-⎰⎰⎰ξξξξξξξξ现在我们可以假设n n n t t n ML t x t y )(!)()(011-≤---,则有 .)()!1()(!)()(),(),()()(10011000+---+=-≤-≤-≤-⎰⎰⎰n nnt t n n t t n t t n t t n ML d t n ML d x y L d x f y f t x t y ξξξξξξξξ故由数学归纳法得知,对于所有的正整数n ,有下面的估计式10)()!1()()(+-+≤-n nn t t n ML t x t y ,于是我们可知在00t t Mbt ≤≤-上有110)()!1()()!1()()(+++≤-+≤-n n n n n Mb n ML t t n ML t x t y , (9)1)()!1(++n n M b n ML 是收敛级数的公项,且当∞→n 时, 0)()!1(1→++n n Mb n ML . 因而)}({t y n 在00t t Mbt ≤≤-上一致收敛于)(t x .根据极限的唯一性,即可知)()(t x t y =,00t t Mbt ≤≤-.命题5证毕.综合命题1~5,即得到Banach 空间中常微分方程解的存在唯一性定理的证明. 例题 求初值问题⎪⎩⎪⎨⎧=--=0)1(22y yt dtdy 其中R :[]0,2-∈t ,[]1,1-∈y 的解的存在区间,并求第二次近似解,给出在解的存在区间的误差估计.解 ()4),(max ,==∈y t f M Ry t则利用本文的结果41==Mbh , 在R 上函数22),(y t y t f -=的利普希茨常数可取2=L ,因为L y yf=≤-=∂∂22. 0)(0=t y ,313))(()(220211+=-=⎰-t d y t y t ξξξ,4211631893))(()(74321212+---=-=⎰-t t t t d y t y t ξξξ.在本文的估计式(9)中令)()(t y t x =,则有误差估计式110)()!1()()!1()()(+++≤-+≤-n n n n n Mb n ML t t n ML t y t y ,从而可得241)41(!324)()(322=⨯⨯≤-t y t y .利用本文结果,初值问题解的存在区间为Mbt t Mbt +≤≤-00为此将10-=t ,41=Mb代入上式,可得解的存在区间为4345-≤≤-t ; 第二次近似解为42116318937432+---=t t t t y ;在解的存在区间的误差估计为2412≤-y y . 结束语在Banach 空间中,通过运用皮卡的逐步逼近法,从证明解的存在性,到解的唯一性,采用严密的逻辑推理和理论证明,得到扩大解的存在区间后Banach 空间中常微分方程解的存在唯一性定理,从而使定理更加实用.当然,展望未来,我们还可以利用所得到的结果进一步作为探究其他问题的可靠性依据.参考文献[1] 王高雄,周之铭,朱思铭,王寿松,编.常微分方程[M].北京:高等教育出版社,2006.[2] 郭大均,孙经先.抽象空间常微分方程[M].济南:山东科学技术出版社,2003.[3] 王兴涛,编.常微分方程[M].哈尔滨:哈尔滨工业大学出版社,2004.[4] 邓海荣,马兆丰.Banach空间中常微分方程解的存在唯一性定理的注[J].扬州大学学报:自然科学版,2007,10(1): 1~3.[5] 房琦贵.关于常微分方程解的存在唯一问题的讨论[J].高校讲坛,2010.[6] 王声望,郑伟行,编.实变函数与泛函分析概要[M].北京:高等教育出版社,2005.如不慎侵犯了你的权益,请联系告知!致谢在完成终稿的今天,在敲完最后一个句号的时刻,我的思想同周围凝固的热气一样停驻了,不知道是慰藉还是悲伤,大学四年的生活就这样结束了,而眼前的路还很长,虽然似乎有些迷茫,但我必须整理心情,背上行囊,坚定的踏上新的征程……我要感谢,非常感谢我的指导老师何老师.在忙碌的教学工作中挤出时间来审查修改我的论文,循循善诱的教导和不拘一格的思路给予我无尽的启迪.他为人随和热情﹑治学严谨细心﹑广博的学识﹑深厚的学术素养,在论文的写作和措辞等方面他也总会以专业标准严格要求,从选题﹑定题﹑开始,一直到论文的反复修改,何老师始终认真负责地给予我深刻而细致地指导,帮助我开拓研究思路,精心点拨﹑热忱鼓励.正是何老师的无私帮助与热忱鼓励,我的毕业论文才能够得以顺利完成,谢谢何老师.再次,我还要认真地谢谢我身边所有的朋友和同学,你们对我的关心﹑帮助和支持是我不断前进的动力之一,我的大学生活因为有你们而更加精彩.最后,向在百忙中抽出时间对本文进行评审并提出宝贵意见的各位专家表示衷心地感谢!(本资料素材和资料部分来自网络,仅供参考。
常微分方程解的存在唯一性定理

常微分方程解的存在唯一性定理一阶微分方程⑴其中. 是在矩形域丄」’叭」上的连续函数。
定义1如果存在常数二11,使得不等式”(础)-/(砒)冏肝川对于所有--■■-1--- 都成立,贝U函数/、•称为在二上关于:'满足Lipschitz 条件。
定理1如果「二,在二上连续且关于「满足Lipschitz 条件,则方程(1)存在唯一的解y=叭心,定义于区间M ■阳卜月上,连续且满足初始条件W八-卄 A = r—)M = max' ■-.,这里」f,•心「。
Picard逐步逼近法来证明这个定理的主要思想首先证明求微分方程的初值冋题的解等价于求积分方程的连续解。
然后去证明积分方程的解的存在唯一性。
任取一个连续函数代入上面积分方程右端的,就得到函数俅沪)Vp(Z()⑴)必,显然J 也是连续函数,如果,那末l:-'就是积分方程的解。
否则,我们又把J二代入积分方程右端的「,得到汀0恥)皿,如果氛沪仍⑴,那末仇⑴就是积分方程的解。
否则我们继续这个步骤。
一般地作函数惦(3.1.1.4)这样就得到连续函数序列,...,〔「」,…如果二, 那末就是积分方程的解。
如果始终不发生这种情况,我们可以证明上面的函数序列有一个极限函数厂:;;1,即'厂…I存在,因而对©Ji/)取极限时,就得到f「打「X FJr=y0+l=y0+祕幼必Jf祕x)=y n+/(X 矶兀))必/ 、即•血,这就是说机x)是积分方程的解。
这种一步一步地求出方程的解的方法就称为逐步逼近法。
函数''■■■■■'称为初值问题的第:次近似解。
命题1设—是方程(1)的定义于区间V —'■'‘上,满足初始条件Jf瞅)=刃的解,则厂曲)是积分方程y=y°+y (2曲碳心砒的定义于V ——'■上的连续解。
反之亦然。
现在取,构造皮卡逐步逼近函数序列如下: 京(X)=丹;保(方=丹+ f于(乙矶_1©)時从“英肿hJ*D(聊=12…)1命题2对于所有的卜,函数在J■:上有定义、连续且满足不等式命题3 函数序列"I「在J ------------ '."上是一致收敛的。
第三章 解的存在唯一性

x
n1(x) n (x) x0 f (,n ( )) f (,n1( ))d
x
L x0 n ( ) n1( )d
MLn
n!
x x0
(
x0 )nd
MLn (x (n 1)!
x0 )n1,
于是由数学归纳法得知,对所有正整数n,有
n (x) n1(x)
MLn1 n!
(x
x0 )n ,
x0 x x0 h,
u' (x) Lu(x), (u' (x) Lu(x))eLx 0,
0 g(x) u(x)
(u' (x) Lu(x))eLx 0,
对最后一个不等式从 x0到x积分得 u(x)eLx u(x0 )eLx0 0,
故g(x) u(x) 0, 即g(x) 0, x [x0, x0 h]. 综合命题1—5得到存在唯一性定理的证明.
现设
lim
n
n
(
x)
(
x),
x0 x x0 h,
则由{n (x)}在[x0, x0 h]的连续性和一致收敛性 得,
(x)在[x0, x0 h]上连续,且
(x) y0 b
命题4 (x)是积分方程 (3.5)定义于[x0, x0 h]上连续解.
证明: 由Lipschitz条件有
f (x,n (x)) f (x,(x)) Ln(x) (x)
以及{n (x)}在[x0, x0 h]的一致收敛性得 ,
函数列{ fn (x)}, ( fn (x) f (x,n (x)))
在[x0, x0 h]上一致收敛于函数 f (x,(x)),
因此对(3.7)两边取极限 ,得
x
lim
n
解的存在唯一性定理

上连续,从而k1(x)在[x0 , x0 h]上连续且
k1(x) y0
x
x0 f ( ,k ( ))d
x x0
f (,k ( ))d
M x x0 Mh b
即当n k 1时成立,命题2成立
综上,命题2得证
二、存在唯一性定理
定理1
dy =f (x, y)
(1)
dx
D :| x x0 | a,| y y0 | b
如果f (x, y)在D上连续且关于y满足利普希茨条件,
则方程(1)存在唯一的连续解y (x),定义在|x x0| h
上,连续且满足初值条件
(x0 ) y0
这里h min(a, b ), M max | f (x, y) |
x
L x0 n ( ) n1( )d
MLn
n!
x x0
(
x0 )nd
MLn (x (n 1)!
x0 )n1,
于是由数学归纳法得知,对所有正整数n,有
n (x) n1(x)
MLn1 n!
(x
x0 )n ,
x0 x x0 h,
(3.11)
从而当x0 x x0 h时,
n (x) n1(x)
于是{n (x)}一致收敛性与级数 (3.9)一致收敛性等价 .
对级数(3.9)的通项进行估计
x
1(x) 0(x) x0 f (,0( ))d M x x0
x
2(x) 1(x) x0 f (,1( )) f (,0 ( ))d
x
L x0 1( ) 0( )d
L
x x0
M (
解的存在唯一性定理证明

解的存在唯一性定理证明以下将从两个方面对解的存在唯一性定理进行证明。
一、解的存在性的证明:首先,我们需要定义一些数学概念:1.解的函数空间:设X是一个函数集合,若对任意的f和g属于X,以及任意的实数a和b,af+bg也属于X,则称X是一个线性函数空间。
2.完备空间:若其中一函数空间X中的Cauchy序列收敛于X中的一个元素,那么该函数空间X就被称为完备空间。
3.有界性:若其中一函数空间X中任意元素的范数有上界,则称该函数空间X是有界的。
现在我们来证明解的存在性:对于方程或问题的解,我们需要构造一个函数空间,并证明该函数空间是完备且有界的。
然后,我们利用一些定理,例如Banach不动点定理或者Peano存在性定理等,来证明解的存在性。
这里以微分方程(dy/dx = f(x, y))为例:1. 构造函数空间X:我们可以选择所有满足函数f(x, y)局部连续和Lipschitz条件的函数f作为函数空间X。
2. 证明函数空间X是完备的:我们需要证明任意在X中的Cauchy序列会收敛于X中的一个元素。
这一步可以通过使用柯西序列或确界原理等方法来完成。
3.证明函数空间X是有界的:我们需要证明X中的任意元素的范数有上界。
这一步可以通过使用函数的有界性条件来证明。
4. 利用定理:利用Banach不动点定理或者其他定理,我们可以找到X中的一个元素y,使得y满足微分方程(dy/dx = f(x, y))。
因此,解的存在性得证。
二、解的唯一性的证明:要证明解的唯一性,我们可以利用函数的局部连续性和Lipschitz条件来证明。
1. 局部连续性:假设存在两个解y1(x)和y2(x),它们满足同一个微分方程(dy/dx = f(x, y))。
首先,我们可以证明y1(x)和y2(x)在其中一区间[α, β]上是局部连续的。
这可以通过反证法来完成。
2. Lipschitz条件:然后,我们需要证明方程(dy/dx = f(x, y))满足Lipschitz条件。
常微分方程课件--解的存在唯一性定理

y ( x) [ s e
0
]ds
x
0
1 2 5 5 [1 ( ) ]ds x 1 2 4 8
例6讨论初始值问题
y 1 y 2 , y(0) 0
的解存在唯一的区间. f ( x, y) 1 y 2 在 解: 对于任意的正数 a, b, 函数
R x, y ) x a, y b (
( 2 )构造 Picard 迭代数列
取0 x) y0 代入(1.2.3)右端后得 (
1 x) y0+ f (s, 0 (s))ds (
x0
x
2 x) y0+ f (s, 1 (s))ds (
x0
x
(x) y0+ f (s, n1 (s))ds n
x0
x
这样就得到一个连续函数列 n ( x ) 它称为 Picard迭代序列。
2
1 4 1 h min { , } 2 5 2
故由解得存在唯一性定理可知,初始值问题的解
1 1 y y( x) 在 x 内存在唯一,当然也在 2 2 1 0 x 内存在唯一。
2
1 对 0 x 2
x
(1.2.11)等价的积分方程得 y( x) 0, 且
y2 (s)
y y( x) 满足 (2.2.2)
构造迭代序列 { yn ( x )} 来证明 (2.2.1) 有解. 取
y0 ( x) 1,
y1 ( x) 1 y0(s)ds 1 x,
0 x
y2 ( x) 1
x
0
x2 y1(s)ds 1 x , 2!
……
yn ( x) 1
解的存在唯一性定理证明
解的存在唯一性定理利用逐次逼近法,来证明微分方程(,),dyf x y dx =的初值问题00(,)()dy f x y dx y y x ==⎧⎨⎩的解存在与唯一性定理。
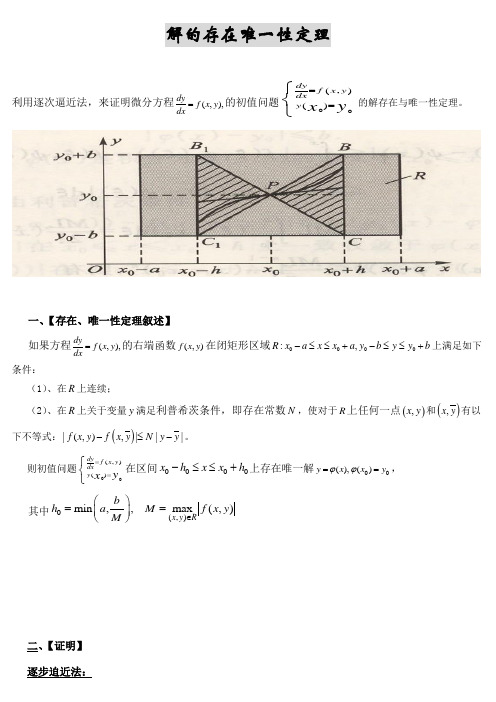
一、【存在、唯一性定理叙述】 如果方程(,),dyf x y dx=的右端函数(,)f x y 在闭矩形区域0000:,R x a x x a y b y y b -≤≤+-≤≤+上满足如下条件:(1)、在R 上连续;(2)、在R 上关于变量y 满足利普希茨条件,即存在常数N ,使对于R 上任何一点(),x y 和(),x y 有以下不等式:()|(,),|||f x y f x y N y y -≤-。
则初值问题00(,)()dyf x y dx y y x ==⎧⎨⎩在区间0000x h x x h -≤≤+上存在唯一解00(),()y x x y ϕϕ==, 其中0(,)min ,,max (,)xy R bh a M f x y M∈⎛⎫== ⎪⎝⎭二、【证明】 逐步迫近法:微分方程(,)dyf x y dx=等价于积分方程00(,)x x y y f x y dx =+⎰。
取00()x y ϕ=,定义001()(,()),1,2,3, (x)n n x x y f x x dx n ϕϕ-=+=⎰可证明lim ()()n n x x ϕϕ→∞=的()y x ϕ=满足积分方程。
通过逐步迫近法可证明解的存在唯一性。
命 题 1:先证积分方程与微分方程等价: 设()y x ϕ=是微分方程(,)dyf x y dx=定义于区间0000x h x x h -≤≤+上满足初值条件00()x y ϕ=的解,则()y x ϕ=是积分方程00(,),x x y y f x y dx =+⎰定义于区间0000x h x x h -≤≤+上的连续解。
反之亦然。
证: 因()y x ϕ=是微分方程(,)dy f x y dx =的解,有'()()(,())d x x f x x dxϕϕϕ== 两边从0x 到x 取定积分,得:000000()()(,()),xx x x f x x dx x h x x h ϕϕϕ-=-≤≤+⎰代入初值条件00()x y ϕ=得:000000()(,()),xx x y f x x dx x h x x h ϕϕ=+-≤≤+⎰即()y x ϕ=是积分方程00(,)xx y y f x y dx =+⎰定义于区间0000x h x x h -≤≤+上的连续解。
常微分方程的解的存在唯一性定理

常微分方程的解的存在唯一性定理常微分方程是数学中的一门重要分支,它涉及到许多实际问题的理论分析和计算求解,尤其是在物理、化学等领域有着广泛的应用。
而常微分方程的解的存在唯一性定理则是研究常微分方程解的基础,下面我将对这一定理进行详细阐述。
1. 常微分方程的定义及初值问题常微分方程(ODE)是指未知函数 $y(t)$ 的某个数量关系式:$$F(t,y,y',y'',\cdots ,y^{(n)})=0$$其中 $y'$,$y''$,$\cdots$,$y^{(n)}$ 分别表示 $y$ 的一阶、二阶、$\cdots$,$n$ 阶导数,$F$ 是已知的函数。
这个方程称为$n$ 阶常微分方程。
方程的初值问题是指,在确定 $n$ 阶常微分方程中的 $n$ 个初始条件:$$y(t_0)=y_0,\ y'(t_0)=y_1,\ \cdots,\ y^{(n-1)}(t_0)=y_{n-1}$$后,求解函数 $y(t)$ 在整个定义域上的解。
2. 解的存在唯一性定理的三个条件常微分方程的解的存在唯一性定理是指在一定的条件下,常微分方程仅有唯一的解。
下面给出常微分方程存在唯一性定理的三个条件。
2.1 连续性设函数 $F(t,y,y',y'',\cdots ,y^{(n)})$ 是定义于某个区域上的$C^{m+1}$ 级函数,即 $F$ 及其 $m$ 个偏导数(一直到$y^{(m)}$)都是连续的。
2.2 局部存在性对于同一初值问题,存在一个足够小的区间 $I$,使得在此区间内存在解 $y(t)$,并且 $y(t)$ 函数及其前 $n-1$ 阶导数都是$C^{m}$ 级函数。
2.3 局部唯一性在区间 $I$ 上,对于同一初值问题,解 $y(t)$ 是唯一的。
3. 解的存在唯一性定理的证明解的存在唯一性定理可转化为证明常微分方程方程的解满足某种 Lipschitz 条件,即:$$\forall \ y_1,y_2\in C([a,b])\ \text{and}\ y_1(t_0)=y_2(t_0)$$$$\Rightarrow \ \exists L>0,\ \text{s.t.}\ |y_1(t)-y_2(t)|\le L\cdot \max_{t\in [t_0,T]}\{|y_1(t)-y_2(t)|\}$$其中,$C([a,b])$ 表示在区间 $[a,b]$ 内连续的函数集合,$L$ 是 Lipschitz 常数。
常微分方程的解的存在唯一性定理

常微分方程的解的存在唯一性定理常微分方程是数学中一个重要的研究对象,它描述了自变量是连续变化的函数与自变量的导数之间的关系。
研究常微分方程的解的存在唯一性定理是常微分方程理论的基石之一,对于解的存在性和唯一性的判断具有重要的意义。
定理一:皮卡尔(Picard)存在定理假设函数f(x, y)在矩形区域D={(x, y):a≤x≤b,α≤y≤β}上连续,且满足利普希茨条件:存在正数L,使得在D上任意点(x, y1)和(x, y2),有|f(x, y1) - f(x, y2)|≤L|y1-y2|。
则初值问题y' = f(x, y),y(x0) = y0在区间[a, b]上存在唯一的解。
证明:(略)定理二:格朗沃尔(Gronwall)不等式假设函数y(x)满足不等式y(x)≤K+∫[a,x]f(t,y(t))dt,其中K为常数且f(x, y)为非负函数。
则有0≤y(x)≤Kexp(∫[a,x]f(t,y(t))dt)。
证明:(略)根据皮卡尔存在定理和格朗沃尔不等式,我们可以推导出常微分方程解的存在唯一性定理。
定理三:常微分方程解的存在唯一性定理假设函数f(x, y)在区域D上连续,且满足利普希茨条件:存在正数L,使得在D上任意点(x, y1)和(x, y2),有|f(x, y1) - f(x, y2)|≤L|y1-y2|。
则对于初值问题y' = f(x, y),y(x0) = y0,在定义区间上存在唯一的解。
证明:(略)常微分方程解的存在唯一性定理的推导过程相对较为复杂,涉及到一些数学理论和定理的运用。
但是这个定理为我们研究和求解常微分方程提供了重要的理论支持,确保了我们在解决实际问题中得到的解是存在且唯一的。
除了皮卡尔存在定理和格朗沃尔不等式外,我们还可以利用其他方法来证明常微分方程解的存在唯一性,比如利用分离变量法、变换方法、级数法等。
在实际应用中,根据具体问题的特点选择适合的方法进行求解。
线性方程组的解存在唯一性定理

线性方程组的解存在唯一性定理线性方程组是数学中常见的问题之一,它与矩阵和向量的概念紧密相关。
对于给定的线性方程组,我们通常会关心解集的存在性和唯一性,这在很多实际问题中具有重要的意义。
本文将探讨线性方程组解的存在唯一性定理,并解释其背后的原理和证明思路。
一、线性方程组的定义和基本性质首先,我们来回顾线性方程组的基本定义。
给定一个包含n个未知数$x_1, x_2, ..., x_n$的线性方程组,可以表示为以下形式:$$\begin{cases}a_{11}x_1 + a_{12}x_2 + ... + a_{1n}x_n = b_1 \\a_{21}x_1 + a_{22}x_2 + ... + a_{2n}x_n = b_2 \\... \\a_{m1}x_1 + a_{m2}x_2 + ... + a_{mn}x_n = b_m \\\end{cases}$$其中,$a_{ij}$表示系数矩阵的元素,$b_i$表示常数向量的元素。
线性方程组的解可以表示为一个n维向量$(x_1, x_2, ..., x_n)$,使得方程组的每个等式都成立。
解集可以是一个空集(即无解)、一个具有无穷多个解的集合,或者只包含一个解。
接下来,我们将研究线性方程组解存在唯一性的情况。
二、线性方程组解存在唯一性定理的表述线性方程组的解存在唯一性定理可以总结为以下表述:对于一个齐次线性方程组,如果系数矩阵的秩等于未知数的个数,即$r(A) = n$,那么方程组的解集只包含零向量;如果系数矩阵的秩小于未知数的个数,即$r(A) < n$,那么方程组的解集包含无穷多个解。
对于一个非齐次线性方程组,如果系数矩阵的秩等于增广矩阵的秩,即$r(A) = r([A|b])$,那么方程组的解集只包含一个解;如果系数矩阵的秩小于增广矩阵的秩,即$r(A) < r([A|b])$,那么方程组的解集包含无穷多个解。
注意,这里的秩指的是矩阵的行秩或列秩,即行向量组或列向量组的最大线性无关组的元素个数。
cauchy问题解的存在唯一性定理的几种证明

cauchy问题解的存在唯一性定理的几种
证明
Cauchy问题解的存在唯一性定理是一个重要的定理,它指出了一个给定的常微分方程的Cauchy问题的解的存在唯一性。
由于它具有重要的应用价值,因此在数学界有很多关于它的证明。
本文将简要介绍几种关于Cauchy问题解的存在唯一性定理的证明。
首先,我们介绍最经典的古典证明:古典证明是由C.F. Gauss于1809年发表的,他通过比较两个解的差分来证明Cauchy问题的解的唯一性。
其次,根据微分方程的函数可微性定理,可以证明Cauchy问题解的唯一性。
函数可微性定理说明了一个多元函数在它的可微点处可以对每个变量做函数导数,因此可以证明Cauchy问题的解的唯一性。
再次,最近的一个证明是由Otto Toeplitz于1903年发表的,他采用“变量变换”的方法。
他证明,Cauchy问题的解的唯一性可以经由一个简单的变量变换,将其转化为一个解析函数,这个函数具有唯一性。
最后,我们介绍最近发现的一种证明:由L.C. Evans于1966年发表的,他使用了“流形理论”的概念来证明Cauchy问题的解的唯一性。
他说,Cauchy问题的解可以看作是一个流
形上的函数,而这个函数的唯一性可以从它的定义域的形状来判断。
以上就是Cauchy问题解的存在唯一性定理的几种证明介绍。
由于它具有重要的应用价值,因此在数学界有很多关于它的证明。
古典证明、函数可微性定理、变量变换、流形理论等等,都是关于Cauchy问题解的存在唯一性定理的有效证明方法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
, 。
设,则 。由数学归纳法,对所有,有 。 因此,对所有,在有成立。但当时。故在上的一致收敛于。由极限的迫近函数序列为: 命 题 2:对所有,函数序列在上有定义、连续且满足不等式
证:当时, 。显然在上有定义、连续且有 ,即命题2当时成立。 由数学归纳法,设命题2当时成立,则对有: 知在上有定义、连续且有 命题2当时也成立。 由数学归纳法原理得命题2对所有均成立。 命 题 3:函数序列在上一致收敛。
解的存在唯一性定理
利用逐次逼近法,来证明微分方程的初值问题的解存在与唯一性定理。
一、【存在、唯一性定理叙述】 如果方程的右端函数在闭矩形区域上满足如下条件:
(1)、在上连续;
(2)、在上关于变量满足利普希茨条件,即存在常数,使对于上任何一点和
有以下不等式:。
则初值问题在区间上存在唯一解, 其中
二、【证明】 逐步迫近法: 微分方程等价于积分方程。 取,定义 可证明的满足积分方程。 通过逐步迫近法可证明解的存在唯一性。 命 题 1:先证积分方程与微分方程等价: 设是微分方程定义于区间上满足初值条件 的解,则是积分方程定义于区间上的连续解。反之亦然。 证: 因是微分方程的解,有 两边从到取定积分,得: 代入初值条件得: 即是积分方程定义于区间上的连续解。 反之,则有 微分得: 且当时有。即是微分方程定义于区间上满足初值条件的解。 现取,代入积分方程的右端,所得函数用表示,则,再将代入积分 方程的右端,所得函数用表示,则,以上称为1次近似, 称为2次近似。以此类推得
证:只须考虑级数-----(*) 在上一致收敛。 因其部分和为:,因, 设对成立。 则当时有 即对所有,在成立 。 其右端组成正项收敛级数
由魏氏判别法,级数(*)在上一致收敛。即在上一致收敛。命题3得 证。 现设 则在上有定义、连续且
命 题 4: 是积分方程在上的连续解。 证: 由利普希茨条件 及在上一致收敛于,知函数序列在上一致收敛 于。 于是即 是积分方程在上的连续解。
