2019届高考数学专题十三三视图与体积表面积精准培优专练.doc

合集下载

2020届高三精准培优专练十三三视图与体积、表面积(理) 学生版

2020届高三好教育精准培优专练例1：中国古建筑借助榫卯将木构件连接起来，构件的凸出部分叫榫头，凹进部分叫卯眼，图中木构件右边的小长方体是榫头．若如图摆放的木构件与某一带卯眼的木构件咬合成长方体，则咬合时带卯眼的木构件的俯视图可以是（）A．B．C．D．例2：如图，在长方体1111ABCD A B C D-中，点P是棱CD上一点，则三棱锥11P A B A-的侧视图是（）A．B．C．D．例3：如图，网格纸的各小格都是正方形，粗实线画出的是一个几何体的三视图，则这个几何体是（）二、根据三视图还原几何体的直观图一、根据几何体的结构特征确认其三视图培优点十三三视图与体积、表面积A．三棱锥B．三棱柱C．四棱锥D．四棱柱例4：若某几何体的三视图如图所示，则这个几何体的直观图可以是（）A．B．C．D．例5：如图是一个空间几何体的正视图和俯视图，则它的侧视图为（）A．B．C．D．例6：一个几何体的三视图中，正视图和侧视图如图所示，则俯视图不可以为（）A．B．C．D．三、已知几何体的三视图中某两个视图，确定另外一种视图例7：如图所示，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则该几何体的表面积为（）A．5π18+B．6π18+C．8π6+D．10π6+例8：如图所示，某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径．若该几何体的体积是28π3，则它的表面积是（）A．17πB．18πC．20πD．28π例9：某几何体的三视图如图所示(单位：cm)，则该几何体的体积(单位：3cm)是（）A．π12+B．π32+C．3π12+D．3π32+例10：如图所示，已知多面体ABCDEFG中，AB、AC、AD两两互相垂直，平面ABC∥平面DEFG，平面BEF∥平面ADGC，2AB AD DG===，1AC EF==，则该多面体的体积为________．五、根据几何体的三视图计算体积四、根据几何体的三视图计算表面积一、选择题1．如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则此几何体的各个面中是直角三角形的个数为（）A．1B．2C．3D．42．某几何体的三视图如图所示，网格纸上小正方形的边长为1，则该几何体的表面积（）A．5πB．6πC．6π2+D．5π2+3．已知一个几何体的三视图如图所示，则其体积为（）A．12πB．16πC．32π3D．403π4．某四棱锥的三视图如图所示，则该四棱锥的体积为（）对点增分集训A ．23B ．43C ．83D5．我国古代《九章算术》将上下两个平行平面为矩形的六面体称为刍童．如图是一个刍童的三视图，其中正视图及侧视图均为等腰梯形，两底的长分别为2和6，高为2，则该刍童的体积为（）A ．1003B ．1043C ．27D ．186．如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的各棱中，最长的棱的长度为（）A ．B ．6C ．D ．47．在正方体1111ABCD A B C D 中，E 、F 、G 分别为棱CD 、1CC 、11A B 的中点，用过点E 、F 、G 的平面截正方体，则位于截面以下部分的几何体的侧视图为（）A．B．C．D．8．如图所示的网格是由边长为1的小正方形构成，粗线画出的是某几何体的三视图，则该几何体的体积为（）A．40B．103C．163D．8039．某几何体的三视图如图所示，则该几何体的外接球的体积是（）A．π3B．π2C．3πD．10．某空间几何体的三视图如图所示，则该几何体的外接球半径为（）ABCD．11．如图，网格纸上小正方形的边长为1，粗线画出的是某四棱锥的三视图，则该四棱锥的体积为（）A．6B．8C．D．12．在棱长为1的正方体1111ABCD A B C D -中，E 、F 分别为线段CD 和11A B 上的动点，且满足1CE A F =，则四边形1D FBE 所围成的图形（如图所示阴影部分）分别在该正方体有公共顶点的三个面上的正投影的面积之和（）A ．有最小值32B ．有最大值52C ．为定值3D ．为定值2二、填空题13．某几何体的三视图如图所示，网格纸上小正方形的边长为1，则该几何体的表面积是．14．《九章算术》是我国古代数学名著，在《九章算术》中将底面为矩形且有一侧棱垂直于底面的四棱锥称为“阳马”．若某“阳马”的三视图如图所示，其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形，则该“阳马”的表面积为．15．已知圆锥的高为3，若该圆锥的顶点与底面的圆周都在同一个球面上，则这个球的体积等于．16．已知点P 、A 、B 、C 是半径为2的球面上的点，2PA PB PC ===，90ABC ∠=︒，点B 在AC 上的射影为D ，则三棱锥P ABD -体积的最大值是．例1：【答案】A【解析】由题意可知带卯眼的木构件的直观图如图所示，由直观图可知其俯视图，应选A．例2：【答案】D【解析】在长方体1111ABCD A B C D-中，从左侧看三棱锥11P A B A-，1B、1A、A的射影分别是1C、1D、D，1AB的射影为1C D，且为实线，1PA的射影为1PD，且为虚线．故选D．例3：【答案】B【解析】由题三视图得直观图如图所示，为三棱柱．故选B．例4：【答案】D【解析】由三视图知该几何体的上半部分是一个三棱柱，下半部分是一个四棱柱．故选D．例5：【答案】A【解析】由正视图和俯视图可知，该几何体是一个圆柱挖去一个圆锥构成的，结合正视图的宽及俯视图的直径知其侧视图应为A．故选A．例6：【答案】C【解析】A中，该几何体是直三棱柱，所以A有可能；B中，该几何体是直四棱柱，所以B有可能；C中，由题干中正视图的中间为虚线知，C不可能；D中，该几何体是直四棱柱，所以D有可能．综上，故选C．例7：【答案】C【解析】由三视图可知该几何体是由一个半圆柱和两个半球构成的，培优点十三三视图与体积、表面积答案故该几何体的表面积为2211124π12π1232π138π6222⨯⨯⨯+⨯⨯⨯+⨯+⨯⨯⨯=+．故选C ．例8：【答案】A【解析】由几何体的三视图可知，该几何体是一个球体去掉上半球的14，得到的几何体如图．设球的半径为R ，则3341428πππ3833R R -⨯=，解得2R =．因此它的表面积为22734ππ17π84R R ⨯+=．故选A ．例9：【答案】A【解析】由几何体的三视图可知，该几何体是一个底面半径为1，高为3的圆锥的一半与一个底面为直角边3的三棱锥的组合体，∴该几何体的体积21111ππ323221331⨯⨯⨯⨯+=+．故选A ．例10：【答案】4【解析】法一：(分割法)因为几何体有两对相对面互相平行，如图所示，过点C 作CH DG ⊥于H ，连接EH ，即把多面体分割成一个直三棱柱DEH ABC -和一个斜三棱柱BEF CHG -．由题意，知三棱柱DEH ABC -的体积11(2221)2DEH V S AD =⨯⨯⨯=⨯=△，三棱柱BEF CHG -的体积21(2221)2BEF V S DE =⨯⨯⨯=⨯=△，故所求多面体ABCDEFG 的体积为12224V V V =+=+=．法二：(补形法)因为几何体有两对相对面互相平行，如图所示，将多面体补成棱长为2的正方体，显然所求多面体的体积即该正方体体积的一半．又正方体ABHI DEKG -的体积328V '==，故所求多面体ABCDEFG 的体积为118422V V '==⨯=．一、选择题 1．【答案】C【解析】三视图还原为如图所示三棱锥A BCD -，由正方体的性质得ABC △、BCD △、ACD △为直角三角形，ABD △为正三角形，故选C ．2．【答案】D【解析】由三视图可知，该几何体为两个半圆柱构成，其表面积为22π1π12π11215π2⨯⨯+⨯⨯+⨯⨯+⨯=+，故选D ． 3．【答案】D【解析】由三视图可知，该几何体为圆柱挖去其16后的剩余部分，该圆柱的底面半径为2，高为4，故其体积为圆柱体积的56，25540ππ16π663V R h ==⨯=．故选D ．4．【答案】C【解析】该三视图还原成直观图后的几何体是如图所示的四棱锥A BCDE -，CBA △和ACD △是两个全等的直角三角形，且2AC CD BC ===，故几何体的体积为1822233⨯⨯⨯=，故选C ．5．【答案】B【解析】由题意几何体原图为正四棱台，底面的边长分别为2和6，高为2，所以几何体体积1104(436233V =++⨯=．故选B ． 6．【答案】B【解析】三视图还原成如图所示的几何体，三棱锥S ABC -，则4SB BC ==，SC =AC AB ==6SA =．故选B ．7．【答案】C【解析】过点E ，F ，G 截正方体的平面为如图所示的平面EFKGHI ，由图知位于截面以下部分的几何体的侧视图为C 选项，故选C ．8．【答案】D【解析】根据几何体三视图可得，该几何体是三棱柱BCE AGF -割去一个三棱锥A BCD -所得的几何体，如图所示，所以其体积为111180444(44)423223V =⨯⨯⨯-⨯⨯⨯⨯⨯=．故选D ．9．【答案】B【解析】根据几何体的三视图知，该几何体是由一个正方体切去正方体的一角得到的，故该几何体的外接球为正方体的外接球，所以球的半径22r ==，则34π3V =⋅⋅=⎝⎭B ． 10．【答案】C【解析】由三视图可知三棱锥的直观图如图，由三视图可知底面三角形是边长为2，顶角120︒的三角形，所以其外接圆半径结合正弦定理可得，224sin30r ==︒，由侧面为两等腰直角三角形，可确定出外接圆圆心，利用球的几何性质可确定出球心，且球心到底面的距离1d =，所以球半径R ==C ．11．【答案】B【解析】由三视图可得四棱锥为如图所示的长方体1111ABCD A B C D -中的四棱锥11C DEE D -，其中在长方体1111ABCD A B C D -中，4AB =，2AD =，13AA =，点E 、1E 分别为AB 、11A B 的中点，由题意得CE DE ==CE DE ⊥，又1CE EE ⊥，所以CE ⊥平面11DEE D ，即线段CE 即为四棱锥11C DEE D -的高，所以四棱锥11C DEE D -的体积1111(3833DEE D V S CE =⋅⋅=⨯⨯⨯=．故选B ．12．【答案】D【解析】依题意，设四边形1D FBE 的四个顶点在后面、上面、左面的投影点分别为'D 、F '、B '、E '，则四边形1D FBE 在上面、后面、左面的投影分别如下图，所以在后面的投影的面积为1111S =⨯=，在上面的投影面积211S D E DE DE ''=⨯=⨯=，在左面的投影面积311S B E CE CE ''=⨯=⨯=，所以四边形1D FBE 所围成的图形分别在该正方体有公共顶点的三个面上的正投影的面积之和为123112S S S S DE CE CD =++=++=+=．故选D ．二、填空题13．【答案】64+【解析】由三视图可知，该几何体的直观图为如图所示的四棱柱，则11111(24)4122ABCD A B C D S S ==⨯+⨯=，11114416BCC B CC D D S S ==⨯=，11428ABB A S =⨯=，114AA D D S =⨯=所以该四棱柱的表面积为2432864S =+++=+14．【答案】2+【解析】由三视图可得该“阳马”的底面是边长为1的正方形，且高为1，故该“阳马”的表面积为11211212122+⨯⨯⨯+⨯=+15．【答案】32π3【解析】设该圆锥的外接球的半径为R ，依题意得，222()3R R +-=，解得2R =，故所求球的体积334432ππ2π333V R ==⨯=．16．【解析】设点P 在平面ABC 上的射影为G ，如图，由2PA PB PC ===，90ABC ∠=︒知，点P 在平面ABC 上的射影G 为ABC △的外心，即AC 的中点，设球的球心为O ，连接PG ，则O 在PG 的延长线上，连接OB 、BG ，设PG h =，则2OG h =-，所以2222OB OG PB PG -=-，即22()424h h --=-，解得1h =，则AG CG ==设AD x =，则GD x AG x =-=BG =所以BD ==12ABD S AD BD ==⋅△令43()f x x =-+，则32()4f x x '=-+，由()0f x '=，得0x =或x =，易知当x =时，函数()f x 取得最大值24316，所以max 1()2ABD S ==△又1PG =，所以三棱锥P ABD -体积的最大值为113=．。

2020届高考数学专题十三三视图与体积表面积精准培优专练文

三视图与体积表面积培优点十三一、三视图与体积的结合1 1：某几何体的三视图如图所示（图中小正方形网格的边长为，则该几何体的体积是（））例8624 C． D．BA．．B【答案】【解析】由三视图可得该几何体为底面是直角梯形的直四棱柱（如图所示），2212其中底面直角梯形的上、下底边分别为，，，高为，直四棱柱的高为2?(12)?6??2．，故选所以该几何体的体积为B2二、三视图与表面积的结合1，粗线画出的是某几何体的三视图，其中俯视图由两个半圆和例2：如图，网格纸上小正方形的边长为两个线段组成，则该几何体的表面积为（）12π?20π?1216?12π17π?1212 D．． CBA．．C【答案】由三视图知，该几何体是一个大半圆柱挖去一个小半圆柱得到的，【解析】331，高均为，两个半圆柱的底面半径分别为和11112212π?202)?2??3?1π?(231?π?33π?2???2???π3??所以该几何体的表面积为．2222对点增分集训一、选择题．某几何体的三视图如图所示，则这个几何体的体积为（）1．ππ4π4π2)8?16(116??16? B． A．D． C．3333C【答案】根据三视图知，该几何体是一个直四棱柱内挖去一个圆锥后剩余的部分，【解析】画出直观图如图所示，VV设四棱柱的体积为，结合图中数据，，圆锥的体积为21π1422??16π?12?V?VV??4??4 C 得该几何体的体积．，故选21331 2．如图，网格纸上小正方形的边长为，粗线条画出的是一个三棱锥的三视图，则该三棱锥中最长棱的长度为（）32252．D ．C ．B ．A．【答案】DA?BCD即为所求几何体，【解析】如图，三棱锥2?2BD1CD?3?AC?2AB5?5BC?AD2，，，，，，根据题设条件，知辅助的正方体棱长为，3AB，长度为则最长棱为．．古人采取“用臼舂米”的方法脱去稻谷的外壳，获得可供食用的大米，用于舂米的“臼”多用石头或木3 头制成．一个“臼”的三视图如图所示，则凿去部分（看成一个简单的组合体）的体积为（）π99π72π7963π．B．．A C ．DA【答案】【解析】由三视图得凿去部分是圆柱与半球的组合体，335，其中圆柱的高为，底面圆的半径为，半球的半径为4132ππ36353π??????A，故选所以组合体的体积为．32．4．某几何体的三视图如图所示，在该几何体的各个面中，面积最小的面与底面的面积的比值为（）4212．C ． A． B．D5335C【答案】ABCDP?4．的四棱锥，如图所示，记为【解析】由三视图可知，该几何体是高为14??1易知面积最小的面为左侧面，其面积为．2115?12??2???(24)?ABCDABCDBCDE的面积为将底面，，则底面补为梯形222所以面积最小的面与底面的面积的比值为C，故选．52的正方形，则该几何体的表5．一个几何体的三视图如图所示，其中正视图和俯视图中的四边形是边长为面积为（）π1513ππ87π．A．．． B D C22B【答案】由三视图可知该几何体是一个圆柱体和一个球体的四分之一的组合体，【解析】1222π?7?1??π?12?2?4π?1??π1π B则所求的几何体的表面积为．，故选41，粗线画出的是某几何体的三视图，则该几何体的表面积6．如图，网格纸上小正方形的边长为为（）π6π?58?48?8?3ππ8． CB．A．．DD【答案】114【解析】由三视图可知，该几何体是由底面半径为的半球得到的，，高为的半圆柱挖去一个半径为111222π6?1?8???????2????2S??π14?π142π1π?4则该几何体的表面积．222．故选B ．某几何体的三视图如图所示，则这个几何体的体积是（）7．16151314 D C．．A．B ．C 【答案】【解析】所求几何体可看作将长方体截去两个三棱柱得到的几何体，在长方体中还原该几何体，????3CABCD?ABD24如图中，所示，长方体的长、宽、高分别为，，1.532两个三棱柱的高为，底面是两直角边长分别为的直角三角形，和31153???2??????V4232C．故该几何体的体积，故选22 8．某装饰品的三视图如图所示，则该装饰品的表面积为（）π16?20?(5?1)ππ5?1)16?(5?1)π16?( BC．A． D．．C【答案】2的正方体，【解析】由装饰品的三视图可知，该装饰品是由一个棱长为12，切去四个四分之一的圆锥所得的几何体，其中圆锥的底面半径为，高为111222?4??2?2?4?π?1?22?4??5?16π?1?(5?1)π，故选则该装饰品的表面积为C．4241，粗线画出的是某几何体的三视图，俯视图中的两条曲线均为圆弧，．如图，网格纸上小正方形的边长为9则该几何体的体积为（）π8π16π32?64?64?64π864? CB．．．A． D 333C【答案】1424圆锥和一个底、高为的【解析】由三视图知，该几何体是由棱长为的正方体截去一个底面半径为4142的面半径为圆柱而得到的，、高为4π1611322?464??V?2π4?(π2????4)所以该几何体的体积，故选．C334．10．我国古代数学名著《九章算术·商功》中阐述：“斜解立方，得两堑堵．斜解堑堵，其一为阳马，一为鳖臑．阳马居二，鳖臑居一，不易之率也．合两鳖臑三而一，验之以棊，其形露矣”若称为“阳马”的1，则对该几何体描述：某几何体的三视图如图所示，图中网格纸上小正方形的边长为①四个侧面都是直角三角形；26；②最长的侧棱长为③四个侧面中有三个侧面是全等的直角三角形；24π．④外接球的表面积为其中正确的个数是（）3021．．．AB ．D CD【答案】【解析】ABCDABCDSA??S所示，其中对于①，由三视图知“阳马”的直观图如图中四棱锥平面，SAD△?BC△SABADABSA?SA?SA，，所以为直角三角形，，所以，SBC△?BCSABBCABBC??SB为直角三角形，，故，所以平面，知结合．△SCD为直角三角形，所以“阳马”的四个侧面均为直角三角形，正确；同理可知22222?SA?25??ABSA??AD22SASB?SD，，，对于②，由三视图及直观图得AC连接，22222?26??AC?SACD?SC?SAAD，则26，正确；所以“阳马”的最长的侧棱长为对于③，由②的侧棱长知，侧面四个直角三角形的斜边均不相等，所以不存在全等的直角三角形，错误；422的长方体，易知长方体的外接球即“阳、、对于④，考虑将“阳马”补形为一个长、宽、高分别为222?24?26?2R?2，马”的外接球其直径22π24(2R)?4πR?π所以“阳马”的外接球的表面积为，正确．3，故选D．综上可知，正确的个数为．某工人现欲用车床将一正方体铁块进行加工处理，加工后成品的三视图如图所示．网格纸上小正方形111的边长为，则加工后成品与去除部分几何体的体积比为（）π48?16?64?32?πππ．．．AB C D ．ππππC 【答案】．4，圆柱的底面【解析】由三视图可知，该几何体为正方体中间挖去一个圆柱后所得，且正方体的棱长为14，，高为半径为VV，，圆柱的体积为设正方体的体积为2132V?V?V?4?π?1?4?64?4π．所以加工后成品的体积2164?4π16?π?．故选C加工后成品与去除部分的体积比为．4ππMA1，其中小正方形的边长均为在俯视图上的对应点为．三棱锥上的点12．某三棱锥的三视图如图所示，NMN B长度的最大值为（）在左视图上的对应点为，则线段点923633．B ．DC ．．AA 【答案】【解析】3根据三视图，在棱长为的正方体中还原该几何体的直观图，N?CNEPB在左视图上对应的点，即点，则点为如图所示的三棱锥．PCCNE MA上的投影，上任意一点点为线段在底面MNPNPCN33M．的长，故线段因为长度的最大值为上的点到点距离的最大值为二、填空题13．已知某几何体的三视图如图所示（侧视图中曲线为四分之一圆弧），则该几何体的体积为．π?1【答案】4111的【解析】由已知三视图得到几何体是棱长为圆柱，的正方体挖去底面半径为4ππ1121π1??1???1．正方体的棱长为，圆柱的体积为，所以几何体体积为44441．如图是某几何体的三视图，图中方格的单位长度为14，则该几何体的表面积为．8?45【答案】【解析】由三视图还原几何体如下图所示，22BD?2?BCDA?BC?2CD52AB??25AD，，，，计算可得，，可得三棱锥111 5225??25S?2?2???2?2S2??2?5?S，，，ABCADC△△BCD△22212262?2?32S??22)3?(25)?(ABD△，为等腰三角形，高为，ABD△25?4825?6?22?5?则该几何体表面积为． 15．一个由半球和四棱锥组成的几何体，其三视图如图所示．则该几何体的体积为．21π?【答案】63211，，高为，正四棱锥的底面边长为由已知，半球的直径为【解析】．1142123???11?ππ?()??．所以其体积为23323612π?．故答案为3616．某几何体的三视图如图所示，则该几何体的体积为．π3【答案】【解析】由题意可知几何体的直观图如图：32π4??3π1??．所以几何体的体积为，故选C4。

2019高考数学二轮复习专题三立体几何第1讲空间几何体的三视图表面积和体积练习

哈哈哈哈哈哈哈哈你好第 1 讲空间几何体的三视图、表面积和体积高考定位 1. 三视图的辨别和简单应用； 2. 简单几何体的表面积与体积计算，主要以选择题、填空题的形式表现，在解答题中，有时与空间线、面地点证明相联合，面积与体积的计算作为此中的一问 .真题感悟1.(2018 ·全国Ⅲ卷) 中国古建筑借助榫卯将木构件连结起来. 构件的凸出部分叫榫头，凹进部分叫卯眼，图中木构件右边的小长方体是榫头. 若如图摆放的木构件与某一带卯眼的木构件咬合成长方体，则咬合时带卯眼的木构件的俯视图能够是()分析由题意知，在咬合时带卯眼的木构件中，从俯视方向看，榫头看不见，所以是虚线，联合榫头的地点知选 A.答案 A2.(2018 ·全国Ⅰ卷 ) 已知圆柱的上、下底面的中心分别为O，O，过直线 OO 的平面截该圆1 2 1 2柱所得的截面是面积为8 的正方形，则该圆柱的表面积为( )A.12 2 πB.12 πC.8 2πD.10 π分析由于过直线 1 2 的平面截该圆柱所得的截面是面积为8 的正方形，所以圆柱的高为OO2 2，底面圆的直径为 2 2. 所以S表面积＝2× π×( 2) 2＋2π ×2×2 2＝ 12π .答案 B3.(2018 ·天津卷 ) 已知正方体ABCD－ A1B1C1D1的棱长为1，除面 ABCD外，该正方体其他各面的中心分别为点E， F， G， H， M(如图)，则四棱锥M－EFGH的体积为________.分析连结 AD1， CD1，B1A，B1C， AC，由于 E，H分别为 AD1，CD1的中点，1 1所以 EH∥ AC， EH＝2AC.由于 F， G分别为 B1A，B1C 的中点，所以FG∥AC， FG＝2AC.所以 EH哈哈哈哈哈哈哈哈你好2正方形 . 又点 M 到平面 EHGF 的距离为1 M － EFGH 的体积为1×2 11，所以四棱锥 3× ＝ .22 2 12 答案1124.(2017 ·全国Ⅰ卷 ) 已知三棱锥 S － ABC 的全部极点都在球 O 的球面上， SC 是球 O 的直径 .若平面⊥平面，＝，＝，三棱锥－的体积为 9，则球O 的表面积为SCA SCB SA AC SB BC S ABC________.分析如图，连结 OA ， OB ，由于 SA ＝AC ， SB ＝BC ， SC 为球 O 的直径，所以 OA ⊥ SC ， OB ⊥ SC .由于平面 SAC ⊥平面 SBC ，平面 SAC ∩平面 SBC ＝SC ，且 OA ? 平面 SAC ，所以 OA ⊥平面 SBC .设球的半径为 r ，则 OA ＝ OB ＝r ， SC ＝2r ，所以A －SBC ＝1× △SBC ×＝1× 1×2 × ×＝1 3，V3SOA 3 2r rr3r1 32所以 3r ＝ 9? r ＝ 3，所以球的表面积为 4π r ＝ 36π .答案 36π考点整合1. 空间几何体的三视图(1) 几何体的摆放地点不一样，其三视图也不一样，需要注意长对正、高平齐、宽相等 .(2) 由三视图复原几何体：一般先从俯视图确立底面，再利用正视图与侧视图确立几何体.2. 空间几何体的两组常用公式(1) 柱体、锥体、台体的表面积公式：①圆柱的表面积 S ＝2π r ( r ＋l ) ；②圆锥的表面积 S ＝π r ( r ＋ l ) ；③圆台的表面积 S ＝π ( r ′ 2＋ r 2＋r ′ l ＋ rl ) ；④球的表面积 S ＝ 4π R 2.(2) 柱体、锥体和球的体积公式：①V 柱体＝Sh ( S 为底面面积， h 为高 ) ；1②V 锥体＝3Sh ( S 为底面面积， h 为高 ) ；43哈哈哈哈哈哈哈哈你好热门一空间几何体的三视图与直观图【例 1】 (1)(2018 ·兰州模拟) 中国古代数学名著《九章算术》中，将底面是直角三角形的直棱柱称为“堑堵”. 已知某“堑堵”的正视图和俯视图如下图，则该“堑堵”的侧视图的面积为()A.18 6B.18 3C.18227 2D.2(2)(2018 ·全国Ⅰ卷 ) 某圆柱的高为 2，底面周长为 16，其三视图如图. 圆柱表面上的点在正视图上的对应点为，圆柱表面上的点 N 在左视图上的对应点为，MAB则在此圆柱侧面上，从到 N 的路径中，最短路径的长度为 ()MA.2 17B.2 5C.3D.2分析(1) 在俯视图 Rt △中，作⊥ 交于.ABC AH BC H由三视图的意义，则 BH ＝ 6，HC ＝ 3，2依据射影定理， AH ＝ BH · HC ，∴ AH ＝ 32.易知该“堑堵”的侧视图是矩形，长为6，宽为＝ 3 2. 故侧视图的面积＝6×3 2＝AHS18 2.(2) 由三视图可知，该几何体为如图①所示的圆柱，该圆柱的高为 2，底面周长为 16. 画出该圆柱的侧面睁开图，如图②所示，连结MN ，则 MS ＝ 2，SN ＝ 4. 则从 M 到 N 的路径中，最短路径的长度为 22225.MS ＋ SN ＝ 2 ＋ 4 ＝ 2答案(1)C (2)B研究提升1. 由直观图确立三视图，一要依据三视图的含义及画法和摆放规则确认. 二要熟悉常有几何体的三视图.(1) 依据俯视图确立几何体的底面.(2)依据正视图或侧视图确立几何体的侧棱与侧面的特点，调整实线和虚线所对应的棱、面的地点 .(3)确立几何体的直观图形状 .【训练 1】 (1) 如图，在底面边长为1，高为 2 的正四棱柱ABCD－ A1B1C1D1中，点 P 是平面A1B1C1D1内一点，则三棱锥 P－ BCD的正视图与侧视图的面积之和为()A.1B.2C.3D.4(2)(2017 ·北京卷 ) 某四棱锥的三视图如下图，则该四棱锥的最长棱的长度为()A.3 2B.2 3C.2 2D.2分析(1) 设点P在平面A1ADD1的射影为P′，在平面 C1CDD1的射影为P″，如下图.∴三棱锥 P－ BCD的正视图与侧视图分别为△P′AD与△ P″ CD，所以所求面积S＝ S△P′AD＋S△P″CD1 1＝×1×2＋×1×2＝ 2.2 2(2)依据三视图可得该四棱锥的直观图( 四棱锥P－ABCD)如下图，将该四棱锥放入棱长为 2 的正方体中 . 由图可知该四棱锥的最长棱为PD，22 2PD＝2＋2＋2＝2 3.考法 1空间几何体的表面积【例 2－ 1】 (1)(2017 ·全国Ⅰ卷) 某多面体的三视图如下图，此中正视图和侧视图都由正方形和等腰直角三角形构成，正方形的边长为2，俯视图为等腰直角三角形，该多面体的各个面中有若干个是梯形，这些梯形的面积之和为()A.10B.12C.14D.16(2)(2018 ·西安模拟) 如图，网格纸上正方形小格的边长为1，粗实线画出的是某几何体的三视图，则该几何体的表面积为()A.20 πB.24 πC.28 πD.32 π分析(1) 由三视图可画出直观图，该直观图各面内只有两个同样的梯形1的面， S 梯＝×(2＋4)×2＝6， S 全梯＝6×2＝12.(2)由三视图知，该几何体由一圆锥和一个圆柱构成的组合体，∵S 圆锥侧＝π ×3×2 2 23 ＋ 4＝15π，S圆柱侧＝2π ×1×2＝ 4π，S圆锥底＝π×3＝9π .故几何体的表面积S＝15π＋4π＋9π＝28π.答案(1)B(2)C研究提升 1. 由几何体的三视图求其表面积：(1) 重点是剖析三视图确立几何体中各元素之间的地点关系及胸怀大小；(2) 复原几何体的直观图，套用相应的面积公式.2.(1) 多面体的表面积是各个面的面积之和；组合体的表面积注意连接部分的办理. (2) 旋转体的表面积问题注意其侧面睁开图的应用.【训练 2】 (1)( 2016·全国Ⅰ卷) 如图，某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径. 若该几何体的体积是28π，则它的表面积是()3哈哈哈哈哈哈哈哈你好A.17 πB.18 πC.20 πD.28 π(2)(2018 ·烟台二模 ) 某几何体的三视图如下图，此中俯视图右边曲线为半圆弧，则几何体的表面积为 ()A.3 π ＋ 4 2－ 2B.3 π ＋ 2 2－ 2 3π3πC. 2 ＋ 2 2－ 2D.2＋22＋ 2分析(1) 由题知，该几何体的直观图如下图，它是一个球 ( 被过球心 O1且相互垂直的三个平面) 切掉左上角的 8后获得的组合体，其表面积是球7172面面积的 8和三个 4圆面积之和，易得球的半径为 2，则得 S ＝ 8×4π ×21 2 ＋3× 4π ×2＝ 17π .(2) 由三视图，该几何体是一个半圆柱挖去向来三棱柱，由对称性，几何体的底面面积S 底22) 2＝ π －2. ＝π ×1－ (∴几何体表面积 S ＝2(2 ×12) ＋ 2(2 π×1×2) ＋ S底＝ 4 2＋2π ＋ π －2＝ 3π ＋4 2－ 2.答案(1)A (2)A考法 2空间几何体的体积【例 2－ 2】 (1)(2018 ·河北衡水中学调研) 某几何体的三视图如下图，则该几何体的体哈哈哈哈哈哈哈哈你好积为()22 20 A.6B.4C. 3D. 3(2) 由一个长方体和两个 1________.4圆柱构成的几何体的三视图如图，则该几何体的体积为分析 (1) 由三视图知该几何体是边长为 2 的正方体挖去一个三棱柱 ( 如图) ，且挖去的三棱柱的高为1，底面是等腰直角三角形，等腰直角三角形的直角边长为 2. 故几何体体积 V ＝ 312 －2×2×2×1＝ 6.1(2) 该几何体由一个长、宽、高分别为 2，1，1 的长方体和两个底面半径为1，高为 1 的 4圆柱体构成 .12π所以 V ＝2×1×1＋2× 4× π ×1×1＝ 2＋ 2 .答案 (1)A(2)2 ＋π2研究提升 1. 求三棱锥的体积：等体积转变是常用的方法，变换原则是其高易求，底面放在已知几何体的某一面上.2. 求不规则几何体的体积：常用切割或补形的思想，将不规则几何体转变成规则几何体以易于求解 .【训练 3】 (1)(2018 ·江苏卷 ) 如下图，正方体的棱长为2，以其全部面的中心为极点的多面体的体积为 ________.哈哈哈哈哈哈哈哈你好(2)(2018 ·北京燕博园质检 ) 某几何体的三视图如下图，则该几何体的体积为 ( )1616A.8 π － 3B.4 π － 38 C.8 π － 4D.4 π ＋ 3分析 (1) 正方体的棱长为2，以其全部面的中心为极点的多面体是正八面体，此中正八面124体的全部棱长都是 2. 则该正八面体的体积为3×( 2)×1×2＝ 3.(2) 该图形为一个半圆柱中间挖去一个四周体，∴体积＝ 1 21 12π ×2 ×4－× ×2×4×4＝ 8πV3216－ 3 .4答案 (1) 3 (2)A热门三多面体与球的切、接问题【例 3】 (2016 ·全国Ⅲ卷) 在关闭的直三棱柱 ABC － A 1B 1C 1 内有一个体积为 V 的球 . 若 AB ⊥BC ， AB ＝ 6， BC ＝ 8，AA 1＝ 3，则 V 的最大值是 ( )9π32πA.4 πB.2C.6 πD. 3分析由 AB ⊥ BC ， AB ＝ 6， BC ＝8，得 AC ＝ 10.要使球的体积 V 最大，则球与直三棱柱的部分面相切，若球与三个侧面相切，设底面△ABC的内切圆的半径为r .1 1 则 ×6×8＝×(6 ＋ 8＋10) · r ，所以 r ＝2.222r ＝ 4＞ 3，不合题意 .球与三棱柱的上、下底面相切时，球的半径R 最大 .由 2 ＝3，即＝ 3. 故球的最大概积＝43＝ 9RRVπ R π .232 答案 B【迁徙研究 1】若本例中的条件变成“直三棱柱ABC －A B C 的 6 个极点都在球 O 的球面1 1 1上”，若 AB ＝ 3， AC ＝ 4， AB ⊥AC ， AA 1＝ 12，求球 O 的表面积 .解将直三棱柱补形为长方体ABEC － A 1B 1E 1C 1，则球 O 是长方体 ABEC － A 1B 1E 1C 1 的外接球 .∴体对角线 BC 1 的长为球 O 的直径 .所以 2R ＝ 32＋ 42＋ 122 ＝13.故 S 球＝ 4π R 2＝ 169π .【迁徙研究 2】若将题目的条件变成“如下图是一个几何体的三视图”试求该几何体外接球的体积 .解该几何体为四棱锥，如下图，设正方形 ABCD 的中心为 O ，连结 OP .由三视图， PH ＝ OH ＝1，2 2则 OP ＝ OH ＋ PH ＝ 2.又 OB ＝ OC ＝ OD ＝ OA ＝ 2.∴点 O 为几何体外接球的球心，4 382则 R ＝ 2， V 球＝ π R ＝3 π .3研究提升1. 与球相关的组合体问题，一种是内切，一种是外接 . 球与旋转体的组合往常是作它们的轴截面解题，球与多面体的组合，经过多面体的一条侧棱和球心，或“切点”、 “接点”作出截面图，把空间问题化归为平面问题.2. 若球面上四点 P ，A ，B ，C 中 PA ，PB ，PC 两两垂直或三棱锥的三条侧棱两两垂直，可结构长方体或正方体确立直径解决外接问题.【训练 4】 (2018 ·广州三模 ) 三棱锥 P － ABC 中，平面PAC ⊥平面 ABC ， AB ⊥ AC ， PA ＝ PC ＝A.23 π23 64B.π C.64 π D. 3π4分析如图，设O′为正△ PAC的中心， D 为Rt△ ABC斜边的中点， H 为AC 中点.由平面PAC⊥平面ABC.则 O′H⊥平面 ABC.作 O′ O∥HD， OD∥2 2 3O′ H，则交点 O为三棱锥外接球的球心，连结OP，又 O′P＝3PH＝3×22 3 1 2 2 2 2 4 16×2＝3，OO′＝DH＝2AB＝ 2. ∴R＝OP＝O′P＋O′O＝3＋ 4＝3 .264故几何体外接球的表面积S＝4π R ＝3π.答案 D1.求解几何体的表面积或体积(1) 关于规则几何体，可直接利用公式计算.(2)关于不规则几何体，可采纳割补法求解；关于某些三棱锥，有时可采纳等体积变换法求解.(3)求解旋转体的表面积和体积时，注意圆柱的轴截面是矩形，圆锥的轴截面是等腰三角形，圆台的轴截面是等腰梯形的应用 .(4)求解几何体的表面积时要注意S 表＝ S 侧＋ S底.2. 球的简单组合体中几何体胸怀之间的关系，如棱长为 a 的正方体的外接球、内切球、棱切3 a 2球的半径分别为，，.2 a2 2 a1 13.锥体体积公式为 V＝3Sh，在求解锥体体积中，不可以遗漏3.一、选择题1.“牟合方盖”是我国古代数学家刘徽在研究球的体积的过程中结构的一个和睦优美的几何体 . 它由完整同样的四个曲面构成，相对的两个曲面在同一个圆柱的侧面上，恰似两个扣合( 牟合 ) 在一同的方形伞 ( 方盖 ). 其直观图如图，图中四边形是为表现其直观性所作的协助线. 当其正视图和侧视图完整同样时，它的俯视图可能是()分析由直观图知，俯视图应为正方形，又上半部分相邻两曲面的交线为可见线，在俯视图中应为实线，所以，选项 B 能够是几何体的俯视图.答案 B2.(2018 ·北京卷 ) 某四棱锥的三视图如下图，在此四棱锥的侧面中，直角三角形的个数为()A.1B.2C.3D.4分析在正方体中作出该几何体的直观图，记为四棱锥P－ABCD，如图，由图可知在此四棱锥的侧面中，直角三角形的个数为3，是△PAD，△PCD，△ PAB.答案 C3.(2018 ·湖南师大附中联考) 某几何体的三视图如下图，则该几何体的表面积为()A.8( π＋ 4)B.8( π＋ 8)C.16( π＋ 4)D.16( π＋ 8)分析由三视图复原原几何体如右图：该几何体为两个空心半圆柱相切，半圆柱的半径为 2，母线长为 4，左右为边长是 4 的正方形 . ∴该几何体的表面积为2×4×4＋ 2π ×2×4＋2(4 ×4 2答案B4.(2017 ·全国Ⅲ卷 ) 已知圆柱的高为 1，它的两个底面的圆周在直径为2 的同一个球的球面上，则该圆柱的体积为( )3ππ πA. πB.4C. 2D. 4分析如图画出圆柱的轴截面ABCD ， O 为球心 . 球半径 R ＝ OA ＝ 1，球心1究竟面圆的距离为 OM ＝ 2.∴底面圆半径r ＝2－2＝ 3 ，故圆柱体积＝ π · 2· ＝ π· 3OAOM 2V r h 223π×1＝4.答案B5.(2018 ·北京燕博园押题 ) 某几何体的三视图如下图，三个视图中的曲线都是圆弧，则该几何体的体积为 ()4π 5π 7π 11π A. 3B. 3C. 6D. 6112分析由三视图可知，该几何体是由半个圆柱与 8个球构成的组合体，其体积为 2× π ×1×31 4π 35π＋ ×3 ×1＝.8 3答案B6.(2018 ·全国Ⅲ卷 ) 设 A ， B ， C ， D 是同一个半径为 4 的球的球面上四点，△ ABC 为等边三哈哈哈哈哈哈哈哈你好角形且其面积为 9 3，则三棱锥 D － ABC 体积的最大值为 ()A.123B.183C.243D.5431 2分析设等边△ ABC 的边长为 x ，则 2x sin 60°＝ 9 3，得 x ＝ 6. 设△ ABC 的外接圆半径为 r ，则 2 ＝ 6 ，解得 r ＝ 2 3，所以球心到△所在平面的距离＝ 42－（ 2 3） 2＝ 2，r sin 60 °ABC d则点 D 到平面 ABC 的最大距离 d ＝ d ＋ 4＝6. 所以三棱锥1－体积的最大值max ＝ 1△ ABC ×6＝ 1 ×9 3×6＝ 18 3.D ABCV3S3答案 B二、填空题7.(2018 ·浙江卷改编 ) 某几何体的三视图如下图( 单位： cm)，则该几何体的体积( 单位：3cm ) 为 ________.分析由三视图可知，该几何体是一个底面为直角梯形的直四棱柱，所以该几何体的体积 V＝ 1×(1 ＋2) ×2×2＝ 6. 2答案68.(2018 ·郑州质检 ) 已知长方体 ABCD － A 1B 1C 1D 1 内接于球 O ，底面 ABCD 是边长为 2 的正方形，E 为 AA 1 的中点， OA ⊥平面 BDE ，则球 O 的表面积为 ________. 分析取 BD 的中点为 O 1，连结 OO 1， OE ， O 1E ， O 1A ，则四边形 OO 1AE 为矩形，∵ OA ⊥平面 BDE ，∴ OA ⊥ EO 1，即四边形 OO 1AE 为正方形，则球O 的2半径 R ＝ OA ＝ 2，∴球 O 的表面积 S ＝ 4π ×2＝ 16π.答案16π9.(2018 ·武汉模拟 ) 某几何体的三视图如下图，此中正视图的轮廓是底边为23，高为 1的等腰三角形，俯视图的轮廓为菱形，侧视图是个半圆 . 则该几何体的体积为 ________.哈哈哈哈哈哈哈哈你好分析由三视图知，几何体是由两个大小同样的半圆锥的组合体 .此中 r ＝ 1，高 h ＝ 3.故几何体的体积＝ 12× 3＝3V 3π ×13 π .3答案3 π三、解答题10. 在三棱柱 ABC － A 1B 1C 1 中，侧面 AA 1C 1C ⊥底面 ABC ，AA 1＝ A 1C＝AC ＝ AB ＝BC ＝ 2，且点 O 为 AC 中点 .(1) 证明： A 1O ⊥平面 ABC ；(2) 求三棱锥 C 1－ ABC 的体积 .(1) 证明由于 AA 1＝ A 1C ，且 O 为 AC 的中点，所以 A 1O ⊥ AC ，又面 AA 1C 1C ⊥平面 ABC ，平面 AA 1C 1C ∩平面 ABC ＝ AC ，且 A 1O ? 平面AA 1C 1C ，∴A 1O ⊥平面 ABC .(2) 解 ∵ A 1C 1∥AC ， A 1C 1?平面 ABC ， AC ? 平面 ABC ，∴A 1C 1∥平面 ABC ，即 C 1 到平面 ABC 的距离等于 A 1 到平面 ABC 的距离 .由(1) 知 AO ⊥平面 ABC 且 A O ＝22AA － AO ＝ 3，11111 1∴VC － ABC ＝VA － ABC ＝3S · A O ＝ 3×2×2× 3× 3＝ 1.11△ABC111.(2018 ·长春模拟 ) 如图，在四棱锥 P － ABCD 中，平面 PAB ⊥平面 ABCD ，＝， ∥ ，＝，＝ 1＝1，＝ 3，∠＝120°， M 为PA PB AD BC AB AC AD 2BCPD BADPC 的中点 .(1) 证明： DM ∥平面 PAB ；(2) 求四周体 MABD 的体积 .(1) 证明取 PB 中点 N ，连结 MN ， AN .1∵M 为 PC 的中点，∴ MN ∥ BC 且 MN ＝ 2BC ，哈哈哈哈哈哈哈哈你好1又 AD∥ BC，且 AD＝2BC，得 MN綉 AD.∴ADMN为平行四边形，∴DM∥AN.又 AN?平面 PAB， DM?平面 PAB，∴ DM∥平面 PAB.(2) 解取AB中点O，连结PO，∵ PA＝PB，∴ PO⊥ AB，又∵平面 PAB⊥平面 ABCD，平面 PAB∩平面 ABCD＝ AB， PO?平面 PAB，则 PO⊥平面 ABCD，取 BC中点 H，连结 AH，∵AB＝ AC，∴ AH⊥ BC，又∵ AD∥BC，∠ BAD＝120°，1∴∠ ABC＝60°，Rt△ ABH中， BH＝2BC＝1， AB＝2，∴AO＝1，又 AD＝1，△AOD中，由余弦定理知，OD＝ 3.Rt△POD中，PO ＝2 2PD－ OD＝ 6.1 3 又 S△ABD＝2AB· AD sin 120°＝2，∴V1 12 －＝· △·＝ .M ABD ABD。

高考专题13 三视图与体积表面积精准培优专练

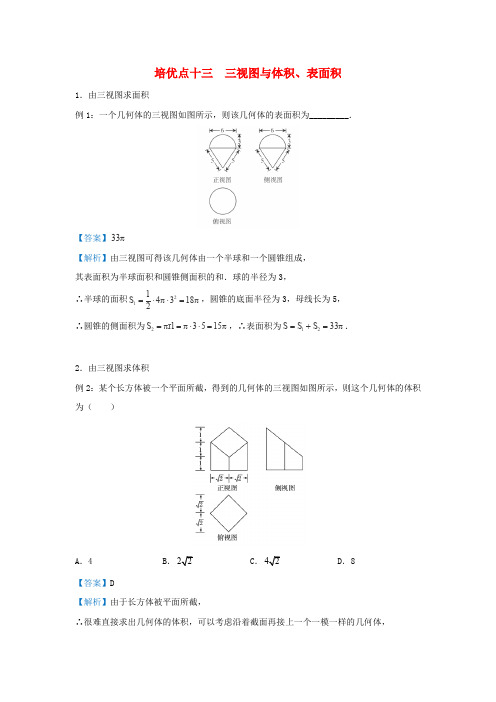
培优点十三三视图与体积、表面积1．由三视图求面积例1：一个几何体的三视图如图所示，则该几何体的表面积为_________．【答案】33π【解析】由三视图可得该几何体由一个半球和一个圆锥组成，其表面积为半球面积和圆锥侧面积的和．球的半径为3， ∴半球的面积21143182S =⋅π⋅=π，圆锥的底面半径为3，母线长为5， ∴圆锥的侧面积为23515S rl =π=π⋅⋅=π，∴表面积为1233S S S =+=π．2．由三视图求体积例2：某个长方体被一个平面所截，得到的几何体的三视图如图所示，则这个几何体的体积为（）A ．4B ．22C ．42D ．8【答案】D【解析】由于长方体被平面所截，∴很难直接求出几何体的体积，可以考虑沿着截面再接上一个一模一样的几何体，从而拼成了一个长方体，∵长方体由两个完全一样的几何体拼成，∴所求体积为长方体体积的一半。

从图上可得长方体的底面为正方形，且边长为2，长方体的高为314+=，∴22416V =⋅=长方体，∴182V V ==长方体，故选D ．一、单选题1．某几何体的三视图如图所示，若该几何体的表面积为，则俯视图中圆的半径为（）A ．1B ．2C ．3D ．4【答案】A【解析】由三视图可知该几何体为一个长方体挖去了一个半球，设圆半径为r ， ∴该几何体的表面积2222242216S r r r r r r =⨯⋅+⨯⋅-π⋅+π⋅=+π，得1r =，故选A ． 2．正方体1111ABCD A B C D -中，E 为棱1AA 的中点（如图）用过点1B E D 、、的平面截去该正方体的上半部分，则剩余几何体的左视图为（）对点增分集训A ．B ．C ．D ．【答案】D【解析】由题意可知：过点B 、E 、1D 的平面截去该正方体的上半部分，如图直观图，则几何体的左视图为D ，故选D ．3．如图，网格纸上小正方形的边长为1，粗线画的是某几何体的三视图，则该几何体的体积为（）A ．236B ．72C ．76D ．4【答案】A【解析】由三视图可得，该几何体是如图所示的三棱柱11ABB DCC -挖去一个三棱锥E FCG -，故所求几何体的体积为()111232221112326⎛⎫⨯⨯⨯-⨯⨯⨯⨯= ⎪⎝⎭，故选A ．4．一个几何体的三视图如图所示，其中正视图是半径为1的半圆，则该几何体的表面积为（）A ．()251++πB ．5212⎛⎫++π ⎪ ⎪⎝⎭C ．51222⎛⎫++π ⎪ ⎪⎝⎭D ．5122⎛⎫+π ⎪ ⎪⎝⎭【答案】C【解析】由三视图可知，其对应的几何体是半个圆锥，圆锥的底面半径为1r =，圆锥的高2h =，其母线长22125l =+=，则该几何体的表面积为：21115111522222222S ⎛⎫=⨯π⨯+⨯π⨯⨯+⨯⨯=++π ⎪ ⎪⎝⎭，本题选择C 选项． 5．若某三棱柱截去一个三棱锥后所剩几何体的三视图如图所示，则所截去的三棱锥．．．．．．的外接球的表面积等于（）A ．34πB ．32πC ．17πD ．172π 【答案】A【解析】由三视图知几何体是底面为边长为3，4，5的三角形，高为5的三棱柱被平面截得的，如图所示，截去的是一个三棱锥，底面是边长为3，4，5的直角三角形，高为3的棱锥，如图蓝色线条的图像是该棱锥，三棱锥上底面外接圆半径52圆心设为M 半径为r ，球心到底面距离为32，设球心为O ，由勾股定理得到2222253342224h R r ⎛⎫⎛⎫⎛⎫=+=+= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，2434S R =π=π，故选A ．6．如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的外接球的表面积为（）A ．32πB ．16πC ．36πD ．72π【答案】C【解析】还原几何体如图所示三棱锥由1B BCD -（如下左图），将此三棱锥补形为直三棱柱111B C D BCD -（如上右图），在直三棱柱111B C D BCD -中取1BC B C 、的中点12O O 、，取12O O 中点O ，()()()22222523R O A OO =+=+=，2244336S R =π=⨯=π表，故答案为C ．7．一个四棱锥的三视图如图所示，则该几何体的表面积为（）A ．642+B ．842+C ．643+D ．843+【答案】B【解析】根据三视图，画出原空间结构图如下图所示：∴表面积为111111111111DA D DA B DB C DC D A B C D S S S S S S =++++11112222222222228422222=⨯⨯+⨯⨯+⨯⨯+⨯⨯+⨯=+，∴故选B ． 8．已知一个三棱锥的三视图如图所示，其中三视图的长、宽、高分别为2，a ，b ，且()520,02a b a b +=>>，则此三棱锥外接球表面积的最小值为（）A ．174π B ．214π C ．4π D ．5π【答案】B【解析】由已知条件及三视图得，此三棱锥的四个顶点位于长方体1111ABCD A B C D -的四个顶点，即为三棱锥11A CB D -，且长方体1111ABCD A B C D -的长、宽、高分别为2，a ，b ，∴此三棱锥的外接球即为长方体1111ABCD A B C D -的外接球，且球半径为222222422a b a b R ++++==， ∴三棱锥外接球表面积为()()222222421445124a b a b a ⎛⎫++ππ=π++=π-+⎪ ⎪⎝⎭， ∴当且仅当1a =，12b =时，三棱锥外接球的表面积取得最小值为214π．故选B ． 9．在四棱锥P ABCD -中，PA ⊥底面ABCD ，底面ABCD 为正方形，PA AB =，该四棱锥被一平面截去一部分后，剩余部分的三视图如图，则截去部分体积与剩余部分体积的比值为（）A ．12 B ．13C ．14 D ．15【答案】B【解析】由三视图知，剩余部分的几何体是四棱锥P ABCD -被平面QBD 截去三棱锥Q BCD -（Q 为PC 中点）后的部分，连接AC 交BD 于O ，连楼OQ ，则OQ PA ∥，且12OQ PA =，设PA AB a ==，则313P ABCD V a -=，23111132212Q BCD V a a a -=⨯⨯=，剩余部分的体积为：3311312a a -，则所求的体积比值为：3331112113312aa a =-．本题选择B 选项．10．如图，画出的是某四棱锥的三视图，网格纸上小正方形的边长为1，则该几何体的体积为（）A ．15B ．16C ．503D ．533【答案】C【解析】由题得几何体原图是下图中的四棱锥A BCDE -，底面四边形BCDE 的面积为114442221022⨯-⨯⨯-⨯⨯=，∴四棱锥的体积为15010533⨯⨯=，故答案为C ．11．某几何体的三视图如图（虚线刻画的小正方形边长为1）所示，则这个几何体的体积为（）A ．94B ．823C ．12D ．83【答案】D【解析】几何体为如图多面体PABCDE ，∴体积为()11118221222132323D PABE A BCD V V --+=⨯⨯⨯⨯++⨯⨯⨯⨯=，故选D ．12．如图为一个多面体的三视图，则该多面体的体积为（）A ．203B ．7C ．223D ．233【答案】B【解析】如图所示，该几何体为正方体去掉两个倒置的三棱锥，∴该多面体的体积为32111121212273232V =-⨯⨯⨯-⨯⨯⨯⨯=；故选B ．二、填空题13．网格纸上小正方形的边长为1，粗虚、实线画出的是某个长方体挖去一个几何体得到的几何图形的三视图，则该被挖去的几何体的体积为__________．【答案】12【解析】根据三视图知长方体挖去部分是一个底面为等腰梯形（上底为2，下底为4，高为2）高为2的直四棱柱，∴()12422122V Sh ==+⨯⨯=． 14．已知某几何体的三视图如图所示，则该几何体的表面积和体积分别为_______与_______．【答案】404+π，4163π+ 【解析】由三视图可知，其对应的几何体是一个组合体，上半部分是一个直径为2的球，下半部分是一个直棱柱，棱柱的底面是边长为2的正方形，高为4，则该几何体的表面积224122424404S =π⨯+⨯+⨯⨯=+π，几何体的体积：32441241633V =π⨯+⨯=+π． 15．某四棱锥的三视图如图所示，则该四棱锥的体积为_________．【答案】1【解析】根据题中所给的三视图，还原几何体，可知其为有一条侧棱垂直于底面的一个四棱锥，该四棱锥的底面就是其俯视图中的直角梯形，根据图中所给的数据，结合椎体的体积公式，可得其体积11212132V +=⨯⨯⨯=，故答案是1． 16．已知某几何体的三视图如图所示，三视图的轮廓均为正方形，则该几何体的体积为__________．【答案】23【解析】由三视图知，该几何体由正方体沿面11AB D 与面11CB D 截去两个角所得，其体积为33112121233-⨯⨯⨯=，故答案为23．。

2020届高三文科数学精准培优专练十三：三视图体积与表面积(解析版)

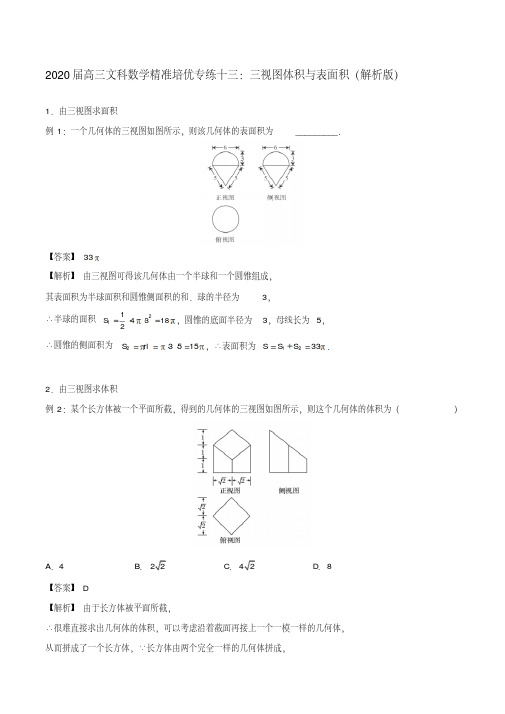
2020届高三文科数学精准培优专练十三：三视图体积与表面积（解析版）1．由三视图求面积例1：一个几何体的三视图如图所示，则该几何体的表面积为_________．【答案】33【解析】由三视图可得该几何体由一个半球和一个圆锥组成，其表面积为半球面积和圆锥侧面积的和．球的半径为3，∴半球的面积21143182S ，圆锥的底面半径为3，母线长为5，∴圆锥的侧面积为23515S rl ，∴表面积为1233SS S ．2．由三视图求体积例2：某个长方体被一个平面所截，得到的几何体的三视图如图所示，则这个几何体的体积为（）A ．4B ．22C ．42D ．8【答案】D【解析】由于长方体被平面所截，∴很难直接求出几何体的体积，可以考虑沿着截面再接上一个一模一样的几何体，从而拼成了一个长方体，∵长方体由两个完全一样的几何体拼成，∴所求体积为长方体体积的一半。

从图上可得长方体的底面为正方形，且边长为2，长方体的高为314，∴22416V长方体，∴182V V长方体，故选D．对点增分集训一、单选题1．某几何体的三视图如图所示，若该几何体的表面积为，则俯视图中圆的半径为（）A．1 B．2 C．3 D．4【答案】A【解析】由三视图可知该几何体为一个长方体挖去了一个半球，设圆半径为r，∴该几何体的表面积2222242216S r r r r r r，得1r，故选A．2．正方体1111ABCD A B C D中，E为棱1AA的中点（如图）用过点1B E D、、的平面截去该正方体的上半部分，则剩余几何体的左视图为（）A．B．C．D．【答案】D【解析】由题意可知：过点B、E、1D的平面截去该正方体的上半部分，如图直观图，则几何体的左视图为D，故选D．3．如图，网格纸上小正方形的边长为1，粗线画的是某几何体的三视图，则该几何体的体积为（）A．236B．72C．76D．4【答案】A【解析】由三视图可得，该几何体是如图所示的三棱柱11ABB DCC挖去一个三棱锥E FCG，故所求几何体的体积为111232221112326，故选A．4．一个几何体的三视图如图所示，其中正视图是半径为1的半圆，则该几何体的表面积为（）A ．251B ．5212C ．51222D ．5122【答案】C【解析】由三视图可知，其对应的几何体是半个圆锥，圆锥的底面半径为1r，圆锥的高2h，其母线长22125l，则该几何体的表面积为：21115111522222222S，本题选择C 选项．5．若某三棱柱截去一个三棱锥后所剩几何体的三视图如图所示，则所截去的三棱锥．．．．．．的外接球的表面积等于（）A ．34B ．32C ．17D ．172【答案】A【解析】由三视图知几何体是底面为边长为3，4，5的三角形，高为5的三棱柱被平面截得的，如图所示，截去的是一个三棱锥，底面是边长为3，4，5的直角三角形，高为3的棱锥，如图蓝色线条的图像是该棱锥，三棱锥上底面外接圆半径52圆心设为M 半径为r ，球心到底面距离为32，设球心为O ，由勾股定理得到2222253342224h Rr，2434SR，故选A ．6．如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的外接球的表面积为（）A ．32B ．16C ．36D ．72【答案】C【解析】还原几何体如图所示三棱锥由1B BCD （如下左图），将此三棱锥补形为直三棱柱111B C D BCD （如上右图），在直三棱柱111B C D BCD 中取1BC B C 、的中点12O O 、，取12O O 中点O ，22222523RO AOO ，2244336SR表，故答案为C ．7．一个四棱锥的三视图如图所示，则该几何体的表面积为（）A ．642B ．842C ．643D ．843【答案】B【解析】根据三视图，画出原空间结构图如下图所示：∴表面积为111111111111DA DDA BDB CDC DA B C DS S S S S S 11112222222222228422222，∴故选B ．8．已知一个三棱锥的三视图如图所示，其中三视图的长、宽、高分别为2，a ，b ，且520,02abab，则此三棱锥外接球表面积的最小值为（）A ．174B ．214C ．4D ．5【答案】B【解析】由已知条件及三视图得，此三棱锥的四个顶点位于长方体1111ABCDA BC D 的四个顶点，即为三棱锥11A CB D ，且长方体1111ABCDA B C D 的长、宽、高分别为2，a ，b ，∴此三棱锥的外接球即为长方体1111ABCD A B C D 的外接球，且球半径为222222422a babR，∴三棱锥外接球表面积为222222421445124ababa ，∴当且仅当1a ，12b 时，三棱锥外接球的表面积取得最小值为214．故选B ．9．在四棱锥PABCD 中，PA 底面ABCD ，底面ABCD 为正方形，PA AB ，该四棱锥被一平面截去一部分后，剩余部分的三视图如图，则截去部分体积与剩余部分体积的比值为（）A ．12B ．13C ．14D ．15【答案】B【解析】由三视图知，剩余部分的几何体是四棱锥PABCD 被平面QBD 截去三棱锥QBCD （Q 为PC中点）后的部分，连接AC 交BD 于O ，连楼OQ ，则OQ PA ∥，且12OQPA ，设PAABa ，则313PABCDV a ，23111132212QBCDV aaa ，剩余部分的体积为：3311312aa ，则所求的体积比值为：3331112113312aaa．本题选择B 选项．10．如图，画出的是某四棱锥的三视图，网格纸上小正方形的边长为1，则该几何体的体积为（）A．15 B．16 C．503D．533【答案】C【解析】由题得几何体原图是下图中的四棱锥A BCDE，底面四边形BCDE的面积为114442221022，∴四棱锥的体积为15010533，故答案为C．11．某几何体的三视图如图（虚线刻画的小正方形边长为1）所示，则这个几何体的体积为（）A．94B．823C．12 D．83【答案】D【解析】几何体为如图多面体PABCDE，∴体积为11118221222132323DPABEABCDV V ，故选D ．12．如图为一个多面体的三视图，则该多面体的体积为（）A ．203B ．7C ．223D ．233【答案】B【解析】如图所示，该几何体为正方体去掉两个倒置的三棱锥，∴该多面体的体积为32111121212273232V；故选B ．二、填空题13．网格纸上小正方形的边长为1，粗虚、实线画出的是某个长方体挖去一个几何体得到的几何图形的三视图，则该被挖去的几何体的体积为__________．【答案】12【解析】根据三视图知长方体挖去部分是一个底面为等腰梯形（上底为2，下底为4，高为2）高为2的直四棱柱，∴12422122VSh．14．已知某几何体的三视图如图所示，则该几何体的表面积和体积分别为_______与_______．【答案】404，4163【解析】由三视图可知，其对应的几何体是一个组合体，上半部分是一个直径为2的球，下半部分是一个直棱柱，棱柱的底面是边长为2的正方形，高为4，则该几何体的表面积224122424404S，几何体的体积：32441241633V．15．某四棱锥的三视图如图所示，则该四棱锥的体积为_________．【答案】1【解析】根据题中所给的三视图，还原几何体，可知其为有一条侧棱垂直于底面的一个四棱锥，该四棱锥的底面就是其俯视图中的直角梯形，根据图中所给的数据，结合椎体的体积公式，可得其体积11212132V ，故答案是1．16．已知某几何体的三视图如图所示，三视图的轮廓均为正方形，则该几何体的体积为__________．【答案】23【解析】由三视图知，该几何体由正方体沿面11AB D 与面11CB D 截去两个角所得，其体积为33112121233，故答案为23．。

2019高考数学二轮复习专题三立体几何第1讲空间几何体的三视图、表面积和体积练习

亲爱的同学：这份试卷将再次记录你的自信、沉着、智慧和收获，我们一直投给你信任的目光……第1讲空间几何体的三视图、表面积和体积高考定位 1.三视图的识别和简单应用；2.简单几何体的表面积与体积计算，主要以选择题、填空题的形式呈现，在解答题中，有时与空间线、面位置证明相结合，面积与体积的计算作为其中的一问.真题感悟1.(2018·全国Ⅲ卷)中国古建筑借助榫卯将木构件连接起来.构件的凸出部分叫榫头，凹进部分叫卯眼，图中木构件右边的小长方体是榫头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体，则咬合时带卯眼的木构件的俯视图可以是( )解析由题意知，在咬合时带卯眼的木构件中，从俯视方向看，榫头看不见，所以是虚线，结合榫头的位置知选A. 答案 A2.(2018·全国Ⅰ卷)已知圆柱的上、下底面的中心分别为O 1，O 2，过直线O 1O 2的平面截该圆柱所得的截面是面积为8的正方形，则该圆柱的表面积为( ) A.122πB.12πC.82πD.10π解析因为过直线O 1O 2的平面截该圆柱所得的截面是面积为8的正方形，所以圆柱的高为22，底面圆的直径为2 2.所以S 表面积＝2×π×(2)2＋2π×2×22＝12π. 答案 B3.(2018·天津卷)已知正方体ABCD －A1B 1C 1D 1的棱长为1，除面ABCD 外，该正方体其余各面的中心分别为点E ，F ，G ，H ，M (如图)，则四棱锥M －EFGH 的体积为________.解析连接AD 1，CD 1，B 1A ，B 1C ，AC ，因为E ，H 分别为AD 1，CD 1的中点，所以EH ∥AC ，EH ＝12AC .因为F ，G 分别为B 1A ，B 1C 的中点，所以FG ∥AC ，FG ＝12AC .所以EH∥FG ，EH ＝FG ，所以四边形EHGF 为平行四边形，又EG ＝HF ，EH ＝HG ，所以四边形EHGF 为正方形.又点M 到平面EHGF 的距离为12，所以四棱锥M －EFGH 的体积为13×⎝ ⎛⎭⎪⎫222×12＝112.答案1124.(2017·全国Ⅰ卷)已知三棱锥S －ABC 的所有顶点都在球O 的球面上，SC 是球O 的直径.若平面SCA ⊥平面SCB ，SA ＝AC ，SB ＝BC ，三棱锥S －ABC 的体积为9，则球O 的表面积为________.解析如图，连接OA ，OB ，因为SA ＝AC ，SB ＝BC ，SC 为球O 的直径，所以OA ⊥SC ，OB ⊥SC .因为平面SAC ⊥平面SBC ，平面SAC ∩平面SBC ＝SC ，且OA ⊂平面SAC ，所以OA ⊥平面SBC .设球的半径为r ，则OA ＝OB ＝r ，SC ＝2r ，所以V A －SBC ＝13×S △SBC ×OA ＝13×12×2r ×r ×r ＝13r 3，所以13r 3＝9⇒r ＝3，所以球的表面积为4πr 2＝36π.答案 36π考点整合1.空间几何体的三视图(1)几何体的摆放位置不同，其三视图也不同，需要注意长对正、高平齐、宽相等. (2)由三视图还原几何体：一般先从俯视图确定底面，再利用正视图与侧视图确定几何体. 2.空间几何体的两组常用公式 (1)柱体、锥体、台体的表面积公式： ①圆柱的表面积S ＝2πr (r ＋l )； ②圆锥的表面积S ＝πr (r ＋l )；③圆台的表面积S ＝π(r ′2＋r 2＋r ′l ＋rl )； ④球的表面积S ＝4πR 2. (2)柱体、锥体和球的体积公式： ①V 柱体＝Sh (S 为底面面积，h 为高)； ②V 锥体＝13Sh (S 为底面面积，h 为高)；③V 球＝43πR 3.热点一空间几何体的三视图与直观图【例1】 (1)(2018·兰州模拟)中国古代数学名著《九章算术》中，将底面是直角三角形的直棱柱称为“堑堵”.已知某“堑堵”的正视图和俯视图如图所示，则该“堑堵”的侧视图的面积为( ) A.18 6 B.18 3 C.18 2D.2722(2)(2018·全国Ⅰ卷)某圆柱的高为2，底面周长为16，其三视图如图.圆柱表面上的点M 在正视图上的对应点为A ，圆柱表面上的点N 在左视图上的对应点为B ，则在此圆柱侧面上，从M 到N 的路径中，最短路径的长度为( )A.217B.2 5C.3D.2解析 (1)在俯视图Rt △ABC 中，作AH ⊥BC 交于H . 由三视图的意义，则BH ＝6，HC ＝3，根据射影定理，AH 2＝BH ·HC ，∴AH ＝3 2.易知该“堑堵”的侧视图是矩形，长为6，宽为AH ＝3 2.故侧视图的面积S ＝6×32＝18 2.(2)由三视图可知，该几何体为如图①所示的圆柱，该圆柱的高为2，底面周长为16.画出该圆柱的侧面展开图，如图②所示，连接MN ，则MS ＝2，SN ＝4.则从M 到N 的路径中，最短路径的长度为MS 2＋SN 2＝22＋42＝2 5.答案 (1)C (2)B探究提高 1.由直观图确定三视图，一要根据三视图的含义及画法和摆放规则确认.二要熟悉常见几何体的三视图. 2.由三视图还原到直观图的思路 (1)根据俯视图确定几何体的底面.(2)根据正视图或侧视图确定几何体的侧棱与侧面的特征，调整实线和虚线所对应的棱、面的位置.(3)确定几何体的直观图形状.【训练1】 (1)如图，在底面边长为1，高为2的正四棱柱ABCD －A 1B 1C 1D 1中，点P 是平面A 1B 1C 1D 1内一点，则三棱锥P －BCD 的正视图与侧视图的面积之和为( )A.1B.2C.3D.4(2)(2017·北京卷)某四棱锥的三视图如图所示，则该四棱锥的最长棱的长度为( )A.3 2B.2 3C.2 2D.2解析 (1)设点P 在平面A 1ADD 1的射影为P ′，在平面C 1CDD 1的射影为P ″，如图所示.∴三棱锥P －BCD 的正视图与侧视图分别为△P ′AD 与△P ″CD ，因此所求面积S ＝S △P ′AD ＋S △P ″CD ＝12×1×2＋12×1×2＝2.(2)根据三视图可得该四棱锥的直观图(四棱锥P －ABCD )如图所示，将该四棱锥放入棱长为2的正方体中.由图可知该四棱锥的最长棱为PD ，PD ＝22＋22＋22＝2 3.答案 (1)B (2)B热点二几何体的表面积与体积考法1 空间几何体的表面积【例2－1】 (1)(2017·全国Ⅰ卷)某多面体的三视图如图所示，其中正视图和侧视图都由正方形和等腰直角三角形组成，正方形的边长为2，俯视图为等腰直角三角形，该多面体的各个面中有若干个是梯形，这些梯形的面积之和为( ) A.10 B.12C.14D.16(2)(2018·西安模拟)如图，网格纸上正方形小格的边长为1，粗实线画出的是某几何体的三视图，则该几何体的表面积为( )A.20πB.24πC.28πD.32π解析 (1)由三视图可画出直观图，该直观图各面内只有两个相同的梯形的面，S 梯＝12×(2＋4)×2＝6，S 全梯＝6×2＝12.(2)由三视图知，该几何体由一圆锥和一个圆柱构成的组合体， ∵S 圆锥侧＝π×3×32＋42＝15π，S 圆柱侧＝2π×1×2＝4π，S 圆锥底＝π×32＝9π.故几何体的表面积S ＝15π＋4π＋9π＝28π. 答案 (1)B (2)C探究提高 1.由几何体的三视图求其表面积：(1)关键是分析三视图确定几何体中各元素之间的位置关系及度量大小；(2)还原几何体的直观图，套用相应的面积公式. 2.(1)多面体的表面积是各个面的面积之和；组合体的表面积注意衔接部分的处理. (2)旋转体的表面积问题注意其侧面展开图的应用.【训练2】 (1)(2016·全国Ⅰ卷)如图，某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径.若该几何体的体积是28π3，则它的表面积是( )A.17πB.18πC.20πD.28π(2)(2018·烟台二模)某几何体的三视图如图所示，其中俯视图右侧曲线为半圆弧，则几何体的表面积为( )A.3π＋42－2B.3π＋22－2C.3π2＋22－2D.3π2＋22＋2解析 (1)由题知，该几何体的直观图如图所示，它是一个球(被过球心O 且互相垂直的三个平面)切掉左上角的18后得到的组合体，其表面积是球面面积的78和三个14圆面积之和，易得球的半径为2，则得S ＝78×4π×22＋3×14π×22＝17π.(2)由三视图，该几何体是一个半圆柱挖去一直三棱柱，由对称性，几何体的底面面积S 底＝π×12－(2)2＝π－2.∴几何体表面积S ＝2(2×2)＋12(2π×1×2)＋S 底＝42＋2π＋π－2＝3π＋42－2. 答案 (1)A (2)A 考法2 空间几何体的体积【例2－2】 (1)(2018·河北衡水中学调研)某几何体的三视图如图所示，则该几何体的体积为( )A.6B.4C.223D.203(2)由一个长方体和两个14圆柱构成的几何体的三视图如图，则该几何体的体积为________.解析 (1)由三视图知该几何体是边长为2的正方体挖去一个三棱柱(如图)，且挖去的三棱柱的高为1，底面是等腰直角三角形，等腰直角三角形的直角边长为2.故几何体体积V ＝23－12×2×2×1＝6.(2)该几何体由一个长、宽、高分别为2，1，1的长方体和两个底面半径为1，高为1的14圆柱体构成.所以V ＝2×1×1＋2×14×π×12×1＝2＋π2.答案 (1)A (2)2＋π2探究提高 1.求三棱锥的体积：等体积转化是常用的方法，转换原则是其高易求，底面放在已知几何体的某一面上.2.求不规则几何体的体积：常用分割或补形的思想，将不规则几何体转化为规则几何体以易于求解.【训练3】 (1)(2018·江苏卷)如图所示，正方体的棱长为2，以其所有面的中心为顶点的多面体的体积为________.(2)(2018·北京燕博园质检)某几何体的三视图如图所示，则该几何体的体积为( )A.8π－163B.4π－163C.8π－4D.4π＋83解析 (1)正方体的棱长为2，以其所有面的中心为顶点的多面体是正八面体，其中正八面体的所有棱长都是 2.则该正八面体的体积为13×(2)2×1×2＝43.(2)该图形为一个半圆柱中间挖去一个四面体，∴体积V ＝12π×22×4－13×12×2×4×4＝8π－163. 答案 (1)43(2)A热点三多面体与球的切、接问题【例3】 (2016·全国Ⅲ卷)在封闭的直三棱柱ABC －A 1B 1C 1内有一个体积为V 的球.若AB ⊥BC ，AB ＝6，BC ＝8，AA 1＝3，则V 的最大值是( )A.4πB.9π2C.6πD.32π3解析由AB ⊥BC ，AB ＝6，BC ＝8，得AC ＝10.要使球的体积V 最大，则球与直三棱柱的部分面相切，若球与三个侧面相切，设底面△ABC 的内切圆的半径为r .则12×6×8＝12×(6＋8＋10)·r ，所以r ＝2. 2r ＝4＞3，不合题意.球与三棱柱的上、下底面相切时，球的半径R 最大.由2R ＝3，即R ＝32.故球的最大体积V ＝43πR 3＝92π.答案 B【迁移探究1】若本例中的条件变为“直三棱柱ABC －A 1B 1C 1的6个顶点都在球O 的球面上”，若AB ＝3，AC ＝4，AB ⊥AC ，AA 1＝12，求球O 的表面积. 解将直三棱柱补形为长方体ABEC －A 1B 1E 1C 1，则球O 是长方体ABEC －A 1B 1E 1C 1的外接球. ∴体对角线BC 1的长为球O 的直径. 因此2R ＝32＋42＋122＝13. 故S 球＝4πR 2＝169π.【迁移探究2】若将题目的条件变为“如图所示是一个几何体的三视图”试求该几何体外接球的体积.解该几何体为四棱锥，如图所示，设正方形ABCD 的中心为O ，连接OP . 由三视图，PH ＝OH ＝1，则OP ＝OH 2＋PH 2＝ 2. 又OB ＝OC ＝OD ＝OA ＝ 2. ∴点O 为几何体外接球的球心，则R ＝2，V 球＝43πR 3＝823π.探究提高 1.与球有关的组合体问题，一种是内切，一种是外接.球与旋转体的组合通常是作它们的轴截面解题，球与多面体的组合，通过多面体的一条侧棱和球心，或“切点”、“接点”作出截面图，把空间问题化归为平面问题.2.若球面上四点P ，A ，B ，C 中PA ，PB ，PC 两两垂直或三棱锥的三条侧棱两两垂直，可构造长方体或正方体确定直径解决外接问题.【训练4】 (2018·广州三模)三棱锥P －ABC 中，平面PAC ⊥平面ABC ，AB ⊥AC ，PA ＝PC ＝AC ＝2，AB ＝4，则三棱锥P －ABC 的外接球的表面积为( )A.23πB.234π C.64π D.643π解析如图，设O ′为正△PAC 的中心，D 为Rt △ABC 斜边的中点，H 为AC 中点.由平面PAC ⊥平面ABC .则O ′H ⊥平面ABC .作O ′O ∥HD ，OD ∥O ′H ，则交点O 为三棱锥外接球的球心，连接OP ，又O ′P ＝23PH ＝23×32×2＝233，OO ′＝DH ＝12AB ＝2.∴R 2＝OP 2＝O ′P 2＋O ′O 2＝43＋4＝163.故几何体外接球的表面积S ＝4πR 2＝643π.答案 D1.求解几何体的表面积或体积(1)对于规则几何体，可直接利用公式计算.(2)对于不规则几何体，可采用割补法求解；对于某些三棱锥，有时可采用等体积转换法求解.(3)求解旋转体的表面积和体积时，注意圆柱的轴截面是矩形，圆锥的轴截面是等腰三角形，圆台的轴截面是等腰梯形的应用.(4)求解几何体的表面积时要注意S 表＝S 侧＋S 底.2.球的简单组合体中几何体度量之间的关系，如棱长为a 的正方体的外接球、内切球、棱切球的半径分别为32a ，a 2，22a . 3.锥体体积公式为V ＝13Sh ，在求解锥体体积中，不能漏掉13.一、选择题1.“牟合方盖”是我国古代数学家刘徽在研究球的体积的过程中构造的一个和谐优美的几何体.它由完全相同的四个曲面构成，相对的两个曲面在同一个圆柱的侧面上，好似两个扣合(牟合)在一起的方形伞(方盖).其直观图如图，图中四边形是为体现其直观性所作的辅助线.当其正视图和侧视图完全相同时，它的俯视图可能是( )解析由直观图知，俯视图应为正方形，又上半部分相邻两曲面的交线为可见线，在俯视图中应为实线，因此，选项B可以是几何体的俯视图.答案 B2.(2018·北京卷)某四棱锥的三视图如图所示，在此四棱锥的侧面中，直角三角形的个数为( )A.1B.2C.3D.4解析在正方体中作出该几何体的直观图，记为四棱锥P－ABCD，如图，由图可知在此四棱锥的侧面中，直角三角形的个数为3，是△PAD，△PCD，△PAB.答案 C3.(2018·湖南师大附中联考)某几何体的三视图如图所示，则该几何体的表面积为( )A.8(π＋4)B.8(π＋8)C.16(π＋4)D.16(π＋8)解析由三视图还原原几何体如右图：该几何体为两个空心半圆柱相切，半圆柱的半径为2，母线长为4，左右为边长是4的正方形.∴该几何体的表面积为2×4×4＋2π×2×4＋2(4×4－π×22)＝64＋8π＝8(π＋8).答案 B4.(2017·全国Ⅲ卷)已知圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的体积为( )A.πB.3π4C.π2D.π4解析如图画出圆柱的轴截面ABCD ，O 为球心.球半径R ＝OA ＝1，球心到底面圆的距离为OM ＝12. ∴底面圆半径r ＝OA 2－OM 2＝32，故圆柱体积V ＝π·r 2·h ＝π·⎝ ⎛⎭⎪⎫322×1＝3π4. 答案 B5.(2018·北京燕博园押题)某几何体的三视图如图所示，三个视图中的曲线都是圆弧，则该几何体的体积为( )A.4π3B.5π3C.7π6D.11π6解析由三视图可知，该几何体是由半个圆柱与18个球组成的组合体，其体积为12×π×12×3＋18×4π3×13＝5π3.答案 B6.(2018·全国Ⅲ卷)设A ，B ，C ，D 是同一个半径为4的球的球面上四点，△ABC 为等边三角形且其面积为93，则三棱锥D －ABC 体积的最大值为( ) A.12 3 B.18 3 C.24 3 D.54 3解析设等边△ABC 的边长为x ，则12x 2sin 60°＝93，得x ＝6.设△ABC 的外接圆半径为r ，则2r ＝6sin 60°，解得r ＝23，所以球心到△ABC 所在平面的距离d ＝42－（23）2＝2，则点D 到平面ABC 的最大距离d 1＝d ＋4＝6.所以三棱锥D －ABC 体积的最大值V max ＝13S △ABC ×6＝13×93×6＝18 3.答案 B二、填空题7.(2018·浙江卷改编)某几何体的三视图如图所示(单位：cm)，则该几何体的体积(单位：cm 3)为________.解析由三视图可知，该几何体是一个底面为直角梯形的直四棱柱，所以该几何体的体积V ＝12×(1＋2)×2×2＝6. 答案 68.(2018·郑州质检)已知长方体ABCD －A 1B 1C 1D 1内接于球O ，底面ABCD 是边长为2的正方形，E 为AA 1的中点，OA ⊥平面BDE ，则球O 的表面积为________.解析取BD 的中点为O 1，连接OO 1，OE ，O 1E ，O 1A ，则四边形OO 1AE 为矩形，∵OA ⊥平面BDE ，∴OA ⊥EO 1，即四边形OO 1AE 为正方形，则球O 的半径R ＝OA ＝2，∴球O 的表面积S ＝4π×22＝16π.答案 16π 9.(2018·武汉模拟)某几何体的三视图如图所示，其中正视图的轮廓是底边为23，高为1的等腰三角形，俯视图的轮廓为菱形，侧视图是个半圆.则该几何体的体积为________.解析由三视图知，几何体是由两个大小相同的半圆锥的组合体. 其中r ＝1，高h ＝ 3.故几何体的体积V ＝13π×12×3＝33π. 答案 33π 三、解答题10.在三棱柱ABC －A 1B 1C 1中，侧面AA 1C 1C ⊥底面ABC ，AA 1＝A 1C ＝AC ＝AB ＝BC ＝2，且点O 为AC 中点.(1)证明：A 1O ⊥平面ABC ；(2)求三棱锥C 1－ABC 的体积.(1)证明因为AA 1＝A 1C ，且O 为AC 的中点，所以A 1O ⊥AC ，又面AA 1C 1C ⊥平面ABC ，平面AA 1C 1C ∩平面ABC ＝AC ，且A 1O ⊂平面AA 1C 1C ， ∴A 1O ⊥平面ABC .(2)解 ∵A 1C 1∥AC ，A 1C 1⊄平面ABC ，AC ⊂平面ABC ，∴A 1C 1∥平面ABC ，即C 1到平面ABC 的距离等于A 1到平面ABC 的距离. 由(1)知A 1O ⊥平面ABC 且A 1O ＝AA 21－AO 2＝3，∴VC 1－ABC ＝VA 1－ABC ＝13S △ABC ·A 1O ＝13×12×2×3×3＝1.11.(2018·长春模拟)如图，在四棱锥P －ABCD 中，平面PAB ⊥平面ABCD ，PA ＝PB ，AD ∥BC ，AB ＝AC ，AD ＝12BC ＝1，PD ＝3，∠BAD ＝120°，M 为PC 的中点.(1)证明：DM ∥平面PAB ；(2)求四面体MABD 的体积.(1)证明取PB 中点N ，连接MN ，AN .∵M 为PC 的中点，∴MN ∥BC 且MN ＝12BC ，又AD ∥BC ，且AD ＝12BC ，得MN 綉AD . ∴ADMN 为平行四边形，∴DM ∥AN .又AN ⊂平面PAB ，DM ⊄平面PAB ，∴DM ∥平面PAB .(2)解取AB 中点O ，连接PO ，∵PA ＝PB ，∴PO ⊥AB ，又∵平面PAB ⊥平面ABCD ，平面PAB ∩平面ABCD ＝AB ，PO ⊂平面PAB ，则PO ⊥平面ABCD ，取BC 中点H ，连接AH ，∵AB ＝AC ，∴AH ⊥BC ，又∵AD ∥BC ，∠BAD ＝120°，∴∠ABC ＝60°，Rt △ABH 中，BH ＝12BC ＝1，AB ＝2， ∴AO ＝1，又AD ＝1，△AOD 中，由余弦定理知，OD ＝ 3.Rt △POD 中，PO ＝PD 2－OD 2＝ 6.又S △ABD ＝12AB ·AD sin 120°＝32， ∴V M －ABD ＝13·S △ABD ·12PO ＝24.。

2020届高三精准培优专练十三三视图与体积表面积(文) 学生版

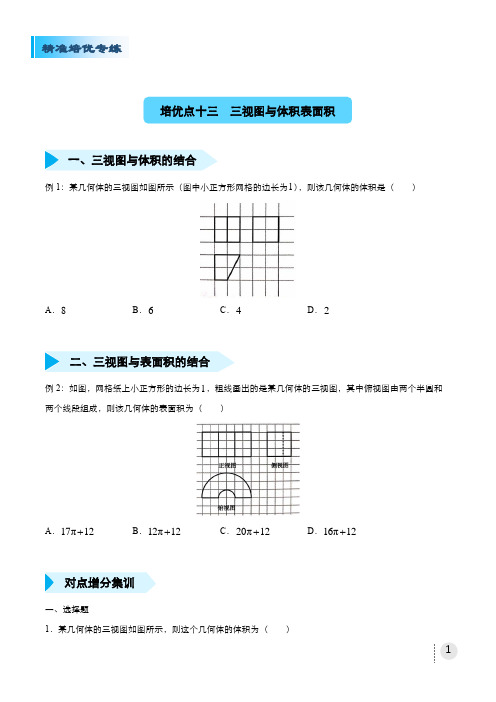
例1：某几何体的三视图如图所示（图中小正方形网格的边长为1），则该几何体的体积是（）A．8B．6C．4D．2例2：如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，其中俯视图由两个半圆和两个线段组成，则该几何体的表面积为（）A．17π12+B．12π12+C．20π12+D．16π12+一、选择题1．某几何体的三视图如图所示，则这个几何体的体积为（）培优点十三三视图与体积表面积一、三视图与体积的结合二、三视图与表面积的结合对点增分集训A．2π163-B．4π83-C．4π163-D．π16(1)3-2．如图，网格纸上小正方形的边长为1，粗线条画出的是一个三棱锥的三视图，则该三棱锥中最长棱的长度为（）A．2B C．D．33．古人采取“用臼舂米”的方法脱去稻谷的外壳，获得可供食用的大米，用于舂米的“臼”多用石头或木头制成．一个“臼”的三视图如图所示，则凿去部分（看成一个简单的组合体）的体积为（）A．63πB．72πC．79πD．99π4．某几何体的三视图如图所示，在该几何体的各个面中，面积最小的面与底面的面积的比值为（）A ．13B ．23C ．25D ．455．一个几何体的三视图如图所示，其中正视图和俯视图中的四边形是边长为2的正方形，则该几何体的表面积为（）A ．13π2B ．7πC ．15π2D ．8π6．如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则该几何体的表面积为（）A ．83π+B ．84π+C ．85π+D ．86π+7．某几何体的三视图如图所示，则这个几何体的体积是（）A ．13B ．14C ．15D ．168．某装饰品的三视图如图所示，则该装饰品的表面积为（）A ．16π+B ．161)π-C ．161)π+D ．201)π+9．如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，俯视图中的两条曲线均为圆弧，则该几何体的体积为（）A ．32π643-B ．648π-C ．16π643-D ．8π643-10．我国古代数学名著《九章算术·商功》中阐述：“斜解立方，得两堑堵．斜解堑堵，其一为阳马，一为鳖臑．阳马居二，鳖臑居一，不易之率也．合两鳖臑三而一，验之以棊，其形露矣”若称为“阳马”的某几何体的三视图如图所示，图中网格纸上小正方形的边长为1，则对该几何体描述： ①四个侧面都是直角三角形；②最长的侧棱长为③四个侧面中有三个侧面是全等的直角三角形； ④外接球的表面积为24π．其中正确的个数是（）A．0B．1C．2D．311．某工人现欲用车床将一正方体铁块进行加工处理，加工后成品的三视图如图所示．网格纸上小正方形的边长为1，则加工后成品与去除部分几何体的体积比为（）A．32ππ-B．64ππ-C．16ππ-D．48ππ-12．某三棱锥的三视图如图所示，其中小正方形的边长均为1．三棱锥上的点M在俯视图上的对应点为A，点N在左视图上的对应点为B，则线段MN长度的最大值为（）A．B．C．9D．6二、填空题13．已知某几何体的三视图如图所示（侧视图中曲线为四分之一圆弧），则该几何体的体积为．14．如图是某几何体的三视图，图中方格的单位长度为1，则该几何体的表面积为．15．一个由半球和四棱锥组成的几何体，其三视图如图所示．则该几何体的体积为．16．某几何体的三视图如图所示，则该几何体的体积为．例1：【答案】B【解析】由三视图可得该几何体为底面是直角梯形的直四棱柱（如图所示），其中底面直角梯形的上、下底边分别为1，2，高为2，直四棱柱的高为2，所以该几何体的体积为(12)2262+⨯⨯=，故选B．例2：【答案】C【解析】由三视图知，该几何体是一个大半圆柱挖去一个小半圆柱得到的，两个半圆柱的底面半径分别为1和3，高均为3，所以该几何体的表面积为112π332π1322⨯⨯⨯+⨯⨯⨯22112(π3π1)22320π1222+⨯⨯-⨯+⨯⨯=+．一、选择题1．【答案】C【解析】根据三视图知，该几何体是一个直四棱柱内挖去一个圆锥后剩余的部分，画出直观图如图所示，设四棱柱的体积为1V，圆锥的体积为2V，结合图中数据，得该几何体的体积221214π24π141633V V V=-=⨯-⨯⨯=-，故选C．2．【答案】D培优点十三三视图与体积表面积答案【解析】如图，三棱锥A BCD -即为所求几何体，根据题设条件，知辅助的正方体棱长为2，1CD =，BD =，BC =，2AC =，3AB =，AD =AB ，长度为3．3．【答案】A【解析】由三视图得凿去部分是圆柱与半球的组合体，其中圆柱的高为5，底面圆的半径为3，半球的半径为3，所以组合体的体积为2314π35π363π23⋅⨯+⨯⨯=，故选A ． 4．【答案】C【解析】由三视图可知，该几何体是高为4的四棱锥，如图所示，记为P ABCD -．易知面积最小的面为左侧面，其面积为1142⨯⨯．将底面ABCD 补为梯形BCDE ，则底面ABCD 的面积为11(24)221522⨯+⨯-⨯⨯=，所以面积最小的面与底面的面积的比值为25，故选C ． 5．【答案】B【解析】由三视图可知该几何体是一个圆柱体和一个球体的四分之一的组合体，则所求的几何体的表面积为22214π1π1π12π127π4⨯⨯+⨯+⨯+⨯⨯=，故选B ． 6．【答案】D【解析】由三视图可知，该几何体是由底面半径为1，高为4的半圆柱挖去一个半径为1的半球得到的，则该几何体的表面积2221112π142π142π14π186π222S =⨯⨯⨯+⨯⨯⨯+⨯-⨯+⨯⨯=+．故选B ． 7．【答案】C 【解析】所求几何体可看作将长方体截去两个三棱柱得到的几何体，在长方体中还原该几何体，如图中ABCD A B C D ''''-所示，长方体的长、宽、高分别为4，2，3，两个三棱柱的高为2，底面是两直角边长分别为3和1.5的直角三角形，故该几何体的体积134232321522V =⨯⨯-⨯⨯⨯⨯=，故选C ． 8．【答案】C【解析】由装饰品的三视图可知，该装饰品是由一个棱长为2的正方体，切去四个四分之一的圆锥所得的几何体，其中圆锥的底面半径为1，高为2，则该装饰品的表面积为222111224π14224π1161)π424+-⨯⨯+⨯⨯⨯+⨯⨯=+，故选C ． 9．【答案】C【解析】由三视图知，该几何体是由棱长为4的正方体截去一个底面半径为2、高为4的14圆锥和一个底面半径为2、高为4的14圆柱而得到的，所以该几何体的体积3221116π4(π24π24)64433V =-⨯⨯+⨯⨯=-，故选C ． 10．【答案】D 【解析】对于①，由三视图知“阳马”的直观图如图中四棱锥S ABCD -所示，其中SA ⊥平面ABCD ，所以SA AB ⊥，SA AD ⊥，SA BC ⊥，所以SAB △，SAD △为直角三角形，结合BC AB ⊥，知BC ⊥平面SAB ，所以BC SB ⊥，故SBC △为直角三角形，同理可知SCD △为直角三角形，所以“阳马”的四个侧面均为直角三角形，正确；对于②，由三视图及直观图得2SA =，SB ==SD ==连接AC ，则SC ===，所以“阳马”的最长的侧棱长为对于③，由②的侧棱长知，侧面四个直角三角形的斜边均不相等，所以不存在全等的直角三角形，错误；对于④，考虑将“阳马”补形为一个长、宽、高分别为4、2、2的长方体，易知长方体的外接球即“阳马”的外接球其直径2R =，所以“阳马”的外接球的表面积为224ππ(2)24πR R ==，正确．综上可知，正确的个数为3，故选D ． 11．【答案】C【解析】由三视图可知，该几何体为正方体中间挖去一个圆柱后所得，且正方体的棱长为4，圆柱的底面半径为1，高为4，设正方体的体积为1V ，圆柱的体积为2V ，所以加工后成品的体积32124π14644πV V V =-=-⨯⨯=-．加工后成品与去除部分的体积比为644π16π4ππ--=．故选C．12．【答案】A【解析】根据三视图，在棱长为3的正方体中还原该几何体的直观图，为如图所示的三棱锥P CNE-，则点B即点N在左视图上对应的点，点A为线段PC上任意一点M在底面CNE上的投影，因为PC上的点M到点N距离的最大值为PN的长，故线段MN长度的最大值为二、填空题13．【答案】π14 -【解析】由已知三视图得到几何体是棱长为1的正方体挖去底面半径为1的14圆柱，正方体的棱长为1，14圆柱的体积为21ππ1144⨯⨯⨯=，所以几何体体积为π14-．14．【答案】8+【解析】由三视图还原几何体如下图所示，可得三棱锥A BCD -，计算可得2BC =，2CD =，BD =，AD =，AB =12222BCD S =⨯⨯=△，122ADC S =⨯⨯=△122ABC S =⨯⨯=△ABD △=162ABD S =⨯=△，则该几何体表面积为268+=+15．【答案】1π36+【解析】，正四棱锥的底面边长为1，高为1，所以其体积为3114111ππ323236⨯⨯+⨯⨯=+．故答案为1π36+．16．【答案】3π【解析】由题意可知几何体的直观图如图：所以几何体的体积为231π43π4⨯⨯⨯=，故选C ．。

高三数学专题三视图与体积

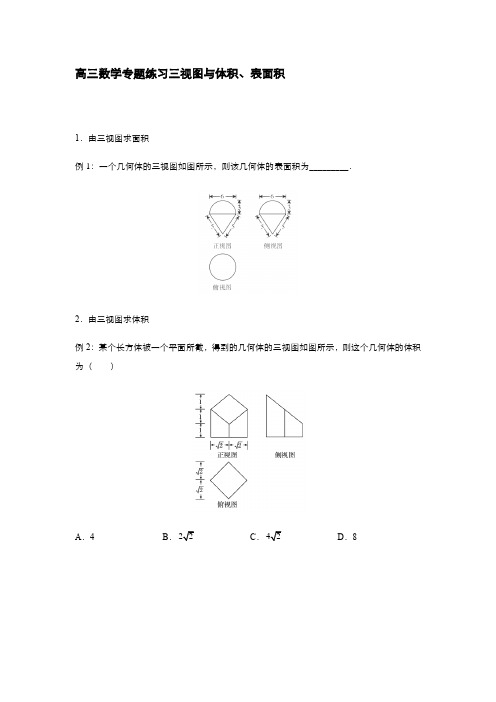
高三数学专题练习三视图与体积、表面积1．由三视图求面积例1：一个几何体的三视图如图所示，则该几何体的表面积为_________．2．由三视图求体积例2：某个长方体被一个平面所截，得到的几何体的三视图如图所示，则这个几何体的体积为（）A ．4B ．C ．D ．8一、单选题1．某几何体的三视图如图所示，若该几何体的表面积为，则俯视图中圆的半径为（）A ．1B ．2C ．3D ．42．正方体中，为棱的中点（如图）用过点的平面截去该正方体的上半部分，则剩余几何体的左视图为（）A ．B ．C ．D ．3．如图，网格纸上小正方形的边长为1，粗线画的是某几何体的三视图，则该几何体的体积为（）1111ABCD A B C D E 1AA 1B E D 、、A ．B ．C ．D ．44．一个几何体的三视图如图所示，其中正视图是半径为1的半圆，则该几何体的表面积为（）A ．B ．C ．D ．5．若某三棱柱截去一个三棱锥后所剩几何体的三视图如图所示，则所截去的三棱锥．．．．．．的外接球的表面积等于（）A ．B ．C ．D ．6．如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的外接球的表面积为（）2367276)21+π21⎫++π⎪⎪⎝⎭122⎫++π⎪⎪⎝⎭12⎫π⎪⎪⎝⎭34π32π17π172πA ．B ．C ．D ．7．一个四棱锥的三视图如图所示，则该几何体的表面积为（）A ．B ．C ．D ．8．已知一个三棱锥的三视图如图所示，其中三视图的长、宽、高分别为2，，，且，则此三棱锥外接球表面积的最小值为（）A ．B ．C ．D ．9．在四棱锥中，底面，底面为正方形，，该四棱锥被一平面截去一部分后，剩余部分的三视图如图，则截去部分体积与剩余部分体积的比值为（）32π16π36π72π6+8+6+8+a b ()520,02a b a b +=>>174π214π4π5πP ABCD -PA ⊥ABCD ABCD PA AB =A ．B ．C ．D ．10．如图，画出的是某四棱锥的三视图，网格纸上小正方形的边长为1，则该几何体的体积为（）A ．15B ．16C ．D ．11．某几何体的三视图如图（虚线刻画的小正方形边长为1）所示，则这个几何体的体积为（）A ．BC ．12D ．12．如图为一个多面体的三视图，则该多面体的体积为（）121314155035339483A ．B ．7C ．D ．二、填空题13．网格纸上小正方形的边长为1，粗虚、实线画出的是某个长方体挖去一个几何体得到的几何图形的三视图，则该被挖去的几何体的体积为__________．14．已知某几何体的三视图如图所示，则该几何体的表面积和体积分别为_______与_______．15．某四棱锥的三视图如图所示，则该四棱锥的体积为_________．20322323316．已知某几何体的三视图如图所示，三视图的轮廓均为正方形，则该几何体的体积为__________．1．由三视图求面积例1：一个几何体的三视图如图所示，则该几何体的表面积为_________．【答案】33【解析】由三视图可得该几何体由一个半球和一个圆锥组成，其表面积为半球面积和圆锥侧面积的和．球的半径为3， ∴半球的面积21143182S =⋅π⋅=π，圆锥的底面半径为3，母线长为5， ∴圆锥的侧面积为23515S rl =π=π⋅⋅=π，∴表面积为1233S S S =+=π．2．由三视图求体积例2：某个长方体被一个平面所截，得到的几何体的三视图如图所示，则这个几何体的体积为（）A ．4B ．C ．D ．8【答案】D【解析】由于长方体被平面所截，∴很难直接求出几何体的体积，可以考虑沿着截面再接上一个一模一样的几何体，从而拼成了一个长方体，∵长方体由两个完全一样的几何体拼成，∴所求体积为长方体体积的一半。

2020届高三文科数学精准培优专练：三视图与体积、表面积(附解析)

2020届高三文科数学精准培优专练：三视图与体积、表面积（附解析）一、三视图与体积的结合例1：某几何体的三视图如图所示（图中小正方形网格的边长为1），则该几何体的体积是（）A ．8B ．6C ．4D ．2二、三视图与表面积的结合例2：如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，其中俯视图由两个半圆和两个线段组成，则该几何体的表面积为（）A ．17π12+B ．12π12+C ．20π12+D ．16π12+对点增分集训一、选择题1．某几何体的三视图如图所示，则这个几何体的体积为（）A．2π163- B．4π83- C．4π163- D．π16(1)3-2．如图，网格纸上小正方形的边长为1，粗线条画出的是一个三棱锥的三视图，则该三棱锥中最长棱的长度为（）A．2 B． D．33．古人采取“用臼舂米”的方法脱去稻谷的外壳，获得可供食用的大米，用于舂米的“臼”多用石头或木头制成．一个“臼”的三视图如图所示，则凿去部分（看成一个简单的组合体）的体积为（）A．63π B．72π C．79π D．99π4．某几何体的三视图如图所示，在该几何体的各个面中，面积最小的面与底面的面积的比值为（）A ．13B ．23 C ．25 D ．455．一个几何体的三视图如图所示，其中正视图和俯视图中的四边形是边长为2的正方形，则该几何体的表面积为（）A ．13π2 B ．7π C ．15π2D ．8π 6．如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则该几何体的表面积为（）A ．83π+B ．84π+C ．85π+D ．86π+7．某几何体的三视图如图所示，则这个几何体的体积是（）A ．13B ．14C ．15D ．168．某装饰品的三视图如图所示，则该装饰品的表面积为（）A ．16π+B ．161)π-C ．161)π+D ．201)π+ 9．如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，俯视图中的两条曲线均为圆弧，则该几何体的体积为（）A ．32π643-B ．648π-C ．16π643-D ．8π643- 10．我国古代数学名著《九章算术·商功》中阐述：“斜解立方，得两堑堵．斜解堑堵，其一为阳马，一为鳖臑．阳马居二，鳖臑居一，不易之率也．合两鳖臑三而一，验之以棊，其形露矣”若称为“阳马”的某几何体的三视图如图所示，图中网格纸上小正方形的边长为1，则对该几何体描述：①四个侧面都是直角三角形；②最长的侧棱长为；③四个侧面中有三个侧面是全等的直角三角形；④外接球的表面积为24π．其中正确的个数是（）A．0 B．1 C．2 D．311．某工人现欲用车床将一正方体铁块进行加工处理，加工后成品的三视图如图所示．网格纸上小正方形的边长为1，则加工后成品与去除部分几何体的体积比为（）A．32ππ-B．64ππ-C．16ππ-D．48ππ-12．某三棱锥的三视图如图所示，其中小正方形的边长均为1．三棱锥上的点M在俯视图上的对应点为A，点N在左视图上的对应点为B，则线段MN长度的最大值为（）A．．．9 D．6二、填空题13．已知某几何体的三视图如图所示（侧视图中曲线为四分之一圆弧），则该几何体的体积为．14．如图是某几何体的三视图，图中方格的单位长度为1，则该几何体的表面积为．15．一个由半球和四棱锥组成的几何体，其三视图如图所示．则该几何体的体积为．16．某几何体的三视图如图所示，则该几何体的体积为．例1：【答案】B【解析】由三视图可得该几何体为底面是直角梯形的直四棱柱（如图所示），其中底面直角梯形的上、下底边分别为1，2，高为2，直四棱柱的高为2，所以该几何体的体积为(12)2262+⨯⨯=，故选B．例2：【答案】C【解析】由三视图知，该几何体是一个大半圆柱挖去一个小半圆柱得到的，两个半圆柱的底面半径分别为1和3，高均为3，所以该几何体的表面积为112π332π1322⨯⨯⨯+⨯⨯⨯22112(π3π1)22320π1222+⨯⨯-⨯+⨯⨯=+．一、选择题1．【答案】C【解析】根据三视图知，该几何体是一个直四棱柱内挖去一个圆锥后剩余的部分，画出直观图如图所示，三视图与体积表面积答案设四棱柱的体积为1V ，圆锥的体积为2V ，结合图中数据，得该几何体的体积221214π24π141633V V V =-=⨯-⨯⨯=-，故选C ． 2．【答案】D【解析】如图，三棱锥A BCD -即为所求几何体，根据题设条件，知辅助的正方体棱长为2，1CD =，BD =，BC =，2AC =，3AB =，AD =AB ，长度为3．3．【答案】A【解析】由三视图得凿去部分是圆柱与半球的组合体，其中圆柱的高为5，底面圆的半径为3，半球的半径为3，所以组合体的体积为2314π35π363π23⋅⨯+⨯⨯=，故选A ． 4．【答案】C【解析】由三视图可知，该几何体是高为4的四棱锥，如图所示，记为P ABCD -．易知面积最小的面为左侧面，其面积为1142⨯⨯．将底面ABCD 补为梯形BCDE ，则底面ABCD 的面积为11(24)221522⨯+⨯-⨯⨯=，所以面积最小的面与底面的面积的比值为25，故选C ． 5．【答案】B【解析】由三视图可知该几何体是一个圆柱体和一个球体的四分之一的组合体，则所求的几何体的表面积为22214π1π1π12π127π4⨯⨯+⨯+⨯+⨯⨯=，故选B ．6．【答案】D【解析】由三视图可知，该几何体是由底面半径为1，高为4的半圆柱挖去一个半径为1的半球得到的，则该几何体的表面积2221112π142π142π14π186π222S =⨯⨯⨯+⨯⨯⨯+⨯-⨯+⨯⨯=+．故选B ． 7．【答案】C 【解析】所求几何体可看作将长方体截去两个三棱柱得到的几何体，在长方体中还原该几何体，如图中ABCD A B C D ''''-所示，长方体的长、宽、高分别为4，2，3，两个三棱柱的高为2，底面是两直角边长分别为3和1.5的直角三角形，故该几何体的体积134232321522V =⨯⨯-⨯⨯⨯⨯=，故选C ． 8．【答案】C【解析】由装饰品的三视图可知，该装饰品是由一个棱长为2的正方体，切去四个四分之一的圆锥所得的几何体，其中圆锥的底面半径为1，高为2，则该装饰品的表面积为222111224π14224π1161)π424+-⨯⨯+⨯⨯⨯+⨯⨯=+，故选C ． 9．【答案】C【解析】由三视图知，该几何体是由棱长为4的正方体截去一个底面半径为2、高为4的14圆锥和一个底面半径为2、高为4的14圆柱而得到的，所以该几何体的体积3221116π4(π24π24)64433V =-⨯⨯+⨯⨯=-，故选C ． 10．【答案】D【解析】对于①，由三视图知“阳马”的直观图如图中四棱锥S ABCD -所示，其中SA ⊥平面ABCD ，所以SA AB ⊥，SA AD ⊥，SA BC ⊥，所以SAB △，SAD △为直角三角形，结合BC AB ⊥，知BC ⊥平面SAB ，所以BC SB ⊥，故SBC △为直角三角形，同理可知SCD △为直角三角形，所以“阳马”的四个侧面均为直角三角形，正确；对于②，由三视图及直观图得2SA =，SB ==SD =连接AC ，则SC ===，所以“阳马”的最长的侧棱长为，正确；对于③，由②的侧棱长知，侧面四个直角三角形的斜边均不相等，所以不存在全等的直角三角形，错误；对于④，考虑将“阳马”补形为一个长、宽、高分别为4、2、2的长方体，易知长方体的外接球即“阳马”的外接球其直径2R =，所以“阳马”的外接球的表面积为224ππ(2)24πR R ==，正确．综上可知，正确的个数为3，故选D ．11．【答案】C【解析】由三视图可知，该几何体为正方体中间挖去一个圆柱后所得，且正方体的棱长为4，圆柱的底面半径为1，高为4，设正方体的体积为1V ，圆柱的体积为2V ，所以加工后成品的体积32124π14644πV V V =-=-⨯⨯=-．加工后成品与去除部分的体积比为644π16π4ππ--=．故选C ． 12．【答案】A【解析】根据三视图，在棱长为3的正方体中还原该几何体的直观图，为如图所示的三棱锥P CNE -，则点B 即点N 在左视图上对应的点，点A 为线段PC 上任意一点M 在底面CNE 上的投影，因为PC 上的点M 到点N 距离的最大值为PN 的长，故线段MN 长度的最大值为二、填空题13．【答案】π14- 【解析】由已知三视图得到几何体是棱长为1的正方体挖去底面半径为1的14圆柱，正方体的棱长为1，14圆柱的体积为21ππ1144⨯⨯⨯=，所以几何体体积为π14-．14．【答案】8+【解析】由三视图还原几何体如下图所示，可得三棱锥A BCD -，计算可得2BC =，2CD =，BD =，AD =，AB =12222BCD S =⨯⨯=△，122ADC S =⨯⨯=△122ABC S =⨯⨯=△ABD △=162ABD S =⨯=△，则该几何体表面积为268+=+15．【答案】1π36+【解析】1，高为1，所以其体积为3114111ππ3233⨯⨯+⨯⨯=+．故答案为13+． 16．【答案】3π【解析】由题意可知几何体的直观图如图：所以几何体的体积为231π43π4⨯⨯⨯=，故选C ．。

2019届高考数学专题十三三视图与体积表面积精准培优专练理

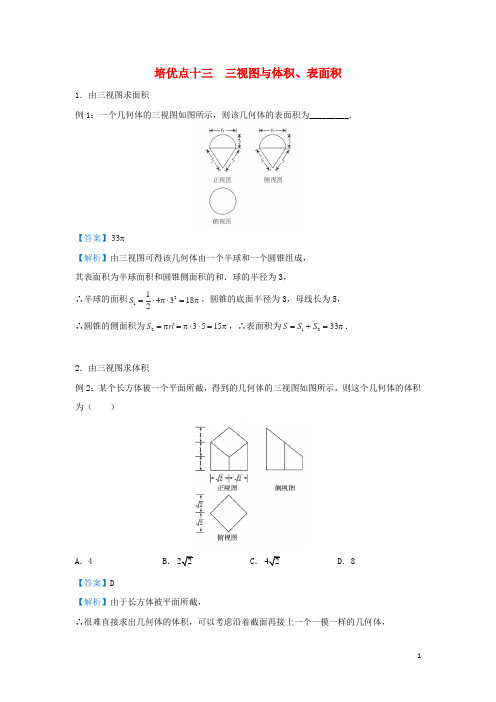
培优点十三三视图与体积、表面积1．由三视图求面积例1：一个几何体的三视图如图所示，则该几何体的表面积为_________．【答案】33π【解析】由三视图可得该几何体由一个半球和一个圆锥组成，其表面积为半球面积和圆锥侧面积的和．球的半径为3， ∴半球的面积21143182S =⋅π⋅=π，圆锥的底面半径为3，母线长为5， ∴圆锥的侧面积为23515S rl =π=π⋅⋅=π，∴表面积为1233S S S =+=π．2．由三视图求体积例2：某个长方体被一个平面所截，得到的几何体的三视图如图所示，则这个几何体的体积为（）A ．4B ．C ．D ．8【答案】D【解析】由于长方体被平面所截，∴很难直接求出几何体的体积，可以考虑沿着截面再接上一个一模一样的几何体，从而拼成了一个长方体，∵长方体由两个完全一样的几何体拼成，∴所求体积为长方体体积的一半。

从图上可得长方体的底面为正方形，且边长为2，长方体的高为314+=，∴22416V =⋅=长方体，∴182V V ==长方体，故选D ．一、单选题1．某几何体的三视图如图所示，若该几何体的表面积为，则俯视图中圆的半径为（）A ．1B ．2C ．3D ．4【答案】A【解析】由三视图可知该几何体为一个长方体挖去了一个半球，设圆半径为r ， ∴该几何体的表面积2222242216S r r r r r r =⨯⋅+⨯⋅-π⋅+π⋅=+π，得1r =，故选A ． 2．正方体1111ABCD A B C D -中，E 为棱1AA 的中点（如图）用过点1B E D 、、的平面截去该正方体的上半部分，则剩余几何体的左视图为（）对点增分集训A ．B ．C ．D ．【答案】D【解析】由题意可知：过点B 、E 、1D 的平面截去该正方体的上半部分，如图直观图，则几何体的左视图为D ，故选D ．3．如图，网格纸上小正方形的边长为1，粗线画的是某几何体的三视图，则该几何体的体积为（）A ．236B ．72C ．76D ．4【答案】A【解析】由三视图可得，该几何体是如图所示的三棱柱11ABB DCC -挖去一个三棱锥E FCG -，故所求几何体的体积为()111232221112326⎛⎫⨯⨯⨯-⨯⨯⨯⨯= ⎪⎝⎭，故选A ．4．一个几何体的三视图如图所示，其中正视图是半径为1的半圆，则该几何体的表面积为（）A ．)21+πB ．21⎫++π⎪⎪⎝⎭C ．122⎫++π⎪⎪⎝⎭D ．12⎫+π⎪⎪⎝⎭【答案】C【解析】由三视图可知，其对应的几何体是半个圆锥，圆锥的底面半径为1r =，圆锥的高2h =，其母线长l =21111112222222S ⎫=⨯π⨯+⨯π⨯⨯⨯=+π⎪⎪⎝⎭，本题选择C 选项． 5．若某三棱柱截去一个三棱锥后所剩几何体的三视图如图所示，则所截去的三棱锥．．．．．．的外接球的表面积等于（）A ．34πB ．32πC ．17πD ．172π 【答案】A【解析】由三视图知几何体是底面为边长为3，4，5的三角形，高为5的三棱柱被平面截得的，如图所示，截去的是一个三棱锥，底面是边长为3，4，5的直角三角形，高为3的棱锥，如图蓝色线条的图像是该棱锥，三棱锥上底面外接圆半径52圆心设为M 半径为r ，球心到底面距离为32，设球心为O ，由勾股定理得到2222253342224h R r ⎛⎫⎛⎫⎛⎫=+=+= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，2434S R =π=π，故选A ．6．如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的外接球的表面积为（）A ．32πB ．16πC ．36πD ．72π【答案】C【解析】还原几何体如图所示三棱锥由1B BCD -（如下左图），将此三棱锥补形为直三棱柱111B C D BCD -（如上右图），在直三棱柱111B C D BCD -中取1BC B C 、的中点12O O 、，取12O O 中点O ，3R ===，2244336S R =π=⨯=π表，故答案为C ．7．一个四棱锥的三视图如图所示，则该几何体的表面积为（）A ．6+B ．8+C ．6+D ．8+【答案】B【解析】根据三视图，画出原空间结构图如下图所示：∴表面积为111111111111DA D DA B DB C DC D A B C D S S S S S S =++++11112222222282222=⨯⨯+⨯⨯⨯⨯⨯⨯+⨯=+，∴故选B ． 8．已知一个三棱锥的三视图如图所示，其中三视图的长、宽、高分别为2，a ，b ，且()520,02a b a b +=>>，则此三棱锥外接球表面积的最小值为（）A ．174π B ．214π C ．4π D ．5π【答案】B【解析】由已知条件及三视图得，此三棱锥的四个顶点位于长方体1111ABCD A B C D -的四个顶点，即为三棱锥11A CB D -，且长方体1111ABCD A B C D -的长、宽、高分别为2，a ，b ，∴此三棱锥的外接球即为长方体1111ABCD A B C D -的外接球，且球半径为R ==，∴三棱锥外接球表面积为()()22222144514a b a ππ=π++=π-+⎝⎭， ∴当且仅当1a =，12b =时，三棱锥外接球的表面积取得最小值为214π．故选B ． 9．在四棱锥P ABCD -中，PA ⊥底面ABCD ，底面ABCD 为正方形，PA AB =，该四棱锥被一平面截去一部分后，剩余部分的三视图如图，则截去部分体积与剩余部分体积的比值为（）A ．12 B ．13C ．14 D ．15【答案】B【解析】由三视图知，剩余部分的几何体是四棱锥P ABCD -被平面QBD 截去三棱锥Q BCD -（Q 为PC 中点）后的部分，连接AC 交BD 于O ，连楼OQ ，则OQ PA ∥，且12OQ PA =，设PA AB a ==，则313P ABCD V a -=，23111132212Q BCD V a a a -=⨯⨯=，剩余部分的体积为：3311312a a -，则所求的体积比值为：3331112113312aa a =-．本题选择B 选项．10．如图，画出的是某四棱锥的三视图，网格纸上小正方形的边长为1，则该几何体的体积为（）A ．15B ．16C ．503D ．533【答案】C【解析】由题得几何体原图是下图中的四棱锥A BCDE -，底面四边形BCDE 的面积为114442221022⨯-⨯⨯-⨯⨯=，∴四棱锥的体积为15010533⨯⨯=，故答案为C ．11．某几何体的三视图如图（虚线刻画的小正方形边长为1）所示，则这个几何体的体积为（）A ．94B C ．12D ．83【答案】D【解析】几何体为如图多面体PABCDE ，∴体积为()11118221222132323D PABE A BCD V V --+=⨯⨯⨯⨯++⨯⨯⨯⨯=，故选D ．12．如图为一个多面体的三视图，则该多面体的体积为（）A ．203B ．7C ．223D ．233【答案】B【解析】如图所示，该几何体为正方体去掉两个倒置的三棱锥，∴该多面体的体积为32111121212273232V =-⨯⨯⨯-⨯⨯⨯⨯=；故选B ．二、填空题13．网格纸上小正方形的边长为1，粗虚、实线画出的是某个长方体挖去一个几何体得到的几何图形的三视图，则该被挖去的几何体的体积为__________．【答案】12【解析】根据三视图知长方体挖去部分是一个底面为等腰梯形（上底为2，下底为4，高为2）高为2的直四棱柱，∴()12422122V Sh ==+⨯⨯=． 14．已知某几何体的三视图如图所示，则该几何体的表面积和体积分别为_______与_______．【答案】404+π，4163π+ 【解析】由三视图可知，其对应的几何体是一个组合体，上半部分是一个直径为2的球，下半部分是一个直棱柱，棱柱的底面是边长为2的正方形，高为4，则该几何体的表面积224122424404S =π⨯+⨯+⨯⨯=+π，几何体的体积：32441241633V =π⨯+⨯=+π． 15．某四棱锥的三视图如图所示，则该四棱锥的体积为_________．【答案】1【解析】根据题中所给的三视图，还原几何体，可知其为有一条侧棱垂直于底面的一个四棱锥，该四棱锥的底面就是其俯视图中的直角梯形，根据图中所给的数据，结合椎体的体积公式，可得其体积11212132V +=⨯⨯⨯=，故答案是1． 16．已知某几何体的三视图如图所示，三视图的轮廓均为正方形，则该几何体的体积为__________．【解析】由三视图知，该几何体由正方体沿面11AB D 与面11CB D 截去两个角所得，。

高考数学专题十三三视图与体积、表面积精准培优专练理-人教版高三全册数学试题

培优点十三三视图与体积、表面积例1：中国古建筑借助榫卯将木构件连接起来，构件的凸出部分叫榫头，凹进部分叫卯眼，图中木构件右边的小长方体是榫头．若如图摆放的木构件与某一带卯眼的木构件咬合成长方体，则咬合时带卯眼的木构件的俯视图可以是（）A ．B ．C ．D ．【答案】A【解析】由题意可知带卯眼的木构件的直观图如图所示，由直观图可知其俯视图，应选A ．例2：如图，在长方体1111ABCD A B C D -中，点P 是棱CD 上一点，则三棱锥11P A B A -的侧视图是（）A ．B ．C ．D ．【答案】D【解析】在长方体1111ABCD A B C D -中，从左侧看三棱锥11P A B A -，一、根据几何体的结构特征确认其三视图1B 、1A 、A 的射影分别是1C 、1D 、D ，1AB 的射影为1C D ，且为实线，1PA 的射影为1PD ，且为虚线．故选D ．例3：如图，网格纸的各小格都是正方形，粗实线画出的是一个几何体的三视图，则这个几何体是（）A ．三棱锥B ．三棱柱C ．四棱锥D ．四棱柱【答案】B【解析】由题三视图得直观图如图所示，为三棱柱．故选B ．例4：若某几何体的三视图如图所示，则这个几何体的直观图可以是（）二、根据三视图还原几何体的直观图A．B．C．D．【答案】D【解析】由三视图知该几何体的上半部分是一个三棱柱，下半部分是一个四棱柱．故选D．三、已知几何体的三视图中某两个视图，确定另外一种视图例5：如图是一个空间几何体的正视图和俯视图，则它的侧视图为（）A．B．C．D．【答案】A【解析】由正视图和俯视图可知，该几何体是一个圆柱挖去一个圆锥构成的，结合正视图的宽及俯视图的直径知其侧视图应为A．故选A．例6：一个几何体的三视图中，正视图和侧视图如图所示，则俯视图不可以为（）A．B．C．D．【答案】C【解析】A中，该几何体是直三棱柱，所以A有可能；B中，该几何体是直四棱柱，所以B有可能；C中，由题干中正视图的中间为虚线知，C不可能；D中，该几何体是直四棱柱，所以D有可能．综上，故选C．例7：如图所示，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则该几何体的表面积为（）四、根据几何体的三视图计算表面积A ．5π18+B ．6π18+C ．8π6+D ．10π6+【答案】C【解析】由三视图可知该几何体是由一个半圆柱和两个半球构成的，故该几何体的表面积为2211124π12π1232π138π6222⨯⨯⨯+⨯⨯⨯+⨯+⨯⨯⨯=+．故选C ．例8：如图所示，某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径．若该几何体的体积是28π3，则它的表面积是（）A ．17πB ．18πC ．20πD ．28π【答案】A【解析】由几何体的三视图可知，该几何体是一个球体去掉上半球的14，得到的几何体如图．设球的半径为R ，则3341428πππ3833R R -⨯=，解得2R =．因此它的表面积为22734ππ17π84R R ⨯+=．故选A ．例9：某几何体的三视图如图所示(单位：cm)，则该几何体的体积(单位：3cm)是（）A．π12+B．π32+C．3π12+D．3π32+【答案】A【解析】由几何体的三视图可知，该几何体是一个底面半径为1，高为3的圆锥的一半与一个底面为直角边的等腰直角三角形，高为3的三棱锥的组合体，∴该几何体的体积21111ππ323221331⨯⨯⨯⨯+=+．故选A．例10：如图所示，已知多面体ABCDEFG中，AB、AC、AD两两互相垂直，平面ABC∥平面DEFG，平面BEF∥平面ADGC，2AB AD DG===，1AC EF==，则该多面体的体积为________．【答案】4【解析】法一：(分割法)因为几何体有两对相对面互相平行，如图所示，五、根据几何体的三视图计算体积过点C 作CH DG ⊥于H ，连接EH ，即把多面体分割成一个直三棱柱DEH ABC -和一个斜三棱柱BEF CHG -．由题意，知三棱柱DEH ABC -的体积11(2221)2DEH V S AD =⨯⨯⨯=⨯=△，三棱柱BEF CHG -的体积21(2221)2BEF V S DE =⨯⨯⨯=⨯=△，故所求多面体ABCDEFG 的体积为12224V V V =+=+=．法二：(补形法)因为几何体有两对相对面互相平行，如图所示，将多面体补成棱长为2的正方体，显然所求多面体的体积即该正方体体积的一半．又正方体ABHI DEKG -的体积328V '==，故所求多面体ABCDEFG 的体积为118422V V '==⨯=．一、选择题1．如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则此几何体的各个面中是直角三角形的个数为（）对点增分集训A ．1B ．2C ．3D ．4【答案】C【解析】三视图还原为如图所示三棱锥A BCD -，由正方体的性质得ABC △、BCD △、ACD △为直角三角形，ABD △为正三角形，故选C ．2．某几何体的三视图如图所示，网格纸上小正方形的边长为1，则该几何体的表面积（）A ．5πB ．6πC ．6π2+D ．5π2+【答案】D【解析】由三视图可知，该几何体为两个半圆柱构成，其表面积为22π1π12π11215π2⨯⨯+⨯⨯+⨯⨯+⨯=+，故选D ． 3．已知一个几何体的三视图如图所示，则其体积为（）A ．12πB ．16πC ．32π3D ．403π【答案】D【解析】由三视图可知，该几何体为圆柱挖去其16后的剩余部分，该圆柱的底面半径为2，高为4，故其体积为圆柱体积的56，25540ππ16π663V R h ==⨯=．故选D ．4．某四棱锥的三视图如图所示，则该四棱锥的体积为（）A ．23B ．43C ．83D【答案】C【解析】该三视图还原成直观图后的几何体是如图所示的四棱锥A BCDE -，CBA △和ACD △是两个全等的直角三角形，且2AC CD BC ===，故几何体的体积为1822233⨯⨯⨯=，故选C ．5．我国古代《九章算术》将上下两个平行平面为矩形的六面体称为刍童．如图是一个刍童的三视图，其中正视图及侧视图均为等腰梯形，两底的长分别为2和6，高为2，则该刍童的体积为（）A ．1003B ．1043C ．27D ．18【答案】B【解析】由题意几何体原图为正四棱台，底面的边长分别为2和6，高为2，所以几何体体积1104(436233V =+⨯=．故选B ． 6．如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的各棱中，最长的棱的长度为（）A ．B ．6C ．D ．4【答案】B【解析】三视图还原成如图所示的几何体，三棱锥S ABC -，则4SB BC ==，SC =AC AB ==6SA =．故选B ．7．在正方体1111ABCD A B C D -中，E 、F 、G 分别为棱CD 、1CC 、11A B 的中点，用过点E 、F 、G 的平面截正方体，则位于截面以下部分的几何体的侧视图为（）A ．B ．C ．D ．【答案】C【解析】过点E ，F ，G 截正方体的平面为如图所示的平面EFKGHI ，由图知位于截面以下部分的几何体的侧视图为C 选项，故选C ．8．如图所示的网格是由边长为1的小正方形构成，粗线画出的是某几何体的三视图，则该几何体的体积为（）A ．40B ．103C ．163D ．803【答案】D【解析】根据几何体三视图可得，该几何体是三棱柱BCE AGF -割去一个三棱锥A BCD -所得的几何体，如图所示，所以其体积为111180444(44)423223V =⨯⨯⨯-⨯⨯⨯⨯⨯=．故选D ．9．某几何体的三视图如图所示，则该几何体的外接球的体积是（）A B C ．3π D ．【答案】B【解析】根据几何体的三视图知，该几何体是由一个正方体切去正方体的一角得到的，故该几何体的外接球为正方体的外接球，所以球的半径22r ==，则34π322V ⎛⎫=⋅⋅= ⎪ ⎪⎝⎭．故选B ．10．某空间几何体的三视图如图所示，则该几何体的外接球半径为（）ABCD．【答案】C【解析】由三视图可知三棱锥的直观图如图，由三视图可知底面三角形是边长为2，顶角120︒的三角形，所以其外接圆半径结合正弦定理可得，224sin30r ==︒，由侧面为两等腰直角三角形，可确定出外接圆圆心，利用球的几何性质可确定出球心，且球心到底面的距离1d =，所以球半径R ==，故选C ．11．如图，网格纸上小正方形的边长为1，粗线画出的是某四棱锥的三视图，则该四棱锥的体积为（）A ．6B ．8C ．D ．【答案】B【解析】由三视图可得四棱锥为如图所示的长方体1111ABCD A B C D -中的四棱锥11C DEE D -，其中在长方体1111ABCD A B C D -中，4AB =，2AD =，13AA =，点E 、1E 分别为AB 、11A B 的中点，由题意得CE DE ==CE DE ⊥，又1CE EE ⊥，所以CE ⊥平面11DEE D ，即线段CE 即为四棱锥11C DEE D -的高，所以四棱锥11C DEE D -的体积1111(3833DEE D V S CE =⋅⋅=⨯⨯⨯=．故选B ．12．在棱长为1的正方体1111ABCD A B C D -中，E 、F 分别为线段CD 和11A B 上的动点，且满足1CE A F =，则四边形1D FBE 所围成的图形（如图所示阴影部分）分别在该正方体有公共顶点的三个面上的正投影的面积之和（）A ．有最小值32B ．有最大值52C ．为定值3D ．为定值2【答案】D【解析】依题意，设四边形1D FBE 的四个顶点在后面、上面、左面的投影点分别为'D 、F '、B '、E '，则四边形1D FBE 在上面、后面、左面的投影分别如下图，所以在后面的投影的面积为1111S =⨯=，在上面的投影面积211S D E DE DE ''=⨯=⨯=，在左面的投影面积311S B E CE CE ''=⨯=⨯=，所以四边形1D FBE 所围成的图形分别在该正方体有公共顶点的三个面上的正投影的面积之和为123112S S S S DE CE CD =++=++=+=．故选D ．二、填空题13．某几何体的三视图如图所示，网格纸上小正方形的边长为1，则该几何体的表面积是．【答案】64+【解析】由三视图可知，该几何体的直观图为如图所示的四棱柱，则11111(24)4122ABCD A B C D S S ==⨯+⨯=，11114416BCC B CC D D S S ==⨯=，11428ABB A S =⨯=，114AA D D S =⨯=所以该四棱柱的表面积为2432864S =+++=+14．《九章算术》是我国古代数学名著，在《九章算术》中将底面为矩形且有一侧棱垂直于底面的四棱锥称为“阳马”．若某“阳马”的三视图如图所示，其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形，则该“阳马”的表面积为．【答案】22【解析】由三视图可得该“阳马”的底面是边长为1的正方形，且高为1，故该“阳马”的表面积为1121121221222+⨯⨯⨯+⨯=+15．已知圆锥的高为33体积等于．【答案】32π3【解析】设该圆锥的外接球的半径为R ，依题意得，222()(3)3R R +-=，解得2R =，故所求球的体积334432ππ2π333V R ==⨯=． 16．已知点P 、A 、B 、C 是半径为2的球面上的点，2PA PB PC ===，90ABC ∠=︒，点B 在AC 上的射影为D ，则三棱锥P ABD -体积的最大值是．33 【解析】设点P 在平面ABC 上的射影为G ，如图，由2PA PB PC ===，90ABC ∠=︒知，点P 在平面ABC 上的射影G 为ABC △的外心，即AC 的中点，设球的球心为O ，连接PG ，则O 在PG 的延长线上，连接OB 、BG ，设PG h =，则2OG h =-，所以2222OB OG PB PG -=-，即22()424h h --=-，解得1h =，则AG CG ==设AD x =，则GD x AG x =-=-BG =所以BD ==12ABD S AD BD ==⋅△令43()f x x =-+，则32()4f x x '=-+，由()0f x '=，得0x =或2x =，易知当2x =时，函数()f x 取得最大值24316，所以max 1()248ABD S =⨯=△．又1PG =，所以三棱锥P ABD -体积的最大值为113=．。

2019年高考数学专题三立体几何与空间向量第1讲空间几何体的三视图、表面积与体积梯度训练新人教A版

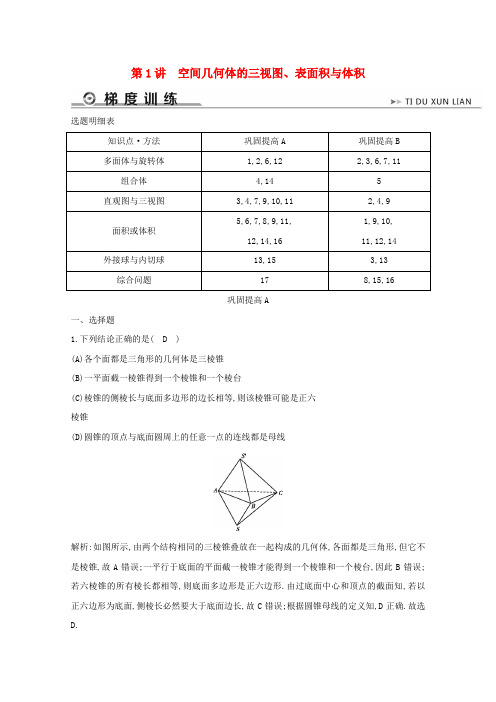
第1讲空间几何体的三视图、表面积与体积选题明细表巩固提高A一、选择题1.下列结论正确的是( D )(A)各个面都是三角形的几何体是三棱锥 (B)一平面截一棱锥得到一个棱锥和一个棱台(C)棱锥的侧棱长与底面多边形的边长相等,则该棱锥可能是正六棱锥(D)圆锥的顶点与底面圆周上的任意一点的连线都是母线解析:如图所示,由两个结构相同的三棱锥叠放在一起构成的几何体,各面都是三角形,但它不是棱锥,故A 错误;一平行于底面的平面截一棱锥才能得到一个棱锥和一个棱台,因此B 错误;若六棱锥的所有棱长都相等,则底面多边形是正六边形.由过底面中心和顶点的截面知,若以正六边形为底面,侧棱长必然要大于底面边长,故C 错误;根据圆锥母线的定义知,D 正确.故选D.2.下列几何体中为棱柱的是( A )解析:A中几何体有两个面互相平行,其余各个面都是平行四边形,是棱柱.故选A.3.(2018·嘉兴模拟)某几何体的三视图如图(单位: m),则该几何体的体积是( A )(A) m3(B)m3(C)2 m3(D)4 m3解析:由三视图可得:该几何体是一个以俯视图为底面的三棱锥,底面的底边长为2 m,底面的高,即为三视图的宽1 m,故底面面积S=×2×1=1 m2,棱锥的高即为三视图的高,故h=2 m,故棱锥的体积V=×1×2= m3,故选A.4.(2017·台州4月调研考试)某几何体的三视图如图所示,其中俯视图是半径为1的圆,则该几何体的体积是( A )(A)π(B)(C)(D)解析:该几何体下部是一个底面半径为1,高为2的圆锥,上部是半径为1的四分之一球体,所以体积V=×π×12×2+××π×13=+=π.故选A.5.长方体ABCD-A1B1C1D1的八个顶点落在球O的表面上,已AB=3,AD=4,BB1=5,那么球O的表面积为( D )(A)25π (B)200π(C)100π(D)50π解析:因为长方体ABCD-A1B1C1D1的八个顶点都在球面上,所以长方体的体对角线为外接球的直径,设半径为r,则长方体的体对角线长为=5,则2r=5,则r=,所以外接球的表面积为4πr2=50π.故选D.6.母线长为1的圆锥的侧面展开图的圆心角等于120°,则该圆锥的体积为( A )(A)π(B)π(C)π(D)π解析:因为母线长为1的圆锥的侧面展开图的圆心角等于120°,120°=,所以侧面展开图的弧长为1×=,弧长=底面周长=2πr,所以r=,所以圆锥的高h==,所以圆锥体积V=×π×r2×h=π.故选A.7.(2018·浙江卷)某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm3)是( C )(A)2 (B)4 (C)6 (D)8解析:由几何体的三视图可知,该几何体是一个底面为直角梯形,高为2的直四棱柱,所以V=2×［×(2+1)×2］=6.故选C.8.已知三棱锥O ABC的顶点A,B,C都在半径为3的球面上,O是球心,∠AOB=150°,当△AOC与△BOC的面积之和最大时,三棱锥O-ABC的体积为( D )(A)(B)(C)(D)解析:设球O的半径为R,由S△AOC+S△BOC=R2(sin∠AOC+sin∠BOC)知,当sin∠AOC=sin∠BOC=90°时,S△AOC+S△BOC取得最大值,此时OA⊥OC,OB⊥OC, 所以OC⊥平面AOB,==R3sin∠AOB=.故选D.二、填空题9.已知一个几何体的三视图如图所示,则此几何体的表面积是,体积是.解析:三视图的直观图如图所示.由题知正方体的棱长为2,点M为棱A′D′的中点,所以AM=B′M=,AB′=2,在等腰三角形AB′M中,底边AB′边上的高为,该几何体的表面积S=2(S正方形ABCD+S△ABB′+S△ADM+S△AB′M)=2×（2×2+×2×2+×2×2+×2×）=16+2,体积V=-2=2×2×2-2×××1×2×2=8-=.答案:16+210. 如图所示,四边形ABCD的直观图四边形A′B′C′D′是一个底角为45°,腰和上底均为1的等腰梯形,那么原平面图形的面积是.解析:根据斜二测画法可知,原图形为直角梯形,其中上底AD=1,高AB=2A′B′=2,下底为BC=1+,所以×2=2+.即原平面图形的面积是+2.答案:+211.(2017·湖州、衢州、丽水三市高三联考)某几何体的三视图如图所示(单位:cm),则此几何体的体积是cm3,表面积是cm2.解析:由三视图可得直观图如图,体积V=×1=3(cm3),表面积S=2×1+(2+1)×2××2+1×1+1×2+1×=2+6+1+2+=(11+)cm2.答案:3 11+12.已知一个正三棱柱的侧面积为18,且侧棱长为底面边长的2倍,则该正三棱柱的体积为.解析:设底面边长为a,则高为2a,侧面积为S侧=3×(a×2a)=6a2=18,所以a=,该三棱柱的体积为V=Sh=（×××sin 60°）×2=.答案:13.体积为8的正方体的顶点都在同一个球面上,则该球的体积为.解析:由题意得球的直径等于正方体的体对角线长,设正方体的边长为a,球的半径为R,即2R=a,而a3=8,所以R=.该球的体积为πR3=π()3=4π.答案:4π14.(2018·杭州二模)一个几何体的三视图如图所示,则该几何体的体积是,表面积是.解析:由三视图知,该几何体是由四分之一球与半个圆锥组合而成,则该组合体的体积为V=·π·23+·π×22·3=π,表面积为S=·4π·22+·π·22+·4·3+··2π·2·=6+(6+)π,从而问题可得解.答案:π6+(6+)π15.(2018·天津卷) 已知正方体ABCD-A1B1C1D1的棱长为1,除面ABCD外,该正方体其余各面的中心分别为点E,F,G,H,M(如图),则四棱锥M-EFGH的体积为.解析:依题意,易知四棱锥M EFGH是一个正四棱锥,且底面边长为,高为.故=×（）2×=.答案:16. 三棱锥P-ABC满足:AB⊥AC,AB⊥AP,AB=2,AP+AC=4,则该三棱锥的体积V的取值范围是.解析:由于AB⊥AP,AB⊥AC,AC∩AP=A,所以AB⊥平面APC,V=S△APC·AB=S△APC,在△APC中,AP+AC=4,要使△APC面积最大,只需AP=AC,∠PAC=90°,AP·AC≤()2=4,所以S△APC的最大值为×4=2,V的最大值为,该三棱锥的体积V的取值范围是(0,］.答案:(0,］三、解答题17. 一个多面体的直观图和三视图如下:(其中M,N分别是AF,BC中点)(1)求证:MN∥平面CDEF;(2)求多面体A-CDEF的体积.(1)证明:由三视图知,该多面体是底面为直角三角形的直三棱柱,且AB=BC=BF=2,DE=CF=2,所以∠CBF=90°.取BF中点G,连MG,NG,由M,N分别是AF,BC中点,可得:NG∥CF,MG ∥EF,所以平面MNG∥平面CDEF,所以MN∥平面CDEF.(2)解:作AH⊥DE于H,由于三棱柱ADE BCF为直三棱柱,所以AH⊥平面CDEF,且AH=,所以=S CDEF·AH=×2×2×=.巩固提高B一、选择题1. 水平放置的△ABC,用斜二测画法作出的直观图是如图所示的△A′B′C′,其中O′A′=O′B′=2,O′C′=,则△ABC绕AB所在直线旋转一周后形成的几何体的表面积为( B )(A)8π (B)16π(C)(8+3)π(D)(16+12)π解析:根据斜二测画法可知,AB=4,OC=2,可知△ABC为等边三角形.△ABC绕AB所在直线旋转一周后形成的几何体是两个对着底的圆锥,其两个侧面积就是这个几何体的表面积,表面积为S=2×π×2×4=16π.故选B.2.(2018·全国Ⅲ卷) 中国古建筑借助榫卯将木构件连接起来,构件的凸出部分叫榫头,凹进部分叫卯眼,图中木构件右边的小长方体是榫头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是( A )解析:由题意可知带卯眼的木构件的直观图如图所示,由直观图可知其俯视图应选A.3.三棱锥P-ABC三条侧棱两两垂直,三个侧面面积分别为,,,则该三棱锥的外接球的表面积为( B )(A)4π(B)6π(C)8π(D)10π解析:三棱锥P-ABC的三条侧棱PA,PB,PC两两互相垂直,它的外接球就是它扩展为长方体的外接球,设PA=a,PB=b,PC=c,则ab=,bc=,ca=,所以①×②×③÷②2得=,即a2=2,所以a=,同理b=1,c=.则长方体的体对角线的长为=.所以球的直径是,半径长R=,则球的表面积S=4πR2=6π.故选B.4.《九章算术》中,将底面是直角三角形的直三棱柱称之为“堑堵”,已知某“堑堵”的三视图如图所示,俯视图中虚线平分矩形的面积,则该“堑堵”的侧面积为( C )(A)2 (B)4+2(C)4+4(D)4+6解析:由三视图知几何体为一三棱柱,底面为一等腰直角三角形,高为1,则底面三角形腰长为,底边长为2,三棱柱高为2,所以侧面积为2×2+2××2=4+4.故选C.5.如图是一个底面半径为1的圆柱被平面截开所得的几何体,截面与底面所成的角为45°,过圆柱的轴的平面截该几何体所得的四边形ABB′A′为矩形,若沿AA′将其侧面剪开,其侧面展开图形状大致为( A )解析:截面方程为x2+=1,截面在轴截面A′ABB′上的投影为圆x2+y2=1,沿AA′剪开,其展开图不可能是B,C,D.故选A.6.正方体ABCD-A1B1C1D1的棱长为1,点E,F分别是棱D1C1,B1C1的中点,过E,F作一平面α,使得平面α∥平面AB1D1,则平面α截正方体的表面所得平面图形为( D )(A)三角形(B)四边形(C)五边形(D)六边形解析:由题意,在正方体ABCD-A1B1C1D1中,E,F分别为棱D1C1,B1C1的中点,取BB1,AB,AD,DD1的中点G,H,M,N,可得正六边形EFGHMN,此时平面AB1D1∥平面EFGHMN.故选D.7.祖暅是南北朝时期的伟大科学家,5世纪末提出体积计算原理,即祖暅原理:“幂势既同,则积不容异”.意思是:夹在两个平行平面之间的两个几何体,被平行于这两个平面的任何一个平面所截,如果截面面积都相等,那么这两个几何体的体积一定相等.现有以下四个几何体:图①是从圆柱中挖出一个圆锥所得的几何体;图②、图③、图④分别是圆锥、圆台和半球,则满足祖暅原理的两个几何体为( D )(A)①② (B)①③ (C)②④ (D)①④解析:设截面与底面的距离为h,则①中截面内圆半径为h,则截面圆环的面积为π(R2-h2);②中截面圆的半径为R-h,则截面圆的面积为π(R-h)2;③中截面圆的半径为R-,则截面圆的面积为π(R-)2;④中截面圆的半径为,则截面圆的面积为π(R2-h2),所以①④中截面的面积相等.故选D.8.(2018·宁波5月模拟)已知x,y均为非负实数,且x+y≤1,则4x2+4y2+(1-x-y)2的取值范围为( A )(A) [,4］(B)[1,4] (C)[2,4] (D)[2,9]解析:因为x,y≥0,所以≤x2+y2≤(x+y)2.令t=x+y,则0≤t≤1.4x2+4y2+(1-x-y)2≤4t2+(1-t)2=5t2-2t+1≤4.当xy=0且t=1,即x=0,y=1或x=1,y=0时取等号;另一方面,4x2+4y2+(1-x-y)2≥2t2+(1-t)2=3t2-2t+1≥.当x=y=时取等号.所以4x2+4y2+(1-x-y)2∈[,4］.故选A.二、填空题9.(2017·温州模拟)如图,一个简单几何体三视图的正视图与侧视图,都是边长为1的正三角形,其俯视图的轮廓为正方形,则该几何体的体积是,表面积是.解析:由正视图和侧视图为等边三角形可得此几何体为锥体,由俯视图为四边形可得此几何体为四棱锥,因为正视图为边长为1的正三角形,所以正三角形的高,也就是棱锥的高为,俯视图的边长为1,所以正四棱锥的体积为V=×1×1×=,表面积为S=1+4××1×1=3.答案: 310.在四面体P-ABC中,PA=PB=PC=BC=1,则该四面体体积的最大值为.解析:由于平面PBC是边长为1的正三角形,=,底面面积固定,要使体积最大,只需高最大,故当PA⊥平面PBC时体积最大,V=××12×1=.答案:11.已知圆锥的母线长为5 cm,侧面积为15π cm2,则此圆锥的体积为cm3.解析:已知圆锥的母线长为5 cm,侧面积为15π cm2,所以圆锥的底面周长为6π cm,底面半径是 3 cm,圆锥的高是 4 cm,此圆锥的体积为×9π×4=12π (cm3).答案:12π12.(2018·全国Ⅱ卷)已知圆锥的顶点为S,母线SA,SB所成角的余弦值为,SA与圆锥底面所成角为45°,若△SAB的面积为5,则该圆锥的侧面积为.解析:如图,因为SA与底面成45°角,所以△SAO为等腰直角三角形.设OA=r,则SO=r,SA=SB=r.在△SAB中,cos∠ASB=,所以sin∠ASB=,所以S△SAB=SA·SB·sin∠ASB=(r)2·=5,解得r=2,所以SA=r=4,即母线长l=4,所以S圆锥侧=πr·l=π×2×4=40π.答案:40π13.有三个球,第一个球内切于正方体,第二个球与这个正方体的各条棱相切,第三个球过这个正方体的各个顶点.则这三个球的半径之比为.解析:设正方体的棱长为a,则正方体的内切球直径为a,则半径为.第二个球与正方体的各条棱相切,由截面知球直径为a,则半径为 a.正方体的外接球,过正方体的各个顶点,其直径为a,则半径为 a.可得三个球的半径之比为1∶∶.答案:1∶∶14.若圆锥的底面直径和高都与一个球的直径相等,圆锥、球的表面积分别记为S1,S2,则的值是.解析:设球的直径为2R,由题意可知,S1=πR2+πR×=(+1)πR2,S2=4πR2,据此可得=.答案:15. 如图,在棱长为1的正方体ABCD A 1B1C1D1中,点P是线段BD1上的动点.当△PAC在平面DC1,BC1,AC上的正投影都为三角形时,将它们的面积分别记为S1,S2,S3.(1)S1S2(填“>”“=”或“<”);(2)S1+S2+S3的最大值为.解析:如图,因=,=,故PO=QN,同理可得RM=PO,所以RM=QN,则S1=S2,特别地当点P与点D1重合时,三个投影面的面积都最大,都是,所以S1+S2+S3=,即最大值是.答案:=三、解答题16. 如图四棱锥P-ABCD中,底面ABCD是平行四边形,∠ACB=90°,PA⊥平面ABCD,PA=BC=1,AB=,F是BC的中点.(1)求证:DA⊥平面PAC;(2)点G为线段PD的中点,证明CG∥平面PAF;(3)求三棱锥A-CDG的体积.(1)证明:因为四边形ABCD是平行四边形,∠ACB=∠DAC=90°,因为PA⊥平面ABCD,所以PA⊥DA,又AC⊥DA,AC∩PA=A,所以DA⊥平面PAC.(2)证明:PD的中点为G,在平面PAD内作GH⊥PA于H,则GH平行且等于AD,连接FH,则四边形FCGH为平行四边形,所以GC∥FH,因为FH⊂平面PAF,CG⊄平面PAF,所以CG∥平面PAF.(3)解:设S为AD的中点,连结GS,则GS平行且等于PA=, 因为PA⊥平面ABCD,所以GS⊥平面ABCD,所以==S△ACD GS=.。

2020届高三数学精准培优专练十三三视图与体积、表面积(理科)学生版

2020届高三例1：中国古建筑借助榫卯将木构件连接起来，构件的凸出部分叫榫头，凹进部分叫卯眼，图中木构件右边的小长方体是榫头．若如图摆放的木构件与某一带卯眼的木构件咬合成长方体，则咬合时带卯眼的木构件的俯视图可以是（）A．B．C．D．例2：如图，在长方体1111ABCD A B C D-中，点P是棱CD上一点，则三棱锥11P A B A-的侧视图是（）A．B．C．D．例3：如图，网格纸的各小格都是正方形，粗实线画出的是一个几何体的三视图，则这个几何体是（）培优点十三三视图与体积、表面积一、根据几何体的结构特征确认其三视图二、根据三视图还原几何体的直观图A．三棱锥B．三棱柱C．四棱锥D．四棱柱例4：若某几何体的三视图如图所示，则这个几何体的直观图可以是（）A．B．C．D．例5：如图是一个空间几何体的正视图和俯视图，则它的侧视图为（）A．B．C．D．例6：一个几何体的三视图中，正视图和侧视图如图所示，则俯视图不可以为（）A．B．C．D．三、已知几何体的三视图中某两个视图，确定另外一种视图例7：如图所示，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则该几何体的表面积为（）A．5π18+B．6π18+C．8π6+D．10π6+例8：如图所示，某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径．若该几何体的体积是28π3，则它的表面积是（）A．17πB．18πC．20πD．28π例9：某几何体的三视图如图所示(单位：cm)，则该几何体的体积(单位：3cm)是（）A．π12+B．π32+C．3π12+D．3π32+例10：如图所示，已知多面体ABCDEFG中，AB、AC、AD两两互相垂直，平面ABC∥平面DEFG，平面BEF∥平面ADGC，2AB AD DG===，1AC EF==，则该多面体的体积为________．四、根据几何体的三视图计算表面积五、根据几何体的三视图计算体积一、选择题1．如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则此几何体的各个面中是直角三角形的个数为（）A．1B．2C．3D．42．某几何体的三视图如图所示，网格纸上小正方形的边长为1，则该几何体的表面积（）A．5πB．6πC．6π2+D．5π2+3．已知一个几何体的三视图如图所示，则其体积为（）A．12πB．16πC．32π3D．403π4．某四棱锥的三视图如图所示，则该四棱锥的体积为（）对点增分集训A ．23B ．43C ．83D 5．我国古代《九章算术》将上下两个平行平面为矩形的六面体称为刍童．如图是一个刍童的三视图，其中正视图及侧视图均为等腰梯形，两底的长分别为2和6，高为2，则该刍童的体积为（）A ．1003B ．1043C ．27D ．186．如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的各棱中，最长的棱的长度为（）A ．B ．6C ．D ．47．在正方体1111ABCD A B C D 中，E 、F 、G 分别为棱CD 、1CC 、11A B 的中点，用过点E 、F 、G 的平面截正方体，则位于截面以下部分的几何体的侧视图为（）A ．B ．C ．D ．8．如图所示的网格是由边长为1的小正方形构成，粗线画出的是某几何体的三视图，则该几何体的体积为（）A ．40B ．103C ．163D ．8039．某几何体的三视图如图所示，则该几何体的外接球的体积是（）A．π3B．π2C ．3π D．10．某空间几何体的三视图如图所示，则该几何体的外接球半径为（）ABCD．11．如图，网格纸上小正方形的边长为1，粗线画出的是某四棱锥的三视图，则该四棱锥的体积为（）A ．6B ．8C ．D ．12．在棱长为1的正方体1111ABCD A B C D -中，E 、F 分别为线段CD 和11A B 上的动点，且满足1CE A F =，则四边形1D FBE 所围成的图形（如图所示阴影部分）分别在该正方体有公共顶点的三个面上的正投影的面积之和（）A ．有最小值32B ．有最大值52C ．为定值3D ．为定值2二、填空题13．某几何体的三视图如图所示，网格纸上小正方形的边长为1，则该几何体的表面积是．14．《九章算术》是我国古代数学名著，在《九章算术》中将底面为矩形且有一侧棱垂直于底面的四棱锥称为“阳马”．若某“阳马”的三视图如图所示，其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形，则该“阳马”的表面积为．15．已知圆锥的高为3 体积等于．16．已知点P 、A 、B 、C 是半径为2的球面上的点，2PA PB PC ===，90ABC ∠=︒，点B 在AC 上的射影为D ，则三棱锥P ABD -体积的最大值是．例1：【答案】A【解析】由题意可知带卯眼的木构件的直观图如图所示，由直观图可知其俯视图，应选A．例2：【答案】D【解析】在长方体1111ABCD A B C D-中，从左侧看三棱锥11P A B A-，1B、1A、A的射影分别是1C、1D、D，1AB的射影为1C D，且为实线，1PA的射影为1PD，且为虚线．故选D．例3：【答案】B【解析】由题三视图得直观图如图所示，为三棱柱．故选B．例4：【答案】D【解析】由三视图知该几何体的上半部分是一个三棱柱，下半部分是一个四棱柱．故选D．例5：【答案】A【解析】由正视图和俯视图可知，该几何体是一个圆柱挖去一个圆锥构成的，结合正视图的宽及俯视图的直径知其侧视图应为A．故选A．例6：【答案】C【解析】A中，该几何体是直三棱柱，所以A有可能；B中，该几何体是直四棱柱，所以B有可能；C中，由题干中正视图的中间为虚线知，C不可能；D中，该几何体是直四棱柱，所以D有可能．综上，故选C．例7：【答案】C【解析】由三视图可知该几何体是由一个半圆柱和两个半球构成的，培优点十三三视图与体积、表面积答案故该几何体的表面积为2211124π12π1232π138π6222⨯⨯⨯+⨯⨯⨯+⨯+⨯⨯⨯=+．故选C ．例8：【答案】A【解析】由几何体的三视图可知，该几何体是一个球体去掉上半球的14，得到的几何体如图．设球的半径为R ，则3341428πππ3833R R -⨯=，解得2R =．因此它的表面积为22734ππ17π84R R ⨯+=．故选A ．例9：【答案】A【解析】由几何体的三视图可知，该几何体是一个底面半径为1，高为3的圆锥的一半与一个底面为直角边的等腰直角三角形，高为3的三棱锥的组合体，∴该几何体的体积21111ππ323221331⨯⨯⨯⨯+=+．故选A ．例10：【答案】4【解析】法一：(分割法)因为几何体有两对相对面互相平行，如图所示，过点C 作CH DG ⊥于H ，连接EH ，即把多面体分割成一个直三棱柱DEH ABC -和一个斜三棱柱BEF CHG -．由题意，知三棱柱DEH ABC -的体积11(2221)2DEH V S AD =⨯⨯⨯=⨯=△，三棱柱BEF CHG -的体积21(2221)2BEF V S DE =⨯⨯⨯=⨯=△，故所求多面体ABCDEFG 的体积为12224V V V =+=+=．法二：(补形法)因为几何体有两对相对面互相平行，如图所示，将多面体补成棱长为2的正方体，显然所求多面体的体积即该正方体体积的一半．又正方体ABHI DEKG -的体积328V '==，故所求多面体ABCDEFG 的体积为118422V V '==⨯=．一、选择题 1．【答案】C【解析】三视图还原为如图所示三棱锥A BCD -，由正方体的性质得ABC △、BCD △、ACD △为直角三角形，ABD △为正三角形，故选C ．2．【答案】D【解析】由三视图可知，该几何体为两个半圆柱构成，其表面积为22π1π12π11215π2⨯⨯+⨯⨯+⨯⨯+⨯=+，故选D ． 3．【答案】D【解析】由三视图可知，该几何体为圆柱挖去其16后的剩余部分，该圆柱的底面半径为2，高为4，故其体积为圆柱体积的56，25540ππ16π663V R h ==⨯=．故选D ．4．【答案】C【解析】该三视图还原成直观图后的几何体是如图所示的四棱锥A BCDE -，CBA △和ACD △是两个全等的直角三角形，且2AC CD BC ===，故几何体的体积为1822233⨯⨯⨯=，故选C ．5．【答案】B【解析】由题意几何体原图为正四棱台，底面的边长分别为2和6，高为2，所以几何体体积1104(436233V =++⨯=．故选B ． 6．【答案】B【解析】三视图还原成如图所示的几何体，三棱锥S ABC -，则4SB BC ==，SC =AC AB ==6SA =．故选B ．7．【答案】C【解析】过点E ，F ，G 截正方体的平面为如图所示的平面EFKGHI ，由图知位于截面以下部分的几何体的侧视图为C 选项，故选C ．8．【答案】D【解析】根据几何体三视图可得，该几何体是三棱柱BCE AGF -割去一个三棱锥A BCD -所得的几何体，如图所示，所以其体积为111180444(44)423223V =⨯⨯⨯-⨯⨯⨯⨯⨯=．故选D ．9．【答案】B【解析】根据几何体的三视图知，该几何体是由一个正方体切去正方体的一角得到的，故该几何体的外接球为正方体的外接球，所以球的半径22r ==，则34π3V =⋅⋅=⎝⎭B ． 10．【答案】C【解析】由三视图可知三棱锥的直观图如图，由三视图可知底面三角形是边长为2，顶角120︒的三角形，所以其外接圆半径结合正弦定理可得，224sin30r ==︒，由侧面为两等腰直角三角形，可确定出外接圆圆心，利用球的几何性质可确定出球心，且球心到底面的距离1d =，所以球半径R ==，故选C ．11．【答案】B【解析】由三视图可得四棱锥为如图所示的长方体1111ABCD A B C D -中的四棱锥11C DEE D -，其中在长方体1111ABCD A B C D -中，4AB =，2AD =，13AA =，点E 、1E 分别为AB 、11A B 的中点，由题意得CE DE ==CE DE ⊥，又1CE EE ⊥，所以CE ⊥平面11DEE D ，即线段CE 即为四棱锥11C DEE D -的高，所以四棱锥11C DEE D -的体积1111(3833DEE D V S CE =⋅⋅=⨯⨯⨯=．故选B ．12．【答案】D【解析】依题意，设四边形1D FBE 的四个顶点在后面、上面、左面的投影点分别为'D 、F '、B '、E '，则四边形1D FBE 在上面、后面、左面的投影分别如下图，所以在后面的投影的面积为1111S =⨯=，在上面的投影面积211S D E DE DE ''=⨯=⨯=，在左面的投影面积311S B E CE CE ''=⨯=⨯=，所以四边形1D FBE 所围成的图形分别在该正方体有公共顶点的三个面上的正投影的面积之和为123112S S S S DE CE CD =++=++=+=．故选D ．二、填空题13．【答案】64+【解析】由三视图可知，该几何体的直观图为如图所示的四棱柱，则11111(24)4122ABCD A B C D S S ==⨯+⨯=，11114416BCC B CC D D S S ==⨯=，11428ABB A S =⨯=，114AA D D S =⨯=所以该四棱柱的表面积为2432864S =+++=+14．【答案】2+【解析】由三视图可得该“阳马”的底面是边长为1的正方形，且高为1，故该“阳马”的表面积为11211212122+⨯⨯⨯+⨯=15．【答案】32π3【解析】设该圆锥的外接球的半径为R ，依题意得，222()3R R +-=，解得2R =，故所求球的体积334432ππ2π333V R ==⨯=．16．【答案】8【解析】设点P 在平面ABC 上的射影为G ，如图，由2PA PB PC ===，90ABC ∠=︒知，点P 在平面ABC 上的射影G 为ABC △的外心，即AC 的中点，设球的球心为O ，连接PG ，则O 在PG 的延长线上，连接OB 、BG ，设PG h =，则2OG h =-，所以2222OB OG PB PG -=-，即22()424h h --=-，解得1h =，则AG CG ==设AD x =，则GD x AG x =-=BG =所以BD ==12ABD S AD BD ==⋅△ 令43()f x x =-+，则32()4f x x '=-+，由()0f x '=，得0x =或2x =，易知当2x =时，函数()f x 取得最大值24316，所以max 1()248ABD S =⨯=△．又1PG =，所以三棱锥P ABD -体积的最大值为113=．。

2019高考真题名校模拟(文数) 空间几何体的三视图、表面积和体积(含答案)

8.1 空间几何体的三视图、表面积和体积五年高考A 组统一命题·课标卷题组考点一几何体的直观图与三视图1．（2018课标全国1,9,5分）某圆柱的高为2，底面周长为16，其三视图如图，圆柱表面上的点M 在正视图上的对应点为A ．圆柱表面上的点N 在左视图上的对应点为B ，则在此圆柱侧面上，从M 到N 的路径中，最短路径的长度为 ( )172.A 52.B 3.C 2.D2．（2018课标全国111.3，5分）中国古建筑借助榫卯将木构件连接起来．构件的凸出部分叫榫头，凹进部分叫卯眼，图中木构件右边的小长方体是榫头，若如图摆放的木构件与某一带卯眼的木构件咬合成长方体，则咬合时带卯眼的木构件的俯视图可以是 ( )3．（2014课标1,8,5分．0.795）如图，网格纸的各小格都是正方形，粗实线画出的是一个几何体的三视图，则这个几何体是( )A ．三棱锥B ．三棱柱C ．四梭锥D ．四棱柱考点二几何体的体积1．（2018课标全国1,10，5分）在长方体1111D C B A ABCD -中，1,2AC BC AB ==与平面C C BB 11所成的角为,30则该长方体的体积为( ) 8.A 26.B 28.C 38.D2．（2018课标全国III ．12，5分）设A ，B ，C ．D 是同一个半径为4的球的球面上四点，△ABC 为等边三角形且其面积为,39则三棱锥D-ABC 体积的最大值为( )312.A 318.B 324.C 354.D3．（2017课标全国11.6，5分）如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，该几何体由一平面将一圆柱截去一部分后所得，则该几何体的体积为 ( )π90.A π63.B π42.C π36.D4．（2014课标Ⅱ．7,5分．0.495）正三棱柱111C B A ABC -的底面边长为2．侧棱长为D ,3为BC 中点，则三棱锥11DC B A -的体积为（ )3.A 23.B 1.C 23.D 5．（2015课标I ，6，5分，0.451）《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题：“今有委米依垣内角，下周八尺，高五尺，问：积及为米几何？”其意思为：“在屋内墙角处堆放米（如图，米堆为一个圆锥的四分之一），米堆底部的弧长为8尺，米堆的高为5尺，问米堆的体积和堆放的米各为多少？”已知1斛米的体积约为1.62立方尺，圆周率约为3．估算出堆放的米约有 ( )14.A 斛 22.B 斛 36.C 斛 66.D 斛6．（2015课标II ，6,5分，0.426）一个正方体被一个平面截去一部分后，剩余部分的三视图如下图，则截去部分体积与剩余部分体积的比值为 ( )81.A 71.B 61.C 51.D 7．（2017课标全国|II ．9，5分）已知圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的体积为( )π.A 43.πB 2.πC 4.πD 8．(2018课标全国II ，16，5分)已知圆锥的顶点为S ．母线SA ，SB 互相垂直．SA 与圆锥底面所成角为.30 若△SAB 的面积为8．则该圆锥的体积为9．（2016课标全国1,18，12分）如图，已知正三棱锥P-ABC 的侧面是直角三角形，PA=6．顶点P 在平面ABC 内的正投影为点D ，D 在平面PAB 内的正投影为点E ，连接PE 并延长交AB 于点C ．(1)证明：C 是AB 的中点；(2)在图中作出点E 在平面PAC 内的正投影F(说明作法及理由)，并求四面体PDEF 的体积，考点三几何体的表面积1．（2018课标全国I ．5，5分）已知圆柱的上、下底面的中心分别为,,21O O 过直线21O O 的平面截该圆柱所得的截面是面积为8的正方形，则该圆柱的表面积为( )π212.A π12.B π28.C π10.D2．（2016课标全国II ．4，5分）体积为8的正方体的顶点都在同一球面上，则该球的表面积为 ( )π12.A π332.B π8.C π4.D 3．（2016课标全国I ．7,5分）如图，某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径．若该几何体的体积是,328π则它的表面积是( )π17.A π18.B π20.C π28.D4．（2016课标全国Ⅲ，10,5分）如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的表面积为 ( )53618.+A 51854.+B 90.C 81.D5．（2014大纲全国，10，5分）正四棱锥的顶点都在同一球面上．若该棱锥的高为4．底面边长为2，则该球的表面积为( )481.πA π16.B π9.C 427.πD6．（2015课标II ．10,5分．0.459）已知A ，B 是球0的球面上两点，C AOB ,90=∠为该球面上的动点，若三棱锥O-ABC 体积的最大值为36．则球O 的表面积为 ( )π36.A π64.B π144.C π256.D7．（2015课标I ，11，5分．0.629）圆柱被一个平面截去一部分后与半球（半径为r ）组成一个几何体，该几何体三视图中的正视图和俯视图如图所示．若该几何体的表面积为,2016π+则=r ( )1.A2.B 4.C 8.D8．（2017课标全国II ．15，5分）长方体的长，宽，高分别为3，2，1，其顶点都在球O 的球面上，则球O 的表面积为______．9．（2017课标全国I ．16,5分）已知三棱锥S-ABC 的所有顶点都在球O 的球面上，SC 是球0的直径．若平面⊥SCA 平面,,,BC SB AC SA SCB ==三棱锥S-ABC 的体积为9．则球0的表面积为_________B 组自主命题·省（区、市）卷题组考点一几何体的直观图与三视图1．（2018北京，6，5分）某四棱锥的三视图如图所示，在此四棱锥的侧面中，直角三角形的个数为 ( )1.A2.B3.C4.D2．（2016天津．3，5分）将一个长方体沿相邻三个面的对角线截去一个棱锥，得到的几何体的正视图与俯视图如图所示，则该几何体的侧（左）视图为 ( )3．（2015北京，7,5分）某四棱锥的三视图如图所示，该四棱锥最长棱的棱长为 ( )1.A2.C2.D.B34．（2014湖南，8,5分）一块石材表示的几何体的三视图如图所示，将该石材切削、打磨，加工成球，则能得到的最大球的半径等于 ( )1.A2.B3.C4.D5．（2014湖北，7，5分）在如图所示的空间直角坐标系O-xyz中，一个四面体的顶点坐标分别是(0，0，2)，(2，2，0)，(1，2，1)，(2，2，2).给出编号为①、②、③、④的四个图，则该四面体的正视图和俯视图分别为 ( )A．①和② B．③和① C．④和③ D．④和②考点二几何体的体积1.(2018浙江．3,4分）某几何体的三视图如图所示（单位：cm ），则该几核体的体积（单位：)3cm 是( )2.A 4.B 6.C 8.D2.(2017北京,6,5分）某三棱锥的三视图如图所示，则该三棱锥的体积为（）60.A 30.B 20.C 10.D3．（2017浙江．3,4分）某几何体的三视图如图所示（单位：cm ），则该几何体的体积（单位：)3cm 是( )12.+πA 32.+πB 123.+πC 323.+πD 4．（2015重庆，5，5分）某几何体的三视图如图所示，则该几何体的体积为 ( )π231.+A 613.πB 37.πC 25.πD 5．（2016山东．5,5分）一个由半球和四棱锥组成的几何体，其三视图如图所示．则该几何体的体积为 ( )π3231.+A π3231.+B π6231.+C π621.+D 6．（2014辽宁，7，5分）某几何体三视图如图所示，则该几何体的体积为 ( )48.πA 28.πB π-8.C π28.-D7．（2014四川，4,5分）某三棱锥的侧视图、俯视图如图所示，则该三棱锥的体积是 ( ) （锥体体积公式：,31Sh V =其中s 为底面面积，h 为高）3.A 2.B 3.C 1.D8．（2018江苏．10,5分）如图所示，正方体的棱长为2，以其所有面的中心为顶点的多面体的体积为9．（2018天津．11,5分）如图，已知正方体1]11D C B A ABCD -的棱长为1．则四棱锥D D BB A l 11- 的体积为___________10.（2017山东．13，5分）由一个长方体和两个41圆柱体构成的几何体的三视图如下图，则该几何体的体积为________11．（2017天津．11，5分）已知一个正方体的所有顶点在一个球面上，若这个正方体的表面积为18．则这个球的体积为___________考点三几何体的表面积1．（2014福建，3,5分）以边长为1的正方形的一边所在直线为旋转轴，将该正方形旋转一周所得圆柱的侧面积等于( )π2.A π.B 2.C 1.D2．（2015安徽，9，5分）一个四面体的三视图如图所示，则该四面体的表面积是 ( )31.+A 221.+B 32.+C 22.D3．（2015陕西，5，5分）一个几何体的三视图如图所示，则该几何体的表面积为 ( )π3.A π4.B 42+πC 43.+πD突破方法方法1 空间几何体表面积与体积的求解方法例1（2014重庆．7，5分）某几何体的三视图如图所示，则该几何体的体积为 ( )12.A 18.B 24.C 30.D1-1 某几何体的三视图如图所示，则该几何体的表面稠等于( )228.+A 2211.+B 2214.+C 15.D1-2 如图所示，在半径为R 的半球内有一内接圆柱，则这个圆柱的体积的最大值是_________方法2 与球有关的切、接问题的求解方法例2（2016课标全国m ．11，5分）在封闭的直三棱柱111C B A ABC -内有一个体积为y 的球，若,8,6,==⊥BC AB BC AB ,31=M 则y 的最大值是( )π4.A 29.πB π6.C 332.πD 2-1 已知直三棱柱11C B A ABC l -的6个顶点都在球O 的球面上．且,12,,4,3=⊥==l AA AC AB AC AB 则球0的表面积是2-2 （2017江苏．6，5分）如图，在圆柱21O O 内有一个球0．该球与圆柱的上、下底面及母线均相切．记圆柱21O O 的体积为,1V 球0的体积为,2V 则2V V l 的值是________三年模拟A 组2016-2018年高考模拟·基础题组考点一几何体的直观图与三视图1．（2018黑龙江佳木斯一中第七次调研）如图所示，网格纸上每个小方格都是边长为1的正方形，粗线画出的是一个几何体的三视图，记该几何体的各棱长度构成的集合为A ，则 ( )A A ∈3. AB ∈3. AC ∈32. AD ∈22.2．（2017内蒙古百校联盟质监卷）已知三棱锥A-BCD 的四个顶点在空间直角坐标系O-xyz 中的坐标分别为 ,2(),2,0,2(B A ),2,2,0(),2,1C ),0,2,1(D 以xOy 平面为投影面，画该三棱锥的俯视图，得到的俯视图可以为 ( )3．（2017黑龙江佳木斯一中三模）一个正方体截去两个角后所得的几何体的主视图，左视图如图所示，则其俯视图为( )4．（2017陕西西安长安一中4月模拟）如图所示的是某几何体的三视图，正视图是等腰直角三角形，侧视图是直角三角形，俯视图是直角梯形，则在几何体中，异面直线PB 与CD 所成角的正切值是 ( )1.A2.B 22.C 21.D 考点二几何体的体积1．（2018东北三省三校二模）如图所示，一个三棱锥的三视图是三个直角三角形，则该三棱锥的体积为( )3.A4.B 6.C 8.D2．（2018甘肃第一次诊断）某几何体挖去两个半球体后的三视图如图所示，若剩余几何体的体积为,32π则a 的值为( )1.A2.B 22.C 32.D3．（2018内蒙古包头一模）某多面体的三视图如图所示，则该多面体的体积为 ( )38.A 332.B 316.C 328.D 4．（2017新疆乌鲁木齐三模）某几何体的三视图如图所示，则该几何体的体积为 ( )221.π+A 21.π+B π+1.C π+2.D 5．（2017陕西咸阳三模）某几何体的三视图如图所示，则这个几何体的体积为 ( )3216.πA 348.πB 3416.πC 316.πD 6．（2017辽宁部分重点中学协作体模拟）棱长为1的正方体截去一部分之后余下的几何体的三视图如图所示，则余下几何体体积的最小值为 ( )65.A 21.B 32.C 31.D 考点三几何体的表面积1．（2018辽宁辽阳一模）如图是某几何体的三视图，则该几何体的表面积为 ( )π848.+A π1648.+B π1696.+C π896.+D2．（2018黑龙江齐齐哈尔一模）如图，网格纸上小正方形的边长为 1，图中画出的是某几何体的三视图，则该几何体的表面积为 ( )18261312.++A 1828139.++B 1826139.++C 1226139.++D3．（2018重庆4月调研（二诊））某几何体的三视图如图所示，其正视图为等腰梯形，则该几何体的表面积是 ( )18.A 388.+B 24.C 5612.+D4．（2017吉林延边高考仿真考试）已知一个几何体的三视图如图所示，则该几何体的表面积为 ( )624.+A 824.+B 1224.+C 1024.+D5．（2017陕西咸阳二模）一个几何体的三视图如图所示，则这个几何体的表面积是 ( )π3.A π4.B π5.C 37.πD 6．（2016黑龙江佳木斯名校联考）在三棱锥P-ABC 中．PA ⊥平面,3,1,,===⊥PA BC AB BC AB ABC 则该三棱锥外接球的表面积为( )π5.A π2.B π20.C π4.DB 组2016-2018年高考模拟·综合题组选择题（每题5分，共55分）1．（2018东北三省三校一模）某几何体的三视图如图所示，且该几何体的体积是，23则正视图中的x 的值是 ( )2.A 29.B 23.C 3.D 2．（2018辽宁辽南协作校一模）某几何体的正视图和侧视图如图(1)所示，它的俯视图的直观图是 ,ABC ∆如图(2)所示，其中,3,20===OC B OA 则该几何体的体积为 ( )38.A 312.B 318.C 324.D3．（2018内蒙古呼和浩特第一次质量普查）某多面体的三视图如图所示，其中正视图和侧视图都是由正方形和等腰直角三角形组成，正方形的边长为2，俯视图为等腰直角三角形．则该多面体的各个面中，面积最大的面的面积为 ( )32.A 6.B 26.C 12.D4．（2018吉林长春质量监测（二））如图，网格纸上小正方形的边长为1．粗线条画出的是一个三棱锥的三视图，则该三棱锥的体积为 ( )34.A 32.B 2.C 23.D 5．（2017辽宁大连双基测试）在空间直角坐标系O-xyz 中，一个四面体的顶点坐标分别是(1，0，2)，(1，2，0)，(1，2，1)，(0，2，2)，若正视图以yoz 平面为投射面，则该四面体侧视图面积为( ) 21.A 1.B2.C 4.D 6．（2017宁夏石嘴山三中三模）如图1所示的是一个棱长为2的正方体被削去一个角后所得到的几何体的直观图，其中=1DD ,1若此几何体的俯视图如图2所示，则可以作为该几何体正视图的是( )7．（2017重庆巴蜀中学三诊）如图，某几何体的三视图都是直角三角形，若几何体的最长棱的长为2，则该几何体的外接球的体积是 ( )π6.A π34.B π4.C π6.D 8．（2017海南海口4月调研）已知一个几何体的三视图如图所示，则该几何体的体积为 ( )316.A 324.B 3380.C 326.D9．（2017陕西黄陵中学考前模拟（一））将一张边长为12,m 的正方形纸片按如图(1)所示将阴影部分的四个全等的等腰司角形裁去，余下部分沿虚线折叠并拼成一个有底的正四棱锥，如图(2)放置，如果正四棱锥的主视图是正三角形，如图(3)所示，则正四棱锥的体积是( )36332.cm A 36364.cm B 32332.cm C 32364.cm D 10.（2017甘肃天水一中三诊）某四面体的三视图如图所示，正视图，俯视图都是腰长为2的等腰直角三角形，侧视图是边长为2的正方形，则此四面体的四个面中面积最大的面的面积为 ( )22.A 32.B 4.C 62.D11.（2017甘肃兰州实战模拟）某几何体的三视图如图所示，则下列说法正确的是 ( ) ①该几何体的体积为;61②该几何体为正三棱锥； ③该几何体的表面积为;323+④该几何体外接球的表面积为.3π①②③.A ①②④.B ①③.C ④ ②③④.D答案。

三视图及体积表面积练习题补习

三视图及体积表面积练习题1、若某空间几何体的三视图如图所示，则该几何体的体积是[ ]（A ）2（B ）1 （C ）23（D ）132、一个几何体的三视图如图，该几何体的表面积是（A ）372 （B ）360 （C ）292 （D ）2803若某几何体的三视图（单位：cm ）如图所示，则此几何体的体积是（A ）3523cm 3 （B ）3203cm 3 （C ）2243cm 3（D ）1603cm 3 4.、个长方体去掉一个小长方体，所得几何体的正（主）视图与侧（左）视图分别如右图所示，则该集合体的俯视图为：C5、如图1，△ ABC 为三角形，AA '//BB ' //CC ' , CC ' ⊥平面ABC 且3AA '=32BB '=CC ' =AB,则多面体△ABC -A B C '''的正视图（也称主视图）是D6．若一个底面是正三角形的三棱柱的正视图如图所示,则其侧面积．．．等于 A ．3 B ．2 C ．23 D ．67、一个几何体的三视图如图，该几何体的表面积为A 、280B 、292C 、360D 、3728、图2中的三个直角三角形是一个体积为20cm 2的几何体的三视图，则h= cm9、已知四棱椎P ABCD -的底面是边长为 6 的正方形，侧棱PA ⊥底面ABCD ，且8PA =，则该四棱椎的体积是。

10.如图，网格纸的小正方形的边长是1，在其上用粗线画出了某多面体的三视图，则这个多面体最长的一条棱的长为 .11、一个几何体的三视图如图所示，则这个几何体的体积为。

12一个几何体的三视图如图所示，则这个几何体的体积为13.圆柱形容器内盛有高度为3cm 的水，若放入三个相同的珠（球的半么与圆柱的底面半径相同）后，水恰好淹没最上面的球（如图所示），则球的半径是____cm.14、图3中的三个直角三角形是一个体积为203cm 的几何体的三视图，则h = cm ．15、若一个底面是正三角形的三棱柱的正视图如图所示,则其表面积等于． 16一个棱锥的三视图如图，则该棱锥的全面积（单位：c 2m ）（A ）48+122 （B ）48+242 （C ）36+122 （D ）36+24217. 一空间几何体的三视图如图所示,则该几何体的体积为( ). A.223π+ B. 423π+ C. 2323π+ D. 2343π+18.某几何体的一条棱长为7，在该几何体的正视图中，这条棱的投影是长为6的线段，在该几何体的侧视图与俯视图中，这条棱的投影分别是长为a 和b 的线段，则a +b 的最大值为（） A ．22 B ．23C ．4D ．2519.右图是一个几何体的三视图，根据图中数据，可得该几何体的表面积是（） A ．9π B ．10π C ．11π D ．12π20.已知某个几何体的三视图如下，根据图中标出的尺寸（单位：cm ），可得这个几何体的体积是（）Ａ．34000cm 3Ｂ．38000cm 3Ｃ．32000cm Ｄ．34000cm21.将正三棱柱截去三个角（如图1所示A B C ，，分别是GHI △三边的中点）得到几何体如图2，则该几何体按图2所示方向的侧视图（或称左视图）为（）22.如图是一个几何体的三视图，若它的体积是33，则=a _______ 23. 设某几何体的三视图如下（尺寸的长度单位为m ），则该几何体的体积为_________m 3。

2019版高考数学(理科)总复习5.1三视图与几何体的体积、表面积练习.docx

2019 版高考数学（理科）总复习5.1三视图与几何体的体积、表面积命题角度 1 空间几何体三视图的识别与画法高考真题体验·对方向1.(2018全国Ⅲ·3)中国古建筑借助榫卯将木构件连接起来,构件的凸出部分叫榫头,凹进部分叫卯眼 ,图中木构件右边的小长方体是榫头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体 ,则咬合时带卯眼的木构件的俯视图可以是()答案 A解析根据三视图原则,从上往下看 ,看不见的线画虚线,则 A 正确 .2.(2018全国Ⅰ·7)某圆柱的高为2,底面周长为16,其三视图如右图.圆柱表面上的点M 在正视图上的对应点为A,圆柱表面上的点N 在左视图上的对应点为B,则在此圆柱侧面上,从 M 到 N的路径中 ,最短路径的长度为()A .2 B.2 C.3 D.2答案 B解析如图所示 ,易知N 为的中点 ,将圆柱的侧面沿母线MC 剪开 ,展平为矩形MCC'M' ,易知CN=CC'= 4,MC= 2,从 M 到 N 的路程中最短路径为MN.2019 版高考数学（理科）总复习在Rt△MCN 中 ,MN== 2.3.(2017北京·7)某四棱锥的三视图如图所示,则该四棱锥的最长棱的长度为()A.3B.2C.2D.2答案 B解析由题意可知 ,直观图为四棱锥A-BCDE (如图所示 ),最长的棱为正方体的体对角线AE== 2.故选 B .4.(2014全国Ⅰ·12)如图 ,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度为()A.6B.6C.4D.4答案 B解析如图所示的正方体ABCD-A 1B1C1D1的棱长为 4.取 B1B 的中点 G,即三棱锥 G-CC 1D 1为满足要2019 版高考数学（理科）总复习求的几何体 ,其中最长棱为D1G,D1G== 6.5.(2013全国Ⅰ·7)一个四面体的顶点在空间直角坐标系O-xyz中的坐标分别是(1,0,1),(1,1,0),(0,1,1),(0,0,0), 画该四面体三视图中的正视图时,以 zOx 平面为投影面,则得到的正视图可以为 ()答案 A解析如图所示 ,该四面体在空间直角坐标系O-xyz 的图象为下图 :则它在平面zOx 上的投影即正视图为,故选 A .新题演练提能·刷高分1.(2018河北衡水调研)某几何体的正视图与俯视图如图,则其侧视图可以为()答案 B解析由俯视图与正视图可知该几何体可以是一个三棱柱挖去一个圆柱,因此其侧视图为矩形内有一条虚线 ,虚线靠近矩形的左边部分,只有选项 B 符合题意 ,故选 B .2.(2018 河南濮阳一模 )如图 ,O1,O2为棱长为 a 的正方体的上、下底面中心,若正方体以 O1O2为轴顺时针旋转 ,则该正方体的所有正视图中最大面积是()2019 版高考数学（理科）总复习22A. aB. aC.a2D.2a2答案 B解析所有正视图中面积最大的是长为a,宽为 a 的矩形 ,面积为 a2,故选 B.3.(2018河北保定模拟)已知一几何体的正视图、侧视图如图所示 ,则该几何体的俯视图不可能是()答案 D解析由图可知 ,选项 D 对应的几何体为长方体与三棱柱的组合,其侧视图中间的线不可视,应为虚线 ,故选 D.4.(2018江西赣州十四县(市 )期中 )某几何体的三视图如图所示,则此几何体的各面中最大面的面积为 ()A.2B.2C.3D.2答案 B解析由三视图可得 ,该几何体为如图所示的三棱锥A1-BCD.结合三视图中的数据可得2S△BCD=×2 = 2,×2×2= 2,×2= 2,故此几何体的各面中最大面的面积为 2.选 B.5.(2018安徽合肥第二次质检)已知某三棱锥的三视图如图所示,则该三棱锥的所有棱中,最短的棱长为 ()A.2B.C.1D.2答案 C解析由三视图可知原几何体是图中的三棱锥P-ABC ,其中 C 为棱的中点 .从图中可以看出棱AC 最短 ,因为 AC= 1,所以最短的棱长为1,故选 C.6.(2018安徽合肥第二次质检)在正方体ABCD-A 1B1C1D1中 ,E 是棱 A1B1的中点 ,用过点A,C,E 的平面截正方体,则位于截面以下部分的几何体的侧(左 )视图为 ()答案 A解析如图所示 ,取 B1C1的中点 F,则 EF∥AC ,即平面 ACFE 亦即平面ACE 截正方体所得的截面,据此可得位于截面以下部分的几何体的侧(左 )视图如选项 A 所示 .7.(2018河南濮阳二模)已知三棱柱HIG-EFD 的底面为等边三角形,且侧棱垂直于底面,该三棱柱截去三个角 (如图①所示 ,A,B,C 分别是△GHI 三边的中点 )后得到的几何体如图②,则该几何体的侧视图为 ()答案 A解析因为平面DEHG ⊥平面EFD ,所以几何体的侧视图为直角梯形,且直角腰在侧视图的左侧,故选 A .命题角度 2 空间几何体的体积、表面积高考真题体验·对方向1.(2015 全国Ⅰ·6)《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角 ,下周八尺 ,高五尺 .问 : 积及为米几何 ?”其意思为 :“在屋内墙角处堆放米 (如图 ,米堆为一个圆锥的四分之一 ),米堆底部的弧长为 8 尺 ,米堆的高为 5 尺 ,问米堆的体积和堆放的米各为多少 ?”已知 1 斛米的体积约为 1.62 立方尺 ,圆周率约为3,估算出堆放的米约有()A .14 斛 B.22 斛 C.36 斛 D.66 斛答案 B解析设底面圆半径为R,米堆高为h.∵米堆底部弧长为8 尺 ,∴·2πR= 8,∴R=.2∴体积 V= ·πR h=×π××5.∴堆放的米约为≈22(斛).2.(2015山东·7)在梯形ABCD中,∠ABC= ,AD∥BC,BC= 2AD= 2AB= 2.将梯形ABCD绕AD所在的直线旋转一周而形成的曲面所围成的几何体的体积为()A. B.C. D.2π答案 C解析由题意可得旋转体为一个圆柱挖掉一个圆锥.22V 圆柱 = π×1 ×2= 2π,V 圆锥 =×π×1 ×1=.∴V 几何体 =V 圆柱 -V 圆锥 = 2π-.2019 版高考数学（理科）总复习3.(2018全国Ⅱ·16)已知圆锥的顶点为S,母线 SA,SB 所成角的余弦值为,SA 与圆锥底面所成角为 45° .若△SAB 的面积为 5.则该圆锥的侧面积为.答案 40π解析设 O 为底面圆圆心 ,∵c os∠ ASB=,∴s in∠ ASB=.∴S△ASB=× |AS|·|BS|·= 5.2∴S A=4.∵SA 与圆锥底面所成的角为45° ,∠ SOA= 90° .∴S O=OA=SA= 2.∴S 圆锥侧 = πrl= 4×2×π= 40π.新题演练提能·刷高分1.(2018云南保山第二次统测)我国古代数学名著《增删算法统宗》中有如下问题: “有个金球里面空 ,球高尺二厚三分,一寸自方十六两,试问金球几许金?”意思是 : 有一个空心金球,它的直径 12 寸 ,球壁厚 0.3 寸 ,1 立方寸金重 1 斤 ,试问金球重是多少斤?(注π≈3)()A.125 .77B.864C.123.23D.369.69答案 C解析由题意知 ,大球半径R=6,空心金球的半径 r= 6-0.3= 5.7,则其体积 V= π(63-5.73)≈123.23(立方寸 ).因为 1 立方寸金重 1 斤 ,所以金球重 123.23 斤 ,故选 C.2.(2018福建宁德期末)我国古代数学名著《孙子算经》中有如下问题:“今有筑城 ,上广二丈 ,下广五丈四尺 ,高三丈八尺 ,长五千五百五十尺 ,秋程人功三百尺.问 :须工几何 ?”意思是 : “现要筑造底面为等腰梯形的直棱柱的城墙,其中底面等腰梯形的上底为 2 丈、下底为 5.4 丈、高为3.8 丈 ,直棱柱的侧棱长为 5 550 尺 .如果一个秋天工期的单个人可以筑出300 立方尺 ,问 :一个秋天工期需要多少个人才能筑起这个城墙?”(注: 一丈等于十尺 )()A.24 642B.26011C.52 022D.78 033答案 B解析根据棱柱的体积公式 ,可得城墙所需土方为×38×5 550= 7 803 300( 立方尺 ),一个秋天工期所需人数为 = 26 011,故选 B .3.(2018山西太原一模)三棱锥D-ABC中 ,CD ⊥底面ABC ,△ABC 为正三角形,若 AE ∥CD,AB=CD=AE=2,则三棱锥 D-ABC与三棱锥E-ABC 的公共部分构成的几何体的体积为()A. B. C. D.答案 B解析根据题意画出如图所示的几何体:2019 版高考数学（理科）总复习∴三棱锥 D-ABC 与三棱锥E-ABC 的公共部分构成的几何体为三棱锥F-ABC.∵△ABC 为正三角形 ,AB= 2,∴S△ABC=×2×2×.∵CD⊥底面 ABC,AE∥ CD ,CD=AE= 2,∴四边形 AEDC 为矩形 ,则 F 为 EC 与 AD 的中点 ,∴三棱锥 F-ABC 的高为 CD= 1, ∴三棱锥 F-ABC 的体积为 V=× 1=. 故选 B .4.(2018四川雅安模拟)《九章算术》是我国古代的数学名著,书中提到一种名为“刍甍”的五面体,如图所示 ,四边形 ABCD 是矩形 ,棱 EF∥ AB ,AB= 4,EF= 2,△ADE 和△BCF 都是边长为 2 的等边三角形 ,则这个几何体的体积是 ()A. B. +2C. D.答案 C解析过点 E 作 EG⊥平面 ABCD ,垂足为点G,过点 F 作 FH ⊥平面 ABCD,垂足为点H,过点 G 作 PQ∥ AD ,交 AB 于点 Q,交 CD 于点 P,过点 H 作 MN ∥BC ,交 AB 于点 N,交 CD 于点 M,如图所示 :∵四边形 ABCD 是矩形 ,棱 EF∥ AB,AB= 4,EF= 2,△ADE 和△BCF 都是边长为 2 的等边三角形 ,∴四边形 PMNQ 是边长为 2 的正方形 ,EG= ,∴这个几何体的体积为V=V E-AQPD +V EPQ-FMN +V F-NBCM =×1×2××2+×2××2=+ 2.故选 C.5.(2018上海虹口期末质量监控)已知M,N 是三棱锥P-ABC 的棱AB,PC 的中点 ,记三棱锥P-ABC 的体积为V1,三棱锥 N-MBC 的体积为V2,则等于.答案解析如图 ,设三棱锥P-ABC 的底面积为S,高为 h.∵M 是 AB 的中点 ,∴S△BMC=S.∵N 是 PC 的中点 ,2019 版高考数学（理科）总复习∴三棱锥 N-MBC 的高为 h,则V1=Sh,V2=S× h=Sh,∴.故填 .6.(2018河北唐山二模)在四棱锥 S-ABCD 中 ,SD⊥底面 ABCD ,底面 ABCD 是正方形 ,SD=AD= 2,三棱柱 MNP-M 1N1 P1的顶点都位于四棱锥S-ABCD 的棱上 ,已知 M,N,P 分别是棱 AB,AD,AS 的中点 ,则三棱柱 MNP-M 1N1P1的体积为.答案 1解析由题得 M1是 BC 中点 ,N1是 DC 中点 ,P1是 SC 中点 ,PN= 1,MN= ,且 PN⊥MN ,所以三棱柱MNP-M 1N1P1的底面积为×1×.由题得正方形的对角线长2,三棱柱 MNP-M 1N1P1的高为×2,所以三棱柱MNP-M 1N1P1的体积为 = 1,故填 1.命题角度 3 三视图还原与几何体的体积、表面积高考真题体验·对方向1.(2017全国Ⅰ·7)某多面体的三视图如图所示,其中正视图和左视图都由正方形和等腰直角三角形组成 ,正方形的边长为 2,俯视图为等腰直角三角形 ,该多面体的各个面中有若干个是梯形,这些梯形的面积之和为()A .10 B.12 C.14 D.16答案 B解析由三视图可还原出几何体的直观图如图所示.该五面体中有两个侧面是全等的直角梯形,且该直角梯形的上底长为2,下底长为4,高为 2,则 S 梯= (2+ 4)×2÷2= 6,所以这些梯形的面积之和为12.2.(2017全国Ⅱ·4)如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为()2019 版高考数学（理科）总复习A .90π B.63π C.42π D.36π答案 B解析由题意 ,可知该几何体由两部分组成,这两部分分别是高为 6 的圆柱截去一半后的图形和高为 4 的圆柱 ,且这两个圆柱的底面圆半径都为3,故其体积为 V=× π×32×6+ π×32×4=63π,故选B.3.(2016全国Ⅰ·6)如图 ,某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径.若该几何体的体积是 ,则它的表面积是 ()A.17 πB.18πC.20πD.28 π答案 A解析由三视图可知该几何体是球截去后所得几何体3,则×R= ,解得 R=2,所以它的表面积为×4πR2+×πR2= 14π+ 3π= 17π.4.(2016全国Ⅱ·6)下图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为()A.20 πB.24πC.28πD.32 π答案 C解析由题意可知 , 该几何体由同底面的一个圆柱和一个圆锥构成 , 圆柱的侧面积为S1= 2π×2×4= 16π,圆锥的侧面积为S2=×2π×2×=8π,圆柱的底面面积为S3= π×22= 4π,故该几何体的表面积为S=S1 +S2+S 3= 28π,故选 C.5.(2016 全国Ⅲ·9)如图 ,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的表面积为()A.18 +36B.54 + 18C.90D.81答案 B解析由三视图知该几何体是平行六面体 ,且底面是边长为 3 的正方形 ,侧棱长为 3,所以该几何体的表面积为 S= 2×3×6+ 2×3×3+ 2×3×3= 54+ 18,故选 B.新题演练提能·刷高分1.(2018河北唐山二模)如下图 ,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图 ,则其表面积为()A.2 πB.5πC.8 πD.10 π答案 C解析由题得几何体原图是球被切割后剩下的, 所以它的表面积由三个部分组成,所以S=×4π×22+×π×22+×π×22= 8π.故选 C.2.(2018山西太原二模)某几何体的三视图如图所示,则该几何体的体积为()A. B. C. D.答案 D解析三视图还原是四棱锥,如图所示 .AC⊥ AD ,PD ⊥底面 ABCD ,PD=AD=BC=AC= 1,所以体积 V=× (1×1)×1= ,故选 D .3.(2018河北石家庄一模)如图 ,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体的表面积为()A.8 + 3πB.8+ 4πC.8+5πD.8+ 6π答案 D解析由题图可知 ,几何体为半圆柱挖去半球体,几何体的表面积为2×+4π+ 2×4-π+= 8+ 6π,故选D.4.(2018东北三省三校二模)如图所示 ,一个三棱锥的三视图是三个直角三角形,则该三棱锥的体积为 ()A.3B.4C.6D.8答案 B解析如图所示 ,在长、宽、高分别为4,2,3 的长方体中 ,三棱锥 P-ABC 对应几何体的三视图即题中的三视图 ,据此可得该几何体的体积:V=×S× PC=× ×2×4×3= 4.故选B.△ABC5.(2018福建福州3月质检)如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图 ,则该几何体的体积为()A. π+ 6B. +6C.+ 6D.+ 2答案 C解析由三视图可知,该几何体为组合体:上方为半个圆锥,下方为放倒的直四棱柱,∴该几何体的体积为×π×2+×(1+ 2)×2×2=+ 6,故选 C.6.(2018江西教学质量监测)若一个空间几何体的三视图如图所示,且已知该几何体的体积为π,则其表面积为 ()A.6 π+4B.6πC.π+ 2D.π+答案 A解析该几何体是半个圆锥 ,则 V=× πr2× r=π,解得 r= 2,母线长为 l= 2r ,所以其表面积为S=πrl+ πr2+×2r × r= r 2=6π+ 4,故选 A .7.(2018湖南、江西十四校第一次联考)已知一个棱长为 2 的正方体被两个平面所截得的几何体的三视图 (单位 :cm) 如图所示 ,则该几何体的体积是 ()A. cm 3B.4 cm 3C. cm3D. cm32019 版高考数学（理科）总复习答案 D解析由三视图得原几何体如图所示 ,在正方体 ABCD-A 1B1C1D 1中 ,由平面 AB1D1 ,平面 CB1D 1截得的几何体 ,它的体积为一个正方体的体积减去两个底面为等腰直角三角形的三棱锥的体积,即 V= 23-2×× S× 8h=-2××2= (cm 3).故选 D.8.(2018安徽江南十校 3 月联考 )某几何体的三视图如图所示,其中正视图由矩形和等腰直角三角形组成 ,侧视图由半圆和等腰直角三角形组成,俯视图的实线部分为正方形,则该几何体的表面积为 ()A.3 π+4B.4( π++ 1)C.4(π+ )D.4( π+ 1)答案 A解析由三视图知几何体的上半部分是半圆柱, 圆柱底面半径为1,高为2,其表面积为S1= π×2×1×+π×12= 3π,下半部分为正四棱锥 ,底面棱长为 2,斜高为 ,其表面积 S2= 4× ×2× = 4,所以该几何体的表面积为S=S1+S 2= 3π+ 4.故选 A .9.(2018山东济南一模)某几何体的三视图如图所示,其中正视图的轮廓是底边为2,高为 1 的等腰三角形 ,俯视图的轮廓为菱形 ,侧视图是个半圆.则该几何体的体积为.答案π解析由三视图可知 ,该几何体是一个组合体 ,它由两个底面重合的半圆锥组成 ,圆锥的底面半径为 1,高为 ,所以组合体的体积为 2××π×12×π,故答案为π.命题角度 4 球与几何体的切、2019 版高考数学（理科）总复习接问题高考真题体验·对方向1.(2018全国Ⅲ·10)设A,B,C,D是同一个半径为 4 的球的球面上四点,△ABC 为等边三角形且其面积为 9,则三棱锥 D-ABC 体积的最大值为()A .12 B.18 C.24 D.54答案 B解析由△ABC 为等边三角形且面积为9,设△ABC 边长为 a,则 S=a·a= 9.∴a= 6,则△ABC 的外接圆半径 r=a= 2<4.设球的半径为R,如图 ,OO 1== 2.当D 在 O 的正上方时 ,V D-ABC =S△ABC·(R+|OO 1|)=×9×6= 18,最大 .故选 B.2.(2017全国Ⅲ·8)已知圆柱的高为1,它的两个底面的圆周在直径为 2 的同一个球的球面上,则该圆柱的体积为()A. πB.C.D.答案 B解析由题意可知球心即为圆柱体的中心,画出圆柱的轴截面如图所示,则AC= 1,AB= ,底面圆的半径r=BC= ,所以圆柱的体积是3.(2016全国Ⅲ·10)在封闭的直三棱柱ABC-A1B1C1 BC,AB= 6,BC= 8,AA1= 3,则 V 的最大值是 ()2V= πr h= π××1= ,故选 B.内有一个体积为V 的球 . 若AB ⊥A.4 πB.C.6 πD.答案 B解析由题意知要使球的体积最大,则它与直三棱柱的若干个面相切 .设球的半径为R,易得△ABC 的内切球的半径为=2,则 R≤ 2.因为 2R≤ 3,即 R≤ ,所以 V max= ,故选 B .4.(2015全国Ⅱ·9)已知A,B是球O的球面上两点,∠AOB= 90°,C为该球面上的动点.若三棱锥O-ABC 体积的最大值为 36,则球 O 的表面积为 ()A.36 πB.64πC.144πD.256π答案 C解析由△AOB 面积确定 ,若三棱锥 O-ABC 的底面 OAB 的高最大 ,则其体积才最大 .因为高最大为半径 R,所以 V O-ABC =R2× R=36,解得 R=6,故 S 球 = 4πR2= 144π.新题演练提能·刷高分1.(2018河南六市一模)在三棱锥S-ABC 中 ,SB⊥ BC,SA⊥ AC,SB=BC,SA=AC ,AB=SC ,且三棱锥。

2019年高考数学二轮专题复习知能专练十三空间几何体的三视图表面积及体积

知能专练（十三）空间几何体的三视图、表面积及体积一、选择题1．一个锥体的正视图和侧视图如图所示，下面选项中，不可能是该锥体的俯视图的是( )解析：选C 注意到在三视图中，俯视图的宽度应与侧视图的宽度相等，而在选项C 中，其宽度为32，与题中所给的侧视图的宽度1不相等，因此选C. 2．一块石材表示的几何体的三视图如图所示，将该石材切削、打磨、加工成球，则能得到的最大球的半径为( )A ．1B ．2C ．3D ．4解析：选B 该几何体为直三棱柱，底面是边长分别为6,8,10的直角三角形，侧棱长为12，故能得到的最大球的半径等于底面直角三角形内切圆的半径，其半径为r ＝2S a ＋b ＋c ＝2×12×6×86＋8＋10＝2，故选B.3．将边长为1的正方形以其一边所在的直线为旋转轴旋转一周，所得几何体的侧面积为( )A ．4πB ．3πC ．2πD ．π解析：选C 由几何体的形成过程知所得几何体为圆柱，底面半径为1，高为1，其侧面积S ＝2πrh ＝2π×1×1＝2π.4．一个四棱锥的侧棱长都相等，底面是正方形，其正视图如图所示，则该四棱锥侧面积和体积分别是( )A ．45，8B ．45，83C ．4(5＋1)，83D ．8,8解析：选B 由题意可知该四棱锥为正四棱锥，底面边长为2，高为2，侧面上的斜高为 22＋12＝5，所以S侧＝4×⎝ ⎛⎭⎪⎫12×2×5＝45，V ＝13×22×2＝83.5.(2017·全国卷Ⅰ)某多面体的三视图如图所示，其中正视图和左视图都由正方形和等腰直角三角形组成，正方形的边长为2，俯视图为等腰直角三角形．该多面体的各个面中有若干个是梯形，这些梯形的面积之和为( )A ．10B ．12C ．14D ．16 解析：选B 由三视图可知该多面体是一个组合体，如图所示，其下面是一个底面为等腰直角三角形的直三棱柱，上面是一个底面为等腰直角三角形的三棱锥，等腰直角三角形的腰长为2，直三棱柱的高为2，三棱锥的高为2，易知该多面体有2个面是梯形，这些梯形的面积之和为＋2×2＝12，故选B.6．如图，三棱锥V ABC 的底面为正三角形，侧面VAC 与底面垂直且VA ＝VC ，已知其正视图的面积为23，则其侧视图的面积为( )A.32B.33。