北邮研究生泛函分析 - 加强版 - 最终稿--2016修改
北京邮电大学学术型硕士研究生培养方案(2016)

2031101036 信息网络安全技术
3111100007 宽带通信网
3111100014 高等通信原理
3111100034 IP/WDM 网络基础理论
选
3111100035 IPv6 与移动计算技术
修
第 6 组至少修 6 学分
3111100036 计算机视觉模型学习与推理
课
(专业方向选修课)
程
3111100042 L硕士研究生培养方案 4、掌握至少一门外国语,能较为熟练地阅读本专业的外文资料,具有一定的
写作能力并具备一定的国际学术交流能力,掌握至少一种计算机语言及编程方法, 熟练运用计算机操作系统和文献检索工具查询技术文献。
四、 学制 3年
五、 课程设置与学分
硕士研究生课程主要划分为学位课、非学位选修课、必修环节三大部分。 硕士研究生应在导师指导下制定个人培养计划和具体选课,应修满不少于 30
二、 研究方向 1、 信息理论与信息处理 2、信息通信网络 3、多媒体与网络大数据 4、无线和移动通信 5、光通信 6、网络服务、管理与安全
三、 培养目标 1、掌握马克思主义的基本理论,树立科学的世界观,坚持四项基本原则,热
爱祖国,遵纪守法,品行端正,学风严谨,团结协作,具有强烈的事业心和献身 精神,积极为社会主义现代化服务,身心健康。
2031100965 工程计算方法
3111100091 电磁场理论
3111100571 现代数字通信
第 4 组, 至少选 1 门 (专业基础课-基础专业
课)
3111100606 3111100941 3111101116
信息论基础 模式识别与机器学习 通信网理论(硕)
3111101119 统计信号处理基础
泛函分析 PPT课件

• 可数基数a,连续基数c。
• 主要结论:1.可数集的子集至多可数; 2.有限或可数多个可数集合的并是可数集; 3.有限个可数集的直积是可数集; 4. 无限集必于它的某真子集对等,含可数子集;
可数集的例子:整数集,有理数集,n维欧式空间中 的有理点集。
实数的基本定理:确界存在原理、单调有界原理、 闭区间套引理、聚点定理、有限覆盖定理等等都 当成已知
距离空间的拓扑
• 空间引入距离,才有了空间上映射的连续性概念 (开集的原像是开集)
• 称X的子集B(x,r)={y;p(x,y)<r}为以x为心半径为r的 开球
• 称X的子集S(x,r)={y; p(x,y)=r}为以x为心半径为r的 有着很大优越和方便之处,但并不完全一致。如:离散距离空间中的球 面只有两种可能:空集或全空间
• 紧集的连续象是紧集 • 紧集上的连续函数是一致连续的,能取到最大值
和最小值。 • 空间X是有限维的当且仅当X的闭单位球是紧集。 • 非紧的空间,可以通过一点紧致化,进而利用紧
空间的性质来研究
小结
• 我们讨论距离空间的基本性质 • 距离空间就是赋予距离的集合,是三维立体空间
概念的推广,二者既有相同又不完全相同。
• Zorn引理是集论的一个重要工具,与选择公理,良序原理都是彼此等价的,主要应用于 数学上存在性定理的证明,而不具体描述寻求的方法。
泛函分析复习与总结

《泛函分析》复习与总结第一部分 空间及其性质泛函分析的主要内容分为空间和算子两大部分. 空间包括泛函分析所学过的各种抽象空间, 函数空间, 向量空间等, 也包括空间的性质, 例如完备性, 紧性, 线性性质, 空间中集合的各种性质等等。
以下几点是对第一部分内容的归纳和总结。
一.空间(1)距离空间 (集合+距离)!验证距离的三个条件:(,)X ρ称为是距离空间,如果对于,,x y z X ∈(i) 【非负性】(,)0x y ρ≥,并且(,)0x y ρ=当且仅当x y =【正定性】;(ii) 【对称性】(,)(,)x y y x ρρ=;(iii) 【三角不等式】(,)(,)(,)x y x y y z ρρρ≤+。
距离空间的典型代表:s 空间、S 空间、所有的赋范线性空间、所有的内积空间。
(2)赋范线性空间 (线性空间 + 范数)!验证范数的三个条件:(,||||)X ⋅称为是赋范线性空间,如果X是数域K =¡(或K =£)上的线性空间,对于a K ∈和,x y X ∈,成立(i) 【非负性】||||0x ≥,并且||||0x =当且仅当0x =【正定性】; (ii) 【齐次性】||||||||||ax a x =⋅;(iii) 【三角不等式】||||||||||||x y x y +≤+。
赋范线性空间的典型代表:n ¡空间(1,2,3,n =L )、n £空间(1,2,3,n =L )、p l 空间(1p ≤≤∞)、([,])p L ab 空间(1p ≤≤∞)、[,]Cab 空间、[,]k C a b 空间、Banach 空间、所有的内积空间(范数是由内积导出的范数)。
(3)内积空间 (线性空间 + 内积)!验证内积的四个条件:(,(,))X ⋅⋅称为是内积空间,如果X 是数域K =¡(或K =£)上的线性空间,对于a K ∈和,,x y z X ∈,成立(i) 【非负性】(,)0x x ≥,并且(,)0x x =当且仅当0x =【正定性】;(ii) 【第一变元可加性】(,)(,)(,)x y z x z x z +=+;(iii) 【第一变元齐次性】(,)(,)ax z a x z =;(iv) 【共轭对称性】(,)(,)x z z x =。
2016年北京邮电大学传播学考研、复试真题,考研真题,考研大纲,考研笔记,考研经验

北邮考研详解与指导名词解释1.编码/解码2.SNS3.沉默的螺旋4.创新扩散5,博客人二。
1.依附理论2.斯蒂分金的游戏论(名字我忘了大体是这么个读法。
好吧,很明显这个题楼主没有看哦)3.非语言符号有什么功能?4.传播学史上主要的三个媒介理论的相互借鉴和异同。
三。
1.施拉姆认识媒介的八个原则,以及他对传播学的贡献。
2.三网融合将会使未来的传播进程和传播格局产生什么样的变化这几天,有很多的考生朋友向笔者咨询关于复试的事,或电话,或邮件,一一答复实在困难,也比较麻烦,于是乎想到利用一段闲暇的时间写下这些文字,如果你有耐心把它看完,那么恭喜你,你已经把很多对手抛弃在后面。
不久全国硕士生招生自划线高校将公布分数线的同时也公布了各自的复试工作办法,国家线也将于近日出炉。
已经上线的朋友应该及时地浏览、查阅招生单位的相关复试文件,及早做好参加复试的准备工作。
自06年教育部就要求复试成绩占总成绩的30%至50%以来,很多自主划线高校积极响应,部分自主划线高校07年的实际复试成绩已经占到了50%。
可想而知,复试的比重只会只升不降,今年更是如此。
复试之所以重要,原因之一是在研究生数量不断增加的今天,教育部和招生高校已经开始往培质量一边添加砝码,使之平衡。
另一方面是招生单位能够在复试更加直观、有效地考查考生综合素质和专业发展潜质,这样更有利于筛选优秀的学生,淘汰那些在初试中考得好但并具有培养潜能的人。
很多朋友认为自己的初试成绩不错,可以松一口气,这是致命的想法,往年很多在初试中取得高分的朋友在复试中也被淘汰出局,在复试结束之前,一切皆有可能。
因此,初试考得好的朋友应该保持清醒的头脑,切不要因为取得高分而沾沾自喜,防止复试中的“黑马”,初试考得不好的朋友更应该利用这段时间,把专业知识再温习一遍,亡羊补牢,为时尚不晚。
虽然今年国家线还没有出来,但根据前几年的分数线判断,今年的分数线的仍然不会出现大幅度的升降,最多也就是3到5分之间波动。
北京邮电大学2016考研复试参考书目
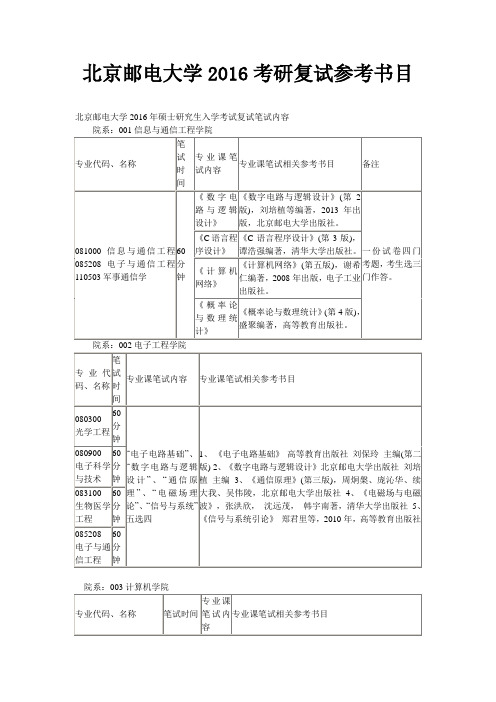
北京邮电大学2016考研复试参考书目
北京邮电大学2016年硕士研究生入学考试复试笔试内容
院系:001信息与通信工程学院
院系:002电子工程学院
院系:004自动化学院
凯程考研集训营,为学生引路,为学员服
务!
院系:005软件学院
第3页共8 页
院系:006数字媒体与艺术设计学院
院系:007理学院
院系:008经济管理学院
凯程考研集训营,为学生引路,为学员服
务!
院系:009公共管理学院
第5页共8 页
院系:011教育技术研究所
院系:012马克思主义学院
院系:013网络技术研究院
凯程考研集训营,为学生引路,为学员服务!
第7页共8 页
院系:014信息光子学与光通信研究院
(责任编辑:田学江)
一分耕耘一分收获。
加油!。
《应用泛函分析》习题解答

1泛函分析与应用-国防科技大学第 一 章第 一 节3.设}{k x 是赋范空间E 中的Cauchy 列,证明}{k x 有界,即∞<N∈k k x sup 。
证明:0>∀ε,0N ∃,当0,N n m >时,有εε<-⇒<-m n m n x x x x ,不妨设m n x x ≥,则0, ,N n m x x m n >+<ε。
取0N m =,则有0 ,0N n x x N n >+<ε,令},,,,m a x {0021ε+=N N x x x x c ,则1 ,≥<n c x n 。
6.设E 是Banach 空间,E 中的点列满足∞<∑∞=1k kx(此时称级数∑∞=1k k x 绝对收敛),证明存在E ∈x ,使∑∞=∞→=1lim k kn xx (此时记x 为∑∞=1k kx,即∑∞==1k kxx ).证明:令∑==nk kn xy 1,则∑∑++=++=+≤=-pn n k kpn n k kn p n xxy y 11。
由于∞<∑∞=1k kx绝对收敛,则它的一般项0→k x 。
因此0>∀ε,总0N ∃,当0,N p n ≥时,有ε<-+n p n y y ,所以}{n y 是E 中的Cauchy 列,又因为E 是Banach 空间,则必存在E ∈x ,使得∑∑∞==∞→==11limk k nk kn x xx 。
9.(Hamel 基)设A 是线性空间E 的非空子集,若A 中任意多个元素都是线性无关的,则称A 是线性无关的。
若A 是线性无关的,且E =A span ,则称A 是E 是的一个Hamel 基。
此时若A 是无穷集,则称E 是无穷维的;若A 是有限集,则称E 是有限维的,并定义E 的维数为A 中所含有的元素个数。
通常用E dim 表示E 的维数,并约定当}0{=E 时,0dim =E ,可以证明任何线性空间都存在Hamel 基。
泛函

泛函分析在数学物理方程、概率论、计算数学、连续介质力学、量子物理学等学科有着广泛的应用。近十几年来,泛函分析在工程技术方面有获得更为有效的应用。它还渗透到数学内部的各个分支中去,起着重要的作用。
泛函分析的起源
泛函分析的源头之一是变分法。18世纪形成的变分法的核心课题是研究形如
连续线性泛函
泛函分析的一个基本概念。围绕对它的研究形成的对偶理论至今仍是泛函分析中心课题之一。对它的研究最早可追溯到C.博莱特(1897)提出要用连续性条件来刻画一定函数类上的连续线性映射T:E→F。1903年阿达马在E是C[α,b]([α,b]上连续函数的全体),F是实数域,当{?n}一致收敛于? 时,T?n→T?的情况下,将T 表示成一列积分的极限的形式。但这种表示不惟一,并且有极大任意性。后来在实l2空间上,弗雷歇和里斯独立地在T 是所谓强连续假设下给出简单而惟一的表示,即希尔伯特空间l2上的连续线性泛函表示定理。里斯在1909~1910年又相继给出C[α,b]、Lp[α,b]、lp(p>1)上的表示定理。在这些表示定理的证明中实质上已蕴含线性子空间(又称向量子空间)上连续线性泛函必可延拓到全空间的事实。E.黑利从1912年开始(中间经过第一次世界大战的中断),直到1921年用“赋范数列空间”(他并未用这个名称)代替具体的C[α,b]、Lp[α,b]、lp等而考虑较抽象形态的延拓问题。他使用了凸性以及在有限维空间情况下早为H.闵科夫斯基用过的术语,如支撑超平面等。
巴拿赫空间
在许多具体的无限维空间以及它们上面相应的收敛性出现之后,抽象形态的线性空间(向量空间)以及按范数收敛的出现就成为自然的了。1922~1923年,E.哈恩和巴拿赫(同时还有N.维纳)独立地引入赋范线性空间。当时的讨论事实上都限于完备的赋范线性空间。1922年哈恩从当时分析数学许多分支已达到的成果和方法中提炼出了共鸣定理。1927年H.施坦豪斯和巴拿赫用完备度量空间的第二纲性代替原来所谓“滑动峰”证明方法,给出现今常见的证明。1922~1923年巴拿赫又得到了压缩映射的不动点定理、开映射定理。1927年哈恩完全解决了完备赋范线性空间上泛函延拓定理的证明,并第一次引入赋范线性空间E的对偶空间(共轭空间)K(当时称为极空间)。两年后,巴拿赫用同样方法也得到同样结果(后来,他承认哈恩的优先权),并看到这个定理可以推广。这个推广形式在后来的局部凸拓扑线性空间理论中起了重要作用。1931年巴拿赫将他1923~1929年的工作以及当时主要成果写成《线性算子理论》一书,书中大部分讨论他1929年开始研究的弱收敛,这又成为局部凸拓扑线性空间理论出现的先导。在同一书中还发表了完备赋范线性空间上连续线性算子值域不是第一纲集便是全空间以及闭图像定理等重要结果。这时,作为完备赋范线性空间理论的独立体系已基本形成,它的许多结果已成为泛函分析应用中的强有力工具。人们为纪念他的功绩,把完备赋范线性空间称为巴拿赫空间。近年来,人们特别感兴趣的一个领域是研究巴拿赫空间的几何学。
泛函分析,泛函分析简介

泛函分析,泛函分析简介泛函分析是20世纪30年代形成的数学分科,是从变分问题,积分方程和理论物理的研究中发展起来的。
它综合运用函数论,几何学,现代数学的观点来研究无限维向量空间上的泛函,算子和极限理论。
它可以看作无限维向量空间的解析几何及数学分析。
泛函分析在数学物理方程,概率论,计算数学等分科中都有应用,也是研究具有无限个自由度的物理系统的数学工具。
1概述泛函分析(FunctionalAnalysis)是现代数学的一个分支,隶属于分析学,其研究的主要对象是函数构成的空间。
泛函分析是由对函数的变换(如傅立叶变换等)的性质的研究和对微分方程以及积分方程的研究发展而来的。
使用泛函作为表述源自变分法,代表作用于函数的函数。
巴拿赫(StefanBanach)是泛函分析理论的主要奠基人之一,而数学家兼物理学家维多·沃尔泰拉(VitoVolterra)对泛函分析的广泛应用有重要贡献。
2拓扑线性空间由于泛函分析源自研究各种函数空间,在函数空间里函数列的收敛有不同的类型(譬如逐点收敛,一致收敛,弱收敛等等),这说明函数空间里有不同的拓扑。
而函数空间一般是无穷维线性空间。
所以抽象的泛函分析研究的是一般的(无穷维的)带有一定拓扑的线性空间。
拓扑线性空间的定义就是一个带有拓扑结构的线性空间,使得线性空间的加法和数乘都是连续映射的空间。
巴拿赫空间这是最常见,应用最广的一类拓扑线性空间。
比如有限闭区间上的连续函数空间,有限闭区间上的k次可微函数空间。
或者对于每个实数p,如果p≥1,一个巴拿赫空间的例子是“所有绝对值的p次方的积分收敛的勒贝格可测函数”所构成的空间。
(参看Lp空间) 在巴拿赫空间中,相当部分的研究涉及到对偶空间的概念,即巴拿赫空间上所有连续线性泛函所构成的空间。
对偶空间的对偶空间可能与原空间并不同构,但总可以构造一个从巴拿赫空间到其对偶空间的对偶空间的一个单同态。
微分的概念可以在巴拿赫空间中得到推广,微分算子作用于其上的所有函数,一个函数在给定点的微分是一个连续线性映射。
2016年北京邮电大学信息与通信工程学院考研、复试真题,考研真题,考研大纲,考研笔记,考研经验

北邮考研详解与指导院系:001信息与通信工程学院专业代码、名称笔试时间专业课笔试内容专业课笔试相关参考书目备注081000信息与通信工程085208电子与通信工程110503军事通信学60分钟《数字电路与逻辑设计》《数字电路与逻辑设计》(第2版),刘培植等编著,2013年出版,北京邮电大学出版社。
一份试卷四门考题,考生选三门作答。
《C 语言程序设计》《C 语言程序设计》(第3版),谭浩强编著,清华大学出版社。
《计算机网络》《计算机网络》(第五版),谢希仁编著,2008年出版,电子工业出版社。
《概率论与数理统计》《概率论与数理统计》(第4版),盛聚编著,高等教育出版社。
1.充分备考2月中上旬2015年全国硕士研究生考试成绩公布后,34所自划线研究生招生单位也将在3月陆续公布复试分数线,3月底,全国各研招单位复试工作陆续进行。
因此你要在这段时间经常浏览招生单位网站,及时获取复试信息,尽可能多地了解复试内容和形式,并尽早做好相应准备。
听力方面可以找历年四、六级或考研真题,在给定的时间内回答所有题目,同时训练自己的语感。
在口语考试方面,可针对下面几个问题做准备(一般都会涉及这几个方面):一是自我介绍,如来自什么地方、毕业学校、所学专业、业余喜好、家庭基本情况等信息;二是做好用英语讲解自己专业的准备。
口语测试时老师有可能就你所报的专业展开话题,考查用英语讲解陌生概念的能力,因此可先用笔头组织回答这些问题的要点,然后再根据这些要点来组织语言。
平时在阅读专业文献时,注意多积累一些专业方面的英语词汇。
2.信息灵通在复试的前期准备中,信息是最重要的。
这些信息除了复试的时间、地点、考官等基本常识外,还包括复试的范围、内容及考查方式等。
具体搜集信息的方法有以下几种:首先,要及时向报考学校的招生办咨询复试的形式及时间,经常浏览所报考学校的网站。
其次,关于复试的范围和内容可以向上届师兄师姐询问,他们亲历过复试,所以由他们提供的信息也最为可靠。
泛函分析---NPU13

1§3 列紧集设),(ρX 是一个距离空间,A 是X 的一个子集,A 称为是有界的,如果X x ∈∃0及0r >,使得0(,)A B x r ⊂,其中00(,){|(,)}B x r x X x x r ρ∈< 。
在有穷维欧氏空间中,有界无穷集必含有一个收敛子列,但这个性质不能推广到任意的距离空间。
例 在[0,1]C 上,考察点列10,,()(1,2,)11,,n t nx t n nt t n ⎧≥⎪⎪==⎨⎪−≤⎪⎩…。
显然)1,(}{θB x n ⊂(因为[]1,0,1∈∀≤t x n ),其中θ表示恒等于0的函数,但是{}n x 不含有收敛子列。
事实上,若{}n x 有收敛子列{()}i n x t ,则{()}i n x t 收敛0,(0,1],()1,0,t x t t ∈⎧=⎨=⎩但()[0,1]x t C ∉,故)}({t x n 在[0,1]C 中无收敛子列。
定义 1.3.1 设),(ρX 是一个距离空间,A 为其一子集,称A 是列紧的,如果A 中的任意点列在X 中有一个收敛子列。
若这个子列还收敛到A 中的点,则称A 是自列紧的。
如果空间X 是列紧的,那么称X 为列紧空间。
命题 1.3.2 在n中任意有界集是列紧集,任意有界闭集是自列紧集。
命题 1.3.3 列紧空间内任意(闭)子集都是(自)列紧集。
2证明 设X A ⊂,X A x n ⊂⊂∀}{,由X 列紧知,}{n x 在X 中有收敛子列}{k n x ,所以A 是列紧集。
若A 还是闭的,由于x x A x k k n n →⊂,}{,由A 是闭,知A x ∈。
从而A 是自列紧集。
□命题1.3.4 列紧空间必是完备空间。
证明 设X 为列紧空间,{}n x 为X 中的基本列。
因为X 列紧,故{}k n x ∃在X 中收敛,极限记为0x ,且X x ∈0,则0x x n →,故X 完备。
(用到P 13 习题1.2.2)□补充性质 在度量空间),(ρX 上,基本列{}n x 是收敛列⇔{}n x 有收敛子列。
泛函分析答案

泛函分析答案:1、 所有元素均为0的n ×n 矩阵2、 设E 为一线性空间,L 是E 中的一个子集,若对任意的x,y ∈L ,以及变数λ和μ均有λx +μy ∈L ,则L 称为线性空间E 的一个子空间。
子空间心室包含零元素,因为当λ和μ均为0时,λx +μy =0∈L ,则L 必定含零元素。
3、 设L 是线性空间E 的子空间,x 0∈E\L,则集合x 0+L={x 0+l,l ∈L}称为E 中一个线性流形。
4、 设M 是线性空间E 中一个集合,如果对任何x,y ∈M ,以及λ+μ=1,λ≥0,μ≥0的λ和μ,都有λx +μy ∈M ,则称M 为E 中的凸集。
5、 设x,y 是线性空间E 中的两个元素,d(x,y)为其之间的距离,它必须满足以下条件:(1) 非负性:d(x,y)>0,且d(x,y)=0<―――>x=y (2) d(x,y)=d(y,x)(3) 三角不等式:d(x,y)≤d(x,z)+d(y,z) for every x,y,z ∈E n 维欧几里德空间常用距离定义:设x={x 1,x 2,…x n }T ,y={y 1y 2,…y n }Td 2(x,y)=(21||niii x y=-∑)1/2d 1(x,y)=1||ni i i x y =-∑d p (x,y) = (1||np iii x y=-∑ )1/p d ∞(x,y)=1max ||i i i nx y ≤≤-6、距离空间(x,d)中的点列{x n }收敛到x 0是指d(x n ,x 0)→0(n →∞),这时记作0lim nn xx -->∞=,或简单地记作x n →x 07、设||x||是线性空间E 中的任何一个元素x 的范数,其须满足以下条件: (1)||x||≥0,且||x||=0 iff x=0 (2)||λx||=λ||x||,λ为常数(3)||x+y||≤||x||+||y||,for every x,y ∈E8、设E 为线性赋范空间,{x n }∞n=1是其中的一个无穷列,如果对于任何ε>0,总存在自然数N ,使得当n>N,m>N 时,均有|x m -x n |<ε,则称序列{x n }是E 中的基本列。
泛函分析讲义

第三章 赋范空间3.1. 范数的概念“线性空间”强调元素之间的运算关系,“度量空间”则强调元素之间的距离关系,两者的共性在于:只研究元素之间的关系,不研究元素本身的属性。
为了求解算子方程,需要深入地了解函数空间的结构与性质,为此,我们不仅希望了解函数之间的运算关系和距离关系,还希望了解函数本身的属性。
那么,究竟需要了解函数的什么属性呢?3.1.1. 向量的长度为了回答上述问题,我们需要从最简单的函数空间——欧氏空间——中寻找灵感。
回想一下,三维欧氏空间中的元素被称为“向量”,向量最重要的两大属性是:长度和方向,向量的许多重要性质都是由其长度和方向所决定的。
这一章的任务就是将欧氏空间中向量的长度推广为(以函数空间为原型的)一般线性空间中元素的广义长度,下一章的任务就是将欧氏空间中向量的方向推广为(以函数空间为原型的)一般线性空间中元素的广义方向。
可以想象:其元素具有广义长度和广义方向的线性空间必将像欧氏空间那样,呈现出丰富多彩的性质,并且这些性质必将有助于求解算子方程。
图3.1.1. 三维欧氏空间中向量的大小和方向矩阵论知识告诉我们:可以为欧氏空间中的向量赋予各种各样的长度,并且可以根据问题需要来选择最合适的向量长度。
实际上,可以在数域F 上的n 维欧式空间n F 上定义向量12(,,,)n x x x x 的如下三种长度(称为“范数”):● 2-范数(也称为欧氏范数):2x =● 1-范数:11n k k x x ==∑;● ∞-范数:1max k k nx x ∞≤≤=。
图3.1.2. 三种向量范数对应的“单位圆” 图3.1.3. “单位圆”集合的艺术形式下一节将谈到:就分析性质而言,这三种向量范数没有任何区别。
我们注意到:通常将2或3中两个向量之间的距离定义为两者的差向量的长度。
由此可知:如果有了长度的概念,就可以诱导出距离;反之则不然。
因此,长度是比距离更本质的概念。
3.1.2. 范数的定义我们希望将向量范数的概念推广到(以函数空间为原型的)无限维线性空间的场合。
最新北邮整理版通信求职、考研复试常见问题---副本

OFDM技术的基本原理在传统的多载波通信系统中,整个系统频带被划分为若干个互相分离的子信道(载波)。
载波之间有一定的保护间隔,接收端通过滤波器把各个子信道分离之后接收所需信息。
这样虽然可以避免不同信道互相干扰,但却以牺牲频率利用率为代价。
而且当子信道数量很大的时候,大量分离各子信道信号的滤波器的设置就成了几乎不可能的事情。
人们提出了频带混叠的多载波通信方案,选择相互之间正交的载波频率作子载波,也就是我们所说的OFDM。
这种“正交”表示的是载波频率间精确的数学关系。
按照这种设想,OFDM既能充分利用信道带宽,也可以避免使用高速均衡和抗突发噪声差错。
OFDM 单个用户的信息流被串/并变换为多个低速率码流,每个码流都用一个子载波发送。
OFDM技术的主要思想就是在频域内将给定信道分成许多正交子信道,在每个子信道上使用一个子载波进行调制,并且各子载波并行传输。
这样,尽管总的信道是非平坦的,具有频率选择性,但是每个子信道是相对平坦的,在每个子信道上进行的是窄带传输,信号带宽小于信道的相应带宽,因此就可以大大消除信号波形间的干扰。
由于在OFDM系统中各个子信道的载波相互正交,它们的频谱是相互重叠的,这样不但减小了子载波间的相互干扰,同时又提高了频谱利用率。
在对每个载波完成调制以后,为了增加数据的吞吐量、提高数据传输的速度,它又采用了一种叫作HomePlug的处理技术,来对所有将要被发送数据信号位的载波进行合并处理,把众多的单个信号合并成一个独立的传输信号进行发送。
另外OFDM 之所以备受关注,其中一条重要的原因是它可以利用离散傅立叶反变换/离散傅立叶变换(IDFT/DFT)代替多载波调制和解调。
OFDM每个载波所使用的调制方法可以不同。
各个载波能够根据信道状况的不同选择不同的调制方式,比如BPSK、QPSK、8PSK、16QAM、64QAM等等,以频谱利用率和误码率之间的最佳平衡为原则。
我们通过选择满足一定误码率的最佳调制方式就可以获得最大频谱效率。
泛函分析讲义

泛函分析讲义第五章Banach代数1代数准备知识2 Banach代数2.1 Banach代数的定义2.2 Banach代数的极大理想与Gelfand表示3例与应用4 c’代数5 Hilbert空间上的正常算子5.1 Hilbert空间上正常算子的连续算符演算5.2正常算子的谱族与谱分解定理5.3正常算子的谱集6在奇异积分算子中的应用第六章无界算子1 闭算子2 cayley变换与自伴算子的谱分解2.1 cayley变换2.2自伴算子的谱分解3无界正常算子的谱分解3.1 B0rel可测函数的算子表示3.2无界正常算子的谱分解?4 自伴扩张4.1 闭对称算子的亏指数与自伴扩张4.2 自伴扩张的判定准则5自伴算子的扰动5.1稠定算子的扰动5.2自伴算子的扰动5.3 自伴算子的谱集在扰动下的变化?6无界算子序列的收敛性6.1预解算子意义下的收敛性6.2图意义下的收敛性第七章算子半群1无穷小生成元1.1无穷小生成元的定义和性质1.2 Hme—Yosida定理2无穷小生成元的例子3单参数酉群和Stone定理3.1单参数酉群的表示——stone定理3.2 stone定理的应用1.B0chner定理2.Schr6dinger方程的解3.遍历(ergodic)定理3.3 Trotter乘积公式4 Markov过程4.1 Markov转移函数4.2扩散过程转移函数5散射理论5.1波算子5.2广义波算子6发展方程第八章无穷维空间上的测度论1 C[O,T]空间上的wiener测度1.1 C[O,T]空间上wiener 测度和wiener积分1.2 Donsker泛函和Donske卜Lions定理1.3 Feynman—Kac公式2 Hilbert空间上的测度2.1 Hilbert—Schmidt算子和迹算子2.2 Hilbert空间上的测度2.3 Hilbert空间的特征泛函3 Hilbert空间上的Gauss测度3.1 Gauss测度的特征泛函3.2 Hilbert空间上非退化Gauss测度的等价性清词丽句必为邻2015-09-21 04:05 | 豆瓣:烟波浩渺1980杜甫的《戏为六绝句》(其五)不薄今人爱古人,清词丽句必为邻。
泛函分析 课件第一章

i 1
Ai x | 0 x 1
Ai x | 0 x 2
1 1 A x | x (2)设 i , i 1, 2,.... i i
则
1 1 Ai x | x , n n i 1
4、逆映射 设 为A到B上的一一映射.作B到A的映射如下:如果 : x | y 令 : y | x , 确实使唯一的
x 与 y 相对应,即 是映射,
11 1 : B A
则称
是 的逆映射 ,也记为
注:逆映射是反函数概念的推广。例如,任何一个严格单调的函数都可
d c 11 : x b ( x a) c a
故(a,b)与(c,d)对等。
定理 1 对任何集合A、B、C均有
(1) (3) A B B
若
(2) A
A
A
(4) A B, B C A C
定理 2 设{An}和{Bn}是两列分别彼此互不相交的集列,
An
Bn , n 1,2,... , 则
集合表示方法:
列举法:将其元素一一列举出来。
特征描述法:将元素所具有的特征义命题的形式描述出来。
p Q {x | x q , p Z , q Z , q 0}
定理1:对任何集合A、B、C,均有
(1)A A
(2)A B,B A,则A = B
(3)A B,B C,则A C 其中(2)是经常用于证明两个集合相等。
§2 集合的运算
1、和集或并集 A B x | x A 或 x B
A x | 存在某个 使x A
2、交集
泛函分析

泛函分析1.范数&线性泛函的定义定义 设X 是线性空间,若对∀x ∈X ,有唯一实数∥x ∥与之应对,且使得(1) ∥x ∥≥0,且x =0⟺∥x ∥=0(2) ∥x +y ∥≤∥x ∥+∥y ∥, x,y ∈X(3) ∥αx ∥=|α|⋅∥x ∥,α∈R or C,x ∈X则称∥x ∥为X 的范数,此时的线性空间X 称为赋范线性空间.2.设x,y 为线性赋范空间,T:x →y 为线性算子.若T 在x 0处连续,则T 在x 上一致连续,且T 连续当且仅当存在M >0,使得∥Tx ∥≤M ∙∥x ∥,x ∈X证明 (1) 因为T 在x 0处连续,则有∀ε>0,∃δ>0,使得当∥x −x 0∥<δ时,有∥Tx −Tx 0∥<ε对∀y,z ∈X ,∥z −y ∥<δ.令x =z −y +x 0,则x −x 0=z −y.∥Tz −Ty ∥=∥T (z −y )∥=∥T (x −x 0)∥=∥Tx −Tx 0∥<ε若T 在x 0处连续,则T 在x 上一致连续(2) 必要性 设T 在x 上一致连续,则在0处也连续。
令ε=1,∃δ>0,当∥u ∥<δ时,∥Tu ∥<1对∀x ∈X,x =∥x∥δ(δ∥x∥⋅x).令c =∥x∥δ,u =δ∥x∥⋅x ,则∥u ∥=δ,x =cu ∥Tx ∥=∥T (cu )∥=c ∥Tu ∥≤c =∥x ∥δ 令δ−1=M ,则∥Tx ∥≤M ∙∥x ∥充分性 若∥Tx ∥≤M ∙∥x ∥,x ∈X ,当x 0=0时,对于∀ε>0,∃δ=εM ,当∥x −0∥<δ时,有 ∥Tx ∥≤M ∙∥x ∥<M ∙δ=M ∙εM=ε 则对x =0,T 是连续的.3.算子范数∥T ∥=sup ∥x∥<1∥Tx ∥,设T:x →y 为连续线性算子,定义∥T ∥为T 的范数,证明: ∥T ∥=sup ∥x∥<1∥Tx ∥=sup ∥x∥=1∥Tx ∥=sup ∥x∥≠0∥Tx ∥∥x ∥证明 sup ∥x∥≠0∥Tx∥∥x∥=sup ∥x∥≠0∥1∥x∥Tx ∥=sup ∥x∥≠0∥T(1∥x∥x)∥≤sup ∥x∥=1∥Tx ∥≤sup ∥x∥≤1∥Tx ∥=∥T ∥ sup∥x∥≠0∥Tx ∥∥x ∥≥sup ∥x∥≤1∥Tx ∥∥x ∥≥sup ∥x∥≤1∥Tx ∥=∥T ∥ 则∥T ∥=sup ∥x∥≠0∥Tx∥∥x∥=sup ∥x∥≤1∥Tx ∥ 4.完备性的证明 什么是柯西列,收敛列,收敛列为什么是柯西列答 度量空间X 中的任意柯西列收敛与X 中的一点,则称X 是完备的柯西列:设空间X 为线性空间,{x n }⊂X ,若∀ε>0,∃N ,当n,m >N 时,有∥x n −x m ∥<ε,则{x n }称为柯西列收敛列:设空间X 有{x n },lim x n =x ,由极限的性质,对∀ε>0,∃N ,当n >N 时,有∥x n −x ∥<ε, 当m >N 时,有∥x −x m ∥<ε. 则当n,m >N 时,有∥x n −x m ∥=∥x n −x +x −x m ∥=∥(x n −x )−(x m −x )∥≤∥x n −x ∥+∥x −x m ∥<2ε 则称{x n }为一个收敛列由定义可知,收敛列必定是柯西列,但柯西列不一定是收敛列.比如:有理数集Q ,级数展开式中e =∑1n!∞n=0=1+1+12+⋯ S n =1n!这个数列是柯西列,但是在Q 上不收敛5.内积空间与赋范线性空间的关系内积空间→赋范线性空间(定义∥x ∥=√(x,x))赋范线性空间→内积空间(满足平行四边形法则)6. 证明:内积空间和线性赋范空间,当∥x ∥=√(x,x)证:(1) ∥x +y ∥2=(x +y,x +y )=(x,x +y )+(y,x +y )=(x,x )+(x,y )+(y,x )+(y,y) 由Cauchy-Schwarz 不等式,可知(x,y )≤√(x,x)√(y,y),则上式有∥x +y ∥2≤(x,x )+√(x,x )√(y,y )+√(y,y )√(x,x )+(y,y )=∥x ∥2+∥y ∥2+2∥x ∥∥y ∥=(∥x ∥+∥y ∥)2即∥x +y ∥≤∥x ∥+∥y ∥(2) ∥αx ∥2=(αx,αx )=αα̅(x,x),因为αα̅=|α|2,则等式=|α|2(x,x)则∥αx ∥=|α|√(x,x )=|α|∥x ∥(3) ∥x ∥=√(x,x ),因为(x,x )≥0,所以∥x ∥≥0(4) 当∥x ∥=√(x,x )=0时,(x,x )=0,即x =07.正交系(集)性质,勾股,三角不等式,线性相关的证明答: 向量集S 称为正交的,是指对于每一对x,y 都有x ⊥y ,其中x ∈S,y ∈S 且x ≠y.若对于每一个x ∈S 还有∥x ∥=1,则称这个集为标准正交集平行四边形法则:∥x +y ∥2+∥x −y ∥2=2∥x ∥2+2∥y ∥2证明: ∥x +y ∥2+∥x −y ∥2=(x +y,x +y )+(x −y,x −y )=(x,x )+(x,y )+(y,x )+(y,y )+(x,x )−(x,y )−((y,x )−(y,y ))=(x,x )+(x,y )+(y,x )+(y,y )+(x,x )−(x,y )−(y,x )+(y,y )=2(x,x )+2(y,y )=2∥x ∥2+2∥y ∥2ε1,ε2,…,εn 为正交向量组,且k 1ε1+k 2ε2+⋯k n εn =0,则0=(0,εi )=(k 1ε1+k 2ε2+⋯k n εn )=k i (εi ,εi )=k i ,即k i =0(i =1,2,…,n),所以ε1,ε2,…,εn 线性无关.8. X 是一个线性空间,S ⊂X,S ⊥={x ′:x ′∈X f |(x,x ′)=0,x ∈S}⊂X f ,证明S ⊥是X f 一个子空间证明 X 是线性空间,则X f 也是线性空间.因为S ⊥⊂X f ,则对任意x ′,y ′∈S ⊥,有x ′,y ′∈X f 而(x ′+y ′)(x )=x ′(x )+y ′(x )=0,故x ′+y ′∈S ⊥.∀α∈R,x ′(αx )=αx ′(x )=0.故αx ′∈S ⊥,则S ⊥是X f 一个子空间。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
泛函分析基础(2015年加强版) ,设(,d x]0,1为闭区间]0,1上赋予度量]为定义在3的哪些子集构成3的线性子空间【[0,2],Cπ【为赋范空间,,,n nx Xαα∈[0,1]上的∞和1不为等价范数∞中除有限个坐标之外均为.p【19】.X '∈【190E 是X 的真闭子空间.y X ∈【23固定,考虑3的线性子空间}33:0x =为赋范空间,M 为X 的线性子空间】 为赋范空间*,.f X ∈【31】Banach 空间Y 为赋范空间为一系列有界线性算子【1,【34】】存在唯一的[0,1],x C ∈,<∞-∞<},n e 为和{:n f n ≥的子空间,,M N ⊥是线性子空间并对于∞中只有有限多个零项的序列构成的子空间,,n x 是赋范空间(,)B xε≠∈使得M,=根据下确界的重要条件,得0inf{d. (略)n n a t .对于n n na t -+2n n b t nb t -++)()g t -<是一个有理数,且().t{()|s f t s 中任何两个不同元素之间的距离均为且有不可数多个.,则这些不相交的小球每一个必含有,,n n x y ∃∈).→+∞②2中元素e 1,0,1,0,.n⎫-⎪⎭{|n e n =≥,0,).下面证明M 是有界闭集但不是紧集.2(,0)1,n d e =<故M 是有界集有2(,)n m d e e ⎛= 2时,则必有0,0,N ∃>当.M .,)d 是完备的的闭子集定义映射,T Tx =,)|Tx Ty Tx =3的哪些子集构成3的线性子空间3).2,x =且3x 11x =+的0≥且2x ≤},1,2.i =)1,0,y M ∈,,1,2,3i =2,1,M α=}:,[,].n n i a t a t a b +∈∈容易验证在通常多项式的加法和与实数的乘法运算下有()(p t p t α且易验证加法与数乘满足线性空间的八个条件},n t 线性无关},n t 是X 的不是Y 的线性子空间∈K ,有()p t α为赋范空间,,n n x y ,y α→→∞和1不为等价范数110|()|max t x t dt ∈=≤⎰⎰使得()[0,1],x t C ∀∈[0,1],C 使得nx ∞>∞中除有限个坐标之外均为不为Banach ∞的线性子空间.1111,,,,,0,0,.23n⎫⎪⎭则()n x ∈})n 是一个Cauchy 列.,n >则()()1110,,0,,,,,0,,12n m x x n n m⎛⎫-= ⎪++⎝⎭10(,).1n m n =→→+∞+故{}()n x 是Cauchy 111,,,,12n n n ⎫⎪++⎭,则()()11sup 0(1n n k k k x x x x n n ≥-=-=→+),n →+∞但x M ∉,故M 不完备.}}:lim 0n n x ∞→∞∈=,由例1.3.6知0C)10,,,,,n n x x C +∈存在),,,0,0,,n x M ∈()11sup sup n k k k k k n x x x ≥≥+-=→时).中稠密.故0C 是M 的完备化空间上定义线性泛函(=(),[1,1].f x x t dt x C ∈-) sup ()sup 212n n f x n ∈∈=- ⎪⎝⎭()x t ⇔在(1,0)-上符号相同且},n e 为,1,i j n ≤≤唯一确定,,n α∈K ,n β∈K 1111n n n nx e e y e e αααββ=++=++,11,,,nni ii i i j i i ij i j ee e βαβαβγ===∑∑∑00,x ⇔=),,n α∈K 12212222120,n n n n n nn n γγαγγγα⎛⎫ ⎪ ⎪⎪ ⎪≥ ⎪⎪ ⎪ ⎪⎪⎪ ⎪⎭⎝⎭⎝⎭①满足①式,则由11nni i ij i j αβγ==∑∑所定义的映射是一个内积Hilbert 空间为H 的闭线性子空间.求证:M 为H[1,1]odd C -[1,1],even C ∈-Hilbert 空间{sup,x y =,,n k 有0,=即j e ),j j x e e e 固定,考虑3的线性子空间}33:0Z x =上的线性泛函2311(,)f x x x a x =到3上的所有保范延拓的有界线性泛函.3中定义范数1x x =首先证{12max ,f a a =因为对12(,,0)x x Z ∀∈∈又若取(sgn x =3,定义F ,Z 有()F x }时,有F故,此时F 是f 到3上的保范延拓.32★4-4.设X 为赋范空间,M 为X 的线性子空间,0.x X ∈ 求证0x M ∈当且仅当任取,0,Mf X f'∈=都有0()0.f x ="":⇒若0,x M ∈则{},n x M ∃⊂且0().n x x n →→∞ 因,f X '∈且0,Mf=则()()0()lim lim 0.n n n n f x f x x →∞→∞===""⇐:反证法.若0,x M ∉因为M 是闭集,故()0,0.x M d ρ=> 则根据定理4.1.7,则,f X '∃∈使得01,0,()0Mf ff x d ===>,与条件矛盾. 34●4-17.设X 为Banach 空间,Y 为赋范空间,(,)n T B X Y ∈为一系列有界线性算子,设任取{},n x X T x ∈都是Y 中的Cauchy 列,求证:存在常数0,C ≥使得任取1,.n n T C ≥≤35 ●4-18.在上题中又设Y 为Banach 空间,求证:存在(,),T B X Y ∈使得任取,,n x X T x Tx ∈→且1sup .n n T T ≥≤因为{}n T x 是Y 中的Cauchy 列,则{}n T x 是有界集,即,x X ∀∈有sup .n n T x ∈<+∞因为X 是Banach 空间,故由一致有界原则有sup ,n n T ∈<+∞即0,c ∃>使得对,n ∀有.n T c ≤若Y 完备,则,Tx Y ∃∈使得n T x Tx →(参考定理2.4.5的证明), 且lim lim sup ,n n n n n n Tx T x T x T x →∞→∞∈==≤⋅故sup .n n T T ∈≤36★4-20.设X 为赋范空间,,,n n x x X x ∈⇀.x 求证:{:1}.n x span x n ∈≥ 若n x ⇀x ,则,f X '∀∈有()().n f x f x →若{}:1,n x span x n ∉≥则{}(),:10.n d x span x n d ≥=> 根据定理4.1.7知,存在{}:1,1,0,n span x n f X f f≥'∈==且()0f x d =>与()()n f x f x →相矛盾.1,级数1n ≥∑.∞)1,,,n x ∈定义1()nn i i i f x y x ==∑是定义在1上的线性泛函且1max n f ≤=1,级数1n n n y x +∞=∑收敛,故lim n →∞1,都有sup (n n f x ∈根据一致有界原则,得sup ,n n f ∈<+∞即1sup max sup .i n i nn y y ≤≤∈∈=<+∞∞中只有有限多个零项的序列构成的子空间)()1,,,,,,,n n x y y y →=式中k y =并计算;T 逆算子定理矛盾?21∞有Tx (1,1,,1,)x =(全为1),111,,,,,2Tx n ⎛⎫= ⎪⎝⎭且1,1,x Tx == 1sup 1,x Tx Tx >=≥=故 1.T =()()1121212:,,,,,2,,,,,,k k k k T y y y y x y y ky ky ky -++=→= 111,1,,1,,,,k k y k k ⎛⎫ ⎪= ⎪⎝⎭项故,k y X ∈且()11,2,,,1,1,,k T y k X -=∈ 11,(),k k k y x T y k k -===→+∞→+∞故1T -无界.这与开映射定理不矛盾,因为X 不完备.取1010,0,,0,,,n n x X n -⎛⎫ ⎪=∈ ⎪⎝⎭个因为110,(,),n m x n m n m =-→→∞所以但是当n →∞时,有(0,0,,0,),n x X →∉故。
