2005年江苏省赣榆高级中学OI校内模拟赛暨网上同步赛

合集下载

江苏省赣榆高级中学20082009学年度第一学期

江苏省赣榆高级中学2008——2009学年度第一学期工作总结在县委、县政府和上级教育主管部门的领导和关心下，学校以邓小平理论和“三个代表”重要思想为指导，认真学习贯彻党的十七届三中全会精神，牢固树立科学发展观和社会主义荣辱观；认真贯彻落实《江苏省中小学管理规范》，以构建和谐校园为主线，以维护安全稳定为保障，以开展“有效教学管理年”活动为抓手，强化教育教学管理，积极推进新课程改革，学校教育教学质量和办学效益稳步提高。

本学期，学校被评为省文明单位、省文明学校、全国作文教学先进单位、省第八届作文大赛优秀组织奖、省2006—2008年度教育学会系统先进单位，市2007—2008学年度高中教学管理质量奖、市星级高中食堂食品卫生等级A级单位，县文明单位、县高三教学工作先进集体、县教科研先进集体、县消防工作先进集体、县“五一巾帼示范岗”，县优质服务科室、县人文奥运·与法同行中小学生学法用法征文活动优秀组织奖等。

本学期，学校还顺利通过省中小学管理规范、省新课程实施专项督导、省学校体育卫生工作专项督导等检查验收，初步完成了四星级高中复审材料的准备工作，展示了学校各个层面的工作实绩，赢得了社会各界的高度评价。

一、加强教职工的思想建设，提高教职工工作的积极性和创造性。

1、积极投身主题教育活动，不断加强政治建设。

本学期，学校组织全体教职工学习了“三个代表”重要思想和市县教育工作会议精神，加强对新形势下党的方针政策和教育发展形势的理解。

学校党委组织学习学习了十七届三中全会和省委十一届五次全会重要精神，组织开展了“讲党性、重品行、作表率”主题教育活动，开展了“三走进，三争创”教育活动，开展了城乡基层组织结对联创活动，开展了行风评议教育活动，开展了党员民主评议活动。

通过学习，教职工的思想觉悟进一步提高。

2、建立健全各规章制度，切实加强作风建设。

本学期，学校修订了并下发了《江苏省赣榆高级中学高考奖励办法》《江苏省赣榆高级中学教职工工作绩效奖励办法》《江苏省赣榆高级中学关于教学质量奖的暂行规定》进一步完善了学校的各项规章制度。

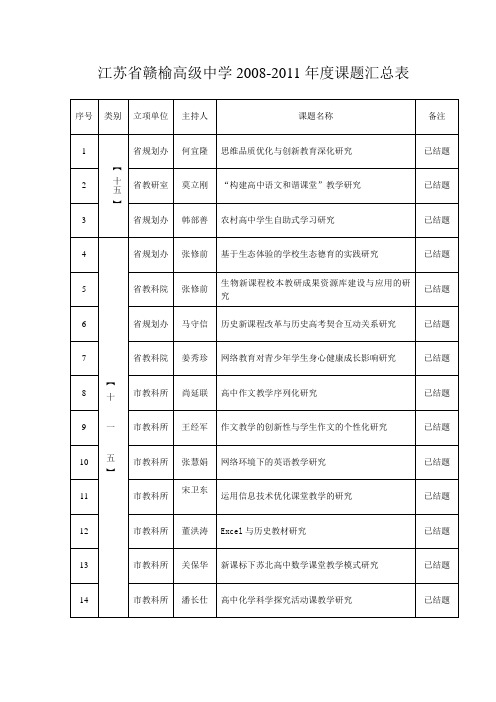
江苏赣榆高级中学2008-2011课题汇总表

已结题
16
市教研室
臧文淑
高中语文课堂和谐氛围创设的研究
已结题
17
市教研室
姜秀珍
信息技术学科中如何帮助青少年摆脱网瘾的研究
已结题
18
市教研室
吴兰红
提高物理教学有效性的策略方法研究
已结题
19
市教研室
潘长仕
高中化学“活动与探究”课型实施策略研究
已结题
20
市教育学会
姜秀珍
新教改技术课程中培养学生创新精神和能力的连之
优化中英物理教学法，提高课堂教学效率
已结题
33
县教研室
王京穆
新教材中扩展性栏目对培养学生思维品质作用研究
已结题
34
县教研室
王军起
加强情境实践提高学生交际能力
已结题
35
县教科室
张春宁
新课程背景下高中物理作业批改方式方法的有效性整改
已结题
36
县教科室
杨宁
高中物理课堂教学中预设与生成的研究
韦文余
高考复习教与学整合研究
已结题
27
县教研室
仲玉梅
“在高中语文教学中构建和谐师生关系”研究
已结题
28
县教研室
张建尚
生物教学中学生信息素养培养的研究
已结题
29
县教研室
崔维云
高中政治课堂小组合作学习的有效性研究
已结题
30
县教研室
祁德志
普通高中课堂教学的重建研究
已结题
31
︻十一五︼
县教研室
于玉和
利用课外实验进行科学探究的尝试
江苏省赣榆高级中学2008-2011年度课题汇总表
序号

江苏省赣榆高级中学高一上学期期中考试物理试题

江苏省赣榆高级中学高一上学期期中考试物理试题一、选择题1．2016年第31届夏季奥运会在巴西的里约热内卢举行，下列比赛中可把研究对象看成质点的是（）A．研究苏炳添在百米跑比赛时的起跑技术B．研究乒乓球男子单打冠军马龙的发球动作C．研究女子3米板冠军施廷懋的跳水动作D．研究女子50米步枪三姿比赛中杜丽射出的子弹轨迹2．诗句“满眼波光多闪灼，看山恰似走来迎，仔细看山山不动，是船行”中，“看山恰似走来迎”和“是船行”所选的参考系分别是A．船和山B．山和船C．地面和山D．河岸和流水3．根据牛顿第一定律，下列说法正确的是（）A．如果物体的速度不断增大，那么物体必受力的作用B．如果物体的位移不断增大，那么物体必受力的作用C．一个竖直向上运动的物体，必受竖直向上的力的作用D．要使物体保持直线运动，一定要对它施加一个大小、方向合适的力4．如图所示，表示五个共点力的有向线段恰分别构成正六边形的两条邻边和三条对角线．已知F1＝10 N，这五个共点力的合力大小为( )A．0B．30 NC．60 ND．90 N5．物块静止在固定斜面上，下图所示的四幅示意图中，正确标明了斜面对物块的支持力的（）A．B．C．D．6．大雪天车轮打滑，车辆难以前进，交警帮忙向前推车，如图所示，在推车的过程中，关于人和车之间的作用力，下列说法正确的一是（）A．车对人有向后的力B．车对人没有作用力C．人对车的力大于车对人的力D．人对车的力小于车对人的力7．物体做匀变速直线运动，相继经过两段距离均为9m的路程，第一段用时3s，第二段用时6 s，则物体加速度的大小是A．16m/s2B．13m/s2C．23m/s2D．43m/s28．下列关于加速度的说法正确的是A．加速度就是增加的速度B．加速度也可以是指减小的速度C．加速度的大小在数值上与单位时间内速度变化量的大小相等D．加速度不断减小，速度一定不断减小9．如图所示，在水平力F的作用下，木块A、B保持静止．若木块A与B的接触面是水平的，且F≠0．则关于木块B的受力个数可能是（）A．3个或4个B．3个或5个C．4个或5个D．4个或6个10．甲、乙、丙三辆汽车同时以相同的速度经过某一路标，此后甲一直做匀速直线运动，乙先加速后减速，丙先减速后加速，它们经过下一路标时的速度仍相同，则A．甲车先经过下一个路标B．乙车先经过下一个路标C．丙车先经过下一个路标D．无法判断谁先经过下一个路标11．在一平直路段检测某品牌汽车的运动性能时，通过传感器发现汽车做直线运动的位移x与时间t的关系为x＝5t＋t2(各物理量均采用国际单位制单位)，则该汽车A．第1 s内的位移是5 mB．前2 s内的平均速度是6 m/sC．任意相邻的1 s内位移差都是1 mD．任意1 s内的速度增量都是2 m/s12．一遥控玩具汽车在平直路上运动的位移﹣时间图象如图所示，则（）A ．15s 内汽车的位移为 300mB ．前10s 内汽车的加速度为3m/s 2C ．20s 末汽车的速度为﹣1m/sD ．前 25s 内汽车做单方向直线运动13．在大枣红了的时候，几个小朋友正在大枣树下用石块投向枣树，若某个小朋友从看到石块击中枣树树枝到听到大枣落地声最少需要0.7 s ，估算一下这课枣树的高度至少是（）A ．1.5 mB ．2.5 mC ．5 mD ．7 m14．有下列几种情景，请根据所学知识选择对情景的分析和判断正确的说法 ( )A ．嫦娥四号运载火箭点火后即将升空，因火箭还没运动，所以加速度一定为零B ．高速公路上高速行驶的轿车紧急刹车，此时轿车速度变化很快，所以加速度也大C ．运行的磁悬浮列车在轨道上高速行驶，因其速度很大，所以加速度也一定很大D ．江泉高架桥的下桥匝道指示牌数字“40”，意思是车辆平均速度限定在40km/h 及以下15．如油画所示是伽利略研究自由落体运动时的情景，他设计并做了小球在斜面上运动的实验，关于这个实验的下列说法中不符合．．．史实的是（）A ．伽利略以实验来检验速度与时间成正比的猜想是否真实B ．伽利略让小球沿阻力很小的斜面滚下是为了“冲淡”重力的影响C ．伽利略通过实验发现小球沿斜面滚下的运动是匀加速直线运动D ．伽利略用实验而不是外推的方法得到斜面倾角增大到90︒小球仍然会保持匀加速运动16．如图所示，质量分别为m 1和m 2的木块A 和B 之间用轻质弹簧相连，在拉力F 作用下，竖直向上做匀速直线运动．某时刻突然撤去拉力F ，撤去F 后的瞬间A 和B 的加速度大小为a A 和aB ，则A ．a A =0，aB =gB ．a A =g ，a B =gC ．a A =0，a B =122m m g m +D．a A=g，a B=122m mgm17．打水漂是人类最古老的游戏之一（如图）．仅需要一块小瓦片，在手上呈水平放置后，用力水平飞出，瓦片擦水面飞行，瓦片不断地在水面上向前弹跳，直至下沉．下列判断正确的是（）A．飞出时的初速度越大，瓦片的惯性一定越大B．飞行时所用时间越长，瓦片的惯性一定越大C．飞出去的距离越长，瓦片的惯性一定越大D．瓦片的质量越大，惯性一定越大18．汽车启动后，某时刻速度计示数如图所示．由此可知此时汽车（）A．行驶了70 hB．行驶了70 kmC．速率是70 m/sD．速率是70 km/h19．一辆汽车由静止开始做匀加速直线运动，4s末速度变为10m/s，则汽车的（）A．加速度为2m/s2B．4s内的位移为40mC．4s内的平均速度为2.5m/sD．2s末的速度为5m/s20．下列说法中正确的是A．平时我们问“现在什么时间？”里的“时间”是指时刻而不是指时间间隔B．“坐地日行八万里”是以地球为参考系C．研究短跑运动员的起跑姿势时，由于运动员是静止的，所以可以将运动员看做质点D．对直线运动的某个过程，路程一定等于位移的大小二、多选题21．物体沿一直线运动，在t时间通过的路程为s，在中间位置2s处的速度为v1，在中间时刻2t 时速度为v 2，则v 1与v 2关系为（） A ．当物体做匀速直线运动时v 1＝v 2B ．当物体做匀加速直线运动时v 1＞v 2C ．当物体做匀减速直线运动时v 1＞v 2D ．当物体做匀减速直线运动时v 1＜v 2 22．如图所示，不计质量的光滑小滑轮用细绳悬挂于墙上O 点，跨过滑轮的细绳连接物块A 、B ，A 、B 都处于静止状态，现将物块B 移至C 点后，A 、B 仍保持静止，下列说法中正确的是（）A ．B 与水平面间的摩擦力变大B ．A 、B 静止时，图中α、β、θ三角始终相等C ．悬于墙上的绳所受拉力大小不变D ．绳子对B 的拉力不变23．长木板上表面的一端放有一个木块，木块与木板接触面上装有摩擦力传感器，如图甲所示，木板由水平位置缓慢向上转动（即木板与地面的夹角α变大），另一端不动，摩擦力传感器记录了木块受到的摩擦力F f 随角度α的变化图像如图乙所示。

江苏省赣榆县一中2024年物理高三第一学期期末联考模拟试题含解析

江苏省赣榆县一中2024年物理高三第一学期期末联考模拟试题注意事项1．考生要认真填写考场号和座位序号。

2．试题所有答案必须填涂或书写在答题卡上，在试卷上作答无效。

第一部分必须用2B 铅笔作答；第二部分必须用黑色字迹的签字笔作答。

3．考试结束后，考生须将试卷和答题卡放在桌面上，待监考员收回。

一、单项选择题：本题共6小题，每小题4分，共24分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1、2017年11月5日，我国用长征火箭成功发射了两颗北斗三号组网卫星(如图所示)，开启了北斗卫星导航系统全球组网的新时代。

下列关于火箭在竖直方向加速起飞阶段的说法，正确的是（）A．火箭只受到重力和空气阻力的作用B．火箭喷出的热气流对火箭的作用力与火箭对热气流的作用力大小相等C．火箭处于失重状态D．保温泡沫塑料从箭壳上自行脱落后，相对地面由静止下落2、如图所示，水平放置的平行板电容器下极板接地，闭合开关S1，S2，平行板电容器两极板间的一个带电粒子恰好能静止在P点．要使粒子保持不动，但粒子的电勢能增加，则下列可行的指施有A．其他条件不变，使电容器上极板下移少许B．其他条件不变，将滑动变阻器滑片向右移少许井将上极板下移少许C．其他条件不变，使开关S2断开，并将电容器下极板上移少许D．其他条件不变，使开关S断开，并将电容器下极板上移少许3、如图，在真空中的绝缘光滑水平面上，边长为L的正三角形的三个顶点上分别固定放置电量为+Q、+Q、-Q的点电荷，以图中顶点为圆心、0. 5L为半径的圆与其腰及底边中线的交点分别为A、B、C、D。

下列说法正确的是（）A ．A 点场强等于C 点场强B ．B 点电势等于D 点电势C ．由A 点静止释放一正点电荷+q ，其轨迹可能是直线也可能是曲线D ．将正点电荷+q 沿圆弧逆时针从B 经C 移到D ，电荷的电势能始终不变4、估算池中睡莲叶面承受雨滴撞击产生的平均压强，小明在雨天将一圆柱形水杯置于露台，测得1小时内杯中水上升了45mm 。

赣榆县2005-2006学年第一学期期末调研考试

赣榆县2005-2006学年第一学期期末调研考试高三物理本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共150分。

第Ⅰ卷 (选择题共40分)一、本题共10小题：每小题4分，共40分。

在每小题给出的四个选项中，有的小题只有一个选项正确，有的小题有多个选项正确，全部选对的得4分，选不全的是2分，有选错或不答的得0分。

1、下列关于变压器的说法中不正确．．．的是 A ．升压变压器在升高电压的同时，也提高了交变电压的频率 B ．若输入电压相同，则输出电压随输入电压频率的增大而增大 C ．降压变压器的副线圈导线比原线圈导线粗D ．变压器输出的电功率由输入的电功率决定2、一束持续电子流在电场力作用下做匀加速直线运动，则在其周围空间（）A. 产生稳定的磁场B. 产生变化的磁场C. 所产生的磁场又可产生电场D. 产生的磁场和电场形成电磁波3、如图所示，设有一分子位于图中的坐标原点O 处不动，另一分子可位于x 轴上不同位置处，图中纵坐标表示这两个行间分子力的大小，两条曲线分别表示斥力和吸力的大小随两分子间距离变化的关系，e 为两曲线的交点，则（）A ．ab 表示吸力，cd 表示斥力，e 点的横坐标可能为10-15mB ．ab 表示斥力，cd 表示吸力，e 点的横坐标可能为10-10mC ．ab 表示吸力，cd 表示斥力，e 点的横坐标可能为10-10mD ．ab 表示斥力，cd 表示吸力，e 点的横坐标可能为10-15m4、用比值法定义物理量是物理学中一种常用的方法。

下面四个物理量都是用比值法定义的，其中定义式正确的是A ．加速度 a =B ．磁感应强度 B ＝C ．电场强度D ．电阻R =5、如图所示，P 、Q 是两个等量异种点电荷，MN 是它们连线的中垂线，在垂直纸面的方向上有磁场．如果某正电荷以初速度V 0沿中垂线MN 运动，不计重力，则A ．若正电荷做匀速直线运动，则所受洛伦兹力的大小不变B ．若正电荷做匀速直线运动，则所受洛伦兹力的大小改变C ．若正电荷做变速直线运动，则所受洛伦兹力的大小不变D ．若正电荷做变速直线运动，则所受洛伦兹力的大小改变 6、如图所示，水平地面上叠放着A 、B 两长方形的物块，F 0是作用在物块B以相同的速度作匀速直线运动，若在运动中突然将F 0改为作用的物块A 上，则此后的运动可能的是（） A 、A 、B仍以相同的速度作匀速直线运动B 、A 作加速运动，B 作减速运动C 、A 、B 最终将分离D 、A 、B 最终以共同的加速度作匀加速运动7、如图所示，质量为m 的小车的水平底板两端各装一根完全一样的弹簧，小车底板上有一质量为的滑块，滑块与小车、小车与地面的摩擦都不计。

赣榆县2004—2005学年度高考临考适应性试卷

赣榆县2004—2005学年度高考临考适应性试卷物理试题本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共150分．考试时间120分钟．一卷(选择题共40分)注意事项：1．答第一卷前，考生务必将自己的姓名、考试证号、考试科目用铅笔涂写在答题卡上。

2．第一卷答案必须填涂在答题卡上，在其他位置作答无效．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑．如需改动，用橡皮擦干净后，再选涂其它答案．3．考试结束，将答题卡和第二卷一并交回．一、本题共10小题，每小题4分，共40分．在每小题给出的四个选项中，有的小题只有一个选项正确，有的小题有多个选项正确．全部选对的得4分，选不全的得2分，有选错或不答的得0分．1、下列说法正确的是：（）A、布朗运动就是分子无规则运动B、大的颗粒在温度较高时有可能做无规则运动C、第一类永动机违反了能量守恒定律，第二类永动机没有违反能量守恒定律D、分子势能最小时，分子间引力与斥力大小相等2.下列说法正确的是（）Ａ．天然放射现象的发现，揭示了原子核是由质子和中子组成的Ｂ．卢瑟福的α粒子散射实验揭示了原子核有复杂结构Ｃ．玻尔的原子结构理论是在卢瑟福核式结构学说基础上引进了量子理论Ｄ．α射线、β射线、γ射线本质上都是电磁波3．一个质点做简谐运动，它的振动图像如图5所示，下列判断不正确的是（）A．图中的曲线部分是质点的运动轨迹B．有向线段OA是质点在t1时间内的位移C．振幅与有向线段OA在x轴的投影之差等于质点在t1时间内的位移大小D．有向线段OA的斜率是质点在t1时刻的瞬时速率4、20世纪80年代初，科学家发明了硅太阳能电池。

如果在太空中设立太阳能卫星站，可24小时发电，利用微波-电能转换装置，将电能转换为微波向地面发送，微波定向性能好，飞机通过微波区不会发生意外，但对飞鸟是致命的，因为微波产生强涡流，那么，飞机外壳能使飞机里的人安然无恙的原因是（）A反射 B吸收 C干涉 D衍射5 . 20 世纪50 年代，科学家提出了地磁场的“电磁感应学说”，认为当太阳强烈活动影响地球而引起磁暴时，磁暴在外地核中感应产生衰减时间较长的电流，此电流产生了地磁场．连续的磁暴作用可维持地磁场．则外地核中的电流方向为（地磁场N 极与S 极在地球表面的连线称为磁子午线）（）A．垂直磁子午线由西向东 B．垂直磁子午线由东向西C．沿磁子午线由南向北 D. 沿磁子午线由北向南6、如图所示，a和b都是厚度均匀的平玻璃板，它们之间的夹角为γ,一条细光束由红光和蓝光组成，以人射角α从O点射人a板，且射出b板后的两束单色光通过空气射在地面上M、N两点，由此可知：A．若射到M、N两点的光分别通过同一双缝发生干涉现象，则射到M点的光形成干涉条纹的间距小，这束光为蓝光，光子的能量大B．若射到M、N两点的光分别通过同一双缝发生干涉现象，则射到M点的光形成干涉条纹的间距大，这束光为红光，光子的能量小C．射到N点的光为蓝光，光子的能量小，较容易发生衍射现象D．射到N点的光为红光，光子的能量大，较难发生衍射现象7．如图所示电路，闭合开关时，灯不亮，已经确定是灯泡断路或短路引起的.在不能拆开电路的情况下（开关可闭合，可断开），现用一个多用表的直流电压挡、直流电流挡和欧姆挡分别对故障作出如下判断（如表所示）：次序操作步骤现象和结论1 闭合开关，选直流电压挡，红黑表笔分别接a、b有示数，灯断路，无示数，灯短路2 闭合开关，选直流电流挡，红黑表笔分别接a、b有示数，灯断路，无示数，灯短路3 闭合开关，选欧姆挡，红黑表笔分别接a、b指针不动，灯断路，指直偏转，灯短路4 断开开关，选欧姆挡，红黑表笔分别接a、b指针不动，灯断路，指直偏转，灯短路A．只有1、2对B．只有3、4对C．只有1、2、4对D．全对8、在谷物的收割和脱粒过程中，小石子、草屑等杂物很容易和谷物混在一起，另外谷粒中也有瘪粒，为了将它们分离，可用扬场机分选，如图，它的分选原理是（）A、小石子质量最大，空气阻力最小，飞得最远B、空气阻力对质量不同的物体影响不同C、瘪谷物和草屑质量最小，在空气阻力作用下，反向加速度最大，飞得最远D、空气阻力使它们的速度变化不同7．如图，从竖直面上大圆的最高点A，引出两条不同的光滑轨道，端点都在大圆上，同一物体由静止开始，从A点分别沿两条轨道滑到底端，则A．到达底端的动量大小相等B．重力的冲量都相同C．动量的变化率都相同D．所用的时间都相同10．如图所示，在光滑的水平面上有质量相等的木块A、B，木块A正以速度V前进，木块B静止。

江苏省连云港市赣榆高级中学2021-2022学年高一物理模拟试卷含解析

江苏省连云港市赣榆高级中学2021-2022学年高一物理模拟试卷含解析一、选择题：本题共5小题，每小题3分，共计15分．每小题只有一个选项符合题意1. 下列关于第一宇宙速度的说法中正确的是（）A、第一宇宙速度的数值是7.9Km/sB、第一宇宙速度的数值是11.2 Km/sC、第一宇宙速度的数值是16.7 Km/sD、第一宇宙速度又称逃逸速度参考答案：A2. 2009年5月，航天飞机在完成对哈勃空间望远镜的维修任务后，在A点从圆形轨道Ⅰ进入椭圆轨道Ⅱ，B为轨道Ⅱ上的一点，如图右所示．关于航天飞机的运动，下列说法中正确的有()A. 在轨道Ⅱ上经过A的速度小于经过B的速度B. 在轨道Ⅱ上经过A的速度大于在轨道Ⅰ上经过A的速度C. 在轨道Ⅱ上运动的周期等于在轨道Ⅰ上运动的周期D. 在轨道Ⅱ上经过A的加速度小于在轨道Ⅰ上经过A的加速度参考答案：A3. 今年国庆黄金周期间，高速公路实施免费政策，小李驾驶汽车外出旅行时,汽车行驶在沪宁高速公路上,两次看到路牌和手表如图所示,则小李驾驶汽车行驶的平均速率为A.16 km/hB.96 km/hC.40 km/hD.120 km/h参考答案：B4. （多选）在宽度为d的河中，水流速度为v2 ，船在静水中速度为v1（且v1＞v2），方向可以选择，现让该船开始渡河，则该船A．可能的最短渡河时间为B．可能的最短渡河位移为dC．只有当船头垂直河岸渡河时，渡河时间才和水速无关D．不管船头与河岸夹角是多少，渡河时间和水速均无关参考答案：BD5. 质量为m的炮弹沿水平方向飞行，其动能为E k，突然在空中爆炸成质量相同的两块，其中一块向后飞去，动能为，另一块向前飞去，则向前的这块的动能为（）A．B．C．D．参考答案：B【考点】动量守恒定律；机械能守恒定律．【分析】由于爆炸产生的作用力远大于重力，在爆炸的瞬间水平方向上动量守恒，根据动量守恒求出另一块炸弹的速度，从而求出动能的大小．【解答】解：炸弹开始动能，解得v=．其中一块动能为=，解得根据动量守恒定律得，mv=﹣解得．则动能．故B正确，A、C、D错误．故选B．二、填空题：本题共8小题，每小题2分，共计16分6. 一个重100N的物体静止在水平桌面上，至少要用40N的水平推力，才能使它从原地开始运动。

赣榆高级中学-高三模拟考试

赣榆高级中学-高三模拟考试数学试卷本试卷分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分.共150分，考试时间120分钟.第Ⅰ卷（选择题，共60分）参考公式：如果事件A 、B 互斥，那么球的表面积公式 24R S π=P(A+B)=P(A)+P(B) 其中R 表示球的半径球的体积公式如果事件A 、B 相互，那么 334R V π=球P(A·B)=P(A)·P(B) 其中R 表示球的半径如果事件A 在一次试验中发生的概率是 P ，那么n 次重复试验中恰好发生k次的概率kn k k n n P P C k P --=)1()(一、选择题（本大题共12小题，每小题5分，共60分，每小题给出的4个选项中，只有1项是符合题要求的）1．命题“若a b >，则88a b ->-”的逆否命题是A.若a b <，则88a b -<-B.若88a b ->-，则a b >C.若a ≤b ，则88a b -≤-D.若88a b -≤-，则a ≤b 2．设函数2()(),()0,(1)f x x x a a R f n f n +=++∈<+满足则的符号是 A 、(1)0f n +< B 、(1)0f n +> C 、0)1(≥+n f D 、(1)0f n +< 3．在等比数列{a n }中，572106,5,a a a a =+=则1810a a 等于 A.23-或32- B.23 C.32 D. 23或324．将函数sin 2y x =的图象按向量a 平移后得到函数sin(2)4y x π=-的图象，则向量a 可以是A.(,0)4πB. (,0)8πC. (,0)4π-D. (,0)8π-5．如图，长方体ABCD -A 1B 1C 1D 1中，∠DAD 1＝45°，∠CDC 1＝30°，那么异面直线AD 1与DC 1所成角的大小是A.2arcsin 4 B. 22arcsin4 C. 2D. 26．101()nknn k C==∑∑的值为AA 1BCDD 1B 1C 1（第5题）A.1022B.1023C.2046D.2047 7．已知sin 0,cos 0,αα>>且1sin cos 4αα>，则α的范围是 A.5(2,2),1212k k k ππππ++∈Z B. 5(,),1212k k k ππππ++∈ZC. (2,2),63k k k ππππ++∈Z D. (,),63k k k ππππ++∈Z 8．定义在R 上函数f （x ）对任意实数x 满足f (x +1)＝－f (x －1)，则下列一定成立的是A. f (x )是以4为周期的周期函数B. f (x )是以6为周期的周期函数C. f (x )的图象关于直线x ＝1对称D. f (x )的图象关于点（1,0）对称9．甲、乙两人玩猜骰子游戏．游戏的规则是：有三个骰子（每个骰子都是正方体，其六个面上分别标有数字1,2,3,4,5,6），乙先从1,2,3,4,5,6这六个数中报一个，然后由甲掷这三个骰子各一次，如果三个骰子中至少有1个骰子的向上一面的数字恰好是乙报的这个数，那么乙获胜，否则甲获胜．若骰子任意一面向上的概率均等，则乙获胜的概率是 A.31216 B. 91216 C. 12 D. 12521610．已知平面上点P ∈(){}22,(2cos )(2sin )16()x y x y ααα-+-=∈R ，则满足条件的点P 在平面上所组成图形的面积是A.36πB.32πC.16πD.4π第Ⅱ卷（非选择题，共100分）二、填空题（本大题共6个小题，每小题5分，共20分，把答案填在题中的横线上.）11．函数()6cos cos 2f x x x =+的最小值是．12．已知椭圆2212516x y +=与双曲线22221(0,0)x y m n m n-=>>具有相同的焦点F 1，F 2，设两曲线的一个交点为Q ,∠QF 1F 2＝90°，则双曲线的离心率为．13．函数2()lg(1)f x x ax =--在区间（1，+∞）上是单调增函数，则a 的取值范围是．14.二项式91()x x-的展开式中3x 的系数是 .15．设函数()f x 的定义域为R .若存在与x 无关的正常数M ，使()f x ≤M x 对一切实数x均成立，则称()f x 为有界泛函．在函数2()2,(),()2,()sin xf x xg x xh x v x x x ====中，属于有界泛函的有． 16.已知向量(,sin )a cosx x =，(cos ,sin )b y y =，若76y x π=+，则向量a 与()a b +的夹角等于__________三、解答题（本大题共6小题，共74分，解答时应写出文字说明、证明过程或演算步骤.）17 某小组中有男生、女生若干人,如果从中选一人参加某项测试，女生被选中的概率是53；如果从中选两人参加测试，两人都是女生的概率为31(每个人被选中是等可能的) .（Ⅰ）求该小组男生、女生各多少人？（Ⅱ）从该小组中选出3人,求男、女生都有的概率；（Ⅲ）若对该小组的同学进行某项测试，其中女生通过的概率为54，男生通过的概率为53，现对该小组中男生甲、乙和女生丙三人进行测试，求至少有2人通过测试的概率。

赣榆高级中学2006-2007学年度高三模拟试卷

赣榆高级中学2006-2007学年度高三模拟试卷数学试卷本试卷分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分.共150分，考试时间120分钟.第Ⅰ卷（选择题，共60分）参考公式：如果事件A 、B 互斥，那么球的表面积公式 24R S π=P(A+B)=P(A)+P(B) 其中R 表示球的半径球的体积公式如果事件A 、B 相互独立，那么 334R V π=球P(A·B)=P(A)·P(B) 其中R 表示球的半径如果事件A 在一次试验中发生的概率是 P ，那么n 次独立重复试验中恰好发生k次的概率k n kk n n P P C k P --=)1()(一、选择题（本大题共12小题，每小题5分，共60分，每小题给出的4个选项中，只有1项是符合题要求的）1．设全集I ={1,2,3,4},集合{1,2}A =,则满足}2{=⋂B A 的集合B 的个数是（） A ．1 B ．3 C ．4 D ．82．已知函数)0(|1|≠-=a ax y 的图象的对称轴方程为x = 2，则a 的值为（）A ．21-B ．21C ．-2D ．23. 教室内有一直尺，无论怎样放置，在地面上总有直线与直尺所在的直线（）A ．异面B ．相交C ．垂直D ．平行4．已知向量)2,1()3,2(-==b a，，若ma b +与 a b -2垂直，则m 等于 ( ）A ． 21-B ． 21C ． 56- D ．565．已知双曲线22a x －22b y ＝1（a ＞0，b ＞0）的右焦点为F ，右准线与一条渐近线交于点A ，△OAF 的面积为22a （O 为原点），则两条渐近线的夹角为（）A ．30ºB ．45ºC ．60ºD ．90º6.若直线02=+-c y x 按向量)1,1(-=平移后与圆522=+y x 相切，则c 的值为（）A ．8或－2B ．6或－4C ．4或－6D ．2或－87.数列{a n }中，a 3=2，a 7=1，且数列}11{+n a 是等差数列，则a 11等于（） A ．—25 B ．12 C ． 23D ．58．函数)(x f 的图象与函数xx g ⎪⎭⎫⎝⎛=21)(的图象关于直线x y =对称，则)2(2x x f -的单调递增区间是 ( )A ． [)+∞,1B (]1,∞-C ． (]1,0D ． [)2,19.某单位要建一圆形喷水池,在水池中央垂直于水面安装一个柱子OP ,OP =1.25m,安置在柱子顶端P 处的喷头向外喷水,抛物线路径如图所示,为使水流形状美观,设计使水流在距离OP 的1m 处到达水的最大高度2.25m,不记其它因素,为使喷出的水不致落到池外,水池的半径至少为 ( ) A ．2.5m B ．4m C ．5m D ．6m 10. 一个棱长都为a 的正三棱柱的六个顶点全部在同一个球面上, 则此球的表面积为( ) A.237a π B. 22a π C ．2411a π D. 234a π第Ⅱ卷（非选择题，共100分）二、填空题（本大题共6个小题，每小题5分，共20分，把答案填在题中的横线上.）11.若P : 2≥x ,Q: 01)2(≥+-x x ,则P 是Q 的 . 12.在n xx )1(-的展开式中，奇数项系数的和为256，则常数项为 .13. 现有6人分乘两辆不同的出租车, 每辆车最多乘4人, 则不同的乘车方案数为 . 14 若316sin =⎪⎭⎫⎝⎛-απ，则⎪⎭⎫ ⎝⎛+απ232cos = ____ _ 15.点C （a ，b ）)0(≠ab 是一定点，过点C 作两条互相垂直的直线1l 和2l ，其中1l 交x 轴于A ，2l 交y 轴于B ，则线段AB 的中点M 的轨迹方程为 . 16．设M 、N 是直角梯形ABCD 两腰的中点，DE ⊥AB 于E (如图)．现将△ADE 沿DE 折起，使二面角A －DE －B 为45°，此时点A 在平面BCDE 内的射影恰为点B ，则M 、N 的连线与AE 所成角的大小等于_________．OABCD EM · · N三、解答题（本大题共6小题，共74分，解答时应写出文字说明、证明过程或演算步骤.）17. （本小题满分12分）某会议室用5盏灯照明，每盏灯各使用灯泡一只，且型号相同.假定每盏灯能否正常照明只与灯泡的寿命有关，该型号的灯泡寿命为1年以上的概率为p 1，寿命为2年以上的概率为p 2.从使用之日起每满1年进行一次灯泡更换工作，只更换已坏的灯泡，平时不换.（1）在第一次灯泡更换工作中，求不需要换灯泡的概率和更换2只灯泡的概率；（2）在第二次灯泡更换工作中，对其中的某一盏灯来说，求该盏灯需要更换灯泡的概率；（3）当p 1=0.8，p 2=0.3时，求在第二次灯泡更换工作，至少需要更换4只灯泡的概率（结果保留两个有效数字）.18. （本小题满分14分）已知向量33(cos,sin ),(cos ,sin )2222x xa x xb ==-，且[0,]2x π∈，设()2||f x a b a b λ=⋅-+．（1）求a b ⋅及||a b +；（2）若()f x 的最小值是32-，求λ的值；（3）若方程()40f x -=有解，求λ的取值范围．19. （本小题满分14分）已知数列{a n }的前n 项和为S n ，且a n 是S n 与2的等差中项；数列{b n }中，b 1=1，点P(b n ,b n+1)在直线x －y ＋2＝0上。

江苏省赣榆高级中学高一数学下学期期末模拟试题苏教版

江苏省赣榆高级中学2012-2013下学期期末模拟高一数学试题一、填空题：本大题共14小题，每小题5分，计70分．1．若{},,sin|RxxyyA∈== ,则自然数=AN I{}1,0．2．函数xxf2tan)(=的单调增区间是Zkkk∈⎪⎭⎫⎝⎛+-;42,42ππππ．3．如下图是样本容量为200的频率分布直方图．根据此样本的频率分布直方图估计，样本数据落在[6,10)内的频数为__64______．4．五个数1，2，3，4，a的平均数是3，这五个数的方差是_ 2 ．5．阅读下图所示的程序框图，运行相应的程序，若输入x的值为－4，则输出y的值为____2____．6．设点P为圆C：4)1(22=+-yx上的任意一点，点Q在直线062=--yx任意一点，则线段PQ长度的取值范围是),25[+∞-．7．已知向量ar，br的夹角为045，且1a=r，210a b-=r r，则b=r23．．8．已知l，m是两条不同的直线，α，β是两个不同的平面，有下列四个命题：①若lβ⊂，且αβ⊥，则lα⊥；②若lβ⊥，且//αβ，则lα⊥；③若lβ⊥，且αβ⊥，则//lα；④若mαβ=I，且//l m，则//lα．则所有正确命题的序号是②．9．正四面体的四个面上分别写有数字1，2，3，4，把两个这样的四面体抛在桌面上，则露在外面的6个数字恰好是2，4，1，3，4，3的概率为81．10．已知圆M：()Rnmnymx∈=-+-,4)()(22，圆M与y轴交于BA,两点，若第5题第3题2||=+,则=|AB 32 ．11．已知,αβ均为锐角，且54cos =α，1tan()3αβ-=-．则βtan 的值等于 913 ．12．已知函数⎪⎩⎪⎨⎧<++≥--=0,0,12)(22x c bx x x x ax x f 是偶函数，直线t y =与函数)(x f y =的图象自左向右依次交于四个不同点D C B A ,,,．若BC AB =，则实数t 的值为 74-．13．已知函数41|1|)(--=x x x f ，则函数)2(x f y =的零点是 1,221log 2-+ ．14．已知O 是锐角△ABC 的外心，AB = 6，AC = 10，若→AO = x →AB ＋y →AC ，且2x ＋10y = 5，则⋅=20 ．二、解答题：本大题6小题，共90分．解答应写出文字说明、证明过程或演算步骤． 15．（本小题满分14分）已知向量)cos ,(cos A B =,)sin ,(sin B A k -=，Csin 53=⋅，其中A 、B 、C 分别是ABC ∆的三内角.（1）求B Atan tan 的值；（2）求tan()A B -的最大值.解析：（1）由Csin 53=⋅CA B B A sin 53cos sin cos sin =-……………………………2分∵π=++C B A ,)sin(sin B A C +=)sin(53cos sin cos sin B A A B B A +=-……………………4分化简得：A B B A cos sin 4cos sin =……………………………………………6分即B Atan tan =4…………………………………………………………………………7分（2）由（1）知：B A tan 4tan =∴B BB A B A B A 2tan 41tan 3tan tan 1tan tan )tan(+=+-=-…………………………………8分B B tan 1tan 43+=…………………………………………………10分由“对勾”函数特性知：函数B B y tan 1tan 4+=，在21tan =B 时的最小值是4. …12分∴43)tan(max =-B A …………………………………………………14分16．（本小题满分14分）已知函数)(,2cos 23cos sin 3)(R x x x x x f ∈-=（1）求函数()f x 的最小正周期；（2）若函数()f x 满足)()(x m f m x f -=+，试求实数m 的最小正值．解x x x x f 2cos 23cos sin 3)(-==]2cos 212sin 23[3x x -………………………… 2分)62sin(3π-=x ………4分∴ T=2π2 =π……………………………6分(Ⅱ) 函数()f x 满足)()(x m f m x f -=+即函数()f x 图像的对称轴是m x =即当m x =时f(x)取最大（小）值时,=-)62sin(πm ±1, ……10分所以=-62πm kπ+π2即322ππ+=k m (k ∈Z) ……………… 13分∴所求实数m 的最小正值是32π, ……………… 14分17．（本小题满分15分）某高校从参加今年自主招生考试的学生中随机抽取容量为50的学生成绩样本，得频率分布表如下：（1）写出表中①②位置的数据；（2）为了选拔出更优秀的学生，高校决定在第三、四、五组中用分层抽样法抽取6名学生进行第二轮考核，分别求第三、四、五各组参加考核人数；（3）在（2）的前提下，高校决定在这6名学生中录取2名学生，求2人中至少有1名是第四组的概率．解：（2）3，2，1 （2）3/5 18．（本小题满分15分）已知关于x 的一元二次方程222(2)160x a x b ---+=. （1）若a b 、是一枚骰子掷两次所得到的点数，求方程有两正根的概率；（2）若[][]6,0,4,2∈∈b a ，求方程没有实根的概率.解：设“方程有两个正根”的事件为A ，（1）由题意知本题是一个古典概型用（a ，b ）表示一枚骰子投掷两次所得到的点数的事件依题意知，基本事件（a ，b ）的总数有36个二次方程x2-2（a-2）x-b2+16=0有两正根，等价于⎪⎩⎪⎨⎧≥-+-=∆>->-0)16(4)2(401602222b a b a ，⎪⎩⎪⎨⎧≥+-<<->16)2(44222b a b a ……………………………4分则事件A 包含的基本事件为（6，1）、（6，2）、（6，3）、（5，3）共4个………6分∴所求的概率为P(A)=91……………………………7分（2）由题意知本题是一个几何概型，试验的全部结果构成区域Ω={（a ，b ）|2≤a≤4，0≤b≤6}，……………………………8分其面积为S （Ω）=12……………………………9分满足条件的事件为：B={（a ，b ）|2≤a≤4，0≤b≤6，（a-2）2+b2＜16}……… ……10分其面积为S(B)=44621⨯⨯⨯π+2224221-⨯⨯=3234+π………………………14分 ∴所求的概率P （B ）=18332+π……………………………15分19．（本小题满分16分）如图，在直角坐标系xOy 中，已知圆O ：x2＋y2＝4，点A(1，0)，B 为直线x ＝4上任意一点，直线AB 交圆O 于不同两点M ，N ．（1）若14=MN ，求点B 的坐标；（2）若→MA ＝2→AN ，求直线AB 的方程；（3）设→AM ＝λ→MB ，→AN ＝μ→NB ，求证：λ＋μ为定值． 25．（1）解: 设直线AB 的方程)1(-=x k y ,即0=--k y kx22,2214,1422=-=∴=d d MN Θ，1,221||2±==+k k k ，直线AB 的方程)1(-±=x y ,因为3,4±=∴=B B y x ,所以)3,4(±B 。

江苏省赣榆高级中学2015～2016学年度高三年级高考前热身训练(无附加部分)

江苏省赣榆高级中学2015～2016学年度高三年级高考前热身训练高三数学试题（必做题）一、填空题：（本大题共14小题，每小题5分，计70分，不需写出解答过程，请把答案写在答题纸的指定位置上.） 1.抛物线214y x =-的准线方程是 ▲ ．1y = 2. 若五个数1,2,3,4，a 的平均数为3，则这五个数的标准差是 ▲ ．3，可知5a =，由()()()()()222222113233343535S ⎡⎤=-+-+-+-+-⎣⎦2=，得标准差S =3.右边程序输出的结果是 ▲ ．【答案】10考点：循环结构流程图4.采用系统抽样方法从420人中抽取21 人做问卷调查，为此将他们随机编号为1，2，…，420，则抽取的21人中，编号落入区间[]241,360上的人数为．6 5.从集合{1，2，3}中随机取一个元素，记为a ，从集合{2，3，4}中随机取一个元素，记为b ，则a ≤b 的概率为 ▲ ．【答案】896. 设{}{}2|230,|10,,A x x x B x ax B A =--==-=⊆则实数a 的取值集合为▲ ．10,1,3⎧⎫-⎨⎬⎩⎭7. 已知矩形ABCD 的边4=AB ，3=BC 若沿对角线AC 折叠，使得平面DAC ⊥平面BAC ,则三棱锥ABC D -的体积为．【命题意图】本题考查棱锥的体积，考查空间想象能力和运算求解能力．【答案】245【解析】因为平面DAC ⊥平面BAC ,所以D 到直线BC 距离为三棱锥ABC D -的高，134123412346,,25555ABC S h h ∆⨯⨯=⨯⨯=====11122463355D ABC ABC V S h -∆=⋅=⨯⨯=．8.已知()π02α∈，，()ππ2β∈，，1cos 3β=-，()7sin 9αβ+=．则=αsin ▲ ．319.已知双曲线)0,0(12222>>=-b a by a x 的渐近线与圆1)2(22=++y x 没有公共点，则该双曲线的离心率的取值范围为 ▲ ．)2,1(10. 在平面直角坐标系xOy 中，已知点,A B 分别为x 轴，y 轴上一点，且2AB =，若点P ，则||++的取值范围是 ▲ ． [7,11]11. 已知数列{}n a 的前n 项和 1 ()n n S k k =-∈R ，且{}n a 既不是等差数列，也不是等比数列，则k 的取值集合是 ▲ ．【答案】{}0．12.在平面直角坐标系x O y 中，若直线l 与圆C 1：221x y +=和圆C 2：((2249x y -+-= 都相切，且两个圆的圆心均在直线l 的下方，则直线l 的斜率为 ▲ ．【答案】7【解析】设两切点分别为A 、B ，连结AC 1、BC 2，过C 1作C 1D //AB 交BC 2于点D ，得到直角三角形C 1C 2D ，易得tan ∠D C 1C 2 =34，而∠xC 1C 2=π4，所以tan ∠D C 1 x=tan ()12DC C π∠+4=7，即直线l 的斜率是7；13. 已知函数),0(|sin |)(R k x kx x x f ∈≥-=有且只有三个零点，设此三个零点中的最大值为0x ，则20(1)sin 2x x x +＝ ▲ ．12B1BANM1C C1A14. 设函数()332x x f x x -=--，则满足12(2)(log )0x f x -<的x 的取值范围是 ▲ ．【答案】(0,1)(2,)+∞【解析】试题分析：()3ln33ln32(33)ln322ln320x x x x f x --'=+-=+-≥->，∴函数()f x 在(,)-∞+∞上单调递增，且(0)0f =，112220(2)(log )0log 0x x f x x ->⎧⎪∴-<⇔⎨<⎪⎩或1220log 0x x -<⎧⎪⎨>⎪⎩，解得2x >或01x <<．二、解答题：（本大题共6小题，计90分.解答应写出必要的文字说明，证明过程或演算步骤，请把答案写在答题纸的指定区域内.）15．（本题满分14分）如图，在xoy 平面上，点(1,0)A ，点B 在单位圆上，AOB θ∠=（0θπ<<）（1）若点34(,)55B -，求tan()4πθ+的值；（2）若=+，1318=⋅，求cos()3πθ-．15. （1）由于34(,)55B -，AOB θ∠=，所以3cos 5θ=-，4sin 5θ= ，所以4tan 3θ=-，所以1tan 1tan()41tan 7πθθθ++==-- ；（2）由于(1,0)OA =,(cos ,sin )OB θθ=,所以(1cos ,sin )OC OA OB θθ=+=+, 22218cos (1cos )sin cos cos sin 13OC OB θθθθθθ⋅=⨯++=++=. 所以5cos 13θ=，所以12sin 13θ=，所以cos()coscos sinsin 333πππθθθ-=+=16．如图，在直三棱柱111C B A ABC -中，BC AC ⊥，41=CC ，M 是棱1CC 上的一点．（1）求证：AM BC ⊥；（2）若N 是AB 的中点，且CN ∥平面M AB 1，求CM 的长．【解】（1）因为111ABC A B C -是直三棱柱，所以1CC ⊥平面ABC ，因为BC ⊂平面ABC ，所以1CC BC ⊥． ……………………2分因为AC BC ⊥，1CC AC C =，1CC AC ⊂，平面11ACC A ，所以BC ⊥平面11ACC A ． ………………………………………………… 4分因为AM ⊂平面11ACC A ，所以BC AM ⊥． …………………………… 6分（2）证法一：如图1，取1AB 的中点P ，连结NP ，PM ．因为N 是AB 的中点，所以1//NP BB ，… 8分因为1//CM BB ，所以//NP CM ，所以NP 与CM 共面． …………………10分因为CN ∥平面1AB M ，平面CNPM平面1AB M MP =，所以//CN MP ．………………………………………………………………12分所以四边形CNPM 为平行四边形，所以1122CM NP CC ===． ……………………………………………… 14分、17．（本题满分14分）现有一个以OB OA , 为半径的扇形池塘，在OB OA , 上分别取点D C , ，作DE ∥OA 、CF ∥OB 交弧AB 于点F E , ，且AC BD =，现用渔网沿着FC OF EO DE ,,, 将池塘分成如图所示的三种的养殖区域．若km OA 1= ，π2AOB ∠=，π(0)2EOF θθ∠=<<．（1）求区域Ⅱ的总面积；PB1BANM1C C图11A（第17题）（2）若养殖区域Ⅰ、Ⅱ、Ⅲ的每平方千米的年收入分别是15万元、20万元、10万元，记年总收入为y 万元．试问当θ为多少时，年总收入最大？【答案】（1）II 1=cos 2S θ区域，π(0)2θ<<．（2）π6【解析】试题分析：（1）由BD = AC 得，OD OC =，所以1π()22COF θ∠=-，1πcos cos[()]22OC OF COF θ=⋅∠=-，11sin cos 24COF S OC OF COF θ∆=⋅⋅⋅∠=，II 1=cos 2S θ区域，定义域为π02θ<<；（2）先分别求出各区域面积，再建立函数关系：I 12S θ=区域，III I II π11cos 422S S S S θθ=--=--总区域区域区域，11π111520cos 10(cos )22422y θθθ=⨯+⨯+⨯--55ππ5cos (0)222θθθ=++<<，，最后利用导数求其最值试题解析：（1）因为BD AC OB OA ==，，所以OD OC =．因为π2EOF ∠=，DE ∥OA ，CF ∥OB ，所以DE OB CF OA ⊥⊥，．又因为OE OF =，所以Rt ODE ∆≌Rt OCF ∆．所以1π()22DOE COF COF θ∠=∠∠=-，． ………………………………2分所以1πcos cos[()]22OC OF COF θ=⋅∠=-．所以11sin cos 24COF S OC OF COF θ∆=⋅⋅⋅∠=，所以II 1=cos 2S θ区域，π(0)2θ<<． …………………………………6分（2）因为I 12S θ=区域，所以III I II π11cos 422S S S S θθ=--=--总区域区域区域．所以11π111520cos 10(cos )22422y θθθ=⨯+⨯+⨯--55ππ5cos (0)222θθθ=++<<，， …………………………………10分所以5(12sin )2y θ'=-，令=0y '，则π=6θ． …………………………………12分当π6θ<<0时，0y '>，当ππ62θ<<时，0y '<．(第18题)故当π=6θ时，y 有最大值．答：当θ为π6时，年总收入最大． …………………………………14分考点：函数应用，利用导数求函数最值18．（本题满分16分）定义：如果一个菱形的四个顶点均在一个椭圆上，那么该菱形叫做这个椭圆的内接菱形，且该菱形的对角线的交点为这个椭圆的中心．如图，在平面直角坐标系xOy 中，设椭圆2214x y +=的所有内接菱形构成的集合为F ．（1）求F 中菱形的最小的面积；（2）是否存在定圆与F 中的菱形都相切?若存在，求出定圆的方程；若不存在，说明理由；（3）当菱形的一边经过椭圆的右焦点时，求这条边所在的直线的方程．解：（1）如图，设11( )A x y ，，22( )B x y ，，1︒当菱形A B C D 142142⨯⨯⨯=； 2︒当菱形ABCD AC 的方程为：y kx =，①则直线BD 的方程为：1y x k=-又椭圆2214x y +=，由①②得，212441x k =+，2212441k y k =+ 从而22221124(1)41k OA x y k +=+=+，同理可得，()()2222222221414(1)4141kk OB x y k k⎡⎤-+⎢⎥+⎣⎦=+==+-+，（3分）所以菱形ABCD 的面积为2OAOB ⨯⨯====≥165=(当且仅当1k =±时等号成立), 综上得，菱形ABCD 的最小面积为165；（6分）（2）存在定圆2245x y +=与F 中菱形的都相切，设原点到菱形任一边的距离为d ，下证：d证明：由(1)知，当菱形ABCD的对角线在坐标轴上时，d ，当菱形ABCD 的对角线不在坐标轴上时，22222OA OB d OA OB ⨯=+222222224(1)4(1)4144(1)4(1)414k k k k k k k k ++⨯++=+++++ 2222224(1)(1)(4)(1)(41)k k k k k +=+++++22224(1)45(1)(55)k k k +==++，即得d =，综上，存在定圆2245x y +=与F 中的菱形都相切；（12分）（3）设直线AD的方程为(y t x =-，即0tx y -=，则点(0 0)O ，到直线AD解得t =所以直线AD的方程为y x =．（16分）19．已知函数()()322152f x x k k x x =--++-，()221g x k x kx =++，其中k ∈R ．（1）设函数()()()p x f x g x =+，若()p x 在区间（0,3）是单调函数，求k 的取值范围；（2）设函数()()(),0,0g x x q x f x x ⎧≥⎪=⎨<⎪⎩，是否存在实数k ，对任意给定的非零实数1x ，存在惟一的非零实数()221x x x ≠，使得()()21q x q x ''=成立？若存在，求k 的值；若不存在，请说明理由．【答案】（1）因32()()()(1)(5)1P x f x g x x k x k =+=+-++- ()232(1)(5)p x x k x k '=+-++， ∵()p x 在区间(0,3)上单调．．恒成立或00≤'≥'∴)()(x P x P)523()12()523()12(22+--≤++--≥+x x x k x x x k 或即恒成立01230>+∴∈x x ),( ∴125231252322++--≤++--≥x x x k x x x k 或恒成立设()()2325391*********x x F x x x x -+⎡⎤=-=-++-⎢⎥++⎣⎦令21,t x =+有()1,7t ∈，记9(),h t t t =+由函数()h t 的图像可知，()h t 在(]1,3上单调递减，在[)3,7上单调递增， ∴()[)6,10h t ∈，于是],()(25--∈x F ∴ 5,2-≤-≥k k 或（2）当0x <时有()()2232(1)5q x f x x k k x ''==--++；当0x >时有()()22q x g x k x k ''==+，因为当0k =时不合题意，因此0k ≠，……8分下面讨论0k ≠的情形，记}|)({},|)({00<'=>'=x x f B x x g A 求得 A (,)k =+∞，B=()5,+∞（ⅰ）当10x >时，()q x '在()0,+∞上单调递增，所以要使()()21q x q x ''=成立，只能20x <且A B ⊆，因此有5k ≥（ⅱ）当10x <时，()q x '在()0,+∞上单调递减，所以要使()()21q x q x ''=成立，只能20x >且A B ⊆，因此5k ≤综合（ⅰ）（ⅱ）5k =当5k =时A=B ，则()110,x q x B A '∀<∈=，即20,x ∃>使得()()21q x q x ''=成立，因为()q x '在()0,+∞上单调递增，所以2x 的值是唯一的；…13分同理，10x ∀<，即存在唯一的非零实数221()x x x ≠，要使()()21q x q x ''=成立，所以5k =满足题意.20.（本小题满分16分）设()k f n 为关于n 的k ()k ∈N 次多项式．数列{a n }的首项11a =，前n 项和为n S ．对于任意的正整数n ，()n n k a S f n +=都成立．（1）若0k =，求证：数列{a n }是等比数列；（2）试确定所有的自然数k ，使得数列{a n }能成等差数列．解：（1）若0k =，则()k f n 即0()f n 为常数，不妨设0()f n c =（c 为常数）．因为()n n k a S f n +=恒成立，所以11a S c +=，即122c a ==．而且当2n ≥时，2n n a S +=， ①112n n a S --+=，② ①－②得 120(2)n n a a n n --=∈N ，≥．若a n =0，则1=0n a -，…，a 1=0，与已知矛盾，所以*0()n a n ≠∈N ．故数列{a n }是首项为1，公比为12的等比数列．（4分）（2）(i) 若k =0，由（1）知，不符题意，舍去．（6分） (ii) 若k =1，设1()f n bn c =+（b ，c 为常数），当2n ≥时，n n a S bn c +=+， ③ 11(1)n n a S b n c --+=-+， ④ ③－④得 12(2)n n a a b n n --=∈N ，≥．要使数列{a n }是公差为d （d 为常数）的等差数列，必须有n a b d =-（常数），而a 1=1，故{a n }只能是常数数列，通项公式为a n =1()*n ∈N ，故当k =1时，数列{a n }能成等差数列，其通项公式为a n =1()*n ∈N ，此时 1()1f n n =+．（9分） (iii) 若k =2，设22()f n an bn c =++（0a ≠，a ，b ，c 是常数），当2n ≥时，2n n a S an bn c +=++， ⑤ 211(1)(1)n n a S a n b n c --+=-+-+， ⑥ ⑤－⑥得 122(2)n n a a an b a n n --=+-∈N ，≥，要使数列{a n }是公差为d （d 为常数）的等差数列，必须有2n a an b a d =+--，且 d =2a ，考虑到a 1=1，所以1(1)2221n a n a an a =+-⋅=-+()*n ∈N ．故当k =2时，数列{a n }能成等差数列，其通项公式为221n a an a =-+()*n ∈N ，此时22()(1)12f n an a n a =+++-（a 为非零常数）．（12分）(iv) 当3k ≥时，若数列{a n }能成等差数列，则n n a S +的表达式中n 的最高次数为2，故数列{a n }不能成等差数列．（14分）综上得，当且仅当k =1或2时，数列{a n }能成等差数列．（16分）附加题（理科做）21B. 选修4—2：矩阵与变换已知矩阵A ＝⎣⎡⎦⎤a 11a ，直线l ：x －y ＋4＝0在矩阵A 对应的变换作用下变为直线l '：x －y ＋2a ＝0．（1）求实数a 的值；（2）求A 2．21C 选修4—3：坐标系与参数方程在直角坐标系中，以原点为极点，x 轴的正半轴为极轴建立极坐标系，两种坐标系取相同的单位长度．已知曲线1325: 45x t C y t ⎧=+⎪⎪⎨⎪=⎪⎩（t 为参数）和曲线22:sin 2cos C ρθθ=相交于A B 、两点，求AB 中点的直角坐标．【必做题】第22题、第23题，每题10分，共计20分.解答应写出必要的文字说明、证明过程或演算步骤．22．设集合{}5,4,3,2,1=S ，从S 的所有非空子集中，等可能地取出一个.（1）设S A ⊆，若A x ∈，则A x ∈-6，就称子集A 满足性质p ，求所取出的非空子集满足性质p 的概率；（2）所取出的非空子集的最大元素为ξ，求ξ的分布列和数学期望()ξE .【命题意图】本题考查子集定义及性质、古典概型及离散型随机变量分布列和期望等基础知识，意在考查分析问题和解决问题能力，运算求解能力，逻辑思维能力．【解析】可列举出集合S 的非空子集的个数为：31125=-个.（2分）（1）满足性质p 的非空子集为：{}3，{}5,1，{}4,2，{}5,3,1，{}4,3,2，{}5,4,2,1，{}5,4,3,2,1共7个，所以所取出的非空子集满足性质p 的概率为： 317=p .（6分）（2）ξ的可能值为1，2，3，4，5.（9分）()31129311653184314331223111=⨯+⨯+⨯+⨯+⨯=ξE .（10分） 23．设()n n n f n -⎪⎭⎫ ⎝⎛+=11，其中n 为正整数．（1）求)1(f ，)2(f ，)3(f 的值；（2）猜想满足不等式0)(<n f 的正整数n 的范围，并用数学归纳法证明你的猜想．由①②可知，对0)11()(,3<-+=≥n n n f n n 成立 .。

江苏省赣榆高级中学2008届高三年级第二次阶段检测数学(理)

20．（本小题满分14分）已知
（Ⅰ）求；（Ⅱ）若，求的取值范围。
21．（本小题满分14分）某厂家拟在2008年举行促销活动，经调查测算，该产品的年销售
量（即该厂的年产量）x万件与年促销费用万元（（k为常数），如果不搞促销活动，则该产品的年销售量只能是1万件。已知2008年生产该产
品的固定投入为8万元，每生产1万件该产品需要再投入16万元，厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍（产品成本包括固定投入和再投入两部分资金,不包括促销费用）．
所以――――――6分（Ⅱ）当时，。转化为：，从而。
――――――――――――――12分
请在各题规定的黑色矩形区域内答题，超出该区域的答案无效！请在各题规定的黑色矩形区域内答题，超出该区域的答案无效！得评卷分人 18.（本小题满
分12分）
解：（Ⅰ） …………………3分 ∴函数f(x)的最小正周期 …………………… 4分令，解得 ∴函数f(x)的单调递减区间是 ……6分
11．_________________；12．___5__________________；
13．_______________；14．______________；
15．____________________；16．________________。
三．解答题
得评分卷
人
17. （本小题满分12分）解：（Ⅰ）
0
1
2
3
0.37
1
2.72 7.39 20.09
1
2
3
4
5
A (—1，0)
B （0，1）
C （1，2）
D
（2，3）
3．若，则下列不等式：①② ③ ④中，正确的不等式有

赣榆

0 0
3
…………1１分
数列{an }是以首项为1, 公差为1的等差数列数列{an }的通项公式为an n
…………10 分
（3） an n,bn 3n (1)n1 2n
所以 60 时， y 取最大值.
0
…………1３分
要使bn 1 bn 恒成立,即bn 1 bn 3n 1 3n (1)n 2n 1 (1)n 1 2n 2 3n 3 (1)n1 2n 0恒成立
3 ②当n为偶数时, 即 ( ) n 1 恒成立 2 3 n 1 3 3 又-( ) 的最大值为- , 2 2 2 3 即- 1，又 0且为整数 2 1, 使得对任意n N , 都有bn 1 bn
…………15 分
①
2 n 1
2 x0 3y2 0 =1， 4 4
F G
R H
F
A
R H
2 | MN |2 x0 ( y0 2) 2 = 2( y0 1) 2 10，其中
3 3 y0 …………11 分 2 2
…………14 分
G 18 题图
18.解析：吊车能把球形工件吊上的高度 y 取决于吊臂的张角，由图可知，
49 ，请写出 x i 的所有项 65
开始输入 x0
.(答:
11 1 或 ) 5 19
．（答：0）
i=1
y x
i=i+1 输出 xi
3．函数 y 3
1 1 x
的值域是
． (0,1) (1, ) .
x1=f （xi-1）
xi∈D 否结束
4．在平行四边形 ABCD 中，点 A, B, C 对应的复数分别是 4 i, 3 4i, 3 5i ，则点 D 对应的复数是（答： 4 8i )

江苏省赣榆县海头高级中学高二下学期期末模拟考试数学理科试题

一、填空题（本大题共16分，每题5分，共80分）1、2(1i)1+i a b +=-（a b ∈R ,，i 是虚数单位），则i a b += ．2、将甲、乙两个球随机放入编号为1，2，3的3个盒子中，每个盒子的放球数量不限，则在1，2号盒子中各有1个球的概率为 .3、将参数方程2sin ,(cos ,x y θθθ=⎧⎨=⎩为参数，且[0,2)θπ∈化为普通方程为 . 4、“/0()0f x =”是“0()f x 是函数()y f x =的极值”的条件.5、已知,a b R ∈，若1 3a b -⎡⎤=⎢⎥⎣⎦M 所对应的变换M T 把直线:23l x y -=变换为自身，则 a b -= .6、某人每次射击命中目标的概率为0.8，现连续射击3次，则击中目标的次数X 的方差为 .7、等差数列{}n a 中，已知158≥a ，139≤a ，则12a 的取值范围是 .8、在ABC ∆中,60ACB ∠=,sin :sin 8:5A B =,则以,A B 为焦点且过点C 的椭圆的离心率为 .9、已知a ，b 为正实数，函数xbx ax x f 2)(3++=在[]1,0上的最大值为4，则)(x f 在[]0,1-上的最小值为 . 10、观察下列等式： 311=， 33129+=， 33312336++=，33331234100+++=，……猜想：3333123n +++⋅⋅⋅+= （n ∈*N ）11、设,x y 满足约束条件1210,0≤+⎧⎪≥-⎨⎪≥≥⎩y x y x x y ,若目标函数()0,0z abx y a b =+>>的最大值为35则a b +的最小值为 .12、已知双曲线2221x y m-=的一条渐近线方程为02=-y x ,则m = .13、数()=+f x x t *∈N ）的最大值是正整数M ，则M = ． 14，则该三角形的面积的最大值是．15、设)(n u 表示正整数n 的个位数，)()(2n u n u a n -=，则数列{}n a 的前2012项和等于 .16、等式2210843≥k x y xy+对于任意正实数x ，y 总成立的必要不充分条件是[),k m ∈+∞，则正整数m 只能取．二、解答题17、（14分）在平面直角坐标系xOy 中，直线y kx =在矩阵0110⎡⎤⎢⎥⎣⎦对应的变换下得到的直线过点(41)P , ，求实数k 的值．18、（14分）已知极坐标系的极点在直角坐标系的原点，极轴与x 轴的正半轴重合，曲线C的极坐标方程2222,cos 3sin 3,(,).1x l t t y tρθρθ⎧=⎪+=∈⎨=+⎪⎩R 直线的参数方程为为参数试在曲线C 上求一点M ，使它到直线l 的距离最大.19、（14分）甲、乙、丙三名射击运动员射中目标的概率分别为1,,2a a (01)a <<，三人各射击一次，击中目标的次数记为ξ. （1）求ξ的分布列及数学期望；（2）在概率()P i ξ=(i =0，1，2，3)中, 若(1)P ξ=的值最大, 求实数a 的取值范围.20、（15分）如图，已知正方形ABCD 和矩形ACEF 所在的平面互相垂直，2AB =，1AF =．（1）求直线DF 与平面ACEF 所成角的正弦值；（2）在线段AC 上找一点P ，使PF 与DA 所成的角为60，试确定点P 的位置．21、（15分）已知230123(1)(1)(1)(1)(1)n n n x a a x a x a x a x +=+-+-+-++-，（其中n N *∈）⑴求0a 及123n n S a a a a =++++；⑵试比较n S 与2(2)22nn n -+的大小，并说明理由．22、（16分）如图，在平面直角坐标系xOy 中，椭圆C ：22221x y a b +=（0a b >>）的左焦点为F ，右顶点为A ，动点M 为右准线上一点（异于右准线与x 轴的交点），设线段FM 交椭圆C 于点P ，已知椭圆C 的离心率为23，点M 的横坐标为92．（1）求椭圆C 的标准方程；（2）设直线PA 的斜率为1k ，直线MA 的斜率为2k ，求12k k ⋅ 的取值范围．23、已知数列{}n a 满足)(11*+∈-=N n a a nn（1）若451=a ，求n a ；（2）若),(),1,(1*∈+∈=N k k k a a ，求{}n a 的前k 3项的和k S 3（用a k ,表示）24、（16分）已知函数2()ln f x x mx n x =++（0x >，实数m ，n 为常数）．（1）若230n m +=（0m >），且函数()f x 在[1,)x ∈+∞上的最小值为0，求m 的值；（2）若对于任意的实数[1,2]a ∈，1b a -=，函数()f x 在区间(,)a b 上总是减函数，对每个给定的n ，求m 的最大值h (n )．。