复旦20002006自主招生数学试题
复旦自主招生试题及答案

复旦自主招生试题及答案一、语文部分阅读理解:1. 阅读下面短文,回答问题。
(1)张謇(1854-1926)是中国现代教育家、政治家、社会活动家和思想家。
张謇曾于光绪十九年(1893年)中策划创办私立南洋公学,为中国留学生出国深造提供了机会,也为中国教育事业的发展做出了巨大贡献。
(2)南洋公学的创建者张謇,生于一般家庭,自小勤奋好学。
他上学时就常常帮助同学,与人为善,仗义疏财。
他在学习中总是能将分散的学习知识联系起来,形成系统地知识体系,且能应用灵活。
在上学期间,他还考取了举人资格。
(3)1875年,张謇考入了南洋公学,他将自己多年的积累展示了出来,并在广大师生的面前,发表了知名的《自力更生》演讲。
这个演讲使他备受赞誉,也为他未来的事业奠定了基础。
(4)张謇毕业后曾出任江西体育局局长,任内积极推行体育运动,提倡健身,改变了当时青年学生体育锻炼不足的状况。
后来,他还出任过官员、教育家等多个职位,努力改革中国教育制度,致力于提高教育的普及率和质量。
(5)张謇还通过创办南京高级工业学堂(复旦大学前身),来培养工科人才。
这一举措对中国的现代工业化进程起到了积极作用。
张謇还参与了辛亥革命,成为众多反清护国的活动家之一。
问题:(1)张謇是中国的哪位教育家和思想家?(2)张謇曾任职的机构有哪些?(3)南京高级工业学堂现在的名称是什么?答案:(1)张謇是中国现代教育家、政治家、社会活动家和思想家。
(2)张謇曾任江西体育局局长,官员和教育家等多个职位。
(3)南京高级工业学堂现在的名称是复旦大学。
二、数学部分选择题:1. 已知函数 f(x) = 2x + 3,求 f(4) 的值。
A. 7B. 9C. 11D. 132. 若 a + b = 20,且 a:b = 2:3,则 a 的值为多少?A. 8B. 10C. 12D. 16填空题:1. C = πd 的公式中,若 d = 10cm,则 C = ______ cm。
2006年复旦大学自主招生数学试题(精校word版,无答案)-历年自主招生考试数学试题大全

2006年复旦大学自主招生考试数学试题选择题(共150分,每题5分,答对得5分,答错倒扣2分,不答得0分)1.在(x2−1x)10的展开式中系数最大的项是_____.A.第4、6项B.第5、6项C.第5、7项D.第6、7项2.设函数y=ƒ (x)对一切实数x均满足ƒ (5+x)=ƒ(5−x),且方程ƒ (x)=0恰好有6个不同的实根,则这6个实根的和为____.学科网A.10 B.12 C.18 D.303.若非空集合X={x|a+1≤x≤3a−5},Y={x|1≤x≤16},则使得X⊆X∪Y成立的所有a的集合是_____.A.{a|0≤a≤7}B.{a|3≤a≤7}C.{a|a≤7}D.空集4.设z为复数,E={z|(z−1)2=|z−1|2},则下列_ __是正确的A.E={纯虚数} B.E={实数}C.{实数}⊆E⊆{复数} D.E={复数}5.把圆x2+(y−1)2=1与椭圆x2+2(1)9y+=1的公共点,用线段连接起来所得到的图形为_____.A.线段B.等边三角形C.不等边三角形D.四边形6.在正三棱柱ABC—A1B1C1中,若AB=2BB1,则AB1与C1B所成的角的大小是___.A.60°B.75°C.90°D.105°7.某厂拟用集装箱托运甲乙两种货物,每箱的体积、重量、可获利润以及托运所受限制如下表所示:货物体积每箱(米3)重量每箱(吨)利润每箱(百元)甲20 10 8乙10 20 10托运限制110 100在最合理的安排下,获得的最大利润是______百元.A.58 B.60 C.62 D.648.若向量a+3b垂直于向量7a−5b,并且向量a−4b垂直于向量7a−2b,则向量a与b的夹角为___ .A .2π; B .3π; C .4π; D .6π. 9.复旦大学外语系某年级举行一次英语口语演讲比赛,共有十人参赛,其中一班有三位,二班有两位,其它班有五位.若采用抽签的方式确定他们的演讲顺序,则一班的三位同学恰好演讲序号相连.问二班的两位同学的演讲序号不相连的概率是____.A .120 B .140 C .160 D .19010.已知sin α,cos α是关于x 的方程x 2−αx +α=0的两个根,这里α∈R .则3sin α+3cos α=___. A .−1−2; B .1+2; C .−2+2 D .2−2 11.设z 1,z 2为一对共轭复数,如果|z 1−z 2|=6且122z z 为实数,那么|z 1|=|z 2|=____. A .2 B .2 C .3 D .612.若四面体的一条棱长是x ,其余棱长都是1,体积是V (x ),则函数V (x )在其定义域上为____. A .增函数但无最大值 B .增函数且有最大值 C .不是增函数且无最大值 D .不是增函数但有最大值 13.下列正确的不等式是____. A .16<12011k k =∑<17; B .18<12011k k =∑<19; C .20<12011k k =∑<21; D .22<12011k k =∑<23. 14.设{αn }是正数列,其前n 项和为S n ,满足:对一切n ∈Z +,αn 和2的等差中项等于S n 和2的等比中项,则limnx n→∞α=______.A .0B .4C .12D .10015.已知x 1,x 2是方程x 2−(α−2)x +(α2+3α+5)=0(α为实数)的两个实根,则x 12+x 22的最大值为______. A .18 B .19 C .20 D .不存在 16.条件甲:1sin θ+=α.条件乙:sin2θ+cos 2θ=α.则下列________是正确的. A .甲是乙的充分必要条件 B .甲是乙的必要条件C .甲是乙的充分条件D .甲不是乙的必要条件,也不是充分条件 17.已知函数ƒ(x )的定义域为(0,1),则函数g (x )= ƒ(x +c )+ƒ(x −c )在0<c<12时的定义域为____.A.(−c,1+c); B.(1−c,c); C.(1+c,−c); D.(c,1−c);18.函数y=2x+12x-的最值为____.A.y min=54-,y ma x=54;B.无最小值,y ma x=54;C.y min=54-,无最大值D.既无最小值也无最大值19.等差数列{αn}中,α5<0,α6>0且α6>|α5|,S n是前n项之和,则下列___是正确的.A.S1,S2,S3均小于0,而S4,S5,…均大于0B.S1,S2,…,S5均小于0,而S6,S7,…均大于0C.S1,S2,…,S9均小于0,而S10,S11,…均大于0D.S1,S2,…,S10均小于0,而S11,S12,…均大于020.已知角θ的顶点在原点,始边为x轴正半轴,而终边经过点Q(3-,y),(y≠0),则角θ的终边所在的象限为___.A.第一象限或第二象限B.第二象限或第三象限C.第三象限或第四象限D.第四象限或第一象限21.在平面直角坐标系中,三角形△ABC的顶点坐标分别为A(3,4),B(6,0),C(−5,−2),则∠A的平分线所在直线的方程为_____.A.7x−y−17=0; B.2x+y+3=0; C.5x+y−6=0; D.x−6y=0.22.对所有满足1≤n≤m≤5的m,n,极坐标方程11cosnmCθρ=-表示的不同双曲线条数为_____.A.6 B.9 C.12 D.1523.设有三个函数,第一个是y=ƒ(x),它的反函数就是第二个函数,而第三个函数的图像与第二个函数的图像关于直线x+y=0对称,则第三个函数是______.A.y=−ƒ(x);B.y=−ƒ(−x);C.y=−ƒ−1(x);D.y=−ƒ−1(−x);24.设ƒ(x)是定义在实数集上的周期为2的周期函数,且是偶函数.已知当x∈[2,3]时,ƒ(x)=x,则当x∈[−2,0]时,ƒ(x)的解析式为_____.A.x+4; B.2−x; C.3−|x+1|; D.2+|x+1|.25.已知α,b为实数,满足(α+b)59=−1,(α−b)60=1,则α59+α60+b59+b60=_____.A .−2B .−1C .0D .126.设αn 是(2−x )n的展开式中x 项的系数(n=2,3,4,…),则极限2323222lim()nx n→∞+++ααα…=________.A .15B .6C .17D .827.设x 1,x 2∈(0,2π),且x 1≠x 2,不等式成立的有 (1)12(tan x 1+tan x 2)>tan 122x x +; (2) 12(tan x 1+tan x 2)<tan 122x x +;(3)12(sin x 1+sin x 2)>sin 122x x +; (4) 12(sin x 1+sin x 2)>sin 122x x +A .(1),(3)B .(1),(4)C .(2),(3)D .(2),(4)28.方程ƒ(x )=213222123333235x x x x x x x x x ---------=0的实根的个数为_______.A .1个B .2个C .3个D .无实根29.如图所示,半径为r 的四分之一的圆ABC 上,分别以AB 和AC 为直径作两个半圆,分别标有α的阴影部分面积和标有b 的阴影部分面积,则这两部分面积α和b 有_____.CBAbaA .α>bB .α<bC .α=bD .无法确定30.设a ,b 是不共线的两个向量.已知PQ =2a +k b ,QR =a +b ,RS =2a −3b .若P ,Q ,S 三点共线,则k 的值为_____.A .−1;B .−3;C .43-; D .35-;历年自主招生考试数学试题大全专题下载链接:/a760682.html链接打开方法:1、按住ctrl键单击链接即可打开专题链接2、复制链接到网页。
复旦大学自主招生试题数学

复旦大学自主招生数学1、当a和b取遍所有实数时,函数f a,b=a+5−3cos+a−2sin所能取到的最小值()2、记2012!=1×2×3×⋯×2012从1到2012之间所有整数的连乘积,则2012!的值的尾部(从个位往前计数)连续的0的个数是()3、已知数列a n满足:3a n+1+a n=4n≥1,且a1=9,其前n项和为S n,则满足不等式S n−n−6<1125的最小整数n是()4、在如果所示三棱柱中,点A、BB1的中点M以及B1C1的中点N所决定的平面把三棱柱切割成体积不相同的两部分,则小部分的体积和大部分的体积之比为()5、方程x−=1有()解6、方程3x2−e x=0的实根是()7、设f x=x8−x5+x2−x+1,则f x有性质()8、证明2是一个无理数9、若对一切实数x都有x−5+x−7>a,则实数a的取值范围是()10、设某个多边形Σ的顶点在复平面中均是形式为1+z+z2+⋯+z k−1的点,其中z≤1,则点z=0有性质()多边形Σ上的点。
11、如图,半径为r的四分之一的圆ABC上,分别以AB和AC为直径作两个半圆,分别标有a的阴影部分面积和标有b的阴影部分面积,则这两部分面积a和b的大小关系是?12、设x,y,z>0满足xyz+y+z=12,则log4x+log2y+log2z的最大值为()13、设实数r>1,如果复平面上的动点z满足z=r,则动点ω=z+1z的轨迹是()焦距的椭圆。
14、对函数f:0,1→0,1,定义f1x=f x,L,f n x=f f n−1x,n=1,2,3,⋯,满足f n x=x的点x∈0,1称为f的一个n周期点,现设f x=2x,0≤x≤122−2x,12≤x≤1,问f的一个n周期点的个数是()15、已知数列a n 满足:a 1=22的等比数列,则k=1na k =()16、设集合X 是实数集R 的子集,如果点x 0∈R 满足:对任意a >0,都存在,使得0<x −x 0<ax 0为集合X 的聚点,则下列集合:①∈Z ,n ≥0,②R \0,∈Z ,n ≠0,④Z 中,以0为聚点的集合有()17、在一个底面半径为12,高为1的圆柱内放入一个直径为1的实心球后,在圆柱内空余的地方放入和实心球、圆柱侧面及两个底面之一都相切的小球,最多可以放入这样的小球个数是()18、经过坐标变换x ‘=x cos θ+y sin θy ’=−x sin θ+y cos θ将二次曲线3x 2−23xy +5y 2−6=0转化为形如x ‘2a 2±y ’2b 2=1的标准方程,求θ并判断二次曲线的类型()19、已知常数k 1,k 2满足0<k 1<k 2,k 1k 2=1.设C 1与C 2分别是以y =±k 1x −1+1和y =±k 2x −1+1为渐近线且通过原点的双曲线,则C 1与C 2的离心率之比等于()20、设非零向量a=a1,a2,a3,b =b1,b2,b3,c=c1,c2,c3为共面向量,x=x1,x2,x3是未知向量,则满足a∙x=0,b ∙x=0,c∙x=0的向量x的个数为()21、将同时满足不等式x−ky−2≤0,2x+3y−6≥0,x+6y−10≤0k>0的点x,y组成的集合D称为可行域,将函数y+1x称为目标函数,所谓规划问题就是求解可行域中的点x,y使目标函数达到在可行域上的最小值。
2016年复旦大学三位一体招生数学试题

2016年复旦大学三位一体招生数学试题1.使得方程32360x x x a +++=有重根的a 的取值情况有 ( )种 A.1 B.2 C.3 D.不存在 2.记()0.00120.010.12xxxf x =-⨯-+,则()0f x <的区间长为 ( ) A.小于0.5 B.大于0.5但小于1 C.大于1但有限 D.无限大3.解析几何的建立意味着 ( ) A.平行公设得到证明 B.代数与几何的结合 C.非欧几何的建立 D.以上均不正确4.记1xy xy y=-,则(2)0x x =的所有根的和为 。
5.两个四位数20XY 、YX 16的积为17817888,则X +Y = 。
6.若ab -1能被2017整除,则称b 是a 的逆。
在集合E ={1,2,3……2016}中,逆是其自身的元素个数为 ( ) A.1 B.2 C.4 D.不存在7.方程5432540x x x ax bx c +-+++=有三根1231,2,3x x x ===-。
则其余两根为( )A.不相等两实根B.共轭复根C.两相等实根D.相等复根 8.|x +3|=2|x -2+yi |,,x y R ∈该方程表示的轨迹为 。
9.A (-1,0),B (3,0),P 在224236x xy y x +++=上,则三角形P AB 面积的最大值为 ( ) A.6 B.7 C.8 D.10 10.222260x x xy y y -++--=上的点到y 轴最小值为 。
11.已知lg2=0.30103,lg5=0.69897,55lg(110)10--->-。
数列满足010,58n n a a a +==+,则2016cos(lg )a π∈ ( )A.[-1, -12] B.(12-,0) C.[0,12) D.[12,1] 12.方程1281940x x+--=的根x ∈ ( ) A.(-2, -1] B.(-1,0) C.[0,1) D.[1,2)13.已知,//,BF BC BD BC BA BF BD ⊥=+则2BC BD =是ABC ∆为等腰三角形的( )A.充分不必要条件B.充要条件C.必要不充分条件D.既不充分也不必要条件 14.参数方程为cos sin {x y θθθθ==的曲线与x 轴非负半轴的交点横坐标由小到大排列为12,,,n a a a⋯,则12ka k +∞-=∑ ( )A.121π- B.141π- C.1121π+- D.1141π+-15.2()3sin 4sin cos f x x x x =+的最小值为 。
2016复旦附中中考自主招生数学试卷(含答案)

2016复旦附中创新拔尖人才培养选拔校园日一.填空题1.已知a b c x b c a c a b===+++,则x =________. 2.已知函数()()225323y x a x b x b =-+-++≤≤图像关于y 轴对称,则a b +=________.3.已知函数()()2221y k x kx k =--++的图像与x 轴只有一个交点,则k =__________.4.在同一个直角坐标系中,已知直线y kx =与函数283233243x x y x x x -⎧⎪=--<<⎨⎪+-⎩,≥,,≤图像恰好有三个公共点,则k 的取值范围是__________.5.如图,在梯形ABCD 中,AB CD ∥CD AB >,,设E F 、分别是AC BD 、的中点,AC 与BD 交于点O ,已知OEF △是边长为1的正三角形,BOC △则梯形ABCD 的面积为__________. 6.已知矩形ABCD 中,1AB BC a ==,,若在边BC 上存在点Q ,满足AQ QD ⊥,则a 的取值范围是__________.7.已知锐角ABC △的三边长恰为三个连续正整数,AB BC CA >>,若BC 边上的高为AD ,则BD DC -=__________.B8. 已知实数m n ,(其中1m n ⋅≠)分别满足:2219991099190m m n n ++=++=,, 则41mn m n++=_____________.9. 若关于x 的方程()()2240x x x m --+=有三个根,且这三个根恰好可以作为一个三角形的三边长,则m 的取值范围是___________.10. 如图,矩形ABCD 中,34AB BC ==,,点E 是BC 边上一点,连接AE ,把B ∠沿AE 折叠,使点B 落在点'B 处,当'CEB △为直角三角形时,BE 的长为__________.11. 如图,OA OD ,是O ⊙的半径,延长OA 至B ,使OA AB C =,是OA 的中点,AOD ∠为锐角α,连接CD BD ,,且CD a =,则_________.BD =12. 已知直角三角形的三边长都是整数,且其面积与周长在数值上相等,若将全等的三角形都作为同一个,那么这样的直角三角形的个数是_________个.13. 设()10n n ≥个机场,每一机场起飞一架飞机,飞到离起飞机场最近的机场降落,且任何两机场之间的距离都不相等,则任意一个机场降落的飞机架数的最大值为__________.二. 解答题14. 关于x 的方程()222120x m x m m --++=的两个根分别为12.x x ,()1若12x x -∣∣求m 的值; ()2若12x x ,均为整数,求m 的值.15. 如图,ABC △中,56AB BC AC ===,,过点A 作AD BC ∥,点P Q ,分别是射线AD 、线段BA 上的动点,且AP BQ =,过点P 作PE AC ∥交线段AQ 于点O ,联结PQ ,记AP x POQ =,△面积为.y ()1求y 关于x 的函数关系式,并写出x 的取值范围;()2联结QE ,若PQE △与POQ △相似,求AP 的长.16. 一幢33层的大楼有一部电梯停在第一层,它一次最多能容纳32人,而且只能在第2层到第33层中的某一层停一次,对于每个人来说,他往下走一层楼感到1分不满意,往上走一层楼梯感到3分不满意. 现在有32个人在第一层,并且他们分别住在第2至第33层的每一层,问:电梯停在哪一层,可以使得这32个人不满意的总分达到最小?最小值是多少?(有些人可以不乘电梯而直接从楼梯上楼)17. 设x 是实数,不大于x 的最大整数叫做x 的整数部分,记作[]x ,如[][][]1.2133 1.32==-=-,,()()()()222111110111111212016201711011111220162017S =+++⎡⎤⎡⎤⎡⎤⨯-⨯-⨯-⎢⎥⎢⎥⎢⎥⨯⨯⨯⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦,求[]90S ;()2解关于x 的方程:212312.2x x x -⎡⎤--=⎢⎥⎣⎦2016复旦附中创新拔尖人才培养选拔校园日一. 填空题 1. 已知a b c x b c a c a b===+++,则x =________. 【答】12或1- 【解析】由题意()()()()2a b c x b a c x a b c a b c x c a b x=+⎧⎪=+⇒++=++⎨⎪=+⎩若0a b c ++=,则1a a x b c a ===-+-, 若0a b c ++≠,则12x =.综上12x =或1-.2. 已知函数()()225323y x a x b x b =-+-++≤≤图像关于y 轴对称,则a b +=________.【答】4【解析】由题意二次函数对称轴0x =,定义域关于原点对称50230a b b ⇒-=++=, 514a b ⇒+=-=.3. 已知函数()()2221y k x kx k =--++的图像与x 轴只有一个交点,则k =__________.【答】2±【解析】若原函数不为二次函数,则2k =43y x ⇒=-+与x 轴只有一个交点成立;若原函数为二次函数,则()()244210202k k k k k =--+=⇒--=⇒=-△综上2k =±4. 在同一个直角坐标系中,已知直线y kx =与函数283233243x x y x x x -⎧⎪=--<<⎨⎪+-⎩,≥,,≤图像恰好有三个公共点,则k 的取值范围是__________.【答】223k <<【解析】原函数图像大致如图,当0k <,y kx =过二四象限不满足题意,显然0k ≠,当y kx =过()32--,则23k =,恰有两交点,当2k =,三条直线平行,于是223k <<.5. 如图,在梯形ABCD 中,AB CD ∥CD AB >,,设E F 、分别是AC BD 、的中点,AC 与BD 交于点O ,已知OEF △是边长为1的正三角形,BOC △则梯形ABCD 的面积为__________.【答】【解析】设BO a =,则2OD OC a ==+,由AOB ODC △、△则()()22sin120222116416sin 604222ABCD a a a a S S a ︒⎧+=⎪⎪⇒++=⇒=⋅=⎨︒⎪=+⎪⎩6. 已知矩形ABCD 中,1AB BC a ==,,若在边BC 上存在点Q ,满足AQ QD ⊥,则a 的取值范围是__________.【答】2a ≥【解析】以AD 中点为圆心2a为半径作圆应与BC 有交点, 122aa ⇒⇒≥≥7. 已知锐角ABC △的三边长恰为三个连续正整数,AB BC CA >>,若BC 边上的高为AD ,则BD DC -=__________.【答】4【解析】设AB BC CA ,,分别为11n n n +-,,,则 ()()222222114n n BD DC AB AC BD DC BD DC BC n+-----====+8. 已知实数m n ,(其中1m n ⋅≠)分别满足:22199********m m n n ++=++=,,则41mn m n++=_____________.【答】5-【解析】由()()2199919190m m +⋅+=19m n ⇒、均为299190x x ++=的解,B若它们为不同解,则1919m n ⋅=矛盾⇒19m n = ⇒原式21941199919551919m m m m m mm m⋅++++-===-9. 若关于x 的方程()()2240x x x m --+=有三个根,且这三个根恰好可以作为一个三角形的三边长,则m 的取值范围是___________.【答】34m <≤【解析】显然2x =是原方程的根,设另两个根分别为a b 、,42a b +=>,0△≥,2a b -<∣∣且0m >,()216441640m a b m ⎧-=-<⎪⇒⎨=-⎪⎩△≥34m ⇒<≤10. 如图,矩形ABCD 中,34AB BC ==,,点E 是BC 边上一点,连接AE ,把B ∠沿AE 折叠,使点B 落在点'B 处,当'CEB △为直角三角形时,BE 的长为__________.【答】32或3【解析】设BE x =,过'B 作'B H BC ⊥于H , ()1'90B E C ∠=︒,45AEB ⇒∠=︒,3x AB ⇒==,()2'90B C E ∠=︒,⇒'B 在CD 上,H 与C 重合,由'BB AE ⊥,'33BB BH ⇒==, 22184291809x BH x x x ==⇒-+=+无解()3'90E B C ∠=︒,则'C B A 、、共线,AE 为BAC ∠33452x x x ⇒=⇒=- 综上32BE =或311. 如图,OA OD ,是O ⊙的半径,延长OA 至B ,使OA AB C =,是OA 的中点,AOD ∠为锐角α,连接CD BD ,,且CD a =,则_________.BD =【答】2a【解析】设1OC =,则42OB OD OA ===,, 2OC OB OD OCD ODB ⋅=⇒△∽△,相似比1:222BD CD a ⇒==12. 已知直角三角形的三边长都是整数,且其面积与周长在数值上相等,若将全等的三角形都作为同一个,那么这样的直角三角形的个数是_________个.【答】2【解析】设直角三角形三边分别为a b c <<,()2222a b cab a b c ⎧+=⎪⎨=++⎪⎩有22222c a b b c =+<⇒<())2227ab b b b b ⇒<++=<7a ⇒<,而()()2205ab a b c b b a =++>++⇒≥,若5a =,()()252511312c b c b c b c b c b =-+⇒+=-=⇒==,,代入两式验证成立; 若6a =,()()36182108c b c b c b c b c b =-+⇒+=-=⇒==,,代入两式验证成立; 综上()()6810a b c =,,,,或()51213,,,满足条件的三角形有2个.13. 设()10n n ≥个机场,每一机场起飞一架飞机,飞到离起飞机场最近的机场降落,且任何两机场之间的距离都不相等,则任意一个机场降落的飞机架数的最大值为__________.【答】5【解析】首先有五架飞机在O 降落是可以构造的,只需O 为正五边形ABCDE 的中心,其他飞机场在较远处即可。
复旦大学自主招生考试数学试题及答案
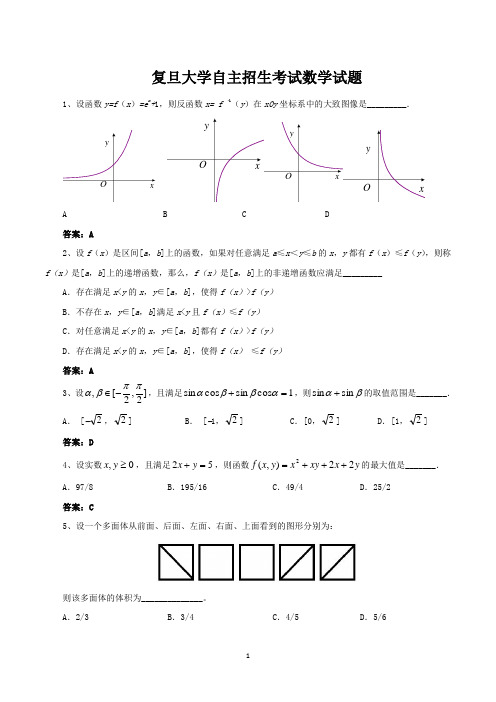
1、设函数y=f(x)=e x+1,则反函数OyxOyxO x答案:A2、设f(x)是区间[a,b]f(x)是[a,b]上的递增函数,那么,f(xA.存在满足x<y的x,y∈[a,b]B.不存在x,y∈[a,b]满足x<y且fC.对任意满足x<y的x,y∈[a,b]D.存在满足x<y的x,y∈[a,b]答案:A3、设]2,2[,ππβα-∈,且满足sinαA. [−2,2] B. [答案:D4、设实数0,≥yx,且满足2=+yxA.97/8 B.答案:C5则该多面体的体积为______________。
A.2/3 B.3/4答案:D6、在一个底面半径为1/2,高为1的圆柱内放入一个直径为1的实心球后,在圆柱内空余的地方放入和实心球、侧面以及两个底面之一都相切的小球,最多可以放入这样的小球个数是___________。
A .32个;B .30个;C .28个;D .26个答案:B7、给定平面向量(1,1),那么,平面向量(231-,231+)是将向量(1,1)经过________. A .顺时针旋转60°所得; B .顺时针旋转120°所得; C .逆时针旋转60°所得;D .逆时针旋转120°所得;答案:C8、在直角坐标系O xy 中已知点A 1(1,0),A 2(1/2,3/2),A 4(−1,0),A 5(−1/2,−3/2)和A6(1/2, −3/2).问在向量−−→−ji A A (i ,j=1,2,3,4,5,6,i≠j)中,不同向量的个数有_____. A .9个; B .15个; C .18个; D .30个答案:C9、对函数f:[0,1]→[0,1],定义f 1(x )=f (x ),……,f n(x ) =f (f n −1(x )),n=1,2,3,…….满足f n (x )=x 的点x ∈[0,1]称为f 的一个n −周期点.现设⎪⎪⎩⎪⎪⎨⎧≤≤-≤≤=121,22,210,2)(x x x x x f 问f 的n −周期点的个数是___________.A .2n 个;B .2n 2个;C .2n个;D .2(2n−1)个.答案:C10、已知复数z 1=1+3i ,z 2=−3+3i ,则复数z 1z 2的幅角__________. A .13π/12 B .11π/12 C .−π/4 D .−7π/12答案:A11、设复数βαβαcos sin ,sin cos i w i z +=+=满足z w =3/2,则sin (β−α)=______. A .±3/2B .3/2,−1/2C .±1/2D .1/2,−3/2答案:D12、已知常数k 1,k 2满足0<k 1<k 2,k 1k 2=1.设C 1和C 2分别是以y =±k 1(x −1)+1和y =±k 2(x −1)+1为渐近线且通过原点的双曲线.则C 1和C 2的离心率之比e 1/e 等于_______.A .222111k k ++ B .212211k k ++ C .1 D .k 1/k 2答案:C13、参数方程0,)cos 1()sin (>⎩⎨⎧-=-=a t a y t t a x 所表示的函数y=f (x )是____________.A .图像关于原点对称;B .图像关于直线x =π对称;C .周期为2a π的周期函数D .周期为2π的周期函数.答案:C14、将同时满足不等式x −k y −2≤0,2x +3y −6≥0,x +6y −10≤0 (k>0)的点(x ,y )组成集合D 称为可行域,将函数(y +1)/x 称为目标函数,所谓规划问题就是求解可行域中的点(x ,y )使目标函数达到在可行域上的最小值.如果这个规划问题有无穷多个解(x ,y ),则k 的取值为_____.A .k≥1;B .k≤2C .k=2D .k=1.答案:C15、某校有一个班级,设变量x 是该班同学的姓名,变量y 是该班同学的学号,变量z 是该班同学的身高,变量w 是该班同学某一门课程的考试成绩.则下列选项中正确的是________.A .y 是x 的函数;B .z 是y 的函数;C .w 是z 的函数;D .w 是x 的函数.答案:B16、对于原命题“单调函数不是周期函数”,下列陈述正确的是________. A .逆命题为“周期函数不是单调函数”; B .否命题为“单调函数是周期函数”; C .逆否命题为“周期函数是单调函数”; D .以上三者都不正确 答案:D17、设集合A={(x ,y )|log a x +log a y >0},B={(x ,y )|y +x <a}.如果A∩B=∅,则a 的取值范围是_______ A .∅ B .a>0,a≠1 C .0<a≤2, a≠1 D .1<a≤2答案:D18、设计和X 是实数集R 的子集,如果点x 0∈R 满足:对任意a>0,都存在x ∈X 使得0<|x −x 0|<a ,则称x 0为集合X 的聚点.用Z 表示整数集,则在下列集合(1){n/(n+1)|n ∈Z , n≥0}, (2) R\{0}, (3){1/n|n ∈Z , n≠0}, (4)整数集Z 中,以0为聚点的集合有_____. A .(2),(3)B .(1),(4)C .(1),(3)D .(1),(2),(4)答案:A19、已知点A (−2,0),B (1,0),C (0,1),如果直线kx y =将三角形△ABC 分割为两个部分,则当k =______时,这两个部分得面积之积最大?A .23-B .43-C .34-D .32-答案:A20、已知x x x x f 2cos 3cos sin )(+=,定义域⎥⎦⎤⎢⎣⎡=ππ127,121)(f D ,则=-)(1x f_____A .π12123arccos 21+⎪⎪⎭⎫ ⎝⎛-x B .π6123arccos 21-⎪⎪⎭⎫ ⎝⎛-x C .π12123arcsin 21+⎪⎪⎭⎫ ⎝⎛--x D .π6123arcsin 21-⎪⎪⎭⎫ ⎝⎛-x 答案:A21、设1l ,2l 是两条异面直线,则直线l 和1l ,2l 都垂直的必要不充分条件是______ A .l 是过点11l P ∈和点22l P ∈的直线,这里21P P 等于直线1l 和2l 间的距离 B .l 上的每一点到1l 和2l 的距离都相等 C .垂直于l 的平面平行于1l 和2lD .存在与1l 和2l 都相交的直线与l 平行 答案:D22、设ABC −A’B’C’是正三棱柱,底面边长和高都为1,P 是侧面ABB’A’的中心,则P 到侧面ACC’A’的对角线的距离是_____A .21B .43C .814D .823答案:C23、在一个球面上画一组三个互不相交的圆,成为球面上的一个三圆组.如果可以在球面上通过移动和缩放将一个三圆组移动到另外一个三圆组,并且在移动过程中三个圆保持互不相交,则称这两个三圆组有相同的位置关系,否则就称有不同的位置关系.那么,球面上具有不同的位置关系的三圆组有______A .2种B .3种C .4种D .5种 答案:A24、设非零向量()()()321321321,,,,,,,,c c c c b b b b a a a a ===为共面向量,),,(31x x x x x = 是未知向量,则满足0,0,0=⋅=⋅=⋅x c x b x a的向量x 的个数为_____A .1个B .无穷多个C .0个D .不能确定 答案:B25、在Oxy 坐标平面上给定点)1,2(),3,2(),2,1(C B A ,矩阵⎪⎪⎭⎫⎝⎛-112k 将向量OC OB OA ,,分别变换成向量,,,如果它们的终点',','C B A 连线构成直角三角形,斜边为''C B ,则k 的取值为______A .2±B .2C .0D .0,−2 答案:B26、设集合A ,B ,C ,D 是全集X 的子集,A∩B≠∅,A∩C≠∅.则下列选项中正确的是______. A .如果B D ⊂或C D ⊂,则D∩A≠∅; B .如果A D ⊂,则C x D∩B≠∅,C x D∩C≠∅; C .如果A D ⊃,则C x D∩B=∅,C x D∩C=∅; D .上述各项都不正确.27、已知数列{}n a 满足21=a 且n a n ⎧⎫⎨⎬⎩⎭是公比为2的等比数列,则∑==nk k a 1______A .221-+n nB .22)1(1+-+n n C .)1(22-+n n n D .n n n 22)1(+-28、复平面上圆周2211=+--iz z 的圆心是_______ A .3+i B .3−iC .1+iD .1−i29.已知C 是以O 为圆心、r 为半径的圆周,两点P 、P *在以O 为起点的射线上,且满足|OP|∙|OP *|=r 2,则称P 、P *关于圆周C 对称.那么,双曲线22x y -=1上的点P (x ,y )关于单位圆周C':x 2+y 2=1的对称点P *所满足的方程是(A )2244x y x y -=+(B )()22222x y x y-=+(C )()22442x y x y-=+(D )()222222x y x y-=+30、经过坐标变换⎩⎨⎧+-=+=θθθθcos sin 'sin cos 'y x y y x x 将二次曲线06532322=-+-y xy x 转化为形如1''2222=±b y a x 的标准方程,求θ的取值并判断二次曲线的类型_______ A .)(6Z k k ∈+=ππθ,为椭圆 B .)(62Z k k ∈+=ππθ,为椭圆C .)(6Z k k ∈-=ππθ,为双曲线D .)(62Z k k ∈-=ππθ,为双曲线31、设k , m , n 是整数,不定方程mx+ny=k 有整数解的必要条件是____________ A .m ,n 都整除kB .m ,n 的最大公因子整除kC .m ,n ,k 两两互素D .m ,n ,k 除1外没有其它共因子。
上海复旦大学2006年自主招生试题及答案

⾯试招⽣考题
1、讨论⼀下《⽆极》、《⼀个馒头的⾎案》给络⽣活带来的启⽰。
2、如果你是校长,会如何激发学⽣的创新能⼒?
3、说出全国政协常委委员名字。
4、说出现任复旦⼤学校长的名字。
5、描述你所希望的⼤学⽣活的⼀天。
6、说说对社会上乞讨者的看法。
7、“两会”是哪两会?
8、评价你校交响乐团成员?
9、简述你理想中的宇宙。
10、在1分钟内列举这瓶⽔的⽤途。
11、请谈⼀下数学以后的发展⽅向。
12、你对“安乐死”有何看法?为何我们要禁⽌“安乐死”?
13、请为你眼前的这个闹钟估价。
14、由你⾃⼰选⼀个话题阐述⼀番。
15、⽤3、4、5、6算24点。
16、请列举钟有哪些⽤途?
17、请说出你⽗母的⽣⽇。
18、简述⽆罪推定和有罪推定。
19、三轮车有⼏个主动轮?哪⼏个?你觉得地球上怎么会产⽣⽣命?
20、说明⽣活是三⾓形物体。
复旦自主招生试题

复旦自主招生试题复旦大学自主招生试题自主招生旨在选拔具有综合素质和潜力的优秀学生,复旦大学自主招生试题考察的是学生的才智、思维能力和学科基础。
以下是几道典型的复旦自主招生试题,帮助大家更好地了解复旦大学自主招生的考察方向和要求。
题一:数学思维某班一共有50名学生,其中有20%的学生参加了足球队,25%的学生参加了篮球队,30%的学生参加了乒乓球队,10%的学生既参加了足球队又参加了篮球队,15%的学生既参加了足球队又参加了乒乓球队,20%的学生既参加了篮球队又参加了乒乓球队,其中没有学生同时参加了三者。
请问有多少学生一个球队都没有参加?解题思路:首先我们可以利用集合论中的容斥原理来解决这个问题。
让A表示参加足球队的学生人数,B表示参加篮球队的学生人数,C表示参加乒乓球队的学生人数,根据题意可得:A +B +C - (A ∩ B) - (A ∩ C) - (B ∩ C) + (A ∩ B ∩ C) = 50其中,我们已知 A = 0.2 * 50 = 10, B = 0.25 * 50 = 12.5(约等于13),C = 0.3 * 50 = 15。
代入上式,可以计算得到:10 + 13 + 15 - (A∩ B) - (A ∩ C) - (B ∩ C) + (A ∩ B ∩ C) = 50。
再根据已知条件,可得到(A ∩ B) = 0.1 * 50 = 5,(A ∩ C) = 0.15 * 50 = 7.5(约等于8),(B ∩ C)= 0.2 * 50 = 10,(A ∩ B ∩ C) = 0。
代入上式,可得:10 + 13 + 15 - 5 - 8 - 10 + 0 = 50。
所以,有多少学生一个球队都没有参加,即(A' ∩ B' ∩ C') = 50 - 35 = 15个学生。
因此,共有15个学生一个球队都没有参加。
题二:文学赏析以下是经典文学作品的一些摘录,请阅读并简要进行评析。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
复旦大学2000年保送生招生测试数学试题(理科)一、填空题(每小题10分,共60分)1.将自然数按顺序分组:第一组含一个数,第二组含二个数,第三组含三个数,……,第n 组含n 个数,即1;2,3;4,5,6;…….令a n 为第n 组数之和,则a n =________________. 2.222sin sin ()sin ()33ππααα+++-=______________.3.222lim[(2)log (2)2(1)log (1)log ]n n n n n n n →∞++-+++=_________________.4.已知平行六面体的底面是一个菱形且其锐角等于60度,又过此锐角的侧棱与锐角两边成等角,和底面成60度角,则两对角面面积之比为__________________.5.正实数x ,y 满足关系式x 2-xy +4=0,又若x ≤1,则y 的最小值为_____________.6.一列火车长500米以匀速在直线轨道上前进,当车尾经过某站台时,有人驾驶摩托车从站台追赶火车给火车司机送上急件,然后原速返回,返回中与车尾相遇时,此人发现这时正在离站台1000米处,假设摩托车车速不变,则摩托车从出发到站台共行驶了______________米. 二、解答题(每小题15分,共90分)1.数列{a n }适合递推式a n +1=3a n +4,又a 1=1,求数列前n 项和S n .2.求证:从椭圆焦点出发的光线经光洁的椭圆壁反射后必经过另一个焦点.你还知道其它圆锥曲线的光学性质吗?请叙述但不必证明.3.正六棱锥的高等于h ,相邻侧面的两面角等于12arcsin 2,求该棱锥的体积.(1cos 124π=)4.设z1,z2,z3,z4是复平面上单位圆上的四点,若z1+z2+z3+z4=0.求证:这四个点组成一个矩形.5.设(1n n x y=+x n,y n为整数,求n→∞时,nnxy的极限.6.设平面上有三个点,任意二个点之间的距离不超过1.问:半径至少为多大的圆盘才能盖住这三个点.请证明你的结论.复旦大学2001年选拔生考试数学试题一、填空(每小题5分,共45分)1.sin x +sin y =0,则cos 2x -sin 2y =___________________.2.平面π1, π2成α的二面角,平面π1中的椭圆在平面π2中的射影是圆,那么椭圆短轴与长轴之比为__________.3.(x 2+2x +2)(y 2-2y +2)=1,则x +y =________________________.4.电话号码0,1不能是首位,则本市电话号码从7位升到8位,使得电话号码资源增加____. 5.2002=83a 3+82a 2+8a 1+a 0,0≤a 0,a 1,a 2,a 3≤7正整数,则a 0=______________. 6.15(x的常数项为_________________.7.n =__________________.8.空间两平面α,β,是否一定存在一个平面均与平面α,β垂直?___________.9.在△ABC 中,cos(2A -C )=cos(2C -B ),则此三角形的形状是________________. 二、解答题(共87分)1.求解:cos3x tan5x =sin7x .2.数列3,3-lg2,…,3-(n -1)lg2.问当n 为几时,前n 项的和最大?3.求证:x ∈R 时,|x -1|≤4|x 3-1|.4.a 为何值时,方程22lg lg()log (1)lg 2lg 2x a x a -+=-有解?只有一解?5.一艘船向西以每小时10公里的速度航行,在它的西南方向有一台风中心正以每小时20公里速度向正北方向移动,船与台风中心距离300米,在台风中心周围100米处将受到影响,问此船航行受台风影响的时间段长度?6.x 3-2y 3=1的所有整数解(x ,y ),试证明:1334|2|||x y y -<.2003年上海交通大学冬令营选拔测试数学试题 2003.1.4一、填空题(本大题共40分,每题4分)1.三次多项式f (x )满足f (3)=2f (1),且有两个相等的实数根2,则第三个根为___________. 2.用长度为12的篱笆围成四边形,一边靠墙,则所围成面积S 的最大值是_______________. 3.已知,x y R +∈,x +2y =1,则22x y+的最小值是______________. 4.有4个数,前3个成等比数列,后3个成等差数列,首末两数和为32,中间两数和为24,则这四个数是___________________.5.已知f (x )=ax 7+bx 5+x 2+2x -1,f (2)=-8,则f (-2)=_______________. 6.投三个骰子,出现三个点数的乘积为偶数的概率是_______________. 7.正四面体的各个面无限延伸,把空间分为________________个部分. 8.有n 个元素的集合分为两部分,空集除外,可有___________种分法.9.有一个整数的首位是7,当7换至末位时,得到的数是原数的三分之一,则原数的最小值是___________.10.100!末尾连续有______________个零. 二、解答题(本大题共60分,每题10分)11.数列{a n }的a 1=1,a 2=3,3a n +2=2a n +1+a n ,求a n 和lim n n a →∞.12.3个自然数倒数和为1.求所有的解.13.已知x 1000+x 999(x +1)+…+(x +1)1000,求x 50的系数.14.化简:(1) 11!22!!n n ⋅+⋅++⋅; (2) 1212k nn n k C C C ++++++.15.求证:342231a aa a +++为最简分式.16.证明不等式()!()23nnn n n >>,当自然数n ≥6时成立.复旦大学2003年暨保送生考试数学试题一、填空题(本大题共80分,每题8分)1.函数1()2y f t x x =-,当x =1时,252t y t =-+,则f (x )=________________. 2.方程x 2+(a -2)x +a +1=0的两根x 1,x 2在圆x 2+y 2=4上,则a =_______________.3.划船时有8人,有3人只能划右边,1人只能划左边,共有________种分配方法. 4.A ={x |log 2(x 2-4x -4)>0},B ={x ||x +1|+|x -3|≥6},则A B ⋂=_______________. 5.数列{a n }的前n 项和为S n ,若a k =k ·p k (1-p ),(p ≠1),则S k =______________. 6.若(x -1)2+(y -1)2=1,则13y x --的范围是___________________. 7.边长为4的正方形ABCD 沿BD 折成60o 二面角,则BC 中点与A 的距离是_________. 8.已知|z 1|=2,|z 2|=3,|z 1+z 2|=4,则12z z =______________. 9.解方程3log 2a xx xa=,x =________________. 10.(a >0),lim 2nn nn a a →∞+=______________.二、解答题(本大题共120分)11.已知|z |=1,求|z 2+z +4|的最小值.12.a 1,a 2,a 3,…,a n 是各不相同的自然数,a ≥2,求证:1231111()()()()2a a a ana a a a ++++<.13.已知sin cos αβ+=cos sin αβ+=tan cot αβ⋅的值.14.一矩形的一边在x 轴上,另两个顶点在函数21xy x=+(x >0)的图象上, 求此矩形绕x 轴旋转而成的几何体的体积的最大值.15.一圆锥的底面半径为12,高为16,球O 1内切于圆锥,球O 2内切于圆锥侧面,与球O 1外切,…,以次类推,(1) 求所有这些球的半径r n 的通项公式;(2) 所有这些球的体积分别为V 1,V 2,…,V n ,….求12lim()n n V V V →∞+++.16.已知数列{a n }的前n 项和为S n ,n a =,求S 2003.17.定义闭集合S ,若,a b S ∈,则a b S +∈,a b S -∈.(1) 举一例,真包含于R 的无限闭集合.(2) 求证对任意两个闭集合S 1,S 2⊂R ,存在c R ∈,但12c S S ∉⋃.复旦大学2004年保送生考试数学试题(150分钟)2003.12.21一、填空题(每题8分,共80分)1.)1)(12(124248++++=+ax x x x x ,则=a _________. 2.已知74535=-++x x ,则x 的范围是___________.3.椭圆191622=+y x ,则椭圆内接矩形的周长最大值是___________. 4.12只手套(左右有区别)形成6双不同的搭配,要从中取出4只正好能形成2双,有____种取法. 5.已知等比数列{}n a 中31=a ,且第一项至第八项的几何平均数为9,则第三项为______. 6.0)1(2<++-a x a x 的所有整数解之和为27,则实数a 的取值范围是___________.7.已知194)4(22=+-y x ,则9422y x +的最大值为____________. 8.设21,x x 是方程053cos 53sin 2=+-ππx x 的两解,则21arctgx arctgx +=__________. 9.z z =3的非零解是___________. 10.x x y +-=112的值域是____________.二、解答题(每题15分,共120分) 1.解方程:1)3(log 5=--x x .2.已知1312)sin(=+βα,54)sin(-=-βα,且2,0,0πβαβα<+>>,求α2tg .3.已知过两抛物线C 1:2)1(1-=+y x ,C 2:2(1)41y x a -=--+的交点的各自的切线互相垂直,求a .4.若存在M ,使任意D t ∈(D 为函数)(x f 的定义域),都有M x f ≤)(,则称函数)(x f 有界.问函数x x x f 1sin 1)(=在)21,0(∈x 上是否有界?5.求证:3131211333<++++n.6.已知E 为棱长为a 的正方体ABCD —A 1B 1C 1D 1的棱AB 的中点,求点B 到平面A 1EC 的距离.7.比较25log 24与26log 25的大小并说明理由.8.已知数列{}n a 、{}n b 满足n n n b a a 21--=+,且n n n b a b 661+=+,又21=a ,41=b , 求 (1) n n b a ,; (2) nnb a lim.简单解答: 一、填空题:1.2- 2.)8.0,6.0(- 3.20 4.31二、解答题: 5.证明1:111))1(1)1(1()1()1(113+-+⋅+--=+-<m m mm m m m m m m=(2111)1111-++⋅⋅+--m m m m m而m m m m m =-++<-++211211111113+--<m m m原式<1+111141213111+--++-+-n n =3111222<+--+n n证明2:)1)(1()1(2--+->+=n n n n n n n11)1(1121---=-+-<n n n n n n n nn n n n n nn 111)1(121--=---<原式〈313)1113121211(21<-=--++-+-+nn n2005年复旦大学考试试卷一、填空题:1.A =(){}22|10x log x x ∈-->R ,B ={}1|221x x x -∈->R ,A CB =______ (C B 表示B 在R 上的补集). 2.数x 满足11-=+x x ,求_______1300300=+xx . 3.求ρ=5cos θθ-的圆心坐标,[)πθ2,0∈4.抛物线2222a ax x y ++=与直线1+=x y 交于A 和B 两点,AB 最大时, a =______. 5.limn →∞=________.6.求1+3+6+…+______2)1(=+n n . 7.一个班20个学生,有3个女生,抽4个人去参观展览馆,恰好抽到1个女生的概率为________. 8.求10003在十进制中最后4位_____________________.9.定义在R 上的函数f (x )(x ≠1)满足 ()x x x f x f -=⎪⎭⎫⎝⎛-++4015120022,则f (2004)=______.10.求xxy cos 2sin 1++=的最大值是__________________.二、解答题1.在四分之一个椭圆12222=+by a x (x >o, y >0)上取一点P ,使过P 点椭圆的切线与坐标轴所围成的三角形的面积最小.2.在ΔABC 中,tan A :tan B :tan C =1:2:3,求ABAC. 3.在正方体A B C D —A 1B 1C 1D 1中,E 、F 、G 点分别为AD 、AA 1、A 1B 1中点, 求:(1) B 到面EFG 距离;(2) 二面角G —EF —D 1平面角θ. 43=的实数根. 5.已知a =+ααcos sin ()20≤≤a ,求ααn n cos sin +关于a 的表达式.6.直线l 与双曲线xy =1交于P 和Q 两点,直线l 与x 轴交于A ,与y 轴交于B ,求证:BQ AP =.7.定义在R 上的函数()244+=x x x f ,⎪⎭⎫ ⎝⎛-++⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛=n n f n f n f S n 121 n =2,3,… (1) 求n S ; (2) 是否存在常数M >0,2≥∀n ,有231111n M S S S ++++≤.11 / 11 2006年复旦大学推优、保送生考试数学试题1.(本题20分)求和:(1) 77777777777n ++++个(2) 2005200520052005200520052005200520052005n ++++个2.(本题15分)试构造函数f(x),g(x)其定域为(0,1),值域为 [0,1](1) 对于任意a ∈[0,1],f (x )=a 只有一解;(2) 对于任意a ∈[0,1],g (x )=a 有无穷多个解.3.(本题15分)对于一个四位数,其各位数字至多有两个不相同,试求共有多少个这种四位数.4.(本题15分)对于任意12,,,n n N x x x ∈均为非负实数,且1212n x x x +++≤, 试用数学归纳法证明:121(1)(1)(1)2n x x x ---≥成立. 5.(本题20分)求证:02122222()()()()n n n n n n n C C C C C ++++=.6.(本题20分)a ,b 满足何条件,可使22122x ax b x x ++<++ 恒成立. 7.(本题20分)下列各式能否在实数范围内分解因式?若能,请作出分解;若不能,请说明理由.(1) x +1 (2) x 2+x +1 (3) x 3+x 2+x +1 (4) x 4+x 3+x 2+x +18.(本题20分)解三角方程:sin()sin 29,4a x x a π+=+为一实常数.9.(本题20分)已知曲线22:14x C y +=,曲线C 关于直线2y x =对称的曲线为曲线C ',曲线C '与曲线C ''关于直线152y x =-+对称,求曲线C '、C ''的方程. 10.(本题20分)已知抛物线2y ax =,直线12,l l 都过点(1,-2)且互相垂直,若抛物线与直线l 1,l 2中至少一条相交,求a 的取值范围.11.(本题15分)f (x )在[1,+∞)上单调递增,且对任意x ,y ∈[1,+∞),都有f (x +y )=f (x )+f (y )成立,证明:存在常数k ,使f (x )=kx 在x ∈[1,+∞)上成立.。
