2018年高考数学复习感知高考刺金四百题：第396—400题(含答案解析)高考

2018年高考数学一轮复习感知高考刺金四百题：第376—380题(含答案解析)

感知高考刺金376题设函数()3,f x x a a a x=--+∈R ,若关于x 的方程()2f x =有且仅有三个不同的实数根,且它们成等差数列,则实数a 的取值构成的集合是．解：3322x a a x a a x x--+=⇒-+=+ 方程的根有且仅有三个,即左右两个函数的交点有且仅有三个, 故考查函数1,2,x x a y x a a a x x a≥⎧=-+=⎨-<⎩与232y x =+的图象这里要注意1y x a a =-+的图象虽然随着a 的变化在移动,但是有规律的移动,“V ”型图的尖底(),a a 是沿着y x =移动的,而232y x =+的图象是确定不变的。

由322a x x+=-解得()11x a =-()21x a =- 由32x x+=解得31x =-,43x = 故画出图象只有两种情况（两个交点在第三象限,一个在第一象限（此时0a <）或三个交点都在第一象限（此时0a >））即1312x +=-⋅（如左图）或1232x x +=（如右图）即()9155a a -=-⇒=-或()()1321a a -=-+24810340a a a a ⇒-⇒--=⇒=又因为此时0a >,故a =综上,95a ⎧⎪∈-⎨⎪⎪⎩⎭感知高考刺金377题已知锐角ABC ∆的内角3A π=,点O 为三角形外接圆的圆心,若OA xOB yOC =+ ,则2x y -的取值范围是．解法一：这是典型的求平面向量基本定理系数和问题,常用“作三点共线”的办法来解决。

由3A π=,得23BOC π∠=,不妨如图固定,,O B C 三点,因为ABC ∆是锐角三角形,所以点A 在 'DC上运动,取OB 的中点为'B ()2''OA xOB yOC xOB y OC =+=+-这样就构造出了系数和2x y -作直线OA 与直线''B C 交于E ,于是作出了',',B C E 三点共线。

2018年高考数学复习题：第386—390题(含答案解析)

感知高考刺金386题在正方形ABCD 中，2AB =，,M N 分别是边,BC CD 上的两个动点，且MN =AM AN 的取值范围是．解：因为MN =所以优先考虑使用极化恒等式设P 为MN 的中点，则222142MNAM AN AP AP =-=- 这来关键就要找到点P 的运动轨迹，注意到MNC ∆为直角三角形，CP 是斜边上的中线等于斜边的一半，即2MNCP ==，故点P 在以C 14圆弧 FEG 上运动故AE AP AG ≤≤ ，即291722AP ≤≤- 所以4,8AM AN ⎡∈-⎣ 感知高考刺金387题在ABC ∆中，,,a b c 分别表示角,,A B C 所对的边长，AD 为BC 边上的高，若AD BC =，则b c的最大值是．解法一：不妨设1c =，则B D (222212b a a a =+=+-这里求2b 的最大值有技巧，因此考虑使用三角换元，设cos ,0,2a πθθ⎛⎫=∈ ⎪⎝⎭，则()22cos 21331cos 2sin cos 1sin 22222b θθθθθθϕ+=+-=+-=++≤+所以b b c = 解法二：建系设点不妨设()0,0B ，()1,0C ，(),1A x 则b c ==要使b c 最大，显然120x ->时b c更大则b c = 解法三：设,BD m CD n ==，则()22222c m b n m n -=-=+ 即22222222,22b m mn n c m mn n =++=++所以2222222222b m mn n c m mn n ++=++ 显然是齐次化了，所以令0m t n =>，则()22222221332212212222212212221t t t t bt t c t t t t t t +++++++===+≤++++++解法四：221sin 22sin ABC a a S bc A b c A∆==⇒=，所以222222cos sin sin b a b c bc A c c A c A+-==，令b t c=，则212cos sin t tA t A +-=，即()21sin 2cos t A A A tϕ+=+=+≤21t t +≤t≤≤点评：这道解三角形的问题，无论是建系还是平面几何，最终都将目标转化为函数求值域的问题求解。

2018年高考数学一轮复习感知高考刺金四百题：第376—380题(含答案解析)

感知高考刺金376题设函数()3,f x x a a a x=--+∈R ，若关于x 的方程()2f x =有且仅有三个不同的实数根，且它们成等差数列，则实数a 的取值构成的集合是．解：3322x a a x a a x x--+=⇒-+=+ 方程的根有且仅有三个，即左右两个函数的交点有且仅有三个，故考查函数1,2,x x a y x a a a x x a≥⎧=-+=⎨-<⎩与232y x =+的图象这里要注意1y x a a =-+的图象虽然随着a 的变化在移动，但是有规律的移动，“V ”型图的尖底(),a a 是沿着y x =移动的，而232y x =+的图象是确定不变的。

由322a x x+=-解得()11x a =- ()21x a =- 由32x x+=解得31x =-，43x = 故画出图象只有两种情况（两个交点在第三象限，一个在第一象限（此时0a <）或三个交点都在第一象限（此时0a >））即1312x +=-⋅（如左图）或1232x x +=（如右图）即()9155a a -=-⇒=-或()()1321a a -=-+24810340a a a a ⇒-⇒--=⇒=又因为此时0a >，故a =综上，95a ⎧⎪∈-⎨⎪⎪⎩⎭感知高考刺金377题已知锐角ABC ∆的内角3A π=，点O 为三角形外接圆的圆心，若OA xOB yOC =+，则2x y -的取值范围是．解法一：这是典型的求平面向量基本定理系数和问题，常用“作三点共线”的办法来解决。

由3A π=，得23BOC π∠=，不妨如图固定,,O B C 三点，因为ABC ∆是锐角三角形，所以点A 在'DC 上运动，取OB 的中点为'B()2''OA xOB yOC xOB y OC =+=+-这样就构造出了系数和2x y -作直线OA 与直线''B C 交于E ，于是作出了',',B C E 三点共线。

2018年高考数学一轮复习感知高考刺金四百题：第296—300题(含答案解析)

感知高考刺金296题若单调递增数列{}n a 满足1236n n n a a a n ++++=-，且2112a a =，则1a 的取值范围是．解：1236n n n a a a n ++++=-，12333n n n a a a n +++++=-两式相减得33n n a a +-=故数列单调递增，只需1234a a a a <<<即可31213332a a a a =---=-- 得不等式1111133322a a a a <<--<+ 解得1123,52a ⎛⎫∈-- ⎪⎝⎭感知高考刺金297题已知,αβ均为锐角，且()sin cos sin ααββ+=，则tan α的最大值是．解：由sin cos cos sin sin sin ααβαββ-=化简得2222sin cos sin cos tan tan 1sin 2sin cos 12tan βββββαββββ===≤=+++当且仅当tan β时取得等号感知高考刺金298题已知函数22 () n n f n n n ⎧⎪=⎨-⎪⎩为奇数为偶数，且()(n af n f n =++，则123a a a a +++⋯+=. 解：当n 为奇数时，1+n 为偶数，22(1)21=-+=--n a n n n当n 为偶数时，1+n 为奇数， 22(1)21=-++=+n a n n n∴ 13=-a ，25=a ，37=-a ，49=a ，511=-a ， 713=a ，……∴ 122+=a a ，342+=a a ，即1220162016a a a ++=感知高考刺金299题在棱长为1的正方体1111ABCD A B C D -中，,M N 分别为111,AC A B 的中点，点P 在正方体的表面上运动，则总能使MP 与BN 垂直的点P 所构成的轨迹的周长为．解：依题意，只需过点M 作直线BN 的垂面即可垂面与正方体表面的交线即为动点P 的轨迹分别取11,CC DD 中点,G H ，易知BN ⊥平面AGHD过M 作平面AGHD 的平行平面''EFG H ，点P 所构成的轨迹即为四边形''EFG H ，其周长与四边形AGHD 的周长相等，所以点P 所构成的轨迹的周长为2点评：本题中面面的交线（截痕）即为动点P 的轨迹，处理问题的关键抓住线面垂直，进行合理转换。

2018年高考数学一轮复习感知高考刺金四百题：第346—350题(含答案解析)

感知高考刺金346题设非零向量,,a b c r r r 满足a b a b +=-r r r r 且1a b a b c ==++=r r r r r ，则a c a r r g r 的取值范围是．解：由a b a b +=-r r r r 得a b ⊥r r ，且1a b ==r r又()1a b c c a b ++=---=r r r r r r ，即c OC =r u u u r 的终点C 在以()a b OD -+=r r u u u r 的终点D 为圆心，1为半径的圆上cos a c c a θ=r r r g r 就是c r 在a r 上的投影，显然[]2,0a c a ∈-r r g r感知高考刺金347题已知()222,0,,f x mx m m m x =++≠∈∈R R ，若1x y +=，则()()f y f x 的取值范围是．解：()()222222222222m y m f y my m f x mx m m x m ⎛⎫+-- ⎪ ⎪++⎝⎭==⎛⎫+++-- ⎪ ⎪⎝⎭()()f y f x 的取值范围问题等价于曲线1x y +=上的点(),P x y 与点2222,22m m A m m ⎛⎫++-- ⎪ ⎪⎝⎭连线的斜率的范围问题．此时点A 在()(),22,y x x ⎤⎡=∈-∞+∞⎦⎣U 上，由图可知：()()21,22f y f x ⎡⎤∈-+⎢⎥⎣感知高考刺金348题若点G 为ABC ∆的重心，且AG BG ⊥，则sin C 的最大值为．解：如图，点G 在以AB 为直径的圆上运动，且由于点G 为ABC ∆的重心，所以3OC OG = 故点G 在以O 为圆心，以32AB 长为半径的圆上运动，问题转化为圆上一点与线段AB 形成的张角问题。

如图，画一个最小圆，即CO AB ⊥时，其余的'C 都在圆外，根据圆外角小于圆上角，可知当CO AB ⊥时，C ∠最大，即sin C 最大此时由11sin 22ABC S AB CO AC BC C ∆=⋅=⋅⋅得3sin 5C = 或二倍角公式3sin 2sin cos 22251010θθθ==⋅⋅=感知高考刺金349题在ABC ∆中，过中线AD 中点E 作一直线分别交边AB ，AC 于,M N 两点，设AM xAB =u u u u r u u u r ，()0AN y AC xy =≠u u u r u u u r ，则4x y +的最小值为．解：因为D 是BC 中点，所以1122AD AB AC =+u u u r u u u r u u u r 又因为E 为AD 中点，所以11114444AE AB AC AM AN x y=+=+u u u r u u u r u u u r u u u u r u u u r 因为,,M E N 三点共线，所以11144x y+= 所以()11594444444y x x y x y x y x y ⎛⎫+=++=++≥ ⎪⎝⎭当且仅当33,84x y ==时等号成立。

2018年高考数学一轮复习感知高考刺金四百题含答案解析)

感知高考刺金361题设x ∈R ，[]x 表示不超过x 的最大整数. 若存在实数t ，使得[]1t =，22t ⎡⎤=⎣⎦，…，n t n⎡⎤=⎣⎦同时成立．．．．，则正整数n 的最大值是．解：由[]1t =得12t ≤<由22t ⎡⎤=⎣⎦得223t ≤< 由44t ⎡⎤=⎣⎦得445t ≤<，所以22t ≤<由33t ⎡⎤=⎣⎦得334t ≤<，所以56t ≤<由55t ⎡⎤=⎣⎦得556t ≤<与56t ≤<n 的最大值是4感知高考刺金362题过点()1,1M -的直线l 交圆()22:11C x y -+=于点,A B ，O 为坐标原点，若在线段AB 上的Q 满足112MA MB MQ+=，则min OQ = ．解：设()11,A x y ，()22,B x y ，(),Q m n ，直线():11l y k x =++则11MA +，21MB =+，1MQ + 由112MA MB MQ +=得12112111x x m +=+++ 由()()221111x y y k x ⎧-+=⎪⎨=++⎪⎩得()()()2222122210k x k k x k +++-++= 所以21222221k k x x k +-+=-+，()212211k x x k +=-+ 所以421k m =-+所以()42111n m m ⎛⎫=-++ ⎪+⎝⎭整理得点(),Q m n 满足的轨迹方程为210m n --=所以min OQ ==感知高考刺金363题如图，已知点D 为ABC ∆的边BC 上一点，3BD DC =u u u r u u u r，()*n E n ∈N 为AC 边上一列点，满足()11324n n n n n E A a E B a E D +=-+u u u u r u u u u r u u u u r，其中数列{}n a 满足0n a >，11a =，则{}n a 的通项公式为．解：由3BD DC =u u u r u u u r可得1344n n n E D E B E C =+u u u u r u u u u r u u u u r又()11324n n n n n E A a E B a E D +=-+u u u u r u u u u r u u u u r，且n n E C E A λ=u u u u r u u u u r故()113132444n n n n n n E D E B a E B a E D λ+⎡⎤=+-+⎢⎥⎣⎦u u u u r u u u u r u u u u r u u u u r即()131********n n n n a E B a E D λλ+⎛⎫⎡⎤+=++ ⎪⎢⎥⎣⎦⎝⎭u u u u r u u u u r 因为,n n E B E D u u u u r u u u u r 不共线，故()1310416313204n na a λλ+⎧+=⎪⎪⎨⎪++=⎪⎩，两式相除消去λ得132n n a a +=+，又11a =，所以1231n n a -=⋅-感知高考刺金364题若点A 在圆C :22(1)(2)4x y -++=上运动,点B 在y 轴上运动,则对定点(3,2)P 而言,||PA PB +u u u r u u u r的最小值为．解法1：设11(,)A x y ,2(0,)B y ,则112(6,4)PA PB x y y +=-+-u u u r u u u r.若设||r PA PB =+u u u r u u u r ,则由题意可得222112(6)(4)x y y r -++-=.即,点A 在以2(6,4)D y -为圆心,以r 为半径的圆D :2222(6)(4)x y y r -++-=上.由圆C与圆D 有公共点A 可得2222||(61)(6)5r CD y +≥=-+-≥,从而3r ≥.解法2：设11(,)A x y ,2(0,)B y ,则112(6,4)PA PB x y y +=-+-u u u r u u u r.从而,22211211||(6)(4)(6)63PA PB x y y x x +=-++-≥-=-≥u u u r u u u r.解法3：由点A 在圆C 上可设(12cos ,22sin )A θθ+-+,(0,)B t ,则(2cos 5,2sin 6)PA PB t θθ+=-+-u u u r u u u r.故222||(2cos 5)(2sin 6)(2cos 5)52cos 3PA PB t θθθθ+=-++-≥-=-≥u u u r u u u r. 解法4：设Q 为AB 的中点,则2PA PB PQ +=u u u r u u u r u u u r,过,,P Q A 作y 轴的垂线,垂足分别为',','P Q A .由于13|'||||'||||'|||22PP PQ QQ PQ AA PQ ≤+=+≤+, 因此33|||'|22PQ PP ≥-=,即||2||3PA PB PQ +=≥u u u r u u u r u u u r .解法5：设'B 为点B 关于点P 的对称点，则|||'||'|PA PB PA PB B A +=-=u u u r u u u r u u u r u u u r u u u u r .由于点'B 在直线6x =上,点A 在圆C :22(1)(2)4x y -++=上可得|'|523B A ≥-=u u u u r.解法6：同解法5，设'A 为点A 关于点P 的对称点,则|||'||'|PA PB PB PA A B +=-=u u u r u u u r u u u r u u u r u u u u r .由于点'A 在圆'C :22(5)(6)4x y -+-=上,点B 在y 轴上可得|'|523A B ≥-=u u u u ryxB'PCOA B感知高考刺金365题设实数,x y 满足2025020x y x y y --≤⎧⎪+-≥⎨⎪-≤⎩，则112u x y =+的取值范围为．解：可行域如图所示，()1,2A ，()4,2B ，()3,1C ，所以14,12x y ≤≤≤≤设点(),P x y 是可行域内一动点，目标函数112u x y=+既是关于x 的减函数，又是关于y 的减函数所以当点P 与点C 重合时，此时x 取得最大值4，同时y 取得最大值2，此时u 取得最小值为1114222+=⋅ 对于每一个固定的y 的值，要使u 取得最大值，应使x 取得最小值，即点P 应位于线段AB 上，此时()5212x y y =-≤≤()()111152522252u y x y y y y y =+=+=--()12y ≤≤ 所以()max 54u y =，此时()1,2P 与点A 重合综上所述，1524u ≤≤感知高考刺金366题已知点,A B 是双曲线22122x y -=右支上两个不同的动点，O为坐标原点，则OA OB u u u r u u u rg的最小值为．解法一：韦达定理当AB k 存在时，设:AB l y kx b =+()222221122022x y k x kbx b y kx b⎧-=⎪⇒----=⎨⎪=+⎩212122222,11kb b x x x x k k ++==-- ()()()()221212*********OA OB x x y y x x kx b kx b k x x kb x x b =+=+++=++++u u u r u u u r g()2222222222222241221111b k b k k b k k k k ++=+++==+>----当AB k 不存在是，222x y x m⎧-=⎨=⎩，则22121222OA OB x x y y m m =+=+-=u u u r u u u r g综上，2OA OB ≥u u u r u u u rg解法二：由于,A B 两点运动，故采取“一定一动”的原则，不妨先在B 点确定的情况下，让A 点运动到最小值，然后再让B 点运动，即取最小值的最小值。

2018年高考数学复习感知高考刺金四百题：第326—330题(含答案解析)高考

感知高考刺金326在△ABC 中，已知BC = 4，AC = 3，cos (A - B) = 34，则△ABC 的面积为．解：在角A 中作出A - B ，即在BC 上取一点D ，使DB = DA ，设DB = x ，则DC = 4 - x ．在△ACD 中，cos ∠CAD = cos (A - B) = 34，∴223(4)9234x x x -=+-⨯⨯⨯，得x = 2．则DA = DC = DB ，∠BAC = 90︒，AB =△ABC ．感知高考刺金327若ABC ∆的外接圆是半径为1的圆O ，且120AOB ∠= ，则AC CB 的取值范围是。

解法一：AC CB CA CB =-是同一个C 点出发的两个向量作点积，且终点连线AB =不错的选择。

222344AB AC CB CA CB CD CD =-=-+=- （其中D 为AB 中点）点C 在圆上运动，故R OD CD R OD -≤≤+ ，即1322CD ≤≤故31,22AC CB ⎡⎤∈-⎢⎥⎣⎦又C 不与,A B 重合，所以0AC CB ≠ ，所以31,00,22AC CB ⎡⎫⎛⎤∈-⎪ ⎢⎥⎣⎭⎝⎦解法二：如图建系设点。

()1,0A ，12B ⎛- ⎝⎭，()cos ,sin C θθ()1cos 1cos sin sin 2111cos sin 2262AC CB θθθθπθθθ⎫⎛⎫=---+⎪ ⎪⎪⎝⎭⎝⎭⎛⎫=+-=+- ⎪⎝⎭ 因为202,0,3πθπθ≤≤≠，所以31,00,22AC CB ⎡⎫⎛⎤∈-⎪ ⎢⎥⎣⎭⎝⎦解法三：基底角度，一问三不知转基底 ()()()111cos 222AC CB OC OA OB OC OC OA OB OC OD θ=--=+-=-=- 由于C 不与,A B 重合，所以31,00,22AC CB ⎡⎫⎛⎤∈-⎪ ⎢⎥⎣⎭⎝⎦ 感知高考刺金328如图，点,,A B C 是以O 为圆心，1为半径的圆O 上任意三点，则AC BC的最小值是。

2018年高考数学复习感知高考刺金四百题：第41—45题(含答案解析)高考

感知高考刺金411．已知m ∈R ，函数()()221,1log 1,1x x f x x x ⎧+<⎪=⎨->⎪⎩，()2221g x x x m =-+-，若函数()y f g x m =-⎡⎤⎣⎦有6个零点，则实数m 的取值范围是．解：令()g x t =，则函数()y f g x m =-⎡⎤⎣⎦有6个零点等价于()f t m =恰有三个实根且对应()g x t =有6个实根．函数()()221,1log 1,1x x f x x x ⎧+<⎪=⎨->⎪⎩与y m =图象有三个交点，其横坐标分别为123,,t t t ．如图所示，其中最小的根112m t +=- 结合图象可知，要满足()g x t =有6个实根需使()1min 1222m t g x m +=->=-，且0m > 解得305m <<2．集合{}321234|101010A x x a a a a ==⨯+⨯+⨯+，其中{}1,2,3,4,14,i a i i ∈≤≤∈N ，则集合A 中满足条件：“i a 中1a 最小，且12233441,,,a a a a a a a a ≠≠≠≠”的元素有个．解：本题可理解为涂色问题，四个格子，相邻两格不同数字，头尾两个数字也不同，且第一格数字最小．第一格填1，则第二格有13C 种选择，第三格填的数字与第一格相同填1，则第四格有13C 种选择，因此共9种选择；第一格填2，则第二格有12C 种选择，第三格填的数字与第一格相同填2，则第四格有12C 种选择，因此共4种选择；第一格填3，则第二格有1种选择填4，第三格填的数字与第一格相同填3，则第四格有1种选择填4，因此共1种选择；第一格填1，则第二格有13C 种选择，第三格填的数字与第一格不同有12C 种选择，，则第四格有12C 种选择，因此共12种选择；第一格填2，则第二格有12C 种选择，第三格填的数字与第一格不同有11C 种选择，，则第四格有1种选择，因此共2种选择；因此共有94112228++++=种．感知高考刺金421．已知函数()()20f x ax bx c a =++≠的图象过点()1,0，且对任意的x ∈R 都有不等式()23231x f x x x --≤≤+-成立．若函数()()222y f x f x mx m =---有三个不同的零点，则实数m 的取值范围是．解：由题夹逼形式知，令23231x x x --=+-，解得1x =-．当1x =-时，()212f -≤-≤-，即()12f -=-，所以2a b c -+=-又()10f =，即0a b c ++=所以1,1b c a ==--再由2231231x ax x a x x --≤+--≤+-对任意的x ∈R 恒成立即2420ax x a ++-≥且()2220a x x a ---≤对任意的x ∈R 恒成立所以()()164204420020a a a a a a --≤⎧⎪+-≤⎪⎨>⎪⎪-<⎩，解得1a =，所以()22f x x x =+-。

2018年高考数学一轮复习感知高考刺金四百题第356—360题(含答案解析)

感知高考刺金题
已知实数满足关系式，则的最小值是．
解法一：题干中出现的全是两数的和、平方和与乘积，所以考虑用均值不等式链条。

由或
所以
点评：这里注意因为题干中没有告诉我们的正负性，所以不能直接用来
求的取值范围，所以改为用重要不等式来来做。

虽然答案正好一样，但做法要注意。

解法二：遇到结构，所以用代数的极化恒等式变形。

令，则问题转变为已知，求的最小值。

因为
所以还需要计算定义域，即
所以
解法三：设，则视为的两根
所以
所以或
当且仅当时取得最小值。

感知高考刺金题
已知点为圆与圆的公共点，圆，圆，若，，则点与直线上任意一点之间的距离的最小值为．
解：设，，则，
所以，即
同理
所以是方程的两个实根
所以
所以点的轨迹方程为
所以点到直线的最短距离为
感知高考刺金题
已知向量满足，，则的取值范围是．
解：（一）几何角度
由和可以画图，找到向量模长的几何意义。

解法一：基底法
因为
因为三者都未知，属于一问三不知问题，所以考虑转基底做。

那么题目中哪些向量适合做基底呢？显然两个
向量长度已知，适合做基底。

（这里夹角未知是应该的，不然整个图就确定下来，就
不会是求最小值了。

）
所以由三点共线，且，可知
所以
解法二：解三角形
设，
则在与中运用余弦定理得
解得
又在中，利用三角形两边之和大于等于第三边得，即
所以
（二）代数角度
解法三：换元思想。

2018年高考数学一轮复习感知高考刺金四百题：第96—100题(含答案解析)

感知高考刺金961．在ABC ∆中,内角,,A B C 所对应的边分别为,,a b c ,且BC,则c b b c+的最大值为 ,此时内角A 的值为。

解法一：由21sin 2ABC S bc A ∆==所以2222cos 2cos 4sin 6c b c b a bc A A A A b c bc bc π++⎛⎫+===+=+ ⎪⎝⎭ 所以当3A π=时,max4c b b c ⎛⎫+= ⎪⎝⎭ 解法二：以BC 为x 轴,BC 中点为原点建系,则,0,,022a a B C ⎛⎫⎛⎫- ⎪ ⎪⎝⎭⎝⎭,A x ⎛⎫ ⎪ ⎪⎝⎭ABAC =所以b c ==当0x =时,1b c= 当0x >时,b c =,当且仅当x =时取等号所以令2b t⎡⎤=∈⎣⎦,1y t=+单调递减,所以当2t =时,即x =时,max 4y = 此时AB =,AC =,则2221cos 22b c a A bc +-==,所以3A π= 由对称性可知,0x <时也一样。

2．某人抛掷一枚硬币,出现正反的概率都是12,构造数列{}n a ,使11n n a n ⎧=⎨-⎩（当第次出现正面时）（当第次出现反面时）,记()12*n n S a a a n =+++∈ N ,则42S =时的概率为。

解：42S =,需四次中有3次正面,1次反面,故344124C P ==感知高考刺金971．点P 为椭圆()222210x y a b a b+=>>在第一象限的弧上的任意一点,过P 引x 轴,y 轴的平行线,分别交直线b y x a=-于,Q R 两点,交y 轴,x 轴于,M N 两点,记OMQ ∆与ONR ∆的面积为12,S S ,当2ab =时,2212S S +的最小值为。

解：设()cos ,sin ,0,2P a b πααα⎛⎫∈ ⎪⎝⎭, 则()()0,sin ,cos ,0M b N a αα,()()sin ,sin ,cos ,cos Q a b R a b αααα-- 所以()()()()1211sin sin ,cos cos 22S a b S a b αααα== ()()22224444122222221sin cos sin cos 411sin cos 2sin cos 1sin 222S S a b ααααααααα+=+=+=+-=-≥ 当且仅当4πα=时取得最小值。

2018年高考数学一轮复习感知高考刺金四百题：第306—310题(含答案解析)

感知高考刺金306如图,矩形OABC 中,AB =1,OA =2,以B 为圆心、BA 为半径在矩形内部作弧,点P 是弧上一动点,PM ⊥OA ,垂足为M ,PN ⊥OC ,,垂足为N ,则四边形OMPN 的周长的最小值为．解：如图,连BP ,则BP=1,设∠CBP =α,(0,2πα⎤∈⎥⎦, cos cos PE DB BP αα===,sin sin PD BP αα== ∴2cos PN α=-,1sin PM α=-四边形OMPN 的周长()22cos 1sin 234L πααα⎡⎤⎛⎫=-+-=+ ⎪⎢⎥⎝⎭⎣⎦ 当4πα=时,min 6L =-感知高考刺金307设1x 、2x 是关于x 的方程022=-++m m mx x 的两个不相等的实数根,那么过两点),(211x x A 、),(222x x B 的直线与圆1)1(22=+-y x 的位置关系是（）(A)相离 (B)相切 (C)相交 (D)随m 的变化而变化解：22121212AB x x k x x x x -==+-,∴直线AB ：))((12121x x x x x y -+=-,即 0)()(2112121=+-+-+x x x x y x x x ,即0)(2121=--+x x y x x x ,圆心()1,0到AB的距离d =,由韦达定理,m x x -=+21,m m x x -=221,∴22d == 取m =0,则d =0⇒相交；取m =2,则1d =>⇒相离,故选D感知高考刺金308 已知函数a x x x x f -+-++=11)(的图像关于垂直于x 轴的直线对称,则a 的取值集合是．解：若11a -<<,则⎪⎪⎩⎪⎪⎨⎧>-≤<-+≤<--+-≤-=1,31,21,21,3)(x a x x a a x a x x a x x a x f ,其图像呈“剑”形,如图,对称轴为x =a ,则1102a -+== 同理,若1a <-时,对称轴是1x =-,∴123a a +=-⇒=- 若1a >时,对称轴是1x =,∴123a a -+=⇒=感知高考刺金309在ABC ∆中,若8,|2|6AB AC AB AC ⋅=-= ,则ABC ∆面积的最大值为．解：在ABC ∆中延长AC 到D ,使AC CD =,所以2A D A C = ,则已知变为16,||6AB AD AB AD ⋅=-= 。

2018年高考数学一轮复习感知高考刺金四百题：第56—60题(含答案解析)

感知高考刺金561．已知正方形1111ABCD A B C D -的棱长为1，,M N 是对角线1AC 上的两点，动点P 在正方体表面上运动，满足PM PN =，则动点P 的轨迹长度的最大值为．解：动点P 的轨迹为线段MN 的中垂面与正方体表面的截痕．2．若5250125(1)(1)(1)...(1)x a a x a x a x +=+-+-++-，则0a = ．答案：32感知高考刺金571．如图，在正方体1111ABCD A B C D -中，当动点M 在底面ABCD 内运动时，总有11DD A DD M ∠=∠，则动点M 在面ABCD 内的轨迹是．A ．椭圆的一部分B ．双曲线的一部分C ．抛物线的一部分D ．圆的一部分解：因为满足条件的动点在底面ABCD 内运动时，动点的轨迹是以1D D 为轴线，以1D A 为母线的圆锥，与平面ABCD 的交线即圆的一部分．2．从6名品学兼优的同学中选出4名去进行为期三天的宣传活动，每人一天，要求星期天有2人参加，星期五、星期六各有1人参加，则不同的选派方案共有种．答案：180感知高考刺金581．已知函数()11f x x =-，()2113f x x =+，()()()()()121222f x f x f x f xg x -+=+，若[],1,5a b ∈-，且当[]12,,x x a b ∈时，()()12120g x g x x x ->-恒成立，则b a -的最大值为．解：()()()()()()()()()111212212(),22(),f x f x f x f x f x f x f x g x f x f x f x ≥⎧-+⎪=+=⎨<⎪⎩即()g x 即为取()11f x x =-，()2113f x x =+中较大者．画出函数图象，且()g x 单调递增，所以单调递增区间[][],0,5a b ⊆，所以b a -的最大值为5． 2．若()()811x x -+的展开式中5x 的系数是．答案：14感知高考刺金591．设正实数,,x y z 满足22340x xy y z -+-=，则当xyz取得最大值时，212x y z +-的最大值为．解：2234z x xy y =-+，所以xyz22134xy xy x xy y xy =≤=-+ 当且仅当2x y =时，等号成立所以222122121222x y z y y y y y +-=+-=-+ 令10t y=>，则原式()2111t =--+≤ 所以212x y z+-的最大值为1. 2．有5名学生站成一列，要求甲同学必须站在乙同学的后面（可以不相邻），则不同的站法有种．答案：60感知高考刺金601．定义{},max ,,a a b a b b a b ≥⎧=⎨<⎩，设实数 ,x y 满足约束条件22x y ⎧≤⎪⎨≤⎪⎩，则{}m a x 4,3z x y x y=+-的取值范围是．解：14,213,2x y y x zx y y x⎧+≥⎪⎪=⎨⎪-<-⎪⎩作出22xy⎧≤⎪⎨≤⎪⎩所对应的区域如图所示：由图可知：{}[]max4,37,10z x y x y=+-∈-2．某外商计划在四个候选城市投资3个不同的项目,且在同一个城市投资的项目不超过2个，则该外商不同的投资方案有种．答案：按条件项目可分配为2,1,0,0与1,1,1,0的结构，∴2223343243362460C C A C A+=+=种．。

2018年高考数学一轮复习感知高考刺金四百题：第336—340题(含答案解析)

感知高考刺金336已知22252259x x a x a x c x x ++≤++≤++对任意x ∈R 恒成立，则a c += ．解：用两边夹逼的方法，令225259x x x x ++=++，解得2x =-故7447a a c ≤-+≤，即7c =所以()()22252712120x x ax ax a x a x ++≤++⇒-+-+≥对任意x ∈R 恒成立，所以 ()()()221013221810230a a a a a a ->>⎧⎧⎪⎪⇒⇒=⎨⎨∆=---≤-≤⎪⎪⎩⎩ 故172a c += 点评：这又是夹逼形式的好题，解法中让不等号两边同时取到，求出临界点的方法要注意。

感知高考刺金337已知非零向量a 与向量 b 的夹角为钝角，2b = ，当2t =-时，()b ta t -∈R 取最小值65，则()a b a -= ．解法一：由当2t =-时，()b ta t -∈R 取最小值65，可知本题是“神图”的应用，如图所示，设,a b θ= ，则()635sin 25πθ-== 即4cos 5θ=-45a = 故()24825a b a a b a -=-=- 解法二：22222b ta b a bt a t -=-+当且仅当22a b t a ==- 时，222364425b ta b a b a -=++= 所以22a b a =- 且3644225a b a b +-= ，得232225a b a =-=- 故()24825a b a a b a -=-=-感知高考刺金338已知椭圆()2211221110,0x y a b a b +=>>和双曲线()2222222210,0x y a b a b -=>>有相同的焦点，且椭圆与双曲线在第一象限的交点为P ，若2222OF OP OF = ，则双曲线的离心率的取值范围是．解：222222222cos ,OF OP OF OF OP OF OP OF =⇒=2222222P P OF c x OF x a =⇒==> 故2222c e a =>感知高考刺金339已知函数()12x f x e x -=+-，()23g x x ax a =--+，若存在实数12,x x 使得()()120f x g x ==，且121x x -≤，则实数a 的取值范围是．解：因为()f x 是增函数，且()10f =，故11x =，所以原条件等价于230x ax a --+=在区间[]0,2上有解，即231x a x +=+在[]0,2上有解因为[]412,0,21y x x x =++-∈+的值域为[]2,3，所以实数a 的取值范围是[]2,3感知高考刺金340在ABC ∆中，1tan 3A =，4B π=，若椭圆E 以AB 为长轴，且过点C ，则椭圆E 的离心率是．解：如图，作CD AB ⊥于D ，则3t a n CD AD CD A==，BD CD =设()2,0B ，则44AB AD BD CD ==+=，所以1OD CD ==，所以()1,1C 设椭圆的方程为22221x y a b+=，将2a =与()1,1C 代入可得24b=，28 3c=故e=。

2018年高考数学一轮复习感知高考刺金四百题：第136—140题(含答案解析)

感知高考刺金136设函数()()2,f x x ax b a b =++∈R ，记(),M a b 为()y f x =在[]1,1-上的最大值（1）设2a ≥，求证：(),2M a b ≥（2）若(),2M a b ≤，请求出a b +的最值。

证明：（1）因为对称轴012a x =-≤-或012ax =-≥ ()()(){}{}maxmax 1,1max 1,1f x f f a b a b =-=++-+证法一：规划视角()()()()()22221112112110a b a b b a b a b a b a a b ++≤-+⇔++++≤+-++⇔+≤故(){}()()max1,410max 1,11,410b a a b f x a b a b b a a b ⎧+++>⎪=++-+=⎨+-+≤⎪⎩，又结合2a ≥，可以从规划视角来解题，以a 为横坐标，b 为横坐标建系，画出可行域()4102a b a +>⎧⎪⎨≥⎪⎩如图1所示，目标函数1122b ab a ++++=视为可行域内的点(),a b 到直线10x y ++=的距离的2倍，显然当(),a b 取点()2,1--时min 1222b a ++=⋅=同理，可行域()4102a b a +≤⎧⎪⎨≥⎪⎩如图2所示，目标函数1a b -+=视为可行域内的点(),a b 到直线10x y -++=的距离(),a b 取点()2,1-时min 12b a +-= 综上，(),2M a b ≥ 证法二：绝对值不等式()()(){}{}()()max max 1,1max 1,11111222f x f f a b a b a b a b a b a ba =-=++-+++--++++-+≥≥=≥解法三：(){},max 1,1M a b a b a b =++-+ 令1b t +=，则()(){},max ,M a b g t t a t a ==+-在同一个坐标系中画出1y t a =+和2y t a =-的图象，两者取其大，则显然当0t =时，()min 2g t a =≥故(),2M a b ≥ （2）解法一：规划视角()()()222211221231,211221231848122424424f a b a b a b a M a b f a b a b a b a a b a a a b f a b ⎧⎧⎪=++≤⎪⎧-≤++≤--≤≤-+⎪⎪⎪⎪≤⇔-=-++≤⇔-≤-++≤⇔-≤≤+⎨⎨⎨⎪⎪⎪-≤-≤⎩⎛⎫⎪⎪-≤≤+-=-≤ ⎪⎩⎪⎝⎭⎩显然又是一个规划问题了。

2018年高考数学一轮复习感知高考刺金四百题：第136—140题(含答案解析)

感知高考刺金136设函数()()2,f x x ax b a b =++∈R ，记(),M a b 为()y f x =在[]1,1-上的最大值（1）设2a ≥，求证：(),2M a b ≥（2）若(),2M a b ≤，请求出a b +的最值。

证明：（1）因为对称轴012a x =-≤-或012ax =-≥ ()()(){}{}max max 1,1max 1,1f x f f a b a b =-=++-+证法一：规划视角()()()()()22221112112110a b a b b a b a b a b a a b ++≤-+⇔++++≤+-++⇔+≤故(){}()()max1,410max 1,11,410b a a b f x a b a b b a a b ⎧+++>⎪=++-+=⎨+-+≤⎪⎩，又结合2a ≥，可以从规划视角来解题，以a 为横坐标，b 为横坐标建系，画出可行域()4102a b a +>⎧⎪⎨≥⎪⎩如图1所示，目标函数1122b ab a ++++=视为可行域内的点(),a b 到直线10x y ++=的距离的2倍，显然当(),a b 取点()2,1--时min 1222b a ++=⋅=同理，可行域()4102a b a +≤⎧⎪⎨≥⎪⎩如图2所示，目标函数1a b -+=视为可行域内的点(),a b 到直线10x y -++=的距离(),a b 取点()2,1-时min 12b a +-=综上，(),2M a b ≥ 证法二：绝对值不等式()()(){}{}()()max max 1,1max 1,11111222f x f f a b a b a b a b a b a b a =-=++-+++--++++-+≥≥=≥解法三：(){},max 1,1M a b a b a b =++-+令1b t +=，则()(){},max ,M a b g t t a t a ==+-在同一个坐标系中画出1y t a =+和2y t a =-的图象，两者取其大，则显然当0t =时，()min 2g t a =≥故(),2M a b ≥ （2）解法一：规划视角()()()222211221231,211221231848122424424f a b a b a b a M a b f a b a b a b a a b a a a b f a b ⎧⎧⎪=++≤⎪⎧-≤++≤--≤≤-+⎪⎪⎪⎪≤⇔-=-++≤⇔-≤-++≤⇔-≤≤+⎨⎨⎨⎪⎪⎪-≤-≤⎩⎛⎫⎪⎪-≤≤+-=-≤ ⎪⎩⎪⎝⎭⎩显然又是一个规划问题了。

2018年高考数学一轮复习感知高考刺金四百题：第236—240题(含答案解析)

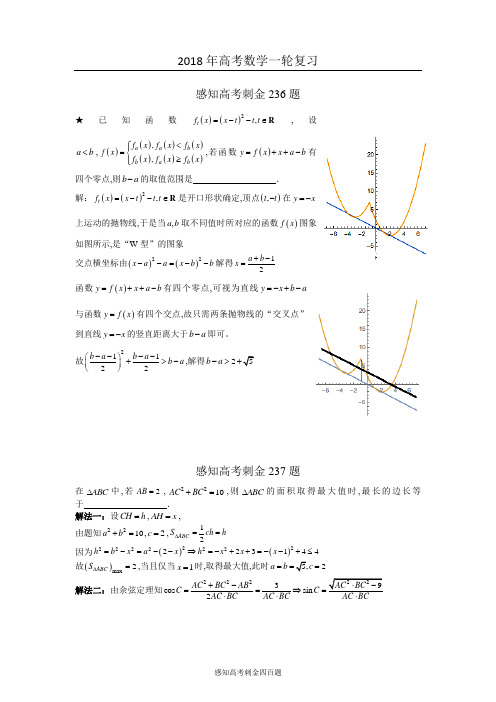
感知高考刺金236题★已知函数()()2,t f x x t t t =--∈R,设a b <,()()()()()()(),,a a b b a b f x f x f x f x f x f x f x <⎧⎪=⎨≥⎪⎩,若函数()y f x x a b =++-有四个零点,则b a -的取值范围是．解：()()2,t f x x t t t =--∈R 是开口形状确定,顶点(),t t -在y x =-上运动的抛物线,于是当,a b 取不同值时所对应的函数()f x 图象如图所示,是“W 型”的图象交点横坐标由()()22x a a x b b --=--解得12a b x +-=函数()y f x x a b =++-有四个零点,可视为直线y x b a =-+-与函数()y f x =有四个交点,故只需两条抛物线的“交叉点”到直线y x =-的竖直距离大于b a -即可。

故21122b a b a b a ----⎛⎫+>- ⎪⎝⎭,解得2b a ->感知高考刺金237题在ABC ∆中,若2AB =,2210AC BC +=,则ABC ∆的面积取得最大值时,最长的边长等于．解法一：设CH h =,AH x =,由题知2210a b +=,2c =,12ABC S ch h ∆==因为()()22222222223144h b x a x h x x x =-=--⇒=-++=--+≤ 故()max 2ABC S ∆=,当且仅当1x =时,取得最大值,此时2a b c ===解法二：由余弦定理知2223cos sin 2AC BC AB C C AC BC AC BC+-==⇒=⋅⋅故1sin 22ABCS AC BC C ∆=⋅⋅=当且仅当AC BC ==,等号成立,感知高考刺金238题如图,,C D 在半径为1的O 上,线段AB 是O 的直径,则AC BD 的取值范围是．解法一：极化恒等式角度 ()AC BD AD DC BD DC DB =+=-显然当,DC DB 均为O 的直径时,DC DB 最大为4；取BC 的中点M ,则由极化恒等式知()2222221111222DM OM OD DC DB DM BM DM OM +=-=+-≥-≥-=-故14,2AC BD ⎡⎤∈-⎢⎥⎣⎦解法二：投影角度 AC BD AC CE =要求max AC BD ,显然在AC 确定的情况下,CE 最大。

2018年高考数学一轮复习感知高考刺金四百题：第396—400题(含答案解析)

感知高考刺金396题已知椭圆22221x y a b +=，12,F F 是椭圆的左、右焦点，,A C 是椭圆上关于x 轴对称的两点，B 为短轴的端点，线段AB 恰好过右焦点，若1AB CF ⊥，则椭圆的离心率e = ．解：设()0,B b ，()2,0F c ，()2,BF c b =- ，()22,F A BF c b λλλ==- ，()(),,A A x c y c b λλ-=-即,A A x c c y b λλ=+=-，则(),C c c b λλ+ 所以12F C bk c c λλ=+，2F B bk c =-1212F C F B bb k kc c c λλ⎛⎫⋅=⋅-=- ⎪+⎝⎭2222cb c λ⇒=- 点A 在椭圆上，所以2222222222222211c c c b b c b c a b ⎛⎫⎛⎫+ ⎪ ⎪--⎝⎭⎝⎭+=化简得2245a c a e =⇒=感知高考刺金397题【2017新课标卷II,理14】若x,y 满足约束条件1020,220,x y x y x y -+≥⎧⎪-≤⎨⎪+-≤⎩，,则z x y =+的最大值为____________。

解：第一步：由约束条件，画出可行域，如图先确定满足约束条件1020,220,x y x y x y -+≥⎧⎪-≤⎨⎪+-≤⎩，的可行域，作出3条直线，围成一个三角形区域；第二步：把目标函数()0z ax by b =+≠化为a z y xb b =-+，作直线a y x b =-将目标函数z x y =+变形为y x z =-+，作直线y x =-；第三步：平移直线a y x b =-，确定目标函数最值把直线y x =-进行平行,确定平移到什么位置截距最大,然后把该点坐标代入z x y =+求最大值.当z 取最大值时，直线y x z =-+的纵截距最大，故将直线尽可能地向上平移到D （1，12），则z x y =+的最大值为23感知高考刺金398题【2017新课标卷II,理14】函数23()sin 4f x x x =-([0,])2x π∈的最大值是____________．解：()22311cos cos 44f x x x x x =--=-+=2(cos 1x -+,由[0,]2x π∈可得cos [0,1]x ∈,当cos x =时,函数()f x 取得最大值1．点评：本题经三角函数式的化简将三角函数的问题转化为二次函数的问题,二次函数、二次方程与二次不等式统称“三个二次”,它们常结合在一起,有关二次函数的问题,数形结合、密切联系图象是探求解题思路的有效方法．一般从：①开口方向；②对称轴位置；③判别式；④端点函数值符号四个方面进行分析．感知高考刺金399题【2017全国Ⅱ，文8】函数2()ln(28)f x x x =--的单调递增区间是____________。

2018年高考数学一轮复习感知高考刺金四百题：第391—395题含解析

感知高考刺金391题在平面直角坐标系xOy 中,,A B 为x 轴正半轴上两个动点，点P （异于原点)为y 轴上的定点，若以AB 为直径的圆与圆()2221x y +-=相外切,且APB ∠的大小为定值，则线段OP的长为．解：设以AB 为直径的圆的圆心为(),0t ，半径为r则()(),0,,0A t r B t r -+ 由两圆外切得241t r +=+而tan t r OPB OP+∠=，tan t r OPA OP-∠=()222222tan tan 231t r t rr OP r OP OP OP APB OPB OPA t r t r OP t r OP r OP OP+--⋅⋅∠=∠-∠===+-+-+-+⋅因为APB ∠的大小为定值，故上式与r 无关，则3OP =，此时tan 3APB ∠=为定值.点评：这又是一个山高模型的好题。

感知高考刺金392题已知()()2131124f x ax x t x t =---≤≤+，若()()maxmin 14fx f x -≥对任意t ∈R 恒成立,则实数a的取值范围是．解:()21324f x ax x =--与2y ax =的图象完全“全等”，即可以通过平移完全重合.因为11t x t -≤≤+且t ∈R ，即用一个区间宽度为2的任意区间去截取函数图象，使得图象的最高点与最低点间的纵坐标之差大于14因此取纵坐标之差最小的状态为()()211f x ax x =-≤≤，此时()()max min 104fx f x a -=-≥故14a ≥点评：本题是考查了二次函数的本质,要充分理解“a 管开口"这句话的真正含义，不仅只管抛物线开口方向，还决定了开口的大小程度.同类型关于“一只碗”的题还有很多，大家要注意，掌握好了,在选择填空题中可以秒杀.但大题要注意书写，至少说清楚每个步骤后面的奥秘。

感知高考刺金393题已知点()3,4P 和圆()22:24C x y -+=，,A B 是圆C 上两个动点，且AB =，则()OP OA OB+（O为坐标原点）的取值范围是．解：取AB 的中点为(),D x y ，则弦心距1CD ，所以点D 的运动轨迹为()2221x y -+=，()268OP OA OB OP OD x y +==+由()2221cos 2,sin x y x y θθ-+=⇒=+=所以()()[]686cos 8sin 1210sin 122,22OP OA OB x y θθθϕ+=+=++=++∈点评：圆的问题,弦心距是必添的辅助线，千万不能忘记。

2018年高考数学一轮复习感知高考刺金四百题：第201—205题(含答案解析)

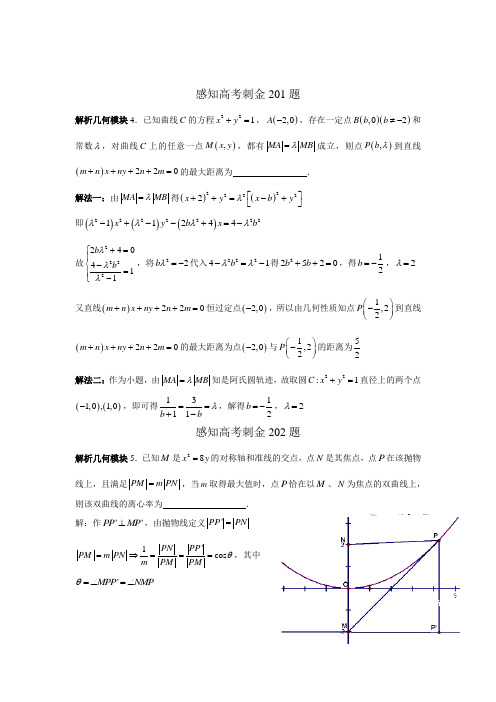
感知高考刺金201题解析几何模块4．已知曲线C 的方程221x y +=，()2,0A -，存在一定点()(),02B b b ≠-和常数λ，对曲线C 上的任意一点(),M x y ，都有MA MB λ=成立，则点(),P b λ到直线()220m n x ny n m ++++=的最大距离为．解法一：由MA MB λ=得()()222222x y x b y λ⎡⎤++=-+⎣⎦即()()()222222211244x y b x b λλλλ-+--+=- 故2222240411b b λλλ⎧+=⎪⎨-=⎪-⎩，将22b λ=-代入22241b λλ-=-得22520b b ++=，得12b =-，2λ= 又直线()220m n x ny n m ++++=恒过定点()2,0-，所以由几何性质知点1,22P ⎛⎫- ⎪⎝⎭到直线()220m n x ny n m ++++=的最大距离为点()2,0-与1,22P ⎛⎫- ⎪⎝⎭的距离为52 解法二：作为小题，由MA MB λ=知是阿氏圆轨迹，故取圆22:1C x y +=直径上的两个点()()1,0,1,0-，即可得1311b b λ==+-，解得12b =-，2λ= 感知高考刺金202题解析几何模块5．已知M 是28x y =的对称轴和准线的交点，点N 是其焦点，点P 在该抛物线上，且满足PM m PN =，当m 取得最大值时，点P 恰在以M 、N 为焦点的双曲线上，则该双曲线的离心率为．解：作''PP MP ⊥，由抛物线定义'PP PN ='1cos PN PP PM m PN m PM PMθ=⇒===，其中'MPP NMP θ=∠=∠要使m 取得最小值，即cos θ最小，即NMP θ=∠最大值，即''2PMP MPP π∠=-∠最小，此时MP 是抛物线的切线．设MP 的方程为2y kx =-，与28x y =联立得()2820x kx --=因为相切，故264640k ∆=-=，解得1k = 故()4,2P，24a PM PN =-= 由24c =，得1e =感知高考刺金203题解析几何模块6．已知斜率为1的直线l 过双曲线()222210,0x y a b a b -=>>的左焦点F ，且与双曲线左、右支分别交于,A B 两点，若A 是线段BF 的中点，则双曲线的离心率为．解：由题意知122y y =()222222422120x y b a y b cy b a b x y c ⎧-=⎪⇒--+=⎨⎪=-⎩ 2121224212122232b c y y y b a b y y y b a ⎧+==⎪⎪-⎨⎪==⎪-⎩所以222492c b a =-，所以2218c a e =⇒=感知高考刺金204题解析几何模块7．已知点P 是双曲线()222210,0x y a b a b -=>>上的动点，12,F F 是其左、右焦点，O 坐标原点，若12PF PF OP +，则此双曲线的离心率是．解：设12,PF m PF n ==，则()22222222122422m n OP F F m n OP c +=+⇒+=+ 又2m n a -=，所以22224m mn n a -+= 所以2222224mn OP c a =+- ()222222222222444m n OP c OP c a OP b +=+++-=+ 所以22244m n b OP OP +⎛⎫=+ ⎪⎝⎭所以m n OP +的最大值在OP a =时取到，所以22446b a +=所以222b a =，即e =感知高考刺金205题解析几何模块8．在平面直角坐标系xOy 中，圆C 的方程为()()22119x y -+-=，直线:3l y kx =+与圆C 相交于,A B 两点，M 为弦AB 上一动点，以M 为圆心，2为半径的圆与圆C 总有公共点，则实数k 的取值范围是．解：两圆有公共点的充要条件是15CM ≤≤，而5CM ≤恒成立，故只要min 1CM ≥时两圆必有公共点．由平面几何知识可知，min CM 为点C 到直线l 的距离d ，所以1d =≥，解得34k ≥-。

2018年高考数学复习感知高考刺金四百题：第356—360题(含答案解析)高考

感知高考刺金356题已知实数,x y 满足关系式1xy x y --=，则22x y +的最小值是．解法一：题干中出现的全是两数的和、平方和与乘积，所以考虑用均值不等式链条。

()()()2222221223x y x y xy xy xy xy +=+-=--=--由()()()2224146103x y xy xy xy xy xy xy +≥⇒-≥⇒-+≥⇒≥+或3xy ≤-所以()()2222233236x y xy +=--≥--=-点评：这里注意因为题干中没有告诉我们,x y 的正负性，所以不能直接用1x y xy +=-≥xy 的取值范围，所以改为用重要不等式来222a b ab +≥来做。

虽然答案正好一样，但做法要注意。

解法二：遇到xy 结构，所以用代数的极化恒等式变形。

令,x a b y a b =+=-，则问题转变为已知22210a b a ---=，求()222a b +的最小值。

因为()2222442a b a a +=-- 所以还需要计算定义域，即2221011b a a a a =--≥⇒≤≥所以()(2min 44216a a f --==-解法三：设,1x y a xy a +==+，则,x y 视为210z az a -++=的两根所以2440a a ∆=--≥所以2a ≥+或2a ≤-()()22222222136x y x y xy a a a +=+-=--=--≥-当且仅当2a =-时取得最小值。

感知高考刺金357题已知点P 为圆1O 与圆2O 的公共点，圆()()2221:1O x a y b b -+-=+，圆()()2222:1O x c y d d -+-=+，若8ac =，a c b d =，则点P 与直线:34250l x y --=上任意一点M 之间的距离的最小值为．解：设(),P m n ，1ac bd k==，则b ak =，d ck = 所以()()22221m a n ka k a -+-=+，即()2222210a m kn a m n -+++-=同理()2222210c m kn c m n -+++-=所以,a c 是方程()2222210x m kn x m n -+++-=的两个实根所以2218ac m n =+-=所以点P 的轨迹方程为229x y +=所以点P 到直线:34250l x y --=的最短距离为min 532PM =-=感知高考刺金358题已知向量,a b 满足23a b += ，22a b -= ，则a b 的取值范围是．解：（一）几何角度由()223a b a b +=--= 和12b a -= 可以画图，找到向量模长的几何意义。