Confidence interval
Confidence interval统计--置信区间

Confidence Intervals—Interpretation
9
• “Probability” means that “in the long run, 95% of these intervals would contain the parameter” • If we repeatedly took random samples using the same method, then, in the long run, in 95% of the cases, the confidence interval will cover (include) the true unknown parameter • For one given sample, we do not know whether the confidence interval covers the true parameter • The 95% probability only refers to the method that we use, but not to the individual sample
σ
µ = population mean and σ = population standard deviation
Confidence Interval
4
• A confidence interval for a parameter is a range of numbers within which the true parameter likely falls • The probability that the confidence interval contains the true parameter is called the confidence coefficient • The confidence coefficient is a chosen number close to 1, usually 0.95 or 0.99
confidence intervals总结置信区间SPSS计算解释 及APA 报告规范-zhaomf

Descriptive statistics (for CIs)
HOW TO REPORT (APA)?
APA, 2009, p117: When reporting confidence intervals, use the format 95% Cl [LL UL]
Displaying results APA, 2009, P130
Inference by Eye
2. For a comparison of two independent means, 1) p < .05 when proportion overlap of the 95% CIs is about .50 or less. (Proportion
overlap is expressed as a proportion of the average margin of error for the two groups.)
1. Identify what the means and error bars represent. Do bars show confidence intervals (CIs) or standard errors (SEs)? What is the experimental design?
Outstanding Issues Complex Experimental Designs
4*2(between) mixed design
References and Tools for this Presentation
• • American Psychological Association (2009). Publication Manual of the American Psychological Association. (6th ed.) American Psychological Association, Washington, DC: Author. Cumming, G., & Finch, S. (2005). Inference by eye: confidence intervals and how to read pictures of data. American Psychologist, 60(2), 170. Thompson, B. (2002). What future quantitative social science research could look like: Confidence intervals for effect sizes. Educational Researcher, 31(3), 25-32. SPSS TOOLS(excel): DANCE WITH p, C(confidence) .au/psy/research/cognitive-anddevelopmental-psychology/esci
Confidence interval统计--置信区间

Confidence Intervals
7
• With 95% probability, the sample mean falls in the interval
µ − 1.96
σ
n
, µ + 1.96
σ
n
• Whenever the sample mean falls within 1.96 standard errors from the population mean, the following interval contains the population mean
Confidence Intervals
6
• To calculate the confidence interval, we use the Central Limit Theorem • Therefore, we need sample sizes of at least, say, n = 30 • Also, we need a z–score that is determined by the confidence coefficient • If we choose 0.95, say, then z = 1.96
Different Confidence Coefficients
15
• We can use Table B3 to construct confidence intervals for other confidence coefficients • For example, there is 99% probability that a normal distribution is within 2.575 standard deviations of the mean (z = 2.575, tail probability = 0.005) • A 99% confidence interval for µ is
统计学之估计与置信区间(英文版)

17
Example: Confidence Interval for a Mean – σ Known
The American Management Association wishes to have information on the mean income of middle managers in the retail industry. A random sample of 256 managers reveals a sample mean of $45,420. The standard deviation of this population is $2,050. The association would like answers to the following questions:
5. Construct a confidence interval for a population proportion(总体比例).
6. Determine the sample size for attribute and variable sampling.
4
Point Estimates and Confidence Intervals for a Mean
7
Population Standard Deviation (σ) Known
A confidence interval estimate is a range of values constructed from sample data so that the population parameter is likely to occur within that range at a specified probability. The specified probability is called the level of confidence(置信水平).
bootstrap置信区间公式

bootstrap置信区间公式## Confidence Intervals for Means Using Bootstrapping.Introduction.Bootstrapping is a technique used to estimatestatistical parameters, such as confidence intervals, by resampling a given dataset with replacement. For example, to calculate a confidence interval for the mean of a population, bootstrapping involves repeatedly sampling from the original dataset, calculating the mean of each sample, and then using the distribution of these sample means to estimate the population mean and the associated confidence interval.Formula.The basic formula for a bootstrap confidence interval for the mean using the percentile method is:CI = (L, U)。
where:L is the lower bound of the confidence interval, which is the _p_th percentile of the sample means, where _p_ is the desired level of confidence.U is the upper bound of the confidence interval, which is the _q_th percentile of the sample means, where _q_ is 1 _p_.For example, if we want a 95% confidence interval, then _p_ = 0.025 and _q_ = 0.975.Steps.The steps for calculating a bootstrap confidence interval for the mean are as follows:1. Resample: Draw B bootstrap samples of size n from the original dataset with replacement.2. Calculate: Compute the mean for each bootstrap sample.3. Percentile: Determine the lower and upper bounds of the confidence interval by finding the _p_th and _q_th percentiles of the sample means.4. Confidence Interval: The interval (L, U) is the bootstrap confidence interval for the mean.Advantages.Bootstrapping has several advantages over traditional methods for estimating confidence intervals, such as:It is non-parametric, so it does not require assumptions about the distribution of the data.It can be used with small sample sizes.It is computationally efficient and easy to implement.Limitations.However, bootstrapping also has some limitations:It can be biased for certain types of data or if the sample size is too small.It can be computationally intensive for large datasets.It may not be accurate if the data is notrepresentative of the population.## 置信区间公式。
Confidence Interval(置信区间)

我们将采用如下所示的单边测试
我们将采用如下所示的单边测试
方法.
方法.
a
1a
a
1a
<
>
置信区间
风险
风险
置信区间
ቤተ መጻሕፍቲ ባይዱ
在此a=.05的例子中,整体风险区域是在一边的. 用适当的Z值写出相对应的不等式.
X 1.645 n
X 1.645 n
7
The Effect Of Level of Significance (a On Confidence Interval
X
Z a
n
X
Za
n
2
2
X Za n or X Za n
A confidence interval describes range of plausible values for a population parameter.
Interval size is based on one of several statistical distributions.
A sample of 10 parts from one of the torsioning stations yielded an average torsion of 198.75lbs with an s=2.333 lbs. Are the parts being made to spec?
Foot Lbs Torque (197.844, 199.627) -2.97 0.008
Variable
95.0% CI
T
P
Foot Lbs Torque 20
Variable
N
198.735 Mean
Confidence_Intervals

Confidence_IntervalsCHAPTER 1: ESTIMATIONAfter completing this chapter, you should be able to1.To construct and interpret confidence interval for the mean when σis known.2.To construct and interpretconfidence interval for the mean when σis unknown.3.To construct and interpretconfidence interval for a proportion. INTRODUCTIONOne aspect of inferential statistics is estimation, which is the process of using sample results to estimate unknown population parameters such as a population mean or a population proportion.General objective:To draw conclusions about the population of study from observations (a sample) obtained from the population.For example;One out of 4 Americans is currently dieting72% of Americans have flown on commercial airlinesThe average kindergarden student has seen more than 5000 hours of television.Since the populations from which these values were obtained are large, these values are only estimates of the true parameters and are derived from data collected from samples.Another example,Suppose we want to estimate the mean GPA of all the students at our university. The mean GPA for all the students is an unknown population mean, denoted by µ. We select a sample of students and find that the sample mean is 2.80.The sample mean, x =2.80, is a point estimate of the population mean, µ.How accurate is 2.80? To answer this question, we must construct a confidence interval estimate.1Point EstimateSuppose a college president wishes to estimate the average age of students attending classes this semester. The president could select a random sample of 100 students and find the average of thse students, say, 22.3 years.From the sample mean, the president could infer that the average age of all the students is 22.3 years.This type of estimate is called a point estimate.A point estimate is a specific numerical value of a parameter.The best point estimate of the population mean µ is the sample mean x.A point estimator draws inference about a population by estimating the value of an unknown parameter using a single value or point.Sample measures (i.e., statistics) are used to estimate population measures (i.e., parameters).These statistics are called estimator.Confident IntervalsAn interval estimate of a parameter is an interval or a range of values used to estimate the parameter. This estimate may or may not contain the value of the parameter being estimated.In an interval estimate, the parameter is specified as being between two values.For example, an interval estimate for the average age of all students might be 26.9 < µ < 27.7, or 27.3 ± 0.4 years.Either the interval contains the parameter or it does not. A degree of confidence (usually a percent) can be assigned before an interval estimate is made.2For example, a 99% confidence level for the mean age of college student might be 26.7 < µ < 27.9, or 27.3 ± 0.6. There is a 1% chance that the mean age of college student is below 26.7 or above 27.9.CONFIDENCE INTERVAL ESTIMATION FOR THE MEANIn practice, we select only one sample of size n, and µ is unknown, we never know for sure whether our specific interval includes the population mean.However, if we take all possible samples of n and compute their 95% confidence intervals, 95% of the intervals will include the population mean, and only 5% of them will not.In other words, we have 95% confidence that the population mean is somewhere in our interval.34Generally, we write the value asLower bound < population parameter < Upper boundA sample of size n is drawn from the population, and its mean x is calculated.By the central limit theorem x is normally distributed (or approximately normallydistributed.), thus…n x Z /σµ-=This leads to the following equivalent statementGraphical Demonstration of the Confidence Interval for µ:In general, the level of confidence is symbolized by (1-α) x 100%, where α is the proportion in thetails of the distribution that is outside the confidence interval.The proportion in the upper tails of the distribution is α/2, and the proportion in the lower tail of the distribution is α/2.The relationship between αand the confidence level is that the stated confidence level is the percentage equivalent to the decimal value of 1 –α, and vice versa.When the 95% confidence interval is to be found, α = 0.05, since 1 - 0.05 =0.95, or 95%.When α = 0.01, then 1 –α= 1 - 0.01 = 0.99, and the 99% confidence interval is being calculated.The term zα/2( / √n ) is called the maximum error of the estimate (also called the margin of error). The maximum error of the estimate is the maximum likely difference between the point estimate ofa parameter and the actual value of the parameterThe value of zα/2needed for constructing a confidence intercal is called the critical value for the distribution.567CONFIDENCE INTERVAL FOR µ WHEN σ KNOWNExample 1:A paper manufacturer has a production process that operates continuously throughout an entire production shift. The paper is expected to have a mean length of 11 inches, and the standard deviation of the length is 0.02 inch. At periodic intervals, a sample is selected to determine whether the mean paper length is still equal to 11 inches or whether something has gone wrong in the production process to change the length of the paper produced. You select a random sample of 11 sheets, and the mean paper length is 10.998 inches. Construct a 95% confidence interval estimate for the population mean paper length. Solution:µ = 11, and σ = 0.02. From the sample, n = 100 and x =10.998, α = 0.05 therefore z 0.025 = 1.96.x ?z ασ√n<µσ√n10.998 – 1.96 x√100< µ < 10.998 + 1.96 x √10010.998 – 0.00392 < µ < 10.998 + 0.00392 10.99408< µ < 11.00192Thus, with 95% confidence, we conclude that the population mean is between10.99408 and 11.00192 inches.Because the interval includes 11, the value indicating that the production process is working properly, you have no reason to believe that anything is wrong with the production process.CONFIDENCE INTERVAL OF THE MEAN FOR THE MEAN WHEN σ IS UNKNOWNCan You Ever Really Know Sigma?We have discussed the concept of confidence interval estimate, how to develop it, and how to interpret it.When the original variable is normally distributed and σ is known, the standard normal distribution can be used to find confidence intervals regardless of the size of the sample.The discussion limited itself to the case where the population standard deviation, sigma, σ, is known. But, can you ever really know sigma?If sigma is known, then we can use the normal distribution to construct confidence intervel. If sigma is unknown, we will use the t distribution instead of the normal distribution.In virtually all real-world business applications, you do not know the standard deviation of the population.If, for a particular case, you knew the population standard deviation, you would also already know (or could compute) the population mean. There would be no need to employ the inductive reasoning interval statistics to estimate the population mean.Just as the mean of the population, µ, is usually unknown, you virtually never know the standard deviation of the population,σ.Therefore, you need to construct a confidence interval estimate of µ, using the sample statistic, s, as an estimate of the population parameter σ.When σ is unknown, we use its point estimator s, and the z-statistic is replaced then by the t-statisticThe symbol d.f. will be used for degrees of freedom.The degrees of freedom for aconfidence interval for the mean are found by subtracting 1 from the sample size.That is, d.f. = n - 1.8Example 2:The data represent a sample of the number of home fires started by candles for the past several years. Find the 99% confidence interval for the mean number of home fires started by candles each year.5460 5900 6090 6310 7160 8440 9930Solution9CONFIDENCE INTERVAL FOR A POPULATION PROPORTIONProportions can be obtained from samples or populations. The following symbols will be used.For example, in a study, 200 people were asked if they were satisfied with their job or profession; 162 said that they were. In this case, n = 200, X = 162, and p? =X/n = 162/200 = 0.81.The sample proportion is p?=0.81.The proportion of people who did not respond favorably when asked if they were satisfied with their job or profession constituted q?, where q? = 1 - p?.For this survey, q? = 1 – 0.81 = 0.19, or 19%.To construct a confidence interval about a proportion, one must use the maximum error of estimate, which isConfidence intervals about proportions must meet the criteria that np ≥5 and nq ≥5.10Example 3:A sample of 500 nursing applications included 60 from men. Find the 90% confidence interval of the true proportion of men who applied to the nursing program.Solution11DETERMINING SAMPLE SIZESample Size Determination for the Mean1213To compute the sample size, you must know three factors:1. The desired confidence level, which determines the value of Z α/2, the critical value from the standardized normal distribution2. The acceptable sampling error, (or margin of error) E.3. The standard deviation, .Sample Size Determination for the ProportionTo compute the sample size, you must know three factors:1. The desired confidence level, which determines the value of Z α/2, the critical value from the standardized normal distribution2. The acceptable sampling error, (or margin of error) E.3. The population proportion, p .Formula for the sample size determination for the proportion:n = z α/22p (1?p )EExample 4:。
confidence interval

置信区间的值
我们用置信区间获得对总体均值、总 体标准差、总体缺陷率和过程能力 (CP,CPK)的区间估计
置信区间方程式均值落 在总体均值的两个“标准误差”内 因此,我们可以说,如果我们从一个过 程中抽取一个样本并计算他们的均值, 我们有95%的把握它落在总体均值真值的 两个误差中 置信区间的一般表达式
总体缺陷的置信区间
举例
假设我们抽取100根针的样品,其中有25个缺陷 点,对这个总体缺陷比例的95%的置信区间是 多少? 答案:该样本的缺陷比例是25/100=0.25,则近 似95%的置信区间是:
0.25±1.96√[0.25(1-0.25)/100]=0.25±0.085
总体缺陷的置信区间
综上所述,95%置信区间近似为
X±1.96s/√N
区间的中点是X 95%的概论获得μ
100个样品的置信区间-95%
16
15
14
1 2 3 4 5 6 7 10 8 9 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 100 99
0.587 0.117 1.39564 0.00444 1.97E-05 -8.4E-02 -1.30902 30 1.38773 1.39116 1.39608 1.39913 1.40248 1.39729 0.00597 1.39849
ConfidenceInterval-GraphingCalculator:置信区间的图形计算器

Confidence IntervalIn practice, the population mean (µ) is hardly ever known. We normally estimate it with a point estimate or an interval estimate.A point estimate is a statistic that estimates a parameter. For example, a sample mean is a point estimate of the parameter population mean (µ).An interval estimate is an interval of values that is believed to contain the population mean. An interval estimate of the population mean (µ) is called a confidence interval.Let's look at an example. Suppose we randomly select 40 SAT math scores and the sample data are as follows: 300 320 350 370 380 380 390 390 400 400420 430 430 440 450 460 470 470 480 500540 550 570 590 600 620 650 650 660 670680 690 700 710 710 720 720 730 730 750The sample average is 536.75 and sample standard deviation is 140.A point estimate for the population of SAT math scores mean would be 536.75.An interval estimate of the population could be (536.75 - 20, 536.75 + 20) = (516.75, 556.75).Question: Can we an interval that is wider that (516.75, 556.75) so that I can more confident aboutcoming up with an interval estimate that contains the population mean?We can make the interval as wide as you want. For example other possible interval estimates might be:a) (536.75 - 30, 536.75 + 30) = (506.75, 566.75)b) (536.75 - 40, 536.75 + 40) = (496.75, 576.75)c) (536.75 - 50, 536.75 + 50) = (486.75, 586.75)Hence, the wider the interval estimate, the more confident you can be about the population mean lying inside the interval.But note that the wider the interval estimate, the less we can be precise about estimating the population mean.Consequently, when constructing an interval estimate, we have to decide which is more important: levelof confidence or precision?To understand the logic behind constructing a confidence interval, we will examine the relationship between sampling distribution and confidence interval.Sampling Distribution and Confidence Interval Illustration of 95% Confidence Intervalx x x x x xxkσand standard deviation =nConfidence interval is defined as follows:/2/2Confidence Interval =, where sample mean;= underlying population standard deviation; = s x z x z x n αασ⎡⎤-+⎢⎥⎣⎦=/2/2ample size; = z-score corresponding to the percentage ofconfidence intervals containing population mean. z z ααmargin of error.=Hence, confidence interval = sample mean ± margin of error .For each sample mean x in the sampling population, we can construct a confidence intervals. For 95% confidence interval, we set /2z α to 1.96. Later on we will see how to figure out the value of /2z α for any confidenceinterval.11/21/2112Sample Mean Confidence Interval, = 1.96, 1.96x x z x z x x x αα⎡⎤⎡⎤-+-+⎢⎥⎢⎥⎣⎦⎣⎦2/22/22233/23/233 , = 1.96, 1.96 , = 1.96, 1.96x z x z x x x x z x z x x αααα⎡⎤⎡⎤-+-+⎢⎥⎢⎥⎣⎦⎣⎦⎡⎤-+-+⎢⎥⎣⎦44/24/24455/25/2 , = 1.96, 1.96 , x x z x z x x x x z x z αααα⎡⎤⎢⎥⎣⎦⎡⎤⎡⎤-+-+⎢⎥⎢⎥⎣⎦⎣⎦-+55= 1.96, 1.96k x x x ⎡⎤⎡⎤-+⎢⎥⎢⎥⎣⎦⎣⎦/2/2 , = 1.96, 1.96k k k k x z x z x x αα⎡⎤⎡⎤-+-+⎢⎥⎢⎥⎣⎦⎣⎦We can see that the number of confidence intervals is very large. Some of these confidence intervals contain the population mean (µ) and some do not. When we construct a confidence interval, we would hope that our confidence interval contains the population mean.In practice we do not know if our constructed confidence interval contains the population mean (µ) or not. We only know what percentage of all possible confidence intervals containing the population mean. The percentage of confidence intervals that contains the population mean is dictated by the quantity /2.z α When calculating the value of /2z α, we will assume that the sampling population is approximately normal. In other words, the sample size is at least 30 or the underlying population is normal.The table below shows some values of /2z α and corresponding percentage of confidence intervals containing the population mean:The percentage containing the population mean is calculated by using the standard normal distribution. For example, for /2z α = 1.96, we would find the area between -1.96 and 1.96. Below the area in yellow is 95% and represents the percentage of confidence intervals containing the population mean.We can find the area between -1.96 and 1.96 by using one of the computational tools at .Question: What would be an appropriate value for /2z?95%As /2z α increases, the width of the confidence intervals also increases. That's the reason why, we see that as/2z α increases, the percentage of the confidence intervals containing the population mean also increases.Thus, if we want to have higher percentage of confidence intervals containing the population mean, then we would choose a large value for /2z α. But note that large value for /2z α will lead to wider confidence intervals; and hence less precision about the estimation of the population mean.In practice, when we want to do an interval estimate of the population mean, we would specify the what percentage of the confidence intervals do we want to contain the population mean. Then we have to figure out the corresponding /2z α.Suppose we want the percentage containing the population mean to be 95%. Normally we would say we want to construct a confidence interval with a level of confidence of 95%./2For level of confidence is 95%:5% = percentage of confidence intervals not containing population mean /2 2.5%0.0251.96.z ααα==== For standard normal distribution, z-score is 1.96 if right-tailed area is 0.025.We can find the z-score corresponding to a right-tailed area of 0.025 by using one of the computational tools at .95%Since the level of confidence is specified at 95%, 95% of confidence intervals contain population mean (µ) and 5% do not. Hence, α = 5%.In practice, to construct a confidence interval, we select a sample of size n at random and then calculate the sample mean and confidence interval. We do not know if our confidence interval is part of the 95% or part of the 5%. All we know is that of all possible confidence intervals -- where level of confidence is set at 95% -- 95% of them contain the population mean and 5% do not.Thus, we can only say that we are 95% confident the our confidence interval contains the population mean (µ).Constructing 95% Confidence IntervalThe population of ACT scores has a standard deviation of 6. Suppose we randomly select a sample of 40 ACT scoresand the data are as follows:6 7 8 10 11 11 12 12 13 1314 15 15 16 16 17 17 18 18 1818 18 19 19 19 20 20 21 21 2222 22 22 23 23 23 24 24 25 27Find a confidence interval with a level of confidence of 95%. Solution:From the population of ACT scores we can form many, many samples of size 40. One these many, many samples is: 6 7 8 10 11 11 12 12 13 13 14 15 15 16 16 17 17 18 18 18 18 18 19 19 19 20 20 21 21 22 22222223232324242527Note: Sample mean = x = 17.48.For each sample of size 40, a sample mean can be calculated. Hence there are many, many sample means. For each samplemean a confidence interval can be formed. Consequently, there are many, many confidence intervals. Since our level of confidence is set 95%, 95% of all confidence intervals will contain the population mean and 5% of the confidence intervals do not contain the population mean.Since the sample size is greater than 30, the distribution of the sample means is approximately normal and 95% of the z-scores will lie between -/2z α and /2z α.Left Area = 2.5% Middle Area = 95% Right Area = 2.5%/2z α is the z-score corresponding to a right area of 0.025. Hence, /2z α= 1.96.From earlier discussion, a confidence interval has the form:/2/2, x z x z αα⎛⎫-+ ⎪⎝⎭where x is the sample mean;/2z α is the number of standard error from the population mean;σ is the standard deviation of the population of ACT scores;n is the sample sizeStandard Error =0.9486=.()()()()/2/2Confidence Interval = , = 17.48 1.960.9486, 17.48 + 1.960.9486 = 15.62, 19.33x z x z αα⎛⎫-+ ⎪⎝⎭-Comments:We do not know if ()15.62, 19.33contains the population mean or not since this interval is one of many, many confidence intervals. However, since we know that 95% of the confidence intervals do contain the population mean, we can be 95% confident that the interval ()15.62, 19.33 does contain the population mean.Also, the interval ()15.62, 19.33 is an interval estimate of the population mean.Illustration of 99% Confidence Intervalx x x x x xxkσand standard deviation =n/2/2Confidence Interval =, x z x z αα⎡⎤⎫-+⎢⎥⎪⎭⎣⎦11/21/2112Sample Mean Confidence Interval, = 2.57, 2.57x x z x z x x x αα⎡⎤⎡⎤-+-+⎢⎥⎢⎥⎣⎦⎣⎦2/22/22233/23/233 , = 2.57, 2.57 , = 2.57, 2.57x z x z x x x x z x z x x αααα⎡⎤⎡⎤-+-+⎢⎥⎢⎥⎣⎦⎣⎦⎡⎤-+-+⎢⎥⎣⎦44/24/24455/25/2 , = 2.57, 2.57 , x x z x z x x x x z x z αααα⎡⎤⎢⎥⎣⎦⎡⎤⎡⎤-+-+⎢⎥⎢⎥⎣⎦⎣⎦-+55= 2.57, 2.57k x x x ⎡⎤⎡⎤-+⎢⎥⎢⎥⎣⎦⎣⎦/2/2 , = 2.57, 2.57 k k k k x z x z x x αα⎡⎤⎡⎤-+-+⎢⎥⎢⎥⎣⎦⎣⎦/2For level of confidence of 99%:1%/20.5%0.0052.57.z ααα==== For standard normal distribution, z-score is 2.57 if right-tailed area is 0.005.99%Using computational tool at :Since the level of confidence is specified at 99%, 99% of confidence intervals contain population mean (µ) and 1% do not. Hence, α = 1%.In practice, to construct a confidence interval, we select a sample of size n at random and then calculate thesample mean and confidence interval. We do not know if our confidence interval is part of the 99% or part of the 1%. All we know is that of all possible confidence intervals -- where level of confidence is set at 99% -- 99% of them contain the population mean and 1% do not.Thus, we can only say that we are 99% confident the our confidence interval contains the population mean (µ).Example:The population of ACT scores has a standard deviation of 6. Suppose we randomly select a sample of 40 ACT scoresand the data are as follows: 6 7 8 10 11 11 12 12 13 13 14 15 15 16 16 17 17 18 18 18 18 18 19 19 19 20 20 21 21 22 22 22 22 23 23 23 24 24 25 27Find a confidence interval with a level of confidence of 99%. Solution:From the population of ACT scores we can form many, many samples of size 40. One these many, many samples is: 6 7 8 10 11 11 12 12 13 13 14 15 15 16 16 17 17 18 18 18 18 18 19 19 19 20 20 21 21 22 22222223232324242527Note: Sample mean = x = 17.48.For each sample of size 40, a sample mean can be calculated. Hence there are many, many sample means. For each sample mean a confidence interval can be formed. Consequently, there are many, many confidence intervals.Since our level of confidence is set 99%, 99% of all confidence intervals will contain the population mean and 1% of the confidence intervals do not contain the population mean.Since the sample size is greater than 30, the distribution of the sample means is approximately normal and 99% of the z-scores will lie between -/2z α and /2z α.Left Area = 0.5% Middle Area = 99% Right Area = 0.5%/2z α is the z-score corresponding to a right area of 0.005. Hence, /2z α= 2.57.From earlier discussion, a confidence interval has the form:/2/2, x z x z αα⎛⎫-+ ⎪⎝⎭where x is the sample mean;/2z α is the number of standard error from the population mean;σ is the standard deviation of the population of ACT scores;n is the sample sizeStandard Error =0.9486=.()()()()/2/2Confidence Interval = , = 17.48 2.570.9486, 17.48 + 2.570.9486 = 15.042, 19.918x z x z αα⎛⎫⎛-+ ⎪⎝⎝⎭-Comments:We do not know if ()15.042, 19.918contains the population mean or not since this interval is one of many, many confidence intervals. However, since we know that 99% of the confidence intervals do contain the population mean, we can be 99% confident that the interval ()15.042, 19.918 does contain the population mean.Also, the interval ()15.042, 19.918 is an interval estimate of the population mean.Illustration of 90% Confidence Intervalx x x x x x/2/2Confidence Interval =,x z x zαα⎡⎤⎫-+⎢⎥⎪⎭⎣⎦kxand standard deviation =nσ11/21/2112Sample Mean Confidence Interval, = 1.645, 1.645x x z x z x x x αα⎡⎤⎡⎤-+-+⎢⎥⎢⎥⎣⎦⎣⎦2/22/22233/23/233 , = 1.645, 1.645 , = 1.645, 1.645x z x z x x x x z x z x x αααα⎡⎤⎡⎤-+-+⎢⎥⎢⎥⎣⎦⎣⎦⎡⎤-+-+⎢⎥⎣⎦44/24/24455/2 , = 1.645, 1.645 , x x z x z x x x xz x ααα⎡⎤⎢⎥⎣⎦⎡⎤⎡⎤-+-+⎢⎥⎢⎥⎣⎦⎣⎦-5/255= 1.645, 1.645k z x x x α⎡⎤⎡⎤+-+⎢⎥⎢⎥⎣⎦⎣⎦/2/2 , = 1.645, 1.645 k k k k x z x z x x αα⎡⎤⎡⎤-+-+⎢⎥⎢⎥⎣⎦⎣⎦/2For level of confidence is 90%:10%/25%0.051.644854.z ααα====For standard normal distribution, z-score is 1.644854 if right-tailed area is 0.05.90%Since the level of confidence is specified at 90%, 90% of confidence intervals contain population mean (µ) and 10% do not.Hence, α = 10%.In practice, to construct a confidence interval, we select a sample of size n at random and then calculate the sample mean and confidence interval. We do not know if our confidence interval is part of the 90% or part of the 10%. All we know is that of all possible confidence intervals -- where level of confidence is set at 90% -- 90% of them contain the population mean and 10% do not.Thus, we can only say that we are 90% confident the our confidence interval contains the population mean (µ).Example:The population of ACT scores has a standard deviation of 6. Suppose we randomly select a sample of 40 ACT scoresand the data are as follows: 6 7 8 10 11 11 12 12 13 13 14 15 15 16 16 17 17 18 18 18 18 18 19 19 19 20 20 21 21 22 22 22 22 23 23 23 24 24 25 27Find a confidence interval with a level of confidence of 90%. Solution:From the population of ACT scores we can form many, many samples of size 40. One these many, many samples is: 6 7 8 10 11 11 12 12 13 13 14 15 15 16 16 17 17 18 18 18 18 18 19 19 19 20 20 21 21 22 22222223232324242527Note: Sample mean = x = 17.48.For each sample of size 40, a sample mean can be calculated. Hence there are many, many sample means. For each sample mean a confidence interval can be formed. Consequently, there are many, many confidence intervals.Since our level of confidence is set 90%, 90% of all confidence intervals will contain the population mean and 10% of the confidence intervals do not contain the population mean.Since the sample size is greater than 30, the distribution of the sample means is approximately normal and 90% of the z-scores will lie between -/2z α and /2z α.Left Area = 5% Middle Area = 90% Right Area = 5%/2z α is the z-score corresponding to a right area of 0.05. Hence, /2z α= 1.644854.From earlier discussion, a confidence interval has the form:/2/2, x z x z αα⎛⎫-+ ⎪⎝⎭ where x is the sample mean;/2z α is the number of standard error from the population mean;σ is the standard deviation of the population of ACT scores; n is the sample sizeStandard Error =0.9486=.()()()()/2/2Confidence Interval = , = 17.48 1.6450.9486, 17.48 + 1.6450.9486 = 15.919, 19.040x z x z αα⎛⎫⎛-+ ⎪⎝⎝⎭-Comments:We do not know if ()15.919, 19.040contains the population mean or not since this interval is one of many, many confidence intervals. However, since we know that 99% of the confidence intervals do contain thepopulation mean, we can be 99% confident that the interval ()15.919, 19.040 does contain the population mean.Also, the interval ()15.919, 19.040 is an interval estimate of the population mean.。
第四章 参数的区间估计(Confidence Interval Estimation)

Chap 4-34
PHStat用于解决此类问题
PHStat | confidence intervals | estimate for the population total Excel spreadsheet for the voucher example
第四章 参数的区间估计 (Confidence Interval Estimation)
阅读教材:第7章
Chap 4-1
本章概要
估计的步骤(Estimation process) 点估计(Point estimates) 区间估计(Interval estimates) 均值的置信区间( 已知) 样本容量的确定(Determining sample size) 均值的置信区间 ( 未知) 比例的置信区间
n
) 1
Chap 4-9
区间估计的要素
置信度
区间内包含未知总体参数的确定程度 与未知参数的接近程度 获得容量为 n 的样本所需付出的代价
精度
成本
Chap 4-10
置信度
以 100 1 %表示,如:90%,95%,99% 相对频率意义上的解释
从长期来看, 所构建的所有置信区间中,100 1 % 的置信区间都将含有未知参数,即未知参数落入区间的 概率;
n
( z 2 ) (1 )
2
E2
其中: E z 2
(1 )
n
2. 3.
E的取值一般小于0.1 (=p) 未知时,可取最大值0.5
比值比和95%置信区间

比值比和95%置信区间英文回答:The ratio estimate and the 95% confidence interval are both statistical measures that are commonly used inresearch and data analysis. These measures provideimportant information about the relationship between two variables and the level of uncertainty associated with the estimate.The ratio estimate is a measure of the relationship between two quantities. It is calculated by dividing one quantity by another. For example, if we want to estimatethe ratio of the number of men to the number of women in a population, we would divide the number of men by the number of women. The resulting ratio estimate gives us an idea of the relative proportions of men and women in the population.The 95% confidence interval, on the other hand,provides a range of values within which we can bereasonably confident that the true population ratio lies.It is calculated based on the sample data and takes into account the variability in the data. The 95% confidence interval is constructed such that we can be 95% confident that the true population ratio falls within the interval.To illustrate these concepts, let's consider an example. Suppose we are interested in estimating the ratio of the number of students who prefer coffee to the number of students who prefer tea in a school. We randomly select a sample of 100 students and find that 60 students prefer coffee and 40 students prefer tea. The ratio estimate would be 60/40, which is 1.5. This means that for every 1 student who prefers tea, there are 1.5 students who prefer coffee.To calculate the 95% confidence interval, we can use statistical software or formulas. Let's say the 95% confidence interval is calculated to be 1.2 to 1.8. This means that we can be 95% confident that the true population ratio of coffee to tea preference lies between 1.2 and 1.8.中文回答:比值比和95%置信区间都是研究和数据分析中常用的统计量。
估计曲线的置信区间

估计曲线的置信区间英文回答:Confidence Intervals for Curves.Introduction.When fitting a curve to a set of data, it is important to be able to estimate the uncertainty in the fitted curve. This can be done by constructing a confidence interval around the curve. A confidence interval is a range of values that is likely to contain the true value of the curve.Methods for Constructing Confidence Intervals.There are a number of different methods that can be used to construct confidence intervals for curves. One common method is to use the bootstrap. The bootstrap is a resampling technique that can be used to estimate thedistribution of a statistic. In the case of curve fitting, the statistic of interest is the fitted curve.To construct a confidence interval using the bootstrap, the following steps are followed:1. Fit the curve to the data.2. Resample the data with replacement.3. Fit the curve to the resampled data.4. Repeat steps 2 and 3 a large number of times (e.g., 1000 times).5. Calculate the confidence interval as the range of values that contains the fitted curve in a specified percentage of the resamples (e.g., 95%).Interpretation of Confidence Intervals.The confidence interval around a curve can be used tomake inferences about the true value of the curve. For example, if the confidence interval is narrow, then it is likely that the true value of the curve is close to thefitted curve. Conversely, if the confidence interval is wide, then it is likely that the true value of the curve is further away from the fitted curve.Confidence intervals can also be used to comparedifferent curves. For example, if the confidence intervals for two curves do not overlap, then it is likely that the curves are different.Example.The following figure shows a fitted curve with a 95% confidence interval. The confidence interval is shown asthe shaded region around the curve.[Image of a fitted curve with a 95% confidence interval]The confidence interval shows that the true value ofthe curve is likely to be within the shaded region.Conclusion.Confidence intervals are a valuable tool for understanding the uncertainty in fitted curves. They can be used to make inferences about the true value of the curve and to compare different curves.中文回答:曲线的置信区间。
CalculateConfidenceInterval:计算置信区间

Confidence IntervalsHow to Calculate Standard Error and Construct Confidence Intervals for MeansAnd Difference in MeansPART 1: Calculating Standard Error for MeansStandard Error for Means = standard deviation of the sample divided by the square root of n = s/√nSTEP I: calculate the mean of the sample:MEAN (aka Average):1) Count the observations in your sample. This is often referred to as n.So here, n = ___2) Add the numbers in your sample. ____+____+____+____+____+____ = ______________.STEP II: calculate the variance of the sample:VARIANCE1)Subtract each observation from the mean.2) Square each of the results.ObservationMean)squared23) Add the numbers from column C: ____+____+____+____+____+____ = ____ Algebraically, this is:4) Divide your result from Step 3 by n – 1.Algebraically, this is:STEP III: Calculate Standard DeviationSTANDARD DEVIATIONTake the square root of the variance (as calculated above).Algebraically, that is:STEP IV: Calculate the Standard Error (SE) of the Mean1)Divide Standard Deviation (result from STEP III) by the square root of n._______/ √______ = _______Part II: Calculating Margin of Error and Constructing Confidence IntervalsSTEP V: Determine the appropriate Confidence Level. In this course, the confidence level will generally be 95%.STEP VI: Recall that the t-statistic (or critical value) that we are using for 95% confidence is 1.96. Sometimes you will see this critical value rounded up to 2.STEP VII: Calculate the margin of error: t- statistic * standard error of the mean1)The t-statistic is: 1.96 (or, if rounding: 2)2)The standard error (SE) of the mean is: ____3)Multiply them: 1.96*SE of the mean1.96 * ________ = _______STEP VII: Construct the Confidence Interval:1)The sample mean () is: _____2)The margin of error is: _____3)Plug these numbers into the following mathematical statement:( - Margin of Error) < μ < ( + Margin of Error)__________ < μ < ____________(lower bound) (upper bound)STEP VIII: Interpret:I am 95% confident that the true population mean lies between [state the value of the lower bound] and [state the value of the upper bound].Calculate Confidence Interval for Difference in MeansSTEP I: Repeat all steps in Part I (above) for the first and second samples. You will need two copies of the worksheet. The steps include the following:[STEP I: calculate the mean of the sampleSTEP II: calculate the varianceSTEP III: calculate standard deviationSTEP IV: calculate standard error of the mean]STEP II: Find the difference in means1) Recall the mean from sample one: 1 = ______2) Recall the mean from sample two: 2 = ______3) Subtract:- 21= ____________STEP III: Calculate the pooled standard error1) Recall the standard error of 1 : _____2) Recall the standard error of 2 : _____3) Plug into the following formula:Pooled Standard Error = Square Root [( standard error of 1 )2 + (standard error of 2 )2]STEP IV: Calculate the Margin of Error1)Recall that the t-statistic is 1.962)The pooled standard error (from above) is: ________Margin of Error = 1.96* Pooled Standard Error= 1.96* ______= ________STEP V: Construct the Confidence Interval1)Recall that the difference in means (STEP II) is = ________2)The margin of error (STEP IV) is: _________3)Plug these numbers into the following mathematical statement:(Difference in Means - Margin of Error) < μ2 - μ1 < (Difference in Means + Margin of Error)___________ < μ2 - μ1 < _________(lower bound) (upper bound)STEP VI: InterpretI am 95% confident that the true difference in means lies between _________ and __________.(lower bound) (upper bound)。
ReviewofConfidenceIntervalConcepts置信区间的概念,综述

One-Proportion and One-Mean Confidence Intervals∙ Say we wanted to estimate the population proportion or percentage of femaleundergraduate students at PSU-UP. I could instruct each of you to take a random sample of say 100 and record the gender of each. Then you would calculate the percentage of your sample that was female. Do you believe that each of these sample proportionswould be the same? No, but each by themselves is a point estimate of the true proportion. What if we wanted to estimate the true population mean age of PSU undergraduatestudents? Again I could instruct you to take a random sample of some size, record each person’s age in your sample and then calculate the sample mean. Again, even thougheach sample mean is a point estimate of the population mean, would you expect eachsample mean to be the same?∙ A confidence interval is an interval of values that is likely to "capture" the unknown value of a population parameter of interest, such as the true population mean, μ, or thetrue difference, μd . Another concept is to estimate the difference between twoindependent samples. However, we will save this discussion for a future lesson.∙ The confidence level is the probability (fraction of times) that the procedure used todetermine an interval gives an interval that actually captures the true population value. For example, say we repeatedly drew samples of the same size from a population andconstructed 95% confidence intervals for each sample, and we repeated this process 1000 times. Then we would expect 95%, or 950, of these confidence intervals to contain the true population parameter. In reality, though, we typically construct only one suchconfidence interval and thus we are X-% confident that this interval has captured the true parameter. However in reality, this interval might or might not contain the true value. As a result, confidence intervals are exactly that: statements of how confident you are. These should not be interpreted, for example, to say that there is a 95% probability that the true value is in this interval. This is not true because the true value is either in the interval (i.e. probability of 1) or not in the interval (probability of 0).∙ For example, In most situations considered in our text, the general format for determininga confidence interval isSample statistic ± Multiplier × Standard error∙ In other words, we form a confidence interval by adding and subtracting an appropriatenumber of standard errors to (and from) the sample estimate. The common levels ofconfidence will be 90%, 95%, 98% and 99%.This week we considered confidence intervals for 1-proportion and 1-mean. For the proportion the formula is:np p Z p )ˆ1(ˆ*ˆ-± and the multipliers are standard.But what if our variable of interest is a quantitative variable (e.g. GPA, Age, Height) and we want to estimate the population mean? In such a situation proportion confidence intervals are not appropriate since our interest is in a mean amount and not a proportion.For 1-mean the confidence interval will involve a new concept: Degrees of Freedom, or df. We will use this df in conjunction with Table A2 to find the multiplier. The formula for a 1-mean confidence interval is:n st x *±Therefore we apply similar techniques but now we are interested in estimating the populationmean, μ, by using the sample statistic and the multiplier is a t-value. Until now we assumed that our random variable came from a normal distribution with a known population standard deviation, σ. However, typically we do not know this parameter and therefore must estimate it. This is done by using the standard deviation of the sample which is expressed as "S ". Since we need to make this estimate we lose our reference to the variable being from a normal distribution. These t-values come from a t-distribution which is similar to the standard normal distribution from which the z-values came. The similarities are that the distribution is symmetrical and centered on 0. The difference is that when using a t-table we need to consider a new feature: degrees of freedom (df ). This degree of freedom will be based on the sample size, n.Example of 1-proportion and 1-mean confidence intervals Assume our class survey represents a random sample taken from the PSU undergraduatepopulation. Find 95% confidence intervals for the following:1. Find 95% confidence interval Do you think marijuana should be legalized?2. Find 90% confidence interval Do you believe in same-sex marriages?3. Find 95% confidence interval for mean GPA.4. Find 99% confidence interval for mean amount of money students spent on books.Solutions : 1. n p p Z p)ˆ1(ˆ*ˆ-± = 65)615.01(615.0*96.1615.0-±= 0.497 ≤ p ≤ 0.734 In Minitab we use Stat > Basic Statistics > 1-ProportionEvent = YesVariable X N Sample p 95% CILegalMJ? 40 65 0.615385 (0.497114, 0.733656)Interpretation: We are 95% confident that the proportion of PSU-UP undergraduate students who think marijuana should be legalized is between 49.7% and 73.4%2. 65)707.01(707.0*65.1707.0-±= 0.614 ≤ p ≤ 0.800Event = YesVariable X N Sample p 90% CISameSexMar 46 65 0.707692 (0.614900, 0.800485)Interpretation: We are 90% confident that the proportion of PSU-UP undergraduate students who agree in same-sex marriage is between 61.5% and 80.0%3. n st x *± = 66473.0*00.238.3+ = 3.26 ≤ u ≤ 3.49In Minitab we use Stat > Basic Statistics > 1-Sample tVariable N Mean StDev SE Mean 95% CIGPA 66 3.3785 0.4733 0.0583 (3.2621, 3.4948)Interpretation: We are 95% confident that the mean GPA of PSU-UP undergraduates is between3.26 and 3.494. n st x *± = 655.153*66.22.350+ = 299.6 ≤ u ≤ 400.8In Minitab we use Stat > Basic Statistics > 1-Sample tVariable N Mean StDev SE Mean 99% CITextSpd 65 350.2 153.5 19.0 (299.6, 400.8)Interpretation: We are 95% confident that the mean amount of money PSU-UP undergraduates spent on books is between $299.6 and $400.8。
CONFIDENCEINTERVALforthemean
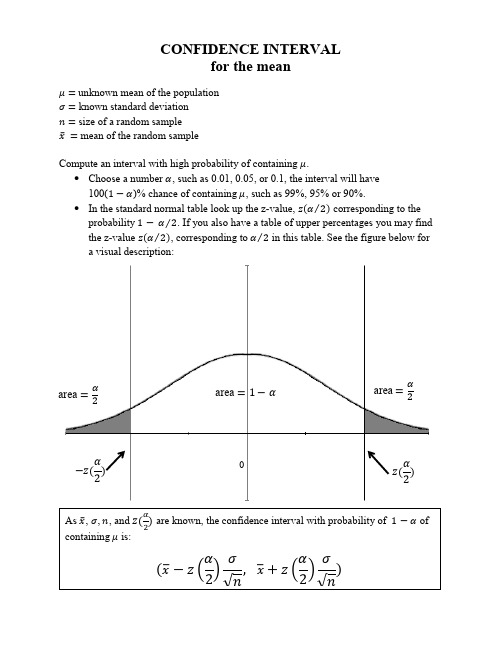
probability
⁄ . If you also have a table of upper percentages you may find
the z-value ⁄ , corresponding to ⁄ in this table. See the figure below for
a visual description:
̅ ̅ ( )√
̅ ̅ ( )√
If the standard deviations, and , of the two populations are unknown and the sample sizes are large enough, the calculated variances and can be substituted for and
Choose a number , such as 0.01, 0.05, or 0.1, the interval will have
100( )% chance of containing , such as 99%, 95% or 90%.
In the standard normal table look up the z-value, ⁄ corresponding to the
of
containing
.Leabharlann FindIf the standard deviation, 1 and 2, of the two populations are known, then
The confidence interval with the probability
of containing
is:
CONFIDENCE INTERVAL for the mean
统计学之估计与置信区间(英文版)

13
Point Estimates and Confidence Intervals for a Mean – σ Known
X 1.96
n
a 99 percent confidence interval :
X 2.58
n
14
10
Finding z-value for 95% Confidence Interval
The area between Z = -1.96 and z= +1.96 is 0.95
11
Interval Estimates Interpretation
For a 95% confidence interval about 95% of the similarly constructed intervals will contain the parameter being estimated. Also 95% of the sample means for a specified sample size will lie within 1.96 standard deviations of the hypothesized population
Point Estimates and Confidence Intervals for a Mean – σ Known
第四章 可信区间

πU =
r +1 r +1+(n−r) / Fα;2(r+1),2(n−r)
2+1 = = 5.2% 2+1+(120 −2) / 2.1371
即该生物制剂的皮疹发生率最大为5.2%。 。 即该生物制剂的皮疹发生率最大为
back11
是以µ为中心的区间, 区间 µ ±u0.05σ X 是以µ为中心的区间,表示从已知的均数 标差为σ的正态分布总体中抽样, 为µ标差为σ的正态分布总体中抽样,每100个样本含量为 个样本含量为 n的样本均数中,理论上有95个被包含在该区间内。从 的样本均数中,理论上有 个被包含在该区间内 个被包含在该区间内。 的样本均数中 逻辑推理上看,是用演绎法解释了样本均数的抽样误差。 逻辑推理上看,是用演绎法解释了样本均数的抽样误差。
正常人(X1) (n1=12) 265.4 264.4 271.5 273.2 215.4 233.8 284.6 270.8 251.8 230.9 291.3 260.5 224.7 240.7 228.3 256.9 231.1 260.7 253.0 224.4 221.7 254.8 275.9 281.7 268.6
s X =253.05µg/g,X =27.18µg/g,求发锌含量总体均数
95%的可信区间。 本例自由度ν=12-1=11,经查表得t0.05,11=2.201,则
µL= X −t0.05,11 ×sX = 253.05 −2.201×27.18 =193.23(µg / g) µU= X +t0.05,11 ×sX = 253.05 +2.201×27.18 = 312.87(µg / g)
x →µ, s →σ
新编文档-Meaning and use of confidence intervals意义与使用的置信区间-精品文档

2
Revision on standard errors
Recall from the previous session that • The standard error provides a measure of the precision of the sample mean • the formula s/n gives the standard error of the mean when simple random sampling is used • A low standard error indicates that the sample mean has high precision, i.e. the sample mean is a “good” estimate of the population mean
10
Using the Central Limit Theorem
Recall this theorem says that the sampling distribution of the mean has a normal distribution, for large sample sizes.
So even when data are not normal, the formula for a 95% confidence interval will give an interval whose “confidence” is still high - approximately 95%. Better attach some measure of uncertainty than worry about exact confidence level.
现代社会调查方法(期末考试重点)

现代社会调查方法在社会科学领域中,最为常见的研究方式主要有以下几种,实验研究、调查研究、实地研究和文献研究。
1。
实验研究:一种经过精心的设计,并在高度控制的条件下,研究者通过操纵某些因素,来研究变量之间因果关系的方法。
在实验过程中,研究者通过操纵一个变量(自变量),以观察和分析它对另一个变量(因变量)所产生的效果.由实验组和对照组、自变量和因变量、前测和后测三组最基本要素构成。
2。
实地研究:一种深入到研究对象的生活背景中,以参与观察和无结构访谈的方式收集资料,并通过这些资料的定性分析来理解和解释社会现象的社会研究方式。
其中最主要的资料收集方法是参与观察和无结构访问。
3。
文献研究:一种通过收集和分析现存的以文字、数字、符号、画面等信息形式出现的文献资料,来探讨和分析各种社会行为、社会关系及其他社会现象的研究方式.包括不同的类型,最常用的有内容分析、二次分析和现存统计资料分析。
(内容分析:是一种对报纸、杂志、广播、电视、网络等各种大众传媒的内容进行客观的、系统的、定量的描述和分析的方法,它通过对文献的抽样,对文献内容的编码、录入和统计分析,来揭示文献所反映的社会现实,探讨社会现象指间的相互关系.)4.社会调查(调查研究):一种采用自填式问卷或结构式访问的方法,通过直接的询问,从一个取自总体的样本那里收集系统的、量化的资料,并通过对这些资料的统计分析来认识社会现象及其规律的社会研究方式。
社会调查的基本要素:抽样问卷统计分析5。
普遍调查:简称普查,指的是对构成总体的所有个体无一例外地逐个进行调查。
特点:(1)工作量大,费时、费力、费钱(2)需要高度集中的组织和高度统一的安排(3)调查项目不能多,只能了解某一方面必不可少的基本情况。
6.抽样调查:从所研究的总体中,按照一定的方式选取一部分个体进行调查,并将在这部分个体中所得到的调查结果推广到总体中去. 优点:(1)非常节省时间、人力和财力(2)十分迅速地获得资料数据(3)比较详细地收集信息,获得内容丰富的资料(4)应用范围十分广泛(5)准确性高7。
