专题32 数列大题解题模板(解析版)
高考数列专题题型讲解及答案

数列题型一、数列的综合问题【例1】已知首项为32的等比数列{a n }不是递减数列,其前n 项和为S n (n ∈N *),且S 3+a 3,S 5+a 5,S 4+a 4成等差数列.(1)求数列{a n }的通项公式;(2)设T n =S n -1S n(n ∈N *),求数列{T n }的最大项的值与最小项的值. 解 (1)设等比数列{a n }的公比为q ,因为S 3+a 3,S 5+a 5,S 4+a 4成等差数列,所以S 5+a 5-S 3-a 3=S 4+a 4-S 5-a 5,即4a 5=a 3,于是q 2=a 5a 3=14. 又{a n }不是递减数列且a 1=32,所以q =-12.故等比数列{a n }的通项公式为a n =32×⎝ ⎛⎭⎪⎫-12n -1 =(-1)n -1·32n .(2)由(1)得S n =1-⎝ ⎛⎭⎪⎫-12n =⎩⎪⎨⎪⎧1+12n ,n 为奇数,1-12n ,n 为偶数,当n 为奇数时,S n 随n 的增大而减小,所以1<S n ≤S 1=32,故0<S n -1S n ≤S 1-1S 1=32-23=56. 当n 为偶数时,S n 随n 的增大而增大,所以34=S 2≤S n <1,故0>S n -1S n ≥S 2-1S 2=34-43=-712.综上,对于n ∈N *,总有-712≤S n -1S n≤56. 所以数列{T n }最大项的值为56,最小项的值为-712.【分析】解决等差数列与等比数列的综合问题,既要善于综合运用等差数列与等比数列的相关知识求解,更要善于根据具体问题情境具体分析,寻找解题的突破口.【即时应用】已知数列{a n }是公差不为零的等差数列,其前n 项和为S n ,满足S 5-2a 2=25,且a 1,a 4,a 13恰为等比数列{b n }的前三项.(1)求数列{a n },{b n }的通项公式;(2)设T n 是数列⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫1a n a n +1的前n 项和,是否存在k ∈N *,使得等式1-2T k =1b k 成立?若存在,求出k 的值;若不存在,请说明理由.解 (1)设等差数列{a n }的公差为d (d ≠0),∴⎩⎪⎨⎪⎧⎝ ⎛⎭⎪⎫5a 1+5×42d -2(a 1+d )=25,(a 1+3d )2=a 1(a 1+12d ),解得a 1=3,d =2,∴a n =2n +1.∵b 1=a 1=3,b 2=a 4=9,∴等比数列{b n }的公比q =3,∴b n =3n .(2)不存在.理由如下:∵1a n a n +1=1(2n +1)(2n +3)=12⎝ ⎛⎭⎪⎫12n +1-12n +3, ∴T n =12⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫13-15+⎝ ⎛⎭⎪⎫15-17+…+⎝ ⎛⎭⎪⎫12n +1-12n +3 =12⎝ ⎛⎭⎪⎫13-12n +3, ∴1-2T k =23+12k +3(k ∈N *), 易知数列⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫12k +3为单调递减数列, ∴23<1-2T k ≤1315,又1b k=13k ∈⎝ ⎛⎦⎥⎤0,13,∴不存在k ∈N *,使得等式1-2T k =1b k成立. 题型二、数列的通项、求和求和要善于分析通项的结构特征,选择合适的求和方法.常用求和方法有:错位相减法、裂项相消法、分组求和法等.【例2】设等差数列{a n }的公差为d ,前n 项和为S n ,等比数列{b n }的公比为q ,已知b 1=a 1,b 2=2,q =d ,S 10=100.(1)求数列{a n },{b n }的通项公式;(2)当d >1时,记c n =a n b n,求数列{c n }的前n 项和T n . (1)解 由题意有⎩⎨⎧10a 1+45d =100,a 1d =2, 即⎩⎨⎧2a 1+9d =20,a 1d =2,解得⎩⎨⎧a 1=1,d =2或⎩⎪⎨⎪⎧a 1=9,d =29. 故⎩⎨⎧a n =2n -1,b n =2n -1或⎩⎪⎨⎪⎧a n =19(2n +79),b n =9·⎝ ⎛⎭⎪⎫29n -1. (2)解 由d >1,知a n =2n -1,b n =2n -1,故c n =2n -12n -1, 于是T n =1+32+522+723+924+…+2n -12n -1,① 12T n =12+322+523+724+925+…+2n -12n .②①-②可得12T n =2+12+122+…+12n -2-2n -12n =3-2n +32n ,故T n =6-2n +32n -1. 【分析】用错位相减法解决数列求和的模板第一步:(判断结构)若数列{a n ·b n }是由等差数列{a n }与等比数列{b n }(公比q )的对应项之积构成的,则可用此法求和.第二步:(乘公比)设{a n ·b n }的前n 项和为T n ,然后两边同乘以q .第三步:(错位相减)乘以公比q 后,向后错开一位,使含有q k (k ∈N *)的项对应,然后两边同时作差. 第四步:(求和)将作差后的结果求和,从而表示出T n .【即时应用】设数列{a n }的前n 项和为S n ,已知a 1=1,a 2=2,且a n +2=3S n -S n +1+3,n ∈N *.(1)证明:a n +2=3a n ;(2)求S 2n .(1)证明 由条件,对任意n ∈N *,有a n +2=3S n -S n +1+3,因而对任意n ∈N *,n ≥2,有a n +1=3S n -1-S n +3.两式相减,得a n +2-a n +1=3a n -a n +1,即a n +2=3a n ,n ≥2.又a 1=1,a 2=2,所以a 3=3S 1-S 2+3=3a 1-(a 1+a 2)+3=3a 1,故对一切n ∈N *,a n +2=3a n .(2)解 由(1)知,a n ≠0,所以a n +2a n=3.于是数列{a 2n -1}是首项a 1=1,公比为3的等比数列;数列{a 2n }是首项a 2=2,公比为3的等比数列.因此a 2n -1=3n -1,a 2n =2×3n -1.于是S 2n =a 1+a 2+…+a 2n=(a 1+a 3+…+a 2n -1)+(a 2+a 4+…+a 2n )=(1+3+…+3n -1)+2(1+3+…+3n -1)=3(1+3+…+3n -1)=32(3n -1).题型三、数列的综合应用3.1 数列与函数的综合问题【例3】 设等差数列{a n }的公差为d ,点(a n ,b n )在函数f (x )=2x 的图象上(n ∈N *).(1)若a 1=-2,点(a 8,4b 7)在函数f (x )的图象上,求数列{a n }的前n 项和S n ;(2)若a 1=1,函数f (x )的图象在点(a 2,b 2)处的切线在x 轴上的截距为2-1ln 2,求数列⎩⎨⎧⎭⎬⎫a n b n 的前n 项和T n . 解 (1)由已知,b 7=2a 7,b 8=2a 8=4b 7,有2a 8=4×2a 7=2a 7+2,解得d =a 8-a 7=2.所以,S n =na 1+n (n -1)2d =-2n +n (n -1)=n 2-3n . (2)函数f (x )=2x 在(a 2,b 2)处的切线方程为y -2a 2=(2a 2ln 2)(x -a 2),它在x 轴上的截距为a 2-1ln 2.由题意知,a 2-1ln 2=2-1ln 2,解得a 2=2.所以,d =a 2-a 1=1.从而a n =n ,b n =2n ,所以T n =12+222+323+…+n -12n -1+n 2n , 2T n =11+22+322+…+n 2n -1 因此,2T n -T n =1+12+122+…+12n -1-n 2n =2-12n -1-n 2n =2n +1-n -22n. 所以,T n =2n +1-n -22n. 热点3.2 数列与不等式的综合问题【例4】 在等差数列{a n }中,a 2=6,a 3+a 6=27.(1)求数列{a n }的通项公式;(2)记数列{a n }的前n 项和为S n ,且T n =S n 3·2n -1,若对于一切正整数n ,总有T n ≤m 成立,求实数m 的取值范围.解 (1)设公差为d ,由题意得:⎩⎨⎧a 1+d =6,2a 1+7d =27,解得⎩⎨⎧a 1=3,d =3,∴a n =3n .(2)∵S n =3(1+2+3+…+n )=32n (n +1),∴T n =n (n +1)2n ,T n +1=(n +1)(n +2)2n +1,∴T n +1-T n =(n +1)(n +2)2n +1-n (n +1)2n=(n +1)(2-n )2n +1,∴当n ≥3时,T n >T n +1,且T 1=1<T 2=T 3=32,∴T n 的最大值是32,故实数m 的取值范围是⎣⎢⎡⎭⎪⎫32,+∞.。
数列大题专题(含解析)

{ n} 1 1数列大题训练一、解答题1.设数列{ a n }的前 n 项和为 S n .已知 S 2 =4, a n +1 =2 S n +1, n ∈ N ∗ . (1)求通项公式 a n ;(2)求数列{| a n − n − 2 |}的前 n 项和.2.已知 a , a , a ,⋅⋅⋅, a为正整数且 a > a > a>⋅⋅⋅> a > 1 ,将等式 (1 − 1 ) + (1 − 1 ) + (1 − 1) +⋅⋅0 12n12na 1a 2a 3⋅ +(1 − 1 ) = 2(1 − 1) 记为 (∗) 式.a na 0(1)求函数 f (x ) = 1 − 1x, x ∈ [2, +∞) 的值域;(2)试判断当 n = 1 时(或 2 时),是否存在 a 0 , a 1 (或 a 0 , a 1 , a 2 )使 (∗) 式成立,若存在,写出对应 a 0 , a 1 (或 a 0 , a 1 , a 2 ),若不存在,说明理由;(3)求所有能使 (∗) 式成立的 a i ( 0 ≤ i ≤ n )所组成的有序实数对 (a 0, a 1, a 2,⋅⋅⋅, a n ) . 3.已知函数 f (x ) = log 3(x +1)(x > 0) 的图象上有一点列 P (x, y )(n ∈ N ∗),点P在 x 轴上的射影是x +1n n nnQ n (x n , 0) , 且 x n = 3x n−1 + 2 ( n ≥ 2 且 n ∈ N ∗ ),x 1 = 2 .(1)求证: {x n + 1} 是等比数列,并求出数列 {x n } 的通项公式;21 (2)对任意的正整数 n ,当 m ∈ [−1,1] 时,不等式 3t − 6mt + > y n 恒成立,求实数 t 的取值范3围.(3)设四边形 P Q QP1 1 的面积是 S ,求证: ++ ⋯ +1< 3 . n n n +1 n +1nS 1 2S 2nS n4.已知 n 为正整数,数列{a }满足 a >0, 4(n + 1)a2− na2= 0 ,设数列{b }满足 b= a n 2nnnn +1nnt na n (1)求证:数列 为等比数列;√(2)若数列{b n }是等差数列,求实数 t 的值;(3)若数列{b n }是等差数列,前 n 项和为 S n , 对任意的 n ∈N * , 均存在 m ∈N * , 使得 8a 2S n ﹣ a 4n 2=16b m 成立,求满足条件的所有整数 a 1 的值. a 2n5.已知数列 {a n } 和 {b n } 满足: a 1 = λ ,数, n 为正整数.n +1 = 3 a n + n − 4, b n = (−1)(a n − 3n + 21) 其中 λ 为实(1)对任意实数 λ ,证明数列 {a n } 不是等比数列; (2)对于给定的实数 λ ,试求数列 {b n } 的前 n 项和 S n ;(3)设 0 < a < b ,是否存在实数 λ ,使得对任意正整数 n ,都有 a < S n < b 成立?若存在,求 λ 的取值范围;若不存在,说明理由.6.已知数列 {a n } 满足 a 1 = 1,a n +1 = 1 − 14a n,其中 n ∈ N ∗ .1 1+a +1Ⅲ 3) (1)设 b n = 22an −1,求证:数列 {b n } 是等差数列,并求出 [a n } 的通项公式 ;(2)设 c n = 4a n n +1 ,数列 {c n c n +2 } 的前 n 项和为 T n ,且存在正整数 m ,使得 T n < 1 c m +1 对 于 n ∈ N ∗ 恒成立,求 m 的最小值.7.设各项均为正数的等比数列 {a n } 中, a 1 + a 3 = 10 , a 3 + a 5 = 40 ,数列 {b n } 的前 n 和 S n =n 2+7n .2(1)求数列 {a n } 、 {b n } 的通项公式;(2)若 c 1 = 1 , c n +1 = c n + b n −3a n,求证: c n< 3 .1(3)是否存在整数 k ,使得 a −b的最大值,若不存在,说明理由.+1a 2−b 2+⋅⋅⋅⋅⋅⋅ +1a n −b n>k 10对任意正整数 n 均成立?若存在,求出 k8.已知数列 {a } 的各项均为非零实数,其前 n 项和为 S,且S n a n .n(1)若 S 3=3 ,求 a 3 的值;nS n 1 = a n +2(2)若 a 2021=2021a 1 ,求证:数列 {a n } 是等差数列;(3)若 a 1=1 , a 2=2 ,是否存在实数 λ ,使得 |2a n − 2a m | ≤ λ|a 2 − a 2 | 对任意正整数 m ,n 恒成立,若存在,求实数 λ 的取值范围,若不存在,说明理由. a 2 −a+2anm9.已知数列 {a n } 和 {b n } , a 1 = 1, a 2 = 3 , a n +1= nn−1nn−1 ,( n ∈ N ∗且n ≥ 2 ), b n =1og 2(a n +1)2−5a n +1(I) 求 a 3, a 4 ;, (n ∈ N ∗) .(Ⅱ)猜想数列 {a n } 的通项公式,并证明;( )设函数 f (x ) = x + 1 x +2, 若 |f (b n ) − t | ≤ 16 35 对任意 n ∈ N ∗恒成立,求 t 的取值范围.210.已知数列 {a n } 满足: a 1 = − 3 , a n +1 =−2a n −3 (n ∈ N ∗ ).3a n+4(1)证明:数列 { 1} 是等差数列,并求 {a} 的通项公式;a n +1n(2)若数列 {b n } 满足: b n = 2 (a n + 1)(n ∈ N ),若对一切 n ∈ N ∗ ,都有 (1 − b 1)(1 − b 2). . . (1 −b n ) ≤λ√2n +1 成立,求实数 λ 的最小值.11.已知数列 {x n } ,如果存在常数 p ,使得对任意正整数 n ,总有 (x n +1 − p )(x n − p ) < 0 成立,那么我们称数列 {x n } 为“p -摆动数列”.(Ⅰ) 设 a n = 2n − 1 , b n = (− 由;1 n2, n ∈ N ∗ ,判断 {a n } 、 {b n } 是否为“p -摆动数列”,并说明理 (Ⅱ)已知“p -摆动数列” {c n} 满足 c n +1 = 1cn +1, c 1= 1 ,求常数 p 的值;∗} 1 2 (Ⅲ)设 d n = (−1)n ⋅ (2n − 1) ,且数列 {d n } 的前 n 项和为 S n ,求证:数列 {S n } 是“p -摆动数列”, 并求出常数 p 的取值范围.12.等差数列 {a n } 的前 n 项和为 S n .(1)求证:数列S n{ n }是等差数列;(2)若 a 1= 1, {√S n 是公差为 的等差数列,求使 S k +1⋅S k +2S k 2为整数的正整数 k 的取值集合;(3)记 b = t a n ( t 为大于 0 的常数),求证:b 1+b 2+⋯…+b n≤b 1+b 2.nn213.已知数列 {a n } 的前 n 项和为 S n ,且 S n = 2a n − 2 . (1)求 {a n } 的通项公式;(2)在 a n 与 a n +1 之间插入 n 个数,使这 n + 2 个数组成一个公差为 d n 的等差数列,在数列 {d n } 中是否存在 3 项 d m , d k , d p (其中 m , k , p 成等差数列)成等比数列?若存在,求出这样的 3 项;若不存在,请说明理由.14.已知递增的等比数列 {a n } 满足 a 2 + a 3 + a 4 = 28 ,且 a 3 + 2 是 a 2 , a 4 的等差中项. (1)求 {a n } 的通项公式;(2)若 b n = a n log 1a n , S n =b 1 + b 2 + b 3 + ⋯ + b n 求使 S n + n ⋅ 2n +1 > 30 成立的 n 的最小值. 15.已知数列 {a n } 中,已知 a 1 = 1 , a 2 = a , a n +1 = k (a n + a n +2) 对任意 n ∈ N ∗ 都成立,数列{a n }的前 n 项和为 S n .(1)若 {a n } 是等差数列,求 k 的值; (2) 若 a = 1 , k = − 12 , 求 S n ;(3)是否存在实数 k ,使数列 {a n } 是公比不为 1 的等比数列,且任意相邻三项 a m , a m +1 , a m +2 按某顺序排列后成等差数列?若存在,求出所有 k 的值;若不存在,请说明理由.16.一列火车从重庆驶往北京,沿途有 n 个车站(包括起点站重庆和终点站北京).车上有一邮政车厢,每停靠一站便要卸下火车已经过的各站发往该站的邮袋各 1 个,同时又要装上该站发往以后各站的邮袋各 1 个,设从第 k 站出发时,邮政车厢内共有邮袋 a k 个(k=1,2,…,n ).(1)求数列{a k }的通项公式;(2)当 k 为何值时,a k 的值最大,求出 a k 的最大值.17.已知等比数列 {a n } 的公比 q > 1 , a 2 , a 3 是方程 x 2 − 6x + 8 = 0 的两根. (1)求数列 {a n } 的通项公式; (2)求数列 {2n ⋅ a n } 的前 n 项和 S n .18.设数列 {a n } 满足 a n 2 = a n +1a n−1 + λ(a 2 − a 1)2 ,其中 n ⩾ 2 ,且 n ∈ N , λ 为常数. (1)若 {a n } 是等差数列,且公差 d ≠ 0 ,求 λ 的值;(2)若 a 1 = 1, a 2 = 2, a 3 = 4 ,且存在 r ∈ [3,7] ,使得 m ⋅ a n ≥ n − r 对任意的 n ∈ N ∗ 都成立,求m 的最小值;(3)若 λ ≠ 0 ,且数列 {a n } 不是常数列,如果存在正整数 T ,使得 a n +T = a n 对任意的 n ∈ N ∗均成立.求所有满足条件的数列{an } 中 T 的最小值.19.已知等差数列 {a n } 满足 a 2 = 5 , a 4 + a 5 = a 3 + 13 .设正项等比数列 {b n } 的前 n 项和为 S n , 且 b 2b 4 = 81 , S 3 = 13 .(1)求数列 {a n } 、 {b n } 的通项公式;(2)设 c n = a n b n ,数列 {c n } 的前 n 项和为 T n ,求 T n .20.公差不为零的等差数列 {a n } 中, a 1 , a 2 , a 5 成等比数列,且该数列的前 10 项和为 100,数列{b n } 的前 n 项和为 S n ,且满足 S n = 2b n − 1, n ∈ N ∗ .( Ⅰ ) 求数列 {a n } , {b n } 的通项公式;( Ⅱ ) 令 c n = 1+a n4b n,数列 {c n } 的前 n 项和为 T n ,求 T n 的取值范围.21.已知数列{a n }的前 n 项和为 S n , 且 S n +a n =4,n ∈N * . (1)求数列{a n }的通项公式;(2)已知 c n =2n+3(n ∈N *),记 d n =c n +log C a n (C >0 且 C≠1),是否存在这样的常数 C ,使得数列{d n }是常数列,若存在,求出 C 的值;若不存在,请说明理由. (3)若数列{b },对于任意的正整数 n ,均有 b a +b a +b a+…+b a =()n ﹣ n +2成立,求证:数n列{b n }是等差数列.1 n2 n ﹣13 n ﹣2n 1 2 222.已知数列 {a n } 满足 a 1 = 1, a n +1 = 1 −14a n,其中 n ∈ N ∗ .(1)设 b n = 22an −1,求证:数列 {b n } 是等差数列,并求出 {a n } 的通项公式;(2)设 c n = 4a nn +1 ,数列 {c n c n +2 } 的前 n 项和为 T n .23.已知数列{a n }的前 n 项和为 S n , 且满足 12S n ﹣36=3n 2+8n ,数列{log 3b n }为等差数列,且 b 1=3,b 3=27. (Ⅰ)求数列{a n }与{b n }的通项公式;(Ⅱ)令c =(﹣1)n (a − 5) + b ,求数列{c }的前 n 项和 T . nn12n n n24.已知 q 和 n 均为给定的大于 1 的自然数,设集合 M ={0,1,2,…,q -1},集合 A ={x|x =x 1+x 2q +…+x n q n -1 , x i ∈M ,i =1,2,…,n}.(1)当 q =2,n =3 时,用列举法表示集合 A.(2)设s ,t ∈A ,s =a 1+a 2q +…+a n q n -1, t =b 1+b 2q +…+b n q n-1, 其中a i ,b i ∈M ,i =1,2,…,n.证明:若 a n <b n , 则 s <t. ∗25.已知数列 {a n } 的首项 a 1 = a (a > 0) ,其前 n 项和为 S n ,设 b n = a n + a n +1(n ∈ N ) . (1)若 a 2 = a + 1 , a 3 = 2a 2 ,且数列 {b n } 是公差为 3 的等差数列,求 S 2n ; (2)设数列 {b n } 的前 n 项和为 T n ,满足 T n = n 2 . ①求数列 {a n } 的通项公式; ②若对 ∀n ∈ N ∗,且n ≥ 2 ,不等式 (a n−1 − 1)(a n +1 − 1) ≥ 2(1 − n ) 恒成立,求 a 的取值范围.12 Ⅱ26.是否存在一个等比数列{a }同时满足下列三个条件:①a +a =11 且 a a =;②a >a (n ∈N *);n163 49 n+1n③至少存在一个 m (m ∈N *且 m >4),使得 2a, a 2 , a + 4依次构成等差数列?若存在,求出通项公式;若不存在,说明理由.3m ﹣1mm+1927.设 {a n } 是等差数列, a 1 = −8 ,且 a 2 + 8 , a 3 + 6 , a 4 + 4 成等比数列. (1)求 {a n } 的通项公式;(2)求 {a n } 的前 n 项和 S n 的最小值;(3)若 {b n } 是等差数列, {b n } 与 {a n } 的公差不相等,且 b 5 = a 5 ,问: {a n } 和 {b n } 中除第 5 项外,还有序号相同且数值相等的项吗?(直接写出结论即可) 28.已知数列 {a } 满足 1a ≤ a≤ 3a , n ∈ N ∗ , a= 1 .n3 n n +1n1(1)若 a 2 = 3 , a 3 = x , a 4 = 6 ,求 x 的取值范围;(2)若 {a } 是公比为 q 的等比数列, S= a + a+ ⋯ + a , 1S ≤ S≤ 3S , n ∈ N ∗ , 求 qn的取值范围;n12n3 nn +1(3)若 a 1, a 2, ⋯ , a k 成等差数列,且 a 1 + a 2 + ⋯ + a k = 2020 ,求正整数 k 的最大值. 29.若数列 {a n } 是公差为 2 的等差数列,数列 {b n } 满足 b 1=1,b 2=2,且 a n b n +b n =nb n +1. (1)求数列 {a n } , {b n } 的通项公式;(2)设数列 {c n} 满足 c n= a n +1 b n +1,数列 {c n } 的前 n 项和为 T n ,若不等式 (-1)n λ < T n+ n 2n−1对一切 n ∈N *恒成立,求实数 λ 的取值范围.30.设 T n 是数列 {a n } 的前 n 项之积,且满足 T n = 3 − a n , n ∈ N ∗ .(1)求证:数列 { 13−a n1− } 是等比数列,并写出数列 {a n } 的通项公式;(2)设 S 是数列 {a } 是前 n 项之和,证明: n + 1 − 1< S< n + 2 − 2.nnT nnT n31.已知数列{a n }满足 a n+1+a n =4n ﹣3,n ∈N * (1)若数列{a n }是等差数列,求 a 1 的值; (2)当 a 1=﹣3 时,求数列{a n }的前 n 项和 S n ; (3)若对任意的n ∈N *, 都 有a n 2+a n +1 2a n +a n +1≥5 成立,求 a 1的取值范围.32.ΔABC 中,内角 A , B , C 的对边分别是 a , b , c ,已知 a , b , c 成等比数列,且B = 3.(Ⅰ)求1tan A+1tan B的值;cos 4( )设 B⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗A ⃗⃗⃗ ⋅ B ⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗C ⃗⃗⃗ = 3 2,求 a + c 的值. 33.已知数列 {a n } 的前 n 和为 S n ,且满足 λS n = a n − 1 ,其中 λ ≠ 0 且 λ ≠ 1 . (1)证明:数列 {a n } 是等比数列;(2)当 λ = 12,令 c n= (n + 1)a n ,数列 {a n } 的前 n 项和为 T n ,若需 Tn> 2019 恒成立,求正整n数 n 的最小值.321+a 2 n a 2 n)34.已知数列 {a n} 满足 a 1 = 1 , a n +1=a n n, n ∈ N ∗, 记Sn, T n分别是数列 {a n} , {a 2} 的前 n 项和,证明:当 n ∈ N ∗ 时,(1)a n +1 < a n ;(2)T n = 1n +1− 2n − 1 ;(3)√2n − 1 < S n < √2n .35.设 q 为不等于 1 的正常数, {a n } 各项均为正,首项为 1 ,且 {a n } 前 n 项和为 S n ,已知对任意的正整数 n , m ,当时 n > m , S n − S m = q m · S n−m 恒成立. (1)求数列 {a n } 的通项公式;(2)若数列 {t n } 是首项为 1 ,公差为 3 的等差数列,存在一列数 k 1, k 2, ⋯ , k n , ⋯ :恰好使得 t k 1 = a 1, t k 2 = a 2, ⋯ , t k n = a n , ⋯, 且 k 1 = 1, k 2 = 2 ,求数列 {k n } 的通项公式;(3)当 q = 3 时,设 b n = na n ,问数列 {b n} 中是否存在不同的三项恰好成等差数列?若存在,求出所 有这样的三项,若不存在,请说明理由36.已知数列 {a} 满足aa− 3 ( n ≥ 2 , 且 n ∈ N ∗), 且 a= − 3, 设 b n + 2 = 3log 1(a n +n4 n = n−1 1441) , n ∈ N ∗,数列{c n } 满足 c n = (a n + 1)b n .(1)求证:数列 {a n + 1} 是等比数列并求出数列 {a n } 的通项公式; (2)求数列 {c n } 的前 n 项和 S n ; (3)对于任意 n ∈ N ∗,t ∈ [0,1], cn⩽ tm 2 − m − 12恒成立,求实数 m 的取值范围.37.已知 {a n } 是递增的等差数列, a 2 , a 4 是方程 x 2-5x +6=0 的根. (1)求 {a n } 的通项公式; a(2)求数列 {2n } 的前 n 项和.38.已知数列 {a } 的满足 a = 1 ,前 n 项的和为 S,且 a n +1−a n = 2 (n ∈ N *) .n1(1)求 a 2 的值;na n an +1 4S n−1(2)设 b n = a na n +1−a n ,证明:数列 {b n} 是等差数列;(3)设 c n = 2b n ⋅ a n ,若 1 ≤ λ ≤ √2 ,求对所有的正整数 n 都有 2λ2 − kλ + 3√2 < c n 成立的 k 的取值范围.39.数列 {a n } 是首项与公比均为 a 的等比数列( a > 0 ,且 a ≠ 1 ),数列 {b n } 满足 b n = a n ⋅ lg a n . (1)求数列 {b n } 的前 n 项和 T n ; (2)若对一切 n ∈ N ∗都有b n < b n +1 ,求 a 的取值范围.40.等差数列{a n }中,其前 n 项和为 S n , 且S n = (a n +1)22,等比数列{b n }中,其前 n 项和为 T n , 且 T n =(b n +1 2 ,(n ∈N *)2(1)求a n ,b n ; (2)求{a n b n }的前 n 项和 M n .n +1 41.已知函数 f (x ) = log 3(ax + b ) 的图象过点 A (2,1) 和 B (5,2 )记 a n = 3f (n ) , n ∈ N * .(1)求数列{ a n }的通项公式.(2)设 b n = a n2n , T n = b 1 + b 2 + ⋯ b n , T n< m ( m ∈ Z ),求 m 的最小值.42.已知公比 q > 0 的等比数列 {a n } 的前 n 项和为 S n ,且 a 1 = 1, S 3 = 13 ,数列 {b n } 中, b 1 = 1, b 3 = 3 .(1)若数列 {a n + b n } 是等差数列,求 a n , b n ; (2)在(1)的条件下,求数列 {b n } 的前 n 项和 T n .43.已知数列{b n }是首项 b 1=1,b 4=10 的等差数列,设 b n +2=3 log 1 4a n (n ∈n *).(1)求证:{a n }是等比数列;(2)记 c n =1 b n b n +1,求数列{c n }的前 n 项和 S n ;(3)记 d n =(3n+1)•S n , 若对任意正整数 n ,不等式的最大值.1n +d 1 1+ n +d 2 +…+ 1n +d nm> 24 恒成立,求整数 m 44.已知各项均不相等的等差数列 {a n } 的前五项和 S 5 = 20 ,且 a 1, a 3, a 7 成等比数列;(1)求数列 {a n } 的通项公式; (2)若 T n 为数列 { 1a n a n +1} 的前 n 项和,且存在 n ∈ N ∗,使得T n− λa n≥ 0 成立,求实数 λ 的取值范围。
专题32 数列中分组求和法问题(解析版)

专题32 数列中分组求和法问题【高考真题】 2022年没考查 【方法总结】 分组转化法求和有些数列,既不是等差数列,也不是等比数列,若将数列通项拆开或变形,可转化为几个可求和的数列,先分别求和,然后再合并.(1)若a n =b n ±c n ,且{b n },{c n }为可求和的数列(等差或等比数列),可采用分组求和法求{a n }的前n 项和.(2)通项公式为a n =⎩⎪⎨⎪⎧b n ,n 为奇数,c n ,n 为偶数的数列,其中数列{b n },{c n }是可求和的数列(等比数列或等差数列),可采用分组求和法求和.【题型突破】1.已知数列{a n }为等差数列,其中a 5=3a 2,a 2+a 3=8. (1)求数列{a n }的通项公式;(2)数列{b n }中,b 1=1,b 2=2,从数列{a n }中取出第b n 项记为c n ,若{c n }是等比数列,求{b n }的前n 项和.1.解析 (1)设等差数列{a n }的公差为d ,依题意有⎩⎪⎨⎪⎧2a 1+3d =8,a 1+4d =3a 1+3d ,解得a 1=1,d =2,从而{a n }的通项公式为a n =2n -1,n ∈N *.(2)c 1=ab 1=a 1=1,c 2=ab 2=a 2=3,从而等比数列{c n }的公比为3,因此c n =1×3n -1=3n -1. 另一方面,c n =a bn =2b n -1,所以2b n -1=3n -1,因此b n =3n -1+12.记{b n }的前n 项和为S n ,则S n =(1+31+…+3n -1)+n 2=3n +2n -14.2.已知递增等比数列{a n }的前三项之积为8,且这三项分别加上1,2,2后又成等差数列. (1)求等比数列{a n }的通项公式;(2)记b n =a n +2n ,求数列{b n }的前n 项和T n .2.解析 (1)设等比数列前三项分别为a 1,a 2,a 3,公比为q ,则a 1+1,a 2+2,a 3+2成等差数列.依题意得⎩⎪⎨⎪⎧a 1a 2a 3=8,2(a 2+2)=(a 1+1)+(a 3+2),即⎩⎪⎨⎪⎧a 1·a 1q ·a 1q 2=8,2(a 1q +2)=a 1+1+a 1·q 2+2,解得⎩⎪⎨⎪⎧a 1=1,q =2或⎩⎪⎨⎪⎧a 1=4,q =12(舍去).∴数列{a n }的通项公式为a n =2n -1.(2)由b n =a n +2n ,得b n =2n -1+2n ,∴T n =b 1+b 2+…+b n =(20+21+22+…+2n -1)+2×(1+2+3+…+n )=20(1-2n )1-2+2×n (1+n )2=2n +n 2+n -1.3.已知数列{a n }是等差数列,S n 是其前n 项和,且a 1=2,S 3=12. (1)求数列{a n }的通项公式;(2)设b n =a n +4n ,求数列{b n }的前n 项和T n .3.解析 (1)∵数列{a n }是等差数列,S n 是其前n 项和,a 1=2,S 3=12, ∴S 3=3×2+3×22d =12,解得d =2,∴a n =2+(n -1)×2=2n .(2)∵b n =a n +4n =2n +4n , ∴T n=2(1+2+3+…+n )+(4+42+43+…+4n )=2×n (n +1)2+4(1-4n )1-4=n 2+n +4n +13-43. 4.已知数列{a n }是各项均为正数的等比数列,且a 1+a 2=2⎝⎛⎭⎫1a 1+1a 2,a 3+a 4=32⎝⎛⎭⎫1a 3+1a 4. (1)求数列{a n }的通项公式;(2)设b n =a 2n +log 2a n ,求数列{b n }的前n 项和T n .4.解析 (1)设等比数列{a n }的公比为q (q >0),则a n =a 1q n -1,且a n >0,由已知得⎩⎨⎧a 1+a 1q =2⎝⎛⎭⎫1a 1+1a 1q ,a 1q 2+a 1q 3=32⎝⎛⎭⎫1a 1q 2+1a 1q 3,化简得⎩⎪⎨⎪⎧ a 21q (q +1)=2(q +1),a 21q 5(q +1)=32(q +1),即⎩⎪⎨⎪⎧a 21q =2,a 21q 5=32,又∵a 1>0,q >0,∴a 1=1,q =2,∴数列{a n }的通项公式为a n =2n -1.(2)由(1)知b n =a 2n +log 2a n=4n -1+n -1, ∴T n=(1+4+42+…+4n -1)+(0+1+2+3+…+n -1)=4n -14-1+n (n -1)2=4n -13+n (n -1)2.5.已知各项都不相等的等差数列{a n },a 6=6,又a 1,a 2,a 4成等比数列. (1)求数列{a n }的通项公式;(2)设b n =2n a+(-1)n a n ,求数列{b n }的前2n 项和T 2n .5.解析 (1)∵{a n }为各项都不相等的等差数列,a 6=6,且a 1,a 2,a 4成等比数列. ∴⎩⎪⎨⎪⎧a 6=a 1+5d =6,a 1+d 2=a 1a 1+3d ,d ≠0,解得a 1=1,d =1,∴数列{a n }的通项公式a n =1+(n -1)×1=n .(2)由(1)知,b n =2n +(-1)n n ,记数列{b n }的前2n 项和为T 2n , 则T 2n =(21+22+…+22n )+(-1+2-3+4-…+2n ). 记A =21+22+…+22n ,B =-1+2-3+4-…+2n , 则A =2(1-22n )1-2=22n +1-2,B =(-1+2)+(-3+4)+…+[-(2n -1)+2n ]=n .故数列{b n }的前2n 项和T 2n =A +B =22n +1+n -2. 6.由整数构成的等差数列{a n }满足a 3=5,a 1a 2=2a 4. (1)求数列{a n }的通项公式;(2)若数列{b n }的通项公式为b n =2n ,将数列{a n },{b n }的所有项按照“当n 为奇数时,b n 放在前面;当n 为偶数时,a n 放在前面”的要求进行“交叉排列”,得到一个新数列{c n },b 1,a 1,a 2,b 2,b 3,a 3,a 4,b 4,…,求数列{c n }的前(4n +3)项和T 4n +3.6.解析 (1)由题意,设数列{a n }的公差为d ,因为a 3=5,a 1a 2=2a 4,可得⎩⎪⎨⎪⎧a 1+2d =5,a 1·a 1+d =2a 1+3d ,整理得(5-2d )(5-d )=2(5+d ),即2d 2-17d +15=0,解得d =152或d =1,因为{a n }为整数数列,所以d =1,又由a 1+2d =5,可得a 1=3, 所以数列{a n }的通项公式为a n =n +2.(2)由(1)知,数列{a n }的通项公式为a n =n +2,又由数列{b n }的通项公式为b n =2n , 根据题意,得新数列{c n },b 1,a 1,a 2,b 2,b 3,a 3,a 4,b 4,…,则T 4n +3=b 1+a 1+a 2+b 2+b 3+a 3+a 4+b 4+…+b 2n -1+a 2n -1+a 2n +b 2n +b 2n +1+a 2n +1+a 2n +2 =(b 1+b 2+b 3+b 4+…+b 2n +1)+(a 1+a 2+a 3+a 4+…+a 2n +2) =2×(1-22n +1)1-2+(3+2n +4)(2n +2)2=4n +1+2n 2+9n +5.7.若数列{a n }的前n 项和S n 满足S n =2a n -λ(λ>0,n ∈N *). (1)证明数列{a n }为等比数列,并求a n ;(2)若λ=4,b n =⎩⎪⎨⎪⎧a n ,n 为奇数,log 2a n ,n 为偶数(n ∈N *),求数列{b n }的前2n 项和T 2n .7.解析 (1)∵S n =2a n -λ,当n =1时,得a 1=λ, 当n ≥2时,S n -1=2a n -1-λ,∴S n -S n -1=2a n -2a n -1,即a n =2a n -2a n -1,∴a n =2a n -1,∴数列{a n }是以λ为首项,2为公比的等比数列,∴a n =λ·2n -1.(2)∵λ=4,∴a n =4·2n -1=2n +1,∴b n =⎩⎪⎨⎪⎧2n +1,n 为奇数,n +1,n 为偶数,∴T 2n =22+3+24+5+26+7+…+22n +2n +1=(22+24+…+22n )+(3+5+…+2n +1) =4-4n ·41-4+n (3+2n +1)2=4n +1-43+n (n +2),∴T 2n =4n +13+n 2+2n -43.8.已知数列{a n }为等比数列,首项a 1=4,数列{b n }满足b n =log 2a n ,且b 1+b 2+b 3=12. (1)求数列{a n }的通项公式;(2)令c n =4b n ·b n +1+a n,求数列{c n }的前n 项和S n .8.解析 (1)由b n =log 2a n 和b 1+b 2+b 3=12,得log 2(a 1a 2a 3)=12,∴a 1a 2a 3=212. 设等比数列{a n }的公比为q ,∵a 1=4,∴a 1a 2a 3=4·4q ·4q 2=26·q 3=212,解得q =4, ∴a n =4·4n -1=4n .(2)由(1)得b n =log 24n =2n ,c n =42n ·2(n +1)+4n =1n (n +1)+4n =1n -1n +1+4n .设数列⎩⎨⎧⎭⎬⎫1n (n +1)的前n 项和为A n ,则A n =1-12+12-13+…+1n -1n +1=nn +1,设数列{4n}的前n 项和为B n ,则B n =4-4n ·41-4=43(4n-1),∴S n =n n +1+43(4n -1).9.已知数列{a n }为等比数列,首项a 1=4,数列{b n }满足b n =log 2a n ,且b 1+b 2+b 3=12. (1)求数列{a n }的通项公式;(2)令c n =4b n ·b n +1+a n,求数列{c n }的前n 项和S n .9.解析 (1)由b n =log 2a n 和b 1+b 2+b 3=12,得log 2(a 1a 2a 3)=12,∴a 1a 2a 3=212. 设等比数列{a n }的公比为q ,∵a 1=4,∴a 1a 2a 3=4·4q ·4q 2=26·q 3=212,解得q =4, ∴a n =4·4n -1=4n .(2)由(1)得b n =log 24n =2n ,c n =42n ·2(n +1)+4n =1n (n +1)+4n =1n -1n +1+4n .设数列⎩⎨⎧⎭⎬⎫1n (n +1)的前n 项和为A n ,则A n =1-12+12-13+…+1n -1n +1=nn +1,设数列{4n}的前n 项和为B n ,则B n =4-4n ·41-4=43(4n-1),∴S n =n n +1+43(4n -1).10.在各项均为正数的等比数列{a n }中,a 1a 3=4,a 3是a 2-2与a 4的等差中项,若a n +1=2n b(n ∈N *).(1)求数列{b n }的通项公式;(2)若数列{}c n 满足c n =a n +1+1b 2n -1·b 2n +1,求数列{}c n 的前n 项和S n .10.解析 (1)设等比数列{a n }的公比为q ,且q >0,由a n >0,a 1a 3=4,得a 2=2,又a 3是a 2-2与a 4的等差中项,故2a 3=a 2-2+a 4,∴2·2q =2-2+2q 2, ∴q =2或q =0(舍).∴a n =a 2q n -2=2n -1, ∴a n +1=2n =2n b,∴b n =n (n ∈N *).(2)由(1)得,c n =a n +1+1b 2n -1·b 2n +1=2n +1(2n -1)(2n +1)=2n +12⎝⎛⎭⎫12n -1-12n +1,∴数列{}c n 的前n 项和S n =2+22+…+2n +12⎣⎡⎦⎤⎝⎛⎭⎫1-13+⎝⎛⎭⎫13-15+…+⎝⎛⎭⎫12n -1-12n +1=2(1-2n )1-2+12⎝⎛⎭⎫1-12n +1=2n +1-2+n 2n +1(n ∈N *). 11.(2019·天津)设{a n }是等差数列,{b n }是等比数列,公比大于0.已知a 1=b 1=3,b 2=a 3,b 3=4a 2+3.(1)求{a n }和{b n }的通项公式;(2)设数列{c n }满足c n =⎩⎪⎨⎪⎧1,n 为奇数,b n 2,n 为偶数.求a 1c 1+a 2c 2+…+a 2n c 2n (n ∈N *).11.解析 (1)设等差数列{a n }的公差为d ,等比数列{b n }的公比为q (q >0).依题意,得⎩⎪⎨⎪⎧3q =3+2d ,3q 2=15+4d ,解得⎩⎪⎨⎪⎧d =3,q =3,故a n =3+3(n -1)=3n ,b n =3×3n -1=3n .所以{a n }的通项公式为a n =3n ,{b n }的通项公式为b n =3n .(2)a 1c 1+a 2c 2+…+a 2n c 2n =(a 1+a 3+a 5+…+a 2n -1)+(a 2b 1+a 4b 2+a 6b 3+…+a 2n b n )=⎣⎡⎦⎤n ×3+n (n -1)2×6+(6×31+12×32+18×33+…+6n ×3n )=3n 2+6(1×31+2×32+…+n ×3n ).记T n =1×31+2×32+…+n ×3n ,① 则3T n =1×32+2×33+…+n ×3n +1,②②-①得,2T n =-3-32-33-…-3n +n ×3n +1=-3(-3n )1-3+n ×3n +1=(2n -1)3n +1+32.所以a 1c 1+a 2c 2+…+a 2n c 2n =3n 2+6T n =3n 2+3×(2n -1)3n +1+32=(2n -1)3n +2+6n 2+92(n ∈N *).12.已知数列{a n }的前n 项和为S n ,若a n =-3S n +4,b n =-log 2a n +1.(1)求数列{a n }和{b n }的通项公式;(2)令c n =b n 2n +1+1n (n +1),其中n ∈N *,若数列{c n }的前n 项和为T n ,求T n .12.解析 (1)由a 1=-3S 1+4=-3a 1+4,得a 1=1,由a n =-3S n +4,知a n +1=-3S n +1+4,两式相减并化简得a n +1=14a n ,∴数列{a n }是首项为1,公比为14的等比数列,∴a n =⎝⎛⎭⎫14n -1,b n =-log 2a n +1=-log 2⎝⎛⎭⎫14n=2n . (2)由题意知,c n =n 2n +1n (n +1).令H n =12+222+323+…+n2n ,①则12H n =122+223+…+n -12n +n2n +1,② ①-②得,12H n =12+122+123+…+12n -n2n +1=1-n +22n +1.∴H n =2-n +22n .又M n =1-12+12-13+…+1n -1n +1=1-1n +1=n n +1,∴T n =H n +M n =2-n +22n +nn +1.13.在数列{a n }中,已知a 1=1,a n ·a n +1=⎝⎛⎭⎫12n,记S n 为{a n }的前n 项和,b n =a 2n +a 2n -1,n ∈N *.(1)判断数列{b n }是否为等比数列,并写出其通项公式; (2)求数列{a n }的通项公式; (3)求S n .13.解析 (1)因为a n ·a n +1=⎝⎛⎭⎫12n ,所以a n +1·a n +2=⎝⎛⎭⎫12n +1,所以a n +2a n =12,即a n +2=12a n . 因为b n =a 2n +a 2n -1,所以b n +1b n =a 2n +2+a 2n +1a 2n +a 2n -1=12a 2n +12a 2n -1a 2n +a 2n -1=12,所以数列{b n }是公比为12的等比数列.因为a 1=1,a 1·a 2=12,所以a 2=12,b 1=a 1+a 2=32,所以b n =32×⎝⎛⎭⎫12n -1=32n ,n ∈N *.(2)由(1)可知a n +2=12a n ,所以a 1,a 3,a 5,…是以a 1=1为首项,12为公比的等比数列;a 2,a 4,a 6,…是以a 2=12为首项,12为公比的等比数列,所以a 2n -1=⎝⎛⎭⎫12n -1,a 2n =⎝⎛⎭⎫12n , 所以a n =11221,21 2n n n n +-⎧⎛⎫⎪ ⎪⎪⎝⎭⎨⎪⎛⎫⎪ ⎪⎝⎭⎩,为奇数,为偶数. (3)因为S 2n =(a 1+a 3+…+a 2n -1)+(a 2+a 4+…+a 2n )=1-⎝⎛⎭⎫12n 1-12+12⎣⎡⎦⎤1-⎝⎛⎭⎫12n 1-12=3-32n ,又S 2n -1=S 2n -a 2n =3-32n -12n =3-42n ,所以S n =21233, 2432n n n n +⎧-⎪⎪⎨⎪-⎪⎩,为偶数,为奇数.14.(2021·新高考Ⅰ)已知数列{a n }满足a 1=1,a n +1=⎩⎪⎨⎪⎧a n +1,n 为奇数,a n +2,n 为偶数.(1)记b n =a 2n ,写出b 1,b 2,并求数列{b n }的通项公式; (2)求{a n }的前20项和.14.解析 (1)因为b n =a 2n ,且a 1=1,a n +1=⎩⎪⎨⎪⎧a n +1,n 为奇数,a n +2,n 为偶数,所以b 1=a 2=a 1+1=2,b 2=a 4=a 3+1=a 2+2+1=5.因为b n =a 2n ,所以b n +1=a 2n +2=a 2n +1+1=a 2n +1+1=a 2n +2+1=a 2n +3,所以b n +1-b n =a 2n +3-a 2n =3,所以数列{b n }是以2为首项,3为公差的等差数列, 所以b n =2+3(n -1)=3n -1,n ∈N *.(2)因为a n +1=⎩⎪⎨⎪⎧a n +1,n 为奇数,a n+2,n 为偶数,所以k ∈N *时,a 2k =a 2k -1+1=a 2k -1+1,即a 2k =a 2k -1+1,①,a 2k +1=a 2k +2,② a 2k +2=a 2k +1+1=a 2k +1+1,即a 2k +2=a 2k +1+1,③ 所以①+②得a 2k +1=a 2k -1+3,即a 2k +1-a 2k -1=3,所以数列{a n }的奇数项是以1为首项,3为公差的等差数列; ②+③得a 2k +2=a 2k +3,即a 2k +2-a 2k =3,又a 2=2,所以数列{a n }的偶数项是以2为首项,3为公差的等差数列. 所以数列{a n }的前20项和S 20=(a 1+a 3+a 5+…+a 19)+(a 2+a 4+a 6+…+a 20)=10+10×92×3+20+10×92×3=300.15.已知等差数列{a n }的前n 项和为S n ,a 5=9,S 5=25.(1)求数列{a n }的通项公式及S n ;(2)设b n =(-1)n S n ,求数列{b n }的前n 项和T n .15.解析 (1)设数列{a n }的公差为d ,由S 5=5a 3=25得a 3=a 1+2d =5,又a 5=9=a 1+4d ,所以d =2,a 1=1, 所以a n =2n -1,S n =n (1+2n -1)2=n 2.(2)结合(1)知b n =(-1)n n 2,当n 为偶数时, T n =(b 1+b 2)+(b 3+b 4)+(b 5+b 6)+…+(b n -1+b n )=(-12+22)+(-32+42)+(-52+62)+…+[-(n -1)2+n 2]=(2-1)(2+1)+(4-3)(4+3)+(6-5)(6+5)+…+[n -(n -1)][n +(n -1)] =1+2+3+…+n =n (n +1)2.当n 为奇数时,n -1为偶数,T n =T n -1+(-1)n ·n 2=(n -1)n 2-n 2=-n (n +1)2.综上可知,T n =(-1)n n (n +1)2.16.在①b n =na n ,②b n =⎩⎪⎨⎪⎧a n ,n 为奇数,log 2a n,n 为偶数,③b n =1(log 2a n +1)(log 2a n +2)这三个条件中任选一个,补充在下面问题中,并解答.问题:已知数列{a n }是等比数列,且a 1=1,其中a 1,a 2+1,a 3+1成等差数列. (1)求数列{a n }的通项公式;(2)记________,求数列{b n }的前2n 项和T 2n .16.解析 (1)设数列{a n }的公比为q ,因为a 1,a 2+1,a 3+1成等差数列,所以2(a 2+1)=a 1+a 3+1.又因为a 1=1,所以2(q +1)=2+q 2,即q 2-2q =0,所以q =2或q =0(舍去),所以a n =2n -1. (2)由(1)知a n =2n -1,若选择条件①,则b n =n ·2n -1, 所以T 2n =1×20+2×21+…+2n ×22n -1, 则2T 2n =1×21+2×22+…+2n ×22n , 两式相减得-T 2n=1×20+1×21+…+1×22n -1-2n ×22n =1-22n1-2-2n ×22n =(1-2n )×22n -1, 所以T 2n =(2n -1)·22n +1.由(1)知a n =2n -1,若选择条件②,则b n =⎩⎪⎨⎪⎧2n -1,n 为奇数,n -1,n 为偶数,所以T 2n =(20+1)+(22+3)+…+(22n -2+2n -1)=(20+22+…+22n -2)+(1+3+…+2n -1) =1-4n 1-4+n (1+2n -1)2=4n 3+n 2-13.由(1)知a n =2n -1,若选择条件③,则b n =1n (n +1),所以T 2n =11×2+12×3+…+12n (2n +1)=⎝⎛⎭⎫1-12+⎝⎛⎭⎫12-13+…+⎝⎛⎭⎫12n -12n +1=1-12n +1=2n2n +1. 17.已知{a n }是等差数列,{b n }是等比数列,且{b n }的前n 项和为S n ,2a 1=b 1=2,a 5=5(a 4-a 3),________.在①b 5=4(b 4-b 3),②b n +1=S n +2这两个条件中任选其中一个,补充在上面的横线上,并完成下面问题的解答.(1)求数列{a n }和{b n }的通项公式; (2)求数列{a n -b n }的前n 项和T n .注:如果选择多个条件分别解答,按第一个解答计分.17.解析 (1)若选条件①,b 5=4(b 4-b 3).设等差数列{a n }的公差为d ,∵2a 1=2,a 5=5(a 4-a 3),∴a 1+4d =5(a 1+3d -a 1-2d ),∴a 1=d =1.∴a n =1+(n -1)×1=n . 设等比数列{b n }的公比为q .由b 1=2,且b 5=4(b 4-b 3),得b 1q 4=4(b 1q 3-b 1q 2).∴q 2-4q +4=0,解得q =2.所以{b n }是首项为2,公比为2的等比数列.故b n =2×2n -1=2n (n ∈N *). 若选条件②,b n +1=S n +2.令n =1,得b 2=S 1+2=b 1+2=4.∴公比q =b 2b 1=2.∴数列{b n }是首项为2,公比为2的等比数列.从而b n =2×2n -1=2n (n ∈N *). (2)由(1)知a n -b n =n -2n ,∴T n =(1+2+3+…+n )-(21+22+23+…+2n ), ∴T n =n (1+n )2-2(1-2n )1-2,∴T n =2-2n +1+n 22+n 2.18.已知在等差数列{a n }中,S n 为其前n 项和,且a 3=5,S 7=49. (1)求数列{a n }的通项公式;(2)若b n =2n a+a n ,数列{b n }的前n 项和为T n ,且T n ≥1 000,求n 的取值范围.18.解析 (1)由等差数列性质知,S 7=7a 4=49,则a 4=7,故公差d =a 4-a 3=7-5=2,故a n =a 3+(n -3)d =2n -1. (2)由(1)知b n =22n -1+2n -1,T n =21+1+23+3+…+22n -1+2n -1=21+23+…+22n -1+(1+3+…+2n -1) =21-22n +11-4+n 1+2n -12=22n +13+n 2-23.易知T n 单调递增,且T 5=707<1 000,T 6=2 766>1 000, 故T n ≥1 000,解得n ≥6,n ∈N *.19.已知等比数列{a n }为递增数列,且a 4=23,a 3+a 5=209,设b n =log 3a n2(n ∈N *).(1)求数列{b n }的前n 项和S n ;(2)令T n =b 1+b 2+b 22+…+b 2n -1,求使T n >0成立的最小值n .19.解析 (1)设等比数列{a n}的公比为q ,由题意知,⎩⎨⎧a 1q 3=23,a 1q 2+a 1q 4=209,两式相除,得q 1+q 2=310, 解得q =3或q =13,∵{a n }为递增数列,∴q =3,a 1=281.∴a n =a 1q n -1=281·3n -1=2·3n -5.∴b n =log 3a n2=n -5,数列{b n }的前n 项和S n =n (-4+n -5)2=12(n 2-9n ).(2)T n =b 1+b 2+b 22+…+b 2n -1=(1-5)+(2-5)+(22-5)+…+(2n -1-5)=1-2n1-2-5n >0, 即2n >5n +1,∵24<5×4+1,25>5×5+1,∴n min =5.20.已知数列{a n }的前n 项和S n 满足关系式S n =ka n +1,k 为不等于0的常数.(1)试判断数列{a n }是否为等比数列; (2)若a 2=12,a 3=1.①求数列{a n }的通项公式及前n 项和S n 的表达式;②设b n =log 2S n ,数列{c n }满足c n =1b n +3b n +4+b n +2·2n b,数列{c n }的前n 项和为T n ,当n >1时,求使4n -1T n <S n +3+n +122成立的最小正整数n 的值.20.解析 (1)若数列{a n }是等比数列,则由n =1得a 1=S 1=ka 2,从而a 2=ka 3.又取n =2,得a 1+a 2=S 2=ka 3,于是a 1=0,显然矛盾,故数列{a n }不是等比数列.(2)①由条件得⎩⎨⎧a 1=12k ,a 1+12=k ,解得⎩⎪⎨⎪⎧a 1=12,k =1,从而S n =a n +1.当n ≥2时,由S n -1=a n ,得a n =S n -S n -1=a n +1-a n ,即a n +1=2a n ,此时数列是首项为a 2=12,公比为2的等比数列.综上所述,数列{a n }的通项公式为a n =⎩⎪⎨⎪⎧12,n =1,2n -3,n ≥2.从而其前n 项和S n =2n -2(n ∈N *). ②由①得b n =n -2,从而c n =1(n +1)(n +2)+n ·2n -2.记C 1=12×3+13×4+…+1(n +1)(n +2)=⎝⎛⎭⎫12-13+⎝⎛⎭⎫13-14+…+⎝⎛⎭⎫1n +1-1n +2=n 2(n +2), 记C 2=1·2-1+2·20+…+n ·2n -2,则2C 2=1·20+2·21+…+n ·2n -1, 两式相减得C 2=(n -1)·2n -1+12,从而T n =n 2(n +2)+(n -1)·2n -1+12=n +1n +2+(n -1)·2n -1,则不等式4n -1T n <S n +3+n +122可化为4(n +1)(n -1)(n +2)+2n +1<2n +1+n +122,即n 2+n -90>0,因为n ∈N *且n ≠1,故n >9, 从而最小正整数n 的值是10.。
部分专题三第二讲高考中的数列解答题型

=a12-1q-k+2q-qk+1, 2Sk-(Sk+2+Sk+1)=2a111--qqk-a12-1q-k+2q-qk+1 =1-a1 q[2(1-qk)-(2-qk+2-qk+1)] =1a-1qkq(q2+q-2)=0, 因此,对任意k∈N+,Sk+2,Sk,Sk+1成等差数列.
返回
2.(2012·山东高考)在等差数列{an}中,a3+a4+a5=84, a9=73. (1)求数列{an}的通项公式; (2)对任意m∈N*,将数列{an}中落入区间(9m,92m)内的项 的个数记为bm,求数列{bm}的前m项和Sm. 解:(1)因为{an}是一个等差数列, 所以a3+a4+a5=3a4=84,故a4=28. 设数列{an}的公差为d, 则5d=a9-a4=73-28=45,故d=9. 由a4=a1+3d得28=a1+3×9,即a1=1. 所以an=a1+(n-1)d=1+9(n-1)=9n-8(n∈N*).
返回
即an=3n-2n,n=1时也适合此式, ∴an=3n-2n. (3)证明:由(2)得a1n=3n-1 2n=2+11n-2n= C1n2n-1+C2n12n-2+…+1<n·21n-1, 所以a11+a12+…+a1n<1+122+1222+…+122n-1=1+121-2n1-1<32.
返回
返回
返回
等差、等比数列的判定与证明
[例1]
ቤተ መጻሕፍቲ ባይዱ
(2012·荆州模拟)已知数列{an}的前n项和为Sn,a1=
1 4
,
且Sn=Sn-1+an-1+
1 2
(n∈N*,n≥2),数列{bn}满足:b1=-
119 4
,
且3bn-bn-1=n(n≥2,且n∈N*). (1)求数列{an}的通项公式; (2)求证:数列{bn-an}为等比数列; (3)求数列{bn}的前n项和的最小值.
2023年高考数学微专题专练32含解析文 (1)

专练32 高考大题专练(三) 数列的综合运用1.[2021·全国乙卷]设{a n }是首项为1的等比数列,数列{b n }满足b n =na n3.已知a 1,3a 2,9a 3成等差数列.(1)求{a n }和{b n }的通项公式;(2)记S n 和T n 分别为{a n }和{b n }的前n 项和.证明:T n <S n2.2.[2022·全国甲(文),18]记S n 为数列{}a n 的前n 项和.已知2S nn+n =2a n +1.(1)证明:{}a n 是等差数列;(2)若a 4,a 7,a 9成等比数列,求S n 的最小值.3.[2022·新高考Ⅰ卷,17]记S n 为数列{}a n 的前n 项和,已知a 1=1,⎩⎨⎧⎭⎬⎫S n an 是公差为13的等差数列.(1)求{}a n 的通项公式; (2)证明:1a 1+1a 2+…+1a n<2.4.[2021·全国甲卷]记S n 为数列{a n }的前n 项和,已知a n >0,a 2=3a 1,且数列{S n }是等差数列,证明:{a n }是等差数列.5.[2022·云南省高三联考(二)]已知正项数列{a n }的前n 项和为S n ,满足4S n =a 2n +2a n-8.(1)求数列{a n }的通项公式;(2)求数列{(-1)n(S n -3n )}的前n 项和T n .专练32 高考大题专练(三) 数列的综合运用1.解析:(1)设{a n }的公比为q ,则a n =qn -1.因为a 1,3a 2,9a 3成等差数列,所以1+9q 2=2×3q ,解得q =13,故a n =13n -1,b n =n 3n .(2)由(1)知S n =1-13n1-13=32(1-13n ),T n =13+232+333+…+n3n ,①13T n =132+233+334+…+n -13n +n3n +1,② ①-②得23T n =13+132+133+…+13n -n 3n +1,即23T n =13(1-13n )1-13-n 3n +1=12(1-13n )-n3n +1, 整理得T n =34-2n +34×3n ,则2T n -S n =2(34-2n +34×3n )-32(1-13n )=-n 3n <0,故T n <S n2.2.解析:(1)证明:由已知条件,得S n =na n -n 22+n2.当n =1时,a 1=S 1.当n ≥2时,a n =S n -S n -1=na n -n 22+n 2-⎣⎢⎡⎦⎥⎤(n -1)a n -1-(n -1)22+n -12,∴(1-n )a n=-n +1-(n -1)a n -1.等式两边同时除以1-n ,得a n =1+a n -1, ∴a n -a n -1=1.∴{a n }是公差为1的等差数列. (2)由(1)可得a n =a 1+(n -1). ∴a 4=a 1+3,a 7=a 1+6,a 9=a 1+8. ∵a 4,a 7,a 9成等比数列,∴a 27 =a 4·a 9, 即(a 1+6)2=(a 1+3)(a 1+8),∴a 1=-12, ∴S n =na 1+n (n -1)2×1=-12n +n 2-n 2=12n 2-252n .当n =12或n =13时,S n 取得最小值,为12×122-252×12=-78.3.解析:(1)∵a 1=1,∴S 1a 1=1.又∵⎩⎨⎧⎭⎬⎫S n a n 是公差为13的等差数列,∴S n a n =S 1a 1+13(n -1), 即S n =(13n +23)a n =13(n +2)a n ,∴当n ≥2时,S n -1=13(n +1)a n -1,∴a n =S n -S n -1=13(n +2)a n -13(n +1)a n -1,n ≥2,即(n -1)a n =(n +1)a n -1,n ≥2,∴a n a n -1=n +1n -1,n ≥2, ∴当n ≥2时,a n a n -1·a n -1a n -2·…·a 3a 2·a 2a 1=n +1n -1·n n -2·…·42·31=n (n +1)2,∴a n =n (n +1)2.当n =1时,a 1=1满足上式,∴a n =n (n +1)2.(2)证明:由(1)知a n =n (n +1)2,∴1a n=2n (n +1)=2(1n -1n +1),∴1a 1+1a 2+…+1a n =2(1-12+12-13+…+1n -1n +1)=2(1-1n +1). ∵n ∈N *,∴0<1n +1≤12,∴1-1n +1<1, ∴2(1-1n +1)<2,∴1a 1+1a 2+…+1a n<2. 4.解析:由题意可知,数列{S n }的首项为a 1,设等差数列{S n }的公差为d ,由题意得S 1=a 1,S 2=a 1+a 2=4a 1=2a 1,则d =S 2-S 1=a 1+a 2-a 1=a 1,所以S n =a 1+(n -1)a 1=n a 1,即S n =a 1·n 2,所以a n =⎩⎪⎨⎪⎧a 1,n =1S n -S n -1=(2n -1)a 1,n ≥2,即a n =(2n -1)a 1,所以a n +1-a n =2a 1,所以数列{a n }是以a 1为首项,2a 1为公差的等差数列.5.解析:(1)由4S n =a 2n +2a n -8, 得4S n -1=a 2n -1 +2a n -1-8(n ≥2), 两式相减得:4a n =a 2n +2a n -a 2n -1 -2a n -1, 则a 2n -a 2n -1 -2(a n +a n -1)=0, 即(a n -a n -1-2)(a n +a n -1)=0, 因为a n >0, 所以a n -a n -1=2,又4a 1=a 21 +2a 1-8,解得a 1=4或a 1=-2(舍去), 所以数列{a n }是以4为首项,以2为公差的等差数列, 所以a n =4+2(n -1)=2n +2;(2)由(1)知:4S n =(2n +2)2+2(2n +2)-8, 所以S n =n (n +3),则(-1)n (S n -3n )=(-1)n n 2,当n 为偶数时,T n =-12+22-32+42-…+n 2, =3+7+…+2n -1,=n2(3+2n -1)2=n (n +1)2;当n 为奇数时,T n =-12+22-32+42-…+(n -1)2-n 2, =3+7+…+2n -3-n 2,=n -12(3+2n -3)2-n 2=-n (n +1)2.所以T n=⎩⎪⎨⎪⎧n (n +1)2,n 为偶数-n (n +1)2,n 为奇数.。
2019年高考文科数学题型秘籍【32】数列的综合应用(解析版)

高考数学精品复习资料2019.5专题三十二数列及其综合应用【高频考点解读】能在具体的问题情境中识别数列的等差关系或等比关系,并能用相关知识解决相应的问题.【热点题型】题型一数列综合应用题例1、已知log2x,log2y,2成等差数列,则M(x,y)的轨迹的图象为()【提分秘籍】数列综合应用题的解题步骤1.审题——弄清题意,分析涉及哪些数学内容,在每个数学内容中,各是什么问题.2.分解——把整个大题分解成几个小题或几个“步骤”,每个小题或每个“步骤”分别是数列问题、函数问题、解析几何问题、不等式问题等.3.求解——分别求解这些小题或这些“步骤”,从而得到整个问题的解答.4.数列的渗透力很强,它和函数、方程、三角形、不等式等知识相互联系,优化组合,无形中加大了综合的力度.解决此类题目,必须对蕴藏在数列概念和方法中的数学思想有所了解.【举一反三】数列1,1+2,1+2+22,1+2+22+23,…,1+2+22+…+2n-1,…的前n项和S n>1 020,那么n的最小值是()A.7B.8C.9D.10【热点题型】题型二常见的数列模型例2、有一种细菌和一种病毒,每个细菌在每秒钟杀死一个病毒的同时将自身分裂为2个,现在有一个这样的细菌和100个这样的病毒,问细菌将病毒全部杀死至少需要() A.6秒钟B.7秒钟C.8秒钟D.9秒钟【提分秘籍】1.等差数列模型:通过读题分析,由题意抽象出等差数列,利用等差数列有关知识解决问题.2.等比数列模型:通过读题分析,由题意抽象出等比数列,利用等比数列有关知识解决问题.3.递推公式模型:通过读题分析,由题意把所给条件用数列递推表达出来,然后通过分析递推关系式求解.4.分期付款模型设贷款总额为a,年利率为r,等额还款数为b,分n期还完,则b=r+r n+r n-1a.【举一反三】等比数列{a n}的前n项和为S n,若a1=1,且4a1,2a2,a3成等差数列,则S4=________.【热点题型】题型三等差与等比数列的综合问题例3、(高考浙江卷)在公差为d 的等差数列{a n }中,已知a 1=10,且a 1,2a 2+2,5a 3成等比数列.(1)求d ,a n ;(2)若d <0,求|a 1|+|a 2|+|a 3|+…+|a n |.【提分秘籍】对于等差、等比数列的综合问题,应重点分析等差、等比数列的通项,前n 项和以及等差、等比数列项之间的关系,往往用到转化与化归的思想方法.【举一反三】已知等差数列{a n }的公差和首项都不等于0,且a 2,a 4,a 8成等比数列,则a 1+a 5+a 9a 2+a 3=( )A .2B .3C .5D .6【热点题型】题型四 数列与函数的综合应用例4、已知函数f(x)=ln x的图象是曲线C,点A n(a n,f(a n))(n∈N*)是曲线C上的一系列点,曲线C在点A n(a n,f(a n))处的切线与y轴交于点B n(0,b n).若数列{b n}是公差为2的等差数列,且f(a1)=3.(1)分别求出数列{a n}与数列{b n}的通项公式;(2)设O为坐标原点,S n表示△OA n B n的面积,求数列{a n S n}的前n项和T n.【提分秘籍】解决函数与数列的综合问题应该注意的事项(1)数列是一类特殊的函数,它的图象是一群孤立的点;(2)转化以函数为背景的条件时,应该注意题中的限制条件,如函数的定义域,这往往是很容易被忽视的问题;(3)利用函数的方法研究数列中的相关问题时,应准确构造相应的函数,注意数列中相关限制条件的转化.【举一反三】(高考全国新课标卷Ⅱ)等差数列{a n}的前n项和为S n,已知S10=0,S15=25,则nS n的最小值为________.【热点题型】题型五数列的实际应用例5、某同学利用暑假时间到一家商场勤工俭学,该商场向他提供了三种付酬方案:第一种,每天支付38元;第二种,第一天付4元,第二天付8元,第三天付12元,依此类推;第三种,第一天付0.4元,以后每天支付的薪酬是前一天薪酬的2倍,工作时间为n天.(1)设工作n天,记三种付酬方式薪酬总金额依次为A n,B n,C n,写出A n,B n,C n关于n 的表达式;(2)如果n=10,你会选择哪种方式领取报酬?【提分秘籍】求解数列应用问题,必须明确属于哪种数列模型,是等差数列,还是等比数列;是求通项问题,还是求项数问题,或者是求和问题.然后将题目中的量建立关系,利用数列模型去解决.【举一反三】根据市场调查结果,预测某种家用商品从年初开始的n 个月内累积的需求量S n (单位:万件)近似地满足S n =n90(21n -n 2-5)(n =1,2,…,12).按此预测,在本年度内,需求量超过1.5万件的月份是( )A .5月、6月B .6月、7月C .7月、8月D .8月、9月【高考风向标】1.(20xx·湖南卷) 已知数列{a n }满足a 1=1,|a n +1-a n |=p n ,n ∈N *. (1)若{a n }是递增数列,且a 1,2a 2,3a 3成等差数列,求p 的值;(2)若p =12,且{a 2n -1}是递增数列,{a 2n }是递减数列,求数列{a n }的通项公式.2.(20xx·安徽卷) 设实数c >0,整数p >1,n ∈N *. (1)证明:当x >-1且x ≠0时,(1+x )p >1+px ;(2)数列{a n }满足a 1>c 1p ,a n +1=p -1p a n +c p a 1-p n ,证明:a n >a n +1>c 1p.3.(20xx·湖北卷) 已知等差数列{a n}满足:a1=2,且a1,a2,a5成等比数列.(1)求数列{a n}的通项公式.(2)记S n为数列{a n}的前n项和,是否存在正整数n,使得S n>60n+800?若存在,求n的最小值;若不存在,说明理由.4.(20xx·江西卷) 已知首项都是1的两个数列{a n },{b n }(b n ≠0,n ∈N *)满足a n b n +1-a n +1b n +2b n +1b n =0.(1)令c n =a nb n ,求数列{c n }的通项公式;(2)若b n =3n -1,求数列{a n }的前n 项和S n .5.(20xx·新课标全国卷Ⅱ] 已知数列{a n }满足a 1=1,a n +1=3a n +1.(1)证明⎩⎨⎧⎭⎬⎫a n +12是等比数列,并求{a n }的通项公式;(2)证明1a 1+1a 2+…+1a n <32.6.(20xx·四川卷) 设等差数列{a n }的公差为d ,点(a n ,b n )在函数f (x )=2x 的图像上(n ∈N *). (1)若a 1=-2,点(a 8,4b 7)在函数f (x )的图像上,求数列{a n }的前n 项和S n ; (2)若a 1=1,函数f (x )的图像在点(a 2,b 2)处的切线在x 轴上的截距为2-1ln 2,求数列⎩⎨⎧⎭⎬⎫a nb n 的前n 项和T n .7.(20xx·浙江卷) 已知数列{a n}和{b n}满足a1a2a3…a n=(2)b n(n∈N*).若{a n}为等比数列,且a1=2,b3=6+b2.(1)求a n与b n.(2)设c n=1a n-1b n(n∈N *).记数列{cn}的前n项和为S n.(i)求S n;(ii)求正整数k,使得对任意n∈均有S k≥S n.8.(高考辽宁卷)下面是关于公差d >0的等差数列{a n }的四个命题: P 1:数列{a n }是递增数列; P 2:数列{na n }是递增数列; P 3:数列{a nn }是递增数列;P 4:数列{a n +3nd }是递增数列. 其中的真命题为( ) A .p 1,p 2 B .p 3,p 4 C .p 2,p 3 D .p 1,p 49.(高考重庆卷)已知{a n }是等差数列,a 1=1,公差d ≠0,S n 为其前n 项和,若a 1,a 2,a 5成等比数列,则S 8=________.10. (高考广东卷)设数列{a n }的前n 项和为S n .已知a 1=1,2S n n =a n +1-13n 2-n -23,n ∈N *.(1)求a 2的值;(2)求数列{a n }的通项公式;(3)证明:对一切正整数n ,有1a 1+1a 2+…+1a n <74.【随堂巩固】1.已知数列{a n},{b n}满足a1=1,且a n,a n+1是函数f(x)=x2-b n x+2n的两个零点,则b8+a9=()A.24 B.32C.48 D.642.已知数列{a n}为等差数列,数列{b n}是各项为正数的等比数列,其公比q≠1,若a4=b4,a12=b12,则()A.a8=b8B.a8>b8C.a8<b8D.a8>b8或a8<b83.已知正项等差数列{a n}满足:a n+1+a n-1=a2n(n≥2),等比数列{b n}满足:b n+1b n-1=2b n(n≥2),则log2(a2+b2)=()A.-1或2 B.0或2C .2D .14.各项都是正数的等比数列{a n }的公比q ≠1,且a 2,12a 3,a 1成等差数列,则q 的值为( )A.1-52B.5-12C.5+12D.5+12或5-125.在△ABC 中,角A ,B ,C 所对的边分别是a ,b ,c ,且a cos C ,b cos B ,c cos A 成等差数列,若b =3,则a +c 的最大值为( )A.32B .3C .2 3D .96.若关于x 的方程x 2-x +a =0与x 2-x +b =0(a ≠b )的四个根组成首项为14的等差数列,则a +b 的值是( )A.38B.1124C.1324D.31727.已知数列{a n }满足a n +2-a n +1=a n +1-a n ,n ∈N *,且a 5=π2.若函数f (x )=sin 2x +2cos 2x2,记y n =f (a n ),则数列{y n }的前9项和为( )A .0B .-9C .9D .18.《九章算术》之后,人们进一步用等差数列求和公式来解决更多的问题,《张丘建算经》卷上第22题为:“今有女善织,日益功疾,且从第2天起,每天比前一天多织相同量的布,若第一天织5尺布,现在一月(按30天计),共织390尺布”,则每天比前一天多织________尺布.(不作近似计算)9.已知数列{a n }满足a n a n +1a n +2a n +3=24,且a 1=1,a 2=2,a 3=3,则a 1+a 2+a 3+…+a 2 013=________.10.已知公比为q 的等比数列{a n }的前6项和S 6=21,且4a 1,32a 2,a 2成等差数列.(1)求a n ;(2)设{b n }是首项为2,公差为-a 1的等差数列,其前n 项和为T n ,求不等式T n -b n >0的解集.11.已知单调递增的等比数列{a n }满足a 2+a 3+a 4=28,且a 3+2是a 2,a 4的等差中项. (1)求数列{a n }的通项公式;(2)若b n =a n log 12a n ,S n =b 1+b 2+…+b n ,求使S n +n ·2n +1>50成立的正整数n 的最小值.12.已知数列{a n }的前n 项和为S n ,点(n ,S n )(n ∈N *)在函数f (x )=12x 2+12x 的图象上.(1)求数列{a n }的通项公式;(2)设数列⎩⎨⎧⎭⎬⎫1a n a n +2的前n 项和为T n ,不等式T n >13log a (1-a )对任意正整数n 恒成立,求实数a 的取值范围.。
专题32 等比数列(解析版)
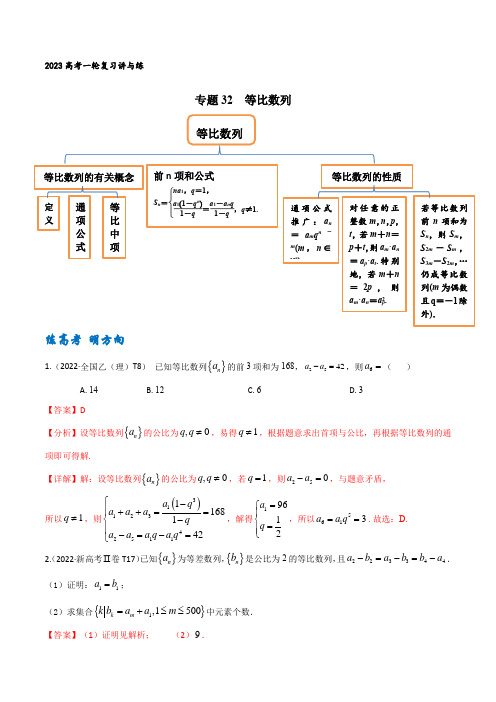
(2)等比中项:如果a,G,b成等比数列,那么G叫做a与b的等比中项.即:G是a与b的等比中项⇔a,G,b成等比数列⇒G2=ab.
【小问2详解】由(1)知, ,所以 ,即 ,亦即 ,解得 ,所以满足等式的解 ,故集合 中的元素个数为 .
3.(2022·浙江卷T20)已知等差数列 的首项 ,公差 .记 的前n项和为 .
(1)若 ,求 ;
(2)若对于每个 ,存在实数 ,使 成等比数列,求d的取值范围.
【答案】(1) (2)
【分析】(1)利用等差数列通项公式及前 项和公式化简条件,求出 ,再求 ;
2023高考一轮复习讲与练
专题32等比数列
练高考 明方向
1.(2022·全国乙(理)T8)已知等比数列 的前3项和为168, ,则 ()
A.14B.12C.6D.3
【答案】D
【分析】设等比数列 的公比为 ,易得 ,根据题意求出首项与公比,再根据等比数列的通项即可得解.
【详解】解:设等比数列 的公比为 ,若 ,则 ,与题意矛盾,
基本方法:
等比数列的三种常用判定方法:
定义法:若 =q(q为非零常数,n∈N*),则{an}是等比数列
等比中项法:若数列{an}中,an≠0,且a =an·an+2(n∈N*),则数列{an}是等比数列
通项公式法:若数列通项公式可写成an=c·qn(c,q均是不为0的常数,n∈N*),则{an}是等比数列
(Ⅰ)证明 是等比数列,并求其通项公式;
(Ⅱ)若 ,求 .
【答案】(Ⅰ) ;(Ⅱ) .
2024年高考数学专项突破数列大题压轴练(解析版)

数列大题压轴练-新高考数学复习分层训练(新高考通用)1.(2023·云南曲靖·宣威市第七中学校考模拟预测)记n S 为数列{}n a 的前n 项和,n T 为数列{}n S 的前n 项和,已知2n n S T +=.(1)求证:数列{}n S 是等比数列;(2)求数列{}n na 的前n 项和n A .2.(2023·辽宁铁岭·校联考模拟预测)已知数列{}n a 中,11a =,214a =,且1(1)(2,3,4,)nn na n n a n a +=-=⋅⋅⋅-.(1)设*111()n n b n N a +=-∈,试用n b 表示1n b +,并求{}n b 的通项公式;(2)设*1sin 3()cos cos n n n n c N b b +=∈,求数列{}n c 的前n 项和n S .3.(2023·湖南株洲·统考一模)数列{}n a 满足13a =,212n n n a a a +-=.(1)若21n bn a =+,求证:{}n b 是等比数列.(2)若1n nnc b =+,{}n c 的前n 项和为n T ,求满足100n T <的最大整数n .4.(2023·河北衡水·河北衡水中学校考模拟预测)已知数列{}n a 满足21n n n a xa ya ++=+()N n +∈,11a =,22a =,n S 为数列{}n a 前n 项和.(1)若2x =,1y =-,求n S 的通项公式;(2)若1x y ==,设n T 为n a 前n 项平方和,证明:214n n n T S S -<恒成立.5.(2023·山西朔州·怀仁市第一中学校校考二模)已知数列{}n a 满足13a =,且12,1,n n na n a a n +⎧=⎨-⎩是偶数是奇数.(1)设221n n n b a a -=+,证明:{}3n b -是等比数列;(2)设数列{}n a 的前n 项和为n S ,求使得不等式2022n S >成立的n 的最小值.6.(2022春·河北衡水·高三校联考阶段练习)已知正项数列{}n a 的前n 项和为n S ,且满足11a =,23a =,2132n n n a a a ++=-,数列{}n c 满足()22221232341n c c c n c n +++++= .2024年高考数学专项突破数列大题压轴练(解析版)(1)求出{}n a ,{}n c 的通项公式;(2)设数列()()1221log 1n n c n a +⎧⎫⋅+⎪⎪⎨⎬+⎡⎤⎪⎪⎣⎦⎩⎭的前n 项和为n T ,求证:516<n T .7.(2022秋·河北衡水·高三河北衡水中学校考阶段练习)已知数列{}n a 的前n 项和n S 满足36S =,2n n S n na =+,*n ∈N .(1)求{}n a 的通项公式;(2)数列{}n b ,{}n c ,{}n d 满足()21211n n n a b a +=+-,12121n n n n n c b b b b --= ,且2nn nc d n =⋅,求数列{}n d 的前n 项和n T .8.(2023·广东·校联考模拟预测)已知数列{}n a 的前n 项和为n S ,且312323n S S S nS n +++⋅⋅⋅+=.(1)求数列{}n a 的通项公式;(2)若n n b na =,且数列{}n b 的前n 项和为n T ,求证:当3n ≥时,()311421n n n T n +≤+--.9.(2022秋·山东青岛·高三山东省莱西市第一中学校考阶段练习)对于项数为m 的数列{}n a ,若满足:121m a a a ≤<<< ,且对任意1i j m ≤≤≤,i j a a ⋅与j ia a 中至少有一个是{}n a 中的项,则称{}n a 具有性质P .(1)如果数列1a ,2a ,3a ,4a 具有性质P ,求证:11a =,423a a a =⋅;(2)如果数列{}n a 具有性质P ,且项数为大于等于5的奇数,试判断{}n a 是否为等比数列?并说明理由.10.(2022秋·山东青岛·高三统考期末)记数列{}n a 的前n 项和为n S ,11a =,______.给出下列两个条件:条件①:数列{}n a 和数列{}1n S a +均为等比数列;条件②:1121222n n n n a a a na -+++⋅⋅⋅+=.试在上面的两个条件中任选一个,补充在上面的横线上,完成下列两问的解答:(注:如果选择多个条件分别解答,按第一个解答计分.)(1)求数列{}n a 的通项公式;(2)记正项数列{}n b 的前n 项和为n T ,12b a =,23b a =,14n n n T b b +=⋅,求211(1)ni i i i b b +=⎡⎤-⎣⎦∑.11.(2022·湖北·黄冈中学校联考模拟预测)已知数列{}n a 满足0n a ≠,*N n ∈.(1)若2210n n n a a ka ++=>且0n a >.(ⅰ)当{}lg n a 成等差数列时,求k 的值;(ⅱ)当2k =且11a =,4a =2a 及n a 的通项公式.(2)若21312n n n n a a a a +++=-,11a =-,20a <,[]34,8a ∈.设n S 是{}n a 的前n 项之和,求2020S 的最大值.12.(2022秋·湖南长沙·高三校考阶段练习)已知数列{}n a 的前n 项和1122n n n S a -⎛⎫=--+ ⎪⎝⎭(n *∈N ),数列{}n b 满足2nn n b a =.(1)求证:数列{}n b 是等差数列,并求数列{}n a 的通项公式;(2)设数列{}n c 满足()()131n nn n a c n λ--=-(λ为非零整数,n *∈N ),问是否存在整数λ,使得对任意n *∈N ,都有1n n c c +>.13.(2022秋·湖南衡阳·高三衡阳市一中校考期中)已知n S 为数列{}n a 的前n 项和,25a =,14n n n S S a +=++;{}n b 是等比数列,29b =,1330bb +=,公比1q >.(1)求数列{}n a ,{}n b 的通项公式;(2)数列{}n a 和{}n b 的所有项分别构成集合A ,B ,将A B ⋃的元素按从小到大依次排列构成一个新数列{}n c ,求2012320T c c c c =++++ .14.(2022·浙江·模拟预测)已知正项数列{}n a 满足11a =,当2n ≥时,22121n n a a n --=-,{}n a 的前n 项和为n S .(1)求数列{}n a 的通项公式及n S ;(2)数列{}n b 是等比数列,q 为数列{}n b 的公比,且13b q a ==,记21n n n nS a c b-+=,证明:122733n c c c ≤++⋅⋅⋅+<15.(2022秋·广东广州·高三校联考阶段练习)已知数列{}n a 的前n 项和为n S ,且12a =,132n n S S +=+,数列{}n b 满足()1122,n n n b b b n++==,其中*n ∈N .(1)分别求数列{}n a 和{}n b 的通项公式;(2)在n a 与1n a +之间插入n 个数,使这2n +个数组成一个公差为n c 的等差数列,求数列{}n n b c 的前n 项和nT16.(2023·辽宁朝阳·校联考一模)已知数列{}n a 的前n 项和为()+N 1=∈+n nS n n ,数列{}n b 满足11b =,且()1+N 2+=∈+nn n b b n b (1)求数列{}n a 的通项公式;(2)求数列{}n b 的通项公式;(3)对于N n +∈,试比较1n b +与n a 的大小.17.(2022秋·广东深圳·高三校考阶段练习)记n S 为数列{}n a 的前n 项和,已知{}12,32n n a a S =-是公差为2的等差数列.(1)求{}n a 的通项公式;(2)若{}11,n n n n n a b b a a ++=的前n 项和为n T ,求证:14n T <.18.(2022秋·江苏常州·高三常州市第一中学校考阶段练习)已知正项数列{}n a满足)1,2n n a a n n -+-∈≥N ,11a =.数列{}n b 满足各项均不为0,14b =,其前n项的乘积112n n n T b -+=⋅.(1)求数列{}n a 通项公式;(2)设2log n n c b =,求数列{}n c 的通项公式;(3)记数列(){}1nn a -的前2m 项的和2m S ,求使得不等式21210m S c c c ≥+++L 成立的正整数m 的最小值.19.(2022秋·江苏宿迁·高三沭阳县建陵高级中学校考期中)已知数列{}n a 满足2123n n n a a a ++=+,112a =,232a =.(1)证明:数列{}1n n a a ++为等比数列,求{}n a 的通项公式.(2)若数列{}n a 的前n 项和为n S ,且()*127N 4n S n n λ⎛⎫+≥-∈ ⎪⎝⎭恒成立,求实数λ的取值范围.20.(2022秋·江苏南通·高三江苏省如东高级中学校考阶段练习)等差数列{}n a 的前n 项和为n S ,且4224,21n n S S a a ==+.数列{}n b 的前n 项和为n T ,且112n n na T ++=(1)求数列{}{},n n ab 的通项公式;(2)数列{}n c 满足cos ,,n n na n n cb n π⎧=⎨⎩为奇数为偶数,求21ni i c =∑.21.(2023秋·广东·高三校联考期末)已知数列1:A a ,2a ,…,n a ,…满足10a =,11i i a a +=+(1,2,,,i n = ),数列A 的前n 项和记为n S .(1)写出3S 的最大值和最小值;(2)是否存在数列A ,使得20221011S =如果存在,写出此时2023a 的值;如果不存在,说明理由.22.(2023秋·山东日照·高三校联考期末)已知数列{}n a 的各项均为非零实数,其前n 项和为(0)n n S S ≠,且21n n n n S a S a ++⋅=⋅.(1)若32S =,求3a 的值;(2)若1a a =,20232023a a =,求证:数列{}n a 是等差数列,并求其前n 项和.23.(2023秋·江苏南京·高三南京市第一中学校考期末)已知数列{}{},n n a b 满足222,1n n n n n a b a b +=-=.(1)求{}{},n n a b 的通项公式;(2)记数列n n a b ⎧⎫⎨⎬⎩⎭的前n 项和为n S ,证明:11121n n S n +≤-+-.24.(2023春·湖南长沙·高三湖南师大附中校考阶段练习)已知数列{}n a 各项都不为0,12a =,24a =,{}n a 的前n 项和为n S ,且满足14n n n a a S +=.(1)求{}n a 的通项公式;(2)若12311231C C CC C n nn nnnn nn nb a a a a a --=+++⋅⋅⋅++,求数列112n n n n b b b ++⎧⎫+⎨⎬⎩⎭的前n 项和n T .25.(2023春·江苏南京·高三校联考阶段练习)已知数列{}n a 中11a =,其前n 项和记为n S ,且满足()()1232n n S S S n S ++⋅⋅⋅+=+.(1)求数列()1n S n n ⎧⎫⎪⎪⎨⎬+⎪⎪⎩⎭的通项公式;(2)设无穷数列1b ,2b ,…n b ,…对任意自然数m 和n ,不等式1m n m n nb b b m a +--<+均成立,证明:数列{}n b 是等差数列.26.(2023·山东·沂水县第一中学校联考模拟预测)在如图所示的平面四边形ABCD 中,ABD △的面积是CBD △面积的两倍,又数列{}n a 满足12a =,当2n ≥时,()()1122n n n n BD a BA a BC --=++- ,记2nn n a b =.(1)求数列{}n b 的通项公式;(2)求证:2221211154n b b b +++< .27.(2022秋·湖北·高三校联考开学考试)已知数列{}n a 满足11a =,1n a +=中*N n ∈)(1)判断并证明数列{}n a 的单调性;(2)记数列{}n a 的前n 项和为n S ,证明:20213522S <<.28.(2022秋·山东潍坊·高三统考阶段练习)定义:对于任意一个有穷数列,在其每相邻的两项间都插入这两项的和,得到的新数列称为一阶和数列,如果在一阶和数列的基础上再在其相邻的两项间插入这两项的和,得到二阶和数列,以此类推可以得到n 阶和数列,如{}2,4的一阶和数列是{}2,6,4,设n 阶和数列各项和为n S .(1)试求数列{}2,4的二阶和数列各项和2S 与三阶和数列各项和3S ,并猜想{}n S 的通项公式(无需证明);(2)设()()()()331321log 3log 3n n n n S n b S S +-+=-⋅-,{}n b 的前m 项和m T ,若20252m T >,求m 的最小值29.(2022秋·湖北黄冈·高三统考阶段练习)已知数列{}1,1,n n a a S =为数列{}n a 的前n 项和,且1(2)3n n S n a =+.(1)求数列{}n a 的通项公式;(2)求证:sin 0n n a a -<;(3)证明:212311111sin 1sin 1sin 1sin e n a a a a ⎛⎫⎛⎫⎛⎫⎛⎫++++< ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭ .30.(2023·浙江温州·统考二模)设n S 为正项数列{}n a 的前n 项和,满足222n n n S a a =+-.(1)求{}n a 的通项公式;(2)若不等式214na n a t ⎛⎫+ ⎪+⎝≥⎭对任意正整数n 都成立,求实数t 的取值范围;(3)设3ln(1)4n a n n b e +=(其中e 是自然对数的底数),求证:123426n n b b b b b b ++++<….数列大题压轴练-新高考数学复习分层训练(新高考通用)1.(2023·云南曲靖·宣威市第七中学校考模拟预测)记n S为数列{}n a的前n项和,n T为S T+=.数列{}n S的前n项和,已知2n n(1)求证:数列{}n S是等比数列;(2)求数列{}n na的前n项和n A.2.(2023·辽宁铁岭·校联考模拟预测)已知数列{}n a 中,11a =,24a =,且1(1)(2,3,4,)nn na n n a n a +=-=⋅⋅⋅-.(1)设*111()n n b n N a +=-∈,试用n b 表示1n b +,并求{}n b 的通项公式;(2)设*sin 3()cos cos n n c N b b =∈,求数列{}n c 的前n 项和n S .3.(2023·湖南株洲·统考一模)数列{}n a 满足13a =,212n n n a a a +-=.(1)若21n bn a =+,求证:{}n b 是等比数列.(2)若1nnc b =+,{}n c 的前n 项和为n T ,求满足100n T <的最大整数n .4.(2023·河北衡水·河北衡水中学校考模拟预测)已知数列{}n a 满足21n n n a xa ya ++=+()N n +∈,11a =,22a =,n S 为数列{}n a 前n 项和.(1)若2x =,1y =-,求n S 的通项公式;(2)若1x y ==,设n T 为n a 前n 项平方和,证明:214n n n T S S -<恒成立.5.(2023·山西朔州·怀仁市第一中学校校考二模)已知数列{}n a 满足13a =,且12,1,n n na n a a n +⎧=⎨-⎩是偶数是奇数.(1)设221n n n b a a -=+,证明:{}3n b -是等比数列;S>成立的n的最小值.(2)设数列{}n a的前n项和为n S,求使得不等式2022n6.(2022春·河北衡水·高三校联考阶段练习)已知正项数列{}n a 的前n 项和为n S ,且满足11a =,23a =,2132n n n a a a ++=-,数列{}n c 满足()22221232341n c c c n c n +++++= .(1)求出{}n a ,{}n c 的通项公式;(2)设数列()()1221log 1n n c n a +⎧⎫⋅+⎪⎪⎨⎬+⎡⎤⎪⎪⎣⎦⎩⎭的前n 项和为n T ,求证:516<n T .7.(2022秋·河北衡水·高三河北衡水中学校考阶段练习)已知数列{}n a 的前n 项和n S 满足36S =,2n n S n na =+,*n ∈N .(1)求{}n a 的通项公式;(2)数列{}n b ,{}n c ,{}n d 满足()21211n n n a b a +=+-,12121n n n n n c b b b b --= ,且2nn nc d n =⋅,求数列{}n d 的前n 项和n T .8.(2023·广东·校联考模拟预测)已知数列{}n a 的前n 项和为n S ,且312323n S S S nS n +++⋅⋅⋅+=.(1)求数列{}n a 的通项公式;(2)若n n b na =,且数列{}n b 的前n 项和为n T ,求证:当3n ≥时,()311421n n n T n +≤+-.9.(2022秋·山东青岛·高三山东省莱西市第一中学校考阶段练习)对于项数为m 的数列{}n a ,若满足:121m a a a ≤<<< ,且对任意1i j m ≤≤≤,i j a a ⋅与j ia a 中至少有一个是{}n a 中的项,则称{}n a 具有性质P .(1)如果数列1a ,2a ,3a ,4a 具有性质P ,求证:11a =,423a a a =⋅;(2)如果数列{}n a 具有性质P ,且项数为大于等于5的奇数,试判断{}n a 是否为等比数列?并说明理由.【答案】(1)证明见解析(2){}n a 为等比数列,理由见解析10.(2022秋·山东青岛·高三统考期末)记数列{}n a 的前n 项和为n S ,11a =,______.给出下列两个条件:条件①:数列{}n a 和数列{}1n S a +均为等比数列;条件②:1121222n n n n a a a na -+++⋅⋅⋅+=.试在上面的两个条件中任选一个,补充在上面的横线上,完成下列两问的解答:(注:如果选择多个条件分别解答,按第一个解答计分.)(1)求数列{}n a 的通项公式;(2)记正项数列{}n b 的前n 项和为n T ,12b a =,23b a =,14n n n T b b +=⋅,求211(1)nii i i b b +=⎡⎤-⎣⎦∑.【答案】(1)12n n a -=(2)288n n+【分析】(1)选择条件①:先由{}1n S a +为等比数列结合等比中项列出式子,再设出等比数列{}n a 的公比,通过等比数列公式化简求值即可得出答案;选择条件②:先由1121222n n n n a a a na -+++⋅⋅⋅+=得出()()12121222212n n n n a a a n a n --++⋅⋅⋅+=-≥,两式做减即可得出()122n n a a n +=≥,再验证1n =时即可利用等比数列通项公式得出答案;(2)通过14n n n T b b +=⋅得出()1142n n n T b b n --⋅≥=,两式相减结合已知即可得出()1142n n b b n +--=≥,即数列{}n b 的奇数项、偶数项分别都成公差为4的等差数列,将211(1)nii i i b b+=⎡⎤-⎣⎦∑转化即可得出答案.【详解】(1)选条件①:数列{}1n S a +为等比数列,()()()2211131S a S a S a ∴+=++,即()()2121123222a a a a a a +=++,11a = ,且设等比数列{}n a 的公比为q ,()()22222q q q ∴+=++,解得2q =或0q =(舍),1112n n n a a q --∴==,选条件②:1121222n n n n a a a na -+++⋅⋅⋅+= ①,()()1212122212n n n n a a a n a n ---++⋅⋅⋅+=-≥∴,即()()12121222212n n n n a a a n a n --++⋅⋅⋅+=-≥ ②,由①②两式相减得:()()12221n n n n a na n a +=-≥-,即()122n n a a n +=≥,令1121222n n n n a a a na -+++⋅⋅⋅+=中1n=得出212a a =也符合上式,故数列{}n a 为首项11a =,公比2q =的等比数列,则1112n n n a a q --==,(2)由第一问可知,不论条件为①还是②,都有数列{}n a 为首项11a =,公比2q =的等比数列,即12n n a -=,11.(2022·湖北·黄冈中学校联考模拟预测)已知数列{}n a 满足0n a ≠,*N n ∈.(1)若2210n n n a a ka ++=>且0n a >.(ⅰ)当{}lg n a 成等差数列时,求k 的值;(ⅱ)当2k =且11a =,4a =2a 及n a 的通项公式.(2)若21312n n n n a a a a +++=-,11a =-,20a <,[]34,8a ∈.设n S 是{}n a 的前n 项之和,求2020S 的最大值.12.(2022秋·湖南长沙·高三校考阶段练习)已知数列{}n a 的前n 项和1122n n n S a -⎛⎫=--+ ⎪⎝⎭(n *∈N ),数列{}n b 满足2nn n b a =.(1)求证:数列{}n b 是等差数列,并求数列{}n a 的通项公式;(2)设数列{}n c 满足()()131n nn n a c n λ--=-(λ为非零整数,n *∈N ),问是否存在整数λ,使得对任意n *∈N ,都有1n n c c +>.13.(2022秋·湖南衡阳·高三衡阳市一中校考期中)已知n S 为数列{}n a 的前n 项和,25a =,14n n n S S a +=++;{}n b 是等比数列,29b =,1330bb +=,公比1q >.(1)求数列{}n a ,{}n b 的通项公式;(2)数列{}n a 和{}n b 的所有项分别构成集合A ,B ,将A B ⋃的元素按从小到大依次排列构成一个新数列{}n c ,求2012320T c c c c =++++ .【答案】(1)43n a n =-,3nn b =(2)660【分析】(1)将14n n n S S a +=++移项作差可得{}n a 是等差数列,结合25a =可求出数列{}n a 的通项公式,将1,b q 代入等式计算,即可求出数列{}n b 的通项公式;(2)由2077a =可判断前20项中最多含有123,,b b b 三项,排除23b a =可确定前20项中14.(2022·浙江·模拟预测)已知正项数列{}n a 满足11a =,当2n ≥时,22121n n a a n --=-,{}n a 的前n 项和为n S .(1)求数列{}n a 的通项公式及n S ;(2)数列{}n b 是等比数列,q 为数列{}n b 的公比,且13b q a ==,记21n n n nS a c b -+=,证明:122733n c c c ≤++⋅⋅⋅+<15.(2022秋·广东广州·高三校联考阶段练习)已知数列{}n a 的前n 项和为n S ,且12a =,132n n S S +=+,数列{}n b 满足()1122,n n n b b b n++==,其中*n ∈N .(1)分别求数列{}n a 和{}n b 的通项公式;(2)在n a 与1n a +之间插入n 个数,使这2n +个数组成一个公差为n c 的等差数列,求数列{}n n b c 的前n 项和nT【答案】(1)1*(2)3n n a n -=⋅∈N ,()*)1(n b n n n =+∈N (2)()*)121(3n n T n n =+-∈N 【分析】(1)由132n n S S +=+可得12)3(2n n S S n -=+≥,两式作差即可得数列{}n a 的递推关系,即可求通项,最后验证1a 是否符合即可;数列{}n b 利用累乘法即可求,最后验证1b 是否符合即可;(2)由题,由等差数列的性质得()11n n n a a n c +-=+,即可求出n c 的通项公式,最后利用错位相减法求n T 即可【详解】(1)由132n n S S +=+可得12)3(2n n S S n -=+≥,两式相减可得13(2)n n a a n +=≥,故数列{}n a 从第3项开始是以首项为2a ,公比3q =的等比数列.又由已知132n n S S +=+,令1n =,得213+2S S =,即12132a a a +=+,得21226a a =+=,故123)2(n n a n -=⋅≥;又12a =也满足上式,则数列{}n a 的通项公式为1*(2)3n n a n -=⋅∈N ;16.(2023·辽宁朝阳·校联考一模)已知数列{}n a 的前n 项和为()+N 1=∈+n nS n n ,数列{}n b 满足11b =,且()1+N 2+=∈+nn n b b n b (1)求数列{}n a 的通项公式;(2)求数列{}n b 的通项公式;(3)对于N n +∈,试比较1n b +与n a 的大小.17.(2022秋·广东深圳·高三校考阶段练习)记n S 为数列{}n a 的前n 项和,已知{}12,32n n a a S =-是公差为2的等差数列.(1)求{}n a 的通项公式;(2)若{}1,n n n a b b a a +=的前n 项和为n T ,求证:14n T <.18.(2022秋·江苏常州·高三常州市第一中学校考阶段练习)已知正项数列{}n a 满足)1,2n n a a n n -+-∈≥N ,11a =.数列{}n b 满足各项均不为0,14b =,其前n项的乘积112n n n T b -+=⋅.(1)求数列{}n a 通项公式;(2)设2log n n c b =,求数列{}n c 的通项公式;(3)记数列(){}1nn a -的前2m 项的和2m S ,求使得不等式21210m S c c c ≥+++L 成立的正整数m 的最小值.19.(2022秋·江苏宿迁·高三沭阳县建陵高级中学校考期中)已知数列{}n a满足2123n n n a a a ++=+,112a =,232a =.(1)证明:数列{}1n n a a ++为等比数列,求{}n a 的通项公式.(2)若数列{}n a 的前n 项和为n S ,且()*127N 4n S n n λ⎛⎫+≥-∈ ⎪⎝⎭恒成立,求实数λ的取值范围.20.(2022秋·江苏南通·高三江苏省如东高级中学校考阶段练习)等差数列{}n a 的前n 项和为n S ,且4224,21n n S S a a ==+.数列{}n b 的前n 项和为n T ,且112n n na T ++=(1)求数列{}{},n n ab 的通项公式;(2)数列{}n c 满足cos ,,n n na n n cb n π⎧=⎨⎩为奇数为偶数,求21ni i c =∑.21.(2023秋·广东·高三校联考期末)已知数列1:A a ,2a ,…,n a ,…满足10a =,11i i a a +=+(1,2,,,i n = ),数列A 的前n 项和记为n S .(1)写出3S 的最大值和最小值;(2)是否存在数列A ,使得20221011S =如果存在,写出此时2023a 的值;如果不存在,说明理由.22.(2023秋·山东日照·高三校联考期末)已知数列{}n a 的各项均为非零实数,其前n 项和为(0)n n S S ≠,且21n n n n S a S a ++⋅=⋅.(1)若32S =,求3a 的值;(2)若1a a =,20232023a a =,求证:数列{}n a 是等差数列,并求其前n 项和.23.(2023秋·江苏南京·高三南京市第一中学校考期末)已知数列{}{},n n a b 满足222,1n n n n n a b a b +=-=.(1)求{}{},n n a b 的通项公式;(2)记数列n n a b ⎧⎫⎨⎬⎩⎭的前n 项和为n S ,证明:11121n n S n +≤-+-.24.(2023春·湖南长沙·高三湖南师大附中校考阶段练习)已知数列{}n a 各项都不为0,12a =,24a =,{}n a 的前n 项和为n S ,且满足14n n n a a S +=.(1)求{}n a 的通项公式;(2)若12311231C C CC C n nn nnnn nn nb a a a a a --=+++⋅⋅⋅++,求数列112n n n n b b b ++⎧⎫+⎨⎬⎩⎭的前n 项和n T .25.(2023春·江苏南京·高三校联考阶段练习)已知数列{}n a 中11a =,其前n 项和记为n S ,且满足()()1232n n S S S n S ++⋅⋅⋅+=+.(1)求数列()1n S n n ⎧⎫⎪⎪⎨⎬+⎪⎪⎩⎭的通项公式;(2)设无穷数列1b ,2b ,…n b ,…对任意自然数m 和n ,不等式1m n m n nb b b m a +--<+均成立,证明:数列{}n b 是等差数列.26.(2023·山东·沂水县第一中学校联考模拟预测)在如图所示的平面四边形ABCD 中,ABD △的面积是CBD △面积的两倍,又数列{}n a 满足12a =,当2n ≥时,()()1122n n n n BD a BA a BC--=++- ,记2nn n a b =.(1)求数列{}n b 的通项公式;(2)求证:22211154b b b +++< .(2)由(1)可得:当1n =时,则1b 当2n ≥时,可得()(2211212n b n n=<-则222121111111114223nb b b ⎛+++=+-+- ⎝L 27.(2022秋·湖北·高三校联考开学考试)已知数列{}n a 满足11a =,1n a +=中*N n ∈)(1)判断并证明数列{}n a 的单调性;(2)记数列{}n a 的前n 项和为n S ,证明:20213522S <<.⎫⎪⎪⎪28.(2022秋·山东潍坊·高三统考阶段练习)定义:对于任意一个有穷数列,在其每相邻的两项间都插入这两项的和,得到的新数列称为一阶和数列,如果在一阶和数列的基础上再在其相邻的两项间插入这两项的和,得到二阶和数列,以此类推可以得到n 阶和数列,如{}2,4的一阶和数列是{}2,6,4,设n 阶和数列各项和为n S .(1)试求数列{}2,4的二阶和数列各项和2S 与三阶和数列各项和3S ,并猜想{}n S 的通项公式(无需证明);(2)设()()()()331321log 3log 3n n n n S n b S S +-+=-⋅-,{}n b 的前m 项和m T ,若20252m T >,求m 的最小值【答案】(1)230S =,384S =,133n n S +=+(2)7【分析】(1)根据123,,S S S 进行猜想,结合等比数列的知识进而求解,并进行推导.(2)利用裂项求和法求得m T ,由此列不等式,从而求得m 的最小值.【详解】(1)一阶和数列:{}2,6,4,对应112S =;二阶和数列:{}2,8,6,10,4,对应230S =;三阶和数列:{}2,10,8,14,6,16,10,14,4,对应384S =;故猜想136n n S S -=-,()1333n n S S --=-,所以数列{}3n S -是首项为139S -=,公比为3的等比数列,所以11393,33n n n n S S -+-=⋅=+.下面证明136n n S S -=-:设112124n m m S a a a a --=++++++ ,则()()()()1112112244n m m m m m S a a a a a a a a a --=+++++++++++++29.(2022秋·湖北黄冈·高三统考阶段练习)已知数列{}1,1,n n a a S =为数列{}n a 的前n 项和,且1(2)3n n S n a =+.(1)求数列{}n a 的通项公式;(2)求证:sin 0n n a a -<;(3)证明:212311111sin 1sin 1sin 1sin e n a a a a ⎛⎫⎛⎫⎛⎫⎛⎫++++< ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭ .30.(2023·浙江温州·统考二模)设n S 为正项数列{}n a 的前n 项和,满足222n n n S a a =+-.(1)求{}n a 的通项公式;(2)若不等式214na n a t ⎛⎫+ ⎪+⎝≥⎭对任意正整数n 都成立,求实数t 的取值范围;(3)设3ln(1)4n a n nb e+=(其中e 是自然对数的底数),求证:123426n n b b b b b b ++++<….。
专题32 数列求和(解析版)
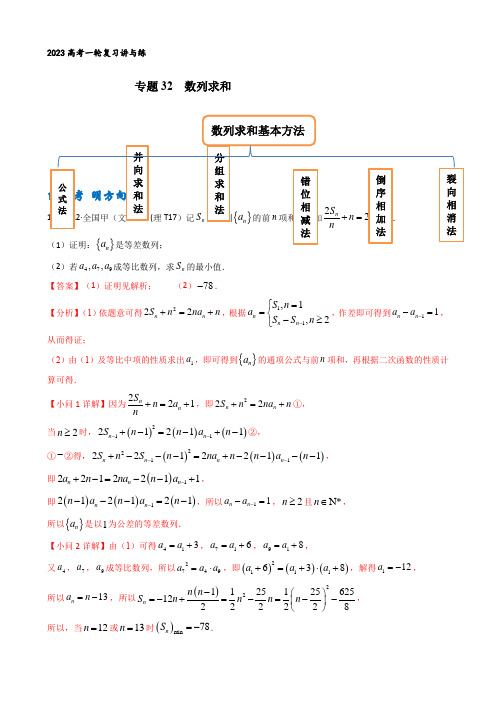
【解析】由题意知数列{2n-1}为1,3,5,7,9,11,13,…,{3n-2}为1,4,7,10,13,16,19,…,所以数列
为1,7,13,19,…,即an=1+6(n-1)=6n-5,所以数列 的前n项和为 =3n2-2n.
8.(2020·全国卷Ⅱ文科·T14)记Sn为等差数列 的前n项和.若a1=-2,a2+a6=2,则S10=.
9.(2020·全国卷Ⅱ文科·T6)记Sn为等比数列{an}的前n项和.若a5-a3=12,a6-a4=24,则 =()
A.2n-1B.2-21-nC.2-2n-1D.21-n-1
【解析】选B.设等比数列的公比为q,由a5-a3=12,a6-a4=24可得: ⇒ ,
所以an=a1qn-1=2n-1,Sn= = =2n-1,因此 = =2-21-n.
答案:25
【解析】设等差数列 的公差为d.因为 是等差数列,且a1=-2,a2+a6=2,根据等差数列通项公式:an=a1+ d,可得a1+d+a1+5d=2,即-2+d+ +5d=2,整理可得:6d=6,解得:d=1.根据等差数列前n项和公式:Sn=na1+ d,n∈N*,可得:S10=10× + =-20+45=25,所以S10=25.
解析:(Ⅰ)当 时, ,因为 ,所以 =3,
当 时, = = ,即 ,因为 ,所以 =2,所以数列{ }是首项为3,公差为2的等差数列,所以 = ;
(Ⅱ)由(Ⅰ)知, = ,
所以数列{ }前n项和为 = = .
讲典例 备高考
类型一、公式法求和
基础知识:
(1)等差数列前n项和公式:Sn=na1+ d= .
2024年高考真题汇总 数列(解析版)

专题数列一、单选题1(全国甲卷数学(文))等差数列a n 的前n 项和为S n ,若S 9=1,a 3+a 7=()A.-2B.73C.1D.29【答案】D【分析】可以根据等差数列的基本量,即将题目条件全转化成a 1和d 来处理,亦可用等差数列的性质进行处理,或者特殊值法处理.【详解】方法一:利用等差数列的基本量由S 9=1,根据等差数列的求和公式,S 9=9a 1+9×82d =1⇔9a 1+36d =1,又a 3+a 7=a 1+2d +a 1+6d =2a 1+8d =29(9a 1+36d )=29.故选:D 方法二:利用等差数列的性质根据等差数列的性质,a 1+a 9=a 3+a 7,由S 9=1,根据等差数列的求和公式,S 9=9(a 1+a 9)2=9(a 3+a 7)2=1,故a 3+a 7=29.故选:D 方法三:特殊值法不妨取等差数列公差d =0,则S 9=1=9a 1⇒a 1=19,则a 3+a 7=2a 1=29.故选:D2(全国甲卷数学(理))等差数列a n 的前n 项和为S n ,若S 5=S 10,a 5=1,则a 1=()A.-2B.73C.1D.2【答案】B【分析】由S 5=S 10结合等差中项的性质可得a 8=0,即可计算出公差,即可得a 1的值.【详解】由S 10-S 5=a 6+a 7+a 8+a 9+a 10=5a 8=0,则a 8=0,则等差数列a n 的公差d =a 8-a 53=-13,故a 1=a 5-4d =1-4×-13 =73.故选:B .3(新高考北京卷)记水的质量为d =S -1ln n,并且d 越大,水质量越好.若S 不变,且d 1=2.1,d 2=2.2,则n 1与n 2的关系为()A.n 1<n 2B.n 1>n 2C.若S <1,则n 1<n 2;若S >1,则n 1>n 2;D.若S <1,则n 1>n 2;若S >1,则n 1<n 2;【答案】C2024年高考真题【分析】根据题意分析可得n 1=eS -12.1n 2=eS -12.2,讨论S 与1的大小关系,结合指数函数单调性分析判断.【详解】由题意可得d 1=S -1ln n 1=2.1d 2=S -1ln n 2=2.2 ,解得n 1=e S -12.1n 2=e S -12.2,若S >1,则S -12.1>S -12.2,可得e S -12.1>e S -12.2,即n 1>n 2;若S =1,则S -12.1=S -12.2=0,可得n 1=n 2=1;若S <1,则S -12.1<S -12.2,可得e S -1 2.1<e S -12.2,即n 1<n 2;结合选项可知C 正确,ABD 错误;故选:C .二、填空题4(新课标全国Ⅱ卷)记S n 为等差数列{a n }的前n 项和,若a 3+a 4=7,3a 2+a 5=5,则S 10=.【答案】95【分析】利用等差数列通项公式得到方程组,解出a 1,d ,再利用等差数列的求和公式节即可得到答案.【详解】因为数列a n 为等差数列,则由题意得a 1+2d +a 1+3d =73a 1+d +a 1+4d =5,解得a 1=-4d =3 ,则S 10=10a 1+10×92d =10×-4 +45×3=95.故答案为:95.5(新高考上海卷)无穷等比数列a n 满足首项a 1>0,q >1,记I n =x -y x ,y ∈a 1,a 2 ∪a n ,a n +1 ,若对任意正整数n 集合I n 是闭区间,则q 的取值范围是.【答案】q ≥2【分析】当n ≥2时,不妨设x ≥y ,则x -y ∈0,a 2-a 1 ∪a n -a 2,a n +1-a 1 ∪0,a n +1-a n ,结合I n 为闭区间可得q -2≥-1q n -2对任意的n ≥2恒成立,故可求q 的取值范围.【详解】由题设有a n =a 1q n -1,因为a 1>0,q >1,故a n +1>a n ,故a n ,a n +1 =a 1q n -1,a 1q n ,当n =1时,x ,y ∈a 1,a 2 ,故x -y ∈a 1-a 2,a 2-a 1 ,此时I 1为闭区间,当n ≥2时,不妨设x ≥y ,若x ,y ∈a 1,a 2 ,则x -y ∈0,a 2-a 1 ,若y ∈a 1,a 2 ,x ∈a n ,a n +1 ,则x -y ∈a n -a 2,a n +1-a 1 ,若x ,y ∈a n ,a n +1 ,则x -y ∈0,a n +1-a n ,综上,x -y ∈0,a 2-a 1 ∪a n -a 2,a n +1-a 1 ∪0,a n +1-a n ,又I n 为闭区间等价于0,a 2-a 1 ∪a n -a 2,a n +1-a 1 ∪0,a n +1-a n 为闭区间,而a n +1-a 1>a n +1-a n >a 2-a 1,故a n +1-a n ≥a n -a 2对任意n ≥2恒成立,故a n +1-2a n +a 2≥0即a 1q n -1q -2 +a 2≥0,故q n -2q -2 +1≥0,故q -2≥-1qn -2对任意的n ≥2恒成立,因q >1,故当n →+∞时,-1q n -2→0,故q -2≥0即q ≥2.故答案为:q ≥2.【点睛】思路点睛:与等比数列性质有关的不等式恒成立,可利用基本量法把恒成立为转为关于与公比有关的不等式恒成立,必要时可利用参变分离来处理.三、解答题6(新课标全国Ⅰ卷)设m 为正整数,数列a 1,a 2,...,a 4m +2是公差不为0的等差数列,若从中删去两项a i 和a j i <j 后剩余的4m 项可被平均分为m 组,且每组的4个数都能构成等差数列,则称数列a 1,a 2,...,a 4m +2是i ,j -可分数列.(1)写出所有的i ,j ,1≤i <j ≤6,使数列a 1,a 2,...,a 6是i ,j -可分数列;(2)当m ≥3时,证明:数列a 1,a 2,...,a 4m +2是2,13 -可分数列;(3)从1,2,...,4m +2中一次任取两个数i 和j i <j ,记数列a 1,a 2,...,a 4m +2是i ,j -可分数列的概率为P m ,证明:P m >18.【答案】(1)1,2 ,1,6 ,5,6 (2)证明见解析(3)证明见解析【分析】(1)直接根据i ,j -可分数列的定义即可;(2)根据i ,j -可分数列的定义即可验证结论;(3)证明使得原数列是i ,j -可分数列的i ,j 至少有m +1 2-m 个,再使用概率的定义.【详解】(1)首先,我们设数列a 1,a 2,...,a 4m +2的公差为d ,则d ≠0.由于一个数列同时加上一个数或者乘以一个非零数后是等差数列,当且仅当该数列是等差数列,故我们可以对该数列进行适当的变形a k =a k -a 1d+1k =1,2,...,4m +2 ,得到新数列a k =k k =1,2,...,4m +2 ,然后对a 1,a 2,...,a 4m +2进行相应的讨论即可.换言之,我们可以不妨设a k =k k =1,2,...,4m +2 ,此后的讨论均建立在该假设下进行.回到原题,第1小问相当于从1,2,3,4,5,6中取出两个数i 和j i <j ,使得剩下四个数是等差数列.那么剩下四个数只可能是1,2,3,4,或2,3,4,5,或3,4,5,6.所以所有可能的i ,j 就是1,2 ,1,6 ,5,6 .(2)由于从数列1,2,...,4m +2中取出2和13后,剩余的4m 个数可以分为以下两个部分,共m 组,使得每组成等差数列:①1,4,7,10 ,3,6,9,12 ,5,8,11,14 ,共3组;②15,16,17,18 ,19,20,21,22 ,...,4m -1,4m ,4m +1,4m +2 ,共m -3组.(如果m -3=0,则忽略②)故数列1,2,...,4m +2是2,13 -可分数列.(3)定义集合A =4k +1 k =0,1,2,...,m =1,5,9,13,...,4m +1 ,B =4k +2 k =0,1,2,...,m =2,6,10,14,...,4m +2 .下面证明,对1≤i <j ≤4m +2,如果下面两个命题同时成立,则数列1,2,...,4m +2一定是i ,j -可分数列:命题1:i ∈A ,j ∈B 或i ∈B ,j ∈A ;命题2:j -i ≠3.我们分两种情况证明这个结论.第一种情况:如果i ∈A ,j ∈B ,且j -i ≠3.此时设i =4k 1+1,j =4k 2+2,k 1,k 2∈0,1,2,...,m .则由i <j 可知4k 1+1<4k 2+2,即k 2-k 1>-14,故k 2≥k 1.此时,由于从数列1,2,...,4m +2中取出i =4k 1+1和j =4k 2+2后,剩余的4m 个数可以分为以下三个部分,共m 组,使得每组成等差数列:①1,2,3,4 ,5,6,7,8 ,...,4k 1-3,4k 1-2,4k 1-1,4k 1 ,共k 1组;②4k 1+2,4k 1+3,4k 1+4,4k 1+5 ,4k 1+6,4k 1+7,4k 1+8,4k 1+9 ,...,4k 2-2,4k 2-1,4k 2,4k 2+1 ,共k 2-k 1组;③4k 2+3,4k 2+4,4k 2+5,4k 2+6 ,4k 2+7,4k 2+8,4k 2+9,4k 2+10 ,...,4m -1,4m ,4m +1,4m +2 ,共m -k 2组.(如果某一部分的组数为0,则忽略之)故此时数列1,2,...,4m +2是i ,j -可分数列.第二种情况:如果i ∈B ,j ∈A ,且j -i ≠3.此时设i =4k 1+2,j =4k 2+1,k 1,k 2∈0,1,2,...,m .则由i <j 可知4k 1+2<4k 2+1,即k 2-k 1>14,故k 2>k 1.由于j -i ≠3,故4k 2+1 -4k 1+2 ≠3,从而k 2-k 1≠1,这就意味着k 2-k 1≥2.此时,由于从数列1,2,...,4m +2中取出i =4k 1+2和j =4k 2+1后,剩余的4m 个数可以分为以下四个部分,共m 组,使得每组成等差数列:①1,2,3,4 ,5,6,7,8 ,...,4k 1-3,4k 1-2,4k 1-1,4k 1 ,共k 1组;②4k 1+1,3k 1+k 2+1,2k 1+2k 2+1,k 1+3k 2+1 ,3k 1+k 2+2,2k 1+2k 2+2,k 1+3k 2+2,4k 2+2 ,共2组;③全体4k 1+p ,3k 1+k 2+p ,2k 1+2k 2+p ,k 1+3k 2+p ,其中p =3,4,...,k 2-k 1,共k 2-k 1-2组;④4k 2+3,4k 2+4,4k 2+5,4k 2+6 ,4k 2+7,4k 2+8,4k 2+9,4k 2+10 ,...,4m -1,4m ,4m +1,4m +2 ,共m -k 2组.(如果某一部分的组数为0,则忽略之)这里对②和③进行一下解释:将③中的每一组作为一个横排,排成一个包含k 2-k 1-2个行,4个列的数表以后,4个列分别是下面这些数:4k 1+3,4k 1+4,...,3k 1+k 2 ,3k 1+k 2+3,3k 1+k 2+4,...,2k 1+2k 2 ,2k 1+2k 2+3,2k 1+2k 2+3,...,k 1+3k 2 ,k 1+3k 2+3,k 1+3k 2+4,...,4k 2 .可以看出每列都是连续的若干个整数,它们再取并以后,将取遍4k 1+1,4k 1+2,...,4k 2+2 中除开五个集合4k 1+1,4k 1+2 ,3k 1+k 2+1,3k 1+k 2+2 ,2k 1+2k 2+1,2k 1+2k 2+2 ,k 1+3k 2+1,k 1+3k 2+2 ,4k 2+1,4k 2+2 中的十个元素以外的所有数.而这十个数中,除开已经去掉的4k 1+2和4k 2+1以外,剩余的八个数恰好就是②中出现的八个数.这就说明我们给出的分组方式满足要求,故此时数列1,2,...,4m +2是i ,j -可分数列.至此,我们证明了:对1≤i <j ≤4m +2,如果前述命题1和命题2同时成立,则数列1,2,...,4m +2一定是i ,j -可分数列.然后我们来考虑这样的i ,j 的个数.首先,由于A ∩B =∅,A 和B 各有m +1个元素,故满足命题1的i ,j 总共有m +1 2个;而如果j -i =3,假设i ∈A ,j ∈B ,则可设i =4k 1+1,j =4k 2+2,代入得4k 2+2 -4k 1+1 =3.但这导致k 2-k 1=12,矛盾,所以i ∈B ,j ∈A .设i =4k 1+2,j =4k 2+1,k 1,k 2∈0,1,2,...,m ,则4k 2+1 -4k 1+2 =3,即k 2-k 1=1.所以可能的k 1,k 2 恰好就是0,1 ,1,2 ,...,m -1,m ,对应的i ,j 分别是2,5 ,6,9 ,...,4m -2,4m +1 ,总共m 个.所以这m +1 2个满足命题1的i ,j 中,不满足命题2的恰好有m 个.这就得到同时满足命题1和命题2的i ,j 的个数为m +1 2-m .当我们从1,2,...,4m+2中一次任取两个数i和j i<j时,总的选取方式的个数等于4m+24m+12=2m+14m+1.而根据之前的结论,使得数列a1,a2,...,a4m+2是i,j-可分数列的i,j至少有m+12-m个.所以数列a1,a2,...,a4m+2是i,j-可分数列的概率P m一定满足P m≥m+12-m2m+14m+1=m2+m+12m+14m+1>m2+m+142m+14m+2=m+12222m+12m+1=18.这就证明了结论.【点睛】关键点点睛:本题的关键在于对新定义数列的理解,只有理解了定义,方可使用定义验证或探究结论.7(新课标全国Ⅱ卷)已知双曲线C:x2-y2=m m>0,点P15,4在C上,k为常数,0<k<1.按照如下方式依次构造点P n n=2,3,...,过P n-1作斜率为k的直线与C的左支交于点Q n-1,令P n为Q n-1关于y轴的对称点,记P n的坐标为x n,y n.(1)若k=12,求x2,y2;(2)证明:数列x n-y n是公比为1+k1-k的等比数列;(3)设S n为△P n P n+1P n+2的面积,证明:对任意的正整数n,S n=S n+1.【答案】(1)x2=3,y2=0(2)证明见解析(3)证明见解析【分析】(1)直接根据题目中的构造方式计算出P2的坐标即可;(2)根据等比数列的定义即可验证结论;(3)思路一:使用平面向量数量积和等比数列工具,证明S n的取值为与n无关的定值即可.思路二:使用等差数列工具,证明S n的取值为与n无关的定值即可.【详解】(1)由已知有m=52-42=9,故C的方程为x2-y2=9.当k=12时,过P15,4且斜率为12的直线为y=x+32,与x2-y2=9联立得到x2-x+322=9.解得x=-3或x=5,所以该直线与C的不同于P1的交点为Q1-3,0,该点显然在C的左支上.故P23,0,从而x2=3,y2=0.(2)由于过P n x n,y n且斜率为k的直线为y=k x-x n+y n,与x2-y2=9联立,得到方程x2-k x-x n+y n2=9.展开即得1-k2x2-2k y n-kx nx-y n-kx n2-9=0,由于P n x n,y n已经是直线y=k x-x n+y n和x2 -y2=9的公共点,故方程必有一根x=x n.从而根据韦达定理,另一根x =2k y n -kx n 1-k 2-x n =2ky n -x n -k 2x n1-k 2,相应的y =k x -x n +y n =y n +k 2y n -2kx n1-k 2.所以该直线与C 的不同于P n 的交点为Q n 2ky n -x n -k 2x n 1-k 2,y n +k 2y n -2kx n1-k 2,而注意到Q n 的横坐标亦可通过韦达定理表示为-y n -kx n 2-91-k 2x n,故Q n 一定在C 的左支上.所以P n +1x n +k 2x n -2ky n 1-k 2,y n +k 2y n -2kx n1-k 2.这就得到x n +1=x n +k 2x n -2ky n 1-k 2,y n +1=y n +k 2y n -2kx n1-k 2.所以x n +1-y n +1=x n +k 2x n -2ky n 1-k 2-y n +k 2y n -2kx n1-k 2=x n +k 2x n +2kx n 1-k 2-y n +k 2y n +2ky n 1-k 2=1+k 2+2k 1-k2x n -y n =1+k1-k x n -y n .再由x 21-y 21=9,就知道x 1-y 1≠0,所以数列x n -y n 是公比为1+k 1-k 的等比数列.(3)方法一:先证明一个结论:对平面上三个点U ,V ,W ,若UV =a ,b ,UW=c ,d ,则S △UVW =12ad -bc .(若U ,V ,W 在同一条直线上,约定S △UVW =0)证明:S △UVW =12UV⋅UW sin UV ,UW =12UV ⋅UW 1-cos 2UV ,UW=12UV ⋅UW 1-UV ⋅UW UV ⋅UW2=12UV 2⋅UW 2-UV ⋅UW 2=12a 2+b 2 c 2+d 2 -ac +bd 2=12a 2c 2+a 2d 2+b 2c 2+b 2d 2-a 2c 2-b 2d 2-2abcd =12a 2d 2+b 2c 2-2abcd =12ad -bc 2=12ad -bc .证毕,回到原题.由于上一小问已经得到x n +1=x n +k 2x n -2ky n 1-k 2,y n +1=y n +k 2y n -2kx n1-k 2,故x n +1+y n +1=x n +k 2x n -2ky n 1-k 2+y n +k 2y n -2kx n 1-k 2=1+k 2-2k 1-k2x n +y n =1-k1+k x n +y n .再由x 21-y 21=9,就知道x 1+y 1≠0,所以数列x n +y n 是公比为1-k 1+k的等比数列.所以对任意的正整数m ,都有x n y n +m -y n x n +m=12x n x n +m -y n y n +m +x n y n +m -y n x n +m -12x n x n +m -y n y n +m -x n y n +m -y n x n +m =12x n -y n x n +m +y n +m -12x n +y n x n +m -y n +m =121-k 1+k m x n -y n x n +y n-121+k 1-k m x n +y n x n -y n =121-k 1+k m -1+k 1-k m x 2n -y 2n=921-k 1+k m -1+k 1-k m.而又有P n +1P n =-x n +1-x n ,-y n +1-y n ,P n +1P n +2 =x n +2-x n +1,y n +2-y n +1 ,故利用前面已经证明的结论即得S n =S △P n P n +1P n +2=12-x n +1-x n y n +2-y n +1 +y n +1-y n x n +2-x n +1=12x n +1-x n y n +2-y n +1 -y n +1-y n x n +2-x n +1=12x n +1y n +2-y n +1x n +2 +x n y n +1-y n x n +1 -x n y n +2-y n x n +2=12921-k 1+k -1+k 1-k +921-k 1+k -1+k 1-k -921-k 1+k 2-1+k 1-k 2 .这就表明S n 的取值是与n 无关的定值,所以S n =S n +1.方法二:由于上一小问已经得到x n +1=x n +k 2x n -2ky n 1-k 2,y n +1=y n +k 2y n -2kx n1-k 2,故x n +1+y n +1=x n +k 2x n -2ky n 1-k 2+y n +k 2y n -2kx n 1-k 2=1+k 2-2k 1-k 2x n +y n=1-k1+k x n +y n .再由x 21-y 21=9,就知道x 1+y 1≠0,所以数列x n +y n 是公比为1-k 1+k的等比数列.所以对任意的正整数m ,都有x n y n +m -y n x n +m=12x n x n +m -y n y n +m +x n y n +m -y n x n +m -12x n x n +m -y n y n +m -x n y n +m -y n x n +m =12x n -y n x n +m +y n +m -12x n +y n x n +m -y n +m =121-k 1+k m x n -y n x n +y n -121+k 1-k m x n +y n x n -y n =121-k 1+k m -1+k 1-k m x 2n -y 2n =921-k 1+k m -1+k 1-k m.这就得到x n +2y n +3-y n +2x n +3=921-k 1+k -1+k1-k =x n y n +1-y n x n +1,以及x n +1y n +3-y n +1x n +3=921-k 1+k 2-1+k 1-k 2=x n y n +2-y n x n +2.两式相减,即得x n +2y n +3-y n +2x n +3 -x n +1y n +3-y n +1x n +3 =x n y n +1-y n x n +1 -x n y n +2-y n x n +2 .移项得到x n +2y n +3-y n x n +2-x n +1y n +3+y n x n +1=y n +2x n +3-x n y n +2-y n +1x n +3+x n y n +1.故y n +3-y n x n +2-x n +1 =y n +2-y n +1 x n +3-x n .而P n P n +3 =x n +3-x n ,y n +3-y n ,P n +1P n +2 =x n +2-x n +1,y n +2-y n +1 .所以P n P n +3 和P n +1P n +2平行,这就得到S △P n P n +1P n +2=S △P n +1P n +2P n +3,即S n =S n +1.【点睛】关键点点睛:本题的关键在于将解析几何和数列知识的结合,需要综合运用多方面知识方可得解.8(全国甲卷数学(文))已知等比数列a n 的前n 项和为S n ,且2S n =3a n +1-3.(1)求a n 的通项公式;(2)求数列S n 的通项公式.【答案】(1)a n =53n -1(2)3253 n -32【分析】(1)利用退位法可求公比,再求出首项后可求通项;(2)利用等比数列的求和公式可求S n .【详解】(1)因为2S n =3a n +1-3,故2S n -1=3a n -3,所以2a n =3a n +1-3a n n ≥2 即5a n =3a n +1故等比数列的公比为q =53,故2a 1=3a 2-3=3a 1×53-3=5a 1-3,故a 1=1,故a n =53n -1.(2)由等比数列求和公式得S n =1×1-53 n1-53=3253 n -32.9(全国甲卷数学(理))记S n 为数列a n 的前n 项和,且4S n =3a n +4.(1)求a n 的通项公式;(2)设b n =(-1)n -1na n ,求数列b n 的前n 项和为T n .【答案】(1)a n =4⋅(-3)n -1(2)T n =(2n -1)⋅3n +1【分析】(1)利用退位法可求a n 的通项公式.(2)利用错位相减法可求T n .【详解】(1)当n =1时,4S 1=4a 1=3a 1+4,解得a 1=4.当n ≥2时,4S n -1=3a n -1+4,所以4S n -4S n -1=4a n =3a n -3a n -1即a n =-3a n -1,而a 1=4≠0,故a n ≠0,故an a n -1=-3,∴数列a n 是以4为首项,-3为公比的等比数列,所以a n =4⋅-3 n -1.(2)b n =(-1)n -1⋅n ⋅4⋅(-3)n -1=4n ⋅3n -1,所以T n =b 1+b 2+b 3+⋯+b n =4⋅30+8⋅31+12⋅32+⋯+4n ⋅3n -1故3T n =4⋅31+8⋅32+12⋅33+⋯+4n ⋅3n所以-2T n =4+4⋅31+4⋅32+⋯+4⋅3n -1-4n ⋅3n=4+4⋅31-3n -11-3-4n ⋅3n =4+2⋅3⋅3n -1-1 -4n ⋅3n=(2-4n )⋅3n -2,∴T n =(2n -1)⋅3n +1.10(新高考北京卷)设集合M =i ,j ,s ,t i ∈1,2 ,j ∈3,4 ,s ∈5,6 ,t ∈7,8 ,2i +j +s +t .对于给定有穷数列A :a n 1≤n ≤8 ,及序列Ω:ω1,ω2,...,ωs ,ωk =i k ,j k ,s k ,t k ∈M ,定义变换T :将数列A 的第i 1,j 1,s 1,t 1项加1,得到数列T 1A ;将数列T 1A 的第i 2,j 2,s 2,t 2列加1,得到数列T 2T 1A ⋯;重复上述操作,得到数列T s ...T 2T 1A ,记为ΩA .(1)给定数列A :1,3,2,4,6,3,1,9和序列Ω:1,3,5,7 ,2,4,6,8 ,1,3,5,7 ,写出ΩA ;(2)是否存在序列Ω,使得ΩA 为a 1+2,a 2+6,a 3+4,a 4+2,a 5+8,a 6+2,a 7+4,a 8+4,若存在,写出一个符合条件的Ω;若不存在,请说明理由;(3)若数列A 的各项均为正整数,且a 1+a 3+a 5+a 7为偶数,证明:“存在序列Ω,使得ΩA 为常数列”的充要条件为“a 1+a 2=a 3+a 4=a 5+a 6=a 7+a 8”.【答案】(1)ΩA :3,4,4,5,8,4,3,10(2)不存在符合条件的Ω,理由见解析(3)证明见解析【分析】(1)直接按照ΩA 的定义写出ΩA 即可;(2)利用反证法,假设存在符合条件的Ω,由此列出方程组,进一步说明方程组无解即可;(3)分充分性和必要性两方面论证.【详解】(1)由题意得ΩA :3,4,4,5,8,4,3,10;(2)假设存在符合条件的Ω,可知ΩA 的第1,2项之和为a 1+a 2+s ,第3,4项之和为a 3+a 4+s ,则a 1+2 +a 2+6 =a 1+a 2+sa 3+4 +a 4+2 =a 3+a 4+s,而该方程组无解,故假设不成立,故不存在符合条件的Ω;(3)我们设序列T k ...T 2T 1A 为a k ,n 1≤n ≤8 ,特别规定a 0,n =a n 1≤n ≤8 .必要性:若存在序列Ω:ω1,ω2,...,ωs ,使得ΩA 为常数列.则a s ,1=a s ,2=a s ,3=a s ,4=a s ,5=a s ,6=a s ,7=a s ,8,所以a s ,1+a s ,2=a s ,3+a s ,4=a s ,5+a s ,6=a s ,7+a s ,8.根据T k ...T 2T 1A 的定义,显然有a k ,2j -1+a k ,2j =a k -1,2j -1+a k -1,2j ,这里j =1,2,3,4,k =1,2,....所以不断使用该式就得到,a 1+a 2=a 3+a 4=a 5+a 6=a 7+a 8,必要性得证.充分性:若a 1+a 2=a 3+a 4=a 5+a 6=a 7+a 8.由已知,a 1+a 3+a 5+a 7为偶数,而a 1+a 2=a 3+a 4=a 5+a 6=a 7+a 8,所以a 2+a 4+a 6+a 8=4a 1+a 2 -a 1+a 3+a 5+a 7 也是偶数.我们设T s ...T 2T 1A 是通过合法的序列Ω的变换能得到的所有可能的数列ΩA 中,使得a s ,1-a s ,2 +a s ,3-a s ,4 +a s ,5-a s ,6 +a s ,7-a s ,8 最小的一个.上面已经证明a k ,2j -1+a k ,2j =a k -1,2j -1+a k -1,2j ,这里j =1,2,3,4,k =1,2,....从而由a 1+a 2=a 3+a 4=a 5+a 6=a 7+a 8可得a s ,1+a s ,2=a s ,3+a s ,4=a s ,5+a s ,6=a s ,7+a s ,8.同时,由于i k +j k +s k +t k 总是偶数,所以a k ,1+a k ,3+a k ,5+a k ,7和a k ,2+a k ,4+a k ,6+a k ,8的奇偶性保持不变,从而a s ,1+a s ,3+a s ,5+a s ,7和a s ,2+a s ,4+a s ,6+a s ,8都是偶数.下面证明不存在j =1,2,3,4使得a s ,2j -1-a s ,2j ≥2.假设存在,根据对称性,不妨设j =1,a s ,2j -1-a s ,2j ≥2,即a s ,1-a s ,2≥2.情况1:若a s ,3-a s ,4 +a s ,5-a s ,6 +a s ,7-a s ,8 =0,则由a s ,1+a s ,3+a s ,5+a s ,7和a s ,2+a s ,4+a s ,6+a s ,8都是偶数,知a s ,1-a s ,2≥4.对该数列连续作四次变换2,3,5,8 ,2,4,6,8 ,2,3,6,7 ,2,4,5,7 后,新的a s +4,1-a s +4,2 +a s +4,3-a s +4,4 +a s +4,5-a s +4,6 +a s +4,7-a s +4,8 相比原来的a s ,1-a s ,2 +a s ,3-a s ,4 +a s ,5-a s ,6 +a s ,7-a s ,8 减少4,这与a s ,1-a s ,2 +a s ,3-a s ,4 +a s ,5-a s ,6 +a s ,7-a s ,8 的最小性矛盾;情况2:若a s ,3-a s ,4 +a s ,5-a s ,6 +a s ,7-a s ,8 >0,不妨设a s ,3-a s ,4 >0.情况2-1:如果a s ,3-a s ,4≥1,则对该数列连续作两次变换2,4,5,7 ,2,4,6,8 后,新的a s +2,1-a s +2,2 +a s +2,3-a s +2,4 +a s +2,5-a s +2,6 +a s +2,7-a s +2,8 相比原来的a s ,1-a s ,2 +a s ,3-a s ,4 +a s ,5-a s ,6 +a s ,7-a s ,8 至少减少2,这与a s ,1-a s ,2 +a s ,3-a s ,4 +a s ,5-a s ,6 +a s ,7-a s ,8 的最小性矛盾;情况2-2:如果a s ,4-a s ,3≥1,则对该数列连续作两次变换2,3,5,8 ,2,3,6,7 后,新的a s +2,1-a s +2,2 +a s +2,3-a s +2,4 +a s +2,5-a s +2,6 +a s +2,7-a s +2,8 相比原来的a s ,1-a s ,2 +a s ,3-a s ,4 +a s ,5-a s ,6 +a s ,7-a s ,8 至少减少2,这与a s ,1-a s ,2 +a s ,3-a s ,4 +a s ,5-a s ,6 +a s ,7-a s ,8 的最小性矛盾.这就说明无论如何都会导致矛盾,所以对任意的j =1,2,3,4都有a s ,2j -1-a s ,2j ≤1.假设存在j =1,2,3,4使得a s ,2j -1-a s ,2j =1,则a s ,2j -1+a s ,2j 是奇数,所以a s ,1+a s ,2=a s ,3+a s ,4=a s ,5+a s ,6=a s ,7+a s ,8都是奇数,设为2N +1.则此时对任意j =1,2,3,4,由a s ,2j -1-a s ,2j ≤1可知必有a s ,2j -1,a s ,2j =N ,N +1 .而a s ,1+a s ,3+a s ,5+a s ,7和a s ,2+a s ,4+a s ,6+a s ,8都是偶数,故集合m a s ,m =N 中的四个元素i ,j ,s ,t 之和为偶数,对该数列进行一次变换i ,j ,s ,t ,则该数列成为常数列,新的a s +1,1-a s +1,2 +a s +1,3-a s +1,4 +a s +1,5-a s +1,6 +a s +1,7-a s +1,8 等于零,比原来的a s ,1-a s ,2 +a s ,3-a s ,4 +a s ,5-a s ,6 +a s ,7-a s ,8 更小,这与a s ,1-a s ,2 +a s ,3-a s ,4 +a s ,5-a s ,6 +a s ,7-a s ,8 的最小性矛盾.综上,只可能a s ,2j -1-a s ,2j =0j =1,2,3,4 ,而a s ,1+a s ,2=a s ,3+a s ,4=a s ,5+a s ,6=a s ,7+a s ,8,故a s ,n =ΩA 是常数列,充分性得证.【点睛】关键点点睛:本题第三问的关键在于对新定义的理解,以及对其本质的分析.11(新高考天津卷)已知数列a n 是公比大于0的等比数列.其前n 项和为S n .若a 1=1,S 2=a 3-1.(1)求数列a n 前n 项和S n ;(2)设b n =k ,n =a kb n -1+2k ,a k <n <a k +1,b 1=1,其中k 是大于1的正整数.(ⅰ)当n =a k +1时,求证:b n -1≥a k ⋅b n ;(ⅱ)求S ni =1b i .【答案】(1)S n =2n -1(2)①证明见详解;②S ni =1b i =3n -1 4n+19【分析】(1)设等比数列a n 的公比为q >0,根据题意结合等比数列通项公式求q ,再结合等比数列求和公式分析求解;(2)①根据题意分析可知a k =2k -1,b n =k +1,b n -1=k 2k -1 ,利用作差法分析证明;②根据题意结合等差数列求和公式可得∑2k -1i =2k -1b i =193k -1 4k -3k -4 4k -1,再结合裂项相消法分析求解.【详解】(1)设等比数列a n 的公比为q >0,因为a 1=1,S 2=a 3-1,即a 1+a 2=a 3-1,可得1+q =q 2-1,整理得q 2-q -2=0,解得q =2或q =-1(舍去),所以S n =1-2n1-2=2n -1.(2)(i )由(1)可知a n =2n -1,且k ∈N *,k ≥2,当n =a k +1=2k≥4时,则a k =2k -1<2k -1=n -1n -1=a k +1-1<a k +1 ,即a k <n -1<a k +1可知a k =2k -1,b n =k +1,b n -1=b a k+a k +1-a k -1 ⋅2k =k +2k 2k -1-1 =k 2k -1 ,可得b n -1-a k ⋅b n =k 2k -1 -k +1 2k -1=k -1 2k -1-k ≥2k -1 -k =k -2≥0,当且仅当k =2时,等号成立,所以b n -1≥a k ⋅b n ;(ii )由(1)可知:S n =2n -1=a n +1-1,若n =1,则S 1=1,b 1=1;若n ≥2,则a k +1-a k =2k -1,当2k -1<i ≤2k -1时,b i -b i -1=2k ,可知b i 为等差数列,可得∑2k -1i =2k -1b i =k ⋅2k -1+2k 2k -12k -1-1 2=k ⋅4k -1=193k -1 4k -3k -4 4k -1 ,所以∑S ni =1b i =1+195×42-2×4+8×43-5×42+⋅⋅⋅+3n -1 4n -3n -4 4n -1=3n -1 4n+19,且n =1,符合上式,综上所述:∑Sni =1b i =3n -1 4n +19.【点睛】关键点点睛:1.分析可知当2k -1<i ≤2k -1时,b i -b i -1=2k ,可知b i 为等差数列;2.根据等差数列求和分析可得∑2k -1i =2k -1b i =193k -1 4k -3k -4 4k -1.12(新高考上海卷)若f x =log a x (a >0,a ≠1).(1)y =f x 过4,2 ,求f 2x -2 <f x 的解集;(2)存在x 使得f x +1 、f ax 、f x +2 成等差数列,求a 的取值范围.【答案】(1)x |1<x <2 (2)a >1【分析】(1)求出底数a ,再根据对数函数的单调性可求不等式的解;(2)存在x 使得f x +1 、f ax 、f x +2 成等差数列等价于a 2=21x +342-18在0,+∞ 上有解,利用换元法结合二次函数的性质可求a 的取值范围.【详解】(1)因为y =f x 的图象过4,2 ,故log a 4=2,故a 2=4即a =2(负的舍去),而f x =log 2x 在0,+∞ 上为增函数,故f 2x -2 <f x ,故0<2x -2<x 即1<x <2,故f 2x -2 <f x 的解集为x |1<x <2 .(2)因为存在x 使得f x +1 、f ax 、f x +2 成等差数列,故2f ax =f x +1 +f x +2 有解,故2log a ax =log a x +1 +log a x +2 ,因为a >0,a ≠1,故x >0,故a 2x 2=x +1 x +2 在0,+∞ 上有解,由a 2=x 2+3x +2x 2=1+3x +2x 2=21x +34 2-18在0,+∞ 上有解,令t =1x ∈0,+∞ ,而y =2t +34 2-18在0,+∞ 上的值域为1,+∞ ,故a 2>1即a >1.一、单选题1(2024·重庆·三模)已知数列a n 的前n 项和为S n ,a 1=1,S n +S n +1=n 2+1n ∈N ∗ ,S 24=()A.276B.272C.268D.266【答案】A【分析】令n =1得S 2=1,当n ≥2时,结合题干作差得S n +1-S n -1=2n -1,从而利用累加法求解S 24=即可.【详解】∵a 1=S 1=1,又∵S n +S n +1=n 2+1,当n =1时,S 1+S 2=12+1=2,解得S 2=1;当n ≥2时,S n -1+S n =(n -1)2+1,作差得S n +1-S n -1=2n -1,∴S 24=S 24-S 22 +S 22-S 20 +⋯+S 4-S 2 +S 2=223+21+⋯+3 -11+1=276.故选:A2(2024·河北张家口·三模)已知数列a n的前n项和为S n,且满足a1=1,a n+1=a n+1,n为奇数2a n,n为偶数,则S100=()A.3×251-156B.3×251-103C.3×250-156D.3×250-103【答案】A【分析】分奇数项和偶数项求递推关系,然后记b n=a2n+a2n-1,n≥1,利用构造法求得b n=6×2n-1-3,然后分组求和可得.【详解】因为a1=1,a n+1=a n+1,n为奇数2a n,n为偶数 ,所以a2k+2=a2k+1+1=2a2k+1,a2k+1=2a2k=2a2k-1+2,k∈N*,且a2=2,所以a2k+2+a2k+1=2a2k+a2k-1+3,记b n=a2n+a2n-1,n≥1,则b n+1=2b n+3,所以b n+1+3=2b n+3,所以b n+3是以b1+3=a1+a2+3=6为首项,2为公比的等比数列,所以b n+3=6×2n-1,b n=6×2n-1-3,记b n的前n项和为T n,则S100=T50=6×20+6×21+6×22+⋅⋅⋅+6×249-3×50=3×251-156.故选:A【点睛】关键点点睛:本题解题关键在于先分奇数项和偶数项求递推公式,然后再并项得b n的递推公式,利用构造法求通项,将问题转化为求b n的前50项和.3(2024·山东日照·三模)设等差数列b n的前n项和为S n,若b3=2,b7=6,则S9=()A.-36B.36C.-18D.18【答案】B【分析】利用等差数列的前n项和公式,结合等差数列的性质求解.【详解】解:S9=b1+b9×92=b3+b7×92=36,故选:B.4(2024·湖北武汉·二模)已知等差数列a n的前n项和为S n,若S3=9,S9=81,则S12=() A.288 B.144 C.96 D.25【答案】B【分析】利用等差数列的前n项和列方程组求出a1,d,进而即可求解S12.【详解】由题意S3=3a1+3×22d=9S9=9a1+9×82d=81,即a1+d=3a1+4d=9,解得a1=1d=2.于是S12=12×1+12×112×2=144.故选:B.5(2024·江西赣州·二模)在等差数列a n中,a2,a5是方程x2-8x+m=0的两根,则a n的前6项和为()A.48B.24C.12D.8【答案】B【分析】利用韦达定理确定a2+a5=8,根据等差数列性质有a2+a5=a1+a6=8,在应用等差数列前n项和公式即可求解.【详解】因为a 2,a 5是方程x 2-8x +m =0的两根,所以a 2+a 5=8,又因为a n 是等差数列,根据等差数列的性质有:a 2+a 5=a 1+a 6=8,设a n 的前6项和为S 6,则S 6=a 1+a 6 ×62=3×8=24.故选:B6(2024·湖南永州·三模)已知非零数列a n 满足2n a n +1-2n +2a n =0,则a 2024a 2021=()A.8B.16C.32D.64【答案】D【分析】根据题意,由条件可得a n +1=4a n ,再由等比数列的定义即可得到结果.【详解】由2n a n +1-2n +2a n =0可得a n +1=4a n ,则a 2024a 2021=4×4×4a 2021a 2021=64.故选:D7(2024·浙江绍兴·二模)汉诺塔(Tower of Hanoi ),是一个源于印度古老传说的益智玩具. 如图所示,有三根相邻的标号分别为A 、B 、C 的柱子,A 柱子从下到上按金字塔状叠放着n 个不同大小的圆盘,要把所有盘子一个一个移动到柱子B 上,并且每次移动时,同一根柱子上都不能出现大盘子在小盘子的上方,请问至少需要移动多少次?记至少移动次数为H n ,例如:H (1)=1,H (2)=3,则下列说法正确的是()A.H (3)=5B.H (n ) 为等差数列C.H (n )+1 为等比数列D.H 7 <100【答案】C【分析】由题意可得H (3)=7,判断A ;归纳得到H n =2n -1,结合等差数列以及等比数列的概念可判断B ,C ;求出H 7 ,判断D .【详解】由题意知若有1个圆盘,则需移动一次:若有2个圆盘,则移动情况为:A →C ,A →B ,C →B ,需移动3次;若有3个圆盘,则移动情况如下:A →B ,A →C ,B →C ,A →B ,C →A ,C →B ,A →B ,共7次,故H (3)=7,A 错误;由此可知若有n 个圆盘,设至少移动a n 次,则a n =2a n -1+1,所以a n +1=2a n -1+1 ,而a 1+1=1+1=2≠0,故a n +1 为等比数列,故a n =2n -1即H n =2n -1,该式不是n 的一次函数,则H (n ) 不为等差数列,B 错误;又H n =2n -1,则H n +1=2n ,H n +1 +1H n +1=2,则H (n )+1 为等比数列,C 正确,H 7 =27-1=127>100,D 错误,故选:C8(2024·云南曲靖·二模)已知S n 是等比数列a n 的前n 项和,若a 3=3,S 3=9,则数列a n 的公比是()A.-12或1 B.12或1 C.-12D.12【答案】A【分析】分别利用等比数列的通项公式和前n 项和公式,解方程组可得q =1或q =-12.【详解】设等比数列a n 的首项为a 1,公比为q ,依题意得a 3=a 1q 2=3S 3=a 1+a 2+a 3=a 1+a 1q +a 1q 2=9 ,解得q =1或q =-12.故选:A .9(2024·四川·模拟预测)已知数列a n 为等差数列,且a 1+2a 4+3a 9=24,则S 11=()A.33B.44C.66D.88【答案】B【分析】将a 1,a 4,a 9用a 1和d 表示,计算出a 6的值,再由S 11=11a 6得S 11的值.【详解】依题意,a n 是等差数列,设其公差为d ,由a 1+2a 4+3a 9=24,所以a 1+2a 1+3d +3a 1+8d =6a 1+30d =6a 6=24,即a 6=4,S 11=11a 1+10×112d =11a 1+5d =11a 6=11×4=44,故选:B .10(2024·北京东城·二模)设无穷正数数列a n ,如果对任意的正整数n ,都存在唯一的正整数m ,使得a m =a 1+a 2+a 3+⋯+a n ,那么称a n 为内和数列,并令b n =m ,称b n 为a n 的伴随数列,则()A.若a n 为等差数列,则a n 为内和数列B.若a n 为等比数列,则a n 为内和数列C.若内和数列a n 为递增数列,则其伴随数列b n 为递增数列D.若内和数列a n 的伴随数列b n 为递增数列,则a n 为递增数列【答案】C【分析】对于ABD :举反例说明即可;对于C :根据题意分析可得a m 2>a m 1,结合单调性可得m 2>m 1,即可得结果.【详解】对于选项AB :例题a n =1,可知a n 即为等差数列也为等比数列,则a 1+a 2=2,但不存在m ∈N *,使得a m =2,所以a n 不为内和数列,故AB 错误;对于选项C :因为a n >0,对任意n 1,n 2∈N *,n 1<n 2,可知存在m 1,m 2∈N *,使得a m 1=a 1+a 2+a 3+⋯+a n 1,a m 2=a 1+a 2+a 3+⋯+a n 2,则a m 2-a m 1=a n 1+1+a n 1+2+⋯+a n 2>0,即a m 2>a m 1,且内和数列a n 为递增数列,可知m 2>m 1,所以其伴随数列b n 为递增数列,故C 正确;对于选项D :例如2,1,3,4,5,⋅⋅⋅,显然a n 是所有正整数的排列,可知a n 为内和数列,且a n 的伴随数列为递增数列,但an 不是递增数列,故D 错误;故选:C.【点睛】方法点睛:对于新定义问题,要充分理解定义,把定义转化为已经学过的内容,简化理解和运算.11(2024·广东茂名·一模)已知T n为正项数列a n的前n项的乘积,且a1=2,T2n=a n+1n,则a5=() A.16 B.32 C.64 D.128【答案】B【分析】利用给定的递推公式,结合对数运算变形,再构造常数列求出通项即可得解.【详解】由T2n=a n+1n,得T2n+1=a n+2n+1,于是a2n+1=T2n+1T2n=a n+2n+1a n+1n,则a n n+1=a n+1n,两边取对数得n lg a n+1=(n+1)lg a n,因此lg a n+1n+1=lg a nn,数列lg a nn是常数列,则lg a nn=lg a11=lg2,即lg a n=n lg2=lg2n,所以a n=2n,a5=32.故选:B12(2024·湖南常德·一模)已知等比数列a n中,a3⋅a10=1,a6=2,则公比q为()A.12B.2 C.14D.4【答案】C【分析】直接使用已知条件及公比的性质得到结论.【详解】q=1q3⋅q4=a3a6⋅a10a6=a3⋅a10a26=122=14.故选:C.二、多选题13(2024·湖南长沙·三模)设无穷数列a n的前n项和为S n,且a n+a n+2=2a n+1,若存在k∈N∗,使S k+1 >S k+2>S k成立,则()A.a n≤a k+1B.S n≤S k+1C.不等式S n<0的解集为n∈N∗∣n≥2k+3D.对任意给定的实数p,总存在n0∈N∗,当n>n0时,a n<p【答案】BCD【分析】根据题意,得到a k+2<0,a k+1>0,a k+1+a k+2>0且a n是递减数列,结合等差数列的性质以及等差数列的求和公式,逐项判定,即可求解.【详解】由S k+1>S k+2>S k,可得a k+2=S k+2-S k+1<0,a k+1=S k+1-S k>0,且a k+1+a k+2=S k+2-S k>0,即a k+2<0,a k+1>0,a k+1+a k+2>0又由a n+a n+2=2a n+1,可得数列a n是等差数列,公差d=a k+2-a k+1<0,所以a n是递减数列,所以a1是最大项,且随着n的增加,a n无限减小,即a n≤a1,所以A错误、D正确;因为当n≤k+1时,a n>0;当n≥k+2时,a n<0,所以S n的最大值为S k+1,所以B正确;因为S2k+1=(2k+1)(a1+a2k+1)2=(2k+1)a k+1>0,S2k+3=(2k+3)a k+2<0,且S 2k +2=a 1+a 2k +22×2k +2 =k +1 ⋅a k +1+a k +2 >0,所以当n ≤2k +2时,S n >0;当n ≥2k +3时,S n <0,所以C 正确.故选:BCD .14(2024·山东泰安·模拟预测)已知数列a n 的通项公式为a n =92n -7n ∈N *,前n 项和为S n ,则下列说法正确的是()A.数列a n 有最大项a 4B.使a n ∈Z 的项共有4项C.满足a n a n +1a n +2<0的n 值共有2个D.使S n 取得最小值的n 值为4【答案】AC【分析】根据数列的通项公式,作差判断函数的单调性及项的正负判断A ,根据通项公式由整除可判断B ,根据项的正负及不等式判断C ,根据数列项的符号判断D .【详解】对于A :因为a n =92n -7n ∈N *,所以a n +1-a n =92n -5-92n -7=-182n -5 2n -7,令a n +1-a n >0,即2n -5 2n -7 <0,解得52<n <72,又n ∈N *,所以当n =3时a n +1-a n >0,则当1≤n ≤2或n ≥4时,a n +1-a n <0,令a n =92n -7>0,解得n >72,所以a 1=-95>a 2=-3>a 3=-9,a 4>a 5>a 6>⋯>0,所以数列a n 有最大项a 4=9,故A 正确;对于B :由a n ∈Z ,则92n -7∈Z 又n ∈N *,所以n =2或n =3或n =4或n =5或n =8,所以使a n ∈Z 的项共有5项.故B 不正确;对于C :要使a n a n +1a n +2<0,又a n ≠0,所以a n 、a n +1、a n +2中有1个为负值或3个为负值,所以n =1或n =3,故满足a n a n +1a n +2<0的n 的值共有2个,故C 正确;对于D :因为n ≤3时a n <0,n ≥4时a n >0,所以当n =3时S n 取得最小值,故D 不正确.故选:AC .15(2024·山东临沂·二模)已知a n 是等差数列,S n 是其前n 项和,则下列命题为真命题的是()A.若a 3+a 4=9,a 7+a 8=18,则a 1+a 2=5B.若a 2+a 13=4,则S 14=28C.若S 15<0,则S 7>S 8D.若a n 和a n ⋅a n +1 都为递增数列,则a n >0【答案】BC【分析】根据题意,求得d =98,结合a 1+a 2=a 3+a 4 -4d ,可判定A 错误;根据数列的求和公式和等差数列的性质,可判定B 正确;由S 15<0,求得a 8<0,可判定C 正确;根据题意,求得任意的n ≥2,a n >0,结合a 1的正负不确定,可判定D 错误.【详解】对于A 中,由a 3+a 4=9,a 7+a 8=18,可得a 7+a 8 -a 3+a 4 =8d =9,所以d =98,又由a 1+a 2=a 3+a 4 -4d =9-4×98=92,所以A 错误;对于B 中,由S 14=14a 1+a 14 2=14a 2+a 132=28,所以B 正确;对于C 中,由S 15=15(a 1+a 15)2=15a 8<0,所以a 8<0,又因为S 8-S 7=a 8<0,则S 7>S 8,所以C 正确;对于D 中,因为a n 为递增数列,可得公差d >0,因为a n a n +1 为递增数列,可得a n +2a n +1-a n a n +1=a n +1⋅2d >0,所以对任意的n ≥2,a n >0,但a 1的正负不确定,所以D 错误.故选:BC .16(2024·山东泰安·二模)已知等差数列a n 的前n 项和为S n ,a 2=4,S 7=42,则下列说法正确的是()A.a 5=4B.S n =12n 2+52n C.a nn为递减数列 D.1a n a n +1 的前5项和为421【答案】BC【分析】根据给定条件,利用等差数列的性质求出公差d ,再逐项求解判断即可.【详解】等差数列a n 中,S 7=7(a 1+a 7)2=7a 4=42,解得a 4=6,而a 2=4,因此公差d =a 4-a 24-2=1,通项a n =a 2+(n -2)d =n +2,对于A ,a 5=7,A 错误;对于B ,S n =n (3+n +2)2=12n 2+52n ,B 正确;对于C ,a n n =1+2n ,a n n 为递减数列,C 正确;对于D ,1a n a n +1=1(n +2)(n +3)=1n +2-1n +3,所以1a n a n +1 的前5项和为13-14+14-15+⋯+17-18=13-18=524,D 错误.故选:BC17(2024·江西·三模)已知数列a n 满足a 1=1,a n +1=2a n +1,则()A.数列a n 是等比数列B.数列log 2a n +1 是等差数列C.数列a n 的前n 项和为2n +1-n -2D.a 20能被3整除【答案】BCD【分析】利用构造法得到数列a n +1 是等比数列,从而求得通项,就可以判断选项,对于数列求和,可以用分组求和法,等比数列公式求和完成,对于幂的整除性问题可以转化为用二项式定理展开后,再加以证明.【详解】由a n +1=2a n +1可得:a n +1+1=2a n +1 ,所以数列a n +1 是等比数列,即a n =2n -1,则a 1=1,a 2=3,a 3=7,显然有a 1⋅a 3≠a 22,所以a 1,a 2,a 3不成等比数列,故选项A 是错误的;由数列a n +1 是等比数列可得:a n +1=2n ,即log 2a n +1 =log 22n =n ,故选项B 是正确的;由a n =2n -1可得:前n 项和S n =21-1+22-1+23-1+⋅⋅⋅+2n-1=21-2n 1-2-n =2n +1-n -2,故选项C是正确的;由a 20=220-1=3-1 20-1=C 020320+C 120319⋅-1 +C 220318⋅-1 2+⋅⋅⋅+C 19203⋅-1 19+C 2020-1 20-1=3×C 020319+C 120318⋅-1 +C 220317⋅-1 2+⋅⋅⋅+C 1920-1 19 ,故选项D 是正确的;方法二:由210=1024,1024除以3余数是1,所以10242除以3的余数还是1,从而可得220-1能补3整除,故选项D 是正确的;故选:BCD .18(2024·湖北·二模)无穷等比数列a n 的首项为a 1公比为q ,下列条件能使a n 既有最大值,又有最小值的有()A.a 1>0,0<q <1B.a 1>0,-1<q <0C.a 1<0,q =-1D.a 1<0,q <-1【答案】BC【分析】结合选项,利用等比数列单调性分析判断即可.【详解】a 1>0,0<q <1时,等比数列a n 单调递减,故a n 只有最大值a 1,没有最小值;a 1>0,-1<q <0时,等比数列a n 为摆动数列,此时a 1为大值,a 2为最小值;a 1<0,q =-1时,奇数项都相等且小于零,偶数项都相等且大于零,所以等比数列a n 有最大值,也有最小值;a 1<0,q <-1时,因为q >1,所以a n 无最大值,奇数项为负无最小值,偶数项为正无最大值.故选:BC 三、填空题19(2024·山东济南·三模)数列a n 满足a n +2-a n =2,若a 1=1,a 4=4,则数列a n 的前20项的和为.【答案】210【分析】数列a n 的奇数项、偶数项都是等差数列,结合等差数列求和公式、分组求和法即可得解.【详解】数列a n 满足a n +2-a n =2,若a 1=1,a 4=4,则a 2=a 4-2=4-2=2,所以数列a n 的奇数项、偶数项分别构成以1,2为首项,公差均为2的等差数列所以数列a n 的前20项的和为a 1+a 2+⋯+a 20=a 1+a 3+⋯+a 19 +a 2+a 4+⋯+a 20=10×1+10×92×2+10×2+10×92×2=210.故答案为:210.20(2024·云南·二模)记数列a n 的前n 项和为S n ,若a 1=2,2a n +1-3a n =2n ,则a 82+S 8=.【答案】12/0.5【分析】构造得a n +12n -1-4=34a n2n -2-4,从而得到a n 2n -2=4,则a n =2n ,再利用等比数列求和公式代入计算即可.【详解】由2a n +1-3a n =2n ,得a n +12n -1=34×a n 2n -2+1,则a n +12n -1-4=34a n2n -2-4,又a 12-1-4=0,则a n 2n -2=4,则a n =2n ,a 8=28,S 8=21-28 1-2=29-2,a 82+S 8=2829=12,故答案为:12.21(2024·上海·三模)数列a n 满足a n +1=2a n (n 为正整数),且a 2与a 4的等差中项是5,则首项a 1=。
2020届高考数学(理)一轮必刷题 专题32 数列的综合问题(解析版)

考点32 数列的综合问题1.(北京市房山区2019年高考第一次模拟测试理)《九章算术》中有如下问题:今有蒲生一日,长三尺,莞生一日,长1尺.蒲生日自半,莞生日自倍.问几何日而长等?意思是:今有蒲第一天长高3尺,莞第一天长高1尺,以后蒲每天长高前一天的一半,莞每天长高前一天的2倍.若蒲、莞长度相等,则所需时间为()(结果精确到0.1.参考数据:lg2=0.3010,lg3=0.4771.)A.天B.天C.天D.天【答案】C【解析】设蒲的长度组成等比数列{a n},其a1=3,公比为,其前n项和为A n,则A n=.莞的长度组成等比数列{b n},其b1=1,公比为2,其前n项和为B n.则B n,由题意可得:,整理得:2n+=7,解得2n=6,或2n=1(舍去).∴n=≈2.6.∴估计2.6日蒲、莞长度相等.故选:C.2.(新疆乌鲁木齐市2018届高三第三次诊断性测验)已知数列,满足,,,则数列的前10项的和为A.B.C.D.【答案】D【解析】由a n+1﹣a n2,所以数列{a n}是等差数列,且公差是2,{b n}是等比数列,且公比是2.又因为=1,所以a n =+(n ﹣1)d =2n ﹣1. 所以b 2n ﹣1=•22n ﹣2=22n ﹣2.设,所以=22n ﹣2,所以4,所以数列{∁n }是等比数列,且公比为4,首项为1.由等比数列的前n 项和的公式得:其前10项的和为(410﹣1).故选:D .3.(安徽省“皖南八校”2018届高三第三次(4月)联考)删去正整数数列 中的所有完全平方数,得到一个新数列,这个数列的第2018项是( ) A .B .C .D .【答案】B 【解析】由题意可得,这些数可以写为:,第个平方数与第个平方数之间有个正整数,而数列共有项,去掉个平方数后,还剩余个数,所以去掉平方数后第项应在后的第个数,即是原来数列的第项,即为,故选B.4.(华大新高考联盟2018届高三上学期11月教学质量测评理)已知等比数列{}n a 的前n 项和为n S ,3123S a a =+,则42S S =( ) A .2 B .3C .4D .5【答案】B 【解析】由3123S a a =+可得312a a =,所以22q =,又因为2123434421212113a a a a a a S q S a a a a ++++==+=+=++,所以选B.5.(湖南省2017届高三高考冲刺预测卷六理)最近各大城市美食街火爆热开,某美食店特定在2017年元旦期间举行特大优惠活动,凡消费达到88元以上者,可获得一次抽奖机会.已知抽奖工具是一个圆面转盘,被分为6个扇形块,分别记为1,2,3,4,5,6,其面积成公比为3的等比数列(即扇形块2是扇形块1面积的3倍),指针箭头指在最小的1区域内时,就中“一等奖”,则一次抽奖抽中一等奖的概率是( ) A .140B .1121C .1364D .11093【答案】C 【解析】由题意,可设1,2,3,4,5,6 扇形区域的面积分别为,3,9,27,81,243x x x x x x ,则由几何概型得,消费88 元以上者抽中一等奖的概率1392781243364x P x x x x x x ==+++++ ,故选C. 6.(湖北省钟祥市2019届高三高考第一次模拟考试理)对于实数x ,[x]表示不超过x 的最大整数,已知正数列{a n }满足S n =12(a n n 1a +),n ∈N*,其中S n 为数列{a n }的前n 项的和,则[12121111S S S ++⋯+]=______.【答案】20 【解析】由题可知0n S >,当1n >时,1111[()]2n n n n n S S S S S --=-+-化简可得2211n n S S --=,当22111,1n S a === 所以数列2{}n S 是以首项和公差都是1的等差数列,即2n n S n S =∴=又1n >时,22nS =<<=记12121111S S S S =++一方面21]1)20S >-=>另一方面1(21)]11)21S <+++-=+=所以2021S << 即[]20S = 故答案为207.(北京市朝阳区2019届高三第一次(3月)综合练习一模)天坛公园是明、清两代皇帝“祭天”“祈谷”的场所.天坛公园中的圜丘台共有三层(如图1所示),上层坛的中心是一块呈圆形的大理石板,从中心向外围以扇面形石(如图2所示).上层坛从第一环至第九环共有九环,中层坛从第十环至第十八环共有九环,下层坛从第十九环至第二十七环共有九环;第一环的扇面形石有9块,从第二环起,每环的扇面形石块数比前一环多9块,则第二十七环的扇面形石块数是______;上、中、下三层坛所有的扇面形石块数是_______.【答案】243 3402 【解析】第一环的扇面形石有9块,从第二环起,每环的扇面形石块数比前一环多9块, 则依题意得:每环的扇面形石块数是一个以9为首项,9为公差的等差数列, 所以,a n =9+(n -1)×9=9n , 所以,a 27=9×27=243, 前27项和为:1272727()27(9243)22a a S ++===3402.格谦教育收集整理,更多优惠资料请搜索淘宝店铺:格谦教育 https://8.(江苏省南京师大附中2018届高三高考考前模拟考试)在数列{a n }中,若a 4=1,a 12=5,且任意连续三项的和都是15,则a 2018=______. 【答案】9【解析】分析:将a n +a n+1+a n+2=15中n 换为n+1,可得数列{a n }是周期为3的数列.求出a 2,a 1,即可得到a 2018详解:由题意可得a n +a n+1+a n+2=15,将n 换为a n+1+a n+2+a n+3=15,可得a n+3=a n ,可得数列{a n 是周期为3的数列.故,由a n +a n+1+a n+2=15,n 取1可得,故,故答案为9.9.(湖北省武昌2018届元月调研考试)对任一实数序列,定义新序列,它的第项为,假设序列的所有项都是,且,则__________.【答案】100. 【解析】 设序列的首项为,则序列,则它的第n 项为,因此序列A 的第项,则是关于的二次多项式,其中的系数为,因为,所以必有,故。
65.高考数学专题32 数列大题解题模板(理)(原卷版)

专题32 数列大题解题模板模板一、由数列的前n 项和n S 与通项n a 的关系求通项n a 例1、已知数列}{n a 的前n 项和n S ,11=a ,121+=+n n S a (+∈N n ),等差数列}{n b 中,0>n b (+∈N n ),且15321=++b b b ,又11b a +、22b a +、33b a +成等比数列。
(1)求数列}{n a 、}{n b 的通项公式;(2)求数列}{n n b a ⋅的前n 项和n T 。
练习1、已知正项数列}{n a 的前n 项和n S 满足2362++=n nn a a S ,且2a 是1a 和6a 的等比中项。
(1)求数列}{n a 的通项公式;(2)已知符合][x 表示不超过实数x 的最大整数,如1]3[log 2=,2]5[log 2=,记]35[log 2+=n n a b ,求数列}2{2n b n ⋅的前n 项和n T 。
模板二、数列求和问题例2、已知数列}{n a 的前n 项和kn n S n +-=221(其中+∈N k ),且n S 的最大值为8。
(1)确定常数k ,并求n a ;(2)求数列}229{n n a -的前n 项和n T 。
练习2、等比数列}{n a 的前n 项和n S ,73=S 且31+a 、23a 、43+a 成等差数列。
(1)求数列}{n a 的公比q 和通项n a ;(2)若}{n a 是递增数列,令128log 12+=n n a b ,求||||||21n b b b +⋅⋅⋅++。
例3、已知数列}{n a 中,11=a ,其前n 项的和为n S ,且满足1222-=n n n S S a (2≥n )。
(1)求证:数列}1{nS 是等差数列; (2)证明:当2≥n 时,2313121321<+⋅⋅⋅+++n S n S S S 。
练习3、已知数列}{n a 的前n 项和为n S ,且满足211=a ,021=⋅+-n n n S S a (2≥n )。
数列大题题型及解题方法

数列大题题型及解题方法数列大题是中学数学中常见的题型之一,主要考察学生对数列概念的理解和运用能力。
数列大题可以分为等差数列和等比数列两种类型。
下面将介绍这两种数列大题的解题方法。
一、等差数列的解题方法:1. 求数列的通项公式:首先,要判断数列是等差数列,可以通过观察数列中的差值是否相等来判断。
如果差值相等,则数列是等差数列。
然后,可以通过观察数列中的前几项来确定数列的首项a和公差d。
有了首项和公差,就可以得到数列的通项公式:an = a + (n-1)d。
2. 求数列的前n项和:数列的前n项和可以通过求和公式来计算。
等差数列的求和公式为Sn = n/2 * (a + an),其中Sn表示前n项和,a表示首项,an 表示第n项。
3. 解题实例:例如,有一个等差数列的前5项分别为1、4、7、10、13,要求求出数列的通项公式和前10项的和。
首先,根据观察,可以确定首项a为1,公差d为3。
其次,根据数列的通项公式an = a + (n-1)d,可以得到数列的通项公式为an = 1 + (n-1)3。
最后,代入n=10,可以计算出前10项的和Sn = 10/2 * (1 + 1 + 9*3) = 100。
二、等比数列的解题方法:1. 求数列的通项公式:判断数列是否是等比数列,可以通过观察数列中的相邻项之间的比值是否相等来判断。
如果比值相等,则数列是等比数列。
然后,可以通过观察数列中的前几项来确定数列的首项a和公比r。
有了首项和公比,就可以得到数列的通项公式:an = a * r^(n-1)。
2. 求数列的前n项和:等比数列的前n项和可以通过求和公式来计算。
等比数列的求和公式为Sn = a * (1 - r^n) / (1 - r),其中Sn表示前n项和,a 表示首项,r表示公比。
3. 解题实例:例如,有一个等比数列的前5项分别为1、2、4、8、16,要求求出数列的通项公式和前10项的和。
首先,根据观察,可以确定首项a为1,公比r为2。
2024年高考数学专项突破数列大题基础练(解析版)

数列大题基础练-新高考数学复习分层训练(新高考通用)1.(2022·浙江·模拟预测)已知数列{}n a 满足,12(1)nn n a a +=+⋅-.(1)若11a =,数列{}2n a 的通项公式;(2)若数列{}n a 为等比数列,求1a .2.(2022·海南省直辖县级单位·校联考一模)等差数列{}n a 的首项11a =,且满足2512a a +=,数列{}n b 满足2n a n b =.(1)求数列{}n a 的通项公式;(2)设数列{}n b 的前n 项和是n T ,求n T .3.(2023·黑龙江大庆·统考一模)设{}n a 是公差不为0的等差数列,12a =,3a 是1a ,11a 的等比中项.(1)求{}n a 的通项公式;(2)设13n n n b a a +=,求数列{}n b 的前n 项和n S .4.(2023·广东惠州·统考模拟预测)数列{}n a 中,12a =,121n n a a +=-.(1)求证:数列{}1n a -是等比数列;(2)若n n b a n =+,求数列{}n b 的前n 项和n T .5.(2023·广东江门·统考一模)已知数列{}n a (N n +∈)满足11a =,133n n n a a n++=,且n n ab n =.(1)求数列{}n b 是通项公式;(2)求数列{}n a 的前n 项和n S .6.(2023·江苏·统考一模)已知等比数列{}n a 的各项均为正数,且23439a a a ++=,54323a a a =+.(1)求{}n a 的通项公式;(2)数列{}n b 满足n nnb a=,求{}n b 的前n 项和n T .2024年高考数学专项突破数列大题基础练(解析版)7.(2023·重庆·统考二模)已知数列{}n a 的前n 项和为n S ,且满足()115n n na n a +-+=,且15a ≠-.(1)求证:数列5n a n +⎧⎫⎨⎬⎩⎭为常数列,并求{}n a 的通项公式;(2)若使不等式20n S >成立的最小整数为7,且1Z a ∈,求1a 和n S 的最小值.8.(2023·海南海口·校考模拟预测)已知数列{}n a 的前n 项和为n S ,14a =,12n n a n S n+=.(1)求数列{}n a 的通项公式;(2)记12nn na c =-,数列{}nc 的前n 项和为n T ,求12111n T T T ++⋅⋅⋅+的值.9.(2023·山东青岛·统考一模)已知等差数列{}n a 的前n 项和为n S ,公差0d ≠,2S ,4S ,54S +成等差数列,2a ,4a ,8a 成等比数列.(1)求n S ;(2)记数列{}n b 的前n 项和为n T ,22n n n n b T S +-=,证明数列1n n b S ⎧⎫-⎨⎬⎩⎭为等比数列,并求{}n b 的通项公式.10.(2023·山东济南·一模)已知数列{}n a 满足111,(1)1n n a na n a +=-+=.(1)若数列{}n b 满足1nn a b n+=,证明:{}n b 是常数数列;(2)若数列{}n c 满足πsin 22n an n c a ⎛⎫=+ ⎪⎝⎭,求{}n c 的前2n 项和2n S .11.(2022·辽宁鞍山·统考一模)已知等差数列{}n a 满足首项为3331log 15log 10log 42-+的值,且3718a a +=.(1)求数列{}n a 的通项公式;(2)设11n n n b a a +=,求数列{}n b 的前n 项和n T .12.(2023·广东·统考一模)已知各项都是正数的数列{}n a ,前n 项和n S 满足()2*2n n n a S a n =-∈N .(1)求数列{}n a 的通项公式.(2)记n P 是数列1n S ⎧⎫⎨⎬⎩⎭的前n 项和,n Q 是数列121n a -⎧⎫⎪⎪⎨⎬⎪⎪⎩⎭的前n 项和.当2n ≥时,试比较n P 与n Q 的大小.13.(2022·吉林长春·东北师大附中校考模拟预测)从①12n a S n n ⎛⎫=+ ⎪⎝⎭;②23S a =,412a a a =;③12a =,4a 是2a ,8a 的等比中项这三个条件中任选一个,补充到下面横线上,并解答.已知等差数列{}n a 的前n 项和为n S ,公差d 不等于零,______.(1)求数列{}n a 的通项公式;(2)若122n n n b S S +=-,数列{}n b 的前n 项和为n W ,求n W .14.(2022·广东珠海·珠海市第三中学统考二模)已知数列{}n a ,{}n b 的前n 项和分别为n S ,n T ,1221n n n a b n -+=+-,221n n n T S n -=--.(1)求11,a b 及数列{}n a ,{}n b 的通项公式;(2)设()*21N 2n n n a n k c k b n k=-⎧=∈⎨=⎩,,,求数列{}n c 的前2n 项和2n P .15.(2022·云南大理·统考模拟预测)已知数列{}n a 的前n 项和为n S ,且满足1121,1nn S a a n+==-.(1)求数列{}n a 的通项公式;(2)若数列2,,23,,n n n C n n ⎧=⎨+⎩为奇数为偶数,求数列{}n C 的前2n 项和2n T .16.(2022·湖南永州·统考一模)已知数列{}{},n n a b 满足:111a b ==,且210n n n n a b a b ++-=.(1)若数列{}n a 为等比数列,公比为121,2q a a -=,求{}n b 的通项公式;(2)若数列{}n a 为等差数列,11n n a a +-=,求{}n b 的前n 项和n T .17.(2022·广东韶关·统考一模)已知数列{}n a 的首项145a =,且满足143n n n a a a+=+,设11nnb a =-.(1)求证:数列{}n b 为等比数列;(2)若1231111140na a a a ++++> ,求满足条件的最小正整数n .18.(2022·河北·模拟预测)已知数列{}n a 的前n 项和为n S ,13a =,且1123n n n S S a +++=-.(1)求数列{}n a 的通项公式;(2)①3log n n nb a a =;②3321log log n n n b a a +=⋅;③3log n n n b a a =-.从上面三个条件中任选一个,求数列{}n b 的前n 项和n T .注:如果选择多个条件分别解答,按第一个解答计分.19.(2022·广东广州·统考一模)已知公差不为0的等差数列{}n a 中,11a =,4a 是2a 和8a 的等比中项.(1)求数列{}n a 的通项公式:(2)保持数列{}n a 中各项先后顺序不变,在k a 与1(1,2,)k a k += 之间插入2k ,使它们和原数列的项构成一个新的数列{}n b ,记{}n b 的前n 项和为n T ,求20T 的值.20.(2023·湖北·荆州中学校联考二模)已知数列{}n a ,若_________________.(1)求数列{}n a 的通项公式;(2)求数列11n n a a +⎧⎫⎨⎬⎩⎭的前n 项和n T .从下列三个条件中任选一个补充在上面的横线上,然后对题目进行求解.①2123n a a a a n ++++= ;②11a =,47a =,()*112,2n n n a a a n n -+=+∈N ≥;③11a =,点(),n A n a ,()11,n B n a ++在斜率是2的直线上.21.(2023·江苏南通·二模)已知正项数列{}n a 的前n 项和为,且11a =,2218n n S S n +-=,*N n ∈.(1)求n S ;(2)在数列{}n a 的每相邻两项1k k a a +,之间依次插入12k a a a ⋯,,,,得到数列{}1121231234n b a a a a a a a a a a ⋯⋯:,,,,,,,,,,,求{}n b 的前100项和.22.(2023·江苏南通·海安高级中学校考一模)已知数列{}n a 满足()1122n n n a a a n -+=+≥,且12342,18a a a a =++=(1)求{}n a 的通项公式;(2)设1000na nb =-,求数列{}n b 的前15项和15T (用具体数值作答).23.(2023·安徽·模拟预测)已知{}n a 为等差数列,{}n b 是公比为2的等比数列,且223344a b a b b a -=-=-.(1)证明:11a b =;(2)求集合{}1,1500k m k b a a m =+≤≤中元素个数.24.(2023·河北衡水·河北衡水中学校考三模)已知{}n a 为等差数列,1154,115n n a n a a n+-==+.(1)求{}n a 的通项公式;(2)若()()1,414n n n n b T a a =++为{}n b 的前n 项和,求n T .25.(2023·广东广州·统考二模)设数列{}n a 的前n 项和为n S ,且()22*n n S a n =-∈N .(1)求{}n a 的通项公式;(2)设2211log log n n n b a a +=⋅,记{}n b 的前n 项和为n T ,证明:1n T <.26.(2023·江苏泰州·统考一模)在①124,,S S S 成等比数列,②4222a a =+,③8472S S S =+-这三个条件中任选两个,补充在下面问题中,并完成解答.已知数列{}n a 是公差不为0的等差数列,其前n 项和为n S ,且满足__________,__________.(1)求{}n a 的通项公式;(2)求12233411111n n a a a a a a a a +++++ .注:如果选择多个方案分别解答,按第一个方案计分.27.(2023·黑龙江·黑龙江实验中学校考一模)已知数列{}n a ,前n 项和为n S ,且满足112n n n a a a +-=-,2n ≥,*N n ∈,1514a a +=,770S =,等比数列{}n b 中,1212b b +=,且12,6b b +,3b 成等差数列.(1)求数列{}n a 和{}n b 的通项公式;(2)记n c 为区间(]()*,N n n a b n ∈中的整数个数,求数列{}n c 的前n 项和n P .28.(2023·吉林·统考二模)已知数列{}n a 的前n 项和为n S ,13a =,数列n S n ⎧⎫⎨⎬⎩⎭是以2为公差的等差数列.(1)求{}n a 的通项公式;(2)设()()112n nn nn a b a a +-+=,求数列{}nb 的前2n 项和2nT .29.(2023·山西·校联考模拟预测)已知数列{}n a 满足0n a >,22112n n n n a a a a ++=+,且13a ,23a +,3a 成等差数列.(1)求{}n a 的通项公式;(2)若12,log ,n n na nb a n ⎧⎪=⎨⎪⎩为奇数为偶数,求数列{}n b 的前2n 项和2n T .30.(2023·黑龙江哈尔滨·哈尔滨三中校考二模)已知数列{}n a 满足:15a =,134n n a a +=-,设2n n b a =-,*N n ∈.(1)求数列{}n b 的通项公式;(2)设3132312log log log n n nb b b T b b b =++⋅⋅⋅+,()*N n ∈,求证:34n T <.数列大题基础练-新高考数学复习分层训练(新高考通用)1.(2022·浙江·模拟预测)已知数列{}n a 满足,12(1)nn n a a +=+⋅-.(1)若11a =,数列{}2n a 的通项公式;(2)若数列{}n a 为等比数列,求1a .【答案】(1)21n a =-;(2)11a =.【分析】(1)利用累加法求2n a 即可;(2)根据()121nn n a a +=+⋅-得到212a a =-,322a a =+,联立得到1q =-,然后代入求1a 即可.【详解】(1)由题意得()121nn n a a +-=⋅-,所以()()()22212122211n n n n n a a a a a a a a ---=-+-++-+ ()()()212212121211n n --=⋅-+⋅-++⨯-+ 211=-+=-.(2)设数列{}n a 的公比为q ,因为()121nn n a a +=+⋅-,所以212a a =-,322a a =+,两式相加得2311a a q a =⋅=,所以1q =±,当1q =时,2112a a a ==-不成立,所以1q =-,2112a a a =-=-,解得11a =.2.(2022·海南省直辖县级单位·校联考一模)等差数列{}n a 的首项11a =,且满足2512a a +=,数列{}n b 满足2n a n b =.(1)求数列{}n a 的通项公式;(2)设数列{}n b 的前n 项和是n T ,求n T .【答案】(1)21n a n =-;3.(2023·黑龙江大庆·统考一模)设{}n a 是公差不为0的等差数列,12a =,3a 是1a ,11a 的等比中项.(1)求{}n a 的通项公式;(2)设3n b a a =,求数列{}n b 的前n 项和n S .4.(2023·广东惠州·统考模拟预测)数列{}n a 中,12a =,121n n a a +=-.(1)求证:数列{}1n a -是等比数列;(2)若n n b a n =+,求数列{}n b 的前n 项和n T .5.(2023·广东江门·统考一模)已知数列{}n a (N n +∈)满足11a =,133n n n a a n++=,且n n ab n =.(1)求数列{}n b 是通项公式;(2)求数列{}n a 的前n 项和n S .【答案】(1)13n n b -=6.(2023·江苏·统考一模)已知等比数列{}n a 的各项均为正数,且23439a a a ++=,54323a a a =+.(1)求{}n a 的通项公式;(2)数列{}n b 满足n nb a =,求{}n b 的前n 项和n T .7.(2023·重庆·统考二模)已知数列{}n a 的前n 项和为n S ,且满足()115n n na n a +-+=,且15a ≠-.(1)求证:数列5n a n +⎧⎫⎨⎬⎩⎭为常数列,并求{}n a 的通项公式;(2)若使不等式20n S >成立的最小整数为7,且1Z a ∈,求1a 和n S 的最小值.8.(2023·海南海口·校考模拟预测)已知数列{}n a 的前n 项和为n S ,14a =,2n n S n=.(1)求数列{}n a 的通项公式;(2)记12nn na c =-,数列{}n c 的前n 项和为n T ,求111T T T ++⋅⋅⋅+的值.9.(2023·山东青岛·统考一模)已知等差数列{}n a 的前n 项和为n S ,公差0d ≠,2S ,4S ,54S +成等差数列,2a ,4a ,8a 成等比数列.(1)求n S ;(2)记数列{}n b 的前n 项和为n T ,22n n n n b T S +-=,证明数列1n n b S ⎧⎫-⎨⎬⎩⎭为等比数列,并求{}n b 的通项公式.10.(2023·山东济南·一模)已知数列{}n a 满足111,(1)1n n a na n a +=-+=.(1)若数列{}n b 满足1nn a b n+=,证明:{}n b 是常数数列;(2)若数列{}n c 满足πsin 22n an n c a ⎛⎫=+ ⎪,求{}n c 的前2n 项和2n S .11.(2022·辽宁鞍山·统考一模)已知等差数列{}n a 满足首项为333log 15log 10log 42-+的值,且3718a a +=.(1)求数列{}n a 的通项公式;(2)设1n b a a =,求数列{}n b 的前n 项和n T .12.(2023·广东·统考一模)已知各项都是正数的数列{}n a ,前n 项和n S 满足()2*2n n n a S a n =-∈N .(1)求数列{}n a 的通项公式.(2)记n P 是数列1n S ⎧⎫⎨⎬⎩⎭的前n 项和,n Q 是数列121n a -⎧⎫⎪⎪⎨⎬⎪⎪⎩⎭的前n 项和.当2n ≥时,试比较n P 与n Q 的大小.【答案】(1)n a n =(2)n nP Q <13.(2022·吉林长春·东北师大附中校考模拟预测)从①12n S n n ⎛⎫=+ ⎪⎝⎭;②23S a =,412a a a =;③12a =,4a 是2a ,8a 的等比中项这三个条件中任选一个,补充到下面横线上,并解答.已知等差数列{}n a 的前n 项和为n S ,公差d 不等于零,______.(1)求数列{}n a 的通项公式;(2)若122n n n b S S +=-,数列{}n b 的前n 项和为n W ,求n W .14.(2022·广东珠海·珠海市第三中学统考二模)已知数列{}n a ,{}n b 的前n 项和分别为n S ,n T ,1221n n n a b n -+=+-,221n n n T S n -=--.(1)求11,a b 及数列{}n a ,{}n b 的通项公式;(2)设()*21N 2n n n a n k c k b n k=-⎧=∈⎨=⎩,,,求数列{}n c 的前2n 项和2n P .15.(2022·云南大理·统考模拟预测)已知数列{}n a 的前n 项和为n S ,且满足111,1nn a a n+==-.(1)求数列{}n a 的通项公式;(2)若数列2,,23,,n n n C n n ⎧=⎨+⎩为奇数为偶数,求数列{}n C 的前2n 项和2n T .16.(2022·湖南永州·统考一模)已知数列{}{},n n a b 满足:111a b ==,且210n n n n a b a b ++-=.(1)若数列{}n a 为等比数列,公比为121,2q a a -=,求{}n b 的通项公式;(2)若数列{}n a 为等差数列,11n n a a +-=,求{}n b 的前n 项和n T .17.(2022·广东韶关·统考一模)已知数列{}n a 的首项15a =,且满足13n n n a a +=+,设1n nb a =-.(1)求证:数列{}n b 为等比数列;(2)若1111140a a a a ++++> ,求满足条件的最小正整数n .18.(2022·河北·模拟预测)已知数列{}n a 的前n 项和为n S ,13a =,且1123n n n S S a +++=-.(1)求数列{}n a 的通项公式;(2)①3log n n n b a a =;②3321log log n n n b a a +=⋅;③3log n n n b a a =-.从上面三个条件中任选一个,求数列{}n b 的前n 项和n T .注:如果选择多个条件分别解答,按第一个解答计分.19.(2022·广东广州·统考一模)已知公差不为0的等差数列{}n a 中,11a =,4a 是2a 和8a 的等比中项.(1)求数列{}n a 的通项公式:(2)保持数列{}n a 中各项先后顺序不变,在k a 与1(1,2,)k a k += 之间插入2k ,使它们和原数列的项构成一个新的数列{}n b ,记{}n b 的前n 项和为n T ,求20T 的值.20.(2023·湖北·荆州中学校联考二模)已知数列{}n a ,若_________________.(1)求数列{}n a 的通项公式;(2)求数列11n n a a +⎧⎫⎨⎬⎩⎭的前n 项和n T .从下列三个条件中任选一个补充在上面的横线上,然后对题目进行求解.①2123n a a a a n ++++= ;②11a =,47a =,()*112,2n n n a a a n n -+=+∈N ≥;③11a =,点(),n A n a ,()11,n B n a ++在斜率是2的直线上.21.(2023·江苏南通·二模)已知正项数列{}n a 的前n 项和为,且11a =,2218n n S S n +-=,*N n ∈.(1)求n S ;(2)在数列{}n a 的每相邻两项1k k a a +,之间依次插入12k a a a ⋯,,,,得到数列{}1121231234n b a a a a a a a a a a ⋯⋯:,,,,,,,,,,,求{}n b 的前100项和.22.(2023·江苏南通·海安高级中学校考一模)已知数列{}n a 满足()1122n n n a a a n -+=+≥,且12342,18a a a a =++=(1)求{}n a 的通项公式;(2)设1000na nb =-,求数列{}n b 的前15项和15T (用具体数值作答).()()1061022166490300022-==--+23.(2023·安徽·模拟预测)已知{}n a 为等差数列,{}n b 是公比为2的等比数列,且223344a b a b b a -=-=-.(1)证明:11a b =;(2)求集合{}1,1500k m k b a a m =+≤≤中元素个数.24.(2023·河北衡水·河北衡水中学校考三模)已知{}n a 为等差数列,11,115n n a a n+==+.(1)求{}n a 的通项公式;(2)若()()1,414n n b T a a =++为{}n b 的前n 项和,求n T .25.(2023·广东广州·统考二模)设数列{}n a 的前n 项和为n S ,且()22*n n S a n =-∈N .(1)求{}n a 的通项公式;(2)设1log log n b a a =⋅,记{}n b 的前n 项和为n T ,证明:1n T <.26.(2023·江苏泰州·统考一模)在①124,,S S S 成等比数列,②4222a a =+,③8472S S S =+-这三个条件中任选两个,补充在下面问题中,并完成解答.已知数列{}n a 是公差不为0的等差数列,其前n 项和为n S ,且满足__________,__________.(1)求{}n a 的通项公式;(2)求12233411111n n a a a a a a a a +++++ .注:如果选择多个方案分别解答,按第一个方案计分.27.(2023·黑龙江·黑龙江实验中学校考一模)已知数列{}n a ,前n 项和为n S ,且满足112n n n a a a +-=-,2n ≥,*N n∈,1514a a +=,770S =,等比数列{}n b 中,1212b b +=,且12,6b b +,3b 成等差数列.(1)求数列{}n a 和{}n b 的通项公式;(2)记n c 为区间(]()*,N n n a b n ∈中的整数个数,求数列{}n c 的前n 项和n P .28.(2023·吉林·统考二模)已知数列{}n a 的前n 项和为n S ,13a =,数列n n ⎧⎫⎨⎬⎩⎭是以2为公差的等差数列.(1)求{}n a 的通项公式;(2)设()()112n n n n n a b a a +-+=,求数列{}n b 的前2n 项和2n T .29.(2023·山西·校联考模拟预测)已知数列{}n a 满足0n a >,22112n n n n a a a a ++=+,且13a ,23a +,3a 成等差数列.(1)求{}n a 的通项公式;(2)若12,log ,n n n a n b a n ⎧⎪=⎨⎪⎩为奇数为偶数,求数列{}n b 的前2n 项和2n T .30.(2023·黑龙江哈尔滨·哈尔滨三中校考二模)已知数列{}n a 满足:15a =,134n n a a +=-,设2n n b a =-,*N n ∈.(1)求数列{}n b 的通项公式;(2)设31323log log log n n b b b T b b b =++⋅⋅⋅+,()*N n ∈,求证:34n T <.。
数列解答题及答案

数列解答题及答案数列是数学中最基础、最常见的概念之一。
它是由一连串数字构成的有序集合,其中每个数字都按照一定规则进行排列。
解题时,我们需要掌握数列的基本概念、求和公式和递推公式等。
下面我们将介绍数列解答题的一般方法,以及一些常见的数列题目及其答案。
一、数列解答题的一般方法要解答数列题目,需要掌握以下几个方面的知识:1.数列的类型:包括等差数列、等比数列、等差数列的前n项和、等比数列的前n项和等。
2.求和公式:包括等差数列求和公式、等比数列求和公式。
3.递推公式:包括等差数列递推公式、等比数列递推公式。
基于上述基本知识点,下面我们将介绍一些常见的数列题目及其解答方法和答案。
二、常见的数列题目及其答案1.等差数列问题题目:3,5,7,9,11……,其中第20项为多少?解答方法:由于该数列的公差为2,所以第20项为15。
2.等比数列问题题目:4,8,16,32,64……,其中第10项为多少?解答方法:由于该数列的公比为2,所以第10项为2^9=512。
3.求和问题(1)等差数列求和问题题目:1,3,5,7……,其中前50项的和为多少?解答方法:该数列的首项为1,公差为2,因此前50项的和为50/2(2×1+49×2)= 1250。
(2)等比数列求和问题题目:2,4,8,16……,其中前10项的和为多少?解答方法:该数列的首项为2,公比为2,因此前10项的和为(2^10-2)÷(2-1)= 1022。
4.递推问题(1)等差数列递推问题题目:3,7,11,15……,其中第10项为多少?解答方法:由于该数列的首项为3,公差为4,所以第10项为(10-1)×4+3=39。
(2)等比数列递推问题题目:4,12,36,108……,其中第6项为多少?解答方法:由于该数列的首项为4,公比为3,所以第6项为4×3^5=1458。
综上所述,数列解答题需要掌握相关的基本概念、公式和递推公式等。
高考数学二轮复习专题32 数列大题解题模板(文)(解析版)

专题32 数列大题解题模板一、递推数列的类型以及求通项方法总结:1、定义法:等差数列的通项公式:d n a a n )1(1-+=或d m n a a m n )(-+=。
等比数列的通项公式:11-⋅=n n q a a (01≠⋅q a )或m n m n q a a -⋅=(m n >)2、做差法:由n a 与n S (即)(21n f a a a n =+⋅⋅⋅++)的关系求n a ,⎩⎨⎧≥-==-2,1,11n S S n S a n nn 。
3、累加法:由)(1n f a a n n =-+求n a ,112211)()()(a a a a a a a a n n n n n +-+⋅⋅⋅+-+-=---(2≥n )。
4、累乘法:已知)(1n f a a n n =+求通项n a ,112211a a aa a a a a n n n n n ⋅⋅⋅⋅⋅=---(2≥n )。
5、已知递推关系求n a ,用构造法(构造等差、等比数列):(1)形如)(1n f pa a n n +=+,只需构造数列}{n b ,消去)(n f 带来的差异,)(n f 的形式有: ①)(n f 为常数,即递推公式为q pa a n n +=+1(其中p 、q 均为常数且0)1(≠-p pq )。
解法:先设参转化为)(1λ+=λ++n n a p a ,其中1-=λp q,再利用换元法转化为等比数列求解。
②)(n f 为一次多项式,即递推公式为s n r a p a n n +⋅+⋅=+1。
③)(n f 为n 的二次式,则可设C Bn An a b n n +++=2。
(2)递推公式为n n n q a p a +⋅=+1(其中p 、q 为常数且0)1)(1(≠--q p pq )或n n n q r a p a ⋅+⋅=+1(其中p 、q 、r 为常数)。
解法:一般地要先在原递推公式两边同除以1+n q ,得:qq a q p q a n n n n 111+⋅=++,引入辅助数列}{n b (其中nn n qa b =),得:q b q p b n n 11+⋅=+,再应用类型(1)的方法解决。
历年数列大题真题答案解析

历年数列大题真题答案解析数列是高中数学中的重要知识点之一,是解决各种数学问题的基础。
对于考生来说,熟练掌握数列的概念和解题方法是取得高分的关键。
为了帮助广大考生更好地掌握数列题型,本文将通过对历年数列大题的真题进行解析,详细介绍解题思路和技巧。
一、等差数列的题目解析等差数列是最基本的数列之一,它的通项公式为an=a1+(n-1)d,其中a1为首项,d为公差。
下面我们通过一道历年真题来解析等差数列的应用。
例题:已知数列{an}的首项为2,公差为3,且a1、a5、a17分别是等差数列,求此数列的通项公式。
解析:首先,根据a1=2和公差d=3,我们可以得到{an}的通项公式为an=2+(n-1)3。
其次,由已知条件a1、a5、a17是等差数列,可推知a5-a1=a17-a5。
将a1=2代入,可得a5-2=a17-a5,整理后可得2a5=a17+2。
由此可以得到a5=(a17+2)/2。
综上所述,数列{an}的通项公式为an=2+(n-1)3,其中n≥1,a5=(a17+2)/2。
二、等比数列的题目解析等比数列与等差数列一样,也是高中数学中的常见题型。
等比数列的通项公式为an=a1*q^(n-1),其中a1为首项,q为公比。
下面我们通过一道历年真题来解析等比数列的应用。
例题:已知数列{an}的首项为2,公比为3,且a1、a3、a5分别是等比数列,求此数列的通项公式。
解析:由已知条件可得a3/a1=a5/a3。
将a1=2代入,可得a3/2 = a5/3。
整理可得a5=9a3/2。
根据等比数列的通项公式可知a3=2*3^(3-1)=18,代入上式可得a5=18*9/2=81。
综上所述,数列{an}的通项公式为an=2*3^(n-1),其中n≥1,a5=81。
三、特殊数列的题目解析除了等差数列和等比数列之外,还有一些特殊的数列题型需要注意。
例如斐波那契数列、等差-等比混合数列等。
下面我们通过一道历年真题来解析特殊数列的应用。
数列典型习题及解题方法【范本模板】

高中数学数列基本题型及解法例2.已知数列{}n a 中,n S 是其前n 项和,并且1142(1,2,),1n n S a n a +=+==,⑴设数列),2,1(21 =-=+n a a b n n n ,求证:数列{}n b 是等比数列; ⑵设数列),2,1(,2==n a c n nn ,求证:数列{}n c 是等差数列; ⑶求数列{}n a 的通项公式及前n 项和。
分析:由于{b n }和{c n }中的项都和{a n }中的项有关,{a n }中又有S 1n +=4a n +2,可由S 2n +-S 1n +作切入点探索解题的途径.解:(1)由S 1n +=4a 2n +,S 2n +=4a 1n ++2,两式相减,得S 2n +—S 1n +=4(a 1n +-a n ),即a 2n +=4a 1n +-4a n .(根据b n 的构造,如何把该式表示成b 1n +与b n 的关系是证明的关键,注意加强恒等变形能力的训练)a 2n +—2a 1n +=2(a 1n +—2a n ),又b n =a 1n +—2a n ,所以b 1n +=2b n ① 已知S 2=4a 1+2,a 1=1,a 1+a 2=4a 1+2,解得a 2=5,b 1=a 2-2a 1=3 ② 由①和②得,数列{b n }是首项为3,公比为2的等比数列,故b n =3·21n -.当n ≥2时,S n =4a 1n -+2=21n -(3n —4)+2;当n=1时,S 1=a 1=1也适合上式.综上可知,所求的求和公式为S n =21n -(3n —4)+2.说明:1.本例主要复习用等差、等比数列的定义证明一个数列为等差,等比数列,求数列通项与前n 项和。
解决本题的关键在于由条件241+=+n n a S 得出递推公式。
2.解综合题要总揽全局,尤其要注意上一问的结论可作为下面论证的已知条件,在后面求解的过程中适时应用.例3.设数列{a n }的前项的和S n =31(a n -1) (n ∈N +),(1)求a 1;a 2; (2)求证数列{a n }为等比数列. 解: (Ⅰ)由)1(3111-=a S ,得)1(3111-=a a ∴=1a 21- 又)1(3122-=a S ,即)1(31221-=+a a a ,得412=a .(Ⅱ)当n >1时,),1(31)1(3111---=-=--n n n n n a a S S a得,211-=-n n a a 所以{}n a 是首项21-,公比为21-的等比数列。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题32 数列大题解题模板一、递推数列的类型以及求通项方法总结:1、定义法:等差数列的通项公式:d n a a n )1(1-+=或d m n a a m n )(-+=。
等比数列的通项公式:11-⋅=n n q a a (01≠⋅q a )或m n m n q a a -⋅=(m n >)2、做差法:由n a 与n S (即)(21n f a a a n =+⋅⋅⋅++)的关系求n a ,⎩⎨⎧≥-==-2,1,11n S S n S a n nn 。
3、累加法:由)(1n f a a n n =-+求n a ,112211)()()(a a a a a a a a n n n n n +-+⋅⋅⋅+-+-=---(2≥n )。
4、累乘法:已知)(1n f a a n n =+求通项n a ,112211a a aa a a a a n n n n n ⋅⋅⋅⋅⋅=---(2≥n )。
5、已知递推关系求n a ,用构造法(构造等差、等比数列):(1)形如)(1n f pa a n n +=+,只需构造数列}{n b ,消去)(n f 带来的差异,)(n f 的形式有: ①)(n f 为常数,即递推公式为q pa a n n +=+1(其中p 、q 均为常数且0)1(≠-p pq )。
解法:先设参转化为)(1λ+=λ++n n a p a ,其中1-=λp q,再利用换元法转化为等比数列求解。
②)(n f 为一次多项式,即递推公式为s n r a p a n n +⋅+⋅=+1。
③)(n f 为n 的二次式,则可设C Bn An a b n n +++=2。
(2)递推公式为n n n q a p a +⋅=+1(其中p 、q 为常数且0)1)(1(≠--q p pq )或n n n q r a p a ⋅+⋅=+1(其中p 、q 、r 为常数)。
解法:一般地要先在原递推公式两边同除以1+n q ,得:qq a q p q a n n n n 111+⋅=++,引入辅助数列}{n b (其中nn n qa b =),得:q b q p b n n 11+⋅=+,再应用类型(1)的方法解决。
(3)递推公式为n n n a q a p a ⋅+⋅=++12(其中p 、q 均为常数)。
解法:先把原递推公式转化为)(112n n n n a s a t a s a ⋅-=⋅-+++,其中s 、t 满足⎩⎨⎧-==+q st pt s ,解出s 、t ,于是}{1n n sa a -+是公比为t 的等比数列,就转化为前面的类型。
6、形如bka a a n n n +=--11或11--⋅⋅=⋅-n n n n a a k a b a 的递推数列都可以用倒数法求通项。
7、形如rn n a p a ⋅=+1型,该类型是等式两边取对数后转化为前边的类型,然后再用递推法或待定系法构造等比数列求通项。
两边取对数n rn n a r p a p a lg lg )lg(lg 1⋅+=⋅=+,设n n a b lg =,原等式变为pb r b n n lg 1+⋅=+即变为基本型。
二、数列常用求和方法 1、等差数列求和:2)1(2)(2)(1)1(1dn n na n a a n a a S m n m n n -+=+=+=--;mnd S S S n m n m ++=+。
2、等比数列求和:⎪⎩⎪⎨⎧≠--=--==)1(11)1()1(111q q q a a q q a q na S n n n ;m n n n m m n m S q S S q S S +=+=+。
3、分组求和法:把数列的每一项分成几项使其转化为几个等差、等比数列,再求和。
对于求||n a 的前n 项和的问题一般都是分类讨论。
4、倒序求和法:将数列的顺序倒过来排列,与原数列两式相加,若有公因式可提,并且剩余项的和易于求出,这样的数列可用倒序相加法求和。
5、裂项相消法:就是把数列的各项分裂成两项之差,相邻的两项彼此相消,只余有限几项,就可以化简后求和。
适用条件:(1)⎭⎬⎫⎩⎨⎧+1n n a a c 其中}{n a 是各项不为0的等差数列,c 为常数,可拆解为)11(11++-=n n n n a a d c a a c ; (2)部分无理数列)(11n n n n a a dca a c -=+++。
(3)一些常用的裂项公式:①111)1(1+-=+n n n n ; ②)121121(21)12)(12(11412+--=+-=-n n n n n ;③)211(21)2(1+-=+n n n n ; ④n n nn -+=++111;⑤)11(1)(1k n n k k n n +-=+; ⑥])2)(1(1)1(1[21)2)(1(1++-+=++n n n n n n n 。
(4)常见放缩公式:①)1(212112)1(2--=-+<<++=-+n n n n n n n n n ;②)1111(2111122+--=-<k k k k ; ③kk k k k k k k k 111)1(11)1(11112--=-<<+=+-; 6、错位相减法:主要用于一个等差数列与一个等比数列对应项相乘得的新数列求和。
7、周期法:有的数列是周期数列,把握了数列的周期则可顺利求和。
模板一、由数列的前n 项和n S 与通项n a 的关系求通项n a例1、已知数列}{n a 的前n 项和n S ,11=a ,121+=+n n S a (+∈N n ),等差数列}{n b 中,0>n b (+∈N n ),且15321=++b b b ,又11b a +、22b a +、33b a +成等比数列。
(1)求数列}{n a 、}{n b 的通项公式; (2)求数列}{n n b a ⋅的前n 项和n T 。
审题路线图:(1)1--=n n n S S a (2≥n )→消去n S →得n n a a 31=+→13-=n n a ;(2)观察}{n n b a ⋅中n a 与n b 的特点→在n T 前乘以}{n a 的公比,构造使用错位相减得条件→n n n T 322⋅-=-→得n T 。
规范解答:【解析】(1)∵11=a ,121+=+n n S a (+∈N n ),∴121+=-n n S a (+∈N n ,2≥n ), 1分∴)(211-+-=-n n n n S S a a ,即n n n a a a 21=-+,∴n n a a 31=+(+∈N n ,2≥n ), 2分 而31212=+=a a ,∴123a a =,∴数列}{n a 是以1为首项、3为公比的等比数列,∴13-=n n a (+∈N n ), 3分 ∴11=a ,32=a ,93=a ,在等差数列}{n b 中,∵15321=++b b b ,∴52=b , 4分 又∵11b a +、22b a +、33b a +成等比数列,设等差数列}{n b 的公差为d ,则有2223311)())((b a b a b a +=++, 5分 ∴64)59)(51(=++-+d d ,解得10-=d 或2=d , 6 又∵0>n b (+∈N n ),∴舍去10-=d ,取2=d ,∴31=b ,∴12+=n b n (+∈N n ); 7分 (2)由(1)知122103)12(3)12(373533--⨯++⨯-+⋅⋅⋅+⨯+⨯+⨯=n n n n n T ①, 8分=n T 3 n n n n 3)12(3)12(3735331321⨯++⨯-+⋅⋅⋅+⨯+⨯+⨯-②, 9分 则①-②得n n n n n T 3)12(3232323233212210⨯+-⨯+⨯+⋅⋅⋅+⨯+⨯+⨯=--- 10分n n n n 3)12()3333(231221⨯+-++⋅⋅⋅++⨯+=--n n n 3)12(31313231⨯+---⨯⨯+=-n n 32⋅-=, 11分∴n n n T 3⋅=。
12分 构建答题模板:第一步:令1=n ,由)(n f S n =求出1a 。
第二步:令2≥n ,构造1--=n n n S S a ,用n a 代换1--n n S S (或用1--n n S S 代换n a ,这要结合题目特点),由递推关系求通项。
第三步:验证当1=n 时的结论是否适合当2≥n 时的结论。
第四步:反复回顾,注意1=n 和2≥n 分类讨论和验证,明确规范书写答题。
练习1、已知正项数列}{n a 的前n 项和n S 满足2362++=n nn a a S ,且2a 是1a 和6a 的等比中项。
(1)求数列}{n a 的通项公式;(2)已知符合][x 表示不超过实数x 的最大整数,如1]3[log 2=,2]5[log 2=,记]35[log 2+=n n a b ,求数列}2{2n b n ⋅的前n 项和n T 。
【解析】(1)由2362++=n nn a a S 得:当1=n 时,2361211++=a a S ,即023121=+-a a ,解得11=a 或21=a , 1分 当2≥n 时,2361211++=---n n n a a S ,633623623121212121-------+=++-++=-=n n n n n n n n n n n a a a a a a a a S S a , 即))(()(3112121-----+=-=+n n n n n n n n a a a a a a a a , 2分又数列}{n a 各项均为正数,∴01≠+-n n a a ,∴31=--n n a a , 3分 当11=a 时,数列}{n a 是首项为1、公差为3的等差数列,∴23-=n a n ,42=a ,166=a ,满足2a 是1a 和6a 的等比中项,可取, 4分 当21=a 时,数列}{n a 是首项为2、公差为3的等差数列,∴13-=n a n ,52=a ,176=a ,不满足2a 是1a 和6a 的等比中项,舍去, 5分 ∴23-=n a n ; 6分(2)由(1)可知)]1([log ]35[log 22+=+=n a b n n , 7分 ∴n b n n =+=)]12([log 22,∴n n n b n 222⋅=⋅, 8分 ∴数列}2{2n b n ⋅的前n 项和n n n T 2232221321⋅+⋅⋅⋅+⨯+⨯+⨯=, 9分=n T 2 14322232221+⋅+⋅⋅⋅+⨯+⨯+⨯n n 10分∴上式减上式得: 132122222+⋅-+⋅⋅⋅+++=-n n n n T122122+⋅--⨯=n n n 22)1(1-⋅-=+n n , 11分∴22)1(1+⋅-=+n n n T 。
