大学物理课件.机械波 下
合集下载
机械波精品PPT课件

震源:是地球内发生地震的地方。
震源深度:震源垂直向上到地表 的距离是震源深度。我们把地震 发生在60公里以内的称为浅源地 震;60-300公里为中源地震; 300公里以上为深源地震。目前有 记录的最深震源达720公里。
地震波主要包含纵波和横波。来自地下的纵波引起地面上下颠簸振动。 来自地下的横波能引起地面的水平晃动。横波是地震时造成建筑物破坏的 主要原因。
(3) 波动曲线与振动曲线不同。
y
yu
o t
振动曲线
o
x
波动曲线
振动的图像
波的图象
研究对象 研究内容
一个振动质点
质点在振动过程中,位移随时间 而变化的规律
波的传播方向上所有的振动质 点
某一时刻连续介质中各质点相 对于平衡位置的位移规律
图象
坐标含义 物理意义
图线的 变化
(t、x)表示t时刻的位移是x
(3) 横波使介质产生切变,只有能承受切变的物体(固体)才能传 递横波。横波仅在固体中传播!
它既不是纵波,也不是横波。
水
它是因重力以及表面张力的作用, 面
在水表面上传播的波。
波
(4) 纵波在介质中引起长变或体变,所有物质都能承受长变和体变 (固、液、气体)。在固体中纵波、横波均可传递,但两种波 速各不相同。
{ 条件
波源:作机械振动的物体 弹性介质:承担传播振动的物质
二、横波和纵波
横波: 介质质点的振动方向与波传播方向相互垂直的波;如 柔绳上传播的波。
纵波:介质质点的振动方向和波传播方向相互平行的波;如空 气中传播的声波。
横波 (transverse wave) 波的传播方向
特点:具有波峰和波谷 ⊥ 质点的振动方向
大学物理(机械波篇)ppt课件

液晶显示
利用偏振光的特性,实现液晶 屏幕对图像的显示和控制。
科学研究
在物理学、化学、生物学等领 域中,利用偏振光研究物质的 光学性质和结构特征。
06
总结回顾与拓展延伸
机械波篇重点知识点总结
机械波的基本概念
机械波是介质中质点间相互作用力引起的振动在介质中的传播。机械波的产生条件、传播方 式、波动方程等基本概念是学习的重点。
驻波形成条件 两列波的频率相同、振幅相等、相位差恒定。
3
驻波特点
波形固定不动,节点和腹点位置固定;相邻节点 间距离等于半波长;能量在节点和腹点之间来回 传递。
03
非线性振动和孤立子简介
非线性振动概念及特点
非线性振动定义
指振动系统恢复力与位移之间不满足线 性关系的振动现象。
振幅依赖性
振动频率和波形随振幅变化而变化。
当障碍物尺寸远大于波长时,衍射现象不 明显。
衍射规律
衍射角与波长成正比,与障碍物尺寸成反 比。
双缝干涉实验原理及结果分析
实验原理:通过双缝让 单色光发生干涉,形成 明暗相间的干涉条纹。
01
干涉条纹间距与光源波 长、双缝间距及屏幕到
双缝的距离有关。
03
05 通过测量干涉条纹间距,
可以计算出光源的波长。
天文学领域
通过测量恒星光谱中谱线的多普勒频移,可以推断出恒星相对于观察 者的径向速度,进而研究恒星的运动和宇宙的结构。
05
光的衍射、干涉和偏振现 象
光的衍射现象及规律总结
衍射现象:光在传播过程中遇到障碍物或 小孔时,会偏离直线传播路径,绕到障碍 物后面继续传播的现象。
当障碍物尺寸与波长相当或更小时,衍射 现象显著。
多个孤立子相互作用后,各自保持 原有形状和速度继续传播。
机械波基础3

大学物理(下)
主讲人:吕波
5
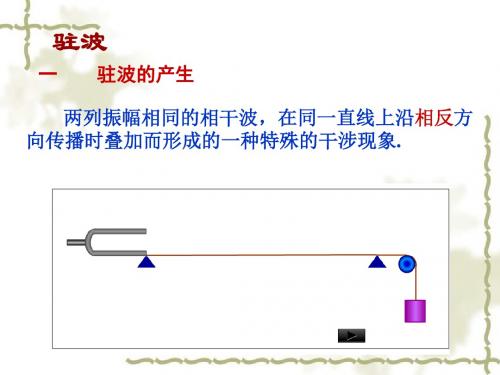
一、驻波的产生
-6
驻波 半波损失
1、演示实验:弦线上的驻波
分别沿X 轴正、负方向传播的同频率、同初相位的两列相干波, 其合成波某些点振幅特大,某些点几乎不动,称为驻波
2、驻波的形成
驻波是一种特殊的干涉现象。 波节——静止不动,振幅为零 波腹——振动最强, 振幅最大
y
t l ( l-x ) y反 A cos[2 ( ) -2 ] T
将l=5λ代入上式得
t x y反 A cos(2 2l-2 ) T t x A cos 2 ( + ) T
(2)驻波的表达式为
t l t x y y入 y反 A cos 2 ( ) A cos 2 ( + ) T T 2 2 2 A sin sin t T
第二步静止的接收器收到行驶的汽车发出的波的频率为:
u v u
v
u u v
u v u v
v
v u
10 1 1 00 330 1 .7 m / s 5 10 1 1 00
例3、车上一警笛发射频率为1500Hz的声波。该车正以20m· -1的 s 速度向某方向运动,某人以5m· -1速度跟踪其后,已知空气中的 s 声速为330 m· -1,求该人听到的警笛发声频率。 s 解:设没有风。根据题目条件已知 =1500Hz,u=330m· -1,观 s 察者向着警笛运动,应取v0=5m· -1,而警笛背着观察者运动, s 应取vs=20m· -1。因而该人听到的频率为 s
y 2 A cos 2
x
cos 2t
使cos(2πx/λ)为正的点,相位为2πνt; 使cos(2πx/λ)为负的点,相位为2πνt+π。
主讲人:吕波
5
一、驻波的产生
-6
驻波 半波损失
1、演示实验:弦线上的驻波
分别沿X 轴正、负方向传播的同频率、同初相位的两列相干波, 其合成波某些点振幅特大,某些点几乎不动,称为驻波
2、驻波的形成
驻波是一种特殊的干涉现象。 波节——静止不动,振幅为零 波腹——振动最强, 振幅最大
y
t l ( l-x ) y反 A cos[2 ( ) -2 ] T
将l=5λ代入上式得
t x y反 A cos(2 2l-2 ) T t x A cos 2 ( + ) T
(2)驻波的表达式为
t l t x y y入 y反 A cos 2 ( ) A cos 2 ( + ) T T 2 2 2 A sin sin t T
第二步静止的接收器收到行驶的汽车发出的波的频率为:
u v u
v
u u v
u v u v
v
v u
10 1 1 00 330 1 .7 m / s 5 10 1 1 00
例3、车上一警笛发射频率为1500Hz的声波。该车正以20m· -1的 s 速度向某方向运动,某人以5m· -1速度跟踪其后,已知空气中的 s 声速为330 m· -1,求该人听到的警笛发声频率。 s 解:设没有风。根据题目条件已知 =1500Hz,u=330m· -1,观 s 察者向着警笛运动,应取v0=5m· -1,而警笛背着观察者运动, s 应取vs=20m· -1。因而该人听到的频率为 s
y 2 A cos 2
x
cos 2t
使cos(2πx/λ)为正的点,相位为2πνt; 使cos(2πx/λ)为负的点,相位为2πνt+π。
大学物理课件第15章 机械波-驻波
x
三 波 疏 介 质
相位跃变(半波损失)
波 密 介 质 较 大
u
较 小
u
当波从波疏介质垂直入射到波密介质, 被反射 到波疏介质时形成波节. 入射波与反射波在此处的相 位时时相反, 即反射波在分界处产生 的相位跃变, 相当于出现了半个波长的波程差,称半波损失.
π
u
较 大 当波从波密介质垂直入射到波疏介质, 被反射 到波密介质时形成波腹. 入射波与反射波在此处的相 位时时相同,即反射波在分界处不产生相位跃变.
15.5 波的衍射
15.5.2 波的衍射
当波长与障碍物 可比拟的时候,波就 可以绕过障碍物而传 播,并且子波的包迹 组成新的波振面
15.5 波的衍射
15.5.3 波的反射和折射
A2 A2 A1 E1 A1 E1 E2
E2
反射:因为在同一介质中波速相同, 所以有
折射:在两种介质中 相等时间内有
t
15.5.1 惠更斯—菲涅耳原理 惠更斯原理:介质中波动传播到的
各点,都可以看成是发射子波的波源, 其后的任一时刻,这些子波的包络面就 是新的波阵面。
水面波的衍射
惠更斯—菲涅耳原理:介质中波 动传播到的各点,都可以看成是发 射子波的波源,其后的任一时刻, 这些子波的包络面就是新的波阵面, 波阵面上的每一点不仅可以看成是 发射子波的波源,而且这些子波波 源是相干波源,它们发出的子波是 相干波,相干波的干涉决定波的强 度。
BC u1
ADC ABC BAC DCA
BAC i
BC t u1
AD u1t BC
AD u2 t
BAC i, ACD
BC u1 t AC sin i AD u 2 t AC sin sin i u1 n2 n21 sin u 2 n1
大学物理下册课件 第15章 机械波

已知振动状态以速度 沿 轴正向传播 。对应同一时刻 ,
振动状态与原点在
时刻的振动状态相同。
点的
因此,在设定坐标系中,波线上任一点、任意时刻的振动规律为
这就是沿 X 轴正向传播的平面简谐波动方程。它是时间和空间的双重周期函数。
15.2.1 平面简谐波的波函数
沿 X 轴正向传播的平面简谐波动方程
t = 7T / 8
t = T
在同一坐标系
XOY 中
正向波
反向波
驻波
点击鼠标,观察在一个周期T 中不同时刻各波的波形图。
每点击一次,
时间步进
合成驻波
15.4.3 驻 波
为简明起见,
设
改写原式得
并用
由
正向波
反向波
驻 波 方 程
注意到三角函数关系
得
驻 波 方 程
驻 波 方 程
波节
波腹
波腹处振幅最大
固体的容变弹性模量
液体和气体:液体可以产生容变,其容变弹性模量如固体一致
对于密度为 的固体,在其中传播横波和纵波的速度为
液体和气体中传播纵波的波速为
15.1.3 波的特征量
关于波速问题: 波速取决于媒质的弹性(弹性模量)和媒质的惯性(密度)
细长棒:沿着棒的长度方向传播纵波的波速取决于杨氏弹性模量及其惯性
上下
抖动
振速 最小
振速 最大
形变最小
形变最大
时刻波形
在波动中,各体积元产生不同程度的 弹性形变,
具有 弹性势能
各体积元以变化的振动速率 上下振动,
具有振动动能
总能量
15.3 波的能量
动能
动能计算
势能计算
大学物理课件:机械波

x u
)
y
A
cos
(t
x u
)
y
u t t t
O
x
x x x ut
“”
“”
u
x
u
x
与计时起点有关。如取位移最大处位计时起点即0时刻:
0 y Acos(t x)
y
u
(6)u
x t
与v
dy dt
不同
x
v ——质元振动速度 u ——波速即位相传播速度
二、波动动力学微分方程
一般说来,波动有其特有的微分方程。对于机械波, 用动力学方法(牛顿定律、胡克定律)可以得到机械平 面波动力学微分方程(推导略):
2
u
可以证明: EP Ek
y y y
证*: 以纵波为例
横波
纵波
为什么会出现横波、纵波呢?主要与媒质弹性有关。
(1)横波产生原因: 媒质可产生切应变
媒质能产生切应变弹性,切应力可 以带动邻近质点振动。形成横波。
固体可以产生切应变——传播横波
液体、气体不能产生切应变 ——不传播横波
切应变
(2)纵波产生原因:媒质可产生正应变 (拉、压、体变弹性)
媒质产生正应变弹性,能发生体积膨胀收缩或拉 伸压缩,从而产生正应力,可形成疏密纵波。
3、简谐波 即简谐振动的传播。 任何复杂波=简谐波叠加
4、几何描述(几个名词)
波线——表示波的传播方向的线(直线或曲线)
波面——位相相同的点组成的面
波前(波阵面)——最前方的波面即 某时刻振动传到的各点构成的同相面。
波线 波面 波前
按波面形状:平面波、球面波、柱面波等。
平面波 球面波
远处的球面波、柱面波的局部可以视为平面波 平面波、球面波、柱面波都是真实波动的理想近似
机械波ppt课件

材料。
机械波在各向异性介质中传播特性
02
机械波在各向异性介质中传播时,其速度、振幅和相位等参数
会受到介质各向异性的影响,表现出复杂的传播行为。
研究意义
03
了解机械波在各向异性介质中的传播特性对于地震学、声学、
材料科学等领域具有重要的理论和应用价值。
地震波在各向异性岩石中传播规律
地震波类型
体波(P波、S波)和面波(L波、R波)是地震波的主要类型,它们在各向异性岩石中的传播 速度、振幅和衰减等特性有所不同。
介质中,波动能量传递无损耗;而在实际介质中,由于阻尼、散射等作
用,波动能量会逐渐衰减。
03
机械波在各向同性介质 中传播特性
纵波和横波传播方式对比
纵波传播方式
对比总结
质点振动方向与波传播方向平行,通 过介质中相邻质点间的相互作用力传 递能量。
纵波和横波在传播方式上存在差异, 主要表现在质点振动方向和能量传递 方式上。
治疗应用
利用高强度聚焦超声(HIFU)技 术,将超声波能量聚焦在病变组织 上,使组织产生热凝固性坏死,达 到治疗目的。
工业自动化领域振动监测技术应用
设备状态监测
通过监测机械设备的振动信号,判断设备的运行状态和故障情况, 实现设备的预防性维护。
质量控制
利用振动检测技术对生产线上的产品进行质量监测和控制,提高 产品质量和生产效率。
横波传播方式
质点振动方向与波传播方向垂直,通 过介质中相邻质点间的剪切力传递能 量。
折射、反射和衍射现象分析
折射现象
当机械波从一种介质传播到另一 种介质时,由于波速的改变,波 的传播方向会发生变化,这种现 象称为折射。折射遵循斯涅尔定
律。
大学物理(II)下册教学课件:机械波2009

x / u表示——————————————。
t时刻x处质点的振动位移
波从原点传播至x处时间 质点在x处比在原点处的振动滞后相位
机械波习题课
注2、波函数中物理量的确定
例1、波动方程 y 0.02cos (4x 50t) ,求
波的振幅,波长,频率,周期和波速
解:用比较法求解
平面谐波的标准方程
y Acos(t x ) Acos 2 ( t x )
dt
t1
2πAsin 2π(1 x / )
v1 sin 2π(1 x1 / ) sin(π / 2) 1 机械波习题课 v2 sin 2π(1 x2 / ) sin(3π / 2)
注4、由波函数确定质元动能和势能
dWk
1 2
dmv2
1 2
dV
v2
1 dVA22 sin2 (t x )
机械波
一、 基本要求
1、 掌握机械波产生条件和传播过程的特点
2 、掌握平面简谐波的波函数及各物理量
3、掌握由已知质点的振动状态得出平面谐波 方程的基本方法
4、理解波的干涉现象及相干条件
5、理解驻波及其形成的条件,了解多普勒效 应
二、 基本内容
1、机械波传播过程中的特点
(1)各质元在各自平衡位置附近振动,而 不沿着波传播方向移动
2
u
dWp
1 2
k dy 2
1 2
ESdx(dy )2 dx
1 2
u 2dV
( dy )2 dx
1 dVA2 2 sin2 (t x )
2
u
dW
dWk
dWp
dVA2 2
sin 2 (t
x) u
机械波习题课
大学物理机械振动和机械波ppt课件

振动系统能量转换关系
动能与势能之间的转换
在振动过程中,物体的动能和势能之间不断 转换。
能量守恒
在理想情况下,振动系统的总能量保持不变 。
能量耗散
在实际情况下,由于阻力的存在,振动系统 的能量会逐渐耗散。
02
机械波传播特性与波动方程
Chapter
机械波产生条件及分类
产生条件
01
振源、介质、传播方向与振动方向关系
天文学
天文学家通过观察恒星光谱的多普勒效应来判断恒星相对于地球的运动速度,进而研究 恒星的运动规律和宇宙结构。
音乐合成
在音乐制作中,可以利用多普勒效应原理来模拟乐器声音的空间感和运动感,使音乐更 加生动和立体。
05
干涉和衍射现象在机械波中表 现
Chapter
干涉现象产生条件及类型划分
产生条件
两列波频率相同,会出现稳定的干涉现 象。
驻波能量分布规律探讨
能量分布
驻波的能量主要集中在波腹处,波节处能量为零。
分布规律
随着时间与空间的变化,能量在波腹与波节之间周 期性传递。
弦线上驻波实验演示
实验装置
弦线、振源、测量仪器等。
实验步骤
激发弦线振动,调整振源频率使弦线上形成驻波,观察并测量驻波 的波形、波腹波节位置等。
实验结果
通过测量得到驻波的波长、频率等参数,验证驻波的产生条件和能量 分布规律。
04
多普勒效应原理及应用举例
Chapter
多普勒效应定义及公式推导
定义
当波源与观察者之间存在相对运动时,观察者接收到的波的频率会发生变化,这种现象 称为多普勒效应。
公式推导
设波源发射频率为f0,波速为v,观察者与波源相对运动速度为vr,则观察者接收到的 频率为f=(v±vr)/v×f0,其中“+”号表示观察者向波源靠近,“-”号表示观察者远离
大学物理课件PPT第16章机械波

不同介质中波动速度的比 较
例如空气中的声速约为340m/s,水中的声速 约为1500m/s。
波动方程在实际问题中应用
波动方程的求解方法
通过分离变量法、行波法等方法求解波动方程。
波动方程在声学、光学等领域的应用
例如声波、光波的传播规律可用波动方程描述。
波动方程的数值解法
利用计算机进行数值模拟,研究复杂波动现象。
折射波的波形与入射波的波形 相同,但传播方向发生改变。
衍射现象及其产生条件
衍射现象
波在传播过程中遇到障碍物或小 孔时,会绕过障碍物或小孔继续 传播的现象。
衍射波的振幅和相位
衍射波的振幅与入射波的振幅和 障碍物的性质有关,相位则与衍 射面的性质有关。
01 02 03 04
产生条件
障碍物或小孔的尺寸与波长相当 或比波长小。
多普勒效应在实际问题中应用
交通警察利用多普勒雷达测速仪 测量车辆的速度,以判断车辆是 否超速行驶。
多普勒效应还广泛应用于声呐、 无线通信、音乐合成等领域。
医学领域 交通领域
天文学领域 其他领域
在医学超声诊断中,利用多普勒 效应可以测量血流速度和方向, 从而判断血管狭窄、血栓等病变 情况。
天文学家利用多普勒效应测量恒 星、行星等天体的径向速度,进 而研究天体的运动规律和宇宙演 化等问题。
关。
反射波的波形
03
反射波的波形与入射波的波形相同,但传播方向相反。
折射现象及其条件分析
折射定律
入射波、折射波和法线在同一 平面内,且入射角的正弦与折 射角的正弦之比等于波在两种
介质中的速度之比。
折射波的振幅和相位
折射波的振幅与入射波的振幅 和两种介质的性质有关,相位
则与折射面的性质有关。
例如空气中的声速约为340m/s,水中的声速 约为1500m/s。
波动方程在实际问题中应用
波动方程的求解方法
通过分离变量法、行波法等方法求解波动方程。
波动方程在声学、光学等领域的应用
例如声波、光波的传播规律可用波动方程描述。
波动方程的数值解法
利用计算机进行数值模拟,研究复杂波动现象。
折射波的波形与入射波的波形 相同,但传播方向发生改变。
衍射现象及其产生条件
衍射现象
波在传播过程中遇到障碍物或小 孔时,会绕过障碍物或小孔继续 传播的现象。
衍射波的振幅和相位
衍射波的振幅与入射波的振幅和 障碍物的性质有关,相位则与衍 射面的性质有关。
01 02 03 04
产生条件
障碍物或小孔的尺寸与波长相当 或比波长小。
多普勒效应在实际问题中应用
交通警察利用多普勒雷达测速仪 测量车辆的速度,以判断车辆是 否超速行驶。
多普勒效应还广泛应用于声呐、 无线通信、音乐合成等领域。
医学领域 交通领域
天文学领域 其他领域
在医学超声诊断中,利用多普勒 效应可以测量血流速度和方向, 从而判断血管狭窄、血栓等病变 情况。
天文学家利用多普勒效应测量恒 星、行星等天体的径向速度,进 而研究天体的运动规律和宇宙演 化等问题。
关。
反射波的波形
03
反射波的波形与入射波的波形相同,但传播方向相反。
折射现象及其条件分析
折射定律
入射波、折射波和法线在同一 平面内,且入射角的正弦与折 射角的正弦之比等于波在两种
介质中的速度之比。
折射波的振幅和相位
折射波的振幅与入射波的振幅 和两种介质的性质有关,相位
则与折射面的性质有关。
大学物理课件-第8章 机械波

引言
机械波:机械振动在连续介质中的传播形 成机械波
电磁波:交变电磁场在空间的传播 ……
本章内容提要
机械波 波动式 波动方程 波强
多普勒效应 叠加干涉 惠更斯原理
8.1 机械波
1. 机械波的产生 2. 横波和纵波 3. 波面和波射线 4. 波长和波数 5. 波速
1. 机械波的产生
(1) 波源 (2) 媒质 y
1Tdt 12A2
T0
2
讨论:
pk1 22A 2sin2(tkx)
1)时间变化: 固定x:εk 、εp均随 t 周期性变化
2A2
2
o
p k x = x0
Tt
y
2)空间变化: 固定t:εk 、εp均 随 x 周期分布
2A2
2
o
u
t = t0
k p
解:能量守恒
I1
1 2
2
A12u
I2
1 2
2 A22u
I14r12I24r22
A 124r12A 224r22
A1 r2 A 2 r1
yA0 cos(tr)
r
u
S1 r1 A1
o
S2 r2 A2
点波源 各向同性介质
三、声波 声强级
声波是纵波
声强: I 1 u 2A2
例:对无吸收媒质:利用 I 1 2 A2 和能量守恒
2 可以证明:
平面波
A const.
球面波 柱面波
Ar const.,A1 r
A r const.,A 1 r
r —— 场点到波源的距离
例:点波源,各向同性媒质中的波速为u,媒质无吸 收,求球面简谐波的波函数 y(r, t)
机械波:机械振动在连续介质中的传播形 成机械波
电磁波:交变电磁场在空间的传播 ……
本章内容提要
机械波 波动式 波动方程 波强
多普勒效应 叠加干涉 惠更斯原理
8.1 机械波
1. 机械波的产生 2. 横波和纵波 3. 波面和波射线 4. 波长和波数 5. 波速
1. 机械波的产生
(1) 波源 (2) 媒质 y
1Tdt 12A2
T0
2
讨论:
pk1 22A 2sin2(tkx)
1)时间变化: 固定x:εk 、εp均随 t 周期性变化
2A2
2
o
p k x = x0
Tt
y
2)空间变化: 固定t:εk 、εp均 随 x 周期分布
2A2
2
o
u
t = t0
k p
解:能量守恒
I1
1 2
2
A12u
I2
1 2
2 A22u
I14r12I24r22
A 124r12A 224r22
A1 r2 A 2 r1
yA0 cos(tr)
r
u
S1 r1 A1
o
S2 r2 A2
点波源 各向同性介质
三、声波 声强级
声波是纵波
声强: I 1 u 2A2
例:对无吸收媒质:利用 I 1 2 A2 和能量守恒
2 可以证明:
平面波
A const.
球面波 柱面波
Ar const.,A1 r
A r const.,A 1 r
r —— 场点到波源的距离
例:点波源,各向同性媒质中的波速为u,媒质无吸 收,求球面简谐波的波函数 y(r, t)
大学物理机械波课件

能流密度
单位时间内通过垂直于传播方向上单位面积的能量,反映机械波传播过程中能量的 流动情况。
衰减原因及影响因素分析
衰减原因
机械波在传播过程中,由于介质阻尼、 内摩擦等因素导致能量逐渐转化为热 能或其他形式的能量而耗散。
影响因素
介质性质(如密度、弹性模量等)、 波的传播速度、波长以及环境温度等 都会对机械波的衰减产生影响。
表面波和体波区别
1 2
传播范围 表面波沿物体表面传播,能量集中在物体表面附 近;体波在物体内部传播,能量分布在物体内部。
传播速度 表面波的传播速度通常小于体波的传播速度。
3
影响因素
表面波的传播特性受物体表面形状、粗糙度等因 素的影响较大;体波的传播特性受物体内部结构 和成分等因素的影响较大。
色散现象和群速度概念
声子与格波关系
声子是格波的量子化形式,描述晶体中原子或分子的集体振动行为。 声子与格波之间存在对应关系。
声子概念及其在固体物理中应用
声子概念
声子是描述晶体中原子或分子集体振动行为的量子化粒子,类似 于光子在电磁场中的角色。
声子与热传导
在固体物理中,声子对热传导起到重要作用。晶体的热传导性能与 声子的传播和散射行为密切相关。
机械波分类
根据质点振动方向与波传播方向的 关系,机械波可分为横波和纵波。
波动现象与振动关系
波动现象
波动是振动在介质中的传播过程,表 现为质点在平衡位置附近的往复运动。
振动与波动关系
振动是波动的起因,波动是振动的传播。 无振动则无波动,有波动则必有振动。
传播介质与波速关系
传播介质
机械波需要在介质中传播,介质可以是固体、液体或气体。
干涉、衍射和叠加原理
单位时间内通过垂直于传播方向上单位面积的能量,反映机械波传播过程中能量的 流动情况。
衰减原因及影响因素分析
衰减原因
机械波在传播过程中,由于介质阻尼、 内摩擦等因素导致能量逐渐转化为热 能或其他形式的能量而耗散。
影响因素
介质性质(如密度、弹性模量等)、 波的传播速度、波长以及环境温度等 都会对机械波的衰减产生影响。
表面波和体波区别
1 2
传播范围 表面波沿物体表面传播,能量集中在物体表面附 近;体波在物体内部传播,能量分布在物体内部。
传播速度 表面波的传播速度通常小于体波的传播速度。
3
影响因素
表面波的传播特性受物体表面形状、粗糙度等因 素的影响较大;体波的传播特性受物体内部结构 和成分等因素的影响较大。
色散现象和群速度概念
声子与格波关系
声子是格波的量子化形式,描述晶体中原子或分子的集体振动行为。 声子与格波之间存在对应关系。
声子概念及其在固体物理中应用
声子概念
声子是描述晶体中原子或分子集体振动行为的量子化粒子,类似 于光子在电磁场中的角色。
声子与热传导
在固体物理中,声子对热传导起到重要作用。晶体的热传导性能与 声子的传播和散射行为密切相关。
机械波分类
根据质点振动方向与波传播方向的 关系,机械波可分为横波和纵波。
波动现象与振动关系
波动现象
波动是振动在介质中的传播过程,表 现为质点在平衡位置附近的往复运动。
振动与波动关系
振动是波动的起因,波动是振动的传播。 无振动则无波动,有波动则必有振动。
传播介质与波速关系
传播介质
机械波需要在介质中传播,介质可以是固体、液体或气体。
干涉、衍射和叠加原理
大学物理(II)下册教学课件:机械波2009

2
u
dWp
1 2
k dy 2
1 2
ESdx(dy )2 dx
1 2
u 2dV
( dy )2 dx
1 dVA2 2 sin2 (t x )
2
u
dW
dWk
dWp
dVA2 2
sin 2 (t
x) u
机械波习题课
4 一平面简谐机械波在弹性介质中传播,
下述各结论哪个正确?
选择( D )
(A)介质质元的振动动能增大时,其弹性势
介质有关? 波源(均匀介质无吸收): A,(T,)
与介质有关: u
(2)式中“+”“-”如何确定 由波的传播方向和 ox 轴的正方向来确定。
当传播方向沿着 ox 轴正方向时,取“-” 号当传播方向沿着 ox 轴负方向时,取“+”
机械波习题课
(3)式中 是否就是波源的初相?
不一定!是坐标原点(不一定是波源) 处振动的初相,( t 0 时,x 0 处的初相)
建立波动方程的问题 y(102m)
(1)由图知
A 2102 m,T
4s,
2
振动方程 (为什么?) 2 o
y0
机械波习题课
2
102
cos(
2
t
2
)
2
2
4
t(s)
(2)由已知某点(坐标原点)
的振动方程得波动方程 ( uT 20m)
y
2 102
cos[
(t
x)
]
给定
x 5
2 52
,得振动方程
y
2 102
y(102 m)
u
2
o
2 Q4
P
大学物理机械波课件-PPT

2、t=t0为定值,y=y(x)
• 表示t0时刻波线上各质点离开各自平衡位置 得位移分布情况,称为该时刻得波形方程
• 对于横波,波形图就就是该时刻各质点在空 间得真实分布
• 对于纵波,波形图仅表示质点得位移分布
3、t与x都在变化
• 波动方程给出了各个质点在不同时刻得位
y 移,或者说包含了不同时刻得波形
结论:机械波传播得就是波 源得振动状态与能量
三、波线与波面
• 波传播到得空间——波场 • 波场中代表波传播方向得射线——波线 • 某时刻振动位相相同得点得轨迹——波面 • 最前方得波面——波前或波阵面 • 横波中,质元振动得轨迹与波线垂直,二者构
成得面——振动面或偏振面
波线
波线
平面波 球面波
波面
• P点t时刻得振动位移与原点 动位移相同
• P点振动方程为
时刻得振
沿x轴正向传播得平面简谐波得波函数
• 也就是x处质点得振ຫໍສະໝຸດ 方程沿x轴负向传播得平面简谐波得波函数
• 常用得波动表达式
(1)如图,已知 P 点得振动方程:
yP
A
y
cos( u
t
0
)
px Q x
O
x
求波动方程即波函数。
(2)如图,已知 P 点得振动方程:
平面简谐波——波面为平面得简谐波
?问题
• 如何用数学表达式描述一个前进中得波动?
• 如何描述各质点得振动位移y随平衡位置x与
t得变换规律
波函数
一、波函数得推导
• 平面简谐波沿x轴正方向传播 • 设原点得振动方程为
• 设平衡位置为x得P点在t时刻得振动位移为y • P点得振动落后于原点,晚了 • 也就就是原点得振动状态传到P点所需得时间 • P点在t时刻将重复原点在 时刻得振动状态
大学物理下册10-1课件

物理学
第五版
10-1 机械波的几个概念
四个物理量的联系
1 T
u
T
u Tu
注意
周期或频率只决定于波源的振动 波速只决定于介质的性质
第十章 波动
14
物理学
第五版
10-1 机械波的几个概念
例1 在室温下,已知空气中的声速 u1 为340 m·s-1,水中的声速 u2 为1 450 m·s-1,求
频率为200 Hz和2 000 Hz 的声波在空气中
和水中的波长各为多少?
Hz
解 由
的声波在
空 气u中,的频波率长为200
Hz和2
000
1
u1 1
340 200
m
1.7 m
第十章 波动
15
物理学
第五版
10-1 机械波的几个概念
2
u1 2
0.17
m
在水中的波长
1
u2 1
Y 为媒质的杨氏弹性模量; 为质量密度。
第十章 波动
12
* 各向同性均匀固体媒质横波波速 c G
G为媒质的切变弹性模量; 为质量密度
在同一种固体媒质中,横波波速比纵波波速小些。
* 在液体和气体只能传播纵波,
其波速为:密度
注意:在一般情况下,如果媒质有切变弹性,它就 能传横波(绳波是例外);如果媒质有体变弹性, 它就能传纵波。一切固体,两种弹性都有,所以两 种波都能传播;流体(液体和气体)没有切变弹性 只有体变弹性,因此只能传纵波(水波是例外)。
波是运动状态的传播,介 质的质点并不随波传播.
第十章 波动
2
物理学
相关主题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
reflection
Angle law
θ =θ'
折射定律: 折射定律:
sinθ1 n2 = = n21 sinθ2 n 1
refract
n21:2介质对1介质的相对折射率; 介质对1介质的相对折射率;
6.5 波的传播规律 干涉
一.波的传播规律[regularity of wave propagation]
x1 < x < x2
F(x)
F
G(x)
只要知道F 只要知道F 值,就可知道 x 值,进一步可知道G 值; 进一步可知道G
F⋅G ≠ 0
在区间
x < x1, x2 < x
F 值与G 值无关联; 值与G 值无关联;
x1 x
x2
X
F⋅G = 0
三.干涉加强、相消的条件 干涉加强、 设两相干波源 设两相干波源 S1 和 S2 的振动表达式为
决定于波源
决定于场点位置
∆ =ϕ2 −ϕ1 −2π ϕ
=∆ 0 − ϕ 2 π
r P −r P 2 1
λ
——恒 ——恒 定
空间各点的 ∆ 不同,因此各不同点有不同的合振幅 A ; ϕ不同,
λ
∆ r
即空间每确定点都 有恒定的合振幅 A ;
I ∝ A2 由波的强度
可认为
I =A
2
A= I
干涉项
[interference term]
δ =r2P −r1P = kλ (k = 0, ±1 ±2,L ) ,
有
A= A ax m
——干涉加强 ——干涉加强[enhance];
δ = r2P −r1P = (2k +1)
有
λ
2
(k = 0, ±1 ±2,L ) ,
A= A in m
——干涉相消 ——干涉相消[abatement] ;
Two speakers constructive 干涉加强
说明宏观形态 独立性[independent]: 几列波(不太强) 几列波(不太强)在媒质 中相遇时, 中相遇时,各个波将保持本 身特性(频率、波长、 身特性(频率、波长、振动 方向等)沿原方向继续传播, 方向等)沿原方向继续传播, 与未相遇一样; 与未相遇一样; 如:可同时听到几种声 看到几种光; 音,看到几种光; 空间每时都存在多种电 磁波; 磁波;
—— Wave front reconstruction
平 面 波
均匀介质中波是直线传播的; 均匀介质中波是直线传播的;
惠更斯原理的理论缺陷 惠更斯原理的理论缺陷[theoretical defect] 1.未能给出严格的证明, 1.未能给出严格的证明,仅是定性地描述了波 未能给出严格的证明 面是如何向前推进,变化的; 面是如何向前推进,变化的; 解决了波的传播方向问题; 即 解决了波的传播方向问题; 2.无法说明 波为何不向后传; 2.无法说明 波为何不向后传; 3.不能说明各子波对传播点的 贡献大小; 3.不能说明各子波对传播点的 贡献大小; 衍射现象; 4.原理给出 原理给出: 4.原理给出:一切波动都具有 衍射现象; 必须指出:该原理适合于任何波动过程; 必须指出:该原理适合于任何波动过程;
已代入坐标
y = y1 + y2 = Acos(ω t +ϕ)
合成效果的确定, 合成效果的确定, 其中 振幅
∆ϕ
r2P −r P 1
A= A + A +2A A cos(ϕ2 −ϕ1 −2π 1 2
2 1 2 2
λ
)
振幅( 振幅(A)分布讨论: 分布讨论: 空间某确定点[overlap point]
y10 = A cos(ωt +ϕ ) 1 1 y20 = A cos(ωt +ϕ2) 2
各自的波动方程 各自的波动方程为: 波动方程为
rP 1
S 1
S2
y1 = A cos(ωt −2π x1 λ +ϕ1) 1
P
rP 2
S1和S2不动
y2 = A cos(ωt −2π x2 λ +ϕ2) 2
频率、波长、波速和位移方向均相同; 频率、波长、波速和位移方向均相同;
消声气管
技术应用:干涉消声; 技术应用:干涉消声; 工业生产,机车,长号等; 如 工业生产,机车,长号等;
激光光学实验模拟 激光光学实验模拟[experimental model]:
He-Ne Laser
两相干波源相对位置不同
[例1] S1和S2是波长为 λ 的两相干波源;相距d= 的两相干波源;相距d (3/4) λ,S1的相位超前S2 π / 2 , 设在S1和S2的连线上不 相位超前 超前S 设在S 则在S 发生波的吸收, 发生波的吸收,且每列波的强度都为I0 , 则在S1和S2连 线两侧合成波的强度分别是多少。 线两侧合成波的强度分别是多少。
Wave front propagation
Diffraction through box opening
Diffraction around door
如何解释此现象呢? 如何解释此现象呢?
6.4 惠更斯原理 波的衍射
一.惠更斯原理[Huygens principle](1678年) 1678年
媒质中波动传到的各点都可以看作是新的“ 论 述:媒质中波动传到的各点都可以看作是新的“次波 源”[secondary source], 这些新波源发射的波称为“子波”[wavelet], 其后 这些新波源发射的波称为“子波” 任一时刻这些子波的“包络面”[wave packet]就是该时刻的新波阵面。 任一时刻这些子波的“包络面” 就是该时刻的新波阵面。
细雨绵绵 独立传播
叠加原理( 叠加原理(振幅要小)[superposition principle]: 在几列波空间相遇区域 在几列波空间相遇区域[overlap zone]内,任一质点的振动是各个 单独在该点引起的振动的合成 在该点引起的振动的合成; 波单独在该点引起的振动的合成; 这种合成是矢量之和; 矢量之和 注:这种合成是矢量之和;
——强度最弱 ——强度最弱 相消干涉; 相消干涉;
如果? 如果
I1 = I2
特例: 特例:如果 ϕ =ϕ2 ,两相干波来自 同一波源; 同一波源; 1 引入“波程差” 引入“波程差”[wave path difference]:
δ = r2P −r1P —— 传播距离之差
相干的条件 可表示成: 可表示成:
能产生相干现象的波 称为“相干 波”[coherent wave]; wave] 称为“ 相干波源” 其波源称为 “相干波源”;
加强
减弱
Interference pattern
只有波的叠加 只有波的叠加合成 才能产生干涉现象; 叠加合成 才能产生干涉现象 干涉现象; 干涉现象 是波动所独有的重要特征之一! 是波动所独有的重要特征之一! 独有的重要特征之一 ——波动的验证性条件 criterion] ——波动的验证性条件[criterion];
将 P 点坐标分别代入方程,可得在 P 点的振动方程; 点坐标分别代入方程, 点的振动方程 振动方程;
传输到 P 点时,振动方程 为 点时,
y1 = Acos(ωt −2π r P λ +ϕ1) 1 1 y2 = A cos(ωt −2π r2P λ +ϕ2) 2
P 点的合振动为(上一章内容): 点的合振动 合振动为 上一章内容):
Water wave interference
说明微观形态
说 明:
振动的叠加仅发 生在单一质点上; 生在单一质点上; 波的叠加发生在两波相 遇范围内的许多质点上; 遇范围内的许多质点上;
二.波的干涉[interference] 干涉现象:波在媒质中叠加时,出现某些地方振动始 干涉现象:波在媒质中叠加时,出现某些地方振动始 始终减弱或完全抵消的现象; 终加强,某些地方振动始终减弱或完全抵消的现象; 加强,某些地方振动始终减弱或完全抵消的现象
历史表明:惠更斯原 历史表明: 理给出了光的波动说; 理给出了光的波动说
惠更斯原理.exe
二.波的衍射、反射和折射 波的衍射、 1.衍 1.衍 射[diffraction] 衍射:波传播过程中遇到障碍物而发生偏 衍射: 离原方向传播的现象; 离原方向传播的现象; ?
Water diffraction
Homework: 一、7.
PxS1dS2解:取 S1 外侧任意点 P ,
3 ∆ϕ =ϕ20 −ϕ10 −2 π = − −2π = − π 2 λ 2 4
P点处干涉加强
r2 −r 1
π
∴A= A + A = 2A , I = 4I0 1 2 0
P
x
S1
d
S2
x’
Q
x
3 ∆ϕ =ϕ20 −ϕ10 −2π = − +2π =π λ 2 4
合成:相遇,叠加 合成:相遇,
相干波的条件[coherent condition]: 频率相同, 频率相同, 振动方向相同, 振动方向相同, 相位相同或相位差恒定; 相位相同或相位差恒定;
——相干三要素 ——相干三要素
需要解释 所谓“相干” 来源于数学中的“相关” 相互关联; 所谓“相干”,来源于数学中的“相关”,即 相互关联; 相关:有两件事, 相关:有两件事,能从其中一个的状况来推算出另一 个的状况,那么就说它们是相关的; 个的状况,那么就说它们是相关的; 如下图,设有两个函数, 如下图,设有两个函数, 在区间
所以叠加波的强度 所以叠加波的强度为(两边平方) 强度为 两边平方)
I = I1 + I2 +2 I1I2 cos∆ϕ 波源一定时, 波源一定时,波的强度只与 ∆ 有关; ϕ 有关;
当
Angle law
θ =θ'
折射定律: 折射定律:
sinθ1 n2 = = n21 sinθ2 n 1
refract
n21:2介质对1介质的相对折射率; 介质对1介质的相对折射率;
6.5 波的传播规律 干涉
一.波的传播规律[regularity of wave propagation]
x1 < x < x2
F(x)
F
G(x)
只要知道F 只要知道F 值,就可知道 x 值,进一步可知道G 值; 进一步可知道G
F⋅G ≠ 0
在区间
x < x1, x2 < x
F 值与G 值无关联; 值与G 值无关联;
x1 x
x2
X
F⋅G = 0
三.干涉加强、相消的条件 干涉加强、 设两相干波源 设两相干波源 S1 和 S2 的振动表达式为
决定于波源
决定于场点位置
∆ =ϕ2 −ϕ1 −2π ϕ
=∆ 0 − ϕ 2 π
r P −r P 2 1
λ
——恒 ——恒 定
空间各点的 ∆ 不同,因此各不同点有不同的合振幅 A ; ϕ不同,
λ
∆ r
即空间每确定点都 有恒定的合振幅 A ;
I ∝ A2 由波的强度
可认为
I =A
2
A= I
干涉项
[interference term]
δ =r2P −r1P = kλ (k = 0, ±1 ±2,L ) ,
有
A= A ax m
——干涉加强 ——干涉加强[enhance];
δ = r2P −r1P = (2k +1)
有
λ
2
(k = 0, ±1 ±2,L ) ,
A= A in m
——干涉相消 ——干涉相消[abatement] ;
Two speakers constructive 干涉加强
说明宏观形态 独立性[independent]: 几列波(不太强) 几列波(不太强)在媒质 中相遇时, 中相遇时,各个波将保持本 身特性(频率、波长、 身特性(频率、波长、振动 方向等)沿原方向继续传播, 方向等)沿原方向继续传播, 与未相遇一样; 与未相遇一样; 如:可同时听到几种声 看到几种光; 音,看到几种光; 空间每时都存在多种电 磁波; 磁波;
—— Wave front reconstruction
平 面 波
均匀介质中波是直线传播的; 均匀介质中波是直线传播的;
惠更斯原理的理论缺陷 惠更斯原理的理论缺陷[theoretical defect] 1.未能给出严格的证明, 1.未能给出严格的证明,仅是定性地描述了波 未能给出严格的证明 面是如何向前推进,变化的; 面是如何向前推进,变化的; 解决了波的传播方向问题; 即 解决了波的传播方向问题; 2.无法说明 波为何不向后传; 2.无法说明 波为何不向后传; 3.不能说明各子波对传播点的 贡献大小; 3.不能说明各子波对传播点的 贡献大小; 衍射现象; 4.原理给出 原理给出: 4.原理给出:一切波动都具有 衍射现象; 必须指出:该原理适合于任何波动过程; 必须指出:该原理适合于任何波动过程;
已代入坐标
y = y1 + y2 = Acos(ω t +ϕ)
合成效果的确定, 合成效果的确定, 其中 振幅
∆ϕ
r2P −r P 1
A= A + A +2A A cos(ϕ2 −ϕ1 −2π 1 2
2 1 2 2
λ
)
振幅( 振幅(A)分布讨论: 分布讨论: 空间某确定点[overlap point]
y10 = A cos(ωt +ϕ ) 1 1 y20 = A cos(ωt +ϕ2) 2
各自的波动方程 各自的波动方程为: 波动方程为
rP 1
S 1
S2
y1 = A cos(ωt −2π x1 λ +ϕ1) 1
P
rP 2
S1和S2不动
y2 = A cos(ωt −2π x2 λ +ϕ2) 2
频率、波长、波速和位移方向均相同; 频率、波长、波速和位移方向均相同;
消声气管
技术应用:干涉消声; 技术应用:干涉消声; 工业生产,机车,长号等; 如 工业生产,机车,长号等;
激光光学实验模拟 激光光学实验模拟[experimental model]:
He-Ne Laser
两相干波源相对位置不同
[例1] S1和S2是波长为 λ 的两相干波源;相距d= 的两相干波源;相距d (3/4) λ,S1的相位超前S2 π / 2 , 设在S1和S2的连线上不 相位超前 超前S 设在S 则在S 发生波的吸收, 发生波的吸收,且每列波的强度都为I0 , 则在S1和S2连 线两侧合成波的强度分别是多少。 线两侧合成波的强度分别是多少。
Wave front propagation
Diffraction through box opening
Diffraction around door
如何解释此现象呢? 如何解释此现象呢?
6.4 惠更斯原理 波的衍射
一.惠更斯原理[Huygens principle](1678年) 1678年
媒质中波动传到的各点都可以看作是新的“ 论 述:媒质中波动传到的各点都可以看作是新的“次波 源”[secondary source], 这些新波源发射的波称为“子波”[wavelet], 其后 这些新波源发射的波称为“子波” 任一时刻这些子波的“包络面”[wave packet]就是该时刻的新波阵面。 任一时刻这些子波的“包络面” 就是该时刻的新波阵面。
细雨绵绵 独立传播
叠加原理( 叠加原理(振幅要小)[superposition principle]: 在几列波空间相遇区域 在几列波空间相遇区域[overlap zone]内,任一质点的振动是各个 单独在该点引起的振动的合成 在该点引起的振动的合成; 波单独在该点引起的振动的合成; 这种合成是矢量之和; 矢量之和 注:这种合成是矢量之和;
——强度最弱 ——强度最弱 相消干涉; 相消干涉;
如果? 如果
I1 = I2
特例: 特例:如果 ϕ =ϕ2 ,两相干波来自 同一波源; 同一波源; 1 引入“波程差” 引入“波程差”[wave path difference]:
δ = r2P −r1P —— 传播距离之差
相干的条件 可表示成: 可表示成:
能产生相干现象的波 称为“相干 波”[coherent wave]; wave] 称为“ 相干波源” 其波源称为 “相干波源”;
加强
减弱
Interference pattern
只有波的叠加 只有波的叠加合成 才能产生干涉现象; 叠加合成 才能产生干涉现象 干涉现象; 干涉现象 是波动所独有的重要特征之一! 是波动所独有的重要特征之一! 独有的重要特征之一 ——波动的验证性条件 criterion] ——波动的验证性条件[criterion];
将 P 点坐标分别代入方程,可得在 P 点的振动方程; 点坐标分别代入方程, 点的振动方程 振动方程;
传输到 P 点时,振动方程 为 点时,
y1 = Acos(ωt −2π r P λ +ϕ1) 1 1 y2 = A cos(ωt −2π r2P λ +ϕ2) 2
P 点的合振动为(上一章内容): 点的合振动 合振动为 上一章内容):
Water wave interference
说明微观形态
说 明:
振动的叠加仅发 生在单一质点上; 生在单一质点上; 波的叠加发生在两波相 遇范围内的许多质点上; 遇范围内的许多质点上;
二.波的干涉[interference] 干涉现象:波在媒质中叠加时,出现某些地方振动始 干涉现象:波在媒质中叠加时,出现某些地方振动始 始终减弱或完全抵消的现象; 终加强,某些地方振动始终减弱或完全抵消的现象; 加强,某些地方振动始终减弱或完全抵消的现象
历史表明:惠更斯原 历史表明: 理给出了光的波动说; 理给出了光的波动说
惠更斯原理.exe
二.波的衍射、反射和折射 波的衍射、 1.衍 1.衍 射[diffraction] 衍射:波传播过程中遇到障碍物而发生偏 衍射: 离原方向传播的现象; 离原方向传播的现象; ?
Water diffraction
Homework: 一、7.
PxS1dS2解:取 S1 外侧任意点 P ,
3 ∆ϕ =ϕ20 −ϕ10 −2 π = − −2π = − π 2 λ 2 4
P点处干涉加强
r2 −r 1
π
∴A= A + A = 2A , I = 4I0 1 2 0
P
x
S1
d
S2
x’
Q
x
3 ∆ϕ =ϕ20 −ϕ10 −2π = − +2π =π λ 2 4
合成:相遇,叠加 合成:相遇,
相干波的条件[coherent condition]: 频率相同, 频率相同, 振动方向相同, 振动方向相同, 相位相同或相位差恒定; 相位相同或相位差恒定;
——相干三要素 ——相干三要素
需要解释 所谓“相干” 来源于数学中的“相关” 相互关联; 所谓“相干”,来源于数学中的“相关”,即 相互关联; 相关:有两件事, 相关:有两件事,能从其中一个的状况来推算出另一 个的状况,那么就说它们是相关的; 个的状况,那么就说它们是相关的; 如下图,设有两个函数, 如下图,设有两个函数, 在区间
所以叠加波的强度 所以叠加波的强度为(两边平方) 强度为 两边平方)
I = I1 + I2 +2 I1I2 cos∆ϕ 波源一定时, 波源一定时,波的强度只与 ∆ 有关; ϕ 有关;
当
