11 三角函数
最全三角函数概念公式、图像大全完整版.doc

初等函数的图形幂函数的图形指数函数的图形各三角函数值在各象限的符号sinα·cscα cosα·secα tanα·cotα三角函数的性质反三角函数的图形反三角函数的性质三角函数公式两角和公式sin(A+B) = sinAcosB+cosAsinB sin(A-B) = sinAcosB-cosAsinB cos(A+B) = cosAcosB-sinAsinB cos(A-B) = cosAcosB+sinAsinBtan(A+B) =tanAtanB -1tanBtanA +tan(A-B) =tanAtanB 1tanBtanA +-cot(A+B) =cotA cotB 1-cotAcotB +cot(A-B) =cotAcotB 1cotAcotB -+倍角公式tan2A =Atan 12tanA2- Sin2A=2SinA•CosACos2A = Cos 2A-Sin 2A=2Cos 2A-1=1-2sin 2A三倍角公式sin3A = 3sinA-4(sinA)3 cos3A = 4(cosA)3-3cosAtan3a = tana ·tan(3π+a)·tan(3π-a)sin(2A )=2cos 1A -cos(2A)=2cos 1A +tan(2A)=A A cos 1cos 1+-cot(2A )=A A cos 1cos 1-+tan(2A )=A A sin cos 1-=A A cos 1sin +和差化积sina+sinb=2sin2b a +cos 2ba - sina-sinb=2cos 2b a +sin 2ba -cosa+cosb = 2cos 2b a +cos 2ba -cosa-cosb = -2sin 2b a +sin 2ba -tana+tanb=ba b a cos cos )sin(+积化和差sinasinb = -21[cos(a+b)-cos(a-b)] cosacosb = 21[cos(a+b)+cos(a-b)]sinacosb = 21[sin(a+b)+sin(a-b)]cosasinb = 21[sin(a+b)-sin(a-b)]sin(-a) = -sina cos(-a) = cosasin(2π-a) = cosacos(2π-a) = sinasin(2π+a) = cosacos(2π+a) = -sinasin(π-a) = sina cos(π-a) = -cosa sin(π+a) = -sina cos(π+a) = -cosatgA=tanA =aacos sin万能公式sina=2)2(tan 12tan2aa + cosa=22)2(tan 1)2(tan 1aa+- tana=2)2(tan 12tan2aa -a•sina+b•cosa=)b (a 22+×sin(a+c) [其中tanc=ab ] a•sin(a)-b•cos(a) = )b (a 22+×cos(a-c) [其中tan(c)=ba ] 1+sin(a) =(sin2a +cos 2a )2 1-sin(a) = (sin 2a -cos 2a)2其他非重点三角函数csc(a) =a sin 1 sec(a) =acos 1双曲函数sinh(a)=2e -e -aacosh(a)=2e e -aa +tg h(a)=)cosh()sinh(a a公式一设α为任意角,终边相同的角的同一三角函数的值相等: sin (2kπ+α)= sinα cos (2kπ+α)= cosα tan (2kπ+α)= tanα cot (2kπ+α)= cotα设α为任意角,π+α的三角函数值与α的三角函数值之间的关系:sin(π+α)= -sinαcos(π+α)= -cosαtan(π+α)= tanαcot(π+α)= cotα公式三任意角α与-α的三角函数值之间的关系:sin(-α)= -sinαcos(-α)= cosαtan(-α)= -tanαcot(-α)= -cotα公式四利用公式二和公式三可以得到π-α与α的三角函数值之间的关系:sin(π-α)= sinαcos(π-α)= -cosαtan(π-α)= -tanαcot(π-α)= -cotα公式五利用公式-和公式三可以得到2π-α与α的三角函数值之间的关系:sin(2π-α)= -sinαcos(2π-α)= cosαtan(2π-α)= -tanαcot(2π-α)= -cotα2π±α及23π±α与α的三角函数值之间的关系:sin (2π+α)= cosαcos (2π+α)= -sinαtan (2π+α)= -cotαcot (2π+α)= -tanαsin (2π-α)= cosαcos (2π-α)= sinαtan (2π-α)= cotαcot (2π-α)= tanαsin (23π+α)= -cosαcos (23π+α)= sinαtan (23π+α)= -cotαcot (23π+α)= -tanαsin (23π-α)= -cosαcos (23π-α)= -sinαtan (23π-α)= cotαcot (23π-α)= tanα(以上k ∈Z)这个物理常用公式我费了半天的劲才输进来,希望对大家有用 A•sin(ωt+θ)+ B•sin(ωt+φ) =)cos(222ϕθ⋅++AB B A ×sin)cos(2)Bsin in arcsin[(As t 22ϕθϕθω⋅++++AB B A三角函数公式证明(全部)公式表达式乘法与因式分解a2-b2=(a+b)(a-b) a3+b3=(a+b)(a2-ab+b2) a3-b3=(a-b)(a2+ab+b2) 三角不等式|a+b|≤|a|+|b||a-b|≤|a|+|b||a|≤b<=>-b≤a≤b|a-b|≥|a|-|b|-|a|≤a≤|a|一元二次方程的解-b+√(b2-4ac)/2a -b-b+√(b2-4ac)/2a根与系数的关系X1+X2=-b/aX1*X2=c/a注:韦达定理判别式b2-4a=0 注:方程有相等的两实根b2-4ac>0 注:方程有一个实根b2-4ac<0 注:方程有共轭复数根三角函数公式两角和公式sin(A+B)=sinAcosB+cosAsinB sin(A-B)=sinAcosB-sinBcosAcos(A+B)=cosAcosB-sinAsinB cos(A-B)=cosAcosB+sinAsinBtan(A+B)=(tanA+tanB)/(1-tanAtanB) tan(A-B)=(tanA-tanB)/(1+tanAtanB) ctg(A+B)=(ctgActgB-1)/(ctgB+ctgA) ctg(A-B)=(ctgActgB+1)/(ctgB-ctgA)倍角公式tan2A=2tanA/(1-tan2A) ctg2A=(ctg2A-1)/2ctgacos2a=cos2a-sin2a=2cos2a-1=1-2sin2a半角公式sin(A/2)=√((1-cosA)/2) sin(A/2)=-√((1-cosA)/2)cos(A/2)=√((1+cosA)/2) cos(A/2)=-√((1+cosA)/2)tan(A/2)=√((1-cosA)/((1+cosA)) tan(A/2)=-√((1-cosA)/((1+cosA))ctg(A/2)=√((1+cosA)/((1-cosA)) ctg(A/2)=-√((1+cosA)/((1-cosA))和差化积2sinAcosB=sin(A+B)+sin(A-B) 2cosAsinB=sin(A+B)-sin(A-B)2cosAcosB=cos(A+B)-sin(A-B) -2sinAsinB=cos(A+B)-cos(A-B)sinA+sinB=2sin((A+B)/2)cos((A-B)/2 cosA+cosB=2cos((A+B)/2)sin((A-B)/2) tanA+tanB=sin(A+B)/cosAcosB tanA-tanB=sin(A-B)/cosAcosBctgA+ctgBsin(A+B)/sinAsinB -ctgA+ctgBsin(A+B)/sinAsinB某些数列前n项和1+2+3+4+5+6+7+8+9+…+n=n(n+1)/21+3+5+7+9+11+13+15+…+(2n-1)=n22+4+6+8+10+12+14+…+(2n)=n(n+1)12+22+32+42+52+62+72+82+…+n2=n(n+1)(2n+1)/6 13+23+33+43+53+63+…n3=n2(n+1)2/41*2+2*3+3*4+4*5+5*6+6*7+…+n(n+1)=n(n+1)(n+2)/3 正弦定理a/sinA=b/sinB=c/sinC=2R注:其中R 表示三角形的外接圆半径余弦定理b2=a2+c2-2accosB注:角B是边a和边c的夹角正切定理[(a+b)/(a-b)]={[Tan(a+b)/2]/[Tan(a-b)/2]}圆的标准方程(x-a)2+(y-b)2=r2 注:(a,b)是圆心坐标圆的一般方程x2+y2+Dx+Ey+F=0 注:D2+E2-4F>0抛物线标准方程y2=2px y2=-2px x2=2py x2=-2py直棱柱侧面积S=c*h斜棱柱侧面积S=c'*h正棱锥侧面积S=1/2c*h'正棱台侧面积S=1/2(c+c')h'圆台侧面积S=1/2(c+c')l=pi(R+r)l球的表面积S=4pi*r2圆柱侧面积S=c*h=2pi*h圆锥侧面积S=1/2*c*l=pi*r*l弧长公式l=a*ra是圆心角的弧度数r >0扇形面积公式s=1/2*l*r锥体体积公式V=1/3*S*H圆锥体体积公式V=1/3*pi*r2h斜棱柱体积V=S'L注:其中,S'是直截面面积,L是侧棱长柱体体积公式V=s*h圆柱体V=pi*r2h-------------------------------------------------------------------------------------------- 三角函数积化和差和差化积公式记不住就自己推,用两角和差的正余弦:cos(A+B)=cosAcosB-sinAsinBcos(A-B)=cosAcosB+sinAsinB这两式相加或相减,可以得到2组积化和差:相加:cosAcosB=[cos(A+B)+cos(A-B)]/2相减:sinAsinB=-[cos(A+B)-cos(A-B)]/2sin(A+B)=sinAcosB+sinBcosAsin(A-B)=sinAcosB-sinBcosA这两式相加或相减,可以得到2组积化和差:相加:sinAcosB=[sin(A+B)+sin(A-B)]/2相减:sinBcosA=[sin(A+B)-sin(A-B)]/2这样一共4组积化和差,然后倒过来就是和差化积了不知道这样你可以记住伐,实在记不住考试的时候也可以临时推导一下正加正正在前正减正余在前余加余都是余余减余没有余还负正余正加余正正减余余余加正正余减还负.3.三角形中的一些结论:(不要求记忆)(1)anA+tanB+tanC=tanA·tanB·tanC(2)sinA+tsinB+sinC=4cos(A/2)cos(B/2)cos(C/2)(3)cosA+cosB+cosC=4sin(A/2)·sin(B/2)·sin(C/2)+1(4)sin2A+sin2B+sin2C=4sinA·sinB·sinC(5)cos2A+cos2B+cos2C=-4cosAcosBcosC-1 ...........................已知sinα=m sin(α+2β), |m|<1,求证tan(α+β)=(1+m)/(1-m)tanβ解:sinα=m sin(α+2β)sin(a+β-β)=msin(a+β+β)sin(a+β)cosβ-cos(a+β)sinβ=msin(a+β)cosβ+mcos(a+β)sinβ sin(a+β)cosβ(1-m)=cos(a+β)sinβ(m+1)tan(α+β)=(1+m)/(1-m)tanβ赠送以下资料《二次函数的应用》中考题集锦10题已知抛物线222(0)y x mx m m =+-≠.(1)求证:该抛物线与x 轴有两个不同的交点;(2)过点(0)P n ,作y 轴的垂线交该抛物线于点A 和点B (点A 在点P 的左边),是否存在实数m n ,,使得2AP PB =?若存在,则求出m n ,满足的条件;若不存在,请说明理由.答案:解:(1)证法1:22229224m y x mx m x m ⎛⎫=+-=+- ⎪⎝⎭,当0m ≠时,抛物线顶点的纵坐标为2904m -<, ∴顶点总在x 轴的下方.而该抛物线的开口向上,∴该抛物线与x 轴有两个不同的交点.(或者,当0m ≠时,抛物线与y 轴的交点2(02)m -,在x 轴下方,而该抛物线的开口向上,∴该抛物线与x 轴有两个不同的交点.)证法2 :22241(2)9m m m ∆=-⨯⨯-=,当0m ≠时,290m >,∴该抛物线与x 轴有两个不同的交点. (2)存在实数m n ,,使得2AP PB =.设点B 的坐标为()t n ,,由2AP PB =知,①当点B 在点P 的右边时,0t >,点A 的坐标为(2)t n -,且2t t -,是关于x 的方程222x mx m n +-=的两个实数根.2224(2)940m m n m n ∴∆=---=+>,即294n m >-.且(2)t t m +-=-(I ),2(2)t t m n -=--(II )由(I )得,t m =,即0m >.将t m =代入(II )得,0n =.∴当0m >且0n =时,有2AP PB =.②当点B 在点P 的左边时,0t <,点A 的坐标为(2)t n ,,且2t t ,是关于x 的方程222x mx m n +-=的两个实数根.2224(2)940m m n m n ∴∆=---=+>,即 294n m >-.且2t t m +=-(I ),222t t m n =--(II )由(I )得,3mt =-,即0m >. 将3m t =-代入(II )得,2209n m =-且满足294n m >-.∴当0m >且2209n m =-时,有2AP PB =第11题一人乘雪橇沿如图所示的斜坡笔直滑下,滑下的距离S (米)与时间t (秒)间的关系式为210S t t =+,若滑到坡底的时间为2秒,则此人下滑的高度为( )A.24米 B.12米C.米 D.6米答案:B第12题我市英山县某茶厂种植“春蕊牌”绿茶,由历年来市场销售行情知道,从每年的3月25日起的180天内,绿茶市场销售单价y (元)与上市时间t (天)的关系可以近似地用如图(1)中的一条折线表示.绿茶的种植除了与气候、种植技术有关外,其种植的成本单价z (元)与上市时间t (天)的关系可以近似地用如图(2)的抛物线表示.关系式;(2)求出图(2)中表示的种植成本单价z (元)与上市时间t (天)(0t >)的函数关系式;(3)认定市场销售单价减去种植成本单价为纯收益单价,问何时上市的绿茶纯收益单价最大?(说明:市场销售单价和种植成本单价的单位:元/500克.))图(1)图(2)天)答案:解:(1)依题意,可建立的函数关系式为:2160(0120)380(120150)220(150180)5t t y t t t ⎧-+<<⎪⎪=<⎨⎪⎪+⎩,,. ≤ ≤≤ (2)由题目已知条件可设2(110)20z a t =-+. 图象过点85(60)3,,2851(60110)203300a a ∴=-+∴=.. 21(110)20300z t ∴=-+ (0)t >. (3)设纯收益单价为W 元,则W =销售单价-成本单价. 故22221160(110)20(0120)3300180(110)20(120150)3002120(110)20(150180)5300t t t W t t t t t ⎧-+---<<⎪⎪⎪=---<⎨⎪⎪+---⎪⎩,,. ≤ ≤≤ 化简得2221(10)100(0120)3001(110)60(120150)3001(170)56(150180)300t t W t t t t ⎧--+<<⎪⎪⎪=-+<⎨⎪⎪--+⎪⎩,,. ≤ ≤≤①当21(10)100(0120)300W t t =--+<<时,有10t =时,W 最大,最大值为100; ②当21(110)60(120150)300W t t =--+<≤时,由图象知,有120t =时,W 最大,最大值为2593;③当21(170)56(150180)300W t t =--+≤≤时,有170t =时,W 最大,最大值为56. 综上所述,在10t =时,纯收益单价有最大值,最大值为100元.第13题如图,足球场上守门员在O 处开出一高球,球从离地面1米的A 处飞出(A 在y 轴上),运动员乙在距O 点6米的B 处发现球在自己头的正上方达到最高点M ,距地面约4米高,球落地后又一次弹起.据实验,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.(1)求足球开始飞出到第一次落地时,该抛物线的表达式. (2)足球第一次落地点C距守门员多少米?(取7=)(3)运动员乙要抢到第二个落点D,他应再向前跑多少米?(取5=)答案:解:(1)(3分)如图,设第一次落地时, 抛物线的表达式为2(6)4y a x =-+. 由已知:当0x =时1y =. 即1136412a a =+∴=-,. ∴表达式为21(6)412y x =--+.(或21112y x x =-++)(2)(3分)令210(6)4012y x =--+=,.212(6)4861360x x x ∴-===-<.≈,(舍去). ∴足球第一次落地距守门员约13米.(3)(4分)解法一:如图,第二次足球弹出后的距离为CD根据题意:CD EF =(即相当于将抛物线AEMFC 向下平移了2个单位)212(6)412x ∴=--+解得1266x x =-=+1210CD x x ∴=-=. 1361017BD ∴=-+=(米). 解法二:令21(6)4012x --+=.解得16x =-,2613x =+.∴点C 坐标为(13,0).设抛物线CND 为21()212y x k =--+.将C 点坐标代入得:21(13)2012k --+=.解得:11313k =-(舍去),2667518k =+++=.21(18)212y x =--+ 令210(18)212y x ==--+,0.118x =-,21823x =+. 23617BD ∴=-=(米). 解法三:由解法二知,18k =, 所以2(1813)10CD =-=, 所以(136)1017BD =-+=. 答:他应再向前跑17米.第14题荆州市“建设社会主义新农村”工作组到某县大棚蔬菜生产基地指导菜农修建大棚种植蔬菜.通过调查得知:平均修建每公顷大棚要用支架、农膜等材料费2.7万元;购置滴灌设备,这项费用(万元)与大棚面积(公顷)的平方成正比,比例系数为0.9;另外每公顷种植蔬菜需种子、化肥、农药等开支0.3万元.每公顷蔬菜年均可卖7.5万元. (1)基地的菜农共修建大棚x (公顷),当年收益(扣除修建和种植成本后)为y (万元),写出y 关于x 的函数关系式.(2)若某菜农期望通过种植大棚蔬菜当年获得5万元收益,工作组应建议他修建多少公项大棚.(用分数表示即可)(3)除种子、化肥、农药投资只能当年受益外,其它设施3年内不需增加投资仍可继续使用.如果按3年计算,是否修建大棚面积越大收益越大?修建面积为多少时可以得到最大收益?请帮工作组为基地修建大棚提一项合理化建议.答案:(1)()227.5 2.70.90.30.9 4.5y x x x x x x =-++=-+. (2)当20.9 4.55x x -+=时,即2945500x x -+=,153x =,2103x =从投入、占地与当年收益三方面权衡,应建议修建53公顷大棚. (3)设3年内每年的平均收益为Z (万元)()()2227.50.90.30.30.3 6.30.310.533.075Z x x x x x x x =-++=-+=--+(10分)不是面积越大收益越大.当大棚面积为10.5公顷时可以得到最大收益.建议:①在大棚面积不超过10.5公顷时,可以扩大修建面积,这样会增加收益. ②大棚面积超过10.5公顷时,扩大面积会使收益下降.修建面积不宜盲目扩大.③当20.3 6.30x x -+=时,10x =,221x =.大棚面积超过21公顷时,不但不能收益,反而会亏本.(说其中一条即可)第15题一家用电器开发公司研制出一种新型电子产品,每件的生产成本为18元,按定价40元出售,每月可销售20万件.为了增加销量,公司决定采取降价的办法,经市场调研,每降价1元,月销售量可增加2万件.(1)求出月销售量y (万件)与销售单价x (元)之间的函数关系式(不必写x 的取值范围);(2)求出月销售利润z (万元)(利润=售价-成本价)与销售单价x (元)之间的函数关系式(不必写x 的取值范围);(3)请你通过(2)中的函数关系式及其大致图象帮助公司确定产品的销售单价范围,使月销售利润不低于480万元.答案:略.第16题一座隧道的截面由抛物线和长方形构成,长方形的长为8m ,宽为2m ,隧道最高点P 位于AB 的中央且距地面6m ,建立如图所示的坐标系(1)求抛物线的解析式;(2)一辆货车高4m ,宽2m ,能否从该隧道内通过,为什么?(3)如果隧道内设双行道,那么这辆货车是否可以顺利通过,为什么?答案:(1)由题意可知抛物线经过点()()()024682A P B ,,,,,设抛物线的方程为2y ax bx c =++ 将A P D ,,三点的坐标代入抛物线方程. 解得抛物线方程为21224y x x =-++ (2)令4y =,则有212244x x -++=解得1244x x =+=-212x x -=>∴货车可以通过.(3)由(2)可知21122x x -=>∴货车可以通过.第17题如图,在矩形ABCD 中,2AB AD =,线段10EF =.在EF 上取一点M ,分别以EM MF ,为一边作矩形EMNH 、矩形MFGN ,使矩形MFGN ∽矩形ABCD .令MN x =,当x 为何值时,矩形EMNH 的面积S 有最大值?最大值是多少?答案:解:矩形MFGN ∽矩形ABCD ,MN MFAD AB∴=. 2AB AD MN x ==,,2MF x ∴=.102EM EF MF x ∴=-=-. (102)S x x ∴=-2210x x =-+ 2525222x ⎛⎫=--+ ⎪⎝⎭.∴当52x =时,S 有最大值为252.第18题某企业信息部进行市场调研发现:信息一:如果单独投资A 种产品,则所获利润A y (万元)与投资金额x (万元)之间存在正比例函数关系:A y kx =,并且当投资5万元时,可获利润2万元.信息二:如果单独投资B 种产品,则所获利润B y (万元)与投资金额x (万元)之间存在二次函数关系:2B y ax bx =+,并且当投资2万元时,可获利润2.4万元;当投资4万元时,可获利润3.2万元.(1)请分别求出上述的正比例函数表达式与二次函数表达式;(2)如果企业同时对AB ,两种产品共投资10万元,请你设计一个能获得最大利润的投资方案,并求出按此方案能获得的最大利润是多少?B A D MF答案:解:(1)当5x =时,12250.4y k k ===,,, 0.4A y x ∴=,当2x =时, 2.4B y =;当4x =时, 3.2B y =.2.4423.2164a ba b =+⎧∴⎨=+⎩解得0.21.6a b =-⎧⎨=⎩∴20.2 1.6B y x x =-+.(2)设投资B 种商品x 万元,则投资A 种商品(10)x -万元,获得利润W 万元,根据题意可得220.2 1.60.4(10)0.2 1.24W x x x x x =-++-=-++ 20.2(3) 5.8W x ∴=--+当投资B 种商品3万元时,可以获得最大利润5.8万元,所以投资A 种商品7万元,B 种商品3万元,这样投资可以获得最大利润5.8万元.第19题如图所示,图(1)是一座抛物线型拱桥在建造过程中装模时的设计示意图,拱高为30m ,支柱3350m A B =,5根支柱1122334455A B A B A B A B A B ,,,,之间的距离均为15m ,1515B B A A ∥,将抛物线放在图(2)所示的直角坐标系中. (1)直接写出图(2)中点135B B B ,,的坐标; (2)求图(2)中抛物线的函数表达式; (3)求图(1)中支柱2244A B A B ,的长度.答案:(1)1(30)B -,0,3(030)B ,,5(300)B ,; (2)设抛物线的表达式为(30)(30)y a x x =-+,把3(030)B ,代入得(030)(030)30y a =-+=.B 图(1)图(2)l130a =-∴. ∵所求抛物线的表达式为:1(30)(30)30y x x =--+. (3)4B ∵点的横坐标为15, 4B ∴的纵坐标4145(1530)(1530)302y =--+=. 3350A B =∵,拱高为30,∴立柱44458520(m)22A B =+=. 由对称性知:224485(m)2A B A B ==。
三角函数公式表(初中物理公式)
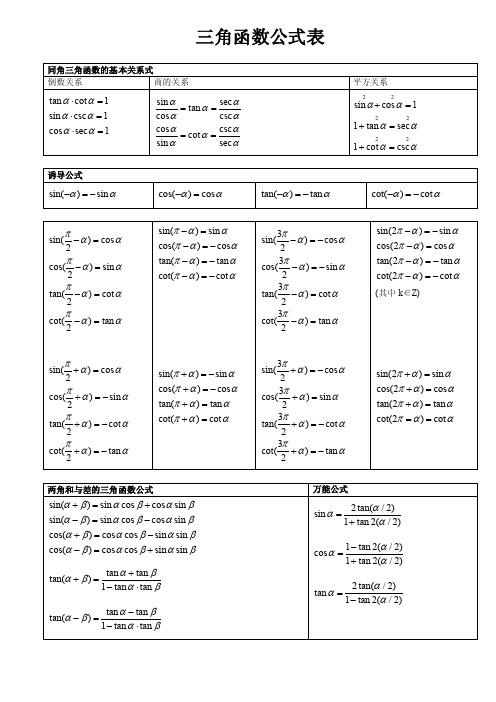
三角函数公式表物理量计算公式备注速度υ= S / t1m / s = 3.6 Km / h声速υ= 340m / s光速C = 3×108 m /s密度ρ= m / V 1 g / c m3 = 103 Kg / m3合力 F = F1 - F2F = F1 + F2 F1、F2在同一直线线上且方向相反F1、F2在同一直线线上且方向相同压强p = F / Sp =ρg h p = F / S适用于固、液、气p =ρg h适用于竖直固体柱p =ρg h可直接计算液体压强1标准大气压= 76 cmHg柱= 1.01×105 Pa = 10.3 m水柱浮力①F浮= G – F②漂浮、悬浮:F浮= G③F浮= G排=ρ液g V排④据浮沉条件判浮力大小(1)判断物体是否受浮力(2)根据物体浮沉条件判断物体处于什么状态(3)找出合适的公式计算浮力物体浮沉条件(前提:物体浸没在液体中且只受浮力和重力):①F浮>G(ρ液>ρ物)上浮至漂浮②F浮=G(ρ液=ρ物)悬浮③F浮<G(ρ液<ρ物)下沉杠杆平衡条件F1 L1 = F2 L 2 杠杆平衡条件也叫杠杆原理滑轮组 F = G / nF =(G动+ G物)/ nSF = n SG 理想滑轮组忽略轮轴间的摩擦n:作用在动滑轮上绳子股数功W = F S = P t 1J = 1N•m = 1W•s功率P = W / t = Fυ1KW = 103 W,1MW = 103KW有用功W有用= G h(竖直提升)= F S(水平移动)= W总– W额=ηW总额外功W额= W总– W有= G动h(忽略轮轴间摩擦)= f L(斜面)总功W总= W有用+ W额= F S = W有用/ η机械效率η= W有用/ W总η=G /(n F)= G物/(G物+ G动)定义式适用于动滑轮、滑轮组中考物理所有的公式特点或原理串联电路并联电路时间:t t=t1=t2 t=t1=t2电流:I I = I 1= I 2 I = I 1+ I 2电压:U U = U 1+ U 2 U = U 1= U 2电荷量:Q电Q电= Q电1= Q电2 Q电= Q电1+ Q电2电阻:R R = R 1= R 2 1/R=1/R1+1/R2 [R=R1R2/(R1+R2)]电功:W W = W 1+ W 2 W = W 1+ W 2电功率:P P = P 1+ P 2 P = P 1+ P 2电热:Q热Q热= Q热1+ Q热 2 Q热= Q热1+ Q热 2物理量(单位)公式备注公式的变形速度V(m/S)v= S:路程/t:时间重力G(N)G=mg m:质量g:9.8N/kg或者10N/kg密度ρ(kg/m3)ρ=m:质量V:体积合力F合(N)方向相同:F合=F1+F2方向相反:F合=F1—F2 方向相反时,F1>F2浮力F浮(N) F浮=G物—G视G视:物体在液体的重力浮力F浮(N) F浮=G物此公式只适用物体漂浮或悬浮浮力F浮(N) F浮=G排=m排g=ρ液gV排G排:排开液体的重力m排:排开液体的质量ρ液:液体的密度V排:排开液体的体积(即浸入液体中的体积)杠杆的平衡条件F1L1= F2L2 F1:动力 L1:动力臂F2:阻力 L2:阻力臂定滑轮F=G物S=h F:绳子自由端受到的拉力G物:物体的重力S:绳子自由端移动的距离h:物体升高的距离动滑轮F= (G物+G轮)S=2 h G物:物体的重力G轮:动滑轮的重力滑轮组F= (G物+G轮)S=n h n:通过动滑轮绳子的段数机械功W(J)W=Fs F:力s:在力的方向上移动的距离有用功W有总功W总W有=G物hW总=Fs 适用滑轮组竖直放置时机械效率η= ×100%功率P(w)P=W:功t:时间压强p(Pa)P=F:压力S:受力面积液体压强p(Pa)P=ρgh ρ:液体的密度h:深度(从液面到所求点的竖直距离)热量Q(J)Q=cm△t c:物质的比热容 m:质量△t:温度的变化值燃料燃烧放出的热量Q(J)Q=mq m:质量q:热值常用的物理公式与重要知识点一.物理公式单位)公式备注公式的变形串联电路电流I(A)I=I1=I2=…… 电流处处相等串联电路电压U(V)U=U1+U2+…… 串联电路起分压作用串联电路电阻R(Ω)R=R1+R2+……并联电路电流I(A)I=I1+I2+…… 干路电流等于各支路电流之和(分流)并联电路电压U(V)U=U1=U2=……并联电路电阻R(Ω)= + +……欧姆定律I=电路中的电流与电压成正比,与电阻成反比电流定义式I=Q:电荷量(库仑)t:时间(S)电功W(J)W=UIt=Pt U:电压 I:电流t:时间 P:电功率电功率P=UI=I2R=U2/R U:电压 I:电流R:电阻电磁波波速与波长、频率的关系C=λν C:波速(电磁波的波速是不变的,等于3×108m/s)λ:波长ν:频率二.知识点1.需要记住的几个数值:a.声音在空气中的传播速度:340m/s b光在真空或空气中的传播速度:3×108m/sc.水的密度:1.0×103kg/m3 d.水的比热容:4.2×103J/(kg•℃)e.一节干电池的电压:1.5V f.家庭电路的电压:220Vg.安全电压:不高于36V2.密度、比热容、热值它们是物质的特性,同一种物质这三个物理量的值一般不改变。
三角函数表

三角函数表你没有看错,这是一个关于紧固件的企业网站,却在讲述三角函数这风牛马不相及的故事.因为......三角函数表用于计算角度和边长的关系,在产品零件的绘图和设计中经常用到,所以我们整理了下表。
此表不仅可供我们机械工人参考,也可供其他工人或学生参考。
先来个定义正弦函数 sin(A)=a/h余弦函数 cos(A)=b/h正切函数 tan(A)=a/b余切函数 cot(A)=b/a正割函数 sec (A) =h/b余割函数 csc (A) =h/a注:a—所研究角的对边b—所研究的邻边h—所研究角的斜边以下是具体的对应参数表:1,正弦函数表 sinsin1=0. sin2=0. sin3=0.sin4=0. sin5=0. sin6=0.sin7=0. sin8=0. sin9=0.sin10=0. sin11=0. sin12=0. sin13=0. sin14=0. sin15=0. sin16=0. sin17=0. sin18=0. sin19=0. sin20=0. sin21=0. sin22=0. sin23=0. sin24=0. sin25=0. sin26=0. sin27=0. sin28=0. sin29=0. sin30=0. sin31=0. sin32=0. sin33=0. sin34=0. sin35=0. sin36=0. sin37=0. sin38=0. sin39=0. sin40=0. sin41=0. sin42=0. sin43=0. sin44=0. sin45=0. sin46=0. sin47=0. sin48=0. sin49=0. sin50=0. sin51=0. sin52=0. sin53=0. sin54=0. sin55=0. sin56=0. sin57=0. sin58=0. sin59=0. sin60=0. sin61=0. sin62=0. sin63=0. sin64=0. sin65=0. sin66=0. sin67=0. sin68=0. sin69=0. sin70=0. sin71=0. sin72=0. sin73=0. sin74=0. sin75=0. sin76=0. sin77=0. sin78=0. sin79=0. sin80=0. sin81=0. sin82=0. sin83=0. sin84=0. sin85=0. sin86=0. sin87=0. sin88=0. sin89=0.sin90=12,余弦函数表 coscos1=0. cos2=0. cos3=0.cos4=0. cos5=0. cos6=0.cos7=0. cos8=0. cos9=0.cos10=0. cos11=0. cos12=0. cos13=0. cos14=0. cos15=0. cos16=0. cos17=0. cos18=0. cos19=0. cos20=0. cos21=0. cos22=0. cos23=0. cos24=0. cos25=0. cos26=0. cos27=0. cos28=0. cos29=0. cos30=0. cos31=0. cos32=0. cos33=0. cos34=0. cos35=0. cos36=0. cos37=0. cos38=0. cos39=0. cos40=0. cos41=0. cos42=0. cos43=0. cos44=0. cos45=0. cos46=0. cos47=0. cos48=0. cos49=0. cos50=0. cos51=0. cos52=0. cos53=0. cos54=0. cos55=0.2 cos56=0. cos57=0.2 cos58=0. cos59=0. cos60=0. cos61=0. cos62=0.6 cos63=0. cos64=0.6 cos65=0. cos66=0. cos67=0. cos68=0.2 cos69=0. cos70=0. cos71=0.5 cos72=0.5cos73=0.7 cos74=0. cos75=0. cos76=0. cos77=0. cos78=0. cos79=0. cos80=0. cos81=0. cos82=0. cos83=0. cos84=0. cos85=0. cos86=0. cos87=0. cos88=0. cos89=0.cos90=03,正切函数表 tantan1=0. tan2=0. tan3=0.tan4=0. tan5=0. tan6=0.tan7=0. tan8=0. tan9=0.tan10=0. tan11=0. tan12=0. tan13=0. tan14=0. tan15=0. tan16=0. tan17=0. tan18=0. tan19=0. tan20=0. tan21=0. tan22=0. tan23=0. tan24=0. tan25=0. tan26=0. tan27=0. tan28=0. tan29=0. tan30=0. tan31=0. tan32=0. tan33=0. tan34=0. tan35=0. tan36=0. tan37=0. tan38=0. tan39=0. tan40=0. tan41=0. tan42=0. tan43=0. tan44=0. tan45=0. tan46=1. tan47=1. tan48=1. tan49=1. tan50=1. tan51=1. tan52=1. tan53=1. tan54=1.tan58=1. tan59=1. tan60=1. tan61=1. tan62=1. tan63=1. tan64=2. tan65=2. tan66=2. tan67=2. tan68=2. tan69=2. tan70=2. tan71=2. tan72=3. tan73=3. tan74=3. tan75=3. tan76=4. tan77=4. tan78=4. tan79=5. tan80=5. tan81=6. tan82=7. tan83=8. tan84=9. tan85=11. tan86=14. tan87=19. tan88=28. tan89=57.tan90=(无限)4,余切函数 cotcot89=0. cot88=0. cot87=0. cot86=0. cot85=0. cot84=0. cot83=0. cot83=0. cot81=0. cot80=0. cot79=0. cot78=0. cot77=0. cot76=0. cot75=0. cot74=0. cot73=0. cot72=0. cot71=0. cot70=0. cot69=0. cot68=0. cot67=0. cot66=0. cot65=0. cot64=0. cot63=0. cot62=0. cot61=0. cot60=0. cot59=0. cot58=0. cot57=0. cot56=0. cot55=0. cot54=0.cot50=0. cot49=0. cot48=0. cot47=0. cot46=0. cot45=0. cot44=1. cot43=1. cot42=1. cot41=1. cot40=1. cot39=1. cot38=1. cot37=1. cot36=1. cot35=1. cot34=1. cot33=1. cot32=1. cot31=1. cot30=1. cot29=1. cot28=1. cot27=1. cot26=2. cot25=2. cot24=2. cot23=2. cot22=2. cot21=2. cot20=2. cot19=2. cot18=3. cot17=3. cot16=3. cot15=3. cot14=4. cot13=4. cot12=4. cot11=5. cot10=5. cot9=6. cot8=7. cot7=8. cot6=9. cot5=11. cot4=14. cot3=19. cot228. cot1=57.cot0=(无限)咨询与留言。
每一个角度的三角函数值表

(1)特殊角三角函数值sin0=0sin30=0.5sin45=0.7071 二分之根号2sin60=0.8660 二分之根号3sin90=1cos0=1cos30=0. 二分之根号3cos45=0. 二分之根号2cos60=0.5cos90=0tan0=0tan30=0. 三分之根号3tan45=1tan60=1. 根号3tan90=无cot0=无cot30=1. 根号3cot45=1cot60=0. 三分之根号3cot90=0(2)0°~90°的任意角的三角函数值,查三角函数表。
(见下)(3)锐角三角函数值的变化情况(i)锐角三角函数值都是正值(ii)当角度在0°~90°间变化时,正弦值随着角度的增大(或减小)而增大(或减小)余弦值随着角度的增大(或减小)而减小(或增大)正切值随着角度的增大(或减小)而增大(或减小)余切值随着角度的增大(或减小)而减小(或增大)(iii)当角度在0°≤α≤90°间变化时,0≤sinα≤1, 1≥cosα≥0,当角度在0°<α<90°间变化时,tanα>0, cotα>0.“锐角三角函数”属于三角学,是《数学课程标准》中“空间与图形”领域的重要内容。
从《数学课程标准》看,中学数学把三角学内容分成两个部分,第一部分放在义务教育第三学段,第二部分放在高中阶段。
在义务教育第三学段,主要研究锐角三角函数和解直角三角形的内容,本套教科书安排了一章的内容,就是本章“锐角三角函数”。
在高中阶段的三角内容是三角学的主体部分,包括解斜三角形、三角函数、反三角函数和简单的三角方程。
无论是从内容上看,还是从思考问题的方法上看,前一部分都是后一部分的重要基础,掌握锐角三角函数的概念和解直角三角形的方法,是学习三角函数和解斜三角形的重要准备。
附:三角函数值表sin0=0,sin15=(√6-√2)/4 ,sin30=1/2,sin45=√2/2,sin60=√3/2,sin75=(√6+√2)/2 ,sin90=1,sin105=√2/2*(√3/2+1/2)sin120=√3/2sin135=√2/2sin150=1/2sin165=(√6-√2)/4sin180=0sin270=-1sin360=0sin1=0. sin2=0. sin3=0.sin4=0.41253 sin5=0. sin6=0.sin7=0. sin8=0. sin9=0.sin10=0. sin11=0.65448 sin12=0.sin13=0. sin14=0. sin15=0.sin16=0. sin17=0.27367 sin18=0.49474sin19=0.71567 sin20=0.56687 sin21=0.sin22=0.5912 sin23=0.92737 sin24=0.sin25=0. sin26=0.90774 sin27=0.sin28=0.58908 sin29=0. sin30=0.sin31=0.00542 sin32=0.32049 sin33=0.5027 sin34=0.07468 sin35=0.1046 sin36=0.24731 sin37=0.20483 sin38=0.56583 sin39=0.98375 sin40=0.65392 sin41=0.05073 sin42=0.88582 sin43=0.24985 sin44=0.89972 sin45=0.65475 sin46=0.86511 sin47=0.91705 sin48=0.73941 sin49=0.27719 sin50=0.8978 sin51=0.69708 sin52=0.67219 sin53=0.72928 sin54=0.49474 sin55=0.89918 sin56=0.50417 sin57=0.54239 sin58=0.6426 sin59=0.21122 sin60=0.44386 sin61=0.93957 sin62=0.89269 sin63=0.83678 sin64=0.9167 sin65=0.66499 sin66=0.26009 sin67=0.24404 sin68=0.67873 sin69=0.72017 sin70=0.59083 sin71=0.93167 sin72=0.51535 sin73=0.30354 sin74=0.83189 sin75=0.90683 sin76=0.59965 sin77=0.52352 sin78=0.38057 sin79=0.7664 sin80=0.2208 sin81=0.51378 sin82=0.15704 sin83=0.1322 sin84=0.82733 sin85=0.17455 sin86=0.98242 sin87=0.45738 sin88=0.90958 sin89=0.63913sin90=1cos1=0.63913 cos2=0.90958 cos3=0.45738 cos4=0.98242 cos5=0.17455 cos6=0.82733 cos7=0.1322 cos8=0.15704 cos9=0.51378cos10=0.2208 cos11=0.7664 cos12=0.38057 cos13=0.52352 cos14=0.59965 cos15=0.90683 cos16=0.83189 cos17=0.30355 cos18=0.51535 cos19=0.93168 cos20=0.59084 cos21=0.72017 cos22=0.67874 cos23=0.24404 cos24=0.26009 cos25=0.66499 cos26=0.9167 cos27=0.83679 cos28=0.8927 cos29=0.93957 cos30=0.44387 cos31=0.21123 cos32=0.6426 cos33=0.5424 cos34=0.50417 cos35=0.89918 cos36=0.49474 cos37=0.72928 cos38=0.67219 cos39=0.69709 cos40=0.8978 cos41=0.2772 cos42=0.73942 cos43=0.91705 cos44=0.86512 cos45=0.65476 cos46=0.89974 cos47=0.24985 cos48=0.88582 cos49=0.05074 cos50=0.65394 cos51=0.98375 cos52=0.56583 cos53=0.20484 cos54=0.24731 cos55=0.10462 cos56=0.07468 cos57=0.50272 cos58=0.32049 cos59=0.00544 cos60=0.00001 cos61=0.63371 cos62=0. cos63=0.95468cos64=0. cos65=0. cos66=0.58004cos67=0.92737 cos68=0.59122 cos69=0.cos70=0.56688 cos71=0. cos72=0.cos73=0. cos74=0. cos75=0.cos76=0. cos77=0. cos78=0.cos79=0. cos80=0. cos81=0.cos82=0. cos83=0. cos84=0.cos85=0. cos86=0. cos87=0.cos88=0. cos89=0.72836cos90=0tan1=0. tan2=0. tan3=0.tan4=0. tan5=0. tan6=0.tan7=0.29046 tan8=0. tan9=0.tan10=0. tan11=0. tan12=0.00221tan13=0.55631 tan14=0. tan15=0.11227tan16=0.88079 tan17=0. tan18=0.29063tan19=0. tan20=0. tan21=0.54158tan22=0.51568 tan23=0.96047 tan24=0.85361 tan25=0.49986 tan26=0.58614 tan27=0.44288 tan28=0.14788 tan29=0.2769 tan30=0.96257 tan31=0.75604 tan32=0.93275 tan33=0.75104 tan34=0.24265 tan35=0.97097 tan36=0.53609 tan37=0.27942 tan38=0.67174 tan39=0.50072 tan40=0.72799 tan41=0.62267 tan42=0.78399 tan43=0.76618 tan44=0.70739 tan45=0.99999 tan46=1.05693 tan47=1.46826 tan48=1.91927 tan49=1.10092 tan50=1.421 tan51=1.5051 tan52=1.30785 tan53=1.04098 tan54=1.11733 tan55=1.21144 tan56=1.27403 tan57=1.45827 tan58=1.10506 tan59=1.05173 tan60=1.88767 tan61=1.14235 tan62=1.63318 tan63=1.51503 tan64=2.9296 tan65=2.95586 tan66=2.4215 tan67=2.3753 tan68=2.62946 tan69=2.38023 tan70=2.46216 tan71=2.5822 tan72=3.52526 tan73=3.41404 tan74=3.09087 tan75=3.88776 tan76=4.58455 tan77=4.4153 tan78=4.8456 tan79=5.0307 tan80=5.7707 tan81=6.5041 tan82=7.4207 tan83=8.4593 tan84=9.2587 tan85=11.132 tan86=14.1942 tan87=19.816 tan88=28.5515 tan89=57.9144tan90=无取值。
高中数学第一章三角函数11任意角和弧度制111任意角知识巧解学案

1。
1.1 任意角疱工巧解牛知识•巧学一、正角、负角、零角1.一条射线的端点是O,它从初始位置OA旋转到终止位置OB,形成一个角α,点O是角α的顶点,射线OA、OB分别是角α的始边、终边。
我们规定,按逆时针方向旋转形成的角叫正角;按顺时针旋转形成的角叫负角;若射线没有作任何旋转,形成的角叫零角,这样就把角的概念推广到了任意角。
旋转一周角的大小记为360°,如图1—1-1.图1—1-12.由于图1-1-1(1)中的α、β分别是按逆时针、顺时针方向旋转的,所以α=45°,β=—315°;图1—1-1(2)中的α=30°,β=390°,γ=-60°。
显然角的大小与旋转的周数有关,角的正负与旋转的方向有关.图1—1—2如图1-1-2,射线OA绕端点O旋转90°到射线OB的位置,接着再旋转-30°到OC的位置,则∠AOC=∠AOB+∠BOC=90°+(-30°)=60°。
学法一得引入正角、负角的概念后,角的减法运算可以转化为角的加法运算,即可以转化α—β为α+(-β),也就是说各角和的旋转量等于各角旋转量的和。
3。
在画图表示角时,常用带箭头的弧来表示旋转的方向,旋转的周数及角的绝对值的大小,旋转生成的角,又常称为转角。
显然,如果以第一个角的终边为始边作第二个角,以第二个角的终边为始边作第三个角,这样一直作下去,那么所有这些角的和等于以第一个角的始边为始边,以最后一个角的终边为终边的角的大小.二、象限角1。
若把角的顶点与原点重合,角的始边与x轴的非负半轴重合,那么,角的终边(除顶点外)在第几象限,我们说这个角是第几象限角.图1—1—3例如:由于图1—1-3甲中的角45°、405°、-315°都是始边与x轴的非负半轴重合,终边落在第一象限的角,所以它们都是第一象限角;同理图1-1-3乙中的角480°是第二象限的角,—70°、290°都是第四象限的角.2。
十一种类型的三角函数最值问题(附题目详解)

十一种类型的三角函数最值问题1.利用三角函数的有界性求最值利用正弦函数、余弦正数的有界性:∣sinx ∣≤1,∣cosx ∣≤1,可求形如y=Asin(ωx+φ),y=Acos(Asin(ωx+φ)(A ≠0, φ≠0)的函数最值.例:已知函数y=12 cos 2x+32 sinxcosx+1,x ∈R,当函数y 取得最大值时,求自变量x 的集合.2.反函数法 例:求函数1cos 21cos 2-+=x x y 的值域[分析] 此为dx c bx a y -+=cos cos 型的三角函数求最值问题,分子、分母的三角函数同名、同角,先用反解法,再用三角函数的有界性去解。
3.配方法—---转化为二次函数求最值例:求函数y=f(x)=cos 22x-3cos2x+1的最值.4.引入辅助角法y=asinx+bcosx 型处理方法:引入辅助角ϕ ,化为y=22b a +sin (x+ϕ),利用函数()1sin ≤+ϕx 即可求解。
Y=asin 2x+bsinxcosx+mcos 2x+n 型亦可以化为此类。
例:已知函数()R x x x x y ∈+⋅+=1cos sin 23cos 212当函数y 取得最大值时,求自变量x 的集合。
[分析] 此类问题为x c x x b x a y 22cos cos sin sin +⋅+=的三角函数求最值问题,它可通过降次化简整理为x b x a y cos sin +=型求解。
5. 利用数形结合 例: 求函数y xx=+s in c o s 2的最值。
解:6、换元法例:若0<x<2π,求函数y=(1+1sinx )(1+1cosx )的最小值.7. 利用函数在区间内的单调性8. 例: 已知()π,0∈x ,求函数xx y sin 2sin +=的最小值。
[分析] 此题为xax sin sin +型三角函数求最值问题,当sinx>0,a>1,不能用均值不等式求最值,适合用函数在区间内的单调性来求解。
三角函数详细讲解

三角函数详细讲解
三角函数是基本初等函数之一,是以角度(最常用的单位是弧度制)为自变量,角度对应任意角终边与单位圆交点坐标或其比值为因变量的函数。
它也可以等价地用与单位圆有关的各种线段的长度来定义。
三角函数在研究三角形和圆等几何形状的性质时有重要作用,也是研究周期性现象的基础数学工具。
三角函数中的正弦函数、余弦函数和正切函数是最常见的。
这些函数的定义可以通过直角三角形来解释,其中θ是要找的角度,对边是指与θ所对应的直角三角形中的最短边,邻边是指与θ所对应的直角三角形中的最长边,斜边是指三角形的最长边。
正弦函数的定义为sinθ=对边/斜边,余弦函数的定义为cosθ=邻边/斜边,正切函数的定义为tanθ=对边/邻边。
这些函数的值是固定的,不会因为三角形的大小改变而改变。
例如,tan45°的值总是等于1,无论三角形的大小如何变化。
这是因为我们用的是直角三角形,所以每个三角形都有成比例的关系。
三角函数不仅用于计算三角形中未知长度的边和未知的角度,在导航、工程学以及物理学方面都有广泛的用途。
另外,以三角函数为模版,可以定义一
类相似的函数,叫做双曲函数。
常见的双曲函数也被称为双曲正弦函数、双曲余弦函数等等。
以上是关于三角函数的详细讲解,如需了解更多信息,建议查阅数学书籍或咨询专业人士。
三角函数对照表

三角函数对照表
三角函数的和差化积公式 三角函数的积化和差公式
sin sin 2sin
cos
22sin sin 2cos sin
22
cos cos 2cos cos
22cos cos 2sin sin
22
αβ
αβ
αβαβαβ
αβαβαβ
αβαβαβ
αβ+-+=⋅+--=⋅+-+=⋅+--=-⋅
[][]
[]
[]
1
sin cos sin()sin()21
cos sin sin()sin()2
1
cos cos cos()cos()21
sin sin cos()cos()2αβαβαβαβαβαβαβαβαβαβαβαβ⋅=
++-⋅=+--⋅=++-⋅=-+--
化asinα ±bcosα为一个角的一个三角函数的形式(辅助角的三角函数的公式)
22sin cos sin()a x b x a b x φ±=+±
其中φ角所在的象限由a 、b 的符号确定,φ角的值由tan b
a
φ=确定
六边形记忆法:图形结构“上弦中切下割,左正右余中间1”;记忆方法“对角线上两个函数的积为1;阴影三角形上两顶点的三角函数值的平方和等于下顶点的三角函数值的平方;任意一顶点的三角函数值等于相邻两个顶点的三角函数值的乘积。
”。
高一第11讲 三角函数概念(学生版)

四.典例剖析:
题型一终边相同的角与象限角
π 例 1 判断真假:(1)将表的分针拨快 10 分钟,则分针转过的角度是 .( ) 3 (2)相等的角终边一定相同,终边相同的角也一定相等.( ) (3)已知 A={小于 90°的角}, B={第一象限角}, 则 A∩B={α|0°<α<90°}. ( (4)终边与坐标轴重合的角 α 的集合为{α|α=k·180°+90°,k∈Z}.( )
)
例2
在 0°~360°范围内,找出与下列各角终边相同的角,并判定它们是第几象限角. (1)-150°;(2)650°;(3)-950°15′.
. 课堂小结: 解答本题可先利用终边相同的角的关系:β=α+k·360°,k∈Z,把所给的 角化归到 0°~360°范围内,然后利用 0°~360°范围内的角分析该角是第几象限角.
(B)2
(C)
1 2
(D) 2
5. (2008 年高考题四川理)设 0≤a<2 .若 sin a> 3 cosα,则 α 的取值范围是
4 3 , ) (C) ( , ) ) (D) ( , 3 3 3 3 2 3 3 cos ( , ) 5 ,且 2 ,则 tanα=__________. 6.(2011 年高考题重庆文)若
课堂小结:1.在弧度制下,计算扇形的面积和弧长比在角度制下更方便、简捷. 1 1 2 2.记住下列公式:①l=αR;②S= lR;③S= αR .其中 R 是扇形的半径,l 是弧长, 2 2 α(0<α<2π)为圆心角,S 是扇形面积.
-4-/8
高一数学上第 11 讲
课堂练习 2:(1)已知扇形的半径为 10 cm,圆心角为 120°,则扇形的弧长为________,面 积为________. 2 (2)设扇形的周长为 8 cm,面积为 4 cm ,则扇形的圆心角的弧度数是________.
三角函数公式(最全)
正弦定理变形可得:
五、其他公式
2、余弦定理
对于如图所示的边长为a、b、c而相应角为α、β、γ的△ABC, 有:
3、降幂公式
sin²α=[1-cos(2α)]/2 cos²α=[1+cos(2α)]/2 tan²α=[1-cos(2α)]/[1+cos(2α)]
4、三角和
sin(α+β+γ)=sinα·cosβ·cosγ+cosα·sinβ·cosγ+ cosα·cosβ·sinγ-sinα·sinβ·sinγ
ln(1+x)=x-x2/2+x3/3-…+(-1)k-1xk/k, x∈(-1,1)
sin x = x-x3/3!+x5/5!-…+(-1)k-1x2k-1/(2k-1)!+…, x∈R
cos x = 1-x2/2!+x4/4!-…+(-1)kx2k/(2k)!+…, x∈R
arcsin x = x + x3/(2*3) + (1*3)x5/(2*4*5) + (1*3*5)x7/(2* 4*6*7)…+(2k+1)!!*x2k+1/(2k!!*(2k+1))+…, x∈(-1,1)(!!表 示双阶乘)
1
一、定义公式
三角函数公式
锐角三角函数 任意角三角函数
正弦(sin) 余弦(cos) 正切(tan或tg) 余切(cot或ctg) 正割(sec) 余割(csc) 正弦(sin) 余弦(cos) 正切(tan或tg) 余切(cot或ctg) 正割(sec) 余割(csc)
1、倒数关系
二、函数关系
三角函数表

1
0
-1
0
cos
1
0.966
0.866
0.707
0.5
0.259
0
-1
0
1
Tg
0
0.268
0.577
1
1.732
3.73
-∞
0
-∞
0
ctg
∞
3.732
1.732
1
0.577
0.268
0
-∞
0
+∞
三.cosΦ与tg的对应值表:
COSΦ
tgΦ
COSΦ
tgΦ
COSΦ
tgΦ
COSΦ
tgΦ
1
0
0.86
正弦sin
余切ctg
正切tg
角度
正弦SinA=a/c=对边/斜边=cosB余弦cosA=b/c=邻边/斜边=sinB
正切tgA=a/b=对边/邻边=ctgB余切ctgA=b/a=邻边/对边=tgB
二.特殊角度函数值:
角度
0
15
30
45
60
75
90
180
270
360
Sin
0
0.259
0.5
0.707
0.866
0.74
0.9089
0.60
1.334
0.30
3.180
0.87
0.5668
0.73
0.9362
0.59
1.638
0.25
3.867
四.公式:A的对边是y,A的邻边是x,A的另一边(斜边)是r
1.α角的正弦=α角的对边/斜边。(塞因)sinα=y/r
三角函数值大全

三角函数值大全(1)特殊角三角函数值sin0=0,sin15=(√6-√2)/4 ,sin30=1/2,sin45=√2/2,sin60=√3/2,sin75=(√6+√2)/2 ,sin90=1,sin105=√2/2*(√3/2+1/2)sin120=√3/2sin135=√2/2sin150=1/2sin165=(√6-√2)/4sin180=0sin270=-1sin360=0cos0=1cos30=0.866025404 二分之根号3cos45=0.707106781 二分之根号2cos60=0.5cos90=0tan0=0tan30=0.577350269 三分之根号3tan45=1tan60=1.732050808 根号3tan90=无cot0=无cot30=1.732050808 根号3cot45=1cot60=0.577350269 三分之根号3cot90=0(2)0°~90°的任意角的三角函数值,查三角函数表。
(3)锐角三角函数值的变化情况(i)锐角三角函数值都是正值(ii)当角度在0°~90°间变化时,正弦值随着角度的增大(或减小)而增大(或减小)余弦值随着角度的增大(或减小)而减小(或增大)正切值随着角度的增大(或减小)而增大(或减小)余切值随着角度的增大(或减小)而减小(或增大)(iii)当角度在0°≤α≤90°间变化时,0≤sinα≤1, 1≥cosα≥0,当角度在0°<α<90°间变化时,tanα>0, cotα>0.附:三角函数值表sin1=0.01745240643728351 sin2=0.03489949670250097 sin3=0.05233595624294383 sin4=0.0697564737441253 sin5=0.08715574274765816 sin6=0.10452846326765346sin7=0.12186934340514747 sin8=0.13917310096006544 sin9=0.15643446504023087 sin10=0.17364817766693033 sin11=0.1908089953765448 sin12=0.20791169081775931 sin13=0.22495105434386497 sin14=0.24192189559966773 sin15=0.25881904510252074 sin16=0.27563735581699916 sin17=0.2923717047227367 sin18=0.3090169943749474 sin19=0.3255681544571567 sin20=0.3420201433256687 sin21=0.35836794954530027 sin22=0.374606593415912 sin23=0.3907311284892737 sin24=0.40673664307580015 sin25=0.42261826174069944 sin26=0.4383711467890774 sin27=0.45399049973954675 sin28=0.4694715627858908 sin29=0.48480962024633706 sin30=0.49999999999999994 sin31=0.5150380749100542 sin32=0.5299192642332049 sin33=0.544639035015027sin34=0.5591929034707468 sin35=0.573576436351046 sin36=0.5877852522924731sin37=0.6018150231520483 sin38=0.6156614753256583 sin39=0.6293203910498375 sin40=0.6427876096865392 sin41=0.6560590289905073 sin42=0.6691306063588582 sin43=0.6819983600624985 sin44=0.6946583704589972 sin45=0.7071067811865475 sin46=0.7193398003386511 sin47=0.7313537016191705 sin48=0.7431448254773941 sin49=0.7547095802227719 sin50=0.766044443118978 sin51=0.7771459614569708sin52=0.7880107536067219 sin53=0.7986355100472928 sin54=0.8090169943749474 sin55=0.8191520442889918 sin56=0.8290375725550417 sin57=0.8386705679454239 sin58=0.848048096156426 sin59=0.8571673007021122 sin60=0.8660254037844386sin61=0.8746197071393957 sin62=0.8829475928589269 sin63=0.8910065241883678 sin64=0.898794046299167 sin65=0.9063077870366499 sin66=0.9135454576426009 sin67=0.9205048534524404 sin68=0.9271838545667873 sin69=0.9335804264972017 sin70=0.9396926207859083 sin71=0.9455185755993167 sin72=0.9510565162951535 sin73=0.9563047559630354 sin74=0.9612616959383189 sin75=0.9659258262890683 sin76=0.9702957262759965 sin77=0.9743700647852352 sin78=0.9781476007338057 sin79=0.981627183447664 sin80=0.984807753012208 sin81=0.9876883405951378 sin82=0.9902680687415704 sin83=0.992546151641322 sin84=0.9945218953682733 sin85=0.9961946980917455 sin86=0.9975640502598242 sin87=0.9986295347545738 sin88=0.9993908270190958 sin89=0.9998476951563913sin90=1cos1=0.9998476951563913 cos2=0.9993908270190958 cos3=0.9986295347545738 cos4=0.9975640502598242 cos5=0.9961946980917455 cos6=0.9945218953682733 cos7=0.992546151641322 cos8=0.9902680687415704 cos9=0.9876883405951378cos10=0.984807753012208 cos11=0.981627183447664 cos12=0.9781476007338057 cos13=0.9743700647852352 cos14=0.9702957262759965 cos15=0.9659258262890683 cos16=0.9612616959383189 cos17=0.9563047559630355 cos18=0.9510565162951535 cos19=0.9455185755993168 cos20=0.9396926207859084 cos21=0.9335804264972017 cos22=0.9271838545667874 cos23=0.9205048534524404 cos24=0.9135454576426009 cos25=0.9063077870366499 cos26=0.898794046299167 cos27=0.8910065241883679 cos28=0.882947592858927 cos29=0.8746197071393957 cos30=0.8660254037844387 cos31=0.8571673007021123 cos32=0.848048096156426 cos33=0.838670567945424cos34=0.8290375725550417 cos35=0.8191520442889918 cos36=0.8090169943749474cos37=0.7986355100472928 cos38=0.7880107536067219 cos39=0.7771459614569709cos40=0.766044443118978 cos41=0.754709580222772 cos42=0.7431448254773942cos43=0.7313537016191705 cos44=0.7193398003386512 cos45=0.7071067811865476cos46=0.6946583704589974 cos47=0.6819983600624985 cos48=0.6691306063588582cos49=0.6560590289905074 cos50=0.6427876096865394 cos51=0.6293203910498375cos52=0.6156614753256583 cos53=0.6018150231520484 cos54=0.5877852522924731cos55=0.5735764363510462 cos56=0.5591929034707468 cos57=0.5446390350150272cos58=0.5299192642332049 cos59=0.5150380749100544 cos60=0.5000000000000001cos61=0.4848096202463371 cos62=0.46947156278589086 cos63=0.4539904997395468 cos64=0.43837114678907746 cos65=0.42261826174069944 cos66=0.4067366430758004 cos67=0.3907311284892737 cos68=0.3746065934159122 cos69=0.35836794954530015 cos70=0.3420201433256688 cos71=0.32556815445715675 cos72=0.30901699437494745 cos73=0.29237170472273677 cos74=0.27563735581699916 cos75=0.25881904510252074 cos76=0.24192189559966767 cos77=0.22495105434386514 cos78=0.20791169081775923 cos79=0.19080899537654491 cos80=0.17364817766693041 cos81=0.15643446504023092 cos82=0.13917310096006546 cos83=0.12186934340514749 cos84=0.10452846326765346 cos85=0.08715574274765836 cos86=0.06975647374412523 cos87=0.052335956242943966 cos88=0.03489949670250108 cos89=0.0174524064372836cos90=0tan1=0.017455064928217585 tan2=0.03492076949174773 tan3=0.052407779283041196 tan4=0.06992681194351041 tan5=0.08748866352592401 tan6=0.10510423526567646tan7=0.1227845609029046 tan8=0.14054083470239145 tan9=0.15838444032453627 tan10=0.17632698070846497 tan11=0.19438030913771848 tan12=0.2125565616700221 tan13=0.2308681911255631 tan14=0.24932800284318068 tan15=0.2679491924311227 tan16=0.2867453857588079 tan17=0.30573068145866033 tan18=0.3249196962329063 tan19=0.34432761328966527 tan20=0.36397023426620234 tan21=0.3838640350354158 tan22=0.4040262258351568 tan23=0.4244748162096047 tan24=0.4452286853085361 tan25=0.4663076581549986 tan26=0.4877325885658614 tan27=0.5095254494944288 tan28=0.5317094316614788 tan29=0.554309051452769 tan30=0.5773502691896257 tan31=0.6008606190275604 tan32=0.6248693519093275 tan33=0.6494075931975104 tan34=0.6745085168424265 tan35=0.7002075382097097 tan36=0.7265425280053609 tan37=0.7535540501027942 tan38=0.7812856265067174 tan39=0.8097840331950072 tan40=0.8390996311772799 tan41=0.8692867378162267 tan42=0.9004040442978399 tan43=0.9325150861376618 tan44=0.9656887748070739 tan45=0.9999999999999999 tan46=1.0355303137905693 tan47=1.0723687100246826 tan48=1.1106125148291927 tan49=1.1503684072210092 tan50=1.19175359259421 tan51=1.234897156535051tan52=1.2799416321930785 tan53=1.3270448216204098 tan54=1.3763819204711733 tan55=1.4281480067421144 tan56=1.4825609685127403 tan57=1.5398649638145827 tan58=1.6003345290410506 tan59=1.6642794823505173 tan60=1.7320508075688767 tan61=1.8040477552714235 tan62=1.8807264653463318 tan63=1.9626105055051503 tan64=2.050303841579296 tan65=2.1445069205095586 tan66=2.246036773904215tan67=2.355852365823753 tan68=2.4750868534162946 tan69=2.6050890646938023 tan70=2.7474774194546216 tan71=2.904210877675822 tan72=3.0776835371752526tan73=3.2708526184841404 tan74=3.4874144438409087 tan75=3.7320508075688776 tan76=4.0107809335358455 tan77=4.331475874284153 tan78=4.704630109478456 tan79=5.144554015970307 tan80=5.671281819617707 tan81=6.313751514675041 tan82=7.115369722384207 tan83=8.144346427974593 tan84=9.514364454222587 tan85=11.43005230276132 tan86=14.300666256711942 tan87=19.08113668772816 tan88=28.636253282915515 tan89=57.289961630759144tan90=无取值。
三角函数公式大全表

三角函数公式大全表三角函数公式大全表:1、正弦函数:正弦函数的定义为:y = sin x这里x表示弧度,y表示正弦函数的值,取值范围为(-1, +1).2、余弦函数:余弦函数的定义为:y = cos x这里x表示弧度,y表示余弦函数的值,取值范围为(-1, +1).3、正割函数:正割函数的定义为:y = tan x这里x表示弧度,y表示正割函数的值,取值范围为(-∞,+∞).4、反正弦函数:反正弦函数的定义为:x = arcsin y这里x表示弧度,y表示反正弦函数的值,取值范围为(-1, +1).5、反余弦函数:反余弦函数的定义为:x = arccos y这里x表示弧度,y表示反余弦函数的值,取值范围为(-1, +1).6、反正割函数:反正割函数的定义为:x = arctan y这里x表示弧度,y表示反正割函数的值,取值范围为(-∞,+∞).7、双曲正弦函数:双曲正弦函数的定义为:y = sinh x这里x表示弧度,y表示双曲正弦函数的值,取值范围为(-∞,+∞).8、双曲余弦函数:双曲余弦函数的定义为:y = cosh x这里x表示弧度,y表示双曲余弦函数的值,取值范围为(1, +∞)9、双曲正割函数:双曲正割函数的定义为:y = tanh x这里x表示弧度,y表示双曲正割函数的值,取值范围为(-1,+1).10、反双曲正弦函数:反双曲正弦函数的定义为:x = arcsinh y这里x表示弧度,y表示反双曲正弦函数的值,取值范围为(-∞,+∞).11、反双曲余弦函数:反双曲余弦函数的定义为:x = arccosh y这里x表示弧度,y表示反双曲余弦函数的值,取值范围为(0, +∞).12、反双曲正割函数:反双曲正割函数的定义为:x = arctanh y这里x表示弧度,y表示反双曲正割函数的值,取值范围为(-1, +1).。
第11讲:三角函数的图像与性质期末高频考点突破

第11讲:三角函数的图像与性质期末高频考点突破高频考点梳理考点一.用五点法作正弦函数和余弦函数的简图正弦函数y =sin x ,x ∈[0,2π]的图象中,五个关键点是:(0,0),(π2,1),(π,0),(3π2,-1),(2π,0).余弦函数y =cos x ,x ∈[0,2π]的图象中,五个关键点是:(0,1),(π2,0),(π,-1),(3π2,0),(2π,1).考点二.正弦函数、余弦函数、正切函数的图象与性质π高频题型归纳题型一:正弦函数图象的应用1.(2022·湖南·高一期末)函数()()0.2sin log 02f x x x x π⎛⎫=->⎪⎝⎭的零点个数为( ) A .1 B .2 C .3 D .42.(2022·福建漳州·高一期末)已知函数()sin (0)f x x ωω=>在()0,π上恰有三个零点,则ω的取值范围为( )A .()2,3B .(]2,3C .()3,4D .(]3,43.(2021·江苏·常州高级中学高一期末)已知函数()21sin sin 4f x x a x =++在区间[]0,π上有4个不同的零点,则实数a 的取值范围是( ) A .514a -<<-B .21a -<<-C .2a <-或1a >-D .514a -<<-或1a >题型二:正弦三角函数的周期和奇偶性问题4.(2022·福建南平·高一期末)将函数π()sin(2)3f x x =+的图象向左平移(0)m m >个单位后得到的图象关于y轴对称,则正数m 的最小值是( )A .π12 B .π3C .5π12 D .5π6 5.(2022·广东揭阳·高一期末)函数()sin 2cos 1xf x x =-的部分图象大致为( )A .B .C .D .6.(2022·广东汕头·高一期末)关于函数()f x x =,下列说法正确的是( )A .()f x 最小值为0B .函数()f x 为奇函数C .函数()f x 是周期为π周期函数D .函数()f x 在区间173(,)72ππ--上单调递减 题型三:求正弦函数的单调区间7.(2022·江西·景德镇一中高一期末)以下四个函数中,在(0)π2,上为减函数,且以π为周期的偶函数为( )A .sin y x =B .cos 2y x =C .|tan |y x =D .cos y x =8.(2022·江西·横峰中学高一期末)函数()2sin 3f x x π⎛⎫=-- ⎪⎝⎭在区间( )上单调递增.A .0,2π⎛⎫⎪⎝⎭B .5,3ππ⎛⎫ ⎪⎝⎭C .23,32ππ⎛⎫ ⎪⎝⎭D .3,22ππ⎛⎫⎪⎝⎭9.(2022·广西柳州·高一期末)将函数()()2sin 203f x x πωω⎛⎫=-> ⎪⎝⎭的图象向左平移6πω个单位,得到函数()y g x =的图象,若()y g x =在0,4⎡⎤⎢⎥⎣⎦π上为增函数,则ω的最大值为( )A .1B .2C .3D .4题型四:余弦函数图象的应用10.(2022·黑龙江·大庆外国语学校高一期末)函数()cos lg f x x x =-零点的个数为( ) A .4B .3C .2D .011.(2021·山西·高一期末)若定义在R 上的奇函数()f x 在()0,∞+上单调递减,且π02f ⎛⎫-= ⎪⎝⎭,则下列取值范围中的每个x 都能使不等式πcos 02f x x ⎛⎫+⋅≥ ⎪⎝⎭成立的是( )A .[]π2π,--B .[]π,0-C .[]0,πD .π,2k x x k Z ⎧⎫=∈⎨⎬⎩⎭12.(2021·湖南·高一期末)函数||2()cos x x f x x⋅=,,22x ππ⎛⎫∈- ⎪⎝⎭的部分图象大致是( )A .B .C .D .题型五:余弦三角函数的周期和奇偶性问题13.(2022·河南开封·高一期末)将函数()cos f x A x ω=图象向右平移6π个单位得到函数()g x 的图象,已知()g x 的图象关于原点对称,则ω的最小正值为( )A .2B .3C .4D .614.(2022·山西运城·高一期末)下列函数中,同时满足:①在0,4π⎛⎫⎪⎝⎭上是增函数,①为奇函数,①最小正周期为π的函数是( ) A .tan 2y x =B .cos 2y x =C .sin y x =D .sin 2y x =15.(2022·河南·商丘市第一高级中学高一期末)将函数()πsin 2f x x ω⎛⎫=+ ⎪⎝⎭,0ω>且()01f =,下列说法错误的是( ) A .()f x 为偶函数B .π02f ⎛⎫-= ⎪⎝⎭C .若()f x 在π0,5⎡⎤⎢⎥⎣⎦上单调递减,则ω的最大值为9D .当5ω=时,()f x 在π0,2⎡⎤⎢⎥⎣⎦上有3个零点题型六:求余弦函数的单调区间16.(2022·广西桂林·高一期末)函数2cos 6y x π⎛⎫=+ ⎪⎝⎭的单调增区间为( )A .()2ππ,2π,Z k k k -∈B .()2π,2ππ,Z k k k +∈C .7ππ(2π,2π),Z 66k k k --∈ D .π5π(2π,2π),Z 66k k k -+∈17.(2022·陕西·宝鸡市陈仓区教育体育局教学研究室高一期末)已知函数()()sin 22f x x x R π⎛⎫=-∈ ⎪⎝⎭,下列结论错误的是( ) A .函数()f x 是偶函数 B .函数()f x 的最小正周期为π C .函数()f x 在区间π02⎡⎤⎢⎥⎣⎦,上单调递增D .函数()f x 的图象关于直线π4x =对称18.(2022·贵州·六盘水市第五中学高一期末)满足不等式2cos 10x +>成立的x 的取值集合为( )A .2222,33x k x k k ππππ⎧⎫-<<+∈⎨⎬⎩⎭Z B .22,33x k x k k ππππ⎧⎫-<<+∈⎨⎬⎩⎭ZC .422,33x k x k k ππππ⎧⎫+<<+∈⎨⎬⎩⎭ZD .522,66x k x k k ππππ⎧⎫-<<+∈⎨⎬⎩⎭Z题型七:正弦、余弦函数的最值(值域)19.(2022·北京平谷·高一期末)已知关于x 的方程2cos sin 20x x a -+=在02π⎛⎤⎥⎝⎦,内有解,那么实数a 的取值范围( )A .58a -≤B .102a -≤≤C .1122a -<≤D .12a -<≤020.(2022·新疆伊犁·高一期末)已知函数()sin cos sin cos f x x x x x =-++,下列结论中错误的是( ) A .函数图像关于直线34x π=对称 B .在区间3,44ππ⎡⎤-⎢⎥⎣⎦上是增函数C .函数是周期函数,最小正周期是2πD .函数的值域是⎡⎤⎣⎦21.(2022·河南·信阳高中高一期末(文))已知函数()2sin 4sin 9sin 2x x f x x -+=-,则函数()f x ( )A .有最小值B .有最大值-C .有最大值92-D .没有最值题型八:正切函数的图像和性质22.(2022·广西梧州·高一期末)在(0,π)内,使tan x >x 的取值范围为( ) A .(3π,2π) B .20,,23πππ⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭C .20,,223πππ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭D .20,3π⎛⎫⎪⎝⎭23.(2022·陕西西安·高一期末)下列关于函数tan 23y x π⎛⎫=-+ ⎪⎝⎭的说法正确的是( )A .最小正周期为πB .图像关于点5,012π⎛⎫⎪⎝⎭成中心对称C .在区间,312ππ⎛⎫-- ⎪⎝⎭上单调递增D .图像关于直线12x π=-成轴对称24.(2022·陕西汉中·高一期末)已知函数()tan 24f x x π⎛⎫=- ⎪⎝⎭,下列说法正确的有( )①函数()f x 最小正周期为2π;①定义域为|R,,Z 28k x x x k ππ⎧⎫∈≠+∈⎨⎬⎩⎭①()f x 图象的所有对称中心为,0,Z 48k k ππ⎛⎫+∈ ⎪⎝⎭;①函数()f x 的单调递增区间为3,,Z 2828k k k ππππ⎛⎫-+∈ ⎪⎝⎭. A .1个 B .2个 C .3个D .4个25.(2022·贵州六盘水·高一期末)已知函数π()sin()(0,0,||)2f x A x A ωϕωϕ=+>><的部分图象如图所示.(1)求函数()f x 的解析式;(2)将函数y x =图象上所有点的横坐标缩短到原来的12,纵坐标不变,再向右平移π3个单位长度,得到函数()h x 的图象.当π0,2x ⎡⎤∈⎢⎥⎣⎦时,求函数()()()F x f x h x =-的最值.26.(2022·安徽·涡阳县第九中学高一期末)已知函数()222cos sin 2f x x x =-+.(1)求函数()f x 的最大值;(2)把()y f x =的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把得到的图象向左平移π3个单位,得到函数()y g x =的图象,求函数()g x 的单调递减区间27.(2022·四川泸州·高一期末)已知函数()()sin (0,0π)f x x ωϕωϕ=+><<的部分图象如图所示.(1)求函数()f x 的解析式;(2)设函数()2π2cos 6g x x x ⎛⎫=-+ ⎪⎝⎭,求使()2g x ≥成立的x 的取值集合.参考答案:1.C【分析】由()0f x =得0.2sin =log 2x x π⎛⎫⎪⎝⎭,再在同一坐标系下画出函数0.2sin log 2y x y x π⎛⎫== ⎪⎝⎭,的图像,观察函数的图像即得解.【详解】解:令()0f x =得0.2sin =log 2x x π⎛⎫⎪⎝⎭, 在同一直角坐标系内画出函数sin 2y x π⎛⎫=⎪⎝⎭和()0.2log 0y x x =>的图象,由图象知,两函数的图象恰有3个交点,即函数()f x 有3个零点, 故选:C.2.D【分析】根据题意,将原问题转化为函数sin y x =在区间()0,ωπ上恰有三个零点,根据正弦函数的性质,即可求出结果.【详解】因为(),00,x πω>∈,所以()0,x ωπω∈,又函数()sin (0)f x x ωω=>在()0,π上恰有三个零点,等价于函数sin y x =在区间()0,ωπ上恰有三个零点, 由正弦函数的性质可知,34πωππ<≤, 所以34ω<≤,即ω的取值范围为(]3,4. 故选:D. 3.A【分析】令sin t x =,分析可知函数()214g t t at =++在[)0,1上有两个不同的零点,根据二次函数的零点分布可得出关于实数a 的不等式组,由此可解得实数a 的取值范围.【详解】①()21sin sin 4f x x a =++,令sin t x =,[]0,1t ∈,令()214g t t at =++,如下图所示:要使得函数()f x 在[]0,π上有4个零点,则函数()214g t t at =++在[)0,1t ∈上有2个不同的零点,显然()1004g =≠,所以,()2Δ100125104a a g a ⎧⎪=->⎪⎪<-<⎨⎪⎪=+>⎪⎩,解得514a -<<-.故选:A. 4.A【分析】图象关于y 轴对称,则其为偶函数,根据三角函数的奇偶性即可求解.【详解】将()sin 23f x x π⎛⎫ ⎪⎝⎭=+的图象向左平移()0m m >个单位后得到()sin 2sin 2233y x m x m ππ⎡⎤⎛⎫ ⎪⎢⎥⎣⎦⎝⎭=++=++,此时图象关于y 轴对称,则232m k k Z πππ∈+=+,,则212k m ππ=+,0m ∴>,当0k =时,m 取得最小值12π, 故选:A. 5.A【分析】先判断奇偶性,再取特殊点得出答案.【详解】①()sin 2cos 1xf x x =-,由cos 10x -≠,所以()f x 的定义域为{|2,Z}x x k k π≠∈, 函数()f x 的定义域关于原点对称,且sin 2()()cos 1xf x f x x --==--,故函数()f x 是奇函数,则排除B ,又()sin 210cos11f =<-,则排除CD. 故选:A. 6.D【分析】根据三角函数的性质,得到()f x的最小值为,可判定A 不正确;根据奇偶性的定义和三角函数的奇偶性,可判定C 不正确;举例可判定C 不正确;根据三角函数的单调性,可判定D 正确. 【详解】由题意,函数(),0,0x x f x x x x ≥==<⎪⎩, 当0x ≥时,可得1sin 1x -≤≤,所以x ≤ 当0x <时,可得1sin 1x -≤≤,所以x ≤≤ 所以函数()f x的最小值为A 不正确;又由()()f x x x f x --==,所以函数()f x 为偶函数,所以B 不正确;因为()144f ππ==,())144f ππππ++=-,所以()()44f f πππ≠+,所以π不是()f x 的周期,所以C 不正确;当0x <时,()f x x =,22,22k x k k Z ππππ-+≤≤+∈,当1k =-时,5322x ππ-≤≤-,即函数()f x 在区间53[,]22ππ--上单调递减, 又因为17353(,)[,]7222ππππ--⊆--,所以函数()f x 在区间173(,)72ππ--上单调递减, 所以D 正确.故选:D. 7.B【分析】根据常见函数的奇偶性,单调性以及周期即可求解.【详解】对A ,最小正周期为2π,且在(0)π2,上为增函数,并为奇函数,不满足要求;对B ,在(0)π2,上为减函数,且以π为周期的偶函数,符合要求;对C ,在(0)π2,上为增函数,且为偶函数,不符合要求;对D,在(0)π2,上为减函数,但是以2π为周期的偶函数,不符合要求;故选:B 8.B【分析】根据正弦函数的单调性逐一代入检验即可得出答案.【详解】解:对于A ,当0,2x π⎛⎫∈ ⎪⎝⎭时,,336x πππ⎛⎫-∈- ⎪⎝⎭,函数()f x 单调递减,故A 不符题意;对于B ,当5,3x ππ⎛⎫∈ ⎪⎝⎭时,24,333x πππ⎛⎫-∈ ⎪⎝⎭,函数()f x 单调递增,故B 符合题意; 对于C ,当23,32x ππ⎛⎫∈ ⎪⎝⎭时,7,336x πππ⎛⎫-∈ ⎪⎝⎭,函数()f x 在23,32x ππ⎛⎫∈ ⎪⎝⎭不是单调函数,故C 不符合题意; 对于D ,当3,22x ππ⎛⎫∈ ⎪⎝⎭时,75,363x πππ⎛⎫-∈⎪⎝⎭,函数()f x 在3,22x ππ⎛⎫∈ ⎪⎝⎭上不是单调函数,故D 不符题意. 故选:B. 9.A【分析】函数()()2sin 203f x x πωω⎛⎫=-> ⎪⎝⎭的图象向左平移6πω个单位,得到函数yg x 的表达式,然后利用在0,4π⎡⎤⎢⎥⎣⎦上为增函数,得到ω的最大值.【详解】函数()()2sin 203f x x πωω⎛⎫=-> ⎪⎝⎭的图象向左平移6πω个单位,得到函数()2sin 22sin 263y g x x x πωωπω⎡⎤⎛⎫==+-= ⎪⎢⎥⎝⎭⎣⎦,若0,4x π⎡⎤∈⎢⎥⎣⎦,则022,πx ωω⎡⎤∈⎢⎥⎣⎦,所以π22ωπ≤,即1ω≤, 所以ω的最大值为1.故选:A. 10.A【分析】由()cos lg 0f x x x =-=,得cos lg x x =,则将函数()f x 零点的个数转化为cos ,lg y x y x ==图象的交点的个数,画出两函数的图象求解即可 【详解】由()cos lg 0f x x x =-=,得cos lg x x =,所以函数()f x 零点的个数等于cos ,lg y x y x ==图象的交点的个数, 函数cos ,lg y x y x ==的图象如图所示,由图象可知两函数图象有4个交点, 所以()f x 有4个零点, 故选:A 11.B【分析】先根据奇函数性质判断函数的单调性和值的正负分布,得到()f x 草图,结合平移得到函数π2f x ⎛⎫+ ⎪⎝⎭的大致草图,再结合余弦函数图象逐一判断四个选项是否恒成立即可. 【详解】由题意可知,奇函数()f x 在()0,∞+上单调递减,且π02f ⎛⎫-= ⎪⎝⎭,则()f x 在(),0∞-上单调递减,且π02f ⎛⎫= ⎪⎝⎭, ()00f =,所以可画出大致草图,而π2f x ⎛⎫+ ⎪⎝⎭可看作()f x 的图象向左平移π2个单位,所以可在同一坐标系中作出π2f x ⎛⎫+ ⎪⎝⎭草图和余弦函数的图象,当3π,2πx ⎡⎤∈--⎢⎥⎣⎦时,满足π0,cos 02f x x ⎛⎫+≥≤ ⎪⎝⎭,即πcos 02f x x ⎛⎫+⋅≤ ⎪⎝⎭,A 不正确; 当ππ,2x ⎡⎤∈--⎢⎥⎣⎦时,满足π0,cos 02f x x ⎛⎫+≤≤ ⎪⎝⎭,即πcos 02f x x ⎛⎫+⋅≥ ⎪⎝⎭, 当π,02x ⎛⎤∈- ⎥⎝⎦时,满足π0,cos 02f x x ⎛⎫+≥> ⎪⎝⎭,即πcos 02f x x ⎛⎫+⋅≥ ⎪⎝⎭, 即当[]π,0x ∈-时,满足πcos 02f x x ⎛⎫+⋅≥ ⎪⎝⎭恒成立,即B 正确; 当π0,2x ⎡⎤∈⎢⎥⎣⎦时,满足π0,cos 02f x x ⎛⎫+≤≥ ⎪⎝⎭,即πcos 02f x x ⎛⎫+⋅≤ ⎪⎝⎭,C 不正确; 当2πx =时,满足π0,cos 12f x x ⎛⎫+<= ⎪⎝⎭,即πcos 02f x x ⎛⎫+⋅< ⎪⎝⎭,D 不正确. 故选:B.12.A【分析】由解析式知()f x 是奇函数且0,2π⎛⎫ ⎪⎝⎭上单调增,即可判断函数图象. 【详解】由于()()()||||22()()cos cos x x x x f x f x x x-⋅-⋅--===-- 所以()f x 为奇函数,故排除B ,D ,而cos y x =,2x y =,y x =在(0,)2π上分别为减函数、增函数、增函数, 且函数值均为正数,所以()f x 在(0,)2π上为增函数, 故选:A13.B【分析】根据图象平移求出g (x )解析式,g (x )为奇函数,则g (0)=0,据此即可计算ω的取值.【详解】根据已知,可得()cos cos 66g x A x A x ππωωω⎛⎫⎛⎫=-=- ⎪ ⎪⎝⎭⎝⎭, ①()g x 的图象关于原点对称,所以()00g =,从而62k πωππ-=+,k ∈Z , 所以36k ω=--,其最小正值为3,此时1k =-.故选:B .14.D【分析】根据三角函数的图像和性质逐项分析即可求解.【详解】A 中tan 2y x =的最小正周期为2π,不满足;B 中cos 2y x =是偶函数,不满足;C 中sin y x =的最小正周期为2π,不满足;D 中sin 2y x =是奇函数﹐且周期22T ππ==,令22222k x k ππππ-+≤≤+,①44k x k ππππ-+≤≤+,①函数sin 2y x =的递增区间为,44k k ππππ⎡⎤-++⎢⎥⎣⎦,k ∈Z ,①函数sin 2y x =在0,4π⎛⎫ ⎪⎝⎭上是增函数,故D 正确. 故选:D.15.C【分析】先求得ω,然后结合函数的奇偶性、单调性、零点对选项进行分析,从而确定正确选项.【详解】()πππ0sin 1,2π,41,Z 222f k k k ωωω===+=+∈, ()()()ππsin 41sin 412π22f x k x k x k ⎡⎤⎛⎫⎡⎤=++=+++ ⎪⎢⎥⎢⎥⎝⎭⎣⎦⎣⎦ ()()πsin 41cos 412k x k x ⎡⎤=++=+⎡⎤⎣⎦⎢⎥⎣⎦, 所以()()f x f x -=,()f x 为偶函数,A 选项正确.()ππππcos 41cos 2π02222f f k k ⎛⎫⎛⎫⎡⎤⎛⎫-==+⨯=+= ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦⎝⎭,B 选项正确. ()()ππ0,0414155x k x k ≤≤≤+≤+⋅,若()f x 在π0,5⎡⎤⎢⎥⎣⎦上单调递减, 则()π41π5k +⋅≤,1k ≤, 由于410k ω=+>,所以1014k k >-⇒≤≤, 所以k 的最大值为1,ω的最大值为415+=,C 选项错误.当5ω=时,()cos5f x x =,π5π0,0522x x ≤≤≤≤,当π3π5π5,,222x =时,()0f x =,所以D 选项正确. 故选:C 16.C【分析】根据给定函数,利用余弦函数的单调性直接列式,求解作答. 【详解】由2ππ2π,Z 6k x k k π-≤+≤∈,解得2π2π,Z 66k x k k 7ππ-≤≤-∈, 所以所求函数的增区间为7ππ(2π,2π),Z 66k k k --∈. 故选:C 17.D 【分析】函数π()sin 2cos 22f x x x ⎛⎫=-=- ⎪⎝⎭,利用余弦函数的周期、奇偶性、对称轴,单调性求解. 【详解】对于函数π()sin 2cos 22f x x x ⎛⎫=-=- ⎪⎝⎭, 由于()cos(2)cos2()f x x x f x -=--=-=,故函数()f x 是偶函数,故A 正确;由()cos2f x x =-知,它的周期等于2ππ2=,故B 正确; 当π02x ⎡⎤∈⎢⎥⎣⎦,时,2[0,π]x ∈,所以()cos2f x x =-单调递增,故C 正确; 令π4x =,则ππ()cos 042f =-=,则π4x =不是()f x 的对称轴,故D 错误. 故选:D18.A【分析】先求出一个周期内不等式的解集,再结合余弦函数的周期性即可求解.【详解】解:由2cos 10x +>得:1cos 2x >- 当[],x ππ∈-时,2233x ππ-<< 因为cos y x =的周期为2π 所以不等式的解集为2222,33x k x k k ππππ⎧⎫-<<+∈⎨⎬⎩⎭Z 故选:A.19.C【分析】可得22sin sin 1a x x =+-在02π⎛⎤ ⎥⎝⎦,内有解,令sin t x =,利用二次函数的性质即可求出. 【详解】方程2cos sin 20x x a -+=在02π⎛⎤ ⎥⎝⎦,内有解,即222cos sin sin sin 1a x x x x =-+=+-在02π⎛⎤ ⎥⎝⎦,内有解, 令sin t x =,(]0,1t ∈,则(]22215sin sin 111,124y x x t t t ⎛⎫=+-=+-=+-∈- ⎪⎝⎭, 所以121a -<≤,解得1122a-<. 故选:C.20.B 【分析】先讨论sin cos y x x =+的正负值去绝对值,可将()f x 表达为分段函数,对A ,计算()32f x f x π⎛⎫-= ⎪⎝⎭即可判断;对BCD ,根据()f x的解析式判断即可 【详解】由题意,当sin cos 04y x x x π⎛⎫=+=+≥ ⎪⎝⎭,即()22Z 4k x k k ππππ≤+≤+∈,()322Z 44k x k k ππππ-≤≤+∈时,()sin cos sin cos 2sin f x x x x x x =-++=;当sin cos 04y x x x π⎛⎫=+=+< ⎪⎝⎭,即()3722Z 44k x k k ππππ+<<+∈时,()sin cos sin cos 2cos f x x x x x x =---=-.即()()()32sin ,22Z 44372cos ,22Z 44x k x k k f x x k x k k ππππππππ⎧-≤≤+∈⎪⎪=⎨⎪-+<<+∈⎪⎩ 对A ,因为33333sin cos sin cos 22222f x x x x x πππππ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫-=---+-+- ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭()cos sin cos sin x x x x f x =-++--=,故函数图像关于直线34x π=对称,故A 正确; 对B ,当3,44x ππ⎡⎤∈-⎢⎥⎣⎦时,()2sin f x x =,在,42x ππ⎡⎤∈-⎢⎥⎣⎦上为增函数,在3,42x ππ⎡⎤∈⎢⎥⎣⎦上为减函数,故B 错误;对C ,由()f x 的解析式可得,最小正周期为7244πππ⎛⎫--= ⎪⎝⎭,故C 正确; 对D ,根据()f x 的解析式可得,当22x k ππ=+与2x k ππ=+时,()f x 取得最大值2,当24x k ππ=-时,()f x取得最小值, 故D 正确;故选:B21.B【分析】换元法后用基本不等式进行求解.【详解】令[]sin 1,1t x =∈-,则()()()22254952222t t t f x g t t t t t -+-+====-+---,因为20t ->,502t >-,故()()522g t t t ⎡⎤=--+≤-=-⎢⎥-⎣⎦当且仅当522t t-=-,即2t =()f x 有最大值- 由对勾函数的性质可得函数()()min 16g t g ==-,即()f x 有最小值6-.故选:B22.B【分析】画出(0π)y tanx x =<<和直线y =.【详解】画出(0π)y tanx x =<<和直线y =由图象可得tanx >,在()0,π上解集为20,,23πππ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭, 故选B. 【点睛】本题考查利用正切函数的图象解不等式,关键是掌握正切函数的图像和性质,利用数形结合思想求解.23.B【分析】根据函数tan(2)tan(2)33y x x ππ=-+=--,结合正切函数的图象与性质,对选项中的命题判断正误即可.【详解】解:函数tan(2)tan(2)33y x x ππ=-+=--, 当512x π=时,521232πππ⨯-=,所以图象关于点5,012π⎛⎫ ⎪⎝⎭成中心对称,选项B 正确; 函数的最小正周期为2T π=,所以A 错误; 当,312x ππ⎛-∈⎫- ⎪⎝⎭时,2,32x πππ⎛⎫-∈-- ⎪⎝⎭,所以函数在,312ππ⎛⎫-- ⎪⎝⎭上单调递减,所以C 错误; 正切函数不是轴对称函数,所以D 错误.故选:B .24.C【分析】根据正切函数的图象与性质,代入周期、定义域、对称中心和单调递增期间的公式即可求解.【详解】对①,函数()tan 24f x x π⎛⎫=- ⎪⎝⎭,可得()f x 的最小正周期为2T π=,所以①正确; 对①,令2,Z 42x k k πππ-≠+∈,解得3,Z 82k x k ππ≠+∈, 即函数()f x 的定义域为3{|,Z}82k x x k ππ≠+∈,所以①错误; 对①,令2,Z 42k x k ππ-=∈,解得,Z 84k x k ππ=+∈,所以函数()f x 的图象关于点,0,Z 48k k ππ⎛⎫+∈ ⎪⎝⎭对称,所以①正确;对①,令2,Z 242k x k k πππππ-<-<+∈,解得3,Z 2828k k x k ππππ-<<+∈,故函数()f x 的单调递增区间为3,,Z 2828k k k ππππ⎛⎫-+∈ ⎪⎝⎭,所以①正确; 故①①①正确;故选:C50.(1)()πsin 23f x x ⎛⎫=+ ⎪⎝⎭ (2)2-【分析】(1)根据图象依次求得,,A ωϕ的值.(2)根据图象变换的知识求得()h x ,化简()F x 的解析式,根据三角函数最值的求法求得正确答案.【详解】(1)由图可知1A =,7πππ2π,π,241234T T ωω=-====,()()sin 2f x x ϕ=+,7π7πsin 1126f ϕ⎛⎫⎛⎫=+=- ⎪ ⎪⎝⎭⎝⎭, ππ2π7π5π,22363ϕϕ-<<<+<,所以7π3ππ,623ϕϕ+==, 所以()πsin 23f x x ⎛⎫=+ ⎪⎝⎭.(2)函数y x =图象上所有点的横坐标缩短到原来的12,纵坐标不变,得到2y x =,再向右平移π3个单位长度,得到()π2π2233h x x x ⎡⎤⎛⎫⎛⎫=-- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦, π2π()()()sin 2233F x f x h x x x ⎛⎫⎛⎫=-=+- ⎪ ⎪⎝⎭⎝⎭ ππsin 22π33x x ⎛⎫⎛⎫=++- ⎪ ⎪⎝⎭⎝⎭ ππsin 2233x x ⎛⎫⎛⎫=++ ⎪ ⎪⎝⎭⎝⎭ ππ2π2sin 22sin 2333x x ⎛⎫⎛⎫=++=+ ⎪ ⎪⎝⎭⎝⎭, π0,2x ⎡⎤∈⎢⎥⎣⎦,2π2π5π2,333x ⎡⎤+∈⎢⎥⎣⎦,所以2π2πsin 2,2sin 233x x ⎡⎛⎫⎛⎫⎡+∈-+∈-⎢ ⎪ ⎪⎣⎝⎭⎝⎭⎣⎦, 所以()f x 在区间π0,2⎡⎤⎢⎥⎣⎦2-. 51.(1)4; (2)π2π2π,2π33k k ⎛⎫-+ ⎪⎝⎭,k ∈Z .【分析】(1)根据降幂公式,结合余弦函数的最值性质进行求解即可; (2)根据余弦型函数图象的变换性质,结合余弦型函数的单调性进行求解即可.【详解】(1)()221cos 2352cos sin 21cos 22cos 2222x f x x x x x -=-+=+-+=+ ①当cos21x =时()f x 取得最大值4;(2)因为把()y f x =的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把得到的图象向左平移π3个单位,得到函数()y g x =的图象, 所以()3π5cos 232g x x ⎛⎫=++ ⎪⎝⎭, 令π2π2ππ(Z)3k x k k ≤+≤+∈,可得函数()g x 的单调递减区间为π2π2π,2π33k k ⎛⎫-+ ⎪⎝⎭,Z k ∈. 52.(1)()πsin 23f x x ⎛⎫=+ ⎪⎝⎭;(2)()ππ,π3k k k ⎡⎤+∈⎢⎥⎣⎦Z .【分析】(1)根据图象先求出周期可得ω,再由特殊点可得ϕ; (2)由三角恒等变换化简出()g x ,解正弦型三角不等式即可得解.(1) 由已知得3π5π3π43124T ⎛⎫=--= ⎪⎝⎭, 所以πT =,所以2π2Tω==, 又因为πππ55sin 1,0126f ϕϕ⎛⎫⎛⎫-=-+=-<< ⎪ ⎪⎝⎭⎝⎭, 所以π3ϕ=,因此()πsin 23f x x ⎛⎫=+ ⎪⎝⎭. (2)因为函数()22cos 6g x x x π⎛⎫=-+ ⎪⎝⎭,222cos 63x x ππ⎡⎤⎛⎫=-++ ⎪⎢⎥⎝⎭⎣⎦cos212sin 216x x x π⎛⎫=++=++ ⎪⎝⎭, 因为()2g x ≥,则1sin 262x π⎛⎫+≥ ⎪⎝⎭, 所以ππ5π2π22π666k x k +≤+≤+, 故πππ,Z 3k x k k ≤≤+∈, 所以符合条件的x 的取值集合为()ππ,π3k k k ⎡⎤+∈⎢⎥⎣⎦Z .。
第11讲 三角函数专题训练

第11讲 三角函数【学习目标】1.掌握直角三角形边角关系和三角函数的定义,发展几何直观; 2.掌握30°,45°,60°这些特殊角的三角函数值;3.能用三角函数解决实际问题,发展应用意识.【学习重难点】锐角三角函数的定义、特殊角的三角函数值、解直角三角形的应用.考点1:三角函数的相关基础知识 知识点与方法技巧梳理:(1)正弦:sin A =∠A 的___边___边=(2)余弦:cos A =∠A 的___边___边=(3)正切:tan A =∠A 的___边∠A 的___边=锐角A 的正弦、余弦和正切都是∠A 的三角函数.正切也经常用来描述山坡的坡度.例如,有一山坡在水平方向上每前进100 m 就升高50m ,那么山坡的坡度就是tan α=50100=12. 【例】在△ABC 中,AB =AC ,AD ⊥BC 于D ,AD =5,BC =24,求tan C 和cos ∠BAD .【变式1】在Rt △ABC 中,∠C =90°,AB =6,BC =2,求sin A 和tan B .【变式2】在Rt △ABC 中,∠C =90°,BC =4,tan A =34,求AB 的长.【变式3】在Rt △ABC 中,∠B =90°,AC =25,cos A =0.8,求BC 的长.【变式4】在Rt △ABC 中,∠C =90°,cos A =1517,AC =10,求AB 的长和tan B 的值.【变式5】某人从山脚下的点A走了300m后到达山顶的点B,已知点B到山脚的垂直距离为75m,求山的坡度.考点2:30°,45°,60°角的三角函数值知识点与方法技巧梳理:【例】计算:(1)cos30°-tan60°(2)6tan230°-3sin60°-2cos45°【变式】计算:(1)cos30sin45sin60cos45︒-︒︒-︒(2)3cos245°-sin30°tan60°+12sin60°考点3:解直角三角形知识点与方法技巧梳理:在直角三角形的6个元素中,直角是已知元素,如果再知道一条边和第三个元素,这个三角形的所有元素就可以确定下来.【例】在Rt△ABC中,∠C为直角,∠A,∠B,∠C所对的边分别为a,b,c,且a=2,c=10,求这个三角形的其他元素.【变式1】在Rt△ABC中,∠C=90°,a=2,b=6,求这个三角形的其他元素.【变式2】在Rt△ABC中,∠C=90°,∠B=30°,a=6,求这个三角形的其他几个元素.考点4:三角函数的应用 知识点与方法技巧梳理:仰角和俯角:在利用测角仪观察目标时,视线在水平线上方和水平线的夹角称为仰角,视线在水平线下方和水平线的夹角称为俯角(如图所示)【例】如图,在一次数学课外实践活动中,要求测教学楼的高度AB .小刚在D 处用高1.5m 的测角仪CD ,测得教学楼顶端A 的仰角为30°,然后向教学楼前进40m 到达E ,又测得教学楼顶端A 的仰角为60°.求这幢教学楼的高度AB .【变式1】如图,两建筑物的水平距离BC 为30m ,从A 点测得D 点的俯角α为35°,测得C 点的俯角β为45°,求这两座建筑物的高度.(tan35°=0.7)【变式2】如图,在一次夏令营活动中,小明从营地A 出发,沿北偏东60°方向走了5003m 到达B 点,然后再沿北偏西30°方向走了500m 到达目的地C 点. (1)求A 、C 两地之间的距离;(2)确定目的地C 在营地A 的什么方向.【能力提升】 1.(2014孝感)如图,在□ABCD 中,对角线AC 、BD 相交成的锐角为α,若AC =a ,BD =b ,则□ABCD 的面积是( )A .12ab sinαB .ab sinαC .ab cosαD .12ab cosα2.如图,SO 是等腰三角形SAB 的高,已知∠ASB =120°,AB =54,则SO 的长为__________. 3.(2016临沂)如图,△ABC 中,cos B =22,sin C =35,AC =5,则△ABC 的面积是__________. 4.在Rt △ABC 中,∠BCA =90°,CD 是AB 边上的中线,BC =8,CD =5,求sin ∠ACD ,cos ∠ACD 和tan∠ACD .5.在△ABC 中,AB =AC =5,BC =6,求sin B ,cos B ,tan B . 6.某阶梯的形状如图所示,其中线段AB =BC ,AB 部分的坡角为45°,BC 部分的坡角为30°,AD =1.5m .如果每个台阶的高不超过20cm ,那么这一阶梯至少有多少个台阶?(最后一个台阶的高不足20cm 时,按一个台阶计算)7.(2016陇南)如图,小山顶上有一信号塔AB ,山坡BC 的倾角为30°,现为了测量塔高AB ,测量人员选择山脚C 处为一测量点,测得塔顶仰角为45°,然后顺山坡向上行走100米到达E 处,再测得塔顶仰角为60°,求塔高AB .8.一副直角三角板如图放置,点C在FD的延长线上,AB∥FC,∠F=∠ACB=90°,∠E=30°,∠A=45°,AC=122,求CD的长.9.如图,已知斜坡AB长为60米,坡角(即∠BAC)为30°,BC⊥AC,现计划在斜坡中点D处挖去部分坡体(图中阴影部分)修建一个平行于水平线CA的平台DE和一条新的斜坡BE.(1)若修建的斜坡BE的坡角(即∠BEF)不大于45°,则平台ED的长最大为_________米;(2)一座建筑物GH距离坡角A点27米远(即AG=27米),小明在D点测得建筑物顶部H的仰角(即∠HDM)为30°,点C、A、G在同一条直线上,且HG⊥CG,问建筑物GH高为多少米?(结果都精确到0.1米,参考数据:3≈1.732)10.(本小题满分8分)北京时间2015年04月25日14时11分,尼泊尔发生8.1级强烈地震,我国积极组织抢险队赴地震灾区参与抢险工作.如图9,某探测队在地面A、B两处均探测出建筑物下方C处有生命迹象,已知探测线与地面的夹角分别是25°和60°,且AB=4米,求该生命迹象所在位置C的深度.(结果精确到1米.参考数据:sin25°≈0.4,cos25°≈0.9,tan25°≈0.5 1.7)【家庭作业】1(2014滨州)在Rt △ACB 中,∠C =90°,AB =10,tan A =34,则BC 的长为( )A .6B .7.5C .8D .12.52.某商场有一自动扶梯,其倾斜角为30°,高为4m ,则扶梯的长度是__________m .3.一个人由山底爬到山顶,需先爬坡度为30°的山坡100m ,再爬坡度为45°的山坡300m ,则山高为______________.(结果保留根号) 4.(2014新疆)如图,在Rt △ABC 中,∠C =90°,∠B =37°,BC =32,则AC =__________.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)5.(2014济宁)如图,在△ABC 中,∠A =30°,∠B =45°,AC =23,则AB 的长为__________.6.(2014重庆)如图,△ABC 中,AD ⊥BC 于D ,若BC =14,AD =12,tan ∠BAD =34,则sin C 的值为_______.7.如图,登山缆车从点A 出发,途经点B 后到达终点C .其中AB 段的运行路程为200m ,BC 段的运行路程为250m ,且AB 段的运行路线与水平面的夹角为30°,BC 段的运行路线与水平面的夹角为37°,求缆车从点A 运行到点C 的垂直上升的距离.(参考数据:tan37°≈0.75)8.为了维护海洋权益,国家海洋局加强了海洋巡逻力度.如图,一艘海监船位于灯塔P 的南偏东45°方向,距离灯塔100海里的A 处,沿正北方向航行一段时间后,到达位于灯塔P 的北偏东30°方向上的B 处. (1)在这段时间内,海监船与灯塔P 的最近距离是多少?(结果保留根号) (2)在这段时间内,海监船航行了多少海里?(结果保留根号)。
11三角函数的诱导公式(二)学案

学习课题:三角函数的诱导公式 日期:2014.2.4三角函数的诱导公式(二)学习目标:1.经历诱导公式五、六的推导过程,体会数学知识的“发现”过程。
2.掌握诱导公式五、六,能初步应用公式解决一些简单的问题。
3.领会数学中转化思想的广泛性,了解诱导公式就是具有一定关系的几何特征关系的代数表示,从而对诱导公式能够达到属性结合的认识高度。
学习重点、难点:重点:诱导公式五、六的推导探究,诱导公式的应用。
难点:发现终边与角α的终边关于直线y x =对称的角与α之间的数量关系。
学习过程:(一)复习(预习教材P26-27,找出疑惑之处,并作记号)回顾旧知,引出新课 上节课我们学习了三角函数的诱导公式二到公式四,大家还记得是哪几个公式吗? 回顾三角函数的诱导公式二到公式四,这几个公式分别体现了角α与角πα+、α-、πα-之间的关系,公式二: 公式三: 公式四: sin()cos()tan()παπαπα+=+=+= sin()cos()tan()ααα-=-=-= sin()cos()tan()παπαπα-=-=-=(二)探究新知:1、诱导公式五:问题1:你能画出角α问题2:的角(终边与单位圆交于点2)可以表示为 问题 3::如图单位圆中,假设点1p 的坐标为()y x ,,你能说出2p 的坐标吗?请用三角函数的定义写出角απ-2的三角函数(诱导公式五):=⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-απαπ2cos 2sin 预习检测1:1、化简1)⎪⎭⎫⎝⎛-βπ25sin 2) )27cos(απ-学习课题:三角函数的诱导公式 日期:2014.2.42、证明:ααπcos 23sin )1-=⎪⎭⎫ ⎝⎛- ααπsin 23cos )2-=⎪⎭⎫ ⎝⎛- 证:2、诱导公式六: 思考:同学们,角2πα+与角α又有怎样的关系呢?你仍然是画图研究吗,还是用已学的公式来探究呢?请试着写出你的推导诱导公式六过程:所以得到公式六:sin()cos 2cos()sin 2πααπαα+=+=-观察可得记忆口诀:把α看成锐角,函数名奇变偶不变,符号看象限。
重难点11 三角函数的图像与性质—2023年高考数学(原卷版)

重难点11 三角函数的图像与性质1.三角函数定义域的求法①以正切函数为例,应用正切函数y =tan x 的定义域求函数y =A tan(ωx +φ)的定义域. ②求复杂函数的定义域转化为求解简单的三角不等式. (2)简单三角不等式的解法 ①利用三角函数线求解. ②利用三角函数的图象求解.2.求解三角函数的值域(最值)常见到以下几种类型:(1)形如y =a sin x +b cos x +c 的三角函数化为y =A sin(ωx +φ)+c 的形式,再求值域(最值); (2)形如y =a sin 2x +b sin x +c 的三角函数,可先设sin x =t ,化为关于t 的二次函数求值域(最值);(3)形如y =a sin x cos x +b (sin x ±cos x )+c 的三角函数,可先设t =sin x ±cos x ,化为关于t 的二次函数求值域(最值).3.函数y =Asin(ωx +φ)(A>0,ω>0)的图象的两种作法五点法设z =ωx +φ,由z 取0,π2,π,32π,2π来求出相应的x ,通过列表,计算得出五点坐标,描点后得出图象图象变 换法由函数y =sin x 的图象通过变换得到y =A sin(ωx +φ)的图象,有两种主要途径“先平移后伸缩”与“先伸缩后平移”多少值.4.确定y =Asin(ωx +φ)+b(A >0,ω>0)的步骤和方法(1)求A ,b ,确定函数的最大值M 和最小值m , 则A =M -m 2,b =M +m2. (2)求ω,确定函数的最小正周期T ,则可得ω=2πT .(3)求φ,常用的方法有:①代入法:把图象上的一个已知点代入(此时A ,ω,b 已知)或代入图象与直线y =b 的交点求解(此时要注意交点在上升区间上还是在下降区间上);②特殊点法:确定φ值时,往往以寻找“最值点”为突破口.具体如下:“最大值点”(即图象的“峰点”)时ωx +φ =π2+2k π(k ∈Z );“最小值点”(即图象的“谷点”)时ωx +φ=3π2+2k π(k ∈Z ).2023年高考仍将重点考查三角函数的图像与性质及三角函数变换,特别是这些知识点的组合考查是考查的热点,题型仍为选择题或填空题,难度可以为基础题或中档题,也可以是压轴题.(建议用时:40分钟)一、单选题1.为了得到函数2sin3y x =的图象,只要把函数π2sin 35y x ⎛⎫=+ ⎪⎝⎭图象上所有的点( )A .向左平移π5个单位长度B .向右平移π5个单位长度C .向左平移π15个单位长度 D .向右平移π15个单位长度 2.函数ππ4sin 33cos 344y x x ⎛⎫⎛⎫=+++ ⎪ ⎪⎝⎭⎝⎭的最小正周期是( )A .6πB .2πC .2π3 D .π33.函数()cos cos 2f x x x =-是( ) A .奇函数,且最大值为2B .偶函数,且最大值为2C .奇函数,且最大值为98D .偶函数,且最大值为984.函数f (x )=sin x 3x (x ∈[﹣π,0])的单调递增区间是( ) A .[﹣π,﹣56π] B .[﹣56π,﹣6π] C .[﹣3π,0] D .[﹣6π,0] 5.将函数π()sin (0)3f x x ωω⎛⎫=+> ⎪⎝⎭的图像向左平移π2个单位长度后得到曲线C ,若C 关于y 轴对称,则ω的最小值是( ) A .16B .14C .13D .126.为得到函数cos 23y x π⎛⎫=+ ⎪⎝⎭的图象,只需将sin 2y x =的图象( )A .向左平移512π个单位长度 B .向右平移512π个单位长度 C .向左平移56π个单位长度 D .向右平移56π个单位长度 7.下列函数中,图象的一部分如图所示的是( )A .sin 6y x π⎛⎫=+ ⎪⎝⎭B .sin 26y x π⎛⎫=- ⎪⎝⎭C .cos 43y x π⎛⎫=- ⎪⎝⎭D .cos 26y x π⎛⎫=- ⎪⎝⎭8.设函数π()sin 3f x x ω⎛⎫=+ ⎪⎝⎭在区间(0,π)恰有三个极值点、两个零点,则ω的取值范围是( ) A .513,36⎫⎡⎪⎢⎣⎭B .519,36⎡⎫⎪⎢⎣⎭C .138,63⎛⎤ ⎥⎝⎦D .1319,66⎛⎤ ⎥⎝⎦9.将函数sin(2)5y x π=+的图象向右平移10π个单位长度,所得图象对应的函数( ) A .在区间35[,]44ππ上单调递增 B .在区间3[,]4ππ上单调递减 C .在区间53[,]42ππ上单调递增 D .在区间3[,2]2ππ上单调递减 10.下列函数中,以2π为周期且在区间(4π,2π)单调递增的是( ) A .f (x )=│cos 2x │ B .f (x )=│sin 2x │ C .f (x )=cos│x │D .f (x )= sin│x │11.设函数f (x )=cos (x +3π),则下列结论错误的是( ) A .f (x )的一个周期为−2π B .f (x )的图像关于直线x=83π对称 C .f (x +π)的一个零点为x=6π D .f (x )在(2π,π)单调递减 12.已知1()sin 22f x x =,关于该函数有下列四个说法:①()f x 的最小正周期为2π;②()f x 在ππ[,]44-上单调递增;③当ππ,63x ⎡⎤∈-⎢⎥⎣⎦时,()f x 的取值范围为33,44⎡⎤-⎢⎥⎣⎦; ④()f x 的图象可由1πg()sin(2)24x x =+的图象向左平移π8个单位长度得到.以上四个说法中,正确的个数为( ) A .1B .2C .3D .4题号 1 2 3 4 5 6 7 8 9 10 11 12 答案二、填空题13.记函数()()cos (0,0π)f x x ωϕωϕ=+><<的最小正周期为T ,若3()2f T =,9x π=为()f x 的零点,则ω的最小值为____________.14.函数()sin 3cos f x x x =+在区间02π⎡⎤⎢⎥⎣⎦,上的最小值为__________.15.已知函数()()2cos f x x ωϕ=+的部分图像如图所示,则2f π⎛⎫= ⎪⎝⎭_______________.16.关于函数f (x )=1sin sin x x+有如下四个命题: ①f (x )的图象关于y 轴对称. ②f (x )的图象关于原点对称. ③f (x )的图象关于直线x =2π对称. ④f (x )的最小值为2.其中所有真命题的序号是__________. 三、解答题17.已知函数22()sin 3cos 2cos ,f x x x x x x =+∈R .(1)求函数()f x 的最小正周期和严格增区间;(2)函数()f x 图像可以由函数sin2()y x x =∈R 的图象经过怎样的变换得到?18.设函数()sin()sin()62f x x x ππωω=-+-,其中03ω<<.已知()06f π=.(1)求ω;(2)将函数()y f x =的图象上各点的横坐标伸长为原来的2倍(纵坐标不变),再将得到的图象向左平移4π个单位,得到函数()y g x =的图象,求()g x 在3[,]44ππ-上的最小值.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
c 2 +θ
1 2 r θ 2 c 2θ = = 2θ 2 + 8θ + 8
8
c2 c2 c2 ≤ = 8 16 2θ + + 8 2 2θ ⋅ 8 + 8
θ
θ
θ 3.若角 θ 的终边与函数 y=-2|x|的图象重合,求 θ 的各三角函数值。 [解] ∵角 θ 的终边与函数 y=2|x|的图象重合 ∴ θ 为第三、四象限的角 若 θ 为第三象限的角,取终边上一点 P(-1,-2),|OP|=r= 5 ,则 θ 的各三角函数值分
5
∴sin α =
2 5
=
2 5 5
cos α =
−1 5
=−
1 5 5
sin 2α = 2 sin α cos α = 2 ×
2 1 4 5 × (− 5) = − 5 5 5 2 3 1 cos 2α = cos 2 α − sin 2 α = ( − 5)2 − ( 5)2 = − 5 5 5 2π 2π 2π + cos 2α sin sin( 2α + ) = sin 2α cos 3 3 3 4 1 3 3 4−3 3 = − × (− ) + (− ) × = 5 2 5 2 10
若 θ 在第四象限,可取点 P(1,-2),易得 θ 的各三角函数值:
sin θ = −
2 5 5 ,cos θ = ,tan θ = −2 5 5 5 1 cot θ = − ,sec θ = 5,csc θ = − 2 2
4.已知角 α 为第一象限的角。确定角
α
2
所在的象限,并画出其变化区别。
o o o
360 − α ,360 ·k+ α 等同角的三角函数之间的关系,其内容相似,极易混淆。
o o
10 k·3600+α, -α, 1800±α, 3600-α的三角函数值等于α的同名三角函数值前面加上一 个把α看作锐角时原函数在相应象限的符号; 20 900±α, 2700±α的三角函数值等于α的相应余函数的值,前面加上一个把α看作 锐角时,原函数在相应象限的符号;
。
[解](1)注意到分式的分子与分母均关于 sin α 、cos α 的一次齐次式,将分子、分母同
2 sin α − 3 cos α 2 tan α − 3 2 × 2 − 3 = = = −1 4 sin α − 9 cos α 4 tan α − 9 4 × 2 − 9 ∴ 应填 − 1
o o
180
π
) o ,1o =
π
180
rad
4.弧长、扇形面积的公式 设扇形的弧长为 l,圆心角大小为 α (rad ) ,半径为 r,则 l=r α 扇形的面积为
S=
1 1 lr = r 2α 2 2
同角三角函数的基本关系式与诱导公式 知识要点 1.同角三角函数的三个基本关系式
sin 2 α + cos 2 α = 1 sin α = tan α cos α tan α ⋅ cot α = 1
综合记之 :
kπ ±α 2
(k ∈ Z )
其记忆规律是:奇变偶不变、符号看象限。 利用诱导公式把任意的三角函数转化为锐角三角函数的基本步骤是:
任意角的三角函数
正角的三角函数 锐角三角函数
0 o ~360 o 的角的三角函数
1.函数 y= A.{-2,4} [解]
sin x cos x tan x cot x 的值域是( ) + + + sin x cos x tan x cot x
说明:新教材对于同角三角函数只有这三个基本关系式,而老教材除此之外,还有如下五 个关系式:
1 + tan 2 α = sec 2 α 1 + cot 2 α = csc 2 α cos α cot α = sin α cos α ⋅ sec α = 1 sin a ⋅ csc α = 1
可见,新教材在三角部分降低了难度,但是,若能掌握这补充的五个关系式,对做题肯定 是有帮助的,这五个关系式,用定义很容易给予证明,在此略。 2.诱导公式 诱导公式是指角 α 的三角函数与诸如— α ,180 ± α ,90 ± α ,270 ± α ,
α
2
<(2m+1) π +
π
4
(m ∈ Z),此
α
2
是第三象限的角;
(2)当 k 为偶数时,设 k=2m(m ∈ Z),则 2m π <
α
2
<2m π +
π
4
(m ∈ Z ) ,此时角
α
2
是第一象限的角。
综上,角
α
2
的第一象限或第三象限的角。
其变化区域如图 16—2 中阴影部分,这样的区域称为一、三象限的前半区域。 5.解答下列问题: (1)若 θ 在第四象限,试判断 sin(cos θ )·cos(sin θ )的符号; (2)若 tan(cos θ )·cot(sin θ )>0,试指出 θ 所在象限。 [解]显然要用到三角函数在各象限内取值符号的结论,其中还应注意 cos θ 、sin θ 本身的 取值限制。 (1)∵ θ 在第四象限 ∴0<cos θ <1<
那么
同角三角函数的基本关系式与诱导公式 1.化简:
(
1 + sin α 1 − sin α sec α + 1 sec α − 1 − − )⋅( ) 1 − sin α 1 + sin α sec α − 1 sec α + 1
[分析]“脱”去根号是我们的目标,这就希望根号下能成为完全平方式,注意到同角三角函数 的平方关系式,利用分式的性质可以达到目标。 [解] 原式 = (
三角函数的概念 知识要点 1.角的有关概念: (1)正角、负角和零角、终边相同的角、象限角等概念. (2)角的度量:包括角的角度制与弧度制及换算关系. 2.任意角的三角函数: 包括三角函数的定义,三角函数线的意义,任意角的三角函数值在各象限中的符号、 特殊角的三角函数值,同角的三角函数的基本关系式及诱导公式.进一步的,应掌握两角 和、差、倍、半的公式.详细内容如下: (1)设 P(x,y)是角 α 终边上任一点,且|PO|=r(r>0),则有
<0 <0
0<cos θ <1, 0<sin θ <1;
即 θ 在第一或第三象限。 6.学科内综合已知角 α 的顶点与直角坐标系的原点重合,始边在 x 轴的正半轴上,终边 经过点 P(-1,2),求 sin(2 α +
2π )的值。 3
(上海高考题)
2 2
[解] ∵P(-1,2)是角 α 终边上一点,由此求得 r=|OP|= (−1) + 2 =
2014-2015 学年
第一学期 第十一周
[课程内容]
三角函数概念、同角三角函数关系、诱导公式
1、准备知识要点: 三角函数的概念、同角三角函数的基本关系式和诱导公式。 2、本阶段知识要点: 理解三角函数概念,熟练使用同角三角函数的基本关系式和诱导公式进行相关计算。
B.{-2,0,4} C.{-2,0,2,4} D.{-4,-2,0,2,4}
当 x 在第一象限时,各种三角函数值均为正值: y=
sin x cos x tan x cot x + + + =4 sin x cos x tan x cot x sin x − cos x tan x − cot x + + + = −2 sin x cos x − tan x cot x
[解]首先写出角 α 的一般形式:2k π < α < 2kπ +
π
2
(k ∈ Z ) ,两边同时除以 2,得 k π <
α
2
< kπ +
π
4
(k ∈ Z ) ,运用分类讨论的数学思想,讨论 k 为奇数和 k 为偶数两种情况。
(1)当 k 奇数时,设 k=2m+1(m ∈ Z),则(2m+1) π < 时角
π
2
,−
π
2
<-1<sin θ <0
∴sin(cos θ )>0,cos(sin θ )>0,∴sin(cos θ )·cos(sin θ )>0 (2)即 ⎨ ∴
⎧tan(cos θ ) >0 ⎩cot(sin θ )
>0
或⎨ 或
⎧tan(cos θ ) ⎩cot(sin θ )
-1<cos θ <0 -1<sin θ <0
⎧4 =⎨ ⎩− 4 (α在第一、 三象限时) (α在第二、 四象限时)
2.已知 f( α ) =
sin(π − a ) cos(2π − α ) tan(−α + cot(− a − π ) sin( −π − α )
3π ) 2
(1)化简 f( α ); (2)若 α 是第三象限的角,且 cos(α − (3)若 α = − 1860 ,求 f( α )的值。
1 =2 sin α 4.已知 tan α =2,则 =−
(1)
2 sin α − 3 cos α = 。 4 sin α − 9 cos α 2 sin 2 α − 3 cos 2 α = 。 (2) 4 sin 2 α − 9 cos 2 α (3)4sin2 α -3sin α cos α -5cos2 α =
(1 + sin α ) 2 (1 − sin α ) 2 (sec α + 1) 2 (sec α − 1) 2 )( − − ) cos 2 α cos 2 α tan 2 α tan 2 α 1 + sin α 1 − sin α | sec α + 1 | | sec α − 1 | )( =( − − ) | cos α | | cos α | | tan α | | tan α | 2 sin α 1 + cos α 1 − cos α = ( − ) | cos α | | cos α | | sin α | 2 sin α 2 cos α = ⋅ | cos α | | sin α |
