有理数复习

合集下载

有理数单元复习

知识点一：有理数的概念（一）有理数：（1）整数与分数统称按定义分类：_______________⎧⎧⎫⎪⎪⎬⎨⎭⎪⎪⎪⎨⎩⎪⎧⎪⎨⎪⎩⎩_ _ _ _ _ _ _ _ _有理数　_ _ _ _ __ _ _ _ _ _ _ _ _ _ 按符号分类：__________⎧⎧⎨⎪⎩⎪⎪⎨⎪⎧⎪⎨⎪⎩⎩_ _ _ _ _ _ _ _有理数零_ _ _ _ _ _ _ _注：①正数和零统称为；②负数和零统称为；③正整数和零统称为；④负整数和零统称为 .（2）认识正数与负数：①正数：像1，1.1，175，2008等大于的数，叫做 .②负数：像-1，-1.1，-175，-2008等在正数前面加上“－”（读作负）号的数，叫注意：都大于零，都小于零.“0”即不是，也不是 .（3）用正数、负数表示相反意义的量：如果用正数表示某种意义的量，那么负数表示其意义的量，如果负数表示某种意义的量，则正数表示其意义的量.如：若-5米表示向东走5米，则+3米表示向走3米；若+6米表示上升6米，则-2米表示；+7C 表示零注意：0既不是_______，也不是____上7C ，-7C 则表示.（4）有理数“0”的作用：作用举例表示数的性质0是自然数、是有理数、是整数表示没有3个苹果用+3表示，没有苹果用0表示表示某种状态00C表示冰点表示正数与负数的界点0非正非负，是一个中性数（二）数轴（1）概念：规定了、和的直线注：①、、称为数轴的三要素，三者缺一不可.②单位长度和长度单位是两个不同的概念，前者指所取度量单位的，后者指所取度量单位的，即是一条人为规定的代表“1’的线段，这条线段，按实际情况来规定，同一数轴上的单位长度一旦确定，则不能再改变.（2）数轴的画法及常见错误分析①画一条水平的；②在这条直线上适当位置取一实心点作为：③确定向右的方向为，用表示；④选取适当的长度作单位长度，用细短线画出，并对应标注各数，同时要注意同一数轴的要一致.⑤数轴画法的常见错误举例：错例原因不统一没有（3）有理数与数轴的关系一切有理数都可以用数轴上的表示出来.在数轴上，右边的点所对应的数总比左边的点所对应的数，正数都大于，负数都小于，正数大于一切负数.注意：数轴上的点不都是有理数，如π.（三）相反数（1）相反数：只有的两个数互称为相反数．特别地，0的相反数是；若a 与b 互为相反数，则___a b += ，反之亦然 .（2）相反数的性质：①代数意义：只有的两个数叫做互为相反数，特别地，O 的相反数是0．相反数必须出现，不能单独存在．例如+5和互为相反数，或者说+5是的相反数，－5是的相反数，而单独的一个数不能说是．另外，定义中的“只有”指除以外，两个数，注意应与“只要符号不同”区分开．例如+3与－3互为相反数，而+3与－2虽然不同，但它们不是相反数．②几何意义：一对相反数在数轴上应分别位于两侧，并且到原点的相等．这两点是关于对称的．③求任意一个数的相反数，只要在这个数的前面添上“”号即可．一般地，数a的相反数是；这里以a表示任意一个数，可以为、、负数，也可以是任意一个代数式．注意－a不一定是．注意：当a＞0时，－a 0(正数的相反数是数)；当a=0时，－a O(0的相反数是)；当a＜0时， a O (负数的相反数是)．④互为相反数的两个数的和为，即若a与b互为，则a+b=0，反之，若a+b=O，则a与b互为．⑤多重符号的化简：一个正数前面不管有多少个“＋”号，都可以全部；一个正数前面有个“－”号，也可以把“－”号全部去掉；一个正数前面有个“－”号，则化简后只保留一个“－”号，即“负正”（其中“奇偶”是指正数前面的“”号的个数的，“负正”是指化简的最后结果的.（四）绝对值（1）绝对值的代数意义及几何意义①绝对值的代数意义：一个正数的绝对值是；一个负数的绝对值是它的；0的绝对值是.②绝对值的几何意义：一个数a的绝对值就是数轴上表示数a的与的距离.数a的绝对值记作.注意：①取绝对值也是一种，这个符号是“ ”，求一个数的绝对值，就是根据性质绝对值符号.②绝对值具有性，取绝对值的结果总是 .③任何一个有理数都是由部分组成：和它的，如：－5，符号是，绝对值是 .（2）字母a 的绝对值的分类___,()___,(0)___,(0)a o a a a >⎧⎪==⎨⎪<⎩ 或___,(0)___,(0)a a a ≥⎧=⎨<⎩ 或___,(0)___,(0)a a a >⎧=⎨≤⎩ （3）利用绝对值比较两个负有理数的大小规则：两个负数，绝对值大的反而 .步骤：①计算两个负数的 .②比较这两个的大小.③写出正确的判断结果.④如果若干个非负数的和为0，那么这若干个非负数都必为 .例如：若0,____,_a b c a b c ++====则知识点二：有理数运算（一）有理数比较大小（1）数轴上的数，右边的数总左边的数．（2）正数大于0，负数小于0，正数大于负数；（3）两个负数，绝对值大的反而；（4）两数比较大小，可按符号情况分类：0⎧⎧⎨⎪⎩⎪⎪⎨⎪⎧⎪⎨⎪⎩⎩同正：__________大的数大两数同号同负：__________大的反而小比较大小两数异号（一正一负）：______大于_______正数与0：_______大于0其中有时负数与0：_______小于0（二）有理数的加减法（1）有理数加法法则①同号两数相加，取相同的，并把绝对值 .②绝对值不相等的异号两数相加，取的加数的符号，并用较大的减去较小的 .③一个数同0相加，仍得 .（2）有理数加法的运算步骤法则是运算的依据，根据有理数加法的运算法则，可以得到加法的运算步骤：①确定和的；②求和的绝对值，即确定是两个加数的绝对值的 .（3）有理数加法的运算律①两个加数相加，交换加数的位置，不变.即a+b=b+a(加法律)②三个数相加，先把前两个数相加，或者先把后两个数相加，不变.即(a+b)+c=a+(b+c)（加法律）（4）有理数加法的运算技巧①分数与小数均有时，应先化为形式.②带分数可分为与两部分参与运算.③多个加数相加时，若有互为相反数的两个数，可先结合得④若有可以凑整的数，即相加得整数时，可先结合.⑤若有同分母的分数或易通分的分数，应先结合在一起.⑥相同的数可以先结合在一起.（5）有理数减法法则减去一个数，等于，即a-b=a+( )（6）有理数减法的运算步骤①把减号变为加号（改变运算符号）②把减数变为它的相反数（改变性质符号）③把减法转化为加法，按照加法运算的步骤进行运算.（7）有理数加减混合运算的步骤①把算式中的减法转化为加法；②省略加号与括号；③利用运算律及技巧简便计算，求出结果.注意：根据有理数减法法则，减去一个数等于加上，因此加减混合运算可以依据上述法则转变为只有的运算，即变为求几个正数，负数和0的和，这个和称为代数和.为了书写简便，可以把加号与每个加数外的括号均省略，写成省略加号和的形式，例如：（+3）+（-0.15）+(-9)+(+5)+(-11)=3-0.15-9+5-11，它的含义是正3，负0.15，负9，正5，负11的和。

有理数总复习

a 10b第一章有理数总复习知识点梳理：1.正数与负数：负数产生的必要性；具有相反意义的量。

2.有理数的分类：3.数轴、相反数、倒数、绝对值：（1）数轴的三要素是：________________________________（2）只有符号不同的两个数叫做互为____________，a 的相反数为___ ；（3）互为倒数的两个数乘积是，没有倒数；（4）一个正数的绝对值是____________；一个负数的绝对值是____________；零的绝对值是_______.（5）有理数的大小比较：方法一：0 一切正数，0 一切负数；两个负数作比较，绝对值大的 .方法二：在数轴上，________表示的数总比________表示的数大。

4.科学记数法：把一个大于10的数表示成a ×10n 的形式，（其中a 是____________ ，n 是____________ ）5.近似数【自主学习、巩固训练】要求：自主完成下列各题，并把自己疑惑的、不懂的做好批注，时间10分钟.1. 在 -1，+7， 0， 23-， 516中，正数有（） A 、1个 B 、2个 C 、3个 D 、4个2.在–2，+3.5，0，32-，–0.7，11中．负分数有…………（） A 、l 个 B 、2个 C 、3个 D 、4个3. 下列数据是近似数的是（）A.小白数学得了90分B. 小明身高约173cmC.数学课本有86页D.（1）班有45名同学4.如图，，那么下列结论正确的是( ) A ．a 比b 大 B ．b 比a 大C ．a 、b 一样大D ．a 、b 的大小无法确定5.我国最长的河流长江全长约为6300千米，用科学记数法表示为（）A. 63×102千米B. 6.3×102千米或者有理数有理数C. 6.3×104千米D. 6.3×103千米6.用数轴上的点表示下列有理数，并求其相反数、倒数和绝对值。

有理数全章复习

有理数全章复习理解有理数的概念和性质：有理数是指可以表示为两个整数的比值的数，这里的整数可以是正整数、负整数或零。

有理数的性质主要包括有理数的加减乘除运算性质、有理数大小的比较，以及有理数的乘方、开方运算等。

一、有理数的加减乘除运算性质：1.有理数的加法性质：-交换律：a+b=b+a-结合律：(a+b)+c=a+(b+c)-存在零元素：a+0=a-存在相反元素：a+(-a)=02.有理数的减法性质：-减法的定义：a-b=a+(-b)-减法与加法的关系：a-b=a+(-b)3.有理数的乘法性质：-交换律：a*b=b*a-结合律：(a*b)*c=a*(b*c)-分配律：a*(b+c)=a*b+a*c4.有理数的除法性质：-除法的定义：a÷b=a*(1/b)二、有理数的大小比较：1.同号比大小：正数大于负数，负数小于正数；正数之间、负数之间，绝对值大的数大。

2.异号比大小：两个数绝对值相比，绝对值大的数小。

三、有理数的乘方和开方运算：1.有理数的乘方：-正数的指数性质：a^m*a^n=a^(m+n)-负数的指数性质：a^(-m)=1/a^m-零的指数性质：a^0=1（a≠0）- 乘方的分配律：(ab)^n = a^n * b^n2.有理数的开方：-非负数的开方：√a*√a=a（a≥0）- 开方的分配律：√(ab) = √a * √b有理数的应用：1.在数轴上表示有理数：-正数表示：从0向右的数轴上的点表示，数值与点的位置对应。

-负数表示：从0向左的数轴上的点表示，数值与点的位置对应。

-零的表示：数轴上的0点表示。

2.数与有理数的运算：-数的加减法：将数转换为有理数进行运算。

-有理数与有理数的加减法：按照有理数的加减法规则进行运算。

3.比例与比例运算：-比例的定义：两个比例相等叫做比例，表示为a:b=c:d。

- 比例的性质：比例的两个比值相等，乘法性质：a:b = ac:bd。

-比例方程的解法：根据比例的性质，设置比例方程求解。

第二章有理数及其运算复习

－4|＋|＋10|)＝×58＝139.2(元)．即该出租车周日下午的营业额是元．
数学·新课标〔BS〕
第二章 |过关测试
数学·新课标〔BS〕
第二章 |过关测试 ►考点十科学记数法例11 用科学记数法表示80 000 000×90 000 000的计算结
果．
解：80 000 000×90 000 000＝7 200 000 000 000 000＝×1015.
＋9，－3，－5，＋4，－8，＋6，－3，－6，－4，＋10. (1)最后出租车离开钟楼多远？在钟楼的什么方向？ (2)假设每千米的收费价格是元，该出租车周日下午的营业额是多少？
数学·新课标〔BS〕
第二章 |过关测试解：(1)＋9－3－5＋4－8＋6－3－6－4＋10＝0，故该出租
车正好在钟楼； ×(|＋9|＋|－3|＋|－5|＋|＋4|＋|－8|＋|＋6|＋|－3|＋|－6|＋|
第二章有理数及其运算复习
第二章 |过关测试
知识归类
1．有理数
(1)有理数
整数
正整数零
负整数
分数
正分数负分数
(2)有理数正零有理数
正整数正分数
负有理数Βιβλιοθήκη 负整数负分数数学·新课标〔BS〕
第二章 |过关测试 2．数轴：(1)数轴的概念：规定了____原__点_、____正__方_、向
所示，则a________b(填“＜〞、“＞〞或“＝〞) .
数学·新课标〔BS〕
第二章 |过关测试 [答案] ＜ [解析] 由图可知，实数a、b都是负数，且表示数a的点在
表示数b的点的左边，所以a＜b.
数学·新课标〔BS〕
第二章 |过关测试例4 有理数a、b在数轴上的位置如图2－2所示，试化简|a

有理数复习

有理数复习课一、有理数的基本概念1.正数和负数2.有理数3.数轴4.互为相反数5.互为倒数6.有理数的绝对值7.有理数大小的比较8.科学记数法、近似数.二、有理数的运算加、减、乘、除、乘方运算正数和负数1.大于0的数叫做正数。

例如：3,1.8%，3.5……2.在正数前面加上“-”号的数叫做负数。

例如：-3，-2.7%，-4.5……3.0既不是正数，也不是负数。

4.在同一个问题中，分别用正数和负数表示两个具有相反意义的量。

有理数1、统称整数，试举例说明。

2、统称分数，试举例说明。

3、_____________统称有理数。

4、统称非负数。

5、统称非正数。

有理数的分类说明：①分类的标准不同，结果也不同；②分类的结果应无遗漏、无重复；③有限小数、无限循环小数属于分数。

④π是无理数。

0的性质：（1）0是整数，是自然数，是有理数。

（2）0既不是正数，也不是负数。

自然数一定是整数吗？自然数一定是正整数吗？整数一定是自然数吗？自然数一定是整数；自然数不一定是正整数，因为零也是自然数；整数不一定是自然数，因为负整数不是自然数。

1.判断：(1)不带“－”号的数都是正数。

( )(2)带“－”号的数都是负数（）(3)如果a是正数，那么－a一定是负数( )(4)在一个数前加上“－”号，这个数变为负数（）(5)一个数如果不是正数，那么这个数是负数。

（）2.增加－20%，实际的意思是．3.甲比乙大－３表示的意思是．4.小明的妈妈在超市买了一瓶消毒液，发现在瓶子上印有这样一段文字：“净含量（750±5）ml”,这瓶消毒液的标准含量是，这瓶消毒液至少有。

5. 把下列各数填在相应额大括号内：1，－0.1，-789，|-25|，0，-(+20)，-3.14，-590，正整数集｛…｝负整数集｛…｝正分数集｛…｝负分数集｛…｝正有理数集｛…｝负有理数集｛…｝自然数集｛…｝6. 以下说法中正确的是（）A．“向东5米”与“向西10米”不是相反意义的量；B．如果汽球上升25米记作+25米，那么-15米的意义就是下降-15米；C．如果气温下降6℃记作-6℃，那么+8℃的意义就是零上8℃；D．若将高1米设为标准0，高1.20米记作+0.20米，那么-0.05米所表示的高是0.95米．7.正数、负数在实际生活中的应用我校对七年级女生进行了仰卧起坐的测试，以能做36个为标准，超过的次数用正数表示，不足的次数用负数表示，其中8名女生的成绩如下：（1）这8名女生的成绩分别是多少？（2）这8名女生有百分之几达到标准？（3）她们共做了多少个仰卧起坐？8. 某检修队从A 地出发，在东西方向的公路上检修线路，如果规定向东行驶为正，向西行驶为负，这个检修队一天中行驶的距离记录如下（单位千米）：－４，＋７，－９，+８，＋６，－５，－３。

第一章有理数的复习

④与原点的距离为三个单位的点有___2____个，他们分别表示的有理数是___-2__和____2___。
近似数的精确度有几种表述方法,分别是什么? 1、一个近似数四舍五入到哪一位,就说这个近似数精确到哪一位 2、用有效数字的个数来表述一个近似数的精确度.
由四舍五入得到的近似数,从左边第一个不是零的数字起,到末位数字为止的所有数字,都叫做这个数的有效数字
有理数的减法
有理数减法法则:减去一个数，等于加上这个数的相反数.
减号变加号
(1)(-32) -(+5)=(-32)+(-5)=-37.
减数变相反数
有理数的乘法
有理数乘法法则：两数相乘，同号得正，异号得负，并把
绝对值相乘. 任何数同0相乘，都得0.
有理数的除法
除以一个数等于乘上这个数的倒数. 两数相除，同号得正，异号得负，并把绝对
例如： 3的相反数是－3
倒数：－4的相反数是－（－4）＝4
乘积是1的两个数互为倒数。0没有倒数。
a
的倒数是
1 a
3、用-a表示的数一定是（D）
A、负数，B 、正数，C、正数或负数，D、都不对
4、一个数的相反数是最小的正整数，那么这个数是（A）
A 、–1， B、 1， C 、±1， D、 0
5、判断题
例:
比较大小:-
2 3
__-0.6
解: 因为: -2 = 2, -0.6 =0.6 33
所以:-
2 3
<-0.6
2 >0.6 3
例5 :
1、数a、b在数轴上的位置如图所示，正确的是（ D）
（A）a>b （B）a+b>0 （C）ab>0 （D）|a|>|b|

有理数复习

5、有理数比较大小、
⑴利用数轴：数轴上两个点表示的数，右边的数总比左边数的大。利用数轴：数轴上两个点表示的数，右边的数总比左边数的大。有理数比较法则： ⑵有理数比较法则：正数大于0 负数小于0 正数大于负数；正数大于0，负数小于0，正数大于负数；两个负数，绝对值大的反而小。两个负数，绝对值大的反而小。比较大小: >”、 <”或 =”填空填空）例10 比较大小: （用“>”、“<”或“=”填空） -3.3 < 0 , 6 > -8 ,0
|=16,则 ____。例7 若|x|=16,则x = ±16 。 |=16, ____ 、、、 __个例8 绝对值不大于3的整数有 7 个，分别是±3、 ±2、 ±1、0 。绝对值不大于3 __ 表示数轴上数a、两点间的距离两点间的距离．表示数轴上数应用： ⑷应用： |a – b|表示数轴上数、b两点间的距离．、。在数轴上与表示- 的点相距4 例9 在数轴上与表示-1的点相距4个单位长度的点表示的数是 3、-5
−12 1) = −4 ( 3 −24 = 3 ( 2) −16 2
⑸乘方：乘方：
①概念：求几个相同因数的积的运算，叫做乘方。概念：求几个相同因数的积的运算，叫做乘方。 a n = a × a × ⋯× a 求法： ②求法：乘方运算可以化为乘法运算进行：乘方运算可以化为乘法运算进行：符号法则：正数的任何次幂都是正数。 ③符号法则：正数的任何次幂都是正数。 n 负数和分数的乘方书写时的乘方书写时，负数和分数的乘方书写时，负数的奇数次幂是负数，偶数次幂是正数。负数的奇数次幂是负数，偶数次幂是正数。一定要把整个负数和分数 0的任何次幂都是。的任何次幂都是0。的任何次幂都是小括号括起来括起来。用小括号括起来。例13 计算：计算：

第一章有理数复习

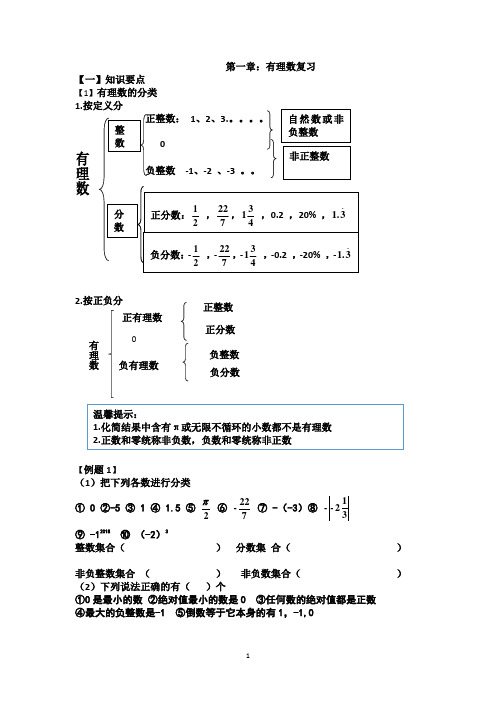
第一章：有理数复习【一】知识要点【1】有理数的分类 1.2.按正负分【例题1】（1）把下列各数进行分类 ① 0 ②-5 ③ 1 ④ 1.5 ⑤2 ⑥ 722- ⑦ -（-3）⑧ 312--⑨ -12018 ⑩ （-2）3整数集合（）分数集合（）非负整数集合（）非负数集合（）（2）下列说法正确的有（）个①0是最小的数 ②绝对值最小的数是0 ③任何数的绝对值都是正数 ④最大的负整数是-1 ⑤倒数等于它本身的有1，-1,0有理数正有理数负有理数温馨提示： 1.化简结果中含有π或无限不循环的小数都不是有理数 2.正数和零统称非负数，负数和零统称非正数正整数正分数负整数负分数有理数【2】相关概念1.数轴：规定了原点、正方向、单位长度的一条直线2.相反数：3.绝对值①几何定义：一个数a 的绝对值就是数轴上表示这个数a 的点离开原点的距离，绝对值越大离原点越远②代数定义：⎩⎨⎧≤-≥=)0()0(a a a a a （注意0）4.倒数：若两个数的积是1，那么这两个数互为倒数5.科学计数法6．近似数和有效数字7.数的大小比较方法：数轴上从左到右依次递增，数轴上的点与实数．．是一一对应 ①代数定义：只有符号不同．．．．．．的两个数叫做相反数 ②几何定义：数轴上在原点的两旁，到原点距离相等的两个点代表的数互为相反数③求一个数或式子的相反数，就在它的前面加上‘-’④a 的相反数是-a ，a-b 的相反数是-（a-b ）=b-a,a+b 的相反数是-(a+b)=-a-b （注意括号），相反数等于它本身的只有0 ⑤性质：若a,b 互为相反数，则a+b=0,或a=-b 1、非负数的绝对值等于它本身，非正数的绝对值是它的相反数 2、绝对值符号去掉规律：非负数各项不变号，非正数各项都变号 3、一个数的绝对值（或者平方）等于正数．．．．．．．．．．．．．，那么这个数有两个．．①a,b 互为倒数 ab=1②倒数等于它本身只有±1，切记0没有倒数形式：ax10n （a 是整数位数只有一位的数，n 是整数），当a ≥10时，n=原数整数位数-1 ，当a <1时，n=-（原数第一个非0数字前所有0的个数） ①保留近似数的方法有：四舍五入法、进一法、去尾法 ②近似数可以用计数单位或科学计数法表示 ③有效数字是从左边第一个不是零的数字起以后的所有数字都是这个数的有效数字 ④通过测量得到的数都是近似数 ①差法 ②数轴法 ③两个负的绝对值法 ④平方法 ⑤商法8.非负数性质【例题2】正负数应用（1）如果提高10分表示+10分，那么下降8分表示____，不升不降用___表示. （2）巴黎与北京的时间差为-7时（正数表示同一时刻比北京时间早的时数），如果北京时间是7月2日14：00，那么巴黎时间是（）A. 7月2日21时B. 7月2日7时C. 7月1日7时D. 7月2日5时（3）某项科学研究，以45分钟为1个时间单位，并记每天上午10时为0，10时以前记为负，10时以后记为正，例如9：15记为-1，10：45记为1等等，依此类推，上午7：45应记为【例题3】数轴、相反数、绝对值、倒数、非负数应用（1）已知 a ,b 互为相反数，c ,d 互为倒数，m-1的绝对值是2，则m dccd b a -+-+222=（2）在数轴上到表示-1的点的距离为7个单位长度的点有_____个，它们表示27（4）绝对值不大于2的整数有________，它们的和是，积是（（6）已知|x|=4，|y|=2且y ＜0，则x+y 的值为（7） ①π-14.3=②20171-2018131-4121-311-21++++。

有理数全章复习(按知识点分类复习)

第一章有理数全章复习考点一：用正负数表示相反意义的量1、七年级一班某次数学测验的平均成绩为80分，数学老师以平均成绩为基准，记作0，把小龙、小聪、小梅、小莉、小刚这五位同学的成绩简记为+10，–15，0，+20，–2．问这五位同学的实际成绩分别是多少分2、如果规定收入为正，支出为负．收入500 元记作500元，那么支出237元应记作( ) A ．－500元B ．－237元C ．237元D ．500元3.有4包真空小包装火腿，每包以标准克数〔450克〕为基准，超过的克数记作正数，不足的克数记作负数，以下数据是记录结果，其中表示实际克数最接近标准克数的( )A ．+2B ．－3C ．+3D ．+44.某商店出售三种不同品牌的大米，米袋上分别标有质量如下表：现从中任意拿出两袋不同品牌的大米，这两袋大米的质量最多相差 ( )A ．B ．C ．D ．考点二：有理数的分类1、_______、_______和_________成为整数，__________和__________统称为分数。

___________和_________统称为有理数。

练习稳固：1、在–2，+3.5，0，32-，–0.7，11中．负分数有……………………〔〕 A 、l 个 B 、2个 C 、3个 D 、4个2、不超过3)23(-的最大整数是………………………………………〔〕 A 、–4 B –3 C 、3 D 、43．在数8.3、－4、0、－〔－5〕、+6、－|－10|、1中,正数有____ 个； 4、以下说法中正确的个数有 ( )①一个有理数不是整数就是分数 ②一个有理数不是正数就是负数 ③一个整数不是正的，就是负的 ④一个分数不是正的，就是负的A 1B 2C 3D 45、在数＋8.3，－4，－0.8，0，90，－｜－24｜中，__________是正数，____________不是整数。

6、比132-大而比123小的所有整数的和为 __________ 。

有理数的运算复习

把一个大于10的数表示成
a 10
n
的形式。
例 (1)用科学记数法表示下列各数:
(2)下列用科学记数法表示的数, 原来各是什么数? 4.315
3 ×10 ;
1.02
(3)计算: (8.1 ×108) ÷ (9 ×105)
{
31个0
230000;
15800…0
6 ×10
对近似数的精确度的两种表述方式：
任何数同0相乘，都得0.
五、有理数除法法则：
1、除以一个不等于0的数，等于乘于这个数的倒数。
2、两数相除，同号得正，异号得负，并把绝对值相除。 0除以任何一个不等于0的数，都得0. 例：用“＞”、“＝”、“＜”填空＞ 1、若ab＞0，则 a ____0 b a ＜ 2、若ab＜0，则 b ____0 ＜，b____0 ＜ 3、若ab＞0，a＋b＜0，则a____0
3、已知两数相乘大于0，相加小于0，则这两数的符号是（ B ） A同正 B同负 C一正一负 D无法确定
4、下列运算中，结果相等的是（ A A（-2）3与－23 C（-3）2与－32 B（-2）3与－32
）
D（-3×2）3与－3×23
5、如果a＞0，b＜0，a+b＜0，那么下列各式中大小关系正确的是（ D ）（A）－b＜－a＜b＜a （B）－a＜b＜a＜－b （C）b＜－a＜－b＜a （D）b＜－a＜a＜－b
例4、若m 5, m n 8, 则n等于（） A、-3 C、-3或13 A、正有理数 C、负有理数 B、13 D、-13或3 B、非正有理数 D、非负有理数
例5、若a是负有理数，则-a 3是（）
1、用计算器填空：你发现什么规律，并根据规律不用计算器计算

有理数复习(有答案)

>有理数综合复习基础训练题一、填空：1、在数轴上表示－2的点到原点的距离等于（）。

2、若∣a ∣=－a,则a （）0.3、任何有理数的绝对值都是（）。

4、如果a+b=0,那么a 、b 一定是（）。

5、将毫米的厚度的纸对折20次，列式表示厚度是（）。

~6、已知||3,||2,||a b a b a b ==-=-，则a b +=（）7、|2||3|x x -++的最小值是（）。

8、在数轴上，点A 、B 分别表示2141，-，则线段AB 的中点所表示的数是（）。

9、若,a b 互为相反数，,m n 互为倒数，P 的绝对值为3，则()20102a b mn p p++-=（）。

10、若abc ≠0，则||||||a b c a b c++的值是（） . 11、下列有规律排列的一列数：1、43、32、85、53、…，其中从左到右第100个数是（）。

二、解答问题：1、已知x+3=0,|y+5|+4的值是4，z 对应的点到-2对应的点的距离是7，求x 、y 、 z 这三个数两两之积的和。

》3、若2|45||13|4x x x +-+-+的值恒为常数，求x 满足的条件及此时常数的值。

4、若,,a b c 为整数，且20102010||||1a b c a -+-=，试求||||||c a a b b c -+-+-的值。

>5、计算：－21 ＋65－127＋209－3011＋4213－5615＋7217能力培训题>知识点一：数轴例1：已知有理数a 在数轴上原点的右方，有理数b 在原点的左方，那么（） A ．b ab < B ．b ab > C ．0>+b a D ．0>-b a 拓展训练：1、如图b a ,为数轴上的两点表示的有理数，在a b b a a b b a ---+,,2,中，负数的个数有（）A ．1B ．2C ．3D ．42、把满足52≤<a 中的整数a 表示在数轴上，并用不等号连接。

有理数专题复习

1.10 有理数专题复习一、有理数的意义及其有关概念这部分内容包括正负数、有理数、数轴、有理数大小的比较、相反数、倒数、科学记数法及近似数和有效数字等。

1. 概念的理解与应用 (1)-213的倒数是；-213的相反数是；-213的绝对值是 ;-(-8)的相反数是；-12的相反数的倒数是 .(2)某种食用油的价格随着市场经济的变化涨落，规定上涨记为正，则-5.8元的意义是；如果这种油的原价是76元，那么现在的卖价是元.(3)上海浦东磁悬浮铁路全长30km ，单程运行时间约为8min,那么磁悬浮列车的平均速度用科学记数法表示约为 m ／min.(4)若a 、b 互为相反数，c 、d 互为倒数，则()++=233cd a b .(5)近似数0.4062精确到位，有个有效数字; 近似数5.47×105精确到位，有个有效数字; 近似数3.5万精确到位，有个有效数字．(6)3.4030×105保留两个有效数字是，精确到千位是 . (7)如图所示的图形为四位同学画的数轴，其中正确的是( )。

(8)在数轴上画出表示下列各数的点，并按从大到小的顺序排列，用“>”号连接起来。

4，-|-2|，-4.5，1，0(9)下列语句中正确的是( )A 数轴上的点只能表示整数B 数轴上的点只能表示分数C 数轴上的点只能表示有理数D 所有有理数都可以用数轴上的点表示出来(10)||=7x ，则x = ；||-=7x ，则x = ．(11)绝对值不大于11的整数有( )A ．11个B ．12个C ．22个D ．23个(12)如果22-=-a a ，则a 的取值范围是( )A ．a >0B ．a ≥0C ．a ≤0D ．a<02．有理数的分类：(1)有理数－3，0，20，－1.25，314， ||--12，()--5中，正整数是，负整数是，正分数是，非负数是。

(2)下列说法正确的个数是 ( )①一个有理数不是整数就是分数 ②一个有理数不是正数就是负数 ③一个整数不是正的，就是负的 ④一个分数不是正的，就是负的 A ．1 B ．2 C ．3 D ．43.有理数的大小比较(1)比大小：-32-54；- [+(-0.75)] _______()--34； * -3.14 -π(2)a，b是有理数，它们在数轴上的对应点的位置如下图所示：把a，-a，b，-b按照从小到大的顺序排列( )A．-b＜-a＜a＜b B．-a＜-b＜a＜bC．-b＜a＜-a＜b D．-b＜b＜-a＜a(3)绝对值最小的有理数是；绝对值等于本身的数是。

七年级第一章有理数全章复习

七年级第一章有理数全章复习
第一章有理数
一、有理数分类
复习练习：
1、下面关于有理数的说法正确的是（ A ）
A. 整数集合和分数集合合在一起就是有理数集合
B. 正数集合与负数集合合在一起就构成整数集合
C. 正数和负数统称为有理数
D. 正数、负数和零统称为有理数
2、若两个有理数的和是正数，那幺一定有结论（ D ）
A. 两个加数都是正数
B. 两个加数有一个是正数
C. 一个加数正数，另外一个加数为零
D. 两个加数不能同为负数
4. 下面说法正确的有（ B ）
①一个有理数不是整数就是分数②一个有理数不是正数就是负数③一个整数不是正数就是负数④一个分数不是正数就是负数
A.1 个
B.2 个
C.3 个
D.4 个
二、数轴
1、像这样规定了原点、正方向和单位长度的直线叫做数轴.
2、数轴的三要素：原点、正方向、单位长度,缺一不可.
3、在数轴上比较两个有理数大小的法则：
①在数轴上表示的两个数，右边的数总比左边的大。

有理数复习

有理数单元复习

有理数总复习

有理数全章复习

第二章 有理数及其运算 复习

有理数复习

第一章 有理数的复习

有理数复习

第一章有理数复习

有理数全章复习(按知识点分类复习)

有理数的运算复习

有理数复习(有答案)

有理数专题复习

七年级第一章有理数全章复习

第二章有理数及其运算复习

第一章有理数的复习