第9届小学希望杯全国数学邀请赛 四年级 第1试
第九届小学“希望杯”全国数学邀请赛四年级第二试真题.

第九届小学“希望杯”全国数学邀请赛四年级第二试真题一填空(每小题5分,共60分)1.计算:234+432-4×8+330÷5=2.四(1)班全体同学站成一排,当从左往右报数时,小华报:18;当从右往左报数时,小华报:13。
那么,该班有学生名。
3.如果25×口÷3×15+5=2005,那么口_________.4.。
图1是由25个面积等于1的小正方形组成的大正方形,图中面积是6的长方形有个。
5.在括号内填上两个相邻的整数,使等式11112()()=-成立。
6.由数字0,3,6组成的所有三位数的和。
7.某种品牌的电脑降价20%后,每台售价为4592元,则该品牌电脑降价前每台售价______元。
8.已知两个自然数的积是35,差是2,则这两个自然数的和是_______。
9.把1991,1992,1993,1994,1995分别填入图2中的5个方格中,使得横排的三个方格中的数的和等于竖列的三个方格中的数的和。
则中间方格中能填的数是。
10.图2是3×3的正方形网格,1与2相比,较大的是__________。
11.小明从家出发,先向东偏北30°的方向跑了350米到达点A ,接着向北偏西30°的方向跑了200米到达点B ,然后又向西偏南30°的方向跑了350米到达点C ,这时小明距家 米。
12.在图5的九个方格里,每行、每列、每条对角线上的三个数的和都相等,则N= 。
二、解答题(每小题15分,共60分)每题都要写出推算过程。
13.将一副三角板摆放在一起(可以叠放),使同时出现15°,30°,45°,60°,75°,90°,105°这七个角,请画图说明并表示出这些角。
14.连续写出从1开始的自然数,写到2008时停止,得到一个多位数:123456789…2008请说明:这个多位数除以3,得到的余数是几?为什么?15.甲、乙、丙三辆车同时从A 地出发驶向B 地,依次在出发后5小时、5512 小时、612小时与迎面驶来的一辆卡车相遇。
第九届小学“希望杯”全国数学邀请赛六年级第1试 答案

x♦ y=x× y-x÷2, x⊕ y= x+ y÷ 2。
按此规则计算:3.6♦2=____________,
0. 12 ♦(7.5⊕4.8)=____________。
g g
4、在方框里分别填入两个相邻的自然数,使下式成立。 □<
1 1 1 1 ×3<□ 150 101 102 103
ห้องสมุดไป่ตู้
19、一批饲料可供 10 只鸭子和 10 只鸡共吃 6 天,或供 12 只鸭子和 6 只鸡共吃 7 天,则这批饲料可供 _________只鸭子吃 21 天。 20、小明从家出发去奶奶家,骑自行车每小时行 12 千米,他走后 2.5 小时,爸爸发现小明忘带作业,便 骑摩托车以每小时 36 千米的速度去追,结果小明到奶奶家后半小时爸爸就赶到了。小明家距离奶奶 家___________千米。
g
5、 在循环小数 0. 1 2345678 9 中, 将表示循环节的圆点移动到新的位置, 使新的循环小数的小数点后第 2011 位上的数字是 6,则新的循环小数是___________。 6、一条项链上共串有 99 颗珠子,如图 1,其中第 1 颗珠子是白色的,第 2、3 颗珠子是红色的,第 4 颗珠 子是白色的,第 5、6、7、8 颗珠子是红色的,第 9 颗珠子是白色的,„„。则这条项链中共有红色珠 子___________颗。
1
11、图 5 中一共有________个长方形(不包含正方形)。
12、图 6 中,每个圆圈内的汉字代表 1~9 中的一个数字,汉字不同,数字也不同,每个小三角形三个顶 点上的数字之和相等。若 7 个数字之和等于 12,则“杯”所代表的数字是____________。 13、如图 7,沿着圆周放置黑、白棋子各 100 枚,并且各自相邻排列。若将圆周上任意两枚棋子换位一次 称为一次交换,则最少经过____________次对换可使全部的黑棋子彼此不相邻。 14、人口普查员站在王阿姨门前问王阿姨:“您的年龄是 40 岁,您收养的三个孤儿的年龄各是多少岁?” 王阿姨说: “他们年龄的乘积等于我的年龄,他们年龄的和等于我家的门牌号。”普查员看了看门牌, 说:“我还是不能确定他们的年龄。”那么,王阿姨家的门牌号是____________。 15、196 名学生按编号从 1 到 196 顺次排成一列。令奇数号位(1,3,5…)上的同学离队,余下的同学顺 序不变,重新自 1 从小到大编号,再令新编号中奇数位上的同学离队,依次重复上面的做法,最后留 下一位同学。这位同学开始的编号是___________号。 16、 甲、 乙两人同时从 A 地出发到 B 地, 若两人都匀速行进,甲用 4 小时走完全程, 乙用 6 小时走完全程。 则当乙所剩路程是甲所剩路程的 4 倍时,他们已经出发了___________小时。 17、某电子表在 6 时 20 分 25 秒时,显示 6:20:25,那么从 5 时到 6 时这 1 个小时里,此表显示的 5 个 数字都不相同的情况共有__________种。 18、有三只蚂蚁外出觅食,发现一堆粮食,要运到蚁洞。根据图 8 中的信息计算,若甲、乙、丙三只蚂蚁 共同搬运这堆粮食,那么,蚂蚁乙搬运粮食__________粒。
2011年第9届小学“希望杯”全国数学邀请赛试卷(四年级第2试)

2011年第9届小学“希望杯”全国数学邀请赛试卷(四年级第2试)一、填空(每小题5分,共60分)1.(5分)计算:234+432﹣4×8+330÷5=.2.(5分)四(1)班全体同学站成一排,当从左往右报数时,小华报:18;当从右往左报数时,小华报:13.那么,该班有学生名.3.(5分)如果25×口÷3×15+5=2005,那么口.4.(5分)如图是由25个面积等于1的小正方形组成的大正方形,图中面积是6的长方形有个.5.(5分)在括号内填上两个相邻的整数,使等式成立.6.(5分)由数字0,3,6组成的所有三位数的和.7.(5分)某种品牌的电脑降价20%后,每台售价为4592元,则该品牌电脑降价前每台售价元.8.(5分)已知两个自然数的积是35,差是2,则这两个自然数的和是.9.(5分)把1991,1992,1993,1994,1995分别填入图中的5个方格中,使得横排的三个方格中的数的和等于竖列的三个方格中的数的和.则中间方格中能填的数是.10.(5分)图是3×3的正方形方格,∠1与∠2相比,较大的是.11.(5分)小明从家出发,先向东偏北30°的方向跑了350米到达点A,接着向北偏西30°的方向跑了200米到达点B,然后又向西偏南30°的方向跑了350米到达点C,这时小明距家米.12.(5分)在图的九个方格里,每行、每列、每条对角线上的三个数的和都相等,则N=.二、解答题(每小题15分,共60分)每题都要写出推算过程.13.(15分)将一副三角板摆放在一起(可以叠放),使同时出现15°,30°,45°,60°,75°,90°,105°这七个角,请画图说明并表示出这些角.14.(15分)连续写出从1开始的自然数,写到2008时停止,得到一个多位数:123456789…2008请说明:这个多位数除以3,得到的余数是几?为什么?15.(15分)甲、乙、丙三辆车同时从A地出发驶向B地,依次在出发后5小时、5小时、6小时与迎面驶来的一辆卡车相遇.已知甲、乙两车的速度分别是80千米/时和70千米/时,求丙车和卡车的速度.16.(15分)将66个乒乓球放入10个盒子中,要求每只盒子都要有乒乓球,有且只有两个盒子中的乒乓球的个数相同,能办到吗?若能办到,请说明一种具体方法.若办不到,请说明理由.2011年第9届小学“希望杯”全国数学邀请赛试卷(四年级第2试)参考答案与试题解析一、填空(每小题5分,共60分)1.(5分)计算:234+432﹣4×8+330÷5=700.【分析】先计算算式中的乘法与除法,得到算式234+432﹣32+66,将这个算式中66使用加法交换律使它与234相加,然后再按照整数的四则混合运算进行计算即可得到答案.【解答】解:234+432﹣4×8+330÷5,=234+432﹣32+66,=234+66+432﹣32,=300+432﹣32,=732﹣32,=700.故答案为:700.2.(5分)四(1)班全体同学站成一排,当从左往右报数时,小华报:18;当从右往左报数时,小华报:13.那么,该班有学生30名.【分析】根据题意,可知小华的左边有17人,右边有12人,由此即可求得该班总人数.【解答】解:小华的左边有17人,右边有12人,17+12+1=30(人);答:该班有学生30名.故答案为:30.3.(5分)如果25×口÷3×15+5=2005,那么口16.【分析】由题目可以看出:25×口÷3×15是2005与5的差,即为2000;25×口÷3是2000与15的商,即为2000÷15;25×口是2000÷15与3的积,即为400;由此可以求出□的值.【解答】解:25×口÷3×15=2005﹣5=200,25×口÷3=2000÷15,25×口=2000÷15×3=400,25×口=400,□=16;答:ϖ应是16.故此题答案为:16.4.(5分)如图是由25个面积等于1的小正方形组成的大正方形,图中面积是6的长方形有24个.【分析】根据方类数图形的计数原理和方法,分别计算出行、列所包含的面积是6的长方形的个数,然后合并起来即可.【解答】解:图形中行所包含的面积是6的长方形是:3×4=12(个);图形中列所包含的面积是6的长方形也是12个;一共有:12+12=24(个);答:图中面积是6的长方形有24个.故答案为:24.5.(5分)在括号内填上两个相邻的整数3、4,使等式成立.【分析】根据题意,由分析分数的拆项,,就可以求出结果.【解答】解:由可知,这两个连续的自然数的积是12,因3×4=12,所以,==,故答案是:3、4.6.(5分)由数字0,3,6组成的所有三位数的和1899.【分析】根据题干,利用枚举法列举出0,3,6可以组成的所有三位数,①0不能为最高位;②3为最高位时可以组成:360;306;③6为最高位时可以组成:603;630.即可计算得出正确答案.【解答】解:根据题干分析可得:360+306+630+603=1899,答:由数字0,3,6组成的所有三位数的和是1899.故答案为:1899.7.(5分)某种品牌的电脑降价20%后,每台售价为4592元,则该品牌电脑降价前每台售价5740元.【分析】“降价20%”是把电脑原来的价格看作单位“1”,按原来价格的1﹣20%=80%出售,所以原来的价格为4592÷80%.【解答】解:4592÷(1﹣20%),=4592÷80%,=5740(元);答:该品牌电脑降价前每台售价5740元.故答案为:5740.8.(5分)已知两个自然数的积是35,差是2,则这两个自然数的和是12.【分析】因为两个自然数的积是35,所以这两个数一定是5和7,故和为:5+7=12.【解答】解:设这两个数分别为a和b,则a×b=35.又a、b都是自然数,在自然数范围内,积为35的只有5和7.所以a+b=12.故答案为:12.9.(5分)把1991,1992,1993,1994,1995分别填入图中的5个方格中,使得横排的三个方格中的数的和等于竖列的三个方格中的数的和.则中间方格中能填的数是1991,1993,1995.【分析】为了便于计算研究,我们把这五个数只取个位上的数字分别为:1、2、3、4、5.因为在横竖排的和中都含有中间的数字,设中间的数字为a,所以根据题意可表示出每排三个数字的和:(1+2+3+4+5+a)÷2=(15+a)÷2,要使(15+a)能被2整除,a只能等于1或3或5;故中间方格中能填的数是:1991,1993,1995.【解答】解:为了便于计算研究,我们把这五个数只取个位上的数字分别为:1、2、3、4、5.设中间的数字为a,所以根据题意可表示出每排三个数字的和:(1+2+3+4+5+a)÷2,=(15+a)÷2,要使(15+a)能被2整除,又因为这五个数是整数,所以a只能等于1或3或5;也就是代表的原数1991,1993,1995.故答案为:1991,1993,1995.10.(5分)图是3×3的正方形方格,∠1与∠2相比,较大的是∠1.【分析】借助正方形和线段构成的角来比较角的大小.:∠1=180°﹣(∠3+∠4),∠2=180°﹣(∠4+∠5)=180°﹣2∠4.很明显∠3<∠4,所以180°﹣(∠3+∠4)>180°﹣2∠4.即∠1>∠2.【解答】解:∠1=180°﹣(∠3+∠4),∠2=180°﹣(∠4+∠5)=180°﹣2∠4.很明显∠3<∠4,所以180°﹣(∠3+∠4)>180°﹣2∠4.即∠1>∠2.11.(5分)小明从家出发,先向东偏北30°的方向跑了350米到达点A,接着向北偏西30°的方向跑了200米到达点B,然后又向西偏南30°的方向跑了350米到达点C,这时小明距家200米.【分析】可根据上北下南,左西右东的方法进行作图,如图可连接C点与小明的家,可以看出小明跑过的路程为一个长方形,根据长方形的对边相等的性质,小明家距离C点有200米.【解答】解:如图小明站在C点时距离小明家的距离=点A到点B的距离,故答案为:200.12.(5分)在图的九个方格里,每行、每列、每条对角线上的三个数的和都相等,则N=18.【分析】先确定每行、每列、每条对角线上的三个数的和,8+6+16=30;再确定对角线上的中心数:30﹣8﹣12=10,然后求出右上角的数:30﹣16﹣10=4;最后得出第一行中间的数N=30﹣8﹣4=18.【解答】解:每行、每列、每条对角线上的三个数的和是:8+6+16=30;中心数是:30﹣8﹣12=10,右上角的数是:30﹣16﹣10=4;第一行中间的数是:N=30﹣8﹣4=18.二、解答题(每小题15分,共60分)每题都要写出推算过程.13.(15分)将一副三角板摆放在一起(可以叠放),使同时出现15°,30°,45°,60°,75°,90°,105°这七个角,请画图说明并表示出这些角.【分析】30°、45°、60°、90°的角在三角板中能找出,可直接利用三角板画出,15°、75°、105°的角要用两个三角板中的角组合画出.【解答】解:所要画出的角如下图:14.(15分)连续写出从1开始的自然数,写到2008时停止,得到一个多位数:123456789…2008请说明:这个多位数除以3,得到的余数是几?为什么?【分析】能被3整除的数的特征,各位数字和被3整除的数,本身能被3整除.各位数字和被3除余几,原数被3除就余几.【解答】解:(1+2+3+ (2008)=(1+2008)×2008÷2=2017036.(2+1+7+3+6)÷3,=19÷3,=6…1;则可推得原数字123…2008被3除余1.答:这个多位数除以3,得到的余数是1.15.(15分)(2010•拱墅区校级自主招生)甲、乙、丙三辆车同时从A地出发驶向B地,依次在出发后5小时、5小时、6小时与迎面驶来的一辆卡车相遇.已知甲、乙两车的速度分别是80千米/时和70千米/时,求丙车和卡车的速度.【分析】已知三车与卡车的相遇时间及甲乙两车的速度,因此可先据速度差×时间=路程差求出甲车与卡车相遇时比乙车多行的路程,即此时卡车和乙车的距离,然后再据路程÷相遇时间=速度和,即能求出卡车的速度;求出卡的速度后再据和丙车的相遇时间即能求出丙的速度.【解答】解:卡车的速度为:[(80﹣70)×5]÷(55)﹣70=50﹣70,=120﹣70,=50(千米/小时).丙车的速度为:[(80+50)×5]÷﹣50=650÷﹣50,=100﹣50,=50(千米).答:卡车的速度与丙车的速度同为每小时50千米.16.(15分)将66个乒乓球放入10个盒子中,要求每只盒子都要有乒乓球,有且只有两个盒子中的乒乓球的个数相同,能办到吗?若能办到,请说明一种具体方法.若办不到,请说明理由.【分析】每个盒子都放,且数目都不一样,至少用1+2+…+10=55个乒乓球,还剩下66﹣55=11个,从1﹣﹣9个的里面任取一个盒子,再放入一个球,例如在放了4个的里面再放一个,这样就有两个盒子有5个球,然后把剩下的10个球都放入最后一个盒子,由此即可得出10个盒子里面的数目.【解答】解:此题的答案有很多,只要把66拆成符合条件的10个数相加即可,这里只说一种方法,首先每个盒子都放,且数目都不一样,至少用的乒乓球的个数是:1+2+…+10=55(个),还剩下:66﹣55=11(个),从1﹣﹣9个的里面任取一个盒子,再放入一个球例如在放了4个的里面再放一个,这样就有两个盒子有5个球,然后把剩下的10个球都放入最后一个盒子,10个盒子里面的数目为:1,2,3,5,5,6,7,8,9,20,答:能将66个乒乓球放入10个盒子中,每只盒子都要有乒乓球,并且只有两个盒子中的乒乓球的个数相同.参与本试卷答题和审题的老师有:pyzq;xiaosh;rdhx;姜运堂;吴涛;齐敬孝;xuetao;春暖花开;admin;zhuyum(排名不分先后)菁优网2017年2月8日第11页(共11页)。
小学四年级希望杯历年数学竞赛试题与答案1-14届(最新全套完整版)

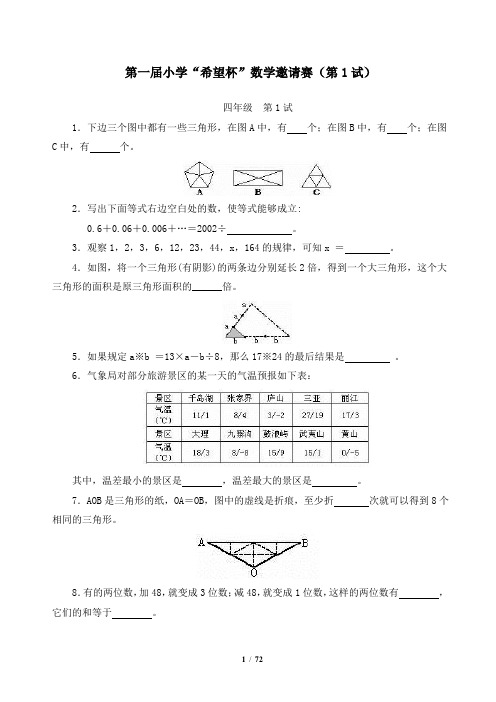
第一届小学“希望杯”全国数学邀请赛(第1试)四年级第1试1.下边三个图中都有一些三角形,在图A中,有个;在图B中,有个;在图C中,有个。
2.写出下面等式右边空白处的数,使等式能够成立:0.6+0.06+0.006+…=2002÷。
3.观察1,2,3,6,12,23,44,x,164的规律,可知x =。
4.如图,将一个三角形(有阴影)的两条边分别延长2倍,得到一个大三角形,这个大三角形的面积是原三角形面积的______倍。
5.如果规定a※b =13×a-b÷8,那么17※24的最后结果是。
6.气象局对部分旅游景区的某一天的气温预报如下表:其中,温差最小的景区是,温差最大的景区是。
7.AOB是三角形的纸,OA=OB,图中的虚线是折痕,至少折次就可以得到8个相同的三角形。
8.有的两位数,加48,就变成3位数;减48,就变成1位数,这样的两位数有,它们的和等于。
9.甲、乙、丙、丁四个学习小组共有图书280本,班主任老师提议让四个组的书一样多,得到拥护,于是从甲调14本给乙,从乙调15本给丙,从丙调17本给丁,从丁调18本给甲。
这时四个组的书一样多。
这说明甲组原来有书本。
10.幼儿园老师给几组小朋友分苹果,每组分7个,少3个;每组分6个,则多4个,苹果有个,小朋友共组。
11.在 a=20032003×2002和 b=20022003×2003中,较大的数是,它比较小的数大。
12.小明的家离学校2千米,小光的家离学校3千米,小明和小光的家相距千米。
13.甲、乙、丙三人中只有1人会开汽车。
甲说:“我会开。
”乙说:“我不会开。
”丙说:“甲不会开。
”三人的话只有一句是真话。
会开车的是。
14.为了支援西部,1班班长小明和2班班长小光带了同样多的钱买了同一种书44本,钱全部用完,小明要了26本书,小光要了18本书。
回校后,小明补给小光28元。
小明、小光各带了元,每本书价元。
小学四年级希望杯历年数学竞赛试题和答案解析1_14届[最新[全套](完整版)]
]](https://img.taocdn.com/s3/m/f473ed0e0912a21614792942.png)
第一届小学“希望杯”全国数学邀请赛(第1试)四年级第1试1.下边三个图中都有一些三角形,在图A中,有个;在图B中,有个;在图C中,有个。
2.写出下面等式右边空白处的数,使等式能够成立:0.6+0.06+0.006+…=2002÷。
3.观察1,2,3,6,12,23,44,x,164的规律,可知x =。
4.如图,将一个三角形(有阴影)的两条边分别延长2倍,得到一个大三角形,这个大三角形的面积是原三角形面积的______倍。
5.如果规定a※b =13×a-b÷8,那么17※24的最后结果是。
6.气象局对部分旅游景区的某一天的气温预报如下表:其中,温差最小的景区是,温差最大的景区是。
7.AOB是三角形的纸,OA=OB,图中的虚线是折痕,至少折次就可以得到8个相同的三角形。
8.有的两位数,加48,就变成3位数;减48,就变成1位数,这样的两位数有,它们的和等于。
9.甲、乙、丙、丁四个学习小组共有图书280本,班主任老师提议让四个组的书一样多,得到拥护,于是从甲调14本给乙,从乙调15本给丙,从丙调17本给丁,从丁调18本给甲。
这时四个组的书一样多。
这说明甲组原来有书本。
10.幼儿园老师给几组小朋友分苹果,每组分7个,少3个;每组分6个,则多4个,苹果有个,小朋友共组。
11.在 a=20032003×2002和 b=20022003×2003中,较大的数是,它比较小的数大。
12.小明的家离学校2千米,小光的家离学校3千米,小明和小光的家相距千米。
13.甲、乙、丙三人中只有1人会开汽车。
甲说:“我会开。
”乙说:“我不会开。
”丙说:“甲不会开。
”三人的话只有一句是真话。
会开车的是。
14.为了支援西部,1班班长小明和2班班长小光带了同样多的钱买了同一种书44本,钱全部用完,小明要了26本书,小光要了18本书。
回校后,小明补给小光28元。
小明、小光各带了元,每本书价元。
第九届小学“希望杯”全国数学邀请赛试卷(四年级第2试)

2011年第九届小学“希望杯”全国数学邀请赛试卷(四年级第2试)一、填空题(每小题5分,共60分)1.(5分)计算:(70÷4+90÷4)÷4=.2.(5分)计算:898+9898+99898+999898=.3.(5分)对运算⊙和㊣,规定:a⊙b=a×b+b,a㊣b=a×b﹣a,那么(2⊙3)⊙(2㊣4)=.4.(5分)若一个能被5整除的两位数既不能被3整除,又不能被4整除,它的97倍是偶数,十位数字不小于6,则这个两位数是.5.(5分)如图中每一横行右面的一个数减去它左面相邻的一个数所得的差都相等,每一数列下面的一个数除以它上面相邻的一个数所得的商都相等,则a+b×c=.6.(5分)如果一个两位数的3倍与4的差是10的倍数,它的4倍与15的差大于60且小于100,则这个两位数是.7.(5分)若四位数的各个数位上的数字都是偶数,并且百位上的数字是2,则这样的四位数有个.8.(5分)将长为12厘米,宽为8厘米的长方形纸片剪去4个同样大小的等腰直角三角形,剩余部分的面积至少是平方厘米.9.(5分)一个除法运算,被除数是10,除数比10小,则可能出现的所有不同的余数的和是.10.(5分)苹果和梨各有若干个,若每袋5个苹果和3个梨,则当梨恰好装完时,还多4个苹果;若每袋装7个苹果和3个梨,则当苹果恰好装完时,梨还多12个,那么苹果和梨共有个.11.(5分)如图,在△ABC中,AB=BC=CA,D、E、F分别是三边的中点,AD、BE、CF交于点O,则图中有个三角形;他们的面积有个不同的值.12.(5分)A、B、C、D四人带着一个手电筒,要通过一个黑暗的只容2人走的隧道,每次先让2人带着手电筒通过,再由一人送回手电筒,又由2人带着手电筒通过…,若A、B、C、D四人单独通过隧道分别需要3、4、5、6分钟,则他们4人都通过至少需要分钟.二、解答题(每小题15分,共60分)13.(15分)摩托车行驶120千米与汽车行驶180千米所用的时间相同,7小时内摩托车行驶的路程比6小时内汽车行驶的路程少80千米,若摩托车先出发2小时,然后汽车从同一出发点开始追赶,那么汽车出发后几小时内可以追上摩托车?14.(15分)将1,10,11,15,18,37,40这7个数分别填入图中的7个圆圈内(每个数都用到),能否使其中两条直线上的三个数的和相等,并且等于另一条直线上的三个数的和的3倍?若可以,请给出一种填法;若不能,请说明理由.15.(15分)100人参加速算测试,共10题.每题答对的人数如下表所示:题号 1 2 3 4 5 6 7 8 9 1093 90 86 91 80 83 72 75 78 59答对人数规定:答对6题或6题以上,为及格,根据上表计算至少有多少人及格.16.(15分)如图,甲乙两只小虫分别从每边长20厘米不透明的正五角星围墙的顶点A、B出发,沿外侧按逆时针方向爬行,甲每秒爬行5厘米,乙每秒爬行4厘米.问:在甲从出发到第一次爬到B的过程中,乙能看到甲的时间有多少秒?2011年第九届小学“希望杯”全国数学邀请赛试卷(四年级第2试)参考答案与试题解析一、填空题(每小题5分,共60分)1.(5分)计算:(70÷4+90÷4)÷4=10 .【分析】可以先从括号里开始运算,而括号里两个除式,可以化成分数的形式,最后再算结果.【解答】解:根据分析,原式=(70÷4+90÷4)÷4=(70+90)÷4÷4=160÷4÷4=40÷4=10.故答案是:10.【点评】本题考查了四则运算的巧算,突破点是,将括号里的运算进行巧算,再求最后的结果.2.(5分)计算:898+9898+99898+999898=1110592 .【分析】此题一看便知,这式子里的数都接近整数,用凑整法把它变成:(898+2﹣2)+(9898+2﹣2)+(99898+2﹣2)+(999898+2﹣2)=(900﹣2)+(9900﹣2)+(99900﹣2)+(999900﹣2)=900+9900+99900+999900﹣8.再根据特点易想到把这些凑整的数化成乘积的形式,便发现了乘法的分配律的运用,计算就简便了.【解答】898+9898+99898+999898=(900﹣2)+(9900﹣2)+(99900﹣2)+(999900﹣2)=900+9900+99900+999900﹣8=9×100+99×100+999×100+9999×100﹣8=(9+99+999+9999)×100﹣8=(10+100+1000+10000﹣4)×100﹣8=(11110﹣4)×100﹣8=11110×100﹣4×100﹣8=1111000﹣400﹣8=1110600﹣8=1110592【点评】此题是反复运用凑整法和乘法的分配律.并且是在解题过程中不断发现所用的运算定律.3.(5分)对运算⊙和㊣,规定:a⊙b=a×b+b,a㊣b=a×b﹣a,那么(2⊙3)⊙(2㊣4)=60 .【分析】按题意,则2⊙3=2×3+3=9;2㊣4=2×4﹣2=6,则(2⊙3)⊙(2㊣4)=9⊙6=9×6+6=60.【解答】解:根据分析,则2⊙3=2×3+3=9,2㊣4=2×4﹣2=6,则(2⊙3)⊙(2㊣4)=9⊙6=9×6+6=60,故答案是:60.【点评】本题考查了定义新运算,突破点是:分别算出2⊙3和2㊣4,再算出结果.4.(5分)若一个能被5整除的两位数既不能被3整除,又不能被4整除,它的97倍是偶数,十位数字不小于6,则这个两位数是70 .【分析】显然,能被5整除,则个位只能是0或5,而它的97倍是偶数,说明此两位数是一个偶数,故可以断定此两位数个位数字为0,而十位不小于6,只能是6、7、8、9,因不能被4整除,则十位不能是6、8,故十位只能是7或9,又因为不能被3整除,故十位上只能是7.【解答】解:根据分析,能被5整除,则个位只能是0或5,而它的97倍是偶数,说明此两位数是一个偶数,故可以断定此两位数个位数字为0,而十位不小于6,只能是6、7、8、9,因不能被4整除,则十位不能是6、8,故十位只能是7或9,又因为不能被3整除,故十位上只能是7.综上,此两位数是70,故答案是:70.【点评】本题考查了数的整除特征,突破点是:从题中已知条件推测出个位数字和十位数字.5.(5分)如图中每一横行右面的一个数减去它左面相邻的一个数所得的差都相等,每一数列下面的一个数除以它上面相邻的一个数所得的商都相等,则a+b×c=540 .【分析】首先分析题意,横行为等差,竖列为等比数列,找到第一行公差和数列的公比即可.【解答】解:依题意可知:横行为等差,竖列为等比.根据横行为等差数列可知第一行的数字为2,4,6,8.竖行是等比数列,故18÷2=9.所以c是2 的3倍即是6.a是4的27倍.4×27=108.b是8的9倍72.a+b×c=108+72×6=540.故答案为:540【点评】本题考查对幻方的理解和运用,关键问题是找到公差和公比问题解决.6.(5分)如果一个两位数的3倍与4的差是10的倍数,它的4倍与15的差大于60且小于100,则这个两位数是28 .【分析】显然,两位数的3倍与4的差是10的倍数,可知此两位数的三倍得到的数的个位数是4,而乘以3得到个位为4的两位数个位数为8,由它的4倍与15的差大于60且小于100,可求得此两位数的范围,不难求得此两位数.【解答】解:根据分析,两位数的3倍与4的差是10的倍数,可知此两位数的三倍得到的数的个位数是4,而乘以3得到个位为4的两位数个位数为8;由它的4倍与15的差大于60且小于100,可求得此两位数的范围:大于:=,小于:=,综上,此两位数为:28.故答案是:28.【点评】本题考查了因数与倍数,突破点是:根据因数与倍数的性质,以及两位数的范围求得两位数.7.(5分)若四位数的各个数位上的数字都是偶数,并且百位上的数字是2,则这样的四位数有100 个.【分析】四位数的最高位是千位,最高位上不能为0,那么可以是2,4,6,8,而百位上只是2,固定好了,那么十位和个位上可以是0,2,4,6,8,根据排列的特点可知:共有4×5×5个不同的四位数.【解答】解:千位可取2,4,6,8,十位和各位都可以取0,2,4,6,8 所以4×5×5=100(个)故答案为:100.【点评】本题考查每个数位数字的特点,注意千位上不能取0.8.(5分)将长为12厘米,宽为8厘米的长方形纸片剪去4个同样大小的等腰直角三角形,剩余部分的面积至少是24 平方厘米.【分析】长为12厘米,宽为8厘米的长方形纸片,显然最多只能剪下4个直角边为6的等腰直角三角形,故剩下的面积不难求得.【解答】解:根据分析,如图,长为12厘米,宽为8厘米的长方形纸片,最多只能剪下4个直角边为6的等腰直角三角形,故剩下的部分的面积至少=12×(8﹣6)=24.故答案是:24【点评】本题考查剪切和拼接,突破点是:利用长方形的长和宽的值,剪切时取最大值,则剩下的部分面积最小.9.(5分)一个除法运算,被除数是10,除数比10小,则可能出现的所有不同的余数的和是10 .【分析】除数比10小,可以将10除以1~9,得出的余数中有2个是0即除以1、5时余数为0,不同的余数为1、2、3、4,再求和即可.【解答】解:根据分析,10÷6=1…4;10÷7=1…3;10÷8=1…2;10÷9=1…1;而10÷3和10÷9余数都是1,10÷4和10÷8余数都是2,故不同的余数只有:1、2、3、4,可能出现的所有不同的余数的和=1+2+3+4=10.故答案是:10【点评】本题考查带余除法,突破点是:将10除以1~9,得出的余数中有2个是0即除以1、5时余数为0,不同的余数为1、2、3、4,再求和.10.(5分)苹果和梨各有若干个,若每袋5个苹果和3个梨,则当梨恰好装完时,还多4个苹果;若每袋装7个苹果和3个梨,则当苹果恰好装完时,梨还多12个,那么苹果和梨共有132 个.【分析】首先分析根据梨的数量是多12个,证明袋子少了12÷3=4袋.再根据少的4袋苹果数量为20加上剩余的4个就是24个平均每袋多2个共12袋子,即可求解.【解答】解:依题意可知:根据梨的数量是多12个,证明袋子少了12÷3=4袋.苹果差是4×5+4=24个.24÷(7﹣5)=12袋,水果总数为10×12+12=132.故答案为:132.【点评】本题考查对分配盈亏问题的理解和运用,关键问题是找到梨的数量差找到袋子的数量差.问题解决.11.(5分)如图,在△ABC中,AB=BC=CA,D、E、F分别是三边的中点,AD、BE、CF交于点O,则图中有16 个三角形;他们的面积有 4 个不同的值.【分析】要求三角形的个数和不同的面积的取值,可以分情况讨论,从只含有一个小三角形的三角形开始算起,面积的不同取值也不难求得.【解答】解:根据分析,由题可知,AB=BC=CA,D、E、F分别是三边的中点,①只含有1个小三角形的三角形有:6个,且每个三角形的面积均相等,且均等于三角形ABC面积的;②含有2个小三角形的三角形有:3个,且每个三角形的面积均相等,且均等于三角形ABC面积的;③含有3个小三角形的三角形有:6个,且每个三角形的面积均相等,且均等于三角形ABC面积的;④含有6个小三角形的三角形有:1个,即三角形ABC,综上,则图中有16个三角形;他们的面积有4个不同的值.故答案是:16、4【点评】本题考查了三角形的面积,突破点是:根据图形的三角形的特点,分情况讨论,不难求得结果.12.(5分)A、B、C、D四人带着一个手电筒,要通过一个黑暗的只容2人走的隧道,每次先让2人带着手电筒通过,再由一人送回手电筒,又由2人带着手电筒通过…,若A、B、C、D四人单独通过隧道分别需要3、4、5、6分钟,则他们4人都通过至少需要21 分钟.【分析】四人要通过的时间要少,过隧道花费时间少的来回跑,即可得出结论.【解答】解:分两种情况讨论:第一种:A和B过,A回,4+3=7(分钟)C和D过,B回,6+4=10(分钟)A和B过,4(分钟)共用7+10+4=21(分钟);第二种:A和B过,A回,4+3=7(分钟)A和C过,A回,5+3=8(分钟)A和D过,6(分钟)共用7+8+6=21分钟.所以,至少需要21分钟;故答案为21.【点评】此题是最大与最小问题,解本题的关键是安排过隧道花费时间少的送手电.二、解答题(每小题15分,共60分)13.(15分)摩托车行驶120千米与汽车行驶180千米所用的时间相同,7小时内摩托车行驶的路程比6小时内汽车行驶的路程少80千米,若摩托车先出发2小时,然后汽车从同一出发点开始追赶,那么汽车出发后几小时内可以追上摩托车?【分析】首先分析两车的路程比即是速度比,根据路程差除以速度差即可求解.【解答】解:依题意可知:摩托车速度:汽车的速度=120:180=2:3.每一份的路程为:80÷(3×6﹣2×7)=20(千米).摩托车7小时的路程为:20×7×2=280(千米).摩托车的速度为:280÷7=40(千米/小时).汽车6小时的路程为:20×6×3=360(千米).汽车的速度是:360÷6=60(千米/小时).40×2÷(60﹣40)=4(小时)答:那么汽车出发后4小时内可以追上摩托车.【点评】本题考查对追及问题的理解和运用,关键问题是找到路程差与速度差问题解决.14.(15分)将1,10,11,15,18,37,40这7个数分别填入图中的7个圆圈内(每个数都用到),能否使其中两条直线上的三个数的和相等,并且等于另一条直线上的三个数的和的3倍?若可以,请给出一种填法;若不能,请说明理由.【分析】首先根据这7个数字求和为132.再根据这些数字除以7的余数和132除以7的余数组成7的倍数即可,【解答】解:依题意可知:设最小的和为1份,那么其他的为3份,最后加的数字和为7的倍数才行.1+10+11+15+18+37+40=132.这7个数字除以7的余数分别为1,3,4,1,4,2,5.132÷7=18…6.根据中间数字多加2次,那么数字和为7的倍数,那么余数是4的可以构成7的倍数.132+11+11=154.154÷7=21.故答案为:【点评】本题考查对凑数谜的理解和运用,关键是找到数字和是7的倍数,问题解决.15.(15分)100人参加速算测试,共10题.每题答对的人数如下表所示:题号 1 2 3 4 5 6 7 8 9 10答对 93 90 86 91 80 83 72 75 78 59人数规定:答对6题或6题以上,为及格,根据上表计算至少有多少人及格.【分析】先确定出答错的总人次,不及格的至少答错5道,即可得出得出结果.【解答】解:各题答错的总人次数为7+10+14+9+20+17+28+25+22+41=193,每有一个人不及格,则他至少答错5题,193÷5=38…3,所以至多有38人不及格,至少有62人及格.为说明是可以的,注意41正好比38多3,所以这38个人全都在第10题上答错,剩余的答错次数恰好平均分配到其他9题上.答:至少有62人及格.【点评】此题是最大与最小问题,主要考查了数的除法,确定出各题答错的总人次是解本题的关键.16.(15分)如图,甲乙两只小虫分别从每边长20厘米不透明的正五角星围墙的顶点A、B出发,沿外侧按逆时针方向爬行,甲每秒爬行5厘米,乙每秒爬行4厘米.问:在甲从出发到第一次爬到B的过程中,乙能看到甲的时间有多少秒?【分析】设五角星的五个顶点按逆时针方向标为B、B1、B2、B3、B4,形成顶点B﹣﹣顶点B1的区间一,顶点B1﹣﹣顶点B2的区间二,以此类推到区间五.根据题意,乙能看到甲的情况是他们必须在同一时间都行走在同一区间.在区间一看到的时间:20÷5=4(秒);区间二看到的时间:20×2÷4=10(秒),20×3﹣10×5=60﹣50=10(厘米),10÷5=2(秒);区间三的情况:甲到达B3的时间是(10+20+20)÷5=10(秒),乙移动距离10×4=40(厘米),此时乙到达B2,乙能看到甲的时间是0,据此可解答.【解答】解:区间一看到的时间:20÷5=4(秒);区间二看到的时间:20×2÷4=10(秒),20×3﹣10×5=60﹣50=10(厘米),10÷5=2(秒);区间三能看到的时间:0总共乙能看到甲的时间有2+4=6(秒)答:乙能看到甲的时间有6秒.【点评】此题一定要结合生活实际去想去思考(什么情况下乙能看到甲),然后确定解题思路,就能顺利解答,这真是生活中的数学.声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布日期:2019/4/22 16:48:13;用户:小学奥数;邮箱:pfpxxx02@;学号:20913800。
历届希望杯全国中学生数学竞赛试题

第三届“希望杯”全国数学邀请赛初一第1试
第三届“希望杯”全国数学邀请赛初一第2试
第四届“希望杯”全国数学邀请赛初一第1试
第四届“希望杯”全国数学邀请赛初一第2试
第五届“希望杯”全国数学邀请赛初一第1试
第五届“希望杯”全国数学邀请赛初一第2试
第六届“希望杯”全国数学邀请赛初一第1试
第六届“希望杯”全国数学邀请赛初一第2试
第七届“希望杯”全国数学邀请赛初一第1试
第七届“希望杯”全国数学邀请赛初一第2试
第八届“希望杯”全国数学邀请赛初一第1试
第八届“希望杯”全国数学邀请赛初一第2试
第九届“希望杯”全国数学邀请赛初一第1试
第九届“希望杯”全国数学邀请赛初一第2试
第十届“希望杯”全国数学邀请赛初一第1试
第十届“希望杯”全国数学邀请赛初一第2试
第十一届“希望杯”全国数学邀请赛初一第1试
第十一届“希望杯”全国数学邀请赛初一第2试。
第1~3届“希望杯”全国数学邀请赛试题详解-小学

前言 目录 小学“希望杯”全国数学邀请赛简介王寿仁、杨乐、龚昇、梅向明题词“ 希望杯”全国数学邀请赛组织委员会、命题委员会前言“希望杯”激励我 走向灿烂的明天试题及解答第一届(2003年) 小学四年级第一试 第二试 小学五年级第一试 第二试 第二届(2004年) 小学四年级第一试 第二试 小学五年级第一试 第二试 第三届(2005年) 小学四年级第一试 第二试 培训题 小学五年级第一试 第二试 培训题 第1~3届“希望杯”全国数学邀请赛获金牌奖学生名单
希望杯数学能力培训教程(小学四年级)例题与习题摘抄

简单方程例1 某数加上6,然后乘以6,再减去6,最后除以6,其结果等于6,则这个数是多少?例2 将4放在一个两位数的右端,得到一个三位数,这个三位数比原来的两位数大445,问原来的两位数是多少?例3 一个数除以8后再减3,得到的数比原来的数少66,问原来的数是多少?例4 一个三位数,个位数字比十位数字大1,比百位数字大3,百位上与十位上的数字交换位置后得到一个新数,这两个三位数的和为787,问原来的三位数是多少?例5 甲筐苹果个数比乙筐苹果多64个,问从甲筐中取出多少个苹果放入乙筐,可使乙筐苹果比甲筐苹果多12个?例6 有三堆棋子,第二堆比第一堆的3倍多4个,第三堆比第一堆的4倍少1个,问当第一堆棋子是多少时,第二、三堆的棋子数相等?例7 有一架飞机,能在空中连续飞行9小时,飞出时的速度是每小时740千米,返回时每小时925千米,问这架飞机最多飞出多少千米就应返回?例8 少年乐团中有170人不是五年级,有135人不是六年级,已知五、六年级学生共205人,则少年乐团中除五、六年级以外的学生共有多少人?习题1 一个四位数abc 2扩大到3倍后,变成了8abc ,问这个四位数是多少?习题2 铁路旁的一条平行小路上,有一汽车人和一开车人同向行进,骑车人速度为每小时14.4千米,开车人速度为每小时72千米.这时有一列火车从他们背后开过来,火车通过骑车人用8秒,通过开车人用24秒,问这列火车车身长多少米?习题3 星期天,妈妈从超市买了4支小梦龙和3支可爱多冰淇淋,用去24元钱.妈妈对小丽说:“上星期我买3支小梦龙和5支可爱多冰淇淋用去29元钱,你算一算,小梦龙和可爱多每支各多少钱?”答:“小梦龙冰淇淋每支______元;可爱多冰淇淋每支_____元.习题4 有兄弟两人今年的年龄之和是50岁,但曾经有一年,哥哥的年龄是弟弟今年的年龄,那时哥哥的岁数恰好是弟弟当年岁数的2倍,问哥哥、弟弟今年分别多少岁?习题5 小明买鸡蛋买了5.40元,后来他觉得鸡蛋太小,又叫小贩无偿添加了2个鸡蛋.这样一来,平均每个鸡蛋降了3分钱,小明共带回多少个鸡蛋?习题6 某工人和老板签了一份30天的劳务合同:工作一天可得报酬48元,休息一天则要从所得报酬中扣掉12元.该工人合同到期后并没有拿到报酬,则他最多工作了多少天?习题7 小明做一道计算题,原题是一个数除以7,再加上72,由于粗心,他把除以算成了乘,加算成了减,凑巧得数是对的,这道题的得数是多少?习题8 将786个桃子分成四堆,第一堆比第二堆多24个,比第三堆多16个,比第四堆多46个,那么第四堆有多少个?习题9 在一堆球中有红、白、黑三种颜色的球,白球和红球合起来是16个,红球比黑球多7个,黑球比白球多5个,那么黑球有多少个?习题10 甲、乙、丙三人参加一次智力测试,甲答对题目最多,他们中任意两个人答对的题目数之和分别是39,50,47.那么甲答对多少到题?应用题1.简单的应用题例1 有一座六层的塔,每一层的灯的盏数都是上一层的3倍,最顶层点了一盏灯,则这座塔一共点了多少盏灯?例2 生产一吨含20%水分的苹果果脯,需要4吨新鲜苹果。
第九届小学“希望杯”全国数学邀请赛试卷(四年级第1试)

2011年第九届小学“希望杯”全国数学邀请赛试卷(四年级第1试)一、解答题(共20小题,满分114分)1.(6分)计算:(7777+8888)÷5﹣(888﹣777)×3=.2.(6分)计算:1+11+21+…+1991+2001+2011=.3.(6分)在小于30的质数中,加3以后是4的倍数的是.4.(6分)小于100的最大的自然数与大于300的最小的自然数的和,是不大于200的最大的自然数的倍.5.既是6的倍数又是8的倍数的所有两位数的和是.6.(6分)四年级一班第2小组共12人,其中5人会打乒乓球,8人会下象棋,3人既会打乒乓球又会下象棋,那么这个小组中既不会打乒乓球又不会下象棋的有人.7.(6分)按照左侧四个图中数的规律,在第五个图中填上适当的数:8.(6分)已知9个数的乘积是800,将其中一个数改为4,这9个数的乘积是200,若再将另外一个数改为30,则这9个数的乘积变为1200,则这两个被改动的数以外的7个数的乘积是.9.(6分)如图,△ABC的面积为36,点D在AB上,BD=2AD,点E在DC 上,DE=2EC,则△BEC的面积是.10.(6分)今年,李林和他爸爸的年龄的和是50岁,4年后,他爸爸的年龄比他的年龄的3倍小2岁,则李林的爸爸比他大岁.11.(6分)某次考试,A、B、C、D、E五人的平均分是90分.若A、B、C 的平均分是86分,B、D、E的平均分是95分,则B的得分是分.12.(6分)如图,已知直线AB和CD交于点O,若∠AOC=20°,∠EOD=60°,则∠AOE=,∠BOC=.13.(6分)如图,四边形ABCD与CEFG是边长相等的正方形,且B、C、G 在一条直线上,则图中共有个正方形,个等腰直角三角形.14.(6分)一个水桶里有水,若将水加到原来的4倍,桶和水共重16千克;若将水加到原来的6倍,桶和水共重22千克.则桶内原有水千克,桶重千克.15.(6分)某个两位数的个位数字和十位数字的和是12,个位数和十位数字交换后所得两位数比原数小36,则原数是.16.(6分)王强步行去公园,回来时坐车,往返用了一个半小时,如果他来回都步行,则需要2个半小时,那么,他来回都坐车,则需分钟.17.(6分)图中“C”形图形的周长是厘米.18.(6分)如图,从1,2,3,4,5,6中选出5个数填在图中空格内,使填好的格内的数右边的比左边的大,下边的比上边的大,则共有种不同的填法.19.(6分)三个连续自然数中最小的数是9的倍数,中间的数是8的倍数,最大的数是7的倍数,则这三个数的和最小是.20.(6分)甲、乙、丙、丁、戊五人猜测全班个人学科总成绩的前五名:甲:“第一名是D,第五名是E.”乙:“第二名是A,第四名是C.”丙:“第三名是D,第四名是A”,丁:“第一名是C,第三名是B.”戊:“第二名是C,第四名是B.”若每个人都是只猜对一个人的名次,且每个名次只有一个人猜对,则第一、二、三、四、五名分别是.2011年第九届小学“希望杯”全国数学邀请赛试卷(四年级第1试)参考答案与试题解析一、解答题(共20小题,满分114分)1.(6分)计算:(7777+8888)÷5﹣(888﹣777)×3=3000 .【分析】把7777+8888与888﹣777,拆成两个数的乘积,再根据乘法分配律进行计算即可.【解答】解:(1111×7+1111×8)÷5﹣(111×8﹣111×7)×3,=1111×(7+8)÷5﹣111×(8﹣7)×3,=1111×(15÷5)﹣111×1×3,=1111×3﹣111×3,=(1111﹣111)×3,=1000×3,=3000.故答案为:3000.【点评】本题主要考查乘法分配律的灵活运用,根据数字特点找出巧算的方法进行计算即可.2.(6分)计算:1+11+21+…+1991+2001+2011=203212 .【分析】通过观察,相邻两个数的差是10,这是一个等差数列,可以用高斯求和公式进行简算.这一数列共有(2011﹣1)÷10+1=202个数,然后运用公式计算即可.【解答】解:1+11+21+…+1991+2001+2011,=(1+2011)×[(2011﹣1)÷10+1]÷2,=2012×202÷2,=203212.故答案为:203212.【点评】此题的关键是先探索出这是一个等差数列,运用“项数=(末项﹣首项)÷公差+1”算出项数.3.(6分)在小于30的质数中,加3以后是4的倍数的是5,13,17,29 .【分析】根据质数的意义,一个自然数,如果只有1和它本身两个因数,这样的数叫做质数.30以内的质数有:2,3,5,7,11,13,17,19,23,29;4的倍数特征是个位上的数是偶数;由此解答.【解答】解:5+3=8;13+3=16;17+3=20;29+3=32;8,16,20,32都是4的倍数;故答案为:5,13,17,29.【点评】此题的解答主要明确质数的意义,掌握30以内的10个质数,和4的倍数的特征.4.(6分)小于100的最大的自然数与大于300的最小的自然数的和,是不大于200的最大的自然数的 2 倍.【分析】此题要找出小于100的最大自然数是99,大于300的最小自然数是301,不大于200(即小于或等于200)的最大自然数是200,由此本题可以看做是:“99和301的和是200的多少倍?”.【解答】解:(99+301)÷200,=400÷200,=2;答:是不大于200的最大的自然数的2倍.故答案为:2.【点评】解决此题的关键是,根据题干先得出“小于100的最大的自然数”是99、“大于300的最小的自然数”是301,“不大于200的最大的自然数”是200.5.既是6的倍数又是8的倍数的所有两位数的和是240 .【分析】既是6的倍数,又是8的倍数,先分解质因数,6分为2×3,8分为2×2×2,再找出最小公倍数,两位数的公倍数只有四个数:24,48,72,96,相加即得答案240.【解答】解:根据分析,先分解质因数6=2×3,8=2×2×2,则两者的最小公倍数即为24,符合条件的所有两位数公倍数为:24,48,72,96;所有这些两位数之和:24+48+72+96=240,故答案为:240.【点评】本题考查了公倍数和数的整除运算知识,本题突破点是:找出两者之间的最小公倍数.6.(6分)四年级一班第2小组共12人,其中5人会打乒乓球,8人会下象棋,3人既会打乒乓球又会下象棋,那么这个小组中既不会打乒乓球又不会下象棋的有 2 人.【分析】只要从总人数12人中,把会打乒乓球和会下象棋的人数减掉,剩下的就是这个小组中既不会打乒乓球又不会下象棋的人数;此题可以画图分析:5+8=13人,这里重复加了一次既会打乒乓球有会下象棋的3人,所以会打乒乓球和会下象棋的人数为13﹣3=10人,则剩下的12=2人就是这个小组中既不会打乒乓球又不会下象棋的人数.【解答】解:12﹣(5+8﹣3)=2(人),答:这个小组中既不会打乒乓球又不会下象棋的有 2人.故答案为:2.【点评】此题考查了利用容斥原理解决实际问题的灵活应用.7.(6分)按照左侧四个图中数的规律,在第五个图中填上适当的数:【分析】(1)根据题干,图中1的位置变化规律是:按顺时针方向依次移动一个格;(2)数字排列规律是:分别按1、3、5、2、4、6的顺序排列的,而且第奇数幅是按顺时针排列,第偶数幅是按逆时针排列;第五幅图是第奇数幅,所以按顺时针排列.【解答】解:根据题干分析可得:(1)图中1的位置变化规律是:按顺时针方向依次移动一个格;所以先确定1的位置如下图所示;(2)第五幅图是第奇数幅,所以按顺时针排列,所以可以在图中添上正确的数字如下图所示:【点评】根据题干得出1的位置变化规律和图中数字1、3、5、2、4、6的排列特点是解决此题的关键.8.(6分)已知9个数的乘积是800,将其中一个数改为4,这9个数的乘积是200,若再将另外一个数改为30,则这9个数的乘积变为1200,则这两个被改动的数以外的7个数的乘积是10 .【分析】只要求出被改动的两个数是多少,即能求出这两个被改动的数以外的7个数的乘积是多少.已知9个数的乘积是800,将其中一个数改为4,这9个数的乘积是200,积缩小了800÷200=4(倍),则这个被改动的数也被缩小了4倍,则被改动的这个数为:4×4=16;同理,1200÷200=6,积扩大了6倍,第二个被改动的数也被扩大了6倍,其原来应为:30÷6=5,所以则这两个被改动的数以外的7个数的乘积是:800÷(16×5)=10.【解答】解:第一个数原来为:(800÷200)×4=16;第二个数原来为:30÷(1200÷200)=5;则两个被改动的数以外的7个数的乘积是:800÷(16×5)=10.故答案为:10.【点评】在乘法算式,其中一个因数扩大(或缩小)多少倍,积也相应的扩大(或缩小)多少倍.9.(6分)如图,△ABC的面积为36,点D在AB上,BD=2AD,点E在DC 上,DE=2EC,则△BEC的面积是8 .【分析】(1)△ABC的面积是36,BD=2AD,根据高一定时,三角形的面积与底成正比的性质即可得出:△ABC的面积:△BDC的面积=3:2,所以:△BDC的面积是:36×2÷3=24;(2)△BDC的面积是36×2÷3=24,DE=2EC,根据高一定时,三角形的面积与底成正比的性质即可得出:△BEC的面积:△BDC的面积=1:3,所以△BEC的面积是24÷3=8.【解答】解:因为BD=2AD,根据高一定时,三角形的面积与底成正比的性质即可得出:△ABC的面积:△BDC的面积=3:2,故△BDC的面积是36×2÷3=24;因为DE=2EC,同理可得:△BEC的面积:△BDC的面积=1:3,故△BEC的面积是24÷3=8.答:△BEC的面积是8.故答案为:8.【点评】此题反复考查了高一定时,三角形的面积与底成正比的性质的灵活应用.10.(6分)今年,李林和他爸爸的年龄的和是50岁,4年后,他爸爸的年龄比他的年龄的3倍小2岁,则李林的爸爸比他大28 岁.【分析】4年后,李林和他爸爸的年龄之和是50+4×2=58岁,设李林4年后的年龄为x岁,则爸爸的年龄是3x﹣2岁,根据他们的年龄之和是58岁列出方程即可解决问题.【解答】解:设李林4年后的年龄为x岁,则爸爸的年龄是3x﹣2岁,根据题意可得方程:x+3x﹣2=50+4×2,4x=60,x=15,3×15﹣2=43(岁),43﹣15=28(岁),答:李林的爸爸比他大28岁.故答案为:28.【点评】此题也可以这样分析,4年后,李林和爸爸的年龄之和就是58岁,把李林的年龄看做1份,那么爸爸的年龄就是3份少2岁,由此可以求出1份即李林的年龄为:(58+2)÷4=15(岁),由此可得爸爸58﹣15=43岁,则爸爸比李林大28岁.11.(6分)某次考试,A、B、C、D、E五人的平均分是90分.若A、B、C 的平均分是86分,B、D、E的平均分是95分,则B的得分是93 分.【分析】根据“平均数×数量=总数”分别计算出A、B、C三个数的和与B、D、E三个数的和与这五个数的和,进而用“A、B、C三个数的和+B、D、E三个数的和﹣五个数的和”进行解答即可.【解答】解:(86×3+95×3)﹣(90×5),=543﹣450,=93(分);故答案为:93.【点评】解答此题的关键:根据平均数和数量、总量之间的关系进行分析解答.12.(6分)如图,已知直线AB和CD交于点O,若∠AOC=20°,∠EOD=60°,则∠AOE=100°,∠BOC=160°.【分析】由图可知,∠AOC=20°、∠EOD=60°与∠AOE相加等于180°,由此即可求得∠AOE的度数;∠BOC与∠AOC=20°互为补角,根据补角的定义即可解答.【解答】解:∠AOE=180°﹣∠AOC﹣∠EOD=180°﹣20°﹣60°=100°.∠BOC=180°﹣∠AOC=180°﹣20°=160°.故答案为:100°;160°.【点评】本题主要考查角的度量与补角的定义,根据几个角的和差关系进行计算是解题关键.13.(6分)如图,四边形ABCD与CEFG是边长相等的正方形,且B、C、G 在一条直线上,则图中共有 3 个正方形,22 个等腰直角三角形.【分析】根据图形可知,正方形有:ABCD、CEFG、BEGD三个;在正方形ABCD、CEFG和BEGD中,单一三角形是10个,有两个小三角形组成的是8个;由3个三角形组成的等腰直角三角形是4个;由此解答.【解答】解:图中共有正方形3个;等腰直角三角形有:10+8+4=22(个);故答案为:3;22【点评】此题主要考查通过分类、观察、思考探寻事物规律的能力.14.(6分)一个水桶里有水,若将水加到原来的4倍,桶和水共重16千克;若将水加到原来的6倍,桶和水共重22千克.则桶内原有水 3 千克,桶重 4 千克.【分析】根据题意知道,桶的重量不变,(22﹣16)千克的水就是水原来的(6﹣4)倍,由此即可求出原来的水的千克数,那桶的重量即可求出.【解答】解:桶内原有水:(22﹣16)÷(6﹣4),=6÷2,=3(千克),桶重:16﹣4×3,=16﹣12,=4(千克);答:桶内原有水3千克,桶重4千克.故答案为:3,4.【点评】解答此题的关键是,根据题意,找出对应的数和对应的倍数,由此列式解答即可.15.(6分)某个两位数的个位数字和十位数字的和是12,个位数和十位数字交换后所得两位数比原数小36,则原数是84 .【分析】设个位数字是x,则十位数字是12﹣x,所以可得:原来两位数是10(12﹣x)+x,交换位置后的新两位数是10x+12﹣x;根据新数比原数小36,列出方程即可解决问题.【解答】解:设个位数字是x,则十位数字是12﹣x,那么原来两位数是10(12﹣x)+x,交换位置后的新两位数是10x+12﹣x;根据题意可得方程:10(12﹣x)+x﹣(10x+12﹣x)=36,18x=72,x=4;12﹣4=8,答:原数是84.故答案为:84.【点评】此题设出个位数字和十位数字,从而得出原两位数和新两位数是解决本题的关键.16.(6分)王强步行去公园,回来时坐车,往返用了一个半小时,如果他来回都步行,则需要2个半小时,那么,他来回都坐车,则需30 分钟.【分析】来回都步行,需要2个半小时说明王强步行单程用:2.5÷2=1.25(小时),又因为步行去公园,回来时坐车,往返用了一个半小时,则坐车单程用:1.5﹣1.25=0.25(小时),则来回都坐车用时:0.25×2=0.5(小时).【解答】解:(1.5﹣2.5÷2)×2,=0.25×2,=0.5(小时);0.5小时=30分钟.故答案为:30.【点评】完成本题的关健是:在求出步行单程所用时间的基础上,求出坐车单程所用时间.17.(6分)图中“C”形图形的周长是32 厘米.【分析】如图,将内部的2厘米边平移到外面红色线段处,这样这个图形的周长就是这个边长为6厘米的正方形的边长与内部横着的两条长为6﹣2=4厘米的线段的长度之和,由此利用正方形周长公式代入数据即可解决问题.【解答】解:根据题干分析可得:6×4+(6﹣2)×2,=24+8,=32(厘米),答:这个图形的周长是32厘米.故答案为:32.【点评】借助平移的性质将图形中的某些线段移动到规则图形的边上,使求这个不规则图形的周长转化成求规则图形的周长是解决此类题目的主要解题思路.18.(6分)如图,从1,2,3,4,5,6中选出5个数填在图中空格内,使填好的格内的数右边的比左边的大,下边的比上边的大,则共有30 种不同的填法.【分析】此题根据乘法原理进行解答,从6个数中选出5个进行填空,共有6×5种.【解答】解:从6个数中选出5个进行填空,共有:6×5=30(种);故答案为:30.【点评】此题运用了乘法原理:做一件事,完成它需要分成n个步骤,做第一步有m1种不同的方法,做第二步有m2种不同的方法,…,做第n步有m n种不同的方法,那么完成这件事共有N=m1×m2×m3×…×m n种不同的方法.19.(6分)三个连续自然数中最小的数是9的倍数,中间的数是8的倍数,最大的数是7的倍数,则这三个数的和最小是1488 .【分析】据题意可知,这是三个相连的自然数,又7、8、9也是相连的自然数,因此先找到7、8、9的最小公倍数:7×8×9=504,则减9是9的倍数,减8是8的倍数,减7是7的倍数,得到495、496、497是符合要求的.【解答】解:7、8、9的最小公倍数为:7×8×9=504;504﹣7=497,504﹣8=496,504﹣9=495;495+496+497=1488.故填:1488.【点评】任何三个连续自然数(零除外)的最小公倍分别减(或加)这三个数得到的三个连续的自然数分别是这三数的倍数.20.(6分)甲、乙、丙、丁、戊五人猜测全班个人学科总成绩的前五名:甲:“第一名是D,第五名是E.”乙:“第二名是A,第四名是C.”丙:“第三名是D,第四名是A”,丁:“第一名是C,第三名是B.”戊:“第二名是C,第四名是B.”若每个人都是只猜对一个人的名次,且每个名次只有一个人猜对,则第一、二、三、四、五名分别是CADBE .【分析】本题可用假设法分两步进行推理:第一步:假设甲说的前半句是真的,那么D是第1名,那么此时丙说的前半句错,后半句对.则A是第4名.同理乙的后半句对,C是第4名.矛盾.由此可知甲的后半句对.第二步:已知E是第5名,D不是第1名.和第一名有关的话只剩下丁说的,设C是第1名.则戊:“第2名是c,第4名是B”.可知前错后对,B 是第4名.且有乙:“第二名是A,第四名是c”.可知,A是第2名.D是第3名.【解答】解:第一步:假设甲说的前半句是真的,那么D是第1名,那么此时丙说的前半句错,后半句对.则A是第4名.同理乙的后半句对,C是第4名.矛盾.由此可知甲的后半句对.即第五名是E;第二步:已知E是第5名,D不是第1名.和第一名有关的话只剩下丁说的,设C是第1名.则戊:“第2名是c,第4名是B”.可知前错后对,B是第4名.且有乙:“第二名是A,第四名是c”.可知,A是第2名.D是第3名.综上可知,第一、二、三、四、五名分别是CADBE.【点评】完成此类题目思路要清晰,根据所给条件中的逻辑关系细心推理,从而得出结论.声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布日期:2019/4/22 16:49:14;用户:小学奥数;邮箱:pfpxxx02@;学号:20913800。
第11~13届小学四年级奥数

第十一届小学“希望杯”全国数学邀请赛四年级 第Ⅰ试试题2013年3月17日 上午8:30至10:00以下每题6分,共120分1.计算:4×37×25= 。
2.某种速印机每小时可以印3600张纸,那么印240张纸需要 分钟。
3.若三个连续奇数的和是111,则其中最小的奇数是 。
4.一个数除以3余2,除以4余3,除以5余4,则这样的数中最小的是 。
5.图1是一个5×5的网格,每个小方格的面积都是1,阴影部分是类似数字“2”的图形,那么阴影部分的面积是 。
6.将两个长4厘米、宽2厘米的长方形拼在一起(彼此不重叠),组成一个新长方形,则新长方形的周长是 厘米,或 厘米。
7.今年,小明12岁,爸爸40岁,在小明 岁的时候,爸爸的年龄是小明的5倍。
8.商店按每个60元购进了50个足球,全部售出后获利1950元,则每个足球的售价是 元。
9.如图2,将数字4,5,6填入正方体的展开图中,使正方形相对的两个面内数字的和都相等,则A 处应该填 ,B 处应该填 ,C 处应该填 。
10.从九位数798056132中任意划去4个数字,使剩下的5个数字顺次组成5位数,则所得五位数最大的是 ,最小的是 。
11.如图3,在一大一小两个正方形拼成的图形中,阴影部分的面积是50平方厘米,则小正方形的面积是 平方厘米。
12.2013的质因数中,最大的质因数与最小的质因数的乘积是 。
13.从边长为5的正方形纸片的四个角剪掉四个小长方形后得到图4,得到新图形的周长是 。
图1图2图3图6图4图514.喜羊羊打开一本书,发现左右两页的页码数的乘积是420,则这两页的页码数的和是。
15.将1到16这16个自然数排成如图5的形状,如果每条斜线是的4个数的和相等,那么a-b-c+d+e+f-g= 。
16.行驶在索马里海域的商船发现在它北偏西60°方向50海里处有一海盗船,于是商船向在它南偏西60°方向50海里处的护航舰呼救,此时,护航舰在海盗船的正(填东、西、南、北)方向海里处。
第一届小学“希望杯”数学邀请赛(第1试)-四年级竞赛试题与答案
第一届小学“希望杯”数学邀请赛(第1试)四年级第1试1.下边三个图中都有一些三角形,在图A中,有个;在图B中,有个;在图C中,有个。
2.写出下面等式右边空白处的数,使等式能够成立:0.6+0.06+0.006+…=2002÷。
3.观察1,2,3,6,12,23,44,x,164的规律,可知x =。
4.如图,将一个三角形(有阴影)的两条边分别延长2倍,得到一个大三角形,这个大三角形的面积是原三角形面积的______倍。
5.如果规定a※b =13×a-b÷8,那么17※24的最后结果是。
6.气象局对部分旅游景区的某一天的气温预报如下表:其中,温差最小的景区是,温差最大的景区是。
7.AOB是三角形的纸,OA=OB,图中的虚线是折痕,至少折次就可以得到8个相同的三角形。
8.有的两位数,加48,就变成3位数;减48,就变成1位数,这样的两位数有,它们的和等于。
9.甲、乙、丙、丁四个学习小组共有图书280本,班主任老师提议让四个组的书一样多,得到拥护,于是从甲调14本给乙,从乙调15本给丙,从丙调17本给丁,从丁调18本给甲。
这时四个组的书一样多。
这说明甲组原来有书本。
10.幼儿园老师给几组小朋友分苹果,每组分7个,少3个;每组分6个,则多4个,苹果有个,小朋友共组。
11.在 a=20032003×2002和 b=20022003×2003中,较大的数是,它比较小的数大。
12.小明的家离学校2千米,小光的家离学校3千米,小明和小光的家相距千米。
13.甲、乙、丙三人中只有1人会开汽车。
甲说:“我会开。
”乙说:“我不会开。
”丙说:“甲不会开。
”三人的话只有一句是真话。
会开车的是。
14.为了支援西部,1班班长小明和2班班长小光带了同样多的钱买了同一种书44本,钱全部用完,小明要了26本书,小光要了18本书。
回校后,小明补给小光28元。
小明、小光各带了元,每本书价元。
希望杯第5-8届四年级数学试题及答案(WORD版)

第五届小学“希望杯”全国数学1. 1只青蛙1张嘴,2只眼睛4条腿:2只青蛙2张嘴,4只眼睛8条腿:……______只青蛙______张嘴,32只眼睛______条腿。
2.在113379902,113379904,113379906,113379908这四个数中,恰好等于六个22的乘积的数是______。
3.2008×2006+2007×2005-2007×2006-2008×2005=______。
4.除法算式□÷□=20…8中,被除数最小等于______。
5.用数字1,2,3可以组成6个没有重复数字的三位数,这6个数的和是______。
6.图中,不含“A”的正方形有______个。
7.把0,1,2,3,4,5,6,7,8这九个数字填入下图的九宫格中,把每行、每列以及每条对角线上的三个数相加,得到8个和,这8个和再相加所得到的和最大是______。
8.如图所示的除法算式中,每个□各代表一个数字,则被除数是______。
9.放寒假了,叔叔送给强强一本有许多个故事的书,强强计划每天看同样个数的故事,用20天可看完。
但强强在看书时发现故事很有趣,实际每天比原计划多看3个故事,结果提前4天看完了故事书。
这本故事书一共有______个故事。
10.欢欢对乐乐说:“我比你大8岁,2年后,我的年龄是你的年龄的3倍。
”欢欢现在______岁。
11.琪琪画了—幅画,请爷爷、奶奶.爸爸和妈妈评分。
爷爷和奶奶评分的平均分是94分,奶奶和爸爸评分的平均分是90分,爸爸和妈妈评分的平均分是92分,那么爷爷和妈妈评分的平均分是______分。
12.养牛场有2007头黄牛和水牛,其中母牛1105头,黄牛1506头,公水牛200头,那么母黄牛有______头。
13.在一段时间里,时针、分针、秒针转动的圈数之和恰好是1466圈,那么这段时间有______秒。
14.甲、乙二人同时从A地去B地,甲每分钟行60米,乙每分钟行90米,乙到达B地后立即返回,并与甲相遇,相遇时,甲还需行3分钟才能到达B地。
历届希望杯试题

第四届小学“希望杯”全国数学邀请赛六年级第1试以下每题5分,共120分。
1.2006×2008×()=________。
2.900000-9=________×99999。
3.=________。
4.如果a=,b=,c=,那么a,b,c中最大的是________,最小的是________。
5.将某商品涨价25%,如果涨价后的销售金额与涨价前的销售金额相同,则销售量减少了________%。
6.小明和小刚各有玻璃弹球若干个。
小明对小刚说:“我若给你2个,我们的玻璃弹球将一样多。
”小刚说:“我若给你2个,我的弹球数量将是你的弹球数量的三分之一。
”小明和小刚共有玻璃弹球________个。
7.一次测验中,小明答错了10道题,小刚答错了8道题,小强答对的题的数量等于小明与小刚答对题的数量之和,且小强答错了3道题。
这次测验共有________道题。
8.一个两位数,加上它的个位数字的9倍,恰好等于100。
这个两位数的各位数字之和的五分之三是________。
9.将一个数A的小数点向右移动两位,得到数B。
那么B+A是B-A的________倍。
(结果写成分数形式)10.用10根火柴棒首尾顺次连接接成一个三角形,能接成不同的三角形有________个。
11.希望小学举行运动会,全体运动员的编号是从1开始的连续整数,他们按图中实线所示,从第1珩第1列开始,按照编号从小到大的顺序排成一个方阵。
小明的编号是30,他排在第3行第6列,则运动员共有________人。
12.将长为5,宽为3,高为1的长方体木块的表面涂上漆,再切成15块棱长为l的小正方体。
则三个面涂漆的小正方体有________块。
13.如图,∠AOB的顶点0在直线l上,已知图中所有小于平角的角之和是400度,则∠AOB=________度。
14.如图,桌面上有A、B、C三个正方形,边长分别为6,8,10。
B的一个顶点在A 的中心处,C的一个顶点在B的中心处,这三个正方形最多能盖住的面积是________。
第一届希望杯-四年级-第一试试卷及解析

第一届小学"希望杯"全国数学邀请赛四年级第1试
一、以下每题4分,共100分1.右边三个图中,都有一些三角形,在图A中,有______个;在图B中,有______个;中图C中,有______ 个. 2.写出下面
等式右边空白处的数,使等式能够成立:0.6+0.06+0.006+……=2002÷______ .
3.观察1、2、3、6、12、23、44、x 、164的规律,可知x =______ .
4.如图2,将一个三角形(有阴影)的两条边分别延长2倍,得到一个大三角形,这个大三角形的面积是原三角形面积的______倍.
5.如果规定a※b =13×a -b ÷8,那么17※24的最后结果是______.
6.气象局对部分旅游景区的某一天的气温预报如下表:
景区千岛湖张家界庐山三亚丽江大理九寨沟鼓浪屿武夷山黄山
气温(℃)11/18/43/-227/1917/318/38/-815/915/10/-5。
2011年第9届小学“希望杯”全国数学邀请赛试卷(五年级第1试)

2011年第9届小学“希望杯”全国数学邀请赛试卷(五年级第1试)一、解答题(共20小题,满分120分)1.(6分)计算:1.25×0.32×2.5=_________.2.(6分)把0.123,按照从小到大的顺序排列:_________<_________<_________<_________.3.(6分)先将从1开始的自然数排成一列:123456789101112131415…然后按一定规律分组:1,23,456,7891,01112,131415,…在分组后的数中,有一个十位数,这个十位数是_________.4.(6分)如图,从A到B,有_________条不同的路线.(不能重复经过同一个点)5.(6分)数一数,图中有多少个正方形?6.(6分)一个除法算式中,被除数、除数、商与余数都是自然数,并且商与余数相等.若被除数是47,则除数是_________,余数是_________.7.(6分)如果六位数1992□□能被105整除,那么它的最后两位数是_________.8.(6分)如果一个自然数的约数的个数是奇数,我们称这个自然数为“希望数”,那么,1000以内最大的“希望数”是_________.9.(6分)将等边三角形纸片按图1所示步骤折叠3次(图1中的虚线是三边的中点的连线),然后沿两边的重点的边减去一角(如图2).将剩下的纸片展开、平铺,得到的图形是_________10.(6分)如图,甲、乙两人按箭头方向从A点同时出发,沿亠正方形ABCD的边行走,正方形ABCD的边长是100米,甲的速度是乙的速度的1.5倍,两人在E点第一次相遇,则三角形ADE的面积比三角形BCE的面积大_________平方米.11.(6分)星期天早晨,哥哥和弟弟去练习跑步,哥哥每分钟跑110米,弟弟每分钟跑80米,弟弟比哥哥多跑了半小时,结果比哥哥多跑了900米,那么,哥哥跑了_________米.12.(6分)小明带了30元钱去买文具,买了3个笔记本和5支笔,剩余的钱,如果再买2支笔还差0.4元,如果再买2个笔记本则还差2元,那么,笔记本每个_________元,笔每支_________元.13.(6分)数学家维纳是控制论的创始人.在他获得哈佛大学博士学位的授予仪式上,有人看他一脸稚气的样子,好奇地询问他的年龄.维纳的回答很有趣,他说:“我的年龄的立方是一个四位数,年龄的四次方是一个六位数,这两个数刚好把0﹣9这10个数字全都用上了,不重也不漏,”那么,维纳这一年_________岁,(注:数a的立方等于a×a×a,数a的四次方等于a×a×a×a)14.(6分)鸡与兔共100只,鸡的脚比兔的脚多26只.那么,鸡有_________只.15.(6分)小松鼠储藏了一些松果过冬.小松鼠原计划每天吃6个松果,实际每天比原计划多吃2个,结果提前5天吃完了松果.小松鼠一共储藏了_________个松果.16.(6分)商店对某饮料推出“第二杯半价”的促销办法.那么,若购买两边这种饮料,相当于在原价的基础上打_________折.17.(6分)A、B、C、D四人进行围棋比赛,每人都要与其他三人各赛一盘,比赛在两张棋盘上同时进行,每人每天只赛一盘.第一天A与C比赛,第二天C与D比赛,第三天B与_________比赛.18.(6分)有白球和红球共300个,纸盒100个.每个纸盒里都放3个球,其中放1个白球的纸盒有27个,放2个或3个红球的纸盒共有42个,放3个白球和3个红球的纸盒数量相同.那么,白球共有_________个.19.(6分)用长是9厘米、宽是6厘米、高是7厘米的长方体木块叠成一个正方体,至少需要这种长方体木块_________块.20.(6分)如图,梯形ABCD的上底AD长12厘米,高BD长18厘米,BE=2DE,则下底BC长_________厘米.2011年第9届小学“希望杯”全国数学邀请赛试卷(五年级第1试)参考答案与试题解析一、解答题(共20小题,满分120分)1.(6分)计算:1.25×0.32×2.5=1.考点:小数的巧算.分析:根据125×8=1000、25×4=100,所以可将算式中的因数0.32改写成0.8×0.4,然后再依据乘法交换律交换因数的位置进行计算比较简便.解答:解:1.25×0.32×2.5=1.25×0.8×0.4×2.5,=(1.25×0.8)×(0.4×2.5),=1×1,=1.故答案为:1.点评:解答此题的关键是将算式中的0.32改写成0.8×0.4,然后用乘法交换律进行计算.2.(6分)把0.123,按照从小到大的顺序排列:0.123<0.2<0.1<0.12.考点:小数大小的比较.分析:为了便于比较这几个小数的大小,应写出循环小数的两个循环节,再按比较小数大小的方法进行比较.解答:解:0.1=0.12323…,0.12=0.12333…,0.2=0.123123…,0.123=0.12300,这些小数的整数部分相同,十分位、百分位、千分位上的数也相同,比较万分位上的数得出:0.123<0.2<0.1<0.12;故答案为:0.123<0.2<0.1<0.12.点评:解答此题关键是把每个循环小数写出两个循环节后再比较大小.3.(6分)先将从1开始的自然数排成一列:123456789101112131415…然后按一定规律分组:1,23,456,7891,01112,131415,…在分组后的数中,有一个十位数,这个十位数是2829303132.考点:数字分组.分析:这是一道操作问题,因为位数不是很多,不用做过多的考虑,按照题目给出的规律,往后数就是了.1617181,92021222,324252627,2829303132,333435363373839方法二:据分组规规可知,每组数的位数购成一个公差为1的等差数列,则十位数之前应该有1+2+3+…+9=45位.1位数有9位,10﹣19有20位,20﹣27有16位,所以十位数的开头应为28,为2829303132.解答:解:方法一:据分组律可得:从131415向后为1617181,92021222,324252627,2829303132(十位数),…;方法二:位数之前应该有1+2+3+…+9=45位.1位数有9位,10﹣19有20位,20﹣27有16位,所以十位数的开头应为28,为2829303132.故填:2829303132.点评:此题要求的结论不是很复杂,所以据分组规则进行直接操作也很容易得出结论.4.(6分)如图,从A到B,有25条不同的路线.(不能重复经过同一个点)考点:排列组合.分析:这是一道数图形问题,采取分类计数的方法;从A到B有5条直连线路,而每条直连线路均有5种不同的路线可以到达B点,由此即可得出答案.解答:解:如图,因为,从A到B有5条直连线路,每条直连线路均有5种不同的路线可以到达B点,所以,共有不同线路:5×5=25(条),答:从A到B,有25条不同的路线,故答案为:25.点评:解答此题的关键是,根据所给图形的特点,运用分类计数的方法,即乘法原理解答即可.5.(6分)数一数,图中有多少个正方形?考点:组合图形的计数.分析:先设最小的正方形的边长为1,分别找出边长为1、2、3的正方形各有多少个;再找出以小正方形的对角线、对角线的一半、3个对角线的一半为边长的正方形各有多少个,最后加起来即可.解答:解:通过有规律的数,得出:(1)边长为1的正方形有4×3=12(个);(2)边长为2的正方形有6个;(3)边长为3的正方形有2个.(4)以小正方形的对角线为边的正方形有8个;(6)以3个对角线的一半为边长的正方形有1个.所以图中共有正方形:12+6+2+8+17+1=46(个).答:图中有46个正方形.点评:按边长找规律,正确的数出正方形的个数.6.(6分)一个除法算式中,被除数、除数、商与余数都是自然数,并且商与余数相等.若被除数是47,则除数是46,余数是1.考点:有余数的除法.分析:设出除数和余数和商,根据被除数=除数×商+余数列出方程,然后化简,再根据它们都是自然数讨论取值.解答:解:设除数为b,商和余数都是c,这个算式就可以表示为:47÷b=c …c,即b×c+c=47,c×(b+1 )=47,所以c一定是47的因数,47的因数只有1和47;c为47肯定不符合条件,所以c=1,即除数是46,余数是1.故答案为:46,1.点评:本题根据被除数=除数×商+余数找出商的取值范围,进而求解.7.(6分)如果六位数1992□□能被105整除,那么它的最后两位数是90.考点:数的整除特征.分析:因为105=3×5×7,根据数的整除性质,可知这个六位数能同时被3、5和7整除.根据能被5整除的数的特征,可知这个六位数的个位数只能是0或5两种,再根据能被3整除的数的特征,可知这个六位数有如下七个可能:199200,199230,199260,199290,199215,199245,199275.最后用7去试除知,199290能被7整除.所以,199290能被105整除,它的最后两位数是90.解答:解:因为105=3×5×7,所以105能同时被3、5和7整除.根据能被5整除的数的特征,可知这个六位数有如下七个可能:199200,199230,199260,199290,199215,199245,199275.最后用7去试除知,199290能被7整除.所以,199290能被105整除,它的最后两位数是90.故答案为:90.点评:此题也可以这样思考:先把后面两个方框中填上0后的199200除以105,根据余数的大小来决定最后两个方框内应填什么.199200÷105=189715,105﹣15=90,如果199200再加上90,199290便可被105整除,最后两位数是90.8.(6分)如果一个自然数的约数的个数是奇数,我们称这个自然数为“希望数”,那么,1000以内最大的“希望数”是961.考点:约数个数与约数和定理.分析:自然数的因数都是成对出现的,比如1和本身是一对,出现奇数个因数的时候是因为其中有一对的因数是相等的,那么这个自然数是完全平方数.所以只有完全平方数的约数个数才是奇数,则这道题就变成了求“1000以内最大的完全平方数是多少”,312=961,322=1024,由此即可得出1000以内最大的完全平方数,从而解决问题.解答:解:根据分析可得:1000以内最大的“希望数”就是1000以内最大的完全平方数,而已知1000以内最大的完全平方数是312=961,根据约数和定理可知,961的约数个数为:2+1=3(个),符合题意,答:1000以内的最大希望数是961.点评:这道题主要考查的知识点是完全平方数的约数个数是奇数这一特点的灵活应用.9.(6分)将等边三角形纸片按图1所示步骤折叠3次(图1中的虚线是三边的中点的连线),然后沿两边的重点的边减去一角(如图2).将剩下的纸片展开、平铺,得到的图形是A考点:重叠问题.分析:找一个等边三角形纸片按图中所示步骤折叠3次,然后用剪刀沿两边的中点的边减去一角,将剩下的纸片展开、平铺看一看,即可得出答案.解答:解:找一剪刀与一等边三角形纸片,按题中所示步骤进行操作,最后得到的图形是A,故答案为:A.点评:解答此题的关键是,根据所给的步骤,进行实际操作,即可得出答案.10.(6分)如图,甲、乙两人按箭头方向从A点同时出发,沿亠正方形ABCD的边行走,正方形ABCD的边长是100米,甲的速度是乙的速度的1.5倍,两人在E点第一次相遇,则三角形ADE的面积比三角形BCE的面积大1000平方米.考点:相遇问题;三角形的周长和面积.分析:这是一道行程与几何结合起来的综合题.要想知道三角形ADE的面积比三角形BCE的面积大多少平方米,就要明确DE及EC的长度是多少,由于相遇问题中,速度比=所行路程的比,因此通过周长及两人的速度比可求出两人相遇时各行的路程是多少,进行求出DE及EC的长度之后,再据三角形的面积公式就能求出三角形ADE的面积比三角形BCE的面积大多少平方米了.解答:解:由于甲的速度是乙的速度的1.5倍所以两人速度比为:1.5:1=3:2,所以两人在E点相遇时,甲行了:(100×4)×=240(米);乙行了:400﹣240=160(米);则EC=240﹣100×2=40(米),DE=160﹣100=60(米);三角形ADE的面积比三角形BCE的面积大:60×100÷2﹣40×100÷2=3000﹣2000,=1000(平方米).点评:根据两人的速度比求出两人相遇时各行了多少千米进而求出DE、EC的长度是完成本题的关健.11.(6分)星期天早晨,哥哥和弟弟去练习跑步,哥哥每分钟跑110米,弟弟每分钟跑80米,弟弟比哥哥多跑了半小时,结果比哥哥多跑了900米,那么,哥哥跑了5500米.考点:列方程解含有两个未知数的应用题.分析:设哥哥跑了X分钟,根据“速度×时间=路程”分别计算出弟弟跑的路程和哥哥跑的路程,进而根据“弟弟跑的路程﹣哥哥跑的路程=多跑的路程(900)”列出方程,解答即可.解答:解:设哥哥跑了X分钟,则有:(X+30)×80﹣110X=900,80x+2400﹣110x=900,2400﹣30x=900,X=50;110×50=5500(米);答:哥哥跑了5500米.故答案为:5500.点评:解答此题的关键是设出要求的量为未知数,进而根据速度、时间和路程的关系,分别计算出弟弟跑的路程和哥哥跑的路程,然后找出数量间的相等关系式,列出方程解答.12.(6分)小明带了30元钱去买文具,买了3个笔记本和5支笔,剩余的钱,如果再买2支笔还差0.4元,如果再买2个笔记本则还差2元,那么,笔记本每个 3.6元,笔每支 2.8元.考点:代换问题.分析:据题意,再加2元就可再买两个笔记本,由此可知,32元就可以买5个笔记本和5支笔,所以,一个笔记本和一支笔的价钱是6.4元;30.4元可以买3个笔记本和7支笔,就是说,30.4﹣3×6.4=11.2元,可以买4支笔,则每支笔的价钱是:2.8元.由此即可求得每个笔记本的价钱解决问题.解答:解:根据题干分析可得:5个笔记本+5支笔=32元;则1个笔记本+1支笔=6.4(元),3个笔记本+3支笔+4支笔=30.4(元),所以4支笔=30.4﹣3×6.4=11.2(元),所以1支笔的价格是:11.2÷4=2.8(元),则每个笔记本的价钱是:6.4﹣2.8=3.6(元).答:每个笔记本3.6元,每支笔2.8元.故答案为:3.6;2.8.点评:此题关键是根据5个笔记本和5支笔的总价格得出1个笔记本和1支笔的价格,再利用等量代换的思想求得1支笔的价格,从而解决问题.13.(6分)数学家维纳是控制论的创始人.在他获得哈佛大学博士学位的授予仪式上,有人看他一脸稚气的样子,好奇地询问他的年龄.维纳的回答很有趣,他说:“我的年龄的立方是一个四位数,年龄的四次方是一个六位数,这两个数刚好把0﹣9这10个数字全都用上了,不重也不漏,”那么,维纳这一年18岁,(注:数a的立方等于a×a×a,数a的四次方等于a×a×a×a)分析:本题先通过缩小范围然后再试验.首先一个数的立方是四位数,四次方是六位数,得出年龄在18~21之间,然后再去掉20、21,因为它的个位数字分别是“0”,“1”;然后再试一试,可得答案为18.解答:解:先用估值的方法大概确定一下维纳的年龄范围.根据174=83521,184=104976,194=130321,根据题意可得:他的年龄大于或等于18岁;再看,183=5832,193=6859,213=9261,223=10648,说明维纳的年龄小于22岁.根据这两个范围可知可能是18、19、20、21的一个数.又因为20、21无论是三次方还是四次方,它们的尾数分别都是:0、1,与“10个数字全都用上了,不重也不漏”不符,所以不用考虑了.只剩下18、19这两个数了.一个一个试,18×18×18=5832,18×18×18×18=104976;19×19×19=6859,19×19×19×19=130321;符合要求是18.故答案为:18.点评:本题需要把实验法用到整个解题过程中,不断的调整,排除不符合题意的情况.14.(6分)鸡与兔共100只,鸡的脚比兔的脚多26只.那么,鸡有71只.考点:鸡兔同笼.分析:这里可以设鸡有x只,则兔就有100﹣x只,根据鸡的脚比兔的脚多26只;即可列出方程解决问题.解答:解:设鸡有x只,则兔就有100﹣x只,根据题意可得方程:2x﹣4×(100﹣x)=26,2x﹣400+4x=26,6x=426,x=71,答:鸡有71只.故答案为:71.点评:此题也可以这样分析:因为鸡脚比兔脚多26,不妨先抓出13只鸡来,这样鸡脚和兔脚就一样多了,则剩下的100﹣13=87只鸡占2份,兔占1份;所以可得兔有87÷3=29只,则鸡就有100﹣29=71只.15.(6分)小松鼠储藏了一些松果过冬.小松鼠原计划每天吃6个松果,实际每天比原计划多吃2个,结果提前5天吃完了松果.小松鼠一共储藏了120个松果.考点:盈亏问题.分析:按计划,最后5天的松果数是5×6=30(个),因为前面每天多吃了2个,这30个松果就匀到前面提前吃掉了,需要15天的时间.实际每天吃的松果数是8个,共吃了15天,所以,共储藏了120个松果.解答:解:(6+2)×[(5×6)÷2]=8×15,=120(个).答:小松鼠一共储藏了120个松果.故答案为:120.点评:本题为较为简单的盈亏问题,关健是根据原计划吃的个数及提前的天数求出小松鼠实际吃了多少天.16.(6分)商店对某饮料推出“第二杯半价”的促销办法.那么,若购买两边这种饮料,相当于在原价的基础上打七五折.考点:折扣问题.分析:用赋值法比较简单;设出设这种饮料每瓶10,两瓶售价是20元;然后根据题意,用“10+10×”计算出实际解答:解:设这种饮料每瓶10,两瓶售价是20元,实际用了:10+10×,=10+5,=15(元),15÷20=0.75=75%,所以是打七五折;故答案为:七五.点评:解答此题的关键:(1)根据单价、数量和总价之间的关系进行解答;(2)根据一个数乘分数的意义,用乘法计算;(3)根据求一个数是另一个数的几分之几是多少,用除法进行解答.17.(6分)A、B、C、D四人进行围棋比赛,每人都要与其他三人各赛一盘,比赛在两张棋盘上同时进行,每人每天只赛一盘.第一天A与C比赛,第二天C与D比赛,第三天B与C比赛.考点:逻辑推理.分析:根据题干,每人每天只赛一盘,①第一天A与C比赛,则B与D比赛;②第二天C与D比赛,则A与B 比赛;根据每人都要与其他三人各赛一盘,即可推理得出第三天比赛情况.解答:解:根据题干分析可得:第一天A﹣与C比赛,则B与D比赛;第二天C与D比赛,则A与B比赛;每人都要和其他三人各赛一盘,而前两天B已经和A、D比赛过了,答:第三天B与C比赛.故答案为:C.点评:根据题干分别得出第一天、第二天中B与其他人的比赛情况,是解决本题的关键.18.(6分)有白球和红球共300个,纸盒100个.每个纸盒里都放3个球,其中放1个白球的纸盒有27个,放2个或3个红球的纸盒共有42个,放3个白球和3个红球的纸盒数量相同.那么,白球共有158个.考点:筛选与枚举.分析:每个个纸盒里放3个球,那么放球的情况有:白白白,红红红,白白红,白红红这4种.又知道放2个红球和放1个白球其实是同一种情况.由此可以知道放3个红球的盒子数是:42﹣27=15个,所以放3个白球的盒子数也是15个,则放2白一红的盒子数是:100﹣15﹣15﹣27=43个,由此即可求得白球的总数.解答:解:根据题干分析可得:3个红球的盒子数是:42﹣27=15(个),所以放3个白球的盒子数也是15(个),则放2白一红的盒子数是:100﹣15﹣15﹣27=43(个),所以白球的总数有:15×3+43×2+27=158(个),答:白球共有158个.故答案为:158.点评:根据题干:放2个红球和放1个白球其实是同一种情况和放2个或3个红球的纸盒共有42个,得出放三个红球和三个白球的盒子数都是15个,是解决本题的关键.19.(6分)用长是9厘米、宽是6厘米、高是7厘米的长方体木块叠成一个正方体,至少需要这种长方体木块5292块.考点:图形的拆拼(切拼).分析:根据题意,正方体的棱长应是9,6,7的最小公倍数,9,6,7的最小公倍数是126;进而根据“正方体的体积=棱长3”求出叠成的正方体的体积,然后根据“长方体的体积=长×宽×高”计算出长方体的体积,用“拼成的正方体的体积÷长方体的体积”即可得出结论.所以,至少需要这种长方体木块:(126×126×126)÷(9×6×7),=2000376÷378,=5292(块);答:至少需要这种长方体木5292块.故答案为:5292.点评:本题利用最小公倍数的概念进行“拼图”的问题,解答时应认真分析题意,然后根据正方体和长方体的体积计算公式进行解答即可.20.(6分)如图,梯形ABCD的上底AD长12厘米,高BD长18厘米,BE=2DE,则下底BC长24厘米.考点:相似三角形的性质(份数、比例).分析:在梯形ABCD中,因为AD∥BC,所以△ADE和△CBE相似,因为BE=2DE,即DE:BE=1:2,所以AD:CB=1:2,又因为AD=12厘米,由此即可求得BC的长度.解答:解:因为AD∥BC,所以△ADE和△CBE相似,因为BE=2DE,即DE:BE=1:2,所以AD:CB=1:2,又因为AD=12厘米,所以BC=12×2=24(厘米),答:下底BC的长为24厘米.故答案为:24.点评:此题考查了相似三角形的对应边成比例的性质的灵活应用.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第九届小学希望杯全国数学邀请赛
四年级 第1试
以下每题6分,共120分.
1. 计算:(7777+8888)÷5—(888—777)×3= . 2. 计算:1+11+21+…+1991+2001+2011= .
3. 在小于30的质数中,加3以后是4的倍数的是 .
4. 小于100的最大的自然数与大于300的最小的自然数的和,是不大于200的最大的自然数的 倍. 5. 既是6的倍数又是8的倍数的所有两位数的和是 .
6. 四年级一班2个小组共12人,其中5人会打乒乓球,8人会下象棋,3人既会打乒乓球又会下象棋,
那么这两个小组中既不会打乒乓球又不会下象棋的有 人. 7. 按照左侧四个图中数的规律,在第五个图中填上适当的数:
6135
2
4
16
4
2
53425
3
1
61
6
42
53
8. 已知9个数的乘积是800,将其中一个数改为4,这9个数的乘积是200,若再将另外一个数改为30,
则这9个数的乘积变为1200.则这两个被改动的数以外的7个数的乘积是 .
9. 如图1,△ABC 的面积为36,点D 在AB 上,BD=2AD ,点E 在DC 上,DE=2EC ,则△BEC 的面积
是 .
E
D
C
B
A
O
60︒20︒
E
D C B
A
F
E
B
图1 图2 图3
10.今年,李林和他爸爸的年龄的和是50岁,4年后,他爸爸的年龄比他的年龄的3倍小2岁,则李林的
爸爸比他大 岁.
11.某次考试,A 、B 、C 、D 、E 五人的平均分是90分.若A 、B 、C 的平均分是86分,B 、D 、E 的平
均分是95分,则B 的得分是 .
12.如图2,已知直线AB 和CD 交于点O ,若∠AOC=20°,∠EOD=60°,则∠AOE= °,
∠BOC= °.
13.如图3,四边形ABCD 与CEFG 是边长相等的正方形,且B 、C 、G 在一条直线上,则图中共有 个
正方形, 个等腰直角三角形.
14.一个水桶里有水,若将水加到原来的4倍,桶和水共重16千克;若将水加到原来的6倍,桶和水共
重22千克.则桶内原有水 千克,桶重 千克.
15.某个两位数的个位数字和十位数字的和是12,个位数字和十位数字交换后所得两位数比原数小36,
则原数是 .
16.王强步行去公园,回来时坐车,往返用了一个半小时,如果他来回都步行,则需要2个半小时,那么
他来回都坐车,则需 分钟.
17.图4中“C ”形图形的周长是 厘米.
图4
18.如图5,从1,2,3,4,5,6,中选出5个数填在图中的空格内,使填好的格内的
数右边的比左边的大,下边的比上边的大,则共有 种不同的填法.
图5
19.三个连续自然数中最小的数是9的倍数,中间的数是8的倍数,最大的数是7的倍数,则这三个数的
和最小是 .
20.甲、乙、丙、丁、戊五人猜测全班个人学科总成绩的前五名:
甲:“第一名是D ,第五名是E .” 乙:“第二名是A ,第四名是C .” 丙:“第三名是D ,第四名是A .” 丁:“第一名是C ,第三名是B .” 戊:“第二名是C ,第四名是B .”
若每个人都只猜对一个人的名次,且每个名次只有一个人猜对,则第一、二、三、四、五名分别是 .
7。
