第6章3 复合求导、隐函数求导及方向导数
复合函数与隐函数的偏导数-PPT

z x
0,
Fy
Fz
z y
0.
因为 Fz 连续,且Fz ( x0 , y0 , z0 ) 0,所以存在
点( x0 , y0 ,
于就是得
z0 ) 得一个邻域,在这个邻域内 z Fx , z Fy .
Fz
0,
x Fz y Fz
隐函数的求导公式
z Fx , x Fz
例
已知 x2 a2
y2 b2
(2) F (0,0) 0; (3) Fy (0,0) 1 0, 隐函数存在定理1 所以方程在点 (0, 0) 附近确定一个有连续导数、 当x 0时y 0得隐函数 y f ( x),且
dy dx
Fx Fy
y x
e e
x y
.
隐函数的求导公式
例 已知ln x2 y2 arctan y ,求 dy . x dx
z f [ ( x, y), ( x, y),( x, y)]在对应点( x, y)
u
v
w
得两个偏导数存在, 且可用下列公式计算:
z x
z u
u x
z v
v x
z w
w x
ux
z y
z u u y
z v
v y
z w
w y
zv wy
多元复合函数的求导法则
例 设z
u2
1 v2
w2
,u
x2
y2,v
x2
x
x
z y z x x y
隐函数的求导公式
设方程 xy yz zx 1 确定了隐函数
z
y
z
z
z(
x,
y),
试求
2z x 2
3复合函数,隐函数求导-PPT精品文档

v(x) v(x) v ( x ) 设 y u(x) 可导 ( u ( x ) 0 ) , 则 y u(x) [ln u ( x ) ]
例 5 求下列函数的导数 : x2 1 (1) y 2 2x x ( 2 ) y (1 2x) , x 0
1 x
3.抽象函数求导法
例2求下列函数的导数
( 1 )y ( x 1 ) .
2 10) ( 3 )y a x arcsin (a0 2 2 a
2 3 ( 4 )y lg arccos x
2
1 (ln x) 例 3求 y ln x 的导数 x
三、求导的方法
• • • • 1.复合函数求导 2.高阶导数 3.隐函数求导法 4.参数求导法
一、复合函数求导法则 • 1.链式法则 • 2.对数求导法 • 3.抽象函数求导法
1.链式法则
性质
如果函数 ug (x ) 在点 x 可导 ,而 yf( u ) 在点 u (x ) 可导 , 则复合函数 yf[ g (x )] 在点 x 可导 , 且其导数为 dy dydu (x f( u )g ). dx dudx
( n ) n y ( 1 ) ( n 1 ) x ( n 1 )
( n ) n y ( 1 ) ( n 1 ) x ( n 1 )
若 为自然数 n ,则
( n ) n( ) n !, y ( x )n
高阶导数求法举例
1.直接法:由高阶导数的定义逐步求高阶导数.
例 1 设 y arctan x , 求 f ( 0 ), f ( 0 ).
注意: 求n阶导数时,求出1-3或4阶后,不要急于合并, 分析结果的规律性,写出n阶导数.(数学归纳法证明) 例2 求下列函数的n阶导数
6.3 多元复合函数和隐函数的求导法则

6.3 多元复合函数和隐函数求导法则6.3.1 复合函数的求导法则思考:设),(v u f z =, 而)(t u ϕ=,)(t v ψ=,如何求dtdz ? 设),(v u f z =,而),(y x u ϕ=,),(y x v ψ=,如何求x z ∂∂和y z ∂∂? 1. 复合函数的中间变量均为一元函数的情形定理1 如果函数)(t u ϕ=及)(t v ψ=都在点t 可导, 函数),(v u f z =在对应点(u , v )具有连续偏导数, 则复合函数)](),([t t f z ψϕ=在点t 可导, 且有dtdv v z dt du u z dt dz ⋅∂∂+⋅∂∂=. 简证1:因为),(v u f z =具有连续的偏导数, 则它是可微的, 即有dv v z du u z dz ∂∂+∂∂=. 又因为)(t u ϕ=,)(t v ψ=都可导, 因而可微, 即有dt dt du du =, dt dt dv dv =, 代入上式得:dt dt dv v z dt dt du u z dz ⋅∂∂+⋅∂∂=dt dtdv v z dt du u z )(⋅∂∂+⋅∂∂=, 从而 dtdv v z dt du u z dt dz ⋅∂∂+⋅∂∂=. 简证2:当t 取得增量∆t 时, u 、v 及z 相应地也取得增量∆u 、∆v 及∆z ,由),(v u f z =、)(t u ϕ=及)(t v ψ=的可微性, 有)(ρo v v z u u z z +∆∂∂+∆∂∂=∆)()]([)]([ρo t o t dtdv v z t o t dt du u z +∆+∆∂∂+∆+∆∂∂= )()()()(ρo t o vz u z t dt dv v z dt du u z +∆∂∂+∂∂+∆⋅∂∂+⋅∂∂=, to t t o v z u z dt dv v z dt du u z t z ∆+∆∆∂∂+∂∂+⋅∂∂+⋅∂∂=∆∆)()()(ρ, 令∆t →0, 上式两边取极限, 即得dtdv v z dt du u z dt dz ⋅∂∂+⋅∂∂=. 注:0)()(0)()()(lim )(lim 222200=+⋅=∆∆+∆⋅=∆→∆→∆dtdv dt du t v u o t o t t ρρρ.推广:设),,(w v u f z =,)(t u ϕ=,)(t v ψ=,)(t w w =,则)](),(),([t w t t f z ψϕ=对t 的导数为:dt dw w z dt dv v z dt du u z dt dz ∂∂+∂∂+∂∂=. 上述dtdz 称为全导数. 2. 复合函数的中间变量均为多元函数的情形定理2:如果函数),(y x u ϕ=,),(y x v ψ=都在点(x , y )具有对x 及y 的偏导数, 函数z =f (u , v )在对应点(u , v )具有连续偏导数, 则复合函数)],(),,([y x y x f z ψϕ=在点(x , y )的两个偏导数存在, 且有x v v z x u u z x z ∂∂⋅∂∂+∂∂⋅∂∂=∂∂,yv v z y u u z y z ∂∂⋅∂∂+∂∂⋅∂∂=∂∂。
多元复合函数求导法则和隐函数求导公式

z
= e [ y ⋅ sin( x + y ) + cos( x + y )]
xy
u x yx
v y
∂ z ∂ z ∂u ∂ z ∂v = ⋅ + ⋅ ∂ y ∂u ∂ y ∂v ∂ y = e u sin v ⋅ x + e u cos v ⋅1 = e [ x ⋅ sin( x + y ) + cos( x + y )]
4
x 2 + y 2 + x 4 sin 2 y
dz . 例3. 设 z = u v + sin t , u = e , v = cos t , 求全导数 dt d z ∂ z du ∂ z dv ∂ z + = ⋅ + ⋅ 解: z d t ∂u d t ∂v dt ∂t
t
= v e t− u sin t + cos t = e t (cos t − sin t ) + cos t
u
x y z
= 2 x (1 + 2 x sin y ) e
2
x 2 + y 2 + x 4 sin 2 y
∂u ∂ f ∂ f ∂ z + ⋅ = ∂ y ∂ y ∂z ∂ y
x
cos y
y
= 2 ye
x2 + y2 + z 2
+2 z e
x2 + y2 + z 2⋅ x 2
= 2 ( y + x sin y cos y ) e
多元复合函数的求导法则
一元复合函数
y = f (u ), u = ϕ ( x)
dy dy d u 求导法则 = ⋅ dx du dx 微分法则 d y = f ′(u ) d u= f ′(u ) ϕ ′ ( x) d x
3多元复合函数与隐函数的求导法则

求 m , m , m
x y z
z z u z v x u x v x
解
m x
m u m v m v u x v x v x
f1 1
f2
y
f3
yz
m m u m v m v
f1 2x
f2 ye xy
z y
f1 2 y
f2 xe xy
例7
设w
f(
x,y yz
),而 u
x ,v y
y z
,求
w x
, w y
, w z
.
z z u z v x u x v x
解
w w u w v x u x v x
于是
2w xz
f11
xyf12
yf2
yz(
f21
xyf22 )
f11 y( x z) f12 xy2zf22 yf2.
例11 设z y F ( x2 y2 ), 验证 y z x z x.
x y
证
z 0 F ( x2 y2 ) ,
由链式法则,
z z u z v , x u x v x
z z u z v , y u y v y
代入,
dz
z x
dx
z y
dy中, 得
dz
z u
u x
z v
v x
dx
z y
z u
多元复合函数求导法和隐函数求导公式

通过练习和案例分析,提 高解决多元复合函数和隐 函数求导问题的能力。
THANKS
感谢观看
通过对方程两边求导,得到隐函数的导数表 达式。
高阶偏导数的计算方法
利用低阶偏导数的计算结果,逐步推导高阶 偏导数的表达式。
学习建议
熟练掌握多元复合函数的 求导法则,能够灵活运用 链式法则、乘积法则等解 决实际问题。
理解偏导数的概念及其性 质,能够正确计算偏导数 并解释其物理意义。
ABCDBiblioteka 学会利用隐函数求导公式, 解决涉及方程组的导数问 题。
04
多元复合函数和隐函数的实际应用
几何应用
曲线和曲面求导
通过多元复合函数求导法,可以求出曲 线和曲面的导数,进而研究它们的几何 性质,如曲线的斜率、曲面的法线等。
VS
参数方程的应用
在几何中,参数方程常常用来描述曲线和 曲面,通过隐函数求导公式,可以方便地 求出参数方程的导数,进而研究曲线的切 线和曲面的法线。
导数
表示函数在某一点附近的变化率,是函数的局部性质。对于隐函数,其导数表示其在某点处的切线斜率。
一阶隐函数求导公式
求导法则
利用链式法则对隐函数进行求导,即对$y$的求导数等于$frac{partial F}{partial x} cdot frac{dx}{dy}$。
举例
若$F(x, y) = 0$,则$frac{dy}{dx} = -frac{frac{partial F}{partial x}}{frac{partial F}{partial y}}$。
全导数的应用
全导数在研究多元函数的性质、优化问题以及偏微分方程等 领域中都有广泛的应用。通过全导数,我们可以更全面地了 解多元复合函数在不同自变量变化情况下的整体行为。
(完整版)3多元复合函数与隐函数的求导法则

z f [φ(t),ψ(t)]
z f (u,v)
u φ(t)
v ψ(t)
dz z du z dv dt u dt v dt
全导数
例 1 设 z eu sin v ,而u xy,v x y 求 z 和z . x y
解 z z u z v eu sin v y eu cos v 1
x y
证
z 0 F ( x2 y2 ) ,
z
1
F ( x2
y2) ,
x
x
y
y
下求 F ( x2 y2 )对x, y的偏导.记u x2 y2,
x u x v x eu ( y sin v cos v)
z y
z u
u y
z v
v y
eu sin v x eu cos v 1
eu( x sin v cos v)
例 2 设 z u2 v2 ,而u x y,v x y ,
求 z 和z . x y
解 z z u z v 2u 1 2v 1 4x x u x v x
§3复合函数与隐函数的偏导数
一、多元复合函数的导数(链式法则)
定理:z f [( x, y),( x, y)]
z f (u,v) u ( x, y)
v (x, y)
z z u z v z z u z v x u x v x y u y v y
链式法则如图示 z f [( x, y),( x, y)]
解 dz z du z dv z dt u dt v dt t
v et u sin t cost
et cos t et sin t cos t
et (cos t sin t ) cos t
例5
复合函数及隐函数求导

1.熟练掌握各种情形下的多元复合函数偏导数的 求法; 2.理解和掌握抽象复合函数的高阶偏导数。
先复习一元函数复合函数求导法则
设 y f (u), u ( x) 则复合函数 y f [ ( x)]的导数为 dy dy du f (u)( x) dx du dx 设 y f (u), u (v) v ( x)
练习形式的隐函数确定的函数为因为所确定的函数设方程确定函数设方程xyxyzyzxzzy确定函数设方程lnln解法1利用隐函数求导求导解法2利用公式三多元复合函数的全微分设函数的全微分为都可微其全微分表达形式都一样这性质叫做全微分形式不变性
第五讲 复合函数与隐函数 的微分法
• 内容提要
1.多元复合函数的求导法则; 2.隐函数的求导法则;
u
y
z
v
x
y
z z u z v z x z y u y v y u v
例8 设
f 具有二阶连续偏导数,
求 w, 2w . x xz
w , f1 , f2
解: 令 u x y z , v xyz , 则
uv
w f (u, v)
3、设 z e sin t2t3 ,则dz ________________. dt
二、设 z
v
ue u ,而u
x2
y2,v
xy ,求z
, z
.
x y
三、设z arctan(xy),而y e x ,求dz . dx
四、设 z f ( x 2 y 2 , e xy ),(其中f具 有一阶连续偏导
wx
y
z y
D9-4,5复合函数求导,隐函数求导
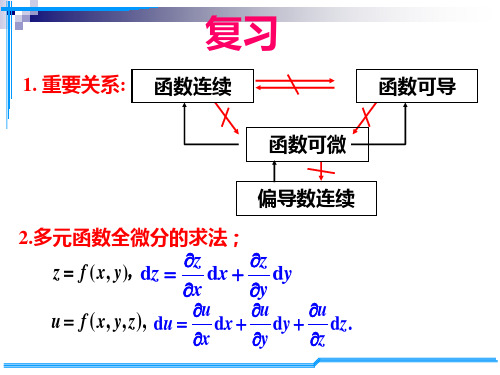
x y zx y z
y z f2 (x y z, xyz)
2w xz
f12 xy
f22 x y
为简便 起f11见
,y引(x入 z记) f号12
f1xy
2zf u
f,22f12yf2u2fv
,
例6 设 z 1 f ( xy) y( x y), f ,具有二阶连续
x 偏导数,求 2z .
xy
解 先求x的偏导数比较复杂,由题意知:
混合偏导数相等,则先求 z , y
z 1 f ( xy) x ( x y) y( x y),
y x
f ( xy) ( x y) y( x y),
2z 2z yf ( xy) ( x y) y( x y).
xy yx
二、多元复合函数的全微分 设函数 z f (u,v) 具有连续偏导数,则全微分
及求导方法 .
例如求由方程e y xy e 0所确定的隐函数y的导数.
两边同时对x求导:e y
dy dx
y
x
dy dx
0,dy dx
x
y ey
.
或用微分法:e ydy
xdy
ydx
0
dy dx
x
y ey
.
一、一个方程所确定的隐函数及其导数
定理1. 设函数
在点
的某一邻域内满足
① 具有连续的偏导数;
( yf1 zf 3)dx ( xf1 zf2)dy ( yf 2 xf 3)dz
u x
yf1
zf 3
u y
xf1
zf 2
u z
yf 2
xf
du u dx u dy u dz x y z
复合函数求导

y x sin x .
方法:
先在方程两边取对数, 然后利用隐函数的求导 方法求出导数.
--------对数求导法
例5: 设 y ( x 1)3 x 1 , 求y. ( x 4)2 e x
解: 等式两边取对数得
ln y ln( x 1) 1 ln( x 1) 2 ln( x 4) x 3
y
x
y y(cos x ln x sin x 1 ) x
x sin x (cos x ln x sin x ) x
四、由参数方程所确定的函数的导数
若参数方程
x y
(t )确定 (t)
y与x间的函数关系
,
称此为由参数方程所确定的函数.
例如
x 2t,
y
t
2
,
t x 2
消去参数 t
2
1 cos
1.
2
当 t 时, x a( 1), y a.
2
2
所求切线方程为
y a x a( 1) 2
即 y x a(2 )
2
谢谢
上式两边对 x求导得
y 1 1 2 1 y x 1 3( x 1) x 4
y
( x 1)3 x ( x 4)2 e x
1[
x
1
1
1 3( x
1)
x
2
4
1]
例6:设 y xsinx ( x 0), 求y.
解: 等式两边取对数得
上式两边对x求导得
1 y cos x ln x sin x 1
dy
dy dx
dy dt
dt dx
dy dt
1 dx
(t) (t)
即
《隐函数的导数》课件

求导过程,提高求解效率。
数的求导规律。
4 常见问题解答
回答一些关于隐函数求导常见问题,帮助大 家更好地理解相关概念。
5 拓展阅读建议
提供一些有趣的拓展阅读建议,让大家可以 继续深入学习隐函数的应用与相关领域。
参数方程
了解参数方程中的隐函数求导 方法,并研究其在曲线上的作 用。
常见问题解答
1 如何判断一个方程是
否为隐函数?
一个方程可以被视为隐函 数,如果它无法通过任何 一种简单的代数方法来直 接解出。
2 如何判断隐函数的导
函数是否存在?
可以通过连续性、准确性 和存在性等条件来判断隐 函数的导函数是否存在。
《隐函数的导数》PPT课 件
通过本课件,我们将深入探讨隐函数的导数,掌握隐函数求导的基本方法和 链式法则的应用,以及常见隐函数的求导规律。让我们一起开启这个有趣的 学习之旅吧!
什么是隐函数?
定义
隐函数是由一个方程表达的,其中变量与方程中 其他变量之间存在一定的关系,但并不直接解出 的函数。
示例
例如,方程x^2 + y^2 = 1是一个隐函数,其中x 和y之间满足关系x^2 + y^2 = 1。
3 如何证明隐函数的导
函数在某点连续?
可以使用极限定义和导数 的连续性来证明隐函数的 导函数在某点连续。
总结
1 隐函数求导的基本方
法
掌握隐函数求导的基本方 法以解决各种复杂的隐函 数导数问题。
2 链式法则在隐函数求
导中的应用
3 常见隐函数及其求导
了解常见隐函数如反三角
运用链式法则简化隐函数
函数、指数函数和对数函
2
例题
我们将通过具体的例题演示如何运用链式法则求解隐函数的导数。
复合函数求导法则与隐函数的求导

1 2 x
.
例11 设 y sin 3 (2 x 1),求y'. 解
y' (sin (2 x 1))'
3
3 sin 2 (2 x 1) (sin3 (2 x 1))' 3 sin 2 (2 x 1) cos( 2 x 1) (2 x 1)' 3 sin (2 x 1) cos( 2 x 1) 2
f' (u ) g' ( x).
复合函数的求导法则一般称为链式法则,它也适 用于多层复合的情况.比如y=f(u),u=g(v),v=h(x),则 只要满足相应的条件,复合函数y=f(g(h(x)))就可导, 且有
dy dy du dv f' (u ) g' (v)h' ( x). dx du dv dx
1 ( sin x) cos x tan x .
例10 设 y e
tan x
,求y' .
y e u , u tan v,v x .则 解 令
dy dy du dv dx du dv dx
e sec v
u 2
1 2 x
2
e
tan x
sec
x
1 x
若完全掌握了复合函数求导的链式法则,那么在
对初等函数求导时,就可以“一步到位”. 例14 计算 [ln( x 2 1 x)]' . 解 [ln( x 2 1 x)]'
1
x2 1 x 2 x2 1
(
1
2 x 1)
1 x ( 2 1) 2 x 1 x x 1 1 x 1
复合函数,隐函数求导

|xx0
f
(u0
)
g(x0
).
即 因变量对自变量求导,等于因变量对中间变 量求导,乘以中间变量对自变量求导.(链式法则)
写成导函数形式为 : y f [g(x)] g(x)
或 dy dy du dx du dx
证
由y
f (u)在点u0可导 ,
lim y u0 u
二、 求下列方程所确定的隐函数 y 的二阶导数dy : dx
1、 y 1 xe y ; 2、 y tan( x y); 3、 x y y x ( x 0,y 0) . 三、 用对数求导法则求下列函数的导数: 1、 y x x2 ; 2、 y x 2(3 x)4 ;
解 y ln u, u sin x.
dy dy du 1 cos x cos x cot x
dx du dx us源自n x例2 求函数 y ( x2 1)10 的导数 .
例3 求函数 y x a2 x2 a2 arcsin x 的导数 .
f (u0 )
故
y u
f (u0
)
o(1)
( lim o(1) 0) u0
则 y f (u0 )u o(1)u
lim
x 0
y x
lim [f
x0
(u0
)
u x
o(1)
u] x
f
(u0
)
lim
x0
u x
lim
x0
o(1)
3.抽象函数求导法
例9 求 y f( x) f (2lnx)的导数 例10 已知y ef 2(x) ,若f (a) 1 ,求证 : y(a) y(a)
3复合函数,隐函数求导

y ( n ) ( 1) ( n 1) x n
( n 1)
若 为自然数n, 则
y ( n ) ( x n )( n ) n! ,
y ( n 1) ( n! ) 0.
nk
n( n 1)( n 2)( n k 1) x y ( x ) n! 0
再设函数x (t ), y (t )都可导, 且 (t ) 0,
由复合函数及反函数的求导法则得
dy dy dt dy 1 ( t ) dx dt dx dt dx ( t ) dt
dy dy dt 即 dx dx dt
x ( t ) 若函数 二阶可导, y ( t )
例求下列参数确定的函 数y f ( x )的二阶导数 x 1 - t3 (1) 3 y t t x f (t) ( 2) y tf (t) - f(t)
x a ( t sin t ) 在t 处的切线 例3 求摆线 2 y a (1 cos t ) 方程 .
加速度a是速度v对时间t的变化率
a(t ) v(t ) [s(t )] .
定义
设f ( x)可导, 则称(f ( x))为函数f ( x)在点x处的二阶导数.
d 2 y d 2 f ( x) . 记作 f ( x ), y , 2 或 2 dx dx
d3y . 二阶导数的导数称为三阶导数, f ( x ), y, 3 dx 4 d y (4) (4) 三阶导数的导数称为四阶导数, f ( x ), y , . 4 dx
------莱布尼兹公式
3.间接法: 利用已知的高阶导数公式, 通过四则
运算, 变量代换等方法, 求出n阶导数. 例5求下列函数的n阶导数
多元函数复合求导和隐函数

fv ( yz
xy z ), x
整理得 z fu yzfv , x 1 fu xyfv
例 3 设z f ( x y z, xyz),求 z ,x ,y . x y z
把x 看成z, y 的函数对y 求偏导数得
0
fu
(
x y
1)
fv ( xz
yz x), y
整理得
x fu xzfv ,
z x x 2 z
再对 x 求导
2
4
2z x2
0
1 (z)2 x
机动 目录 上页 下页 返回 结束
例2.
设
x2
y
2
z2
4z
0,
求
2z x2
.
解法3. 利用全微分形式不变性同时求出各偏导数. d(x2 y2 z2 4z) 0, dx2 dy2 dz2 4dz 0,
2xdx 2 ydy 2zdz 4dz 0,
z f (u,v)
z
uv
( 全导数公式 )
tt
机动 目录 上页 下页 返回 结束
推广: 设下面所涉及的函数都可微 .
1) 中间变量多于两个的情形. 例如, z f (u,v, w) ,
u (t), v (t), w (t)
dz z du z dv z dw d t u d t v dt w dt
机动 目录 上页 下页 返回 结束
例 6. 利用全微分形式不变性再解例1.
解: dz d( eu sin v ) eu cos v dv
d (xy)
d (x y)
(yd x xdy) exy[ y sin(x y) cos(x y)]d x
(dx dy)
复合函数导数公式及运算法则

复合函数导数公式及运算法则复合函数导数公式极其运算法则同学们还记得吗,如果不记得了,请往下看。
下面是由小编为大家整理的“复合函数导数公式及运算法则”,仅供参考,欢迎大家阅读。
复合函数导数公式.常用导数公式1.y=c(c为常数) y'=02.y=x^n y'=nx^(n-1)3.y=a^x y'=a^xlnay=e^x y'=e^x4.y=logax y'=logae/xy=lnx y'=1/x5.y=sinx y'=cosx6.y=cosx y'=-sinx7.y=tanx y'=1/cos^2x8.y=cotx y'=-1/sin^2x9.y=arcsinx y'=1/√1-x^210.y=arccosx y'=-1/√1-x^211.y=arctanx y'=1/1+x^212.y=arccotx y'=-1/1+x^2在推导的过程中有这几个常见的公式需要用到:1.y=f[g(x)],y'=f'[g(x)]•g'(x)『f'[g(x)]中g(x)看作整个变量,而g'(x)中把x看作变量』2.y=u/v,y'=u'v-uv'/v^23.y=f(x)的反函数是x=g(y),则有y'=1/x'证:1.显而易见,y=c是一条平行于x轴的直线,所以处处的切线都是平行于x的,故斜率为0。
用导数的定义做也是一样的:y=c,⊿y=c-c=0,lim⊿x→0⊿y/⊿x=0。
2.这个的推导暂且不证,因为如果根据导数的定义来推导的话就不能推广到n为任意实数的一般情况。
在得到 y=e^x y'=e^x和y=lnx y'=1/x这两个结果后能用复合函数的求导给予证明。
3.y=a^x,⊿y=a^(x+⊿x)-a^x=a^x(a^⊿x-1)⊿y/⊿x=a^x(a^⊿x-1)/⊿x如果直接令⊿x→0,是不能导出导函数的,必须设一个辅助的函数β=a^⊿x-1通过换元进行计算。
3多元复合函数与隐函数的求导法则

du ? dx
解
du u u dy u dz dx x y dx z dx
ae (y z) e e ax a cos x ( 2 ) ( sin x ) 2 2 a 1 a 1 a 1
ax
ax
例6 设 z f ( x y , e ) ,而u x y , v e ,
e cos t e sin t cos t
t t
e t (cos t sin t ) cos t
e ax(y z) , y a sin x, z cos x 例5 设 u 2 a 1
z z u z v x u x v x
z u z v dx z u z v dy dz u x v x u y v y
z u u z v v dx dy dx dy u x y v x y
z z u z v 2u (1) 2v 1 4 y y u y v y
z z x 例3 设 z u ln v ,而 u , v 3 x 2 y ,求 , x y y
2
解
z z u z v 1 u2 2u ln v 3 y v x u x v x
2x 3x2 2 ln ( 3 x 2 y) y ( 3 x 2 y)y 2
z z u z v y u y v y
x u2 2u ln v ( 2 ) ( 2 ) y v
2x2 2x2 3 ln ( 3 x 2 y) y ( 3 x 2 y)y 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第六章
人民邮电出版社Advanced mathematics 多元函数微分学高等数学
内容导航
第六章第四节 多元函数微分学的应用
第一节 多元函数的概念、极限与连续
第二节 多元函数的偏导数与全微分
第三节 复合求导、隐函数求导及方向导数
一、多元函数复合求导
第六章 多元函数微分学1、复合函数的中间变量为一元函数的情形
第六章 多元函数微分学1、复合函数的中间变量为一元函数的情形
z u
v
t
t
第六章 多元函数微分学
z
u
w t t
v t 1、复合函数的中间变量为一元函数的情形
1、复合函数的中间变量为一元函数的情形
第六章 多元函数微分学
第六章 多元函数微分学z u
w t t
v
t 1、复合函数的中间变量为一元函数的情形
1、复合函数的中间变量为一元函数的情形
第六章 多元函数微分学
z u
v x
y x
y
z u
v x
y y
z
x
u x x
y y
y
z u v x
x y
、、等记号
r r r
r
r
r
Ɵ(1)
r r r
r
二、隐函数的求导公式
第六章 多元函数微分学
F x
y x x
第六章 多元函数微分学1、一个方程的情形。
