用倒数法解题举例-

合集下载

倒数法练习题

倒数法练习题简介：本文将提供一些倒数法练习题，帮助读者巩固和提高倒数法的运用能力。

倒数法是一种在数学和逻辑推理中常用的方法，通过将问题转换为倒数的形式，能够简化解题思路，提高解题效率。

在本文中，我们将介绍一些常见的倒数法应用例题，并给出详细解答，以便读者更好地理解和掌握倒数法。

一、题目一一辆汽车以每小时120公里的速度行驶，若汽车从A市出发到B市需要2小时，那么从A市到B市的距离是多少公里？解答：根据题目中所给的信息，我们可以将问题转换为倒数的形式。

汽车以每小时120公里的速度行驶，意味着汽车每1小时能行驶120公里。

而从A市到B市需要2小时，因此从A市到B市的距离可以表示为120公里/小时 × 2小时 = 240公里。

答案：从A市到B市的距离是240公里。

二、题目二甲、乙、丙三人合作完成一项工作，若甲独立完成需要10天，乙独立完成需要15天，丙独立完成需要20天。

如果三人一起合作完成该工作，需要多少天？解答：将问题转换为倒数形式，甲独立完成该工作需要10天，即甲每天能完成工作量的1/10。

同理，乙每天能完成工作量的1/15，丙每天能完成工作量的1/20。

若三人一起合作完成工作，他们的工作效率将累加，即每天完成工作量的1/10 + 1/15 + 1/20 = 11/60。

根据倒数法的原则，他们合作完成工作所需的时间为60/11 ≈ 5.45天。

答案：三人合作完成该工作需要约5.45天。

三、题目三某数的一半加上三分之一等于这个数本身减去5，求这个数。

解答：假设这个数为x，根据题目中所给的条件，我们可以建立方程：1/2x + 1/3x = x - 5。

为了方便计算，我们可以将方程两边的分数转换为相同的分母，即3/6x + 2/6x = 6/6x - 5。

合并同类项得到5/6x = 6/6x - 5，进一步简化为-1/6x = -5。

将方程两边都乘以-6，得到x = 30。

答案：这个数为30。

数学解题方法谈18：倒数法解题

数学解题方法谈18：倒数法解题■说明：这里的数学式不是用公式编辑器编辑的，而都是用EQ 码编打的，它可以变文字的颜色和调整文字的大小。

这些编辑法,你不仿下载试试，一些心得供参考。

■由于网络原因,先前发的已打不开,故修整后重发例1、已知a 、b 、c 为实数，且ab a ＋b =13, bc b ＋c =14, ca c ＋a =15 求abc ab ＋bc ＋ca的值（1997年第八届“希望杯”竞赛试题）解：由题设知：a 、b 、c 均不为零，对已知条件取倒数得：1a ＋1b =3, 1b ＋1c =4, 1c ＋1a=4 ∴2⎝ ⎛⎭⎪⎫1a ＋1b ＋1c =12 1a ＋1b ＋1c =6 ab ＋bc ＋ca abc =1a ＋1b ＋1c =6 ∴abc ab ＋bc ＋ca =16例2、实数a 、b 、c 、d 满足：abcd a ＋b ＋c =1 abcd a ＋b ＋d =2 abcd a ＋c ＋d =3 abcd b ＋c ＋d=6 则abcd =解：由题设知：a 、b 、c 均不为零，对已知条件取倒数得：a ＋b ＋c abcd =1, a ＋b ＋d abcd =12, a ＋c ＋d abcd =13 ,b ＋c ＋d abcd =16……(1) 四式相加得：3(a ＋b ＋c ＋d)abcd =2 ∴a ＋b ＋c ＋d abcd =23分别减去倒数式(1)可得：a abcd =12 b abcd =13 c abcd =16 d abcd =－13四式相乘得：abcd (abcd)4=－1108(abcd)3=－108 ∴abcd=3－108=－334 例3、设x x 2－2x ＋1=1求x 3x 6－22x ＋1的值. 解：∵x ≠0∴x 2－2x ＋1x =1 ∴x ＋1x=2＋1∴原式=x 3＋1x 3－22=(x ＋1x )3－3(x ＋1x )－22=(2＋1)3－3(2＋1)―22=4 例4、设x x 2－mx ＋1=1求x 3x 6－m 3x 3＋1的值解：由已知得：x 2－mx ＋1x =1则有x ＋1x=m ＋1 ∵x 6－m 3x 3＋1x 3=x 3－m 3＋1m 3=(x+1x )[(x ＋1x )2―3]－m 3 =(m ＋1)3－3(m ＋1)－m 3=3m 3－2 ∴原式=13m 2－2例10、已知：x 2x 2－2=11－3－2，求⎝ ⎛⎭⎪⎫11－x －11＋x ÷⎝ ⎛⎭⎪⎫x x 2－1＋x 的值解：把已知式两边都取倒数得x 2－2x 2=1－3－ 2 即1－2x 2=1－3－ 2 ∴－2x 2=－(3＋2) ∴原式=2x 1－x 2·x 2－1x 3=－2x 2=－(3＋2)=－3－2 得x=32x=－52（舍去）。

六年级数学上册分数应用题转化单位1的五种解题方法

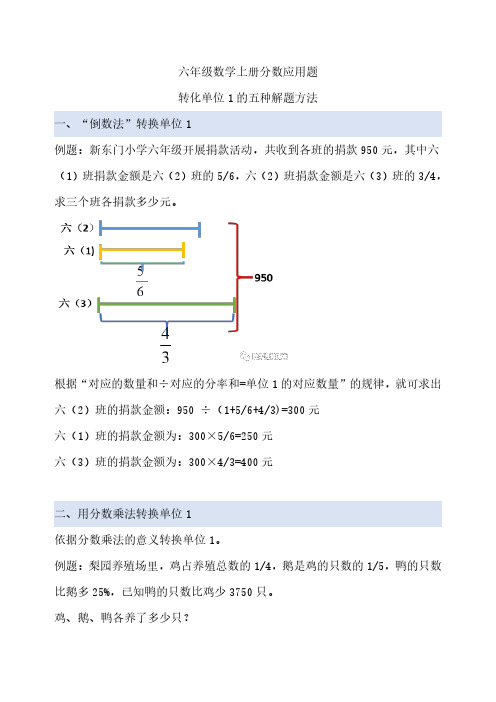
六年级数学上册分数应用题转化单位1的五种解题方法一、“倒数法”转换单位1例题：新东门小学六年级开展捐款活动，共收到各班的捐款950元，其中六（1）班捐款金额是六（2）班的5/6，六（2）班捐款金额是六（3）班的3/4，求三个班各捐款多少元。

根据“对应的数量和÷对应的分率和=单位1的对应数量”的规律，就可求出六（2）班的捐款金额：950÷（1+5/6+4/3)=300元六（1）班的捐款金额为：300×5/6=250元六（3）班的捐款金额为：300×4/3=400元二、用分数乘法转换单位1依据分数乘法的意义转换单位1。

例题：梨园养殖场里，鸡占养殖总数的1/4，鹅是鸡的只数的1/5，鸭的只数比鹅多25%，已知鸭的只数比鸡少3750只。

鸡、鹅、鸭各养了多少只？以养殖总数为单位1，依据分数乘法的意义，鹅占养殖总数的1/4×1/5=1/20，鸭占养殖总数的1/20×(1+25%)=1/16。

鸡、鹅、鸭的分率如下图：这样，鸡与鸭就统一单位1了，都是以养殖总数为单位1的，用鸡与鸭的数量差与分率差相除，就能求出养殖总数了：3750÷（1/4-1/16)=20000只。

鸡的只数：20000×1/4=5000只鹅的只数：20000×1/20=1000只鸭的只数：20000×1/16=1250只三、用份数法转换单位1例题：乌江泥厂有甲、乙、丙、丁四个车间，甲车间人数是其他三个车间的1/4，乙车间人数是其他三个车间的4/11，丙车间人数是其他三个车间的1/2,已知丁车间有60人，该厂有职工多少人？我们可以用全厂职工总数为单位1，用份数法，分别求出甲、乙、丙三车间人数各占全厂职工总数的几分之几，然后，再求出丁车间人数占全厂职工总数的几分之几。

三个车间的分率转换如下：甲车间人数是全厂职工的1÷（1+4）=1/5，乙车间人数占全厂职工的4÷（4+11）=4/15丙车间人数占全厂职工的1÷(1+2)=1/3.现在，本题的数量关系已简化成下图：看图可知，60人的对应分率为1-1/5-4/15-1/3。

分式方程的求解掌握解含有分式的一元一次方程的方法

分式方程的求解掌握解含有分式的一元一次方程的方法在数学中，分式方程是指方程中涉及到分式的方程。

解决这类方程需要掌握解含有分式的一元一次方程的方法。

本文将介绍一些常见的求解分式方程的方法供参考。

1. 清除分母法清除分母法是处理涉及到分式的方程的常见方法之一。

该方法的思路是通过乘以适当的公倍数，将方程两侧的分式的分母消除，从而得到一个整式方程。

举例说明：假设要解决如下分式方程：(3/x) - (2/x - 1/2) = (1/3)首先，我们可以观察到方程中都是关于x的分式。

为了消除分母，我们可以找到这两个分式的公倍数，即2x。

接下来，我们将方程两侧乘以2x，得到：2x * (3/x) - 2x * (2/x - 1/2) = 2x * (1/3)6 - 4 + x = 2x/3化简方程得到：x + 2x/3 = 10/33x/3 + 2x/3 = 10/3合并同类项得到：5x/3 = 10/3接下来，我们可以将上述方程两侧乘以3，得到整数方程：5x = 10最后，解得：x = 2所以，原始的分式方程的解为x = 2。

2. 倒数法倒数法是求解含有分式的方程的另一种常用方法。

该方法的思路是用公式将含有分式的方程转化为以未知数的倒数为变量的整式方程。

举例说明：假设我们要解决如下分式方程：(1/x) + (1/x + 1/2) = (2/3)首先，我们可以观察到方程中都是关于x的分式。

为了使用倒数法，我们令y = (1/x)，将方程转化为：y + (y + 1/2) = 2/32y + 1/2 = 2/3接下来，我们可以将上述方程两侧乘以6，得到整数方程：12y + 3 = 4继续化简得到：12y = 4 - 312y = 1最后，解得：y = 1/12由于我们令y = (1/x)，所以：1/x = 1/12交叉相乘得到：12 = x所以，原始的分式方程的解为x = 12。

除了清除分母法和倒数法，还有一些其他的方法可以用于求解分式方程，如代入法、直接比较法等。

数学(心得)之巧用倒数解题举隅

数学论文之巧用倒数解题举隅一、巧用倒数使计算简便。

例如：计算2002÷（2002+2002/2003），如果我们按照四则运算顺序直接进行计算的话，计算起来也比较繁杂。

我们不妨利用倒数的知识使计算简便。

分析：根据2002÷（2002+2002/2003）的商与（2002+2002/2003）÷2002的商是互为倒数的这一特点，我们只需求出（2002+2002/2003）÷2002的商后再求出这个商的倒数即可。

（2002+2002/2003）÷2002=2002÷2002+2002/2003÷2002=1+1/2003=2004/20031÷2004/2003=2003/2004即：2002÷（2002+2002/2003）=2003/2004二、巧用倒数巧比较大小。

例如：人教版第十一册《倒数的认识》后面的练习五有这样一道星号题：已知a×4/3 = 11/12×b=15/15×c并且a﹑b﹑c都不等于零。

把a﹑b﹑c这三个数按从大到小的顺序排列，并说明为什么。

假设a×4/3 = 11/12×b=15/15×c=1，这样可以得到以下三个等式：a×4/3 =1，11/12×b=1，15/15×c=1。

根据乘积是1的两个数互为倒数可知a=3/4，b=12/11，c=1。

即b>c>a。

当然，此题也可用分数乘法的意义来推想：观察题目可以看出15/15=1，这样可以得到以下两个等式：a×4/3 =cb ×11/12=c第一个等式表示a的4/3等于c，可知c>a，第二个等式表示b的11/12等于c，可知b>c。

由此推出b>c>a。

显然，利用倒数来解此题学生更容易接受，同时也巩固了刚学过的倒数的知识。

巧用倒数转化法解答分数应用题_

巧用倒数转化法解答分数应用题_－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－某些较复杂的分数应用题，一般思路就是先要转化分率，然后才能解答。

若采用倒数转化法来解答，既能巧妙地统一单位“1”，又可减少分率转化的繁琐计算，往往能出奇制胜，使思路清晰，解法简捷。

现举几例如下：例1 某电器厂男工占总人数的2/3，后来又招进20名女工，这时男工占总人数的6/11。

这个厂原来有男、女工各多少名?分析与解答：用一般方法的解题思路是，因为这个厂总人数前后有所变化，题中两个分率所涉及的单位“1”不统一，而男工人数前后没有变化，所以把男工人数看作单位“1”，再把前后两次的女工人数转化成占男工的分率，然后再求解。

如果采用倒数法，立即可统一单位“1”，即原来工厂总人数占男工人数的5/3，后来工厂总人数占男工人数的11/6。

则：男工人数：20÷(11/6-5/3)=20÷1/6=120(名)女工人数：120×5/3-120=80(名)例2 电视机厂生产一批电视机，原计划30天完成，实际每天比原计划多生产1/4，实际多少天完成?分析与解答：这道题中的“30天”是原计划的工作时间，“1/4”所对应的单位“1”是原计划的工作效率，已知数量和已知分率不相对应，这就需要将某个条件进行转化。

设这批电视机的台数为“1”，我们可以将“原计划30天完成”转化为“原计划每天完成这批电视机的1/30(即30的倒数，也就是工作效率)”。

“倒数法”的应用

２．已知：口＋ ÷ Ｄ＝４，求．－ — ４３ｊａ叶＋３２ａ口／出，６＋一４３ｊ＿６６￣ｇ。
３・已知：．老＋＋ｌ，求：＋ｌ的值。
经检验一２是原方程的根。
为掌握以上方法，可以尝试练习以下几题：
１．解方程：盟一二！一１＝０。
ｘ－１ｘ＋ｌ
所以ｙｌ＝２，ｙ２＝ｌ，
当ｙ２＝２时，即￣ｉｙ２＝１１ｔ；］＂，即
＝２，￣１２２ｘ＝一２，＝ｌ，此方程无解，
＋，ｌｉｐ；ｌ时。
例３解方程（ ÷ ）＋２（）一３－－０
故原式最大值为、／了一、／。
三、练习
凄兔 ●
）
解：设之，则盟：１，
于是三一３－－０，所以产３２＝ｏ，
０
技法点拨
● ・・
大家分享一下：
一
● ● 倒数法＂的应用
■ 张生苗加朋
：，得：
（）２＋９９ｓ＋ｌ９：０。
Ｓ
・ ●
在解决代数问题时，适当使用 “ 倒数法 ” 会起到
事半功倍的作用，笔者现将教学实践中相关感悟与
４．已知：去＝叶６ ÷ ３，羔＝６＋ｃ４，旦＝ａ＋ｃ了５１，一求： … 代数一
式一的值。如果灵活运用此法，它会给我们解题带来简便，会收到较好的效果。

小学数学挑战解决分数除法的高效方法

小学数学挑战解决分数除法的高效方法在小学数学中，分数除法是一个相对较难的概念，对于很多学生来说，理解和解决分数除法问题是一项挑战。

然而，通过学会一些高效的方法，我们可以更轻松地解决分数除法问题。

本文将介绍一些解决分数除法的高效方法。

一、通分法通分法是解决分数除法问题常用的一种方法。

当被除数和除数分别为分数时，我们可以通过通分，将分数转化为整数，从而简化计算过程。

举个例子，假设我们要计算2/3 ÷ 1/4 ，我们可以先将2/3和1/4通分为8/12 和 3/12，然后将除法转化为乘法：8/12 × 12/3，最后我们得到答案为8/3，也可以化简为2⅔。

二、倒数法倒数法是另一种解决分数除法问题的高效方法。

倒数法的原理是将除法问题转化为乘法问题，通过将除数的倒数乘以被除数，从而简化计算过程。

以1/2 ÷ 1/3 为例，我们可以将除法转化为乘法：1/2 × 3/1，最后我们得到答案为3/2，也可以化简为1½。

三、画图法画图法是一个直观而又有效的方法来解决分数除法问题。

通过画图，我们可以更好地理解分数除法的概念，并帮助我们解决问题。

以2/3 ÷ 1/4 为例，我们可以画两个长方形，一个长方形代表被除数2/3，另一个长方形代表除数1/4。

然后，我们将被除数的长方形分成3等分，将除数的长方形分成4等分，最后我们找到两个长方形的交集。

交集的面积表示答案，即8/3。

四、分数除法的应用掌握了解决分数除法问题的高效方法后，我们还可以应用这些方法解决一些实际问题，例如比例问题、面积问题等。

比如，我们要计算长方形A的面积是长方形B面积的几倍，其中长方形A的长是3/4，宽是1/2，长方形B的长是2/3，宽是1/3。

我们可以先计算出长方形A的面积为1/2 × 3/4 = 3/8，长方形B的面积为1/3 ×2/3 = 2/9。

然后，我们将长方形A的面积除以长方形B的面积，即3/8 ÷ 2/9。

倒数知识点和题型总结

倒数知识点和题型总结一、倒数基础知识点总结1. 基本概念倒数是指从整数起始数值递减至零的过程或数值。

在数学中，倒数是指一个数的倒数，即这个数的倒数是1/这个数。

例如，2的倒数是1/2，3的倒数是1/3，以此类推。

倒数在日常生活和数学中都有广泛的应用，如计时器的倒计时、商业活动的倒数计时等。

2. 倒数的概念在数学中，倒数是指一个数除以1，通常记作1/x，其中x是一个非零数。

倒数是数学中一个重要的概念，它与整数、分数等相关联，广泛应用于代数、数论、几何等领域。

3. 倒数的性质- 非零数的倒数是小数。

- 任意数的倒数是1与这个数的倒数的积等于1。

4. 倒数的运算- 计算倒数：要计算一个数的倒数，只需要将1除以这个数即可得到其倒数。

- 倒数的性质：对于任意非零数a，其倒数记作1/a，即a的倒数是1/a。

二、常见倒数题型总结1. 计算倒数问题描述：计算给定数的倒数。

解题方法：将1除以给定数即可得到其倒数。

例题：计算以下数的倒数：a) 2; b) 5; c) 1/3; d) 0.25。

2. 倒数的运算问题描述：运用倒数概念，对数进行加、减、乘、除的运算。

解题方法：先求出各数的倒数，然后进行常规的加、减、乘、除运算。

例题：计算以下数的和的倒数：a) 1/2 + 1/3; b) 2*3; c) 1/4 ÷ 1/5。

3. 倒数的应用问题描述：运用倒数的概念解决实际问题。

解题方法：根据问题描述，找出倒数的应用场景，并分析实际解决方法。

例题：若甲乙两人相约在某地见面，甲离目的地有5公里，乙离目的地有8公里。

若两人同时起步，那么两人能在多长时间后相遇？三、倒数题型解题方法1. 计算倒数- 例题1：计算以下数的倒数：a) 2; b) 5; c) 1/3; d) 0.25。

解题方法：a) 1/2; b) 1/5; c) 3; d) 4。

2. 倒数的运算- 例题2：计算以下数的和的倒数：a) 1/2 + 1/3; b) 2*3; c) 1/4 ÷ 1/5。

巧用倒数法快速解题

巧用倒数法快速解题一、题目1。

1. 题目。

- 已知x+(1)/(x)=3，求x^2+(1)/(x^2)的值。

2. 解析。

- 我们可以根据完全平方公式(a + b)^2=a^2+2ab + b^2来求解。

- 对于x+(1)/(x)=3，将其两边平方得(x+(1)/(x))^2 = 3^2。

- 展开(x+(1)/(x))^2得到x^2+2× x×(1)/(x)+(1)/(x^2)=x^2+2+(1)/(x^2)。

- 因为(x +(1)/(x))^2=9，即x^2+2+(1)/(x^2) = 9，所以x^2+(1)/(x^2)=9 - 2=7。

二、题目2。

1. 题目。

- 若a-(1)/(a)=2，求a^2+(1)/(a^2)的值。

2. 解析。

- 对a-(1)/(a)=2两边平方，根据(a - b)^2=a^2-2ab + b^2。

- (a-(1)/(a))^2=2^2，展开得到a^2-2× a×(1)/(a)+(1)/(a^2)=a^2-2+(1)/(a^2)。

- 因为(a-(1)/(a))^2 = 4，即a^2-2+(1)/(a^2)=4，所以a^2+(1)/(a^2)=4 + 2=6。

三、题目3。

1. 题目。

- 已知x+(1)/(x)=5，求x^4+(1)/(x^4)的值。

- 先由x+(1)/(x)=5两边平方得(x+(1)/(x))^2 = 5^2。

- 展开(x+(1)/(x))^2=x^2+2+(1)/(x^2)，所以x^2+(1)/(x^2)=25 - 2 = 23。

- 再对x^2+(1)/(x^2) = 23两边平方，(x^2+(1)/(x^2))^2=23^2。

- 展开(x^2+(1)/(x^2))^2=x^4+2+(1)/(x^4)，所以x^4+(1)/(x^4)=23^2-2=529 - 2 = 527。

四、题目4。

1. 题目。

- 若m-(1)/(m)=4，求(m^2+(1)/(m^2))(m^4+(1)/(m^4))的值。

实际应用训练：如何运用倒数知识解题,全方位教案

实际应用训练：如何运用倒数知识解题倒数（reciprocal）是高中数学里的一个基本概念，它的数学定义是一个数的倒数就是它的倒数。

例如，数3的倒数是1/3，数5的倒数是1/5。

在日常生活或工作中，倒数的应用非常广泛，例如计算比例、速度、密度等等。

在数学考试中，倒数也是很常见的题型。

但是，很多学生对倒数的应用掌握不够熟练，导致出现一些应该能解出的题目答错的情况。

在这篇文章中，我们将讲解如何运用倒数知识解题，并设计一份全方位的教案，帮助学生更好地掌握这一知识点。

一、倒数的定义及基本概念在数学上，倒数就是一个数的倒数。

一个数a的倒数是1/a。

例如，数3的倒数是1/3，数5的倒数是1/5。

通常，我们用字母x表示一个数，则x的倒数为1/x。

在应用中，倒数也有很多种形式，例如：1、比例：比例是两个数的倒数的比，如3:2表示3的倒数是2的1.5倍。

2、时速：时速就是单位时间内走过的路程与该时间的倒数的乘积，如每小时60公里表示每分钟走1公里。

3、密度：密度是物体的质量与其体积的倒数的比，如1克/立方厘米表示每个立方厘米的体积中有1克的质量。

了解基本的倒数概念对于解题很有帮助。

下面是几道常见的倒数应用题：例1：甲乙两人分别在8：10的速度下跑了2400米，谁用的时间更短？解答：根据速度=路程/时间的公式，可以列出甲、乙两人的速度的式子：甲的速度为8/x，乙的速度为10/x，其中x为甲、乙两人的时间。

由于路程相等，可以列出一个方程：8/x=10/x，解得x=20/3。

因为甲的速度比乙的速度低，所以甲所用的时间更长，乙用的时间更短。

例2：已知物体的密度为3克/立方厘米，其质量为27克，它的体积是多少？解答：物体的密度为质量与体积的比，即3=27/体积，解得体积=9立方厘米。

以上两个例子都使用了数学中的“倒数”概念来解题。

二、倒数的应用范围倒数在学科和领域中广泛应用：1、在数学中，倒数可以用来求解比例、速度、密度等相关题目。

总结求倒数的方法

总结求倒数的方法
1. 嘿，你知道不，求倒数就像是找一个数的“好伙伴”！比如说 2 的倒数就是 1/2 呀！
2. 求倒数其实超简单啦！就像给每个数找个“相反的朋友”，像 3 的倒数不就是 1/3 嘛！
3. 哎呀呀，求倒数不就是把数“翻个个儿”嘛！比如 4 的倒数就是1/4 呀，这多容易理解！
4. 哇塞，求倒数其实就是一种神奇的“变身法”！就像 5 变成 1/5 一样！
5. 嘿，你想想，求倒数不就跟找数的“小跟班”似的！比如 6 的倒数就是 1/6 呢！
6. 求倒数呀，就如同给数配个“小搭档”！像 7 的倒数就是 1/7 ，这不难吧？
7. 哎呀，求倒数不就是让数有个“对应物”嘛！比如 8 的倒数就是1/8 呀！
8. 哇哦，求倒数就好像给数找个“另一半”！像 9 的倒数就是 1/9 呢！
9. 嘿，求倒数其实就是一种简单的“配对游戏”呀！像 10 的倒数就是 1/10 哦！
10. 哈哈，求倒数不就是给数找个“反一反的伙伴”嘛！比如 1/11 就是 11 的倒数呀！。

取倒数法求数列的通向公式

取倒数法求数列的通向公式
在数学中，取倒数法是一种用于生成数列的方法。

它可以产生
一系列的数，这些数的倒数之和是一个常数。

这个常数通常被称为
通项公式，它可以用来计算数列中任意项的值。

取倒数法的数列通
向公式可以用来描述这种数列的规律和特点。

假设我们有一个数列a₁, a₂, a₃, ...，其中aₙ表示数列
的第n项。

如果我们对数列中的每一项取倒数，得到1/a₁, 1/a₂, 1/a₃, ...。

如果这些倒数之和是一个常数，我们可以用通项公式
来表示原数列。

数列的通项公式通常用符号表示，比如aₙ = f(n)，其中f(n)
是一个关于n的函数。

取倒数法求数列的通向公式可以表示为
1/aₙ = g(n)，其中g(n)是另一个关于n的函数。

通过研究g(n)的
特点和规律，我们可以得出原数列的通项公式。

举个例子，假设我们有一个数列1, 2, 3, 4, ...。

对这个数
列的每一项取倒数，得到1/1, 1/2, 1/3, 1/4, ...。

如果我们计
算这些倒数的和，可以发现它是一个无穷级数，1 + 1/2 + 1/3 +
1/4 + ...。

这个级数被称为调和级数，它的和是无穷的。

因此，我
们可以得出结论，原数列1, 2, 3, 4, ...的通项公式是aₙ = n。

通过取倒数法求数列的通向公式，我们可以发现一些有趣的数学规律和性质。

这种方法不仅可以帮助我们理解数列的生成规律，还可以拓展我们对数学的认识和理解。

因此，取倒数法求数列的通向公式是数学中一个重要且有趣的概念。

倒数的计算方法

倒数的计算方法
倒数是什么呢？嘿，这可太有意思啦！倒数啊，就像是数字世界里的一场奇妙反转游戏。

你看哦，一个数的倒数，不就是用 1 除以这个数嘛。

这就好像是数字们在玩一个特殊的魔术，一下子就把原来的数变得不一样了。

比如说 2 的倒数就是 1 除以 2 等于 0.5 呀。

这多神奇呀！就好比我们在生活中，有时候换个角度看问题，整个世界都变得不一样了呢。

计算倒数也是这样，给了我们一个全新的视角去认识那些熟悉的数字。

那怎么计算倒数呢？其实很简单啦！对于整数，就直接用 1 除以它。

那分数呢？嘿嘿，那就把分子分母调换位置就行啦！像三分之二的倒数就是二分之三嘛。

这不是挺容易的嘛。

那小数怎么办呢？也不难呀，把小数转换成分数，然后再按照分数的方法去算倒数。

是不是感觉像打开了一扇通往数字奇妙世界的大门？
再想想，倒数的存在是不是让数字之间的关系变得更加丰富多样了呢？每个数都有它独特的倒数，就像每个人都有自己独特的性格一样。

而且倒数之间也有着有趣的规律呢，两个互为倒数的数相乘，结果肯定是 1 呀，这就像是数字世界里的一个永恒定律。

在数学的海洋里，倒数就像是一颗颗闪耀的星星，照亮着我们探索的道路。

我们可以通过计算倒数来解决各种各样的问题，是不是超级厉害？难道我们不应该好好去了解它、掌握它吗？
总之，倒数的计算方法并不复杂，但却有着无穷的魅力和乐趣。

让我们尽情享受在数字的奇妙世界里，去发现更多关于倒数的奥秘吧！。

求倒数的方法

求倒数的方法
首先，最简单直接的方法是利用倒数的定义进行计算。

对于一
个数a，它的倒数可以表示为1/a。

这种方法适用于任何数，但是在
实际计算中可能会比较繁琐，特别是对于复杂的分数或者小数。

其次，我们可以利用分数的性质来求倒数。

对于一个分数a/b，它的倒数可以表示为b/a。

这种方法适用于分数的倒数计算，可以
简化计算过程，特别是对于涉及到分数的复杂计算。

另外，对于小数的倒数计算，我们可以利用小数的性质来求倒数。

对于一个小数0.abc，它的倒数可以表示为1/0.abc。

这种方法
适用于小数的倒数计算，可以通过移位和乘法来求得倒数。

此外，我们还可以利用倒数的性质来简化计算。

对于两个数a
和b的乘积，它们的倒数之积等于它们倒数的和。

即(1/a)(1/b) =
1/(ab)。

这种方法适用于复杂的计算，可以通过简化计算过程来求
得倒数。

最后，我们还可以利用计算器或者电脑软件来求倒数。

现代的
计算器和电脑软件都具有求倒数的功能，可以帮助我们进行复杂的
倒数计算，特别是对于涉及到大量数据和复杂运算的情况。

综上所述，求倒数的方法有很多种，我们可以根据具体的情况
选择合适的方法来进行计算。

无论是利用倒数的定义、分数的性质、小数的性质，还是倒数的性质，都可以帮助我们简化计算过程，提
高计算效率。

当然，在实际应用中，我们也可以利用现代的工具来
进行倒数计算，以便更快更准确地得到结果。

希望以上内容能够帮
助大家更好地理解和应用倒数的概念。

数字的倒数应用题

数字的倒数应用题在数学中，倒数是指一个数除以它自己，即1除以这个数。

倒数可以表示两个数之间的比例关系，也可以应用于各种实际问题中。

本文将介绍一些数字的倒数应用题，探讨其在生活和学习中的实际意义。

1. 加法问题假设小明去菜市场买了一些蔬菜，他先买了3千克的土豆，然后又买了它的倒数。

问小明总共买了多少千克土豆？解答：所谓土豆的倒数，即1除以土豆的重量。

因此，土豆的倒数为1/3千克。

小明总共买了3千克土豆加上1/3千克土豆，即3 + 1/3 = 10/3千克土豆。

2. 减法问题小红的房间里有一批书，其中有10本是她的，其余的是弟弟的。

小红决定借给朋友3本书，问剩下的书中她的书和弟弟的书比例是多少？解答：小红决定借给朋友的书是自己的，所以剩下的书中小红的数量为10-3=7本。

整个过程可以看作是总数减去借出去的数量。

因此，剩下的书中她的书和弟弟的书比例是7:3。

3. 乘法问题小明每天都要跑步训练，他决定每天跑的距离是30米的十分之一。

问小明每天跑了多少米？解答：小明每天跑的距离是30米的十分之一，即1/10 * 30 = 3米。

因此，小明每天跑了3米。

4. 除法问题小明想把一箱苹果平均分给他的5位朋友，每人分得15个苹果。

问小明一共有多少个苹果？解答：小明想把一箱苹果平均分给5位朋友，每人分得15个苹果。

因此，一共有5 * 15 = 75个苹果。

5. 比例问题小王参加了一场模拟考试，他的总分是80分，题目数量是20个。

问小王每个题目的平均得分是多少？解答：小王的总分是80分，题目数量是20个。

因此，小王每个题目的平均得分是80/20 = 4分。

结论通过以上几个数字的倒数应用题，我们可以看到数字的倒数在生活和学习中有着广泛的应用。

它能够帮助我们解决各种问题，了解事物之间的比例关系，以及进行计算和分析。

对于数学的学习，理解和应用数字的倒数是非常重要的。

总结本文主要介绍了数字的倒数应用题，通过分析不同类型的题目，我们了解了数字的倒数在解决实际问题中的作用。

用比例法和倒数法解题

用比例法和倒数法解题
比例法和倒数法是两种重要的数学运算方法，也是科学计算中不可或缺的必备技巧。

比例法是一种解决比例问题的方法，也叫比率法，它与单纯比较不同，它允许我们使用一系列的比率来比较两个或多个数字，从而得出比率之间的关系和差距。

比例法可以帮助我们发现事物之间的关系，并使用此关系来解决一些问题，这些关系可用一个数组表示，比如2:3、3:5或1:2.5，其准确的含义是第一个比率的一部分和第二个比率的一部分之比。

倒数法也叫比倒数，是一种用数字把一个数倒过来的方法，也可以看作把该数倒转过来。

倒数法可以帮助我们进行相关数学计算，用数字来表示倒数的运算方式如下：把数字分解成1和数字的乘积，取出数字的乘积，然后把乘积的倒数表示出来即可。

比如： 1/4=1/4; 1/9=1/9。

两种方法各有优劣，比例法可以方便我们计算比例之间的差异，而倒数法可以解决和数学运算有关的问题。

当然，这两种方法只是作为一种辅助手段来计算数学知识，并不能代替理解学习数学，必须积极发挥自己的学习能力，能够有效地提升学习效果。