八年级数学上册竞赛试题
初二数学竞赛试题7套整理版(含答案)

初二数学竞赛试题7套整理版(含答案)初二数学竞赛试题7套整理版(含答案)第一套试题1. 某数与它的四分之一之和的和是28,求这个数是多少?解:设这个数为x,根据题意可得方程 x + (1/4)x + x = 28,化简得9/4x = 28,解得 x = 44.2. 有一个矩形,长是宽的3倍,如果长再加上宽再加上1的和等于50,求矩形的长和宽各是多少?解:设矩形的宽为x,则长为3x,根据题意可得方程 3x + x + 1 = 50,化简得 4x + 1 = 50,解得 x = 12,所以长为3 * 12 = 36,宽为12.3. 某个数的三次方减去它自身等于608,求这个数是多少?解:设这个数为x,根据题意可得方程 x^3 - x = 608,化简得 x^3 - x - 608 = 0,因此需求解该方程的解x.4. 甲数和乙数之和是300,甲数比乙数大30,求甲数和乙数各是多少?解:设甲数为x,乙数为y,根据题意可得方程 x + y = 300,x - y = 30,联立这两个方程可以解得甲数x和乙数y.5. 家长购买某品牌的饮料,每瓶售价为5元,如果购买10瓶,优惠50%,那么需要支付的价格是多少?解:购买10瓶优惠50%,相当于购买5瓶的价格,所以需要支付 5 * 10 * (1 - 50%) = 25元.第二套试题1. 学校图书馆购买300本新书,若图书馆中已有书籍500本,现将这些书按每排放10本的方式摆放,共需要多少排?解:新书300本加上原有书籍500本,共计800本书,每排放10本,所以需要 800 / 10 = 80排.2. 小明每天早上跑步30分钟,下午骑自行车25分钟,晚上游泳40分钟,求他一天中运动的总时长是多少分钟?解:小明一天早上跑步30分钟,下午骑自行车25分钟,晚上游泳40分钟,总时长为 30 + 25 + 40 = 95分钟.3. 甲、乙两人开始一起钓鱼,甲每分钟能钓2条鱼,乙每分钟能钓1条鱼,如果他们一起钓了45分钟,那么他们一共钓到了多少条鱼?解:甲每分钟能钓2条鱼,乙每分钟能钓1条鱼,他们一起钓了45分钟,所以甲和乙一共钓到了 2 * 45 + 1 * 45 = 135 条鱼.4. 某商品原价100元,现在打8折,过了一段时间后再降价,降到原价的85%,现在这个商品的售价是多少?解:原价100元,打8折后为 100 * (1 - 80%) = 80元,再降到原价的85%为 80 * 85% = 68元.5. 某人的年收入为12000元,每月生活费占月收入的1/5,那么这个人每月的生活费用是多少元?解:年收入12000元,月收入为 12000 / 12 = 1000元,生活费占收入的1/5,所以生活费用为 1000 * 1/5 = 200元.第三套试题1. 甲、乙两个人合作修一个房子,甲一个人修需要8天,乙一个人修需要12天,问他们一起修需要多少天?解:甲一个人修需要8天,乙一个人修需要12天,他们一起修需要的时间为 1/(1/8 + 1/12) = 4.8天.2. 甲购买一本书花费了原价的3/4,折后价格为60元,问这本书的原价是多少?解:折后价格为60元,花费原价的3/4,所以原价为 60 / (3/4) = 80元.3. 甲、乙两人比赛,甲第一轮跑步用时1分钟,第二轮用时50秒,第三轮用时40秒;乙第一轮跑步用时55秒,第二轮用时45秒,第三轮用时35秒,问谁的平均速度更快?解:甲第一轮跑步用时1分钟,第二轮用时50秒,第三轮用时40秒,平均速度为 (60 + 50 + 40) / 3 = 50 秒/轮;乙第一轮跑步用时55秒,第二轮用时45秒,第三轮用时35秒,平均速度为 (55 + 45 + 35) / 3 = 45 秒/轮;所以甲的平均速度更快.4. 一只小狗每小时能跑5公里,一只小猫每小时能跑8公里,如果它们从同一地点同时出发并分别向东和西跑,4小时后它们相距了多少公里?解:小狗每小时能跑5公里,4小时后跑了5 * 4 = 20公里,小猫每小时能跑8公里,4小时后跑了8 * 4 = 32公里,所以它们相距了 32 -20 = 12 公里.5. 三个连续的偶数相加的和是60,求这三个数分别是多少?解:设第一个偶数为x,那么第二个偶数为x + 2,第三个偶数为x+ 4,根据题意可得方程 x + (x + 2) + (x + 4) = 60,求解该方程可得x及其对应的三个连续偶数.第四套试题1. 一个数的2倍加上5等于13,求这个数是多少?解:设这个数为x,根据题意可得方程 2x + 5 = 13,解得 x = 4.2. 甲乙两数相差22,乙数的2倍与甲数的3倍之和等于70,求甲、乙两数各是多少?解:设甲数为x,乙数为y,根据题意可得方程 y - x = 22,2y + 3x= 70,联立这两个方程可以解得甲数x和乙数y.3. 一辆汽车以每小时80千米的速度行驶,行驶了1小时20分钟后停下来休息,求这段时间内汽车行驶的路程?解:汽车以每小时80千米的速度行驶,1小时20分钟共1.33 小时,所以汽车行驶的路程为 80 * 1.33 = 106.4 千米.4. 甲、乙两个人一起做一件工作,甲单独完成需要4小时,乙单独完成需要6小时,他们一起完成这件工作需要多少小时?解:甲单独完成需要4小时,乙单独完成需要6小时,他们一起完成需要的时间为 1/(1/4 + 1/6) = 2.4小时.5. 一个数加上它的四分之一之和的和是28,求这个数是多少?解:设这个数为x,根据题意可得方程 x + (1/4)x + x = 28,化简得9/4x = 28,解得 x = 44.第五套试题1. 一条宽10米的路,两边分别种植了向阳向每排7棵树或9棵树,每棵树之间距离相等,而且与路两边相邻树之间距离也相等,问道路中间最宽的地方有多宽?解:分别种植7棵树和9棵树,每棵树之间距离相等,所以道路中间最宽的地方为两排树之间的距离.2. 一个数与4的乘积减去2等于18,求这个数是多少?解:设这个数为x,根据题意可得方程 4x - 2 = 18,解得 x = 5.3. 甲、乙、丙三人合作种田,甲一个人种地需要10天,乙一个人种地需要12天,丙一个人种地需要15天,问他们三个人一起种地需要多少天?解:甲一个人种地需要10天,乙一个人种地需要12天,丙一个人种地需要15天,他们一起种地需要的时间为 1/(1/10 + 1/12 + 1/15) =4.8天.4. 某人共有100元,买了一本书花掉了原价的3/5,剩下的钱还能买另一本原价为80元的书吗?解:100元买了一本书花掉了原价的3/5,剩下的钱为 100 * (1 - 3/5) = 40元,剩下的钱不足以购买另一本80元的书.5. 一团面粉重800克,其中水分为15%,求这团面粉中水分的重量是多少克?解:面粉重800克,其中水分为15%,所以水分的重量为800 * 15% = 120克.第六套试题1. 一个数与它的五分之一之和的和是40,求这个数是多少?解:设这个数为x,根据题意可得方程 x + (1/5)x + x = 40,化简得7/5x = 40,解得 x = 28.57.2. 甲、乙两个人分别完成一项工作需要的时间比为2:5,如果他们一起完成这项工作需要3小时,求乙单独完成这项工作需要多少时间?解:甲、乙两个人分别完成一项工作需要的时间比为2:5,设甲单独完成需要的时间为x,乙单独完成需要的时间为y,根据题意可得方程 2x + 5x = 3,解得 y = 7.5.3. 有两个相交的圆,圆心之间的距离为8,两圆的半径分别为5和3,求两圆相交的弦的长度是多少?解:两个圆的半径分别为5和3,圆心之间的距离为8,利用勾股定理可以求得两圆相交的弦的长度.4. 甲乙两个人一起做一件工作,甲单独完成需要10小时,乙单独完成需要15小时,他们一起完成这件工作需要多少小时?解:甲单独完成需要10小时,乙单独完成需要15小时,他们一起完成需要的时间为 1/(1/10 + 1/15) = 6小时.5. 甲给乙20元,乙给丙30元,丙给甲10元,这三个人一共交易了多少元?解:甲给乙20元,乙给丙30元,丙给甲10元,所以一共交易了20 + 30 + 10 = 60元.第七套试题1. 某数比它的2/3小12,求这个数是多少?解:设这个数为x,根据题意可得方程 x - (2/3)x = 12,化简得 1/3x = 12,解得 x = 36.2. 甲、乙两个人一起修一条路,甲单独修需要8小时,乙单独修需要12小时,也有可能甲的速度是乙的倍数,问他们一起修需要多少小时?解:甲单独修需要8小时,乙单独修需要12小时,他们一起修需要的时间为 1/(1/8 + 1/12) = 4.8小时.3. 某品牌的衣服原价为200元,现在打折8折,过了一段时间后再降价,降到原价的85%,现在这件衣服的售价是多少?解:原价200元,打8折后为 200 * (1 - 80%) = 160元,再降到原价的85%为 160 * 85% = 136元.4. 甲、乙两个人一起做工,甲一个小时能做1/3的工作量,乙一个小时能做1/4的工作量,问他们一起做一份工作需要多少时间?解:甲一个小时能做1/3的工作量,乙一个小时能做1/4的工作量,他们一起做一份工作需要的时间为 1/(1/3 + 1/4) = 12/7小时.5. 某人的年收入为12000元,每月花销占收入的1/4,那么这个人每月的花销是多少元?解:年收入12000元,。
八年级(上)数学竞赛试题及答案(新人教版)
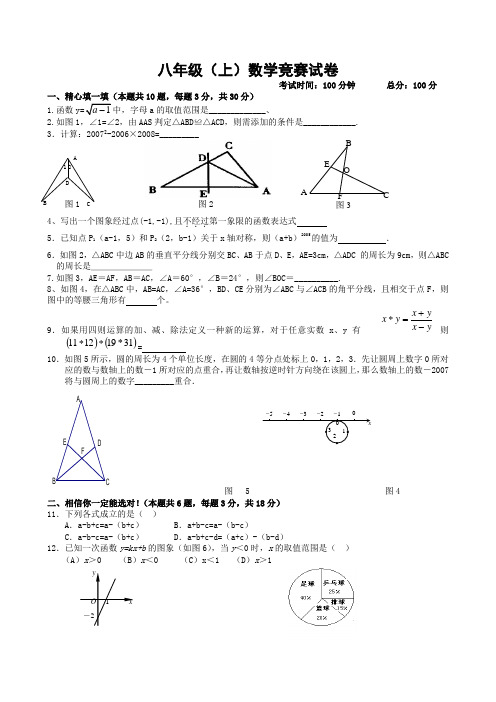
八年级(上)数学竞赛试卷考试时间:100分钟 总分:100分一、精心填一填(本题共10题,每题3分,共30分)1.函数a 的取值范围是_____________、2.如图1,∠1=∠2,由AAS 判定△ABD ≌△ACD ,则需添加的条件是____________. 3.计算:20072-2006×2008=_________图1 图24、写出一个图象经过点(-1,-1),且不经过...第一象限的函数表达式 5.已知点P 1(a-1,5)和P 2(2,b-1)关于x 轴对称,则(a+b )2005的值为 .6.如图2,△ABC 中边AB 的垂直平分线分别交BC 、AB于点D 、E ,AE=3cm ,△ADC•的周长为9cm ,则△ABC 的周长是_______7.如图3,AE =AF ,AB =AC ,∠A =60°,∠B =24°,则∠BOC =__________.8、如图4,在△ABC 中,AB=AC ,∠A=36°,BD 、CE 分别为∠ABC 与∠ACB 的角平分线,且相交于点F ,则图中的等腰三角形有 个。
9.如果用四则运算的加、减、除法定义一种新的运算,对于任意实数x 、y 有y x y x y x -+=* 则()()31*191211**=10.如图5所示,圆的周长为4个单位长度,在圆的4等分点处标上0,1,2,3.先让圆周上数字0所对应的数与数轴上的数-1所对应的点重合,再让数轴按逆时针方向绕在该圆上,那么数轴上的数-2007将与圆周上的数字_________重合.FEDACB图 5图4 二、相信你一定能选对!(本题共6题,每题3分,共18分) 11.下列各式成立的是( )A .a-b+c=a-(b+c )B .a+b-c=a-(b-c )C .a-b-c=a-(b+c )D .a-b+c-d=(a+c )-(b-d ) 12.已知一次函数y=kx+b 的图象(如图6),当y <0时,x 的取值范围是( )(A )x >0 (B )x <0 (C )x <1 (D )x >1A B C D12 AEBO F C图3图6 图713.在△ABC 中,∠B =∠C ,与△ABC 全等的三角形有一个角是100°,那么在△ABC 中与这100°角对应相等的角是 ( )A.∠AB.∠BC.∠CD.∠B 或∠C 14.某校八(2)班的全体同学喜欢的球类运动用图7所示的扇形统计图来表示,下面说法正确的是( ) A 、从图中可以直接看出喜欢各种球类的具体人数; B 、从图中可以直接看出全班的总人数;C 、从图中可以直接看出全班同学初中三年来喜欢各种球类的变化情况;D 、从图中可以直接看出全班同学现在喜欢各种球类的人数的大小关系 15.已知一次函数y=mx+│m+1│的图像与y 轴交于点(0,3),且y 随x 的增大而减小,则m 的值为( ). A .2 B .-4 C .-2或-4 D .2或-416.设y=ax 15+bx 13+cx 11-5(a 、b 、c 为常数),已知当x=7时,y=7,则x= -7时,y 的值等于( )A 、-7B 、-17C 、17D 、不确定 三、认真解答,一定要细心哟!(各6分,共18分) 17. 先化简再求值:[]y y x y x y x 4)4()2)(2(2÷+--+,其中x =5,y=2。
人教版 八年级数学上册 竞赛专题分式方程(含答案)

人教版 八年级数学上册 竞赛专题:分式方程(含答案)【例1】 若关于x 的方程22x ax +-=-1的解为正数,则a 的取值范围是______.解题思路:化分式方程为整式方程,注意增根的隐含制约.【例2】 已知()22221111x x A B Cx x x x x +-=++--,其中A ,B ,C 为常数.求A +B +C 的值.解题思路:将右边通分,比较分子,建立A ,B ,C 的等式.【例3】解下列方程: (1)596841922119968x x x x x x x x ----+=+----; (2)222234112283912x x x x x x x x ++-+=+-+; (3)2x +21x x ⎛⎫⎪+⎝⎭=3.解题思路:由于各个方程形式都较复杂,因此不宜于直接去分母.需运用解分式问题、分式方程相关技巧、方法解.【例4】(1)方程18272938x x x x x x x x +++++=+++++的解是___________. (2)方程222111132567124x x x x x x x ++=+++++++的解是________.解题思路:仔细观察分子、分母间的特点,发现联系,寻找解题的突破口.【例5】若关于x 的方程2211k x kx x x x x+-=--只有一个解,试求k 的值与方程的解. 解题思路:化分式方程为整式方程,解题的关键是对原方程“只有一个解”的准确理解,利用增根解题.【例6】求方程11156x y z ++=的正整数解. 解题思路:易知,,x y z 都大于1,不妨设1<x ≤y ≤z ,则111x y z≥≥,将复杂的三元不定方程转化为一元不等式,通过解不等式对某个未知数的取值作出估计.逐步缩小其取值范围,求出结果.能力训练A 级1.若关于x 的方程1101ax x +-=-有增根,则a 的值为________. 2.用换元法解分式方程21221x x x x --=-时,如果设21x x-=y ,并将原方程化为关于y 的整式方程,那么这个整式方程是___________. 3.方程2211340x x x x ⎛⎫+-++= ⎪⎝⎭的解为__________. 4.两个关于x 的方程220x x --=与132x x a=-+有一个解相同,则a =_______.5.已知方程11x a x a+=+的两根分别为a ,1a ,则方程1111x a x a +=+--的根是( ). A .a ,11a - B .11a -,1a - C .1a ,1a - D .a ,1aa -6.关于x 的方程211x mx +=-的解是正数,则m 的取值范围是( ) A .m >-1 B .m >-1且m ≠0C .m <-1D .m <-l 且m ≠-27.关于x 的方程22x c x c +=+的两个解是x 1=c ,x 2=2c ,则关于x 的方程2211x a x a +=+--的两个解是( ) . A .a ,2a B .a -1,21a - C .a ,21a - D .a ,11a a +- 8.解下列方程:(1)()2221160x x x x+++-=; (2)2216104933x x x x ⎛⎫+=-- ⎪⎝⎭.9.已知13x x+=.求x 10+x 5+51011x x +的值.10.若关于x 的方程2211k x kx x x x x+-=--只有一个解(相等的两根算作一个),求k 的值.11.已知关于x 的方程x2+2x +221022m x x m-=+-,其中m 为实数.当m 为何值时,方程恰有三个互不相等的实数根?求出这三个实数根.12.若关于x 的方程()()122112x x ax x x x x ++-=+--+无解,求a 的值.B 级1.方程222211114325671221x x x x x x x x +++=+++++++的解是__________.2.方程222111011828138x x x x x x ++=+-+---的解为__________.3.分式方程()()1112x m x x x -=--+有增根,则m 的值为_________. 4.若关于x 的分式方程22x ax +-=-1的解是正数,则a 的取值范围是______.5.(1)若关于x 的方程2133mx x =---无解,则m =__________. (2)解分式方程225111mx x x +=+--会产生增根,则m =______. 6.方程33116x x x x ⎛⎫+=+ ⎪⎝⎭的解的个数为( ). A .4个 B .6个 C .2个 D .3个7.关于x 的方程11ax =+的解是负数,则a 的取值范围是( ) . A .a <l B .a <1且a ≠0 C .a ≤1 D .a ≤1且a ≠08.某工程,甲队独做所需天数是乙、丙两队合做所需天数的a 倍,乙队独做所需天数是甲、丙两队合做所需天数的b 倍,丙队独做所需天数是甲、乙两队合做所需天数的c 倍,则111111a b c +++++的值是( ).A .1B .2C .3D .49.已知关于x 的方程(a 2-1)()2271011x x a x x ⎛⎫⎛⎫-++= ⎪ ⎪--⎝⎭⎝⎭有实数根.(1)求a 的取值范围;(2)若原方程的两个实数根为x 1,x 2,且121231111x x x x +=--,求a 的值.10.某电脑公司经销甲种型号电脑,受经济危机影响,电脑价格不断下降. 今年三月份的电脑售价比去年同期每台降价1 000元.如果卖出相同数量的电脑,去年销售额为10万元.今年销售额只有8万元. (1)今年三月份甲种电脑每台售价多少元?(2)为了增加收入,电脑公司决定再经销乙种型号电脑.已知甲种电脑每台进价为3500元,乙种电脑每台进价为3000元,公司预计用不多于5万元且不少于4.8万元的资金购进这两种电脑共15台,有几种进货方案?(3)如果乙种电脑每台售价为3 800元,为打开乙种电脑的销路,公司决定每售出一台乙种电脑,返还顾客现金a元.要使(2)中所有方案获利相同,a值应是多少?此时,哪种方案对公司更有利?参考答案例1 a <2且a ≠-4例2 原式右边=22(1)+B(1)(1Ax x x Cx x x --+-)=2222()()211(1)(1)A C x B A x B x x x x x x ++--+-=-- 得2111A C B A B +=⎧⎪-=⎨⎪-=-⎩∴1011,8.A B C =⎧⎪=⎨⎪=-⎩,∴A +B +C =13.例3 (1)x =12314提示:1155(5)(1)(4)(2)191968x x x x -++=++-----.(2)1,2x =,x 3=-1,x 4=-4 提示:令223.4x xy x x +=+-(3)1,2x =提示222222()().111x x x x x x x +=++++例4 (1)原方程化为11111+111+2+9+3+8x x x x --=-+-,即1111+3+2+9+8x x x x -=-,进一步可化为(x +2) (x +3)=(x +8) (x +9),解得x =-112.(2)原方程化为1111111+1+2+2+3+3+4+4x x x x x x x -+-+-=,即12+14x x =+,解得x =2. 例5 原方程化为kx 2-3kx +2x -1=0①,当k =0时,原方程有唯一解x =12;当k ≠0,Δ=5k 2+4(k -1)2>0.由题意知,方程①必有一根是原方程的曾根,即x =0或x =1,显然0不是①的根,故x =1是方程①的根,代入的k =12.∴当k =0或12时,原方程只有一个解. 例6 11113x x y z x <++≤,即1536x x <≤,因此得x =2或3.当x =2时,111x x y <+=511112623y y y -=≤+=,即1123y y<≤,由此可得y =4或5或6;同理,当x =3时,y =3或4,由此可得当1≤x ≤y ≤z 时,(x ,y ,z )共有(2,4,12),(2,6,6),(3,3,6),(3,4,4)4组;由于x ,y ,z 在方程中地位平等,可得原方程组的解共15组:(2,4,12),(2,12,4), (4,2,12),(4,12,2),(12,2,4),(12,4,2),(2,6,6),(6,2,6),(6,6,2),(3,3,6),(3,6,3),(6,3,3),(3,4,4) ,(4,4,3) ,(4,3,4).A 级1.-1 2.y 2-2y -1=0 3.1 4.-8 5.D 6.D 7.D8.(1)12123x x ==-, (2)1226x x ==-,,3,43x =-±9.15250 提示:由x +13x =得2217.x x +=则2211()()21x x x x ++=,得33118x x+=. 于是221()x x+331()126x x +=,得551123x x +=.进一步得1010115127x x +=.故原式=15250.10.k =0或k =12提示:原方程化为kx 2-3kx +2x -1=0,分类讨论. 11.设x +2x =y ,则原方程可化为y 2-2my +m 2-1=0,解得y 1=m +1,y 2=m -1.∵x 2+2x -m -1=0①,x 2+2x -m +1=0②,从而Δ1=4m +8,Δ2=4m 中应有一个等于零,一个大于零.经讨论,当Δ2=0即m =0时,Δ1>0,原方程有三个实数根.将m =0代入原方程,解得12321211.x x x ⎧=-⎪⎪=--⎨⎪=⎪⎩12 原方程“无解”内涵丰富:可能是化得的整式方程无解,亦可能是求得的整式方程的解为増根,故需全面讨论.原方程化为(a+2)x =-3 ① , ∵原方程无解,∴a+2=0或x -1=0,x+2=0,得B 级1. 3或 - 72. x₁=8 , x₁=-1 , x₁=-8 , x₁=1 提示: 令x ²-8=y3. 3 提示:由有増根可得m=0或 m=3,但当 m=0,化为整式方程时无解4. a<2 且 a ≠-45. ⑴ -2 ⑵ -4 或 -106. A7.8. 设甲单独做需要x 天完成,乙单独做需要y 天完成,丙单独做需要z 天完成则.解 . 当a ≠±1时,则Δ≥0,原方程有实数解.由Δ=[-﹙2a+7﹚]²-4﹙a ²-1﹚≥0,解得.21-5,2,21-a 5,-=a 分别别代入①2-= x 1,=x 把 2,-=a 或综上知--==a 0≠1a ∴ 0,≠11 0≠1x 1a 01-a x ∴,111x a: a a x a B 且即且由提示<+-+<⇒<=+=⇒=+1x y +=++a yz yzxz 得⑥⑤④, ⑥11yz x z x y x y ⑤,11yz x z x y x z ④.11yz x z x y yz ∴+++=+++=+++=++c b a 同理可得111111a 1=+++++c b 得,01.01)72(1)t -(a 1,≠,1⑴....9222=-=++-=-a t a t t x x当原方程可化为则设.,?=a , 41-=x 81-=x ∴, 51=1-x 91=1-x 0=1+5-0=1+9-, ?=原方程有实数解时当故或或即或则方程为时即x x t t a 且当综上可知由于解得时但当又,2853-≥,,2853->22±1,22±1=a ,1=t 1,≠t ,2853-≥a a .,22±1≠原方程有实数解时a。
八年级数学竞赛试题及参考答案

八年级数学竞赛试题及参考答案八年级数学竞赛试题(一)一、选择题(每小题5分,共30分) 1.已知2220082008,2ca b a b c k k +=-==++=,且那么的值为( ). A .4 B .14 C .-4 D .14- 2.若方程组312433x y k x y k x y x y +=+⎧<<-⎨+=⎩的解为,,且,则的取值范围是( ). A .102x y <-<B .01x y <-<C .31x y -<-<-D .11x y -<-< 3.计算:2399100155555++++++=( ).A .10151- B .10051- C .101514- D .100514-4.如图,已知四边形ABCD 的四边都相等,等边△AEF 的顶点E 、F 分别在BC 、CD 上,且AE=AB ,则∠C=( ). A .100° B .105° C .110° D .120°5.已知5544332222335566a b c d a b c d ====,,,,则、、、的大小关系是( ). A .a b c d >>> B .a b d c >>> C .b a c d >>> D .a d b c >>> 6.如果把分数97的分子、分母分别加上正整数913a b 、,结果等于,那么a b +的最小 值是( ).A .26B .28C .30D .32 二、填空题:(每小题5分,共30分)(第4题图)DCB(第15题图)EDCBA7.方程组200820092007200720062008x y x y -=⎧⎨-=⎩的解是 .8.如图,已知AB 、CD 、EF 相交于点O ,EF ⊥AB ,OG 为∠COF 的平分线,OH 为∠DOG 的平分线,若∠AOC :∠COG=4:7,则∠GOH= .9.小张和小李分别从A 、B 两地同时出发,相向而行,第一次在距A 地5千米处相遇,继续往前走到各地(B 、A )后又立即返回,第二次在距B 地4千米处两人再次相遇,则A 、B 两地的距离是 千米.10.在△ABC 中,∠A 是最小角,∠B 是最大角,且2∠B=5∠A ,若∠B 的最大值为m °,最小值为n °,则m °+n °= .11.已知21()()()04b c b c a b c a a a+-=--≠=,且,则 . 12.设p q ,均为正整数,且7111015p q <<,当q 最小时,pq 的值为 . 以下三、四、五题要求写出解题过程. 三、(本题满分20分)13.在一次抗击雪灾而募捐的演出中,晨光中学有A 、B 、C 、D 四个班的同学参加演出,已知A 、B 两个班共16名演员,B 、C 两个班共20名演员,C 、D 两个班共34名演员,且各班演员的人数正好按A 、B 、C 、D 次序从小到大排列,求各班演员的人数. 四、(本题满分20分)14.已知2211x x y y x y =+=+≠,,且. ⑴ 求证:1x y +=. ⑵ 求55x y +的值.五、(本题满分20分)15.如图,在△ABC 中AC >BC ,E 、D 分别是AC 、BC 上的点,且∠BAD=∠ABE ,AE=BD .求证:∠BAD=12∠C .G(第8题图)HOFED CBA参考答案一、选择题1.A 2.B 3.C 4.A 5.A 6.B 二、填空题: 7、21x y =⎧⎨=⎩ 8、72.5° 9、11 10、175° 11、2 12、68213、解:依题意得:A+B=16,B+C=20,C+D=34∵A <B <C <D ,∴A <8,B >8,B <10,C >10,C <17,D >17 由8<B <10且B 只能取整数得,B=9 ∴C=11,D=23,A=7答:A 、B 、C 、D 各班演员人数分别是7人、9人、11人、23人。
八年级上学期数学竞赛试题(含答案)

八年级上学期数学竞赛试题(含答案)题号 一 二 三 四 五 得分 得分一、选择题(每题3分,共42分)将唯一正确答案的代号字母填在下面的表格内: 题号 1 2 345 6 7 8 9 10 11 12 13 14 答案1.在以下绿色食品、回收、节能、节水四个标志中,是轴对称的图形有2.已知三角形两边长分别为3和5,则第三边a 的取值范围是 A .53<<a B .83<<a C .52<<a D .82<<a 3.下列运算错误的是 A .333532a a a -=B .633a a a ÷=C .325()()()a b b a a b --=-D .236m n m n +⨯=4. 一个正多边形的外角与它相邻的内角之比为1:4,那么这个多边形的边数为 A .8 B .9 C .10 D .125. 计算45(210)(410)-⨯⨯⨯的正确结果是A. 20210-⨯B. 9210⨯C. 9810⨯D. 9810-⨯ 6.下列各式由左边到右边的变形中,是分解因式的为A B C DA .ay ax y x a +=+)(B .4)4(442+-=+-x x x xC .)12(55102-=-x x x xD .x x x x x 3)4)(4(3162++-=+-7. 若321()44m n x y x y x ÷=,则,m n 的值分别是A.6,1m n ==B.5,1m n ==C.5,0m n ==D.6,0m n ==8.下列分式运算中正确的是 A. a acb bc= B.x y y x x y x y --=+- C.321x y x xy x +=+ D. 0.33100.20.525a b a ba b a b++=++9.如图,∠1=∠2,要证明△ABC≌△ADE,还需补充的条件是A. AB =AD ,AC =AEB. AB =AD ,BC =DEC. AC =AE ,BC =DED. 以上都不对10.在平面直角坐标系中,已知点(,3)A m 与点(4,)B n 关于y 轴对称,那么2015()m n + 的值为A .1-B .1C .20157-D .2015711.如果214x x c ++是一个完全平方式,那么常数c 的值可以是 A .49 B .169 C .49±D .169±12.对于任何整数a ,多项式2(35)4a +-都能第9题图A.被9整除B.被a 整除C.被1a +整除D.被1a -整除13.如图,在直角ABC △中,90C =∠,30B =∠,AB 的垂直平分线交AB 于点D ,交BC 于点E ,若3AC =,1CE =,则△DBE 的周长为 A .13+ B .23+C .231+D .33+14. 如图为杨辉三角系数表,它的作用是指导读者按规律写出形如()n a b +(其中 n 为正整数)展开式的系数,例如:(a +b )=a +b ,(a +b )2=a 2+2ab +b 2,(a +b )3=a 3+3a 2b +3ab 2+b 3,那么6()a b +展开式中前四项系数分别为A .1,5,6,8B .1,5,6,10C .1,6,15,18D .1,6,15,20二、填空题:(每题3分,共15分)答案直接填在题中横线上. 15. 计算:()2323x x ⋅-= .16. 分解因式:(1)(3)4x x -++=___________. 17.若分式2244x x x --+的值为0,则x 的值为 .18. 如图,在△ABC 中,AB =6,BC =8,∠B =60°,将第18题图第13题图E DCBA△ABC沿射线BC 的方向平移2个单位后,得到△'''A B C ,连 接'A C ,则△''A B C 的周长为________.19. 新定义一种运算:22@()()a b a b a b =+--,下面给出关于这种运算的几个结论:①1@(2)8-=-;②@@a b b a =;③若@0a b =,则a 一定为0;④若0a b +=,那么2(@)(@)8a a b b a +=.其中正确结论的序号是 . 三、开动脑筋,你一定能做对!(本大题共3小题,共19分)20. (本题共6分)如图,在△ABC 和△BDE 中,点C 在边BD 上,边AC 交边BE 于点F ,若AC =BD , AB =ED ,BC =BE ,求证:∠ACB =12∠AFB .21.(本题共7分)先化简再求值:已知y x A +=2,y x B -=2,求代数式22()(2)A B x y --的值,其中1x =-,2y =.F E DCBA第20题图22.(本题共6分)如图所示,ABC △中,110BAC ∠=︒,点D,E,F 分别在线段AB 、BC 、AC 上,且BD =BE ,CE =CF ,求DEF ∠的度数.四、认真思考,你一定能成功!(本大题共2小题,共21分)23.(12分)如图,在平面直角坐标系中,直线l 是第一、三象限的角平分线. 实验与探究:(1)由图观察易知A (0,4)关于直线l 的对称点A '的坐标为(4,0),请在图中分别 标明B(5,2) 、C(-2,3) 关于直线l 的对称第22题图FEDCBA点B'、C'的位置,并写出他们的坐标:B'、C';归纳与发现:(2)结合图形观察以上三组点的坐标,你会发现:坐标平面内任一点(,)P a b关于第一、三象限的角平分线l的对称点P'的坐标为(不必证明);运用与拓广:(3)已知两点D(1,-2)、E(-1,-3),试在直线l上确定一点Q,使点Q到D、E两点的距离之和最小.(要有必要的画图说明,并保留作图痕迹)24.(本题共9分)设kxy=,是否存在实数k,使得代数式5x?若能,请求出所有满足条件的k的值;----能化简为2()(2)3(2)x y x y x x y若不能,请说明理由.五、相信自己,加油呀!(本大题共2小题,共23分)25. (11分)已知:△ABC中,∠A=90°,AB=AC,D为BC的中点.(1)如图1,E,F分别是AB,AC上的点,且BE=AF,求证:△DEF为等腰直角三角形.(2)如图2,若E,F分别为AB,CA延长线上的点,仍有BE=AF,其他条件不变,那么,△DEF是否仍为等腰直角三角形?如果是,请写出证明过程;如果不是,请说明理由.26.(本题12分)阅读材料: 分解因式:223x x +-解:原式=22113x x ++-- =2(21)4x x ++-=2(1)4x +- =(12)(12)x x +++-=(3)(1)x x +-此种方法抓住了二次项和一次项的特点,然后加一项,使这三项成为完全平方式,我们把这种分解因式的方法叫配方法.请仔细体会配方法的特点,然后尝试用配方法解决下列问题: (1)分解因式: 2243m mn n -+;(2)无论m 取何值,代数式232015m m -+总有一个最小值,请你尝试用配FE DCBA方法求出它的最小值.八年级数学试题参考答案及评分建议15. 518x 16. 2(1)x + 17. 2x =- 18. 18 19.①②④三、解答题(共63分)20. (本题共6分)证明:∵AC =BD , AB =ED ,BC =BE , ∴△ABC ≌△DEB ,……………………………………………2分 ∴∠ACB=∠EBD,…………………………………………………3分 ∵∠AFB 是△BFC 的外角,∴∠AFB=∠ACB+∠EBD , ∴∠AFB=2∠ACB ,即∠ACB =12∠AFB.…………………………………………………6分 21.(本题共7分)解:原式=8(2)xy x y -=22816x y xy -…………………………… 5 分当1,2x y =-=时,原式=16+64=80. ……………………………… 7 分 22.(本题共6分)解:不妨设∠B=x ,∠C =y ,则在△BDE 中,∵BD =BE ,∴∠B ED =12(180°-x ),同理在在△CEF中,∵CE =CF ,∴∠CEF =12(180°-y ),………………2分 因为∠B ED +∠DEF +∠CEF =180°,FEDCBA∴∠DEF =180°-(∠B ED +∠CEF )=180°-11(180)(180)22x y ⎡⎤-+-⎢⎥⎣⎦=1()2x y +……………………………4分 又∵110BAC ∠=︒,∴18011070x y +=︒-︒=︒,故∠DEF =170352⨯︒=︒.………6分 23.(本题共9分)解:能.……………………………………………………………1分假设存在实数k ,因为()(2)3(2)x y x y x x y ----=224x y -+,………………3分将kx y =代入,原式=224()x kx -+=22(4)k x -,………………………………5分∵22(4)k x -=25x ,∴245k -=,………………………………………………7分29k =,得3k =±.……………………………………………………………………9分24.(12分) 解:(1)由图可知,'(2,5)B ,'(3,2)C -;…………………………4分(2)由(1)可知,关于直线l 对称的点'(,)P b a ;……………………………………7分(3)作出点E 关于直线l 对称点F ,连接FD ,则QF =QE ,故EQ +QD =FQ +QD =FD.……………………………………………………12分25. (11分)证明:(1)连结AD , ∵AB AC =,∠BAC =90°,D 为BC 的中点,∴AD ⊥ BC ,BD =AD ,∴∠B =∠DAC =45°又BE =AF ,∴△BDE ≌△ADF (SAS )∴ED =FD ,∠BDE =∠ADF∴∠EDF =∠EDA +∠ADF =∠EDA +∠BDE =∠BDA =90°∴△DEF 为等腰直角三角形 …………………………… 5分(2)若E ,F 分别是AB ,CA 延长线上的点,如图所示.连结AD ∵AB =AC ,∠BAC =90°, D 为BC 的中点,∴AD =BD ,AD ⊥BC ∴∠DAC =∠ABD =45°,∴∠DAF =∠DBE =135°,又AF =BE ,∴△DAF ≌△DBE (SAS ),∴FD =ED ,∠FDA =∠EDB , ∴∠EDF =∠EDB +∠FDB =∠FDA +∠FDB =∠ADB =90°,∴△DEF 仍为等腰直角三角形.…………………………………………………11分26.(本题12分)解:(1)222224344m mn n m mn n n -+=-+- …………1分22(2)m n n =-- ………………………………3分 (3)()m n m n =--;………………………………6分(2)232015m m -+222333()()201522m m =-+-+…………………………7分 2233()()201522m =--+233()201224m =-+,………………………………8分 ∵23()02m -≥,∴2333()20122012244m -+≥,…………………………11分 即代数式232015m m -+的最小值为320124.…………………………………12分(备注:在解答题中,考生若用其它解法,应参照本评分标准给分)。
八年级数学竞赛试题(附答案)

八年级数学竞赛试题(本卷满分150分,时间120分钟)一、填空题(每小题5分,共50分)1.点P (3,-5)关于y 轴对称的点的坐标为( )A . (3,5)--B .(5,3)C .(3,5)-D .(3,5) 2.下列四组数据中,不能..作为直角三角形的三边长的是( ) A . 7,24,25 B .6,8,10 C .9,12,15 D .3,4,6 3.已知△ABC 中,AB=AC ,高BD ,CE 交于点O ,连接AO ,则图中全等三角形的对数为( )A .3B .4C .5D .6 4.如图,在△ABC 中,∠C=90°,∠BAC=30°,AB=8,AD 平分∠BAC ,点PQ 分别是AB 、AD 边上的动点,则PQ+BQ 的最小值是( )A .4B .5C .6D .7 5.设M=(x -3)(x -7),N=(x -2)(x -8),则M 与N 的关系为( )A.M <NB.M >NC.M=N D .不能确定 6.用三种边长相等的正多边形地砖铺地,其顶点拼在一起,刚好能完全铺满地面,已知正多边形的边数为x ,y ,z ,则zy x 111++的值为( ) A .1 B .32 C .21 D .317.如图,长方形ABCD 中,△ABP 的面积为a ,△CDQ 的面积为b ,则阴影四边形的面积等于( )A .b a +B . b a -C .2ba + D .无法确定 8.若实数x 、y 、z 满足2()4()()0x z x y y z ----=.则下列式子一定成立的是( )A .0x y z ++=B .20x y z +-=C . 20y z x +-=D . 20z x y +-=9.已知3030--+-+-=a x x a x y ,其中0<a <30,30≤≤x a ,那么y 的最小值为.( ) A .10 B .20C .30D .4010.如图,ABE ∆和ADC ∆是ABC ∆分别沿着AB ,AC 边翻折0180形成的,若∠1:∠2:∠3=28:5:3,则a ∠的度数为.( )A .60oB .70oC .80oD .90o二、填空题(每小题7分,共49分)11.如果2222(2)(2)45a b a b +++-=,则a 2+b 2的值为 .12.将五个分数:23 ,58 ,1523 ,1017 ,1219 ;由小到大或由大到小排列,排在中间位置的分数是13.x 表示a 与b 的和的平方,y 表示a 与b 的平方的和,则a=7,b=-5时,x -y 的值是14.计算:|11992 -11991 |+|11993 -11992 |-|11993 -11991 |=15.观察下列运算:12=1;22=1+3;32=1+3+5;42=1+3+5+7;52=1+3+5+7+9;则n 2= (n 为正整数)。
八年级上册数学竞赛试题

八年级上册数学竞赛试题一、选择题(每题3分,共30分)1. 下列哪个数是无理数?A. 3.1416B. πC. 0.33333D. √22. 如果a和b是两个实数,且a > b,那么下列哪个不等式是正确的?A. a + 1 > b + 1B. 3a > 3bC. a - b > 0D. 所有选项都是正确的3. 一个数的平方根是它本身的数有几个?A. 0个B. 1个C. 2个D. 3个4. 以下哪个是二次根式?A. √3xB. 3√xC. √x²D. √x/25. 一个直角三角形的两条直角边分别为3和4,斜边的长度是多少?A. 5C. 7D. 86. 一个数的立方根是它本身的数有几个?A. 0个B. 1个C. 2个D. 3个7. 一个圆的半径是5,那么它的面积是多少?A. 25πB. 50πC. 100πD. 125π8. 下列哪个不是有理数?A. 1/2B. -3C. 0D. √39. 如果一个数的绝对值是5,那么这个数是?A. 5B. -5C. 5或-5D. 不存在10. 一个数的倒数是1/2,那么这个数是?A. 2B. 1/2D. 1/4二、填空题(每题2分,共20分)11. 一个数的相反数是-8,这个数是_________。
12. 一个数的绝对值是7,这个数可以是_________或_________。
13. 一个数的平方是25,这个数可以是_________或_________。
14. 一个数的立方是-64,这个数是_________。
15. 如果一个数的平方根是4,那么这个数是_________。
16. 一个数的倒数是2,那么这个数是_________。
17. 一个圆的直径是14,它的半径是_________。
18. 一个直角三角形的斜边是13,一条直角边是5,另一条直角边是_________。
19. 如果一个数的立方根是3,那么这个数是_________。
八年级上册数学竞赛试题
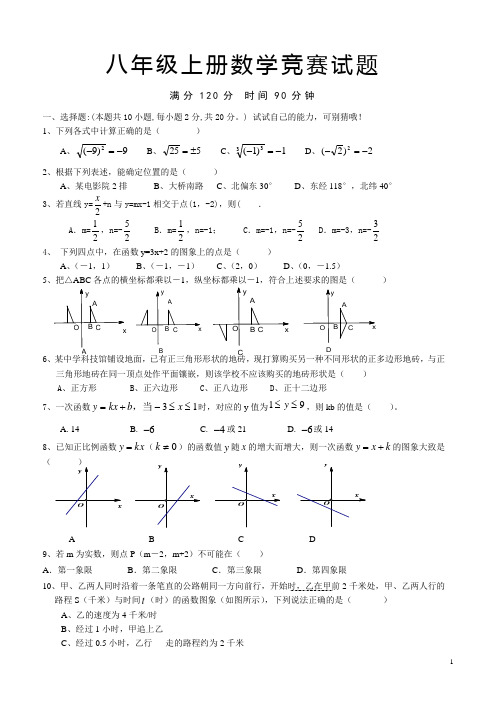
八年级上册数学竞赛试题满分120分 时间90分钟一、选择题:(本题共10小题,每小题2分,共20分。
) 试试自己的能力,可别猜哦! 1、下列各式中计算正确的是( )A 、9)9(2-=-B 、525±=C 、1)1(33-=-D 、2)2(2-=-2、根据下列表述,能确定位置的是( )A 、某电影院2排B 、大桥南路C 、北偏东30°D 、东经118°,北纬40°3、若直线y=2x+n 与y=mx-1相交于点(1,-2),则( . A .m=12,n=-52 B .m=12,n=-1; C .m=-1,n=-52 D .m=-3,n=-324、 下列四点中,在函数y=3x+2的图象上的点是( )A 、(-1,1)B 、(-1,-1)C 、(2,0)D 、(0,-1.5)5、把△ABC 各点的横坐标都乘以-1,纵坐标都乘以-1,符合上述要求的图是( )6、某中学科技馆铺设地面,已有正三角形形状的地砖,现打算购买另一种不同形状的正多边形地砖,与正三角形地砖在同一顶点处作平面镶嵌,则该学校不应该购买的地砖形状是( ) A 、正方形B 、正六边形C 、正八边形D 、正十二边形7、一次函数y kx b x =+-≤≤,当31时,对应的y 值为91≤≤y ,则kb 的值是( )。
A. 14B. -6C. -4或21D. -6或148、已知正比例函数kx y =(0≠k )的函数值y 随x 的增大而增大,则一次函数k x y +=的图象大致是( )A B C D 9、若m 为实数,则点P (m -2,m+2)不可能在( )A .第一象限B .第二象限C .第三象限D .第四象限10、甲、乙两人同时沿着一条笔直的公路朝同一方向前行,开始时,乙在甲前2千米处,甲、乙两人行的路程S (千米)与时间t (时)的函数图象(如图所示),下列说法正确的是( ) A 、乙的速度为4千米/时 B 、经过1小时,甲追上乙x yxy x y xyOO OO Dy x C B A O Cy x C B A O By x C B A O Ayx C B A OD 、经过1.5小时,乙在甲的前面二、填空题(每小题3分,共15分)11、若无理数a 满足14a <<,请你写出一个满足条件的无理数a :12、汽车开始行驶时,油箱中有油30升,如果每小时耗油4升,那么油箱中的剩余油量y(升)和工作时间x (时)之间的函数关系式是 ; 13、⎩⎨⎧==1,2y x 是方程2x -ay=5的一个解,则a = ; 14、已知直角三角形两边的长分别为3cm,4cm, 则以第三边为边长的正方形的面积为 。
初中数学八年级上数学竞赛试题含答案

初中数学八年级上数学竞赛试题含答案Newly compiled on November 23, 20200 1 2-1A 八年级(上)数学竞赛试题一、填空题:(40分)1、在ABC Rt ∆中,b a 、为直角边,c 为斜边,若14=+b a ,10=c ,则ABC ∆的面积是 ;2、计算:=⋅27 311 ;3 313÷⨯= ;2 3 2 +-= ; 3、某位老师在讲实数时,画了一个图(如图1),即以数轴的单位长线段为边作一个正方形,然后以0点为圆心,正方形的对角线长为半径画图,交x 轴于一点A ,作这样的图是用来说明 ;42,又出现了一个方格体正向下运动,为了使所有图案消失,你必须按 后 才能拼一个完整图案,从而使图案自动消失(游戏机有此功能)。
5、如图3,=∠+∠+∠+∠+∠+∠F E D C B A ;6、图4是一住宅小区的长方形花坛图样,阴影部分是草地,空地是四块同样的菱形,则草地与空地的面积之比为 ;(6)7、如图5,一块白色的正方形木板,边长是cm 18,上面横竖各有两根木条(阴影部分),宽都是cm 2,则白色部分面积是 2cm ;8、如图6,一块正方形地板由全等的正方形瓷砖铺成,这地板上的两条对角线上的瓷砖全是黑色,其余的瓷砖是白色的,如果有101块黑色瓷砖,那么瓷砖的总数是 ; 二、选择题:(30分)9、CD 是ABC Rt ∆斜边AB 上的高,若2=AB ,1:3:=BC AC ,则CD 为( )A 、51B 、52 C 、53D 、5410、如图,长方形ABCD 中,3=AB ,4=BC ,若将该矩形折叠,使C 点与A 点重合,则折痕EF 的长为( )A 、B 、3.75C 、D 、 11、如果a a -=-1 1 ,则a 的取值范围是( )A 、1=aB 、10<<aC 、0≥aD 、10≤≤a 12、若2 2 -+-x x 有意义,则x 的取值为( )A 、2>xB 、2<xC 、2≤xD 、2=x13、如上中图所示,一块边长为cm 10的正方形木板ABCD ,在水平桌面上绕点D 按顺时针方向转到D C B A ''''的位置时,顶点B 从开始到结束所经过的路径为( ) A 、cm 20 B 、cm 220 C 、cm 10π D 、cm 25π14、如上右图所示,设ABCD 边上任意一点,设CMB ∆的面积为2S ,CDM ∆的面积为S ,AMD ∆的面积为1S ,则有( )A 、21S S S +=B 、21S S S +> C 、21S S S +< D 、不能确定 三、画图题:(12分)15、如图,历史上最有名的军师诸葛亮,率精骑兵与司马懿对阵,诸葛亮一挥羽扇,军阵瞬时由左图变为右图,其实只移动了其中的3骑而己,请问如何移动(在图形上画出来即可)16、有一等腰梯形纸片,其上底和腰长都是a ,下底的长是a 2,你能将它剪成形状、大小完全一样的四块吗若能,请画出图形。
八年级上册数学奥林匹克竞赛题

八年级上册数学奥林匹克竞赛题1.八年级奥数题精选大全1、某厂向银行申请甲、乙两种贷款共40万元,每年需付利息5万元。
甲种贷款年利率为12%,乙种贷款年利率为14%。
该厂申请甲、乙两种贷款的金额各是多少?2、商店进了一批钢笔,用零售价10元卖出20支与用零售价11元卖出15支的利润相同。
这批钢笔的进货价每支多少元?3、某种蜜瓜大量上市,这几天的价格每天都是前一天的80%。
妈妈第一天买了2个,第二天买了3个,第三天买了5个,共花了38元。
若这10个蜜瓜都在第三天买,则能少花多少钱?4、商店以每双13元购进一批凉鞋,售价为14.8元,卖到还剩5双时,除去购进这批凉鞋的全部开销外还获利88元。
问:这批凉鞋共多少双?5、体育用品商店用3000元购进50个足球和40个篮球。
零售时足球加价9%,篮球加价11%,全部卖出后获利润298元。
问:每个足球和篮球的进价是多少元?6、甲、乙两个油桶各装了15千克油,售货员卖了14千克。
后来,售货员从剩下较多油的甲桶倒一部分给乙桶,使乙桶的油增加一倍;然后又从乙桶倒一部分给甲桶,使甲桶的油也增加一倍;这时甲桶的油恰好是乙桶油的3倍。
问售货员从两个油桶里各卖了多少千克油?2.八年级奥数题精选大全1.平整一块土地,原计划8人平整,每天工作7.5小时,6天可以完成任务。
由于急需播种,要求5天完成,并且增加1人。
问:每天要工作多少小时?2.妈妈买了2斤苹果,4斤菠萝,花去14元;爸爸买了3斤苹果,2斤菠萝,花去13元;那么1斤苹果,1斤菠萝各多少钱?3.修一段路计划16人20天完成,这16人工作了5天后,增加4人,如果这些人的工作效率相同,问提前几天完成修路任务?4.某饭店要安装空调240台,已知10名工程技术人员8小时能安装空调64台,现饭店要求安装公司在12小时内装完,需要增派同样工作效率的技术人员多少名?5.某工程原计划42人12天(每天按8小时工作)完成,工作7天后因支持其它紧急任务调走了12人,那么剩下的工作还要几天才能完成?若要求按原定日期完工,那么每天得工作多少小时?6.小强家住三层,从一层到三层需要走60秒钟,按此速度,从一层到六层需要多少秒钟?3.八年级奥数题精选大全1、小明放学回家,他沿一电车的路线步行,他发现每6分钟,有一辆电车迎面开来;每12分钟,有一辆电车从背后开来。
八年级(上)竞赛数学试题(含答案)

八年级竞赛数学试题及答案一、选择题:(每小题3分,本题满分共36分,)下列每小题中有四个备选答案,其中只有一个....是符合题意的,把正确答案前字母序号填在下面表格相应的题号下。
题号 1 2 3 4 5 6 7 8 9 10 11 12答案1.分式有意义,则x的取值范围是()A.x>1 B.x≠1 C.x<1 D.一切实数2.下列运算正确的是()A.3a+2a=5a2B.x2﹣4=(x+2)(x﹣2)C.(x+1)2=x2+1 D.(2a)3=6a33.把x3﹣2x2y+xy2分解因式,结果正确的是( )A.x(x+y)(x﹣y)B.x(x2﹣2xy+y2)C.x(x+y)2D.x(x﹣y)2 4.如图,将等腰直角三角形沿虚线裁去顶角后,∠ 1+∠ 2=()A.225°B.235°C.270°D.300°5.如图,△ABC和△DEF中,AC=DE,∠B=∠DEF,添加下列哪一个条件无法证明△ABC≌△DEF( )A.AC∥DF B.∠A=∠D C.AB=DE D.∠ACB=∠F 6.如图,在△ABC中,∠A=50°,∠ABC=70°,BD平分∠ABC,则∠BDC的度数是( )A.85°B.80°C.75°D.70°7.如图,小敏做了一个角平分仪ABCD,其中AB=AD,BC=D C.将仪器上的点A与∠PRQ 的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过点A,C画一条射线AE,AE就是∠PRQ的平分线.此角平分仪的画图原理是:根据仪器结构,可得△ABC≌△ADC,这样就有∠QAE=∠P AE.则说明这两个三角形全等的依据是( ) A.SAS B.ASA C.AAS D.SSS8.若3x=4,9y=7,则3x﹣2y的值为( )A.B.C.﹣3 D.9.如图,在方格纸中,以AB为一边作△ABP,使之与△ABC全等,从P1,P2,P3,P4四个点中找出符合条件的点P,则点P有( )A.1个B.2个C.3个D.4个10.如图,在△ABC中,AD是角平分线,DE⊥AB于点E,△ABC的面积为7,AB=4,DE=2,则AC的长是()A.4 B.3 C.6 D.511.如图,平面直角坐标系中,已知定点A(1,0)和B(0,1),若动点C在x轴上运动,则使△ABC为等腰三角形的点C有( )个A. 5B. 4C. 3D. 212、.当x=1时,ax+b+1的值为﹣2,则(a+b﹣1)(1﹣a﹣b)的值为()A.﹣16 B.﹣8 C.8D.16二、填空(每题4分,共32分)13. 如图,直线a ∥b ,一块含60°角的直角三角板ABC (∠A =60°)按如图所示放置.若∠1=55°,则∠2的度数为 .14.如图,△ABC 中,∠C =90°,∠BAC =60°,AD 是角平分线,若BD =8,则CD 等于 .15.分解因式:﹣x 2+4xy ﹣4y 2= .16.若9x 2﹣kxy +4y 2是一个完全平方式,则k 的值是 . 17.一个多边形的内角和是它的外角和的4倍,这个多边形是 边形. 18.已知x 为正整数,当时x = 时,分式的值为负整数.19. 已知1024x y xy +==,,则()2x y -的值是 .20.比较255,344,433,522的大小,用“<”号连接为: 三、解答下列各题(满分52分)21.(每小题4分,本题满分8分)分解因式: (1)3x 2﹣12x +12 (2)ax 2﹣4a .22. (每小题5分,本题满分15分)计算与化简 (1)(3-x )(3+x )+(1+x )2,(2)(﹣)÷.(3)÷23. (本题满分8分)如图,△ACB和△ECD都是等边三角形,点A、D、E在同一直线上,连接BE.(1)求证:△ACD≌△BCE;(2)若CE=16,BE=21,求AE的长.24.(本题满分10分)如图,AD为△ABC的角平分线,DE⊥AB于点E,DF⊥AC于点F,连接EF交AD 于点G.(1)求证:AD垂直平分EF;(2)若∠BAC=60°,猜测DG与AG间有何数量关系?请说明理由.25. (本题满分5分)阅读材料:若m2﹣2mn+2n2﹣8n+16=0,求m、n的值.解:∵m2﹣2mn+2n2﹣8n+16=0,∴(m2﹣2mn+n2)+(n2﹣8n+16)=0∴(m﹣n)2+(n﹣4)2=0,∴(m﹣n)2=0,(n﹣4)2=0,∴n=4,m=4.根据你的观察,探究下面的问题:已知x2﹣2xy+2y2+6y+9=0,求xy的值;26. (本题满分6分).我们在学习完全平方公式(a+b)2=a2+2ab+b2时,了解了一下它的几何背景,即通过图来说明上式成立.在习题中我们又遇到了题目“计算:(a+b+c)2”,你能将知识进行迁移,从几何背景说明(大致画出图形即可)并计算(a+b+c)2吗?八年级数学试题参考答案及评分标准(这里只提供了一种解法或证法,其他证法,只要合理,照常得分)一、1-12,BBDCC A DACB BA二、13.115°14.4 15. ﹣(x﹣2y)2.16、±12.17、十.18、3,4,5,8;19、4;20、522<255<433<344三、解答题.21、(1)解:原式=3(x2﹣4x+4)--------------------2分=3(x﹣2)2,-------------4分(2)解:ax2﹣4a=a(x2﹣4)--------------------------2分=a(x﹣2)(x+2).-----------------------4分22、(1)解:原式=9-x2+1+2x+x2 -------------------3分=2x+10 ---------------------------5分(2)解:原式=•--------------------3分=•---------------------------4分=,------------------------------5分(3)解:÷=--------------------3分=----------------------------5分23、(1)证明:∵△ACB和△ECD都是等边三角形,∴AC=BC,CD=CE,∠ACB=∠DCE=60°,----------------1分∵∠ACD=∠ACB﹣∠DCB,∠BCE=∠DCE﹣∠DCB,∴∠ACD=∠BCE,--------------------2分在△ACD和△BCE中,,∴△ACD≌△BCE(SAS);----------------------5分(2)∵△ACD≌△BCE,∴AD=BE=21,----------------6分∵△ECD是等边三角形,∴DE=CE=16,----------------------------7分∴AE=AD+DE=21+16=37.--------------------------8分24、(1)证明:∵ A D为△ABC的角平分线,DE⊥AB,DF⊥AC,∴DE=DF,∠AED=∠AFD=90°,---------1分∴∠DEF=∠DFE,∴∠AEF=∠AFE,∴AE=AF------------------------------------3分∴点A、D都在EF的垂直平分线上,∴AD垂直平分EF.--------------------------------5分(2)答:AG=3DG.-----------------------6分理由:∵∠BAC=60°,AD平分∠BAC,∴∠EAD=30°,∴AD=2DE,∠EDA=60°,-------------7分∵AD⊥EF,∴∠EGD=90°,∴∠DEG=30°--------------8分∴DE=2DG,∴AD=4DG,∴AG=3DG.---------------------------------10分25解:∵x2﹣2xy+2y2+6y+9=0,∴(x2﹣2xy+y2)+(y2+6y+9)=0,---------------------2分∴(x﹣y)2+(y+3)2=0,∴x﹣y=0,y+3=0,∴x=﹣3,y=﹣3,---------------------------------4分∴xy=(﹣3)×(﹣3)=9,即xy的值是9.--------------------------------5分26.解:(a+b+c)2的几何背景如图,-----------------------3分整体的面积为:(a+b+c)2,用各部分的面积之和表示为:(a+b+c)2=a2+b2+c2+2ab+2ac+2bc,所以(a+b+c)2=a2+b2+c2+2ab+2ac+2bc.-----------------------6分。
初二数学上册竞赛试题
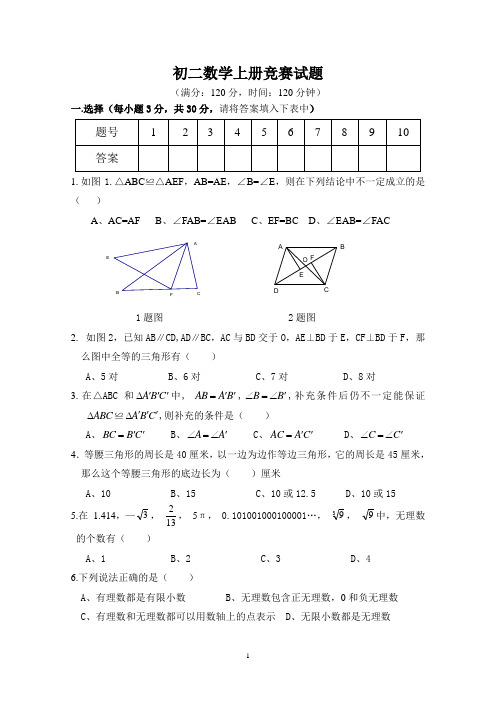
O F EDCBA初二数学上册竞赛试题(满分:120分,时间:120分钟)一.选择(每小题3分,共30分,请将答案填入下表中)1.如图1.△ABC ≌△AEF ,AB=AE ,∠B=∠E ,则在下列结论中不一定成立的是( )A 、AC=AFB 、∠FAB=∠EABC 、EF=BCD 、∠EAB=∠FAC1题图 2题图2. 如图2,已知AB ∥CD,AD ∥BC ,AC 与BD 交于O ,AE ⊥BD 于E ,CF ⊥BD 于F ,那么图中全等的三角形有( )A 、5对B 、6对C 、7对D 、8对3.在△ABC 和A B C '''∆中, AB A B ''=,B B '∠=∠,补充条件后仍不一定能保证A B C∆≌A B C '''∆,则补充的条件是( )A 、BC B C ''= B 、A A '∠=∠ C 、A C A C ''=D 、C C '∠=∠ 4.等腰三角形的周长是40厘米,以一边为边作等边三角形,它的周长是45厘米,那么这个等腰三角形的底边长为( )厘米A 、10B 、15C 、10或12.5D 、10或15 5.在 1.414,—3, 132, 5π, 0.101001000100001…, 39, 9中,无理数的个数有( )A 、1B 、2C 、3D 、4 6.下列说法正确的是( )A 、有理数都是有限小数B 、无理数包含正无理数,0和负无理数C 、有理数和无理数都可以用数轴上的点表示D 、无限小数都是无理数FECBA7.已知一次函数y=kx+k,且y 随x 的增大而减小,则该函数的图像经过( ) A 、第一、二、三象限 B 、第一、二、四象限C 、第二、三、四象限D 、第一、三、四象限8.已知正比例函数y=(2m -1)x 的图像上有两点A (x 1,y 1),B (x 2,y 2),当x 1<x 2时,有y 1>y 2,那么m 的取值范围是( ) A 、m <2B 、m >2C 、m <21 D 、m >21 9.下列四个图是函数y=kx+b 的图像,已知k ·b >0,其中正确的是( )A 、B 、C 、D 、10.某班同学在探究弹簧的长度与外力的变化关系时,实验得到相应数据如下表:则y 与x 的函数图像是( )A 、B 、 C、 D 、二.填空(每小题3分,共24分)11.△ABC 和△A ′B ′C ′,已知AB=A ′B ′,BC=B ′C ′,•则增加条件___________(只填一个),使△ABC ≌△A ′B ′C ′。
初中数学八年级(上)数学竞赛试题(含答案)

1 2-1A 八年级〔上〕数学竞赛试题一、填空题:〔40分〕1、在ABC Rt ∆中,b a 、为直角边,c 为斜边,若14=+b a ,10=c ,则ABC ∆的面积是;2、计算:=⋅27 311 ;3 313÷⨯=;2 3 2 +-=;3、某位老师在讲实数时,画了一个图〔如图1〕,即以数轴的单位长线段为边作一个正方形,然后以0点为圆心,正方形的对角线长为半径画图,交x 轴于一点A ,作这样的图是用来说明;〔1〕4、在电子游戏中有一种方格拼图游戏,若在游戏过程中,已拼好的图案如图2,又出现了一个方格体正向下运动,为了使所有图案消失,你必须按后才能拼一个完整图案,从而使图案自动消失〔游戏机有此功能〕。
5、如图3,=∠+∠+∠+∠+∠+∠F E D C B A ;6、图4是一住宅小区的长方形花坛图样,阴影部分是草地,空地是四块同样的菱形,则草地与空地的面积之比为;<4> <5> <6>7、如图5,一块白色的正方形木板,边长是cm 18,上面横竖各有两根木条〔阴影部分〕,宽都是cm 2,则白色部分面积是2cm ;8、如图6,一块正方形地板由全等的正方形瓷砖铺成,这地板上的两条对角线上的瓷砖全是黑色,其余的瓷砖是白色的,如果有101块黑色瓷砖,则瓷砖的总数是; 二、选择题:〔30分〕9、CD 是ABC Rt ∆斜边AB 上的高,若2=AB ,1:3:=BC AC ,则CD 为〔 〕A 、51B 、52 C 、53 D 、5410、如图,长方形ABCD 中,3=AB ,4=BC ,若将该矩形折叠,使C 点与A 点重合,则折痕EF 的长为〔 〕A 、3.74B 、3.75 C 、3.76 D 、3.77DFD)(A '11、如果a a -=-1 1 ,则a 的取值范围是〔 〕A 、1=aB 、10<<aC 、0≥aD 、10≤≤a 12、若2 2 -+-x x 有意义,则x 的取值为〔 〕A 、2>xB 、2<xC 、2≤xD 、2=x13、如上中图所示,一块边长为cm 10的正方形木板ABCD ,在水平桌面上绕点D 按顺时针方向转到D C B A ''''的位置时,顶点B 从开始到结束所经过的路径为〔 〕A 、cm 20B 、cm 220C 、cm 10πD 、cm 25π14、如上右图所示,设M 是边上任意一点,设CMB ∆的面积为2S ,CDM ∆的面积为S ,AMD ∆的面积为1S ,则有〔 〕A 、21S S S +=B 、21S S S +>C 、21S S S +<D 、不能确定 三、画图题:〔12分〕15、如图,历史上最有名的军师诸葛亮,率精骑兵与司马懿对阵,诸葛亮一挥羽扇,军阵瞬时由左图变为右图,其实只移动了其中的3骑而己,请问如何移动?〔在图形上画出来即可〕16、有一等腰梯形纸片,其上底和腰长都是a ,下底的长是a 2,你能将它剪成形状、大小完全一样的四块吗?若能,请画出图形。
人教版 八年级数学上册 竞赛专题:整式的乘除(含答案)

人教版 八年级数学上册 竞赛专题:整式的乘除(含答案)【例1】(1)若n 为不等式2003006n>的解,则n 的最小正整数的值为 .(2)已知21x x +=,那么432222019x x x x +--+= .(3)把26(1)x x -+展开后得121121211210a x a x a x a x a +++++,则121086420a a a a a a a ++++++= .(4)若543237629()()()()()x x x x x x a x b x c x d x e -+-++=-----则ab ac ad ae bc bd be cd ce de +++++++++= .解题思路:对于(1),从幂的乘方逆用入手;对于(2),目前无法求x 值,可考虑高次多项式用低次多项式表示;对于(3),它是一个恒等式,即在x 允许取值范围内取任何一个值代入计算,故可考虑赋值法;对于(4),可考虑比较系数法.【例2】已知252019x=,802019y=,则11x y+等于( ) A .2 B .1 C .12D .32解题思路:,x y 为指数,我们无法求出,x y 的值,而11x y x y xy++=,所以只需求出,x y xy +的值或它们的关系,于是自然想到指数运算律.【例3】设,,,a b c d 都是正整数,并且5432,,19a b c d c a ==-=,求d b -的值.(江苏省竞赛试题) 解题思路:设5420326,a b m c d n ====,这样,a b 可用m 的式子表示,,c d 可用n 的式子表示,通过减少字母个数降低问题的难度.【例4】已知多项式2223286(2)(2)x xy y x y x y m x y n +--+-=++-+,求3211m n +-的值.解题思路:等号左右两边的式子是恒等的,它们的对应系数对应相等,从而可考虑用比较系数法.【例5】是否存在常数,p q 使得42x px q ++能被225x x ++整除?如果存在,求出,p q 的值,否则请说明理由.解题思路:由条件可推知商式是一个二次三项式(含待定系数),根据“被除式=除式×商式”,运用待定系数法求出,p q 的值,所谓,p q 是否存在,其实就是关于待定系数的方程组是否有解.【例6】已知多项式432237x x ax x b -+++能被22x x +-整除,求ab的值. (北京市竞赛试题) 解题思路:本题主要考查了待定系数法在因式分解中的应用.本题关键是能够通过分析得出当2x =-和1x =时,原多项式的值均为0,从而求出,a b 的值.当然本题也有其他解法.能力训练A 级1.(1)24234(0.25)1⨯--= . (2)若23n a=,则621n a -= .2.若2530x y +-=,则432xy. 3.满足200300(1)3x ->的x 的最小正整数为 .4.,,,a b c d 都是正数,且23452,3,4,5a b c d ====,则,,,a b c d 中,最大的一个是 . 5.探索规律:133=,个位数是3;239=,个位数是9;3327=,个位数是7;4381=,个位数是1;53243=,个位数是3;63729=,个位数是9;…那么73的个位数字是 ,303的个位数字是 . 6.已知31416181,27,9a b c ===,则,,a b c 的大小关系是( ) A .a b c >>B .a c b >>C .a b c <<D .b c a >>7.已知554433222,3,5,6a b c d ====,那么,,,a b c d 从小到大的顺序是( ) A .a b c d <<< B .a b d c <<< C .b a c d <<< D .a d b c <<<8.若11222,22n n n n x y +--=+=+,其中n 为整数,则x 与y 的数量关系为( )A .4x y =B .4y x =C .12x y =D .12y x =9.已知23,26,212,abc===则,,a b c 的关系是( ) A .2b a c <+B .2b a c =+C .2b a c >+D .a b c +>10.化简4322(2)2(2)n n n ++-得( ) A .1128n +- B .12n +-C .78D .7411.已知2233447,49,133,406ax by ax by ax by ax by +=+=+=+=, 试求171995()6()2x y xy a b ++-+的值.12.已知2267314(23)(3)x xy y x y a x y b x y c --+++=-+++.试确定,,a b c 的值.13.已知323x kx ++除以3x +,其余数较被1x +除所得的余数少2,求k 的值.B 级1.已知23,45,87,abc===则28a c b+-= .2.(1)计算:2019201920192019201973153735+⎛⎫⨯ ⎪+⎝⎭= . (2)如果5555555555555554444666666233322n ++++++++⨯=+++,那么n = . 3.(1)1615与1333的大小关系是1615 1333(填“>”“<”“=”).(2)201920193131++与201920203131++的大小关系是:201920193131++ 201920203131++(填“>”“<”“=”).4.如果210,x x +-=则3223x x ++= .5.已知55432(2)x ax bx cx dx ex f +=+++++,则164b d f ++= . 6.已知,,a b c 均为不等于1的正数,且236,a b c -==则abc 的值为( )A .3B .2C .1D .127.若3210x x x +++=,则27261226271x x x x x x x ---+++++++++的值是( )A .1B .0C .—1D .28.如果328x ax bx +++有两个因式1x +和2x +,则a b +=( ) A .7B .8C .15D .219.已知12320182019,,,,a a a a a 均为正数,又122018232019()()M a a a a a a =++++++,122019232020()()N a a a a a a =++++++,则M 与N 的大小关系是( )A .M N =B .M N <C .M N >D .关系不确定10.满足22(1)1n n n +--=的整数n 有( )个A .1B .2C .3D .411.设,,,a b x y 满足2233443,7,16,42,ax by ax by ax by ax by +=+=+=+=求55ax by +的值.12.若,,,x y z w 为整数,且x y z w >>>,52222208xyzw+++=,求2020(1)x y z w +++-的值.13.已知,,a b c 为有理数,且多项式32x ax bx c +++能够被234x x +-整除. (1)求4a c +的值; (2)求22a b c --的值;(3)若,,a b c 为整数,且1c a >≥.试比较,,a b c 的大小.参考答案例1(1)(n 2)100>(63)100,n 2 >216,n 的最小值为15.(2)原式=x 2(x 2+x )+x (x 2 +x )-2(x 2+x ) +2019= x 2+x -2+2019=2018 (3)令x =1时,a 12+a 11+a 10+…+a 2+a 1+a 0=1, ① 令x =-1时,a 12 –a 11+a l 0-…+n 2-a l +a 0 =729 ② 由①+②得:2(a 12+a l 0+a 8+…+a 2 +a 0)=730. ∴a 12 +a 10 +a 8 +a 6+a 4 +a 2+a 0 =365. (4)所有式子的值为x 3项的系数,故其值为7. 例2 B 提示:25xy =2 019y , ① 80xy =2 019x , ②①×②,得:(25×80)xy =2019x +y ,得:x + y =xy .例3 设a =m 4,b =m 5,c =n 2,d =n 3,由c -a =19得,n 2-m 4=19,即(n +m 2) (n -m 2)=19,因19是质数,n +m 2,n -m 2是自然数,且n +m 2>n -m 2,得⎩⎪⎨⎪⎧n +m 2=19n -m 2=1,解得n =10,m =3,所以d -b =103-35 =757例4 -78提示:由题意知:2x 2+3xy -2y 2-x +8y -6=2x 2+3xy -2y 2+(2m +n )x +(2n -m )y +mn .∴⎩⎪⎨⎪⎧2m +n =-12n -m =8mn =-6,解得⎩⎨⎧m =-2n =3,∴m 3+1n 2-1 =-78倒5提示:假设存在满足题设条件的p ,q 值,设(x 4+px 2+q )=(x 2+2x +5)(x 2+mx +n ),即 x 4+px 2+q =x 4+(m +2)x 3+(5+n +2m )x 2+(2n +5m )x +5n ,得⎩⎨⎧m +2=05+n +2m =p 2n +5m =05n =q ,解得⎩⎨⎧m =-2n =5p =6q =25,故存在常数p ,q 且p =6,q =25,使得x 4+px 2+q 能被x 2+2x +5整除.例6解法1 ∵x 2+x -2=(x +2) (x -1),∴2x 4-3x 3+ax 2+7x +b 能被(x +2)(x -1)整除,设商是A . 则2x 4-3x 3+ax 2+7x +b =A (x +2)(x -l ),则x =-2和x =1时,右边都等于0,所以左边也等于0.当x =-2时,2x 4-3x 3+ax 2+7x +b =32+24+4a -14+b =4a +b +42=0, ① 当x =1时, 2x 4-3x 3+ax 2+7x +b =2-3+a +7+b =a +b +6=0. ② ①-②,得3a +36=0,∴ a =-12, ∴ b =-6-a =6. ∴a b =-126=-2 解法2 列竖式演算,根据整除的意义解2243243232322225(9)22372245(4)75510(9)3(9)(9)2(9)(12)2(9)x x a x x x x ax x bx x x x a x x b x xx a x x ba x a x a a xb a -+++--++++--++++--++-++-+-+--+++∵2x 4-3x 3+ax 2+7x +b 能被x 2+x -2整除,∴⎩⎨⎧-12-a =0b +2(a +9)=0,即⎩⎨⎧a =-12b =6,∴a b =-2A 级1.(1) -5 (2)53 2.8 3.7 4.6 5.7 9 6.A 7.D 提示:a =(25)11,b -(34)11,c =(53)11,d =(62)11 8.A 9.B 10.C 11.4800 12.a =4.b =4,c =113. 提示:令x 3 +kx 2+3=(x +3) (x 2+ax +6)+r 1,x 3+kx 2+3=( x +1) (x 2+cx +d )+r 2,令x =-3,得r 1=9k -24.令x =-1,得r 2=k +2,由9k -24+2=k +2, 得k =3.B 级1.1891252. (1)949(2)123.(1) < 1516 <1615=264,3 313 >3213=265 >264. (2) > 提示:设32 000 =x .4.4 5.512 提示:令x =±2. 6.C 提示:由条件得a =c -3 ,b =c 2 ,abc =c -3·c 2·c =1 7.C 8.D 9.C 10.D11.由ax 2+by 2 =7,得(ax 2+by 2)(x +y )=7(x +y ),即ax 3-ax 2y +bxy 2+by 3 =7(x +y ),(ax 3+by 3)-xy (ax +by )-7(x +y ). ∴16+3xy = 7(x +y ). ①由ax 3 +by 3=16,得(ax 3+by 3)(x +y ) =16(x +y ),即ax 4 +ax 3 y +bxy 3+by 4 =16(x +y ),(ax 4+by 4)+xy (a 2x +b 2y )=16(x +y ). ∴42+7xy =16(x +y ). ② 由①②可得,x +y =-14,xy =-38.由a 2x +b 2y =42,得(a 4x +b 4y )(x +y )=42×(-14), (a 5x +b 5y )+xy (a 3x +b 3y )=-588,55ax by ++16×(-38)=-588.故55ax by +=20. 12. ()20191x y z w +++-=()201942131+---=1.13.(1)∵(x -1)(x +4)=2x +3x -4, 令x -1=0,得x =1;令x +4=0,得x =-4. 当x =1时,得1+a +b +c =0; ① 当x =-4时,得-64+16a -4b +c =0. ② ②-①,得15a -5b =65,即3a -b =13. ③ ①+③,得4a +c =12.(2)③-①,得2a -2b -c =14.(3)∵c ≥a >1,4a +c =12,a ,b ,c 为整数, ∴1<a ≤125,则a =2,c =4. 又a +b +c =-1,∴b =-7,.∴c >a >b .。
初二上数学竞赛试题及答案

初二上数学竞赛试题及答案一、选择题(每题3分,共30分)1. 下列哪个数是最小的正整数?A. 0B. 1C. -1D. 22. 如果一个数的平方等于9,那么这个数是多少?A. 3B. -3C. ±3D. 93. 一个直角三角形的两条直角边分别为3和4,斜边的长度是多少?A. 5B. 6C. 7D. 84. 一个数的绝对值是5,这个数可以是?A. 5B. -5C. ±5D. 05. 以下哪个是合数?A. 2B. 3C. 4D. 56. 一个数的立方等于-8,这个数是多少?A. -2B. 2C. -8D. 87. 一个数除以2余1,除以3余2,这个数最小是多少?A. 5B. 7C. 8D. 98. 一个圆的半径是5,那么它的面积是多少?A. 25πB. 50πC. 75πD. 100π9. 一个数的平方根是4,这个数是多少?A. 16B. -16C. ±4D. ±1610. 以下哪个是偶数?A. 1B. 2C. 3D. 5答案:1-5 B C A C B;6-10 A B B D B二、填空题(每题2分,共20分)1. 一个数的平方是16,这个数是______。
2. 如果一个数的绝对值是4,那么这个数可以是______或______。
3. 一个数的立方是27,这个数是______。
4. 一个数的倒数是1/2,这个数是______。
5. 一个数的平方根是2,这个数是______。
6. 如果一个数除以4余3,那么这个数可以是______(答案不唯一)。
7. 一个数的平方是25,这个数是______或______。
8. 一个数的立方根是3,这个数是______。
9. 一个数的平方根是-3,这个数是______。
10. 如果一个数的绝对值是3,那么这个数可以是______或______。
答案:1. ±4 2. 4, -4 3. 3 4. 2 5. 4 6. 7(答案不唯一) 7.±5 8. 27 9. 无实数解 10. 3, -3三、计算题(每题10分,共40分)1. 计算下列表达式的值:(2+3)² - 4×5 + 6。
初中八年级上册数学竞赛试题.doc

墨希(A) AD//BC (B) 最新初中八年级上册数学竞赛试题一、填空题(每题4分)1、篆刻是中国独特的传统艺术,篆刻出来的艺术品叫印章.印章的文字刻成凸状的称为“阳文",刻成 凹状的称为“阴文如图1的“希望''即为阳文印章在纸上盖出的效果,此印章是下列选项中的(阴 影表示印章中的实体部分,白色表示印章中的镂空部分)()2、若线段MN // y 轴,点A (3,2)是线段奶 的中点,且MN=4,则M 点的坐标是( )A. (3,2)B. (-3,2)C. (3,4)或(3,0)D. (5,2)或(1,2) 3、一次函数y = kx+b 的图象经过点(0, 5)和点B (4, 0),则在该图象和坐标轴围成的三角形内,横坐标和纵坐标都是正整数的点有()A 、6 个B 、7 个C 、8 个 ,D 、9 个4、如图,在平面直角坐标系中,线段AB 的端点坐标为A (-2,4),3(4,2),直线y = kx -2与线段AB 有交点,则*的值不可能是(). A. 3 B. 5 C. -5 D. -2 5、如图(七),将某四边形纸片菌CZ )的AB 向BC 方向折过去(其中AB<BC ),使得A 点落在BC ±, 展开,后出现折线BD,如图(A )o 将B 点折向O,使得B 、。
两点重迭,如图(九),.展开后出现折线 CE,如图(十)。
根据图(十),判断下列关系何者正确? ( .)(C) ZADB=ZBDC (D) ZADB>ZBDC6、如图,ZBAC 与ZCBE 的平分线相交于点P, BE=BC, PB 与CE 交于点H, PG 〃AD 交BC 于时在x 轴上找一点D,F,.交 AB 于 G,下列结论:①GA=GP;② S — ■ S PAB = AC : AB ■, ®BP 垂直平分 CE; @FP=FC; 其中正确的判断有() A.只有①②③B.只有②③④C.只有①③④D.①②③④7、7条长度均为整数厘米的线段:ai ,<23, at ,a 5, aj,满足ai<a2<a 3<a4<a 5<a 6<a 7,且这7条线段中的任意3条都不能构成三角形.若a\=\厘米,您=2 厘米,则的的最小值为() (A )21厘米 (B )18厘米 (C )15厘米 (D )12厘米8. 如图 1 在ZS.ABC 中,AB=BC=CA,且AD=BE=CF,但D, E, F 不是AB, BC, CA 的中点.又 AE, BF, CD 分别交于M, N, P,如果把找出的三个全等三角形叫做一组全等三角联,那么从图中能找出全等三角形( )A. 4组B. 5组.C. 6组D. 7组。
八年级数学上学期竞赛试题含解析试题

分宜中学2021-2021学年八年级数学上学期竞赛试题创作人:历恰面日期:2020年1月1日一、选择题〔一共10小题,每一小题3分,一共30分〕1.三角形三边长为a、b、c,且满足a2﹣4b=7,b2﹣4c=﹣6,c2﹣6a=﹣18,那么此三角形的形状是〔〕A.等腰三角形B.等边三角形C.直角三角形D.无法确定2.在平面直角坐标系中,点A〔m,3〕与点B〔4,n〕关于y轴对称,那么〔m+n〕2021的值是〔〕A.﹣1 B.1 C.﹣72021D.720213.,那么=〔〕A.1 B.﹣1 C.2 D.﹣24.如图,∠DAE=∠ADE=15°,DE∥AB,DF⊥AB,假设AE=8,那么DF等于〔〕A.5 B.4 C.3 D.25.如图,等边△ABC的边长为4,AD是BC边上的中线,F是AD边上的动点,E是AC边上一点,假设AE=2,当EF+CF获得最小值时,那么∠ECF的度数为〔〕A.15° B.22.5°C.30° D.45°6.假设m+n﹣p=0,那么的值是〔〕A.﹣3 B.﹣1 C.1 D.37.如图,M是线段AD、CD的垂直平分线交点,AB⊥BC,∠D=65°,那么∠MAB+∠MCB的大小是〔〕A.120°B.130°C.140°D.160°8.如图,在等边△ABC中,AC=9,点O在AC上,且AO=3,点P是AB上一动点,连接OP,以O为圆心,OP长为半径画弧交BC于点D,连接PD,假如PO=PD,那么AP的长是〔〕A.5 B.8 C.7 D.69.如图,过边长为1的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,当PA=CQ时,连PQ交AC边于D,那么DE的长为〔〕A.B.C.D.不能确定10.如图,AB=4,射线BM和AB互相垂直,点D是AB上的一个动点,点E在射线BM上,2BE=DB,作EF⊥DE并截取EF=DE,连结AF并延长交射线BM于点C.设BE=x,BC=y,那么y关于x 的函数解析式是〔〕A.y=﹣B.y=﹣C.y=﹣D.y=﹣二、填空题〔本大题一一共6个小题,每一小题3分,一共18分〕11.〔3分〕如图,△ABC中,BD平分∠ABC,BC的中垂线交BC于点E,交BD于点F,连接CF.假设∠A=60°,∠ABD=24°,那么∠ACF= .12.等腰三角形一边长为3cm,周长7cm,那么腰长是.13.如图,在△ABC中,AH⊥BC于H,∠C=35°,且AB+BH=HC,那么∠B度数为.14.10x=m,10y=n,那么102x+3y等于.15.a﹣b=b﹣c=,a2+b2+c2=1,那么ab+bc+ca的值等于.16.如图,∠AOB=30°,点P为∠AOB内一点,OP=8.点M、N分别在OA、OB上,那么△PMN 周长的最小值为.三、解答题〔一共8题,一共72分〕17.〔8分〕先化简,再求值:,其中x是的整数局部.18.如下图,点D为等边△ABC的AC边上的一点,∠1=∠2,BD=CE.求证:△DAE是等边三角形.19.〔8分〕如图,△ABC为等边三角形,D在BC的延长线上,∠ADE=60°,∠ACD的平分线交DE于E,求证:AD=DE.20.〔8分〕如图,AB=AC,∠BAC=60°,∠BDC=120°,求证:AD=BD+CD.21.如图,在等边三角形△ABC中,AE=CD,AD、BE交于P点,BQ⊥AD于Q,〔1〕求证:BP=2PQ;〔2〕连PC,假设BP⊥PC,求的值.22.在△ABC中,AD平分∠BAC交BC于D.〔1〕如图1,∠MDN的两边分别与AB、AC相交于M、N两点,过D作DF⊥AC于F,DM=DN,证明:AM+AN=2AF;〔2〕如图2,假设∠C=90°,∠BAC=60°,AC=9,∠MDN=120°,ND∥AB,求四边形AMDN 的周长.23.如图1,在平面直角坐标系中,点A、B分别在x轴、y轴上.〔1〕如图1,点A与点C关于y轴对称,点E、F分别是线段AC、AB上的点〔点E不与点A、C重合〕,且∠BEF=∠BAO.假设∠BAO=2∠OBE,求证:AF=CE;〔2〕如图2,假设OA=OB,在点A处有一等腰△AMN绕点A旋转,且AM=MN,∠AMN=90°.连接BN,点P为BN的中点,试猜测OP和MP的数量关系和位置关系,说明理由.24.如图,在平面直角坐标系中,A〔0,a〕、B〔﹣b,0〕且a、b满足+|a﹣2b+2|=0.〔1〕求证:∠OAB=∠OBA;〔2〕如图1,假设BE⊥AE,求∠AEO的度数;〔3〕如图2,假设D是AO的中点,DE∥BO,F在AB的延长线上,∠EOF=45°,连接EF,试探究OE和EF的数量和位置关系.2021-2021学年分宜中学八年级〔上〕竞赛数学试卷参考答案与试题解析一、选择题〔一共10小题,每一小题3分,一共30分〕1.三角形三边长为a、b、c,且满足a2﹣4b=7,b2﹣4c=﹣6,c2﹣6a=﹣18,那么此三角形的形状是〔〕A.等腰三角形B.等边三角形C.直角三角形D.无法确定【考点】因式分解的应用.【分析】将a2﹣4b=7,b2﹣4c=﹣6,c2﹣6a=﹣18相加后利用因式分解分别求得a、b、c的值即可.【解答】解:∵a2﹣4b=7,b2﹣4c=﹣6,c2﹣6a=﹣18,∴a2﹣4b+b2﹣4c+c2﹣6a=7﹣6﹣18,整理得:a2﹣6a+9+b2﹣4b+4+c2﹣4c+4=0,因式分解得:〔a﹣3〕2+〔b﹣2〕2+〔c﹣2〕2=0,解得:a=3,b=2,c=2.∴此三角形为等腰三角形.【点评】此题考察了实数的运算及因式分解的应用,解题的关键是正确的进展因式分解.2.在平面直角坐标系中,点A〔m,3〕与点B〔4,n〕关于y轴对称,那么〔m+n〕2021的值是〔〕A.﹣1 B.1 C.﹣72021D.72021【考点】关于x轴、y轴对称的点的坐标.【分析】根据关于y轴对称的点,纵坐标一样,横坐标互为相反数,可得答案.【解答】解:由点A〔m,3〕与点B〔4,n〕关于y轴对称,得n=3,m=﹣4.〔m+n〕2021=〔3﹣4〕2021=﹣1,应选:A.【点评】此题考察了关于y轴对称的点的坐标,解决此题的关键是掌握好对称点的坐标规律:〔1〕关于x轴对称的点,横坐标一样,纵坐标互为相反数;〔2〕关于y轴对称的点,纵坐标一样,横坐标互为相反数;〔3〕关于原点对称的点,横坐标与纵坐标都互为相反数.3.,那么=〔〕A.1 B.﹣1 C.2 D.﹣2【考点】分式的化简求值.【专题】计算题.【分析】等式左边通分并利用同分母分式的加法法那么计算,整理得到关系式,所求式子通分并利用同分母分式的加法法那么变形,将得出的关系式代入计算即可求出值.【解答】解:∵+==,∴〔p+q〕2=pq,那么+====﹣1.应选B.【点评】此题考察了分式的化简求值,分式的加减运算关键是通分,通分的关键是找最简公分母.4.如图,∠DAE=∠ADE=15°,DE∥AB,DF⊥AB,假设AE=8,那么DF等于〔〕A.5 B.4 C.3 D.2【考点】三角形的外角性质;角平分线的性质;直角三角形斜边上的中线.【分析】过D作DG⊥AC于G,根据三角形的一个外角等于和它不相邻的两个内角的和求出∠DEG=30°,再根据直角三角形30°角所对的直角边等于斜边的一半求出DG的长度是4,又DE∥AB,所以∠BAD=∠ADE,所以AD是∠BAC的平分线,根据角平分线上的点到角的两边的间隔相等,得DF=DG.【解答】解:如图,∵∠DAE=∠ADE=15°,∴∠DEG=∠DAE+∠ADE=15°+15°=30°,DE=AE=8,过D作DG⊥AC于G,那么DG=DE=×8=4,∵DE∥AB,∴∠BAD=∠ADE,∴∠BAD=∠CAD,∵DF⊥AB,DG⊥AC,∴DF=DG=4.应选:B.【点评】此题主要考察三角形的外角性质,直角三角形30°角所对的直角边等于斜边的一半的性质,平行线的性质和角平分线上的点到角的两边的间隔相等的性质,纯熟掌握性质是解题的关键.5.如图,等边△ABC的边长为4,AD是BC边上的中线,F是AD边上的动点,E是AC边上一点,假设AE=2,当EF+CF获得最小值时,那么∠ECF的度数为〔〕A.15° B.22.5°C.30° D.45°【考点】轴对称-最短道路问题;等边三角形的性质.【分析】过E作EM∥BC,交AD于N,连接CM交AD于F,连接EF,推出M为AB中点,求出E和M关于AD对称,根据等边三角形性质求出∠ACM,即可求出答案.【解答】解:过E作EM∥BC,交AD于N,∵AC=4,AE=2,∴EC=2=AE,∴AM=BM=2,∴AM=AE,∵AD是BC边上的中线,△ABC是等边三角形,∴AD⊥BC,∵EM∥BC,∴AD⊥EM,∵AM=AE,∴E和M关于AD对称,连接CM交AD于F,连接EF,那么此时EF+CF的值最小,∵△ABC是等边三角形,∴∠ACB=60°,AC=BC,∵AM=BM,∴∠ECF=∠ACB=30°,应选C.【点评】此题考察了轴对称﹣最短道路问题,等边三角形的性质,等腰三角形的性质,平行线分线段成比例定理等知识点的应用.6.假设m+n﹣p=0,那么的值是〔〕A.﹣3 B.﹣1 C.1 D.3【考点】分式的化简求值.【分析】先根据题意把原式化为+﹣的形式,再由m+n﹣p=0得出m﹣p=﹣n,m﹣p=﹣n,n﹣p=﹣m,m+n=p,代入原式进展计算即可.【解答】解:原式=﹣+﹣﹣﹣=+﹣,∵m+n﹣p=0,∴m﹣p=﹣n,m﹣p=﹣n,n﹣p=﹣m,m+n=p,∴原式=﹣1﹣1﹣1=﹣3.应选A.【点评】此题考察的是分式的化简求值,熟知分式混合运算的法那么是解答此题的关键.7.如图,M是线段AD、CD的垂直平分线交点,AB⊥BC,∠D=65°,那么∠MAB+∠MCB的大小是〔〕A.120°B.130°C.140°D.160°【考点】三角形的外接圆与外心;多边形内角与外角;圆周角定理.【分析】过M作射线DN,根据线段垂直平分线的性质得出AM=DM,CM=DM,推出∠DAM=∠ADM,∠DCM=∠CDM,求出∠MAD+∠MCD=∠ADM+∠CDM=∠ADC=65°,根据三角形外角性质求出∠AMC,根据四边形的内角和定理求出即可.【解答】解:过M作射线DN,∵M是线段AD、CD的垂直平分线交点,∴AM=DM,CM=DM,∴∠DAM=∠ADM,∠DCM=∠CDM,∴∠MAD+∠MCD=∠ADM+∠CDM=∠ADC,∵∠ADC=65°,∴∠MAD+∠MCD=∠ADC=65°,∴∠AMC=∠AMN+∠CMN=∠DAM+∠ADM+∠DCM+∠CDM=65°+∠ADC=65°+65°=130°∵AB⊥BC,∴∠B=90°,∴∠MAB+∠MCB=360°﹣∠B﹣∠AMC=360°﹣90°﹣130°=140°,应选C.【点评】此题考察了线段垂直平分线性质,等腰三角形性质,三角形的外角性质的应用,主要考察学生的推理才能,8.如图,在等边△ABC中,AC=9,点O在AC上,且AO=3,点P是AB上一动点,连接OP,以O为圆心,OP长为半径画弧交BC于点D,连接PD,假如PO=PD,那么AP的长是〔〕A.5 B.8 C.7 D.6【考点】全等三角形的断定与性质;等边三角形的性质.【专题】压轴题.【分析】连接OD,由题意可知OP=DP=OD,即△PDO为等边三角形,所以∠OPA=∠PDB=∠DPA ﹣60°,推出△OPA≌△PDB,即可求出AP的长度.【解答】解:连接OD,∵PO=PD,∴OP=DP=OD,∴∠DPO=60°,∵等边△ABC,∴∠A=∠B=60°,AC=AB=9,∴∠OPA=∠PDB=∠DPA﹣60°,∴△OPA≌△PDB,∵AO=3,∴AO=PB=3,∴AP=6.应选D.【点评】此题主要考察全等三角形的断定和性质、等边三角形的性质,关键在于求证△OPA≌△PDB.9.如图,过边长为1的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,当PA=CQ时,连PQ交AC边于D,那么DE的长为〔〕A.B.C.D.不能确定【考点】等边三角形的性质;平行线的性质;全等三角形的断定与性质.【专题】计算题.【分析】过P作BC的平行线,交AC于M;那么△APM也是等边三角形,在等边三角形APM 中,PE是AM上的高,根据等边三角形三线合一的性质知AE=EM;易证得△PMD≌△QCD,那么DM=CD;此时发现DE的长正好是AC的一半,由此得解.【解答】解:过P作PM∥BC,交AC于M;∵△ABC是等边三角形,且PM∥BC,∴△APM是等边三角形;又∵PE⊥AM,∴AE=EM=AM;〔等边三角形三线合一〕∵PM∥CQ,∴∠PMD=∠QCD,∠MPD=∠Q;又∵PA=PM=CQ,在△PMD和△QCD中∴△PMD≌△QCD〔AAS〕;∴CD=DM=CM;∴DE=DM+ME=〔AM+MC〕=AC=,应选B.【点评】此题考察了平行线的性质、等边三角形的性质、全等三角形的断定和性质;可以正确的构建出等边三角形△APM是解答此题的关键.10.如图,AB=4,射线BM和AB互相垂直,点D是AB上的一个动点,点E在射线BM上,2BE=DB,作EF⊥DE并截取EF=DE,连结AF并延长交射线BM于点C.设BE=x,BC=y,那么y关于x 的函数解析式是〔〕A.y=﹣B.y=﹣C.y=﹣D.y=﹣【考点】相似三角形的断定与性质;函数关系式;全等三角形的断定与性质.【分析】作FG⊥BC于G,根据条件求得△DBE≌△EGF,得出FG=BE=x,EG=DB=2x,然后根据平行线的性质即可求得.【解答】解:作FG⊥BC于G,∵∠DEB+∠FEC=90°,∠DEB+∠DBE=90°;∴∠BDE=∠FEG,在△DBE与△EGF中,,∴△DBE≌△EGF〔AAS〕,∴EG=DB,FG=BE=x,∴EG=DB=2BE=2x,∴GC=y﹣3x,∵FG⊥BC,AB⊥BC,∴FG∥AB,CG:BC=FG:AB,即=,∴y=﹣.应选A.【点评】此题考察了三角形全等的断定和性质,以及平行线的性质,辅助线的做法是解题的关键.二、填空题〔本大题一一共6个小题,每一小题3分,一共18分〕11.〔3分〕如图,△ABC中,BD平分∠ABC,BC的中垂线交BC于点E,交BD于点F,连接CF.假设∠A=60°,∠ABD=24°,那么∠ACF=48°.【考点】线段垂直平分线的性质.【分析】根据角平分线定义求出∠ABC=2∠ABD=48°,∠DBC=∠ABD=24°,根据三角形内角和定理求出∠ACB,根据线段垂直平分线性质求出FC=FB,求出∠FCB,即可求出答案.【解答】解:∵BD平分∠ABC,∠ABD=24°,∴∠ABC=2∠ABD=48°,∠DBC=∠ABD=24°,∵∠A=60°,∴∠ACB=180°﹣∠A﹣∠ACB=180°﹣60°﹣48°=72°,∵FE是BC的中垂线,∴FB=FC,∴∠FCB=∠DBC=24°,∴∠ACF=∠ACB﹣∠FCB=72°﹣24°=48°,故答案为:48°.【点评】此题考察了三角形内角和定理,线段垂直平分线性质,角平分线定义,等腰三角形性质的应用,能熟记知识点是解此题的关键,题目比拟好,难度适中.12.等腰三角形一边长为3cm,周长7cm,那么腰长是3cm或者2cm .【考点】等腰三角形的性质;三角形三边关系.【分析】题中给出了周长和一边长,而没有指明这边是否为腰长,那么应该分两种情况进展分析求解.【解答】解:①当3cm为腰长时,那么腰长为3cm,底边=7﹣3﹣3=1cm,因为1+3>3,所以能构成三角形;②当3cm为底边时,那么腰长=〔7﹣3〕÷2=2cm,因为2+2>3,所以能构成三角形.故答案为:3cm或者2cm.【点评】此题主要考察等腰三角形的性质及三角形三边关系的综合运用,关键是利用三角形三边关系进展检验.13.如图,在△ABC中,AH⊥BC于H,∠C=35°,且AB+BH=HC,那么∠B度数为70°.【考点】等腰三角形的断定与性质.【专题】探究型.【分析】在CH上截取DH=BH,连接AD,即可得到△ABH≌△ADH,进而得到CD=AD,再由三角形外角的性质即可得出∠B的大小.【解答】解:在CH上截取DH=BH,连接AD,∵AH⊥BC,∴∠AHB=∠AHD=90°,在△ABH≌△ADH中,∵∴△ABH≌△ADH,∴AD=AB∵AB+BH=HC,HD+CD=CH∴AD=CD∴∠C=∠DAC,又∵∠C=35°∴∠B=∠ADB=70°.【点评】此题考察的是等腰三角形的断定与性质及三角形外角的性质,根据题意作出辅助线,构造出等腰三角形是解答此题的关键.14.10x=m,10y=n,那么102x+3y等于m2n3.【考点】幂的乘方与积的乘方;同底数幂的乘法.【分析】先根据同底数幂的乘法进展变形,再根据幂的乘方变形,最后整体代入求出即可.【解答】解:∵10x=m,10y=n,∴102x+3y=102x×103y=〔10x〕2×〔10y〕3=m2n3.故答案为:m2n3.【点评】此题考察了同底数幂的乘法,幂的乘方的应用,能灵敏运用法那么进展变形是解此题的关键,用了整体代入思想.15.a﹣b=b﹣c=,a2+b2+c2=1,那么ab+bc+ca的值等于﹣.【考点】完全平方公式.【专题】压轴题.【分析】先求出a﹣c的值,再利用完全平方公式求出〔a﹣b〕,〔b﹣c〕,〔a﹣c〕的平方和,然后代入数据计算即可求解.【解答】解:∵a﹣b=b﹣c=,∴〔a﹣b〕2=,〔b﹣c〕2=,a﹣c=,∴a2+b2﹣2ab=,b2+c2﹣2bc=,a2+c2﹣2ac=,∴2〔a2+b2+c2〕﹣2〔ab+bc+ca〕=++=,∴2﹣2〔ab+bc+ca〕=,∴1﹣〔ab+bc+ca〕=,∴ab+bc+ca=﹣=﹣.故答案为:﹣.【点评】此题考察了完全平方公式,解题的关键是要由a﹣b=b﹣c=,得到a﹣c=,然后对a﹣b=,b﹣c=,a﹣c=三个式子两边平方后相加,化简求解.16.如图,∠AOB=30°,点P为∠AOB内一点,OP=8.点M、N分别在OA、OB上,那么△PMN 周长的最小值为8 .【考点】轴对称-最短道路问题.【分析】分别作点P关于OA、OB的对称点P1、P2,连P1、P2,交OA于M,交OB于N,△PMN 的周长=P1P2,然后证明△OP1P2是等边三角形,即可求解.【解答】解:分别作点P关于OA、OB的对称点P1、P2,连P1、P2,交OA于M,交OB于N,那么OP1=OP=OP2,∠P1OA=∠POA,∠POB=∠P2OB,MP=P1M,PN=P2N,那么△PMN的周长的最小值=P1P2∴∠P1OP2=2∠AOB=60°,∴△OP1P2是等边三角形.△PMN的周长=P1P2,∴P1P2=OP1=OP2=OP=8.故答案为:8.【点评】此题考察了轴对称﹣最短道路问题,正确正确作出辅助线,证明△OP1P2是等边三角形是关键.三、解答题〔一共8题,一共72分〕17.〔8分〕先化简,再求值:,其中x是的整数局部.【考点】分式的化简求值;估算无理数的大小.【分析】首先将括号里面进展通分,再将能因式分解的进展因式分解,进而化简求出答案.【解答】解:原式=÷=×=,∵﹣3<﹣<﹣2,2<5﹣<3,那么x=2,∴原式=.【点评】此题主要考察了分式的化简求值以及估算无理数的大小,正确化简分式是解题关键.18.如下图,点D为等边△ABC的AC边上的一点,∠1=∠2,BD=CE.求证:△DAE是等边三角形.【考点】等边三角形的断定与性质.【专题】证明题.【分析】由条件可证明△ABE≌△ACD,从而AE=AD,∠BAE=∠CAD=60°,所以可知△DAE是等边三角形.【解答】证明:∵三角形ABC为等边三角形∴AB=AC在△ABD和△ACE中∴△ABD≌△ACE〔SAS〕∴AE=AD,∠BAD=∠DAE=60°∴△ADE是等边三角形.【点评】此题主要考察三角形全等的断定和性质及等边三角形的断定,解题的关键是证△ABD≌△ACE.19.〔8分〕如图,△ABC为等边三角形,D在BC的延长线上,∠ADE=60°,∠ACD的平分线交DE于E,求证:AD=DE.【考点】全等三角形的断定与性质;等边三角形的性质.【专题】证明题.【分析】由条件可以容易证明△ABD≌△ACE,进一步得出AD=AE,加上∠DAE=60°,即可证明△ADE为等边三角形.【解答】证明:∵△ABC为等边三角形,∴∠B=∠ACB=60°,AB=AC,即∠ACD=120°,∵CE平分∠ACD,∴∠ACE=∠ECD=60°,在△ABD和△ACE中,,∴△ABD≌△A CE〔SAS〕,∴AD=AE,∵∠DAE=60°,∴△ADE为等边三角形,∴AD=DE.【点评】此题考察了等边三角形的断定与性质,难度适中,关键找出断定三角形等边的条件.20.〔8分〕如图,AB=AC,∠BAC=60°,∠BDC=120°,求证:AD=BD+CD.【考点】全等三角形的断定与性质.【专题】证明题.【分析】先延长DB,使BE=CD,连接AE,BC,根据条件得出A,B,D,C四点一共圆,得出∠ACB=∠ADE,再根据等边三角形的性质得出△ABC是等边三角形,在△ABE和△ACD中,根据SAS得出△ABE≌△ACD,得出△ADE是等边三角形,得出AD=DE,再根据DE=BD+BE,即可证出AD=BD+CD.【解答】解:延长DB,使BE=CD,连接AE,BC,∵∠BAC+∠ACD+∠BDC+∠ABD=360°,∠BAC=60°,∠BDC=120°,∴∠ABD+∠ACD=180°,∴A,B,D,C四点一共圆,∴∠ACB=∠ADE,∵∠ABD+∠ABE=180°,∴∠ABE=∠ACD,∵AB=AC,∴△ABC是等边三角形,∴∠ACB=60°,∴∠ADE=60°,在△ABE和△ACD中,,∴△ABE≌△ACD〔SAS〕,∴AE=AD,∴△ADE是等边三角形,∴AD=DE,∵DE=BD+BE,∴AD=BD+CD.【点评】此题考察了全等三角形的断定与性质,用到的知识点是等边三角形的性质,全等三角形的断定与性质和三角形内角和定理,关键是根据题意作出辅助线.21.如图,在等边三角形△ABC中,AE=CD,AD、BE交于P点,BQ⊥AD于Q,〔1〕求证:BP=2PQ;〔2〕连PC,假设BP⊥PC,求的值.【考点】全等三角形的断定与性质;等边三角形的性质.【分析】〔1〕根据全等三角形的断定定理SAS可得△BAE≌△ACD,得∠ABE=∠CAD,即可得出∠BPQ=60°,再根据BQ⊥AD,得出BP=2PQ;〔2〕根据∠ABE=∠CAD,得∠PBC=∠BAQ,利用AAS可证明△BAQ和△CBP,从而得出AP=PQ,即可得出的值.【解答】证明:〔1〕在等边△ABC中,AB=AC,∠BAE=∠ACD=60°,在△BAE和△ACD中,,∴△BAE≌△ACD〔SAS〕,∴∠ABE=∠CAD,∴∠BPQ=∠ABE+∠BAP=∠CAD+∠BAP=∠BAC=60°,∵BQ⊥AD于Q,∴∠BPQ=30°,∴BP=2PQ;〔2〕∵∠ABE=∠CAD,∴∠ABC﹣∠ABE=∠BAC﹣∠CAD,即∠PBC=∠BAQ,在△BAQ和△CBP中,,∴△BAQ和△CBP〔AAS〕,∴AQ=BP=2PQ,∴AP=PQ,即.【点评】此题考察了全等三角形的性质和断定,以及等边三角形的性质,掌握全等三角形的断定定理:SSS,SAS,ASA,AAS以及HL是解题的关键.22.在△ABC中,AD平分∠BAC交BC于D.〔1〕如图1,∠MDN的两边分别与AB、AC相交于M、N两点,过D作DF⊥AC于F,DM=DN,证明:AM+AN=2AF;〔2〕如图2,假设∠C=90°,∠BAC=60°,AC=9,∠MDN=120°,ND∥AB,求四边形AMDN 的周长.【考点】全等三角形的断定与性质.【分析】〔1〕过点D作DG⊥AB于G,证明Rt△DFN≌Rt△DGM,得MG=NF,AG=AF,再把AM+AN 变形即可得出等于2AF;〔2〕过点D作DE⊥AB于E,可证明△MDE≌△NDC,得DM=DN,再证明△BDM为等腰三角形,根据直角三角形的性质,30°所对的直角边等于斜边的一半,从而得出AB=18,AM=12,BM=DM=6,同理得:AN=DN=DM=6,即可求得四边形AMDN的周长.【解答】证明:〔1〕过点D作DG⊥AB于G,如图1,∵AD平分∠BAC,DF⊥AC,∴DF=DG,在Rt△DFN和Rt△DGM中,∴Rt△DFN≌Rt△DGM〔HL〕,∴MG=NF又∵AG=AF,∴AM+AN=AG+MG+AN=AF+NF+AN=2AF;〔2〕过点D作DE⊥AB于E,如图2,在四边形ACDE中,∠EDC=360°﹣60°﹣90°﹣90°=120°,∴∠EDN+∠MDE=120°,又∠EDN+∠NDC=120°,∴∠MDE=∠NDC,∵AD平分∠BAC,∴DE=DC,在△MDE和△NDC中,,∴△MDE≌△NDC〔ASA〕,∴DM=DN,∵ND∥AB,∴∠NDC=∠B=30°,∠DNC=60°,∴∠MDB=180°﹣120°﹣30°=50°,∴△MDB为等腰三角形,∴MB=MD,∴∠ADM=90°,∴AM=2DM,在Rt△ABC中,∠B=30°,∴AB=2AC=18,AM=AB=12,BM=AB=DM=6,同理:AN=DN=DM=6,∴四边形AMDN的周长为12+6+6+6=30.【点评】此题考察了全等三角形的性质和断定,纯熟运用角平分线的性质定理、直角三角形的性质,要充分挖掘隐含条件,此类题学生丢分率较高,需注意.23.如图1,在平面直角坐标系中,点A、B分别在x轴、y轴上.〔1〕如图1,点A与点C关于y轴对称,点E、F分别是线段AC、AB上的点〔点E不与点A、C重合〕,且∠BEF=∠BAO.假设∠BAO=2∠OBE,求证:AF=CE;〔2〕如图2,假设OA=OB,在点A处有一等腰△AMN绕点A旋转,且AM=MN,∠AMN=90°.连接BN,点P为BN的中点,试猜测OP和MP的数量关系和位置关系,说明理由.【考点】全等三角形的断定与性质;坐标与图形性质;等腰直角三角形.【分析】〔1〕设∠OBE=α,∠AEF=β,证明∠EBC=∠AEF,EB=EF,进而可以证明△AEF和△CBE 〔AAS〕,利用全等三角形的对应边相等,即可解答;〔2〕OP=MP且OP⊥MP,延长MP至C,且使PC=MP,连接BC、MO,延长AM交BC于D,连接CO,NO,证明△MPN≌△CPB〔SAS〕,得到BC=MN=AM,∠MNP=∠CBP,再证明△MOC为等腰直角三角形,根据MP=CP,即可得到OP⊥MP且OP=MP.【解答】证明:〔1〕如图1,设∠OBE=α,∠AEF=β,∴∠BAO=∠BEF=2α,∵点A、C关于y轴对称,∴BA=BC,∴∠BAO=∠BCO=2α∵∠AEB=2α+β=∠BCO+∠EBC∴∠EBC=β,即∠EBC=∠AEF∵∠BFE=∠BAO+∠FEA=2α+β又∠ABO=∠CBO=α+β∴∠FBE=α+β+α=2α+β∴∠BFE=∠FBE∴EB=EF,在△AEF和△CBE中∴△AEF和△CBE〔AAS〕∴AF=CE〔2〕OP=MP且OP⊥MP,理由如下:延长MP至C,且使PC=MP,连接BC、MO,延长AM交BC于D,连接CO,NO,∵点P为BN的中点,∴PN=PB,在△MPN和△CPB中∴△MPN≌△CPB〔SAS〕∴BC=MN=AM,∠MNP=∠CBP,∴MN∥BC,∵∠AMN=90°∴AD⊥BC,∴∠MAO=∠CBO,∴∠MOA=∠COB,MO=CO,∴∠MOC=∠MOB+∠BOC=∠MOB+∠MOA=∠AOB=90°∴△MOC为等腰直角三角形,∵MP=CP,∴OP⊥MP且OP=MP.【点评】此题考察了全等三角形的性质定理与断定定理,等腰三角形的性质、直角三角形的性质,解决此题的关键是作出辅助线,构建全等三角形.24.如图,在平面直角坐标系中,A〔0,a〕、B〔﹣b,0〕且a、b满足+|a﹣2b+2|=0.〔1〕求证:∠OAB=∠OBA;〔2〕如图1,假设BE⊥AE,求∠AEO的度数;〔3〕如图2,假设D是AO的中点,DE∥BO,F在AB的延长线上,∠EOF=45°,连接EF,试探究OE和EF的数量和位置关系.【考点】全等三角形的断定与性质;坐标与图形性质;等腰直角三角形.【分析】〔1〕根据非负数的性质得到,解得,确定A〔0,2〕、B〔﹣2,0〕,得到OA=OB,所以△AOB为等腰直角三角形,即可解答;〔2〕如图1,过点O作OF⊥OE交AE于F,利用条件证明△OBE≌△OAF〔ASA〕,得到OE=OF,即△OEF为等腰直角三角形,即可解答;〔3〕过点F作FG⊥OF交OE的延长线于G,过点F作FH⊥FB交x轴于H,延长DE交HG于I,利用条件证明△HFG≌△BFO〔SAS〕,得到FG=FO,GH=OB=OA,进而得到△FGO为等腰直角三角形,再证明△EIG≌△EDO〔SAS〕得到EG=EO,进而FE=EO且FE⊥EO〔三线合一〕.【解答】解:〔1〕∵a、b满足+|a﹣2b+2|=0.∴∴,∴A〔0,2〕、B〔﹣2,0〕,∴OA=OB,∴△AOB为等腰直角三角形∴∠OAB=∠OBA=45°,〔2〕如图1,过点O作OF⊥OE交AE于F,∵∠AOF+∠BOF=90°,∠BOE+∠BOF=90°∴∠AOF=∠BOE,∵BE⊥AE,∴∠AEB=90°又∠AOB=90°∴∠BOE=∠OAF〔八字型〕在△OBE和△OAF中,∴△OBE≌△OAF〔ASA〕∴OE=OF∴△OEF为等腰直角三角形∴∠AEO=45°〔3〕过点F作FG⊥OF交OE的延长线于G,过点F作FH⊥FB交x轴于H,延长DE交HG于I,∵∠EOF=45°,∠HBF=∠ABO=45°,∴△OFG、△HFB为等腰直角三角形,∵∠HFG+∠GFB=90°,∠BFO+∠GFB=90°∴∠HFG=∠BFO,在△HFG和△BFO中,∴△HFG≌△BFO〔SAS〕∴FG=FO,GH=OB=OA∴△FGO为等腰直角三角形,又∠GHF=∠OBF=135°∴∠GHO=90°∴HI=OD=IG在△EIG和△EDO中,∴△EIG≌△EDO〔SAS〕∴EG=EO∴FE=EO且FE⊥EO〔三线合一〕.【点评】此题考察了非负数的性质、全等三角形的性质定理与断定定理,解决此题的关键是作出辅助线,构建全等三角形,利用全等三角形的对应边相等得到相等的线段.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A
E
C
D F 图6
1
2八年级数学上册竞赛试题
(时间120分钟,满分120分)
一、填空题(每小题3分,共30分) 1、8l 的平方根为____________
2、已知点 P 在第二象限,它的横坐标与纵坐标的和为1,则点 P 的坐标是________. (写出符合条件的一个点即可)
3、一个多边形的内角和为12600 ,则它的边数是____________.
4、已知b
a
82=(b a ,是正整数)且,52=+b a 那么28a
b
+的值是 5、如图,在Rt △ABC 中,∠C=90°,∠A=35°,以直角顶点C
为旋转中心,将△ABC 旋转到△A ’B ’C 的位置,其中A ’、B ’分别是A 、B 的对应点,且点B 在斜边A ’B ’上,直角边CA ’交AB 于点D ,则∠DCA 的度数_____。
6、小王与同学约好下午4:30在学校门口见,不见不散,为此,
他们在早上8:00钟两人均把自己的表对准,小王于4:30正点走到学校门口,可是同学没来,原来同学的手表比正确时间每小时慢4分钟,如果同学按他自己的手表4:30到达,则小王还要等 分钟(正确时间)
7、甲、乙两位探险者到沙漠进行探险。
某日早晨7∶00甲先出发,他以6千米/时的速度向东
行走,1小时后乙出发,他以5千米/时的速度向北行进。
上午10∶00,甲、乙二人的距离的平方是_____。
8、一个等腰三角形的周长为16,底边上的高是4,则 这个三角形的三边长分别是______,_____,_______。
9、已知:如图2,E 、F 分别是正方形ABCD 的边BC 、 CD 上的点,AE 、AF 分别与对角线BD 相交于M 、N ,
若∠EAF=500,则∠CME +∠CNF = ________。
10、如图3,将面积为2a 的正方形与面积为2
b 的正方形
(b>a)放在一起,则△ABC 的面积是__________。
二、选择题(每小题3分,共30分) 1、ΔABC 中三边之比为1: 1: ,则ΔABC 形状一定不是 ( )
A 、等腰三角形
B 、直角三角形
C 、等腰直角三角形
D 、锐角三角形 2、.将图4中的图案甲变成图案乙,正确的说法是 ( )
A 、“扶正”后即可
B 、“扶正”后向右平移即可
C 、“扶正”后作直线 MN 的轴对称图形即可
D 、以上三种方法都可
3、如图5,正方形ABCD 的边长为1cm ,以对角线AC 为边长再作一个正方形,则正方形ACEF
的面积是( ) A 、3cm 2 B 、4cm 2 C 、5cm 2 D 、2cm 2
4、以线段16,13,10,6a b c d ====为边,
且使a ∥c 作四边形,这样的四边形( )
A 、能作两个
B 、能作三个
C 、能作无数个
D 、不能作 5、如图6,正方形的面积为256,点F 在AD 上,点
E 在AB 的延
长线上,Rt △CEF 的面积为200,则BE 的值为( ) A 、10 B 、11 C 、12 D 、15 6、实数a 、b 满足ab =1,若11,1111a b
M N a b a b
=
+=+
++++, 则M 、N 的关系为( )
A 、M>N
B 、M=N
C 、M<N
D 、不确定 7、一块等边三角形的木板,边长为1,现将木板沿
水平线翻滚(如左图),那么B 点从开始至结束走过的路径长度为( ) A 、23π B 、23π C 、 4 D 、2 +2
3π
8、在甲组图形的4个图中,每个图示由4种简单图形A 、B 、C 、D (不同的线段或圆) 中的某两个图形组成的,例如由A 、B 组成的图形记为B A ∙,在乙组图形的(a )、(b)、 (c)、(d )4个图中,表示“D A ∙”和“C A ∙”的是( )
A 、 (a),(b)
B 、 (b),(c)
C 、 (c),(d)
D 、 (b),(d) 9、如图所示的4个的半径均为1,那么图中的阴影部分的
面积为( )
A 、1+π
B 、π
2 C 、 4 D 、6
10、正ΔABC 的顶点A 、B 的坐标分别为A (0,0),B(2,
0),则点
C 的
坐标为 ( ) A 、(1, ) B 、(1,- )
C 、(1, ) 或(1,- )
D 、(-1, ) 或 (-1,- )
三、(每题10分, 计30分)
1、已知四边形ABCD 中 ,AB=AD ,∠BAD=60°,∠BCD=120°,请说明:BC+DC=AC
A E D
B F
C 图3
A B C
D F
E
图5
A B C D F E N M
图2
2、如图,两条等宽的长纸条倾斜地重叠着, 试说明重叠部分ABCD为菱形.
3、已知:四边形 ABCD,从下列给出的条件中任取 (个数不限) 几个组合,使四边形ABCD为
矩形,并说明理由.(写出两种组合)
① AB// CD ② AD // BC ③ AB= CD
④ AO = CO = BO =DO ⑤∠ABC =∠DCB
⑥ AC =2 AB ⑦AC =BD ⑧AO = CO,BO =DO
四、(每题15分, 计30分)
4、如图, 已知正方形ABCD的对角线AC、BD 相交于点O ,E 是AC 上一点,过 A 作AG ⊥
EB,垂足为G,AG 交 BD 于点 F,则 OE=OF.(对上述命题,可证 RtΔBOE ≌ Rt ΔAOF,可得OE=OF.) 若点 E 在 AC 的延长线上,AG ⊥ EB 交 EB的延长线于点 G,AG的延长线交 DB的延长线于点F,其他条件不变,则结论“OE = OF ”还成立吗 ? 如果成立,请说明理由;如果不成立,也请说明理由.
5、ΔABC中, ∠C=900,∠A, ∠B, ∠C 的对边分别为 a, b, c,设A4BC的面积为s,周长
为 l ,探索与 a + b-c 的值之间的关系.
(1)计算后填表: (6分)
(2) 观察分析后猜想: 若设 a + b-c = m(m为正实数), 则=_________.(用m表
示). (4分)
(3) 写出(2)中结论的推导过程.(5分)
八年级数学竞赛答案
一、填空题。
1、±9
2、(略)
3、9
4、16
5、70
6、
7
3
36 7、 424
8、 5,5,6 9、 1000 10、2
1
2
b
二、选择题
D、C、D、
E、D、B、B、D、C、C
三、
1、已知四边形ABCD中,AB=AD,∠BAD=60°,∠BCD=120°,请说明:BC+DC=AC
由AB=AD,∠BAD=60°可得ABD
∆是等边三角形,把ADC
∆绕点D逆时针旋转60°,点A与点B重合,点C转到点E,连接EC,则DCE
∆是等边三角形,∠BAD=60°,又因为∠BCD=120°,
所以∠BAD+∠BCD=180°,故B、C、
E共线,
所以AC=BE=BC+CE=BC+DC
2-3、(略)
四、
4-5 (略)
E。
