第二章_光学答案提示
《应用光学》第2章课后答案全文

12. 由两个透镜组成的一个倒像系统,设第一组透镜的焦距 为f1′,第二组透镜的焦距为f2′,物平面位于第一组透镜 的物方焦面上,求该倒像系统的垂轴放大率。
解:
1
1
1
1
F2
1
1
第一组透镜
第二组透镜
1
第二组透镜
13. 由两个同心的反射球面(二球面球心重合)构成的光学系 统,按照光线反射的顺序第一个反射球面是凹的,第二个 反射球面是凸的,要求系统的像方焦点恰好位于第一个反 射球面的顶点,求两个球面的半径r1,r2和二者之间的间隔 d之间的关系。
B′
面,如图示.
l ′ = 2f′
4 试用作图法对位于空气中的正透镜组( f 0 )分别求 下列不同物距的像平面位置.
l = −f′
B
……
F
F′
A
H H′
像平面在像 空间无限远 处.
l′=∞
4 试用作图法对位于空气中的正透镜组( f 0 )分别求 下列不同物距的像平面位置.
l f' 2
B′
r1 无穷远物点
r2
r1/2
最终像点
11 2
l2 l2 r2
l2
l2
2 r2
(l2l2 )
14. 假定显微镜物镜由相隔20mm的两个薄透镜组构成,物平 面和像平面之间的距离为180mm,放大率β=-10×,要求近 轴光线通过二透镜组时的偏角Δu1和Δu2相等,求二透镜 组的焦距。
y n1u1 u1 10
l = −f′
B
……
F′
F
H H′
A
像平面在像 空间无限远 处.
5 试用作图法对位于空气中的负透镜组( f 0 )分别求 下列不同物距的像平面位置.
光学第二章习题解答

∆y = y2 − y1 ≈ 2 f ′
λ
b
− f′
λ
b
= f′
λ
b
∆y ⋅ b 0.02 × 0.885 ɺ λ= = = 5900 A f′ 300
(2)波长为 波长为0.1nm的x射线时,相邻最小值间的距离为 射线时, 波长为 的 射线时
′λ 300 × 0.1×10−9 f ∆y = = 0.02 b −6 −4 = 1.5 × 10 m = 1.5 × 10 cm
主焦点
还有次焦点: 还有次焦点:± f ′ /3,
± f ′ /5, ± f ′ / 7⋯
故:光强极大值出现在轴上 1/3m,1/5m,1/7m……1/(2k+1)m等处 , , 等处
2.6 波长为 的点光源波带片成一个像点,该波带 波长为λ的点光源波带片成一个像点 的点光源波带片成一个像点, 个透明奇数半波带(1, , )。另外 有100个透明奇数半波带 ,3,5 ……199)。另外 个透明奇数半波带 )。 100个不透明偶数半波带。比较用波带片换上同样焦 个不透明偶数半波带。 个不透明偶数半波带 距和口径的透镜时像点的强度比I: 距和口径的透镜时像点的强度比 :I0 解:(1) 只有 ) 只有100个透明奇数半波带透过 个透明奇数半波带透过
∵
θ3 < θ 2
∴
二级和三级光谱部分重叠 二级和三级光谱部分重叠
2.14 用波长为 用波长为589nm的单色光照射一衍射光栅, 的单色光照射一衍射光栅 的单色光照射一衍射光栅, 其光谱的中央最大值和第二十级主最大值之间的衍 射角为15 10′。试求该光栅1cm内的缝数是多少? 15° cm内的缝数是多少 射角为15°10′。试求该光栅 cm内的缝数是多少? 解: 由光栅方程 d sin θ = jλ
工程光学习题参考答案第二章理想光学系统
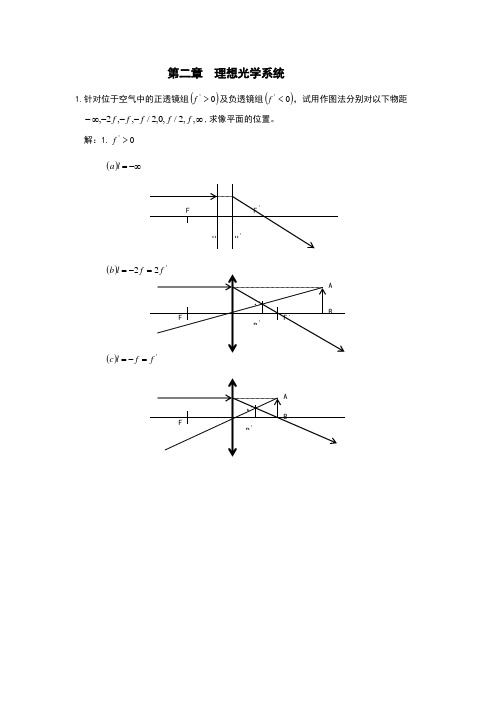
第二章 理想光学系统1.针对位于空气中的正透镜组()0'>f 及负透镜组()0'<f ,试用作图法分别对以下物距 ∞---∞-,,2/,0,2/,,2,f f f f f ,求像平面的位置。
解:1.0'>f ()-∞=l a()'2f l b -=()f f l c =-=()/f l d -=()0=l e()/f l f =')(f f l g -=='22)(f f l h -==+∞=l i )(2.0'<f -∞=l a )(l b )(=l c =)(/)(f l d -=0 el(=)f=l2/ (f)()fg=l(=h)ll i)(+∞=2. 已知照相物镜的焦距f’=75mm,被摄景物位于(以F 点为坐标原点)=x ,2,4,6,8,10,m m m m m -----∝-处,试求照相底片应分别放在离物镜的像方焦面多远的地方。
解: (1)x= -∝ ,xx ′=ff ′ 得到:x ′=0 (2)x ′= (3)x ′= (4)x ′= (5)x ′=(6)x ′=3.设一系统位于空气中,垂轴放大率*-=10β,由物面到像面的距离(共轭距离)为7200mm , 物镜两焦点间距离为1140mm 。
求该物镜焦距,并绘出基点位置图。
解:∵ 系统位于空气中,f f -='10''-===ll y y β 由已知条件:1140)('=+-+x f f7200)('=+-+x l l解得:mm f 600'= mm x 60-=4.已知一个透镜把物体放大*-3投影到屏幕上,当透镜向物体移近18mm 时,物体将被放大*-4,试求透镜的焦距,并用图解法校核之。
解:方法一:31'11-==l l β ⇒ ()183321'1--=-=l l l ①42'22-==l l β ⇒ 2'24l l -= ② 1821+-=-l l ⇒ 1821-=l l ③ '/1/1/11'1f l l =-'/1/1/12'2f l l =-将①②③代入④中得 mm l 2702-= mm l 1080'2-= ∴ mm f 216'=方法二: 311-=-=x fβ 422-=-=x fβ ⇒ mm f 216-= 1812=-x x方法三: 12)4)(3(21''=--==∆∆=ββαnn x x2161812'-=⨯=∆x''fx -=β143''''2'121=+-=∆=+-=-∴fx fx x ββ mm x f 216''=∆=∴5.一个薄透镜对某一物体成实像,放大率为⨯-1,今以另一个薄透镜紧贴在第一个透镜上,则见像向透镜方向移动,放大率为原先的3/4倍,求两块透镜的焦距为多少 解:⇒ 2'21'1/1/1/1/1l l l l -=- ④6.有一正薄透镜对某一物成倒立的实像,像高为物高的一半,今将物面向物体移近100mm , 则所得像与物同大小,求该正透镜组的焦距。
光学课件全部习题

解:三列平面波的复振幅分别为
选z=0平面
~ E1 = A1e i ( − k sin θx + k cosθz ) = A1e − ik sin θx ~ ikz E2 = A2 e = 2 A1
~ E3 = A3e i ( k sin θx + k cosθz ) = A1e ik sin θx
~ ~* ~ ~ ~ ~* ~* ~* I = EE = ( E1 + E2 + E3 )( E1 + E2 + E3 )
wwwwenku1comview9c970f097eb60a1分布a2sinkz221有三列在xz平面内传播的同频率单色平面波其振幅分别为a1a2a3传播方向如图求xy平面上的光强分布可设三列波在坐标原点初相均为0
第二章部分典型习题答案
2h1 +
λ1
2
= m1λ1
2h1 +
λ2
2
= m2 λ2
2h2 + 2h2 +
λ1
2
kλ1 = (k + 1)λ2
= (m1 + k )λ1 = (m2 + k + 1)λ2
980λ1 = 981λ2
λ2
2
λ1 = 589.6nm λ1 = 589nm
第四章部分典型习题答案
4.10 单色平面波垂直照射图示的衍射屏,图中标出的是该处到轴上场点 的光程,屏中心到场点的光程为ro,阴影区为不透光区.试用矢量图解 法求场点的光强与波自由传播时该场点的光强的比值.
2
2
I = 5I F
r0 + λ r0 + λ / 4
1 A= 2 AF 4
光学蔡履中第二章习题答案

光学蔡履中第二章习题答案光学蔡履中第二章习题答案第一题:题目:一束平行光通过一块平面玻璃板,入射角为45°,折射角为30°,求该玻璃的折射率。
解答:根据折射定律,得到sin30°/sin45°=n,解得n=0.577。
第二题:题目:一束光从空气射入玻璃,入射角为30°,折射角为20°,求该玻璃的折射率。
解答:根据折射定律,得到sin20°/sin30°=n,解得n=0.667。
第三题:题目:一束光从空气射入水,入射角为45°,折射角为30°,求水的折射率。
解答:根据折射定律,得到sin30°/sin45°=n,解得n=0.667。
第四题:题目:一束光从水射入空气,入射角为30°,折射角为45°,求水的折射率。
解答:根据折射定律,得到sin45°/sin30°=n,解得n=1.155。
第五题:题目:一束光从空气射入玻璃,入射角为60°,折射角为45°,求该玻璃的折射率。
解答:根据折射定律,得到sin45°/sin60°=n,解得n=0.866。
第六题:题目:一束光从玻璃射入空气,入射角为45°,折射角为60°,求该玻璃的折射率。
解答:根据折射定律,得到sin60°/sin45°=n,解得n=1.155。
第七题:题目:一束光从水射入玻璃,入射角为30°,折射角为45°,求该玻璃的折射率。
解答:根据折射定律,得到sin45°/sin30°=n,解得n=1.155。
第八题:题目:一束光从玻璃射入水,入射角为45°,折射角为30°,求该玻璃的折射率。
解答:根据折射定律,得到sin30°/sin45°=n,解得n=0.866。
《应用光学》第2章课后答案解析

l = 2f′
B F′ B′ A A′ H H′
F
像平面为 A’B’所在平 面,如图示.
5 试用作图法对位于空气中的负透镜组( f 0 )分别求 下列不同物距的像平A′ H
H′
F
像平面为 A’B’所在平 面,如图示.
5 试用作图法对位于空气中的负透镜组( f 0 )分别求 下列不同物距的像平面位置.
第二章 部分习题答案
牛顿公式 一、物像位置关系 二、物像大小关系 1、垂轴放大率 2、轴向放大率 3、角放大率 三、物方像方焦距关系 四、物像空间不变式
f' n' f n
y nl y nl
高斯公式
f' f 1 l' l
nuy n' u' y'
2. 有一放映机,使用一个凹面反光镜进行聚光照明,光源经过反
f' l 2
B
B′ A F′ A′ H H′
F
像平面为 A’B’所在平 面,如图示.
5 试用作图法对位于空气中的负透镜组( f 0 )分别求 下列不同物距的像平面位置.
l=0
B
B′
F′ H A
A′ H′
F
像平面为: 像方主平面
5 试用作图法对位于空气中的负透镜组( f 0 )分别求 下列不同物距的像平面位置.
考虑物镜组二主面之间的距离)。 解:
9. 已知航空照相机物镜的焦距f′=500mm,飞机飞行高度为
6000m,相机的幅面为300×300mm2,问每幅照片拍摄的地
面面积。 解:
10. 由一个正透镜组和一个负透镜组构成的摄远系统,前组
正透镜的焦距f1′=100,后组负透镜的焦距f2 ′=-50,要 求由第一组透镜到组合系统像方焦点的距离D与系统的组合 焦距之比为1∶1.5,求二透镜组之间的间隔d应为多少?组 合焦距等于多少?
仪器分析答案整理

第二章 光学分析法导论3. 计算:(1)670.7nm 锂线的频率;(2)3300cm -1谱线的波长; (3)钠588.99nm 共振线的激发电位。
解:(1)ν = λc = cm s cm 710107.670/1099792.2-⨯⨯ = 4.470 ×1014 s -1 (2)λ = σ1 = 133001-cm = 3030 nm (3)E = h λc = 4.136×10-15eV·s×cm s cm 7101099.588/1099792.2-⨯⨯ = 2.105 eV第三章 紫外-可见吸收光谱法2.何谓生色团及助色团?试举例说明。
解:含有π键的不饱和基团叫做生色团.例如C =C ;C =O ;C =N ;—N =N — 有一些含有n 电子的基团,它们本身没有生色功能,但当它们与生色团相连时,就会发生n —π共轭作用,增强生色团的生色能力(吸收波长向长波方向移动,且吸收强度增加),这样的基团称为助色团。
如—OH 、—OR 、—NH 2、—NHR 、—X 等。
3.作为苯环的取代基,―NH 3+不具有助色作用,―NH 2却具有助色作用;―OH 的助色作用明显小于―O -。
试说明原因。
解:助色团至少要有一对非键n 电子,这样才能与苯环上的π电子相作用,产生助色作用。
例如,苯胺中的氨基(―NH 2)含有一对非键n 电子,具有助色作用,当形成苯胺正离子(―NH 3+)时,非键n 电子消失了,助色作用也随之消失。
苯酚负离子中的氧原子(―O -)比酚羟基中的氧原子(―OH )多了一对非键n 电子,其助色效果也就更显著。
7. 比较双光束分光光度计与单光束分光光度计各有何优点。
解:双光束分光光度计对参比信号和试样信号的测量几乎是同时进行的,补偿了光源和检测系统的不稳定性,具有较高的测量精密度和准确度。
同时自动记录,可进行快速全波段扫描。
单光束分光光度计仪器结构简单,价廉,容易操作,比较适用于定量分析。
光学教程答案(第二章)

1. 单色平面光照射到一小圆孔上,将其波面分成半波带。
求第к个带的半径。
若极点到观察点的距离r 0为1m ,单色光波长为450nm ,求此时第一半波带的半径。
解:2022rr k k +=ρ 而20λkr r k +=20λk r r k =-20202λρk r r k =-+将上式两边平方,得422020202λλρk kr r r k++=+ 略去22λk 项,则 λρ0kr k=将cm104500cm,100,1-80⨯===λr k 带入上式,得cm 067.0=ρ2. 平行单色光从左向右垂直射到一个有圆形小孔的屏上,设此孔可以像照相机光圈那样改变大小。
问:(1)小孔半径满足什么条件时,才能使得此小孔右侧轴线上距小空孔中心4m 的P 点的光强分别得到极大值和极小值;(2)P 点最亮时,小孔直径应为多大?设此时的波长为500nm 。
解:(1)根据上题结论ρρ0kr k =将cm105cm,400-50⨯==λr 代入,得cm 1414.01054005k k k =⨯⨯=-ρ 当k 为奇数时,P 点为极大值; k 为偶数时,P 点为极小值。
(2)P 点最亮时,小孔的直径为 cm2828.02201==λρr3.波长为500nm 的单色点光源离光阑1m ,光阑上有一个内外半径分别为0.5mm 和1mm 的透光圆环,接收点P 离光阑1m ,求P 点的光强I 与没有光阑时的光强度I 0之比。
解:根据题意m 1=R 500nmmm 1R mm 5.0R m 121hk hk 0====λr有光阑时,由公式⎪⎪⎭⎫ ⎝⎛+=+=R r R R r r R R k h h 11)(02002λλ得11000110001105005.011620211=⎪⎭⎫ ⎝⎛+⨯=⎪⎪⎭⎫ ⎝⎛+=-R r R k hk λ4100011000110500111620222=⎪⎭⎫ ⎝⎛+⨯=⎪⎪⎭⎫ ⎝⎛+=-R r R k hk λ按圆孔里面套一个小圆屏幕()13221312121212121a a a a a a a a p =+=⎥⎦⎤⎢⎣⎡+-+=没有光阑时210a a =所以 42/211200=⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛=a a a a I I p4.波长为632.8nm 的平行光射向直径为2.76mm 的圆孔,与孔相距1m 处放一屏。
光学作业答案

I = 0.37% ,此时接近消反射。 I0
2π λ0 λ0 = π , λ0 = 500nm λ 2 λ
(2)反射两光束相位差
δ=
2π
λ
2n 2 h =
将 λ = 400nm 和 λ = 700 nm 分别代入上式,得到相位差分别是 1.375πrad 和 0.7857πrad 20.砷化镓发光管制成半球形,以增加位于球心的发光区对外输出功率,减少反射损耗,已 知砷化镓发射光波长 930nm,折射率为 3.4,为了进一步提高光输出功率,常在球形表面涂 一层增透膜。 (1)不加增透膜时,球面的强度反射率多大? (2)增透膜折射率和厚度应取多大? (3)如果用氟化镁(1.38)作为增透膜,能否增透?强度反射率多大? (4)如果用硫化锌(2.35) ,情况又如何? 解:
此光学系统成像在 L1 之右 10cm 处。
, s1, s2 10 10 = − = −1 , V2 = − = − = 2, 横向放大率分别为 V1 = − −5 s1 10 s2
总放大率 V = V1 • V2 = −2 27.用作图法求本题各图中的 Q 像。 (a)
(b)
(c)
(d)
35.(1)用作图法求图中光线 1 共轭线 (2)在图上标出光具组节点 N,N’位置
与屏幕交点(零级)随之移动,即以 M 为中心转了角 β ≈ δs / B ,反映在屏幕上零级位移
C δs ,即幕上条纹总体发生一个平移。 B (5)设扩展光源 b,即其边缘两点间隔 δs = b ,若这两套条纹错开的距离(零级平移量) δx = Δx ,则幕上衬比度降为零,据此有, B+C C δx = b , Δx = λ 2aB B 令 δx = Δx ,
36.已知 1-1’是一对共轭光线,求光线 2 的共轭线。
工程光学基础 习题参考答案-第二章_02

3、设一系统位于空气中, 设一系统位于空气中,垂轴放大 率 β = −10 × , 由物面到像面的距离 (共轭距) 共轭距)为 7200mm,物镜两焦点 间距离为 1140mm。求该物镜焦距, 求该物镜焦距, 并绘出基点位置图。 并绘出基点位置图。 解: 由公式 β = − x' f = − (2-4) , f' x
f 2 ' = −240mm
8、一短焦距物镜 一短焦距物镜, 焦距物镜,已知其焦距为 35mm,筒长 L=65mm,工作距离 l k ' = 50mm ,按 最简单结构的薄透镜系统考虑, 最简单结构的薄透镜系统考虑,求系统结构。 求系统结构。 解: (仿照 (仿照 P32 P32 例 2) 利用正切计算法,设 h1 = 100mm ,有公式:
1 1 1 d (2-33) = + − f ' f1 ' f 2 ' f1 ' f 2 '
f1 ' f 2 ' nr1 r2 f ' = − f = − ∆ = ( n − 1)[n( r − r ) + ( n − 1)d ] 2 1 1 Φ = f ' − dr2 l ' = H n( r2 − r1 ) + ( n − 1)d − dr1 l = H n( r2 − r1 ) + ( n − 1)d
xx' = ff ' = − f ' 2 ∴ x' = − f2 x
代入数据得:
x = −∞, x' = 0.5625mm x = −10m, x' = 0.703mm x = −6m, x' = 0.9375mm x = −4m, x' = 1.406mm x = −2m, x' = 2.813mm
大学物理-游璞-于国萍-光学-课后习题-答案

第一章 习题
1.2 解:从图中可以看出: i2=i1+q
激光器
i2+q=i1+a
∴a=2q
又
tana = 5
50
a=5.71o ∴ q=2.86o
i2 q
q
i1 i1
i2
O
a
50cm
A 5cm
B
用途:平面镜微小的角度改变,转化为屏幕上可测量的长度改 变。力学中钢丝杨氏模量的测量、液体表面张力的测量等。
)2
=
( n1 n1
− +
n2 n2
)2
=
0.04
Rp
=
rp 2
=
( n1 cos i1 n1 cos i1
− n2 + n2
cos i2 cos i2
)2
=
( n2 n2
− n1 )2 + n1
=
0.03
3.4 解:(1)不加树脂胶时,两个透镜之间有空气,所以当自然光正入射
时,在第一个透镜与空气的分界面I上,
R2 + f 2 = nz + x2 + y2 + ( f − z)2 (n2 −1)z2 − z(n R2 + f 2 − f )z − (x2 + y2 ) = −R2
1.11 证明 n' − n = n' − n p' p r
1 +1 =2 p' p r
f = f= r 2
1.13 解:
f '=
Ey
=
A cos[ (t
−
z) c
应用光学 课后题,作业答案

第二章作业:1、一个玻璃球直径为400mm,玻璃折射率为1.5。
球中有两个小气泡,一个在球心,一个在1/2半径处。
沿两气泡连线方向,在球的两侧观察这两个气泡,它们应在什么位置?如在水中观察(水的折射率为1.33)时,它们又应在什么位置?答案:空气中:80mm、200mm;400mm、200mm水中:93.99mm、200mm;320.48mm、200mm3、一个玻璃球直径为60mm,玻璃折射率为1.5,一束平行光射到玻璃球上,其汇聚点在何处?答案:l'=15mm4、一玻璃棒(n=1.5),长500mm,两端面为凸的半球面,半径分别为r1=50mm, r2= -100mm,两球心位于玻璃棒的中心轴线上。
一箭头高y=1mm,垂直位于左端球面顶点之前200mm处,垂直于玻璃棒轴线。
试画出结构简图,并求a)箭头经玻璃棒成像在什么位置(l2')?b)整个玻璃棒的垂轴放大率为多少?答案:l2'= -400mm、-3第三章作业:1、已知一个透镜把物体放大-3⨯,当透镜向物体移近18mm时,物体将被放大-4⨯,试求透镜的焦距。
答案:216mm2、一个薄透镜对某一物体成实像,放大率为-1⨯。
以另一薄透镜紧贴此薄透镜,则见像向透镜方向移动了20mm,放大率为原来的3/4,求两薄透镜的焦距。
答案:40mm、240mm3、一束平行光入射到平凸透镜上,汇聚于透镜后480mm处。
如在此透镜凸面上镀反射膜,则平行光汇聚于透镜前80mm处,求透镜折射率和凸面曲率半径。
答案:1.5、-240mm5、一块厚透镜,n=1.6,r1=120mm,r2=-320mm,d=30mm,试求该透镜的焦距及基点位置。
如果物距l1= -5m,像在何处?如果平行光入射时,使透镜绕一和光轴垂直的轴转动,而要求像点位置不变,问该轴安装在何处?答案:f'=149.27mm、l F'=135.28mm、l F= -144.02mm、l H'= -13.99mm、l H=5.25mm l2'=139.87mm像方节点,即像方主点6、由两薄透镜组成的对无穷远物成像的短焦距物镜,已知其焦距为35mm,筒长T=65mm,后工作距为50mm,求系统结构。
浙教版科学七年级下第二章光学之平面镜易错题整理(含答案)解析版

浙教版科学七年级下第二章光学之平面镜易错题整理(含答案)解析版一、选择题1.如图所示,墙面上挂着标有“255”数字的牌子,在其相邻的一墙面上挂着一平面镜,地面上也放有一平面镜,通过平面镜不可能看到的数字是().A.522 B.552 C.225 D.252【答案】D【解析】墙面上挂着标有“255”数字的牌子,若平面镜是相对牌子是竖直方向的,则通过平面镜看到的数字是225,若平面镜是相对牌子是水平方向的,则通过平面镜看到的数字是522,若平面镜是相对牌子是倾斜方向的,则通过平面镜看到的数字有可能是552,总之,通过平面镜不可能看到的数字是252.故选2.如图所示,一平面镜放在圆筒的中心处,平面镜正对筒壁上的一点光源S,点光源S发出一细光束垂直射向平面镜。
平面镜从图示的位置开始绕圆筒的中心轴O匀速转动,在转动30º时,点光源在平面镜中所成的像在镜中转过的角度为θ1,照射到筒壁上的反射光转过的角度为θ2,则()A.θ1=30º,θ2=30ºB.θ1=30º,θ2=60ºC.θ1=60º,θ2=30ºD.θ1=60º,θ2=60º【答案】D【解析】如右图所示,平面镜旋转30°,相当于入射角增大30°,因为原先入射角为0°,(如左图)则入射角和反射角的夹角为60°,照射到筒壁上的反射光斑转过的角度θ2即为60°(如右图)由左右两图的“虚像”的位置可知:点光源在镜中所成的像转过的角度θ1为60°.3.如图所示,两面竖直放置的平面镜互成直角,在镜前A点有一只没有数字的钟指示为3点,在A点的人向O点看()第1 页,共6 页。
2023年大学_《光学》(赵凯华钟锡华著)课后习题答案下载

2023年《光学》(赵凯华钟锡华著)课后习题答案
下载
《光学》(赵凯华钟锡华著)内容简介
绪论
第一章几何光学
第二章波动光学基本原理
第三章干涉装置光场的时空相干性
第四章衍射光栅
第五章傅里叶变换光学
第六章全息照相
第七章光在晶体中的传播
第八章光的吸收、色散和散射
第九章光的量子性激光
《光学》(赵凯华钟锡华著)目录
《光学(上下)》分上、下两册。
上册主要内容:几何光学、波动光学基本原理、干涉装置和光场的`时空相干性。
下册主要内容:衍射光栅、傅里叶变换光学、全息照相、光在晶体中的传播、光的吸收、色散和散射、光的量子性和激光。
《仪器分析》第二章 光学分析法导论习题答案

第二章光学分析法导论1. 已知1电子伏特=1. 602×10-19J,试计算下列辐射波长的频率(以兆赫为单位),波数(以cm-1为单位)及每个光子的能量(以电子伏特为单位):(1)波长为900pm的单色X射线;(2)589.0nm的钠D线;(3)12.6µm的红外吸收峰;(4)波长为200cm的微波辐射。
解:已知1eV=1.602×10-19J, h=6.626×10-34J·s, c=3.0×108m·s-1①λ=900pm的X射线Hz,即3.333×1011MHzcm-1J用eV表示,则eV②589.0nm的钠D线Hz,即5.093×108MHzcm-1J用eV表示,则eV③12.6µm的红外吸收峰Hz,即2.381×107MHzcm-1J用eV表示,则eV④波长为200cm的微波辐射Hz,即1.50×102MHzcm-1J用eV表示,则eV2. 一个体系包含三个能级,如果这三个能级的统计权重相同,体系在300K温度下达到平衡时,试计算在各能级上的相对分布(N i/N).能级的相对能量如下。
(1) 0eV,0.001eV,0.02eV;(2) 0eV,0.01eV,0.2eV;(3) 0eV,0.1eV, 2eV。
解:已知T=300K, k=1.380×10-23J·K-1=8.614×10-5eV·K-1,kT=8.614×10-5×300=0.0258eV①E0=0eV, E1=0.001eV, E2=0.02eV②E0=0eV, E1=0.01eV, E2=0.2eV③E0=0eV, E1=01eV, E2=2eV3. 简述下列术语的含义电磁辐射电磁波谱发射光谱吸收光谱荧光光谱原子光谱分子光谱自发发射受激发射受激吸收电致发光光致发光化学发光热发光电磁辐射――电磁辐射是一种以巨大速度通过空间传播的光量子流,它即有波动性,又具有粒子性.电磁波谱――将电磁辐射按波长顺序排列,便得到电子波谱.电子波谱无确定的上下限,实际上它包括了波长或能量的无限范围.发射光谱――原来处于激发态的粒子回到低能级或基态时,往往会发射电磁辐射,这样产生的光谱为发射光谱.吸收光谱――物质对辐射选择性吸收而得到的原子或分子光谱称为吸收光谱.荧光光谱――在某些情形下,激发态原子或分子可能先通过无辐射跃迁过渡到较低激发态,然后再以辐射跃迁的形式过渡到基态,或者直接以辐射跃迁的形式过渡到基态。
光学实验知到章节答案智慧树2023年潍坊学院

光学实验知到章节测试答案智慧树2023年最新潍坊学院第一章测试1.光学实验室中常见的光源有()。
参考答案:热辐射光源;气体放电光源;激光光源2.钠光光源的波长为589.3nm。
()参考答案:对3.氦氖激光器发出的光波波长为632.8nm()。
参考答案:对4.光具座需要调节各个元件的等高共轴。
()参考答案:对5.使用测微目镜的过程中,将螺旋沿同一个方向旋转,目的是为了防止回城误差。
()参考答案:对6.分光计在使用前要进行调整,调整之前,要把仪器上的所有螺丝都调到中间的位置。
()参考答案:对7.借助双面镜调整垂直时,可随意放置。
()参考答案:错8.显微镜镜筒改变后,放大率也会随之改变。
()参考答案:对9.钠灯和汞灯点燃后一般要预热3~4分钟才能正常工作,熄灭后也需冷却3~4分钟后,方可重新开启。
()参考答案:对10.读数显微镜的读数鼓轮上每一个小格是0.1mm。
()参考答案:错第二章测试1.凸透镜成像时,物距在大于一倍焦距且小于两倍焦距处,成()。
参考答案:倒立放大实像2.用共轭法测凸透镜的焦距,不需要测量物距、像距。
()参考答案:对3.自准法测量凸透镜焦距,平面镜的位置最好在()。
参考答案:凸透镜近距离后面4.使用读数显微镜时,要单方向移动测量螺丝,以避免回程差。
()参考答案:对5.显微镜光学部分的照明系统由哪几部分构成?()参考答案:反射镜;聚光镜;可变光阑6.显微镜的转动手轮顺时针时会下降,逆时针时会上升。
()参考答案:对7.干涉和衍射是光具有波动性的具体表现。
()参考答案:对8.用测节器测定光具组基点时不需要准直物镜。
()参考答案:错9.分光计的主要结构包括( )。
参考答案:载物平台;望远镜;平行光管10.分光计的平线光管的作用是产生平行光,望远镜的作用是接收平行光,载物平台上放置光学元件。
()参考答案:对11.调整分光计至可以使用需要满足那几个条件?()参考答案:平行光管发出的平行光与主光轴垂直;载物平台与主光轴垂直;望远镜接收的光与主光轴垂直12.仪器调整好之后,望远镜的仰角螺丝,平行光管的仰角螺丝,载物平台底下的三个螺丝是不能再动的。
工程光学基础教程_习题参考答案

工程光学基础教程_习题参考答案工程光学基础教程_习题参考答案第一章光学基本知识与技术1.1 什么是光学?光学在人类生活中有哪些应用?答:光学是研究光的行为和性质的物理学科。
它涉及到光的产生、传播、变换、干涉、衍射、偏振以及光在介质中的行为等问题。
光学在人类生活中有着广泛的应用,如眼镜、镜头、显示器、照明、医疗器械、天文望远镜等。
1.2 光的波动性是如何描述的?答:光的波动性是指光是一种电磁波,具有振幅、频率、波长等特征。
它可以在空间中传播,并且可以表现出干涉、衍射等波动性质。
光的波动性可以通过波长、频率、振幅等参数进行描述。
1.3 什么是光的干涉?举例说明其应用。
答:光的干涉是指两列或两列以上的光波在空间中叠加时,由于光波的叠加产生明暗相间的干涉条纹的现象。
光的干涉在很多领域都有应用,例如光学干涉仪、双缝干涉实验、全息照相、光学通信等。
1.4 什么是光的衍射?举例说明其应用。
答:光的衍射是指光在遇到障碍物或孔径时,会绕过障碍物或孔径边缘,产生明暗相间的衍射图案的现象。
光的衍射在很多领域也有应用,例如光学透镜、衍射光学器件、全息照相、光学存储等。
1.5 什么是光的偏振?举例说明其应用。
答:光的偏振是指光波的电矢量在振动时,只在某个方向上振动,而在其他方向上振动为零的现象。
光的偏振在很多领域也有应用,例如偏振眼镜、偏振片、偏振光学器件等。
第二章光学透镜与成像2.1 什么是透镜?列举几种常见的透镜及其特点。
答:透镜是一种光学器件,它由一块透明材料制成,可以聚焦或发散光线。
常见的透镜包括凸透镜、凹透镜、平凸透镜、平凹透镜等。
2.2 凸透镜的成像原理是什么?如何计算凸透镜的焦距?答:凸透镜的成像原理是光线经过凸透镜后,平行于主轴的光线会聚于一点,这个点称为焦点。
焦距是指从透镜中心到焦点的距离。
凸透镜的焦距可以通过公式 f=1/v+1/u 进行计算,其中f为焦距,u为物距,v为像距。
2.3 凹透镜的成像原理是什么?如何计算凹透镜的焦距?答:凹透镜的成像原理是光线经过凹透镜后,平行于主轴的光线会朝透镜中心方向会聚于一点,这个点称为虚焦点。
高等光学教程-第2章参考答案

0.82
d
pd Z 0
Z 0 2.95 mm p
sin
(3)
V
pd Z 0
sin 3.19 4.76 10 3 3.19
2.6
有两束振幅相等的平行光,设它们相干,在原点处这两束光的初相位 10 20 0 , 偏振方向均垂直于 xoy 平面,这两束光的入射方向与 x 轴的夹角大小相等(如图 p2-6 所示) ,对称地斜射在记录面 yoz 上,光波波长为 633 nm 。 (1) 作出 yoz 平面,并在该平面上大致画出干涉条纹的形状,画三条即可。 (2) 当两束光的夹角 10 和 30 时,求 yoz 平面上干涉条纹的间距和空间频率。 (3) 设置于 yoz 平面上记录面感光物质的空间分辨率为 2000 条/mm,若要记录干涉条 纹,问上述相干涉的两束光波波矢方向的夹角 最大不能超过多少度。
第二章 干涉理论基础和干涉仪
2.1 用迈克耳逊干涉仪进行精密测长,光源波长为 633nm,其谱线宽度为 10
4
nm,光电接
收元件的灵敏度可达 1/10 个条纹, 问这台仪器测长精度是多少?一次测长量程是多少? 解答:设测长精度为 l ,则 l 由探测器接受灵敏度 N 10 所决定, 2 l N
所以电矢量的振幅以及电能密度的时间平均值沿 z 方向是周期变化的。由(1-81)式,电能 密度的时间平均值
Re( E D * )
1 4
0n2
4
(i ) Re( E E * ) 0 n 2 E 0
2
2 sin 2 2 kz
结果与坐标 z 有关,与坐标 x 、 y 无关。
2
工程光学第二章练习参考答案

(5)
n sinU NA sinU 0.1
U 5.73917 D 2( ltgU ) 2(45 tg 5.73917 ) 9.045mm
(5)
lz 160 D D' 1.667 9.00mm lz ' 29.63
(6)
-l (6)
l’ 180 -lz
h3 h2 d 2 tgu2 ' 12 10 0.04 11.6 tgu3 ' tgu3 h3 11.6 0.04 0.156 f3' 100
第二章 17
F’ 求物方参数。反向算。 h1=10
H’
u3’
f’
h1 10 f ' 64.102564 tgu3 ' 0.156 h3 11.6 lF ' 74.35897 tgu3 ' 0.156
第二章 17
求物方参数。反向算。
h1=10
H’
u3’
F’
f1 ' 50, f 2 ' 50, f 3 ' 100 d1 d 2 10
f’
lF’
tgu1 ' tgu2
h1
f1 '
10
50
0.2
h2 h1 d1tgu1 ' 10 10 ( 0.2) 12 tgu2 ' tgu3 tgu2 h2 f2' 0.2 12 50 0.04
第二章 3
y H -f d 1140mm 7200mm H’ f’ y’
l ' l 10
l d l ' 7200 2 f ' d 1140 1 1 1 l' l f'
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《激光导论》第二章 光学谐振腔
Download: FTP Server: 202.120.52.67 User: optics Password: optics Port: 8021
习题答案提示:
1. He-Ne 激光器的中心频率Hz 1401074.4×=ν,荧光线宽,今腔长
,问它可能输出的纵模数为多少?为获得单纵模输出,腔长最长为多长? Hz 9105.1×=∆νm d 1=提示: (1) n=10
(2)因为考虑腔长最长的情况,故只要νν∆>∆2
1q 即可,于是有 m d 2.0=2. 试证高斯光束基横模中有效截面内的光能占该模总光能的86.5%。
提示:高斯光束基横模的振幅部分为:
⎟⎟⎠
⎞⎜⎜⎝⎛+−=)(exp )(222000z w y x z w w C U 在任意z=constant 处,)
(000z w w C =constant ,w z w =)(=constant 。
所以 ⎟⎟⎠
⎞⎜⎜⎝⎛−=⎟⎟⎠⎞⎜⎜⎝⎛+−=220022200exp exp w r N w y x N U 在任意一截面上,高斯光束基横模中有效截面内的光能占该模总光能的百分比为
%5.8611424422exp 2exp 222002222002002220020022200=−=⋅⋅⎟⎟⎠⎞⎜⎜⎝⎛−⋅⋅=⎟⎟⎠⎞⎜⎜⎝⎛−⎟⎟⎠⎞⎜⎜⎝⎛−∫∫∫∫∞e w N e w w N drd w r N drd w r N w
ππϕϕππ 3. (1)计算腔长为的共焦腔基横模的远场发散角以及处的光斑面积。
设
;
m 1km 10o A 6328=λ(2)有一普通探照灯,设发散角为,则远处的光斑面积多大。
o 2km 1提示:(1) 远场发散半角为rad d w f 401035.62−×===λππ
λπλθ 远场发散角为
rad f 31027.12−×=θ 处的光斑面积为
2
2)tan (f L r S θππ⋅==km 102127m (2)请注意发散半角 远处的光斑面积为
o 1=f θkm 12957m 4. 考虑一用于氩离子激光器的稳定球面腔,波长m µλ5145.0=,腔长,腔镜曲率m d 1=
半径,。
试计算:
m R 5.11=m R 42=(1) 该球面腔的束腰半径和位置;
(2) 两镜面上的光斑尺寸;
(3) 画出等效共焦腔的位置。
提示:(1)
m z 86.01=mm w 348.00= (2)
mm w s 53.01=mm w s 35.02=5. 欲设计一对称光学谐振腔,波长m µλ06.1=,两反射镜间距m d 2=,如选择凹面镜曲
率半径,试求镜面上光斑尺寸。
若保持不变,选择,并使镜面上光斑尺寸,问此时镜的曲率半径和腔中心光斑尺寸多大?
d R =d d R >>cm w s 3.0=注意:请将原题中波长改为m µλ06.1=,否则不能满足题目中的条件
d R >>提示: 2120])2(1[)(d
z w z w += 镜面上光斑尺寸即2
d z =时的值 )(z w mm d w 58.0)2(= 根据教材P.46 式(2.6.21) ()412141
22
141221'22222242⎥⎦⎤⎢⎣⎡⎟⎠⎞⎜⎝⎛≈⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎟⎠⎞⎜⎝⎛−⎟⎠⎞⎜⎝⎛=⎥⎦⎤⎢⎣⎡−⎟⎠⎞⎜⎝⎛=d R d d d R R d d d R R d w s πλπλπλ 4
121'2058.03.02⎥⎦⎤⎢⎣⎡≈=⎟⎠⎞⎜⎝⎛d R d w s
πλ 所以
m R 8.715= 根据教材P.45 式(2.6.11)和(2.6.20)
mm d d R d w 32241210=⎟⎠
⎞⎜⎝⎛−⎟⎠⎞⎜⎝⎛=πλ 6. (1)要制作一个腔长的对称稳定腔,反射镜的曲率半径取值范围如何?
cm d 60=(2)稳定腔的一块反射镜的曲率半径d R 41=,求另一面镜的曲率半径取值范围。
(提示:请注意考虑另一面镜为凹面镜或凸面镜两种不同情况)
提示:(1)
cm R 30> (2) 凹透镜,凸透镜d R >2d R 32−<。
