模糊跟踪控制综合设计报告
《智能控制》-模糊控制实验报告

课程名称:智能控制实验名称:模糊控制一、实验目的:(1)了解在Simulink 仿真环境下建立控制系统方框图的方法,熟悉Matlab 和Simulink 仿真环境(2)掌握模糊控制器的设计方法。
(3)比较PID 控制和模糊控制的特点。
二、实验内容和步骤 已知s e s s s G 2.0214820)(-++=,分别设计PID 控制与模糊控制,使系统达到较好性能,并比较两种方法的结果。
结构如下图。
(1)模糊控制规则设计针对该定位系统,设计二维模糊控制规则,使性能达到最佳。
模糊控制规则如下:(2)设计未加PID或FUZZY控制器时,设计系统如下:输入阶跃信号,观测与分析仿真结果。
(3)加入PID控制器如下:对应的仿真结构图为:调整参数,观测与分析仿真结果。
PID控制的仿真曲线如下:(4)设计FUZZY控制器在simulink仿真环境下,设计模糊控制系统,包括模糊控制规则、隶属函数、比例因子、量化因子、论域等参数设计。
FUZZY控制仿真结构图如下:其中黄色部分具体为:利用simulink设计的模糊控制的仿真结构图为:其中对于模糊控制器的设计:E=[-6 6] EC=[-6 6] U=[-6 6],并且其隶属函数分别为:E的隶属函数EC的隶属函数U的隶属函数再将其中一个学生的比较好的实验结果作为参考实例:首先仿真图如下:模糊控制器的设计:E=[-6 6] EC=[-6 6] U=[-6 6],并且其隶属函数分别为:E和EC的隶属函数U的隶属函数控制规则:ECNB NM NS ZE PS PM PB ENB PB PB PB PB PM ZE ZENM PB PB PB PB PM ZE ZENS PM PM PM PM ZE NS NSZE PM PM PS ZE NS NM NMPS PS PS ZE NM NM NM NMPM ZE ZE NM NB NB NB NBPB ZE ZE NM NB NB NB NB设计好模糊控制器后,运行仿真图形,得到的仿真曲线如下(step time=1):模糊控制的仿真曲线由仿真可知,通过选择合适的PID参数可以达到较好的控制性能。
模糊控制实验报告

模糊控制实验报告本实验通过使用模糊控制器来控制直流电机的转速。
模糊控制是一种基于模糊推理的控制方法,该方法可以处理一些无法准确数学建模的系统控制。
模糊控制的输入和输出都是模糊变量,这样可以考虑到系统存在的不确定性和模糊性。
实验装置包括模糊控制器、直流电机、转速测量装置、实验板等。
模糊控制器由模糊推理机、偏差和变化率输入模糊化模块、输出反模糊化模块、规则库组成。
实验板可通过控制开关选择转速和方向。
在实验中,通过设置转速值和方向,记录电机的真实转速和输出控制信号,来验证模糊控制器的控制效果。
通过不同的控制变量和规则库来对比不同的控制方案。
实验结果表明,模糊控制器对于直流电机转速的控制具有较好的效果。
当控制变量为偏差和变化率时,规则库中的设定合理,输出控制信号的变化平稳,电机转速较为稳定。
当增加控制变量或修改规则库时,控制效果也发生了变化。
同时,实验还验证了模糊控制的重要性和优越性,可以解决一些无法准确建模的系统控制问题。
在实验中,还需要注意一些实验细节,例如校准直流电机转速传感器的准确度,保证实验板电路的正常工作和实验数据的准确性,减少误差的影响。
总之,本实验通过实际操作验证了模糊控制器在直流电机转速控制中的应用,对于学习模糊控制的控制方法和实验操作具有很好的参考意义。
同时,本实验也展示了模糊控制对于处理模糊问题的效果。
在直流电机转速控制中,存在许多因素的影响导致控制过程不确定和模糊,例如负载的变化、外部干扰的存在等等。
而模糊控制可以将这些不确定因素转化为模糊变量进行处理,从而提高控制精度和鲁棒性。
此外,本实验也强调了规则库的重要性。
规则库是模糊控制中很关键的一部分,其中包含了专家经验和数学模型的映射关系。
规则库中的设定需要充分考虑被控对象的特性,才能够保证模糊控制器的控制效果。
而实验中不同的规则库设计对于控制效果的影响也展现了模糊控制的灵活性和可定制性。
最后,本实验的数据记录和实验结果分析也为后续工程实际应用提供了很好的参考。
模糊控制实验报告

模糊控制系统实验报告学院:班级::学号:、实验目的1.通过本次实验,进一步了解模糊控制的基本原理、模糊模型的建立和模糊控制器的设计过程。
2.提高有关控制系统的程序设计能力;3.熟悉Matlab语言以及在智能控制设计中的应用。
二、实验内容设计一个采用模糊控制的加热炉温度控制系统。
被控对象为一热处理工艺制作中的加热炉,加热设备为三相交流调压供电装置,输入控制信号电压为0-5V,输出相电压为0-220V,输出最大功率180kW炉内变化室温~625C。
三、实验过程及步骤1.用Matlab中的Simulink工具箱,组成一个模糊控制系统,如图所示2.采用模糊控制算法,设计出能跟踪给定输入的模糊控制器,对被控系统进行仿真,绘制出系统的阶跃响应曲线(1)模糊集合及论域的定义对误差E、误差变化EC机控制量U的模糊集合及其论域定义如下: E、EC和U的模糊集合均为:{NB、NM NS 0、PS PM PB}E和EC的显示范围为:[-6 6]结果如下图所示FIS Editor: UntitledFile Edit Viev;FIS VariablesEMECin put variable "E"Current VariableNameTypeRangeDisplay RangeEinput[-6 6]Help Close Select etl variable "E"File Edit Viev^Current VariableNsrueTypeRangeDitsptey RangeSelected variable 'U"打开Rule编辑器,并将49条控制规则输入到Rule编辑器中FIS VariablesLIoutput06】[-6 6]Rule Editor: UntitledECouiput variable "U1利用编辑器的” View T Rules”和” View^Surface ”得到模糊推理系统的模糊规则和输入输出特性曲面,分别如下图所示Fil e Edit Viev; OptionsFile Edit Viev^ OptionsRule Viewer Untitled忻珅:[□ g]Plot points: 101left down up ReadySurface Viewer: UntitledE "U = 1.a3e-D0&Move:Help Close口从图中可以看出,输出变量U 是关于两个输入变量E 、EC 的非线性函 数,输入输出特性曲面越平缓、光滑,系统的性能越好。
移动机器人路径跟踪模糊控制系统设计及仿真

( nigUn e i f otadT lcmmu i t n nig20 0 hn) Naj i rt o P s e o n v sy sn e nc i s j 103C ia a o Na n
Absr t t ac :The m an c nt n ft spa ri i o e t o hi pe sAppi a on off z o i ,U nd rt ond to o lc t i uz y l g c e he c ii n fkno n goba t w l lpah
i ood c sg oncuso . l i ns K ey o ds i u a on; r bot pah—f Ho i w r :sm lt i o ; t —o w ng
2口1 . 19
De i n & Re e r h sg s ac
0 引言
利用模糊逻辑在移动机器人运动控制 中的优越性,采
点的位 置 ; 预瞄点确定以后 ,再根据移动机器人当前点相
具独特的优势 , 本文结合 驾驶 员的丰富经验设计了移动机 器人的模 糊控制器 。设计 出移动机器人运 动控制进行仿真 的方法及程序流程 , 然后对仿真结果进行了分析比较 , 说
明模 糊控制器 的有效 性。
对于预瞄点的距离长短和方向偏差大小由角速度 ,线速度
模糊控制 器控制输 出移 动机器人 的线 速度 V和 角速度 ∞, 再 由移动机器人的运动模块完成运动控制。
1 移动机器人模糊控制 系统设计
对于移动机器人的运动控制 问题 ,首先是要对经过机 器视觉检测和处理而成的规划路径进 行分析 ,其次就是根
踪运动 中的应用 。利用模糊逻辑在移动机器人运动控制中的优越性 ,结合驾驶员的丰富经验设计 了移动机器人 的模 糊控制器 ,包括一个预 瞄距 离确定器和一个 运动模糊控 制器 。设 计出移动机器人运 动控制进行仿真 的方 法及程 序流程 ,对其进行 计算机仿真验证控 制效 果, 对仿真 结果进行 了分析比较 , 出模糊控制器达 到设 计要 得
智能控制--模糊控制实验报告

clear all;close all;T=0; %ʱ¼ä³£Êýa=newfis('fuzz_temperatrue');a=addvar(a,'input','e',[-3,3]); %Parameter e a=addmf(a,'input',1,'NB','zmf',[-3,-1]);a=addmf(a,'input',1,'NM','trimf',[-3,-2,0]);a=addmf(a,'input',1,'NS','trimf',[-3,-1,1]);a=addmf(a,'input',1,'Z','trimf',[-2,0,2]);a=addmf(a,'input',1,'PS','trimf',[-1,1,3]);a=addmf(a,'input',1,'PM','trimf',[0,2,3]);a=addmf(a,'input',1,'PB','smf',[1,3]);a=addvar(a,'output','u',[72,78]); %Parameter u a=addmf(a,'output',1,'NB','zmf',[72,74]);a=addmf(a,'output',1,'NM','trimf',[72,73,75]);a=addmf(a,'output',1,'NS','trimf',[73,74,75]);a=addmf(a,'output',1,'Z','trimf',[74,75,76]);a=addmf(a,'output',1,'PS','trimf',[75,76,77]);a=addmf(a,'output',1,'PM','trimf',[75,77,78]);a=addmf(a,'output',1,'PB','smf',[76,78]);rulelist=[1 1 1 1; %Edit rule base2 2 1 1;3 3 1 1;4 4 1 1;5 5 1 1;6 6 1 1;7 7 1 1];a=addrule(a,rulelist);a1=setfis(a,'DefuzzMethod','mom'); %Defuzzywritefis(a1,'temperatrue'); %Save to fuzzy file "tank.fis" a2=readfis('temperatrue');figure(1);plotfis(a2);figure(2);plotmf(a,'input',1);figure(3);plotmf(a,'output',1);flag=1;if flag==1showrule(a) %Show fuzzy rule baseruleview('temperatrue'); %Dynamic Simulationenddisp('-------------------------------------------------------');disp(' fuzzy controller table:e=[-3,+3],u=[-4,+4] ');disp('-------------------------------------------------------');for i=1:1:7e(i)=i-4;Ulist(i)=evalfis([e(i)],a2);endUlist=round(Ulist)e=-3; % Erroru=evalfis([e],a2) %Using fuzzy inference四、Simulink仿真模型五、实验结果令T=0;1、模糊控制器为一维控制器,输入输出变量的量化等级为7级,取5个模糊集。
模糊控制课程设计报告
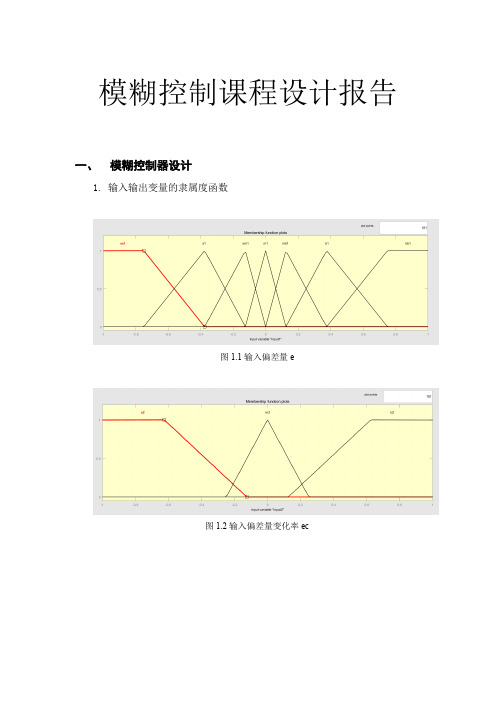
模糊控制课程设计报告一、模糊控制器设计1.输入输出变量的隶属度函数图1.1输入偏差量e图1.2输入偏差量变化率ec图1.3输出控制量u2.模糊规则设置1.if(input1 is ss1 ) and (input2 is s2)then (output1is b3)2.if(input1 is ss1 )and (input2 is m2)then (output1 is b3)3.if(input1 is ss1 )and (input2 is b2)then (output1 is mb3)4.if(input1 is s1 ) and (input2 is s2)then (output1 is b3)5.if(input1 is s1 )and (input2 is m2)then (output1 is mb3)6.if(input1 is s1 ) and (input2 is b2)then (output1 is m3)7.if(input1 is sm1) and (input2 is s2)then (output1 is mb3)8.if(input1 is sm1)and (input2 is m2)then (output1 is mb3)9.if(input1 is sm1)and (input2 is b2)then (output1 is m3)10.if(input1 is bb1)and (input2 is b2)then (output1 is s3)11.if(input1 is bb1)and (input2 is m2)then (output1 is s3)12.if(input1 is bb1)and (input2 is s2)then (output1 is sm3)13.if(input1 is b1) and (input2 is b2)then (output1 is s3)14.if(input1 is b1)and (input2 is m2)then (output1 is sm3)15.if(input1 is b1)and (input2 is s2)then (output1 is m3)16.if(input1 is mb1)and (input2 is b2)then (output1 is sm3)17.if(input1 is mb1)and (input2 is m2)then (output1 is sm3)18.if(input1 is mb1)and (input2 is s2)then (output1 is m3)19.if(input1 is m1)and (input2 is m2)then (output1 is m3)20.if(input1 is m1)and (input2 is s2)then (output1 is mb3)21.if(input1 is m1)and (input2 is b2)then (output1 is sm3)二、Simulink回路设计1.设计思路按照书中所示的基本结构将偏差、控制器、被控对象连接成一个回路,通过将偏差和偏差变化率输入模糊控制器,得到输出控制力矩u输入到被控对象中,最终得到理想的控制结果。
模糊控制实验报告

西安交通大学实验报告第1页(共13页)课程:智能控制实验日期:年月日专业班号:自动化交报告日期:年月日姓名:学号:报告退发:(订正、重做)同组者:教师审批签字:实验一模糊控制仿真系统设计实验目的:理解和掌握模糊控制系统的构成和设计方法,为实际工程应用打下基础。
基本要求:掌握以误差及其变化率为输入的典型模糊控制器的设计方法,了解影响模糊控制器性能的关键参数及调节方法。
针对被控对象,构建合适的模糊控制器,搭建模糊控制系统。
实验内容提要:针对典型的二阶以上被控对象,设计模糊控制器。
包括控制器输入输出量的选择,输入输出论域的模糊划分,模糊规则库的建立等。
利用设计完成的模糊控制在Simulink中搭建模糊控制系统,要求该系统稳定且具有良好的动态及稳态特性。
实验工作概述:主要针对倒立摆进行了建模与模糊控制仿真,其中实验1-1是仅针对角度的模糊PID控制,实验1-2是针对位置与角度的分段模糊控制。
后面也尝试进行了二级倒立摆的模糊控制设计,但由于知识水平不够没能完全实现,仅实现了第一级的直立控制。
实验1-1 单级倒立摆的PID模糊控制一、被动对象数学描述与特性分析关于倒立摆的相关背景:倒立摆,Inverted Pendulum ,是典型的多变量、高阶次、非线性、强耦合、自然不稳定系统。
倒立摆系统的稳定控制是控制理论中的典型问题,在倒立摆的控制过程中能有效反映控制理论中的许多关键问题 ,如非线性问题、鲁棒性问题、随动问题、镇定、跟踪问题等。
因此倒立摆系统作为控制理论教学与科研中典型的物理模型 ,常被用来检验新的控制理论和算法的正确性及其在实际应用中的有效性。
所以我此次实验采用一阶倒立摆来验证。
当摆杆夹角很小时,近似线性化处理:(I +ml 2)θ+mglθ=mlẍ (M +m )ẍ+bẋ−mlθ=u根据微分方程组做拉普拉斯变换联立求得外力针对角度的传递函数:Φ(s)U(s)=ml 2qs 2s 4+b(I +ml 2)q s 3−(M +m )mgl q s2−bmql q s将各种参数输入matlab ,编辑一个函数脚本GetPendulum 来求传递函数的系数:当M=2,m=0.8,l=0.25时,求得:这是一个典型的二阶系统二、模糊控制器的设计步骤与具体参数选择模糊集合设计:总共有两个输入三个输出,输入角度和角度微分的模糊集合划分都相同,论域为[-5,5],模糊集合为3个,分别命名为:[N Z P],输出P I D三个参数的范围分别为[110,120],[115,125],[80,90],模糊集合为3个命名为:[S M B]它们的分布如上图所示。
实验三 模糊控制实验报告示例

实验三模糊控制实验班别:自动化081 姓名:覃健学号:200800301031一实验过程1 对模糊控制模块建立模糊规则的步骤(1)在Command window 命令窗口中输入fuzzy,按enter弹出模糊规则窗口;(2)加入一个输入,在弹出的窗口中选择Edit→Add V ariable→input;(3)在name中更改input1为“e”,input2为“ec”,output为“u”;(4)双击e对e的设置:a, 选择Edit→Add MFs→numbers of MFs 中选择4;b,在range和display range中设置隶属函数图的取值范围;c,更改mf1~mf7的参数,分别命名为“NB”、“NM”、“NS”、“Z”、“PS”、“PM”、“PB”,并设置三角形的顶点值,其中'NB'的类型为'zmf','PB'为'smf'其他的都为'trimf',结果如下图所示:(5)重复步骤(4)对ec、u进行设置,结果如下图所示:(6)双击mamdani,设置49条Rules命令语句,结果如下图所示:(7)在Defuzzification中选择mom;(8)最后完成模糊规则的建立如下图所示,然后选择file→export→to workspace,保存到工作路径中;2simulink仿真(1)打开simulink模块库浏览器窗口,然后选择菜单file→new→model,新建空白的模型窗口;我们所需要画的模块框图,框图如下所示,按下图在simulink模块库中查找我们所需的模块,拉到模型窗口中,然后连接各个模块,画好图形。
(2)画好图形后,设定载入模糊控制模块的模糊规则:a,双击模糊控制模块,输入文件名为之前设计好的模糊规则fuzza;b,右键选择look under mask,在弹出的窗口中双击模糊控制木块,在弹出的选择框中输入fuzza;然后就可以进行仿真。
T-S模糊系统H∞跟踪控制器设计

关键 词 : T—S模 糊 系统 ; 积分 型模 糊 L y a p u n o v函数 ; H 跟 踪控 制 ; 线性 矩 阵不等 式
最 近几 年 , T—s模 糊控 制器 非线 性 系 统 正被 成 功应 用 ] .在 大 多数 应 用 中 , 模 糊 系 统 被 看作 是 非 线
性 系统 的通 用逼 近技 术 .正如 文献 所述 , T—S模糊 模型 对 于描述 非线性 系 统 的动态 是准确 的 .因此 , 模 糊技 术 也被 成功 的用 于研 究跟 踪控 制 问题 .
中图分类 号 : T P 2 7 3 . 4 文献 标志 码 : A 文 章编 号 : 1 6 7 3—0 5 6 9 ( 2 0 1 7 ) 0 1— 0 0 1 3— 0 6
0 引 言
稳 定 和跟踪 是 两类 典型 的控 制 问题 .一般 而 言 , 跟 踪要 比稳 定 更加 困难 , 特别 是 对 于非 线性 系 统.对
M d i 的 隶 属度 且满 足 ( ( ) ) ≥0 , ∑h i ( ( ) )= 1 .
那 么 根据上 述 的 阐述 , 系统 ( 1 )可 以重 新 写为 :
f ( £ )=A ( ) ( )+B ( ) “ ( )+ ( ^ ) ( )
t z ( )= C ( ) ( £ )+D( ) ∞( £ )
, 、
、
其 中, A( )= h ( ( ) ) A , A =A, B, C, D, E . 设 参考模 型 为 ( )=A r , ( )+r ( ) ( 3 )
自适应模糊跟踪系统的设计

“ = -() y’ k ] ‘ ÷[f + 4 r x -e
收稿 日期 :0 1 0 2 1 — 7—1 1 修回 日期 :0 1 0—1 2 1 —1 2
() 3
作者简介 : 段玉垒 (9 0 ) 男 , 18一 , 河南修武人 , 士 , 硕 讲师 , 研究方 向 : 自适应模糊系统及应用
从 仿 真 中得 到验 证. 尤其 是 当 系统 的参 考轨 线 是变 化 的值 时候 ( 跟踪 系统 设计 ) 即使参 数 自调 整器 始终 运 ,
行着 , 选取 X 作为输入变量的 自适应模糊控制系统的控制效果也有可能很差. 当要求实现系统跟踪设计时, 文献¨ 中提 出了一个改进 的方法, , 即 将系统 的参考轨线 Y 也作为模糊
() 5
其 中 , =1 2 Z , ,… , m; 1 2 , ,… , ; 意 , 果实 际应用 中采 用模 糊 规则 来 描述 系 统 的控制 知 识 可 以获 n注 如 得到 , 则可 将其嵌 入 到模 糊 系统 的初 始参 数 中去.
2 白适应模糊跟踪 系统 的实现
它的结构模型 的重要特征. 这里主要讨论基于 Lauo 综合法 的 白 ypnv 适应模糊控制系统 , 其绝大多数文 献 “资料 中, 卜 模糊系统的结构都是选取状态向量 x 作为输入变量的, 而且此方法都假设了存在着一个最优 控制律. 但是 , 选取 x 作为输入变量的 自 适应模糊控制系统 的控制律并不是收敛到某个 固定的最优值 , 而是 不停地调整参数 0 来消除控制误差 的( 系统控制 目标的参考轨线为常数值 的情况下除外 ) 我们通过实验结 , 果可 以明显 地看 出这 一 问题 , 只需 经过 一段 时 间的参数 自调 整后 , 止其 参数 的 自调 整 功 能 , 可 以简单 地 停 便
《模糊控制》课程实验报告

《模糊控制》课程实验报告学院:___________________专业:___________________班级:___________________学号:___________________姓名:___________________同组:___________________成绩:___________________指导教师:_______________提交日期:_______________批改日期:_______________存档日期:_______________Harbi n In stitute of Tech no logy2005.1一、实验目的利用Matlab软件实现模糊控制系统仿真实验,了解模糊控制的查询表方法和在线推理方法的基本原理及实现过程,并比较模糊控制和传统PID控制的性能,得出结论。
二、实验要求设计一个二维模糊控制器分别控制一个一阶被控对象和二阶被控对象。
先用模糊控制器进行控制,然后改变控制对象参数的大小,观察模糊控制的鲁棒性。
为了进行对比,再设计PID控制器,同样改变控制对象参数的大小,观察PID 控制的鲁棒性。
三、实验步骤叙述查询表式模糊控制系统仿真及在线推理模糊控制的仿真的主要步骤。
四、实验内容(一)查询表式模糊控制系统仿真实验11、一阶对象Gi(s) 米用查询表式方法进行仿真实验,自己选定Ke,Ts + 1Ku,Kec的值,通过仿真实验观察它们各自对控制性能的影响。
从而确定一组较好的参数值并填入表中。
然后按下表中给出的数值调整对象参数并观察输出响应曲线,将实验结果填入下表。
控制参数:Ke二Ku二Kec二2、给定对象参数T1二2,通过调整两组控制参数Ke, Ku, Kec 使其得到较 好的响 应 曲 线 , 将 结 果 填 入 下 表 中 。
(二)给定二阶对象G 2 (s ): 仃2+1皿+1)1、采用在线模糊推理方法进行仿真实验,自己选定对象参数,调整控制参数Ke ,Ku ,Kec ,得到较好的响应曲线,并把实验结果填入下表。
模糊控制实验报告

模糊控制实验报告1.引言随着科技的不断发展,模糊控制理论在控制系统中的应用越来越广泛。
模糊控制通过将精确的数学模型转化为模糊的规则,可以更好地适应复杂、非线性的控制系统。
本实验旨在通过设计一个模糊控制系统来实现对一个简单的水温控制过程的控制,以验证模糊控制在实际系统中的有效性。
2.实验原理本实验将一个简化的水温控制过程作为被控对象,控制目标是使得水温保持在一个设定的温度范围内。
水温的变化是由水流量和加热功率两个因素决定的。
因此,控制系统的输入变量为水流量、加热功率,输出变量为水温。
通过模糊控制器根据当前的水温及其变化率来调节水流量和加热功率,从而实现对水温的控制。
模糊控制器的输入变量为当前的水温和水温变化率,输出变量为水流量和加热功率的控制信号。
通过设定一系列模糊规则,模糊控制器可以根据当前的输入变量来决定输出变量的值,并调整其大小以实现对水温的精确控制。
3.实验步骤1)设定水温的设定值及其变化率,作为模糊控制器的输入变量。
2)使用模糊推理方法,通过设定一系列模糊规则,将输入变量映射到输出变量。
3)根据输出变量的值,调节水流量和加热功率的控制信号。
4)监测水温的变化,根据测量结果对模糊控制器进行调整,以提高控制的精度。
5)重复步骤3和4,直到水温稳定在设定的范围内。
4.实验结果经过多次实验,我们成功地设计出了一个能够稳定控制水温的模糊控制系统。
在不同的设定值和变化率下,模糊控制器都能够根据当前的输入变量来自适应地调节输出变量的值,使水温保持在设定的范围内。
通过对实验数据的分析,我们发现模糊控制系统具有较好的动态性能和鲁棒性。
在水温变化较快的情况下,模糊控制器能够及时地调整输出变量的值,使水温能够迅速回到设定的范围内。
而在水温变化较慢的情况下,模糊控制器能够稳定地控制输出变量的值,使水温能够保持在设定的范围内。
对比传统的PID控制器,我们发现模糊控制系统在对非线性系统和难以建模的系统进行控制方面具有明显的优势。
简单的模糊控制实验报告

实验报告课程名称智能控制学院自动化学院班级姓名学号日期2019.4.9基于mamdani 型模糊控制器线性系统的位置跟踪一、实验目的1.熟悉mamdani 模糊控制器的设计原理;2.掌握模糊控制器的设计步骤;3.熟悉模糊控制规则对控制系统效果的影响 ;4.熟悉模糊控制器设计的Matlab 命令;5.掌握用MATLAB 实现模糊控制系统仿真的方法。
二、设备及条件 计算机系统Matlab 仿真软件三、实验原理根据跟踪误差及其变化率,设计模糊控制器使得跟踪误差趋近于零。
四、设计要求 已知某一线性系统2400500s s+,根据误差及其变化率来设计模糊控制器,使得闭环系统的输出跟踪正弦信号0.5sin(10)t ,已知:误差及其变化率的范围初步定为[]33-,要求分为7个模糊集; 输出的范围初步定为[]4.5 4.5-,要求分为9个模糊集;设计隶属度函数误差变化划分表,控制电压变化划分表和模糊控制规则表,基于MATLAB 实现该控制器,并对控制效果进行仿真,根据仿真结果对模糊控制规则、控制信号范围、误差及其变化率进行调整。
五、实验环境I Simulink 介绍1.1 Simulink 简介Simulink 是MATLAB 中的一种可视化仿真工具, 是一种基于MATLAB 的框图设计环境,是实现动态系统建模、仿真和分析的一个软件包,被广泛应用于线性系统、非线性系统、数字控制及数字信号处理的建模和仿真中。
1.2 Simulink 优点Simulink 提供一个动态系统建模、仿真和综合分析的集成环境。
在该环境中,无需大量书写程序,而只需要通过简单直观的鼠标操作,就可构造出复杂的系统。
对各种时变系统,包括通讯、控制、信号处理、视频处理和图像处理系统,Simulink 提供了交互式图形化环境和可定制模块库来对其进行设计、仿真、执行和测试。
II模糊控制工具箱介绍2.1 模糊控制工具箱简介MATLAB模糊控制工具箱为模糊控制器的设计提供了一种非常便捷的途径,通过它我们不需要进行复杂的模糊化、模糊推理及反模糊化运算,只需要设定相应参数,就可以很快得到我们所需要的控制器,而且修改也非常方便。
基于模糊控制的环境监测与控制系统设计

基于模糊控制的环境监测与控制系统设计近年来,环境污染问题日益严重,为了改善环境质量、保护生态环境,环境监测与控制越来越受到人们的关注。
为了实现对环境的准确监测和有效控制,我们可以运用模糊控制技术,设计一种基于模糊控制的环境监测与控制系统。
一、环境监测与控制系统的必要性环境污染已经成为制约经济社会可持续发展的重要因素之一。
环境问题的解决需要依靠环境监测和控制。
通过环境监测,我们可以了解环境的污染状况以及变化趋势;通过环境控制,我们可以对环境进行相应的治理,以达到保护环境、保障人类健康的目的。
现在的环境监测和控制手段依然存在很多问题,其中最主要的是单一控制。
单一控制的特点就是只有在系统的一些方面上进行监测与控制,而不是全面监测。
这会导致一些“盲区”没有被发现也就没有被解决。
另外,传统的控制方法存在许多问题,比如说反应时间较长、操作难度较大等。
二、基于模糊控制的环境监测与控制系统的设计1、系统的功能基于模糊控制的环境监测与控制系统,可以完成环境条件的准确检测和相应的治理。
系统通过传感器进行感知,将数据传递到控制板中,再通过模糊识别和控制算法进行处理和分析,反馈控制信号调节作用执行机构,来达到控制治理的目的。
2、系统的构成一个基于模糊控制的环境监测与控制系统,主要包括四个部分:检测与传输模块、模糊控制模块、执行机构模块、用户界面模块。
(1)检测与传输模块:主要负责采集环境情况,并将采集到的数据传输到系统中。
(2)模糊控制模块:主要根据环境数据分析和研究,确定操作指令和相应的控制策略。
(3)执行机构模块:主要负责执行控制策略,完成环境治理任务。
(4)用户界面模块:主要提供人机交互的界面,操作人员可以通过这个界面来设置控制参数、查看控制效果等。
3、系统的工作原理系统中的检测与传输模块可以采集环境的数据,包括温度、湿度、空气质量等信息。
得到这些数据后,系统将自动根据预设的模糊控制算法进行计算,判断当前环境状况下所需要的治理措施,并将计算结果反馈给执行机构模块。
模糊跟踪控制综合设计报告

自动化专业综合设计报告设计题目:模糊跟踪控制一、设计目的学习模糊控制的理论基础,了解模糊控制的概念,掌握模糊控制的基本方法;熟悉Matlab,学习模糊控制的Matlab仿真,设计模糊控制器,实现控制系统输出跟踪期望信号;熟悉模糊跟踪控制器的基本原理,学会通过改变跟踪信号,看仿真结果;学会改变控制系统,看仿真结果。
二、设计要求熟悉Matlab ,参考教材的第三章和第四章4.1,4.3;设计模糊控制器,实现控制系统输出跟踪期望信号;熟悉模糊跟踪控制器的基本原理,熟悉模糊跟踪控制的程序和结构框图;改变跟踪信号,看仿真结果;改变控制系统,看仿真结果。
三、设计内容(可加附页)(一)、设计模糊控制器,实现控制系统输出跟踪期望信号。
通过设计模糊跟踪控制程序实现跟踪控制功能。
其中模糊控制器组成原理框图如下图设计的控制器原理结构图如下根据以上原理图进行编程,并绘制以下结构框图,通过修改程序参数完成模糊跟踪控制器的设计。
其中原程序为:%Fuzzy Controller Designclear all;close all;a=newfis('fuzzf');f1=1;a=addvar(a,'input','e',[-3*f1,3*f1]); %Parameter ea=addmf(a,'input',1,'NB','zmf',[-3*f1,-1*f1]);a=addmf(a,'input',1,'NM','trimf',[-3*f1,-2*f1,0]);a=addmf(a,'input',1,'NS','trimf',[-3*f1,-1*f1,1*f1]);a=addmf(a,'input',1,'Z','trimf',[-2*f1,0,2*f1]);a=addmf(a,'input',1,'PS','trimf',[-1*f1,1*f1,3*f1]);a=addmf(a,'input',1,'PM','trimf',[0,2*f1,3*f1]);a=addmf(a,'input',1,'PB','smf',[1*f1,3*f1]);f2=1;a=addvar(a,'input','ec',[-3*f2,3*f2]); %Parameter ec a=addmf(a,'input',2,'NB','zmf',[-3*f2,-1*f2]);a=addmf(a,'input',2,'NM','trimf',[-3*f2,-2*f2,0]);a=addmf(a,'input',2,'NS','trimf',[-3*f2,-1*f2,1*f2]);a=addmf(a,'input',2,'Z','trimf',[-2*f2,0,2*f2]);a=addmf(a,'input',2,'PS','trimf',[-1*f2,1*f2,3*f2]);a=addmf(a,'input',2,'PM','trimf',[0,2*f2,3*f2]);a=addmf(a,'input',2,'PB','smf',[1*f2,3*f2]);f3=1.5;a=addvar(a,'output','u',[-3*f3,3*f3]); %Parameter u a=addmf(a,'output',1,'NB','zmf',[-3*f3,-1*f3]);a=addmf(a,'output',1,'NM','trimf',[-3*f3,-2*f3,0]);a=addmf(a,'output',1,'NS','trimf',[-3*f3,-1*f3,1*f3]);a=addmf(a,'output',1,'Z','trimf',[-2*f3,0,2*f3]);a=addmf(a,'output',1,'PS','trimf',[-1*f3,1*f3,3*f3]);a=addmf(a,'output',1,'PM','trimf',[0,2*f3,3*f3]);a=addmf(a,'output',1,'PB','smf',[1*f3,3*f3]);rulelist=[1 1 1 1 1; %Edit rule base1 2 1 1 1;1 32 1 1;1 42 1 1;1 5 3 1 1;1 6 3 1 1;1 7 4 1 1;2 1 1 1 1;2 2 2 1 1;2 3 2 1 1;2 43 1 1;2 53 1 1;2 6 4 1 1;2 7 5 1 1;3 1 2 1 1;3 2 2 1 1;3 3 3 1 1;3 4 3 1 1;3 54 1 1;3 6 5 1 1;3 7 5 1 1;4 1 2 1 1;4 2 3 1 1;4 3 3 1 1;4 4 4 1 1;4 5 5 1 1;4 65 1 1;4 7 6 1 1;5 1 3 1 1;5 2 3 1 1;5 3 4 1 1;5 4 5 1 1;5 5 5 1 1;5 6 6 1 1;5 76 1 1;6 1 3 1 1;6 2 4 1 1;6 3 5 1 1;6 4 5 1 1;6 5 6 1 1;6 6 6 1 1;6 7 7 1 1;7 1 4 1 1;7 2 5 1 1;7 3 5 1 1;7 4 6 1 1;7 5 6 1 1;7 6 7 1 1;7 7 7 1 1];a=addrule(a,rulelist);%showrule(a) % Show fuzzy rule base a1=setfis(a,'DefuzzMethod','mom'); % Defuzzywritefis(a1,'fuzzf'); % save to fuzzy file "fuzz.fis" which can be% simulated with fuzzy toola2=readfis('fuzzf');disp('-------------------------------------------------------');disp(' fuzzy controller table:e=[-3,+3],ec=[-3,+3] ');disp('-------------------------------------------------------');Ulist=zeros(7,7);for i=1:7for j=1:7e(i)=-4+i;ec(j)=-4+j;Ulist(i,j)=evalfis([e(i),ec(j)],a2);endendUlist=ceil(Ulist)figure(1);plotfis(a2);figure(2);plotmf(a,'input',1);figure(3);plotmf(a,'input',2);figure(4);plotmf(a,'output',1);通过Matlab仿真软件绘制结构框图实现以上功能,如下图(二)、改变跟踪信号,看仿真结果;将原有正弦信号改成锯齿波信号,看仿真结果。
模糊控制算法研究

模糊控制算法研究——实验报告一、实验目的1、通过本次综合设计,进一步了解模糊控制的基本原理、模糊模型的建立和模糊控制的设计过程。
2提高学生有关控制系统的程序设计能力。
3熟悉MATLAB语言以及在智能控制设计中的应用。
二、实验内容1、用MATLAB中的SIMULINK工具箱,组成一个模糊控制系统。
如图:2、采用模糊控制算法,设计出能跟踪给定输入的模糊控制器,对被控系统进行仿真,绘制出系统的阶跃响应曲线。
3、改变模糊控制器中模糊变量的隶属度函数,分析隶属度函数和模糊控制规则对模糊控制效果的影响。
三、实验步骤1、启动SIMULINK。
打开MATLAB程序,并在该窗口键入SIMULINK来运行SIMULINK,或单击工具栏上SIMULINK按钮,这时SIMULINK就显示其所包含的子模块库。
2、创建一个新模型。
在FILE菜单中选择NEW-MODEL,SIMULINK就创建一个新的窗口。
3、向窗口复制模块。
例如,复制阶跃输入Step模块,具体操作为:在SIMULINK 窗口中用鼠标单击Source图标,这样就打开了Source Library中所有的模块;要从Source Library中复制Step模块,可以用鼠标单击该模块,然后拖动鼠标把它移到自己的模型窗口中,并在所需要放的位置松开鼠标,这时Step模块就出现在自己的模型窗口中。
其他需要复制的模块可参考上图,这些模块分别在Math库、Continuous库、Discontinuous库、Signal Routing库以及Sink库中找到,方法同Step模块。
在MATLAB的命令窗口输入命令Fuzzy,进入图形用户界面(GUI)窗口。
根据控制规则和所选择的隶属度函数,利用模糊推理系统(FIS)编辑器可以建立一个FIS文件,取名为fuzzycontrol.fis。
在Fuzzy Logic Toolbox中将Fuzzy Logic Controller模块找到,用鼠标将相应模块拖入窗口中即可。
模糊控制程序设计报告

模糊控制程序设计报告自研112班 麻世博 2201100387题目:已知被控对象为0.51()101s G s e s −=+。
假设系统给定为阶跃值r =30,采样时间为0.5s ,系统的初始值r(0)=0。
试分别设计:(1)常规的PID 控制器;(2)常规的模糊控制器;分别对上述2种控制器进行Matlab 仿真,并比较控制效果解答:1 常规PID 控制器的设计与SIMULINK 仿真如图1所示,使用SIMULINK 工具对已知系统的PID 控制系统进行仿真。
图1 PID 控制系统的SIMULIK 仿真其中PID 控制器为离散型,采样时间T=0.5s ,参数P=14,I=3,D=0。
阶跃信号幅值为30,被控对象传递函数为0.51()101s G s e s −=+。
该系统的阶跃响应如图2。
图2 PID控制系统的输出该控制系统上升时间T r=1.5s,调节时间T s=8s,超调量σ%=70%,没有稳态误差。
该系统中PID控制器的输出曲线如图3。
图3 PID控制器的输出曲线输出最大值为465,最小值为-208。
2 模糊控制器的设计在本文中,我通过MATLAB提供的模糊逻辑工具箱(Fuzzy Logic Toolbox)编辑隶属函数、控制规则,设计了一个双输入单输出的模糊控制器,如下图所示。
图4 模糊控制器概览2.1 隶属度函数的确立。
选择偏差E和偏差变化率EC作为控制器的输入,控制量U为输出。
取E、EC和U的模糊子集为{NB, NM, NS, ZO, PS, PM, PL} ,它们的论域为{-3, -2, -1, 0, 1, 2, 3}。
在 MATLAB的命令窗口输入命令Fuzzy,进入模糊逻辑编辑窗口。
取输入量E、EC的隶属函数为高斯型(gaussmf),输出U的隶属函数为三角形(trimf),如下图所示。
图5 输入模糊变量E的隶属度函数图6 输入模糊变量EC的隶属度函数图7 输出模糊变量U的隶属度函数2.2 模糊控制规则与决策方法的确立。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
自动化专业综合设计报告设计题目:模糊跟踪控制一、设计目的学习模糊控制的理论基础,了解模糊控制的概念,掌握模糊控制的基本方法;熟悉Matlab,学习模糊控制的Matlab仿真,设计模糊控制器,实现控制系统输出跟踪期望信号;熟悉模糊跟踪控制器的基本原理,学会通过改变跟踪信号,看仿真结果;学会改变控制系统,看仿真结果。
二、设计要求熟悉Matlab ,参考教材的第三章和第四章4.1,4.3;设计模糊控制器,实现控制系统输出跟踪期望信号;熟悉模糊跟踪控制器的基本原理,熟悉模糊跟踪控制的程序和结构框图;改变跟踪信号,看仿真结果;改变控制系统,看仿真结果。
三、设计内容(可加附页)(一)、设计模糊控制器,实现控制系统输出跟踪期望信号。
通过设计模糊跟踪控制程序实现跟踪控制功能。
其中模糊控制器组成原理框图如下图设计的控制器原理结构图如下根据以上原理图进行编程,并绘制以下结构框图,通过修改程序参数完成模糊跟踪控制器的设计。
其中原程序为:%Fuzzy Controller Designclear all;close all;a=newfis('fuzzf');f1=1;a=addvar(a,'input','e',[-3*f1,3*f1]); %Parameter ea=addmf(a,'input',1,'NB','zmf',[-3*f1,-1*f1]);a=addmf(a,'input',1,'NM','trimf',[-3*f1,-2*f1,0]);a=addmf(a,'input',1,'NS','trimf',[-3*f1,-1*f1,1*f1]);a=addmf(a,'input',1,'Z','trimf',[-2*f1,0,2*f1]);a=addmf(a,'input',1,'PS','trimf',[-1*f1,1*f1,3*f1]);a=addmf(a,'input',1,'PM','trimf',[0,2*f1,3*f1]);a=addmf(a,'input',1,'PB','smf',[1*f1,3*f1]);f2=1;a=addvar(a,'input','ec',[-3*f2,3*f2]); %Parameter ec a=addmf(a,'input',2,'NB','zmf',[-3*f2,-1*f2]);a=addmf(a,'input',2,'NM','trimf',[-3*f2,-2*f2,0]);a=addmf(a,'input',2,'NS','trimf',[-3*f2,-1*f2,1*f2]);a=addmf(a,'input',2,'Z','trimf',[-2*f2,0,2*f2]);a=addmf(a,'input',2,'PS','trimf',[-1*f2,1*f2,3*f2]);a=addmf(a,'input',2,'PM','trimf',[0,2*f2,3*f2]);a=addmf(a,'input',2,'PB','smf',[1*f2,3*f2]);f3=1.5;a=addvar(a,'output','u',[-3*f3,3*f3]); %Parameter u a=addmf(a,'output',1,'NB','zmf',[-3*f3,-1*f3]);a=addmf(a,'output',1,'NM','trimf',[-3*f3,-2*f3,0]);a=addmf(a,'output',1,'NS','trimf',[-3*f3,-1*f3,1*f3]);a=addmf(a,'output',1,'Z','trimf',[-2*f3,0,2*f3]);a=addmf(a,'output',1,'PS','trimf',[-1*f3,1*f3,3*f3]);a=addmf(a,'output',1,'PM','trimf',[0,2*f3,3*f3]);a=addmf(a,'output',1,'PB','smf',[1*f3,3*f3]);rulelist=[1 1 1 1 1; %Edit rule base1 2 1 1 1;1 32 1 1;1 42 1 1;1 5 3 1 1;1 6 3 1 1;1 7 4 1 1;2 1 1 1 1;2 2 2 1 1;2 3 2 1 1;2 43 1 1;2 53 1 1;2 6 4 1 1;2 7 5 1 1;3 1 2 1 1;3 2 2 1 1;3 3 3 1 1;3 4 3 1 1;3 54 1 1;3 6 5 1 1;3 7 5 1 1;4 1 2 1 1;4 2 3 1 1;4 3 3 1 1;4 4 4 1 1;4 5 5 1 1;4 65 1 1;4 7 6 1 1;5 1 3 1 1;5 2 3 1 1;5 3 4 1 1;5 4 5 1 1;5 5 5 1 1;5 6 6 1 1;5 76 1 1;6 1 3 1 1;6 2 4 1 1;6 3 5 1 1;6 4 5 1 1;6 5 6 1 1;6 6 6 1 1;6 7 7 1 1;7 1 4 1 1;7 2 5 1 1;7 3 5 1 1;7 4 6 1 1;7 5 6 1 1;7 6 7 1 1;7 7 7 1 1];a=addrule(a,rulelist);%showrule(a) % Show fuzzy rule base a1=setfis(a,'DefuzzMethod','mom'); % Defuzzywritefis(a1,'fuzzf'); % save to fuzzy file "fuzz.fis" which can be% simulated with fuzzy toola2=readfis('fuzzf');disp('-------------------------------------------------------');disp(' fuzzy controller table:e=[-3,+3],ec=[-3,+3] ');disp('-------------------------------------------------------');Ulist=zeros(7,7);for i=1:7for j=1:7e(i)=-4+i;ec(j)=-4+j;Ulist(i,j)=evalfis([e(i),ec(j)],a2);endendUlist=ceil(Ulist)figure(1);plotfis(a2);figure(2);plotmf(a,'input',1);figure(3);plotmf(a,'input',2);figure(4);plotmf(a,'output',1);通过Matlab仿真软件绘制结构框图实现以上功能,如下图(二)、改变跟踪信号,看仿真结果;将原有正弦信号改成锯齿波信号,看仿真结果。
发现模糊跟踪控制系统无法再跟踪输入信号,所以调节程序参数使模糊跟踪控制器重新跟踪输入信号。
结构框图如下:(三)、改变控制系统,看仿真结果在原有信号不变的条件下,改变控制系统,观察仿真结果;改变控制系统后,通过重新调节是控制系统重新跟踪输入信号。
例如我们将被控对象改为实现了跟踪控制功能。
四、设计实验结果及分析(一)、刚编程后试验结果与分析如下实验结果:通过编程实现模糊跟踪控制,其中原程序模糊跟踪控制实验现象如下图实验分析:初始程序在坐标范围内可以实现模糊跟踪控制,但模糊跟踪控制并未能实现完全跟踪,仍有一定的误差,需要调节相关参数消除误差从而实现跟踪控制。
(二)、改变跟踪信号,看仿真结果;将原有正弦信号改成锯齿波信号,看仿真结果。
发现模糊跟踪控制系统无法再跟踪输入信号,所以调节程序参数使模糊跟踪控制器重新跟踪输入信号。
调整参数后实验结果和分析如下。
实验结果:将跟踪信号改为锯齿波后,改变相关系数后,实验结果如下图实验分析:通过改变程序的f值控制e和ec,我们可以使模糊跟踪控制器很好的实现跟踪锯齿波型的功能,其中锯齿波的幅值为0.45,周期为0.5,这很好的体现了模糊跟踪控制器的优点。
(三)、改变控制系统,看仿真结果,在原有信号不变的条件下,改变控制系统,通过重新调节是控制系统重新跟踪输入信号后实验结果和分析如下。
实验结果:改变控制对象后实验结果如下图实验分析:以上模糊跟踪控制程序通过改变参数从而很好的达到预期效果,该系统实现了对输入的正弦信号的准确跟踪。
五、结论模糊控制是一种反映人类智慧的智能控制方法,能够很好的实现模糊跟踪控制,有其一定的优越性。
模糊控制的基本原理为1、确定观测量和控制量;2、输入量和输出量的模糊化;3、模糊规则的描述;4、求模糊关系;5、模糊决策;6、控制量的反模糊化。
我们进行模糊设计应根据模糊控制的基本原理,通过Matlab语言编程和仿真实现跟踪功能。
编程完成后,程序很好的实现了跟踪控制功能,我们通过改变跟踪信号,看仿真结果,发现改变跟踪信号后,只需改变相应参数,模糊跟踪控制依然能够很好的实现对输入信号的准确跟踪。
