4组合变形和强度理论
强度理论与组合变形ppt

通过监测桥梁的变形、裂缝等指标,及时发现 并解决潜在的安全隐患。
3
桥梁修复和加固
根据强度理论分析,针对受损或老化桥梁采取 适当的修复和加固措施。
强度理论在建筑物中的应用
建筑设计
01
考虑建筑物结构的强度、刚度和稳定性,以确保建筑物在使用
过程中的安全性。
抗震设计
02
强度理论在地震作用下用于评估建筑物的抗震性能,设计合理
02
组合变形
组合变形的定义与特点
定义
组合变形是指结构或构件在复杂受力或温度变化等作用下,由平面弯曲、拉 伸、压缩、扭转等基本变形组合而形成的变形形式。
特点
组合变形具有复杂性、多变性、综合性等特点,变形形式多种多样,影响因 素较为复杂,需要综合考虑多种因素进行分析和计算。
组合变形的影响因素
材料性质
组合变形对强度理论的影响
组合变形过程中,材料内部的应力 、应变和裂缝等状态是不断变化的 ,这些因素对强度理论的应用和验 证产生一定的影响。
VS
在复杂应力状态下,材料的强度和 稳定性受到多种因素的影响,因此 需要综合考虑各种因素来评估材料 的强度和稳定性。
强度理论与组合变形的相互作用
强度理论是组合变形的基础,它为组合变形的分析 和设计提供了重要的理论依据。
强度理论分类
根据不同的破坏特征和受力条件,强度理论可分为最大拉应 力理论、最大伸长线应变理论、最大剪切应力理论和形状改 变比能理论等。
强度理论的重要性
强度理论是工程应用中设计、制造、使用和维护各种材料的 关键依据之一,可以指导人们合理地选择材料、制定工艺和 优化结构。
强度理论能够为各种工程结构的分析、设计和优化提供理论 基础,从而提高工程结构的可靠性、安全性和经济性。
四大强度理论
六、例题: 例题1、薄壁容器,厚度 δ<< 平均直径D,在容器中贮满
水,水结冰后,将容器涨破,而冰不碎,解释原因。
解:⑴、水结冰时,发生膨胀,容器将受到内压作用,其单 元体的应力状态为二向拉应力状态。
15
p
李禄昌
p
1
p
1
2
1
由纵向截面上的静力平衡条件
Y 0 2 l p D l 0
轴向拉伸时
1 s , 2 3 0 ud 1 2 s2
6E
11
李禄昌
3、强度条件:
1 s 2 1 1 2 2 2 2 22 2 s uf (21 3 3 ) (3 ) u 1 2( 2 6 f 2) 3 11 E n 2 6E s
1
b
n
4、存在问题:⑴、该理论只考虑σ1 ,而没有考虑σ2 、σ3的 影响。⑵、当σ1<0,即没有拉应力的应力状态时,它不能对 材料的压缩破坏作出合理解释。⑶、 σ1必须是拉应力。
4
李禄昌 试验证明,这一理论与铸铁、岩石、砼、陶瓷、玻璃等脆 性材料的拉断试验结果相符,这些材料在轴向拉伸时的断裂 破坏发生于拉应力最大的横截面上。 脆性材料的扭转破坏,也是沿拉应力最大的斜面发生断裂, 这些都与最大拉应力理论相符。
x
x
得主应力
1 =14.5 103 F ( MPa) 2 0 3 1.8 10 F ( MPa)
3
19
李禄昌
⑶、对于钢材,利用第三强度理论强度条件:
r 3 1 3 [ ]
代入有关参数得:
[ ] F 9.8 KN 3 16.3 10
强度理论及组合变形

(3)强度条件 1 [ ] (4)特点 该理论较好的解释了脆性材料在拉伸和扭转时的破坏 现象,但没有考虑其它两个主应力的影响,且对没有拉 应力的状态也不适用。
2、最大伸长线应变理论(第二强度理论)
(1)内容 无论材料处于何种应力状态,只要其上某点的最大伸长线 应变ε1达到其极限值,材料即发生断裂破坏。 (2)破坏条件
又由第二强度理论 取μ=0.27
也即
0.787 ] [
则
[ ] 0.787 ] 0.8[ ] [
对于塑性材料,由第三强度理论
1 3 ( ) 2 [ ]
与纯剪切强度条件比较 则
[ ] 0.5[ ]
又由第四强度理论
1 [( 1 2 )2 ( 2 3 )2 ( 1 3 )2 ] 3 [ ] 2
(1)内容 无论材料处于何种应力状态,只要形状改变比能μf达到单 向拉伸相应于极限应力σ0的形状改变比能μ0f时,材料即发生 屈服破坏。 (2)破坏条件 在三向应力状态下,弹性体的形状改变比能为
1 u uf [( 1 2 )2 ( 2 3 )2 ( 1 3 ) 2 ] 6E
max 1 3
2
方法: 叠加法
σ2 σ3
σ2
σ3
由虎克定律, σ1 单独作用下,在σ1方向的主应变可表示为
E 在σ 2 σ 3单独作用下,沿σ1方向的引起的主应变为
1 2
E 1
3
E
由叠加原理,在σ1σ2σ3三个主应力共同作用下σ1方向的主 应变为:
A 双向拉伸
p
σ A
p
σ
B
B
m
(完整版)四大强度理论基本内容介绍

四大强度理论基本内容介绍:1、最大拉应力理论(第一强度理论):这一理论认为引起材料脆性断裂破坏的因素是最大拉应力,无论什么应力状态,只要构件内一点处的最大拉应力σ1达到单向应力状态下的极限应力σb,材料就要发生脆性断裂。
于是危险点处于复杂应力状态的构件发生脆性断裂破坏的条件是:σ1=σb。
σb/s=[σ]所以按第一强度理论建立的强度条件为:σ1≤[σ]。
2、最大伸长线应变理论(第二强度理论):这一理论认为最大伸长线应变是引起断裂的主要因素,无论什么应力状态,只要最大伸长线应变ε1达到单向应力状态下的极限值εu,材料就要发生脆性断裂破坏。
εu=σb/E;ε1=σb/E。
由广义虎克定律得:ε1=[σ1-u(σ2+σ3)]/E 所以σ1-u(σ2+σ3)=σb。
按第二强度理论建立的强度条件为:σ1-u(σ2+σ3)≤[σ]。
3、最大切应力理论(第三强度理论):这一理论认为最大切应力是引起屈服的主要因素,无论什么应力状态,只要最大切应力τmax达到单向应力状态下的极限切应力τ0,材料就要发生屈服破坏。
依轴向拉伸斜截面上的应力公式可知τ0=σs/2(σs——横截面上的正应力)由公式得:τmax=τ1s=(σ1-σ3)/2。
所以破坏条件改写为σ1-σ3=σs。
按第三强度理论的强度条件为:σ1-σ3≤[σ]。
4、形状改变比能理论(第四强度理论):这一理论认为形状改变比能是引起材料屈服破坏的主要因素,无论什么应力状态,只要构件内一点处的形状改变比能达到单向应力状态下的极限值,材料就要发生屈服破坏。
四大强度理论适用的范围各种强度理论的适用范围及其应用第一理论的应用和局限1、应用材料无裂纹脆性断裂失效形势(脆性材料二向或三向受拉状态;最大压应力值不超过最大拉应力值或超过不多)。
2、局限没考虑σ2、σ3对材料的破坏影响,对无拉应力的应力状态无法应用。
第二理论的应用和局限1、应用脆性材料的二向应力状态且压应力很大的情况。
应力状态分析 、强度理论、组合变形

Page57
BUCT
解:1 T=3×0.25 = 0.75KN.M
2 MxY =7×0.22 = 1.54KN.M
3 MxY中=7×0.22×0.5 =0.77KN.M
4 MxZ=3.5×0.4= 1.4KN.M
5
M总
M
2 z
M
2 y
=1.6
6
r3
1 W
M 2 T 2 [ ]
Page28
BUCT
化工设备机械 基础
然后叠加
= + = Pcos / A + Pl sin y / Iz
1 = N / A + M / Wz
2 = N / A - M / Wz
Page29
BUCT
例题5-5
化工设备机械 基础
Page30
BUCT
化工设备机械 基础
Page31
BUCT
uf 达到某一数值时,材料失效。
强度条件:
1 2
[(1
2
)2
(
2
3
)2
(
3
1)2
]
[]
Page21
BUCT
化工设备机械 基础
r1 1
r2 1-μ(σ2 - σ3 )
r3 1 3 2 4 2
r4
1 2
2 3 2
r3
( M )2 4( T )2 1
W
Wp
W
M 2 T 2 [ ]
Page2
BUCT
§1 应力状态的概念
化工设备机械 基础
一、问题的提出
杆件在基本变形时横截面上应力的分布规律
1. 轴向拉压:
精选-四大强度理论基本内容介绍

四大强度理论基本内容介绍:1、最大拉应力理论(第一强度理论):这一理论认为引起材料脆性断裂破坏的因素是最大拉应力,无论什么应力状态,只要构件内一点处的最大拉应力σ1达到单向应力状态下的极限应力σb,材料就要发生脆性断裂。
于是危险点处于复杂应力状态的构件发生脆性断裂破坏的条件是:σ1=σb。
σb/s=[σ]所以按第一强度理论建立的强度条件为:σ1≤[σ]。
2、最大伸长线应变理论(第二强度理论):这一理论认为最大伸长线应变是引起断裂的主要因素,无论什么应力状态,只要最大伸长线应变ε1达到单向应力状态下的极限值εu,材料就要发生脆性断裂破坏。
εu=σb/E;ε1=σb/E。
由广义虎克定律得:ε1=[σ1-u(σ2+σ3)]/E 所以σ1-u(σ2+σ3)=σb。
按第二强度理论建立的强度条件为:σ1-u(σ2+σ3)≤[σ]。
3、最大切应力理论(第三强度理论):这一理论认为最大切应力是引起屈服的主要因素,无论什么应力状态,只要最大切应力τmax达到单向应力状态下的极限切应力τ0,材料就要发生屈服破坏。
依轴向拉伸斜截面上的应力公式可知τ0=σs/2(σs——横截面上的正应力)由公式得:τmax=τ1s=(σ1-σ3)/2。
所以破坏条件改写为σ1-σ3=σs。
按第三强度理论的强度条件为:σ1-σ3≤[σ]。
4、形状改变比能理论(第四强度理论):这一理论认为形状改变比能是引起材料屈服破坏的主要因素,无论什么应力状态,只要构件内一点处的形状改变比能达到单向应力状态下的极限值,材料就要发生屈服破坏。
四大强度理论适用的范围各种强度理论的适用范围及其应用第一理论的应用和局限1、应用材料无裂纹脆性断裂失效形势(脆性材料二向或三向受拉状态;最大压应力值不超过最大拉应力值或超过不多)。
2、局限没考虑σ2、σ3对材料的破坏影响,对无拉应力的应力状态无法应用。
第二理论的应用和局限1、应用脆性材料的二向应力状态且压应力很大的情况。
工程力学四大强度理论的基本内容

工程力学中四大强度理论的基本内容一、四大强度理论基本内容介绍:1、最大拉应力理论(第一强度理论):这一理论认为引起材料脆性断裂破坏的因素是最大拉应力,无论什么应力状态,只要构件内一点处的最大拉应力σ1达到单向应力状态下的极限应力σb,材料就要发生脆性断裂。
于是危险点处于复杂应力状态的构件发生脆性断裂破坏的条件是:σ1=σb。
σb/s=[σ] ,所以按第一强度理论建立的强度条件为:σ1≤[σ]。
2、最大伸长线应变理论(第二强度理论):这一理论认为最大伸长线应变是引起断裂的主要因素,无论什么应力状态,只要最大伸长线应变ε1达到单向应力状态下的极限值εu,材料就要发生脆性断裂破坏。
εu=σb/E;ε1=σb/E。
由广义虎克定律得:ε1=[σ1-u(σ2+σ3)]/E 所以σ1-u(σ2+σ3)=σb。
按第二强度理论建立的强度条件为:σ1-u(σ2+σ3)≤[σ]。
3、最大切应力理论(第三强度理论):这一理论认为最大切应力是引起屈服的主要因素,无论什么应力状态,只要最大切应力τmax达到单向应力状态下的极限切应力τ0,材料就要发生屈服破坏。
依轴向拉伸斜截面上的应力公式可知τ0=σs/2(σs——横截面上的正应力)由公式得:τmax=τ1s=(σ1-σ3)/2。
所以破坏条件改写为σ1-σ3=σs。
按第三强度理论的强度条件为:σ1-σ3≤[σ]。
4、形状改变比能理论(第四强度理论):这一理论认为形状改变比能是引起材料屈服破坏的主要因素,无论什么应力状态,只要构件内一点处的形状改变比能达到单向应力状态下的极限值,材料就要发生屈服破坏。
二、四大强度理论适用的范围1、各种强度理论的适用范围及其应用(1)、第一理论的应用和局限应用:材料无裂纹脆性断裂失效形势(脆性材料二向或三向受拉状态;最大压应力值不超过最大拉应力值或超过不多)。
局限:没考虑σ2、σ3对材料的破坏影响,对无拉应力的应力状态无法应用。
(2)、第二理论的应用和局限应用:脆性材料的二向应力状态且压应力很大的情况。
第9章 强度理论及组合变形

第9章 强度理论及组合变形概述如图9-1所示的各种处于复杂应力状态的点,当单元体微分面上的正应力满足正应力强度条件][σσ≤i,同时切应力满足切应力强度条件][ττ≤ij 时,依然不能判别其在强度上是否安全。
那么它们在什么情况下安全?又在什么情况下危险?本章的强度理论部分就要回答这个问题。
材料力学主要研究杆件以及杆件结构系统在外力作用下的强度,刚度和稳定性问题,而材料力学最复杂的问题是杆件的组合变形问题,最一般的组合变形杆件危险点的应力状态通常是复杂应力状态,如图9-2所示。
因此,本章强度理论的诸多结论主要用于组合变形杆件的强度计算和设计,所以,本章组合变形部分主要研究杆件各种组合变形情况下的强度计算。
9.1 强度理论概念根据材料力学的强度观点,构件在强度方面的安全性实质上可考察构件中的危险点是否安全,若危险点安全,则整个构件也安全;若危险点不安全,则整个构件就不安全。
假设构件中A 点是最危险的点,问题:当A 点处于任意应力状态时,亦即A 点的应力状态可以是简单应力状态,也可以是复杂应力状态,那么该点在什么情况下强度是安全的?又在什么情况下强度是不安全的?如何判断?如果A 点的应力状态是简单应力状态,如图9-3所示。
那么可以根据强度条件:][σσ≤ ][ττ≤ (9-1)判别A 点的安全性。
如果危险点是单向应力状态,则σ是A 点处的最大正应力(图9-3(a));如果危险点是纯剪应力状态,则τ是A 点处的最大切应力(图9-3(b))。
从而也就知道杆件在强度上是否安全。
][σ是材料的许用正应力;][τ是材料的许用切应力。
大量事实说明,工程材料的破坏形式图9-1 复杂应力状态yσxσz σxy τxzτyxτyz τzxτzy τxσy σxy τστ(a)(b(c)ABFMm图9-2 组合变形危险点的应力状态στ主要有两种,一是脆性断裂,二是塑性屈服,脆性断裂的极限应力为强度极限)(b b τσ,而塑性屈服的极限应力为屈服应力)(s s τσ,考虑到诸多偶然因素的影响(如材料缺陷,加工误差,实际工作环境,载荷非理想化等等),所以通常将极限应力除以一个适当的安全系数1>n ,这样就得到材料的许用正应力][σ和许用切应力][τ。
广义胡克定律、强度理论、组合变形

解:1. 解析法
已知:
x 70 MPa x 50 MPa y0
max min
x
2
y
x
2
y
2 x
26 96
MPa MPa
0
arctan
max
x
y
62.5
1 26 MPa 3 96 MPa 2 0
2. 图解法
先画出应力圆, 在圆上找出主应力大小与方位, 并标在截面图上
0 62.5
定义: 构件内一点处的变形均发生在同一平面内
时的应变状态,称为 平面应变状态
z xz yzz 0xz yz 0 z xzz xyzz 0yz 0 z xz yz 0
平面应变状态
一点处任意方位应变:
xy2x源自y2cos2
xy
2
sin2
x y sin2 xy cos2
1 26 MPa 2 0
3 96 MPa
§5 复杂应力状态的最大应力
三向应力圆 最大应力
三向应力圆 (三向应力状态, 所有斜截面的应力)
主平面微体
平面应力状态: 与主
应力σ3平行的斜截面上 的应力,位于σ1和σ2所 确定的应力圆上
三向应力状态:与主应
力均不平行的斜截面上的
应力,位于三圆所构成的 阴影区域内
0
2
=
εx
- εy 2
2
+
γ xy 2
2
Cε
εx
+ εy 2
,0
Rε =
εx
- εy 2
2
+
γ xy 2
2
最大应变与主应变
max
min
x
2
第九章强度理论和组合变形讲解学习

b.剪应力强度校核(K2)点
C截面
m a x Q I C Z S b Z * 1 7 .2 1 1 0 0 0 2 1 0 7 3 1 0 3 8 3 .1 M p a 9 5 M p a
正应力和剪应力强度条件均满足。
c.校核腹板和翼板交接处(K3)点的强度。 K3点处的复杂应力状态,绘出K3点的应力状态图。
变为 0,则外力偶m=?
m
CL10mTU60
解:(1)将应变片贴于与母线成45°角的外表面上
(2) 1 ,2 0 ,3
1E 11(23) max
min
1
E
1
E
m
d3
0
16
m d 3E 0 16(1 )
9.4组合变形的概念
在外力的作用下,构件若同时产生两种或 两种以上基本变形的情况,就是组合变形
解:1.梁的内力分析 首先,将载荷F沿x和y轴分
解,得相应分力为
Fx Fcos30=8.66103N Fy Fsin305.00103N
然后,将Fx平移到梁的轴线上, 得轴向力Fc和附加力偶Me。
(4)选用适当的强度理论计算相当应力eq。 (5)确定材料的许用拉应力[] ,将其与eq比较。
例 从某构件的危险点处取出一单元体如图7-8a 所示,已知钢
材的屈服点s = 280MPa.试按最大剪应力理论和形状改变比能
理论计算构件的工作安全系数。
先计算 oxy 平面内的主应力,然后 计算工作安全系数
Tm
a
x
15000
6000
3.140.1252 3.140.1235
4
32
32.4106 32.4MPa35MPa
满足强度条件,最后选用立柱直 d = 12.5cm
知识资料材料力学知识资料应力状态分析和强度理论(三)组合变形压杆稳定(新版)

需要课件请或强度理论(一)强度理论的概念1.材料破坏的两种类型材料破坏型式不仅与材料本身的材质有关,而且与材料所处的应力状态、加载速度温度环境等因素有关。
材料在常温、静载荷下的破坏型式主要有以下两种:脆性断裂材料在无显然的变形下骤然断裂。
塑性屈服(流动) 材料浮上显著的塑性变形而丧失其正常的工作能力。
2.强度理论在复杂应力状态下关于材料破坏缘故的假设,称为强度理论。
研究强度理论的目的,在于利用容易应力状态下的实验结果,来建立材料在复杂应力状态下的强度条件。
(二)四个常用的强度理论四个常用强度理论的强度条件可以统一地写成式中σr称为相当应力,其表达式为最大拉应力理论σr1=σ1(第一强度理论)最大拉应变理论σr2=σ1-ν(σ1+σ2)(第二强度理论)最大剪应力理论σr3=σ1-σ3(第三强度理论)形状改变比能理论(第四强度理论)[σ]为材料的许用应力。
第1 页/共18 页对于工程上常见的一种二向应力状态如图5—9—3所示,其特点是平面内某一方向的正应力为零。
设σy=0,则该点的主应力为代入(5—9-15)式得:第三强度理论(最大剪应力理论)的相当应力为第四强度理论(形状改变比能理论)的相当应力为最大拉应力理论、最大拉应变理论是关于脆性断裂的强度理论;最大剪应力理论、形状改变比能理论是关于塑性屈服的强度理论。
强度理论的选用在三向拉应力作用下,材料均产生脆性断裂,故宜用第一强度理论;而在三向压缩应力状态下,材料均产生屈服破坏,故应采用第三或第四强度理论。
当材料处于二向应力状态作用下时:脆性材料易发生断裂破坏,宜用第一或第二强度理论;塑性材料易发生塑性屈服破坏,宜用第三或第四强度理论。
[例5-9-1] 已知构件上某点的应力单元体如图5-9-4(a),(b)所示(图中应力单位为MPa)。
试求指定斜截面上的应力。
[解] 图示单元体处于平面应力状态。
(1)在图示坐标中代人公式(5-9-1)、(5-9-2)得σα、τσ方向如图中所示。
材料力学 强度理论与组合变形

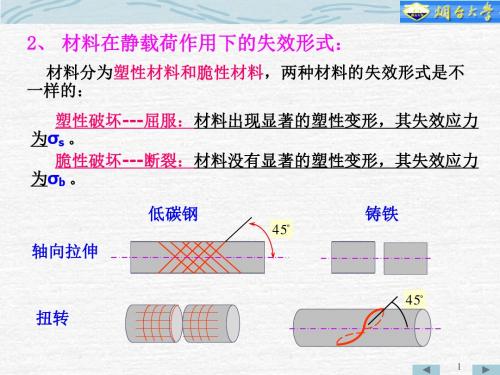
第八章强度理论与组合变形§8-1 强度理论的概念1.不同材料在同一环境及加载条件下对“破坏”(或称为失效)具有不同的抵抗能力(抗力)。
例1常温、静载条件下,低碳钢的拉伸破坏表现为塑性屈服失效,具有屈服极限σ,s铸铁破坏表现为脆性断裂失效,具有抗拉强度σ。
图9-1a,bb2.同一材料在不同环境及加载条件下也表现出对失效的不同抗力。
例2常温静载条件下,带有环形深切槽的圆柱形低碳钢试件受拉时,不再出现塑性变形,而沿切槽根部发生脆断,切槽导致的应力集中使根部附近出现两向和三向拉伸型应力状态。
图(9-2a,b)例3 常温静载条件下,圆柱形铸铁试件受压时,不再出现脆性断口,而出现塑性变形,此时材料处于压缩型应力状态。
图(9-3a )例4 常温静载条件下,圆柱形大理石试件在轴向压力和围压作用下发生明显的塑性变形,此时材料处于三向压缩应力状态下。
图9-3b3.根据常温静力拉伸和压缩试验,已建立起单向应力状态下的弹性失效准则,考虑安全系数后,其强度条件为 []σσ≤ ,根据薄壁圆筒扭转实验,可建立起纯剪应力状态下的弹性失效准则,考虑安全系数后,强度条件为 []ττ≤ 。
建立常温静载一般复杂应力状态下的弹性失效准则——强度理论的基本思想是: 1)确认引起材料失效存在共同的力学原因,提出关于这一共同力学原因的假设; 2)根据实验室中标准试件在简单受力情况下的破坏实验(如拉伸),建立起材料在复杂应力状态下共同遵循的弹性失效准则和强度条件。
3)实际上,当前工程上常用的经典强度理论都按脆性断裂和塑性屈服两类失效形式,分别提出共同力学原因的假设。
§8-2四个强度理论1.最大拉应力准则(第一强度理论)基本观点:材料中的最大拉应力到达材料的正断抗力时,即产生脆性断裂。
表达式:u σσ=+max复杂应力状态321σσσ≥≥, 当01>σ, 1m a xσσ=+简单拉伸破坏试验中材料的正断抗力b u σσσ==1,032==σσ 最大拉应力脆断准则: b σσ=1(9-1a)相应的强度条件:[]bb n σσσ=≤1(9-1b)适用范围:虽然只突出 1σ 而未考虑 32,σσ 的影响,它与铸铁,工具钢,工业陶瓷等多数脆性材料的实验结果较符合。
四大强度理论

四大强度理论1、最大拉应力理论(第一强度理论)(材料脆性断裂的强度理论):()这一理论认为引起材料脆性断裂破坏的因素是最大拉应力,无论什么应力状态,只要构件内一点处的最大拉应力σ1达到单向应力状态下的极限应力σb,材料就要发生脆性断裂。
于是危险点处于复杂应力状态的构件发生脆性断裂破坏的条件是:σ1=σb。
σb/s=[σ]所以按第一强度理论建立的强度条件为:σ1≤[σ]。
2、最大伸长线应变理论(第二强度理论)(材料塑性屈服的强度理论):这一理论认为最大伸长线应变是引起断裂的主要因素,无论什么应力状态,只要最大伸长线应变ε1达到单向应力状态下的极限值εu,材料就要发生脆性断裂破坏。
εu=σb/E;ε1=σb/E。
由广义虎克定律得:ε1=[σ1-u(σ2+σ3)]/E所以σ1-u(σ2+σ3)=σb。
按第二强度理论建立的强度条件为:σ1-u(σ2+σ3)≤[σ]。
3、最大切应力理论(第三强度理论):这一理论认为最大切应力是引起屈服的主要因素,无论什么应力状态,只要最大切应力τmax 达到单向应力状态下的极限切应力τ0,材料就要发生屈服破坏。
τmax=τ0。
依轴向拉伸斜截面上的应力公式可知τ0=σs/2(σs——横截面上的正应力)由公式得:τmax=τ1s=(σ1-σ3)/2。
所以破坏条件改写为σ1-σ3=σs。
按第三强度理论的强度条件为:σ1-σ3≤[σ]。
4、形状改变比能理论(第四强度理论)(最大歪形能理论):这一理论认为形状改变比能是引起材料屈服破坏的主要因素,无论什么应力状态,只要构件内一点处的形状改变比能达到单向应力状态下的极限值,材料就要发生屈服破坏。
发生塑性破坏的条件为:所以按第四强度理论的强度条件为:sqrt(σ1^2+σ2^2+σ3^2-σ1σ2-σ2σ3-σ3σ1)<[σ]Von mise应力Von Mises 应力是基于剪切应变能的一种等效应力其值为(((a1-a2)^2+(a2-a3)^2+(a3-a1)^2)/2)^0.5 其中a1,a2,a3分别指第一、二、三主应力。
《建筑力学》最新备课课件:第四章:四大强度理论

第四章 强度理论
(2)主应力、主平面
y xy
max
x
2
y
(
x
y
)
2
2
xy
2
68.3MPa
x
m in
x
2
y
(
x
y
)2
2
xy
2
48.3MPa
1 68.3MPa, 2 0, 3 48.3MPa
第四章 强度理论
y xy
主平面的方位:
tg20
2 xy x
y
x
60 0.6 60 40
y xy
x
第四章 强度理论
解:(1) 斜面上的应力
y xy
x
y
2
x
y
2
cos 2
xy
sin 2
60 40 60 40 cos(60 ) 30sin(60 )
2
2
x
9.02MPa
x
y
2
sin
2
xy
cos
2
60 40 sin(60 ) 30cos(60 ) 2
58.3MPa
-形状改变比能的极限值,由单拉实验测得
第四章 强度理论
形状改变比能理论(第四强度理论) 屈服条件 强度条件
实验表明:对塑性材料,此理论比第三强度理 论更符合试验结果,在工程中得到了广泛应用。
第四章 强度理论
强度理论的统一表达式: r [ ]
相当应力
r ,1 1 [ ] r,2 1 ( 2 3 ) [ ]
第四章 强度理论
2
1
0 3
2
3
由三向应力圆可以看出:
max
图中的四种话中当材料强度

图中的四种话中当材料强度由于材料的破坏按其物理本质分为脆断和屈服两类形式,所以,强度理论也就相应地分为两类,下面就来介绍目前常用的四个强度理论。
1、最大拉应力理论(第一强度理论即最大主应力)这一理论又称为第一强度理论。
这一理论认为破坏主因是最大拉应力。
不论复杂、简单的应力状态,只要第一主应力达到单向拉伸时的强度极限,即断裂。
破坏形式:断裂。
破坏条件:σ1 =σb强度条件:σ1≤[σ]实验证明,该强度理论较好地解释了石料、铸铁等脆性材料沿最大拉应力所在截面发生断裂的现象;而对于单向受压或三向受压等没有拉应力的情况则不适合。
缺点:未考虑其他两主应力。
使用范围:适用脆性材料受拉。
如铸铁拉伸,扭转。
2、最大伸长线应变理论(第二强度理论即最大主应变)这一理论又称为第二强度理论。
这一理论认为破坏主因是最大伸长线应变。
不论复杂、简单的应力状态,只要第一主应变达到单向拉伸时的极限值,即断裂。
破坏假设:最大伸长应变达到简单拉伸的极限(假定直到发生断裂仍可用胡克定律计算)。
破坏形式:断裂。
脆断破坏条件:ε1= εu=σb/Eε1=1/E[σ1−μ(σ2+σ3)]破坏条件:σ1−μ(σ2+σ3) = σb强度条件:σ1−μ(σ2+σ3)≤[σ]实验证明,该强度理论较好地解释了石料、混凝土等脆性材料受轴向拉伸时,沿横截面发生断裂的现象。
但是,其实验结果只与很少的材料吻合,因此已经很少使用。
缺点:不能广泛解释脆断破坏一般规律。
使用范围:适于石料、混凝土轴向受压的情况。
3、最大切应力理论(第三强度理论即Tresca强度)这一理论又称为第三强度理论。
这一理论认为破坏主因是最大切应力ma xτ。
不论复杂、简单的应力状态,只要最大切应力达到单向拉伸时的极限切应力值,即屈服。
破坏假设:复杂应力状态危险标志最大切应力达到该材料简单拉、压时切应力极限。
破坏形式:屈服。
破坏因素:最大切应力。
τmax=τu=σs/2屈服破坏条件:τmax=1/2(σ1−σ3 )破坏条件:σ1−σ3 = σs强度条件:σ1−σ3≤[σ]实验证明,这一理论可以较好地解释塑性材料出现塑性变形的现象。
四种强度理论(1)讲课教案

由于材料的破坏按其物理本质分为脆断和屈服两类形式,所以,强度理论也就相应地分为两类,下面就来介绍目前常用的四个强度理论。
1、最大拉应力理论:这一理论又称为第一强度理论。
这一理论认为破坏主因是最大拉应力。
不论复杂、简单的应力状态,只要第一主应力达到单向拉伸时的强度极限,即断裂。
破坏形式:断裂。
破坏条件:σ1 =σb强度条件:σ1≤[σ]实验证明,该强度理论较好地解释了石料、铸铁等脆性材料沿最大拉应力所在截面发生断裂的现象;而对于单向受压或三向受压等没有拉应力的情况则不适合。
缺点:未考虑其他两主应力。
使用范围:适用脆性材料受拉。
如铸铁拉伸,扭转。
2、最大伸长线应变理论这一理论又称为第二强度理论。
这一理论认为破坏主因是最大伸长线应变。
不论复杂、简单的应力状态,只要第一主应变达到单向拉伸时的极限值,即断裂。
破坏假设:最大伸长应变达到简单拉伸的极限(假定直到发生断裂仍可用胡克定律计算)。
破坏形式:断裂。
脆断破坏条件:ε1=εu=σb/Eε1=1/E[σ1−μ (σ2+σ3)]破坏条件:σ1−μ(σ2+σ3) =σb强度条件:σ1−μ(σ2+σ3)≤[σ]实验证明,该强度理论较好地解释了石料、混凝土等脆性材料受轴向拉伸时,沿横截面发生断裂的现象。
但是,其实验结果只与很少的材料吻合,因此已经很少使用。
缺点:不能广泛解释脆断破坏一般规律。
使用范围:适于石料、混凝土轴向受压的情况。
3、最大切应力理论:这一理论又称为第三强度理论。
这一理论认为破坏主因是最大切应力maxτ。
不论复杂、简单的应力状态,只要最大切应力达到单向拉伸时的极限切应力值,即屈服。
破坏假设:复杂应力状态危险标志最大切应力达到该材料简单拉、压时切应力极限。
破坏形式:屈服。
破坏因素:最大切应力。
τmax=τu=σs/2屈服破坏条件:τmax=1/2(σ1−σ3)破坏条件:σ1−σ3=σs强度条件:σ1−σ3≤[σ]实验证明,这一理论可以较好地解释塑性材料出现塑性变形的现象。
四大强度理论对比

四大强度理论1、最大拉应力理论(第一强度理论):这一理论认为引起材料脆性断裂破坏的因素是最大拉应力,无论什么应力状态,只要构件内一点处的最大拉应力σ1达到单向应力状态下的极限应力σb,材料就要发生脆性断裂.于是危险点处于复杂应力状态的构件发生脆性断裂破坏的条件是:σ1=σb。
σb/s=[σ]所以按第一强度理论建立的强度条件为:σ1≤[σ].2、最大伸长线应变理论(第二强度理论):这一理论认为最大伸长线应变是引起断裂的主要因素,无论什么应力状态,只要最大伸长线应变ε1达到单向应力状态下的极限值εu,材料就要发生脆性断裂破坏.εu=σb/E;ε1=σb/E.由广义虎克定律得:ε1=[σ1-u(σ2+σ3)]/E所以σ1—u(σ2+σ3)=σb.按第二强度理论建立的强度条件为:σ1-u(σ2+σ3)≤[σ]。
3、最大切应力理论(第三强度理论):这一理论认为最大切应力是引起屈服的主要因素,无论什么应力状态,只要最大切应力τmax达到单向应力状态下的极限切应力τ0,材料就要发生屈服破坏。
τmax=τ0.依轴向拉伸斜截面上的应力公式可知τ0=σs/2(σs——横截面上的正应力)由公式得:τmax=τ1s=(σ1—σ3)/2。
所以破坏条件改写为σ1—σ3=σs。
按第三强度理论的强度条件为:σ1—σ3≤[σ]。
4、形状改变比能理论(第四强度理论):这一理论认为形状改变比能是引起材料屈服破坏的主要因素,无论什么应力状态,只要构件内一点处的形状改变比能达到单向应力状态下的极限值,材料就要发生屈服破坏.发生塑性破坏的条件为:所以按第四强度理论的强度条件为:2、sqrt(σ1^2+σ2^2+σ3^2—σ1σ2—σ2σ3-σ3σ1)〈[σ]四个强度理论的比较材料极限值获得方法通过任意一种使试件发生破坏的试验来确定通过任意一种使试件发生脆断破坏的试验来确定通过任意一种使试件发生屈服破坏的试验来确定表示极限应力σjx由简单的拉伸试验知σjx =σb极限应变εjx由单向拉伸试件在拉断时其横截面上的正应力σjx决定εjx =σjx /E极限剪应力τjx由单向拉伸试验知τjx =σs /2σs为材料的屈服极限极限形状改变比能μd jx在简单拉伸条件下因σ1=σs,σ2 =σ3=0μd jx =材料破坏条件脆断破坏σ1=σb (a)脆断破坏ε1=εjx=σjx /E(b)屈服破坏τmax =τjx =σs /2(c)屈服破坏μd =μd jx强度条件σ1≤[σ](1—59)[σ]由b除以安全系数得到公式中的σ1必须为拉应力[σ1—μ(σ2+σ3)]≤[σ](1-60)[σ]由σjx 除以安全系数得到(σ1—σ3)≤[σ](1-61)[σ]由σs 除以安全系数得到说明该理论在17世纪就已提出,是最早的强度理论;此理论基本上能正确反映出某些脆性材料的强度特性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
不比第一强度理论好,一般不用。
2012-7-1 29
3、最大剪应力理论 (第三强度理论)
最大剪应力达到极限值, 材料就发生屈服破坏 。 破坏条件: max jx
max
1
3 2
jx
s
2
强度条件:
1 3
虽然没考虑σ2,但能较好地解释塑性屈服, 在工程中得到广泛的应用。
23
正应力拉为正,压为负;剪应力以对单元 体内任一点的矩顺时针为正,反之为负。
2012-7-1 24
第三节 强度理论
一、强度理论的概念 单向应力状态可通过试验建立强度条件
max
N A
,
n
0
破坏原因的假说
2012-7-1 25
二、材料的两种破坏形式
脆断破坏 屈服破坏 三向拉应力的塑性材料发生脆性断裂 三向压应力的脆性材料有时也发生明 显的塑性变形
f max l f l
d f
2012-7-1
2
dx
2
M (x) EJ
Z
df dx
f ( x )
2
小结
1、受力分析,变形类型,求支座反力 2、截面法求内力,画内力图 3、确定应力分布规律 4、强度计算
最大工作应力 危险截面上最大内力 相应的截面几何性质 许用应力
平 面 应 力 状 特例 态
单向应力状态
纯剪应力状态
应力状态/应力状态的概念及其描述
示例一 F
S面
F
1
1
F A
1
S面
F 1
应力状态/应力状态的概念及其描述 n
F
1
90
同一点的应力状态可以有各种各样的描述方式.
二、平面应力状态
1、斜截面上的应力
2012-7-1
2012-7-1 33
用强度理论解决实际问题步骤:
(1)分析外力与变形,分成基本变形 (2)内力与应力,计算危险点的应力, 画出应力单元体,正应力与剪应力 (3)各基本变形应力叠加后确定主应力 (4)根据危险点应力状态及构件材料性 质,用适当强度理论计算相当应力 (5)应用强度条件进行强度校核
2012-7-1 34
平面弯曲
FN
M
z
FS
横截面上正应力分析和切应力分析 的结果表明:同一面上不同点的应力 各不相同,此即 应力的点的概念 。
应力状态/应力状态的概念及其描述
应 力
指明
哪一个面上? 哪一点?
哪一点? 哪个方向面?
过一点不同方向面上应力的集合, 称之为这一点的应力状态(State of the Stresses of a Given Point)。
限小的几何体,常用的是六
面体。
z
z
xy
x
x
应力状态/应力状态的概念及其描述
可以认为:
1、各个面上的应力都是均布的;
2、单元体每一对相互平行的两个
y
y
z
z
xy
x
x
面上应力大小相等,方向相反。
若单元体各个面上的应力已知, 由平 衡条件即可确定任意方向面上的正应力和
切应力。
应力状态/应力状态的概念及其描述
第四章 组合变形和强度理论
第一节 基本变形小结 受力与变形 内力—轴力图 正应力与强度
N A
虎克定律与刚度 E
2012-7-1
L
NL EA1
受力与变形 内力—剪力图 和弯矩图 正应力与强度
max
刚度
M
max
WZ
f max f
或
max
2012-7-1 28
2、最大伸长线应变理论(第二强度理论)
最大伸长线应变达到材料的极限值,材料 就发生脆性断裂破坏 。满足虎克定律。 jx 1 破坏条件:
1
jx
E
E
1 2 3
jx
E
强度条件:
1 2 3
2
强度条件:
1 2
1
2 2 2
3 3 1
2
2
考虑σ2,得到广泛的应用。
2012-7-1 32
一般原则如下:
1、脆性材料,常用第一、第二强度理论; 2、塑性材料,常用第三、第四强度理论; 3、在接近三向等拉应力状态下,不论是塑 性材料还是脆性材料,都将发生脆性断裂, 应采用第一强度理论; 4、在接近三向等压应力状态下,不论是塑 性材料还是脆性材料,都将发生塑性流动 破坏,应采用第三或第四强度理论。
2012-7-1 30
4、形状改变比能理论(第四强度理论)
变形体单位体积内所积蓄变形能称变形比 能。包括形状改变比能和体积改变比能
ud u 1 6E 1 2 E
1
2
2
2 2
3 3 1
2
2
1 2
3
形状改变比能达到极限值,就发生屈服 破坏条件: u d max u djx
校核强度、设计截面、确定许可载荷
2012-7-1 3
小结
5、截面对强度和刚度的影响,A、Wz、 Jz,材料远离中性轴。 6、许用应力 7、虎克定律 8、刚度条件
变形
载荷( P , q , M ) 长度( l ) 常数 许用值 截面几何性质 弹性模量 ( l , , f , ) ( A, J Z , J ) ( E,G)
三向(空间)应力状态
( Three-Dimensional State of Stresses )
x
z
z
xy
yx
zy
yz
垂直于x轴 的截面上 的正应力
x
zx
xz
x
x y
y
y
垂直于x轴的 截面上的切 应力,其方 向平行于y 轴
应力状态/应力状态的概念及其描述
平面(二向)应力状态 ( Plane State of Stresses )
9、材料力学试验
2012-7-1 4
第二节 复杂应力状态
弯曲和 压缩
2012-7-1
5
拉伸与压缩
扭转
弯曲
2012-7-1
6
扭转 弯曲
2012-7-1
7
一、一点处的应力状态
受力构件内任一点各个不同方位截面上的 应力及其相互关系称为一点的应力状态
2012-7-1 8
应力状态/应力状态的概念及其描述
z
z x
切应力为零的截面。
主应力(Principal Stress ):
2 1
主平面上的正应力。
主应力排列规定:按代数值大小,
3
1 2
3
应力状态/应力状态的概念及其描述 三向(空间)应力状态(Three—Dimensional State of Stress):
三个主应力都不为零的应力状态。
1 s ,
2012-7-1
2 3 0
u djx
1 6E
2
2 s
Hale Waihona Puke 311 6E
1
1
2 2 3 3 1
2 2
2
1 6E
2
2
2 s
s
2
1
2
2
2 3 3 1
应力状态/应力状态的概念及其描述
应力的三个重要的概念 1、应力的面的概念 2、应力的点的概念 3、应力状态的概念
应力状态/应力状态的概念及其描述
一点应力状态的描述
• 单元体(微元)
(Element)
dx , dy , dz 0
y
dz dx dy
y
单元体——构件内的点的代
表物,是包围被研究点的无
2012-7-1
26
三、四个基本的强度理论
一类是解释材料断裂破坏的强度理论, 有最大拉应力理论和最大拉应变理论; 另一类是解释材料流动破坏的强度理论, 最大剪应力理论和形状改变比能理论。
2012-7-1
27
1、最大拉应力理论(第一强度理论)
在十七世纪提出 ,针对建筑材料 只要最大拉应力达到材料的极限值, 材料就发生脆性断裂破坏 。 破坏条件: 1 b 强度条件: 1 用于受拉应力的某些脆性材料,铸铁、 石料、混凝土 没有考虑其它两个主应力的影响,也不 适用于三向压缩应力状态。
例1 画出下列图中的A、B、C点的已知单元体。 P y B C P M x P
A
x
A
x yx
x
zx
B
xz
x
C
xy
z
应力状态/应力状态的概念及其描述 主单元体、主面、主应力: y
y x
主单元体(Principal bidy): 各侧面上切应力均为零的单元体。 主平面(Principal Plane):
2 1 3
二向(平面)应力状态(Plane State of Stress): 只有一个主应力为零的应力状态。 单向应力状态(Unidirectional State of Stress): 只有一个主应力不为零的应力状态。
