ch05a_Gauss消去法
Gauss列主元素消去法实验

Lab06.Gauss 列主元素消去法实验【实验目的和要求】1.使学生深入理解并掌握Gauss 消去法和Gauss 列主元素消去法步骤; 2.通过对Gauss 消去法和Gauss 列主元素消去法的程序设计,以提高学生程序设计的能力;3.对具体问题,分别用Gauss 消去法和Gauss 列主元素消去法求解。
通过对结果的分析比较,使学生感受Gauss 列主元素消去法优点。
【实验内容】1.根据Matlab 语言特点,描述Gauss 消去法和Gauss 列主元素消去法步骤。
2.编写用不选主元的直接三角分解法解线性方程组Ax=b 的M 文件。
要求输出Ax=b 中矩阵A 及向量b ,A=LU 分解的L 与U ,det A 及解向量x 。
3.编写用Gauss 列主元素消去法解线性方程组Ax=b 的M 文件。
要求输出Ax=b 中矩阵A 及向量b 、PA=LU 分解的L 与U 、det A 及解向量x ,交换顺序。
4.给定方程组(1) ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--11134.981.4987.023.116.427.199.103.601.3321x x x(2) ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----15900001.582012151********.23107104321x x x x 先用编写的程序计算,再将(1)中的系数3.01改为3.00,0.987改为0.990;将(2)中的系数2.099999改为2.1,5.900001改为9.5,再用Gauss 列主元素消去法解,并将两次计算的结果进行比较。
【实验仪器与软件】1.CPU 主频在1GHz 以上,内存在128Mb 以上的PC ;2.Matlab 6.0及以上版本。
实验讲评:实验成绩:评阅教师:200 年 月 日Lab06.Gauss 列主元素消去法实验第一题:1、算法描述:Ⅰ、Gauss 消去法由书上定理5可知 设Ax=b ,其中A ∈R^(n(1)如果()0(1,2,....,1)k kka k n ≠=-,则可通过高斯消去法将Ax=b 约化为等价的 角形线性方程组,且计算公式为:① 消元计算(k=1,2,….,n-1)()()(1)()()(1)()()/,1,...,,,,1,...,,,1,...,.k k ik ik kk k k k ij ij ik kj k k k iiik k m a a i k n a a m a i j k n b b m b i k n ++==+=-=+=-=+② 回带公式()()()()()1/,()/,1,...,2,1.n n n n nn ni i i i iii j ii j i x b a x ba x a i n =+==-=-∑(2)如果A 为非奇异矩阵,则可通过高斯消去法将方程组Ax=b 约化方程组为上三角矩阵以上消元和回代过程总的乘除法次数为332333nn nn +-≈,加减法次数为32353263nnn n+-≈以上过程就叫高斯消去法。
数值分析课件ch05高斯消去法

( ) n
xi
b(i) i
a(i) ij
x
j
a(i) ii
(
i
=
k+1,
…,
n
)
j i 1
顺序Gauss 消去法的乘除运算量为:n3 n2 n
3
3
14
顺序高斯消去法的计算步骤
1 . 顺序消元
k 1,L , n 1
i k 1,L , n
(1)mik
a (k) ik
/ akk(k )
end
16
MATLAB For Gaussian Elimination
X(n)=b(n)/A(n,n); for i=n-1:-1:1
X(i)=(b(i)-A(i,i+1:n)* X(i+1:n))/A(i,i); end
A的第i行、第i+1到n列元素
构成的行向量
xn bn / ann
n
xi (bi aik xk ) / aii k i 1 i n 1, ,1
[n,n]=size(A);
% 确定A的维数
X=zeros(n,1); for k=1:n-1
for i=k+1:n
% 消元过程
m=A(i,k)/ A(k,k); % A(k,k) ≠0
A(i,k+1:n)= A(i,k+1:n)-m*A(k,k+1:n);
b(i)= b(i)-m*b(k);
end
for i=k+1:n
r=k;
det=abs(aug(k,k)); for j=k+1:n
%选主元
if det<abs(aug(j,k))
(完整word版)Gauss消去法Matlab

实验一 用列主元Gauss 消去法求解线性方程组实验目的会使用Matlab 语言编程使用列主元Gauss 消去法求解线性方程组.实验原理1、 列主元Gauss 消去法记线性方程组1112111212222212n n n n nn n n a a a x b a a a x b a a a x b ⎛⎫⎛⎫⎛⎫⎪⎪ ⎪ ⎪⎪ ⎪=⎪⎪ ⎪⎪⎪ ⎪⎝⎭⎝⎭⎝⎭ 为Ax=b, 其中A =111212122212n n n n nn a a a a a a a a a ⎛⎫ ⎪ ⎪ ⎪⎪⎝⎭,x=12n x x x ⎛⎫⎪ ⎪ ⎪⎪⎝⎭, b=12n b b b ⎛⎫ ⎪ ⎪ ⎪ ⎪⎝⎭, 记其增广矩阵为()(1)(1)(1)1111(1)(1)(1)(1)(1)2122(1)(1)(1)1n nn nnn a a b aa b Ab a a b ⎛⎫ ⎪ ⎪= ⎪ ⎪ ⎪⎝⎭。
设主元(1)11a 0≠,记(1)11(1)11(2,3,,)i i a l i n a =-=,用1i l 乘增广矩阵()(1)(1)A b 的第1行,再分别与第i 行相加,得()(1)(1)(1)(1)111211(1)(1)(2)(2)(2)2222(2)(2)(2)2b 00n nn nnn a a a a a b Ab a a b ⎛⎫ ⎪⎪= ⎪ ⎪ ⎪⎝⎭, 其中(2)(1)(1)1,ij ij i ij a a l a =+ i ,j=2,3,,n(2)(1)(1)11,i i i b b l b =+ i=2,3,,n又设主元(2)(2)i222i2(2)22a 0,l =-a a≠用乘矩阵()(2)(2)A b 的第二行,再与第i 行相加(i=3,4,,n ),得()(1)(1)(1)(1)(1)1112131n 1(2)(2)(2)(2)22232n 2(3)(3)(3)(3)(3)333n3(3)(3)(3)n3nnn b 0b Ab =0b 00b a a a a a a a a a a a ⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭. 经过n-1步消去后,增广矩阵最终变为()=)()( n n b A实验程序function x=gaussc(A ,b ) [n,m ]=size(A); A=[A ,b]; for k=1:n —1for p=k+1:nif abs(A (p ,k))>abs(A(k ,k )) for j=k :n+1 t=A(k,j );A (k,j)=A(p,j ); A(p,j)=t; end endend %搜索主元并交换 for i=k+1:nl=-A(i ,k )/A(k,k); for j=k+1:n+1A (i,j )=A(i ,j )+l*A(k,j); end endend %消去过程结束 x(n)=A (n,n+1)/A (n ,n); for i=n —1:-1:1 s=0;for j=i+1:ns=s+A (i,j)*x(j ); endx (i)=(A (i,n+1)-s )/A (i,i); end实验结果设A=[2,5;4,6],b=[3;4],求解线形方程组Ax=b.实验步骤:1) 先在matlab 里输入上面的程序;2) 然后输入A=[2,5;4,6] b=[3;4]3)再输入x=gaussc(A,b)命令即得出结果.由以上程序可求解得到x=( 0.2500 0。
研究生数值分析第四版第二章2.1Gauss消去法

2 x1 2 x2 3x3 3 3x2 x3 5 6 x2 8 x3 4
消元2
(1) ×2-(2)
(1)+(3)
3x2 x3 5 6 x2 8x3 4
6 x3 6
x3 1 x 2 2 x 2 1
(1)
a23 a33
(1)
a2 n1 a3n1
(1)
a2 n a3n(1)(1)()(1)(1)
ann1
a1n1
(1) ( 2)
ann
a1n
(1)
(1)
an 3
a13
(1) ( 2)
(1)
(1)
(1) b2 (1) b3 (1) bn
(1)
x3 1 x 2 2 x 2 1
二、Gauss消去法 1、Gauss消去法的基本思想: 消元与回代。 Gauss消去法分为: 顺序Gauss消去法,列主元素Gauss消去法 2、顺序Gauss消去法 例1在四位十进制的限制下,试用顺序Gauss消去法求 解下列线性方程组
天河一号 曾经的王者
2011年6月21日日本理化学研究所20日宣布,与富士 通共同研发中的超级计算机“京”以每秒8612万亿次的 运算速度在最新全球超级计算机500强排名中位列第一。
9.707 10 31 4 8 3600 8612 10 10
20
由170个机 柜组成的 天河二号 整齐排列, 气势恢宏。
a13
a1n
(1) (1)
b1
a23 a33
a2 n1 a3n1
a2 n a3n
(1)
(1)
(1)
ann1
gauss列主元素消去法matlab

高斯列主元素消去法是一种解线性方程组的常用方法,特别在数值分析和线性代数中应用广泛。
在Matlab中,我们可以使用该方法来解决大规模的线性方程组,包括矩阵的求解和矩阵的反转。
一、高斯列主元素消去法的基本原理高斯列主元素消去法是一种基于矩阵消元的方法,它通过一系列的矩阵变换将原始的线性方程组转化为上三角形式,然后再进行回代求解。
这个方法的核心就是通过矩阵的变换来简化原始的线性方程组,使得求解过程更加简单高效。
在Matlab中,我们可以利用矩阵运算和函数来实现高斯列主元素消去法,如`lu`分解函数和`\"`运算符等。
通过这些工具,我们能够快速地求解各种规模的线性方程组并得到准确的结果。
二、高斯列主元素消去法在Matlab中的实现在Matlab中,我们可以通过调用`lu`函数来实现高斯列主元素消去法。
该函数返回一个上三角矩阵U和一个置换矩阵P,使得PA=LU。
通过对U进行回代求解,我们可以得到线性方程组的解。
除了`lu`函数之外,Matlab还提供了一些其他的函数和工具来帮助我们实现高斯列主元素消去法,比如`\"`运算符和`inv`函数等。
通过这些工具的组合使用,我们能够更加灵活地进行线性方程组的求解,并且可以方便地处理特殊情况和边界条件。
三、高斯列主元素消去法的应用与局限性高斯列主元素消去法在实际应用中具有广泛的适用性,特别是对于大规模的线性方程组或者稀疏矩阵的求解。
通过Matlab中的工具和函数,我们可以快速地求解各种规模的线性方程组,并得到高精度的数值解。
然而,高斯列主元素消去法也存在一些局限性,比如对于奇异矩阵或者接近奇异矩阵的情况时,该方法的求解精度可能会下降。
在实际应用中,我们需要结合具体的问题和矩阵特性来选择合适的求解方法,以确保得到准确的结果。
四、个人观点和总结作为一种经典的线性方程组求解方法,高斯列主元素消去法在Matlab 中具有较好的实现和应用效果。
通过对其原理和实现细节的深入理解,我们能够更加灵活地应用该方法,并且能够更好地理解其适用性和局限性。
数值分析-Gauss消去法

数值分析上机报告1. 考虑方程组⎪⎪⎩⎪⎪⎨⎧-=+++=+++=+++=+++2557.03927.02786.04002.01784.04240.00643.03781.01920.03645.01550.01129.04015.03872..02246.04043.02943.03678.01234.04069.04.3214.3214.3214.321x x x x x x x x x x x x x x x x (1) 用Gauss 消去法解所给方程组(用四位小数计算);(2) 用列主元素消去法解所给方程组并且与(1)比较结果。
1. Matlab 程序>> clearA=input('输入系数矩阵A :');b=input('输入b 向量(按行向量):');B=[A b'];n=length(b);RA=rank(A);RB=rank(B);zhica=RB-RA;if zhica>0,disp('请注意:因为RA~=RB ,所以此方程组无解.\n')returnendif RA==RBif RA==nfprintf('请注意:因为RA=RB=%d ,所以此方程组有唯一解.\n',n) X=zeros(n,1);for p=1:n-1for k=p+1:nm= B(k,p)/ B(p,p);B(k,p:n+1)= B(k,p:n+1)-m* B(p,p:n+1);endend%把方程组系数矩阵A 化为同解的上三角矩阵b=B(1:n,n+1);A=B(1:n,1:n);X(n)=b(n)/A(n,n);for q=n-1:-1:1X(q)=(b(q)-sum(A(q,q+1:n)*X(q+1:n)))/A(q,q);end%从xn 至x1逐个求解上三角方程组elsedisp('请注意:因为RA=RB<n,所以此方程组有无穷多解.')returnendenddisp('方程组的解为:');X运行后输入系数矩阵A:[0.4096 0.1234 0.3678 0.2943;0.2246,0.3872,0.4015,0.1129;0.3645 0.1920 0.3781 0.0643;0.1784 0.4002 0.2786 0.3927]输入b向量(按行向量):[0.4043 0.1550 0.4240 -0.2667]请注意:因为RA=RB=4,所以此方程组有唯一解.方程组的解为:X =-0.2603-1.73242.3280-0.44712.Matlab程序>> clearA=input('输入系数矩阵A:');b=input('输入b向量(按行向量):');B=[A b'];n=length(b);RA=rank(A);RB=rank(B);zhica=RB-RA;if zhica>0,disp('请注意:因为RA~=RB,所以此方程组无解.\n')endif RA==RBif RA==nfprintf('请注意:因为RA=RB=%d,所以此方程组有唯一解.\n',n)X=zeros(n,1); C=zeros(1,n+1);for p= 1:n-1[Y,j]=max(abs(B(p:n,p))); C=B(p,:);B(p,:)= B(j+p-1,:); B(j+p-1,:)=C;for k=p+1:nm= B(k,p)/ B(p,p);B(k,p:n+1)= B(k,p:n+1)-m* B(p,p:n+1);endend%把方程组系数矩阵A化为同解的上三角矩阵b=B(1:n,n+1);A=B(1:n,1:n);X(n)=b(n)/A(n,n);for q=n-1:-1:1X(q)=(b(q)-sum(A(q,q+1:n)*X(q+1:n)))/A(q,q);end%从xn至x1逐个求解上三角方程组elsedisp('请注意:因为RA=RB<n,所以此方程组有无穷多解.')returnendenddisp('方程组的解为:');X运行结果输入系数矩阵A:[0.4096 0.1234 0.3678 0.2943;0.2246,0.3872,0.4015,0.1129;0.3645 0.1920 0.3781 0.0643;0.1784 0.4002 0.2786 0.3927]输入b向量(按行向量):[0.4043 0.1550 0.4240 -0.2667]请注意:因为RA=RB=4,所以此方程组有唯一解.方程组的解为:X =-1.7324 2.3280 -0.4471。
高斯消元法与列主元消去法实验报告

实验报告:Gauss消元法小组成员:李岚岚、邱粉珊、缪晓浓、杨水清学号:0917020040、0917010078、0917010073、0917010112一、实验问题编写两个程序,分别利用Gauss消元法和列主元消去法求解方程组二、分析及其计算过程Gauss顺序消元法:源程序:function [x]=gaussl(A,b)[n1,n2]=size(A);n3=size(b);if n1~=n2|n2~=n3|n1~=n3disp('A的行和列的维数不同!');return;endif det(A)==0disp('系数矩阵A奇异');return;end%消元过程L=eye(n1);for j=2:n1for i=j:n1L(i,j-1)=A(i,j-1)/A(j-1,j-1);A(i,:)=A(i,:)-L(i,j-1)*A(j-1,:);b(i)=b(i)-L(i,j-1)*b(j-1);endend%回代过程x(n1)=b(n1)/A(n1,n1);for t=n1-1:-1:1for k=n1:-1:t+1b(t)=b(t)-A(t,k)*x(k);endx(t)=b(t)/A(t,t);end程序的运行以及结果:>>A=[1 2/3 1/3;9/20 1 11/20;2/3 1/3 1];>>b=[2 2 2];>> [x]=gaussl(A,b)x =1 1 1Gauss列主元消去法:源程序:function [x]=gaussll(A,b) [n1,n2]=size(A);n3=size(b);if n1~=n2|n1~=n3|n2~=n3disp('输入的方程错误!');return;endif det(A)==0disp('系数矩阵A奇异');return;endmax=zeros(n1);for m=1:n1%找主元for i=m:n1if abs(A(i,m))>maxmax=A(i,:);A(i,:)=A(m,:);A(m,:)=max;maxb=b(i);b(i)=b(m);b(m)=maxb;endend%消元过程L=eye(n1);for j=2:n1for i=j:n1L(i,j-1)=A(i,j-1)/A(j-1,j-1);A(i,:)=A(i,:)-L(i,j-1)*A(j-1,:);b(i)=b(i)-L(i,j-1)*b(j-1);endendend%回代过程x(n1)=b(n1)/A(n1,n1);for t=n1-1:-1:1for k=n1:-1:t+1b(t)=b(t)-A(t,k)*x(k);endx(t)=b(t)/A(t,t);end程序的运行以及结果:>>A=[-0.002 2 2;1 0.78125 0;3.996 5.5625 4]; >>b=[0.4 1.3816 7.4178];>>[x]= gaussll(A,b)x =1.9273 -0.6985 0.9004。
数学实验题目5 相对Gauss列主元消去法

数学实验题目5 相对Gauss 列主元消去法摘要由一般线性方程组在使用Gauss 消去法求解时,从求解过程中可以清楚地看到,若(1)0k kk a -=,必须施以行交换的手续,才能使消去过程继续下去。
有时既使(1)0k kk a -≠,但其绝对值很小,由于舍入误差的影响,消去过程也会出现不稳定现象。
因此,为使这种不稳定现象发生的可能性减至最小,在施行消去过程时每一步都要选主元素,即要寻找行r ,使(1)(1)||max ||k k rk ik i ka a -->=并将第r 行与第k 行交换,以使(1)k kka -的当前值(即(1)k ika -的数值)远大于0。
这种列主元消去法的主要步骤如下: 1.消元过程 对1,2,,1k n =-,做1º 选主元,记||max ||rk ik i ka a >=若0rk a =,说明方程组系数矩阵奇异,则停止计算,否则进行2º。
2º 交换A (增广矩阵)的,r k 两行元素,,1rj kja a j k n ↔=+3º 计算/ij ij ik kj kk a a a a a =-1,,i k n =+1,,1j k n =++2.回代过程 对,1,,2,1k n n =-,计算,11(/)nk k n kjj kk j k x a ax a +=-=-∑前言利用Gauss 列主元消去法、显式相对Gauss 列主元消去法、隐式相对Gauss 列主元消去法求解线性方程组程序设计流程是否否是开 始输入A (增广矩阵)1k = ||max ||rk ik i ka a >=rk a =1,,1,,1/ij ij ik kj kk i k n j k n a a a a a =+=++=-交换A 中,r k 两行1k n <-,11,1,,2,1()/nk k n kjj kkj k k n n x a ax a +=+=-=-∑输出x结 束 1k =问题1(1)程序运行如下:x = GaussSysSolve(Mat1_1,b1_1)x = 1.0000 1.0000 1.0000 1.0000x = GaussExpSysSolve(Mat1_1,b1_1)x = 1.0000 1.0000 1.0000 1.0000x = GaussIneSysSolve(Mat1_1,b1_1)x = 1.0000 1.0000 1.0000 1.0000 (2)程序运行如下:x = GaussSysSolve(Mat1_2,b1_2)x = 1.0000 1.0000 1.0000 1.0000x = GaussExpSysSolve(Mat1_2,b1_2)x = 1.0000 1.0000 1.0000 1.0000x = GaussIneSysSolve(Mat1_2,b1_2)x = 1.0000 1.0000 1.0000 1.0000 (3)程序运行如下:x = GaussSysSolve(Mat1_3,b1_3)x = 1.0000 1.0000 1.0000 1.0000x = GaussExpSysSolve(Mat1_3,b1_3)x = 1.0000 1.0000 1.0000 1.0000x = GaussIneSysSolve(Mat1_3,b1_3)x = 1.0000 1.0000 1.0000 1.0000 (4)程序运行如下:x = GaussSysSolve(Mat1_4,b1_4)x = 1.0000 1.0000 1.0000 1.0000x = GaussExpSysSolve(Mat1_4,b1_4)x = 1.0000 1.0000 1.0000 1.0000x = GaussIneSysSolve(Mat1_4,b1_4)x = 1.0000 1.0000 1.0000 1.0000问题2(1)程序运行如下:= GaussSysSolve(Mat2_1,b2_1)x = 1.0915 0.2832 1.1463 -0.1008x = GaussExpSysSolve(Mat2_1,b2_1)x = 1.0915 0.2832 1.1463 -0.1008x = GaussIneSysSolve(Mat2_1,b2_1)x = 1.0915 0.2832 1.1463 -0.1008 (2)程序运行如下:x = GaussSysSolve(Mat2_2,b2_2)x = 0.5162 0.4152 0.1100 1.0365x = GaussExpSysSolve(Mat2_2,b2_2)x = 0.5162 0.4152 0.1100 1.0365x = GaussIneSysSolve(Mat2_2,b2_2)x = 0.5162 0.4152 0.1100 1.0365 (3)程序运行如下:x = GaussSysSolve(Mat2_3,b2_3)x = 1.0000 1.0000 1.0000x = GaussExpSysSolve(Mat2_3,b2_3)x = 1 1 1x = GaussIneSysSolve(Mat2_3,b2_3)x = 1.0000 1.0000 1.0000(4)程序运行如下:x = GaussSysSolve(Mat2_4,b2_4)x = 1 1 1x = GaussExpSysSolve(Mat2_4,b2_4)x = 1.0000 1.0000 1.0000x = GaussIneSysSolve(Mat2_4,b2_4)x = 1 1 1使用的函数function x = GaussSysSolve(A, b)% GaussSysSolve 用Gauss消去法解线性方程组Ax = b%% Synopsis: x = GaussSysSolve(A, b)%% Input: A = 系数矩阵% b = 方程组右端%% Output: x = 线性系统的解向量[m,n] = size(A);b = b(:); %将b变为列向量if m ~= n %A必须为方阵error('Argument matrix A must be square!');elseif m ~= length(b) %b的长度应与A维度相同error('The dimentions of A and b do not agree!');endAb = [A b]; %构造增广矩阵for i = 1:n[amax, imax] = max(Ab(i:n, i)); %选择主元if amax == 0 %主元为0,矩阵奇异error('Tne Linear System is singular!');elseif i ~= imax+i-1 %主元行数与i不同时,交换这两行Ab([i imax+i-1],:) = Ab([imax+i-1 i], :);endfor j = i+1:n %向下消元Ab(j,:) = Ab(j,:) - Ab(i,:) * Ab(j,i)/amax;endendx = zeros(n,1);x(n) = Ab(n,n+1)/Ab(n,n);for k = n-1:-1:1 %计算x x(k) = ( Ab(k,n+1) - Ab(k,k+1:n)*x(k+1:n) ) / Ab(k,k);endfunction x = GaussExpSysSolve(A, b)% GaussExpSysSolve 用显式Gauss列主元消去法解线性方程组Ax = b%% Synopsis: x = GaussExpSysSolve(A, b)%% Input: A = 系数矩阵% b = 方程组右端%% Output: x = 线性系统的解向量[m,n] = size(A);b = b(:); %将b变为列向量if m ~= n %A必须为方阵error('Argument matrix A must be square!');elseif m ~= length(b) %b的长度应与A维度相同error('The dimentions of A and b do not agree!');endAb = [A b]; %构造增广矩阵for i = 1:n %显式平衡技术s = max(Ab(i,1:n));Ab(i,:) = Ab(i,:)/s;endfor i = 1:n[amax, imax] = max(Ab(i:n, i)); %选择主元if amax == 0 %主元为0,矩阵奇异error('Tne Linear System is singular!');elseif i ~= imax+i-1 %主元行数与i不同时,交换这两行Ab([i imax+i-1],:) = Ab([imax+i-1 i], :);endfor j = i+1:n %向下消元Ab(j,:) = Ab(j,:) - Ab(i,:) * Ab(j,i)/amax;endendx = zeros(n,1);x(n) = Ab(n,n+1)/Ab(n,n);for k = n-1:-1:1 %计算xx(k) = ( Ab(k,n+1) - Ab(k,k+1:n)*x(k+1:n) ) / Ab(k,k);endfunction [x,det] = GaussIneSysSolve(A, b)% GaussIneSysSolve 用隐式Gauss列主元消去法解线性方程组Ax = b%% Synopsis: x = GaussIneSysSolve(A, b)%% Input: A = 系数矩阵% b = 方程组右端%% Output: x = 线性系统的解向量% det = 系数矩阵行列式的值[m,n] = size(A);b = b(:); %将b变为列向量if m ~= n %A必须为方阵error('Argument matrix A must be square!');elseif m ~= length(b) %b的长度应与A维度相同error('The dimentions of A and b do not agree!');endAb = [A b]; %构造增广矩阵det = 1; %初始化系数矩阵行列式为1for i = 1:n %隐式平衡技术s(i) = max(abs(Ab(i,1:n)));if s(i) == 0error('Tne Linear System is singular!'); %系数矩阵某行全为0时,矩阵奇异endends = s(:);for k = 1:n-1[c, kmax] = max(abs(Ab(k:n, k)./s(k:n))); %选择主元if c == 0 %主元为0,矩阵奇异det = 0;error('Tne Linear System is singular! det(A) = 0');elseif k ~= kmax+k-1 %主元行数与k不同时,交换这两行s([k kmax+k-1]) = s([kmax+k-1 k]);Ab([k kmax+k-1],:) = Ab([kmax+k-1 k], :);det = -det;endfor j = k+1:n %向下消元Ab(j,:) = Ab(j,:) - Ab(k,:) * Ab(j,k)/Ab(k,k);enddet = Ab(k,k)*det;endif Ab(n,n) == 0det = 0;error('Tne Linear System is singular!'); %最后一行唯一非0元素为0时,矩阵奇异endx = zeros(n,1);x(n) = Ab(n,n+1)/Ab(n,n);for k = n-1:-1:1 %计算x x(k) = ( Ab(k,n+1) - Ab(k,k+1:n)*x(k+1:n) ) / Ab(k,k);enddet = Ab(n,n)*det;思考题(1)在各主元不是非常小的时候,三种方法结果一致(2)隐式平衡列选主元法最好,应为当主元很小时,普通的Gauss消元法会产生很大误差;显式平衡列选主元法每一行除以其绝对值最大元素时会引入额外的舍入误差。
gauss消去法求解方程组matlab

高斯消去法是一种用于求解线性方程组的经典方法,它可以通过矩阵的初等变换将方程组化为上三角形式,然后通过回代的方式求解方程组。
在Matlab中,我们可以利用高斯消去法求解方程组,这样可以更加高效地进行数值计算。
下面我们将简要介绍高斯消去法的原理,并通过Matlab代码演示如何使用高斯消去法求解方程组。
一、高斯消去法原理及步骤高斯消去法是一种通过矩阵的初等变换将线性方程组化为上三角形式的方法,其求解过程主要包括以下几个步骤:1. 将系数矩阵增广为增广矩阵;2. 首先通过初等行变换将增广矩阵化为上三角矩阵;3. 然后通过回代的方式求解方程组。
通过这样的步骤,我们可以将原始的线性方程组化简为上三角形式,从而更容易求解方程组。
二、Matlab代码演示在Matlab中,我们可以通过编写代码实现高斯消去法来求解线性方程组。
下面是一个简单的例子代码,用来演示如何在Matlab中使用高斯消去法求解方程组:```matlabfunction x = gauss_elimination(A, b)[n, m] = size(A);if n ~= merror('A must be a square matrix');endAb = [A, b];for k = 1 : n - 1for i = k + 1 : nfactor = Ab(i, k) / Ab(k, k);Ab(i, k : n + 1) = Ab(i, k : n + 1) - factor * Ab(k, k : n + 1); endendx = zeros(n, 1);x(n) = Ab(n, n + 1) / Ab(n, n);for i = n - 1 : -1 : 1x(i) = (Ab(i, n + 1) - Ab(i, i + 1 : n) * x(i + 1 : n)) / Ab(i, i); endend```通过以上的Matlab代码,我们可以实现高斯消去法的求解过程,并得到方程组的解。
Gauss消去法求解线性方程组

Gauss消去法求解线性方程组
Gauss消去法,又称高斯-约旦消去法,是求解线性方程组的一种常用方法。
其基本思想是通过行变换将线性方程组转化为行最简形式,然后利用回代法求解。
以下是Gauss消去法求解线性方程组的详细步骤:
1. 将线性方程组的系数矩阵和常数向量组成增广矩阵。
2. 从第一行开始,将第一列的元素作为主元,并通过初等行变换将其它行的第一元素消成0。
3. 将第二行的第二个元素作为主元,并通过初等行变换将其它行的第二元素消成0。
4. 以此类推,直到将增广矩阵转化为行最简形式。
5. 利用回代法求解,即从最后一行开始,解出未知数依次代入上面的方程中求解。
其中,初等行变换包括以下三种:
1. 交换矩阵中两行的位置。
表示为 Ri<->Rj。
2. 将矩阵中某一行的每个元素乘以一个非零常数k。
表示为Ri*k。
3. 将矩阵中某一行的每个元素加上另一行对应元素的k倍。
表
示为 Ri+k*Rj。
Gauss消去法是一种较为常用的求解线性方程组的方法,但当系数矩阵存在奇异现象或行列式为0时,此方法无法求解。
此时可以采用LU分解法、SOR迭代法等其他方法进行求解。
数值分析3 Gauss消去法

§1 Gauss 消去法它是以行初等变换为基础,整理而成的计算机算法。
由它改进和变形得到的高斯选主元消去法及三角分解法,仍然是目前计算机上常用的解低阶稠密矩阵的线性方程组的有效方法。
一、 引例:解方程组:⎪⎩⎪⎨⎧-=-+-=+-=+-4336425294321321321x x x x x x x x x用Matlab 先画出空间三个平面,并找出三平面的交点clear,clf,x=[-9 –9 9 9 -9];y=[-9 9 9 –9 -9];z=5-4*x+9*y;plot3(x,y,z),hold on,grid on z=3-2*x+4*y;plot3(x,y,z) z=-4+x-y;plot3(x,y,z)A=[4 –9 2;2 –4 6;-1 1 –3];b=[5 3 –4]';x=A\b; plot3(x(1),x(2),x(3),'r*')解:方程组的增广矩阵是[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-----=431136425294b A消元运算:[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--−−−→−⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----−−→−-----5.110005.055.00529475.25.225.105.055.0052942313125.025.14142r r r r r r b A回代求解:0.15,1.5/103-=-=x [],5.25.0/)15.0(55.0x 2=-⨯-=95.64/)15.025.295(x 1=⨯+⨯+=。
【注】Gauss 消元的基本思想:用初等行变换方法化一般的方程组为上三角方程组,然后求解;Gauss 消去法步骤:先消元计算,再回代求解二、Gauss 消去法设n阶线性代数方程组为Ax=b (1)其中系数矩阵A(n 阶非奇异矩阵)和右端列向量b 分别为A=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡nn n n n n a a a a a a a a a 212222111211 , b=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡n b b b 21 (一)上三角方程组的回代求解:⎪⎪⎩⎪⎪⎨⎧==++=+++n n nn n n n n b x u b x u x u b x u x u x u 2222211212111 ………………(2) 假设u ii ≠0(i=1,2,…,n ),则回代解得:⎪⎩⎪⎨⎧-==∑+=ii ni j j ij i innn n u x u b x u b x /)(/11,2,2,1 --=n n i ………………(3) (二)GAUSS消元过程:(行变换)记方程组(1)为⎪⎪⎩⎪⎪⎨⎧=+++=+++=+++)1()1(2)1(21)1(1)1(2)1(22)1(221)1(21)1(1)1(12)1(121)1(11nn nn n n n n n n b x a xa x ab x a x a x a b x a x a x a (4)对应的增广矩阵为[]⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡=)1()1()1(2)1(1)1(2)1(2)1(22)1(21)1(1)1(1)1(12)1(11)1()1(,n nn n n nn b a a a b a a a b a a a bA…………………(5) 第一轮消元:若)1(11a ≠0,利用)1(11a 消下面的)1(1i a (i=2,3,…n), 消元因子:)1(11)1(11/a a l i i = (i=2,3,…n)[]⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡=)2()2()2(2)2(2)2(2)2(22)1(1)1(1)1(12)1(11)2()2(00,n nn n nnb a a b a a b a a a bA………………(6) 其中)1(11)1()2(j i ij ij a l a a -= n j i ,,3,2, =)1(11)1()2(b l b b i i i -= n i ,,3,2 = (7)第二轮消元:若0)2(22≠a ,用第i 行减去第二行的)2(22)2(22/a a l i i =(i=3,4,…n)倍,得到[]⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=)3()3()3(3)3(3)3(3)3(33)2(2)2(2)2(23)2(22)1(1)1(1)1(13)1(12)1(11)3()3(00000,n nnn nn nb a a b a a b a a a b a a a a b A……………(8) 其中n j i b l b b a l a a i i ij i ij ij ,,4,3,,,)2(22)2()3()2(22)2()3( =-=-= …………(9) 已进行k-1轮消元后,得[]⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=)()()()()()()2(2)2(2)2(2)2(22)1(1)1(1)1(1)1(12)1(11)()(,k n k nnk nk k k k knk kk nkn k k K b a a b a a b a a a b a a a a b A……………(10) 第k 轮消元:若)(k kk a ≠0,用第i 行元素减去第k 行元素的)()(/k kk k ik ik a a l = (i=k+1,k+2,…,n)倍,得[]⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=++++++++++++++++)1()1()1(111)1(1)1(11)()()(1)()2(2)2(2)2(12)2(2)2(22)1(1)1(1)1(11)1(1)1(12)1(11)1()1(,k n k nnk nk k k k nk k k k k k kn knk kk k kknk kn k kk K b a a b a a b a a a b a a a a b a a a a a b A…(11) 其中⎪⎩⎪⎨⎧-=-=++,)()()1()()()1(k k ik k i k ik kjik k ij k ij b l b b a l a a ,,,1,n k j i += (12)最后,得[]⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡=)()()2(2)2(2)2(22)1(1)1(1)1(12)1(11)()(,n n n nnnnn n b a b a a b a a a bA消元过程:[][][][])()()()()2()2()1()1(,,,,n n k k b A b A b A b A−→−−→−−→−−→−−→− (三)算法公式消元公式:对k=1,2,…,n-1若)(k kk a ≠0 )()(/k kk k ik ik a a l =⎪⎩⎪⎨⎧-=-=++,)()()1()()()1(k k ik k i k ik kj ik k ij k ij b l b b a l a a ,,,1,n k j i +=回代公式:)(n nn a ≠0⎪⎩⎪⎨⎧-==∑+=)(1)()()()(/)(/i ii n i j j i ij i i in nn n n n a x a b x a b x1,2,2,1 --=n n i三、GAUSS 消去法得以实现的前提(可行性分析)1、0a )()2(22(1)11≠n nn a a 或 2、,0,,0,,0,02122221112112221121111≠≠=≠≠A a a a aa a a a a D a a a a a kkk k k kk (13)这是因为:⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡→⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡)()2(2)2(22)1(1)1(12)1(11212222111211k kk n k kk k k k k a a a a a a a a a a a a a a a 行变换 k i a D n k i ii k ,,2,1,0,0,,,2,1)( =≠≠=则有若令【如】对称正定矩阵、严格对角占优矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡632351214 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-103131021310四、Gauss 消去法的运算量消元过程乘法:[])1(31)()1(211-=-⨯+-∑-=n n k n k n n k 除法:)1(2)(11-=-∑-=n nk n n k 回代过程乘除法总运算量:),1(221+=+++n nnGauss 消去法的总运算量为:3)3(31)1(2)1(2)1(313232n n n n n n n n n n ≈-+=++-+- 对比克莱姆法则的总运算量为(n+1)!【注】对比:当n=10时,克莱姆法则(n+1)!=39916800,而Gauss 消去法,运算430次五、算法及例子步1,定义数组A,B,x ; 步2,输入A,B,Eps ;步3,对k=1到n-1进行消元:⎪⎩⎪⎨⎧++=-⇐>-⇐n k k j i a b a b b Eps a a a a a a kkk ik i i kk kk kj ik ij ij ,,2,1,/,,/ 步4,nn n n a b x /=;对i=n-1到1回代解ij ni j j iji i a x ab x /)(1∑+=-=步5,输出n i x i ,,2,1, =; 步6,结束。
Gauss消去法
determinantal
D det(A) | A |
行列式的记号
若用初等变换法求解,则对其增广矩阵作行初等变换:
A ( A, b) ( A(1) , b(1) )
( A(2) , b(2) )
经过n-1次
( A(n) , b(n) ) 目标:A(n)为上三角阵
则方程组 A(n) x b(n) 的解不难得到
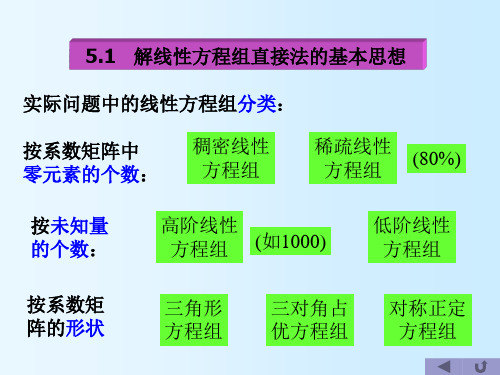
§ 5.1 解线性方程组直接法的基本思想
实际问题中的线性方程组分类:
按系数矩阵中
稠密线性
零元素的个数: 方程组
稀疏线性 方程组 (80%)
按未知量 的个数:
高阶线性 方程组 (如1000)
低阶线性 方程组
按系数矩 阵的形状
三角形 方程组
三对角占 优方程组
对称正定 方程组
一、直接法概述
直接法是将原方程组化为一个或若干个三角形 方程组的方法,共有若干种.
Lx b
l11 l21 l22
x1 b1
x2
b2
ln1
ln2
lnn
xn
bn
l11x1
b1
前
即
l21x1 l22 x2 li1x1 li2 x2 lii xi
b2 bi
推 方 向
ln1x1 ln2 x2 lnnxn bn
其解为
对于线性方程组
Ax b ------------(1)
其中
a11
A
a21
a12
a22
a1n a2n
x1
x
x2
b1
b
b2
an1
an2
ann
xnCramer(克莱姆)法则,若
Gauss消去法解方程组

Gauss消去法解方程组// Gauss消去法解方程组// 采用列主元Gauss消去法解线性方程组// 版本 1.0// copyright 2009 by zhangjl#includeusing namespace std;// 用二维数组Matrix[4][5]储存增广矩阵double Matrix[4][5]={{1 , -1 , 1 , -4 , 2 },{5 , -4 , 3 , 12 , 4 },{2 , 1 , 1 , 11 , 3 },{2 , -1 , 7 , -1 , 0 }};////void Show_Matrix(); //显示矩阵void FS_result$zjl$(); //方程组的解int main(){cout<<"增广矩阵初等变换:"<<endl;// 原始矩阵Show_Matrix();// 矩阵变换过程// 用于储存矩阵中特殊值的变量double D_Value=0; //变量double Maxcell=0; //储存主元int Index=0; //标记主元int Matrix_ROW=0; //行 Rowint Matrix_COLUMN=0; //列 Column//===================================== =====================// 令detA==1double detA=1;//储存矩阵第一行double FRow[5]={1 , -1 , 1 , -4 , 2};//矩阵变换过程先选主元再交换行cout<<"\n选主元交换行=>"<<endl;//选主元Maxcell=Matrix[0][0];for( Matrix_ROW=0 ; Matrix_ROW<4 ; Matrix_ROW ++ ){if( Maxcell <= Matrix[Matrix_ROW][0]){Maxcell = Matrix[Matrix_ROW][0]; //储存主元Index = Matrix_ROW; //标记主元}}if(Index){for( Matrix_COLUMN=0 ; Matrix_COLUMN<5 ; Matrix_COLUMN++ )//交换行{Matrix[0][Matrix_COLUMN] = Matrix[Index][Matrix_COLUMN];Matrix[Index][Matrix_COLUMN] = FRow[Matrix_COLUMN];}detA= -1;}detA=detA*Matrix[0][0];//Show_Matrix();//消元计算cout<<"\n消元计算=>"<<endl;for( Matrix_ROW=1 ; Matrix_ROW<4 ; Matrix_ROW++ ){for( Matrix_COLUMN=0 ; Matrix_COLUMN<5 ;Matrix_COLUMN++ )Matrix[Matrix_ROW][Matrix_COLUMN] -= (Matrix[Matrix_ROW][Matrix_COLUMN]/Matrix[0][0])*Matrix[0][ Matrix_COLUMN];}//===================================== =====================Show_Matrix();////储存矩阵第二行Matrix[1][Matrix_COLUMN]double SRow[5];for(Matrix_COLUMN=0 ; Matrix_COLUMN<5 ; Matrix_COLUMN++ ){SRow[Matrix_COLUMN] = Matrix[1][Matrix_COLUMN];}//选主元cout<<"\n选主元交换行=>"<<endl;Index=1;Maxcell=Matrix[1][1];for(Matrix_ROW=1 ; Matrix_ROW<4 ; Matrix_ROW++ ){if( Maxcell <= Matrix[Matrix_ROW][1]){Maxcell = Matrix[Matrix_ROW][1];Index = Matrix_ROW;//标记主元}}if(Index!=1){for(Matrix_COLUMN=0 ; Matrix_COLUMN<5 ; Matrix_COLUMN++)//交换行{Matrix[1][Matrix_COLUMN] = Matrix[Index][Matrix_COLUMN];Matrix[Index][Matrix_COLUMN] = SRow[Matrix_COLUMN];}detA= -detA;}//detA=detA*Matrix[1][1];Show_Matrix();//消元计算cout<<"\n消元计算=>"<<endl;D_Value=Matrix[2][1];for(Matrix_COLUMN=1 ; Matrix_COLUMN<5 ; Matrix_CO</endl;</endl;</endl;</endl;</endl;LUMN++)Matrix[2][Matrix_COLUMN] -= Matrix[1][Matrix_COLUMN]/Matrix[1][1]*D_Value;D_Value=Matrix[3][1];for(Matrix_COLUMN=1 ; Matrix_COLUMN<5 ; Matrix_COLUMN++)Matrix[3][Matrix_COLUMN] -= Matrix[1][Matrix_COLUMN]/Matrix[1][1]*D_Value;//===================================== =====================Show_Matrix();//储存矩阵第三行Matrix[2][Matrix_COLUMN]double TRow[5];for(Matrix_COLUMN=0 ; Matrix_COLUMN<5 ; Matrix_COLUMN++ ){TRow[Matrix_COLUMN] = Matrix[2][Matrix_COLUMN];}//选主元cout<<"\n选主元交换行=>"<<endl;Index=2;Maxcell=Matrix[2][2];for(Matrix_ROW=2 ; Matrix_ROW<4 ; Matrix_ROW++ ){if( Maxcell <= Matrix[Matrix_ROW][2]){Maxcell = Matrix[Matrix_ROW][2];Index = Matrix_ROW;//标记主元}}if(Index!=2){for(Matrix_COLUMN=0 ; Matrix_COLUMN<5 ; Matrix_COLUMN++ )//交换行{Matrix[2][Matrix_COLUMN] = Matrix[Index][Matrix_COLUMN];Matrix[Index][Matrix_COLUMN] = TRow[Matrix_COLUMN];}detA= -detA;}//detA=detA*Matrix[2][2];Show_Matrix();//消元计算cout<<"\n消元计算=>"<<endl;D_Value=Matrix[3][2];for(Matrix_ROW=3 ; Matrix_ROW<4 ; Matrix_ROW++ ){for(Matrix_COLUMN=2 ; Matrix_COLUMN<5 ; Matrix_COLUMN++ )Matrix[Matrix_ROW][Matrix_COLUMN] -= Matrix[2][Matrix_COLUMN]/Matrix[2][2]*D_Value;}//==========================================================Show_Matrix();FS_result$zjl$();//return 0 ;}void Show_Matrix(){//行:i_Row//列: i_Columncout<<"\t"<<"============================= ========="<<endl;for(int i_Row=0 ; i_Row<4 ; i_Row++ ){for(int i_Column=0 ; i_Column<5 ; i_Column++ ){cout<<"\t"<<matrix;}cout<<endl;}cout<<"\t"<<"============================= ========="<<endl;}void FS_result$zjl$(){double X1,X2,X3,X4;//方程组的解X4=Matrix[3][4]/Matrix[3][3];X3=(Matrix[2][4]-X4*Matrix[2][3])/Matrix[2][2];X2=(Matrix[1][4]-X4*Matrix[1][3]-X3*Matrix[1][2])/Matrix[1][1];X1=(Matrix[0][4]-X4*Matrix[0][3]-X3*Matrix[0][2]-X2*Matrix[0][1])/Matrix[0][0];cout<<"方程组的解:"<<endl;cout<<"X=("<<x1<<","<<x2<<","<<x3<<","<<x4<<")t"< <endl;}</x1<<","<<x2<<","<<x3<<","<<x4<<")t"<<endl;</endl;</endl;</endl;</matrix;</endl;</endl;</endl;。
实验一Gauss消元法解方程组

{ int n,i,j,k,m,h,t,q; double a[N][N],b[N],x[N],w,v,p; cout<<"请输入矩阵的阶数:"<<endl; while(cin>>n) //以下为数据输入,并显示所求方程以下为数据输入,并显示所求方程{ cout<<"请输入增广矩阵:"<<endl; for(i=1;i<=n;i++) { for(j=1;j<=n;j++) { cin>>a[i][j]; } cin>>b[i]; } k=1; for(i=1;i<=n;i++) //消元的第一重循环消元的第一重循环{ p=0; q=0; for(m=i;m<n+1;m++) { if(p<abs(a[m][i])) { p=abs(a[m][i]); q=m; } } cout<<"第"<<k<<"个系数矩阵为:"<<endl; //开始矩阵消元的过程开始矩阵消元的过程 for(m=1;m<=n;m++) { for(h=1;h<=n;h++) { cout<<setiosflags(ios::left)<<setw(10)<<a[m][h]; } cout<<b[m]<<endl; } for(t=i;t<=n-1;t++) //从此处开始时具体的消元算法从此处开始时具体的消元算法{ w=a[t+1][i]; for(j=i;j<=n;j++) 。
用高斯消元法求解线性代数方程组

用高斯消元法求解线性代数方程组12341115-413-2823113-21041513-21719x x x x ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦ 1111X *⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦(X*是方程组的精确解)1 高斯消去法1.1 基本思想及计算过程高斯(Gauss )消去法是解线性方程组最常用的方法之一,它的基本思想是通过逐步消元,把方程组化为系数矩阵为三角形矩阵的同解方程组,然后用回代法解此三角形方程组得原方程组的解。
为便于叙述,先以一个三阶线性方程组为例来说明高斯消去法的基本思想。
⎪⎩⎪⎨⎧=++II =++I =++III)(323034)(5253)(6432321321321x x x x x x x x x 把方程(I )乘(23-)后加到方程(II )上去,把方程(I )乘(24-)后加到方程(III )上去,即可消去方程(II )、(III )中的x 1,得同解方程组⎪⎩⎪⎨⎧=+-II -=-I =++III)(20223)(445.0)(64323232321x x x x x x x将方程(II )乘(5.03)后加于方程(III ),得同解方程组: ⎪⎩⎪⎨⎧-=-II -=-I =++III)(42)(445.0)(6432332321x x x x x x由回代公式(3.5)得x 3 = 2,x 2 = 8,x 1 = -13。
下面考察一般形式的线性方程组的解法,为叙述问题方便,将b i 写成a i , n +1,i = 1, 2,…,n 。
⎪⎪⎩⎪⎪⎨⎧=++++=++++=+++++++1,3322111,223232221211,11313212111n n n nn n n n n n n n n n a x a x a x a x a a x a x a x a x a a x a x a x a x a(1-1)如果a 11 ≠ 0,将第一个方程中x 1的系数化为1,得)1(1,1)1(12)1(121+=+++n n n a x a x a x其中)0(11)0()1(1aa aijj=, j = 1, …, n + 1(记ij ij a a =)0(,i = 1, 2, …, n ; j = 1, 2, …, n + 1)从其它n –1个方程中消x 1,使它变成如下形式⎪⎪⎩⎪⎪⎨⎧=++=++=++++++)1(1,)1(2)1(2)1(1,2)1(22)1(22)1(1,1)1(12)1(121n n n nn n n n n n n n a x a x a a x a x a a x a x a x(1-2)其中n i a m a aij i ij ij ,,2)1(1)1( =⋅-=,1,,3,211)1(11+==n j a a m i i由方程(1-1)到(1-2)的过程中,元素11a 起着重要的作用,特别地,把11a 称为主元素。
数值分析实验作业,gauss消去法的数值稳定性分析之欧阳学文创编

实验3.1 Gauss 消去法的数值稳定性试验欧阳歌谷(2021.02.01)实验目的:观察和理解Gauss 消元过程中出现小主元(即)(k kka 很小)时引起的方程组解的数值不稳定性。
实验内容:求解方程组b Ax =,其中(1)⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡⨯=11212592.1121-130.6-291.51314.59103.015-1A ,⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=2178.4617.591b ; (2)⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----=2010151526990999999999.23107102A ,⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=15019000000000.582b . 实验要求:(1) 计算矩阵的条件数,判断系数矩阵是良态的还是病态的。
(2) 用Gauss 列主元消去法求得L 和U 及解向量421,R x x ∈.(3) 用不选主元的Gauss 消去法求得L ~和U ~及解向量421~,~R x x ∈.(4)观察小主元并分析其对计算结果的影响.程序如下:计算矩阵条件数及Gauss列主元消去法:format longengA1=[0.3e-15 59.14 3 1;5.291 -6.130 -1 2;11.2 9 5 2;1 2 1 1];b1=[59.17;46.78;1;2];n=4;k2=cond(A1) %k2为矩阵的条件数;for k=1:n-1a=max(abs(A1(k:n,k)));[p,k]=find(A1==a);B=A1(k,:);c=b1(k);A1(k,:)=A1(p,:);b1(k)=b1(p);A1(p,:)=B;b1(p)=c;if A1(k,k)~=0A1(k+1:n,k)=A1(k+1:n,k)/A1(k,k);A1(k+1:n,k+1:n)=A1(k+1:n,k+1:n)-A1(k+1:n,k)*A1(k,k+1:n); elsebreakendendL1=tril(A1,0);for i=1:nL1(i,i)=1;endL=L1U=triu(A1,0)for j=1:n-1b1(j)=b1(j)/L(j,j);b1(j+1:n)=b1(j+1:n)-b1(j)*L(j+1:n,j);endb1(n)=b1(n)/L(n,n);for j=n:-1:2b1(j)=b1(j)/U(j,j);b1(1:j-1)=b1(1:j-1)-b1(j)*U(1:j-1,j);endb1(1)=b1(1)/U(1,1);x1=b1运行结果如下:K2=68.43;x=[18.9882;3.3378;-34.747;-33.9865]1不选主元的Gauss消去法程序:clearformat longengA1=[0.3e-15 59.14 3 1;5.291 -6.130 -1 2;11.2 9 5 2;1 2 1 1];b1=[59.17;46.78;1;2];n=4;for k=1:n-1A1(k+1:n,k)=A1(k+1:n,k)/A1(k,k);A1(k+1:n,k+1:n)=A1(k+1:n,k+1:n)-A1(k+1:n,k)*A1(k,k+1:n); endL1=tril(A1,0);for i=1:nL1(i,i)=1;endL=L1U=triu(A1,0)for j=1:n-1b1(j)=b1(j)/L(j,j);b1(j+1:n)=b1(j+1:n)-b1(j)*L(j+1:n,j);endb1(n)=b1(n)/L(n,n);for j=n:-1:2b1(j)=b1(j)/U(j,j);b1(1:j-1)=b1(1:j-1)-b1(j)*U(1:j-1,j);endb1(1)=b1(1)/U(1,1);x1=b1程序运行结果如下:同理可得A对应的系数矩阵条件数及Gauss列主元消去法求解结2果:K2=8.994;不选主元的Gauss消去法结果:实验4.5 三次样条插值函数的收敛性问题提出:多项式插值不一定收敛的,即插值的节点多,效果不一定就好。
gauss消去法及其某些变形时解低阶稠密方程组的有效方法。

gauss消去法及其某些变形时解低阶稠密方程组的有效方法。
一、引言Gauss消去法作为一种经典的线性方程组求解方法,在数学、物理、计算机科学等领域具有广泛的应用。
其在低阶稠密方程组求解中表现出了较高的效率,成为了一种有效的解决方法。
本文将对Gauss消去法及其某些变形进行详细介绍,并分析其在低阶稠密方程组解中的应用情况,以期为相关领域的研究提供参考。
二、Gauss消去法原理Gauss消去法是一种基于高斯消元的过程,通过初等行变换将增广矩阵转化为阶梯形矩阵,从而求解线性方程组。
具体步骤如下:1.选取一个方程的系数矩阵,将其与增广矩阵进行相乘,得到一个新的矩阵。
2.用新矩阵减去原矩阵,得到一个上三角矩阵。
3.重复步骤1和2,直到所有方程的系数矩阵都被替换为1。
4.将上三角矩阵的右侧部分替换为对应的方程右端项,得到一个新的增广矩阵。
5.按照步骤2-4的方法,将新矩阵转化为阶梯形矩阵。
6.从阶梯形矩阵中提取线性方程组的解。
三、Gauss消去法的变形1.列文逊-逆平方根法:在Gauss消去法的基础上,对矩阵进行列文逊分解,然后求解低阶线性方程组。
该方法在一定程度上提高了求解速度,但计算过程中需要进行多次矩阵乘法,可能导致计算量大。
2.列文逊-逆平方根法的改进型:针对原方法的时间复杂度问题,通过对列文逊分解过程中的矩阵进行优化,降低了计算量。
这种改进型在低阶稠密方程组求解中具有较高的效率。
3.其他相关变形方法:例如列文逊-托马斯法、托马斯算法等,这些方法在低阶稠密方程组求解中也有一定的应用价值。
四、低阶稠密方程组的解法1.低阶稠密方程组的定义和特点:低阶稠密方程组指的是系数矩阵的阶数较小,且元素较多的线性方程组。
这类方程组在实际应用中具有一定的特点,如系数矩阵非奇异、右端项较小等。
2.Gauss消去法在低阶稠密方程组中的应用:Gauss消去法在低阶稠密方程组中具有较好的解题效果,能够有效克服直接求解所带来的计算量大、存储空间不足等问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
k i, j n
② if ik k then 交换第 k 行和第 ik 行 if jk k then 交换第 k 列和第 jk 列 ③ 消元 列交换改变了 xi 的顺序,须记录交换次序,解完后 再换回来
全主元高斯消去法具有更好的稳定性,但很费时, 在实际计算中很少使用
21
1 1 记: L L 1 L2
1 ( n) L , U A ,则 n
A LU
LU 分解 (杜利脱尔Doolittle分解)
其中:L --- 单位下三角矩阵,U --- 上三角矩阵
16
LU 分解存在唯一性
LU 分解存在
高斯消去法不被中断
(k) akk 0
所有顺序主子式不为零
定理:若 A 的所有顺序主子式不为零,则 A 存在 唯一的 LU分解
(i) ii
(1) (i) 推论: a11 D1, aii Di Di 1 , i 2,
,n
13
运算量
计算机中做乘除运算的时间远远超过做加减运算时间, 故我们只估计 乘除运算 的次数
第 k 步:消第 k 列 2次 (k) (k ) ( n – k ) 计算 mik aik akk (i k 1, ..., n) ( k 1) (k ) (k ) 计算 aij aij mikakj ( i = k+1, …, n ) n–k次 ( k 1) (k ) (k )
相关性质
Ax x A x x
1 1
tr( A) 1 2 det( A) 12
n
n
A 与 AT 有相同的特征值
6
特殊矩阵
一些特殊矩阵
对角矩阵、三角矩阵、三对角矩阵 对称矩阵、Hermite对称矩阵、对称正定矩阵 正交矩阵、酉矩阵 初等置换阵、置换阵(排列阵) 上 Hessenberg 矩阵
列主元 Gauss 消去法比普通 Gauss 消去法要多一些比 较运算,但比普通高斯消去法稳定 列主元 Gauss 消去法是目前直接法的首选算法
20
全主元Gauss消去法
全主元高斯消去法:
第 k 步消元时,在剩余的 n-k 阶子矩阵中选取主元 (k) (k) max | a ① 先选取全主元:| ai j | = ij | 0
矩阵形式
Ax b
高斯消去法的主要思路:
将系数矩阵 A 化为上三角矩阵,然后回代求解。
=
10
(1) ) nn A, b(1) 记 A(1) (aij
Gauss 消去法
第一步:消去第一列 (1) (1) (1) 设 a11 0 ,计算 mi1 ai1 a11 (i 2, ..., n) 依次将增广矩阵的 第 i 行 + mi1 第 1 行,得 (2) (1) (1) ( 1) ( 1) ( 1) ( 1) 其中 aij a11 a12 ... a1 b1 aij mi1a1 n j
aij 0 for i j 1
a11 a 21 a12 a22 a32 a13 a23 a33 an, n1 a1n a2 n a3 n ann
7
性质
定理 1 定理 2 定理 3 定理 4
(解的存在唯一性,教材 141 页) (对称正定矩阵的性质,教材 141 页) (对称正定矩阵的充分条件,教材 141 页) (Jordan 标准型,教材 142 页)
8
Gauss 消去法
例:直接法解线性方程组 解:
x1 2 x2 2 x3 2 2 x1 3 x2 3 x3 4 4 x1 x2 6 x3 3
2 2 1 2 0 1 7 8 0 9 2 1 1
1 2 2 2 ( A, b) 2 3 3 4 4 1 6 3 2 2 1 2 0 1 7 8 0 0 61 61
bi bi mikbk
n
n–k次
回代求解:
( n) ( n) xn bn ann
xi bi(i )
(
j i 1
(i) a ij x j
)
n (n+1)/2 次
(i) aii ( i = k+1, …, n )
3 n n2 n Gauss 消去法的乘除运算量为: 3 3
(1) b1 b (1) (1) a a , b bi 。 ,即 ij ij i (1) b n
A
( 2)
b
(2)
(1) bi(2) bi(1) mi1b1
(i, j 2, ..., n)
第二步:消去第二列 (2) (2) (2) 设 a22 0 ,计算 mi 2 ai2 a22 (i 3, ..., n) 依次将上述矩阵的 第 i 行 + mi2 第 2 行,得
(证:板书)
17
列主元 Gauss 消去法
Gauss 消去法有效的条件是: 主元全不为零 例:解线性方程组 0 1 x1 1
1 0 x2 1
列主元 Gauss 消去法 在第 k 步消元时,在第 k 列的剩余部分选取主元
① 先选取列主元: | a
k in
) if ai( k =0 then stop kk if ik k then swap k-th and ik-th row (including b) for i=k+1 to n
aij aij mikakj , j k 1, k 2, ..., n bi bi mikbk end end
x3 1 x2 8 7 x3 1 x1 2 2x2 2x3 2
9
Gauss 消去法
考虑 n 阶线性方程组:
x ... 1a n xn 1 b a11 x 1 a 12 2 x ... 2a n xn 2 b a21 x 1 a 22 2 an1 x1 an 2 x 2 ... ann x n bn
A( k )
( k = 1, …, n-1)
( k 1)
则 其中:
A(k) 与
A(k+1) 之间的关系式可以表示为:
1 mk 1, k
Lk A
(k)
(k) (k) mik aik akk
( i = k + 1, …, n )
第五章 解线性方程组的直接方法
—— Gauss 消去法
1
本章内容
预备知识 Gauss 消去法 矩阵三角分解法 误差分析
2
本讲内容
预备知识
向量与矩阵 特征值与谱半径 一些特殊矩阵
Gauss 消去法
一般过程 对应的矩阵三角分解
列主元Gauss消去法
3
线性方程组直接解法
(k) ik k
(k) max | a | = k i n ik | 0
② if ik k then 交换第 k 行和第 ik 行
③ 消元
18
列主元 Gauss 消去法
算法 (列主元Gauss消去法 )
for k=1 to n-1 (k) | ai(kkk) | = max | aik | 0
依此类推,直到第 n-1 步,原方程化为
(1) (1) a11 a12 (2) a22 (1) a1(1) b x n 1 1 (2) b(2) x a2 n 2 2 ( n) ( n) x b ann n n
Ax b
A R
nn
, b R
n
自然科学和工程计算中, 很多问题最终都需要求解 一个线性代数方程组
目前使用的数值解法:
(1) 直接法: 适合低阶方程组或某些特殊大型稀疏方程组 (2) 迭代法: 解大型稀疏方程组的主流算法
在本章中,我们总是假定 A 是 n 阶方阵
4
预备知识
预备知识
(i, j 3, ..., n)
11
第 k 步:消去第 k列 高斯消去法 (k) (k) (k) 0,计算 mik aik akk 设 akk
( k 1) (k) (k) 计算 aij aij mikakj
Gauss 消去法
(i k 1, ..., n)
( k ) ( i = k+1, …, n ) bi( k 1) bi( k ) mikbk
回代求解: x b(n) a(n) n n nn
xi bi(i )
(
j i 1
(i) a ij x j
n
)
(i) aii ( i = n-1, …, 1 )
12
几点注记
主元: a
(i) ii
(i 1, 2, ..., n)
Gauss 消去法能进行到底的条件:主元全不为 0 定理: a 0 (i=1, 2, ..., n)的充要条件是 A 的顺 序主子式不为零,即 a11 a1i D1 a11 0, Di 0, i 1, 2, , n ai1 aii
15
( n) A 分解 Ln1 L2L1 A(1) 于是有: LU LU 分解
A A(1) ( Ln1
容易验证:
1 1 L k
L2L1)1 A(n)
1
1 mk 1, k mn, k 1
( k = 1, …, n-1)
xn bn an , xi bi
mik aik akk
(
j i 1
a x)
ij j
