【小初高学习】高中数学人教A版必修5习题:第三章不等式3.3.2.2
高中数学必修5第三章不等式精选习题
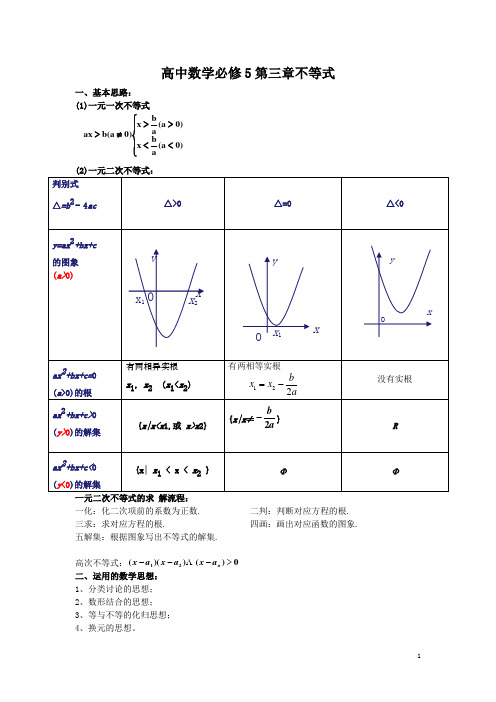
高中数学必修5第三章不等式一、基本思路: (1)一元一次不等式(2)一元二次不等式:一化:化二次项前的系数为正数. 二判:判断对应方程的根. 三求:求对应方程的根. 四画:画出对应函数的图象. 五解集:根据图象写出不等式的解集.高次不等式:二、运用的数学思想:1、分类讨论的思想;2、数形结合的思想;3、等与不等的化归思想;4、换元的思想。
⎪⎩⎪⎨⎧<<>>≠>)0a (a bx )0a (ab x )0a (b ax 0)())((21>---n a x a x a x高中数学必修5第三章不等式精选习题一、选择题1.若02522>-+-x x ,则221442-++-x x x 等于( ) A .54-x B .3- C .3 D .x 45- 2.设a >1>b >-1,则下列不等式中恒成立的是 ( )A .ba 11< B .b a 11> C .a >b 2 D .a 2>2b3.a > b > 0, 下列不等式一定成立的是 ( )A .a +b b a 11+> B .bc a c < C .b a b a b a >++22 D .b a abab b a +>>+22 4.如果实数x,y 满足x 2+y 2=1,则xy 有 ( )A .最大值21和最小值21- B .最大值21和最小值-1 C .最大值21没有最小值 D .以上都不对5.如果实数x,y 满足x 2+y 2=1,则(1-xy) (1+xy)有 ( )A .最小值21和最大值1 B .最大值1和最小值43 C .最小值43而无最大值 D .最大值1而无最小值6.如果x 2+y 2=1,则3x -4y 的最大值是 ( )A .3B .51C .4D .5 7.函数)1(log 21xx y += ,(x > 0)的最大值是 ( ) A .-1 B .-2 C .-3 D .0 8.函数y =log 21(x +11+x +1) (x >-1)的最大值是 ( )A .-2B .2C .-3D .3 9.不等式lgx 2<lg 2x 的解集是 ( )A .(1001,1) B .(100,+∞) C . (1001,1)∪(100,+∞) D .(0,1)∪(100,+∞) 10.若不等式x 2-log a x <0在(0,21)内恒成立,则a 的取值范围是 ( )A .161≤a <1B .161<a <1C .0<a ≤161D .0<a <161二、填空题11.不等式组⎩⎨⎧->-≥32x x 的负整数解是 .12.若方程05)2(2=++++m x m x 只有正根,则m 的取值范围是 . 13.若不等式0≤x 2-ax +a ≤1有唯一解,则a 的取值为 . 14.函数221x xy +=的值域是 . 15.不等式0)1()10)(3(2≥---x x x x 的解集是 .三、求下列不等式的解集:16、0122>+-x x 17、0522<-+-x x18、2017122>-x x 19、022<++x x20、0)1)(1)(2(>+--x x x三、解答题21.求证:ca bc ab c b a ++≥++222.22.求函数4522++=x x y 的最小值.23.已知2>a ,求证:()()1log log 1+>-a a a a24.已知:a 、b 都是正数,且1a b +=,1a a α=+,1b bβ=+,求αβ+的最小值25.设0a b +>,n 为偶数,证明 11n n n n b a a b--+≥11a b +26≥证:设向量(,4),(4,6)p a q a ==- ,由 ||||||p q p q +≥+,得||||p q =+ ||p q ≥+|(,4)(4,6)||(4,10)|a a =+-===∴原不等式成立,证毕。
高中数学 第三章 不等式单元测试题 新人教A版必修5

第三章《不等式》测试题1.设a<b<0,则下列不等式中不能成立的是( )A .1a >1bB .1a-b >1aC .a b >D .22b a > 2.关于x 的不等式(x-2)(ax-2)>0的解集为{x ︱x ≠2,x ∈R },则a=( )A .2B .-2C .-1D .13.不等式022>++bx ax 的解集是)31,21(-,则b a -的值等于( ) A .-14 B .14 C .-10 D .104.若实数a 、b 满足a+b=2,是3a +3b 的最小值是( )A .18B .6C .23D .2435.已知直角三角形的周长为2,则它的最大面积为( )A .3-2 2B .3+2 2C .3- 2D .3+ 26.f x a x a x ()=+-21在R 上满足f x ()<0,则a 的取值范围是( ) A a ≤0 B a <-4 C -<<40a D -<≤40a7.如果方程02)1(22=-+-+m x m x 的两个实根一个小于‒1,另一个大于1,那么实数m 的取值范围是( )A )22(,-B (-2,0)C (-2,1)D (0,1)8.若角α,β满足-2π<α<β<2π,则2α-β的取值范围是( ) A (-π,0) B (-π,π) C (-23π,2π) D (-π23,23π) 9.目标函数y x z +=2,变量y x ,满足⎪⎩⎪⎨⎧≥<+≤+-12553034x y x y x ,则有( )A 3,12min max ==z zB ,12max =z z 无最小值C z z ,3min =无最大值D z 既无最大值,也无最小值10.设M=)11)(11)(11(---cb a ,且a+b+c=1,(a 、b 、c ∈R +),则M 的取值范围是 ( ) A [0,81] B [81,1] C [1,8] D [8,+∞) 11.设.11120,0的最小值,求且yx y x y x +=+>> 12.若x ,y 为正实数,且2x +5y =20,则lgx +lgy 的最大值为13.若函数()f x =R ,则实数k 的取值范围是14.解不等式:(1)22740x x ++>;(2)2830x x -+->;(3)ax 2-(a +1)x +1<0.15.已知关于x 的方程(k-1)x 2+(k+1)x+k+1=0有两个相异实根,求实数k 的取值范围16.已知x 、y 满足不等式⎪⎩⎪⎨⎧≥≥≥+≥+0,01222y x y x y x ,求z=3x+y 的最小值。
人教A版高中数学必修五章节素质测试题——第三章 不等式.doc

新课标高中数学人教A 版必修5章节素质测试题——第三章 不等式(考试时间:120分钟 满分:150分)姓名__________评价_________一、选择题(本大题共12小题,每小题5分,共60分. 以下给出的四个备选答案中,只有一个正确) 1.(11广东文5)不等式0122>--x x 的解集是( )A .1(,1)2-B .(1, +∞)C .(-∞,1)∪(2,+∞)D .1(,)(1,)2-∞-⋃+∞2.(11上海理15)若,a b R ∈,且0ab >,则下列不等式中,恒成立的是( )A. 222a b ab +>B. a b +≥C.11a b +> D. 2b a a b +≥ 3.(11陕西文3)设0a b <<,则下列不等式中正确的是( )A.2a b a b +<<<B.2a ba b +<<< C.2a b a b +<<< D2a ba b +<<<4.(11重庆文7)若函数)2(21)(>-+=x x x x f 在x a =处取最小值,则a =( )A.1+B.1.3D .45.(12福建理5)下列不等式一定成立的是( )A .)0(lg )41lg(2>>+x x x B .),(2sin 1sin Z k k x xx ∈≠≥+π C .)(||212R x x x ∈≥+ D .)(1112R x x ∈>+6.(12广东理5)已知变量,x y 满足约束条件211y x y x y ≤⎧⎪+≥⎨⎪-≤⎩,则3z x y =+的最大值为( )A .12B .11C .3D .1-7.(09湖北文8)在“家电下乡”活动中,某厂要将100台洗衣机运往邻近的乡镇,现有4辆甲型货车和8辆乙型货车可供使用,每辆甲型货车运输费用400元,可装洗衣机20台;每辆乙型货车运输费用300元,可装洗衣机10台,若每辆车至多只运一次,则该厂所花的最少运输费用为( )A.2000元B.2200元C.2400元D.2800元 8.(10重庆理7)已知822,0,0=++>>xy y x y x ,则y x 2+的最小值是( )A.3B.4C.29 D.211 9.(10全国Ⅰ文7)已知函数()|lg |f x x =.若a b ≠且,()()f a f b =,则a b +的取值范围是( )A.(1,)+∞B.[1,)+∞C. (2,)+∞D. [2,)+∞ 10.(09山东文5)在R 上定义运算⊙: a ⊙b a ab b ++=2,则满足x ⊙)2(-x <0的实数x 的取值范围为( )A. {}20<<x xB. {}12<<x x - C. {}12>-<x x x ,或 D. {}21<<x x -11.(11浙江理理5)设实数y x 、满足不等式组250270,0x y x y x +-⎧⎪+-⎨⎪⎩>>≥,y ≥0,若y x 、为整数,则34x y +的最小值是( ) A .14B .16C .17D .1912.(09陕西理11)若x ,y 满足约束条件1122x y x y x y +≥⎧⎪-≥-⎨⎪-≤⎩,目标函数2z ax y =+仅在点(1,0)处取得最小值,则a 的取值范围是( )A. (1-,2 )B. (4-,2 )C. (4,0]-D. (2,4)- 二、填空题(每小题5分,共20分. 将你认为正确的答案填写在空格上) 13.(10山东文14)已知+∈R y x ,,且满足134x y+=,则xy 的最大值为____________. 14.(08江苏4)A={}73)1(x 2+<-x x ,则Z A I 的元素的个数为 . 15.(11新课标理13)若变量,x y 满足约束条件329,69,x y x y ≤+≤⎧⎨≤-≤⎩则2z x y =+的最小值为 .16.(10安徽文15)若200=+>>b a b a ,,,则下列不等式对一切满足条件的b a ,恒成立的是 . (写出所有正确命题的编号).①1≤ab ; ②2≤+b a ; ③222≥+b a ; ④333≥+b a ;⑤211≥+ba 三、解答题(本大题共6小题,共70分,解答应写出文字说明.证明过程或演算步骤) 17.(本题满分10分)已知R a ∈,试比较a+24与a -2的大小. 18.(本题满分12分,07江西文17)已知函数21(0)()21(1)x c cx x c f x c x -+<<⎧⎪=⎨⎪+<⎩≤满足29()8f c =.(Ⅰ)求常数c 的值;(Ⅱ)解不等式()18f x >+.19.(本题满分12分,11安徽理19)(Ⅰ)设1,1≥≥y x ,证明xy yx xy y x ++≤++111; (Ⅱ)设c b a ≤≤<1,证明c b a a c b a c b c b a log log log log log log ++≤++.20.(本题满分12分,08福建文20)已知{}n a 是正整数组成的数列,11a =,且点*1)()n a n N +∈在函数21y x =+的图像上: (Ⅰ)求数列{}n a 的通项公式;(Ⅱ)若数列{}n b 满足111,2na n nb b b +==+,求证:221n n n b b b ++⋅<.21.(本题满分12分,福建文21)设函数f (θ)cos θθ+,其中,角θ的顶点与坐标原点重合,始边与x 轴非负半轴重合,终边经过点P (x,y ),且0θπ≤≤. (1)若点P 的坐标为1(,22,求f ()θ的值; (II )若点P (x ,y )为平面区域Ω:x+y 1x 1y 1≥⎧⎪≤⎨⎪≤⎩,上的一个动点,试确定角θ的取值范围,并求函数()f θ的最小值和最大值.22.(本题满分12分,10广东19)某营养师要求为某个儿童预订午餐和晚餐.已知一个单位的午餐含12个单位的碳水化合物,6个单位的蛋白质和6个单位的维生素C;一个单位的晚餐含8个单位的碳水化合物,6个单位的蛋白质和10个单位的维生素C.另外,该儿童这两餐需要的营状中至少含64个单位的碳水化合物和42个单位的蛋白质和54个单位的维生素C.如果一个单位的午餐、晚餐的费用分别是2.5元和4元,那么要满足上述的营养要求,并且花费最少,应当为该儿童分别预订多少个单位的午餐和晚餐?13.__3__. 14. 6 . 15. -6 . 16. ①,③,⑤. 三、解答题 17.解:aa a a a +-+-=--+2)2)(2(4)2(24 ,22)4(422+=+--=a a a a ①当2-<a 时,0)2(24<--+a a ,<+a24a -2; ②当02≠->a a 且时,0)2(24>--+a a ,>+a 24a -2;③当0=a 时,0)2(24=--+a a ,=+a24a -2.18. 解:(Ⅰ)因为01c <<,所以2c c <; 由29()8f c =,即3918c +=, 12c =. (Ⅱ)由(Ⅰ)得411122()211x x x f x x -⎧⎛⎫+0<< ⎪⎪⎪⎝⎭=⎨1⎛⎫⎪+< ⎪⎪2⎝⎭⎩,,≤,由()18f x >+得, ①当102x <<时,121+x >182+,解得x >42,所以142x <<; ②当112x <≤时,124+-x >182+, 即x42->25321222-=,x 4->25-,解得x <85,所以1528x <≤.综上所述,不等式()18f x >+的解集为58x ⎧⎫⎪⎪<<⎨⎬⎪⎪⎩⎭.19. 证明:(Ⅰ)由于x ≥1,y ≥1,所以xy yx xy y x ++≤++111 2)(1)(xy x y y x xy ++≤++⇔将上式中的右式减左式,得)1)(1)(1()1)(1()1)(()1)(1())()(()1)(()1)(())((22---=+---=-+--+=+-+--=++-++y x xy y x xy xy xy y x xy xy y x y x xy xy y x xy xy x y 既然x ≥1,y ≥1,所以0)1)(1)(1(≥---y x xy ,从而所要证明的不等式成立. (Ⅱ)设y c x b b a ==log ,log ,由对数的换底公式得xy c yb x a xy a ac b c ====log ,1log ,1log ,1log 于是,所要证明的不等式即为xy yx xy y x ++≤++111 其中1log ,1log ≥=≥=c y b x b a 故由(Ⅰ)立知所要证明的不等式成立.20. 解:(Ⅰ)由已知得1)(21+=+n n a a ,即11=-+n n a a ,又11a =, 所以数列{}n a 是以1为首项,公差为1的等差数列. 因此.1)1(1)1(1n n d n a a n =⋅-+=-+=故数列{}n a 的通项公式为).(*N n n a n ∈= (Ⅱ)由(Ⅰ)知:n a n =,从而nn n b b 21=-+.)()()()(12123121----+-⋯⋯+-+-+=n n n n n b b b b b b b b b b.1221)21(1222112-=--⋅=++⋯⋯++=--n n n n因为212212)12()12)(12(----=-⋅++++n n n n n n b b b.02)1222()1222(122222<-=+⋅--+--=++++n n n n n n 所以b n ·b n +2<b 21+n .21. 解:(Ⅰ)由点P的坐标和三角函数的定义可得sin 1cos .2θθ⎧=⎪⎪⎨⎪=⎪⎩于是1()cos 2.22f θθθ=+=+= (Ⅱ)作出平面区域Ω(即三角形区域ABC )如图所示,其中A (1,0),B (1,1),C (0,1).于是0.2πθ≤≤又()cos 2sin()6f πθθθθ=+=+,且2,663πππθ≤+≤故当,623πππθθ+==即,()f θ取得最大值,且最大值等于2;当,066ππθθ+==即时,()f θ取得最小值,且最小值等于1.22. 解:设为该儿童分别预订x 个单位的午餐和y 个单位的晚餐,设费用为z 元,则目标函数为y x z 45.2+=,由题意知:⎪⎪⎩⎪⎪⎨⎧∈≥+≥+≥+Ny x y x y x y x 、54106426664812,即⎪⎪⎩⎪⎪⎨⎧∈≥+≥+≥+N y x y x y x y x 、275371623. 画出可行域:由⎩⎨⎧=+=+27537y x y x 得⎩⎨⎧==34y x ,所以直线7=+y x 与2753=+y x 的交点为)3,4(A .当直线045.20=+y x l :自左至右平行移动经过点)3,4(A 时,.2245.2min =+=y x z 答:应当为儿童分别预定4个单位午餐和3个单位晚餐,能满足上述的营养要求,并且花费最少.。
高中数学必修5(人教A版)第三章不等式3.3知识点总结含同步练习及答案

描述:例题:高中数学必修5(人教A版)知识点总结含同步练习题及答案第三章 不等式 3.3 二元一次不等式(组)与简单的线性规划问题一、学习任务1. 能从实际情景中抽象出二元一次不等式组;了解二元一次不等式组的集合意义,能用平面区域表示二元一次不等式组.2. 能从实际情景中抽象出一些简单的二元线性规划问题,并能加以解决.二、知识清单平面区域的表示 线性规划 非线性规划三、知识讲解1.平面区域的表示二元一次不等式表示的平面区域已知直线 :,它把坐标平面分为两部分,每个部分叫做开半平面,开半平面与 的并集叫做闭半平面.以不等式解 为坐标的所有点构成的集合,叫做不等式表示的区域或不等式的图象.对于直线 : 同一侧的所有点 ,代数式 的符号相同,所以只需在直线某一侧任取一点 代入 ,由 符号即可判断出 (或)表示的是直线哪一侧的点集.直线 叫做这两个区域的边界(boundary).二元一次不等式组表示的平面区域二元一次不等式组所表示区域的确定方法:①直线定界②由几个不等式组成的不等式组所表示的平面区域,是各个不等式所表示的平面区域的公共部分.l Ax +By +C =0l (x ,y )l Ax +By +C =0(x ,y )Ax +By +C (,)x 0y 0Ax +By +C A +B +C x 0y 0A +B +C >0x 0y 0<0Ax +By +C =0画出下列二元一次不等式表示的平面区域.(1) ;(2).解:(1)① 画出直线 ,因为这条直线上的点不满足 ,所以画成虚线.② 取原点 ,代入 ,所以原点在不等式 所表示的平面区域内,不等式表示的区域如图.3x +2y +6>0y ⩾3x 3x +2y +6=03x +2y +6>0(0,0)3x +2y+6=6>03x +2y +6>0描述:2.线性规划线性规划的有关概念若约束条件是关于变量的一次不等式(方程),则称为线性约束条件(objective function).一般地,满足线性约束条件的解 叫做可行解(feasible solution),由所有可行解组成的集合叫做可行域(feasible region).要求最大(小)值所涉及的关于变量 , 的一次解析式叫做线性目标函数(linearobjectives).使目标函数取得最大值或最小值的可行解叫做最优解.在线性约束条件下,求线性目标函数的最大值或最小值问题叫做线性规划问题(linearprogram).(2)① 画出直线 ,画成实线.② 取点 ,代入 ,所以 不在不等式 表示的平面区域内,不等式表示的区域如图.y =3x (1,0)y −3x =−3<0(1,0)y ⩾3x 画出不等式组 表示的平面区域.解:不等式 表示直线 及右下方的平面区域; 表示直线及右上方的平面区域; 表示直线 及左方的平面区域;所以不等式组表示的平面区域如图中阴影部分.⎧⎩⎨x −y +5⩾0x +y ⩾0x ⩽3x −y +5⩾0x −y +5=0x +y ⩾0x +y =0x ⩽3x =3(x ,y )xy⎩⎨4x+y+10⩾0作出可行域如图中阴影部分所示:可知,图可知,答案:解析:1. 下列各点中,不在 表示的平面区域的是 A .B .C .D .C将 代入得 ,故 不在 表示的平面区域内.x +y −1⩽0()(0,0)(−1,1)(−1,3)(2,−3)x =−1,y =3x +y −1−1+3−1=1>0(−1,3)x +y −1⩽02. 在平面直角坐标系 中,满足不等式组 ,点 的集合用阴影表示为下列图中的 A.B .C .xOy {|x |⩽|y ||x |<1(x ,y )()高考不提分,赔付1万元,关注快乐学了解详情。
(人教版)高中数学必修5检测第3章 不等式3.2 Word版含答案

第三章一、选择题(每小题分,共分).不等式-->的解集是( ).{≥或≤-} .{>或<-}.{-<<} .{-≤≤}解析:不等式-->化为-->,解得>或<-.答案:.设集合={+-<},={≤≤},则∩等于( ).[) .[].(] .[]解析:易知=(-),∴∩=[).故选.答案:.设集合={-<},={<},则( ).∩=∅.∩=.∪=.∪=解析:={-<}={<<},={<}={-<<},所以∩=.答案:.函数=+(-+)的定义域为( ).[-) .[-)∪(,+∞) .[-,+∞) .(-∞,-)∪(,+∞) 解析:由题意得(\\(+≥,-+>,))解得(\\(≥-,<或>.))∴-≤<或>,故其定义域为[-)∪(,+∞).故选.答案:二、填空题(每小题分,共分).满足不等式≤-≤的的取值范围是.解析:原不等式等价于(\\(-≥,--≤.))解得-≤≤或≤≤.答案:[-]∪[].二次函数=++(∈)的部分对应值如下表:解析:由题表得方程++=的两根为-,∴=++=(+)(-).将(-)代入二次函数得=>,∴不等式++>的解集为{<-,或>}.答案:{<-,或>}三、解答题(每小题分,共分).解下列不等式:()-->;()-+>;()--+≥;()-≥-;()-+<.解析:()∵Δ=(-)-××(-)=>,∴方程--=有两个不同实根,分别是-,,∴原不等式的解集为.()∵Δ=(-)-×=-<,∴-+>的解集为.()原不等式可化为+-≤,∵Δ=-××(-)=>,∴方程+-=有两个不同实根,分别是-,,∴原不等式的解集为.()原不等式可化为-+≤,即(-)≤.∴原不等式的解集是.()∵Δ=(-)-××=-<,∴不等式-+<的解集为∅..若不等式++>的解集为{-<<},求不等式+--<的解集.。
人教A版高中数学必修五 第三章 不等式.docx

人教A 版必修5 第三章 不等式
3.2一元二次不等式及其解法
对于一元二次方程()20y ax bx c a =++≠,设2
4b ac ∆=-,填表格:
1.求不等式24410x x -+>的解集.
2.求不等式2230x x -+->的解集.
3.求解下列不等式的解集.
(1)23710x x -≤; (2)2
250x x -+-<; (3)2440x x -+-<; (4)2
0.250x x -+>; (5)223x x -+<-; (6)2
1231200x x -+>; 4.自变量x 取何值时,对应的函数值为正数.零.负数.
(1)2362y x x =-+; (2)2
25y x =-; (3)2610y x x =++;
(4)2
31212y x x =-+-; 5.求下列函数的定义域:
(1)y = (2)y =
6.①若关于x 的一元二次方程()210x m x m -+-=有两个不同的实数根,求m 的范围; ②若关于x 的方程有()210mx m x m -++=两个不同的实数根,求m 的范围;
7.某文具店购进一批钢笔,若按每支15的价格销售,每天可卖30支;若售价每提高1元,则销售量减少2支.为了使这批钢笔每天获得400元以上的销售收入,售价应该定为多少?
8.若不等式2
2180x bx --<的解集为()1.5,6-,求b。
人教A版高中数学必修5第三章不等式

精选资料精选资料精选资料精选资料3.5 二元一次不等式 (组)与简单的线性规划问题知识梳理1.平面地区的表示方法(1)当 B>0 时,Ax+By+C>0 表示直线 Ax+By+C=0上方的地区 ;Ax+By+C<0表示直线 Ax+By+C=0下方的地区 .当 B<0 时,Ax+By+C>0 -Ax-By-C<0,表示直线下方的地区 ;Ax+By+C<0 - Ax-By-C>0,表示直线上方的地区 .(2)已知 M(x1,y1),N(x2,y2),直线 l:Ax+By+C=0,①若(Ax1+By1+C) × (Ax2+By2+C)>0,则点M、N在直线l 的同侧;②若(Ax1+By1+C) × (Ax2+By2+C)<0,则点M、N在直线l 的异侧;2.线性规划(1)对于变量 x,y 的拘束条件,都是对于 x,y 的一次不等式,称其为线性拘束条件; z=f(x,y)是欲达到最值所波及的变量 x,y 的分析式,叫目标函数 . 当f(x,y)是对于 x,y 的一次函数分析式时, z=f(x,y)叫做线性目标函数 .(2)求线性目标函数在线性拘束条件下的最大值和最小值问题,统称为线性规划 .知足线性拘束条件的解( x,y)叫做可行解,由全部可行解构成的会合叫做可行域,使目标函数获得最大值或最小值的解叫做最优解 .知识导学能正确地画出给定的二元一次不等式(组)表示的平面地区是学习简单线性规划问题图解法的重要基础;理解线性规划及线性拘束条件、线性目标函数、可行解、可行域、最优解等观点是解决实质生活中简单的最优化问题的有效方法,在本节的学习过程中,要注意领会数形联合与化归转变的数学思想.疑难打破1.二元一次不等式表示的平面地区.分析:在平面直角坐标系中,已知直线l:Ax+By+C=0,坐标平面内的点 P(x 0,y0).如有 Ax0+By0+C=0,则点 P 在直线 lxx;如有 Ax0+By0+C>0 或许 Ax0+By0+C<0,则点 P 在直线 l 的某一侧 .即二元一次不等式Ax+By+C>0 和 Ax+By+C <0分别表示直线 l 双侧的平面地区 .往常把直线画成虚线以表示地区不包含界限直线 ,若画不等式 Ax+By+C≥0或 Ax+By+C≤0表示的平面地区时 ,此地区包含界限直线,则把界限直线画成实线 .2.利用线性规划解决实质问题的问题种类及步骤.分析:利用线性规划来进行优化设计 ,解决生活中的实质问题往常有以下几种种类 :第一类 :给定必定数目的人力、物力资源 ,分析如何合理利用这些资源 ,才能使收到的效益最大 ;第二类 :给定一项任务 ,分析如何安排 ,能使达成这项任务的人力、物力资源最小,还要依据条件求最优解 ,有时还要分析整数解 .解线性规划应用题的步骤以下:第一步 :列表 ,转变为线性规划问题 ;第二步 :设出有关变元 ,列出线性拘束条件对应的不等式(组),写出目标函数 ;第三步 :正确画出可行域 ,依据条件求出目标函数的最大值或最小值及对应的变元 ;第四步 :写出实质问题的答案 .最新精选资料。
人教A版高中数学必修五本章练测:第3章不等式(含答案详解).docx

第3章 不等式(苏教版必修5)建议用时 实际用时满分 实际得分90分钟160分一、填空题(每小题5分,共70分)1.不等式2104x x ->-的解集是. 2.设01b a <<<,则下列不等式中成立的是.①21a ab <<;②1122log log 0b a <<;③21ab b <<;④222b a <<.3.不等式组()()002x y x y x -+>⎧⎨≤≤⎩,表示的平面区域是一个.4.不等式组0,34,34x x y x y ≥⎧⎪+≥⎨⎪+≤⎩所表示的平面区域的面积等于.5.已知函数2log (1)fx x =+()且0a b c >>>,则()()(),,f a f b f c a b c的大小关系是. 6.已知不等式1()9a x y x y ⎛⎫++≥ ⎪⎝⎭对任意正实数,x y恒成立,则正实数a 的最小值为.7.若函数1,0,()1,0,x x f x x x -+<⎧=⎨-≥⎩则不等式(1)x x ++∙(1)1f x +≤的解集是.8.设111111M a b c ⎛⎫⎛⎫⎛⎫=---⎪⎪⎪⎝⎭⎝⎭⎝⎭,且1a b c ++=(,a ,b c +∈R ),则M 的取值范围是.9.对于满足等式22(1)1x y +-=的一切实数,x y ,不等式0x y c ++≥恒成立,则实数c 的取值范围是. 10.若正数,,,a b c d 满足4a b cd +==,则ab c d +(填“≥”或“≤”),且等号成立时,,,a b c d 的取值(填“唯一”或“不唯一”).11.不等式224122xx +-≤的解集为. 12.已知函数1x y a -=(01)a a >≠,的图象恒过定点A ,若点A 在直线10(0)mx ny mn +-=>上,则11m n+的最小值为.13.设函数25z x y =+,其中,x y 满足条件280403x y x y +≤⎧⎪≤≤⎨⎪≤≤⎩,,,则z 的最大值是. 14.用两种材料做一个矩形框,按要求其长和宽分别选用价格为每米3元和5元的两种材料,且长和宽必须为整数米,现预算花费不超过100元,则做成的矩形框所围成的最大面积是 .二、解答题(解答应写出文字说明,证明过程或演算步骤,共90分)15.(14分)解关于x的不等式22---+30a a x(2)(23)x a+>.a16.(14分)如图,要设计一张矩形广告,该广告含有大小相等的左右两个矩形栏目(图中阴影部分),这两个栏目的面积之和为18 000 cm2,四周空白的宽度为10 cm,两栏之间的中缝空白的宽度为5 cm.怎样确定广告的高与宽的尺寸(单位:cm)能使矩形广告的面积最小?第16题图17.(14分)不等式22(23)(3)10m m x m x -----<对一切x ∈R 恒成立,求实数m 的取值范围.18.(16分)制定投资计划时,不仅要考虑可能获得的盈利,而且要考虑可能出现的亏损.某投资人打算投资甲、乙两个项目,根据预测,甲、乙两个项目可能的最大盈利率分别为100%和50%,可能的最大亏损率分别为30%和10%,投资人计划投资金额不超过10万元,要求确保可能的资金亏损不超过1.8万元,则投资人对甲、乙两个项目各投资多少万元才能使可能的盈利最大?19.(16分)已知二次函数()f x 满足(2)0f -=,且2422x x f x +≤≤()对一切实数x 都成立. (1)求(2)f 的值; (2)求()f x 的解析式;(3)设1()n b f n =,数列{}n b 的前n 项和为n S ,求证:43(3)n nS n >+.20.(16分)某村计划建造一个室内面积为72 m 2的矩形蔬菜温室.在温室内,沿左、右两侧与后侧内墙各保留1 m 宽的通道,沿前侧内墙保留3 m 宽的空地.当矩形温室的边长各为多少时蔬菜的种植面积最大?最大种植面积是多少?第3章 不等式(苏教版必修5)答题纸得分:一、填空题1. 2.3. 4.5. 6.7.8.9.10.11.12. 13. 14.二、解答题15.16.17.18.19.20.第3章 不等式(苏教版必修5)参考答案1.(-2,1)∪(2,+∞)解析:原不等式化为(2)(1)(2)0x x x +-->,解得21x -<<或2x >.2.④解析:∵2x y =是增函数,而01b a <<<,∴1222b a <<<.3.三角形 解析:原不等式组可化为0002x y x y x -⎧⎪+⎨⎪≤≤⎩>,>,或000 2.x y x y x -⎧⎪+⎨⎪≤≤⎩<,<,在平面直角坐标系中作出符合上面两个不等式组的平面区域,如图中的阴影部分所示,∴不等式组()()002x y x y x -+>⎧⎨≤≤⎩,表示的平面区域是一个三角形.第3题图第4题图4.43解析:不等式组表示的平面区域如图所示,由34,34x y x y +=⎧⎨+=⎩得交点A 的坐标为(1,1),又,B C 两点的坐标分别为(0,4),40,3⎛⎫ ⎪⎝⎭,故14441233ABC S ⎛⎫=⨯-⨯= ⎪⎝⎭△. 5.()()()f c f b f a c b a >>解析:特殊值法.令7a =,31b c ==,,满足0a b c >>>,∴ 2log (11)1+>2log (31)3+>2log (71)7+.故()()()f c f b f a c b a>>. 6.4 解析:不等式1()9a x y x y ⎛⎫++≥ ⎪⎝⎭对任意正实数,x y 恒成立,则1219y ax a a a x y +++≥++≥,∴a ≥2或4a ≤-(舍去),∴ 正实数a 的最小值为4.7.21x ≤-解析:依题意得10,10,(1)()1(1)1x x x x x x x x +<+≥⎧⎧⎨⎨++-≤++≤⎩⎩或,所以1,1,2121R x x x x ≥-⎧<-⎧⎪⇒⎨⎨∈--≤≤-⎪⎩⎩或1x <-或12121x x -≤≤-⇒≤-. 8.8 解析:M =b c a +·a c b +·a bc+≥8ab bc ac abc ∙∙=8.9.[21,)-+∞解析:令cos x θ= ,1sin y θ=+,则()sin cos 1x y θθ-+=---=π2sin 4θ⎛⎫-+ ⎪⎝⎭-1,∴ max ()2x y -+=-1.∵0x y c ++≥恒成立,∴ max ()2c x y ≥-+=-1. 10.≤ 唯一 解析:因为4a b cd +==,由基本不等式得2a b ab +≥,故4ab ≤.又2()4c d cd +≤,故4c d +≥,所以ab c d ≤+,当且仅当2a b c d ====时,等号成立.11.{|31}x x -≤≤解析:依题意得2241(3)(1)031x x x x x +-≤-⇒+-≤⇒∈-,[].12.4 解析:由题意知(11)A ,,∴10m n +-=,∴1m n +=, ∴1m +1n =11()2224n m n m m n m n m n m n ⎛⎫++=++≥+∙= ⎪⎝⎭.13.19解析:先在平面直角坐标系xOy 内画出不等式组所表示的平面区域,即可行域(如图中阴影部分).把25z x y =+变形为5152y x z =-+,得斜率为25-,在y 轴上的截距为15z ,随z 变化的一族平行直线.由图可以看出,当直线5152y x z =-+经过可行域上的点M 时,截距15z 最大,即z 最大. 解方程组283x y y +=⎧⎨=⎩,,得23.x y =⎧⎨=⎩,故23M (,).此时max z =2×2+5×3=19.第13题图14.40解析:设长为x 米,宽为y 米,则610100x y +≤,即3550x y +≤.∵0255335x y x y +≥∙≥,当且仅当35x y =时等号成立,,x y 为正整数,∴只有当324525x y ==,时面积最大,此时面积40xy =平方米. 15.解:由22(2)(23)x a a a x ---+30a +>,得[(2)3]()0a x x a --->. ①当2a =时,20x -<,解得2x <. ②当2a >时,原不等式可以化为32()0a x x a ⎛⎫⎪⎭--⎝->. 因为2323(3)(1)222a a a a a a a a -++-+--==---, 所以当3a =时,2(03)x ->,则x ∈R 且3x ≠. 当23a <<时,32a a >-,解得32x a >-或x a <.当3a >时,32a a <-,解得32x a <-或x a >. ③当2a <时,原不等式可以化为3(2)0a x x a ⎛⎫⎪⎭--⎝-<. 因为2323(3)(1)222a a a a a a a a -++-+--==---,所以当12a -<<时,32a a <-,所以32a x a -<<;当1a =-时,2(01)x +<,不等式无解;当1a <-时,32a a >-,所以32a a x <<-. 所以原不等式的解集为: 当1a <-时,32a x a x ⎧⎫⎨⎬-⎩<<⎭; 当1a =-时,不等式无解; 当12a -<<时,32xa x a <<⎧⎫⎨⎬-⎩⎭;当2a =时,{|2}x x <; 当23a <<时,32a x x a x ⎧⎫<>⎨⎩⎭-⎬或; 当3a =时,{|3}x x x ∈≠且R ; 当3a >时,32x x x a a ⎧⎫<>⎨-⎬⎩⎭或. 16.解:设矩形栏目的高为a cm ,宽为b cm ,则ab =9 000.① 广告的高为a +20,宽为2b +25,其中a >0,b >0. 广告的面积(20)(225)2402550018 500254018 5002254018 500S a b ab b a a b a b =++=+++=++≥+∙=+2 1 00024 500ab =,当且仅当2540a b =时等号成立,此时58b a =,将其代入①式得120a =,从而75b =,即当12075a b ==,时,S 取得最小值24 500.故广告的高为140 cm ,宽为175 cm 时,可使广告的面积最小. 17.解:若2230m m --=,则1m =-或3m =. 当1m =-时,不合题意;当3m =时,符合题意.若2230m m --≠,设22()(23)(3)1f x m m x m x =-----,则由题意,得22230,230,m m m m m ∆2⎧--<⎪⎨=[-(-3)]+4(--)<⎪⎩解得135m -<<. 综合以上讨论,得135m -<≤.18.解:设投资人分别用x y ,万元投资甲、乙两个项目,由题意,得10,0.30.1 1.8,0,0,x y x y x y +≤⎧⎪+≤⎪⎨≥⎪⎪≥⎩目标函数为0.5z x y =+.上述不等式组表示的平面区域如图所示,阴影部分(含边界)即为可行域.作直线0:0.50l x y +=,并作平行于直线0l 的一组直线0.5x y z +=,z ∈R ,与可行域相交,其中有一条直线经过可行域上的点M ,此时z 最大,这里点M 是直线10x y +=与直线0.30.1 1.8x y +=的交点.解方程组10,0.30.1 1.8,x y x y +=⎧⎨+=⎩得4,6,x y =⎧⎨=⎩此时,40.567z =+⨯=(万元).∴ 当46x y ==,时,z 取得最大值.答:投资人用4万元投资甲项目,6万元投资乙项目,才能使可能的盈利最大. 第18题图19.(1)解:∵ 2422x x f x +≤≤()对一切实数都成立, ∴4(2)4f ≤≤,∴(2)4f =.(2)解:设2()(0)f x ax bx c a =++≠.∵(2)0(2)4f f -==,,∴424,1,42024.a b c b a b c c a ++==⎧⎧⇒⎨⎨-+==-⎩⎩∵22ax bx c x ++≥,即2240ax x a -+-≥,∴214240410aa a ∆=--≤⇒-≤()(), ∴ 14a =,241c a =-=,故2()14x f x x =++.(3)证明:∵ 2144114()(2)(2)(3)23n b f n n n n n n ⎛⎫==>=- ⎪+++++⎝⎭, ∴ 1211111111444344523333(3)n n n S b b b n n n n ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=+++-+-++-=⨯-= ⎪ ⎪ ⎪ ⎪⎢⎥++++⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦>. 20.解:设矩形温室的左侧边长为a m ,后侧边长为b m,则72ab =,蔬菜的种植面积(4)(2)428802(2)8042S a b ab b a a b ab =--=--+=-+≤-=32(m 2).当且仅当2a b =,即126a b ==,时,max 32S =.答:当矩形温室的边长为6 m ,12 m 时,蔬菜的种植面积最大,最大种植面积是32 m 2.。
人教A版高中数学必修五第三章不等式

式的解法求解
人教A版数学 ·必修5
课前自主预习
高效互动课堂
课时演练广场
【规范解答】(1)由题意知 Δ=a2-16.
①当 Δ<0,即-4<a<4 时,方程 2x2+ax+2=0 无实根, 所以原不等式的解集为 R;2 分 ②当 Δ≥0,即 a≤-4 或 a≥4 时,方程 2x2+ax+2=0 的 1 2 根为 x1=4-a- a -16, 1 x2=4-a+ a -16 .
人教A版数学 ·必修5
课前自主预习
高效互动课堂
课时演练广场
(1)(2012 广东高考)已知变量 x,y 满足约束条件 x+y≤1, x-y≤1, x+1≥0, A.3 C.-5
则 z=x+2y 的最小值为( B.1 D.-6
)
人教A版数学 ·必修5
课前自主预习
高效互动课堂
课时演练广场
人教A版数学 ·必修5
课前自主预习
高效互动课堂
课时演练广场
二、有关一元二次不等式恒成立的问题
1.关于 x 的不等式 f(x)≥0(≤0)对于 x 在某个范围内的每个 值不等式都成立,就叫不等式在这个范围内恒成立. 2.一元二次不等式恒成立的类型及解法. 设 f(x)=ax2+bx+c(a≠0). (1)f(x)>0 在 x∈R 上恒成立⇔
解:原不等式可化为(x-a)(x-a2)>0.
∴当a<0时,a<a2,解集为{x|x<a或x>a2}; 当a=0时,a2=a,解集为{x|x≠0}; 当0<a<1时,a2<a,解集为{x|x<a2或x>a}; 当a=1时,a2=a,解集为{x|x≠1};
当a>1时,a<a2,解集为{x|x<a或x>a2}.
新版高中数学人教A版必修5习题:第三章不等式 3.3.1.2

第2课时二元一次不等式(组)表示平面区域的应用课时过关·能力提升基础巩固1不等式组---表示的平面区域的面积是A.3 B答案:C2点(a,1)在直线x-2y+4=0的右下方,则a的取值范围是().A.(-2,+∞)B.(-∞,-2)C.(1,+∞)D.(-∞,1)解析:如图,原点(0,0)在直线x-2y+4=0的右下方,则点(a,1)与原点在直线x-2y+4=0的同侧.把原点(0,0)代入x-2y+4,得4>0.于是把点(a,1)代入x-2y+4>0,即a-2+4>0,得a>-2.答案:A3如果点P在平面区域---上点在曲线上那么的最小值为AC.答案:A4在平面直角坐标系xOy中,M为不等式组----所表示的区域上一动点则直线斜率的最小值为A.2B.1C.解析:不等式组表示的区域如图阴影部分所示,结合斜率变化规律,当M位于C点时OM斜率最小,且为故选C.答案:C5若x,y满足条件-则的取值范围是解析:不等式组表示的平面区域如图阴影部分所示.表示原点与阴影部分中点的连线的斜率的2倍.又k OA=2,k OB所以1≤≤4.答案:[1,4]6已知实数x,y满足----则的取值范围是解析:画出约束条件对应的可行域(如图中阴影部分所示),x2+y2表示原点到可行域中的点的距离的平方,由图知原点到直线2x+y-2=0的距离的平方为x2+y2的最小值,为原点到点(2,3)的距离的平方为x2+y2的最大值,为22+32=13.因此x2+y2的取值范围是答案:7已知点P(x,4)到直线x-2y+2=0的距离为且点在不等式所表示的平面区域内则解析:由条件知即或答案:168某家具厂制造甲、乙两种型号的桌子,每张桌子需木工和漆工两道工序完成.已知木工做一张甲、乙型号的桌子分别需要1 h和2 h,漆工油漆一张甲、乙型号的桌子分别需要3 h和1 h.又木工、漆工每天工作分别不得超过8 h和9 h.请列出满足生产条件的数学关系式,并画出相应的平面区域.解设家具厂每天生产甲、乙型号的桌子的张数分别为x和y,它们满足的数学关系式为∈∈分别画出不等式组中各不等式表示的平面区域,然后取交集,如图中的阴影部分所示,生产条件是图中阴影部分的整数点.9有粮食和石油两种货物,可用轮船和飞机两种方式运输,每天每艘轮船和每架飞机的运输量如下表:现在要在一天之内运输2 000 t粮食和1 500 t石油,列出表示运输工具和运输数量的数学关系式,并画出相应的平面区域.解设需要x艘轮船,y架飞机,代数关系式和几何描述(如图阴影部分中的整数点)分别为∈∈能力提升1不等式组所表示的平面区域的面积等于AC解析:画出不等式组表示的平面区域,如图中的阴影部分所示.∵直线x+3y=4和3x+y=4的交点为(1,1),∴S-答案:C2若不等式组---表示的平面区域为三角形且其面积等于则的值为A.-3B.1 C解析:如图,要使不等式组表示的平面区域为三角形,则不等式x-y+2m≥0表示的平面区域为直线x-y+2m=0下方的区域,且-2m<2,即m>-1.这时平面区域为三角形ABC.由--解得则A(2,0).由解得则B(1-m,1+m).同理-因为S△ABC=S△ABM-S△ACM·(2+2m)·-由已知得解得m=1(m=-3<-1舍去).答案:B3设则满足条件≤1,0≤≤1的动点P的变动范围(下图中阴影部分,含边界)是().解析:设P点坐标为(x,y),则由可得即其表示的区域为选项A中的阴影部分.答案:A★4若不等式组所表示的平面区域被直线分为相等的两部分则的值为A解析:不等式组表示的平面区域如图所示阴影部分△ABC,由得A(1,1).又B(0,4),则直线y=kx过点C.要使直线y=kx平分△ABC,则直线y=kx过AB的中点.又线段AB的中点为故解得k答案:C5若实数x,y满足条件-则的最大值为解析:画出平面区域,如图中的阴影部分所示.设点P(x,y)为平面区域内一点,则--由-得交点A(2,1).由图,得0≤k OP≤k OA答案:6在平面直角坐标系中,不等式组--所表示的平面区域的面积为解析:原不等式组化为--或-画出其表示的平面区域如图阴影部分所示,由条件得A(-1,-2),-故所求平面区域的面积S答案:7当投资生产A 产品时,每生产100吨需要资金200万元,需场地200平方米;当投资生产B 产品时,每生产100米需要资金300万元,需场地100平方米.现某单位可使用资金1 400万元,场地900平方米,列出满足题意的数学关系式,并在直角坐标系中画出相应的平面区域. 解先将已知数据列成表,如下表所示:然后根据此表设未知数,列出限制条件,最后作图即可.设生产A 产品x 百吨,生产B 产品y 百米,则用图形表示以上限制条件,得其表示的平面区域如图所示(阴影部分).★8已知α,β是方程x 2+ax+2b=0的两根,且α∈[0,1],β∈[1,2],a ,b ∈R ,求--的最大值和最小值 解 - -∵0≤α≤1,1≤β≤2,∴1≤α+β≤3,0≤αβ≤2.- - 建立平面直角坐标系aOb , 则上述不等式组表示的平面区域如图所示.令k-- 可以看成动点P (a ,b )与定点A (1,3)的连线的斜率. ∵k AB- -故的最大值是最小值是。
2018秋新版高中数学人教A版必修5习题:第三章不等式 3.3.2.1 Word版含解析

3.3.2 简单的线性规划问题第1课时 简单的线性规划问题课时过关·能力提升基础巩固1若x ,y 满足{2x -y ≤0,x +y ≤3,x ≥0,则2x +y 的最大值为( ).A .0B .3C .4D .5解析:由不等式组可作出如图的可行域(阴影部分),将z=2x+y 变形为y=-2x+z ,这是斜率为-2,随z 变化的一族平行直线,如图,可知当y=-2x+z 经过点P 时,z 取最大值.由{2x -y =0,x +y =3,可得P 点坐标为(1,2),故z max =2×1+2=4. 答案:C2设变量x ,y 满足约束条件{x -y +2≥0,x -5y +10≤0,x +y -8≤0,则目标函数z =3x −4y 的最大值和最小值分别为( ).A.3,-11B.-3,-11C.11,-3D.11,3解析:画出可行域,如图中阴影所示.可知当直线z=3x-4y 平移到过点A (5,3)时,目标函数z=3x-4y 取得最大值3;当直线平移到过点B (3,5)时,目标函数z=3x-4y 取得最小值-11.答案:A3已知x ,y 满足不等式组{2x -y +1≥0,x -2y -1≤0,x +y ≤1,z =x −y 取得最大值的可行解为( ). A.(0,1) B.(-1,-1) C.(1,0) D .(12,12)解析:画出可行域如图所示的阴影部分.由图可知,当直线z=x-y 平移到过点(1,0)时,目标函数z=x-y 取得最大值. 答案:C4设x ,y 满足{2x +y ≥4,x -y ≥-1,x -2y ≤2,则z =x +y( ).A.有最小值2,最大值3B.有最小值2,无最大值C.有最大值3,无最小值D.既无最大值,也无最小值解析:画出可行域,如图中的阴影部分所示.作直线l 0:x+y=0,平移l 0,当l 0过点A (2,0)时,z 有最小值2,无最大值. 答案:B5已知x ,y 满足约束条件{x -y ≥0,x +y ≤2,y ≥0.若z =ax +y 的最大值为4,则a =(). A.3 B.2 C.-2 D.-3解析:由约束条件画出可行域,如图阴影部分所示.线性目标函数z=ax+y ,即y=-ax+z.设直线l 0:ax+y=0.。
人教A版高中数学必修五本章练测:第三章不等式(含答案详解).docx

第三章不等式(数学人教实验A版必修5)7.已知函数f(x)=1,1,0,x xx x-+<0,⎧⎨-≥⎩则不等式x+(x+1)f(x+1)≤1的解集是()A.{x|-1≤x-1}B.{x|x≤1}C.{x|x-1}D.{x|1≤x-1}8. 设,且a b (a、b、),则M的取值范围是()A.,18B. [,1)C.[,)D.[8,+∞)9.对于满足等式x2+(y-1)2=1的一切实数x、y,不等式x+y+c≥0恒成立,则实数c的取值范围是()A.(-∞,0]B.+∞)C.-1,+∞)D.[1,+∞)10.如果正数a,b,c,d满足a+b=cd=4,那么()A.ab≤c+d,且等号成立时a,b,c,d的取值唯B.ab≥c+d,且等号成立时a,b,c,d的取值唯一C.ab≤c+d,且等号成立时a,b,c,d 的取值不唯一D.ab≥c+d,且等号成立时a,b,c,d 的取值不唯一11. 一个直角三角形的周长为2p,则其斜边长的最小值为()A.B.C.D.12.某市的一家报刊摊点,从报社买进一种晚报的价格是每份0.20元,卖出的价格是每份0.30元,卖不掉的报纸可以以每份0.05元的价格退回报社.在一个月(按30天计算)里,有20天每天卖出量可达400份,其余10天每天只能卖出250份,但每天从报社买进的份数必须相同,为使每月所获利润最大,这个摊主应每天从报社买进( )份晚报. A.250 B.400C.300D.350二、填空题(本大题共4小题,每小题4分,共16分.把答案填在题中横线上)13.不等式2242x x+-≤12的解集为.14.函数y=1xa-(a>0,a≠1)的图像恒过定点A,若点A在直线mx+ny-1=0(mn>0)上,则1m+1n 的最小值为.15.若不等式x22a x a>0对x∈R恒成立,则关于t的不等式a2t1<a t22t3的解集为 .16.设x,y,z∈R,则最大值是 .三、解答题(解答应写出文字说明,证明过程或演算步骤,共74分)告含有大小相等的左右两个矩形栏目(即图中阴影部分),这两栏目的面积之和为18 000 cm 2,四周空白的宽度为10 cm ,两栏之间的中缝空白的宽度为5 cm.怎样确定广告版面的高与宽的尺寸(单位:cm )能使矩形广告的面积最小? 18.(12分)不等式(m 2-2m-3)x 2-(m-3)x-1<0对一切x ∈R 恒成立,求实数m 的取值范围.19.(12分)某人上午7时乘摩托艇以匀速 v km/h(4≤v ≤20)从A 港出发到距50 km 的B 港去,然后乘汽车以匀速w km/h(30≤w ≤100)从B 港向距 300 km 的C 市驶去.应该在同一天下午4至9点到达C 市.设乘摩托艇、汽车去所需要的时间分别是x h 、y h.若所需的经费p =100+3(5-y )+2(8-x )元,那么v ,w 分别为多少时,所需经费最少?并求出这时所花的经费.20.(12分)已知二次函数f(x)满足f(-2)=0,且2x≤f(x)≤242x+对一切实数x都成立.(1)求f(2)的值;(2)求f(x)的解析式;(3)设b n=1()f n,数列{b n}的前n项和为S n,求证:S n>43(3)nn+.21.(12分)制定投资计划时,不仅要考虑可能获得的盈利,而且要考虑可能出现的亏损.某投资人打算投资甲、乙两个项目,根据预测,甲、乙两个项目可能的最大盈利率分别为100%和50%,可能的最大亏损率分别为30%和10%,投资人计划投资金额不超过10万元,要求确保可能的资金亏损不超过1.8万元,则投资人对甲、乙两个项目各投资多少万元才能使可能的盈利最大?22.(14分)某村计划建造一个室内面积为72 m2的矩形蔬菜温室.在温室内,沿左、右两侧与后侧内墙各保留1 m宽的通道,沿前侧内墙保留3 m宽的空地.当矩形温室的边长各为多少时蔬菜的种植面积最大?最大种植面积是多少?第三章不等式(数学人教实验A版必修5)答题纸得分:一、选择题二、填空题13. 14. 15. 16.三、解答题17.18.19.20.21.22.第三章 不等式(数学人教实验A 版必修5)参考答案一、选择题1.D 解析:∵ y 2x 是增函数,而0<b <a <1,∴ 1<2b <2a <2.2.D 解析:∵ t-s =a+2b-a-b 2-1=-(b-1)2≤0,∴ t ≤s .3.C 解析:不等式组表示的平面区域如图所示, 由34,34x y x y +=⎧⎨+=⎩得交点A 的坐标为(1,1),又B ,C 两点的坐标分别为(0,4),(0,43), 故S △ABC =12 (4-43)×1=43. 第3题答图 4.B 解析:特殊值法.令a =7,b =3,c =1,满足a >b >c >0,∴2log (11)1+>2log (31)3+>2log (71)7+. 5. A 解析:不等式组可化为 xy >0,x y >0,或 xy <0,x y <0,在平面直角坐标系中作出符合上面两个不等式组的平面区域,如图中的阴影部分所示, ∴ 不等式组(x y )(x y )>0,0 x2表示的平面区域为三角形. 第5题答图6.B 解析:取测试点(0,1)可知C ,D 错,再取测试点(0,-1)可知A 错,故选B.7.C 解析:依题意得10,10,(1)()1(1)1x x x x x x x x +<+≥⎧⎧⎨⎨++-≤++≤⎩⎩或,所以1,1,11x x x x ≥-⎧<-⎧⎪⇒⎨⎨∈≤≤⎪⎩⎩R 或x <-1或-1≤x-1 x-1,故选C. 8. D 解析:M≥9.C 解析:令x = cos θ,y =1+ sin θ,则-(x+y )=- sinθ-cos θ-1=sin (θ+π4)-1.∴ -(x+y )max-1.∵ x+y+c ≥0恒成立,故c ≥-(x+y )max-1,故选C.10.A 解析:因为a+b =cd =4,由基本不等式得a+b ≥ab ≤4.又cd ≤2()4c d +,故c+d ≥4,所以ab ≤c+d ,当且仅当a =b =c =d =2时,等号成立.故选A.11.A 解析:设直角三角形的一个锐角为θ,斜边长为c , 则根据题意得c (sin θ+cos θ+1)=2p , ∴ c =2sin cos 1p θθ++∵ π,当θ=π时,等号成立,∴ c,当此三角形为等腰直角三角形时,等号成立. ∴ 斜边c.故选A. 12. B 解析:若设每天从报社买进x (250≤x ≤400,x ∈N )份晚报,则每月共可销售(20x +10×250)份,每份可获利润0.10元,退回报社10(x -250)份,每份亏损0.15元,建立月利润函数f (x ),再求f (x )的最大值,可得一个月的最大利润.设每天从报社买进x 份晚报,每月获得的总利润为y 元,则依题意,得 y =0.10(20x +10×250)-0.15×10(x -250)=0.5x +625,x ∈[250,400].∵ 函数y =0.5x +625在[250,400]上单调递增,∴ 当x =400时,y =825. 即摊主每天从报社买进400份晚报时,每月所获得的利润最大,最大利润为825元.13.{x |-3≤x ≤1} 解析:依题意x 2+2x-4≤-1 (x+3)(x-1)≤0 x ∈[-3,1]. 14.4 解析:由题意知A (1,1),∴ m+n-1=0,∴ m+n =1,∴1m +1n =(1m +1n )(m+n )=2+n m +mn≥2+=4. 15.(-2,2) 解析:由x 2-2ax +a >0对x ∈R 恒成立得Δ 4a 24a <0,即0<a <1, ∴ 函数y ax是R 上的减函数,∴ 2t 1>t22t3,解得-2<t <2.16.222 解析: x22y 2z222221 22xy z 2x 22y 2z21122xy z 2.17.解:设矩形栏目的高为a cm ,宽为b cm ,则ab =9 000.①广告版面的高为a+20,宽为2b+25,其中a >0,b >0.广告的面积S =(a+20)(2b+25)=2ab+40b+25a+500=18 500+25a+40b ≥18 500+=18 500+当且仅当25a =40b 时等号成立,此时b =58a ,代入①式得a =120,从而b =75,即当a =120,b =75时,S 取得最小值24 500.故广告版面的高为140 cm ,宽为175 cm 时,可使广告的面积最小. 18.解:若m 2-2m-3=0,则m =-1或m =3.当m =-1时,不合题意;当m =3时,符合题意.若m 2-2m-3≠0,设f (x )=(m 2-2m-3)x 2-(m-3)x-1,则由题意,得22230,230,m m m m m ∆2⎧--<⎨=[-(-3)]+4(--)<⎩ 解得-15<m <3.综合以上讨论,得-15<m ≤3.19.解:依题意得 4 50x 20,30 300y 100, 9 x y 14,x >0,y >0,考察z =2x +3y 的最大值,作出可行域,平移直线2x +3y =0, 当直线经过点(4,10)时,z 取得最大值38.故当v =12.5,w =30时所需要经费最少,此时所花的经费为93元. 20.(1)解:∵ 242()2+≤≤x x f x 对一切实数都成立,∴ 4≤f (2)≤4,∴ f (2)=4.(2)解:设f (x )=ax 2+bx+c (a ≠0).∵ f (-2)=0,f (2)=4,∴424,1,42024.a b c b a b c c a ++==⎧⎧⇒⎨⎨-+==-⎩⎩ ∵ ax 2+bx+c ≥2x ,即ax 2-x+2-4a ≥0,∴ Δ=1-4a (2-4a )≤0⇒(4a-1)2≤0,∴ a =14,c =2-4a =1,故f (x )=24x +x+1. (3)证明:∵ b n =1()f n =24(2)n +>4(2)(3)n n ++=4(12n +-13n +), ∴ S n =b 1+b 2+…+b n >4[(13-14)+(14-15)+…+(12n +-13n +)] =4×13-13n +=43(3)n +. 21.解:设投资人分别用x ,y 万元投资甲,乙两个项目,由题意,得10,0.30.1 1.8,0,0,x y x y x y +≤⎧⎪+≤⎪⎨≥⎪⎪≥⎩目标函数为z =x+0.5y . 上述不等式组表示的平面区域如图所示,阴影部分(含边界)即为可行域.作直线l 0:x+0.5y =0,并作平行于直线l 0的一组直线x+0.5y =z ,z ∈R ,与可行域相交,其中有一条直线经过可行域上的点M ,此时z 最大,这里点M 是直线x+y =10与直线0.3x+0.1y =1.8的交点. 第21题答图解方程组10,0.30.1 1.8,x y x y +=⎧⎨+=⎩得4,6,x y =⎧⎨=⎩此时,z =4+0.5×6=7(万元).∴ 当x =4,y =6时,z 取得最大值.答:投资人用4万元投资甲项目,6万元投资乙项目,才能使可能的盈利最大.22.解:设矩形温室的左侧边长为a m,后侧边长为b m,则ab=72,蔬菜的种植面积S=(a-4)(b-2)=ab-4b-2a+8=80-2(a+2b)≤80-(m2).当且仅当a=2b,即a=12,b=6时,S max=32.答:矩形温室的边长为6 m,12 m时,蔬菜的种植面积最大,最大种植面积是32 m2.。
【人教A版】高中数学必修5第三章课后习题解答

新课程标准数学必修5第三章课后习题解答第三章 不等式3.1不等关系与不等式 练习(P74)1、(1)0a b +≥; (2)4h ≤; (3)(10)(10)3504L W L W ++=⎧⎨>⎩.2、这给两位数是57.3、(1)>; (2)<; (3)>; (4)<;习题3.1 A 组(P75)1、略.2、(1)24<; (2>.3、证明:因为20,04x x >>,所以21104x x x ++>+>因为22(1)02x +>>,所以12x+>4、设A 型号帐篷有x 个,则B 型号帐篷有(5)x +个,050448054853(5)484(4)48x x x x x x >⎧⎪+>⎪⎪<⎪⎨<-<⎪⎪+<⎪+⎪⎩≥5、设方案的期限为n 年时,方案B 的投入不少于方案A 的投入.所以,(1)5105002n n n -+⨯≥ 即,2100n ≥.习题3.1 B 组(P75)1、(1)因为222259(56)30x x x x x ++-++=+>,所以2225956x x x x ++>++ (2)因为222(3)(2)(4)(69)(68)10x x x x x x x ----=-+--+=>所以2(3)(2)(4)x x x ->--(3)因为322(1)(1)(1)0x x x x x --+=-+>,所以321x x x >-+(4)因为22222212(1)1222(1)(1)10x y x y x y x y x y ++-+-=++-+-=-+-+> 所以2212(1)x y x y ++>+-2、证明:因为0,0a b c d >>>>,所以0ac bd >>又因为0cd >,所以10cd >于是0a bd c>>>3、设安排甲种货箱x 节,乙种货箱y 节,总运费为z .所以 352515301535115050x y x y x y +⎧⎪+⎨⎪+=⎩≥≥ 所以28x ≥,且30x ≤所以 2822x y =⎧⎨=⎩,或2921x y =⎧⎨=⎩,或3020x y =⎧⎨=⎩所以共有三种方案,方案一安排甲种货箱28节,乙种货箱22节;方案二安排甲种货箱29节,乙种货箱21节;方案三安排甲种货箱30节,乙种货箱20节. 当3020x y =⎧⎨=⎩时,总运费0.5300.82031z =⨯+⨯=(万元),此时运费较少. 3.2一元二次不等式及其解法 练习(P80) 1、(1)1013x x ⎧⎫-⎨⎬⎩⎭≤≤; (2)R ; (3){}2x x ≠; (4)12x x ⎧⎫≠⎨⎬⎩⎭; (5)31,2x x x ⎧⎫<->⎨⎬⎩⎭或; (6)54,43x x x ⎧⎫<>⎨⎬⎩⎭或; (7)503x x ⎧⎫-<<⎨⎬⎩⎭.2、(1)使2362y x x =-+的值等于0的x的集合是1⎧⎪⎨⎪⎪⎩⎭;使2362y x x =-+的值大于0的x的集合为11x x x ⎧⎪<>⎨⎪⎪⎩⎭或;使2362y x x =-+的值小于0的x的集合是11x x ⎧⎪<<+⎨⎪⎪⎩⎭.(2)使225y x =-的值等于0的x 的集合{}5,5-; 使225y x =-的值大于0的x 的集合为{}55x x -<<; 使225y x =-的值小于0的x 的集合是{}5,5x x x <->或. (3)因为抛物线2+610y x x =+的开口方向向上,且与x 轴无交点 所以使2+610y x x =+的等于0的集合为∅; 使2+610y x x =+的小于0的集合为∅; 使2+610y x x =+的大于0的集合为R. (4)使231212y x x =-+-的值等于0的x 的集合为{}2; 使231212y x x =-+-的值大于0的x 的集合为∅;使231212y x x =-+-的值小于0的x 的集合为{}2x x ≠. 习题3.2 A 组(P80)1、(1)35,22x x x ⎧⎫<->⎨⎬⎩⎭或; (2)x x ⎧⎪<<⎨⎪⎪⎩⎭;(3){}2,5x x x <->或; (4){}09x x <<.2、(1)解2490x x -+≥,因为200∆=-<,方程2490x x -+=无实数根所以不等式的解集是R ,所以y R. (2)解2212180x x -+-≥,即2(3)0x -≤,所以3x =所以y {}3x x =3、{33m m m <-->-+或;4、R.5、设能够在抛出点2 m 以上的位置最多停留t 秒. 依题意,20122v t gt ->,即212 4.92t t ->. 这里0t >. 所以t 最大为2(精确到秒)答:能够在抛出点2 m 以上的位置最多停留2秒. 6、设每盏台灯售价x 元,则15[302(15)]400x x x ⎧⎨-->⎩≥. 即1520x <≤.所以售价{}1520x x x ∈<≤习题3.2 B 组(P81)1、(1)52x ⎧+⎪<<⎨⎪⎪⎩⎭; (2){}37x x <<; (3)∅; (4)113x x ⎧⎫<<⎨⎬⎩⎭. 2、由22(1)40m m ∆=--<,整理,得23210m m +->,因为方程23210m m +-=有两个实数根1-和13,所以11m <-,或213m >,m 的取值范围是11,3m m m ⎧⎫<->⎨⎬⎩⎭或.3、使函数213()324f x x x =--的值大于0的解集为3322x x x ⎧⎪<-<+⎨⎪⎪⎩⎭或.4、设风暴中心坐标为(,)a b ,则a =22450b +<,即150150b -<<151)13.72=≈(h ),3001520=.所以,经过约13.7小时码头将受到风暴的影响,影响时间为15小时.3.3二元一次不等式(组)与简单的线性规划问题 练习(P86) 1、B . 2、D . 3、B .4解:设家具厂每天生产A 类桌子x 张,B 类桌子y 张.对于A 类桌子,x 张桌子需要打磨10x min ,着色6x min ,上漆6x min 对于B 类桌子,y 张桌子需要打磨5y min ,着色12y min ,上漆9y min 而打磨工人每天最长工作时间是450min ,所以有105450x y +≤. 类似地,612480x y +≤,69450x y +≤ 在实际问题中,0,0x y ≥≥;所以,题目中包含的限制条件为 1054506124806945000x y x y x y x y +⎧⎪+⎪⎪+⎨⎪⎪⎪⎩≤≤≤≥≥练习(P91)1、(1)目标函数为2z x y =+,可行域如图所示,作出直线2y x z =-+,可知z 要取最大值,即直线经过点C 时,解方程组11x y y +=⎧⎨=-⎩得(2,1)C -,所以,max 222(1)3z x y =+=⨯+-=.(2)目标函数为35z x y =+,可行域如图所示,作出直线35z x y =+ 可知,直线经过点B 时,Z 取得最大值. 直线经过点A 时,Z 取得最小值. 解方程组 153y x x y =+⎧⎨-=⎩,和15315y x x y =+⎧⎨+=⎩(第1题)可得点(2,1)A --和点(1.5,2.5)B .所以max 3 1.55 2.517z =⨯+⨯=,min 3(2)5(1)11z =⨯-+⨯-=-2、设每月生产甲产品x 件,生产乙产品y 件,每月收入为z 元,目标函数为30002000z x y =+,需要满足的条件是 2400250000x y x y x y +⎧⎪+⎪⎨⎪⎪⎩≤≤≥≥,作直线30002000z x y =+当直线经过点A 时,z 取得最大值. 解方程组 24002500x y x y +=⎧⎨+=⎩可得点(200,100)A ,z 的最大值为800000元. 习题3.3 A 组(P93)1、画图求解二元一次不等式:(1)2x y +≤; (2)22x y ->; (3)2y -≤; (4)3x ≥2、3(第2题)解:设每周播放连续剧甲x 次,播放连续剧乙y目标函数为6020z x y =+,所以,题目中包含的限制条件为8040320600x y x y x y +⎧⎪+⎪⎨⎪⎪⎩≤≥≥≥可行域如图. 解方程组80403206x y x y +⎧⎨+⎩==得点M 的坐标为(2,4),所以max 6020200z x y =+= 答:电视台每周应播放连续剧甲2次,播放连续剧乙4次,才能获得最高的收视率. 4、设每周生产空调器x 台,彩电y 台,则生产冰箱120x y--台,产值为z . 则,目标函数为432(120)2240z x y x y x y =++--=++ 所以,题目中包含的限制条件为111(120)402341202000x y x y x y x y ⎧++--⎪⎪⎪--⎨⎪⎪⎪⎩≤≥≥≥即,312010000x y x y x y +⎧⎪+⎪⎨⎪⎪⎩≤≤≥≥ 可行域如图,解方程组3120100x y x y +⎧⎨+⎩==得点M 的坐标为(10,90),所以max 2240350z x y =++=(千元)答:每周应生产空调器10台,彩电90台,冰箱20台,才能使产值最高,最高产值是350千元.习题3.3 B 组(P93)1、画出二元一次不等式组 231223600x y x y x y +⎧⎪+>-⎪⎨⎪⎪⎩≤≥≥,所表示的区域如右图2、画出(21)(3)0x y x y +--+>表示的区域.3、设甲粮库要向A 镇运送大米x 吨、向B 镇运送大米y 吨,总运费为z . 则乙粮库要向A 镇运送大米(70)x -吨、向B 镇运送大米(110)y -吨,目标函数(总运费)为122025101512(70)208(110)60z x y x y x y =⨯⨯+⨯⨯+⨯⨯-+⨯⨯-=++. 所以,题目中包含的限制条件为 100(70)(110)800700x y x y x y +⎧⎪-+-⎪⎨⎪⎪⎩≤≤≤≤≥.所以当70,30x y ==时,总运费最省 min 37100z =(元) 所以当0,100x y ==时,总运费最不合理 max 39200z =(元)使国家造成不该有的损失2100元.答:甲粮库要向A 镇运送大米70吨,向B 镇运送大米30吨,乙粮库要向A 镇运送大米0吨,向B 镇运送大米80吨,此时总运费最省,为37100元. 最不合理的调运方案是要向A 镇运送大米0吨,向B 镇运送大米100吨,乙粮库要向A 镇运送大米70吨,向B 镇运送大米10吨,此时总运费为39200元,使国家造成损失2100元.3.42a b+练习(P100)1、因为0x >,所以12x x +≥当且仅当1x x =时,即1x =时取等号,所以当1x =时,即1x x+的值最小,最小值是2. 2、设两条直角边的长分别为,a b ,0,a >且0b >,因为直角三角形的面积等于50.即 1502ab =,所以20a b +==≥,当且仅当10a b ==时取等号.答:当两条直角边的长均为10时,两条直角边的和最小,最小值是20.(第2题)3、设矩形的长与宽分别为a cm ,b cm. 0a >,0b > 因为周长等于20,所以10a b +=所以 2210()()2522a b S ab +===≤,当且仅当5a b ==时取等号.答:当矩形的长与宽均为5时,面积最大.4、设底面的长与宽分别为a m ,b m. 0a >,0b >因为体积等于323m ,高2m ,所以底面积为162m ,即16ab =所以用纸面积是 222324()32323264S ab bc ac a b =++=+++=+=≥ 当且仅当4a b ==时取等号答:当底面的长与宽均为4米时,用纸最少. 习题3.4 A 组(P100) 1、(1)设两个正数为,a b ,则0,0a b >>,且36ab =所以 12a b +==≥,当且仅当6a b ==时取等号. 答:当这两个正数均为6时,它们的和最小.(2)设两个正数为,a b ,依题意0,0a b >>,且18a b +=所以2218()()8122a b ab +==≤,当且仅当9a b ==时取等号.答:当这两个正数均为9时,它们的积最大. 2、设矩形的长为x m ,宽为y m ,菜园的面积为S 2m . 则230x y +=,S x y =⨯由基本不等式与不等式的性质,可得211219002252()222242x y S x y +=⨯⨯=⨯=≤. 当2x y =,即1515,2x y ==时,菜园的面积最大,最大面积是22522m . 3、设矩形的长和宽分别为x 和y ,圆柱的侧面积为z ,因为2()36x y +=,即18x y +=. 所以222()1622x y z x y πππ+=⨯⨯⨯=≤, 当x y =时,即长和宽均为9时,圆柱的侧面积最大.4、设房屋底面长为x m ,宽为y m ,总造价为z 元,则12xy =,12y x=123600312006800580048000012480058000z y x x x⨯=⨯+⨯+=+++=≥ 当且仅当1236004800x x⨯=时,即3x =时,z 有最小值,最低总造价为34600元. 习题3.4 B 组(P101)1、设矩形的长AB 为x ,由矩形()ABCD AB AD >的周长为24,可知,宽12AB x =-. 设PC a =,则DP x a =-所以 222(12)()x x a a -+-=,可得21272x x a x -+=,1272x DP x a x-=-=.所以ADP ∆的面积 211272187272(12)66[()18]2x x x S x x x x x--+-=-=⨯=⨯-++ 由基本不等式与不等式的性质6[18]6(18108S ⨯-=⨯-=-≤ 当72x x=,即x =m 时,ADP ∆的面积最大,最大面积是(108-2m . 2、过点C 作CD AB ⊥,交AB 延长线于点D .设BCD α∠=,ACB β∠=,CD x =.在BCD ∆中,tan b c x α-=. 在ACD ∆中,tan()a cxαβ-+= 则tan()tan tan tan[()]1tan()tan αβαβαβααβα+-=+-=++⋅()()1a c b ca b x x a c b c a c b c x x x x----==----+⋅+))c =当且仅当()()a cbc x x--=,即x =tan β取得最大,从而视角也最大.第三章 复习参考题A 组(P103)1<2、化简得{}23A x x =-<<,{}4,2B x x x =<->或,所以{}23A B x x =<<3、当0k <时,一元二次不等式23208kx kx +-<对一切实数x 都成立,即二次函数2328y kx kx =+-在x 轴下方,234(2)()08k k ∆=--<,解之得:30k -<<.当0k >时,二次函数2328y kx kx =+-开口朝上一元二次不等式23208kx kx +-<不可能对一切实数x 都成立,所以,30k -<<. 4、不等式组438000x y x y ++>⎧⎪<⎨⎪<⎩表示的平面区域的整点坐标是(1,1)--.5、设每天派出A 型车x 辆,B 型车y 辆,成本为z .所以 070494860360x y x y x y ⎧⎪⎪⎨+⎪⎪+⎩≤≤≤≤≤≥,目标函数为160252z x y =+把160252z x y =+变形为40163252y x z =-+,得到斜率为4063-,在y 轴上的截距为1252z ,随z 变化的一族平行直线. 在可行域的整点中,点(5,2)M 使得z 取得最小值. 所以每天派出A 型车5辆,B 型车2辆,成本最小,最低成本为1304元.6、设扇形的半径是x ,扇形的弧长为y ,因为 12S xy =扇形的周长为2Z x y =+≥ 当2x y =,即x =y =Z可以取得最小值,最小值为. 7、设扇形的半径是x ,扇形的弧长为y ,因为2P x y =+扇形的面积为221112(2)()244216x y P Z xy x y +===≤当2x y =,即4P x =,2P y =时,Z 可以取得最大值,半径为4P时扇形面积最大值为216P .8、设汽车的运输成本为y , 2()s say bv a sbv v v=+⨯=+当sasbv v=时,即v =c 时,y 有最小值.2sa y sbv v =+=≥2c 时,由函数sa y sbv v =+的单调性可知,v c =时y 有最小值,最小值为sa sbc c+. 第三章 复习参考题B 组(P103)1、D2、(1)32264x x x x ⎧⎫<--<<>⎨⎬⎩⎭或或 (2)⎧⎨⎩3、1m =4、设生产裤子x 条,裙子y 条,收益为z .则目标函数为2040z x y =+,所以约束条件为 10210600x y x y x y x y +⎧⎪+⎪⎪+⎨⎪⎪⎪⎩≤≤≤≥≥人教A 版高中数学课后习题解答答案11 5、因为22x y +是区域内的点到原点的距离的平方所以,当240330x y x y -+=⎧⎨--=⎩ 即2,3A A x y ==时,22x y +的最大值为13. 当4525x y ⎧=⎪⎪⎨⎪=⎪⎩时,22x y +最小,最小值是45. 6、按第一种策略购物,设第一次购物时的价格为1p ,购n kg ,第二次购物时的价格为2p ,仍购n kg ,按这种策略购物时两次购物的平均价格为121222p n p n p p n ++=. 若按第二种策略购物,第一次花m 元钱,能购1m p kg 物品,第二次仍花m 元钱,能购2m p kg 物品,两次购物的平均价格为12122211m m m p p p p =++ 比较两次购物的平均价格:221212121212121212121222()4()011222()2()p p p p p p p p p p p p p p p p p p p p +++---=-==++++≥ 所以,第一种策略的平均价格高于第二种策略的平均价格,因而,用第二种策略比较经济. 一般地,如果是n 次购买同一种物品,用第二种策略购买比较经济.。
人教A版高中数学必修5《三章 不等式 复习参考题》示范课件_22

x x 3或x 4
x 3 x 1
(3) x2 2x 1 0
x x 1
(4) x 2 2x 2 0
解一元二次不等式有哪些基本步骤?
问题1、解一元二次不等式有哪些基本步骤?
一、解原不等式对应的一元二次方程。
二、看原不等式对应的二次函数的图象。
解题点拨:该不等式对应方程的根是什么?其根的大小确定吗?
a (1)解:原不等式(2)对分析应:方原程不的等根式对应方程的根为 和 1
为 m 和 m1
原不等式对应二次函数当a 1时, 解集为
ya(x1 m)[x (m 1)]
的简图为
m a m1 1当a 1时, 解集{x a x 1}
0
y 0 x
无实数根
R
x 例1.解关于 的不等式:a(x 1)(x 3) 0(a 0)
分析: 原不等式对应方程的根 为1和3。
当a 0时
当a 0时
1
3
解集为{x x 1或x 3}
1
3
解集为{x1 x 3}
例2. 解下列关于 x 的不等式:
(1) (x m)x (m 1) 0(m R) (2) (x a)(x 1) 0(a R)
解: 原不等式对应方程的根为a和a2 当a a2即a 0或1时, 对应二次函数的简图为: a
原不等式的解集为{x x a} 当a a2,即0 a 1时,
原不等式对应二次函数的简图为: a2 a 原不等式的解集为{x a2 x a} 当a a2,即a 0或a 1时,
的解集
0
0
y
y
0 x1 x2 x
【K12小初高学习】新版高中数学人教A版必修5习题:第三章不等式 3.4.2

第2课时基本不等式的应用课时过关·能力提升基础巩固1已知p,q∈R,若pq=100,则p2+q2的最小值是().A.200B.100C.50D.20解析:p2+q2≥2pq=200,当且仅当p=q=10或p=q=-10时,等号成立.答案:A2在下列函数中,最小值为2的是().A.y=xB.y=3x+3-xC.y=lg xD.y=sin x解析:选项A中,由于x可能为负,因此y=x2;选项B中,3x,3-x都大于零,且3x+3-x≥3x=3-x,即x=0时,等号成立,故B正确;选项C中,lg x<0,因此最小值不是2;选项D中,由于sin x∈(0,1),故sin x2.答案:B3若a≥0,b≥0,且a+b=2,则().A.ab≤C.a2+b2≥2D.a2+b2≤3解析:取a=1,b=1,则ab=1,排除A项;取a=0,b=2,则ab=0,a2+b2=4,排除B,D两项,故选C.答案:C4将一根铁丝切割成三段做一个面积为2 m2、形状为直角三角形的框架,在下列四种长度的铁丝中,选用最合理(够用且浪费最少)的是().A.6.5 mB.6.8 mC.7 mD.7.2 m解析:设直角三角形框架的两直角边分别为a m,b m,则ab=4.所用铁丝长度l=a+b=4+≈6.828,当且仅当a=b=2时取等号.答案:C5两直角边之和为4的直角三角形面积的最大值等于.答案:26如图,有一张单栏的竖向张贴的海报,若它的印刷面积为72 dm2(图中阴影部分),上、下空白各宽2 dm,左、右空白各宽1 dm,则四周空白部分面积的最小值是 dm2.答案:567有一块半径为2 m的半圆形钢板,若裁成矩形的钢板,则矩形钢板的最大面积为m2. 解析:设垂直于直径的边长为x m,则另一边长m,则S=2≤4x2=4-x2,即x,等号成立,故当x,S=4,即S的最大值为4.答案:48已知a,b,c都是实数,求证:a2+b2+c2≥证明因为a,b,c∈R,所以a2+b2≥2ab,b2+c2≥2bc,c2+a2≥2ac.将以上三式两边分别相加,得2(a2+b2+c2)≥2(ab+bc+ca),在上式两边同时加上a2+b2+c2,得3(a2+b2+c2)≥(a+b+c)2,即a2+b2+c2≥9某单位用木料制作如图所示的框架,框架的下部是边长分别为x,y(单位:m)的矩形,上部是等腰直角三角形,如果要求框架围成的总面积为8 m2,那么x,y分别为多少时用料最省?解由题意则y则框架用料长度为l=2x+2y+2x=8-,等号成立,此时y=因此,当x=8-.10若a>0,b>0,(1)求a3+b3的最小值;(2)是否存在a,b,使得2a+3b=6?并说明理由.解(1)ab≥2,且当a=b,等号成立.故a3+b3≥a=b,等号成立.所以a3+b3的最小值(2)由(1)知,2a+3b≥由a,b,使得2a+3b=6.能力提升1若a,b是实数,且a+b=3,则2a+2b的最小值是().A.6B.解析:2a+2b≥2a=2b,即a=b,等号成立.答案:B2在三棱锥O-ABC中,OA,OB,OC两两垂直,若OC=1,OA=x,OB=y,x+y=4,则三棱锥O-ABC体积的最大值是().A解析:V·OA·S△OBC·OA··OB·OC·x··y·1因为x+y=4,x>0,y>0,所以4=x+y≥xy≤4.所以V x=y=2时,等号成立.答案:A3某公司租地建仓库,每月租金y1与仓库到车站的距离成反比,而每月库存货物的运费y2与到车站的距离成正比.如果在距离车站10千米处建仓库,这两项费用y1与y2分别为2万元和8万元,那么,要使这两项费用之和最小,仓库应建在离车站千米处.解析:设仓库建在离车站d千米处,设y1由y1=2k1=20,∴y1由y2=8=10k2,得k2∴y1+y2当且仅d=5时,两项费用之和最小.答案:54一批货物随17列货车从A市以v千米/时匀速直达B市,已知两地铁路线长400千米,为了安全,两列货车的间距不得小解析:设这批货物从A市全部运到B市的时间为t,则t≥),当且仅v=100时等号成立,此时t=8小时.答案:8★5某种汽车的购车费用为10万元,每年的保险费、养路费、汽油费约为0.9万元,年维修费第一年是0.2万元,以后逐年递增0.2万元.求这种汽车使用多少年时,它的年平均费用最少.解设汽车使用x年时,它的年平均费用最少.由年维修费第一年是0.2万元,以后逐年递增0.2万元,可知汽车每年维修费构成以0.2万元为首项,0.2万元为公差的等差数列,因此,汽车使用x年时总的维修费用.设汽车的年平均费用为y万元,则y=1≥1+当且仅x=10时,y取得最小值.故这种汽车使用10年时,它的年平均费用最少.★6(1)已知a,b,c>0,求证≥a+b+c;(2)已知a>0,b>0,a+b=1,求证≥8.证明(1)∵a,b,c0,a=b时等号成立;b=c时等号成立;a=c时等号成立.以上三式相加≥2a+2b+2c,当且仅当a=b=c时等号成立.≥a+b+c.(2∵a+b=1,a>0,b>0,≥2+2=4,7如图,公园想建一块面积为144平方米的矩形草地,一边靠墙,另外三边用铁丝网围住,现有44米铁丝网可供使用(铁丝网可以剩余),若利用x米墙,(1)求x的取值范围;(2)求最少需要多少米铁丝网.(精确到0.1米)解(1)由于矩形草地的面积是144平方米,一边长是x米,则另一边长,则矩形草地所需铁丝网长度为y=x+2令y=x+2≤44(x>0),解得8≤x≤36,故x的取值范围是[8,36].(2)由基本不等式,得y=x≥2当且仅当x x≈17.0时,等号成立,则y min=2≈34.0,故最少需要约34.0米铁丝网.。
人教A版高中数学必修五第三章不等式题组训练.doc

高中数学学习材料鼎尚图文*整理制作高中数学必修5第三章不等式题组训练[基础训练A 组]一、选择题(六个小题,每题5分,共30分)1.若02522>-+-x x ,则221442-++-x x x 等于( )A .54-xB .3-C .3D .x 45-2.函数y =log 21(x +11+x +1) (x > 1)的最大值是 ( )A .-2B .2C .-3D .33.不等式xx --213≥1的解集是 ( ) A .{x|43≤x ≤2} B .{x|43≤x <2} C .{x|x >2或x ≤43} D .{x|x <2} 4.设a >1>b >-1,则下列不等式中恒成立的是 ( )A .b a 11<B .ba 11> C .a >b 2 D .a 2>2b 5.如果实数x,y 满足x 2+y 2=1,则(1-xy) (1+xy)有 ( )A .最小值21和最大值1 B .最大值1和最小值43 C .最小值43而无最大值 D .最大值1而无最小值 6.二次方程x 2+(a 2+1)x +a -2=0,有一个根比1大,另一个根比-1小, 则a 的取值范围是 ( )A .-3<a <1B .-2<a <0C .-1<a <0D .0<a <2二、填空题(五个小题,每题6分,共30分)1.不等式组⎩⎨⎧->-≥32x x 的负整数解是____________________。
2.一个两位数的个位数字比十位数字大2,若这个两位数小于30,则这个两位数为____________________。
3.不等式0212<-+xx 的解集是__________________。
4.当=x ___________时,函数)2(22x x y -=有最_______值,其值是_________。
5.若f(n)=)(21)(,1)(,122N n nn n n n g n n ∈=--=-+ϕ,用不等号 连结起来为____________.三、解答题(四个小题,每题10分,共40分)1.解log (2x – 3)(x 2-3)>02.不等式049)1(220822<+++++-m x m mx x x 的解集为R,求实数m 的取值范围。
【专业资料】新版高中数学人教A版必修5习题:第三章不等式 3.2.2 含解析

第2课时一元二次不等式的应用课时过关·能力提升基础巩固1若集合M=(-1,+∞),集合N={x|x(x+2)≤0},则M∩N=().A.[0,2]B.(0,+∞)C.(-1,0]D.(-1,0)解析:N={x|-2≤x≤0},所以M∩N=(-1,0].答案:C2若关于x的不等式x2+mx+1≥0的解集为R,则实数m的取值范围是().A.m≥2B.m≤-2C.m≤-2或m≥2D.-2≤m≤2解析:∵不等式x2+mx+1≥0的解集为R,∴Δ=m2-4≤0,即-2≤m≤2.答案:D3若关于x的不等式x2-4x-m≥0对任意x∈(0,1]恒成立,则m的最大值为().A.1B.-1C.-3D.3解析:由x2-4x-m≥0对任意x∈(0,1]恒成立,得m≤x2-4x对任意x∈(0,1]恒成立.设f(x)=x2-4x,则m≤f(x)min,∵f(x)=x2-4x在(0,1]上是减函数,∴f(x)min=f(1)=-3.∴m≤-3.答案:C=0有两个不相等的实数根,4若关于x的一元二次方程x2-(t+2)x+94则实数t的取值范围是.答案:(-∞,-5)∪(1,+∞)的定义域是.5函数y=√6-x-x2解析:由6-x-x2>0,得x2+x-6<0,∴-3<x<2.答案:{x|-3<x<2}6若关于x的不等式x2-2x+3≤a2-2a-1在R上的解集是⌀,则实数a的取值范围是.解析:∵x 2-2x-(a 2-2a-4)≤0的解集是⌀,∴Δ=4+4(a 2-2a-4)<0.∴a 2-2a-3<0,∴-1<a<3.答案:(-1,3)7若关于x 的一元二次方程x 2+(m-3)x+m+5=0的实数根均是正数,则实数m 的取值范围是 .解析:由题意得{Δ=(m -3)2-4(m +5)≥0,-(m -3)>0,m +5>0,解得-5<m ≤-1.答案:(-5,-1]8已知关于x 的函数y =√kx 2-6kx +(k +8)的定义域为R ,求k 的取值范围.解函数y =√kx 2的定义域为R ,即kx 2-6kx+(k+8)≥0恒成立.当k=0时,显然8>0恒成立;当k ≠0时,则{k >0,Δ≤0,即{k >0,36k 2-4k (k +8)≤0,解得0<k ≤1.综上所述,k 的取值范围是[0,1].9某校园内有一块长为800 m,宽为600 m 的长方形地面,现要对该地面进行绿化,规划四周种花卉(花卉带的宽度相同),中间种草坪,若要求草坪的面积不小于总面积的一半,求花卉带宽度的范围. 解设花卉带的宽度为x m(0<x<300),则草坪的长为(800-2x )m,宽为(600-2x )m .所以草坪的面积为(800-2x )(600-2x ).依题意有(800-2x )(600-2x )≥12×800×600,所以(400-x )(300-x )≥60000,整理得x 2-700x+60000≥0.解得x ≤100或x ≥600,又因为0<x<300,所以x 的取值范围是0<x ≤100,答:花卉带宽度的范围应是0~100m .10你能用一根长为100 m 的绳子围成一个面积大于600 m 2的矩形吗?解设围成的矩形一边的长为x m,则另一边的长为(50-x )m,且0<x<50.由题意,得围成矩形的面积S=x (50-x )>600,即x 2-50x+600<0,解得20<x<30.所以,当矩形一边的长在(20,30)的范围内取值时,能围成一个面积大于600m 2的矩形.能力提升1设M={x|x 2-x ≤0},若函数f (x )=ln(1-x )的定义域为N ,则M ∩N=( ).A.[0,1)B.(0,1)C.[0,1]D.(-1,0]解析:M={x|0≤x ≤1},N={x|x<1},所以M ∩N={x|0≤x<1}=[0,1).答案:A2若集合A={x|ax 2-ax+1<0}=⌀,则实数a 的取值集合为( ).A.{a|0<a<4}B.{a|0≤a<4}C.{a|0<a ≤4}D.{a|0≤a ≤4}解析:依题意应有{a >0,Δ≤0或a=0,即{a >0,a 2-4a ≤0或a=0. 解得0≤a ≤4.答案:D3某产品的总成本为C (单位:万元),它与产量x (单位:台)的关系是C=3 000+20x-0.1x 2,其中x ∈(0,240),且x 为正整数,若每台售价为25万元,则生产厂家不亏本的最低产量是( ).A.60台B.90台C.120台D.150台解析:由题意,有25x-C ≥0,即25x-3000-20x+0.1x 2≥0,解此不等式,得x ≥150,且x 为正整数或x ≤-200(舍去).答案:D4若关于x 的不等式ax 2+bx+c>0的解集是(-∞,-1)∪(3,+∞),则对函数f (x )=ax 2+bx+c ,下列不等式成立的是( ).A.f (4)>f (0)>f (1)B.f (4)>f (1)>f (0)C.f (0)>f (1)>f (4)D.f (0)>f (4)>f (1)解析:由题意知-1,3是方程ax 2+bx+c=0的两根,且a>0,∴{-1+3=-b a ,-1·3=c a ,∴{b a =-2,c a =-3. 对二次函数f (x )=ax 2+bx+c 来说,其对称轴x=−b 2a =1,且开口向上.由于|4-1|>|1-0|,∴f (4)>f (0)>f (1).答案:A5若关于x 的方程x 2m +x +m −1=0有一个正实数根和一个负实数根,则实数m 的取值范围是 .解析:由题意得,{ Δ=1-4·1m ·(m -1)>0,m-11m <0,m ≠0,解得0<m<1.答案:(0,1)6若点P (m ,1)到直线3x+4y=0的距离大于1,则实数m 的取值范围是 .解析:点P (m ,1)到直线3x+4y=0的距离d =|3m+4|√3+4=|3m+4|5, 则有|3m+4|5>1,即|3m+4|>5,则(3m+4)2>25,解得m<-3或m >13.答案:(-∞,-3)∪(13,+∞) ★7有纯农药液一桶,倒出8升后用水补满,然后又倒出4升后再用水补满,此时桶中的纯农药液不超过容积的28%,则桶的容积V (单位:升)的取值范围是 .解析:设桶的容积为x 升,那么第一次倒出8升纯农药液后,桶内还有(x-8)升纯农药液,用水补满后,桶内纯农药液占容积的x -8x. 第二次又倒出4升药液,则倒出的纯农药液为4(x -8)x 升, 此时桶内有纯农药液[(x -8)-4(x -8)x ]升. 依题意,得(x-8)−4(x -8)x≤28%x. 由于x>0,因而原不等式化简为9x 2-150x+400≤0,即(3x-10)(3x-40)≤0,解得103≤x ≤403.答案:103升≤V ≤403升8某蛋糕厂生产某种蛋糕的成本为40元/个,出厂价为60元/个,日销售量为1 000个.为适应市场需求,计划提高蛋糕档次,适度增加成本.若每个蛋糕成本增加的百分率为x (0<x<1),则每个蛋糕的出厂价相应提高的百分率为0.5x ,同时预计日销售量增加的百分率为0.8x ,已知日利润=(出厂价-成本)×日销售量,且设增加成本后的日利润为y.(1)写出y 与x 的关系式;(2)为使日利润有所增加,求x 的取值范围.解(1)由题意,得y=[60×(1+0.5x )-40×(1+x )]×1000×(1+0.8x )=2000(-4x 2+3x+10)(0<x<1).(2)要保证日利润有所增加,则{y >(60-40)×1000,0<x <1,即{-4x 2+3x >0,0<x <1,解得0<x <34. 所以为保证日利润有所增加,x 的取值范围是(0,34). ★9当x ∈(1,2)时,关于x 的不等式x 2+mx+4<0恒成立,求m 的取值范围. 解(方法一)设f (x )=x 2+mx+4,则f (x )<0在x ∈(1,2)内恒成立等价于{f (1)=m +5≤0,f (2)=2m +8≤0,解得m ≤-5. 故所求m 的取值范围为(-∞,-5].(方法二)∵x ∈(1,2),∴不等式x 2+mx+4<0恒成立等价于m<−x 2+4x =−(x +4x )在x ∈(1,2)内恒成立. 令g (x )=−(x +4x),则g (x )在(1,2)内单调递增. 故g (x )>g (1)=-5,∴m ≤-5.故所求m 的取值范围为(-∞,-5].。
高二数学人教A必修5练习:第三章 不等式 复习课 Word版含解析
第三章 章末复习课【课时目标】1.熟练掌握一元二次不等式的解法,并能解有关的实际应用问题. 2.掌握简单的线性规划问题的解法.3.能用基本不等式进行证明或求函数最值.不等式—⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪—不等关系—⎪⎪⎪⎪—不等式的性质—实数比较大小—一元二次不等式—⎪⎪⎪—一元二次不等式的解法—一元二次不等式的应用—简单线性规划—⎪⎪⎪⎪—二元一次不等式(组)与平面区域—简单线性规划—简单线性规划的应用—基本不等式—⎪⎪⎪⎪—算术平均数与几何平均数—基本不等式的应用一、选择题1.设a >b >0,则下列不等式中一定成立的是( )A .a -b <0B .0<ab<1C.ab <a +b2D .ab >a +b答案 C2.已知不等式ax 2-bx -1≥0的解是[-12,-13],则不等式x 2-bx -a <0的解是( )A .(2,3)B .(-∞,2)∪(3,+∞)C .(13,12)D .(-∞,13)∪(12,+∞)答案 A解析 由题意知,a <0,b a =-56,-1a =16,∴a =-6,b =5.∴x 2-5x +6<0的解是(2,3).3.若变量x ,y 满足⎩⎪⎨⎪⎧2x +y ≤40,x +2y ≤50,x ≥0,y ≥0,则z =3x +2y 的最大值是( )A .90B .80C .70D .40答案 C解析 作出可行域如图所示 .由于2x +y =40、x +2y =50的斜率分别为-2、-12,而3x +2y =0的斜率为-32,故线性目标函数的倾斜角大于2x +y =40的倾斜角而小于x +2y =50的倾斜角,由图知,3x +2y =z 经过点A (10,20)时,z 有最大值,z 的最大值为70.4.不等式x -1x≥2的解为( )A .[-1,0)B .[-1,+∞)C .(-∞,-1]D .(-∞,-1]∪(0,+∞) 答案 A解析 x -1x ≥2⇔x -1x -2≥0⇔-x -1x≥0⇔x +1x ≤0⇔⎩⎪⎨⎪⎧x (x +1)≤0x ≠0⇔-1≤x <0.5.设a >1,b >1且ab -(a +b )=1,那么( ) A .a +b 有最小值2(2+1) B .a +b 有最大值(2+1)2 C .ab 有最大值2+1 D .ab 有最小值2(2+1) 答案 A解析 ∵ab -(a +b )=1,ab ≤(a +b 2)2,∴(a +b 2)2-(a +b )≥1,它是关于a +b 的一元二次不等式,解得a +b ≥2(2+1)或a +b ≤2(1-2)(舍去). ∴a +b 有最小值2(2+1).又∵ab -(a +b )=1,a +b ≥2ab ,∴ab -2ab ≥1,它是关于ab 的一元二次不等式,解得ab ≥2+1,或ab ≤1-2(舍去), ∴ab ≥3+22,即ab 有最小值3+2 2. 6.设x ,y 满足约束条件⎩⎪⎨⎪⎧3x -y -6≤0,x -y +2≥0,x ≥0,y ≥0,若目标函数z =ax +by (a >0,b >0)的最大值为12,则2a +3b 的最小值为( )A.256B.83C.113 D .4 答案 A 解析不等式表示的平面区域如图所示阴影部分,当直线ax +by =z (a >0,b >0)过直线x -y +2=0与直线3x -y -6=0的交点(4,6)时,目标函数z =ax +by (a >0,b >0)取得最大值12,即4a +6b =12,即2a +3b =6,而2a +3b =(2a +3b )·2a +3b 6=136+(b a +a b )≥136+2=256(a =b=65时取等号). 二、填空题7.已知x ∈R ,且|x |≠1,则x 6+1与x 4+x 2的大小关系是________. 答案 x 6+1>x 4+x 2 解析 x 6+1-(x 4+x 2) =x 6-x 4-x 2+1 =x 4(x 2-1)-(x 2-1) =(x 2-1)(x 4-1) =(x 2-1)2(x 2+1)∵|x |≠1,∴x 2-1>0,∴x 6+1>x 4+x 2.8.若函数f (x )=2x 2-2ax -a -1的定义域为R ,则a 的取值范围为________. 答案 [-1,0]解析 由f (x )=2x 2-2ax -a -1的定义域为R .可知2x 2-2ax -a ≥1恒成立,即x 2-2ax -a ≥0恒成立,则Δ=4a 2+4a ≤0,解得-1≤a ≤0.9.若x ,y ,z 为正实数,x -2y +3z =0,则y 2xz的最小值为____.答案 3解析 由x -2y +3z =0,得y =x +3z 2,将其代入y 2xz,得x 2+9z 2+6xz 4xz ≥6xz +6xz 4xz =3,当且仅当x =3z 时取“=”,∴y 2xz的最小值为3.10.铁矿石A 和B 的含铁率a ,冶炼每万吨铁矿石的CO 2的排放量b 及每万吨铁矿石的价格c 如下表: a b /万吨 c /百万元A 50% 1 3B 70% 0.5 6某冶炼厂至少要生产1.9(万吨)铁,若要求CO 2的排放量不超过2(万吨),则购买铁矿石的最少费用为________(百万元).答案 15解析 设购买A 、B 两种铁矿石分别为x 万吨、y 万吨,购买铁矿石的费用为z 百万元,则z =3x +6y .由题意可得约束条件为⎩⎪⎨⎪⎧12x +710y ≥1.9,x +12y ≤2,x ≥0,y ≥0.作出可行域如图所示,由图可知,目标函数z =3x +6y 在点A (1,2)处取得最小值,z min=3×1+6×2=15.三、解答题11.已知关于x 的不等式ax -5x 2-a<0的解集为M .(1)若3∈M ,且5∉M ,求实数a 的取值范围. (2)当a =4时,求集合M .解 (1)∵3∈M ,∴3a -59-a<0,解得a <53或a >9;若5∈M ,则5a -525-a<0,解得a <1或a >25.则由5∉M ,知1≤a ≤25,因此所求a 的范围是1≤a <53或9<a ≤25.(2)当a =4时,4x -5x 2-4<0.4x -5x 2-4<0⇔⎩⎪⎨⎪⎧ 4x -5>0x 2-4<0或⎩⎪⎨⎪⎧4x -5<0x 2-4>0.⇔⎩⎪⎨⎪⎧ x >54-2<x <2或⎩⎪⎨⎪⎧x <54x <-2或x >2⇔54<x <2或x <-2. ∴M ={x |x <-2或54<x <2}.12.当x >3时,求函数y =2x 2x -3的值域.解 ∵x >3,∴x -3>0.∴y =2x 2x -3=2(x -3)2+12(x -3)+18x -3=2(x -3)+18x -3+12≥22(x -3)·18x -3+12=24.当且仅当2(x -3)=18x -3,即x =6时,上式等号成立,∴函数y =2x 2x -3的值域为[24,+∞).【能力提升】13.设a >b >0,则a 2+1ab +1a (a -b )的最小值是( )A .1B .2C .3D .4 答案 D解析 a 2+1ab +1a (a -b )=a 2-ab +ab +1ab +1a (a -b )=a (a -b )+1a (a -b )+ab +1ab ≥2+2=4.当且仅当a (a -b )=1且ab =1,即a =2,b =22时取等号. 14.若关于x 的不等式(2x -1)2<ax 2的解集中的整数恰有3个,则实数a 的取值范围是________.答案 (259,4916]解析 由(2x -1)2<ax 2成立可知a >0,整理不等式可得(4-a )x 2-4x +1<0,由于该不等式的解集中的整数恰有3个,则有4-a >0,即a <4,故0<a <4,解得不等式有2-a 4-a <x <2+a4-a,即2-a (2+a )(2-a )<x <2+a(2+a )(2-a ), 亦即14<12+a <x <12-a ,要使该不等式的解集中的整数恰有3个,那么3<12-a ≤4,解得259<a ≤4916.1.不等式是高中数学的重要内容,其中蕴含着许多重要的思想方法,是高考考查的重点.2.本章内容主要有以下四个方面:①不等式的性质,②一元二次不等式的解法,③简单的线性规划问题,④基本不等式及应用.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第2课时线性规划的实际应用
课时过关·能力提升
基础巩固
1某所学校计划招聘男教师x名,女教师y名,若x和y须满足约束条
A.6
B.8
C.10
D.12
解析:该校招聘男教师x名,女教师y名,此时该校招聘的教师人数为z名,
则z=x+y,且x≥0,y≥0,x,y均为自然数,画出可行域如图阴影部分中的整数点所示,可得M(3,1),
所以可行解有(3,1),(4,2),(4,3),(5,3),(5,4),(5,5),
则z=4,6,7,8,9,10,所以z的最大值是10,即该校招聘的教师人数最多是10.
答案:C
2在一次促销活动中,某厂要将100台洗衣机运往邻近的乡镇.现有4辆甲型货车和8辆乙型货车可供使用.每辆甲型货车运输费用400元,可装洗衣机20台;每辆乙型货车运输费用300元,可装洗衣机10台.若每辆车至多只运一次,则该厂所花的最少运输费用为().
A.2 000元
B.2 200元
C.2 400元
D.2 800元
答案:B
3已知签字笔2元一支,练习本1元一本.某学生欲购买的签字笔不少于3支,练习本不少于5本,但买签字笔和练习本的总数量不超过10,则支出的钱数最多是元.
答案:15
4某公司租赁甲、乙两种设备生产A,B两类产品,甲种设备每天能生产A类产品5件和B类产品10件,乙种设备每天能生产A类产品6件和B类产品20件.已知设备甲每天的租赁费为200元,设备乙每天的租赁费为300元.现该公司至少要生产A类产品50件,B类产品140件,所需租赁费最少为元.
答案:2 300
5某家具厂有方木料90 m3,五合板600 m2,准备加工成书桌和书橱出售.已知生产每张书桌需要方木料0.1 m3,五合板2 m2,生产每个书橱需要方木料0.2 m3,五合板1 m2,出售一张书桌可获利润80元,出售一个书橱可获利润120元.设生产书桌x张,书橱y个,利润总额为z元,则线性约束条件
是,线性目标函数是.
答案:
6某高科技企业生产产品A和产品B需要甲、乙两种新型材料.生产一件产品A需要甲材料1.5 kg,乙材料1 kg,用5个工时;生产一件产品B需要甲材料0.5 kg,乙材料0.3 kg,用3个工时.生产一件产品A的利润为2 100元,生产一件产品B的利润为900元.该企业现有甲材料150 kg,乙材料90 kg,则在不超过600个工时的条件下,生产产品A、产品B的利润之和的最大值为元.
解析:设生产产品A x件,生产产品B y件,
由题意
目标函数z=2100x+900y,画出约束条件对应的可行域(如图阴影部分中的整数点所示),作直线y=5x+3y=600与10x+3y=900的交点时,z取最大值,
所以z max=2100×60+900×100=216000.
答案:216 000
7某公司有60万元资金,计划投资甲、乙两个项目,按要求对项目甲的投资不小于对项目乙投资
解设投资项目甲x万元,投资项目乙y万元,可获得利润为z万元,
z=0.4x+0.6y.
由图知,目标函数z=0.4x+0.6y在A点取得最大值.
A(24,36).
故y max=0.4×24+0.6×36=31.2(万元),
即获得的最大利润为31.2万元.
8某投资人打算投资甲、乙两个项目,根据预测,甲、乙两个项目可能的最大盈利率分别为100%和50%,可能的最大亏损率分别为30%和10%,投资人计划投资金额不超过10万元,要求确保可能的资金亏损不超过1.8万元,问投资人对甲、乙两个项目各投资多少万元,才能使可能的盈利最大?
解设投资人分别用x万元、y万元投资甲、乙两个项目,由题意
z=x+0.5y.
上述不等式组表示的平面区域如图所示,阴影部分(含边界)即可行域.
作直线l0:x+0.5y=0,并作平行于直线l0的一族直线x+0.5y=z,z∈R,与可行域相交,其中有一条直线经过可行域上的M点,且与直线x+0.5y=0的距离最大,这里M点是直线x+y=10和0.3x+0.1y=1.8的交点.
解方程
得x=4,y=6,此时z=4+0.5×6=7(万元).
∵7>0,∴当x=4,y=6时,z取得最大值.
故投资人用4万元投资甲项目,6万元投资乙项目,才能在确保亏损不超过1.8万元的前提下,使可能的盈利最大.
能力提升
1某企业生产甲、乙两种产品均需用A,B两种原料,已知生产1吨每种产品所需原料及每天原料的可用限额如表所示.如果生产1吨甲、乙产品可获利润分别为3万元、4万元,则该企业每天可获得最大利润为().
A.12万元
B.16万元
C.17万元
D.18万元
解析:设该企业每天生产甲、乙两产品分别为x吨、y吨,由题意知,x,y需满足约束条
z=3x+4y.
由约束条件画出可行域,如图所示,l0:y=l0得点C,使z取得最大值.
C(2,3),
故z max=6+12=18(万元).
答案:D
★2如图,目标函数z=ax-y的可行域为四边形OACB(含边界),若
A
C
解析:最优解为C点,则目标函数表示的直线斜率在直线BC与AC的斜率之间.
因为k BC=a∈
答案:B
3某运输公司有12名驾驶员和19名工人,有8辆载重量为10吨的甲型卡车和7辆载重量为6吨的乙型卡车.某天需送往A地至少72吨的货物,派用的每辆车需满载且只运送一次,派用的每辆甲型卡车需配2名工人,运送一次可得利润450元;派用的每辆乙型卡车需配1名工人,运送一次可得利润350元.该公司合理计划当天派用两类卡车的车辆数,可得最大利润z等于().
A.4 650元
B.4 700元
C.4 900元
D.5 000元
解析:设派用甲型卡车x辆,乙型卡车y辆,
z=450x+350y.画出可行域,如图阴影部分的整数点.当目标函数经过A(7,5)时,利润z最大,为4900元.
答案:C
4铁矿石A和B的含铁率a,冶炼每万吨铁矿石的CO2的排放量b及每万吨铁矿石的价格c如下表:
某冶炼厂至少要生产1.9万吨铁,若要求CO2的排放量不超过2万吨,则购买铁矿石的最少费用为
百万元.
解析:可设需购买A铁矿石x万吨,B铁矿石y万吨,
则根据题意得到约束条件
目标函数为z=3x+6y.当目标函数对应的直线经过点(1,2)时,目标函数取最小值,最小值为
z min=3×1+6×2=15.
答案:15
5某电脑用户计划使用不超过500元的资金购买单价分别为60元,70元的单片软件和盒装磁盘.根据需要,软件至少买3片,磁盘至少买2盒,则不同的选购方式有种.
解析:设购买软件x片,磁盘y盒.
由题意,
∴3≤x≤6.∴x=3,4,5,6.
当x=3时,2≤y y=2,3,4.
当x=4时,2≤y y=2,3.
当x=5时,2≤y y=2.
当x=6时,y=2.
∴整点为(3,2),(3,3),(3,4),(4,2),(4,3),(5,2),(6,2),则不同的选购方式有7种.
答案:7
6已知甲、乙两煤矿每年的产量分别为200万吨和260万吨,需经过东车站和西车站两个车站运往外地.东车站每年最多能运280万吨煤,西车站每年最多能运360万吨煤,甲煤矿运往东车站和西车站的运费价格分别为1元/吨和1.5元/吨,乙煤矿运往东车站和西车站的运费价格分别为0.8元/吨和1.6元/吨.煤矿应怎样编制调运方案,能使总运费最少?
解设甲煤矿向东车站运x万吨煤,乙煤矿向东车站运y万吨煤,那么总运费
z=x+1.5(200-x)+0.8y+1.6(260-y)(万元),
即z=716-0.5x-0.8y.
x,y应满
作出上面的不等式组所表示的平面区域,如图.
设直线x+y=280与y=260的交点为M,则M(20,260).把直线l0:5x+8y=0向上平移至经过平面区域上的点M时,z的值最小.
因为点M的坐标为(20,260),
所以甲煤矿生产的煤向东车站运20万吨,向西车站运180万吨,乙煤矿生产的煤全部运往东车站时,能使总运费最少.
★7甲、乙两公司生产同一种产品,但由于设备陈旧,需要更新,经测算,对于函数f(x),g(x)及任意的x≥0,当甲公司投入x万元改造设备时,若乙公司投入改造设备费用小于f(x)万元,则乙有倒闭的风险,否则无倒闭的风险;同样当乙公司投入x万元改造设备时,若甲公司投入改造设备费用小于g(x)万元,则甲有倒闭的风险,否则无倒闭的风险.
(1)请解释f(0),g(0)的实际意义;
(2)设
f(x)=x+5,g(x)
解(1)f(0)表示当甲公司不投入资金改造设备时,乙公司要避免倒闭,至少要投入f(0)万元的资金;g(0)表示当乙公司不投入资金改造设备时,甲公司要避免倒闭,至少要投入g(0)万元的资金.
(2)设甲公司投入的资金为x万元,乙公司投入的资金为y万元.
依题意,甲、乙两公司均无倒闭风险,
改造设备资金为z=x+y,此不等式组表示的平面区域如图阴影部分所示.
作直线l0:x+y=0,平移直线l0,在可行域中的点P处z=x+y取得最小值.
故在双方均无倒闭风险的情况下,甲公司至少要投入25万元,乙公司至少要投入30万元,此时改
造设备资金最少为55万元.。
