必修5数学不等式典型例题解析(整理)

合集下载

高中数学必修5第三章不等式练习题含答案解析

高中数学必修5第三章不等式练习题含答案解析人教版高中数学必修5第三章不等式单元测试题及答案一、选择题(本大题共10小题，每小题5分，共50分) 1．不等式x 2≥2x 的解集是( )A ．{x |x ≥2}B ．{x |x ≤2}C ．{x |0≤x ≤2}D ．{x |x ≤0或x ≥2} 2．下列说法正确的是( )A ．a >b ?ac 2>bc 2B ．a >b ?a 2>b 2C ．a >b ?a 3>b 3D ．a 2>b 2?a >b3．直线3x ＋2y ＋5＝0把平面分成两个区域，下列各点与原点位于同一区域的是( ) A ．(－3,4) B ．(－3，－4) C ．(0，－3) D ．(－3,2) ·4．不等式x －1x ＋2>1的解集是( )A ．{x |x <－2}B ．{x |－2<1}<="" p="">C ．{x |x <1}D ．{x |x ∈R } 5．设M ＝2a (a －2)＋3，N ＝(a －1)(a －3)，a ∈R ，则有( ) A ．M >N B ．M ≥N C ．M <="" d="" p="" ≤n="" ．m="">2x －y ＋2≥0，x ＋y －2≤0，y ≥0表示的平面区域的形状为( )A ．三角形B ．平行四边形C ．梯形D ．正方形7．设z ＝x －y ，式中变量x 和y 满足条件?x ＋y －3≥0，x －2y ≥0，则z 的最小值为( )A ．1B ．－1C ．3D ．－3.8．若关于x 的函数y ＝x ＋m 2x 在(0，＋∞)的值恒大于4，则( )A ．m >2B ．m <－2或m >2C ．－2<2<="" p="">D ．m <－2 9．已知定义域在实数集R 上的函数y ＝f (x )不恒为零，同时满足f (x ＋y )＝f (x )·f (y )，且当x >0时，f (x )>1，那么当x <0时，一定有( )A ．f (x )<－1B ．－1<0<="" p="">C ．f (x )>1D ．0<1<="" p="">10．若x ＋23x －5<0，化简y ＝25－30x ＋9x 2－(x ＋2)2－3的结果为( )A ．y ＝－4xB ．y ＝2－xC ．y ＝3x －4D ．y ＝5－x二、填空题(本大题共5小题，每小题5分，共25分) 【11．对于x ∈R ，式子1kx 2＋kx ＋1恒有意义，则常数k 的取值范围是_________．12．不等式log 12(x 2－2x －15)>log 12(x ＋13)的解集是_________．13．函数f (x )＝x －2x －3＋lg 4－x 的定义域是__________．14．x ≥0，y ≥0，x ＋y ≤4所围成的平面区域的周长是________．15．某商家一月份至五月份累计销售额达3860万元．预测六月份销售额为500万元，七月份销售额比六月份递增x %，八月份销售额比七月份递增x %，九、十月份销售总额与七、八月份销售总额相等．若一月份至十月份销售总额至少达7000万元，则x 的最小值是________．三、解答题(本大题共6小题，共75分) "16．(12分)已知a >b >0，c <="" －c="">b －d的大小．17．(12分)解下列不等式：(1)－x 2＋2x －23>0； (2)9x 2－6x ＋1≥0.18．(12分)已知m ∈R 且m <－2，试解关于x 的不等式：(m ＋3)x 2－(2m ＋3)x ＋m >0.、19．(12分)已知非负实数x ，y 满足?2x ＋y －4≤0，x ＋y －3≤0.(1)在所给坐标系中画出不等式组所表示的平面区域；(2)求z ＝x ＋3y 的最大值．%20．(13分)经市场调查，某超市的一种小商品在过去的近20天内的销售量(件)与价格(元)均为时间t (天)的函数，且销售量近似满足g (t )＝80－2t (件)，价格近似满足f (t )＝20－12|t －10|(元)．(1)试写出该种商品的日销售额y 与时间t (0≤t ≤20)的函数表达式；(2)求该种商品的日销售额y 的最大值与最小值．21．(14分)某工厂有一段旧墙长14 m ，现准备利用这段旧墙为一面建造平面图形为矩形，面积为126 m 2的厂房，工程条件是：(1)建1 m 新墙的费用为a 元；(2)修1 m 旧墙的费用为a4元；…(3)拆去1 m 的旧墙，用可得的建材建1 m 的新墙的费用为a2元．经讨论有两种方案：①利用旧墙x m(0<="">必修5第三章《不等式》单元测试题（1．解析：原不等式化为x 2－2x ≥0，则x ≤0或x ≥2. 答案：D2．解析：A 中，当c ＝0时，ac 2＝bc 2，所以A 不正确；B 中，当a ＝0>b ＝－1时，a 2＝0(－1)2时，－2<－1，所以D 不正确．很明显C 正确．答案：C3．解析：当x ＝y ＝0时，3x ＋2y ＋5＝5>0，所以原点一侧的平面区域对应的不等式是3x ＋2y ＋5>0，可以验证，仅有点(－3,4)的坐标满足3x ＋2y ＋5>0.答案：A4．解析：x －1x ＋2>1?x －1x ＋2－1>0?－3x ＋2>0?x ＋2<0?x <－2.答案：A -5．解析：M －N ＝2a (a －2)＋3－(a －1)(a －3)＝a 2≥0，所以M ≥N . 答案：B6．解析：在平面直角坐标系中，画出不等式组表示的平面区域，如下图中的阴影部分．则平面区域是△ABC . 答案：A7．解析：画出可行域如下图中的阴影部分所示．解方程组?x ＋y －3＝0，x －2y ＝0.得A (2,1)．由图知，当直线y＝x －z 过A 时，－z 最大，即z 最小，则z 的最小值为2－1＝1.>答案：A8．解析：∵x ＋m 2x ≥2|m |，∴2|m |>4. ∴m >2或m <－2. 答案：B9．解析：令x ＝y ＝0得f (0)＝f 2(0)，若f (0)＝0，则f (x )＝0·f (x )＝0与题设矛盾．∴f (0)＝1.又令y ＝－x ，∴f (0)＝f (x )·f (－x )，、故f (x )＝1f (－x ).∵x >0时，f (x )>1，∴x <0时，0<="">10．解析：∵x ＋23x －5<0，∴－2<5<="" p="">3.而y ＝25－30x ＋9x 2－(x ＋2)2－3＝|3x －5|－|x ＋2|－3＝5－3x －x－2－3＝－4x .∴选A.答案：A二、填空题（填空题的答案与试题不符）11．对于x ∈R ，式子1kx 2＋kx ＋1恒有意义，则常数k 的取值范围是__________．；解析：式子1kx 2＋kx ＋1恒有意义，即kx 2＋kx ＋1>0恒成立．当k ≠0时，k >0且Δ＝k 2－4k <0，∴00恒成立，故0≤k <4，选C.答案：C12．函数f (x )＝x －2x －3＋lg 4－x 的定义域是__________．解析：求原函数定义域等价于解不等式组x －2≥0，x －3≠0，4－x >0，解得2≤x <3或3<4.<="" p="">∴定义域为[2,3)∪(3,4)．答案：[2,3)∪(3,4)13．x ≥0，y ≥0，x ＋y ≤4所围成的平面区域的周长是________． &解析：如下图中阴影部分所示，围成的平面区域是Rt △OAB .可求得A (4,0)，B (0,4)，则OA ＝OB ＝4，AB ＝42，所以Rt △OAB 的周长是4＋4＋42＝8＋4 2. 答案：8＋42f (x )＋f (y )≤0，f (x )－f (y )≥0的点(x ，y )所形成区域14．已知函数f (x )＝x 2－2x ，则满足条件的面积为__________．解析：化简原不等式组(x －1)2＋(y －1)2≤2，(x －y )(x ＋y －2)≥0，…所表示的区域如右图所示，阴影部分面积为半圆面积．答案：π 15．(2010·浙江高考)某商家一月份至五月份累计销售额达3860万元．预测六月份销售额为500万元，七月份销售额比六月份递增x %，八月份销售额比七月份递增x %，九、十月份销售总额与七、八月份销售总额相等．若一月份至十月份销售总额至少达7000万元，则x 的最小值是________．解析：由已知条件可得，七月份销售额为500×(1＋x %)，八月份销售额为500×(1＋x %)2，一月份至十月份的销售总额为3860＋500＋2[500(1＋x %)＋500(1＋x %)2]，可列出不等式为4360＋1000[(1＋x %)＋(1＋x %)2]≥7000.令1＋x %＝t ，则t 2＋t －6625≥0，即? ????t ＋115? ??t －65≥0.又∵t ＋115≥0，∴t ≥65，∴1＋x %≥65，∴x %≥，∴x ≥20.故x 的最小值是20. 答案：20三、解答题(本大题共6小题，共75分) }16．(12分)已知a >b >0，c <="" －c="">b －d的大小．解：e a －c －eb －d ＝e (b －d )－e (a －c )(a －c )(b －d )＝(b －a )＋(c －d )(a －c )(b －d )e .∵a >b >0，c <0，<="" p="">∴a －c >0，b －d >0，b －a <0，c －d <0.又e <0，∴e a －c －e b －d >0.∴e a －c >eb －d.17．(12分)解下列不等式：(1)－x 2＋2x －23>0； (2)9x 2－6x ＋1≥0. ；解：(1)－x 2＋2x －23>0?x 2－2x ＋23<0?3x 2－6x ＋2<0.Δ＝12>0，且方程3x 2－6x ＋2＝0的两根为x 1＝1－33，x 2＝1＋33，∴原不等式解集为{x |1－33<1＋3<="" p="">3}． (2)9x 2－6x ＋1≥0?(3x －1)2≥0. ∴x ∈R .∴不等式解集为R .18．(12分)已知m ∈R 且m <－2，试解关于x 的不等式：(m ＋3)x 2－(2m ＋3)x ＋m >0. 解：当m ＝－3时，不等式变成3x －3>0，得x >1；当－3<=""－m ]>0，得x >1或x <m< p="">m ＋3；当m <－3时，得1<m<="" p="">m ＋3.综上，当m ＝－3时，原不等式的解集为(1，＋∞)；当－3<="" －∞，m="" m="" p="" ＋3∪(1，＋∞)；当m="">1，m m ＋3.19．(12分)已知非负实数x ，y 满足?2x ＋y －4≤0，x ＋y －3≤0.(1)在所给坐标系中画出不等式组所表示的平面区域；(2)求z ＝x ＋3y 的最大值．;解：(1)由x ，y 取非负实数，根据线性约束条件作出可行域，如下图所示阴影部分．(2)作出直线l ：x ＋3y ＝0，将直线l 向上平移至l 1与y 轴的交点M 位置时，此时可行域内M 点与直线l 的距离最大，而直线x ＋y －3＝0与y 轴交于点M (0,3)．∴z max ＝0＋3×3＝9. 20．(13分)(2009·江苏苏州调研)经市场调查，某超市的一种小商品在过去的近20天内的销售量(件)与价格(元)均为时间t (天)的函数，且销售量近似满足g (t )＝80－2t (件)，价格近似满足f (t )＝20－12|t －10|(元)．(1)试写出该种商品的日销售额y 与时间t (0≤t ≤20)的函数表达式；(2)求该种商品的日销售额y 的最大值与最小值．解：(1)y ＝g (t )·f (t ) #＝(80－2t )·(20－12|t －10|) ＝(40－t )(40－|t －10|)＝(30＋t )(40－t )，0≤t <10，(40－t )(50－t )，10≤t ≤20.(2)当0≤t <10时，y 的取值范围是[1200,1225]，在t ＝5时，y 取得最大值为1225；当10≤t ≤20时，y 的取值范围是[600,1200]，在t ＝20时，y 取得最小值为600.21．(14分)某工厂有一段旧墙长14 m ，现准备利用这段旧墙为一面建造平面图形为矩形，面积为126 m 2的厂房，工程条件是：￥(1)建1 m 新墙的费用为a 元；(2)修1 m 旧墙的费用为a4元；(3)拆去1 m 的旧墙，用可得的建材建1 m 的新墙的费用为a2元．经讨论有两种方案：①利用旧墙x m(0<="">解：方案①：修旧墙费用为ax4(元)，拆旧墙造新墙费用为(14－x )a2(元)，其余新墙费用为(2x ＋2×126x －14)a (元)，则总费用为y ＝ax 4＋(14－x )a 2＋(2x ＋2×126x －14)a ＝7a (x 4＋36x －1)(0<="" 4＋36x=""x ＝6，∴当且仅当x 4＝36x 即x ＝12时，y min ＝35a ，方案②：利用旧墙费用为14×a 4＝7a2(元)，建新墙费用为(2x ＋252x －14)a (元)，则总费用为y ＝7a 2＋(2x ＋252x －14)a ＝2a (x ＋126x )－21 2a (x ≥14)，可以证明函数x ＋126x 在[14，＋∞)上为增函数，∴当x ＝14时，y min ＝. ∴采用方案①更好些．</m<>。

高二数学人教A必修5练习及解析：3-2 一元二次不等式及其解法

∴a=2.
∴不等式
+1
2+1
+2
>1 可化为
>1,移项通分得 >0,
-1
-1
-1
∴(x+2)(x-1)>0,解得 x<-2 或 x>1.
∴所求解集为{x|x<-2 或 x>1}.
8.解关于 x 的不等式 2x2+ax+2>0.
解:对于方程 2x2+ax+2=0,其判别式 Δ=a2-16=(a+4)(a-4).
【解析】

1
由题意知，一元二次不等式 f(x)>0 的解集为x－1<x<2 .

而 f(10x)>0，
1
∴－1<10x<2，
1
解得 x<lg 2，即 x<－lg 2.
【答案】
D
二、填空题
6．(2015·广东高考)不等式－x2－3x＋4>0 的解集为________．(用区间表示)
①当 a>4 或 a<-4 时,Δ>0,方程 2x2+ax+2=0 的两根为:
1
4
1
4
x1= (-a-√2 -16),x2= (-a+√2 -16).
∴原不等式的解集为
1
4
1
4
{ | < (--√2 -16)或 > (- + √2 -16)}.
②当 a=4 时,Δ=0,方程有两个相等实根,x1=x2=-1;
1
1
∴不等式 bx2-ax-1>0 的解集是(- 2 ,- 3).

必修5基本不等式(含答案)

基本不等式及其应用[考点梳理]1．如果a ＞0，b ＞0，那么________叫做这两个正数的算术平均数． 2．如果a ＞0，b ＞0，那么________叫做这两个正数的几何平均数．3．重要不等式：a ，b ∈R ，则a 2＋b 2≥________ (当且仅当a ＝b 时取等号)．4．基本不等式：a ＞0，b ＞0，则________，当且仅当a ＝b 时等号成立，即两个正数的算术平均数不小于它们的几何平均数．5．求最小值：a >0，b >0，当ab 为定值时，a ＋b ，a 2＋b 2有________，即a ＋b ≥________，a 2＋b 2≥________.简记为：积定和最小．6．求最大值：a ＞0，b ＞0，当a ＋b 为定值时，ab 有最大值，即________，亦即________；或a 2＋b 2为定值时，ab 有最大值(a ＞0，b ＞0)，即_____.简记为：和定积最大．7．拓展：若a ＞0，b ＞0时，21a ＋1b≤________≤a ＋b 2≤________，当且仅当a ＝b 时等号成立．自查自纠： 1.a ＋b 2 2.ab 3.2ab 4.a ＋b 2≥ab 5．最小值 2ab 2ab6．ab ≤⎝ ⎛⎭⎪⎫a ＋b 22 ab ≤14(a ＋b )2 ab ≤a 2＋b 22 7.ab a 2＋b 22[基础自测]设a ，b ∈R ，且a ＋b ＝3，则2a ＋2b 的最小值是( )A ．6B ．4 2C ．2 2D ．2 6解：因为2a ＞0，2b ＞0，由基本不等式得2a ＋2b ≥22a ·2b ＝22a ＋b ＝42，当且仅当a ＝b ＝32时取等号，故选B.已知向量m ＝(2，1)，n ＝(2－b ，a )(a ＞0，b ＞0)．若m ∥n ，则ab 的最大值为( ) A.12B ．1C ．2D ．4 解：依题意得2a ＝2－b ，即2a ＋b ＝2(a ＞0，b ＞0)，∴2＝2a ＋b ≥22ab ，∴ab ≤12，当且仅当2a ＝b ＝1时取等号，∴ab 的最大值是12.故选A.设f (x )＝lnx ，0＜a ＜b ，若p ＝f (ab )，q ＝f ⎝⎛⎭⎪⎫a ＋b 2，r ＝12(f (a )＋f (b ))，则下列关系式中正确的是( )A ．q ＝r ＜pB ．q ＝r ＞pC ．p ＝r ＜qD ．p ＝r ＞q 解：p ＝f (ab )＝ln ab ，q ＝f ⎝ ⎛⎭⎪⎫a ＋b 2＝ln a ＋b 2，r ＝12(f (a )＋f (b ))＝12ln ab ＝ln ab ，函数f (x )＝ln x 在(0，＋∞)上单调递增，∵a ＋b 2＞ab ，∴f ⎝⎛⎭⎪⎫a ＋b 2＞f (ab )．∴q ＞p ＝r.故选C. 若实数x ，y 满足xy ＝1，则x 2＋2y 2的最小值为________．解：由xy ＝1得x 2＋2y 2＝x 2＋2x2≥22，当且仅当x ＝±42时等号成立．故填22.已知函数f (x )＝4x ＋ax (x ＞0，a ＞0)在x ＝3时取得最小值，则实数a ＝________. 解：f (x )＝4x ＋ax ≥24x ·a x ＝4a (x ＞0，a ＞0)，当且仅当4x ＝a x ，即x ＝a2时等号成立，∴a2＝3，∴a ＝36.故填36. [典例解析]类型一利用基本不等式求最值(1)函数y ＝（x ＋5）（x ＋2）x ＋1(x ＞－1)的值域为________．解：∵x ＞－1，∴x ＋1＞0，令m ＝x ＋1，则m ＞0，且y ＝（m ＋4）（m ＋1）m ＝m ＋4m ＋5≥2m ·4m ＋5＝9，当且仅当m ＝2时取等号，故y min ＝9.又当m →＋∞或m →0时，y →＋∞，故原函数的值域是[9，＋∞)．故填[9，＋∞)．(2)若a >b >0，则代数式a 2＋1b （a －b ）的最小值为( )A ．2B ．3C ．4D ．5解：∵b (a －b )≤⎝ ⎛⎭⎪⎫b ＋（a －b ）22＝a 24，∴a 2＋1b （a －b ）≥a 2＋1a 24＝a 2＋4a 2≥4，当且仅当b＝a －b 且a 2＝4a 2，即a ＝2，b ＝22时等号成立．故选C.小结：基本不等式的应用在于“定和求积，定积求和”，必要时可以通过变形(拆补)、配凑，常数代换、构造“和”或者“积”，使之为定值．(1)已知t ＞0，则函数f (t )＝t 2－4t ＋1t的最小值为________．解：∵t ＞0，∴f (t )＝t 2－4t ＋1t ＝t ＋1t －4≥－2，当且仅当t ＝1时，f (t )min ＝－2，故填－2.(2)已知x ＞0，y ＞0，且2x ＋8y －xy ＝0，求： (Ⅰ)xy 的最小值； (Ⅱ)x ＋y 的最小值．解：(Ⅰ)由2x ＋8y －xy ＝0，得8x ＋2y ＝1，又x ＞0，y ＞0，则1＝8x ＋2y ≥28x ·2y ＝8xy，得xy ≥64，当且仅当x ＝4y ，即x ＝16，y ＝4时等号成立．(Ⅱ)解法一：由2x ＋8y －xy ＝0，得x ＝8yy －2，∵x ＞0，∴y ＞2，则x ＋y ＝y ＋8y y －2＝(y －2)＋16y －2＋10≥18，当且仅当y －2＝16y －2，即y ＝6，x ＝12时等号成立．解法二：由2x ＋8y －xy ＝0，得8x ＋2y ＝1，则x ＋y ＝⎝ ⎛⎭⎪⎫8x ＋2y ·(x ＋y )＝10＋2x y ＋8y x ≥10＋22x y ·8yx ＝18，当且仅当y ＝6，x ＝12时等号成立．类型二利用基本不等式求参数范围已知a >0，b >0，若不等式m 3a ＋b－3a －1b ≤0恒成立，则m 的最大值为( ) A ．4 B ．16 C ．9 D ．3解：∵a >0，b >0，∴由m 3a ＋b －3a －1b ≤0恒成立得m ≤⎝ ⎛⎭⎪⎫3a ＋1b (3a ＋b )＝10＋3b a ＋3a b 恒成立．∵3b a ＋3ab ≥23b a ·3a b ＝6，当且仅当a ＝b 时等号成立，故10＋3b a ＋3a b ≥16，∴m ≤16，即m 的最大值为16.故选B.小结：一般地，对含参的不等式求范围问题通常采用分离变量转化为恒成立问题，对于“恒成立”的不等式，一般的解题方法是先分离然后求函数的最值．另外，要记住几个常见的有关不等式的等价命题：(1)a ＞f (x )恒成立⇔a ＞f (x )max ；(2)a ＜f (x )恒成立⇔a ＜f (x )min ；(3)a ＞f (x )有解⇔a ＞f (x )min ；(4)a ＜f (x )有解⇔a ＜f (x )max .已知函数f (x )＝e x ＋e －x ，其中e 是自然对数的底数．若关于x 的不等式mf (x )≤e－x＋m －1在(0，＋∞)上恒成立，则实数m 的取值范围为________．解：由条件知m (e x ＋e －x －1)≤e －x －1在(0，＋∞)上恒成立．令t ＝e x (x ＞0)，则t ＞1，且m ≤－t －1t 2－t ＋1＝－1t －1＋1t －1＋1对任意t ＞1成立．∵t －1＋1t －1＋1≥2（t －1）·1t －1＋1＝3，∴－1t －1＋1t －1＋1≥－13，当且仅当t ＝2，即x ＝ln 2时等号成立．故实数m 的取值范围是⎝ ⎛⎦⎥⎤－∞，－13.故填⎝ ⎛⎦⎥⎤－∞，－13.类型三利用基本不等式解决实际问题某小区想利用一矩形空地ABCD 建市民健身广场，设计时决定保留空地边上的一水塘(如图中阴影部分)，水塘可近似看作一个等腰直角三角形，其中AD ＝60 m ，AB ＝40 m ，且△EFG 中，∠EGF ＝90°，经测量得到AE ＝10 m ，EF ＝20 m ，为保证安全同时考虑美观，健身广场周围准备加设一个保护栏，设计时经过点G 作一直线分别交AB ，DF 于M ，N ，从而得到五边形MBCDN 的市民健身广场，设DN ＝x (m)．(1)将五边形MBCDN 的面积y 表示为x 的函数；(2)当x 为何值时，市民健身广场的面积最大？并求出最大面积．解：(1)作GH ⊥EF ，垂足为H. ∵DN ＝x ，∴NH ＝40－x ，NA ＝60－x ，∵NH HG ＝NAAM ，∴40－x 10＝60－x AM ，∴AM ＝600－10x 40－x.S 五边形MBCDN ＝S 矩形ABCD －S △AMN ＝40×60－12·AM ·AN ＝2 400－5（60－x ）240－x .∵N 与F 重合时，AM ＝AF ＝30适合条件，∴x∈(0，30]．(2)y ＝2 400－5（60－x ）240－x ＝2 400－5[(40－x )＋40040－x ＋40]，当且仅当40－x ＝40040－x ，即x ＝20∈(0，30]时，y 取得最大值2 000, ∴当DN ＝20 m 时，得到的市民健身广场面积最大，最大面积为 2 000 m 2.小结：建立关于x 的函数关系式是解决本题的关键，在运用基本不等式求最小值时，除了“一正，二定，三相等”以外，在最值的求法中，使用基本不等式次数要尽量少，最好是在最后一步使用基本不等式，如果必须使用几次，就需要查看这几次基本不等式等号成立的条件是否有矛盾，有矛盾则应调整解法．如图，为处理含有某种杂质的污水，要制造一个底宽2 m 的无盖长方体的沉淀箱，污水从A 孔流入，经沉淀后从B 孔排出，设箱体的长度为a m ，高度为b m ，已知排出的水中该杂质的质量分数与a ，b 的乘积ab 成反比．现有制箱材料60 m 2，问a ，b 各为多少m 时，经沉淀后排出的水中该杂质的质量分数最小(A ，B 孔面积忽略不计)．解法一：设y 为排出的水中杂质的质量分数，根据题意可知：y ＝kab ，其中k 是比例系数且k ＞0.依题意要使y 最小，只需ab 最大．由题设得：4b ＋2ab ＋2a ≤60(a ＞0，b ＞0)，即a ＋2b ≤30－ab (a ＞0，b ＞0)．∵a ＋2b ≥22ab ， ∴22·ab ＋ab ≤30，得0＜ab ≤32.当且仅当a ＝2b 时取“＝”号，ab 最大值为18，此时得a ＝6，b ＝3. 故当a ＝6 m ，b ＝3 m 时经沉淀后排出的水中杂质最少．解法二：同解法一得b ≤30－a a ＋2，代入y ＝kab 求解．[归纳小结]1．要熟悉基本不等式的变式和推广，这对提高解题能力是有帮助的，常见的基本不等式的变式和推广有：①a 2＋b 2≥（a ＋b ）22；②ab ≤a 2＋b 22；③ab ≤ 14(a ＋b )2；④⎝ ⎛⎭⎪⎫a ＋b 22≤a 2＋b 22；⑤(a ＋b )2≥4ab ；⑥ab ≥21a ＋1b；⑦a ＋b ＋c 3≥3abc ；⑧abc ≤a 3＋b 3＋c 33等．对于以上各式，要明了其成立的条件和取“＝”的条件．2．在利用基本不等式求最值时，要注意一正，二定，三相等．“一正”是指使用均值不等式的各项(必要时，还要考虑常数项)必须是正数；“二定”是指含变数的各项的和或积必须是常数；“三相等”是指具备等号成立的条件，使待求式能取到最大或最小值．3．基本不等式的应用在于“定和求积，定积求和；和定积最大，积定和最小”，必要时可以通过变形(拆补)、配凑、常数代换、运算(指数、对数运算、平方等)构造“和”或者“积”，使之为定值．4．求1a ＋1b 型最值问题，常通过“1”来进行转化，但不是所有的最值都可以通过基本不等式解决，有一些看似可以通过基本不等式解决的问题，由于条件的限制，等号不能够成立，这时就不能用基本不等式来解决，而要借助于其他求值域的方法来解决．5．基本不等式除具有求最值的功能外，还具有将“和式”转化为“积式”以及将“积式”转化为“和式”的放缩功能，常用于比较数(式)的大小或证明不等式，解决问题的关键是抓住不等式两边的结构特征，找准利用基本不等式的切入点． [课后作业]1．若a ＞1，则a ＋1a －1的最小值是( )A ．2B ．aC ．3 D.2aa －1解：∵a ＞1，∴a ＋1a －1＝a －1＋1a －1＋1≥2（a －1）·1a －1＋1＝2＋1＝3，当且仅当a ＝2时等号成立．故选C.2．已知a >0，b >0，且2a ＋b ＝4，则1ab 的最小值为( ) A.14 B ．4 C.12D ．2 解：∵a >0，b >0，∴4＝2a ＋b ≥22ab ，得ab ≤2，∴1ab ≥12，当且仅当a ＝1，b ＝2时等号成立．故选C.3．函数f (x )＝5－4x ＋x 22－x在(－∞，2)上的最小值是( )A ．0B ．1C ．2D ．3解：当x ＜2时，2－x ＞0，因此f (x )＝1＋（4－4x ＋x 2）2－x ＝12－x ＋(2－x )≥2·12－x·（2－x ）＝2，当且仅当12－x ＝2－x 时上式取等号．而此方程有解x ＝1∈(－∞，2)，因此f (x )在(－∞，2)上的最小值为2，故选C.4．小王从甲地到乙地往返的时速分别为a 和b (a ＜b )，其全程的平均时速为v ，则( )A ．a ＜v ＜abB ．v ＝ab C.ab ＜v ＜a ＋b 2 D ．v ＝a ＋b2解：设甲、乙两地之间的距离为s.∵a ＜b ，∴v ＝2s s a ＋s b＝2ab a ＋b＜2ab2ab ＝ab.又v －a ＝2aba ＋b －a ＝ab －a 2a ＋b ＞a 2－a 2a ＋b＝0，∴v ＞a.故选A.5．已知a ＞0，b ＞0，a ＋b ＝2，则1a ＋4b 的最小值是( ) A.72 B ．4 C.92D ．5解：依题意，得1a ＋4b ＝12⎝ ⎛⎭⎪⎫1a ＋4b ·(a ＋b )＝12[5＋⎝ ⎛⎭⎪⎫b a ＋4a b ]≥12⎝⎛⎭⎪⎫5＋2b a ·4a b ＝92，当且仅当⎩⎪⎨⎪⎧a ＋b ＝2，b a ＝4a b ，a ＞0，b ＞0，即⎩⎪⎨⎪⎧a ＝23，b ＝43时取等号，即1a ＋4b 的最小值是92.故选C.6．若log 4(3a ＋4b )＝log 2ab ，则a ＋b 的最小值是( )A ．6＋2 3B ．7＋2 3C ．6＋4 3D ．7＋4 3解：因为log 4(3a ＋4b )＝log 2ab ，所以log 4(3a ＋4b )＝log 4(ab )，即3a ＋4b ＝ab ，且⎩⎪⎨⎪⎧3a ＋4b ＞0，ab ＞0，即a ＞0，b ＞0，所以4a ＋3b ＝1(a ＞0，b ＞0)，a ＋b ＝(a ＋b )⎝ ⎛⎭⎪⎫4a ＋3b ＝7＋4b a ＋3a b ≥7＋24b a ·3a b ＝7＋43，当且仅当4b a ＝3ab 时取等号．故选D.7．点(m ，n )在直线x ＋y ＝1位于第一象限内的图象上运动，则log 2m ＋log 2n 的最大值是________．解：由条件知，m ＞0，n ＞0，m ＋n ＝1，∴mn ≤⎝⎛⎭⎪⎫m ＋n 22＝14，当且仅当m ＝n ＝12时取等号，∴log 2m ＋log 2n ＝log 2mn ≤log 214＝－2.故填－2.8．设m ∈R ，过定点A 的动直线x ＋my ＝0和过定点B 的动直线mx －y －m ＋3＝0交于点P (x ，y )，则|PA |·|PB |的最大值是________．解：易知定点A (0，0)，B (1，3)．且无论m 取何值，两直线垂直．所以无论P 与A ，B 重合与否，均有|PA |2＋|PB |2＝|AB |2＝10(P 在以AB 为直径的圆上)．所以|PA |·|PB |≤12(|PA |2＋|PB |2)＝5.当且仅当|PA |＝|PB |＝5时，等号成立．故填5.9．(1)已知0＜x ＜43，求x (4－3x )的最大值；(2)点(x ，y )在直线x ＋2y ＝3上移动，求2x ＋4y 的最小值．解：(1)已知0＜x ＜43，∴0＜3x ＜4.∴x (4－3x )＝13(3x )(4－3x )≤13⎝⎛⎭⎪⎫3x ＋4－3x 22＝43，当且仅当3x ＝4－3x ，即x ＝23时“＝”成立．∴当x ＝23时，x (4－3x )取最大值为43.(2)已知点(x ，y )在直线x ＋2y ＝3上移动，所以x ＋2y ＝3. ∴2x ＋4y ≥22x ·4y ＝22x ＋2y ＝223＝42. 当且仅当⎩⎪⎨⎪⎧2x ＝4y ，x ＋2y ＝3，即⎩⎪⎨⎪⎧x ＝32，y ＝34时“＝”成立．∴当⎩⎪⎨⎪⎧x ＝32，y ＝34时，2x ＋4y 取最小值为42.10．已知a＞0，b＞0，且2a＋b＝1，求S＝2ab－4a2－b 2的最大值．解：∵a＞0，b＞0，2a＋b＝1，∴4a2＋b2＝(2a＋b)2－4ab＝1－4ab.且1＝2a＋b≥22ab，即ab≤24，ab≤18，∴S＝2ab－4a2－b2＝2ab－(1－4ab)＝2ab＋4ab－1≤2－12.当且仅当a＝14，b＝12时，等号成立．11．如图，动物园要围成相同的长方形虎笼四间，一面可利用原有的墙，其他各面用钢筋网围成．(1)现有可围36 m长网的材料，每间虎笼的长、宽各设计为多少时，可使每间虎笼面积最大？(2)若使每间虎笼面积为24 m2，则每间虎笼的长、宽各设计为多少时，可使围成四间虎笼的钢筋总长度最小？解：(1)设每间虎笼长为x m，宽为y m，则由条件，知4x＋6y＝36，即2x＋3y＝18.设每间虎笼的面积为S，则S＝xy.解法一：由于2x＋3y≥22x×3y＝26xy，∴26xy≤18，得xy≤272，即S≤272.当且仅当2x＝3y时等号成立．由⎩⎪⎨⎪⎧2x＝3y，2x＋3y＝18，解得⎩⎪⎨⎪⎧x＝4.5，y＝3.故每间虎笼长为4.5 m，宽为3 m时，可使每间虎笼面积最大．解法二：由2x＋3y＝18，得x＝9－32y.∵x＞0，∴0＜y＜6.S＝xy＝⎝⎛⎭⎪⎫9－32y y＝32(6－y)y.∵0＜y＜6，∴6－y＞0.∴S≤32⎣⎢⎡⎦⎥⎤（6－y）＋y22＝272.当且仅当6－y＝y，即y＝3时，等号成立，此时x＝4.5.故每间虎笼长4.5 m，宽3 m时，可使每间虎笼面积最大．(2)由条件知S＝xy＝24.设钢筋网总长为l，则l＝4x＋6y.解法一：∵2x＋3y≥22x·3y＝26xy＝24，∴l＝4x＋6y＝2(2x＋3y)≥48，当且仅当2x＝3y时，等号成立．由⎩⎪⎨⎪⎧2x＝3y，xy＝24，解得⎩⎪⎨⎪⎧x＝6，y＝4.故每间虎笼长6 m，宽4 m时，可使钢筋网总长度最小．解法二：由xy＝24，得x＝24y.∴l＝4x＋6y＝96y＋6y＝6⎝⎛⎭⎪⎫16y＋y≥6×216y×y＝48，当且仅当16y＝y，即y＝4时，等号成立，此时x＝6.故每间虎笼长6 m，宽4 m时，可使钢筋网总长度最小．如图所示，已知树顶A离地面212米，树上另一点B离地面112米，某人在离地面32米的C处看此树，则该人离此树________米时，看A，B的视角最大．解：问题转化为求△ABC中∠BCA的取值范围．过点C作CD⊥AB交AB的延长线于点D.设该人距离此树的距离CD＝x米，看A，B的视角最大，即∠BCA最大．不妨设∠BCD＝α，∠ACD＝β，则∠BCA＝β－α，且tanα＝4x ，tanβ＝9x，所以tan(β－α)＝9x－4x1＋9x×4x＝5xx2＋36＝5 x＋36x≤52x×36x＝512，当且仅当x＝36x，即x＝6时取等号，此时∠BCA最大．故填6.不等式检测1．已知集合A ＝{x |y ＝x 2－2x －3}，B ＝⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x |x ＋2x －2≤0，则A ∩B ＝( )A ．[－1，1]B ．[－1，2)C ．[1，2)D ．[－2，－1]解：依题意，集合A ＝{x |x ≤－1或x ≥3}，B ＝{x |－2≤x <2}，A ∩B ＝{x |－2≤x ≤－1}．故选D.2．不等式x ＋5()x －12≥2的解集是( )A.⎣⎢⎡⎦⎥⎤－3，12B.⎣⎢⎡⎦⎥⎤－12，3C.⎣⎢⎡⎭⎪⎫12，1∪(1，3]D.⎣⎢⎡⎭⎪⎫－12，1∪(1，3] 解：x ＋5（x －1）2≥2⇔（x ＋5）－2（x －1）2（x －1）2≥0⇔－2x 2＋5x ＋3（x －1）2≥0⇔－2x 2＋5x ＋3≥0(x ≠1)⇔2x 2－5x －3≤0(x ≠1)⇔－12≤x ≤3且x ≠1.故选D.3．若f (x )是偶函数，且当x ∈[0，＋∞)时，f (x )＝x －1，则不等式f (x 2－1)<0的解集为( ) A ．(－1，0) B ．(－2，0)∪(0，2) C ．(0，2) D ．(1，2)解：∵f (x )是偶函数，∴f (x )＝f (|x |)＝|x |－1.∴f (x 2－1)＝|x 2－1|－1.解不等式|x 2－1|－1<0，得0<x 2<2，∴x ∈(－2，0)∪(0，2)．故选B.4．若一个矩形的对角线长为常数a ，则其面积的最大值为( )A ．a 2 B.12a 2 C ．a D.12a解：如图，设矩形的长和宽分别为x ，y ，则x 2＋y 2＝a 2，其面积S ＝xy ，由基本不等式得S ≤12(x 2＋y 2)＝12a 2，当且仅当x ＝y 时取等号，此时为正方形．故选B.5．若正数x ，y 满足x 2＋3xy －1＝0，则x ＋y 的最小值是( )A.23 B .223 C.33 D.233解：∵x 2＋3xy －1＝0，∴y ＝13⎝ ⎛⎭⎪⎫1x －x ，∴x ＋y ＝2x 3＋13x ≥229＝223(当且仅当x ＝22时等号成立)．故选B.6．执行如图所示的程序框图，如果输入的x ，y ∈R ，那么输出的S 的最大值为( )A ．0B ．1C ．2D ．3解：由程序框图知，当⎩⎪⎨⎪⎧x ≥0，y ≥0，x ＋y ≤1时，目标函数S ＝2x ＋y ∈[0，2]，否则，S ＝1.因此，输出的S的最大值为2.故选C.7．若不等式x 2＋ax －2>0在区间[1，5]上有解，则实数a 的取值范围是( )A.⎝ ⎛⎭⎪⎫－235，＋∞B.⎣⎢⎡⎦⎥⎤－235，1 C ．(1，＋∞) D.⎝ ⎛⎦⎥⎤－∞，－235 解法一：∵x ∈[1，5]，∴不等式变形为a >－x ＋2x ，∵x ∈[1，5]时，y ＝－x ＋2x 单调递减，∴y ∈⎣⎢⎡⎦⎥⎤－235，1，∴要使不等式在[1，5]上有解，应有a >－235.解法二：一元二次方程x 2＋ax －2＝0的两根之积为－2，两根一正一负．对于二次函数y ＝f (x )＝x 2＋ax －2，开口向上．与x 轴交点一正一负，y ＞0，在区间[1，5]上有解，只需y ＝f (5)＞0即可.52＋5a －2＞0，∴a ＞－235.故选A.8．已知实数x ，y 满足⎩⎨⎧y ≥1，y ≤2x －1，x ＋y ≤m ，如果目标函数z ＝x －y 的最小值为－1，则实数m ＝()A ．2B ．3C ．4D ．5解：显然m ＞2，作出⎩⎪⎨⎪⎧y ≥1，y ≤2x －1，x ＋y ≤m 的可行域，当⎩⎨⎧x ＝m ＋13，y ＝2m －13 时z ＝x －y 的最小值为－1，解得m ＝5.故选D.9．若直线ax －by ＋2＝0(a ＞0，b ＞0)被圆x 2＋y 2＋2x －4y ＋1＝0截得的弦长为4，则1a ＋1b 的最小值为( )A.14B. 2C.32＋ 2 D.32＋2 2解：圆的直径是4，说明直线过圆心(－1，2)，故12a ＋b ＝1，1a ＋1b ＝⎝ ⎛⎭⎪⎫12a ＋b ⎝ ⎛⎭⎪⎫1a ＋1b ＝32＋b a ＋a2b ≥32＋2(当且仅当a ＝22－2，b ＝2－2时等号成立)，故选C. 10．设函数f (x )＝3sin πx m ，若存在f (x )的极值点x 0满足x 20＋[f (x 0)]2＜m 2，则m 的取值范围是( )A ．(－∞，－6)∪(6，＋∞)B ．(－∞，－4)∪(4，＋∞)C ．(－∞，－2)∪(2，＋∞)D ．(－∞，－1)∪(1，＋∞)解：函数f (x )的极值点满足πx m ＝π2＋k π，即x ＝m ⎝ ⎛⎭⎪⎫k ＋12，k ∈Z ，且极值为±3，问题等价于存在k 0使之满足不等式m 2⎝ ⎛⎭⎪⎫k 0＋122＋3<m 2，即⎝ ⎛⎭⎪⎫k 0＋122＜m 2－3m 2，因为⎝ ⎛⎭⎪⎫k ＋122的最小值为14，∴只要m 2－3m 2＞14即可，得m 2>4，解得m >2或m <－2，故m 的取值范围是(－∞，－2)∪(2，＋∞)．故选C.11．已知O 是坐标原点，点A (－1，0)，若点M (x ，y )为平面区域⎩⎨⎧x ＋y ≥2，x ≤1，y ≤2上的一个动点，则|OA→＋OM →|的取值范围是( ) A ．[1，5] B ．[2，5] C ．[1，2] D ．[0，5]解：OA →＋OM →＝(－1，0)＋(x ，y )＝(x －1，y )，设z ＝|OA →＋OM →|＝（x －1）2＋y 2，则z 2的几何意义为M 到定点E (1，0)的距离，由约束条件作出平面区域如图，由图象可知当M 位于点D (0，2)时，z 取得最大值z max ＝1＋4＝5，易知最小值z min ＝1，∴1≤z ≤5，即|OA→＋OM →|的取值范围是[1，5]．故选A. 12．设M 是△ABC 内一点，且AB →·AC →＝23，∠BAC ＝30°.定义f (M )＝(m ，n ，p )，其中m ，n ，p 分别是△MBC ，△MCA ，△MAB 的面积．若f (Q )＝⎝ ⎛⎭⎪⎫12，x ，y ，则log 2x ＋log 2y 的最大值是( )A ．－5B ．－4C ．－3D ．－2解：∵AB→·AC →＝|AB →||AC →|cos ∠BAC ＝32|AB →||AC →|＝23，∴|AB →||AC →|＝4，∴S △ABC ＝12AB ·AC ·sin ∠BAC ＝12×4×12＝1，∵f (Q )＝⎝ ⎛⎭⎪⎫12，x ，y ，∴12＋x ＋y ＝1，∴x ＋y ＝12，∵x >0，y >0，∴log 2x ＋log 2y ＝log 2(xy )≤log 2⎝⎛⎭⎪⎫x ＋y 22＝log 2⎝ ⎛⎭⎪⎫142＝－4.故选B.13．已知集合A ＝{x ∈R|||x ＋2<3}，集合B ＝{x ∈R|(x －m )(x －2)<0}，且A ∩B ＝(－1，n )，则m ＝__________，n ＝__________．解：∵A ＝{x ∈R|||x ＋2<3}＝{x |－5<x <1}，又∵A ∩B ＝(－1，n )，画数轴可知m ＝－1，n ＝1.故填－1；1.14．设x ，y 满足约束条件⎩⎨⎧x －y ≤0，x ＋y －1≥0，x －2y ＋2≥0，若z ＝x ＋3y ＋m 的最小值为4，则实数m ＝________.解：画出可行域如图所示，设z ′＝x ＋3y ，当平行直线系z ′＝x ＋3y 过点C ⎝ ⎛⎭⎪⎫12，12时取最小值，有z ′min ＝12＋3×12＝2，此时，目标函数z ＝x ＋3y ＋m 取最小值，有z min ＝z ′min ＋m ＝2＋m ＝4，m ＝2.故填2.15．从等腰直角三角形纸片ABC 上，剪下如图所示的两个正方形，其中BC ＝2，∠A ＝90°，则这两个正方形的面积之和的最小值为________．解：设两个正方形边长分别为a ，b (a ≤b )，则由题可得2a ＋2b ＝2，即a ＋b ＝1，S ＝a 2＋b 2≥2×⎝⎛⎭⎪⎫a ＋b 22＝12，当且仅当a ＝b ＝12时取等号．故填12. 16．某项研究表明：在考虑行车安全的情况下，某路段车流量F (单位时间内经过测量点的车辆数，单位：辆/小时)与车流速度v (假设车辆以相同速度v 行驶，单位：米/秒)、平均车长l (单位：米)的值有关，其公式为F ＝76 000v v 2＋18v ＋20l.(1)如果不限定车型，l ＝6.05，则最大车流量为________辆/小时；(2)如果限定车型，l ＝5，则最大车流量比(1)中的最大车流量增加________辆/小时．解：(1)F ＝76 000v ＋20×6.05v＋18≤76 00022＋18＝1 900，当且仅当v ＝11时等号成立．(2)F ＝76 000v ＋20×5v ＋18≤76 00020＋18＝2 000，当且仅当v ＝10时等号成立，2 000－1 900＝100.故填(1)1 900；(2)100.17．已知不等式kx 2－x ＋4k ＜0(k ≠0)．(1)若不等式的解集为{x |x ＜－4或x ＞－1}，求实数k 的值； (2)若不等式的解集为∅，求实数k 的取值范围．解：(1)因为不等式的解集为{x |x ＜－4或x ＞－1}，所以－1和－4是方程kx 2－x ＋4k ＝0的两个实根，由韦达定理得x 1＋x 2＝1k ，解得k ＝－15.(2)不等式的解集为∅，则kx 2－x ＋4k ≥0恒成立，所以k ＞0且Δ＝1－16k 2≤0，解得k ≥14.18．某种饮料分两次提价，提价方案有两种，方案甲：第一次提价p %，第二次提价q %；方案乙：每次都提价p ＋q2%.若p >q >0，则提价多的方案是哪一种？解：设原价为a ，则提价后的价格为方案甲：(1＋p %)(1＋q %)a ，方案乙：⎝ ⎛⎭⎪⎫1＋p ＋q 2%2a ，∵1＋p %·1＋q %≤1＋p %2＋1＋q %2＝1＋p ＋q2%(当且仅当p ＝q 时取等号)，∵p ＞q ＞0，∴1＋p %·1＋q %＜1＋p ＋q2%，即(1＋p %)(1＋q %)a ＜⎝ ⎛⎭⎪⎫1＋p ＋q 2%2a ，∴提价多的方案是方案乙．答：提价多的方案是方案乙．19．(1)解不等式4x －1≤x －1；(2)求函数y ＝2x ＋91－2x ⎝ ⎛⎭⎪⎫x ∈⎝ ⎛⎭⎪⎫0，12的最小值．解：(1)4x －1≤x －1⇔4－（x －1）2x －1≤0⇔（x －3）（x ＋1）x －1≥0⇔⎩⎪⎨⎪⎧（x ＋1）（x －1）（x －3）≥0，x ≠1⇔ x ≥3或－1≤x ＜1. ∴此不等式的解集为{x |x ≥3或－1≤x ＜1}．(2)∵x ∈⎝ ⎛⎭⎪⎫0，12，∴2x ＞0，1－2x ＞0，∴y ＝42x ＋91－2x ＝⎝ ⎛⎭⎪⎫42x ＋91－2x [2x ＋(1－2x )]＝13＋9×2x 1－2x ＋4×（1－2x ）2x ≥25，当且仅当x ＝15时，等号成立，即函数的最小值为25.20．已知x ，y 满足约束条件⎩⎨⎧x －y －1≤0，2x －y －3≥0，当目标函数z ＝ax ＋by (a ＞0，b ＞0)在该约束条件下取到最小值25时，求a 2＋b 2的最小值．解法一：不等式组表示的平面区域如图所示，由于－ab ＜0，所以目标函数在点A (2，1)处取得最小值，故2a ＋b ＝25，两端平方得4a 2＋b 2＋4ab ＝20，又4ab ＝2×a ×2b ≤a 2＋4b 2，所以20≤4a 2＋b 2＋a 2＋4b 2＝5(a 2＋b 2)，所以a 2＋b 2≥4，当且仅当a ＝2b ，即a ＝45，b ＝25时等号成立．解法二：同解法一得2a ＋b ＝25.把2a ＋b ＝25看作平面直角坐标系aOb 中的直线，则a 2＋b 2的几何意义是直线上的点与坐标原点距离的平方，显然a 2＋b 2的最小值是坐标原点到直线2a ＋b ＝25距离的平方，即⎝⎛⎭⎪⎫|－25|52＝4. 21．某工厂生产甲、乙两种产品．已知生产甲种产品1 t 需耗A 种矿石10 t ，B 种矿石5 t ，煤4 t ；生产乙种产品1 t 需耗A 种矿石4 t ，B 种矿石4 t ，煤9 t ．每1 t 甲种产品的利润是600元，每1 t 乙种产品的利润是1 000元．工厂在生产这两种产品的计划中要求消耗A 种矿石不超过300 t ，B 种矿石不超过200 t ，煤不超过360 t ．甲、乙两种产品应各生产多少(精确到0.1 t )，能使利润总额达到最大？解：设生产甲、乙两种产品分别为x t ，y t ，利润总额为z 元，那么⎩⎪⎨⎪⎧10x ＋4y ≤300，5x ＋4y ≤200，4x ＋9y ≤360，x ≥0，y ≥0；z ＝600x ＋1 000y.作出以上不等式组所表示的平面区域(如图)，即可行域．作直线l ：600x ＋1 000y ＝0，即直线l ：3x ＋5y ＝0，把直线l 向右上方平移至l 1的位置时，直线经过可行域上的点M ，且与原点距离最大．此时z ＝600x ＋1 000y 取最大值．解方程组⎩⎪⎨⎪⎧5x ＋4y ＝200，4x ＋9y ＝360，得M 的坐标为x ＝36029≈12.4，y ＝1 00029≈34.4.故应生产甲产品约12.4 t ，乙产品34.4 t ，能使利润总额达到最大．22．已知函数f (x )＝x 3＋2bx 2＋cx ＋1的两个极值点为x 1和x 2，x 1∈[－2，－1]，x 2∈[1，2]，求f (－1)的取值范围．解：f ′(x )＝3x 2＋4bx ＋c ，由题可得⎩⎪⎨⎪⎧f ′（－2）＝12－8b ＋c ≥0，f ′（－1）＝3－4b ＋c ≤0，f ′（1）＝3＋4b ＋c ≤0，f ′（2）＝12＋8b ＋c ≥0.在平面直角坐标系bOc 中作图，图中阴影部分所示为可行域，易知f (－1)＝2b －c 在点(0，－3)取得最小值3，在点(0，－12)取得最大值12.∴3≤f (－1)≤12.故f (－1)的取值范围为[3，12]．。

高中数学必修5不等式解答题专项练习附答案学生版

淇淋供不应求．
第 1 页共 35 页
（1）求冰淇淋店进一次货，经加工售卖后所得净利润 w 与车速 v 和进货量 x 之间的关系式；（2）每次至少进货多少千克，才能使得销售后不会亏本（净利润 w≥0）？（3）当一次进货量 x 与车速 v 分别为多少时，能使得冰淇淋店有最大净利润？并求出最大值．（提示：
（I）用 x，y 列出满足题目条件的数学关系式，并画出相应的平面区域；（II）问电视台每周播出甲、乙两套连续剧各多少次，才能使总收视人次最多？
19.已知动点到定点
和到直线
2 的距离之比为 2 ，设动点的轨迹为曲线，过点作
2
垂直于轴的直线与曲线相交于两点，直线
ā 与曲线交于 h 两点，与相交于
第 4 页共 35 页
18.电视台播放甲、乙两套连续剧，每次播放连续剧时，需要播放广告．已知每次播放甲、乙两套连续剧时，连续剧播放时长、广告播放时长、收视人次如下表所示：
连续剧播放时长（分钟）广告播放时长（分钟）收视人次（万）
甲
70
5
60
乙
60
5
25
已知电视台每周安排的甲、乙连续剧的总播放时间不多于 600 分钟，广告的总播放时间不少于 30 分钟，且甲连续剧播放的次数不多于乙连续剧播放次数的 2 倍．分别用 x，y 表示每周计划播出的甲、乙两套连续剧的次数．（13 分）
一点（交点位于线段上，且与不重合）.
（1）求曲线的方程；值？若有，求出其最大值及对
应的直线的方程；若没有，请说明理由.
20.已知函数
2
（1）若
，求关于
（2）若不等式 ⩽
2
2
的不等式
对任意实数

高中数学必修5一元二次不等式及其解法精选题目(附答案)

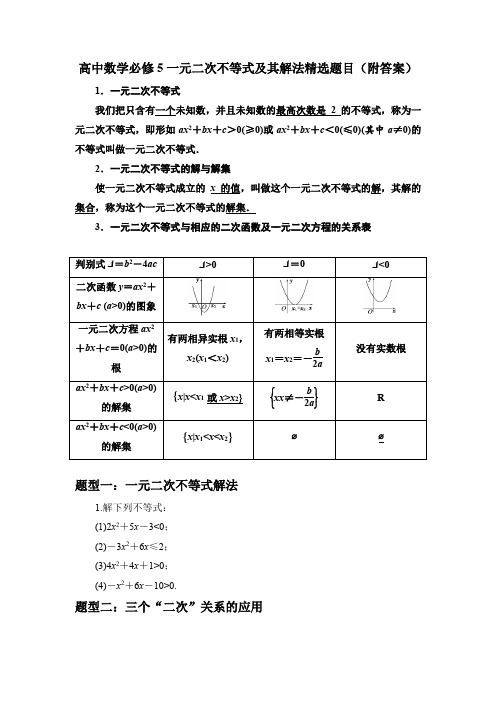
高中数学必修5一元二次不等式及其解法精选题目（附答案）1．一元二次不等式我们把只含有一个未知数，并且未知数的最高次数是2的不等式，称为一元二次不等式，即形如ax2＋bx＋c＞0(≥0)或ax2＋bx＋c＜0(≤0)(其中a≠0)的不等式叫做一元二次不等式．2．一元二次不等式的解与解集使一元二次不等式成立的x的值，叫做这个一元二次不等式的解，其解的集合，称为这个一元二次不等式的解集．3．一元二次不等式与相应的二次函数及一元二次方程的关系表题型一：一元二次不等式解法1.解下列不等式：(1)2x2＋5x－3<0；(2)－3x2＋6x≤2；(3)4x2＋4x＋1>0；(4)－x2＋6x－10>0.题型二：三个“二次”关系的应用2.若不等式ax 2＋bx ＋2>0的解集是⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪－12<x <13，则a ＋b 的值为( )A ．14B ．－10C ．10D ．－143.已知一元二次不等式x 2＋px ＋q ＜0的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪－12＜x ＜13，求不等式qx 2＋px ＋1＞0的解集．题型三：解含参数的一元二次不等式4.解关于x 的不等式x 2＋(1－a )x －a ＜0.巩固练习：1．不等式6x 2＋x －2≤0的解集为( )A.⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪－23≤x ≤12B.⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x ≤－23或x ≥12 C.⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x ≥12D.⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x ≤－23 2．设a <－1，则关于x 的不等式a (x －a )⎝ ⎛⎭⎪⎫x －1a <0的解集为( )A.⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x <a 或x >1a B ．{x |x >a } C.⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x >a 或x <1aD.⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x <1a 3．在R 上定义运算⊙：a ⊙b ＝ab ＋2a ＋b ，则满足x ⊙(x －2)<0的实数x 的取值范围为( )A ．(0,2)B ．(－2,1)C ．(－∞，－2)∪(1，＋∞)D ．(－1,2)4．不等式mx 2－ax －1>0(m >0)的解集可能是( )A.⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x <－1或x >14 B ．R C.⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪－13<x <32 D ．∅5．函数y ＝17－6x －x 2的定义域为( )A ．[－7,1]B ．(－7,1)C ．(－∞，－7]∪[1，＋∞)D ．(－∞，－7)∪(1，＋∞)6．已知全集U ＝R ，A ＝{x |x 2－1≥0}，则∁U A ＝________.7．若二次函数y ＝ax 2＋bx ＋c (a <0)的图象与x 轴的两个交点为(－1,0)和(3,0)，则不等式ax 2＋bx ＋c <0的解集是________．8．已知函数f (x )＝⎩⎨⎧x 2＋2x ，x ≥0，－x 2＋2x ，x <0.若f (a )≤3，则a 的取值范围是________．9．解关于x 的不等式x 2－3ax －18a 2>0. 10．若函数f (x )＝2 018ax 2＋2ax ＋2的定义域是R ，求实数a 的取值范围．参考答案：1.[解] (1)Δ＝49>0，方程2x 2＋5x －3＝0的两根为x 1＝－3，x 2＝12，作出函数y ＝2x 2＋5x －3的图象，如图①所示．由图可得原不等式的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪－3<x <12.(2)原不等式等价于3x 2－6x ＋2≥0.Δ＝12>0，解方程3x 2－6x ＋2＝0，得x 1＝3－33，x 2＝3＋33，作出函数y ＝3x 2－6x ＋2的图象，如图②所示，由图可得原不等式的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x ≤3－33或x ≥3＋33. (3)∵Δ＝0，∴方程4x 2＋4x ＋1＝0有两个相等的实根x 1＝x 2＝－12.作出函数y ＝4x 2＋4x ＋1的图象如图所示．由图可得原不等式的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x ≠－12，x ∈R.(4)原不等式可化为x 2－6x ＋10<0，∵Δ＝－4<0， ∴方程x 2－6x ＋10＝0无实根，∴原不等式的解集为∅. 2.解：由已知得，ax 2＋bx ＋2＝0的解为－12，13，且a <0. ∴⎩⎪⎨⎪⎧－b a ＝－12＋13，2a ＝⎝ ⎛⎭⎪⎫－12×13，解得⎩⎨⎧a ＝－12，b ＝－2，∴a ＋b ＝－14.3.解：因为x 2＋px ＋q ＜0的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪－12＜x ＜13，所以x 1＝－12与x 2＝13是方程x 2＋px ＋q ＝0的两个实数根，由根与系数的关系得⎩⎪⎨⎪⎧13－12＝－p ，13×⎝ ⎛⎭⎪⎫－12＝q ，解得⎩⎪⎨⎪⎧p ＝16，q ＝－16 .所以不等式qx 2＋px ＋1＞0即为－16x 2＋16x ＋1＞0，整理得x 2－x －6＜0，解得－2＜x ＜3.即不等式qx 2＋px ＋1＞0的解集为{x |－2＜x ＜3}．4.[解] 方程x 2＋(1－a )x －a ＝0的解为x 1＝－1，x 2＝a ，函数y ＝x 2＋(1－a )x －a 的图象开口向上，则当a ＜－1时，原不等式解集为{x |a ＜x ＜－1}；当a ＝－1时，原不等式解集为∅；当a ＞－1时，原不等式解集为{x |－1＜x ＜a }． 5.设a ∈R ，解关于x 的不等式ax 2＋(1－2a )x －2>0.5.解：(1)当a ＝0时，不等式可化为x －2>0，解得x >2，即原不等式的解集为{x |x >2}．(2)当a ≠0时，方程ax 2＋(1－2a )x －2＝0的两根分别为2和－1a .①当a <－12时，解不等式得－1a <x <2，即原不等式的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪－1a <x <2；②当a ＝－12时，不等式无解，即原不等式的解集为∅；③当－12<a <0时，解不等式得2<x <－1a ，即原不等式的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪2<x <－1a ； ④当a >0时，解不等式得x <－1a 或x >2，即原不等式的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x <－1a 或x >2. 练习：1.解析：选A 因为6x 2＋x －2≤0⇔(2x －1)·(3x ＋2)≤0，所以原不等式的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪－23≤x ≤12. 2.解析：选A ∵a <－1，∴a (x －a )·⎝ ⎛⎭⎪⎫x －1a <0⇔(x －a )·⎝ ⎛⎭⎪⎫x －1a >0.又a <－1，∴1a >a ，∴x >1a 或x <a .3.解析：选B 由a ⊙b ＝ab ＋2a ＋b ，得x ⊙(x －2)＝x (x －2)＋2x ＋x －2＝x 2＋x －2<0，所以－2<x <1.4.解析：选A 因为Δ＝a 2＋4m >0，所以函数y ＝mx 2－ax －1的图象与x 轴有两个交点，又m >0，所以原不等式的解集不可能是B 、C 、D ，故选A.5.解析：选B 由7－6x －x 2>0，得x 2＋6x －7<0，即(x ＋7)(x －1)<0，所以－7<x <1，故选B.6.解析：∁U A ＝{x |x 2－1<0}＝{x |－1<x <1}．答案：{x |－1<x <1}7.解析：根据二次函数的图象知所求不等式的解集为(－∞，－1)∪(3，＋∞)．答案：(－∞，－1)∪(3，＋∞)8.解析：当a ≥0时，a 2＋2a ≤3，∴0≤a ≤1；当a <0时，－a 2＋2a ≤3，∴a <0.综上所述，a 的取值范围是(－∞，1]．9.解：将x 2－3ax －18a 2>0变形得(x －6a )(x ＋3a )>0，方程(x －6a )(x ＋3a )＝0的两根为6a ，－3a .所以当a >0时，6a >－3a ，原不等式的解集为{x |x <－3a 或x >6a }；当a ＝0时，6a ＝－3a ＝0，原不等式的解集为{x |x ≠0}；当a <0时，6a <－3a ，原不等式的解集为{x |x <6a 或x >－3a }． 10.解：因为f (x )的定义域为R ，所以不等式ax 2＋2ax ＋2>0恒成立． (1)当a ＝0时，不等式为2>0，显然恒成立；(2)当a ≠0时，有⎩⎨⎧ a >0，Δ＝4a 2－8a <0，即⎩⎨⎧a >0，0<a <2，所以0<a <2.综上可知，实数a 的取值范围是[0,2)．。

高二数学必修5第三章不等式章末训练题精选（含解析）

⼀、选择题(本⼤题共12⼩题，每⼩题5分，共60分)1.原点和点(1,1)在直线x+y=a两侧，则a的取值范围是( )A.a<0或a>2B.0答案　B2.若不等式ax2+bx-2>0的解集为x|-2A.-18B.8C.-13D.1答案　C解析　∵-2和-14是ax2+bx-2=0的两根.∴-2+-14=-ba -2 ×-14=-2a，∴a=-4b=-9.∴a+b=-13.3.如果a∈R，且a2+a<0，那么a，a2，-a，-a2的⼤⼩关系是( )A.a2>a>-a2>-aB.-a>a2>-a2>aC.-a>a2>a>-a2D.a2>-a>a>-a2答案　B解析　∵a2+a<0，∴a(a+1)<0，∴-1a2>-a2>a.4.不等式1x<12的解集是( )A.(-∞，2)B.(2，+∞)C.(0,2)D.(-∞，0)∪(2，+∞)答案　D解析　1x<12⇔1x-12<0⇔2-x2x<0⇔x-22x>0⇔x<0或x>2.5.设变量x，y满⾜约束条件x+y≤3，x-y≥-1，y≥1，则⽬标函数z=4x+2y的值为( )A.12B.10C.8D.2答案　B解析　画出可⾏域如图中阴影部分所⽰，⽬标函数z=4x+2y可转化为y=-2x+z2，作出直线y=-2x并平移，显然当其过点A时纵截距z2.解⽅程组x+y=3，y=1得A(2,1)，∴zmax=10.6.已知a、b、c满⾜cA.ab>acB.c(b-a)>0C.ab2>cb2D.ac(a-c)<0答案　C解析　∵c0，c<0.⽽b与0的⼤⼩不确定，在选项C中，若b=0，则ab2>cb2不成⽴.7.已知集合M={x|x2-3x-28≤0}，N={x|x2-x-6>0}，则M∩N为( )A.{x|-4≤xB.{x|-4C.{x|x≤-2或x>3}D.{x|x答案　A解析　∵M={x|x2-3x-28≤0}={x|-4≤x≤7}，N={x|x2-x-6>0}={x|x3}，∴M∩N={x|-4≤x8.在R上定义运算⊗：x⊗y=x(1-y)，若不等式(x-a)⊗(x+a)<1对任意实数x成⽴，则( )A.-1答案　C解析　(x-a)⊗(x+a)=(x-a)(1-x-a)<1⇔-x2+x+(a2-a-1)<0恒成⽴⇔Δ=1+4(a2-a-1)<0⇔-129.在下列各函数中，最⼩值等于2的函数是( )A.y=x+1xB.y=cos x+1cos x (0C.y=x2+3x2+2D.y=ex+4ex-2答案　D解析　选项A中，x>0时，y≥2，x<0时，y≤-2;选项B中，cos x≠1，故最⼩值不等于2;选项C中，x2+3x2+2=x2+2+1x2+2=x2+2+1x2+2，当x=0时，ymin=322.选项D中，ex+4ex-2>2ex•4ex-2=2，当且仅当ex=2，即x=ln 2时，ymin=2，适合.10.若x，y满⾜约束条件x+y≥1x-y≥-12x-y≤2，⽬标函数z=ax+2y仅在点(1,0)处取得最⼩值，则a的取值范围是( )A.(-1,2)B.(-4,2)C.(-4,0]D.(-2,4)答案　B解析　作出可⾏域如图所⽰，直线ax+2y=z仅在点(1,0)处取得最⼩值，由图象可知-1即-411.若x，y∈R+，且2x+8y-xy=0，则x+y的最⼩值为( )A.12B.14C.16D.18答案　D解析　由2x+8y-xy=0，得y(x-8)=2x，∵x>0，y>0，∴x-8>0，得到y=2xx-8，则µ=x+y=x+2xx-8=x+ 2x-16 +16x-8=(x-8)+16x-8+10≥2 x-8 •16x-8+10=18，当且仅当x-8=16x-8，即x=12，y=6时取“=”.12.若实数x，y满⾜x-y+1≤0，x>0，则yx-1的取值范围是( )A.(-1,1)B.(-∞，-1)∪(1，+∞)C.(-∞，-1)D.[1，+∞)答案　B解析　可⾏域如图阴影，yx-1的⼏何意义是区域内点与(1,0)连线的斜率，易求得yx-1>1或yx-1⼆、填空题(本⼤题共4⼩题，每⼩题4分，共16分)13.若A=(x+3)(x+7)，B=(x+4)(x+6)，则A、B的⼤⼩关系为________.答案　A14.不等式x-1x2-x-30>0的解集是________________________________________________________________________.答案　{x|-56}15.如果a>b，给出下列不等式：①1a<1b;②a3>b3;③a2>b2;④2ac2>2bc2;⑤ab>1;⑥a2+b2+1>ab+a+b.其中⼀定成⽴的不等式的序号是________.答案　②⑥解析　①若a>0，b<0，则1a>1b，故①不成⽴;②∵y=x3在x∈R上单调递增，且a>b.∴a3>b3，故②成⽴;③取a=0，b=-1，知③不成⽴;④当c=0时，ac2=bc2=0,2ac2=2bc2，故④不成⽴;⑤取a=1，b=-1，知⑤不成⽴;⑥∵a2+b2+1-(ab+a+b)=12[(a-b)2+(a-1)2+(b-1)2]>0，∴a2+b2+1>ab+a+b，故⑥成⽴.16.⼀批货物随17列货车从A市以v千⽶/⼩时匀速直达B市，已知两地铁路线长400千⽶，为了安全，两列货车的间距不得⼩于v202千⽶，那么这批货物全部运到B市，最快需要________⼩时.答案　8解析　这批货物从A市全部运到B市的时间为t，则t=400+16v202v=400v+16v400≥2 400v×16v400=8(⼩时)，当且仅当400v=16v400，即v=100时等号成⽴，此时t=8⼩时.三、解答题(本⼤题共6⼩题，共74分)17.(12分)若不等式(1-a)x2-4x+6>0的解集是{x|-3(1)解不等式2x2+(2-a)x-a>0;(2)b为何值时，ax2+bx+3≥0的解集为R.解　(1)由题意知1-a<0且-3和1是⽅程(1-a)x2-4x+6=0的两根，∴1-a<041-a=-261-a=-3，解得a=3.∴不等式2x2+(2-a)x-a>0即为2x2-x-3>0，解得x32.∴所求不等式的解集为x|x32.(2)ax2+bx+3≥0，即为3x2+bx+3≥0，若此不等式解集为R，则b2-4×3×3≤0，∴-6≤b≤6.18.(12分)解关于x的不等式56x2+ax-a2<0.解　原不等式可化为(7x+a)(8x-a)<0，即x+a7x-a8<0.①当-a70时，-a7②当-a7=a8，即a=0时，原不等式解集为∅;③当-a7>a8，即a<0时，a8综上知，当a>0时，原不等式的解集为x|-a7当a=0时，原不等式的解集为∅;当a<0时，原不等式的解集为x|a819.(12分)证明不等式：a，b，c∈R，a4+b4+c4≥abc(a+b+c).证明　∵a4+b4≥2a2b2，b4+c4≥2b2c2，c4+a4≥2c2a2，∴2(a4+b4+c4)≥2(a2b2+b2c2+c2a2)即a4+b4+c4≥a2b2+b2c2+c2a2.⼜a2b2+b2c2≥2ab2c，b2c2+c2a2≥2abc2，c2a2+a2b2≥2a2bc.∴2(a2b2+b2c2+c2a2)≥2(ab2c+abc2+a2bc)，即a2b2+b2c2+c2a2≥abc(a+b+c).∴a4+b4+c4≥abc(a+b+c).20.(12分)某投资⼈打算投资甲、⼄两个项⽬，根据预测，甲、⼄项⽬可能的盈利率分别为100%和50%，可能的亏损率分别为30%和10%，投资⼈计划投资⾦额不超过10万元，要求确保可能的资⾦亏损不超过1.8万元，问投资⼈对甲、⼄两个项⽬各投资多少万元，才能使可能的盈利?解　设投资⼈分别⽤x万元、y万元投资甲、⼄两个项⽬，由题意知x+y≤10，0.3x+0.1y≤1.8，x≥0，y≥0.⽬标函数z=x+0.5y.上述不等式组表⽰的平⾯区域如图所⽰，阴影部分(含边界)即可⾏域.作直线l0：x+0.5y=0，并作平⾏于直线l0的⼀组直线x+0.5y=z，z∈R，与可⾏域相交，其中有⼀条直线经过可⾏域上的M点，且与直线x+0.5y=0的距离，这⾥M点是直线x+y=10和0.3x+0.1y=1.8的交点.解⽅程组x+y=10，0.3x+0.1y=1.8，得x=4，y=6，此时z=1×4+0.5×6=7(万元).∵7>0，∴当x=4，y=6时，z取得值.答　投资⼈⽤4万元投资甲项⽬、6万元投资⼄项⽬，才能在确保亏损不超过1.8万元的前提下，使可能的盈利.21.(12分)设a∈R，关于x的⼀元⼆次⽅程7x2-(a+13)x+a2-a-2=0有两实根x1，x2，且0解　设f(x)=7x2-(a+13)x+a2-a-2.因为x1，x2是⽅程f(x)=0的两个实根，且0所以f 0 >0，f 1 <0，f 2 >0⇒a2-a-2>0，7- a+13 +a2-a-2<0，28-2 a+13 +a2-a-2>0⇒a2-a-2>0，a2-2a-8<0，a2-3a>0⇒a2，-23⇒-2所以a的取值范围是{a|-222.(14分)某商店预备在⼀个⽉内分批购买每张价值为20元的书桌共36台，每批都购⼊x台(x是正整数)，且每批均需付运费4元，储存购⼊的书桌⼀个⽉所付的保管费与每批购⼊书桌的总价值(不含运费)成正⽐，若每批购⼊4台，则该⽉需⽤去运费和保管费共52元，现在全⽉只有48元资⾦可以⽤于⽀付运费和保管费.(1)求该⽉需⽤去的运费和保管费的总费⽤f(x);(2)能否恰当地安排每批进货的数量，使资⾦够⽤?写出你的结论，并说明理由.解　(1)设题中⽐例系数为k，若每批购⼊x台，则共需分36x批，每批价值20x.由题意f(x)=36x•4+k•20x，由x=4时，y=52，得k=1680=15.∴f(x)=144x+4x (0(2)由(1)知f(x)=144x+4x (0∴f(x)≥2144x•4x=48(元).当且仅当144x=4x，即x=6时，上式等号成⽴.故只需每批购⼊6张书桌，可以使资⾦够⽤.。

(典型题)高中数学必修五第三章《不等式》测试卷(含答案解析)(1)

一、选择题1．已知正数x ，y 满足1431x y +=+，则x y +的最小值为（） A ．53B ．2C ．73D ．62．设实数x ，y 满足约束条件21,22,x y x y -≤⎧⎨-≥⎩则x y +的最小值是（）A ．2B ．-2C ．1D ．-13．已知a b >，不等式220ax x b ++≥对于一切实数x 恒成立，且0x R ∃∈，使得20020ax x b ++=成立，则22a b a b+-的最小值为（）A ．1BC ．2D．4．若x ､y 满足约束条件36022x y x y y +-≤⎧⎪+≥⎨⎪≤⎩，则22x y +的最小值为（）A ．5B ．4C ．2D5．已知实数,x y 满足24240x y x y y -≥⎧⎪+≤⎨⎪≤⎩，则32z x y =-的最小值是（）A ．4B ．5C ．6D ．76．设,x y 满足约束条件321104150250x y x y x y +-≥⎧⎪-+≥⎨⎪--≤⎩，则z x y =+的最小值为（）A ．3B ．4C ．5D ．107．若函数()1xy a a =>的图象与不等式组40,20,1x y y x -≤⎧⎪-≥⎨⎪≤+⎩，表示的区域有公共点，则a 的取值范围为（） A ．[]2,4B．⎤⎦C ．(][)1,24,⋃+∞D．([)2,⋃+∞8．已知函数()32f x x ax bx c =+++，且()()()01233f f f <-=-=-≤，则( )A ．c 3≤B ．3c 6<≤C ．6c 9<≤D ．c 9>9．设x ，y 满足约束条件261322x y x y y -≤⎧⎪⎪+≥⎨⎪≤⎪⎩，则1z x y =-+的最小值是（）A ．1-B ．0C ．1D ．210．在ABC 中，BAC ∠的平分线交BC 于D .若3BAC π∠=，4AB AC +=，则AD 长度的最大值为（） AB ．2C ．3D．11．设函数2()1f x mx mx =--，若对于任意的x ∈{x |1 ≤ x ≤ 3}，()4f x m <-+恒成立，则实数m 的取值范围为（） A ．m ≤0 B ．0≤m <57C ．m <0或0<m <57D ．m <5712．已知不等式230ax bx a --≥的解集是[]4,1-，则b a 的值为（） A ．-64B ．-36C ．36D ．64二、填空题13．若正实数x 、y 、z ，满足3z x y +=，4z y x +=，则x y x y z++-的最小值为_______.14．已知x ，y 满足不等式组220,10,30x y x y x +-≥⎧⎪-+≥⎨⎪-≤⎩，则11x z y -=+，则z 的最大值为________.15．若关于x 的不等式250ax x b -+< 的解集为{|23}x x << ，则+a b 的值是__________．16．若不等式20++≥x mx m 在[1,2]x ∈上恒成立，则实数m 的最小值为________ 17．在下列函数中， ①1y x x=+②1123212y x x x ⎛⎫=++< ⎪-⎝⎭③()2114141x y x x x x ⎛⎫=++> ⎪+⎝⎭ ④22221πsin cos 0,sin cos 2y x x x x x ⎛⎫⎛⎫=+∈ ⎪ ⎪⎝⎭⎝⎭其中最小值为2的函数是__________.18．若关于x 的不等式()0f x <和()0g x <的解集分别为(),a b 和11,b a ⎛⎫⎪⎝⎭,则称这两个不等式为“对偶不等式”.若不等式()2220x x θ-+<和不等式()224sin 210x x θ++<为“对偶不等式”,且,2πθπ⎛⎫∈ ⎪⎝⎭,则θ=______.19．若实数x ，y 满足约束条件103030x y x y x -+≥⎧⎪+-≥⎨⎪-≤⎩，则3z x y =-的最小值为__________．20．记等差数列{}n a 的前n 项和为n S ，满足570a a ，1122S =，则7811572a a a a a 的最小值为_________.三、解答题21．2020年受疫情影响，全球经济均受到不同程度的冲击.为稳妥有序地推进复工复产，2月11日晚，郑州市相关政府部门印发了《郑州市关于应对新型冠状病毒肺炎疫情促进经济平稳健康发展的若干举措》的通知，并出台多条举措促进全市经济平稳健康发展.某工厂为拓宽市场，计划生产某种热销产品，经调查，该产品一旦投入市场就能全部售出.若不举行促销活动，该产品的年销售量为28万件，若举行促销活动，年销售量y (单位；万件)与年促销费用()0x x ≥(单位；万元)满足3010(ky k x =-+为常数).已知生产该产品的固定成本为80万元，每生产1万件该产品需要再投入生产成本160万元，厂家将每件产品的销售价格定为每件产品平均成本的1.5倍(产品成本包括固定成本和生产成本，不包括促销成本). （1）求k 的值，并写出该产品的利润L (单位:万元)与促销费用x (单位:万元)的函数关系﹔ （2）该工厂计划投入促销费用多少万元，才能获得最大利润?22．已知m R ∈，命题p ：对任意[]0,1x ∈，不等式2223x m m -≥-恒成立；命题q ：存在[]1,1x ∈-，使得m ax ≤成立．（1）若p 为真命题，求m 的取值范围；（2）当1a =时，若p q ∨为真，p q ∧为假，求m 的取值范围． 23．已知()f x 是偶函数，()g x 是奇函数，且2()()2f x g x x x +=+-. （1）求()f x 和()g x 的解析式；（2）设2()33h x mx mx =+-（其中m R ∈），解不等式()()h x g x <.24．已知函数2221,()?23,x ax x af x x ax x a ⎧-+<⎪⎪=⎨⎪+-≥⎪⎩，其中 0a >．（1）若()()01ff =，求a 的值．（2）若函数()f x 的图象在x 轴的上方，求a 的取值范围． 25．已知函数()()21,4f x ax bx a b R =++∈，且()10f -=，对任意实数x ，()0f x ≥成立.（1）求函数()f x 的解析式；（2）若0c ≥，解关于x 的不等式()2131424f x c x x c ⎛⎫⎛⎫>+-++ ⎪ ⎪⎝⎭⎝⎭. 26．某单位计划建造一间背面靠墙的小屋，其地面面积为12m 2，墙面的高度为3m ，经测算，屋顶的造价为5800元，房屋正面每平方米的造价为1200元，房屋侧面每平方米的造价为800元，设房屋正面地面长方形的边长为x m ，房屋背面和地面的费用不计. （1）用含x 的表达式表示出房屋的总造价；（2）当x 为多少时，总造价最低？最低造价是多少？【参考答案】***试卷处理标记，请不要删除一、选择题 1．B 解析：B 【分析】化简114[(1)]()131x y x y x y +=++⨯+-+，再利用基本不等式求解. 【详解】由题得1114(1)1[(1)]31[(1)]()1331x y x y x y x y x y +=++-=++⨯-=++⨯+-+ 1141(5)1(5)123131y x x y y +=++-≥+-=++ 当且仅当1x y ==时取等. 所以x y +的最小值为2. 故选：B 【点睛】方法点睛：利用基本不等式求最值时，常用到常量代换，即把所求代数式中的某一常量换成已知中的代数式，再利用基本不等式求解.2．C解析：C 【分析】先作出约束条件对应的可行域，然后分析目标函数的几何意义，结合图形即可求解. 【详解】作出约束条件2122x y x y -≤⎧⎨-≥⎩所表示的平面区域如图所示：移动直线x y z +=，可知当其过点A 时取得最小值，解方程组2122x y x y -≤⎧⎨-≥⎩，求得10x y =⎧⎨=⎩，即(1,0)A ，代入求得101=+=z ，所以x y +的最小值是1，故选：C. 【点睛】方法点睛：该题考查的是有关线性规划的问题，解题方法如下：（1）根据题中所给的约束条件画出可行域；（2）根据目标函数的意义找到最优解；（3）解方程组求得最优解的坐标；（4）代入求得最小值，得到结果.3．D解析：D 【分析】根据条件对于一切实数x 不等式恒成立和0x R ∃∈使得方程成立结合二次不等式、二次方程、二次函数，可得1ab =，将22a b a b+-化成2a b a b -+-，再结合基本不等式求解即可.【详解】解：因为不等式220ax x b ++≥对于一切实数x 恒成立，所以0440a ab >⎧⎨-≤⎩，又因为0x R ∃∈，使得20020ax x b ++=成立，所以440ab -≥，所以440ab -=，即0,0,1a b ab >>=，所以222()2222a b a b ab a b a b a b a b+-+==-+≥---，当且仅当2a b a b-=-时取得最小值. 故选：D. 【点睛】易错点睛：利用基本不等式求最值时，要注意其必须满足的三个条件：（1）“一正二定三相等”“一正”就是各项必须为正数；（2）“二定”就是要求和的最小值，必须把构成和的二项之积转化成定值；要求积的最大值，则必须把构成积的因式的和转化成定值；（3）“三相等”是利用基本不等式求最值时，必须验证等号成立的条件，若不能取等号则这个定值就不是所求的最值，这也是最容易发生错误的地方.4．C解析：C 【分析】由不等式组作出可行域，如图,目标函数22xy +可视为可行域中的点与原点距离的平方，故其最小值应为原点到直线2x y +=的距离平方，根据点到直线的距离公式可得选项. 【详解】由不等式组做出可行域如图，目标函数22xy +可视为可行域内的点与原点距离的平方，故其最小值为原点到直线2x y +=的距离的平方，由点到直线的距离公式可知，原点到直线2x y +=的距离为22d ==，所以所求最小值为2. 故选:C.【点睛】本题主要考查线性规划问题，首先由不等式组作出相应的可行域，作图时，可将不等式0Ax By C ++≥转化为y kx b ≤+（或y kx b ≥+），明确可行域对应的是封闭区域还是开放区域、分界线是实线还是虚线，其次确定目标函数的几何意义，是求直线的截距、两点间距离的平方、直线的斜率、还是点到直线的距离等等，最后结合图形确定目标函数最值取法、值域范围.5．C解析：C【分析】由约束条件画出可行域，化目标函数为直线方程的斜截式，数形结合得到最优解，联立方程组得到最优解的坐标，代入目标函数得到答案.【详解】由实数x，y满足2424x yx yy-≥⎧⎪+≤⎨⎪≤⎩得到可行域如图：z＝3x﹣2y变形为y＝32x﹣2z，由24yx y=⎧⎨-=⎩，解得B（2，0）当此直线经过图中B时，在y轴的截距最大，z最小，所以z的最小值为3×2﹣2×0＝6；故选C．【点睛】本题主要考查线性规划中利用可行域求目标函数的最值，求目标函数最值的一般步骤是“一画、二移、三求”：（1）作出可行域（一定要注意是实线还是虚线）；（2）找到目标函数对应的最优解对应点（在可行域内平移变形后的目标函数，最先通过或最后通过的顶点就是最优解）；（3）将最优解坐标代入目标函数求出最值.6．B解析：B【分析】结合题意画出可行域，然后运用线性规划知识来求解【详解】如图由题意得到可行域，改写目标函数得y x z =-+，当取到点(3,1)A 时得到最小值，即314z =+=故选B 【点睛】本题考查了运用线性规划求解最值问题，一般步骤：画出可行域，改写目标函数，求出最值，需要掌握解题方法7．B解析：B 【分析】由约束条件作出可行域，再由指数函数的图象经过A ，B 两点求得a 值，则答案可求．【详解】解：由约束条件40,20,1x y y x -⎧⎪-⎨⎪+⎩作出可行域如图：当1x =时，2y a =≤；当4x =时，42y a =≥，则42a ≥故a 的取值范围为42,2⎡⎤⎣⎦.故选：B ．【点睛】本题考查简单的线性规划，考查数形结合的解题思想方法，属于中档题．8．C解析：C 【分析】由()()()123f f f -=-=-可求得a b ，的值，代回不等关系得出c 的取值范围【详解】由()()()123f f f -=-=-可得184********a b c a b ca b c a b c -+-+=-+-+⎧⎨-+-+=-+-+⎩解得611a b =⎧⎨=⎩则()32611f x x x x c =+++ 所以()16f c -=-，()013f <-≤所以0c 63-≤＜，解得6c 9≤＜，故选C . 【点睛】本题主要考查了函数的性质，运用待定系数法求出参量的值，然后结合题意求出取值范围，较为基础．9．C解析：C 【分析】作出约束条件所表示的平面区域，结合图象确定目标函数的最优解，代入求解，即可得到答案. 【详解】作出x ，y 满足约束条件261322x y x y y -≤⎧⎪⎪+≥⎨⎪≤⎪⎩，所对应的可行域，如图所示，目标函数1z x y =-+可化为1y x z =+-，当直线1y x z =+-过点A 时，此时直线在y 轴上的截距最大值，此时目标函数取得最小值，又由2132y x y =⎧⎪⎨+=⎪⎩，解得(2,2)A ，所以目标函数的最小值为min 2211z =-+=. 故选：C.【点睛】本题主要考查简单线性规划求解目标函数的最值问题．其中解答中正确画出不等式组表示的可行域，利用“一画、二移、三求”，确定目标函数的最优解是解答的关键，着重考查了数形结合思想，及推理与计算能力，属于基础题．10．A解析：A 【分析】根据题意，设,,,AD t AB c AC b ===由三角形面积公式1sin 2S a b θ=⋅⋅可表示出,,ACD ABD ABC ∆∆∆三者之间的关系，进而得边长关系为3,t bc =最后通过基本不等式求得AD 的最大值。

高中数学必修5基本不等式精选题目(附答案)

高中数学必修5基本不等式精选题目(附答案）1．重要不等式当a ，b 是任意实数时，有a 2＋b 2≥2ab ，当且仅当a ＝b 时，等号成立． 2．基本不等式(1)有关概念：当a ，b 均为正数时，把a ＋b2叫做正数a ，b 的算术平均数，把ab 叫做正数a ，b 的几何平均数．(2)不等式：当a ，b 是任意正实数时，a ，b 的几何平均数不大于它们的算术平均数，即ab ≤a ＋b2，当且仅当a ＝b 时，等号成立．(3)变形：ab ≤⎝ ⎛⎭⎪⎫a ＋b 22≤a 2＋b 22，a ＋b ≥2ab (其中a ＞0，b ＞0，当且仅当a＝b 时等号成立)．题型一：利用基本不等式比较大小1.已知m ＝a ＋1a －2(a >2)，n ＝22－b 2(b ≠0)，则m ，n 之间的大小关系是( ) A ．m >n B ．m <n C ．m ＝nD ．不确定2.若a >b >1，P ＝lg a ·lg b ，Q ＝12(lg a ＋lg b )，R ＝lg a ＋b 2，则P ，Q ，R 的大小关系是________．题型二：利用基本不等式证明不等式3.已知a ，b ，c 均为正实数，求证：2b ＋3c －a a ＋a ＋3c －2b 2b ＋a ＋2b －3c3c ≥3.4.已知a ，b ，c 为正实数，且a ＋b ＋c ＝1，求证：⎝ ⎛⎭⎪⎫1a －1⎝ ⎛⎭⎪⎫1b －1⎝ ⎛⎭⎪⎫1c －1≥8.题型三：利用基本不等式求最值5.已知lg a ＋lg b ＝2，求a ＋b 的最小值．6.已知x ＞0，y ＞0，且2x ＋3y ＝6，求xy 的最大值．7.已知x ＞0，y ＞0，1x ＋9y ＝1，求x ＋y 的最小值．8．已知a >0，b >0，2a ＋1b ＝16，若不等式2a ＋b ≥9m 恒成立，则m 的最大值为( )A ．8B ．7C ．6D ．5题型四：利用基本不等式解应用题9.某单位决定投资3 200元建一仓库(长方体状)，高度恒定，它的后墙利用旧墙不花钱，正面用铁栅，每米长造价40元，两侧墙砌砖，每米长造价45元，顶部每平方米造价20元，求：(1)仓库面积S 的最大允许值是多少？(2)为使S 达到最大，而实际投资又不超过预算，那么正面铁栅应设计为多长？巩固练习：1．下列结论正确的是( ) A ．当x >0且x ≠1时，lg x ＋1lg x ≥2 B ．当x >0时，x ＋1x≥2 C ．当x ≥2时，x ＋1x 的最小值为2 D ．当0<x ≤2时，x －1x 无最大值2．下列各式中，对任何实数x 都成立的一个式子是( ) A ．lg(x 2＋1)≥lg(2x ) B ．x 2＋1>2x C.1x 2＋1≤1 D ．x ＋1x ≥23．设a ，b 为正数，且a ＋b ≤4，则下列各式中正确的一个是( ) A.1a ＋1b <1 B.1a ＋1b ≥1 C.1a ＋1b <2D.1a ＋1b ≥24．四个不相等的正数a ，b ，c ，d 成等差数列，则( ) A.a ＋d2>bcB.a ＋d2<bcC.a＋d2＝bc D.a＋d2≤bc5．若x>0，y>0，且2x＋8y＝1，则xy有()A．最大值64B．最小值1 64C．最小值12D．最小值646．若a>0，b>0，且1a＋1b＝ab，则a3＋b3的最小值为________．7．(2017·江苏高考)某公司一年购买某种货物600吨，每次购买x吨，运费为6万元/次，一年的总存储费用为4x万元．要使一年的总运费与总存储费用之和最小，则x的值是________．8．若对任意x>0，xx2＋3x＋1≤a恒成立，则a的取值范围是________．9．(1)已知x<3，求f(x)＝4x－3＋x的最大值；参考答案：1.解：因为a>2，所以a－2>0，又因为m＝a＋1a－2＝(a－2)＋1a－2＋2，所以m≥2(a－2)·1a－2＋2＝4，由b≠0，得b2≠0，所以2－b2<2，n＝22－b2<4，综上可知m>n.2.解：因为a>b>1，所以lg a>lg b>0，所以Q＝12(lg a＋lg b)>lg a·lg b＝P；Q＝12(lg a＋lg b)＝lg a＋lg b＝lg ab<lga＋b2＝R.所以P<Q<R.3.[证明]∵a，b，c均为正实数，∴2ba＋a2b≥2(当且仅当a＝2b时等号成立)，3c a＋a3c≥2(当且仅当a＝3c时等号成立)，3c 2b ＋2b3c ≥2(当且仅当2b ＝3c 时等号成立)，将上述三式相加得⎝ ⎛⎭⎪⎫2b a ＋a 2b ＋⎝ ⎛⎭⎪⎫3c a ＋a 3c ＋⎝ ⎛⎭⎪⎫3c 2b ＋2b 3c ≥6(当且仅当a ＝2b ＝3c时等号成立)，∴⎝ ⎛⎭⎪⎫2b a ＋a 2b －1＋⎝ ⎛⎭⎪⎫3c a ＋a 3c －1＋⎝ ⎛⎭⎪⎫3c 2b ＋2b 3c －1≥3(当且仅当a ＝2b ＝3c 时等号成立)，即2b ＋3c －a a ＋a ＋3c －2b 2b ＋a ＋2b －3c 3c ≥3(当且仅当a ＝2b ＝3c 时等号成立)．4.证明：因为a ，b ，c 为正实数，且a ＋b ＋c ＝1，所以1a －1＝1－a a ＝b ＋c a ≥2bc a . 同理，1b －1≥2ac b ，1c －1≥2abc . 上述三个不等式两边均为正，相乘得⎝ ⎛⎭⎪⎫1a －1⎝ ⎛⎭⎪⎫1b －1⎝ ⎛⎭⎪⎫1c －1≥2bc a ·2ac b ·2abc ＝8，当且仅当a ＝b ＝c ＝13时，取等号.5.解：由lg a ＋lg b ＝2可得lg ab ＝2，即ab ＝100，且a ＞0，b ＞0，因此由基本不等式可得a ＋b ≥2ab ＝2100 ＝20，当且仅当a ＝b ＝10时，a ＋b 取到最小值20. 6.解：∵x ＞0，y ＞0,2x ＋3y ＝6， ∴xy ＝16(2x ·3y )≤16·⎝⎛⎭⎪⎫2x ＋3y 22＝16·⎝ ⎛⎭⎪⎫622＝32，当且仅当2x ＝3y ，即x ＝32，y ＝1时，xy 取到最大值32. 7.解：∵1x ＋9y ＝1， ∴x ＋y ＝(x ＋y )·⎝ ⎛⎭⎪⎫1x ＋9y＝1＋9x y ＋y x ＋9＝y x ＋9xy ＋10，又∵x ＞0，y ＞0， ∴y x ＋9xy ＋10≥2y x ·9xy ＋10＝16，当且仅当y x ＝9xy ，即y ＝3x 时，等号成立．由⎩⎪⎨⎪⎧y ＝3x ，1x ＋9y＝1，得⎩⎨⎧x ＝4，y ＝12，即当x ＝4，y ＝12时，x ＋y 取得最小值16.8.解析：选C 由已知，可得6⎝ ⎛⎭⎪⎫2a ＋1b ＝1，∴2a ＋b ＝6⎝ ⎛⎭⎪⎫2a ＋1b ·(2a ＋b )＝6⎝ ⎛⎭⎪⎫5＋2a b ＋2b a ≥6×(5＋4)＝54，当且仅当2a b ＝2b a 时等号成立，∴9m ≤54，即m ≤6，故选C.9.[解] (1)设铁栅长为x 米，一堵砖墙长为y 米，而顶部面积为S ＝xy ，依题意得，40x ＋2×45y ＋20xy ＝3 200，由基本不等式得3 200≥240x ×90y ＋20xy ＝120xy ＋20xy ，＝120S ＋20S .所以S ＋6S －160≤0，即(S －10)(S ＋16)≤0，故S ≤10，从而S ≤100，所以S 的最大允许值是100平方米，(2)取得最大值的条件是40x ＝90y 且xy ＝100，求得x ＝15，即铁栅的长是15米．练习：1.解析：选B A 中，当0<x <1时，lg x <0，lg x ＋1lg x ≥2不成立；由基本不等式知B 正确；C 中，由对勾函数的单调性，知x ＋1x 的最小值为52；D 中，由函数f (x )＝x －1x 在区间(0,2]上单调递增，知x －1x 的最大值为32，故选B.2.解析：选C 对于A ，当x ≤0时，无意义，故A 不恒成立；对于B ，当x ＝1时，x 2＋1＝2x ，故B 不成立；对于D ，当x <0时，不成立．对于C ，x 2＋1≥1，∴1x 2＋1≤1成立．故选C. 3.解析：选B 因为ab ≤⎝⎛⎭⎪⎫a ＋b 22≤⎝ ⎛⎭⎪⎫422＝4，所以1a ＋1b ≥21ab ≥214＝1.4.解析：选A 因为a ，b ，c ，d 成等差数列，则a ＋d ＝b ＋c ，又因为a ，b ，c ，d 均大于0且不相等，所以b ＋c >2bc ，故a ＋d2>bc .5.解析：选D 由题意xy ＝⎝ ⎛⎭⎪⎫2x ＋8y xy ＝2y ＋8x ≥22y ·8x ＝8xy ，∴xy ≥8，即xy 有最小值64，等号成立的条件是x ＝4，y ＝16.6.解析：∵a >0，b >0，∴ab ＝1a ＋1b ≥21ab ，即ab ≥2，当且仅当a ＝b ＝2时取等号，∴a 3＋b 3≥2(ab )3≥223＝42，当且仅当a ＝b ＝2时取等号，则a 3＋b 3的最小值为4 2.7.解析：由题意，一年购买600x 次，则总运费与总存储费用之和为600x ×6＋4x ＝4⎝ ⎛⎭⎪⎫900x ＋x ≥8900x ·x ＝240，当且仅当x ＝30时取等号，故总运费与总存储费用之和最小时x 的值是30.8.解析：因为x >0，所以x ＋1x ≥2.当且仅当x ＝1时取等号，所以有xx 2＋3x ＋1＝1x ＋1x ＋3≤12＋3＝15，即x x 2＋3x ＋1的最大值为15，故a ≥15. 答案：⎣⎢⎡⎭⎪⎫15，＋∞(2)已知x ，y 是正实数，且x ＋y ＝4，求1x ＋3y 的最小值． 9.解：(1)∵x <3， ∴x －3<0，∴f (x )＝4x －3＋x ＝4x －3＋(x －3)＋3 ＝－⎣⎢⎡⎦⎥⎤43－x ＋(3－x )＋3≤－243－x·(3－x )＋3＝－1，当且仅当43－x＝3－x ，即x ＝1时取等号， ∴f (x )的最大值为－1. (2)∵x ，y 是正实数，∴(x ＋y )⎝ ⎛⎭⎪⎫1x ＋3y ＝4＋⎝ ⎛⎭⎪⎫y x ＋3x y ≥4＋2 3.当且仅当y x ＝3xy ，即x ＝2(3－1)，y ＝2(3－3)时取“＝”号．又x ＋y ＝4， ∴1x ＋3y ≥1＋32，故1x ＋3y 的最小值为1＋32.。

高中数学人教版必修5——第十三讲：均值不等式(解析版)

均值不等式教学重点：掌握均值不等式的证明及应用，会用均值不等式求函数的最大值或最小值；教学难点：利用均值不等式的证明。

1. 算术平均值与几何平均值（1）算术平均值：对任意两个正实数,a b ，数2a b+ 叫做,a b 的算术平均值（2）几何平均值：对任意两个正实数,a b,a b 的几何平均值 2. 均值定理如果,a b R +∈，那么2a b+≥a b =时，等号成立 3. 均值不等式的常见变形（1）),a b a b R ++≥∈（2）()2,2a b ab a b R +⎛⎫≤∈ ⎪⎝⎭（3）2b aa b+≥（,a b 同号且不为0）（4）)2,11a b R a b+≤∈+类型一：均值不等式的理解例1. 设0,0a b >>，则下列不等式不成立的是（）A.2b a a b +≥B.44222a b a b +≥ C. 22b a a b a b +≥+ D.1122a b a b+≥++ 解析：特值法，令1a b ==，则A,B,C 项都成立，而D 项中，1122,23a b a b+=+=+ 显然不成立，故D 项不成立。

答案：D练习1. 若a 、b ∈R ，且ab >0，则下列不等式中，恒成立的是( )A ．a 2＋b 2>2abB ．a ＋b ≥2abC ．1a ＋1b >2abD ．b a ＋ab ≥2答案：D练习2. 设0<a <b ，则下列不等式中正确的是( )A ．a <b <ab <a ＋b 2B ．a <ab <a ＋b 2<bC ．a <ab <b <a ＋b 2D ．ab <a <a ＋b2<b答案：B类型二：均值不等式与最值例2. 若正数x 、y 满足x ＋3y ＝5xy ，则3x ＋4y 的最小值是( ) A ．245 B ．285 C ．5 D ．6解析：由x ＋3y ＝5xy 得15y ＋35x ＝1，∴3x ＋4y ＝(3x ＋4y )·(15y ＋35x )＝3x 5y ＋12y 5x ＋95＋45≥23x 5y ·12y 5x ＋135＝125＋135＝5，当且仅当3x 5y ＝12y5x时，得到最小值5. 答案：C练习3. 设x 、y ∈R ，且x ＋y ＝5，则3x ＋3y 的最小值为( ) A ．10 B ．63 C ．46 D ．183答案：D练习4. 已知正项等差数列{a n }中，a 5＋a 16＝10则a 5a 16的最大值为( ) A ．100 B ．75 C ．50 D ．25 答案：D类型三：利用均值不等式证明不等式及应用例3. 已知a 、b 、c ∈R ，求证：a 2＋b 2＋b 2＋c 2＋c 2＋a 2≥2(a ＋b ＋c )．解析：∵a ＋b2≤a 2＋b 22，∴a 2＋b 2≥a ＋b2＝22(a ＋b )(a ，b ∈R 等号在a ＝b 时成立)．同理b 2＋c 2≥22(b ＋c )(等号在b ＝c 时成立)． a 2＋c 2≥22(a ＋c )(等号在a ＝c 时成立)．三式相加得a 2＋b 2＋b 2＋c 2＋a 2＋c 2 ≥22(a ＋b )＋22(b ＋c )＋22(a ＋c ) ＝2(a ＋b ＋c )(等号在a ＝b ＝c 时成立). 答案：见解析练习5. 已知a 、b 是正数，试比较21a ＋1b 与ab 的大小．答案：∵a >0，b >0，∴1a ＋1b ≥21ab >0. ∴21a ＋1b ≤221ab ＝ab .即21a ＋1b≤ab . 练习6.若x >0，y >0，x ＋y ＝1，求证：(1＋1x )·(1＋1y)≥9..答案：证法一：左边＝(1＋1x )(1＋1y)＝1＋1x ＋1y ＋1xy ＝1＋x ＋y xy ＋1xy＝1＋2xy ≥1＋2(x ＋y 2)2＝9＝右边．当且仅当x ＝y ＝12时，等号成立．证法二：∵x ＋y ＝1，∴左边＝(1＋1x )(1＋1y)＝(1＋x ＋y x )(1＋x ＋y y )＝(2＋y x )(2＋xy )＝5＋2(y x ＋xy )≥5＋4＝9＝右边．当且仅当x ＝y ＝12时，等号成立．例4. 在面积为S (S 为定值)的扇形中，当扇形中心角为θ，半径为r 时，扇形周长最小，这时θ、r 的值分别是( )A ．θ＝1，r ＝SB ．θ＝2，r ＝4SC ．θ＝2，r ＝3S D ．θ＝2，r ＝S解析：S ＝12θr 2⇒θ＝2Sr2，又扇形周长P ＝2r ＋θr ＝2⎝⎛⎭⎫r ＋Sr ≥4S ，当P 最小时，r ＝Sr ⇒r ＝S ，此时θ＝2.答案：D练习7. 设计用32m 2的材料制造某种长方体车厢(无盖)，按交通规定车厢宽为2m ，则车厢的最大容积是( )A ．(38－373)m 3B ．16m 3C ．42m 3D ．14m 3 答案：B练习8. 将进货单价为80元的商品按90元一个售出时，能卖出400个，每涨价1元，其销售量就减少20个，为获得最大利润，售价应定在( )A ．每个95元B ．每个100元C ．每个105元D ．每个110元答案：A1. 若x ＞0，y ＞0，且x ＋y ≤4，则下列不等式中恒成立的是( ) A ．1x ＋y ≤14 B ．1x ＋1y ≥1 C ．xy ≥2 D ．1xy ≥1答案：B2. 已知m 、n ∈R ，m 2＋n 2＝100，则mn 的最大值是( )A ．100B ．50C ．20D ．10 答案：B3. 若a >0，b >0且a ＋b ＝4，则下列不等式恒成立的是( )A ．1ab >12B ．1a ＋1b ≤1C ．ab ≥2D ．1a 2＋b 2≤18答案：D4. 实数x 、y 满足x ＋2y ＝4，则3x ＋9y 的最小值为( )A ．18B ．12C ．23D ．43 答案：A5．设x ＋3y －2＝0，则3x ＋27y ＋1的最小值为( )A ．7B ．339 C ．1＋22 D ．5 答案：A6. 设a ＞0，b ＞0，若3是3a 与3b 的等比中项，则1a ＋1b 的最小值为( )A ．8B ．4C ．1D ．14答案：B__________________________________________________________________________________________________________________________________________________________________基础巩固1. 若0<a <1,0<b <1，且a ≠b ，则a ＋b,2ab ，2ab ，a 2＋b 2中最大的一个是( ) A ．a 2＋b 2 B ．2ab C ．2ab D ．a ＋b 答案：D2. 若2x ＋2y ＝1，则x ＋y 的取值范围是( )A ．[0,2]B ．[－2,0]C ．[－2，＋∞)D ．(－∞，－2] 答案：D3. 已知x 、y ∈R ＋，且满足x 3＋y 4＝1，则xy 的最大值为________．答案：34. 已知a 、b 为实常数，函数y ＝(x －a )2＋(x －b )2的最小值为__________ 答案：12(a －b )25. a 、b 、c 是互不相等的正数，且a 2＋c 2＝2bc ，则下列关系中可能成立的是( ) A ．a >b >c B ．c >a > b C ．b >a >cD ．a >c >b答案：C6. 设{a n }是正数等差数列，{b n }是正数等比数列，且a 1＝b 1，a 21＝b 21，则( ) A ．a 11＝b 11 B ．a 11>b 11 C ．a 11<b 11 D ．a 11≥b 11 答案：D7. 已知a >1，b >1，且lg a ＋lg b ＝6，则lg a ·lg b 的最大值为( ) A ．6 B ．9 C ．12 D ．18答案：B8. 某车间分批生产某种产品，每批的生产准备费用为800元．若每批生产x 件，则平均仓储时间为x8天，且每件产品每天的仓储费用为1元．为使平均到每件产品的生产准备费用与仓储费用之和最小，每批应生产产品( )A ．60件B ．80件C ．100件D ．120件答案：B9. 已知2x ＋3y＝2(x >0，y >0)，则xy 的最小值是________．答案：610. 若实数x 、y 满足x 2＋y 2＋xy ＝1，则x ＋y 的最大值是________．答案：23311. 做一个面积为1 m 2，形状为直角三角形的铁架框，在下面四种长度的铁管中，最合理(够用，又浪费最少)的是( )A ．4.6 mB ．4.8 mC ．5 mD ．5.2 m 答案：C12. 光线透过一块玻璃，其强度要减弱110.要使光线的强度减弱到原来的13以下，至少需这样的玻璃板________块．(参考数据：lg2＝0.3010，lg3＝0.4771) 答案：1113. 一个矩形的周长为l ，面积为S ，给出下列实数对：①(4,1)；②(8,6)；③(10,8)；④(3，12)．其中可作为(l ，S )的取值的实数对的序号是________．答案：①④14. 已知正常数a 、b 和正实数x 、y ，满足a ＋b ＝10，a x ＋by ＝1，x ＋y 的最小值为18，求a 、b 的值．答案：x ＋y ＝(x ＋y )·1＝(x ＋y )·(a x ＋by)＝a ＋b ＋ay x ＋bxy ≥a ＋b ＋2ab ＝(a ＋b )2，等号在ay x ＝bx y 即y x＝ba时成立． ∴x ＋y 的最小值为(a ＋b )2＝18，又a ＋b ＝10，∴ab ＝16.∴a 、b 是方程x 2－10x ＋16＝0的两根， ∴a ＝2，b ＝8或a ＝8，b ＝2.能力提升15. 已知x >0，y >0，lg2x ＋lg8y ＝lg2，则 1x ＋13y 的最小值是( )A ．2B ．22C ．4D ．23 答案：C16. 设函数f (x )＝2x ＋1x－1(x <0)，则f (x )( )A ．有最大值B ．有最小值C ．是增函数D ．是减函数答案：A17. 已知x >0，y >0，x 、a 、b 、y 成等差数列，x 、c 、d 、y 成等比数列，则(a ＋b )2cd的最小值是( )A ．0B ．1C ．2D ．4 答案：D18. 若a 、b 、c 、d 、x 、y 是正实数，且P ＝ab ＋cd ，Q ＝ax ＋cy ·b x ＋dy，则有( ) A ．P ＝Q B ．P ≥Q C ．P ≤Q D ．P >Q 答案：C19. 已知x ≥52，则f (x )＝x 2－4x ＋52x －4有( )A ．最大值54B ．最小值54 C ．最大值1 D ．最小值1答案： D20. 已知y >x >0，且x ＋y ＝1，那么( )A ．x <x ＋y 2<y <2xyB ．2xy <x <x ＋y 2<yC ．x <x ＋y 2<2xy <yD ．x <2xy <x ＋y2<y答案：D21. 设a 、b 是正实数，给出以下不等式：①ab >2ab a ＋b；②a >|a －b |－b ；③a 2＋b 2>4ab －3b 2；④ab ＋2ab >2，其中恒成立的序号为( )A ．①③B ．①④C ．②③D ．②④ 答案：D22. 已知a >0，b >0，且a ＋b ＝1，则⎝⎛⎭⎫1a 2－1⎝⎛⎭⎫1b 2－1的最小值为( ) A ．6 B ．7 C ．8 D ．9 答案：D23.若直线2ax －by ＋2＝0(a >0，b >0)被圆x 2＋y 2＋2x －4y ＋1＝0截得的弦长为4，则1a ＋1b 的最小值为( )A ．14B ．12 C ．2 D ．4答案：D24. 当x >1时，不等式x ＋1x －1≥a 恒成立，则实数a 的取值范围是( ) A ．(－∞，2] B ．[2，＋∞) C ．[3，＋∞) D ．(－∞，3] 答案：D25. 已知正数x 、y 满足1x ＋4y＝1，则xy 有( )A ．最小值116B ．最大值16C ．最小值16D ．最大值116答案：C26. 若正实数x 、y 满足2x ＋y ＋6＝xy ，则xy 的最小值是________ 答案：1827. 已知函数f (x )＝lg x (x ∈R ＋)，若x 1、x 2∈R ＋，判断12[f (x 1)＋f (x 2)]与f (x 1＋x 22)的大小并加以证明．答案：12[f (x 1)＋f (x 2)]≤f (x 1＋x 22)∵f (x 1)＋f (x 2)＝lg x 1＋lg x 2＝lg(x 1·x 2)， f (x 1＋x 22)＝lg x 1＋x 22，而x 1、x 2∈R ＋，x 1x 2≤(x 1＋x 22)2，而f (x )＝lg x 在区间(0，＋∞)上为增函数． ∴lg(x 1x 2)≤lg(x 1＋x 22)2，∴12lg(x 1x 2)≤lg x 1＋x 22. 即12(lg x 1＋lg x 2)≤lg x 1＋x 22. 因此，12[f (x 1)＋f (x 2)]≤f (x 1＋x 22)．28. 已知a 、b 、c ∈R ＋，求证：a 2b ＋b 2c ＋c 2a≥a ＋b ＋C答案：∵a 、b 、c ∈R ＋，a 2b ，b 2c ，c 2a均大于0，又a 2b ＋b ≥2a 2b ·b ＝2a ， b 2c ＋c ≥2b 2c·c ＝2b ， c 2a＋a ≥2c 2a·a ＝2c ，三式相加得a 2b ＋b ＋b 2c ＋c ＋c 2a ＋a ≥2a ＋2b ＋2c ，∴a 2b ＋b 2c ＋c 2a ≥a ＋b ＋C ． 29．求函数y ＝1－2x －3x的值域．答案：y ＝1－2x －3x ＝1－(2x ＋3x)．①当x >0时，2x ＋3x≥22x ·3x＝2 6. 当且仅当2x ＝3x ，即x ＝62时取等号．∴y ＝1－(2x ＋3x)≤1－2 6.②当x <0时，y ＝1＋(－2x )＋(－3x )．∵－2x ＋(－3x)≥2(－2x )·(－3x)＝2 6.当且仅当－2x ＝－3x 时，即x ＝－62时取等号．∴此时y ＝1－2x －3x≥1＋26综上知y ∈(－∞，1－26]∪[1＋26，＋∞)．∴函数y ＝1－2x －3x的值域为(－∞，1－26)∪[1＋26，＋∞)．30. 某单位决定投资3 200元建一仓库(长方体状)，高度恒定，它的后墙利用旧墙不花钱，正面用铁栅，每米长造价40元，两侧墙砌砖，每米长造价45元，顶部每平方米造价20元．试求：(1)仓库面积S 的取值范围是多少？(2)为使S 达到最大，而实际投资又不超过预算，那么正面铁栅应设计多长？答案：(1)设正面铁栅长x m ，侧面长为y m ，总造价为z 元，则z ＝40x ＋2×45y ＋20xy ＝40x ＋90y ＋20xy ，仓库面积S ＝xy .由条件知z ≤3 200，即4x ＋9y ＋2xy ≤320. ∵x >0，y >0，∴4x ＋9y ≥24x ·9y ＝12xy .∴6S ＋S ≤160，即(S )2＋6S －160≤0. ∴0<S ≤10，∴0<S ≤100. 故S 的取值范围是(0,100]．(2)当S ＝100 m 2时，4x ＝9y ，且xy ＝100. 解之得x ＝15(m)，y ＝203(m)．答：仓库面积S 的取值范围是(0,100]，当S 取到最大允许值100 m 2时，正面铁栅长15 m.31. 某渔业公司年初用98万元购买一艘捕鱼船，第一年各种费用为12万元，以后每年增加4万元，每年捕鱼收益50万元．(1)问第几年开始获利？(2)若干年后，有两种处理方案：①年平均获利最大时，以26万元出售该渔船；②总纯收入获利最大时，以8万元出售该渔船．问哪种方案最合算？答案：由题设知每年的费用是以12为首项，4为公差的等差数列．设纯收入与年数的关系为f (n )，则f (n )＝50n －[12＋16＋…＋(8＋4n )]－98＝40n －2n 2－98.(1)由f (n )>0得，n 2－20n ＋49<0，∴10－51<n <10＋51，又∵n ∈N ，∴n ＝3,4， (17)即从第3年开始获利．(2)①年平均收入＝f (n )n ＝40－2(n ＋49n)≤40－2×14＝12，当且仅当n ＝7时，渔船总收益为12×7＋26＝110(万元)．②f (n )＝－2(n －10)2＋102.因此当n ＝10时，f (n )max ＝102，总收益为102＋8＝110万元，但7<10，所以第一种方案更合算．。

(压轴题)高中数学必修五第三章《不等式》测试题(包含答案解析)(1)

一、选择题1．设正数m ，n ，2m n u +=，222v m n mn =++，则2u v ⎛⎫ ⎪⎝⎭的最大值是（） A ．14B ．13C ．12D ．12．已知x ，y 满足约束条件20030x y x y m x -+≥⎧⎪+-≥⎨⎪-≤⎩，若34z x y =-的最大值为9，则m 的值为（） A ．32-B ．28-C ．2D ．33．已知正实数a ，b 满足231a b +=，则12a b+的最小值为（） A ．15B．8+C ．16D．8+4．已知实数,x y 满足24240x y x y y -≥⎧⎪+≤⎨⎪≤⎩，则32z x y =-的最小值是（）A ．4B ．5C ．6D ．75．当02x π<<时，函数21cos 28sin ()sin 2x xf x x++=的最小值为（）A ．2B．C ．4D．6．已知函数()()log 31a f x x =+-（0a >且1a ≠）的图象恒过定点A ，若点A 在直线40mx ny ++=上，其中0mn >，则12m n+的最小值为（） A ．23B ．43C ．2D ．47．已知实数x y 、满足不等式组21010x x y m x y ≤⎧⎪-+≥⎨⎪+-≥⎩,若目标函数2z x y =-+的最大值不超过4,则实数m 的取值范围是 A．(B．⎡⎣ C．⎡⎤⎣⎦D ．[ 8．在ABC 中，BAC ∠的平分线交BC 于D .若3BAC π∠=，4AB AC +=，则AD 长度的最大值为（） AB ．2C ．3D．9．对于任意实数a ，b ，若a ＞b ，则下列不等式一定成立的是（） A ．11a b< B ．a 2＞b 2 C ．a 3＞b 3 D ．a b b a> 10．设m 1>，在约束条件1y x y mx x y ≥⎧⎪≤⎨⎪+≤⎩下，目标函数z=x+my 的最大值小于2，则m 的取值范围为（） A．(1,1 B．()1++∞ C ．（1，3）D ．（3，+∞）11．设变量,x y 、满足约束条件236y xx y y x ≤⎧⎪+≥⎨⎪≥-⎩，则目标函数2z x y =+的最大值为（）A ．2B ．3C ．4D ．912．若a ，b ，c ∈R ，a >b ，则下列不等式恒成立的是（） A ．1a <1bB ．a 2>b 2C ．21a c +>21b c + D ．a |c |>b |c |二、填空题13．123,,x x x 为实数，只要满足条件1230x x x >>>，就有不等式121233log 20202log 2020log 2020x x x x x x k +≥恒成立，则k 的最大值是__________．14．若x ，y ，z 满足约束条件4802400x y x y y --≤⎧⎪-+≥⎨⎪≤⎩，则z =__________．15．已知x ，y 满足041x y x y x -≤⎧⎪+≤⎨⎪≥⎩，则2z x y =+的最大值为________.16．已知实数x ，y 满足约束条件2020220x y x y x y +-≥⎧⎪--≤⎨⎪--≥⎩，则2z x y =+的最小值为________.17．已知实数,x y 满足不等式组201030y x y x y -≤⎧⎪--≤⎨⎪+-≥⎩，则yx 的取值范围为__________．18．记等差数列{}n a 的前n 项和为n S ，满足570a a ，1122S =，则7811572a a a a a 的最小值为_________.19．某港口的水深y （米）随着时间t （小时）呈现周期性变化，经研究可用sincos66y a t b t c ππ=++来描述，若潮差（最高水位与最低水位的差）为3米，则+a b的取值范围为_______．20．已知正实数x ，y 满足22462x y xy ++=，则2x y +的最小值是_________.三、解答题21．设矩形ABCD 的周长为20，其中AB AD >，如图所示，把它沿对角线AC 对折后，AB 交DC 于点P .设AD x =，DP y =.（1）将y 表示成x 的函数，并求定义域；（2）求ADP △面积的最大值. 22．选修4-5 不等式选讲已知函数f (x )＝|x －1|－2|x ＋1|的最大值为m . (1)求m ；(2)若a ，b ，c ∈(0，＋∞)，a 2＋2b 2＋c 2＝2m ，求ab ＋bc 的最大值． 23．已知函数()243f x ax ax =--(1)当a=-1时,求不等式f(x)>0的解集;(2)若对于任意的x ∈R,均有不等式f(x)≤0成立,求实数a 的取值范围.24．若不等式2122x x mx -+>的解集为{}|02x x <<. （1）求m 的值；（2）已知正实数a ，b 满足4a b mab +=，求+a b 的最小值. 25．已知函数2()2,,f x x ax x R a R =-∈∈．（1）当1a =时，求满足()0f x <的x 的取值范围；（2）解关于x 的不等式2()3f x a <．26．（1）已知()2f x kx =+，不等式()3f x <的解集为()1,5-，不等式()1xf x ≥的解集为A .求集合A ；（2）解关于x 的不等式()2220ax a x +--≥.【参考答案】***试卷处理标记，请不要删除一、选择题 1．B 解析：B 【分析】化简22211()44u mn vm n mn=+⨯++，再结合基本不等式，即可求解. 【详解】由题意，正数m ，n ，2m nu +=，222v m n mn =++，则2222222222()12112()444m n u m n mn mn v m n mn m n mn m n mn+++===+⨯++++++ 2111111111444444213()11mnm m m n n n n m=+⨯=+⨯≤+⨯=+++++，当且仅当m n n m =时，即m n =时，等号成立,所以2u v ⎛⎫ ⎪⎝⎭的最大值是为13.故选：B . 【点睛】利用基本不等式求最值时，要注意其满足的三个条件：“一正、二定、三相等”：（1）“一正”：就是各项必须为正数；（2）“二定”：就是要求和的最小值，必须把构成和的二项之积转化成定值；要求积的最大值，则必须把构成积的因式的和转化成定值；（3）“三相等”：利用基本不等式求最值时，必须验证等号成立的条件，若不能取等号则这个定值就不是所求的最值，这也是最容易发生错误的地方.2．D解析：D 【分析】作出x ，y 满足约束条件20030x y x y m x -+≥⎧⎪+-≥⎨⎪-≤⎩，表示的可行域如图中阴影部分所示，再利用数形结合分析得()max 33439z m =⨯--=，解得参数即可. 【详解】作出x ，y 满足约束条件20030x y x y m x -+≥⎧⎪+-≥⎨⎪-≤⎩，表示的可行域如图中阴影部分所示，由z ＝3x -4y 得344z yx =-，它表示斜率为34纵截距为4z-的一系列直线，当直线经过点A 时，直线的纵截距4z-最小，z 最大.由03x y m x +-=⎧⎨=⎩，解得A (3，m －3)，故()max 33439z m =⨯--=，解得3m =. 故选：D. 【点睛】方法点睛：线性规划问题一般用图解法，其步骤如下：（1）根据题意，设出变量,x y ；（2）列出线性约束条件；（3）确定线性目标函数(,)z f x y =；（4）画出可行域（即各约束条件所示区域的公共区域）；（5）利用线性目标函数作平行直线系()(y f x z =为参数).3．D解析：D 【分析】妙用“1”的代换，利用()121223a b a b a b ⎛⎫+=++ ⎪⎝⎭拼凑基本不等式，求和式的最小值即可. 【详解】正实数a ，b 满足231a b +=，则()12122388282343412843a b a b a b a b a b a b a b⎛⎫+=++=++≥+⋅=+=+ ⎪⎝⎭，当且仅当34b a b a =，即3133,46a b --==时等号成立，故12a b +的最小值为843+. 故选：D. 【点睛】思路点睛：利用基本不等式求最值时，需注意取等号条件是否成立. （1）积定，利用2x y xy +≥，求和的最小值；（2）和定，利用()24x y xy +≤，求积的最大值；（3）已知和式（倒数和）或为定值时，妙用“1”拼凑基本不等式求最值.4．C解析：C 【分析】由约束条件画出可行域，化目标函数为直线方程的斜截式，数形结合得到最优解，联立方程组得到最优解的坐标，代入目标函数得到答案. 【详解】由实数x ，y 满足24240x y x y y -≥⎧⎪+≤⎨⎪≤⎩得到可行域如图：z ＝3x ﹣2y 变形为y ＝32x ﹣2z，由024y x y =⎧⎨-=⎩，解得B （2，0）当此直线经过图中B 时，在y 轴的截距最大，z 最小，所以z 的最小值为3×2﹣2×0＝6；故选C ．【点睛】本题主要考查线性规划中利用可行域求目标函数的最值，求目标函数最值的一般步骤是“一画、二移、三求”：（1）作出可行域（一定要注意是实线还是虚线）；（2）找到目标函数对应的最优解对应点（在可行域内平移变形后的目标函数，最先通过或最后通过的顶点就是最优解）；（3）将最优解坐标代入目标函数求出最值.5．C解析：C 【解析】0,tan 02xx π<∴，()21cos28sin sin2x x f x x++=2222cos 8sin 28tan 14tan 42sin cos 2tan tan x x x x x x x x ++===+≥=，当且仅当1tan 2x =时取等号，函数()21cos28sin sin2x x f x x ++=的最小值为4，选C.6．C解析：C 【分析】由对数函数的图象得出A 点坐标，代入直线方程得,m n 的关系，从而用凑出基本不等式形式后可求得最小值．【详解】令31+=x ，2x =-，(2)1f -=-，∴(2,1)A --，点A 在直线40mx ny ++=上，则240m n --+=，即24m n +=， ∵0mn >，24m n +=，∴0,0m n >>，∴12112141(2)442444n m m n m n m n m n ⎛⎛⎫⎛⎫+=++=++≥+= ⎪ ⎪ ⎝⎭⎝⎭⎝，当且仅当4n mm n=，即1,2m n ==时等号成立．故选：C ．【点睛】本题考查对数函数的性质，考查点在直线上，考查用基本不等式求最小值．是一道综合题，属于中档题．7．D解析：D 【分析】将2z x y =-+化为2y x z =+,作出可行域和目标函数基准直线2y x =(如图所示),当直线2y x z =+将左上方平移时,直线2y x z =+在y 轴上的截距z 增大,由图象,得当直线2y x z =+过点A 时,z 取得最大值,联立2010x y m x y ⎧-+=⎨+-=⎩,得2211,22m m A ⎛⎫-+ ⎪⎝⎭,则22112422m m -+-⨯+≤,解得33m -≤≤;故选D.点睛：线性规划的实质是把代数问题几何化，即数形结合的思想.需要注意的是：一、准确无误地作出可行域；二、画标准函数所对应的直线时，要注意与约束条件中的直线的斜率进行比较，避免出错；三、一般情况下，目标函数的最大或最小会在可行域的端点或边界上取得.8．A解析：A 【分析】根据题意，设,,,AD t AB c AC b ===由三角形面积公式1sin 2S a b θ=⋅⋅可表示出,,ACD ABD ABC ∆∆∆三者之间的关系，进而得边长关系为3,t bc =最后通过基本不等式求得AD 的最大值。

高一数学必修5基本不等式总结和例题[1]

高一数学必修5基本不等式总结和例题(word版可编辑修改)编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（高一数学必修5基本不等式总结和例题(word版可编辑修改)）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为高一数学必修5基本不等式总结和例题(word版可编辑修改)的全部内容。

基本不等式典题精讲例1(1）已知0＜x ＜31，求函数y=x （1—3x)的最大值;(2)求函数y=x+x1的值域。

思路分析：（1）由极值定理，可知需构造某个和为定值，可考虑把括号内外x 的系数变成互为相反数;(2）中,未指出x ＞0,因而不能直接使用基本不等式，需分x ＞0与x ＜0讨论. （1）解法一：∵0＜x ＜31，∴1—3x ＞0。

∴y=x （1—3x ）= 31·3x(1-3x)≤31［2)31(3x x -+］2=121，当且仅当3x=1-3x ，即x=61时，等号成立.∴x=61时，函数取得最大值121. 解法二:∵0＜x ＜31,∴31-x ＞0。

∴y=x（1-3x ）=3x(31—x ）≤3［231x x -+］2=121，当且仅当x=31-x,即x=61时，等号成立. ∴x=61时，函数取得最大值121. （2)解：当x ＞0时，由基本不等式，得y=x+x 1≥2xx 1•=2,当且仅当x=1时，等号成立. 当x ＜0时，y=x+x1=—［（—x ）+)(1x -］。

∵—x ＞0,∴(—x)+)(1x -≥2，当且仅当-x=x-1,即x=—1时,等号成立。

∴y=x+x1≤—2. 综上,可知函数y=x+x1的值域为（—∞,—2］∪［2，+∞). 绿色通道：利用基本不等式求积的最大值，关键是构造和为定值,为使基本不等式成立创造条件，同时要注意等号成立的条件是否具备.变式训练1当x ＞-1时，求f （x)=x+11+x 的最小值. 思路分析：x ＞—1⇒x+1＞0,变x=x+1-1时x+1与11+x 的积为常数。

数学：3.1.1《不等关系与不等式》(新人教a版必修5)

作差比较法其一般步骤是: 作差→变形→判断符号→确定大小.
例1．比较x2－x与x－2的大小。解：(x2－x)－(x－2)=x2－2x+2
=(x－1)2+1，
因为(x－1)2≥0，所以(x2－x)－(x－2)>0，因此x2－x>x－2.
例2．当p，q都是正数且p+q=1时，试比较代数式(px+qy)2与px2+qy2的大小。解：(px+qy)2－(px2+qy2)
p q 读作“p等价于q或q等价于p”。
上述结论可以写成：
a b 0 a b a b 0 a b
a b 0 a b
判断两个实数大小的依据是： a b ab 0
a b ab 0 a b ab 0
作差比较法
这既是比较大小 ( 或证明大小 ) 的基本方法,又是推导不等式的性质的基础.
3.1.1 不等关系与不等式
在考察事物之间的数量关系时，经常
要对数量的大小进行比较，我们来看下
面的例子。国际上常用恩格尔系数（记为n）来衡量一个国家和地区人民的生活水平的高低。它的计算公式是
食品消费额 n 100% 消费支出总额
。
有关机构还制定了各种类型的家庭应达到的恩格尔系数的取值范围：
40
5、某品牌酸奶的质量检查规定，酸奶中脂肪的含量f应不少于2.5%，蛋白质的含量p应不少于 2.3%，用不等式可以表示为：( )
A. f ≥p ≥ 2.3%
f ≥ 2.5% C. p ≥ 2.3%
某人为自己制定的月支出计划中，规定
=p(p－1)x2+q(q－1)y2+2pqxy. 因为p+q=1，所以p－1=－q，q－1=－p，因此(px+qy)2－(px2+qy2) =－pq(x2+y2－2xy)=－pq(x－y)2，

高中数学必修5解不等式习题精选精讲----均值定理的拓广

均值定理的拓广在高中数学教材中，均值不等式几乎涉及高中数学的所有章节，且在每年的高考题中常考常新，其题型主要以大小判断、求最值、求参数的取值范围以及最值时刻等几个方面出现，在高考的考试说明中也明确地要求学生能熟练地掌握均值不等式的适用条件及适用情境。

高中教材中对均值定理的叙述是：（1）定理：如果a 、b 是正数，那么ab ba ≥+2（当且仅当a=b 时取“＝”号）（2）定理：如果a 、b 、c 是正数，那么33abc c b a ≥++（当且仅当a=b=c 时取“＝”号）我们称2b a +（3c b a ++）为a 、b （a 、b 、c ）的算术平均数，称ab （3abc ）为a 、b(a 、b 、c)的几何平均数，因而这一定理又可叙述为“两个（或三个）正数的算术平均数不小于它们的几何平均数。

”事实上，由数学归纳法可把这一定理拓广为“n 个正数的算术平均数不小于它们的几何平均数” 。

用均值不等式求函数的最大（小）值是高中数学的一个重点，在运用均值定理求函数的最大（小）值时，往往需要掌握“凑”（凑项、凑因子）的技巧，其目的（一）是创造一个应用不等式的情境；（二）是使等号成立的条件。

例1．边长为c b a ,,的三角形，其面积等于41，而外接圆半径为1，若c b a t c b a S 111,++=++=，则S 与t 的大小关系是（） A. t S >B. t S =C. t S <D.不确定（1986年全国高中数学联赛题）解：在三角形中，由正弦定理和面积公式可得C C R C sin 2sin 2==，又∵41sin 21==C ab S ，∴1=abc ∴ab ac bc cb a t ++=++=111∴)()()(2ac bc bc ab ac ab t +++++=S c b a bc a abc c ab 2)(2222222=++=++≥∵1====R c b a 不可能成立故上式取不到等号，∴S t >即t S <，故选C例2．若正数b a ,满足3++=b a ab ，则ab 的取值范围是（1999年全国高考题第15题）解：∵+∈R b a ,，∴ab b a 2=+，∴323+≥++=ab b a ab ∴032≥--ab ab ，∴0)1)(3(≥+-ab ab ∴1-≤ab （舍去）或3≥ab ∴3≥ab然而有些题由于解析式自然，从形态上看根本凑不出定值，或虽凑出定值而其等号又不能成立，对于这样的题目，学生往往为很难用甚至不能用均值定理而感到束手无策。

高中数学必修5(人教A版)第三章不等式3.2知识点总结含同步练习及答案

（2）因为
为整式不等式
解得 x <
3 或 x > 4，所以原不等式的解集为 2 3 ∣ {x ∣ x < 或x > 4} . ∣ 2
4.高次不等式的解法描述：高次不等式的解法解一元高次不等式一般利用数轴穿根法（或称根轴法）求解，其步骤是：（1）将 f (x) 最高次项系数化为正数；（2）将 f (x) 分解为若干个一次因式的乘积或二次不可分因式的乘积；（3）求出各因式的零点，并在数轴上依次标出；（4）从最右端上方起，自右至左依次通过各根画曲线，遇到奇次重根要一次穿过，遇到偶次重根要穿而不过；（5）记数轴上方为正，下方为负，根据曲线显现出的 f (x) 的值的符号变化规律，写出不等式的解集．例题：解不等式 (x + 2)(x + 1)2 (x − 1)3 (x − 2) < 0 ．解：不等式中各因式的实数根为 −2，−1，1 ，2 ．利用根轴法，如图所示．
2 )(x − a) ⩽ 0 ． a 2 2 ① 当 < a ，即 a > √2 时，原不等式的解集为 {x| ⩽ x ⩽ a}． a a 2 2 ② 当 > a ，即 0 < a < √2 时，原不等式的解集为 {x|a ⩽ x ⩽ }． a a 2 ③ 当 = a ，即 a = √2 时，原不等式的解集为 {x|x = √2 } ． a 2 （3）当 a < 0 时，原不等式化为 (x − )(x − a) ⩾ 0 ． a 2 2 ① 当 < a ，即 −√2 < a < 0 时，原不等式的解集为 {x|x ⩽ 或x ⩾ a} ． a a 2 2 ② 当 > a ，即 a < −√2 时，原不等式的解集为 {x|x ⩽ a或x ⩾ }． a a 2 ③ 当 = a ，即 a = −√2 时，原不等式的解集为 R． a

高二数学必修五单元测试03不等式(A卷)(解析版).doc

班级_________ 姓名_____________ 学号____________ 分数 ___________ 《必修五单元测试三不等式》测试卷（A卷）（测试时间：120分钟满分：150分）第I卷（共60分）一、选择题：本大题共12个小题，每小题5分，共60分•在每小题给出的四个选项中，只有一项是符合题目要求的.1.在不等式x + 2y-1>0表示的平面区域内的点是（）A. （1,-1）B. （0,1）C. （1,0）D. （-2,0）【答案】B【解析】试题分析：・・・1+2><（_1）_1〈0；0+2><1_1血1 + 2><0-1 = 0；-2 + 2><0-1<0,二可知点（0丄）在不等式x+2y-l >0表示的平面区域內.故B正确.2.已知集合A = [xeN\x2-5x + 4<0], B = {x\x2-4 = o],下列结论成立的是（）A. Be A B_. A\J B = A C. Ar\B = A D. AcB = {2}【答案】D【解析】由已知得A = {123,4}, B = {-2,2},则AcB = {2},故选D.x>l3.区域｛y>\构成的儿何图形的面积是（）x+y<3A. 2B. 1C. 一D.-4 2【答案】D【解析】画出不等式组表示的区域如图，结合图形对知区域三角形的面积是S=-xlxl=l,应选答案D.2 24.[2018届河南省中原名校高三上学期第一次质】若a<b<0,则下列不等关系屮，不能成立的是1 ] ] ] 1 1A. ->-B. -------------------- >-C. a3 <b3D. a2 > b2a b a~b a【答案】B【解析]Va<b<0,.\a<a - b<0由y =丄在（一a,0）上单调递减知：一-— < 丄x a~b a因此B不成立.故选：B.5.不等式乞二L>0的解集是（）x + 3A. _,+8B. （4,+00）、2（J 、C. （-00, -3）U（4, +oo）D. （-00,-3）u —,+oo【答案】D【解析】分式不等式可转换为二次不等式：（2兀一1）（兀+3）>0,（\ \据此可得不等式的解集为：（-00,-3）u -,+a）>本题选择D选项.6.已知关于兀的不等式x2-4x>m对任意XG（O,1]恒成立，则有（）A. m <一3B. m >—3C. —3 < m < 0D. m > ~4【答案】A【解析1 vx2-4x> w对任意xe[O3l]恒成立，令/（x）=x2-4x s xe[0a l], v f（x）的对称轴为x = 2 ,二/ （x）在[0 J]单调递减，二当* 1时取到最小值为-3 ,:.实数w的取值范围是w<-3,故选A.X>1x + y<47.【2018届四川省南充市高三零诊】若实数俎y满足lx-2y-lS0 ,贝ljz = 2x + y的最大值为（）A. 2B. 5C. 7D. 8【答案】C【解析】作出可行域：学@科网rf]Z = 2x +儿可得：y=- 2x + z,平行移动丿=-2兀+ z,由图象可知当直线经过点A时，直线的纵截距最大, 即z最大；易得A（3, 1）,带入目标惭数z = 2咒+儿得：z = 2x3 + l = 7,即z = 2兀+ y的最大值为7故选：C.8.已知/（兀）=0?+加，且满足：15/（1）53,-1</（-1）<1,则/（2）的取值范围是（）A. [0,12] B. [2,10] C. [0,10] D. [2,12]【答案】B【解析】・・・/（兀）=血2+加且15/（1）53, -1</（-1）<1, ：.\<a + b<3, -\<a-b<\,JV+V =4 x— 3/（2）= 4a + 2b,令4d + " = x（Q+b） + y（a—b）,可得｛7-,解得｛—,即x-y=2 y=l4a + 2/? = 3（Q+b）+（o—b）, ・・・353（d+b）59, 253（a+b）+（d—b）510,则/（2）的取值范围是[2,10],故选B.F — r — 69.不等式一<0的解集为（）兀—1A. {兀|兀（一2或»1}B. {兀| 兀<一2或vxv3}C. {兀|-2v兀〈1或x〉3}D. {%|-2VJVV1或lcxv3}【答案】B【解析】不等式即：（〒）（节2）<0（-1）转化为高次不等式：（x-3）（x+2）（x-l）<0利用数轴穿根法解得x < —2或1 v尢v 3 ,本题选择B选项.点睛：解不等式的基本思路是等价转化，分式不等式整式化，使要求解的不等式转化为一元一次不等式或一元二次不等式，进而获得解决.10.若a，bER且必>0,则下列不等式中，恒成立的是（）11 2 b a9 9.—— +「> ~严= —d—二2A. a + b > 2ab g a + b > Q a b ^Jab D. Q b'【答案】D【解析】对于选项A,当a = b时不成立；对于选项巧当a<0.b<0或a = b > 0时不成立；对于选项C, 当aV0,b<0时不成立：对于选项D,因为ab>0,所以;>0^>0,由基本不等式有恒成立, 故选D.y>0尤-y + 1 二011.[2018届广东省茂名市五大联盟学校高三9月】设绘y满足约束条件U + y-3<0,贝ijz = x-3y的最大值为（）A. 3B. -5C. 1D. -1【答案】Ax - y +1 > 0 y = _x —z —z画出不等•式组k + 表示的区域如图，则问题转化为求动直线 3 B 在y 上的截距B 的最小值 1 1的问题，结合图形可知：当动直线一孑经过点P （3,0）^, z nlax = 3-3x0 = 3,应选答案A .12. [2018届云南省师范大学附属中学高三月考一】若直线ax + by-2 = Q （d>0』>0）始终平分圆第II 卷（共90分）二、填空题（每题5分，满分20分，将答案填•在答题纸上）13.【2018届江苏省泰州屮学高三上学期开学】已知点PU ，y ）满足<-XI y>>-+ y Xy z ~~ _贝I 」X 的最大值为 __________【解析】画出满足条件的半面区域，如图示：由z【答案】D【解析】x 2+y 2-2x-2y = 2 的周长,则眾的最小值为（3-2^2 43-2^2 ~2-D.【解析】直线平分圆周，则直线过圆心（1」），所以有G + b = 2,-!- +丄二丄(d + b) — 2ci b 2、)"(1 1)• -I 2G b )b = y[2a 时取“二”），故选 D.y咒表示过平面区域的点Qy）与（°，°）的直线的斜率,显然直线过力仃，3)时，z取得最大值，x故答案为：3.14. [2018届河南省中原名校高三上学期第一次联考】某学生计划用不超过50元钱购买单价分别为6元、7元的软皮和硬皮两种笔记本，根据需要软皮笔记本至少买3本，硬皮笔记本至少买2本，则不同的选购方式共有. _________ 种.【答案】7.(6x + 7y < 50% > 3沖2【解析】根据题意，设买x本软皮笔记本，y本硬皮笔记本，则有I ,32y <——当x=3时，7 ,可取的值.为2、3、4；26y < —当x=4时，7,可取的值为2、3；20y <——当x=5时，一7,可取的值为2；14y <——当X二6时，7,可取的值为2；共7种不同的选购方式；故答案为：7.15.若不等式x2-ax-b< 0的解集为何2VXV3},则不等式bx2-ax-l>0的解集为_____________________【答案】【解析】.••不等式x2-ax-b<0的解集为{x|2<x<3})・・・2,3是一元二次方程x2-ax-b = 0的两个实数根,2 +3 = a[2 x 3 =- b ,解得。

高中数学必修5不等式精选题目(附答案)

高中数学必修5不等式精选题目（附答案）一、一元二次不等式(1)确定ax 2＋bx ＋c >0(a >0)或ax 2＋bx ＋c <0(a >0)在判别式Δ>0时解集的结构是关键．在未确定a 的取值情况下，应先分a ＝0和a ≠0两种情况进行讨论．(2)若给出了一元二次不等式的解集，则可知二次项系数a 的符号和方程ax 2＋bx ＋c ＝0的两个根，再由根与系数的关系就可知a ，b ，c 之间的关系．(3)解含有参数的一元二次不等式，要注意对参数的取值进行讨论：①对二次项系数与0的大小进行讨论；②在转化为标准形式的一元二次不等式后，对判别式与0的大小进行讨论；③当判别式大于0，但两根的大小不确定时，对两根的大小进行讨论．1. (1)已知不等式ax 2＋bx ＋2>0的解集为{x |－1<x <2}，则不等式2x 2＋bx ＋a <0的解集为( )A.⎩⎨⎧⎭⎬⎫x －1<x <12B.⎩⎨⎧⎭⎬⎫xx <－1或x >12 C ．{x |－2<x <1} D ．{x |x <－2或x >1}(2)解关于x 的不等式ax 2－2ax ＋a ＋3＞0.1.[解析] (1)由题意知x ＝－1，x ＝2是方程ax 2＋bx ＋2＝0的根．由根与系数的关系得⎩⎪⎨⎪⎧ －1＋2＝－b a ，(－1)×2＝2a ⇒⎩⎨⎧a ＝－1，b ＝1. ∴不等式2x 2＋bx ＋a <0，即2x 2＋x －1<0.解得－1<x <12.[答案] A(2)解：当a ＝0时，解集为R ；当a ＞0时，Δ＝－12a ＜0，∴解集为R ；当a ＜0时，Δ＝－12a ＞0，方程ax 2－2ax ＋a ＋3＝0的两根分别为a ＋－3a a ，a －－3a a ，∴此时不等式的解集为x a ＋－3a a ＜x ＜a －－3a a. 综上所述，当a ≥0时，不等式的解集为R ；a ＜0时，不等式的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪⎪ a ＋－3a a ＜x ＜a －－3a a . 注：解一元二次不等式时，当二次项系数为负时要先化为正，再根据判别式符号判断对应方程根的情况，然后结合相应二次函数的图象写出不等式的解集．2．函数f (x )＝1ln (－x 2＋4x －3)的定义域是( ) A ．(－∞，1)∪(3，＋∞) B ．(1,3)C ．(－∞，2)∪(2，＋∞)D ．(1,2)∪(2,3) 解析：选D 由题意知⎩⎨⎧ －x 2＋4x －3>0，－x 2＋4x －3≠1，即⎩⎨⎧ 1<x <3，x ≠2，故函数f (x )的定义域为(1,2)∪(2,3)．3．若关于x 的不等式ax 2－6x ＋a 2<0的解集是(1，m )，则m ＝________.解析：根据不等式与方程之间的关系知1为方程ax 2－6x ＋a 2＝0的一个根，即a 2＋a －6＝0，解得a ＝2或a ＝－3，当a ＝2时，不等式ax 2－6x ＋a 2<0的解集是(1,2)，符合要求；当a ＝－3时，不等式ax 2－6x ＋a 2<0的解集是(－∞，－3)∪(1，＋∞)，不符合要求，舍去．故m ＝2.答案：24．已知不等式ax 2－3x ＋6>4的解集为{x |x <1或x >b }．(1)求a ，b 的值；(2)解不等式ax 2－(ac ＋b )x ＋bc <0.解：(1)因为不等式ax 2－3x ＋6>4的解集为{x |x <1或x >b }，所以x 1＝1与x 2＝b 是方程ax 2－3x ＋2＝0的两个实数根，b >1且a >0.由根与系数的关系，得⎩⎪⎨⎪⎧ 1＋b ＝3a ，1×b ＝2a .解得⎩⎨⎧a ＝1，b ＝2. (2)不等式ax 2－(ac ＋b )x ＋bc <0，即x 2－(2＋c )x ＋2c <0，即(x －2)(x －c )<0.当c >2时，不等式(x －2)(x －c )<0的解集为{x |2<x <c }；当c <2时，不等式(x －2)(x －c )<0的解集为{x |c <x <2}；当c ＝2时，不等式(x －2)(x －c )<0的解集为∅.所以，当c >2时，不等式ax 2－(ac ＋b )x ＋bc <0的解集为{x |2<x <c }；当c <2时，不等式ax 2－(ac ＋b )x ＋bc <0的解集为{x |c <x <2}；当c ＝2时，不等式ax 2－(ac ＋b )x ＋bc <0的解集为∅.二、简单的线性规划问题1．确定二元一次不等式表示平面区域的方法与技巧确定二元一次不等式表示的平面区域时，经常采用“直线定界，特殊点定域”的方法．2．利用线性规划求最值，一般用图解法求解，其步骤是(1)在平面直角坐标系内作出可行域．(2)考虑目标函数的几何意义，将目标函数进行变形．(3)确定最优解：在可行域内平行移动目标函数变形后的直线，从而确定最优解．(4)求最值：将最优解代入目标函数即可求出最大值或最小值．5.(1)设变量x ，y 满足约束条件：⎩⎨⎧ x ＋y ≥3，x －y ≥－1，2x －y ≤3，则目标函数z ＝y ＋1x 的最小值为( )A ．1B ．2C ．3D ．4 (2)某公司有60万元资金，计划投资甲、乙两个项目，按要求对项目甲的投资不小于对项目乙投资的23倍，且对每个项目的投资不能低于5万元．对项目甲每投资1万元可获得0.4万元的利润，对项目乙每投资1万元可获得0.6万元的利润，该公司正确规划投资后，在这两个项目上共可获得的最大利润为( )A ．36万元B ．31.2万元C ．30.4万元D ．24万元5.[解析] (1)不等式组所表示的平面区域如图中的△ABC ，目标函数的几何意义是区域内的点与点P (0，－1)连线的斜率，显然图中AP 的斜率最小．由⎩⎨⎧x ＋y ＝3，2x －y ＝3解得点A 的坐标为(2,1)，故目标函数z ＝y ＋1x 的最小值为1＋12＝1.(2)设对项目甲投资x 万元，对项目乙投资y 万元，则⎩⎪⎨⎪⎧ x ＋y ≤60，x ≥23y ，x ≥5，y ≥5.目标函数z ＝0.4x ＋0.6y .作出可行域如图所示，由直线斜率的关系知目标函数在A 点取最大值，代入得z max ＝0.4×24＋0.6×36＝31.2，所以选B.[答案] (1)A (2)B注：(1)求目标函数最值的一般步骤为：一画、二移、三求．其关键是准确作出可行域，理解目标函数的意义．(2)在约束条件是线性的情况下，线性目标函数只有在可行域的顶点或者边界上取得最值．在解答选择题或者填空题时也可以根据可行域的顶点直接进行检验．6．不等式组⎩⎨⎧ 2x ＋y －6≤0，x ＋y －3≥0，y ≤2表示的平面区域的面积为( ) A ．4B ．1C ．5D ．无穷大解析：选B 不等式组⎩⎨⎧ 2x ＋y －6≤0，x ＋y －3≥0，y ≤2表示的平面区域如图所示(阴影部分)，△ABC 的面积即为所求．求出点A ，B ，C 的坐标分别为(1,2)，(2,2)，(3,0)，则△ABC 的面积为S ＝12×(2－1)×2＝1.7．已知实数x ，y 满足⎩⎨⎧ x ≥0，y －x ＋1≤0，y －2x ＋4≥0，若z ＝y －ax 取得最大值时的最优解(x ，y )有无数个，则a ＝________. 解析：依题意，在坐标平面内画出题中的不等式组表示的平面区域，如图所示．要使z ＝y －ax 取得最大值时的最优解(x ，y )有无数个，则直线z ＝y －ax 必平行于直线y －x ＋1＝0，于是有a ＝1.答案：18．某公司用两种机器来生产某种产品，第一种机器每台需花3万日元及人民币50元的维护费；第二种机器则需5万日元及人民币20元的维护费．第一种机器的年利润每台有9万日元，第二种机器的年利润每台有6万日元，但政府核准的外汇日元为135万元，并且公司的总维护费不得超过1 800元，为了使年利润达到最大值，第一种机器应购买________台，第二种机器应购买________台．解析：设第一种机器购买x 台，第二种机器购买y 台，总的年利润为z 万日元，则⎩⎨⎧ 3x ＋5y ≤135，50x ＋20y ≤1 800，x ，y ∈N ，目标函数为z＝9x ＋6y . 不等式组表示的平面区域如图阴影部分中的整点．当直线z ＝9x ＋6y 经过点M ⎝ ⎛⎭⎪⎫63019，13519，即到达l 1位置时，z 取得最大值，但题目要求x ，y 均为自然数，故进行调整，调整到与M 邻近的整数点(33,7)，此时z ＝9x ＋6y 取得最大值，即第一种机器购买33台，第二种机器购买7台获得年利润最大．答案：33 7三、基本不等式基本不等式的常用变形(1)a ＋b ≥2ab (a >0，b >0)，当且仅当a ＝b 时，等号成立；(2)a 2＋b 2≥2ab ，ab ≤⎝ ⎛⎭⎪⎫a ＋b 22(a ，b ∈R)，当且仅当a ＝b 时，等号成立； (3)b a ＋a b ≥2(a ，b 同号且均不为零)，当且仅当a ＝b 时，等号成立；(4)a ＋1a ≥2(a >0)，当且仅当a ＝1时，等号成立；a ＋1a ≤－2(a <0)，当且仅当a ＝－1时，等号成立．9.(1)若正数x ，y 满足x ＋3y ＝5xy ，则3x ＋4y 的最小值是( )A.245B.285 C ．5 D ．6(2)若正数x ，y 满足4x 2＋9y 2＋3xy ＝30，则xy 的最大值是( )A.43B.53 C ．2 D.54[解析] (1)由x ＋3y ＝5xy 可得15y ＋35x ＝1，∴3x ＋4y ＝(3x ＋4y )⎝ ⎛⎭⎪⎫15y ＋35x ＝95＋45＋3x 5y ＋12y 5x ≥135＋125＝5当且仅当3x 5y ＝12y 5x ，即x ＝1，y ＝12时，等号成立， ∴3x ＋4y 的最小值是5.(2)由x >0，y >0，得4x 2＋9y 2＋3xy ≥2×(2x )×(3y )＋3xy (当且仅当2x ＝3y 时等号成立)，∴12xy ＋3xy ≤30，即xy ≤2，∴xy 的最大值为2.[答案] (1)C (2)C注：条件最值的求解通常有两种方法：一是消元法，即根据条件建立两个量之间的函数关系，然后代入代数式转化为函数的最值求解；二是将条件灵活变形，利用常数代换的方法构造和或积为常数的式子，然后利用基本不等式求解最值．10．已知2x ＋2y ＝1(x >0，y >0)，则x ＋y 的最小值为( )A ．1B ．2C ．4D ．8解析：选D ∵x >0，y >0，∴x ＋y ＝(x ＋y )·⎝ ⎛⎭⎪⎫2x ＋2y ＝4＋2⎝ ⎛⎭⎪⎫x y ＋y x ≥4＋4 x y ·yx ＝8.当且仅当x y ＝y x ，即x ＝y ＝4时取等号．11．设x ，y ∈R ，且xy ≠0，则⎝ ⎛⎭⎪⎫x 2＋1y 2⎝ ⎛⎭⎪⎫1x 2＋4y 2的最小值为________．解析：⎝ ⎛⎭⎪⎫x 2＋1y 2⎝ ⎛⎭⎪⎫1x 2＋4y 2＝5＋1x 2y 2＋4x 2y 2≥5＋21x 2y 2·4x 2y 2＝9，当且仅当x 2y 2＝12时“＝”成立．答案：912．某种商品原来每件售价为25元，年销售8万件． (1)据市场调查，若价格每提高1元，销售量将相应减少2 000件，要使销售的总收入不低于原收入，该商品每件定价最多为多少元？(2)为了扩大该商品的影响力，提高年销售量．公司决定明年对该商品进行全面技术革新和营销策略改革，并提高定价到x 元．公司拟投入16(x 2－600)万元作为技改费用，投入50万元作为固定宣传费用，投入15x 万元作为浮动宣传费用．试问：当该商品明年的销售量a 至少应达到多少万件时，才可能使明年的销售收入不低于原收入与总投入之和？并求出此时每件商品的定价．解：(1)设每件定价为t 元，依题意，有[8－(t －25)×0.2]t ≥25×8，整理得t 2－65t ＋1 000≤0，解得25≤t ≤40.因此要使销售的总收入不低于原收入，每件定价最多为40元．(2)依题意，x >25时，不等式ax ≥25×8＋50＋16(x 2－600)＋15x 有解，等价于x>25时，a≥150x＋16x＋15有解．∵150x＋16x≥2150x·16x＝10(当且仅当x＝30时，等号成立)，∴a≥10.2.因此当该商品明年的销售量a至少应达到10.2万件时，才可能使明年的销售收入不低于原收入与总投入之和，此时该商品的定价为每件30元．巩固练习：1．若1a＜1b＜0，则下列不等式不正确的是()A．a＋b＜ab B.ba＋ab＞0C．ab＜b2D．a2＞b2解析：选D由1a＜1b＜0，可得b＜a＜0，故选D.2．已知不等式x2－2x－3＜0的解集为A，不等式x2＋x－6＜0的解集为B，不等式x2＋ax＋b＜0的解集是A∩B，那么a＋b等于()A．－3 B．1C．－1 D．3解析：选A由题意：A＝{x|－1＜x＜3}，B＝{x|－3＜x＜2}．A∩B＝{x|－1＜x＜2}，由根与系数的关系可知：a＝－1，b＝－2，∴a＋b＝－3.3．函数y＝x2＋2x－1(x＞1)的最小值是()A．23＋2 B．23－2 C．2 3 D．2解析：选A∵x＞1，∴x－1＞0.∴y＝x2＋2x－1＝x2－2x＋2x＋2x－1＝x2－2x＋1＋2(x－1)＋3x－1＝(x－1)2＋2(x－1)＋3x－1＝x －1＋3x －1＋2≥23＋2当且仅当x －1＝3x －1，即x ＝3＋1时等号成立． 4．(2017·浙江高考)若x ，y 满足约束条件⎩⎨⎧ x ≥0，x ＋y －3≥0，x －2y ≤0，则z ＝x ＋2y 的取值范围是( )A ．[0,6]B ．[0,4]C ．[6，＋∞)D ．[4，＋∞) 解析：选D 作出不等式组所表示的平面区域如图中阴影部分所示，由z ＝x ＋2y ，得y ＝－12x ＋z 2，∴z 2是直线y ＝－12x ＋z 2在y 轴上的截距，根据图形知，当直线y ＝－12x ＋z 2过A 点时，z 2取得最小值．由⎩⎨⎧ x －2y ＝0，x ＋y －3＝0，得x ＝2，y ＝1，即A (2,1)，此时，z ＝4，∴z ＝x ＋y 的取值范围是[4，＋∞)．5．已知圆C ：(x －a )2＋(y －b )2＝1，平面区域Ω：⎩⎨⎧ x ＋y －7≤0，x －y ＋3≥0，y ≥0.若圆心C∈Ω，且圆C 与x 轴相切，则a 2＋b 2的最大值为( )A ．5B ．29C ．37D ．49解析：选C 由已知得平面区域Ω为△MNP 内部及边界．∵圆C 与x 轴相切，∴b ＝1.显然当圆心C 位于直线y＝1与x ＋y －7＝0的交点(6,1)处时，a max ＝6.∴a 2＋b 2的最大值为62＋12＝37.故选C.6．设正实数x ，y ，z 满足x 2－3xy ＋4y 2－z ＝0，则当xy z 取得最大值时，2x ＋1y －2z 的最大值为( )A ．0B ．1C.94 D ．3 解析：选B 由x 2－3xy ＋4y 2－z ＝0，得z ＝x 2－3xy ＋4y 2， ∴xy z ＝xy x 2－3xy ＋4y 2＝1x y ＋4yx －3. 又x ，y ，z 为正实数，∴x y ＋4y x ≥4，即xy z ≤1，当且仅当x ＝2y 时取等号，此时z ＝2y 2.∴2x ＋1y －2z ＝22y ＋1y －22y2 ＝－⎝ ⎛⎭⎪⎫1y 2＋2y ＝－⎝ ⎛⎭⎪⎫1y －12＋1，当1y ＝1，即y ＝1时，上式有最大值1.7．若x ，y 满足约束条件⎩⎨⎧ x －1≥0，x －y ≤0，x ＋y －4≤0，则y x 的最大值为________．解析：画出可行域如图阴影部分所示， ∵y x 表示过点(x ，y )与原点(0,0)的直线的斜率，∴点(x ，y )在点A 处时y x 最大．由⎩⎨⎧ x ＝1，x ＋y －4＝0，得⎩⎨⎧ x ＝1，y ＝3.∴A (1,3)．∴y x 的最大值为3.答案：38．设正数a ，使a 2＋a －2>0成立，若t >0，则12log a t ________log a t ＋12(填“>”“≥”“≤”或“<”)．解析：因为a 2＋a －2>0，所以a <－2或a >1，又a >0，所以a >1，因为t >0，所以t ＋12≥ t ，所以log a t ＋12≥log a t ＝12log a t .答案：≤9．(2017·全国卷Ⅲ)若x ，y 满足约束条件⎩⎨⎧ x －y ≥0，x ＋y －2≤0，y ≥0，则z ＝3x －4y 的最小值为________．解析：作出约束条件表示的可行域如图中阴影部分所示，作出直线l ：3x －4y ＝0，平移直线l ，当直线z ＝3x －4y 经过点A (1,1)时，z 取得最小值，最小值为3－4＝－1.答案：－110．某玩具生产公司每天计划生产卫兵、骑兵、伞兵这三种玩具共100个，生产一个卫兵需5 min ，生产一个骑兵需7 min ，生产一个伞兵需4 min ，已知总生产时间不超过10 h ．若生产一个卫兵可获利润5元，生产一个骑兵可获利润6元，生产一个伞兵可获利润3元．(1)用每天生产的卫兵个数x 与骑兵个数y 表示每天的利润W (元)．(2)怎样分配生产任务才能使每天的利润最大，最大利润是多少？解：(1)依题意每天生产的伞兵个数为100－x －y ，所以利润W ＝5x ＋6y ＋3(100－x －y )＝2x ＋3y ＋300.(2)约束条件为：⎩⎨⎧ 5x ＋7y ＋4(100－x －y )≤600，100－x －y ≥0，x ∈N ，y ∈N ，整理得⎩⎨⎧ x ＋3y ≤200，x ＋y ≤100，x ∈N ，y ∈N ，目标函数为W ＝2x ＋3y ＋300，如图所示，作出可行域．初始直线l 0：2x ＋3y ＝0，平移初始直线经过点A 时，W 有最大值，由⎩⎨⎧x ＋3y ＝200，x ＋y ＝100，得⎩⎨⎧x ＝50，y ＝50.最优解为A (50,50)，所以W max ＝550(元)．故每天生产卫兵50个，骑兵50个，伞兵0个时利润最大，为550元．11．某外商到一开发区投资72万美元建起一座蔬菜加工厂，第一年各种经费12万美元，以后每年增加4万美元，每年销售蔬菜收入50万美元．设f (n )表示前n 年的纯利润总和．(注：f (n )＝前n 年的总收入－前n 年的总支出－投资额)(1)从第几年开始获利？(2)若干年后，外商为开发新项目，有两种处理方案：①年平均利润最大时以48万美元出售该厂；②纯利润总和最大时，以16万美元出售该厂；问哪种方案最合算？为什么？解：由题意知，每年的经费是以12为首项，4为公差的等差数列，∴f (n )＝－2n 2＋40n －72.(1)获利就是要求f (n )>0，所以－2n 2＋40n －72>0，解得2<n <18.由n ∈N 知从第三年开始获利．(2)①年平均利润＝f (n )n ＝40－2⎝ ⎛⎭⎪⎫n ＋36n ≤16. 当且仅当n ＝6时取等号．故此方案共获利6×16＋48＝144(万美元)，此时n ＝6.②f (n )＝－2(n －10)2＋128.当n ＝10时，f (n )max ＝128.故第②种方案共获利128＋16＝144(万美元)，故比较两种方案，获利都是144万美元．但第①种方案只需6年，而第②种方案需10年，故选择第①种方案最合算．12．已知α，β是方程x 2＋ax ＋2b ＝0的两根，且α∈[0,1]，β∈[1,2]，a ，b ∈R ，求b －3a －1的最大值和最小值．解：设f (x )＝x 2＋ax ＋2b ，由题意f (x )在[0,1]和[1,2]上各有一个零点，∴⎩⎨⎧ f (0)≥0，f (1)≤0，f (2)≥0，即⎩⎨⎧ b ≥0，a＋2b ＋1≤0，a ＋b ＋2≥0，建立平面直角坐标系aOb ，则上述不等式组表示的平面区域如图．由⎩⎨⎧ a ＋2b ＋1＝0，a ＋b ＋2＝0，解得⎩⎨⎧ a ＝－3，b ＝1，即C (－3,1)．令k ＝b －3a －1，可以看成动点P (a ，b )与定点A (1,3)的连线的斜率．又B (－1,0)，C (－3,1)，则k AB ＝32，k AC ＝12，∴12≤b －3a －1≤32.故b －3a －1的最大值是32，最小值是12.。

高一数学必修5不等式易错题及错解分析

必修5不等式易错题及错解分析一、选择题：1．设()lg ,f x x =若0<a<b<c,且f(a)>f(b)>f(c),则下列结论中正确的是A (a-1)(c-1)>0B ac>1C ac=1D ac>1错解原因是没有数形结合意识,正解是作出函数()lg f x x =的图象,由图可得出选D. 2．设,,1x y R x y ∈+>则使成立的充分不必要条件是A 1x y +≥B 1122x y >>或 C 1x ≥ D x<-1 错解:选B,对充分不必要条件的概念理解不清,“或”与“且”概念不清，正确答案为D 。

3．不等式(0x -≥的解集是A {|1}x x >B {|1}x x ≥C {|21}x x x ≥-≠且D {|21}x x x =-≥或错解：选B ，不等式的等价转化出现错误，没考虑x=-2的情形。

正确答案为D 。

4．某工厂第一年的产量为A ，第二年的增长率为a,第三年的增长率为b ，这两年的平均增长率为x,则A 2a b x +=B 2a b x +≤C 2a b x +>D 2a bx +≥ 错解：对概念理解不清，不能灵活运用平均数的关系。

正确答案为B 。

5．已知1324a b a b -<+<<-<且，则2a+3b 的取值范围是A 1317(,)22-B 711(,)22-C 713(,)22-D 913(,)22- 错解：对条件“1324a b a b -<+<<-<且”不是等价转化，解出a,b 的范围，再求2a+3b的范围，扩大了范围。

正解：用待定系数法，解出2a+3b=52(a+b)12-(a-b),求出结果为D 。

6．若不等式ax 2+x+a ＜0的解集为 Φ，则实数a 的取值范围（）A a ≤-21或a ≥21B a ＜21C -21≤a ≤21D a ≥ 21正确答案：D 错因：学生对一元二次不等式与二次函数的图象之间的关系还不能掌握。