燕山地区2015年初中毕业考试答案
北京市燕山区2015年中考一模英语试题word版 含答案

北京市燕山2015年初中毕业考试英 语 试 卷 2015年4月听力理解(共30分)一、听对话,从下面各题所给的A 、B 、C 三幅图片中选择与对话内容相符的图片。
每段对话你将听两遍。
(共5分,每小题1分)1.2.3.4.5.C.A. B. C.B. C. A. B. C.请听一段对话,完成第6至第7小题。
6. Who bought the sweater?A. The man’s daughter.B. The man’s sonC. The man’s wife.7. What size should the man try?A. Size 14.B. Size 16.C. Size 18.请听一段对话,完成第8至第9小题。
8. Why is the boy back hom e early today?A. Because he wants to have a short break.B. Because he wants to help for the dinner.C. Because the classroom is too noisy to study9. What will the boy do to help his mother?A. Wash the dishes.B. Wash the tomatoes.C. Set the table.请听一段对话,完成第10至第11小题。
10. Why is the woman unhappy with the dog?A. It looks very dirty and sick.B. It will make a mess in the house.C. It will make troubles with the neighbor.11. What are they going to do with the dog?A. Keep it.B. Send it back.C. Give it away.请听一段对话,完成第12至第13小题。
2014-2015年燕山区初三数学期末考试及答案

燕山地区2014—2015学年度第一学期九年级期末考试 数 学 试 卷 2015年1月考 生 须 知1.本试卷共8页,共五道大题,25道小题,满分120分。
考试时间120分钟。
2.答题纸共6页,在规定位置准确填写学校名称、班级、姓名和学号。
3.试题答案一律书写在答题纸上,在试卷上作答无效。
4.考试结束,请将答题纸交回,试卷和草稿纸可带走。
一、选择题(本题共32分,每小题4分)下面各题均有四个选项,其中只有一个....是符合题意的,请将符合题意的答案代号写在答题纸的相应位置上.1.观察下列图形,是中心对称图形的是A .B .C .D .2.某校举办中学生汉字听写大会,准备从甲、乙、丙、丁4套题中随机抽取一套题对选手进行训练,则抽中甲套题的概率是A .41B .31C .21 D .1 3.右图是某几何体的三视图,该几何体是A .圆锥B .圆柱C .棱柱D .正方体4.已知△ABC ∽△DEF ,相似比为1∶2,△ABC 的周长为4,则△DEF 的周长为A .2B .4C .8D .16 5.如图,点A ,B ,C 均在⊙O 上,∠ACB =35°,则∠AOB 的度数为A .20°B .40°C .60°D .70° 6.如图,在Rt △ABC 中,∠C =90°,AC =1,BC =2,则cos B 的值是A .55 B .552 C .21 D .2 O CBAAB俯视图左视图正视图7.某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18℃的条件下生长最快的新品种.如图是某天恒温系统从开启到关闭及关闭后,大棚内温度y (℃)随时间x (小时)变化的函数图象,其中BC 段是双曲线)0(≠=k xky 的一部分,则当x =16时,大棚内的温度约为A .18℃B .15.5℃C .13.5℃D .12℃ 8.如图,在Rt △OAB 中,∠AOB =90°,OA =4,OB =. ⊙O 的半径为2,点P 是线段AB 上的一动点,过点P 作 ⊙O 的一条切线PQ ,Q 为切点.设AP =x ,PQ 2=y , 则y 与x 的函数图象大致是A .B .C .D . 二、填空题(本题共16分,每小题4分) 9.若y x 54=,则yx= . 10.已知反比例函数)0(≠=k xky 的图象在其每一分支上,y 随x 的增大而减小,则此反比例函数的解析式可以是 .(注:只需写出一个正确答案即可) 11.如图,小明在打网球时,要使球恰好能打过网,且落点恰好在离网4米的位置上,则球拍击球的高度h 为 米.(已知网高为0.8米,击球点到网的水平距离为3米)12.在函数)0(8>=x xy 的图象上有点P 1,P 2,P 3,…,18122y (℃)x (时)CBO APOB AQh 米0.8米3米4米5512Oxy5512OxyyxO 12555512OxyS 1S 2P 3P 1P 2y 初四数学期末试卷第1页(共8页)P n ,P n +1,它们的横坐标依次为1,2,3,…,n ,n +1.过点P 1,P 2,P 3,…,P n ,P n +1分别作x 轴、y 轴的垂线段,构成如图所示的若干个矩形,将图中阴影部分的面积从左至右依次记为1S ,2S ,3S ,…,n S ,则点P 1的坐标为 ;2S = ;n S = .(用含n 的代数式表示)三、解答题(本题共30分,每小题5分) 13.计算:2sin45°-tan60°·cos30°.14.如图,点D 是△ABC 的边AC 上的一点,AB 2=AC ·AD .求证:△ADB ∽△ABC .15.如图,正比例函数y=2x 与反比例函数)0(≠=k xky 的图象的一个交点为A (2,m ). 求m 和k 的值.16.如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,点A ,B ,C 的坐标分别为(0,1),(1,-1),(5,1).yxO11A初四数学期末试卷第3页(共8页)DCAy(1)直接写出点B 关于原点的对称点D 的坐标;(2)将△ABC 绕点C 顺时针旋转90º得到△A 1B 1C .请在网格中画出△A 1B 1C ,并直接写出点A 1和B 1的坐标.17.如图,在半径为6cm 的⊙O 中,圆心O 到弦AB 的距离OE 为3cm .(1)求弦AB 的长;(2)求劣弧AB ⌒的长.18.在燕房线地铁施工期间,交管部门在施工路段设立了矩形路况警示牌(如图所示).已知立杆AB 的高度是3米,从路侧点D 处测得路况警示牌顶端C 点和底端B 点的仰角分别是60°和45°,求路况警示牌宽BC 的值.(精确到0.1米) (参考数据:2≈1.41,3≈1.73)四、解答题(本题共20分,每小题5分)19.如图,四边形ABCD 的对角线AC ,BD 交于点F ,点E 是BD 上一点,且∠BAC =∠BDC=∠DAE .(1)求证:△ABE ∽△ACD ;(2)若BC =2,AD =6,DE =3,求AC 的长.20.根据某网站调查,2014年网民们最关注的热点话题分别有:消费、教育、环保、反腐及其它共五类.根据调查的部分相关数据,绘制的统计图表如下:根据以上信息解答下列问题:(1)请补全条形统计图并在图中标明相应数据;(2)若北京市约有2100万人口,请你估计最关注环保问题的人数约为多少万人? (3)在这次调查中,某单位共有甲、乙、丙、丁四人最关注教育问题,现准备从这四人中随机抽取两人进行座谈,则抽取的两人恰好是甲和乙的概率为 .21.如图,AB 为⊙O 的直径,直线l 与⊙O 相切于点C ,过点A 作AD ⊥l于点D ,交⊙O 于点E . (1)求证:∠CAD =∠BAC ;(2)若sin ∠BAC =53,BC =6,求DE 的长.22.阅读下面材料:小辉遇到这样一个问题:如图1,在Rt △ABC 中,∠BAC =90°,AB =AC ,点D ,E 在边BC 上,∠DAE =45°.若BD =3,CE =1,求DE 的长.反腐20%消费30%环保10%教育25%其他15%网民关注的热点问题情况统计图 140280210420人数(万人)420350280210140700关注各类热点问题的网民人数统计图lE D AOBC初四数学期末试卷第5页(共8页)ABDEF FD小辉发现,将△ABD 绕点A 按逆时针方向旋转90º,得到△ACF ,连接EF (如图2),由图形旋转的性质和等腰直角三角形的性质以及∠DAE =45°,可证△FAE ≌△DAE ,得FE =DE .解△FCE ,可求得FE (即DE )的长.请回答:在图2中,∠FCE 的度数是 ,DE 的长为 . 如图3,在四边形ABCD 中,AB =AD ,∠B +∠D =180°.E ,F 分别是边BC ,CD 上的点,且∠EAF =21∠BAD .猜想线段BE ,EF ,F D 之间的数量关系并说明理由.五、解答题(本题共22分,第23、24题每题7分,第25题8分) 23.已知关于x 的方程012=-+-k kx x .(1)求证:当2>k 时,方程总有两个不相等的实数根;(2)若二次函数)2(12>-+-=k k kx x y 的图象与x 轴交于A ,B 两点(A 在B 的左侧),与y 轴交于点C ,且tan ∠OAC =4,求该二次函数的解析式;(3)已知点P (m ,0)是x 轴上的一个动点,过点P 作垂直于x 轴的直线交(2)中的二次函数图象于点M ,交一次函数q px y +=的图象于点N .若只有当51<<m 时,点M 位于点N 的下方,求一次函数q px y +=的解析式.11Oxy(1)如图1,求证:EF=FG,且EF⊥FG;(2)如图2,若点H在线段BC的延长线上,猜想线段BH,EF,EK之间满足的数量关系,并证明你的结论.(3)若点H在线段BC的反向延长线上,请在图3中补全图形并直接写出线段BH,EF,EK之间满足的数量关系.25.在平面直角坐标系xOy中,对于任意三点A,B,C,给出如下定义:y D1D2D3CC2C1若矩形的任何一条边均与某条坐标轴平行,且A ,B ,C 三点都在矩形的内部或边界上,则称该矩形为点A ,B ,C 的外延矩形.点A ,B ,C 的所有外延矩形中,面积最小的矩形称为点A ,B ,C 的最佳外延矩形.例如,右图中的矩形1111D C B A ,2222D C B A ,333CD B A 都是点A ,B ,C 的外延矩形,矩形333CD B A 是点A ,B ,C 的最佳外延矩形.(1)如图1,已知A (-2,0),B (4,3),C (0,t ).①若2=t ,则点A ,B ,C 的最佳外延矩形的面积为 ; ②若点A ,B ,C 的最佳外延矩形的面积为24,则t 的值为 ; (2)如图2,已知点M (6,0),N (0,8).P (x ,y )是抛物线542++-x x y =上一点,求点M ,N ,P 的最佳外延矩形面积的最小值,以及此时点P 的横坐标x 的取值范围;(3)如图3,已知点D (1,1).E (m ,n )是函数)0(4>=x xy 的图象上一点,矩形OFEG 是点O ,D ,E 的一个面积最小的最佳外延矩形,⊙H 是矩形OFEG 的外接圆,请直接写出⊙H 的半径r 的取值范围.数学试卷参考答案与评分标准 2015年1月一、选择题(本题共32分,每小题4分)yxO11BA 图1图3OxyH G DE F图211O xyNMB .A .B .C .D .B .C .A .二、填空题(本题共16分,每小题4分) 9.45 10.x y 1-= )0(<=k xky (答案不唯一)11.1.4 12.(1,8);34;)1(8+n n . 三、解答题(本题共30分,每小题5分) 13.解:原式=233222⨯-⨯……………………………………3分 =123-=21-. ……………………………………5分14.证明:∵AB 2=AC ·AD ,∴AC AB =ABAD. ……………………………………2分 又∵∠A =∠A , ……………………………………4分 ∴△ADB ∽△ABC . ……………………………………5分 15.解:将点A (2,m )的坐标代入y=2x 中,得m =2×2,即m =4. ……………………………………2分 ∴A (2,4). ……………………………………3分将点A (2,4)的坐标代入xky =,得 k =2×4,即k =8. ………………5分 16.解:(1)D (-1,1); ………………2分(2)画出△A 1B 1C ,如图; ………………3分A 1(5,6),B 1(3,5). ………………5分 17.解:(1)∵AB 为⊙O 的弦,OE ⊥AB 于E ,∴AE =BE =21AB . ……………………………………1分 在Rt △AOE 中,OA =6,OE =3,∴AE =22OE OA -=2236-=27=33, ………………2分 ∴AB =2AE =36. ……………………………………3分(2)由(1)知,在Rt △AOE 中,∠AEO =90°,OA =6,OE =3, ∴cos ∠AOE =OA OE =21, ∴∠AOE =60°,∴∠AOB =2∠AOE =120°, ……………………………………4分O 5342x y 1BA B1CA 1-1-1∴AB ⌒的长l=1806120⨯π=π4. ……………………………………5分18.解:由题意,在Rt △ABD 中,∠DAB =90°,∠ADB =45°,AB =3米,∴AD =AB =3米, ……………………………………2分 又∵Rt △ACD 中,∠DAC =90°,∠ADC =60°,∴AC =AD ·tan ∠ADC =3·tan60°=33米, ………………4分 ∴BC =AC -AB =33-3≈2.2米. ………………5分 即路况警示牌宽BC 的值约为2.2米. 四、解答题(本题共20分,每小题5分) 19.(1)证法一:∵∠BAC =∠DAE ,∴∠BAC +∠CAE =∠DAE +∠CAE ,即∠BAE =∠CAD . ……………………………………1分 又∵∠BAC =∠BDC ,∠BFA =∠CFD ,∴180°-∠BAC -∠BFA =180°-∠BDC -∠CFD ,即∠ABE =∠ACD . ……………………………………2分 ∴△ABE ∽△ACD . ……………………………………3分 证法二:∵∠BAC =∠DAE , ∴∠BAC +∠CAE =∠DAE +∠CAE ,即∠BAE =∠CAD . ……………………………………1分 又∵∠BEA =∠DAE +∠ADE ,∠ADC =∠BDC +∠ADE ,∠DAE =∠BDC ,∴∠AEB =∠ADC . ……………………………………2分 ∴△ABE ∽△ACD . ……………………………………3分 (2)∵△ABE ∽△ACD ,∴AC AB=ADAE . 又∵∠BAC =∠DAE ,∴△ABC ∽△AED , ……………………………………4分 ∴DE BC =ADAC, ∴AC =AD DE BC ⋅=632⨯=4. ……………………………………5分 20.(1)补全条形统计图如图; ………………2分(2)2100×10%=210万人; ………………4分(3)61. ………………5分 21.(1)证明:连接OC ,350140280210420 人数(万人)42035028021014070∵CD 为⊙O 的切线,∴OC ⊥CD , ……………………………………1分 ∵AD ⊥CD ,∴OC ∥AD , ∴∠CAD =∠ACO . 又∵OC =OA , ∴∠ACO =∠OAC ,∴∠CAD =∠OAC ,即∠CAD =∠BAC . ……………………………………2分 (2)解法一:过点B 作BF ⊥l 于点F ,连接BE , ∵AB 为⊙O 的直径,∴∠AEB =90°, 又AD ⊥l 于点D ,∴∠AEB =∠ADF =∠BFD =90°, ∴四边形DEBF 是矩形,∴DE =BF . ……………………………………3分∵AB 为⊙O 的直径,∴∠ACB =90°,∴∠ACD +∠BCF =90°.∵∠ADC =90°,∴∠ACD +∠CAD =90°, ∴∠BCF =∠CAD . ∵∠CAD =∠BAC ,∴∠BCF =∠BAC . ……………………………………4分 在Rt △BCF 中,BC =6,sin ∠BCF =BC BF =sin ∠BAC =53, ∴BF =BC 53=518,∴DE =BF =518. ……………………………………5分解法二:连接CE ,∵AB 为⊙O 的直径,∴∠ACB =90°. ∵A ,B ,C ,E 四点共圆, ∴∠AEC +∠ABC =180°. 又∵∠AEC +∠DEC =180°,∴∠DEC =∠ABC ,∴Rt △CDE ∽Rt △ACB , ……………………………………3分 ∴BC DE =ACCD. 在Rt △ABC 中,sin ∠BAC =AB BC =53,BC =6, ∴AB =BC 35=10,∴AC =22BC AB =8. lEDA O BClF E D AOBClEDA O BC在Rt △ADC 中,∵∠DAC =∠BAC ,∴sin ∠DAC =AC CD =sin ∠BAC =53, ∴CD =AC 53=524. ……………………………………4分∴DE =AC BC CD ⋅=86524⨯=518. ……………………………………5分22.90°;10. ……………………………………2分猜想:EF =BE +FD ; ……………………………………3分 理由如下:如图,将△ABE 绕点A 按逆时针方向旋转,使AB 与AD 重合,得到△ADG , ∴BE =DG ,AE =AG ,∠DAG =∠BAE ,∠B =∠ADG , ∵∠B +∠ADC =180°,∠B =∠ADG ,∴∠ADG +∠ADC =180°,即点F ,D ,G 在同一条直线上. ∵∠EAF =21∠BAD , ∴∠GAF =∠DAG +∠DAF =∠BAE +∠DAF =∠BAD -∠EAF =∠EAF , 即∠GAF =∠EAF . ……………………………………4分在△AEF 和△AGF 中,⎪⎩⎪⎨⎧∠∠AF AF GAF EAF AG AE =,=,=∴△AEF ≌△AGF , ∴EF =FG .∵FG =DG +FD =BE +DF ,∴EF =BE +FD . ……………………………………5分五、解答题(本题共22分,第23题8分,第24、25题每小题7分)23.(1)证明:∵)1(14)(2-⨯⨯--=∆k k =2)2(-k , ………………1分又∵2>k ,∴02>-k , ∴0)2(2>-k ,即0>∆,∴当2>k 时,方程总有两个不相等的实数根. ………………2分 (2)解:∵)2(12>-+-=k k kx x y 与x 轴交于A 、B 两点,∴令0y =,有210x kx k -+-=,解得 1=x ,或1-=k x . ………………3分EFD GABC C1yN∵2>k ,点A 在点B 的左侧, ∴A (1,0),B (1-k ,0). ∵抛物线与y 轴交于点C ,∴C (0,1-k ). ……………………………………4分 在Rt △AOC 中,tan ∠OAC =OA OC =11-k =4, 解得5=k .∴抛物线的解析式为452+-=x x y . ……………………………………5分 (3)依题意并结合图象可知,一次函数的图象与二次函数的图象交点的横坐标分别为1和5,由此可得交点坐标为(1,0)和(5,4). ………………6分 将交点坐标分别代入一次函数解析式q px y +=中,得⎩⎨⎧+=+q p q p 54,0=, 解得⎩⎨⎧-1,1==q p , ∴一次函数的解析式为1-=x y . ……………………………………7分 24.(1)证明:∵正方形ABCD ,E ,F ,G 分别是边AD ,AB ,BC 的中点,∴AE =AF =FB =BG ,∠A =∠B =90°,∴△AEF ≌△BGF , ……………………………………1分 ∴EF =FG ,∠AFE =∠BFG =45°,∴∠EFG =180°-∠AFE -∠BFG =90°,即EF ⊥FG . ………………2分 (2)BH =22EF +EK ; ……………………………………3分 证明:将线段FH 绕点F 逆时针旋转90º,得到线段FK , ∴FH =FK ,∠HFK =90°, ∴∠KFE +∠EFH =90°,∵∠EFG =90°,∴∠HFG +∠EFH =90°, ∴∠KFE =∠HFG , 在△EFK 和△GFH 中,FK =FH ,∠KFE =∠HFG ,EF =FG ,∴△EFK ≌△GFH , ……………………………………4分 ∴EK =GH .∵△BFG 是等腰直角三角形,∴BG =22FG ,∴BH =BG +GH =22FG +EK =22EF +EK , 即BH =22EF +EK . ……………………………………5分(3)补全图形如图; ……………………………………6分BH =EK -22EF . ……………………………………7分25.(1)①18; ……………………………………1分②4=t 或1-=t ; ……………………………………3分 (2)如图,过M 点作x 轴的垂线与过N 点垂直于y 轴的直线交于点Q ,则当点P 位于矩形OMQN 内部或边界时,矩形OMQN 是点M ,N ,P 的最佳外延矩形,且面积最小.∵S 矩形OMQN =OM ·ON =6×8=48,∴点M ,N ,P 的最佳外延矩形面积的最小值为48.………………4分抛物线542++-x x y =与y 轴交于点T (0,5). 令0y =,有0542=++-x x , 解得 1-=x (舍),或5=x . 令8=y ,有8542=++-x x , 解得 1=x ,或3=x .∴10≤≤x ,或53≤≤x . ……………………………………6分 (3)2172≤≤r . ……………………………………8分 说明:各解答题的其他正确解法请参照以上标准按分步给分的原则酌情评分.第一课件网系列资料 yxO 11J RS N MTQK PK G E F C D BA H。
2015初三数学毕业考题目-燕山1
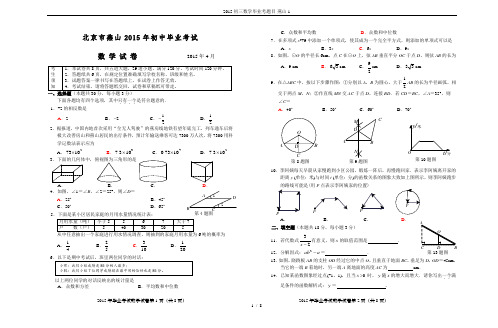
∴ ;………………………1分
∵抛物线 的对称轴为 ,
∴ ,
解得 ,………………………2分
∴抛物线 的解析式为 .………………………3分
(2)由题意,抛物线 的解析式为 .………………………4分
∴BE=DF.………………………5分
18.解:原式= ………………………4分
=4.………………………5分
19.解:解不等式①,得 ,………………………2分
解不等式②,得 ,………………………4分
∴原不等式组的解集为 .………………………5分
20.解:
= ………………………2分
=
= .………………………3分
∴S△DCB= = =12.………………………3分
在Rt△OBC中,
BC= =5,sin∠OCB= = .
作OG⊥BC于点G,
∵CF=CO=4,∴BF=BC−CF=5−4=1.
在Rt△OCG中,sin∠OCG= = ,
∴OG= OC= .………………………4分
∴S△OBF= = = .
∴S四边形OFCD=S△DCB−S△OBF
(2)证明:延长PD至点F,使EF=PE,连接BF.………………………3分
∵BE=AE,∠BEF=∠AEP,
∴△BEF≌△AEP,
∴∠APE=∠F,BF=PA.
又∵∠BDF=∠CDP,
∴△BDF∽△CDP.………………………4分
∴ = ,
∴ = ,
即PA·CD=PC·BD.………………………5分
五、解答题(本题共22分,第27、28题每小题7分,第29题8分)
B
A
D
二、填空题(本题共18分,每小题3分)
2015年北京市燕山区初三毕业考试数学试题及答案

学校 班级 姓名 学号密 封 线 内 不 要 答 题足条件的函数解析式:y15内10元;超出3到离家1016.定义:对于任意一个不为1211-=-,1-差倒数,4a 是3a三、解答题(本题共3017.如图,点E ,F 在线段AC 求证:BE =DF .18.计算:13|3|)31(--+-19.解不等式组:⎩⎨⎧≤-<-.21512x x20.已知022=--x x21用时间比自驾车多53速度是自行车速度的2AC ,CE ∥BD .上截取6,亿件,比2013年增长52%,跃居2014年全国直接丢弃的快递2015学校 班级 姓名 学号29题8分)x 轴交于点A (2,0). D (0,k ).已知点B (2,2),k 的取值范围.密 封 线 内 不 要 答 题28.△ABC 中,∠ABC =45对应点为点D ,直线BD(1)如图1,当∠BAC ①求证:BE ⊥AC ; ②求∠BEH 的度数; (2)当∠BAC 为钝角时,P 为和谐点.例如(23,23),)0(43≠a 的最小值为-3,最大值D ,与反比例函数xn y G =:的P 的横坐标为1,且2015图1A BHCED学校 班级 姓名 学号≥x ∴原不等式组的解集为)(1+x )1 ………………………1分………………………2分 ………………………3分 ………………………4分 ………………………5分 ………………………1分=9>0,原方程总有两个不相等的实数根. ………………………2分 03)3=--k x 中,. ………………………3分32+x ; ………………………4分32-x ………………………5分 ,由求根公式,得19)±k =,………………………3分 ………………………4分 ………………………5分………………………1分 ………………………2分密 封 线 内 不 要 答 题(2)解法一:∵菱形∴AC 与BD ∴OD =OB =21BD =3,∴S △DOC =OC OD ⋅21在Rt △OBC 中,BC =22OC OB +=5作FH ⊥OC 于点H ,在Rt △CFH 中,CF =∴FH =53CF =512.∴S △OCF =FH OC ⋅21∴S 四边形OFCD =S △DOC +S △解法二:∵菱形ABCD ,∴AC 与BD ∴OD =OB =21BD =3,∴S △DCB =OC DB ⋅21在Rt △OBC 中,BC =22OC OB +=5作OG ⊥BC 于点G ,∵CF =CO =4,∴BF =在Rt △OCG 中,sin ∠学校 班级 姓名 学号………………………3分 ………………………4分………………………5分 ………………………6分 ………………………7分 ………………………1分 ………………………2分 图1-1密 封 线 内 不 要 答 题3, (0,-3), 由对称性,该函数图………………………5在对称轴右侧y 随x 的增3的最小值为-3,最大值为1, ………………………6分 ………………………8分 . 图2-2。
北京市燕山区中考一模题及答案2015界0506132148_38597要点

F 列各小题均有四个选项,其中只有一个选项符合题意。
1.在国际单位制中,电压的单位是A .安培B .伏特2•下列物品中,通常情况下属于导体的是A •塑料笔杆B •橡胶手套3.下列现象中,质量发生变化的是A .铁水凝固成铁块 C .菜刀被磨光以后4•下列现象中,属于光的反射现象的是A .岸边景物在水中形成倒影 C •小孔成像5.下列四个实例中,能够使蒸发减慢的是A •将湿衣服晾在通风向阳处 C .将新鲜的黄瓜装入塑料袋6•下列用电器中,利用电流热效应工作的是A .电视机B .电热毯7•下列实例中,目的是为了减小压强的是A•上学出发前,将不用的书本从书包中取出C •把酸奶吸管的一端切成斜口 8.A •两手相互摩擦,手的温度升高B .用煤气炉给水加热,水的温度升高9.如图1所示的四种情景中,所使用的杠杆属于费力杠杆的是2015年北京市燕山地区初中毕业考试物理试卷2015年4月C .把蔬菜放进冰箱,蔬菜的温度降低D .用炭火将肉烤熟 (共30分,每小题2分)C .焦耳D .瓦特C .不锈钢尺D .陶瓷碗B .将一块矿石由地球运到太空 D .将铁丝用拔丝机拉长B .放大镜把字体放大 D .雨后天空出现彩虹B .将湿手伸到干手器下方吹 D .将新收获的玉米摊开晾晒C .电风扇D .电脑B .啄木鸟的喙坚硬而细长 D .把菜刀磨得很锋利F 列实例中,通过做功的方式改变物体内能的是10.下列事例中,由弹性势能转化为动能的是A .风吹动树叶B .拉弯的弓把箭射出C .汽车在盘山公路匀速前进D .秋千从高处向低处摆动11•生活中需要对一些物理量进行估测,以下估测接近实际的是A .一个鸡蛋的质量约为 0.5kg C •人正常体温约27 C 12.下列能源中属于不可再生能源的是 A •风能B •太阳能 B .教室门框的高度接近于 2mD .一般初中生的体重大约是 600gC .水能D .核能13•图2中两个小灯泡串联接入电路,闭合开关后小灯泡均发光,它们一定相等的是14. 龙卷风的实质是高速旋转的气流.它能把地面上的人、动物或物体等入空中,如图3所示。
北京市燕山区2015届九年级上期末考试数学试题及答案

数学试卷
2015 年 1 月
考 1.本试卷共 8 页,共五道大题,25 道小题,满分 120 分。考试时间 120 分钟。 生 2.答题纸共 6 页,在规定位置准确填写学校名称、班级、姓名和学号。 须 3.试题答案一律书写在答题纸上,在试卷上作答无效。 知 4.考试结束,请将答题纸交回,试卷和草稿纸可带走。
D,E 在边 BC 上,∠DAE=45°.若 BD=3,CE=1,求 DE 的长.
C E
D
C E
F D
D F
C E
B
D C
15.如图,正比例函数 y=2x 与反比例函数 y kx (k 0) 的图象的一个交点为 A(2,m).
求 m 和 k 的值.
y
A
1
O1
x
y 16.如图,在边长为 1 的小正方形组成的网格中,△ABC
A
C
O 12 3 4 5
x
B
的三个顶点均在格点上,点 A,B,C 的坐标分别为(0,1),(1,-1),(5,1). (1)直接写出点 B 关于原点的对称点 D 的坐标; (2)将△ABC 绕点 C 顺时针旋转 90º 得到△A B1 C1.请在网格中画出△A B 1C,1 并直
A
BF
E
D
C
20.根据某网站调查,2014 年网民们最关注的热点话题分别有:消费、教育、环保、反腐 及其它共五类.根据调查的部分相关数据,绘制的统计图表如下:
科*网]网民关注的热点来自题情况统计万万万万 万 万
420
关注各类热点问题的网民人数统计图 420
万万
万 万 30%
15%
万万
北京市燕山区2015届九年级上学期期末考试化学试题及答案

北京市燕山区2015届九年级上学期期末考试化学试卷一、选择题(每小题只有1个选项符合题意.共25个小题,每小题1分,共25分.)3CaO+CO+4Al3CaO+CO+4Al3Mn+2Al放出氧气的过程,叫做光合作用.光合作用的反应式为:二氧化碳﹢水12.(1分)反应H2+Cl22HCl中,反应前后没有改变的是().16.(1分)氟元素的相关信息如图所示.下列说法中,不正确的是()20.(1分)A、B、C三只小烧杯内依次盛有一定体积的浓氨水、酚酞溶液、酚酞溶液,按图所示进行探究活动,不能得到的结论是()23.(1分)密闭容器中有甲、乙两种物质各10g,加热一段时间后测得容器中各物质的质量24.(1分)氨基钠(NaNH2)常用于医药制造,根据其性质,氨基钠应该用时制备,不要长时间贮存.工业上制取氨基钠是将钠于97~100℃熔融,向反应容器中缓慢通入无水液氨3.用酒精灯加热一定量KMnO4固体将等质量的镁片和铁片投入到足量稀H2SO4中用等质量、等浓度的双氧水分别制取氧气.2H二、填空题(共5个小题,共30分.)26.(5分)(1)凡是碳或含碳物质在氧不充分时燃烧,均可产生一种毒气.请写出碳在氧气不充足的条件下,不完全燃烧的化学方程式2C+O22CO.(2)用石灰浆抹墙,一段时间后墙壁变得又白又硬,原因是Ca(OH)2+CO2=CaCO3↓+H2O (用化学方程式回答).(3)取一朵用石蕊溶液染成紫色的干燥小花,将小花的一半用水喷湿,放入盛有CO2的集气瓶中,可观察到的实验现象是小花干燥的一半无变化,湿润的一半变为红色,此现象说明CO2具有的化学性质是能与水反应生成酸性物质.2227.(7分)建立宏观、微观和符号之间联系是学习化学的一种方法.(1)在汞、水、氯化钠三种物质中,由离子构成的物质是氯化钠.(2)属于单质的是汞.属于氧化物的是水.(3)乙基雌烯醇是一种参赛运动员禁用的兴奋剂,其化学式为C20H32O.乙基雌烯醇由三种元素组成,分子中H、O两种元素的质量比为32:1.下列说法正确的是AB(填数字序号).A.该反应中元素化合价都不变B.化学变化中分子和原子均可再分C.4种物质中属于氧化物的是B和CD.若反应后生成1.8gD,则生成C的质量为8.4gE.B与C物质的化学性质不同,是因为分子构成不同.OCO+3HO28.(5分)水和溶液在生产生活中有着重要的作用.(1)水是生命之源,如图是用来净化河水的简易装置,其中活性炭的主要作用是吸附.下列说法错误的是BCD.A.水是一种重要的溶剂B.利用如图装置能把硬水变为软水C.通过过滤可以除去水中所有的杂质D.利用如图装置能对水杀菌消毒(2)生活中可以用肥皂水检验某水样是硬水还是软水.(3)20℃时,将等质量的甲、乙固体,分别加入到盛有100g水的烧杯中,充分搅拌后现象如图1,加热到50℃时现象如图2(不考虑水分蒸发),甲、乙固体溶解度曲线如图3.下列说法正确的是C(填字母序号).A.图3中N表示的是甲的溶解度曲线B.图2中的甲溶液是不饱和溶液C.图2中甲、乙溶液的溶质质量分数相等D.将图2中两溶液降温至30℃,甲一定会析出晶体E.图1中甲溶液一定是饱和溶液,乙溶液一定是不饱和溶液.29.(8分)金属具有广泛的应用.(1)下列金属制品中,利用金属导热性的是B(填字母序号).A.黄金饰品B.铝蒸锅C.铜导线(2)铁制品在沙漠地区不易锈蚀的原因是缺少水分.(3)工业上用一氧化碳和赤铁矿炼铁反应的化学方程式为3CO+Fe2O32Fe+3CO2.(4)某化学实验室废液缸里的废液含有CuSO4、ZnSO4、FeSO4,将废液直接排放既造成浪费,又造成污染.小红利用课余时间进行废液处理,实验过程如图所示.①固体A的成分是Fe、Cu、Zn,滤液1和滤液2中含有一种相同的溶质,该溶质是ZnSO4.②写出下面流程中发生反应的化学方程式:加入过量锌粉后:Zn+CuSO4=ZnSO4+Cu(写出一个即可).③若所加锌粉量不足,则滤液1中的溶质可能是AD(填字母).A.ZnSO4和FeSO4 B.ZnSO4和CuSO4C.CuSO4和FeSO4D.ZnSO4、CuSO4和FeSO4.32Fe+3CO330.(6分)下列A~H 为初中化学常见的8种物质,由H、C、O、Ca、Cl五种元素中的一种或几种组成.(1)A是一种单质,在自然界硬度最大,A的名称是金刚石.(2)B和C为由两种相同元素组成的化合物,B能发生分解反应能生成C,该反应的化学方程式为2H2O22H2O+O2↑.(3)D、E、F、G为含一种相同元素的化合物,其中E、F含不同的原子团,其转化关系为D→E→F→G.写出D→E反应的化学方程式CaO+H2O═Ca(OH)2;D、E、F、G中含有的相同元素为氧元素、钙元素.(4)H具有可燃性,则下列说法正确的是①(填数字序号).①H可能有毒②H一定为气体③H一定由碳元素和氢元素组成.22三、实验题(共3个小题,共19分)31.(6分)根据如图回答问题.(1)仪器a的名称是集气瓶.(2)实验室用高锰酸钾制取氧气的化学方程式为2KMnO4K2MnO4+MnO2+O2↑,选用的发生装置是B,收集装置是D或E(填字母序号,下同).(3)实验室制取二氧化碳时,选用的收集装置是D.将燃着的木条放在瓶口,若观察到燃烧的木条熄灭,说明瓶中已充满二氧化碳.4K4K32.(5分)通常情况下,燃烧需要三个条件.【查阅资料】(1)白磷和红磷燃烧,都能生成白色的五氧化二磷.(2)白磷的着火点40℃,常温下在空气中也能与氧气反应;红磷的着火点260℃.【进行实验】某化学兴趣小组同学设计并完成了如下图所示实验验证可燃物燃烧与氧气和温度有关.【解释与结论】(1)实验②和实验④(填序号)证明了可燃物燃烧必须要接触氧气.(2)实验③和实验④(填序号)证明了可燃物燃烧必须要达到一定温度.(3)写出白磷燃烧的化学方程式4P+5O22P2O5.【反思与评价】以上四个实验中,实验①(填序号)省略不做也可达到实验目的.【拓展延伸】白磷在储存时必须注意密封,少量时可保存在水里.22P33.(7分)某实验小组对“载人宇宙飞船或潜水艇中一般都要安装盛放过氧化钠(Na2O2)颗粒的装置”感到非常好奇,设计实验进行探究.【提出问题】过氧化钠是否为一种制氧剂?与人呼出的哪种气体发生反应?【查阅资料】①人呼出的气体中主要成分是N2、O2、CO2和水蒸气等.②CO2+2NaOH Na2CO3+H2O.【提出猜想】过氧化钠与人呼出的N2或CO2或水蒸气反应并生成氧气.【进行实验】实验Ⅰ:验证过氧化钠与氮气反应并生成氧气.(1)实验操作如图1所示.(2)实验现象及结论:观察到燃着木条熄灭现象,判断过氧化钠与氮气没有生成氧气.实验Ⅱ:验证过氧化钠与水蒸气反应并生成氧气.(1)同学们在老师的指导下设计了如图2所示装置.其中A装置的作用是提供水蒸气.(2)实验现象及结论:C瓶口带火星的木条复燃;过氧化钠与水蒸气发生化学反应并生成氧气.(3)查资料得知过氧化钠与水蒸气反应,除氧气外还产生了另一种物质,请写出该反应的化学方程式2Na2O2+2H2O=4NaOH+O2↑.实验Ⅲ:验证过氧化钠与二氧化碳反应并生成氧气.(1)同学们在老师的指导下设计了如图3所示装置.某同学对实验Ⅲ的设计提出疑问:该实验不能证明二氧化碳与过氧化钠确实发生了反应,你认为他的理由是二氧化碳中混有水蒸气,而水蒸气与过氧化钠反应也生成氧气.四、计算题(共6分)34.(3分)(2013•北京)甲醇(CH3OH)是基础的化工原料,制备原理为:CO+2H2CH3OH.当消耗5.6kgCO时,计算生成甲醇的质量.235.(3分)某校化学兴趣小组同学用一瓶含有少量氯化钠的硫酸钠固体样品,进行如图所示的实验.已知:Na2SO4+BaCl2═BaSO4↓+2NaCl,请根据以上信息,计算反应后所得溶液中溶质的质量分数.滤液中氯化钠的质量分数为:。
北京市燕山区2015届九年级上学期期末考试语文试题(附答案)

燕山地区2014—2015学年度第一学期九年级期末考试语文试卷2015年1月一、选择。
下面各题均有四个选项,其中只有一个..符合题意,将选出答案字母项填在答题纸上相应位置。
(共12分。
每小题2分)1.下列词语中加点字的读音完全正确的一项是A.翘.首(qiáo)粗犷.(kuàng)耳濡.目染(rú)B.脂.肪(zhī)颠簸.(bǒ)随声附和.(hé)C.自诩.(yǔ)涨.红(zhàng)杳.无消息(yǎo)D.修葺.(qì)参.差(cēn)迥.然不同(jiǒng)2.结合语境,对下面语段中加点的错别字修改有误的一项是因为贪睡,错过了欣赏那变换.莫测的海市蜃楼的机会,想象着碧海中忽然涌出星罗旗.布的房屋,听着有幸目睹了这奇观的人兴至.勃勃的谈论,我满心的懊诲.无以言表。
A.换——“变换莫测”这一词语在文段中描写的是海市蜃楼无规律可循的奇异变化,此处加点的“换”应改为“幻”。
B.旗——“星罗旗布”这一词语在文段中描写的是海市蜃楼中房屋排列的样子,此处加点的“旗”应改为“棋”。
C.至——“兴至勃勃”这一词语在文段中描写的是人们谈论海市蜃楼时高兴的情趣,此处加点的“至”应改为“志”。
D.诲——“懊诲”这一词语在文段中写的是“我”没有看到海市蜃楼的心情,此处加点的“诲”应改为“悔”。
3.在下面语段中,依次填入关联词语最恰当的是前方是二个古老的球场。
岁月和风雨的侵蚀,球场的大部分建筑已倾塌,但是透过这些断壁残垣,依稀可以想见当年比赛的热烈场面。
可以说,古代体育运动,开启了人类逐步进入有序竞争的序幕,是人类力与美结合最早开出的二朵灿烂之花。
A.由于不仅也B.由于因为所以C.虽然不仅也D.虽然因为所以4.结合语境,在下面语段中的横线处填写句子,最恰当的一项是苇塘的秋天到了,苇顶上的穗子由绿变黄继而变白,①。
一些带着绒毛的草籽在风中②,要人带它们到远方去落户。
2015年北京市燕山区初三语文一模及答案

北京市燕山2015年初中毕业考试语文试卷201504考生须知1.本试卷共8页,共四道大题,24道小题。
满分120分。
考试时间150分钟。
2.在试卷和答题卡上准确填写学校名称、姓名和准考证号。
3.试题答案一律书写在答题卡上,在试卷上作答无效。
4.考试结束,将试卷、答题卡和草稿纸一并交回。
一、基础·运用(共26分)(一)选择。
(共14分)阅读下面的文字,完成第1-3题。
(8分)《朱子治家格言》又称《治家格言》、《朱子家训》。
作者朱用纯(1617-1688),字致一,自号柏庐,江苏省昆山县人,生于明万历四十五年(1617)。
其父朱集璜是明末学者。
朱氏自幼致力读书,曾考取秀才志于仕途。
清入关明亡,遂不再求取功名,居乡教授学生并潜心程朱理学,主张知行并进,一时颇负盛名。
康熙曾多次征召,均为先生所拒绝。
著有《删补易经蒙引》、《四书讲义》、《劝言》、《耻耕堂诗文集》和《愧纳集》。
《朱子家训》通篇意在劝人要勤俭持家,安分守己。
讲中国几千年形成的道德教育思想,以名言警句的形式表达出来,可以口头传训,也可以写成对联条幅挂在大门、厅堂和居室,作为治理家庭和教育子女的座右铭。
因此,。
《朱子家训》仅522字,却以警句、箴言的形式讲述了许多为人处世、修身治家的道理,精辟地阐明了修身治家之道,是一篇家教名著。
其中许多内容继承了中国传统文化的优秀特点,比如勤俭持家、邻里和睦、公平厚道、与人为善,力戒色欲和浮华,反对见利忘义、谄媚权贵等等,在今天仍然有现实意义,当然其中封建性的糟粕如迷信报应、自得守旧等是那个时代的历史局限,我们是不能苛求于前人的。
1.加点字注音全都正确的一项是()(2分)A.征召.(zhāo)报应.(yīng)为.人处.世(wéi chǔ)B.苛求(kē)报应.(yìng)为.人处.世(wèi chù)C.潜.心(qián)报应.(yīng)为.人处.世(wèi chù)D.箴言(zhēn)报应.(yìng)为.人处.世(wéi chǔ)2.在第一段横线处补充句子,次序比较恰当的一项是()(2分)①很为士绅、官宦和书香门第乐道②自问世以来流传甚广③被历代士大夫尊为“治家之经”④清至民国年间一度成为童蒙必读课本之一A.①②③④B.②③①④C.①③④D.④③②①3.某大户人家新筑大屋,拟将《朱子家训》中的一个句子挂在厅堂里训示子孙勤俭持家。
2015年北京燕山初三一模数学试题及答案整理版

2015年北京燕山初三一模数学试题及答案整理版D从中任意抽出一个家庭进行用水情况调查,则抽到的家庭月用水量为6吨的概率为A .41B .52C .103D .201以上两位同学的对话反映出的统计量是A .众数和方差B .平均数和中位数C .众数和平均数D .众数和中位数7.在多项式x 2+9中添加一个单项式,使其成为一个完全平方式,则添加的单项式可以是A .xB .3xC .6xD .9x 8.如图,⊙O 的半径长6cm ,点C 在⊙O 上,弦AB垂直平分OC 于点D ,则弦AB 的长为A .9 cmB .36cmC .29cm D .33cm 9.在△ABC 中,按以下步骤作图:①分别以A ,B为圆心,大于21AB 的长为半径画弧,相交于两点M ,N ;②作直线MN 交AC 于点D ,连接BD .若CD =BC ,∠A =35°,则 ∠C = A .40° B .50° C .60° D .70°10.李阿姨每天早晨从家慢跑到小区公园,锻炼一阵y (单位:)点表示李阿姨家的位置)A .B .C .NM ABD C第9第8题分第10二、填空题(本题共18分,每小题3分)11.若代数式23-x 有意义,则x 的取值范围是 .12.分解因式:a ab -2= .13.如图,跷跷板AB 的支柱OD 经过它的中点O ,且垂直于地面BC ,垂足为D ,OD =45cm ,当它的一端B 着地时,另一端A 离地面的高度AC 为 cm . 14.已知某函数图象经过点(-1,1),且当x >0时,y 随x的增大而增大.请你写出一个..满足条件的函数解析式:y = .15.为了节能减排,近期纯电动出租车正式上路运行.某地纯电动出租车的运价为3公里以内10元;超出3公里后每公里2元;单程超过15公里,超过部分每公里3元.小周要到离家10公里的博物馆参观,若他往返都乘坐纯电动出租车,共需付车费 元.16.定义:对于任意一个不为1的有理数a ,把a-11称为a 的差倒数,如2的差倒数为1211-=-,1-的差倒数为)1(11--=21.记211=a ,2a 是1a 的差倒数,3a 是2a 的差倒数,4a 是3a 的差倒数,…,ABEF依此类推,则2a = ;2015a = .三、解答题(本题共30分,每小题5分)17.如图,点E ,F 在线段AC 上,AB ∥CD ,AB =CD ,AE =CF .求证:BE =DF .18.计算:01)3(30tan 3|3|)31(π-+︒--+-.19.解不等式组:⎩⎨⎧≤-<-.21512x x ,20.已知022=--x x ,求代数式)1)(1()12(-+--x x x x 的值. 21.列方程或方程组解应用题:赵老师为了响应市政府“绿色出行”的号召,改骑自行车上下班,结果每天上班所用时间比自驾车多53小时.已知赵老师家距学校12千米,上下班高峰时段,自驾车的速度是自行车速度的2倍.求赵老师骑自行车的速度.22.已知关于x 的方程03)32(22=-+--k k x k x .(1)求证:方程总有两个不相等的实数根; (2)已知方程有一个根为0,请求出方程的另DO FECAB一个根.四、解答题(本题共20分,每小题5分)23.如图,菱形ABCD 中,对角线AC ,BD 交于O点,DE ∥AC ,CE ∥BD .(1)求证:四边形OCED 为矩形;(2)在BC 上截取CF =CO ,连接OF ,若AC=8,BD =6,求四边形OFCD 的面积.24.根据国家邮政局相关信息,2014年我国快递业务量达140亿件,比2013年增长52%,跃居世界第一,而快递产生的包装垃圾也引起了邮政管理部门的重视.以下是根据相关数据绘制的统计图的一部分.根据以上信息,解答下列问题:(1)请补全条形统计图并标明相应数据;(结果保留整数) 市民收到快递后对包装处理方式统计图D :其他C :留着下次寄件 使用;B :收集整理后作 为废品卖掉;A:直接丢弃;60%20%8%12%AB C D1601401208060100402002014140年)业务量(亿件2012201120132357372010-2014年全国快递业务量统计图(2)每件快递专用包装的平均价格约为1.2元,据此计算2014年全国直接丢弃的快递包装造成了约多少亿元的损失? (3)北京市2014年的快递业务量约为6亿件,预计2015年的增长率与近五年全国快递业务量年增长率的平均值近似相等,据此估计2015年北京市快递业务量将达到 亿件.(直接写出结果,精确到0.1)25.如图,△ABC 中,AB =AC ,以AB 为直径作⊙O 交BC 于点D ,过点D 作⊙O 的切线DE 交AC 于点E .(1)求证:∠CDE =90°; (2)若AB =13,sin ∠C =135,求CE 的长.26.阅读下面材料:小军遇到这样一个问题:如图1,△ABC 中,AB =6,AC =4,点D 为BC的中点,求AD 的取值范围.AB DC E ABP小军发现老师讲过的“倍长中线法”可以解决这个问题.他的做法是:如图2,延长AD 到E ,使DE =AD ,连接BE ,构造△BED ≌△CAD ,经过推理和计算使问题得到解决.请回答:AD 的取值范围是 .参考小军思考问题的方法,解决问题: 如图3,△ABC 中,E 为AB 中点,P 是CA 延长线上一点,连接PE 并延长交BC 于点D .求证:PA •CD =PC •BD .五、解答题(本题共22分,第27题7分,第28题7分,第29题8分)27.抛物线cbx x y C ++=2121:与y 轴交于点C (0,3),其对称轴与x 轴交于点A (2,0). (1)求抛物线1C 的解析式; (2)将抛物线1C 适当平移,使平移后的抛物线2C 的图ABC图顶点为D (0,k ).已知点B (2,2),若抛物线2C 与△OAB 的边界总有两个公共点,请结合函数图象,求k 的取值范围.28.△ABC 中,∠ABC =45°,AH ⊥BC 于点H ,将△AHC 绕点H 逆时针旋转90°后,点C 的对应点为点D ,直线BD 与直线AC 交于点E ,连接EH .AB H CA BHCED(1)如图1,当∠BAC 为锐角时,①求证:BE ⊥AC ;②求∠BEH 的度数; (2)当∠BAC 为钝角时,请依题意用实线补全图2,并用等式表示出线段EC ,ED ,EH 之间的数量关系29.在平面直角坐标系中,如果点P 的横坐标和纵坐标相等,则称点P 为和谐点.例如点(1,1),(31-,31-),(2-,2-),…,都是和谐点.(1)分别判断函数12+-=x y 和12+=x y 的图象上是否存在和谐点,若存在,求出其和谐点的坐标; (2)若二次函数)0(42≠++=a c x ax y 的图象上有且只有一个和谐点(23,23),且当m x ≤≤0时,函数)0(4342≠-++=a c x axy 的最小值为-3,最大值为1,求m 的取值范围.(3)直线2:+=kx y l 经过和谐点P ,与x 轴交于点D ,与反比例函数xny G =:图图的图象交于M,N两点(点M在点N 的左侧),若点P的横坐标为1,且+DNDM,请直接写出n的取值范围.32<燕山地区2015年初中毕业考试数学试卷参考答案与评分标准 2015年4月一、 选择题(本题共30分,每小题3分)二、填空题(本题共18分,每小题3分) 11.2≠x 12.)1)(1(-+b b a ; 13.90; 14.答案不唯一:xy 1-=,2x y =,2+=x y ,… 15.48; 16.2;2.三、解答题(本题共30分,每小题5分)17.证明:∵AB ∥CD ,∴∠A =∠C . ………………………1分在△BAE 和△DCF 中,⎪⎩⎪⎨⎧∠=∠=,=,CF AE C A CD AB ,∴△BAE ≌△DCF(SAS ), ………………………4分∴BE =DF . ………………………5分18.解:原式=133333+⨯-+ ………………………4分=4.………………………5分 19.解:解不等式①,得3<x , ………………………2分解不等式②,得1-≥x , ………………………4分∴原不等式组的解集为31<≤-x . ………………………5分20.解:)1)(1()12(-+--x x x x=)1(222---x x x ………………………2分=1222+--x x x =12+-x x . ………………………3分∵022=--x x ,即22=-x x . ………………………4分∴原式=1)(2+-x x =2+1=3. ………………………5分21.解:设赵老师骑自行车的速度为x 千米/小时, ………………………1分依题意得5321212=-x x , ………………………2分解方程得 x =10. ………………………3分经检验,x =10是原方程的解且符合实际意义. ………………………4分答:赵老师骑自行车的速度是10千米/小时. ………………………5分22.解:(1)Δ=)3(14)32(22k k k -⨯⨯-- ………………………1分=k k k k 124912422+-+-=9>0,∴ 原方程总有两个不相等的实数根. ………………………2分(2)解法一: 把0=x 代入方程03)32(22=-+--k k x k x中, 得 032=-k k , 解得=k ,或3=k . ………………………3分当0=k 时,原方程化为032=+x x ,解得31-=x ,2=x ; ………………………4分当3=k 时,原方程化为032=-x x ,解得31=x ,02=x.综上,原方程的另一个根3-=x ,或3=x . ………………………5分解法二:∵Δ=9,由求根公式,得 23)32(129)32(21±-=⨯±-=k k x ,, ∴原方程的根为kx =1,32-=k x . ………………………3分当1==k x 时,332-=-=k x ; ………………………4分当032=-=k x时,31==k x.综上,原方程的另一个根3-=x ,或3=x . ………………………5分四、解答题(本题共20分,每小题5分) 23.(1)证明:∵DE ∥AC ,CE ∥BD ,∴四边形OCED 为平行四边形. ………………………1分又∵四边形ABCD 是菱形, ∴AC ⊥BD .∴∠DOC =90°.∴四边形OCED 为矩形. ………………………2分(2)解法一:∵菱形ABCD ,∴AC 与BD 互相垂直平分于点O ,∴OD =OB =21BD =3,OA =OC =21AC =4, ∴S △DOC=OC OD ⋅21=4321⨯⨯=6. ………………………3分在Rt △OBC 中,BC =22OC OB +=5,sin ∠OCB =BCOB =53.作FH ⊥OC 于点H ,在Rt △CFH 中,CF =CO =4,sin ∠HCF=FCFH =53,HB ACDE FO∴FH=53CF =512. ………………………4分∴S △OCF =FH OC ⋅21=512421⨯⨯=524.∴S四边形OFCD =S △DOC +S △OCF =6+524=554. ………………………5分解法二:∵菱形ABCD ,∴AC 与BD 互相垂直平分于点O , ∴OD =OB =21BD =3,OA =OC =21AC =4, ∴S △DCB=OC DB ⋅21=4621⨯⨯=12. ………………………3分在Rt △OBC 中,BC =22OCOB +=5,sin ∠OCB =BCOB =53.作OG ⊥BC 于点G ,∵CF =CO =4,∴BF =BC − CF =5− 4=1. 在Rt △OCG 中,sin ∠OCG =OCOG =53,∴OG =53OC=GB ACDE FO512. ………………………4分∴S △OBF =OGBF ⋅211211⨯⨯6∴S 四边形OFCD =S=56=554. …………5分24.解:(1)140÷(1+52%)=92;补全条形统计图如图; …………2分(2)140×60%×1.2=100.8亿元; …………4分答:2014年全国直接丢弃的快递包装造成了约100.8亿元的损失.(3)9.1,9.2,9.3,9.4,9.5,9.6,9.7其中之一. ………………………5分 25.(1)证明:如图,连接OD ,∵DE 切⊙O 于D ,OD 是⊙O 的半径, ∴∠EDO =90°. ……(年)(亿件)…………………1分∵OD=OB错误!未找到引用源。
北京市燕山区215届九年级(上)期末考试数学试题(含答案)

燕山地区2014—2015学年度第一学期九年级期末考试 数 学 试 卷 2015年1月考 生 须 知1.本试卷共8页,共五道大题,25道小题,满分120分。
考试时间120分钟。
2.答题纸共6页,在规定位置准确填写学校名称、班级、姓名和学号。
3.试题答案一律书写在答题纸上,在试卷上作答无效。
4.考试结束,请将答题纸交回,试卷和草稿纸可带走。
一、选择题(本题共32分,每小题4分)下面各题均有四个选项,其中只有一个....是符合题意的,请将符合题意的答案代号写在答题纸的相应位置上.1.观察下列图形,是中心对称图形的是A .B .C .D .2.某校举办中学生汉字听写大会,准备从甲、乙、丙、丁4套题中随机抽取一套题对选手进行训练,则抽中甲套题的概率是A .41 B .31C .21 D .13.右图是某几何体的三视图,该几何体是A .圆锥B .圆柱C .棱柱D .正方体4.已知△ABC ∽△DEF ,相似比为1∶2,△ABC 的周长为4,则△DEF 的周长为A .2B .4C .8D .16 5.如图,点A ,B ,C 均在⊙O 上,∠ACB =35°,则∠AOB 的度数为A .20°B .40°C .60°D .70°6.如图,在Rt △ABC 中,∠C =90°,AC =1,BC =2,则cos B 的值是A .55 B .552 C .21 D .27.某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18℃的条件下生长最快的新品种.如图是某天恒温系统从开启到关闭及关闭后,大棚内温度y (℃)随时间x (小时)O CBAACB18122y (℃)x (时)CBO A俯视图左视图正视图变化的函数图象,其中BC 段是双曲线)0(≠=k xky 的一部分,则当x =16时,大棚内的温度约为A .18℃B .15.5℃C .13.5℃D .12℃ 8.如图,在Rt △OAB 中,∠AOB =90°,OA =4,OB =3. ⊙O 的半径为2,点P 是线段AB 上的一动点,过点P 作 ⊙O 的一条切线PQ ,Q 为切点.设AP =x ,PQ 2=y , 则y 与x 的函数图象大致是 A . B . C . D . 二、填空题(本题共16分,每小题4分) 9.若y x 54=,则yx= . 10.已知反比例函数)0(≠=k xky 的图象在其每一分支上,y 随x 的增大而减小,则此反比例函数的解析式可以是 .(注:只需写出一个正确答案即可) 11.如图,小明在打网球时,要使球恰好能打过网,且落点恰好在离网4米的位置上,则球拍击球的高度h 为 米.(已知网高为0.8米,击球点到网的水平距离为3米)12.在函数)0(8>=x xy 的图象上有点P 1,P 2,P 3,…,P n ,P n +1,它们的横坐标依次为1,2,3,…,n ,n +1.过点P 1,P 2,P 3,…,P n ,P n +1分别作x 轴、y 轴的垂线段,构成如图所示的若干个矩形,将图中阴影部分的面积从左至右依次记为1S ,2S ,3S ,…,n S ,则点P 1的坐标为 ;2S = ;n S = . (用含n 的代数式表示)POB AQh 米0.8米3米4米5512Oxy5512OxyyxO 12555512OxyP 5P 4S 1S 2P 3P 1P 2S 3 (56)3421Oxy三、解答题(本题共30分,每小题5分) 13.计算:2sin45°-tan60°·cos30°.14.如图,点D 是△ABC 的边AC 上的一点,AB 2=AC ·AD .求证:△ADB ∽△ABC .15.如图,正比例函数y=2x 与反比例函数)0(≠=k xky 的图象的一个交点为A (2,m ). 求m 和k 的值.yxO11ADCAB16.如图,在边长为1的小正方形组成的网格中,△ABC 的三个顶点均在格点上,点A ,B ,C 的坐标分别为(0,1),(1,-1),(5,1). (1)直接写出点B 关于原点的对称点D 的坐标; (2)将△ABC 绕点C 顺时针旋转90º得到△A 1B 1C .请在网格中画出△A 1B 1C ,并直接写出点A 1和B 1的坐标.17.如图,在半径为6cm 的⊙O 中,圆心O 到弦AB 的距离OE 为3cm .(1)求弦AB 的长;(2)求劣弧AB ⌒的长.E OABO5342xy1BAC18.在燕房线地铁施工期间,交管部门在施工路段设立了矩形路况警示牌(如图所示).已知立杆AB 的高度是3米,从路侧点D 处测得路况警示牌顶端C 点和底端B 点的仰角分别是60°和45°,求路况警示牌宽BC 的值.(精确到0.1米) (参考数据:2≈1.41,3≈1.73)四、解答题(本题共20分,每小题5分)19.如图,四边形ABCD 的对角线AC ,BD 交于点F ,点E 是BD 上一点,且∠BAC =∠BDC =∠DAE .(1)求证:△ABE ∽△ACD ;(2)若BC =2,AD =6,DE =3,求AC 的长.地 铁 施 工请绕道慢行CAB D ABCDEF20.根据某网站调查,2014年网民们最关注的热点话题分别有:消费、教育、环保、反腐及其它共五类.根据调查的部分相关数据,绘制的统计图表如下:根据以上信息解答下列问题:(1)请补全条形统计图并在图中标明相应数据;(2)若北京市约有2100万人口,请你估计最关注环保问题的人数约为多少万人? (3)在这次调查中,某单位共有甲、乙、丙、丁四人最关注教育问题,现准备从这四人中随机抽取两人进行座谈,则抽取的两人恰好是甲和乙的概率为 .21.如图,AB 为⊙O 的直径,直线l 与⊙O 相切于点C ,过点A 作AD ⊥l 于点D ,交⊙O于点E .(1)求证:∠CAD =∠BAC ;(2)若sin ∠BAC =53,BC =6,求DE 的长.反腐20%消费30%环保10%教育25%其他15%网民关注的热点问题情况统计图反腐140280210420其他教育环保消费人数(万人)热点问题420350280210140700关注各类热点问题的网民人数统计图lE D AOBC22.阅读下面材料:小辉遇到这样一个问题:如图1,在Rt △ABC 中,∠BAC =90°,AB =AC ,点D ,E 在边BC 上,∠DAE =45°.若BD =3,CE =1,求DE 的长.小辉发现,将△ABD 绕点A 按逆时针方向旋转90º,得到△ACF ,连接EF (如图2),由图形旋转的性质和等腰直角三角形的性质以及∠DAE =45°,可证△FAE ≌△DAE ,得FE =DE .解△FCE ,可求得FE (即DE )的长.请回答:在图2中,∠FCE 的度数是 ,DE 的长为 . 参考小辉思考问题的方法,解决问题:如图3,在四边形ABCD 中,AB =AD ,∠B +∠D =180°.E ,F 分别是边BC ,CD 上的点,且∠EAF =21∠BAD .猜想线段BE ,EF ,FD 之间的数量关系并说明理由.初四数学期末试卷第5页(共8页)图1ABC DE图2FABC DE图3EFDABC五、解答题(本题共22分,第23、24题每题7分,第25题8分) 23.已知关于x 的方程012=-+-k kx x .(1)求证:当2>k 时,方程总有两个不相等的实数根;(2)若二次函数)2(12>-+-=k k kx x y 的图象与x 轴交于A ,B 两点(A 在B 的左侧),与y 轴交于点C ,且tan ∠OAC =4,求该二次函数的解析式;(3)已知点P (m ,0)是x 轴上的一个动点,过点P 作垂直于x 轴的直线交(2)中的二次函数图象于点M ,交一次函数q px y +=的图象于点N .若只有当51<<m 时,点M 位于点N 的下方,求一次函数q px y +=的解析式.11Oxy24.在正方形ABCD 中,点E ,F ,G 分别是边AD ,AB ,BC 的中点,点H 是直线BC 上一点.将线段FH 绕点F 逆时针旋转90º,得到线段FK ,连接EK .(1)如图1,求证:EF =FG ,且EF ⊥FG ;(2)如图2,若点H 在线段BC 的延长线上,猜想线段BH ,EF ,EK 之间满足的数量关系,并证明你的结论.(3)若点H 在线段BC 的反向延长线上,请在图3中补全图形并直接写出线段BH ,EF ,EK 之间满足的数量关系.G EFC D BAH图3KGE FC D BAH图2G E FC D BA图125.在平面直角坐标系xOy 中,对于任意三点A ,B ,C ,给出如下定义:若矩形的任何一条边均与某条坐标轴平行,且A ,B ,C 三点都在矩形的内部或边界上,则称该矩形为点A ,B ,C 的外延矩形.点A ,B ,C 的所有外延矩形中,面积最小的矩形称为点A ,B ,C 的最佳外延矩形.例如,右图中的矩形1111D C B A ,2222D C B A ,333CD B A 都是点A ,B ,C 的外延矩形,矩形333CD B A 是点A ,B ,C 的最佳外延矩形. (1)如图1,已知A (-2,0),B (4,3),C (0,t ).①若2=t ,则点A ,B ,C 的最佳外延矩形的面积为 ; ②若点A ,B ,C 的最佳外延矩形的面积为24,则t 的值为 ; (2)如图2,已知点M (6,0),N (0,8).P (x ,y )是抛物线542++-x x y =上一点,求点M ,N ,P 的最佳外延矩形面积的最小值,以及此时点P 的横坐标x 的取值范围;(3)如图3,已知点D (1,1).E (m ,n )是函数)0(4>=x xy 的图象上一点,矩形OFEG 是点O ,D ,E 的一个面积最小的最佳外延矩形,⊙H 是矩形OFEG 的外接圆,请直接写出⊙H 的半径r 的取值范围.yxO11BA 图1图3OxyH G DE FO xyD 1D 2B 3A 3D 3C A B A 2B 2A 1B 1C 2C 1图211O xyNM数学试卷参考答案与评分标准 2015年1月一、选择题(本题共32分,每小题4分)B .A .B .C .D .B .C .A . 二、填空题(本题共16分,每小题4分) 9.45 10.x y 1-= )0(<=k xky (答案不唯一)11.1.4 12.(1,8);34;)1(8+n n . 三、解答题(本题共30分,每小题5分) 13.解:原式=233222⨯-⨯……………………………………3分 =123-=21-. ……………………………………5分14.证明:∵AB 2=AC ·AD ,∴AC AB =ABAD. ……………………………………2分 又∵∠A =∠A , ……………………………………4分 ∴△ADB ∽△ABC . ……………………………………5分 15.解:将点A (2,m )的坐标代入y=2x 中,得m =2×2,即m =4. ……………………………………2分 ∴A (2,4). ……………………………………3分将点A (2,4)的坐标代入xky =,得 k =2×4,即k =8. ………………5分 16.解:(1)D (-1,1); ………………2分(2)画出△A 1B 1C ,如图; ………………3分 A 1(5,6),B 1(3,5). ………………5分 17.解:(1)∵AB 为⊙O 的弦,OE ⊥AB 于E ,∴AE =BE =21AB . ……………………………………1分 在Rt △AOE 中,OA =6,OE =3,∴AE =22OE OA -=2236-=27=33, ………………2分 ∴AB =2AE =36. ……………………………………3分 (2)由(1)知,在Rt △AOE 中,∠AEO =90°,OA =6,OE =3, ∴cos ∠AOE =OA OE=21, ∴∠AOE =60°,O 5342x y 1BA B1CA 1-1-1∴∠AOB =2∠AOE =120°, ……………………………………4分 ∴AB⌒的长l =1806120⨯π=π4. ……………………………………5分18.解:由题意,在Rt △ABD 中,∠DAB =90°,∠ADB =45°,AB =3米,∴AD =AB =3米, ……………………………………2分 又∵Rt △ACD 中,∠DAC =90°,∠ADC =60°,∴AC =AD ·tan ∠ADC =3·tan60°=33米, ………………4分 ∴BC =AC -AB =33-3≈2.2米. ………………5分 即路况警示牌宽BC 的值约为2.2米. 四、解答题(本题共20分,每小题5分) 19.(1)证法一:∵∠BAC =∠DAE ,∴∠BAC +∠CAE =∠DAE +∠CAE ,即∠BAE =∠CAD . ……………………………………1分 又∵∠BAC =∠BDC ,∠BFA =∠CFD ,∴180°-∠BAC -∠BFA =180°-∠BDC -∠CFD ,即∠ABE =∠ACD . ……………………………………2分 ∴△ABE ∽△ACD . ……………………………………3分 证法二:∵∠BAC =∠DAE , ∴∠BAC +∠CAE =∠DAE +∠CAE ,即∠BAE =∠CAD . ……………………………………1分 又∵∠BEA =∠DAE +∠ADE ,∠ADC =∠BDC +∠ADE ,∠DAE =∠BDC ,∴∠AEB =∠ADC . ……………………………………2分 ∴△ABE ∽△ACD . ……………………………………3分 (2)∵△ABE ∽△ACD ,∴AC AB =ADAE . 又∵∠BAC =∠DAE ,∴△ABC ∽△AED , ……………………………………4分 ∴DE BC =ADAC, ∴AC =AD DE BC ⋅=632⨯=4. ……………………………………5分 20.(1)补全条形统计图如图; ………………2分(2)2100×10%=210万人; ………………4分(3)61. ………………5分21.(1)证明:连接OC ,350反腐140280210420其他教育环保消费 人数(万人)热点问题42035028021014070∵CD 为⊙O 的切线,∴OC ⊥CD , ……………………………………1分 ∵AD ⊥CD ,∴OC ∥AD , ∴∠CAD =∠ACO . 又∵OC =OA , ∴∠ACO =∠OAC ,∴∠CAD =∠OAC ,即∠CAD =∠BAC . ……………………………………2分 (2)解法一:过点B 作BF ⊥l 于点F ,连接BE , ∵AB 为⊙O 的直径,∴∠AEB =90°, 又AD ⊥l 于点D ,∴∠AEB =∠ADF =∠BFD =90°, ∴四边形DEBF 是矩形,∴DE =BF . ……………………………………3分∵AB 为⊙O 的直径,∴∠ACB =90°,∴∠ACD +∠BCF =90°.∵∠ADC =90°,∴∠ACD +∠CAD =90°, ∴∠BCF =∠CAD . ∵∠CAD =∠BAC ,∴∠BCF =∠BAC . ……………………………………4分在Rt △BCF 中,BC =6,sin ∠BCF =BC BF =sin ∠BAC =53, ∴BF =BC 53=518,∴DE =BF =518. ……………………………………5分解法二:连接CE ,∵AB 为⊙O 的直径,∴∠ACB =90°. ∵A ,B ,C ,E 四点共圆, ∴∠AEC +∠ABC =180°. 又∵∠AEC +∠DEC =180°,∴∠DEC =∠ABC ,∴Rt △CDE ∽Rt △ACB , ……………………………………3分 ∴BC DE =ACCD. 在Rt △ABC 中,sin ∠BAC =AB BC =53,BC =6, ∴AB =BC 35=10,∴AC =22BC AB =8. lEDA O BClF E D A OBClEDA O BC在Rt △ADC 中,∵∠DAC =∠BAC ,∴sin ∠DAC =AC CD =sin ∠BAC =53, ∴CD =AC 53=524. ……………………………………4分∴DE =AC BC CD ⋅=86524⨯=518. ……………………………………5分22.90°;10. ……………………………………2分猜想:EF =BE +FD ; ……………………………………3分 理由如下:如图,将△ABE 绕点A 按逆时针方向旋转,使AB 与AD 重合,得到△ADG , ∴BE =DG ,AE =AG ,∠DAG =∠BAE ,∠B =∠ADG , ∵∠B +∠ADC =180°,∠B =∠ADG ,∴∠ADG +∠ADC =180°,即点F ,D ,G 在同一条直线上. ∵∠EAF =21∠BAD , ∴∠GAF =∠DAG +∠DAF =∠BAE +∠DAF =∠BAD -∠EAF =∠EAF , 即∠GAF =∠EAF . ……………………………………4分在△AEF 和△AGF 中,⎪⎩⎪⎨⎧∠∠AF AF GAF EAF AG AE =,=,=∴△AEF ≌△AGF , ∴EF =FG .∵FG =DG +FD =BE +DF ,∴EF =BE +FD . ……………………………………5分五、解答题(本题共22分,第23题8分,第24、25题每小题7分)23.(1)证明:∵)1(14)(2-⨯⨯--=∆k k =2)2(-k , ………………1分又∵2>k ,∴02>-k ,∴0)2(2>-k ,即0>∆,∴当2>k 时,方程总有两个不相等的实数根. ………………2分 (2)解:∵)2(12>-+-=k k kx x y 与x 轴交于A 、B 两点,∴令0y =,有210x kx k -+-=,解得 1=x ,或1-=k x . ………………3分EFD GABC C1yP N∵2>k ,点A 在点B 的左侧, ∴A (1,0),B (1-k ,0). ∵抛物线与y 轴交于点C ,∴C (0,1-k ). ……………………………………4分 在Rt △AOC 中,tan ∠OAC =OA OC =11-k =4, 解得5=k .∴抛物线的解析式为452+-=x x y . ……………………………………5分 (3)依题意并结合图象可知,一次函数的图象与二次函数的图象交点的横坐标分别为1和5,由此可得交点坐标为(1,0)和(5,4). ………………6分 将交点坐标分别代入一次函数解析式q px y +=中,得⎩⎨⎧+=+q p q p 54,0=, 解得⎩⎨⎧-1,1==q p , ∴一次函数的解析式为1-=x y . ……………………………………7分 24.(1)证明:∵正方形ABCD ,E ,F ,G 分别是边AD ,AB ,BC 的中点,∴AE =AF =FB =BG ,∠A =∠B =90°,∴△AEF ≌△BGF , ……………………………………1分 ∴EF =FG ,∠AFE =∠BFG =45°,∴∠EFG =180°-∠AFE -∠BFG =90°,即EF ⊥FG . ………………2分 (2)BH =22EF +EK ; ……………………………………3分 证明:将线段FH 绕点F 逆时针旋转90º,得到线段FK , ∴FH =FK ,∠HFK =90°, ∴∠KFE +∠EFH =90°,∵∠EFG =90°,∴∠HFG +∠EFH =90°, ∴∠KFE =∠HFG , 在△EFK 和△GFH 中,FK =FH ,∠KFE =∠HFG ,EF =FG ,∴△EFK ≌△GFH , ……………………………………4分 ∴EK =GH .∵△BFG 是等腰直角三角形,∴BG =22FG ,∴BH =BG +GH =22FG +EK =22EF +EK , 即BH =22EF +EK .……………………………………5分(3)补全图形如图; ……………………………………6分BH =EK -22EF . ……………………………………7分25.(1)①18; ……………………………………1分②4=t 或1-=t ; ……………………………………3分 (2)如图,过M 点作x 轴的垂线与过N 点垂直于y 轴的直线交于点Q ,则当点P 位于矩形OMQN 内部或边界时,矩形OMQN 是点M ,N ,P 的最佳外延矩形,且面积最小.∵S 矩形OMQN =OM ·ON =6×8=48,∴点M ,N ,P 的最佳外延矩形面积的最小值为48.………………4分 抛物线542++-x x y =与y 轴交于点T (0,5). 令0y =,有0542=++-x x , 解得 1-=x (舍),或5=x . 令8=y ,有8542=++-x x , 解得 1=x ,或3=x .∴10≤≤x ,或53≤≤x . ……………………………………6分 (3)2172≤≤r . ……………………………………8分 说明:各解答题的其他正确解法请参照以上标准按分步给分的原则酌情评分.yxO 11J R SN M TQK PK G E F C D BA H。
2014-2015学年北京市燕山区七年级下学期期末考试数学试题(含答案)

燕山地区2014—2015学年度第二学期七年级期末考试数 学 试 卷 2015月7月一、选择题(本题共30分,每小题3分)下面各题均有四个选项,其中只有一个....是符合题意的,请将正确答案前的字母填入下面的答题表中.题号 1 2 3 4 5 6 7 8 9 10 选项1.9的平方根是 A .±3B .3C .-3D .92.不等式2x -4 ≤ 0的解集是 A .x <2B .x >2C .x ≤ 2D .x ≥ 23.在平面直角坐标系中,点P (-2,3)位于 A .第一象限B .第二象限C .第三象限D .第四象限4.下列调查中,适合采用全面调查(普查)方式的是 A .对长江水质情况的调查B .对端午节期间市场上粽子质量情况的调查C .对某班40名同学体重情况的调查D .对某类烟花爆竹燃放安全情况的调查 5.下列各数中,是无理数的是 A .16B .3.14C .311D .76.已知1,1x y =⎧⎨=-⎩是方程2x -ay =3的一组解,那么a 的值为A .1B .3C .-3D .-157.下列各式中,运算正确的是 A .235a b ab +=B .220a b ab -=C .222(2)4ab a b =D .222()a b a b +=+ 8.如果a <b ,那么下列不等式成立的是 A .a -b >0B .a -3>b -3C .1133a b >D .-3a >-3b初二数学试卷第1页(共8页)9.若2(5)(20)x x x mx n -+=++,则m ,n 的值分别为A .15m =-,100n =-B .15m =,100n =-C .25m =,100n =D .25m =,100n =-10.在日常生活中如取款、上网等都需要密码.有一种用“因式分解法”产生的密码,方便记忆.原理是:如对于多项式44y x -,因式分解的结果是22()()()x y x y x y -++,取99==y x ,时,各个因式的值是:()0x y -=,()18x y +=,22()162x y +=,于是就可以把“018162”作为一个六位数的密码.对于多项式4229x x y -,取8x =,11y =时,用上述方法产生的密码不可能...是 A .643513 B .643153 C .641335 D .356413 二、填空题(本题共18分,每小题3分)11.已知x 的一半与5的差小于3,用不等式表示为 . 12.已知方程5x -y =7,用含x 的代数式表示y ,y = . 13.不等式2x +5>4x -1的正整数解是 . 14.点A (4,-3)到x 轴的距离为 . 15.若162++mx x 是完全平方式,则m = .16.已知关于x ,y 的方程组34,3x y a x y a +=-⎧⎨-=⎩,其中-3 ≤ a ≤ 1,给出下列命题:① 5,1x y =⎧⎨=-⎩是方程组的解;② 当a =-2时,x ,y 的值互为相反数;③ 当a =1时,方程组的解也是方程x +y =4-a 的解; ④ 若x ≤ 1,则1 ≤ y ≤ 4.其中正确命题的序号是 .(把所有正确命题的序号都填上)三、解答题(本题共52分.第17题~18题,每题各6分,每小题各3分;第19题~26题,每题各5分)17.计算:(1) 34825-; (2) 232(2)x y xy ⋅÷.18.因式分解:(1) 24x-;(2) 2()()a ab b b a---.19.解方程组:320,1. x yx y-=⎧⎨-=⎩20.解不等式组:2734532xx x+>⎧⎨-≤-⎩,,并把它的解集在数轴上表示出来.0 1 2 3 4-1-2-3 x3090120频数(人)0m (条)DC B A1201008060402021.先化简,再求值:24(1)(2)x x x ---,其中3x =.22.列方程组...解应用题: 随着人民生活水平的不断提高,外出采摘成了近郊旅游新时尚.端午节期间,小王一家去某农场采摘樱桃,已知A 品种樱桃采摘价格为80元/千克,B 品种樱桃采摘价格为60元/千克.若小王一家采摘A ,B 两种樱桃共8千克,共消费580元,那么他们采摘A ,B 两种樱桃各多少千克?23.在某项针对18~35岁的青年人每天发微博数量的调查中,设一个人的“日均发微博条数”为m ,规定:当0 ≤ m <5时为A 级,5 ≤ m <10时为B 级,10 ≤ m <15时为C 级,15 ≤ m <20时为D 级.现随机抽取部分符合年龄条件的青年人开展每人“日均发微博条数”的调查,根据调查数据整理并制作图表如下:m 频数 百分数 A 级(0 ≤ m <5) 90 0.3 B 级(5 ≤ m <10) 120 a C 级(10 ≤ m <15) b 0.2 D 级(15 ≤ m <20) 300.1请你根据以上信息解答下列问题:(1)在表中:a = ,b = ;青年人日均发微博条数直方图青年人日均发微博条数统计表(2)补全频数分布直方图;(3)若北京市常住人口中18~35岁的青年人大约有530万人,试估计其中“日均发微博条数”不少于10条的大约有多少万人.24.如图,在直角坐标系xOy中,A(﹣1,0),B(3,0),将A,B同时分别向上平移2个单位,再向右平移1个单位,得到的对应点分别为D,C,连接AD,BC.(1)直接写出点C,D的坐标:C(,),D(,);(2)四边形ABCD的面积为;(3)点P为线段BC上一动点(不含端点),连接PD,PO.求证:∠CDP+∠BOP=∠OPD.25.图①是一个长为2m,宽为2n(m>n)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它平均分成形状和大小都一样的四块小长方形,然后按图②那样拼成一个正方形.n n m mmm nn图①图②21O xPD CBAy(1)观察图②,请用两种不同的方法表示图②中阴影部分的面积:方法1: ; 方法2: ;(2)直接写出三个代数式2)(n m +,2)(n m -,mn 之间的等量关系:; (3)根据(2)中的等量关系,解决如下问题:若7=+b a ,5=ab ,求b a -的值.26.在平面直角坐标系中,已知点A (-2,0),B (2,0),若在坐标轴上存在点C ,使得AC +BC =m ,则称点C 为点A ,B 的“m 和点”,例如当点C 的坐标为(0,0)时,有 AC +BC =4,则称点C (0,0)为点A ,B 的“4和点”. 请根据上述规定回答下列问题:(1) 若点C 为点A ,B 的“m 和点”,且△ABC 为等边三角形,求m 的值;(2) 点E 是点A ,B 的“5和点”,且点E 在x 轴上,则点E 的坐标为 ; (3) 若点A ,B 的“m 和点”有且只有4个,则m 的取值范围是 .以 下 为 草 稿 纸参考答案及评分标准 2015.07说明: 与参考答案不同,但解答正确相应给分. 一、选择题(本题共30分,每小题3分)ACBCD ACDBB二、填空题(本题共18分,每小题3分) 11.3521<-x 12.75-x y = 13.1,2 14.3 15.±8 16.②③④三、解答题(本题共52分.17题~18题,每小题各3分;19题~26题,每题各5分)17.(1) 原式=522-……………………2分 =58. ……………………3分 (2) 原式=2324xy y x ÷⋅ ……………………1分=xy 4. ……………………3分18.(1) 42-x =)2)(2(-+x x ……………………3分 (2) 原式=)()(2b a b b a a -+- ……………………1分=)2)((b a b a +-. ……………………3分19.⑴解法一:⎩⎨⎧=-=-②.1①,023y x y x ,②×2得,2x -2y =2,③①-③得,x =-2; ……………………2分频数(人)30901206012010080604020把x =-2代入①得,02)2(3=--⨯y ,解得y =-3. ……………………4分∴方程组的解是⎩⎨⎧-=-=.3,2y x . ……………………5分解法二:⎩⎨⎧=-=-②.1①,023y x y x ,由②得,x =1+y ,③ ……………………2分 把③代入①得,3(1+y )-2y =0,解得y =-3. ……………………4分 把y =-3代入③得,x =-2. ∴方程组的解是⎩⎨⎧-=-=.3,2y x . ……………………5分20.解:解不等式①,得x >-2, ……………………1分解不等式②,得3≤x , ……………………2分 ∴这个不等式组的解集是32≤<x -. ……………………3分 在数轴上表示解集如图: ………5分 21.原式=)44()44(22+---x x x x ……………………2分=444422-+--x x x x=432-x ……………………3分 当3=x 时,原式=4)3(32-⨯=5. ……………………5分 22.解:设小王一家采摘A 品种樱桃x 千克,B 品种樱桃y 千克,……………………1分依题意,得⎩⎨⎧=+=+.5806080,8y x y x ……………………3分解得⎩⎨⎧==.3,5y x ……………………4分答:小王一家采摘A 品种樱桃5千克,B 品种樱桃3千克. ……………………5分23.(1)在表中:a =0.4,b =60; ……………………2分(2)补全频数分布直方图如图; ……………………3分(3)530×(0.2+0.1)=159(万人). ……………………5分-3-2x 43210-124.(1) C (4,2),D (0,2); ……………………2分(2) 四边形ABCD 的面积为 8 ; ……………………3分(3) 证明:如图,过点P 作PQ ∥AB , …………4分由题意,CD ∥AB , ∴CD ∥PQ ,AB ∥PQ , ∴∠CDP =∠1,∠BOP =∠2,∴∠CDP +∠BOP =∠1+∠2=∠OPD . ……………………5分 25.(1) 2)(n m -; mn n m 4)(2-+; ……………………2分 (2) 2)(n m -=mn n m 4)(2-+; ……………………3分 (3) 2)(b a -=ab b a 4)(2-+=5472⨯-=29,∴ b a -=29±. ……………………5分26.(1) ∵ 点A (-2,0),B (2,0),∴AB =4,∵ △ABC 为等边三角形, ∴AC =BC =AB =4,∴ m =AC +BC =8. ……………………2分 (2) E (-2.5,0),或E (2.5,0). ……………………4分 (3) 4>m . ……………………5分12Q 21OxP DC BA y。
2015年北京燕山初三一模数学试题及答案整理版
燕山2015年4月 一、选择题(本题共30分,每小题3分) 1.-2的相反数是 A .2B .2-C .12-D .122.据报道,中国内地首次采用“全无人驾驶”的燕房线地铁有望年底完工,列车通车后将极大改善房山和燕山居民的出行条件,预计年输送乘客可达7300万人次,将7300用科学记数法表示应为A .21073⨯B .3103.7⨯C .41073.0⨯D .2103.7⨯3.下面的几何体中,俯视图为三角形的是A . B .C . D . 4.如图,∠1=∠B ,∠2=25°,则∠D =A .25°B .45°C .50°D .65°5.下面是某小区居民家庭的月用水量情况统计表:12ABCD从中任意抽出一个家庭进行用水情况调查,则抽到的家庭月用水量为6吨的概率为A .41 B .52 C .103 D .2016A .众数和方差B .平均数和中位数C .众数和平均数D .众数和中位数7.在多项式x 2+9中添加一个单项式,使其成为一个完全平方式,则添加的单项式可以是 A .xB .3xC .6xD .9x8.如图,⊙O 的半径长6cm ,点C 在⊙O 上,弦AB 垂直平分OC 于点D ,则弦AB 的长为A .9 cmB .36cmC .29cmD .33cm9.在△ABC 中,按以下步骤作图:①分别以A ,B 为圆心,大于21AB 的长为半径画弧,相交于两点M ,N ;②作直线MN 交AC 于点D ,连接BD .若CD =BC ,∠A =35°,则∠C = A .40° B .50° C .60° D .70°10.李阿姨每天早晨从家慢跑到小区公园,锻炼一阵后,再y (t (单位:分)的函数关系P 点表示李阿姨家的位置)A .B .C .二、填空题(本题共18分,每小题3分)11.若代数式23-x有意义,则x 的取值范围是 . 12.分解因式:aab -2= .13.如图,跷跷板AB 的支柱OD 经过它的中点O ,且垂直于地面BC ,垂足为D ,OD =45cm ,当它的一端B 着地时,另一端A 离地面的高度AC 为 cm .14.已知某函数图象经过点(-1,1),且当x >0时,y 随x 的增大而增大.请你写出一个..满足条件的函数解析式:y = .15.为了节能减排,近期纯电动出租车正式上路运行.某地纯电动出租车的运价为3公里以内10元;超出3公里后每公里2元;单程超过15公里,超过部分每公里3元.小周要到离家10公里的博物馆参观,若他往返都乘坐纯电动出NM ABDCB分租车,共需付车费 元.16.定义:对于任意一个不为1的有理数a ,把a-11称为a 的差倒数,如2的差倒数为1211-=-,1-的差倒数为)1(11--=21.记211=a ,2a 是1a 的差倒数,3a 是2a 的差倒数,4a 是3a 的差倒数,…,依此类推,则2a = ;2015a = .三、解答题(本题共30分,每小题5分)17.如图,点E ,F 在线段AC 上,AB ∥CD ,AB =CD ,AE =CF . 求证:BE =DF .18.计算:01)3(30tan 3|3|)31(π-+︒--+-.19.解不等式组:⎩⎨⎧≤-<-.21512x x ,20.已知022=--x x ,求代数式)1)(1()12(-+--x x x x 的值. 21.列方程或方程组解应用题:赵老师为了响应市政府“绿色出行”的号召,改骑自行车上下班,结果每天上班所用时间比自驾车多53小时.已知赵老师家距学校12千米,上下班高峰时段,自驾车的速度是自行车速度的2倍.求赵老师骑自行车的速度.22.已知关于x 的方程03)32(22=-+--k k x k x . (1)求证:方程总有两个不相等的实数根;ABCDEFDO FECAB(2)已知方程有一个根为0,请求出方程的另一个根.四、解答题(本题共20分,每小题5分)23.如图,菱形ABCD 中,对角线AC ,BD 交于O 点,DE ∥AC ,CE ∥BD . (1)求证:四边形OCED 为矩形;(2)在BC 上截取CF =CO ,连接OF ,若AC =8,BD =6,求四边形OFCD 的面积.24.根据国家邮政局相关信息,2014年我国快递业务量达140亿件,比2013年增长52%,跃居世界第一,而快递产生的包装垃圾也引起了邮政管理部门的重视.以下是根据相关数据绘制的统计图的一部分.根据以上信息,解答下列问题:(1)请补全条形统计图并标明相应数据;(结果保留整数)(2)每件快递专用包装的平均价格约为1.2元,据此计算2014年全国直接丢弃的快递包装造成了约多少亿元的损失?(3)北京市2014年的快递业务量约为6亿件,预计2015年的增长率与近五年全国快递业务量年增长率的平均值近似相等,据此估计2015年北京市快递业务量将达到亿件.(直接写出结果,精确到0.1)25.如图,△ABC 中,AB =AC ,以AB 为直径作⊙O 交BC 于点D ,过点D 作⊙O 的切线DE 交AC 于点E .市民收到快递后对包装处理方式统计图D :其他C :留着下次寄件使用;B :收集整理后作 为废品卖掉;A:直接丢弃;(1)求证:∠CDE =90°;(2)若AB =13,sin ∠C =135,求CE的长.26.阅读下面材料:小军遇到这样一个问题:如图1,△ABC 中,AB =6,AC =4,点D 为BC的中点,求AD 的取值范围.小军发现老师讲过的“倍长中线法”可以解决这个问题.他的做法是:如图2,延长AD 到E ,使DE =AD,连接BE ,构造△BED ≌△CAD ,经过推理和计算使问题得到解决.参考小军思考问题的方法,解决问题:如图3,△ABC 中,E 为AB 中点,P 是CA 延长线上一点,连接PE 并延长交BC 于点D .求证:PA?CD =PC?BD .五、解答题(本题共22分,第27题7分,第28题7分,第29题8分) 27.抛物线c bx x y C ++=2121:与y 轴交于点C (0,3),其对称轴与x 轴交于点A (2,0).(1)求抛物线1C 的解析式;ABDCAB D CEE ABDP(2)将抛物线1C 适当平移,使平移后的抛物线2C 的顶点为D (0,k ).已知点B (2,2),若抛物线2C 与△OAB 的边界总有两个公共点,请结合函数图象,求k 的取值范围.28.△ABC 中,∠ABC =45°,AH ⊥BC 于点H ,将△AHC 绕点H 逆时针旋转90°后,点C 的对应点为点D ,直线BD 与直线AC 交于点E ,连接EH .(1)如图1,当∠BAC 为锐角时,①求证:BE ⊥AC ;②求∠BEH 的度数; (2)当∠BAC 为钝角时,请依题意用实线补全图2,并用等式表示出线段EC ,ED ,EH 之间的数量关系29.在平面直角坐标系中,如果点P 的横坐标和纵坐标相等,则称点P 为和谐点.例如点(1,1),(31-,31-),(2-,2-),…,都是和谐点.(1)分别判断函数12+-=x y 和12+=x y 的图象上是否存在和谐点,若存在,求出其和谐点的坐标;(2)若二次函数)0(42≠++=a c x ax y 的图象上有且只有一个和谐点(23,23),且当m x ≤≤0时,函数)0(4342≠-++=a c x ax y 的最小值为-3,最大值为1,求m 的取值范围.交于点(3)直线2:+=kx y l 经过和谐点P ,与x 轴D ,与反比例函数xn y G =:的图象交于M ,N 两点(点M 在点N 的左侧),若点P的横坐标为1,且23<+DN DM ,请直接写出n 的取值范围.燕山地区2015年初中毕业考试数学试卷参考答案与评分标准 2015年4月一、选择题(本题共30分,每小题3分)1D二、填空题(本题共18分,每小题3分) 11.2≠x 12.)1)(1(-+b b a ; 13.90; 14.答案不唯一:xy 1-=,2x y =,2+=x y ,…15.48; 16.2;2.三、解答题(本题共30分,每小题5分) 17.证明:∵AB∥CD ,∴∠A =∠C . ………………………1分在△BAE 和△DCF 中,⎪⎩⎪⎨⎧∠=∠=,=,CF AE C A CD AB ,∴△BAE ≌△DCF (SAS ), ………………………4分∴BE =DF . ………………………5分 18.解:原式=133333+⨯-+ ………………………4分 =4. ………………………5分19.解:解不等式①,得3<x , ………………………2分解不等式②,得1-≥x , (4)分∴原不等式组的解集为31<≤-x . ………………………5分 20.解:)1)(1()12(-+--x x x x=)1(222---x x x ………………………2分=1222+--x x x=12+-x x . ………………………3分∵022=--x x ,即22=-x x . ………………………4分 ∴原式=1)(2+-x x =2+1=3. ………………………5分21.解:设赵老师骑自行车的速度为x 千米/小时, ………………………1分依题意得5321212=-x x , ………………………2分 解方程得 x =10. ………………………3分经检验,x =10是原方程的解且符合实际意义. ………………………4分答:赵老师骑自行车的速度是10千米/小时. ………………………5分22.解:(1)Δ=)3(14)32(22k k k -⨯⨯-- ………………………1分=k k k k 124912422+-+-=9>0,∴ 原方程总有两个不相等的实数根. ………………………2分 (2)解法一: 把0=x 代入方程03)32(22=-+--k k x k x 中, 得 032=-k k , 解得 0=k ,或3=k .………………………3分当0=k 时,原方程化为032=+x x ,解得 31-=x ,02=x ; ………………………4分 当3=k 时,原方程化为032=-x x ,解得 31=x ,02=x .综上,原方程的另一个根3-=x ,或3=x . (5)分解法二:∵Δ=9,由求根公式,得23)32(129)32(21±-=⨯±-=k k x ,,∴原方程的根为k x =1,32-=k x . ………………………3分 当01==k x 时,332-=-=k x ; ………………………4分 当032=-=k x 时,31==k x .综上,原方程的另一个根3-=x ,或3=x . (5)分四、解答题(本题共20分,每小题5分) 23.(1)证明:∵DE ∥AC ,CE ∥BD ,∴四边形OCED 为平行四边形. ………………………1分 又∵四边形ABCD 是菱形, ∴AC ⊥BD .∴∠DOC =90°.∴四边形OCED 为矩形. ………………………2分 (2)解法一:∵菱形ABCD ,HACD E O∴AC 与BD 互相垂直平分于点O ,∴OD =OB =21BD =3,OA =OC =21AC =4,∴S △DOC =OC OD ⋅21=4321⨯⨯=6. ………………………3分 在Rt △OBC 中,BC =22OC OB +=5,sin ∠OCB =BCOB=53.作FH ⊥OC 于点H ,在Rt △CFH 中,CF =CO =4,sin ∠HCF =FCFH=53,∴FH =53CF =512. ………………………4分 ∴S △OCF =FH OC ⋅21=512421⨯⨯=524. ∴S 四边形OFCD =S △DOC +S △OCF =6+524=554. ………………………5分解法二:∵菱形ABCD ,∴AC 与BD 互相垂直平分于点O ,∴OD =OB =21BD =3,OA =OC =21AC =4,∴S △DCB =OC DB ⋅21=4621⨯⨯=12. ………………………3分 GB ACDEFO在Rt △OBC 中,BC =22OC OB +=5,sin ∠OCB =BCOB=53.作OG ⊥BC 于点G ,∵CF =CO =4,∴BF =BC ? CF =5? 4=1. 在Rt △OCG 中,sin ∠OCG =OCOG=53,∴OG =53OC =512. ………………………4分∴S △OBF =OG BF ⋅21=512121⨯⨯=56. ∴S 四边形OFCD =S △DCB ?S △OBF=12?56=554.…………5分 24.解:(1)140÷(1+52%)=92;补全条形统计图如图; …………2分(2)140×60%×1.2=100.8亿元; …………4分答:2014年全国直接丢弃的快递包装造成了约100.8亿元的损失.(年)(亿件(3)9.1,9.2,9.3,9.4,9.5,9.6,9.7其中之一. ………………………5分25.(1)证明:如图,连接OD , ∵DE 切⊙O 于D ,OD 是⊙O 的半径,∴∠EDO =90°.………………………1分∵OD =OB , ∴∠ABC =∠ODB . ∵AB =AC , ∴∠ABC =∠C , ∴∠ODB =∠C , ∴DO ∥AC ,∴∠CED =∠EDO =90°. ………………………2分 (2)如图,连接AD ,∵AB 为⊙O 直径,∴∠ADB =90°,即AD ⊥BC . ………………………3分 在Rt △CED 和Rt △BDA 中,∠C =∠ABC ,∠DEC =∠ADB =90°, ∴△CED ∽△BDA ,∴sin∠ABC =AB =sin ∠C =13, ∴AD =135AB =5, ∴CD =BD =22AD AB -=12.∴131212⨯=CE =13144. ………………………5分26.(1)1<AD <5; ………………………2分(2)证明:延长PD 至点F ,使EF =PE ,连接BF . ………………………3分∵BE =AE ,∠BEF =∠AEP , ∴△BEF ≌△AEP , ∴∠APE =∠F ,BF =PA . 又∵∠BDF =∠CDP ,即PA ·CD =PC ·BD . ………………………5分 五、解答题(本题共22分,第27、28题每小题7分,第29题8分) 27.解:(1)∵抛物线c bx x y ++=221与y 轴交于点C (0,3),∴3=c ; ………………………1分∵抛物线c bx x y ++=221的对称轴为2=x ,∴2212=⨯-b ,解得2-=b , ………………………2分 ∴抛物线1C 的解析式为32212+-=x x y . ………………………3分(2)由题意,抛物线2C 的解析式为k x y +=221. ………………………4分当抛物线经过点A (2,0)时,02212=k +⨯,解得2-=k . ………………………5分 ∵O (0,0),B (2,2),∴直线OB 的解析式为x y =由⎪⎩⎪⎨⎧+==k x y x y 221,,得0222=+-k x x ,(*)当Δ=k 214)2(2⨯⨯--=0,即21=k 时, ………………………6分抛物线2C 与直线OB 只有一个公共点, 此时方程(*)化为0122=+-x x , 解得1=x ,即公共点P 的横坐标为1,点P 在线段OB 上.∴k 的取值范围是212<<-k .7分28.(1)①证明:∵AH ⊥BC 于点H ∴△ABH 为等腰直角三角形, ∴AH =BH ,∠BAH =45°,∴△AHC 绕点H 逆时针旋转90°得△BHD , 由旋转性质得,△BHD ≌△AHC ,∴∠1=∠2. ………………………1分 ∵∠1+∠C =90°, ∴∠2+∠C =90°,∴∠BEC =90°,即BE ⊥AC . ………………………2分 ②解法一:如图1-1, ∵∠AHB =∠AEB =90°,∴A ,B ,H ,E 四点均在以AB 为直径的圆上, ………………………3分 ∴∠BEH =∠BAH =45°. ………………………4分 解法二:如图1-2,过点H 作HF ⊥HE 交BE 于F 点,∴∠FHE即∠4+∠5=90°.又∵∠3+∠5=∠AHB =90°, ∴∠3=∠4.在△AHE 和△BHF 中,⎪⎩⎪⎨⎧∠=∠=∠=∠,,,3421BH AH ∴△AHE ≌△BHF , ………………………3分 ∴EH =FH .∵∠FHE =90°,∴△FHE 是等腰直角三角形,∴∠BEH =45°. ………………………4分29.解:(1)令x x =+-12,解得31=x ,∴函数12+-=x y 的图象上有一个和谐点(31,31); ………………………2分令x x =12+,即012=+-x x ,∵根的判别式Δ=114)1(2⨯⨯--=-3<0, ∴方程012=+-x x 无实数根,∴函数12+=x y ………………………3分(2)令x c x ax =++42,即32ax +由题意,Δ=ac 432-=0,即4ac 又方程的根为2323=-a , 解得1-=a ,49-=c . ………………………4分∴函数4342-++=c x ax y ,即342-+-=x x y ,如图,该函数图象顶点为(2,1),与y 轴交点为(0,-3), 由对称性,该函数图象也经过点(4,-3). ………………………5分由于函数图象在对称轴2=x 左侧y 随x 的增大而增大,在对称轴右侧y 随x 的增大而减小,且当m x ≤≤0时,函数342-+-=x x y 的最小值为-3,最大值为1,∴42≤≤m . ………………………6分(3)045<<n -,或10<<n . ………………………8分说明:各解答题的其他正确解法请参照以上标准按分步给分的原则酌情评分. 2020-2-8。
北京市燕山一模2015年初中毕业考试
北京市燕山一模2015年初中毕业考试 数 学 试 卷 2015年4月一、选择题(本题共30分,每小题3分)下面各题均有四个选项,其中只有..一个..是符合题意的. 1.-2的相反数是A .2B .2-C .12-D .122.据报道,中国内地首次采用“全无人驾驶”的燕房线地铁有望年底完工,列车通车后将极大改善房山和燕山居民的出行条件,预计年输送乘客可达7300万人次,将7300用科学记数法表示应为A .21073⨯ B .3103.7⨯ C .41073.0⨯ D .2103.7⨯ 3A .B .C .D . 4.如图,∠1=∠B ,∠2=25°,则∠D =A .25°B .45°C .50°D .65° 5.下面是某小区居民家庭的月用水量情况统计表:从中任意抽出一个家庭进行用水情况调查,则抽到的家庭月用水量为6吨的概率为 A .41 B .52 C .103 D .201 6以上两位同学的对话反映出的统计量是A .众数和方差B .平均数和中位数C .众数和平均数D .众数和中位数7.在多项式x 2+9中添加一个单项式,使其成为一个完全平方式,则添加的单项式可以是A .xB .3xC .6xD .9x 8.如图,⊙O 的半径长6cm ,点C 在⊙O 上,弦AB 垂直平分OC 于点D ,则弦AB 的长为第4题图12ABCDA .9 cmB .36cmC .29cm D .33cm9.在△ABC 中,按以下步骤作图:①分别以A ,B 为圆心,大于21AB 的长为半径画弧,相交于两点M ,N ;②作直线MN 交AC 于点D ,连接BD .若CD =BC ,∠A =35°,则 ∠C = A .40°B .50°C .60°D .70°10.李阿姨每天早晨从家慢跑到小区公园,锻炼一阵后,再慢跑回家.表示李阿姨离开家的距离y (单位:米)与时间t (单位:分)的函数关系的图象大致如上图所示,则李阿姨跑步的路线可能是(用)A .B .C .D .二、填空题(本题共18分,每小题3分) 11.若代数式23-x 有意义,则x 的取值范围是. 12.分解因式:a ab -2=.13.如图,跷跷板AB 的支柱OD 经过它的中点O ,且垂直于地面BC ,垂足为D ,OD =45cm ,当它的一端B 着地时,另一端A 离地面的高度AC 为 cm .14.已知某函数图象经过点(-1,1),且当x >0时,y 随x 的增大而增大.请你写出一个..满足条件的函数解析式:y = .15.为了节能减排,近期纯电动出租车正式上路运行.某地纯电动出租车的运价为3公里以内10元;超出3公里后每公里2元;单程超过15公里,超过部分每公里3元.小周要到离家10公里的博物馆参观,若他往返都乘坐纯电动出租车,共需付车费 元. 16.定义:对于任意一个不为1的有理数a ,把a -11称为a 的差倒数,如2的差倒数为1211-=-,NM ABD C第9题图B CD第13题图第8题图分第10题图1-的差倒数为)1(11--=21.记211=a ,2a 是1a 的差倒数,则2a 3a 是2a 的差倒数,4a 是3a 的差倒数,…,依此类推,= ;2015a = .三、解答题(本题共30分,每小题5分)17.如图,点E ,F 在线段AC 上,AB ∥CD ,AB =CD ,AE =CF . 求证:BE =DF .18.计算:01)3(30tan 3|3|)31(π-+︒--+-.19.解不等式组:⎩⎨⎧≤-<-.21512x x ,20.已知022=--x x ,求代数式)1)(1()12(-+--x x x x 的值.21.列方程或方程组解应用题:赵老师为了响应市政府“绿色出行”的号召,改骑自行车上下班,结果每天上班所用时间比自驾车多53小时.已知赵老师家距学校12千米,上下班高峰时段,自驾车的速度是自行车速度的2倍.求赵老师骑自行车的速度.22.已知关于x 的方程03)32(22=-+--k k x k x .(1)求证:方程总有两个不相等的实数根;(2)已知方程有一个根为0,请求出方程的另一个根. 四、解答题(本题共20分,每小题5分)23.如图,菱形ABCD 中,对角线AC ,BD 交于O 点,DE ∥AC ,CE ∥BD .(1)求证:四边形OCED 为矩形;(2)在BC 上截取CF =CO ,连接OF ,若AC =8,BD =6,求四边形OFCD 的面积.ABCDE F D O FECAB24.根据国家邮政局相关信息,2014年我国快递业务量达140亿件,比2013年增长52%,跃居世界第一,而快递产生的包装垃圾也引起了邮政管理部门的重视.以下是根据相关数据绘制的统计图的一部分.根据以上信息,解答下列问题:(1)请补全条形统计图并标明相应数据;(结果保留整数)(2)每件快递专用包装的平均价格约为1.2元,据此计算2014年全国直接丢弃的快递包装造成了约多少亿元的损失?(3)北京市2014年的快递业务量约为6亿件,预计2015年的增长率与近五年全国快递业务量年增长率的平均值近似相等,据此估计2015年北京市快递业务量将达到 亿件.(直接写出结果,精确到0.1)25.如图,△ABC 中,AB =AC ,以AB 为直径作⊙O 交BC 于点D ,过点D 作⊙O 的切线DE 交AC于点E .(1)求证:∠CDE =90°;(2)若AB =13,sin ∠C =135,求CE 的长.市民收到快递后对包装处理方式统计图D :其他C :留着下次寄件 使用;B :收集整理后作 为废品卖掉;A:直接丢弃;(年)(亿件)2010-2014年全国快递业务量统计图26.阅读下面材料:小军遇到这样一个问题:如图1,△ABC 中,AB =6,AC =4,点D 为BC 的中点,求AD的取值范围.小军发现老师讲过的“倍长中线法”可以解决这个问题.他的做法是:如图2,延长AD 到E ,使DE =AD ,连接BE ,构造△BED ≌△CAD ,经过推理和计算使问题得到解决.如图3,△ABC 中,E 为AB 中点,P 是CA 延长线上一点,连接PE 并延长交BC 于点D .求证:PA •CD =PC •BD .五、解答题(本题共22分,第27题7分,第28题7分,第29题8分) 27.抛物线c bx x y C ++=2121:与y 轴交于点C (0,3),其对称轴与x 轴交于点A (2,0). (1)求抛物线1C 的解析式;(2)将抛物线1C 适当平移,使平移后的抛物线2C 的顶点为D (0,k ).已知点B (2,2),若抛物线2C 与△OAB 的边界总有两个公共点,请结合函数图象,求k 的取值范围.图1AB CABDCE 图2图3E ABP28.△ABC 中,∠ABC =45°,AH ⊥BC 于点H ,将△AHC 绕点H 逆时针旋转90°后,点C 的对应点为点D ,直线BD 与直线AC 交于点E ,连接EH .(1)如图1,当∠BAC 为锐角时,①求证:BE ⊥AC ; ②求∠BEH 的度数; (2)当∠BAC 为钝角时,请依题意用实线补全图2,并用等式表示出线段EC ,ED ,EH 之间的数量关系.29.在平面直角坐标系中,如果点P 的横坐标和纵坐标相等,则称点P 为和谐点.例如点(1,图1图2ABH CABHCED1),(31-,31-),(2-,2-),…,都是和谐点. (1)分别判断函数12+-=x y 和12+=x y 的图象上是否存在和谐点,若存在,求出其和谐点的坐标;(2)若二次函数)0(42≠++=a c x ax y 的图象上有且只有一个和谐点(23,23),且当m x ≤≤0时,函数)0(4342≠-++=a c x ax y 的最小值为-3,最大值为1,求m 的取值范围.(3)直线2:+=kx y l 经过和谐点P ,与x 轴交于点D ,与反比例函数xny G =:的图象交于M ,N 两点(点M 在点N 的左侧),若点P 的横坐标为1,且23<+DN DM ,请直接写出n 的取值范围.燕山地区2015年初中毕业考试数学试卷参考答案与评分标准 2015年4月一、 选择题(本题共30分,每小题3分)二、填空题(本题共18分,每小题3分)11.2≠x 12.)1)(1(-+b b a ; 13.90; 14.答案不唯一:xy 1-=,2x y =,2+=x y ,… 15.48; 16.2;2.三、解答题(本题共30分,每小题5分)17.证明:∵AB ∥CD ,∴∠A =∠C . ………………………1分在△BAE 和△DCF 中,⎪⎩⎪⎨⎧∠=∠=,=,CF AE C A CD AB ,∴△BAE ≌△DCF (SAS ), ………………………4分 ∴BE =DF . ………………………5分18.解:原式=133333+⨯-+ ………………………4分 =4.………………………5分19.解:解不等式①,得 3<x , ………………………2分解不等式②,得1-≥x , ………………………4分∴原不等式组的解集为31<≤-x . ………………………5分20.解:)1)(1()12(-+--x x x x=)1(222---x x x ………………………2分 =1222+--x x x=12+-x x . ………………………3分 ∵022=--x x ,即22=-x x . ………………………4分 ∴原式=1)(2+-x x =2+1=3. ………………………5分 21.解:设赵老师骑自行车的速度为x 千米/小时, ………………………1分依题意得5321212=-x x , ………………………2分解方程得 x =10. ………………………3分 经检验,x =10是原方程的解且符合实际意义. ………………………4分 答:赵老师骑自行车的速度是10千米/小时. ………………………5分 22.解:(1)Δ=)3(14)32(22k k k -⨯⨯--………………………1分=k k k k 124912422+-+-=9>0,∴ 原方程总有两个不相等的实数根. ………………………2分(2)解法一: 把0=x 代入方程03)32(22=-+--k k x k x 中,得 032=-k k ,解得 0=k ,或3=k. ………………………3分 当0=k 时,原方程化为032=+x x ,解得 31-=x ,02=x ; ………………………4分 当3=k 时,原方程化为032=-x x , 解得 31=x ,02=x .综上,原方程的另一个根3-=x ,或3=x . ………………………5分 解法二:∵Δ=9,由求根公式,得23)32(129)32(21±-=⨯±-=k k x ,,∴原方程的根为k x =1,32-=k x . ………………………3分 当01==k x 时,332-=-=k x ; ………………………4分 当032=-=k x 时,31==k x .综上,原方程的另一个根3-=x ,或3=x . ………………………5分四、解答题(本题共20分,每小题5分) 23.(1)证明:∵DE ∥AC ,CE ∥BD ,∴四边形OCED 为平行四边形. ………………………1分 又∵四边形ABCD 是菱形, ∴AC ⊥BD .∴∠DOC =90°.∴四边形OCED 为矩形. ………………………2分 (2)解法一:∵菱形ABCD ,∴AC 与BD 互相垂直平分于点O ,∴OD =OB =21BD =3,OA =OC =21AC =4,∴S △DOC =OC OD ⋅21=4321⨯⨯=6. ………………………3分在Rt △OBC 中,HB ACD EFOBC =22OC OB +=5,sin ∠OCB =BC OB =53. 作FH ⊥OC 于点H ,在Rt △CFH 中,CF =CO =4,sin ∠HCF =FC FH =53, ∴FH =53CF =512. ………………………4分 ∴S △OCF =FH OC ⋅21=512421⨯⨯=524. ∴S 四边形OFCD =S △DOC +S △OCF =6+524=554. ………………………5分解法二:∵菱形ABCD ,∴AC 与BD 互相垂直平分于点O , ∴OD =OB =21BD =3,OA =OC =21AC =4, ∴S △DCB =OC DB ⋅21=4621⨯⨯=12. ………………………3分 在Rt △OBC 中,BC =22OC OB +=5,sin ∠OCB =BC OB =53. 作OG ⊥BC 于点G ,∵CF =CO =4,∴BF =BC − CF =5− 4=1. 在Rt △OCG 中,sin ∠OCG =OC OG =53, ∴OG =53OC =512. ………………………4分 ∴S △OBF =OG BF ⋅21=512121⨯⨯=56.∴S 四边形OFCD =S △DCB −S △OBF=12−56=554. …………5分 24.解:(1)140÷(1+52%)=92;GB ACDEFO (亿件)补全条形统计图如图;…………2分 (2)140×60%×1.2=100.8亿元; …………4分答:2014年全国直接丢弃的快递包装造成了约100.8亿元的损失.(3)9.1,9.2,9.3,9.4,9.5,9.6,9.7其中之一. ………………………5分 25.(1)证明:如图,连接OD ,∵DE 切⊙O 于D ,OD 是⊙O 的半径,∴∠EDO =90°. 1分 ∵OD =OB , ∴∠ABC =∠ODB . ∵AB =AC , ∴∠ABC =∠C , ∴∠ODB =∠C , ∴DO ∥AC ,∴∠CED =∠EDO =90°. ………………………2分 (2)如图,连接AD ,∵AB 为⊙O 直径,∴∠ADB =90°,即AD ⊥BC . ………………………3分 在Rt △CED 和Rt △BDA 中,∠C =∠ABC ,∠DEC =∠ADB =90°, ∴△CED ∽△BDA ,∴CD =BD =22AD AB -=12. ∴131212⨯=CE =13144. ………………………5分 26.(1)1<AD <5; ………………………2分(2)证明:延长PD 至点F ,使EF =PE ,连接BF . ………………………3分∵BE =AE ,∠BEF =∠AEP , ∴△BEF ≌△AEP , ∴∠APE =∠F ,BF =PA . 又∵∠BDF =∠CDP ,P∴△BDF ∽△CDP . ………………………4分即PA ·CD =PC ·BD . ………………………5分五、解答题(本题共22分,第27、28题每小题7分,第29题8分) 27.解:(1)∵抛物线c bx x y ++=221与y 轴交于点C (0,3), ∴3=c ; ………………………1分 ∵抛物线c bx x y ++=221的对称轴为2=x , ∴2212=⨯-b ,解得2-=b , ………………………2分 ∴抛物线1C 的解析式为32212+-=x x y . ………………………3分 (2)由题意,抛物线2C 的解析式为k x y +=221. ………………………4分 当抛物线经过点A (2,0)时,02212=k +⨯, 解得2-=k . ………………………5分∵O (0,0),B (2,2),∴直线OB 的解析式为x y =.由⎪⎩⎪⎨⎧+==k x y x y 221,, 得0222=+-k x x ,(*) 当Δ=k 214)2(2⨯⨯--=0,即21=k 时, ………………………6分 抛物线2C 与直线OB 只有一个公共点,此时方程(*)化为0122=+-x x , 解得1=x ,即公共点P 的横坐标为1,点P 在线段OB 上. ∴k 的取值范围是212<<-k .分 28.(1)①证明:∵AH ⊥BC 于点H ,∠ABC =45°,∴△ABH 为等腰直角三角形, ∴AH =BH,∠BAH =45°,∴△AHC 绕点H 逆时针旋转90°得△BHD , 由旋转性质得,△BHD ≌△AHC,∴∠1=∠2. ………………………1分 ∵∠1+∠C =90°, ∴∠2+∠C =90°,∴∠BEC =90°,即BE ⊥AC . ………………………2分 ②解法一:如图1-1,∵∠AHB =∠AEB =90°,∴A ,B ,H ,E 四点均在以AB 为直径的圆上, ………………………3分 ∴∠BEH =∠BAH =45°. ………………………4分解法二:如图1-2,过点H 作HF ⊥HE 交BE 于F 点,∴∠FHE =90°即∠4+∠5=90°.又∵∠3+∠5=∠AHB =90°, ∴∠3=∠4. 在△AHE 和△BHF 中,⎪⎩⎪⎨⎧∠=∠=∠=∠,,,3421BH AH ∴△AHE ≌△BHF , ………………………3分 ∴EH =FH .∵∠FHE =90°,∴△FHE 是等腰直角三角形,∴∠BEH =45°. ………………………4分 29.解:(1)令x x =+-12,解得31=x , 图1-2图1-1图2∴函数12+-=x y 的图象上有一个和谐点(31,31); ………………………2分 令x x =12+,即012=+-x x ,∵根的判别式Δ=114)1(2⨯⨯--=-3<0,∴方程012=+-x x 无实数根, ∴函数12+=x y 的图象上不存在和谐点.3分 (2)令x c x ax =++42,即032=c x ax ++,由题意,Δ=ac 432-=0,即94=ac ,又方程的根为2323=-a ,解得1-=a ,49-=c . ………………………4分 ∴函数4342-++=c x ax y ,即342-+-=x x y , 如图,该函数图象顶点为(2,1),与y 轴交点为(0,-3), 由对称性,该函数图象也经过点(4,-3). ………………………5分由于函数图象在对称轴2=x 左侧y 随x 的增大而增大,在对称轴右侧y 随x 的增大而减小,且当m x ≤≤0时,函数342-+-=x x y 的最小值为-3,最大值为1, ∴42≤≤m . ………………………6分 (3)045<<n -,或10<<n . ………………………8分说明:各解答题的其他正确解法请参照以上标准按分步给分的原则酌情评分.。
2015英语毕业试题答案

北京市燕山2015年初中毕业考试英语试卷参考答案2015、04听力理解(共30分)一、听对话,选图片。
(共5分,每小题1分)1—5 CBACA二、听对话或独白,选答案。
(共15分,每小题1.5分)6—7 AB;8—9 CA;10—11 BA;12—13 BC;14—15 AB三、听对话,记录关键信息。
(共10分,每小题2分)16. Andrew 17. Blue 18. 3809 19. Chinese 20. Monday知识运用(共25分)四、单项选择。
(共10分,每小题1分)21—25 ABACC; 26—30 DDDCB五、完形填空. (共15分,每小题1.5分)31—35 BACAA; 36—40 DCBAD阅读理解(共50分)六、阅读理解。
(共30分,每小题2分)41—43 BDB; 44—47 ACBA; 48—51 CADB; 52—55 BAAC七、阅读短文,还原句子。
(共10分,每小题2分)56. B 57. A 58. D 59. E 60. C八、阅读短文,回答问题。
(共10分,每小题2分)61. Lighting.62. In the morning or wait till the 2 o’clock shadow has passed.63. Learn what angles suit your face.64. Keep shoulders back.65. How to look nice in a photo. / How to have a nice photo taken.书面表达(共15分)十、文段表达。
(共15分)As a child, I often do chores at home because I think it can not only improve my ability of looking after myself well but also make my parents relax.In my opinion, it’s important to do chores at home. On one hand, it can improve the relationship between my parents and me. In this way, we can understand each other. On the other hand, doing chores can also keep my room tidy, so I can have a comfortable environment to study.In short, it’s really good for me to do chores at home. It can help me a lot.书面表达评分标准:第一档:(15~13分)完全符合题目要求,观点正确,要点齐全。
北京市燕山区2015-2016学年度期末考试初三英语试卷含答案

燕山2015—2016学年第一学期初四年级期末考试英语试卷2016.01听力理解(共30分)一、听对话,选择与对话内容相符的图片。
(共5分,每小题1分)1.A B C2.A B C3.A B C4.A B C5.A B C二、听对话或独白,选择正确答案。
(共15分,每小题1.5分)请听一段对话,完成第6至第7小题。
6. What does the woman want to buy?A.Apples.B. Beef.C. Tomatoes.7. How much should the woman pay?A. $ 3.B. $ 20.C. $ 15.请听一段对话,完成第8至第9小题。
8. What sport is Mike going to do?A. Running.B. Sit-ups.C. High jump.9. What sport is Kathy going to do?A. Running.B. Sit-ups.C. High jump.10. What did the boy lose?A. His bike.B. His computer.C. His schoolbag.11. Where did the boy lose it?A. In the library.B. In the park.C. In the bookstore.12. Where are the two speakers going?A. To the cinema.B. To the club.C. To the hospital.13. What will the weather be like?A. Rainy.B. Sunny.C. Snowy.14. Where will Kate probably work after she leaves the school?A. In a hospital.B. In a school.C. In a bank.15. Who is Sandy in the story?A. She is the school teacher.B. She is Kate’s classmate.C. She is the school cleaner.三、听独白,记录关键信息。
燕山物理初三试卷答案
1分
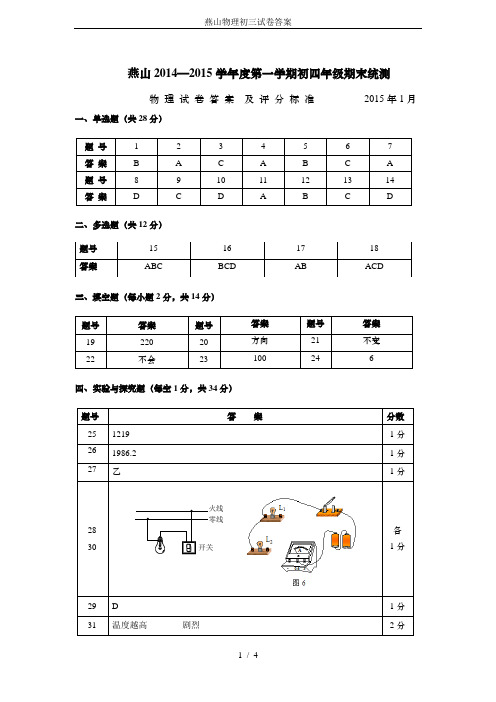
(3) I P 176W 0.8A
1分
U 220V
P热 I 2 R1 0.8A 0.8A 55 35.2W
1分
(4)
43
W
P煮 t1
P保 t 2
0.88KW
15 h 60
0.176KW
1h
0.396kW
h
1分
3/4
燕山物理初三试卷答案 4/4
S。
40
5分
(3)用装置乙替换电路中的装置甲,改变滑动变阻器滑片的位置,观
察并记录装置乙中温度计的示数 t0。仿照步骤(2),做一次实验。
(4)用装置丙替换电路中的装置乙,再次改变滑动变阻器滑片的位置, 观察并记录装置丙中温度计的示数 t0。仿照步骤(2),再做一次实验。 实验数据记录表:
U/V
t0/℃ t/℃
三、填空题(每小题 2 分,共 14 分)
题号 19 22
答案 220 不会
题号 20 23
答案 方向 100
四、实验与探究题(每空 1 分,共 34 分)
题号 25 1219 26 1986.2 27 乙
答案
题号 21 24
答案 不变
6
分数 1分 1分 1分
火线
零线
28
各
30
开关
1分
29 D
1分
31 温度越高
剧烈
2分
1/4
燕山物理初三试卷答案
32 导体的电阻可能与导体的长度、横截面积有关
33 b
电压
0.5
34 白雾
35 质量
时间
小
在玻璃板后移动
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
燕山地区2015年初中毕业考试数学试卷参考答案与评分标准 2015年4月一、 选择题(本题共30分,每小题3分)二、填空题(本题共18分,每小题3分)11.2≠x 12.)1)(1(-+b b a ; 13.90; 14.答案不唯一:xy 1-=,2x y =,2+=x y ,… 15.48; 16.2;2.三、解答题(本题共30分,每小题5分)17.证明:∵AB ∥CD ,∴∠A =∠C . ………………………1分在△BAE 和△DCF 中,⎪⎩⎪⎨⎧∠=∠=,=,CF AE C A CD AB ,∴△BAE ≌△DCF (SAS ), ………………………4分 ∴BE =DF . ………………………5分18.解:原式=133333+⨯-+ ………………………4分 =4.………………………5分19.解:解不等式①,得 3<x , ………………………2分解不等式②,得1-≥x , ………………………4分∴原不等式组的解集为31<≤-x . ………………………5分20.解:)1)(1()12(-+--x x x x=)1(222---x x x ………………………2分 =1222+--x x x=12+-x x . ………………………3分 ∵022=--x x ,即22=-x x . ………………………4分 ∴原式=1)(2+-x x =2+1=3. ………………………5分 21.解:设赵老师骑自行车的速度为x 千米/小时, ………………………1分依题意得5321212=-x x , ………………………2分 解方程得 x =10. ………………………3分 经检验,x =10是原方程的解且符合实际意义. ………………………4分 答:赵老师骑自行车的速度是10千米/小时. ………………………5分 22.解:(1)Δ=)3(14)32(22k k k -⨯⨯--………………………1分=k k k k 124912422+-+-=9>0,∴ 原方程总有两个不相等的实数根. ………………………2分(2)解法一: 把0=x 代入方程03)32(22=-+--k k x k x 中,得 032=-k k ,解得 0=k ,或3=k. ………………………3分当0=k 时,原方程化为032=+x x ,解得 31-=x ,02=x ; ………………………4分当3=k 时,原方程化为032=-x x ,解得 31=x ,02=x .综上,原方程的另一个根3-=x ,或3=x . ………………………5分 解法二:∵Δ=9,由求根公式,得23)32(129)32(21±-=⨯±-=k k x ,,∴原方程的根为k x =1,32-=k x . ………………………3分 当01==k x 时,332-=-=k x ; ………………………4分 当032=-=k x 时,31==k x .综上,原方程的另一个根3-=x ,或3=x . ………………………5分四、解答题(本题共20分,每小题5分) 23.(1)证明:∵DE ∥AC ,CE ∥BD ,∴四边形OCED 为平行四边形. ………………………1分 又∵四边形ABCD 是菱形, ∴AC ⊥BD .∴∠DOC =90°.∴四边形OCED 为矩形. ………………………2分 (2)解法一:∵菱形ABCD ,∴AC 与BD 互相垂直平分于点O ,∴OD =OB =21BD =3,OA =OC =21AC =4,HB ACD EFO∴S △DOC =OC OD ⋅21=4321⨯⨯=6. ………………………3分在Rt △OBC 中,BC =22OC OB +=5,sin ∠OCB =BC OB =53. 作FH ⊥OC 于点H ,在Rt △CFH 中,CF =CO =4,sin ∠HCF =FCFH=53, ∴FH =53CF =512. ………………………4分 ∴S △OCF =FH OC ⋅21=512421⨯⨯=524. ∴S 四边形OFCD =S △DOC +S △OCF =6+524=554. ………………………5分解法二:∵菱形ABCD ,∴AC 与BD 互相垂直平分于点O ,∴OD =OB =21BD =3,OA =OC =21AC =4,∴S △DCB =OC DB ⋅21=4621⨯⨯=12. ………………………3分 在Rt △OBC 中,BC =22OC OB +=5,sin ∠OCB =BC OB =53. 作OG ⊥BC 于点G ,∵CF =CO =4,∴BF =BC − CF =5− 4=1. 在Rt △OCG 中,sin ∠OCG =OC OG =53, ∴OG =53OC =512. ………………………4分 ∴S △OBF =OG BF ⋅21=512121⨯⨯=56.GB ACDEFO (亿件)∴S 四边形OFCD =S △DCB −S △OBF=12−56=554. …………5分 24.解:(1)140÷(1+52%)=92;补全条形统计图如图; …………2分 (2)140×60%×1.2=100.8亿元; …………4分答:2014年全国直接丢弃的快递包装造成了约100.8亿元的损失.(3)9.1,9.2,9.3,9.4,9.5,9.6,9.7其中之一. ………………………5分 25.(1)证明:如图,连接OD ,∵DE 切⊙O 于D ,OD 是⊙O 的半径,∴∠EDO =90°.1分 ∵OD =OB , ∴∠ABC =∠ODB . ∵AB =AC , ∴∠ABC =∠C , ∴∠ODB =∠C , ∴DO ∥AC ,∴∠CED =∠EDO =90°. ………………………2分 (2)如图,连接AD ,∵AB 为⊙O 直径,∴∠ADB =90°,即AD ⊥BC . ………………………3分 在Rt △CED 和Rt △BDA 中,∠C =∠ABC ,∠DEC =∠ADB =90°, ∴△CED ∽△BDA , ∴CD =BD =22AD AB -=12. ∴131212⨯=CE =13144. ………………………5分 26.(1)1<AD <5; ………………………2分(2)证明:延长PD 至点F ,使EF =PE ,连接BF . ………………………3分∵BE =AE ,∠BEF =∠AEP , ∴△BEF ≌△AEP , ∴∠APE =∠F ,BF =PA . 又∵∠BDF =∠CDP ,即PA ·CD =PC ·BD . ………………………5分五、解答题(本题共22分,第27、28题每小题7分,第29题8分) 27.解:(1)∵抛物线c bx x y ++=221与y 轴交于点C (0,3), ∴3=c ; ………………………1分 ∵抛物线c bx x y ++=221的对称轴为2=x , ∴2212=⨯-b ,解得2-=b , ………………………2分 ∴抛物线1C 的解析式为32212+-=x x y . ………………………3分 (2)由题意,抛物线2C 的解析式为k x y +=221. ………………………4分 当抛物线经过点A (2,0)时,02212=k +⨯, 解得2-=k . ………………………5分∵O (0,0),B (2,2),∴直线OB 的解析式为x y =.由⎪⎩⎪⎨⎧+==k x y x y 221,,得0222=+-k x x ,(*) 当Δ=k 214)2(2⨯⨯--=0,即21=k 时, ………………………6分 抛物线2C 与直线OB 只有一个公共点, 此时方程(*)化为0122=+-x x , 解得1=x ,即公共点P 的横坐标为1,点P 在线段OB 上. ∴k 的取值范围是212<<-k .分 28.(1)①证明:∵AH ⊥BC 于点H ,∠ABC =45°,∴△ABH 为等腰直角三角形, ∴AH =BH,∠BAH =45°,∴△AHC 绕点H 逆时针旋转90°得△BHD , 由旋转性质得,△BHD ≌△AHC ,∴∠1=∠2. ………………………1分 ∵∠1+∠C =90°, ∴∠2+∠C =90°,∴∠BEC =90°,即BE ⊥AC . ………………………2分 ②解法一:如图1-1,∵∠AHB =∠AEB =90°,∴A ,B ,H ,E 四点均在以AB 为直径的圆上, ………………………3分 ∴∠BEH =∠BAH =45°. ………………………4分解法二:如图1-2,过点H 作HF ⊥HE 交BE 于F 点,∴∠FHE =90°即∠4+∠5=90°.又∵∠3+∠5=∠AHB =90°, ∴∠3=∠4. 在△AHE 和△BHF 中, ⎪⎩⎪⎨⎧∠=∠=∠=∠,,,3421BH AH ∴△AHE ≌△BHF , ………………………3分 ∴EH =FH .∵∠FHE =90°,∴△FHE 是等腰直角三角形,∴∠BEH =45°. ………………………4分 图1-2图1-129.解:(1)令x x =+-12,解得31=x , ∴函数12+-=x y 的图象上有一个和谐点(31,31); ………………………2分 令x x =12+,即012=+-x x , ∵根的判别式Δ=114)1(2⨯⨯--=-3<0,∴方程012=+-x x 无实数根, ∴函数12+=x y 的图象上不存在和谐点. 3分 (2)令x c x ax =++42,即032=c x ax ++,由题意,Δ=ac 432-=0,即94=ac ,又方程的根为2323=-a , 解得1-=a ,49-=c . ………………………4分 ∴函数4342-++=c x ax y ,即342-+-=x x y , 如图,该函数图象顶点为(2,1),与y 轴交点为(0,-3), 由对称性,该函数图象也经过点(4,-3). ………………………5分由于函数图象在对称轴2=x 左侧y 随x 的增大而增大,在对称轴右侧y 随x 的增大而减小,且当m x ≤≤0时,函数342-+-=x x y 的最小值为-3,最大值为1, ∴42≤≤m . ………………………6分 (3)045<<n -,或10<<n . ………………………8分说明:各解答题的其他正确解法请参照以上标准按分步给分的原则酌情评分.图2。
