11:数值分析试题2009~2010
(完整版)2009研究生数值分析试题及答案-石家庄铁道大学,推荐文档
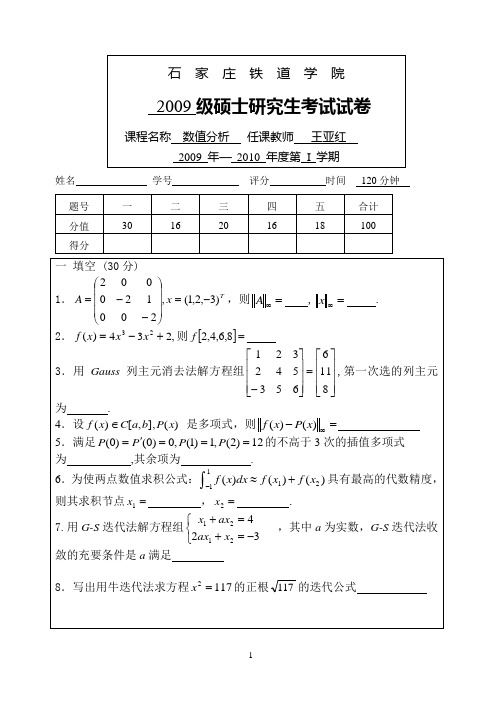
姓名学号评分时间120分钟石家庄铁道学院 2009 级硕士研究生考试试卷参考答案及评分标准课程名称 数值分析 任课教师 王亚红一.(1-6题 2分/空;7-10题 3分/空)1. 3,32. 43. -34. )()(max x P x f bx a -≤≤5. )2)(1(!4)(),2(2)4(2--+-x x x f x x ξ 6. 33,3321=-=x x 7. 21<a8.Λ,2,1,0,211721=--=+k x x x x kkk k 9. ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=323/22/3212L 10.1,...,2,1,1--=⎩⎨⎧-==+n n k x d x d x k k k kn n β 二(16分).1. 解 :⎢⎢⎢⎣⎡221213112⎥⎥⎥⎦⎤ =⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-32/12/1112132/112/31------8分解,b Ly =得⎪⎪⎪⎭⎫⎝⎛=304y解,y Ux =得⎪⎪⎪⎭⎫ ⎝⎛=111x . -----------------------------------------------12分2.Jacobi 迭代法计算公式:初始向量)0(x⎪⎩⎪⎨⎧--=--=--=+++2/)25()236(2/)4()(2)(1)1(3)(3)(1)1(2)(3)(2)1(1k k k k k k k k k x x x x x x x x x , Λ,2,1,0=k ------------------------------16分-----------------------------------7分)2)(1)(1(245)1)(1(65)1(233))()(](,,,[))(](,,[)](,[)()(21032101021001003--+--++++-=---+--+-+=x x x x x x x x x x x x x x x x f x x x x x x x f x x x x f x f x N--------------------10分2.(10分)根据最小二乘原理∑=--=302))((i i i y b ax I 最小,----2分有⎪⎪⎩⎪⎪⎨⎧=∂∂=∂∂00aI bI即⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛∑∑∑∑∑i i i ii i x y y a b xxx 24----------------------8分即⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛36915554a b ,解得b =1.2857,a =2.8286 拟合曲线2857.18286.2+=x y ----------------------10分 四(16分)解: 1.+----=))(())(()()(2010210x x x x x x x x x f x L ))(())(()(2101201x x x x x x x x x f ----+))(())(()(1202102x x x x x x x x x f ---- ------------------------------6分计算=)(0'x L ()()()()2104321x f x f x f h-+- ----------------9分 )()(0'0'x L x f ≈=()()()()2104321x f x f x f h-+- ------------------------------------------12分2.)()(),,(210x L x f x x x ≈∈,))()!1()(()()(1)1(2'++'='++x n f x L x f n n ωξ, x x n f n n 与ξωξ,))()!1()((1)1('+++有关, )()(),,(210x L x f x x x '≈'∈无法估计. )(,2x L x '不是插值节点时当的值不能作为)('x f 的近似值.-----------------16分 五. 解 1.(8分)Λ004.041.10=-I 21021-⨯≤------------------2分 2000011102110)~(10)1~10(110~-⨯⨯≤-=---=-I I I I I I ------------------------4分22111122102110)~(10)1~10(110~-⨯⨯≤-=---=-I I I I I I类推有 8210999910101021102110~10)1~10(110~--⨯=⨯⨯≤-=---=-I I I I I I-----------6分计算到10I 时,误差限为初始0I 的误差限的1010倍,每递推一次误差扩大10倍, 所以这个计算过程是不稳定的。
研究生《数值分析》试卷(带答案)

2009级研究生《数值分析》试卷一.(6分) 已知描述某实际问题的数学模型为xy y x y x u 223),(+=,其中,y x ,由统计方法得到,分别为4,2==y x,统计方法的误差限为0.01,试求出u 的误差限)(u ε和相对误差限)(u r ε.解:)(23)(6)(),()(),()(222y x y x x x y xy y y y x u x x y x u u εεεεε⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛-=∂∂+∂∂≈ 6.016.044.001.0)412(01.0)448(=+=⨯++⨯-= 0.010714566.03)()(22=≈+=xy y x u u r εε 二.(6分) 已知函数13)(3+=x x f 计算函数)(x f 的2阶均差]2,1,0[f ,和4阶均差]4,3,2,1,0[f .解:21142512)1()2(]2,1[,311401)0()1(]1,0[=-=--==-=--=f f f f f f9232102]1,0[]2,1[]2,1,0[=-=--=f f f ,0!4)(]4,3,2,1,0[)4(==ξff 三.(6分)试确定求积公式: )]1(')0('[121)]1()0([21)(1f f f f dx x f -++≈⎰的代数精度.解:记⎰=10)(dx x f I )]1(')0('[121)]1()0([21f f f f I n -++= 1)(=x f 时:1110==⎰dx I1]00[121]2[21=-+=n I x x f =)(时:2110==⎰xdx I 21]11[121]1[21=-+=n I2)(x x f =时:31102==⎰dx x I 31]20[121]1[21=-+=n I3)(x x f =时:41103==⎰dx x I 41]30[121]1[21=-+=n I 4)(x x f =时:51104==⎰dx x I 61]40[121]1[21=-+=n I求积公式)]1(')0('[121)]1()0([21)(1f f f f dx x f -++≈⎰具有3次代数精度. 四.(12分) 已知函数122)(23-++=x x x x f 定义在区间[-1,1]上,在空间},,1{)(2x x Span x =Φ上求函数)(x f 的最佳平方逼近多项式.其中,权函数1)(=x ρ,154))(),((,1532))(),((,34))(),((210-==-=x x f x x f x x f ϕϕϕ.解:0))(),(())(),((21))(),((1101101100=====⎰⎰--dx x x x x x dx x x ϕϕϕϕϕϕ32))(),(())(),(())(),((112110220====⎰-dx x x x x x x x ϕϕϕϕϕϕ0))(),(())(),((1131221===⎰-dx x x x x x ϕϕϕϕ 52))(),((11422==⎰-dx x x x ϕϕ解方程组⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛154153234520320320320221a a a 得⎪⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛15161210a a a 则)(x f 的最佳平方逼近多项式为:1516)(2-+=x x x p 五.(16分) 设函数)(x f 满足表中条件:(1) 填写均差计算表((2) 分别求出满足条件22k k k k 的 2次 Lagrange 和 Newton 差值多项式.(3) 求出一个四次插值多项式)(4x H ,使其满足表中所有条件.并用多项式降幂形式表示. 解:12)12)(02()1)(0()20)(10()2)(1()(22+-=----+----=x x x x x x x L12)1)(0(1)0)(1(1)(22+-=--+--+=x x x x x x N 令)2)(1()(12)(24--+++-=x x x b ax x x x H则)2()()2)(1)(()2)(1(22)('4-++--++--+-=x x b ax x x b ax x x ax x x H)1()(-++x x b ax由 ⎩⎨⎧-=+=+⇒⎩⎨⎧=-++-=-=-++-=1220)12(2)2(24)2('2)21)((22)1('44b a b a b a H b a H ,解得 5,3=-=b a 因此1820143)2)(1()53(12)(23424++-+-=--+-++-=x x x x x x x x x x x H 六.(16分)(1). 用Romberg 方法计算⎰31dx x ,将计算结果填入下表(*号处不填).(2). 试确定三点 Gauss-Legender 求积公式⎰∑-=≈110)()(k k k x f A dx x f 的Gauss 点k x 与系数k A ,并用三点 Gauss-Legender 求积公式计算积分: ⎰31dx x .解:过点(1,-1)和点(3,1)作直线得 y t x +=所以积分⎰⎰-+=11312dt t dx x由三次Legendre 多项式 )35(21)(33x x x p -=得得Gauss 点: ,515,0,515210==-=x x x再由代数精度得 ⎪⎪⎪⎩⎪⎪⎪⎨⎧==+==+-==++⎰⎰⎰---32535305155152111220112011210dt x A A dt x A A dt A A A即 ⎪⎩⎪⎨⎧=+=-=++9/10022020210A A A A A A A 解得 ,95,98,95210===A A A所以三点Gauss-Legendre 求积公式为:()⎪⎪⎭⎫⎝⎛++⎪⎪⎭⎫ ⎝⎛-≈⎰-5159509851595)(11f f f dx x f 因此 79746.2515295298515295211=+++-≈+=⎰-dx t I七.(14分)(1) 证明方程02ln =--x x 在区间(1,∞)有一个单根.并大致估计单根的取值范围. (2) 写出Newton 迭代公式,并计算此单根的近似值.(要求精度满足: 5110||-+<-k k x x ). 解:令 2ln )(--=x x x f),1(,011)('∞∈>-=x xx f > 即)(x f 在区间 ),1(∞ 单调增又 04)(,02ln )2(22>-=<-=e e f f 所以 02ln =--x x 在区间 ),1(∞有一单根 ),1(20e x ∈ Newton 迭代公式为1ln 112ln 1-+=----=+k k k k kk k k k x x x x x x x x x令 20=x 计算得八. (12分) 用追赶法求解方程组:⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎪⎭⎫ ⎝⎛022112111131124321x x x x 的解. 解: 由计算公式 ⎪⎩⎪⎨⎧-===+====-1,,2,,,2,,111111n i c n i b a c b i i ii i i i i i βααβγγβαα得 ,2,1,1,21,1,24321111======γγγββαα25211322212=⨯-=⇒=+ααβγb 52222222==⇒=αββαc c 53521133323=⨯-=⇒=+ααβγb 35333333==⇒=αββαc c37352144434-=⨯-=⇒=+ααβγb因此 ⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛-=⎪⎪⎪⎪⎪⎭⎫⎝⎛135152121137253125121211113112即 LU A = 令 b Ly = 解 ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛-022137253125124321y y y y 得⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛23753214321y y y y 令 y Ux =解 ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛237532113515212114321x x x x 得⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛21104321x x x x九. (12分) 设求解初值问题⎩⎨⎧==00)(),('y x y y x f y 的计算格式为:)],(),([111--+++=n n n n n n y x bf y x af h y y ,假设11)(,)(--==n n n n y x y y x y ,试确定参数b a ,的值,使该计算格式的局部截断误差为二阶,即截断部分为: )(3h o .解:)],(),([111--+++=n n n n n n y x bf y x af h y y )](')('[)(1-++=n n n x by x ay h x y])('''21)('')('[)(')(2++-++=n nn n n x y h x hy x y hb x hay x y ++-++=)('''21)('')(')()(32n n n n x by h x by h x y b a h x y对比 ++++=+)('''61)(''21)(')()(321n n n n n x y h x y h x hy x y x y得 ⎩⎨⎧==+2/11b b a , 即 2/1==b a 时该计算格式具有二阶精度.。
(完整版)2009研究生数值分析试题及答案-石家庄铁道大学,推荐文档

姓名学号评分时间120分钟石家庄铁道学院 2009 级硕士研究生考试试卷参考答案及评分标准课程名称 数值分析 任课教师 王亚红一.(1-6题 2分/空;7-10题 3分/空)1. 3,32. 43. -34. )()(max x P x f bx a -≤≤5. )2)(1(!4)(),2(2)4(2--+-x x x f x x ξ 6. 33,3321=-=x x 7. 21<a8.Λ,2,1,0,211721=--=+k x x x x kkk k 9. ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=323/22/3212L 10.1,...,2,1,1--=⎩⎨⎧-==+n n k x d x d x k k k kn n β 二(16分).1. 解 :⎢⎢⎢⎣⎡221213112⎥⎥⎥⎦⎤ =⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-32/12/1112132/112/31------8分解,b Ly =得⎪⎪⎪⎭⎫⎝⎛=304y解,y Ux =得⎪⎪⎪⎭⎫ ⎝⎛=111x . -----------------------------------------------12分2.Jacobi 迭代法计算公式:初始向量)0(x⎪⎩⎪⎨⎧--=--=--=+++2/)25()236(2/)4()(2)(1)1(3)(3)(1)1(2)(3)(2)1(1k k k k k k k k k x x x x x x x x x , Λ,2,1,0=k ------------------------------16分-----------------------------------7分)2)(1)(1(245)1)(1(65)1(233))()(](,,,[))(](,,[)](,[)()(21032101021001003--+--++++-=---+--+-+=x x x x x x x x x x x x x x x x f x x x x x x x f x x x x f x f x N--------------------10分2.(10分)根据最小二乘原理∑=--=302))((i i i y b ax I 最小,----2分有⎪⎪⎩⎪⎪⎨⎧=∂∂=∂∂00aI bI即⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛∑∑∑∑∑i i i ii i x y y a b xxx 24----------------------8分即⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛36915554a b ,解得b =1.2857,a =2.8286 拟合曲线2857.18286.2+=x y ----------------------10分 四(16分)解: 1.+----=))(())(()()(2010210x x x x x x x x x f x L ))(())(()(2101201x x x x x x x x x f ----+))(())(()(1202102x x x x x x x x x f ---- ------------------------------6分计算=)(0'x L ()()()()2104321x f x f x f h-+- ----------------9分 )()(0'0'x L x f ≈=()()()()2104321x f x f x f h-+- ------------------------------------------12分2.)()(),,(210x L x f x x x ≈∈,))()!1()(()()(1)1(2'++'='++x n f x L x f n n ωξ, x x n f n n 与ξωξ,))()!1()((1)1('+++有关, )()(),,(210x L x f x x x '≈'∈无法估计. )(,2x L x '不是插值节点时当的值不能作为)('x f 的近似值.-----------------16分 五. 解 1.(8分)Λ004.041.10=-I 21021-⨯≤------------------2分 2000011102110)~(10)1~10(110~-⨯⨯≤-=---=-I I I I I I ------------------------4分22111122102110)~(10)1~10(110~-⨯⨯≤-=---=-I I I I I I类推有 8210999910101021102110~10)1~10(110~--⨯=⨯⨯≤-=---=-I I I I I I-----------6分计算到10I 时,误差限为初始0I 的误差限的1010倍,每递推一次误差扩大10倍, 所以这个计算过程是不稳定的。
统计第十一章(1)练习题

第十一章 对比分析与指数分析(1)(一)单项选择题(在下列备选答案中,只有一个是正确的,请将其顺序号填入括号内) 1.总量指标按其反映时间状况不同,可以分为( )。
①总体总量和标志总量 ②总体总量和时期指标 ③标志总量和时期指标 ④时点指标和时期指标 2.总量指标按其反映内容的不同,可以分为( )。
①时点指标和时期指标 ②时期指标和标志总量 ③总体单位总量和总体标志总量 ④总体总量和时点指标 3.某企业某月产品销售额为20万元,月末库存商品为30万元,这两个总量指标是( )。
①时期指标 ②时点指标 ③前者为时期指标,后者为时点指标 ④前者为时点指标,后者为时期指标 4.下列属于总量指标的是( )。
①出勤率 ②合格率 ③人均产粮 ④工人人数 5.在相对指标中,主要用有名数表示的指标是( )。
①结构相对指标 ②强度相对指标 ③比较相对指标 ④动态相对指标 6.按人口平均计算的钢产量是( )。
①算术平均数 ②比例相对数 ③比较相对数 ④强度相对数7.第五次人口普查结果,我国每10万人中具有大学程度的为3611人。
该数字资料为( )。
①绝对数 ②比较相对数 ③强度相对数 ④结构相对数8.某地区有40个工业企业,职工人数为8万人,工业总产值为4.5亿元,在研究工业企业职工分布和劳动生产率的情况时 ①40个企业既是标志总量又是总体单位总量 ②8万人既是标志总量又是总体单位总量③4.5亿元既是标志总量又是总体单位总量 ④每个企业的产值既是标志总量又是总体单位总量 9.产品合格率,设备利用率这两个相对数是( )。
①结构相对数 ②强度相对数 ③比例相对数 ④比较相对数10.我国第五次人口普查结果,我国男女之间的对比关系为1.063:1,这个指标是( )。
①比较相对数 ②比例相对数 ③强度相对数 ④结构相对数 11.某月份甲工厂的工人出勤率属于( )。
①结构相对数 ②强度相对数 ③比例相对数 ④计划完成相对数12.某厂的劳动生产率计划比去年提高5%,执行结果提高8%,则劳动生产率计划执行提高程度为( )。
高等数值分析

高等数值分析历年考题高值试题一,填空题(4*7)1.求矩阵的二范数,条件数。
矩阵A=[0,2;3,0]2.把一个矩阵SVD,然后求个广义逆算个结果3.CG法,求余量的方向二、简答1.三类矩阵哪些能被Householder变换变换出来2.GMRES的性质,每次余量是否变小3.本质上是证明牛顿迭代的超线性收敛三、计算1.strum算法的使用,比书上习题还简单2.Arnoldi过程中断时的若干性质证明3.第八章Galerkin方法的求解,边值条件改成一阶导数。
定理8.4.3的变形。
答疑的时候一定要去听听,李老师在讲牛顿迭代的超线性收敛和Galerkin方法时眉飞色舞,果断就考了。
2012高等数值分析1. 用householder和givens变换做QR分解,由于矩阵特殊,非常简单。
如果拿不准,不妨用GS方法做一遍验证一下,因为不同的QR分解只是符号有差异而已,GS还是比householder简单很多的。
2.1证明rayleigh商最大值等于A的最大特征值,将x拆成各个特征向量之和就容易证。
2.2幂法求一个特征值,一步收敛4.1 去年考题。
注意到Ak*R(k-1)=R(k-1)*A(k-1),那么就类似冒泡算法把Ak移到最右边变成一个A4.2 有点小恶心,去年这个问号问的是Qk第一列是特征向量x1,只需要两边同乘以e1即可,但今年问的是最后一行是特征向量xn,顿时就不会证了,当时打眼一看觉得貌似A也不能说明是可逆的,就没往反幂法这个方向去,但是后来想想其实最多也就是lamdaN=0,其他不为0,也许可以分情况讨论下?后来有同学说假设可逆用了反幂法也没得到什么结论...不知道...还好就是5分,丢了就丢了吧5 考过多年的经典背诵题,默写rayleigh ritz方法和贾哥定理,以及Arnolid和精化Arnolid算法6.1 lagrange差值,三个点而已6.2 最佳平方逼近,解一个2*2的法方程组就完事2003高等数值分析1 证明不动点定理(存在唯一性)2 第三章习题83 共扼剃度法ak的选取,以及正交的证明4 梯形法(迭代,相容,稳定区间)具体为dy/dt + y=0 y(0)=1?5 求正交阵使H*(2/3 1/3 2/3)'=e1求I-2ww' (w的二范数为1)的特征值已知H,问计算Ha的运算量6 摄动原理误差分析7 拉各朗日插值(这里实际考的是代数基本定理的应用)8 忘了2005高等数值考题下面是B卷内容,总共六道题1.用Givens变换QR分解一个3*2的矩阵,并求解一个最小二乘2.证明:对于Minres和Gmres(1)A有k个特征值时,至多k步收敛(2)A有n个不同的特征值,r0由k个属于不同特征值的特征向量构成时,k步收敛(这里没有“至多”)3.A为m*n矩阵,m>n(1)用完全QR分解,不完全QR分解以及SVD表示A+(2)用完全QR分解以及SVD得到min||Ax-b||问题的xls和rls,并加以证明4.(1)证明Arnoldi过程中断时找到准确解(2)证明Arnoldi过程中断时不会发生方法中断(3)当A为正定对称阵时,证明Lanczos方法不会发生方法中断(即W'AV非奇异,讲义上有的)5.A=uv'。
哈工大研究生2009-2010数值分析

+
(������������
−
������������
������
������
)
(������ ������ )������ ������������ (������ ������ )������ ������������ ������
������
2������13 − ������22 − 1 = 0 ������1������23 − ������2 − 4 = 0
哈工大研究生数值分析
2010 年硕士研究生《数值分析》
1.(10
分)应用
Hermite
迭 代 法 于 方 程 ������ ������
= ������������ − ������ = 0 和 ������ ������
=
1
−
������ ������ ������
=
0 ������ > 0 ,分别导出求������ ������的迭代公式;并讨论迭代公式的收敛速度。
Байду номын сангаас
������������
+
ℎ 2
,
������������
+
ℎ 2
������(������������ , ������������ )
1) 讨论其稳定性,步长 h 应取何值方能保证方法的绝对稳定性?
2) 对������ = 1,取 h=0.2 求方程的数值解。
第 9 页 共 20 页
哈工大研究生数值分析
������������
=
1 ������ !
1−
������������=0(−������)������ ������������ + ������ ������������=−1(−������)������−1������������ ,r=2,3···
中国石油大学《数值分析》2011年考试试题A卷及答案

f (4)(x)
1 2880
1 n
4
6
1 2
104
,
仅要 n 4 1 101 2.54 ,取 n 3 即对将[1,2] 作 6 等分,则有 240
(8 分)
2
1 ln xdx
1 [0 4(ln 7 ln 3 ln 11) 2(ln 4 ln 5) ln 2] 0.38628716327880 .
0.000040074
( 4 分)
七、(10 分)(1)牛顿迭代格式
x(k 1)
x(k)
f f
(x(k ) ) '(x(k) )
x(k)
x(k) 1 (2
(x(k) )2 )(x(k) )1
1
(1 (2
)(
x( )(
)k ) 2 x(k ) )1
(2)
x(k 1)
lim
k
x(k)
1 1
fgdx
,取( x) ax bx3 , f ( x) sin x ,则法方程为
(0 ,0 )
(1
,
0
)
(0 ,1) (1 , 1 )
a b
( (
f f
,0 ,1
) )
( 4 分)
其中 0,0
1
x xdx
1
2, 3
0 ,1
(1 )(x(k) )2
lim
k
1
(2
)(x(k ) )1
c0
2
c 1
(5 分) (5 分)
1
x(k) 2
x(k) 3
1
x(k) 1
x(k) 3
/2
x3( k
1)
数值分析考试题

山东科技大学2008-2009 学年第一学期《数值分析》考试一、设 x9.1234, y10.486均具有 5位有效数字。
试分析x y和 x3y3的绝对误差限和相对误差限。
二、求一条拟合3点 A(0,1), B(1,3), C( 2,2)的直线。
三、设 n 2为正整数, c为正数,记 x*n c1)说明不能用下面的迭代格式1 nx k 1cx k, k0,1,22)构造一个可以求x*的迭代格式,证明所构造迭代格式的收敛性,并指出收敛阶数。
四、给定线性方程组4- 10x12-1a1x26014x32其中 a为非零常数。
1)写出 Jacobi迭代格式与 Gauss- Seidel迭代格式并分析其收敛性。
2)分析 a在什么范围取值时以上迭代格式收敛。
五、做一个 5次多项式 H (x)使得H (1) 3,H (2)1,H (4) 3,H '(1) 2,H '(2) 1,H *(2) 2,六、求 f ( x) x2在区间 0,1上的一次最佳一致逼近多项式。
七、给定积分公式:1f ( x)d x Af (1) Bf (0) f (1)1)试确定求积系数A, B,C ,使其具有尽可能高的代数精度,并指出其代数精度。
12)试判断该求积公式是否为高斯型求积公式,并说明理由。
)将区间,作n等分,并记h2 1 ih ,i0,1,,n,利用该求积公式3-11, x in构造一个复化求积公式。
八、考虑常微分方程初值问题y'f ( x, y),ax b取正整数,y( a)n记h b a, x i a ih ,0 i n. n试确定常数使得下列数值求解公式hf ( x i , y i ) 2 f (x i h, y i hf (x i , y i )) ,0 i n 1y i 1 y i3y0具有最高阶精度,指出相应的阶数,并给出此时局部截断误差的表达式。
九用矩阵的三角分解法,求解方程组x12x23x3142x15x22x3183x1x25x320山东科技大学 2009-2010学年第一学期《数值分析》考试试卷一、设近似值 x 1.1021, y 56.430均有 5位有效数字。
数值分析典型习题

题型一:有效数字1,的首位数字x 1,x *的相对误差不超过0.5×10-5,至少要保留几位有效数字.(2010-2011)1*1151211||10100.5102226n n r x n e x n ---=≤⨯=⨯≤⨯⨯≥=解答:设至少要保留位有效数字,则有解得, n 5.7取位有效数字.2,0.5×10-4,至少要保留几位有效数字?(2009-2010)3,已知21.787654为有效数,确定其绝对误差界与相对误差界.(2007-2008)*6*118711||102111||1010102224n r e e x ----=⨯=⨯=⨯=⨯⨯解答:4,已知30.49876为有效数,确定其绝对误差界.(2006-2007B) 5,设有效数x=12.4567,确定x 的绝对误差界.(2004-2005)题型二:插值多项式1,已知f(x)的函数值:f(0)=-2, f(1)=1, f(2)=5, 用反插值法求f(x)=0在[0,2]内的近似根x *.(2010-2011)11111202012012010210122021()()()()()()()()()()()()()()()()()(2)(5)(2)(1)012(12)(15)(52)(51)2991422884y y y y y y y y y y y y y L y f y f y f y y y y y y y y y y y y y y y y y y ----------=⋅+⋅+⋅------+-+-=+⨯+⨯+-+-=+-解答:对y=f(x)的反函数x=f 进行二次插值2*229(0)42y x L ≈=故,2,已知f(x)的如下函数值及导数值:f(-1)=1, f(0)=2, f ’(0)=3, f(1)=7; (1),建立不超过3次的埃尔米特插值多项式H 3(x);(2),x ∈[-1,1], 确定用H 3(x)代替f(x)的误差界(已知|f (4)(x)|≤M 4,x ∈[-1,1]).(2010-2011)32001001201232233)),(0,1,2)()()[,]()[,,]()()1(1)2(1)(0)232()()(1)(0)(1)232()'(i i H x f x i N x f x f x x x x f x x x x x x x x x x x x H x N x k x x x x x k x x H ===+-+--=++++-=++=++--=+++-解答:(1),满足插值条件((的二次插值多项式为:也可用拉格朗日插值法满足题设插值条件的插值多项式为:2323(4)23443)43(31)'(0)'(0)3()232()(2),(1)(0)(1),(1,1)4!1||=4!496x x k x H f H x x x f R x x x M M R ζζ=++-===+++--∈-≤⨯由得:k=0故:误差(x)=则误差界(x)3,已知f(x)的函数值:f(0)=2, f(1)=4, f(2)=9, 写出二次拉格朗日插值多项式及余项.(2009-2010)4,已知f(x)的如下函数值及导数值:f(1)=1, f(2)=2, f ’(1)=3, f(3)=9; (1),建立不超过3次的埃尔米特插值多项式;(2)计算f(1.6)的近似值;若M 4=0.5,估计f(1.6)的误差界.(已知|f (4)(x)|≤M 4).(2009-2010)5,写出满足条件H(0)=1, H(1)=0, H ’(1)=1, H(2)=1的三次插值多项式,并给出误差估计式.(2008-2009B)6,已知一组数据,求函数f(x)=0的根.(2008-2009B)7,已知f(x)的如下函数值及导数值:f(0)=1, f(1)=3, f ’(1)=1, f(2)=9, (1),建立不超过3次的埃尔米特插值多项式,写出误差估计式;(2),计算f(1.8)的近似值:若M 4=1,估计f(1.8)的误差界.(已知|f (4)(x)|≤M 4).(2007-2008)8,已知f(x)的如下函数值及导数值:f(1)=2, f(2)=4, f ’(2)=5, f(3)=8, (1),建立不超过3次的埃尔米特插值多项式;(2),计算f(2.5)的近似值:若M 4=0.5,估计f(2.5)的误差界.(已知|f (4)(x)|≤M 4).(2006-2007)9,已知f(x)的如下函数值表选取合适的插值节点,用二次插值多项式计算f(0.35)的近似值.(2005-2006) 10,已知f(x)=sinx 的如下函数值表用插值多项式计算sin1.8, 并估计误差界.(2004-2005)11,用f(x)的关于互异节点集112{}{}n ni i i i x x -==和的插值多项式g(x)和h(x)构造出关于节点集1{}ni i x =的插值多项式.(2005-2006)(课后习题)-11111121111{}(),()(){}(),()()()()))()())]()n n i i i i n n n n n n n n n n n n n n q x q x g x x x x x x x x x g A x x g x ==------=----=-解答:法一:设关于节点集x 的插值多项式为则与有共同插值节点x ,则设:q(x)=g(x)+Aw w f(x (x )由q(x )=f(x 得,w w 故:q(x)=g(x)+[f(x (x )w 法二:设q(x)=g(x)+1-122311111()()(){}()()()()(),01()=()[()()]()[()()]()()()()()()[()()]=-n n i i n n n n n n n n n n x g x h x B g x h x B x x x x x x B x x x g x h x BAx x g x h x Bq x f x h x Ah x g x x x g x h x BA B -=---=---≠----===+--Aw 由于和有共同插值节点x ,则存在常数,使得则,w 故:q(x)=g(x)+由得得1111()[()()]()n n x x x x h x g x x x ----则:q(x)=g(x)+12,(1),已知f(x)的如下函数值:f(0)=1,f(1)=3,f(3)=5,写出二次拉格朗日插值多项式L 2(x);(2),若同时已知:f ’(1)=1,用待定系数法求埃尔米特插值多项式H 3(x);(3),当(3)(4)1|()|2|()|4,[0,3]f x f x x ≤≤≤≤∈及3时,x 不取节点,[0,3]x ∈,求32()()||()()f x H x f x L x --的上界.(2011-2012)题型三:最佳平方逼近多项式及最小二乘法1,已知函数值表:用二次多项式y=C 0+C 1X+C 2X 2按最小二乘法拟合改组数据,并求平方逼近误差.(2010-2011)(2005-2006)()000102030410111213142021222324012()()()()()11111()()()()()21012()()()()()4101401210,5010010010034T T T T x x x x x A x x x x x x x x x x y A AC A y c c c ϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕ⎛⎫⎛⎫ ⎪ ⎪==-- ⎪ ⎪⎪ ⎪⎝⎭⎝⎭==⎛⎫⎛ ⎪ ⎪ ⎪⎝⎭⎝解答:法一:线性拟合的法方程组为:即()()01222*20000100011402583,0,3575833570581358||||=(y,y)-Y 01210402023531701(,)0,(,)(T c c y x C x xx δϕϕϕαϕαϕϕϕα⎫⎛⎫⎪ ⎪=⎪ ⎪⎪ ⎪⎭⎝⎭===-=-⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪=-= ⎪ ⎪ ⎪ ⎪- ⎪ ⎪⎝⎭⎝⎭====解得:c 则平方逼近误差:法二:构造首项系数为的正交多项式:(x)=1(x)=x-111211021100002*22022220,)0(,)(,)2,()()2(,)(,)46583()()0(2)(,)514357(,)8||||=(y,y)-(,)35i i i i i i i i ix x y x x x x y ϕϕϕϕϕβααϕβϕϕϕϕϕϕϕϕϕδϕϕ======----==++-=-=∑∑(x)(x)=x 则,平方逼近误差:2,求21()1f x x =+在区间[0,1]上的一次最佳平方逼近多项式及平方逼近误差(去权函数ρ(x)=x).(2009-2010) 3,通过实验获得以下数据:请用最小二乘法求形如y=a+bx 2的经验公式.(2008-2009)T T A AC A y =解析:4,利用正交多项式的性质构造首项系数为1的正交多项式1{()}i i g x ∞=,有下列公式:010111()1()()()()(),(1,2,...)k k k k k g x g x x g x x g x g x k ααβ+--==-=--=其中:111(,),(0,1,2...)(,)(,),(1,2...)(,)k k k k k k k k k k xg g k g g g g k g g αβ---==== (1),求[0,1]上首项系数为1的正交多项式(权函数ρ(x)=1),g 0(x),g 1(x),g 2(x) (2),以上述正交多项式为基,求sinx 在区间[0,1]上的二次最佳平方逼近多项式,并求平方逼近误差.(2008-2009B)(2004-2005)010000110001201111211021102110000*010001(1),()1(,)11,()(,)221()(,)121(,)2()2(,)11,()()()()(,)126(,)(,)(2),()(,)(g x xdx xg g g x x x g g dx x x dx xg g g g x dx g g g x x g x g x x x g g g f g f x g g g g αααβαβϕ=====-=--===-===--=-+=+⎰⎰⎰⎰解答:21212211120020111222000222*220(,),)(,)11()sin ()sin sin 11621()()1126()()260.00746 1.09130.23546(,)||||(,)0.000623.(,)i i i ig f g g g g g x x xdx x xdx xdx x x x dx x dx x x dx x x f g f f f g g ϕ=+-+-=⋅+⋅-+⋅-+--+=-+--=-=⎰⎰⎰⎰⎰⎰∑平方逼近误差:5,以正交多项式为基,求函数21()1f x x =+在区间[0,1]上的二次最佳平方逼近多项式,并求平方逼近误差.(2007-2008)(权函数ρ(x)=x,(2011-2012))20120122201201()1,(),(),111()2,()1,()2242211112234211113454111112224561.0656,0.503x x x x x f In f f In C F In c c c In ϕϕϕπϕϕϕπ=====-=-=⎛⎫⎛⎫⎪ ⎪⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪⋅=- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭ ⎪ ⎪- ⎪ ⎪⎝⎭⎝⎭==-解答:法一:取解得,,,正规方程组为:H 即:解得:c c 2*222*00001000111110110002,0.07423() 1.06560.503020.07423=(f,f)-F 0.000029041()11(,)223,()1(,)332(,)8(,)1,(,)15(,)T n p x x x C g x xg g g x x x g g xg g g g g g g g δαααβ=-=--======-=-====c 故二次最佳平方逼近多项式:平方逼近误差:法二:构造首项系数为的正交多项式:221100*201220120011222*1882163()()()()()()15318510(,)(,)(,)()()()() 1.06560.503020.07423(,)(,)(,)=(f,f)-F 0.00002904T n g x x g x g x x x x x f g f g f g p x g x g x g x x x g g g g g g C αβδ=--=---=-+=++=--=则:平方逼近误差:6,通过实验获得以下数据:请用最小二乘法求形如v =的经验公式,并求平方误差.(2006-2007)01:c c v=+解答转化题型四:代数精确度1,确定参数α,使求积公式20()[(0)()]['(0)'()]2hhf x dx f f h h f f h α≈++-⎰的代数精确度尽可能高,并求其代数精确度.(2010-2011)23322442320()1,,()1(),=121()()(0)(03)2121()()0+)(04)212()[(0)()]['(0)'()]2h h h f x x f x f x x h f x x f x dx h h h h f x x f x dx h h h hf x dx f f h h f f h αα====++-=≠+-≈++-⎰⎰⎰解答:令显然成立令得又时:时:(故具有三次代数精确度.2,确定参数A 1,A 2,使求积公式12()()(0)()3hh hf x dx A f h A f f h -≈-++⎰的代数精确度尽可能高,并求其代数精确度.(2009-2010)3,建立高斯型求积公式1211221()()()x f x dx A f x A f x -≈+⎰.(2009-2010)23121211311221122411221133511221121200010001,232513()1(,)0,()(,)xA A x dxA x A x x dxA x A x x dxA x A x x dxx A Ag xxg gg x x xg gααα----+==+==+==+===-=======-=⎰⎰⎰⎰解答:法一:已知求积公式有3次代数精确度,令f(x)=1,x,x得解上述方程组得:x法二:构造二次正交多项式1111110022110021211222112111221121(,)(,)30,(,)(,)53()()()()5()0,11,331()[(3xg g g gg g g gg x x g x g x xg x xx x x xA x dx A x dxx x x xx f x dx f fβαβρ---=====--=-==-=--=⋅==⋅=--≈+⎰⎰⎰令得高斯点: x故高斯型求积公式为:方法三:设[-1,1]上权(x)2221221122122121122221122331122212121().223()0,+0,5352()0,0,053().52:325()()(),(g x x ax bbx g x dx bax xg x dx ag x xA AA x A xA x A xA x A xx x x x x x c x c xϕϕ--=++===-⋅====-+=+=+=+==--=++⎰⎰=x,首项系数为1的二次正交多项式为则有:即即所以剩下步骤同法二.法四显然222221122111122212211221112221222332211122211221112221122112)()0()()()()()()()2230,535()()()()()20,053(),5xA x A x A x c x c A x c x c A x A x c A x A x c A AccA x x A x x A x A x c A x A x c A x A xccx xϕϕϕϕϕϕ==+=+++++=+++++=+==-+=+++++====-剩下步骤同法二.4,确定求积公式()()(0)()hh f x dx Af h Bf Cf h -≈-++⎰中的参数A,B,C ,使其代数精度尽量高,并指出其代数精确度.(2008-2009B) 5,确定求积公式10211123()()()()343234f x dx f f f ≈-+⎰的代数精确度.(2006-2007B) 6,确定下列求积公式中的参数,使求积公式的代数精确度尽可能高,并求出代数精确度10120113()()()()424f x dx A f A f A f ≈++⎰.(2005-2006) 7,确定下列求积公式中的参数,使求积公式的代数精确度尽可能高,并求出代数精确度101()()(0)()hh f x dx A f h A f A f h --≈-++⎰.(2004-2005) 8,已知h>0,建立高斯型求积公式:21122()()()hhx f x dx A f x A f x -≈+⎰.(2011-2012)题型五:求积公式的最少节点数1,设定积分320x e dx -⎰,问用复化辛普森(Simpson)求积公式进行计算,要求误差小于10-6,所需要的最少节点数为多少?(2010-2011)(4)2244(4)461(),()16301[]||()|101801801696017.0519.x xS f x e f x e b a h f h f h b ahη---==--=-≤⋅=<-=解答:复化辛普森公式截断误差:|R 解得:h<0.176,n>故应取个节点 2,设定积分130x e dx -⎰,问用复化梯形求积公式进行计算,要求误差小于10-6,所需要的最少节点数为多少?(2009-2010)(2)3322(2)261(),()9101[]||()|10121891622.8.x x T f x e fx eb a h f h f h b ahη---==--=-≤⋅=<-=解答:复化梯形公式截断误差:|R 解得:h<0.357,n>故应取4个节点3,给定积分20cos2xdx ⎰,问用复化梯形求积公式和复化辛普森(Simpson)求积公式进行计算,要求误差小于10-6,所需要的最少节点数各为多少? (注:2(2)4(4)[](),[](),[,]122880T S b a b a R f h f R f h f a b ηηη--=-=-∈)(2008-2009B) 4,给定积分140x e dx -⎰,问用复化梯形求积公式和复化辛普森(Simpson)求积公式进行计算,要求误差小于10-6,所需要的最少节点数各为多少?(2007-2008) 5,给定积分21Inxdx ⎰,问用复化梯形求积公式和复化辛普森(Simpson)求积公式进行计算,要求误差小于10-6,所需要的最少节点数各为多少? (已知:2(2)4(4)1212[](),[](),,(,)12180T S b a b a R f h f R f h f a b ηηηη--=-=-∈)(2006-2007) 6,用积分82122dx In x=⎰计算In2,要使所得近似值具有7位有效数字,问用复化辛普森求积公式至少需要取多少个节点?(2005-2006)4(4)8(4)52(4)-744(4)4-7[](),[2,8]18011122,(),()223|()|,[2,8]817[]102631[]||()|101801808802820.04472,S S S b a R f h f In dx f x f x x x xf x x R f b a h R f h f h h n hηηη-=-∈===≤∈≤⨯-=-≤⋅=≤⨯-≤≥=⎰解答:复化辛普森公式截断误差公式:则使所得的近似值具有位有效数字,即令:|134.2137故至少需要取个节点.7,用积分6213dx In x=⎰计算In3,要使所得近似值具有5位有效数字,问用复化梯形求积公式至少需要取多少个节点?(2004-2005)8,对于定积分10()I f x dx =⎰,当M 2=1/8,M 4=1/32,用11点的复化辛普森(Simpson)求积公式求I 的截断误差为R s [f],用n 个节点的复化梯形求积公式求I 的截断误差为R T [f],要使R T [f]≤R s [f],n 至少是多少?(M 2=max|f ”(x)|,M 4=max|f (4)(x)|,[0,1]x ∈).(2011-2012)题型六:Doolittle 分解及方程组求解1,求矩阵212454635⎛⎫⎪ ⎪⎪-⎝⎭的Doolittle 分解.(2010-2011)212100212454210030635321001LU ⎛⎫⎛⎫⎛⎫ ⎪ ⎪⎪== ⎪ ⎪⎪ ⎪ ⎪⎪---⎝⎭⎝⎭⎝⎭解答:A=2,求矩阵114103241⎛⎫⎪- ⎪⎪⎝⎭的Doolittle 分解.(2009-2010)3,设线性方程组123410135114152410162116x x x x ---⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪- ⎪⎪ ⎪⋅= ⎪ ⎪ ⎪- ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭ (1),对方程组的系数矩阵A 作Doolittle 分解;(2),用所得的Doolittle 分解求该线性方程组的解.(2007-2008&2005-2006)12341234101013101311000132114124100013224101119162116210001313191,,,)(5,0,11,)13,,,)(1,1,1,1).T TT T A LU LY b y y y UX Y x x x --⎛⎫⎛⎫--⎛⎫ ⎪⎪- ⎪ ⎪⎪-⎪=== ⎪⎪--- ⎪ ⎪⎪ ⎪ ⎪⎪-- ⎪⎪⎝⎭⎝⎭⎝⎭==---==--解答:由得:(y 由得:(x4,设线性方程组123411415101312410762118x x x x -⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪-- ⎪⎪ ⎪⋅=⎪ ⎪ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭ (1),对方程组的系数矩阵A 作Doolittle 分解;(2),用所得的Doolittle 分解求该线性方程组的解.(2006-2007)5,设线性方程组:12312312323153478113x x x x x x x x x ++=+-=-++=-(1),对方程组的系数矩阵A 作Doolittle 分解; (2),利用上述分解结果求解该线性方程组.(2004-2005)6,用高斯顺序消去法求解线性方程组:13241234242532431737x x x x x x x x x x +=+=+++=+=.(2010-2011)4321102051020510205010130101301013=124317022312002160103701037000242,2,1, 1.x x x ⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪⎪ ⎪ ⎪→→ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭====解答:增广矩阵回代求解:x7,用高斯顺序消去法求解线性方程组:1231231233472212320x x x x x x x x x -+=-+-=---=.(2009-2010)题型七:条件数及范数1,求线性方程组1212391078981510x x x x x --=+==的系数矩阵A 的条件数cond 1(A),并说明其含义.(2010-2011)1111191008900015910089010015()||||||||19193611A A cond A A A A b ----⎛⎫ ⎪= ⎪⎪⎝⎭⎛⎫ ⎪-- ⎪= ⎪⎪⎪⎝⎭==⨯=解答:系数矩阵条件数远大于,这说明当和有小扰动时会引起解的较大误差,即该方程组是病态的.2,设矩阵15000910089A ⎛⎫ ⎪=-- ⎪⎪⎝⎭,求cond ∞(A).(2009-2010)3,设三阶对称矩阵A 的特征值分别为:-2,1,3,求||A||2及cond 2(A).(2007-2008)2121222||||3||||()|||||||| 3.A A cond A A A --========解答:则:4,若n 元线性方程组Ax=b 为病态的,可以得到关于系数矩阵A 的什么性质.(2006-2007)5,若111123124A ⎛⎫⎪= ⎪⎪⎝⎭,求cond 1(A).(2005-2006)求cond ∞(A).(2004-2005)6,设1231032475A -⎛⎫⎪=-- ⎪⎪-⎝⎭,求1||||||||A A ∞与.(2007-2008)7,若1234A ⎛⎫= ⎪⎝⎭,求谱半径()A ρ.(2005-2006) 52ρ解答:最大特征值:(A)=题型八:雅可比迭代与高斯-赛德尔迭代1,写出求解方程组1231231237321241021534818x x x x x x x x x -+=--=--=的雅可比迭代公式,并说明其收敛性.(2010-2011)(1)()()123(1)()()213(1)()()312(0)1(3212)71(4215)101(3418)87324102348.k k k k k k k k k J x x x x x x x x +++=-+=--++=--++-⎛⎫ ⎪=-- ⎪ ⎪--⎝⎭解答:雅可比迭代公式为:x 雅可比迭代法迭代矩阵:B 严格对角占优,故求解该方程组的雅可比迭代法关于任意初始向量x 收敛 2,设有方程组:132********2112212x x x x x x x -=+=-++=,讨论用雅可比迭代法和高斯-赛德尔迭代法解此方程组的收敛性.(2010-2011)112330200030000202100002000121221000200020031()0021102||0,=0=-J J J L D U B D L U E B B λλλλρ---⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪=++=++ ⎪ ⎪ ⎪ ⎪⎪ ⎪ ⎪ ⎪--⎝⎭⎝⎭⎝⎭⎝⎭⎛⎫ ⎪ ⎪⎪=-+=- ⎪ ⎪⎪- ⎪⎝⎭-=解答:A=雅可比迭代矩阵:得,()<1,故用雅可比迭代法解答此方程组对任意(0)1123(0)20031-()00211001211||0,=012-S S S B D L U E B B λλλλρ-⎛⎫ ⎪ ⎪⎪=-+=- ⎪ ⎪⎪ ⎪⎝⎭-===初始向量x 都收敛.高斯赛德尔迭代矩阵:得,()<1,故用高斯赛格尔迭代法解答此方程组对任意初始向量x 都收敛.3,写出求解方程组:123123123532124721535818x x x x x x x x x -+=--=--=的高斯-赛德尔迭代公式,并说明收敛性.(2009-2010)4,用雅可比迭代法求解以313132323A ⎛⎫⎪= ⎪ ⎪-⎝⎭为系数矩阵的线性方程组时,确定其收敛性.(2009-2010)5,设线性方程组123123123221162222x x x x x x x x x -+=-+-=--+=-,讨论分别用雅可比迭代法和高斯-赛德尔迭代法解此线性方程组的收敛性,若收敛,请给出迭代格式.(2008-2009B)6,设线性方程组:1231231232215202225x x x x x x x x x +-=-++=++=-(1),证明求解该方程组的雅可比迭代法关于任意初始向量收敛;相应的高斯-赛德尔迭代法不是关于任意初始向量收敛; (2),取(0)(0,0,0)T x=,用雅可比迭代法进行求解,要求(1)()5||||10k k x x +--<.(2007-2008)11231123022()101220||0,===0)1022()023002||0,0,2,)1-J J J S S S D L U E B D L U E λλλλρλλλλρ---⎛⎫ ⎪=-+=-- ⎪⎪--⎝⎭-=<-⎛⎫⎪=-+=- ⎪⎪⎝⎭-====>解答:(1):B B 解得:,(B B 解得:(B 所以用雅可比迭代法解此方程组对任意初始向量都收敛,而用高斯赛德尔迭代法解此方程组不是对任意初始向量都收敛.(2):(1)()()123(1)()()213(1)()()312(0)(1)(2)(3)(4)2215202225(0,0,0)(15,20,25)(105,60,35)(205,160,65)(205,160,65)k k k k k k k k k T T T TTx x x xx x x x x x x x x +++=-+-=--+=---==--=--=-=-雅可比迭代公式:x 当时,计算得:(精确解).7,设线性方程组:123123123821027325431111x x x x x x x x x ++=--++=-+=-(1),写出求解该方程组的雅可比迭代法的迭代公式和高斯-赛德尔迭代法的迭代公式,并确定其收敛性; (2),取(0)(0,0,0)T x=,用高斯-赛德尔迭代法计算x (3).(2006-2007)8,设线性方程组Ax=b 的系数矩阵232131t A t t ⎛⎫ ⎪= ⎪ ⎪-⎝⎭,其中t<0,问t 取何值时雅可比迭代法关于任意初始向量都收敛.(2006-2007)12122223021()0310422||()0=0=-,=)12||<1,t<-2,or t>20, 2.J J J t t D L U t t t t E B t t ttt t λλλλλλρ-⎛⎫-- ⎪ ⎪ ⎪=-+=-- ⎪ ⎪ ⎪- ⎪⎝⎭-=-=<<<-解答:雅可比迭代矩阵B 得,,雅可比迭代法对于任意初始向量都收敛,则(B 即:得又故9,1),设线性方程组:121232343243430424x x x x x x x +=+-=-+=-写出求解该方程组的雅可比迭代法的迭代公式,并确定该迭代法的收敛性;2),设线性方程组:123123123104413410811481025x x x x x x x x x ++=++=++=写出求解该方程组的高斯-赛德尔迭代法的迭代公式,并确定该迭代法的收敛性.(2004-2005)10,给定方程组:1231231232251223x x x x x x x x x +-=++=++=(1),用三角分解法解此方程组;(2),写出解此方程组的雅可比迭代公式,说明收敛性;取初始向量x 0=(0,0,0)T,当21||||10k k x x -+-<时,求其解.(2011-2012)11,设()21253sin 3421sincos 43tan 5k k k k k k k Ak k k kk⎛⎫- ⎪+ ⎪ ⎪= ⎪+⎪⎪⎪⎭,求()lim k k A →∞.(2007-2008)()020lim 021205K k A →∞⎛⎫⎪= ⎪ ⎪⎝⎭解答: 12,若()()11,lim 1sin sin k k k k k k AA k k k k →∞⎛⎫⎪+=⎪ ⎪⎪⎝⎭求.(2004-2005) ()01lim 10K k A →∞⎛⎫= ⎪⎝⎭解答: 题型九:非线性迭代1,设计一个算法求.(2008-2009B)101125(),0.2k k kx x x +=+>解答:牛顿迭代公式:x2,给出用牛顿法求围.(2010-2011)661556'5"4"*00001050517001701170[5]66()170,()60,()300()()0,.1170(5)61170()(5)6k k k k k kx x x x x x x x f x x f x x f x x x f x f x x x x x x g x x x +=-=-=-=+=-=>=>>⋅><=+=+解答:的正根.由牛顿迭代法得迭代公式:当故此时收敛到当0<设'611*01850()(5)0,()0,6:0,.0.x g x x g x g xx x x x x ∈=-<∈>=>>∈>故故回到前段.所以当迭代公式也收敛到综上:3,给出用牛顿法求近似值的迭代公式,并给出初值的取值范围.(2009-2010) 解答:方法同上.4,设φ(x)=x+c(x 2-5),当c 为何值时,x k+1=φ(x k ),(k=0,1,2…)产生的序列{x k }收敛于c 为何值时收敛最快?(2010-2011)2''**1**'*5),||<1,||<110,0;.k k cx x c ϕϕϕϕϕ+-=-<<<<解答:(x)=x+c(x (x)=1+2cxx (x )收敛,则有(x )即1+2cx 又当(x )=0,即5,设2()(3)x x c x ϕ=+-,应如何选取常数c 才能使迭代1(),(0,1,2)k k x xk ϕ+==具有局部收敛性?C 取何值时,这个迭代收敛最快?取x 0=2,c =计算()x ϕ的不动点,要求当61||10k k x x -+-<时结束迭代.(2004-2005)****21*2'****'**1(),(3)()(3)()|1|12|1,11,0,,033(2),()0+0,6(3),k kkx x x x c xx x x c x xcx cx x c or cxxϕϕϕϕ++==+-==+-<+<-<<=<<<<==±±解答:(1),令x收敛于则故要局部收敛,即|又得根据收敛阶定理,当时,迭代至少二阶收敛,即12cx得c=故c=.迭代公式为:212346*433)21.7113248651.7319268031.7320508041.732050808|10,: 1.732050808.k kx xxxxxxx x x-=-=====-<=又因为|故6,方程x3-3x-1=0在x=2附近有一根,构造一个局部收敛的不动点迭代法,并说明收敛的理由.(2009-2010)'2(1.5) 1.765174168,(2.5) 2.040827551[1.5,2.5]()[1.5,2.5]()|0.33,xx xxϕϕϕϕϕ===∈∈=≤<解答:取的邻域[1.5,2.5]当时,又因为|故迭代在[1.5,2.5]上整体收敛.7,已知方程42()440f x x x=-+=有一个两重根0x=,请以初值x0=1.5,用m重根的牛顿迭代法计算其近似值,要求51||10k kx x-+-<.(2008-2009B)(P204例7.7)8,(1),已知方程240xe x+-=在0.6附近有一根x,迭代法214,0,1,2kxkx e k+=-=是否局部收敛?如果不收敛,试构造一个局部收敛的不动点迭代法,并说明收敛的理由.(2),取x 0=0.6,用你所构造的不动点迭代法求解该方程,迭代至x 5. (3),给出牛顿法求围.(2007-2008)2'2'**1'''1(1):()4,()2|()|1,(0),1(4)211(4),()22(4)1(0)2,(1)3()[0,1]21()||(1)|161(4)2x xk k k k x e x e x x x In x In x x x In In x x x In x ϕϕϕϕϕϕϕϕϕϕ++=-=->>=---=-==∈≤=<=-解答:故该迭代公式不是局部收敛的.构造:理由:取邻域[0,1](x)=故又|故迭代式在[0,1]上整体收敛11021324354101(2),(4),21(4)0.61188771521(4)0.61013645921(4)0.61039483321(4)0.61035672221(4)0.61036234421120(3),(),0.2k k k k kx In x x In x x In x x In x x In x x In x x x x x ++=-=-==-==-==-==-==+>.则9,给定方程x 2+x-2=0,[0,2]x ∈,采用迭代公式x k+1=x k +c(x k 2+x k -2),(k=0,1,2…)求其根,问当c 为何值时,迭代法收敛?又当c 为何值时,迭代法收敛最快?(2011-2012)*2'''1,()(2)()1(21)2(1)||1(21)|1,-0.31(1)=03x x x c x x x c x c c ϕϕϕϕ==++-=++=++<<<解答:当|即时,线性收敛当,即c=-时收敛最快.10,给定方程230xx e -=,[3,4]x ∈(1),构造一种线性收敛的不动点迭代公式求该方程的根(含迭代公式,初值取何值或何区间,迭代法收敛的原因);(2),构造一种二次收敛的不动点迭代公式求该方程的根(含迭代公式,初值取何值或何区间,迭代法收敛的原因).(2011-2012)21111'12102'"0(1),()(3),3.29(3)()(4) 3.8712(),[3,4]23(3),(0,1,2,)[3,4].(2),()3,[3,4](3)0,(4)0()60,()60,[3,4]3k k x x x x In x x x x In x k x f x x e x f f f x x e f x e x x ϕϕϕϕϕ+==≤≤=≤≤∈==∈=-∈><=-<=-<∈=解答:故不动点迭代公式:x 对于任意初值收敛取初值时,牛顿213.6kkx kk k x k x ex x x e +-=--迭代法:收敛,且二次收敛11,方程x 3-x 2-1=0在x=1.5附近有根,建立一个收敛的迭代公式,并证明其收敛性.(2004-2005)122''33312111.51()1(1.3) 1.591715976,(1.6) 1.390625[1.3,1.6]()[1.3,1.6]222(),|()|||0.921.311k k k kx x x x x x x x x x x x x ϕϕϕϕϕϕ++=+==+==∈∈=-=-≤<=+解答:取的邻域[1.3,1.6]故当时,又故迭代公式:在[1.3,1.5]上整体收敛.12,(1),已知方程1020xex +-=在0.09附近有一根x,迭代法1(210),(0,1,2)k k x In x k +=-=是否局部收敛?如果不收敛,请构造一个局部收敛的不动点迭代法,并说明收敛的理由; (2),取x 0=0.09,用局部收敛的迭代法计算x 5;(3),用牛顿法求的近似值,并给出初值的取值.(2006-2007)'''*1''5(1),()(210),()15|()|1,[0,1],|()|>1.11510111(),()51010(0)0.1,(0.12)0.087250323[0,0.12]()[0,0.12]()|kx k x xx In x x xx x x x e x e x e x x x ϕϕϕϕϕϕϕϕϕϕ+-=-=->∈=-=-=-==∈∈≤解答:显然故该迭代公式不是局部收敛的构造:因为取[0,0.12]邻域考察故当时,又|'0.12110.09010.09058257820.09051881530.0905241|(0.12)|||0.1131101151011(2),510110.09,0.090582578510110.090518815510110.09052579651011510k kx k x k e x e x e x x e x e x e x e ϕ++=-<<=-=-==-==-==-==-故迭代公式:在[0,0.12]上整体收敛.57960.09052503151200.090525031110.0905251155102117(3),()30.k k k x e x x x +==-==+>使用迭代公式:进行求解.初值:x13,设方程x 3-3x-1=0在x=2附近有根;1),证明该方程在区间[1.5,2.5]内有唯一根x *;2),确定迭代函数φ(x).当初始值x 0在何区间取值时,迭代公式x k+1=φ(x k ),(k=0,1,2…)收敛到x *,并说明理由.3),写出求解该方程组的牛顿法迭代公式,当初始值x 0在何区间取值时,牛顿法迭代公式收敛到x,并说明理由.取x 0=1.8,用牛顿法迭代公式计算x,要求(1)()4||||10k k x x +--<.4),写出求解该方程的弦截法迭代公式,当初始值在何区间取值时,弦截法迭代公式收敛到x,并说明理由.(2005-2006)3'2'331223(1),()31,()33(1.5) 2.125,(2.5)7.125(1.5)(2.5)0,()0()0,[1.5,2.5][1.5,2.5].(2),3121(3),,3333()3k k k k k k k f x x x f x x f f f f f x f x x x x x x x x x f x x +=--=-=-=⋅<=>∈--+=-=--=-解答:证明:故在[1.5,2.5]内有根.又故方程在区间内有唯一根牛顿法迭代公式:'2"1,()33,()6x f x x f x x-=-=题型十:稳定算法1,对给定的x ,下列两式能否直接计算,说明理由;如果不能,请给出变换算式:(1x ,x 很大;(21,|x|很小.(2010-2011)3(1)x =解答:不能直接计算,因为两个相近的数相减,会产生较大的误差:2,为了提高计算精度,当正数x.(2005-2006)3,给出计算积分10,(0,1,2,10)10nn x I dx n x ==+⎰的递推稳定算法和初值.(2010-2011)1111111000-11110002010101101010101=101011111)11101010(1)11121[].2111)101)220(1)n n n n n n n n n n x x dx x dx x dx I I x x nn n x x x dx dx dx n x n n n n ----+-===-=-++-=<<=+++=+=+++⎰⎰⎰⎰⎰⎰解:I 该算法不稳定,变形得:I 因为(取初值I ((4,设计一种求10x nn I e x dx =⎰(n 为非负整数)稳定的递推算法,包括递推公式,初值的确定;当初值201221e I =⋅时,利用上述稳定的递推公式计算三个连续的积分值.(2011-2012)题型十一:部分证明题1,利用差分的性质证明:12+22+…n 2=n(n+1)(2n+1)/6222()12,g n n n =++证明:设函数对任意的建立差分表:函数g(n)的三阶差分是与n 无关的非零常数,故g(n)是n 的三次多项式:3(1)1,(2)5,(3)14,(4)30111()()14521231(1)(2)(1)(2)(3)(1)(21)14521!2!3!6g g g g n n n g n N n n n n n n n n n n ====---⎛⎫⎛⎫⎛⎫==+++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭------++=+⋅+⋅+⋅=按等距节点牛顿向前插值公式建立三次插值多项式,则2,证明:n+1个互异节点的插值型求积公式的代数精确度至少为n.(2010-2011)(1)0()(),.(1)!n nb i ai f x x dx n ζ+=-+∏⎰证明:截断误差R[f]=易证 3,若0{()}ni i l x =是关于互异节点0{}ni i x =的拉格朗日插值基函数组,函数0011()()()(),(1)n n f x x l x x l x x l x n =++≥,证明:f(x)≡x.(2009-2010)00110()()()()()()()()n n i i n n i f x L x f x l x x l x x l x x l x f x x=≈==+++≡∑证明:故:4,证明:0101'()[()()]"()2hf x f x f x f h ζ=--,其中h=x 1-x 0,01(,)x x ζ∈.(2009-2010)"'20000"'211001010'"010())()()()2!(),())()()()2!1()[()()]()2f f x x x x x f x x f x f x x x x x hf x f x f x f h ζζζ+-+-==+-+-=--证明:由泰勒公式得f(x)=f(x 令则f(x 整理得: 5,证明:关于互异节点0{}ni i x =的拉格朗日插值基函数0{()}ni i l x =满足恒等式012()()()()1n l x l x l x l x +++≡.(2008-2009B)(2006-2007B)(2004-2005)120(1)(1)1010()1,(),,1=L ()()()()()()()1,()0,()()0(1)!()()()()1n nn n i n i n n n n ni n i f x f x x x x x R x l x f x R x f f x fx R x W x n l x l x l x l x ζ=+++==+=+=≡==+=+++≡∑∑证明:令对在上进行拉格朗日插值,有因故故:6,证明求积公式()[()()]2ba b af x dx f a f b -≈+⎰的截断误差:3"()[](),12f R f b a ηη=--∈其中:(a,b).(2007-2008) (1)001(2)(2)(2)33()()(1)!1,,()()()1"()()()()()()()2!2!2!612n nb i ai b b aa f x x dx n n x a xb f f f f x a x b dx x a x b dx a b b a ζζηηη+=-+===--=--=⋅-=--∏⎰⎰⎰证明:插值型求积公式截断误差R[f]=R[f]=7,设矩阵A 为可逆上三角阵,证明A -1仍为上三角阵,并导出求逆算法.(2006-2007B)8,设x k =a+kh(k=0,1,2;h>0),f(x)的三阶导数连续,证明:2(3)102021'()[()()](),(,)26h f x f x f x f x x h ζζ=-+-∈其中为中值.(2011-2012)001122120201201201021012202112020101222,),,),,)()()()()()()()()()()()()()()()()()()()()()()()()(22x y x y x y x x x x x x x x x x x x x f x f x f x x x x x x x x x x x x x x x x x x x x x x x x x f x f x f x h h h ------=++------------=-+证明:过(((的拉格朗日插值多项式为:L 12'2102(3)201202(3)'''1210122'(3)10202)1()[()()]2()()()()()(),(,)3!()()()[()()()]3!1()[()()](),(,)26x x L x f x f x hf f x L x x x x x x x x x f f x L x x x x x x x h f x f x f x f x x h ηηηζζ==-+-=---∈-=---=-+-∈又故:。
北京理工大学2009级数值分析试题及答案

课程编号:12000044 北京理工大学2010-2011学年第一学期2009级计算机学院《数值分析》期末试卷A 卷班级 学号 姓名 成绩注意:① 答题方式为闭卷。
② 可以使用计算器。
请将填空题和选择题的答案直接填在试卷上,计算题答在答题纸上。
一、 填空题 (2 0×2′)1. 设x =0.231是精确值x *=0.229的近似值,则x 有 位有效数字。
2. 设⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡-=32,1223X A ,‖A ‖∞=___ ____,‖X ‖∞=__ _____,‖AX ‖∞≤____ ___ (注意:不计算‖AX ‖∞的值) 。
3. 非线性方程f (x )=0的迭代函数x =ϕ(x )在有解区间满足 ,则使用该迭代函数的迭代解法一定是局部收敛的。
4. 若f (x )=x 7-x 3+1,则f [20,21,22,23,24,25,26,27]= ,f [20,21,22,23,24,25,26,27,28]= 。
5. 区间[a ,b ]上的三次样条插值函数S (x )在[a ,b ]上具有直到 阶的连续导数。
6. 当插值节点为等距分布时,若所求节点靠近首节点,应该选用等距节点下牛顿差商公式的 (填写前插公式、后插公式或中心差分公式),若所求节点靠近尾节点,应该选用等距节点下牛顿差商公式的 (填写前插公式、后插公式或中心差分公式);如果要估计结果的舍入误差,应该选用插值公式中的 。
7. 拉格朗日插值公式中f (x i )的系数a i (x )的特点是:=∑=ni i x a 0)( ;所以当系数a i (x )满足 ,计算时不会放大f (x i )的误差。
8. 要使20的近似值的相对误差小于0.1%,至少要取 位有效数字。
9. 对任意初始向量X (0)及任意向量g ,线性方程组的迭代公式x (k +1)=Bx (k )+g (k =0,1,…)收敛于方程组的精确解x *的充分必要条件是 。
数值分析试题(卷)和答案解析

试题__2009___年~__2010___年第 一学期课程名称: 数值分析 专业年级: 2009级(研究生) 考生学号: 考生: 试卷类型: A 卷 √ B 卷 □ 考试方式: 开卷 √ 闭卷 □………………………………………………………………………………………………………一. 填空题(本大题共4小题,每小题4分,共16分)1.设有节点012,,x x x ,其对应的函数()y f x =的值分别为012,,y y y ,则二次拉格朗日插值基函数0()l x 为 。
2.设()2f x x =,则()f x 关于节点0120,1,3x x x ===的二阶向前差分为 。
3.设110111011A -⎡⎤⎢⎥=--⎢⎥⎢⎥-⎣⎦,233x ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦,则1A = ,1x = 。
4. 1n +个节点的高斯求积公式的代数精确度为 。
二.简答题(本大题共3小题,每小题8分,共24分)1. 哪种线性方程组可用平方根法求解?为什么说平方根法计算稳定?2. 什么是不动点迭代法?()x ϕ满足什么条件才能保证不动点存在和不动点迭代序列收敛于()x ϕ的不动点?3. 设n 阶矩阵A 具有n 个特征值且满足123n λλλλ>≥≥≥,请简单说明求解矩阵A 的主特征值和特征向量的算法及流程。
三.求一个次数不高于3的多项式()3P x ,满足下列插值条件:i x 1 2 3 i y 2 4 12 i y '3并估计误差。
(10分)四.试用1,2,4n =的牛顿-科特斯求积公式计算定积分1011I dx x=+⎰。
(10分) 五.用Newton 法求()cos 0f x x x =-=的近似解。
(10分) 六.试用Doolittle 分解法求解方程组:12325610413191963630x x x -⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥-=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥----⎣⎦⎣⎦⎣⎦(10分) 七.请写出雅可比迭代法求解线性方程组123123123202324812231530x x x x x x x x x ++=⎧⎪++=⎨⎪-+=⎩ 的迭代格式,并判断其是否收敛?(10分)八.就初值问题0(0)y yy y λ'=⎧⎨=⎩考察欧拉显式格式的收敛性。
2009-2016数值分析真题

∑A
k =0
2
K f ( xk ) ≈ ∫ f ( x )dx 是高斯型的,则其余项为 a
b
∫
b
a
f ( x)dx − ∑ AK f ( xk ) = .
k =0
二、(15 分) 已知函数 f ( x) 在 0,1,2 处的函数值分别是 1,2,15,且 f ′′(1) = 12 . (1) 利用 Newton 均差插值思想,求满足以上四个插值条件的插值多项式 H ( x) ;
f ( x) − P2 ( x) (假设 f ( x) 三阶连续可导).
二、(15 分) 确定求积公式
∫
h
0
f ( x)dx=
h [ f (0) + f (h)] + α h 2 [ f ′(0) − f ′(h)] 中的待定参数 α,使该 2
公式的代数精度尽量的高,并指出该公式的代数精度是多少. 三、(15 分) 用平方根法求解方程组
五、(20 分) 已知线性方程组
1 x1 + 2 x2 − 2 x3 = 3 x1 + x2 + x3 = 2 x + 2 x + x = 5 2 3 1
(1) 判断用 J 方法、GS 方法求解该方程组是否收敛; (2) 若 J 方法、GS 方法中有收敛公式,用一收敛公式求解;若两种公式都不收敛,构造收敛迭
∫
4
1
x −1 dx 的近似值. x+x
4 −2 −4 x1 10 −2 17 10 x = 2 3 . −4 10 9 x3 −7
5、(15 分) 已知线性方程组
−12 5 x1 + 2 x2 + x3 = 9 − x1 + 4 x2 + 2 x3 = 2 x − 3 x + 10 x = 1 2 3 1
福州大学2010以及2011年数值分析考题及答案

课程名称 数值分析 考生姓名
题号 题分 得分 一 15
考00 累分人 签名
学号
二 20
生注意事项:1、本试卷共 6 页,请查看试卷中是否有缺页。 、考试结束后,考生不得将试卷、答题纸和草稿纸带出考场。
一、选择题(每小题3分,共18分)
3、 确定求积公式中的待定参数,使其代数精度尽量高, 则A0=___________, A1=__________, A2=________,代数精度 =__2_________。
4、 为减少误差的影响应将表达式改写为 。 5、 用两点的高斯-勒让德求积公式计算积 分=__________ 5、 应用牛顿法求解,迭代公式是 6、 已知由数据(0,0),(0.5,y),(1,3),(2,2)构造出的 三次插值多项式则y=___4.25_______ ,其余项表达式 R(x)=_________________________________ 三、计算题(共 40分) 2、 设,求矩阵A的LU分解,其中L为单位下三角矩 得分 评卷人 阵,U为上三角矩阵(6分)
2、(8分)用复合梯形公式计算积分,(n=2),并估计误差。 解:
3、(10分)用最小二乘法求拟合函数使其与下列数据相拟合 -1 0 1 2 1 2 2 1
4、(8分)用改进的欧拉方法求解初值问题 取步长h=0.2(小数点后保留4位有效数字)
5、设,试用平面旋转矩阵对矩阵A进行QR分解,其中Q为正交矩阵,R 为上三角阵(8分)
( ) (A) 0.001% (B) 0.333% (C) 1% (D) 6、用高斯消元法解线性方程组,能进行到底的充分必要条件是 ( ) (A) 系数矩阵各阶顺序主子式不为零 (B) 系数矩阵主对角线元素不为零
(完整word版)三峡大学2010-2011数值分析试题

二、(10分)求下列超定线性方程组的最小二乘解. ⎪⎩⎪⎨⎧=+=+=+00212212121x x x x x x三、(10分) 在区间[]4,2上利用压缩映像原理判断迭代格式Λ,2,1,0,321=+=+k x x k k 的敛散性.四、(14分)设n n ij R a A ⨯∈=)(对称,顺序主子式),,2,1(0n i i Λ=≠∆则T LDL A =分解存在,其中L 为单位下三角形矩阵,D 为对角阵,试写出求方程组b Ax =解的计算步骤(用矩阵表示), 此法称为改进平方根法. 试用它求解方程组:⎩⎨⎧=+=+1710712752121x x x x五、(10分) 已知)(x f y =的函数值如下表: 28.44.54.79.77.888.74.52.10)(20181614121086420x f x利用所有数据,用复合辛普森(Simpson )公式计算积分dx x f ⎰20)(的近似值.六、(10分) 取节点1,010==x x ,写出xe x y -=)(的一次插值多项式),(1x L 并估计插值误差.七、(10分)分别写出解线性方程组⎪⎩⎪⎨⎧=++-=-+=+-1874165321321321x x x x x x x x x 收敛的Jacobi 迭代格式和Seidel Gauss -迭代格式,并说明其收敛的理由.八、(10分)设初值问题:⎩⎨⎧=+='1)0(y yx y )10(≤≤x(1) 写出用欧拉(Euler )方法、取步长1.0=h 解上述初值问题数值解的公式; (2) 写出用改进欧拉(Euler )方法、取步长1.0=h 解上述初值问题数值解的公式.九、(10分)求线性代数方程组Ax b =的数值解法主要有矩阵的直接分解法(如LU 分解法、Crout 分解法、Cholesky 分解法等)和迭代法(如Jacobi 迭代法、Gauss-Seidel 迭代法).请你简述求解线性代数方程组Ax b =的直接分解法和迭代法这两类方法的不同点和相同点.。
2009数值分析试卷A答案

南京工业大学 数值分析 试题(A )答案2009--2010 学年第一学期学年第一学期 使用班级使用班级 信科0701应数0701 一、填空题 (每小题3分,共30分)1.已知974997.999995»,则»-9995100 0.025003126 具有 8 位有效数字。
2.对f(x)=2x 4+x+1,差商f[0,1,2,3,4]= 2 ;f[0,1,2,3,4,5]= 0 。
3.设方程x=j (x)有根x *,且设j (x)在含x *的区间(a,b)内可导,设x 0Î(a,b)则迭代格式x k+1=j (x k )收敛的充要条件为 1|)(|*<¢x j 。
4.÷÷øöççèæ=011001001001....A ,||A||µ= 2.01 ,cond(A)µ= 404.01 。
5.中矩形公式:)()2()(a b b a f dx x f ba-+=ò的代数精度为 2 。
6.在区间[1,2]上满足插值条件îíì==1)2(2)1(P P 的一次多项式P(x)= 3-x 。
7.设å==nk k k n x f A f I 0)()(是函数f(x)在区间[a,b]上的插值型型求积公式,则å=nk kA= a b - 。
8.梯形公式和改进的Euler 公式都是 2 阶的。
9.在区间[0,1]上,函数ax x +=)(1j与函数22)(x x =j 正交,则a= -0.75 。
10.求解线性方程组Ax=b 的迭代格式x (k+1)=Jx (k)+f 收敛的充要条件为1)(<J r 。
二、计算题 (每题8分,共48分)1.试用Gauss 消元法解下列方程组,计算过程按5位小数进行:÷÷÷øöçççèæ=÷÷÷øöçççèæ÷÷÷øöçççèæ---08.255.190.05.11.40.10.15.26.15.05.12.3321x x x (写出详细过程!)解:A=÷÷÷øöçççèæ--2524.01010.0001000.12500.12500.309000.05000.05000.12000.3 (4分)分) ÷÷÷øöçççèæ 2.5000 1.0000 0 0 1.3000 0 1.0000 0 0.5000 0 0 1.0000~ (3分)分) 所以方程组的解为:5.2,3000.1,5000.0321===x x x (1分)分) 2. 给出f(x)f(x)的函数表,的函数表,(1)在表中填上指定阶的差商;(2)写出f(x)f(x)的的2次牛顿插值多项式;(3)给出截断误差。
安徽大学2009-2010(1)数值分析A卷

L2 (x) =
Putting these values of the Lagrange coefficients in p2 (x), we have p2 (x) = 1 (37x2 − 55x + 168), 84 . . . . . . 10 marks (b) Now taking x = 4 in the polynomial above, we have p2 (4) = 1 (37(4)2 − 55(4)x + 168) = 6.4286, 84 . . . . . . 15 marks 4. (15 marks) Using the method of least squares, fit a straight line to the four points, (1, 1), (2, 2), (3, 2), and (4, 3). Solution. The sums required for normal equation are easily obtained using the values in table i xi yi x2 xi yi i 1 1.0000 1.0000 1.0000 1.0000 2 2.0000 2.0000 4.0000 4.0000 3 3.0000 2.0000 9.0000 6.0000 4 4.0000 3.0000 16.000 12.000 ∑ ∑ ∑ 2 ∑ n=4 xi = 10 yi = 8 xi = 30 xi yi = 23
The bound f ′′ (x) on [1, 2] is M = max |f ′′ (x)| = max
∫
2
I (f ) =
1
ln(x + 1)dx,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中国石油大学(北京)2009--2010学年第一学期研究生期末考试试题A (闭卷考试)课程名称:数值分析注:计算题取小数点后四位一、填空题(共30分,每空3分)1、 已知x =0.004532是由准确数a 经四舍五入得到的近似值,则x 的绝对误差界为_______________。
2、数值微分公式()()'()i i i f x h f x f x h+-≈的截断误差为 。
3、已知向量T x =,求Householder 变换阵H ,使(2,0)T Hx =-。
H = 。
4、利用三点高斯求积公式11()0.5556(0.7746)0.8889(0)0.5556(0.7746)f x d x f f f -≈-++⎰导出求积分40()f x dx⎰的三点高斯求积公式 。
5、42()523,[0.1,0.2,0.3,0.4,0.5]_____.f x x x f =+-=若则6、以n + 1个互异节点x k ( k =0,1,…,n ),(n >1)为插值节点的 Lagrange 插值基函数为l k (x)( k =0,1,…,n ),则(0)(1)__________.nkk k lx =+=∑7、已知3()P x 是用极小化插值法得到的cos x 在[0,4]上的三次插值多项式,则3()P x 的截断误差上界为3()cos ()R x x P x =-≤_________.8、已知向量(3,2,5)T x =-,求Gauss 变换阵L ,使(3,0,0)T Lx =。
L =_________. 9、设32()(7)f x x =-, 给出求方程()0f x =根的二阶收敛的迭代格式_________。
10、下面M 文件是用来求解什么数学问题的?________________________.function [x,k]=dd (x0) for k=1:1000 x=cos (x0);if abs(x-x0)<0.00001, break end x0=x; end二、(15分)已知矛盾方程组Ax=b ,其中11120,1211A b ⎡⎤⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦,(1)用施密特正交化方法求矩阵A 的正交分解,即A=QR 。
(2)用此正交分解求矛盾方程组Ax=b 的最小二乘解。
三、(10分)已知求解线性方程组Ax=b 的分量迭代格式1(1)(1)()1+1/,121,,i nk k k ii ij jijj ii j j i x b a xax a i n n -++===--=-∑∑(),,(1)试导出其矩阵迭代格式及迭代矩阵; (2)若11a A a⎛⎫=⎪⎝⎭,推导上述迭代格式收敛的充分必要条件。
四、(15分)(1)证明对任何初值0x R ∈,由迭代公式111sin ,0,1,2, (2)k k x x k +=+=所产生的序列{}0k k x ∞=都收敛于方程11sin 2x x =+的根。
(2)迭代公式1121sin ,0,1,2, (2)k k k x x x k +=--=是否收敛。
五、(15分)用最小二乘法确定一条经过原点(0,0)的二次曲线,使之拟合下列数据-2-11230.81 3.4iix y ⎧⎨⎩并求平方误差22δ。
六、(15分)(1)写出以0,1,2为插值节点的二次Lagrange 插值多项式2()P x ; (2)以0,1,2为求积节点,建立求积分3()I f x dx =⎰的一个插值型求积公式,并推导此求积公式的截断误差。
中国石油大学(北京)2009--2010学年第一学期 研究生期末考试试题标准答案A (闭卷考试)课程名称:数值分析一、(30分) 1、61102-⨯; 2、()O h ; 3、1121H ⎡-=⎢⎢⎥⎣⎦; 4、4() 1.1112(0.4508) 1.7778(2) 1.1112(3.5492)f x dx f f f ≈++⎰;5、 5;6、1;7、112; 8、10021035013L ⎛⎫⎪⎪=- ⎪ ⎪ ⎪⎝⎭;9、 3231522(7)726(7)3k k k k k k k kx x x x x x x x +--=-=-- 10、用简单迭代法1cos()k k x x +=求方程cos()x x =的根。
二、(15分)(1)1211122211212211212(1,2,2),(1,0,1)1(1,2,2),(1,2,2)311(,)(2,-2,1),=(2,-2,1)333123112-230121T TT T T Tu u v u v u u u v u u A QR εεεεεεεε======-=-===⎧⎨=+⎩⎡⎤⎡⎤⎢⎥==⎢⎥⎢⎥⎣⎦⎢⎥⎣⎦,(10分)5/341(2),,1/393TTRx Q b x ⎡⎤⎡⎤===⎢⎥⎢⎥⎣⎦⎣⎦(5分)三、(10分) (1) 1(1)()(+1)1+1,,1,,2,1i nk k k ii ii ij jijj j j i a x b a xax i n n -+===--=-∑∑(1)(1)()(1)()(1)1()1)()()()k k k k k k k Dx b Lx Ux D L x Ux bx D L Ux D L b++++--=++-=+=-+-(1)()11112221111211,()()000,00000k k nn n nn n n n x Bx g B D L Ug D L ba a a D L a a a a a U a +----=+=-=-⎛⎫⎛⎫⎪⎪⎪ ⎪==- ⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎛⎫ ⎪ ⎪=- ⎪ ⎪⎝⎭迭代矩阵右端向量其迭代法的矩阵形式中 (6分)112100(2)()10010001000a B D L U aa a a a ---⎛⎫⎛⎫=-=⎪ ⎪⎝⎭⎝⎭--⎛⎫⎛⎫⎛⎫== ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭迭代矩阵22(),()1,101B a B a a ρρ=<<→<<迭代格式收敛的充分必要条件是即 (4分)四、(15分)(1)记1()1sin 2x x ϕ=+,则1'()cos 2x x ϕ=。
先考虑区间[0.5,1.5],当[0.5,1.5]x ∈时,1()1sin [0.5,1.5]2x x ϕ=+∈ ,11'()cos 122x x ϕ=≤< 。
故对任意初值[0.5,1.5]x ∈,由迭代公式111sin ,0,1,2, (2)k k x x k +=+=产生的序列{}0k k x ∞= 都收敛于方程11sin 2x x=+的根。
(9分)对任意初值0x R ∈,有1011sin [0.5,1.5]2x x =+∈,将此1x 看成新的迭代初值,则由(1)可知,由迭代公式111sin ,0,1,2, (2)k k x x k +=+=产生的序列{}0k k x ∞= 都收敛于方程11sin 2x x =+的根。
(3分) (2)记1()21sin 2x x x ϕ=--,则1'()2cos 2x x ϕ=-,对任意x R ∈,有'() 1.5x ϕ≥ 所以迭代公式1121sin ,0,1,2, (2)k k k x x x k +=--=不收敛。
(3分)五、(15分)212122(),()-243-110.8,,,11124 3.40.110010.1,=27.403427.40.805934()0.1+0.8059x x x x Y a a b b s x x x ϕϕ==⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥Φ=Φ==⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦= (10分)2212(,)(,)(,)22.20.10.805927.40.0183Y Y a Y b Y δ=-Φ-Φ=--⨯= (5分)六、(15分) (1)2(1)(2)(0)(2)(1)(0)()(0)(1)(2)(01)(02)(10)(12)(21)(20)x x x x x x P x f f f ------=++------ ( 5分)(2)3321039()()(0)(2)=44I f x dx P x dx f f I =≈=+⎰⎰ (5分)34319()=32442.f x x =⨯≠⨯=取,代入求积公式,左边右边代数精度为 构造一个二次插值多项式p 2(x)满足下列条件222(0)(0),(2)(2),'(2)'(2)p f p f p f ===(3)2(3)2()23!333()23!0()()(2),()()(2)f f f x p x x x a b f x dx p x dx x x dxξξξ-=-≤≤-=-⎰⎰⎰因为p 2(x)为二次多项式,所以322203939()(0)(2)(0)(2)4444p x dx p p f f =+=+⎰(3)3210(3)(3)32(3)0()(2)3!()()93(2)()3!3!48f I I x x dxf f x x dx f ξξξη-=-=-==⎰⎰ (5分)。
