金融工程答案翻译
金融工程答案翻译

金融工程答案翻译1.4的第1章详细解释了卖出看涨期权和买入看跌期权之间的区别卖出看跌期权意味着给予其他人购买你的部分房产的权利,这将给你带来-max(st-k,0)=min(k-st,0)买入看跌期权意味着从其他人那里购买期权,回报是max(k-st,0) 。
他们都有一个可能的收入k-st。
当你卖出看涨期权时,收入为负或0,因为交易对手可以选择是否执行。
当你购买看跌期权时,你的收入是0,或者仅仅因为你选择是否执行它。
你认为股票价格会上涨。
股票的当前价格是29美元,三个月期间,执行价格为30美元的看涨期权的价格是2.9美元,你总共有5800美元,这表明两种投资模式。
并简要说明两种模式的优缺点,有两种选择,即购买XXXX年期远期合同执行价格为800美元,一次套利可以以每年10%的利率借入资金,套利应该如何做才能达到套利的目的?这里我们假设黄金的储存成本是0。
同时,黄金不会带来任何利息收入。
这位套利者可以借入资金购买100盎司黄金现货,并出售一份一年内交割的100盎司期货合约。
这意味着黄金以每盎司600美元的价格买进,以每盎司800美元的价格卖出,收益率约为33.3%,远高于10%的准入率。
这是一个很好的获利机会。
仲裁员应该购买尽可能多的1.27股票的期货合约,与预期的黄金现货数量相匹配。
目前的价格是94美元。
与此同时,执行价格为95美元的三个月期欧洲期权是4.7美元。
一位投资者认为股价会上涨,但他不知道是在7月份买入100只股票还是XXXX。
一家矿业公司刚刚发现了一个小金矿。
决定在六个月内建起这座矿井。
黄金将在明年继续开发。
纽约期货交易所有黄金期货合约。
从XXXX的一月到二月,总共将生产3000盎司黄金。
卖出30长期货合约可以锁定其价格2.26一家公司进入了空头期货头寸。
在合同中,该公司以每蒲式耳250美分的价格出售了5000蒲式耳小麦。
初始保证金为3000美元,XXXX的维持保证金为6%,股息收益率为每年3%,当前3个月期货价格为1259美元。
金融工程常用术语(中英对照)

金融工程常用术语中英对照AABS Asset-Backed Security 资产支持证券ABS CDO 由ABS所派生出的份额产品Accrual Swap 计息互换Accrued Interest 应计利息Actuaries 保险精算师Adaptive Mesh Model 自适应网格模型Adjusted Present Value 调整现值法Adverse Selection 逆向选择After-tax Interest Rate 税后利润Agency Costs 代理费用American Option 美式期权Amortization 分期偿付Amortization Schedule 分期偿付时间表Amortizing Swap 分期偿还互换Analytic Result 解析结果APR Annual Percentage Rate 年度百分率Annualized Capital Cost 按年折算的资本成本Arbitrage 套利Arbitrageur 套利者Asian Option 亚式期权Ask Price 卖盘价Asset 资产Asset Allocation 资产分配Asset-or-Nothing Call Option 资产或空手看涨期权Asset-or-Nothing Put Option 资产或空手看跌期权Asset Swap 资产互换As-You-Like-It Option 任选期权At-the-Money Option 平值期权Average Price Call Option 平均价格看涨期权Average Price Put Option 平均价格看跌期权Average Strike Option 平均执行价格期权BBackdating 倒填日期Back Testing 回顾测试Backwards Induction 倒推归纳Barrier Option 障碍期权Base Correlation 基础相关系数Basel Committee 巴塞尔委员会Basis 基差Basis Point 基点Basis Risk 基差风险Basis Swap 基差互换Basket Credit Default Swap 篮筐式信用违约互换Basket Option 篮筐式期权Bear Spread 熊市差价Bermudan Option 百慕大式期权Before-tax Interest Rate 税前利率Beta 贝塔Bid-Ask Spread 买入卖出差价Bid Price 买入价Bilateral Clearing 双边结算Binary Credit Default Swap 两点式信用违约互换Binary Option 两值期权Binomial Model 二项式模型Binomial Option Pricing Model 二项期权定价模型Binomial Tree 二叉树Bivariate Normal Distribution 二元正态分布Black’s Approximation 布莱克近似Black’s Model 布莱克模型Black-Scholes-Merton Model 布莱克-斯科尔斯-莫顿模型Bond Option 债券期权Bond Yield 债券收益率Book Value 账面价值Bootstrap Method 票息剥离方法Boston Option 波士顿期权BOT Build-Operate-Transfer 建设-经营-转让Box Spread 合式差价Break-even point 盈亏平衡点Break Forward 断点远期Brownian Motion 布朗运动Bull Spread 牛市差价Butterfly Spread 蝶式差价CCalendar Spread 日历差价Calibration 校正Callable Bond 可赎回债券Call Option 看涨期权Cancelable Swap 可取消互换Cap 上限Cap Rate 上限利率CAPM Capital Asset Pricing Model 资本资产定价模型Caplet 上限单元Capital gain 资本收藏Capital less 资本损失Capital Market 资本市场Capital Market Line 资本市场线Caps 赔付限额Case-Shiller Index 凯斯-席勒指数Cash budget 现金预算Cash cycle time 现金周转时间Cash Dividend 现金股利Cash Flow Mapping 现金流映射Cash-or-Nothing Call Option 现金或空手看涨期权Cash-or-Nothing Put Option 现金或空手看跌期权Cash Settlement 现金交割或现金清算CCP Central Clearing Party 中央结算对手CDD Cooling Degree Days 降温天数CDO Collateralized Debt Obligation 债务抵押债券CDS Credit Default Swap 信用违约互换CEBO Credit Event Binary Option 信用事件两点式期权Central Clearing 中心结算Central Clearing Party 中央结算对手Central Counterparty 中央交易对手CEV Model Constant Elasticity of Variance Model 常方差弹性模型Cheapest-to-Deliver Bond 最便宜可交割债券Cholesky Decomposition 乔里斯基分解Chooser Option 选择人期权Class of Options 期权分类Clean Price of Bond 债券除息价格Clearing House 结算中心Clearing Margin 结算保证金Cliquet Option 棘轮期权CMO Collateralized Mortgage Obligation 见房产抵押债券CMS Constant Maturity Swap 固定期限国债互换Collar 双限Collateral 抵押品Collateralization 抵押品策略Collateralized Debt Obligation 债务抵押债券Collateralized Mortgage Obligation 房产抵押债券Combination 组合Commercial Banks 商业银行Commercial Loan Rate 商业贷款利率Commodity Futures Trading Commission 商品期货交易管理委员会Commodity Swap 商品互换Compound Interest 复利Compounding 复利计息Compounding Frequency 复利利率Compound Correlation 复合相关系数Compound Option 复合期权Confidence interval 置信区间Continuous Probability Distribution 连续概率分布Confirmation 交易确认书Consumption Asset 消费资产Contango 期货溢价Continuous Compounding 连续复利Control Variate Technique 控制变量技术Convenience Yield 便利收益率Conversion Factor 转换因子Convertible Bond 可转换债券Convexity 曲率Convexity Adjustment 曲率调整Cornish-Fisher Expansion 科尼什-费雪展开Copayments 赔付比例Corporation 公司Correlation 相关性Cost of Capital 资本成本Cost of Carry 持有成本Controller 审计官Counterparty 交易对手Coupon 券息Coupon bond 付息债券Covariance 协方差Covarance Matrix 协方差矩阵Covered Call 备保看涨期权Crash phobia 暴跌恐惧症Credit Contagion 信用蔓延Credit Default Swap 信用违约互换Credit Derivative 信用衍生产品Credit Event 信用事件Credit Event Binary Option 信用事件两点式期权Credit Index 信用指数Credit Rating 信用等级Credit Ratings Transition Matrix 信用评级转移矩阵Credit Risk 信用风险Credit Spread Option 信用差价期权CSA Credit Support Annex 信用支持附约CVA Credit Value Adjustment 信用价值调节量Credit Value at Risk 信用风险价值度Cross Hedging 交叉对冲Currency Swap 货币互换Current yield 本期收益率DDay Count 计天方式Day Trade 即日交易DCF Discounted Cash flow Model 现金流折现模型DDM Dividend Discount Model 股利贴现模型DVA Debt Value Adjustment 债务价值调节量Decision Tree 决策树Deductible 免赔额Default Risk 违约风险Defined-benefit Pension Plan 规定受益型养老金计划Defined-contribution Pension Plan 规定缴费型养老金计划Delivery Price 交割价格Delta Hedging Delta对冲Delta-Neutral Portfolio Delta 中性交易组合Derivative 衍生产品Deterministic Variable 确定性变量Diagonal Spread 对角差价Differential Swap 交叉货币度量互换Diffusion Process 扩散过程Dirty Price of Bond 带息价格Discount Bond 折扣债券Discount Instrument 折扣产品Discounted Cash Flow Analysis 贴现现金流分析Discounted Dividend Model 股利贴现模型Diversifiable Risk 可分散风险Diversification 分散化Diversification Principle 分散化原则Diversifying 分散投资Discount Rate 贴现率Dividend 股息Dividend Yield 股息收益率Dodd-Frank Act 多德-弗兰克法案Dollar Duration 绝对额久期DOOM Option DOOM期权Down-and-In Option 下降-敲入期权Down-and-Out Option 下降-敲出期权Downgrade Trigger 降级触发Drift Rate 漂移变化率Duration 久期Duration Matching 久期匹配Dynamic Hedging 动态对冲EEAR/ EFF Effective Annual Rate 实际年利率Early Exercise 提前行使EBIT Earnings Before Interest and Tax 息税前利润Effective Federal Funds Rate 有效联邦基金利率Efficient Portfolio 有效投资组合Efficient Portfolio Frontier 有效投资组合边界Electronic Trading 电子交易Embedded Option 内含期权EMH Efficient Markets Hypothesis 有效市场假说Empirical Research 实证研究Employee Stock Option 雇员股票期权Equilibrium Model 均衡模型Equity Swap 股权互换Equity Tranche 股权份额Equivalent Annual Interest Rate 等价年利率Eurocurrency 欧洲货币Eurodollar 欧洲美元Eurodollar Futures Contract 欧洲美元期货合约Eurodollar Interest Rate 欧洲美元利率Euro LIBOR 欧元同业拆借利率European Option 欧式期权Exchange Option 互换期权Exchange Rate 汇率Exclusions 免赔条款Ex-dividend Date 除息日Exercise Limit 行使限额Exercise Multiple 行使倍数Exercise Price 执行价格Exotic Option 特种期权Expectations Theory 预期理论Expected Shortfall 预期亏损Expected Rate of Return 预期回报率Expected Value of a Variable 变量的期望值Expiration Date 到期日Explicit Finite Difference Method 显式有限差分方法Exponentially Weighted Moving Average Model 指数加权移动平均模型Exponential Weighting 指数加权Exposure 风险敞口Extendable Bond 可展期债券Extendable Swap 可延期互换External Financing 外部投资FFace Value 面值Factor 因子Factor Analysis 因子分析Federal Funds Rate 联邦基金利率FEI Financial Executives Institute 财务执行官组织Finance 金融学Financial Futures 金融期货Financial Guarantees 财务担保Financial Intermediary 金融媒介Financial System 金融系统Finite Difference Method 有限差分法Fixed-Income Instrument 固定收益证券Flat Volatility 单一波动率Flex Option 灵活期权Flexi Cap Flexi上限Floor 下限Floor-Ceiling Agreement 下限上限协议Floor let 下限单元Floor Rate 下限利率Flow of funds 资金流Foreign Currency Option 外汇期权Forward Contract 远期合约Forward Exchange Rate 远期汇率Forward Interest Rate 远期利率Forward Price 远期价格Forward Rate 远期率FRA Forward Rate Agreement 远期利率合约Forward Risk-Neutral World 远期风险中性世界Forward Start Option 远期开始期权Forward Swap 远期互换Fundamental Value 基本价值Futures Commission Merchants 期货佣金经纪人Futures Contract 期货合约Futures Option 期货期权Futures-Style Option 期货式期权FV Final Value 终值GGrowth annuity 增长年金GAP Management 制品管理Gap Option 缺口期权Gaussian Copula Model 高斯Copula 模型Gaussian Quadrature 高斯求积公式Generalize Wiener Process 广义维纳过程Geometric Average 几何平均Geometric Brownian Motion 几何布朗运动Girsanov’s Theorem 哥萨诺夫定理Guaranty Fund 担保基金HHaircut 折扣Hazard Rate 风险率Hedge 对冲Hedge Funds 对冲基金Hedger 对冲者Hedge Ratio 对冲比率Hedgers 套期保值者Historical Simulation 历史模拟Historical Volatility 历史波动率Holiday Calendar 假期日历Human Capital 人力资本IImmediate Annuity 即时年金Implicit Finite Difference Method 隐式有限差分Implied Correlation 隐含相关系数Implied Distribution 隐含分布Implied Dividend 隐含股利Implied Tree 隐含树形Implied Volatility 隐含波动率Inception Profit 起始盈利Index Amortizing Swap 指数递减互换Index Arbitrage 指数套利Index Futures 指数期货Index-linked Bonds 指数化债券Index Option 指数期权Index Principal Swap 指数本金互换Initial Margin 初始保证金Instantaneous Forward Rate 瞬时远期利率Insuring 保险Intangible Assets 无形资产Interest-rate Arbitrage 利率套利Interest Rate Cap 利率上限Interest Rate Collar 利率双限Interest Rate Derivative 利率衍生产品Interest Rate Floor 利率下限Interest Rate Swap 利率互换Internal Financing 内部融资International Swap and Derivatives Association 国际互换和衍生产品协会In-the-Money Option 实值期权Intrinsic Value 内涵价值Inverted Market 反向市场Investment Asset 投资资产Investment Banks 投资银行ISDA International Swap and Derivatives Association 国际互换和衍生产品协会IRR Internal Rate of Return 内部收益率JJump-Diffusion Model 跳跃扩散模型Jump Process 跳跃过程LLaw of One Price 一价原则Liability 负债LIBID London Inter Bank Bid Rate 伦敦同业借款利率LIBOR London Inter Bank Offered Rate 伦敦同业拆出利率LIBOR Curve LIBOR曲线LIBOR-in-Arrears Swap LIBOR后置互换Life Annuity 人寿年金Limited Liability 有限责任Limit Move 涨跌停版变动Limit Order 限价指令Liquidity 流动性Liquidity Preference Theory 流动性偏好理论Liquidity Premium 流动性溢价Liquidity Risk 流动性风险Locals 自营经纪人Lognormal Distribution 对数正态分布Long Hedge 多头对冲Long Position 多头Look back option 回望期权Low Discrepancy Sequence 低偏差序列MMaintenance Margin 维持保证金Margin 保证金Margin Call 保证金催付Market Capitalization Rate 市场资本化利率MSU Market-Leveraged Stock Unit 市场股票凭据Market Maker 做市商Market Model 市场模型Market Portfolio 市场投资组合Market Price of Risk 风险市场价格Market Segmentation Theory 市场分隔理论Market-weighted Stock Indexes 市场加权股票指数Marking to Market 按市场定价Markov Process 马尔科夫过程Martingale 鞅Maturity 期限Maturity Date 到期日Maximum Likelihood Method 极大似然方法Mean Reversion 均值回归Measure 测度Merger 合并Mezzanine Tranche 中层份额Minimum Variance 最小方差组合Modified Duration 修正久期Money Market 货币市场Money Market Account 货币市场帐户Monte Carlo Simulation 蒙特卡罗模拟Moral Hazard 道德风险Mortgage-Backed Security 房产抵押贷款证券Mutual Fund 共同基金NNaked Position 裸露期权Netting 净额结算Net Present Value 净现值Net Worth 净资产No-Arbitrage Assumption 无套利假设No-Arbitrage Interest Rate Model 无套利假设Nominal Future Value 名义终值Nominal Interest Rate 名义利率Nominal Prices 名义价格Nondiversifiable Risk 不可分割风险Nonstationary Model 非平稳模型Non Systemic Risk 非系统风险Normal Backwardation 正常现货溢价NPV Net Present Value 净现值Normal Distribution 正态分布Normal Market 正常市场Notional Principal 面值(本金)Numeraire 计价单位Numerical Procedure 数值方法OOCC Option Clearing Corporation 期权结算中心Offer Price 卖出价格Open Interest 未平仓合约Open Outcry 公开喊价Opportunity Cost of Capital 资金的机会成本Optimal Combination of risky assets 风险资产的最优组合Option 期权Option-Adjusted Spread 期权调整差价Option Class 期权种类Ordinary Annuity 普通年金Out-of-the-Money Option 虚值期权Overnight Indexed Swap 隔夜指数互换Over-the-Counter Market 场外交易市场PPackage 组合期权Par bonds 等价债券Par Value 面值Par Yield 面值收益Parallel Shift 平行移动Parisian Option 巴黎期权Partnership 合伙制Path-Dependent Option 路径依赖型期权Payoff 收益Pay off Diagram 收益图Percent-of-sales method 销售收入百分比法Permanent Income 持久收入Perpetuity 永续年金Perpetual Derivatives 永续衍生品Portfolio Immunization 组合免疫Portfolio Insurance 证券组合保险Portfolio selection 投资组合选择Portfolio theory 投资组合理论Position Limit 头寸限额Premium 期权付费Premium Bond 溢价债券Present Value 现值Principal-agent Problem 委托人-代理人问题Prepayment Function 提前偿付函数Principal 本金Principal Components Analysis 主因子分析Principal Protected Notes 保本型证券Probability Distributions 概念分布Program Trading 程序交易Protective Put 保护看跌期权Pull-to-Par 收敛于面值现象Purchasing-power Parity 购买力评价Pure Discount Bonds 纯贴现债券Put-Call Parity 看跌-看涨期权平价关系式Put Option 看跌期权Puttable Bond 可提前退还债券Puttable Swap 可赎回互换President 总裁PMT Payment(Returns the periodic payment for an annuity)年金PPP Public-Private Partnership 政府和社会资本合作PV Present Value 现值QQuansi-Random Sequences 伪随机序列RRate of Return on capital 资本收益率Rainbow Option 彩虹期权Range-Forward Contract 远期范围合约Ratchet Cap 执行价格调整上限Real Future Value 实际终值Real Interest Rate 实际利率Real Option 实物期权Real Prices 实际价格Rebalancing 再平衡Recovery Rate 回收率Reference Entity 参考实体Reinvestment Rate 再投资利率Residual Claim 剩余索取权Repo 再回购Repo Rate 再回购利率Reset Date 重置日(定息日)RSU Restricted Stock Unit 受限股票单位Reversion Level 回归水平Risk Aversion 风险厌恶Risk-adjusted discount rate 风险调整贴现率Risk Exposure 风险暴露Rights Issue 优先权证Risk-Free Rate 无风险利率Risk Management 风险管理Risk Management Process 风险管理过程Risk-Neutral Valuation 风险中性定价Risk-Neutral World 风险中性世界Roll Back 倒推ROS Ratio of income as percentage of sales 销售利润率ROA Return On Assets 资产收益率ROE Rate of Return on Common Stockholders’ Equity 净资产收益率SScalper 投机者Scenario Analysis 情形分析Securitization 证券化Security Market Line 证券市场线Sensitivity Analysis 敏感性分析Self-financing Investment Strategy 自筹资金投资策略Settlement Price 结算价格Share Repurchase 股票回购Short Hedge 空头头寸对冲Short Position 空头头寸Short Rate 短期利率Short Selling 卖空交易Short-Term Risk-Free Rate 短期无风险利率Shout Option 喊价期权Simple Interest 单利Sole Proprietorship 独资企业Specialist 专家Speculator 投机者Spot futures price parity relation 现货期货价格平价关系。
金融学14章金融答案翻译

CHAPTER 14FORWARD AND FUTURES PRICESObjectives∙ To explain the economic role of futures markets∙ To show what information can and cannot be inferred from forward and futures prices.∙Outline14.1 Distinctions Between Forward and Futures Contracts14.2 The Economic Function of Futures Markets14.3 The Role of Speculators14.4 Relation Between Commodity Spot and Futures Prices14.5 Extracting Information from Commodity Futures Prices14.6 Spot-Futures Price Parity for Gold14.7 Financial Futures14.8 The Implied Risk-Free Rate14.9 The Forward Price Is Not a Forecast of the Spot Price14.10 Forward-Spot Parity with Cash Payouts14.11 Implied Dividends14.12 The Foreign-Exchange Parity Relation14.13 The Role of Expectations in Determining Exchange RatesSummary∙ Futures contracts make it possible to separate the decision of whether to physically store a commodity from thedecision to have financial exposure to its price changes.∙ Speculators in futures markets improve the informational content of futures prices and make futures marketsmore liquid than they would otherwise be.∙ The futures price of wheat cannot exceed the spot price by more than the cost of carry:∙ The forward-spot price parity relation for gold is that the forward price equals the spot price times the cost ofcarry:This relation is maintained by the force of arbitrage . ∙One can infer the implied cost of carry and the implied storage costs from the observed spot and forward prices and the risk-free interest rate. ∙ The forward-spot parity relation for stocks is that the forward price equals the spot price times 1 plus the risk-free rate less the expected cash dividend.This relation can therefore be used to infer the implied dividend from the observed spot and forward prices and the risk-free interest rate. ∙ The forward-spot price parity relation for the dollar/yen exchange rate involves two interest rates:where F is the forward price of the yen, S is the current spot price, r Y is the yen interest rate, and r $ is the dollarinterest rate. ∙ If the forward dollar/yen exchange rate is an unbiased forecast of the future spot exchange rate, then one caninfer that forecast either from the forward rate or from the dollar-denominated and yen-denominated risk-free interest rates.F S C -≤F S r s =++()1F S r D=+-()1F r S r Y11+=+$Solutions to Problems at End of ChapterForward Contracts and Forward-Spot Parity.1. Suppose that you are planning a trip to England. The trip is a year from now, and you have reserved a hotel room in London at a price of ₤50 per day. You do not have to pay for the room in advance. The exchange rate is currently $1.50 to the pound sterling.a.Explain several possible ways that you could completely hedge theexchange rate risk in this situation.b.Suppose that r₤=.12 and r$=.08. Because S=$1.50, what must theforward price of the pound be?c.Show that if F is $0.10 higher than in your answer to part b, therewould be an arbitrage opportunity.SOLUTION:a.Ways to hedge the exchange rate risk:Pay for the room in advanceBuy the pounds you will need in the forward market.Invest the present value of the rental payments in a pound-denominated riskless asset.对冲外汇风险的几种方法:提前对这个房间付款;在期货市场购买英镑;将与现期价值的租金同等的英镑投资于无风险资产。
金融工程名词解释英文版

Terms in Financial Engineering1. Derivatives: an instrument whose value depends on the values of other more basic underlying variables. It derives its value from the performance of the underlying asset.2. Option: the right, but not the obligation, to buy (for a call option) or sell (for a put option) a specific amount of a given stock, commodity, currency, index, or debt, at a specified price (the strike price) during a specified period of time.3. American Options: can be exercised at any time up to the expiration date. European Options: can be exercised only on the expiration date itself.4. Forward Contract: an over-the-counter agreement between two parties, a buyer and a seller, that calls for the delivery of an asset at a future point in time with a price agreed upon today.5. Long Party: the party agrees to buy. Short Party: sell.6. Futures Contract: a forward contract that has standardized terms, is traded on an organized exchange, and follows a daily settlement procedure in which the losses of one party to the contract are paid to the other party.7. Swap: an over-the-counter derivative in which two parties make a series of payments to each other at specific dates.8. Financial Engineering: the notion that you can use a combination of assets and financial derivatives to construct cash flow streams that would otherwise be difficult or impossible to obtain.9. Hedger: If someone bears an economic risk and uses derivative markets to reduce that risk, the person is a hedger.10. Speculators: bet on the movement of the market to make windfall profits. Speculators attempt to profit from guessing the direction of the market.11. Arbitrage: a type of transaction in which an investor seeks to make a riskless profit when the same good sells for two different prices.12. Arbitrageurs: persons actively engaged in the arbitrage seeking out minor pricing discrepancies.13. Offsetting: most traders close out a position prior to the delivery period14. Underlying Asset: 衍生品合约中约定的资产,可以是实物商品、金融资产、利率、汇率、价格指数等等。
金融工程课后题7习题解答zhoujiaLite

CH 77.1 一位投资者购买了一个执行价格为X的看涨期权并出售了一个相同执行价格的看跌期权。
请描述他的头寸情况。
解:投资者头寸状况为:max(S T-X,0)-max(X-S T,0)此头寸相当于执行价格为X的远期合约。
当X与远期合约价格相同时,合约价值为0,此时看涨期权与看跌期权价值相等。
7.2请说明为什么欧式期权总是不如有相同标的物、相同执行价格、相同到期日的美式期权值钱。
解:美式期权持有者除具有欧式期权持有者所拥有的所有权利外,还有提早执行权。
因此,美式期权至少应与相应的欧式期权有相同的价值。
7.3请解释为什么美式期权的价值总是大于等于它的内在价值。
解:美式期权的持有者有立即执行期权,实现期权内在价值的权利,因此,美式期权的价值至少应等于其内在价值。
7.4列举影响期权价格的6个因素。
解:影响期权价格的6个因素有:标的资产价格、期权的执行价格、无风险利率、资产价格的波动率、期限以及持有期间收益。
7.5基于无红利支付股票的看涨期权,期限为4个月,执行价格为$25,股票价格为$28,无风险利率为8%。
该看涨期权价格下限为多少?解:该看涨期权的价格下限为:28-25×0.08*0.3333e-=$3.667.6基于无红利支付股票的欧式看跌期权,期限为1个月,股票价格为$12,执行价格为$15,无风险年利率6%,该期权的价格下限为多少?解:该看跌期权价格下限为:15×0.06*0.083333e--12=$2.937.7请给出两个原因说明为什么早执行无红利支付股票的美式看涨期权不是最好的。
第一条原因应包括货币时间价值。
第二条原因在利率为零时也成立。
解:1)推迟执行可推迟支付期权的执行价格,期权持有者可赚取执行价格更长时间的时间价值;2)推迟执行可提供保值价值,避免执行日时股价低于执行价格。
假设期权购买者有现金X ,且利率为0。
提早执行会使期权购买者头寸在到期日为T S , 而推迟执行买方头寸在到期日则为max (X,T S )7.8 “提前执行美式看跌期权是在货币的时间价值与看跌期权的保险价值之间的权衡。
【精品】金融工程第七版课后习题答案(中文

第1章导言练习题1.1请解释远期多头与远期空头的区别。
答:远期多头指交易者协定将来以某一确定价格购入某种资产;远期空头指交易者协定将来以某一确定价格售出某种资产。
1.2请详细解释套期保值、投机与套利的区别。
答:套期保值指交易者采取一定的措施补偿资产的风险暴露;投机不对风险暴露进行补偿,是一种“赌博行为”;套利是采取两种或更多方式锁定利润。
1.3请解释签订购买远期价格为$50的远期合同与持有执行价格为$50的看涨期权的区别。
答:第一种情况下交易者有义务以50$购买某项资产(交易者没有选择),第二种情况下有权利以50$购买某项资产(交易者可以不执行该权利)。
1.4一位投资者出售了一个棉花期货合约,期货价格为每磅50美分,每个合约交易量为50,000磅。
请问期货合约结束时,当合约到期时棉花价格分别为(a)每磅48.20美分;(b)每磅51.30美分时,这位投资者的收益或损失为多少?答:(a)合约到期时棉花价格为每磅$0.4820时,交易者收入:($0.5000-$0.4820)×50,000=$900;(b)合约到期时棉花价格为每磅$0.5130时,交易者损失:($0.5130-$0.5000)×50,000=$6501.5假设你出售了一个看跌期权,以$120执行价格出售100股IBM的股票,有效期为3个月。
IBM股票的当前价格为$121。
你是怎么考虑的?你的收益或损失如何?答:当股票价格低于$120时,该期权将不被执行。
当股票价格高于$120美元时,该期权买主执行该期权,我将损失100(st-x)。
1.6你认为某种股票的价格将要上升。
现在该股票价格为$29,3个月期的执行价格为$30的看跌期权的价格为$2.90.你有$5,800资金可以投资。
现有两种策略:直接购买股票或投资于期权,请问各自潜在的收益或损失为多少?答:股票价格低于$29时,购买股票和期权都将损失,前者损失为$5,800$29×(29-p),后者损失为$5,800;当股票价格为(29,30),购买股票收益为$5,800$29×(p-29),购买期权损失为$5,800;当股票价格高于$30时,购买股票收益为$5,800 $29×(p-29),购买期权收益为$$5,800$29×(p-30)-5,800。
金融工程学各章习题及答案

金融工程学各章习题及答案第一章综合远期外汇协议(SAFE交易)1.请简述金融衍生产品的功能。
2.金融工程的应用领域。
3.金融远期合约有哪些优点?又有哪些缺点?4.请简述远期外汇市场的卖出者包括那些人。
5.请简述远期外汇市场的买入者包括那些人。
6.常见的远期合约有哪几种?7.远期交易主要应用在哪些领域?8.某交易商拥有1亿日元远期空头,远期汇率为0.008美元/日元.如果合约到期时汇率分别为0.0074美元/日元和0.0090美元/日元,请计算该交易商的盈亏状况。
9.某日美元对瑞郎即期汇率为USD/CHF1.2200-1.2210,若l个月美元对瑞郎远期汇率点数为20-30,l个月美元对瑞郎远期汇率点数为45-40,分别求l 个月和3个月美元对瑞郎远期汇率。
10.有些学者认为,远期汇率是对未来汇率的无偏预测。
请问在什么情况下这种观点是正确的?11.请简述影响期货汇率波动的主要因素。
12.请简述有效的外汇风险管理步骤。
第一章答案1.答:1.规避市场风险2.套利3.投机4.提高效率5.促进金融市场的完善2.答:1.公司理财方面2.金融工具及其交易策略3.投资与货币管理方面4.风险管理技术与手段3.答:优点主要是具有较大的灵活性;缺点是市场效率较低、流动性较差、违约风险较高。
4.答:1.有远期外汇收入的出口商2.持有未到期外汇的债权人3.输出短期资本的牟利者4.对远期外汇看跌的投机者5.答:1.有远期外汇支出的进口商2.负有未到期外汇的债务人3.输入短期资本的牟利者4.对远期外汇看涨的投机者6.常见的远期合约主要包括远期利率协议和远期外汇协议。
7.主要应用于利率风险和外汇风险防范。
8.若合约到期时汇率为0.0075美元/日元,则他赢利1亿(0.008-0.0074)=6万美元。
若合约到期时汇率为0.0090美元/日元,则他赢利1亿(0.008-0.009)=-10万美元。
9. l个月美元对瑞郎远期汇率为USD/CHF:(1.2200+0.0020)-(1.2210+30)=1.2220-1.2240。
金融工程课后题13-20习题解答renzhengliang(Lite)

Ch1313.1不是可交易证券价格的变量的风险价格是如何定义的?解:不是可交换证券价格的变量的风险市场价格是通过求可交换证券的风险市场价格而来,但必须满足该可交换证券的价格与不是可交换证券价格的变量瞬态完全正相关。
13.2假设黄金的风险市场价格为零,如果贮存成本为每年1%,无风险年利率为6%,那么黄金价格的期望增长率为多少?解:由公式m-λs=r-y+u,而λ=0,r=0.06,y=0,u=0.01所以m=0.07.即期望增长率为0.07。
13.3一个证券的价格与以下两个变量正相关:铜的价格和日元兑美元的汇率,假设这两个变量的风险市场价格分别为0.5和0.1。
若铜的价格固定,则该证券的波动率为每年8%;如果日元对美元的汇率固定,则该证券的波动率为每年12%。
无风险利率为每年7%。
证券的预期回报率为多少?如果两个变量彼此之间是不相关的,该证券的波动率为多少?解:(1)令u为证券的预期收益率,已知无风险利率r=0.07,铜价和日圆兑美圆汇率的风险市场价格分别为λ1=0.5和λ2=0.1,铜价固定时汇率引起的证券波动率为σ2=0.08,汇率固定时铜价引起的证券波动率为σ1=0.12。
因此由公式u-r=λ1σ1+λ2σ2可得u=0.138即证券的预期收益率为每年0.138(2)由σ1dz1+σ2dz2=dz3代入σ1,σ2的值可得(s)*T m TS S eλ-⨯为0.144即铜价和日圆兑美圆汇率不相关时证券的波动率为0.14413.4某个石油公司只是为了开发德克萨斯一个很小区域的石油。
其价值主要依赖于如下两个随机变量:石油的价格和以探明石油的储存量。
讨论:这两个变量中的风险市场价格为正数、负数还是零?解:第二个变量的风险市场价格为0。
这是因为这种风险是非系统的,它与经济社会的其他风险完全不相关,投资者不能因为承担这种不可转换的风险而要求更高的回报。
13.5通过两个无红利支付的交易证券和两个依赖于这两个无红利支付交易证券价格的衍生工具构成一个无风险组合,推导出这个衍生工具的微分方程。
金融工程 相关习题及答案教学文案

金融工程相关习题及答案Chapter 1 Market Organization and Structure PRACTICE PROBLEMS FOR CHAPTER 11. Akihiko Takabe has designed a sophisticated forecasting model, which predicts the movements in the overall stock market, in the hope of earning a return in excess of a fair return for the risk involved. He uses the predictions of the model to decide whether to buy, hold, or sell the shares of an index fund that aims to replicate the movements of the stock market. Takabe would best be characterized as a (n):A. hedger.B. investor.C. information-motivated trader.2. James Beach is young and has substantial wealth. A significant proportion of his stock portfolio consists of emerging market stocks that offer relatively high expected returns at the cost of relatively high risk. Beach believes that investment in emerging market stocks is appropriate for him given his ability and willingness to take risk. Which of the following labels most appropriately describes Beach?A. Hedger.B. Investor.C. Information-motivated trader.3. Lisa Smith owns a manufacturing company in the United States. Her company has sold goods to a customer in Brazil and will be paid in Brazilian real (BRL) in three months. Smith is concerned about the possibility of the BRL depreciating more than expected against the U.S. dollar (USD). Therefore, she is planning to sell three-month futures contracts on the BRL. The seller of such contracts generally gains when the BRL depreciates against the USD. If Smith were to sell these future contracts, she would most appropriately be described as a (n):A. hedger.B. investor.C. information-motivated trader.4. Which of the following is not a function of the financial system?A. To regulate arbitrageurs’ profits (excess returns).B. To help the economy achieve allocational efficiency.C. To facilitate borrowing by businesses to fund current operations.5. An investor primarily invests in stocks of publicly traded companies. The investor wants to increase the diversification of his portfolio. A friend has recommendedinvesting in real estate properties. The purchase of real estate would best be characterized as a transaction in the:A. derivative investment market.B. traditional investment market.C. alternative investment market.6. A hedge fund holds its excess cash in 90-day commercial paper and negotiable certificates of deposit. The cash management policy of the hedge fund is best described as using:A. capital market instruments.B. money market instruments.C. intermediate-term debt instruments.7. An oil and gas exploration and production company announces that it is offering 30 million shares to the public at $45.50 each. This transaction is most likely a sale in the:A. futures market.B. primary market.C. secondary market.8. Consider a mutual fund that invests primarily in fixed-income securities that have been determined to be appropriate given the fund’s investment goal. Which of the following is least likely to be a part of this fund?A. Warrants.B. Commercial paper.C. Repurchase agreements.9. A friend has asked you to explain the differences between open-end and closed-end funds. Which of the following will you most likely include in your explanation?A. Closed-end funds are unavailable to new investors.B. When investors sell the shares of an open-end fund, they can receive a discount or a premium to the fund’s net asset value.C. When selling shares, investors in an open-end fund sell the shares back to the fund whereas investors in a closed-end fund sell the shares to others in the secondary market.10. The usefulness of a forward contract is limited by some problems. Which of the following is most likely one of those problems?A. Once you have entered into a forward contract, it is difficult to exit from the contract.B. Entering into a forward contract requires the long party to deposit an initial amount with the short party.C. If the price of the underlying asset moves adversely from the perspective of the long party, periodic payments must be made to the short party.11. Tony Harris is planning to start trading in commodities. He has heard about the use of futures contracts on commodities and is learning more about them. Which of the following is Harris least likely to find associated with a futures contract?A. Existence of counterparty risk.B. Standardized contractual terms.C. Payment of an initial margin to enter into a contract.12. A German company that exports machinery is expecting to receive $10 million in three months. The firm converts all its foreign currency receipts into euros. The chief financial officer of the company wishes to lock in a minimum fixed rate for converting the $10 million to euro but also wants to keep the flexibility to use the future spot rate if it is favorable. What hedging transaction is most likely to achieve this objective?A. Selling dollars forward.B. Buying put options on the dollar.C. Selling futures contracts on dollars.13. A book publisher requires substantial quantities of paper. The publisher and a paper producer have entered into an agreement for the publisher to buy and the producer to supply a given quantity of paper four months later at a price agreed upon today. This agreement is a:A. futures contract.B. forward contract.C. commodity swap.14. The Stand ard & Poor’s Depositary Receipts (SPDRs) is an investment that tracks the S&P 500 stock market index. Purchases and sales of SPDRs during an average trading day are best described as:A. primary market transactions in a pooled investment.B. secondary market transactions in a pooled investment.C. secondary market transactions in an actively managed investment.15. The Standard & Poor’s Depositary Receipts (SPDRs) is an exchange-traded fund in the United States that is designed to track the S&P 500 stock market index. The current price of a share of SPDRs is $113. A trader has just bought call options on shares of SPDRs for a premium of $3 per share. The call options expire in five months and have an exercise price of $120 per share. On the expiration date, the trader will exercise the call options (ignore any transaction costs) if and only if the shares of SPDRs are trading:A. below $120 per share.B. above $120 per share.C. above $123 per share.16. Which of the following statements about exchange-traded funds is most correct?A. Exchange-traded funds are not backed by any assets.B. The investment companies that create exchange-traded funds are financial intermediaries.C. The transaction costs of trading shares of exchange-traded funds are substantially greater than the combined costs of trading the underlying assets of the fund.17. Jason Schmidt works for a hedge fund and he specializes in finding profit opportunities that are the result of inefficiencies in the market for convertible bonds—bonds that can be converted into a predetermined amount of a company’s common stock. Schmidt tries to find convertibles that are priced inefficiently relative to the underlying stock. The trading strategy involves the simultaneous purchase of the convertible bond and the short sale of the underlying common stock. The above process could best be described as:A. hedging.B. arbitrage.C. securitization.18. Pierre-Louis Robert just purchased a call option on shares of the Michelin Group.A few days ago he wrote a put option on Michelin shares. The call and put options have the same exercise price, expiration date, and number of shares underlying. Considering both positions, Robert’s exposure to the risk of the stock of the Michelin Group is:A. long.B. short.C. neutral.19. An online brokerage firm has set the minimum margin requirement at 55 percent. What is the maximum leverage ratio associated with a position financed by this minimum margin requirement?A. 1.55.B. 1.82.C. 2.22.20. A trader has purchased 200 shares of a non-dividend-paying firm on margin at a price of $50 per share. The leverage ratio is 2.5. Six months later, the trader sells these shares at $60 per share. Ignoring the interest paid on the borrowed amount and the transaction costs, what was the return to the trader during the six-month period?A. 20 percent.B. 33.33 percent.C. 50 percent.21. Jason Williams purchased 500 shares of a company at $32 per share. The stock was bought on 75 percent margin. One month later, Williams had to pay interest on the amount borrowed at a rate of 2 percent per month. At that time, Williams receiveda dividend of $0.50 per share. Immediately after that he sold the shares at $28 per share. He paid commissions of $10 on the purchase and $10 on the sale of the stock. What was the rate of return on this investment for the one-month period?A. −12.5 percent.B. –15.4 percent.C. –50.1 percent.22. Caroline Rogers believes the price of Gamma Corp. stock will go down in the near future. She has decided to sell short 200 shares of Gamma Corp. at the current market price of €47. The initial margin requirement is 40 percent. Which of the following is an appropriate statement regarding the margin requirement that Rogers is subject to on this short sale?A. She will need to contribute €3,760 as margin.B. She will need to contribute €5,640 as margin.C. She will only need to leave the proceeds from the short sale as deposit and does not need to contribute any additional funds.23. The current price of a stock is $25 per share. You have $10,000 to invest. You borrow an additional $10,000 from your broker and invest $20,000 in the stock. If the maintenance margin is 30 percent, at what price will a margin call first occur?A. $9.62.B. $17.86.C. $19.71.24. You have placed a sell market-on-open order—a market order that would automatically be submitted at the market’s open tomorrow and would fill at the market price. Your instruction, to sell the shares at the market open, is a(n):A. execution instruction.B. validity instruction.C. clearing instruction.25. A market has the following limit orders standing on its book for a particular stock. The bid and ask sizes are number of shares in hundreds.What is the market?A. 9.73 bid, offered at 10.14.B. 9.81 bid, offered at 10.10.C. 9.95 bid, offered at 10.02.26. Consider the following limit order book for a stock. The bid and ask sizes are number of shares in hundredsA new buy limit order is placed for 300 shares at ¥123.40. This limit order issaid to:A. take the market.B. make the market.C. make a new market.27. Currently, the market in a stock is "$54.62 bid, offered at $54.71." A new sell limit order is placed at $54.62. This limit order is said to:A. take the market.B. make the market.C. make a new market.28. Jim White has sold short 100 shares of Super Stores at a price of$42 per share. He has also simultaneously placed a "good-till-cancelled, stop 50, limit 55 buy" order. Assume that if the stop condition specified by White is satisfied and the order becomes valid, it will get executed. Excluding transaction costs, what is the maximum possible loss that White can have?A. $800.B. $1,300.C. Unlimited.29. You own shares of a company that are currently trading at $30 a share. Your technical analysis of the shares indicates a support level of $27.50. That is, if the price of the shares is going down, it is more likely to stay above this level rather than fall below it. If the price does fall below this level, however, you believe that the price may continue to decline. You have no immediate intent to sell the shares but are concerned about the possibility of a huge loss if the share price declines below thesupport level. Which of the following types of orders could you place to most appropriately address your concern?A. Short sell order.B. Good-till-cancelled stop sell order.C. Good-till-cancelled stop buy order.30. In an underwritten offering, the risk that the entire issue may not be sold to the public at the stipulated offering price is borne by the:A. issuer.B. investment bank.C. buyers of the part of the issue that is sold.31 . A British company listed on the Alternative Investment Market of the London Stock Exchange, announced the sale of 6,686,665 shares to a small group of qualified investors at £0.025 per share. Which of the following best describesthis sale?A. Shelf registration.B. Private placement.C. Initial public offering.32. A German publicly traded company, to raise new capital, gave its existing shareholders the opportunity to subscribe for new shares. The existing shareholders could purchase two new shares at a subscription price of €4.58 per share for every 15 shares held. This is an example of a(n):A. rights offering.B. private placement.C. initial public offering.33. Consider an order-driven system that allows hidden orders. The following four sell orders on a particular stock are currently in the system's limit order book. Based on the commonly used order precedence hierarchy, which of these orders will have precedence over others?A. Order I (time of arrival of 9:52:01 ).B. Order II (time of arrival of 9:52:08).C. Order III (time of arrival of 9:53:04)34. Zhenhu Li has submitted an immediate-or-cancel buy order for 500 shares of a company at a limit price of CNY 74.25. There are two sell limit orders standing in that stock's order book at that time. One is for 300 shares at a limit price of CNY 74.30 and the other is for 400 shares at a limit price of CNY 74.35. How many shares in Li's order would get cancelled?A. None (the order would remain open but unfilled).B. 200 (300 shares would get filled).C. 500 (there would be no fill).35. A market has the following limit orders standing on its book for a particular stock:Ian submits a day order to sell 1,000 shares, limit £19.83. Assuming that no more buy orders are submitted on that day after Ian submits his order, what would be Ian's average trade price?A. £19.70.B. £19.92.C. £20.05.36. A financial analyst is examining whether a country's financial market is well functioning. She finds that the transaction costs in this market are low and trading volumes are high. She concludes that the market is quite liquid. In such a market:A. traders will find it hard to make use of their information.B. traders will find it easy to trade and their trading will make the market less informationally efficient.C. traders will find it easy to trade and their trading will make the marketmore informationally efficient.37. The government of a country whose financial markets are in an early stage of development has hired you as a consultant on financial market regulation. Your first task is to prepare a list of the objectives of market regulation. Which of the following is least likely to be included in this list of objectives?A. Minimize agency problems in the financial markets.B. Ensure that financial markets are fair and orderly.C. Ensure that investors in the stock market achieve a rate of return that is at least equal to the risk-free rate of return.Chapter 2 Portfolio Management: An Overview PRACTICE PROBLEMS FOR CHAPTER 21. Investors should use a portfolio approach to:A. reduce risk.B. monitor risk.C. eliminate risk.2. Which of the following is the best reason for an investor to be concerned with the composition of a portfolio?A. Risk reduction.B. Downside risk protection.C. Avoidance of investment disasters.3. With respect to the formation of portfolios, which of the following statements is most accurate?A. Portfolios affect risk less than returns.B. Portfolios affect risk more than returns.C. Portfolios affect risk and returns equally.4. Which of the following institutions will on average have the greatest need for liquidity?A. Banks.B. Investment companies.C. Non-life insurance companies.5. Which of the following institutional investors will most likely have the longest time horizon?A. Defined benefit plan.B. University endowment.C. Life insurance company.6. A defined benefit plan with a large number of retirees is likely to have a high need forA. income.B. liquidity.C. insurance.7. Which of the following institutional investors is most likely to manage investments in mutual funds?A. Insurance companies.B. Investment companies.C. University endowments.8. With respect to the portfolio management process, the asset allocation is determined in the:A. planning step.B. feedback step.C. execution step9. The planning step of the portfolio management process is least likely to include an assessment of the client'sA. securities.B. constraints.C. risk tolerance.10. With respect to the portfolio management process, the rebalancing of a portfolio's composition is most likely to occur in the:A. planning step.B. feedback step.C. execution step.11. An analyst gathers the following information for the asset allocations of three portfolios:Which of the portfolios is most likely appropriate for a client who has a high degree of risk tolerance?A. Portfolio 1.B. Portfolio 2.C. Portfolio 3.12. Which of the following investment products is most likely to trade at their net asset value per share?A. Exchange traded funds.B. Open-end mutual funds.C. Closed-end mutual funds.13. Which of the following financial products is least likely to have a capital gain distribution?A. Exchange traded funds.B. Open-end mutual funds.C. Closed-end mutual funds.14. Which of the following forms of pooled investments is subject to the least amount of regulation?A. Hedge funds.B. Exchange traded funds.C. Closed-end mutual funds.15. Which of the following pooled investments is most likely characterized by a few large investments?A. Hedge funds.B. Buyout funds.C. Venture capital funds.Chapter 3 Portfolio Risk and Return: Part I PRACTICE PROBLEMS FOR CHAPTER 31. An investor purchased 100 shares of a stock for $34.50 per share at the beginning of the quarter. If the investor sold all of the shares for $30.50 per share after receiving a $51.55 dividend payment at the end of the quarter, the holding period return is closest to:A. - 13.0%.B. - 11.6%.C. - 10.1%.2. An analyst obtains the following annual rates of return for a mutual fund:The fund's holding period return over the three-year period is closest to:A. 0.18%.B. 0.55%.C. 0.67%.3. An analyst observes the following annual rates of return for a hedge fund:The hedge fund's annual geometric mean return is closest to:A. 0.52%.B. 1.02%.C. 2.67%.4. Which of the following return calculating methods is best for evaluating the annualized returns of a buy-and-hold strategy of an investor who has made annual deposits to an account for each of the last five years?A. Geometric mean return.B. Arithmetic mean return.C. Money-weighted return.5. An investor evaluating the returns of three recently formed exchange-traded funds gathers the following information:The ETF with the highest annualized rate of return is:A. ETF 1.B. ETF 2.C. ETF 3.6. With respect to capital market theory, which of the following asset characteristics is least likely to impact the variance of an investor's equally weighted portfolio?A. Return on the asset.B. Standard deviation of the asset.C. Covariances of the asset with the other assets in the portfolio.7. A portfolio manager creates the following portfolio:If the correlation of returns between the two securities is 0.40, the expected standard deviation of the portfolio is closest to:A. 10.7%.B. 11.3%.C. 12.1%.8. A portfolio manager creates the following portfolio:If the covariance of returns between the two securities is - 0.0240, the expected standard deviation of the portfolio is closest to:A. 2.4%.B. 7.5%.C. 9.2%.The following information relates to Questions 9-10A portfolio manager creates the following portfolio:9. If the standard deviation of the portfolio is 14.40%, the correlation between the two securities is equal to:A. - 1.0.B. 0.0.C. 1.0.10. If the standard deviation of the portfolio is 14.40%, the covariance between the two securities is equal to:A. 0.0006.B. 0.0240.C. 1.0000.The following information relates to Questions 11-14An analyst observes the following historic geometric returns:11 . The real rate of return for equities is closest to:A. 5.4%.B. 5.8%.C. 5.9%.12. The real rate of return for corporate bonds is closest to:A. 4.3%.B. 4.4%.C. 4.5%.13. The risk premium for equities is closest to:A. 5.4%.B. 5.5%.C. 5.6%.14. The risk premium for corporate bonds is closest to:A. 3.5%.B. 3.9%.C. 4.0%.15. With respect to trading costs, liquidity is least likely to impact the:A. stock price.B. bid-ask spreads.C. brokerage commissions.16. Evidence of risk aversion is best illustrated by a risk-return relationship that is:A. negative.B. neutral.C. positive.17. With respect to risk-averse investors, a risk-free asset will generate a numerical utility that is:A. the same for all individuals.B. positive for risk-averse investors.C. equal to zero for risk seeking investors18. With respect to utility theory, the most risk-averse investor will have an indifference curve with the:A. most convexity.B. smallest intercept value.C. greatest slope coefficient.19. With respect to an investor's utility function expressed as:21=E(r)-2u A , whichof the following values for the measure for risk aversion has the least amount of risk aversion?A. - 4.B. 0.C. 4.The following information relates to Questions 20-23A financial planner has created the following data to illustrate the application of utility theory to portfolio selection:20. A risk-neutral investor is most likely to choose:A. Investment 1.B. Investment 2.C. Investment 3.ExpectedStandard Deviation (% )28153021. If an investor's utility function is expressed as U = E(r) ~A& and the measure for risk aversion has a value of- 2, the risk-seeking investor is most likely to choose:A. Investment 2.B. Investment 3.C. Investment 4.22. If an investor's utility function is expressed as U = E(r) - ~A& and the measure for risk aversion has a value of2, the risk-averse investor is most likely to choose:A. Investment 1.B. Investment 2.C. Investment 3.23. If an investor's utility function is expressed as U =E(r) - ~A& and the measure for risk aversion has a value of4, the risk-averse investor is most likely to choose:A. Investment 1.B. Investment 2.C. Investment 3.24. With respect to the mean-variance portfolio theory, the capital allocation line, CAL, is the combination of the risk-free asset and a portfolio of all:A. risky assets.B. equity securities.C. feasible investments.25. Two individual investors with different levels of risk aversion will have optimal portfolios that are:A. below the capital allocation line.B. on the capital allocation line.C. above the capital allocation line.The following information relates to Questions 26-28A portfolio manager creates the following portfolio:26. If the portfolio of the two securities has an expected return of15%, the proportion invested in Security 1 is:A. 25%.B. 50%.C. 75%.27. If the correlation of returns between the two securities is - 0.15, the expected standard deviation of an equal-weighted portfolio is closest to:A. 13.04%.B. 13.60%.C. 13.87%.28. If the two securities are uncorrelated, the expected standard deviation of an equal-weighted portfolio is closest to:A. 14.00%.B. 14.14%.C. 20.00%.29. As the number of assets in an equally-weighted portfolio increases, the contribution of each individual asset's variance to the volatility of the portfolio:A. increases.B. decreases.C. remains the same.30. With respect to an equally-weighted portfolio made up of a large number of assets, which of the following contributes the most to the volatility of the portfolio?A. Average variance of the individual assets.B. Standard deviation of the individual assets.C. Average covariance between all pairs of assets.31. The correlation between assets in a two-asset portfolio increases during a market decline. If there is no change in the proportion of each asset held in the portfolio or the expected standard deviation of the individual assets, the volatility of the portfolio is most likely to:A. increase.B. decrease.C. remain the same.The following information relates to Questions 32-34An analyst has made the following return projections for each of three possible outcomes with an equal likelihood of occurrence:32. Which pair of assets is perfectly negatively correlated?A. Asset 1 and Asset 2.B. Asset 1 and Asset 3.C. Asset 2 and Asset 3.33. If the analyst constructs two-asset portfolios that are equally-weighted, which pair of assets has the lowest expected standard deviation?A. Asset 1 and Asset 2.B. Asset 1 and Asset 3.C. Asset 2 and Asset 3.34. If the analyst constructs two-asset portfolios that are equally weighted, which pair of assets provides the least amount of risk reduction?A. Asset 1 and Asset 2.B. Asset 1 and Asset 3.C. Asset 2 and Asset 3.35. Which of the following statements is least accurate? The efficient frontier is the set of all attainable risky assets with the:A. highest expected return for a given level of risk.B. lowest amount of risk for a given level of return.C. highest expected return relative to the risk-free rate.36. The portfolio on the minimum-variance frontier with the lowest standard deviation is:A. unattainable.B. the optimal risky portfolio.C. the global minimum-variance portfolio.37. The set of portfolios on the minimum-variance frontier that dominates all sets of portfolios below the global minimum-variance portfolio is the:A. capital allocation line.B. Markowitz efficient frontier.C. set of optimal risky portfolios.38. The dominant capital allocation line is the combination of the risk-free asset and the:A. optimal risky portfolio.B. levered portfolio of risky assets.C. global minimum-variance portfolio.39. Compared to the efficient frontier of risky assets, the dominant capital allocation line has higher rates of return for levels of risk greater than the optimal risky portfolio because of the investor's ability to:A. lend at the risk-free rate.B. borrow at the risk-free rate.C. purchase the risk-free asset.40. With respect to the mean-variance theory, the optimal portfolio is determined by each individual investor's:A. risk-free rate.B. borrowing rate.C. risk preference.Chapter 4 Portfolio Risk and Return: Part II PRACTICE PROBLEMS FOR CHAPTER 41. The line depicting the risk and return of portfolio combinations of a risk-free asset and any risky asset is the:A. security market line.B. capital allocation line.C. security characteristic line.2. The portfolio of a risk-free asset and a risky asset has a better risk-return tradeoff than investing in only one asset type because the correlation between the risk-free asset and the risky asset is equal to:A. - 1.0.B. 0.0.C. 1.0.3. With respect to capital market theory, an investor's optimal portfolio is the combination of a risk-free asset and a risky asset with the highest:A. expected return.B. indifference curve.C. capital allocation line slope.4. Highly risk-averse investors will most likely invest the majority of their wealth in:A. risky assets.B. risk-free assets.C. the optimal risky portfolio.5. The capital market line, CML, is the graph of the risk and return of portfolio combinations consisting of the risk-free asset and:A. any risky portfolio.B. the market portfolio.C. the leveraged portfolio.6. Which of the following statements most accurately defines the market portfolio in capital market theory? The market portfolio consists of all:A. risky assets.B. tradable assets.C. investable assets.7. With respect to capital market theory, the optimal risky portfolio:。
金融工程教材英文版课后习题

END-OF-CHAPTER QUESTIONS AND PROBLEMSChapter 11. Business risk is the risk associated with a particular line of business, whereas financial risk is the risk associated with stock prices, exchange rates, interest rates and commodity prices. An example would be that a firm might be in the business of manufacturing furniture. Business risk would reflect the uncertainty of the furniture market, whereas financial risk would reflect the risk associated with the interest rates that would impact their borrowing costs. In addition a business might also be affected by exchange rates. Some of the financial risks can also be business risks. The business risk of a bank, for example, is highly affected by interest rate and exchange rate risk.2. Real assets consist of the tangible assets of the economy; however, for our purposes we also define them to include such intangible assets as management talent, ideas, brand names, etc. They are distinguished from financial assets, which are securities. These securities represent claims on business firms, which own the real assets, or on governments.3. An investor who is risk averse does not like risk and will not take on additional risk without the expectation of higher return. Such an individual will try to get the highest return for a given amount of risk or the lowest risk for a given amount of return. An individual who is risk neutral will simply seek the highest return without regard to risk.4. Financial markets distinguish the qualities of stocks and bonds by their prices. The markets set the price so that the return expected by investors is appropriate for the level of risk. In competitive and efficient markets, the expected return will vary directly with the level of risk. If one wishes to earn a higher return, it is necessary to assume more risk. This is the risk-return trade-off. Investors trade off risk against return.The risk-return trade-off will also hold in derivative markets. The risk-return trade-off is a fundamental result of the nature of competition in the marketplace. Attractive, low-risk investments will have their prices driven up and this will lower the expected returns. High-risk investments will have their prices driven down and this will result in higher expected returns.5. The expected return consists of the risk-free rate and a risk premium. The risk-free rate is the return one expects from investing money today and, thereby, foregoing the consumption that could be obtained. A risk premium is the additional return that one expects to receive by virtue of assuming risk.6. An efficient market is one in which prices reflect the true economic values of the assets trading therein. Inefficient markets, no one can earn returns that are more than commensurate with the level of risk. Efficient markets are characterized by low transaction costs and by the rapid rate at which new information is incorporated into prices.7. Arbitrage is a type of investment transaction that seeks to profit when identical goods are priced differently. Buying an item at one price and immediately selling it at another is a type of arbitrage. Because of the combined activities of arbitrageurs, identical goods, primarily financial assets, cannot sell for different prices for long. This is the law of one price. Arbitrage helps make our markets efficient by assuring that prices are in line with what they are supposed to be. In short, we cannot get something for nothing. A situation involving two identical goods or portfolios that are not priced equivalently would be exploited by arbitrageurs until their prices were equal. The "one price" that an asset must be is called the "theoretical fair value."11. Derivative markets provide a means of adjusting the risk of spot market investments to a more acceptable level and identifying the consensus market beliefs. They make trading easier and less costly and spot markets more efficient. These markets also provide a means of speculating.Chapter 33. European call: We know that its price cannot exceed S0 but must exceed Max(0, S0 - X(1+r)-T). With an infinite time to expiration, the present value of X is zero so the lower bound is S0 and, since the upper bound is S0, the call price must be S0. American call: We know that its price cannot exceed S0 but it must be at least as valuable as a European call. Thus its value must also be S0. Note that if exercised early it would be worth only S0 - X so it will never be exercised early.4. Ordinarily the option with the longer time to expiration would sell for more. If both options were deep out of-the-money, however, they could both sell for essentially nothing. The market would be expecting that both the shorter- and longer-lived options will expire out-of-the-money.5. If both options were deep out-of-the-money, they might have prices of zero. As in the previous question, the two options are expected to expire out-of-the-money.6. The call is underpriced, so buy the call, sell short the stock, and buy risk-free bonds with face value of X. The cash received from the stock is greater than the cost of the call and bonds. Thus, there is a positive cash flow up front. The payoffs from the portfolio at expiration are as follows:If S T < X,- S T (from the stock)X (from the bonds)the total, X - S T, is positive3-2If S T ≥ XS T - X (from the call)- S T (from the stock)X (from the bonds)the total is zero.The portfolio generates a positive cash flow up front and there is no cash outflow at expiration.7. Time value is a measure of the amount of uncertainty in an option. Uncertainty relates to whether the option will expire in- or out-of-the-money. When the option is deep in-the-money, there is little uncertainty about the fact that the option will expire in-the-money. The option will then begin to behave about like the stock. Then the option is deep-out-the-money, there is also little uncertainty since it is likely to finish out-of-the money. When the option is at-the-money there is considerable uncertainty about how it will finish.8. Assuming the stock pays no dividends, there is no reason to exercise a call early (this obviously presumes the call is American). The tendency to believe that exercising an option because the stock can go up no further ignores the fact that an option can generally be sold. Exercising an option throws away any chance that the stock can go up further. If the stock falls, the option holder would be hurt, but if the option holder exercised and became a stock holder, he would also be hurt by a falling stock price. There is simply no reason to give away the time value that arises because of the possibility that the stock can always go further upward. In simple, mathematical terms, exercising captures only the intrinsic value S0 - X. The call can always be sold for at least S0 - X (1 + r) -T.9. The paradox is resolved by recalling that if the option expires out-of-the-money, it does not matter how far out-of-the-money it is. The loss to the option holder is limited to the premium paid. For example, suppose the stock price is $24, the exercise price is $20, and the call price is $6. Higher volatility increases the chance of greater gains to the holder of the call. It also increases the chance of a larger stock price decrease. If, however, the stock price does end up below $20, the investor's loss is the same regardless of whether the stock price at expiration is $19 or $1. If the stock were purchased instead of the call, the loss would obviously be greater if the stock price went to $1 than if it went to $19. For this reason, holders of stocks dislike volatility, while holders of calls like volatility. A similar argument applies to puts.10. The minimum value of an American put is Max(0, X - S0). This is always higher than the lower bound of a European put, X (1 + r) -T - S0, except at expiration when the two are equal.11. When buying a call option, one hopes to exercise it at a later date. Thus, the exercise price will be paid out later. If interest rates are higher, additional interest can be earned on the money that will eventually be paid out as the exercise price. When buying a put option, one hopes to exercise it later, thus receiving the exercise price. If interest rates are higher, the put is less valuable because the holder is foregoing interest by having to wait to exercise the put. Higher interest rates make the present value of the exercise price be lower. In the case of the call, this is good because the call holder anticipates having to pay out the exercise price. For the put holder this is bad because the put holder anticipates receiving the exercise price.12. If the put price is higher than predicted by the model, the put is overpriced. Then the put should be sold. The funds should be used to construct a portfolio consisting of a long call and risk-free bonds with face value of X, and a short position in the stock. You can (and should) verify that this portfolio has a payoff at expiration that is the same as that of the put. Thus, if you sell the put for more than it costs to construct this portfolio, you can create a portfolio that offsets your put and have some money left over.13. An American call is exercised early only to capture a dividend. When a stock goes ex-dividend, the call will lose value as the stock drops. This will cause a loss in value to the holder of the call. The call holder knows this loss will be incurred as soon as the stock goes ex-dividend. If the call were exercised just before the stock goes ex-dividend, however, the call holder would capture the stock and the dividend, which might be enough to offset the otherwise loss in the value of the call. For a put, however, dividends are not necessary to make the argument that it might be optimal to exercise early. The holder of an American put faces a situation in which the gains are limited to the exercise price. Since the stock price can go down only to zero, early exercise of a put on a bankrupt firm would obviously be advisable. But the firm does not have to go bankrupt. If the stock price is low enough, the gains from waiting for it to go lower are not worth the wait. If dividends were added to the picture, however, they would discourage early exercise. The more dividends paid, the lower the stock price is driven and the more valuable it is to hold on to the put.Chapter 41. When we price an option according to its boundary conditions, we do not find an exact price for the option. We provide only limits on the maximum and minimum price of an option or group of options. In the case of options differing by exercise prices or in the case of put-call parity, we can price only the relationship or difference between the option prices. We cannot price each option individually without an option pricing odel; however, an option pricing model must provide prices that conform to the boundary conditions. Because boundary condition rules require fewer assumptions, we can say that they are more generally applicable and are more likely to hold in practice. They are incomplete, however, in the sense that they do not tell us exactly what the option price should be, which is what an option pricing model does tell us.2. A binomial option pricing model enables us to see the relationship between the stock price and the call price. The model shows, in a simple framework, how to construct a riskless portfolio by appropriately weighting the stock against the option. By noting that the riskless portfolio should return the risk-free rate, we can see what the call price must be. We can also understand the forces that bring the call option price in line if it is not priced according to the model. In addition, the model illustrates the importance of revising the hedge ratio. Finally, the model is probably the best way to handle the problem of pricing an American option.3. For a call, a hedge portfolio will consist of n shares of stock and one short call. The shares of stock, n, will be a long position that will reflect the next two possible values of the call and stock. The call is short because the call and stock move opposite each other, so a short position in the call is needed to offset a long position in the stock. If the option is a put, a long position in n shares will be hedged by a long position in one put. The number of shares, n, is also a reflection of the next two possible option and stock values. The put is long because it already moves opposite to the stock.4. This means that the option is trading in the market for a price that is lower than its theoretical fair value. Consequently, the option is underpriced. An underpriced option should be bought. To hedge the position, one should sell n shares of stock, where n is the hedge ratio as defined in the chapter.5. At each point in the binomial tree, the option price is computed based on the next two possible prices, weighted by the appropriate probability values and discounted back one period. If the option can be exercised early, we determine its intrinsic value, i.e., the value it would have if it were exercised at that point. If the intrinsic value is greater, it replaces the computed value. This is done at all nodes. Note that it is quite possible that the option will be exercised at many different nodes.6. A path independent problem is one in which the only values that matter in determining the current price are the values at expiration. A particular expiration value is the same regardless of the sequence of up and down moves the stock took to get to that point. A path dependent model is one in which the sequence of up and down moves does matter. For example, suppose the stock goes down, up and then up. Contrast that with up, up and down. If the option is a European put, it does not matter which sequence the stock followed. Where it is at expiration is the only thing that matters. If the option is, however, an American put, the down, up, up sequence could lead to early exercise when it makes that first move down, whereas the up, up, down sequence is unlikely to lead to early exercise.Chapter 51. In a discrete time model, the stock price can make a jump to only one of two possible values. The length of time over which the move can be made is finite. In a continuous time model, the stock price can jump to an infinite number of possibilities. The length of time over which the move can be made is infinitesimal (very, very small). The difference between the two models is perhaps best described as in the text as the difference between still photos and a movie.2. The familiar normal or bell-shaped distribution is a symmetric probability distribution that depends only on the mean and variance. A lognormal distribution is skewed, having more extreme right values. A lognormal distribution, however, is normal in the logarithm. Thus, if x is lognormally distributed, its logarithm, lnx, is normally distributed. With respect to stock prices, the logarithm is of the rate of return. That is, let (S1 –S0)/S0 be defined as the return over period 0 to period 1. Then if it is lognormally distributed, ln(S1/S0) is normally distributed. Note what appears to be slight inconsistency: (S1 – S0)/S0 is a percentage return whereas S1/S0 is 1.0 plus the percentage return. That does not matter as we can always shift a normal distribution by adding a constant such as 1.0 and it does not affect the fact that it is normally distributed. It just slides it over.3. The Black-Scholes model assumes no dividends, but actually this was just for convenience to allow us to start at the simplest level. If the dividends are appropriately modeled, the Black-Scholes model handles stocks with dividends with only the minor adjustment that we must remove the present value of the dividends from the stock price before using it in the model. We can do this by subtracting the present value of the stream of discrete dividends over the life of the model or by discounting the stock price by the dividend yield rate over the life of the model.4. The variables in the binomial model are S0 (the stock price), X (the exercise price), r (the discrete risk-free rate), u (one plus the return on the stock if it goes up), d (one plus the return on the stock if it goes down) and n, the number of time periods. The variables in the Black-Scholes model are S0 (the stock price), X (the exercise price), r c (the continuously compounded risk-free rate), ó (the standard deviation of the continuously compounded return on the stock) and T (the time to expiration). The variables S0 and X are the same in both models. In the binomial model, r is the discrete interest rate per period. In the Black-Scholes model, the interest rate must be expressed in continuously compounded form. The annual discrete interest rate (r) is related to the annual continuously compounded rate (r c) by the formula, r c = ln(1 + r). Then the binomial rate per period is found as (1 + r)T/n - 1. The up and down factors in the binomial model are directly related to ó in the Black-Scholes model by the formula u = T/n ó e – 1 and d = (1/(1+u)) – 1. The time to expiration (T) in the Black-Scholes model is related to the length of each binomial period by the relationship T/n where n is the number of periods. Thus, all of the Black-Scholes variables are either equal to or directly convertible to binomial variables.Chapter6Chapter7Chapter 8Chapter9Chapter 10。
金融工程教材英文版课后习题

END-OF-CHAPTER QUESTIONS AND PROBLEMSChapter 11. Business risk is the risk associated with a particular line of business, whereas financial risk is the risk associated with stock prices, exchange rates, interest rates and commodity prices. An example would be that a firm might be in the business of manufacturing furniture. Business risk would reflect the uncertainty of the furniture market, whereas financial risk would reflect the risk associated with the interest rates that would impact their borrowing costs. In addition a business might also be affected by exchange rates. Some of the financial risks can also be business risks. The business risk of a bank, for example, is highly affected by interest rate and exchange rate risk.2. Real assets consist of the tangible assets of the economy; however, for our purposes we also define them to include such intangible assets as management talent, ideas, brand names, etc. They are distinguished from financial assets, which are securities. These securities represent claims on business firms, which own the real assets, or on governments.3. An investor who is risk averse does not like risk and will not take on additional risk without the expectation of higher return. Such an individual will try to get the highest return for a given amount of risk or the lowest risk for a given amount of return. An individual who is risk neutral will simply seek the highest return without regard to risk.4. Financial markets distinguish the qualities of stocks and bonds by their prices. The markets set the price so that the return expected by investors is appropriate for the level of risk. In competitive and efficient markets, the expected return will vary directly with the level of risk. If one wishes to earn a higher return, it is necessary to assume more risk. This is the risk-return trade-off. Investors trade off risk against return.The risk-return trade-off will also hold in derivative markets. The risk-return trade-off is a fundamental result of the nature of competition in the marketplace. Attractive, low-risk investments will have their prices driven up and this will lower the expected returns. High-risk investments will have their prices driven down and this will result in higher expected returns.5. The expected return consists of the risk-free rate and a risk premium. The risk-free rate is the return one expects from investing money today and, thereby, foregoing the consumption that could be obtained. A risk premium is the additional return that one expects to receive by virtue of assuming risk.6. An efficient market is one in which prices reflect the true economic values of the assets trading therein. Inefficient markets, no one can earn returns that are more than commensurate with the level of risk. Efficient markets are characterized by low transaction costs and by the rapid rate at which new information is incorporated into prices.7. Arbitrage is a type of investment transaction that seeks to profit when identical goods are priced differently. Buying an item at one price and immediately selling it at another is a type of arbitrage. Because of the combined activities of arbitrageurs, identical goods, primarily financial assets, cannot sell for different prices for long. This is the law of one price. Arbitrage helps make our markets efficient by assuring that prices are in line with what they are supposed to be. In short, we cannot get something for nothing. A situation involving two identical goods or portfolios that are not priced equivalently would be exploited by arbitrageurs until their prices were equal. The "one price" that an asset must be is called the "theoretical fair value."11. Derivative markets provide a means of adjusting the risk of spot market investments to a more acceptable level and identifying the consensus market beliefs. They make trading easier and less costly and spot markets more efficient. These markets also provide a means of speculating.Chapter 33. European call: We know that its price cannot exceed S0 but must exceed Max(0, S0 - X(1+r)-T). With an infinite time to expiration, the present value of X is zero so the lower bound is S0 and, since the upper bound is S0, the call price must be S0. American call: We know that its price cannot exceed S0 but it must be at least as valuable as a European call. Thus its value must also be S0. Note that if exercised early it would be worth only S0 - X so it will never be exercised early.4. Ordinarily the option with the longer time to expiration would sell for more. If both options were deep out of-the-money, however, they could both sell for essentially nothing. The market would be expecting that both the shorter- and longer-lived options will expire out-of-the-money.5. If both options were deep out-of-the-money, they might have prices of zero. As in the previous question, the two options are expected to expire out-of-the-money.6. The call is underpriced, so buy the call, sell short the stock, and buy risk-free bonds with face value of X. The cash received from the stock is greater than the cost of the call and bonds. Thus, there is a positive cash flow up front. The payoffs from the portfolio at expiration are as follows:If S T < X,- S T (from the stock)X (from the bonds)the total, X - S T, is positive3-2If S T ≥ XS T - X (from the call)- S T (from the stock)X (from the bonds)the total is zero.The portfolio generates a positive cash flow up front and there is no cash outflow at expiration.7. Time value is a measure of the amount of uncertainty in an option. Uncertainty relates to whether the option will expire in- or out-of-the-money. When the option is deep in-the-money, there is little uncertainty about the fact that the option will expire in-the-money. The option will then begin to behave about like the stock. Then the option is deep-out-the-money, there is also little uncertainty since it is likely to finish out-of-the money. When the option is at-the-money there is considerable uncertainty about how it will finish.8. Assuming the stock pays no dividends, there is no reason to exercise a call early (this obviously presumes the call is American). The tendency to believe that exercising an option because the stock can go up no further ignores the fact that an option can generally be sold. Exercising an option throws away any chance that the stock can go up further. If the stock falls, the option holder would be hurt, but if the option holder exercised and became a stock holder, he would also be hurt by a falling stock price. There is simply no reason to give away the time value that arises because of the possibility that the stock can always go further upward. In simple, mathematical terms, exercising captures only the intrinsic value S0 - X. The call can always be sold for at least S0 - X (1 + r) -T.9. The paradox is resolved by recalling that if the option expires out-of-the-money, it does not matter how far out-of-the-money it is. The loss to the option holder is limited to the premium paid. For example, suppose the stock price is $24, the exercise price is $20, and the call price is $6. Higher volatility increases the chance of greater gains to the holder of the call. It also increases the chance of a larger stock price decrease. If, however, the stock price does end up below $20, the investor's loss is the same regardless of whether the stock price at expiration is $19 or $1. If the stock were purchased instead of the call, the loss would obviously be greater if the stock price went to $1 than if it went to $19. For this reason, holders of stocks dislike volatility, while holders of calls like volatility. A similar argument applies to puts.10. The minimum value of an American put is Max(0, X - S0). This is always higher than the lower bound of a European put, X (1 + r) -T - S0, except at expiration when the two are equal.11. When buying a call option, one hopes to exercise it at a later date. Thus, the exercise price will be paid out later. If interest rates are higher, additional interest can be earned on the money that will eventually be paid out as the exercise price. When buying a put option, one hopes to exercise it later, thus receiving the exercise price. If interest rates are higher, the put is less valuable because the holder is foregoing interest by having to wait to exercise the put. Higher interest rates make the present value of the exercise price be lower. In the case of the call, this is good because the call holder anticipates having to pay out the exercise price. For the put holder this is bad because the put holder anticipates receiving the exercise price.12. If the put price is higher than predicted by the model, the put is overpriced. Then the put should be sold. The funds should be used to construct a portfolio consisting of a long call and risk-free bonds with face value of X, and a short position in the stock. You can (and should) verify that this portfolio has a payoff at expiration that is the same as that of the put. Thus, if you sell the put for more than it costs to construct this portfolio, you can create a portfolio that offsets your put and have some money left over.13. An American call is exercised early only to capture a dividend. When a stock goes ex-dividend, the call will lose value as the stock drops. This will cause a loss in value to the holder of the call. The call holder knows this loss will be incurred as soon as the stock goes ex-dividend. If the call were exercised just before the stock goes ex-dividend, however, the call holder would capture the stock and the dividend, which might be enough to offset the otherwise loss in the value of the call. For a put, however, dividends are not necessary to make the argument that it might be optimal to exercise early. The holder of an American put faces a situation in which the gains are limited to the exercise price. Since the stock price can go down only to zero, early exercise of a put on a bankrupt firm would obviously be advisable. But the firm does not have to go bankrupt. If the stock price is low enough, the gains from waiting for it to go lower are not worth the wait. If dividends were added to the picture, however, they would discourage early exercise. The more dividends paid, the lower the stock price is driven and the more valuable it is to hold on to the put.Chapter 41. When we price an option according to its boundary conditions, we do not find an exact price for the option. We provide only limits on the maximum and minimum price of an option or group of options. In the case of options differing by exercise prices or in the case of put-call parity, we can price only the relationship or difference between the option prices. We cannot price each option individually without an option pricing odel; however, an option pricing model must provide prices that conform to the boundary conditions. Because boundary condition rules require fewer assumptions, we can say that they are more generally applicable and are more likely to hold in practice. They are incomplete, however, in the sense that they do not tell us exactly what the option price should be, which is what an option pricing model does tell us.2. A binomial option pricing model enables us to see the relationship between the stock price and the call price. The model shows, in a simple framework, how to construct a riskless portfolio by appropriately weighting the stock against the option. By noting that the riskless portfolio should return the risk-free rate, we can see what the call price must be. We can also understand the forces that bring the call option price in line if it is not priced according to the model. In addition, the model illustrates the importance of revising the hedge ratio. Finally, the model is probably the best way to handle the problem of pricing an American option.3. For a call, a hedge portfolio will consist of n shares of stock and one short call. The shares of stock, n, will be a long position that will reflect the next two possible values of the call and stock. The call is short because the call and stock move opposite each other, so a short position in the call is needed to offset a long position in the stock. If the option is a put, a long position in n shares will be hedged by a long position in one put. The number of shares, n, is also a reflection of the next two possible option and stock values. The put is long because it already moves opposite to the stock.4. This means that the option is trading in the market for a price that is lower than its theoretical fair value. Consequently, the option is underpriced. An underpriced option should be bought. To hedge the position, one should sell n shares of stock, where n is the hedge ratio as defined in the chapter.5. At each point in the binomial tree, the option price is computed based on the next two possible prices, weighted by the appropriate probability values and discounted back one period. If the option can be exercised early, we determine its intrinsic value, i.e., the value it would have if it were exercised at that point. If the intrinsic value is greater, it replaces the computed value. This is done at all nodes. Note that it is quite possible that the option will be exercised at many different nodes.6. A path independent problem is one in which the only values that matter in determining the current price are the values at expiration. A particular expiration value is the same regardless of the sequence of up and down moves the stock took to get to that point. A path dependent model is one in which the sequence of up and down moves does matter. For example, suppose the stock goes down, up and then up. Contrast that with up, up and down. If the option is a European put, it does not matter which sequence the stock followed. Where it is at expiration is the only thing that matters. If the option is, however, an American put, the down, up, up sequence could lead to early exercise when it makes that first move down, whereas the up, up, down sequence is unlikely to lead to early exercise.Chapter 51. In a discrete time model, the stock price can make a jump to only one of two possible values. The length of time over which the move can be made is finite. In a continuous time model, the stock price can jump to an infinite number of possibilities. The length of time over which the move can be made is infinitesimal (very, very small). The difference between the two models is perhaps best described as in the text as the difference between still photos and a movie.2. The familiar normal or bell-shaped distribution is a symmetric probability distribution that depends only on the mean and variance. A lognormal distribution is skewed, having more extreme right values. A lognormal distribution, however, is normal in the logarithm. Thus, if x is lognormally distributed, its logarithm, lnx, is normally distributed. With respect to stock prices, the logarithm is of the rate of return. That is, let (S1 –S0)/S0 be defined as the return over period 0 to period 1. Then if it is lognormally distributed, ln(S1/S0) is normally distributed. Note what appears to be slight inconsistency: (S1 – S0)/S0 is a percentage return whereas S1/S0 is 1.0 plus the percentage return. That does not matter as we can always shift a normal distribution by adding a constant such as 1.0 and it does not affect the fact that it is normally distributed. It just slides it over.3. The Black-Scholes model assumes no dividends, but actually this was just for convenience to allow us to start at the simplest level. If the dividends are appropriately modeled, the Black-Scholes model handles stocks with dividends with only the minor adjustment that we must remove the present value of the dividends from the stock price before using it in the model. We can do this by subtracting the present value of the stream of discrete dividends over the life of the model or by discounting the stock price by the dividend yield rate over the life of the model.4. The variables in the binomial model are S0 (the stock price), X (the exercise price), r (the discrete risk-free rate), u (one plus the return on the stock if it goes up), d (one plus the return on the stock if it goes down) and n, the number of time periods. The variables in the Black-Scholes model are S0 (the stock price), X (the exercise price), r c (the continuously compounded risk-free rate), ó (the standard deviation of the continuously compounded return on the stock) and T (the time to expiration). The variables S0 and X are the same in both models. In the binomial model, r is the discrete interest rate per period. In the Black-Scholes model, the interest rate must be expressed in continuously compounded form. The annual discrete interest rate (r) is related to the annual continuously compounded rate (r c) by the formula, r c = ln(1 + r). Then the binomial rate per period is found as (1 + r)T/n - 1. The up and down factors in the binomial model are directly related to ó in the Black-Scholes model by the formula u = T/n ó e – 1 and d = (1/(1+u)) – 1. The time to expiration (T) in the Black-Scholes model is related to the length of each binomial period by the relationship T/n where n is the number of periods. Thus, all of the Black-Scholes variables are either equal to or directly convertible to binomial variables.Chapter6Chapter7Chapter 8Chapter9Chapter 10。
《金融工程》(第三版)课后习题参考答案.doc

《金融工程》高等教育出版社郑振龙陈蓉主编(第三版)课后习题参考答案《金融工程》高等教育出版社(郑振龙、陈蓉主编/第三版)课后习题参考答案第1章金融工程概述7.该说法是正确的。
从图1.3中可以看出,如果将等式左边的标的资产多头移至等式右边,整个等式左边就是看涨期权空头,右边则是看跌期权空头和标的资产空头的组合。
9. lOOOOe 5% 4.u82元M2725.21 10.每年计一次复利的年利率=(1+0.14/4) 4-1=14.75% 连续复利年利率= 41n(l+0.14/4)=13.76%o 11,连续复利年利率=121n(l+0.15/12)=14.91%。
12. 12%连续复利利率等价的每季度支付一次利息的年利率=4 (0.03e-l) =12.18%。
因此每个季度可得的利息=10000xl2.8%/4=304.55元。
第2章远期与期货概述1.2007年4月16日,该公司向工行买入半年期美元远期,意味着其将以764.21人民币/100美元的价格在2007年10月18日向工行买入美元。
合约到期后,该公司在远期合约多头上的盈亏=10000 (71)52。
,637 64 .21)11 5,8 0 0 2,收盘时,该投资者的盈亏= (1528.9 —1530.0)x250=-275美元;保证金账户余额=19,688-275 = 19,413美元。
若结算后保证金账户的金额低于所需的维持保证金,即19,688 (S &P时5(即S&0P5000指数指期货结算价数<1514.3期时),货结算价1 530 )250 lv5,750交易商会收到追缴保证金通知,而必须将保证金账户余额补足至19,688美元。
3.他的说法是不对的。
首先应该明确,期货(或远期)合约并不能保证其投资者未来一定盈利,但投资者通过期货(或远期)合约获得了确定的未来买卖价格,消除了因价格波动带来的风险。
本例中,汇率的变动是影响公司跨国贸易成本的重要因素,是跨国贸易所面临的主要风险之一,汇率的频繁变动显然不利于公司的长期稳定运营(即使汇率上升与下降的概率相等);而通过买卖外汇远期(期货),跨国公司就可以消除因汇率波动而带来的风险,锁定了成本,从而稳定了公司的经营。
最新金融工程答案翻译

第一章1.4 仔细解释卖出一个看涨期权与买入一个看跌期权的差别卖出一个看涨期权涉及到给他人一个买入你某项财产的权利,它将给你带来的收益为-max (st-k,0)=min(k-st,0)买入一个看跌期权涉及到从他人手里买入一个期权,带来的收益为max(k-st,0)他们都有一个可能性的收入k-st,当你卖出看涨期权,收入为负值或0,这是因为交易对手可以选择是否执行。
当你买入一个看跌期权,你的收入为0或正直,这是因为你选择执行与否1.5 你认为某股票价格将要上升,股票当前价格为29美元,三个月期限,执行价格为30美元的看涨期权价格为2.9美元,你共有美金5800元,说明两种投资模式,并简单说明一下两种模式的优缺点有两种方案,即买入200股股票或买入2000份看涨期权,当股票价格上涨航行好,第二种方案将得到更高的回报。
举例来说,当股价上涨为40元,此时收益为2000(40-30)-5800=14200 而第一种反感只有200(40-29)=2200元收益,但当股价下跌,第二种方案将有更大的损失。
当股票价格下跌至25元,第一种方案损失为200(29-25)=800元,第二种方案则带来5800元的损失,这个例子证明了期权有一定的杠杆效率1.26当前黄金市价为每盎司600美元,一个一年期远期合约的执行价格为800美元,一个套利者能以每年10%的利率借入资金,套利者应如何做才能达到套利目的?这里我们假设黄金存储费用为0.同时黄金不会带来任何利息收入这个套利者可以借入资金买入100盎司黄金现货和卖出一个100盎司于一年后交割的期货合约,这就意味着黄金以600美元每盎司买入以800美元每盎司卖出,收益率约为33.3%,远高于10%的接入率,这是一个很好的盈利机会,套利者应尽可能多的买入黄金现货及预期数量相匹配的期货合约1.27 股票当前价格为94美金,同时,三个月期,执行价格为95美元的欧式期权价格为4.7美元,一个投资者认为股价会上涨,但他并不知道应该买入100股股票或买入2000个(20份)期权,这两种投资所需资金均为9400美元,此时你会给出什么建议?股价涨到什么样的水平会使得期权投资盈利更好?投资于看涨期权会带来高收益但是会有高风险,如果股价停止在94美元,买入看涨期权的投资者损失9400美元,儿买入股票的投资者什么也没有损失,如果股价上涨到120美元,买入期权的投资者会得到2000(120-95)-9400=40600美元的收益,而买入股票的投资者会得到100(120-94)-9400=2600元,当股价为s时,这两种投资的收益相等,100(s-94)=2000(s-95),s-100。
金融工程学课后答案

金融工程学课后答案-07121.5 答:当股票价格低于$120时,该期权将不被执行。
当股票价格高于$120 美元时,该期权买主执行该期权,我将损失 100(st-x)。
1.9 答:如果投资者预期价格将会上涨,可以通过远期多头来降低风险暴 露,反之, 预期价格下跌,通过远期空头化解风险。
如果投资者资产无潜在的 风险暴露,远期合约交易就成为投机行为。
1.19答:这句话是说期权和期货的一方损失程度等于另一方的盈利程度,总的收入为零。
1.21答:假设ICON 中外汇汇率为S T ,则ICON 勺收益为1000,若S T V X1000-a(S r -Xk vIC0N 的收益來自:普通债券执厅价格为X 的欧式个头看涨期权 1.25答:由欧式看涨期权和看跌期权的损益公式得,一个欧式看涨期权的 多头和一个欧式看跌期权的空头组合的损益为:max(S r - A\0) + 一 $八 0)当S T > X 时,总收入为S T -X+X -S T =0;当S T < X 时,总收入亦为0。
与远期合约多头相一致2.19答:平仓是从事一个与初始交易头寸相反的头寸,如果双方购入新的合 约,未平仓数就会增加一个,如果交易双方结平头寸,未平仓数就会减少一个, 如果一方购入新的合约,一方结平已有的头寸,未平仓数就保持不变。
当C S =2 cF, p= 0.5时,套期保值率为1.0,但是由于p <1.0,因此该套期保 值不是完全的。
2.25 答:该陈述是正确的,如果套期保值率为1.0,则套期保值者将价格 锁定在F1 + b2,由于F1和b2都是确定的,因此风险为零。
2.33答:套期保值既可能导致公司利润的增加也可能导致公司利润的降 低。
而公司衡如FI 引所示: 普通侑券空头看涨期权 峯头看涨期权 总收益 S T <X 1000 0 01000 v 1000 c . A + ---- >S T >}「 1000 S T - X)1000-3( ) c . 「1000 S T >X +- 1000 5L-A ) } 0(c) 执行价必为V +竺时欧式多头石•洙期权 a1^1 lit, (a)2.24答:该陈述错误,最小风险的套期保值比率为量财务经理的标准是他们为公司作出的贡献,因此,如果其它管理者不理解财务经理所作的行为,财务经理还会收到责备。
金融学第十五章课后答案翻译
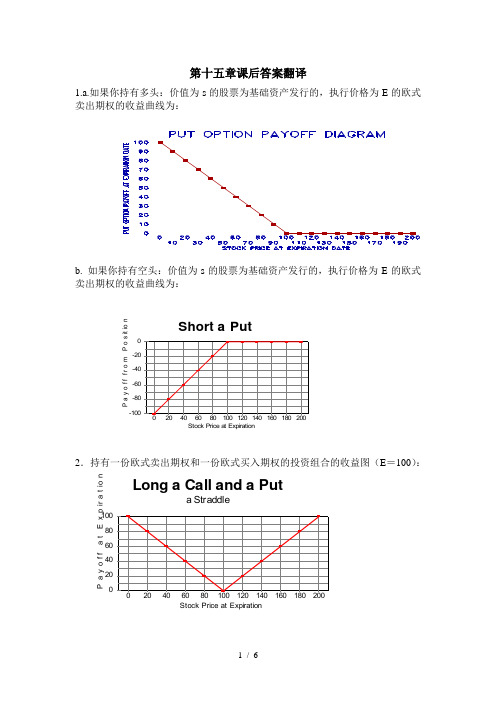
第十五章课后答案翻译1.a.如果你持有多头:价值为s的股票为基础资产发行的,执行价格为E的欧式卖出期权的收益曲线为:卖出期权的收益曲线为:2.持有一份欧式卖出期权和一份欧式买入期权的投资组合的收益图(E=100):3.a .为了保证你至少能够收回你初始的一百万美元,你需要投资在till 股票上。
你可以购买的期权。
104股指的报酬线斜率是4807.69,正如图表所显示的。
B .4.a.要复制一个面值为100美元的纯贴现债券,应买一份股票:其欧式买入期权价格和欧式卖出期权价格均为100。
b. S = $100, P = $10, and C = $15.E/(1+r) = S + P- C$100/(1+r) = $100 + $10 - $15 = $95 r = 100/95 -1 =0 .053 or 5.3%c.如果1年期无风险利率小于b 的答案,则说明纯贴现债券的价格过高,人们便会通过便宜购买综合性产品(一份其欧式买入期权价格和欧式卖出期权价格均为100的股票)来替换价格较高的纯贴现债券以从中套利。
5.用P = -S + E/(1+r)T + C 这个表达式来表示卖出期权S 是股价,P 是卖出的执行价,C 是买入期权的价格,E 是执行价格,既然政府债券是以9855日元每10000日元的价格出售,这就是计算执行价格现值的贴现率,而无须用风险利率进行折现。
用平价的替代等式来计算,我们可以得到:P = -2,400 + 500 x .9855 +2,000 = 92.75 yen6.a.根据卖出-买入平价,Gekko 投资组合中买入期权的价格: C = S - E/(1+r)T + P = $215 - $50 ×0 .9901 + $25 = $190.495b. Gekko 的投资组合的总价值:10 x $990.10 + 200 x $190.495 = $48,000,而300股股票的总价值:$64,500。
金融工程答案翻译

第一章1.4 仔细解释卖出一个看涨期权与买入一个看跌期权的差别卖出一个看涨期权涉及到给他人一个买入你某项财产的权利,它将给你带来的收益为-max 〔st-k,0=min〔k-st,0买入一个看跌期权涉及到从他人手里买入一个期权,带来的收益为max〔k-st,0他们都有一个可能性的收入k-st,当你卖出看涨期权,收入为负值或0,这是因为交易对手可以选择是否执行。
当你买入一个看跌期权,你的收入为0或正直,这是因为你选择执行与否1.5 你认为某股票价格将要上升,股票当前价格为29美元,三个月期限,执行价格为30美元的看涨期权价格为2.9美元,你共有美金5800元,说明两种投资模式,并简单说明一下两种模式的优缺点有两种方案,即买入200股股票或买入2000份看涨期权,当股票价格上涨航行好,第二种方案将得到更高的回报。
举例来说,当股价上涨为40元,此时收益为2000〔40-30-5800=14200 而第一种反感只有200〔40-29=2200元收益,但当股价下跌,第二种方案将有更大的损失。
当股票价格下跌至25元,第一种方案损失为200〔29-25=800元,第二种方案则带来5800元的损失,这个例子证明了期权有一定的杠杆效率1.26当前黄金市价为每盎司600美元,一个一年期远期合约的执行价格为800美元,一个套利者能以每年10%的利率借入资金,套利者应如何做才能达到套利目的?这里我们假设黄金存储费用为0.同时黄金不会带来任何利息收入这个套利者可以借入资金买入100盎司黄金现货和卖出一个100盎司于一年后交割的期货合约,这就意味着黄金以600美元每盎司买入以800美元每盎司卖出,收益率约为33.3%,远高于10%的接入率,这是一个很好的盈利机会,套利者应尽可能多的买入黄金现货及预期数量相匹配的期货合约1.27 股票当前价格为94美金,同时,三个月期,执行价格为95美元的欧式期权价格为4.7美元,一个投资者认为股价会上涨,但他并不知道应该买入100股股票或买入2000个〔20份期权,这两种投资所需资金均为9400美元,此时你会给出什么建议?股价涨到什么样的水平会使得期权投资盈利更好?投资于看涨期权会带来高收益但是会有高风险,如果股价停止在94美元,买入看涨期权的投资者损失9400美元,儿买入股票的投资者什么也没有损失,如果股价上涨到120美元,买入期权的投资者会得到2000〔120-95-9400=40600美元的收益,而买入股票的投资者会得到100〔120-94-9400=2600元,当股价为s时,这两种投资的收益相等,100〔s-94=2000〔s-95,s-100。
金融工程答案翻译

金融工程答案翻译金融工程答案翻译1.4的第1章详细解释了卖出看涨期权和买入看跌期权之间的区别卖出看跌期权意味着给予其他人购买你的部分房产的权利,这将给你带来-max(st-k,0)=min(k-st,0)买入看跌期权意味着从其他人那里购买期权,回报是max(k-st,0) 。
他们都有一个可能的收入k-st。
当你卖出看涨期权时,收入为负或0,因为交易对手可以选择是否执行。
当你购买看跌期权时,你的收入是0,或者仅仅因为你选择是否执行它。
你认为股票价格会上涨。
股票的当前价格是29美元,三个月期间,执行价格为30美元的看涨期权的价格是2.9美元,你总共有5800美元,这表明两种投资模式。
并简要说明两种模式的优缺点,有两种选择,即购买XXXX年期远期合同执行价格为800美元,一次套利可以以每年10%的利率借入资金,套利应该如何做才能达到套利的目的?这里我们假设黄金的储存成本是0。
同时,黄金不会带来任何利息收入。
这位套利者可以借入资金购买100盎司黄金现货,并出售一份一年内交割的100盎司期货合约。
这意味着黄金以每盎司600美元的价格买进,以每盎司800美元的价格卖出,收益率约为33.3%,远高于10%的准入率。
这是一个很好的获利机会。
仲裁员应该购买尽可能多的1.27股票的期货合约,与预期的黄金现货数量相匹配。
目前的价格是94美元。
与此同时,执行价格为95美元的三个月期欧洲期权是4.7美元。
一位投资者认为股价会上涨,但他不知道是在7月份买入100只股票还是XXXX。
一家矿业公司刚刚发现了一个小金矿。
决定在六个月内建起这座矿井。
黄金将在明年继续开发。
纽约期货交易所有黄金期货合约。
从XXXX的一月到二月,总共将生产3000盎司黄金。
卖出30长期货合约可以锁定其价格2.26一家公司进入了空头期货头寸。
在合同中,该公司以每蒲式耳250美分的价格出售了5000蒲式耳小麦。
初始保证金为3000美元,XXXX的维持保证金为6%,股息收益率为每年3%,当前3个月期货价格为1259美元。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章1.4 仔细解释卖出一个看涨期权与买入一个看跌期权的差别卖出一个看涨期权涉及到给他人一个买入你某项财产的权利,它将给你带来的收益为-max (st-k,0)=min(k-st,0)买入一个看跌期权涉及到从他人手里买入一个期权,带来的收益为max(k-st,0)他们都有一个可能性的收入k-st,当你卖出看涨期权,收入为负值或0,这是因为交易对手可以选择是否执行。
当你买入一个看跌期权,你的收入为0或正直,这是因为你选择执行与否1.5 你认为某股票价格将要上升,股票当前价格为29美元,三个月期限,执行价格为30美元的看涨期权价格为2.9美元,你共有美金5800元,说明两种投资模式,并简单说明一下两种模式的优缺点有两种方案,即买入200股股票或买入2000份看涨期权,当股票价格上涨航行好,第二种方案将得到更高的回报。
举例来说,当股价上涨为40元,此时收益为2000(40-30)-5800=14200 而第一种反感只有200(40-29)=2200元收益,但当股价下跌,第二种方案将有更大的损失。
当股票价格下跌至25元,第一种方案损失为200(29-25)=800元,第二种方案则带来5800元的损失,这个例子证明了期权有一定的杠杆效率1.26当前黄金市价为每盎司600美元,一个一年期远期合约的执行价格为800美元,一个套利者能以每年10%的利率借入资金,套利者应如何做才能达到套利目的?这里我们假设黄金存储费用为0.同时黄金不会带来任何利息收入这个套利者可以借入资金买入100盎司黄金现货和卖出一个100盎司于一年后交割的期货合约,这就意味着黄金以600美元每盎司买入以800美元每盎司卖出,收益率约为33.3%,远高于10%的接入率,这是一个很好的盈利机会,套利者应尽可能多的买入黄金现货及预期数量相匹配的期货合约1.27 股票当前价格为94美金,同时,三个月期,执行价格为95美元的欧式期权价格为4.7美元,一个投资者认为股价会上涨,但他并不知道应该买入100股股票或买入2000个(20份)期权,这两种投资所需资金均为9400美元,此时你会给出什么建议?股价涨到什么样的水平会使得期权投资盈利更好?投资于看涨期权会带来高收益但是会有高风险,如果股价停止在94美元,买入看涨期权的投资者损失9400美元,儿买入股票的投资者什么也没有损失,如果股价上涨到120美元,买入期权的投资者会得到2000(120-95)-9400=40600美元的收益,而买入股票的投资者会得到100(120-94)-9400=2600元,当股价为s时,这两种投资的收益相等,100(s-94)=2000(s-95),s-100。
所以当股价高于一百时,期权盈利更好2.9 设计一个新的期货合约时需要考虑那些方面?合约规模,交割安排,交割月份2.19在期货市场,投机就是纯粹的赌博,为了公众利益,不应该让投机者在交易场所交易齐国,评价这种说法投机者是期货市场重要的参与者,因为他们增加了期货市场的流动性,和投机一样合约对于对冲来说必须是有用的。
因为总的来说,和投机这类似,当合约对风险对冲者有利益时才会得到监管部门的通过2.25 现在是2008年7月,一个矿物公司刚刚发现了一个小型金矿,决定用六个月时间建矿,黄金将在今后的一年内连续被开发出,nyce有关于黄金期货的合约,从2008.8-2009.12月,每两个月有一个期货交割月,每一个合约规模为100盎司黄金,讨论矿业公司将采用何种期货产品来对冲风险。
矿业公司应该连续按月估计出黄金的产量,今儿通过卖出与黄金产量想等的期货合约来锁定近期黄金价格,比如2009年1、2月共产出黄金三千盎司,卖出30长期货合约可以锁定其价格2.26 一家公司进入一个期货短头寸,合约中,公司以每蒲式耳250美分卖出5000蒲式耳小麦,初始保证金为3000美金,维持保证金为2000美金,价格如何变化会导致保证金的催收?什么情况下,公司可以从保证金账户中提取1500美金?在期货市场损失1000美金,即小麦期货没蒲式耳上涨二十美分时,会导致保证金的催收,当小麦期货价格每蒲式耳下降30美分时,可以从保证金账户中提取1500美金。
3.7:一家公司持有价值为2000万美元,β值为1.2的股票组合,该公司想要采用S&P500期货来对冲风险,股指期货的当前价格为1080,每一个期货是关于250美元倍的股指,什么样的对冲可以使风险极小化?公司怎么做才可以将组合的beta值降为0.6?N*=1.2*20000000/(250*1080)=88.89所以进入89份的期货短头寸。
N`=(1.2-0.6)*20000000/(250*1080)=44.4所以公司只需持有44份期货短头寸就可以将beta值降为0.6.3.17:一个玉米农场的农场主有以下观点,我们不能采用期货来对冲我面临的风险,我的真正风险并不是玉米价格的变化,而是气候原因使我颗粒无收。
讨论这一观点,这个农民是否应该对玉米的预期产量有所估计然后采用对冲策略来锁定预期价格。
由于气候原因使得玉米颗粒无收,但是气候的影响对于所有的玉米农场主来说都是一样的。
因此玉米的总产量下降,导致玉米价格会有个相当大的提高。
相对于实际的玉米产量,这个农民很有可能会过度对冲了。
这样一来农民在期货市场上的损失会增加自己整体的损失。
因此这个农场主的观点是正确的,也即是这个农民不应该对玉米预期产量有所估计然后采用对冲策略来锁定预期价格。
3.23下表关于某商品的即期以及期货每月价格变化的数据,利用这些数据来计算使方差最小化即期价格变化期货价格变化即期价格变化期货价格变化δF估计值为δS估计值为3.25一个基金经理持有一价值为5000万美元,Beta等于0.87的股票组合。
该经理担心在今后两个月内市场的表现,因此打算采用3个月期的关于S&P500的期货合约来对冲其风险。
股指的当前水平为1250,期货合约是关于250倍的指数,无风险利率未每年6%,股息收益率为每年3%,当前3个月期的期货价格为1259.(a)基金经理应采用什么样的头寸来对冲今后两个月内的市场风险?(b)当股指在两个月后分别为1000、1100、1200、1300和1400时,你的策略对于基金经理的收益影响会如何?假定一个月期的期货价格比现在的股指水平高0.25%。
(a)...N*=0.87*50000000/(1259*250)=138.2 ...进入期货合约的短头寸,数量为138份。
(b)当股指为1000时:期货市场上投资效果=250×(1259-1000×1.0025)×138=8849250现货市场上的效果:由于股指在这两个月的亏损率=3%×2/12-{(1000-1250)/1250}-6%×2/12=0.5%-21%=-20.5%而基金经理所持有的股票组合的beta值为0.87,所以该股票组合的亏损率为20.5%×0.87=17.835%,减去其中的无风险利率1%,那么现货市场的实际亏损率为16.835%亏损价值=16.835%×5000×10000=8417500则总效果=8849250-8417500=431750美元其他情形雷同。
4.8从久期你能知道债券组合对于利率有什么样的敏感度?久期有什么局限性?久期提供的信息是一个小的收益率曲线的平行移动对债券投资组合价值的影响。
投资组合价值减少的百分比等于久期乘以相对应的平行移动的利率的变化。
久期的局限性是只能在利率的平行移动中适用。
4.21解释为什么一个FRA等价于以浮动利率交换固定利率?一个FRA是约定在将来某一段时间交易的一方将以某一个特定的利率RK借入或者借出一个固定的资金L的协议。
不管市场上的利率如何变化,订立FRA协议者就有权在约定的时间以利率为RK这一固定利率借入或者借出资金。
相当于以浮动利率交换固定利率。
4.25:6个月、12个月、18个月和24个月期限的零息利率分别为4%、4.5%、4.75%和5%,这里利率为每半年复利一次。
(a)相应的连续复利利率为多少?(b)在18个月开始的6个月期的远期利率为多少?(a)R6=2ln1.02=0.039605,R12=2ln1.0225=0.044501,R18=2ln1.02375=0.046945,R24=2ln1.025=0.049385.(b)远期利率=(4.9385*2-4.9645*1.5)/0.5=0.05670718个月开始的6个月期的远期利率=2(e0.056707*0.5-1)=0.0575184.27下表给出了债券价格表中,每6个月支付所示利息的一半。
(a )计算对应于6个月、12个月、18个月和24个月期限的零息利率。
(b )以下时间段的远期利率为多少?6~12个月;12~18个月;18~24个月。
(c )对于每半年支付一次券息,期限分别为6个月、12个月、18个月和24个月的债券平价收益率为多少?(d )估算年券息率未10%,每半年支付一次券息,2年期限债券的收益率。
(a )零息利率:R 0.5=2ln(1+2/98)=4.0405%; R 1=ln(1+5/95)=5.1293%,;R 1.5满足3.1e -0.0405*0.5+3.1e -0.051293*1+103.1e -R*1.5=101,得出,R 1.5=5.4429%;R 2满足4-0.0405*0.5+4e -0.051293*1+4e -0.054429*1+104e -R*2=104,得出,R 1.5=5.8085%; (b )远期利率:R 0.5=4.0405%,R 1=6.2181%,R 1.5=6.0700%,R 2=6.9054%;(c )票面利率:R 0.5=4.0816%,R 1=5.1813%,R 1.5=5.4986%,R 2=5.8620%;(第二问和第三问的解题方式找不到,直接给出了答案。
)(d )债券价格:债券收益率y 满足:y=0.057723,所以,收益率未5.7723%5.6 仔细解释便利收益与持有成本两个术语的含义。
期货价格、即期价格、便利收益与持有成本的关系式是什么?便利收益率反映了市场对未来商品可获得性的预期也可以说是因持有商品而带来的好处。
持有成本包括储存成本加上资产的融资利息,再减去资产的收益。
期货价格:F0. 即期价格:S0.便利收益:y持有成本:c关系式为T是期货合约到期时间5.15 白银的限价为每盎司9美元,每年储存费用为每盎司0.24美元,储存费要每季度预先支付一次。
假定所有期限的利率均为每年10%(连续复利),计算9个月后到期的期货价格。
答:九个月的存储成本现值为:9月后到期的期货价格:5.17 当一家公司采用远期合约对于将来已知的外汇现金流进行对冲时,就不存在汇率风险。
