(完整版)北师大版七年级数学全等三角形练习题
最新北师大版七年级下册三角形全等的证明试题以及答案(SSS、AAS、ASA、SAS、HL)(各10题)
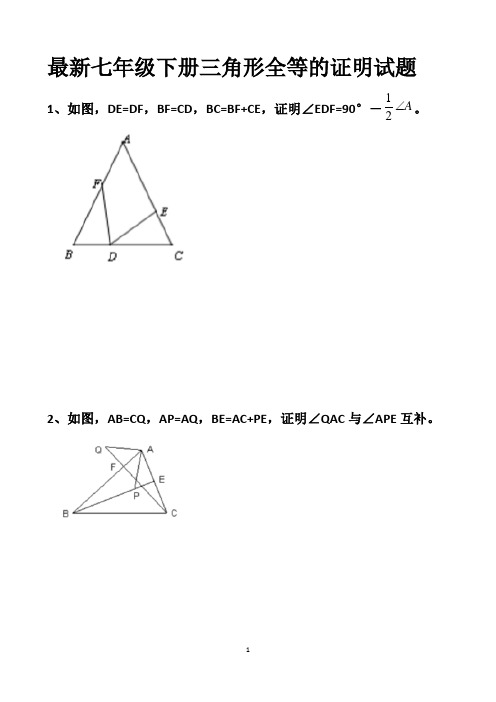
最新七年级下册三角形全等的证明试题1、如图,DE=DF ,BF=CD ,BC=BF+CE ,证明∠EDF=90°-A 21。
2、如图,AB=CQ ,AP=AQ ,BE=AC+PE ,证明∠QAC 与∠APE 互补。
3、如图,AB=CD,AC=BD,BE=CE,证明AE=DE。
4、如图,AE=CF,AD=BC,DF=BE,证明AE∥CF。
5、如图,AB=AD,AC=AE,BD+DC=DE,证明∠1=∠EDC。
6、如图,AB=BD,AC=BE,BC=DE,∠D=90°,证明AC⊥BE。
7、如图,O是BD的中点,OE=OF,DE=BF,证明AD∥BC。
8、如图,O是EF、BD的公共中点,AD=BC,AF=EC,证明AV=CD。
9、如图,AC=BF,AD=DF,BD=DC,证明∠B=∠C。
10、如图DF=DE,AC=BC,AF=BE,证明∠A=∠B。
11、如图,F是CD的中点,A点到C点与A点到D点到距离相等,AB=AE,∠BAF=∠EAF,证明∠B=∠E。
1、如图,AC∥DF,且AC=DF,∠C=∠F,说明BC和EF关系。
2、如图,AB=AC,∠BAC=∠DAE,∠ABD=∠2,证明∠3=∠1+∠2.3、如图,AB=AC,∠BAC=∠DAE,∠ADB=∠AEC,证明∠ADE=∠ACB。
4、如图,E在△ABC的边AC上,且∠AEB=∠ABC.求证:(1)∠ABE=∠C;(2)求∠BAE的平分线AF交BE于点F,FD∥BC交AC于点D,设AB=8,AC=10,求DC的长。
5、如图,MQ、NR是△PMN的高线,且MQ=NQ,证明PM=HN。
6、如图,BD⊥AC,CE⊥AB,AB=AC,证明∠B=∠C。
7、如图,BC=CD,∠BCE=∠ACD,∠B=∠D,证明AB=ED。
8、如图,AB∥CF,AD=CF,说明E是AC、DF的公共中点。
9、如图,BD⊥DE,CE⊥DE,AB⊥AC,且AB=AC,说明BD、CE和DE 关系。
新北师大版七年级数学下册第三章全等三角形练习题

七年级数学周周清一、填空题1、若△ABC ≌△DEF ,△DEF 的周长为32 cm ,DE =9 cm ,EF =12 cm ,则AB =_____ cm ,BC =_____ cm,AC =_____ cm.2、若△ABC ≌△DEF ,AB =DE ,AC =DF ,∠A =80°,BC =9 cm,则∠D =_____,∠D 的对边是_____=_____ cm.3、已知如图1,在△ABF 和△DEC 中,∠A =∠D ,AB =DE ,若再添加条件_____=_____,则可根据边角边公理证得△ABF ≌△DEC .4、如图2,△ABC 中,∠C=90°,CD ⊥AB 于点D ,AE 是∠BAC 的平分线,点E 到AB 的距离等于3cm ,则CE=_____cm 。
图1图2 图35、如图3,△ABC ≌△ADE ,延长BC 交DA 于F ,交DE 于G ,∠D=25°,∠E=105°,∠DAC=16°,则∠DGB=____________。
6、为了使一扇旧木门不变形,木工师傅在木门的背面 加钉了一根木条,这样做的道理是 。
二、选择题1、有下列长度的三条线段,能组成三角形的是( )A 、 2cm ,3cm ,4cmB 、 1cm ,4cm ,2cmC 、1cm ,2cm ,3cmD 、 6cm ,2cm ,3cm 2、下列命题中正确的是( )①全等三角形对应边相等; ②三个角对应相等的两个三角形全等; ③三边对应相等的两三角形全等;④有两边对应相等的两三角形全等。
A .4个 B 、3个 C 、2个 D 、1个3、已知△ABC ≌△DEF ,∠A=70°,∠E=30°,则∠F 的度数为 ( )(A ) 80° (B ) 70° (C ) 30° (D ) 100°4、如图4,△ABD 和△ACE 都是等边三角形,那么△ADC ≌△ABE 的根据是( )图4A.SSSB.SASC.ASAD.AAS 5、如图所示,某同学把一块三角形玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是( )F EDC BAA.带①去B. 带②去C. 带③去D. 带①和②去 6、下列说法:①所有的等边三角形都全等 ②斜边相等的直角三角形全等③顶角和腰长对应相等的等腰三角形全等 ④有两个锐角相等的直角三角形全等其中正确的个数是( )A .1个B .2个C .3个D .4个第7题 第8题 第9题7、如图,AB 平分∠CAD ,E 为AB 上一点,若AC=AD ,则下列结论错误的是( )A.BC=BDB.CE=DEC.BA 平分∠CBDD.图中有两对全等三角形8、如图,D 在AB 上,E 在AC 上,且∠B=∠C ,则在下列条件中,无法判定△ABE ≌△ACD 的是( ) (A )AD=AE (B )AB=AC(C )BE=CD (D )∠AEB=∠ADC9、如图,AB=AC ,BE ⊥AC 于E ,CF ⊥AB 于F ,则①△ABE ≌△ACF ;②△BOF ≌△COE ;③点O 在∠BAC 的角平分线上,其中正确的结论有( ) A .3个 B .2个 C .1个 D .0个10、下列条件中能确定两个三角形全等的是( )A.一边及这条边上的高相等B.一边及这条边上的中线对应相等C.两角及第三个角平分线对应相等D.两条边及夹角的平分线对应相等11、下列各组图形中,一定全等的是( )A.各有一个角是45°的两个等腰三角形B.两个等边三角形C.各有一个角是40°,腰长都为3 cm 的两个等腰三角形D.腰和顶角对应相等的两个等腰三角形 三、解答题1、已知,如图,∠1=∠2,BD=CD,求证:AD 是∠BAC 的平分线.2、如图,点E 在△ABC 外部,点D 在BC 边上,DE 交AC 于点F ,若∠1=∠2=∠3,AC=AE ,求证:△ABC ≌△ADEA B C D EC B A E F O3、已知线段a 和∠1,作一个△ABC ,使得AB=a ,AC=2a ,∠A=∠ 1.4、如图,已知AB =DC ,AC =DB ,E 是BC 的中点,求证:AE =DE5、如图,在△ABC 中,BE 、CF 分别是AC 、AB 两边上的高,在BE 上截取BD=AC ,在CF 的延长线上截取CG=AB ,连结AD 、AG 。
最新北师大版七年级下册三角形全等(SSS)的证明试题以及答案(共41道证明题)
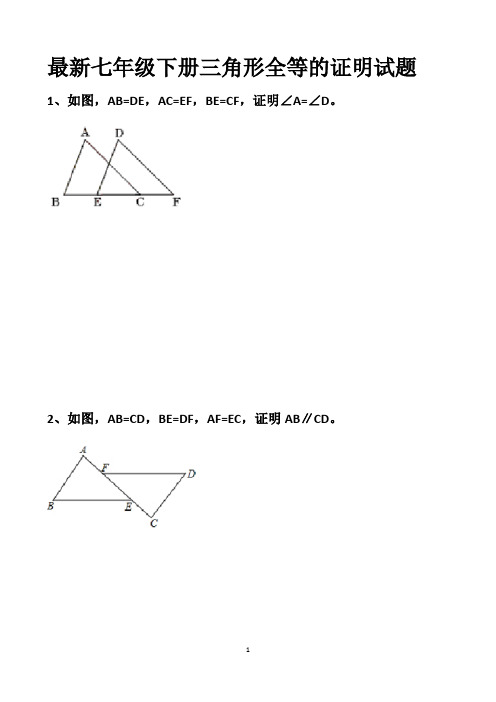
最新七年级下册三角形全等的证明试题1、如图,AB=DE,AC=EF,BE=CF,证明∠A=∠D。
2、如图,AB=CD,BE=DF,AF=EC,证明AB∥CD。
3、如图,AC=DF,EF=BC,AD=BE,证明∠F=∠C。
4、如图,AB=AC,AD=AE,BE=DC,证明∠ABD=∠AEC。
5、如图,AB=AD,AE=AC,BC=ED,证明∠ABE=∠ACD。
6、如图,AD=AB,DC=BC,证明∠B=∠D。
7、如图,AB=AC,BD=DC,证明∠1=∠2.8、如图,∠C=90°,AD=BD,DE=DC,AE=BC,说明AB和DE的关系。
9、如图,AB=DE,BC=EF,AF=CD,证明AB∥DE。
10、如图,AB=AC,D是BC的中点,证明AD⊥BC。
11、如图,AE=DF,AB=CD,CE=BF,证明AE∥DF。
12、如图,AB=AD,AE=AC,BC=DE,证明∠E=∠C。
13、如图,BC=BE,DE=DC,∠C=90°,证明(1)DE⊥AB(2)BD是∠ABC的角平分线。
14、如图,AB=EF,AD=CF,DE=BC,证明∠B=∠E。
15、如图,OA=OB,AC=BD,AD=BC,证明∠ACB=∠ADB。
16、如图,AD=BC,A0=OB,OC=OD,证明∠BAD=∠ABC。
17、如图,AD=BD,BE=AC,AD+DE=BC,AD⊥BC,证明BE⊥AC。
18、如图,AD=BC,AF=EC,DE=BF,证明DE∥BF,AD∥BC。
19、如图,AB=DC,AC=BD,AO=OD,证明∠B=∠C。
20、如图,AB=AD,AE=AC,BC=DE,证明∠1=∠2.21、如图,AC⊥CE,AC=CE,AB=CD,且AB+DE=BD,AB∥DE。
22、如图,AE=AB,AC=AF,EC=BF,证明∠BAE=∠CAF。
23、如图,AD=BC,AC=BD,证明∠ADO=∠BCO。
24、如图,AB=AC,BD=CE,AD=AE,证明∠ABC=∠ADE。
北师大版七年级下册三角形全等的证明练习题以及答案

最新北师大版七年级下册三角形全等的证明练习题以及答案最新七年级下册三角形全等的证明1、已知:如图,四边形ABCD中,AC平分角BAD,CE垂直AB 于E,且角B+角D=180度,求证:AE=AD+BEA B DCE 122、已知,如图,AB=CD,DF⊥AC于F,BE⊥AC于E,DF=BE。
求证:AF=CE。
F EA CDB3、已知,如图,AB ⊥AC ,AB =AC ,AD ⊥AE ,AD =AE 。
求证:BE =CD 。
AEDCB4、如图,DE⊥AB,DF⊥AC,垂足分别为E、F,请你从下面三个条件中任选出两个作为已知条件,另一个为结论,推出一个正确的命题。
① AB=AC ② BD=CD ③ BE=CF5、如图,△ABC中,AB=AC,过A作GE∥BC,角平分线BD、CF交于点H,它们的延长线分别交GE于E、G,试在图中找出三对全等三角形,并对其中一对给出证明。
E6、如图,在△ABC中,点D在AB上,点E在BC上,BD=BE。
(1)请你再添加一个条件,使得△BEA≌△BDC,并给出证明。
你添加的条件是:________ ___(2)根据你添加的条件,再写出图中的一对全等三角形:______________(不再添加其他线段,不再标注或使用其他字母,不必写出证明过程)7、已知:如图,AB⊥BC,AD⊥DC,AB=AD,若E是AC上一点。
求证:EB=ED。
DA E CB8、已知:如图,AB、CD交于O点,CE//DF,CE=DF,AE=BF。
求证:∠ACE=∠BDF。
AB CDEFO9、已知:如图,△ABC中,AD⊥BC于D,E是AD上一点,BE的延长线交AC于F,若BD=AD,DE=DC。
求证:BF⊥AC。
AE FDB C10、. 已知:如图,△ABC 和△A 'B 'C '中,∠BAC=∠B 'A 'C ',∠B=∠B ',AD 、A 'D '分别是∠BAC 、∠B 'A 'C '的平分线,且AD=A 'D '。
最新北师大版七年级下册三角形全等的证明试题以及答案(SSS、AAS、ASA、SAS、HL)(各10题)

最新七年级下册三角形全等的证明试题1、如图,AB=DE,AC=EF,BE=CF,证明∠A=∠D。
2、如图,AB=CD,BE=DF,AF=EC,证明AB∥CD。
3、如图,AC=DF,EF=BC,AD=BE,证明∠F=∠C。
4、如图,AB=AC,AD=AE,BE=DC,证明∠ABD=∠AEC。
5、如图,AB=AD,AE=AC,BC=ED,证明∠ABE=∠ACD。
6、如图,AD=AB,DC=BC,证明∠B=∠D。
7、如图,AB=AC,BD=DC,证明∠1=∠2.8、如图,∠C=90°,AD=BD,DE=DC,AE=BC,说明AB和DE的关系。
9、如图,AB=DE,BC=EF,AF=CD,证明AB∥DE。
10、如图,AB=AC,D是BC的中点,证明AD⊥BC。
1、如图,AB∥CD,且AB=CD,证明O是AD、BC的公共中点。
2、如图,CA⊥OM,CB⊥ON,OC平分∠MON,证明(1)OA=OB(2)连接AB,证明AB⊥OC。
3、如图,∠B=∠C,AD=AE,证明BD=CE。
4、如图,AC平分∠BAD,AB⊥BC,AD⊥DC,证明CA平分∠BCD。
5、如图,AB∥DE,BF=CE,∠A=∠D,试着说明AC和DF的关系。
6、如图,AB=CD,∠A=∠D,证明∠1=∠2.7、如图,∠A=∠D,∠BCE=∠ACD,CB=CE,证明AB=ED。
8、如图,DE⊥AB,DF⊥AC,D是BC的中点,∠BDF=∠CDE,证明AB=AC。
9、如图,∠1=∠2,AB=AE,∠B=∠E,证明∠D=∠C。
10、如图,AB⊥BC,DC⊥BC,BE=CF,∠BED=∠ACF,证明AF⊥DE。
1、如图,∠1=∠2,AE=AD,AC=AB,证明∠C=∠B。
2、如图,OA=OC,OD=OB,证明AD=BC。
3、如图,AD平分∠BAC,AB=AC,证明BD=CD。
4、如图,OD=OC,OA=OB,证明∠OBA=∠OAB。
5、如图,AB=AC,AD平分∠BAC,证明AD⊥BC。
(完整word版)北师大版七年级数学全等三角形练习题

全等三角形练习题一、选择题1.如图,给出下列四组条件:①AB DE BC EF AC DF ===,,;②AB DE B E BC EF =∠=∠=,,; ③B E BC EF C F ∠=∠=∠=∠,,;④AB DE AC DF B E ==∠=∠,,.其中,能使ABC DEF △≌△的条件共有( ) A .1组B .2组C .3组D .4组2.如图,D E ,分别为ABC △的AC ,BC 边的中点,将此三 角形沿DE 折叠,使点C 落在AB 边上的点P 处.若48CDE ∠=°, 则APD ∠等于( )A .42°B .48°C .52°D .58° 3.如图(四),点P 是AB 上任意一点,ABC ABD ∠=∠,还应补 充一个条件,才能推出APC APD △≌△.从下列条件中补充 一个条件,不一定能....推出APC APD △≌△的是( ) A .BC BD = B.AC AD = C.ACB ADB ∠=∠ D.CAB DAB ∠=∠ 4.如图,在△ABC 与△DEF 中,已有条件AB=DE ,还需添加两 个条件才能使△ABC ≌△DEF ,不能添加的一组条件是( ) (A)∠B=∠E,BC=EF (B )BC=EF ,AC=DF (C)∠A=∠D ,∠B=∠E (D )∠A=∠D ,BC=EF5.如图,△ABC 中,∠C = 90°,AC = BC ,AD 是∠BAC 的平分线, DE⊥AB 于E ,若AC = 10cm ,则△DBE 的周长等于( ) A .10cm B .8cm C .6cm D .9cm6. 如图所示,表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有() A.1处B.2处C.3处D.4处EDCBA④①② ③CADP B图(四)7.某同学把一块三角形的玻璃打碎了3块,现在要到玻璃店去配 一块完全一样的玻璃,那么最省事的方法是( )A .带①去B .带②去C .带③去D .带①②③去8.如图,在Rt ABC △中,ο90=∠B ,ED 是AC 的垂直平分线,交AC 于 点D ,交BC 于点E .已知ο10=∠BAE ,则C ∠的度数为( ) A .ο30 B .ο40 C .ο50 D .ο60 9.如图,ACB A C B '''△≌△,BCB ∠'=30°,则ACA '∠的度数为( ) A .20° B .30°C .35°D .40°10.如图,AC =AD ,BC =BD ,则有( ) A .AB 垂直平分CD B .CD 垂直平分AB C .AB 与CD 互相垂直平分D .CD 平分∠ACB12.如图, ∠C=90°,AD 平分∠BAC 交BC 于D,若BC=5cm,BD=3cm,则点D 到AB 的距离为( ) A. 5cmB. 3cmC. 2cmD. 不能确定13.如图,OP 平分AOB ∠,PA OA ⊥,PB OB⊥,垂足分别为A ,B .下列结论中不一定成立的是( )A .PA PB = B .PO 平分APB ∠C .OA OB =D .AB 垂直平分OP14.如图,已知AB AD =,那么添加下列一个条件后,仍无法判定( )A .CB CD = B .BAC DAC =∠∠ C .BCA DCA =∠∠D .90B D ==︒∠∠ADCEBABCDABCDAB CDC ABB 'A 'OBAP15.观察下列图形,则第n 个图形中三角形的个数是( )A .22n +B .44n +C .44n -D .4n二、填空题1.如图,已知AD AB =,DAC BAE ∠=∠,要使 ABC △≌ADE △,可补充的条件是 (写出一个即可).2.如图,在△ABC 中,∠C=90°,AC=BC,AD 平分∠BAC 交BC 于D,DE ⊥AB 于E,且AB=5cm,则△DEB 的周长为 ________3.如图,BAC ABD ∠=∠,请你添加一个条件: ,使OC OD =(只添一个即可).4.如图,在ΔABC 中,∠C=90°∠ABC 的平分线BD 交AC 于点D,若BD=10厘米,BC=8厘米,DC=6厘米,则点D 到直线AB 的距离是__________厘米。
(完整版)北师大七年级下全等三角形测试题(50分钟)
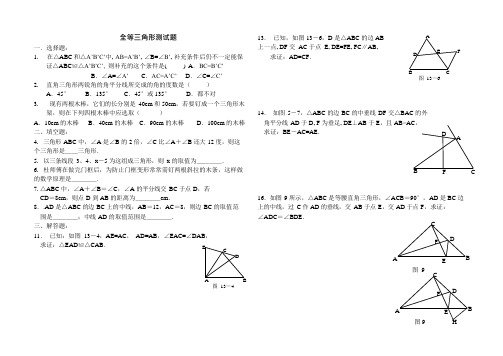
DACFD D EC FDE 图 9H一.选择题: 全等三角形测试题13. 已知,如图 13-6,D 是△ABC 的边 ABA上一点, DF 交 AC 于点 E, DE=FE, FC ∥AB,F 1.在△ABC 和△A’B’C’中, AB=A’B’, ∠B=∠B’, 补充条件后仍不一定能保 证△ABC ≌△A’B’C’, 则补充的这个条件是( ) A .BC=B’C’ B .∠A=∠A’ C .AC=A’C’ D .∠C=∠C’2. 直角三角形两锐角的角平分线所交成的角的度数是( )A .45°B .135°C .45°或 135°D .都不对 3.现有两根木棒,它们的长分别是 40cm 和 50cm ,若要钉成一个三角形木 求证:AD=CF .BC图 13-6 架,则在下列四根木棒中应选取( ) A .10cm 的木棒 B .40cm 的木棒 C .90cm 的木棒 D .100cm 的木棒二、填空题: 4. 三角形 ABC 中,∠A 是∠B 的 2 倍,∠C 比∠A +∠B 还大 12 度,则这个三角形是__三角形.5. 以三条线段 3、4、x -5 为这组成三角形,则 x 的取值为____.6. 杜师傅在做完门框后,为防止门框变形常常需钉两根斜拉的木条,这样做的数学原理是____.7. △ABC 中,∠A +∠B =∠C ,∠A 的平分线交 BC 于点 D ,若CD =8cm ,则点 D 到 AB 的距离为____cm .8..AD 是△ABC 的边 BC 上的中线,AB =12,AC =8,则边 BC 的取值范围是____;中线 AD 的取值范围是____. 三、解答题:11. 已知:如图 13-4,AE=AC , AD=AB ,∠EAC=∠DAB , 14. 如图 5-7,△ABC 的边 BC 的中垂线 DF 交△BAC 的外角平分线 AD 于 D, F 为垂足, DE ⊥AB 于 E ,且 AB>AC , 求证:BE -AC=AE .BF C16.如图 9 所示,△ABC 是等腰直角三角形,∠ACB =90°,AD 是 BC 边上的中线,过 C 作 AD 的垂线,交 AB 于点 E ,交 AD 于点 F ,求证: ∠ADC =∠BDE .求证:△EAD ≌△CAB . EB图 13-4AEB图 9AB CD⎪⎩六、参考答案提示1. C .(提示:边边角不能判定两个三角形全等.)2. C .(提示:由三角形内角和为 180°可求,要注意有两个不同的角.)3. B .(提示:利用三角形三边的关系,第三根木棒 x 的取值范围是:10cm <x <90cm .= ∠ECB , 又 ∵∠ABE=∠ACE ,∴∠ABC=∠ACB , ∴AB=AC. 在△ AEB 和△AEC 中, AE=AE. BE=CE, AB=AC, ∴△AEB ≌△AEC,∠BAE=∠CAE. C16.如图 11 所示,过 B 点作 BH ⊥BC 交 CE 的延长线于 H 点.∵∠CAD +∠ACF =90°,∠BCH +∠ACF =90°,FD∴∠CAD =∠BCH .在△ACD 与△CBH 中,AEB4.C . (提示:A 不能构成三角形,B 满足边边角,不能判定三角形全等,D 项 可 画 出 无 数 个 三 角 形 .) 5.B .(提示:∠CDE =∠B +∠-∠=∠-∠B ,故得到 2(∠B -∠)+∠=0.又∵∠-∠B =∠-∠C =∠CDE ,所以可得到∠CDE = ,故当∠为定值时,∠CDE 为定值.)∵∠CAD =∠BCH ,AC =CB ,∠ACD =∠CBH =90°,∴△ACD ≌△CBH .∴∠ADC =∠H ① CD =BH , ∵CD =BD ,∴BD =BH .∵△ABC 是等腰直角三角形,∠CBA =∠HBE =45°⎧BD = BH ,图 11H 26.钝角.(提示:由三角形的内角和可求出∠A 、∠B 和∠C 的度数) 7.6<x<12.(提示:由三边关系可知:4-3<x -5<4+3. 8.三角形的稳定性.9.8.(提示:点 D 到 AB 的距离与 CD 的长相等.) 10.4<BC <20;2<AD <10.(提示:要注意三角形一边上的中线的取值范围是大于另两边之差的一半,小于两边之和的一半.) 11. 提示:先证∠EAD=∠CAB ,再由 SAS 即可证明.12. ①△ABC ≌△DBE ,BC=BE ,∠ABC=∠DBE=90°,AB=BD ,符合SAS ;②△ACB 与△ABD 不全等,因为它们的形状不相同,△ACB 只是直角三角形,△ABD 是等腰直角三角形;③△CBE 与△BED 不全等, 理由同②;④△ACE 与△ADE 不全等,它们只有一边一角对应相等. 13. 提示:由 ASA 或 AAS ,证明△ADE ≌△CFE .14. 过 D 作 DN ⊥AC, 垂足为 N, 连结 DB 、DC 则 DN=DE ,DB=DC ,又 ∵DE ⊥AB, DN ⊥AC, ∴Rt △DBE ≌Rt △DCN , ∴BE=CN .又 ∵AD=AD ,DE=DN ,∴Rt △DEA ≌Rt △DNA ,∴AN=AE ,∴BE=AC+AN=AC+AE ,∴BE -AC=AE . 15. 上面证明过程不正确; 错在第一步. 正确过程如下:在△BEC 中, ∵BE=CE , ∴∠EBC=∴在△BED 和 BEH 中, ⎨∠EBD =∠EBH, ,∴△BED ≌△BEH .⎪BE =BE, ∴∠BDE =∠H , ② 由①②得,∠ADC =∠BDE .。
七年级数学全等及全等三角形(北师版)(基础)(含答案)

全等及全等三角形(北师版)(基础)一、单选题(共10道,每道10分)1.下列说法中正确的是( )A.面积相等的两个图形是全等图形B.周长相等的两个图形是全等图形C.所有正方形都是全等图形D.能够完全重合的两个图形是全等图形答案:D解题思路:全等图形的定义:能够完全重合的两个图形称为全等图形.所以D选项正确.选项A:面积相等的两个图形不一定能完全重合,故A选项错误;选项B:周长相等的两个图形不一定能完全重合,故B选项错误;选项C:所有正方形都是全等图形说法错误,边长不相等时两个正方形不能完全重合,故C 选项错误;故选D.试题难度:三颗星知识点:全等图形2.下列说法不正确的是( )A.全等三角形的对应边相等,对应角相等B.图形全等,只与形状、大小有关,而与它们的位置无关C.全等三角形的面积相等D.形状相同的两个三角形全等答案:D解题思路:全等三角形的定义:能够完全重合的两个三角形叫做全等三角形.全等三角形的性质:全等三角形的对应边相等,对应角相等.所以选项A、C正确.选项B:图形全等,只与形状、大小有关,而与它们的位置无关,正确.选项D:形状相同的两个三角形不一定是全等三角形,比如一张照片,放大以后还是原来的形状,但是不全等,所以选项D错误.故选D.试题难度:三颗星知识点:全等三角形3.如图,已知△ABC≌△CDE,其中AB=CD,那么下列结论中,不正确的是( )A.AC=CEB.∠BAC=∠ECDC.∠ACB=∠ECDD.∠B=∠D答案:C解题思路:全等三角形的性质:全等三角形的对应边相等,对应角相等.因为△ABC≌△CDE,对应边相等,所以AC=CE;对应角相等,所以∠BAC=∠ECD,∠B=∠D,故选项A、B、D正确.选项C:∠ACB和∠ECD不是对应角,不能证明两个角相等.故选项C错误.故选C.试题难度:三颗星知识点:全等三角形的性质4.如图,△ABC≌△DEF,则此图中相等的线段有( )A.1对B.2对C.3对D.4对答案:D解题思路:全等三角形的性质:全等三角形的对应边相等,对应角相等.因为△ABC≌△DEF,全等三角形对应边相等,所以AB=DE,AC=DF,BC=EF.因为BC=EF,所以BC-EC=EF-EC,即BE=CF.所以图中相等的线段有4对.故选D.试题难度:三颗星知识点:全等三角形的性质5.如图,已知△ABE≌△ACD,下列结论不一定成立的是( )A.AB=ACB.∠BAD=∠CAEC.∠ADB=∠AECD.AD=DE答案:D解题思路:本题考查全等三角形的性质:全等三角形对应边相等,对应角相等.A选项:由△ABE≌△ACD可得AB=AC,依据是全等三角形对应边相等,所以A选项正确;B选项:由△ABE≌△ACD可得∠BAE=∠CAD,依据是全等三角形对应角相等.等式两边同时减去∠DAE,可得∠BAD=∠CAE,所以B选项正确;C选项:由△ABE≌△ACD可得∠BEA=∠CDA,依据是全等三角形对应角相等.然后利用补角的定义可得∠AEC=∠ADB,所以C选项正确;D选项:AD的对应边是AE,和DE不是对应边,因此AD=DE不一定成立,所以D选项错误.故选D.试题难度:三颗星知识点:全等三角形的性质6.如图,△ADB≌△EDB,△BDE≌△CDE,B,E,C在一条直线上.下列结论:①BD是∠ABE 的平分线;②点E是BC的中点;③DE⊥BC.其中正确的有( )A.0个B.1个C.2个D.3个答案:D解题思路:本题考查全等三角形的性质:全等三角形对应边相等,对应角相等.因为△ADB≌△EDB,全等三角形对应角相等,可得∠ABD=∠EBD,即BD是∠ABE的平分线;故①正确;因为△BDE≌△CDE,全等三角形对应边相等,可得BE=CE,所以点E是BC的中点;对应角相等,∠BED=∠CED=90°,所以DE⊥BC;故②③正确;故选D.试题难度:三颗星知识点:全等三角形的性质7.如图,若△ABC≌△DEF,∠A=45°,∠F=35°,则∠E等于( )A.35°B.45°C.60°D.100°答案:D解题思路:全等三角形的性质:全等三角形对应边相等,对应角相等.因为△ABC≌△DEF,所以∠D=∠A=45°.在△DEF中,依据三角形内角和等于180°,∠D+∠E+∠F=180°,可得∠E=180°-45°-35°=100°.故选D.试题难度:三颗星知识点:全等三角形的性质8.已知△ABC的三边长分别为3,4,5,△DEF的三边长分别为3,3x-2,2x+1,若这两个三角形全等,则x的值为( )A.2B.C. D.答案:A解题思路:本题考查全等三角形的性质:全等三角形对应边相等,对应角相等.根据全等三角形对应边相等,可知△DEF的三边长也分别为3,4,5.而题中条件给出△DEF的三边长分别为3,3x-2,2x+1,3和3对应,但4是和还是和对应,无法确定,所以要分两种情况进行讨论:①,解得;②,x不存在.综上,.故选A.试题难度:三颗星知识点:全等三角形的性质9.如图,若△ABC≌△DEF,BE=22,BF=5,则FC的长度是( )A.10B.12C.8D.16答案:B解题思路:要求线段FC的长度,首先由△ABC≌△DEF可得BC=EF.则BC-FC=EF-FC,即BF=CE.由已知条件BE=22,BF=5可得CE=5,FC=BE-BF-CE=22-5-5=12.故选B.试题难度:三颗星知识点:全等三角形的性质10.如图,N,C,A三点在同一直线上,△ABC中,∠A:∠ABC:∠ACB=3:5:10.若△MNC≌△ABC,则∠BCM的度数为( )A.20°B.25°C.28°D.30°答案:A解题思路:要求∠BCM的度数.首先由三角形内角和180°,∠A:∠ABC:∠ACB=3:5:10得∠A=30°,∠ABC=50°,∠ACB=100°.由△MNC≌△ABC可得∠MCN=∠ACB=100°.观察图形,可以利用平角是180°,求出∠BCN=80°.∴∠BCM=∠MCN-∠BCN=100°-80°=20°故选A.试题难度:三颗星知识点:全等三角形的性质。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
全等三角形练习题
一、选择题
1.如图,给出下列四组条件:
①AB DE BC EF AC DF ===,,;②AB DE B E BC EF =∠=∠=,,; ③B E BC EF C F ∠=∠=∠=∠,,;④AB DE AC DF B E ==∠=∠,,.
其中,能使ABC DEF △≌△的条件共有( ) A .1组
B .2组
C .3组
D .4组
2.如图,D E ,分别为ABC △的AC ,BC 边的中点,将此三 角形沿DE 折叠,使点C 落在AB 边上的点P 处.若48CDE ∠=°, 则APD ∠等于( )
A .42°
B .48°
C .52°
D .58° 3.如图(四),点P 是AB 上任意一点,ABC ABD ∠=∠,还应补 充一个条件,才能推出APC APD △≌△.从下列条件中补充 一个条件,不一定能....
推出APC APD △≌△的是( ) A .BC BD = B.AC AD = C.ACB ADB ∠=∠ D.CAB DAB ∠=∠ 4.如图,在△ABC 与△DEF 中,已有条件AB=DE ,还需添加两 个条件才能使△ABC ≌△DEF ,不能添加的一组条件是( ) (A)∠B=∠E,BC=EF (B )BC=EF ,AC=DF (C)∠A=∠D ,∠B=∠E (D )∠A=∠D ,BC=EF
5.如图,△ABC 中,∠C = 90°,AC = BC ,AD 是∠BAC 的平分线, DE⊥AB 于E ,若AC = 10cm ,则△DBE 的周长等于( ) A .10cm B .8cm C .6cm D .9cm
6. 如图所示,表示三条相互交叉的公路,现要建一个货物中
转站,要求它到三条公路的距离相等,则可供选择的地址有( ) A.1处
B.2处
C.3处
D.4处
E
D
C
B
A
④
①② ③
C
A
D
P B
图(四)
7.某同学把一块三角形的玻璃打碎了3块,现在要到玻璃店去配 一块完全一样的玻璃,那么最省事的方法是( )
A .带①去
B .带②去
C .带③去
D .带①②③去
8.如图,在Rt ABC △中,
90=∠B ,ED 是AC 的垂直平分线,交AC 于 点D ,交BC 于点E .已知
10=∠BAE ,则C ∠的度数为( ) A .
30 B .
40 C .
50 D .
60 9.如图,ACB A C B '''△≌△,BCB ∠'=30°,则ACA '∠的度数为( ) A .20° B .30°
C .35°
D .40°
10.如图,AC =AD ,BC =BD ,则有( ) A .AB 垂直平分CD B .CD 垂直平分AB C .AB 与CD 互相垂直平分
D .CD 平分∠ACB
12.如图, ∠C=90°,AD 平分∠BAC 交BC 于D,若BC=5cm,BD=3cm,则点D 到AB 的距离为( ) A. 5cm
B. 3cm
C. 2cm
D. 不能确定
13.如图,OP 平分AOB ∠,PA OA ⊥,PB OB
⊥,垂足分别为A ,B .下列结论中不一定成立的是( )
A .PA P
B = B .PO 平分APB ∠
C .OA OB =
D .AB 垂直平分OP
14.如图,已知AB AD =,那么添加下列一个条件后,仍无法判定( )
A .C
B CD = B .BA
C DAC =∠∠ C .BCA DCA =∠∠
D .90B D ==︒∠∠
A
D
C
E
B
A
B
C
D
A
B
C
D
A
B C
D
C A
B
B '
A '
O
B
A
P
15.观察下列图形,则第n 个图形中三角形的个数是( )
A .22n +
B .44n +
C .44n -
D .4n
二、填空题
1.如图,已知AD AB =,DAC BAE ∠=∠,要使 ABC △≌ADE △,可补充的条件是 (写出一个即可).
2.如图,在△ABC 中,∠C=90°,AC=BC,AD 平分∠BAC 交BC 于D,DE ⊥AB 于E,且AB=5cm,则△DEB 的周长为 ________
3.如图,BAC ABD ∠=∠,请你添加一个条件: ,使OC OD =(只添一个即可).
4.如图,在ΔABC 中,∠C=90°∠ABC 的平分线BD 交AC 于点D,若BD=10厘米,BC=8厘米,DC=6厘米,则点D 到直线AB 的距离是__________厘米。
5.观察图中每一个大三角形中白色三角形的排列规律,则第5个大三角形中白色三角形有 个 .
……
第1个
第2个
第3个
第1个第2个
第3个
A
C
E
B
D
D
O C
B A
A
B
C
D E
6.已知:如图,△OAD ≌△OBC ,且∠O =70°,∠C =25°,则∠AEB =________度.
7如图,C 为线段AE 上一动点(不与点A ,E 重合),在AE 同侧分别作正三角形ABC 和正三角形CDE 、AD 与BE 交于点O ,AD 与BC 交于点P ,BE 与CD 交于点Q ,连结PQ.以下五个结论:①AD=BE ;②PQ ∥AE ;③AP=BQ ;④DE=DP ;⑤∠AOB=60°.恒成立的结论有_______________________(把你认为正确的序号都填上)。
8.如图所示,AB = AD ,∠1 = ∠2,添加一个适当的条件,使△ABC ≌ △ADE,则需要添加的条件是________. 三、解答题
1.如图,已知AB=AC ,AD=AE ,求证:BD=CE.
2.如图,在ABC △中,40AB AC BAC =∠=,°,分别以AB AC ,为边作两个等腰直角三角形ABD 和ACE ,使90BAD CAE ∠=∠=°. (1)求DBC ∠的度数;(2)求证:BD CE =.
O A
B
C D
E
Q
P
O B
E D
C A
A
B D E C
4.如图,D 是等边△ABC 的边AB 上的一动点,以CD 为一边向上作等边△EDC ,连接AE ,找出图中的一组全等三角形,并说明理由.
5.如图,在△ABC 和△DCB 中,AB = DC ,AC = DB ,AC 与DB 交于点M .
(1)求证:△ABC ≌△DCB ;(2)过点C 作CN ∥BD ,过点B 作BN ∥AC ,CN 与BN 交于点N ,试判断线段BN 与CN 的数量关系,并证明你的结论.
9.如图,△ABC 中,∠BAC =90度,AB =AC ,BD 是∠ABC 的平分线,BD 的延长线
垂直于过C 点的直线于E ,直线CE 交BA 的延长线于F . 求证:BD =2CE .
B C
A D
M
N
E
D
C
B
A
F
E D C
B
A
10.如图,,AB AC AD BC D AD AE AB DAE DE F =⊥=∠于点,,平分交于点,请你写出图中三对..全等三角形,并选取其中一对加以证明.
11.(7分)已知:如图,DC ∥AB ,且DC =AE ,E 为AB 的中点, (1)求证:△AED ≌△EBC .
(2)观看图前,在不添辅助线的情况下,除△EBC 外,请再写出两个与△AED 的面积相等的三角形.(直接写出结果,不要求证明):
12.如图①,E 、F 分别为线段AC 上的两个动点,且DE ⊥AC 于E ,BF ⊥AC 于F ,若AB =CD ,AF =CE ,BD 交AC 于点M . (1)求证:MB =MD ,ME =MF
(2)当E 、F 两点移动到如图②的位置时,其余条件不变,上述结论能否成立?若成立请给予证明;若不成立请说明理由.
O
E
D
C
B
A
B
D C
F A
郜
E。
