08级线代期末试题A

合集下载

2008年线性代数考试A卷

2
第 2 页共 7页
学院
姓名
学号
任课老师
选课号
………密………封………线………以………内………答………题………无………效……
0 0⎞ ⎛ 1 ⎟ ⎜ P = ⎜ 2 −1 0⎟ ， ⎜ − 4 1 1⎟ ⎠ ⎝
−1
所以有
0 0⎞ ⎛ 1 0 0 ⎞⎛ 1 0 0 ⎞⎛ 1 ⎟ ⎟⎜ ⎟⎜ ⎜ A = PBP = ⎜ 2 − 1 0 ⎟⎜ 0 0 0 ⎟⎜ 2 − 1 0 ⎟ ⎜ 2 1 1 ⎟⎜ 0 0 − 1⎟⎜ − 4 1 1 ⎟ ⎠ ⎠⎝ ⎠⎝ ⎝
⎛ λ1 0 ⎜ ⎜ 0 λ2 T −1 P AP = P AP = ⎜ " " ⎜ ⎜0 0 ⎝
0⎞ ⎟ " 0⎟ ， " "⎟ ⎟ " λn ⎟ ⎠ "
3．设 n 元非齐次线性方程组是 Ax = b ，它对应的齐次线性方程组是 Ax = 0 ，则下面结论中正确的是( ② ). ① 若 Ax = 0 有惟一解，则 Ax = b 也有惟一解； ② 若 Ax = b 有无穷多个解，则 Ax = 0 也有无穷多个解； ③ 若 Ax = 0 有无穷多个解，则 Ax = b 也有无穷多个解； ④ 若 Ax = 0 有惟一解，则 Ax = b 无解. 分析：A 未必是方阵。 4．设 α 1 , α 2 , β 线性无关， α 2 , α 3 , β 线性相关，则下面结论正确的是( ④ )。 ① ③ k1α 1 + k 2α 2 + k 3α 3 = 0 仅有零解； k1α 2 + k 2α 3 = β 必有解； ② ④ k1α 1 + k 2α 2 + k 3α 3 = 0 必有非零解； k1α 1 + k 2α 2 + k 3 β = α 3 必有解。

武汉理工2008年末-线代-A

武汉理工大学教务处试题标准答案及评分标准用纸| 课程名称——线性代数—— （ A 卷） |一、填空题：（每小题3分，共15分）1．6；2．⎪⎪⎪⎪⎪⎭⎫⎝⎛--233421（未写出的元素为0）；3．-128；4．2；5．.3535<<-t二、选择题： 1.B ； 2.C ； 3.B ； 4.C ； 5.A （每小题3分，共15分）三、计算题： 1．()20092008000020082008000200920091200800020092008000020092008200820082007⨯⨯-+⨯=D （5分）=2007200720092008+ (10分)2．首先，11)(6---=E A B （3分）其次，⎪⎪⎪⎭⎫⎝⎛=-7431A ，（5分）⎪⎪⎪⎭⎫ ⎝⎛=--6321E A ，（7分）()⎪⎪⎪⎭⎫ ⎝⎛=---6/13/12/111EA，（9分）最后， .123⎪⎪⎪⎭⎫ ⎝⎛=B (10分) 注：矩阵中未写出的元素为0。

3．方程组的系数行列式()()⇒≠+-=---=012111111λλλλλA （3分）（1）21≠-≠λλand，时，方程组有唯一解；（5分）（2）当2=λ时，方程组的增广矩阵)()(100021104211~B R A R B <⇒⎪⎪⎪⎭⎫ ⎝⎛--此时方程组无解；（7分）（3）当1-=λ时，方程组的增广矩阵⇒<=⇒⎪⎪⎪⎭⎫ ⎝⎛3)()(000000001111~B R A R B此时方程组有无穷多个解，其通解为.),(0011010112121R k k k k X ∈⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎪⎭⎫ ⎝⎛-= （10分）4．解：观察知，矩阵A 的第一列加上第二列的（-1）倍，然后再交换第二列和第三列即得B ，（4分）根据初等方阵的定义，两次初等列变换所对应的初等方阵分别为：⎪⎪⎪⎭⎫⎝⎛⎪⎪⎪⎭⎫ ⎝⎛-1111111，；（8分）再根据初等行变换的实质得，⎪⎪⎪⎭⎫⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛-=11111111111X . （10分）注：矩阵中未写出的元素为0。

2008线性代数A参考答案

2007~2008学年第二学期《线性代数》A 卷参考答案及评分标准一、单项选择（每小题2分，共20分）请将正确选项前的字母填入下表中1、2-。

2、159206915-⎛⎫⎪-⎝⎭。

3、4。

4、213/21/2-⎛⎫⎪-⎝⎭。

5、 3 。

6、3。

7、 0 。

8、2。

9、1/λ。

10、222123122344x x x x x x x ++++ 三、计算题（1、2每小题6分，其余每小题6分，共40分）1、解：212223242322A A A A +++=1222232********* ……3分122201220011001---=1=- ……6分2、解：由AX A X =+有()A E X A -=()1002001002001101200101201111120112A E A ⎛⎫⎛⎫⎪ ⎪-=→- ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭ ……4分 200120012X ⎛⎫⎪∴=- ⎪ ⎪-⎝⎭……6分 3、解：由225A A E O --=有()()32A E A E E -+= ……3分320A E A E -+=≠有30A E -≠ 所以3A E -可逆 ……6分且11(3)()2A E A E --=+ ……7分4、解：()1234310111512112370122318100001397000TTTTαααα⎛⎫ ⎪--⎛⎫⎪⎪- ⎪ ⎪-=→ ⎪ ⎪- ⎪ ⎪- ⎪⎝⎭ ⎪⎝⎭……3分 ∴1234,,,αααα线性相关，1234(,,,)2R αααα=，12,αα是它的一个极大无关组，……4分且31241237, 222αααααα=-=+. ……7分5、解：矩阵A 的特征方程为0)1)(2(163530642=--=-+--=-λλλλλλA E得特征值 12321==-=λλλ ……3分当21-=λ时有⎩⎨⎧=-=+⎪⎩⎪⎨⎧=-+=+=--00,036303306632313212121x x x x x x x x x x x 即它的基础解系是⎪⎪⎪⎭⎫ ⎝⎛-111，所以对应于21-=λ的全部特征向量是)0(111≠⎪⎪⎪⎭⎫⎝⎛-c c ……5分当132==λλ时有 02,6306306321212121=+⎪⎩⎪⎨⎧=+=+=--x x x x x x x x 即它的基础解系是向量⎪⎪⎪⎭⎫⎝⎛⎪⎪⎪⎭⎫ ⎝⎛-100012及，所以对应于132==λλ的全部特征向量是不全为零）2121,(100012c c c c ⎪⎪⎪⎭⎫⎝⎛+⎪⎪⎪⎭⎫ ⎝⎛- ……7分6、解： 22020021201002000410011201001201001A E -⎛⎫⎛⎫⎪ ⎪---⎪⎪⎪⎪-⎛⎫=→⎪ ⎪⎪-⎝⎭⎪ ⎪- ⎪ ⎪⎪ ⎪⎝⎭⎝⎭……3分112012001P -⎛⎫⎪∴=- ⎪ ⎪⎝⎭……6分 222123123(,,)24f x x x y y y=-+ ……7分四、证明题（每题5分，共10分）1、证明：由 AB O = 有 12(,,,)s A X X X O = 即12(,,,)s AX AX AX O = 得i AX O = ()1,2,i s =即i X 为A X O =的s 个解 ……2分显然12()(,,,)()s R B R X X X n R A =≤-即()()R A R B n +≤ ……3分 2、证明：()123,,3R ααα= ，()1234,,,3R αααα= 123,,ααα 线性无关 1234,,,αααα线性相关则有 4112233m m m αααα=++ 成立 ……2分设 112233454()0k k k k ααααα+++-=有 112233454112233()0k k k k k m m m ααααααα+++-++= 1411242234334()()()0k k m k k m k k m kαααα-+-+-+=……3分 ()1235,,,4R αααα=1235,,,αααα 线性无关则有141242343400k k m k k m k k m k -=⎧⎪-=⎪⎨-=⎪⎪=⎩ 解之有 12340k k k k ==== ……4分故 12354,,,ααααα-线性无关即12354(,,,)4R ααααα-=……5分。

2008-2009学年线性代数试卷A及答案

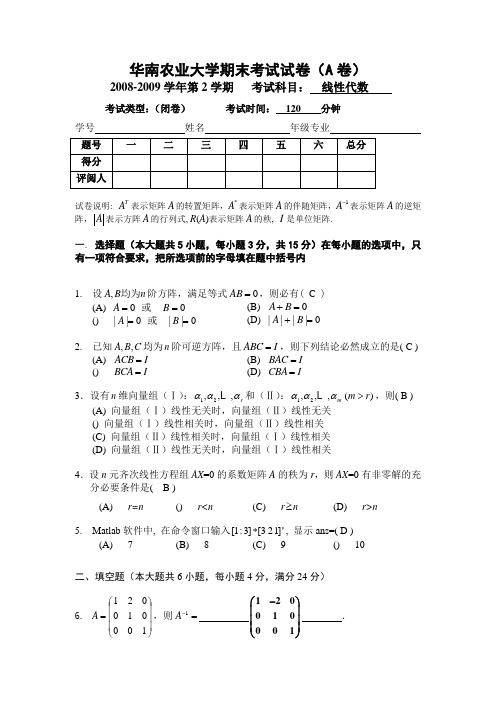
华南农业大学期末考试试卷（A 卷）2008-2009学年第2学期考试科目：线性代数考试类型：（闭卷）考试时间： 120 分钟学号姓名年级专业题号一二三四五六总分得分评阅人试卷说明: T A 表示矩阵A 的转置矩阵，*A 表示矩阵A 的伴随矩阵，1A -表示矩阵A 的逆矩阵，A 表示方阵A 的行列式, R (A )表示矩阵A 的秩, I 是单位矩阵.一. 选择题（本大题共5小题，每小题3分，共15分）在每小题的选项中，只有一项符合要求，把所选项前的字母填在题中括号内1. 设n B A 均为,阶方阵，满足等式0=AB ，则必有( C )(A) 0=A 或 0=B(B) 0=+B A () 0||=A 或 0||=B(D) 0||||=+B A2. 已知,,A B C 均为n 阶可逆方阵，且ABC I =，则下列结论必然成立的是( C )(A) ACB I = (B) BAC I = () BCA I = (D) CBA I =3．设有n 维向量组（Ⅰ）：12,,,r ααα 和（Ⅱ）：12,,,()m m r ααα> ，则( B )(A) 向量组（Ⅰ）线性无关时，向量组（Ⅱ）线性无关() 向量组（Ⅰ）线性相关时，向量组（Ⅱ）线性相关 (C) 向量组（Ⅱ）线性相关时，向量组（Ⅰ）线性相关 (D) 向量组（Ⅱ）线性无关时，向量组（Ⅰ）线性相关4．设n 元齐次线性方程组AX =0的系数矩阵A 的秩为r ，则AX =0有非零解的充分必要条件是( B )5. Matlab 软件中, 在命令窗口输入[1:3][321]'*, 显示ans=( D )二、填空题（本大题共6小题，每小题4分，满分24分）6. ⎪⎪⎪⎭⎫ ⎝⎛=100010021A ，则=-1A120010001-⎛⎫⎪ ⎪ ⎪⎝⎭． (A) r=n() r<n(C) r ≥n(D) r>n(A) 7 (B) 8 (C) 9 () 107. 设t ηηη,,,21 及t t ηληληλ+++ 2211都是非齐次线性方程组b A =X 的解向量，则=+++t λλλ 21______1__________.8. 矩阵20002023A a ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦与矩阵10002000B b ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦相似, 则a b += . 9. 设123,1,1),0,2,3),1,0,1),k ααα===（（（则当k = 时，α1,α2,α3 线性相关.10.设A 为三阶方阵，其特征值2,1,3,- 则*A = ．11.已知二次型222123112132233(,,)2245f x x x x tx x x x x x x x =+-+++正定, 则t 的取值范围为．三、计算题12.(7分) 已知100110,021A ⎛⎫ ⎪=- ⎪ ⎪⎝⎭131011,002B ⎛⎫⎪=- ⎪ ⎪⎝⎭求:2T A AB +13.（8分）计算下列行列式3214214314324321四、解方程组14. (10分)求方程组123412341234311232x x x xx x x xx x x x⎧⎪--+=⎪-+-=⎨⎪⎪--+=-⎩的通解.五、解答题15.（10分）求下列向量组的秩，并求一个最大无关组：a1=(1, 2,-1, 4)T,a2=(9, 100, 10, 4)T, a3= (-2,-4, 2,-8)T．16. (8分) 已知1121 342 012A--⎛⎫⎪= ⎪⎪-⎝⎭，求A的伴随矩阵*A．17.(12分) 设212122221A ⎛⎫ ⎪= ⎪ ⎪⎝⎭，求一个正交阵P ，使1P AP -=Λ为对角阵．六、证明题18.(6分) 设向量组322211,a a b a a b +=+= 433,a a b += 144,a a b +=, 证明向量组4321,,,b b b b 线性相关.2008—2009第二学期《线性代数》（A ）参考答案和评分标准一. 选择题（本大题共5小题，每小题3分，共15分）1. C2. C3. B4. B5. D二、填空题（本大题共6小题，每小题4分，满分24分）6. 120010001-⎛⎫⎪ ⎪⎪⎝⎭ 7. 18. 8 9. -1/2 10. 36 11. 405t -<<三、计算题12.T T A AB A E B 2(2)+=+=1001001001102010310021001112⎡⎤⎛⎫⎛⎫⎛⎫⎢⎥⎪ ⎪ ⎪-+⎢⎥ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎢⎥-⎝⎭⎝⎭⎝⎭⎣⎦3分100300110330021114⎛⎫⎛⎫ ⎪⎪=- ⎪⎪ ⎪⎪-⎝⎭⎝⎭ 5分 300030754⎛⎫ ⎪= ⎪ ⎪⎝⎭7分 13.将行列式第2、3、4列加到第1列上，得3214214314324321=32110214101431043210=101110222031104321------ 4分=10400440311--- 6分=160 8分14.11110111101111011131002410024111231/200121/200000⎛⎫⎛⎫⎛⎫------ ⎪ ⎪ ⎪--→-→- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪-----⎝⎭⎝⎭⎝⎭ 4分 x x x x x x 1234340241--+=⎧⎨-=⎩，x x x x x x x x 1324132431-=-⎧⎨+=++⎩， 5分取x x 2400⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭，得*120120η⎛⎫ ⎪ ⎪⎪= ⎪ ⎪ ⎪ ⎪⎝⎭， 6分取x x 2410,01⎛⎫⎛⎫⎛⎫= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，x x 1311,02⎛⎫⎛⎫⎛⎫= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭， 8分得齐次方程组基础解系为121110,0201ξξ⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪== ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭, 9分通解为x x k kx x 12123411120101022010⎛⎫⎪⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪=++ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎪⎝⎭10分 15. 192192192210040820010110201900004480320000A ---⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦6分rank(A)=2 7分所以向量组的秩为2． 8分 a 1=(1, 2, -1, 4)T , a 2=(9, 100, 10, 4)T 不成比例，所以 a 1，a 2为最大无关组. 10分16. 因为1*1,||A A A -=2分*1111||||A A AA A ---==4分 1||1A -=- 6分*1||1*A A -=-=121342012--⎛⎫ ⎪--- ⎪ ⎪-⎝⎭8分17.123(1)(1)(5),1,1,5A E λλλλλλλ-=-+--=-==， 3分对应于11λ=-，由 ()0A E x += 得111122ξ-⎛⎫ ⎪=- ⎪ ⎪⎝⎭，单位化，得111162p -⎛⎫ ⎪=- ⎪ ⎪⎝⎭； 6分对应于21λ=，由 ()0A E x -= 得2110ξ-⎛⎫ ⎪= ⎪ ⎪⎝⎭，单位化，得211120p -⎛⎫⎪= ⎪ ⎪⎝⎭ 8分对应于35λ=，由 (5)0A E x -= 得3111ξ⎛⎫ ⎪= ⎪ ⎪⎝⎭，单位化，得311131p ⎛⎫⎪= ⎪ ⎪⎝⎭． 10分 11162311162321063P ⎛⎫-- ⎪ ⎪ ⎪=- ⎪ ⎪ ⎪ ⎪⎝⎭，有1100010005TP AP P AP --⎛⎫⎪==Λ= ⎪ ⎪⎝⎭． 12分18. 设有4321,,,x x x x 使得044332211=+++b x b x b x b x即0)()()()(144433322211=+++++++a a x a a x a a x a a x 3分整理得 01100011000111001)(43214321=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎪⎭⎫ ⎝⎛x x x x a a a a 4分而011000110001110014321=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎪⎭⎫⎝⎛x x x x 有非零解，所以结论成立 6分。

线性代数2008A答案

上海财经大学成人高等教育线性代数试题参考答案（2008A 卷）姓名学号专业班级一、单选题(每小题2分，共计10分)1. 设,A B 均为方阵，且0AB =, 则以下结论中正确的是 ( 4 ) .(1) 0AB = (2) 0,0A B == (3) 0A =或0B = (4) 0A =或0B =2. 以下矩阵中是对称矩阵的是 ( 2 ).(1) 123212025⎛⎫ ⎪-- ⎪ ⎪-⎝⎭ (2)123204341⎛⎫⎪ ⎪ ⎪-⎝⎭ (3) 123211301⎛⎫⎪ ⎪ ⎪⎝⎭ (4) 111011001⎛⎫⎪ ⎪ ⎪⎝⎭3. 以下矩阵中是初等矩阵的是 ( 2 ).(1) 100010000⎛⎫ ⎪- ⎪ ⎪⎝⎭ (2)100010001⎛⎫⎪ ⎪ ⎪-⎝⎭ (3) 101010001⎛⎫⎪ ⎪ ⎪-⎝⎭ (4) 101011001⎛⎫⎪ ⎪ ⎪⎝⎭4. 下列不是n 阶矩阵A 可逆的充分必要条件的为 ( 1 ) .(1) 0A ≠ (2) 0A ≠ (3) ()R A n = (4) A 与单位阵E 等价5. 下列矩阵中是分块矩阵00A B ⎛⎫⎪⎝⎭的逆矩阵为 ( 4 ). (1) 1100A B --⎛⎫⎪⎝⎭ (2) 1100B A --⎛⎫⎪⎝⎭(3) 1100A B--⎛⎫⎪⎝⎭(4) 1100B A --⎛⎫ ⎪⎝⎭二、填选题(每小题3分，共计30分)6. 行列式 111253_____.4259= （- 6）7. 设4阶行列式的第三行元素为1，2，3，4，其对应的余子式为4，3，2，1，则该行列式的值等于______.（ 0 ）……………………………………………………………装订线…………………………………………………8. 设A 是3阶方阵，TA 是A 的转置矩阵且 2,A =则 3____.T A =；（ 54 ）9. 设211123223,322141113A B ⎛⎫⎛⎫⎪⎪=-=- ⎪ ⎪ ⎪ ⎪---⎝⎭⎝⎭, 则 _____________AB =；（487731112514⎛⎫ ⎪- ⎪ ⎪-⎝⎭）10．设矩阵 120340002A ⎛⎫ ⎪= ⎪ ⎪⎝⎭，则1A -=__________. ；（312212210000--⎛⎫⎪ ⎪ ⎪⎝⎭） 11. 设矩阵 200030004A ⎛⎫⎪= ⎪ ⎪⎝⎭，则*A =__________.（*A 是A 的伴随矩阵）；（12000800012⎛⎫⎪ ⎪ ⎪⎝⎭） 12. 设矩阵 123024003A ⎛⎫ ⎪= ⎪ ⎪⎝⎭，则*1()A -=__________；（12310246003⎛⎫⎪ ⎪ ⎪⎝⎭）13. 设矩阵 121211212112121,a a a a a A b b B b b b c c c c c -⎛⎫⎛⎫⎪ ⎪==- ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭，且AP B =,则初等阵P _____________；（1101-⎛⎫ ⎪⎝⎭） 14. 设 123(1,1,1),(2,3,4),(3,4,5)ααα===，则 123,,ααα的秩等于_______.；（ 2 ） 15. 设123(1,1,1),(1,3,4),(3,4,5)ααα===，则 123,,ααα的极大无关组的个数为 _____.（ 3 ）三、计算题（共计47分)16. 求解方程:2452450245x x x++=+ (本题满分10分)解：由于311113111132245(1)024500(1)47245(1)245047x r r x xx x x x x x c c x x a A x xx r r x x ++-+--+=-+-==-++-+++则原方程即2(11)0x x += 因而原方程的解为：120,11x x ==。

山东建筑大学07-08线性代数试题A卷参考答案

2007-2008学年第二学期线性代数试卷A 参考答案和评分标准一、单项选择题（每小题4分，本大题共20分） 1．C ； 2．C ； 3. A ； 4. A ； 5. C 二、填空题（每小题4分，本大题共20分）1. 5 ；2、4444⎛⎫⎪⎝⎭；3. 1 ；4．⎥⎦⎤⎢⎣⎡4331 ；5．正数. 三、（本题10分）计算行列式efcf bf de cdbd aeacab ---. 解：ef cfbf de cdbd aeac ab ---=ec b e c bec b adf ---……….…….…..…………（3分） =111111111---adfbce ……………………………………………………………………………….（6分） =abcdef 4……….………………………………………………………....……（10分）四、（本题10分）求方阵⎪⎪⎪⎪⎪⎭⎫ ⎝⎛2500380000120025的逆矩阵. 解：,21⎪⎪⎭⎫ ⎝⎛=A O O A A ,112251==A ,125382==A .……….……..……..（3分） ,5221111⎪⎪⎭⎫⎝⎛--==*-A A .……….……………………………………………（5分）,8532212⎪⎪⎭⎫ ⎝⎛--==*-A A .…………………………………………..……..…（7分）⎪⎪⎪⎪⎪⎭⎫⎝⎛-=- 8 5-003-2000000 2- 1 521A .……….…………………………………….…（10分）五、（本题12分）求线性方程组 ⎪⎩⎪⎨⎧=++-=++-=++-211117847246373542432143214321x x x x x x x x x x x x 通解.解.对方程组的增广矩阵作初等行变换⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛--→⎪⎪⎪⎭⎫ ⎝⎛---=0000175100172021211117847246373542A ………………………..（4分）于是方程组的同解方程组为⎪⎪⎩⎪⎪⎨⎧-=++=434217517221x x x x x ，42,x x 为自由未知量……………………..………..（8分）所以方程组的通解为：21432117507200120101k k x x x x ⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛-+⎪⎪⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛ . …………….…..….（12分）六、（本题12分）解：A 的特征方程为2103411||----+=-λλλλA E =0)1)(2(2=--λλ，……………..………....（2分）故A 的特征值为21=λ，132==λλ. ……………..………………….……..（5分）(1) 对于特征值21=λ，得到齐次线性方程组 ⎪⎩⎪⎨⎧=-=-=-0040312121x x x x x ，它的基础解系是⎪⎪⎪⎭⎫ ⎝⎛100，所以属于特征值2的全部特征向量为,100⎪⎪⎪⎭⎫ ⎝⎛k (0≠k ).………..…….（7分） (2) 对于特征值132==λλ，得到齐次线性方程组 ⎪⎩⎪⎨⎧=--=-=-002402312121x x x x x x ，它的基础解系是⎪⎪⎪⎭⎫ ⎝⎛-121，所以属于特征值1的全部特征向量为,121⎪⎪⎪⎭⎫ ⎝⎛-k (0≠k ).………...（9分）因此A 不与对角形矩阵相似. .…………….…………………………….（12分）七、（本题8分）设321,,ααα线性无关，证明3213221,,ααααααα++++也线性无关.证明：设0)()()(3213322211=++++++αααααααk k k ，………..…….（2分）则有0)()()(3322321131=++++++αααk k k k k k k ， ……………….（4分）321,,ααα 线性无关，⎪⎩⎪⎨⎧=+=++=+∴0003232131k k k k k k k ，0321===∴k k k ……….….（6分）所以3213221,,ααααααα++++线性无关. …………………………..….（8分）八、（本题8分）证明：若A 为n n ⨯阶非零矩阵，则秩（A ）=1的充分必要条件是A 可写为一列向量与一行向量的积.证明：必要性：因为秩（A ）=1，所以存在可逆矩阵P 和Q ，使得10010000(100)0000PAQ ⎛⎫⎛⎫ ⎪ ⎪⎪ ⎪== ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭，.……………………..….（2分）得到11)001(001--⎪⎪⎪⎪⎪⎭⎫⎝⎛=Q P A=)(2121n n b b b a a a ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛，这里⎪⎪⎪⎪⎪⎭⎫ ⎝⎛n a a a 21=⎪⎪⎪⎪⎪⎭⎫⎝⎛-0011 P ，)(21n b b b =1)001(-Q 。

西安交通大学2008年线性代数期末考试试题(含答案)

有唯一解、无解、有无穷多解?并在有无穷多解时,求出该方程组的结构式通解.
共6页第3页
五、(12分).设二次型，其中
(1)写出二次型的矩阵 ;
(2)求一个正交矩阵，使成对角矩阵;
(3)求一个合同矩阵，写出在线性变换下的规范形.
共6页第4页
六、(12分)向量组， ,能否由向量组，，线性表示。若能，求出它们的表达式。
(3).若向量组线性相关,则 =.
(4).设矩阵为正定矩阵，则的取值范围
是.
共6页第1页
二、单项选择题(每小题4分,共16分)
(1).设，则必有
(A) .(B) .
(C) .(D) .【】
(2).直线和直线
(A)重合.(B)相交.(C)平行.(D)异面.【】
(3). 只有零解的充分必要条件是
(A) 的列向量线性相关;(B) 的行向量线性相关;
(C) 是行满秩的;(D) 是列满秩的;【】
(4).设矩阵，则＝
(A) .(B) .(C) .(D) .【】
三、(12分)写出以为顶点，为准线的锥面方程。并指出其在平面上的投影曲线的名称。
.
共6页第2页
四、(12分) 取何值时,线性方程组
成绩
西安交通大学考试题
课程线性代数与解析几何（A卷）
系别考试日期2008年1月10日
专业班号
姓名学号期中期末√
说明: 指方阵的行列式, 指方阵的伴随矩阵, 指矩阵的秩, 指矩阵的转置矩阵, 为单位矩阵.
题号
一
二
三
四
五
六
七
八
九
得分
一、填空题(每小题4分,共16分)

2007-2008第二学期线代试卷A及答案)

武汉理工大学教务处试题标准答案及评分标准用纸课程名称:线性代数（ A 卷）一、填空题（每小题3分，共12分）1、 2；2、 1；3、 21t ≠；4、k >二、选择题（每小题3分，共12分）1、 A ；2、 C ；3、 B ；4、 D 三、解答题（每小题9分，共36分）1、11(2,,)(2,,)1100011111100100020012000200011i in i n i n r r r r n nn n n D n nn n nn n==+++---=-------…..…（4分）()(1)(2)(1)1122000001(1)1(1)(1)()(1)1222000n n n n n n n n n n n n n n nn n n n -------+++=⋅=⋅⋅-⋅-=⋅⋅---...….（9分）2、记 121624,1713A A ---⎛⎫⎛⎫==⎪ ⎪-⎝⎭⎝⎭，则121,1A A =-=；…..…………………………………..…..……...（4分）又1112767637,111112A A -----⎛⎫⎛⎫⎛⎫=-==⎪ ⎪ ⎪---⎝⎭⎝⎭⎝⎭，所以1760011000037012A --⎛⎫ ⎪ ⎪= ⎪- ⎪-⎝⎭－。

………………………...（9分）3、由题意有010100001A B ⎛⎫⎪= ⎪ ⎪⎝⎭，100011001B C ⎛⎫⎪= ⎪ ⎪⎝⎭，……………..…………………………………………...（4分）于是 010100100011001001A C ⎛⎫⎛⎫⎪ ⎪= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭，所以011100001X ⎛⎫⎪= ⎪ ⎪⎝⎭。

……….……………………………………...（9分）4、()123403481011,,,21043211αααα⎛⎫ ⎪- ⎪= ⎪ ⎪⎝⎭～1011034801220244-⎛⎫ ⎪ ⎪ ⎪ ⎪⎝⎭～10110122002200-⎛⎫ ⎪⎪ ⎪- ⎪⎝⎭～10000104001100⎛⎫ ⎪ ⎪ ⎪- ⎪⎝⎭………...（4分）则()1234,,,3R αααα=，且123,,ααα线性无关，所以123,,ααα即为1234,,,αααα的一个极大无关组，（7分）且412304αααα=+-；…………………………………………………………………………………..………...（9分）或者取124,,ααα，312404αααα=+-；还可以取134,,ααα，2341144ααα=+四、解()2111,1111tA b t t tt -⎛⎫⎪=-- ⎪ ⎪-⎝⎭～2223110110111t tt t t t t t t ⎛⎫- ⎪--+-- ⎪ ⎪+-++⎝⎭～ 22321101100(1)(2)1t tt t t t t t t t t ⎛⎫- ⎪--+-- ⎪ ⎪-+---+⎝⎭…………………………….…………..………...（4分）所以当12t t ≠-≠且时，方程组有唯一解；…………………………………..…………………………….……...（6分）当2t ＝时，(),A b ～112403360001-⎛⎫⎪-- ⎪ ⎪⎝⎭()(),32R A b R A =≠=，所以方程组无解。

沈阳建筑大学08秋-线性代数试卷A答案

沈阳建筑大学考试评分标准专用纸2008年秋季学期科目：线性代数1（A 卷）适用年级、专业：07级土木、环境、交通机械、管理、信息（除计算机）学院 ————————————————————————————————一、填空（每小题4分，共20分） 1．0； 2．AA； 3．-4； 4．!n ； 5．22t -<< 二、选择题（每小题4分，共20分） 1． D ； 2．D ； 3．B ； 4．C ；5．C 三、（6分）原式＝222222()(()())16x y x yx y x y x y x y x y x y-+-=--+=+- ．．．．．．．．．．．．．．．．．．6' 四、（6分）证明：设存在121,,,s l l l - 满足 1122110s s l l l βββ--+++=．．．．．．．．．．．．．．．．．．．2' 则有111222111()()()s s s s s s l k l k l k αααααα---++++++112211112211()0s s s s s l l l l k l k l k αααα----=+++++++=因为 12,,,s ααα无关，．．．．．．．．．．．．．．．．．．．2' 所以 1211122110s s s l l l l k l k l k ---====+++=故 121,,,s βββ-无关. ．．．．．．．．．．．．．．．．．．．2'五、（6分）解：32213211111111122200()3203200r r r r A a b aba b a a b aa ba ab a b+----=+--=-=-=--+-+-．．2'当()0a a b -=时，即0a =或a b =时，()3R A < （1）若0a b ==，则111100010000A -⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦，()1()2R A R =<=，无解. .．．．．．．．．．．．．2' （2）若0,0a b =≠，则2132221 1 1 1111 1222300100 23002311 1100100 01r r r r A b b b b b -+--⎡⎤⎡⎤⎢⎥⎢⎥=---⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦-⎡⎤⎢⎥-⎢⎥⎢⎥-⎣⎦()2()3R A R A =<=，无解. ．．．．．．．．．．．．．2' 六、（6分）解：()12341525100236330101,,,2215001110110000a a a a --⎡⎤⎡⎤⎢⎥⎢⎥-⎢⎥⎢⎥=⎢⎥⎢⎥--⎢⎥⎢⎥-⎣⎦⎣⎦.．．．．．．．．．．．．．3' 秩为3，123,,a a a 为一个最大无关组，41232a a a a =-+. ..．．．．．．．．．．．．．3' 七、（6分）解：1122r n n n D D D --=-按展..．．．．．．．．．．．．．3'232232(2)32n n n n n D D D D D -----=--=-34334213(2)243(1)(2)n n n n n D D D D D n D n D -----=--=-==---21(1)(2)2(1)32(2) 1.12n n n n n =---=---=+ ..．．．．．．．．．．．．．3' 八、（6分）解：由2AX E A X +=+，得到2()A E X A E -=- ..．．．．．．．．．．．．．2' 由于001010,0100A E A E ⎡⎤⎢⎥-=-≠⎢⎥⎢⎥⎣⎦201030102X A E ⎡⎤⎢⎥=+=⎢⎥⎢⎥⎣⎦. ..．．．．．．．．．．．．．4' (或者)由2AX E A X +=+，得到2()A E X A E -=- ..．．．．．．．．．．．．．2'11001001001010,()010010100100100A E A E --⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥-=-==⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦..．．．．．．．．．．．．．2'12()()X A E A E -=--001102201010030030100201102⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦． ..．．．．．．．．．．．．．2' 九、（6分）解：222222A B αααηζηζβββ+=+=+4444A B ααηζββ=+=+ .．．．．．．．．．．．．．4' 454(2)12.=⨯+⨯-= ..．．．．．．．．．．．．．2'十、（8分）解：100023032A ⎛⎫⎪= ⎪ ⎪⎝⎭， (5)(1)(1)E A λλλλ-=--+ ..．．．．．．．．．．．．．1' 5λ=的特征向量1011ξ⎛⎫⎪= ⎪ ⎪⎝⎭1λ=特征向量2100ξ⎛⎫ ⎪= ⎪ ⎪⎝⎭1λ=-特征向量3011ξ⎛⎫⎪= ⎪ ⎪-⎝⎭单位化11011q β⎛⎫⎪==⎪⎪⎭ ，222q βξ==，333011q βξ⎛⎫⎪===⎪⎪-⎭..．．．．．．．．．．．．．4'正交变换01000X Y ⎛⎫⎪⎪⎪=⎪⎪..．．．．．．．．．．．．．1'2221235f y y y =+-. ..．．．．．．．．．．．．．1' 由顺序主子式不全大于等于0或标准形中有负项，得不是正定的...．．．．．．．．．．1' 十一、（6分）解：由 ,P PA Λ=故11,k k A P P A P P --=Λ=Λ所以 175()(62)A P E P ϕ-=Λ-Λ+又10,11P -⎡⎤=⎢⎥⎣⎦ 所以110,11P --⎡⎤=⎢⎥⎣⎦..．．．．．．．．．．．．3' 75175101010()62010(1)0(1)103010110711A P P ϕ-⎛⎫⎡⎤⎡⎤⎡⎤=-+ ⎪⎢⎥⎢⎥⎢⎥ ⎪--⎣⎦⎣⎦⎣⎦⎝⎭---⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦30.107-⎡⎤=⎢⎥⎣⎦..．．．．．．．．．．．．3' 十二、（4分）解：由1234b αααα=+++得线性方程组Ax b = 的特解*T (1,1,1,1)η= . 由234,,ααα 线性无关，1232ααα=-知()3R A =，线性方程组0Ax = 的基础解系含有431-=个解向量。

线性代数期末考试试卷A答案

…………(2分)
它的特征多项式为
，
…………(4分)
由于其有一特征值，故，所以A的特征值为
，。
…………(6分)
当时，解方程。
，
得基础解系，，
…………(8分)
单位化即得，；
…………(10分)
当时，解方程。
，
得基础解系，单位化即得； …………(12分)
于是正交变换为，
且其标准型为.
…………(13分) …………(15分)
八、证明（本题13分）
1、设A、B都是n阶矩阵，且A为对称阵，证明也是对称阵。
得分
（本小题7分）
证明：由于，
A是n次对称阵，故有。
…………(3分)
于是
即是对称阵，故也是对称阵。 …………(7分)
2、设，证明：A的特征值只能取1或2。
（本题6分）
得分
证明：设是A的特征值，是A的属于的特征向量，则
…………(2分)
A） ACB B）ABC C）BAC D）CBA
3、设矩阵A =，则 D 。
A）8 B） -8 C）-16 D）16
4、设三元非齐次程组AX=B的两个解分别为，且系数矩阵A的秩为2，
则对任意常数方程组的通解可表为 C 。
A）
B）
C） D）
5、矩阵A=非零特征值是 B 。
A）4 B）3 C）2
D）1
二、填空题：（每题2分共10分）
…………(6分)
当时，解方程。，
得基础解系，故的全部特征向量为…………(8分) 当时，解方程。，
得基础解系，故的全部特征向量为…………(10分) 当时，解方程。，
得基础解系，故的全部特征向量为………(12分)

广工2008线代试题A-答案

七、(8分)
解：设有关系式，即
则有
因为线性无关，所以
………………………………………….4分
齐次线性方程组的系数行列式为
…………….….…6分
即当为奇数时，齐次线性方程组只有零解，从而，即向量组线性无关；
即当为偶数时，齐次线性方程组有非零解，从而存在不全为零的数，使，即向量组线性无关………………………………………………………………..……………8分
解答
一、单项选择题（每题4分，共20分）
1、D；2、D；3、D；4、B；5、B；
二、填空题（每题4分，共24分）
1、；2、；3、；4、；5、；6、
三、（11分）法一：
解： = --------------------------------------------4分
---------------------------------------------7分
五、（13分）
解：对增广矩阵进行初等行变换
…………3分
（1）；……………5分
(2) ；………………………………7分
(3) ；………………………9分
----------------------------------------11分
方程组的通解为：
-----------------------------------------------------13分
4、设是齐次线性方程组的一个基础解系，则（）也是它的基础解系
（A）；（B）；
ห้องสมุดไป่ตู้(C) (D) .
5、设A是n阶正交矩阵，则下列结论不正确的是（）
（A） ;（B）A的行列式等于1
（C）A的行向量都是单位向量且两两正交；

线性代数试题(济南大学2008～2009学年第二学期课程考试试卷(A卷))

济南大学2008～2009学年第二学期课程考试试卷（A 卷）一、选择题（每小题3分，共15分）1．D 2333231232221131211==a a a a a a a a a ，则333132312321222113111211322322322a a a a a a a a a a a a ---的值为 [ C ] (A ) 4; (B ) 6; (C ) 8; (D ) 10.2. 设n 阶方阵A ，B ，C ，满足ABC=E ，则必有 [ D ](A ) ACB=E ; (B ) CBA=E ; (C ) BAC=E ; (D ) BCA=E .二、填空题（每空3分，共24分）1. 行列式225144196151214111=_________.2. 设矩阵A ，⎥⎦⎤⎢⎣⎡=1102,230311⎥⎦⎤⎢⎣⎡-=B 则=B A T .6. 4阶行列式D 某一行的所有元素都相等且它们对应的余子式也相等，则D = 0 . 三、（本题满分10分）计算4阶行列式 b b a a -+-+1111111111111111.四、（本题满分12分）设矩阵A =⎪⎪⎪⎭⎫⎝⎛400021012，矩阵B 满足：AB=A+2B ，求矩阵B .五、（本题满分14分）试求b 为何值时, 线性方程组⎪⎪⎩⎪⎪⎨⎧=+++-=---=++=+++bx x x x x x x x x x x x x x 43214324324321223121220有解,并求其通解.一、选择题（每小题3分，共18分） 1．若622211211=a a a a ，则120020221221112--a a a a 的值为 [ A ] (A ) 12-; (B )12; (C ) 18; (D ) 0.3. 设n 元齐次线性方程组=Ax 0的系数矩阵的秩为r ，则方程组=Ax 0有非零解的充分必要条件是 [ D ] (A ) n r =； (B ) n r ≥； (C ) n r >； (D ) n r <. 5. 设n 阶方阵A ，B ，C 满足ABC=E ，则必有 [ B ](A ) ACB=E ; (B ) BCA =E ; (C ) BAC=E ; (D ) CBA =E .二、填空题（每空3分，共24分）1. 行列式222111c b a c b a=_________. 2. 设A ，B 均为3阶方阵,且A =2,21=B ，则12-A B T =_____ __.4. 非齐次线性方程组b Ax =有解的充分必要条件是 . 56. 设n 阶矩阵A 满足=-+E A A 102320，则1)2(--E A = .三、（本题满分10分）计算4阶行列式aa a a a a a a aa a a 0000. 四、（本题满分12分）设AX +B =X ，其中A =，⎪⎪⎪⎭⎫ ⎝⎛---101111010B =⎪⎪⎪⎭⎫ ⎝⎛3-5021-1，求矩阵X .五、（本题满分14分）试求a 为何值时, 线性方程组⎪⎩⎪⎨⎧-=++-=++-=++322321321321a x x ax x ax x ax x x有唯一解、无解、有无穷多解？并在无穷多解时求其通解.一、填空题（每小题3分，共18分）2. 设⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=100020101A ，则(A +3E )-1 (A 2-9E )=.3. 设⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=200031021A ，则A -1=.二、选择题（每小题3分，共18分）1. 若矩阵A 有一个r 阶子式不为零，则下列结论正确的是 [ ](A ) R (A )<r ； (B ) R (A )≤ r ； (C ) R (A )>r ； (D ) R (A )≥ r .2. 设A ，B 为同阶可逆矩阵，则下列结论一定成立的是 [ D ](A ) AB = BA ； (B ) 存在可逆矩阵P ，使P -1 AP =B ； (C ) 存在可逆矩阵C ，使C T AP =B ； (D ) 存在可逆矩阵P 和Q ，使P -AQ =B . 5. 矩阵方程AX =B 有解的充分必要条件是 [ C ](A ) R (A )= R (B )； (B ) R (B )=R (A , B )； (C ) R (A )=R (A , B )； (D ) R (A )<R (A , B ).6. ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+++=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=133312321131131211232221333231232221131211,a a a a a a a a a a a a a a a a a a a a a B A ,,101010001,10000101021⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=P P 则[ D ](A ) B =P 1AP 2； (B ) B =P 2AP 1； (C ) B =A P 1P 2； (D ) B =P 1P 2A .三、计算题（第1、2题每小题10分，第3小题12分，共32分）1. 计算行列式3321322132113211111b a a a a b a a a a b a a a a +++.2. 求齐次线性方程组⎪⎩⎪⎨⎧=++=++=+++000224214324321x x x x x x x x x x 的全部解.3. 已知矩阵⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡--=2001,1121B P 满足P -1AP=B ，计算： (1) |-A 5|； (2) A 3.济南大学2011～2012学年第二学期课程考试试卷（A 卷）课程线性代数考试时间 2012 年 7 月 2 日一、填空题（每小题3分，满分27分）1、设行列式==11110342226111304z y xzy x，则行列式_________. 4、设矩阵A =⎪⎪⎪⎪⎪⎭⎫⎝⎛1100120000120025，则A -1=________________. 6、三元线性方程x 1+ x 2+ x 3=1的全部解是_______________.三、计算题（每小题9分，满分18分）（1）D =cc b b a a ------1100110011001.（2）设矩阵A =⎪⎪⎪⎭⎫⎝⎛161020101,而X 满足AX +E =A 2+X ，求X .四、应用题（每小题10分，满分20分）（2）设A =⎪⎪⎪⎭⎫ ⎝⎛-1-11020011-λλλ, b =⎪⎪⎪⎭⎫⎝⎛11-a ，已知非齐次线性方程组Ax=b 存在两个不同的解，求（I ）a ，λ的值；（II ）Ax =b 的通解.。

2008-2009学年第2学期期末考试 A卷试卷及解答

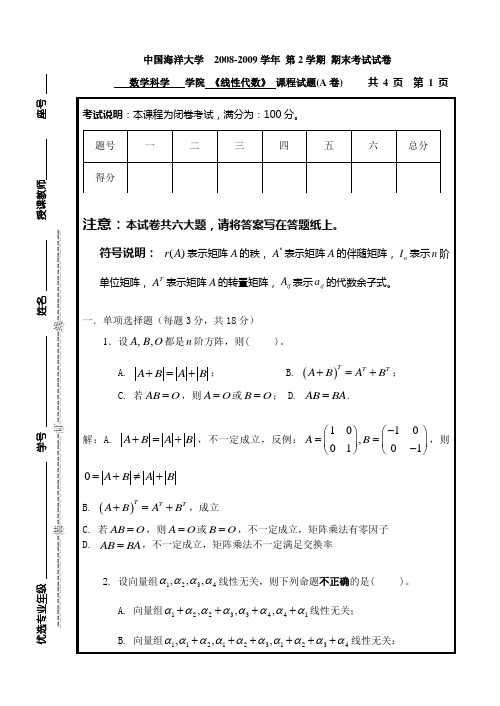
中国海洋大学2008-2009学年第2学期期末考试试卷数学科学学院《线性代数》课程试题(A卷) 共4 页第2 页中国海洋大学 2008-2009学年第2学期期末考试试卷数学科学学院《线性代数》课程试题(A 卷) 共 4 页第 3 页解： 1X A B -=，根据初等行变换求解可得 ()()213132132323102211022110221311133,201570015702,521891014510012110021010351,100121rr r r r r r r r r r r ⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪-------+---+-⎪ ⎪ ⎪ ⎪ ⎪ ⎪----⎝⎭⎝⎭⎝⎭--⎛⎫ ⎪-⨯-⨯-⎪ ⎪---⎝⎭uuuuuuuuuuuuu r uuuuu r uuuuuuuuuuuuu r uuuuu r 100210103500121--⎛⎫ ⎪--⎪ ⎪⎝⎭uuuuuuuuuuu因此213521X --⎛⎫ ⎪=-- ⎪ ⎪⎝⎭4. 已知3R 的两组基为()()()1231,0,0,1,1,0,1,1,1TTTααα==-=与()()()1231,2,1,2,3,3,3,7,1T T Tβββ===，求：（1）基{}123,,ααα到基{}123,,βββ的过渡矩阵；（2）向量()5,2,1Tα=在基{}123,,ααα下的坐标。

解：（1）设基{}123,,ααα到基{}123,,βββ的过渡矩阵为C ，则()()123123,,,,C βββααα=，即123111237011131001C ⎛⎫⎛⎫⎪ ⎪=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭，因此1111123011237001131C -⎛⎫⎛⎫⎪ ⎪=- ⎪ ⎪⎪ ⎪⎝⎭⎝⎭，利用初等变换法求解得()2313122111123110012100118011237,010106,1010106001131001131001131r r r r r r r --⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪----+⨯--- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭uuuuuuuuuuu r uuuuuuuuuuuuur12,,,,n αααβL 线性无关；（2）若1β可由12,,,n αααL 表出，而2β不能由12,,,n αααL 表出，则1212,,,,n αααββ+L 线性无关。

2008-2009(1)广州大学线性代数期末考试试卷A卷

广州大学2008-2009学年第一学期考试卷一．填空题（每小题3分，共15分）1．行列式524210321--中（2，3）元的代数余子式A 23的值为______ 2．设A 是4阶方阵，A =-2，则*A -=________3．向量组α1=(1,2,-1,1), α2=(2,0,3,0), α3=(-1,2,-4,1)的秩为________4．若α1，α2，α3都是齐次线性方程组Ax=0的解向量，则A （3α1-5α2+2α3）=______. 5．已知0=λ是方阵A 的一个特征值，则|A|= ___ 二．单项选择题（每小题3分，共15分）1．设n 阶方阵A 中有n 2-n 个以上元素为零，则A 的值【】A ．大于零B ．等于零C ．小于零D ．不能确定2．设n 阶方阵A ，B ，C 满足ABC=E ，则必有【】A ．ACB=EB ．CBA=EC ．BAC=ED ．BCA=E3．设3阶矩阶A=（α1，β，γ），B=（α2，β，γ），且A =2，B =-1，则B A += 【】A ．4B ．2C ．1D ．-44．设A 是3阶可逆矩阵, A 的第2行乘以2为矩阵B ，则1-A 的【】为1-BA ．第2列乘以2; B. 第2行乘以2; C. 第2列乘以21; D. 第2行乘以21. 5．设A 为m ×n 矩阵，则非齐次线性方程组Ax=b 有惟一解的充分必要条件是【】A ．m=nB ．Ax=0只有零解C ．向量b 可由A 的列向量组线性表出D ．A 的列向量组线性无关，而增广矩阵A 的列向量组线性相关三．（本题8分）计算行列式3351110243152113------=D .四．（本题8分）设矩阵3400430000200022A ⎛⎫ ⎪-⎪= ⎪ ⎪ ⎪⎝⎭，求4A 五．（本题10分）已知向量1110α-⎛⎫⎪=- ⎪ ⎪⎝⎭，⎪⎪⎪⎭⎫ ⎝⎛=1322α，⎪⎪⎪⎭⎫ ⎝⎛=2133α，⎪⎪⎪⎭⎫ ⎝⎛=7054α，（1）试判定1α，2α，3α是向量组1α，2α，3α，4α的一个最大无关组（2）将4α用1α，2α，3α线性表出六．（本题10分）已知⎪⎪⎪⎭⎫ ⎝⎛-=321011330A ，B A AB 2+=，求B七．（本题12分）求齐次线性方程组⎪⎩⎪⎨⎧=++-=++-=--+0377023520432143214321x x x x x x x x x x x x 的基础解系与通解八．（本题12分）设矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=00111100x A ，问x 为何值时，矩阵A 能对角化？九．证明下列各题（每小题5分，共计10分）1．已知向量组α1，α2，α3线性无关，证明向量组α1+2α2，2α2+3α3，3α3+α1线性无关.2．已知n 阶方阵A 的各行元素之和均为a ，证明向量x=(1，1，…，1)T 为A 的一个特征向量，并求相应的特征值.广州大学2007-2008学年第一学期考试卷一．填空题（每小题3分，本大题满分15分） 1．设A 为3阶方阵，且||4A =, 则|2|A =________.2．设1234⎛⎫=⎪⎝⎭AB , 则T T =B A3．已知200*220421⎛⎫ ⎪= ⎪ ⎪⎝⎭A ，则1-=A4．n 元齐次线性方程组=Ax 0的解空间的维数等于____________.5．若2阶方阵A 满足方程256-+=A A E O ，且A 的两个特征值不相等,则||=A ________.二．选择题 (每小题3分, 本大题满分15分)1．设123,,ααα为3维列向量, 且123|,,|4ααα=, 则1322|2,23,|-=αααα( ). (A) 16； (B) 16-； (C) 24 (D) 24-.2. 二次多项式281175413561081x x ---中2x 项的系数是( ).(A) 7； (B) 7-； (C) 5 (D) 5-.3. 设,,A B C 均为n 阶方阵, 且ABC E =, 则必有( ).(A) BCA E =; (B) BAC E =; (C) CBA E =; (D) ACB E =.4. 矩阵方程=AX B 有解的充分必要条件是( ).(A) ()(,)R R <A A B ; (B) ()(,)R R <B A B ; (C) ()(,)R R =A A B ; (D) ()(,)R R =B A B .5. 若向量组1,,ααm 线性相关, 且110ααm m k k ++= , 则( ). (A) 1,,m k k 全为0; (B) 1,,m k k 全不为0; (C) 1,,m k k 不全为0; (D) 前述情况都可能出现.三．（本题满分8分）计算行列式0000a b ca b cD b a c c a b =.四．（本题满分10分）设1200010000240012⎛⎫ ⎪⎪= ⎪ ⎪⎝⎭A , 求8A . 五．（本题满分10分）设12341314(,,,)431010561114⎛⎫⎪= ⎪ ⎪⎝⎭αααα, 求向量组1234,,,αααα的秩和一个最大无关组, 再把其余向量用该最大无关组线性表示.六．（本题满分10分）已知矩阵3000130011301113⎛⎫ ⎪⎪= ⎪ ⎪⎝⎭A , 解矩阵方程2=+AX X A . 七．（本题满分12分）求方程组12341234123432434537761171513x x x x x x x x x x x x -+-=⎧⎪-+-=⎨⎪-+-=⎩的通解.八．（本题满分12分）已知矩阵9226A ⎛⎫= ⎪⎝⎭,(1) 求矩阵A 的特征值和特征向量;(2) 求可逆矩阵P , 使1P AP -为对角矩阵. 九．（本题满分8分）设η是非齐次线性方程组=Ax b 的一个解, 1,,n r -ξξ 是=Ax 0的一个基础解系. 证明 1,,,n r -++ηηξηξ 线性无关.2006----2007广大线性代数广州大学2005-2006学年第一学期考试卷一．填空题（每小题3分，本大题满分15分）1．=000000000000dc b a ________.2．已知⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=321021001A , 则=-||1A ________.3．已知34⨯矩阵A 的秩2)(=A R ，而⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=504030201B ，则=)(AB R ________. 4．设向量T )2,2,1(=α, A 为三阶正交矩阵, 则长度=αA ________.5．设方阵A 满足方程O aE A A =+-32，且已知A 的一个特征值为1=λ，则常数=a ________.二．选择题 (每小题3分, 本大题满分15分)1. 设n 阶方阵B A ,满足关系式O AB =, 且O B ≠, 则必有( ).(A) O A =; (B) 0||≠B ; (C) 222)(B A B A +=+; (D) 0||=A .2. 设三阶方阵],,[21ααα=A , ],,[21ααβ=B , 其中βααα,,,21为3 维列向量, 且5||=A , 1||-=B , 则=+||B A ( ). (A) 4; (B) 6; (C) 16; (D) 24.3. 设A 为可逆矩阵, 则=-1*)(A ( ).(A)A A ||1; (B) A A ||; (C) 1||1-A A ; (D) 1||-A A . 4. 设向量组0A 为向量组A 的部分组, 下列命题正确的是( ). (A) 若向量组A 线性相关，则向量组0A 必线性相关;(B) 若向量组0A 线性相关，则向量组A 必线性相关; (C) 向量组A 线性无关，而向量组0A 可能线性相关; (D) 向量组0A 线性相关，而向量组A 可能线性无关;5. 设A 是n m ⨯矩阵, 若线性方程组0=Ax 仅有零解, 则必有( ). (A) m A R =)(; (B) m A R <)(; (C) n A R =)(; (D) n A R <)(.三．（本题满分8分）1) 设⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=000100010A , 计算2A 和3A ;2) 设⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=λλλ001001B , 求nB .四．计算下列行列式（每小题6分，本大题满分12分）1．0741512090318512-----=D .2．110000010001121nn n a a a a D -=. 五．（本题满分8分）求线性变换⎪⎩⎪⎨⎧++=++=++=3213321232113432232xx x y x x x y x x x y 的逆变换.六．（本题满分10分）设⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--==12212228324131),,,(4321ααααA .1) 求矩阵A 的行最简形和秩;2) 求向量组4321,,,αααα的一个最大无关组, 再把其余向量用该最大无关组线性表示.七．（本题满分10分）求方程组⎪⎩⎪⎨⎧-=+-+=-+-=-+-253443233423432143214321x x x x x x x x x x x x 的通解.八．（本题满分12分）已知矩阵⎥⎦⎤⎢⎣⎡=3113A , 1) 求矩阵A 的特征值和特征向量;2) 求可逆矩阵P , 使AP P 1-为对角矩阵, 并计算10A . 九．（每小题5分, 本大题满分10分）1．设向量组321,,ααα线性无关，证明向量组32112αααβ++=，3212432αααβ--=，321343αααβ-+=也线性无关.2．设A ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡---=7600054000320001，E 为4阶单位阵，且)()(1A E A E B -+=-，求1)(-+B E .广州大学2004-2005学年第一学期考试卷-1广州大学2003-2004学年第二学期考试卷一．填充题（每小题3分，共15分）6．多项式=)(x f 3273121x x x-中2x 的系数为_______. 7．设A 为3阶方阵，且2||=A , 则=-|2|1A _______. 8．当=a _______时, 下列齐次方程组有非零解.12312312332023020x x x x x x x x ax ++=⎧⎪-+=⎨⎪++=⎩9．矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--121240321的秩为_______. 10．二次型2221231223226T x Ax x x x x x x x =+-+-中对称阵A =_______二．选择题（每小题3分，共15分）1. 设n 阶方阵B A ,满足关系式O AB =, 则必有( ). (A) O A =或O B =; (B) O B A =+;(C) 0||=A 或0||=B ; (D) 0||||=+B A .2. 设三阶方阵],,[21ααα=A , ],,[21ααβ=B ,其中βααα,,,21为3维列向量, 且1||=A , 2||=B , 则=+||B A ( ).(A) 3; (B) 6; (C) 9; (D) 12. 3. 设A 是3阶矩阵, 则必有( ).(A) *2)*2(A A =; (B) *21)*2(A A =; (C) *4)*2(A A =; (D) *8)*2(A A =.4. 设向量组r A ααα,,,:21 可由向量组s B βββ,,,:21 线性表示, 则( ).(A) 当s r <时, 向量组A 必线性相关; (B) 当s r >时, 向量组A 必线性相关;(C) 当s r <时, 向量组B 必线性相关; (D) 当s r >时, 向量组B 必线性相关. 5. 设A 是n m ⨯矩阵, 则线性方程组0=Ax ( ).(A) 当m n >时仅有零解; (B) 当m n >时必有非零解; (C) 当m n <时仅有零解; (D) 当m n <时必有非零解. 三．解答下列各题(每小题7分，共21分) 1．设⎥⎦⎤⎢⎣⎡=4321A , ⎥⎦⎤⎢⎣⎡=9531B , B AC -=2, 求2003C . 2．计算行列式2342013241102121----=D .3．讨论向量组1(1,1,1)α=,2(1,2,3)α=,)2,1,(3a =α的线性相关性.四．（12分）求下列方程组的通解⎪⎪⎩⎪⎪⎨⎧-=+++-=+++=+++=+++13345323173324321432143214321x x x x x x x x x x x x x x x x五．（12分）已知矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=122112,321212431B A , 1）求矩阵A 的逆阵;2）解矩阵方程AX=B.六．（12分）求方阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=442442221A 的特征值和特征向量. 七．（7分）设A 为n 阶正定矩阵，r αα,,1 是n 维非零列向量, 且0=j T i A αα ),,2,1,,(r j i j i =≠, 证明:r αα,,1 线性无关.八. (6分) 设方阵A 满足O E A A =+-232, 证明A 的特征值只能取值1或2.。

2008-2009学年试题__线性代数

五、证明题（每小题 5 分，共 10 分）
17. 设有向量组
a1 , a2 , a3 , a 4
，
b1 = a1 + a2 , b2 = a2 + a3 , b3 = a3 + a4 , b4 = a4 + a1 ，证明向量组
b1 , b2 , b3 , b 4 线性相关。
18. 证明：二次型
f = X T AX
在
X = 1 时的最大值为 A 的最大特征值，最小值为 A 的最小特征值。
2008-2009-2 线性代数期末试卷(A) 一、单项选择题（每小题 3 分，共 15 分）
1．设 A，B 都是 n 阶方阵，且|A|=3，|B|=-1,则
AT B -1 =(
2008-2009-1 年秋线性代数期末试卷(A) 一、单项选择题（每小题 3 分，共 15 分）
1.设
A 中有 n 2 - n
个以上元素为零，则
A 的值为（
）
A.大于零; B. 等于零; C. 小于零; D. 不能确定. 2.设
C.16； D. 16.
A. 4 B. 4；
3. 已知
A 为 n 阶方阵，且满足 A2 - A - 2 E = 0 则必有（
B.
）
A. C. 4. 设
A 不可逆； A = E ；
A - E 可逆； D. A = - E 。
）
A, B 均为 n 阶方阵，若 R ( A ) = R ( B ) ，则必有（
x 0 6． 0 y
y x 0 0
0 y x 0
0 0 = y x
;
æ 1 2 2 ö ç ÷ 7．设矩阵 A = 2 t 3 ÷ ，若齐次线性方程组 Ax = 0 有非零解，则数 t = ç ç 3 4 5 ÷ è ø æ 1 0 0 ö ç ÷ 8．矩阵 A = 0 1 3 ÷ 的逆矩阵为 ç ç 0 1 2 ÷ è ø

线性代数2007-2008第二学期试卷A答案

n 4, 有唯一解 III)a 2且a 1时，r r
综上，a 2且b 1时，方程组无解。
1 0 (2)a 2, b 1时，A 0 0
1 0 a 1时，A 0 0 0 0 1 1 0 0 1 0 0 2 0 0
3、设 A, B 均为 3 阶方阵，且满足 A 2, B 3 ，则 ( AB ) 6 ； ( AB ) ＝ 36 。

1 1 1 1 1 1 2 3 的秩为 4、矩阵 3 1 5 1 1 3 4 2
4
1 0 ，它的行最简形是 0 0
1
1 3 6 0 0 1 和 2 。 3 6 1 1 3 6
6,3,2
8、设三阶方阵 A 、B 相似，A 的特征值为 1、 2、 3，则 B* 的特征值为
。
二、单项选择题（每小题 2 分，共 12 分）得分
1 3 0
2 3 2 ( 1) 3
3 1 2 1 0 1 1 0 1 A E 5 2 3 0 1 1 0 1 1 1 0 1 0 2 2 0 0 0 1 ( A E ) x 0的基础解系为 1 ， 1 A只有一个线性无关的特征向量，因此A不能对角化。
3310分分设为一向量组12341131151?21893??????317?????????????????????????????????????????????????????????????????1
浙江工业大学
《线性代数》试卷 (A)

2007-2008第一学期线代试卷A及标答

武汉理工大学教务处试题标准答案及评分标准用纸课程名称:线性代数（ A 卷）一、填空题（每小题3分，共15分）1、23-； 2、E ； 3、-15； 4、5t ≠； 5、 2 二、选择题（每小题3分，共15分）1、C2、A3、B4、C 5 、D 三、解答题（每小题8分，共32分）1、 121000121000(1)2121000121121n n n x xn x n xn n D x x n n x x n nn n-+-++⎡⎤==+⎢⎥⎣⎦+-+--………………（4分） (1)12(1)(1)2n n n n n x x --+⎡⎤=-+⎢⎥⎣⎦………………………………………………………………（8分） 2、由题意(1,2)B AE = ……………………………………………………………………………………（4分）又BX A =，即(1,2)A E X A =，所以1(1,2)X E -=(1,2)E =……………………………………………（8分） 3、记1200A A A ⎛⎫=⎪⎝⎭，则1111200A A A ---⎛⎫= ⎪⎝⎭， ……………………………………………………………（2分）又*11211,10A A ⎛⎫== ⎪-⎝⎭，故112110A -⎛⎫= ⎪-⎝⎭ …………………………………………………………（4分）*21211,31A A -⎛⎫=-= ⎪-⎝⎭，故122131A --⎛⎫= ⎪-⎝⎭………………………………………………………（6分）所以12100100000210031A -⎛⎫⎪-⎪= ⎪- ⎪-⎝⎭。

…………………………………………………………………（8分） 4、记()1234,,,A αααα=，对A 进行行初等变换，将其化为行最简形：1211241012213631A -⎛⎫ ⎪-⎪= ⎪--- ⎪-⎝⎭～1211003200320064-⎛⎫ ⎪- ⎪ ⎪- ⎪-⎝⎭～121100320000000-⎛⎫⎪- ⎪ ⎪⎪⎝⎭～11203201300000000⎛⎫-⎪⎪⎪-⎪ ⎪⎪ ⎪⎝⎭…………………（4分）()2R A =，又显然13,αα线性无关，所以13,αα即为原向量组的一个最大无关组；………………………（6分）且212αα=，4131233ααα=--。

2008级线性代数试题和答案 A卷

经济学院本科生09-10学年第一学期线性代数期末考试试卷 (A 卷)答案及评分标准一、填空题（每小题4分、本题共28分）1. 设A 为n 阶方阵, *A 为其伴随矩阵, 31det =A , 则=⎪⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛*-A A 1541det 1_____ 2. 已知12,αα均为2维列向量, 矩阵),2(2121αααα-+=A , ),(21αα=B . 若行列式6A =, 则B = _____3.若,),,,(),,,,(2121k r r s s ==αααβααα,1),,,,(21+=k r s γααα 则),,,,,(21γβαααs r = _____4. 设A 为5阶方阵, 且4)(=A r , 则齐次线性方程组0*=x A （*A 是A 的伴随矩阵）的基础解系所包含的线性无关解向量的个数为 _____5. 设33()ij A a ⨯=是实正交矩阵, 且,a b T11=1,=(1,0,0)则线性方程组Ax b =的解是_____6. 若使二次型31212322213212242),,(x tx x x x x x x x x f ++++=为正定的, 则 t 的取值范围是 _____7. 设3阶方阵A 满足0322=--E A A , 且0<A <5, 则=A _____ 答案：（1） 3)1(n - （2）-2 （3） k +1 （4） 4（5） T)0,0,1( （6） 2<t （7）3二、单项选择题（每小题4分、本题共28分）1. 设A 为n 阶方阵, B 是A 经过若干次矩阵的初等变换后所得到的矩阵, 则有（） (A) B A = (B) B A ≠(C) 若0=A , 则一定有0=B (D) 若0>A , 则一定有0>B 2. 设行列式3040222207005322D =--, 则第四行各元素代数余子式之和的值为 ( ) (A) 28 (B) -28 (C) 0 (D) 336 3. 设A 为m 阶方阵, B 为n 阶方阵, ⎪⎪⎭⎫ ⎝⎛=00BA C , 则 C 等于 ( )(A) B A (B) B A - (C) B A m n )1(- (D) B A n m +-)1( 4. 设n 维列向量组)(,,21n m m <ααα 线性无关, 则n 维列向量组m βββ ,,21线性无关的充分必要条件是（）(A) 向量组m ααα ,,21可由向量组m βββ ,,21线性表示 (B) 向量组m βββ ,,21可由向量组m ααα ,,21线性表示 (C) 矩阵),,(21m ααα 与矩阵),,(21m βββ 等价 (D) 向量组m ααα ,,21与向量组m βββ ,,21等价 5．设A 、B 为n 阶方阵, 且)()(B r A r =, 则（）(A) 0)(=-B A r (B) )(2)(A r B A r =+ (C) )()()(B r A r B A r +≤ (D) )(2)(A r AB r =6. 设矩阵⎪⎪⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎪⎪⎭⎫⎝⎛=0000000000000004,1111111111111111B A , 则A 与B （）（A ）合同且相似（B ）合同但不相似( C ) 不合同但相似（D) 不合同且不相似7．设21,λλ是矩阵A 的两个不同的特征值, 对应的特征向量分别为21,αα, 则221),(ααα+A 线性无关的充分必要条件是（）（A ）01≠λ （B ）02≠λ ( C )01=λ (D) 02=λ 答案：CCC CCA A三、计算题（每小题8分、本题共32分）1．计算n +1阶行列式 nn n n d b d b d b a a a a D 00000022112101=+.解分三种情况讨论：（1）当n d d d ,,,21 全不为0时，D 为箭型行列式且∑∑==--=-=====nk n kkk nn nk k k k c c d d d d b a a d d d a a a d b a a D jjd jb 1210212110;)(0000001（2）当n d d d ,,,21 中只有一个为0时，不妨假设0=i d ，则ni i i i ni i i inni i i i ni i ic cd d d d b a d d b d d a d b d b b d b d a a a a a a D i111111111111011000011+-+-+--+-↔-=-=-====+（3）当n d d d ,,,21 中有两个以上为0时，显然0=D .综合以上三种情况，我们有⎪⎩⎪⎨⎧=∃-=≠-=+-=∑0,;...),...,2,1(0;)(11211210i n i i i i k nk n kk k d i d d d d d b a n k d d d d d b a a D 2. 设矩阵A 满足关系式11)2(--=-C A B C E T , 其中⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡---=1000210002101021,1000210032102321C B , 求A ？解在等式11)2(--=-C A B C E T 等号两边同时乘以C , 得[]TB C A 1)2(--=,⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡---=-⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=--100021********21)2(,100021003210432121B C B C ,[]⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡---=-=-1210012100120001)2(1TB C A . 3．设线性方程组 ⎪⎪⎩⎪⎪⎨⎧=+++=+++-=+--=+--bx x x x x ax x x x x x x x x x x 43214321432143217107141253032（1）问：a , b 取何值时, 线性方程组无解、有解?（2）当线性方程组有解时, 试用基础解系表示通解.解设题中线性方程组为.Ax b =用消元法, 对线性方程组Ax b =的增广矩阵A 施以行初等变换，化为阶梯形矩阵：⎪⎪⎪⎪⎪⎭⎫⎝⎛--−−−→−⎪⎪⎪⎪⎪⎭⎫⎝⎛----=ｂ－４０１００００００－１００１３２０ｂ１－１０初等行变换a a A 32117107141125313211 由此可知：当b ≠4时,)()(A r A r ≠ 线性方程组Ax b =无解; 当b =4时, 恒有)()(A r A r = 线性方程组Ax b =有解.若,3)()(,1==≠A r A r a 方程组有无穷多个解，通解为：T T )1,0,21,27()0,0,21,21(--+k k 为任意实数若,2)()(,1===A r A r a 方程组有无穷多个解，通解为：T 2T 1T )1,0,21,27()0,1,23,21()0,0,21,21(--+-+k k 21k k 、为任意实数 4．设矩阵,,321101210,324202423*1Q A Q B Q A -=⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛= 求E B 2010+的特征值和特征向量. 其中*A 是A 的伴随矩阵, E 为3阶单位矩阵. 解计算A 的特征多项式32422423--------=-λλλλA E .)1()8(2+-=λλ故A 的特征值为1,8321-===λλλ. 因为.,,8*X AX A X AX A i λλλ====∏则若所以*A 的特征值为1,-8,-8.由于Q A Q B *1-=与*A 相似, 相似矩阵有相同的特征值，所以E B 2010+的特征值为：2011，2002，2002.下面求特征向量, 因为X Q A X A Q X Q Q A Q X Q B 1*11*11||))(()(-----===λ,我们有矩阵B 的属于λA的特征向量为X Q 1-, 因此矩阵E B 2010+的属于2010+λA的特征向量为X Q 1-第三步求出A 的全部特征向量对于81=λ，求解线性方程组0)8(=-x A E 得特征向量 .2121⎪⎪⎪⎭⎫ ⎝⎛=α 对于132-==λλ，求解线性方程组0)(=--x A E 得特征向量.021,10132⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛-=αα第四步求出E B 2010+ 的全部特征向量，即计算312111,,ααα---Q Q Q .,012,23223,23121,21211111212113121111⎪⎪⎪⎭⎫⎝⎛-=⎪⎪⎪⎪⎪⎭⎫⎝⎛--=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛----=----αααQ Q Q Q综合以上分析我们有：矩阵E B 2010+属于特征值2011的特征向量为k ⎪⎪⎪⎪⎪⎭⎫⎝⎛--27121, k 为任意实数属于特征值2002的特征向量为 ,0122322321⎪⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎪⎪⎪⎭⎫⎝⎛--k k 21k k 、为任意实数四、证明题（每题6分，共12分）1. 已知向量组)1(,,,121>+s s s αααα 线性无关, 向量组s βββ,,21 可表示为),,2,1(1s i t i i i i =+=+ααβ, 其中i t 是实数. 证明s βββ,,21 线性无关.证明用定义. 假设存在 s 个数s k k k ,,21 , 使 02211=+++s s k k k βββ , 即 0)()()(132222111=+++++++s s s s t k t k t k αααααα , 也就是0)()()(11133212221111=++++++++++--s s s s s s s t k k t k k t k k t k k ααααα .又因为)1(,,,121>+s s s αααα 线性无关, 所以上式中系数部分都为0, 即⎪⎪⎪⎩⎪⎪⎪⎨⎧==+=+=--0000112111s s s s s t k k t k k t k k 解得 021====s k k k , 故s βββ,,21 线性无关. 2. 设n 阶矩阵 A 满足022=-+E A A 且E A ≠. 证明A 相似于对角矩阵.证由022=-+E A A 可得 ))(2(0)2)((E A A E A E A E ---==+- (1)可得A 的特征值为 1或 -2，要证明A 相似于对角矩阵，也就是A 可以对角化，即要证明A 有n 个线性无关的特征向量。

北京工业大学线性代数07-08二学期末考试题

北京工业大学2007-2008学年第二学期期末线性代数(工) 课程试卷（A ）考试方式：闭卷考试时间：2008年06月25日学号姓名成绩注：本试卷共8大题，满分100分. 得分登记（由阅卷教师填写）一. 填空题（每小题3分，共30 分）.1. 矩阵乘积100123401056783019101112⎛⎫⎛⎫ ⎪⎪= ⎪⎪ ⎪⎪-⎝⎭⎝⎭2. 设n 阶方阵A B 、满足AB A B =+，则A E -可逆，且1()A E --=3. 如果2阶方阵A 的特征值是1,1-，*A 为其伴随矩阵，则行列式*2A E -=4. 设3维列向量组321,,ααα和21,ββ满足122123123αβαββαββ=⎧⎪=-+⎨⎪=-⎩，则由向量组321,,ααα构成的矩阵123()ααα的行列式等于（写出具体数值）5. 如果211110139pp =-，而且0p >，则p = 6.如果实系数方程组112233100b xc y b x c y b x c y +=-⎧⎪+=⎨⎪+=⎩有实数解，则行列式2233b c b c =7. 设121,0λλ=-=是实对称矩阵A 的特征值，(2,2,1),(1,1,2)T Tt t αβ=+=+--是分别属于1,1-的特征向量，则t =8. 如果(1,1,1)Tα=-是实方阵A 的一个特征向量，则223A E -必有一个特征向量等于9.如果13133a ⎛⎫ ⎪⎪ ⎪- ⎪⎝⎭是正交矩阵，则a = 10. 二次型112323233(,,)112341x x x x x x ⎛⎫⎛⎫ ⎪⎪- ⎪⎪ ⎪⎪--⎝⎭⎝⎭的正惯性指数与负惯性指数之和是二. 单项选择题（每小题3分，共15分）。

将正确答案的字母填入括号内。

1. 如果n 阶实矩阵A 满足30A =，E 是n 阶单位矩阵，则【】（A ）A E +可逆，但A E -不可逆（B ）A E +不可逆，但A E -可逆（C ）A E +、A E -都可逆（D ）A E +、A E -都不可逆2. 如果向量组1234,,,αααα线性无关，而且其中的每一个向量都与向量β正交，则向量组1234,,,,ααααβ 【】 (A) 一定线性相关（B ）一定线性无关（C ）可能线性相关，也可能线性无关（D ）前三个选项都不正确 3. 设A 是n 阶方阵，则下列选项中不正确的是【】（A ）当线性方程组b AX =无解时，行列式0A =。

线性代数2007-2008第一学期试卷A

浙江工业大学《线性代数》试卷 (A)(2007—2008学年第一学期) 2008.6一、填空(每空2分,共24分)1、在四阶行列式中，乘积项43213412a a a a 的符号为号。

2、设,B C 为n 阶可逆方阵，00B A C⎛⎫=⎪⎝⎭，则T A = ；1A -= 。

3、设,A B 均为n 阶方阵，且满足2,3A B ==，则()AB *= 。

4、设 100010b A ac ⎛⎫⎪= ⎪ ⎪⎝⎭，当,,a b c 分别为时，A 为对称阵；A 的伴随阵为；当,,a b c 满足条件时，A 为正交阵。

5、向量组⎛⎫ ⎪ ⎪ ⎪⎝⎭141、k ⎛⎫ ⎪ ⎪ ⎪⎝⎭14、⎛⎫ ⎪ ⎪⎪⎝⎭120为3R 的一组基, 则k 必须满足的条件是。

6、线性方程组AX β=有无穷多解的充要条件是。

7向量TT)0,1,0,1,0(,)1,0,1,0,1(==βα8、设二阶方阵A 、B 相似，A 的特征值为2、3，则1-B 的特征值为，而*B 的特征值为。

二、单项选择题（每小题2分，共12分）1、以下结论正确的是（）。

A 、若2=A 0，则A =0；B 、若方阵A 的行列式0=A ，则A =0；C 、若=A B 0，则A =0或B =0；D 、若方阵A 对称，则2A 也对称。

2、下列四项中，向量组T 线性相关的充分必要条件是（）。

A 、向量组T 中至少有一个是零向量；B 、向量组T 中至少有两个向量的分量成比例；C 、向量组T 中至少有一个向量能由其余向量线性表示；D 、向量组T 中至少有一个部分向量组线性相关。

3、下列矩阵中，（）不是初等矩阵。

A 、100001010⎛⎫ ⎪ ⎪ ⎪⎝⎭ ； B 、001010101⎛⎫ ⎪ ⎪ ⎪⎝⎭； C 、100015001⎛⎫ ⎪ ⎪ ⎪⎝⎭； D 、001010100⎛⎫⎪ ⎪ ⎪⎝⎭。

4、若n 阶方阵A 可逆，则下列各项中不是A 可逆的充分必要条件的是（）。