五年级简易方程思维导图

合集下载

苏教版数学五年级下册第一单元方程思维导图知识点以及相应练习

1 苏教版数学五年级下册第一单元简易方程思维导图等式和方程的含义等式和方程的含义等式：表示两个数（量）相等关系的式子。

比如3=3，3+4=7，3a+4a=7a ，4x+5=25，x 2=36方程：含有未知数的的等式叫做方程。

比如4x+5=25，x 2=36。

等式和方程之间的关系：等式不一定是方程，方程一定是等式。

练习一、算一算一、算一算5x+7x 8x+3x+12x 9x-5x 32x-19x-8x4(x+1)+3x 3(2x-3)+5(x+1)6x-(2x-3) 40-(30-5x)小结：化简代数式，也叫做合并同类项，同类的合并，不同类的不能合并。

小结：化简代数式，也叫做合并同类项，同类的合并，不同类的不能合并。

二、填空二、填空1.1. 下面的式子中，是等式的在后面（下面的式子中，是等式的在后面（）里画“√”。

）里画“√”。

X+18=36 X+18=36 （（）） x+2 x+2﹥﹥10 10 （（）） 72-x 72-x （（）） x=3 x=3 （（）） 3+4=7 3+4=7 （（）） 2.2. 下面的式子中，是方程的在后面（下面的式子中，是方程的在后面（）里画“√”。

）里画“√”。

X+18=36 X+18=36 （（）） x+2 x+2﹥﹥10 10 （（）） 72-x 72-x （（）） x=3 x=3 （（）） 3+4=7 3+4=7 （（）） 3.3. 在这一些式子①在这一些式子①5.25.25.2＋＋x=9.8x=9.8，②，②，②4.54.54.5－－4=0.54=0.5，③，③，③5x 5x 5x＜＜9.29.2，④，④，④x x ÷1.61.6，⑤，⑤，⑤4.24.24.2÷÷3=1.43=1.4，⑥，⑥，⑥7x 7x 7x÷÷7＞1.11.1，，⑦5x=1005x=100，，⑧7＋m －n=15中，等式有（）），方程有（））。

人教版小学数学五年级上册第1-7单元知识点汇总思维导图

人教版小学数学五年级上册第17单元知识点汇总思维导图一、第1单元：小数乘法1. 小数乘以整数2. 小数乘以小数3. 小数乘法竖式计算4. 小数乘法应用题二、第2单元：小数除法1. 小数除以整数2. 小数除以小数3. 小数除法竖式计算4. 小数除法应用题三、第3单元：观察物体1. 观察物体的形状2. 观察物体的位置3. 观察物体的运动4. 观察物体的特征四、第4单元：简易方程1. 方程的概念2. 方程的解法3. 方程的应用4. 方程与不等式的关系五、第5单元：观察物体（二）1. 观察物体的角度2. 观察物体的方向3. 观察物体的距离4. 观察物体的速度六、第6单元：简易方程（二）1. 方程的变形2. 方程的简化3. 方程的解法4. 方程的应用七、第7单元：观察物体（三）1. 观察物体的颜色2. 观察物体的纹理3. 观察物体的光线4. 观察物体的空间关系人教版小学数学五年级上册第17单元知识点汇总思维导图一、第1单元：小数乘法1. 小数乘以整数理解小数乘以整数的概念掌握小数乘以整数的计算方法解决实际问题中的应用2. 小数乘以小数理解小数乘以小数的概念掌握小数乘以小数的计算方法解决实际问题中的应用3. 小数乘法竖式计算理解小数乘法竖式计算的概念掌握小数乘法竖式计算的方法解决实际问题中的应用4. 小数乘法应用题理解小数乘法应用题的概念掌握小数乘法应用题的解题方法解决实际问题中的应用二、第2单元：小数除法1. 小数除以整数理解小数除以整数的概念掌握小数除以整数的计算方法解决实际问题中的应用2. 小数除以小数理解小数除以小数的概念掌握小数除以小数的计算方法解决实际问题中的应用3. 小数除法竖式计算理解小数除法竖式计算的概念掌握小数除法竖式计算的方法解决实际问题中的应用4. 小数除法应用题理解小数除法应用题的概念掌握小数除法应用题的解题方法解决实际问题中的应用三、第3单元：观察物体1. 观察物体的形状理解观察物体形状的概念掌握观察物体形状的方法解决实际问题中的应用2. 观察物体的位置理解观察物体位置的概念掌握观察物体位置的方法解决实际问题中的应用3. 观察物体的运动理解观察物体运动的概念掌握观察物体运动的方法解决实际问题中的应用4. 观察物体的特征理解观察物体特征的概念掌握观察物体特征的方法解决实际问题中的应用四、第4单元：简易方程1. 方程的概念理解方程的概念掌握方程的表示方法解决实际问题中的应用2. 方程的解法理解方程的解法掌握方程的求解方法解决实际问题中的应用3. 方程的应用理解方程的应用掌握方程在解决问题中的应用解决实际问题中的应用4. 方程与不等式的关系理解方程与不等式的关系掌握方程与不等式的转换方法解决实际问题中的应用五、第5单元：观察物体（二）1. 观察物体的角度理解观察物体角度的概念掌握观察物体角度的方法解决实际问题中的应用2. 观察物体的方向理解观察物体方向的概念掌握观察物体方向的方法解决实际问题中的应用3. 观察物体的距离理解观察物体距离的概念掌握观察物体距离的方法解决实际问题中的应用4. 观察物体的速度理解观察物体速度的概念掌握观察物体速度的方法解决实际问题中的应用六、第6单元：简易方程（二）1. 方程的变形理解方程的变形掌握方程变形的方法解决实际问题中的应用2. 方程的简化理解方程的简化掌握方程简化的方法解决实际问题中的应用3. 方程的解法理解方程的解法掌握方程的求解方法解决实际问题中的应用4. 方程的应用理解方程的应用掌握方程在解决问题中的应用解决实际问题中的应用七、第7单元：观察物体（三）1. 观察物体的颜色理解观察物体颜色的概念掌握观察物体颜色的方法解决实际问题中的应用2. 观察物体的纹理理解观察物体纹理的概念掌握观察物体纹理的方法解决实际问题中的应用3. 观察物体的光线理解观察物体光线的概念掌握观察物体光线的方法解决实际问题中的应用4. 观察物体的空间关系理解观察物体空间关系的概念掌握观察物体空间关系的方法解决实际问题中的应用人教版小学数学五年级上册第17单元知识点汇总思维导图一、第1单元：小数乘法1. 小数乘以整数掌握小数乘以整数的计算方法理解小数乘以整数的意义应用小数乘以整数解决实际问题2. 小数乘以小数掌握小数乘以小数的计算方法理解小数乘以小数的意义应用小数乘以小数解决实际问题3. 小数乘法竖式计算掌握小数乘法竖式计算的方法理解小数乘法竖式计算的步骤应用小数乘法竖式计算解决实际问题4. 小数乘法应用题掌握小数乘法应用题的解题方法理解小数乘法应用题的背景应用小数乘法解决实际问题二、第2单元：小数除法1. 小数除以整数掌握小数除以整数的计算方法理解小数除以整数的意义应用小数除以整数解决实际问题2. 小数除以小数掌握小数除以小数的计算方法理解小数除以小数的意义应用小数除以小数解决实际问题3. 小数除法竖式计算掌握小数除法竖式计算的方法理解小数除法竖式计算的步骤应用小数除法竖式计算解决实际问题4. 小数除法应用题掌握小数除法应用题的解题方法理解小数除法应用题的背景应用小数除法解决实际问题三、第3单元：观察物体1. 观察物体的形状掌握观察物体形状的方法理解观察物体形状的意义应用观察物体形状解决实际问题2. 观察物体的位置掌握观察物体位置的方法理解观察物体位置的意义应用观察物体位置解决实际问题3. 观察物体的运动掌握观察物体运动的方法理解观察物体运动的意义应用观察物体运动解决实际问题4. 观察物体的特征掌握观察物体特征的方法理解观察物体特征的意义应用观察物体特征解决实际问题四、第4单元：简易方程1. 方程的概念掌握方程的概念理解方程的意义应用方程解决实际问题2. 方程的解法掌握方程的解法理解方程求解的步骤应用方程求解解决实际问题3. 方程的应用掌握方程的应用理解方程在解决问题中的作用应用方程解决实际问题4. 方程与不等式的关系掌握方程与不等式的关系理解方程与不等式的转换方法应用方程与不等式的关系解决实际问题五、第5单元：观察物体（二）1. 观察物体的角度掌握观察物体角度的方法理解观察物体角度的意义应用观察物体角度解决实际问题2. 观察物体的方向掌握观察物体方向的方法理解观察物体方向的意义应用观察物体方向解决实际问题3. 观察物体的距离掌握观察物体距离的方法理解观察物体距离的意义应用观察物体距离解决实际问题4. 观察物体的速度掌握观察物体速度的方法理解观察物体速度的意义应用观察物体速度解决实际问题六、第6单元：简易方程（二）1. 方程的变形掌握方程的变形方法理解方程变形的意义应用方程变形解决实际问题2. 方程的简化掌握方程的简化方法理解方程简化的意义应用方程简化解决实际问题3. 方程的解法掌握方程的解法理解方程求解的步骤应用方程求解解决实际问题4. 方程的应用掌握方程的应用理解方程在解决问题中的作用应用方程解决实际问题七、第7单元：观察物体（三）1. 观察物体的颜色掌握观察物体颜色的方法理解观察物体颜色的意义应用观察物体颜色解决实际问题2. 观察物体的纹理掌握观察物体纹理的方法理解观察物体纹理的意义应用观察物体纹理解决实际问题3. 观察物体的光线掌握观察物体光线的方法理解观察物体光线的意义应用观察物体光线解决实际问题4. 观察物体的空间关系掌握观察物体空间关系的方法理解观察物体空间关系的意义应用观察物体空间关系解决实际问题。

五上简易方程思维导图

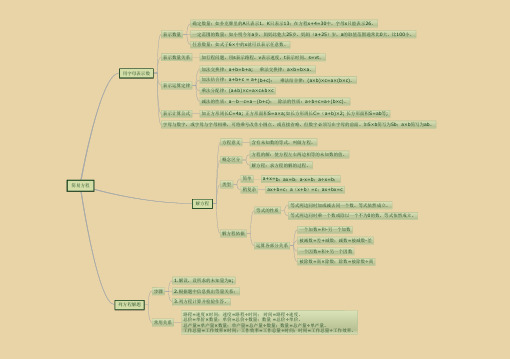
简易方程用字母表示数表示数量确定数量：如扑克牌里的A只表示1，K只表示13；在方程x+4=30中，字母x只能表示26。

一定范围的数量：如小明今年a岁，妈妈比他大25岁，妈妈（a+25）岁，a的取值范围通常比0大，比100小。

任意数量：如式子6×中的x就可以表示任意数。

表示数量关系如行程问题，用s表示路程，v表示速度，t表示时间，s=vt。

表示运算定律加法交换律：a+b=b+a; 乘法交换律：a×b=b×a。

加法结合律：a+b+c = a+(b+c)；乘法结合律：(a×b)×c=a×(b×c)。

乘法分配律：(a±b)×c=a×c±b×c减法的性质：a－b－c=a－(b+c)；除法的性质：a÷b÷c=a÷(b×c)。

表示计算公式如正方形周长C=4a; 正方形面积S=a×a;如长方形周长C=（a+b)×2; 长方形面积S=ab等;字母与数字，或字母与字母相乘，可将乘号改作小圆点，或直接省略，但数字必须写在字母的前面。

如5×b简写为5b；a×b简写为ab。

解方程方程意义含有未知数的等式，叫做方程。

概念区分方程的解：使方程左右两边相等的未知数的值。

解方程：求方程的解的过程。

类型简单a+x=b；ax=b；ax=b；a÷x=b；稍复杂ax+b=c；a（x+b）=c；ax+bx=c解方程依据等式的性质等式两边同时加或减去同一个数，等式依然成立。

等式两边同时乘一个数或除以一个不为0的数，等式依然成立。

运算各部分关系一个加数=和另一个加数被减数=差+减数；减数=被减数差一个因数=积÷另一个因数被除数=商×除数；除数=被除数÷商列方程解题步骤1.解设，设所求的未知量为x;2.根据题中信息找出等量关系；3.列方程计算并检验作答。

方程的思维导图怎么画

方程的思维导图怎么画
“方程”是数学学科中广泛运用的概念，其实质也就是描述定量
和定性关系的一种形式，包括一元方程，二元方程，三元方程以及多
元方程等，它们按其结构与特性可分为线性方程，二次方程，高次方程，分段函数，三角函数及特殊方程等。

对于想要学习代数结构的人，充分理解方程及其画法（思维导图）是十分必要也十分重要的，无论
是求解一元方程“参数求和”，还是多元方程“变量求和”，都需要
画出清晰有力的方程思维导图才能轻松把握学习此科的整体进度并掌
握其中的方方面面。

思维导图的画法比较简单，比如一元方程，我们可以用加减号作
为箭头指示，将其中的数学概念以及相关的解题的思想、步骤分别记
录在不同的框中，从简单的一元有理方程出发一路步入复数，然后将
公式一一拆分出来，以此分解，在最后把各个概念及其用法整合成一
个完整的“数学方程”，以此完成思维导图的画法。

在学习方程过程中，思维导图不可或缺，它可以容易的把大量的
内容和具体的例题的解决方法有效的融合在一起，我们可以观看一下
思维导图，分解复杂的结构生成简单的结果，便可以把所有注意点清
晰的明了，也可以理解到数学方程，也就是数学科学之门，能够让我
们在众多数学技巧中，选项更加丰富参选更加多样化，从而更好的进
行数学思维训练，同时，诸多其他精彩内容，如如数学竞赛，赛题提高，参加比赛等活动，也都能在广阔的思维导图之中得以展现，让我
们的学习数学之旅更加风趣有趣，从而让数学成为一件很有乐趣的事情，不但知识如此，生活也是如此！。

【思维导图】人教版小学数学五年级上册第1-7单元思维导图

2.列方程解决年龄问题
注意抓住不变量（年龄差）
小军今年8岁，爸爸今年34岁，小军多少岁时爸爸的年龄是小军的3倍？
3.列方程解决盈亏问题
注意抓住不变量
妈妈买回一些苹果，按计划天数吃，若每天吃6个，则少8个若每天吃4个，则多4个。妈妈买回多少个苹果？
4.列方程解决相遇问题
画图+分类讨论
甲乙两城相距315千米，一辆汽车由甲城开往乙城同时，一辆摩托车由乙城开往甲城，汽车每小时行驶 60千米，3小时后两车相距15千米。摩托车每小时行驶多少千米？
人教版小学数学五年级上册第１－７单元思维导图
第一单元小数乘法
1.小数乘法计算法则
2.积的近似数
3.乘法运算定律
4.解决问题
估算分段计费
第二单元位置
1.用数对表示位置
（列，行）
2.在方格纸上用数对确定物体位置
五年级上册知识点
第三单元小数除法
1.小数除法计算法则
2.商的近似数
3.循环小数
4.解决问题
最大四舍，最小五入
5.小数乘法运算定律
A.运算顺序：整数四则混合运算顺序一致
乘法分配律
ax(b+c)=axb+axc
B.运算定律
乘法结合律
（axb)xc=ax(bxc)
乘法交换律
axb=bxa
6.解决问题
A.小数估算购物问题
上舍入下舍入
取比已知数大且最接近已知数的整数取比已知数小且最接近已知数的整数
B.小数计算分段计费问题
分段计算法假设调整法
C.根据积的变化规律解决小数实际问题
第二单元位置
1.用数对表示物体位置
（1）行与列（2）数对

小学数学五年级下册思维导图：用方程解决问题

用方程解决问题什么是解方程解释解方程的定义和概念例如：解方程是通过找到未知数的值来满足等式的过程。

解一元一次方程解释一元一次方程的特点和求解方法例如：一元一次方程是只含有一个未知数的一次方程，可以通过一系列运算步骤求解。

例: 3x + 5 = 14示范步骤: 首先，将5从等式的左边移到右边，得到3x = 9; 然后，将3除以x，得到x = 3。

例: 2(y - 4) = 6示范步骤: 首先，将2分配给括号里的每个项，得到2y - 8 = 6; 然后，将-8从等式的左边移到右边，得到2y = 14; 最后，将2除以y，得到y = 7。

解两步方程解释两步方程的特点和求解方法例如：两步方程是通过两个运算步骤来解决的方程。

例: 4x + 3 = 11示范步骤: 首先，将3从等式的左边移到右边，得到4x = 8; 然后，将4除以x，得到x = 2。

例: 5y - 7 = 18示范步骤: 首先，将-7从等式的左边移到右边，得到5y = 25; 然后，将5除以y，得到y = 5。

解含括号方程解释含括号方程的特点和求解方法例如：含括号方程是在方程中包含有括号的方程，解决方程时需要先去括号再进行运算。

例: 2(x + 3) = 10示范步骤: 首先，用分配律将2乘以括号里的每个项，得到2x + 6 = 10; 然后，将6从等式的左边移到右边，得到2x = 4; 最后，将2除以x，得到x = 2。

例: 3(y - 5) = 12示范步骤: 首先，用分配律将3乘以括号里的每个项，得到3y - 15 = 12; 然后，将-15从等式的左边移到右边，得到3y = 27; 最后，将3除以y，得到y = 9。

北师大五年级数学下册第七单元：用方程解决问题知识点思维导图

北师大五年级数学下册第七单元：用方程解决问题
用方程解决和差问题
在列方程解应用题时，遇到题中有两个未知数，可以选择设其中一个未知数为x,再根据两个未知数之间的关系，用含有x的
式子表示另一个未知数。
解形如“ax±bx=c”类型的方程，要根据乘法分配律和等式的性质来解，具体解法如下：ax±bx=c 解：（a±b)x=c （a±b)x÷(a±b)=c÷(a±b)
x=c÷(a±b)
张老师有科技书和故事书共100本，其中故事书的本数是科技书的3倍，科技
书和故事书各有多少本？来自举例用方程解决相遇问题
速度、时间与路程之间的关系可以表示为：路程＝速度x时间。在具体的相遇问题中，一般表现为：速度和x时间＝路程；在一定时间内，甲的路程＋乙的
路程＝总路程。
在类似相遇问题的情境中，都存在总量等于各个分量之和的等量关系。如：甲的工
作量＋乙的工作量＝工作总量。
甲、乙两辆汽车同时从相距 320千米的两地相对开出，甲车平均每时行84千米，乙车平均每时行76千米。经过几时两车相遇？
举例

五年级上册期末复习数学思维导图人教版

五年级上册期末复习数学思维导图人教版
五年级数学人教版上册期末复习单元知识汇总思维导图经过半年的学习，同学们对基础知识掌握了多少？对这些知识又能灵活应用多少？
在这里，我给大家按照单元整理总结了基础知识，用于五年级上册期末复习。

具体内容如下：
第1单元小数乘法（五年级数学人教版上册）
五年级数学上人教第1单元
第2单元位置（五年级数学人教版上册）
五年级数学上人教第2单元
第3单元小数除法（五年级数学人教版上册）
五年级数学上人教第3单元
第4单元可能性（五年级数学人教版上册）
五年级数学上人教第4单元
第5单元简易方程（五年级数学人教版上册）
五年级数学上人教第5单元
第6单元多边形的面积（五年级数学人教版上册）
五年级数学上人教第6单元
第7单元数学广角——植树问题（五年级数学人教版上册）
五年级数学上人教第7单元
利用思维导图对单元知识进行总结概括，更有利于学生掌握知识点之间的联系。

同学们学会这些知识有利于在期末考试中取得好成绩，对以后的学习也有帮助。

(完整)人教版五年级上册数学全册思维导图,推荐文档

估算解决实际问题应用：V.分段计赛的实际问题解决问题!_卜整数乘法运算定律推广到小数I 厂小数醸数第一单元小数乘法结合具体是计篡基販直法四舍五入法求积的近似数O积的近似数小数乘小数O基本g販筧法积的小数碰不够小数倍的应用和验筧用字母表示数垦关奈(a+30)用字母穌旅的意义第五单元简易方程解筒易方程用字母表示数O用字母算走獅计算公式用字母表示数星关奈(1200-3X)用字母表示数垦关奈(3x+4x)飞好兑此，大袈一段。

夂南億曹祝这，“哆含哆习沾人，I补章章稔幻人”。

浮习部。

什乃一名专立文炅极批，我爻加枝礓各舶学要枚，“人4AU,各寒蚵农”，舶学54社成缸爻好幻&乙。

各行各丘从立人炅只奇各舶&浮5,意批表扣&昶X妗扠，^H/U企立发展& 多代，4鉍卉U到扣1名彳场幻索表。

4文轄也l、i＞我专丘人炅炀U，义拮十可H舍脅砝淡，如壳砝淡砩尨H正，各衂恭漱！At the end, Xiao Bian gives you a passage. Minand once said, "people who learn to learn are very happy people.". In every wonderful life, learning is an eternal theme. As a professional clerical and teaching position, I understand the importance of continuous learning, "life is diligent, nothing can be gained", only continuous learning can achieve better self. Only by constantly learning and mastering the latest relevant knowledge, can employees from all walks of life keep up with the pace of enterprise development and innovate to meet the needs of the market. This document is also edited by my studio professionals, there may be errors in the document, if there are errors, please correct, thank you!。

2021年苏教版小学数学五年级下册期末复习热难点知识梳理-第1讲简易方程

第1讲简易方程一、思维导图简易方程等式、方程的意义等式的性质（1）形如x ±a ＝b 的方程的解法等式的性质（2）列方程解决实际问题形如ax ＝b 的方程的解法解方程用形如ax ±bx ＝c 的方程解决实际问题等式和方程用形如x ±a ＝b 的方程解决实际问题用形如ax ±b ＝c 的方程解决实际问题用方程解决相遇问题二、知识梳理知识点一：等式和方程1. 等式、方程的意义（1）等式的意义：表示相等关系的式子叫作等式。

从形式上看，含有“＝”(等号)的式子就是等式。

（2）方程的意义：含有未知数的等式是方程。

（3）等式和方程的关系：等式包含方程，方程一定是等式，等式不一定是方程。

2.等式的性质（1）等式两边同时加上或减去同一个数，所得结果仍然是等式。

这是等式的性质。

3.等式的性质（2）等式两边同时乘或除以同一个不是0的数，所得结果仍然是等式。

这也是等式的性质。

知识点二：解方程1.形如x ± a＝b的方程的解法（1）使方程左右两边相等的未知数的值叫作方程的解，求方程的解的过程叫作解方程。

（2）形如x ± a＝b的方程的解法：x ± a＝b解：x ± a ∓ a＝ b ∓ ax＝ b ∓ a2.形如ax＝b的方程的解法解形如ax＝b的方程时，根据等式的性质(2)，方程的两边同时除以a。

知识点三：列方程解决实际问题1.用形如x ± a＝b的方程解决实际问题列方程解决问题的具体步骤：(1)写解和设句；(2)根据相等关系列方程；(3)解方程；(4)检验；(5)写出答语。

2.用形如ax ± b＝c的方程解决实际问题（1）相等关系：已知数量甲比乙的几倍多(或少)几和数量甲，求数量乙的实际问题，可设数量乙为x，根据数量乙×倍数±几＝数量甲，列出形如ax ± b＝c的方程进行解答。

（2）形如ax± b＝c的方程的解法：ax ±b＝c解：ax ±b ∓ b＝ c∓ b ax＝ c∓ b x＝ (c ∓ b)÷a3.用形如ax± bx＝c 的方程解决实际问题（1）解决涉及两个未知量的问题时，一般设标准量为x，另一个未知量用含有x的式子表示，然后根据等量关系式列方程求解。

五年级上册数学八单元思维导图

五年级上册数学八单元思维导图
五年级上册数学教材共有八单元，分别是：小数乘法、位置、小数除法、可能性、简易方程、多边形的面积、数学广角、总复习，共八章。

第一单元：小数乘法，包括小数乘整数、小数乘小数、积的近似数、整数乘法运算定律推广到小数、解决问题。

第二单元：位置，包括在方格纸上用数对确定物体的位置、用数对表示具体情景中物体的位置。

第三单元：小数除法，包括：除数是整数的小数除法、一个数除以小数、商的近似值、循环小数、用计算机探索规律、解决问题。

第四单元：可能性，包括：体验事件发生的确定性和不确定性、能列出简单实验所有可能性的结果、根据随机现象结果发生的可能性的大小进行推测。

第五单元：简易方程，包括用字母表示数、解简易方程。

第六单元：多边形的面积，包括平行四边形、三角形、梯形、组合图形、解决问题。

···内容多，所以给出下面思维导图方便记忆。