Hyperchem学习
化学信息学——第八讲hyperchem 软件学习

HyperChem程序简介 7.5版新增功能 OpenGL绘图: 基础演示模式:已全部转换为全新的 OpenGL模式,使分子演示图形具有更高 质量支持自定义色彩,1600万种颜色代替 了传统的8种标准色。 混合演示:棒型,球型或组合型等分子 演示手段可以用于该分子的任意原子及链 段的演示,及全新的适用于原子的"管型" 演示。增强的蛋白质模型构建功能,支持 多种蛋白质二级结构演示,大分子的电子 密度近似方法。
13
工具 条 •使用图标工具可以简化操作 •从左至右分别是绘制、选择、旋转、平面 转动、平移
14
工作状态
•工作 区: •状态 行:
15
2、打开已存在的数据文件 •File-Open
16
浏览文件夹
17
C60分子
18
选择分子图形的显示方式 •Display- Labels可以选择原子、化学键等 标记方式:
39
计算几何构型 •COMPUTE---GEOMETRY
40
计算结果 •优化结束
41
测量键长、键角、二面角等结构参数 •数值显示在底部状态栏
42
单点能计算
•对给定体系优化构型后,可对优化后的构 型再进行单点计算。
43
单点能结果 •单点能结果
44
输出结果
45
计算结果的输出文件
• • • • • • • • • • • • • • • HyperChemlog start -- Sun May 28 21:38:15 2000. Geometry optimization, SemiEmpirical, molecule = (untitled). CNDO PolakRibiere optimizer Convergence limit = 0.0001000 Iteration limit = 50 Accelerate convergence = YES Optimization algorithm = Polak-Ribiere Criterion of RMS gradient = 0.0100 kcal/(A mol) Maximum cycles = 150 RHF Calculation: Singlet state calculation Number of electrons = 22 Number of Double Occupied Levels = 11 Charge on the System = 0 Total Orbitals = 22
hyperchem应用-辛烷

Hyperchem程序应用-辛烷1、画辛烷分子模型:辛烷分子碳碳骨架结构:加氢并模型化:2、用半经验方法CNDO进行优化3、选用从头算计算方法进行单点计算:4、显示原子电荷、显示键长、显示键角、二面角:5、分子性质:6、分子轨道图-最高占据轨道2D、3D图:7、分子轨道图-最低空轨道2D、3D图:8辛烷分子总电荷密度图(2D、3D):8、辛烷分子2D、3D静电势图、等值面图:9、分子结构模型表示:10、计算输出结果:HyperChem log start -- Mon Dec 13 18:37:31 2010.Geometry optimization, SemiEmpirical, molecule = (untitled).CNDOFletcherReeves optimizerConvergence limit = 0.0001000 Iteration limit = 50Accelerate convergence = YESOptimization algorithm = Fletcher-ReevesCriterion of RMS gradient = 0.1000 kcal/(A mol) Maximum cycles = 345RHF Calculation:Singlet state calculationNumber of electrons = 44Number of Double Occupied Levels = 22Charge on the System = 0Total Orbitals = 44Starting CNDO calculation with 44 orbitalsE=0.0000 Grad=0.000 Conv=NO(0 cycles 0 points) [Iter=1 Diff=14292.75153]E=0.0000 Grad=0.000 Conv=NO(0 cycles 0 points) [Iter=2 Diff=9.35887]E=0.0000 Grad=0.000 Conv=NO(0 cycles 0 points) [Iter=3 Diff=0.54071]E=0.0000 Grad=0.000 Conv=NO(0 cycles 0 points) [Iter=4 Diff=0.03993]E=0.0000 Grad=0.000 Conv=NO(0 cycles 0 points) [Iter=5 Diff=0.00066]E=0.0000 Grad=0.000 Conv=NO(0 cycles 0 points) [Iter=6 Diff=0.00004]E=-5569.6934 Grad=74.633 Conv=NO(0 cycles 1 points) [Iter=1 Diff=115.68581] E=-5569.6934 Grad=74.633 Conv=NO(0 cycles 1 points) [Iter=2 Diff=9.46473] E=-5569.6934 Grad=74.633 Conv=NO(0 cycles 1 points) [Iter=3 Diff=0.86416] E=-5569.6934 Grad=74.633 Conv=NO(0 cycles 1 points) [Iter=4 Diff=0.10244] E=-5569.6934 Grad=74.633 Conv=NO(0 cycles 1 points) [Iter=5 Diff=0.00180] E=-5569.6934 Grad=74.633 Conv=NO(0 cycles 1 points) [Iter=6 Diff=0.00012] E=-5569.6934 Grad=74.633 Conv=NO(0 cycles 1 points) [Iter=7 Diff=0.00001] E=-5516.4321 Grad=113.901 Conv=NO(0 cycles 2 points) [Iter=1 Diff=46.41182] E=-5516.4321 Grad=113.901 Conv=NO(0 cycles 2 points) [Iter=2 Diff=3.63947]E=-5516.4321 Grad=113.901 Conv=NO(0 cycles 2 points) [Iter=3 Diff=0.32064] E=-5516.4321 Grad=113.901 Conv=NO(0 cycles 2 points) [Iter=4 Diff=0.03685] E=-5516.4321 Grad=113.901 Conv=NO(0 cycles 2 points) [Iter=5 Diff=0.00059] E=-5516.4321 Grad=113.901 Conv=NO(0 cycles 2 points) [Iter=6 Diff=0.00003] E=-5613.0083 Grad=6.496 Conv=NO(1 cycles 3 points) [Iter=1 Diff=0.06673] E=-5613.0083 Grad=6.496 Conv=NO(1 cycles 3 points) [Iter=2 Diff=0.00512] E=-5613.0083 Grad=6.496 Conv=NO(1 cycles 3 points) [Iter=3 Diff=0.00050] E=-5613.0083 Grad=6.496 Conv=NO(1 cycles 3 points) [Iter=4 Diff=0.00007] E=-5613.5781 Grad=3.499 Conv=NO(1 cycles 4 points) [Iter=1 Diff=0.06718] E=-5613.5781 Grad=3.499 Conv=NO(1 cycles 4 points) [Iter=2 Diff=0.00516] E=-5613.5781 Grad=3.499 Conv=NO(1 cycles 4 points) [Iter=3 Diff=0.00050] E=-5613.5781 Grad=3.499 Conv=NO(1 cycles 4 points) [Iter=4 Diff=0.00007] E=-5613.6587 Grad=4.830 Conv=NO(1 cycles 5 points) [Iter=1 Diff=0.00755] E=-5613.6587 Grad=4.830 Conv=NO(1 cycles 5 points) [Iter=2 Diff=0.00058] E=-5613.6587 Grad=4.830 Conv=NO(1 cycles 5 points) [Iter=3 Diff=0.00006] E=-5613.6865 Grad=3.874 Conv=NO(2 cycles 6 points) [Iter=1 Diff=0.09278] E=-5613.6865 Grad=3.874 Conv=NO(2 cycles 6 points) [Iter=2 Diff=0.00694] E=-5613.6865 Grad=3.874 Conv=NO(2 cycles 6 points) [Iter=3 Diff=0.00063] E=-5613.6865 Grad=3.874 Conv=NO(2 cycles 6 points) [Iter=4 Diff=0.00008] E=-5613.8223 Grad=3.477 Conv=NO(2 cycles 7 points) [Iter=1 Diff=0.00902] E=-5613.8223 Grad=3.477 Conv=NO(2 cycles 7 points) [Iter=2 Diff=0.00067] E=-5613.8223 Grad=3.477 Conv=NO(2 cycles 7 points) [Iter=3 Diff=0.00006] E=-5613.8574 Grad=2.075 Conv=NO(3 cycles 8 points) [Iter=1 Diff=0.00837] E=-5613.8574 Grad=2.075 Conv=NO(3 cycles 8 points) [Iter=2 Diff=0.00083] E=-5613.8574 Grad=2.075 Conv=NO(3 cycles 8 points) [Iter=3 Diff=0.00010] E=-5613.8574 Grad=2.075 Conv=NO(3 cycles 8 points) [Iter=4 Diff=0.00002] E=-5613.9468 Grad=1.293 Conv=NO(3 cycles 9 points) [Iter=1 Diff=0.00837] E=-5613.9468 Grad=1.293 Conv=NO(3 cycles 9 points) [Iter=2 Diff=0.00083] E=-5613.9468 Grad=1.293 Conv=NO(3 cycles 9 points) [Iter=3 Diff=0.00010] E=-5613.9468 Grad=1.293 Conv=NO(3 cycles 9 points) [Iter=4 Diff=0.00002] E=-5613.9312 Grad=2.539 Conv=NO(3 cycles 10 points) [Iter=1 Diff=0.00351] E=-5613.9312 Grad=2.539 Conv=NO(3 cycles 10 points) [Iter=2 Diff=0.00035] E=-5613.9312 Grad=2.539 Conv=NO(3 cycles 10 points) [Iter=3 Diff=0.00004] E=-5613.9531 Grad=1.581 Conv=NO(4 cycles 11 points) [Iter=1 Diff=0.03067] E=-5613.9531 Grad=1.581 Conv=NO(4 cycles 11 points) [Iter=2 Diff=0.00315] E=-5613.9531 Grad=1.581 Conv=NO(4 cycles 11 points) [Iter=3 Diff=0.00041] E=-5613.9531 Grad=1.581 Conv=NO(4 cycles 11 points) [Iter=4 Diff=0.00007] E=-5614.0254 Grad=1.729 Conv=NO(4 cycles 12 points) [Iter=1 Diff=0.03082] E=-5614.0254 Grad=1.729 Conv=NO(4 cycles 12 points) [Iter=2 Diff=0.00317] E=-5614.0254 Grad=1.729 Conv=NO(4 cycles 12 points) [Iter=3 Diff=0.00041] E=-5614.0254 Grad=1.729 Conv=NO(4 cycles 12 points) [Iter=4 Diff=0.00007] E=-5613.9551 Grad=3.772 Conv=NO(4 cycles 13 points) [Iter=1 Diff=0.03047] E=-5613.9551 Grad=3.772 Conv=NO(4 cycles 13 points) [Iter=2 Diff=0.00314] E=-5613.9551 Grad=3.772 Conv=NO(4 cycles 13 points) [Iter=3 Diff=0.00041]E=-5614.0254 Grad=1.739 Conv=NO(5 cycles 14 points) [Iter=1 Diff=0.10421] E=-5614.0254 Grad=1.739 Conv=NO(5 cycles 14 points) [Iter=2 Diff=0.00961] E=-5614.0254 Grad=1.739 Conv=NO(5 cycles 14 points) [Iter=3 Diff=0.00112] E=-5614.0254 Grad=1.739 Conv=NO(5 cycles 14 points) [Iter=4 Diff=0.00018] E=-5614.0254 Grad=1.739 Conv=NO(5 cycles 14 points) [Iter=5 Diff=0.00000] E=-5614.0059 Grad=2.873 Conv=NO(5 cycles 15 points) [Iter=1 Diff=0.02966] E=-5614.0059 Grad=2.873 Conv=NO(5 cycles 15 points) [Iter=2 Diff=0.00274] E=-5614.0059 Grad=2.873 Conv=NO(5 cycles 15 points) [Iter=3 Diff=0.00032] E=-5614.0059 Grad=2.873 Conv=NO(5 cycles 15 points) [Iter=4 Diff=0.00005] E=-5614.0864 Grad=0.979 Conv=NO(6 cycles 16 points) [Iter=1 Diff=0.00695] E=-5614.0864 Grad=0.979 Conv=NO(6 cycles 16 points) [Iter=2 Diff=0.00061] E=-5614.0864 Grad=0.979 Conv=NO(6 cycles 16 points) [Iter=3 Diff=0.00007] E=-5614.1025 Grad=0.870 Conv=NO(6 cycles 17 points) [Iter=1 Diff=0.00052] E=-5614.1025 Grad=0.870 Conv=NO(6 cycles 17 points) [Iter=2 Diff=0.00005] E=-5614.1055 Grad=0.577 Conv=NO(7 cycles 18 points) [Iter=1 Diff=0.00479] E=-5614.1055 Grad=0.577 Conv=NO(7 cycles 18 points) [Iter=2 Diff=0.00048] E=-5614.1055 Grad=0.577 Conv=NO(7 cycles 18 points) [Iter=3 Diff=0.00006] E=-5614.1069 Grad=0.931 Conv=NO(7 cycles 19 points) [Iter=1 Diff=0.00096] E=-5614.1069 Grad=0.931 Conv=NO(7 cycles 19 points) [Iter=2 Diff=0.00010] E=-5614.1108 Grad=0.447 Conv=NO(8 cycles 20 points) [Iter=1 Diff=0.00213] E=-5614.1108 Grad=0.447 Conv=NO(8 cycles 20 points) [Iter=2 Diff=0.00018] E=-5614.1108 Grad=0.447 Conv=NO(8 cycles 20 points) [Iter=3 Diff=0.00002] E=-5614.1177 Grad=0.476 Conv=NO(8 cycles 21 points) [Iter=1 Diff=0.00213] E=-5614.1177 Grad=0.476 Conv=NO(8 cycles 21 points) [Iter=2 Diff=0.00018] E=-5614.1177 Grad=0.476 Conv=NO(8 cycles 21 points) [Iter=3 Diff=0.00002] E=-5614.1167 Grad=0.939 Conv=NO(8 cycles 22 points) [Iter=1 Diff=0.00085] E=-5614.1167 Grad=0.939 Conv=NO(8 cycles 22 points) [Iter=2 Diff=0.00007] E=-5614.1182 Grad=0.627 Conv=NO(9 cycles 23 points) [Iter=1 Diff=0.02140] E=-5614.1182 Grad=0.627 Conv=NO(9 cycles 23 points) [Iter=2 Diff=0.00201] E=-5614.1182 Grad=0.627 Conv=NO(9 cycles 23 points) [Iter=3 Diff=0.00022] E=-5614.1182 Grad=0.627 Conv=NO(9 cycles 23 points) [Iter=4 Diff=0.00003] E=-5614.1118 Grad=1.125 Conv=NO(9 cycles 24 points) [Iter=1 Diff=0.00758] E=-5614.1118 Grad=1.125 Conv=NO(9 cycles 24 points) [Iter=2 Diff=0.00071] E=-5614.1118 Grad=1.125 Conv=NO(9 cycles 24 points) [Iter=3 Diff=0.00008] E=-5614.1235 Grad=0.266 Conv=NO(10 cycles 25 points) [Iter=1 Diff=0.00049] E=-5614.1235 Grad=0.266 Conv=NO(10 cycles 25 points) [Iter=2 Diff=0.00005] E=-5614.1260 Grad=0.299 Conv=NO(10 cycles 26 points) [Iter=1 Diff=0.00049] E=-5614.1260 Grad=0.299 Conv=NO(10 cycles 26 points) [Iter=2 Diff=0.00005] E=-5614.1245 Grad=0.624 Conv=NO(10 cycles 27 points) [Iter=1 Diff=0.00036] E=-5614.1245 Grad=0.624 Conv=NO(10 cycles 27 points) [Iter=2 Diff=0.00004] E=-5614.1260 Grad=0.339 Conv=NO(11 cycles 28 points) [Iter=1 Diff=0.00379] E=-5614.1260 Grad=0.339 Conv=NO(11 cycles 28 points) [Iter=2 Diff=0.00040] E=-5614.1260 Grad=0.339 Conv=NO(11 cycles 28 points) [Iter=3 Diff=0.00005]E=-5614.1328 Grad=0.318 Conv=NO(11 cycles 29 points) [Iter=2 Diff=0.00040] E=-5614.1328 Grad=0.318 Conv=NO(11 cycles 29 points) [Iter=3 Diff=0.00005] E=-5614.1348 Grad=0.524 Conv=NO(11 cycles 30 points) [Iter=1 Diff=0.01513] E=-5614.1348 Grad=0.524 Conv=NO(11 cycles 30 points) [Iter=2 Diff=0.00160] E=-5614.1348 Grad=0.524 Conv=NO(11 cycles 30 points) [Iter=3 Diff=0.00020] E=-5614.1348 Grad=0.524 Conv=NO(11 cycles 30 points) [Iter=4 Diff=0.00003] E=-5614.1270 Grad=1.092 Conv=NO(11 cycles 31 points) [Iter=1 Diff=0.01436] E=-5614.1270 Grad=1.092 Conv=NO(11 cycles 31 points) [Iter=2 Diff=0.00152] E=-5614.1270 Grad=1.092 Conv=NO(11 cycles 31 points) [Iter=3 Diff=0.00019] E=-5614.1270 Grad=1.092 Conv=NO(11 cycles 31 points) [Iter=4 Diff=0.00003] E=-5614.1348 Grad=0.538 Conv=NO(12 cycles 32 points) [Iter=1 Diff=0.14614] E=-5614.1348 Grad=0.538 Conv=NO(12 cycles 32 points) [Iter=2 Diff=0.01365] E=-5614.1348 Grad=0.538 Conv=NO(12 cycles 32 points) [Iter=3 Diff=0.00158] E=-5614.1348 Grad=0.538 Conv=NO(12 cycles 32 points) [Iter=4 Diff=0.00025] E=-5614.1348 Grad=0.538 Conv=NO(12 cycles 32 points) [Iter=5 Diff=0.00000] E=-5613.9834 Grad=4.088 Conv=NO(12 cycles 33 points) [Iter=1 Diff=0.11050] E=-5613.9834 Grad=4.088 Conv=NO(12 cycles 33 points) [Iter=2 Diff=0.01032] E=-5613.9834 Grad=4.088 Conv=NO(12 cycles 33 points) [Iter=3 Diff=0.00120] E=-5613.9834 Grad=4.088 Conv=NO(12 cycles 33 points) [Iter=4 Diff=0.00019] E=-5613.9834 Grad=4.088 Conv=NO(12 cycles 33 points) [Iter=5 Diff=0.00000] E=-5614.1387 Grad=0.255 Conv=NO(13 cycles 34 points) [Iter=1 Diff=0.00190] E=-5614.1387 Grad=0.255 Conv=NO(13 cycles 34 points) [Iter=2 Diff=0.00021] E=-5614.1387 Grad=0.255 Conv=NO(13 cycles 34 points) [Iter=3 Diff=0.00003] E=-5614.1421 Grad=0.289 Conv=NO(13 cycles 35 points) [Iter=1 Diff=0.00190] E=-5614.1421 Grad=0.289 Conv=NO(13 cycles 35 points) [Iter=2 Diff=0.00021] E=-5614.1421 Grad=0.289 Conv=NO(13 cycles 35 points) [Iter=3 Diff=0.00003] E=-5614.1431 Grad=0.532 Conv=NO(13 cycles 36 points) [Iter=1 Diff=0.00010] E=-5614.1431 Grad=0.532 Conv=NO(13 cycles 36 points) [Iter=2 Diff=0.00001] E=-5614.1431 Grad=0.470 Conv=NO(14 cycles 37 points) [Iter=1 Diff=0.03041] E=-5614.1431 Grad=0.470 Conv=NO(14 cycles 37 points) [Iter=2 Diff=0.00300] E=-5614.1431 Grad=0.470 Conv=NO(14 cycles 37 points) [Iter=3 Diff=0.00038] E=-5614.1431 Grad=0.470 Conv=NO(14 cycles 37 points) [Iter=4 Diff=0.00007] E=-5614.1255 Grad=1.489 Conv=NO(14 cycles 38 points) [Iter=1 Diff=0.01674] E=-5614.1255 Grad=1.489 Conv=NO(14 cycles 38 points) [Iter=2 Diff=0.00165] E=-5614.1255 Grad=1.489 Conv=NO(14 cycles 38 points) [Iter=3 Diff=0.00021] E=-5614.1255 Grad=1.489 Conv=NO(14 cycles 38 points) [Iter=4 Diff=0.00004] E=-5614.1455 Grad=0.166 Conv=NO(15 cycles 39 points) [Iter=1 Diff=0.00113] E=-5614.1455 Grad=0.166 Conv=NO(15 cycles 39 points) [Iter=2 Diff=0.00010] E=-5614.1455 Grad=0.166 Conv=NO(15 cycles 39 points) [Iter=3 Diff=0.00001] E=-5614.1465 Grad=0.312 Conv=NO(15 cycles 40 points) [Iter=1 Diff=0.00011] E=-5614.1465 Grad=0.312 Conv=NO(15 cycles 40 points) [Iter=2 Diff=0.00001] E=-5614.1465 Grad=0.207 Conv=NO(16 cycles 41 points) [Iter=1 Diff=0.00191] E=-5614.1465 Grad=0.207 Conv=NO(16 cycles 41 points) [Iter=2 Diff=0.00016]E=-5614.1465 Grad=0.338 Conv=NO(16 cycles 42 points) [Iter=1 Diff=0.00053]E=-5614.1465 Grad=0.338 Conv=NO(16 cycles 42 points) [Iter=2 Diff=0.00005]E=-5614.1470 Grad=0.118 Conv=NO(17 cycles 43 points) [Iter=1 Diff=0.00009]E=-5614.1475 Grad=0.087 Conv=NO(17 cycles 44 points) [Iter=1 Diff=0.00010]E=-5614.1479 Grad=0.135 Conv=NO(17 cycles 45 points) [Iter=1 Diff=0.00000]E=-5614.1479 Grad=0.125 Conv=NO(18 cycles 46 points) [Iter=1 Diff=0.00045]E=-5614.1479 Grad=0.125 Conv=NO(18 cycles 46 points) [Iter=2 Diff=0.00004]E=-5614.1475 Grad=0.250 Conv=NO(18 cycles 47 points) [Iter=1 Diff=0.00015]E=-5614.1475 Grad=0.250 Conv=NO(18 cycles 47 points) [Iter=2 Diff=0.00001]E=-5614.1479 Grad=0.080 Conv=YES(19 cycles 48 points) [Iter=1 Diff=0.00000] ENERGIES AND GRADIENTTotal Energy = -39107.4530564 (kcal/mol)Total Energy = -62.5 (a.u.)Binding Energy = -5614.1480863 (kcal/mol)Isolated Atomic Energy = -33493.3049701 (kcal/mol)Electronic Energy = -151855.7014212 (kcal/mol)Core-Core Interaction = 112748.2483647 (kcal/mol)Heat of Formation = -3584.2860863 (kcal/mol)Gradient = 0.0797574 (kcal/mol/Ang) MOLECULAR POINT GROUPC2VEIGENV ALUES(eV)Symmetry: 1 A1 1 B2 2 A1 2 B2 3 A1 Eigenvalue: -48.228653 -44.921967 -39.969822 -34.146118 -30.883162 Symmetry: 1 B1 4 A1 3 B2 1 A2 5 A1 Eigenvalue: -28.682699 -28.469046 -28.056545 -25.610565 -24.098553 Symmetry: 4 B2 2 B1 5 B2 6 A1 2 A2 Eigenvalue: -23.099024 -21.719042 -20.119864 -18.474934 -18.154465 Symmetry: 7 A1 3 B1 6 B2 3 A2 8 A1 Eigenvalue: -16.890295 -15.730311 -15.627211 -14.505156 -14.398620 Symmetry: 7 B2 4 B1 5 B1 4 A2 9 A1 Eigenvalue: -14.220551 -14.122036 6.037422 6.486364 6.984152 Symmetry: 6 B1 8 B2 10 A1 9 B2 11 A1 Eigenvalue: 7.209129 7.266216 7.494792 7.807704 7.893167 Symmetry: 10 B2 5 A2 12 A1 11 B2 13 A1 Eigenvalue: 8.082231 8.194494 8.242883 8.928360 9.149508 Symmetry: 7 B1 14 A1 6 A2 12 B2 8 B1 Eigenvalue: 9.358259 9.783697 10.395283 10.967291 11.024303 Symmetry: 13 B2 15 A1 16 A1 14 B2Eigenvalue: 11.812114 11.856253 12.302794 12.332813ATOMIC ORBITAL ELECTRON POPULATIONSAO: 1 S C 1 Px C 1 Py C 1 Pz C 2 S C1.017689 0.970367 1.030565 0.973715 0.968621AO: 2 Px C 2 Py C 2 Pz C 3 S C 3 Px C1.012650 1.023395 0.956421 0.974890 1.013266AO: 3 Py C 3 Pz C 4 S C 4 Px C 4 Py C1.016258 0.960073 0.976386 1.014955 1.017676AO: 4 Pz C 5 S C 5 Px C 5 Py C 5 Pz C0.959603 0.974890 1.014978 1.014546 0.960073AO: 6 S C 6 Px C 6 Py C 6 Pz C 7 S C0.968622 1.017895 1.018150 0.956422 1.017688AO: 7 Px C 7 Py C 7 Pz C 8 S H 9 S H1.024900 0.976031 0.973714 1.011286 1.004890AO: 10 S H 11 S H 12 S H 13 S H 14 S H1.004890 1.014996 1.014996 1.015570 1.015570AO: 15 S H 16 S H 17 S H 18 S H 19 S H1.015582 1.015582 1.015570 1.015570 1.014996AO: 20 S H 21 S H 22 S H 23 S H1.014995 1.011287 1.004890 1.004890NET CHARGES AND COORDINATESAtom Z Charge Coordinates(Angstrom) Massx y z1 6 0.007665 1.27026 -2.99875 0.00000 12.011002 6 0.038912 1.22452 -1.53312 0.00000 12.011003 6 0.035512 -0.13502 -0.95607 0.00000 12.011004 6 0.031379 -0.21279 0.51953 0.00000 12.011005 6 0.035513 -1.57806 1.08470 -0.00000 12.011006 6 0.038911 -1.66895 2.55885 0.00000 12.011007 6 0.007667 -3.03551 3.09050 -0.00000 12.011008 1 -0.011286 2.31779 -3.39733 -0.00000 1.008009 1 -0.004890 0.76635 -3.44042 0.89791 1.0080010 1 -0.004890 0.76635 -3.44042 -0.89790 1.0080011 1 -0.014996 1.80141 -1.14693 0.88746 1.0080012 1 -0.014996 1.80141 -1.14693 -0.88746 1.0080013 1 -0.015570 -0.70523 -1.35564 0.88637 1.0080014 1 -0.015570 -0.70523 -1.35564 -0.88637 1.0080015 1 -0.015582 0.35562 0.92145 0.88644 1.0080016 1 -0.015582 0.35562 0.92145 -0.88643 1.0080017 1 -0.015570 -2.14485 0.68030 -0.88638 1.0080018 1 -0.015570 -2.14486 0.68029 0.88636 1.0080019 1 -0.014996 -1.11255 2.97401 0.88746 1.0080020 1 -0.014995 -1.11254 2.97402 -0.88745 1.0080021 1 -0.011287 -3.06212 4.21099 0.00000 1.0080022 1 -0.004890 -3.61989 2.76263 -0.89791 1.0080023 1 -0.004890 -3.61990 2.76263 0.89790 1.00800ATOMIC GRADIENTSAtom Z Gradients(kcal/mol/Angstrom)x y z1 6 -0.23321 0.17204 -0.000102 6 -0.05131 -0.05641 -0.000493 6 -0.12340 0.09713 -0.000494 6 0.05576 0.06527 -0.000275 6 0.07533 -0.18029 0.000046 6 -0.08613 -0.00112 -0.000097 6 0.10150 -0.28460 -0.000148 1 0.04407 0.00197 -0.000029 1 -0.01228 0.07302 0.0311010 1 -0.01224 0.07324 -0.0309911 1 -0.05895 -0.04436 -0.1303212 1 -0.05946 -0.04468 0.1308613 1 0.06288 0.03734 -0.0218714 1 0.06334 0.03765 0.0223715 1 0.05153 0.03609 0.1191916 1 0.05140 0.03583 -0.1189617 1 0.05580 0.04741 0.0218218 1 0.05573 0.04738 -0.0218019 1 -0.06188 -0.04176 -0.1312320 1 -0.06184 -0.04172 0.1312321 1 0.01654 0.04341 -0.0000122 1 0.06347 -0.03639 -0.0327523 1 0.06334 -0.03647 0.03294Dipole (Debyes) x y z TotalPoint-Chg. -0.024 -0.017 -0.000 0.030sp Hybrid 0.011 0.008 -0.000 0.013pd Hybrid 0.000 0.000 0.000 0.000Sum -0.013 -0.009 -0.000 0.016Single Point, AbInitio, molecule = (untitled).Convergence limit = 0.0001000 Iteration limit = 50Accelerate convergence = YESFull MP2 correlation energy is requested.The initial guess of the MO coefficients is from eigenvectors of the core Hamiltonian. Shell Types: S, S=P.RHF Calculation:Singlet state calculationNumber of electrons = 58Number of Doubly-Occupied Levels = 29Charge on the System = 0Total Orbitals (Basis Functions) = 95Primitive Gaussians = 153Starting HyperGauss calculation with 95 basis functions and 153 primitive Gaussians. 2-electron Integral buffers will be 3200 words (double precision) long.Two electron integrals will use a cutoff of 1.00000e-010Regular integral format is used.Computing the one-electron integrals ...Computing 2e integrals (s and p orbitals only): done 0%.Computing 2e integrals (s and p orbitals only): done 10%.Computing 2e integrals (s and p orbitals only): done 20%.Computing 2e integrals (s and p orbitals only): done 30%.Computing 2e integrals (s and p orbitals only): done 40%.Computing 2e integrals (s and p orbitals only): done 50%.Computing 2e integrals (s and p orbitals only): done 60%.Computing 2e integrals (s and p orbitals only): done 70%.Computing 2e integrals (s and p orbitals only): done 80%.Computing 2e integrals (s and p orbitals only): done 90%.5631113 integrals have been produced.Computing the initial guess of the MO coefficients ...Iteration = 1 Difference = 1032.07Iteration = 2 Difference = 1938.56Iteration = 3 Difference = 189.33Iteration = 4 Difference = 632.45Iteration = 5 Difference = 171.79Iteration = 6 Difference = 24.01Iteration = 7 Difference = 2.02Iteration = 8 Difference = 0.35Iteration = 9 Difference = 0.03Iteration = 10 Difference = 0.00Iteration = 11 Difference = 0.0002403903Iteration = 12 Difference = 0.0000084763Computing MP2 energy with 29 occupied and 66 virtual orbitals ... Transfering the 2e integrals from AO to MO: done 0%.Transfering the 2e integrals from AO to MO: done 10%.Transfering the 2e integrals from AO to MO: done 20%.Transfering the 2e integrals from AO to MO: done 30%.Transfering the 2e integrals from AO to MO: done 40%.Transfering the 2e integrals from AO to MO: done 50%.Transfering the 2e integrals from AO to MO: done 60%.Transfering the 2e integrals from AO to MO: done 70%.Transfering the 2e integrals from AO to MO: done 80%.Transfering the 2e integrals from AO to MO: done 90%.Energy=-171223.093981 MP2 Correlation Energy=-414.861844 Symmetry=C2V ENERGIES AND GRADIENT========== SCF RESULTS ==========Total Energy = -171223.0939809 (kcal/mol)Total Energy = -272.0 (a.u.)Electronic Kinetic Energy = 170947.5590687 (kcal/mol)Electronic Kinetic Energy = 272.2 (a.u.)The Virial (-V/T) = 2.0016eK, ee and eN Energy = -367133.0518992 (kcal/mol)Nuclear Repulsion Energy = 195909.9579183 (kcal/mol)======== POST SCF RESULTS ========MP2 Correlation Energy = -414.8618444 (kcal/mol)MP2 Correlation Energy = -0.0 (a.u.)Total Energy (with MP2 energy) = -171637.9558252 (kcal/mol)Total Energy (with MP2 energy) = -273.5224594 (a.u.)Occupied and Virtual Orbitals in MP2 = 29, 66========== SCF RESULTS ==========MOLECULAR POINT GROUPC2VEIGENV ALUES(eV)Symmetry: 1 B2 1 A1 2 B2 2 A1 3 A1 Eigenvalue: -303.674866 -303.674713 -303.631775 -303.630157 -303.627747 Symmetry: 3 B2 4 A1 5 A1 4 B2 6 A1 Eigenvalue: -303.623016 -303.612946 -30.261747 -29.204332 -27.434654 Symmetry: 5 B2 7 A1 8 A1 6 B2 1 B1 Eigenvalue: -25.107853 -22.681458 -21.177843 -21.160900 -17.947813 Symmetry: 1 A2 9 A1 7 B2 2 B1 8 B2 Eigenvalue: -16.982294 -16.493128 -16.444221 -15.528235 -15.090984 Symmetry: 10 A1 2 A2 11 A1 9 B2 3 B1 Eigenvalue: -14.549708 -13.900264 -13.511187 -12.866585 -12.585258 Symmetry: 12 A1 10 B2 3 A2 4 B1 13 A1 Eigenvalue: -12.306542 -12.249912 -11.875375 -11.724080 7.087684 Symmetry: 5 B1 11 B2 14 A1 15 A1 4 A2 Eigenvalue: 7.258967 7.333437 7.768019 8.007830 8.335639 Symmetry: 12 B2 16 A1 13 B2 6 B1 14 B2 Eigenvalue: 8.724559 9.351191 9.442577 9.514703 9.899670 Symmetry: 5 A2 7 B1 17 A1 6 A2 8 B1 Eigenvalue: 10.156153 10.202340 10.277209 10.321597 10.688224 Symmetry: 18 A1 19 A1 15 B2 16 B2 20 A1 Eigenvalue: 11.894808 12.191500 12.239221 13.969515 14.873546 Symmetry: 17 B2 18 B2 21 A1 9 B1 7 A2 Eigenvalue: 14.943412 24.174065 24.497423 25.322130 25.437565 Symmetry: 22 A1 10 B1 19 B2 23 A1 8 A2 Eigenvalue: 25.885952 26.483768 27.062307 27.959761 28.765862 Symmetry: 20 B2 24 A1 21 B2 25 A1 26 A1 Eigenvalue: 28.808775 29.825521 30.151628 30.719355 31.761393 Symmetry: 11 B1 22 B2 9 A2 23 B2 12 B1 Eigenvalue: 31.900881 32.902023 33.776600 33.784996 33.892372 Symmetry: 27 A1 13 B1 10 A2 28 A1 24 B2 Eigenvalue: 33.973347 35.433430 36.171829 36.518166 36.652103Symmetry: 14 B1 11 A2 29 A1 30 A1 15 B1 Eigenvalue: 36.898243 37.728039 37.748863 38.017197 38.224873 Symmetry: 25 B2 31 A1 26 B2 32 A1 27 B2 Eigenvalue: 38.257149 38.725616 38.931732 39.085808 40.204521 Symmetry: 12 A2 28 B2 16 B1 33 A1 29 B2 Eigenvalue: 41.526394 43.364548 49.700970 49.825069 55.635876 Symmetry: 34 A1 30 B2 35 A1 31 B2 36 A1 Eigenvalue: 60.068157 62.722443 64.506859 69.455078 77.091454 ATOMIC ORBITAL ELECTRON POPULATIONSC 1 S C 1 S C 1 Px C 1 Py C 1 Pz1.988309 0.353594 0.528720 0.555717 0.528189C 1 S C 1 Px C 1 Py C 1 Pz C 2 S1.112087 0.573252 0.345988 0.569138 1.989476C 2 S C 2 Px C 2 Py C 2 Pz C 2 S0.348915 0.547487 0.559715 0.527539 1.107065C 2 Px C 2 Py C 2 Pz C 3 S C 3 S0.400466 0.350437 0.582624 1.989604 0.349376C 3 Px C 3 Py C 3 Pz C 3 S C 3 Px0.546579 0.556665 0.525439 1.094947 0.398869C 3 Py C 3 Pz C 4 S C 4 S C 4 Px0.337608 0.578260 1.989672 0.349268 0.546835C 4 Py C 4 Pz C 4 S C 4 Px C 4 Py0.556721 0.525498 1.098025 0.397285 0.340660C 4 Pz C 5 S C 5 S C 5 Px C 5 Py0.579368 1.989603 0.349377 0.546403 0.556843C 5 Pz C 5 S C 5 Px C 5 Py C 5 Pz0.525439 1.094939 0.396197 0.340286 0.578257C 6 S C 6 S C 6 Px C 6 Py C 6 Pz1.989476 0.348915 0.551136 0.556063 0.527539C 6 S C 6 Px C 6 Py C 6 Pz C 7 S1.107065 0.406435 0.344470 0.582624 1.988310C 7 S C 7 Px C 7 Py C 7 Pz C 7 S0.353594 0.551270 0.533168 0.528188 1.112088C 7 Px C 7 Py C 7 Pz H 8 S H 8 S0.376075 0.543161 0.569141 0.455906 0.350817H 9 S H 9 S H 10 S H 10 S H 11 S0.455789 0.354839 0.455790 0.354841 0.454201H 11 S H 12 S H 12 S H 13 S H 13 S0.350338 0.454202 0.350338 0.453928 0.354491H 14 S H 14 S H 15 S H 15 S H 16 S0.453928 0.354490 0.453952 0.354422 0.453952H 16 S H 17 S H 17 S H 18 S H 18 S0.354420 0.453928 0.354491 0.453928 0.354491H 19 S H 19 S H 20 S H 20 S H 21 S0.454202 0.350338 0.454202 0.350338 0.455904H 21 S H 22 S H 22 S H 23 S H 23 S0.350817 0.455789 0.354840 0.455789 0.354840NET CHARGES AND COORDINATESAtom Z Charge Coordinates(Angstrom) Mass (Mulliken) x y z1 6 -0.554993 1. -2. 0.00000244 12.011002 6 -0.413723 1. -1. 0.00000350 12.011003 6 -0.377347 -0. -0. 0.00000361 12.011004 6 -0.383332 -0. 0. 0.00000283 12.011005 6 -0.377344 -1. 1.08469892 -0.00000218 12.011006 6 -0.413724 -1. 2. 0.00000175 12.011007 6 -0.554995 -3.03550863 3.09049869 -0.00000256 12.011008 1 0.193277 2. -3. -0.00000215 1.008009 1 0.189371 0. -3. 0. 1.0080010 1 0.189370 0. -3. -0. 1.0080011 1 0.195461 1. -1. 0. 1.0080012 1 0.195460 1. -1. -0. 1.0080013 1 0.191581 -0. -1. 0. 1.0080014 1 0.191582 -0. -1. -0. 1.0080015 1 0.191626 0. 0. 0. 1.0080016 1 0.191628 0. 0. -0. 1.0080017 1 0.191581 -2. 0. -0. 1.0080018 1 0.191581 -2. 0. 0. 1.0080019 1 0.195461 -1. 2. 0. 1.0080020 1 0.195461 -1. 2. -0. 1.0080021 1 0.193278 -3.06212473 4. 0.00000114 1.0080022 1 0.189371 -3. 2. -0. 1.0080023 1 0.189371 -3. 2. 0. 1.00800Net Charge (Electrons):0.0000Dipole Moment (Debye):X: 0.0374 Y: 0.0265 Z: -0.0000 Ttl: 0.0458 Quadrupole Moment (Debye-Ang):XX: -50.1060 YY: -50.0433 ZZ: -49.0744XY: -0.0137 XZ: -0.0000 YZ: -0.0000Octapole Moment (Debye-Ang^2):XXX: 92.7823 YYY: -33.3817 ZZZ: -0.0002XYY: 30.1231 XXY: -13.8770 XXZ: -0.0000XZZ: 29.0156 YZZ: -12.3621 YYZ: -0.0000 XYZ: -0.0000 Hexadecapole Moment (Debye-Ang^3):XXXX: -913.8107 YYYY: -1448.3551 ZZZZ: -99.1216XXXY: 473.6560 XXXZ: -0.0005 YYYX: 469.1867YYYZ: 0.0004 ZZZX: -0.0003 ZZZY: 0.0004XXYY: -394.9777 XXZZ: -163.0937 YYZZ: -256.2102 XXYZ: 0.0002 YYXZ: -0.0002 ZZXY: 158.8551 HyperChem log stop -- Mon Dec 13 18:51:44 2010.。
HyperChem基本操作 Setup设置

HyperChem基本操作Setup设置Charge和Spin Multiplicity在Ab initio和Semi-empirical计算的对话框中出现。
Charge:指定额外的净剩电荷。
额外电荷定义当前的分子系统是一个电中性系统,正电系统(阳离子),还是一个负电系统(阴离子)。
Spin Multiplicity:自旋多重度。
闭壳分子的自旋多重度为1(单重态)。
一个自由基,有一个未成对电子,自旋多重度为2(双重态)。
有两个未成对电子的系统,自旋多重度一般为3(三重态)。
然而在某些情况下,例如两个自由基,两个未成对电子也可能产生单态。
State描述系统中价电子的状态。
包括指定分子处于第一激发单态(Next lowest)或者Lowest电子态。
Lowest给定自旋多重度的最低电子态。
它不一定是基态。
Next lowest给定自旋多重度(单重、双重、三重或四重态)的第一电子激发态。
在HyperChem 6.0中,semi-empirical方法通常需要给定多重度的最低能态(lowest)或者次最低能态(next lowest)的计算。
由于偶数个电子的分子没有未成对电子,是闭壳层单态,所以只有最低三重态是有效的,而次最低三重态是无效的。
例如,苯有偶数个电子,并且基态是闭壳层单重态。
我们可以计算基态(最低单重态),第一激发单重态(次最低单重态),或者第一激发三重态(最低三重态)。
也就是说,或者HOMO被两个电子占据,或者一个电子在HOMO,另一个电子在LUMO,产生了激发单重态或者三重态。
对双重态和四重态,只有给定多重度的最低态(lowest)可用。
UHF选项仅允许给定多重度的最低态(lowest)可用。
例如,可以用UHF选项研究苯的最低三重激发态,但是不能用来计算单重激发态。
这是因为HyperChem中的UHF选项不允许任意的轨道占据,也不允许CI计算。
对于RHF选项,可以计算CI波函数。
这个计算由一系列计算得到的RHF轨道开始,或者从最低单态(或双重态),或者从half electron的单态和三态(或双态和四重态)轨道。
HyperChem

分子图形与分子模型设计——HyperChem使用简介厦门大学化学系2005年3月HyperChem使用简介HyperChem是HyperCube Inc.的产品,它具有非常强大的综合计算与分析功能,是优秀的分子图形和分子设计的工具软件之一。
HyperChem是运行在Windows系统的分子计算与建模软件,具有量子化学(半经验和从头算)、分子力学、分子动力学、随机动力学、Monte Carlo模拟等计算功能,计算结果可以用三维图形显示。
它还提供用户VB、C/C++和FORTRAN等语言的应用程序接口。
HyperChem 7.5版本已经推出。
图1是HyperChem的工作窗口,最下部是工作状态档。
在菜单下面是常用工具档。
图1 HyperChem的工作窗口HyperChem的操作可以使用鼠标和键盘两种。
在工具档从左开始有8个工具图标,当鼠标点图标之后,鼠标在工作区的形状也改变为该图标的形状:1.绘图工具。
鼠标双击该图标可直接进入缺省元素周期表,选择所要绘制元素。
2.选择工具。
3.xy轴方向旋转工具,也可使用键盘的上下左右光标键进行相同的操作。
4.z轴方向旋转工具,也可使用键盘的Home和End键进行相同的操作。
5.xy轴平移工具,也可使用键盘的Shift+上下左右光标键进行相同的操作。
6.z轴平移工具。
7.缩放工具,也可使用键盘的PgUp和PgDn键进行相同的操作。
8.z轴截片工具。
鼠标操作有较为多样:左点击、右点击、左拖拉、右拖拉、左右拖拉、Shift+左点击、Shift+右点击、双击等。
一般的旋转和平移操作是使用鼠标的左键进行,当完成了某个基团、分子的选择之后,可以使用右键对所选部分进行旋转和平移操作。
HyperChem的详细操作将结合具体的实例进行讲解。
以下通过对HyperChem 5.1的菜单命令的介绍,说明它的主要功能和使用方法。
一、File1.New (Ctrl+N):新建一个沿尚未命名文件。
HyperChem

分子图形与分子模型设计——HyperChem使用简介厦门大学化学系2005年3月HyperChem使用简介HyperChem是HyperCube Inc.的产品,它具有非常强大的综合计算与分析功能,是优秀的分子图形和分子设计的工具软件之一。
HyperChem是运行在Windows系统的分子计算与建模软件,具有量子化学(半经验和从头算)、分子力学、分子动力学、随机动力学、Monte Carlo模拟等计算功能,计算结果可以用三维图形显示。
它还提供用户VB、C/C++和FORTRAN等语言的应用程序接口。
HyperChem 7.5版本已经推出。
图1是HyperChem的工作窗口,最下部是工作状态档。
在菜单下面是常用工具档。
图1 HyperChem的工作窗口HyperChem的操作可以使用鼠标和键盘两种。
在工具档从左开始有8个工具图标,当鼠标点图标之后,鼠标在工作区的形状也改变为该图标的形状:1.绘图工具。
鼠标双击该图标可直接进入缺省元素周期表,选择所要绘制元素。
2.选择工具。
3.xy轴方向旋转工具,也可使用键盘的上下左右光标键进行相同的操作。
4.z轴方向旋转工具,也可使用键盘的Home和End键进行相同的操作。
5.xy轴平移工具,也可使用键盘的Shift+上下左右光标键进行相同的操作。
6.z轴平移工具。
7.缩放工具,也可使用键盘的PgUp和PgDn键进行相同的操作。
8.z轴截片工具。
鼠标操作有较为多样:左点击、右点击、左拖拉、右拖拉、左右拖拉、Shift+左点击、Shift+右点击、双击等。
一般的旋转和平移操作是使用鼠标的左键进行,当完成了某个基团、分子的选择之后,可以使用右键对所选部分进行旋转和平移操作。
HyperChem的详细操作将结合具体的实例进行讲解。
以下通过对HyperChem 5.1的菜单命令的介绍,说明它的主要功能和使用方法。
一、File1.New (Ctrl+N):新建一个沿尚未命名文件。
谷晓明 物理化学HyperChem
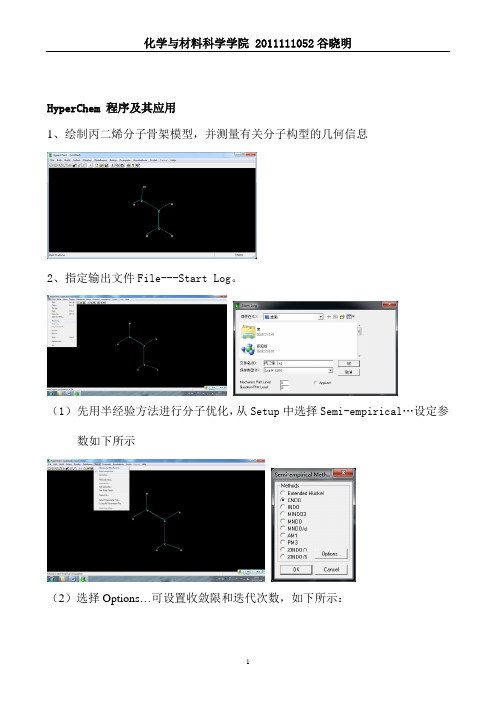
HyperChem 程序及其应用1、绘制丙二烯分子骨架模型,并测量有关分子构型的几何信息2、指定输出文件File---Start Log。
(1)先用半经验方法进行分子优化,从Setup中选择Semi-empirical…设定参数如下所示(2)选择Options…可设置收敛限和迭代次数,如下所示:(3)从Compute中选择Geometry Optimzation…进行集合构型优化:(4)优化完成之后,在Compute选择Single Point可进行单点计算。
3、采用从头算的方法:(1)Setup中选择Ab Initio…设定参数如下:(2)从Compute中选择Geometry Optimzation…进行集合构型优化:(3)完成集合构型优化后,从Compute选择Single Point可进行单点计算。
4、计算结束后,停止数据输出,从File---Stop Log。
5、分析有关分子的性质并简单分析讨论分子性质(1)采用从头算方法后,分析振动光谱:(该图显示谱线的位置、强度和振动模式)虚振动频率-185.84意味着,此结构不是一个稳定结构,而是一个过渡态。
(2)计算电子光谱最低能量跃迁π-π*在373.90,是禁阻跃迁允许的跃迁是116.84单态π-π*跃迁。
(3)分子偶极矩(4)轨道特征1、最高占据轨道2、最低空轨道(5)绘分子图,测电子光谱从Comput选择Plot Molecular Graphs1、2D图像2、3D图像6、结论与经验1、丙烯分子为一平面型分子,并且其振动频率存在虚频-185.84,意味着此平面结构不是一个稳定结构,而是一个过渡态。
2、半经验算法计算分子总能量为-16180.6852898 (kcal/mol),从头算方法计算分子总能量为-72576.4084722 (kcal/mol),所以计算方法的选择很重要。
3、计算分子的电子光谱能够得到该分子最低能量跃迁π-π*在373.90,是禁阻跃迁;允许的跃迁是116.84单态π-π*跃迁。
hyperchem教案3

一、建立H2O2模型双击Draw—选择O原子---双击选择图标---选择H1-O1-O2-H2四个原子----edit---set bond torsion ----bond torsion=60度---OK---save as 到指定文件夹(用英语或汉语拼音命名。
扩展名为.hin)二、优化H2O2的结构1、先进行MM+优化File----start log----命名H2O2----append----OKSetup----molecular mechanics----MM+---OK----OKComput---optimization----OKFile----stop log2、进行semi-empirical优化File---start log---OKSetup----semi-empirical----AM1---OKComput---optimization----OKFile----stop log3、进行ab-initio优化File---start log---OKSetup----ab-initio---将basis set 设置为6-31g*---OKComput---optimization----OKFile----stop log三、进行单点能计算、振动光谱(IR)计算和电子光谱(UV)计算1、单点能计算File---start log---OKSetup----ab-initio---将basis set 设置为6-31g*---OKComput---single point----OKFile----stop log2振动光谱(IR)File---start log---OKSetup----ab-initio---将basis set 设置为6-31g*---OKComput---vibrations----OKFile----stop log3、电子光谱(UV)计算File---start log---OKSetup----ab-initio---将basis set 设置为6-31g*---options---configration intereaction—singly exicited—将energy criterion 设置为100eVeV—OKComput---single point----OKFile----stop log三、输出和保存结果File----export----勾选有关项后---OK----命名为*****.ext 文件----四、观察和输出体系能量、原子电荷、键长、键级、键角、HOMO、LUMO、分子静电势、IR、UV在display----lable中可看到原子电荷、键长、键级、键角在comput的中部可以看到体系能量、HOMO、LUMO、分子静电势、IR、UV. (copy----paste)。
HyperChem应用-水分子轨道计算

HyperChem应用水分子轨道计算构造水分子1. 在Display菜单,确保Show Hydrogens打开,Rendering对话框Sticks栏中的Perspe ctive关闭。
2. 关闭Default Element对话框中的Explicit Hydrogens,设置缺省元素为O。
3. 在工作区画一个氧原子。
4. 双击Selection激活Model Builder。
它自动为氧原子添加氢原子。
5. 设置Label添加元素符号。
结果是这样:∣H∣∣∣O╲╲╲H键角是109度。
结构校准1. 在Edit菜单选择Align Molecules。
2. 在Align对话框选择Secondary,With对话框选择Y Axis。
3. 关闭Minor Axis。
4. 选择OK。
得到这样的水分子:H H╲╱╲╱╲╱╲╱O5. 把这个结构保存为h2o.hin。
显示原子电荷1. 打开Labels对话框。
2. 把Charge作为Atom的选项,单击OK。
计算波函1. 在Setup菜单选择Semi-empirical。
2. 选择CNDO方法。
选择Options。
当然也可以选择其他方法。
3. 在Semi-empirical的Options的对话框中使用下面的值:Total charge: 0, Spin multiplicity: 1, Spin Pairing: RHF,State: Lowest, Convergence limit: 0.0001, Iteration limit: 50,Accelerate convergence: NO。
这意味着两次叠代计算的值的差小于0.0001 kcal/mol,叠代次数已经达到了最大的次数5 0次。
4. 选择OK回到工作区。
5. 选择Compute菜单中的Single Point。
结果:能量,梯度,和原子电荷如图所示:0.145 0.145╲╱╲╱╲╱╲╱-0.290窗口左下角:Energy=-320.414117, Gradient=124.385845, Symmetry=C2V(结果可能会有略微差别。
HyperChem基本操作 一、画原子

HyperChem基本操作一、画原子HyperChem基本操作一、画原子作者:水云间文章来源:本站原创点击数:571 更新时间:2005-11-11HyperChem基本操作画原子1. 打开Element Table对话框。
这里有两种方法:在Build菜单中选择Default Element,或者双击Drawing工具。
DefaultElement对话框允许从周期表中选择缺省元素。
2. 如果单击Properties...按钮,将显示当前选择元素的物理属性。
也可以按下Shift键同时单击元素按钮,结果是一样的。
单击OK键,物理属性框消失。
3. 如果Allow Ions或者Explicit Hydrogens打开(用对勾选择),左键单击这些选项使其关闭。
4. 在缺省元素列表中选择Carbon,接着关闭元素对话框。
缺省元素将设置为碳。
当然也可以把打开的Default Element对话框移走,这样可以看到HyperChem工作区。
当画原子非常多的分子时,这是非常有效的。
5. 左键单击Drawing工具,把指针移到工作区。
6. 左键单击工作区左下角,将出现一个小圈,代表未成键的碳原子。
7. 在工作区不同位置画更多的原子。
画价键1. 把指针移到刚才画的第一个碳上。
2. 按下鼠标左键。
这是价键在第一个原子的位置。
3. 保持鼠标按钮按下的同时拖向工作区的顶端。
4. 放开鼠标按钮。
这是价键在第二个原子的位置。
一条线代表两个碳原子之间的价键。
5. 用仍旧停留在价键末端的指针, 用左键拖向工作区右下角。
6. 放开鼠标按钮。
这是第三个原子的位置。
7. 在空白工作区画六个价键,形成一个环。
现在你清楚了如何画原子和分子,并且学会了一些基本技巧。
选择原子在这个练习中,通过选择原子,你可以学到基本的选择技巧。
首先必须设置选择的级别[原子(atoms),基(residues),或分子(molecules)]。
这里设置为原子(atoms)。
HyperChem程序及其应用
河北师范大学计算量子化学研究所蔡新华教授量子化学在线教学.100/qc/lzhx-0.htmHyperChem 程序及其应用一、HyperChem 程序的运行环境HyperChem 程序包,用C++写源程序,具有工作站、微机等不同的版本,作为教学示例,我们向大家介绍适用于微机运行的程序版本。
可以通过网络选购HyperChem程序包,也可以免费下载演示版本以供学习只用,现在该公司提供的最新版本为V6.0。
该公司的网址为:该公司与98年诺贝尔奖金得主Pople的关系可以参看其网页有关介绍。
1、软件环境Windows95、Windows98或Windows2000系统。
2、硬件环境486以上的微机,内存应在8M以上,硬盘至少有32M以上自由空间。
为了能够以最佳方式显示分子图像,最好有VGA以上显示器。
3、程序安装使用该程序应注意程序版权(注册)。
安装程序默认子目录为:C:\hyper6安装完成后,该目录可以看到如下文件,其中,绿色烧杯为执行程序图标。
有关该程序的使用说明、参考手册等全套文档均可免费获得。
二、程序基本使用方法我们以演示版本为例,说明该程序的基本使用方法。
1、启动程序在屏幕上,双击绿色烧杯可以得到如下画面:点击 Try进入工作区窗口窗口各部分功能简介标题名称:最大、最小化、退出按钮菜单条:FILE、EDIT、BUILD、SELECT、DISPLAY、DATABASE、SETUP 、COMPUTE、CANCEL、SCRIPT、HELP工具条:工作区:状态行:2、打开已存在的数据文件File-Open选择分子图形的显示方式Display- Labels可以选择原子、化学键等标记方式:Dispay-RenderingRenderings-BallsRendering—Balls and Cylinders3、建立计算分子的数据文件以丁二烯为例:选择Build-Default Element可以显示指定元素的基本性质:选择绘图工具后,得到碳碳骨架。
Hyperchem学习

OK Thr Mutate
谢谢观赏
胡非非
hyperchem学习 hyperchem
*保存文件
• File→Save As→
保存←
*改变键型连接
• 将鼠标移动至需要修改键型的原子上面,左击鼠标同时移 动至另一个原子上面,则
*制作苯环
• 用鼠标单击环形结构中的任一原子,则可画出苯环
*标记原子
• Display→Labels ↓ →→Symbol→OK ↑ ↓ ↑ ↑ →→↑
*编辑个人原子
Line Options→ 移动鼠标 ← ↓ ←
→Turn on Perspective ↓ ←确定
*缩放工具的使用
按着鼠标左键移 动鼠标
*定心和缩放
• Display Select to Y轴的旋转
*Z轴的旋转
将鼠标移动至工作区, 则可以对分子进行旋转
原子间距离显示在 状态栏
*键角测量
• 按住鼠标左键从碳原子拖到氢原子,接着放开鼠标则
键角显示
六、创建多肽
• • • •
Amino Acids对话框的使用 创建一个多肽 创建一个两性分子 位点专一诱变
*Amino Acids对话框的使用
• Databases→Amino Acids→
不同氨基酸结构
• 双击鼠标左键→Element Table→选择原子→关闭Element Table→将鼠标移动至想要编辑的原子上面,单击左键, 则该原子变为自己后面所选原子,如
*选用模型生成器
• Build→Add H and Model Build→
如果没有显示相应原子,则进入 Display→Show Hydrogens
Hyperchem学习
HyperChem基本操作 单点计算

HyperChem基本操作单点计算单点计算,仅仅执行势能曲面上的一个单个点的计算。
例如对一个双原子分子来说,这可能是在点a原子间距离R=2.0埃的计算。
单点计算的结果给出系统在当前几何构型的势能,以及那个点的梯度。
在点b,c,d,或e的单点计算可能将给出更高的能量。
如果在关键的部分取足够多的点,利用Origin或者Matlab等数学工具软件,就能描出势能曲线,从而精确算出离解能De和核平衡距离re,利用公式就能得到震动参数ωe。
对多原子系统来说,状况更加复杂,但是本质是一样的。
Orbital中显示的轨道信息Alpha & Beta显示选择的轨道是alpha自旋还是beta自旋。
LUMO+显示选择轨道相对于LUMO的位置关系。
例如,选择能量在LUMO之上的轨道,文本框依次显示+1,+2,+3......;如果选择能量低于LUMO的轨道,文本框显示-1,-2,-3......。
HOMO-显示选择轨道相对于HOMO的位置关系。
例如,选择能量在HOMO之上的轨道,文本框依次显示-1,-2,-3......;如果选择能量低于HOMO的轨道,文本框显示+1,+2,+3......。
Number显示从能量最低轨道开始的选择轨道绝对数值。
对于UHF计算,轨道的alpha和beta列编号分开显示,对HOMO-和LUMO+选项也是这样。
Energy以eV为单位显示选择轨道的能量。
Symmetry显示选择轨道的不可约表示。
Labels在轨道显示窗口中,显示每个轨道的电子占据情况和每个轨道的能量。
按照约定俗成,向上的箭头代表alpha自旋,向下的箭头代表beta自旋。
对于RHF计算,最大轨道占据是2;对于UHF计算,最大轨道占据是1。
Zoom Out和轨道的放大如果轨道间距太密,在使用Labels时,文字符号会重合在一起,看起来很不方便。
通过鼠标左键圈出一个或相邻几个选择的轨道,这些轨道就会被放大。
放大之后,Zoom Out选项可以在窗口中重新回到显示全部轨道范围。
HyperChem软件的应用2011

5.模拟分子光谱 分子光谱(振动光谱、电子光谱)是结构 化学中非常重要的内容之一。 研究物质的分子光谱,可以使我们了解分 子中电子的运动,分子中各原子核的相对振动 以及整个分子的转动情况。分子光谱也是现代 研究分子结构和进行定性、定量分析的重要方 法之一。 HyperChem能够对分子进行振动分析,对振 动频率、振动模式、红外吸收强度、电子跃迁 等进行计算,
6. 数据库(Database) 数据库( ) 氨基酸、核酸、糖类。 氨基酸、核酸、糖类。
6. 其它模块:晶体构造器;糖类构造器,构 其它模块:晶体构造器;糖类构造器, 像搜寻, 特性, 像搜寻,QSAR特性,脚本编辑器。 特性 脚本编辑器。
ห้องสมุดไป่ตู้
2.建立与显示分子骨架模型: 结构输入和对分子操作。 除了能绘制分子的平面结构,还能够获得 分子的空间构型、键长、键角、扭转角、氢键 等参数。建立起3D或2D分子结构模型。 几何优化
3. 化学计算: 化学计算: 量子化学计算(从头计算,半经验方法, 量子化学计算(从头计算,半经验方法,密度 泛函计算):单点计算、 ):单点计算 泛函计算):单点计算、几何优化和过渡态寻 找计算; 找计算; 分子力学计算; 分子力学计算; 分子动力学模拟计算( 分子动力学模拟计算(Langevin,Metropolis , Monte Carlo模拟)。 模拟)。 模拟
4. 可以用来研究的分子特性: 可以用来研究的分子特性: 同位素的相对稳定性;生成热;活化能; 同位素的相对稳定性;生成热;活化能;原 子电荷; 能量间隔; 子电荷;HOMO-LUMO能量间隔;电离势; 能量间隔 电离势; 电子亲和力;偶极矩;电子能级; 电子亲和力;偶极矩;电子能级;过渡态结 构和能量;非键相互作用能; 构和能量;非键相互作用能;
计算化学教程01Gaussian和Hyperchem使用

双击在跳出的对话框中选择相应的元素,如下图选择了C,同时把对话框底部Allow Ions 选项选上,这样就可以任意画键。
然后右上角关闭对话框。
意结构图选择按钮,旋转图形成近平面,如左图们同平面三个原子连接起来。
如下7. 删除键的方法:鼠标在Draw模式下放至要删除的键的中部,点击右键。
Hyperchem搭建初步构型的粗模型,在键长和键角上可能很不合理,我们可通过中的几何优化功能,粗略优化一下构型。
如下选择菜单Compute →在跳出的对话框中选择Ok,程序就会对刚才的模型进行优化。
这样就得到了化学上相对合理构型,如右。
(比较一下可以看出,程序对键长自动作了一定的调整)用Hyperchem9. 保存构型。
选择菜单File →Save,保存为10. 用Gaussview打开,C5.mol 如右,在Gaussview中可以进行一定的修改。
打开时注意选择*.mol 扩展名。
中选择File →Save 保存为C5.gjf,文件用Scite编辑器打开,内容如下第1行%开头定义chk文件,类似还可以定义内存%mem,%rwf等。
第2行#开头定义计算关键字第3行空第4行说明性文字第5行空第6行0 指体系电荷,如负1价离子则写-1. 1 为体系多重度= 2s+1 s为体系总自旋第7-11行为原子坐标。
第12空行用Gaussian优化构型下面以优化C5为例进行说明:1. 编辑C5.gjf文件,内容如右%mem定义内存为4GB%nprocshared=8定义使用CPU数目#P B3LYP/6-31+G*定义了优化Freq。
文件传到计算服务器上。
转换文件格式(注意Linux上区分大小写)5. 运行ps x 查看,如果正常,则显示如下:Gaussian优化构型传回文件。
查看工作是否计算完可以通过类似5步中的ps 录下运行tail C5.out 查看文件末尾信息,如果最后一行显示如下:Normal termination …说明任务正常结束,结果文件可用。
HyperChem应用 乙烯最低电子激发态的从头计算

HyperChem应用乙烯最低电子激发态的从头计算优化乙烯的基态通过前面几个例子的学习,你已经对从头计算有了初步的了解,所以下面的一些指令将省略。
用STO-3G基组构造乙烯:1. 在File菜单中选择New,刷新工作区。
2. 确保Explicit Hydrogens没有选择。
3. 从Default Element中选择碳,并画一条C-C单键。
单击碳键中部使它变成双键。
4. 从Build菜单选择Add H和Model Build构造乙烯。
5. 从Setup菜单选择Ab Initio,并选基组为Minimal (STO-3G)。
同时令Total charge = 0,Spin multiplicity = 1,Spin pairing = RHF,Accelerate convergence =Yes,SCF Convergence limit = 0.0001. 按下CI按钮选择CI Method 为None。
优化乙烯基态:1. 选择Compute菜单的Geometry Optimization。
选择Polak-Ribiere方法,RMS gr adient 为0.01。
选择OK关闭对话框。
得到的结果为:C-C bond length:1.31埃,C-H bond length:1.08埃,H-C-H angle:115.7度。
计算相关能:1. 在Setup菜单选择Ab Initio,按下Options按钮并选择MP2 correlation energy。
单击OK回到工作区。
2. 在Compute菜单选择Single Point。
得到结果:SCF能量:-48364.64 kcal/mol ,MP2总能量:-48438.61 kcal/mol,包括-74.97kc al/mol相关能。
具体运算结果可能会与这个值有微小的差别。
乙烯基态轨道观察乙烯的轨道和轨道能量图:1. 从Compute菜单选择Orbitals。
化学软件——HyperChem(分子模拟)介绍

化学软件——HyperChem(分子模拟)介绍HyperChem是一款以高质量,灵活易操作而闻名的分子模拟软件。
通过利用3D对量子化学计算,分子力学及动力学进行模拟动画,HyperChem 为您提供比其它 Windows 软件更多的模拟工具。
图形界面:图形界面,有半经验方法( AM1 , PM3 等), UHF , RHF 和 CI 和7.0 版新增加的密度泛函。
可进行单点能,几何优化,分子轨道分析,预测可见- 紫外光谱,蒙特卡罗和分子力学计算。
主要功能:1. 结构输入和对分子操作。
2. 显示分子。
3. 化学计算。
用量子化学或经典势能曲面方法,进行单点、几何优化和过渡态寻找计算。
可以进行的计算类型有:单点能,几何优化,计算振动频率得到简正模式,过渡态寻找,分子动力学模拟 Langevin 动力学模拟, Metropolis Monte Carlo 模拟。
支持的计算方法有:从头计算,半经验方法,分子力学,混合计算。
4. 可以用来研究的分子特性有:同位素的相对稳定性;生成热;活化能;原子电荷; HOMO-LUMO能量间隔;电离势;电子亲和力;偶极矩;电子能级; MP2 电子相关能; CI 激发态能量;过渡态结构和能量;非键相互作用能; UV-VIS 吸收谱; IR 吸收谱;同位素对振动的影响;对结构特性的碰撞影响;团簇的稳定性。
5. 支持用户定制的外部程序。
6. 其它模块: RAYTRACE 模块, RMS Fit , SEQUENCE 编辑器,晶体构造器;糖类构造器,构像搜寻,QSAR 特性,脚本编辑器。
7. 新的力场方法: Amber 2 , Amber 3 ,用于糖类的 Amber , Amber 94 ,Amber 96 。
8. ESR 谱。
9. 电极化率。
10. 二维和三维势能图。
11. 蛋白质设计。
12. 电场。
13. 梯度的图形显示。
14. 新增功能:密度泛函理论 (DFT) 计算; NMR 模拟;数据库; Charmm 蛋白质模拟;半经验方法TNDO ;磁场中分子计算;激发态几何优化; MP2 相关结构优化;新的芳香环图;交互式参数控制;增强的聚合物构造功能;新增基组。
hyperchem使用方法

HyperC hem应用HyperC hem应用水中质子的从头计算用expli cit hydrog ens画H3O+:1. 在Build菜单选择E xplic it Hydrog ens。
2.选择Allo w Ions。
3. 在Displ ay菜单选择Labe ls打开L abels对话框。
4. 选择Symb ols单击OK。
5. 在Build菜单选择D efaul t Elem en t打开周期表,设置氧元素为缺省元素。
6. 左键单击Dr awing工具。
画H3O+1. 左键单击工作区创建氧原子。
2. 从氧原子画三个价键得到H3O。
在量子力学计算中添加正电荷:1. 在Setup菜单选择A b Initio。
2. 单击Opti ons按钮。
3. 设置总电荷(Totalcharge)值为1,单击OK关闭Optio ns对话框。
4. 单击OK按钮关闭AbInitio对话框。
这样就得到了H3O+。
选择基组1. 在Setup菜单选择A b Initio。
2. 为基组选择O ther。
3. 按下Assi gn OtherBasisSet按钮。
4. 从列表中选择4-31G 单击OK。
5. 为基组选择M inima l (STO-3G)。
6. 选择Appl y BasisSet接着单击OK,或者直接选择OK关闭A b Initio对话框。
观察每个原子应用的基组:1. 在Displ ay菜单选择Labe ls。
2. 选择Basi s Set,单击OK。
最小化能量结构计算H3O+的几何优化:1. 从Setup菜单选择A b Initio。
2. 单击Opti ons按钮,保证Tota l charge = 1,Spin m ultip licit y = 1,Spin pairin g = RHF,Conver-gencelim it= 0.01,Iterat ion lim it= 50,Accele rateconver-gence= Yes,为几何优化选择合适的选项。
利用Hyperchem软件进行分子结构构建及性质计算

利用Hyperchem软件进行分子结构构建及性质计算实验目的1.初步了解分子模型方法的原理和应用。
2.学习使用Hyperchem软件构建简单的分子并使用适当方法优化结构。
3.学习使用Hyperchem软件计算简单分子的几何和电子性质。
实验原理化学的学习使我们认识了许多分子的分子式及二维结构,如何得到分子的三维结构,以及分子在空间的几何特征和电子特征,则可以借助于理论计算的工具和方法去模拟计算。
HyperChem软件是HyperCube公司开发的Windows界面程序。
是常用的分子设计和模拟软件。
它可以应用于构建简单及复杂的分子模型并进行综合计算与分析。
分子构建过程可以通过熟练各个菜单及工具栏的操作来实现,计算和分析需要我们了解常用的计算方法。
在本实验室中我们需要了解一下计算方法,这些方法位于HyperChem的Setup菜单下。
(1)分子力学(Molecular Mechanics)方法:分子力学又叫力场方法,目前广泛地用于计算分子的构象和能量。
适用于超大规模体系,超低精度计算。
分子力学的基本假设:玻恩-奥本海默近似,原子核的运动与电子的运动可以看成是独立的;分子是一组靠各种作用力维系在一起的原子集合。
这些原子在空间上若过于靠近,便相互排斥;但又不能远离,否则连接它们的化学键以及由这些键构成的键角等会发生变化,即出现键的拉伸或压缩、键角的扭变等,会引起分子内部应力的增加。
每个真实的分子结构,都是在上述几种作用达到平衡状态的表现。
分子力学从几个主要的典型结构参数和作用力出发来讨论分子结构,即用位能函数来表示当键长、键角、二面角等结构参数以及非键作用等偏离“理想”值时分子能量的变化。
不同的分子力场方法采用不同的势能函数。
MM+:适用于有机分子的计算。
Amber:适用于有机分子、蛋白质和核酸等大分子的计算。
(2)半经验计算(Semi-empirical)方法:是求解HF(Hartree-Fock)方程时采用各种近似,或者直接使用拟合的经验参数来近似求解自洽场。
《量子化学计算软件HyperChem程序及其应用》

HyperChem 程序及其应用一、HyperChem 程序的运行环境HyperChem 程序包,用C++写源程序,具有工作站、微机等不同的版本,作为教学示例,我们向大家介绍适用于微机运行的程序版本。
可以通过网络选购HyperChem程序包,也可以免费下载演示版本以供学习只用,现在该公司提供的最新版本为V6.0。
该公司的网址为:该公司与98年诺贝尔奖金得主Pople的关系可以参看其网页有关介绍。
1、软件环境Windows95、Windows98或Windows2000系统。
2、硬件环境486以上的微机,内存应在8M以上,硬盘至少有32M以上自由空间。
为了能够以最佳方式显示分子图像,最好有VGA以上显示器。
3、程序安装使用该程序应注意程序版权(注册)。
安装程序默认子目录为:C:\hyper6安装完成后,该目录可以看到如下文件,其中,绿色烧杯为执行程序图标。
有关该程序的使用说明、参考手册等全套文档均可免费获得。
二、程序基本使用方法我们以演示版本为例,说明该程序的基本使用方法。
1、启动程序在屏幕上,双击绿色烧杯可以得到如下画面:点击 Try进入工作区窗口窗口各部分功能简介标题名称:最大、最小化、退出按钮菜单条:FILE、EDIT、BUILD、SELECT、DISPLAY、DATABASE、SETUP 、COMPUTE、CANCEL、SCRIPT、HELP工具条:工作区:状态行:2、打开已存在的数据文件File-OpenDisplay- Labels可以选择原子、化学键等标记方式:Dispay-RenderingRenderings-BallsRendering—Balls and Cylinders3、建立计算分子的数据文件以丁二烯为例:选择Build-Default Element可以显示指定元素的基本性质:选择绘图工具后,得到碳碳骨架。
左键、右键增减键序把2D骨架转换为3D图像Select选定原子后,状态行提示原子标号、坐标等结构信息。
环戊烷Hyperchem程序应用
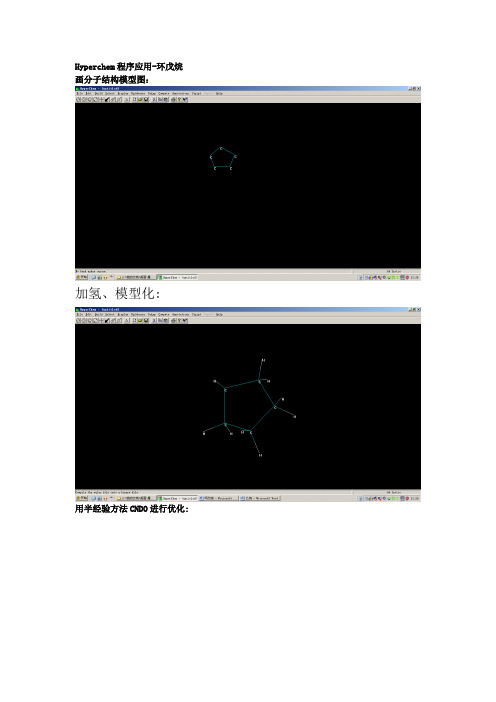
Hyperchem程序应用-环戊烷画分子结构模型图:加氢、模型化:用半经验方法CNDO进行优化:用从头算计算方法进行单点计算:显示原子电荷:测键长、键角、二面角:分子性质:戊烷分子2D、3D静电势图:分子总电荷密度图(2D、3D):等值面图:分子轨道图-最高占据轨道2D、3D图:分子轨道图-最低空轨道2D 、3D 图:分子结构模型表示:输出结果:HyperChem log start -- Sun Dec 12 21:25:30 2010.Geometry optimization, SemiEmpirical, molecule = (untitled).CNDOFletcherReeves optimizerConvergence limit = 0.0001000 Iteration limit = 50Accelerate convergence = YESOptimization algorithm = Fletcher-ReevesCriterion of RMS gradient = 0.1000 kcal/(A mol) Maximum cycles = 225RHF Calculation:Singlet state calculationNumber of electrons = 30Number of Double Occupied Levels = 15Charge on the System = 0Total Orbitals = 30Starting CNDO calculation with 30 orbitalsE=0.0000 Grad=0.000 Conv=NO(0 cycles 0 points) [Iter=1 Diff=9872.30361]E=0.0000 Grad=0.000 Conv=NO(0 cycles 0 points) [Iter=2 Diff=6.19972]E=0.0000 Grad=0.000 Conv=NO(0 cycles 0 points) [Iter=3 Diff=0.35983]E=0.0000 Grad=0.000 Conv=NO(0 cycles 0 points) [Iter=4 Diff=0.02932]E=0.0000 Grad=0.000 Conv=NO(0 cycles 0 points) [Iter=5 Diff=0.00064]E=0.0000 Grad=0.000 Conv=NO(0 cycles 0 points) [Iter=6 Diff=0.00003]E=-3902.0813 Grad=75.208 Conv=NO(0 cycles 1 points) [Iter=1 Diff=50.66003] E=-3902.0813 Grad=75.208 Conv=NO(0 cycles 1 points) [Iter=2 Diff=3.70425] E=-3902.0813 Grad=75.208 Conv=NO(0 cycles 1 points) [Iter=3 Diff=0.31058] E=-3902.0813 Grad=75.208 Conv=NO(0 cycles 1 points) [Iter=4 Diff=0.03342] E=-3902.0813 Grad=75.208 Conv=NO(0 cycles 1 points) [Iter=5 Diff=0.00075] E=-3902.0813 Grad=75.208 Conv=NO(0 cycles 1 points) [Iter=6 Diff=0.00012] E=-3902.0813 Grad=75.208 Conv=NO(0 cycles 1 points) [Iter=7 Diff=0.00000] E=-3854.4941 Grad=131.923 Conv=NO(0 cycles 2 points) [Iter=1 Diff=20.67949] E=-3854.4941 Grad=131.923 Conv=NO(0 cycles 2 points) [Iter=2 Diff=1.47203] E=-3854.4941 Grad=131.923 Conv=NO(0 cycles 2 points) [Iter=3 Diff=0.11775] E=-3854.4941 Grad=131.923 Conv=NO(0 cycles 2 points) [Iter=4 Diff=0.01208] E=-3854.4941 Grad=131.923 Conv=NO(0 cycles 2 points) [Iter=5 Diff=0.00021] E=-3854.4941 Grad=131.923 Conv=NO(0 cycles 2 points) [Iter=6 Diff=0.00001] E=-3929.7410 Grad=5.160 Conv=NO(1 cycles 3 points) [Iter=1 Diff=0.02148]E=-3929.7410 Grad=5.160 Conv=NO(1 cycles 3 points) [Iter=2 Diff=0.00163]E=-3929.7410 Grad=5.160 Conv=NO(1 cycles 3 points) [Iter=3 Diff=0.00015]E=-3929.7410 Grad=5.160 Conv=NO(1 cycles 3 points) [Iter=4 Diff=0.00002]E=-3930.0144 Grad=3.723 Conv=NO(1 cycles 4 points) [Iter=1 Diff=0.02156]E=-3930.0144 Grad=3.723 Conv=NO(1 cycles 4 points) [Iter=2 Diff=0.00164]E=-3930.0144 Grad=3.723 Conv=NO(1 cycles 4 points) [Iter=3 Diff=0.00016]E=-3930.0144 Grad=3.723 Conv=NO(1 cycles 4 points) [Iter=4 Diff=0.00002]E=-3930.1650 Grad=3.794 Conv=NO(1 cycles 5 points) [Iter=1 Diff=0.08681]E=-3930.1650 Grad=3.794 Conv=NO(1 cycles 5 points) [Iter=2 Diff=0.00661]E=-3930.1650 Grad=3.794 Conv=NO(1 cycles 5 points) [Iter=3 Diff=0.00063]E=-3930.1650 Grad=3.794 Conv=NO(1 cycles 5 points) [Iter=4 Diff=0.00008]E=-3930.0955 Grad=7.526 Conv=NO(1 cycles 6 points) [Iter=1 Diff=0.03555]E=-3930.0955 Grad=7.526 Conv=NO(1 cycles 6 points) [Iter=2 Diff=0.00271]E=-3930.0955 Grad=7.526 Conv=NO(1 cycles 6 points) [Iter=3 Diff=0.00026]E=-3930.0955 Grad=7.526 Conv=NO(1 cycles 6 points) [Iter=4 Diff=0.00003]E=-3930.1970 Grad=4.816 Conv=NO(2 cycles 7 points) [Iter=1 Diff=0.31929]E=-3930.1970 Grad=4.816 Conv=NO(2 cycles 7 points) [Iter=2 Diff=0.02495]E=-3930.1970 Grad=4.816 Conv=NO(2 cycles 7 points) [Iter=3 Diff=0.00236]E=-3930.1970 Grad=4.816 Conv=NO(2 cycles 7 points) [Iter=5 Diff=0.00001] E=-3930.0500 Grad=8.453 Conv=NO(2 cycles 8 points) [Iter=1 Diff=0.10464] E=-3930.0500 Grad=8.453 Conv=NO(2 cycles 8 points) [Iter=2 Diff=0.00818] E=-3930.0500 Grad=8.453 Conv=NO(2 cycles 8 points) [Iter=3 Diff=0.00078] E=-3930.0500 Grad=8.453 Conv=NO(2 cycles 8 points) [Iter=4 Diff=0.00010] E=-3930.0500 Grad=8.453 Conv=NO(2 cycles 8 points) [Iter=5 Diff=0.00000] E=-3930.3799 Grad=2.276 Conv=NO(3 cycles 9 points) [Iter=1 Diff=0.00575] E=-3930.3799 Grad=2.276 Conv=NO(3 cycles 9 points) [Iter=2 Diff=0.00059] E=-3930.3799 Grad=2.276 Conv=NO(3 cycles 9 points) [Iter=3 Diff=0.00007] E=-3930.4749 Grad=1.731 Conv=NO(3 cycles 10 points) [Iter=1 Diff=0.00574] E=-3930.4749 Grad=1.731 Conv=NO(3 cycles 10 points) [Iter=2 Diff=0.00059] E=-3930.4749 Grad=1.731 Conv=NO(3 cycles 10 points) [Iter=3 Diff=0.00007] E=-3930.5400 Grad=1.433 Conv=NO(3 cycles 11 points) [Iter=1 Diff=0.02291] E=-3930.5400 Grad=1.433 Conv=NO(3 cycles 11 points) [Iter=2 Diff=0.00237] E=-3930.5400 Grad=1.433 Conv=NO(3 cycles 11 points) [Iter=3 Diff=0.00030] E=-3930.5400 Grad=1.433 Conv=NO(3 cycles 11 points) [Iter=4 Diff=0.00005] E=-3930.5815 Grad=1.970 Conv=NO(3 cycles 12 points) [Iter=1 Diff=0.00052] E=-3930.5815 Grad=1.970 Conv=NO(3 cycles 12 points) [Iter=2 Diff=0.00005] E=-3930.5830 Grad=1.813 Conv=NO(4 cycles 13 points) [Iter=1 Diff=0.13831] E=-3930.5830 Grad=1.813 Conv=NO(4 cycles 13 points) [Iter=2 Diff=0.01226] E=-3930.5830 Grad=1.813 Conv=NO(4 cycles 13 points) [Iter=3 Diff=0.00133] E=-3930.5830 Grad=1.813 Conv=NO(4 cycles 13 points) [Iter=4 Diff=0.00019] E=-3930.5830 Grad=1.813 Conv=NO(4 cycles 13 points) [Iter=5 Diff=0.00000] E=-3930.4128 Grad=6.041 Conv=NO(4 cycles 14 points) [Iter=1 Diff=0.06925] E=-3930.4128 Grad=6.041 Conv=NO(4 cycles 14 points) [Iter=2 Diff=0.00614] E=-3930.4128 Grad=6.041 Conv=NO(4 cycles 14 points) [Iter=3 Diff=0.00066] E=-3930.4128 Grad=6.041 Conv=NO(4 cycles 14 points) [Iter=4 Diff=0.00010] E=-3930.6182 Grad=1.216 Conv=NO(5 cycles 15 points) [Iter=1 Diff=0.00777] E=-3930.6182 Grad=1.216 Conv=NO(5 cycles 15 points) [Iter=2 Diff=0.00071] E=-3930.6182 Grad=1.216 Conv=NO(5 cycles 15 points) [Iter=3 Diff=0.00008] E=-3930.6323 Grad=1.558 Conv=NO(5 cycles 16 points) [Iter=1 Diff=0.00082] E=-3930.6323 Grad=1.558 Conv=NO(5 cycles 16 points) [Iter=2 Diff=0.00007] E=-3930.6365 Grad=0.975 Conv=NO(6 cycles 17 points) [Iter=1 Diff=0.00493] E=-3930.6365 Grad=0.975 Conv=NO(6 cycles 17 points) [Iter=2 Diff=0.00053] E=-3930.6365 Grad=0.975 Conv=NO(6 cycles 17 points) [Iter=3 Diff=0.00007] E=-3930.6555 Grad=0.993 Conv=NO(6 cycles 18 points) [Iter=1 Diff=0.00493] E=-3930.6555 Grad=0.993 Conv=NO(6 cycles 18 points) [Iter=2 Diff=0.00053] E=-3930.6555 Grad=0.993 Conv=NO(6 cycles 18 points) [Iter=3 Diff=0.00007] E=-3930.6479 Grad=2.055 Conv=NO(6 cycles 19 points) [Iter=1 Diff=0.00305] E=-3930.6479 Grad=2.055 Conv=NO(6 cycles 19 points) [Iter=2 Diff=0.00033] E=-3930.6479 Grad=2.055 Conv=NO(6 cycles 19 points) [Iter=3 Diff=0.00004] E=-3930.6563 Grad=1.187 Conv=NO(7 cycles 20 points) [Iter=1 Diff=0.02653] E=-3930.6563 Grad=1.187 Conv=NO(7 cycles 20 points) [Iter=2 Diff=0.00282]E=-3930.6563 Grad=1.187 Conv=NO(7 cycles 20 points) [Iter=4 Diff=0.00008] E=-3930.6553 Grad=1.447 Conv=NO(7 cycles 21 points) [Iter=1 Diff=0.00680] E=-3930.6553 Grad=1.447 Conv=NO(7 cycles 21 points) [Iter=2 Diff=0.00072] E=-3930.6553 Grad=1.447 Conv=NO(7 cycles 21 points) [Iter=3 Diff=0.00010] E=-3930.6553 Grad=1.447 Conv=NO(7 cycles 21 points) [Iter=4 Diff=0.00002] E=-3930.6733 Grad=0.377 Conv=NO(8 cycles 22 points) [Iter=1 Diff=0.00126] E=-3930.6733 Grad=0.377 Conv=NO(8 cycles 22 points) [Iter=2 Diff=0.00013] E=-3930.6733 Grad=0.377 Conv=NO(8 cycles 22 points) [Iter=3 Diff=0.00002] E=-3930.6770 Grad=0.591 Conv=NO(8 cycles 23 points) [Iter=1 Diff=0.00126] E=-3930.6770 Grad=0.591 Conv=NO(8 cycles 23 points) [Iter=2 Diff=0.00013] E=-3930.6770 Grad=0.591 Conv=NO(8 cycles 23 points) [Iter=3 Diff=0.00002] E=-3930.6760 Grad=1.185 Conv=NO(8 cycles 24 points) [Iter=1 Diff=0.00060] E=-3930.6760 Grad=1.185 Conv=NO(8 cycles 24 points) [Iter=2 Diff=0.00006] E=-3930.6772 Grad=0.765 Conv=NO(9 cycles 25 points) [Iter=1 Diff=0.01277] E=-3930.6772 Grad=0.765 Conv=NO(9 cycles 25 points) [Iter=2 Diff=0.00156] E=-3930.6772 Grad=0.765 Conv=NO(9 cycles 25 points) [Iter=3 Diff=0.00022] E=-3930.6772 Grad=0.765 Conv=NO(9 cycles 25 points) [Iter=4 Diff=0.00004] E=-3930.6943 Grad=0.537 Conv=NO(9 cycles 26 points) [Iter=1 Diff=0.01278] E=-3930.6943 Grad=0.537 Conv=NO(9 cycles 26 points) [Iter=2 Diff=0.00156] E=-3930.6943 Grad=0.537 Conv=NO(9 cycles 26 points) [Iter=3 Diff=0.00022] E=-3930.6943 Grad=0.537 Conv=NO(9 cycles 26 points) [Iter=4 Diff=0.00004] E=-3930.7007 Grad=0.713 Conv=NO(9 cycles 27 points) [Iter=1 Diff=0.05107] E=-3930.7007 Grad=0.713 Conv=NO(9 cycles 27 points) [Iter=2 Diff=0.00624] E=-3930.7007 Grad=0.713 Conv=NO(9 cycles 27 points) [Iter=3 Diff=0.00088] E=-3930.7007 Grad=0.713 Conv=NO(9 cycles 27 points) [Iter=4 Diff=0.00017] E=-3930.7007 Grad=0.713 Conv=NO(9 cycles 27 points) [Iter=5 Diff=0.00000] E=-3930.6814 Grad=1.564 Conv=NO(9 cycles 28 points) [Iter=1 Diff=0.04619] E=-3930.6814 Grad=1.564 Conv=NO(9 cycles 28 points) [Iter=2 Diff=0.00565] E=-3930.6814 Grad=1.564 Conv=NO(9 cycles 28 points) [Iter=3 Diff=0.00080] E=-3930.6814 Grad=1.564 Conv=NO(9 cycles 28 points) [Iter=4 Diff=0.00015] E=-3930.6814 Grad=1.564 Conv=NO(9 cycles 28 points) [Iter=5 Diff=0.00000] E=-3930.7007 Grad=0.746 Conv=NO(10 cycles 29 points) [Iter=1 Diff=0.30872] E=-3930.7007 Grad=0.746 Conv=NO(10 cycles 29 points) [Iter=2 Diff=0.03123] E=-3930.7007 Grad=0.746 Conv=NO(10 cycles 29 points) [Iter=3 Diff=0.00379] E=-3930.7007 Grad=0.746 Conv=NO(10 cycles 29 points) [Iter=4 Diff=0.00060] E=-3930.7007 Grad=0.746 Conv=NO(10 cycles 29 points) [Iter=5 Diff=0.00001] E=-3930.4949 Grad=5.995 Conv=NO(10 cycles 30 points) [Iter=1 Diff=0.22743] E=-3930.4949 Grad=5.995 Conv=NO(10 cycles 30 points) [Iter=2 Diff=0.02299] E=-3930.4949 Grad=5.995 Conv=NO(10 cycles 30 points) [Iter=3 Diff=0.00279] E=-3930.4949 Grad=5.995 Conv=NO(10 cycles 30 points) [Iter=4 Diff=0.00044] E=-3930.4949 Grad=5.995 Conv=NO(10 cycles 30 points) [Iter=5 Diff=0.00001] E=-3930.7065 Grad=0.567 Conv=NO(11 cycles 31 points) [Iter=1 Diff=0.00702] E=-3930.7065 Grad=0.567 Conv=NO(11 cycles 31 points) [Iter=2 Diff=0.00087]E=-3930.7065 Grad=0.567 Conv=NO(11 cycles 31 points) [Iter=4 Diff=0.00002] E=-3930.7183 Grad=0.492 Conv=NO(11 cycles 32 points) [Iter=1 Diff=0.00702] E=-3930.7183 Grad=0.492 Conv=NO(11 cycles 32 points) [Iter=2 Diff=0.00087] E=-3930.7183 Grad=0.492 Conv=NO(11 cycles 32 points) [Iter=3 Diff=0.00013] E=-3930.7183 Grad=0.492 Conv=NO(11 cycles 32 points) [Iter=4 Diff=0.00002] E=-3930.7261 Grad=0.615 Conv=NO(11 cycles 33 points) [Iter=1 Diff=0.02813] E=-3930.7261 Grad=0.615 Conv=NO(11 cycles 33 points) [Iter=2 Diff=0.00348] E=-3930.7261 Grad=0.615 Conv=NO(11 cycles 33 points) [Iter=3 Diff=0.00050] E=-3930.7261 Grad=0.615 Conv=NO(11 cycles 33 points) [Iter=4 Diff=0.00010] E=-3930.7292 Grad=1.133 Conv=NO(11 cycles 34 points) [Iter=1 Diff=0.00269] E=-3930.7292 Grad=1.133 Conv=NO(11 cycles 34 points) [Iter=2 Diff=0.00033] E=-3930.7292 Grad=1.133 Conv=NO(11 cycles 34 points) [Iter=3 Diff=0.00005] E=-3930.7300 Grad=0.957 Conv=NO(12 cycles 35 points) [Iter=1 Diff=0.34365] E=-3930.7300 Grad=0.957 Conv=NO(12 cycles 35 points) [Iter=2 Diff=0.04173] E=-3930.7300 Grad=0.957 Conv=NO(12 cycles 35 points) [Iter=3 Diff=0.00599] E=-3930.7300 Grad=0.957 Conv=NO(12 cycles 35 points) [Iter=4 Diff=0.00114] E=-3930.7300 Grad=0.957 Conv=NO(12 cycles 35 points) [Iter=5 Diff=0.00002] E=-3930.5986 Grad=5.283 Conv=NO(12 cycles 36 points) [Iter=1 Diff=0.21604] E=-3930.5986 Grad=5.283 Conv=NO(12 cycles 36 points) [Iter=2 Diff=0.02624] E=-3930.5986 Grad=5.283 Conv=NO(12 cycles 36 points) [Iter=3 Diff=0.00377] E=-3930.5986 Grad=5.283 Conv=NO(12 cycles 36 points) [Iter=4 Diff=0.00071] E=-3930.5986 Grad=5.283 Conv=NO(12 cycles 36 points) [Iter=5 Diff=0.00001] E=-3930.7395 Grad=0.780 Conv=NO(13 cycles 37 points) [Iter=1 Diff=0.01219] E=-3930.7395 Grad=0.780 Conv=NO(13 cycles 37 points) [Iter=2 Diff=0.00152] E=-3930.7395 Grad=0.780 Conv=NO(13 cycles 37 points) [Iter=3 Diff=0.00022] E=-3930.7395 Grad=0.780 Conv=NO(13 cycles 37 points) [Iter=4 Diff=0.00004] E=-3930.7498 Grad=0.615 Conv=NO(13 cycles 38 points) [Iter=1 Diff=0.01218] E=-3930.7498 Grad=0.615 Conv=NO(13 cycles 38 points) [Iter=2 Diff=0.00152] E=-3930.7498 Grad=0.615 Conv=NO(13 cycles 38 points) [Iter=3 Diff=0.00022] E=-3930.7498 Grad=0.615 Conv=NO(13 cycles 38 points) [Iter=4 Diff=0.00004] E=-3930.7446 Grad=1.320 Conv=NO(13 cycles 39 points) [Iter=1 Diff=0.00844] E=-3930.7446 Grad=1.320 Conv=NO(13 cycles 39 points) [Iter=2 Diff=0.00105] E=-3930.7446 Grad=1.320 Conv=NO(13 cycles 39 points) [Iter=3 Diff=0.00016] E=-3930.7446 Grad=1.320 Conv=NO(13 cycles 39 points) [Iter=4 Diff=0.00003] E=-3930.7500 Grad=0.705 Conv=NO(14 cycles 40 points) [Iter=1 Diff=0.04089] E=-3930.7500 Grad=0.705 Conv=NO(14 cycles 40 points) [Iter=2 Diff=0.00529] E=-3930.7500 Grad=0.705 Conv=NO(14 cycles 40 points) [Iter=3 Diff=0.00080] E=-3930.7500 Grad=0.705 Conv=NO(14 cycles 40 points) [Iter=4 Diff=0.00016] E=-3930.7500 Grad=0.705 Conv=NO(14 cycles 40 points) [Iter=5 Diff=0.00000] E=-3930.7607 Grad=1.074 Conv=NO(14 cycles 41 points) [Iter=1 Diff=0.00206] E=-3930.7607 Grad=1.074 Conv=NO(14 cycles 41 points) [Iter=2 Diff=0.00027] E=-3930.7607 Grad=1.074 Conv=NO(14 cycles 41 points) [Iter=3 Diff=0.00004] E=-3930.7620 Grad=0.819 Conv=NO(15 cycles 42 points) [Iter=1 Diff=0.05678]E=-3930.7620 Grad=0.819 Conv=NO(15 cycles 42 points) [Iter=3 Diff=0.00116] E=-3930.7620 Grad=0.819 Conv=NO(15 cycles 42 points) [Iter=4 Diff=0.00024] E=-3930.7620 Grad=0.819 Conv=NO(15 cycles 42 points) [Iter=5 Diff=0.00000] E=-3930.7861 Grad=1.072 Conv=NO(15 cycles 43 points) [Iter=1 Diff=0.05676] E=-3930.7861 Grad=1.072 Conv=NO(15 cycles 43 points) [Iter=2 Diff=0.00749] E=-3930.7861 Grad=1.072 Conv=NO(15 cycles 43 points) [Iter=3 Diff=0.00116] E=-3930.7861 Grad=1.072 Conv=NO(15 cycles 43 points) [Iter=4 Diff=0.00024] E=-3930.7861 Grad=1.072 Conv=NO(15 cycles 43 points) [Iter=5 Diff=0.00000] E=-3930.7898 Grad=2.033 Conv=NO(15 cycles 44 points) [Iter=1 Diff=0.00627] E=-3930.7898 Grad=2.033 Conv=NO(15 cycles 44 points) [Iter=2 Diff=0.00083] E=-3930.7898 Grad=2.033 Conv=NO(15 cycles 44 points) [Iter=3 Diff=0.00013] E=-3930.7898 Grad=2.033 Conv=NO(15 cycles 44 points) [Iter=4 Diff=0.00003] E=-3930.7908 Grad=1.690 Conv=NO(16 cycles 45 points) [Iter=1 Diff=0.94010] E=-3930.7908 Grad=1.690 Conv=NO(16 cycles 45 points) [Iter=2 Diff=0.12528] E=-3930.7908 Grad=1.690 Conv=NO(16 cycles 45 points) [Iter=3 Diff=0.01931] E=-3930.7908 Grad=1.690 Conv=NO(16 cycles 45 points) [Iter=4 Diff=0.00389] E=-3930.7908 Grad=1.690 Conv=NO(16 cycles 45 points) [Iter=5 Diff=0.00006] E=-3930.7996 Grad=2.454 Conv=NO(16 cycles 46 points) [Iter=1 Diff=0.20799] E=-3930.7996 Grad=2.454 Conv=NO(16 cycles 46 points) [Iter=2 Diff=0.02769] E=-3930.7996 Grad=2.454 Conv=NO(16 cycles 46 points) [Iter=3 Diff=0.00427] E=-3930.7996 Grad=2.454 Conv=NO(16 cycles 46 points) [Iter=4 Diff=0.00086] E=-3930.7996 Grad=2.454 Conv=NO(16 cycles 46 points) [Iter=5 Diff=0.00001] E=-3930.8279 Grad=1.061 Conv=NO(17 cycles 47 points) [Iter=1 Diff=0.38133] E=-3930.8279 Grad=1.061 Conv=NO(17 cycles 47 points) [Iter=2 Diff=0.04968] E=-3930.8279 Grad=1.061 Conv=NO(17 cycles 47 points) [Iter=3 Diff=0.00754] E=-3930.8279 Grad=1.061 Conv=NO(17 cycles 47 points) [Iter=4 Diff=0.00150] E=-3930.8279 Grad=1.061 Conv=NO(17 cycles 47 points) [Iter=5 Diff=0.00002] E=-3930.7996 Grad=2.058 Conv=NO(17 cycles 48 points) [Iter=1 Diff=0.15114] E=-3930.7996 Grad=2.058 Conv=NO(17 cycles 48 points) [Iter=2 Diff=0.01968] E=-3930.7996 Grad=2.058 Conv=NO(17 cycles 48 points) [Iter=3 Diff=0.00298] E=-3930.7996 Grad=2.058 Conv=NO(17 cycles 48 points) [Iter=4 Diff=0.00060] E=-3930.7996 Grad=2.058 Conv=NO(17 cycles 48 points) [Iter=5 Diff=0.00001] E=-3930.8440 Grad=0.360 Conv=NO(18 cycles 49 points) [Iter=1 Diff=0.00912] E=-3930.8440 Grad=0.360 Conv=NO(18 cycles 49 points) [Iter=2 Diff=0.00133] E=-3930.8440 Grad=0.360 Conv=NO(18 cycles 49 points) [Iter=3 Diff=0.00022] E=-3930.8440 Grad=0.360 Conv=NO(18 cycles 49 points) [Iter=4 Diff=0.00005] E=-3930.8372 Grad=1.580 Conv=NO(18 cycles 50 points) [Iter=1 Diff=0.00413] E=-3930.8372 Grad=1.580 Conv=NO(18 cycles 50 points) [Iter=2 Diff=0.00060] E=-3930.8372 Grad=1.580 Conv=NO(18 cycles 50 points) [Iter=3 Diff=0.00010] E=-3930.8462 Grad=0.452 Conv=NO(19 cycles 51 points) [Iter=1 Diff=0.00463] E=-3930.8462 Grad=0.452 Conv=NO(19 cycles 51 points) [Iter=2 Diff=0.00056] E=-3930.8462 Grad=0.452 Conv=NO(19 cycles 51 points) [Iter=3 Diff=0.00008] E=-3930.8523 Grad=0.372 Conv=NO(19 cycles 52 points) [Iter=1 Diff=0.00463]E=-3930.8523 Grad=0.372 Conv=NO(19 cycles 52 points) [Iter=3 Diff=0.00008] E=-3930.8562 Grad=0.471 Conv=NO(19 cycles 53 points) [Iter=1 Diff=0.01854] E=-3930.8562 Grad=0.471 Conv=NO(19 cycles 53 points) [Iter=2 Diff=0.00225] E=-3930.8562 Grad=0.471 Conv=NO(19 cycles 53 points) [Iter=3 Diff=0.00032] E=-3930.8562 Grad=0.471 Conv=NO(19 cycles 53 points) [Iter=4 Diff=0.00006] E=-3930.8567 Grad=0.916 Conv=NO(19 cycles 54 points) [Iter=1 Diff=0.00397] E=-3930.8567 Grad=0.916 Conv=NO(19 cycles 54 points) [Iter=2 Diff=0.00048] E=-3930.8567 Grad=0.916 Conv=NO(19 cycles 54 points) [Iter=3 Diff=0.00007] E=-3930.8577 Grad=0.692 Conv=NO(20 cycles 55 points) [Iter=1 Diff=0.20944] E=-3930.8577 Grad=0.692 Conv=NO(20 cycles 55 points) [Iter=2 Diff=0.02334] E=-3930.8577 Grad=0.692 Conv=NO(20 cycles 55 points) [Iter=3 Diff=0.00318] E=-3930.8577 Grad=0.692 Conv=NO(20 cycles 55 points) [Iter=4 Diff=0.00059] E=-3930.8577 Grad=0.692 Conv=NO(20 cycles 55 points) [Iter=5 Diff=0.00001] E=-3930.7786 Grad=3.886 Conv=NO(20 cycles 56 points) [Iter=1 Diff=0.14055] E=-3930.7786 Grad=3.886 Conv=NO(20 cycles 56 points) [Iter=2 Diff=0.01566] E=-3930.7786 Grad=3.886 Conv=NO(20 cycles 56 points) [Iter=3 Diff=0.00214] E=-3930.7786 Grad=3.886 Conv=NO(20 cycles 56 points) [Iter=4 Diff=0.00040] E=-3930.7786 Grad=3.886 Conv=NO(20 cycles 56 points) [Iter=5 Diff=0.00001] E=-3930.8616 Grad=0.408 Conv=NO(21 cycles 57 points) [Iter=1 Diff=0.00370] E=-3930.8616 Grad=0.408 Conv=NO(21 cycles 57 points) [Iter=2 Diff=0.00046] E=-3930.8616 Grad=0.408 Conv=NO(21 cycles 57 points) [Iter=3 Diff=0.00007] E=-3930.8633 Grad=0.323 Conv=NO(21 cycles 58 points) [Iter=1 Diff=0.00040] E=-3930.8633 Grad=0.323 Conv=NO(21 cycles 58 points) [Iter=2 Diff=0.00005] E=-3930.8638 Grad=0.167 Conv=NO(22 cycles 59 points) [Iter=1 Diff=0.00047] E=-3930.8638 Grad=0.167 Conv=NO(22 cycles 59 points) [Iter=2 Diff=0.00005] E=-3930.8640 Grad=0.335 Conv=NO(22 cycles 60 points) [Iter=1 Diff=0.00009] E=-3930.8643 Grad=0.175 Conv=NO(23 cycles 61 points) [Iter=1 Diff=0.00088] E=-3930.8643 Grad=0.175 Conv=NO(23 cycles 61 points) [Iter=2 Diff=0.00010] E=-3930.8643 Grad=0.175 Conv=NO(23 cycles 61 points) [Iter=3 Diff=0.00001] E=-3930.8647 Grad=0.288 Conv=NO(23 cycles 62 points) [Iter=1 Diff=0.00010] E=-3930.8647 Grad=0.182 Conv=NO(24 cycles 63 points) [Iter=1 Diff=0.00091] E=-3930.8647 Grad=0.182 Conv=NO(24 cycles 63 points) [Iter=2 Diff=0.00011] E=-3930.8647 Grad=0.182 Conv=NO(24 cycles 63 points) [Iter=3 Diff=0.00002] E=-3930.8652 Grad=0.280 Conv=NO(24 cycles 64 points) [Iter=1 Diff=0.00010] E=-3930.8655 Grad=0.179 Conv=NO(25 cycles 65 points) [Iter=1 Diff=0.00055] E=-3930.8655 Grad=0.179 Conv=NO(25 cycles 65 points) [Iter=2 Diff=0.00007] E=-3930.8655 Grad=0.210 Conv=NO(25 cycles 66 points) [Iter=1 Diff=0.00011] E=-3930.8655 Grad=0.210 Conv=NO(25 cycles 66 points) [Iter=2 Diff=0.00001] E=-3930.8657 Grad=0.087 Conv=YES(26 cycles 67 points) [Iter=1 Diff=0.00000]ENERGIES AND GRADIENTTotal Energy = -27282.0711491 (kcal/mol)Total Energy = -43.475879746 (a.u.)Binding Energy = -3930.8657598 (kcal/mol)Isolated Atomic Energy = -23351.2053892 (kcal/mol)Electronic Energy = -94220.9390162 (kcal/mol)Core-Core Interaction = 66938.8678671 (kcal/mol)Heat of Formation = -2555.3957598 (kcal/mol)Gradient = 0.0868837 (kcal/mol/Ang)MOLECULAR POINT GROUPC1EIGENV ALUES(eV)Symmetry: 1 A 2 A 3 A 4 A 5 A Eigenvalue: -52.653831 -37.028770 -37.023975 -29.824509 -27.272388Symmetry: 6 A 7 A 8 A 9 A 10 A Eigenvalue: -27.244719 -26.948746 -21.098186 -21.075989 -16.563450Symmetry: 11 A 12 A 13 A 14 A 15 A Eigenvalue: -16.429049 -15.312742 -15.311525 -14.240474 -14.069750Symmetry: 16 A 17 A 18 A 19 A 20 A Eigenvalue: 5.680637 7.398578 7.487293 7.505365 7.740531Symmetry: 21 A 22 A 23 A 24 A 25 A Eigenvalue: 7.752286 8.286099 8.289171 9.845991 9.896807Symmetry: 26 A 27 A 28 A 29 A 30 A Eigenvalue: 10.778082 10.850065 11.798207 11.810519 12.510362ATOMIC ORBITAL ELECTRON POPULATIONSAO: 1 S C 1 Px C 1 Py C 1 Pz C 2 S C0.981183 0.980386 1.020323 0.985765 0.981165AO: 2 Px C 2 Py C 2 Pz C 3 S C 3 Px C1.010096 1.020040 0.956455 0.981115 1.023187AO: 3 Py C 3 Pz C 4 S C 4 Px C 4 Py C0.979342 0.984885 0.981080 0.987665 1.025378AO: 4 Pz C 5 S C 5 Px C 5 Py C 5 Pz C0.975304 0.981111 1.027103 0.981545 0.978970AO: 6 S H 7 S H 8 S H 9 S H 10 S H1.011723 1.021239 1.021008 1.011737 1.012302AO: 11 S H 12 S H 13 S H 14 S H 15 S H1.018996 1.014655 1.015266 1.012561 1.018415NET CHARGES AND COORDINATESAtom Z Charge Coordinates(Angstrom) Massx y z1 6 0.032343 -1.39292 -0.40536 -0.29632 12.011002 6 0.032244 -1.34981 1.07050 -0.40720 12.011003 6 0.031471 -0.25570 -0.75893 0.58456 12.011004 6 0.030573 0.74650 0.32324 0.42738 12.011005 6 0.031272 0.08522 1.42651 -0.31184 12.011006 1 -0.011723 -1.26616 -0.87726 -1.31021 1.008007 1 -0.021239 -2.38081 -0.80365 0.06269 1.008008 1 -0.021008 -1.85072 1.46941 -1.33095 1.008009 1 -0.011737 -1.92795 1.54160 0.43564 1.0080010 1 -0.012302 -0.59748 -0.82756 1.65452 1.0080011 1 -0.018996 0.16333 -1.78099 0.37672 1.0080012 1 -0.014655 1.66579 -0.03935 -0.10959 1.0080013 1 -0.015266 1.14721 0.66647 1.42046 1.0080014 1 -0.012561 0.53113 1.53877 -1.33889 1.0080015 1 -0.018415 0.25658 2.43292 0.15858 1.00800ATOMIC GRADIENTSAtom Z Gradients(kcal/mol/Angstrom)x y z1 6 0.18896 -0.01485 -0.037312 6 -0.06992 0.15860 0.124113 6 -0.04983 -0.22042 0.046674 6 -0.23309 0.00363 -0.055545 6 -0.07703 0.10066 0.046146 1 -0.03418 -0.07446 -0.091057 1 0.04834 -0.03494 -0.000568 1 0.08235 0.00353 0.067629 1 0.01803 -0.00056 0.0062910 1 -0.02103 0.03455 0.0719511 1 -0.01904 0.16346 0.0392112 1 0.08853 0.01197 -0.0319613 1 -0.01082 -0.02264 0.0098214 1 0.07787 0.03463 -0.1507815 1 0.01086 -0.14317 -0.04460Dipole (Debyes) x y z TotalPoint-Chg. 0.032 0.003 0.010 0.034sp Hybrid 0.028 0.003 0.010 0.030pd Hybrid 0.000 0.000 0.000 0.000Sum 0.061 0.007 0.020 0.064Geometry optimization, SemiEmpirical, molecule = (untitled).CNDOFletcherReeves optimizerConvergence limit = 0.0001000 Iteration limit = 50Accelerate convergence = YESOptimization algorithm = Fletcher-ReevesCriterion of RMS gradient = 0.1000 kcal/(A mol) Maximum cycles = 225 RHF Calculation:Singlet state calculationNumber of electrons = 30Number of Double Occupied Levels = 15Charge on the System = 0Total Orbitals = 30Starting CNDO calculation with 30 orbitalsE=0.0000 Grad=0.000 Conv=NO(0 cycles 0 points) [Iter=1 Diff=9901.38267] E=0.0000 Grad=0.000 Conv=NO(0 cycles 0 points) [Iter=2 Diff=8.52345]E=0.0000 Grad=0.000 Conv=NO(0 cycles 0 points) [Iter=3 Diff=0.51968]E=0.0000 Grad=0.000 Conv=NO(0 cycles 0 points) [Iter=4 Diff=0.04223]E=0.0000 Grad=0.000 Conv=NO(0 cycles 0 points) [Iter=5 Diff=0.00150]E=0.0000 Grad=0.000 Conv=NO(0 cycles 0 points) [Iter=6 Diff=0.00007]E=-3930.8657 Grad=0.087 Conv=YES(0 cycles 1 points) [Iter=1 Diff=0.00000]ENERGIES AND GRADIENTTotal Energy = -27282.0711491 (kcal/mol) Total Energy = -43.475879746 (a.u.)Binding Energy = -3930.8657598 (kcal/mol) Isolated Atomic Energy = -23351.2053892 (kcal/mol) Electronic Energy = -94220.9363559 (kcal/mol)Core-Core Interaction = 66938.8652068 (kcal/mol)Heat of Formation = -2555.3957598 (kcal/mol) Gradient = 0.0868814 (kcal/mol/Ang)MOLECULAR POINT GROUPC1EIGENV ALUES(eV)Symmetry: 1 A 2 A 3 A 4 A 5 A Eigenvalue: -52.653828 -37.028770 -37.023975 -29.824505 -27.272387Symmetry: 6 A 7 A 8 A 9 A 10 A Eigenvalue: -27.244719 -26.948744 -21.098185 -21.075987 -16.563450Symmetry: 11 A 12 A 13 A 14 A 15 A Eigenvalue: -16.429049 -15.312742 -15.311525 -14.240474 -14.069750Symmetry: 16 A 17 A 18 A 19 A 20 A Eigenvalue: 5.680636 7.398577 7.487292 7.505364 7.740530Symmetry: 21 A 22 A 23 A 24 A 25 A Eigenvalue: 7.752286 8.286098 8.289171 9.845991 9.896806Symmetry: 26 A 27 A 28 A 29 A 30 A Eigenvalue: 10.778081 10.850063 11.798207 11.810519 12.510361ATOMIC ORBITAL ELECTRON POPULATIONSAO: 1 S C 1 Px C 1 Py C 1 Pz C 2 S C0.981183 0.980386 1.020323 0.985765 0.981165AO: 2 Px C 2 Py C 2 Pz C 3 S C 3 Px C1.010096 1.020040 0.956455 0.981115 1.023187AO: 3 Py C 3 Pz C 4 S C 4 Px C 4 Py C0.979342 0.984885 0.981080 0.987665 1.025378AO: 4 Pz C 5 S C 5 Px C 5 Py C 5 Pz C0.975304 0.981111 1.027103 0.981545 0.978970AO: 6 S H 7 S H 8 S H 9 S H 10 S H1.011723 1.021239 1.021008 1.011737 1.012302AO: 11 S H 12 S H 13 S H 14 S H 15 S H1.018996 1.014655 1.015266 1.012561 1.018415NET CHARGES AND COORDINATESAtom Z Charge Coordinates(Angstrom) Massx y z1 6 0.032343 -1.39292 -0.40536 -0.29632 12.011002 6 0.032244 -1.34981 1.07050 -0.40720 12.011003 6 0.031471 -0.25570 -0.75893 0.58456 12.011004 6 0.030573 0.74650 0.32324 0.42738 12.011005 6 0.031272 0.08522 1.42651 -0.31184 12.011006 1 -0.011723 -1.26616 -0.87726 -1.31021 1.008007 1 -0.021239 -2.38081 -0.80365 0.06269 1.008008 1 -0.021008 -1.85072 1.46941 -1.33095 1.008009 1 -0.011737 -1.92795 1.54160 0.43564 1.0080010 1 -0.012302 -0.59748 -0.82756 1.65452 1.0080011 1 -0.018996 0.16333 -1.78099 0.37672 1.0080012 1 -0.014655 1.66579 -0.03935 -0.10959 1.0080013 1 -0.015266 1.14721 0.66647 1.42046 1.0080014 1 -0.012561 0.53113 1.53877 -1.33889 1.0080015 1 -0.018415 0.25658 2.43292 0.15858 1.00800ATOMIC GRADIENTSAtom Z Gradients(kcal/mol/Angstrom)x y z1 6 0.18903 -0.01497 -0.037262 6 -0.06997 0.15884 0.124053 6 -0.04990 -0.22039 0.046734 6 -0.23292 0.00362 -0.055475 6 -0.07709 0.10066 0.046006 1 -0.03420 -0.07453 -0.091207 1 0.04821 -0.03497 -0.000488 1 0.08237 0.00350 0.067629 1 0.01799 -0.00054 0.0063110 1 -0.02104 0.03449 0.0720411 1 -0.01899 0.16335 0.0391512 1 0.08855 0.01194 -0.0319513 1 -0.01082 -0.02262 0.0098114 1 0.07792 0.03468 -0.1508315 1 0.01087 -0.14306 -0.04451Dipole (Debyes) x y z TotalPoint-Chg. 0.032 0.003 0.010 0.034sp Hybrid 0.028 0.003 0.010 0.030pd Hybrid 0.000 0.000 0.000 0.000Sum 0.061 0.007 0.020 0.064Single Point, AbInitio, molecule = (untitled).Convergence limit = 0.0001000 Iteration limit = 50Accelerate convergence = YESFull MP2 correlation energy is requested.The initial guess of the MO coefficients is from eigenvectors of the core Hamiltonian. Shell Types: S, S=P.RHF Calculation:Singlet state calculationNumber of electrons = 40Number of Doubly-Occupied Levels = 20Charge on the System = 0Total Orbitals (Basis Functions) = 65Primitive Gaussians = 105Starting HyperGauss calculation with 65 basis functions and 105 primitive Gaussians.2-electron Integral buffers will be 3200 words (double precision) long.Two electron integrals will use a cutoff of 1.00000e-010Regular integral format is used.Computing the one-electron integrals ...Computing 2e integrals (s and p orbitals only): done 0%.Computing 2e integrals (s and p orbitals only): done 10%.Computing 2e integrals (s and p orbitals only): done 20%.Computing 2e integrals (s and p orbitals only): done 30%.Computing 2e integrals (s and p orbitals only): done 40%.Computing 2e integrals (s and p orbitals only): done 50%.Computing 2e integrals (s and p orbitals only): done 60%.Computing 2e integrals (s and p orbitals only): done 70%.Computing 2e integrals (s and p orbitals only): done 80%.Computing 2e integrals (s and p orbitals only): done 90%.2173889 integrals have been produced.Computing the initial guess of the MO coefficients ...Iteration = 1 Difference = 155.0197070573Iteration = 2 Difference = 660.9952921963Iteration = 3 Difference = 0.9379147588Iteration = 4 Difference = 0.7714439436Iteration = 5 Difference = 0.4010571545Iteration = 6 Difference = 0.0020506989Iteration = 7 Difference = 0.0001176669Iteration = 8 Difference = 0.0000087172Computing MP2 energy with 20 occupied and 45 virtual orbitals ...Transfering the 2e integrals from AO to MO: done 0%.Transfering the 2e integrals from AO to MO: done 10%.Transfering the 2e integrals from AO to MO: done 20%.Transfering the 2e integrals from AO to MO: done 30%.Transfering the 2e integrals from AO to MO: done 40%.Transfering the 2e integrals from AO to MO: done 50%.Transfering the 2e integrals from AO to MO: done 60%.Transfering the 2e integrals from AO to MO: done 70%.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
*保存文件
• File→Save As→
保存←
*改变键型连接
• 将鼠标移动至需要修改键型的原子上面,左击鼠标同时移 动至另一个原子上面,则
*制作苯环
• 用鼠标单击环形结构中的任一原子,则可画出苯环
*标记原子
• Display→Labels ↓ →→Symbol→OK ↑ ↓ ↑ ↑ →→↑
*编辑个人原子
Ala为丙氨酸 Val为缬氨酸 Gly为甘氨酸
构造• • • •
进入Amino Acids选择Beta Sheet 选择两个以上氨基酸建立肽链 关闭Amino Acids Display→Labels→确认Atoms和Redidues选择的是 None→OK
*创建一个两性分子
Hyperchem学习
小组成员:
胡非非 王珊珊 张鹏程 杨素 邓超 张春洪 花木兴 李庆湖 龙继亮
概况:
• HyperChem用户界面的介绍 • 讨论如何使用工具、菜单和菜单项建立、编辑、显示和操 纵分子
学习内容:
• 打开——打开、关闭某一文件,使用标签和分子效果图 • 基本绘图和编辑——画图、选择、复制及删除原子连接 • 创建小分子的2D和3D模型——绘制和编辑2D图将其转 为3D模型 • 交换、旋转、缩放分子——移动和操纵分子 • 测量结构属性——测量和调整分子几何结构 • 创建一个多肽——创造生物聚合物,学会使用氨基酸和 酸数据库
*Z轴的剪辑
双击
意移 观动 察两 变侧 化红 框 部 分 注
OK
五、测量结果属性
• • • • • • 创建2D结构 编辑此结构 建立3D框架 查看某个原子 键长 键角测量
*创建2D结构
*编辑此结构
双击环状结构
Build
Default Element
N
将一个 碳原子 换成氧原子, 同时点击 DISPLAY 接着 点击Labers 选 择Symbol
四、交换、旋转、缩放分子
• • • • • • • XY轴工具的使用 Z轴工具的使用 缩放工具的使用 定心和缩放 XY轴旋转 Z轴旋转 Z轴剪辑
*XY轴工具的使用
• →工作区→移动鼠标,则所画图像随着移动→双击 ↓
输入XY轴的变化量 如: ↓ OK
←
*Z轴工具的使用
• Display→Rendering→ →Vector and
*多原子的选择
• Select→Turn off Select Sphere→同时点击鼠标的左右键, 圈出想要的多个原子→Select→Turn on Multiple Selections→同时点击鼠标的左右键→放开鼠标
*删除原子
• 将鼠标移动至
点击左键
• 选择所要删除的原子或者键型右击鼠标
*复制原子到Clipboard
• 双击鼠标左键→Element Table→选择原子→关闭Element Table→将鼠标移动至想要编辑的原子上面,单击左键, 则该原子变为自己后面所选原子,如
*选用模型生成器
• Build→Add H and Model Build→
如果没有显示相应原子,则进入 Display→Show Hydrogens
原子间距离显示在 状态栏
*键角测量
• 按住鼠标左键从碳原子拖到氢原子,接着放开鼠标则
键角显示
六、创建多肽
• • • •
Amino Acids对话框的使用 创建一个多肽 创建一个两性分子 位点专一诱变
*Amino Acids对话框的使用
• Databases→Amino Acids→
不同氨基酸结构
OK Thr Mutate
谢谢观赏
胡非非
hyperchem学习 hyperchem
Line Options→ 移动鼠标 ← ↓ ←
→Turn on Perspective ↓ ←确定
*缩放工具的使用
按着鼠标左键移 动鼠标
*定心和缩放
• Display Select to Fit
恢复原来大小
*XY轴转换
移动鼠标
可进行XY轴的旋转
*Z轴的旋转
将鼠标移动至工作区, 则可以对分子进行旋转
*画原子
Build→Default Element→
↓ ← Properties Ok←
*画原子
• Ok→工作区→左键→
*连接
• 将鼠标移动至某一画好的碳原子上,按住鼠标将其拖至另 一相连的碳原子上边,放开鼠标,则:
*选择原子
Select→Atoms→Turn off Multiple Selections→ ↓ 将鼠标移动至想要的原 子或者其他原子上面则 可对相应原子进行选择
• Edit→Rotate→ →
调整X Y Z轴 的数据点击 OK
Make Zwitterion Databases
*位点专一诱变
• Display→Labels→在Residues里选择Name+Seq→OK
Select
Residues
接 下 页
*位点专一诱变
接上图 右击鼠标 点击GLY3
Databases
*打开文件
• File→Open→Hyperchem→Samples→c60.hin→
*使用laber
• Display→Labels→
*使用不同Moleculer Renderings
• Display→Rendering→
↓ ←
Balls
一、打开
二、基本绘图和编辑
• • • • • • Drawing Atoms Drawing Bonds Selecting Atoms Selecting Groups of Atoms Deleting Atoms Copying Atoms to the Clipboard
• 将鼠标移动至
点击左键
• 将鼠标移动至某一原子或键型,点击左键
三、小分子的2D和3D模型
1,画2D图 2,保存文件 3,改变键型连接 4,制作苯环 5,标记原子 6,编辑个人原子 7,调用模型生成器
*画2D图
• Build→Turn on Arbitray Valence→Turn off Explicit Hydrogens→Default Element→Element Table→选择原 子→ →画图如下
*建立3D框架
• Build→Turn off Explicit Hydrogens→双击
*查看某个原子
• Select→关闭Atoms和Multiple Seltctions→
点击氧原子
注意此处
*键长
• 单击碳氧键
键长表示在 此处
*键长测量
• Select→Turn on Multiple Selections→右击鼠标(选中所 有原子)→左击鼠标两个原子→
