人教版数学九年级上同步练习 24.1.3 弧、弦、圆心角

合集下载

人教版九年级上《24.1.3弧、弦、圆心角》同步练习(含答案解析)

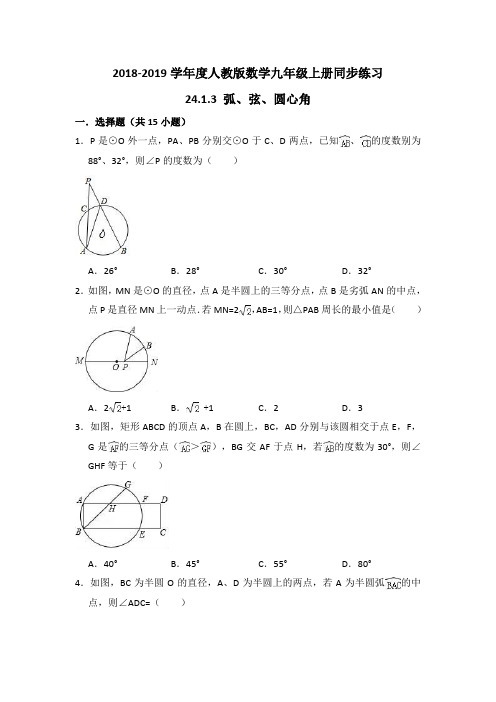
2018-2019学年度人教版数学九年级上册同步练习24.1.3 弧、弦、圆心角一．选择题（共15小题）1．P是⊙O外一点，PA、PB分别交⊙O于C、D两点，已知、的度数别为88°、32°，则∠P的度数为（）A．26°B．28°C．30°D．32°2．如图，MN是⊙O的直径，点A是半圆上的三等分点，点B是劣弧AN的中点，点P是直径MN上一动点．若MN=2，AB=1，则△PAB周长的最小值是（）A．2+1B． +1C．2D．33．如图，矩形ABCD的顶点A，B在圆上，BC，AD分别与该圆相交于点E，F，G是的三等分点（＞），BG交AF于点H，若的度数为30°，则∠GHF等于（）A．40°B．45°C．55°D．80°4．如图，BC为半圆O的直径，A、D为半圆上的两点，若A为半圆弧的中点，则∠ADC=（）A．105°B．120°C．135°D．150°5．如果两个圆心角相等，那么（）A．这两个圆心角所对的弦相等B．这两个圆心角所对的弧相等C．这两个圆心角所对的弦的弦心距相等D．以上说法都不对6．下列语句，错误的是（）A．直径是弦B．相等的圆心角所对的弧相等C．弦的垂直平分线一定经过圆心D．平分弧的半径垂直于弧所对的弦7．点A、C为半径是4的圆周上两点，点B为的中点，以线段BA、BC为邻边作菱形ABCD，顶点D恰在该圆半径的中点上，则该菱形的边长为（）A．或2B．或2C．2或2D．2或28．将一个圆分割成三个扇形，它们的圆心角的度数比为1：2：3，则这个扇形中圆心角度数最大的是（）A．30°B．60°C．120°D．180°9．如图所示，△ABC的三个顶点在⊙O上，D是上的点，E是上的点，若∠BAC=50°．则∠D+∠E=（）A．220°B．230°C．240°D．250°°10．如图，AB是⊙O的直径，==，∠COD=38°，则∠AEO的度数是（）A．52°B．57°C．66°D．78°11．如图，已知A，B，C，D是圆上的点，弧AD=弧BC，AC，BD交于点E，则下列结论正确的是（）A．AB=AD B．BE=CD C．AC=BD D．BE=AD12．如图，圆心角∠AOB=25°，将AB旋转n°得到CD，则∠COD等于（）A．25°B．25°+n°C．50°D．50°+n°13．如图，⊙O的半径为1，动点P从点A处沿圆周以每秒45°圆心角的速度逆时针匀速运动，即第1秒点P位于如图所示的位置，第2秒中P点位于点C 的位置，……，则第2018秒点P所在位置的坐标为（）A．（，）B．（0，1）C．（0，﹣1）D．（，﹣）14．下列语句中不正确的有（）①相等的圆心角所对的弧相等；②平分弦的直径垂直于弦；③圆是轴对称图形，任何一条直径都是它的对称轴；④长度相等的两条弧是等弧．A．3个B．2个C．1个D．4个15．如图所示，在⊙O中，A，C，D，B是⊙O上四点，OC，OD交AB于点E，F，且AE=FB，下列结论：①OE=OF；②AC=CD=DB；③CD∥AB；④=，其中正确的有（）A．4个B．3个C．2个D．1个二．填空题（共10小题）16．如图，AB，CD是⊙O的直径，弦CE∥AB，弧CE的度数为40°，∠AOC的度数．17．⊙O的半径为5，弦AB与弦CD相等，且AB⊥CD于H，若OH=3，则线段BH长为．18．如图，C为弧AB的中点，CN⊥OB于N，CD⊥OA于M，CD=4cm，则CN= cm．19．将一个圆分割成三个扇形，它们圆心角度数之间的关系为2：3：4，则这三个扇形中圆心角最小的度数是度．20．如图，⊙O中，已知弧AB=弧BC，且弧AB：弧AmC=3：4，则∠AOC=度．21．如图，在⊙O中，=，∠1=30°，则∠2=．22．如图，在四边形ABCD中，∠BAD=∠CDA=90°，AB=1，CD=2，过A，B，D三点的⊙O分别交BC，CD于点E，M，下列结论：①DM=CM；②；③⊙O的直径为2；④AE=AD．其中正确的结论有（填序号）．23．如图，在⊙O中，AB=DC，∠AOB=50°，则∠COD=．24．如图，已知AB、CD是⊙O中的两条直径，且∠AOC=50°，过点A作AE∥CD交⊙O于点E，则的度数为．25．如图，已知⊙O中，直径AB平分弦CD，且交CD于点E，如果OE=BE，那么弦CD所对的圆心角是度．三．解答题（共6小题）26．如图，在⊙O中，弦AB与DC相交于E，且BE=DE，求证：=．27．如图，OA、OB、OC都是⊙O的半径，∠AOB=2∠BOC．探索∠ACB与∠BAC 之间的数量关系，并说明理由．28．如图，在⊙O中，AB=CD．求证：AD=BC．29．如图，在⊙O中，弦AD、BC相交于点E，连接OE，已知AD=BC，AD⊥CB．（1）求证：AB=CD；（2）如果⊙O的半径为5，DE=1，求AE的长．30．将一个圆分割成甲、乙、丙、丁四个扇形，使它们的圆心角的度数比为1：2：3：4，分别求出这四个扇形的圆心角的度数．31．如图，已知⊙O的弦AB，E，F是弧AB上两点，=，OE、OF分别交于AB于C、D两点，求证：AC=BD．参考答案与试题解析一．选择题（共15小题）1．【解答】解：∵和所对的圆心角分别为88°和32°，∴∠A=×32°=16°，∠ADB=×88°=44°，∵∠P+∠A=∠ADB，∴∠P=∠ADB﹣∠A=44°﹣16°=28°．故选：B．2．【解答】解：作点A关于MN的对称点A′，连接A′B，交MN于点P，连接OA′，OA，OB，PA，AA′，∵点A与A′关于MN对称，点A是半圆上的一个三等分点，∴∠A′ON=∠AON=60°，PA=PA′，∵点B是弧AN的中点，∴∠BON=30°，∴∠A′OB=∠A′ON+∠BON=90°，又∵OA=OA′=，∴A′B=2．∴PA+PB=PA′+PB=A′B=2，∴△PAB周长的最小值是2+1=3，故选：D．3．【解答】解：连接BF，∵的度数为30°，∴的度数为150°，∠AFB=15°，∵G是的三等分点，∴的度数为50°，∴∠GBF=25°，∴∠GHF=∠GBF+∠AFB=40°，故选：A．4．【解答】解：连接AC，∵BC为半圆的直径，∴∠BAC=90°，又A为半圆弧的中点，∴AB=AC，∴∠B=∠ACB=45°，∵A、B、C、D四点共圆，∴∠ADC+∠B=180°，∴∠ADC=180°﹣45°=135°．故选：C．5．【解答】解：在同圆和等圆中，相等的圆心角所对的弧相等，所对的弦也相等，所对的弦的弦心距相等．故选：D．6．【解答】解：直径是弦，A正确，不符合题意；在同圆或等圆中，相等的圆心角所对的弧相等，B错误，符合题意；弦的垂直平分线一定经过圆心，C正确，不符合题意；平分弧的半径垂直于弧所对的弦，D正确，不符合题意；故选：B．7．【解答】解：过B作直径，连接AC交AO于E，∵点B为的中点，∴BD⊥AC，如图①，∵点D恰在该圆直径上，D为OB的中点，∴BD=×4=2，∴OD=OB﹣BD=2，∵四边形ABCD是菱形，∴DE=BD=1，∴OE=1+2=3，连接OC，∵CE===，在Rt△DEC中，由勾股定理得：DC===2；如图②，OD=2，BD=4+2=6，DE=BD=3，OE=3﹣2=1，由勾股定理得：CE===，DC===2，故选：C．8．【解答】解：由题意可得，三个圆心角的和为360°，∵三个圆心角的度数比为1：2：3，∴最大的圆心角度数为：360°×=180°．故选：D．9．【解答】解：连接OA、OB、OC，如图所示：∵∠BAC=50°，∴∠BOC=2∠BAC=100°，∴∠AOB+∠AOC=360°﹣100°=260°，∵∠D=（∠BOC+∠AOC），∠E=（∠BOC+∠AOB），∴∠D+∠E=（∠BOC+∠AOC+∠BOC+∠AOB）=（260°+100°+100°）=230°．故选：B．10．【解答】解：∵==，∠COD=38°，∴∠BOC=∠EOD=∠COD=38°，∴∠AOE=180°﹣∠EOD﹣∠COD﹣∠BOC=66°．又∵OA=OE，∴∠AEO=∠OAE，∴∠AEO=×（180°﹣66°）=57°．故选：B．11．【解答】解：连接BC，∵，∴，∴，∴AC=BD，故选：C．12．【解答】解：∵将AB旋转n°得到CD，∴=，∴∠COD=∠AOB=25°，故选：A．13．【解答】解：作PE⊥OA于E，∵OP=1，∠POE=45°，∴OE=PE=，即点P的坐标为（，），则第2秒P点为（0，1），根据题意可知，第3秒P点为（﹣，），第4秒P点为（﹣1，0），第5秒P点为（﹣，﹣），第6秒P点为（0，﹣1），第7秒P点为（，﹣），第8秒P点为（1，0），2018÷8=252……2，∴第2018秒点P所在位置的坐标为（0，1），故选：B．14．【解答】解：①和④、错误，应强调在同圆或等圆中；②、错误，应强调不是直径的弦；③、错误，应强调过圆心的直线才是它的对称轴．故选D．15．【解答】解：连接OA，OB，∵OA=OB，∴∠OAB=∠OBA．在△OAE与△OBF中，，∴△OAE≌△OBF（SAS），∴OE=OF，故①正确；∠AOE=∠BOF，即∠AOC=∠BOD，∴，故④正确；连结AD．∵，∴∠BAD=∠ADC，∴CD∥AB，故③正确；∵∠BOD=∠AOC不一定等于∠COD，∴弧AC=弧BD不一定等于弧CD，∴AC=BD不一定等于CD，故②不正确．正确的有3个，故选B．二．填空题（共10小题）16．【解答】解：连接OE，如图，∵弧CE的度数为40°，∴∠COE=40°，∵OC=OE，∴∠OCE=∠OEC，∴∠OCE=（180°﹣40°）÷2=70°，∵弦CE∥AB，∴∠AOC=∠OCE=70°．17．【解答】解：①过点O作OE⊥AB，OF⊥CD，∴AE=BE，∵AB=CD，∴OE=OF，∵OH=3，OA=5，∴OE=3，∴AE=BE=4，∴BH=BE﹣HE=4﹣3=1；②根据①得出BE=4，HE=3，∴BH=HE+BE=3+4=7．18．【解答】解：∵CM⊥OA，即OM⊥CD，由垂径定理得：CD=2CM=4cm，连接OC，∵C为弧AB的中点，∴弧AC=弧BC，∴∠AOC=∠BOC，∵CN⊥OB，CD⊥OA∴∠CMO=∠CNO∴∴△CMO≌△CNO∴CN=CM=2cm，故答案为：2．19．【解答】解：∵周角的度数是360°，∴这三个扇形中圆心角最小的度数是，故答案为：80．20．【解答】解：∵弧AB=弧BC，且弧AB：弧AmC=3：4，∴弧ABC：弧AmC=6：4，∴∠AOC的度数为（360°÷10）×4=144°．21．【解答】解：∵在⊙O中，=，∴=，∴∠1=∠2=30°．故答案是：30°．22．【解答】解：如下图，连接AM，连接MB，过点O作OG⊥AM，OH⊥AM，∵∠BAD=∠CDA=90°，∴AM过圆心O，而A、D、M、B四点公圆，∴四边形ADMB为矩形，而AB=1，CD=2，∴CM=2﹣1=1=AB=DM，即：①DM=CM，正确；又AB∥CD，∴四边形ABMC为平行四边形，∴∠AEB=∠MAE，=，故②正确；∵四边形ADMB为矩形，∴AB=DM，∴=，∴∠DAM=∠EAM，过点O作OG⊥AM，OH⊥AM，∴OG=OH，∴AD=AE，∴④正确；由题设条件求不出直径的大小，故③⊙O的直径为2，错误；故答案为①②④．23．【解答】解：∵AB=CD，∴∠COD=∠AOB，∵∠AOB=50°，∴∠COD=50°，故答案是：50°．24．【解答】解：∵AEE∥CD，∠AOC=50°，∴∠EAO=∠C=50°，∵OA=OE，∴∠AEO=∠EAO=50°，∴∠AOE=180°﹣∠EAO﹣∠AEO=80°，即的度数为80°，故答案为：80°．25．【解答】解：连接OC，BC，OD，∵直径AB平分弦CD，OE=BE，∴OC=BC=OB，∴△OCB是等边三角形，∴∠COB=60°，∴∠COD=120°，即弦CD所对的圆心角是120°，故答案为：120三．解答题（共6小题）26．【解答】证明：在△AED和△CEB中，，∴△AED≌△CEB（AAS）．∴AD=BC，∴=．27．【解答】解：∠ACB=2∠BAC．证明：∵∠ACB=∠AOB，∠BAC=∠BOC；又∵∠AOB=2∠BOC，∴∠ACB=2∠BAC．28．【解答】证明：∵AB=CD，∴=，∴﹣=﹣，即=，∴AD=BC．29．【解答】（1）证明：如图，∵AD=BC，∴=，∴﹣=﹣，即=，∴AB=CD；（2）如图，过O作OF⊥AD于点F，作OG⊥BC于点G，连接OA、OC．则AF=FD，BG=CG．∵AD=BC，∴AF=CG．在Rt△AOF与Rt△COG中，，∴Rt△AOF≌Rt△COG（HL），∴OF=OG，∴四边形OFEG是正方形，∴OF=EF．设OF=EF=x，则AF=FD=x+1，在直角△OAF中．由勾股定理得到：x2+（x+1）2=52，解得x=3．则AF=3+1=4，即AE=AF+3=7．30．【解答】解：∵甲、乙、丙、丁四个扇形的面积之比为1：2：3：4，∴各个扇形的面积分别占整个圆面积的，，，，∴各个扇形的圆心角的度数分别360°×=36°，360°×=72°，360°×=108°，360°×=144°，答：甲、乙、丙、丁四个扇形的圆心角的度数分别是36°，72°，108°，144°．31．【解答】证明：连接OA、OB，∵OA=OB，∴∠A=∠B，∵=，∴∠AOC=∠BOD，在△AOC和△BOD中，，∴△AOC≌△BOD，∴AC=BD．。

人教版九年级数学上册 24.1.3 弧、弦、圆心角同步练习卷

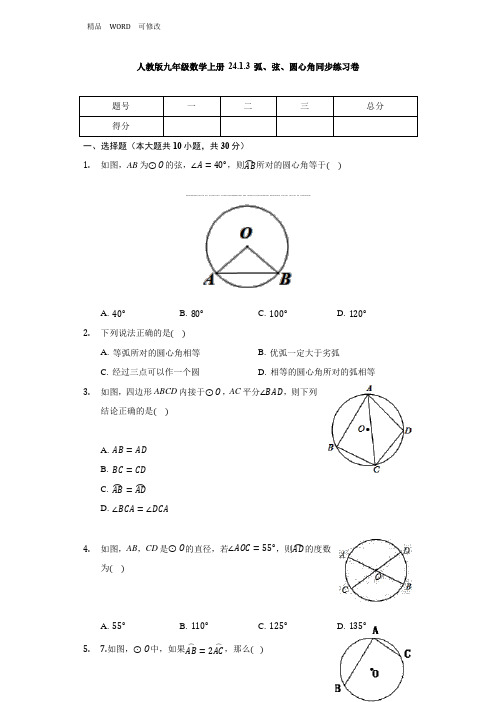
人教版九年级数学上册24.1.3 弧、弦、圆心角同步练习卷题号一二三总分得分一、选择题（本大题共10小题，共30分）1.如图，AB为⊙O的弦，∠A=40°，则AB⏜所对的圆心角等于()A. 40°B. 80°C. 100°D. 120°2.下列说法正确的是()A. 等弧所对的圆心角相等B. 优弧一定大于劣弧C. 经过三点可以作一个圆D. 相等的圆心角所对的弧相等3.如图，四边形ABCD内接于⊙O，AC平分∠BAD，则下列结论正确的是()A. AB=ADB. BC=CDC. AB⏜=AD⏜D. ∠BCA=∠DCA4.如图，AB，CD是⊙O的直径，若∠AOC=55°，则AD⏜的度数为()A. 55°B. 110°C. 125°D. 135°5.7.如图，⊙O中，如果AB⌢=2AC⌢，那么()A. AB=ACB. AB=2ACC. AB<2ACD. AB>2AC6.如图，在⊙O中AC⏜=BD⏜，∠AOB=40°，则∠COD的度数()A. 20°B. 40°C. 50°D. 60°7.如图，AB，CD是⊙O的直径，AE⏜=BD⏜.若∠AOE=32°，则∠COE的度数是()A. 32°B. 60°C. 68°D. 64°8.如图，在⊙O中，已知弦AB长为16cm，C为弧AB的中点，OC交AB于点M，且OM∶MC=3∶2，则CM长为()A. 2cmB. 4cmC. 6cmD. 8cm9.如图，AB是⊙O的直径，C，D分别是⊙O上的两点，OC⊥OD，AC=2cm，BD=√2cm，则⊙O的半径是()A. √3cmB. 2cmC. √5cmD. 3cm10.如图，AB是⊙O的直径，C是AB⏜的中点，连接OC，点E，F分别是OA，OC上的点，若EF//AC，则∠EFC的度数为()A. 45°B. 60°C. 135°D. 160°二、填空题（本大题共5小题，共15分）11.已知圆O的半径长为6，若弦AB=6√3，则弦AB所对的圆心角等于______ ．12.如图，在⊙O中，点C为弧AB的中点，OC交弦AB于D，如果AB=8，OC=5，那么OD的长为______．13.如图，在⊙O中，AB⏜=CD⏜，∠AOB与∠COD的关系是______．14.如图，AB是⊙O的直径，弦CD⊥AB于点E，如果AC⏜=CD⏜，则∠ACD的度数是______．15.如图所示，PO是⊙O直径所在的直线，且PO平分∠BPD，OE⊥AB，OF⊥CD，则：①AB=CD；②AB⌢=CD⌢；③PO=PE；④BG⌢=DG⌢；⑤PB=PD.其中结论正确的是_________.(填序号)三、解答题（本大题共5小题，共55分）16.如图，已知AB为圆O的直径，M，N分别为OA，OB的中点，CM⊥AB，DN⊥AB，垂足分别为M，N，连结OC，OD，求证：AC⏜=BD⏜．17.如图，已知⊙O的弦AB，E，F是弧AB上两点，AE⏜=BF⏜，OE、OF分别交于AB于C、D两点，求证：AC=BD．18.如图，在⊙O中，AB⏜=BC⏜，∠BOC=32°，求∠D的度数．19.如图，以□ABCD的顶点A为圆心，AB为半径作⊙A，分别交BC，AD于E，F两点，交BA的延长线于G，判断EF⌒和FG⌒是否相等，并说明理由．20.已知：在△ABC中，以AC边为直径的⊙O交BC于点D，在劣弧AD⏜上到一点E使∠EBC=∠DEC，延长BE依次交AC于G，交⊙O于H．(1)求证：AC⊥BH；(2)若∠ABC=45°，⊙O的直径等于10，BD=8，求①CGCD的值；②EH的长．1、最困难的事就是认识自己。

(人教版数学)初中9年级上册-同步练习-24.1.3 弧、弦、圆心角-九年级数学人教版(上)(解析版

第二十四章圆24.1.3弧、弦、圆心角一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的．1．如图，已知AB是O的直径，D，C是劣弧EB的三等分点，∠BOC=40°，那么∠AOE=A．40°B．60°C．80°D．120°【答案】B2．将一个圆分割成四个大小相同的扇形，则每个扇形的圆心角是（）度．A．45 B．60C．90 D．120【答案】C【解析】∵圆心处构成一个周角,∴圆心角为360°,∵将圆分割成四个大小相同的扇形,∴每个扇形的圆心角是90°,故选C.【名师点睛】本题考查了扇形和圆心角的定义，解题的关键是掌握一个圆的圆心角为360°.3．已知AB与A′B′分别是O与O′的两条弦,AB=A′B′,那么∠AOB与∠A′O′B′的大小关系是A．∠AOB=∠A′O′B′ B．∠AOB>∠A′O′B′C．∠AOB<∠A′O′B′ D．不能确定【答案】D【解析】由弦相等推弦所对的圆心角相等,必须保证在同圆或等圆中.此题没有限制,所以不能确定∠AOB 和∠A′O′B′的大小关系.4．下列图形中表示的角是圆心角的是A ．AB ．BC ．CD ．D【答案】A【解析】根据圆心角的定义:顶点在圆心的角是圆心角可知,B,C,D 项图形中的顶点都不在圆心上,所以它们都不是圆心角.故选A. 5．如果两个圆心角相等，那么 A ．这两个圆心角所对的弦相等B ．这两个圆心角所对的弧相等C ．这两个圆心角所对的弦的弦心距相等D ．以上说法都不对【答案】D6．在同圆中，下列四个命题:(1)圆心角是顶点在圆心的角；(2)两个圆心角相等，它们所对的弦也相等；(3)两条弦相等，它们所对的弧也相等；(4)等弧所对的圆心角相等.其中真命题有A ．4个B ．3个C ．2个D ．1个【答案】B【解析】圆心角是顶点在圆心的角，所以①正确，为真命题；在同圆中，两个圆心角相等，它们所对的弦也相等，所以②正确，为真命题；在同圆中，两条弦相等，所对的劣弧也相等，所以③错误，为假命题；等弧所对的圆心角相等，所以④正确，为真命题．故选B ．7．如图，已知A 、B 、C 、D 是⊙O 上的点，∠1＝∠2，则下列结论中正确的有 ①AB CD =；②BD AC =；③AC ＝BD ；④∠BOD ＝∠AO C ．A．1个B．2个C．3个D．4个【答案】D二、填空题：请将答案填在题中横线上．8．如图，AB是⊙O的直径，点C在⊙O上，∠AOC=40°，D是弧BC的中点，则∠ACD= ________．【答案】125°【解析】连接OD，∵AB是⊙O的直径，∠AOC=40°，∴∠BOC=140°，∠ACO=（180°-40°）÷2=70°，∵D是弧BC的中点，∴∠COD=70°，∴∠OCD=（180°-70°）÷2=55°，∴∠ACD=∠ACO+∠OCD=70°+55°=125°，故答案为125°．9．在半径为R的⊙O中，有一条弦等于半径，则弦所对的圆心角为 ________．【答案】60°【解析】如图，AB=OA=OB，所以△ABC为等边三角形，所以∠AOB=60°．故答案为60°．10．弦AB将⊙O分成度数之比为1：5的两段弧，则∠AOB= _________°.【答案】60三、解答题：解答应写出文字说明、证明过程或演算步骤．11．如图,AB,CD,EF都是O的直径,且∠1=∠2=∠3,求证:AC=EB=DF.【解析】在O中,∵∠1=∠2=∠3,又∵AB,CD,EF都是O的直径,∴∠FOD=∠AOC=∠BOE.∴DF=AC=EB,∴AC=EB=DF.。

2020年人教版九年级数学上册24.1.3《弧、弦、圆心角》同步练习学生版

别交 BC，CD 于点 E，M，下列结论：①DM=CM；② AE=AD．其中正确的结论有（填序号）．
；③⊙O 的直径为 2；④
23．如图，在⊙O 中，AB=DC，∠AOB=50°，则∠COD= ．
24．如图，已知 AB、CD 是⊙O 中的两条直径，且∠AOC=50°，过点 A 作 AE∥CD 交⊙O 于点 E，则的度数为．
B．BE=CD
C．AC=BD
D．BE=AD
12．如图，圆心角∠AOB=25°，将 AB 旋转 n°得到 CD，则∠COD 等于（）
A．25°
B．25°+n°
C．50°
D．50°+n°
13．如图，⊙O 的半径为 1，动点 P 从点 A 处沿圆周以每秒 45°圆心角的速度逆时针匀速运动，即第 1 秒点 P 位于如图所示的位置，第 2 秒中 P 点位于点 C 的位置，……，则第 2018 秒点 P 所在位置的坐标为（）
下列结论：①OE=OF；②AC=CD=DB；③CD∥AB；④ = ，其中正确的有（）
A．4 个
B．3 个
C．2 个
D．1 个
二．填空题
16．如图，AB，CD 是⊙O 的直径，弦 CE∥AB，弧 CE 的度数为 40°，∠AOC 的度
数．
17．⊙O 的半径为 5，弦 AB 与弦 CD 相等，且 AB⊥CD 于 H，若 OH=3 ，则线段 BH 长为． 18．如图，C 为弧 AB 的中点，CN⊥OB 于 N，CD⊥OA 于 M，CD=4cm，则 CN= cm．
A．40°
B．45°
C．55°
D．80°
4．如图，BC 为半圆 O 的直径，A、D 为半圆上的两点，若 A 为半圆弧 ADC=（）

人教版九年级上数学《24.1.3弧、弦、圆心角》练习题(含答案)

24．1.3　弧、弦、圆心角01 基础题知识点1　圆心角的概念及其计算1．下面图形中的角是圆心角的是(D)A B C D2．已知⊙O 的半径为5 cm ，弦AB 的长为5 cm ，则弦AB 所对的圆心角∠AOB ＝60°.知识点2　弧、弦、圆心角之间的关系3．下列说法正确的是(B)A ．相等的圆心角所对的弧相等B ．在同圆中，等弧所对的圆心角相等C ．弦相等，圆心到弦的距离相等D ．圆心到弦的距离相等，则弦相等4．(兰州中考)如图，在⊙O 中，点C 是的中点，∠A ＝50°，则∠BOC ＝(A)AB ︵ A ．40° B ．45° C ．50° D ．60°5．(教材P85练习T2变式)(贵港中考)如图，AB 是⊙O 的直径，＝＝，∠COD ＝34°，则∠AEO 的BC ︵ CD ︵ DE ︵度数是(A)A ．51°B ．56°C ．68°D ．78°6．如图，已知A ，B ，C ，D 是⊙O 上的点，∠1＝∠2，则下列结论中正确的有(D)①＝；②＝；③AC ＝BD ；④∠BOD ＝∠AOC.AB ︵ CD ︵ BD ︵ AC ︵ A ．1个 B ．2个 C ．3个 D ．4个7．如图，AB 是⊙O 的直径，BC ，CD ，DA 是⊙O 的弦，且BC ＝CD ＝DA ，则∠BCD 的度数为(C)A ．100°B ．110°C ．120°D ．135°8．如图，AB ，DE 是⊙O 的直径，C 是⊙O 上的一点，且＝.BE 与CE 的大小有什么关系？为什么？AD ︵ CE ︵解：BE ＝CE.理由如下：∵AB ，DE 是⊙O 的直径，∴∠AOD ＝∠BOE.∴＝.AD ︵ BE ︵ ∵＝，∴＝.AD ︵ CE ︵ BE ︵ CE ︵ ∴BE ＝CE.9．如图，M 为⊙O 上一点，OD ⊥AM 于点D ，OE ⊥BM 于点E.若OD ＝OE ，求证：＝.AM ︵ BM ︵证明：连接OM.∵OD ⊥AM ，OE ⊥BM ，∴AD ＝MD ，ME ＝BE ，∠ODM ＝∠OEM ＝90°.在Rt △DMO 和Rt △EMO 中，{OD ＝OE ，OM ＝OM ，)∴Rt △DMO ≌Rt △EMO(HL)．∴DM ＝EM.∴AM ＝BM.∴＝.AM ︵ BM ︵易错点　对圆中的有关线段的关系运用不当而致错10．如图，A ，B ，C ，D 是⊙O 上的四点，且AD ＝BC ，则AB 与CD 的大小关系为(B)A ．AB>CDB ．AB ＝CDC ．AB<CDD ．不能确定02 中档题11．如图，已知A ，B ，C 在圆O 上，D ，E ，F 是三边的中点．若＝，则四边形AEDF 的形状是(B)AB ︵ AC ︵ A ．平行四边形B ．菱形C ．正方形D ．矩形12．已知⊙O 中，M 为的中点，则下列结论正确的是(C)AB ︵ A ．AB ＞2AMB ．AB ＝2AMC ．AB ＜2AMD ．AB 与2AM 的大小不能确定13．如图，AB 是半圆O 的直径，E 是OA 的中点，F 是OB 的中点，ME ⊥AB 于点E ，NF ⊥AB 于点F.在下列结论中：①＝＝；②ME ＝NF ；③AE ＝BF ；④ME ＝2AE.AM ︵ MN ︵ BN ︵正确的有①②③．14．如图，AB 是⊙O 的直径，＝，∠COD ＝60°.AC ︵ CD ︵ (1)△AOC 是等边三角形吗？请说明理由；(2)求证：OC ∥BD.解：(1)△AOC 是等边三角形．理由：∵＝，AC ︵ CD ︵ ∴∠AOC ＝∠COD ＝60°.又∵OA ＝OC ，∴△AOC 是等边三角形．(2)证明：∵∠AOC ＝∠COD ＝60°，∴∠BOD ＝180°－(∠AOC ＋∠COD)＝60°.∵OD ＝OB ，∴△ODB 为等边三角形．∴∠ODB ＝60°.∴∠ODB ＝∠COD ＝60°.∴OC ∥BD.15．(教材P84例3变式)如图，A ，B ，C 为圆O 上的三等分点．(1)求∠BOC 的度数；(2)若AB ＝3，求圆O 的半径长及S △ABC .解：(1)∵A ，B ，C 为圆O 上的三等分点，∴＝＝.AB ︵ BC ︵ AC ︵ ∴∠BOC ＝×360°＝120°.13(2)过点O 作OD ⊥AB 于点D ，∵A ，B ，C 为圆O 上的三等分点，∴AB ＝AC ＝BC ＝3，即△ABC 是等边三角形．∴∠BAO ＝∠OBA ＝30°.则AD ＝，故DO ＝，OA ＝，即圆O 半径长为.323233∴S △ABC ＝3××DO·AB ＝.1293403 综合题16．如图，∠AOB ＝90°，C ，D 是的三等分点，连接AB 分别交OC ，OD 于点E ，F ，求证：AB ︵ AE ＝BF ＝CD.证明：连接AC ，BD.∵C ，D 是的三等分点，AB ︵ ∴＝＝.AC ︵ CD ︵ DB ︵ ∴AC ＝CD ＝DB.又∠AOB ＝90°，∴∠AOC ＝∠COD ＝∠BOD ＝∠AOB ＝×90°＝30°.1313∵OA ＝OB ，∴∠OAB ＝∠OBA ＝45°.∴∠AEC ＝∠AOC ＋∠OAB ＝75°.在△AOC 中，OA ＝OC ，∴∠ACO ＝＝＝75°.180°－∠AOC 2180°－30°2∴∠AEC ＝∠ACO.∴AE ＝AC.同理BF ＝BD.∴AE ＝BF ＝CD.。

人教版数学九年级上册：24.1.3 弧、弦、圆心角同步练习(附答案)

24.1.3 弧、弦、圆心角1．如图，图中的圆心角(小于平角的)有( )A ．1个B ．2个C ．3个D ．4个2．已知⊙O 的半径为5 cm ，弦AB 的长为5 cm ，则弦AB 所对的圆心角∠AOB ＝． 3．如图，A ，B ，C ，D 是⊙O 上的四点，且AD ＝BC ，则AB 与CD 的大小关系为( )A ．AB>CDB ．AB ＝CDC ．AB<CD D ．不能确定4．如图，在⊙O 中，点C 是AB ︵的中点，∠A ＝50°，则∠BOC ＝( )A ．40°B ．45°C ．50°D ．60°5．如图，AB 是⊙O 的直径，BC ︵＝CD ︵＝DE ︵，∠COD ＝34°，则∠AEO 的度数是( )A ．51°B ．56°C ．68°D ．78°6．如图，在⊙O 中，AB ︵＝AC ︵，∠A ＝30°，则∠B ＝( )A ．150°B ．75°C ．60°D ．15°7．如图，AB 是⊙O 的直径，C ，D 为半圆的三等分点，CE ⊥AB 于点E ，则∠ACE 的度数为．8．如图，AB ，DE 是⊙O 的直径，点C 是⊙O 上的一点，且AD ︵＝CE ︵，求证：BE ＝CE.9．如图，在⊙O 中，AB ︵＝2CD ︵，试判断AB 与2CD 的大小关系，并说明理由．10．如图，在⊙O 中，已知弦AB ＝DE ，OC ⊥AB ，OF ⊥DE ，垂足分别为C ，F ，则下列说法中正确的个数为( )①∠DOE ＝∠AOB ；②AB ︵＝DE ︵；③OF ＝OC ；④AC ＝EF. A ．1个 B ．2个 C ．3个 D ．4个11．如图，点A ，B ，C 是⊙O 上的三点，且四边形ABCO 是平行四边形，OF ⊥AB 交⊙O 于点F ，则∠BAF 等于( )A ．12.5°B ．15°C ．20°D ．22.5°12．如图，AB 是半圆O 的直径，E 是OA 的中点，F 是OB 的中点，ME ⊥AB 于点E ，NF ⊥AB 于点F.下列结论：①AM ︵＝MN ︵＝BN ︵；②ME ＝NF ；③AE ＝BF ；④ME ＝2AE.其中正确结论的序号是．13．如图，以▱ABCD 的顶点A 为圆心，AB 为半径作圆，交AD ，BC 于E ，F ，延长BA 交⊙A 于点G ，求证：GE ︵＝EF ︵.14．如图，AB 是⊙O 的直径，AC ︵＝CD ︵，∠COD ＝60°. (1)△AOC 是等边三角形吗？请说明理由； (2)求证：OC ∥BD.15．如图，∠AOB ＝90°，C ，D 是AB ︵的三等分点，连接AB 分别交OC ，OD 于点E ，F ，求证：AE ＝BF ＝CD.参考答案：1．B 2． 60°． 3．B 4．A 5．A 6．B 7． 30°．8．证明：∵∠BOE ＝∠AOD ， ∴BE ︵＝AD ︵. 又∵AD ︵＝CE ︵， ∴BE ︵＝CE ︵. ∴BE ＝CE.9．解：∵在同圆或等圆中，同弧或等弧所对的弦相等，∴当AB ︵＝2CD ︵时，AB ＝2CD. 以上解答是否正确？若不正确，请改正．解：不正确．AB ＜2CD.理由：取AB ︵的中点E ，连接AE ，BE ， ∵AB ︵＝2CD ︵，∴AE ︵＝BE ︵＝CD ︵，∴AE ＝BE ＝CD. ∵AE ＋BE ＞AB ，∴AB ＜2CD. 10．D 11．B 12．①②③．13．证明：连接AF.∵四边形ABCD 为平行四边形， ∴AD ∥BC. ∴∠GAE ＝∠B ， ∠EAF ＝∠AFB.又∵AB ，AF 为⊙A 的半径，AB ＝AF ， ∴∠B ＝∠AFB. ∴∠GAE ＝∠EAF. ∴GE ︵＝EF ︵.14．解：(1)△AOC 是等边三角形． ∵AC ︵＝CD ︵，∴∠AOC ＝∠COD ＝60°. 又∵OA ＝OC ，∴△AOC 是等边三角形． (2)证明：∵AC ︵＝CD ︵，∴OC ⊥AD. ∵∠AOC ＝∠COD ＝60°，∴∠BOD ＝180°－(∠AOC ＋∠COD )＝60°. ∵OD ＝OB ，∴△ODB 为等边三角形． ∴∠ODB ＝60°. ∴∠ODB ＝∠COD ＝60°. ∴OC ∥BD.15．证明：连接AC ，BD. ∵AC ︵＝CD ︵＝DB ︵，∠AOB ＝90°，∴∠AOC ＝∠COD ＝∠DOB ＝13∠AOB ＝13×90°＝30°，AC ＝CD ＝BD.∵OA ＝OB ，∴∠OAB ＝∠ABO ＝45°. ∴∠AEC ＝∠AOC ＋∠OAB ＝75°. ∵在△AOC 中，OA ＝OC ，∴∠ACO ＝180°－∠AOC 2＝180°－30°2＝75°.∴∠AEC ＝∠ACO. ∴AE ＝AC. 同理BF ＝BD. ∴AE ＝BF ＝CD.。

初三数学九年级上册同步练习24.1.3 弧、弦、圆心角

24.1.3 弧、弦、圆心角一、课内练习：1．下列命题中，正确的有（）A．圆只有一条对称轴B．圆的对称轴不止一条，但只有有限条C．圆有无数条对称轴，每条直径都是它的对称轴D．圆有无数条对称轴，经过圆心的每条直线都是它的对称轴2．下列说法中，正确的是（）A．等弦所对的弧相等B．等弧所对的弦相等C．圆心角相等，所对的弦相等D．弦相等所对的圆心角相等3．下列命题中，不正确的是（）A．圆是轴对称图形B．圆是中心对称图形C．圆既是轴对称图形，又是中心对称图形D．以上都不对4．如果两个圆心角相等，那么（）A．这两个圆心角所对的弦相等; B．这两个圆心角所对的弧相等C．这两个圆心角所对的弦的弦心距相等; D．以上说法都不对5．如图1，半圆的直径AB=4，O为圆心，半径OE⊥AB，F为OE的中点，CD∥AB，则弦CD的长为（）A．23B．3C．5D．256．已知：如图2，⊙O的直径CD垂直于弦AB，垂足为P，且AP=4cm，PD=2cm，则⊙O 的半径为（）A．4cm B．5cm C．42cm D．23cm7．如图3，同心圆中，大圆的弦AB交小圆于C、D，已知AB=4，CD=2，AB的弦心距等于1，那么两个同心圆的半径之比为（）A．3：2 B．5：2 C．5：2D．5：48．在⊙O中，圆心角∠AOB=90°，点O到弦AB的距离为4，则⊙O的直径的长为（）A．42B．82C．24 D．169．如果两条弦相等，那么（）A．这两条弦所对的弧相等B．这两条弦所对的圆心角相等C．这两条弦的弦心距相等D．以上答案都不对10．半径为5的⊙O内有一点P，且OP=4，则过点P的最短的弦长是，最长的弦长是．11．弓形的弦长6cm，高为1cm，则弓形所在圆的半径为 cm．12．一条弦把圆分成1：3两部分，则弦所对的圆心角为．13．弦心距是弦的一半时，弦与直径的比是，弦所对的圆心角是．14．如图，∠AOB=90°，C、D是弧AB的三等分点，AB分别交OC、OD于点E、F，求证：AE=BF=CD．O。

人教版九年级上册上册数学 24.1.3弧、弦、圆心角同步测试(含解析)

24.1.3弧、弦、圆心角同步测试一．选择题（共10小题）1．如图所示，AB是⊙O直径，CM是AO的垂直平分线，DN是OB的垂直平分线，则下列结论正确的是（）A．＝＝B．＝＜C．＝＞D．＜＜2．已知，如图，∠AOB＝∠COD，下列结论不一定成立的是（）A．AB＝CDB．＝C．△AOB≌△CODD．△AOB、△COD都是等边三角形3．如果两个圆心角相等，那么（）A．这两个圆心角所对的弦相等B．这两个圆心角所对的弧相等C．这两个圆心角所对的弦的弦心距相等D．以上说法都不对4．⊙O中，M为的中点，则下列结论正确的是（）A．AB＞2AMB．AB＝2AMC．AB＜2AMD．AB与2AM的大小不能确定5．下列说法中正确的有（）①直径相等的圆一定是等圆；②两个半圆一定是等弧；③平分弦的直径垂直于弦；④等弧所对的弦相等；⑤相等的圆心角所对的弦相等．A．①②③B．①③④C．①④⑤D．①④6．如图，A，B，C，D是⊙O上的四个点，AD∥BC．那么与的数量关系是（）A．＝B．＞C．＜D．无法确定7．如图⊙O的半径为1cm，弦AB、CD的长度分别为，则弦AC、BD所夹的锐角α为（）A．75°B．45°C．60°D．30°8．已知AB是⊙O的直径，弧AC的度数是30°．如果⊙O的直径为4，那么AC2等于（）A．B．C．D．29．如图，AB是半圆的直径，∠BAC＝20°，D是的中点，则∠DAC的度数是（）A．30°B．35°C．45°D．70°10．下列说法中正确的是（）①圆心角是顶点在圆心的角；②两个圆心角相等，它们所对的弦相等；③两条弦相等，圆心到这两弦的距离相等；④在等圆中，圆心角不变，所对的弦也不变．A．①③B．②④C．①④D．②③二．填空题（共5小题）11．已知圆O的半径为5，弦AB的长为5，则弦AB所对的圆心角∠AOB＝．12．如图，在⊙O中，直径AB∥弦CD，若∠COD＝120°，则∠BOD＝°．13．如图，AB是直径，＝＝，∠BOC＝50°，∠AOE的度数是．14．如图，AB是⊙O的直径，如果∠COA＝∠DOB＝60°，那么与线段OA相等的线段是；与相等的弧是．15．如图，AD为直径，∠AOB＝∠BOC＝∠COD，O为圆心，那么（1）弧AB所对的圆心角是；（2）弧BD所对的圆心角是．三．解答题（共3小题）16．如图，已知⊙O中，点A，B，C，D在圆上，且AB＝CD，求证：AC＝BD．17．已知，如图，⊙O的两条弦AB，CD相交于点E，且AB＝CD，连结BC，AD，求证：AE＝CE．18．如图，在⊙O中，弦AB∥弦CD，∠A＝28°，∠B＝45°，＝3，求的度数．参考答案1．解：连接AC，OC，OD，BD，∵CM是AO的垂直平分线，DN是OB的垂直平分线，∴AC＝OC，BD＝OD，∵OC＝OD＝OA＝OB，∴△AOC，△BOD是等边三角形，∴∠AOC＝∠BOD＝60°，∵AB是⊙O直径，∴∠COD＝60°，∴＝＝，故选：A．2．解：∵∠AOB＝∠COD，∴AB＝CD，＝，∵OA＝OB＝OC＝OD，∴△AOB≌△COD，∴ABC成立，则D不成立，故选：D．3．解：在同圆和等圆中，相等的圆心角所对的弧相等，所对的弦也相等，所对的弦的弦心距相等．故选：D．4．解：连接BM．∵M为的中点，∴AM＝BM，∵AM+BM＞AB，∴AB＜2AM．故选：C．5．解：①直径相等的圆一定是等圆，本小题说法正确；②两个半径相等的半圆一定是等弧，本小题说法错误；③平分弦（不是直径）的直径垂直于弦，本小题说法错误；④等弧所对的弦相等，本小题说法正确；⑤在同圆或等圆中，相等的圆心角所对的弦相等，本小题说法错误；故选：D．6．证明：连接AC，∵AD∥BC，∴∠DAC＝∠ACB，∴＝．故选：A．7．解：连接OA、OB、OC、OD，∵OA＝OB＝OC＝OD＝1，AB＝，CD＝1，∴OA2+OB2＝AB2，∴△AOB是等腰直角三角形，△COD是等边三角形，∴∠OAB＝∠OBA＝45°，∠ODC＝∠OCD＝60°，∵∠CDB＝∠CAB，∠ODB＝∠OBD，∴α＝180°﹣∠CAB﹣∠OBA﹣∠OBD＝180°﹣∠OBA﹣（∠CDB+∠ODB）＝180°﹣45°﹣60°＝75°．8．解：如图，连接OC．过点C作CD⊥OA于点D．∵⊙O的直径为4，∴AB＝4，∴OA＝OC＝2．∵弧AC的度数是30°，∴∠COD＝30°，∴CD＝1，∴OD＝＝，则AD＝2﹣，∵AB是直径，∴∠ACB＝90°．∴AC2＝AD•AB＝（2﹣）×4＝8﹣4．故选：C．9．解：连接BC，∵AB是半圆的直径，∴∠C＝90°，∵∠BAC＝20°，∴∠CBA＝90°﹣∠BAC＝70°，∵D是的中点，∴∠DAC＝∠ABC＝35°．10．解：圆心角是顶点在圆心的角，所以①正确；在同圆和等圆中，两个圆心角相等，它们所对的弦相等，所以②错误；③在同圆和等圆中，两条弦相等，圆心到这两弦的距离相等，所以③错误；在等圆中，圆心角不变，所对的弦也不变，所以④正确．故选：C．11．解：如图，∵OA＝OB＝5，AB＝5，∴OA＝OB＝AB，∴△OAB为等边三角形，∴∠AOB＝60°．故答案为60°．12．解：∵OC＝OD，∴∠C＝∠D，∵∠COD＝120°，∴∠C＝∠D＝30°，∵AB∥CD，∴∠BOD＝∠D＝30°，故答案为30．13．解：∵＝＝，∴∠BOC＝∠COD＝∠DOE＝50°，∴∠AOE＝180°﹣3×50°＝30°．故答案为30°．14．解：∵AB是⊙O的直径，∠COA＝∠DOB＝60°，∴∠AOC＝∠COD＝∠BOD＝60°；又∵OA＝OC＝OD＝OB，∴△OAC、△OCD、△BOD是全等的等边三角形；∴OA＝AC＝OC＝CD＝OD＝BD＝OB；∴，故答案为：AC，OC，CD，OD，BD，OB；、．15．解：（1）弧AB所对的圆心角是∠AOB＝60°；（2）弧BD所对的圆心角是∠BOD＝120°．故答案为60°，120°．16．解：∵AB＝CD，∴＝，∴+＝+，即＝，∴AC＝BD．17．证明：∵AB＝CD，∴＝，∴﹣＝﹣，即＝，∴AD＝BC，在△AED和△CEB中，，∴△AED≌△CEB，∴AE＝CE．18．解：连接AE，DE，∵∠A＝28°，＝3，∴∠AED＝3∠A＝84°，∠ADE＝∠B＝45°，∴∠EAD＝180°﹣∠ADE﹣∠AED＝51°，∴的度数是102°．。

人教版数学九年级上册第二十四章圆 24.1.3 弧、弦、圆心角同步测试

人教版数学九年级上册第二十四章圆 24.1.3 弧、弦、圆心角同步测试一、选择题1. 下面四个图中的角，为圆心角的是( )A B C D2. 在两个圆中有两条相等的弦，则下列说法正确的是( ) A. 圆心到这两条弦的距离相等 B. 这两条弦所对的圆心角相等 C. 这两条弦所对的弧相等D. 这两条弦都被垂直于弦的半径平分 3. 如果两个圆心角相等，那么( ) A. 这两个圆心角所对的弦相等 B. 这两个圆心角所对的弧相等 C. 这两个圆心角所对的弦的弦心距相等 D. 以上说法都不对4. 如图所示，在⊙O 中，AB ︵＝CD ︵，则在①AB ＝CD ，②AC ＝BD ，③∠AOC ＝∠BOD ，④AC ︵＝BD ︵说法中，正确的个数是( )A. 1个B. 2个C. 3个D. 4个第4题第5题5. 如图，AB 是⊙O 的直径，BC ︵＝CD ︵＝DE ︵，∠COD ＝34°，则∠AEO 的度数是( ) A. 51° B. 56° C. 68° D. 78°6. 如图，AB 是⊙O 的直径，BC ，CD ，DA 是⊙O 的弦，若BC ＝CD ＝DA ＝4cm ，则⊙O 的周长为( )A. 5πcmB. 6πcmC. 9πcmD. 8πcm第6题第7题7. 如图所示，在⊙O 中，弦AB ＞CD ，OM ⊥AB ，ON ⊥CD ，M ，N 分别为垂足，那么OM ，ON 的大小关系是( )A. OM ＞ONB. OM ＝ONC. OM ＜OND. 无法确定 8. 在⊙O 中，M ，N 分别为弦AB ，CD 的中点，如果OM ＝ON ，那么在结论：①AB ＝CD ；②AB ︵＝CD ︵；③∠AOB ＝∠COD 中，正确的是( )A. ①②B. ①③C. ②③D. ①②③ 9. 在半径为2的⊙O 中，弦AB 的长为2，则弦AB 所对的圆心角的度数为度.10. 如果⊙O 的半径为R ，则⊙O 中60°的圆心角所对的弦长为，120°的圆心角所对的弦长为 .11. 弦AB 分圆为1∶3两部分，则劣弧所对的圆心角等于 .12. 如图，AC 是⊙O 的直径，AB ，CD 是⊙O 的两条弦，且AB ∥CD ，若∠BAC ＝52°，则∠AOD ＝ .第12题第13题13. 如图，MN 是⊙O 的直径，MN ＝2，点A 在⊙O 上，AN ︵的度数为60°，点B 为AN ︵的中点，点P 是直径MN 上的一个动点，则P A ＋PB 的最小值为 .14. 如图所示，在⊙O 中，AB ︵＝CD ︵，∠AOC ＝100°，求∠BOD 的度数.15. 如图所示，已知在⊙O 中，AC ︵＝BC ︵，D ，E 分别为半径OA ，OB 的中点，你认为CD 和CE 有何关系？为什么？16. 如图所示，⊙O 1和⊙O 2为两个等圆，O 1A ∥O 2D ，O 1O 2与AD 相交于点E ，AD 与⊙O 1和⊙O 2分别交于点B ，C .求证：AB ＝CD .17. 如图所示，已知AB 为⊙O 的直径，M ，N 分别为OA ，OB 的中点，MC ⊥AB ，DN ⊥AB ，垂足分别为M ，N .求证：AC ︵＝BD ︵.18. 如图所示，以等边三角形ABC 的边BC 为直径作⊙O 交AB 于点D ，交AC 于点E ，判断BD ︵，DE ︵，EC ︵之间的大小关系，并说明理由.19. 如图，∠AOB ＝90°，C ，D 是AB ︵的三等分点，AB 分别交OC ，OD 于点E ，F . 求证：AE ＝BF ＝CD .20. 如图，已知P 是直径AB 上的一点，EF ，CD 是过点P 的两条弦，∠CPB ＝∠EPB ，试说明： (1)弦CD 与EF 相等吗？为什么？ (2)DE ︵与CF ︵相等吗？为什么？1. D2. D3. D4. D5. A6. D7. C8. D9. 60 10. R R 11. 90° 12. 104° 13.14. 解：∵︵AB ＝︵CD ，∴︵AB ＋︵BC ＝︵CD ＋︵BC ，即︵AC ＝︵BD，∴∠BOD ＝∠AOC ＝100°.15. 解：CD ＝CE .理由：连接CO ，∵AO ＝BO ，D ，E 分别为AO ，BO 的中点，∴DO ＝EO .∵︵AC ＝︵BC ，∴∠DOC ＝∠EOC .又OC ＝OC ，∴△DOC ≌△EOC ，∴CD ＝CE .16. 证明：∵O 1A ∥O 2D ，∴∠A ＝∠D .∴∠AO 1B ＝∠DO 2C .又∵⊙O 1和⊙O 2为两个等圆，∴AO 1＝BO 1＝CO 2＝DO 2，∴△AO 1B ≌△CO 2D .∴AB ＝CD .17. 解：连接OC ，OD ，则OC ＝OD .∵OA ＝OB ，且OM ＝21OA ，ON ＝21OB ，∴OM ＝ON .在Rt △CMO 与Rt △DNO 中，OM ＝ON ，OC ＝OD ，∴Rt △CMO ≌Rt △DNO ，∴∠COM ＝∠DON ，∴︵AC ＝︵BD. 18. 解：︵BD ＝︵DE ＝︵EC.理由：连接DO ，EO ，∵△ABC 是等边三角形，∴∠ABC ＝∠ACB ＝60°，∴在△DOB 中，OD ＝OB ，∴∠BDO ＝∠DBO ＝60°，∴∠DOB ＝60°.同理在△EOC 中，∠OEC ＝∠OCE ＝60°，∴∠EOC ＝60°，∴∠DOE ＝180°－∠BOD －∠EOC ＝60°，∴︵BD ＝︵DE ＝︵EC .19. 证明：连接AC ，BD .∵C ，D 是︵AB 的三等分点，∠AOB ＝90°，∴︵AC ＝︵CD ＝︵DB ，∠AOC ＝∠COD ＝∠DOB ＝30°，∴AC ＝CD ＝DB .又∵OA ＝OB ，∠AOB ＝90°，∴∠OAB ＝∠OBA ＝45°.∴∠AEC ＝∠AOC ＋∠OAB ＝75°.在△AOC 中，OA ＝OC ，∴∠ACO ＝2180°－30°＝75°，∴∠AEC ＝∠ACO ，∴AE ＝AC .同理BF ＝BD ，∴AE ＝BF ＝CD .20. 解：(1)CD ＝EF .理由：过点O 作OM ⊥EF ，ON ⊥DC ，垂足分别为M ，N ，∵∠EPB ＝∠CPB ，∠OMP ＝∠ONP ＝90°，OP ＝OP ，∴△OPM ≌△OPN (AAS )，∴OM ＝ON ，连接OE ，OC ，∵OE ＝OC ，由勾股定理得EM ＝NC ，∴由垂径定理得EF ＝2EM ，CD ＝2NC ，∴CD ＝EF . (2) ︵DE ＝︵CF .理由：∵CD ＝EF ，∴︵CD ＝︵EF ，∴︵CD －︵DF ＝︵EF －︵DF ，∴︵CF ＝︵DE ，即︵DE ＝︵CF .。

人教版数学九年级上册24.1.3《弧、弦、圆心角》同步测试

弧、弦、圆心角1．若AB ︵，CD ︵是同一圆上的两段弧，且AB ︵＝CD ︵，则弦AB 与弦CD 之间的关系是( C )A ．AB ＜CD B ．AB ＞CDC ．AB ＝CD D ．不能确定【解析】同圆或等圆中等弧所对的弦相等．2．如图24－1－27所示，AB 是⊙O 的直径，C ，D 是BE ︵上的三等分点，∠AOE ＝60°，则∠COE 为( C )A ．40°B ．60°C ．80°D ．120°【解析】易知∠EOB＝180°－60°＝120°.∵C ，D 是BE ︵的三等分点，∴BC ︵＝CD ︵＝DE ︵，∴∠BOC ＝∠COD＝∠DOE，∴∠COE ＝23∠EOB ，∴∠COE ＝23×120°＝80°.故选C.图24－1－27图24－1－28图24－1－293．如图24－1－28，AB 是⊙O 的弦，OD ⊥AB 于D ，延长OD 交⊙O 于E ，则下列说法错误的是( D )A ．AD ＝BDB ．∠AOE ＝∠BOE C.AE ︵＝BE ︵D ．OD ＝DE【解析】由垂径定理得A ，C 正确．又由AE ︵＝BE ︵得∠AOE＝∠BOE，故B 正确，故选D.4．如图24－1－29，AB 是⊙O 的直径，点C ，D 在⊙O 上，∠BOC ＝110°，AD ∥OC ，则∠AOD＝( D ) A ．70° B ．60° C ．50° D ．40° 【解析】 ∠AOC＝180°－∠BOC＝180°－110°＝70°.∵AD ∥OC ，∴∠A ＝∠AOC ＝70°.∵OA ＝OD ，∴∠A ＝∠D＝70°.∴∠AOD ＝180°－∠A－∠D＝180°－70°×2＝40°.故选D.5．已知AB ︵，CD ︵是同圆的两段弧，且AB ︵＝2CD ︵，则弦AB 与2CD 之间的关系为( B ) A ．AB ＝2CD B ．AB ＜2CD C ．AB ＞2CD D ．不能确定【解析】如图，在圆上截取DE ︵＝CD ︵，则有AB ︵＝CE ︵，∴AB ＝CE.∵CD＋DE ＝2CD ＞CE ＝AB ，∴AB ＜2CD.6．如图24－1－30，AB 是⊙O 的直径，BC ，CD ，DA 是⊙O 的弦，且BC ＝CD ＝DA ，则∠BCD＝( B ) A ．105° B ．120° C ．135° D ．150°图24－1－30图24－1－317．如图24－1－31所示，AB 是⊙O 的直径，如果∠COA＝∠DOB＝60°，那么与线段OA 相等的线段有__OC ，OD ，OB ，AC ，CD ，DB__；与AC ︵相等的弧有__CD ︵和DB ︵__． 8．如图24－1－32，在⊙O 中，AB ︵＝AC ︵，∠A ＝42°，则∠B＝__69°__．【解析】 ∵AB ︵＝AC ︵，∴AB ＝AC ，∴∠B ＝∠C＝12(180°－∠A)＝12×(180°－42°)＝69°.图24－1－32图24－1－339．如图24－1－33，AB为半圆O的直径，OC⊥AB，OD平分∠BOC，交半圆于点D，AD交OC于点E，则∠AEO的度数是__67.5°__．【解析】因为OD平分∠BOC，所以∠BOD＝12∠BOC＝12×90°＝45°.因为OA＝OD，所以∠A＝∠D.又因为∠BOD＝∠A＋∠D＝2∠A，所以∠A＝12∠BOD＝12×45°＝22.5°，所以∠AEO＝90°－22.5°＝67.5°.10．如图24－1－34所示，D，E分别是⊙O的半径OA，OB上的点，CD⊥OA，CE ⊥OB，CD＝CE，则AC与CB的大小关系是__AC＝CB__．图24－1－34图24－1－3511．如图24－1－35，已知在△ABC中，∠ACB＝90°，∠B＝35°，以C为圆心、CA为半径的圆交AB于D点，则弧AD为__70__度．【解析】连接CD，∵∠ACB＝90°，∠B＝35°，∴∠A＝90°－∠B＝55°.∵CA＝CD，∴∠A＝∠CDA＝55°，∴∠ACD＝180°－2∠A＝70°.12．如图24－1－36，AB ，BC ，AC 都是⊙O 的弦，且∠AOB＝∠BOC.求证：(1)∠BAC ＝∠BCA；(2)∠ABO＝∠CBO.图24－1－36 【解析】 (1)在⊙O 中，有圆心角∠AOB＝∠BOC，则可知该圆心角所对的弦相等，即AB ＝BC ，在△ABC 中，AB ＝BC ，则∠BAC＝∠BCA.(2)图中共有4个等腰三角形，根据它们的底角分别相等，可以得出结论．证明：(1)∵∠AOB＝∠BOC， ∴AB ＝BC ，∴∠BAC ＝∠BCA. (2)∵OB＝OA ，∴∠ABO ＝∠BAO，同理得∠CBO＝∠BCO，∠CAO ＝∠ACO. 又∵∠BAC＝∠BCA，∴∠BAO ＝∠BCO， ∴∠ABO ＝∠CBO.13．如图24－1－37所示，已知AB 为⊙O 的直径，M ，N 分别为OA ，OB 的中点，CM ⊥AB ，DN ⊥AB ，垂足分别为M ，N.求证：AC ︵＝BD ︵.图24－1－37第13题答图【解析】证两弧相等，可根据其定义和圆心角、弦、弧三者之间的关系定理与推论来证明．证明：如图所示，连接OC ，OD ，则OC ＝OD. 又OM ＝12OA ，ON ＝12OB ，OA ＝OB ，∴OM ＝ON ，∴Rt △CMO ≌Rt △DNO ， ∴∠COA ＝∠DOB，∴AC ︵＝BD ︵.14．如图24－1－38所示，A ，B ，C 为⊙O 上的三点，且有AB ︵＝BC ︵＝CA ︵，连接AB ，BC ，CA.(1)试确定△ABC 的形状； (2)若AB ＝a ，求⊙O 的半径．图24－1－38第14题答图解： (1)∵AB ︵＝BC ︵＝CA ︵(已知)，∴AB ＝BC ＝CA(在同圆中相等的弧所对的弦相等)，∴△ABC 为等边三角形． (2)如图，连接OA ，OB ，OC ，过O 作OE⊥BC，垂足为E.∵AB ︵＝BC ︵＝CA ︵(已知)， ∴∠AOB ＝∠BOC＝∠COA(在同圆中相等的弧所对的圆心角相等)．又∵∠AOB＋∠BOC＋∠COA ＝360°(周角的定义)， ∴∠BOC ＝120°.又∵OB＝OC ，OE ⊥BC ，∴∠BOE ＝∠C OE ＝60°，BE ＝EC ＝12BC ＝12AB ＝12a(等腰三角形三线合一)．∴∠OBE ＝90°－∠BOE＝30°.∴OE ＝12OB.根据勾股定理得BE 2＋OE 2＝OB 2， ∴⎝ ⎛⎭⎪⎫12a 2＋⎝ ⎛⎭⎪⎫12OB 2＝OB 2，解得OB ＝33a(负值已舍)，即⊙O 的半径为33a. 15．如图24－1－39，A ，B ，C ，D ，E ，F 是⊙O 的六等分点．连接AB ，AD ，AF ，求证：AB ＋AF ＝AD.【解析】连接OB ，OF ，得到等边△AOB，△AOF ，据此并结合圆的性质，即可推理出AB ＝AF ＝AO ＝OD ，从而得到AB ＋AF ＝AD.图24－1－39解：连接OB ，OF.∵A ，B ，C ，D ，E ，F 是⊙O 的六等分点，∴AD 是⊙O 的直径，且∠AOB＝∠AOF＝60°，又∵OA＝OB ，OA ＝OF ，∴△AOB ，△AOF 是等边三角形，∴AB ＝AF ＝AO ＝OD ，∴AB ＋AF ＝AO ＋OD ＝AD.16．已知如图24－1－40，A 点是半圆上一个三等分点，B 点是AN ︵的中点，P 是直径MN 上一动点，⊙O 的半径为1，则AP ＋BP 的最小值为多少？图24－1－40第16题答图【解析】利用圆的对称性，找到AP ＋BP 取最小值时的P 点，再结合弧与圆心角的关系得到直角三角形，运用勾股定理求解．解：作A 关于MN 的对称点A′，根据圆的对称性，则A′必在圆上，连接BA′交MN 于P ，连接PA ，则PA ＋PB 最小，此时PA ＋PB ＝PA′＋PB ＝A′B，连接OA ，OA ′，OB.∵AN ︵＝13MN ︵，∴∠AON ＝∠A′ON＝60°.∵AB ︵＝BN ︵，∴∠BON ＝12∠AON ＝30°，∴∠A ′OB ＝90°，∴A ′B ＝OA ′2＋OB 2＝12＋12＝2，即AP ＋BP 的最小值是 2.。

人教版九年级上册数学弧、弦、圆心角同步训练(含答案)

人教版九年级上册数学24.1.3弧、弦、圆心角同步训练一、单选题1．在半径为1的⊙O中，若弦AB的长为1，则弦AB所对的圆心角的度数为（）A．90°B．60°C．30°D．15°2．如图，⊙O中，如果⊙AOB＝2⊙COD，那么（）A．AB＝DC B．AB＜DC C．AB＜2DC D．AB＞2DC 3．如图，AB为O的直径，C，D为O上的两点，且C为AD的中点，若BAD∠=︒，则ACO20∠的度数是（）A．45︒B．55︒C．50︒D．60︒4．如图，已知⊙O中，CD，AB是⊙O的两条弦，AOB∠与COD∠互补，若AB=8，CD=6，则⊙O的半径长为（）．A．5B．6C．7D．85．如图，在⊙O中，AB是直径，AC是弦，连接OC，若⊙ACO＝25°，则⊙BOC的度数是（）A ．40°B ．50°C ．55°D ．60° 6．如图，在O 中，AB BC CD ==，40AOB ∠=︒，则CAD ∠的度数为（）A ．10°B ．20°C ．30°D ．40°7．如图，在⊙O 中，=AC BD ，⊙AOD =150°，⊙BOC =80°，则⊙AOB 的度数是（）A ．20°B ．25°C ．30°D ．35° 8．如图，AB 为⊙O 直径，CD 为弦，AB⊙CD 于E ，连接CO ，AD ，⊙BAD ＝25°，下列结论中正确的有（）⊙CE ＝OE ；⊙⊙C ＝40°；⊙ACD ＝ADC ；⊙AD ＝2OEA．⊙⊙B．⊙⊙C．⊙⊙⊙D．⊙⊙⊙⊙二、填空题9．在同圆或等圆中，相等的圆心角所对的弧_________，所对的弦也_______．同样，还可以得到：在同圆或等圆中，如果两条弧相等，那么它们所对的圆心角_____，所对的弦________；在同圆或等圆中，如果两条弦相等，那么他们所对的圆心角______，所对的弧_________．10．半径为5的O中，弦AB的长为5，则弦AB所对的圆心角的度数为________．11．如图，AB为⊙O的直径，△P AB的边P A，PB与⊙O的交点分别为C、D．若AC CD DB，则∠P的大小为_____度．==⊥,垂足为点12．如图，已知半O的直径AB为3，弦AC与弦BD交于点E，OD AC =，则弦AC的长为_____________．F，AC BD13．已知在⊙O中,AB=BC,且:3:4AB AMC=,则⊙AOC=________.14．如图，⊙O中OA⊙BC，⊙CDA=25°，则⊙AOB的度数为________．15．如图，AB 为⊙O 直径，E 是BC 中点，OE 交BC 于点D ，BD=3，AB=10，则AC=________．16．P 为⊙O 内一点，OP ＝3cm ，⊙O 的半径为5cm ，则经过P 点的最短弦长为_____cm ，最长弦长为_____cm ．三、解答题17．如图，AD 是O 的一条弦，,B C 是弦AD 上的点，AB CD =，连接,OB OC ，分别延长,OB OC 交O 于,E F 两点．求证：AE DF =．18．如图，过O 的直径AB 上两点,M N ，分别作弦,CD EF ，//,CD EF AC BF =．求证：（1）BC AF =；（2）AM BN =．19．已知：如图，AB是⊙O的直径，M、N分别为AO、BO的中点，CM⊙AB，DN⊙AB，垂足分别为M、N，连接OC、OD．求证：AC BD20．如图，AD=CB，求证：AB=CD．参考答案：1．B2．C3．B4．A5．B6．B7．D8．B9．相等相等相等相等相等相等10．60°11．601213．144°14．50°15．816．810答案第1页，共1页。

九年级数学人教版(上册)24.1.3 弧、弦、圆心角

易错点对弧、弦、圆心角的关系理解有误致错 9．如图，在⊙O 中，A︵C＝2A︵B，试判断 AC 与 2AB 的大小关系，并说明理由．解：∵在同圆或等圆中，同弧或等弧所对的弦相等， ∴当A︵C＝2A︵B时，AC＝2AB.
以上解答是否正确？若不正确，请改正．
解：不正确，2AB＞AC.
理由：连接 BC， ∵A︵C＝2A︵B， ∴A︵B＝B︵C. ∴AB＝BC. ∵在△ABC 中，AB＋BC＞AC，
∴△OAD 是等边三角形． ∴OA＝AD. 同理可证△OBD 是等边三角形． ∴OB＝BD. ∴AD＝BD＝OA＝OB. ∴四边形 OADB 是菱形．
13．如图，MN 是⊙O 的直径，点 A 是半圆上一个三等分点，点 B 是A︵N的中点，点 B′是点 B 关于 MN 的对称点，⊙O 的半径为 1，则 AB′的长为 2 ．
第二十四章圆
24.1 圆的有关性质 24.1.3 弧、弦、圆心角
知识点 1 圆心角的概念及其计算 1．下图中∠ACB 是圆心角的是( B )
2．如图，已知 AB 为⊙O 的直径，点 D 为半圆周上的一点，且 A︵D所对圆心角的度数是B︵D所对圆心角度数的 2 倍，则圆心角∠BOD ＝ 60° ．
33
E，OD⊥AC，垂足为 F，AC＝BD，则弦 BD 的长为 2 ．
12．如图，在⊙O 中，A︵B＝A︵C，∠ACB＝60°.
(1)求证：∠AOB＝∠BOC＝∠AOC. 证明：∵A︵B＝A︵C， ∴AB＝AC. 又∵∠ACB＝60°， ∴△ABC 是等边三角形． ∴AB＝BC＝AC. ∴∠AOB＝∠AOC＝∠BOC.
(2)若 D 是A︵B的中点，求证：四边形 OADB 是菱形．证明：∵∠AOB＋∠AOC＋∠BOC＝360°， ∴∠AOB＝∠AOC＝∠BOC＝120°. 连接 OD，交 AB 于点 M. ∵D 是A︵B的中点， ∴A︵D＝B︵D.

24.1.3 弧、弦、圆心角人教版数学九年级上册同步练习(含答案)

24.1.3弦.弧.圆周角1．如图，在⊙O中，AB是弦，C是弧AB上一点．若∠OAB＝25°，∠OCA＝40°，则∠BOC的度数为（）A．30°B．40°C．50°D．60°2．如图，«Skip Record If...»是«Skip Record If...»的直径，弦«Skip Record If...»交«Skip Record If...»于点E，若«Skip Record If...»，则«Skip Record If...»的度数为（）A．«Skip Record If...»B．«Skip Record If...»C．«Skip Record If...»D．«Skip Record If...»3．如图1是一座立交桥的示意图（道路宽度忽略不计）A为入口，F，G为出口，其中直行道为AB，CG，EF，且AB＝CG＝EF，弯道为以点O为圆心的一段弧，且«Skip Record If...»，«Skip Record If...»，«Skip Record If...»，所对的圆心角均为90°，甲、乙两车由A 口同时驶入立交桥，均以10m/s的速度行驶，从不同出口驶出，其间两车到点O的距离y（m）与时间x（s）的对应关系如图2所示，结合题目信息，下列说法正确的是（）A．甲车从F口出，乙车从G口出B．甲车驶出立交桥时，乙车在«Skip Record If...»上C．甲乙两车同时在立交桥上的时间为10sD．图中立交桥总长为140 m4．如图，«Skip Record If...»为«Skip Record If...»的直径，点D是弧«Skip Record If...»的中点，过点D作«Skip Record If...»于点E，延长«Skip Record If...»交«Skip Record If...»于点F，若«Skip Record If...»．则«Skip Record If...»的直径长为（）A．15B．13C．10D．165．如图，AB是⊙O的直径，C.D是⊙O上的两点，且点C为弧BAD的中点，连接CD.CB.OD，CD与AB交于点F．若∠AOD＝100°，则∠ABC的度数为（）A．15°B．20°C．25°D．30°6．如图，在⊙O中，«Skip Record If...»，∠AOD=150°，∠BOC=80°，则∠AOB的度数是（）A．20°B．25°C．30°D．35°7．下列说法中，正确的是（）A．等弦所对的弧相等B．等弧所对的弦相等C．圆心角相等，所对的弦相等D．弦相等所对的圆心角相等8．如图，A.B是⊙O上的两点，∠AOB＝120°，C是«Skip Record If...»的中点，则四边形OACB是（）A．梯形B．矩形C．菱形D．正方形9．如图，半径为5的⊙A中，弦«Skip Record If...»所对的圆心角分别是«Skip Record If...»，«Skip Record If...»．已知«Skip Record If...»，«Skip Record If...»，则弦«Skip Record If...»的弦心距等于（）A．«Skip Record If...»B．«Skip Record If...»C．4D．310．如图，⊙O中，弦AB⊥CD，垂足为E，F为«Skip Record If...»的中点，连接AF、BF、AC，AF交CD于M，过F作FH⊥AC，垂足为G，以下结论：①«Skip Record If...»；②HC＝BF：③MF＝FC：④«Skip Record If...»，其中成立的个数是（）A．1个B．2个C．3个D．4个11．若将一个圆等分成三个扇形，则其中一个扇形圆心角的度数为________«Skip Record If...»．12．如图，在半径为5的«Skip Record If...»中，«Skip Record If...»，则弦«Skip Record If...»的长度为______．13．如图，在⊙O中，若«Skip Record If...» ，则AC与2CD的大小关系是：AC__2CD．（填“＞”，“＜”或“＝”）14．如图，在圆«Skip Record If...»中，若«Skip Record If...»，且«Skip Record If...»，求«Skip Record If...»的长度．15．如图，MB，MD是⊙O的两条弦，点A，C分别在弧MB，弧MD上，且AB＝CD，点M是弧AC的中点．（1）求证：MB＝MD；（2）过O作OE⊥MB于E，OE＝1，⊙O的半径是2，求MD的长．参考答案1．A【分析】根据等腰三角形的性质求出∠OBA＝∠OAB＝25°，∠OAC＝∠OCA＝40°，再根据三角形内角和定理求出∠AOB和∠AOC，再求出答案即可．【详解】解：∵OA＝OB，∠OAB＝25°，∴∠OBA＝∠OAB＝25°，∴∠AOB＝180°﹣∠OAB﹣∠OBA＝130°，∵OA＝OC，∠OCA＝40°，∴∠OAC＝∠OCA＝40°，∴∠AOC＝180°﹣∠OAC﹣∠OCA＝100°，∴∠BOC＝∠AOB﹣∠AOC＝130°﹣100°＝30°，故选：A．【点拨】本题考查圆心角的定义，等腰三角形的性质，三角形内角和定理，解题关键是掌握圆心角的定义．2．B【分析】连接OC，根据圆周角定理求出∠AOC，求出«Skip Record If...»的度数，根据直角三角形的性质求出∠BCD=70°，根据平行线的性质求出∠D，求出«Skip Record If...»的度数，求出«Skip Record If...»的度数可得∠AOE，再求出答案即可．【详解】解：连接OC，∵AB⊥CD，∴∠CFB=90°，∵∠CBA=15°，∴∠AOC=2∠CBA=30°，∠BCD=90°-∠CBA=75°，∴«Skip Record If...»的度数是30°，∵DE∥BC，∴∠BCD+∠D=180°，∴∠D=105°，∴«Skip Record If...»的度数是210°，∴«Skip Record If...»的度数是360°-210°=150°，∴«Skip Record If...»的度数是150°-30°=120°，∴∠AOE=120°，∴«Skip Record If...»故选：B．【点拨】本题考查了圆周角定理，圆心角、弧、弦之间的关系等知识点，能熟记知识点是解此题的关键．3．B【分析】结合题意函数图象可分析出在直道AB，CG以及EF上的行驶时间均为3s，在弯道BC，CD，DE上的行驶时间均为2s，从而结合速度进行逐项分析即可．【详解】A.分析图2可知，甲车先驶出立交桥，乙车后驶出，因此甲车从G口出，乙车从F口出，原说法错误，不符合题意；B.根据图2甲的图象可知甲车在立交桥上由A到G共计用时5+3=8s，其中由B到C用时2s，由于甲乙的速度相同，则乙从A到D用时3+2×2=7s，从A到E用时3+3×2=9s，因此第8s 时，乙车在«Skip Record If...»上，原说法正确，符合题意；C.根据B选项的分析可知，两车同时在立交桥上的时间为8s，原说法错误，不符合题意；D.根据题意，立交桥总长为：«Skip Record If...»，原说法错误，不符合题意；故选：B．【点拨】考本题考查函数图象与实际行程问题，涉及到圆心角等相关知识点，理解函数图象对应的实际意义是解题关键．4．A【分析】连接«Skip Record If...»，首先证明«Skip Record If...»，设«Skip Record If...»，在«Skip Record If...»中，利用勾股定理构建方程即可解决问题．【详解】解：如图，连接«Skip Record If...»．«Skip Record If...»，«Skip Record If...»，«Skip Record If...»，«Skip Record If...»点«Skip Record If...»是弧«Skip Record If...»的中点，«Skip Record If...»«Skip Record If...»，«Skip Record If...»«Skip Record If...»，«Skip Record If...»，«Skip Record If...»，设«Skip Record If...»，在«Skip Record If...»中，则有«Skip Record If...»，解得«Skip Record If...»，«Skip Record If...»，故答案是：A．【点拨】本题考查勾股定理，垂径定理，圆心角，弧，弦之间的关系等知识，解题的关键是学会利用参数构建方程解决问题，属于中考常考题型．5．B【分析】先根据邻补角的性质求出∠BOD，再根据点C为弧BAD的中点，求出∠BOC的度数，再根据等腰三角形的性质即可求出∠ABC的度数．【详解】∵∠AOD＝100°，∴∠BOD=180°-∠AOD＝80°，∵点C为弧BAD的中点∴∠BOC=∠DOC=«Skip Record If...»（360°-80°）=140°∵OC=OB∴∠ABC=∠BCO=«Skip Record If...»（180°-140°）=20°故选B．【点拨】此题主要考查圆内角度求解，解题的关键是熟知圆心角、弧的关系．6．D【分析】首先根据题意得出«Skip Record If...»，然后得到«Skip Record If...»，然后利用角度之间的关系求解即可．【详解】«Skip Record If...»，«Skip Record If...»，«Skip Record If...»，«Skip Record If...»．∵∠AOD=150°，∠BOC=80°，«Skip Record If...»，故选：D．【点拨】本题主要考查圆心角、弧、弦的关系，准确识图并灵活运用相关知识是解题的关键．7．B【分析】根据圆心角，弦，弧之间的关系判断，注意条件．【详解】A中，等弦所对应的弧可以相等也可以互补构成新圆；B中，等弧所对应的弦相等，故选BC中，圆心角相等所对应的弦可能互补；D中，弦相等，圆心角可能互补；故选B【点拨】本题考查了圆心角，弧，弦之间的观，此类试题属于难度较大的试题，其中，弦和圆心角等一些基本知识容易混淆，从而很难把握．8．C【分析】连接OC，如图，利用圆心角、弧的关系得到∠AOC＝∠BOC＝«Skip Record If...»∠AOB＝60°，可判断△OAC和△OCB都是等边三角形，所以OA＝AC＝OB＝BC，于是可判断四边形OACB 为菱形．【详解】解：连接OC，如图，∵C是«Skip Record If...»的中点，∴∠AOC＝∠BOC＝«Skip Record If...»∠AOB＝«Skip Record If...»×120°＝60°，∵OA＝OC，OC＝OB，∴△OAC和△OCB都是等边三角形，∴OA＝AC＝OB＝BC，∴四边形OACB为菱形．故选：C．【点拨】本题考查了圆心角、弧、弦的关系：在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对应的其余各组量都分别相等．也考查了菱形的判定．9．D【分析】作AH⊥BC于H，作直径CF，连结BF，先利用等角的补角相等得到∠DAE=∠BAF，再利用圆心角、弧、弦的关系得到DE=BF=6，由AH⊥BC，根据垂径定理得CH=BH，易得AH 为△CBF的中位线，然后根据三角形中位线性质得到AH=«Skip Record If...»BF=3.【详解】解：作AH⊥BC于H，作直径CF，连结BF，如图，∵∠BAC+∠EAD=180°，∠BAC+∠BAF=180°，∴∠DAE=∠BAF，∴«Skip Record If...»，∴DE=BF=6，∵AH⊥BC，∴CH=BH，而CA=AF，∴AH为△CBF的中位线，∴AH=«Skip Record If...»BF=3，故选：D．【点拨】本题考查了圆心角、弧、弦的关系．也考查了垂径定理和三角形中位线性质，解题的关键是熟练运用相应的定理．10．C【分析】根据弧，弦，圆心角之间的关系，圆周角定理以及三角形内角和定理一一判断即可．【详解】解：∵F为«Skip Record If...»的中点，∴«Skip Record If...»，故①正确，∴∠FCM＝∠FAC，∵∠FCG＝∠ACM+∠FCM，∠AME＝∠FMC＝∠ACM+∠FAC，∴∠AME＝∠FMC＝∠FCG＞∠FCM，∴FC＞FM，故③错误，∵AB⊥CD，FH⊥AC，∴∠AEM＝∠CGF＝90°，∴∠CFH+∠FCG＝90°，∠BAF+∠AME＝90°，∴∠CFH＝∠BAF，∴«Skip Record If...»，∴HC＝BF，故②正确，∵∠AGF＝90°，∴∠CAF+∠AFH＝90°，∴«Skip Record If...»＝180°，∴«Skip Record If...»＝180°，∴«Skip Record If...»，故④正确，故选：C．【点评】本题考查圆心角，弧，弦之间的关系，三角形内角和定理等知识，解题的关键是熟练掌握基本知识，属于中考选择题中的压轴题．11．120【分析】根据圆的性质计算，即可得到答案．【详解】根据题意，将一个圆等分成三个扇形，则其中一个扇形圆心角的度数为：«Skip Record If...» 故答案为：120．【点拨】本题考查了圆的知识；解题的关键是熟练掌握圆和圆心角的性质，从而完成求解．12．«Skip Record If...»【分析】作OC⊥AB，根据垂径定理得到AC=BC=«Skip Record If...»AB，根据直角三角形的性质求出OC，根据勾股定理求出AC，得到答案.【详解】解：作«Skip Record If...»于C，则«Skip Record If...»，«Skip Record If...»，«Skip Record If...»，«Skip Record If...»，«Skip Record If...»，由勾股定理得，«Skip Record If...»，«Skip Record If...»，故答案为：«Skip Record If...»【点拨】本题考查的是垂径定理、圆心角、弧、弦的关系定理，正确作出辅助性、灵活运用定理是解题的关键.13．«Skip Record If...»【分析】如图，连接AB.BC，根据题意知，AB＝BC＝CD，又由三角形三边关系得到AB+BC＞AC得到：AC＜2CD．【详解】解：如图，连接AB.BC，∵«Skip Record If...»∴AB＝BC＝CD，在△ABC中，AB+BC＞AC．∴AC＜2CD．故答案是：＜．【点拨】本题主要考查了圆心角、弧、弦的关系，解题的关键是利用三角形三边关系得到AB+BC＞AC．14．«Skip Record If...»【分析】由弦与弧的关系，得到«Skip Record If...»，然后得到«Skip Record If...»，即可得到«Skip RecordIf...»．【详解】解：∵«Skip Record If...»，∴«Skip Record If...»，∴«Skip Record If...»即«Skip Record If...»∴«Skip Record If...»．【点拨】本题考查了弦与弧的关系，解题的关键是熟练掌握所学的知识，正确得到«Skip Record If...»．15．（1）见解析；（2）«Skip Record If...»【分析】（1）根据圆心角、弦、弧、弦心距之间的关系得出«Skip Record If...»即可；（2）根据垂径定理，勾股定理求出ME，进而求出MB即可．【详解】证明：（1）∵AB＝CD，∴«Skip Record If...»，又∵点M是弧AC的中点，∴«Skip Record If...»，∴«Skip Record If...»，即：«Skip Record If...»，∴MB＝MD；（2）过O作OE⊥MB于E，则ME＝BE，连接OM，在Rt△MOE中，OE＝1，⊙O的半径OM＝2，∴ME＝«Skip Record If...»＝«Skip Record If...»＝«Skip Record If...»，∴MD＝MB＝2ME＝2«Skip Record If...»．【点拨】本题考查圆心角、弦、弧之间的关系，垂径定理、勾股定理等知识，掌握垂径定理、勾股定理是正确计算的前提．。

人教版九年级上册数学24.1.3 弧、弦、圆心角同步练习(含解析)

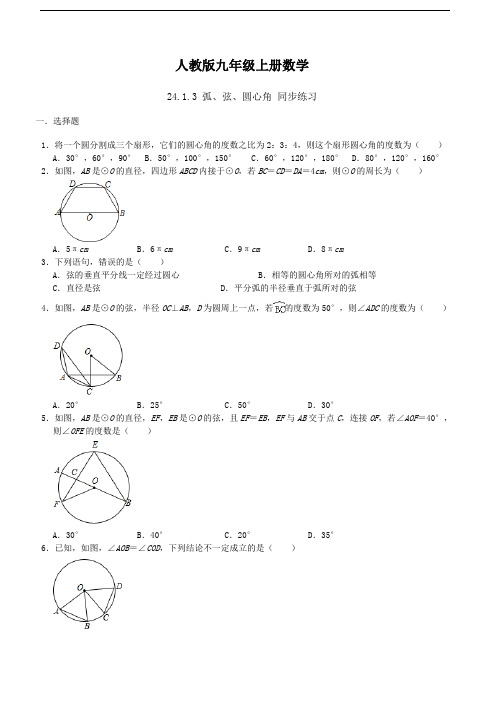
人教版九年级上册数学24.1.3 弧、弦、圆心角同步练习一．选择题1．将一个圆分割成三个扇形，它们的圆心角的度数之比为2：3：4，则这个扇形圆心角的度数为（）A．30°，60°，90° B．50°，100°，150°C．60°，120°，180° D．80°，120°，160°2．如图，AB是⊙O的直径，四边形ABCD内接于⊙O，若BC＝CD＝DA＝4cm，则⊙O的周长为（）A．5πcm B．6πcm C．9πcm D．8πcm3．下列语句，错误的是（）A．弦的垂直平分线一定经过圆心 B．相等的圆心角所对的弧相等C．直径是弦 D．平分弧的半径垂直于弧所对的弦4．如图，AB是⊙O的弦，半径OC⊥AB，D为圆周上一点，若的度数为50°，则∠ADC的度数为（）A．20°B．25°C．50°D．30°5．如图，AB是⊙O的直径，EF，EB是⊙O的弦，且EF＝EB，EF与AB交于点C，连接OF，若∠AOF＝40°，则∠OFE的度数是（）A．30°B．40°C．20°D．35°6．已知，如图，∠AOB＝∠COD，下列结论不一定成立的是（）A．＝ B．AB＝CD C．△AOB≌△COD D．△AOB、△COD都是等边三角形7．如图，已知AB是⊙O的直径，BC是弦，∠ABC＝30°，过圆心O作OD⊥BC交弧BC于点D，连接DC，则∠DCB的度数为（）度．A．45 B．30 C．50 D．608．如图，AB为半圆⊙O的直径，AB＝10，AC为⊙O的弦，AC＝8，D为的中点，DM⊥AC于M，则DM的长为（）A．B．C．1 D．9．如图，半径为R的⊙O的弦AC＝BD，且AC⊥BD于E，连结AB、AD，若AD＝，则半径R的长为（）A．1 B．C．D．10．如图，⊙O的半径为1，动点P从点A处沿圆周以每秒45°圆心角的速度逆时针匀速运动，即第1秒点P位于如图所示位置，第2秒B点P位于点C的位置，……，则第2017秒点P所在位置的坐标为（）A．（，）B．（）C．（0，﹣1）D．（）二．填空题11．圆上有四个点，若它们两两连结后得到的所有线段只有两个不同的长度，则这四个点依次分圆弧的比为．12．如图，在⊙O中，，AB＝3，则AC＝．13．如图，已知点C是⊙O的直径AB上的一点，过点C作弦DE，使CD＝CO．若的度数为35°，则的度数是．14．如图，已知四边形ABCD外接圆⊙O的半径为5，对角线AC与BD交于点E，BE＝DE，AB＝BE，且AC ＝8，则四边形ABCD的面积为．15．如图，已知AB、CD是⊙O的直径，，∠AOE＝32°，那么∠COE的度数为度．三．解答题16．如图，AB、AC是⊙O的两条弦，M是的中点，N是的中点，弦MN分别交AB、AC于点P、D．（1）求证：AP＝AD；（2）连接PO，当AP＝3，OP＝，⊙O的半径为5，求MP的长．17．如图，A、B、C、D是⊙O上四点，且AB＝CD，求证：AD＝BC．18．如图，AB、AC是⊙O的两条弦，且AB＝AC，点D是的中点，连接并延长BD、CD，分别交AC、AB的延长线于点E、F．（1）求证：DF＝DE；（2）若BD＝6，CE＝8，求⊙O的半径．参考答案1．解：设圆心角的度数分别为2x、3x、4x，由题意得，2x+3x+4x＝360°，解得，x＝40°，则这个扇形圆心角的度数为80°、120°、160°，故选：D．2．解：如图，连接OD、OC．∵AB是⊙O的直径，四边形ABCD内接于⊙O，若BC＝CD＝DA＝4cm，∴＝＝，∴∠AOD＝∠DOC＝∠BOC＝60°．又OA＝OD，∴△AOD是等边三角形，∴OA＝AD＝4cm，∴⊙O的周长＝2×4π＝8π（cm）．故选：D．3．解：直径是弦，A正确，不符合题意；在同圆或等圆中，相等的圆心角所对的弧相等，B错误，符合题意；弦的垂直平分线一定经过圆心，C正确，不符合题意；平分弧的半径垂直于弧所对的弦，D正确，不符合题意；故选：B．4．解：∵的度数为50°，∴∠BOC＝50°，∵半径OC⊥AB，∴＝，∴∠ADC＝∠BOC＝25°．故选：B．5．解：如图，连接BF，OE．∵EF＝EB，OE＝OE，OF＝OB，∴△OEF≌△OEB（SSS），∴∠OFE＝∠OBE，∵OE＝OB＝0F，∴∠OEF＝∠OFE＝∠OEB＝∠OBE，∠OFB＝∠OBF，∵∠ABF＝∠AOF＝20°，∴∠OFB＝∠OBE＝20°，∵∠OFB+∠OBF+∠OFE+∠OBE+∠BEF＝180°，∴4∠EFO+40°＝180°，∴∠OFE＝35°，故选：D．6．解：∵∠AOB＝∠COD，∴AB＝CD，＝，∵OA＝OB＝OC＝OD，∴△AOB≌△COD，∴ABC成立，则D不成立，故选：D．7．解：∵OD⊥BC，∠ABC＝30°，∴在直角三角形OBE中，∠BOE＝60°（直角三角形的两个锐角互余），即∠DOB＝60°．又∵∠DCB＝∠DOB（同弧所对的圆周角是所对的圆心角的一半），∴∠DCB＝30°；故选：A．8．解：如图，连接OD交AC于H，连接BC．∵AB是直径，∴∠ACB＝90°，∴BC＝＝6，∵＝，∴OD⊥AB，∵∠OAH＝∠CAB，∠AOH＝∠ACB＝90°，∴△AOH∽△ACB，∴＝＝∴＝＝∴OH＝，AH＝，∵DH＝OD﹣OH＝5﹣＝，∵DM⊥AC，∵∠DMH＝∠AOH＝90°，∠DHM＝∠AHO，∴△DMH∽△AOH，∴＝，∴＝，∴DM＝1，故选：C．9．解：∵弦AC＝BD，∴，∴，∴∠ABD＝∠BAC，∴AE＝BE；连接OA，OD，∵AC⊥BD，AE＝BE，∴∠ABE＝∠BAE＝45°，∴∠AOD＝2∠ABE＝90°，∵OA＝OD，∴AD＝R，∵AD＝，∴R＝1，故选：A．10．解：2017÷8＝252…1，即第2017秒点P所在位置如图：过P作PM⊥x轴于M，则∠PMO＝90°，∵OP＝1，∠POM＝45°，∴PM＝OM＝1×sin45°＝，即此时P点的坐标是（，），故选：A．11．解：∵四个点两两连结后得到的所有线段只有两个不同的长度，∴圆上的四个点构成了圆的内接正方形，∵正方形的边长相等，即四条弦长相等，∴这四个点依次分圆弧的比为1：1：1：1．故答案为1：1：1：1．12．解：∵在⊙O中，，∴AC＝AB＝3，故答案为：313．解：连接OD、OE，∵的度数为35°，∴∠AOD＝35°，∵CD＝CO，∴∠ODC＝∠AOD＝35°，∵OD＝OE，∴∠ODC＝∠E＝35°，∴∠DOE＝110°，∴∠AOE＝75°，∴∠BOE＝105°，∴的度数是105°．故答案为105°．14．解：∵BE＝DE，AB＝BE，∴AB2＝2BE2＝BE•BD，∴AB：BE＝BD：AB，又∠EBA＝∠ABD，∴∠ADB＝∠BAE，∵∠ADB＝∠ACB，∴∠ACB＝∠CAB，∴AB＝BC．连接BO，交AC于H，连接OA，∵AB＝BC，∴BO⊥AC，∴CH＝AH，∴CH＝AH＝AC＝4∵AO＝5，∴OH＝＝3，BH＝OB﹣OH＝5﹣3＝2．∴S△ABC＝AC•BH＝×8×2＝8，∵E是BD的中点，∴S△ABE＝S△ADE，S△BCE＝S△DCE，∴S△ABC＝S△ADC，∴S四边形ABCD＝2S△ABC＝16，故答案为16．15．解：∵，（已知）∴∠AOE＝∠COA（等弧所对的圆心角相等）；又∠AOE＝32°，∴∠COA＝32°，∴∠COE＝∠AOE+∠COA＝64°．故答案是：64°．16．（1）证明：连AM，AN，∵＝，＝，∴∠BAM＝∠ANM，∠AMN＝∠CAN，∵∠APD＝∠AMN+∠BAM，∠ADP＝∠CAN+∠ANM，∴AP＝AD．（2 ）解：连AO，OM交AB于E，设PE＝x，∵＝，∴OM⊥AB，∴∠AEO＝90°，∵OE2＝OA2﹣AE2＝OP2﹣PE2∴52﹣（x+3）2＝（）2﹣x2，∴x＝1，∴AE＝4，OE＝3，ME＝2，∴MP＝＝＝．17．证明：∵AB＝CD，∴＝，∴+＝+，∴＝，∴AD＝BC．18．（1）证明：连接AD，∵点D是的中点，∴∠CAD＝∠BAD，∴CD＝BD，在△CAD和△BAD中，，∴△CAD≌△BAD（SAS），∴∠ACD＝∠ABD，∴∠DCE＝∠DBF，在△CED和△BFD中，，∴△CED≌△BFD（ASA），∴DF＝DE；（2）解：∵四边形ABDC是圆内接四边形，∴∠DBF＝∠ACD，∵∠ACD＝∠ABD，∴∠ABD＝∠DBF，∴∠ABD＝90°，∴∠ECD＝∠ABD＝90°，∴AD是⊙O的直径，∵CD＝BD＝6，CE＝8，∴DE＝＝10，∴EB＝10+6＝16，在Rt△ABE中，AB2+BE2＝AE2，设AB＝AC＝x，则x2+162＝（x+8）2，解得x＝12，∴AB ＝12，在Rt△ABD 中，AB2+BD2＝AD2，∴AD＝＝6，∴⊙O的半径为3．。

人教版九年级数学上册级24.1.3《弧、弦、圆心角》同步练习(有答案)

九年级24.1.3《弧、弦、圆心角》同步练习一、选择题：1、如图，⊙O的半径为5，点C在弦AB上，AC=2，BC=6，则OC的长是( )．A. 2B. √13C. 3D. √152、已知在⊙O中，弦AB的长为8，圆心O到AB的距离为3，则⊙O的面积是（）A．9π B．16πC．25πD．64π3、如图，⊙O中，直径CD=20cm，弦AB⊥CD于点M，OM:MD=3：2，则AB的长是( )cm.A. 16B. 15C. 13D. 144、下列说法中正确的是( )A．等弦所对的弧相等B．等弧所对的弦相等C．圆心角相等，所对的弦相等D．弦相等，所对的圆心角相等5、如图，AB为⊙O的直径，弦AB⊥CD，垂足为点E，连接OC，若OC=5，CD=8，则AE的长度为（）A. 2B. 1C. 3D. 46、如图，已知⊙O的半径为5，弦AB，CD所对的圆心角分别是∠AOB，COD，若∠AOB与∠COD互补，弦CD=6，则弦AB的长为（）A．6 B．8 C．5√2 D．5√37、如图，坐标平面上，A、B两点分别为圆P与x轴、y轴的交点，有一直线L通过P点且与AB垂直，C点为L与y轴的交点．若A、B、C的坐标分别为（a，0），（0，4），（0，﹣5），其中a＜0，则a的值为（）A．﹣2√14 B．﹣2√15 C．﹣8 D．﹣78、如图，AB是⊙O的直径，，∠COD＝34°，则∠AEO的度数是（）A. 51°B. 56°C. 68°D. 78°二、填空题：9、蔬菜基地圆弧形蔬菜大棚的剖面如图所示，已知AB=16m，半径OA=10m，则高度CD为________m．10、如图所示，⊙O的半径为13，弦的长度是24，ON⊥AB,垂足为N，则ON= .11、如图，C，D为半圆上的三等分点，下列说法中：①AD=CD=BC②∠AOD=∠DOC=∠BOC③AD=CD=OC④△AOD沿OD翻折与△COD重合，正确的有，正确的有个。

人教版九年级数学上册24.1.3弧弦圆心角同步练习题

24.1.3弧弦圆心角同步练习题姓名：__________ 班级：__________考号：__________题号一二总分评分一、单选题（共15题；共60分）1.如图，在⊙O中，AB⌢＝AC⌢，∠A＝40°，则∠B的度数是（）A. 60°B. 40°C. 50°D. 70°2.如图，已知点A，B，C，D，E是⊙O的五等分点，则∠BAD的度数是（）A. 36°B. 48°C. 72°D. 96°3.如图，四边形ABCD内接于⊙O，AC平分∠BAD，则下列结论正确的是（）A. AB=ADB. BC=CDC. AB⌢=AD⌢ D. ∠BCA=∠DCA4.下图中∠ACB是圆心角的是( )A. B. C. D.5.如图，在△ABC中，∠C＝90°，DE⌢的度数为α，以点C为圆心，BC长为半径的圆交AB于点D，交AC 于点E，则∠A的度数为（）A. 45º－12α B. 12α C. 45º＋12α D. 25º＋12α6.如果两条弦相等，那么( )A. 这两条弦所对的圆心角相等B. 这两条弦所对的弧相等C. 这两条弦所对的弦心距相等D. 以上说法都不对7.如图，在⊙O中AĈ= BD̂，∠AOB=40°，则∠COD的度数（）A. 20°B. 40°C. 50°D. 60°8.如图，△ABC内接于⊙O，连接AO并延长交BC于点D，若∠B=70°，∠C=50°，则∠ADB的度数是（）A. 70°B. 80°C. 82°D. 85°9.如图，在⊙O中，若点C是AB⌢的中点，∠A=50°，则∠BOC=( )A. 40°B. 45°C. 50°D. 60°10.如图，AB是⊙O的直径，弦CD⊥AB于点E，若AB=10，AE=2，则弦CD的长是（）A. 4B. 6C. 8D. 1011.如图，已知AB是⊙O的直径，∠CBA=25°，则∠D的度数为（）A. B. C. D.12.如图，在⊙O中，AB̂= AĈ，∠AOB=40°，则∠ADC的度数是（）A. 40°B. 30°C. 20°D. 15°13.已知，如图，∠AOB=∠COD，下列结论不一定成立的是（）A. AB=CDB. AB⌢=CD⌢ C. △AOB≅△COD D. △AOB、△COD都是等边三角形14.下列命题中，正确的分别是（）A. 相等的圆心角，所对的弧也相等B. 两条弦相等，它们所对的弧也相等C. 在等圆中，圆心角相等，它们所对的弦也相等D. 顶点在圆周的角是圆周角15.在两个圆中有两条相等的弦，则下列说法正确的是（）A. 这两条弦所对的弦心距相等B. 这两条弦所对的圆心角相等C. 这两条弦所对的弧相等D. 这两条弦都被垂直于弦的半径平分第1题图第7题第2题图第8题第9题第10题第11题第13题第12题二、填空题（共15题；共60分）16.如图，在⊙O中，AĈ=BD̂，若∠AOB＝40°，则∠COD＝________．17.如图，AB是⊙O的直径，∠AOE＝78°，点C、D是弧BE的三等分点，则∠COE＝________．18.如图的齿轮有30个齿，每两齿之间的间隔相等，则相邻两齿间的圆心角α等于________度.19.如图，在⊙O中，点C是弧AB的中点，∠A＝50°，则∠BOC等于________度．20.某校全体同学的综合素质评价的等级统计如图所示,其中评价为C等级所在扇形的圆心角是________度.21.如图，在⊙O中，AĈ = BD̂，若∠AOB=40°，则∠COD=________°．22.过圆内的一点(非圆心)有________条弦，有________条直径．23.如图，⊙O经过五边形OABCD的四个顶点，若∠AOD=150°，∠A=65°，∠D=60°，则BC⏜的度数为________．24.如图，一块含45°角的直角三角板，它的一个锐角顶点A在⊙O上，边AB，AC分别与⊙O交于点D，E.则∠DOE 的度数为________.25.在⊙O中，弦AB的长恰好等于半径，弦AB所对的圆心角为________．26.如图，在⊙O中，半径OA垂直于弦BC，点D在圆上且∠ADC=30∘，则∠AOB的度数为________．27.如图，在⊙O中，直径AB∥弦CD，若∠COD=110°，则AC∧的度数为________ ．28.在⊙O中，弦AB=2cm，圆心角∠AOB=60°，则⊙O的直径为 ________cm．29.已知弦AB把圆周分成1：5的两部分，则弦AB所对的圆心角的度数为 ________°.30.如图，在△ABC中，∠ACB=90°，∠B=36°，以C为圆心，CA为半径的圆交AB于点D，交BC于点E．求弧AD所对的圆心角的度数________．答案解析部分一、单选题1.【答案】D【解析】【解答】解：∵AB⌢=AC⌢，∴AB＝AC，∴∠B＝∠C，∴∠B＝12（180°﹣∠A）＝12×（180°﹣40°）＝70°.故答案为：D.【分析】先利用等腰三角形的性质得∠B＝∠C，然后根据三角形内角和计算∠B的度数.2.【答案】C【解析】【解答】解：∵点A，B，C，D，E是⊙O的五等分点，∴弧BD的度数为144度，∴∠A＝72°.故答案为：C.【分析】根据圆周角的度数等于其所对的弧的度数的一半即可算出答案.3.【答案】B【解析】【解答】解：A.∵∠ACB与∠ACD的大小关系不确定，∴AB与AD不一定相等，故本选项错误；B.∵AC平分∠BAD，∴∠BAC=∠DAC，∴BC=CD，故本选项正确；C.∵∠ACB与∠ACD的大小关系不确定,∴AB⌢与AD⌢不一定相等，故本选项错误；D.∠BCA与∠DCA的大小关系不确定，故本选项错误。

人教版数学九年级上同步练习 24.1.3 弧、弦、圆心角

人教版九年级上《24.1.3弧、弦、圆心角》同步练习(含答案解析)

人教版九年级数学上册 24.1.3 弧、弦、圆心角 同步练习卷

(人教版数学)初中9年级上册-同步练习-24.1.3 弧、弦、圆心角-九年级数学人教版(上)(解析版

2020年人教版九年级数学上册24.1.3《弧、弦、圆心角》同步练习 学生版