如果你的计算器上没有pi
如何使用自己的计算器解决数学问题

如何使用自己的计算器解决数学问题在现代社会中,计算器已经成为数学学习和工作中必不可少的工具。
虽然现在的手机也具备计算器的功能,但使用专门的计算器更加方便,尤其是在考试时。
在本文中,我们将讨论如何使用自己的计算器解决数学问题,包括基本的运算、解方程、微积分等。
一、基本的运算使用计算器进行基本的运算非常简单。
包括加减乘除,指数和根号等。
一般来说,计算器的操作符和数字键位很容易理解。
例如,在大多数计算器中,加号是“+”,减号是“-”,乘号是“×”,除号是“÷”,指数键是“×y”,根号键是“√”。
例如,要计算“3+4”,只需按下数字键“3”、“+”、“4”和“=”即可。
对于一些较大的运算,也可以使用括号键“()”来进行分组。
二、解方程对于方程的求解,计算器也提供了一些辅助功能。
例如,方程求根功能。
对于形如“ax²+bx+c=0”的二次方程,只需按键“a”、“x ²”、“+”、“b”、“x”、“+”、“c”、“=”、“x”、“=”即可得到方程的根。
一般来说,计算器会显示出两个根:一个是解析解,另一个是数字近似解。
对于更加复杂的方程,看起来似乎无法使用计算器进行计算时,可以尝试使用计算器的图形功能来帮助解决问题。
例如,对于形如“y=sin(x)”或“y=x²”的函数,可以根据名为绘图函数的功能在平面直接上进行图形绘制。
通过观察图形,我们可以获得一些粗略的解析结果,甚至可以用图形进行验证。
三、微积分实际上,许多计算器都提供微积分的计算功能,包括导数和积分等。
例如,对于函数“y =x²”,我们要求它在点“x =3”的导数,只需按键“y = x ²”、“=”、按下“2nd”、“x”、“d/dx”、“=>”、“3”、“=”即可得到它在点“x =3”的导数。
同样,我们也可以使用计算器的积分功能来解决问题。
例如,对于形如“y = sin(x)”的函数,我们要求它在一个区间“[0,π]”内的积分,只需按键“y = sin x”、“=”、“2nd”、“quad”、“=>”、“0”、“,”、“π”、“)”、“=”,即可得到所求区间的积分。
windows自带计算器详细使用方法-图文并茂Word版
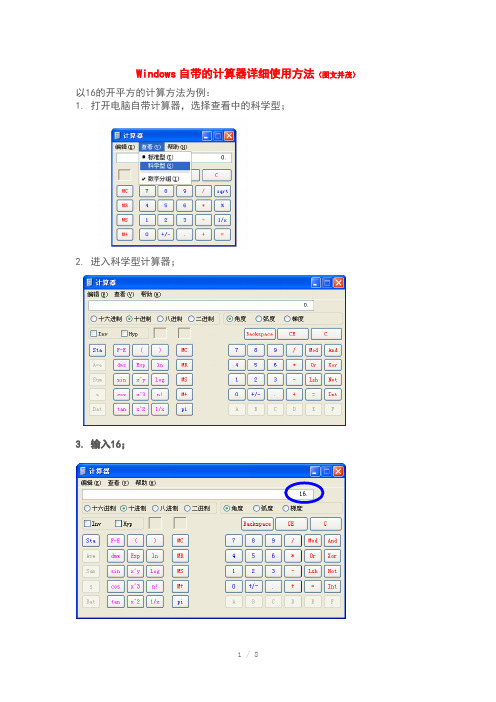
Windows自带的计算器详细使用方法(图文并茂)以16的开平方的计算方法为例:1.打开电脑自带计算器,选择查看中的科学型;2.进入科学型计算器;3.输入16;4.勾选Inv;5.按按钮;6.输入2,注意了,不是输入1/2,一定要是2,才正确;7.按按钮。
结果计算完成。
其他:一、进行复杂运算我们平时使用计算器时,往往进行简单计算,如8×9=72。
如果复杂些,就一步步进行计算,如要计算(4+5)×6时,就需要先算4+5=9,再算9×6=120。
现在我们使用计算器的高级功能就可以一步实现这个运算。
我们打开计算器,是默认的界面。
点击计算器的“查看”下拉菜单,点中“科学型”,就会出现更大的窗口:首先,我们在记事本里编写好我们要的计算式,如: (4+5)×6,然后将它复制。
打开计算器的“编辑”菜单,再点击“粘贴”,做完这些操作后,按下计算器的“=”按纽,计算器就会将最后的计算结果显示在输出文本框中。
二、数学计算普通的计算器具有很强的数学计算功能,它可以计算角度的正弦值、余弦值、正切值等,Windows计算器也具备了这些功能,并且使用起来也很方便。
假如我们要计算正弦值,我们输入角度或弧度的数值后,直接点“sin”按纽,结果就会输出。
同时我们还可以方便进行平方、立方、对数、阶数、倒数运算。
三、逻辑运算Windows计算器可以方便快捷地进行二进制、八进制、十进制、十六进制之间的任意转换。
假如我们要把十进制数69转换成到二进制数,我们首先通过计算器输入69,完毕后点“二进制”单选按纽,计算器就会输出对应的二进制数。
如果要转换成其他进制,点击对应的按纽就可以了。
需要注意的是在四个进制按纽后面还有四个按纽,它们的作用是定义数的长度,“字节”把要转换数的长度限制为一个字节,即八位二进制数,“单字”刚是指两个字节长度,“双字”是四个字节长度,“四字”是八个字节长度。
除了可以进行进制转换外,还可以进行与、或、非等逻辑运算。
Python-3.5.2--官方入门指南-中文版

Python 入门指南目录Python 入门指南 (1)1. 开胃菜 (5)2. 使用Python 解释器 (6)2.1. 调用Python 解释器 (6)2.1.1. 参数传递 (8)2.1.2. 交互模式 (8)2.2. 解释器及其环境 (8)2.2.1. 源程序编码 (8)3. Python 简介 (9)3.1. 将Python 当做计算器 (10)3.1.1. 数字 (10)3.1.2. 字符串 (12)3.1.3. 列表 (16)3.2. 编程的第一步 (18)4. 深入Python 流程控制 (19)4.1. if 语句 (20)4.2. for 语句 (20)4.3. range() 函数 (21)4.4. break 和continue 语句, 以及循环中的else 子句 (22)4.5. pass 语句 (23)4.6. 定义函数 (24)4.7. 深入Python 函数定义 (26)4.7.1. 默认参数值 (26)4.7.2. 关键字参数 (28)4.7.3. 可变参数列表 (30)4.7.4. 参数列表的分拆 (30)4.7.5. Lambda 形式 (31)4.7.6. 文档字符串 (31)4.7.7. 函数注解 (32)4.8. 插曲:编码风格 (33)5. 数据结构 (34)5.1. 关于列表更多的内容 (34)5.1.1. 把列表当作堆栈使用 (35)5.1.2. 把列表当作队列使用 (36)5.1.3. 列表推导式 (37)5.1.4. 嵌套的列表推导式 (39)5.2. del 语句 (40)5.3. 元组和序列 (40)5.4. 集合 (42)5.6. 循环技巧 (44)5.7. 深入条件控制 (46)5.8. 比较序列和其它类型 (46)6. 模块 (47)6.1. 深入模块 (48)6.1.1. 作为脚本来执行模块 (49)6.1.2. 模块的搜索路径 (50)6.1.3. “编译的” Python 文件 (51)6.2. 标准模块 (51)6.3. dir() 函数 (52)6.4. 包 (55)6.4.1. 从* 导入包 (57)6.4.2. 包内引用 (58)6.4.3. 多重目录中的包 (58)7. 输入和输出 (58)7.1. 格式化输出 (59)7.1.1. 旧式的字符串格式化 (63)7.2. 文件读写 (63)7.2.1. 文件对象方法 (63)7.2.2. 使用json 存储结构化数据 (66)8. 错误和异常 (67)8.1. 语法错误 (67)8.2. 异常 (67)8.3. 异常处理 (68)8.4. 抛出异常 (71)8.5. 用户自定义异常 (71)8.6. 定义清理行为 (73)8.7. 预定义清理行为 (74)9. 类 (75)9.1. 术语相关 (75)9.2. Python 作用域和命名空间 (76)9.2.1. 作用域和命名空间示例 (78)9.3. 初识类 (78)9.3.1. 类定义语法 (79)9.3.2. 类对象 (79)9.3.3. 实例对象 (80)9.3.4. 方法对象 (81)9.3.5. 类和实例变量 (82)9.4. 一些说明 (83)9.5. 继承 (85)9.5.1. 多继承 (86)9.6. 私有变量 (87)9.7. 补充 (88)9.9. 迭代器 (89)9.10. 生成器 (91)9.11. 生成器表达式 (91)10. Python 标准库概览 (92)10.1. 操作系统接口 (92)10.2. 文件通配符 (93)10.3. 命令行参数 (93)10.4. 错误输出重定向和程序终止 (93)10.5. 字符串正则匹配 (94)10.6. 数学 (94)10.7. 互联网访问 (95)10.8. 日期和时间 (95)10.9. 数据压缩 (96)10.10. 性能度量 (96)10.11. 质量控制 (97)10.12. “瑞士军刀” (98)11. 标准库浏览– Part II (98)11.1. 输出格式 (98)11.2. 模板 (100)11.3. 使用二进制数据记录布局 (101)11.4. 多线程 (102)11.5. 日志 (103)11.6. 弱引用 (103)11.7. 列表工具 (104)11.8. 十进制浮点数算法 (105)12. 虚拟环境和包 (106)12.1. 简介 (106)12.2. 创建虚拟环境 (107)12.3. 使用pip 管理包 (108)13. 接下来? (110)14. 交互式输入行编辑历史回溯 (112)14.1. Tab 补全和历史记录 (112)14.2. 其它交互式解释器 (112)15. 浮点数算法:争议和限制 (112)15.1. 表达错误 (116)16. 附录 (118)16.1. 交互模式 (118)16.1.1. 错误处理 (118)16.1.2. 可执行Python 脚本 (118)16.1.3. 交互式启动文件 (119)16.1.4. 定制模块 (119)Python 是一门简单易学且功能强大的编程语言。
Calc 计算器说明

Calc 计算器说明“计算器”概述使用“计算器”可以完成任意的通常借助手持计算器来完成的标准运算。
“计算器”可用于基本的算术运算,比如加减运算等。
同时它还具有科学计算器的功能,比如对数运算和阶乘运算等。
执行简单的计算键入计算的第一个数字。
单击“+”执行加、“-”执行减、“*”执行乘或“/”执行除。
键入计算的下一个数字。
输入所有剩余的运算符和数字。
单击“=”。
注意通过按 NUM LOCK 键,数字键盘也可以用来输入数字和运算符。
执行科学计算单击“查看”菜单中的“科学型”。
单击某一数制。
单击要使用的显示大小,然后继续计算。
注意对于十六进制、八进制及二进制来说,有四种可用的显示类型:四字(64 位表示法)、双字(32 位表示法)、单字(16 位表示法)和字节(8 位表示法)。
对于十进制来说,有三种可用的显示类型:角度、弧度和梯度。
通过按 NUM LOCK 键,数字键盘也可以用来输入数字和运算符。
执行统计计算单击“查看”菜单中的“科学型”。
键入首段数据,然后单击“Sta”打开“统计框”。
单击“返回(R)”返回到“计算器”,再单击“Dat”保存该数值。
键入其余的数据,每次输入之后单击“Dat”。
单击“Ave”、“Sum”或“s”。
注意通过按 NUM LOCK 键,数字键盘也可以用来输入数字和运算符。
“Ave”计算保存在“统计框”中值的平均数,“Sum”计算值的总和,而“s”计算标准误差。
当所有的数据录入完成后,单击“Sta”可以看到数据列表。
“统计框”可以记录您在对话框底部保存的数值个数。
要从列表中删除某个数值,请单击“清零(c)”。
如果要删除所有数值,请单击“全清(A)”。
单击“加载(L)”可将计算器显示区的数字改为在“统计框”内选定的数字。
在标准型和科学型间转换数据单击“MS”存储显示的数字。
在“查看”菜单上,单击所需的视图。
单击“MR”再次调用存储的数字。
注意在标准型和科学型视图之间切换时,“计算器”将清除它所显示的内容。
振动单位换算
0.00097 mm rms. x 1000 = 0.97 um rms. (micro-meters rms.)
从图#2 的后缀转换方式, 这个条件可以正确 地表达为:
(0.97 um rms./ 0.707) x 2 = 2.74 um 峰-峰值
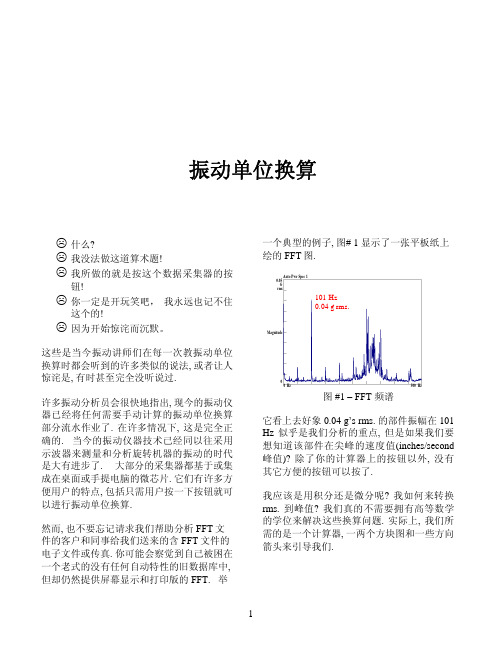
2.74 um 峰-峰值是图#1 在 101 Hz 处振幅组成 部分位移的 SI 单位值.
÷ 9807 加速度 (mm/s2)
x 2(Pi)f 加速 (mm/s)
x 2(Pi)f
加速度 (g’s) 位移 (mm)
x 9807 加速度 (mm/s2)
÷ 2(Pi)f 加速 (mm/s)
÷ 2(Pi)f
图 #4 – SI 单位尺度换算
转换 SI 单位方式:
单位尺度经常指加速度, 速度或位移. SI 单位 通常指国际单位系统并有以下表示:
显然我们可以将这个 0.00097 mm rms.位移值 按照方块图#4 的箭头方向将它乘以 2(Pi)f 来 转换(微分)为 0.618 mm/sec rms.,这个速度值, 另外我们也可以将速度值按照方块图#4 的箭 头方向转换(微分)为加速度值, 只需将速度值 乘 以 2(Pi)f 就 可 以 得 到 加 速 度 值 392.28 mm/sec2 rms. 了. 如果你想要知道以 g’s rms. 为 单 位 的 加 速 度 值 , 那 么 你 需 要 用 392.28 mm/sec2 rms. 来除以 9807 来得到原来的 0.04 g’s rms.
0.024 in/sec rms. 是图#1 中用英制单位表示的 振幅组成的速度值.
我们现在可以将速度值 0.024 in/sec rms.除以 以计算式中的 2(Pi)f 值来(积分)转换成位移值:
计算器使用说明书

k平方根﹑立方根﹑根﹑平方﹑立方﹑倒数﹑阶乘﹑
随机数﹑圆周率(π)及排列/组合....................20
k角度单位转换.......................................................21
使用注意事项
?在首次使用本计算器前务请按5键。
?即使操作正常﹐MODEx。115MS/MODEx。570MS/MODEx。991MS型计算器也必须至少每3年更换一次电池。而MODEx。95MS/MODEx。100MS型计算器则须每2年更换一次电池。
电量耗尽的电池会泄漏液体﹐使计算器造成损坏及出现故障。因此切勿将电量耗尽的电池留放在计算器内。
k输入时的错误订正..................................................9
k重现功能.................................................................9
k错误指示器.............................................................9
?在开始进行计算之前﹐必须检查目前的计算模式(SD﹑
REG﹑COMP)及角度单位设定(Deg﹑Rad﹑Gra)。
用于储存计算输入的记忆区可储存79“步”。每当您按下
数字键或算术运算键 时便会占用
一步 键的操作不占用一步。例如﹐输入 只占用一步。您可为一个单独计算输入最多79步。每当您输入到任何
计算的第73步时﹐游标即会由“_”变为“ ”以表示记忆容量快用完了。若您需要的输入多于79步﹐请将计算分割为两个或多个计算部分进行。
电脑系统自带科学计算器使用方法

电脑的科学计算器函数名:ln在数学中ln(x)是以e为底的x的对数。
e是一个常数函数名: exp功能: 指数函数exp就是以e为底的指数,exp(0)=1, exp(1)=e, exp(2)=en!代表一个数的阶乘,例如:5!就是5*4*3*2*1;sta代表统计算法;x^3代表x的3次方;x^y代表x的y次方。
sin正弦,cos余弦,tan正切,dms度分秒切换Lsh左移ln自然对数,F-E科学计数法开关,Xor异或,Int整数部分,Exp允许输入用科学计数法表示的数字1/x倒数,log常用倒数mod余数Pi是圆周率,Exp是科学计数法exp代表以e为幂指数函数例如:exp10就是e的10次方;ln是以e为底的对数函数例如:ln10就是以e为底10的对数;M+是计算结果并加上已经储存的数;M-是计算结果并用已储存的数字减去目前的结果;MR是读取储存的数据;MC是清除储存数据;AC,CE归零是有一个是清除现有数据重新输入,另一个是清除全部数据结果和运算符.数学计算度量衡换算百度计算器为用户提供常用的数学计算功能。
您可在任何地方的网页搜索栏内,输入需要计算的数学表达式(例如:3+2),点击搜索,即可获得结果。
百度计算器支持实数范围内的计算,支持的运算包括:加法(+或+),减法(-或-),乘法(*或×),除法(/),幂运算(^),阶乘(!或!)。
支持的函数包括:正弦,余弦,正切,对数。
支持上述运算的混合运算。
例:加法:3+2减法:3-2乘法:3*2除法:3/2阶乘:4! 4的阶乘电脑自带计算器开根号:1,调到科学型。
2,开方:(1)选一下INV这个。
(2)按一个数字。
(3)再按х^у。
(4)开几次方就按几然后等于就行了!平方:4^2 4的平方立方:4^3 4的立方开平方:4^(1/2) 4的平方根开立方:4^(1/3) 4的立方根倒数:1/4 4的倒数幂运算:2^8 2的8次方常用对数:log(8) 以10 为底8的对数以自然底数为底的对数:ln(8) 以e为底8的对数求弧度的正弦:sin(10) 10弧度角正弦值求弧度的余弦:cos(10) 10弧度角余弦值求弧度的正切:tan(10) 10弧度角正切值上述运算的混合运算:log((5+5)^2)-3+pi圆周率pi=3.自然底数e=2.您可以直接使用常数字符,比如:如果您输入的算式不符合上述格式,则不会得到计算结果,而只得到算式的搜索结果。
计算器 标准正态分布

计算器标准正态分布在统计学中,正态分布是一种非常重要的概率分布,也被称为高斯分布。
它具有许多重要的特性,因此在各种领域都有着广泛的应用。
在实际应用中,我们经常需要计算正态分布的各种统计量,比如均值、标准差、累积概率等。
而计算这些统计量的过程通常需要借助计算器来进行,接下来我们将介绍如何使用计算器来进行标准正态分布的计算。
首先,我们需要明确正态分布的概率密度函数和累积分布函数。
正态分布的概率密度函数可以表示为:\[f(x) = \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}}\]其中,\( \mu \) 为均值,\( \sigma \) 为标准差。
而正态分布的累积分布函数则可以表示为:\[F(x) = \frac{1}{2}[1+erf(\frac{x-\mu}{\sigma\sqrt{2}})]\]其中,\( erf(x) \) 为误差函数。
在实际的计算过程中,我们通常将正态分布转化为标准正态分布进行计算,即均值为0,标准差为1的情况。
这样可以简化计算的复杂度,使得计算过程更加方便快捷。
接下来,我们将介绍如何使用计算器来进行标准正态分布的计算。
首先,我们需要确定所要计算的统计量,比如给定一个数值,我们需要计算其对应的累积概率。
在这种情况下,我们可以使用计算器上的标准正态分布表,直接查找对应数值的累积概率。
如果计算器上没有预置标准正态分布表,我们也可以使用计算器上的正态分布累积概率函数来进行计算。
另外,我们还可以使用计算器上的逆正态分布函数来进行计算。
逆正态分布函数可以帮助我们求解给定累积概率对应的数值。
这在实际应用中也是非常常见的情况,比如在质量控制中,我们需要确定一个产品的质量指标,使得其累积概率达到一定的要求,这时就需要用到逆正态分布函数来进行计算。
总之,标准正态分布在统计学中有着非常重要的地位,而计算器在进行标准正态分布的计算时起着非常重要的作用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
如果你的计算器上没有pi
下面是一个有趣的小把戏:拿出一个科学型计算器(就比如说 Windows 计算器),确认你的计算器使用的是角度制。
然后,输入 55555555 ,按 1/x ,再按 sin ,然后看看你的屏幕……神奇吧!如果你觉得还不够精确,输入55555555555555555555 ,再依次按下 1/x 和 sin 看看……
事实上,sin( (1 / 55555555555555555555)° ) =
3.141592653589793238494059.. * 10-22,前 20 位都和 pi 的值一模一样。
显然,这绝对不可能是一个巧合。
那么,这究竟是为什么呢?
注意到 1/180 = 0.00555555... ,换句话说 55555..55 (连续 n 个 5 )的倒数就近似于 180 * 10-n-2。
另外,当 x 很小很小的时候, sin(x) 会与 x 非常接近,但在角度制中,我们必须写作sin(x) ≈ (pi / 180) x 。
因此, sin(1 / 55555..555) ≈ (pi / 180) * (180 * 10-n-2) = pi * 10-n-2
来源:
/2010/02/17/the-math-behind-a-neat-calculator-t rick/。
