辽宁省沈阳市城郊市重点联合体2012-2013学年高一下学期期中考试数学试题

合集下载

2013沈阳市高一数学统考试题

2013年沈阳市高中一年级教学质量监测数学本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，第Ⅰ卷第1至2页，第Ⅱ卷第3至6页. 满分150分. 考试时间为120分钟.注意事项： 1.答题前，考生务必将自己的姓名、班级、座位号用2B 铅笔填写在答题卡上，并将条形码粘贴在答题卡指定区域。

2.第Ⅰ卷每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑，如需改动用橡皮擦干净后，再选涂其他答案标号。

第Ⅱ卷用黑色墨水签字笔在答题卡指定位置书写作答，在试题卷上作答，答案无效。

3.考试结束后，考生将答题卡交回。

第Ⅰ卷（选择题共60分）一、选择题（本大题共12个小题，每小题5分，共60分. 在每个小题给出的四个选项中只有一个是符合题目要求的）1．若集合A={}|∈x y =-x,x 2R ， B={}|∈x x <,x 4R 错误！未找到引用源。

，则A ，B 间的关系为（） A ．A ⊆B B ．B ⊆AC ．A ⊆ðR BD ．B ⊆ðR A 2．若过点()A -m 2,和()B m 4，的直线与直线2x+y-1=0平行，则实数m 的值为（） A ．0 B ．8-C ．2D ．10 3．在斜四棱柱的四个侧面中，矩形的个数最多有（）个A ．1B ．4C ．3D ．2 4．圆O 1∶x 2+y 2-2x=0与圆O 2∶x 2+y 2-4y=0的位置关系是（）A ．相离B ．相交C ．外切D ．内切5．如果一个几何体的主（正）视图，左（侧）视图，俯视图都是全等的图形，那么称这个几何体为“完美几何体”. 在下面选项中，可以由“完美几何体”组成的选项是（）A ．正方体、球、侧棱两两垂直且相等的正三棱锥B ．正方体、球、各棱长都相等的正三棱柱C ．球、高和底面半径相等的圆柱、高和底面半径相等的圆锥D ．正方体、正四棱台、棱长相等的平行六面体6．若直线l 1∶(a-2)x+3y+a=0，l 2∶ax+(a-2)y-1=0相互垂直，错误！未找到引用源。

2012-2013高一数学下期中试卷及答案

振阳公学2012—2013学年第二学期期中考试高一数学试题（考试时间：120分钟试卷分值：150分）第Ⅰ卷一、选择题（本大题共10小题，每小题5分，共50分）1. 在ABC ∆中，若::1:2:3A B C ∠∠∠=，则::a b c 等于（）A.1:2:3B.3:2:1C.D.2 2.不等式x 2-2x +3<0的解集是（）A.{x |－1＜x ＜3}B.{x |－3＜x ＜1}C.{x |x ＜－3或x ＞1}D.∅ 3．数列{}n a 的通项公式32-=n a n 则=+31a a （）A ．0B ．2C ．5D ．－14．等比数列｛a n ｝中，a 3=7，前3项之和S 3=21，则公比q 的值为（）A ．1B ．－21C ．1或－21D ．－1或215．在等差数列{a n }中，若a 1＋a 2＋a 12＋a 13＝24，则7a 为( )．A ．6B ．7C ．8D ．96．若x y ，满足约束条件03003x y x y x ⎧+⎪-+⎨⎪⎩，，，≥≥≤≤则2z x y =-的最大值为（） A ．０ B ．6 C ．9 D ．157．在△ABC 中，222a b c bc =++ ，则A 等于（）A ．60°B ．45°C ．120°D ．30°8．在△ABC 中，若222sin sin sin A B C +<，则△ABC 的形状是（）A 、钝角三角形B 、直角三角形C 、锐角三角形D 、不能确定 9．设0<<b a ，则下列不等式中不成立的是（）A ．b a 11>B ．ab a 11>- C ．b a -> D ．b a ->- 10．若称na 1＋a 2＋…＋a n为n 个正数a 1＋a 2＋…＋a n 的“均倒数”已知数列{a n }的各项均为正，且其前n 项的“均倒数”为12n －1则数列{a n }的通项公式为( )．A ．2n －1B ．4n －3C ．4n －1D ．4n －5第Ⅱ卷非选择题（共100分）二、填空题：本大题共5小题，每小题5分，共25分，把答案填在横线上。

2012年沈阳中考数学真题卷含答案解析

2012年沈阳市中等学校招生统一考试试卷数学13A(满分:150分时间:120分钟)参考公式:抛物线y=ax 2+bx+c 的顶点是(-b2a ,4ac -b 24a),对称轴是直线x=-b2a .第Ⅰ卷(选择题,共24分)一、选择题(下列各题的备选答案中,只有一个答案是正确的.每小题3分,共24分)1.下列各数中比0小的数是( )A.-3B.13 C.3 D.√32.如图是由四个相同的小立方块搭成的几何体,这个几何体的左视图是( )3.沈阳地铁2号线的开通,方便了市民的出行.从2012年1月9日到2月7日的30天里,累计客运量约达3 040 000人次,将3 040 000用科学记数法表示为( ) A.3.04×105 B.3.04×106 C.30.4×105 D.0.304×1074.计算(2a)3·a 2的结果是( ) A.2a 5 B.2a 6 C.8a 5 D.8a 65.在平面直角坐标系中,点P(-1,2)关于x 轴的对称点的坐标为( ) A.(-1,-2) B.(1,-2) C.(2,-1) D.(-2,1)6.气象台预报“本市明天降水概率是30%”,对此消息下列说法正确的是( ) A.本市明天将有30%的地区降水 B.本市明天将有30%的时间降水 C.本市明天有可能降水 D .本市明天肯定不降水7.一次函数y=-x+2的图象经过( ) A.一、二、三象限 B .一、二、四象限 C.一、三、四象限 D .二、三、四象限8.如图,正方形ABCD 中,对角线AC,BD 相交于点O,则图中的等腰直角三角形有( )A.4个B.6个C.8个D.10个第Ⅱ卷(非选择题,共126分)二、填空题(每小题4分,共32分)9.分解因式:m 2-6m+9= .10.一组数据1,3,3,5,7的众数是 . 11.五边形的内角和为度. 12.不等式组{x +1>0,1-2x >0的解集是 .13.已知△ABC ∽△A'B'C',相似比为3∶4,△ABC 的周长为6,则△A'B'C'的周长为 .14.已知点A 为双曲线y=kx 图象上的点,点O 为坐标原点,过点A 作AB ⊥x 轴于点B,连结OA.若△AOB 的面积为5,则k 的值为 .15.有一组多项式:a+b 2,a 2-b 4,a 3+b 6,a 4-b 8,…,请观察它们的构成规律,用你发现的规律写出第10个多项式为 .16.如图,菱形ABCD 的边长为8 cm,∠A=60°,DE ⊥AB 于点E,DF ⊥BC 于点F,则四边形BEDF 的面积为 cm 2.三、解答题(本大题共9小题,共94分)17.(本题8分)计算:(-1)2+|√2-1|+2sin 45°.18.(本题8分)小丁将中国的清华大学、北京大学及英国的剑桥大学的图片分别贴在3张完全相同的不透明的硬纸板上,制成名校卡片,如图,小丁将这3张卡片背面朝上洗匀后放在桌子上,从中随机抽取一张卡片,放回后洗匀,再随机抽取一张卡片.(1)小丁第一次抽取的卡片上的图片是剑桥大学的概率是多少?(请直接．．写出结果) (2)请你用列表法或画树状图(树形图)法,帮助小丁求出两次抽取的卡片上的图片一个是国内大学、一个是国外大学的概率.(卡片名称可用字母表示)19.(本题10分)已知,如图,在▱ABCD中,延长DA到点E,延长BC到点F,使得AE=CF,连结EF,分别交AB,CD 于点M,N,连结DM,BN.(1)求证:△AEM≌△CFN;(2)求证:四边形BMDN是平行四边形.20.(本题10分)为了提高沈城市民的节水意识,有关部门就“你认为最有效的节水措施”随机对部分市民进行了问卷调查.其中调查问卷设置以下选项(被调查者只能选择其中的一项):A.出台相关法律法规;B.控制用水大户数量;C.推广节水技改和节水器具;D.用水量越多,水价越高;E.其他.根据调查结果制作了统计图表的一部分如下:你认为最有效的节水措施的条形统计图(1)此次抽样调查的人数为人;(2)结合上述统计图表可得m=,n=;(3)请根据以上信息直接．．补全条形统计图.13B21.(本题10分)甲、乙两人加工同一种机器零件,甲比乙每小时多加工10个零件,甲加工150个零件所用时间与乙加工120个零件所用时间相等,求甲、乙两人每小时各加工多少个机器零件?22.(本题10分)如图,☉O是△ABC的外接圆,AB是☉O的直径,D为☉O上一点,OD⊥AC,垂足为E,连结BD.(1)求证:BD平分∠ABC;(2)当∠ODB=30°时,求证:BC=OD.23.(本题12分)已知,如图,在平面直角坐标系内,点A的坐标为(0,24),经过原点的直线l1与经过点A的直线l2相交于点B,点B坐标为(18,6).(1)求直线l1,l2的表达式;(2)点C为线段OB上一动点(点C不与点O,B重合),作CD∥y轴交直线l2于点D,过点C,D 分别向y轴作垂线,垂足分别为F,E,得到矩形CDEF.①设点C的纵坐标为a,求点D的坐标(用含a的代数式表示);②若矩形CDEF的面积为60,请直接．．写出此时点C的坐标.24.(本题12分)已知,如图①,∠MON=60°,点A,B为射线OM,ON上的动点(点A,B不与点O重合),且AB=4√3,在∠MON的内部、△AOB的外部有一点P,且AP=BP,∠APB=120°.(1)求AP的长;(2)求证:点P在∠MON的平分线上;(3)如图②,点C,D,E,F分别是四边形AOBP的边AO,OB,BP,PA的中点,连结CD,DE,EF,FC,OP.①当AB⊥OP时,请直接．．写出四边形CDEF的周长的值;②若四边形CDEF的周长用t表示,请直接．．写出t的取值范围.25.(本题14分)已知,如图,在平面直角坐标系中,点A坐标为(-2,0),点B坐标为(0,2),点E为线段AB上的动点(点E不与点A,B重合),以E为顶点作∠OET=45°,射线ET交线段OB于点F,C为y轴正半轴上一点,且OC=AB,抛物线y=-√2x2+mx+n的图象经过A,C两点.(1)求此抛物线的函数表达式;(2)求证:∠BEF=∠AOE;(3)当△EOF为等腰三角形时,求此时点E的坐标;(4)在(3)的条件下,当直线EF交x轴于点D,P为(1)中抛物线上一动点,直线PE交x轴于点G,在直线EF上方的抛物线上是否存在一点P,使得△EPF的面积是△EDG面积的(2√2+1)倍.若存在,请直接．．写出点P的坐标;若不存在,请说明理由.温馨提示:考生可以根据题意,在备用图中补充图形,以便作答.2012年沈阳市中等学校招生统一考试试卷一、选择题1.A正数大于0,0大于负数.故选A.2.D从几何体的左侧看,第1列为2个方块,第2列为1个方块,故选D.3.B用科学记数法表示较大的数,正确的表示形式为a×10n(1≤|a|<10,n为正整数).所以3040 000=3.04×106,故选B.4.C由幂的运算法则得(2a)3·a2=8a3·a2=8a5,故选C.5.A在平面直角坐标系中,关于x轴对称的两个点横坐标相同,纵坐标互为相反数.所以点P(-1,2)关于x轴的对称点的坐标为(-1,-2),故选A.6.C本市明天降水概率是指降水发生的可能性大小而不是指多少地区或多少时间降水,故选C.7.B因为k=-1<0,b=2>0,所以y=-x+2的图象经过第一、二、四象限.故选B.8.C正方形的两条对角线把正方形分成四个相同的小等腰直角三角形.这四个小等腰直角三角形又可以拼成四个等腰直角三角形,故选C.二、填空题9.答案(m-3)2解析m2-6m+9=(m-3)2.10.答案3解析众数是出现次数最多的数据,所以这组数据的众数为3.11.答案540解析五边形的内角和=(5-2)×180°=540°.12.答案-1<x<12解析解不等式x+1>0得x>-1;解不等式1-2x>0得x<12,所以原不等式组的解集为-1<x<12.13.答案8解析相似三角形的周长比等于相似比.由题意得△ABC的周长△A'B'C'的周长=34,因为△ABC的周长为6,所以△A'B'C'的周长=4×63=8.14.答案10或-10解析设点A坐标为(x,y).因为点A在双曲线y=kx图象上,所以xy=k.当k>0时,点A在第一、三象限,S△AOB=12xy=5,∴k=10;当k<0时,点A在第二、四象限,S△AOB=-12xy=5,∴k=-10.评析本题考查反比例函数的几何意义.解决本题的关键在于对点A所在象限的分类讨论.15.答案a10-b20解析观察多项式的首项:a,a2,a3,a4,…,显然第10个多项式的首项为a10;观察多项式的末项:b2,-b4,b6,-b8,…,第10个多项式的末项为-b20.故第10个多项式为a10-b20.评析本题是规律探索问题.主要关注单项式的系数、次数的变化情况,同时注意符号的改变与否.16.答案16√3解析连结BD.在菱形ABCD中,AD=AB,又∵∠A=60°,∴△ABD为等边三角形,∴S△ADE=S△BDE,同理S△CDF=S△BDF,∴S四边形BEDF=12S菱形ABCD=S△ABD.∵∠A=60°,∴DE=AD·sin60°=4√3cm,∴S四边形BEDF=S△ABD=12×8×4√3=16√3cm2.三、解答题17.解析原式=1+√2-1+2×√22=2√2.18.解析(1)13.(2)列表得第二次第一次A B CA(A,A)(A,B)(A,C)B(B,A)(B,B)(B,C)C(C,A)(C,B)(C,C)或画树状(形)图得由表格(或树状图/树形图)可知,共有9种可能出现的结果,每种结果出现的可能性相同,其中两次抽取的卡片上的图片一个是国内大学,一个是国外大学的结果有4种:(A,C)、(B,C)、(C,A)、(C,B).∴P(两次抽取的卡片上的图片一个是国内大学、一个是国外大学)=49.19.证明(1)∵四边形ABCD是平行四边形,∴∠DAB=∠BCD,∴∠EAM=∠FCN.又∵AD∥BC,∴∠E=∠F.∵AE=CF,∴△AEM≌△CFN.(2)由(1)得AM=CN,又∵四边形ABCD是平行四边形,∴AB△CD,∴BM△DN,∴四边形BMDN是平行四边形.20.解析(1)500.(2)35%;5%.(3)21.解析设乙每小时加工机器零件x个,则甲每小时加工机器零件(x+10)个,根据题意得150 x+10=120x,解得x=40.经检验,x=40是原方程的解,x+10=40+10=50.答:甲每小时加工50个零件,乙每小时加工40个零件.22.证明(1)∵OD⊥AC,OD为半径,∴CD⏜=AD ⏜, ∴∠CBD=∠ABD,∴BD 平分∠ABC. (2)∵OB=OD,∴∠OBD=∠ODB=30°,∴∠AOD=∠OBD+∠ODB=30°+30°=60°. 又∵OD ⊥AC 于E,∴∠OEA=90°, ∴∠A=180°-∠OEA-∠AOD=180°-90°-60°=30°. 又∵AB 为☉O 的直径,∴∠ACB=90°, 则在Rt △ACB 中BC=12AB,∵OD=12AB,∴BC=OD.评析本题考查垂径定理、圆周角定理、等边对等角等知识的综合运用.解决(2)问的关键在于对“30°角所对直角边等于斜边的一半”的认识.23.解析 (1)设直线l 1的表达式为y=k 1x,它过B(18,6),得18k 1=6,k 1=13,∴y=13x.设直线l 2的表达式为y=k 2x+b,它过A(0,24),B(18,6), 得{b =24,18k 2+b =6,解得{k 2=-1,b =24,y=-x+24. (2)①∵点C 在直线l 1上,且点C 的纵坐标为a, ∴a=13x,x=3a,∴点C 的坐标为(3a,a).∵CD ∥y 轴,∴点D 的横坐标为3a. ∵点D 在直线l 2上,∴y=-3a+24, ∴D(3a,-3a+24). ②C(3,1)或C(15,5).24.解析 (1)过点P 作PQ ⊥AB 于点Q.∵PA=PB,∠APB=120°,AB=4√3, ∴AQ=12AB=12×4√3=2√3, ∠APQ=12∠APB=12×120°=60°. 在Rt △APQ 中,sin ∠APQ=AQAP , ∴AP=AQsin △APQ =2√3sin60°=√3√32=4.(2)证明:过点P 分别作PS ⊥OM 于点S,PT ⊥ON 于点T, ∴∠OSP=∠OTP=90°,在四边形OSPT 中, ∠SPT=360°-∠OSP-∠SOT-∠OTP=360°-90°-60°-90°=120°,∴∠APB=∠SPT=120°,∴∠APS=∠BPT.又∵∠ASP=∠BTP=90°,AP=BP, ∴△APS ≌△BPT,∴PS=PT, ∴点P 在∠MON 的平分线上. (3)①8+4√3.②4+4√3<t ≤8+4√3.评析本题考查角平分线性质定理、中垂线性质定理、全等三角形的判定和性质、锐角三角函数、三角形中位线定理等知识,综合性强,对学生要求较高.第(3)问的解题关键在于随∠APB 的位置变化寻找特殊图形,确定t 的取值范围. 25.解析 (1)如图①,∵A(-2,0),B(0,2),图①∴OA=OB=2,∴AB 2=OA 2+OB 2=22+22=8,∴AB=2√2,∵OC=AB, ∴OC=2√2,即C(0,2√2).又∵抛物线y=-√2x 2+mx+n 的图象经过A 、C 两点,则可得{-4√2-2m +n =0,n =2√2,解得{m =-√2,n =2√2.∴抛物线的表达式为y=-√2x 2-√2x+2√2. (2)证明:∵OA=OB,∠AOB=90°,∴∠BAO=∠ABO=45°. 又∵∠BEO=∠BAO+∠AOE=45°+∠AOE, ∠BEO=∠OEF+∠BEF=45°+∠BEF,∴∠BEF=∠AOE. (3)当△EOF 为等腰三角形时,分三种情况讨论: ①当OE=OF 时,∠OFE=∠OEF=45°, 在△EOF 中,∠EOF=180°-∠OEF-∠OFE=180°-45°-45°=90°.又∵∠AOB=90°, 则此时点E 与点A 重合,不符合题意,此种情况不成立. ②如图②,当FE=FO 时,∠EOF=∠OEF=45°.图②在△EOF 中, ∠EFO=180°-∠OEF-∠EOF=180°-45°-45°=90°, ∴∠AOF+∠EFO=90°+90°=180°, ∴EF ∥AO,∴∠BEF=∠BAO=45°. 又∵由(2)可知,∠ABO=45°,∴∠BEF=∠ABO,∴BF=EF,∴EF=BF=OF=12OB=12×2=1,∴E(-1,1).③如图③,当EO=EF时,过点E作EH⊥y轴于点H.图③在△AOE和△BEF中,∠EAO=∠FBE,EO=EF,∠AOE=∠BEF,∴△AOE≌△BEF,∴BE=AO=2.∵EH⊥OB,∴∠EHB=90°,∴∠AOB=∠EHB,∴EH∥AO,∴∠BEH=∠BAO=45°.在Rt△BEH中,∵∠BEH=∠ABO=45°,∴EH=BH=BEcos45°=2×√22=√2,∴OH=OB-BH=2-√2,∴E(-√2,2-√2).综上所述,当△EOF为等腰三角形时,所求E点坐标为(-1,1)或(-√2,2-√2).(4)P(0,2√2)或P(-1,2√2).评析本题综合考查二次函数的图象和性质、勾股定理、全等三角形、等腰三角形、锐角三角函数等知识,尤其侧重考查分类讨论的思想.。

2019-2020学年辽宁省沈阳市郊联体高一下学期期中考试数学(文)试题Word版含答案

2019-2020学年辽宁省沈阳市郊联体高一下学期期中考试数学（文）试题第Ⅰ卷（共60分）一、选择题：本大题共12个小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知0cos ,0sin <>αα，则α的终边落在（）A ．第一象限角B ．第二象限角C ．第三象限角D ．第四象限角2．已知向量)1,2(),2,1(-==a ，则=+2（）A ．)5,0(B ．)1,5(-C ．)3,1(-D ．)4,3(-3．已知βα,为锐角，且51cos ,101cos ==βα，则βα+的值是（） A ．π32B ．π43C ．4πD ．3π4．已知b a ,均为单位向量，它们的夹角为060，那么=+|3|b a （）A ．7B ．10C ．13D ．45．函数)(cos sin 42sin )(3R x x x x x f ∈-=的最小正周期为（）A ．2πB ．4π C ．8π D ．π 6．=-+000084tan 36tan 384tan 36tan （）A ．3-B ．3C ．33-D ．33 7．已知3sin 1cos =+αα，则1sin cos -αα的值为（） A ．33 B ．33- C ．3 D ．3- 8．为得到函数)3sin(π+=x y 的图象可将函数x y cos =的图象向右平移)0(>m m 个单位长度，则m 的最小值是（）A ．611πB ．65πC ．3πD ．6π9．已知2)tan(=-απ，则ααααcos sin cos sin +-的值为（） A ．3 B ．2 C ．3- D ．31 10．若点)tan ,cos (sin ααα-P 在第一象限，则在)2,0[π内α的取值范围是（）A ．)45,()43,2(ππππY B ．)45,()2,4(ππππY C ．)23,45()43,2(ππππY D ．),43()43,2(ππππY 11．函数x x y cos 12sin -=的部分图像大致为（）12．已知AB 是圆1)1(:22=+-y x C 的直径，点P 为直线01=+-y x 上任意一点，则PB PA ⋅的最小值是（）A ．12-B ．2C ．0D ．1 二、填空题（每题4分，满分20分，将答案填在答题纸上）13．已知非零向量b a ,满足||||b a b a -=+，则>=<b a ,| .14．函数)2||,0)(sin(πϕϕω<>+=A x A y 的部分图象如图，则函数解析式为 .15．若41)6sin(=+πx ，则=++-+-)32cos()3(sin )65sin(2πππx x x . 16．三角形ABC 是锐角三角形，若角θ终边上一点P 的坐标为)sin cos ,cos (sin B A B A --，则|tan |tan |cos |cos |sin |sin θθθθθθ++的值是 . 三、解答题（本大题共6题，共70分．解答应写出文字说明、证明过程或演算步骤．）17．已知向量)3,2(-=OA ，)4,5(-=OB ，)23,1(+-=λλOC .（1）若ABC ∆为直角三角形，且B ∠为直角，求实数λ的值；（2）若点C B A ,,能构成三角形，求实数λ应满足的条件.18．已知),2(ππα∈，51cos sin =+αα. （1）求ααcos sin -的值；（2）求)3sin(πα+的值.19．如图所示，以向量b OB a OA ==,为边作平行四边形OADB ，又BC BM 31=，CD CN 31=，用b a ,表示MN ON OM ,,.20．已知函数)2||,0,0)(sin(πϕωϕω<>>+=A x A y 的图象过点)0,12(πP ，且图象上与P 点最近的一个最高点坐标为)5,3(π. （1）求函数的解析式；（2）若将此函数的图象向左平移6π个单位长度后，再向下平移2个单位长度得到)(x g 的图象，求)(x g 在]3,6[ππ-∈x 上的值域.21．已知函数)0(21cos sin 3sin )(2>+-=ωωωωx x x x f ，)(x f y =的图象与直线2=y 相交，且两相邻交点之间的距离为π. （1）求)(x f 的解析式，并求)(x f 的单调区间；（2）已知函数2)3cos()(+-+=m x m x g π，若对任意],0[,21π∈x x ，均有)()(21x g x f ≥，求m 的取值范围.22．已知向量)2sin ,2(cos ),23sin ,23(cos x x x x ==且]2,0[π∈x （1）求b a ⋅及||+；（2）若λ2)(-⋅=x f ||+的最小值是23-，求实数λ的值.2019-2020学年辽宁省沈阳市郊联体高一下学期期中考试数学（文）试题参考答案1-6,BDBCAA,7-12,BDABCD二、填空题13 . 错误!未找到引用源。

12～2013学年度下学期期中联考

2012～2013学年度下学期期中联考高一生物试卷本试题卷共8页，二大题38小题，本试卷全卷满分90分。

考试用时90 分钟考生注意：1.答题前，考生务必将自己的准考证号、姓名填写在答题卡上。

2.第I 卷每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号。

第II 卷用黑色墨水签字笔在答题卡上书写作答，在试题卷上作答，答案无效。

第Ⅰ卷选择题（共50分）一、选择题（选出最适合的答案。

1-25题每题1分，26-30题每题2分，31-35题每题3分，共50分）1、“假说—演绎法”是现代科学研究中常用的一种方法，下列属于孟德尔在发现基因分离定律时的“演绎”过程的是（）A ．生物的性状是遗传因子决定的B ．由F 2出现了3∶1的性状分离推测，生物体产生配子时成对遗传因子彼此分离C ．若F 1产生配子时成对遗传因子分离，则测交后代会出现两种性状，比例接近1∶1D ．若F 1产生配子时成对遗传因子分离，则F 2中三种基因型个体比接近1∶2∶1 2、关于孟德尔豌豆杂交试验的叙述中，不正确的是（） A ．孟德尔在豌豆花蕾期进行去雄和授粉，实现亲本的杂交B ．孟德尔提出等位基因控制相对性状的假设，来解释所观察到的现象。

C ．孟德尔做了正交和反交试验，增强了实验的严谨性。

xK b1 .C omD ．孟德尔设计了测交实验来验证自己的假说。

3、孟德尔利用豌豆作为实验材料进行植物杂交实验，成功地发现了两大遗传规律。

下列各项中不属于豌豆作为遗传实验材料的优点的是（）A ．豌豆是严格的自花传粉、闭花受粉植物B ．豌豆在自然状态下一般是纯合的C ．豌豆具有许多易于区分的相对性状D ．杂种豌豆自交后代容易发生性状分离 4、下列各组中不属于相对性状的是（）A.水稻的早熟和晚熟B.豌豆的紫花和红花C.小麦的抗病和不抗病D.绵羊的长毛和细毛 5、下列杂交组合中，后代只有一种基因型的是（）A ．Aabb ×aabbB ．AABb ×aabbC ．AaBb ×AaBbD ．AAbb ×aaBB 6、下图为鼠的毛色（黑色和白色）的遗传图解。

【政治】辽宁省沈阳市城郊市重点联合体2012-2013学年高一下学期期中考试试题

辽宁省沈阳市城郊市重点联合体2012-2013学年高一下学期期中考试试题第Ⅰ卷（选择题，共70分）一、单项选择题：本题有35小题，每小题2分，共70分。

在每题给出的四个选项中，只有一个选项是最符合题意的。

1、我国是人民民主专政的社会主义国家，人民民主专政的本质是人民当家作主，对“人民当家作主”应当这样理解A．人民是国家的主人B．公民是国家的主人C．国家保护全体公民的民主和自由D．人民当家作主是我国的国家性质2、我国人民民主专政的最大特点是A．人民当家作主B．实现了对绝大多数人民主，对极少数人的专政C．民主与专政的统一D．尊重和保障人权3、在我国，既是公民基本的民主权利，又是公民参与国家管理的基础和标志的是A．生存权和劳动权 B. 选举权和被选举权C. 言论、集会等自由权利D. 对国家机关及其工作人员的监督权4．下列说法正确的是A．在我国，公民享有同样的权利B．公民的权利可以放弃，但义务必须履行C．履行义务比享有权利更重要D．任何公民的权利都应该受到保护5．发展社会主义民主政治，建设社会主义政治文明，最根本的就是A. 公民参与政治生活的积极性B. 正确地处理权利和义务的关系C. 坚持党的领导、人民当家作主和依法治国的有机统一D. 不允许任何人有超越宪法和法律的特权6.近年来，我国的一些省市陆续向群众开放政府“红头文件”的查阅，这一举措被人们称为“阳光工程”。

对推行“阳光工程”的认识正确的是A.有利于增强政府工作的透明度B.势必会限制政府权力的行使C.说明政府的群众意识、服务意识已经很强D.消除腐败现象的治本之策7、差额选举与等额选举相比的优点是①可以比较充分地考虑当选者结构的合理②为选民行使选举权提供了选择的余地③能更真实地反映民主的实质和要求④通过竞选有助于选民了解候选人A. ②③B. ②④C. ①④D. ①②8、直接选举、间接选举、等额选举、差额选举是公民参与民主选举的方式。

采取什么样的选举方式，要根据以下条件来确定①社会经济制度②物质生活条件③选民的文化水平④选民的意愿A.①②③B.②③④C.①②④D.①③④9、我国中央和地方政府在预算中逐年扩大了对居民生活补助的支出。

沈阳数学高一下期中经典题(含答案解析)

一、选择题1．(0分)[ID ：12411]已知m ，n 是空间中两条不同的直线，α，β为空间中两个互相垂直的平面，则下列命题正确的是（） A ．若m α⊂，则m β⊥B ．若m α⊂，n β⊂，则m n ⊥C ．若m α⊄，m β⊥，则//m αD ．若m αβ=，n m ⊥，则n α⊥2．(0分)[ID ：12408]已知两点()A 3,4-，()B 3,2，过点()P 1,0的直线l 与线段AB 有公共点，则直线l 的斜率k 的取值范围是( ) A ．()1,1- B ．()(),11,∞∞--⋃+ C ．[]1,1-D ．][(),11,∞∞--⋃+3．(0分)[ID ：12379]已知点(),P x y 是直线()400kx y k ++=>上一动点，,PA PB 是圆22:20C x y y +-=的两条切线，切点分别为,A B ，若四边形PACB 的面积最小值为2，则k 的值为（）A ．3B ．212C ．22D ．24．(0分)[ID ：12376]设α表示平面，a ，b 表示直线，给出下列四个命题：①a α//，a b b α⊥⇒//；②a b //，a b αα⊥⇒⊥；③a α⊥，a b b α⊥⇒⊂；④a α⊥，b a b α⊥⇒//，其中正确命题的序号是（） A ．①② B ．②④ C ．③④ D ．①③5．(0分)[ID ：12358]如图，已知正方体1111ABCD A B C D -中，异面直线1AD 与1A C 所成的角的大小是( )A ．30B ．60C ．90D ．1206．(0分)[ID ：12352]已知直线20ax y a +-+=在两坐标轴上的截距相等，则实数(a =)A ．1B ．1-C ．2-或1D ．2或17．(0分)[ID ：12349]已知三棱锥S ABC -的每个顶点都在球O 的表面上，ABC ∆是边长为43的等边三角形，SA ⊥平面ABC ，且SB 与平面ABC 所成的角为6π，则球O 的表面积为（） A ．20π B ．40π C ．80π D ．160π 8．(0分)[ID ：12396]若a ＞b ＞0，0＜c ＜1，则A ．log a c ＜log b cB ．log c a ＜log c bC ．a c ＜b cD ．c a ＞c b9．(0分)[ID ：12389]在长方体1111ABCD A B C D -中，11111,2AA A D a A B a ===，点P 在线段1AD 上运动，当异面直线CP 与1BA 所成的角最大时，则三棱锥11C PA D -的体积为（）A ．34aB ．33aC ．32aD ．3a 3a10．(0分)[ID ：12386]已知AB 是圆22620x y x y +-+=内过点(2,1)E 的最短弦，则||AB 等于（）A ．3B ．22C ．23D ．2511．(0分)[ID ：12384]若圆22240x y x y +--=的圆心到直线0x y a -+=的距离为22，则a 的值为( ) A ．-2或2B ．12或32C ．2或0D ．-2或012．(0分)[ID ：12419]陀螺是汉族民间最早的娱乐工具之一，也称陀罗，北方叫做“打老牛”.陀螺的主体形状一般是由上面部分的圆柱和下面部分的圆锥组成.如图画出的是某陀螺模型的三视图，已知网格纸中小正方形的边长为1，则该陀螺模型的体积为（）A ．1073πB ．32453π+ C ．16323π+ D ．32333π+ 13．(0分)[ID ：12415]已知ABC 的三个顶点在以O 为球心的球面上，且2AB =，4AC =，25BC =,三棱锥O ABC -的体积为43，则球O 的表面积为（）A ．22πB ．743πC ．24πD ．36π14．(0分)[ID ：12402]如图，在正方体1111ABCD A B C D -中，M ，N 分别是1BC ，1CD 的中点，则下列说法错误．．的是( )A ．MN 与1CC 垂直B ．MN 与AC 垂直 C ．MN 与BD 平行D ．MN 与11A B 平行15．(0分)[ID ：12370]如图1，ABC ∆是以B 为直角顶点的等腰直角三角形，T 为线段AC 的中点，G 是BC 的中点，ABE ∆与BCF ∆分别是以AB 、BC 为底边的等边三角形，现将ABE ∆与BCF ∆分别沿AB 与BC 向上折起（如图2），则在翻折的过程中下列结论可能正确的个数为（）图1 图2（1）直线AE ⊥直线BC ；（2）直线FC ⊥直线AE ；（3）平面//EAB 平面FGT ；（4）直线//BC 直线AE . A ．1个B ．2个C ．3个D ．4个二、填空题16．(0分)[ID ：12463]已知圆22:20(0)M x y ay a +-=>截直线0x y +=所得线段的长度是2M 与圆22:(1)(1)1N x y -+-=的位置关系是_________．17．(0分)[ID ：12462]若一个圆柱的侧面展开图是边长为2的正方形，则此圆柱的体积为 .18．(0分)[ID ：12523]已知在直角梯形ABCD 中，AB AD ⊥，CD AD ⊥，224AB AD CD ===，将直角梯形ABCD 沿AC 折叠，使平面BAC ⊥平面DAC ，则三棱锥D ABC -外接球的体积为__________．19．(0分)[ID ：12486]以(3,2)a =-方向向量的直线平分圆2220x y y =++，直线l 的方程为________.20．(0分)[ID ：12467]已知,m n 为直线，,αβ为空间的两个平面，给出下列命题：①,//m n m n αα⊥⎧⇒⎨⊥⎩；②,////m n m n αβαβ⊂⎧⎪⊂⇒⎨⎪⎩；③,//m m ααββ⊥⎧⇒⎨⊥⎩；④,//m m n n ββ⊥⎧⇒⎨⊥⎩．其中的正确命题为_________________． 21．(0分)[ID ：12506]在各棱长均为1的正四棱锥P ABCD -中，M 为线段PB 上的一动点，则当AM MC +最小时，cos AMC ∠=_________ 22．(0分)[ID ：12437]在正方体1111ABCD A B C D -中， ①BD平面11CB D ②直线AD 与1CB 所成角的大小为60︒③1AA BD ⊥ ④平面11A BC ∥平面1ACD 请把所有正确命题的序号填在横线上________．23．(0分)[ID ：12456]已知四面体ABCD 的外接球球心O 在棱CD 上，AB=3，CD=2，则A 、B 两点在四面体ABCD 的外接球上的球面距离是________.24．(0分)[ID ：12468]如图：点P 在正方体1111ABCD A B C D -的面对角线1BC 上运动，则下列四个命题：①三棱锥1A D PC -的体积不变； ②1A P ∥面1ACD ；③1DP BC ；④面1PDB 面1ACD ．其中正确的命题的序号是__________.25．(0分)[ID ：12438]已知PA 垂直于平行四边形ABCD 所在平面，若PC BD ⊥，则平行四边形ABCD 一定是___________.三、解答题26．(0分)[ID ：12595]如图，在三棱锥S ABC -中，SAC ∆为等边三角形，4AC =，43BC =，BC AC ⊥，3cos 4SCB ∠=-，D 为AB 的中点．（1）求证：AC SD ⊥；（2）求直线SD 与平面SAC 所成角的大小．27．(0分)[ID ：12565]已知点()1,0P ，()4,0Q ，一动点M 满足2MQ MP =. （1）求点M 的轨迹方程；（2）过点()2,3A 的直线l 与（1）中的曲线有且仅有一个公共点，求直线l 的方程. 28．(0分)[ID ：12553]如图，已知三棱锥A BPC -中，AP PC ⊥，AC BC ⊥，M 为AB 的中点，D 为PB 的中点，且PMB △为正三角形.（1）求证：//DM 平面APC ；（2）求证：BC ⊥平面APC ；（3）若4BC =，10AB =，求三棱锥D BCM -的体积.29．(0分)[ID ：12615]若圆M 的方程为22(2)(5)10x y -+-=，△ABC 中，已知(1,1)A ，(4,2)B ，点C 为圆M 上的动点．（1）求AC 中点D 的轨迹方程；（2）求△ABC 面积的最小值．30．(0分)[ID ：12532]如图，在直三棱柱ABC -A 1B 1C 1中，∠ACB ＝90°，∠BAC ＝30°，BC ＝1，A 1A 6，M 是CC 1的中点．(1)求证：A1B⊥AM；(2)求二面角B--AM--C的平面角的大小．.【参考答案】2016-2017年度第*次考试试卷参考答案**科目模拟测试一、选择题1．C2．D3．D4．B5．C6．D7．C8．B9．B10．D11．C12．D13．C14．D15．C二、填空题16．相交【解析】【分析】根据直线与圆相交的弦长公式求出的值结合两圆的位置关系进行判断即可【详解】解：圆的标准方程为则圆心为半径圆心到直线的距离圆截直线所得线段的长度是即则圆心为半径圆的圆心为半径则即两个17．2π【解析】试题分析：设圆柱的底面半径为r高为h底面积为S体积为V则有2πr=2⇒r=1π故底面面积S=πr2=π×(1π)2=1π故圆柱的体积V=Sh=1π×2=2π考点：圆柱的体积18．【解析】结合题意画出折叠后得到的三棱锥如图所示由条件可得在底面中取AB的中点OAC的中点E连OCOE则∵∴∵平面平面∴平面∴又∴∴∴点O为三棱锥外接球的球心球半径为2∴答案：点睛：（1）本题是一道关19．【解析】【分析】由为方向向量设直线的方程为：若要求直线平分圆则圆心在要求的直线上故得解【详解】根据题意要求的直线的方向向量为：设直线的方程为：圆即圆心为若要求直线平分圆则圆心在要求的直线上则有：则直20．③④【解析】关于①也会有的结论因此不正确；关于②也会有异面的可能的结论因此不正确；容易验证关于③④都是正确的故应填答案③④21．【解析】【分析】将侧面和侧面平展在一个平面上连即可求出满足最小时点的位置以及长解即可求出结论【详解】将侧面和侧面平展在一个平面上连与交点即为满足最小正四棱锥各棱长均为在平展的平面中四边形为菱形且在正22．①③④【解析】【分析】利用线面平行的判定定理判断①；由异面直线所成角判断②；由线面垂直的性质判断③；由面面平行的判定定理判断④【详解】对于①如下图所示由于则四边形为平行四边形则面面所以平面故①正确；23．【解析】【分析】根据球心到四个顶点距离相等可推断出O为CD的中点且OA＝OB＝OC＝OD进而在△A0B中利用余弦定理求得cos∠AOB的值则∠AOB可求进而根据弧长的计算方法求得答案【详解】解：球心24．①②④【解析】对于①因为从而平面故上任意一点到平面的距离均相等以为顶点平面为底面则三棱锥的体积不变正确；对于②连接容易证明且相等由于①知：平面平面所以可得面②正确；对于③由于平面若则平面则为中点与动25．菱形【解析】【分析】【详解】根据题意画出图形如图∵PA垂直平行四边形ABCD所在平面∴PA⊥BD又∵PC⊥BDPA⊂平面PACPC⊂平面PACPA∩PC=P∴BD⊥平面PAC又∵AC⊂平面PAC∴A三、解答题 26． 27． 28． 29． 30．2016-2017年度第*次考试试卷参考解析【参考解析】**科目模拟测试一、选择题 1．C 解析：C 【解析】由题设，,αβ⊥ 则A. 若m α⊂，则m β⊥，错误；B. 若m α⊂，n β⊂，则m n ⊥ 错误；D. 若m αβ⋂=，n m ⊥，当n β⊄ 时不能得到n α⊥，错误. 故选C.2．D解析：D 【解析】分析：根据两点间的斜率公式，利用数形结合即可求出直线斜率的取值范围．详解：∵点A （﹣3，4），B （3，2），过点P （1，0）的直线L 与线段AB 有公共点， ∴直线l 的斜率k≥k PB 或k≤k PA ，∵PA 的斜率为4031--- =﹣1，PB 的斜率为2031--=1， ∴直线l 的斜率k≥1或k≤﹣1，故选：D ．点睛：本题主要考查直线的斜率的求法，利用数形结合是解决本题的关键，比较基础．直线的倾斜角和斜率的变化是紧密相联的，tana=k,一般在分析角的变化引起斜率变化的过程时，是要画出正切的函数图像，再分析.3．D解析：D 【解析】【分析】当且仅当PC 垂直于()400kx y k ++=>时，四边形PACB 的面积最小，求出PC 后可得最小面积，从而可求k 的值. 【详解】圆C 方程为()2211x y +-=，圆心()0,1C ，半径为1．因为PA ，PB 为切线，221PC PA ∴=+且1=2122PACB S PA PA ⨯⨯⨯==四边形．∴当PA 最小时，PACB S 四边形最小，此时PC 最小且PC 垂直于()400kx y k ++=>．又min 21PC k =+，222221+1k ⎛⎫∴=+，2k ∴=，故选D. 【点睛】圆中的最值问题，往往可以转化圆心到几何对象的距离的最值来处理，这类问题属于中档题.4．B解析：B 【解析】【分析】【详解】①a ∥α，a ⊥b ⇒b 与α平行，相交或b ⊂α，故①错误； ②若a ∥b ，a ⊥α，由直线与平面垂直和判定定理得b ⊥α，故②正确； ③a ⊥α，a ⊥b ⇒b 与α平行，相交或b ⊂α，故③错误； ④若a ⊥α，b ⊥α，则由直线与平面垂直的性质得a ∥b ，故④正确．故选B ．5．C解析：C 【解析】【分析】在正方体1111ABCD A B C D -中，利用线面垂直的判定定理，证得1AD ⊥平面1A DC ，由此能求出结果．【详解】如图所示，在正方体1111ABCD A B C D -中，连结1A D ，则1AD DC ⊥，11A D AD ⊥，由线面垂直的判定定理得1AD ⊥平面1A DC ，所以11AD AC ⊥, 所以异面直线1AD 与1A C 所成的角的大小是90．故选C ．【点睛】本题主要考查了直线与平面垂直的判定与证明，以及异面直线所成角的求解，其中解答中牢记异面直线所成的求解方法和转化思想的应用是解答的关键，平时注意空间思维能力的培养，着重考查了推理与论证能力，属于基础题．6．D解析：D 【解析】【分析】根据题意讨论直线它在两坐标轴上的截距为0和在两坐标轴上的截距不为0时，求出对应a 的值，即可得到答案．【详解】由题意，当2a 0-+=，即a 2=时，直线ax y 2a 0+-+=化为2x y 0+=，此时直线在两坐标轴上的截距都为0，满足题意；当2a 0-+≠，即a 2≠时，直线ax y 2a 0+-+=化为122x ya a a+=--，由直线在两坐标轴上的截距相等，可得2a 2a a-=-，解得a 1=；综上所述，实数a 2=或a 1=．故选：D ．【点睛】本题主要考查了直线方程的应用，以及直线在坐标轴上的截距的应用，其中解答中熟记直线在坐标轴上的截距定义，合理分类讨论求解是解答的关键，着重考查了运算与求解能力，属于基础题.7．C解析：C【解析】【分析】根据线面夹角得到4SA =，计算ABC ∆的外接圆半径为42sin a r A==，2222SA R r ⎛⎫=+ ⎪⎝⎭，解得答案. 【详解】 SA ⊥平面ABC ，则SB 与平面ABC 所成的角为6SBA π∠=，故4SA =.ABC ∆的外接圆半径为42sin a r A ==，设球O 的半径为R ，则2222SA R r ⎛⎫=+ ⎪⎝⎭，解得R =O 的表面积为2480R ππ=. 故选：C .【点睛】本题考查了三棱锥的外接球问题，意在考查学生的计算能力和空间想象能力.8．B解析：B【解析】试题分析：对于选项A ，a b 1gc 1gc log c ,log c lg a lg b==，01c <<，10gc ∴<，而0a b >>，所以lg lg a b >，但不能确定lg lg a b 、的正负，所以它们的大小不能确定;对于选项B ，c lg lg log ,log lg lg c a b a b c c ==,lg lg a b >，两边同乘以一个负数1lg c改变不等号方向，所以选项B 正确;对于选项C ，利用c y x =在第一象限内是增函数即可得到c c a b >，所以C 错误;对于选项D ，利用xy c =在R 上为减函数易得a b c c <，所以D 错误.所以本题选B.【考点】指数函数与对数函数的性质【名师点睛】比较幂或对数值的大小,若幂的底数相同或对数的底数相同,通常利用指数函数或对数函数的单调性进行比较；若底数不同,可考虑利用中间量进行比较.9．B解析：B【解析】【分析】当P 与A 重合时，异面直线CP 与BA 1所成的角最大，由此能求出当异面直线CP 与BA 1所成的角最大时，三棱锥C ﹣PA 1D 1的体积．【详解】如图，当P 与A 重合时，异面直线CP 与BA 1所成的角最大，∴当异面直线CP 与BA 1所成的角最大时，三棱锥C ﹣PA 1D 1的体积：11C PA D V -=11C AA D V -=1113AA D S AB ⨯⨯=1111132AA A D AB ⎛⎫⨯⨯⨯⨯ ⎪⎝⎭=11232a a a ⎛⎫⨯⨯⨯⨯ ⎪⎝⎭=33a ．故选:B ．【点睛】求锥体的体积要充分利用多面体的截面和旋转体的轴截面，将空间问题转化为平面问题求解，注意求体积的一些特殊方法——分割法、补形法、等体积法. ①割补法：求一些不规则几何体的体积时，常用割补法转化成已知体积公式的几何体进行解决．②等积法：等积法包括等面积法和等体积法．等积法的前提是几何图形(或几何体)的面积(或体积)通过已知条件可以得到，利用等积法可以用来求解几何图形的高或几何体的高，特别是在求三角形的高和三棱锥的高时，这一方法回避了通过具体作图得到三角形(或三棱锥)的高，而通过直接计算得到高的数值．10．D解析：D【解析】【分析】求出圆的标准方程，确定最短弦的条件，利用弦长公式进行求解即可．圆的标准方程为（x ﹣3）2+（y +1）2＝10，则圆心坐标为C （3，﹣1），半径为过E 的最短弦满足E 恰好为C 在弦上垂足，则CE ==，则|AB |==，故选D ．【点睛】本题主要考查圆的标准方程的求解，以及直线和圆相交的弦长问题,属于中档题．11．C解析：C【解析】【分析】把圆的方程化为标准方程,找出圆心坐标,根据点到直线的距离公式列出关于a 的方程,求出方程的解得到a 的值即可.【详解】把圆的方程化为标准式为:22(1)(2)5x y -+-=,所以圆心坐标为(1,2).则圆心到直线0x y a -+=的距离2d ==, 即11a -=,化简得11a -=或11a -=-,解得:2a =或0a =.所以a 的值为0或2.故选C.【点睛】本题考查学生会将圆的一般式方程化为标准式方程,灵活运用点到直线的距离公式化简求值.12．D解析：D【解析】【分析】由三视图可知，该陀螺模型是由一个正四棱锥、一个圆柱、一个圆锥组合而成.根据柱体、锥体的体积计算公式即得该陀螺模型的体积.【详解】由三视图可知，该陀螺模型是由一个正四棱锥、一个圆柱、一个圆锥组合而成. 所以该陀螺模型的体积222113242333233333V πππ=⨯⨯+⨯⨯+⨯⨯⨯=+. 故选：D .【点睛】本题考查三视图，考查学生的空间想象能力，属于基础题. 13．C【解析】【分析】由已知可得三角形ABC 为直角三角形，斜边BC 的中点O '就是ABC 的外接圆圆心，利用三棱锥O ABC -的体积，求出O 到底面的距离，可求出球的半径，然后代入球的表面积公式求解．【详解】在ABC 中，∵2AB =，4AC =，25BC =得AB AC ⊥，则斜边BC 的中点O '就是ABC 的外接圆的圆心，∵三棱锥O ABC -的体积为43， 11424323OO '⨯⨯⨯⨯=，解得1OO '=，221(5)6R =+=，球O 的表面积为2424R ππ=．故选C ．【点睛】本题考查球的表面积的求法，考查锥体体积公式的应用，考查空间想象能力和计算能力，属于基础题.14．D解析：D【解析】【分析】先利用三角形中位线定理证明//MN BD ，再利用线面垂直的判定定理定义证明MN 与1CC 垂直，由异面直线所成的角的定义证明MN 与AC 垂直，即可得出结论.【详解】如图：连接1C D ，BD ，在三角形1C DB 中，//MN BD ，故C 正确．1CC ⊥平面ABCD ，1CC BD ∴⊥，MN ∴与1CC 垂直，故A 正确；AC BD ，//MN BD ，MN ∴与AC 垂直，B 正确；∵//MN BD ，MN ∴与11A B 不可能平行，D 错误故选：D ．【点睛】本题主要考查了正方体中的线面关系，线线平行与垂直的证明，异面直线所成的角及其位置关系，熟记正方体的性质是解决本题的关键.15．C解析：C【解析】【分析】（1）翻折时使得平面ABE ⊥平面ABC ，由面面垂直的性质定理得出BC ⊥平面ABE ，从而使得（1）有可能；（2）翻折时使得点E 、F 两点重合，利用勾股定理可证得此时AE CE ⊥，即AE FC ⊥；（3）翻折时使得平面ABE 和平面BCF 同时与平面ABC 垂直，利用面面垂直的性质定理、直线与平面平行的判定定理以及面面平行的判定定理可证明出平面//EAB 平面FGT ；（4）利用反证法，可推出//BC AE 不成立.【详解】（1）翻折时，若平面ABE ⊥平面ABC ，由于ABC ∆是以B 为直角顶点的等腰直角三角形，则BC AB ⊥，又平面ABE 平面ABC AB =，BC ⊂平面ABC ，BC ∴⊥平面ABE ，AE ⊂平面ABC ，此时AE BC ⊥；（2）设AB BC a ==，则2AC a =，且有AE CF a ==，翻折时，若点E 、F 重合，则AE CE a ==，222AE CE AC ∴+=，此时，AE CE ⊥，即AE FC ⊥；（3）如下图所示：翻折时，若平面ABE 和平面BCF 同时与平面ABC 垂直，取AB 的中点D ，连接DE 、FG 、GT 、FT .ABE ∆是等边三角形，且D 为AB 的中点，DE AB ⊥∴.平面ABE ⊥平面ABC ，平面ABE 平面ABC AB =，DE ⊂平面ABE .DE ∴⊥平面ABC ，同理可证FG ⊥平面ABC ，//DE FG ∴，DE ⊄平面FGT ，FG ⊂平面FGT ，//DE ∴平面FGT . G 、T 分别为BC 、AC 的中点，//AB GT ∴，AB ⊄平面FGT ，GT ⊂平面FGT ，//AB ∴平面FGT .DE AB D =，∴平面//EAB 平面FGT ；（4）假设AE 与BC 可能平行，BC AB ⊥，则AE AB ⊥，事实上60BAE ∠=，即AE 与AB 不垂直，假设不成立，因此，AE 与BC 不可能平行. 因此，可能正确命题的个数为3.故选：C.【点睛】本题考查的是线面位置关系的判定，判断时要熟悉线面、面面平行与垂直的判定、性质定理，考查推理能力，属于中等题.二、填空题16．相交【解析】【分析】根据直线与圆相交的弦长公式求出的值结合两圆的位置关系进行判断即可【详解】解：圆的标准方程为则圆心为半径圆心到直线的距离圆截直线所得线段的长度是即则圆心为半径圆的圆心为半径则即两个解析：相交【解析】【分析】根据直线与圆相交的弦长公式，求出a 的值，结合两圆的位置关系进行判断即可．【详解】解：圆的标准方程为222:()(0)M x y a a a +-=>，则圆心为(0,)a ，半径R a =，圆心到直线0x y +=的距离2d =，圆22:20(0)M x y ay a +-=>截直线0x y +=所得线段的长度是∴即24a =，2a =，则圆心为(0,2)M ，半径2R =，圆22:(1)(1)1N x y -+-=的圆心为(1,1)N ，半径1r =，则MN =3R r +=，1R r -=，R r MN R r ∴-<<+，即两个圆相交．故答案为：相交．【点睛】本题主要考查直线和圆相交的应用，以及两圆位置关系的判断，根据相交弦长公式求出a 的值是解决本题的关键．17．2π【解析】试题分析：设圆柱的底面半径为r 高为h 底面积为S 体积为V 则有2πr=2⇒r=1π故底面面积S=πr2=π×(1π)2=1π故圆柱的体积V=Sh=1π×2=2π考点：圆柱的体积解析：2π【解析】试题分析：设圆柱的底面半径为r ，高为h ，底面积为S ，体积为V ，则有2πr =2⇒r =1π，故底面面积S =πr 2=π×(1π)2=1π，故圆柱的体积V =Sh =1π×2=2π. 考点：圆柱的体积 18．【解析】结合题意画出折叠后得到的三棱锥如图所示由条件可得在底面中取AB 的中点OAC 的中点E 连OCOE 则∵∴∵平面平面∴平面∴又∴∴∴点O 为三棱锥外接球的球心球半径为2∴答案：点睛：（1）本题是一道关解析：323π 【解析】结合题意画出折叠后得到的三棱锥D ABC -如图所示，由条件可得在底面ACB ∆中，90,ACB AC BC ∠=︒==AB 的中点O ，AC 的中点E ，连OC,OE 。

辽宁省沈阳二中2012-2013学年高一下学期期中考试数学Word版含答案

沈阳二中2012——2013学年度下学期期中考试高一（15届）数学试题说明：1.测试时间：120分钟总分：150分2.客观题涂在答题纸上，主观题答在答题纸的相应位置上第Ⅰ卷（60分）一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知为第三象限角，则所在的象限是（）A．第一或第二象限 B.第二或第三象限C.第一或第三象限D.第二或第四象限2. 一个扇形的圆心角为，半径为，则此扇形的面积为（）A. B. C. D.3. 已知，则=（）A. B. C. D.4.的值为（）A. B. C.3 D.5. 已知是夹角为60°的两个单位向量，则与的夹角的余弦值是（）A. B. C. D.6. 使函数为奇函数，且在上是减函数的的一个值是（）A. B. C. D.7. 已知函数的最小正周期为，为了得到函数的图象，只要将的图象（） A ．向左平移个单位长度 B ．向右平移个单位长度 C ．向左平移个单位长度 D ．向右平移个单位长度8. 函数的部分图象如图所示，点、是最高点，点是最低点．若△是直角三角形，则的值为（）A ．B ．C ．D ．9. 在平行四边形ABCD 中，E 、F 分别是BC 、CDAH →＝（）A. B. C. D.10.在锐角中，设则大小关系为（）A. B. C . D.11.已知为平面上不共线的三点，是△ABC 的垂心，动点满足，则点一定为△ABC 的（） A.边中线的中点 B.边中线的三等分点（非重心） C. 重心 D.边的中点12.平面向量的集合到的映射，其中为常向量．若映射满足对任意的恒成立，则的坐标可能是（）A.(，)B.(，)C.(，)D. (，)（第8题）第Ⅱ卷（90分）二、填空题: 本大题共4小题，每小题5分，共20分.13. 若角的终边经过点，则的值为______________．14. 函数的定义域为．15. 已知且，则．16. 如图，在平面斜坐标系xOy中，，平面上任意一点P关于斜坐标系的斜坐标这样定义：若（其中，分别是x轴，y轴正方向的单位向量），则P点的斜坐标为(x，y)，向量的斜坐标为(x，y)．给出以下结论：①若，P(2,－1)，则；②若，，则；③若(x，y)，，则；④若，，则；⑤若，以O为圆心，1为半径的圆的斜坐标方程为．其中所有正确的结论的序号是______________．三、解答题：本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.17. （本小题满分10分）设（Ⅰ）若，求实数的值；（Ⅱ）求在方向上的正射影的数量．18. （本小题满分12分）已知向量与互相垂直，其中.（Ⅰ）求和的值；（Ⅱ）若，，求的值．19. （本小题满分12分）在中，.（Ⅰ）求的取值范围；（Ⅱ）若为锐角，求的最大值并求出此时角的大小．20. （本小题满分12分）已知函数，且函数的图象相邻两条对称轴之间的距离为.（Ⅰ）求的对称中心；（Ⅱ）当时，求的单调增区间．21. （本小题满分12分）已知向量（Ⅰ）用含x的式子表示及；（Ⅱ）求函数的值域；（Ⅲ）设，若关于x的方程有两个不同的实数解，求实数的取值范围．22. （本小题满分12分）如图，在平面直角坐标系中，以轴为始边，两个锐角,的终边分别与单位圆相交于A,B 两点．（Ⅰ）若，，求的值；（Ⅱ）若角的终边与单位圆交于点，设角的正弦线分别为，试问：以作为三边的长能否构成一个三角形？若能，请加以证明；若不能，请说明理由.沈阳二中2012——2013学年度下学期期中考试高一（15届）数学试题参考答案一、选择题DACBD BABDC BB二、填空题13.14.15. 0 16. ①②③⑤三、解答题17.解：（Ⅰ）故所以……5分（Ⅱ）……10分 18.解：（Ⅰ） (1)∵，∴＝sin θ－2cos θ＝0，即sin θ＝2cos θ，又∵sin 2θ＋cos 2θ＝1，∴4cos 2θ＋cos 2θ＝1，即cos 2θ＝15，∴sin 2θ＝45，又θ∈⎝⎛⎭⎫0，π2，∴sin θ＝255，cos θ＝55. ……6分（Ⅱ）∵5cos(θ－φ)＝5(cos θcos φ＋sin θsin φ)＝5cos φ＋25sin φ＝35cos φ， ∴cos φ＝sin φ，∴cos 2φ＝sin 2φ＝1－cos 2φ，即cos 2φ＝12.∵0<φ<π2，∴cos φ＝22.……12分19解：（Ⅰ）且所以……6分（Ⅱ）令由得……8分所以，则，于是，所以当时，，此时.……12分 20.解：（Ⅰ）. 由题意，，即，所以，即. 从而，……4分令，则所以对称中心为……6分（Ⅱ）由可得：时为单调递增函数……8分 ∴单调递增区间为，……12分 21.解：（Ⅰ）……2分 (4)分（Ⅱ）又 ∴ ……8分（Ⅲ）由得：令 ∴ ……10分 ∴ ……12分22.解：（Ⅰ）∵0<α<π2，tan α＝17，∴cos α＝7210，sin α＝210.又∵0<β<π2，sin β＝1010，∴0<2β<π，cos2β＝1－2sin 2β＝45，sin2β＝1－cos 22β＝35.于是cos(α＋2β)＝cos αcos2β－sin αsin2β＝7210×45－210×35＝22.由已知条件知0<α＋2β<32π，∴α＋2β＝π4.……6分另解：由0<2β<π，cos2β＝1－2sin 2β＝45，可得出，，则，所以，又，故α＋2β＝π4……6分（Ⅱ）解：以作为三边的长能构成一个三角形，证明如下：∵，∴ ∴，，∵，所以，，于是有：①……8分又∵，∴，于是有：()()()()sin sin sin cos cos sin sin sin ααββαββαββαββ=+-=+-+<++⎡⎤⎣⎦②同理：③由①②③可知，以作为三边的长能构成一个三角形.……12分。

2023-2024学年辽宁省沈阳市五联考高一下学期期中考试数学质量检测模拟试题(含解析)

2023-2024学年辽宁省沈阳市五校联考高一下册期中考试数学模拟试题一、单选题1．已知3sin 375︒=，则sin 593︒=（）A ．35B ．35-C ．45D ．45-【正确答案】D【分析】利用三角函数诱导公式和同角三角函数基本关系即可求得sin 593︒的值.【详解】()sin 593sin 360233sin 233︒︒=+︒=︒()()sin 18053sin 53sin 9037cos37︒+︒︒=︒-︒︒==--=-又3sin 375︒=，则4cos 375︒=，则4sin 5935=-︒故选：D2．圆的一条弧的长度等于圆内接正六边形的边长，则这条弧所对的圆心角的弧度数为（）A ．1B ．π6C ．π3D 【正确答案】A【分析】首先求弧长，再根据圆心角公式，即可求解.【详解】设圆的半径为r ，由于圆内接正六边形每条边长对应的圆心角为60︒，则圆内接正六边形的边长为r ，所以这条弧长所对的圆心角为1r r=.故选：A3．已知tan 2θ=，则22sin sin cos 2cos θθθθ+-=A ．43-B ．54C ．34-D ．45【正确答案】D【详解】试题分析：22222222sin sin cos 2cos tan tan 24sin sin cos 2cos sin cos tan 15θθθθθθθθθθθθθ+-===++＋－＋－同角间三角函数关系4．已知π1sin 34α⎛⎫-= ⎪⎝⎭，则πcos 23α⎛⎫+= ⎪⎝⎭（）A ．58B ．78-C ．58-D ．78【正确答案】B利用诱导公式以及二倍角的余弦公式即可求解.【详解】π1sin sin cos 32664πππααα⎛⎫⎛⎫⎛⎫-=--=+= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，所以2π17cos 22cos 113688παα⎛⎫⎛⎫+=+-=-=- ⎪ ⎪⎝⎭⎝⎭，故选：B5．在ABC 中2,6AB AC ==，若O 为外接圆的圆心，则AO BC ⋅的值为（）A ．-16B ．-8C ．8D ．16【正确答案】D【分析】根据给定条件，利用向量数量积的运算律，结合圆的性质计算作答.【详解】取AB ，AC 的中点D ，E ，连接,OD OE ，如图，当圆心O 与点E 不重合时，则OD ⊥AB ，OE ⊥AC ，1,3AD AE ==，则()AO BC AO AC AB AO AC AO AB ⋅=⋅-=⋅-⋅＝()2()2AE EO AE AD DO AD +⋅-+⋅ 222222AE EO AE AD DO AD =+⋅--⋅ 2223021016=⨯+-⨯-=，当圆心O 与点E 重合时，AB BC ⊥，2222111()()(62)16222AO BC AC AC AB AC AB ⋅=⋅-=-=-= ，所以16AO BC ⋅=.故选：D.6．已知α，()0,βπ∈，cos 10α=-，若()1sin sin 22αββ=+，则αβ+=（）A ．54πB ．23πC ．76πD ．74π【正确答案】A【分析】由()1sin sin 22αββ=+可得1sin[sin[()]2()]αβααβα++=+-，然后利用两角和与差的正弦公式展开化简可得()cos sin ααβ++()3sin co 0s ααβ+=，由cos 10α=-可得10sin α=，代入化简得()()sin cos αβαβ+=+，由题意可知cos()0αβ+≠，所以()tan 1αβ+=，再结合,αβ的范围可求得结果【详解】由题意可知，()1sin sin 22αββ=+，可化为1sin[sin[()]2()]αβααβα++=+-，展开得()()()()11sin cos cos sin cos sin sin cos 22ααβααβααβααβ+++=++-，则()cos sin ααβ++()3sin co 0s ααβ+=，因为α，()0,βπ∈，且cos 10α=-，所以sin 10α=，则()()301010αβαβ-++⨯+=，且,2παπ⎛⎫∈ ⎪⎝⎭，所以()()sin cos αβαβ+=+，当cos()0αβ+=时不满足题意，所()tan 1αβ+=，因为,2παπ⎛⎫∈ ⎪⎝⎭，()0,βπ∈，所以,22παβπ⎛⎫+∈ ⎪⎝⎭，则54αβπ+=，故选：A.7．已知函数()1tan 26f x x π⎛⎫=- ⎪⎝⎭，则下列说法正确的是（）A ．()f x 的最小正周期是2πB ．()f x 的值域是{}0y y y ∈≠R 且C ．直线53x π=是函数()f x 图像的一条对称轴D ．()f x 的递减区间是22,233k k ππππ⎛⎤-+ ⎥⎝⎦，k ∈Z 【正确答案】D根据函数()f x 的解析式，得到其最小正周期，值域，对称轴和递减区间，然后对四个选项分别进行判断，得到答案.【详解】函数()1tan 26f x x π⎛⎫=- ⎪⎝⎭所以函数()f x 的最小正周期212T ππ==，所以选项A 错误；由()f x 解析式可知()0f x ≥，所以()f x 的值域为[)0,∞+，所以选项B 错误；当53x π=时，122632k x πππ-=≠，k ∈Z ，53x π∴=不是函数()f x 图像的对称轴，所以选项C 错误.令1226k x k ππππ-<-≤，k ∈Z ，可得22233k x k ππππ-<≤+，k ∈Z ，()f x \的递减区间是22,233k k ππππ⎛⎤-+ ⎥⎝⎦，k ∈Z ，所以选项D 正确.故选：D.本题考查正切型函数的周期、值域、对称性和单调区间，属于简单题.8．中国传统扇文化有着极其深厚的底蕴．一般情况下，折扇可看作是从一个圆面中剪下的扇形制作而成，如图，设扇形的面积为1S ，其圆心角为θ，圆面中剩余部分的面积为2S ，当1S 与2S 的比时，扇面为“美观扇面”，则下列结论错误的是（）2.236≈）A ．122S S θπθ=-B ．若1212S S =，扇形的半径3R =，则13πS =C ．若扇面为“美观扇面”，则138θ≈︒D ．若扇面为“美观扇面”，扇形的半径20R =，则此时的扇形面积为(2003【正确答案】D 【分析】求得12S S 判断选项A ；求得满足条件的1S 的值判断选项B ；求得满足条件的θ的值判断选项C ；求得满足条件的扇形面积的值判断选项D.【详解】扇形的面积为1S ，其圆心角为θ，半径为R ，圆面中剩余部分的面积为2S ，选项A.()212212=12π2π2S R S R θθθθ=--故A 正确；选项B ：由1212S S =，可得12π2θθ=-，解得2π3θ=，又扇形的半径3R =，则2112π33π23S =⨯=.故B 正确；选项C ：若扇面为“美观扇面”，则1212π2S S θθ==-，解得(()3π3 2.236180138θ⎡⎤=≈-⨯≈⎣⎦.故C 正确；选项D ：若扇面为“美观扇面”，则(3πθ=，又扇形的半径20R =，则此时的扇形面积为((213π202003π2⨯⨯=-.故D 错误.故选：D 二、多选题9．下列各式的值等于2的有（）A ．2sin 67.5cos67.5︒︒B ．22cos 67.51︒-C ．212sin 22.5︒-D ．22tan 22.51tan 22.5︒︒-【正确答案】AC利用二倍角的正弦公式分析A ；利用二倍角的余弦公式的变形式分析BC ；利用二倍角的正切公式分析D.【详解】因为2sin 67.5cos 67.sin13525︒︒=︒=，故A的值等于2；因为22cos 67.51cos1352︒-=︒=-，故B的值不等于2；因为212sin 22.5cos 452︒=︒=-，故C的值等于2；因为22tan 22.5tan 4511tan 22.5︒︒=︒=-，故D的值不等于2，故选：AC.10．已知((),cos ,sin a b θθ==，则下列命题正确的有（）A ．若a b ⊥，则π3θ=B ．a b ⋅的最大值为2C ．存在θ，使||||||a b a b +=+D ．a b - 的最大值为3【正确答案】BCD【分析】根据向量的数量积公式即可求解AB ，当,a b 同向时，则有||||||a b a b +=+，将a b - 转化为三角函数的最值问题即可求解.【详解】依题意，对于A ：0a b a b ⊥⇒⋅=，即(()πcos ,sin sin cos 2sin 06a b θθθθ=θ⎛⎫⋅=⋅++= ⎪⎝⎭ ，所以()()πππ,Z πZ 66k k k k θθ+=∈⇒=-∈，故A 错误；对于B ：由A 知π2sin 6a b θ⎛⎫⋅=+ ⎪⎝⎭ ，所以当()()πππ2π,Z 2πZ 623k k k k θθ+=+∈⇒=+∈时，有最大值2，故B 正确；对于C ：当π3θ=时，(1,2a b ⎛== ⎝⎭，(1322a b ⎛⎛+=+= ⎝⎭⎝⎭，所以||3a b += ，2,1a b ==，所以||||||a b a b +=+，故C 正确；对于D ：(()()cos ,sin 1cos ,sin a b θθθθ-=-=- ，所以())2221cos sin a b θθ-=-+=()π52cos 54sin 6θθθ⎛⎫-+=-+ ⎪⎝⎭，当πsin 16θ⎛⎫+=- ⎪⎝⎭，即()()ππ2π2π,Z 2π,Z 623k k k k θθ+=-+∈⇒=-+∈时，2a b - 取得最大值9，所以a b - 的最大值为3，故D 正确.故选：BCD.11．已知函数()()πsin 0,0,2f x A x A ωϕωϕ⎛⎫=+>>< ⎪⎝⎭的部分图像如图所示，下列说法正确的是（）A ．()f x 的图像关于点π,03⎛⎫- ⎪⎝⎭对称B ．()f x 的图像关于直线5π12x =-对称C ．将函数2cos 2y x =的图像向右平移π12个单位长度得到函数()f x 的图像D ．若方程()f x m =在π,02⎡⎤-⎢⎥⎣⎦上有两个不相等的实数根，则m 的取值范围是(2,-【正确答案】BCD【分析】根据图中的信息求出,ωϕ，再根据正弦函数的性质逐项分析.【详解】由图可知：2A =，()f x 的周期ππ2π4π,2312T T ω⎛⎫=⨯-=∴== ⎪⎝⎭，当π12x =时，()ππ2π,Z ,22π22x k k x k ωϕϕ+=+∈∴+=+，ππ,23ϕϕ∴=＜，()π2sin 23f x x ⎛⎫∴=+ ⎪⎝⎭；对于A ，π2ππ2sin 0333f ⎛⎫⎛⎫-=-+=≠ ⎪ ⎪⎝⎭⎝⎭，错误；对于B ，5π5ππ2sin 21263f ⎛⎫⎛⎫-=-+=- ⎪ ⎪⎝⎭⎝⎭，正确；对于C ，将2cos 2y x =向右平移π12：ππππ2cos 22cos 22cos 212623y x x x ⎡⎤⎛⎫⎛⎫⎛⎫=-=-=-+ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦πππ2cos 22sin 2233x x ⎡⎤⎛⎫⎛⎫⎛⎫=--+=+⎢⎥ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎣⎦，正确；对于D ，()f x 的大致图像如下：欲使得在π,02⎡⎤-⎢⎥⎣⎦内方程()f x m =有2个不相等的实数根，则2m -≤＜故选：BCD.12．平面向量,m n 满足||||1m n ==，对任意的实数t ，1||2m n m tn -≤+ 恒成立，则（）A ．m 与n的夹角为60︒B ．22()()m tn m tn ++- 为定值C ．||n tm - 的最小值为12D ．m 在m n + 上的投影向量为1()2m n + 【正确答案】AD【分析】由题意可得：m 与n的夹角60θ=︒，然后根据向量的运算逐项进行检验即可求解.【详解】设平面向量m 与n的夹角为θ，因为对任意的实数t ，1||2m n m tn -≤+ 恒成立，即22222124m m n n m tm n t n -+≤++ 恒成立，又||||1m n ==，也即212cos cos 04t t θθ++-≥对任意的实数t 恒成立，所以224cos 4cos 1(2cos 1)0θθθ∆=-+=-≤，则1cos 2θ=，所以60θ=︒，故选项A 正确；对于B ，因为2222212co ()s ()6012cos 6022t t t m tn m tn t t =+︒++++++=--︒随t 的变化而变化，故选项B 错误；对于C ，因为||n tm -=== 由二次函数的性质可知：当12t =时，||n tm - 取最小值2，故选项C 错误；对于D ，m n +向量上的一个单位向量m n e m n+==+11()2cos ,()2m m n m m n m m n++<+>==+ ，由投影向量的计算公式可得：m 在m n +上的投影向量为1cos ,()1()2m m m n e m n ⋅<+>==+，故选项D 正确，故选.AD 三、填空题13．若向量()()(),3,1,4,2,1a k b c === ，已知23a b - 与c的夹角为钝角，则k 的取值范围是________．【正确答案】99,,322⎛⎫⎛⎫-∞-- ⎪ ⎪⎝⎭⎝⎭ 【分析】根据23a b - 与c 的夹角为钝角，由()230a b c -⋅< ，且23a b - 与c 的不共线求解.【详解】解：由()(),3,1,4a k b == ，得()2323,6a b k -=--．又23a b - 与c的夹角为钝角，∴()22360k --<，得3k <，若()23//a b c - ，则2312k -=-，即92k =-．当92k =-时，23a b - 与c 共线且反向，不合题意．综上，k 的取值范围为99,,322⎛⎫⎛⎫-∞-- ⎪ ⎪⎝⎭⎝⎭ ，故99,,322⎛⎫⎛⎫-∞-- ⎪ ⎪⎝⎭⎝⎭ ．14．若x α=时，函数()cos f x x x =-取得最小值，则sin α=____．【正确答案】3-/【分析】利用题给条件列出关于sin α的方程，解之即可求得sin α的值.【详解】()()cos f x x x x ϕ=-=-（sin ,cos 33ϕϕ=）x α=时，函数()cos f x x x =-取得最小值，cos αα-=cos αα=+则22sin 1αα++=，解之得sin 3α=-故3-15．一半径为3.6米的水轮如图所示，水轮圆心O 距离水面1.8米．已知水轮按逆时针做匀速转动，每60秒转动一圈，如果当水轮上点P 从水面浮现时（图中点0P 位置）开始计时，则P 点离开水面的高度h 关于时间t 的函数解析式为____．【正确答案】ππ3.6sin() 1.8306h =-+【分析】先设P 点离开水面的高度h 关于时间t 的函数解析式为πsin()0,0,2h A t B A ωϕωϕ⎛⎫=++>>< ⎪⎝⎭，再利用题给条件求得各参数值，即可得到该解析式.【详解】P 点离开水面的高度h 关于时间t 的函数解析式可设为πsin()0,0,2h A t B A ωϕωϕ⎛⎫=++>>< ⎪⎝⎭由题给条件可得， 5.41.8A B A B +=⎧⎨-+=-⎩，解之得 3.61.8A B =⎧⎨=⎩水轮按逆时针做匀速转动，每60秒转动一圈，则运动周期为60秒，则2ππ6030ω==，又1sin 2ϕ=-，π2ϕ<，则π6ϕ=-则ππ3.6sin() 1.8306h =-+故ππ3.6sin() 1.8306h =-+16．如图所示,正方形ABCD 边长为6,圆D 的半径为1,E 是圆D 上任意一点,则AE CE ⋅的最小值为________.【正确答案】162-【分析】以D 为原点建立直角坐标系,然后结合三角函数的定义将所求向量坐标化,就可以求出最值.【详解】如图以D 为原点坐标,DC 为x 轴,AD 为y 轴建立直角坐标系:则()0,6A -,()6,0C ,设()cos ,sin E θθ,[)0,2πθ∈,则()()cos ,sin 6cos 6,sin AE CE θθθθ⋅=+⋅-=22πcos 6cos sin 6sin 211624θθθθθ⎛⎫-++=-+≥- ⎪⎝⎭当且仅当π3π42θ-=即7π4θ=时等号成立.∴AE CE ⋅的最小值为162-故答案为:162-四、解答题17．已知向量a 与b 的夹角3π4θ=，且3a = ，2b = (1)求()(2)a b a b +⋅-；(2)a 与a b +的夹角的余弦值．【正确答案】(1)1-55【分析】（1）由向量数量积定义及运算律求结果；（2）由向量夹角公式、数量积的运算律求夹角余弦值.【详解】（1）已知向量a 与b 的夹角3π4θ=，且3a =，b =则3πcos 3642a b a b ⎛⎫⋅=⋅⋅=⨯⨯-=- ⎪ ⎪⎝⎭，所以()22()(2)296281a b a b a a b b +⋅-=-⋅-=---⨯=-；（2）由（1）知：6a b ⋅=-，所以a b +== ，所以a 与a b + 的夹角的余弦值为()2cos ,a a b a a b a a b a a b a a b ⋅++⋅+====⋅+⋅+18．已知sin θ、cos θ是方程221)0x x m -+=的两个实数根.(1)求实数m 的值；(2)求sin cos 11tan 1tan θθθθ+--的值；(3)若3(,2)2θππ∈，求cos 2θ的值.【正确答案】(1)m =(2)12-；(3)12.【分析】（1）根据韦达定理及同角关系式即得；（2）根据同角关系式化简即得；（3）由题可得cos sin θθ-=.【详解】（1）因为sin θ、cos θ是方程221)0x x m -+=的两个实数根，由韦达定理得1sin cos 2sin cos 2m θθθθ⎧+=⎪⎪⎨⎪=⎪⎩，由22(sin cos )θθ+=，则212sin cos 1m θθ+=+=，所以m =（2）sin cos 11tan 1tan θθθθ+--22sin cos sin cos cos sin θθθθθθ=+--22sin cos sin cos θθθθ-=-sin cos θθ=+；（3）因为m =所以sin cos sin cos θθθθ⎧+⎪⎪⎨⎪=⎪⎩，所以2(sin cos )12sin cos θθθθ-=-21=+，因为3(,2)2θππ∈，所以cos 0θ>，sin 0θ<，cos sin θθ-所以221cos 2cos sin (cos +sin )(cos sin )2θθθθθθθ=-=-=.19．已知cos 2βα⎛⎫-= ⎪⎝⎭1sin 22αβ⎛⎫-= ⎪⎝⎭，2απ<<π，02βπ<<，求：(1)cos 2αβ+的值；(2)()tan αβ+的值.【正确答案】(1)14-(2)11【分析】（1）先由已知条件判断,22βααβ--的范围，再利用同角三角函数的关系求出sin ,cos 22βααβ⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭，则由cos cos 222αββααβ⎡⎤+⎛⎫⎛⎫=--- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦利用两角差的余弦公式可求得cos2αβ+，（2）由同角三角函数的关系求出sin 2αβ+，从而可求得tan2αβ+的值，再利用正切的二倍角公式可求得()tan αβ+的值.【详解】（1）因为2απ<<π，02βπ<<，所以42πβαπ<-<，422παπβ-<-<，所以sin 27βα⎛⎫-= ⎪⎝⎭，cos 22αβ⎛⎫-= ⎪⎝⎭，所以coscos 222αββααβ⎡⎤+⎛⎫⎛⎫=--- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦cos cos sin .sin 2222βαβααβαβ⎛⎫⎛⎫⎛⎫⎛⎫=--+-- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭17214=⨯=-.（2）因为3424παβπ+<<，cos2αβ+=，所以sin2αβ+==所以sin2tan23cos 2αβαβαβ++==-+，所以2222tan 2tan()111tan12αβαβαβ⎛+⨯ ⎝⎭+===+⎛-- ⎝⎭.20．已知(sin ,cos )(sin ,sin )a x x b x x ==，，函数()f x a b =⋅ ．（1）求()f x 的对称轴方程；（2）求使()1f x ≥成立的x 的取值集合；（3）若对任意实数[]63x ππ∈,，不等式()2f x m -<恒成立，求实数m 的取值范围．【正确答案】(1)3,28k x k Z ππ=+∈(2){|,}42x k x k k Z ππππ+≤≤+∈(3))+∞【分析】（1）由向量的数量积的运算公式及三角恒等变换，化简得1())242f x x π=-+，利用三角函数的性质，即可求解函数()f x 的对称轴方程；（2）由()1f x ≥，得到sin(242x π-≥，即可求得x 的取值集合；（3）由[]63x ππ∈,,则5212412x πππ≤-≤，利用三角函数的性质，求得函数的最大值，即可求得实数m 的取值范围.【详解】（1）由题意，向量(sin ,cos )(sin ,sin )a x x b x x ==，，可得21cos 211()sin sin cos sin 2)2242x f x a b x x x x x π-=⋅=+⋅=+=-+r r ，令2,42x k k Z πππ-=+∈，解得3,28k x k Z ππ=+∈，所以函数()f x 的对称轴方程为3,28k x k Z ππ=+∈.（2）由()1f x ≥，可得1)1242x π-+≥，即sin(242x π-≥，故3,444k x k k Z πππππ+≤-≤+∈222，解得,42k x k k Z ππππ+≤≤+∈，所以x 的取值集合为{|,}42x k x k k Z ππππ+≤≤+∈.（3）因为[]63x ππ∈,,则5212412x πππ≤-≤，又因为sin y x =在[0,]2π上是增函数，则5sin sin(sin 12412x πππ≤-≤2，又因为5sinsin()12644πππ=+=所以()f x 在[,63x ππ∈时的最大值是max 1(x)2f +又由()2f x m -<恒成立，可得()2max m f x >-，即54m >，故实数m 的取值范围是)+∞.本题主要考查了向量的数量积的运算公式，以及三角函数的图象与性质的综合应用，其中解答熟记向量的数量积的运算求得函数的解析，合理应用三角函数的图象与性质是解答的关键，着重考查了推理与运算能力，属于中档试题.21．某公司欲生产一款迎春工艺品回馈消费者，工艺品的平面设计如图所示，该工艺品由直角ABC 和以BC 为直径的半圆拼接而成，点P 为半圆上一点（异于BC ），点H 在线段AB 上，且满足CH AB ⊥．已知90ACB ∠=︒，1dm AB =，设ABC θ∠=．(1)为了使工艺礼品达到最佳观赏效果，需满足ABC PCB ∠=∠，且CA CP +达到最大．当θ为何值时，工艺礼品达到最佳观赏效果，并求最大值；(2)为了工艺礼品达到最佳稳定性便于收藏，需满足60PBA ∠=︒，且CH CP +达到最大．当θ为何值时，CH CP +取得最大值，并求该最大值．【正确答案】(1)π6θ=，AC CP +的最大值为54(2)π12θ=，CH CP +【分析】（1）设ABC PCB θ∠=∠=，则在直角ABC 中，sin AC θ=，cos BC θ=，计算得到2sin sin 1AC CP θθ+=-++，计算最值得到答案.（2）计算sin cos CH θθ=⋅，得到πsin 23CH CP θ⎛⎫+=+ ⎪⎝⎭.【详解】（1）设ABC PCB θ∠=∠=，则在直角ABC 中，sin AC θ=，cos BC θ=.在直角PBC 中，2cos cos co s cos PC BC θθθθ=⋅=⋅=，sin sin cos sin cos PB BC θθθθθ=⋅=⋅=.22sin cos sin 1sin AC CP θθθθ+=+=+-2sin sin 1θθ=-++，π0,2θ⎛⎫∈ ⎪⎝⎭，所以当1sin 2θ=，即π6θ=，AC CP +的最大值为54.（2）在直角ABC 中，由1122ABC S CA CB AB CH =⋅=⋅ ，可得sin cos sin cos 1CH θθθθ⋅==⋅.在直角PBC 中，πsin 3PC BC θ⎛⎫=⋅- ⎪⎝⎭ππcos sin cos cos sin 33θθθ⎛⎫=⋅- ⎪⎝⎭，所以1sin cos cos cos sin 22CH CP θθθθθ⎛⎫+=+- ⎪ ⎪⎝⎭，π0,3θ⎛⎫∈ ⎪⎝⎭，所以211sin2sin cos 222CH CP θθθθ+=+-11πsin2cos2sin 2444243θθθ⎛⎫==++ ⎪⎝⎭，所以当π12θ=，CH CP +达到最大值24.22．已知函数()4sincos122xxf x ωω=+，其中常数0ω>．（1）()y f x =在3,44ππ⎡⎤-⎢⎥⎣⎦上单调递增，求ω的取值范围；（2）若4ω<，将函数()y f x =图象向左平移3π个单位，得到函数()y g x =的图象，且过,16πP ⎛⎫⎪⎝⎭，若函数()g x 在区间[,]a b （a ，b ∈R 且a b <）满足：()y g x =在[,]a b 上至少含30个零点，在所上满足上述条件的[,]a b 中，求b a -的最小值；（3）在（2）问条件下，若对任意的,612ππx ⎡⎤∈-⎢⎥⎣⎦，不等式()()210g x mg x --≤恒成立，求实数m的取值范围．【正确答案】（1）203ω<≤；（2）433π；（3）83m ≥．【分析】(1)由二倍角正弦公式化简原函数()2sin()1f x x ω=+，0ω>即知最小正周期，找到其中一个递增区间，由已知区间属于递增区间列不等式组求ω的范围即可；(2)根据函数图象平移得到()2sin 13πg x x ω⎛⎫=++ ⎪⎝⎭，由其过P 点且04ω<<求出ω值，()y g x =在[,]a b 上至少含30个零点，根据三角函数的图象及性质分析即可知b a -的最小值；(3)由不等式恒成立，令()21t t mt ϕ=--，即()max 0t ϕ≤成立即可求m 的范围【详解】解（1）由题意，有()2sin()1f x x ω=+，又0ω>则最小正周期2T πω=由正弦函数的性质，当2πx ω=-，函数取得最小值，2x πω=函数取得最大值∴,22ππωω⎡⎤-⎢⎥⎣⎦是函数2sin y x ω=的一个单调递增区间若函数()2sin 0y x ωω=>在3,34ππ⎡⎤-⎢⎥⎣⎦上单调递增，则23ππω-≤-且324ππω≥解得203ω<≤（2）∵由（1）：()2sin 1f x x ω=+∴将函数()y f x =图象向左平移3π个单位，得到函数()2sin 13πy g x x ωω⎛⎫==++ ⎪⎝⎭的图象∵()g x 的图象过,16πP ⎛⎫⎪⎝⎭．∴2sin 11663g πππωω⎛⎫⎛⎫=++= ⎪ ⎪⎝⎭⎝⎭，可得：sin 02πω=，解得：2k πωπ=，Z k ∈，即：2k ω=，Z k ∈，∵04ω<<∴2ω=，可得()g x 的解析式为：()22sin 213πg x x ⎛⎫=++ ⎪⎝⎭∴()g x 的周期为22T ππ==在区间[,]a b （a ，b ∈R 且a b <）满足：()y g x =在[,]a b 上至少有30个零点，即21sin 232πx ⎛⎫+=- ⎪⎝⎭在[,]a b 上至少有30个解．∴有252236ππx kπ+=-或22236ππx kπ+=-解得：34πx kπ=-或512πx kπ=-分析：直线与三角函数图象的一个周期内的交点中，两个交点距离：最小为波谷跨度53()1243k k πππππ---=，最大为波峰跨度：233πππ-=∴当交点正好跨过15个波谷，即跨过14个整周期和一个波谷时，b a -有最小值即，在所有满足上述条件的[,]a b 中b a -的最小值为431433πππ⨯+=（3）()[]2,3g x ∈，设()21t t mt ϕ=--，[]2,3t ∈∵()()(){}max max 2,30t ϕϕϕ=≤即可只需要()()2030ϕϕ≤⎧⎪⎨≤⎪⎩解得83m ≥综上所述83m ≥本题考查了三角函数的图象及性质，1、应用二倍角正弦公式化简，结合正弦函数的单调性求参数范围；2、根据函数图象平移得到新函数的解析式，由函数的零点个数求最值；3、将不等式恒成立转化为函数的最值情况下不等式成立，进而求参数范围。

辽宁沈阳城郊市重点联合体12-13学年高一下期中考试-生物(.

2012—2013学年度下学期城郊市重点联合体期中考高一年级生物试卷1.考试时间：90分钟，分数：100分2.第I 卷为客观题60分;第n 卷为主观题40分一.单项选择题（本题包括30小题，每小题2分，共60分。

每小题给出的四个选项中，只有一个选项最符合题U 要求。

）1. 肝细胞内含量最多的有机化合物是（） A.糖类 B.核酸D.蛋白质2. 下列四组生物中，都属于真核生物的一组是（）A.病毒和柳树B.细菌和草履虫C.蓝藻和酵母菌D.青蛙和酵母菌 3. 生物体的基本组成物质中，作为生命活动主要承担者的是（） A.无机盐B.水C.蛋白质D.核酸3.参与有氧呼吸的氧气用''0标记，结果最先发现含‘七的物质是（） A CO ： B 丙酮酸C 水5. 染色体和染色质的关系是（） A.不同时期，不同物质的不同形态 C.同一时期，同一物质的不同形态6. 玉米叶肉细胞中，具有色素的一组细胞器是（）A 、线粒体和高尔基体B 、叶绿体和液泡C 、中心体和核糖体D 、内质网和液泡7. 食醋中的醋酸成分是活细胞不需要的小分子物质，蔗糖不是活细胞需要的大分子物质。

用食醋和蔗糖可将新鲜的大蒜头很快地腌成糖醋蒜，其原因是A. 醋酸和蔗糖分子均能存在于活细胞的间隙中B. 醋酸和蔗糖分子均能被吸附在活细胞的表面C. 醋酸能固定和杀死活细胞，细胞膜失去了选择性D. 因腌的时间过久，两种物质均慢慢地进入活细胞 8.下列核昔酸中，在DNA 结构中可能具有的是（C.脂类D 乳酸B ・不同时期，同一物质的不同形态 D.同一时期，不同物质的不同形态A.氨基酸、核昔酸、核糖核甘酸昔酸C.氨基酸、核糖核昔酸、脱氧核昔酸昔酸10.生物体进行生命活动的主要能源物质和细胞内&好的储能物质分别是（）A.蛋白质、脂肪B.糖类、脂肪C.脂肪、糖类D.糖类、蛋0 质A.控制物质进出细胞B.将产生的抗体分泌到细胞外C.维持细胞内的小环境的稳定D.使细胞内的各种生物化学反应加快12.观察DXA 和RXA 在细胞中的分布，所运用的原理是A 、单独利用屮基绿对细胞染色，可显示DNA 在细胞中的分布，从而推知RNA 的分布B 、单独利用毗罗红对细胞染色，可显示RNA 在细胞中的分布，从而推知DNA 的分布C 、利用屮基绿和毗罗红混合染色剂对细胞染色，同时显示DXA 和RM 在细胞中的分布D 、在细胞核和细胞质内可以分别提取到DNA 和RNA,山此说明DXA 和RXA 的分布13. 当植物山代谢旺盛的生长期转入休眠期时，体内结合水与自山水的比值通常会（）A.升高B.下降C.无变化D.产生波动 14. "观察DXA 和RXA 在细胞中的分B.核昔酸、脱氧核昔酸、核糖核 D.氨基酸、脱氧核昔酸、核糖核11项不属于细胞膜的功能取口腔上皮细胞制片f 水解f 冲洗f 染色f 观察取口腔上皮细胞制片f 染色f 冲洗f 水解f 观察取口腔上皮细胞制片f 水解f 染色f 冲洗f 观察取口腔上皮细胞制片f 冲洗f 水解f 染色f 观察布”实验中，正确的实验步骤是（）A.B.C.D.15.人体某些白细胞可以祚噬病菌，这一生理过程的完成依赖于细胞膜的（）A.选择透过性B.主动运输C.保护性D.流动性16.有一种物质能顺浓度梯度进出细胞膜，但却不能顺浓度梯度进出无蛋0质的磷脂双层膜。

辽宁省沈阳二中2012-2013学年高一12月月考数学试题

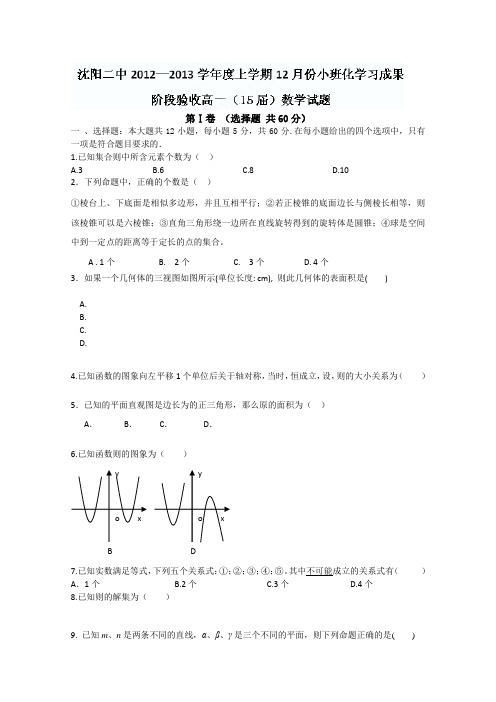
第Ⅰ卷（选择题共60分）一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的．1.已知集合则中所含元素个数为（）A.3B.6C.8D.102．下列命题中，正确的个数是（）①棱台上、下底面是相似多边形，并且互相平行；②若正棱锥的底面边长与侧棱长相等，则该棱锥可以是六棱锥；③直角三角形绕一边所在直线旋转得到的旋转体是圆锥；④球是空间中到一定点的距离等于定长的点的集合。

A . 1个 B. 2个 C. 3个 D. 4个3．如果一个几何体的三视图如图所示(单位长度: cm), 则此几何体的表面积是( )A.B.C.D.4.已知函数的图象向左平移1个单位后关于轴对称，当时，恒成立，设，则的大小关系为（）5．已知的平面直观图是边长为的正三角形，那么原的面积为（）A．B．C．D．6.已知函数则的图象为（）7.已知实数满足等式，下列五个关系式：①；②；③；④；⑤。

其中不可能成立的关系式有（）A．1个 B.2个 C.3个 D.4个8.已知则的解集为（）9. 已知m、n是两条不同的直线，α、β、γ是三个不同的平面，则下列命题正确的是()A．若α⊥γ，α⊥β，则γ∥βB．若m∥n，m⊂α，n⊂β，则α∥βC．若m∥n，m∥α，则n∥αD．若m∥n，m⊥α，n⊥β，则α∥β10. 如图所示，在正四棱锥S-ABCD中，是的中点，P点在侧面△SCD内及其边界上运动，并且总是保持．则动点的轨迹与△组成的相关图形最有可有是图中的()11.已知球的直径SC=4，A，B是该球球面上的两点，AB=，，则棱锥S—ABC的体积为( )A. B. C. D.112.定义在R上的函数满足当（）A.335B.338C.1678D.2012第Ⅱ卷（非选择题共90分）二填空题（本大题共4小题，每小题5分，共20分）13．当x＞0时，函数的值总大于1，则a的取值范围是．14.已知函数—是增函数，则实数的取值范围是。

辽宁省沈阳市城郊市重点联合体2012-2013学年高一物理下学期期中试题

2012-2013学年度下学期城郊市重点联合体期中考试高一年级物理试卷试卷说明：1.命题范围：人教版高中物理必修2第六章完毕；2.试卷分两卷，第I卷为选择题，请将正确答案用2B铅笔涂在答题卡上，第II卷为非选择题，请将答案按照题序用黑色水性签字笔填写在答题纸上；本卷总分为为100分，考试时间为90分钟。

第1卷〔选择题共60分〕一、单项选择题〔此题共10小题。

每一小题4分，共40分。

在每一小题给出的四个选项中，只有一个选项正确〕1．如下说法中，正确的答案是：( )A.托勒密引入了“本轮〞“均轮〞“偏心等距点〞等概念，丰富和完善了“地心说〞理论B.开普勒发表《天体运行论》一书，创立了行星运行三定律C.哈勃望远镜的问世，彻底终结了“地心说〞的理论D.牛顿创立万有引力定律，并通过实验准确测定引力常量G=6.67×10-11N﹒m2/kg22．如下列图的曲线为运动员抛出的铅球运动轨迹(铅球视为质点)，A、B、C为曲线上的三点，关于铅球在B点的速度方向，说法正确的答案是 ( )A．为AB的方向 B．为BC的方向C．为BD的方向 D．为BE的方向3．物体做曲线运动的条件为 ( )A．物体所受的合外力为恒力B．物体所受的合外力为变力C．物体所受的合外力的方向与速度的方向不在同一条直线上D．物体所受的合外力的方向与加速度的方向不在同—条直线上4．一个做匀速直线运动的物体，突然受到一个与运动方向不在同一直线上的恒力作用时，如此物体将()A．继续做直线运动 B．一定做曲线运动C．可能做直线运动，也可能做曲线运动D．运动的形式不能确定5．一船以恒定的速率渡河，水流速度恒定(小于船速)，要使船垂直到达对岸，如此( )A．船应垂直河岸航行B．船的航行方向应偏向上游一侧C．船不可能沿直线到达对岸D ．河的宽度一定时，船到对岸的时间是任意的6．关于平抛物体的运动，如下说法中正确的答案是 ( )A ．平抛物体运动的速度和加速度都随时间的增加而增大B ．平抛物体的运动是变加速运动C ．做平抛运动的物体仅受到重力的作用，所以加速度保持不变D ．做平抛运动的物体水平方向的速度逐渐增大7．飞机以150 m/s 的水平速度匀速飞行，某时刻让A 球落下，相隔1 s 又让B 球落下，不计空气阻力.在以后的运动中，关于A 球与B 球的相对位置关系，正确的答案是〔取g=10 m/s 2)〔〕A ．A 球在B 球前下方 B ．A 球在B 球后下方C ．A 球在B 球正下方5 m 处D ．A 球在B 球的正下方，距离随时间增加而增加8．某行星绕太阳运行的椭圆轨道如下列图，F 1和F 2是椭圆轨道的两个焦点，行星在A 点的速率比在B 点的大，如此太阳是位于( )A ．F 2B ．AC ．F 1D ．B9．由于通信和广播等方面的需要，许多国家发射了地球同步轨道卫星，这些卫星的( )A ．质量可以不同B ．轨道半径可以不同C ．轨道平面可以不同D ．速率可以不同10．物体做匀速圆周运动的条件是：〔〕A.物体有一定的初速度，且受到一个始终和初速度垂直的恒力作用B.物体有一定的初速度，且受到一个大小不变，方向变化的力的作用C.物体有一定的初速度，且受到一个方向始终指向圆心的力的作用D.物体有一定的初速度，且受到一个大小不变方向始终跟速度垂直的力的作用二、多项选择题〔此题共5小题。

辽宁省沈阳市城郊市重点联合体高一物理下学期期中试题

2012-2013学年度下学期城郊市重点联合体期中考试高一年级物理试卷试卷说明：1.命题范围：人教版高中物理必修2第六章结束；2.试卷分两卷，第I卷为选择题，请将正确答案用2B铅笔涂在答题卡上，第II卷为非选择题，请将答案按照题序用黑色水性签字笔填写在答题纸上；本卷满分为100分，考试时间为90分钟。

第Ⅰ卷（选择题共60分）一、单项选择题（本题共10小题。

每小题4分，共40分。

在每小题给出的四个选项中，只有一个选项正确）1．下列说法中，正确的是：( )A.托勒密引入了“本轮”“均轮”“偏心等距点”等概念，丰富和完善了“地心说”理论B.开普勒发表《天体运行论》一书，创立了行星运行三定律C.哈勃望远镜的问世，彻底终结了“地心说”的理论D.牛顿创立万有引力定律，并通过实验精确测定引力常量G=6.67×10-11N﹒m2/kg22．如图所示的曲线为运动员抛出的铅球运动轨迹(铅球视为质点)，A、B、C为曲线上的三点，关于铅球在B点的速度方向，说法正确的是 ( ) Array A．为AB的方向 B．为BC的方向C．为BD的方向 D．为BE的方向3．物体做曲线运动的条件为 ( )A．物体所受的合外力为恒力B．物体所受的合外力为变力C．物体所受的合外力的方向与速度的方向不在同一条直线上D．物体所受的合外力的方向与加速度的方向不在同—条直线上4．一个做匀速直线运动的物体，突然受到一个与运动方向不在同一直线上的恒力作用时，则物体将 ( )A．继续做直线运动 B．一定做曲线运动C．可能做直线运动，也可能做曲线运动 D．运动的形式不能确定5．一船以恒定的速率渡河，水流速度恒定(小于船速)，要使船垂直到达对岸，则( )A．船应垂直河岸航行B．船的航行方向应偏向上游一侧C．船不可能沿直线到达对岸D ．河的宽度一定时，船到对岸的时间是任意的6．关于平抛物体的运动，下列说法中正确的是 ( )A ．平抛物体运动的速度和加速度都随时间的增加而增大B ．平抛物体的运动是变加速运动C ．做平抛运动的物体仅受到重力的作用，所以加速度保持不变D ．做平抛运动的物体水平方向的速度逐渐增大7．飞机以150 m/s 的水平速度匀速飞行，某时刻让A 球落下，相隔1 s 又让B 球落下，不计空气阻力.在以后的运动中，关于A 球与B 球的相对位置关系，正确的是（取g=10 m/s 2)（）A ．A 球在B 球前下方 B ．A 球在B 球后下方C ．A 球在B 球正下方5 m 处D ．A 球在B 球的正下方，距离随时间增加而增加8．某行星绕太阳运行的椭圆轨道如图所示，F 1和F 2是椭圆轨道的两个焦点，行星在A 点的速率比在B 点的大，则太阳是位于( )A ．F 2B ．AC ．F 1D ．B 9．由于通信和广播等方面的需要，许多国家发射了地球同步轨道卫星，这些卫星的( )A ．质量可以不同B ．轨道半径可以不同C ．轨道平面可以不同D ．速率可以不同10．物体做匀速圆周运动的条件是：（）A.物体有一定的初速度，且受到一个始终和初速度垂直的恒力作用B.物体有一定的初速度，且受到一个大小不变，方向变化的力的作用C.物体有一定的初速度，且受到一个方向始终指向圆心的力的作用D.物体有一定的初速度，且受到一个大小不变方向始终跟速度垂直的力的作用二、多项选择题（本题共5小题。

2019-2020学年辽宁省沈阳市郊联体高一下学期期中考试数学试题(解析版)

2019-2020学年辽宁省沈阳市郊联体高一下学期期中考试数学试题一、单选题1．一个半径是R 的扇形，其周长为3R ，则该扇形圆心角的弧度数为（） A ．1 B ．3C ．πD ．3π 【答案】A【解析】设扇形的弧长为l ，根据半径是R ，周长为3R 的扇形，求出l ，再由公式计算出弧度数. 【详解】设扇形的弧长为l ，则23R l R +=，得l R =，则扇形圆心角的弧度数为1lR=. 故选：A. 【点睛】本题考查了扇形的弧长相关的计算，弧度的计算，属于基础题. 2．函数1tan 24y x π⎛⎫=+⎪⎝⎭的定义域是（）A ．4,2xx k k Z ππ⎧⎫≠-+∈⎨⎬⎩⎭∣ B ．2,2xx k k Z ππ⎧⎫≠+∈⎨⎬⎩⎭∣ C ．32,2xx k k Z ππ⎧⎫≠+∈⎨⎬⎩⎭∣ D ．,2xx k k Z ππ⎧⎫≠+∈⎨⎬⎩⎭∣ 【答案】B 【解析】将124x π+看成整体，由正切函数的定义域，知1,242x k k Z πππ+≠+∈，求出x 的取值范围，得到答案. 【详解】令1,242x k k Z πππ+≠+∈，则2,2x k k Z ππ≠+∈，故选：B. 【点睛】本题考查了正切型函数的定义域的求法，属于基础题.3．已知tan 4α=-，则4sin 2cos 5cos 3sin αααα-=+（）A ．2-B ．187C ．1817D ．1417【答案】B【解析】利用齐次式技巧化简求值. 【详解】由题4sin 2cos 5cos 3sin αααα-=+4tan 253tan αα-+162512--=-187=. 故选：B. 【点睛】本题考查了同角三角函数的基本关系式，利用正余弦齐次式技巧化简求值，属于基础题. 4．已知(1,1)a =-，(1,2)b =，若()a b b λ+⊥，则实数λ=（） A ．4 B ．5C ．-4D ．-5【答案】D【解析】先由平面向量的坐标运算得到a b λ+，再由()a b b λ+⊥，则()0a b b λ+⋅=，由数量积的坐标表示，求得答案. 【详解】由题(1,1)a =-，(1,2)b =，则(1,2)a b λλλ+=-+，又由()a b b λ+⊥，则()0a b b λ+⋅=，得(1)1(2)20λλ-⨯++⨯=，得5λ=-. 故选：D. 【点睛】本题考查了平面向量的坐标运算，向量垂直的坐标表示，属于基础题. 5．下列关系式中，正确的是（） A ．sin1cos1tan1<< B ．cos1sin1tan1<< C ．tan1sin1cos1<< D ．cos1tan1sin1<<【答案】B【解析】画出1弧度的正弦线，余弦线和正切线，比较长度得到答案. 【详解】画出1弧度的正弦线，余弦线和正切线，如图所示：则sin1,cos1,tan1MP OM AT ===，比较,,OM MP AT 的长度，得cos1sin1tan1<< . 故选：B. 【点睛】本题考查了三角函数线的应用，属于基础题. 6．下列函数中最小正周期为π的是（） A ．sin y x = B ．1sin y x =+C ．cos y x =D ．tan 2y x =【答案】C【解析】对A 选项，对x 赋值，即可判断其最小正周期不是π；利用三角函数的周期公式即可判断B 、D 的最小正周期不是π，问题得解. 【详解】对A 选项，令32x π=-，则33sin 122f ππ⎛⎫-=-=- ⎪⎝⎭ 3sin 122f πππ⎛⎫-+=-= ⎪⎝⎭，不满足3322f f πππ⎛⎫⎛⎫-=-+ ⎪ ⎪⎝⎭⎝⎭，所以sin y x =不是以π为周期的函数，其最小正周期不为π；对B 选项，1sin y x =+的最小正周期为：2T π=；对D 选项，tan 2y x =的最小正周期为：2T π=；排除A 、B 、D故选C 【点睛】本题主要考查了三角函数的周期公式及周期函数的定义，还考查了赋值法，属于基础题． 7．设2πθπ<<，1cos 3θ=-，则sin2θ=（）A ．6 B ．6C 3D ．63±【答案】A 【解析】先求出2θ的范围，确定sin 2θ的符号，再用半角公式求解.【详解】由2πθπ<<，则22πθπ<<，则sin02θ>，所以sin2θ=3==. 故选：A. 【点睛】本题考查了半角公式，属于基础题. 8．已知α为锐角，β为钝角且cos α=，tan 3β=-，则αβ+的值为（） A ．34π B ．23π C ．3π D ．4π 【答案】A【解析】先由α为锐角且cos 5α=，求得tan α，再利用两角和的正切公式求出tan()αβ+，再结合αβ+的范围，得到答案.【详解】由α为锐角且cos α=，得sin 5α==，则sin 1tan cos 2ααα==，则1(3)tan tan 2tan()111tan tan 1(3)2αβαβαβ+-++===---⨯-，又(0,),(,)22ππαβπ∈∈，则3(,)22ππαβ+∈，得34αβπ+=.故选：A. 【点睛】本题考查了同角三角函数的基本关系式，两角和的正切公式，已知三角函数值求角，属于中档题.9．已知函数()()2cos 0,2f x x πωϕωϕ⎛⎫=+><⎪⎝⎭的部分函数图像如图所示，点()0,3,,06A B π⎛⎫⎪⎝⎭，则函数()f x 图像的一条对称轴方程为（）A ．12x π=-B ．3x π=-C ．18x π=D ．24x π=【答案】D【解析】由条件确定函数()()2cos f x x ωϕ=+的解析式，再根据余弦函数图象的对称性，可得结果．【详解】由()()2cos f x x ωϕ=+的图象知，f （0）＝2cos 3ϕ=3cos ϕ=，又2πϕ<，∴6πϕ=或6πϕ=-；又由五点作图可知，函数()f x 在A 点附近呈上升趋势，应满足6πϕ=-，当6πϕ=-时，f （6π）＝2cos （6πω6π-）＝0，∴6πω62ππ-=，解得ω＝4；∴()2cos 46f x x π⎛⎫=- ⎪⎝⎭；令46x π-=k π，k ∈Z ，求得x 424k ππ=+，k ∈Z ； k ＝0时，得函数g （x ）图象的一条对称轴方程为x 24π=．故选D ．【点睛】本题主要考查由图像及性质确定解析式，关键是ϕ的确定，考查了余弦函数图象的对称性问题，是中档题．10．已知ABC 3的等边三角形，点D ，E 分别是AB ，BC 上的点，且13AD AB =，23BE BC =，连接DE 并延长到点F ，使得DE EF =，则AF BC ⋅的值为（） A ．32-B ．92C ．32D ．92-【答案】C【解析】设,a AB b AC ==，以,a b 为基底，根据已知的关系，利用向量的线性运算表示出,AF BC ，再利用向量的数量积的运算律化简求值. 【详解】作示意图如图所示：设,a AB b AC ==，则13||3,||3,3322a b a b ==⋅=⨯=，由13AD AB =，23BE BC =，得//DE AC ，且23DE AC =，又DE EF =，则43DF AC =，即43DF b =，又13AD a =，得1433AF AD DF a b =+=+， BC AC AB b a =-=-，则14()()33A BC a F b b a ⋅=+⋅-221433a ab b =--⋅+1343333232=-⨯-+⨯=.故选：C. 【点睛】本题考查了平面向量的基本定理，平面向量的基本定理，数量积的运算，属于中档题. 11．在平面直角坐标系xOy 中，角α的顶点为坐标原点，始边为x 轴的非负半轴，终边与单位圆O 交于点34,55A ⎛⎫ ⎪⎝⎭，将角α的终边绕原点按逆时针方向旋转3π，交单位圆O 于点()00,B x y ，则0x =（）A ．B C ．310+ D ．410+ 【答案】B【解析】由已知条件可求出sin ,cos αα的值，由三角函数的定义可得0cos()3x πα=+，从而可求出结果【详解】解：因为角α的终边与单位圆O 交于点34,55A ⎛⎫⎪⎝⎭，所以43sin ,cos 55αα==，由题意可知0314cos()cos cos sin sin 333525x πππααα=+=-=⨯-=故选：B 【点睛】此题考查三角函数的定义的应用，考查两角和的正弦公式，属于基础题 12．将函数()sin f x x =的图像先向右平移3π个单位，再把所得函数图像横坐标变为原来的1(0)ωω>，纵坐标不变，得到函数()g x 的图像，若函数()g x 在3,22ππ⎛⎫⎪⎝⎭上没有零点，则ω的取值范围是（） A ．(0,1]B ．20,9⎛⎤ ⎥⎝⎦C ．2280,,939⎛⎤⎡⎤⋃ ⎥⎢⎥⎝⎦⎣⎦D ．280,,199⎛⎤⎡⎤⋃ ⎥⎢⎥⎝⎦⎣⎦【答案】C【解析】先由图象的变换求出()g x 的解析式，再由定义域求出3x πω-的范围，再利用正弦函数的图象和性质，求得ω的取值范围. 【详解】函数()sin f x x =的图象先向右平移3π个单位长度，可得sin 3y x π⎛⎫=- ⎪⎝⎭的图象，再将图象上每个点的横坐标变为原来的1ω(0)>ω倍(纵坐标不变)，得到函数()sin 3g x x πω⎛⎫=-⎪⎝⎭的图象，∴周期2T πω=，由3,22x ππ⎛⎫∈⎪⎝⎭，则3(,)32323x πωππωππω-∈--，若函数()g x 在3(,)22ππ上没有零点，结合正弦函数sin y x =的图象观察则3(,)(,)2323k k ωππωπππππ--⊆+∴ 323232T ωππωπππω⎛⎫⎛⎫---≤=⎪ ⎪⎝⎭⎝⎭，21ω∴≤，解得01ω<≤，又23323k k ωπππωππππ⎧≤-⎪⎪⎨⎪+≥-⎪⎩，解得3412323k ωω-≤≤-，当0k =时，解2839ω≤≤，当1k =-时，01ω<≤，可得209ω<≤， ω∴∈228(0,][,]939.故选：C. 【点睛】本题考查正弦型的图象变换及零点问题，此类问题通常采用数形结合思想，构建不等关系式求解，属于较难题.二、填空题13．把时钟拨快1小时，则时针走过的弧度数是_____________. 【答案】6π-【解析】根据题意，求得角度，结合角度和弧度的相互转化，即可求得结果. 【详解】始终拨快1小时，则时针顺时针旋转30︒，故走过的弧度数为6π-.故答案为：6π-. 【点睛】本题考查角度和弧度的转化，属简单题.14．化简tan 20tan 25tan 20?tan 25︒+︒+︒︒=_____. 【答案】1 【解析】【详解】分析：首先从式子中分析得出2025︒︒+角的大小，借助于两角和的正切公式，得到tan 20tan 25︒︒+与tan 20tan 25︒︒⋅之间的关系，借助于45︒角的正切值，求得结果. 详解：因为tan 20tan 25tan(2025)1tan 20tan 25︒︒︒︒︒︒++=-，所以1tan 20tan 25tan 20tan 25︒︒︒︒-=+，所以有tan 20tan 25tan 20tan 251︒︒︒︒++=，故答案为：1.点睛：该题考查的是有关三角函数化简求值问题，在解题的过程中，涉及到的知识点有两角和的正切公式的逆用，注意45︒角的正切值的大小.15．已知2cos sin 2αβ+=，32sin cos 2αβ-=，则sin()αβ-=_____________.【答案】12【解析】对两个等式两边同时平方相加，再结合同角的三角函数关系式中的平方和公式、逆用两角差的正弦公式求解即可【详解】222232cos sin (2cos sin )(4cos 4cos sin sin (1)224αβαβααββ+=⇒+=⇒++=，22223392sin cos (2sin cos )()4sin 4sin cos cos (2),224αβαβααββ-=⇒-=⇒-+=(1)(2)+得：144cos sin 4sin cos 134(sin cos cos sin )2sin()2αβαβαβαβαβ+-+=⇒-=⇒-=.故答案为：12【点睛】本题考查了逆用两角差的正弦公式，考查了同角的三角函数关系式的应用，考查了数学运算能力.16．已知(cos 2,1)a x =，(1,sin 1)b x =+，,3x ππ⎛⎤∈ ⎥⎝⎦，则a b ⋅的取值范围是_____________. 【答案】171,8⎡⎤⎢⎥⎣⎦【解析】由已知得21172sin 48a b x ⎛⎫⋅=--+ ⎪⎝⎭，然后由,3x ππ⎛⎤∈ ⎥⎝⎦得sin [0,1]x ∈，再根据二次函数的性质可求出函数的最值【详解】解：因为(cos 2,1)a x =，(1,sin 1)b x =+，所以2cos 2sin 12sin sin 2a b x x x x ⋅=++=-++21172sin 48x ⎛⎫=--+ ⎪⎝⎭因为,3x ππ⎛⎤∈⎥⎝⎦，所以sin [0,1]x ∈，所以当1sin 4x =时，21172sin 48x ⎛⎫--+ ⎪⎝⎭有最大值178，当sin 1x =时，21172sin 48x ⎛⎫--+ ⎪⎝⎭有最小值1，所以171,8a b ⎡⎤⋅∈⎢⎥⎣⎦，故答案为：171,8⎡⎤⎢⎥⎣⎦【点睛】此题考查向量的数量积运算，考查三角函数恒等变换公式的应用，考查二次函的性质的应用，属于基础题三、解答题17．已知3tan()sin(2)cos 2()9cos tan(3)2x x x f x x x πππππ⎛⎫+-- ⎪⎝⎭=⎛⎫+-+ ⎪⎝⎭（1）化简()f x ；（2）若α是第三象限角，5sin 213απ⎛⎫-= ⎪⎝⎭，求()f α的值.【答案】（1）()f x sin x =；（2）1213-. 【解析】（1）直接利用诱导公式化简；（2）利用诱导公式化简，再利用同角三角函数基本关系求值. 【详解】（1）()()()()3tan sin 2cos 29cos tan 32x x x f x x x πππππ⎛⎫+-- ⎪⎝⎭=⎛⎫+-+ ⎪⎝⎭tan (sin )(sin )sin (sin )(tan )x x x x x x --==--（2）5sin cos 213παα⎛⎫-=-= ⎪⎝⎭，得5cos 13α=- ∵α为第三象限角，∴12sin 13α==-，∴12()sin 13f αα==- 【点睛】本题考查了诱导公式，同角三角函数的基本关系式，属于基础题.18．已知1e 、2e 是两个单位向量，其夹角为60︒，1232a e e =-+，122b e e =+. （1）求||a ；（2）求a 与b 的夹角. 【答案】（1；（2）120︒. 【解析】（1）由于()222121122||329124a e e e e e e =-+=-+⋅+，然后代值可得答案；（2）先求出,b a b ⋅，然后利用向量夹角公式求解即可【详解】（1）()222121122||3291247a e e e e e e =-+=-+⋅+=（2）222121122||(2)447b e e e e e e =+=+⋅+=22121211227(32)(2)622a b e e e e e e e e ⋅=-+⋅+=-+⋅+=-则712cos ,2||||7a b a b a b -⋅<>===-⨯∵[],0,180a b 〈〉∈︒︒ ∴,120a b 〈〉=︒ 【点睛】此题考查向量模的计算，向量的夹角的计算，属于基础题19．已知函数()sin()f x A x ωϕ=+，x ∈R （其中0A >，0>ω，02πϕ<<）的图像上一个最低点为2,23P π⎛⎫- ⎪⎝⎭，且()y f x =的图像与x 轴的交点中，两相邻交点之间的距离为2π. （1）求()f x 的解析式；（2）求()f x 在区间,122ππ⎡⎤⎢⎥⎣⎦上的最大值和最小值，并求出相应的x 的值. 【答案】（1）()2sin 26f x x π⎛⎫=+ ⎪⎝⎭；（2）max ()2f x =；此时6x π=；min ()1f x =-，此时2x π=【解析】（1）根据五点作图法的五个关键点的性质，先得到A ，再求得周期T ，求得ω，再代入最低点为2,23P π⎛⎫- ⎪⎝⎭，结合02πϕ<<，求得ϕ，得到()f x 的解析式；（2）由（1）得到()2sin 26f x x π⎛⎫=+⎪⎝⎭，将26x π+看成整体，求出范围，由正弦函数的性质，求得最大值和最小值及相应的x 的值. 【详解】（1）由题意可知2A =，22T π=，T π=，2ω=，()2sin(2)f x x ϕ=+， 2,23P π⎛⎫- ⎪⎝⎭代入得，43232k πϕππ+=+，k Z ∈，得26k πϕπ=+，k Z ∈∵02πϕ<<，∴6π=ϕ，∴()2sin 26f x x π⎛⎫=+⎪⎝⎭（2）∵122x ππ≤≤，∴π72366x ππ≤+≤ 当262x ππ+=，即6x π=时，max ()2f x =当7266x ππ+=，即2x π=时，min ()1f x =-.【点睛】本题考查了由正弦型函数的图象性质求解析式，正弦型函数的最值问题，属于中档题. 20．已知2παπ<<，且1cos sin 5=.（1）求sin cos αα-的值；（2）求223sin 4sincoscos 122221tan tan αααααα--+++的值.【答案】（1）15；（2）168125. 【解析】（1）利用同角三角函数的基本关系式， sin cos αα±与sin cos αα之间的关系，结合角度的范围，化简求值；（2）利用同角三角函数的基本关系式，倍角公式化简求值. 【详解】（1）cos sincos sin =1sin 1cos cos sin |cos ||sin |αααααα-+=+由2παπ<<原式1sin 11cos sin cos 5αααα=-++=+= 平方得112sin cos 25αα+=，即242sin cos 25αα=- ∵2παπ<<，∴7sin cos 5αα-==（2）223sin4sin cos cos1 22221tantanαααααα--+++(3)(1cos)1cos2sint1tanan122ααααα--+-+++=2(cos sin)2sin cos(cos sin)sin coscos sinαααααααααα-==-+247168255125⎛⎫=-⨯-=⎪⎝⎭【点睛】本题考查了同角三角函数的基本关系式，二倍角公式，sin cosαα±与sin cosαα之间的关系，三角函数式的化简与求值，属于中档题.21．函数()3cos3sin(0)f x x xωωω=+>在一个周期内的图像如图所示，A为图像的最高点，B 、C为图像与x轴的交点，且ABC为正三角形.（1）求ω的值；（2）求()f x的单调增区间；（3）若()035f x=且0102,33x⎛⎫∈-⎪⎝⎭，求()1f x+的值.【答案】（1）4πω=；（2）1028,833k k k Z⎡⎤-++∈⎢⎥⎣⎦；（376.【解析】（1）由()3cos3(0)f x x xωωω=+>，利用辅助角化简，再由ABC为正三角形，求得BC，求出周期，从而求得ω的值；（2）用整体代入法求正弦型函数的单调增区间；（3）先求()083f x=，再利用两角和的正弦公式求出()1f x+.【详解】（1）由已知可得()3cos 3f x x x x πωωω⎛⎫=+=+⎪⎝⎭，因为正三角形的高为4BC =,即42T =，8T =，284ππω==，()43f x x ππ⎛⎫=+ ⎪⎝⎭（2）令222432k x k ππππππ-+≤+≤+，k Z ∈，即1028833k x k -+≤≤+，k Z ∈， ∴()y f x =的单调增区间为1028,833k k k Z ⎡⎤-++∈⎢⎥⎣⎦，（3）由（1）有()00543ππ⎛⎫=+⎪⎝⎭=f x x 即04sin 435x ππ⎛⎫+= ⎪⎝⎭，由0102,33x ⎛⎫∈- ⎪⎝⎭，得0,4322x ππππ⎛⎫+∈- ⎪⎝⎭ 则03cos 435x ππ⎛⎫+=⎪⎝⎭()001443f x x πππ⎛⎫+=++ ⎪⎝⎭0434x πππ⎡⎤⎛⎫=++ ⎪⎢⎥⎝⎭⎣⎦432555⎫=+=⎪⎝⎭ 【点睛】本题考查了辅助角公式，正弦型函数的图象及性质，两角和差公式，属于中档题. 22．已知向量(2cos ,0)a x =，sin ,16b x π⎛⎫⎛⎫=-⎪ ⎪⎝⎭⎝⎭，若()f x a b =⋅. （1）求4f π⎛⎫⎪⎝⎭的值；（2）求函数()f x 的对称中心；（3）若方程102x m ⎛⎫-= ⎪⎝⎭在[]0,π上恰有两个不相等的实数根，求实数m 的取值范围.【答案】（1）12；（2）1,1222k k Z ππ⎛⎫+-∈ ⎪⎝⎭；（3）1,12⎡⎫+⎪⎢⎪⎣⎭. 【解析】先利用数量积的坐标表示，降次公式，辅助角公式化简()f x . （1）代入4x π=，计算4f π⎛⎫⎪⎝⎭；（2）整体代入法求正弦型函数的对称中心；（3）将方程102x m ⎛⎫-=⎪⎝⎭在[]0,π上恰有两个不相等的实数根，转化为sin ,[0,]6y x x ππ⎛⎫=-∈ ⎪⎝⎭与12y =+有两个不同交点，再结合正弦函数的图象性质，求出m 的范围. 【详解】1()2cos sin 2cos cos 62f x a b x x x x x π⎫⎛⎫=⋅=-=-⎪ ⎪⎪⎝⎭⎝⎭2111sin cos 2cos 2sin 22262x x x x x x π⎛⎫=-=--=-- ⎪⎝⎭11sin 4322f ππ⎛⎫⎛⎫=-= ⎪ ⎪⎝⎭⎝⎭ （2）令26x k ππ-=，k Z ∈即122k x ππ=+，k Z ∈， ∴()f x 的对称中心为1,1222k k Z ππ⎛⎫+-∈⎪⎝⎭（3）()162g x m x π⎛⎫=--+ ⎪⎝⎭， ()y g x =在[0,]π上恰有两个零点，即1,[0,2]26m x x π⎛⎫-+=-∈ ⎪⎝⎭有两个不等实根，即sin ,[0,]6y x x ππ⎛⎫=-∈ ⎪⎝⎭与12y =有两个不同交点，令,[0,]6t x x ππ=-∈则5sin ,,66y t t ππ⎡⎤=∈-⎢⎥⎣⎦，由正弦函数的图象性质，可知111222≤<，得211m≤<，即实数m的取值范围是2 1,12⎡⎫+⎪⎢⎪⎣⎭【点睛】本题考查了数量积的坐标表示，三角恒等变换，辅助角公式，正弦型函数的图象与性质，已知函数零点个数求参问题，属于中档题.。