第十章 方差分析
方差分析的基本思想

1
第一节 方差分析的基本思想
方差分析的基本思想是,首先将总 变异分解为几个部分,每部分与特 定的因素相联系。之后构造检验统 计量F,实现对总体均数的推断。 方差分析的应用条件是各组资料取 自正态分布,各总体方差齐同。
2
现以随机设计为例来说明方差分析基 本思想。
3
每个观察值与总均值的离均差平
,
MSTR SSTR / TR (10.5)
10
数学上可以证明
SST SSTR SSe (10.6)
,
,,
T
TR
e (10.7)
F MS TR MS e
(10.8)
11
式(10.8)反映了组间变异与组内变 异的比值,可以应用式对检验假设
H0: 1 2 c
H1: i(i=1,…,c)不全相等
不同处理组样本均数之间的差异称 为组间变异。产生组间变异的原因 一方面是个体变异,另一方面是各 组总体均数之间可能存在的实质性 差异差别。用组间离均差平方和反 映组间变异。
8
c
SSTR ni (xi x)2 (10.4) i 1
相应的自由度为 TR c 1
9
显然,组间离均差平方和的大小与自 由度有关。能够客观反映组间ST
( X ij x)2
i1 j1
(10.1)
相应的自由度为νT=N-1。
4
处理组内每个观察值之间的差异来源 于同一总体内的个体变异,称为组内
变异,可用组内离均差平方和表示:
c ni
SSe
( X ij xi ) 2 (10.2)
i1 j1
相应的自由度νe=N-c。 5
由于的大小与自由度有关,能够客观 反映组内变异的是组内均方:
医学科研中的统计方法(第十章)协方差分析

Y X
大学生 肺活量Y (ml) 身高X (cm) 3650 168.7 4300 170.8 4000 165.0 4150 169.0 4280 171.5 3450 166.5 3800 165.0 3400 165.0 4300 173.0 4050 169.0 4050 173.8 4100 174.0 3450 170.5 4300 176.0 3850 169.0 4150 176.0 3700 163.0 4100 172.5 3650 177.0 4050 173.0 3939
混 杂 因 素 ?
协 变 量 ?
处理因素 三种饲料
观察指标 体重增加量
干扰因素 实际进食量
研究男性篮球运动员与男性大学生的平均肺活 量的差异 由于肺活量与身高有一定的关系(一般来说肺活 量随身高增加而增大),而篮球运动员的身高高于大 学生。 因此在比较两组肺活量时的差异时,必须先验 证身高是否对肺活量有影响,并且符合协变量的条 件,如果是,要把身高作为协变量做协方差分析。
分组 Model 运动员 1 (Constant) 身高 大学生 1 (Constant) 身高
F 12.023
Sig. .001
结论 p = 0.001,差异有统计学意义。即不考虑身高对肺活量 的影响,篮球运动员与大学生的肺活量之差异有统计学意义。
二、作协方差分析
但是,在本例中,我们注意到两组的平均身高水平 不同,分别为 178.09 和170.42。而一般认为身高较高者 其肺活量亦较大。本例 X1> X 2 如果 X1 = X 2 则 Y1 与 Y2 之差应小于470。因此上述直接比较 Y1 与 Y2 差的假设检 验,不太合理。应当考虑身高为协变量作方差分析。 下面对本例作协方差分析,其步骤如下: ⑴ 作肺活量与身高的线性回归,验证肺活量与身 高存在线性回归,且回归系数近 似相同,即
统计学第十章答案解析

第十章习题10.1H0:三个总体均值之间没有显著差异。
H1: 三个总体均值之间有显著差异。
答:方差分析可以看到,由于P=0.1078>0.01, 所以接受原假设H0。
说明了三个总体均值之间没有显著差异。
10.2H 0 :五个个总体均值之间相等。
H1: 五个总体均值之间不相等。
P=1.02E-05<0.01, H0值之间不相等。
10.3H 0 :四台机器的装填量相等。
H1: 四台机器的装填量不相等答:方差分析可以看到,由于P=0.00068<0.01, 所以拒接原假设H0。
说明了四台机器装填量不相同。
10.4H 0 :不同层次管理者的满意度没有差异。
H1: 不同层次管理者的满意度有差异P=0.000849<0.05, H0理者的满意度有差异。
10.5H0:3 个企业生产的电池平均寿命之间没有显著差异。
H1: 3 个企业生产的电池平均寿命之间有显著差异单因素方差分析多重比较因变量: VAR00002*. 0.05答:方差分析可以看到,由于P=0.00031<0.01, 所以拒接原假设H0。
说明了不同 3 个企业生产的电池平均寿命之间有显著差异。
通过SPSS分析(1,2,3代表A,B,C公司),通过显著性对比可知道A和B以及B和C 公司有差异。
10.6H0:不同培训方式对产品组装的时间没有显著影响。
答:方差分析可以看到,由于P=0.00196<0.05, 所以拒接原假设H0。
说明了不同培训方式对产品组装的时间没有显著影响。
10.8H 0:u 1=u 2=u 3=u 4=u 5 H 1:u i (i=1,2,3,4,5) 不全相等 H 0:u 1=u 2=u 31i对于行因素, P=0.000236<0.01, 所以拒绝原假设。
说明不同供应商生产的轮胎对磨损 程度有显著影响。
对于列因素, p=2.39E-06<0.01 ,所以拒绝原假设,说明不同车速对磨损程度有显著 影响。
统计学第十章(方差分析)

第十章方差分析一、单项选择题:1.在方差分析中,( )反映的是样本数据与其组平均值的差异。
A.总离差平方和B.组间离差平方和C.抽样误差D.组内离差平方和2.∑∑=⎪⎪⎭⎫⎝⎛k1i 21-j ij n i i x x ——是( )。
A.组内平方和 B.组间平方和C.总离差平方和D.因素B 的离差平方和3.∑∑=⎪⎪⎭⎫⎝⎛k1i 21-j ij n i i x x ——是( )。
A.组内平方和 B.组间平方和 C.总离差平方和D.总方差4.单因素方差分析中,计算F 统计量,其分子与分母的自由度各位( )。
A.k ,nB.k ,n-kC.k-1,n-kD.n-k ,k-15.方差分析基本原理是( )首先提出的。
A.费雪B.皮尔逊C.泰勒D.凯特勒6.组间离差平方和反映的是( )。
A.抽样误差B.系统误差C.随机误差D.总误差7.组内离差平方和反映的是( )。
A.抽样误差B.系统误差C.随机误差D.总误差8.单因素方差分析的对立和假设是( )。
A.μμμk 21===B.差距不显著,,,μμμk 21C.不是全部相等,,,μμμk 21D.全部不相等,,,μμμk 219.单因素方差分析的零假设是( )。
A.μμμk 21===B.差距不显著,,,μμμk 21C.不是全部相等,,,μμμk 21D.全部不相等,,,μμμk 2110.在方差分析中,若F k -n 1,-k 05.0F )(>,则统计推论是( )。
A.各组间的总体均数不全相等B.各组间的总体均数都不相等C.各组间的样本均数都不相等D.各组间的总体方差不全相等11.为研究温度对菌种生产率的影响,将温度控制在三个水平上,则应该使用( )。
A.单因素方差分析B.双因素方差分析C.独立样本t 检验D.三因素方差分析12.为分析学历对收入的影响,调查了50个职工,按学历高低分成四组,使用单因素方差分析,则F 检验临界值为( )。
管理统计学10 第十章 方差分析

问:不同的方案是否对汽车销售量产生影响。
星蓝海学习网
10.1 方差分析的内容和思想
10.1.1 方差分析的内容
这是一个方差分析问题。即对四种方案下的电话交易频数的均值是否相等进 行检验。 由于汽车是同一厂家生产的,它们的质量、外形设计、价格、内装修等所有
可能影响销售量的因素全部相同,如果检验结果 1,2,3,4
2
(xij - x)
2
(xij x j )
2
(x j x)
即
SST = SSE+SSA
关键是如何确定各离差平方的自由度:
对总离差平方和(SST)来说,它是n个离差平方之和,共同拥有一个
平均数,也就失去了一个自由度,其自由度应为n—1。因为它只有一
个约束条件,即 SST
(xij - x) 0
星蓝海学习网
10.2 单因素方差分析
10.2.2 F分布与F值的计算
对水平离差平方和(SSA)来说,它是4组水平(即四种不同方案)离差平方
(x j - x)2之和,共同拥有一个平均数,也失去1个自由度,其自由度为4-1。
用r表示组数,则有 r = 4,4-1 = r-1。它也有一个约束条件,即要求:
为了将方差分析的主要过程表现的更清楚,通常把有关计算结果列成方差分 析表,如表10-3所示。
表10-3 方差分析表
星蓝海学习网
10.2 单因素方差分析
10.2.3 样本容量不等下方差分析
进行方差分析时,各个水平下的样本容量可以相同,也可以不同。 进行方差分析时,可以把方差分析的因素放在列的位置,也可以放在行的位 置,但通常放在列的位置。这样与计算机中数据库的结构相一致,便于计算 机处理。
第10章方差分析习题解答

第10章方差分析习题解答一.选择题1. 下列关于方差分析的说法不正确的是( A ).A. 方差分析是一种检验若干个正态分布的均值和方差是否相等的一种统计方法.B. 方差分析是一种检验若干个独立正态总体均值是否相等的一种统计方法.C. 方差分析实际上是一种F 检验.D. 方差分析基于偏差平方和的分解和比较.2. 设,1,2,,;1,2,,ij i ij i X i a j n µε=+== ,2(0,)ij i N εσ ,且ij ε相互独立,进行单因子方差分析是( C ) . A . 对假设012:a H µµµ=== 作检验. B . 对假设222012:a H σσσ=== 作检验. C . 假定2(0,)ij N εσ ,2σ为未知,对假设012:a H µµµ=== 作检验. D . 假定2(0,)ij N εσ 12a µµµµ==== ,µ为未知,对假设222012:a H σσσ=== 作检验.3. 对因子A 取r 个不同的水平进行试验,每个水平观测t 次,结果,1,2,,,1,2,,ij y i r j t == .对()ij r t y ×的偏差有分解:2211111()()()ˆr t r trTijij i i E A i j i j i SS y y y y t y y SS SS ⋅⋅======−=−+−=+∑∑∑∑∑ 其中11111, r t ti i ij i j j y y y y rt t ⋅=====∑∑∑对假设012:r H µµµ=== 进行检验时,如下说法错误 的是( B ) .A .E SS 表示0H 为真时,由随机性引起的y ij 的波动.B .A SS 表示0H 为真时,所引起的由各水平间ij y 波动.C . E SS 表示各水平上随机性误差的总和.D . A SS 表示各水平之间系统误差的总和.4. 对某因素进行方差分析,由所得试验数据算得下表: 方差来源 平方和自由度F 值组间 4623.7 4 组内 4837.25 15 总和9460.9519采用F 检验法检验,且知在0.05α=时F 的临界值0.05(4,15) 3.06F =,则可以认为因素的不同水平对试验结果( B ).A. 没有影响.B. 有显著影响.C. 没有显著影响.D. 不能作出是否有显著影响的判断.5. 设在双因子A 和B 的方差分析模型:ij i j ij X µαβε=+++,10ai i α==∑,10bjj β==∑,2(0,)ij N εσ ,且ij ε相互独立,检验假设:0112:,0rH ααα==== ,和0212:,0sH βββ==== 检验时,下列结论中错误的是( D ) . A . 若拒绝域01H ,则认为因子A 的不同水平对结果有显著影响. B . 若拒绝域02H ,则认为因子B 的不同水平对结果有显著影响.C . 若不拒绝01H 和02H ,则认为因子A 与B 的不同水平的组合对结果无显著影响.D . 若不拒绝01H 或02H ,则认为因子A 与B 的不同水平组合对结果无显著影响.6. 某结果可能受因素A 及B 的影响.现对A 取4个不同的水平, B 取3个不同水平,对A 与B 每一种水平组合重复二次试验,对观测结果的双因子有交互作用的方差分析模型计算得:44.3A SS =,11.5B SS =,27.0A B SS ×=,65.0E SS =.且0.05(2,12) 3.89F =,0.05(3,12) 3.49F =,0.05(6,12) 3.00F =,则在显著性水平0.05α=时,检验的结果是( B ).A. 只有A 因素对结果有显著性影响.B. 只有B 因素对结果有显著性影响.C. 只有交互作用对结果有显著性影响.D. A 、B 及A 和B 的交互作用都对结果无显著性影响.7.设某结果可能受因素A 及B 的影响,现对A 取4个不同的水平, B 取3个不同的水平配对作试验,按双因子方差分析模型的计算结果: 5.29A SS =, 2.22B SS =,7.77T SS =.且0.05(3,6) 4.80F =,0.05(2,6) 5.10F =,则在显著性水平0.05α=时,检验的结果是( C ). A. 只有A 因素的不同水平对结果有显著影响. B. 只有B 因素的不同水平对结果有显著影响.C. A 的不同水平及B 的不同水平都对结果有显著影响.D. A 、B 因素不同水平组合对结果没有显著影响.8. 对因子A 取r 个不同水平,因子B 取s 个不同水平,A 与B 的每种水平组合重复次试验后,对结果进行双因子有重复试验的方差分析,则以下关于各偏差平方和自由度的结论错误的是( D ).A. A 因子的偏差平方和A SS 的自由度为.B.B 因子的偏差平方和B SS 的自由度为.C. 交互作用的偏差平方和A B SS ×的自由度为(1)(1)r s −−.D. 误差平方和E SS 的自由度为(1)(1)(1)r s t −−−. 二.填空题9. 进行单因素方差分析的前提之一是要求表示r 个水平的r 个总体的方差 相等 . 10. 进行方差分析时,将离差平方和211()in r Tiji j SS XX ===−∑∑表示为TA E SS SS SS =+,其中A SS =21()ri ii n XX =−∑,E SS =211()in riji i j XX ==−∑∑.11. 进行方差分析时,将离差平方和211()in rT iji j SS XX ===−∑∑表示为TA E SS SS SS =+,则2ESS σ~2(n r)χ−.12. 进行方差分析时,如果所有2~(,)ij X N µσ,则222111()in r T iji j SSXX σσ===−∑∑~21(1)ri i n χ=−∑.13. 进行方差分析时,选取统计量2 1211()()(1)()(1)()i ri i i A n rE ij i i j n r n X X SS r FSS n r r X X ===−−−==−−−∑∑∑,则F ~(r 1,n r)F −−.14. 在单因素方差分析中,如果因素A 有a 个水平,其中在第i 个水平下作了i n 次试验,12a n n n n +++= ,总的偏差平方和T SS 分解为A SS 和E SS ,则A SS 的自由度为1a −,E SS 的自由度为n a−,检验统计量A F =/(1)/(1)A E SS a SS n −−,若A F 大于给定的临界值水平,则说明 因素A 的a 个水平对试验指标有显著影响 .15. 某企业准备用三种方法组装一种新的产品,为确定哪种方法每小时生产的产品数量最多,随机抽取了30名工人,并指定每个人使用其中一种方法.在显著水平α=0.05下,通过对每个工人生产的产品数量进行方差分析得到下面的部分结果.请完成方差分析表,由于 1.70 3.354131F =< 或P=0.245946>0.05 ,可判断不同的组装方法对产品数量的影响 不显著 (显著,不显著). 差异源 SS df MS F P-value F crit 组 间 420 2 210 1.70 0.245946 3.354131 组 内 3836 27 142.07 — — — 总 计425629————16. 在双因素方差分析中,因素A 有三个水平,因素B 有四个水平,每个水平搭配各做一次试验.请完成下列方差分析表,在显著水平α=0.05下,由于0.05(25.7,6)508.1A F F ==>,可判断因素A 的影响 显著 (显著,不显著);由于0.05(35.8,6)405.8B F F ==>,可判断因素B 的影响 显著 (显著,不显著). 来 源 平方和 自由度 均方 F 值 因素A 54 2 27 5.78 因素B 82 3 27.33 5.85 误差e 28 6 4.67 — 总 和16411——17. 在某种化工产品的生产过程中,选择3种不同的浓度:1A =2%,2A =4%,3A =6%;4种不同的温度:1B =100C ,2B =240C ,3B =380C ,4B =520C ;在每种浓度与温度配合下各做两次试验,观测产品的收取率.现由试验数据计算出如下结果:总偏差平方和147.8333T SS =,因素A (浓度)的偏差平方和44.3333A SS =,因素B (温度)的偏差平方和11.50B SS =,交互作用A B ×的偏差平方和27.00A B SS ×=,则误差平方和E SS = 65 ,检验统计量A F = 4.09 , B F = 0.708 ,A B F ×= 0.831 ,在显著性水平0.05α=下.由于0.05(2,4.0912) 3.89A F F ==>,可判断因素A 的影响 显著 (显著,不显著);由于0.05(30.7,12)908 3.4B F F ==<,可判断因素B 的影响 不显著 (显著,不显著);由于0.050.831(6,12) 3.00A B F F ×==<,可判断因因素A 与因素B 的交互作用影响不显著 (显著,不显著).18. 为了分析不同操作方法生产某种产品节约原料是否相同,在其余条件尽可能相同的情况下,安排了五种不同的操作方法生产某种产品,测量原料节约额,得到实验结果如下表所示.在显著水平α=0.05下,由于0.00410.05P =<,可判断不同操作方法生产某种产品节约原料 有 (有,无)显著差异.差异源 SS df MS F P-value F crit 操作方法55.5370 4 13.8842 6.05900.00414.8932组内 34.3725 15 2.2915总计89.90951919. 对腐乳的味道、口感等只能通过感观来确定其产品质量.为了检验专业评议员对腐乳评分标准是否存在显著差异,不同的腐乳质量是否存在显著差异,得到4位专业评议员对4种腐乳的评分结果,得到实验结果如下表所示.在显著水平α=0.05下,由于0.0005690.05P =<,可判断专业评议员对腐乳评分标准 有 (有,无)显著差异;由于 1.020.0505E P −=<,可判断不同的腐乳质量 有 (有,无)显著差异.差异源 SS df MS F P-value F crit 专业评议员54 3 18.0000 16.2 0.000569 3.8625 腐乳 148 3 49.3333 44.4 1.02E-053.8625误差 10 9 1.1111总计2121520.为了分析时段、路段以及时段与路段的交互作用对行车时间的影响,某市一名交通警察分别在两个路段和高峰期与非高峰期驾车试验,共获得20个行车时间数据,得到实验结果如下表所示.在显著水平α=0.05下,由于 5.700.056E P =<−,可判断时段因素对行车时间的影响 显著 (显著,不显著);由于0.0001.0805P =<,可判断路段因素对行车时间的影响 显著 (显著,不显著);由于0.9118.0105P =>,可判断时段与路段因素对行车时间交互作用的影响 不显著 (显著,不显著). 差异源SSdfMS F P-value F crit时段 174.05 1 174.05 44.0632 5.7E-06 4.49399 路段 92.45 1 92.45 23.4050 0.00018 4.49399 交互 0.05 1 0.05 0.01260.911814.49399内部 63.20 16 3.95总计329.7519三.应用计算题21.比较四种肥料1234,,,A A A A 对作物产量的影响,每一种肥料做5次试验,得产量(公斤/小区)如下表.试检验四种肥料对产量的影响有无显著差异?肥料 1A2A3A4A样 本 观 测 值5.56.5 8.0 5.5 5.0 6.0 6.5 6.5 6.07.0 7.5 6.0 4.5 6.5 7.0 5.0 7.05.56.05.5解:设使用四种不同肥料后作物的产量2~(,),1,2,3,4i i Y N i µσ=.则需检验的问题为43210:µµµµ===H ,:1H 4321,,,µµµµ不全相等.首先由样本直接计算有关值如下表作物产量计算表肥料样本观测值行和i A T1A 5.5 5.0 6.0 4.5 7.0 28 2A 6.5 6.0 7.0 6.5 5.5 31.5 3A 8.0 6.5 7.5 7.0 6.0 35 4A5.56.56.05.05.528.5 411in ij i j T x ===∑∑1232756.45T C n ==4211771.5756.4515.05in Tiji j SS xC ===−=−=∑∑22222412831.53528.5756.45 6.255555iA A i iT SS C n ==−=+++−=∑15.05 6.258.8E T A SS SS SS =−=−=列出相应的方差分析表.作物产量方差分析表方差来源 平方和 自由度 均方MS F 值临界值因素A 6.25 3 2.08 3.79 0.05(3,16) 3.24F = 0.01(3,16) 5.29F =误差 8.8 16 0.55 总和15.0519由于0.053.79(3,16)A F F =>,认为四种肥料对产量有显著影响.22.取四个种系未成年雌性大白鼠各三只,每只按一种剂量注射雌激素,一月后,解剖秤其子宫重量,结果如下表.试检验不同剂量和不同白鼠种系对子宫重量有无显著影响?解设注射不同剂量的不同白鼠种系的子宫重量2~(,),1,2,3,4ij i j Y N i µαβσ++=;1,2,3j =.则需检验的问题为01234:0A H αααα==== ,11234:,,,A H αααα不全为零 0123:0B H βββ===,1123:,,B H βββ不全为零为了计算各平方和,列出如下表.子宫重量计算表本题中4,3,12a b n ab ====22109810046712T C n ===4321111354210046713075Tiji j SS xC ===−=−=∑∑242222.11(367225314192)1004676457.66733i Ai T SS C ==−=+++−=∑ 23.22211(260358480)100467607444j Bj T SS C==−=++−=∑130756457.6676074543.33E T A B SS SS SS SS =−−=−−=得到相应的无交互作用双因素方差分析表.子宫重量双因素方差分析表方差来源 平方和 自由度 均方MS F 值 临界值因素A(种系) 6457.6732152.5623.770.05(3,6) 4.76F =0.01(3,6)9.78F =因素B60742303733.540.05(2,6) 5.14F =(剂量)0.01(2,6)10.92F =误差E 543.33 6 90.56 总和1307511因为0.0123.77(3,6)A F F =>,认为种系对子宫重量有极显著影响;0.0133.54(2,6)B F F =>,认为剂量对子宫重量有极显著影响.由此可知,种系和剂量对子宫重量都有极显著影响.23.为检验广告媒体和广告方案对产品销售量的影响,一家营销公司做了一项试验,考察三种广告方案和两种广告媒体,获得的销售量数据如下表.试检验广告方案.广告媒体或其交互作用对销售量的影响是否显著.广告方案广告媒体报纸电视 A8,12 12,8 B22,14 26,30 C10,1818,14解 设不同广告方案和广告媒体的产品销售量2~(,)ij i j ij Y N µαβγσ+++,1,2i =,3;1,2j =.则需检验的问题为0111221223132:0A B H γγγγγγ×======,1111221223132:,,,,,A B H γγγγγγ×不全为零. 0123:0A H ααα===,1123:,,A H ααα不全为零, 012:0B H ββ==,112:,B H ββ不全为零, 本题计算过程如下表:销售量数据方差分析计算表2A22,14 (36) 26, 30(56) 9284643A10,18 (28)18, 14(32)603600 列和..j x84 108 154 136642..j x705611664 1872032221113616ijti j t x====∑∑∑32221111()307212ijt i j t x ====∑∑∑ 322.117040ij i j x===∑∑36163072544T SS =−=11336430723444A SS =×−=1187203072486B SS =×−=17040307234448562A B SS ×=×−−−=得如下方差分析表:销售量数据双因素方差分析表方差来源 平方和 自由度 均方和 F 值 广告方案A 344 2 172 10.75 广告媒体B 48 1 48 3 交互效应A B ×56 2 28 1.75 误差 96 6 16 总和54411查表得0.05(2,6) 5.14F =,0.05(1,6) 5.99F =,因此,广告方案对产品销售量的影响显著;广告媒体对产品销售量的影响不显著;广告方案和广告媒体对产品销售量没有交互作用.。
最新人大版_贾俊平_第五版_统计学_第10章_方差分析PPT课件

பைடு நூலகம்
10.1.3 方差分析中的基本假定 1.每个总体都应服从正态分布
• 对于因素的每一个水平,其观察值是来自服从正态 分布总体的简单随机样本。
• 比如,每种颜色饮料的销售量必需服从正态分布 2.各个总体的方差必须相同
• 对于各组观察数据,是从具有相同方差的总体中抽 取的
10.2 单因素方差分析
10.2.1 数据结构
观察值 ( j )
1 2 : : n
水平A1
x11 x21 : : xn1
因素(A) i
水平A2
…
x12
…
x22
…
:
:
:
:
xn2
…
水平Ak
x1k x2k : : xnk
10.2.2 分析步骤
1.提出假设
• 一般提法 H0: m1 = m2 =…= mk (因素有k个水平) H1: m1 ,m2 ,… ,mk不全相等
身所造成的,后者所形成的误差是由系统性因素造成的, 称为系统误差
2.两类方差 (1)组内方差(误差平方和 、残差平方和、 SSE)
– 因素的同一水平(同一个总体)下样本数据的方差 – 比如,无色饮料A1在5家超市销售数量的方差 – 组内方差只包含随机误差
(2)组间方差(因素平方和、SSA)
– 因素的不同水平(不同总体)下各样本之间的方差 – 比如,四种颜色饮料销售量之间的方差 – 组间方差既包括随机误差,也包括系统误差
水平A ( i ) 粉色(A2) 橘黄色(A3)
绿色(A4)
1
26.5
31.2
27.9
30.8
第十章协方差分析

第十章协方差分析协方差分析(Analysis of Covariance,简称ANCOVA)是一种多元统计方法,用于在考虑一个或多个共变量(covariates)的情况下,评估一个或多个自变量(independent variables)对于因变量(dependent variable)的影响。
在实际研究中,常常会遇到一些与因变量相关但未被考虑的其他变量,而这些变量可能会对因变量与自变量之间的关系产生干扰。
ANCOVA通过引入共变量来修正这种干扰,从而提高自变量对因变量的解释效果。
ANCOVA的基本思想是通过构建一个线性回归模型,将自变量、共变量以及其交互项作为预测变量,将因变量作为被预测变量,进而评估自变量对因变量的影响。
在这个过程中,共变量的作用是控制或削弱对因变量的影响,从而更准确地评估自变量的效果。
在进行ANCOVA分析之前,需要满足一些前提条件。
首先,因变量和自变量之间应该存在线性关系。
其次,各个共变量与自变量和因变量之间也应该存在线性关系。
最后,自变量与因变量之间的差异不能完全由共变量解释。
在进行ANCOVA分析时,需要进行一些统计检验来评估因变量与自变量、共变量之间的关系。
例如,可以计算自变量和因变量之间的相关系数,使用方差分析来比较组间差异,以及计算共变量与因变量的相关系数等。
ANCOVA的优势在于可以更准确地评估自变量对因变量的影响,同时控制其他可能干扰的因素。
此外,ANCOVA还可以用于提高实验的统计效力,减少研究中可能出现的偏差。
然而,ANCOVA也存在一些局限性。
首先,ANCOVA要求共变量与自变量和因变量之间存在线性关系,因此如果数据不符合线性假设,则ANCOVA可能不适用。
其次,ANCOVA要求样本量足够大,才能保证结果的可信度。
此外,ANCOVA对于共变量和自变量之间的交互作用也存在敏感性。
总结来说,协方差分析是一种有效的多元统计方法,可以用于控制共变量的干扰,评估自变量对因变量的影响。
第十章 方差分析
dft n 1
SSt MSt dft
SSw X X
SSt SSb
随机误差
SSw dfw n k , MSw dfw
个体差异 实验误差
第二节 方差齐性检验
一、意义
• 定义:检验各总体方差是否一致的统计方法。
目的:保证样本组的同质性
假设: Ho: σ12=σ22 =…=σk2 Ha:至少两个总体方差有显著差异。
组间变异 实验因素 随机误差
组间变异 ? 组内变异
X X
t
总变异
X
i
Xt
X X
i
组内变异
随机误差 实验误差 个体差异
二、基本过程
• 总变异: – 总方差、变异数(V)或均方(MS)
S
2 t
X X
t
2
N
X X
t
2
dft
(一)总变异的分解
S
2 t
X X MS
t t
2
dft
SSt dft
2
S
2 b
MSb
SSb X X
t
dfb
S MS w
2 w
X X
dfw
dfb
2
SSw dfw
例10-3
SSt 48 6 MSt 8 dft
SSb 42 MSb 21 dfb 2
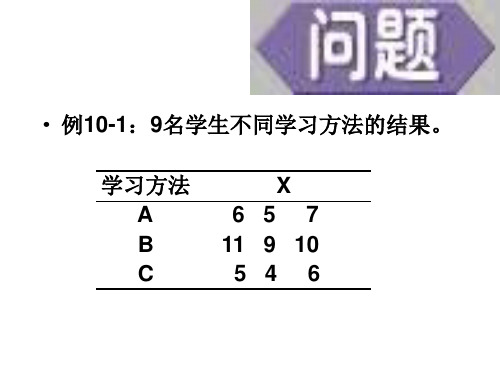
• 例10-1:9名学生不同学习方法的结果。 学习方法 A B C X 6 5 7 11 9 10 5 4 6
基本原理与过程 方差齐性检验 完全随机设计方差分析 随机区组设计方差分析 多重比较
第10章单因素方差分析

第10章单因素方差分析单因素方差分析(0ne-Way ANOV A),又称一维方差分析,它能够对单因素多个独立样本的均数进行比较,可以用10种检验方法对变量间的均数进行两两比较(即多重比较检验)并给出方差分析表,还可以作出5种类型图形(Type of plots)和2种均数图形(Means plot options)10.1 单因素方差分析的计量资料[例10—1] 某社区随机抽取了30名糖尿病患者、IGT异常人和正常人进行载脂蛋白(mg/dL)测定,结果示于表10—1。
试问3组人群的载脂蛋白测定结果含量是否相同?(倪宗瓒.卫生统计学.第4版,北京:人民卫生出版社,2001.50)本例是一个完全随机设计的单因素方差分析。
已建立SAS数据集文件并保存Sasuser.onewav4。
(1)进入SAS/Win(v8)系统,单击Solutions-Analysis-Analyst,得到分析家窗口。
(2)单击File-open By SAS Name—Sasuser-0neway4—0K,调入数据文件。
(3)在“分析家”窗口单击Statistics-ANOV A-One way ANOV A,得到图10—1所示对话框。
本例因变量(Dependent)为A(载脂蛋白),单击A—Dependent。
自变量(1ndependent):B(3种人的组别),单击B—Independent 。
图10.1 0ne—way ANOV A:0neway4(单因素方差分析)对话框(4)单击Tests按钮,得到图10—2所示对话框。
在此对话框的ANOV A(F—检验)选项中可进行如下设置。
Analysis of variance,方差分析。
Welch’s variance-weighted ANOV A,威尔奇方差—权重方差分析。
Tests for equal variance,相等方差检验,即方差齐性检验。
Barlett’s test,巴特尼特检验。
第十章 方差分析

表中每个水平的平均值与 总均值之间差距的平方和
构造检验的统计量
(三个平方和的关系)
总离差平方和(SST)、组间平方和 (SSA)、
组内平方和(SSE)之间的关系:
x
k i1 j1
3;xji xi
2 k 2 k i1 i1 j1
第一自由度df1=k-1、第二自由度df2=n-k 相应的 临界值 Fa ; 若F>Fa ,则拒绝原假设H0 ,表明均值之间的 差异是显著的,所检验的因素对观察值有显著 影响; 若F<Fa ,则不能拒绝原假设H0 ,表明所检验 的因素对观察值没有显著影响 ;
统计决策
(标准二)
如果概率P值小于显著性水平α,则拒绝零 假设,认为控制变量不同水平下观测变量 各总体均值存在显著差异,表明控制变量 对观测变量有显著影响; 如果概率P值大于显著性水平α,则不能拒 绝零假设,认为控制变量不同水平下观测 变量各总体均值不存在显著差异,表明控 制变量对观测变量没有显著影响;
方差分析的基本思想和原理
(两类方差)
数据的误差用平方和(sum of squares)表示,称为 方差 组内方差(within groups)
因素的同一水平(同一个总体)下样本数据的方差 比如,采用报纸广告时产品销量的方差 组内方差只包含随机误差 因素的不同水平(不同总体)下各样本之间的方差 比如,四种广告形式之间的产品销售量的方差 组间方差既包括随机误差,也包括系统误差
如果组间均方显著大于组内均方,说明各水平(总
体)之间的差异不仅有随机误差,还有系统误差; 表明观测变量的变动主要是由控制变量引起的。
构造检验的统计量
(计算检验统计量 F )
十章节方差分析

1 q
q j 1
ij
j
j
1 p
p
ij
j 1
,
ij (ij ) i j
称 为理论总均值, 表达所考虑旳 pq个总体
数学期望旳总平均;称i为原因 A 旳第i 个水平
Ai 对试验成果旳效应; 称 j为原因 B 旳第 j个 水平 Bj 对试验成果旳效应。 ij 反应了水
平搭配 Ai Bj 对试验成果旳总效应, ij 是总效
)
(
p
1)(q
1)
2
r
2 ij
i1 j1
定理15.5 对模型(**)有
(1) SE , SA , SB , SAB相互独立。
(2)
SE
2
~
2
(
pq(r
1)).
(3)
当H
成立时,
01
SA
2
~ 2( p 1).
(4)
当H
成立时,
02
SB
2
~
2(q 1).
(5)
当H
成立时,
03
S AB
2
~ 2(( p 1)(q 1)).
E(SE ) ( p 1)(q 1) 2
p
E(SA
)
(
p
1)
2
q
2 i
i 1
q
E(SB)
(q 1)
2
p
2 j
j1
定理15.3 对模型(**)有
(1) SE , SA , SB相互独立。
(2)
SE
2
~
2 ((
p
1)(q
1)).
(3)
当H
成立时,
第10章-方差分析PPT课件

1.正态性的检验
各组数据的直方图 峰度系数、偏度系数 Q-Q图, 非参数检验
2021/3/9
2.等方差性的检验
经验方法:计算各组数据的标准差,如果最大值 与最小值的比例小于2:1,则可认为是同方差的。 最大值和最小值的比例等于1.83<2
Levene检验 *
N
均值 标准差
第10章 方差分析
2021/3/9
学习目标
掌握方差分析中的基本概念; 掌握方差分析的基本思想和原理; 掌握单因素、双因素方差分析的应用条件、
意义及计算方法; 熟悉多重比较方法的意义及方法; 掌握用Excel,spss进行方差分析的操作
方法。
2021/3/9
一、方差分析引论
为什么要进行方差分析?
2021/3/9
(续)组间方差和组内方差
组间离差平方和
k
SSA ni(xi x)2 i1
组内离差平方和
k ni
SSE
(xij xi)2
பைடு நூலகம்i1 j1
组间方差
MSA SSA k 1
2021/3/9
受因素A和 随 机
因素的影响
组内方差
MSE SSE nk
只受随机 因素的影响
(续)方差分析的基本思想
F=
组间方差 MSA SSA k 1
组内方差 MSE SSE
nk
如果因素A的不同水平对结果没有影响,那么在组间方差中 只包含有随机误差,两个方差的比值会接近1
如果不同水平对结果有影响,组间方差就会大于组内方差, 组间方差与组内方差的比值就会大于1
当这个比值大到某种程度时,就可以说不同水平之间存在显 著差异,或者说因素A对结果有显著影响。
第10章 方差分析

郑州轻工业学院数学与信息科学系第十章:方差分析概率统计教研组方差分析是英国大统计学家费歇尔(R.A.Fisher)在20世纪20年代创立的.起初用于农田间试验结果的分析,随后迅速发展完善,被广泛应用于在工、农业生产,经济、管理领域,工程技术和科学研究中.方差分析与回归分析方法有许多相似之处,但又有本质区别,回归分析研究两个或多个数值型变量之间的关系,而方差分析是研究分类变量对数值型变量的影响,从形式上看,方差分析是比较多个总体均值是否相等,但本质上它所研究的是变量之间的关系.本章学习单因素方差分析和双因素方差分析的基本理论和方法.●【营销策略问题】某苹果汁厂家开发了一种新产品——浓缩苹果汁,一包该果汁与水混合可产生1升的普通苹果汁.该产品有三点特性可以吸引消费者的注意:1.它比目前市场销售的罐装苹果汁方便.2.由于市场上的罐装苹果汁事实上也是通过浓缩果汁制造而成,因此新产品的质量至少不会差于罐装果汁.3.新产品的生产成本要略低于罐装苹果汁.营销经理需要决定的是如何宣传这种新产品,她可以通过强调产品的便利性、高品质或价格优势的广告来推销,还可以使用两种媒体中的一种来刊登广告:电视和报●【营销策略问题】为了决定采用何种广告战略,她分别在6个小城市开展试验.在城市1,营销的重点是宣传浓缩果汁的便利性(例如很方便地就可以从商店搬回家,占用更少的冰箱空间等),广告采用电视形式;在城市2,营销的重点依然是便利性,但广告采用报纸形式;在城市3,营销的重点是大力宣传产品的质量(画面上“普通的”购买者正在讨论果汁的口味如何纯正),广告采用电视形式;●【营销策略问题】在城市4,营销的重点也是质量,但广告采用报纸形式; 城市5和6的营销重点都是产品的另一亮点——相对较低的成本,但城市5采用电视形式,而城市6采用报纸形式.记录下每个城市10周中每周的销售情况.数据如表10-1所示(1-6列分别是每个城市的10个观测值).●【营销策略问题】表10-1 不同营销策略及广告媒体下的销售情况城市1城市2城市3城市4城布5城市6491464677689575803712559627650614584558759590704706525447557632652484498479528683576478812624670760836650565546534690628583708444657548798536546582557579497579616672474644841795587 从这些数据来看:(1)采用不同的营销策略对销售是否有显著的差异?【营销策略问题】表10-1 不同营销策略及广告媒体下的销售情况城市1城市2城市3城市4城布5城市6491464677689575803712559627650614584558759590704706525447557632652484498479528683576478812624670760836650565546534690628583708444657548798536546582557579497579616672474644841795587(2)采用不同的广告媒体对销售是否有显著的差异?(3)不同营销策略与不同广告媒体之间有无交互作用?主要内容§10.1方差分析中的基本概念§10.2单因素方差分析§10.3双因素方差分析在实际问题中,影响一个数值型随机变量的因素一般会有很多,例如影响农作物产量的因素就有种子品种,肥料、雨水等;影响化工产品的产出率的因素可能有原料成分、剂量、催化剂、反应温度、机器设备和操作水平等;影响儿童识记效果的因素有教学材料、教学方法等.为了找出影响结果(效果)最显著的因素,并指出它们在什么状态下对结果最有利,就要先做些试验,然后对测试的数据进行统计推断,方差分析就是对实测数据进行统计分析,鉴别各个因素对试验结果影响程度的方法.方差分析采用的方法是通过检验各总体的均值是否相等,来判断分类型自变量对数值型因变量(响应变量)是否有显著影响.由于检验各总体的均值是否相等的方法是通过计算分析观测数据的变差而实现的,所以称之为方差分析.当方差分析中只涉及一个分类型自变量时,称为单因素方差分析,当涉及两(多)个分类自变量时称为双(多)因素方差分析.●10.2.1单因素方差分析的问题单因素方差分析用来检验根据某一个分类变量得到的多个分类总体的均值是否相等.下面以一简例说明方差分析的原理.10.2.1单因素方差分析的问题【例10-1】某化肥生产商要检验三种新产品的效果,在同一地区选取18块大小相同,土质相近的农田中播种同样的种子,用等量的甲乙丙化肥各施于六块农田,试验结果每块农田的粮食产量如下所示.产量甲化肥504649524848乙化肥495047474649丙化肥515049465050根据试验数据推断甲乙丙三种化肥的肥效是否存在差异●10.2.1单因素方差分析的问题【例10-1】根据试验数据推断甲乙丙三种化肥的肥效是否存在差异本例中,只考虑化肥这一个因素(记为A )对粮食产量的影响,三种不同的化肥称为该因素的三个不同水平(分别记为A 1,A 2,A 3).从表中数据看出,即使是施同一种化肥,由于随机因素(温度,湿度等)的影响,产量也不同.因而有:产量甲化肥504649524848乙化肥495047474649丙化肥51504946505010.2.1单因素方差分析的问题【例10-1】根据试验数据推断甲乙丙三种化肥的肥效是否存在差异(1)粮食产量是随机变量,是数值型的变量;(2)把同一化肥(A 的同一水平)得到的粮食产量看作同一总体抽得的样本,不同化肥下的测得粮食产量视为不同总体下抽得的样本,故表中数据应看成从三个总体X 1,X 2,X 3中分别抽了容量为6的样本的观测值.产量甲化肥504649524848乙化肥495047474649丙化肥515049465050●10.2.1单因素方差分析的问题【例10-1】根据试验数据推断甲乙丙三种化肥的肥效是否存在差异推断甲乙丙三种化肥的肥效是否存在差异的问题,就是要辨别粮食产量之间的差异主要是由随机误差造成的,还是由不同化肥造成的,这一问题可归结为三个总体是否有相同分布的讨论.产量甲化肥504649524848乙化肥495047474649丙化肥515049465050●10.2.1单因素方差分析的问题【例10-1】根据试验数据推断甲乙丙三种化肥的肥效是否存在差异由于在实际中有充分的理由认为粮食产量从正态分布,且在安排试验时,除所关心的因素(这儿是化肥)外,其它试验条件总是尽可能做到一致,这就使我们可以认为每个总体的方差相同,即X i ~N (μi ,σ2),i =1,2,3.产量甲化肥504649524848乙化肥495047474649丙化肥515049465050●10.2.1单因素方差分析的问题【例10-1】根据试验数据推断甲乙丙三种化肥的肥效是否存在差异因此,推断三个总体是否具有相同分布的问题就简化为:检验几个具有相同方差的正态总体均值是否相等的问题,即只需检验H 0:μ1= μ2= μ3产量甲化肥504649524848乙化肥495047474649丙化肥515049465050●10.2.1单因素方差分析的问题【例10-1】根据试验数据推断甲乙丙三种化肥的肥效是否存在差异象这类检验若干同方差的正态母体均值是否相等的一种统计分析方法称为方差分析.当只有两个正态总体时,这类问题也可以用第八章讲过的两正态总体均值比较的方法来解决.产量甲化肥504649524848乙化肥495047474649丙化肥515049465050●10.2.2单因素方差分析的数学模型进行单因素方差分析时,需得到表10-2所示的数据结构表10-2 单因素方差分析中数据结构表中用A 表示因素,A 的m 个取值称为m 个水平分别用A 1,A 2,…,A m 表示,每个水平对应一个总体.22n x mmn x .1x .2x .m x 观测值(j )A 因素(i )A 1A 2…A m1x 11x 21…x m 12x 12x 22…x m 2……………n i …平均值11n x●10.2.2单因素方差分析的数学模型进行单因素方差分析时,需得到表10-2所示的数据结构表10-2 单因素方差分析中数据结构从不同水平(总体)中抽出的样本容量可以相同,也可以不同.若不同水平抽出的样本容量相同则称为均衡数据,否则称非均衡数据.22n x mmn x .1x .2x .m x 观测值(j )A 因素(i )A 1A 2…A m1x 11x 21…x m 12x 12x 22…x m 2……………n i …平均值11n x●10.2.2单因素方差分析的数学模型单因素方差分析问题的一般提法为:因素A 有m 个水平A 1,A 2,…,A m ,在A i 水平下,总体X i ~N (μi ,σ2),i =1,2,…,m .其中μi 和σ2均未知,但方差相等,希望对不同水平下总体的均值进行比较.设x ij 表示第i 个总体的第j 个观测值(j =1,2,…,n i ,i =1,2,…,m ),由于X ij ~N (μi ,σ2),i =1,2,…,m .单因素方差分析模型常可表示为:x ij = μi + εij 相互独立,1≤i ≤m ,1≤j ≤n i .其中μi 表示第i 个总体的均值,εij 为随机误差.●10.2.3方差分析的方法为了方便起见,可将μi 记为:μi = μ+ νi 其中称为总均值,νi =μi –μ(i =1,2,…,m )称为因素A 的第i 个水平的附加效应,这样对不同水平下均值是否相同的检验H 0:μ1= μ2= …= μm ,H 1:μ1, μ2, …, μm 不全相等就可以表示为:H 0:ν1= ν2= …= νm = 0, H 1:ν1, ν2,…, νm 不全为零∑==m i i i n m 11μμ●10.2.3方差分析的方法下面简单介绍检验统计量及检验方法.以表示所有x ij 的总平值,表示第i 组数据的组内平均值即 其中n =n 1+n 2+…+n m .统计量称为总离差平方和,或简称总平方和.它反映了全部试验数据之间的差异.x .i x ,111∑∑===m i n j ij i x n x ∑==i n j iji i x n x 1.1∑∑==-=m i n j ij i x x SST 112)(●10.2.3方差分析的方法另外 反映了每组数据均值和总平均值的误差,称为组间离差平方和,简称组间平方和,或称因素A 平方和.反映了组内数据和组内平均的随机误差,称为组内离差平方和,或称为误差平方和.可以证明SST = SSM A + SSE∑∑∑===-=-=m i i i m i n j i A x x n x x SSM i 12.112.)()(∑∑==-=m i n j i ij i x x SSE 112.)(●10.2.3方差分析的方法构造检验统计量可以证明,在H 0成立下当原假设成立时,各总体均值相等,各样本均值间的差异应该较小,模型平方和也应较小,F 统计量取很大值应该是稀有的情形.所以对给定显著性水平α∈(0,1),H 0的拒绝域为:)()1(m n SSE m SSM F A --=),1(~)()1(m n m F m n SSE m SSM F A ----=⎭⎬⎫⎩⎨⎧--≥--=),1()()1(m n m F m n SSE m SSM F A α●10.2.3方差分析的方法若由观测数据xij(j=1,2,…,n i,i=1,2,…,m),计算得到F的观测值为F0,当F落入拒绝域时拒绝原假设H,可以认为所考虑的因素A对响应变量有显著影响;否则不能拒绝H,认为所考虑的因素A对响应变量无显著影响.另外,F统计量的P值为P=P{F≥F},在显著水平α下,若P=P{F≥F}<α,则拒绝原假设H0,可以认为所考虑的因素对响应变量有显著影响;否则不能拒绝H,认为所考虑的因素对响应变量无显著影响.●10.2.3方差分析的方法通常将上述计算结果表示为表10-3所示的方差分析表.表10-3 单因素方差分析表 其中,MS A =SSM A /(m –1),MSE =SSE /(n –m ).利用方差分析表中的信息,就可以对因素各水平间的差异是否显著做出判断.来源Source 平方和Sun ofSquare自由度DF 平均平方和Mean Square F 统计量F value P 值Pr > F 组间SSM Am –1SSM A / (m –1)MS A / MSE P 组内SSE n –m SSE / (n –m )全部SSM A +SSE n –1●10.2.3方差分析的方法【实验10-1】利用Excel的数据分析工具对例10-1作方差分析.Excel的数据分析工具作方差分析的步骤如下:1)将例10-1中数据输入Excel中,如图10-1所示.2)在Excel主菜单中选择“工具” “数据分析”,打开“数据分析”对话框,在“分析工具”列表中选择“方差分析:单因素方差分析”选项,单击“确定”按钮.图10-1 18块农田产量●10.2.3方差分析的方法【实验10-1】利用Excel的数据分析工具对例10-1作方差分析.3)在打开的“方差分析:单因素方差分析”对话框中,输入“输入区域”:B2:D8,“分组方式”取默认的“列”方式,选中“标志位于第一行”复选框,如图10-2所示,单击“确定”按钮.得到单因素方差分析的结果如图10-3所示.图10-2 ―方差分析:单因素方差分析”对话框●10.2.3方差分析的方法【实验10-1】利用Excel的数据分析工具对例10-1作方差分析.4)结果分析第一部分“SUMMARY‖提供拟合模型的一般信息,包括各分组的名称、观测数、和、均值和方差,如图10-3上所示.图10-3 单因素方差分析的结果10.2.3方差分析的方法【实验10-1】利用Excel的数据分析工具对例10-1作方差分析.4)结果分析第二部分为方差分析表,其中各项含义可参见表10-4的说明.最右边的多了一列:在α=0.05的显著水平下,单因素方差分析F检验的临界值(即F统计量的上α分位点:Fα)●10.2.3方差分析的方法【实验10-1】利用Excel的数据分析工具对例10-1作方差分析.4)结果分析从方差分析表可以看出,P值大于0.05(显著水平),所以不能拒绝原假设,没有足够的证据证明三种化肥的肥效有显著差异.●10.2.3方差分析的方法【实验10-1】利用Excel 的数据分析工具对例10-1作方差分析. 实验操作:甲化肥乙化肥丙化肥594951465050494749524746484650484950产量18块农田产量10.2.3方差分析的方法【例10-2】消费者与产品生产者、销售者或服务的提供者之间经常发生纠纷.当发生纠纷后,消费者常常会向消费者协会投诉.为了对几个行业的服务质量进行评价,消费者协会在零售业、旅游业、航空公司、家电制造业分别抽取了不同的企业作为样本.每个行业各抽取5家企业,所抽取的这些企业在服务对象、服务内容、企业规模等方面基本上是相同的.然后统计出最近一年中消费者对总共20家企业投诉的次数,结果如下:10.2.3方差分析的方法【例10-2】行业投诉次数零售业5766494044旅游业6839294556航空公司3149213440家电制造业4451657758通常,受到投诉的次数越多,说明服务的质量越差,消费者协会想知道这几个行业之间的服务质量是否有显著差异,试进行方差分析.10.2.3方差分析的方法【例10-2】行业投诉次数零售业5766494044旅游业6839294556航空公司3149213440家电制造业4451657758本例采用单因素方差分析法,只考虑行业这一个因素对投诉次数的影响,四个不同的行业称为该因素的四个不同的水平.原假设是:不同行业对服务质量的投诉次数没有显著差异10.2.3方差分析的方法【实验10-2】利用Excel的数据分析工具对例10-2作方差分析.1)将数据输入Excel中,如图10-4所示.2)在Excel主菜单中选择“工具” “数据分析”,打开“数据分析”对话框,在“分析工具”列表中选择“方差分析:单因素方差分析”选项,单击“确定”按钮.图10.4 消费者对四个行业的投诉次数●10.2.3方差分析的方法【实验10-2】利用Excel的数据分析工具对例10-2作方差分析.3)在打开的“方差分析:单因素方差分析”对话框中,输入“输入区域”:A2:D7,“分组方式”取默认的“列”方式,选中“标志位于第一行”复选框,如图10-5所示,单击“确定”按钮.得到单因素方差分析的结果如图10-6所示.图10-5 “方差分析:单因素方差分析”对话框●10.2.3方差分析的方法【实验10-2】利用Excel的数据分析工具对例10-2作方差分析.4)结果分析:从方差分析表可以看出,P值=0.047647<0.05(显著水平),所以拒绝原假设,即4个行业之间的服务质量有显著差异.从平均投诉的次数来看,家电制造业最高(59),航空公司最低(35),从各分组的方差来看,航空公司的服务最稳定(方差最小)图10-6 单因素方差分析的结果●10.2.3方差分析的方法【实验10-2】利用Excel的数据分析工具对例10-2作方差分析.实验操作:消费者对四个行业的投诉次数零售业旅游业航空公司家电制造业5768314466394951492921654045347744564058单因素方差分析研究的是总体的均值受一个因素不同水平的影响.但在一些实际问题中,影响总体均值的因素不止一个,这些因素间还可能存在交互作用,这就要考虑两个或多个因素的问题.为简单起见,仅考虑两个因素的情况.对于两因素问题,通常考虑等重复观测的情形,若第一个因素A有l个水平,第二个因素B有m个水平.在因素A 的第i个水平和因素B的第j个水平下均进行了n次观测,记为{x,1≤i≤l,1≤j≤m,1≤k≤n}.其数据结构如表10-4所ijk示.对于两因素问题,通常考虑等重复观测的情形,若第一个因素A 有l 个水平,第二个因素B 有m 个水平.在因素A 的第i 个水平和因素B 的第j 个水平下均进行了n 次观测,记为{x ijk ,1≤i ≤l ,1≤j ≤m ,1≤k ≤n }.其数据结构如表10-4所示..1.x .2.x ..m x ..1x ..2x ..l x x观测值A 因素(i )平均值A 1A 2…A lB 因素(j )B 1x 111…x 11nx 211…x 21n…x l 11…x l 1nB 2x 121…x 12nx 221…x 22n…x l 21…x l 2n……………B mx 1m 1…x 1mn x 2m 1…x 2mn…x lm 1…x lmn平均值表10-4 双因素方差分析中数据结构●10.3.1无交互作用的双因素方差分析无交互作用的双因素方差分析的数学模型可以表示为:x ijk =μ+ αi + τj + εijkεijk ~N (0, σ2),且相互独立1≤i ≤l ,1≤j ≤m ,1≤k ≤n,其中μ表示平均的效应,αi 和τj 分别表示因素A 的第i 个水平和因素B 的第j 个水平的附加效应,εijk 为随机误差,同样这里的随机误差也假定它是独立的并且服从等方差的正态分布.,01=∑=li ia1=∑=mj jτ●10.3.1无交互作用的双因素方差分析要说明因素A 有无显著影响,就是要检验如下假设:H 0A :α1= α2= …= αl ,H 1A :α1, α2, …,αl 不全相等 要说明因素B 有无显著影响,就是要检验如下假设:H 0B :τ1= τ2= …= τm ,H 1B :τ1, τ2,…,τm 不全相等与单因素方差分析类似,引进以下统计量: 总平均值: 组内平均值:∑∑∑====l i m j nk ijk x lmn x 1111,11.∑==in k ijk ij x n x ,111..∑∑===m j n k ijk i x mn x ∑∑===l i nk ijkj x n l x 11..1●10.3.1无交互作用的双因素方差分析因素A平方和:因素B平方和:交互作用平方和: 误差平方和:总离差平方和:∑=-=liiAxxmnSSM12..)(∑=-=mjjBxxn lSSM12..)(∑∑==+--=limjjiijBAxxxxlmSSM112.....*)(∑∑∑===-=limjnkijijkxxSSE1112.) (∑∑∑===-=li mjnkijkxxSST1112) (●10.3.1无交互作用的双因素方差分析可以证明SST = SSM A + SSM B +SSM A*B + SSE构造检验统计量可以证明:在H 0A 成立时,检验统计量:,)1()1(+---=m l lmn SSE l SSM F A A )1()1(+---=m l lmn SSE m SSM F B B ))1(,1(~)1()1(0+---+---=m l lmn l F m l lmn SSE l SSM F A H A A 真●10.3.1无交互作用的双因素方差分析可以证明SST = SSM A + SSM B +SSM A*B + SSE构造检验统计量在H 0B 成立时,检验统计量,)1()1(+---=m l lmn SSE l SSM F A A )1()1(+---=m l lmn SSE m SSM F B B ))1(,1(~)1()1(0+---+---=m l lmn m F m l lmn SSE m SSM F B H B B 真●10.3.1无交互作用的双因素方差分析要说明因素A 有无显著影响,就是要检验如下假设:H 0A :α1= α2= …= αl ,H 1A :α1, α2, …,αl 不全相等 可以证明:在H 0A 成立时,检验统计量:对于给定的显著性水平α,H 0A 的拒绝域为:))1(,1(~)1()1(0+---+---=m l lmn l F m l lmn SSE l SSM F A H A A 真⎭⎬⎫⎩⎨⎧+---≥+---=))1(,1()1()1(m l lmn l F m l lmn SSE l SSM F A A α●10.3.1无交互作用的双因素方差分析要说明因素B 有无显著影响,就是要检验如下假设:H 0B :τ1= τ2= …= τm ,H 1B :τ1, τ2,…,τm 不全相等 在H 0B 成立时,检验统计量H 0B 的拒绝域为:))1(,1(~)1()1(0+---+---=m l lmn m F m l lmn SSE m SSM F B H B B 真⎭⎬⎫⎩⎨⎧+---≥+---=))1(,1()1()1(m l lmn m F m l lmn SSE m SSM F B B α●10.3.1无交互作用的双因素方差分析另外,若F A ,F B 统计量的观测值分别为F A 0,F B 0,则 当值P =P {F A ≥F A 0}<α时拒绝H 0A ,否则不能拒绝H 0A 当值P =P {F B ≥F B 0}<α时拒绝H 0B ,否则不能拒绝H 0B . 无交互作用的双因素方差分析表见表10-5.来源Source+自由度DF 平方和Sun of Square平均平方和Mean Square F 统计量F value p 值Pr > F 因素A l –1SSM A SSM A / (l –1)MS A / MSE P (A )因素B m –1SSM B SSM B / (m –1)MS B / MSE P (B )随机误差lmn –l –m + l SSESSE / (lmn –l –m + 1)全部lmn –1SSM A + SSM B +SSE表10-5 无交互作用的双因素方差分析表。
第十章 统计学 方差分析

经济、管理类 基础课程
二、方差分析的基本思想和原理
(一)图形描述
不同行业被投诉的次数是有明显差异的 同一个行业,不同企业被投诉的次数也明显不同
统计学
1. 从散点图上可以看出(仍以例10.1为例)
家电制造被投诉的次数较高,航空公司被投诉的次数 较低
2. 行业与被投诉次数之间有一定的关系
3. 系统误差
经济、管理类 基础课程
统计学
1. 数据的误差用平方和(sum of squares)表示,称 为方差 2. 组内方差(within groups) 因素的同一水平(同一个总体)下样本数据的方差 比如,零售业被投诉次数的方差 组内方差只包含随机误差 3. 组间方差(between groups) 因素的不同水平(不同总体)下各样本之间的方差 比如,四个行业被投诉次数之间的方差 组间方差既包括随机误差,也包括系统误差
经济、管理类 基础课程
统理类 基础课程
统计学
第十章 方差分析
第一节 方差分析的基本问题 第二节 单因素方差分析 第三节 双因素方差分析
10 - 2
经济、管理类 基础课程
统计学
1. 2. 2. 3.
学习目标
解释方差分析的概念 解释方差分析的基本思想和原理 掌握单因素方差分析的方法及应用 掌握双因素方差分析的方法及应用
(analysis of variance)
统计学
1. 检验多个总体均值是否相等 通过分析数据的误差判断各总体均值是否相
等
2. 研究分类型自变量对数值型因变量的影响
一个或多个分类尺度的自变量
两个或多个 (k 个) 处理水平或分类
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
F值
FA SA SE SB SE
因素A
SA
i 1
( xij ) 2
j 1
s
s
n( X )2
r 1
s 1
因素B 误差 总和
SB
j 1
s
( xij ) 2
i 1
r
r
n( X )2
SB
SB nr
FB
S E R S A S B ( r 1)( s 1)
S A 761.205 724.808 36.397 SB 725.128 724.808 0.32 S E 38.352 36.397 0.32 1.635
20
计算方差的第二种方法
材质
淬火温度 a1 a2 a3 a4 a5 b1 4.4 5.3 5.8 6.6 8.4 b2 5.2 5 5.5 6.9 8.3 b3 4.3 5.1 4.8 6.6 8.5 b4 4.9 4.7 4.9 7.3 7.9 行合计 行均值 18.8 20.1 21 27.4 33.1 4.7 5.025 5.25 6.85 8.275
i 1 j 1
r
ni
构造F统计量: FA S A
SE
FB
SB SE
15
三、检验
在H 01为真时 FA S A ~ F (( r 1, ( r 1)( s 1))
SE
在给定的显著性水平 0.05下, 查F分布表,得临界值F
若FA F ( r 1, ( r 1)( s 1)), 因素A的水平有显著影响;反之则没有影响。
F F ( r 1, n r ),拒绝原假设, 这三种机器产量之间存在差异
10
具体分析步骤 ① 首先在A1:F4单元格中输入上表中数据; ② 在菜单中选取“工具→数据分析→方差分析:单因 素重复方差分析”,单击“确定”按钮; ③ 在弹出的“方差分析:单因素方差分析”对话框中, 设置“输入区域”为A1:F4,“分组方式”选择列,显 著性水平,输出区域设定为H1:J11,单击“确定” 按钮,输出单因素方差分析结果:
i 1 j 1 r ni
r
i 1
3、检验
S A /( r 1) S A 构造F统计量:F S E /( n r ) S E
在给定的显著性水平 0.05下, 查F分布表,得临界值 F ( r 1, n r )
若F F ( r 1, n r ),接受原假设, A因素影响不显著,均值相等
影响的显著性水平。
, Bs 设因素A有r个水平 A1 , A2 , , Ar ,因素B有s个水平 B1 , B2 ,,
用 X ij 表示两个因素的各水平的每一种配合下 ( Ai , B j ) 的总体, r, j 1,2, s ) 假定各个总体都都服从正态分布 X ij ~ N ( ij , 2 )(i 1,2,, 也要求样本是简单随机样本,样本之间相互独立,但在无 交互作用的方差分析中,忽略两个因素之间相互影响所带 来的效应。
2
3 为什么不能 检验上面三个总体有相同的均值 H 0 : 1 2 ,
3 将它们简单地配对,然后每次检验两个 ,即检验 H 0 : 1 , 3 这样就要需要三次不 然后H 0 : 1 2 ,再检验 H 0 : 2 , 同地假设检验,置信度将会下降到 0.953 0.8574
9
SA F SE
( r 1) (n r )
380.9333 456.8
(3 1)
(15 3)
190.4667 5.0035 38.0667
在给定的显著性水平 0.05下, 查F分布表,得临界值
F ( r 1, n r ) F0.05 ( 2,12) 3.89
2 ST xij n( X ) i 1 j 1 r ni 2
SE
SE ( r 1)( s 1)
rs 1
17
例12.1对钢材进行拉伸变形实验,选择五种不同的淬火
温度 以及四种不同的材质。数据如下,试检验淬火温度 和材质对拉伸变形是否有显著影响。 s=4(列)
材质 b1 4.4 b2 5.2 b3 4.3 b4 4.9
b3 4.3 5.1 4.8 6.6 8.5 29.3
b4 4.9 4.7 4.9 7.3 7.9 29.7
x
j 1 ij
4
x
j 1
4
2
( x ) 2
j 1 ij
4
ij
18.8 20.1 21 27.4 33.1 120.4
353.44 404.01 441 750.76 1095.61 3044.82
若F F ( r 1, n r ),拒绝原假设, A因素影响显著,均值不相等
5
方差分析表ANOVA 方差来源 组间 组内 平方和
r
自由度 平均平方 和
F值
SA
i 1
( xij ) 2
j 1
ni
ni
n( X ) 2
r 1
nr
SA
SE
SA r 1
SE nr
列合计
列均值
在H 02为真时
FB
SB ~ F (( s 1, ( r 1)( s 1)) SE
若FB F ( s 1, ( r 1)( s 1)), 因素B的水平有显著影响;反之则没有影响。
16
无交互作用的方差分析表
方差来源 平方和
r
自由度
平均平方和
S SA A r 1
i 1 j 1 2 ij
r
ni
SA
i 1
r
( xij ) 2
j 1
ni
ni
n( X ) 2 380.9333
SE ST S A 456.8
8
计算方差的第二种方法:
机器 A1 138 144 日产量 135 149 143 行合计 709 行均值 141.8
A2
S E ST S A
2 ST xij n( X ) i 1 j 1 r ni 2
SA F SE
总和
n 1
X
x
i 1 j 1
r
ni
ij
n
6
例10.1三台机器制造同一产品,记录五天的产量如下,试判
断这三台机器的产量是否有显著差异。
r 3, ni 5
88.9 101.19 110.94 188.02 274.11 763.16
( x )
i 1 ij
5
930.25 954.81 858.49 882.09
19
5 4 1 (120.4) 2 2 n( X ) ( xij ) 724.808 5 4 i 1 j 1 20 2
11
Excel输出的方差分析结果
方差分析 差异源 组间 组内 总计 SS 380.9 456.8 837.7 df 2 12 14 MS 190.4667 38.06667 F 5.0035 P-value 0.0263 F crit 3.8853
从结果中可得到 F 5.0035
F值的伴随概率p 0.0263(小概率) =0.05
1 3044.82 ( x ) 761.205 ij 4 i 1 j 1 4
5
4
2
1 3625.64 ( x ) 725.128 ij 5 j 1 i 1 5
4
5
2 x ij 763.16 i 1 j 1
5
4
ST 763.16 724.808 38.352
A3
163
155
148
144
152
159
146
147
157
153
766
758 2233
153.2
151.6
总和
总均值
148.8667
2233 X 148.8667 15
ST ( X ij X ) (138 148.8667) 2 (144 148.6667) 2 (153 148.6667) 2 837.7333
(以95%的置信度为例);如果检验四个总体也采用这样 方法,那将需要作6次不同的假设,置信度会降低 到 0.956 0..7351,同时随着检验次数的增多,偶然因素导 致差别的可能性将会增大。而方差分析通过使用一个针对 多个样本均值相对的检验避开了这个问题。
3
10.1 单因素方差分析
单因素方差分析研究一个因素对某种指标的影响,在实验中
14
二、构造统计量
计算总离差平方和ST ( xij X ) 2
i 1 j 1
r
r
ni
因素A的偏差平方和S A s ( X i . X ) 2
i 1
因素B的偏差平方和S B r ( X . j X ) 2
j 1
s
误差平方和S E ( X ij X i . X . j X ) 2
i 1
r
( xij ) 2
j 1
ni
ni
ni 2 ij
100536.2 117351.2 114912.8 332800.2
x
i 1 j 1
r
106655 117542 115060 333257
2
ST x n( X ) 837.7333
第十章 方差分析
1
前面我们介绍了检验两个总体均值相等的假设的方
法,但是在检验三个或更多总体均值相等的时候, 就要使用方差分析方法。 比如测量三组不同的人(如吸烟者、暴露在吸烟环境 种的不吸烟者和没有暴露在吸烟环境中的吸烟者)身 体中含有的尼古丁水平,检验他们是否具有不同的 尼古丁水平。既然可以使用两样本均值相等的检验 方法,为什么还要使用这种方差分析方法?
