2005年广东省中考数学试题及答案

合集下载

2005年-2014年广州市中考数学选择填空题汇编(有答案)

广州市2005年初中毕业生学业考试一、选择题（本大题共10小题，每小题3分，满分30分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

）1. 下列四个数中，在-2和1之间的数是（）A. –3B. 0C. 2D. 32. 如图，将一块正方形纸片沿对角线折叠一次，然后在得到的三角形的三个角上各挖去一个圆沿，最后将正方形纸片展开，得到的图案是（）3. 下列各点中，在函数72-=x y 的图像上的是（）A. （2，3）B. （3，1）C. （0，-7）D. （-1，9）4. 不等式组⎩⎨⎧>-≥+0101x x 的解集是（）A. 1-≥xB. 1->xC. 1≥xD. 1>x5. 已知12112-=+=b a ，，则a 与b 的关系是（）A. a=bB. ab=1C. a=-bD. ab=-16. 如图，AE 切圆O 于E ，AC=CD=DB=10，则线段AE 的长为（）A. 210B. 15C. 310D. 207. 用计算器计算，，，，15151414131312122222--------…，根据你发现的规律，判断112--=n n P 与1)1(1)1(2-+-+=n n Q （n 为大于1的整数）的值的大小关系为（） A. P<QB. P=QC. P>QD. 与n 的取值有关8. 当k>0时，双曲线xk y =与直线kx y -=的公共点有（）A. 0个B. 1个C. 2个D. 3个9. 如图，多边形的相邻两边均互相垂直，则这个多边形的周长为（）A. 21B. 26C. 37D. 4210. 如图，已知点A （-1，0）和点B （1，2），在坐标轴上确定点P ，使得△ABP 为直角三角形，则满足这样条件的点P 共有（）A. 2个B. 4个C. 6个D. 7个第二部分非选择题（共120分）二、填空题（本题共6小题，每小题3分，满分18分）11. 如图，点A 、B 、C 在直线l 上，则图中共有__________条线段。

广东省中考数学试题与答案(2005年)

2005年广东省初中毕业生学业考试数学试卷一、选择题（本题共５小题，每小题３分，共15分）１．计算的结果是1-的式子是（）Ａ．1-- Ｂ．0(1)- Ｃ．(1)--Ｄ．11-２．已知1O 的半径为１，2O 的半径为２，两圆的圆心距12O O 为３，则两圆的位置关系是（）Ａ．相交Ｂ．相离Ｃ．外切Ｄ．内切３．函数1y x=与函数y x =的图象在同一平面直角坐标系内的交点个数是（）Ａ．１个Ｂ．２个Ｃ．３个Ｄ．０个４．如图所示几何体的左视图是（）５．４个红球、３个白球、２个黑球放入一个不透明袋子里，从中摸出８个球，恰好红球、白球、黑球都摸到，这件事情（）Ａ．可能发生Ｂ．不可能发生Ｃ．很可能发生Ｄ．必然发生二、填空题（本题共５小题，每小题４分，共20分）6.三峡工程电站的总装机容量是18 200 000千瓦，用科学记数法表示电站的总装机容量，应记为千瓦．７．方程2x =的解是．８．若数据8，9，7，8，x ，3的平均数是７，则这组数据的众数是．９．如图，已知CD AB ⊥，BEAC ⊥，垂足分别为D 、E ，BE 、CD 交于点O ，且AO 平分BAC ∠，那么图中全等三角形共有对．10．如图，PA 、PB 是O 的切线，点A 、B 为切点，AC 是O 的直径，20BAC ∠=，则P ∠的大小是度．三、解答题（一）（本题共５小题，每小题６分，共30分） 11．分解因式224ax ay -； 12．解方程11121x x x ++=-+ 13．将方格中的图案作下列变换，请画出相应的图案：⑴沿y 轴正向平移４个单位；⑵平移后关于y 轴轴对称图形；Ａ． B ． C ． D ．（第4题图） xy B第9题图第10题图14．如图，某长方形广场的四角都有一块半径相同的四分之一圆形的草地，若圆形的半径为宽为b 米．请用代数式表示空地的面积．若长方形长为300米，宽为200米，圆形的半径为10米，求广场空地的面积。

2005年广东广州市中考数学试题及答案.doc

广州市2005年高中阶段学校招生考试数学第一部分选择题（共30分）一、选择题（本大题共10小题，每小题3分，满分30分．在每小题给出的四个选项中，只有一项是符合题目要求的．）1.下列四个数中，在一2和1之间的数是（＊）．(A ）-3 （B ）0 （C ）2 （D ）32.如图1，将一块正方形纸片沿对角线折叠一次，然后在得到的三角形的三个角上各挖去一个圆洞，最后将正方形纸片展开，得到的图案是（＊）．3.下列各点中，在函数y ＝2x-7的图象上的是（＊）．(A ）（2，3）（B ）（3，1）（C ）（0，-7）（D ）（一1，9)4.不等式组⎩⎨⎧>-≥+0101x x 的解集是（＊）．(A)1-≥x (B)1->x (C)1≥x (D) 1>x5.已知,12+=a 121-=b ，则,a 与b 的关系是（）(A)a ＝b （B ）ab ＝1 （C ）a ＝-b （D ）ab ＝一16.如图2，AE 切⊙D 于点E ，AC ＝CD ＝DB ＝10，则线段AE 的长为（＊）．(A) 210 (B ）15 (C) 310 (D ）207.用计算器计算,12122--,13132--,14142--,15152--…，根据你发现的规律，判断,112--=n n P 与,1)1(1)1(2-+-+=n n Q （n 为大于1的整数）的值的大小关系为（＊）．(A) P ＜Q (B ）P ＝Q (C ）P ＞Q (D)与n 的取值有关8.当 k>0时，双曲线x ky =与直线kx y -=的公共点有（＊）(A ）0个（B ）1个（C ）2个（D ）3个9.如图3，多边形的相邻两边均互相垂直，则这个多边形的周长为（＊）．（A ）21 （B ）26 （C ）37 （D ）4210.如图4，已知点A （一1，0）和点B （1，2），在坐标轴上确定点P ，使得△ABP 为直角三角形，则满足这样条件的点P 共有（＊）．(A ）2个（B ）4个（C ） 6个（D ）7个二、填空题（本大题共6小题，每小题3分，满分18分．）11.如图5，点A 、B 、C 在直线l 上，则图中共有______条线段．12.若0122=+-a a ，则a a 422-=__________．13．函数x y 1=中，自变量x 的取值范围是________· 14.假设电视机屏幕为矩形．”某个电视机屏幕大小是64 cm"的含义是矩形对角线长为64 cm.如图6，若该电视机屏幕A BCD 中,BC CD ＝0.6，则电视机屏幕的高CD 为______cm.（精确到l cm ）15.方程2122=+xx 的解是_________· 16.如图7，在直径为6的半圆AB 上有两动点M 、N ，弦AM,BN 相交于点P ，则AP.AM + BP.BN 的值为__________．三、解答题（本大题共9小题，满分102分．解答应写出文字说明、证明过程或演算步骤．）17．（本小题满分9分）计算：222ba ab a -+ 18．（本小题满分9分）如图8，AB 是⊙0的弦，直线DE 切⊙0于点C ：AC=BC ，求证：DE//A B.19.（本小题满分10分）解方程组：⎩⎨⎧-==+103xy y x 20．（本小题满分10分）以下统计图中数据来源于2004年12月广州市教育局颁布的《广州市2004/2005学年教育事业统计简报》．其中，小学按6年制，初中、高中均按3年制统计，2004年底广州市管辖各类学校的在校学生人数情况统计图（1)请回答，截止2004年底，广州市在校小学生、在校初中生平均每个年级的人数哪一个更多？多多少？(2)根据该统计图，你还能得到什么信息？请你写出两条不同于（1)的解答的信息．21．（本小题满分12分）某次知识竞赛共有20道选择题．对于每一道题，若答对了，则得10分；若答错了或不答，则扣3分．请问至少要答对几道题，总得分才不少于70分？22.（本小题满分12分）如图9，点D 是线段AB 的中点，点C 是线段AB 的垂直平分线上的任意一点，DE ⊥AC 于点E ，DF ⊥ BC 于点F.（1)求证：CE ＝CF;(2）点C 运动到什么位置时，四边形CEDF 成为正方形？请说明理由．23．（本小题满分12分）已知二次函数c bx ax y ++=2(1）当a=1，b 二一2，c=1时，请在图10的直角坐标系中画出此时二次函数的图象；（2）用配方法求该二次函数（＊）的图象的顶点坐标．24.（本小题满分14分）如图1I ，某学校校园内有一块形状为直角梯形的空地A BCD ，其中AB//DC ， ∠B=90°，AB=100m ，BC ＝80m ，CD ＝40m ，现计划在上面建设一个面积为s 的矩形综合楼PMBN ，其中点P 在线段AD 上，且PM 的长至少为36m.（1）求边AD 的长；(2）设PA = x （m ），求S 关于二的函数关系式，并指出自变量x 的取值范围；(3）若S ＝3300m 2,求PA 的长．（精确到0.lm ）25，（本小题满分14分）如图12，已知正方形ABCD 的面积为S.（1）求作：四边形A 1B 1C 1D 1，使得点A 1和点A 关于点B 对称,点B 1和点B 关于点C 对称，点C 1和点C 关于点D 对称，点D 1和点D 关于点A 对称；（只要求画出图形，不要求写作法）(2）用S 表示（1）中作出的四边形A 1B 1C 1D 1的面积S 1;(3)若将已知条件中的正方形改为任意四边形，面积仍为S并按（1）的要求作出一个新的四边形，面积为S 2,则S 2与S 1是否相等？为什么？。

2005年广东中考数学卷

2005年广东试验区数学中考试卷一、选择题：（本大题共10小题，每小题4分，共40分，每小题给出四个答案，其中只有一个正确） 1、已知，－5的相反数是a ，则a 是A 、5，B 、51-， C 、51， D 、－5；2、下列各式由左边到右边的变形中，是分解因式的为：A 、ay ax y x a +=+)(，B 、4)4(442+-=+-x x x xC 、)12(55102-=-x x x xD 、x x x x 3)4)(4(3162+-+=+-3、下列三个事件属于必然事件的是（）：① 今年冬天，茂名会下雪； ② 将花生油滴入水中，花生油会浮在水面上；③ 任意投掷一枚质地均匀的硬币，硬币停止后，正面朝上； A 、①②， B 、①③ , C 、 ②③ ，D 、② ；4、下列四幅图形中，表示两颗小树在同一时刻阳光下的影子的图形可能是：5、下列分式的运算中，其中结果正确的是： A 、ba b a +=+211， B 、323)(a aa =， C 、b a ba b a +=++22，D 、319632-=+--a a a a ；6、某同学把下图所示的几何体的三种视图画出如下（不考虑尺寸）；在这三种是图中，其正确的是：A 、①②,B 、①③ ，C 、②③ ，D 、② ；7、若关于x 的一元二次方程的两个根为x 1=1,x 2=2,则这个方程是：A 、0232=-+x x ， B 、0232=+-x x ，C 、0322=+-x x ， D 、0232=++x x ； 8、如图，梯形ABCD 内接于◎○，AB//CD ，AB 为直径，DO 平分∠ADC ，则∠DAO 的度数是 A 、900， B 、800， C 、700， D 、600； 9、下列三个命题：① 园既是轴对称图形，又是中心对称图形；③ 相等圆心角所对的弧相等；其中是真命题的是A 、①② ，B 、②③ ，C 、①③ ，D 、①②③； 10、下列四个函数：① );0( k k kx y 为常数，= ② );0,( k b k b kx y 为常数，+= ③ );0( k k xk y 为常数，=④ );0(2a a ax y 为常数，=其中，函数y 的值随着x 值得增大而减少的是 A 、 ① ， B 、② ， C 、③ ， D 、④ ；二、填空题：（本大题共5小题，每小题4分，共20分，请你把答案填在横线的上方）11、用一个平面去截一个正方体其截面形状不可能的是（请你在三角形、四边形、五边形、六边形、七边形这五种图形中选择符合题意的图形填上即可）；12、若x=1时一元二次方程ax 2+bx －2=0的根，则a+b= ； 13、如图是一口直径AB 为4米，深BC 为2米的圆柱形养蛙池，小青蛙们晚上经常坐在池底中心O 观赏月亮，则它们看见月亮的最大视角 ∠COD= 度，（不考虑青蛙的身高）；14、《广东省工伤保险条例》规定：职工有依法享受工伤保险待遇的权利，某单位一名职工因公受伤住院治疗了一个月（按30天计），用去医疗费5000元，伙食费500元，工伤保险基金按规定给他补贴医疗费4500元，其单位按因公出差标准（每天30元）的百分之七十补助给他做伙食费，则在这次工伤治疗中他自己只需支付；15、用同样大小的黑、白两种颜色的棋子摆设如下图所示的正方形图案，则第n 个图案需要用白色棋子枚（用含有n 的代数式表示）三、解答下列各题（本大题共5小题，每小题8分，共40分） 16、已知)216(2),2)(2(2a B a a A -=-+=，求A+B ；解：17、如图所示，转盘被等分成六个扇形，并在上面依次写上数字1、2、3、4、5、6；（1）若自由转动转盘，当它停止转动时，指针指向奇数区的概率是多少？（4分）（2）请你用这个转盘设计一个游戏，当自由转动的转盘停止时，指针指向的区域的概率为32，（4分）解：18、如图，有一条小船，（1）若把小船平移，使点A 平移到点B ，请你在图中画出平移后的小船；（5分）（2）若该小船先从点A 航行到达岸边L 的点P 处补给后，再航行到点B ，但要求航程最短，试在图中画出点P 的位置（3分）19、如图，一张边长为16㎝的正方形硬纸板，把它的四个角都剪去一个边长为x ㎝的小正方形，然后把它折成一个无盖的长方体，设长方体的容积为V ㎝3，请回答下列问题：（1）若用含有X 的代数式表示V ，则V= （2分）（2）完成下表：（4分）(3) 观察上表，容积V 的值是否随x 值得增大而增大？当x 取什么值时，容积V 的值最大？（2分）解：20、四、（本大题共3小题，每小题10分，共30分）21、某校要从小王和小李两名同学中挑选一人参加全国数学竞赛，在最近的五次选拔测试中，他俩的成绩分别如下表：根据上表解答下列问题：小李在这五次测试中的优秀率各是多少？（3分）（3）历届比赛表明，成绩达到80分以上（含80分）就很可能获奖，成绩达到90分以上（含90分）就很可能获得一等奖，那么你认为应选谁参加比赛比较合适？说明你的理由（2分）22、（本小题满分10分）如图，用三个全等的菱形ABGH、BCFG、CDEF拼成平行四边形ADEH，连接AE与BG、CF分别交于P、Q，（1）若AB=6，求线段BP的长；（6分）（2）观察图形，是否有三角形与ΔACQ全等？并证明你的结论，（4分）解：23、（本小题满分10分）今年6月份，我市某果农收获荔枝30吨，香蕉13吨，现计划租用甲、乙两种货车共10辆将这批水果全部运往深圳，已知甲种货车可装荔枝4吨和香蕉1吨，一种货车可装荔枝香蕉各2吨；（1）该果农按排甲、乙两种货车时有几种方案？请你帮助设计出来（6分）（2）若甲种货车每辆要付运输费2000元，乙种货车每辆要付运输费1300元，则该果农应选择哪种方案？使运费最少？最少运费是多少元？（4分）解：五、（本大题共2小题，每小题10分，共20分）24（本小题10分）如图，已知直线L与◎○相切于点A，直径AB=6，点P在L上移动，连接OP交◎○于点C，连接BC并延长BC交直线L于点D，（1）若AP=4，求线段PC的长（4分）（2）若ΔPAO与ΔBAD相似，求∠APO的度数和四边形OADC的面积（答案要求保留根号）（6分）解：25、（本小题满分10分）如图，已知二次函数322++=x ax y 的图像与x 轴交于点A 、点B （点B 在X 轴的正半轴上），与y 轴交于点C ，其顶点为D ，直线DC 的函数关系式为3+=kx y ，又tan ∠OBC=1，（1）求a 、k 的值；（5分）（2）探究：在该二次函数的图像上是否存在点P （点P 与点B 、C 补重合），使得ΔPBC 是以BC 为一条直角边的直角三角形？若存在，求出点P 的坐标，若不存在，请你说明理由（5分）解：茂名是2005年课改实验区初中毕业生学业考试与高中招生考试数学试题参考答案及评分标准说明：1、如果考生的解法与本解法不同，可根据试题的主要内容，并参照评分标准制定相应的评分细则后评卷。

广州2005年中考试卷真题及答案

秘密★启用前广州市2005年初中毕业生学业考试数学本试卷分选择题和非选择题两部分，共三大题25小题，满分150分．考试时间120分钟．注意事项：1．答卷前，考生务必在答题卡第1面、第3面、第5面上用黑色字迹的钢笔或签字笔填写自己的考生号、姓名；填写考场试室号、座位号，再用2B 铅笔把对应这两个号码的标号涂黑．2．选择题每小题选出答案后，用2B 铅笔把答题卡上对应题同的答案标号涂黑；如需改动，用橡皮擦干净后，再选涂其他答案标号；不能答在试卷上．3．非选择题必须用黑色字迹的钢笔或签字笔作答，涉及作图的题目，用2B 铅笔画图．答案必须写在答题卡各题目指定区域内的相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；改动的答案也不能超出指定的区域．不准使用铅笔、圆珠笔和涂改液．不按以上要求作答的答案无效．4．考生必须保持答题卡的整洁，考试结束后，将本试卷和答题卡一并交回．第一部分选择题（共30分）一、选择题（本大题共10小题，每小题3分，满分30分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

）1. 下列四个数中，在-2和1之间的数是（）A. –3B. 0C. 2D. 32. 如图，将一块正方形纸片沿对角线折叠一次，然后在得到的三角形的三个角上各挖去一个圆沿，最后将正方形纸片展开，得到的图案是（）3. 下列各点中，在函数72-=x y 的图像上的是（）A. （2，3）B. （3，1）C. （0，-7）D. （-1，9）4. 不等式组⎩⎨⎧>-≥+0101x x 的解集是（）A. 1-≥xB. 1->xC. 1≥xD. 1>x5. 已知12112-=+=b a ，，则a 与b 的关系是（）A. a=bB. ab=1C. a=-bD. ab=-16. 如图，AE 切圆O 于E ，AC=CD=DB=10，则线段AE 的长为（）A. 210B. 15C. 310D. 207. 用计算器计算，，，，15151414131312122222--------…，根据你发现的规律，判断112--=n n P 与1)1(1)1(2-+-+=n n Q （n 为大于1的整数）的值的大小关系为（） A. P<QB. P=QC. P>QD. 与n 的取值有关8. 当k>0时，双曲线xky =与直线kx y -=的公共点有（） A. 0个 B. 1个 C. 2个 D. 3个9. 如图，多边形的相邻两边均互相垂直，则这个多边形的周长为（）A. 21B. 26C. 37D. 4210. 如图，已知点A （-1，0）和点B （1，2），在坐标轴上确定点P ，使得△ABP 为直角三角形，则满足这样条件的点P 共有（）A. 2个B. 4个C. 6个D. 7个第二部分非选择题（共120分）二、填空题（本题共6小题，每小题3分，满分18分）11. 如图，点A 、B 、C 在直线l 上，则图中共有__________条线段。

2005年广东省中考数学试卷(扫描版)(含答案)(课改实验区)

一、选择题（本题共5小题，每小题3分，共15分） 1. A2. C3. B4. C5. D二、填空题（本题共5小题，每小题4分，共20分）6. 71.82107. 0或8. 7和8 9. 4 10. 40三、解答题（本题共5小题，每小题6分，共30分） 11.解：ax 2-4ay 2=a(x 2-4y 2)………………3分 =a(x+2y)(x-2y)………………6分12.解：方程两边同乘（x ﹣2）（x+1），得（x+1）2+x ﹣2=（x ﹣2）（x+1）， ………………2分整理，得 4x=﹣1， ………………4分解得 x=﹣，………………5分检验：当x=﹣时，（x ﹣2）（x+1）≠0，∴原分式方程的解为x=﹣． ………………6分13.解：如图所示.200514.解：(1) 由题意可知：空地的面积为(ab-πr2)平方米；………………3分(2)当a=300，b=200，r=10时，ab-πr2=300×200-100π=60000-100π(平方米). …………5分答：广场空地的面积是(60000-100π)平方米. ………………6分15.解：（1）由题意可知：每次翻动正面一个数字共9种情况，其中有1种情况是“翻到奖金1000元”，故“翻到奖金1000元”的概率为；………………2分（2）由题意可知：每次翻动正面一个数字共9种情况，其中有3种情况是“翻到奖金”，故“翻到奖金”的概率；………………4分（3）由题意可知：每次翻动正面一个数字共9种情况，其中有6种情况是“翻不到奖金”，故“翻不到奖金”的概率．………………6分四、解答题（本题共4小题，每小题7分，共28分）16.解：（1）当0≤x≤15时，函数的图象过点A（15，27）设y=kx，∴27=15k，∴k=，∴y=x（0≤x≤15）．………………2分当x≥15时，函数的图象过点A（15，27），B（20，39.5）设y=k1x+b则解得∴y=2.5x﹣10.5（x≥15）；………………4分（2）∵x=21＞15，………………5分∴当x=21时，y=2.5×21﹣10.5=42（元）．答：某用户该月用水21吨，应交水费42元. ………………7分17.解：（1）过点A作AD⊥BC于点D．在Rt△ABD中，∵∠ABC=45°，∴BD=AD，………………2分∵BC=20，∴CD=BC﹣BD=20﹣AD，在Rt△ACD中，∠ACD=30°，tan∠ACD=，∴AD=CDtan∠ACD，∴AD=10（﹣1）≈7.32（米）．答：小河的宽度为10（﹣1）米．………………5分（或：答：小河的宽度约为7.32米．）.说明：分母有理化可不作要求，使用计算器的地区结果近似7.32米（2）先取点A，测量得∠ABC=90°处取点B，然后取∠ACB=30°，量出BC的长度即可．………………7分说明：答案开放，能用数学知识且符合生活实际便可酌情给分.18.解：（1）a2=AC，且在直角△ABC中，AB2+BC2=AC2，∴a2=a1=，………………2分同理a3=a2=a1=2，………………3分a4=a3=a1=2；………………4分（2）由（1）结论可知：a2=a1=，a3=a2=a1=2，a4=a3=a1=2；……故找到规律：a n =a1=．………………7分19.解：(1)说明：完整填空作图给3分；………………3分(2)从图中可以清楚地看出79.5分到89.5分这个分数段的学生数最多，49.5分到59.5分这个分数段的学生数最少；………………5分(3)及格率：×100%=95%；优秀率：×100%=12.5%. ………………7分五、解答题（本题共3小题，每小题9分，共27分）20.解：（1）证明：∵四边形ABCD为等腰梯形，∴AB=CD，∠A=∠D．∵M为AD的中点，∴AM=DM．………………2分∴△ABM≌△DCM．………………3分∴BM=CM．………………4分∵E、F、N分别是MB、CM、BC的中点，∴EN、FN分别为△BMC的中位线，∴EN=MC，FN=MB，且ME=BE=MB，MF=FC=MC．∴EN=FN=FM=EM．∴四边形ENFM是菱形．………………5分（2）等腰梯形ABCD的高是底边BC的一半．证明：连接MN，∵BM=CM，BN=CN，∴MN⊥BC．∴MN是梯形ABCD的高．………………7分又∵四边形MENF是正方形，∴∠EMF=90°，∴△BMC为直角三角形．又∵N是BC的中点，∴MN=BC．………………8分即等腰梯形ABCD的高是底边BC的一半．21.解：设原计划某间宿舍每天开空调时间为x小时，依题意，得………………1分………………6分解得8＜x＜10 ………………8分答：原计划某间宿舍每天开空调时间为8至10小时. ………………9分22.解：(1)顶点P (2,4)，点M (4,0). ………………2分设抛物线的解析式为y=a(x-2)2+4，因为抛物线经过点M(4,0)，所以0=a(4-2)2+4，解得a=-1，∴抛物线的解析式是y=-(x-2)2+4=-x2+4x. ………………4分(2)设点的坐标是A(x,y)，其中0＜x＜4.则AD=BC=2x-4(x≠2，否则A、D两点重合)，AB=CD=y.矩形的周长为：l=2(AB+AD)=2(y+2x-4)=2(-x2+4x+2x-4)=-2x2+12x-8=-2(x-3)2+10.∵0＜3＜4，∴当x=3时，矩形的周长l的最大值是10. ………………7分(3)存在.理由：作OP的中垂线一定能与抛物线相交，或以O点为圆心，以OP为半径画弧也能与抛物线相交. ………………9分。

2005年广东中考数学试题与答案(实验区)

2005年广东省基础教育课程改革实验区初中毕业生学业考试数学试卷一、选择题(本题共5小题，每小题3分，共15分，每小题给出的4个选项中只有一个是正确的，请将所选选项的字母写在题目后面的括号内)1、计算的结果是1-的式子是( )A 、1--B 、()01- C 、()1-- D 、11- 2、已知⊙1O 的半径为1，⊙2O 的半径为2，两圆的圆心距21O O 为3，则两圆的位置关系是( ) A 、相交 B 、相离 C 、外切 D 、内切3、函数xy 1=与函数x y =的图象在同一平面直角坐标系内的交点的个数是( ) A 、1个 B 、2个 C 、3个 D 、0个4、如图所示几何体的左视图是( )5、4个红球、3个白球、2个黑球放入一个不透明的袋子里，从中摸出8个球，恰好红球、白球、黑球都摸到，这件事情( )A 、可能发生B 、不可能发生C 、很可能发生D 、必然发生二、填空题(本题共5小题，每小题4分，共20分，请把下列各题的正确答案填写在横线上)千瓦。

7、方程x x 22=的解是。

8、若数据3,,8,7,9,8x 的平均数是7，则这组数据的众数是。

9、如图，已知CD ⊥AB ，BE ⊥AC ，垂足分别为D 、E ，BE 、CD 交于点O ，且AO 平分∠BAC ，那么图中全等三角形共有对。

10、如图，PA 、PB 是⊙O 的切线，点A 、B 为切点，AC 是⊙O 的直径，∠BAC=°20，则P 的大小是度。

三、解答题(本题共5小题，每小题6分，共30分)11、分解因式224ay ax - 12、解方程11121=++-+x x x 解：解：13、将方格中的图案作下列变换，请画出相应的图案：⑴沿y 轴正向平移4个单位；⑵关于y 轴轴对称；14、如图，某长方形广场的四角都有一块半径相同的四分之一的圆形的草地，若圆形的半径为r 米，长方形长为a 米，宽为b 米。

⑴请用代数式表示空地的面积；⑵若长方形的长为300米，宽为200米，圆的半径为10米。

2005年广东省中考数学试卷

2005年广东省中考数学试卷（课标卷）一、选择题（共5小题，每小题3分，满分15分）3．（3分）（2005•中山）函数y=与y=x 的图象在同一平面直角坐标系内的交点的个数是（） 4．（3分）（2005•中山）如图所示的几何体的左视图是（）．CD ．5．（3分）（2005•中山）将4个红球、3个白球、2个黑球放入一个不透明的袋子里，从中摸出8个球，恰好红球、二、填空题（共5小题，每小题4分，满分20分） 6．（4分）（2005•中山）长江三峡水电站的总装机容量是18 200 000千瓦，用科学记数法表示为 _________ 千瓦．7．（4分）（2005•中山）方程x 2=2x 的解是 _________ ． 8．（4分）（2005•中山）若一组数据8，9，7，8，x ，3的平均数是7，则这组数据的众数是 _________ ． 9．（4分）（2005•中山）如图，已知CD ⊥AB ，BE ⊥AC ，垂足分别为D 、E ，BE 、CD 交于点O ，且AO 平分∠BAC ，那么图中全等三角形共有 _________ 对．10．（4分）（2005•中山）如图，PA、PB是⊙O的切线，点A、B为切点，AC是⊙O的直径，∠BAC=20°，则∠P 的大小是_________度．三、解答题（共12小题，满分85分）11．（6分）（2005•中山）分解因式：ax2﹣4ay2．12．（6分）（2005•中山）解方程：13．（6分）（2005•中山）将方格中的图案作下列变换，请画出相应的图案：（1）沿y轴正向平移4个单位；（2）关于y轴轴对称．14．（6分）（2005•中山）如图，某长方形广场的四个角都有一块半径相同的四分之一圆形的草地，若圆形的半径为r米，长方形长为a米，宽为b米．（1）分别用代数式表示草地和空地的面积；（2）若长方形长为300米，宽为200米，圆形的半径为10米，求广场空地的面积（计算结果保留到整数）．15．（6分）（2005•中山）某电视台的娱乐节目《周末大放送》有这样的翻奖牌游戏，数字的背面写有祝福语或奖金数，游戏规则是：每次翻动正面一个数字，看看反面对应的内容，就可知是得奖还是得到温馨祝福．计算：（2）“翻到奖金”的概率；（3）“翻不到奖金”的概率．16．（7分）（2005•中山）某市选自来水公司为鼓励居民节约用水，采取按月用水量收费办法，若某户居民应交消费y（元）与用水量x（吨）的函数关系如图所示．（1）分别写出当0≤x≤15和x≥15时，y与x的函数关系式；（2）若某用户该月用水21吨，则应交水费多少元？17．（7分）（2005•中山）如图，为测量小河的宽度，先在河岸边任意取一点A，再在河的另一岸取两点B、C，测得∠ABC=45°，∠ACB=30°，量得BC长为20米．（1）求小河的宽度（使用计算器的地区，结果保留三位有效数字；不使用计算器的地区，结果保留根号）；（2）请再设计一种测量河宽度的方案，画出设计草图并作简要说明．18．（7分）（2005•中山）如图，设四边形ABCD是边长为1的正方形，以正方形ABCD的对角线AC为边作第二个正方形ACEF，再以第二个正方形的对角线AE为边作第三个正方形AEGH，如此下去…．（1）记正方形ABCD的边长为a1=1，依上述方法所作的正方形的边长依次为a2，a3，a4，…，a n，求出a2，a3，a4的值．（2）根据以上规律写出第n个正方形的边长a n的表达式．19．（7分）（2005•中山）初三（1）班某一次数学测验成绩如下：63，84，91，53，69，81，61，69，91，78，75，81，80，67，76，81，79，94，61，69，89，70，70，87，81，86，90，88，85，67，71，82，87，75，87，95，53，65，74，77．（2）请说明哪个分数段的学生最多？哪个分数段的学生最少？（3）请你帮老师统计一下这次数学考试的及格率（60分以上含60分为及格）及优秀率（90分以上含90分为优秀）．20．（9分）（2005•中山）如图，等腰梯形ABCD中，AD∥BC，M、N分别是AD、BC的中点，E、F分别是BM、CM中点．（1）求证：四边形MENF是菱形；（2）若四边形MENF是正方形，请探索等腰梯形ABCD的高和底边BC的数量关系，并证明你的结论．21．（9分）（2005•中山）某夏令营的活动时间为15天，营员的宿舍安装了空调．如果某间宿舍每天比原计划多开2个小时的空调，那么开空调的总时间超过150小时；如果每天比原计划少开2个小时的空调，那么开空调的总时间不足120小时，问原计划每天开空调的时间为多少小时？22．（9分）（2005•中山）如图所示，在平面直角坐标中，抛物线的顶点P到x轴的距离是4，抛物线与x轴相交于O、M两点，OM=4；矩形ABCD的边BC在线段的OM上，点A、D在抛物线上．（1）请写出P、M两点坐标，并求出这条抛物线的解析式；（2）设矩形ABCD的周长为l，求l的最大值；（3）连接OP、PM，则△PMO为等腰三角形，请判断在抛物线上是否存在点Q（除点M外），使得△OPQ也是等腰三角形，简要说明你的理由．2005年广东省中考数学试卷（课标卷）参考答案与试题解析一、选择题（共5小题，每小题3分，满分15分）3．（3分）（2005•中山）函数y=与y=x的图象在同一平面直角坐标系内的交点的个数是（）y=中，4．（3分）（2005•中山）如图所示的几何体的左视图是（）．C D．5．（3分）（2005•中山）将4个红球、3个白球、2个黑球放入一个不透明的袋子里，从中摸出8个球，恰好红球、二、填空题（共5小题，每小题4分，满分20分）6．（4分）（2005•中山）长江三峡水电站的总装机容量是18 200 000千瓦，用科学记数法表示为 1.82×107千瓦．7．（4分）（2005•中山）方程x2=2x的解是x1=0，x2=2．8．（4分）（2005•中山）若一组数据8，9，7，8，x，3的平均数是7，则这组数据的众数是7和8．9．（4分）（2005•中山）如图，已知CD⊥AB，BE⊥AC，垂足分别为D、E，BE、CD交于点O，且AO平分∠BAC，那么图中全等三角形共有4对．10．（4分）（2005•中山）如图，PA、PB是⊙O的切线，点A、B为切点，AC是⊙O的直径，∠BAC=20°，则∠P 的大小是40度．三、解答题（共12小题，满分85分）11．（6分）（2005•中山）分解因式：ax2﹣4ay2．12．（6分）（2005•中山）解方程：．是原方程的解．．13．（6分）（2005•中山）将方格中的图案作下列变换，请画出相应的图案：（1）沿y轴正向平移4个单位；（2）关于y轴轴对称．14．（6分）（2005•中山）如图，某长方形广场的四个角都有一块半径相同的四分之一圆形的草地，若圆形的半径为r米，长方形长为a米，宽为b米．（1）分别用代数式表示草地和空地的面积；（2）若长方形长为300米，宽为200米，圆形的半径为10米，求广场空地的面积（计算结果保留到整数）．×π15．（6分）（2005•中山）某电视台的娱乐节目《周末大放送》有这样的翻奖牌游戏，数字的背面写有祝福语或奖金数，游戏规则是：每次翻动正面一个数字，看看反面对应的内容，就可知是得奖还是得到温馨祝福．计算：（2）“翻到奖金”的概率；（3）“翻不到奖金”的概率．的概率为=16．（7分）（2005•中山）某市选自来水公司为鼓励居民节约用水，采取按月用水量收费办法，若某户居民应交消费y（元）与用水量x（吨）的函数关系如图所示．（1）分别写出当0≤x≤15和x≥15时，y与x的函数关系式；（2）若某用户该月用水21吨，则应交水费多少元？y=，x解得17．（7分）（2005•中山）如图，为测量小河的宽度，先在河岸边任意取一点A，再在河的另一岸取两点B、C，测得∠ABC=45°，∠ACB=30°，量得BC长为20米．（1）求小河的宽度（使用计算器的地区，结果保留三位有效数字；不使用计算器的地区，结果保留根号）；（2）请再设计一种测量河宽度的方案，画出设计草图并作简要说明．ACD=（（18．（7分）（2005•中山）如图，设四边形ABCD是边长为1的正方形，以正方形ABCD的对角线AC为边作第二个正方形ACEF，再以第二个正方形的对角线AE为边作第三个正方形AEGH，如此下去…．（1）记正方形ABCD的边长为a1=1，依上述方法所作的正方形的边长依次为a2，a3，a4，…，a n，求出a2，a3，a4的值．（2）根据以上规律写出第n个正方形的边长a n的表达式．====a a=a=2=，=a=a=2=．19．（7分）（2005•中山）初三（1）班某一次数学测验成绩如下：63，84，91，53，69，81，61，69，91，78，75，81，80，67，76，81，79，94，61，69，89，70，70，87，81，86，90，88，85，67，71，82，87，75，87，95，53，65，74，77．（2）请说明哪个分数段的学生最多？哪个分数段的学生最少？（3）请你帮老师统计一下这次数学考试的及格率（60分以上含60分为及格）及优秀率（90分以上含90分为优秀）．可计算出数学考试的及格率与优秀率．）及格率为：优秀率为：20．（9分）（2005•中山）如图，等腰梯形ABCD中，AD∥BC，M、N分别是AD、BC的中点，E、F分别是BM、CM中点．（1）求证：四边形MENF是菱形；（2）若四边形MENF是正方形，请探索等腰梯形ABCD的高和底边BC的数量关系，并证明你的结论．MC MBMB MCMN=21．（9分）（2005•中山）某夏令营的活动时间为15天，营员的宿舍安装了空调．如果某间宿舍每天比原计划多开2个小时的空调，那么开空调的总时间超过150小时；如果每天比原计划少开2个小时的空调，那么开空调的总时间不足120小时，问原计划每天开空调的时间为多少小时？小时，依题意可得22．（9分）（2005•中山）如图所示，在平面直角坐标中，抛物线的顶点P到x轴的距离是4，抛物线与x轴相交于O、M两点，OM=4；矩形ABCD的边BC在线段的OM上，点A、D在抛物线上．（1）请写出P、M两点坐标，并求出这条抛物线的解析式；（2）设矩形ABCD的周长为l，求l的最大值；（3）连接OP、PM，则△PMO为等腰三角形，请判断在抛物线上是否存在点Q（除点M外），使得△OPQ也是等腰三角形，简要说明你的理由．。

2005年广东省深圳市中考数学试卷+答案

2005年广东省深圳市中考数学试卷一、选择题（共10小题，每小题3分，满分30分）1．（3分）在0，﹣1，1，2这四个数中，最小的数是（）A．﹣1 B．0 C．1 D．22．（3分）我们从不同的方向观察同一物体时，可以看到不同的平面图形，如图，从图的左面看这个几何体的左视图是（）A．B．C．D．3．（3分）方程x2﹣2x=0的解是（）A．x=2 B．x1=−√2，x2=0 C．x1=2，x2=0 D．x=04．（3分）长城总长约为6 700 010米，用科学记数法表示是（保留两个有效数字）（）A．6.7×105米B．6.7×106米C．6.7×107米D．6.7×108米5．（3分）函数y=kk xx（k≠0）的图象过点（2，﹣2），则此函数的图象在平面直角坐标系中的（）A．第一、三象限B．第三、四象限C．第一、二象限D．第二、四象限6．（3分）下面所列图形中是中心对称图形的为（）A．B．C．D．7．（3分）中央电视台“幸运52”栏目中的“百宝箱”互动环节，是一种竞猜游戏，游戏规则如下：在20个商标中，有5个商标牌的背面注明了一定的奖金额，其余商标的背面是一张苦脸，若翻到它就不得奖、参加这个游戏的观众有三次翻牌的机会．某观众前两次翻牌均得若干奖金，如果翻过的牌不能再翻，那么这位观众第三次翻牌获奖的概率是（）A．14B．16C．15D．3208．（3分）实数a、b在数轴上的位置如图所示，那么化简|a﹣b|﹣�aa2的结果是（）A．2a﹣b B．b C．﹣b D．﹣2a+b9．（3分）一件衣服标价132元，若以9折降价出售，仍可获利10%，则这件衣服的进价是（）A．106元B．105元C．118元D．108元10．（3分）如图，AB是⊙O的直径，点D、E是半圆的三等分点，AE、BD的延长线交于点C，若CE=2，则图中阴影部分的面积是（）A．43π﹣√3B．23πC．23π﹣√3D．13π二、填空题（共5小题，每小题3分，满分15分）11．（3分）一组数据3，8，8，19，19，19，19的众数是．12．（3分）下图是根据某地相邻两年6月上旬日平均气温情况绘制的折线统计图，通过观察图形，可以判断这两年6月上旬气温比较稳定的年份是年．13．（3分）如图，已知，在△ABC和△DCB中，AC=DB，若不增加任何字母与辅助线，要使△ABC≌△DCB，则还需增加一个条件是．14．（3分）已知：21×2=21+2，32×3=32+3，43×4=43+4，…，若aa bb×10=aa bb+10（a、b 都是正整数），则a+b的值是．15．（3分）如图，▱ABCD中，点E在边AD上，以BE为折痕，将△ABE向上翻折，点A正好落在CD上的F点，若△FDE的周长为8 cm，△FCB的周长为20cm，则FC的长为cm．三、解答题（共7小题，满分55分）16．（6分）计算：（√3−1）0+（13）﹣1﹣�(−√5)2﹣|﹣1|．17．（6分）先化简，再求值：（xx xx−2−xx xx+2）÷4xx xx−2，其中x=2005．18．（8分）大楼AD的高为10米，不远处有一塔BC，某人在楼底A处测得塔顶B处的仰角为60°，爬到楼顶D点测得塔顶B点的仰角为30°，求塔BC的高度．19．（8分）如图是某班学生外出乘车、步行、骑车的人数分布直方图和扇形分布图．（1）求该班有多少名学生？（2）补上步行分布直方图的空缺部分；（3）在扇形统计图中，求骑车人数所占的圆心角度数；（4）若全年级有500人，估计该年级步行人数．20．（9分）某工程，甲工程队单独做40天完成，若乙工程队单独做30天后，甲、乙两工程队再合作20天完成．（1）求乙工程队单独做需要多少天完成？（2）将工程分两部分，甲做其中一部分用了x天，乙做另一部分用了y天，其中x、y均为正整数，且x＜15，y＜70，求x、y．21．（9分）已知△ABC是边长为4的等边三角形，BC在x轴上，点D为BC的中点，点A在第一象限内，AB与y轴的正半轴相交于点E，点B（﹣1，0），P 是AC上的一个动点（P与点A、C不重合）（1）求点A、E的坐标；（2）若y=−6�37x2+bx+c过点A、E，求抛物线的解析式；（3）连接PB、PD，设L为△PBD的周长，当L取最小值时，求点P的坐标及L 的最小值，并判断此时点P是否在（2）中所求的抛物线上，请充分说明你的判断理由．22．（9分）AB是⊙O的直径，点E是半圆上一动点（点E与点A、B都不重合），点C是BE延长线上的一点，且CD⊥AB，垂足为D，CD与AE交于点H，点H与点A不重合．（1）求证：△AHD∽△CBD；（2）连HO，若CD=AB=2，求HD+HO的值．2005年广东省深圳市中考数学试卷参考答案与试题解析一、选择题（共10小题，每小题3分，满分30分）1．（3分）在0，﹣1，1，2这四个数中，最小的数是（）A．﹣1 B．0 C．1 D．2【分析】一切负数小于0，两个负数作比较，绝对值大的反而小．【解答】解：∵在0，﹣1，1，2这四个数中，0，1，2均大于0，﹣1＜0，故﹣1最小．故选A．【点评】本题很简单，只要熟知正数都大于0，负数都小于0，正数大于一切负数即可．2．（3分）我们从不同的方向观察同一物体时，可以看到不同的平面图形，如图，从图的左面看这个几何体的左视图是（）A．B．C．D．【分析】找到从左面看所得到的图形即可．【解答】解：从左边看时，因为左边是3竖列，右边1竖列，所以左边三个正方形叠一起，右边一个正方形．故选B．【点评】本题考查了三视图的知识，左视图是从物体的左面看得到的视图．3．（3分）方程x2﹣2x=0的解是（）A．x=2 B．x1=−√2，x2=0 C．x1=2，x2=0 D．x=0【分析】本题应对方程进行移项，等式右边化为0，即为x2﹣2x=0，提取公因式x，将原式化为两式相乘的形式，x（x﹣2）=0，再根据“两式相乘值为0，这两式中至少有一式值为0”来求解．【解答】解：原方程变形为：x2﹣2x=0，x（x﹣2）=0，x1=0，x2=2．故本题选C．【点评】本题考查了一元二次方程的解法．解一元二次方程常用的方法有直接开平方法，配方法，公式法，因式分解法，要根据方程的特点灵活选用合适的方法，本题运用的是因式分解法．4．（3分）长城总长约为6 700 010米，用科学记数法表示是（保留两个有效数字）（）A．6.7×105米B．6.7×106米C．6.7×107米D．6.7×108米【分析】在实际生活中，许多比较大的数，我们习惯上都用科学记数法表示，使书写、计算简便．将一个绝对值较大的数写成科学记数法a×10n的形式时，其中1≤|a|＜10，n为比整数位数少1的数．而且a×10n（1≤|a|＜10，n为整数）中n的值是易错点，∵6 700 010有7位，所以可以确定n=7﹣1=6．【解答】解：根据题意6 700 010≈6.7×106．（保留两个有效数字）故本题选B．【点评】本题考查了科学记数法，把一个数M记成a×10n（1≤|a|＜10，n为整数）的形式，这种记数的方法叫做科学记数法．5．（3分）函数y=kk xx（k≠0）的图象过点（2，﹣2），则此函数的图象在平面直角坐标系中的（）A．第一、三象限B．第三、四象限C．第一、二象限D．第二、四象限【分析】本题考查反比例函数的图象和性质，k=﹣4＜0，函数位于二四象限．【解答】解：将（2，﹣2）代入y=kk xx（k≠0）得k=﹣4，根据反比例函数的性质，函数的图象在平面直角坐标系中的第二、四象限．故选D．【点评】本题考查了反比例函数的性质，①、当k＞0时，图象分别位于第一、三象限；当k＜0时，图象分别位于第二、四象限．②、当k＞0时，在同一个象限内，y随x的增大而减小；当k＜0时，在同一个象限，y随x的增大而增大．6．（3分）下面所列图形中是中心对称图形的为（）A．B．C．D．【分析】根据中心对称与轴对称的概念和各图形的特点即可求解．【解答】解：A、是轴对称图形；B、有五个角，但有旋转，所以既不是轴对称图形也不是中心对称图形；C、即是轴对称图形，又是中心对称图形；D、是轴对称图形．故选C．【点评】注意区别轴对称图形与中心对称图形的概念．【链接】轴对称的关键是寻找对称轴，图象沿对称轴折叠后可重合，中心对称是要寻找对称中心，旋转180度后与原图重合．7．（3分）中央电视台“幸运52”栏目中的“百宝箱”互动环节，是一种竞猜游戏，游戏规则如下：在20个商标中，有5个商标牌的背面注明了一定的奖金额，其余商标的背面是一张苦脸，若翻到它就不得奖、参加这个游戏的观众有三次翻牌的机会．某观众前两次翻牌均得若干奖金，如果翻过的牌不能再翻，那么这位观众第三次翻牌获奖的概率是（）A．14B．16C．15D．320【分析】分别求出所剩商标数与中奖商标的个数，再根据概率公式解答即可．【解答】解：因为20个商标有5个中奖，翻了两个都中奖，所以还剩18个，其中还有3个会中奖，所以这位观众第三次翻牌获奖的概率是318=16．故选B．【点评】概率等于所求情况数与总情况数之比．8．（3分）实数a、b在数轴上的位置如图所示，那么化简|a﹣b|﹣�aa2的结果是（）A．2a﹣b B．b C．﹣b D．﹣2a+b【分析】首先能根据数轴看出：a＜0，b＞0，且a的绝对值大于b的绝对值，化简�aa−bb�和�aa2即可．【解答】解：根据数轴可知：a＜0，b＞0，且�aa�＞�bb�，∴�aa−bb�﹣�aa2，=﹣（a﹣b）﹣（﹣a），=b，故选：B．【点评】解此题的关键是（1）确定a b的大小及之间的关系，（2）利用绝对值的性质和二次根式的性质进行化简，难点是（1）确定a b的大小及之间的关系，题目很好，有一定难度．9．（3分）一件衣服标价132元，若以9折降价出售，仍可获利10%，则这件衣服的进价是（）A．106元B．105元C．118元D．108元【分析】本题等量关系：利润=售价﹣进价．【解答】解：设这件衣服的进价为x元，则132×0.9=x+10%x解得：x=108故选D．【点评】注意售价有两种表示方式：标价×折数；进价+利润．10．（3分）如图，AB是⊙O的直径，点D、E是半圆的三等分点，AE、BD的延长线交于点C，若CE=2，则图中阴影部分的面积是（）A．43π﹣√3B．23πC．23π﹣√3D．13π【分析】已知D、E是半圆的三等分点，如果连接DE、OE、OD，那么△OAE、△ODE、△OBD、△CDE都是等边三角形，由此可求出扇形OBE的圆心角的度数和圆的半径长；由于∠AOE=∠BOD，则AB∥DE，S△ODE =S△BDE；可知阴影部分的面积=S扇形OAE ﹣S△OAE+S扇形ODE求解．【解答】解：连接OE、OD，点D、E是半圆的三等分点，∴∠AOE=∠EOD=∠DOB=60°∵OA=OE=OD=OB∴△OAE、△ODE、△OBD、△CDE都是等边三角形，∴AB∥DE，∴S△ODE =S△BDE；∴图中阴影部分的面积=S扇形OAE ﹣S△OAE+S扇形ODE=60⋅ππ⋅22360×2﹣12×2×√3=43π﹣√3．故选：A．【点评】本题考查了扇形面积公式的运用．关键是将阴影部分面积转化为扇形ODE的面积．二、填空题（共5小题，每小题3分，满分15分）11．（3分）一组数据3，8，8，19，19，19，19的众数是19．【分析】根据众数的定义就可以求解．【解答】解：在这一组数据中19是出现次数最多的，故众数是19．故填19．【点评】本题为统计题，考查众数的意义．众数是一组数据中出现次数最多的数．12．（3分）下图是根据某地相邻两年6月上旬日平均气温情况绘制的折线统计图，通过观察图形，可以判断这两年6月上旬气温比较稳定的年份是2005年．【分析】折线统计图中折线越起伏的表示数据越不稳定，相反，折线越平稳的表示数据越稳定；从两幅图中可以看出：2004年6月上旬折线起伏较大，所以2004年6月上旬气温比较不稳定，则2005年6月上旬折线较平稳，则2005年6月上旬气温比较稳定．【解答】解：从两幅图中可以看出：2004年6月上旬折线起伏较大，所以2004年6月上旬气温比较不稳定，则2005年6月上旬折线较平稳，则2005年6月上旬气温比较稳定．【点评】本题考查的是折线统计图的综合运用．从折线统计图中不仅能看出数据的多少，还能看出数据的变化情况．13．（3分）如图，已知，在△ABC和△DCB中，AC=DB，若不增加任何字母与辅助线，要使△ABC≌△DCB，则还需增加一个条件是AB=DC．【分析】要使△ABC≌△DCB，已知有两对边对应相等，则可根据全等三角形的判定方法添加合适的条件即可．【解答】解：∵AC=BD，BC=BC，∴可添加AB=DC利用SSS判定△ABC≌△DCB．故填AB=DC．【点评】本题考查三角形全等的判定方法；判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．添加时注意：AAA、SSA不能判定两个三角形全等，不能添加，根据已知结合图形及判定方法选择条件是正确解答本题的关键．14．（3分）已知：21×2=21+2，32×3=32+3，43×4=43+4，…，若aa bb×10=aa bb+10（a、b 都是正整数），则a+b的值是19．【分析】根据题意可知，a=10，b=9，所以a+b的值是=19．【解答】解：∵aa bb×10=aa bb+10∴a+b=1910a∵（a、b都是正整数）∴a=10，b=9∴a+b的值是19．故答案为：19．【点评】主要考查了学生的分析、总结、归纳能力，规律型的习题一般是从所给的数据和运算方法进行分析，从特殊值的规律上总结出一般性的规律．15．（3分）如图，▱ABCD中，点E在边AD上，以BE为折痕，将△ABE向上翻折，点A正好落在CD上的F点，若△FDE的周长为8 cm，△FCB的周长为20cm，则FC的长为6cm．【分析】根据折叠的性质，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．【解答】解：AE=EF，AB=BF；△FDE的周长为DE+FE+DF=AD+DF=8cm，△FCB的周长为FC+AD+AB=20 cm，分析可得：FC=12[FC+AD+AB﹣（AD+DF）]=12（2FC）=12（△FCB的周长﹣△FDE 的周长）=12（20﹣8）=6cm．故答案为6．【点评】本题通过折叠变换考查学生的逻辑思维能力，解决此类问题，应结合题意，最好实际操作图形的折叠，易于找到图形间的关系．三、解答题（共7小题，满分55分）16．（6分）计算：（√3−1）0+（13）﹣1﹣�(−√5)2﹣|﹣1|．【分析】按照实数的运算法则依次计算：（√3−1）0=1，（13）﹣1=3，﹣�(−√5)2=√5，﹣|﹣1|=﹣1．将其代入原式易得答案．【解答】解：原式=1+3﹣√5﹣1=3﹣√5．【点评】本题考查绝对值的定义：一个正数的绝对值是它本身；一个负数的绝对值是它的相反数；0的绝对值是0；互为相反数的绝对值相等．17．（6分）先化简，再求值：（xx xx−2−xx xx+2）÷4xx xx−2，其中x=2005．【分析】先通分，然后进行四则运算，最后将x=2005代入．【解答】解：原式=xx2+2xx−xx2+2xx(xx+2)(xx−2)•xx−24xx=1xx+2=12007．【点评】解答此题的关键是把分式化到最简，然后代值计算．18．（8分）大楼AD的高为10米，不远处有一塔BC，某人在楼底A处测得塔顶B处的仰角为60°，爬到楼顶D点测得塔顶B点的仰角为30°，求塔BC的高度．【分析】过点B作BE⊥AD交AD延长线于点E，构造两个直角三角形．设DE=x，分别求解可得AD与DE的值，再利用BC=AD+DE，即可求出答案．【解答】解：过点B作BE⊥AD，交AD延长线于点E．（1分）在Rt△BED中，∵D点测得塔顶B点的仰角为30°，∴∠BDE=60度．设DE=x，则BE=√3x．（2分）在Rt△BEA中，∠BAE=30度，BE=√3x．∴AE=3x．（3分）∴AD=AE﹣DE=3x﹣x=2x=10．∴x=5．（4分）∴BC=AD+DE=10+5=15（米）．（5分）答：塔BC的高度为15米．【点评】本题考查俯角、仰角的定义，要求学生能借助俯角、仰角构造直角三角形并结合图形利用三角函数解直角三角形．19．（8分）如图是某班学生外出乘车、步行、骑车的人数分布直方图和扇形分布图．（1）求该班有多少名学生？（2）补上步行分布直方图的空缺部分；（3）在扇形统计图中，求骑车人数所占的圆心角度数；（4）若全年级有500人，估计该年级步行人数．【分析】（1）根据骑车12人占百分比30%，即可计算学生总数；（2）根据学生总数进行计算，然后补全统计图即可；（3）根据骑车所占的百分比乘以360°即可；（3）根据样本中步行所占的百分比进行估算500人中步行的人数．【解答】解：（1）12÷30%=40人；（2）见图；（3）圆心角度数=20100×360°=72°；（4）估计该年级步行人数=500×30%=150（人）．【点评】本题考查的是条形统计图和扇形统计图的综合运用．读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小．20．（9分）某工程，甲工程队单独做40天完成，若乙工程队单独做30天后，甲、乙两工程队再合作20天完成．（1）求乙工程队单独做需要多少天完成？（2）将工程分两部分，甲做其中一部分用了x天，乙做另一部分用了y天，其中x、y均为正整数，且x＜15，y＜70，求x、y．【分析】本题的等量关系为：工作时间=工作总量÷工作效率，由题意可知：甲工程队的总工程量+乙工程队的总工程量=1．其中（1）甲做的天数为20天，乙做的天数50天；（2）甲做的天数为x天，乙做的天数为y天．【解答】解：（1）设乙工程队单独做需要a天完成，则30×1aa+20（140+1aa）=1，解之得：a=100经检验，a=100是所列方程的解，答：乙工程队单独做需要100天完成．（2）甲做其中一部分用了x天，乙做另一部分用了y天，则xx40+yy100=1，即：y=100﹣52xx，又x＜15，y＜70所以�100−52xx＜70xx＜15，解之得：12＜x＜15，因为x是整数，所以x=13或14，又∵y也为正整数，∴当x=13时，y=100﹣52xx=1352（舍去）当x=14时，y=100﹣52xx=65．∴x=14，y=65．答：x=14，y=65．【点评】列分式方程解应用题与所有列方程解应用题一样，重点在于准确地找出相等关系，这是列方程的依据．找到关键描述语，找到等量关系是解决问题的关键．本题主要考查的等量关系为：工作时间=工作总量÷工作效率．21．（9分）已知△ABC是边长为4的等边三角形，BC在x轴上，点D为BC的中点，点A在第一象限内，AB与y轴的正半轴相交于点E，点B（﹣1，0），P 是AC上的一个动点（P与点A、C不重合）（1）求点A、E的坐标；（2）若y=−6�37x2+bx+c过点A、E，求抛物线的解析式；（3）连接PB、PD，设L为△PBD的周长，当L取最小值时，求点P的坐标及L 的最小值，并判断此时点P是否在（2）中所求的抛物线上，请充分说明你的判断理由．【分析】（1）△ABC是边长为4的等边三角形，则BC=4，而点D为BC的中点，BD=2，点B（﹣1，0），则OD=1，就可以求出A的横坐标，等边三角形的高线长，就是A的纵坐标．在直角三角形OBE中，根据三角函数可以求出OE的长，即得到E点的纵坐标．（2）已经求出A，E的坐标，根据待定系数法就可以求出函数的解析式．（3）先作点D关于AC的对称点D'，连接BD'交AC于点P，则PB与PD的和取最小值，即△PBD的周长L取最小值．根据三角函数求的D′的坐标，再求出直线BD′的解析式，以及直线AC的解析式，两直线的交点就是P的坐标．把点P的坐标代入二次函数的解析式，就可以判断是否在函数的图象上．【解答】解：（1）连接AD，∵△ABC是边长为4的等边三角形，又B的坐标为（﹣1，0），BC在x轴上，A 在第一象限，∴点C在x轴的正半轴上，∴C的坐标为（3，0），由中点坐标公式，得：D的坐标为（1，0）．显然AD⊥BC且AD=√3BD=2√3，∴A的坐标是（1，2√3）．OE=12AD，得E（0，√3）；（2）因为抛物线y=−6�37x2+bx+c过点A、E，由待定系数法得：c=√3，b=13√37，抛物线的解析式为y=−6�37xx2+13�37xx+√3；（3）大家记得这样一个常识吗？“牵牛从点A出发，到河边l喝水，再到点B处吃草，走哪条路径最短”即确定l 上的点P，方法是作点A关于l的对称点A'，连接A'B与l的交点P即为所求．本题中的AC就是“河”，B、D分别为“出发点”和“草地”．由引例并证明后，得先作点D关于AC的对称点D'，连接BD'交AC于点P，则PB与PD的和取最小值，即△PBD的周长L取最小值．∵D、D′关于直线AC对称，∴DD′⊥AC，即∠D′DC=30°，DF=√3，DD'=2√3，求得点D'的坐标为（4，√3），直线BD'的解析式为：yy=�35x+√35，直线AC的解析式为：yy=−√3xx+3√3，求直线BD'与AC的交点可得点P的坐标（73，2√33）．此时BD'=�BBGG2+DD′GG2=�52+(√3)2=2√7，所以△PBD的最小周长L为2√7+2，把点P的坐标代入y=−6�37xx2+13�37xx+√3成立，所以此时点P在抛物线上．【点评】本题主要考查了待定系数法求函数的解析式，求两条线段的和最小的问题，一般是转化为两点之间线段最短的问题．22．（9分）AB是⊙O的直径，点E是半圆上一动点（点E与点A、B都不重合），点C是BE延长线上的一点，且CD⊥AB，垂足为D，CD与AE交于点H，点H与点A不重合．（1）求证：△AHD∽△CBD；（2）连HO，若CD=AB=2，求HD+HO的值．【分析】（1）要证△AHD∽△CBD，只要证明这两个三角形的两组对边的比相等，就可以证出；（2）①设OD=x，则BD=1﹣x，AD=1+x，由Rt△AHD∽Rt△CBD可用x表示出DH的值，在Rt△HOD中利用勾股定理可用x表示出OH的值，进而可得出结论；②当点E移动到使D与O重合的位置时，这时HD与HO重合，由Rt△AHO∽Rt △CBO，利用对应边的比例式为方程，可以算出HD=HO=12，即HD+HO=1；③当D在OA段时BD=1+x，AD=1﹣x，证明同①．【解答】（1）证明：AB是⊙O的直径∴∠AEB=90°，则∠ABC+∠BAE=90°，又∵CD⊥AB，∴∠BAE+∠AHD=90°，∴∠AHD=∠ABC，又∵∠ADH=∠CDB=90°，∴△AHD∽△CBD．（2）解：设OD=x，则BD=1﹣x，AD=1+x，∵Rt△AHD∽Rt△CBD，则HD：BD=AD：CD，即HD：（1﹣x）=（1+x）：2，即HD=1−xx22，在Rt△HOD中，由勾股定理得：OH=�OODD2+HHDD2=�xx2+(1−xx22)2=1+xx22，所以HD+HO=1−xx22+1+xx22=1；②当点E移动到使D与O重合的位置时，这时HD与HO重合，由Rt△AHO∽Rt △CBO，利用对应边的比例式为方程，可以算出HD=HO=12，即HD+HO=1；③当D在OA段时BD=1+x，AD=1﹣x，证明同①∵Rt△AHD∽Rt△CBD，则HD：BD=AD：CD，即HD：（1﹣x）=（1+x）：2，即HD=1−xx22，在Rt△HOD中，由勾股定理得：OH=�OODD2+HHDD2=�xx2+(1−xx22)2=1+xx22，所以HD+HO=1−xx22+1+xx22=1．【点评】本题主要考查了三角形相似的证明方法，有两组对应角相等的三角形相似；在第二问中根据三角形相似，对应边的比相等，把问题转化为解方程的问题．第21页（共21页）。

2005年广州市中考数学试题及参考答案(word版)

2005广东省数学中考试题与答案（非课改区）一、选择题（本题共5小题、每小题3分，共15分）1、计算的结果是－1的式子是（）A 、－∣－1∣B 、（－1）0C 、－（－1）D 、1－12、已知梯形的上底边长是6cm ，它的中位线长是8cm ，则它的下底边长是（）A 、8cmB 、10cmC 、12cmD 、14cm3、函数y ＝x 1与函数y ＝x 的图象在同一平面直角坐标系内的交点的个数是（）A 、一个B 、二个C 、三个D 、零个4、如图，⊙O 中弧AB 的度数为60°，AC 是⊙O 的直径，那么∠BOC 等于（）A 、150°B 、130°C 、120°D 、60°5、在△ABC 中，∠C ＝90°，若∠A ＝2∠B ，则cosB 等于（）A 、3B 、33C 、23D 、21二、填空题（本题共5小题，每小题4分，共20分）6、纳米是一种长度单位，常用于度量物质原子的大小，1纳米＝10－9米，已知某种植物孢子的直径为45000纳米，用科学记数法表示该孢子的直径为＿＿＿＿＿＿米。

7、若一组数据8、9、7、8、x 、3的平均数是7，则这组数据的众数是＿＿＿。

8、如图，△ABC 中，AC ＝BC ，∠BAC 的外角平分线交BC的延长线于点D ，若∠ADC ＝21∠CAD ，则∠ABC 等于＿＿＿度。

9、计算：012)121()21()2(---÷--＝＿＿＿＿。

10、一条抛物线经过原点，请写出它的一个函数解析式＿＿＿＿＿＿＿。

三、解答题（本题5小题，每小题6分，共30分）11、先分解因式，再求值：2212a b b -+-，其中a ＝－3，b ＝3＋412、如图，AB ∥CD ，直线EF 分别交AB 、CD 于点E 、F ，EG 平分∠AEF ，∠1＝40°，求∠2的度数。

13、解不等式组：⎪⎩⎪⎨⎧-≤-->-x x x x 2214315，并求它的整数解的和。

2005年广东省汕头市中考数学试卷及答案

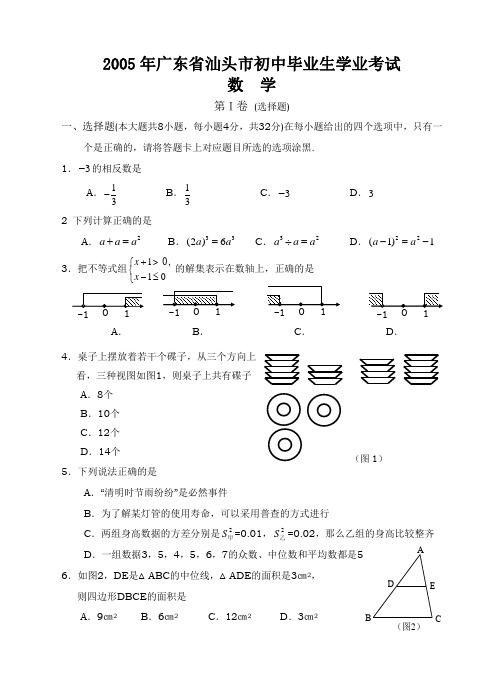
（图1）（图2）E DCBA2005年广东省汕头市初中毕业生学业考试数学第Ⅰ卷 (选择题)一、选择题(本大题共8小题，每小题4分，共32分)在每小题给出的四个选项中，只有一个是正确的，请将答题卡上对应题目所选的选项涂黑. 1．3-的相反数是A ．13-B ．13C ．3-D ．32 下列计算正确的是A ．2a a a +=B ．33(2)6a a =C ．32a a a ÷=D ．22(1)1a a -=-3．把不等式组110x x +⎧⎨-≤⎩>0 ,的解集表示在数轴上，正确的是A ．B ．C ．D ．4．桌子上摆放着若干个碟子，从三个方向上看，三种视图如图1，则桌子上共有碟子 A ．8个B ．10个C ．12个D ．14个 5．下列说法正确的是A ．“清明时节雨纷纷”是必然事件B ．为了解某灯管的使用寿命，可以采用普查的方式进行C ．两组身高数据的方差分别是2甲S =0.01，2乙S =0.02，那么乙组的身高比较整齐D ．一组数据3，5，4，5，6，7的众数、中位数和平均数都是5 6．如图2，DE 是△ABC 的中位线，△ADE 的面积是3㎝2，则四边形DBCE 的面积是A ．9㎝2B ．6㎝2C ．12㎝2D ．3㎝27．如图3，P 是双曲线xk y =上一点，PA ⊥x 轴于A ，△OPA 的面积是1，则k 的值是A ．1B ．2C ．21D ．－28．已知两圆的半径分别是一元二次方程0652=+-x x 的两个根，两圆的圆心距是1，那么这两个圆的位置关系是 A ．内切 B ．内含 C ．相交 D ．外切第Ⅱ卷(非选择题)二、填空题(本大题共5小题，第小题4分，共20分)请把下列各题的正确答案填写在答卷对应的横线上.9．北京2008年第29届奥运会火炬接力活动历时130天，传递总里程约13.7万千米，传递总里程用科学记数法表示为_________千米. 10．函数x y -=2的自变量x 的取值范围是． 11．化简：222111a a a a a -+--+=___________.12．如图4，△ABC 和△ADE 都是等腰直角三角形，∠C 和∠E都是直角，点C 在AD 上，如果△ABC 经旋转后能与△ADE 重合，那么旋转中心是点________，旋转了_________度. 13 认真观察图5的四个图中阴影部分构成的图案，请写出这四个图案都具有的一个共同特征:____________．三、解答题(本大题共5小题，每小题7分，共35分)解答须写出文字说明、证明过程和演算步骤.1411(π1)2cos 454-⎛⎫--+ ⎪⎝⎭°15．解方程：32211xx x +=-+16．已知，如图，在平行四边形ABCD 中，BAD ∠的平分线交BC 边于点E ．（图5）（图3）EDCBA图4)BA求证：BE CD =．17．李强和张新都喜爱看足球、篮球、排球三大球比赛，现有三个频道的电视节目分别在直播这三类球赛，假设他俩同时在各自家里看球赛. (1)李强正在看足球比赛的概率是多少?(2)试用树状图或列表法求李强和张新恰好都在看足球比赛的概率.18．园林工人在对一块半圆形场地进行绿化时遇到难题，需将如图所示的半圆面分成面积相等的三个扇形，以种上不同花草.(1)请你帮该工人在图上作出圆弧的三等分点C 、D ，画出等分线(用直尺和圆规作图，不写作法，保留作图痕迹).(2)已知直径AB 长24m ，请你帮该工人算出其中一份的面积.四、解答题(本大题共3小题，每小题9分，共27分)19．如图，在Rt △ABC 中，∠C=90o ，M 是AB 的中点，AM=AN ，MN//AC ． (1)求证：MN=AC ；(2)如果把条件“AM=AN ”改为“AM ⊥AN ”，其它条件不变，那么MN=AC 不一定成立．如果再改变一个条件，就能使MN=AC 成立．请你写出改变的条件并说明理由．20．如图，一被冰雪压垮的高压铁塔从A 处折断，塔尖着地. 经测量，折断部分AC 与地面的夹角α=43°，塔身部分AB BD=12米，而在同一时刻身高1.82.7米。

广州市2005年2017年中考十年数学试卷真题(打印版附答案)

在每小题给出的四个选项中，只有一项是符合题目要求的。

）1. 下列四个数中，在-2和1之间的数是（）A. –3B. 0C. 2D. 32. 如图，将一块正方形纸片沿对角线折叠一次，然后在得到的三角形的三个角上各挖去一个圆沿，最后将正方形纸片展开，得到的图案是（）3. 下列各点中，在函数72-=x y 的图像上的是（）A. （2，3）B. （3，1）C. （0，-7）D. （-1，9）4. 不等式组⎩⎨⎧>-≥+0101x x 的解集是（）A. 1-≥xB. 1->xC. 1≥xD. 1>x5. 已知12112-=+=b a ，，则a 与b 的关系是（） A. a=bB. ab=1C. a=-bD. ab=-16. 如图，AE 切圆O 于E ，AC=CD=DB=10，则线段AE 的长为（）A. 210B. 15C. 310D. 207. 用计算器计算，，，，15151414131312122222--------…，根据你发现的规律，判断112--=n n P 与1)1(1)1(2-+-+=n n Q （n 为大于1的整数）的值的大小关系为（） A. P<QB. P=QC. P>QD. 与n 的取值有关8. 当k>0时，双曲线x ky =与直线kx y -=的公共点有（） A. 0个 B. 1个 C. 2个 D. 3个9. 如图，多边形的相邻两边均互相垂直，则这个多边形的周长为（）A. 21B. 26C. 37D. 4210. 如图，已知点A （-1，0）和点B （1，2），在坐标轴上确定点P ，使得△ABP 为直角三角形，则满足这样条件的点P 共有（）A. 2个B. 4个C. 6个D. 7个第二部分非选择题（共120分）二、填空题（本题共6小题，每小题3分，满分18分）11. 如图，点A 、B 、C 在直线l 上，则图中共有__________条线段。

2005年佛山市中考数学试题及答案

佛山市2005年高中阶段学校招生考试数学试卷（课改实验区用）说明：本试卷分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共6页，满分130分，考试时间90分钟。

注意事项：1．试卷的选择题和非选择题都在答题卡上作答，不能答在试卷上．2．要作图（含辅助线）或画表，先用铅笔画线、绘图，再用黑色字迹的钢笔或签字笔描黑． 3．其余注意事项，见答题卡．第Ⅰ卷（选择题共30分）一、选择题（本大题共10小题，每小题3分，共30分．在每小题给出的四个选项中，只有一项是符合题目要求的）.1．－2的绝对值是（）。

A ．2 B ．－2 C ．±2 D ．212．1海里等于1852米．如果用科学记数法表示，1海里等于（）米． A ．4101852.0⨯ B ．310852.1⨯ C ．21052.18⨯ D ．1102.185⨯ 3．下列运算中正确的是（）。

A ．532a a a =+ B ．842a a a =⋅ C ．632)(a a = D ．326a a a =÷4．要使代数式32-x 有意义，则x 的取值范围是（）。

A ．2≠x B ．2≥x C ．2>x D ．2≤x5．小明从正面观察下图所示的两个物体，看到的是（）。

ABC D6．方程11112-=-x x 的解是（）。

A ．1 B ．－1C．±1D．07．下列各组图形，可经平移变换由一个图形得到另一个图形的是（）。

A B C D8．对角线互相垂直平分且相等的四边形一定是（）。

A ．正方形B ．菱形C ．矩形D ．等腰梯形9．下列说法中，正确的是（）。

A ．买一张电影票，座位号一定是偶数B ．投掷一枚均匀的硬币，正面一定朝上C ．三条任意长的线段可以组成一个三角形D ．从1，2，3，4，5这五个数字中任取一个数，取得奇数的可能性大 10．如图，是象棋盘的一部分。

若位于点（1，－2）上，位于点（3，－2）上，则位于点（）上。