中考数学模拟分类汇编48 探索规律型问题

合集下载

中考规律探索型问题及

规律探索型问题1. 如，下面是依照必然律画出的“数形〞，察可以：A 2 比 A 1 多出 2 个“ 枝〞， A 3 比 A 2 多出 4 个“ 枝〞，律，A 6 比 A 2 多出“ 枝〞〔〕A 4 比A 3 多出8 个“ 枝〞，⋯⋯，照此D. 124【答案】 C2. 将一些半径相同的小按如所示的律放，小 .〔用含 n的代数式表示〕仔察，第n个形有个第 1个形第 2个形第3个形第 4个形【答案】 n(n1) 4 或 n 2 n 43. 察以下算式：① 1 × 3 - 2 2=3-4=-1 ② 2 × 4 - 3 2=8-9=-1③ 3 × 5 - 4 2=15-16=-1④ ⋯⋯〔 1〕你按以上律写出第 4 个算式；（ 2〕把个律用含字母的式子表示出来；（ 3〕你〔 2〕中所写出的式子必然成立？并明原由．2 24 25 1 ；【答案】解： ⑴ 4 6 5⑵ 答案不唯一 . 如 n n 221；n 1 ⑶ n n 22n22n n 22n 1n 1n 2 2n n 22n 11.4. 察上面的形，它是按必然律排列的，依照此律，第_____个形共有 120 个。

【答案】 155. 先找律，再填数：1 1 1 11 1 1 1 1 11 11 1 1 112,4 2,63,8 4 ,2 3 12 5 30 7 56............那么1+ 1 _______ 2021 1 .2021 20212021【答案】110066. 察下面的形律：1 ＝1－1；2 1 ＝1－1； 1＝1－1；⋯⋯1223233 4 34解答下面的：〔1〕假设 n 正整数，你猜想1 ＝；n(n1)〔2〕明你猜想的；〔3〕求和：11 ＋11.＋23 ＋⋯＋2021 2021123 4【答案】〔1〕11n n 1〔2〕明： 1－1 ＝ n1 － n ＝ n 1 n ＝ 1 .nn 1 n(n 1) n(n 1) n(n1)n(n 1)〔3〕原式＝ 1－1＋1－1＋1－1＋⋯＋1－1＝112021 . 2233420212021202120217.S1=111S2=111=111S n =111222,222,S3242 ,⋯,n22 133(n 1)S S1S2...S n，S=_________ (用含 n 的代数式表示，其中n 正整数 ) ．【答案】n22nn ．1S n 111=11]221=1 [1]21 2( n2 1 [(n n(n2n1)n1)n(n 1)1)n(n 1)=[11]2n( n1)∴S= (11)+(121)+(11) +⋯+(11)n22n .1 2334n(n1)n1接下去利用拆法111即可求和．n(n1) n n18. 以下数表是由从1开始的自然数成，察律并完成各的解答.〔1〕表中第 8 行的最后一个数是〔2〕用含n 的代数式表示：第行共有个数；，它是自然数n 行的第一个数是的平方，第 8 行共有，最后一个数是个数；，第 n〔 3〕求第n行各数之和．【解】〔 1〕 64， 8，15；〔 2〕( n1)2 1 ， n2，2n1；〔 3〕第 2 行各数之和等于3×3；第 3 行各数之和等于5×7；第 4 行各数之和等于7×7-13 ；似的，第 n 行各数之和等于(2 n1)(n2n 1) = 2n33n23n 1 .9. 求 1+2+22+23 +⋯+22021的，可令S=1+2+22+23+⋯+22021， 2S=2+22+23+24+⋯+22021，因此 2S S=22021 1．模拟以上推理，算出1+5+52+53+⋯+52021的〔〕A． 52021 1B． 52021 1C．D．【剖析】 S=1+5+52+53+⋯+52021， 5S=5+52+53 +54+⋯+52021，因此，5S S=520211，S=【答案】 C．10. 察以下一数： 2 ， 4，6，8， 10，⋯⋯，它是按必然律排列的，那么一357911数的第 k 个数是．2k【答案】12k11.察以下面一列数： 1，-2 ，3，-4 ，5，-6 ，⋯依照你的律，第 2021 个数是 ___________【答案】 -202112. 在下中，每个案均由 1 的小正方形按必然的律堆叠而成，照此律，第10个案中共有个小正方形。

中考数学模拟分类汇编48 探索规律型问题

中考数学模拟分类汇编48 探索规律型问题一、选择题1、（2011年北京四中中考模拟20）32，33和34分别可以按如图所示方式“分裂”成2个、3个和4个连续奇数的和，36也能按此规律进行“分裂”，则36“分裂”出的奇数中最大的是( ) A 、41 B 、39 C 、31 D 、29答案A2、（2011年北京四中模拟26）观察下列算式：21=2，22=4，23=8，24=16，25=32，26=64，27=128，28=256，……。

通过观察，用作所发现的规律确定212的个位数字是（） A ．2 B.4 C.6 D.8 3．（2011年浙江省杭州市模拟）如图，，过上到点的距离分别为的点作的垂线与相交，得到并标出一组黑色梯形，它们的面积分别为．观察图中的规律，求出第10个黑色梯形的面积( )A.32B.54C.76D.8632 3 5 733 9 11 34 1315 1719（第1题图）…① ② ③4. （2011浙江杭州模拟7）图①是一块边长为1，周长记为P 1的正三角形纸板，沿图①的底边剪去一块边长为12的正三角形纸板后得到图②，然后沿同一底边依次剪去一块更小的正三角形纸板（即其边长为前一块被剪如图掉正三角形纸板边长的21）后，得图③，④，…，记第n(n≥3) 块纸板的周长为P n ，则P n -P n-1的值为（）A ．1n 41-）（B ．n 41）（C ．1n 21-）（D ．n21）（答案:C5 (2011浙江省杭州市10模)公务员行政能力测试中有一类图形规律题，可以运用我们初中数学中的图形变换再结合变化规律来解决，下面一题问号格内的图形应该是（ ▲ ）（ (第2题）答案:B（第2题图）…① ② ③6. (2011浙江省杭州市10模)对于每个非零自然数n ，抛物线2211(1)(1)n n n n n y x x +++=-+与x轴交于A n 、B n 两点，以n n A B 表示这两点间的距离，则112220092009A B A B A B +++的值是 ▲答案: 200920107、（2011年浙江杭州二模）（2011年浙江杭州三模）对于每个非零自然数n ，抛物线2211(1)(1)n n n n n y x x +++=-+与x 轴交于A n 、B n 两点，以n n A B 表示这两点间的距离，则112220112011A B A B A B +++的值是（）A ．20112010B ．20102011 C ．20122011 D ．20112012答案：D8、（2011年浙江杭州七模）图①是一块边长为1，周长记为P 1的正三角形纸板，沿图①的底边剪去一块边长为12的正三角形纸板后得到图②，然后沿同一底边依次剪去一块更小的正三角形纸板（即其边长为前一块被剪如图掉正三角形纸板边长的21）后，得图③，④，…，记第n (n ≥3) 块纸板的周长为P n ，则P n -P n-1的值为（）A ．1n 41-）（ B ．n 41）（ C ．1n 21-）（ D ．n 21）（答案：C二、填空题1、（2011年黄冈中考调研六）瑞士的一位中学教师巴尔末从光谱数据95，1612，2521，3632，中，成功地发现了其规律，从而得到了巴尔末公式，继而打开了光谱奥妙的大门．请你根据这个规律写出第9个数答案1171212、（北京四中模拟）一组按规律排列的数：2，0，4，0，6，0，…，其中第7个数是，第n个数是（n为正整数）．答案：())1(2111+-++nn3、（2011杭州模拟26）如图，将矩形沿图中虚线（其中x y>）剪成①②③④四块图形，用这四块图形恰能拼一个．．．．．正方形．若 y = 2，则x 的值等于 .514、（2011杭州模拟26）若【x】表示不超过x的最大整数（如【∏】=3，【223-】=-3等），212 -⨯】+323-⨯+…+200120002001-⨯= .答案：20005、（2011年浙江杭州三模）如图，在平面直角坐标系上有个点P(1，0)，点P第1次向上跳动1个单位至点P1(1，1)，紧接着第2次向左跳动2个单位至点P2(―1，1)，第3次向上跳动1个单位，第4次向右跳动3个单位，第5次又向上跳动1个单位，第6次向左跳动4个单位，……，依此规律跳动下去，点P第100次跳动至点P100的坐标是。

中考数学专题复习探索规律问题

专题探索规律问题解读考点考点归纳归纳 1：数字猜想型基础知识归纳：数字规律问题主要是在分析比较的基础上发现题目中所蕴涵的数量关系,先猜想,然后通过适当的计算回答问题．注意问题归纳：要认真分析比较,从而发现题中蕴涵的数量关系,通过猜想,再通过计算解决问题．例1一列数：0,-1,3,-6,10,-15,21,……,按此规律第n个数为归纳 2：数式规律型基础知识归纳：数式规律问题主要是通过观察、分析、归纳、验证,然后得出一般性的结论,以列代数式即函数关系式为主要内容．注意问题归纳：要注意观察、分析、归纳、并验证得出结论．例2有一个计算程序,每次运算都是把一个数先乘以2,再除以它与1的和,多次重复进行这种运算的过程如下：则第n次运算的结果yn= 用含字母x和n的代数式表示．归纳 3：图形规律型基础知识归纳：图形规律问题主要是观察图形的组成、分拆等过程中的特点,分析其联系和区别,用相应的算式描述其中的规律,要注意对应思想和数形结合．注意问题归纳：要注意分析图形的组成与分拆过程中的特点,要注意数形结合．例3如图,是由一些点组成的图形,按此规律,在第n个图形中,点的个数为．归纳 4：数形结合猜想型基础知识归纳：数形结合猜想型问题首先要观察图形,从中发现图形的变化方式,再将图形的变化以数或式的形式反映出来,从而得出图形与数或式的对应关系,数形结合总结出图形的变化规律,进而解决相关问题．注意问题归纳：要注意观察图形,发现图形的变化方式,用好数形结合思想解决问题．例4如图,等腰Rt△ABC中,∠ACB=90°,AC=BC=1,且AC边在直线a上,将△ABC绕点A顺时针旋转到位置①可得到点P1,此时AP1=；将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2,此时AP2=1+；将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时AP3=2+；……,按此规律继续旋转,直至得到点P2014为止．则AP2014= ．归纳5：动态规律型基础知识归纳：动态规律问题是探求图形在运动变换过程中的变化规律,解答此类问题时,要将图形每一次的变化与前一次变化进行比较,明确哪些结果发生了变化,哪些结果没有发生变化,从而逐步发现规律．注意问题归纳：要注意探求图形的变化规律,明确发生变化的与没有发生变化的量,从而逐步发现规律．例5如图,在x轴的正半轴上依次间隔相等的距离取点A1,A2,A3,A4,……,An分别过这些点做x轴的垂线与反比例函数y=1x的图象相交于点P1,P2,P3,P4,……Pn作P2B1⊥A1P1,P3B2⊥A2P2,P4B3⊥A3P3,……,PnBn﹣1⊥An﹣1Pn﹣1,垂足分别为B1,B2,B3,B4,……,Bn﹣1,连接P1P2,P2P3,P3P4,……,Pn﹣1Pn,得到一组Rt△P1B1P2,Rt△P2B2P3,Rt△P3B3P4,……,Rt△Pn﹣1Bn﹣1Pn,则Rt△Pn﹣1Bn﹣1Pn的面积为．2年中考2015年题组1．2015绵阳将一些相同的“○”按如图所示的规律依次摆放,观察每个“龟图”中的“○”的个数,若第n个“龟图”中有245个“○”,则n=A．14 B．15 C．16 D．17考点：1．规律型：图形的变化类；2．综合题．2．2015十堰如图,分别用火柴棍连续搭建正三角形和正六边形,公共边只用一根火柴棍．如果搭建正三角形和正六边形共用了2016根火柴棍,并且正三角形的个数比正六边形的个数多6个,那么能连续搭建正三角形的个数是A．222 B．280 C．286 D．2923．2015荆州把所有正奇数从小到大排列,并按如下规律分组：1,3,5,7,9,11,13,15,17,19,21,23,25,27,29,31,…,现有等式Am=i,j表示正奇数m 是第i组第j个数从左往右数,如A7=2,3,则A2015=A．31,50 B．32,47 C．33,46 D．34,424．2015包头观察下列各数：1,43,97,1615,…,按你发现的规律计算这列数的第6个数为A．2531 B．3635 C．47 D．6263考点：1．规律型：数字的变化类；2．综合题．5．2015重庆市下列图形都是由同样大小的小圆圈按一定规律组成的,其中第①个图形中一共有6个小圆圈,第②个图形中一共有9个小圆圈,第③个图形中一共有12个小圆圈,…,按此规律排列,则第⑦个图形中小圆圈的个数为A．21 B．24 C．27 D．306．2015泰安下面每个表格中的四个数都是按相同规律填写的：根据此规律确定x的值为A．135 B．170 C．209 D．252考点：1．规律型：数字的变化类；2．综合题．7．2015重庆市下列图形都是由几个黑色和白色的正方形按一定规律组成,图①中有2个黑色正方形,图②中有5个黑色正方形,图③中有8个黑色正方形,图④中有11个黑色正方形,…,依次规律,图⑩中黑色正方形的个数是A．32 B．29 C．28 D．26考点：1．规律型：图形的变化类；2．综合题．8．2015崇左下列图形是将正三角形按一定规律排列,则第4个图形中所有正三角形的个数有A．160 B．161 C．162 D．1639．2015贺州观察下列等式：21=2,22=4,23=8,24=16,25=32,26=64,27=128,…,解答下面问题：2+22+23+24+…+22015﹣1的末位数字是A．0 B．3 C．4 D．8考点：1．尾数特征；2．规律型；3．综合题．10．2015宜宾如图,以点O为圆心的20个同心圆,它们的半径从小到大依次是1、2、3、4、…、20,阴影部分是由第1个圆和第2个圆,第3个圆和第4个圆,…,第19个圆和第20个圆形成的所有圆环,则阴影部分的面积为A ．231π B．210π C．190π D．171π11．2015鄂州在平面直角坐标系中,正方形A1B1C1D1、D1E1E2B2、A2B2C2D2、D2E3E4B3、A3B3C3D3…按如图所示的方式放置,其中点B1在y 轴上,点C1、E1、E2、C2、E3、E4、C3…在x 轴上,已知正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3…则正方形A2015B2015C2015D2015的边长是A ．201421）（B ．201521）（C ．201533）（D ．201433）（答案D ．考点：1．正方形的性质；2．规律型；3．综合题．12．2015庆阳在如图所示的平面直角坐标系中,△OA1B1是边长为2的等边三角形,作△B2A2B1与△OA1B1关于点B1成中心对称,再作△B2A3B3与△B2A2B1关于点B2成中心对称,如此作下去,则△B2nA2n+1B2n+1n 是正整数的顶点A2n+1的坐标是A ．4n ﹣3．2n ﹣3．3 D ．313．2015宁德如图,在平面直角坐标系中,点A1,A2,A3…都在x 轴上,点B1,B2,B3…都在直线y x 上,△OA1B1,△B1A1A2,△B2B1A2,△B2A2A3,△B3B2A3…都是等腰直角三角形,且OA1=1,则点B2015的坐标是A ．20142,20142B ．20152,20152C ．20142,20152D ．20152,20142考点：1．一次函数图象上点的坐标特征；2．等腰直角三角形；3．规律型；4．综合题．14．2015河南省如图所示,在平面直角坐标系中,半径均为1个单位长度的半圆O1、O2、O3,…组成一条平滑的曲线,点P 从原点O 出发,沿这条曲线向右运动,速度为每秒2π个单位长度,则第2015秒时,点P 的坐标是A ．2014,0B ．2015,﹣1C ．2015,1D ．2016,0考点：1．规律型：点的坐标；2．规律型；3．综合题；4．压轴题．15．2015张家界任意大于1的正整数m 的三次幂均可“分裂”成m 个连续奇数的和,如：5323+=,119733++=,1917151343+++=,…按此规律,若3m 分裂后其中有一个奇数是2015,则m 的值是A ．46B ．45C ．44D ．4316．2015邵阳如图,在矩形ABCD 中,已知AB=4,BC=3,矩形在直线l 上绕其右下角的顶点B 向右旋转90°至图①位置,再绕右下角的顶点继续向右旋转90°至图②位置,…,以此类推,这样连续旋转2015次后,顶点A 在整个旋转过程中所经过的路程之和是A ．2015π B．π C ．3018π D．3024π17．2015威海如图,正六边形A1B1C1D1E1F1的边长为2,正六边形A2B2C2D2E2F2的外接圆与正六边形A1B1C1D1E1F1的各边相切,正六边形A3B3C3D3E3F3的外接圆与正六边形A2B2C2D2E2F2的各边相切,…按这样的规律进行下去,A10B10C10D10E10F10的边长为A ．92432B ．98132C ．9812 D ．88132考点：1．正多边形和圆；2．规律型；3．综合题．18．2015日照观察下列各式及其展开式：222()2a b a ab b +=++；33223()33a b a a b ab b +=+++；4432234()464a b a a b a b ab b +=++++；554322345()510105a b a a b a b a b ab b +=+++++；…请你猜想10()a b +的展开式第三项的系数是A ．36B ．45C ．55D ．66考点：1．完全平方公式；2．规律型；3．综合题．19．2015宁波如图,将△ABC 沿着过AB 中点D 的直线折叠,使点A 落在BC 边上的A2处,称为第1次操作,折痕DE 到BC 的距离记为h1；还原纸片后,再将△ADE 沿着过AD 中点D1的直线折叠,使点A 落在DE 边上的A2处,称为第2次操作,折痕D1E1到BC 的距离记为h2；按上述方法不断操作下去…,经过第2015次操作后得到的折痕D2014E2014到BC 的距离记为h2015,到BC 的距离记为h2015．若h1=1,则h2015的值为A ．201521B ．201421C ．2015211- D ．2014212-考点：1．相似三角形的判定与性质；2．三角形中位线定理；3．翻折变换折叠问题；4．规律型；5．综合题．20．2015常州数学家歌德巴赫通过研究下面一系列等式,作出了一个着名的猜想． 4=2+2； 12=5+7；6=3+3； 14=3+11=7+7；8=3+5； 16=3+13=5+11；10=3+7=5+5 18=5+13=7+11；…通过这组等式,你发现的规律是请用文字语言表达．21．2015淮安将连续正整数按如下规律排列：若正整数565位于第a 行,第b 列,则a+b= ．22．2015雅安若1m ,2m ,…,2015m 是从0,1,2这三个数中取值的一列数,若122015...m m m +++=1525,222122015(1)(1)...(1)1510m m m -+-++-=,则1m ,2m ,…,2015m 中为2的个数是．23．2015桂林如图是一个点阵,从上往下有无数多行,其中第一行有2个点,第二行有5个点,第三行有11个点,第四行有23个点,…,按此规律,第n 行有个点．24．2015梧州如图是由等圆组成的一组图,第①个图由1个圆组成,第②个图由5个圆组成,第③个图由12个圆组成…按此规律排列下去,则第⑥个图由个圆组成．25．2015百色观察下列砌钢管的横截面图：则第n 个图的钢管数是用含n 的式子表示26．2015北海如图,直线22y x =-+与两坐标轴分别交于A 、B 两点,将线段OA 分成n等份,分点分别为P1,P2,P3,…,Pn﹣1,过每个分点作x 轴的垂线分别交直线AB 于点T1,T2,T3,…,Tn ﹣1,用S1,S2,S3,…,Sn ﹣1分别表示Rt△T1OP1,Rt△T2P1P2,…,Rt△Tn ﹣1Pn ﹣2Pn ﹣1的面积,则当n=2015时,S1+S2+S3+…+Sn﹣1= ．考点：1．一次函数图象上点的坐标特征；2．规律型；3．综合题．27．2015南宁如图,在数轴上,点A 表示1,现将点A 沿x 轴做如下移动,第一次点A向左移动3个单位长度到达点A1,第二次将点A1向右移动6个单位长度到达点A2,第三次将点A2向左移动9个单位长度到达点,按照这种移动规律移动下去,第n次移动到点An,如果点An 与原点的距离不小于20,那么n 的最小值是．28．2015常德取一个自然数,若它是奇数,则乘以3加上1,若它是偶数,则除以2,按此规则经过若干步的计算最终可得到1．这个结论在数学上还没有得到证明．但举例验证都是正确的．例如：取自然数5．最少经过下面5步运算可得1,即：,如果自然数m 最少经过7步运算可得到1,则所有符合条件的m 的值为．29．2015株洲“皮克定理”是用来计算顶点在整点的多边形面积的公式,公式表达式为12b S a =+-,孔明只记得公式中的S 表示多边形的面积,a 和b 中有一个表示多边形边上含顶点的整点个数,另一个表示多边形内部的整点个数,但不记得究竟是a 还是b 表示多边形内部的整点个数,请你选择一些特殊的多边形如图1进行验证,得到公式中表示多边形内部的整点个数的字母是 ,并运用这个公式求得图2中多边形的面积是．30．2015内江填空：()()a b a b -+= ；22()()a b a ab b -++= ；3223()()a b a a b ab b -+++= ．2猜想：1221()(...)n n n n a b a a b ab b -----++++= 其中n 为正整数,且2n ≥．3利用2猜想的结论计算：98732222...222-+-+-+． 31．2015南平定义：底与腰的比是51-的等腰三角形叫做黄金等腰三角形．如图,已知△ABC 中,AB=BC,∠C=36°,BA1平分∠ABC 交AC 于A1．AB=AA1A C；122探究：△ABC是否为黄金等腰三角形请说明理由；提示：此处不妨设AC=13应用：已知AC=a,作A1B1∥AB交BC于B1,B1A2平分∠A1B1C交AC于A2,作A2B2∥AB 交B2,B2A3平分∠A2B2C交AC于A3,作A3B3∥AB交BC于B3,…,依此规律操作下去,用含a,n的代数式表示An﹣1An．n为大于1的整数,直接回答,不必说明理由考点：1．相似形综合题；2．新定义；3．探究型；4．综合题；5．压轴题；6．规律型．33．2015重庆市如果把一个自然数各数位上的数字从最高位到个位依次排出的一串数字,与从个位到最高位依次排出的一串数字完全相同,那么我们把这样的自然数称为“和谐数”．例如自然数12321,从最高位到个位依次排出的一串数字是：1,2,3,2,1,从个位到最高位依次排出的一串数字仍是：1,2,3,2,1,因此12321是一个“和谐数”,再加22,545,3883,345543,…,都是“和谐数”．1请你直接写出3个四位“和谐数”；请你猜想任意一个四位“和谐数”能否被11整除并说明理由；2已知一个能被11整除的三位“和谐数”,设其个位上的数字x1≤x≤4,x为自然数,十位上的数字为y,求y与x的函数关系式．2014年题组1．2014年南平中考如图,将1,若规定a,b表示第a排第b列的数,则8,2与2014,2014表示的两个数的积是A．B．C． D．12．2014年株洲中考在平面直角坐标系中,孔明做走棋的游戏,其走法是：棋子从原点出发,第1步向右走1个单位,第2步向右走2个单位,第3步向上走1个单位,第4步向右走1个单位……依此类推,第n步的走法是：当n能被3整除时,则向上走1个单位；当n被3除,余数为1时,则向右走1个单位；当n被3除,余数为2时,则向右走2个单位,当走完第100步时,棋子所处位置的坐标是A．66,34 B．67,33 C．100,33 D．99,343．2014年宜宾中考如图,将n个边长都为2的正方形按如图所示摆放,点A1,A2,……An分别是正方形的中心,则这n个正方形重叠部分的面积之和是A．n B．n-1 C.n11()4D．n1()4考点：1．正方形的性质；2．全等三角形的判定与性质．4．2014年崇左中考如图,在平面直角坐标系中,A1,1,B﹣1,1,C﹣1,﹣2,D1,﹣2．把一条长为2014个单位长度且没有弹性的细线线的粗细忽略不计的一端固定在点A处,并按A﹣B﹣C﹣D﹣A……的规律绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是A．﹣1,0 B．1,﹣2 C．1,1 D．﹣1,﹣15．2014年百色中考观察以下等式：32﹣12=8,52﹣12=24,72﹣12=48,92﹣12=80,……由以上规律可以得出第n个等式为．6．2014年衡阳中考如图,在平面直角坐标系xOy 中,已知点0M 的坐标为()10，,将线段0OM 绕原点O 逆时针方向旋转45,再将其延长至点1M ,使得100M M OM ⊥,得到线段1OM ；又将线段1OM 绕原点O 逆时针方向旋转45,再将其延长至点2M ,使得211M M OM ⊥,得到线段2OM ；如此下去,得到线段3OM 、4OM 、5OM 、……．根据以上规律,请直接写出线段2014OM 的长度为．答案2014．7．2014年抚顺中考如图,已知CO1是△ABC 的中线,过点O1作O1E1∥AC 交BC 于点E1,连接AE1交CO1于点O2；过点O2作O2E2∥AC 交BC 于点E2,连接AE2交CO1于点O3；过点O3作O3E3∥AC 交BC 于点E3,……,如此继续,可以依次得到点O4,O5,……,On 和点E4,E5,……,En ．则OnEn= AC ．用含n 的代数式表示考点：1．相似三角形的判定与性质；2．三角形中位线定理．8．2014年资阳中考如图,以O0,0、A2,0为顶点作正△OAP1,以点P1和线段P1A 的中点B 为顶点作正△P1BP2,再以点P2和线段P2B 的中点C 为顶点作△P2CP3,……,如此继续下去,则第六个正三角形中,不在第五个正三角形上的顶点P6的坐标是9．2014年宜宾中考在平面直角坐标系中,若点Px,y 的坐标x 、y 均为整数,则称点P 为格点,若一个多边形的顶点全是格点,则称该多边形为格点多边形．格点多边形的面积记为S,其内部的格点数记为N,边界上的格点数记为L,例如图中△ABC 是格点三角形,对应的S=1,N=0,L=4．1求出图中格点四边形DEFG 对应的S,N,L 的值．2已知格点多边形的面积可表示为S=N+aL+b,其中a,b为常数,若某格点多边形对应的N=82,L=38,求S的值．考点：1．规律型：图形的变化类； 2．二元一次方程组的应用．10．2014年凉山中考实验与探究：三角点阵前n行的点数计算如图是一个三角点阵,从上向下数有无数多行,其中第一行有1个点,第二行有2个点……第n行有n个点……容易发现,10是三角点阵中前4行的点数约和,你能发现300是前多少行的点数的和吗如果要用试验的方法,由上而下地逐行的相加其点数,虽然你能发现1+2+3+4+……+23+24=300．得知300是前24行的点数的和,但是这样寻找答案需我们先探求三角点阵中前n行的点数的和与n的数量关系前n行的点数的和是1+2+3+……+n﹣2+n﹣1+n,可以发现．2×1+2+3+……+n﹣2+n﹣1+n=1+2+3+……+n﹣2+n﹣1+n+n+n﹣1+n﹣2+……3+2+1把两个中括号中的第一项相加,第二项相加……第n项相加,上式等号的后边变形为这n个小括号都等于n+1,整个式子等于nn+1,于是得到1+2+3+……+n﹣2+n﹣1+n=12nn+1这就是说,三角点阵中前n项的点数的和是12nn+1下列用一元二次方程解决上述问题设三角点阵中前n行的点数的和为300,则有12nn+1整理这个方程,得：n2+n﹣600=0解方程得：n1=24,n2=25根据问题中未知数的意义确定n=24,即三角点阵中前24行的点数的和是300．请你根据上述材料回答下列问题：1三角点阵中前n行的点数的和能是600吗如果能,求出n；如果不能,试用一元二次方程说明道理．2如果把图中的三角点阵中各行的点数依次换成2、4、6、……、2n、……,你能探究处前n行的点数的和满足什么规律吗这个三角点阵中前n行的点数的和能使600吗如果能,求出n；如果不能,试用一元二次方程说明道理．1年模拟1．2015届山东省济南市平阴县中考二模在平面直角坐标系xOy中,对于点Px,y,我们把点P-y+1,x+1叫做点P的伴随点．已知点A1的伴随点为A2,点A2的伴随点为A3,点A3的伴随点为A4,…,这样依次得到点A1,A2,A3,…,An,…．例如：点A1的坐标为3,1,则点A2的坐标为0,4,…；若点A1的坐标为a,b,则点A2015的坐标为A．-b+1,a+1 B．-a,-b+2 C．b-1,-a+1 D．a,b2．2015届山东省潍坊市昌乐县中考一模如图,下面是按照一定规律画出的“树形图”,经观察可以发现：图A2比图A1多出2个“树枝”,图A3比图A2多出4个“树枝”,图A4比图A3多出8个“树枝”,…,照此规律,图A6比图 A2多出“树枝”A．32 B．56 C．60 D．643．2015届山西省晋中市平遥县九年级下学期4月中考模拟如图,四边形ABCD 中,AC=a,BD=b,且AC⊥BD,顺次连接四边形ABCD各边中点,得到四边形A1B1C1D1,再顺次连接四边形A1B1C1D1各边中点,得到四边形A2B2C2D2,如此进行下去,得到四边形AnBnCnDn．下列结论正确的是①四边形A4B4C4D4是菱形；②四边形A3B3C3D3是矩形；③四边形A7B7C7D7周长为；④四边形AnBnCnDn面积为．A．①②③ B．②③④ C．①③④ D．①②③④4．2015届广东省深圳市龙华新区中考二模如图,已知直线y=-12x+2与x轴交于点B,与y轴交于点A．过线段AB的中点A1做A1B1⊥x轴于点B1,过线段A1B的中点A2作A2B2⊥x轴于点B2,过线段A2B的中点A3作A3B3⊥x轴于点B3…,以此类推,则△AnBnBn-1的面积为A ．112n -B ．12nC ．114n -D ．14n5．2014-2015学年山东省潍坊市诸城市实验中学中考三模如图放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为2的等边三角形,边AO 在y 轴上,点B1,B2,B3,…都在直线y=33x 上,则A2015的坐标是．考点：1．一次函数图象上点的坐标特征；2．等边三角形的性质；3．规律型．6．2015届北京市平谷区中考二模在平面直角坐标系中,点A,B,C 的坐标分别为()1,0,()0,1,()1,0-．一个电动玩具从坐标原点O 出发,第一次跳跃到点P1,使得点P1与点O 关于点A 成中心对称；第二次跳跃到点P2,使得点P2与点P1关于点B 成中心对称；第三次跳跃到点P3,使得点P3与点P2关于点C 成中心对称；第四次跳跃到点P4,使得点P4与点P3关于点A 成中心对称；第五次跳跃到点P5,使得点P5与点P4关于点B 成中心对称；．…照此规律重复下去．则点P3的坐标为；点Pn 在y 轴上,则点Pn 的坐标为．7．2015届北京市门头沟区中考二模在平面直角坐标系xOy 中,矩形OABC 如图放置,动点P 从0,3出发,沿所示方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角,当点P 第2次碰到矩形的边时,点P 的坐标为；当点P 第6次碰到矩形的边时,点P 的坐标为；当点P 第2015次碰到矩形的边时,点P 的坐标为____________．答案7,4, 0,3 ,1,4．8．2015届安徽省安庆市中考二模一组按规律排列的式子：,,,,…则第n 个式子是 n为正整数．9．2015届山东省威海市乳山市中考一模在直角坐标系xOy中,对于点Px,y,我们把点P′y+1,-x+1叫做点P的影子点．已知点A1的影子点为A2,点A2的影子点为A3,点A3的影子点为A4,…,这样依次得到点A1,A2,A3,…,An,…若点A1的坐标为a,b,对于任意的正整数n,点An均在y轴的右侧,则a,b应满足的条件是．10．2015届山东省日照市中考模拟如图,在直角坐标系中,第一次将△OAB变换成△OA1B1,第二次将△OA1B1变换成△OA2B2,第三次将△OA2B2变换成△OA3B3,已知A1,3,A12,3,A24,3,A38,3,B2,0,B14,0,B28,0,B316,0．1观察每次变换前后的三角形有何变化,找出规律,按此变换规律再将△OA3B3变换成△OA4B4,则A4的坐标是．2若按1题找到的规律将△OAB进行了n次变换,得到的△OAnBn,比较每次变换中三角形顶点坐标有何变化,找出规律,推出Bn的坐标是．11．2015届广东省佛山市初中毕业班综合测试如图,依次连接第一个矩形各边的中点得到一个菱形,再依次连接菱形各边的中点得到第二个矩形,按照此方法继续下去．已知第一个矩形的两条邻边长分别为6和8,则第n个菱形的周长为．12．2015届湖北省黄石市6月中考模拟如图,点A1,A2,A3,A4,…,An在射线OA上,点B1,B2,B3,…,Bn﹣1在射线OB上,且A1B1∥A2B2∥A3B3∥…∥An﹣1Bn﹣1,A2B1∥A3B2∥A4B3∥…∥AnBn﹣1,△A1A2B1,△A2A3B2,…,△An﹣1AnBn﹣1为阴影三角形,若△A2B1B2,△A3B2B3的面积分别为1、4,则△A1A2B1的面积为__________；面积小于2011的阴影三角形共有__________个．13．2015届广东省佛山市初中毕业班综合测试若a是不为1的有理数,我们把11a-称为a的差倒数．如：2的差倒数是112-=-1,-1的差倒数是111(1)2=--．已知a1=-13,a2是a1的差倒数,a3是a2的差倒数,a4是a3的差倒数,…,依此类推．1分别求出a2,a3,a4的值；2求a1+a2+a3+…+a2160的值．。

中考数学探索规律题分类及解析

中考数学探索规律题分类及解析中考数学探索规律题是指通过观察一组数或一组图形，发现其中存在的规律或者推导出下一个数字或图形的解题方法。

这类题目不是通过直接计算或者运用公式来得到答案，而是通过观察和推理来寻找规律并进行推导。

这类题目在中考数学中比较常见，考察学生的观察力、逻辑推理能力和发现规律的能力。

中考数学探索规律题可以分为数列规律、形状规律和操作规律等几个分类。

数列规律题是指给出一组数字，要求学生根据已知数字的特点推导出下一个数字或者补全数列。

这类题目常常通过给出一定的条件或者变化规律，让学生去寻找数字之间的关系。

学生可以通过计算差值、比值等方式来找到规律。

比如，给出一个数列1，3，5，7，要求学生推导出下一个数字。

学生可以发现，每两个数字之间差值都是2，所以下一个数字应该是9。

形状规律题是指给出一组图形，要求学生根据已知图形的特点推导出下一个图形或者补全图形。

这类题目常常通过给出一定的条件或者变化规律，让学生去寻找图形之间的关系。

学生可以通过观察图形边长、角度、对称性等特点找到规律。

比如，给出一个图形如下：1 2 34 5 67 8 ?要求学生填空。

学生可以发现，每一行的数字是依次递增的，所以下一个数字应该是9。

操作规律题是指通过一系列操作或者变换，让学生来探索操作之间的关系从而推导出答案。

这类题目常常通过给出一系列数字或者图形的变化过程，让学生去寻找变化之间的规律。

比如，给出一系列数字1，4，9，16，要求学生推导下一个数字。

学生可以发现，每一个数字都是前一个数字的平方，所以下一个数字应该是25。

总之，中考数学探索规律题要求学生通过观察和推理来寻找规律，需要学生具备较强的观察力、逻辑推理能力和发现规律的能力。

在解题过程中，学生可以采用数列差值、比值等方式来寻找数列规律；可以通过观察图形的边长、角度、对称性等特点来寻找形状规律；可以通过寻找操作之间的关系来寻找操作规律。

通过不断的练习和思考，可以提高解决这类问题的能力。

中考数学复习指导：探索规律型问题归类解析

探索规律型问题归类解析探索规律型问题是历年中考数学试题中的重要题型之一，其特点是给出一组变化了的数字、式子、表格、图形等，要求学生通过观察、归纳、猜想、验证、类比，探求其内在规律．1.通用的解题策略解答规律型问题一般要从特殊情况入手→探索发现规律→综合归纳→猜想得出结论→验证结论．这种“特殊——一般——特殊”的解题模式，体现了总结归纳的数学思想，也正是人们认识新事物的一般过程．具体来说，就是先写出开头几个数式的基本结构，然后通过横比或纵比找出各部分的特征，写出符合要求的结果．例1 如图1，房间地面的图案是用大小相同的黑、白正方形镶嵌而成．图中，第1个黑色“L”形由3个正方形组成，第2个黑色“L”形由7个正方形组成，…那么组成第6个黑色“L”形的正方形个数是( )(A)22 (B)23 (C)24 (D)25解析从特例入手：如图1．纵比正方形的个数3，7，11，15中，后一个数比前一个大4（即相邻两数的差为4），猜想与4有关．横比3与1，7与2，11与3，15与4之间有何关系？联想到与4有关，故改写为：3＝4×1－1，7＝4×2－1．11＝4×3－1，15＝4×4－1．猜想组成第6个黑色L形的正方形个数是4 ×6－1＝23个．故选B．点评考察相邻两数的差（或商）是探究数字规律的常用手段．常见的类型有：相邻两数的差（或商）相等或成倍数关系，相邻两数的差相等与商相等交替出现等．2.关注特殊数列(1)斐波那契数列：1，1，2，3，5，8，13，21…（其规律为：从第三项开始，每一项都等于前两项之和）；(2)平方数数列：1，4，9，16，25，36…（其规律为：n2，即每一项都等于项数的平方）．例2 有一组数：1，2，5，10，17，26…请观察这组数的构成规律，用你发现的规律确定第8个数为_______．解析规律为：n2＋1（n＝0，1，2…）．答案：50．点评此类题要注意n2，n2＋1，n2－1等(3)三角形数列：1，3，6，10，15，21，…（其规律为1＋2＋3＋…＋n）例3 世界上著名的莱布尼茨三角形如图2所示，则排在第10行从左边数第3个位置上的数是：( )（A）（B）（C）（D）解析从第3行起，从左边数第3位置上的数分别为，，，，…它们的分母可分别改写为：1×3，3×4，6×5，10×6，15×7，21×8，…，而1，3，6，10，15，21，…，正是三角形数，故答案为：．选B．(4)杨辉三角形，杨辉三角形斜边上1以外的各数，都等于它“肩上”的两数之和，如图3．(5)与等差等比数列有关的数列．如例1中3，7，11，15…就是一个等差数列．例4 数字解密：第一个数是3＝2＋1，第二个数是5＝3＋2，第三个数是9＝5＋4，第四个数是17＝9＋8，……观察并猜想第六个数应是_______．解析第二个加数1，2，4，8…规律为2n（为一等比数列，也要关注这一数列），第一个加数2，3，5，9…比第二个加数大1．所以第六个数为(25＋1)＋25＝65．例5 一组按规律排列的数：…请你推断第9个数是________．解析这列数的分母为2，3，4，5，6…的平方数，分子形成二阶等差数列，依次相差2，4，6，8…故第9个数分子为1＋2＋4＋6＋8＋10＋12＋14＋16＝73，分母为100，故答案为．(6)与循环有关的问题例6 让我们轻松一下，做一个数字游戏：第一步：取一个自然数n1＝5，计算n12＋1得a1；第二步：算出a1的各位数字之和得n2，计算n22＋1得a3；第三步：算出a2的各位数字之和得n3，再计算n32＋1得a3；……依此类推，则a2008＝_______．解析根据题意可算出a1＝26，a2＝65，a3＝122，a4＝26，a5＝65，a6＝122，…发现每3个数就出现一次循环．所以由2008＝669×3＋1，可得a2008＝a1＝26．点评一列数由某m个数循环出现组成，可依据同余等值(由n＝p·m＋r得a n＝a r)实施转换．(7)分奇数项偶数项的问题例7 一组按规律排列的式子：，…(a b≠0)，其中第7个式子是________，第n个式子是_(n为正整数)．解析6的指数2，5，8，11…，相邻两数差为3，是等差数列，其规律为3n－1；再注意到奇数项为负，偶数项为正，则第n个式子为第七个式子为3.特殊数列的迁移例8 把数字按如图4所示排列起来，从上开始，依次为第一行、第二行、第三行、…，中间用虚线围的一列，从上至下依次为1.5.13.25.…，则第10个数为_______．解析1 中间框出的一列数的规律为：第n个数为1＋4＋8＋12＋…＋4（n－1）．所以第10个数为1＋4＋8＋12＋…＋36＝．解析2 用虚线圈出的一列数1，5，13，25可改写为：02＋12，12＋22，22＋32，32＋42，猜想第10个数为92＋102＝181．点评此列数可看成是平方数数列的迁移．例9 图5中是与杨辉三角有类似性质的三角形数垒．a，b，c，d是相邻两行的前四个数，那么当a＝8时，c＝_______，d＝_______．解析除两边外，中间的每个数等于肩上两数的和．答案：9；32．点评此列数可看成是杨辉三角形的迁移．4.关注中考新题型例10 观察图6所示表格，依据表格数据排列的规律，数2008在表格中出现的次数共有_______次．解析从特例入手，通过扩充表格可得：数1，2，3，4，5，6，7，8，9，10出现次数分别为1，2，2，3，2，4，2，4，3，4．出现的次数恰为给定数的所有因数的个数，而2008的因数为1，2，4，8，251，502，1004，2008等8个．故答案为8．点评本例中新产生的数为自然数的倍数，因此，其出现的次数与其因数的多少有关，仔细观察便会发现，其出现次数就是给定数所有因数的个数，本题规律的隐蔽性较强，因而有一定的难度．。

中考数学必考题型《规律探索》分类专项练习含答案

中考数学必考题型《规律探索》分类专项练习类型一数式规律1. 我国战国时期提出了“一尺之棰，日取其半，万世不竭”这一命题，用所学知识来解释可理解为：设一尺长的木棍，第一天折断一半，其长为12尺，第二天再折断一半，其长为14尺，…，第n 天折断一半后得到的木棍长应为________尺． 12n2. 如图，是按一定规律排成的三角形数阵，按图中数阵的排列规律，第9行从左至右第5个数是________．第2题图41【解析】由图形可知，第n 行最后一个数为1＋2＋3＋…＋n ＝n （n ＋1）2，∴第8行最后一个数为8×92＝36＝6，则第9行从左至右第5个数是36＋5＝41.3. 观察下列关于自然数的式子：第一个式子：4×12－12 ① 第二个式子：4×22－32 ② 第三个式子：4×32－52 ③ …根据上述规律，则第2019个式子的值是______．8075 【解析】∵4×12－12＝3①，4×22－32＝7②，4×32－52＝11③，…，4n 2－(2n －1)2＝4n －1，∴第2019个式子的值是4×2019－1＝8075. 4. 将数1个1，2个12，3个13，…，n 个1n (n 为正整数)顺次排成一列：1，12，12，13，13，13，…，1n ，1n ，…，记a 1＝1，a 2＝12，a 3＝12，…，S 1＝a 1，S 2＝a 1＋a 2，S 3＝a 1＋a 2＋a 3，…，S n ＝a 1＋a 2＋…＋a n ，则S 2019＝________．63364 【解析】根据题意，将该数列分组，1个1的和为1，2个12的和为1，3个13的和为1，…；∵1＋2＋3＋…＋63＝2016个数，则第2019个数为64个164的第3个数，则此数列中，S 2019＝1×63＋3×164＝63364. 类型二图形规律5. 如图，在平面直角坐标系中，第一次将△OAB 变换成△OA 1B 1，第二次将△OA 1B 1变换成△OA 2B 2，第三次将△OA 2B 2变换成△OA 3B 3，…，已知A (1，3)，A 1(2，3)，A 2(4，3)，A 3(8，3)，B (2，0)，B 1(4，0)，B 2(8，0)，B 3(16，0)．观察每次变换前后的三角形的变化，按照变换规律，则点A n 的坐标是________．第5题图(2n，3)【解析】∵A(1，3)，A1(2，3)，A2(4，3)，A3(8，3)，…，∴纵坐标不变，为3，横坐标都和2有关，为2n，即点An的坐标是(2n，3)．6. 如图，把正方形铁片OABC置于平面直角坐标系中，顶点A的坐标为(3，0)，点P(1，2)在正方形铁片上，将正方形铁片绕其右下角的顶点按顺时针方向依次旋转90°，第一次旋转至图①位置，第二次旋转至图②位置，…，则正方形铁片连续旋转2019次后，点P的坐标为________．第6题图(6058，1)【解析】∵铁片OABC为正方形，A(3，0)，P(1，2)，∴正方形铁片OABC 的边长为3，如解图第一个循环周期内的点P1，P2，P3，P4的坐标分别为(5，2)，(8，1)，(10，1)，(13，2)，每增加一个循环，对应的点的横坐标就增加12.而2019÷4＝504……3，即504个循环周期后点P2016的横坐标为504×12＋1＝6049，纵坐标为2，所以点P2019的横坐标为6049＋9＝6058，纵坐标为1.故P2019(6058，1)．第6题解图7. 如图，在平面直角坐标系中，半径均为1个单位长度的半圆O 1，O 2，O 3，…，组成一条平滑的曲线，点P 从原点O 出发，沿这条曲线向右运动，速度为每秒π2个单位长度，则第2019秒时，点P 的坐标是________．第7题图(2019，－1) 【解析】∵圆的半径都为1，∴半圆的周长＝π，以时间为点P 的下标．观察发现规律：P 0(0，0)，P 1(1，1)，P 2(2，0)，P 3(3，－1)，P 4(4，0)，P 5(5，1)，…，∴P 4n (4n ，0)，P 4n ＋1(4n ＋1，1)，P 4n ＋2(4n ＋2，0)，P 4n ＋3(4n ＋3，－1)．∵2019÷4＝504……3，∴第2019秒时，点P 的坐标为(2019，－1)．8. 如图，已知菱形OABC 的顶点O (0，0)，B (2，2)，若菱形绕点O 逆时针旋转，每秒旋转45°，则第60秒时，菱形的对角线交点D 的坐标为________．第8题图(－1，－1) 【解析】∵菱形OABC 的顶点O (0，0)，B (2，2)，∴BO 与x 轴的夹角为45°，∵菱形的对角线互相垂直平分，∴点D是线段OB的中点，∴点D的坐标是(1，1)，∵菱形绕点O逆时针旋转，每秒旋转45°，360°÷45°＝8，∴每旋转8秒，菱形的对角线交点就回到原来的位置(1，1)，∵60÷8＝7……4，∴第60秒时是把菱形绕点O 逆时针旋转了7周回到原来位置后，又旋转了4秒，即又旋转了4×45°＝180°，∴点D 的对应点落在第三象限，且对应点与点D关于原点O成中心对称，∴第60秒时，菱形的对角线交点D的坐标为(－1，－1)．9. 如图，∠MON＝60°，作边长为1的正六边形A1B1C1D1E1F1，边A1B1、F1E1分别在射线OM、ON上，边C1D1所在的直线分别交OM、ON于点A2、F2，以A2F2为边作正六边形A2B2C2D2E2F2，边C2D2所在的直线分别交OM、ON于点A3、F3，再以A3F3为边作正六边形A3B3C3D3E3F3，…，依此规律，经第n次作图后，点B n到ON的距离是________．第9题图3n－13【解析】由题可知，∠MON＝60°，设B n到ON的距离为h n，∵正六边形A1B1C1D1E1F1的边长为1，∴A1B1＝1，易知△A1OF1为等边三角形，∴A1B1＝OA1＝1，∴OB1＝2，则h1＝2×32＝3，又∵OA2＝A2F2＝A2B2＝3，∴OB2＝6，则h2＝6×32＝33，同理可得：OB3＝18，则h3＝18×32＝93，…，依此可得OB n＝2×3n－1，则h n＝2×3n －1×32＝3n －1 3.∴B n 到ON 的距离h n ＝ 3n －1 3.10. 如图，正方形AOBO 2的顶点A 的坐标为A (0，2)，O 1为正方形AOBO 2的中心；以正方形AOBO 2的对角线AB 为边，在AB 的右侧作正方形ABO 3A 1，O 2为正方形ABO 3A 1的中心；再以正方形ABO 3A 1的对角线A 1B 为边，在A 1B 的右侧作正方形A 1BB 1O 4，O 3为正方形A 1BB 1O 4的中心；再以正方形A 1BB 1O 4的对角线A 1B 1为边，在A 1B 1的右侧作正方形A 1B 1O 5A 2，O 4为正方形A 1B 1O 5A 2的中心；…；按照此规律继续下去，则点O 2018的坐标为________．第10题图(21010－2，21009) 【解析】由A (0，2)和A 1(2，4)可知直线AA 1的解析式为y ＝x ＋2，由图可知点A 1，A 2，…，A n 的纵坐标分别为22，23，…，2n ＋1，将y ＝2n ＋1代入y ＝x ＋2，得2n ＋1＝x ＋2，∴x ＝2n ＋1－2，∴点A n 的坐标为(2n ＋1－2，2n ＋1)，由图可知O 2n 横坐标与A n 的横坐标相同，O 2n 纵坐标是A n 的纵坐标的12，∴O 2n 的坐标为(2n ＋1－2，2n)，∴当n ＝1009时，O 2018的坐标为(21010－2，21009)．真题反馈：1. 观察下列一组数：，，，，，…，它们是按一定规律排列的，那么这一组数的第n个数是．2. 如图，用黑白两种颜色的菱形纸片，按黑色纸片数逐渐增加1的规律拼成下列图案，若第n个图案中有2017个白色纸片，则n的值为( )A．671 B．672 C．673 D．6743. 观察下列一组图形，其中图形①中共有2颗星，图形②中共有6颗星，图形③中共有11颗星，图形④中共有17颗星，…，按此规律，图形⑧中星星的颗数是( )A．43 B．45 C．51 D．534. 请你计算:(1-x)(1+x),(1-x)(1+x+x2),…,猜想(1-x)(1+x+x2+…+x n)的结果是( ).A. 1-x n+1B. 1+x n+1C. 1-x nD. 1+x n5. 如图,已知正方形ABCD,顶点A(1,3),B(1,1),C(3,1).规定“把正方形ABCD先沿x轴翻折,再向左平移1个单位”为一次变换,如此这样,连续经过2019次变换后,正方形ABCD的对角线交点M的坐标变为().A. (-2012,2)B. (-2012,-2)C. (-2013,-2)D. (-2013,2)6. 观察下列数据：－2，52，－103，174，－265，…，它们是按一定规律排列的，依照此规律，第11个数据是．7. 观察下列数据：－2，52，－103，174，－265，…，它们是按一定规律排列的，依照此规律，第11个数据是．8. 正方形A1B1C1O，A2B2C2C1，A3B3C3C2，…按如图的方式放置．点A1，A2，A3，…和点C1，C2，C3，…分别在直线y＝x＋1和x轴上，则点B6的坐标是．9. 如图,将若干个正三角形、正方形和圆按一定规律从左向右排列,那么第2015个图形是.10. 如图,弹性小球从点P(0,3)出发,沿所示方向运动,每当小球碰到矩形OABC的边时反弹,反弹时反射角等于入射角,当小球第1次碰到矩形的边时的点为P1,第2次碰到矩形的边时的点为P2,…,第n 次碰到矩形的边时的点为P n,则点P3的坐标是;点P2 019的坐标是.11.观察下列关于自然数的等式：32-4×12=5 ①52-4×22=9 ②72-4×32=13 ③…根据上述规律解决下列问题：（1）完成第四个等式：（2）写出你猜想的第n个等式（用含n的式子表示），并验证其正确性．12.(1)证明三角形中位线定理:三角形的中位线平行于第三边,且等于第三边的一半;[要求根据图(1)写出已知、求证、证明;在证明过程中,至少有两处写出推理依据(“已知”除外)(2)如图(2),在▱ABCD中,对角线焦点为O,A1,B1,C1,D1分别是OA,OB,OC,OD的中点,A2,B2,C2,D2分别是OA1,OB1,OC1,OD1的中点,…,以此类推.若▱ABCD的周长为1,直接用算式表示各四边形的周长之和l;(3)借助图形(3)反映的规律,猜猜l可能是多少?(1)(2) (3)。

历年初三数学中考规律探索问题试题汇编及答案

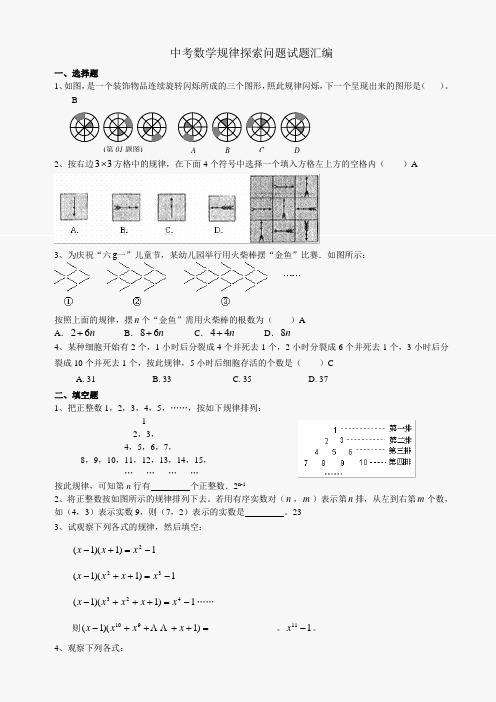
中考数学规律探索问题试题汇编一、选择题 1、如图，是一个装饰物品连续旋转闪烁所成的三个图形，照此规律闪烁，下一个呈现出来的图形是（）。

B2、按右边33⨯方格中的规律，在下面4个符号中选择一个填入方格左上方的空格内（）A3、为庆祝“六g 一”儿童节，某幼儿园举行用火柴棒摆“金鱼”比赛．如图所示：按照上面的规律，摆n 个“金鱼”需用火柴棒的根数为（）A A ．26n + B ．86n + C ．44n + D ．8n4、某种细胞开始有2个，1小时后分裂成4个并死去1个，2小时分裂成6个并死去1个，3小时后分裂成10个并死去1个，按此规律，5小时后细胞存活的个数是（）C A. 31 B. 33 C. 35 D. 37 二、填空题1、把正整数1，2，3，4，5，……，按如下规律排列：1 2，3， 4，5，6，7，8，9，10，11，12，13，14，15，… … … …按此规律，可知第n行有个正整数．2n-12、将正整数按如图所示的规律排列下去。

若用有序实数对（n ，m ）表示第n 排，从左到右第m 个数，如（4，3）表示实数9，则（7，2）表示的实数是。

233、试观察下列各式的规律，然后填空：1)1)(1(2-=+-x x x 1)1)(1(32-=++-x x x x1)1)(1(423-=+++-x x x x x ……则=++++-)1)(1(910x x xx ΛΛ_______________。

111-x 。

4、观察下列各式：(第01题图) A B C D11235...22151(11)1005225=⨯+⨯+= 22252(21)1005625=⨯+⨯+= 22353(31)10051225=⨯+⨯+=……依此规律，第n 个等式（n 为正整数）为．22(105)(1)1005n n n +=+⨯+5、意大利著名数学家斐波那契在研究兔子繁殖问题时，发现有这样一组数：1，1，2，3，5，8，13，…，其中从第三个数起，每一个数都等于它前面两上数的和。

全国各地市中考数学模拟试题分类汇编48探索规律型问题

探索规律型问题一、选择题1、（2012年浙江金华五模）已知a ≠0，12S a =，212S S =，322S S =，…，201220112S S =，则2012S = ▲ (用含a 的代数式表示)．答案：1a2（2012年江苏海安县质量与反馈）如图所示，已知直线133+-=x y 与x 、y 轴交于B 、C 两点,(00)A ，，在ABC △内依次作等边三角形，使一边在x 轴上，另一个顶点在BC 边上，作出的等边三角形分别是第1个11AA B △，第2个122B A B △，第3个233B A B △，……则第n 个等边三角形的边长等于A ．32nB ．132n -C ．12nD ．132n +答案：A.3（2012荆州中考模拟）．如图，正方形ABCD 的边长是3cm ，一个边长为1cm 的小正方形沿着正方形ABCD 的边AB →BC →CD →DA →AB 连续地翻转，那么这个小正方形第一次回到起始位置时，它的方向是( )A. B. C. D. 答案：A4、（2012广西贵港）对于每个非零自然数n ，抛物线2211(1)(1)n n n n n y x x +++=-+与x 轴交于A n 、B n 两点，以n n A B 表示这两点间的距离，则112220112011A B A B A B +++的值是第1题图D CBAA ．20112010B ．20102011 C ．20122011 D ．20112012答案：D5. （2012年广东模拟）如图，在直角坐标系中，射线OA 与x 轴正半轴重合，以O 为旋转中心，将OA 逆时针旋转:OA ⇒OA 1⇒OA 2⇒…⇒OA n …，旋转角∠AOA 1＝2°， ∠A 1OA 2＝4°， ∠A 2OA 3＝8°，… 要求下一个旋转角(不超过360°)是前一个旋转角的2倍.当旋转角大于360°时，又从2°开始旋转，即∠A 8OA 9＝2°， ∠A 9OA 10＝4°，… 周而复始.则当OA n 与y 轴负半轴第一次重合时，n 的值为（）（提示：2+22+23+24+25+26+27＋28＝510）（改编） A ．28 B ．32 C ．36 D ．40答案C二、填空题 1、(2012年南京建邺区一模)如图，正方形ABCD 的边长为2，将长为2的线段QF 的两端放在正方形相邻的两边上同时滑动．如果点Q 从点A 出发，沿图中所示方向按A D C B A →→→→滑动到点A 为止，同时点F 从点B 出发，沿图中所示方向按B A DC B →→→→滑动到点B 为止，那么在这个过程中，线段QF 的中点M 所经过的路线长为．答案： 2π2、(2012年香坊区一模)观察下列图形：[来源:]它们是按一定规律排列的，依照此规律，第20个图形共有个★．答案：603、(2012年福州模拟卷)如图，∠AOB ＝30°，n 个半圆依次外切，它们的圆心都在射线OA上并与射线OB 相切，设半圆C 1、半圆C 2、半圆C 3、…、半圆C n 的半径分别是r 1、r 2、4224685x O A 8A 9A nyA 7A 6A 5A 4A 3A 2A 1Ar 3、、r n ，则r 2012r 2011＝___________．答案：34、(徐州市2012年模拟)右图为手的示意图，在各个手指间标记字母A 、B 、C 、D 。

中考数学复习《探索规律问题》经典题型及测试题(含答案)

中考数学复习《探索规律问题》经典题型及测试题（含答案）阅读与理解探索规律问题是中考数学中的常考问题，往往以选择题或填空题中的压轴题形式出现，主要命题方向有数式规律、图形变化规律、点的坐标规律等．基本解题思路为：从简单的、局部的、特殊的情形出发，通过分析、比较、提炼，发现其中的规律，进而归纳或猜想出一般性的结论，最后验证结论的正确性．即“从特殊情形入手→探索发现规律→猜想结论→验证”．类型一数式规律这类问题通常是先给出一组数或式子，通过观察、归纳这组数或式子的共性规律，写出一个一般性的结论．解决这类题目的关键是找出题目中的规律，即不变的和变化的，变化部分与序号的关系．例1 (2016·绥化)古希腊数学家把数1，3，6，10，15，21，…叫做三角数，它有一定的规律性．若把第一个三角数记为a1，第二个三角数记为a2，…，第n个三角数记为an ，计算a1＋a2，a2＋a3，a3＋a4，…，由此推算a399＋a400＝．【分析】首先计算a1＋a2，a2＋a3，a3＋a4的值，然后总结规律根据规律得出结论，进而求出a399＋a400的值．【自主解答】∵a1＋a2＝1＋3＝4＝22，a2＋a3＝3＋6＝9＝32，a3＋a4＝6＋10＝16＝42，…，∴an ＋an＋1＝(n＋1)2.∴a399＋a400＝4002＝160 000.故答案为160 000.变式训练：1．(2017·遵义)按一定规律排列的一列数依次为：，1，，，，，…，按此规律，这列数中的第100个数是．2．(2017年黄石)观察下列格式：=1﹣=+=1﹣+﹣=++=1﹣+﹣+﹣=…请按上述规律，写出第n个式子的计算结果（n为正整数）．（写出最简计算结果即可）类型二图形规律这类题目通常是给出一组图形的排列(或通过操作得到一系列的图形)，探求图形的变化规律，以图形为载体考查图形所蕴含的数量关系．解决此类问题先观察图案的变化趋势是增加还是减少，然后从第一个图形进行分析，运用从特殊到一般的探索方式，分析归纳找出增加或减少的变化规律，并用含有字母的代数式进行表示，最后用代入法求出特殊情况下的数值．例2 (2016·重庆)下列图形都是由同样大小的小圆圈按一定规律所组成的，其中第①个图形中一共有4个小圆圈，第②个图形中一共有10个小圆圈，第③个图形中一共有19个小圆圈，…，按此规律排列，则第⑦个图形中小圆圈的个数为( )A．64 B．77 C．80 D．85【分析】观察图形特点，可将图形分为两部分：上面的三角形和下面的正方形，因此小圆圈的个数分别是3＋12，6＋22，10＋32，15＋42，…，据此总结出规律求解即可．【自主解答】解：通过观察，得到小圆圈的个数分别是：第一个图形为：+12=4，第二个图形为：+22=6，第三个图形为：+32=10，第四个图形为：+42=15 …，所以第n个图形为：+n2，当n=7时，+72=85，故选D．变式训练：3．(2017·随州)在公园内，牡丹按正方形种植，在它的周围种植芍药，如图反映了牡丹的列数(n)和芍药的数量规律，那么当n＝11时，芍药的数量为( )A．84株 B．88株 C．92株 D．121株4．(2015·德州)如图1，四边形ABCD中，AB∥CD，AD＝DC＝CB＝a，∠A＝60°.取AB的中点A1，连接A1C，再分别取A1C，BC的中点D1，C1，连接D1C1，得到四边形A1BC1D1.如图2，同样方法操作得到四边形A2BC2D2，如图3，…，如此进行下去，则四边形An BCnDn的面积为_______类型三点的坐标规律这类问题要求探索图形在运动过程中的规律，通常以平面直角坐标系为载体探索点的坐标的变化规律．解答时，应先写出前几次的变化过程，并将相邻两次的变化过程进行比对，明确哪些地方发生了变化，哪些地方没有发生变化，逐步发现规律，从而使问题得以解决．例3 (2017·东营)如图，在平面直角坐标系中，直线l：y=x﹣与x轴交于点B1，以OB1为边长作等边三角形A1OB1，过点A1作A1B2平行于x轴，交直线l于点B2，以A1B2为边长作等边三角形A2A1B2，过点A2作A2B3平行于x轴，交直线l于点B3，以A2B3为边长作等边三角形A3A2B3，…，则点A2017的横坐标是．21433an【分析】先根据直线l：y=x﹣与x轴交于点B1，可得B1（1，0），OB1=1，∠OB1D=30°，再，过A1作A1A⊥OB1于A，过A2作A2B⊥A1B2于B，过A3作A3C⊥A2B3于C，根据等边三角形的性质以及含30°角的直角三角形的性质，分别求得A1的横坐标为，A2的横坐标为，A3的横坐标为，进而得到An的横坐标为，据此可得点A2017的横坐标．【自主解答】解：由直线l：y=x﹣与x轴交于点B1，可得B1（1，0），D（﹣，0），∴OB1=1，∠OB1D=30°，如图所示，过A1作A1A⊥OB1于A，则OA=OB1=，即A1的横坐标为=，由题可得∠A1B2B1=∠OB1D=30°，∠B2A1B1=∠A1B1O=60°，∴∠A1B1B2=90°，∴A1B2=2A1B1=2，过A2作A2B⊥A1B2于B，则A1B=A1B2=1，即A2的横坐标为+1==，过A3作A3C⊥A2B3于C，同理可得，A2B3=2A2B2=4，A2C=A2B3=2，即A3的横坐标为+1+2==，同理可得，A4的横坐标为+1+2+4==，由此可得，An的横坐标为，∴点A2017的横坐标是，故答案为：．变式训练5．(2016·德州)如图，在平面直角坐标系中，函数y＝2x和y＝－x的图象分别为直线l1，l2，过点(1，0)作x轴的垂线交l1于点A1，过点A1作y轴的垂线交l2于点A2，过点A2作x轴的垂线交l1于点A3，过点A3作y轴的垂线交l2于点A4，…，依次进行下去，则点A2 017的坐标为__6．(2017·安顺)如图，在平面直角坐标系中，直线l：y＝x＋2交x轴于点A，交y轴于点A1，点A2，A3，…在直线l上，点B1，B2，B3，…在x轴的正半轴上，若△A1OB1，△A2B1B2，△A3B2B3，…，依次均为等腰直角三角形，直角顶点都在x轴上，则第n个等腰直角三角形An Bn－1Bn顶点Bn的横坐标为___。

2011年全国中考数学模拟汇编48探索规律型问题(2份)

222123323321x s O x s O x s O O s x A BC D P55.动态综合型问题A 组一选择题1. （2011广州六校一摸）如图，O 的半径为5，弦AB 的长为8，M 是弦AB 上的动点，则线段OM 长的最小值为（）Ａ．2 Ｂ．3Ｃ．4Ｄ．5答案:B2．（南京市溧水县2011年中考一模）如图，A ，B ，C ，D 为⊙O 的四等分点，动点P 从圆心O 出发，沿O —C —D —O 路线作匀速运动，设运动时间为x (秒)，∠APB ＝y (度)，右图函数图象表示y 与x 之间函数关系，则点M 的横坐标应为（ ▲ ）A ．2B ．2πC ．12π+ D ．2π＋2 答案：C3．（南京市雨花台2011年中考一模）如图，矩形ABCD 中，1AB =，2BC =，点P 从点B 出发，沿B C D →→向终点D 匀速运动，设点P 走过的路程为x ，△ABP 的面积为S ，能正确反映S 与x 之间函数关系的图象是A ．B ．C ．D ．(第2题)答案：C4、(2011海淀一模) 如图，在Rt ABC △中，∠C =90°，AB =5cm ，BC =3cm ，动点P 从点A 出发，以每秒1cm 的速度，沿A →B →C 的方向运动，到达点C 时停止.设2y PC =, 运动时间为t 秒，则能反映y 与t 之间函数关系的大致图象是DB CO A90 1 M x y45O （第1题） PAPBCyO 58916yO58916yO58916yO 58916OA MB考查内容: 答案：A 二、填空题：1、(2011广东化州二模)15．如图,正方形ABCD的边长为2，将长为2的线段QR 的两端放在正方形的相邻的两边上同时滑动．如果Q 点从A 点出发，沿图中所示方向按A →B →C →D →A 滑动到A 止，同时点R 从B 点出发，沿图中所示方向按 B →C →D →A →B 滑动到B 止，在这个过程中，线段BM 的长为线段，QR 的中点M 所经过的路线围成的图形的面积为考查内容：答案：2 4π三、解答题1．（南京市鼓楼区2011年中考一模）（10分）如图，在矩形ABCD 中，AB ＝43，BC ＝4．点M 是AC 上动点（与点A 不重合），设AM ＝x ，过点M 作AC 的垂线，交直线AB 于点N ．（1）当△AND 的面积为833时，求x 的值；（2）以D 、M 、N 三点为顶点的△DMN 的面积能否达到矩形ABCD 面积的18？若能，请求出此时x 的值，若不能，请说明理由．答案：（本题10分）＝BCAB＝解：（1）在Rt △ABC 中，AB ＝43，BC ＝4，∠B ＝90°，∴tan ∠BAC 443．∴tan ∠BAC ＝33．∵∠BAC 是锐角，∴∠BAC ＝30°．在Rt △AMN 中，AM ＝x ，∠AMN ＝90°， ∴MN ＝AM·tan ∠BAC ＝33x ，AN ＝MN sin ∠BAC ＝23x3．………………………2分 ∴S △ADN ＝12·AD ·AN ＝12·4·23x 3＝833．∴x ＝2． ………………………3分（2）设DN 交AC 于点E ．当点E 、M 重合时，x ＝AM =12×4=2 ………………………4分ABCDMNA BC QRM D①当0＜x ＜2时，点M 在△ADN 的内部．过D 作DF ⊥AC ，垂足为F ． ∴DF ＝AD ·sin60°＝4×32＝23．∵S △AMN ＝12×x ×33x ＝36x 2，S △ADN ＝12×4×23x 3x ＝433x ，S △ADM ＝12× x ×23＝3x ，∴S △DMN ＝S △ADN －S △AMN －S △ADM ＝433x －36x 2－3x ＝33x －36x 2．设S △DMN ＝18S 矩形ABCD ，33x －36x 2＝18×43×4＝23，2x －x 2＝12．∴x 2－2x ＋12＝0．∵ (－2)2－4×1×12＜0，∴该方程无实数根． ………6分②当2＜x ≤8时，点M 在△ADN 的外部． ∴S △DMN ＝S △AMN ＋S △ADM －S △ADN ＝36x 2＋3x －433x ＝36x 2－33x ．设S △DMN ＝18S 矩形ABCD ，36x 2－33x ＝23， x 2－2x ＝12．∴x 2－2x －12＝0．∴x 1＝1－13＜0，舍去，x 2＝1＋13．∵3＜13＜4，∴4＜1＋13＜5． ∴x ＝1＋13满足条件．∴当S △DMN ＝18S 矩形ABCD 时，x ＝1＋13．…………………………………10分2．（南京市建邺区2011年中考一模）（12分）如图，在Rt △ABC 中，∠C =90°，AC =BC =4cm ，点D为AC 边上一点，且AD =3cm ，动点E 从点A 出发，以1cm/s 的速度沿线段AB 向终点B 运动，运动时间为x s ．作∠DEF =45°，与边BC 相交于点F ．设BF 长为y cm ．（1）当x = ▲ s 时，DE ⊥AB ；（2）求在点E 运动过程中，y 与x 之间的函数关系式及点F 运动路线的长；（3）当△BEF 为等腰三角形时，求x 的值．答案：（本题12分）A BC DEF（第4题图）（第4题备用图）ABCD解：（1）32 2 ····························································································· 2分（2）∵在△ABC 中，∠C =90°，AC =BC =4．∴∠A ＝∠B ＝45°，AB =4 2 ，∴∠ADE ＋∠AED ＝135°；又∵∠DEF ＝45°，∴∠BEF ＋∠AED ＝135°，∴∠ADE ＝∠BEF ；∴△ADE ∽△BEF ··························································································· 4分 ∴AD BE ＝AE BF ， ∴3 4 2 －x＝x y ，∴y ＝－13 x 2+43 2 x ···························································· 5分∴y ＝－13 x 2+43 2 x ＝－13 ( x －2 2 )2+83∴当x ＝2 2 时，y 有最大值＝83 ······································································ 6分∴点F 运动路程为163 cm ·················································································· 7分（3）这里有三种情况：①如图，若EF ＝BF ，则∠B ＝∠BEF ；又∵△ADE ∽△BEF ，∴∠A ＝∠ADE ＝45°∴∠AED ＝90°，∴AE ＝DE ＝32 2 ，∵动点E 的速度为1cm/s ，∴此时x ＝32 2 s ；②如图，若EF ＝BE ，则∠B ＝∠EFB ；又∵△ADE ∽△BEF ，∴∠A ＝∠AED ＝45° ∴∠ADE ＝90°，∴AE ＝3 2 ， ∵动点E 的速度为1cm/s ∴此时x ＝3 2 s ；A B CDE F 第4题（1）（2）图A BCDEF第4题（3）①图ABCDE FA BCDE F③如图，若BF ＝BE ，则∠FEB ＝∠EFB ；又∵△ADE ∽△BEF ，∴∠ADE ＝∠AED ∴AE ＝AD ＝3，∵动点E 的速度为1cm/s ∴此时x ＝3s ；综上所述，当△BEF 为等腰三角形时，x 的值为322 s 或3 2 s 或3s ．（注：求对一个结论得2分，求对两个结论得4分，求对三个结论得5分）3．（南京市溧水县2011年中考一模）（9分）已知24AB AD ==，，90DAB ∠=，AD BC ∥（如图）．E 是射线BC 上的动点（点E 与点B 不重合），M 是线段DE 的中点．（1）设BE x =，ABM △的面积为y ，求y 关于x 的函数关系式，并写出自变量x 的取值范围；（2）如果以线段AB 为直径的圆与以线段DE 为直径的圆外切，求线段BE 的长；（3）连结BD ，交线段AM 于点N ，如果以A N D ，，为顶点的三角形与BME △相似，求线段BE 的长．答案：解：（1）取AB 中点H ，连结MH ，M 为DE 的中点，MH BE ∴∥，1()2MH BE AD =+． ······························· 1分又AB BE ⊥ ，MH AB ∴⊥． ······································································· 2分12ABM S AB MH ∴=△，得12(0)2y x x =+>； ·············································· 3分（2）过D 作DP ⊥BC ，垂足为P ， ∠DAB =∠ABC =∠BPD =90°，∴四边形ABPD 是矩形．以线段AB 为直径的圆与以线段DE 为直径的圆外切，1122MH AB DE ∴=+，又1()2MH BE AD =+，∴DE=BE+AD -AB =x +4-2=x +2……4分PD =AB=2，PE= x -4，DE 2= PD 2+ PE 2，…………………………………………………5分∴（x +2）2=22+（x -4）2，解得：34=x ．∴线段BE 的长为34．…………………………………………………………………………6分（3）由已知，以A N D ，，为顶点的三角形与BME △相似，又易证得DAM EBM ∠=∠． ········································································ 7分B A D M EC 第28题图BADC备用图由此可知，另一对对应角相等有两种情况：①ADN BEM ∠=∠；②ADB BME ∠=∠． ①当ADN BEM ∠=∠时，AD BE ∥，ADN DBE ∴∠=∠．DBE BEM ∴∠=∠． DB DE ∴=，易得2BE AD =．得8BE =； ··················································· 8分 ②当ADB BME ∠=∠时，AD BE ∥，ADB DBE ∴∠=∠．DBE BME ∴∠=∠．又BED MEB ∠=∠，BED M EB ∴△∽△．DE BE BE EM ∴=，即2BE EM DE = =221DE ，得x 2=21[22+（x -4）2]．解得12x =，210x =-（舍去）．即线段BE 的长为2． ········································ 9分综上所述，所求线段BE 的长为8或2．4．（南京市六合区2011年中考一模）（9分）如图1，△ABC 中，AB =AC =5cm ，BC =6cm ，边长为2cm 的菱形DEFG 两边DG 、DE 分别在AC 、AB 上．若菱形DEFG 以1cm/s 的速度沿射线AC 方向平移．（1）经过 ▲ 秒菱形DEFG 的顶点F 恰好在BC 上；（2）求菱形DEFG 的面积；（3）设菱形DEFG 与△ABC 的重合部分为S cm 2，菱形DEFG 平移的时间为t 秒．求S 与t 的函数关系式．答案：解：（1）1．…………………………2分（2）方法一：如图，连接GE 、AF ，交于点O ，并延长AF 交BC 于点H ． ∵由AG =AE 得∠AGE=∠AEG ，由AB=AC 得∠B=∠C ， ∴∠AEG=∠C=180°–∠A2 ． ∴GE ∥BC ， ∴AE AC =GEBC ，得GE= 125 ．………………3分 ∵菱形AEFG 中，GE ⊥AF ，可得AH ⊥BC ，故CH=12BC=3． ∴Rt △ACH 中，AH=AC 2–CH 2=4．∴AO AH =AE AC ，得AO=85，于是AF=165．……………………4分 ∴S 菱形AEFG =12⨯GE ⨯AF=9625． …………………………5分方法二：易求S △ABC =12．………………3分由△AGE ∽△ABC 得S △AGE S △ABC=(AE AC )2 ，即S △AGE 12=(25)2．……………4分所以，S △AGE =4825得S 菱形AEFG =9625．…………………………5分（3）①当0≤t ≤1时，S=9625 ．…………………………6分②当1<t ≤3时，AD=t ，则CE=5–t –2=3–t ，EN=EC=3–t ，故FN=2–（3–t ）=t –1 ．由△FMN ∽△ABC 可得S △FMN S △ABC =(FN AC)2．即S △FMN 12=(t –15)2，所以S △FMN =1225(t –1)2 ．所以S= S 菱形AEFG –S △FMN =9625 –1225(t –1)2．……………7分 ③当3<x ≤5时，AD=t ，则CD=5–t ，由△DMC ∽△ABC 可得SS △ABC=(DCAC )2．即S12=(5–t5)2，所以S=1225(5–t)2．……………………8分 ④当t>5时，S=0．…………………………9分5．（南京市浦口区2011年中考一模）（10分）如图，已知直角梯形ABCD 中，AD //BC ， DC ⊥BC ，AB ＝5，BC ＝6，∠B ＝53°．点O 为BC 边上的一个动点，连结OD ，以O 为圆心，BO 为半径的⊙O 分别交边AB 于点P ，交线段OD 于点M ，交射线BC 于点N ，连结MN ．（1）当BO ＝AD 时，求BP 的长；（2）在点O 运动的过程中，线段 BP 与MN 能否相等？若能，请求出当BO 为多长时BP ＝MN ；若不能，请说明理由；（3）在点O 运动的过程中，以点C 为圆心，CN 为半径作⊙C ，请直接写出．．．．当⊙C 存在时，⊙O 与⊙C 的位置关系，以及相应的⊙C 半径CN 的取值范围.(参考数据：cos53°≈0．6；sin53°≈0．8；tan74°≈3.5)A D AD答案：（本题10分）解：（1）∵AD//BC,BO=AD∴四边形AB0D 为平行四边形-------------------------------------------------------------------------1分 ∴AB//OD, ∠COD=∠ABO=53°，DO=AB=5在Rt ∆OCD 中，36.05cos =⨯=∠⨯=COD DO CO , BO=BC-CO=3.-----------------2分在RtPOB 中，BO=PO, ∴BP=.6.353cos 20=⨯⨯BO -------------------------------------------3分（2）不存在.---------------------------------------------------------------4分如图,过A 点作AE ⊥BC 交BC 于E 点.若BP = MN ，则△BOP ≌△MON --------------------------------5分 ∴∠BOP=∠MON=180°- 2∠B = 74°DC=AE=.453sin 0=⨯AB -------------------------------------------------------------------------6分在Rt ∆OCD 中，7874tan 0==DC CO . BO=BC-CO=734在△POB 中,BP=83.56.0734253cos 20≈⨯⨯=⨯⨯BO 因为AB=5,所以BP>AB.又因为P 点在边AB 上，即BP ＜AB.所以BP 与MN 不可能相等.--------------------------------------------------------------------------- 8分（3）当时，30<<BO ⊙O 与⊙C 外切，CN 取值范围为 0< CN < 6 ------------ 9分当时，6253≤<BO ⊙O 与⊙C 内切，CN 取值范围为 370≤<CN ------------- 10分6. （南京市玄武区2011年中考一模）（9分）如图，小明将一张直角梯形纸片沿虚线剪开，得到矩形ABCD 和三角形EGF 两张纸片，测得AB=5，AD=4，EF=55．在进行如下操作时遇到了下面的几个问题，请你帮助解决．(1) 请你求出FG 的长度．(2)在(1)的条件下，小明先将三角形的边EG 和矩形边AB 重合，然后将△EFG 沿直线BC 向右平移，至F 点与B 重合时停止．在平移过程中，设G 点平移的距离为x ，两纸片重叠部分面积为．y ，求在平移的整个过程中，y 与x 的函数关系式，并求当重叠部分面积为10时，平移距离x 的值．A B C DO PM N E(3)在(2)的操作中，小明发现在平移过程中，虽然有时平移的距离不等，但两纸片重叠的面积却是相等的；而有时候平移的距离不等，两纸片重叠部分的面积也不可能相等．请探索这两种情况下重叠部分面积y 的范围(直接写出结果)．答案：(1)∵在R t △EGF 中，EG=AB=5，EF=55, ∴FG=105)55(2222=-=-EGEF ……………..2分(2)当0≤x ≤4时，2154y x x =-+；………………….3分当4＜x ≤10时，y=－2x+24，…………..4分当y=10时，x=7或10215x =-．……………….6分 (3)当0≤x ≤4时，()22115102544y x x x =-+=--+，顶点为(10，25)，…….7分 ∴当0≤x ≤4时，0≤y ≤16．当4＜x ≤10时，y=－2x+24，4≤y ＜16．∴当4≤y<16时，平移的距离不等，两纸片重叠的面积y 可能相等．………8分当0≤y ＜4或y=16时，平移的距离不等，两纸片重叠部分的面积也不可能相等．…..9分 7．（南京市雨花台2011年中考一模）（14分）如图，在□ABCD 中，cm AB 6=，cm AC AD 5==．点P 由C 出发沿CA 方向匀速运动，速度为1/cm s ；同时，线段EF 由AB 出发沿AD 方向匀速运动，速度为1/cm s ，交AC 于Q ，连接PE 、PF ．若设运动时间为t （s ）（50<<t ）．解答下列问题：（1）当t 为何值时，PE ∥CD ？并求出此时PE 的长; （2）试判断△PEF 的形状，并请说明理由．（3）当5.20<<t 时，(ⅰ)在上述运动过程中，五边形ABFPE 的面积 ▲ (填序号)①变大 ②变小 ③先变大,后变小 ④不变(ⅱ)设PEQ △的面积为2()y cm ，求出2()y cm 与()t s 之间的函数关系式及y 的取值范围．QPEDA（第9题）解：（1）由题意知AE BF CP t ===，5AP t =-, 在□ABCD 中，5AD BC AC ===，6AB EF CD ===，当PE ∥CD 时，APE ∆∽ACD ∆,∴555t t -=，∴ 2.5t =…………………3分 (或当PE ∥CD 时，AE AP =,∴t t -=5，∴ 2.5t =)此时，点P 、E 分别为AC 、AD 的中点， ∴113()22EF CD AB cm ===……………………………………4分 (2)△PEF 是等腰三角形 ………………………………………………………5分证明：在□ABCD 中，AD BC AC ==，AB EF CD ==，∴CBA CAB ∠=∠, ∵AB ∥EF ,∴,,CBA CFQ CAB CQF ∠=∠∠=∠∴,CQF CFQ ∠=∠∴CQ CF =, ∴AQ BF AE ==，∴AP CQ CF ==， ∵AD ∥BC ,∴PAEFCP ??，∴PAE ∆≌)(SAS FCP ∆,∴PF PE =……8分(3) (ⅰ)在上述运动过程中，五边形ABFPE 的面积 ④ (填序号)…………10分(ⅱ) ∵△AQE ∽△ACD ，∴QE AQ CD AC =，∴65AQ QE CD t AC == …………11分过点P 作PH EF ⊥于点H ，过点C 作CG AB ⊥于点G ，∴△PQH ∽△CAG ，∴PH PQ CG CA =，∴()4525PQ PH CG t CA ==- ∴23)45(25245122524)25(54562122+--=+-=-⋅⋅=t t t t t y ……………13分 ∴当45=t 时，最大y 23=，∴230≤<y ……………………………………14分（其它解法，正确合理可参照给分。

【精品】48.中考真题探索规律型问题.docx

探索规律型问题一、选择题1.（2010安徽省中中考）下面两个多位数1248624……、6248624……，都是按照如下方法得到的：将第一位数字乘以2,若积为一位数，将其写在第2位上，若积为两位数，则将其个位数字写在第2位。

对第2位数字再进行如上操作得到第3位数字……，后面的每一位数字都是由前一位数字进行如上操作得到的。

当第1位数字是3时，仍按如上操作得到一个多位数，则这个多位数前100位的所有数字之和是............................. （）A） 495 B） 497 C） 501 D） 503【答案】A2.（2010江苏盐城）填在下面各正方形中的四个数之间都有相同的规律，根据此规律，m 的值是（）A.38B. 52C. 66D. 74【答案】D3. （2010山东威海）在平面直角坐标系中，正方形ABCD的位置如图所示，点A的坐标为（1, 0）,点。

的坐标为（0, 2）.延长CB交x轴于点A1，作正方形A J B J C I C；延长GBi交x轴于点A?,作正方形A2B2C2G...按这样的规律进行下去，第2010个正方形的面积为（）、B IB2A A,【答案】D4.（2010福建晋江）如图，将一张正方形纸片剪成四个小正方形，得到4个小正方形，称为第一次操作；然后，将其中的一个正方形再剪成四个小正方形，共得到7个小正方形，称为第二次操作；再将其中的一个正方形再剪成四个小正方形，共得到10个小正方形，称为第三次操作；…，根据以上操作，若要得到2011个小正方形，则需要操作的次数是（）■【答案】B5. （2010山东日照）古希腊人常用小石子在沙滩上摆成各种形状来研究数，例如:I 3 6 10图11 4 9 16图210, …，由于这些数能够表示成三角形，将其称为三角形数;16,…，这样的数为正方形数.下列数中既是三角形数又是正方形数的是()(A) 15 (B) 25(C) 55 (D) 1225【答案】D6. （2010山东烟台）如图，一串有■趣的图案按一定的规律排列，请仔细观察，按此规律第 2010个图案是（）【答案】B7. （2010河北）将正方体骰子（相对面上的点数分别为1和6、2和5、3和4）放置于水平桌面上，如图6-1.在图6-2中，将骰子向右翻滚90°,然后在桌面上按逆时针方向旋转90。

2022中考数学最新重点汇编48-探索规律型问题

2022中考数学最新重点汇编48-探索规律型问题一、选择题1、（2020年浙江一模）如图，一只青蛙在圆周上标有数字的五个点上跳，若它停在奇数点上，则下次沿顺时针方向跳两个点；若停在偶数点上，则下次沿逆时针方向跳一个点．若青蛙从5这点开始跳，则通过2020次后它停在哪个数对应的点上（） A ．1 B ．2 C ．3 D ．5 答案：D2、（2020年浙江金华模拟）将1、2、3、6按右侧方式排列．若规定（m ，n ）表示第m 排从左向右第n 个数，则（4，2）与（21，2）表示的两数之积是（ ▲ )． A ．1 B ．2 C ．2 3 D ．6 答案：D3、（2020年重庆外国语学校九年级第二学期期中）下列图形差不多上由同样大小的正方形按一定的规律组成，其中，第①个图形中一共有1个正方形，第②个图形中一共有5个正方形，第③个图形中一共有14个正方形，……则第⑦个图形中正方形的个数为A 、49B 、 100C 、140D 、91 答案：C4、(2020年荆州模拟)如图，已知直线l ：y =x ，过点A （0，1）作y 轴的垂线交直线l 于点B ，过点B 作直线l 的垂线交y 轴于点A 1；过点A 1作y 轴的垂线交直线l 于点B 1，过点B 1作直线l 的垂线交y 轴于点A 2；…；按此作法连续下去，则点A 4的坐标为（）134第1题图111122663263323第1排第2排第3排第4排第5排……A 、（0，64）B 、（0，128）C 、（0，256）D 、（0，512）答案： C5、（2020江苏江阴华士片九年级下期中检测，10,3分）如图，直线xy 33=，点1A 坐标为（1，0），过点1A 作x 轴的垂线交直线于点1B ，以原点O 为圆心，1OB 长为半径画弧交x 轴于点2A ；再过点2A 作x 轴的垂线交直线于点2B ，以原点O 为圆心，2OB 长为半径画弧交x 轴于点3A ，…，按此做法进行下去，点nA 的横坐标为（）A ．1)332(-n B ．23()3nC ．32()3n D ．132()3n答案：A6、（2020浙江温岭三中一模）如图，电子跳蚤游戏盘为△ABC ，AB=8，AC=9，BC=10，假如电子跳蚤开始时在BC 边上的P 0点，BP 0=4．第一步跳蚤跳到AC 边上P 1点，且CP 1=CP 0；第二步跳蚤从P 1跳到AB 边上P 2点，且AP 2=AP 1；第三步跳蚤从P 2 跳回到BC 边上P 3点，且BP 3=BP 2；…跳蚤按上述规则跳下去，第n 次落点为P n （n 为正整数），则点B 与P 2020之间的距离为（）第10题图（第1题）A ．3B ．4C ．5D ．6答案：C7. (2020年浙江新昌县毕业考试)如图，△ABC 是边长为1的等边三角形．取BC 边中点E ，作ED ∥AB ，EF ∥AC ，得到四边形EDAF ，它的面积记作S 1；取BE 中点E 1，作E 1D 1∥FB ，E 1F 1∥EF ，得到四边形E 1D 1FF 1，它的面积记作S 2．照此规律作下去，S 2020=A ．201023 B ．201223C ．402423 D. 402523 答案：D8. （2020重庆市渝北区二中检测）观看下列图形：若图形（1）中阴影部分的面积为1，图形（2）中阴影部分的面积为43，图形（3）中阴影部分的面积为169，图形（4）中阴影部分的面积为6427，…，则第n 个图形中阴影部分的面积用字母表示为（）⑷⑶⑵⑴1第7题图（第3题）A．n43B．n)43(C．1)43(-n D．1)43(+n答案：C9、．下列图形差不多上由同样大小的等边三角形按一定的规律组成，其中，第①个图形中一共有3根小棒，第②个图形中一共有9根小棒，第③个图形中一共有18根小棒，……，则第⑥个图形中小棒的根数为①②③A．60B．63C．69D．72答案B10、．下列图形差不多上由同样大小的等边三角形按一定的规律组成，其中，第①个图形中一共有3根小棒，第②个图形中一共有9根小棒，第③个图形中一共有18根小棒，……，则第⑥个图形中小棒的根数为①②③A．60B．63C．69D．72答案B二、填空题1、（2020年浙江五模）已知a≠0，12S a=，212SS=，322SS=，…，201220112SS=，则2012S=(用含a的代数式表示)．…………xyO A 1A 2 A 3l 2 l 1l 31 423 答案：1a2、（保沙中学2020二模）如图，n +1个上底、两腰长皆为1，下底长为2的等腰梯形的下底均在同一直线上，设四边形P 1M 1N 1N 2面积为S 1，四边形P 2M 2N 2N 3的面积为S 2，……，四边形P n M n N n N n +1的面积记为S n ，则S n = ▲答案：3、（保沙中学2020二模）如图，在平面直角坐标系中，点A 1是以原点O 为圆心，半径为2的圆与过点（0，1）且平行于x 轴的直线l 1的一个交点；点A 2是以原点O 为圆心，半径为3的圆与过点（0，2）且平行于x 轴的直线l 2的一个交点；……按照如此的规律进行下去，点An 的坐标为_________ ．答案：(√2n+1,n)4、（广州海珠区2020毕业班综合调研）定义：a 是不为1的有理数，我们把11a-称为a 的差倒数．．．．如：2的差倒数是1112=--，1-的差倒数是111(1)2=--．已知113a =-，2a 是1a 的差倒数，3a 是2a 的差倒数，4a 是3a 的差倒数，……，依此类推，则2012a = ．答案：435、（2020 年福州市初中毕业班质量检查）如图，∠AOB ＝30°，n 个半圆依次外切，它们的圆心都在射线OA 上并与射线OB 相切，设半圆C 1、半圆C 2、半圆C 3、…、半圆C n 的半径分别是r 1、r 2、r 3、、r n ，则r 2020r 2011＝___________．答案：36、（2020年周口二模）图11－1是三个直立于水平面上的形状完全相同的几何体（下底面为圆面，单位：cm ）．将它们拼成如图11－2的新几何体，则该新几何体的体积为 ____cm 3．（运算结果保留π）答案： 60π7、（2020年周口二模）如图，n +1个上底、两腰长皆为1，下底长为2的等腰梯形的下底均在同一直线上，设四边形P 1M 1N 1N 2面积为S 1，四边形P 2M 2N 2N 3的面积为S 2，……，四边形P n M n N n N n +1的面积记为S n ，则S n = ▲答案：331221n n +⋅+8、（2020年孝感模拟）设12211=112S ++,22211=123S ++,32211=134S ++,…,2211=1(1)n S n n +++，若12...n S S S S =+++，则S =_________ (用含n 的代数式表示，其中n 为正整数)．答案：)1()2(2++n n n9、（2020年北京门头沟一模）如图，对面积为1的△ABC 逐次进行以下操作：第一次操作，分别延长AB 、BC 、CA 至A 1、B 1、C 1，使得A 1B =2AB ，B 1C =2BC ，C 1A =2CA ，顺次连接A 1、 B 1、C 1，得到△A 1B 1C 1，记其面积为S 1；第二次操作，分别延长A 1B 1，B 1C 1，C 1A 1至A 2，B 2，C 2，使得 A 2B 1=2A 1B 1，B 2C 1=2B 1C 1，C 2A 1=2C 1A 1，顺次连接 A 2，B 2，C 2，得到△A 2B 2C 2，记其面积为S 2……，按此规律连续下去，可得到△A 5B 5C 5，则其面积为 S 5=_________. 第n 次操作得到△A n B n C n ，则△A n B n C n 的面积S n = . 答案：195 19n第13题64464464410、（2020北京市密云初三一模）在∠A （0°＜∠A ＜90°）的内部画线段，并使线段的两端点分别落在角的两边AB 、AC 上，如图所示，从点A 1开始，依次向右画线段，使线段与线段在两端点处互相垂直，A 1A 2为第1条线段．设AA 1=A 1A 2=A 2A 3=1，则∠A =；若记线段A 2n-1A 2n 的长度为a n （n 为正整数），如A 1A 2=a 1,A 3A 4=a 2，则现在a 2= ，a n = （用含n 的式子表示）．答案：22．5；12+1(12)n -+11、（2020北京市延庆县初三一模）将1、2、3、6按右侧方式排列．若规定（m,n ）表示第m 排从左向右第n 个数，则（7,3）所表示的数是；（5，2）与（20，17）表示的两数之积是答案：6；2312、（2020南京江宁区九年级调研卷）已知,...,154415431,83314321,32213211321=+⨯⨯==+⨯⨯==+⨯⨯=a a a 依据上述规律，则=99a ▲ ．答案：100999913、（2020北京市石景山区初三一模）一个正整数数表如下（表中下一行中数的个数是上一行中数的个数的2倍）：第1行 1 第2行 3 5 第3行 7 9 11 13……则第4行中的最后一个数是，第n 行中共有个数，第n 行的第n 个数是．答案：29；12-n ；322-+n n111122663263323第1排第2排第3排第4排第5排（第1题）D 2D 3E 2E 3E 1D 1ABC14、（2020双柏县一模）有一组数列：2，3-，2，3-，2，3-，2，3-，…… ，依照那个规律，那么第2020个数是__________．答案：-315. （2020年犍为县五校联考）若x y 31=，123y y =，233y y =，343y y =，……，200720083y y =，则=⋅20081yy ___. 答案：316. (2020湛江调研测试)下图中的实心点个数1，5，12，22，…，被称为五角形数，若按此规律连续下去，则第5个五角形数是．答案：3517. (2020浙江绍兴县3时期)信息需要加密传输，发送方由明文→密文（加密），接收方由密文→明文（解密），已知加密规则为：明文d c b a ,,,对应密文d d c c b b a 4,32,2,2+++，例如，明文1,2,3,4对应密文5,7,18,16，当接收方收到密文14,9,23,28时，则解密得到的明文为 ▲ .答案：6,4，1,718、（2020江苏省无锡市期中）如图，已知Rt △ABC ，D 1是斜边AB 的中点，过D 1作 D 1E 1⊥AC 于E 1，连结BE 1交CD 1于D 2；过D 2作D 2E 2⊥AC 于E 2，连结BE 2交CD 1于D 3；过D 3作D 3E 3⊥AC 于E 3，…，如此连续，能够依次得到点E 4、E 5、…、E n ，分别记△BCE 1、 △BCE 2、△BCE 3···△BCE n 的面积为S 1、S 2、S 3、…S n . 则S n ＝ S △ABC （用含n 的代数式表示）．答案：19、（2020北京市大兴区）如图所示的10-三角数表．从上往下数，第1次全行的数都为1（第3题）5121 22的是第1行，第2次全行的数都为1的是第3行，第3次全行的数都为1的是第行，… ，第n 次全行的数都为1的是第行．第1行第2行第3行第4行第5行…………………………………… 答案：7, 21n -20. （2020北京市怀柔区）一组按规律排列的数：2，0，4，0，6，0，…，其中第7个数是，第n 个数是 . （用含字母n 的代数式表示，n 为正整数）．答案：8，())1(2111+-++n n22．（2020北京市通州区）已知如图，△ABC 和△DCE 差不多上等边三角形，若△ABC 的边长为1，则△BAE 的面积是 .四边形ABCD 和四边形BEFG 差不多上正方形，若正方形ABCD 的边长为4，则△FAC 的面积是 . ……假如两个正多边形ABCDE …和BPKGY …ABCDE …的边长是2a ，则△KCA 的面积是 .（结果用含有a 、n 的代数式表示）答案：43，8，n a ︒360sin 22或（n n n n a )2(90cos)2(90sin 42-︒⨯-︒⋅）三、解答题1、（广东省2020初中学业水平模拟六）友爱的同学，你能比较20112020和20202011的大P H AE DC EF C ACG BF小吗？为了解决那个问题，我们先把它抽象成数学问题，写出它的一样形式，即比较n n+1和（n+1）n的大小（n是自然数）然后，我们分析n=1,n=2,n=3…这些简单情形入手，从中发觉规律，通过归纳、猜想，得出结论。