全国各地高考数学试题分类汇编10 排列、组合及二项式定理 文
2013年高考理科数学试题分类汇编:10排列、组合及二项式定理

实用文档 2013年高考理科数学试题分类汇编:10排列、组合及二项式定理一、选择题1、13年高考江西卷(理))(x 2-32x )5展开式中的常数项为 ( ) A .80B .-80C .40D .-402、13年山东数学(理)试题,用0,1,,9十个数字,可以组成有重复数字的三位数的个数为 ( )A .243B .252C .261D .2793、设m 为正整数,2()m x y +展开式的二项式系数的最大值为a ,21()m x y ++展开式的二项式系数的最大值为b ,若137a b =,则m =( ) A .5B .6C .7D .84、13年大纲版数学(理))()()8411+x y +的展开式中22x y 的系数是 ( )A .56B .84C .112D .1685、13年福建数学(理)试题)满足{},1,0,1,2a b ∈-,且关于x 的方程220ax x b ++=有实数解的有序数对(,)a b 的个数为( )A .14B .13C .12D .10实用文档6、13年上海市春季高考数学)10(1)x +的二项展开式中的一项是( ) A .45xB .290xC .3120xD .4252x7、辽宁数学(理))使得()3n x n N n +⎛+∈ ⎝的展开式中含有常数项的最小的为 ( ) A .4B .5C .6D .78、高考四川卷(理))从1,3,5,7,9这五个数中,每次取出两个不同的数分别为,a b ,共可得到lg lg a b-的不同值的个数是( ) A .9B .10C .18D .209、13年高考陕西卷(理))设函数61,00.,()x x f x x x ⎧⎛⎫-<⎪ ⎪=⎝≥⎭⎨⎪⎩ , 则当x >0时, [()]f f x 表达式的展开式中常数项为( ) A .-20B .20C .-15D .1510、13年新课标Ⅱ卷数学(理)已知5)1)(1(x ax ++的展开式中2x 的系数为5,则=a( ) A .4-B .3-C .2-D .1-实用文档二、填空题11、二项式5()x y +的展开式中,含23x y 的项的系数是_________.(用数字作答)12、大纲版数学(理)6个人排成一行,其中甲、乙两人不相邻的不同排法共有____________种.(用数字作答).13、从4名男同学和6名女同学中随机选取3人参加某社团活动,选出的3人中男女同学都有的概率为________(结果用数值表示).14、考试浙江数学(理)试题(纯WORD 版))将F E D C B A ,,,,,六个字母排成一排,且B A ,均在C的同侧,则不同的排法共有________种(用数字作答)15、重庆数学(理)试题)从3名骨科.4名脑外科和5名内科医生中选派5人组成一个抗震救灾医疗小组,则骨科.脑外科和内科医生都至少有1人的选派方法种数是___________(用数字作答)16、天津数学(理)试题)6x ⎛ ⎝ 的二项展开式中的常数项为______.实用文档17、试浙江数学(理)试题)设二项式53)1(xx -的展开式中常数项为A ,则=A ________.18、13年高考上海卷(理))设常数a R ∈,若52a x x ⎛⎫+ ⎪⎝⎭的二项展开式中7x 项的系数为10-,则______a =19、高考北京卷(理))将序号分别为1,2,3,4,5的5张参观券全部分给4人,每人至少1张,如果分给同一人的2张参观券连号,那么不同的分法种数是_________.20、安徽数学(理)若8x ⎛+ ⎝的展开式中4x 的系数为7,则实数a =______.21、36的所有正约数之和可按如下方法得到:因为2236=23⨯,所以36的所有正约数之和为22222222(133)(22323)(22323)(122)133)91++++⨯+⨯++⨯+⨯=++++=(参照上述方法,可求得2000的所有正约数之和为________________________以下是答案一、选择题1、C2、B3、B4、D5、B6、C7、B8、C9、A10、D二、填空题11、1012、48013、45实用文档14、48015、59016、1517、-10a=-18、219、961 20、2 21、4836实用文档。
全国高考数学 试题分类汇编 排列、组合及二项式定理

2010排列、组合、二项式定理1.(2010·陕西高考理科·T4)5()ax x+(x R ∈)展开式中3x 的系数为10,则实数a 等于( ) (A )-1 (B )12(C) 1 (D) 2 【命题立意】本题考查二项式定理的通项公式的应用及运算能力,属保分题。
【思路点拨】5()ax x+⇒5215r r r r T a C x -+=⇒523r -=⇒11510 2.a C a =⇒= 【规范解答】选D 552155,(0,1,2,3,4,5)rr r r r r r a T C x a C x r x --+⎛⎫=== ⎪⎝⎭Q ,令523r -=,所以1r =,所以11510 2.a C a =⇒=2.(2010·北京高考理科·T4)8名学生和2位老师站成一排合影,2位老师不相邻的排法种数为( ) (A )8289A A (B )8289A C (C )8287A A (D )8287A C【命题立意】本题考查排列组合的相关知识。
所用技巧:有序排列无序组合、不相邻问题插空法。
【思路点拨】先排8名学生,再把老师插入到9个空中去。
【规范解答】选A 。
8名学生共有88A 种排法,把2位老师插入到9个空中有29A 种排法,故共有8289A A 种排法。
【方法技巧】解决排列组合问题常用的方法与技巧:(1)有序排列无序组合;(2)不相邻问题插空法:可以把要求不相邻的元素插入到前面元素间的空中;(3)相邻问题捆绑法。
3.(2010·山东高考理科·T8)某台小型晚会由6个节目组成,演出顺序有如下要求:节目甲必须排在前两位、节目乙不能排在第一位,节目丙必须排在最后一位,该台晚会节目演出顺序的编排方案共有( ) (A )36种(B )42种(C)48种(D )54种【命题立意】本题考查排列组合的基础知识,考查分类与分步计数原理,考查了考生的分析问题解决问题的能力和运算求解能力.【思路点拨】根据甲的位置分类讨论.【规范解答】选B ,分两类:第一类:甲排在第一位,共有44A =24种排法;第二类:甲排在第二位,共有1333A A =18⋅种排法,所以共有编排方案241842+=种,故选B. 【方法技巧】排列问题常见的限制条件及对策1、有特殊元素或特殊位置,先满足特殊元素或特殊位置的要求,再考虑其他元素或位置.2、元素必须相邻的排列,将必须相邻的的元素捆绑,作为一个整体,但要注意其内部元素的顺序.3、元素不相邻的排列,先排其他元素,然后“插空”.4、元素有顺序限制的排列.4.(2010·天津高考理科·T10)如图,用四种不同颜色给图中的A,B,C,D,E,F 六个点涂色,要求每个点涂一种颜色,且图中每条线段的两个端点涂不同颜色,则不同的涂色方法用( )(A )288种 (B )264种 (C )240种 (D )168种【命题立意】本题考查分类计数原理,排列组合等基础知识,考查分析问题、解决问题的能力。
高考数学试题分类详解排列组合二项式定理

高考数学试题分类详解排列组合二项式定理1、(全国1理10)的展开式中,常数项为15,则n= A.3 B.4 C.5D.6解.的展开式中,常数项为15,则,所以n可以被3整除,当n=3时,,当n=6时,,选D。
2、(全国1文5)甲、乙、丙3位同学选修课程,从4门课程中,甲选修2门,乙、丙各选修3门,则不同的选修方案共有A.36种 B.48种 C.96种 D.192种解.甲、乙、丙3位同学选修课程,从4门课程中,甲选修2门,乙、丙各选修3门,则不同的选修方案共有种,选C。
3、(全国2理10)从5位同学中选派4位同学在星期五、星期六、星期日参加公益活动,每人一天,要求星期五有2人参加,星期六、星期日各有1人参加,则不同的选派方法共有(A)40种 (B) 60种 (C) 100种 (D) 120种解.从5位同学中选派4位同学在星期五、星期六、星期日参加公益活动,每人一天,要求星期五有2人参加,星期六、星期日各有1人参加,则不同的选派方法共有种,选B。
4、(全国2文10)5位同学报名参加两个课外活动小组,每位同学限报其中的一个小组,则不同的报名方法共有()A.10种 B.20种 C.25种 D.32种解.5位同学报名参加两个课外活动小组,每位同学限报其中的一个小组,则不同的报名方法共有25=32种,选D。
5、(北京文5)某城市的汽车牌照号码由2个英文字母后接4个数字组成,其中4个数字互不相同的牌照号码共有()A.个B.个C.个D.个解析:某城市的汽车牌照号码由2个英文字母后接4个数字组成,其中4个数字互不相同的牌照号码共有个,选A。
6、(北京理5)记者要为5名志愿者和他们帮助的2位老人拍照,要求排成一排,2位老人相邻但不排在两端,不同的排法共有()A.1440种B.960种C.720种D.480种解析:5名志愿者先排成一排,有种方法,2位老人作一组插入其中,且两位老人有左右顺序,共有=960种不同的排法,选B。
高考数学试题分类汇编---- 排列组合二项式定理

高考数学试题分类汇编---- 排列组合二项式定理一. 选择题:1.(全国一3)512x ⎛⎫+ ⎪⎝⎭的展开式中2x 的系数为( C ) A .10 B .5 C .52 D .12.(全国一12)将1,2,3填入33⨯的方格中,要求每行、每列都没有重复数字,下面是一种填法,则不同的填写方法共有( B ) A .6种 B .12种 C .24种 D .48种3.(全国二9)44)1()1(x x +-的展开式中x 的系数是( A )A .4-B .3-C .3D .44.(安徽卷7)设88018(1),x a a x a x +=+++则0,18,,a a a 中奇数的个数为( A ) A .2 B .3 C .4 D .55.(安徽卷12)12名同学合影,站成前排4人后排8人,现摄影师要从后排8人中抽2人调整到前排,若其他人的相对顺序不变,则不同调整方法的总数是 ( C )A . 2686C AB . 2283C A C .2286C AD .2285C A6.(福建卷9)某班级要从4名男士、2名女生中选派4人参加某次社区服务,如果要求至少有1名女生,那么不同的选派方案种数为AA.14B.24C.28D.487.(湖北卷9)从5名男生和5名女生中选3人组队参加某集体项目的比赛,其中至少有一名女生入选的组队方案数为BA.100B.110C.120D.1808.(湖南卷8)某市拟从4个重点项目和6个一般项目中各选2个项目作为本年度启动的项目,则重点项目A 和一般项目B 至少有一个被选中的不同选法种数是( C )A .15B .45C .60D .759.(江西卷8)10101(1)(1)x x++展开式中的常数项为 D A .1 B .1210()C C .120C D .1020C10.(辽宁卷7)4张卡片上分别写有数字1,2,3,4,从这4张卡片中随机抽取2张,则取出的2张卡片上的数字之和为奇数的概率为( C )A .13B .12C .23D .3411.(辽宁卷10)一生产过程有4道工序,每道工序需要安排一人照看.现从甲、乙、丙等6名工人中安排4人分别照看一道工序,第一道工序只能从甲、乙两工人中安排1人,第四道工序只能从甲、丙两工人中安排1人,则不同的安排方案共有( B )A .24种B .36种C .48种D .72种12.(浙江卷6)在)5)(4)(3)(2)(1(-----x x x x x 的展开式中,含4x 的项的系数是(A )-15 (B )85 (C )-120 (D )27413.(重庆卷10)若(x +12x)n 的展开式中前三项的系数成等差数,则展开式中x 4项的系数为B(A)6 (B)7 (C)8 (D)9 二. 填空题:1.(全国二14)从10名男同学,6名女同学中选3名参加体能测试,则选到的3名同学中既有男同学又有女同学的不同选法共有 种(用数字作答)4202.(北京卷12)5231x x ⎛⎫+ ⎪⎝⎭的展开式中常数项为 ;各项系数之和为 .(用数字作答)10, 323.(福建卷13)(x +1x)9展开式中x 2的系数是 .(用数字作答)84 4.(湖南卷13)记n x x )12(+的展开式中第m 项的系数为m b ,若432b b =,则n =__________.55.(辽宁卷15)6321(1)x x x ⎛⎫++ ⎪⎝⎭展开式中的常数项为 .356.(陕西卷14)72(1)x -的展开式中21x的系数为 84 .(用数字作答) 7.(陕西卷16)某地奥运火炬接力传递路线共分6段,传递活动分别由6名火炬手完成.如果第一棒火炬手只能从甲、乙、丙三人中产生,最后一棒火炬手只能从甲、乙两人中产生,则不同的传递方案共有 96 种.(用数字作答).8.(四川卷13)()()34121x x +-展开式中x 的系数为______2_________。
十年高考真题分类汇编 数学 专题 排列组合与二项式定理

十年高考真题分类汇编(2010—2019)数学专题13 排列组合与二项式定理一、选择题1.(2019·全国3·理T4)(1+2x 2)(1+x)4的展开式中x 3的系数为( ) A.12B.16C.20D.24【答案】A【解析】(1+2x 2)(1+x)4的展开式中x 3的系数为C 43+2C 41=4+8=12.故选A.2.(2018·全国3·理T5) (x 2+2x)5的展开式中x 4的系数为( )A.10B.20C.40D.80【答案】C【解析】由展开式知T r+1=C 5r (x 2)5-r(2x -1)r=C 5r2r x10-3r.当r=2时,x 4的系数为C 5222=40.3.(2017·全国1·理T6)(1+1x 2)(1+x)6展开式中x 2的系数为( ) A.15B.20C.30D.35【答案】C【解析】(1+x )6的二项展开式通项为T r+1=C 6rx r,(1+1x2)(1+x )6的展开式中含x 2的项的来源有两部分,一部分是1×C 62x 2=15x 2,另一部分是1x 2×C 64x 4=15x 2,故(1+1x2)(1+x )6的展开式中含x 2的项为15x 2+15x 2=30x 2,其系数是30.4.(2017·全国3·理T4)(x+y)(2x-y)5的展开式中x 3y 3的系数为( ) A.-80 B.-40 C.40 D.80【答案】C【解析】(2x-y )5的展开式的通项公式T r+1=C 5r(2x )5-r(-y )r.当r=3时,x (2x-y )5的展开式中x 3y 3的系数为C 53×22×(-1)3=-40;当r=2时,y (2x-y )5的展开式中x 3y 3的系数为C 52×23×(-1)2=80.故展开式中x 3y 3的系数为80-40=40.5.(2017·全国2·理T6)安排3名志愿者完成4项工作,每人至少完成1项,每项工作由1人完成,则不同的安排方式共有( )A .12种B .18种C .24种D .36种 【答案】D【解析】先把4项工作分成3份有C 42C 21C 11A 22种情况,再把3名志愿者排列有A 33种情况,故不同的安排方式共有C 42C 21C 11A 22·A 33=36种,故选D .6.(2016·四川·理T2)设i 为虚数单位,则(x+i)6的展开式中含x 4的项为( ) A.-15x 4B.15x 4C.-20i x 4D.20i x 4【答案】A【解析】二项式(x+i)6展开的通项T r+1=C 6rx 6-r i r,则其展开式中含x 4是当6-r=4,即r=2,则展开式中含x 4的项为C 62x 4i 2=-15x 4,故选A .7.(2016·全国2·理T5)如图,小明从街道的E 处出发,先到F 处与小红会合,再一起到位于G 处的老年公寓参加志愿者活动,则小明到老年公寓可以选择的最短路径条数为( )A.24B.18C.12D.9【答案】B【解析】由题意知,小明从街道的E 处出发到F 处的最短路径有6条,再从F 处到G 处的最短路径有3条,则小明到老年公寓可以选择的最短路径条数为6×3=18,故选B .8.(2016·全国3·理T12)定义“规范01数列”{a n }如下:{a n }共有2m 项,其中m 项为0,m 项为1,且对任意k ≤2m ,a 1,a 2,…,a k 中0的个数不少于1的个数.若m=4,则不同的“规范01数列”共有( )A.18个B.16个C.14个D.12个【答案】C【解析】由题意知a 1=0,a 8=1,则满足题意的a 1,a 2,…,a 8的可能取值如下:综上可知,不同的“规范01数列”共有14个.9.(2016·四川·理T4)用数字1,2,3,4,5组成没有重复数字的五位数,其中奇数的个数为()A.24B.48C.60D.72【答案】D【解析】要组成没有重复数字的五位奇数,则个位数应该为1,3,5中的一个,其他位置共有A44种排法,所以其中奇数的个数为3A44=72,故选D.10.(2015·四川·理T6)用数字0,1,2,3,4,5组成没有重复数字的五位数,其中比40 000大的偶数共有()A.144个B.120个C.96个D.72个【答案】B【解析】当首位数字为4,个位数字为0或2时,满足条件的五位数有C21A43个;当首位数字为5,个位数字为0或2或4时,满足条件的五位数有C31A43个.故满足条件的五位数共有C21A43+C31A43=(2+3)A43=5×4×3×2×1=120个.故选B.11.(2015·全国1·理T10)(x2+x+y)5的展开式中,x5y2的系数为()A.10B.20C.30D.60【答案】C【解析】(x2+x+y)5=[(x2+x)+y]5的展开式通项为T r+1=C5r(x2+x)5-r y r(r=0,1,2,…,5).由题意,y的幂指数为2,故r=2.对应的项为C52(x2+x)3y2=10(x2+x)3y2.记(x2+x)3的展开式通项为T s+1=C3s(x2)3-s x s=C3s x6-s(s=0,1,2,3),由题意令6-s=5,得s=1.故所求项的系数为10C31=30.12.(2015·陕西·理T4)二项式(x+1)n(n∈N*)的展开式中x2的系数为15,则n=()A.7B.6C.5D.4【答案】B【解析】(x+1)n的展开式通项为T r+1=C n r x n-r.令n-r=2,即r=n-2.则x2的系数为C n n-2=C n2=15,解得n=6,故选B.13.(2015·湖北·理T3)已知(1+x)n的展开式中第4项与第8项的二项式系数相等,则奇数项的二项式系数和为( )A.212B.211C.210D.29【答案】D【解析】由条件知C n3=C n7,∴n=10.∴(1+x)10中二项式系数和为210,其中奇数项的二项式系数和为210-1=29.14.(2014·大纲全国·理T5)有6名男医生、5名女医生,从中选出2名男医生、1名女医生组成一个医疗小组,则不同的选法共有()A.60种B.70种C.75种D.150种【答案】C【解析】从6名男医生中选出2名有C62种选法,从5名女医生中选出1名有C51种选法,故共有C62·C51=6×5×5=75种选法,选C.2×115.(2014·辽宁·理T6)6把椅子摆成一排,3人随机就座,任何两人不相邻的坐法种数为()A.144B.120C.72D.24【答案】D【解析】插空法.在已排好的三把椅子产生的4个空档中选出3个插入3人即可.故排法种数为A43=24.故选D.16.(2014·四川·理T6)六个人从左至右排成一行,最左端只能排甲或乙,最右端不能排甲,则不同的排法共有()A.192种B.216种C.240种D.288种【答案】B【解析】(1)当最左端排甲的时候,排法的种数为A55;(2)当最左端排乙的时候,排法种数为C41A44.因此不同的排法的种数为A 55+C 41A 44=120+96=216.17.(2014·重庆·理T9)某次联欢会要安排3个歌舞类节目、2个小品类节目和1个相声类节目的演出顺序,则同类节目不相邻的排法种数是( ) A.72B.120C.144D.168【答案】B【解析】第1步,先排歌舞类节目,有A 33=6种排法,排好后有4个空位.第2步,排另3个节目,因为3个歌舞节目不相邻,则中间2个空位必须安排2个节目.分两类情况:①中间两个空位安排1个小品类节目和1个相声节目,有C 21A 22=4种排法,最后一个小品类节目排两端,有2种方法.共有6×4×2=48种排法. ②中间两个空位安排2个小品类节目,有A 22=2种排法,排好后有6 个空位,选1个将相声类节目排上,有6种排法.共有6×2×6=72种排法. 所以一共有48+72=120种排法.18.(2014·四川·理T2)在x(1+x)6的展开式中,含x 3项的系数为( ) A.30B.20C.15D.10【答案】C【解析】含x 3的项是由(1+x)6展开式中含x 2的项与x 相乘得到,又(1+x)6展开式中含x 2的项的系数为C 62=15,故含x 3项的系数是15. 19.(2014·湖南·理T4) (12x -2y)5的展开式中x 2y 3的系数是( )A .-20B .-5C .5D .20【答案】A 【解析】由已知,得T r+1=C 5r (12x)5-r(-2y)r=C 5r(12)5-r(-2)r x 5-r y r(0≤r≤5,r∈Z),令r=3,得T 4=C 53(12)2(-2)3x 2y 3=-20x 2y 3.20.(2014·浙江·理T5)在(1+x)6(1+y)4的展开式中,记x m y n项的系数为f(m,n),则f(3,0)+f(2,1)+f(1,2)+f(0,3)=( ) A.45 B.60 C.120 D.210【答案】C【解析】∵(1+x )6展开式的通项公式为T r+1=C 6rx r ,(1+y )4展开式的通项公式为T h+1=C 4ℎy h,∴(1+x )6(1+y )4展开式的通项可以为C 6r C 4ℎx r y h. ∴f (m ,n )=C 6m C 4n .∴f (3,0)+f (2,1)+f (1,2)+f (0,3)=C 63+C 62C 41+C 61C 42+C 43=20+60+36+4=120.故选C .21.(2013·全国1·理T9)设m 为正整数,(x+y)2m 展开式的二项式系数的最大值为a,(x+y)2m+1展开式的二项式系数的最大值为b.若13a=7b,则m=( ) A.5 B.6 C.7 D.8 【答案】B【解析】由题意可知,a=C 2m m ,b=C 2m+1m ,∵13a=7b,∴13·(2m )!m !m !=7·(2m+1)!m !(m+1)!, 即13=2m+1,解得m=6.故选B.22.(2013·山东·理T10)用0,1,…,9十个数字,可以组成有重复数字的三位数的个数为( ) A.243 B.252 C.261 D.279 【答案】B【解析】构成所有的三位数的个数为C 91C 101C 101=900,而无重复数字的三位数的个数为C 91C 91C 81=648,故所求个数为900-648=252,应选B .23.(2013·全国2·理T5)已知(1+ax)(1+x)5的展开式中x 2的系数为5,则a=( ) A.-4B.-3C.-2D.-1【答案】D【解析】因为(1+x)5的二项展开式的通项为C 5r x r(0≤r≤5,r∈Z),则含x 2的项为C 52x 2+ax·C 51x=(10+5a)x 2,所以10+5a=5,a=-1.24.(2013·辽宁·理T7)使(3x x √x )n(n ∈N *)的展开式中含有常数项的最小的n 为( )A.4B.5C.6D.7 【答案】B【解析】(3x +x √x )n 展开式中的第r+1项为C nr (3x)n-rx -32r =C n r 3n-rx n -52r ,若展开式中含常数项,则存在n ∈N *,r ∈N,使n-5r=0,故最小的n 值为5,故选B.25.(2013·大纲全国·理T7)(1+x)8(1+y)4的展开式中x 2y 2的系数是( ) A.56B.84C.112D.168【解析】因为(1+x)8的展开式中x 2的系数为C 82,(1+y)4的展开式中y 2的系数为C 42,所以x 2y 2的系数为C 82C 42=168.故选D.26.(2012·湖北·理T5)设a ∈Z,且0≤a<13,若512 012+a 能被13整除,则a=( )A.0B.1C.11D.12 【答案】D 【解析】∵512 012可化为(52-1)2 012,其二项式系数为T r+1=C 2012r522 012-r·(-1)r .故(52-1)2 012被13除余数为C 20122012·(-1)2 012=1,则当a=12时,512 012+12被13整除.27.(2012·安徽·理T7)(x 2+2) (1x 2-1)5的展开式的常数项是()A.-3B.-2C.2D.3【答案】D【解析】通项为T r+1=C 5r(1x 2)5-r(-1)r=(-1)rC 5r1x 10-2r.令10-2r=2或0,此时r=4或5.故(x 2+2)(1x 2-1)5的展开式的常数项是(-1)4×C 54+2×(-1)5×C 55=3.28.(2012·全国·理T2)将2名教师,4名学生分成2个小组,分别安排到甲、乙两地参加社会实践活动,每个小组由1名教师和2名学生组成,不同的安排方案共有( ) A.12种 B.10种 C.9种 D.8种 【答案】A【解析】将4名学生均分为2个小组共有C 42C 22A 22=3种分法,将2个小组的同学分给两名教师带有A 22=2种分法,最后将2个小组的人员分配到甲、乙两地有A 22=2种分法,故不同的安排方案共有3×2×2=12种.29.(2012·辽宁·理T5)一排9个座位坐了3个三口之家,若每家人坐在一起,则不同的坐法种数为( ) A.3×3! B.3×(3!)3C.(3!)4D.9!【答案】C【解析】完成这件事可以分为两步,第一步排列三个家庭的相对位置,有A 33种排法;第二步排列每个家庭中的三个成员,共有A 33A 33A 33种排法.由乘法原理可得不同的坐法种数有A 33A 33A 33A 33,故选C .30.(2012·安徽·理T10)6位同学在毕业聚会活动中进行纪念品的交换,任意两位同学之间最多交换一次,进行交换的两位同学互赠一份纪念品.已知6位同学之间共进行了13次交换,则收到4份纪念品的同学人数为( )A .1或3B .1或4C .2或3D .2或4【解析】6人之间互相交换,总共有C 62=15种,而实际只交换了13次,故有2次未交换.不妨设为甲与乙、丙与丁之间未交换或甲与乙、甲与丙之间未交换,当甲与乙、丙与丁之间未交换时,甲、乙、丙、丁4人都收到4份礼物;当甲与乙、甲与丙之间未交换时,只有乙、丙两人收到4份礼物,故选D . 31.(2011·全国·理T8) (x +a x )(2x -1x)5的展开式中各项系数的和为2,则该展开式中常数项为( )A.-40B.-20C.20D.40【答案】D【解析】令x=1得(1+a)(2-1)5=2,∴a=1.原式=x·(2x -1x)5+1x (2x -1x)5,故常数项为 x·C 53(2x)2(-1x )3+1x ·C 52(2x)3(-1x )2=-40+80=40.32.(2010·山东·理T8)某台小型晚会由6个节目组成,演出顺序有如下要求:节目甲必须排在前两位,节目乙不能排在第一位,节目丙必须排在最后一位,该台晚会节目演出顺序的编排方案共有( ) A.36种 B.42种 C.48种 D.54种 【答案】B【解析】若乙排在第二位,则有A 33种方案;若乙不排在第二位,则乙只能排在第三、四、五位,此时共有A 31A 21A 33种方案,故共有A 33+A 31A 21A 33=42(种).二、填空题1.(2019·天津·理T10)(2x-18x 3)8的展开式中的常数项为 【答案】28【解析】T r+1=C 8r (2x)8-r(1-8x3)r=C 8r ·28-r·(-18)r·x8-4r.需8-4r=0,r=2.常数项为C 8226(-18)2=C 8226126=C 82=28.2.(2018·天津·理T10)在(x 2√x )5的展开式中,x 2的系数为.【答案】52【解析】展开式的通项为T r+1=C 5r x 5-r(2x)r =(-12)r C 5r x 5-3r2.令5-3r 2=2,可得r=2.所以(x 2x )5的展开式中的x 2的系数为(-12)2C 52=52.3.(2018·浙江·T14)二项式(√x 3+12x)8的展开式的常数项是 .【答案】7 【解析】通项为T r+1=C 8r (x 13)8-r (12x -1)r =(12)r C 8r x 8-4r3,当r=2时,8-4r3=0. 故展开式的常数项为(12)2C 82=14×8×72=7.4.(2018·上海·T3)在(1+x)7的二项展开式中,x 2项的系数为 (结果用数值表示). 【答案】21【解析】由(1+x)7的二项展开式的通项,得(1+x)7的二项展开式的x 2项的系数为C 72=21.5.(2018·全国1·理T15)从2位女生,4位男生中选3人参加科技比赛,且至少有1位女生入选,则不同的选法共有 种.(用数字填写答案) 【答案】16【解析】方法一:①恰有1位女生时,有C 21C 42=12种选法. ②恰有2位女生时,有C 22C 41=4种选法.故不同的选法共有12+4=16种.方法二:6人中选3人共有C 63种选法,3人全是男生时有C 43种选法,所以至少有1位女生入选时有C 63−C 43=16种选法.6.(2018·浙江·T16)从1,3,5,7,9中任取2个数字,从0,2,4,6中任取2个数字,一共可以组成 个没有重复数字的四位数.(用数字作答) 【答案】1260 【解析】分两类:第一类:从0,2,4,6中取到0,则没有重复数字的四位数有C 31C 52A 31A 33=540;第二类:从0,2,4,6中不取0,则没有重复数字的四位数有C 32C 52A 44=720.所以没有重复数字的四位数共有540+720=1260种.7.(2017·山东·理T11)已知(1+3x)n的展开式中含有x 2项的系数是54,则n= .【答案】4【解析】二项展开式的通项T r+1=C n r (3x)r=3r·C n r ·x r,令r=2,得32·C n 2=54,解得n=4.8.(2017·浙江·T13)已知多项式(x+1)3(x+2)2=x 5+a 1x 4+a 2x 3+a 3x 2+a 4x+a 5,则a 4= ,a 5= . 【答案】16 4【解析】由二项式展开式可得通项公式为C 3r x 3-rC 2m x 2-m 2m,分别取r=3,m=1和r=2,m=2可得a 4=4+12=16,令x=0可得a 5=13×22=4.9.(2017·天津·理T14)用数字1,2,3,4,5,6,7,8,9组成没有重复数字,且至多有一个数字是偶数的四位数,这样的四位数一共有 个.(用数字作答) 【答案】1080【解析】①没有一个数字是偶数的四位数有A 54=120个;②有且只有一个数字是偶数的四位数有C 41C 53A 44=960个.所以至多有一个数字是偶数的四位数有120+960=1 080个.10.(2017·浙江·T16)从6男2女共8名学生中选出队长1人,副队长1人,普通队员2人组成4人服务队,要求服务队中至少有1名女生,共有 种不同的选法.(用数字作答) 【答案】660【解析】由题意可得,总的选择方法为C 84C 41C 31种方法,其中不满足题意的选法有C 64C 41C 31种方法,则满足题意的选法有C 84C 41C 31−C 64C 41C 31=660种.11.(2016·全国1·理T14)(2x+√x )5的展开式中,x 3的系数是 .(用数字填写答案) 【答案】10【解析】二项式的通项公式T r+1=C 5r (2x)5-rx r 2=C 5r 25-rx 5-r2,令5-r2=3,解得r=4,故x 3的系数为C 54×25-4=10.12.(2016·天津·理T10) (x 2-1x )8的展开式中x 7的系数为 .(用数字作答)【答案】-56【解析】展开式通项为T r+1=C 8r (x 2)8-r(-1)r=(-1)rC 8r x16-3r,令16-3r=7,得r=3,所以展开式中x 7的系数为(-1)3C 83=-56.13.(2015·广东·理T12)某高三毕业班有40人,同学之间两两彼此给对方仅写一条毕业留言,那么全班共写了 条毕业留言.(用数字作答) 【答案】1560【解析】共有A 402=40×39=1 560条毕业留言.14.(2015·天津·理T12)在(x -1)6的展开式中,x 2的系数为. 【答案】 1516【解析】由题意知T r+1=C 6r x 6-r ·(-14x )r =C 6r ·x 6-2r ·(-14)r .令6-2r=2,可得r=2. 故所求x 2的系数为C 62(-14)2=1516. 15.(2015·重庆·理T12)(x32√x )5的展开式中x 8的系数是(用数字作答). 【答案】52【解析】展开式的通项公式T r+1=C 5r ·(x 3)5-r ·(2√x )r =C 5r ·2-r ·x 15-72r (r=0,1,2,…,5). 令15-72r=8,得r=2,于是展开式中x 8项的系数是C 52·2-2=52. 16.(2015·全国2·理T15)(a+x)(1+x)4的展开式中x 的奇数次幂项的系数之和为32,则a= .【答案】3【解析】∵(1+x)4=x 4+C 43x 3+C 42x 2+C 41x+C 40x 0=x 4+4x 3+6x 2+4x+1, ∴(a+x)(1+x)4的奇数次幂项的系数为4a+4a+1+6+1=32,∴a=3.17.(2014·安徽·理T13)设a ≠0,n 是大于1的自然数, (1+x a )n 的展开式为a 0+a 1x+a 2x 2+…+a n x n .若点A i (i,a i )(i=0,1,2)的位置如图所示,则a= .【答案】3 【解析】由题意得a 1=1a ·C n 1=n a =3,∴n=3a; a 2=1a 2C n 2=n (n -1)2a 2=4, ∴n 2-n=8a 2.将n=3a 代入n 2-n=8a 2得9a 2-3a=8a 2,即a 2-3a=0,解得a=3或a=0(舍去).∴a=3.18.(2014·北京·理T13)把5件不同产品摆成一排.若产品A 与产品B 相邻,且产品A 与产品C 不相邻,则不同的摆法有 种.【答案】36【解析】产品A,B 相邻时,不同的摆法有A 22A 44=48种.而A,B 相邻,A,C 也相邻时的摆法为A 在中间,C,B 在A的两侧,不同的摆法共有A 22A 33=12(种).故产品A 与产品B 相邻,且产品A 与产品C 不相邻的不同摆法有48-12=36(种).19.(2014·全国1·理T13)(x-y)(x+y)8的展开式中x 2y 7的系数为 .(用数字填写答案)【答案】-20【解析】(x+y)8的通项公式为T r+1=C 8r x 8-r y r (r=0,1,…,8,r ∈Z).当r=7时,T 8=C 87xy 7=8xy 7,当r=6时,T 7=C 86x 2y 6=28x 2y 6, 所以(x-y)(x+y)8的展开式中含x 2y 7的项为x·8xy 7-y·28x 2y 6=-20x 2y 7,故系数为-20.20.(2014·全国2·理T13)(x+a)10的展开式中,x 7的系数为15,则a= .(用数字填写答案)【答案】12【解析】设展开式的通项为T r+1=C 10r x10-r a r , 令r=3,得T 4=C 103x 7a 3,即C 103a 3=15,得a=12. 21.(2013·浙江·理T11)设二项式(√x -√x 3)5的展开式中常数项为A,则A= . 【答案】-10【解析】T r+1=C 5r (√x )5-r ·(-1√x 3)r =C 5r x 5-r 2·(-1)r ·x -r 3=(-1)r C 5r x 5-r 2-r 3=(-1)r C 5r x 15-5r 6. 令15-5r=0,得r=3,所以A=(-1)3C 53=-C 52=-10. 22.(2013·北京·理T12)将序号分别为1,2,3,4,5的5张参观券全部分给4人,每人至少1张,如果分给同一人的2张参观券连号,那么不同的分法种数是 .【答案】96【解析】分给同一人的2张参观券连号的情况共有12,23,34,45四种情况,从4人中选一人得到连号参观券,有4C 41种方法.其余3张分给3人可以全排列,有A 33种方法,所以不同的分法有4C 41×A 33=96种.23.(2013·大纲全国·理T14)6个人排成一行,其中甲、乙两人不相邻的不同排法共有 种.(用数字作答)【答案】480【解析】先排除甲、乙外的4人,方法有A 44种,再将甲、乙插入这4人形成的5个间隔中,有A 52种排法,因此甲、乙不相邻的不同排法有A 44·A 52=480(种).24.(2013·浙江·理T14)将A ,B ,C ,D ,E ,F 六个字母排成一排,且A ,B 均在C 的同侧,则不同的排法共有 种(用数字作答).【答案】480【解析】按C 的位置分三类情况:①当C 在第一或第六位时,有A 55=120种排法;②当C 在第二或第五位时,有A 42A 33=72种排法;③当C 在第三或第四位时,有A 22A 33+A 32A 33=48种排法.所以共有2×(120+72+48)=480种排法.25.(2012·福建·理T11)(a+x)4的展开式中x 3的系数等于8,则实数a= .【答案】2【解析】∵T r+1=C 4r a r x 4-r ,∴当4-r=3,即r=1时,T 2=C 41·a·x 3=4ax 3=8x 3.故a=2. 26.(2012·浙江·理T14)若将函数f(x)=x 5表示为f(x)=a 0+a 1(1+x)+a 2(1+x)2+…+a 5(1+x)5,其中a 0,a 1,a 2,…,a 5为实数,则a 3= .【答案】10【解析】由x 5=a 0+a 1(1+x)+a 2(1+x)2+…+a 5(1+x)5可得,{x 5=a 5·C 55x 5,0·x 4=a 4C 44x 4+a 5C 54x 4,0·x 3=a 3C 33x 3+a 4C 43x 3+a 5C 53x 3, 可解得{a 5=1,a 4=-5,a 3=10.27.(2012·大纲·理T15)若(x +1)n 的展开式中第3项与第7项的二项式系数相等,则该展开式中12的系数为 .【答案】56【解析】∵C n 2=C n 6,∴n=8.T r+1=C 8r x 8-r (1)r =C 8r x 8-2r ,当8-2r=-2时,r=5.∴系数为C 85=56.28.(2011·北京·理T12)用数字2,3组成四位数,且数字2,3至少都出现一次,这样的四位数共有 个.(用数字作答)【答案】14【解析】可用排除法,这个四位数每一位上的数字只能是2或3,则共有24个,而这其中要求数字2或3至少出现一次,所以全是2和全是3不满足,即满足要求的四位数有24-2=14个.。
十年高考真题分类汇编(2010-2019) 数学 专题13 排列组合与二项式定理 Word版及答案

十年高考真题分类汇编(2010—2019)数学专题13 排列组合与二项式定理一、选择题1.(2019·全国3·理T4)(1+2x 2)(1+x)4的展开式中x 3的系数为( ) A.12B.16C.20D.242.(2018·全国3·理T5) (x 2+2x)5的展开式中x 4的系数为( )A.10B.20C.40D.803.(2017·全国1·理T6)(1+1x2)(1+x)6展开式中x 2的系数为( )A.15B.20C.30D.354.(2017·全国3·理T4)(x+y)(2x-y)5的展开式中x 3y 3的系数为( ) A.-80 B.-40C.40D.805.(2017·全国2·理T6)安排3名志愿者完成4项工作,每人至少完成1项,每项工作由1人完成,则不同的安排方式共有( )A .12种B .18种C .24种D .36种6.(2016·四川·理T2)设i 为虚数单位,则(x+i)6的展开式中含x 4的项为( ) A.-15x 4B.15x 4C.-20i x 4D.20i x 47.(2016·全国2·理T5)如图,小明从街道的E 处出发,先到F 处与小红会合,再一起到位于G 处的老年公寓参加志愿者活动,则小明到老年公寓可以选择的最短路径条数为( )A.24B.18C.12D.98.(2016·全国3·理T12)定义“规范01数列”{a n }如下:{a n }共有2m 项,其中m 项为0,m 项为1,且对任意k ≤2m ,a 1,a 2,…,a k 中0的个数不少于1的个数.若m=4,则不同的“规范01数列”共有( )A.18个B.16个C.14个D.12个9.(2016·四川·理T4)用数字1,2,3,4,5组成没有重复数字的五位数,其中奇数的个数为( ) A.24B.48C.60D.7210.(2015·四川·理T6)用数字0,1,2,3,4,5组成没有重复数字的五位数,其中比40 000大的偶数共有()A.144个B.120个C.96个D.72个11.(2015·全国1·理T10)(x2+x+y)5的展开式中,x5y2的系数为()A.10B.20C.30D.6012.(2015·陕西·理T4)二项式(x+1)n(n∈N*)的展开式中x2的系数为15,则n=()A.7B.6C.5D.413.(2015·湖北·理T3)已知(1+x)n的展开式中第4项与第8项的二项式系数相等,则奇数项的二项式系数和为( )A.212B.211C.210D.2914.(2014·大纲全国·理T5)有6名男医生、5名女医生,从中选出2名男医生、1名女医生组成一个医疗小组,则不同的选法共有()A.60种B.70种C.75种D.150种15.(2014·辽宁·理T6)6把椅子摆成一排,3人随机就座,任何两人不相邻的坐法种数为()A.144B.120C.72D.2416.(2014·四川·理T6)六个人从左至右排成一行,最左端只能排甲或乙,最右端不能排甲,则不同的排法共有()A.192种B.216种C.240种D.288种17.(2014·重庆·理T9)某次联欢会要安排3个歌舞类节目、2个小品类节目和1个相声类节目的演出顺序,则同类节目不相邻的排法种数是()A.72B.120C.144D.16818.(2014·四川·理T2)在x(1+x)6的展开式中,含x3项的系数为( )A.30B.20C.15D.1019.(2014·湖南·理T4) (12x-2y)5的展开式中x2y3的系数是( )A.-20B.-5C.5D.2020.(2014·浙江·理T5)在(1+x)6(1+y)4的展开式中,记x m y n项的系数为f(m,n),则f(3,0)+f(2,1)+f(1,2)+f(0,3)=( )A.45B.60C.120D.21021.(2013·全国1·理T9)设m 为正整数,(x+y)2m 展开式的二项式系数的最大值为a,(x+y)2m+1展开式的二项式系数的最大值为b.若13a=7b,则m=( ) A.5 B.6 C.7 D.822.(2013·山东·理T10)用0,1,…,9十个数字,可以组成有重复数字的三位数的个数为( ) A.243 B.252 C.261 D.27923.(2013·全国2·理T5)已知(1+ax)(1+x)5的展开式中x 2的系数为5,则a=( ) A.-4B.-3C.-2D.-124.(2013·辽宁·理T7)使(3x x x )n(n ∈N *)的展开式中含有常数项的最小的n 为( )A.4B.5C.6D.725.(2013·大纲全国·理T7)(1+x)8(1+y)4的展开式中x 2y 2的系数是( ) A.56B.84C.112D.16826.(2012·湖北·理T5)设a ∈Z,且0≤a<13,若512 012+a 能被13整除,则a=( )A.0B.1C.11D.12 27.(2012·安徽·理T7)(x 2+2) (1x 2-1)5的展开式的常数项是()A.-3B.-2C.2D.328.(2012·全国·理T2)将2名教师,4名学生分成2个小组,分别安排到甲、乙两地参加社会实践活动,每个小组由1名教师和2名学生组成,不同的安排方案共有( ) A.12种 B.10种 C.9种 D.8种29.(2012·辽宁·理T5)一排9个座位坐了3个三口之家,若每家人坐在一起,则不同的坐法种数为( ) A.3×3! B.3×(3!)3C.(3!)4D.9!30.(2012·安徽·理T10)6位同学在毕业聚会活动中进行纪念品的交换,任意两位同学之间最多交换一次,进行交换的两位同学互赠一份纪念品.已知6位同学之间共进行了13次交换,则收到4份纪念品的同学人数为( )A .1或3B .1或4C .2或3D .2或431.(2011·全国·理T8) (x +a)(2x -1)5的展开式中各项系数的和为2,则该展开式中常数项为( ) A.-40 B.-20C.20D.4032.(2010·山东·理T8)某台小型晚会由6个节目组成,演出顺序有如下要求:节目甲必须排在前两位,节目乙不能排在第一位,节目丙必须排在最后一位,该台晚会节目演出顺序的编排方案共有( ) A.36种 B.42种 C.48种 D.54种二、填空题1.(2019·天津·理T10)(2x-18x 3)8的展开式中的常数项为 2.(2018·天津·理T10)在(x 2x )5的展开式中,x 2的系数为.3.(2018·浙江·T14)二项式(√x 3+12x )8的展开式的常数项是.4.(2018·上海·T3)在(1+x)7的二项展开式中,x 2项的系数为 (结果用数值表示).5.(2018·全国1·理T15)从2位女生,4位男生中选3人参加科技比赛,且至少有1位女生入选,则不同的选法共有 种.(用数字填写答案)6.(2018·浙江·T16)从1,3,5,7,9中任取2个数字,从0,2,4,6中任取2个数字,一共可以组成 个没有重复数字的四位数.(用数字作答)7.(2017·山东·理T11)已知(1+3x)n的展开式中含有x 2项的系数是54,则n= . 8.(2017·浙江·T13)已知多项式(x+1)3(x+2)2=x 5+a 1x 4+a 2x 3+a 3x 2+a 4x+a 5,则a 4= ,a 5= .9.(2017·天津·理T14)用数字1,2,3,4,5,6,7,8,9组成没有重复数字,且至多有一个数字是偶数的四位数,这样的四位数一共有 个.(用数字作答)10.(2017·浙江·T16)从6男2女共8名学生中选出队长1人,副队长1人,普通队员2人组成4人服务队,要求服务队中至少有1名女生,共有 种不同的选法.(用数字作答)11.(2016·全国1·理T14)(2x+√x )5的展开式中,x 3的系数是 .(用数字填写答案) 12.(2016·天津·理T10) (x 2-1x)8的展开式中x 7的系数为 .(用数字作答)13.(2015·广东·理T12)某高三毕业班有40人,同学之间两两彼此给对方仅写一条毕业留言,那么全班共写了 条毕业留言.(用数字作答)14.(2015·天津·理T12)在(x -14x )6的展开式中,x 2的系数为.15.(2015·重庆·理T12)(x32√x)5的展开式中x 8的系数是(用数字作答).16.(2015·全国2·理T15)(a+x)(1+x)4的展开式中x 的奇数次幂项的系数之和为32,则a= . 17.(2014·安徽·理T13)设a ≠0,n 是大于1的自然数, (1+x a )n的展开式为a 0+a 1x+a 2x 2+…+a n x n.若点A i (i,a i )(i=0,1,2)的位置如图所示,则a= .18.(2014·北京·理T13)把5件不同产品摆成一排.若产品A 与产品B 相邻,且产品A 与产品C 不相邻,则不同的摆法有 种.19.(2014·全国1·理T13)(x-y)(x+y)8的展开式中x 2y 7的系数为 .(用数字填写答案) 20.(2014·全国2·理T13)(x+a)10的展开式中,x 7的系数为15,则a= .(用数字填写答案) 21.(2013·浙江·理T11)设二项式(√x -1√x3)5的展开式中常数项为A,则A= .22.(2013·北京·理T12)将序号分别为1,2,3,4,5的5张参观券全部分给4人,每人至少1张,如果分给同一人的2张参观券连号,那么不同的分法种数是 .23.(2013·大纲全国·理T14)6个人排成一行,其中甲、乙两人不相邻的不同排法共有 种.(用数字作答)24.(2013·浙江·理T14)将A ,B ,C ,D ,E ,F 六个字母排成一排,且A ,B 均在C 的同侧,则不同的排法共有 种(用数字作答).25.(2012·福建·理T11)(a+x)4的展开式中x 3的系数等于8,则实数a= .26.(2012·浙江·理T14)若将函数f(x)=x 5表示为f(x)=a 0+a 1(1+x)+a 2(1+x)2+…+a 5(1+x)5,其中a 0,a 1,a 2,…,a 5为实数,则a 3= .27.(2012·大纲·理T15)若(x +1x )n的展开式中第3项与第7项的二项式系数相等,则该展开式中1x 2的系数为.28.(2011·北京·理T12)用数字2,3组成四位数,且数字2,3至少都出现一次,这样的四位数共有 个.(用数字作答)十年高考真题分类汇编(2010—2019)数学专题13 排列组合与二项式定理一、选择题1.(2019·全国3·理T4)(1+2x 2)(1+x)4的展开式中x 3的系数为( ) A.12B.16C.20D.24【答案】A【解析】(1+2x 2)(1+x)4的展开式中x 3的系数为C 43+2C 41=4+8=12.故选A.2.(2018·全国3·理T5) (x 2+2x)5的展开式中x 4的系数为( )A.10B.20C.40D.80【答案】C【解析】由展开式知T r+1=C 5r (x 2)5-r(2x -1)r=C 5r2r x10-3r.当r=2时,x 4的系数为C 5222=40.3.(2017·全国1·理T6)(1+1x 2)(1+x)6展开式中x 2的系数为( ) A.15B.20C.30D.35【答案】C【解析】(1+x )6的二项展开式通项为T r+1=C 6rx r,(1+1x2)(1+x )6的展开式中含x 2的项的来源有两部分,一部分是1×C 62x 2=15x 2,另一部分是1x 2×C 64x 4=15x 2,故(1+1x2)(1+x )6的展开式中含x 2的项为15x 2+15x 2=30x 2,其系数是30.4.(2017·全国3·理T4)(x+y)(2x-y)5的展开式中x 3y 3的系数为( ) A.-80 B.-40 C.40 D.80【答案】C【解析】(2x-y )5的展开式的通项公式T r+1=C 5r(2x )5-r(-y )r.当r=3时,x (2x-y )5的展开式中x 3y 3的系数为C 53×22×(-1)3=-40;当r=2时,y (2x-y )5的展开式中x 3y 3的系数为C 52×23×(-1)2=80.故展开式中x 3y 3的系数为80-40=40.5.(2017·全国2·理T6)安排3名志愿者完成4项工作,每人至少完成1项,每项工作由1人完成,则不同的安排方式共有( )A .12种B .18种C .24种D .36种 【答案】D【解析】先把4项工作分成3份有C 42C 21C 11A 22种情况,再把3名志愿者排列有A 33种情况,故不同的安排方式共有C 42C 21C 11A 22·A 33=36种,故选D .6.(2016·四川·理T2)设i 为虚数单位,则(x+i)6的展开式中含x 4的项为( ) A.-15x 4B.15x 4C.-20i x 4D.20i x 4【答案】A【解析】二项式(x+i)6展开的通项T r+1=C 6rx 6-r i r,则其展开式中含x 4是当6-r=4,即r=2,则展开式中含x 4的项为C 62x 4i 2=-15x 4,故选A .7.(2016·全国2·理T5)如图,小明从街道的E 处出发,先到F 处与小红会合,再一起到位于G 处的老年公寓参加志愿者活动,则小明到老年公寓可以选择的最短路径条数为( )A.24B.18C.12D.9【答案】B【解析】由题意知,小明从街道的E 处出发到F 处的最短路径有6条,再从F 处到G 处的最短路径有3条,则小明到老年公寓可以选择的最短路径条数为6×3=18,故选B .8.(2016·全国3·理T12)定义“规范01数列”{a n }如下:{a n }共有2m 项,其中m 项为0,m 项为1,且对任意k ≤2m ,a 1,a 2,…,a k 中0的个数不少于1的个数.若m=4,则不同的“规范01数列”共有( )A.18个B.16个C.14个D.12个【答案】C【解析】由题意知a 1=0,a 8=1,则满足题意的a 1,a 2,…,a 8的可能取值如下:综上可知,不同的“规范01数列”共有14个.9.(2016·四川·理T4)用数字1,2,3,4,5组成没有重复数字的五位数,其中奇数的个数为()A.24B.48C.60D.72【答案】D【解析】要组成没有重复数字的五位奇数,则个位数应该为1,3,5中的一个,其他位置共有A44种排法,所以其中奇数的个数为3A44=72,故选D.10.(2015·四川·理T6)用数字0,1,2,3,4,5组成没有重复数字的五位数,其中比40 000大的偶数共有()A.144个B.120个C.96个D.72个【答案】B【解析】当首位数字为4,个位数字为0或2时,满足条件的五位数有C21A43个;当首位数字为5,个位数字为0或2或4时,满足条件的五位数有C31A43个.故满足条件的五位数共有C21A43+C31A43=(2+3)A43=5×4×3×2×1=120个.故选B.11.(2015·全国1·理T10)(x2+x+y)5的展开式中,x5y2的系数为()A.10B.20C.30D.60【答案】C【解析】(x2+x+y)5=[(x2+x)+y]5的展开式通项为T r+1=C5r(x2+x)5-r y r(r=0,1,2,…,5).由题意,y的幂指数为2,故r=2.对应的项为C52(x2+x)3y2=10(x2+x)3y2.记(x2+x)3的展开式通项为T s+1=C3s(x2)3-s x s=C3s x6-s(s=0,1,2,3),由题意令6-s=5,得s=1.故所求项的系数为10C31=30.12.(2015·陕西·理T4)二项式(x+1)n(n∈N*)的展开式中x2的系数为15,则n=()A.7B.6C.5D.4【答案】B【解析】(x+1)n的展开式通项为T r+1=C n r x n-r.令n-r=2,即r=n-2.则x2的系数为C n n-2=C n2=15,解得n=6,故选B.13.(2015·湖北·理T3)已知(1+x)n的展开式中第4项与第8项的二项式系数相等,则奇数项的二项式系数和为( )A.212B.211C.210D.29【答案】D【解析】由条件知C n3=C n7,∴n=10.∴(1+x)10中二项式系数和为210,其中奇数项的二项式系数和为210-1=29.14.(2014·大纲全国·理T5)有6名男医生、5名女医生,从中选出2名男医生、1名女医生组成一个医疗小组,则不同的选法共有()A.60种B.70种C.75种D.150种【答案】C×【解析】从6名男医生中选出2名有C62种选法,从5名女医生中选出1名有C51种选法,故共有C62·C51=6×52×15=75种选法,选C.15.(2014·辽宁·理T6)6把椅子摆成一排,3人随机就座,任何两人不相邻的坐法种数为()A.144B.120C.72D.24【答案】D【解析】插空法.在已排好的三把椅子产生的4个空档中选出3个插入3人即可.故排法种数为A43=24.故选D.16.(2014·四川·理T6)六个人从左至右排成一行,最左端只能排甲或乙,最右端不能排甲,则不同的排法共有()A.192种B.216种C.240种D.288种【答案】B【解析】(1)当最左端排甲的时候,排法的种数为A55;(2)当最左端排乙的时候,排法种数为C41A44.因此不同的排法的种数为A 55+C 41A 44=120+96=216.17.(2014·重庆·理T9)某次联欢会要安排3个歌舞类节目、2个小品类节目和1个相声类节目的演出顺序,则同类节目不相邻的排法种数是( ) A.72B.120C.144D.168【答案】B【解析】第1步,先排歌舞类节目,有A 33=6种排法,排好后有4个空位.第2步,排另3个节目,因为3个歌舞节目不相邻,则中间2个空位必须安排2个节目.分两类情况:①中间两个空位安排1个小品类节目和1个相声节目,有C 21A 22=4种排法,最后一个小品类节目排两端,有2种方法.共有6×4×2=48种排法. ②中间两个空位安排2个小品类节目,有A 22=2种排法,排好后有6 个空位,选1个将相声类节目排上,有6种排法.共有6×2×6=72种排法. 所以一共有48+72=120种排法.18.(2014·四川·理T2)在x(1+x)6的展开式中,含x 3项的系数为( ) A.30B.20C.15D.10【答案】C【解析】含x 3的项是由(1+x)6展开式中含x 2的项与x 相乘得到,又(1+x)6展开式中含x 2的项的系数为C 62=15,故含x 3项的系数是15. 19.(2014·湖南·理T4) (12x -2y)5的展开式中x 2y 3的系数是( )A .-20B .-5C .5D .20【答案】A 【解析】由已知,得T r+1=C 5r (12x)5-r(-2y)r=C 5r(12)5-r(-2)r x 5-r y r(0≤r ≤5,r ∈Z),令r=3,得T 4=C 53(12)2(-2)3x 2y 3=-20x 2y 3.20.(2014·浙江·理T5)在(1+x)6(1+y)4的展开式中,记x m y n项的系数为f(m,n),则f(3,0)+f(2,1)+f(1,2)+f(0,3)=( ) A.45 B.60 C.120 D.210【答案】C【解析】∵(1+x )6展开式的通项公式为T r+1=C 6rx r ,(1+y )4展开式的通项公式为T h+1=C 4ℎy h,∴(1+x )6(1+y )4展开式的通项可以为C 6r C 4ℎx r y h. ∴f (m ,n )=C 6m C 4n .∴f (3,0)+f (2,1)+f (1,2)+f (0,3)=C 63+C 62C 41+C 61C 42+C 43=20+60+36+4=120.故选C .21.(2013·全国1·理T9)设m 为正整数,(x+y)2m 展开式的二项式系数的最大值为a,(x+y)2m+1展开式的二项式系数的最大值为b.若13a=7b,则m=( ) A.5 B.6 C.7 D.8 【答案】B【解析】由题意可知,a=C 2m m ,b=C 2m+1m ,∵13a=7b,∴13·(2m )!m !m !=7·(2m+1)!m !(m+1)!, 即13=2m+1,解得m=6.故选B.22.(2013·山东·理T10)用0,1,…,9十个数字,可以组成有重复数字的三位数的个数为( ) A.243 B.252 C.261 D.279 【答案】B【解析】构成所有的三位数的个数为C 91C 101C 101=900,而无重复数字的三位数的个数为C 91C 91C 81=648,故所求个数为900-648=252,应选B .23.(2013·全国2·理T5)已知(1+ax)(1+x)5的展开式中x 2的系数为5,则a=( ) A.-4B.-3C.-2D.-1【答案】D【解析】因为(1+x)5的二项展开式的通项为C 5r x r(0≤r ≤5,r ∈Z),则含x 2的项为C 52x 2+ax ·C 51x=(10+5a)x 2,所以10+5a=5,a=-1.24.(2013·辽宁·理T7)使(3x x √x )n(n ∈N *)的展开式中含有常数项的最小的n 为( )A.4B.5C.6D.7 【答案】B【解析】(3x +x √x )n 展开式中的第r+1项为C nr (3x)n-rx -32r =C n r 3n-rx n -52r ,若展开式中含常数项,则存在n ∈N *,r ∈N,使n-5r=0,故最小的n 值为5,故选B.25.(2013·大纲全国·理T7)(1+x)8(1+y)4的展开式中x 2y 2的系数是( ) A.56B.84C.112D.168【解析】因为(1+x)8的展开式中x 2的系数为C 82,(1+y)4的展开式中y 2的系数为C 42,所以x 2y 2的系数为C 82C 42=168.故选D.26.(2012·湖北·理T5)设a ∈Z,且0≤a<13,若512 012+a 能被13整除,则a=( )A.0B.1C.11D.12 【答案】D 【解析】∵512 012可化为(52-1)2 012,其二项式系数为T r+1=C 2012r522 012-r·(-1)r .故(52-1)2 012被13除余数为C 20122012·(-1)2 012=1,则当a=12时,512 012+12被13整除.27.(2012·安徽·理T7)(x 2+2) (1x 2-1)5的展开式的常数项是()A.-3B.-2C.2D.3【答案】D【解析】通项为T r+1=C 5r(1x 2)5-r(-1)r=(-1)rC 5r1x 10-2r.令10-2r=2或0,此时r=4或5.故(x 2+2)(1x 2-1)5的展开式的常数项是(-1)4×C 54+2×(-1)5×C 55=3.28.(2012·全国·理T2)将2名教师,4名学生分成2个小组,分别安排到甲、乙两地参加社会实践活动,每个小组由1名教师和2名学生组成,不同的安排方案共有( ) A.12种 B.10种 C.9种 D.8种 【答案】A【解析】将4名学生均分为2个小组共有C 42C 22A 22=3种分法,将2个小组的同学分给两名教师带有A 22=2种分法,最后将2个小组的人员分配到甲、乙两地有A 22=2种分法,故不同的安排方案共有3×2×2=12种.29.(2012·辽宁·理T5)一排9个座位坐了3个三口之家,若每家人坐在一起,则不同的坐法种数为( ) A.3×3! B.3×(3!)3C.(3!)4D.9!【答案】C【解析】完成这件事可以分为两步,第一步排列三个家庭的相对位置,有A 33种排法;第二步排列每个家庭中的三个成员,共有A 33A 33A 33种排法.由乘法原理可得不同的坐法种数有A 33A 33A 33A 33,故选C .30.(2012·安徽·理T10)6位同学在毕业聚会活动中进行纪念品的交换,任意两位同学之间最多交换一次,进行交换的两位同学互赠一份纪念品.已知6位同学之间共进行了13次交换,则收到4份纪念品的同学人数为( )A .1或3B .1或4C .2或3D .2或4【解析】6人之间互相交换,总共有C 62=15种,而实际只交换了13次,故有2次未交换.不妨设为甲与乙、丙与丁之间未交换或甲与乙、甲与丙之间未交换,当甲与乙、丙与丁之间未交换时,甲、乙、丙、丁4人都收到4份礼物;当甲与乙、甲与丙之间未交换时,只有乙、丙两人收到4份礼物,故选D . 31.(2011·全国·理T8) (x +a x )(2x -1x)5的展开式中各项系数的和为2,则该展开式中常数项为( )A.-40B.-20C.20D.40【答案】D【解析】令x=1得(1+a)(2-1)5=2,∴a=1.原式=x ·(2x -1x)5+1x (2x -1x)5,故常数项为 x ·C 53(2x)2(-1x )3+1x ·C 52(2x)3(-1x )2=-40+80=40.32.(2010·山东·理T8)某台小型晚会由6个节目组成,演出顺序有如下要求:节目甲必须排在前两位,节目乙不能排在第一位,节目丙必须排在最后一位,该台晚会节目演出顺序的编排方案共有( ) A.36种 B.42种 C.48种 D.54种 【答案】B【解析】若乙排在第二位,则有A 33种方案;若乙不排在第二位,则乙只能排在第三、四、五位,此时共有A 31A 21A 33种方案,故共有A 33+A 31A 21A 33=42(种).二、填空题1.(2019·天津·理T10)(2x-18x 3)8的展开式中的常数项为 【答案】28【解析】T r+1=C 8r (2x)8-r(1-8x3)r=C 8r ·28-r·(-18)r·x8-4r.需8-4r=0,r=2.常数项为C 8226(-18)2=C 8226126=C 82=28.2.(2018·天津·理T10)在(x 2√x )5的展开式中,x 2的系数为.【答案】52【解析】展开式的通项为T r+1=C 5r x 5-r(2x)r =(-12)r C 5r x 5-3r2.令5-3r 2=2,可得r=2.所以(x 2x )5的展开式中的x 2的系数为(-12)2C 52=52.3.(2018·浙江·T14)二项式(√x 3+12x)8的展开式的常数项是 .【答案】7 【解析】通项为T r+1=C 8r (x 13)8-r (12x -1)r =(12)r C 8r x 8-4r3,当r=2时,8-4r3=0. 故展开式的常数项为(12)2C 82=14×8×72=7.4.(2018·上海·T3)在(1+x)7的二项展开式中,x 2项的系数为 (结果用数值表示). 【答案】21【解析】由(1+x)7的二项展开式的通项,得(1+x)7的二项展开式的x 2项的系数为C 72=21.5.(2018·全国1·理T15)从2位女生,4位男生中选3人参加科技比赛,且至少有1位女生入选,则不同的选法共有 种.(用数字填写答案) 【答案】16【解析】方法一:①恰有1位女生时,有C 21C 42=12种选法. ②恰有2位女生时,有C 22C 41=4种选法.故不同的选法共有12+4=16种.方法二:6人中选3人共有C 63种选法,3人全是男生时有C 43种选法,所以至少有1位女生入选时有C 63−C 43=16种选法.6.(2018·浙江·T16)从1,3,5,7,9中任取2个数字,从0,2,4,6中任取2个数字,一共可以组成 个没有重复数字的四位数.(用数字作答) 【答案】1260 【解析】分两类:第一类:从0,2,4,6中取到0,则没有重复数字的四位数有C 31C 52A 31A 33=540;第二类:从0,2,4,6中不取0,则没有重复数字的四位数有C 32C 52A 44=720.所以没有重复数字的四位数共有540+720=1260种.7.(2017·山东·理T11)已知(1+3x)n的展开式中含有x 2项的系数是54,则n= .【答案】4【解析】二项展开式的通项T r+1=C n r (3x)r=3r·C n r ·x r,令r=2,得32·C n 2=54,解得n=4.8.(2017·浙江·T13)已知多项式(x+1)3(x+2)2=x 5+a 1x 4+a 2x 3+a 3x 2+a 4x+a 5,则a 4= ,a 5= . 【答案】16 4【解析】由二项式展开式可得通项公式为C 3r x 3-rC 2m x 2-m 2m,分别取r=3,m=1和r=2,m=2可得a 4=4+12=16,令x=0可得a 5=13×22=4.9.(2017·天津·理T14)用数字1,2,3,4,5,6,7,8,9组成没有重复数字,且至多有一个数字是偶数的四位数,这样的四位数一共有 个.(用数字作答) 【答案】1080【解析】①没有一个数字是偶数的四位数有A 54=120个;②有且只有一个数字是偶数的四位数有C 41C 53A 44=960个.所以至多有一个数字是偶数的四位数有120+960=1 080个.10.(2017·浙江·T16)从6男2女共8名学生中选出队长1人,副队长1人,普通队员2人组成4人服务队,要求服务队中至少有1名女生,共有 种不同的选法.(用数字作答) 【答案】660【解析】由题意可得,总的选择方法为C 84C 41C 31种方法,其中不满足题意的选法有C 64C 41C 31种方法,则满足题意的选法有C 84C 41C 31−C 64C 41C 31=660种.11.(2016·全国1·理T14)(2x+√x )5的展开式中,x 3的系数是 .(用数字填写答案) 【答案】10【解析】二项式的通项公式T r+1=C 5r (2x)5-rx r 2=C 5r 25-rx 5-r2,令5-r2=3,解得r=4,故x 3的系数为C 54×25-4=10.12.(2016·天津·理T10) (x 2-1x )8的展开式中x 7的系数为 .(用数字作答)【答案】-56【解析】展开式通项为T r+1=C 8r (x 2)8-r(-1)r=(-1)rC 8r x16-3r,令16-3r=7,得r=3,所以展开式中x 7的系数为(-1)3C 83=-56.13.(2015·广东·理T12)某高三毕业班有40人,同学之间两两彼此给对方仅写一条毕业留言,那么全班共写了 条毕业留言.(用数字作答) 【答案】1560【解析】共有A 402=40×39=1 560条毕业留言.14.(2015·天津·理T12)在(x -1)6的展开式中,x 2的系数为.【答案】 1516 【解析】由题意知T r+1=C 6r x 6-r·(-14x )r =C 6r·x 6-2r ·(-14)r .令6-2r=2,可得r=2.故所求x2的系数为C 62(-14)2=1516. 15.(2015·重庆·理T12)(x 32√x)5的展开式中x 8的系数是(用数字作答).【答案】52【解析】展开式的通项公式T r+1=C 5r·(x 3)5-r ·(2√x )r =C 5r·2-r ·x 15-72r (r=0,1,2,…,5).令15-72r=8,得r=2,于是展开式中x 8项的系数是C 52·2-2=52.16.(2015·全国2·理T15)(a+x)(1+x)4的展开式中x 的奇数次幂项的系数之和为32,则a= . 【答案】3【解析】∵(1+x)4=x 4+C 43x 3+C 42x 2+C 41x+C 40x 0=x 4+4x 3+6x 2+4x+1,∴(a+x)(1+x)4的奇数次幂项的系数为4a+4a+1+6+1=32,∴a=3.17.(2014·安徽·理T13)设a ≠0,n 是大于1的自然数, (1+x a )n的展开式为a 0+a 1x+a 2x 2+…+a n x n.若点A i (i,a i )(i=0,1,2)的位置如图所示,则a= .【答案】3【解析】由题意得a 1=1a ·C n 1=n a=3,∴n=3a; a 2=1a 2C n 2=n (n -1)2a 2=4, ∴n 2-n=8a 2.将n=3a 代入n 2-n=8a 2得9a 2-3a=8a 2, 即a 2-3a=0,解得a=3或a=0(舍去).∴a=3.18.(2014·北京·理T13)把5件不同产品摆成一排.若产品A 与产品B 相邻,且产品A 与产品C 不相邻,则不同的摆法有 种. 【答案】36【解析】产品A,B 相邻时,不同的摆法有A 22A 44=48种.而A,B 相邻,A,C 也相邻时的摆法为A 在中间,C,B 在A 的两侧,不同的摆法共有A 22A 33=12(种).故产品A 与产品B 相邻,且产品A 与产品C 不相邻的不同摆法有48-12=36(种).19.(2014·全国1·理T13)(x-y)(x+y)8的展开式中x 2y 7的系数为 .(用数字填写答案) 【答案】-20【解析】(x+y)8的通项公式为T r+1=C 8r x 8-r y r(r=0,1,…,8,r ∈Z).当r=7时,T 8=C 87xy 7=8xy 7,当r=6时,T 7=C 86x 2y 6=28x 2y 6,所以(x-y)(x+y)8的展开式中含x 2y 7的项为x ·8xy 7-y ·28x 2y 6=-20x 2y 7,故系数为-20.20.(2014·全国2·理T13)(x+a)10的展开式中,x 7的系数为15,则a= .(用数字填写答案) 【答案】12【解析】设展开式的通项为T r+1=C 10r x10-r a r ,令r=3,得T 4=C 103x 7a 3,即C 103a 3=15,得a=12.21.(2013·浙江·理T11)设二项式(√x -√x3)5的展开式中常数项为A,则A= .【答案】-10【解析】T r+1=C 5r(√x )5-r ·(-1√x3)r =C 5r x5-r2·(-1)r·x-r 3=(-1)r C 5r x 5-r 2-r 3=(-1)r C 5r x 15-5r6.令15-5r=0,得r=3,所以A=(-1)3C 53=-C 52=-10.22.(2013·北京·理T12)将序号分别为1,2,3,4,5的5张参观券全部分给4人,每人至少1张,如果分给同一人的2张参观券连号,那么不同的分法种数是 . 【答案】96【解析】分给同一人的2张参观券连号的情况共有12,23,34,45四种情况,从4人中选一人得到连号参观券,有4C 41种方法.其余3张分给3人可以全排列,有A 33种方法,所以不同的分法有4C 41×A 33=96种.23.(2013·大纲全国·理T14)6个人排成一行,其中甲、乙两人不相邻的不同排法共有 种.(用数字作答) 【答案】480【解析】先排除甲、乙外的4人,方法有A 44种,再将甲、乙插入这4人形成的5个间隔中,有A 52种排法,因此甲、乙不相邻的不同排法有A 44·A 52=480(种).24.(2013·浙江·理T14)将A ,B ,C ,D ,E ,F 六个字母排成一排,且A ,B 均在C 的同侧,则不同的排法共有 种(用数字作答). 【答案】480【解析】按C 的位置分三类情况:①当C 在第一或第六位时,有A 55=120种排法;②当C 在第二或第五位时,有A 42A 33=72种排法;③当C 在第三或第四位时,有A 22A 33+A 32A 33=48种排法.所以共有2×(120+72+48)=480种排法.25.(2012·福建·理T11)(a+x)4的展开式中x 3的系数等于8,则实数a= . 【答案】2【解析】∵T r+1=C 4r a r x 4-r,∴当4-r=3,即r=1时,T 2=C 41·a ·x 3=4ax 3=8x 3.故a=2.26.(2012·浙江·理T14)若将函数f(x)=x 5表示为f(x)=a 0+a 1(1+x)+a 2(1+x)2+…+a 5(1+x)5,其中a 0,a 1,a 2,…,a 5为实数,则a 3= . 【答案】10【解析】由x 5=a 0+a 1(1+x)+a 2(1+x)2+…+a 5(1+x)5可得,{x 5=a 5·C 55x 5,0·x 4=a 4C 44x 4+a 5C 54x 4,0·x 3=a 3C 33x 3+a 4C 43x 3+a 5C 53x 3,可解得{a 5=1,a 4=-5,a 3=10.27.(2012·大纲·理T15)若(x +1x)n的展开式中第3项与第7项的二项式系数相等,则该展开式中1x2的系数为 . 【答案】56【解析】∵C n2=C n 6,∴n=8.T r+1=C 8r x 8-r (1x)r=C 8r x8-2r,当8-2r=-2时,r=5.∴系数为C 85=56.28.(2011·北京·理T12)用数字2,3组成四位数,且数字2,3至少都出现一次,这样的四位数共有 个.(用数字作答) 【答案】14【解析】可用排除法,这个四位数每一位上的数字只能是2或3,则共有24个,而这其中要求数字2或3至少出现一次,所以全是2和全是3不满足,即满足要求的四位数有24-2=14个.。
2012-2013年高考真题汇编:排列、组合及二项式定理

2012-2013高考真题分类汇编:排列、组合及二项式定理一、选择题1.(2013年新课标Ⅱ)已知5)1)(1(x ax ++的展开式中2x 的系数为5,则=a( )A .4-B .3-C .2-D .1-2.(2013年山东)用0,1,,9十个数字,可以组成有重复数字的三位数的个数为( )A .243B .252C .261D .2793.(2013新课标)设m 为正整数,2()mx y +展开式的二项式系数的最大值为a ,21()m x y ++展开式的二项式系数的最大值为b ,若137a b =,则m =( )A .5B .6C .7D .84 .(2013年福建)满足{},1,0,1,2a b ∈-,且关于x 的方程220ax x b ++=有实数解的有序数对(,)a b 的个数为 ( )A .14B .13C .12D .105 .(2013年辽宁)使得()3nx n N n +⎛+∈ ⎝的展开式中含有常数项的最小的为 ( )A .4B .5C .6D .76.(2013年四川)从1,3,5,7,9这五个数中,每次取出两个不同的数分别为,a b ,共可得到lg lg a b -的不同值的个数是 ( ) A .9 B .10 C .18 D .207.(2013年高考陕西卷(理))设函数61,00.,()x x f x x x ⎧⎛⎫-<⎪ ⎪=⎝≥⎭⎨⎪⎩ , 则当x >0时, [()]f f x 表达式的展开式中常数项为 ( )A .-20B .20C .-15D .158(2013年江西)(x 2-32x)5展开式中的常数项为 ( )A .80B .-80C .40D .-40 9.(2013年大纲版)()()8411+x y +的展开式中22x y 的系数是( ) A .56B .84C .112D .16810.【2012重庆】821⎪⎪⎭⎫⎝⎛+x x 的展开式中常数项为 A.1635 B.835 C.435 D.105 11.【2012浙江】若从1,2,3,…,9这9个整数中同时取4个不同的数,其和为偶数,则不同的取法共有 A.60种 B.63种 C.65种 D.66种12.【2012新课标】将2名教师,4名学生分成2个小组,分别安排到甲、乙两地参加社会实践活动,每个小组由1名教师和2名学生组成,不同的安排方案共有( )()A 12种 ()B 10种()C 9种 ()D 8种13.【2012四川】7(1)x +的展开式中2x 的系数是( )A 、42B 、35C 、28D 、2114.【2012陕西】两人进行乒乓球比赛,先赢三局着获胜,决出胜负为止,则所有可能出现的情形(各人输赢局次的不同视为不同情形)共有( ) A. 10种 B.15种 C. 20种 D. 30种15.【2012山东】现有16张不同的卡片,其中红色、黄色、蓝色、绿色卡片各4张.从中任取3张,要求这3张卡片不能是同一种颜色,且红色卡片至多1张.不同取法的种数为 (A )232 (B)252 (C)472 (D)48416.【2012辽宁】一排9个座位坐了3个三口之家,若每家人坐在一起,则不同的坐法种数为(A)3×3! (B) 3×(3!)3 (C)(3!)4 (D) 9!17.【2012湖北】设a ∈Z ,且013a ≤<,若201251a +能被13整除,则a =A .0B .1C .11D .1218.【2012北京】从0,2中选一个数字.从1.3.5中选两个数字,组成无重复数字的三位数.其中奇数的个数为( )A. 24B. 18C. 12D. 6 19.【2012安徽】2521(2)(1)x x+-的展开式的常数项是( ) ()A 3- ()B 2- ()C 2 ()D 3[20.【2012高考真题安徽理10】6位同学在毕业聚会活动中进行纪念品的交换,任意两位同学之间最多交换一次,进行交换的两位同学互赠一份纪念品,已知6位同学之间共进行了13次交换,则收到4份纪念品的同学人数为( )()A 1或3 ()B 1或4 ()C 2或3 ()D 2或4 21.【2012高考真题天津理5】在52)12(xx -的二项展开式中,x 的系数为 (A )10 (B )-10 (C )40 (D )-4022.【2012高考真题全国卷理11】将字母a,a,b,b,c,c,排成三行两列,要求每行的字母互不相同,每列的字母也互不相同,则不同的排列方法共有 (A )12种(B )18种(C )24种(D )36种二、填空题23、(2013四川)二项式5()x y +的展开式中,含23x y 的项的系数是_________.(用数字作答) 24.(2013年浙江)将F E D C B A ,,,,,六个字母排成一排,且B A ,均在C 的同侧,则不同的排法共有________种(用数字作答) 25.(2013重庆)从3名骨科.4名脑外科和5名内科医生中选派5人组成一个抗震救灾医疗小组,则骨科.脑外科和内科医生都至少有1人的选派方法种数是_______(用数字作答) 26.(2013年理)6x⎛- ⎝的二项展开式中的常数项为______.27.(2013年浙江)设二项式53)1(xx -的展开式中常数项为A ,则=A ________. 28.(2013上海)常数a R ∈,若52a x x ⎛⎫+ ⎪⎝⎭的二项展开式中7x 项的系数为10-,则______a =29.(2013年北京)将序号分别为1,2,3,4,5的5张参观券全部分给4人,每人至少1张,如果分给同一人的2张参观券连号,那么不同的分法种数是_________.30.(2013年安徽)若8x ⎛ ⎝的展开式中4x 的系数为7,则实数a =______. 31.(2013大纲)6个人排成一行,其中甲、乙两人不相邻的不同排法共有____________种.32【2012重庆】某艺校在一天的6节课中随机安排语文、数学、外语三门文化课和其他三门艺术课各1节,则在课表上的相邻两节文化课之间最多间隔1节艺术课的概率为 . 33.【2012高考陕西】5()a x +展开式中2x 的系数为10, 则实数a 的值为 .34.【2012上海】在6)2(x x -的二项展开式中,常数项等于 。
2023年高考数学真题分训练 排列组合、二项式定理(理)(含答案含解析)

专题 30 排列组合、二项式定理(理)年 份题号 考 点考 查 内 容2011 理 8 二项式定理 二项式定理的应用,常数项的计算 2023 理 2排列与组合 简单组合问题卷 1 理 9 二项式定理 二项式定理的应用以及组合数的计算 2023卷 2理 5 二项式定理 二项式定理的应用 卷 1 理 13 二项式定理 二项式展开式系数的计算2023卷 2 理 13 二项式定理 二项式展开式系数的计算 卷 1 理 10 二项式定理 三项式展开式系数的计算2023卷 2 理 15 二项式定理 二项式定理的应用卷 1 理 14 二项式定理 二项式展开式指定项系数的计算 卷 2 理 5 排列与组合 计数原理、组合数的计算2023卷 3理 12 排列与组合 计数原理的应用 卷 1 理 6 二项式定理 二项式展开式系数的计算 卷 2 理 6 排列与组合 排列组合问题的解法2023卷 3理 4 二项式定理 二项式展开式系数的计算 卷 1 理 15 排列与组合 排列组合问题的解法2023 卷 3 理 5 二项式定理 二项式展开式指定项系数的计算2023卷 3 理 4 二项式定理 利用展开式通项公式求展开式指定项的系数 卷 1 理 8 二项式定理 利用展开式通项公式求展开式指定项的系数2023 卷 3理 14二项式定理利用展开式通项公式求展开式常数项考点出现频率2023 年预测考点 102 两个计数原理的应用 23 次考 2 次 考点 103 排列问题的求解 23 次考 0 次 考点 104 组合问题的求解23 次考 4 次 考点 105 排列与组合的综合应用 23 次考 2 次 考点 106 二项式定理23 次考 11 次命题角度:(1)分类加法计数原理;(2)分步乘法计数原 理;(3)两个计数原理的综合应用.核心素养:数学建模、数学运算考点102 两个计数原理的应用1.(2023 全国II 理)如图,小明从街道的E 处出发,先到F 处与小红会合,再一起到位于G 处的老年公寓参加志愿者活动,则小明到老年公寓可以选择的最短路径条数为A.24 B.18 C.12 D.9(答案)B(解析)由题意可知E →F 有6 种走法,F →G 有3 种走法,由乘法计数原理知,共有6 ⨯ 3 = 18 种走法,应选B.2.(2023 新课标理1 理)4 位同学各自在周六、周日两天中任选一天参加公益活动,则周六、周日都有同学参加公益活动的概率为A.18B.3824 - 2 7C.58D.78(答案)D(解析)P ==.24 83.(2023 湖北理)回文数是指从左到右读与从右到左读都一样的正整数.如22,121,3443,94249 等.显然2位回文数有9 个:11,22,33,…,99.3 位回文数有90 个:101,111,121,…,191,202,…,999.则(Ⅰ)4 位回文数有个;(Ⅱ) 2n +1 (n ∈N+) 位回文数有个.(解析)(Ⅰ)4 位回文数只用排列前面两位数字,后面数字就可以确定,但是第—位不能为0,有9(1~9)种情况,第二位有10(0~9)种情况,所以4 位回文数有9 ⨯10 = 90 种.答案:90(Ⅱ)解法一:由上面多组数据研究发觉,2n +1 位回文数和2n + 2 位回文数的个数相同,所以可以算出2n + 2位回文数的个数.2n + 2 位回文数只用看前n +1位的排列情况,第—位不能为0 有9 种情况,后面n 项每项有10 种情况,所以个数为9 ⨯10n .解法二:可以看出2 位数有9 个回文数,3 位数90 个回文数。
2020年全国高考理科数学试题分类汇编10:排列、组合及二项式定理 Word版含答案

2020年全国高考理科数学试题分类汇编10:排列、组合及二项式定理一、选择题1 .(2020年普通高等学校招生统一考试新课标Ⅱ卷数学(理)(纯WORD版含答案))已知5)1(x+的展开式中2x的系数为5,ax+)(1则=a()A.4-B.3-C.2-D.1-【答案】D2 .(2020年普通高等学校招生统一考试山东数学(理)试题(含答案))用0,1,,9十个数字,可以组成有重复数字的三位数的个数为()A.243 B.252 C.261 D.279【答案】B3 .(2020年高考新课标1(理))设m为正整数,2+展开式的x y()m二项式系数的最大值为a,21+展开式的二项式系数的x y+()m最大值为b,若137=,则m=()a bA.5 B.6 C.7 D.8【答案】B4 .(2020年普通高等学校招生统一考试大纲版数学(理)WORD版含答案(已校对))()()84x y的系数是()+的展开式中22x y11+A .56B .84C .112D .168【答案】D5 .(2020年普通高等学校招生统一考试福建数学(理)试题(纯WORD 版))满足{},1,0,1,2a b ∈-,且关于x 的方程220ax x b ++=有实数解的有序数对(,)a b 的个数为 ( )A .14B .13C .12D .10【答案】B6 .(2020年上海市春季高考数学试卷(含答案))10(1)x +的二项展开式中的一项是 ( )A .45xB .290xC .3120xD .4252x【答案】C7 .(2020年普通高等学校招生统一考试辽宁数学(理)试题(WORD版))使得()13nx n N n x x +⎛⎫+∈ ⎪⎝⎭的展开式中含有常数项的最小的为 ( )A .4B .5C .6D .7【答案】B8 .(2020年高考四川卷(理))从1,3,5,7,9这五个数中,每次取出两个不同的数分别为,a b ,共可得到lg lg a b -的不同值的个数是 ( )A .9B .10C .18D .20【答案】C9 .(2020年高考陕西卷(理))设函数61,00.,(),x x f x x x x ⎧⎛⎫-<⎪ ⎪=⎝-≥⎭⎨⎪⎩ , 则当x>0时, [()]f f x 表达式的展开式中常数项为 ( )A .-20B .20C .-15D .15【答案】A10.(2020年高考江西卷(理))(x 2-32x )5展开式中的常数项为( )A .80B .-80C .40D .-40【答案】C 二、填空题11.(2020年上海市春季高考数学试卷(含答案))36的所有正约数之和可按如下方法得到:因为2236=23⨯,所以36的所有正约数之和为22222222(133)(22323)(22323)(122)133)91++++⨯+⨯++⨯+⨯=++++=(参照上述方法,可求得2000的所有正约数之和为________________________【答案】483612.(2020年高考四川卷(理))二项式5()x y +的展开式中,含23x y 的项的系数是_________.(用数字作答)【答案】1013.(2020年上海市春季高考数学试卷(含答案))从4名男同学和6名女同学中随机选取3人参加某社团活动,选出的3人中男女同学都有的概率为________(结果用数值表示).【答案】4514.(2020年普通高等学校招生统一考试浙江数学(理)试题(纯WORD 版))将F E D C B A ,,,,,六个字母排成一排,且B A ,均在C的同侧,则不同的排法共有________种(用数字作答)【答案】48015.(2020年普通高等学校招生统一考试重庆数学(理)试题(含答案))从3名骨科.4名脑外科和5名内科医生中选派5人组成一个抗震救灾医疗小组,则骨科.脑外科和内科医生都至少有1人的选派方法种数是___________(用数字作答)【答案】59016.(2020年普通高等学校招生统一考试天津数学(理)试题(含答案))61x x ⎛⎫- ⎪⎝⎭ 的二项展开式中的常数项为______.【答案】1517.(2020年普通高等学校招生统一考试浙江数学(理)试题(纯WORD 版))设二项式53)1(xx -的展开式中常数项为A ,则=A ________.【答案】10-18.(2020年高考上海卷(理))设常数a R ∈,若52a x x ⎛⎫+ ⎪⎝⎭的二项展开式中7x 项的系数为10-,则______a =【答案】2a =-19.(2020年高考北京卷(理))将序号分别为1,2,3,4,5的5张参观券全部分给4人,每人至少1张,如果分给同一人的2张参观券连号,那么不同的分法种数是_________.【答案】9620.(2020年普通高等学校招生统一考试安徽数学(理)试题(纯WORD 版))若83a x x ⎛⎫+ ⎪⎝⎭的展开式中4x 的系数为7,则实数a =______.【答案】2121.(2020年普通高等学校招生统一考试大纲版数学(理)WORD 版含答案(已校对))6个人排成一行,其中甲、乙两人不相邻的不同排法共有____________种.(用数字作答).【答案】480。
高考数学试题分类汇编——概率统计与排列组合二项式定理

布列、均值等基本知识,考查在复杂情境下处理问题的能力以及抽象概括能力、合
情推理与演绎推理,分类读者论论思想,应用意识与创新意识
.
解:( I)无论以怎样的顺序派出人员,任务不能被完成的概率都是
(1 p1 )(1 p2 )(1 p3 ) ,所以任务能被完成的概率与三个被派出的先后顺序无关,
并等于
1 (1 p1 )(1 p2 )(1 p 3) p1 p 2 p3 p1 p2 p2 p3 p 3 p1 p1 p 2 p3.
数字作答 )
【解析】个数为 24 2 14 。
17. 以下茎叶图记录了甲、乙两组各四名同学的植树棵数。乙组记录中有一个数据模糊,无
法确认,在图中以 X 表示。
(1)如果 X 8 ,求乙组同学植树棵数的平均数和方差;
3 / 36
(2)如果 X 9 ,分别从甲、乙两组中随机选取一名同学,求这两名同学的植树总棵数
q , q , q ,其中
q , q , q 是 p , p , p 的一个排列, 求所需派出人员数 目 X 的分布列和均值 (数字
期望) EX ;
(Ⅲ)假定
p p p ,试分析以怎样的 先后顺序派出人员,可使所需派出的人员
数目的均值(数字期望)达到最小。
(20)(本小题满分 13 分)本题考查相互独立事件的概率计算, 考查离散型随机变量及其分
事实上,
(3 2 q1 q 2 q1q 2 ) (3 2 p1 p 2 p1 p 2)
2( p1 q1 ) ( p 2 q 2 ) p1 p 2 q1q 2 2( p1 q1 ) ( p 2 q 2 ) ( p1 q1 ) p 2 q1 ( p 2 q2 ) (2 p2 )( p1 q1) (1 q1)(( p2 q2 ) (1 q1)[( p1 p 2 ) ( q1 q2 )] 0.
十年高考真题分类汇编(2010-2019) 数学 专题13 排列组合与二项式定理 含解析

十年高考真题分类汇编(2010—2019)数学专题13 排列组合与二项式定理一、选择题1.(2019·全国3·理T4)(1+2x2)(1+x)4的展开式中x3的系数为( )A.12B.16C.20D.24【答案】A【解析】(1+2x2)(1+x)4的展开式中x3的系数为+2=4+8=12.故选A.2.(2018·全国3·理T5) 的展开式中x4的系数为( )A.10B.20C.40D.80【答案】C【解析】由展开式知T r+1=(x2)5-r(2x-1)r=2r x10-3r.当r=2时,x4的系数为22=40.3.(2017·全国1·理T6)(1+x)6展开式中x2的系数为( )A.15B.20C.30D.35【答案】C【解析】(1+x)6的二项展开式通项为T r+1=x r,(1+x)6的展开式中含x2的项的来源有两部分,一部分是1×x2=15x2,另一部分是x4=15x2,故(1+x)6的展开式中含x2的项为15x2+15x2=30x2,其系数是30.4.(2017·全国3·理T4)(x+y)(2x-y)5的展开式中x3y3的系数为()A.-80B.-40C.40D.80【答案】C【解析】(2x-y)5的展开式的通项公式T r+1=(2x)5-r(-y)r.当r=3时,x(2x-y)5的展开式中x3y3的系数为×22×(-1)3=-40;当r=2时,y(2x-y)5的展开式中x3y3的系数为×23×(-1)2=80.故展开式中x3y3的系数为80-40=40.5.(2017·全国2·理T6)安排3名志愿者完成4项工作,每人至少完成1项,每项工作由1人完成,则不同的安排方式共有()A.12种B.18种C.24种D.36种【答案】D【解析】先把4项工作分成3份有种情况,再把3名志愿者排列有种情况,故不同的安排方式共有=36种,故选D.6.(2016·四川·理T2)设i为虚数单位,则(x+i)6的展开式中含x4的项为()A.-15x4B.15x4C.-20i x4D.20i x4【答案】A【解析】二项式(x+i)6展开的通项T r+1=x6-r i r,则其展开式中含x4是当6-r=4,即r=2,则展开式中含x4的项为x4i2=-15x4,故选A.7.(2016·全国2·理T5)如图,小明从街道的E处出发,先到F处与小红会合,再一起到位于G处的老年公寓参加志愿者活动,则小明到老年公寓可以选择的最短路径条数为()A.24B.18C.12D.9【答案】B【解析】由题意知,小明从街道的E处出发到F处的最短路径有6条,再从F处到G处的最短路径有3条,则小明到老年公寓可以选择的最短路径条数为6×3=18,故选B.8.(2016·全国3·理T12)定义“规范01数列”{a n}如下:{a n}共有2m项,其中m项为0,m项为1,且对任意k≤2m,a1,a2,…,a k中0的个数不少于1的个数.若m=4,则不同的“规范01数列”共有()A.18个B.16个C.14个D.12个【答案】C【解析】由题意知a1=0,a8=1,则满足题意的a1,a2,…,a8的可能取值如下:综上可知,不同的“规范01数列”共有14个.9.(2016·四川·理T4)用数字1,2,3,4,5组成没有重复数字的五位数,其中奇数的个数为()A.24B.48C.60D.72【答案】D【解析】要组成没有重复数字的五位奇数,则个位数应该为1,3,5中的一个,其他位置共有种排法,所以其中奇数的个数为3=72,故选D.10.(2015·四川·理T6)用数字0,1,2,3,4,5组成没有重复数字的五位数,其中比40 000大的偶数共有()A.144个B.120个C.96个D.72个【答案】B【解析】当首位数字为4,个位数字为0或2时,满足条件的五位数有个;当首位数字为5,个位数字为0或2或4时,满足条件的五位数有个.故满足条件的五位数共有=(2+3)=5×4×3×2×1=120个.故选B.11.(2015·全国1·理T10)(x2+x+y)5的展开式中,x5y2的系数为()A.10B.20C.30D.60【答案】C【解析】(x2+x+y)5=[(x2+x)+y]5的展开式通项为T r+1=(x2+x)5-r y r(r=0,1,2,…,5).由题意,y的幂指数为2,故r=2.对应的项为(x2+x)3y2=10(x2+x)3y2.记(x2+x)3的展开式通项为T s+1=(x2)3-s x s=x6-s(s=0,1,2,3),由题意令6-s=5,得s=1.故所求项的系数为10=30.12.(2015·陕西·理T4)二项式(x+1)n(n∈N*)的展开式中x2的系数为15,则n=()A.7B.6C.5D.4【答案】B【解析】(x+1)n的展开式通项为T r+1=x n-r.令n-r=2,即r=n-2.则x2的系数为=15,解得n=6,故选B.13.(2015·湖北·理T3)已知(1+x)n的展开式中第4项与第8项的二项式系数相等,则奇数项的二项式系数和为( )A.212B.211C.210D.29【答案】D【解析】由条件知,∴n=10.∴(1+x)10中二项式系数和为210,其中奇数项的二项式系数和为210-1=29.14.(2014·大纲全国·理T5)有6名男医生、5名女医生,从中选出2名男医生、1名女医生组成一个医疗小组,则不同的选法共有()A.60种B.70种C.75种D.150种【答案】C【解析】从6名男医生中选出2名有种选法,从5名女医生中选出1名有种选法,故共有×5=75种选法,选C.15.(2014·辽宁·理T6)6把椅子摆成一排,3人随机就座,任何两人不相邻的坐法种数为()A.144B.120C.72D.24【答案】D【解析】插空法.在已排好的三把椅子产生的4个空档中选出3个插入3人即可.故排法种数为=24.故选D.16.(2014·四川·理T6)六个人从左至右排成一行,最左端只能排甲或乙,最右端不能排甲,则不同的排法共有()A.192种B.216种C.240种D.288种【答案】B【解析】(1)当最左端排甲的时候,排法的种数为;(2)当最左端排乙的时候,排法种数为.因此不同的排法的种数为=120+96=216.17.(2014·重庆·理T9)某次联欢会要安排3个歌舞类节目、2个小品类节目和1个相声类节目的演出顺序,则同类节目不相邻的排法种数是()A.72B.120C.144D.168【答案】B【解析】第1步,先排歌舞类节目,有=6种排法,排好后有4个空位.第2步,排另3个节目,因为3个歌舞节目不相邻,则中间2个空位必须安排2个节目.分两类情况:①中间两个空位安排1个小品类节目和1个相声节目,有=4种排法,最后一个小品类节目排两端,有2种方法.共有6×4×2=48种排法.②中间两个空位安排2个小品类节目,有=2种排法,排好后有6个空位,选1个将相声类节目排上,有6种排法.共有6×2×6=72种排法.所以一共有48+72=120种排法.18.(2014·四川·理T2)在x(1+x)6的展开式中,含x3项的系数为( )A.30B.20C.15D.10【答案】C【解析】含x3的项是由(1+x)6展开式中含x2的项与x相乘得到,又(1+x)6展开式中含x2的项的系数为=15, 故含x3项的系数是15.19.(2014·湖南·理T4) 的展开式中x2y3的系数是( )A.-20B.-5C.5D.20【答案】A【解析】由已知,得T r+1=(-2y)r=(-2)r x5-r y r(0≤r≤5,r∈Z),令r=3,得T4=(-2)3x2y3=-20x2y3.20.(2014·浙江·理T5)在(1+x)6(1+y)4的展开式中,记x m y n项的系数为f(m,n),则f(3,0)+f(2,1)+f(1,2)+f(0,3)=( )A.45B.60C.120D.210【答案】C【解析】∵(1+x)6展开式的通项公式为T r+1=x r,(1+y)4展开式的通项公式为T h+1=y h,∴(1+x)6(1+y)4展开式的通项可以为x r y h.∴f(m,n)=.∴f(3,0)+f(2,1)+f(1,2)+f(0,3)==20+60+36+4=120.故选C.21.(2013·全国1·理T9)设m为正整数,(x+y)2m展开式的二项式系数的最大值为a,(x+y)2m+1展开式的二项式系数的最大值为b.若13a=7b,则m=( )A.5B.6C.7D.8【答案】B【解析】由题意可知,a=,b=,∵13a=7b,∴13·=7·,即,解得m=6.故选B.22.(2013·山东·理T10)用0,1,…,9十个数字,可以组成有重复数字的三位数的个数为()A.243B.252C.261D.279【答案】B【解析】构成所有的三位数的个数为=900,而无重复数字的三位数的个数为=648,故所求个数为900-648=252,应选B.23.(2013·全国2·理T5)已知(1+ax)(1+x)5的展开式中x2的系数为5,则a=()A.-4B.-3C.-2D.-1【答案】D【解析】因为(1+x)5的二项展开式的通项为x r(0≤r≤5,r∈Z),则含x2的项为x2+ax·x=(10+5a)x2,所以10+5a=5,a=-1.24.(2013·辽宁·理T7)使 (n∈N*)的展开式中含有常数项的最小的n为( )A.4B.5C.6D.7【答案】B【解析】展开式中的第r+1项为(3x)n-r3n-r,若展开式中含常数项,则存在n∈N*,r∈N,使n-r=0,故最小的n值为5,故选B.25.(2013·大纲全国·理T7)(1+x)8(1+y)4的展开式中x2y2的系数是( )A.56B.84C.112D.168【答案】D【解析】因为(1+x)8的展开式中x2的系数为,(1+y)4的展开式中y2的系数为,所以x2y2的系数为=168.故选D.26.(2012·湖北·理T5)设a∈Z,且0≤a<13,若512 012+a能被13整除,则a=( )A.0B.1C.11D.12【答案】D【解析】∵512 012可化为(52-1)2 012,其二项式系数为T r+1=522 012-r·(-1)r.故(52-1)2 012被13除余数为·(-1)2 012=1,则当a=12时,512 012+12被13整除.27.(2012·安徽·理T7)(x2+2) 的展开式的常数项是( )A.-3B.-2C.2D.3【答案】D【解析】通项为T r+1=(-1)r=(-1)r.令10-2r=2或0,此时r=4或5.故(x2+2)的展开式的常数项是(-1)4×+2×(-1)5×=3.28.(2012·全国·理T2)将2名教师,4名学生分成2个小组,分别安排到甲、乙两地参加社会实践活动,每个小组由1名教师和2名学生组成,不同的安排方案共有()A.12种B.10种C.9种D.8种【答案】A【解析】将4名学生均分为2个小组共有=3种分法,将2个小组的同学分给两名教师带有=2种分法,最后将2个小组的人员分配到甲、乙两地有=2种分法,故不同的安排方案共有3×2×2=12种.29.(2012·辽宁·理T5)一排9个座位坐了3个三口之家,若每家人坐在一起,则不同的坐法种数为()A.3×3!B.3×(3!)3C.(3!)4D.9!【答案】C【解析】完成这件事可以分为两步,第一步排列三个家庭的相对位置,有种排法;第二步排列每个家庭中的三个成员,共有种排法.由乘法原理可得不同的坐法种数有,故选C.30.(2012·安徽·理T10)6位同学在毕业聚会活动中进行纪念品的交换,任意两位同学之间最多交换一次,进行交换的两位同学互赠一份纪念品.已知6位同学之间共进行了13次交换,则收到4份纪念品的同学人数为()A.1或3B.1或4C.2或3D.2或4【答案】D【解析】6人之间互相交换,总共有=15种,而实际只交换了13次,故有2次未交换.不妨设为甲与乙、丙与丁之间未交换或甲与乙、甲与丙之间未交换,当甲与乙、丙与丁之间未交换时,甲、乙、丙、丁4人都收到4份礼物;当甲与乙、甲与丙之间未交换时,只有乙、丙两人收到4份礼物,故选D.31.(2011·全国·理T8) 的展开式中各项系数的和为2,则该展开式中常数项为( )A.-40B.-20C.20D.40【答案】D【解析】令x=1得(1+a)(2-1)5=2,∴a=1.原式=x·,故常数项为x·(2x)2(2x)3=-40+80=40.32.(2010·山东·理T8)某台小型晚会由6个节目组成,演出顺序有如下要求:节目甲必须排在前两位,节目乙不能排在第一位,节目丙必须排在最后一位,该台晚会节目演出顺序的编排方案共有()A.36种B.42种C.48种D.54种【答案】B【解析】若乙排在第二位,则有种方案;若乙不排在第二位,则乙只能排在第三、四、五位,此时共有种方案,故共有=42(种).二、填空题1.(2019·天津·理T10)(2x-8的展开式中的常数项为【答案】28【解析】T r+1=(2x)8-r(r=·28-r·(-r·x8-4r.需8-4r=0,r=2.常数项为26(-2=26=28.2.(2018·天津·理T10)在的展开式中,x2的系数为.【答案】【解析】展开式的通项为T r+1=x5-r.令5-=2,可得r=2.所以的展开式中的x2的系数为.3.(2018·浙江·T14)二项式的展开式的常数项是.【答案】7【解析】通项为T r+1=,当r=2时,=0.故展开式的常数项为=7.4.(2018·上海·T3)在(1+x)7的二项展开式中,x2项的系数为(结果用数值表示).【答案】21【解析】由(1+x)7的二项展开式的通项,得(1+x)7的二项展开式的x2项的系数为=21.5.(2018·全国1·理T15)从2位女生,4位男生中选3人参加科技比赛,且至少有1位女生入选,则不同的选法共有种.(用数字填写答案)【答案】16【解析】方法一:①恰有1位女生时,有=12种选法.②恰有2位女生时,有=4种选法.故不同的选法共有12+4=16种.方法二:6人中选3人共有种选法,3人全是男生时有种选法,所以至少有1位女生入选时有=16种选法.6.(2018·浙江·T16)从1,3,5,7,9中任取2个数字,从0,2,4,6中任取2个数字,一共可以组成个没有重复数字的四位数.(用数字作答)【答案】1260【解析】分两类:第一类:从0,2,4,6中取到0,则没有重复数字的四位数有=540;第二类:从0,2,4,6中不取0,则没有重复数字的四位数有=720.所以没有重复数字的四位数共有540+720=1260种.7.(2017·山东·理T11)已知(1+3x)n的展开式中含有x2项的系数是54,则n= .【答案】4【解析】二项展开式的通项T r+1=(3x)r=3r··x r,令r=2,得32·=54,解得n=4.8.(2017·浙江·T13)已知多项式(x+1)3(x+2)2=x5+a1x4+a2x3+a3x2+a4x+a5,则a4= ,a5= .【答案】16 4【解析】由二项式展开式可得通项公式为x3-r x2-m2m,分别取r=3,m=1和r=2,m=2可得a4=4+12=16,令x=0可得a5=13×22=4.9.(2017·天津·理T14)用数字1,2,3,4,5,6,7,8,9组成没有重复数字,且至多有一个数字是偶数的四位数,这样的四位数一共有个.(用数字作答)【答案】1080【解析】①没有一个数字是偶数的四位数有=120个;②有且只有一个数字是偶数的四位数有=960个.所以至多有一个数字是偶数的四位数有120+960=1 080个.10.(2017·浙江·T16)从6男2女共8名学生中选出队长1人,副队长1人,普通队员2人组成4人服务队,要求服务队中至少有1名女生,共有种不同的选法.(用数字作答)【答案】660【解析】由题意可得,总的选择方法为种方法,其中不满足题意的选法有种方法,则满足题意的选法有=660种.11.(2016·全国1·理T14)(2x+)5的展开式中,x3的系数是.(用数字填写答案)【答案】10【解析】二项式的通项公式T r+1=(2x)5-r25-r,令5-=3,解得r=4,故x3的系数为×25-4=10.12.(2016·天津·理T10) 的展开式中x7的系数为.(用数字作答)【答案】-56【解析】展开式通项为T r+1=(x2)8-r=(-1)r x16-3r,令16-3r=7,得r=3,所以展开式中x7的系数为(-1)3=-56.13.(2015·广东·理T12)某高三毕业班有40人,同学之间两两彼此给对方仅写一条毕业留言,那么全班共写了条毕业留言.(用数字作答)【答案】1560【解析】共有=40×39=1 560条毕业留言.14.(2015·天津·理T12)在的展开式中,x2的系数为.【答案】【解析】由题意知T r+1=x6-r··x6-2r·.令6-2r=2,可得r=2.故所求x2的系数为.15.(2015·重庆·理T12)的展开式中x8的系数是(用数字作答).【答案】【解析】展开式的通项公式T r+1=·(x3)5-r··2-r·(r=0,1,2,…,5).令15-r=8,得r=2,于是展开式中x8项的系数是·2-2=.16.(2015·全国2·理T15)(a+x)(1+x)4的展开式中x的奇数次幂项的系数之和为32,则a= .【答案】3【解析】∵(1+x)4=x4+x3+x2+x+x0=x4+4x3+6x2+4x+1,∴(a+x)(1+x)4的奇数次幂项的系数为4a+4a+1+6+1=32,∴a=3.17.(2014·安徽·理T13)设a≠0,n是大于1的自然数, 的展开式为a0+a1x+a2x2+…+a n x n.若点A i(i,a i)(i=0,1,2)的位置如图所示,则a= .【答案】3【解析】由题意得a1==3,∴n=3a;a2==4,∴n2-n=8a2.将n=3a代入n2-n=8a2得9a2-3a=8a2,即a2-3a=0,解得a=3或a=0(舍去).∴a=3.18.(2014·北京·理T13)把5件不同产品摆成一排.若产品A与产品B相邻,且产品A与产品C不相邻,则不同的摆法有种.【答案】36【解析】产品A,B相邻时,不同的摆法有=48种.而A,B相邻,A,C也相邻时的摆法为A在中间,C,B在A的两侧,不同的摆法共有=12(种).故产品A与产品B相邻,且产品A与产品C不相邻的不同摆法有48-12=36(种).19.(2014·全国1·理T13)(x-y)(x+y)8的展开式中x2y7的系数为.(用数字填写答案)【答案】-20【解析】(x+y)8的通项公式为T r+1=x8-r y r(r=0,1,…,8,r∈Z).当r=7时,T8=xy7=8xy7,当r=6时,T7=x2y6=28x2y6,所以(x-y)(x+y)8的展开式中含x2y7的项为x·8xy7-y·28x2y6=-20x2y7,故系数为-20.20.(2014·全国2·理T13)(x+a)10的展开式中,x7的系数为15,则a= .(用数字填写答案)【答案】【解析】设展开式的通项为T r+1=x10-r a r,令r=3,得T4=x7a3,即a3=15,得a=.21.(2013·浙江·理T11)设二项式的展开式中常数项为A,则A= .【答案】-10【解析】T r+1=)5-r··(-1)r·=(-1)r=(-1)r.令15-5r=0,得r=3,所以A=(-1)3=-=-10.22.(2013·北京·理T12)将序号分别为1,2,3,4,5的5张参观券全部分给4人,每人至少1张,如果分给同一人的2张参观券连号,那么不同的分法种数是.【答案】96【解析】分给同一人的2张参观券连号的情况共有12,23,34,45四种情况,从4人中选一人得到连号参观券,有4种方法.其余3张分给3人可以全排列,有种方法,所以不同的分法有4=96种.23.(2013·大纲全国·理T14)6个人排成一行,其中甲、乙两人不相邻的不同排法共有种.(用数字作答)【答案】480【解析】先排除甲、乙外的4人,方法有种,再将甲、乙插入这4人形成的5个间隔中,有种排法,因此甲、乙不相邻的不同排法有=480(种).24.(2013·浙江·理T14)将A,B,C,D,E,F六个字母排成一排,且A,B均在C的同侧,则不同的排法共有种(用数字作答).【答案】480【解析】按C的位置分三类情况:①当C在第一或第六位时,有=120种排法;②当C在第二或第五位时,有=72种排法;③当C在第三或第四位时,有=48种排法.所以共有2×(120+72+48)=480种排法.25.(2012·福建·理T11)(a+x)4的展开式中x3的系数等于8,则实数a= .【答案】2【解析】∵T r+1=a r x4-r,∴当4-r=3,即r=1时,T2=·a·x3=4ax3=8x3.故a=2.26.(2012·浙江·理T14)若将函数f(x)=x5表示为f(x)=a0+a1(1+x)+a2(1+x)2+…+a5(1+x)5,其中a0,a1,a2,…,a5为实数,则a3= .【答案】10【解析】由x5=a0+a1(1+x)+a2(1+x)2+…+a5(1+x)5可得,可解得27.(2012·大纲·理T15)若的展开式中第3项与第7项的二项式系数相等,则该展开式中的系数为.【答案】56【解析】∵,∴n=8.T r+1=x8-r x8-2r,当8-2r=-2时,r=5.∴系数为=56.28.(2011·北京·理T12)用数字2,3组成四位数,且数字2,3至少都出现一次,这样的四位数共有个.(用数字作答)【答案】14【解析】可用排除法,这个四位数每一位上的数字只能是2或3,则共有24个,而这其中要求数字2或3至少出现一次,所以全是2和全是3不满足,即满足要求的四位数有24-2=14个.。
高二数学下学期期末考试分类汇编排列组合与二项式定理新人教A版

专题10 排列组合与二项式定理一、单选题1.(2022·浙江宁波·高二期中)甲、乙、丙、丁四名同学分别从篮球、足球、排球、羽毛球四种球类项目中选择一项进行活动,则四名同学所选项目各不相同且只有乙同学选篮球发生的概率( )A.B.C.D.【答案】B【解析】四名同学从四种球类项目中选择一项,每人有4种选择,由分步乘法计数原理可得总的选法有种,由于乙同学选篮球,且四名同学所选项目各不相同,所以问题相当于将足球、排球、羽毛球三种球类项目分别分配给甲、丙、丁3位同学,共种,所以所求概率.故选:B2.(2022·黑龙江·海伦市第一中学高二期中)的值是( )A.0B.1C.-1D.【答案】B.故选:B.3.(2022·重庆·高二阶段练习)在的展开式中,的系数为( )A.B.30C.D.60【答案】C【解析】的展开式通项为,的展开式通项为,由,解得,所以的系数为.故选:C.4.(2022·河北·沧县中学高二阶段练习)的展开式中的系数为( )A.B.C.40D.80【答案】C【解析】解:,由展开式的通项公式,当时,,不含有项.所以展开式中的系数为;故选:.5.(2022·北京八十中高二期中)今年中国空间站将进入到另一个全新的阶段—正式建造阶段,首批参加中国空间站建造的6名航天员,将会分别搭乘着神舟十四号和神舟十五号载人飞船,接连去往中国空间站,并且在上面“会师”.中国空间站的主体结构包括天和核心舱、问天实验舱和梦天实验舱. 假设中国空间站要安排甲,乙,丙,丁等6名航天员开展实验,其中天和核心舱安排3人,问天实验舱安排2人,梦天实验舱安排1人.若甲、乙两人不能同时在一个舱内做实验,则不同的安排方案共有( )A.44种B.48种C.60种D.50种【答案】A【解析】解:由题意,要安排甲,乙,丙,丁等6名航天员开展实验,其中天和核心舱安排3人,问天实验舱安排2人,梦天实验舱安排1人,共有种方案;若甲、乙两人同时在天和核心舱做实验,则有种方案;若甲、乙两人同时在问天实验舱做实验,则有种方案.所以甲、乙两人不能同时在一个舱内做实验,则共有不同的安排方案.故选:A.6.(2022·浙江·高二阶段练习)25某高中举办2022年“书香涵泳,润泽心灵”读书节活动,设有“优秀征文”、“好书推荐语展示”和“演讲”三个项目.某班级有7名同学报名参加,要求每人限报一项,每个项目至少2人参加,则报名的不同方案有( )A.420种B.630种C.1260种D.1890种【答案】B【解析】由题7名同学分成3个组,每组分别有2,2,3人,共有种分组方式.再排列有种方案.故选:B.7.(2022·河北保定·高二期中)4月1日,根据当前疫情防控工作需要,定州市新冠肺炎疫情防控工作总指挥部发布通告,要求我市全域内除特殊人员外,所有人员保持居家,不出小区(村)等待全员核酸检测.为了保障广大居民的生活需要,某小区征集了多名志愿者,现有5名志愿者承包A,B,C三栋居民楼,每位志愿者负责一栋楼,且每栋楼至少一名志愿者,则分派方法的种数为( )A.90B.150C.180D.300【答案】B【解析】先分组:按照居民楼人数分为3,1,1和2,2,1两类3,1,1:从5名志愿者中选出3名作为一个组,其余2人各自一组,有种2,2,1:从5名志愿者中选出4名平均分为两组,剩下1人一组,有种再分配:3个组到三栋居民楼有种所以总的分派方法数有种故选:B8.(2022·全国·高二课时练习)设a∈Z,且0≤a<13,若512012+a能被13整除,则a=A.0B.1C.11D.12【答案】D【解析】由于,又由于13|52,所以只需13|1+a,0≤a<13,所以a=12.故选:D.9.(2022·湖北·高二阶段练习)若,则=( )A.244B.1C.D.【答案】D【解析】根据,令时,整理得:令x = 2时,整理得:由①+②得,,所以.故选:D.10.(2022·黑龙江·大庆实验中学高二阶段练习)展开式中常数项为( )A.B.0C.15D.80【答案】B【解析】的通项为当时,;当时,则展开式中常数项为故选:B11.(2022·全国·高二课时练习)设n为正奇数,则被7整除的余数为( ).A.B.0C.3D.5【答案】D.∵为整数,故被7整除的余数为5;故选:D.12.(2022·全国·高二课时练习)在的展开式中,偶数项的二项式系数的和为128,则展开式的中间项为( )A.B.C.D.【答案】C【解析】【分析】解:因为二项展开式中,奇数项的二项式系数与偶数项的二项式系数相等,所以,偶数项的二项式系数的和为,即,所以,展开式的中间项为.故选:C13.(2022·山西临汾·高二期中)若,,则下列结论中正确的是( )A .B.C.D.【答案】D【解析】令,可得.又,所以,A错误;展开式的通项公式为因为,所以,B错误;令,可得,C错误;对两边同时求导,得,令,可得,D正确.故选:D.14.(2022·江苏·东海县教育局教研室高二期中)设,则( )A.10206B.5103C.729D.728【答案】A【解析】解:因为,两边同时取导数得,其中展开式的通项为,所以当为奇数时系数为负数,为偶数时系数为正数,即,,,,,,,令,则,所以;故选:A一、单选题1.(2022·河南新乡·高二期中(理))展开式中的常数项为( )A.-70B.-56C.56D.70【答案】D【解析】的通项公式为,当时,得到展开式的常数项为,故选:D 2.(2022·全国·高二课时练习)化简多项式的结果是( )A .B.C.D.【答案】D【解析】依题意可知,多项式的每一项都可看作,故该多项式为的展开式,化简.故选:D.3.(2022·天津·南开大学附属中学高二期中)如图为我国数学家赵爽(约3世纪初)在为《周髀算经》作注时验证勾股定理的示意图,现在提供5种颜色给其中5个小区域涂色,规定每个区域只涂一种颜色,相邻区域颜色不相同,则不同的涂色方案共有种A.120B.260C.340D.420【答案】D由题意可知上下两块区域可以相同,也可以不同,则共有故选4.(2022·全国·高二课时练习)我国古代“五行”学说认为:“物质分金、木、土、水、火五种属性,金克木,木克土,土克水,水克火,火克金.”将这五种不同属性的物质任意排成一排,设事件表示“排列中属性相克的两种物质均不相邻”,则事件发生的概率为( )A.B.C.D.【答案】B【解析】由题意知,五种不同属性的物质任意排成一列有种排法,事件表示“排列中属性相克的两种物质均不相邻”可看作五个位置排列五个元素,第一位置有五种排列方法,不妨假设是金,则第二步只能从土与水两者中选一种排放,有两种选择,不妨假设排上的是水,第三步只能排上木,第四步只能排上火,第五步只能排上土,∴总的排列方法种数为,∴事件发生的概率为.故选:B.5.(2022·四川省绵阳南山中学高二期中(理))中国空间站的主体结构包括天和核心舱、问天实验舱和梦天实验舱.假设中国空间站要安排甲,乙,丙,丁,戊5名航天员开展实验,其中天和核心舱安排3人,问天实验舱与梦天实验舱各安排1人.若甲、乙两人不能同时在一个舱内做实验,则不同的安排方案共有( )A.8种B.14种C.20种D.116种【答案】B【解析】按照甲是否在天和核心舱划分,①若甲在天和核心舱,天和核心舱需要从除了甲乙之外的三人中选取两人,剩下两人去剩下两个舱位,则有种可能;②若甲不在天和核心舱,需要从问天实验舱和梦天实验舱中挑选一个,剩下四人中选取三人进入天和核心舱即可,则有种可能;根据分类加法计数原理,共有6+8=14种可能.故选:B.6.(2022·江苏·海安县实验中学高二期中)2022年北京冬奥会和冬残奥会给世界人民留下了深刻的印象,其吉祥物“冰墩墩”和“雪容融的设计好评不断,这是一次中国文化与奥林匹克精神的完美结合.为了弘扬奥林匹克精神,某学校安排甲、乙等5名志愿者将吉祥物“冰墩墩”和“雪容融”安装在学校的体育广场,每人参与且只参与一个吉祥物的安装,每个吉祥物都至少由两名志愿者安装.若甲、乙必须安装不同的吉祥物,则不同的分配方案种数为( )A.8B.10C.12D.14【答案】C【解析】甲和乙必须安装不同的吉祥物,则有种情况,剩余3人分两组,一组1人,一组2人,有,然后分配到参与两个吉祥物的安装,有,则共有种,故选:.二、多选题7.(2022·重庆市万州第二高级中学高二阶段练习)第24届冬奥会于2022年2月4日在中国北京市和张家口市联合举行.甲,乙等5名志愿者计划到高山滑雪、自由式滑雪、短道速滑和花样滑冰4个比赛区从事志愿者活动,则下列说法正确的有( )A.若短道速滑赛区必须安排2人,其余各安排1人,则有60种不同的方案B.若每个比赛区至少安排1人,则有240种不同的方案C.安排这5人排成一排拍照,若甲、乙相邻,则有42种不同的站法D.已知这5人的身高各不相同,若安排5人拍照,前排2人,后排3人,且后排3人中身高最高的站中间,则有40种不同的站法【答案】ABD【解析】【详解】若短道速滑赛区必须安排2人,其余各安排1人,则先从5人中任选2人安排在短道速滑赛区,剩余3人在其余三个比赛区全排列,故有种,A正确:若每个比赛区至少安排1人,则先将5人按“2,1,1,1”形式分成四组,再分配到四个岗位上,故有种,B正确:若甲、乙相邻,可把2人看成一个整体,与剩下的3人全排列,有种排法,甲、乙两人相邻有种排法,所以共有种站法,C错误;前排有种站法,后排3人中最高的站中间有种站法,所以共有种站法,D 正确.故选:ABD8.(2022·全国·高二课时练习)(多选)某校以大课程观为理论基础,以关键能力和核心素养的课程化为突破口,深入探索普通高中创新人才培养的校本化课程体系.本学期共开设了八大类校本课程,具体为学科拓展()、体艺特长()、实践创新(S)、生涯规划()、国际视野()、公民素养()、大学先修()、PBL项目课程(),假期里决定继续开设这八大类课程,每天开设一类且不重复,连续开设八天,则( )A.某学生从中选两类,共有种选法B.课程“”“”排在不相邻两天,共有种排法C.课程中“S”“”“”排在相邻三天,且“”只能排在“S”与“”的中间,共有720种排法D.课程“”不排在第一天,课程“”不排在最后一天,共有种排法【答案】BD【解析】对于A,某学生从中选两类,如选“”“”与选“”“”是一种选法,没有顺序之分,所以种选法计算重复,故A错误;对于B,课程“”“”排在不相邻两天,先将剩余六类课程全排列,产生7个空隙,再将课程“”“”插空,共有种排法,故B正确;对于C,课程“S”,“”,“”排在相邻三天,且“”只能排在“S”与“”的中间,采用捆绑法,共有种排法,故C错误;对于D,课程“”不排在第一天,课程“”不排在最后一天,则分两类情况:①课程“”排在第一天,②课程“”排在除第一天和最后一天之外的某一天,则共有种排法,故D正确.故选:BD.9.(2022·黑龙江·铁人中学高二期中)已知的展开式中第项与第项的二项数系数相等,且展开式的各项系数之和为,则下列说法正确的是( )A.展开式中有理项有6项B.展开式中第项的系数最大C .展开式中奇数项的二项式系数和为D.展开式中含项的系数为【答案】ABD【解析】依题意可得,得,得,得,得.在展开式中,令,得,因为,所以,所以.展开式的通项为,,对于A,由为整数,得,所以展开式中有理项有6项,故A正确;对于B,因为展开式中各项的系数等于各项的二项式系数,且为奇数,所以展开式中第6项的二项式系数最大,所以展开式中第6项的系数最大,故B正确;对于C,根据二项式系数的性质可得,展开式中奇数项的二项式系数和为,故C 不正确;对于D,令,得,所以展开式中含项的系数为,故D正确.故选:ABD.10.(2022·江苏·连云港高中高二期中)下列结论正确的是( )A.B.多项式展开式中的系数为40C.若,则展开式中各项的二项式系数的和为1 D.被5除所得的余数是1【答案】ABD【解析】解:因为,故A项正确;多项式的展开式通项为:,要求的系数,则,当时,有,的系数为,当时,有,不存在,当时,有,的系数为,当时,有,不存在,故展开式中的系数为,故B项正确;,其展开式中各项的二项式系数之和为,故C项错误;因为,其展开式的通项公式为:,只有当时,即,不能被5整除,且256被5整除的余数为1,故D项正确.故选:ABD.11.(2022·广东·深圳市南山外国语学校(集团)高级中学高二期中)已知,则( )A.B.C.D.【答案】AD【解析】解:因为,令,则,故A正确;令,则,所以,故B错误;令,则,所以,故C错误;对两边对取导得,再令得,故D正确;故选:AD三、解答题12.(2022·安徽·高二期中)已知.(1)求;(2)求.【答案】(1)(2)令x=1,得,令x=0,得,所以.(2)两边同时求导得:,令x=1,得.。
高考数学试题分类汇编——排列组合、二项式定理排列组合

高考数学试题分类汇编——排列组合、二项式定理排列组合1. 由数字2,3,4,5,6所组成的没有重复数字的四位数中5,6相邻的奇数共有( )A .10个B .14个C .16个D .18个B (简析:分两类。
若末位数字为5,则倒数第二位为6,前两位数字排法有623=A 种;若末位数字为3,将5,6视为一个元素,排法有2×22A ×2=8种,故5,6相邻的奇数的个数共有6+8=14个)2. 如图所示,某城镇由6条东西方向的街道和6条南北方向的街道组成,其中有一个池塘,街道在此变成一个菱形的 环池大道.现要从城镇的A 处走到B最多可以有 种不同的走法.35 3. 已知集合A ={1,2,3},集合B ={4,5,6,7,8},映射f :A →B 满足f (1)<f (2)<f (3),则这样的映射f 共有( )A 、35个B 、15个C 、53个D 、10个4. 3名女生与2名男生排成一排照相,其中女生不相邻的排法种数有 ;女生有33A 种排法,男生插空排列有22A 种排法,故共有323212A A ⋅=种排法5. 电视台某段时间连续播放5个广告,其中有3个不同的商业广告和2个不同的奥运宣传广告,要求最后播放的必须是奥运宣传广告,且2个奥运宣传广告不能连续播放,则不同的播放方式有A .120种B .48种C .36种D .18种二项式定理一、填空题:上海市浦东新区2007学年度第一学期期末质量抽测2008/11、若8(1)tg θ+展开式的第4项为7,则θ2sin 的值为 . 542、山东省潍坊市2007—2008学年度高三第一学期期末考试 已知532)51(xx -1的展开式中的常数项为T ,)(x f 是以T 为周期的偶函数,且当k kx x f x g x x f x --=-=∈)()(,]3,1[,)(,]1,0[函数内若在区间时有4个零点,则实数ABk 的取值范围是 。
高考数学专题:排列、组合与二项式定理问题练习试题、答案

高考数学专题:排列、组合与二项式定理问题练习试题一.排列与组合问题1.某科技小组有四名男生两名女生,现从中选出三名同学参加比赛,其中至少一名女生入选的不同选法种数为( )A .36CB .1225C C C .12212424C C C CD .36A2.某校需要在5名男生和5名女生中选出4人参加一项文化交流活动,由于工作需要,男生甲与男生乙至少有一人参加活动,女生丙必须参加活动,则不同的选人方式有( )A .56种B .49种C .42种D .14种 3.五人排成一排,甲与乙不相邻,且甲与丙也不相邻的不同排法有( )A .60种B .48种C .36种D .24种4.某单位有7个连在一起的停车位,现有3辆不同型号的车需要停放,如果要求剩余的4个空车位连在一起,则不同的停放方法有( )A .16种B .18种C .24种D .32种5.为迎接2008年北京奥运会,某校举行奥运知识竞赛,有6支代表队参赛,每队2名同学,若12名参赛同学中有4人获奖,且这4人来自3个不同的代表队,则不同获奖情况种数共有( )A .412CB .3111162223C C C C C C .31116322C C C C D .311112622232C C C C C A 6.A 、B 两点之间有6条网线并联,它们能通过的最大信息量分别为1,1,2,2,3,4,现从中任取三条网线且使这三条网线通过最大信息量的和大于等于6的方法共有( )A .13种B .14种C .15种D .16种7.有一排7只发光二级管,每只二级管点亮时可发出红光或绿光,若每次恰有3只二级管点亮,但相邻的两只二级管不能同时点亮,根据这三只点亮的二级管的不同位置或不同颜色来表示不同的信息,则这排二级管能表示的信息种数共有( )A .10B .48C .60D .808.数列{}n a 共七项,其中五项为1,两项为2,则满足上述条件的数列{}n a 共有( )A .21个B .25个C .32个D .42个 9.三个人踢毽,互相传递,每人每次只能踢一下,由甲开始踢,经过5次传递后,毽又踢回给甲,则不同的传递方式共有( )A .6种B .8种C .10种D .16种 10.5个大小都不同的数按如图形式排列,设第一行中的最大数为a ,第二行中的最大数为b ,则满足a b <的所有排列的个数是( )A .144B .72C .36D .2411.有A ,B ,C ,D ,E ,F 共6个不同的油气罐准备用甲,乙,丙3台卡车运走,每台卡车运两个,但卡车甲不能运A 罐,卡车乙不能运B 罐,此外无其它限制. 要把这6个油气罐分配给这3台卡车,则不同的分配方案种数为( )A .168B .84C .56D .4212.若m 、2210{|1010}n x x a a a ∈=⨯+⨯+,其中(0,1,2){1,2,3,4,5,6}i a i =∈,并且606m n +=,则实数对(,)m n 表示平面上不同点的个数为( )A .32个B .30个C .62个D .60个 13.由0、1、2、3这四个数字,可组成无重复数字的三位偶数有_______个.14.从1,2,…,9这九个数中,随机抽取3个不同的数,则这3个数的和为奇数的概率是____________(用数字作答).15.如图所示,画中的一朵花,有五片花瓣.现有四种不同颜色的画笔可供选择,规定每片花瓣都要涂色,且只涂一种颜色.若涂完的花中颜色相同的花瓣恰有三片,则不同涂法种数为_______(用数字作答).二.二项式定理1.已知23132nx x ⎛⎫- ⎪⎝⎭的展开式中含有常数项(非零),则正整数n 的可能值是( )A .6B .5C .4D .32.已知622x x p ⎛⎫- ⎪⎝⎭的展开式中,不含x 的项是2720,那么正数p 的值是( ) A .1 B .2 C .3 D .43.已知31nx ⎛⎫ ⎪⎝⎭的展开式中第二项与第三项的系数之和等于27,则n 等于______,系数最大的项是第___________项.4.621x x ⎛⎫- ⎪⎝⎭的展开式中第四项的系数为___________.(用数字作答) 5.6)21(x -展开式中所有项的系数之和为________;63)21)(1(x x -+展开式中5x 的系数为__________.6.62)21(x x -展开式中5x 的系数为______________.7.已知n x )21(+的展开式中含3x 项的系数等于含x 项的系数的8倍,则n 等于__________.8.已知n+的二项展开式的第6项是常数项,那么n =_______. 9.62)2(x x+的展开式中的常数项是______________(用数字作答). 10. 在6(12)x -的展开式,含2x 项的系数为_________________;所有项的系数的和为_______________. 11.在n的展开式中,前三项的系数的绝对值依次组成一个等差数列,则n =______,展开式中第五项的二项式系数为_____(用数字作答). 12.82)2(x +的展开式中12x 的系数等于______________(用数字作答). 13.210(1)x -的展开式中2x 的系数是______________,如果展开式中第4r 项和第2r +项的二项式系数相等,则r 等于____________. 14. 若62a x x ⎛⎫- ⎪⎝⎭的展开式中常数项为160-,则常数a 的值为_________,展开式中各项系数之和为_________.答案一.1.C2.B3.C4.C5.C6.C7.D8.A9.C10.B11.D12.D13.1014.10 2115.240二1.B2.C 3.9,5 4.-20 5.1,-132 6.-160 7.58.10 9.60 10.60,111.8,70 12.112 13.-10,2 14.1,1。
高考数学 全国统考区(甘肃、贵州、云南)精选试题分类汇编10 排列、组合及二项式定理

备战2014年高考之2013届全国统考区(甘肃、贵州、云南)精选理科试题(大部分详解)分类汇编10:排列、组合及二项式定理一、选择题1 .(【解析】贵州省四校2013届高三上学期期末联考数学(理)试题)将甲、乙、丙、丁四名学生分到三个不同的班,每个班至少分到一名学生,且甲、乙两名学生不能分到同一个班,则不同的分法的种数为( ) A .24种 B .30种 C .36种 D .81种【答案】B 【解析】甲、乙、丙、丁四名学生分到三个不同的班,每个班至少分到一名学生则,从4人中先选2人一个班,然后在分班,有234336C A =种。
若甲乙两人分在一个班则有336A =种,所以甲、乙两名学生不能分到同一个班,则不同的分法的种数为36630-=种,选 B .2 .(云南省玉溪一中2013届高三第五次月考理科数学)从0,2中选一个数字.从1.3.5中选两个数字,组成无重复数字的三位数.其中奇数的个数为( ) A .24 B .18 C .12 D .6【答案】B 【解析】若选0,0只能放在十位上,此时从1,3,5中选2个奇数的排成三位奇数有236A =种。
若选2,从1,3,5中选1个奇数排在个位,然后从剩下俩个奇数选一个和2进行全排列放在十位和百位,共有2232=12A ⨯⨯种,所以共有18种排法,选B .3 .(【解析】云南省玉溪一中2013届高三上学期期中考试理科数学)某教师一天上3个班级的课,每班一节,如果一天共9节课,上午5节、下午4节,并且教师不能连上3节课(第5和第6节不算连上),那么这位教师一天的课的所有排法有( ) A .474种 B .77种 C .462种 D .79种【答案】A 【解析】首先求得不受限制时,从9节课中任意安排3节,有39504A =种排法,其中上午连排3节的有33318A =种,下午连排3节的有33212A =种,则这位教师一天的课表的所有排法有504-18-12=474种,故选A .4 .(甘肃省兰州一中2013届高三上学期12月月考数学(理)试题)51()(2)a x x x x +-展开式中各项系数的和为2,则该展开式中的常数项为( )A .40-B .20-C .20D .40【答案】D 【解析】令1x =,得12a +=,所以1a =,所以55111()(2)()(2)a x x x x x x x x +-=+-,51(2)x x -的展开通项为:()()5552551212rr rrr rr C x C x x ---⎛⎫-=- ⎪⎝⎭,由521,2,52-1,3,r r r r -==-==得由得所以51(2)x x -展开式中x 项的系数为80,51(2)x x -展开式中1x -项的系数为-40,所以511()(2)x x x x +-的展开式中常数项为80-40=40。
高考数学选择题试题分类汇编排列组合与二项式定理

2010年高考数学选择题试题分类汇编——排列组合与二项式定理 (2010全国卷2理数)(6)将标号为1,2,3,4,5,6的6张卡片放入3个不同的信封中.若每个信封放2张,其中标号为1,2的卡片放入同一信封,则不同的方法共有(A )12种 (B )18种 (C )36种 (D )54种【答案】B【命题意图】本试题主要考察排列组合知识,考察考生分析问题的能力.【解析】标号1,2的卡片放入同一封信有种方法;其他四封信放入两个信封,每个信封两个有种方法,共有种,故选B.(2010全国卷2文数)(9)将标号为1,2,3,4,5,6的6张卡片放入3个不同的信封中,若每个信封放2张,其中标号为1,2的卡片放入同一信封,则不同的方法共有(A ) 12种 (B)18种 (C) 36种 (D)54种【解析】B :本题考查了排列组合的知识∵先从3个信封中选一个放1,2有3种不同的选法,再从剩下的4个数中选两个放一个信封有246C =,余下放入最后一个信封,∴共有24318C =(2010江西理数)6.(82展开式中不含..4x 项的系数的和为( ) A.-1 B.0 C.1 D.2【答案】B【解析】考查对二项式定理和二项展开式的性质,重点考查实践意识和创新能力,体现正难则反。
采用赋值法,令x=1得:系数和为1,减去4x 项系数80882(1)1C -=即为所求,答案为0.(2010重庆文数)(10)某单位拟安排6位员工在今年6月14日至16日(端午节假期)值班,每天安排2人,每人值班1天 . 若6位员工中的甲不值14日,乙不值16日,则不同的安排方法共有(A )30种 (B )36种(C )42种 (D )48种解析:法一:所有排法减去甲值14日或乙值16日,再加上甲值14日且乙值16日的排法即2212116454432C C C C C C -⨯+=42法二:分两类甲、乙同组,则只能排在15日,有24C =6种排法甲、乙不同组,有112432(1)C C A +=36种排法,故共有42种方法(2010重庆文数)(1)4(1)x +的展开式中2x 的系数为 (A )4 (B )6(C )10 (D )20解析:由通项公式得2234T C 6x x ==(2010重庆理数)(9)某单位安排7位员工在10月1日至7日值班,每天1人,每人值班1天,若7位员工中的甲、乙排在相邻两天,丙不排在10月1日,丁不排在10月7日,则不同的安排方案共有A. 504种B. 960种C. 1008种D. 1108种 解析:分两类:甲乙排1、2号或6、7号 共有4414222A A A ⨯种方法甲乙排中间,丙排7号或不排7号,共有)(43313134422A A A A A +种方法 故共有1008种不同的排法(2010北京理数)(4)8名学生和2位第师站成一排合影,2位老师不相邻的排法种数为(A )8289A A (B )8289A C (C ) 8287A A (D )8287A C答案:A(2010四川理数)(10)由1、2、3、4、5、6组成没有重复数字且1、3都不与5相邻的六位偶数的个数是(A )72 (B )96 (C ) 108 (D )144解析:先选一个偶数字排个位,有3种选法①若5在十位或十万位,则1、3有三个位置可排,32232A A =24个②若5排在百位、千位或万位,则1、3只有两个位置可排,共32222A A =12个算上个位偶数字的排法,共计3(24+12)=108个答案:C(2010天津理数)(10) 如图,用四种不同颜色给图中的A,B,C,D,E,F 六个点涂色,要求每个点涂一种颜色,且图中每条线段的两个端点涂不同颜色,则不同的涂色方法用(A )288种 (B )264种 (C )240种 (D )168种【答案】D【解析】本题主要考查排列组合的基础知识与分类讨论思想,属于难题。
高考数学试题分类汇编10 排列、组合及二项式定理 文 试题

本卷贰O 贰贰年贰月捌日编写; 出题人:令狐学复;欧阳化语;令狐理总。
本卷贰O 贰贰年贰月捌日编写; 出题人:令狐学复;欧阳化语;令狐理总。
2021年全国各地高考文科数学试题分类汇编10:排列、组合及二项式定理
本卷贰O 贰贰年贰月捌日编写; 出题人:令狐学复;欧阳化语;令狐理总。
一、选择题
1 .〔2021年高考大纲卷〔文〕〕()862x x +的展开式中的系数是 〔 〕
A .28
B .56
C .112
D .224
【答案】C
二、填空题
2 .〔2021年高考数学试题〔文科〕〕设常数a ∈R .假设5
2a x x ⎛⎫+ ⎪⎝
⎭的二项展开式中7x 项的系数为-10,那么a =_______.
【答案】2-
3 .〔2021年高考大纲卷〔文〕〕从进入决赛的6名选手中决出1名一等奖,2名二等奖,3名三等奖,那么
可能的决赛结果一共有____种.(用数字答题)
【答案】60
本卷贰O 贰贰年贰月捌日编写; 出题人:令狐学复;欧阳化语;令狐理总。
2019年全国高考理科数学试题分类汇编10:排列、组合及二项式定理

2019年全国高考理科数学试题分类汇编10:排列、组合及二项式定理一、选择题1 .(2019年普通高等学校招生统一考试新课标Ⅱ卷数学(理)(纯W ORD 版含答案))已知5)1)(1(x ax ++的展开式中2x 的系数为5,则=a ( )A .4-B .3-C .2-D .1-【答案】D2 .(2019年普通高等学校招生统一考试山东数学(理)试题(含答案))用0,1,,9十个数字,可以组成有重复数字的三位数的个数为( )A .243B .252C .261D .279【答案】B3 .(2019年高考新课标1(理))设m 为正整数,2()m x y +展开式的二项式系数的最大值为a ,21()m x y ++展开式的二项式系数的最大值为b ,若137a b =,则m =( )A .5B .6C .7D .8【答案】B4 .(2019年普通高等学校招生统一考试大纲版数学(理)WORD 版含答案(已校对))()()8411+x y +的展开式中22x y 的系数是 A .56B .84C .112D .168【答案】D5 .(2019年普通高等学校招生统一考试福建数学(理)试题(纯WORD 版))满足{},1,0,1,2a b ∈-,且关于x的方程220ax x b ++=有实数解的有序数对(,)a b 的个数为 ( )A .14B .13C .12D .10【答案】B6 .(2019年上海市春季高考数学试卷(含答案))10(1)x +的二项展开式中的一项是( )A .45xB .290xC .3120xD .4252x【答案】C7 .(2019年普通高等学校招生统一考试辽宁数学(理)试题(WORD 版))使得()3nx n N n+⎛+∈ ⎝的展开式中含有常数项的最小的为( )A .4B .5C .6D .7【答案】B8 .(2019年高考四川卷(理))从1,3,5,7,9这五个数中,每次取出两个不同的数分别为,a b ,共可得到lg lg a b -的不同值的个数是( )A .9B .10C .18D .20【答案】C9 .(2019年高考陕西卷(理))设函数61,00.,()x x f x x x ⎧⎛⎫-<⎪ ⎪=⎝≥⎭⎨⎪⎩ , 则当x >0时, [()]f f x 表达式的展开式中常数项为( )A .-20B .20C .-15D .15【答案】A10.(2019年高考江西卷(理))(x 2-32x )5展开式中的常数项为 ( )A .80B .-80C .40D .-40【答案】C 二、填空题11.(2019年上海市春季高考数学试卷(含答案))36的所有正约数之和可按如下方法得到:因为2236=23⨯,所以36的所有正约数之和为222222(133)(22323)(++++⨯+⨯++⨯+(参照上述方法,可求得2000的所有正约数之和为________________________【答案】483612.(2019年高考四川卷(理))二项式5()x y +的展开式中,含23x y 的项的系数是_________.(用数字作答)【答案】1013.(2019年上海市春季高考数学试卷(含答案))从4名男同学和6名女同学中随机选取3人参加某社团活动,选出的3人中男女同学都有的概率为________(结果用数值表示).【答案】4514.(2019年普通高等学校招生统一考试浙江数学(理)试题(纯WORD 版))将F E D C B A ,,,,,六个字母排成一排,且B A ,均在C 的同侧,则不同的排法共有________种(用数字作答)【答案】48015.(2019年普通高等学校招生统一考试重庆数学(理)试题(含答案))从3名骨科.4名脑外科和5名内科医生中选派5人组成一个抗震救灾医疗小组,则骨科.脑外科和内科医生都至少有1人的选派方法种数是___________(用数字作答) 【答案】59016.(2019年普通高等学校招生统一考试天津数学(理)试题(含答案))6x ⎛⎝的二项展开式中的常数项为______.【答案】1517.(2019年普通高等学校招生统一考试浙江数学(理)试题(纯WORD 版))设二项式53)1(xx -的展开式中常数项为A ,则=A ________【答案】10。
排列组合与二项式定理(教师卷)- 十年(2015-2024)高考真题数学分项汇编(全国通用)
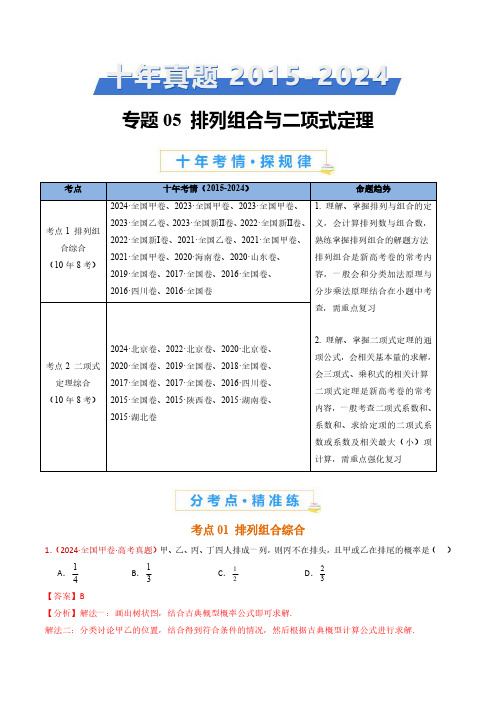
专题05排列组合与二项式定理考点十年考情(2015-2024)命题趋势考点1排列组合综合(10年8考)2024·全国甲卷、2023·全国甲卷、2023·全国甲卷、2023·全国乙卷、2023·全国新Ⅱ卷、2022·全国新Ⅱ卷、2022·全国新Ⅰ卷、2021·全国乙卷、2021·全国甲卷、2021·全国甲卷、2020·海南卷、2020·山东卷、2019·全国卷、2017·全国卷、2016·全国卷、2016·四川卷、2016·全国卷1.理解、掌握排列与组合的定义,会计算排列数与组合数,熟练掌握排列组合的解题方法排列组合是新高考卷的常考内容,一般会和分类加法原理与分步乘法原理结合在小题中考查,需重点复习2.理解、掌握二项式定理的通项公式,会相关基本量的求解,会三项式、乘积式的相关计算二项式定理是新高考卷的常考内容,一般考查二项式系数和、系数和、求给定项的二项式系数或系数及相关最大(小)项计算,需重点强化复习考点2二项式定理综合(10年8考)2024·北京卷、2022·北京卷、2020·北京卷、2020·全国卷、2019·全国卷、2018·全国卷、2017·全国卷、2017·全国卷、2016·四川卷、2015·全国卷、2015·陕西卷、2015·湖南卷、2015·湖北卷考点01排列组合综合1.(2024·全国甲卷·高考真题)甲、乙、丙、丁四人排成一列,则丙不在排头,且甲或乙在排尾的概率是()A .14B .13C .12D .23【答案】B【分析】解法一:画出树状图,结合古典概型概率公式即可求解.解法二:分类讨论甲乙的位置,结合得到符合条件的情况,然后根据古典概型计算公式进行求解.【详解】解法一:画出树状图,如图,由树状图可得,甲、乙、丙、丁四人排成一列,共有24种排法,其中丙不在排头,且甲或乙在排尾的排法共有8种,故所求概率81=243P =.解法二:当甲排在排尾,乙排第一位,丙有2种排法,丁就1种,共2种;当甲排在排尾,乙排第二位或第三位,丙有1种排法,丁就1种,共2种;于是甲排在排尾共4种方法,同理乙排在排尾共4种方法,于是共8种排法符合题意;基本事件总数显然是44A 24=,根据古典概型的计算公式,丙不在排头,甲或乙在排尾的概率为81243=.故选:B2.(2023·全国甲卷·高考真题)现有5名志愿者报名参加公益活动,在某一星期的星期六、星期日两天,每天从这5人中安排2人参加公益活动,则恰有1人在这两天都参加的不同安排方式共有()A .120B .60C .30D .20【答案】B【分析】利用分类加法原理,分类讨论五名志愿者连续参加两天公益活动的情况,即可得解.【详解】不妨记五名志愿者为,,,,a b c d e ,假设a 连续参加了两天公益活动,再从剩余的4人抽取2人各参加星期六与星期天的公益活动,共有24A 12=种方法,同理:,,,b c d e 连续参加了两天公益活动,也各有12种方法,所以恰有1人连续参加了两天公益活动的选择种数有51260⨯=种.故选:B.3.(2023·全国甲卷·高考真题)某校文艺部有4名学生,其中高一、高二年级各2名.从这4名学生中随机选2名组织校文艺汇演,则这2名学生来自不同年级的概率为()A .16B .13C .12D .23【答案】D【分析】利用古典概率的概率公式,结合组合的知识即可得解.【详解】依题意,从这4名学生中随机选2名组织校文艺汇演,总的基本事件有24C 6=件,其中这2名学生来自不同年级的基本事件有1122C C 4=,所以这2名学生来自不同年级的概率为4263=.故选:D.4.(2023·全国乙卷·高考真题)甲乙两位同学从6种课外读物中各自选读2种,则这两人选读的课外读物中恰有1种相同的选法共有()A .30种B .60种C .120种D .240种【答案】C【分析】相同读物有6种情况,剩余两种读物的选择再进行排列,最后根据分步乘法公式即可得到答案.【详解】首先确定相同得读物,共有16C 种情况,然后两人各自的另外一种读物相当于在剩余的5种读物里,选出两种进行排列,共有25A 种,根据分步乘法公式则共有1265C A 120⋅=种,故选:C.5.(2023·全国新Ⅱ卷·高考真题)某学校为了解学生参加体育运动的情况,用比例分配的分层随机抽样方法作抽样调查,拟从初中部和高中部两层共抽取60名学生,已知该校初中部和高中部分别有400名和200名学生,则不同的抽样结果共有().A .4515400200C C ⋅种B .2040400200C C ⋅种C .3030400200C C ⋅种D .4020400200C C ⋅种【答案】D【分析】利用分层抽样的原理和组合公式即可得到答案.【详解】根据分层抽样的定义知初中部共抽取4006040600⨯=人,高中部共抽取2006020600⨯=,根据组合公式和分步计数原理则不同的抽样结果共有4020400200C C ⋅种.故选:D.6.(2022·全国新Ⅱ卷·高考真题)有甲、乙、丙、丁、戊5名同学站成一排参加文艺汇演,若甲不站在两端,丙和丁相邻,则不同排列方式共有()A .12种B .24种C .36种D .48种【答案】B【分析】利用捆绑法处理丙丁,用插空法安排甲,利用排列组合与计数原理即可得解【详解】因为丙丁要在一起,先把丙丁捆绑,看做一个元素,连同乙,戊看成三个元素排列,有3!种排列方式;为使甲不在两端,必须且只需甲在此三个元素的中间两个位置任选一个位置插入,有2种插空方式;注意到丙丁两人的顺序可交换,有2种排列方式,故安排这5名同学共有:3!2224⨯⨯=种不同的排列方式,故选:B7.(2022·全国新Ⅰ卷·高考真题)从2至8的7个整数中随机取2个不同的数,则这2个数互质的概率为()A.16B.13C.12D.23【答案】D【分析】由古典概型概率公式结合组合、列举法即可得解.【详解】从2至8的7个整数中随机取2个不同的数,共有27C21=种不同的取法,若两数不互质,不同的取法有:()()()()()()()2,4,2,6,2,8,3,6,4,6,4,8,6,8,共7种,故所求概率2172213 P-==.故选:D.8.(2021·全国乙卷·高考真题)将5名北京冬奥会志愿者分配到花样滑冰、短道速滑、冰球和冰壶4个项目进行培训,每名志愿者只分配到1个项目,每个项目至少分配1名志愿者,则不同的分配方案共有()A.60种B.120种C.240种D.480种【答案】C【分析】先确定有一个项目中分配2名志愿者,其余各项目中分配1名志愿者,然后利用组合,排列,乘法原理求得.【详解】根据题意,有一个项目中分配2名志愿者,其余各项目中分配1名志愿者,可以先从5名志愿者中任选2人,组成一个小组,有25C种选法;然后连同其余三人,看成四个元素,四个项目看成四个不同的位置,四个不同的元素在四个不同的位置的排列方法数有4!种,根据乘法原理,完成这件事,共有2 54!240C⨯=种不同的分配方案,故选:C.【点睛】本题考查排列组合的应用问题,属基础题,关键是首先确定人数的分配情况,然后利用先选后排思想求解.9.(2021·全国甲卷·高考真题)将3个1和2个0随机排成一行,则2个0不相邻的概率为()A.0.3B.0.5C.0.6D.0.8【答案】C【分析】利用古典概型的概率公式可求概率.【详解】解:将3个1和2个0随机排成一行,可以是:00111,01011,01101,01110,10011,10101,10110,11001,11010,11100,共10种排法,其中2个0不相邻的排列方法为:01011,01101,01110,10101,10110,11010,共6种方法,故2个0不相邻的概率为6=0.610,故选:C.10.(2021·全国甲卷·高考真题)将4个1和2个0随机排成一行,则2个0不相邻的概率为()A .13B .25C .23D .45【答案】C【详解】将4个1和2个0随机排成一行,可利用插空法,4个1产生5个空,若2个0相邻,则有155C =种排法,若2个0不相邻,则有2510C =种排法,所以2个0不相邻的概率为1025103=+.故选:C.11.(2020·海南·高考真题)要安排3名学生到2个乡村做志愿者,每名学生只能选择去一个村,每个村里至少有一名志愿者,则不同的安排方法共有()A .2种B .3种C .6种D .8种【答案】C【分析】首先将3名学生分成两个组,然后将2组学生安排到2个村即可.【详解】第一步,将3名学生分成两个组,有12323C C =种分法第二步,将2组学生安排到2个村,有222A =种安排方法所以,不同的安排方法共有326⨯=种故选:C【点睛】解答本类问题时一般采取先组后排的策略.12.(2020·山东·高考真题)6名同学到甲、乙、丙三个场馆做志愿者,每名同学只去1个场馆,甲场馆安排1名,乙场馆安排2名,丙场馆安排3名,则不同的安排方法共有()A .120种B .90种C .60种D .30种【答案】C【分析】分别安排各场馆的志愿者,利用组合计数和乘法计数原理求解.【详解】首先从6名同学中选1名去甲场馆,方法数有16C ;然后从其余5名同学中选2名去乙场馆,方法数有25C ;最后剩下的3名同学去丙场馆.故不同的安排方法共有126561060C C ⋅=⨯=种.故选:C【点睛】本小题主要考查分步计数原理和组合数的计算,属于基础题.13.(2019·全国·高考真题)我国古代典籍《周易》用“卦”描述万物的变化.每一“重卦”由从下到上排列的6个爻组成,爻分为阳爻“——”和阴爻“——”,如图就是一重卦.在所有重卦中随机取一重卦,则该重卦恰有3个阳爻的概率是A .516B .1132C .2132D .1116【答案】A【分析】本题主要考查利用两个计数原理与排列组合计算古典概型问题,渗透了传统文化、数学计算等数学素养,“重卦”中每一爻有两种情况,基本事件计算是住店问题,该重卦恰有3个阳爻是相同元素的排列问题,利用直接法即可计算.【详解】由题知,每一爻有2种情况,一重卦的6爻有62情况,其中6爻中恰有3个阳爻情况有36C ,所以该重卦恰有3个阳爻的概率为3662C =516,故选A .【点睛】对利用排列组合计算古典概型问题,首先要分析元素是否可重复,其次要分析是排列问题还是组合问题.本题是重复元素的排列问题,所以基本事件的计算是“住店”问题,满足条件事件的计算是相同元素的排列问题即为组合问题.14.(2017·全国·高考真题)安排3名志愿者完成4项工作,每人至少完成1项,每项工作由1人完成,则不同的安排方式共有()A .12种B .18种C .24种D .36种【答案】D【详解】4项工作分成3组,可得:24C =6,安排3名志愿者完成4项工作,每人至少完成1项,每项工作由1人完成,可得:36363A ⨯=种.故选D.15.(2016·全国·高考真题)如图,小明从街道的E 处出发,先到F 处与小红会合,再一起到位于G 处的老年公寓参加志愿者活动,则小明到老年公寓可以选择的最短路径条数为A .24B .18C .12D .9【答案】B【详解】解:从E 到F ,每条东西向的街道被分成2段,每条南北向的街道被分成2段,从E 到F 最短的走法,无论怎样走,一定包括4段,其中2段方向相同,另2段方向相同,每种最短走法,即是从4段中选出2段走东向的,选出2段走北向的,故共有C 42C 22=6种走法.同理从F 到G ,最短的走法,有C 31C 22=3种走法.∴小明到老年公寓可以选择的最短路径条数为6×3=18种走法.故选B .【考点】计数原理、组合【名师点睛】分类加法计数原理在使用时易忽视每类中每一种方法都能完成这件事情,类与类之间是相互独立的;分步乘法计数原理在使用时易忽视每步中某一种方法只是完成这件事的一部分,而未完成这件事,步步之间是相互关联的.16.(2016·四川·高考真题)用数字1,2,3,4,5组成没有重复数字的五位数,其中奇数的个数为A .24B .48C .60D .72【答案】D【详解】试题分析:由题意,要组成没有重复数字的五位奇数,则个位数应该为1或3或5,其他位置共有44A 种排法,所以奇数的个数为44372A =,故选D.【考点】排列、组合【名师点睛】利用排列、组合计数时,关键是正确进行分类和分步,分类时要注意不重不漏,分步时要注意整个事件的完成步骤.在本题中,个位是特殊位置,第一步应先安排这个位置,第二步再安排其他四个位置.17.(2016·全国·高考真题)定义“规范01数列”{an }如下:{an }共有2m 项,其中m 项为0,m 项为1,且对任意2k m ≤,12,,,,k a a a 中0的个数不少于1的个数.若m =4,则不同的“规范01数列”共有A .18个B .16个C .14个D .12个【答案】C【详解】试题分析:由题意,得必有10a =,81a=,则具体的排法列表如下:,01010011;010101011,共14个【点睛】求解计数问题时,如果遇到情况较为复杂,即分类较多,标准也较多,同时所求计数的结果不太大时,往往利用表格法、树状图将其所有可能一一列举出来,常常会达到出奇制胜的效果.考点02二项式定理综合1.(2024·北京·高考真题)在(4x x 的展开式中,3x 的系数为()A .6B .6-C .12D .12-【答案】A【分析】写出二项展开式,令432r-=,解出r 然后回代入二项展开式系数即可得解.【详解】(4x x 的二项展开式为(()()442144C C1,0,1,2,3,4r rrr rrr T x xxr --+==-=,令432r-=,解得2r =,故所求即为()224C 16-=.故选:A.2.(2022·北京·高考真题)若443243210(21)x a x a x a x a x a -=++++,则024a a a ++=()A .40B .41C .40-D .41-【答案】B【分析】利用赋值法可求024a a a ++的值.【详解】令1x =,则432101a a a a a ++++=,令=1x -,则()443210381a a a a a -+-+=-=,故420181412a a a +++==,故选:B.3.(2020·北京·高考真题)在52)-的展开式中,2x 的系数为().A .5-B .5C .10-D .10【答案】C【分析】首先写出展开式的通项公式,然后结合通项公式确定2x 的系数即可.【详解】)52展开式的通项公式为:()()55215522r rrrrr r T CC x --+=-=-,令522r -=可得:1r =,则2x 的系数为:()()11522510C -=-⨯=-.故选:C.【点睛】二项式定理的核心是通项公式,求解此类问题可以分两步完成:第一步根据所给出的条件(特定项)和通项公式,建立方程来确定指数(求解时要注意二项式系数中n 和r 的隐含条件,即n ,r 均为非负整数,且n ≥r ,如常数项指数为零、有理项指数为整数等);第二步是根据所求的指数,再求所求解的项.4.(2020·全国·高考真题)25()()x x y xy ++的展开式中x 3y 3的系数为()A .5B .10C .15D .20【答案】C【分析】求得5()x y +展开式的通项公式为515r rrr T C xy -+=(r N ∈且5r ≤),即可求得2y x x ⎛⎫+ ⎪⎝⎭与5()x y +展开式的乘积为65r rr C xy -或425r r r C x y -+形式,对r 分别赋值为3,1即可求得33x y 的系数,问题得解.【详解】5()x y +展开式的通项公式为515r rr r T C xy -+=(r N ∈且5r ≤)所以2y x x ⎛⎫+ ⎪⎝⎭的各项与5()x y +展开式的通项的乘积可表示为:56155r rrr rrr xT xC xy C xy --+==和22542155r r rr r r r T C x y xC y y y x x --++==在615rrr r xT C xy -+=中,令3r =,可得:33345xT C x y =,该项中33x y 的系数为10,在42152r r r r T C x x y y -++=中,令1r =,可得:521332T C y x xy =,该项中33x y 的系数为5所以33x y 的系数为10515+=故选:C【点睛】本题主要考查了二项式定理及其展开式的通项公式,还考查了赋值法、转化能力及分析能力,属于中档题.5.(2019·全国·高考真题)(1+2x 2)(1+x )4的展开式中x 3的系数为A .12B .16C .20D .24【答案】A【分析】本题利用二项展开式通项公式求展开式指定项的系数.【详解】由题意得x 3的系数为314424812C C +=+=,故选A .【点睛】本题主要考查二项式定理,利用展开式通项公式求展开式指定项的系数.6.(2018·全国·高考真题)522x x ⎛⎫+ ⎪⎝⎭的展开式中4x 的系数为A .10B .20C .40D .80【答案】C【详解】分析:写出103152r r rr T C x -+=⋅⋅,然后可得结果详解:由题可得()5210315522rrrr r r r T C xC x x --+⎛⎫== ⋅⋅⎪⎝⎭⋅⋅令103r 4-=,则r 2=所以22552240r r C C ⋅⋅==故选C.点睛:本题主要考查二项式定理,属于基础题.7.(2017·全国·高考真题)(x +y )(2x -y )5的展开式中x 3y 3的系数为A .-80B .-40C .40D .80【答案】C【详解】()()()()555222x y x y x x y y x y +-=-+-,由()52x y -展开式的通项公式()()515C 2rrrr T x y -+=-可得:当3r =时,()52x x y -展开式中33x y 的系数为()3325C 2140⨯⨯-=-;当2r =时,()52y x y -展开式中33x y 的系数为()2235C 2180⨯⨯-=,则33x y 的系数为804040-=.故选C.【名师点睛】(1)二项式定理的核心是通项公式,求解此类问题可以分两步完成:第一步根据所给出的条件(特定项)和通项公式,建立方程来确定指数(求解时要注意二项式系数中n 和r 的隐含条件,即n ,r 均为非负整数,且n ≥r ,如常数项指数为零、有理项指数为整数等);第二步是根据所求的指数,再求所求解的项.(2)求两个多项式的积的特定项,可先化简或利用分类加法计数原理讨论求解.8.(2017·全国·高考真题)621(1)x x++展开式中2x 的系数为A .15B .20C .30D .35【答案】C【分析】化简已知代数式,利用二项式展开式的通项公式可以求出展开式中2x 的系数.【详解】因为6662211(1)(1)(1)(1)x x x x x ++=++⨯+,则6(1)x +展开式中含2x 的项为2226C 15x x =;621(1)x x⨯+展开式中含2x 的项为442621C 15x x x ⨯=,故2x 的系数为151530+=,故选:C .9.(2016·四川·高考真题)设i 为虚数单位,则(x +i)6的展开式中含x 4的项为()A .-15x 4B .15x 4C .-20i x 4D .20i x 4【答案】A【详解】试题分析:二项式6()x i +的展开式的通项为616r r r r T C xi -+=,令64r -=,则2r =,故展开式中含4x 的项为2424615C x i x =-,故选A.【考点】二项展开式,复数的运算【名师点睛】本题考查二项式定理及复数的运算,复数的概念及运算也是高考的热点,几乎是每年必考的内容,属于容易题.一般来说,掌握复数的基本概念及四则运算即可.二项式6()x i +可以写为6()i x +,则其通项为66r r r C i x -,则含4x 的项为46444615C i x x -=-.10.(2015·全国·高考真题)()52x x y ++的展开式中,52x y 的系数为A .10B .20C .30D .60【答案】C【详解】在25()x x y ++的5个因式中,2个取因式中2x 剩余的3个因式中1个取x ,其余因式取y,故52x y 的系数为212532C C C =30,故选C.考点:本题主要考查利用排列组合知识计算二项式展开式某一项的系数.【名师点睛】本题利用排列组合求多项展开式式某一项的系数,试题形式新颖,是中档题,求多项展开式式某一项的系数问题,先分析该项的构成,结合所给多项式,分析如何得到该项,再利用排列组知识求解.11.(2015·陕西·高考真题)二项式()()1n x n N *+∈的展开式中2x 项的系数为15,则n =A .4B .5C .6D .7【答案】C 【详解】二项式()1n x +的展开式的通项是1C r rr n x +T =,令2r =得2x 的系数是2C n ,因为2x 的系数为15,所以2C 15n =,即,解得:6n =或5n =-,因为n +∈N ,所以6n =,故选C .【考点定位】二项式定理.12.(2015·湖南·高考真题)已知5的展开式中含32x 的项的系数为30,则a 等于().AB .C .6D .6-【答案】D 【详解】5215C 1r r r r r T a x -+=-(),令1r =,可得530a -=解得6a =-.故选:D.【点睛】本题主要考查了二项式定理的运用,属于容易题.13.(2015·湖北·高考真题)已知(1)n x +的展开式中第4项与第8项的二项式系数相等,则奇数项的二项式系数和为().A .122B .112C .102D .92【答案】D【详解】因为(1)n x +的展开式中第4项与第8项的二项式系数相等,所以,解得,所以二项式10(1)x +中奇数项的二项式系数和为.考点:二项式系数,二项式系数和.。
