2020春七年级数学下册 第九章 不等式与不等式组 9.2 一元一次不等式 9.2.1 一元一次不等
2020年-人教版七年级数学下册 学案 9.2 第4课时 一元一次不等式的应用--含答案

第9章不等式与不等式组9.2 一元一次不等式第4课时一元一次不等式的应用核心提要在列不等式解应用题的时候要注意:(1)要根据题目中的关键字(如“大于”“不大于”“至多”“不超过”等)所表示的不等关系列出________.(2)在设未知数的时候,不能出现“至多”“不超过”等字眼.典例精讲知识点:一元一次不等式的应用1.小明准备用22元钱买笔和笔记本,已知每支笔3元,每本笔记本2元,他买了3本笔记本后,其余的钱用来买笔,那么他最多可以买()A.3支笔B.4支笔C.5支笔D.6支笔2.某文具店计划购进学生用的甲、乙两种圆规80只,进货总价要求不超过384元.两种圆规的进价和售价如下表:甲种乙种进价(元) 4 5售价(元) a(6≥a>4) 7(1)问该文具店至少应购进甲种圆规多少只?(2)在全部可销售完的情况下,针对a的不同取值,应怎样的进货所获利润最大?变式训练变式1某种商品的进价为800元,出售时标价为1200元,后来由于该商品积压,商店准备打折销售,但要保证利润率不低于5%,则至多可打()A.6折B.7折C.8折D.9折变式2某蔬菜经营户从蔬菜批发市场批发蔬菜进行零价,其中西红柿与西兰花的批发价格与零售价格如表.蔬菜品种西红柿西兰花批发价(元/kg) 3.68零售价(元/kg) 5.414蔬菜当天全部售完后,一共能赚多少钱?(请列方程组求解)(2)第二天该经营户用1520元仍然批发西红柿和西兰花,要想当天全部售完后所赚钱数不少于1050元,则该经营户最多能批发多少千克的西红柿?基础巩固1.有10名菜农,每人种茄子3亩或辣椒2亩,已知茄子每亩可收入0.5万元,辣椒每亩可收入0.8万元,要使总收入不低于15.6万元,则最多只能安排________人种茄子.2.小王家鱼塘有可出售的大鱼和小鱼共800千克,大鱼每千克售价10元,小鱼每千克售价6元,若将这800千克鱼全部出售,收入可以超过6 800元,则其中售出的大鱼至少有多少千克?若设售出的大鱼为x千克,则可列式为:________________________.3.某大型超市从生产基地购进一批水果,运输及销售中估计有10%的苹果正常损耗,苹果的进价是每千克1.8元,商家要避免亏本,需把售价至少定为____元.4.为增强市民的节水意识,某市对居民用水实行“阶梯收费”:规定每户每月不超过月用水标准部分的水价为1.5元/吨,超过月用水标准量部分的水价为2.5元/吨.该市小明家5月份用水12吨,缴水费20元.请问:该市规定的每户月用水标准量是多少吨?5.某职业高中机电班共有学生42人,其中男生人数比女生人数的2倍少3人.(1)该班男生和女生各有多少人?(2)某工厂决定到该班招录30名学生,经测试,该班男、女生每天能加工的零件数分别为50个和45个,为保证他们每天加工的零件总数不少于1 460个,那么至少要招录多少名男学生?能力提升6.某小区为更好地提高业主垃圾分类的意识,管理处决定在小区内安装垃圾分类的温馨提示牌和垃圾箱,若购买3个温馨提示牌和4个垃圾箱共需580元,且每个温馨提示牌比垃圾箱便宜40元.(1)问购买1个温馨提示牌和1个垃圾箱各需多少元?(2)如果需要购买温馨提示牌和垃圾箱共100个,费用不超过8000元,问最多购买垃圾箱多少个?培优训练7.为了加强对校内外安全监控,创建荔湾平安校园,某学校计划增加15台监控摄像设备,现有甲、乙两种型号的设备,其中每台价格,有效监控半径如表所示,经调查,购买1台甲型设备比购买1台乙型设备多150元,购买2台甲型设备比购买3台乙型设备少400元.(2)若购买该批设备的资金不超过11 000元,且两种型号的设备均要至少买一台,学校有哪几种购买方案?(3)在(2)问的条件下,若要求监控半径覆盖范围不低于1 600米,为了节约资金,请你设计一种最省钱的购买方案.第4课时 一元一次不等式的应用----答案【核心提要】 不等式 【典例精讲】 1.C2.解:(1)设该文具店应购进甲种圆规x 个,则乙种圆规的个数为80-x 个, 由题意得,4x +5(80-x)≤384, 解得:x ≥16, 答:该文具店至少应购进甲种圆规16个; (2)设购进甲种圆规x 个,利润为y ,则y =x(a -4)+(7-5)(80-x)=(a -6)x +160, ∵6≥a >4,∴a -6≤0, 故x 越小,y 值越大, 当x =16时,y 值最大.答:该文具店应购进甲种圆规16个,乙种圆规64个,所获利润最大.【变式训练】1.B2.解:(1)设批发西红柿x kg ,西兰花y kg ,由题意得⎩⎪⎨⎪⎧x +y =3003.6x +8y =1 520, 解得:⎩⎪⎨⎪⎧x =200y =100 ,故批发西红柿200 kg ,西兰花100 kg ,则这两种蔬菜当天全部售完一共能赚:200×1.8+100×6=960(元),答:这两种蔬菜当天全部售完一共能赚960元;(2)设批发西红柿a kg ,由题意得,(5.4-3.6)a +(14-8)×1 520-3.6a8≥1 050,解得:a ≤100,答:该经营户最多能批发西红柿100 kg.【基础巩固】 1.42.10x +6(800-x)>6 800 3.24.解:设该市规定的每户每月标准用水量为x 吨,∵12×1.5=18<20, ∴x <12. 则1.5x +2.5(12-x)=20, 解得:x =10. 答:该市规定的每户每月标准用水量为10吨. 5.解:(1)设该班男生有x 人,女生有y 人,依题意得:⎩⎪⎨⎪⎧x +y =42,x =2y -3,解得:⎩⎪⎨⎪⎧x =27,y =15.∴该班男生有27人,女生有15人.(2)设招录的男生为m 名,则招录的女生为(30-m)名,依题意得:50m +45(30-m)≥1 460, 即5m +1 350≥1 460, 解得:m ≥22.答:工厂在该班至少要招录22名男生.【能力提升】6.(1)解:设购买1个温馨提示牌需要x 元,购买1个垃圾箱需要y 元,依题意得⎩⎪⎨⎪⎧3x +4y =580x =y -40,解得:⎩⎪⎨⎪⎧x =60y =100 答:购买1个温馨提示牌需要60元,购买1个垃圾箱需要100元. (2)解:设购买垃圾箱m 个,则购买温馨提示牌(100-m)个,依题意得60(100-m)+100m ≤8 000,解得m ≤50, 答:最多购买垃圾箱50个.【培优训练】7.解:(1)由题意得:⎩⎪⎨⎪⎧a -b =1503b -2a =400, 解得⎩⎪⎨⎪⎧a =850b =700;(2)设购买甲型设备x 台,则购买乙型设备(15-x)台,依题意得 850x +700(15-x)≤11 000, 解得x ≤313,∵两种型号的设备均要至少买一台,∴x=1,2,3,∴有3种购买方案:①甲型设备1台,乙型设备14台;②甲型设备2台,乙型设备13台;③甲型设备3台,乙型设备12台;(3)依题意得:150x+100(15-x)≥1 600,解得x≥2,∴x取值为2或3.当x=2时,购买所需资金为:850×2+700×13=10 800(元),当x=3时,购买所需资金为:850×3+700×12=10 950(元),∴最省钱的购买方案为:购买甲型设备2台,乙型设备13台.。
人教版七年级数学下册课件 第九章 不等式与不等式组 一元一次不等式 第2课时 一元一次不等式的应用

购买数量(件)
A
第一次 第二次
B
购买总费用(元)
2
1
55
1
3
65
解:(1)设 A 种商品的单价为 x 元,B 种商品的单价为 y 元,根据题 意,可得2xx++3yy= =5655, , 解得xy==1250,,
答:A 种商品的单价为 20 元,B 种商品的单价为 15 元
(2)设第三次购买商品A种a件,则购买B种商品(12-a)件,根据题意, 可得a≥2(2y=y=59940000,,
解得xy==13
500, 200,
答:每台 A 型电脑
的价格为 3 500 元,每台 B 型打印机的价格为 1 200 元
(2)设学校购买 a 台 B 型打印机,则购买 A 型电脑为(a-1)台,根据题 意,得 3 500(a-1)+1 200a≤20 000,解得 a≤5.答:该学校至多能购买 5 台 B 型打印机
9.某大型超市从生产基地购进一批水果,运输过程中质量损失10%, 假设不计超市其他费用,如果超市要想至少获得20%的利润,那么这种水 果的售价在进价的基础上应至少提高( B )
A.40% B.33.4% C.33.3% D.30%
10.马师傅计划用10天时间加工320个零件,前两天每天加工20个零件, 后改进了工作方式,结果提前一天完成了加工任务,马师傅在两天后每天 至少加工__4_0_个零件.
∵m=20a+15(12-a)=5a+180,∴当a=8时所花钱数最少,即购买 A商品8件,B商品4件
(1)求每台A型电脑和每台B型打印机的价格分别是多少元? (2)如果学校购买A型电脑和B型打印机的预算费用不超过20 000元,并 且购买B型打印机的台数要比购买A型电脑的台数多1台,那么该学校至 多能购买多少台B型打印机?
人教版七年级下册数学课件 第九章 不等式与不等式组 一元一次不等式 第1课时 一元一次不等式的解法

第九章 不等式与不等式组
9.2 一元一次不等式
第1课时 一元一次不等式的解法
1.(3 分)下列各式中,是一元一次不等式的是( B)
A.x2-2x>1
B.x3 -1>x-2 1
C.1x -2≥0 D.x+y2 <-1
2.(3 分)已知 xa-1+3<5 是关于 x 的一元一次不等式,则 a=_2__.
9.若点 P(3a-2,2b-3)在第二象限,则(C )
A.a>23 ,b>32
B.a>23 ,b<32
C.a<23 ,b>32
D.a<23 ,b<32
10.(呼和浩特中考)若不等式2x+ 3 5 -1≤2-x 的解集中 x 的每一个值, 都能使关于 x 的不等式 3(x-1)+5>5x+2(m+x)成立,则 m 的取值范围是(C )
三、解答题(共 36 分) 13.(10 分)当 x 取何值时,代数式6x-4 1 -2x 的值:(1)大于-2;(2)不大于 1-2x.
解:(1)由题意,得6x-4 1 -2x>-2,解得 x<72 (2)由题意,得6x-4 1 -2x≤1-2x,解得 x≤56
14.(10 分)已知关于 x 的方程x+3m -2x-2 1 =m 的解为负数,求 m 的取值范围. 解:解方程得 x=-m+34 ,∵方程的解为负数,∴-m+34 <0,解得 m>34
6.(12分)解下列不等式,并在数轴上表示出解集: (1)3x-1≥2(x-1); 解:去括号,得3x-1≥2x-2,移项,得3x-2x≥-2+1,合并同类项,得x≥-1. 将不等式的解集表示在数轴上如下:
x-2 (2) 5
-ቤተ መጻሕፍቲ ባይዱ+2 4
>-3.
解:去分母,得2(x-2)-5(x+4)>-30,去括号,得2x-4-5x-20>-30, 移项,得2x-5x>-30+4+20,合并同类项,得-3x>-6, 系数化为1,得x<2.将不等式的解集表示在数轴上如下:
人教版 数学 七年级 下册 第九章 不等式与不等式组 知识点
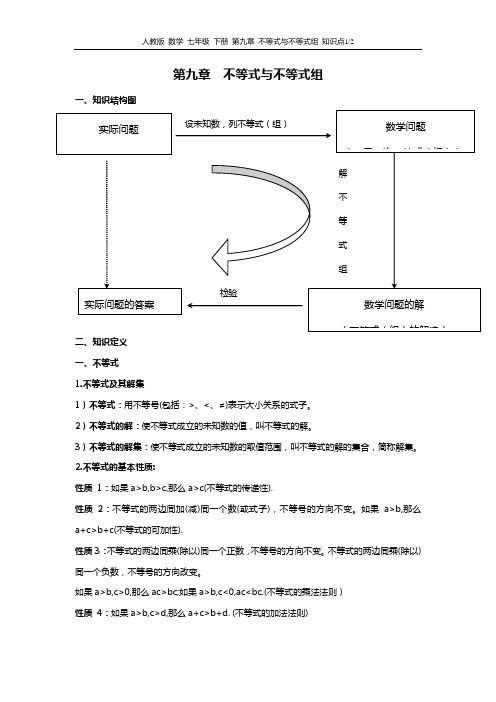
第九章不等式与不等式组一、知识结构图二、知识定义一、不等式1.不等式及其解集1)不等式:用不等号(包括:>、<、≠)表示大小关系的式子。
2)不等式的解:使不等式成立的未知数的值,叫不等式的解。
3)不等式的解集:使不等式成立的未知数的取值范围,叫不等式的解的集合,简称解集。
2.不等式的基本性质:性质 1:如果a>b,b>c,那么a>c(不等式的传递性).性质2:不等式的两边同加(减)同一个数(或式子),不等号的方向不变。
如果a>b,那么a+c>b+c(不等式的可加性).性质3:不等式的两边同乘(除以)同一个正数,不等号的方向不变。
不等式的两边同乘(除以)同一个负数,不等号的方向改变。
如果a>b,c>0,那么ac>bc;如果a>b,c<0,ac<bc.(不等式的乘法法则)性质 4:如果a>b,c>d,那么a+c>b+d.(不等式的加法法则)性质5:如果a>b>0,c>d>0,那么ac>bd.(可乘性)性质6:如果a>b>0,n∈N,n>1,那么an>bn,且.当0<n<1时也成立.(乘方法则)二、一元一次不等式1.一元一次不等式:含有一个未知数,未知数的次数是1的不等式。
2.解一元一次不等式的一般方法:可以先把其中的不等式逐条算出各自的解集,然后分别在数轴上表示出以两条不等式组成的不等式组为例,①若两个未知数的解集在数轴上表示同向左,就取在左边的未知数的解集为不等式组的解集,此乃“同小取小”②若两个未知数的解集在数轴上表示同向右,就取在右边的未知数的解集为不等式组的解集,此乃“同大取大”③若两个未知数的解集在数轴上相交,就取它们之间的值为不等式组的解集。
若x表示不等式的解集,此时一般表示为a<x<b,或a≤x≤b。
此乃“相交取中”④若两个未知数的解集在数轴上向背,那么不等式组的解集就是空集,不等式组无解。
人教版七年级数学下册 第九章 不等式与不等式组 一元一次不等式 第2课时 实际问题与一元一次不等式

5.(2021·焦作期末)一种苹果的进价是每千克1.9元,销售中估计有5%的苹果 正常损耗,商家把售价至少定为__2__元,才能避免亏本.
解:因为1.5×10=15<25,所以小明家这个月的用水量超过10立方米.设小明 家这个月的用水量至少为x立方米,根据题意有15+2(x-10)≥25,解得x≥15,答: 他家这个月的用水量至少是15立方米
11.(2021·河北)已知训练场球筐中有A,B两种品牌的乒乓球共101个,设A品 牌乒乓球有x个.
(1)淇淇说:“筐里B品牌球是A品牌球的两倍.”嘉嘉根据她的说法列出了方 程:101-x=2x.请用嘉嘉所列方程分析淇淇的说法是否正确;
(2)据工作人员透露:B品牌球比A品牌球至少多28个,试通过列不等式的方法 说明A品牌球最多有几个.
解:(1)嘉嘉所列方程为 101-x=2x,解得 x=3323 ,又∵x 为整数,∴x=3323 不合题意,∴淇淇的说法不正确 (2)设A品牌乒乓球有x个,则B品牌乒乓球有(101-x)个,依题意,得101-x- x≥28,解得x≤36.5,又∵x为整数,∴x可取的最大值为36.答:A品牌球最多有36 个
8.红旗中学组织本校师生参加红色研学实践活动,现租用11辆甲、乙两种型 号的大客车(每种型号至少一辆)送549名学生和11名教师参加此次实践活动.
甲、乙两种型号的大客车的载客量如表所示:
则最多可以租用多少辆甲种型号大客车?有几种租车方案?
解:设租用x辆甲种型号大客车,则租用(11-x)辆乙种型号大客车,依题意得: 40x+55(11-x)≥549+11,解得x≤3,∴x可以取的最大值为3.∵x为正整数,∴x= 1或2或3,∴有3种租车方案.答:最多可以租用3辆甲种型号大客车.有3种租车 方案,方案1:租用1辆甲种型号大客车,10辆乙种型号大客车;方案2:租用2辆 甲种型号大客车,9辆乙种型号大客车;方案3:租用3辆甲种型号大客车,8辆乙 种型号大客车
2023~2024学年 9.2 课时1 一元一次不等式(15页)

问题(6) 对比第(1)小题和第(2)小题的解题过程,系数 化为1时应注意些什么?
要看未知数系数的符号,若未知数的系数是正数, 则不等号的方向不变;若未知数系数是负数,则不 等号的方向要改变.
问题7 解一元一次不等式每一步变形的依据 是什么?
步骤
依据
去分母 去括号 移项 合并同类项 系数化为1
(1) 2(1 x) 3
解:去括号,得 移项,得
合并同类项,得
系数化为1,得
2
例 解下列不等式,并在数轴上表示解集:
(2) 2 x 2x 1
2
3
问题(3)
对比不等式
2 x 2x 1
2
3
与
2(1 x) 3的两边,
它们在形式上有什么不同?
问题(4)
怎样将不等式 2 x 2x 1 变形,使变形后的不等
第九章 不等式与不等式组 9.2 课时1 一元一次不等式
学习目标
1. 了解一元一次不等式的概念,掌握一元一次不等式的解法. 2. 在依据不等式的性质探究一元一次不等式解法过程中,加深 对化归思想的体会.
引入概念
问题1 观察下面的不等式,它们有哪些共同特征?
x 7 26, 3x 2x 1,
4x 3, 2 x 50
不等式的性质2 去括号法则 不等式的性质1 合并同类项法则 不等式的性质2或3
问题8 解一元一次不等式和解一元一次方程 有哪些相同和不同之处?
相同之处: 基本步骤相同:去分母,去括号,移项,合并同类项, 系数化为1. 基本思想相同:都是运用化归思想,将一元一次方程 或一元一次不等式变形为最简形式.
3
一元一次不等式的概念: 含有一个未知数,未知数次数是1的不等式,叫做一元一
初中数学 人教版七年级下册 9.2一元一次不等式 课件

⑤
两边同除以a
不等式的基本性质2,3
写不等式的解时,要把表示未知数的字母写在不等号的左边。
练习反馈
4.解下列不等式,并在数轴上表示解集.
(1) -5x ≤10 ;
x ≥ -2
(2)4x-3 < 10x+7 .
x
>
-
5 3
(3) 3x -1 > 2(2-5x) ;
5
x > 13
(4) x 32≥2x23
合并同类项,得 系数化为1,得
2x 1 x 1
2
移项,得 合并同类项,得 系数化为1,得
3x 4x 2 6, x 8,
x 8.
归纳总结 归纳解不等式的一般步骤,并指出每个步骤的根据,完成下表.
步骤
根据
①
去分母
不等式的基本性质2,3
②
去括号
去括号法则
③
移项
不等式的基本性质1
④
合并同类项
合并同类项法则
-5x >-10
x=2
系数化为1
x<2
总结归纳
解一元一次不等式与解一元一次方程的依据和步骤有什么异同点?
相同之处:
议
基本步骤相同:去分母,去括号,移项,合并同类项,
一 议
系数它化们为的1依这.据些不步相骤同中. ,要特别注意的是:
解一元一不次等方式程两的边依都乘(或除以)同一个 据是等式负的数性,质必,须解改变不等号的方向.这是 一元一次与不解等一式元的一依次方程不同的地方.
✓ (2)5x+3<5(x-y) ✓
✕ (4)x(x–1)< x2 -2x ✓
✕ (6) x2-3x-5<6
七年级下册数学第九章《不等式与不等式组》教案

9.1.1不等式及其解集学习目标知识:不等式及其解集和一元一次不等式。
方法:渗透数形结合的思想。
情感:培养学生的数感,促进合作交流意识的形成。
学习重点:不等式、不等式解与解集的意义,并把解集正确地表示在数轴上。
学习难点:正确理解不等式的解集意义。
.教具准备:多媒体课件。
教学流程一、【情境引入】1、ppt出示题目:某班同学去植树,原计划每位同学植树4棵,但由于某组的10名同学另有任务,未能参加植树,其余同学每位植树6棵,结果仍未能完成计划任务,若以该班同学的人数为x,此时的x应满足怎样的关系式?依题意得4x>6(x−10)2、你能举出生活中不相等关系的一些实例吗?3、怎样来表示这些不等关系呢?这就是我们今天探讨的问题。
(板书课题:不等式及其解集)。
二、【自主探究】学生阅读121——123页。
自读提纲:(1)什么叫做不等式及不等式的解?(2)什么叫做不等式的解集?什么叫做一元一次不等式?(3)怎样在数轴上表示不等式的解集?三、【合作探究】以上问题让学生展示,先让学困生回答,中等生补充,优等生总结;教师适当指导汇总得出:1、不等式的概念:用“<”“>”“≠”表示大小关系的式子叫做不等式。
(让学生回忆等式的概念。
)2、使不等式成立的未知数的值叫做不等式的解。
3、使不等式成立的所有的解的集合叫做不等式的解集。
4、含有一个未知数,未知数的次数是1的不等式,叫做一元一次不等式。
(让学生回忆一元一次方程的概念。
)例1、用不等式表示。
(1)a与1的和是正数。
(2)y的2倍与1的和大于3;(3)x的一半与x的2倍的和是非正数;(4)c与4的和不大于-2;2x>50的解例2、判断下列数中哪些是不等式376,73,79,80,74,75.1,90,60例3、在数轴上表示下列不等式的解集(1)x>1;(2)x≥1;(3)x<1;(4)x≤1教师分析指点:按画数轴,定界点,走方向答。
五、【当堂训练】1、课本P123页1,2,3。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(5)x2>2;
(6)x4+x2+x>1.
(4)2x+2≥2x;
解:(1)(3)(6)是一元一次不等式;(2)(4)(5)不是一元一次不等式.
-3-
一元一次不等式的解集
同步考点手册 P33
3.下列未知数的值中,是一元一次不等式 3-2x<7 的解的是( C )
A.x=-4
B.x当 y 为何值时,x<12? 解:由方程 2x-3-y=0 移项,得 2x=y+3,所以 x=y+2 3.令 x<12得y+2 3 <12,所以 y+3<1,解得 y<-2,所以当 y<-2 时,x<12.
-16-
13.已知 3m-2x3+2m>1 是关于 x 的一元一次不等式. (1)求 m 的值; 解:∵3m-2x3+2m>1 是关于 x 的一元一次不等式,∴3+2m=1,解得 m=-1. (2)求出不等式的解集,并把解集表示在数轴上. 解:由(1)可知,题目中的不等式是-3-2x>1,-2x>4,解得 x<-2.
第九章 不等式与不等式组 9.2 一元一次不等式 第1课时 一元一次不等式
-1-
一元一次不等式的定义
1.下列不等式是一元一次不等式的是( A )
A.2x+1>3
B.2+x2<2x
C.2x-2>3x
D.3-x=78
同步考点手册 P33
-2-
2.判断下列各式是否是一元一次不等式?
(1)-x≥5; (2) y-3x<0;(3)x+1<0;
-7-
7.解下列不等式,并把它们的解集分别表示在数轴上. (1)5x>-10; 解:两边同时除以 5,得 x>-2.这个不等式的解集在数轴上表示为:
(2)-3x+12≤0; 解:移项,得-3x≤-12,两边都除以-3,得 x≥4,这个不等式的解 集在数轴上表示为:
-8-
(3)x-2 1<4x3-5; 解:去分母,得 3(x-1)<2(4x-5),去括号,得 3x-3<8x-10,移项、 合并同类项,得 5x>7,两边都除以 5,得 x>75,不等式的解集在数轴上表
D.x=-8
-4-
4.(1)已知关于 x 的不等式3-x+13a<3-2 x的解为 x<7,求 a 的值; 解:由3-x+13a<3-2 x得:x<39+7 2a,又∵此不等式的解集为 x<7,故 39+7 2a=7,∴39+2a=49,∴a=5. (2)如果(a+1)x>a+1 的解为 x<1,求 a 的取值范围. 解:∵(a+1)x>a+1 的解集为 x<1,∴a+1<0,∴a<-1.
解集在数轴上表示如图.
14.是否存在整数 m,使关于 x 的不等式 1+m3x2>mx +m92与x-23+m<x +1 的解集相同,如果存在,求出 m 的整数值和不等式的解集;如果不存 在,请说明理由.[提示:m2-9=(m+3)(m-3)]
解:假设存在符合条件的整数 m,由x-23+m<x+1,解得 x>m-2 5. 又由 1+m3x2>mx +m92,整理得:m2+3x>mx+9,所以 mx-3x<m2-9,(m -3)x<(m+3)(m-3).由不等式的解集相同,可得当 m<3 时,x>m+3. 因与第一个不等式的解集同解,故 m+3=m-2 5,所以 m=-11,把 m=- 11 代入两个已知不等式,都解得 x>-8,因此存在符合题意的整数 m,当 m=-11 时,两个不等式的解相同,解集为 x>-8.
同步考点手册 P34
-11-
9.若 x=2 是不等式 2x-a-2<0 的一个解,则 a 可取的最小正整数为
(B) A.2
B.3
C.4
D.5
-12-
10. 求不等式 3(x+1)≥5x-9 的非负整数解. 解:∵3(x+1)≥5x-9,∴3x+3≥5x-9,∴-2x≥-12,x≤6.故不等 式 3(x+1)≥5x-9 的非负整数解为:0,1,2,3,4,5,6.
-13-
判断一元一次不等式时忽视隐含条件
11.下列不等式中,是一元一次不等式的是( C )
A.2x2-5>0
B.1x+x<5
C.-5y+8>0
D.2x+3>2(1+x)
-14-
12.已知 x,y 满足方程 2x-3-y=0,试求: (1)当 x 为何值时,y>0? 解:由方程 2x-3-y=0 移项,得 y=2x-3.令 y>0 得 2x-3>0,解得 x>32.所以当 x>32时,y>0.
-5-
一元一次不等式的解法
同步考点手册 P34
5.不等式 4-2x>0 的解集在数轴上表示为( D )
-6-
6.解不等式:x-2 2≤7-3 x. 解:去分母,得 3(x-2)≤2(7-x).去括号,得 3x-6≤14-2x.移项, 得 3x+2x≤14+6.合并同类项,得 5x≤20.两边都除以 5,得 x≤4.
示为:
-9-
(4)x+2 7-1<3x2+2. 解:去分母,得 x+7-2<3x+2,移项、合并同类项,得 2x>3,两 边都除以 2,得 x>32,不等式的解集在数轴上表示为:
-10-
一元一次不等式的特殊解
8.不等式 3x-5<3+x 的正整数解有( C )
A.1 个
B.2 个
C.3 个
D.4 个
