2.5逻辑函数的化简(2011)
合集下载
2011数字电子技术试题及答案(题库)
2011数字电子技术基础试题（一）一、填空题 : （每空1分，共10分）1． (30.25) 10 = ( ) 2 = ( ) 16 。
2 . 逻辑函数L = + A+ B+ C +D = 。
3 . 三态门输出的三种状态分别为：、和。
4 . 主从型JK触发器的特性方程= 。
5 . 用4个触发器可以存储位二进制数。
6 . 存储容量为4K×8位的RAM存储器，其地址线为条、数据线为条。
二、选择题： (选择一个正确的答案填入括号内，每题3分，共30分 )1.设图1中所有触发器的初始状态皆为0，找出图中触发器在时钟信号作用下,输出电压波形恒为0的是：（）图。
图 12.下列几种TTL电路中，输出端可实现线与功能的电路是（）。
A、或非门B、与非门C、异或门D、OC门3.对CMOS与非门电路，其多余输入端正确的处理方法是（）。
A、通过大电阻接地（>1.5KΩ）B、悬空C、通过小电阻接地（<1KΩ）D、通过电阻接VCC4.图2所示电路为由555定时器构成的（）。
A、施密特触发器B、多谐振荡器C、单稳态触发器D、T触发器5.请判断以下哪个电路不是时序逻辑电路（）。
图2A、计数器B、寄存器C、译码器D、触发器6．下列几种A/D转换器中，转换速度最快的是（）。
图2A、并行A/D转换器B、计数型A/D转换器C、逐次渐进型A/D转换器D、双积分A/D转换器7．某电路的输入波形 u I 和输出波形 u O 如图 3所示，则该电路为（）。
图3A、施密特触发器B、反相器C、单稳态触发器D、JK触发器8．要将方波脉冲的周期扩展10倍，可采用（）。
A、10级施密特触发器B、10位二进制计数器C、十进制计数器D、10位D/A转换器9、已知逻辑函数与其相等的函数为（）。
A、B、C、D、10、一个数据选择器的地址输入端有3个时，最多可以有（）个数据信号输出。
A、4B、6C、8D、16三、逻辑函数化简（每题5分，共10分）1、用代数法化简为最简与或式Y= A +2、用卡诺图法化简为最简或与式Y= + C +A D，约束条件：A C + A CD+AB=0四、分析下列电路。
第二章 逻辑函数及其简化
L 表示。
利用反演规则，可以非常方便地求得一个函数的反函数 求函数 L AC B D 的反函数：
解： L ( A C) ( B D) 例 求函数 解：
L A B D
在应用反演规则求反函数时要注意以下两点： （1）保持运算的优先顺序不变，必要时加括号表明；
A B
如：串联开关电路
逻辑符号和表达式
A B C
P
P = A ·B · C=A×B ×C = A B C
&
真值表：列出输入的所
有状态和输出值。
逻辑1: 表示开关”闭”,灯的” 亮”. 逻辑0: 表示开关”断”,灯的”
A B
断 断 断 闭 闭 断 闭 闭
P
灭 灭 灭 亮
A B 0 0 0 1 1 0 1 1
B
逻辑符号和表达式
A B C ≥1
真值表：
A B 0 0 0 1 P 0 1 1 1
P = A + B+ C
或逻辑也称逻辑加运算，相当于 集合中的并集，根据并集的概念， 不难确定逻辑加的运算规则： A+B = P 0+ 0 = 0 0+ 1 = 1 1+ 0 = 1
A B P 00 0 0 1 1 1 0 1
第二章 逻辑函数及其简化
2.1 基本概念
2.2 逻辑代数 2.3 逻辑函数的表示方法 2.4 代数法化简逻辑函数 2.5 逻辑函数的卡诺图化简
2.1 基本概念
逻辑门电路：在数字电路中，实现逻辑运算功能的电路。 如：与门、或门、非门。 逻辑状态：在数字电路中；把一个状态分为两种，一种 状态叫逻辑1，另一种状态叫逻辑0 。
名称
逻辑函数的化简
卡诺图化简法：
优：简单、直观、有一定的步骤、不易出错 缺: ５变量以上无法用
作 业
• p.121 • p.121 3.2.2 (a)(b)(e)(g) 3.3.4
异或逻辑
同或逻辑
定义：只有当两个输入变量A、 定义：只有当两个输入变量A、 B取值相异时，输出为1 B取值相同时，输出为1 逻辑式—— L A B 逻辑符号
国 标
逻辑式—— 逻辑符号
国 标
L=A ⊙B
A B
=1
参与运算 为两变量
L
A B
A B
=1 L
A 国 B
外
L
国 外
L
注意
当多个变量作异或运算时： 若变量中有奇数个1，则运算结果为1； 若变量中有偶数个1，则运算结果为0。
当多个变量作同或运算时： 若变量中有偶数个0，则运算结果为1； 若变量中有奇数个0，则运算结果为0。
方法： （1）找出真值表中使逻辑函数Z=1的那些输入变量 取值的组合； （2）每组输入变量取值的组合对应一个乘积项，其中 取值为1的写为原变量，取值为0的写为反变量；
（3）将这些乘积项相加，即得Z的逻辑函数式。
练习
A
0 0 0 0
B
0 0 1 1
C
0 1 0 1
Z
1 0 1 0
1 1
1 1
0 0
1 1
3.1.3
函数
逻辑函数的简化
一、化简的必要性
Y A B C A B C A BC A B C A B C
化简后
Y B AC
降低成本
必要性 逻辑电路所用门的数量少 每个门的输入端个数少 提高电路的工作 速度和可靠性 逻辑电路构成级数少 逻辑电路保证能可靠地工作
第三讲 逻辑函数的公式化简法
(二) 逻辑函数的代数化简法
（1）并项法
运用公式 A A 1，将两项合并为一项，消去一个变量。如
L A(BC BC) A(BC BC) ABC ABC ABC ABC AB(C C) AB(C C)
AB AB A(B B) A
A BC CB BD DB ADE(F G)
（利用 A AB A B ）
A BC CB BD DB
（利用A+AB=A） （配项法）
A BC(D D) CB BD DB(C C)
A BCD BC D CB BD DBC DBC
A BC D CB BD DBC
（利用A+AB=A）
A C D(B B) CB BD
A C D CB BD
（利用 A A 1 ）
例3
化简逻辑函数： L AB BC BC AB
解法1：
解法2：
由上例可知，逻辑函数的化简结果不是唯一的。代数化 简法的优点是不受变量数目的限制。 缺点是：没有固定的步骤可循；需要熟练运用各种公式 和定理；在化简一些较为复杂的逻辑函数时还需要一定的技 巧和经验；有时很难判定化简结果是否最简。
知识点导入
这一讲，我们将学习如何使用代数法来 化简逻辑函数，从而使逻辑电路达到最简 洁合理。 首先，我们要熟悉和掌握逻辑代数的基 本公式和基本定律；在此基础上，大家要 灵活运用这些公式和定律对逻辑函数进行 化简。
一、逻辑代数中的基本公式和定律 (一) 基本公式 1．逻辑变量和常量的关系
2．与普通代数相似的定律 1) 交换律
二、逻辑函数的化简与变换（代数法） (一)化简与变换的意义 对逻辑函数进行化简和变换，可以得到最 简的逻辑函数式和所需要的形式，设计出最 简洁的逻辑电路。 1．逻辑函数的五种表达式 除了与或表达式外还有或与表达式、与 非—与非表达式、或非—或非表达式、与或 非表达式等。
逻辑函数的公式法化简
=AB + (A + B )C
=AB + ABC
=AB + C
数字电路与逻辑设计
电子工 程学院
School of Electronic Engineering
厚夜博学
第二章逻辑函数及其简化
数字电路与逻辑设计
4 .配项法：
利用公式 A + A = 1、A - A = 0、AB + AC = AB + AC + BC，将某一
数字电路与逻辑设计
! !!在化简逻辑函数时，要灵活运用上述方法，才能将逻辑函数化为最简。
例7:化简逻辑函数： L = AD + AD + AB + AC + BD + ABEF + BEF
解：L = A + AB + AC + BD + ABEF + BEF
（利用 A + A = 1 ）
=A + AC + BD + BEF （利用A+AB=A）
乘积项展开为两项，或添加某乘积项，再与其它乘积项进行合并化简。
例 6： L = AB + AC + BCD
=AB + AC + BCD( A + A)
=AB + AC + ABCD + ABCD
=AB + AC
电子工 程学院
School of Electronic Engineering
厚夜博学
第二章逻辑函数及其简化
=AC+CD
电子工 程学院
School of Electronic Engineering
=AB + ABC
=AB + C
数字电路与逻辑设计
电子工 程学院
School of Electronic Engineering
厚夜博学
第二章逻辑函数及其简化
数字电路与逻辑设计
4 .配项法：
利用公式 A + A = 1、A - A = 0、AB + AC = AB + AC + BC，将某一
数字电路与逻辑设计
! !!在化简逻辑函数时，要灵活运用上述方法，才能将逻辑函数化为最简。
例7:化简逻辑函数： L = AD + AD + AB + AC + BD + ABEF + BEF
解：L = A + AB + AC + BD + ABEF + BEF
（利用 A + A = 1 ）
=A + AC + BD + BEF （利用A+AB=A）
乘积项展开为两项，或添加某乘积项，再与其它乘积项进行合并化简。
例 6： L = AB + AC + BCD
=AB + AC + BCD( A + A)
=AB + AC + ABCD + ABCD
=AB + AC
电子工 程学院
School of Electronic Engineering
厚夜博学
第二章逻辑函数及其简化
=AC+CD
电子工 程学院
School of Electronic Engineering
逻辑函数及其简化
消去法
运用吸收律 A AB A B 消去多余因子。
L A AB BE A B BE ABE
L AB AC BC
AB A B C
AB ABC
AB C
AB AB C C ABC ABC
AB AC AB AC BC
将某一乘积项展开为两项，或添加某乘积项，再与其它乘积项 进行合并化简。
AB
A
C 00 01 11 10
00 0 1 0
C1 0 1 1 1
B
从逻辑表达式到卡诺图
（1）如果表达式为最小项表达式，则可直接填入卡诺图,方法如下：
逻辑函数包含的最小项，其对应的方格填1。 逻辑函数不包含的最小项，其对应的方格填0。
用卡诺图表示3变量逻辑函数： F ABC ABC ABC ABC
所以：F F * * AC B D B F
不受变量数目的限制。
没有固定的步骤可循； 需要熟练运用各种公式和定理； 复杂的逻辑函数化简时需要技巧和经验； 有时很难判定化简结果是否最简。
1. 逻辑函数化简的意义和目标； 2. 逻辑函数的化简方法； 3. 公式法化简的方法和步骤。
逻辑函数的 卡诺图法化简
从真值表到卡诺图
已知某逻辑函数的真值表，用卡诺图表示该逻辑函数。
解 该函数有3个变量，先 画出3变量卡诺图，然 后根据真值表将8个最 小项的取值0或者1填入 卡诺图中对应的8个方 格中即可。
真值表
ABC L
000 0 001 0 010 0 011 1 100 0 101 1 110 1 111 1
A AC BD BEF （利用 A AB A ） A C BD BEF （利用 A AB A B ）
化简函数
F A A B A C B D A C E F B F D E F
2.5 逻辑函数表达式的形式 2.6 逻辑函数的化简方法
20
例1
F1 = ABC + AB C =BC (A+ A) =BC
例2. 化简函数 F = A BC + AC + B C 解： = + +
F A B C AC B C = A BC + A + B ）C （
= A BC + A BC =C
21
2. 吸收法 利用公式： 吸收多余项。 利用公式：A+AB= A ，吸收多余项。 例. 化简函数 解：
14
三变量最小项的真值表
m0 m1 m2 m3 m4 m5 m6 m7 ABC ABC ABC ABC ABC ABC ABC ABC ABC 000 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 001 010 0 0 0 0 1 0 0 0 011 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 100 101 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 110 0 0 0 0 0 0 0 1 111
19
2.6 逻辑函数的化简方法 与或式最简的标准: 两个最少原则) 与或式最简的标准:(两个最少原则) 与项个数最少; 1) 与项个数最少; 每个与项中的变量个数最少. 2) 每个与项中的变量个数最少. 2.6.1 逻辑函数的代数化简方法： 2.6.1 逻辑函数的代数化简方法： 1、并项法 利用公式 AB+AB =B 可将函数的两个与项合并成一项。 可将函数的两个与项合并成一项。
= B( A + C ) + B = A+ B +C
24
例. 化简函数
F = AB + A B + ABCD + A B CD
逻辑函数的卡诺图化简
F ( A, B,C) m1 m4 m6
1 1 0 01
=ABC+ABC+ABC
图 2.6.4
F ( A, B,C) M 0 M 2 M3 M5 M 7 =( A + B + C )( A + B + C )( A + B + C )
( A + B + C )( A + B + C )
2.5 逻辑函数的卡诺图化简 ：
1.逻辑函数的卡诺图表示 (1) 卡诺图的构成
卡诺图实质上是将逻辑函数的最小项按逻 辑相邻的原则排列而成的方格图。
1
两个特点： 1、将真值表中的变量分成两组，构成两维图表 。一个方格对应一个最小项（对应两轴上的变 量）。 2、行、列的组合排列顺序按循环码排列。（几 何相邻、对称相邻和头尾相邻）。 约定：高位权变量在斜下角。
0
11
1
11
7
③ 方法三：观察法 方法：在包含乘积项中全部变量的小格中填 1 例2.6.12 试将 F(A,B,C,D) = ABCD + ABD + AC 用卡诺图表示。
解：
CD
AB 00 01 11 10 00
01 1 1
11 1
1 1 图 2.6.5
10
11
8
练习：将F（ABCD）=ABCD + BC D +AC + A 添入卡诺图。
解：
CD AB 00 01 11 10
00 1 1
01 1 1
11 1 1 1 1 10 1 1 1 1
9
b. 一般或与式的卡诺图填写方法 方法：在包含和项中全部变量的小格中填 0 例2.6.13 试将 F(A,B,C,D) = (A+B+C+D)(A+B+D) 用卡诺图表示。
电工电子技术-逻辑函数的化简
（2）吸收法
运用公式 A AB A 消去多余的项，其中，A、B可以是
任意一个复杂的逻辑式。例如：
Y1 AB AC DEB AB
Y2 AB ABC ABD AB D E AB AB C D D E AB
（3）消去法
运用公式 A AB A B 消去多余的因子。例如：
例如：逻辑函数Y的卡诺图。 Y ABCD ABCD ABCD ABCD
ABCD ABCD ABCD ABCD
（3）用卡诺图化简逻辑函数式 使用卡诺图化简逻辑函数所依据的原理是：具有相邻性 的最小项可以合并消去不同的因子。 ①2个相邻的最小项结合（用一个包围圈表示），可以消 去1个取值不同的变量而合并为1项，如下图所示。
00 01 11 10 00
01 11 10
②4个相邻的最小项结合（用一个包围圈表示），可以消 去2个取值不同的变量而合并为l项，如下图所示。
00 01 11 10 00
01 11 10
③8个相邻的最小项结合（用一个包围圈表示），可以消 去3个取值不同的变量而合并为l项，如下图所示。
00 01 11 10 00
②化简具有无关项的逻辑函数 在卡诺图中用×表示无关项。使用卡诺图化简逻辑函数 式时，要充分利用无关项可以当0也可以当1的特点，尽量扩 大卡诺圈，使逻辑函数式更简。
（2）卡诺图
卡诺图就是将n变量的全部最小项各用一个小方块表示，
并使具有逻辑相邻性的最小项在几何位置上也相邻的排列起 来所得的图形。下图所示为2到4变量最小项的卡诺图。
若要画出某一逻辑函数的卡诺图，只需将该逻辑函数式 化为最小项之和的标准形式后，在卡诺图中这些最小项对应 的位置上填入1，在其余的位置上填入0即可。
1．公式化简法
逻辑函数的公式化简法(经典实用)
逻辑函数的公式化简法（经典实用）逻辑函数公式化简法是一种在数字逻辑设计中常用的方法，用于简化逻辑函数表达式，以便更有效地进行逻辑电路设计。
以下是一些经典实用的逻辑函数公式化简法：
1.摩根定律
摩根定律可以将两个逻辑函数表达式进行等价转换。
它有两个版本：
① 0-1律：¬(A+B) = ¬A * ¬B
② A律：¬(A*B) = ¬A + ¬B
使用摩根定律可以将复杂的逻辑函数表达式转换为更简单的形式。
2.吸收律
吸收律可以用来简化逻辑函数表达式中的冗余项。
它有两个版本：
① A+AB=A
② A+A'B=A+B
使用吸收律可以消除逻辑函数表达式中的冗余项，使表达式更简洁。
3.分配律
分配律可以将逻辑函数表达式中的括号展开，使表达式更易于分析。
它有两个版本：
① A*(B+C)=AB+AC
② A+(B C)=(A+B)(A+C)
使用分配律可以简化逻辑函数表达式中的括号，使表达式更简洁。
4.反演律
反演律可以用来求得一个逻辑函数的反函数。
它在数字逻辑设计中非常有用，因为它允许我们在一个逻辑函数和它的反函数之间进行转换。
反演律的公式为：A' * (A * B) = B。
通过使用以上经典实用的逻辑函数公式化简法，我们可以将复杂的逻辑函数表达式转换为更简单的形式，从而更有效地进行逻辑电路设计。
知识点1.逻辑函数化简的意义及最简式
逻辑函数的常用表达式：
F=AB+AC =(A+C)(A+B) =AB·AC =A+C+A+B =AB+AC
与或式
或与式 与非－与非式 或非－或非式 与或非式
最常用的为“与或”逻辑表达式。
逻辑函数的化简 ——化简的意义
最简“与或”式的标准： （1）所得与或表达式中，乘积项（与项）数目最少；
——门最少 （2）每个乘积项中所含的变量数最少。
逻辑函数的化简——化简的意义
一个逻辑函数有多种不同的表达式: F1=AB+AC F2=AB+AC+BC F3= ABC+ABC+ABC+ABC
+ F1
+ F2
Байду номын сангаас
+ F3
逻辑函数的化简 ——化简的意义
化简的意义:
① 节省元器件,降低电路成本; ② 提高电路可靠性; ③ 减少连线,制作方便。
逻辑函数的化简 ——化简的意义
——门的输入端最少
F1=AB+AC F2=AB+AC+BC F3= ABC+ABC+ABC+ABC
逻辑函数的化简
A BC (A B)(A C)
注意：在运用反演规则和对偶规则时，必须按照逻辑运算 的优先顺序进行：先算括号，接着与运算，然后或运算，最后非 运算，否则容易出错。
逻辑函数的表达式
一个逻辑函数的表达式可以有与或表达式、或与表达式、 与非-与非表达式、或非-或非表达式、与或非表达式5种表示 形式。
（１）利用公式Ａ＋ＡＢ＝Ａ，消去多余的项。
是另项是
Y1 AB ABCD(E F ) AB
多外的另
运用摩根定律 余 一 因 外 如
的个子一果
。乘，个乘
Y2 A B CD ADB A BCD AD B ( A AD) (B BCD) A B
积则乘积 项这积项
（２）利用公式Ａ＋ＡＢ＝Ａ+Ｂ，消去多余的变量。
m4 ABC、m5 ABC、m6 ABC、m7 ABC
最小项的编号： 把与最小项对应的变量取值当成二进制数，与之
相应的十进制数，就是该最小项的编号，用 mi 表示。 对应规律：原变量 1 反变量 0
ABC ABC ABC ABC ABC ABC ABC ABC
000 001 010 011 100 101 110 111
例如： Y AB AC
= AB• AC
与-或 与非-与非
A B•A C AB AC
AB AC AB• AC A B AC
与-或-非 或-与
A BA C A B A C或非-或非
2、最简与-或表达式
所谓最简与-或表达式，是指乘积项的个数是最少 的，而且每个乘积项中变量的个数也是最少的与-或 表达式。这样的表达式逻辑关系更明显，而且便于 用最简的电路加以实现（因为乘积项最少，则所用 的与门最少；而每个乘积项中变量的个数最少，则 每个与门的输入端数也最少），所以化简有其实用 意义。
逻辑化简(公式)
核心
二、逻辑函数的最简表达式及相互转换 最简与或式
Y AB AC BC
最简 与非-与非式 最简或与非式 最简与或非式 最简或与式
AB AC
( A B)( A C )
AB A C
A B A C
最简或非-或式 最简或非-或非式
AB AC BC
( A B) ( A C )
ABC ABC ABC ABC
最小项
标准与或式就是最小项之和的形式
标准与 或式
1. 最小项的概念： 包括所有变量的乘积项，每个变量均以原变量或反变量的形式出现且仅出现一次。
Y F ( A ,B )
AB AB AB
( 2 变量共有 4 个最小项)
AB
( 3 变量共有 8 个最小项)
ABC ABC ABC ABC ABC ABC AB C ABC
1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1
Y ABC ABC ABC ABC ABC
4. 最小项的编号： 把与最小项对应的变量取值当成二进制数，与之相应的十进制数，就是该最小项的 编号，用 mi 表示。
对应规律：原变量 1
反变量 0
ABC ABC ABC ABC ABC ABC AB C ABC
000 0 m0 001 1 m1 010 2 m2 011 3 m3 100 4 m4 101 5 m5 110 6 m6 111 7 m7
E BC D AE BC D
逻辑函数的化简
逻辑相邻
根据逻辑相邻的定义,不难由图8-10看出, 几何相邻的两个方格的最小项满足逻辑相邻性. 而不直接相邻的方格,但以卡诺图中心轴对称 的方格对应的最小项也满足逻辑相邻,如图810c中m0与m2,m0与m8,m3与m11等,称这种相 邻叫对称相邻.所以卡诺图可看作是立体图. 这是卡诺图巧妙之所在 .
由图8-12中可以看出卡诺图覆盖过的变量以0 和1两种取值出现,则该变量被消去;只以0出 现,则该变量用反变量表示;只以1出现,则 以原变量出现.卡诺圈越大消去的变量越多, 能够合并相邻项的一个正确的卡诺圈必须符合 以下要求.
(1) 卡诺圈里的1方格数必须是2m个.m=0,1, 2,…. (2) 2m个1方格必须排列成方阵或矩阵. (3) 2m个1方格必须是方格相邻或对称相邻的.
二,公式化简
1.并项法 利用 A + A =1将两项合并成一 项并消去一个变量. 2.吸收法 3.消去法 F= = 利用A+AB=A,消去多余项. 利用A+AB=A+B,消去多余项.
AB + A B + A BD + ABD
AB + AB + D AB + A B
= AB + A B + D
4. 配项法
二,三,四个变量的函数的卡诺图
a.二变量函数的卡诺图 b.三变量函数的卡诺图. c.四变量函数的卡诺图
构造卡诺图时应遵循以下规则
① n变量函数有2n个最小项,则卡诺图有2n方 格,即方格与最小项一一对应. ② 2n个方格必须排列成方阵或矩阵. ③ 变量分成两组,行变量和列变量组,行变 量为高位组,列变量为低位组.如图8-10中C 中,为行变量,为列变量. ④ 变量取值遵守反射码的形成规则.
逻辑函数的公式化简法
分配律 吸收律 分配律 吸收律 并项 吸收律
逻辑函数的公式化简法
化简逻辑函数表达式的方法 ◇公式化简法
◆没有固定的步骤可以遵循 ◆依赖于对逻辑代数公式的熟练掌握 ◆需要一些化简技巧 ◆难以确定被化简过的逻辑函数是否最简 ◇卡诺图化简法 √简便、直观
= B (A+AC)+ AC + BCD = B (A+C)+ AC + BCD = AB + AC + BC (1 + D) = AB + AC + BC = AB + AC
化简逻辑函数表达式的方法 公式化简法 卡诺图化简法
逻辑函数的公式化简法
(1) 并项、配项 A + A = 1 ； 1 = A + A
逻辑函数的公式化简法
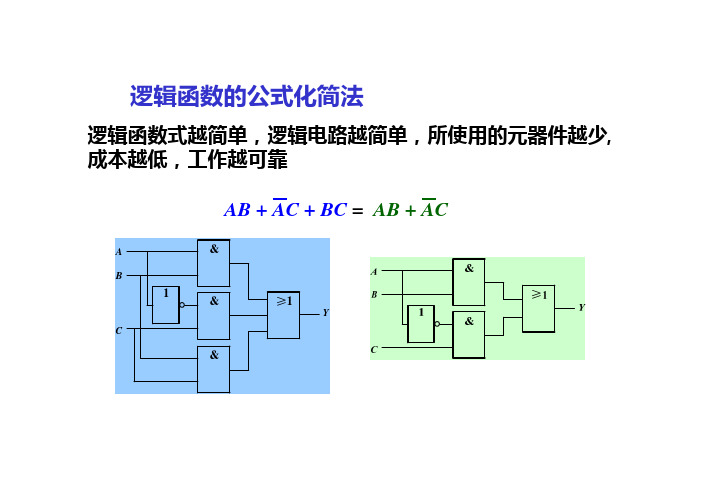
逻辑函数式越简单，逻辑电路越简单，所使用的元器件越少, 成本越低，工作越可靠
AB + AC + BC = AB + AC
A
&
B
1 &
C
&
1
Y
逻辑函数的公式化简法
☆最简与—或表达式 也最少
Y = AB + AC + BCD + ABC
分配律 吸收律
逻辑函数的公式化简法
Y = ABCD + ABD + BCD + ABC + BD + BC = ABC(D + 1)+ BD(A + 1)+ BCD + BC = ABC+ BD + BCD + BC = B(AC + C)+ B(D + CD) = B(A + C)+ B(D + C) = AB + BD + B(C + C) =B
卡诺图化简逻辑表达式
表2-18 三变量最小项的编号表
2019/6/8
7
（3）最小项表达式 任何一个逻辑函数都可以表示为最小项之和的
形式——标准与或表达式。而且这种形式是惟一的， 就是说一个逻辑函数只有一种最小项表达式。
例 将Y=AB+BC展开成最小项表达式。
解： Y AB BC AB(C C) (A A)BC
③圈要尽可能的大（消去的变量就越多）;
④ 圈要尽可能的少（与项就少）；
⑤一般是先圈孤立的1 ，再画只有一种圈法的1，最
后画大圈。
2019/6/8
20
（4）由卡诺圈写出最简与或表达式的方法：
① 将每个圈用一个与项表示 圈内各最小项中互补的因子消去， 相同的因子保留， 相同取值为1用原变量， 相同取值为0用反变量； ② 将各与项相或，便得到最简与或表达式。
2019/6/8
21
例2-10 用卡诺图化简逻辑函数 Y(A、B、C、D)=∑m(0,1,2,3,4,5,6,7,8,10,11) 解：
A
2019/6/8
相邻
22
2019/6/8
A
BC
相邻
23
A
BC
B D
Y A BC B D
2019/6/8
24
例2-11 化简图示逻辑函数。 解：
m(9,13)
（4）从一般形式表达式画卡诺图 先将表达式变换为与或表达式，则可画出卡诺图。
2019/6/8
15
2.5.3 用卡诺图化简逻辑函数
由于卡诺图两个相邻最小项中，只有一个变量 取值不同，而其余的取值都相同。所以，合并相邻 最小项，利用公式A+A=1，AB＋AB＝A，可以消去 一个或多个变量，从而使逻辑函数得到简化。
2019/6/8
7
（3）最小项表达式 任何一个逻辑函数都可以表示为最小项之和的
形式——标准与或表达式。而且这种形式是惟一的， 就是说一个逻辑函数只有一种最小项表达式。
例 将Y=AB+BC展开成最小项表达式。
解： Y AB BC AB(C C) (A A)BC
③圈要尽可能的大（消去的变量就越多）;
④ 圈要尽可能的少（与项就少）；
⑤一般是先圈孤立的1 ，再画只有一种圈法的1，最
后画大圈。
2019/6/8
20
（4）由卡诺圈写出最简与或表达式的方法：
① 将每个圈用一个与项表示 圈内各最小项中互补的因子消去， 相同的因子保留， 相同取值为1用原变量， 相同取值为0用反变量； ② 将各与项相或，便得到最简与或表达式。
2019/6/8
21
例2-10 用卡诺图化简逻辑函数 Y(A、B、C、D)=∑m(0,1,2,3,4,5,6,7,8,10,11) 解：
A
2019/6/8
相邻
22
2019/6/8
A
BC
相邻
23
A
BC
B D
Y A BC B D
2019/6/8
24
例2-11 化简图示逻辑函数。 解：
m(9,13)
（4）从一般形式表达式画卡诺图 先将表达式变换为与或表达式，则可画出卡诺图。
2019/6/8
15
2.5.3 用卡诺图化简逻辑函数
由于卡诺图两个相邻最小项中，只有一个变量 取值不同，而其余的取值都相同。所以，合并相邻 最小项，利用公式A+A=1，AB＋AB＝A，可以消去 一个或多个变量，从而使逻辑函数得到简化。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
BC = 0
F = ∑ m(2, 4) + ∑ d (3, 5, 6, 7) F = ∏ M (2, 4) • ∏ d (3, 5, 6, 7)
AC = 0 AB = 0
ABC = 0
任意项：某些输入变量的取值下，其函数值为1或为0都可以，并不影响 电路的功能，这些取值对应的最小项称为～。 约束项和任意项统称为无关项。
（3）将函数变换成与或非式
F = F = D + AB + AC
作业： 2-8（c，e，f） 2-9（2，4，6 ） 2-10（1，3，5 ） 2-11 （1，2） 2-12 2-13（1，2） 2-14（2）
13
AB
C
构成特点： （1）将输入变量分成两组，取值分别按格雷码排列。 （2）n个变量的K图有 2 个小方格，每格对应一个最小项或最大项。
n
卡诺图与真值表的一一对应关系：
AB
C
ABC ABC ABC A BC
A BC ABC ABC A BC
AB
A B C
最小项
mi
0 0 0 0 0 1 0 1 0
ABC ABC ABC ABC ABC ABC ABC ABC
ABC DE
00 01
11
1
1 1 1 1* 1 1
1
1 1* 1 1
1 1 1 1
1
1
1
10
9
（2）求最简或与式（圈0） 【例3】 将逻辑函数化简成最简或与式： F = ∑ m (1, 3, 4, 5, 6, 7, 9, 11, 13 ) 解： 1）作K图（填1） 2）圈K圈（圈0） 3）写或与式 （0——原变量，1——反变量）
消去A、B、D
4、 用卡诺图化简逻辑函数 （1）求最简与或式 化简的步骤： • 作出逻辑函数的卡诺图； • 圈卡诺圈； • 将每个卡诺圈中的最小项合并成相应的与项。 圈卡诺圈的原则： 在卡诺图上，以最少的卡诺圈数和尽可能大的卡诺圈覆盖所有填1的 方格。（即：最小覆盖原则） 注释： • 将 2 n个相邻的填1方格圈起来，圈子尽可能大； • 所有填1格都必须被圈过，在此前提下K圈的个数尽可能少； • 任何一个填1格可以被不同的K圈多次圈过，但如果在一个K圈中， 所有的1格均已被别的K圈圈过，则该圈为多余的。
1 1
1 1
0 1
0 1
0 1
0 1
0 1
0 1
0 1
F1
F2
F = F1 • F2
作业： 2-3（2，4，6 ） 2-5（1） 2-7（1，3，5，7） 2-9（1、3、5、7）只填K图 2-12
5
3、最小项合并规律 怎样利用卡诺图化简逻辑函数？进一步了解K图的特点。 逻辑相邻： 对于两个输入变量相同的最小项，若只有一个变量互补，其余变量均 相同， 则称这两个最小项逻辑相邻。 举例：
1 0 1 0
0 1 0 1 1 1 1 1 1 1 1 1 1 1
原则：分别寻找各与项中变量相交的小方格填1. （0——反变量，1——原变量）
（3）由或与式填卡诺图（填0） 举例：
F = ∏ M (0, 2, 6) = ( A + B + C )( A + B + C )( A + B + C )
吸收法：
A + AB = A
举例：
A + AB = A + B
AB + AC + BC = AB + AC
F = AB + AC + BC = AB + ( A + B )C = AB + ABC = AB + C
配项法：
A + A = A A + A = 1 AB + AC + BC = AB + AC
10
2.5.2 非完全描述的逻辑函数及其化简
1、非完全描述的逻辑函数 完全描述的逻辑函数：对于输入变量的每一组取值，逻辑函数都有确定的 值与之对应，这样的逻辑函数称为～。
非完全描述的逻辑函数：由于输入变量的某些取值，逻辑函数没有确定的 值与之对应，这样的逻辑函数称为～。
举例： 十字路口的红绿灯，正常工作时不允许有两个或两个以上的灯亮。 规定： A： 红灯 B：黄灯 C：绿灯
m0 m1 m2 m3 m4 m5 m6 m7
C
m0
m1
AB
m2 m3
m6 m7
m4 m5
0 1 1 1 0 0 1 0 1 1 1 0 1 1 1
C
0 1
2 3
6 7
4 5
2
CD 00 AB
01
11
10
00
01
11
0 4 12 8
1 5 13 9
3 7 15 11
2 6 14 10
ABC DE
00
举例：
F = AC + AD + BD + BC = AC + BC + ( A + B) D = AC + BC + ABD = AC + BC + AB + ABD = AC + BC + AB + D = AC + BC + D
（消去AB） （填AB）
1
2.5.2 卡诺图化简法
1、卡诺图的构成 举例：三变量卡诺图
AB
AB
C
0 1 0 1 0 1 1 1
C
1 1
0 1
0 1
0 1
举例：
F = ( A + C )( B + C )
原则：分别寻找各或项中变量相交的小方格填0. （0——原变量，1——反变量）
4
（4）复杂的混合形式填卡诺图 举例：
卡诺图的性质：
F = AB + BC + AC + [( A + B)( A + C )( B + C ) ⊕ AC ] F2 F3 F1
1、K图中所有的小方格填1时，F=1 K图中所有的小方格填0时，F=0 2、逻辑函数F的K图中，所有的小方格中的0换1，1换0，得到 F 的K图。 3、若 F = F1 ? F2 ，则F的卡诺图可由 F1和F2 的卡诺图运算得到。 即：相应小方格中的数分别进行运算。
AB
AB
C
C
AB
C
0 1
0 1
0 1
1
1 1
答案不唯一，还可以如红笔所示。
• 任何一个填1格可以被不同的K圈多次圈过，但每个K圈中至少有一个 填1格只被圈过一次。
8
【例3】
求 F = ∑ m(0, 4, 5, 6, 7, 8, 11, 13, 15, 16, 20, 21, 22, 23, 24, 25, 27, 29, 31)
的最简与或式。 解： 1） 作K图 2） 圈K圈 原则： 先从左半K图中只有 一种圈法的最小项圈 起，同时关注右半K 图中对称位置上的方 格是否可以同圈。
1 1 0 0 1 1 0 0
AB
C
1 1 0 0 0 0 1 1
3
（2）由与或式填卡诺图（填1） 举例：
F = ∑ m (0, 2, 4, 7, 9, 10, 12, 15)
AB 00 CD
F = A BC + ABC + D + AD
AB CD
01
11
10
00 01
11 10
1 0 0 1
1 0 1 0
AB 00 CD
01
11
10
00 01
11
0 1 1 0
1 1 1 1
0 1 0 0
0 1 1 0
F = ( B + D )( A + D )( A + B + C )
10
【例4】 求 F = ( A + B + C + D )( A + B )( A + C )C 的最简或与式。 解： 1）作K图（填0） 2）圈K圈（圈0） 3）写或与式 （0——原变量，1——反变量）
01
11
10
0 1 3 2
4 5 7 6
12 13 15 14
8 9 11 10
24 25 27 26
28 29 31 30
20 21
16 17
23 19 22 18
10
2 、逻辑函数的卡诺图表示法 （1）由真值表填卡诺图（一一对应）
A B C
F
0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1
AB 00 CD
01
11
10
00 01
11 10
0
0 0
F = C • ( A + B + D )( A + B )
总结：
0 0
0 0
0 0
0 0
根据题目要求，确定“填什么”和“圈什么”。 【例5】 求 F = ( A + B + C + D )( A + B )( A + C )C 的最简与或式。
= BC D + BC D = BD
消去B
11 10
结论： 1、 2 n 个最小项合并，消去n 个变量。 2、消去K圈中变量取值发生过 变化的量。保留取值没有变 化的量。
ABC D + ABC D + ABC D + ABC D
消去A、C
A BCD + ABCD + ABCD + A BCD + ABC D + ABC D + ABC D + ABC D = ACD + ACD + AC D + AC D = CD + C D = C